Dan Winske
Lynn B. Wilson - 1Retired Laboratory Fellow, Los Alamos National Laboratory, Los Alamos, NM, United States
- 2Heliophysics Science Division, NASA Goddard Space Flight Center, Greenbelt, MD, United States
We discuss Peter Gary’s contributions to the understanding of the origin and properties of ultra-low frequency (ULF) waves in the Earth’s foreshock during the period when the International Sun Earth Explorer spacecraft (ISEE-1 and -2) provided unique data about the plasma and wave environment in this region. Peter’s work concerning the linear theory of electromagnetic ion beam instabilities is contained in five journal articles and then summarized in a review article, all of which are discussed here. Brief summaries of observations and theory prior to ISEE as well as to later work are also included.
Introduction
As this collection of articles emphasizes, Peter Gary is best known for his work on linear Vlasov theory of plasma instabilities. In the early days of plasma physics (i.e., 1950s–1970s) plasma instabilities were often studied using a reduced fluid approach that yielded simplified equations that could be solved analytically. As plasma theory matured, a more complete, and complex theory developed based on the Vlasov equation that could be sometimes solved in reduced forms. Peter was one of the first to solve the complete Vlasov equation exactly using numerical methods and displaying the results with simple line plots. Nowadays, this is the common technique, and there are a number of widely available computer programs to do this with sophisticated graphical interfaces, e.g., WHAMP (Rönmark, 1982). But back in the 70s his method was a unique approach.
This article discusses Peter Gary’s contributions to understanding the linear theory of ultra-low frequency (ULF) electromagnetic waves driven by ion beams in the Earth’s foreshock. The foreshock is the broad region upstream of the bow shock where the solar wind interacts with electrons and ions flowing away from the shock and generating a wide spectrum of plasma waves. This work covers the period of time from the late 1970s to the late 1980s, when the three ISEE (International Sun Earth Explorer) spacecraft provided very significant and unique measurements in the foreshock as well as other regions both inside and outside of the magnetosphere. Much information about the observations in the foreshock has been published over the years and our goal here is only to emphasize a few key results, using appropriate references and reviews of this effort, to define the outstanding theoretical issues that Peter’s work addressed and contributed to their understanding. So in this sense, this paper is a not a review article, but hopefully it summarizes a key feature of Peter’s work, the legacy of which continues to the present. Peter and one of us (Dan) worked together during this time period on a number of these investigations. While he can report the results of these studies, they cannot convene the sense of excitement, wonder, and achievement that they shared as theory, simulations and observations came together to produce new understanding. The other author here (Lynn) is much more familiar with work on more recent observations related to ion beams and low frequency waves in the foreshock from the Cluster and Magnetospheric Multiscale missions and how they relate to Peter’s legacy.
We begin with a little background—a simplified version of the geometry of the foreshock, as shown in Figure 1. This figure is taken from Figure 16.1 of Wilson, (2016) and which in turn was adapted from Tsurutani and Rodriguez (Plate 1, 1981). The slanted straight lines are the magnetic field embedded in the solar wind that is flowing downward in the figure and encounters the curved bow shock (green curve). The angle between the magnetic field and the normal direction at the shock is denoted as θBn. The portion of the bow shock where θBn > 45° (i.e., the region to the left of the Earth in the figure) is termed the “quasi-perpendicular shock”, while the region to the right, θBn < 45°, is the “quasi-parallel shock” that extends all the way down to θBn ∼ 0°—the “parallel shock”. At the shock near θBn ∼ 90°, some of the incoming solar wind electrons, which have small gyroradii, are reflected and propagate back upstream creating the region known as the ‘electron foreshock’. Some of the solar wind ions impinging on the bow shock near θBn ∼ 90° are also reflected, but because they have larger gyroradii, quickly gyrate into the downstream. At somewhat smaller θBn, but still associated with the quasi-perpendicular bow shock, a fraction of the solar wind ions are also reflected and travel back upstream along the magnetic field as well as being convected in the solar wind (VE×B in the figure) to form the quasi-perpendicular portion of the ion foreshock. Farther to the right of the ion foreshock boundary shown in Figure 1, ions originating at the shock at even smaller θBn, e.g., on the quasi-parallel portion of the shock, also propagate upstream (dots in the figure), generating larger amplitude waves in the magnetic field (blue wavy lines), to form the quasi-parallel portion of the ion foreshock. These backstreaming ions may have been from the solar wind and reflected at the shock or could have leaked out of the magnetosheath. This process extends deep in the foreshock to θBn ∼ 0°, where the shock normal is essentially parallel to the solar wind magnetic field.
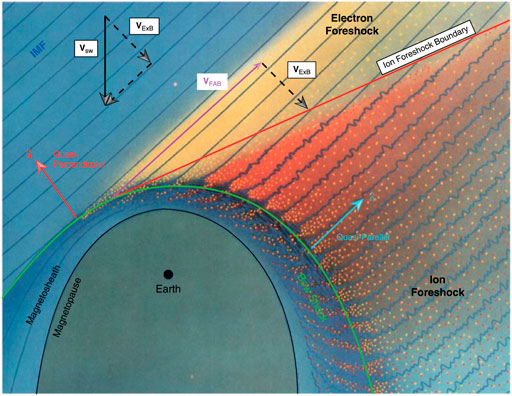
FIGURE 1. Foreshock configuration showing incident solar wind magnetic field (blue lines), impinging on the bow shock (green curved line), producing backstreaming ions (yellow dots), leaked magnetosheath ions (red dots), and upstream waves (wavy blue lines). The ion foreshock boundary is shown as the red line. Figure is from Wilson, (2016), adapted from Tsurutani and Rodriguez (1981), and is reproduced with permission from The American Geophysical Union.
In this article we discuss only electromagnetic instabilities that Peter studied during this time period that are driven by ion beams that are cold and fast, characteristically produced in the quasi-perpendicular portion of the foreshock. Electromagnetic ion beam instabilities with somewhat different properties are also found deeper in the foreshock on magnetic field lines that connect to the nearly parallel portion of the bow shock. Here the ion beams are slower and hotter and instead of being generated by reflection at the shock, are more likely to result from heating and scattering of the cold beam ions, processes related to the unsteady nature of the parallel shock, or from magnetosheath ions that leaked out into the foreshock. Other types of ion beam instabilities arise elsewhere in space, e.g., in the plasma sheet boundary layer upstream of slow-mode shocks in the magnetotail and in the vicinity of comets. Waves resulting from such instabilities were observed by ISEE-3 late in its mission. See, for example, articles by Smith et al. (1984) related to observations of slow-mode shocks in the magnetotail, by Tsurutani et al. (1985) concerning waves in the plasma sheet boundary layer, and by Smith et al. (1986) related to wave observations at Comet Giacobini-Zinner. As we discuss later, in his review article (Gary, 1991), Peter summarizes his contributions to relevant theory and simulations of all of these environments.
International Sun Earth Explorer
In the decade before ISEE, numerous spacecraft observed ion beams streaming away from the Earth along the interplanetary magnetic field outward from the bow shock through the foreshock, e.g., measurements by the Vela satellites (Asbridge et al., 1968). In this region, low-frequency (0.01–0.05 Hz) transverse hydromagnetic waves were also observed (Greenstadt et al., 1968) and data from Explorer 34 led to the conclusion that these waves were indeed associated with the bow shock since they were seen only on field lines that intersect the shock (Fairfield, 1969). A direct correlation was subsequently established (Scarf et al., 1970) between the presence of the waves and a portion of the solar wind that was reflected at the bow shock by a process which had been demonstrated theoretically by Sonnerup (1969). While the early work suggested that the waves could be produced by an ion cyclotron resonance involving the beam ions, Barnes (1970) provided a detailed model for this wave generation process based on stochastic scattering and acceleration of the beam ions. Years later, Watanabe and Terasawa (1984) verified the correctness of the cyclotron resonance process using IMP-5 data from 1969.
During the late 60s and early 70s, Peter developed his linear theory of instabilities in magnetized plasmas, numerically solving the complete dispersion equation for both electrostatic and electromagnetic waves, excited by various sorts of free energy: i.e., Beams of electrons or ions, temperature anisotropies in either the background or beam species, etc. Using Fried-Conte functions to characterize the various species as Maxwellians, he solved the resulting equation numerically without approximations. The full dispersion equation he used is found in the appendix of his review article (Gary, 1991). An early application of his methodology was to electromagnetic ion streaming instabilities in the solar wind (Montgomery et al., 1974). Both instabilities associated with magnetosonic and Alfvenic wave modes were investigated.
The early spacecraft observations in the foreshock helped motivate the International Space Earth Explorer (ISEE) mission which consisted of three spacecraft, ISEE-1 and ISEE-3 that were designed and built by the U.S., and ISEE-2 that was built and managed by the European Space Agency (ESA) (Ogilvie et al., 1977). It was realized from the earlier missions that with two spacecraft with similar instruments (ISEE-1 and -2), which when in essentially the same orbit but with variable spacing, would be able to measure the thickness of thin boundaries, such as the bow shock and the magnetopause that had been discovered earlier. And a third spacecraft (ISEE-3) could be positioned much far upstream to monitor the solar wind conditions. ISEE-1 and ISEE-2 were launched together in October 1977, in almost identical orbits around the earth with periods of approximately 57 h, and their separation in orbit could be altered by maneuvering ISEE-2. ISEE-3 was launched in August 1978, and inserted into orbit about the libation point situated ∼240 Earth radii upstream of the Earth so that disturbances detected by ISEE-3 arrive at the Earth about 1 hour later. The satellites all carried a wide variety of instrumentation to measure not only the density and velocity distribution of the backstreaming ions and low frequency waves of interest to us here, but also to measure very energetic electrons and ions, ion composition, as well as a broad spectrum of both electrostatic and electromagnetic waves. All three spacecraft enjoyed long and successful lives. The ISEE-1 and ISEE-2 spacecraft reentered the Earth’s atmosphere in September 1987 after more than 1,500 orbits of the Earth. ISEE-3 was taken out of its libation point orbit in the summer of 1983 and after a series of deep passes down the magnetotail, encountered Comet Giacobini-Zinner in September 1985.
In just its first few years, ISEE-1 and -2 greatly expanded on the earlier discoveries and understanding of backstreaming ions and low-frequency waves in the foreshock. The fast-plasma instruments on these satellites were able to show there are two main populations of backstreaming ions, termed “reflected” and “diffuse” (Gosling et al., 1978). The reflected ions have a sharply peaked energy spectrum and relatively collimated flow coming from the bow shock along the interplanetary magnetic field with number densities ∼ 1.5% of the solar wind. In contrast, the diffuse ions have a much flatter energy spectrum and broad angular distributions, with lower density ∼ 0.7% of the solar wind. These two populations occur in separate regions of the foreshock, with reflected ions in the quasi-perpendicular portion and the diffuse ions in the more nearly parallel portion of the foreshock, suggesting different mechanisms of origin and acceleration. Bonifazi and Moreno (1981) carried out a statistical analysis of these distributions, also showing that the reflected beams tended to be found in the quasi-perpendicular portion of the foreshock. In between the reflected and diffuse ion populations, were ‘intermediate’ ions that had a crescent shape in velocity space (Paschmann et al., 1981), the origin of which will be discussed later. Paschmann et al. also show examples of the velocity distributions of all three populations. The reflected ions were so named, because backstreaming beams of ions were observed traveling upstream in a direction determined by the interplanetary magnetic field and the convection velocity (VE×B), consistent with simple models of specular reflection at the bow shock (Sonnerup, 1969; Paschmann et al., 1980). Thomsen et al. (1983) examined the backstreaming ions to show that these simple models of reflection, along with the conservation of magnetic moment, could account for a number of the observations, although other observations indicated that backstreaming ions could instead arise from the leakage of shock-heated magnetosheath ions.
The ISEE spacecraft likewise produced new, detailed information about the low frequency waves associated with the backstreaming ions and the correlation between magnetic field and plasma density in wave events, expanding on the early work of Greenstadt et al. (1968). Paschmann et al. (1979) reported that there were usually weak waves occurring with reflected beam ions, while with diffuse ions large amplitude, compressive waves often occurred. Hoppe et al. (1981) and Hoppe and Russell (1983) further examined the waves associated with ion beam populations, measuring polarizations and frequencies. They observed magnetosonic waves that are right-hand polarized in the plasma rest frame but left-hand polarized in spacecraft frame and sometimes with large amplitudes. These waves have frequencies ∼0.03 Hz and are often referred to as “30-s waves.” Obliquely propagating waves were also observed, often in the form of steepened waves, termed shocklets. In addition, deeper in the foreshock Alfven waves were also generated in associated with the diffuse ions. Early theoretical analysis of the magnetosonic waves generated by the reflected ions was provided by Gary (1981), which will be discussed later in some detail. Sentman et al. (1981) also carried out linear analysis of both reflected and diffuse ion beams and examined both unstable magnetosonic and Alfvenic wave modes. And years later, Le and Russell (1992) determined the location in the foreshock where the low frequency waves begin to appear, the so-called ULF foreshock boundary, near the ion foreshock boundary.
A few years after the initial ISEE observations of backstreaming ions and associated waves in the foreshock, a closer examination of the intermediate ion distributions found that sometimes the backstreaming ions were gyrating in the magnetic field in the presence of large amplitude waves (Gurgiolo et al., 1981; Thomsen et al., 1985; Fuselier et al., 1986a). Fuselier et al. (1986b) carried out a large survey of intermediate ion observations and showed that roughly half involved ions gyrating in the magnetic field which could be due to how they interact with the bow shock, while other events, characterized by gyrophase-bunched beam ions that could be due to disruption of the beam later in time by the instability-generated waves. The issue of gyrophase-bunching will be discussed later in relation to Peter’s theoretical work.
Further details and summaries of the many publications that came out of the ISEE mission concerning observations of foreshock ions and waves [including ions and waves produced deep in the foreshock near the quasi-parallel bow shock, termed “short large-amplitude magnetic structures” (SLAMS) by Schwartz et al. (1992), that we are not addressing here] were given by Tsurutani and Rodriguez (1981) discussing the early results, by Russell and Hoppe (1983) focusing on wave measurements, and Thomsen (1984) emphasizing the plasma measurements.
Peter Gary’s Contributions
During the ISEE period, Peter made a number of significant contributions to the interpretation of the foreshock observations in terms of linear theory of electromagnetic ion beam instabilities, which were published in five journal articles and later summarized in a review article. We describe each of these publications in a short paragraph.
1. S. P. Gary, J. Geophys. Res. (1981): Microinstabilities Upstream of the Earth’s Bow Shock: A Brief Review (Gary, 1981).
This first paper was part of a collection of papers summarizing the first several years of results from ISEE -1 and -2 observations in the Earth’s foreshock (e.g., Tsurutani and Rodriguez, 1981). Part of Peter’s paper is tutorial in nature, defining and contrasting terms such as: micro/macro plasma instabilities, linear/nonlinear fluctuations, weak/strong turbulence. He also describes his framework for studying instabilities: namely identifying the source of free energy, determining which instabilities can be excited from this energy source, understanding the properties of the instabilities as they grow and then saturate in such a way as to reduce the free energy. In the Earth’s foreshock the free energy source is the ion beams streaming back from the bow shock along the magnetic field. As discussed earlier, the observations show two main classes of backstreaming ions, denoted as reflected and diffuse (e.g., Gosling et al., 1978) and that the reflected ions are energetically consistent with their being specularly reflected at the bow shock. Linear theory discussed in this paper shows the beam ions can excite unstable magnetosonic waves that are in cyclotron resonant with the beam ions. This instability is denoted as the “right-hand resonant electromagnetic ion beam instability” or simply as the “right-hand resonant instability”. During the initial growth of the instability, the excited electromagnetic waves have group velocities close to the beam speed, so that the field energy propagates with the beam. The waves pitch-angle scatter the beam reducing the free energy. Based on this simplified picture, Peter suggested that this process could explain many of the general features of the observations: The magnetic field fluctuations observed in the foreshock, the deceleration and deflection of the solar wind, and the scattering of the beam to produce velocity distributions that were characteristic of intermediate and diffuse ions. However, his preliminary model assumed parallel propagating waves, which do not produce the observed large fluctuations in the solar wind density.
2. S. P. Gary, J. T. Gosling, and D. W. Forslund, J. Geophys. Res. (1981): The Electromagnetic Ion Beam Instability Upstream of the Earth’s Bow Shock (Gary et al., 1981).
To address the question of the observed density fluctuations, in this paper the linear theory is extended to include oblique wave propagation. After summarizing the observations (e.g., Tsurutani and Rodriguez, 1981), the basic instability model is reviewed. Recalling that the basic physics of waves in cyclotron resonance with the beam that grow and scatter the beam (e.g., Barnes, 1970), the linear theory presented in Peter’s previous paper provides a detailed description ion of wave properties (i.e., wavenumbers and real and imaginary frequencies of the unstable waves, that show how a weak (∼1% density beam) initially produces a low level of waves and growth times > 25 s. Because the growth rate of the waves is small, the ion beam propagates a long distance upstream from the bow shock before the waves grow to large amplitude. But in the process of propagating upstream, the beam ions and the waves are convected deep into the quasi-parallel portion of the foreshock, where they are slowed. The beam ions loses parallel momentum as they are pitch-angle scattered by the waves, producing intermediate velocity distributions (kidney shaped). This loss of energy and momentum by the beam, and the waves, causes the solar wind to be deflected and slowed, as observed by Bame et al. (1980). An example of results of linear theory are shown in Figure 2. Taken from Figure 1 in this paper, the real (ωr) and imaginary (γ) frequencies of the unstable waves are plotted as a function of wavenumber (k), showing the instability is sharply peaked in wavenumber. In the vicinity of this peak the real frequency is about a factor of two larger than the imaginary part and the dispersion of the wave is also modified in this region. The parameters of this calculation are given in the figure caption. The figure also shows the effect of extending the linear theory to include oblique wave propagation. Parallel (θ = 0°) and obliquely (θ ∼ 45°) propagating unstable waves are compared, showing the maximum growth rate at large oblique angles is reduced by less than a factor of two and that maximum growth in both cases occurs essentially at the same wavenumber. But even at small oblique angles, ∼ 15°, the compressibility (i.e., the density fluctuations computed from linear theory) is significantly larger than for parallel propagation, so oblique waves can grow and produce density fluctuations in agreement with observations.
3. S. P. Gary, C. W. Smith, M. A. Lee, M. L. Goldstein and D. W. Forslund, Phys. Fluids (1984): Electromagnetic Ion Beam Instabilities (Gary et al., 1984).
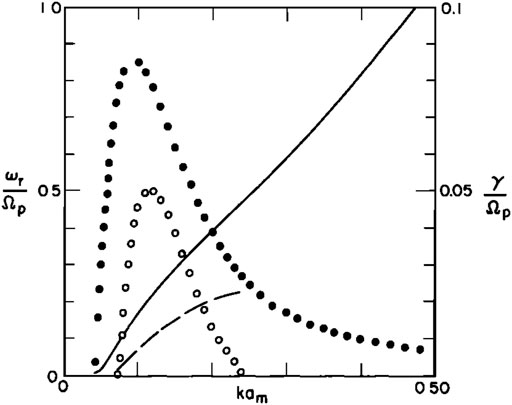
FIGURE 2. Complex frequency (ω = ωr + iγ) computed from linear theory for the right-hand resonant ion beam instability as a function of wavenumber (k). The beam density is 1% of the background ion density and beam speed is 10 vA (vA = Alfven speed). The frequencies are normalized by the background ion cyclotron frequency (Ωi) and the wavenumbers to the background ion gyroradius (ai). Two cases are shown: (a) parallel propagation (θ = 0°) -- real frequencies are given by the solid line, growth rates by the solid circles; (a) oblique propagation (θ = 45o) -- real frequencies are given by the dashed line, growth rates by the open circles. Figure is reproduced from Gary et al., 1981, with permission from The American Geophysical Union.
In this paper Peter and his coauthors consider the linear properties four electromagnetic ion beam instabilities: the previously discussed right-hand resonant magnetosonic instability, the right-hand non-resonant Alfvenic instability that was studied by Sentman et al. (1981), a left-hand resonant Alfvenic hot beam instability, and a left-hand ion cyclotron anisotropy instability. To clarify these different modes, the concept of resonance and polarization are carefully defined. Numerical solutions of the linear dispersion relation are presented to show that for parallel propagation the righthand resonant instability has a lower instability threshold than the non-resonant instability unless the beam speed or beam density is sufficiently large. For hot ion beams a left-hand resonant instability is also excited, and if there is a large temperature anisotropy in the beam (Tb,⊥>> Tb,||), a left-hand ion cyclotron instability is also possible. For parallel propagation, analytic solutions for the unstable modes are also presented. At oblique propagation and high beam speeds, it is demonstrated that an instability associated with the m = 2 cyclotron resonance is also excited for both the right-hand resonant and non-resonant instabilities.
4. S. P. Gary, M. F. Thomsen, and S. A. Fuselier, Phys. Fluids (1986): Electromagnetic Instabilities and Gyrophase-Bunched Particles (Gary et al., 1986a).
In this paper, linear theory of both the right-hand resonant and non-resonant instabilities driven by an energetic, cool ion beam is used to calculate the phase angle between the fluctuating velocity of the beam ions relative to the fluctuating magnetic field in order to determine whether gyrophase bunching of the beam ions is observable. As mentioned earlier, distinct gyrophase-bunched ions have been observed in the foreshock by ISEE (Gurgiolo et al., 1981; Thomsen et al., 1985; Fuslerier et al., 1986a). Hoshino and Terasawa (1985) investigated whether the right-hand resonant instability in the foreshock could lead to the observed gyrophase bunching. They demonstrated in their one-dimensional full particle simulations that during the growth of the instability the perpendicular component of the beam ions’ velocity had a well-defined phase angle relationship relative to the growing waves. Peter’s linear calculations showed that for the non-resonant mode, the phase angle is ∼ 0°, while for the resonant mode it is ∼ 90° for the most unstable wavenumber. From these results it is concluded that the right-hand resonant instability will give rise to observable gyrophase bunching of the ion beam for foreshock conditions—consistent with the observations of Fuselier et al. (1986a) and the simulations of Hoshino and Terasawa (1985).
5. S. P. Gary, C. D. Madland, D. Schriver, and D. Winske, J. Geophys. Res. (1986): Computer Simulations of Electromagnetic Cool Ion Beam Instabilities (Gary et al., 1986b).
In this paper the authors discuss results of 1-D hybrid (particle ions, massless fluid electrons) simulations of the right-hand resonant and non-resonant electromagnetic ion beam instabilities. Unlike earlier simulations of these instabilities (Winske and Leroy, 1984), this study considers small-scale simulations, a system length of only one wavelength of the most unstable linear mode. In this way two issues can be addressed: 1) The properties of the instability at small relative drift of the beam ions relative to the background ions (Vb in terms of the Alfven speed vA), and 2) gyrophase bunching of the beam ions. Three regimes common to the foreshock are considered: 1) low beam drift speed (Vb = 3 vA and beam density nb = 0.05), where the resonant instability dominates and the development of the system is quasilinear—the beam heats in the perpendicular direction, while the parallel velocity decreases (Gary and Tokar, 1985); 2) higher beam drift velocity (nb = 0.02, Vb = 10 vA) with the resonant instability still dominating that shows gyrophase bunching of the beam at 90° with respect to the wave magnetic field is clearly visible; and 3) higher beam speeds or densities (nb = 0.10, Vb = 10 vA) where the non-resonant instability dominates—here bunching still occurs, but is different as the phase angle is near 0°. The gyrophase bunching measured in the simulations is consistent with results from linear theory. In addition, a scaling for the magnetic fluctuation amplitudes at saturation of the instability is obtained from simulations that is valid in all three regimes: The energy in the perturbed magnetic fields is roughly half of the initial kinetic energy of the beam ions. The longer time behavior of the instability in each of the three cases is also discussed. While at later times, the resonant instability in the strong regime leads to a shift of the dominant unstable mode to shorter wavelengths, for both the resonant instability in the quasilinear regime and the non-resonant instability at higher beam energies, a shift to longer wavelengths after saturation is found.
6. S. P. Gary, Space Science Rev. (1991): Electromagnetic Ion/Ion Instabilities and Their Consequences in Space Plasmas: A Review (Gary, 1991).
This review article summarizes the work that Peter had done concerning low frequency (less than the ion cyclotron frequency) electromagnetic ion beam instabilities and their presence in various environments. While we have been dealing here only with Peter’s work in the foreshock, Peter has also applied the same methodology to the solar wind, interplanetary shocks, the plasma sheet boundary layer, and near comets. These last two situations derived from observations from ISEE-3 after its position was moved from far upstream of the bow shock to the deep magnetotail, where it encountered ion beams upstream of slow mode shocks in the plasma sheet boundary layer, and then later near Comet Giacobini-Zinner where heavy ions were emitted. Peter emphasizes throughout the review the characteristics of the various ion beam instabilities that can occur in space and compares their properties, such as growth rates, saturation levels, and the polarization/helicity of the unstable waves. His review gives appropriate and extensive references to observations as well as theory/simulation work that had been done in the last decade. He concentrates on cases where the background and beam ions are described as Maxwellians and focuses on parallel propagating modes, but does include some discussion of oblique modes as well. In addition, he treats cases that include anisotropic (T⊥ > T||) ions, ring-beams, and heavy ion beams. He gives a review of quasilinear theory as applied to these instabilities where appropriate and discusses results from hybrid computer simulations. Finally, in the appendix a very detailed discussion of the derivation and form of the linear dispersion equation used in all his studies is provided. This review also includes work on transport ratios, such as polarization, helicity, compressibility in stable plasmas (details in Gary, 1986) as well as unstable plasmas (in Gary, 1992). Finally, this article formed the basis of Peter’s major opus, the monograph “Theory of Space Plasma Microinstabilities” published in the Cambridge Atmospheric and Space Science Series (Gary, 1993) that summarized his work on a large number of electromagnetic as well as electrostatic instabilities, with consistent methodology and notation throughout.
Recent Work
We conclude this article with some brief comments about more recent work, following the era of ISEE and Peter’s publications concerning electromagnetic ion beam instabilities in the foreshock, which demonstrate Peter’s continuing legacy. New insights have been gained from observations from of multi-spacecraft missions, such as Cluster, THEMIS, and the Magnetospheric Multi-Scale (MMS) missions. For example, the four Cluster spacecraft have observed field-aligned beams in the foreshock, but also gyrating ions that can be associated with the quasi-parallel bow shock (Meziane et al., 2004; Kis et al., 2007). Gyrophase-bunched ions have also been observed by Cluster in the foreshock (Mazelle et al., 2003). Cluster has also made interesting observations of ULF waves. The four spacecraft are able to more accurately show that most of the waves, consistent with earlier observations, are low frequency, left-hand polarized in the spacecraft frame, but right-hand polarized in the plasma frame (Eastwood, 2002, 2005a; Eastwood, 2005b; Hobara et al., 2007a; Hobara et al., 2007b). It has also been possible with the ARTEMIS spacecraft orbiting the moon to measure the growth rate of the waves as they propagate out farther in the foreshock (Dorfman et al., 2017) The observed waves are consistent with the linear theory of Gary et al. (1981), although reduced forms of the linear dispersion relation that ignore thermal effects need to be modified in cases of high-beta solar wind plasma beta to get better agreement (Hobara et al., 2007a; Hobara et al., 2007b). Wilson, (2016) has reached similar conclusions in his recent review of foreshock waves.
However, a major problem remains—the observed ULF waves are primarily propagating oblique to the magnetic field, contrary to linear theory that says the parallel mode has the largest growth rate and thus in time will grow to be the dominant mode. Measurements by the four Cluster spacecraft have been able to make this more quantitative, indicating that for some data-sets the mean angle of wave propagation is 21° (Eastwood et al., 2005b). One resolution of this issue was proposed some years ago by Hada et al. (1987). They suggested that the parallel propagating waves refract as they are carried by the solar wind deeper into the foreshock and become increasingly more oblique and compressive. This remains the most accepted explanation and is consistent with THEMIS observations of ULF waves in the foreshock (Hsieh and Shue, 2013). But multi-dimensional hybrid simulations have provided alternative explanations. Very early 2-D hybrid simulations by Winske and Quest (1986) show that the development of the instability in 2-D is not much different than in 1-D, but their rudimentary diagnostics of the spectrum of unstable waves, as well as the relatively small size of the simulations, limit the discussion on the development of oblique unstable modes. Hellinger and Mangeney (1999) observe in their simulations in a uniform background, but with slightly different beam parameters than are usually assumed, that oblique waves, even though their linear growth rates are smaller, grow to larger amplitudes. Blanco-Cano et al. (2006) include the bow shock in their calculations and show that parallel propagating ULF waves dominate far upstream from the bow shock, but oblique waves are excited relatively close to the shock. An even more interesting suggestion is given later by Strumik et al. (2015). In their foreshock simulations they assume that the solar wind is essentially radial so that the Hada et al. (1987) refraction mechanism is minimalized. They find that while parallel unstable modes dominate, oblique waves are also generated, and when properly averaged over phase space density, the “average” propagation direction is ∼ 20°, consistent with Eastwood et al. (2005b). The bottom line from all this recent work is that the linear theory as worked out by Peter Gary and others years ago is sufficient to explain the origin of the ULF waves observed far upstream from the shock, but more realistic, probably 3-D, simulations in a foreshock geometry and maybe new observations will be needed to resolve this remaining issue of propagation direction. Perhaps other articles in this topical series will also shed new light on this problem.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
DW wrote much of the text, provided Figure 2 and put the manuscript together. LWIII provided text, references, and Figure 1.
Funding
LBW was partially supported by Wind MO&DA funds
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Asbridge, J. R., Bame, S. J., and Strong, I. B. (1968). Outward Flow of Protons from the Earth's bow Shock. J. Geophys. Res. 73, 5777–5782. doi:10.1029/ja073i017p05777
Bame, S. J., Asbridge, J. R., Feldman, W. C., Gosling, J. T., Paschmann, G., and Sckopke, N. (1980). Deceleration of the Solar Wind Upstream from the Earth's bow Shock and the Origin of Diffuse Upstream Ions. J. Geophys. Res. 85, 2981–2990. doi:10.1029/ja085ia06p02981
Barnes, A. (1970). Theory of Generation of bow-shock-associated Hydromagnetic Waves in the Upstream Interplanetary Medium. Cosmic Electrodyn 1, 90–114.
Blanco-Cano, X., Omidi, N., and Russell, C. T. (2006). Macrostructure of Collisionless bow Shocks: 2. ULF Waves in the Foreshock and Magnetosheath. J. Geophys. Res. 111, A10205. doi:10.1029/2005ja011421
Bonifazi, C., and Moreno, G. (1981). Reflected and Diffuse Ions Backstreaming from the Earth's bow Shock 2. Origin. J. Geophys. Res. 86, 4405–4413. doi:10.1029/ja086ia06p04405
Dorfman, S., Hietala, H., Astfalk, P., and Angelopoulos, V. (2017). Growth Rate Measurement of ULF Waves in the Ion Foreshock. Geophys. Res. Lett. 44, 2120–2128. doi:10.1002/2017gl072692
Eastwood, J. P., Balogh, A., Dunlop, M. W., Horbury, T. S., and Dandouras, I. (2002). Cluster Observations of Fast Magnetosonic Waves in the Terrestrial Foreshock. Geophys. Res. Lett. 29, 2046. doi:10.1029/2002gl015582
Eastwood, J. P., Balogh, A., Lucek, E. A., Mazelle, C., and Dandouras, I. (2005a). Quasi-monochromatic ULF Foreshock Waves as Observed by the Four-Spacecraft Cluster mission: 1. Statistical Properties. J. Geophys. Res. 110, A11219. doi:10.1029/2004ja010617
Eastwood, J. P., Balogh, A., Lucek, E. A., Mazelle, C., and Dandouras, I. (2005b). Quasi-monochromatic ULF Foreshock Waves as Observed by the Four-Spacecraft Cluster mission: 2. Oblique Propagation. J. Geophys. Res. 110, A11220. doi:10.1029/2004ja010618
Fairfield, D. H. (1969). Bow Shock Associated Waves Observed in the Far Upstream Interplanetary Medium. J. Geophys. Res. 74, 3541–3553. doi:10.1029/ja074i014p03541
Fuselier, S. A., Thomsen, M. F., Gary, S. P., Bame, S. J., Russell, C. T., and Parks, G. K. (1986a). The Phase Relationship between Gyrophase-Bunched Ions and MHD-like Waves. Geophys. Res. Lett. 13, 60–63. doi:10.1029/gl013i001p00060
Fuselier, S. A., Thomsen, M. F., Gosling, J. T., Bame, S. J., and Russell, C. T. (1986b). Gyrating and Intermediate Ion Distributions Upstream from the Earth's bow Shock. J. Geophys. Res. 91, 91–99. doi:10.1029/ja091ia01p00091
Gary, S. P. (1991). Electromagnetic Ion/ion Instabilities and Their Consequences in Space Plasmas: A Review. Space Sci. Rev 56, 373–415. doi:10.1007/bf00196632
Gary, S. P., Gosling, J. T., and Forslund, D. W. (1981). The Electromagnetic Ion Beam Instability Upstream of the Earth's bow Shock. J. Geophys. Res. 86, 6691–6696. doi:10.1029/ja086ia08p06691
Gary, S. P. (1986). Low-frequency Waves in a High-Beta Collisionless Plasma: Polarization, Compressibility and Helicity. J. Plasma Phys. 35, 431–447. doi:10.1017/s0022377800011442
Gary, S. P., Madland, C. D., Schriver, D., and Winske, D. (1986b). Computer Simulations of Electromagnetic Cool Ion Beam Instabilities. J. Geophys. Res. 91, 4128–4200. doi:10.1029/ja091ia04p04188
Gary, S. P. (1981). Microinstabilities Upstream of the Earth's bow Shock: A Brief Review. J. Geophys. Res. 86, 4331–4336. doi:10.1029/ja086ia06p04331
Gary, S. P., Smith, C. W., Lee, M. A., Goldstein, M. L., and Forslund, D. W. (1984). Electromagnetic Ion Beam Instabilities. Phys. Fluids 27, 1852–1862. doi:10.1063/1.864797
Gary, S. P. (1993). Theory of Space Plasma Microinstabilities. New York: Cambridge University Press.
Gary, S. P., Thomsen, M. F., and Fuselier, S. A. (1986a). Electromagnetic Instabilities and Gyrophase-Bunched Particles. Phys. Fluids 29, 531–535. doi:10.1063/1.865441
Gary, S. P., and Tokar, R. L. (1985). The Second-Order Theory of Electromagnetic Hot Ion Beam Instabilities. J. Geophys. Res. 90, 65–72. doi:10.1029/ja090ia01p00065
Gary, S. P., and Winske, D. (1992). Correlation Function Ratios and the Identification of Space Plasma Instabilities. J. Geophys. Res. 97, 3103–3111. doi:10.1029/91ja02752
Gosling, J. T., Asbridge, J. R., Bame, S. J., Paschmann, G., and Sckopke, N. (1978). Observations of Two Distinct Populations of bow Shock Ions in the Upstream Solar Wind. Geophys. Res. Lett. 5, 957–960. doi:10.1029/gl005i011p00957
Greenstadt, E. W., Green, I. M., Inouye, G. T., Hundhausen, A. J., Bame, S. J., and Strong, I. B. (1968). Correlated Magnetic Field and Plasma Observations of the Earth's bow Shock. J. Geophys. Res. 73, 51–60. doi:10.1029/ja073i001p00051
Gurgiolo, C., Parks, G. K., Mauk, B. H., Lin, C. S., Anderson, K. A., Lin, R. P., et al. (1981). Non-E × Bordered Ion Beams Upstream of the Earth's bow Shock. J. Geophys. Res. 86, 4415–4424. doi:10.1029/ja086ia06p04415
Hada, T., Kennel, C. F., and Terasawa, T. (1987). Excitation of Compressional Waves and the Formation of Shocklets in the Earth's Foreshock. J. Geophys. Res. 92, 4423–4435. doi:10.1029/ja092ia05p04423
Hellinger, P., and Mangeney, A. (1999). Electromagnetic Ion Beam Instabilities: Oblique Pulsations. J. Geophys. Res. 104, 4669–4680. doi:10.1029/1998ja900157
Hobara, Y., Walker, S. N., Balikhin, M., Pokhotelov, O. A., Dunlop, M., Nilsson, H., et al. (2007a). Characteristics of Terrestrial Foreshock ULF Waves: Cluster Observations. J. Geophys. Res. 112, A07202. doi:10.1029/2006ja012142
Hobara, Y., Walker, S. N., Dunlop, M., Balikhin, M., Pokhotelov, O. A., Nilsson, H., et al. (2007b). Mode Identification of Terrestrial ULF Waves Observed by Cluster: A Case Study. Planet. Space Sci. 55, 2257–2260. doi:10.1016/j.pss.2007.05.020
Hoppe, M. M., Russell, C. T., Frank, L. A., Eastman, T. E., and Greenstadt, E. W. (1981). Upstream Hydromagnetic Waves and Their Association with Backstreaming Ion Populations: ISEE 1 and 2 Observations. J. Geophys. Res. 86, 4471–4492. doi:10.1029/ja086ia06p04471
Hoppe, M. M., and Russell, C. T. (1983). Plasma Rest Frame Frequencies and Polarizations of the Low-Frequency Upstream Waves: ISEE 1 and 2 Observations. J. Geophys. Res. 88, 2021–2028. doi:10.1029/ja088ia03p02021
Hoshino, M., and Terasawa, T. (1985). Numerical Study of the Upstream Wave Excitation Mechanism: 1. Nonlinear Phase Bunching of Beam Ions. J. Geophys. Res. 90, 57–64. doi:10.1029/ja090ia01p00057
Hsieh, W.-C., and Shue, J.-H. (2013). Dependence of the Oblique Propagation of ULF Foreshock Waves on Solar Wind Parameters. J. Geophys. Res. Space Phys. 118, 4151–4160. doi:10.1002/jgra.50225
Kis, A., Scholer, M., Klecker, B., Kucharek, H., Lucek, E. A., and Rème, H. (2007). Scattering of Field-Aligned Beam Ions Upstream of Earth's bow Shock. Ann. Geophys. 25, 785–799. doi:10.5194/angeo-25-785-2007
Le, G., and Russell, C. T. (1992). A Study of ULF Wave Foreshock Morphology-I: ULF Foreshock Boundary. Planet. Space Sci. 40, 1203–1213. doi:10.1016/0032-0633(92)90077-2
Mazelle, C., Meziane, K., LeQuéau, D., Wilber, M., Eastwood, J. P., Rème, H., et al. (2003). Production of Gyrating Ions from Nonlinear Wave-Particle Interaction Upstream from the Earth's bow Shock: A Case Study from Cluster-CIS. Planet. Space Sci. 51, 785–795. doi:10.1016/j.pss.2003.05.002
Meziane, K., Wilber, M., Mazelle, C., LeQueau, D., Kucharek, H., Lucek, E. A., et al. (2004). Simultaneous Observations of Field-Aligned Beams and Gyrating Ions in the Terrestrial Foreshock. J. Geophys. Res. 109, A05107. doi:10.1029/2003ja010374
Montgomery, M. D., Gary, S. P., Forslund, D. W., and Feldman, W. C. (1974). Electromagnetic Ion-Beam Instabilities in the Solar Wind. Phys. Rev. Lett. 35, 667–670. doi:10.1103/physrevlett.35.667
Ogilvie, K. W., von Rosenvinge, T., and Durney, A. C. (1977). International Sun-Earth Explorer: A Three-Spacecraft Program. Science 198, 131–138. doi:10.1126/science.198.4313.131
Paschmann, G., Sckopke, N., Asbridge, J. R., Bame, S. J., and Gosling, J. T. (1980). Energization of Solar Wind Ions by Reflection from the Earth's bow Shock. J. Geophys. Res. 85, 4689–4693. doi:10.1029/ja085ia09p04689
Paschmann, G., Sckopke, N., Bame, S. J., Asbridge, J. R., Gosling, J. T., Russell, C. T., et al. (1979). Association of Low-Frequency Waves with Suprathermal Ions in the Upstream Solar Wind. Geophys. Res. Lett. 6, 209–212. doi:10.1029/gl006i003p00209
Paschmann, G., Sckopke, N., Papamastorakis, I., Asbridge, J. R., Bame, S. J., and Gosling, J. T. (1981). Characteristics of Reflected and Diffuse Ions Upstream from the Earth's bow Shock. J. Geophys. Res. 86, 4355–4364. doi:10.1029/ja086ia06p04355
Rönmark, K. (1982). Whamp-waves in Homogeneous, Anisotropic, Multicomponent Plasmas (Tech. Rep.). Sweden: Kiruna Geofysiska Inst.
Russell, C. T., and Hoppe, M. M. (1983). Upstream Waves and Particles. Space Sci. Rev. 34, 155–172. doi:10.1007/978-94-009-7096-0_12
Scarf, F. L., Fredricks, R. W., Frank, L. A., Russell, C. T., Coleman, P. J., and Neugebauer, M. (1970). Direct Correlations of Large-Amplitude Waves with Suprathermal Protons in the Upstream Solar Wind. J. Geophys. Res. 75, 7316–7322. doi:10.1029/ja075i034p07316
Schwartz, S. J., Burgess, D., Wilkinson, W. P., Kessel, R. L., Dunlop, M., and Lühr, H. (1992). Observations of Short Large-Amplitude Magnetic Structures at a Quasi-Parallel Shock. J. Geophys. Res. 97, 4209–4227. doi:10.1029/91ja02581
Sentman, D. D., Edmiston, J. P., and Frank, L. A. (1981). Instabilities of Low Frequency, Parallel Propagating Electromagnetic Waves in the Earth's Foreshock Region. J. Geophys. Res. 86, 7487–7497. doi:10.1029/ja086ia09p07487
Smith, E. J., Slavin, J. A., Tsurutani, B. T., Feldman, W. C., and Bame, S. J. (1984). Slow Mode Shocks in the Earth' Magnetotail: ISEE-3. Geophys. Res. Lett. 11, 1054–1057. doi:10.1029/gl011i010p01054
Smith, E. J., Tsurutani, B. T., Slavin, J. A., Jones, D. E., Siscoe, G. L., and Mendis, D. A. (1986). International Cometary Explorer Encounter with Giacobini-Zinner: Magnetic Field Observations. Science 232, 382–385. doi:10.1126/science.232.4748.382
Sonnerup, B. U. Ö. (1969). Acceleration of Particles Reflected at a Shock Front. J. Geophys. Res. 74, 1301–1304. doi:10.1029/ja074i005p01301
Strumik, M., Roytershteyn, V., Karimabadi, H., Stasiewicz, K., Grzesiak, M., and Przepiórka, D. (2015). Identification of the Dominant ULF Wave Mode and Generation Mechanism for Obliquely Propagating Waves in the Earth's Foreshock. Geophys. Res. Lett. 42, 5109–5116. doi:10.1002/2015gl064915
Thomsen, M. F. (1984). Upstream Suprathermal Waves” in Collisionless Shocks in the Heliosphere: Reviews of Current Research, Geophys. Monogr. Ser. Editors B. T. Tsurutani, and R. Stone (Washington, DC: Amer. Geophys. Union), 35, 253–270.
Thomsen, M. F., Gosling, J. T., Bame, S. J., and Russell, C. T. (1985). Gyrating Ions and Large-Amplitude Monochromatic MHD Waves Upstream of the Earth's bow Shock. J. Geophys. Res. 90, 267–273. doi:10.1029/ja090ia01p00267
Thomsen, M. F., Schwartz, S. J., and Gosling, J. T. (1983). Observational Evidence on the Origin of Ions Upstream of the Earth's bow Shock. J. Geophys. Res. 88, 7843–7852. doi:10.1029/ja088ia10p07843
Tsurutani, B. T., Richardson, I. G., Thorne, R. M., Butler, W., Smith, E. J., Cowley, S. W. H., et al. (1985). Observations of the Right-Hand Resonant Ion Beam Instability in the Distant Plasma Sheet Boundary Layer. J. Geophys. Res. 90, 12159–12172. doi:10.1029/ja090ia12p12159
Tsurutani, B. T., and Rodriguez, P. (1981). Upstream Waves and Particles: An Overview of ISEE Results. J. Geophys. Res. 86, 4319–4324. doi:10.1029/ja086ia06p04317
Watanabe, Y., and Terasawa, T. (1984). On the Excitation Mechanism of the Low-Frequency Upstream Waves. J. Geophys. Res. 89, 6623–6630. doi:10.1029/ja089ia08p06623
Wilson, L. B. (2016). “Low Frequency Waves at and Upstream of Collisionless Shocks,” in Low-frequency Waves at and Upstream of Collisionless Shocks” in Low-Frequency Waves in Space Plasmas, Geophys. Monogr. Ser. Editors A. Keiling, D.-H. Lee, and V. Nakariakov (Washington, DC: Amer. Geophys. Union), 216, 269–291. doi:10.1002/9781119055006.ch16
Winske, D., and Leroy, M. M. (1984). Diffuse Ions Produced by Electromagnetic Ion Beam Instabilities. J. Geophys. Res. 89, 2673–2688. doi:10.1029/ja089ia05p02673
Keywords: earth foreshock, ULF waves, plasma theory, plasma instabilities, electromagnetic waves, ion beams in space
Citation: Winske D and Wilson LB (2022) Linear Theory of Electromagnetic Ion Beam Instabilities in the Earth’s Forshock: Peter Gary’s Contributions (1981–1991). Front. Astron. Space Sci. 9:899642. doi: 10.3389/fspas.2022.899642
Received: 18 March 2022; Accepted: 11 April 2022;
Published: 16 May 2022.
Edited by:
Joseph E. Borovsky, Space Science Institute, United StatesReviewed by:
Xochitl Blanco-Cano, National Autonomous University of Mexico, MexicoStephen A. Fuselier, Southwest Research Institute (SwRI), United States
Copyright © 2022 Winske and Wilson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dan Winske, winske@losalamos.com