W. M. C. Sameera1,2*
Bethmini Senevirathne1,3Thanh Nguyen1
Yasuhiro Oba1Atsuki Ishibashi1
Masashi Tsuge1
Hiroshi Hidaka1Naoki Watanabe1- 1Institute of Low Temperature Science, Hokkaido University, Sapporo, Japan
- 2Department of Chemistry, University of Colombo, Colombo, Sri Lanka
- 3Department of Chemistry and Molecular Biology, University of Gothenburg, Gothenburg, Sweden
Heterogeneous radical processes on ice surfaces play a vital role in the formation of building blocks of the biologically relevant molecules in space. Therefore, quantitative mechanistic details of the radical binding and radical reactions on ices are crucial in rationalizing the chemical evolution in the Universe. The radical chemistry on ice surfaces was explored at low temperatures by combining quantum chemical calculations and laboratory experiments. A range of binding energies was observed for OH, HCO, CH3, and CH3O radicals binding on ices. Computed reaction paths of the radical reactions on ices, OCS + H and PH3 + D, explained the experimentally observed products. In both radical reactions, quantum tunnelling plays a key role in achieving the reactions at low temperatures. Our findings give quantitative insights into radical chemistry on ice surfaces in interstellar space and the planetary atmospheres.
1 Introduction
The mechanisms of the heterogeneous chemical reactions on dust and ice surfaces in space are essential in understanding the molecular evolution in the Universe that leads to the origin of life. A number of molecular species have been detected in interstellar space (Herbst and van Dishoeck, 2009; Guélin and Cernicharo, 2022; Herbst and Garrod, 2022) and the planetary atmospheres. (Zapata Trujillo et al., 2021) However, their origin and chemical reactions, giving rise to complex organic molecules (COM), are not fully understood. The most plausible theory for COMs formation in interstellar circumstances is the radical-driven chemistry on ice dust particles. (Garrod and Herbst, 2006; Garrod et al., 2009; Chuang et al., 2016) At the early stage of the COMs formation, the hydrogen atoms addition reactions on the primordial species, such as C, N, O, and CO is occurred on ices at very low-temperatures (∼10 K). The hydrogen addition processes give rise to various small radical species (e.g., OH, HCO, CH3O, NH, NH2, CH, CH2, and CH3) (Herbst and van Dishoeck, 2009) and stable molecules (e.g., methanol, formaldehyde, ammonia, methane). As the temperature rises, i.e., during the warming-up stage, small molecules or radicals begin to diffuse on ice to form COMs when they encounter. Thus, the elementary chemical processes on ices, such as radical adsorption, radical diffusion, and radical reaction mechanisms are required to rationalize the mechanisms of the COMs formation. However, radical processes on ices are challenging to characterize from laboratory experiments alone. For example, radical species are highly reactive and consume quickly, and therefore the number density of the radical species is too low for detection. Also, the temperature-programmed desorption method cannot be used to determine the binding energies of radicals on ices. Therefore, computational methods employing ab-initio calculations become critical in quantitative determination of the radical processes on ices. (Sameera et al., 2017; Enrique-Romero et al., 2019; Lamberts et al., 2019; Duflot et al., 2021)
The quantum chemical methods have been the most successful approaches in calculating molecule structures and their properties. High-level ab-initio calculations, configuration interaction (CI), multireference CI, coupled-cluster singles doubles perturbative triples CCSD(T), (Pople and Raghavachari, 1987) for instance, can be performed for a small molecular system with few atoms. For large molecular systems, density functional theory (DFT) would be the method of choice. The quantum mechanics/molecular mechanics (QM/MM) methods can be used for modelling relatively large molecular systems. (Sameera and Maseras, 2012; Chung et al., 2015; Sameera et al., 2017; Sameera and Maseras, 2018) In a QM/MM calculation, the electronically important part of the molecular system is calculated using a QM method, and the remaining part of the molecule is calculated by a MM method. Therefore, QM/MM calculations give accurate results at a low computational cost. Chemical processes on ices can be computed using DFT or DFT/MM methods, employing ice cluster models or periodic ice structures.
The first step of a computational study is to calculate the potential energy surface (PES) of the molecular system, which is a geometric hypersurface representing the potential energy as a function of the coordinates of the molecular system. The PES consists of stationary points, specifically local minima (LM, i.e., reactant, intermediates, product) or first-order saddle points (i.e., transition states, TS). A simplified potential energy surface of a single-step reaction is shown in Figure 1. In this PES, the LM1 represents the reactant(s), and LM2 is the product(s) of the reaction. The LM1 and LM2 are connected through the TS1. The molecular structures of LM1, LM2, and TS1 can be optimized using the ab-initio computations. (Schlegel, 2011) Also, the connectivity between the LM can be confirmed, for instance, by employing the intrinsic reaction coordinate (IRC) calculations. (Fukui, 1981) Then, the reaction barrier (i.e., the relative energy difference between LM1 and TS1) and the reaction rate can be calculated.
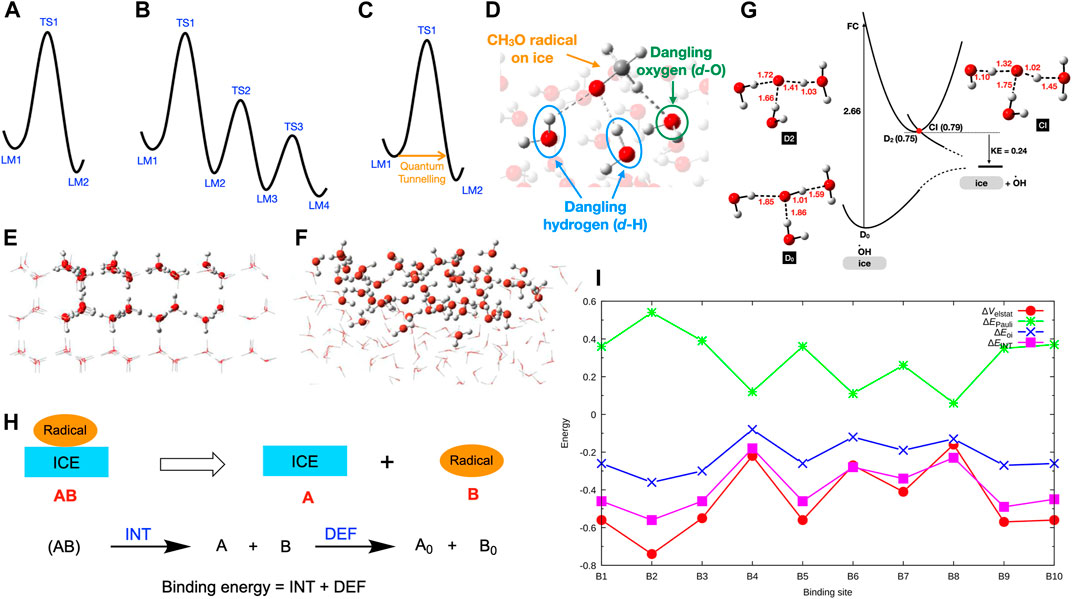
FIGURE 1. (A) Potential energy surface for a single-step reaction. (B) Potential energy surface for a multistep reaction. (C) Quantum tunnelling at low temperatures. (D) Interactions between the dangling-H (d-H) and dangling-O (d-O) atoms and a radical on ice. (E) Ih cluster model (side view). (F) ASW cluster model (side view). (G) Ground and excited potential energy surfaces for the OH radical on ice. (H) Decomposition of binding energy into interaction energy (INT) and deformation energy (DEF). (I) Computed INT, electrostatic interactions (ΔEelstat), Pauli repulsion (ΔEPauli), and orbital interactions (ΔEOi) of CH3O-ice systems in eV. Reprinted (adapted) with permission from J. Phys. Chem. A, 2021, 125, 387–393. Copyright 2021 American Chemical Society.
Multistep chemical reactions, consisting of several chemical steps, can proceed on ices in interstellar space and planetary atmospheres. PES of a multistep reaction is challenging to calculate, as it goes through several LM and TS (Figure 1B). There are two methods for calculating reaction paths of multistep chemical reactions, specifically conventional or systematic approaches. The conventional method uses chemical knowledge and intuition to sketch the possible reaction mechanisms. (Sameera and Maseras, 2012) Then, PESs of the guessed reaction paths are calculated. After that, the lowest energy path connecting the reactant and the product, the so-called reaction mechanism, can be determined. The conventional approach is the most common method in calculating reaction mechanisms. However, the accuracy of the computed reaction mechanism depends on the guessed reaction paths. On the other hand, systematic methods determine the PESs of all possible reaction paths (known, unknown, or unexpected) in an automated way. (Sameera et al., 2016) Therefore, systematic approaches are vital for investigating complex chemical networks. As the systematic methods explored reaction paths in a broad sense, the computational cost of a systematic reaction path survey is substantial.
Once the reaction paths are determined from conventional or systematic methods, PESs of the reaction mechanisms can be prepared. Then, reaction rates can be calculated using the transition state theory (TST). (Eyring, 1934) Quantum tunnelling is very important for the reactions if the system temperature is very low (Figure 1C). The classical TST does not include tunneling effects. However, a semiclassical approach can be used for including tunneling effects. (Senevirathne et al., 2017; Nyman, 2021) After determining the PESs for the radical process on ices from quantum chemical methods, computed data must be compared with the available experimental results. Then, an accurate picture of the radical chemistry on ices can be achieved. This mini-review focuses on our recent progress on radical binding and radical reaction mechanisms on ices. The main focus of the article is the computational results and their implications. Relevant experimental results were described briefly to compare with the computational results.
2 Computational Methods
LM and TS on the ground state PESs were optimized using QM or QM/MM methods as implemented in the Gaussian16 program. (Frisch et al., 2016) The two-layer Our own N-layered Integrated molecular Orbital and molecular Mechanics (ONIOM) (Chung et al., 2015; Sameera and Maseras, 2018) method was employed for QM/MM calculations. We have used density functional theory (DFT) and standard double-zeta (Ditchfield et al., 1971; Hehre et al., 1972) or triple-zeta basis sets (Schäfer et al., 1992; Schäfer et al., 1994) for QM calculations. The ωB97X-D (Chai and Head-Gordon, 2008) or M062X (Zhao and Truhlar, 2008) density functionals were employed for QM calculations. The AMOEBA09 polarizable force field was used for MM computations, employing the SICTWO interface. (Sameera and Maseras, 2018) Vibrational frequency calculations were performed to confirm the nature of the stationary points (i.e., no imaginary frequency for LM and one imaginary frequency for TS) and to calculate zero-point energies. Connectivity between the LM was confirmed by performing IRC calculations. (Fukui, 1981) Excited-state PESs were calculated using the time-dependent DFT method. The energy decomposition analysis (EDA) (Morokuma, 1971; Ziegler Rauk, 1977) was performed using the ADF program. (te Velde et al., 2001) The excited states seam crossing calculations were performed using the GRRM program. (Maeda et al., 2018) We have used the ice structure models of Andersson et al. (Andersson et al., 2006) to make ice cluster models for crystalline hexagonal water ice (Ih) and amorphous solid water (ASW). In ONIOM(QM:MM) structure optimizations, the H2O molecules in the MM region were frozen (i.e., kept as in the ice structure models of Andersson et al. (Andersson et al., 2006)).
3 Radical Binding on Ices
The binding energy of the radical species on ices gives some insights into their desorption and diffusion. These properties are vital in understanding radical reactions on ices. Radical species interact with the dangling-H (d-H) and dangling-O (d-O) atoms on ice surfaces (Figure 1D). To understand the roles of the dangling atoms on the binding energy, binding energy of OH, HCO, and CH3 radicals on Ih (Figure 1E) was calculated. (Sameera et al., 2017) Computed binding energies of OH (0.20–0.67 eV, 2321–7775 K), HCO (0.12–0.47 eV, 1393–5454 K), and CH3 (0.11–0.26 eV, 1277–3017 K) on Ih indicated a range of binding energies. According to the calculated averaged binding energies, binding preference follows the order of OH (0.46 eV, 5338 K) > HCO (0.30 eV, 3481 K) > CH3 (0.20 eV, 2321 K). Recently, both Ih and ASW models (Figure 1F) were employed to calculate the binding energy of OH on ices. (Miyazaki et al., 2020) Moreover, a broader range of binding energies (0.06–0.74 eV, 696–8587 K) was observed relative to the previous work that employed only Ih models (0.20–0.67 eV, 2321–7775 K). The computed binding energies of the other radical species are also in a broad range, CH3O: 0.10–0.50 eV (1160–5802 K), (Sameera et al., 2021) PH2: 0.13–0.21 eV (1503–2406 K), (Nguyen et al., 2021a) PH: 0.10–0.19 eV (1105–2205 K), (Nguyen et al., 2021a) P: 0.07–0.16 eV (831–1800 K), (Nguyen et al., 2021a) and OCSH: 0.19–0.46 eV (2205–5338 K), (Nguyen et al., 2021b).
Understanding the origin of the strong or weak radical binding energies on ices is essential. During the radical binding on ices, the radical and ice structures can be deformed that cost some energy. Also, the interactions between the radical and the ice surface are vital for the binding energy. We have performed an energy decomposition analysis (EDA, Figure 1H) (Morokuma, 1971; Ziegler Rauk, 1977) to rationalize the deformation energy and interaction energy of CH3O radical binding on ASW. (Sameera et al., 2021) The energy difference between ice-CH3O complex and the energy sum of the isolated ice structure (A) and CH3O (B), without changing their internal geometries, is defined as the interaction energy, INT. The INT term was further decomposed into electrostatic interactions (ΔEelstat), Pauli repulsion (ΔEPauli), and orbital interactions (ΔEOi). The deformation energy (DEF) is defined as the energy sum of the isolated ice and CH3O structures at the ice-CH3O complex and the energy sum of the fully optimized ice and CH3O structures (i.e., A0 and B0). According to EDA, the deformation energy of the CH3O radical or ice is almost zero. (Sameera et al., 2021) Thus, the radical bonding process does not require geometric or electronic preparation. On the other hand, the interaction energy between CH3O and ASW is significant, and therefore the interaction energy controls the strength of the binding energy. According to the computed data, the ΔEelstat and ΔEOi overcome the ΔEPauli, giving rise to strong or weak binding energy (Figure 1I).
The physicochemical behaviour of OH radicals on ices depends on the adsorption sites. (Miyazaki et al., 2020; Tsuge and Watanabe, 2021) Recent experiments observed photodesorption of OH radicals on ASW upon absorption of 532 nm photons. However, 532 nm photons cannot be absorbed by isolated OH and H2O molecules. Computed ground and excited-state PESs of the OH radical on ices suggested that one-photon absorption of the OH-(H2O)n complex (Figure 1G), having strong hydrogen bonds between OH and surrounding H2O molecules, leads to OH desorption. Further, the excited OH radical enters a dissociation channel through the conical intersection (CI) near the excited state minima (Figure 1G), leading to the OH desorption from the ASW with the kinetic energy (KE) of 0.24 eV, which is in agreement with the experimentally determined KE.
4 Radical Reactions on Ices
Radical reactions in interstellar space and the planetary atmospheres produce small molecules or radical species. Thus, reaction mechanisms of the radical reactions on ices are crucial in understanding the chemical evolution in the Universe. We have performed experimental and quantum chemical studies side-by-side to rationalize the radical reactions on ices. The following section focuses on the characterization of two radical reaction mechanisms on ices.
4.1 Carbonyl Sulphide + H
Chemistry of the sulphur (S)-bearing species in space has been an active topic in the astrochemical community. (Oba et al., 2018; Laas and Caselli, 2019; Cabezas et al., 2021) A number of S-bearing species have been detected in space. Carbonyl sulphide (OCS), a S-bearing molecule, was detected in the gas (Goldsmith and Linke, 1981) and solid phases of the ISM. (Palumbo et al., 1995) According to the laboratory experiments under the ISM conditions, OCS can be produced through the photon and cosmic ray-induced processes of H2S-containing ices. (Palumbo et al., 1995; Ferrante et al., 2008; Jiménez-Escobar et al., 2014) The reactivity of OCS is, however, not well established. Thus, we have performed experiments on the surface reaction of OCS solid with H atoms on icy surfaces at 10 K. (Nguyen et al., 2021b) We found that the addition of H atoms to OCS solid proceeded via quantum tunnelling. The main products were H2S, CO, H2CO, and CH3OH. Thioformic acid (HC(O)SH) was also observed as a minor product. Reaction paths for the formation of H2S, CO, and HC(O)SH are unknown. The H2CO and CH3OH molecules may be formed by successive H addition to CO. (Watanabe and Kouchi, 2002) Quantum chemical calculations were performed to rationalize the reaction mechanisms. Calculated potential energy surfaces are shown in Figure 2A.
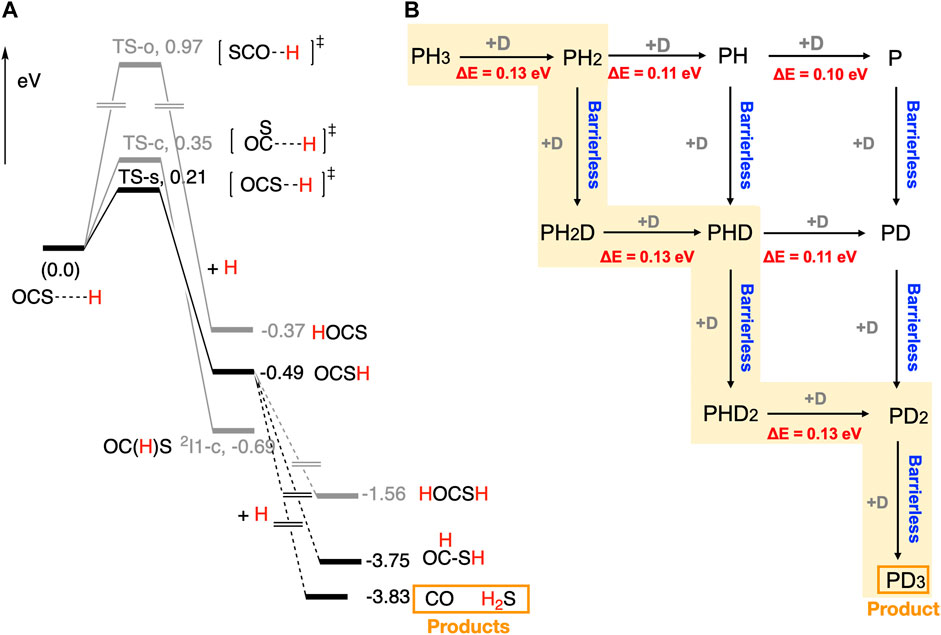
FIGURE 2. (A) Computed potential energy surfaces for the reaction between OCS and H on ASW. (Nguyen et al., 2021b) (B) Possible reaction pathways and reaction barriers for the reaction between PH3 and D on ASW, giving rise to PD3. (Nguyen et al., 2021a) ZPE-corrected energies were used for making energy profiles.
Three reaction paths are possible for the reactions between OCS and H on ASW. The lowest energy path, OCS + H → OCS-H, has a barrier of 0.21 eV (2437 K). Computed reaction barrier for the second-lowest energy path, OCS + H → OC(H)S, is 0.35 eV (4062 K). The highest energy path, OCS + H → H-OCS, shows a significant energy barrier (0.97 eV, 11256 K). The main product of the reaction is OCS-H. Our experimental results indicated a large kinetic isotope effect. (Nguyen et al., 2021b) Therefore, OCS reacts with the H atom on ASW through quantum tunnelling. The computed PESs indicated three barrierless reaction paths for the reaction between OCS-H and H. Among them, OCS-H + H → CO + H2S reaction path gives rise to the most stable products. Other possible products, HC(O)SH and H-OCSH, are 0.08 eV (928 K) and 2.27 eV (26342 K) above CO + H2S, respectively. Thus, the main products of the reaction are CO and H2S, and the minor product would be HC(O)SH. These results are in agreement with our experimental data. The OCS-H radical interacts with the d-Hs and d-Os of the water molecules on ices. Thus, H atom abstraction reaction channel, i.e., OCS-H + H → OCS + H2 is unlikely to occur. Even though some of the reported radical-radical reactions showed barriers, H addition processes described above would operate at low temperatures, (Enrique-Romero et al., 2022) as the H atom diffusion rate on ice is the highest. Our study gives mechanistic insights to understand the evolution of S-bearing species in interstellar space and planetary atmospheres.
4.2 Phosphine + D
Phosphine (PH3) is an important phosphorus-bearing molecule in space. PH3 was detected in the atmosphere of Jupiter, Saturn, and Venus. (Sousa-Silva et al., 2020; Greaves et al., 2021) The formation of PH3 in the gas phase of the ISM is a matter of controversy. (Thorne et al., 1984; Millar, 1991) Therefore, the chemistry of PH3 in space is very important in understanding its origin and the chemical evolution of the phosphorus-bearing species in space. We have performed a combined experimental and computational study to rationalize the reactions between PH3 and D on ASW at low temperatures. According to our experimental data, PD3 is formed on ice and partly released into the gas phase by chemical desorption. We have also detected PH2D and PHD2, but their concentration is relatively low compared to PD3 since their deuteration is fast on icy surfaces. (Nguyen et al., 2021a) However, the mechanism of the reaction between PH3 and D is unknown. Thus, we have performed quantum chemical calculations to rationalize the mechanism.
Computed reaction pathways for the reaction between PH3 and D are shown in Figure 2B. The computed reaction barrier for the PH3 + D → PH2 + HD reaction is 0.13 eV (1509 K). After the formation of PH2 radical, two reaction paths are possible; 1) PH2 + D → PH2D and 2) PH2 + D → PH + HD. The former reaction is barrierless, while the latter reaction has a barrier of 0.11 eV (1277 K). Thus, PH2D is the main product of the reaction. Similar vein, PH2D + D → PHD + HD and PHD2 + D → PD2 + HD reactions occur through the reaction barriers of 0.13 eV (1509 K). Finally, a barrierless reaction between PD2 radical and D leads to PD3. It is important to note that we have performed electronic structure calculations, where zero-point energy of the systems was calculated introducing the mass of H and D. Computed reaction paths explained the mechanism for the formation of PD3 that goes through the experimentally characterized PH2D and PHD2 intermediates. Our findings give implications to understand chemical networks that include phosphine in interstellar space and planetary atmospheres.
5 Summary
Modern computational methods, employing quantum chemical computations, allow quantitative determination of the heterogeneous radical processes on ice surfaces, such as the binding energies of radicals on ices and radical reaction mechanisms. Thus, theory and computations play a crucial role in modern astrochemistry. Computed binding energies of the radical species are summarized in Table 1. In all cases, a range of binding energies were found. Thus, a distribution of binding energies would be used in developing astrochemical models.
TABLE 1. Summary of the computed binding energies.
Reported binding energies of Ferrero et al.(Ferrero et al., 2020) [OH (1551–5321 K), HCO (1315–3081 K), CH3 (1119–1654 K)] and Enrique-Romero et al.(Enrique-Romero et al., 2022) [CH3O (3139–4582 K)] are also in a range, where a few binding sites of a large water ice cluster model were taken into account for calculating binding energies. Wakelam et al.(Wakelam et al., 2015) also reported a range of binding energies for OH (3300–5300 K) and HCO (2300–2700 K) using small water ice cluster models. Compared to their computed binding energies, we have found a broader range of binding energies due to the fact that our studies employed a number of binding sites in large water ice clusters.
We have rationalized the radical reaction mechanisms on ice surfaces by combining laboratory experiments and quantum chemical calculations. According to the calculated potential energy surfaces for the reaction between OCS and H on ices, the first hydrogenation gives rise to OCS-H, where the reaction barrier is relatively high. Therefore, quantum tunnelling is critical. The second hydrogenation yields CO and H2S as the major products and HC(O)SH as the minor product. A recent astronomical observation indicated the presence of HC(O)SH in space.
Computed reaction mechanisms suggested that the reaction between PH3 and D yields PD3, where step-wise dehydrogenation is occurred with a relatively high reaction barrier. Thus, quantum tunnelling is critical for the mechanism to operate at very low temperatures. Deuterated isotopologues of phosphine have not been detected in astronomical observations. However, based on our experimental and computational studies, we argue that the deuterated isotopologues of phosphine can be formed on ices. Thus, we suspect that astronomical observations would detect the deuterated isotopologues of phosphine in the near future.
Author Contributions
WMCS made the first draft of the manuscript. All authors revised the manuscript and were approved the final version of the manuscript.
Funding
This work was partly supported by JSPS KAKENHI Grant Numbers JP19K03940 and JP21H05416 (to WS), JP17H06087 (to NW), JP21H04501 (to YO), and JP21K13974 (to TN).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
Supercomputing resources at the Institute for Molecular Science (IMS) in Japan, the Institute for Information Management and Communication at Kyoto University in Japan are acknowledged.
References
Andersson, S., Al-Halabi, A., Kroes, G.-J., and van Dishoeck, E. F. (2006). Molecular-Dynamics Study of Photodissociation of Water in Crystalline and Amorphous Ices. J. Chem. Phys. 124, 064715. doi:10.1063/1.2162901
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., et al. (2016). Gaussian 16, Revision C.01, Wallingford CT: Gaussian, Inc.
Cabezas, C., Cernicharo, J., Agúndez, M., Tercero, B., Pardo, J. R., Marcelino, N., et al. (2021). TMC-1, the Starless Core Sulfur Factory: Discovery of NCS, HCCS, H2CCS, H2CCCS, and C4S and Detection of C5S. Astron. Astrophys. 648, L3. doi:10.1051/0004-6361/202140642
Chai, J.-D., and Head-Gordon, M. (2008). Long-range Corrected Hybrid Density Functionals with Damped Atom-tom Dispersion Corrections. Phys. Chem. Chem. Phys. 10, 6615–6620. doi:10.1039/B810189B
Chuang, K.-J., Fedoseev, G., Ioppolo, S., van Dishoeck, E. F., and Linnartz, H. (2016). H-atom Addition and Abstraction Reactions in Mixed CO, H2CO and CH3OH Ices—an Extended View on Complex Organic Molecule Formation. Mon. Not. R. Astron. Soc. 455, 1702–1712. doi:10.1093/mnras/stv2288
Chung, L. W., Sameera, W. M. C., Ramozzi, R., Page, A. J., Hatanaka, M., and Petrova, G. P. (2015). The ONIOM Method and its Applications. Chem. Rev. 115, 5678–5796. doi:10.1021/cr5004419
Ditchfield, R., Hehre, W. J., and Pople, J. A. (1971). Self‐Consistent Molecular‐Orbital Methods. IX. An Extended Gaussian‐Type Basis for Molecular‐Orbital Studies of Organic Molecules. J Chem Phys 54, 724–728. doi:10.1063/1.1674902
Duflot, D., Toubin, C., and Monnerville, M. (2021). Theoretical Determination of Binding Energies of Small Molecules on Interstellar Ice Surfaces. Front. Astron. Space Sci. 8, 645243. doi:10.3389/fspas.2021.645243
Enrique-Romero, J., Rimola, A., Ceccarelli, C., Ugliengo, P., Balucani, N., and Skouteris, D. (2022). Quantum Mechanical Simulations of the Radical-Radical Chemistry on Icy Surfaces. Astrophys J Suppl Ser. 259, 39. doi:10.3847/1538-4365/ac480e10.3847/1538-4365/ac480e
Enrique-Romero, J., Rimola, A., Ceccarelli, C., Ugliengo, P., Balucani, N., and Skouteris, D. (2019). Reactivity of HCO with CH3 and NH2 on Water Ice Surfaces. A Comprehensive Accurate Quantum Chemistry Study. ACS Earth Space Chem. 3, 2158–2170. doi:10.1021/acsearthspacechem.9b00156
Eyring, H. (1935). The Activated Complex in Chemical Reactions. J Chem Phys 3, 107–115. doi:10.1063/1.1749604
Ferrante, R. F., Moore, M. H., Spiliotis, M. M., and Hudson, R. L. (2008). Formation of Interstellar OCS: Radiation Chemistry and IR Spectra of Precursor Ices. Astrophys. J. 684, 1210–1220. doi:10.1086/590362
Ferrero, S., Zamirri, L., Ceccarelli, C., Witzel, A., Rimola, A., and Ugliengo, P. (2020). Binding Energies of Interstellar Molecules on Crystalline and Amorphous Models of Water Ice by Ab Initio Calculations. Astrophys. J. 904, 11. doi:10.3847/1538-4357/abb953
Fukui, K. (1981). The Path of Chemical Reactions - the IRC pproach. Acc. Chem. Res. 14, 363–368. doi:10.1021/ar00072a001
Garrod, R. T., and Herbst, E. (2006). Formation of Methyl Formate and Other Organic Species in the Warm-Up Phase of Hot Molecular Cores. Astron. Astrophys. 457, 927–936. doi:10.1051/0004-6361:20065560
Goldsmith, P. F., and Linke, R. A. (1981). A Study of Interstellar Carbonyl Sulfide. Astrophys. J. 245, 482. doi:10.1021/jp908321210.1086/158824
Greaves, J. S., Richards, A. M. S., Bains, W., Rimmer, P. B., Sagawa, H., and Clements, D. L. (2021). Phosphine Gas in the Cloud Decks of Venus. Nat. Astron. 5, 655–664. doi:10.1038/s41550-020-1174-4
Guélin, M., and Cernicharo, J. (2022). Organic Molecules in Interstellar Space: Latest Advances. Front. Astron. Space Sci. 9, 787567. doi:10.3389/fspas.2022.787567
Hehre, W. J., Ditchfield, R., and Pople, J. A. (1972). Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-ype Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J Chem Phys 56, 2257–2261. doi:10.1063/1.1677527
Herbst, E., and Garrod, R. T. (2022). Synthetic Approaches to Complex Organic Molecules in the Cold Interstellar Medium. Front. Astron. Space Sci. 8, 789428. doi:10.3389/fspas.2021.789428
Herbst, E., and van Dishoeck, E. F. (2009). Complex Organic Interstellar Molecules. Annu. Rev. Astron. Astrophys. 47, 427–480. doi:10.1146/annurev-astro-082708-101654
Jiménez-Escobar, A., Muñoz Caro, G. M., and Chen, Y.-J. (2014). Sulphur Depletion in Dense Clouds and Circumstellar Regions. Organic Products made from UV Photoprocessing of Realistic ice Analogs Containing H2S. Mon. Not. R. Astron. Soc. 443, 343–354. doi:10.1093/mnras/stu1100
Laas, J. C., and Caselli, P. (2019). Modeling Sulfur Depletion in Interstellar Clouds. Astron. Astrophys. 624, A108. doi:10.1051/0004-6361/201834446
Lamberts, T., Markmeyer, M. N., Kolb, F. J., and Kästner, J., 2019, Formation of Acetaldehyde on CO-Rich Ices, ACS Earth Space Chem. 3, 958–963. doi:10.1021/acsearthspacechem.9b00029
Maeda, S., Harabuchi, Y., Takagi, M., Saita, K., Suzuki, K., and Ichino, T. (2018). Implementation and Performance of the Artificial Force Induced Reaction Method in the GRRM17 Program. J. Comput. Chem. 39, 233–251. doi:10.1002/jcc.25106
Millar, T. J. (1991). Phosphorus Chemistry in Dense Interstellar Clouds. Astron. Astrophys. 242, 241.
Miyazaki, A., Watanabe, N., Sameera, W. M. C., Nakai, Y., Tsuge, M., Hama, T., et al. (2020). Photostimulated Desorption of OH Radicals from Amorphous Solid Water: Evidence for the Interaction of Visible Light with an OH-ice Complex. Phys. Rev. A 102, 052822. doi:10.1103/PhysRevA.102.052822
Morokuma, K. (1971). Molecular Orbital Studies of Hydrogen Bonds. III. C=O···H-O Hydrogen Bond in H2CO···H2O and H2CO···2H2O. J Chem Phys 55, 1236. doi:10.1063/1.1676210
Nguyen, T., Oba, Y., Sameera, W. M. C., Kouchi, A., and Watanabe, N. (2021a). Experimental and Computational Studies on the Physicochemical Behavior of Phosphine Induced by Reactions with H and D Atoms on Interstellar Ice Grains. Astrophys. J. 918, 73. doi:10.3847/1538-4357/ac0cf4
Nguyen, T., Oba, Y., Sameera, W. M. C., Kouchi, A., and Watanabe, N. (2021b). Successive H-tom Addition to Solid OCS on Compact Amorphous Solid Water. Astrophys. J. 922, 146. doi:10.3847/1538-4357/ac2238
Nyman, G. (2021). Tunneling of Hydrogen and Deuterium Atoms on Interstellar Ices (Ih and ASW). Front. Astron. Space Sci. 8, 738264. doi:10.3389/fspas.2021.738264
Oba, Y., Tomaru, T., LambertsKouchi, T.A, Kouchi, A., and Watanabe, N. (2018). An Infrared Measurement of Chemical Desorption from Interstellar Ice Analogues. Nat. Astron. 2, 228–232. doi:10.1038/s41550-018-0380-9
Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., and Linnartz, H. (2009). Formation Rates of Complex Organics in UV Irradiated CH3OH-rich Ices. Astron. Astrophys. 504, 891–913. doi:10.1051/0004-6361/200912559
Palumbo, M. E., Tielens, A. G. G. M., and Tokunaga, A. T. (1995). Solid Carbonyl Sulphide (OCS) in W33A. Astrophys. J. 449, 674. doi:10.1086/176088
Pople, J. A., Head‐Gordon, M., and Raghavachari, K. (1987). Quadratic Configuration Interaction. A General Technique for Determining Electron Correlation Energies. J Chem Phys 87, 5968–5975. doi:10.1063/1.453520
Sameera, W. M. C., Maeda, S., and Morokuma, K. (2016). Computational Catalysis Using the Artificial Force Induced Reaction Method. Acc. Chem. Res. 49, 763–773. doi:10.1021/acs.accounts.6b00023
Sameera, W. M. C., and Maseras, F. (2018). Expanding the Range of Force Fields Available for ONIOM Calculations: The SICTWO Interface. J. Chem. Inf. . 58, 1828–1835. doi:10.1021/acs.jcim.8b00332
Sameera, W. M. C., and Maseras, F. (2012).Transition etal atalysis by ensity unctional heory and ensity unctional heory/molecular echanics. Comput. Mol. Sci. 2, 375–385. doi:10.1002/wcms.1092
Sameera, W. M. C., Senevirathne, B., Andersson, S., Al-lbadi, M., Hidaka, H., and Kouchi, A. (2021). CH3O Radical Binding on Hexagonal Water Ice and Amorphous Solid Water. J. Phys. Chem. A 125, 387–393. doi:10.1021/acs.jpca.0c09111
Sameera, W. M. C., Senevirathne, B., Andersson, S., Maseras, F., and Nyman, G. (2017). ONIOM(QM:AMOEBA09) Study on Binding Energies and Binding Preference of OH, HCO, and CH3 Radicals on Hexagonal Water Ice (Ih). J. Phys. Chem. C 121, 15223–15232. doi:10.1021/acs.jpcc.7b04105
Schäfer, A., Horn, H., and Ahlrichs, R. (1992). Fully Optimized Contracted Gaussian Basis Sets for Atoms Li to Kr. J Chem Phys 97, 2571–2577. doi:10.1063/1.463096
Schäfer, A., Huber, C., and Ahlrichs, R. (1994). Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J Chem Phys 100, 5829–5835. doi:10.1063/1.467146
Senevirathne, B., Andersson, S., Dulieu, F., and Nyman, G. (2017). Hydrogen Atom Mobility, Kinetic Isotope Effects and Tunneling on Interstellar Ices (Ih and ASW). Mol Astrophys 6, 59–69. doi:10.1016/j.molap.2017.01.005
Sousa-Silva, C., Seager, S., Ranjan, S., Petkowski, J. J., Zhan, Z., and Hu, R. (2020). Phosphine as a Biosignature Gas in Exoplanet Atmospheres. Astrobiology 20, 235–268. doi:10.1089/ast.2018.1954
te Velde, G., Bickelhaupt, F. M., Baerends, E. J., Fonseca Guerra, C., van Gisbergen, S. J. A., and Snijders, J. G. (2001). Chemistry with ADF. J. Comput. Chem. 22, 931–967. doi:10.1002/jcc.1056
Thorne, L. R., Anicich, V. G., Prasad, S. S., and Huntress, W. T. J. (1984). The Chemistry of Phosphorus in Dense Interstellar Clouds. Astrophys. J. 280, 139. doi:10.1086/161977
Tsuge, M., and Watanabe, N. (2021). Behavior of Hydroxyl Radicals on Water Ice at Low Temperatures. Acc. Chem. Res. 54, 471–480. doi:10.1021/acs.accounts.0c00634
Wakelam, V., Loison, J.-C., Herbst, E., Pavone, B., Bergeat, A., Béroff, K., et al. (2015). The 2014 KIDA Network for Interstellar Chemistry. Astrophys J Suppl Ser. 217, 20. doi:10.1088/0067-0049/217/2/20
Watanabe, N., and Kouchi, A. (2002). Efficient Formation of Formaldehyde and Methanol by the Addition of Hydrogen Atoms to CO in H2O-CO Ice at 10 K. Astrophys. J. 571, L173–L176. doi:10.1086/341412
Zapata Trujillo, J. C., Syme, A.-M., Rowell, K. N., Burns, B. P., Clark, E. S., Gorman, M. N., et al. (2021). Computational Infrared Spectroscopy of 958 Phosphorus-Bearing Molecules. Front. Astron. Space Sci. 8, 639068. doi:10.3389/fspas.2021.639068
Zhao, Y., and Truhlar, D. G. (2008). The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-lass Functionals and 12 Other Functionals. Theor Chem Acc 120, 215–241. doi:10.1007/s00214-007-0310-x
Keywords: DFT, QM/MM, radicals on ice surfaces, binding energy, reaction mechanisms, quantum tunnelling
Citation: Sameera WMC, Senevirathne B, Nguyen T, Oba Y, Ishibashi A, Tsuge M, Hidaka H and Watanabe N (2022) Modelling the Radical Chemistry on Ice Surfaces: An Integrated Quantum Chemical and Experimental Approach. Front. Astron. Space Sci. 9:890161. doi: 10.3389/fspas.2022.890161
Received: 05 March 2022; Accepted: 25 April 2022;
Published: 30 May 2022.
Edited by:
Martin Robert Stewart McCoustra, Heriot-Watt University, United KingdomReviewed by:
Albert Rimola, Universitat Autònoma de Barcelona, SpainJennifer Noble, Aix Marseille Université, France
Copyright © 2022 Sameera, Senevirathne, Nguyen, Oba, Ishibashi, Tsuge, Hidaka and Watanabe. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: W. M. C. Sameera, wmcsameera@lowtem.hokudai.ac.jp