Five Dimensional Bianchi Type-I Anisotropic Cloud String Cosmological Model With Electromagnetic Field in Saez-Ballester Theory

F

Within the context of Saez-Ballester theory, we explored the interaction of a five-dimensional Bianchi type-I anisotropic cloud string cosmological model Universe with an electromagnetic field. With an electromagnetic field, the energy momentum tensor is assumed to be the sum of the rest energy density and string tension density in this paper. We use the average scale factor as an integrating function of time to get exact answers to Saez-Ballester equations. The dynamics and importance of the model’s many physical parameters are also examined.

1 Introduction

Many authors have been attracted by the possibility of space-time having more than four dimensions. This has piqued the curiosity of cosmologists and theoretical physicists to the point where, in recent decades, there has been a trend among authors to investigate cosmology in higher-dimensional space-time. In an attempt to combine gravity and electromagnetism, the higher-dimensional model was introduced in (Kaluza, 1921; Klein, 1926). The late time expedited expanding paradigm can be illustrated using a higher dimensional model (Banik and Bhuyan, 2017). Investigation of higher dimensional space-time is a critical undertaking, as the cosmos may have passed through a higher dimensional epoch during its early history (Singh et al., 2004). Extra dimensions generate a large quantity of entropy, according to (Guth, 1981; Alvax and Gavela, 1983), which may provide a solution to the flatness and horizon problems. The discovery of time-varying fundamental constants can perhaps provide us the proof for extra dimensions, according to (Marciano, 1984). (Shinkai and Torii, 2015; Singh and Singh, 2019; Montefalcone et al., 2020; Daimary and Baruah, 2021; Singh and Baro, 2021) are a few of the noteworthy studies on higher dimensional space-time published in the previous few years.

Our Universe is growing at an accelerated rate, according to various types of literature. The Saez-Ballester theory of gravitation is regarded a perfect explanation to describe our expanding Universe in FRW space-time. Bull et al. (Bull et al., 2016) researched alternative cosmology and summarised the current position of ΛCDM as a physical theory in addition to the standard model ΛCDM in extending cosmology. Only an isotropic and homogeneous Universe is described by FRW space-time on a huge scale. However, recent discoveries and reasoning show that throughout the cosmic expansion of the Universe, an anisotropic phase exists before it transitions to an isotropic one. The homogeneous and anisotropic universes are represented by Bianchi typecosmological models, and their isotropy nature can be examined across time. In addition, anisotropic worlds have more generality than isotropic model universes from a theoretical standpoint. Several publications (Singh et al., 2021; Amirhashchi et al., 2009; Akarsu and Kilinc, 2010b,a; Sahoo and Mishra, 2015) looked at the anisotropic Bianchi type cosmological model from various angles. Kibble (Kibble, 1976) identified the stable topological flaws that occurred throughout the phase shift as strings in his study “Topology of Cosmic Domains and Strings.” He also shown that the homogeneity group of the manifold of degenerate vacua affects the topological defects of domain structure. Letelier (Letelier, 1983) used the Bianchi type I and Kantowski-Sachs space-time cosmological models to research String Cosmology. The Bianchi type VII models, according to Collins and Hawking (Collins and Hawking, 1972), are the most generic uniform cosmological models that are infinite in all three spatial directions. These models include wide class initial conditions, allowing for the largest number of arbitrary constants imaginable. He also demonstrated that while all initial anisotropic universes do not attain isotropy, a subclass of universes with escape velocity does.

Because of the importance of string in characterising the early stages of our Universe’s evolution, several authors have recently focused on string cosmological models. The string can describe the nature and fundamental configuration of the early cosmos at the same time. The most actively explored approach to quantum gravity is string theory, and it can be used to discuss the mechanics of the early cosmos. String theory unifies all matter and forces into a single theoretical structure and describes the early stages of our cosmos in terms of vibrating strings rather than particles. According to Kibble (Kibble, 1976), cosmic strings are stable line-like topological objects/defects that arise at some point during the phase transition in our Universe’s early history. According to GUT (grand unified theories) [Zel’dovich et al. (Zel’dovich et al., 1974), Kibble (Kibble, 1976; Kibble, 1980), Everett (Everett, 1981), Vilenkin (Vilenkin, 1981a; Vilenkin, 1981b)], symmetry is broken during the phase transition in the early stages of the Universe after the big bang, and these strings appear when the cosmic temperature drops below a critical temperature. Strings can thus play an important part in studying the early stages of the Universe. Massive closed loops of strings also produce huge scale structures like galaxies and clusters of galaxies. The gravitational field couples with the cosmic strings, which may include stress-energy. As a result, one of the most exciting projects is the investigation of gravitational effects coming from cosmic strings.

Letelier (Letelier, 1983) succeeded in obtaining enormous string cosmological models in Bianchi type-I and Kantowski-Sachs space-times in 1983. Following Letelier, a slew of authors investigated string cosmological models in a variety of settings.

Krori (Krori et al., 1990) and Wang (Wang, 2003) explored the Letelier string cosmological model and obtained their exact solutions using Bianchi type-II, -VI0, -VIII, and -IX space-times. By taking the coefficient of bulk viscosity as a power function of energy density, Xing (Xing-Xiang, 2004) developed an exact solution string cosmological model with bulk viscosity using the LRS Bianchi type-I metric. Yavuz (Yavuz et al., 2005) investigated charged weird quark matter linked to the string cloud in spherical symmetric space-time and demonstrated the existence of a one-parameter group of conformal motions. In the setting of general relativity, Yilmaz (Yilmaz, 2006) established the Kaluza-Klein cosmological solutions for quark matter connected to the string cloud. Rao (Rao et al., 2008) established an exact perfect fluid cosmological model based on Lyra manifold where the displacement vector is a constant while investigating a Bianchi type-V space-time in a scalar-tensor theory. However, if β is a function of cosmic time t, then this model occurs solely in the case of radiation. In Saez-Ballester Scalar-Tensor theory, Tripathy (Tripathy et al., 2009) investigated an anisotropic and spatially homogeneous Bianchi type-VI0 space-time and developed string cloud cosmological models. In the Brans-Dicke theory of gravitation, Adhav et al. (Adhav et al., 2007) produced string cosmological models by solving the field equations with the condition that the sum of the tension density and energy density is zero. Pawar (Pawar et al., 2018) investigated the Kaluza–Klein string cosmological model in the context of the f (R, T) theory of gravity and solved the field equations using a power law relationship between scale factor and a time-varying deceleration parameter.

In the presence of an electromagnetic field, the cosmological model plays a critical role in the evolution of the cosmos and the construction of large scale structures such as galaxies and other celestial bodies. The presence of a cosmic electromagnetic field formed during inflation is responsible for the current phase of accelerated expansion of the cosmos. On cosmological scales, Jimenez and Maroto (Jimenez and Maroto, 2009) shown that the presence of a electromagnetic field provides an effective cosmological constant, which accounts for the Universe’s accelerated expansion. In general relativity, Tripathy et al. (Tripathi et al., 2017) investigated an inhomogeneous string cosmological model with electromagnetic field. Parikh (Parikh et al., 2018) recently investigated a Bianchi type II string dust cosmological model in Lyra’s Geometry with an electromagnetic field. Pradhan (Pradhan and Jaiswal, 2018) investigated a class of anisotropic and homogeneous Bianchi type-V cosmological models with heavy strings in the presence of a magnetic field in the f (R, T) theory of gravity. Grasso (Grasso and Rubinstein, 2000) looked into a wide range of characteristics of magnetic fields in the early Universe, as well as modern temporal fields and their evolution in galaxies and clusters. The magnetic field also contributes to the breakdown of statistical homogeneity and isotropy. Magnetic fields can be found in large scale galaxies and galaxy clusters. In his study, Subramanian (Subramanian, 2016) demonstrated that primordial magnetic fields have a significant impact on the creation of star structures, particularly on dwarf galaxy scales.

Alternative theories of gravity, such as the Brans-Dicke gravity theory (Brans and Dicke, 1961), the Saez-Ballester theory of gravity (Saez and Ballester, 1986), f (R) gravity (Capozziello et al., 2003; Nojiri and Odintsov, 2003), f (R,T) gravity (Harko et al., 2011) are all important. Each of these gravity theories has its own significance. We built a cosmological model in the Saez-Ballester theory of gravity to examine several features of the cosmos in this research. As it is known, the metric is easily coupled with a dimensionless scalar field in Sáez and Ballester theory. Despite the scalar field’s dimensionless behaviour, this coupling affords a fair description of weak fields in which an accelerated growth regime arises. Many authors, including our peers, have built cosmological models based on the Saez-Ballester theory of gravity to investigate various features of the Universe (Singh and Agrawal, 1991; Aditya and Reddy, 2018; Mishra and Dua, 2019; Mishra and Chand, 2020; Rasouli et al., 2020). Santhi and Sobhanbabu (Santhi and Sobhanbabu, 2020) looked at the dynamics of the Bianchi type-III Tsallis holographic dark energy model in the Saez-Ballester theory of gravity and came up with some interesting findings. In the Saez-Ballester theory of gravity, Naidu et al. (Naidu et al., 2021) explored the behaviour of Kaluza-Klein FRW dark energy models, finding the solution of field equations utilising I hybrid expansion law and (ii) variable deceleration parameter. Saez-Ballester gives the Einstein field equations for the combined scalar and tensor fields

$R_{ij}-\frac{1}{2}R{g}_{ij}-\omega {\varphi }^m\left({\varphi }_{,i}{\varphi }_{,j}-\frac{1}{2}{g}_{ij}{\varphi }_{,k}{\varphi }^{,k}\right)=-T_{ij}(1)$

and the scalar field also fulfils the equation

$2{\varphi }^m{\varphi }_{;i}^{,i}+m{\varphi }^{m-1}{\varphi }_{,k}{\varphi }^{,k}=0(2)$

We solved the Saez-Ballester equations for energy momentum tensor for cloud string interacting with electromagnetic field and addressed in depth all elements of physical and kinematic properties in this article, which was motivated by the study of the above literatures. The following is how the paper is structured: The metric and field equations are presented in Section 2; the solution of the field equations is offered in Section 3; physical features of our model Universe are presented in Section 4; and illustrations and figures are presented in Section 5. Finally, in Section 6, we review the findings and provide some last observations.

2 Metric and Field Equations

We consider the Bianchi type-I metric, which is spatially homogenous and anisotropic

$d{s}^2=-d{t}^2+A^2\left(d{x}^2+d{y}^2\right)+B^{2}d{z}^2+C^{2}d{\psi }^2(3)$

A, B, and C are all functions of cosmic time t.

For the metric (3) we assume

x¹ = x, x² = y, x³ = z, x⁴ = ψ, and x⁵ = t

A cloud string’s energy-momentum tensor (Reddy, 2003) is of the form

$T_{ij}=\rho u_i{u}_j-\lambda x_i{x}_j+E_{ij}(4)$

where ${\rho }_p$ is the particle density and λ is the string tension density, and ρ is the rest energy density of the cloud of strings with particles attached to them ρ = ρ_p + λ. x_i is a unit space-like vector that represents the direction of strings, with x² = 0 = x³ = x⁴ = x⁵ and x¹ ≠ 0, and u_i is the five velocity vector that meets the following conditions

$u^i{u}_i=-x^i{x}_i=-1(5)$

and

$u^i{x}_i=0(6)$

The five velocity vectors uⁱ as well as the string’s direction xⁱ, are given by

$u^i=\left(\mathrm{0,0,0,0,1}\right)(7)$

and

$x^i=\left(\frac{1}{A},\mathrm{0,0,0,0}\right)(8)$

where the strings direction are parallel to the x-axis.

The electromagnetic field E_ij, which is a component of the energy momentum tensor, is referred to as

$E_{ij}=\frac{1}{4\pi }\left(g^{\alpha \beta }{F}_{i\alpha }{F}_{i\beta }-\frac{1}{4}{g}_{ij}{F}_{\alpha \beta }{F}^{\alpha \beta }\right)(9)$

Here F_αβ is denoted the electromagnetic field tensor.

F₁₅ is the only non-vanishing component of the electromagnetic field tensor F_ij if we quantize the magnetic field along the x axis. Assuming infinite electromagnetic conductivity, it can be obtain that F₁₂ = F₁₃ = F₁₄ = F₂₃ = F₂₄ = F₂₅ = F₃₄ = F₃₅ = 0 (Singh et al., 2020).

As a result, the nontrivial components of the electromagnetic field E_ij can be calculated using Eq. 9 as given below

$E_1^1=-E_2^2=-E_3^3=-E^4=E_1^1=-\frac{1}{2}{g}^{11}{g}^{55}{F}_{15}^2=\frac{1}{2A^2}{F}_{15}^2(10)$

Or, If we take the magnetic field along the x-axis in co-moving coordinates, F₃₄ is the only non-vanishing component of the electromagnetic field tensor F_ij. Assuming infinite electromagnetic conductivity, it can be define that F₁₅ = F₂₅ = F₃₅ = F₁₂ = F₁₃ = F₁₄ = 0 (Singh et al., 2020).

As a result, the nontrivial components of the electromagnetic field E_ij can be calculated using Eq. 9

$E_1^1=-E_2^2=-E_3^3=-E^4=E_1^1=-\frac{1}{2A^2}{F}_{34}^2(11)$

Important physical quantities for the metric (3) include the spatial volume V, the average scale factor R, the expansion scalar θ, the Hubble parameter H, the deceleration parameter q, the shear scalar σ² and the mean anisotropy parameter △:

$V=R^4=A^{2}BC(12)$

$\theta =u_{;i}^i=2\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}(13)$

$H=\frac{\dot{R}}{R}=\frac{1}{4}\left(2\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right)(14)$

$q=-\frac{R\ddot{R}}{{\dot{R}}^2}=\frac{d}{dt}\left(\frac{1}{H}\right)-1(15)$

${\sigma }^2=\frac{1}{2}{\sigma }_{ij}{\sigma }^{ij}=\frac{1}{2}\left(2\frac{{\dot{A}}^2}{A^2}+\frac{{\dot{B}}^2}{B^2}+\frac{{\dot{C}}^2}{C^2}\right)-\frac{{\theta }^2}{8}(16)$

$△=\frac{1}{4}\sum _{i=1}^4{\left(\frac{H_i-H}{H}\right)}^2(17)$

With regard to cosmic time t, an over head dot represents the first derivative, while a double over head dot represents the second. Also, H_i(i = 1, 2, 3, 4) denotes the directional Hubble Parameters in the direction of x, y, z and ψ axes and are obtained for metric (1) as $H_1=H_2=\frac{\dot{A}}{A}$, $H_3=\frac{\dot{B}}{B}$, and $H_4=\frac{\dot{C}}{C}$.

The Saez-Ballester field Eqs 1, 2 are reduced to the following system of equations when combined with Eq. 4 for the line-element Eq. 3:

$\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\dot{A}}{A}\frac{\dot{B}}{B}+\frac{\dot{A}}{A}\frac{\dot{C}}{C}+\frac{\dot{B}}{B}\frac{\dot{C}}{C}=\lambda -\frac{1}{2A^2}{F}_{15}^2+\omega {\varphi }^m\frac{{\dot{\varphi }}^2}{2}(18)$

$\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\dot{A}}{A}\frac{\dot{B}}{B}+\frac{\dot{A}}{A}\frac{\dot{C}}{C}+\frac{\dot{B}}{B}\frac{\dot{C}}{C}=\frac{1}{2A^2}{F}_{15}^2+\omega {\varphi }^m\frac{{\dot{\varphi }}^2}{2}(19)$

$2\frac{\ddot{A}}{A}+\frac{{\dot{A}}^2}{A^2}+\frac{\ddot{C}}{C}+2\frac{\dot{A}}{A}\frac{\dot{C}}{C}=\frac{1}{2A^2}{F}_{15}^2+\omega {\varphi }^m\frac{{\dot{\varphi }}^2}{2}(20)$

$2\frac{\ddot{A}}{A}+\frac{{\dot{A}}^2}{A^2}+\frac{\ddot{B}}{B}+2\frac{\dot{A}}{A}\frac{\dot{B}}{B}=\frac{1}{2A^2}{F}_{15}^2+\omega {\varphi }^m\frac{{\dot{\varphi }}^2}{2}(21)$

$\frac{{\dot{A}}^2}{A^2}+2\frac{\dot{A}}{A}\frac{\dot{B}}{B}+2\frac{\dot{A}}{A}\frac{\dot{C}}{C}+\frac{\dot{B}}{B}\frac{\dot{C}}{C}=\rho -\frac{1}{2A^2}{F}_{15}^2-\omega {\varphi }^m\frac{{\dot{\varphi }}^2}{2}(22)$

$\ddot{\varphi }+\dot{\varphi }\left(2\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\right)+\frac{m}{2}\frac{{\dot{\varphi }}^2}{\varphi }=0(23)$

3 Solution of the Field Equations

The field Eqs 18–22 are a set of five equations with seven unknown parameters (A, B, C, ρ, λ, ϕ and F₁₅). As a result, two additional constraints linking these parameters are necessary in order to achieve explicit system solutions. These two relationships are considered to be

1) We can take advantage of the fact that the shear scalar σ is proportional to the scalar expansion θ (Collins et al., 1983; Rao et al., 2015).

$B=C^n(24)$

here n is constant.2) Berman (Berman, 1983) and Ram et al. (Ram et al., 2010) derived a relationship between the Hubble parameter H and the average scale factor R. Berman, and Gomide (Berman and Gomide, 1988), and Ram et al. (Ram et al., 2010) solved FRW models using this type of relation, whereas Ram et al. (Ram et al., 2010) solved Bianchi Type V cosmological models in Lyra’s Geometry.

$H=a{R}^{-k_1}(25)$

a ≥ 0, k₁ ≥ 0 are constants.

Equation 25 provides us with

$R={\left(a{k}_{1}t+k_2\right)}^{\frac{1}{k_1}}if{k}_1\ne 0(26)$

and

$R=k_3{e}^{at}if{k}_1=0(27)$

k₂ and k₃ are constants.

As a result of Equation 15, the deceleration parameter q is determined

$q=\left(k_1-1\right)if{k}_1\ne 0(28)$

$q=-1if{k}_1=0(29)$

Case I. Case I: When k₁ ≠ 0, we haveThe Eqs 19, 20, 24, 26 will provide us with the following result

$C=k_5{e}^{\frac{k_4{\left(a{k}_{1}t+k_2\right)}^{\frac{k_1-4}{k_1}}}{a\left(k_1-4\right)}}(30)$

k₄, k₅ are constants in this equation. We can assume k₄ = k₅ = 1 without losing generality, giving us

$C=e^{\frac{{\left(a{k}_{1}t+k_2\right)}^{\frac{k_1-4}{k_1}}}{a\left(k_1-4\right)}}(31)$

As a result, the Eqs 12, 24, 26 will provide us with

$A={\left(a{k}_{1}t+k_2\right)}^{\frac{2}{k_1}}{e}^{-\frac{{\left(a{k}_{1}t+k_2\right)}^{\frac{k_1-4}{k_1}}\left(n+1\right)}{2a\left(k_1-4\right)}}(32)$

and

$B=e^{\frac{n{\left(a{k}_{1}t+k_2\right)}^{\frac{k_1-4}{k_1}}}{a\left(k_1-4\right)}}(33)$

As a result, the line element Eq. 3 is transformed into

$\begin{array}{ll}\hfill d{s}^2& =-d{t}^2+{\left(a{k}_{1}t+k_2\right)}^{\frac{4}{k_1}}{e}^{-\frac{{\left(a{k}_{1}t+k_2\right)}^{\frac{k_1-4}{k_1}}\left(n+1\right)}{a\left(k_1-4\right)}}\left(d{x}^2+d{y}^2\right)\hfill \\ \hfill & +e^{\frac{2n{\left(a{k}_{1}t+k_2\right)}^{\frac{k_1-4}{k_1}}}{a\left(k_1-4\right)}}d{z}^2+e^{\frac{2{\left(a{k}_{1}t+k_2\right)}^{\frac{k_1-4}{k_1}}}{a\left(k_1-4\right)}}d{\psi }^2\hfill \end{array}(34)$

Equation 34 is a Bianchi Type I cosmological model Universe with electromagnetic field and Hubble parameter special law which is becomes singular for k₁ = 4.

4 Some Physical Properties of the Model

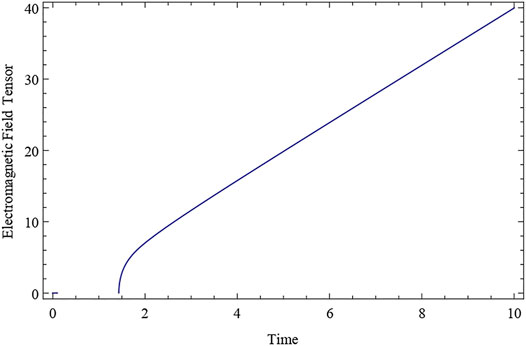
Now, using Equations 18–22, we can calculate the values of energy density ρ, String tension density λ, and electromagnetic field tensor F₁₅ for our model Universe provided by Equation 34.

$\rho =-4a^2\left(k_1-4\right){\left(a{k}_{1}t+k_2\right)}^{-2}(35)$

$\begin{array}{ll}\hfill \lambda & =\frac{1}{2}\left(3n^2+2n+3\right){\left(a{k}_{1}t+k_2\right)}^{\frac{-8}{k_1}}-2a^2\left(3k_1-8\right){\left(a{k}_{1}t+k_2\right)}^{-2}\hfill \\ \hfill & -4a\left(n+1\right){\left(a{k}_{1}t+k_2\right)}^{-\left(\frac{k_1+4}{k^1}\right)}-\omega k_6^2{\left(a{k}_{1}t+k_2\right)}^{-\frac{8}{k_1}}\hfill \end{array}(36)$

$\begin{array}{ll}\hfill F_{15}& =\sqrt{2}\left[\frac{1}{4}\left(3n^2+2n+3\right){\left(a{k}_{1}t+k_2\right)}^{-\frac{4}{k_1}}\right.\hfill \\ \hfill & -4a^2\left(k_1-3\right){\left(a{k}_{1}t+k_2\right)}^{-2\left(\frac{k_1-2}{k_1}\right)}\hfill \\ \hfill & {\left.-2a\left(n+1\right){\left(a{k}_{1}t+k_2\right)}^{-1}-\omega \frac{k_6^2}{2}{\left(a{k}_{1}t+k_2\right)}^{-\frac{8}{k_1}}\right]}^{\frac{1}{2}}\hfill \\ \hfill & \times e^{\frac{{\left(a{k}_{1}t+k_2\right)}^{\frac{k_1-4}{k_1}}\left(n+1\right)}{a\left(k_1-4\right)}}\hfill \end{array}(37)$

Using the relationship ρ = ρ_p + λ we now obtain

$\begin{array}{l}\hfill {\rho }_p=2a^2{k}_1{\left(a{k}_{1}t+k_2\right)}^{-2}-\frac{1}{2}\left(3n^2+2n+3\right){\left(a{k}_{1}t+k_2\right)}^{-\frac{8}{k_1}}+\\ \hfill 4a\left(n+1\right){\left(a{k}_{1}t+k_2\right)}^{-\left(\frac{k_1+4}{k_1}\right)}+\omega k_6^2{\left(a{k}_{1}t+k_2\right)}^{-\frac{8}{k_1}}\end{array}(38)$

The physical quantities proper volume V, Hubble parameter H, expansion scalar θ, scalar field ϕ shear scalar σ², and mean anisotropy parameter △ are calculated as follows:

$V=R={\left(a{k}_{1}t+k_2\right)}^{\frac{4}{k_1}}(39)$

$H=\frac{a}{\left(a{k}_{1}t+k_2\right)}(40)$

$\theta =\frac{4a}{\left(a{k}_{1}t+k_2\right)}(41)$

$\varphi ={\left[\frac{k_6\left(m+2\right)}{2a\left(k_1-4\right)}\right]}^{\frac{2}{m+2}}\left[{\left(a{k}_{1}t+k_2\right)}^{\left(\frac{k_1-4}{k_1}\right)}\left(\frac{2}{m+2}\right)\right](42)$

$\begin{array}{cc}\hfill {\sigma }^2& =\frac{\left(3n^2+2n+3\right)}{4}{\left(a{k}_{1}t+k_2\right)}^{-\frac{8}{k_1}}\hfill \\ \hfill & -2a\left(n+1\right){\left(a{k}_{1}t+k_2\right)}^{-\left(\frac{k_1+4}{k_1}\right)}+2a^2{\left(a{k}_{1}t+k_2\right)}^{-2}\hfill \end{array}(43)$

$\begin{array}{cc}\hfill △& =1-\frac{\left(n+1\right)}{a}{\left(a{k}_{1}t+k_2\right)}^{\left(\frac{k_1-4}{k_1}\right)}\hfill \\ \hfill & +\frac{\left(3n^2+2n+3\right)}{2a^2}{\left(a{k}_{1}t+k_2\right)}^{2\left(\frac{k_1-4}{k_1}\right)}\hfill \end{array}(44)$

From Equations 41, 43, we get

$\underset{t\to \infty }{\lim }\frac{{\sigma }^2}{{\theta }^2}\ne 0(45)$

The fluctuation of some of the parameters is depicted using the values a = k₁ = k₆ = n = 1 and k₂ = 0.

5 Physical Interpratation

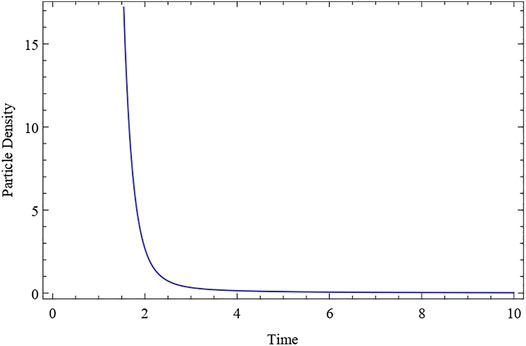
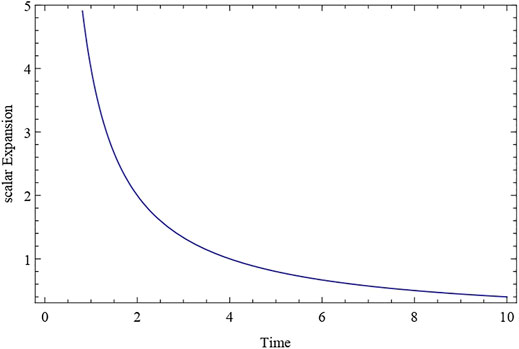
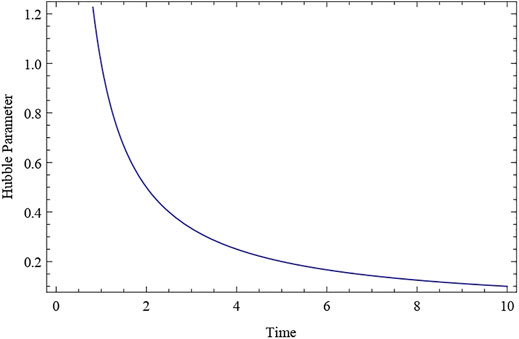
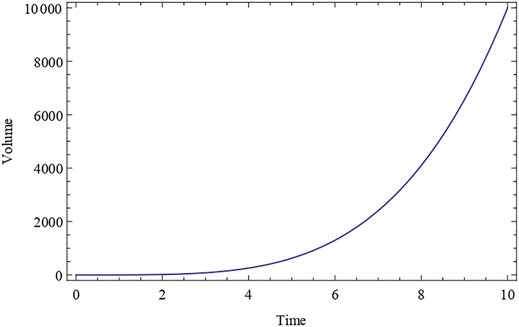
The deceleration parameter q is constant and negative, as shown in the expression Eq. 28. This indicates that since cosmic time t = 0, our proposed model Universe has been inflating and expanding at a constant rate. Throughout the course of evolution, the Universe’s expansion rate is constant. q = constant (negative value) for k₁ < 1. Also, at t = 0 at the time of the big bang, the particle density has a huge positive value. It approaches a positive value as time passes, eventually reaching a finite constant value at t → ∞ (As shown in Figure 1). This demonstrates that the particle continues to dominate the cosmos as time passes, and that the total number of particles in the Universe remains constant. The expansion scalar, a Hubble parameter, exhibits similar fluctuations throughout time. After evolving from infinity at t = 0 to a finite value at t→∞, both the Hubble’s parameter H and the expansion scalar diminish with cosmic time t (shown in Figures 2, 3). The expansion of the cosmos appears to be accelerating, and the deceleration parameter is negative in this scenario, $\ddot{R}>0$. Our model satisfies the energy conditions ρ ≥ 0 and ρ_p ≥ 0. The electromagnetic field changes the behaviour of the model, as well as the physical parameter expressions. In the presence of an electromagnetic field, the rest energy density and string tension tensity decrease (As shown in Figures 4, 5). Particle density and string tension density are also comparable, although string tension density vanishes faster than particle density. This shows that our model displays a matter-dominated Universe at a late time scale, which is in line with current observational data. We can see from the expression Eq. 39, that the proper volume $V=k_2^{\frac{4}{k_1}}$ at t = 0 increases with cosmic time t (Shown in Figure 6). This implies that the Universe begins with a finite volume at t = 0 and then grows as cosmic time passes. The appropriate volume V becomes infinite at time t. Equation 37 illustrates that the non-vanishing electromagnetic field tensor F₁₅ grows exponentially as a function of cosmic time t (Shown in Figure 7). If a ≠ 0, we can see that the electromagnetic field tensor F₁₅ does not vanish. It has a significant impact on the formation of strings during the early stages of the Universe’s evolution. In this scenario, the string and electromagnetic field are found to coexist.

FIGURE 1

FIGURE 1. Particle Density ρ_p vs. time.

FIGURE 2

FIGURE 2. Scalar Expansion θ vs. time.

FIGURE 3

FIGURE 3. Hubble Parameter H vs. time.

FIGURE 4

FIGURE 4. Energy density ρ vs. time.

FIGURE 5

FIGURE 5. Tension Density λ vs. time.

FIGURE 6

FIGURE 6. Volume V vs. time.

FIGURE 7

FIGURE 7. Electromagnetic Field tensor F₁₅ vs. time.

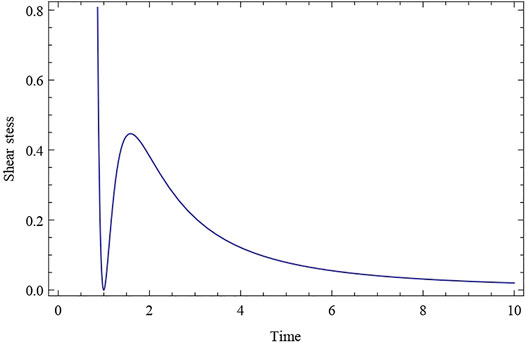
At the first singularity, the parameters shear scalar σ² and mean anisotropy parameter △ diverge (As shown in Figures 8, 9). The model depicts a shearing, non-rotating cosmos with the potential for a large crunch at some t = 0 beginning epoch. Also, we can observe from the mathematical statement Eq. 45, the isotropic condition ${\lim }_{t\to \infty }\frac{{\sigma }^2}{\theta 2}\ne 0$(constant), remains constant throughout the Universe’s evolution (from early to late-time), indicating the model does not attain isotropy (Sahoo et al., 2017).

FIGURE 8

FIGURE 8. Shear Stress σ² vs. time.

FIGURE 9

FIGURE 9. Anisotropy Parameter △ vs. time.

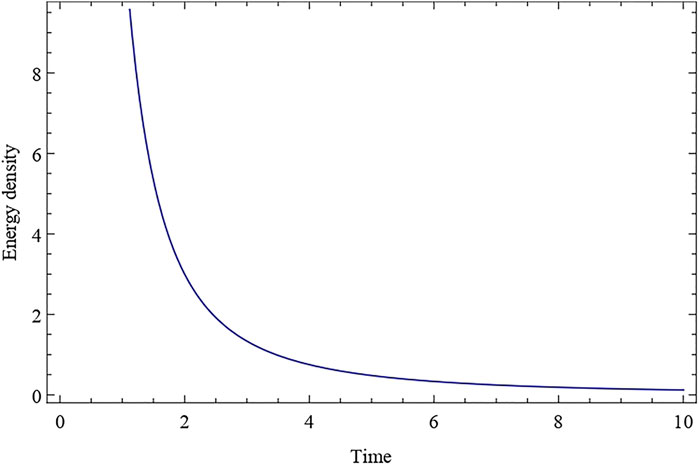
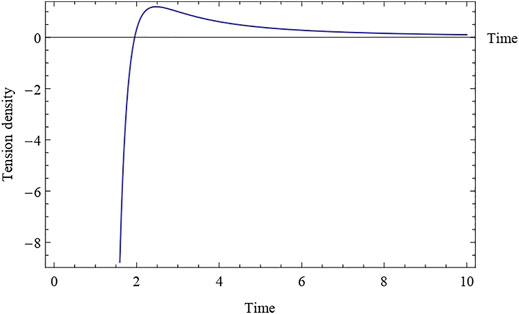
6 Conclusion

The interaction of an anisotropic Bianchi Type-I string cosmological model Universe with an electromagnetic field is investigated in the general theory of relativity. In the above cosmological model H > 0 and q < 0, which demonstrates that the Universe expands according to a power law after the big bang, starting with a finite volume at cosmic time t = 0 and expanding with an acceleration. For the above cosmological model Universe, the hypothesised relationship between Hubble’s parameter and average scale factor results in a constant negative value of the deceleration parameter. A point type (MacCallum, 1971) singularity exists in the derived model at time t = 0. The density of particles and the tension density of the string are comparable, but tension density falls off more quickly than particle density, showing that particles dominate the cosmos as time passes. In our hypothesis, the Universe has a chance of being anisotropic at any point during its existence, from the beginning to the end. According to recent research, there is a discrepancy in estimating microwave intensities emitted from various directions of the sky. This prompted us to investigate the world using the anisotropic Bianchi Type-I metric to better describe our Universe. Several CMB (de Bernardis et al., 2000; Hanany et al., 2000) anomalies, such as temperature anisotropies in the CMB that are inconsistent with the exact homogeneous and isotropic FRW model recorded by COBE/WMAP (Bennet et al., 2003) satellites, foregrounds/systematics, and novel topologies, are also evidence that we live in a globally anisotropic Universe. Shear reduces during inflation, finally resulting in an isotropic phase with no shear. In order to produce any significant amount of shear in recent years, one must first induce anisotropy in space-time.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author Contributions

All of the authors listed have contributed a significant, direct, and intellectual contribution to the work and have given their permission for it to be published.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adhav, K. S., Nimkar, A. S., and Dawande, M. V. (2007). N-Dimensional String Cosmological Model in Brans-Dicke Theory of Gravitation. Astrophys. Space Sci. 310, 231–235. doi:10.1007/s10509-007-9506-8

CrossRef Full Text | Google Scholar

Aditya, Y., and Reddy, D. R. K. (2018). Anisotropic New Holographic Dark Energy Model in Saez-Ballester Theory of Gravitation. Astrophys. Space Sci. 363 (10), 1–11. doi:10.1007/s10509-018-3429-4

CrossRef Full Text | Google Scholar

Akarsu, Ö., and Kılınç, C. B. (2010a). Bianchi Type III Models with Anisotropic Dark Energy. Gen. Relativ. Gravit. 42 (4), 763–775. doi:10.1007/s10714-009-0878-7

CrossRef Full Text | Google Scholar

Akarsu, Ö., and Kılınç, C. B. (2010b). LRS Bianchi Type I Models with Anisotropic Dark Energy and Constant Deceleration Parameter. Gen. Relativ. Gravit. 42 (1), 119–140. doi:10.1007/s10714-009-0821-y

CrossRef Full Text | Google Scholar

Alvarez, E., and Gavela, M. B. (1983). Entropy from Extra Dimensions. Phys. Rev. Lett. 51, 931–934. doi:10.1103/PhysRevLett.51.931

CrossRef Full Text | Google Scholar

Amirhashchi, H., Zainuddin, H., and Dezfouli, H. N. S. (2009). Geometrical Behaviors of Lrs Bianchi Type-I Cosmological Model. E. J. Theor. Phys. 6 (22), 79–84. Available at: http://www.ejtp.com/articles/ejtpv6i22p79.pdf.

Google Scholar

Banik, S. K., and Bhuyan, K. (2017). Dynamics of Higher-Dimensional FRW Cosmology in R^p exp(λR) Gravity. Pramana - J. Phys. 88, 1–17. doi:10.1007/s12043-016-1335-2

CrossRef Full Text | Google Scholar

Bennett, C. L., Halpern, M., Hinshaw, G., Jarosik, N., Kogut, A., Limon, M., et al. (2003). First‐Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results. Astrophys J. Suppl. S 148, 1–27. doi:10.1086/377253

CrossRef Full Text | Google Scholar

Berman, M. S. (1983). A Special Law of Variation for Hubble's Parameter. Nuov. Cim. B 74 (2), 182–186. doi:10.1007/BF02721676

CrossRef Full Text | Google Scholar

Berman, M. S., and de Mello Gomide, F. (1988). Cosmological Models with Constant Deceleration Parameter. Gen. Relat. Gravit. 20 (2), 191–198. doi:10.1007/BF00759327

CrossRef Full Text | Google Scholar

Brans, C., and Dicke, R. H. (1961). Mach's Principle and a Relativistic Theory of Gravitation. Phys. Rev. 124 (3), 925–935. doi:10.1103/PhysRev.124.925

CrossRef Full Text | Google Scholar

Bull, P., Akrami, Y., Adamek, J., Baker, T., Bellini, E., Jimenez, J. B., et al. (2016). Beyond λcdm Problems, Solutions, and the Road Ahead, Physics of the Dark Universe. Phys. Dark Universe 12, 56–99. doi:10.1016/j.dark.2016.02.001

CrossRef Full Text | Google Scholar

Capozziello, S., Carloni, S., and Troisi, A. (2003). Quintessence without Scalar fields. Recent Res. Dev. Astron. Astrophys. 1, 1–46. arXiv:astro-ph/0303041.

Google Scholar

Collins, C. B., Glass, E. N., and Wilkinson, D. A. (1983). Exact Spatially Homogeneous Cosmologies. Gen. Relativ. Gravit. 12, 805–823.

Google Scholar

Collins, C. B., and Hawking, S. W. (1973). Why Is the Universe Isotropic? ApJ 180, 317–334. doi:10.1086/151965

CrossRef Full Text | Google Scholar

Daimary, J., and Baruah, R. R. (2021). Five Dimensional Bianchi Type-I String Cosmological Model with Electromagnetic Field. J. Math. Comput. Sci. 11, 6599–6613. doi:10.28919/jmcs/6267

CrossRef Full Text | Google Scholar

de Bernardis, P., Ade, P. A. R., Bock, J. J., Bond, J. R., Borrill, J., Boscaleri, A., et al. (2000). A Flat Universe from High-Resolution Maps of the Cosmic Microwave Background Radiation. Nature 404, 955–959. doi:10.1038/35010035

PubMed Abstract | CrossRef Full Text | Google Scholar

Everett, A. E. (1981). Cosmic Strings in Unified Gauge Theories. Phys. Rev. D 24, 858–868. doi:10.1103/PhysRevD.24.858

CrossRef Full Text | Google Scholar

Grasso, D., and Rubinstein, H. R. (2000). Magnetic Fields in the Early Universe. Phys. Rep. 348 (3), 163–266. doi:10.1016/S0370-1573(00)00110-1

CrossRef Full Text | Google Scholar

Guth, A. H. (1981). Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 23, 347–356. doi:10.1103/physrevd.23.347

CrossRef Full Text | Google Scholar

Hanany, S., Ade, P., Balbi, A., Bock, J., Borrill, J., Boscaleri, A., et al. (2000). MAXIMA-1: A Measurement of the Cosmic Microwave Background Anisotropy on Angular Scales of 10[arcmin]-5°. Astrophys. J. Lett. 545, L5–L9. doi:10.1086/317322

CrossRef Full Text | Google Scholar

Harko, T., Lobo, F. S. N., Nojiri, S. i., and Odintsov, S. D. (2011). f(R,T) Gravity. Phys. Rev. D 84 (2), 1–11. doi:10.1103/PhysRevD.84.024020

CrossRef Full Text | Google Scholar

Jimenez, J. B., and Maroto, A. L. (2009). Cosmological Electromagnetic fields and Dark Energy. arXiv:0811.0566v2 [astro-ph] 2009, 1–13. doi:10.1088/1475-7516/2009/03/016

CrossRef Full Text | Google Scholar

Kaluza, T. (2018). On the Unification Problem in Physics. Int. J. Mod. Phys. D 27, 1870001–1870972. doi:10.1142/S0218271818700017

CrossRef Full Text | Google Scholar

Kibble, T. W. B. (1980). Some Implications of a Cosmological Phase Transition. Phys. Rep. 67, 183–199. doi:10.1016/0370-1573(80)90091-5

CrossRef Full Text | Google Scholar

Kibble, T. W. B. (1976). Topology of Cosmic Domains and Strings. J. Phys. A: Math. Gen. 9 (8), 1387–1398. doi:10.1088/0305-4470/9/8/029

CrossRef Full Text | Google Scholar

Kiran, M., Reddy, D. R. K., and Rao, V. U. M. (2015). Minimally Interacting Holographic Dark Energy Model in Brans-Dicke Theory. Astrophys Space Sci. 356 (2), 407–411. doi:10.1007/s10509-014-2213-3

CrossRef Full Text | Google Scholar

Klein, O. (1926). Quantentheorie und fünfdimensionale Relativitätstheorie. Z. Physik 37, 895–906. doi:10.1007/BF01397481

CrossRef Full Text | Google Scholar

Krori, K. D., Chaudhury, T., Mahanta, C. R., and Mazumdar, A. (1990). Some Exact Solutions in String Cosmology. Gen. Relat. Gravit. 22, 123–130. doi:10.1007/BF00756203

CrossRef Full Text | Google Scholar

Letelier, P. S. (1983). String Cosmologies. Phys. Rev. D 28, 2414–2419. doi:10.1103/PhysRevD.28.2414

CrossRef Full Text | Google Scholar

MacCallum, M. A. H. (1971). A Class of Homogeneous Cosmological Models Iii: Asymptotic Behaviour. Commun.Math. Phys. 20, 57–84. doi:10.1007/bf01646733

CrossRef Full Text | Google Scholar

Marciano, W. J. (1984). Time Variation of the Fundamental "Constants" and Kaluza-Klein Theories. Phys. Rev. Lett. 52, 489–491. doi:10.1103/PhysRevLett.52.489

CrossRef Full Text | Google Scholar

Mishra, R. K., and Chand, A. (2020). Cosmological Models in Sáez-Ballester Theory with Bilinear Varying Deceleration Parameter. Astrophys. Space Sci. 365, 1–9. doi:10.1007/s10509-020-03790-w

CrossRef Full Text | Google Scholar

Mishra, R. K., and Dua, H. (2019). Bulk Viscous String Cosmological Models in Saez-Ballester Theory of Gravity. Astrophys. Space Sci. 364 (11), 1951. doi:10.1007/s10509-019-3689-7

CrossRef Full Text | Google Scholar

Montefalcone, G., Steinhardt, P. J., and Wesley, D. H. (2020). Dark Energy, Extra Dimensions, and the Swampland. J. High Energ. Phys. 91, 1–12. doi:10.1007/JHEP06(2020)091

CrossRef Full Text | Google Scholar

Naidu, R. L., Aditya, Y., Deniel Raju, K., Vinutha, T., and Reddy, D. R. K. (2021). Kaluza-Klein FRW Dark Energy Models in Saez-Ballester Theory of Gravitation. New Astron. 85, 101564–101567. doi:10.1016/j.newast.2020.101564

CrossRef Full Text | Google Scholar

Nojiri, S. i., and Odintsov, S. D. (2003). Modified Gravity with Negative and Positive powers of Curvature: Unification of Inflation and Cosmic Acceleration. Phys. Rev. D 68 (12), 1–10. doi:10.1103/PhysRevD.68.123512

CrossRef Full Text | Google Scholar

Parikh, S., Tyagi, A., and Tripathi, B. R. (2018). Lyra’s Geometry in a Bianchi Type Ii String Dust Cosmological Model. Prespacetime J. 9 (4), 288–296. Available at: https://prespacetime.com/index.php/pst/article/viewFile/1423/1365.

Google Scholar

Pawar, D. D., Bhuttampalle, G. G., and Agrawal, P. K. (2018). Kaluza-Klein f(R, T) Theory of Gravity. New Astron. 65, 1–6. doi:10.1016/j.newast.2018.05.002

CrossRef Full Text | Google Scholar

Priyokumar, S. K., Baro, J., and Jiten, B. (2021). Higher Dimensional Lrs Bianchi Type-I String Cosmological Model with Bulk Viscosity in General Relativity. Indian J. Sci. Technol. 14, 1239–1249. doi:10.17485/IJST/v14i16.240

CrossRef Full Text | Google Scholar

Ram, S., Zeyauddin, M., and Singh, C. P. (2010). Anisotropic Bianchi Type V Perfect Fluid Cosmological Models in Lyra's Geometry. J. Geometry Phys. 60 (11), 1671–1680. doi:10.1016/j.geomphys.2010.06.010

CrossRef Full Text | Google Scholar

Rao, V. U. M., Vinutha, T., and Vijaya Santhi, M. (2008). Bianchi Type-V Cosmological Model with Perfect Fluid Using Negative Constant Deceleration Parameter in a Scalar Tensor Theory Based on Lyra Manifold. Astrophys. Space Sci. 314, 213–216. doi:10.1007/s10509-008-9757-z

CrossRef Full Text | Google Scholar

Rasouli, S. M. M., Pacheco, R., Sakellariadou, M., and Moniz, P. V. (2020). Late Time Cosmic Acceleration in Modified Sáez–Ballester Theory. Phys. Dark Universe 27, 1–20. doi:10.1016/j.dark.2019.100446

CrossRef Full Text | Google Scholar

Reddy, D. R. K. (2003). A String Cosmological Model in a Scalar-Tensor Theory of Gravitation. Astrophys. Space Sci. 286, 359–363. doi:10.1023/A:1026370732619

CrossRef Full Text | Google Scholar

Sáez, D., and Ballester, V. J. (1986). A Simple Coupling with Cosmological Im-plications. Phys. Lett. A 113 (9), 467–470. doi:10.1016/0375-9601(86)90121-0

CrossRef Full Text | Google Scholar

Sahoo, P. K., and Mishra, B. (2015). Higher-Dimensional Bianchi Type-III Universe with Strange Quark Matter Attached to String Cloud in General Relativity. Turk J. Phys. 39, 43–53. doi:10.3906/fiz-1403-5

CrossRef Full Text | Google Scholar

Sahoo, P. K., Sahoo, P., and Bishi, B. K. (2017). Anisotropic Cosmological Models in f(R,T) Gravity with Variable Deceleration Parameter. Int. J. Geom. Methods Mod. Phys. 14, 1750097. doi:10.1142/S0219887817500979

CrossRef Full Text | Google Scholar

Santhi, M. V., and Sobhanbabu, Y. (2020). Bianchi Type-III Tsallis Holographic Dark Energy Model in Saez-Ballester Theory of Gravitation. Eur. Phys. J. C 80 (12), 1–15. doi:10.1140/epjc/s10052-020-08743-9

CrossRef Full Text | Google Scholar

Shinkai, H.-A., and Torii, T. (2015). Wormhole in Higher-Dimensional Space-Time. J. Phys. Conf. Ser. 600, 012038. doi:10.1088/1742-6596/600/1/012038

CrossRef Full Text | Google Scholar

Singh, G. P., Deshpande, R. V., and Singh, T. (2004). Higher-Dimensional Cosmological Model with Variable Gravitational Constant and Bulk Viscosity in Lyra Geometry. Pramana - J. Phys. 63, 937–945. doi:10.1007/BF02704332

CrossRef Full Text | Google Scholar

Singh, K. P., Baro, J., and Meitei, A. J. (2021). Higher Dimensional Bianchi Type-I Cosmological Models with Massive String in General Relativity. Front. Astron. Space Sci. 8, 1–6. doi:10.3389/fspas.2021.777554

CrossRef Full Text | Google Scholar

Singh, K. P., Mollah, M. R., Baruah, R. R., and Daimary, M. (2020). Interaction of Bianchi Type-I Anisotropic Cloud String Cosmological Model Universe with Electromagnetic Field. Int. J. Geom. Methods Mod. Phys. 17 (8), 2050133. doi:10.1142/S0219887820501339

CrossRef Full Text | Google Scholar

Singh, K. P., and Singh, P. S. (2019). Dark Energy on Higher Dimensional Spherically Symmetric Brans-Dicke Universe. Chin. J. Phys. 60, 239–247. doi:10.1016/j.cjph.2019.05.003

CrossRef Full Text | Google Scholar

Singh, T., and Agrawal, A. K. (1991). Some Bianchi-Type Cosmological Models in a New Scalar-Tensor Theory. Astrophys. Space Sci. 182 (2), 289–312. doi:10.1007/bf00645008

CrossRef Full Text | Google Scholar

Subramanian, K. (2016). The Origin, Evolution and Signatures of Primordial Magnetic Fields. Rep. Prog. Phys. 79 (7), 076901–076957. doi:10.1088/0034-4885/79/7/076901

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripathi, B. R., Parikh, S., and Tyagi, A. (2017). Bianchi Type-I Inhomogeneous String Cosmological Model with Electromagnetic Field in General Relativity. Prespacetime J. 8 (4), 474–483. Available at: https://www.prespacetime.com/index.php/pst/article/viewFile/1220/1201.

Google Scholar

Tripathy, S. K., Nayak, S. K., Sahu, S. K., and Routray, T. R. (2009). Massive String Cloud Cosmologies in Saez-Ballester Theory of Gravitation. Int. J. Theor. Phys. 48, 213–225. doi:10.1007/s10773-008-9796-9

CrossRef Full Text | Google Scholar

Vilenkin, A. (1981a). Cosmic Strings. Phys. Rev. D 24, 2082–2089. doi:10.1103/PhysRevD.24.2082

CrossRef Full Text | Google Scholar

Vilenkin, A. (1981b). Gravitational Field of Vacuum Domain walls and Strings. Phys. Rev. D 23 (24), 852–857. doi:10.1103/PhysRevD.23.852

CrossRef Full Text | Google Scholar

Xing-Xiang, W. (2003). Exact Solutions for String Cosmology. Chin. Phys. Lett. 20 (5), 615–617. doi:10.1088/0256-307X/20/5/307

CrossRef Full Text | Google Scholar

Xing-Xiang, W. (2004). Locally Rotationally Symmetric Bianchi Type-I String Cosmological Model with Bulk Viscosity. Chin. Phys. Lett. 21 (7), 1205–1207. doi:10.1088/0256-307X/21/7/006

CrossRef Full Text | Google Scholar

Yavuz, İ., Yilmaz, İ., and Baysal, H. (2005). Strange Quark Matter Attached to the String Cloud in the Spherical Symmetric Space-Time Admitting Conformal Motion. Int. J. Mod. Phys. D 14 (1), 1365–1372. doi:10.1142/S0218271805007061

CrossRef Full Text | Google Scholar

Yilmaz, İ. (2006). String Cloud and Domain walls with Quark Matter in 5-D Kaluza-Klein Cosmological Model. Gen. Relativ. Gravit. 38 (9), 1397–1406. doi:10.1007/s10714-006-0322-1

CrossRef Full Text | Google Scholar

Zel’dovich, Y. B., Kobzarev, I. Y., and Okun, L. B. (1974). Cosmological Consequences of the Spontaneous Breakdown of Discrete Symmetry. Zh. Eksp. Teor. Fiz. 67, 3–11. Available at: http://www.jetp.ras.ru/cgi-bin/dn/e_040_01_0001.pdf.

Google Scholar

Zia, R., Maurya, D. C., and Pradhan, A. (2018). Transit Dark Energy String Cosmological Models with Perfect Fluid in F(R,T)-Gravity. Int. J. Geom. Methods Mod. Phys. 15, 1850168. doi:10.1142/S0219887818501682

CrossRef Full Text | Google Scholar