
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci., 20 May 2022
Sec. Space Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.875985
This article is part of the Research TopicApplications of Statistical Methods and Machine Learning in the Space SciencesView all 17 articles
 Kiley L. Yeakel1*
Kiley L. Yeakel1* Jon D. Vandegriff1
Jon D. Vandegriff1 Tadhg M. Garton2,3
Tadhg M. Garton2,3 Caitriona M. Jackman3
Caitriona M. Jackman3 George Clark1
George Clark1 Sarah K. Vines1
Sarah K. Vines1 Andrew W. Smith4
Andrew W. Smith4 Peter Kollmann1
Peter Kollmann1Several machine learning algorithms and feature subsets from a variety of particle and magnetic field instruments on-board the Cassini spacecraft were explored for their utility in classifying orbit segments as magnetosphere, magnetosheath or solar wind. Using a list of manually detected magnetopause and bow shock crossings from mission scientists, random forest (RF), support vector machine (SVM), logistic regression (LR) and recurrent neural network long short-term memory (RNN LSTM) classification algorithms were trained and tested. A detailed error analysis revealed a RNN LSTM model provided the best overall performance with a 93.1% accuracy on the unseen test set and MCC score of 0.88 when utilizing 60 min of magnetometer data (|B|, Bθ, Bϕ and BR) to predict the region at the final time step. RF models using a combination of magnetometer and particle data, spanning H+, He+, He++ and electrons at a single time step, provided a nearly equivalent performance with a test set accuracy of 91.4% and MCC score of 0.84. Derived boundary crossings from each model’s region predictions revealed that the RNN model was able to successfully detect 82.1% of labeled magnetopause crossings and 91.2% of labeled bow shock crossings, while the RF model using magnetometer and particle data detected 82.4 and 74.3%, respectively.
Preliminary to any detailed studies of space physics phenomena is the detection and statistical quantification of large quantities of example “events” in data sets from orbiting spacecraft. At present, the detection and cataloging of such events is done primarily by visual inspection of the data sets by domain experts. Yet, as the current and near-future space missions continue to fly evermore data-intensive sensors, the space physics community is rapidly approaching a point in which the data volume vastly exceeds the analysis capacity of the domain experts (Azari et al., 2020). Additionally, manual detection and cataloging of the events embeds the bias of the individual observer into the curated catalog, consequently precluding the inter-comparison of results from two independent observers. Semi-automation of the event detection by using, for instance, a set of explainable threshold criteria to define an event, has helped to combat some of the inter-observer bias and reduce the time needed to build event catalogs relative to a purely manual method. Yet, it can be the case that such rigid threshold criteria fail to replicate the subtle event detection/inspection process of the domain experts, or to appropriately account for the complexities introduced by the varying observer (spacecraft) position. Machine learning (ML) presents a viable alternative to the current best practice of manual inspection or semi-automated methodologies given the proven ability in other fields to comb through vast data reserves to find events of interest. In the space domain, with its exponentially increasing data archives, ML is becoming a necessity.
A common feature to identify in spacecraft data sets is the encounter of a spacecraft with magnetospheric boundaries such as the bow shock or magnetopause. The regions adjacent to these boundaries have very particular characteristics: the magnetosphere is dominated by planetary field and plasma; the magnetosheath is a region of turbulent, compressed, heated, shocked solar wind plasma, and the solar wind upstream of the bow shock can reflect a pattern of regular corotating interaction regions as well as revealing the presence of solar wind transients such as coronal mass ejections. There are many physical phenomena which occur in these different regions—e.g., from magnetic reconnection to wave-particle interactions—and robust region identification (magnetosphere vs magnetosheath vs solar wind) is often a necessary step prior to doing focused event detection surveys. At Earth, various studies have developed algorithms to detect magnetopause and bow shock boundaries based on changes in the time-based variance of the magnetic field, orientation of the magnetic field and the composition and properties of the local plasma from in situ spacecraft data (Ivchenko et al., 2000; Jelínek et al., 2012; Case and Wild, 2013; Olshevsky et al., 2021). Similar studies have been applied to splitting heliospheric measurements into categories based on in situ solar wind observation and using techniques such as Gaussian process classification (Xu and Borovsky, 2015; Camporeale et al., 2017). On the sun-ward side of the bow shock there is also a foreshock region, which displays properties similar to the magnetosheath. This is especially prominent at Earth where the orientation of interplanetary magnetic field (IMF) drives a quasi-parallel bow shock over a large extent of the boundary, and the resulting foreshock propagates shocked ions and magnetic field perturbations far upstream, obfuscating the solar wind population. The distinct characteristics of the quasi-parallel foreshock region at Earth has prompted ML-based region classification algorithm approaches to identify the foreshock as a fourth region in addition to the magnetopshere, magnetosheath and solar wind (Olshevsky et al., 2021). In contrast to Earth, the Parker spiral angle at Saturn is found to be larger at approximately 86.8 ± 0.3° (Jackman et al., 2008). Thus, Saturn’s bow shock is primarily quasi-perpendicular to the IMF, and the foreshock will be pushed to the dawn side of the planet. While some studies have found evidence of quasi-parallel foreshocks at Saturn present in the Cassini data (Bertucci et al., 2007), in general, quasi-perpendicular bow shock crossings dominate (Sulaiman et al., 2016).
At Saturn, there are still large unknowns concerning physically processes within Saturn’s magnetosphere as well as its interaction with the solar wind. For example, the role of dayside reconnection in controlling the magnetospheres of giant planets is still not fully understood (Guo et al., 2018). Increasing the event list that can enable detailed studies of physical phenomena, i.e., magnetic reconnection, can have impactful results in our understanding of physical drivers of magnetospheric dynamics such as particle injections and auroral pulsations (Guo et al., 2018). Therefore, in this study, we will focus on observations from the Cassini-Huygens mission, which orbited the Saturn system from 2004–2017, sampling Saturn’s dynamic magnetosphere from a diversity of vantage points as highlighted in Figure 1. The variable orbit design of the Cassini mission meant that while most of the mission was spent taking measurements within the planetary magnetosphere, the magnetosheath and upstream solar wind was also frequently sampled. Each of the three regimes all have uniquely identifying characteristics of field and plasma, with transitions between the three regimes occasionally seen to occur at different times depending on the identifying data set being used (i.e., magnetometer data versus low-energy plasma or energetic particle data). Early studies included the publication of lists of boundary crossings (Pilkington et al., 2015), while other work included the development of empirical models to describe the shape and location of the magnetopause (Kanani et al., 2010) and bow shock (Went et al., 2011).
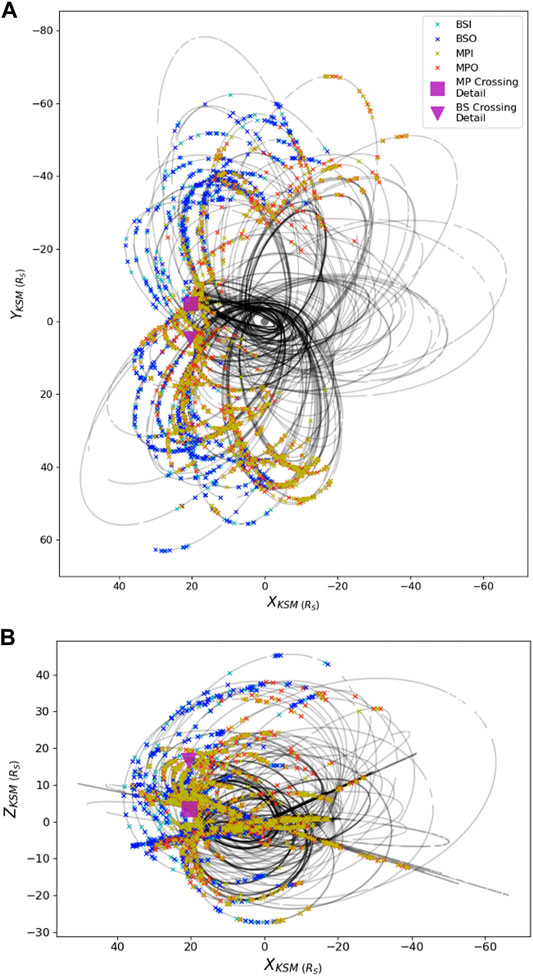
FIGURE 1. Depiction of Cassini’s orbits spanning 1 November 2004 (the end of the first capture orbit) through 15 September 2017 along with associated labeled boundary crossings in the X-Y KSM plane (A) and X-Z KSM plane (B). The legend refers to the color denoting the four types of crossings in the data set: bow shock inbound (BSI, cyan), bow shock outbound(BSO, blue), magnetopause inbound (MPI, yellow) and magnetopuase outbound (MPO, red). The magenta box and triangle highlight case study MP and BS crossings, which were fully encapsulated in the test set and occurred on 3 May 2008 and 8 March 2008, respectively. These case studies are highlighted in Figure 2.
Since the conclusion of the Cassini mission in 2017, the full data set has been visually inspected and a list of bow shock and magnetopause crossings has been made available (Jackman et al., 2019). This list uses magnetometer data as the primary descriptor, with augmentation from plasma data (electron spectrometer) until the failure of the CAPS sensor in 2012. The list focuses on clear crossings of the boundaries and does not consider very short excursions (with duration
In an effort to explore whether machine learning (ML) algorithms may be able to replicate the selection processes of the scientists, we explored classifying segments within Cassini’s orbit according to one of three regions - the solar wind (upstream of the bow shock), magnetosheath (between the bow shock and magnetopause) or the magnetosphere (inside of the magnetopause). There are four possible types of crossings as identified by Jackman et al. (2019) - bow shock out (BSO; spacecraft is moving across the bow shock boundary from the magnetosheath to the solar wind), bow shock in (BSI; spacecraft is moving from the solar wind into the magnetosheath), magnetopause in (MPI; spacecraft is moving across the magnetopause from the magnetosheath into the magnetosphere) and magnetopause out (MPO; spacecraft is moving from the magnetosphere into the magnetosheath). Despite the long length of the Cassini mission, there were relatively few crossings - in total Jackman et al. (2019) found approximately 3,300 crossings over a span of twelve years (see Figure 1 for a depiction of Cassini’s orbit path and the locations of the boundary crossings). Structuring the ML approach to identify the three distinct regions in lieu of directly identifying crossings ensured much larger data sets were available for training, validation and testing, enabling a much greater variety of ML algorithms to be utilized. However, as a consequence of this approach, algorithm performance is optimized for identifying the bulk region (i.e., the mean conditions for each region) and can be expected to suffer in the vicinity of boundary transitions.
To identify the regions, we explored various combinations of data from four sensors: 1) the Cassini magnetometer (MAG) (Dougherty et al., 2005); 2) the Ion Mass Spectrometer (IMS) of the Cassini Plasma Spectrometer (CAPS) (Young et al., 2004) instrument suite; and two sensors from the Magnetospheric Imaging Instrument (MIMI) (Krimigis et al., 2004) suite: 3) the Low Energy Magnetospheric Measurement System (LEMMS) and 4) the Charge Energy Mass Spectrometer (CHEMS). For completeness, we briefly describe the instruments and the associated data products used for this study below but more detailed descriptions can be found in the instrument papers.
MAG: MAG consists of a fluxgate magnetometer (MAG) and vector helium magnetometer (VHM) also capable of operating in a scalar mode. For this study, we utilize MAG data interpolated to a one-minute sampling cadence in the KRTP coordinate frame.
CAPS/IMS: The Ion Mass Spectrometer (IMS), measures energy and mass resolved fluxes over an energy-per-charge range of 1 eV/q to 50 keV/q and consists of eight look directions. In this study, we use the ion singles data product averaged over a ten-minute window, and utilize directional data specifically from anode four spanning an energy range of
MIMI/LEMMS: LEMMS is a particle detector with two separate telescopes, a low-energy telescope (LET) and a high-energy telescope (HET). We utilize both LET and HET data as well as pulse height analyzed (PHA) data. The selected subset of LET and HET data capture proton fluxes spanning energy ranges of 27–158,700 keV, while the PHA data spans 25.7–67.7 keV, over which the dominate species present will be protons.
MIMI/CHEMS: CHEMS is an instrument designed to characterize the suprathermal ion population in Saturn’s magnetosphere by measuring the charge state, energy, mass and angular distributions of ions (Krimigis et al., 2004). Double and triple count incidence data is utilized for H+, He+ and He++ over energy ranges of 2.81–220.2 keV.
Figure 2 shows two example 24-h periods from 8 March 2008 and 3 May 2008, in which the spacecraft crossed through a bow shock and magnetopause crossing, respectively, with only the selected subsets of data from the MAG, CHEMS, LEMMS and CAPS instruments used in the later algorithm approaches shown. Note that LEMMS data below 35 keV is not shown in Figure 2 due to known spurious instrument artifacts in those channels, however that data was included in the ML data sets to avoid embedding bias of known instrument performance issues in the training, validation and test data sets. Immediately evident is the rapidity with which the transitions into and out of regions can occur, with the spacecraft briefly transitioning into the solar wind over the span of just an hour (Figure 2A, at approximately 04:30) and likewise moving rapidly between the magnetosheath and magnetosphere (Figure 2I). We also see that the changes in the running mean and variance in the magnetic field magnitude closely align with the observed crossings as to be expected since the MAG data was used predominately by the scientists when discerning boundary crossings. In addition to the total field magnitude, the components of the magnetic field (shown in Figure 2B) can reveal particular characteristics of the regions. For example, the magnetosphere will primarily reflect the orientation of the planetary field, while the solar wind may reveal features such as field rotations associated with the crossings of the heliospheric current sheet (Jackman et al., 2004). Bow shock crossings are generally much clearer in the magnetometer data than magnetopause crossings as the character of the solar wind is typically vastly different to the character of the magnetosheath. In contrast, crossings of the magnetopause may be more or less clear in the magnetometer data depending on the relative orientations of the planetary field (inside the magnetosphere) versus the shocked interplanetary magnetic field (IMF; in the magnetosheath). From the perspective of ion observations, regions can generally be identified based on different characteristic energies, spectral profiles, and composition. For example, the bulk solar wind ion populations are typically in a narrow range of 1–2 keV and thus below the minimum energy bin of CHEMS. However, the solar wind bulk ion population becomes heated while crossing the bow shock such that H+ and He++ ions are within the energy range of the CHEMS instrument (a few to 10’s keV). For magnetosphere to magnetosheath transitions, boundary transitions tend to appear most clearly in magnetometer data (Figure 2). For populations near the magnetopause, suprathermal and energetic ions and electrons have much larger gyroradii and lower densities, and so consequently will not always move in the direction of the bulk plasma flow. This can at times result in boundary transitions that appear “fuzzier” (Liou et al., 2021) as compared to low-energy, bulk species (particularly electrons) or the magnetometer data which can demonstrate sharp discontinuities between the various regions.
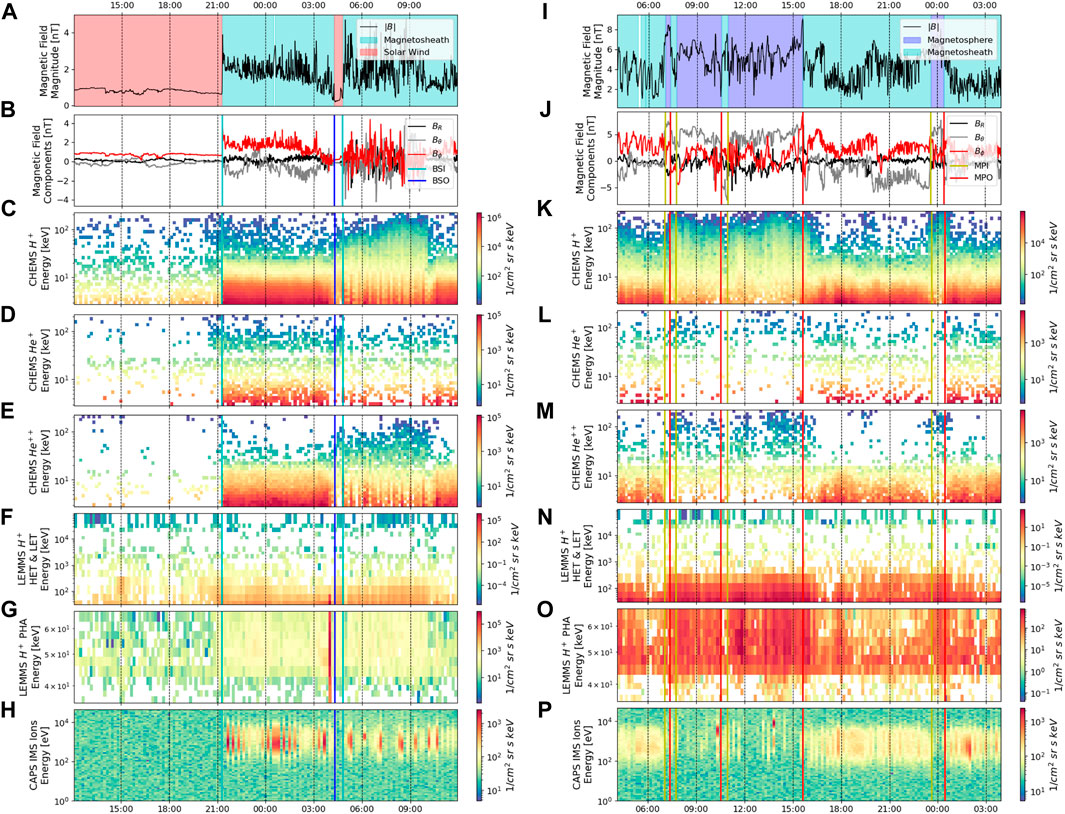
FIGURE 2. Detailed view of MAG, MIMI CHEMS & LEMMS data, and CAPS/IMS data from two example 24-h periods on 8 March 2008 (left column) and 3 May 2008 (right column) in which the spacecraft passed through the BS and MP, respectively. The regions (magnetosphere, magnetosheath and solar wind) are denoted by shaded bands (A) and (I), with vertical lines in panels (B–H) and (J–P) denoting the labeled crossings. The MAG data are shown on a 1-min interpolated sampling rate, while all other data are shown on a 10-min interpolated sampling rate. The only data shown from CAPS, CHEMS, and LEMMS are those utilized by the ML algorithms, and specifically spans targeted energy ranges of H+, He+ and He++ ions.
Initial preprocessing of the data set consisted of applying background subtraction and calibration factors to convert instrument voltages to physical units. Data gaps which were noted in the reference crossing list from Jackman et al. (2019) were excluded from contention. Being sampled at a much higher cadence, the MAG data was interpolated to a 1-min sampling rate, with the other data features (CAPS/IMS, MIMI LEMMS and CHEMS) being interpolated to a 10-min sampling rate. MAG data were formatted in the Kronian Radial-Theta-Phi (KRTP) coordinates, a spherical polar coordinate system. BR (the radial component) is positive radially outward from Saturn to the spacecraft, Bθ (the meridional component) is positive southward, and Bϕ (the azimuthal component) is positive in the direction of corotation. Specific combinations of the features were then considered to elucidate feature importance in model prediction capability. Those subsets included (and their abbreviated name):
1) MAG at 1 min cadence
2) MAG at 10 min cadence
3) MAG with subset of CAPS/IMS and MIMI/LEMMS/CHEMS at 10 min cadence (MAG & subset particle)
4) Subset of CAPS/IMS and MIMI/LEMMS/CHEMS at 10 min cadence (Subset particle)
5) All CAPS/IMS and MIMI/LEMMS/CHEMS data at 10 min cadence (Full particle)
6) MAG with all CAPS/IMS and MIMI/LEMMS/CHEMS data at 10 min cadence (MAG & full particle)
For the MAG data, the features used consisted of the MAG field components in the KRTP system (BR, Bθ, and Bϕ) as well as the total magnitude of the magnetic field (|B|), giving a total of four total features. The specific “subset” of CAPS/IMS and MIMI/LEMMS/CHEMS data chosen were:
1) CAPS/IMS 8.002 eV ions
2) CAPS/IMS 107.654 eV ions
3) CAPS/IMS 16.387 keV ions
4) MIMI/CHEMS 3.78 keV protons
5) MIMI/CHEMS 6.75 keV protons
6) MIMI/LEMMS 44.27 keV protons
With this list of features specifically chosen due to their significantly divergent behavior from one another, and ability to provide the minimum set of representative channels. The “full particle” data set refers to the entire set of species and energy levels—specifically H+, He+ and He++ ions—as previously mentioned in the instrument descriptions. When all of the MIMI CHEMS, LEMMS and CAPS/IMS data were made available to the machine learning algorithms there were a total of 194 features. When combined with the magnetic field data, there were a total of 198 features. Given that CAPS data is included in all subsets of data featuring particle data, and that the CAPS sensor failed in 2012, all “particle” data sets only span through 2012, while MAG-only data sets span the entirety of the mission.
Spacecraft position data were never used as features within any of the ML approaches, given the sparsity of the space around Saturn through which Cassini flew relative to the entire region under the influence of Saturn’s magnetic field. However, spacecraft position data were used to correct for sample imbalance within the three regions, ensuring that there was not an orbit bias to the training, validation or test data sets, and finally to interpret model results. The spacecraft position was calculated in the Kronocentric Solar Magnetospheric (KSM) coordinate system. In KSM coordinates, the X axis is the line from Saturn’s center to the Sun, with positive X pointing in the direction of the Sun. The Y axis is the cross product of Saturn’s magnetic axis with the X axis, and Z completes the triad. The XYZ KSM coordinates were then converted to spherical polar coordinates (R, θ, and ϕ) and θ was converted to magnetic local time, with noon along the line from Saturn’s center to the Sun.
Initial data exploration revealed that there were far more data present within the magnetosphere than within either the solar wind or magnetosheath once the data from before the end of the first capture orbit (i.e., data collected before 1 November 2004) were removed. To correct for the sample discrepancy, regions within the orbit regime that were exclusively within the magnetosphere (and therefore the likelihood of a boundary crossing were zero), were removed from consideration. Those magnetosphere-exclusive regions were restricted to radial locations less than 15.1 Saturn radii (RS = 60,268 km) and local time regions less than 2.81 h and greater than 20.8 h—corresponding exclusively to the nightside of the planet, far from the flanks and deep in the center of the magnetotail. The radial and magnetic local time thresholds were the location of the minimum radial and minimum/maximum local time positions of magnetopause crossings from our labeled crossings list. While removing these orbit regimes vastly improved the sample imbalance present in the data set, the resulting data set still had more samples from the magnetosphere than from within the magnetosheath or solar wind. Additionally, orbit locations in close proximity to Saturn’s moon Titan were excluded. Titan orbits Saturn at a radial distance of
Two fundamental approaches were undertaken with regards to framing the ML classification problem: 1) classifying the region based on a single time point or 2) using a time series of points to classify the region the spacecraft was in at the last time step. The time series approach was motivated by the observation that the running mean and variance of a time series of features can provide indication of the region the spacecraft is transiting. For instance, in Figure 2, we see the total magnetic field magnitude (|B|) varies significantly in amplitude and variance in each of the three regions, with the magnetosheath having a very large running variance in |B| while the magnetosphere has a higher mean |B| but lower variance. Similarly, a single time step of data, if rich in features, may provide sufficient information to classify the region. Therefore, the two different approaches can be viewed as assessing the predictive capability of the time-related variance (i.e., gradients) of a small subset of features versus the predictive capability of many features at a single snapshot in time. The two approaches were also motivated by data availability, with only MAG data available at a 1-min cadence, and therefore the only set of features available in sufficient quantities for a deep learning, time-series approach. In contrast, many more features were available at a 10-min cadence, including data from MAG, CAPS/IMS and MIMI CHEMS and LEMMS.
To classify a single time point, several different combinations of algorithms and data sets were used. Algorithms that were tested include the multi-class implementation of logistic regression (LR), linear-kernel support vector machine (SVM), and a random forest (RF). For the LR approach, the multi-class implementation utilized a multinomial loss fit and a L2 norm penalization (Pedregosa et al., 2011). For the SVM model, the multi-class implementation utilized a one-versus-rest methodology in which 3 different one-versus-rest classifiers were trained (one classifier for each region) (Pedregosa et al., 2011). For the RF approach, hyperparameter tuning consisted of iterating on the number of trees in the forest and the minimum number of samples to define a leaf node. All combinations of the data mentioned in Section 2.2 at a 10-min cadence were utilized. By varying the features that were used in the algorithm development, it was possible to assess whether certain sensor data (or combinations of sensor data) provided more predictive capability.
To classify the last time-point in a time series, a recurrent neural network (RNN) with long short-term memory (LSTM) cells was utilized. Because of the quantities of data required to appropriately train a RNN algorithm, only the 1-min MAG data was utilized with a total of four features—total magnetic field magnitude (|B|), and the magnetic field components in KRTP coordinates (BR, Bθ, and Bϕ). Variations in the number of LSTM layers (1–4) and the number of neurons per layer were explored, with a dropout layer (with a 50% drop rate) utilized after every LSTM layer. All neural network approaches were implemented via the TensorFlow module (Abadi et al., 2015). For multiple RNN layers, the full sequence (i.e., the output from all the neurons in the layer) was returned and passed along to the next layer. The output of the final neuron of the last RNN layer was passed to a dense fully-connected network with three neurons and a softmax activation. The Adam optimizer (Kingma and Ba, 2017) was used to train all variations of the RNN network, with the categorical cross entropy loss function and unweighted classification accuracy used to assess algorithm training progress. An early stopping criteria was implemented to prevent over-fitting, with training stopped if validation loss failed to achieve a minimum decrease of 0.001 over a period of two epochs.
For the time-series-based approach, it was necessary to sample from continuous segments of data, particularly because time-series ML approaches such as the RNNs used here have no concept of time other then the ordering of the samples fed to the algorithm (i.e., time stamps are not supplied). Within continuous segments of data, care was taken to sample the data such that the training, validation and test splits were not biased with regards to orbit location. It was found that reserving large continuous segments of data—such as an entire year—for the validation or test set produced an algorithm that was significantly biased. This is due to the large year-to-year variation in Cassini’s orbit, which results in some years being biased towards an orbit scheme that was closer to Saturn (i.e., low R) or a more equatorial orbit scheme (i.e., low latitude). To reduce the bias between the three sets as much as possible, a weekly split was used (depicted in Figure 3) in which one week of continuous data was split into 105 h of training data, and 22.5 h each for the testing and validation data sets. A 6 h buffer between each of the sets was then discarded (18 h of data in total), which ensured that there was no overlap between the training, validation or test sets. When splitting the continuous data for the time-series-based approach, different sample lengths (20 versus 40 versus 60 min) were explored. A 5-sample “stride”, where “stride” refers to the number of samples skipped over before the next sample is indexed, was used for all iterations. As an example, using a 20 min sample length with a five sample stride, sample one would utilize the data indexed from 0 to 19, while sample two would utilize the data indexed from 5 to 24. Offsetting the samples in this way ensured that there were still enough samples to attempt more data-intensive methods such as RNNs, but that samples were not so closely overlapped that over-fitting was a concern. By analyzing the distribution of spacecraft positions in KSM coordinates for the overall data set as well as across the training, validation and test sets, it could be deduced whether the time-based splicing induced any bias. Figure 4 shows the spacecraft position histograms for the 1-min-interpolated MAG data that was utilized by the RNN (a—c) and the 10-min-interpolated data used in the SVM/LR/RF algorithms (d—f). Generally, the time-based splitting produced a relatively equal distribution across the overall sets and the three subsets for the 1-minute-interpolated data. There does appear to be some slight aliasing in the local time for the three sets (Figures 4B,E) which is may be related to the periodicity of Cassini’s orbit and the week period chosen to do the time splitting.

FIGURE 3. Depiction of time-based splitting of data set into training, validation and test splits. 105 h of continuous data from each week were reserved for the training set, and 22.5 h each for the validation and test sets. A 6 h buffer period between each of the three sets was discarded, ensuring that there was no overlap between the sets.
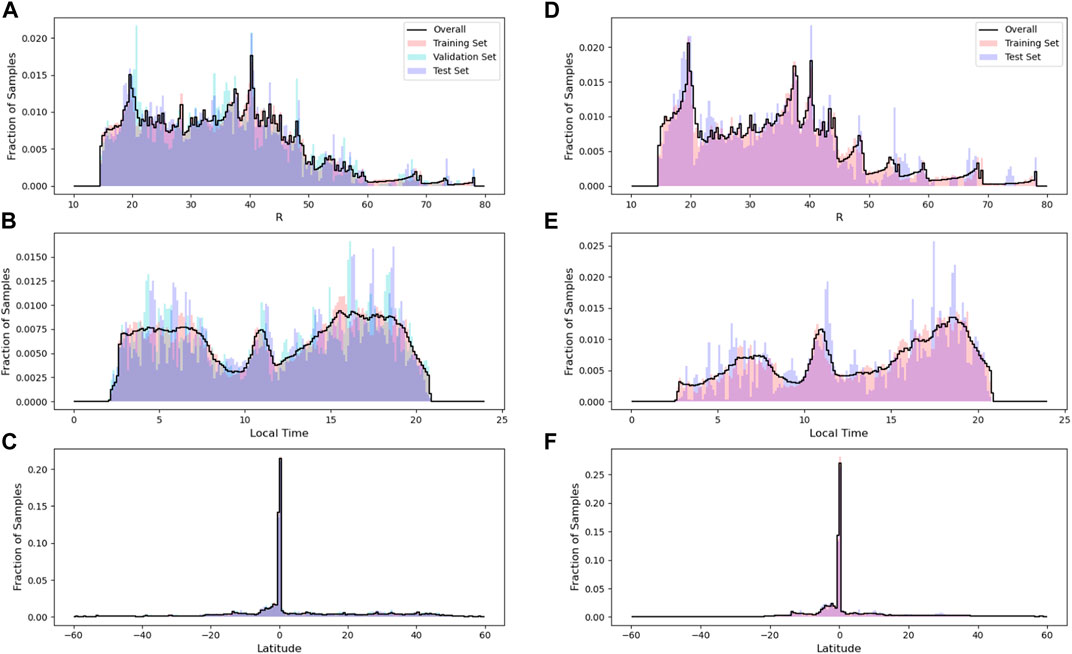
FIGURE 4. Histogram of spacecraft position in KSM coordinates for Saturn radius [R; (A) and (D)], local time [(B,E)] and latitude [(C,F)] for the 1-min interpolated MAG-only data used in the RNN approaches (left panels) and 10-min interpolated MAG and full particle data set used in the RF/SVM/LR approach. For the RNN approach the data is split across the overall data set (black line), training set (red), validation set (cyan) and test set (blue). For the RF approach, a validation set was not used but the time periods of the test and training sets were matched as closely as possible to the RNN data sets for the sake of comparison. The histograms are scaled relative to the total number of samples in each set (for the 1-min interpolated data: Ntrain = 504,338, Nval = 109,582, and Ntest = 109,259; for the 10-min interpolated data Ntrain = 103,665 and Ntest = 32,475).
While all iterations of the RNN approach used the same four features derived from the MAG data, the SVM, LR and RF approaches used solely the 10-min interpolated data sets (previously mentioned in Section 3.2) since even at a lower sampling cadence there were still sufficient amounts of training and test data. Both approaches used the time-based splitting procedure previously described, with the sets spanning the same intervals whether at a 1-min or 10-min cadence to allow comparisons across the algorithms. In other words, the same time span used for training a RNN algorithm with the 1-min-interpolated data was used to train the SVM/LR/RF algorithms with 10-min-interpolated data. One deviation between the two approaches was to ignore the validation data for the SVM/LR/RF algorithms since these algorithms do not require epoch-based training.
The final pre-processing step that was completed prior to ML algorithm development was to standardize and scale each of the features independently. This was done using the python scikit-learn “Robust Scaler” algorithm, which operates on each feature independently, removing the median and scaling the data to the range of the 1st (25%) and 3rd quartiles (75%) (Pedregosa et al., 2011). After scaling the features, the training, validation and test sets were randomly shuffled. The final breakdown of the number of samples in each region for the training, validation and test sets is shown in Table 1. As is evident in Table 1, there remained approximately three times as many samples from within the magnetosphere than either the magnetosheath or the solar wind even after removing samples within a low radial or near midnight local time position.

TABLE 1. Number of samples in each region for the training, validation and test sets. Note that for the 10-min interpolated data sets, which were only used by the SVM, RF, and LR classifier, a validation data set was not used. The time spans of the training, validation and test sets remained as close as possible across the different sets to allow for intracomparison of the model results.
The algorithms report a confidence in each of the three regions, the maximum of which was taken as the prediction and compared to the accompanying label for the sample. We measured the effectiveness of the various ML models on the unseen test samples using four different metrics: accuracy, balanced accuracy, Matthew’s Correlation Coefficient (MCC) and the F1 score. Accuracy is simply the ratio of the number of correct samples to the total number of test samples, where no weighting has been applied to any samples from a particular class. Balanced accuracy, in contrast, accounts for the sample imbalance in the test set and weights samples from a particular class according to the occurrence of that class within the test set. The weighting for a sample from a particular class is simply the fraction of test samples which belong to that class. In this instance, in which magnetosphere samples outnumber the magnetosheath and solar wind samples by a factor of roughly three, it can be expected that the balanced accuracy will give a more appropriate depiction of the model’s performance across all the classes.
In the binary case, the F1 score is the harmonic mean of the precision and recall:
where precision is defined as:
and can be interpreted as the ability of the model to maximize the detection of true events while minimizing the detection of false events. Recall is defined as:
and can be interpreted as the ability of the model to correctly identify all the events in the test set. The subcomponents for precision and recall are also best described in the binary case: True Positives (TP) are positive-class samples that have been correctly identified as positive by the model, False Positives (FP) are negative class samples that have been incorrectly identified as positive by the model, with True Negatives (TN) and False Negatives (FN) defined similarly for the negative samples. In the multi-class setting, the F1 score was calculated for each class independently, and then combined into a single metric using a weighted average. The “weight” of a class’s F1 was scaled as the ratio of the samples from a particular class to the total number of test samples.
Matthew’s Correlation Coefficient (MCC) was derived in the binary case as a means of encompassing the confusion matrix within a singular number (Matthews, 1975). The MCC in the binary case is described by the following equation:
For a model which has predictions which are perfectly anti-correlated with the labels, MCC will return a value of −1, while for a model in which the predictions are perfectly correlated with the labels MCC will return a value of +1. For a model in which there is no relationship evident between the predictions and the labels (i.e. predictions are equivalent to a random guess), MCC will return a value of 0. MCC was extended to the multi-class setting by Gorodkin (2004), and in such cases the lower limit for anti-correlation may range between 0 and −1, but the maximum remains +1 for perfect correlation. For the sake of brevity, the equation for MCC in the multi-class setting which was used in our model evaluation is not shown here (see (Gorodkin, 2004) for details). Recent evidence has pointed to MCC being a more informative and less misleading metric than F1 or accuracy (Chicco and Jurman, 2020). All of the classification metrics were implemented via scikit-learn (Pedregosa et al., 2011).
Table 2 provides a breakdown in the performance of the SVM, LR, and RF models for different combinations of feature sets. We find that across all feature sets, the RF model, when appropriately tuned, performs the best. Figure 5 illustrates the accuracy of the RF models at predicting the three regions when utilizing different combinations of feature sets. We find generally that utilizing the CAPS/IMS and MIMI/CHEMS/LEMMS data alone, without any magnetic field data, leads to a model which over-predicts the magnetosphere region. This is particularly the case when utilizing only the small subset of features (6 total) from the CAPS/IMS and MIMI/LEMMS/CHEMS data set (see Section 3.2 for a list of features). In contrast, using the magnetic field data alone provides some physical interpretation of the different regions, since the magnitude of the magnetic field acts as a proxy for the radial distance from the planet. However, we see there is still confusion between the adjoining regions - solar wind being confused for magnetosheath or magnetosheath being confused for magnetosphere, and vice versa. The best performance is found when the MAG and full particle data set is used as shown in Figure 5E. While the model using this feature set still confuses magnetosheath samples for magnetosphere, we generally see a much improved performance over the models using either only the magnetometer data or only the CAPS/IMS and MIMI/CHEMS/LEMMS data. In contrast to the RF models, the SVM and LR models fail to approach the same accuracy level on the test set predictions, except for when the MAG data is used alone.
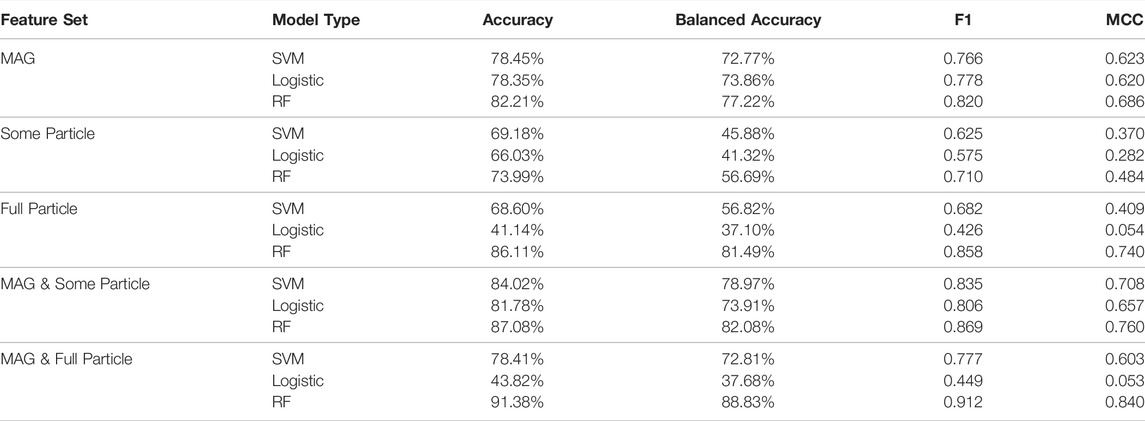
TABLE 2. Comparison of SVM, Logistic Regression and RF models using various feature sets as described in the Methods section. Depending on the feature sets used, the amount of training and test data available will change, however all the time intervals used for training and testing are consistent across the different feature sets.
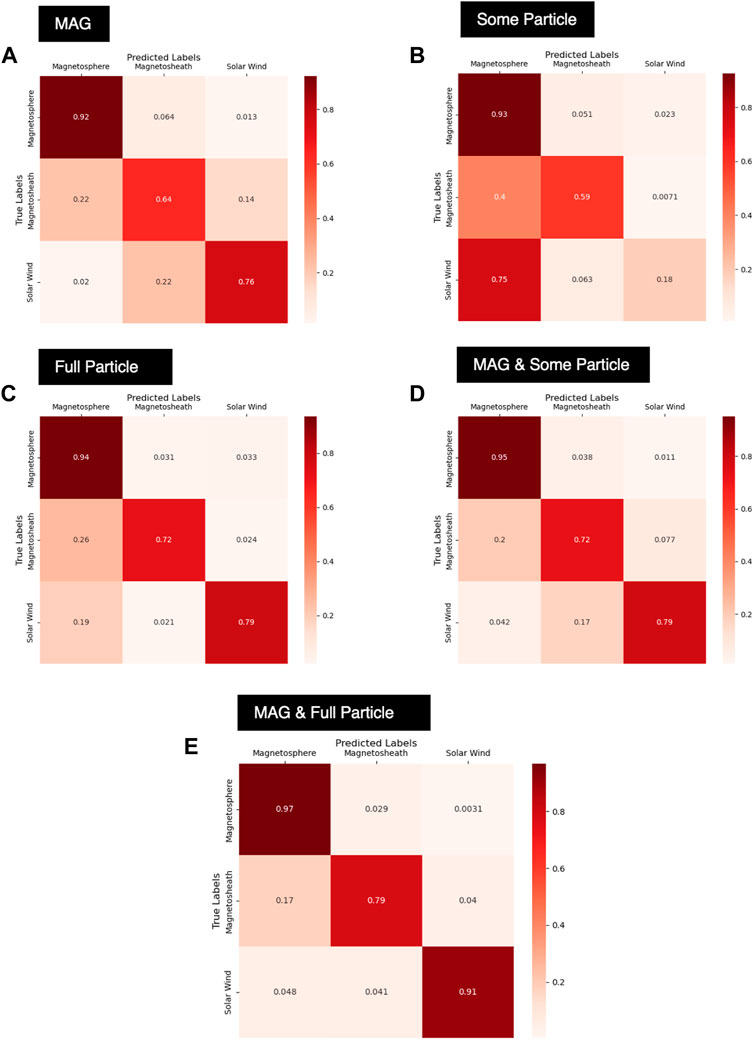
FIGURE 5. Normalized confusion matrices for different combinations of data, all using the RF model which was the best performing model across all feature sets [(A) MAG-only, (B) Some particle, (C) Full particle, (D) MAG & some particle, and (E) MAG & full particle]. The comparisons here are shown as normalized confusion matrices in which each row is divided by the number of “true” samples in the class. A perfect model would have all ones on the diagonal and all zeros on the off-diagonal.
When comparing the performance of different input sets it needs to be considered that boundaries and regions can appear different in different measurements. Boundaries can appear generally more gradual in energetic particle data (Mauk et al., 2019; Liou et al., 2021) and show dependencies on particle energy and direction that are still under scientific investigation (Mauk et al., 2016, 2019). Results from particle measurements that disagree from magnetic measurements are therefore not necessarily wrong from the scientific perspective but are a signature of physical processes such as particle escape that effectively soften up boundaries. However, our goal here is not to understand the underlying physics but to find the best defined boundaries, which can be found through magnetic field measurements. We therefore calculate our error measures relative the manually derived list that relied on magnetic field data.
Table 3 shows the RNN model performances for varying time sequence lengths along with the hyperparameters for the best-performing model at each time segment length. As mentioned in the Methods section, the number of layers and number of neurons per layer was iterated on to find the best performing model without overfitting. An exhaustive search for the optimal number of layers and neurons per layer was not performed due to the limitations on time and computational resources. However, general trends in test accuracy and test loss were observed by iterating over various combinations of neurons and layers. Overall, it can be observed that the 60-min RNN model provides the best performance on the test set. There was some slight overfitting (as can be seen by comparing the training loss with the validation and test set loss), however, stopping criteria were implemented to prevent substantial over-fitting. It also should be noted that the number of samples for the training, validation and test sets changed slightly between the 20-, 40-, and 60-min models due to the length of the time sample and allowed overlap between samples.

TABLE 3. Comparison of RNN model performance for differing time sequence lengths as well as relevant model parameters.
As the length of the time segment increases from 20 to 40–60 min, we see overall accuracy slightly increases, as indicated in Table 3. Therefore, it can be reasonably concluded that the gradients of the individual features and amount of variance in the features over the selected time frame is important for correctly classifying the region. Essentially, the longer the time segment, the more contextual information is provided to the model which allows for correct prediction of the region at the last time step. This is even more noticeable when we consider the samples which contain a boundary transition, which are a very small subset of the overall sample set. As shown in Figure 6, there is a drastic improvement in the model’s accuracy for the small subset of samples containing a listed boundary transition as we increase the length of the sample. The improvement in accuracy is most drastic when moving from a 20-min sample to a 40-min sample, but incremental improvements are also observed as we increase the sample length from 40 to 60 min. Most notably, the confusion between the magnetosphere and magnetosheath regions decreases, which is where most of the confusion lies for the 20-min model. The number of samples containing a boundary transition is only approximately 1.5% of the total samples in the test set (1,619 samples out of 109,200 test samples for the 60-min model), however we see the improvement in accurately predicting the sample jumps from 62.28% for the 20-min model to 81.03% for the 40-min model to 84.25% for the 60-min model.
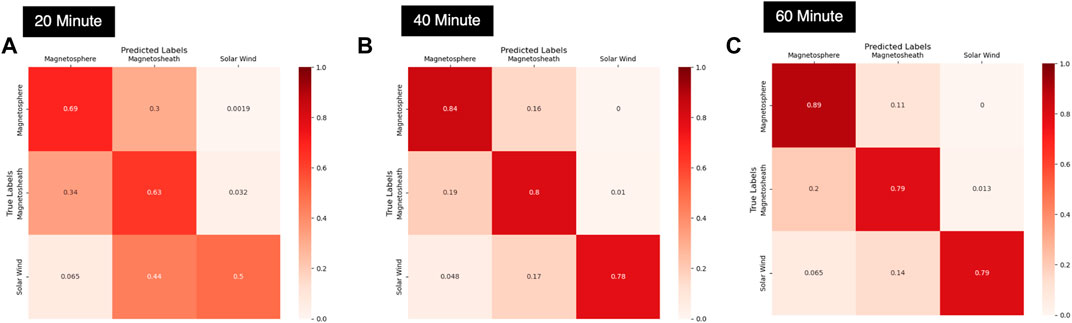
FIGURE 6. Comparison of length of the time sample used with overall prediction performance on samples containing a boundary transition for the 20-min (A), 40-min (B) and 60-min (C) RNN models. The comparisons here are shown as normalized confusion matrices.
All remaining analysis is focused on three models in particular—RF MAG, RF MAG & full particle, and RNN 60-min MAG model. These models were chosen as the best performers for time series classification (RNN 60-min) and single time point classification (RF MAG & full particle). The results from the RF MAG model are shown given that they are the closest comparison in feature space to the RNN model. Figure 7 shows the spatial discrepancies between the model predictions and the labeled data for three models in particular—the RF model with only MAG data [predictions (b) and difference from actual (c)], the RF model with MAG and full particle data set [predictions (d) and difference from actual (e)] and the RNN 60-min model with only MAG data [predictions (f) and difference from actual (g)]. The data has been binned according to local time and R, with the total number of predictions or labels of a particular region (magnetosphere, magnetosheath or solar wind) in a particular polar bin scaled to the total number of observations across all regions in that bin. The discrepancy plots have been scaled to highlight differences between the actual fraction of a region in a polar bin to the predicted fraction exceeding +/− 0.25. Despite having no information about the spacecraft position, we see in all cases that the models are generally able to correctly discern the physical layering of the problem, with the magnetosphere most commonly predicted radially close to the planet, the solar wind farthest from the planet, and the magnetosheath sandwiched in between.
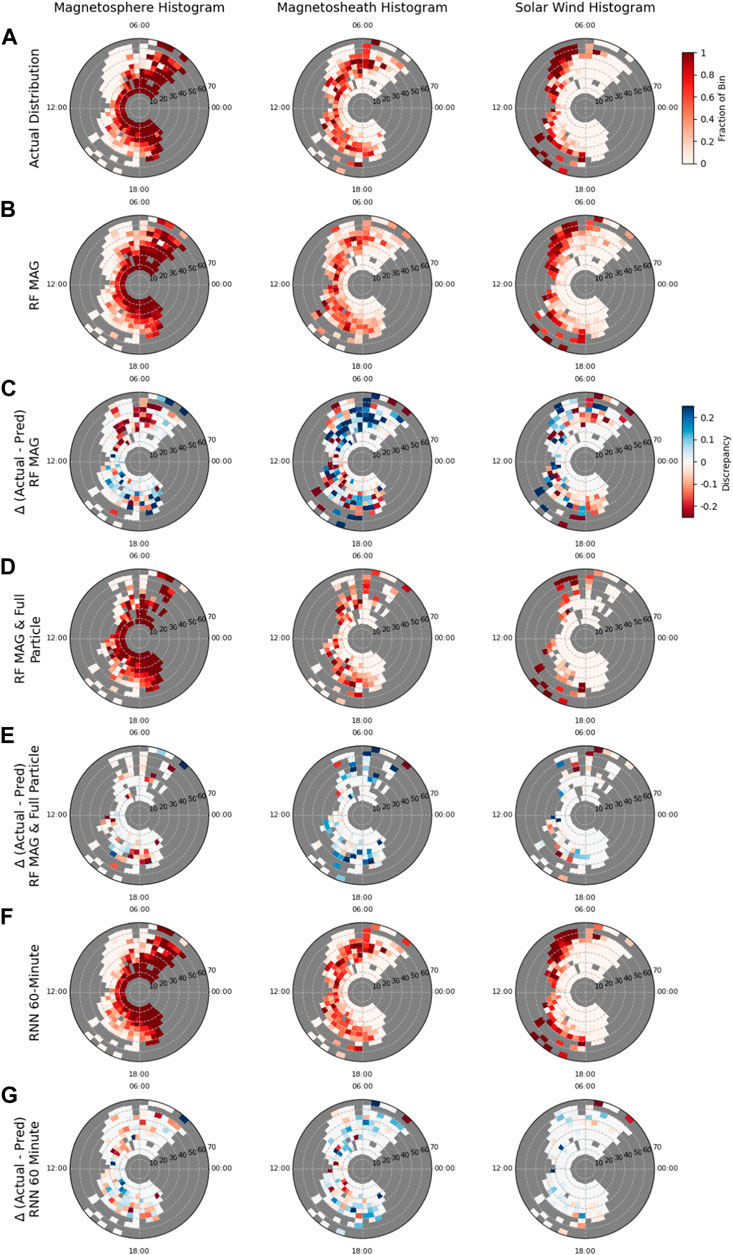
FIGURE 7. Comparison on the spatial distribution of predictions for the magnetsophere (left column), magnetosheath (middle column) and solar wind (right column), for the true labels (A), RF MAG-only model (B), RF MAG & full particle model (D) and RNN 60-min MAG-only model (F). The predictions for a particular region have been binned by local time (0.5 h increment) and radial distance (5 RS increment), with bins in gray indicating where there is no data. The discrepancy polar histograms (C,E,G) shows the difference between the observed fraction of a bin labeled as a particular region (A) and the predicted fraction (B,D,or,F), highlighting model errors. Discrepancy bins trending toward red indicate where the model has over-predicted a region, while blue indicates where a model has under-predicted a region. Panels (B,D,F) share the colorbar in panel (A), while panels (E,G) share the colorbar for panel (C).
The discrepancy polar histograms (Figures 7C,E,G) show the differences between the binning of the model predictions of particular regions and the binning of the labeled data (a), revealing where the model has under-predicted (in blue) or over-predicted (in red) a particular region. It is clear the RF model utilizing only MAG data performs the worst (as is also evident in comparing it’s test accuracy with that of the RF MAG & full particle model and the RNN 60-min model). Utilizing only the MAG data set at a single time step, the model has much greater confusion on the spatial location of the magnetosphere and magnetosheath regions. We see a strong tendency to over-predict the magnetosphere and under-predict the magnetosheath on the dawn side of the planet. This confusion between the magnetosheath and the magnetsphere is then reversed on the dusk side of the planet, where there is a preference to under-predict the magnetosphere and over-predict the magnetosheath. Dawn-side errors could be due to the presence of the foreshock, which, as previously mentioned, causes large perturbations in the solar wind magnetic field. When the full particle data set is added to the RF model, we see that the spatial discrepancies are drastically improved as compared to the MAG data alone. Figure 7E shows that instead of the strong dawn/dusk preferences in the model predictions that we see with the MAG-only RF model (c) for the magnetosphere and magnetsheath predictions, that generally the MAG & full particle RF model tends to over-predict the magnetosphere and under-predict the magnetosheath at all radial and local time bins. Finally, the RNN 60-min model demonstrates the best spatial accuracy of the three (Figure 7G), with the least amount of spatial discrepancy from the true labels. It can be observed, however, that the 60-min RNN model, using the same feature set as the RF MAG model, again shows the dawn/dusk confusion between the magnetosphere and magnetosheath regions, though to a much lesser degree than the RF MAG model. In particular, there appears to be a very spatially narrow (14:00 to 16:00 h LT and 20–40 RS) but discernible preference to over-predict magnetosheath and under-predict magnetosphere. Outside of this spatially-narrow region, however, we find that the RNN model tends to underestimate the magnetosheath and overestimate the magnetosphere across all areas, similar to the Mag & full particle RF model. Confusion at low radial positions does not appear to be driven by traversals of the cusp region (see Supplemental Material and Figure ??), though previous studies have shown that Saturn’s cusp shows a depressed magnetic field relative to the surrounding magnetosphere (Jasinski et al., 2017) and contains magnetosheath plasma (Arridge et al., 2016; Jasinski et al., 2016). In the case of the MAG-only models, a depressed magnetic field may cause the algorithm to predict magnetosheath in lieu of magnetosphere, while the RF MAG & full particle model would likewise predict magnetosheath due to the presence of magnetosheath plasma. The 60-min RNN model demonstrates by far the best spatial accuracy in predictions of the solar wind (Figure 7G, right), with virtually no discrepancy from the label set with the exception of a few large radial, dawn side bins where the solar wind is over-predicted. It is important to note that the RF model utilizing the MAG & full particle data set has far fewer samples than the MAG-only RF and RNN models due to the failure of the CAPS sensor in 2012.
To investigate temporal consistency in the model predictions, each continuous segment of testing data (22.5 h of data per week) was individually analyzed. Example segments demonstrating a bow shock and magnetopause crossing are shown in Figure 8 and are directly corollary to the crossing shown in Figure 2, showing the temporal evolution of the predictions for the three models in particular. Within each continuous segment of data the time points in which predictions changed from one region to another can be used to derive the model’s predicted crossings. Counting the number of predicted crossings in the continuous time frame and comparing with the labeled crossings over the same segment can thus provide an indication of the temporal consistency of the model’s output. The example test segments shown in Figure 8 is one such example of how a worse-performing model will have much less consistency in its predictions, with the RF models predicting far more transitions than the RNN 60-min model, as well as being largely incorrect in the case of the BS crossing. The numbers of predicted and actual transitions in each weekly test period were counted and summed up to the encompassing month for ease of comparison across the entire length of the mission. The results are shown in Figure 9 for RF MAG (b), RF MAG & full particle (c) and RNN 60-min MAG (d). Here there are four possible types of transitions (as defined earlier)—BSI, BSO, MPI, and MPO. It is important to note, however, that these inbound/outbound notations simply refer to the spacecraft direction of travel at the time of the boundary encounter, and there is no expectation that the character of the regions on either side of the transition would be biased by the travel direction of the spacecraft.
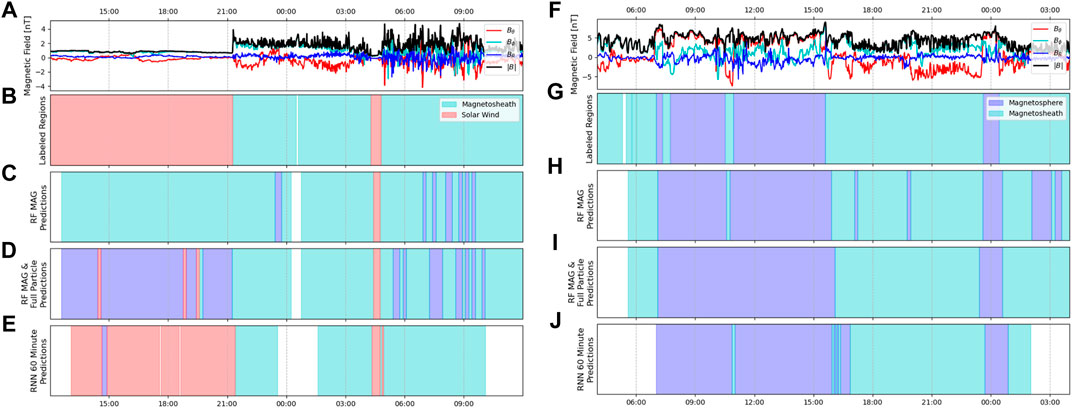
FIGURE 8. An example BS crossing is shown from 8 March 2008 (left column) and an example MP crossing is shown from 3 May 2008 (right column), coincident with the transitions shown in Figure 2. Magnetic field magnitude and KRTP components are shown (A,F) along with regions as denoted by the labeled MP and BS crossings (B,G) and the model predictions from three selected models - RF MAG (C,H), RF MAG & full ion (D,I), and RNN MAG 60-min model (E,J). Time periods which do not have any predictions due to a lack of data are denoted by white. Ideally the time periods of the model-predicted regions would coincide directly with the labeled regions. Here, we see that the RNN 60-min model comes closest to the labeled test set, while the RF models predict significantly more transitions, and particularly with the BS crossing, they are incorrect in their prediction of the solar wind region.
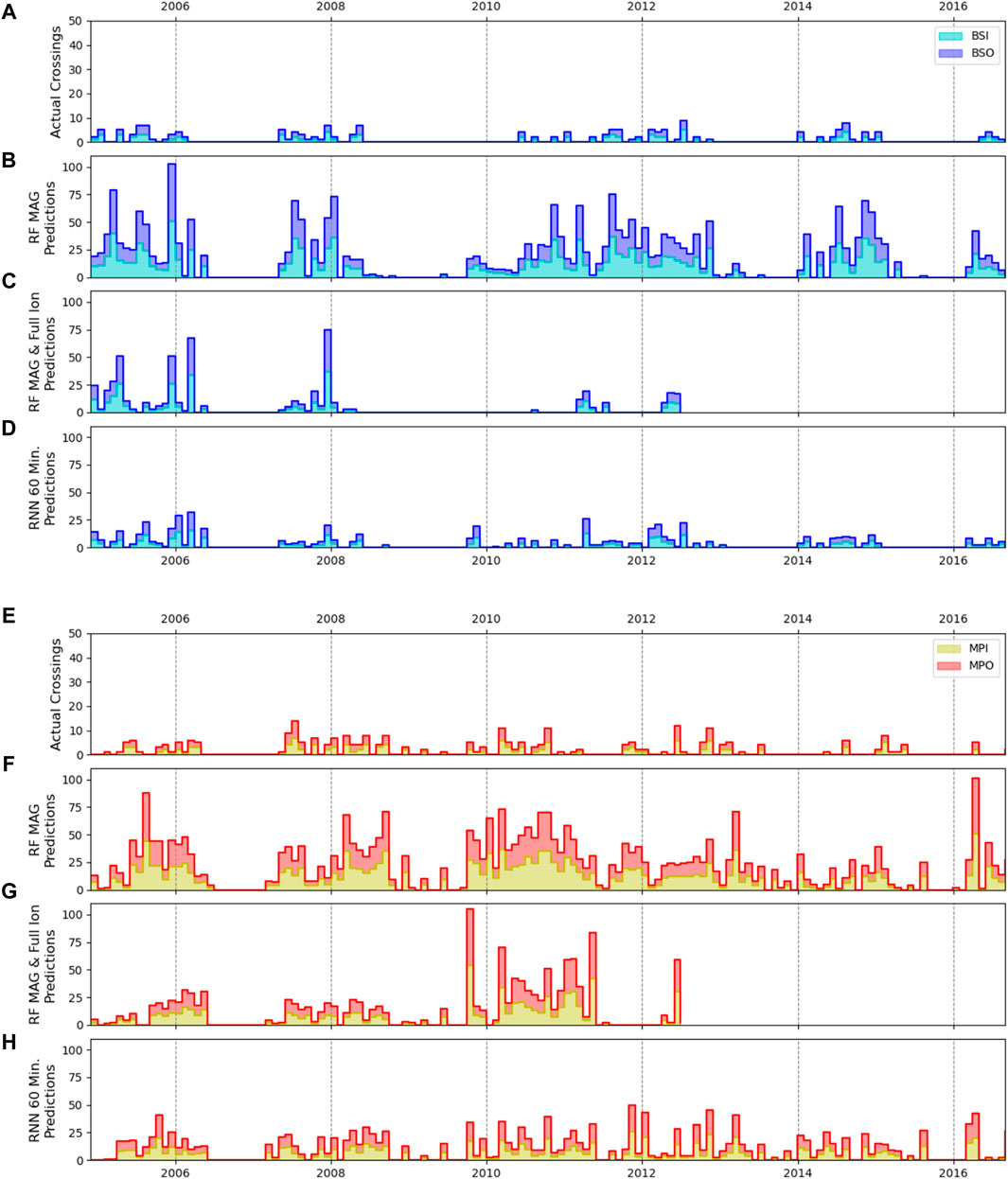
FIGURE 9. For the bow shock transitions, comparison of the numbers of crossings from the labeled data set (A) and those predicted by the RF MAG model (B), RF MAG & full particle model (C) and RNN 60-min model (D) are shown in the top grouping of panels. The numbers of crossings were computed per each continuous segment of test data and grouped by month. Panels (E–H) show the corollary for the magnetopause crossings, with the number of actual magnetopause crossings shown in (E). The number of actual crossings is then compared with predicted crossings from the RF MAG model (F), RF MAG & full ion (G) and RNN 60-min models (H). The vertical scaling of panels (A,E) are significantly smaller than the other panels to allow for ease of comparison. All models over-predict the number of crossings, however we find of the three shown that the RNN 60-min model has the best performance, with the least amount of crossings predicted and closest crossing type alignment to the true crossings shown in (A) and (E).
All the models analyzed drastically over-predicted the number of transitions occurring, with the RF models demonstrating more false boundary transitions than the RNN 60-min model. The MAG-only RF model performs the worst of all, with significantly higher numbers of false transitions predicted at every time interval. Of all the RF models analyzed (see the appendix for all possible feature combinations), we find that the MAG & full particle data set (Figure 9C) produces the greatest consistency in region prediction (i.e., least false transitions). The RNN 60-min MAG model performs better yet (Figure 9D), while still predicting vastly more transitions than present in the labeled data set. However, comparisons between the labeled transitions and the RNN-predicted transitions qualitatively reveal that the general trends of BSI/BSO-dominant periods (such as 2011–2012) versus MPI/MPO-dominant periods (2010) seen in the labeled data set are echoed in the model results, giving confidence that the model is capturing the underlying physics of the system. We also note that the Jackman et al. (2019) list, upon which this supervised learning approach is based, was formulated to capture the clearest and longest duration boundary crossings, and was not optimised to select multiple short-duration (2–3 min) crossings. While the aim of our ML approach is to determine what method best classifies the bulk of the regions, and the models demonstrate proficiency at doing so, the multiple short-duration “false” crossings predicted by the models could be actual phenomena (e.g. boundary-layer dynamics) that are not fully labeled and thus require further investigation (see Supplemental Material). In our investigation, the prediction for a particular sample was taken as the maximum of the algorithm confidence in the three regions, as is standard practice in the machine learning community. However, examining the algorithm confidence in the three regions rather than the maximum, as well as the inter-sample variance in the confidence, could eliminate many “false” crossings as well as highlight the need for SITL-intervention in the case where confidence in any one particular region is not high.
To understand whether the boundary crossings identified by the temporal error analysis aligned with those in our labeled data set, we analyzed each of the model’s boundary crossings shown in Figure 9 to see if they were a “matched” event (coincided with a boundary crossing of the same type identified in the labeled data set), an “unmatched” event (a labeled boundary which did not have a corresponding match in the model’s boundary crossings), or a “False Boundary,” (FB) i.e., a model boundary without a corresponding match in the labeled boundary list. A model-identified boundary crossing would be considered a “match” if it occurred within an hour before or after a list boundary crossing of the same type. In the case that the model identified multiple boundary crossings of the same time within the +/− hour span surrounding a labeled event, we chose the model crossing that was closest in absolute time. Table 4 shows the results for the RF MAG, RF MAG & full particle and RNN 60-min MAG model. For labeled boundaries which were matched to a model prediction, the time difference between the model-predicted boundary and the true boundary was calculated, with a positive difference indicating that the model transition occurred after the list transition (i.e., the model was delayed).
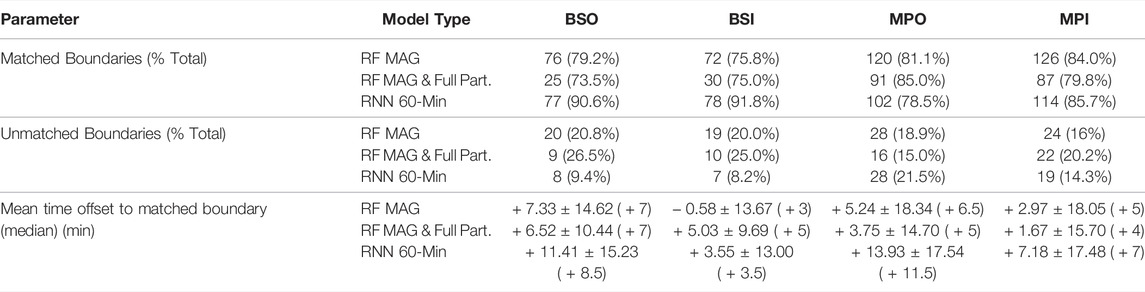
TABLE 4. Performance of the RF MAG, RF MAG & full particle, and 60-min RNN model at correctly detecting labeled boundary crossings. A boundary crossing was considered “matched” if there was the same type of boundary in the model predictions within one hour of the labeled crossing. The mean time offset of the matched boundaries is positive if the detected boundary crossing occurred after the labeled boundary (i.e., the model was delayed in its prediction). Noted is the shorter length of the RF MAG & full particle test set (extending only through 2012) and fewer labeled boundary crossings.
In general, we find that all the models perform relatively well at identifying the crossings manually identified by Jackman et al. (2019), however, there were a high number of FBs across all models and all boundary types. The number of FBs was especially pronounced for the RF MAG model, echoing the large amount of spatial and temporal variability in model predictions seen in Figures 7,9, respectively. The RNN MAG model, which covers the same duration of the mission as the RF MAG model (2004–2016), observes much fewer FBs, particularly of BSO and BSI transitions. The RF MAG & full particle model observes much fewer FBs than the MAG-only RF model, likely as a consequence of the addition of the CAPS/IMS and MIMI/CHEMS/LEMMS data. Relative to the total number of test samples provided to the respective models, the RNN model shows the least FBs by far, indicating it has far more temporal accuracy and consistency than the RF approach. Investigating the RNN performance more closely, an interesting observation is the greater lag observed on outward transitions (BSO and MPO) as opposed to inward transitions (BSI and MPI), as well as a greater lag observed at the magnetopause transitions as opposed to the bow shock transitions. The lag suggests that the model needs at least a few minutes of data from the new region before it is able to shift its prediction, with the running variance and mean of the features within the new region “learned” by the model. Therefore, it can be assumed that RNN-based approaches for predicting region transitions may lag on their exact prediction of the boundary crossing, particularly when the boundary between the regions is only subtly hinted at by the behavior of the features. This is especially the case at the magnetopause boundary, where the transition between the magnetosheath and magnetopause can be somewhat ambiguous when using the MAG data alone for times of small magnetic shear and/or highly turbulent boundary layers. In contrast, a sharp difference between the solar wind and the magnetosheath is typically observed, particularly in the enhancement of the running variance across all MAG field components as we move into the magnetosheath. We see that consequently the BSI transition appears to be the easiest transition for the RNN model to discern, with a lag of only ≈3.6 min.
It should also be noted that the five-minute stride present within the test sample data for the RNN to prevent over sampling means that the “labeled” boundary may be slightly offset from the “true” boundary depending on whether the timing of the “true” boundary falls on the same sample cadence of the test data. In cases where the true boundary timing does not directly coincide with a test sample, the nearest following sample was indicated as the location of the boundary, which was at most 4 min away from the true boundary location. For the RF models, the sampling cadence of 10 min results in the model’s first sample within a new region being at most 9 min away from the true boundary. A secondary point to note is how the model results are interpreted, which impacts the determination of predicted boundary crossings. The output of the models is a three component vector, representing the model’s confidence in each of the three regions; the maximum of these three components is interpreted as the model’s predicted region. The confidence in a particular region would have to exceed 0.33 before it is interpreted as the current region, yet the model’s confidence in a region would increase prior to it becoming the dominant region. Therefore, the lag in recognizing a transition may not be as severe as suggested when we only interpret the maximum as the model’s prediction, since investigating the individual confidence levels may reveal an increasing trend in a particular region before it overtakes the confidence levels of the other regions and becomes the maximum.
Again focusing only on the RNN 60-min model, Figures 10,11 show the corresponding behavior of the magnetic field features at the bow shock and magnetopause boundary crossings, respectively for both the matched and unmatched boundaries. Outward transitions (i.e., the spacecraft is encountering the boundary on an outward trajectory) and inward transitions are overlaid in the figures, such that all transitions are oriented to be inwards. The sharp division between the solar wind and magnetosheath is present in Figure 10, with the cross over into the magnetosheath resulting in a much more variable and higher magnitude magnetic field. As indicated in Table 4, we see that the RNN 60-min model is easily able to detect the BS in most cases as revealed by the high confidence levels in the solar wind and magnetosheath before and after the transition, respectively (Figure 10E). In the few cases (N = 7 for BSI, N = 8 for BSO) when the BS was missed, we see that it was because the model failed to register it was in the solar wind before the transition, seemingly due to elevated Bθ values.
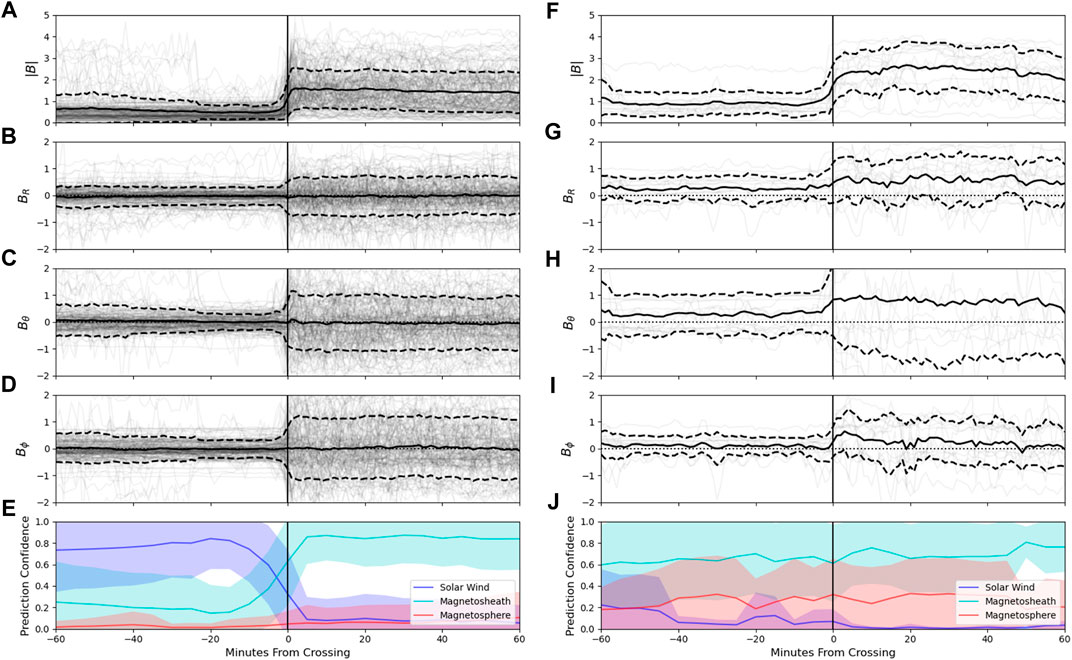
FIGURE 10. Comparison of the bow shock crossings in the labeled data set which were matched to a predicted crossing (A-E), versus those which were not matched (F–J) in the RNN 60-min model predictions. Panels (A–D) and (F–I) show the magnetic field conditions in a 1-h vicinity surrounding the labeled crossing, with individual instances plotted as transparent black lines. The average conditions ± the standard deviation are shown as thick black solid and dotted lines, respectively. Panels (E,J) show the prediction confidence of the model surrounding the labeled crossing for matched (E) and unmatched (J) crossings, with the average ± the standard deviation shown in the shaded region. Here the inwards and outwards crossings have been overlaid, such that all crossings are oriented in a inwards trajectory. In total there were 155 matched crossings and 15 unmatched crossings (see Table 4).
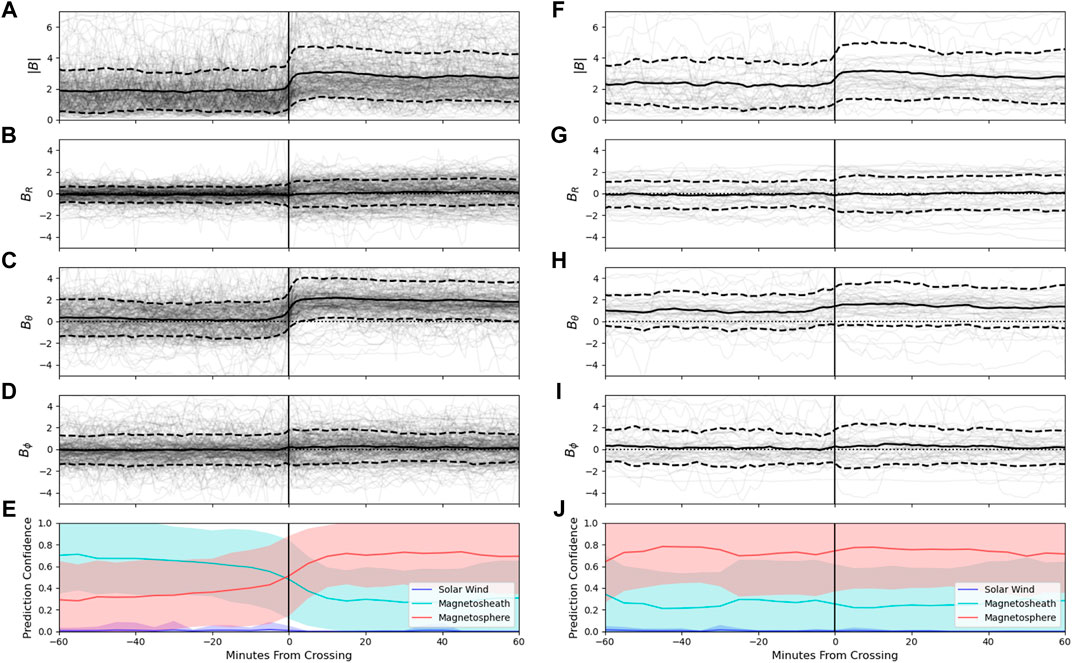
FIGURE 11. Comparison of the magnetopause crossings in the labeled data set which were matched to a predicted crossing (A–E), versus those which were not matched (F–J) in the RNN 60-min model predictions. Panels (A–D) and (F–I) show the magnetic field conditions in a 1-h vicinity surrounding the labeled crossing, with individual instances plotted as transparent black lines. The average conditions ± the standard deviation are shown as thick black solid and dotted lines, respectively. Panels (E,J) show the prediction confidence of the model surrounding the labeled crossing for matched (E) and unmatched (J) crossings, with the average ± the standard deviation shown in the shaded region. Here the inwards and outwards crossings have been overlaid, such that all crossings are oriented in a inwards trajectory. In total there were 216 matched crossings and 47 unmatched crossings (see Table 4).
The boundary between the magnetosheath and the magnetosphere is much more subtle than that between the solar wind and magnetosheath as revealed in Figure 11. The subtle nature of the boundary is underscored by the greater percentage of missed MPI (14.3%) and MPO (21.1%) transitions relative to the BSI (9.1%) and BSO (10.4%) transitions (see Table 4), and the greater delay in the matched transitions from the timing of the actual boundary crossing and the model detection of the new region. The MP crossings that were successfully identified demonstrate a sharp increase in |B| as the spacecraft moves into the magnetosphere, which is principally driven by an increase in Bθ. The missed MP transitions show a slightly more gradual increase in |B| and particularly in Bθ, with the model failing to recognize the magnetosheath is present before the transition. For all four boundary transition types, we see that the missed transitions exhibit confusion mainly between the magnetosphere and the magnetosheath, even for bow shock boundaries.
Here we have found that a variety of ML algorithms are capable of producing relatively accurate classifications of the region the spacecraft is inhabiting using only instrument data as the model input. Architecting the problem as a region-classification task instead of attempting to directly classify the boundary crossings afforded a much larger data set for both training and testing, enabling a broader swath of algorithms to be explored. However, as a consequence, assessment of where and how well the model predicted boundary crossings required a more-complicated post processing methodology and ultimately led to a large number of FBs. Daigavane et al. (2020) performed a complementary study in which they attempted to directly detect magnetopause and bow shock crossings in the CAPS-ELS data set using an anomaly detection methodology. Similar to the results contained herein, they found that bow shock crossings were substantially easier to detect than magnetopause crossings.
Comparing the predictive value of different feature sets, as was possible with the simpler and less data-intensive RF models, we find that the inclusion of more features clearly increases the predictive capability of the model, as expected. It should be noted that the specific subset of features from the plasma data chosen is important for this type of classification scheme. Ultimately, the best models will have inputs derived from the most physically relevant measurements, which given the architecture of this problem would be those features showing distinctly different characteristics in the bulk regions. We find that ultimately a time-series-based approach, as is possible with the RNN LSTM algorithm, produces a model with the greatest accuracy and temporal consistency, indicating that the temporal trends and variances of the MAG data alone provides sufficient predictive capability. This is further underscored by the improvement in the model performance as the length of the time sample fed to the RNN models is increased from 20 to 40 and, finally, 60 min. Though outside the scope of this study, we urge future studies to consider algorithm approaches which can leverage the benefits of both time-variance of the features and a richer feature set encompassing multiple instruments. While the scope of the algorithms explored in this study was relatively limited, other algorithms such as 1-D Convolutional Neural Networks (CNNs) or hybrid CNN-LSTM architectures should be explored given their utility in other sequence classification tasks, such as natural language processing and speech recognition (Sainath et al., 2015; Yin et al., 2017).
We have also shown the necessity of doing a full error analysis of the results and expand beyond the scope of analysis typically done in multi-class ML classification tasks. Blanket accuracy metrics fail to measure the algorithm prediction consistency over temporal or spatial scales. Nor do such metrics capture the feature context leading to model errors, or attempt to elucidate whether model predictions are tied to particular physical phenomena. By investigating the errors on spatial and temporal scales, we have found that models only slightly different in their overall accuracy metrics have demonstrably different performance in terms of temporal or spatial cohesion. The RF models in particular are only slightly worse than the RNN 60-min model in terms of their overall accuracy, and yet their predictions exhibit much more temporal volatility and undesirable patterns in spatial errors.
Given that there was an intentional decision to not apply filtering or smoothing techniques such as a centered running mean to the data prior to implementing the ML methods, the algorithms presented here could be run in a real-time scenario (ignoring the computational limitations of current spacecraft). As such, the instability of the model output could be addressed in real-time by implementing a persistence counter, i.e., a prediction of a different region would have to persist for a set number of continuous samples before the model were to shift its predictions. Such persistence measures are already widely used in spacecraft fault management autonomy systems to prevent outlier measurements from driving operational fault containment measures to the detriment of science or broader mission objectives (Fesq, 2009). Similarly, a threshold on the model’s confidence in a particular region needed before shifting the region prediction from one region to another, as would be the case in a boundary crossing, could be implemented. Both of these measures would reduce the rapid, and likely incorrect, false boundary crossings observed here—reducing risk with the side effect of potentially lengthening the lag between the true boundary crossing and the model’s recognition of the boundary crossing.
As noted by several studies (Azari et al., 2020; Hook et al., 2020; Theiling et al., 2021; Vandegriff et al., 2021), current missions are already facing severe downlink constraints and more data-intensive sensors. Without increased capabilities in on-board storage and deep space communications, missions may ultimately require the use of on-board autonomy to sift through the deluge of collected data to prioritize the most relevant observations for downlink or optimize the science collection of the sensors for the environment the spacecraft or lander is currently inhabiting. Examples of automated decisions the spacecraft could complete with on-board AI could be changing the sampling rate of an instrument or changing the binning scheme of plasma data. Already, research is being done to optimize data downlink using AI on earth-orbiting missions such as MMS, where only 4% of the high-rate data collected daily can be sent to the ground (Argall et al., 2020). In these cases, where predictions from an on-board AI system could contribute to mission operations, model stability becomes critical else undue risk is embedded in the mission. The results shown here illustrate that while simpler algorithms such as a RF can replicate the overall accuracy of more complicated RNNs and are more apt for on-board application due to their ability to operate in low-Size, Weight and Power (SWaP) embedded applications, they fail to replicate the accuracy and temporal stability of neural network approaches. Therefore, assessments of candidate algorithm performance must not only assess model performance using an unbiased, representative test set but also fully evaluate the context of the predictions.
Publicly available datasets were analyzed in this study. This data can be found here: https://pds-ppi.igpp.ucla.edu/mission/Cassini-Huygens.
KY and JV conceptualized the study. KY developed the models and resulting analysis of model predictions. All authors contributed to the interpretation of the results and writing of the manuscript.
KY, JV, GC, SV, and PK were supported by an JHU APL internal research and development grant, funded by the Civil Space Mission Area within the Space Exploration Sector. KY and JV were additionally supported by NASA Cassini/MIMI mission contract NNN06AA01C. GC was additionally supported by NASA’s Cassini Data Analysis program under grant 80NSSC18K1234, which also partially supported KY and SV was additionally supported by NASA grant 80NSSC19K0899. TG’s work at the University of Southampton was supported by the Alan Turing Institute and the Science and Technology Facilities Council (STFC). CJ’s work at DIAS was supported by the Science Foundation Ireland (SFI) Grant 18/FRL/6199. AS was supported by STFC Consolidated Grant ST/S000240/1 and NERC grants NE/P017150/1 and NE/V002724/1.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We are thankful to the institutions and personnel that made the Cassini-Huygens mission and the associated instruments a success.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.875985/full#supplementary-material
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2015). TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. doi:10.48550/arXiv.1603.04467
Argall, M. R., Small, C., Piatt, S., Breen, L., Petrik, M., Kokkonen, K., et al. (2020). Mms Sitl Ground Loop: Automating the Burst Data Selection Process. doi:10.3389/fspas.2020.00054
Arridge, C. S., Jasinski, J. M., Achilleos, N., Bogdanova, Y. V., Bunce, E. J., Cowley, S. W. H., et al. (2016). Cassini Observations of Saturn's Southern Polar Cusp. J. Geophys. Res. Space Phys. 121, 3006–3030. doi:10.1002/2015ja021957
Azari, A. R., Biersteker, J. B., Dewey, R. M., Doran, G., Forsberg, E. J., Harris, C. D. K., et al. (2020). Integrating Machine Learning for Planetary Science: Perspectives for the Next Decade. doi:10.48550/arXiv.2007.15129
Bertucci, C., Achilleos, N., Mazelle, C., Hospodarsky, G., Thomsen, M., Dougherty, M., et al. (2007). Low-frequency Waves in the Foreshock of Saturn: First Results from Cassini. J. Geophys. Res. Space Phys. 112. doi:10.1029/2006ja012098
Camporeale, E., Carè, A., and Borovsky, J. E. (2017). Classification of Solar Wind with Machine Learning. J. Geophys. Res. Space Phys. 122 (10), 910–920. doi:10.1002/2017JA024383
Case, N. A., and Wild, J. A. (2013). The Location of the Earth's Magnetopause: A Comparison of Modeled Position and In Situ Cluster Data. J. Geophys. Res. Space Phys. 118, 6127–6135. doi:10.1002/jgra.50572
Chicco, D., and Jurman, G. (2020). The Advantages of the Matthews Correlation Coefficient (Mcc) over F1 Score and Accuracy in Binary Classification Evaluation. BMC genomics 21, 6–13. doi:10.1186/s12864-019-6413-7
Dougherty, M. K., Achilleos, N., Andre, N., Arridge, C. S., Balogh, A., Bertucci, C., et al. (2005). Cassini Magnetometer Observations during Saturn Orbit Insertion. Science 307, 1266–1270. doi:10.1126/science.1106098
Fesq, L. M. (2009). “Current Fault Management Trends in Nasa’s Planetary Spacecraft,”, 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7-14 March 2020 (IEEE), 1–9. doi:10.1109/AERO.2009.4839530
Gorodkin, J. (2004). Comparing Two K-Category Assignments by a K-Category Correlation Coefficient. Comput. Biol. Chem. 28, 367–374. doi:10.1016/j.compbiolchem.2004.09.006
Guo, R. L., Yao, Z. H., Wei, Y., Ray, L. C., Rae, I. J., Arridge, C. S., et al. (2018). Rotationally Driven Magnetic Reconnection in Saturn's Dayside. Nat. Astron 2, 640–645. doi:10.1038/s41550-018-0461-9
Hook, J. V., Castillo-Rogez, J., Doyle, R., Vaquero, T. S., Hare, T. M., Kirk, R. L., et al. (2020). “Nebulae: A Proposed Concept of Operation for Deep Space Computing Clouds,”. 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7-14 March 2020 (IEEE), 1–14. doi:10.1109/AERO47225.2020.9172264
Ivchenko, N. V., Sibeck, D. G., Takahashi, K., and Kokubun, S. (2000). A Statistical Study of the Magnetosphere Boundary Crossings by the Geotail Satellite. Geophys. Res. Lett. 27, 2881–2884. doi:10.1029/2000gl000020
Jackman, C., Forsyth, R., and Dougherty, M. (2008). The Overall Configuration of the Interplanetary Magnetic Field Upstream of Saturn as Revealed by Cassini Observations. J. Geophys. Res. Space Phys. 113. doi:10.1029/2008ja013083
Jackman, C. M., Achilleos, N., Bunce, E. J., Cowley, S. W. H., Dougherty, M. K., Jones, G. H., et al. (2004). Interplanetary magnetic field at 9 au during the declining phase of the solar cycle and its implications for saturn’s magnetospheric dynamics. J. Geophys. Res. Space Phys. 109. doi:10.1029/2004JA0106110.1029/2004ja010614
Jackman, C. M., Thomsen, M. F., and Dougherty, M. K. (2019). Survey of Saturn's Magnetopause and Bow Shock Positions over the Entire Cassini Mission: Boundary Statistical Properties and Exploration of Associated Upstream Conditions. J. Geophys. Res. Space Phys. 124, 8865–8883. doi:10.1029/2019JA026628
Jasinski, J. M., Arridge, C. S., Coates, A. J., Jones, G. H., Sergis, N., Thomsen, M. F., et al. (2016). Cassini Plasma Observations of Saturn’s Magnetospheric Cusp. J. Geophys. Res. Space Phys. 121, 12–047. doi:10.1002/2016ja023310
Jasinski, J. M., Arridge, C. S., Coates, A. J., Jones, G. H., Sergis, N., Thomsen, M. F., et al. (2017). Diamagnetic Depression Observations at Saturn's Magnetospheric Cusp by the Cassini Spacecraft. J. Geophys. Res. Space Phys. 122, 6283–6303. doi:10.1002/2016ja023738
Jelínek, K., Němeček, Z., and Šafránková, J. (2012). A New Approach to Magnetopause and Bow Shock Modeling Based on Automated Region Identification. J. Geophys. Res. 117, a–n. doi:10.1029/2011JA017252
Kanani, S. J., Arridge, C. S., Jones, G. H., Fazakerley, A. N., McAndrews, H. J., Sergis, N., et al. (2010). A New Form of Saturn's Magnetopause Using a Dynamic Pressure Balance Model, Based on In Situ, Multi-Instrument Cassini Measurements. J. Geophys. Res. 115, a–n. doi:10.1029/2009JA014262
Kingma, D. P., and Ba, J. (2017). Adam: A Method for Stochastic Optimization. doi:10.48550/arXiv.1412.6980
Krimigis, S. M., Mitchell, D. G., Hamilton, D. C., Livi, S., Dandouras, J., Jaskulek, S., et al. (2004). Magnetosphere Imaging Instrument (MIMI) on the Cassini Mission to Saturn/Titan. Dordrecht: Springer Netherlands, 233–329. doi:10.1007/978-1-4020-2774-1_3
Liou, K., Paranicas, C., Vines, S., Kollmann, P., Allen, R. C., Clark, G. B., et al. (2021). Dawn-dusk Asymmetry in Energetic (> 20 Kev) Particles Adjacent to Saturn’s Magnetopause. J. Geophys. Res. Space Phys. 126, e2020JA028264. doi:10.1029/2020ja028264
Matthews, B. W. (1975). Comparison of the Predicted and Observed Secondary Structure of T4 Phage Lysozyme. Biochimica Biophysica Acta (BBA) - Protein Struct. 405, 442–451. doi:10.1016/0005-2795(75)90109-9
Mauk, B. H., Cohen, I. J., Haggerty, D. K., Hospodarsky, G. B., Connerney, J. E. P., Anderson, B. J., et al. (2019). Investigation of Mass‐/Charge‐Dependent Escape of Energetic Ions across the Magnetopauses of Earth and Jupiter. J. Geophys. Res. Space Phys. 124, 5539–5567. doi:10.1029/2019JA026626
Mauk, B. H., Cohen, I. J., Westlake, J. H., and Anderson, B. J. (2016). Modeling Magnetospheric Energetic Particle Escape across Earth's Magnetopause as Observed by the MMS Mission. Geophys. Res. Lett. 43, 4081–4088. doi:10.1002/2016gl068856
Olshevsky, V., Khotyaintsev, Y. V., Lalti, A., Divin, A., Delzanno, G. L., Anderzén, S., et al. (2021). Automated Classification of Plasma Regions Using 3d Particle Energy Distributions. J. Geophys. Res. Space Phys. 126, e2021JA029620. doi:10.1029/2021ja029620
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 12, 2825–2830.
Pilkington, N. M., Achilleos, N., Arridge, C. S., Guio, P., Masters, A., Ray, L. C., et al. (2015). Internally Driven Large-Scale Changes in the Size of Saturn's Magnetosphere. J. Geophys Res. Space Phys. 120, 7289–7306. doi:10.1002/2015JA021290
Sainath, T. N., Vinyals, O., Senior, A., and Sak, H. (2015). Convolutional, Long Short-Term Memory, Fully Connected Deep Neural Networks , 4580–4584. doi:10.1109/icassp.2015.7178838
Simon, S., Roussos, E., and Paty, C. S. (2015). The Interaction between Saturn's Moons and Their Plasma Environments. Phys. Rep. 602, 1–65. doi:10.1016/j.physrep.2015.09.005
Sulaiman, A. H., Masters, A., and Dougherty, M. K. (2016). Characterization of Saturn's Bow Shock: Magnetic Field Observations of Quasi-Perpendicular Shocks. J. Geophys. Res. Space Phys. 121, 4425–4434. doi:10.1002/2016ja022449
Theiling, B., Brinckerhoff, W., Castillo-Rogez, J., Chou, L., Poian, V. D., Graham, H., et al. (2021). Non-robotic Science Autonomy Development. Bull. AAS 53. doi:10.3847/25c2cfeb.ee4e6b64
Vandegriff, J., Smith, B., Yeakel, K., Vines, S., Ho, G., Clark, G., et al. (2021). Developing Smarter Techniques to Deal with the Heliophysics Science Data Flood.
Went, D. R., Hospodarsky, G. B., Masters, S., Hansen, K. C., and Dougherty, M. K. (2011). A New Semiempirical Model of Saturn’s Bow Shock Based on Propagated Solar Wind Parameters. J. Geophys. Res. Space Phys. 116. doi:10.1029/2010ja016349
Xu, F., and Borovsky, J. E. (2015). A New Four-Plasma Categorization Scheme for the Solar Wind. J. Geophys. Res. Space Phys. 120, 70–100. doi:10.1002/2014JA020412
Yin, W., Kann, K., Yu, M., and Schütze, H. (2017). Comparative Study of Cnn and Rnn for Natural Language Processing. doi:10.48550/arXiv.1702.01923
Keywords: recurrent neural network (RNN) long short-term memory (LSTM), random forest, machine learning, magnetosphere, boundary crossings, Saturn, Cassini-Huygens
Citation: Yeakel KL, Vandegriff JD, Garton TM, Jackman CM, Clark G, Vines SK, Smith AW and Kollmann P (2022) Classification of Cassini’s Orbit Regions as Magnetosphere, Magnetosheath, and Solar Wind via Machine Learning. Front. Astron. Space Sci. 9:875985. doi: 10.3389/fspas.2022.875985
Received: 14 February 2022; Accepted: 19 April 2022;
Published: 20 May 2022.
Edited by:
Olga Verkhoglyadova, NASA Jet Propulsion Laboratory (JPL), United StatesReviewed by:
Tomas Karlsson, Royal Institute of Technology, SwedenCopyright © 2022 Yeakel, Vandegriff, Garton, Jackman, Clark, Vines, Smith and Kollmann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kiley L. Yeakel, a2lsZXkueWVha2VsQGpodWFwbC5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.