Domain-Agnostic Outlier Ranking Algorithms—A Configurable Pipeline for Facilitating Outlier Detection in Scientific Datasets

Automatic detection of outliers is universally needed when working with scientific datasets, e.g., for cleaning datasets or flagging novel samples to guide instrument acquisition or scientific analysis. We present Domain-agnostic Outlier Ranking Algorithms (DORA), a configurable pipeline that facilitates application and evaluation of outlier detection methods in a variety of domains. DORA allows users to configure experiments by specifying the location of their dataset(s), the input data type, feature extraction methods, and which algorithms should be applied. DORA supports image, raster, time series, or feature vector input data types and outlier detection methods that include Isolation Forest, DEMUD, PCA, RX detector, Local RX, negative sampling, and probabilistic autoencoder. Each algorithm assigns an outlier score to each data sample. DORA provides results interpretation modules to help users process the results, including sorting samples by outlier score, evaluating the fraction of known outliers in n selections, clustering groups of similar outliers together, and web visualization. We demonstrated how DORA facilitates application, evaluation, and interpretation of outlier detection methods by performing experiments for three real-world datasets from Earth science, planetary science, and astrophysics, as well as one benchmark dataset (MNIST/Fashion-MNIST). We found that no single algorithm performed best across all datasets, underscoring the need for a tool that enables comparison of multiple algorithms.

1 Introduction

The ability to automatically detect out-of-distribution samples in large data sets is of interest for a wide variety of scientific domains. Depending on the application setting, this capability is also commonly referred to as anomaly detection, outlier detection, or novelty detection. More broadly, this is referred to as out-of-distribution (OOD) detection. In general, the goal of OOD detection systems is to identify samples that deviate from the majority of samples in a dataset in an unsupervised manner (Pimentel et al., 2014). In machine learning, these methods are commonly used for identifying mislabeled or otherwise invalid samples in a dataset (Liang et al., 2018; Böhm and Seljak, 2020). When working with science datasets, OOD detection can be used for cleaning datasets, e.g., flagging ground-truth labels with GPS or human entry error or identifying wrongly categorized objects in a catalog (Wagstaff et al., 2020a; Lochner and Bassett, 2021). It could also be used for discovery, e.g., to flag novel samples in order to guide instrument acquisition or scientific analysis (Wagstaff et al., 2013; Kerner et al., 2020a; Kerner et al., 2020b; Wagstaff et al., 2020b). Another application is the detection of rare objects that are known to exist but the known examples are too few to create a large enough labeled dataset for supervised classification algorithms (Chein-I Chang and Shao-Shan Chiang, 2002; Zhou et al., 2016).

Despite wide differences in applications, data types, and dimensionality, the same underlying machine learning algorithms can be employed across all of these domains. A challenge for applying them however is that domain scientists do not always have the programming or machine learning background to apply the algorithms themselves using existing tools. Given the widespread applicability and transferability of OOD methods, the scientific community would benefit from a tool that made it easy for them to apply popular outlier detection algorithms to their science datasets. We created DORA (Domain-agnostic Outlier Ranking Algorithms) to provide a tool for applying outlier detection algorithms to a variety of scientific data sets with minimal coding required. Users need only to specify details for their data/application including the data type, location, and algorithms to run in an experiment configuration file. DORA supports image, raster, time series, or feature vector input data types and outlier detection methods that include Isolation Forest, Discovery via Eigenbasis Modeling of Uninteresting Data (DEMUD) (Wagstaff et al., 2013), principal component analysis (PCA), Reed-Xiaoli (RX) detector (Reed and Yu, 1990), Local RX, negative sampling (Sipple, 2020), and probabilistic autoencoder (PAE). Each algorithm assigns an outlier score to each sample in a given dataset. DORA provides results organization and visualization modules to help users process the results, including sorting samples by outlier score, evaluating outlier recall for a set of known/labeled outliers, clustering groups of similar outliers together, and web visualization. We demonstrated how DORA facilitates application, evaluation, and interpretation of outlier detection methods by performing experiments for three real-world datasets from Earth science, planetary science, and astrophysics, as well as one benchmark dataset (MNIST/Fashion-MNIST).

The key contributions of this paper are:

• A new pipeline, DORA, for performing outlier detection experiments using several AI algorithms that reduces the effort and expertise required for performing experiments and comparing results from multiple algorithms

• Using experiments for a diverse set of real world datasets and application areas, we show that no single algorithm performs best for all datasets and use cases, underscoring the need for a tool that compares multiple algorithms

• We provide publicly available code for running and contributing to the DORA pipeline and datasets that can be used for reproducing experiments or benchmarking outlier detection methods

2 Related Work

Methods for outlier detection have been surveyed extensively and can be differentiated primarily based on how they score outliers (Markou and Singh, 2003a; Markou and Singh, 2003b; Chandola et al., 2009; Pimentel et al., 2014). Reconstruction-based methods construct a model of a dataset by learning a mapping between the input data and a lower-dimensional representation that minimizes the loss between the input and its reconstruction from the low-dimensional representation (Kerner et al., 2020a). The reconstruction error is used as the outlier score because samples that are unlike the data used to fit the model will be more poorly reconstructed compared to inliers. Reconstruction-based methods include PCA (Jablonski et al., 2015), autoencoders (Richter and Roy, 2017), and generative adversarial networks (Akcay et al., 2018). Distance-based methods score outliers based on their distance from a “background” which can be defined in a variety of ways. For example, the Reed-Xiaoli (RX) detector computes the Mahalanobis distance between each sample and the background dataset defined by its mean and covariance matrix (Reed and Yu, 1990). Sparsity-based methods such as isolation forest (Liu et al., 2008) and local outlier factor (Breunig et al., 2000) score outliers based on how isolated or sparse samples are in a given feature space. Probability distribution and density based methods estimate the underlying distribution or probability density of a dataset and score samples using likelihood. Examples include the probabilistic autoencoder, which scores samples based on the log likelihood under the latent space distribution (Böhm and Seljak, 2020), Gaussian mixture Models, and kernel density estimators (Chandola et al., 2009). Other methods formulate outlier detection as supervised classification, usually with only one class constituted by known normal samples. Such methods include one-class support vector machines (Schölkopf et al., 1999) and negative sampling (Sipple, 2020).

In astrophysics, outlier detection methods have been used to identify astrophysical objects with unique characteristics (Hayat et al., 2021) as well as data or modeling artifacts in astronomical surveys (Wagstaff et al., 2020a; Lochner and Bassett, 2021). Example outlier detection applications in Earth science include detecting anomalous objects or materials (Zhou et al., 2016), data artifacts or noise (Liu et al., 2017), change (Touati et al., 2020), and ocean extremes (Prochaska et al., 2021). Planetary science applications have mostly focused on prioritizing samples with novel geologic or geochemical features for follow-up targeting or analysis (Wagstaff et al., 2013; Kerner et al., 2020a). These examples show the benefit of applying outlier detection methods in a variety of real-world science use cases. However, the effort required to apply and evaluate the many available algorithms is non-trivial and can be daunting for non-ML experts, thus impeding the uptake of outlier detection methods in science applications. There is a need for tools that make it easier for domain scientists to apply outlier detection methods as well as compare results across datasets. While there have been some efforts to develop tools for facilitating the application of outlier detection methods (Zhao et al., 2019), they cover limited data formats and algorithms. DORA aims to fill the need for tools that facilitate application, evaluation, and interpretation of outlier detection methods.

3 Methods

Figure 1 illustrates the architecture of DORA including data loading, feature extraction, outlier ranking, and results organization and visualization modules. In order to improve the readability and execution speed of the code, we adopted object-oriented and functional programming practices. We designed DORA to be readily extensible to support additional data types or formats, outlier detection algorithms, and results organization or visualization methods by writing new modules that follow the DORA API. Experimental settings are controlled by configuration files in which users can specify the input data, feature extraction methods, normalization method, outlier ranking methods, and results organization methods. DORA is implemented in Python 3.

FIGURE 1

FIGURE 1. DORA pipeline architecture.

3.1 Data Loaders

We chose to implement data loaders for four data types that are commonly used by the machine learning and domain science communities: time series, feature vectors, images (grayscale or RGB), and N-band rasters. N-band rasters are images or grids in which every pixel is associated with a location (e.g., latitude/longitude in degrees); most satellite data are distributed as rasters. A data loader for each data type locates the data by the path(s) defined in the configuration file and loads samples into a dictionary of numpy arrays indexed by the sample id. This data_dict is then passed to each of the ranking algorithms.

3.2 Outlier Ranking Algorithms

We implemented seven unsupervised algorithms for scoring and ranking samples by outlierness. We chose these algorithms to include a diverse set of approaches to scoring outliers since different algorithms may perform better for different datasets and use cases. We describe each approach to scoring outliers and the associated methods below.

3.2.1 Reconstruction Error

Principal component analysis (PCA) has been used for outlier detection by scoring samples using the reconstruction error (here, the L2 norm) between inputs and their inverse transformation from the principal subspace (Kerner et al., 2020a). DEMUD (Wagstaff et al., 2013) differs from other outlier ranking methods: instead of independently scoring all observations, DEMUD incrementally identifies the most unusual remaining item, then incorporates it into the model of “known” (non-outlier) observations before selecting the next most unusual item. DEMUD’s goal is to identify diverse outliers and avoid redundant selections. Once an outlier is found, repeated occurrences of that outlier are deprioritized. Methods that score samples independently maximize coverage of outliers, while DEMUD maximizes fast discovery of distinct outlier types.

3.2.2 Distance

The Reed-Xiaoli (RX) detector is commonly used for anomaly detection in multispectral and hyperspectral remote sensing. RX scores samples using the Mahalanobis distance between a sample and a background mean and covariance (Reed and Yu, 1990). The local variant of RX (Local RX or LRX) can be used for image or raster data and scores each pixel in an image with respect to a window “ring” of pixels surrounding it (Molero et al., 2013). LRX requires two parameters to define the size of the outer window surrounding the pixel and the inner window around the target pixel to exclude from the background distribution.

3.2.3 Sparsity

Isolation forest (iForest) is a common sparsity-based method that constructs many random binary trees from a dataset (Liu et al., 2008). The outlier score for a sample is quantified as the average distance from the root to the item’s leaf. Shorter distances are indicative of outliers because the number of random splits required to isolate the sample is small.

3.2.4 Probability

The negative sampling algorithm is implemented by converting the unsupervised outlier ranking problem into a semi-supervised problem (Sipple, 2020). Negative (anomalous) examples are created by sampling from an expanded space defined by the minimum and maximum values of each dimension of the positive (normal) examples. The negative and positive examples are then used to train a random forest classifier. We use the posterior probabilities of the random forest classifier as outlier scores, which means that the observations with higher posterior probabilities are more likely to be outliers. The probabilistic autoencoder is a generative model consisting of an autoencoder trained to reconstruct input data which is interpreted probabilistically after training using a normalizing flow on the autoencoder latent space (Böhm and Seljak, 2020). Samples are scored as outliers using the log likelihood in the latent distribution, the autoencoder reconstruction error, or a combination of both.

3.3 Results Interpretation

Each of the outlier ranking algorithms returns an array containing the sample index, outlier score, and selection index (index after sorting by outlier score). DORA provides organization and visualization modules intended to help users interpret and make decisions based on these outputs. The simplest module saves a CSV of the samples sorted by their outlier score (i.e., selection order). Clustering the top N outlier selections can enable users to investigate the different types of outliers that might be present in the dataset; this could be especially useful for separating outliers caused by noise or data artifacts vs scientifically interesting samples. We implemented the K-means and self-organizing maps (SOMs) algorithms for clustering the top-N outliers. For use cases in which an evaluation dataset containing known outliers is available, we provide a module to assess how well algorithm selections correlate with known outliers. This is done by plotting the number of known outliers vs number of selections made. We provide a module for plotting histograms of outlier scores to visualize the distribution of scores in the dataset (which may be, e.g., multimodal or long-tailed). We developed a desktop application to easily visualize DORA results with the Electron application framework and React frontend library. This enables fast and easy comparison of the results from different methods. We developed a desktop application to easily visualize DORA results with the Electron application framework and React frontend library. The application loads the DORA configuration file to locate the dataset and result CSVs. Then, it displays the ranked samples and their scores in a table sorted by their selection order. This allows for fast and easy comparison of the results of different methods. Figure 2 shows a screenshot of the “Aggregate Table” view, which displays all results from different algorithms side-by-side.

FIGURE 2

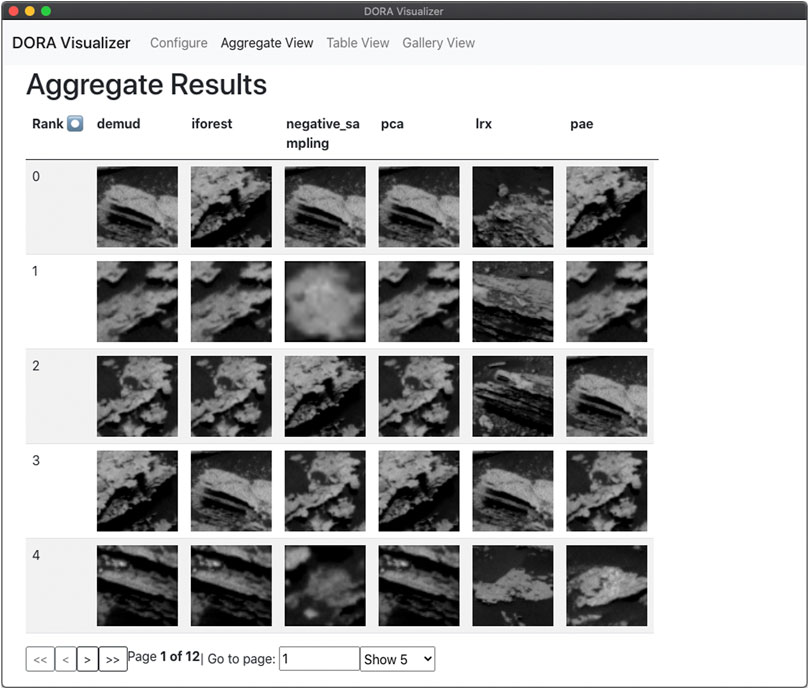
FIGURE 2. A screenshot of the DORA visualizer displaying results from the planetary science dataset.

4 Datasets

We constructed three datasets to evaluate the utility of DORA and algorithm performance for a variety of scientific domains (astrophysics, planetary science, and Earth science). We also included a benchmark dataset that uses MNIST and Fashion-MNIST. Table 1 summarizes the number of unlabeled samples used for training and evaluation for each dataset. We describe each dataset in detail below.

TABLE 1

TABLE 1. Number of samples in the training and test sets for each dataset.

4.1 Astrophysics: Objects in Dark Energy Survey

Astronomical data sets are large and growing. Large modern optical imaging surveys are producing catalogs of order 10⁸ stars and galaxies, with dozens or hundreds of distinct measured features for each entry. Discovery science becomes difficult at this data volume: the scale is too large for expert human inspection, and separating real astrophysical anomalies from non-astrophysical sources like detector artifacts or satellite trails is a challenging problem for current methods.

The Dark Energy Survey (DES) is an ongoing imaging survey of 5,000 deg² of the southern sky from the Cerro-Tololo Inter-American Observatory in Chile (Zuntz et al., 2018). The resulting galaxy catalogs produced have provided some of the strongest constraints to date on the physical properties of dark energy and accelerated expansion of the Universe. The first version of this catalog, released June 2018, incorporated only cuts on signal-to-noise and resolution, masks against known detector anomalies and data quality indicators, and the automated data quality flags produced during processing to filter outliers. In December 2019, the full catalog was released after 18 months of extensive manual vetting. We used the samples that were removed in the second version of the catalog as a set of known outliers for evaluating anomaly detection methods on the first version.

We compared all methods on a dataset of 100K galaxy objects observed by the Dark Energy Survey (DES) sampled from the initial June 2018 release. We labeled the 25,339 objects from this 100 K set that did not appear in the later December 2019 release, thus were likely eliminated during the manual vetting process, as outliers. While the remaining 74,661 objects may also contain outliers, we assume them to be inliers in this experiment. We used publicly-available photometry from the g −, r −, i − and z − band DES exposures. We transformed the photometry into luptitudes¹. The input features were the r-band luptitude, colors computed as band differences between g − r, i − r, and z − r, and associated observational errors, for a total of eight features.

4.2 Planetary: Targets in Mars Rover Images

Mars exploration is fundamentally an exercise in discovery with the goal of increasing our understanding of Mars’s history, evolution, composition, and currently active processes. Outliers identified in Mars observations can inspire new discoveries and inform the choice of which areas merit follow-up or deeper investigation (Kerner et al., 2020a; Wagstaff et al., 2020b). We collected 72 images from the Navigation camera (Navcam) on the Mars Science Laboratory (MSL) rover and employed Rockster (Burl et al., 2016) (currently used by onboard rover software) to identify candidate rock targets with an area of at least 100 pixels, yielding 1,050 targets. We cropped out a 64 × 64 pixel image centered on each target.

We simulated the operational setting in which the rover has observed targets up through mission day (sol) s and the goal is to rank all subsequent targets (after sol s) to inform which recent targets merit further study. Our rover image data covers sols 1,343 to 1703. We partitioned the images chronologically to assess outlier detection in the 10 most recent sols, using “prior” set D_1343−1693 (n = 992) and “assessment” set D_1694−1703 (n = 58) for evaluation. We collaborated with an MSL science team member to independently review the targets in D_1694−1703 and identify those considered novel by the mission (n_outlier = 9). Our goal for this application is to assess how well the selections made by each algorithm correlate with human novelty judgments to determine which methods would be most suitable for informing onboard decisions about follow-up observations.

4.3 Earth: Satellite Time Series for Ground Observations

Many Earth science applications using satellite Earth observation (EO) data require ground-truth observations for identifying and modeling ground-identified objects in the satellite observations. These ground observations also serve as labels that are paired with satellite data inputs for machine learning models. For example, a model trained to classify crop types in satellite observations requires ground-annotated labels of crop type. A widespread challenge for ground-annotated labels is that there are often points with erroneous location or label information (e.g., due to GPS location error or human entry error) that need to be cleaned before the labels can be used for machine learning or other downstream uses. Automatically detecting these outliers could save substantial time required for cleaning datasets and improve the performance of downstream analyses that rely on high-quality datasets.

We used a dataset of ground annotations of maize crops collected by the UN Food and Agriculture Organization (FAO). This dataset includes 6,757 samples with location (latitude/longitude) metadata primarily in Africa and Southeast Asia. Most locations coincide with crop fields but there are many outliers that coincide with other land cover types such as water, buildings, or forests. We constructed an evaluation set of all samples in Kenya (n = 113) and manually annotated whether each sample was located in a crop field (inlier) or not (outlier) using high-resolution satellite images in Collect Earth Online (n_inlier = 76, n_outlier = 37). We used the Sentinel-1 synthetic aperture radar (SAR) monthly median time series for each sample location from the year the sample was collected. We used SAR data because it is sensitive to ground texture and penetrates clouds, which is important for the often-cloudy region covered by the dataset. Our goal for this application was to assess how well the selections made by each algorithm correlate with outliers determined by visual inspection of the satellite images.

4.4 Benchmark: MNIST and Fashion-MNIST

We used MNIST and Fashion-MNIST (F-MNIST) to demonstrate DORA with a traditional benchmark dataset. We used 60,000 images from F-MNIST as the training set and a test set of 1,000 images each from MNIST (outliers) and F-MNIST (inliers).

5 Results

The experimental setup for each dataset was to fit or train a model for each ranking algorithm using a larger unlabeled dataset and then apply the models to compute the outlier scores for a smaller test dataset for which labels of known outliers were available (Table 1). For each test set, we created a plot of the number of known outliers detected out of the top N selections. We also reported the Mean Discovery Rate (MDR) in the legend for each algorithm to give a quantitative comparison across the datasets. We defined MDR as:

$MDR=\frac{{\sum }_{i=1}^{N_s}{n}_i}{{\sum }_{i=1}^{N_s}{s}_i}(1)$

where i ∈ [1, N_s] is the selection index, N_s is the total number of selections, s_i is the number of selections made up to index i, and n_i is the number of known outliers (true positives) among s_i selections. We also reported the precision at N = n_outlier for each test set where n_outlier is the number of known outliers, i.e., the precision obtained when the number of selections is the same as the total number of outliers. Precision at N is the number of known outliers divided by the number of selections N (Campos et al., 2016). Table 2 compares the precision at N = n_outlier for each dataset and ranking algorithm. We calculated a random selection baseline which we refer to as “Theoretical Random” using the expected value of n_i for i random selections:

$\mathbf{E}\left[n_i,i\in \left[1,N_s\right]\right]=\frac{{\sum }_{j=0}^i\left(\begin{array}{c}{n}_{outlier}\\ j\end{array},\right)\left(\begin{array}{c}D-n_{outlier}\\ i-j\end{array},\right)j}{\left(\begin{array}{c}D\\ i\end{array},\right)}(2)$

$=\frac{n_{outlier}i}{D}(3)$

TABLE 2

TABLE 2. Precision at N = n_outlier for four datasets; the best result for each data set is in bold.

For the astrophysics dataset (Figure 3A), DEMUD was omitted due to computational time and LRX was omitted as it applies only to image data. Of the remaining methods, PCA achieved the highest precision, followed by RX. Negative sampling performs well initially before its performance drops off. The PAE finds the most outliers overall.

FIGURE 3

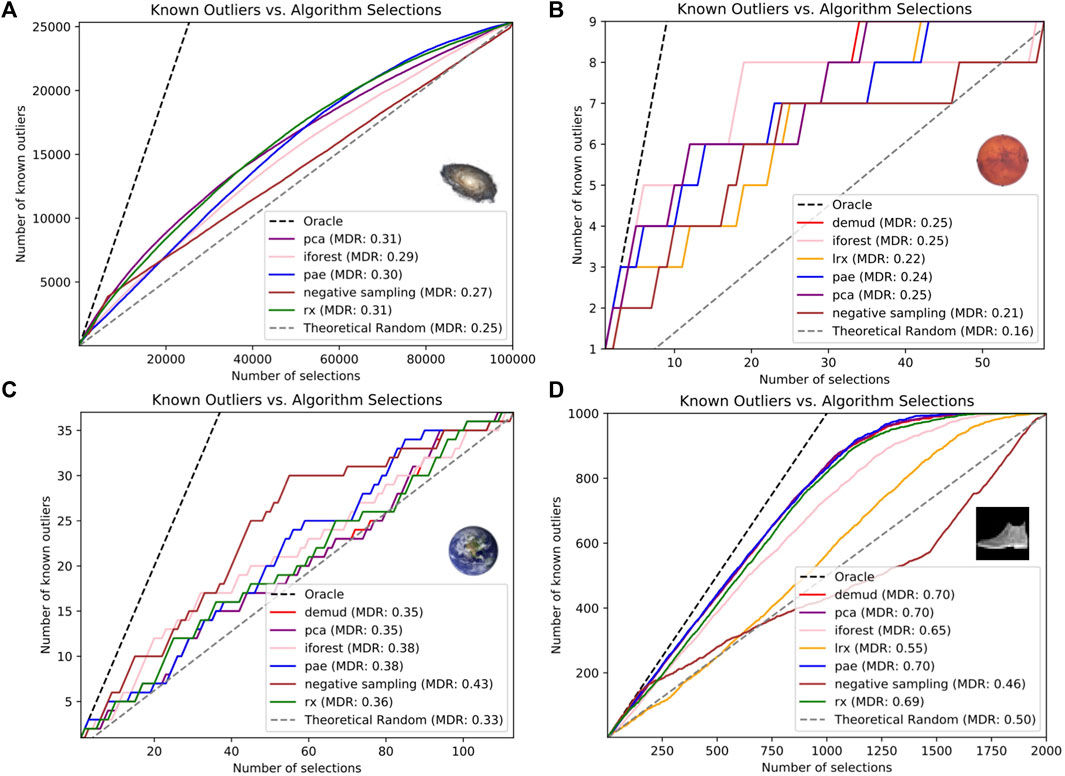
FIGURE 3. Number of known outliers ranked in top N selections for the (A) astrophysics, (B) planetary, (C) Earth, and (D) FMNIST datasets.

For the planetary dataset, we found that the Isolation Forest achieved the highest precision (best outlier detection) when allowed to select only 9 images. Figure 3B shows the complete (cumulative) outlier detection performance for each algorithm when ranking all 58 target images in D_1694−1703. We could not employ RX since the data dimensionality (64 × 64 = 4,096) exceeded the data set size.

For the Earth dataset, negative sampling had the best performance in both metrics. DEMUD, PCA, and PAE tied for the lowest precision at N = n_outlier while DEMUD and PCA tied for the lowest MDR (Figure 3C). We did not evaluate LRX for this time series dataset because LRX can only be applied to gridded image or raster data types.

For the MNIST and F-MNIST dataset, PCA and DEMUD tied for the highest precision at N = n_outlier while DEMUD, PCA, and PAE tied for the highest MDR (Figure 3D). Negative sampling had the lowest performance in both metrics.

6 Discussion

6.1 Algorithm Performance

No one algorithm had the best performance across all four datasets. PCA had the best performance for the astrophysics and F-MNIST datasets, while negative sampling and isolation forest was best for the Earth science and planetary datasets respectively. This illustrates the importance of including a diverse set of algorithms and tools for easily inter-comparing them in DORA, since the best algorithm will vary for different datasets. The purpose of this study was to demonstrate how DORA could be used to facilitate outlier detection experiments and compare results across datasets from different domains. Thus we did not perform hyperparameter tuning which could improve results for each dataset; we leave this for future work.

6.2 Evaluation in Outlier Detection

Prior work has emphasized the difficulty of creating standardized metrics for outlier detection that represents how models will perform in real world settings while also enabling intercomparison between datasets (Campos et al., 2016). We chose two complementary metrics with this in mind: precision at N = n_outliers, which measures the fraction of selections that are known outliers when the number of selections is equivalent to the number of outliers, and Mean Discovery Rate, which measures the fraction of selections that are known outliers on average. Designing experiments to evaluate outlier detection methods for real-world use cases is also difficult because it is difficult, or sometimes impossible, to obtain labeled samples of outliers, inliers, or both for evaluation. In addition, labels are often subjective or uncertain, especially in the case of scientific datasets. For example, a dataset of known outliers was available for the astrophysics dataset from human annotation in prior work, but the remainder of samples in the dataset used for evaluation were not known to be inliers or outliers. This can result in evaluation metrics that are deceptively low because unlabeled samples that might actually be outliers (as was found to be common in prior work (Wagstaff et al., 2020a)) are counted as false positives.

6.3 Open Code and Data

Our goal is for DORA to enable increased application and benefit of outlier detection methods in real-world scientific use cases. We have designed DORA to make it as easy as possible for scientists to apply algorithms and to compare and interpret their results. Users need only to specify the specifics of their data (e.g., path, data type) in a configuration file to start running experiments and seeing results for their own datasets and use cases. DORA is publicly available and can be installed using pip via Github, making it easy to integrate into existing scientific workflows. The datasets used in this study are also publicly available via Zenodo. This enables DORA to be improved and expanded by the machine learning and domain science communities. If a researcher wants to use DORA for a dataset with a type that is not yet supported, they can contribute a new data loader by creating a subclass that extends the DataLoader abstract base class. Similarly, new results interpretation modules can be added by creating a subclass of the ResultsOrganization abstract base class. A new outlier ranking algorithm can be added by writing a new python module that defines a subclass of the OutlierDetection abstract base class and implements the required functions for scoring and ranking samples, following the existing algorithm modules named *_outlier_detection.py. In addition, DORA will be infused into the scientific workflows for the three use cases we demonstrated results for in this study. The DORA code can be accessed at https://github.com/nasaharvest/dora and datasets at https://doi.org/10.5281/zenodo.5941338.

7 Conclusion

The ability to automatically find outliers in large datasets is critical for a variety of scientific and real-world use cases. We presented Domain-agnostic Outlier Ranking Algorithms (DORA), a configurable pipeline that facilitates application and evaluation of outlier detection methods in a variety of domains. DORA minimizes the coding and ML expertise required for domain scientists since users need only to specify their experiment details in a configuration file to get results from all available algorithms. This is particularly important because the experiments for three cross-domain science datasets in this study showed that no one algorithm performs best for all datasets. DORA will be publicly accessible as a python package to make it easy to integrate into existing scientific workflows. The will be open-sourced to enable continued improvement and expansion of DORA to serve the needs of the science community. The datasets used in this study will also be public and can serve as real-world benchmarks for future outlier detection methods.In future work, we will continue to improve DORA based on the experience of deploying it in the workflows of the domain scientists associated with the datasets in this study and add additional interpretation modules including causal inference graphs.

Data Availability Statement

The datasets generated and analyzed for this study can be found in the “Multi-Domain Outlier Detection Dataset” repository on Zenodo (https://doi.org/10.5281/zenodo.5941338).

Author Contributions

HK, UR, and KW developed the conception of the project. HK oversaw the overall implementation and led the analysis of the Earth science dataset. UR led the analysis of the astrophysics dataset. KW led the analysis of the planetary science dataset. SL led the development of the DORA software architecture. BD led the analysis of the FMNIST/MNIST dataset. EH supported the analysis of the astrophysics dataset. JL developed the desktop application for results visualization. VR supported the analysis of the Earth science dataset. SK supported the analysis of the planetary science dataset. All authors contributed to the overall system implementation and manuscript writing/editing.

Funding

This work was funded by a grant from the NASA Science Mission Directorate (under the NASA Cross-Divisional AI Use Case Demonstration grants; Grant No. 80NSSC21K0720). Part of this research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the UN Food and Agriculture Organization (FAO) and Ritvik Sahajpal (University of Maryland/NASA Harvest) for providing the maize ground observation dataset. We thank Raymond Francis for analyzing the Navcam rover images to identify targets considered to be “novel” for evaluating outlier detection in the planetary rover scenario.

Footnotes

¹A “Luptitude” (Lupton et al., 1999) is an arcsinh-scaled flux, with properties quantitatively equal to traditional astronomical magnitudes for bright sources, but which gracefully handles non-detections and negative fluxes.

References

Akcay, S., Atapour-Abarghouei, A., and Breckon, T. P. (2018). “Ganomaly: Semi-supervised Anomaly Detection via Adversarial Training,” in Asian Conference on Computer Vision (Springer), 622–637.

Google Scholar

Böhm, V., and Seljak, U. (2020). Probabilistic Auto-Encoder. arXiv preprint arXiv:2006.05479.

Google Scholar

Breunig, M. M., Kriegel, H.-P., Ng, R. T., and Sander, J. (2000). “Lof,” in Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, 29. 93–104. SIGMOD Rec. doi:10.1145/335191.335388

CrossRef Full Text | Google Scholar

Burl, M. C., Thompson, D. R., deGranville, C., and Bornstein, B. J. (2016). Rockster: Onboard Rock Segmentation through Edge Regrouping. J. Aerospace Inf. Syst. 13, 329–342. doi:10.2514/1.i010381

CrossRef Full Text | Google Scholar

Campos, G. O., Zimek, A., Sander, J., Campello, R. J. G. B., Micenková, B., Schubert, E., et al. (2016). On the Evaluation of Unsupervised Outlier Detection: Measures, Datasets, and an Empirical Study. Data Min Knowl Disc 30, 891–927. doi:10.1007/s10618-015-0444-8

CrossRef Full Text | Google Scholar

Chandola, V., Banerjee, A., and Kumar, V. (2009). Anomaly Detection. ACM Comput. Surv. 41, 1–58. doi:10.1145/1541880.1541882

CrossRef Full Text | Google Scholar

Chein-I Chang, C. I., and Shao-Shan Chiang, S. S. (2002). Anomaly Detection and Classification for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sensing 40, 1314–1325. doi:10.1109/tgrs.2002.800280

CrossRef Full Text | Google Scholar

Hayat, M. A., Stein, G., Harrington, P., Lukić, Z., and Mustafa, M. (2021). Self-supervised Representation Learning for Astronomical Images. ApJL 911, L33. doi:10.3847/2041-8213/abf2c7

CrossRef Full Text | Google Scholar

Jablonski, J. A., Bihl, T. J., and Bauer, K. W. (2015). Principal Component Reconstruction Error for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sensing Lett. 12, 1725–1729. doi:10.1109/lgrs.2015.2421813

CrossRef Full Text | Google Scholar

Kerner, H., Hardgrove, C., Czarnecki, S., Gabriel, T., Mitrofanov, I., Litvak, M., et al. (2020). Analysis of Active Neutron Measurements from the mars Science Laboratory Dynamic Albedo of Neutrons Instrument: Intrinsic Variability, Outliers, and Implications for Future Investigations. J. Geophys. Res. Planets 125, e2019JE006264. doi:10.1029/2019je006264

CrossRef Full Text | Google Scholar

Kerner, H. R., Wagstaff, K. L., Bue, B. D., Wellington, D. F., Jacob, S., Horton, P., et al. (2020). Comparison of novelty Detection Methods for Multispectral Images in Rover-Based Planetary Exploration Missions. Data Min Knowl Disc 34, 1642–1675. doi:10.1007/s10618-020-00697-6

CrossRef Full Text | Google Scholar

Liang, S., Li, Y., and Srikant, R. (2018). “Enhancing the Reliability of Out-Of-Distribution Image Detection in Neural Networks,” in 6th International Conference on Learning Representations (ICLR 2018).

Google Scholar

Liu, F. T., Ting, K. M., and Zhou, Z. H. (2008). “Isolation forest,” in 2008 8th IEEE International Conference on Data Mining (IEEE), 413–422. doi:10.1109/icdm.2008.17

CrossRef Full Text | Google Scholar

Liu, Q., Klucik, R., Chen, C., Grant, G., Gallaher, D., Lv, Q., et al. (2017). Unsupervised Detection of Contextual Anomaly in Remotely Sensed Data. Remote Sensing Environ. 202, 75–87. doi:10.1016/j.rse.2017.01.034

CrossRef Full Text | Google Scholar

Lochner, M., and Bassett, B. A. (2021). Astronomaly: Personalised Active Anomaly Detection in Astronomical Data. Astron. Comput. 36, 100481. doi:10.1016/j.ascom.2021.100481

CrossRef Full Text | Google Scholar

Lupton, R. H., Gunn, J. E., and Szalay, A. S. (1999). A Modified Magnitude System that Produces Well-Behaved Magnitudes, Colors, and Errors Even for Low Signal-To-Noise Ratio Measurements. Astronomical J. 118, 1406–1410. doi:10.1086/301004

CrossRef Full Text | Google Scholar

Markou, M., and Singh, S. (2003). Novelty Detection: a Review-Part 1: Statistical Approaches. Signal. Process. 83, 2481–2497. doi:10.1016/j.sigpro.2003.07.018

CrossRef Full Text | Google Scholar

Markou, M., and Singh, S. (2003). Novelty Detection: a Review-Part 2:. Signal. Process. 83, 2499–2521. doi:10.1016/j.sigpro.2003.07.019

CrossRef Full Text | Google Scholar

Molero, J. M., Garzon, E. M., Garcia, I., and Plaza, A. (2013). Analysis and Optimizations of Global and Local Versions of the Rx Algorithm for Anomaly Detection in Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 6, 801–814. doi:10.1109/jstars.2013.2238609

CrossRef Full Text | Google Scholar

Pimentel, M. A. F., Clifton, D. A., Clifton, L., and Tarassenko, L. (2014). A Review of novelty Detection. Signal. Process. 99, 215–249. doi:10.1016/j.sigpro.2013.12.026

CrossRef Full Text | Google Scholar

Prochaska, J. X., Cornillon, P. C., and Reiman, D. M. (2021). Deep Learning of Sea Surface Temperature Patterns to Identify Ocean Extremes. Remote Sensing 13, 744. doi:10.3390/rs13040744

CrossRef Full Text | Google Scholar

Reed, I. S., and Yu, X. (1990). Adaptive Multiple-Band Cfar Detection of an Optical Pattern with Unknown Spectral Distribution. IEEE Trans. Acoust. Speech, Signal. Process. 38, 1760–1770. doi:10.1109/29.60107

CrossRef Full Text | Google Scholar

Richter, C., and Roy, N. (2017). Safe Visual Navigation via Deep Learning and novelty Detection. Robotics: Sci. Syst. doi:10.15607/rss.2017.xiii.064

CrossRef Full Text | Google Scholar

Schölkopf, B., Williamson, R. C., Smola, A. J., Shawe-Taylor, J., Platt, J. C., et al. (1999). Support Vector Method for novelty Detection. Neural Inf. Process. Syst. (Citeseer) 12, 582–588.

Google Scholar

Sipple, J. (2020). “Interpretable, Multidimensional, Multimodal Anomaly Detection with Negative Sampling for Detection of Device Failure,” in Proceedings of the 37th International Conference on Machine Learning, 119. 9016–9025.

Google Scholar

Touati, R., Mignotte, M., and Dahmane, M. (2020). Anomaly Feature Learning for Unsupervised Change Detection in Heterogeneous Images: A Deep Sparse Residual Model. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 13, 588–600. doi:10.1109/jstars.2020.2964409

CrossRef Full Text | Google Scholar

Wagstaff, K. L., Francis, R., Kerner, H., Lu, S., Nerrise, F., et al. (2020). “Novelty-driven Onboard Targeting for mars Rovers,” in Proceedings of the International Symposium on Artificial Intelligence (Robotics and Automation in Space).

Google Scholar

Wagstaff, K. L., Huff, E., and Rebbapragada, U. (2020). “Machine-assisted Discovery through Identification and Explanation of Anomalies in Astronomical Surveys,” in Proceedings of the Astronomical Data Analysis Software and Systems Conference.

Google Scholar

Wagstaff, K. L., Lanza, N. L., Thompson, D. R., Dietterich, T. G., and Gilmore, M. S. (2013). “Guiding Scientific Discovery with Explanations Using DEMUD,” in Proceedings of the Twenty-Seventh Conference on Artificial Intelligence, 905–911.

Google Scholar

Zhao, Y., Nasrullah, Z., and Li, Z. (2019). Pyod: A python Toolbox for Scalable Outlier Detection. J. Machine Learn. Res. 20, 1–7.

Google Scholar

Zhou, J., Kwan, C., Ayhan, B., and Eismann, M. T. (2016). A Novel Cluster Kernel Rx Algorithm for Anomaly and Change Detection Using Hyperspectral Images. IEEE Trans. Geosci. Remote Sensing 54, 6497–6504. doi:10.1109/tgrs.2016.2585495

CrossRef Full Text | Google Scholar

Zuntz, J., Sheldon, E., Samuroff, S., Troxel, M. A., Jarvis, M., MacCrann, N., et al. (2018). Dark Energy Survey Year 1 Results: Weak Lensing Shape Catalogues. Monthly Notices R. Astronomical Soc. 481, 1149–1182.

Google Scholar