- National Institute for Astrophysics, Astrophysical Observatory of Torino, Pino Torinese, Italy
Space Weather is receiving more and more attention from the heliophysical scientific community, as it is now well established that an adequate capability of monitoring any Earth-directed heliospheric event and forecasting the most severe perturbations produced by solar activity and their impact on the geo-spatial environment is crucial, given the human increasing reliance on space-related technologies and infrastructures. Predicting how the Sun affects life on Earth and human activities in the short term relies on establishing empirical laws to forecast not only the arrival time on Earth of potentially geo-effective solar drivers, but also, and more importantly, the intensity of induced geomagnetic disturbance (if any). Scientific studies performed on a statistical basis are the key to providing such empirical laws and analytically relating solar-wind properties to geomagnetic indices. This paper summarizes the results achieved by the author in the last few years in the context of Space Weather science, and based on statistical analyses of interplanetary and geomagnetic data.
1 Introduction
The Sun influences conditions in the near-Earth environment, including the magnetosphere, ionosphere and thermosphere, and can pose a persistent hazard in the form of damaging radiation to both space- or ground-based stations and human health. More specifically, Space Weather (as commonly referred to the science dealing with the complex Sun-Earth interaction and forecasting of potentially geo-effective events) covers the geo-space disturbances caused by the release of solar energy into the Earth’s magnetosphere during geomagnetic storms, and all related phenomena. Sun-related environmental impacts include a potential slowdown and orbital decay of the low-Earth-orbiting satellites (due to an additional aerodynamic drag force induced by solar activity), induction of very harmful electric currents in power transmission grids and pipelines, disruption of satellite signal propagation with severe implications for positioning systems, and unrecoverable failures of electronics onboard spacecraft. The ionosphere reflectivity can also be altered by the arrival of solar energetic particles, impairing radio communication systems. Finally, Space Weather deals with radiation produced by solar storms that can endanger the astronauts’ health.
Interplanetary counterparts of Coronal Mass Ejections (ICMEs, large eruptions of magnetized plasma from the Sun into interplanetary space Webb and Howard, 2012), which occur much more frequently at solar maximum than at minimum, and Corotating Interaction Regions (CIRs, forming at the interface between high- and low-speed streams), which are instead typical of low activity phases of the solar cycle, are the largest interplanetary manifestations of the solar activity (Gosling et al., 1990; Tsurutani et al., 1995; Gonzalez et al., 1999; Yermolaev et al., 2005, 2012). These interplanetary structures, which can be seen as propagating regions of space of enhanced density and magnetic field strength, are characterized by an intense and long-lasting South-directed magnetic field, which thus magnetically reconnects with the oppositely (North-)oriented Earth’s magnetic field, according to the scenario first proposed by Dungey (1961). This process allows a net transfer of energy from the solar wind to Earth, triggering “de facto” the most severe geomagnetic disturbances (Russell and McPherron, 1973; Gonzalez et al., 1994; Baker et al., 1996). However, the old-fashioned paradigm that the level of geomagnetic storming depends primarily on how pronounced in the southern direction the interplanetary magnetic field is (Fairfield and Cahill, 1966) is not quite correct. Other solar wind-related parameters, such as the dynamic pressure (e.g., Burton et al., 1975), the transported kinetic/magnetic energy (Telloni et al., 2020), and turbulence (e.g., D’Amicis et al., 2020), play a crucial role in driving the geomagnetic activity.
Although one-to-one studies have been often performed so far, a statistical approach is needed for forecasting Space Weather phenomena, with particular reference to predicting the geomagnetic response to the impact of geo-effective solar structures, the relativistic electron flux (which may cause irreparable damage to the geosynchronous satellites, Forsyth et al., 2020), the occurrence of solar flares, the propagation time of CMEs, the transit of high-speed streams to Earth, and the crossing of the heliospheric current sheet (the latter two also being sources of geomagnetic disturbances, though to a lesser extent). In fact, by means of the analysis of a large amount of solar, interplanetary, and geomagnetic data of past events, it is possible to establish empirical laws, a sort of analytical functions relating the different quantities involved, that allow the prediction of the onset of new solar events and/or their effects on the Earth’s magnetosphere.
Most forecasting methods rely on remote-sensing observations of solar phenomena, i.e., CMEs, causing geomagnetic storms, and can be roughly divided into three main classes, namely, physics-based, event-based, and drag-based models, depending on the approach used to provide expectations of CME arrival times. Physics-based models rely on photospheric magnetic field observations to initiate numerical MagnetoHydroDynamic (MHD) simulations of the eruption of the CME and its propagation from Sun to Earth. Predictions of the CME transit time can be thus provided. These numerical codes require the use of supercomputers to run efficiently. In addition, their reliability obviously depends on a correct representation of the physical processes within the models, i.e., the understanding (unfortunately not yet full) of the physics of the corona and the solar wind. The MHD models currently used for operational Space Weather predictions are the well-known Enlil (Odstrcil, 2003) and the EUropean Heliospheric FORecasting Information Asset (EUHFORIA, Pomoell and Poedts, 2018). Simpler and much less computationally expensive (but no less reliable) event-based (or empirical) models rely on statistical studies of past CMEs and essentially relate the CME Sun-Earth transit times to their propagation speeds, as inferred from coronagraphic images. This allows the establishment of empirical laws, say analytical functions, that (assuming that past observations are analogous to future ones, i.e., that CMEs share common kinematic characteristics) allow prediction of the impact time on Earth of a new CME, once its coronagraphic speed is measured (e.g., Manoharan et al., 2004; Schwenn et al., 2005; Vršnak and Žic, 2007). Similar empirically-derived relations to forecast the geo-effectiveness of CMEs are also available (e.g., Dumbović et al., 2015). Observational evidence for an adjustment of the CME propagation speed to the background solar wind and its interpretation in terms of aerodynamic drag, stimulated the development of the so-called drag-based models (e.g., Vršnak and Gopalswamy, 2002; Vršnak et al., 2013), which basically assume that the CME propagation in the heliosphere is governed by aerodynamic drag (one of the most refined drag-based model is 3D COronal Rope Ejection (3DCORE) introduced by Möstl et al., 2018). That is, the dynamics/kinematics of the CME can be analytically described through a pretty simple equation of motion, which can thus provide real-time prediction of the CME arrival time and impact speed at Earth (in spite of various drawbacks associated with the approximations intrinsic to this approach).
Regardless of the pros and cons of the different approaches (whose discussion is beyond the scope of this paper, but the interested reader is refereed to Verbeke et al., 2019), all these methods provide alerts 1–4 days in advance of the geomagnetic storm, although the predictions are significantly model-dependent and affected by large uncertainties. On the other hand, expectations of CME arrival and storminess level based on in-situ solar wind data at the Lagrangian point L1, i.e., Space Weather now-casting methods, are not widely used, although they could provide much more accurate warnings. This is essentially due to the difficulty of identifying CMEs locally in the interplanetary medium with in-situ measurements. Interplanetary scintillation (IPS), which is scattering phenomenon of solar wind density irregularities, serves as a remote sensing method for observing the solar wind. Thus, IPS observations have the potential to bridge a gap between the Sun and the near-Earth solar wind. Some efforts to improve CME arrival time predictions already have been performed using IPS observations (e.g., Iwai et al., 2021). However, in in-situ data, many of the CME distinctive properties (i.e., higher magnetic fields and lower plasma densities/temperatures with respect to the ambient solar wind in which they propagate, Burlaga et al., 1981) are common to a variety of other interplanetary structures, such as high-speed streams. What really distinguishes them is a rotation of the magnetic field vector in the plane perpendicular to the direction of propagation. This is due to the presence of a flux rope (which generally all CMEs embed and carry during their expansion, Vourlidas, 2014), a helical structure that can be revealed as a region of space with high magnetic helicity (an MHD quantity that measures the degree of twisting of magnetic field lines). However, unlike the shock front of a CME, which provides a prompt signal, in order for the flux rope-related magnetic field rotation to be detected, the CME must have entirely passed the spacecraft orbiting at L1, thus drastically reducing forecasting capabilities: indeed, at least for the largest structures (which can have a radial extension at Earth of even 0.25 au, Klein and Burlaga, 1982, much larger than the L1 point-Earth distance of only 0.01 au), the front may have already impacted Earth by the time diagnostic codes based on magnetic helicity measurements identified the presence of a CME at L1. This issue, along with difficulties associated with measuring the magnetic helicity (the reader is referred to Telloni et al., 2012, 2013, for a detailed discussion) have limited the development of now-casting methods based on in-situ L1 measurements of the solar wind for Space Weather purposes. This lack motivated the works by Telloni et al. (2019, 2020, 2021) (hereafter Papers I, II, and III), all appeared on The Astrophysical Journal and based on statistical surveys of solar wind and geomagnetic data (the period analyzed in each case covers more than one solar cycle) with the aim of obtaining statistical relationships, i.e., empirical laws, that can be used in the Space Weather framework to predict the onset and the time evolution of geomagnetic storming.
The present paper summarizes the results obtained in the aforementioned three papers. Ideally following the title, section 2 reports the statistical results obtained in the three studies, while section 3 discusses their applications to Space Weather science. section 4 is devoted to future developments of the application of statistical methods and machine learning in Space Weather science in the framework of the Space Weather Service Network (SWESNET) project.
2 Statistical Results
Paper I addressed the detection, characterization, and geo-effectiveness likelihood of ICMEs. The localization of ICMEs in the near-Earth space environment was accomplished by comparing some MHD quantities measured at L1 with those typical of the unperturbed solar wind plasma. Specifically, ICMEs were identified as structures with a large magnetic helicity content (representative of the embedded flux rope) that also have a total (thermal plus magnetic) internal pressure higher than the medium in which they propagate (Gosling et al., 1994). The potential geo-effectiveness of the so identified ICMEs was ascertained by looking at their energy budget: only those ICMEs carrying an amount of kinetic and/or magnetic energy far exceeding that characteristic of the quiet solar wind (thus ensuring a remarkable energy transfer to the Earth’s magnetosphere during magnetic reconnection processes) were in fact defined as able of inducing geomagnetic perturbations. In the 12-year period from 2005 to 2016, 106 likely geo-effective ICMEs were thus revealed in the Wind spacecraft data by the in-situ data-based tool developed in Paper I. The actual geomagnetic disturbances driven by those ICMEs were verified by inspecting the Earth’s magnetospheric activity through the Dst (disturbance storm time) and Ap indices, both indicative (albeit at different ground latitudes) of the intensification of ring current systems caused by solar storms. Specifically, sustained periods of either Dst
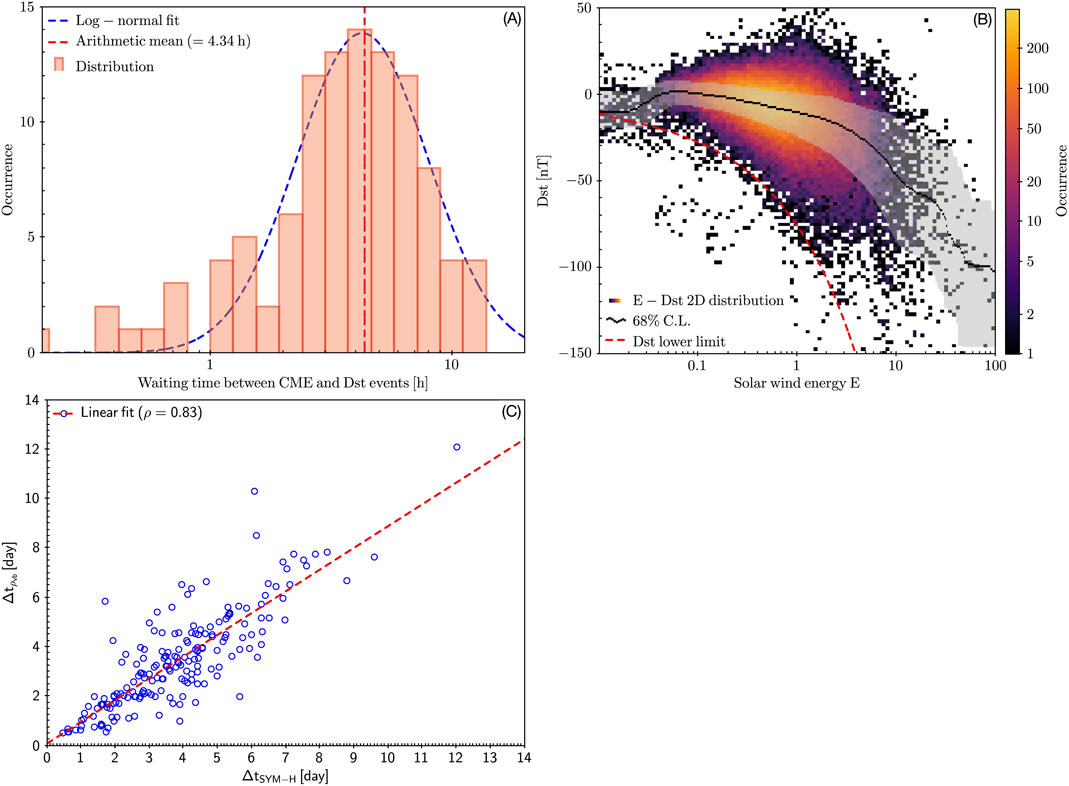
FIGURE 1. (A) Distribution of the waiting times between the detection of the geo-effective CME and the onset of the induced geomagnetic storm; the arithmetic mean (vertical dashed red line) and the best-fitting lognormal function (blue dashed curve) are also displayed. (B) E − Dst 2D distribution; the most probable Dst value and the lower Dst threshold are marked, as a function of E, as a black solid and red dashed line, respectively; the gray dashed area denotes the 68% probability interval of Dst per energy bin. (C)
Paper II extended the study to any likely geo-effective solar event (not just CMEs), focusing, in the same 2005–2006 interval, on the relationship existing between solar wind energy and geomagnetic activity. Panel (B) of Figure 1 displays the 2D histogram of a dimensionless measure of the total (kinetic plus magnetic) energy E carried by the solar wind (see Telloni et al., 2020, for more details on how E was derived from Wind in-situ data) and the Dst index. Superimposed are the Dst most likely value (black solid line) and 68% probability range (gray shaded area) for each energy bin. It appears evident that a clean statistical correlation exists between the energy content of the solar wind impacting Earth and the perturbation level of the magnetospheric current system: that is, the larger the energy stored in the solar wind plasma, the more severe the induced geomagnetic perturbations. It follows that in the solar wind-magnetosphere coupling, energy is to be thus regarded as a crucial parameter in solar-terrestrial interactions.
Finally, unlike the above two papers that addressed the topic of what triggers the geomagnetic storms, Paper III dealt with the study of their recovery phase and specifically what determines a slow restoration of the Earth’s magnetosphere to its equilibrium conditions. Specifically, the aim was to establish, on a statistical basis, the relationship between long recovery phases and sustained periods of Alfvénic plasma streams that follow the solar event (either recurrent, such as CIRs, or non-recurrent, such as CMEs) driving the geomagnetic disturbance. By defining thresholds for the magnetospheric quiet state and Alfvénicity (i.e., the level of correlation between magnetic and velocity fluctuations, Grappin et al., 1982, measured by the Wind spacecraft), it was possibile to quantify the extent of magnetospheric recovery phases (through inspection of the SYM-H geomagnetic index, which is essentially the same as the Dst index, but provided at a higher time resolution, ΔtSYM-H) and concurrent Alfvénic solar wind flows
3 Applications to Space Weather Science
Studies of the solar wind and its effects on Earth performed on a statistical basis allow both a deeper understanding of the physical processes underlying the Sun–Earth relations and an advanced capability in forecasting geomagnetic storm events within the framework of Space Weather science. Panel (A) of Figure 1 sheds light, for instance, on the time delay between the CME passage and the onset of its magnetospheric effect. This waiting time is the combination of the time interval the CME needs to travel the distance between L1 and Earth with the time required for the CME to trigger the geomagnetic storm, perturbing the magnetospheric current system. As a conclusion, Paper I clearly pointed out that, once detected at L1, 98% of CMEs take between 2 and 8 h to initiate the geomagnetic disturbance, with an average time of about 4 h. This piece of information is particularly important in Space Weather perspective. Subtracting from this delay the CME transit time to Earth (about 30 min (1 h) for the fastest (slowest) CMEs), it appears that the complex (and not yet fully understood) processes involved in intensifying the magnetospheric ring currents take on average 3 −3 h and a half to lead the magnetosphere out of its equilibrium configuration. This result can be easily extended to any solar event, because it can be argued that the processes involved in the response of the Earth’s magnetosphere to the Sun’s activity do not depend on the particular type of solar driver triggering the geomagnetic storm.
Another crucial question for Space Weather is: once destabilized by a solar event how long does it take the magnetosphere to recover its equilibrium condition? The answer, by no means straightforward since the recovery phase is governed by multiple and competing restoring forces, is nevertheless of paramount importance for all those ground or space-based facilities that, in addition to being affected by the episodic and abrupt magnetospheric reconfiguration due to the impact (in most cases, but not only) of CMEs on Earth, are equally affected by time-integrated effects throughout the whole storm. Paper III established that a correlation between long recovery phases of geomagnetic storms and the presence of Alfvénic turbulent plasma flows exists on a statistical basis (Panel (C) of Figure 1). Specifically, the duration of the recovery phase, when controlled by Alfvénic fluctuations, is 0.88 (which is the slope inferred from the
However, the most important capability that any forecasting model must have is to predict the likelihood for the solar events to impact the Earth and, if so, the intensity of the resulting geomagnetic storm. Paper III provided in this regard a useful Space Weather diagnostic tool. From the measurement at L1 of the energy load of the incoming solar wind, it is indeed possible to assess not only what will be the most likely geomagnetic activity (with the required confidence interval, black solid curve and gray shaded area in panel (B) of Figure 1), but also and especially the maximum response the Earth’s magnetosphere could have. In fact, it is clear from the figure that the E − Dst distribution is bounded on the bottom side (red dashed curve). From a physical perspective this means that the perturbations of the ring current system are limited and strictly related to the energy input from the Sun. From a more predictive perspective, it instead allows the assessment of what will be the most severe geomagnetic disturbance that can be expected from the interaction with the magnetosphere of a solar wind carrying an energy E; or, otherwise, whether there is no need to provide an alert. Based on the above considerations, and because the measurement of solar wind energy can be performed in quasi real-time, any alert might be provided, with a confidence level of 98%, between 2 and 8 h in advance of the likely geomagnetic event.
The application of statistical methods to data acquired in situ from space missions orbiting L1 in the Space Weather science is being further explored and exploited in the ongoing SWESNET project of the European Space Agency, which involves about 50 research institutes/universities throughout Europe. A brief introduction of SWESNET and the author’s tasks in delivering novel statistically-driven services/tools is provided in the following section.
4 Outlook: The SWESNET Project
The Space Weather Service Network (SWESNET) project aims at the further development of the Space Weather services provided by the European Space Agency (ESA), drawing on the results of the Space Situational Awareness (SSA) Program. Activities include the delivery of Space Weather products and toolkits, for a timely, reliable and accurate monitoring, prediction and dissemination of Space Weather conditions and influences, via the dedicated ESA portal (https://swe.ssa.esa.int/web/guest/), which is the main resource for Space Weather in Europe. The Heliospheric Weather Expert Service Centre (ESC) is one of the five ESCs (along with Solar Weather, Space Radiation, Ionospheric Weather, and Geomagnetic Conditions) contributing to the network and deals with the effects on the Earth’s environment of solar wind-related events, such as high-speed streams, CIRs, and CMEs. Characterizing, tracking, and predicting all of these interplanetary structures is vitally important for promptly reacting to the impacts of Space Weather events, thereby protecting critical infrastructures and mitigating their potentially deleterious effects.
The Solar Physics group, at the Astrophysical Observatory of Turin, part of the National Institute for Astrophysics, is one of the expert groups involved in the SWESNET Heliospheric Weather ESC and is in charge of developing several tools/prototype services for real-time analysis of space data to provide results of interest to the ESA-SSA SWESNET program and the end users. Based on the results of the three papers reviewed in this article, the author will lead the implementation into SWESNET of three new services: 1) development of diagnostic code for automatic detection and characterization of ICMEs at L1 with in-situ data acquired from near-Earth space observatories (arising from Paper I); 2) development of algorithm for predicting the likely geo-effectiveness of ICMEs based on local estimation of their energy content with in-situ data provided by spacecraft orbiting at L1 (arising from Paper II); 3) development of a tool for predicting the length of the recovery phase of the geomagnetic storm and thus estimating the time-integrated effects of sustained periods of albeit low geomagnetic activity (arising from Paper III). In addition, a preliminary investigation for the design of a machine learning-based tool for real-time prediction of geomagnetic events from solar wind measurements acquired in situ at L1 will be carried out, thus approaching the challenging field of machine learning techniques for Space Weather, which has received a significant boost in recent years (e.g., Camporeale, 2019).
As a conclusion, this paper reports on the statistical approach necessary to study the magnetospheric response to any solar driver and the benefits this approach may have in Space Weather studies. Only through statistical analyses it is indeed possible to ascertain which solar and geomagnetic parameters are correlated (and to what extent) in the complex solar wind-magnetosphere interaction and, specifically, to establish empirical laws useful for Space Weather purposes, with the final aim to improve the prediction capabilities and increase the robustness of the ESA-SSA SWESNET forecasting service system.
Data Availability Statement
The results summarized in this paper refer to publicly available solar wind and geomagnetic data, stored at the NASA’s Space Physics Data Facility (https://cdaweb.gsfc.nasa.gov/index.html/).
Author Contributions
The author confirms being the sole contributor to this paper, having conceived and written it, and approved it for publication.
Funding
The author was partially supported by the Italian Space Agency (ASI) under contract 2018–30-HH.0.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The author is grateful to R. D’Amicis for helpful discussions in conceiving this work.
References
Baker, D. N., Pulkkinen, T. I., Angelopoulos, V., Baumjohann, W., and McPherron, R. L. (1996). Neutral Line Model of Substorms: Past Results and Present View. J. Geophys. Res. 101, 12975–13010. doi:10.1029/95JA03753
Burlaga, L., Sittler, E., Mariani, F., and Schwenn, R. (1981). Magnetic Loop behind an Interplanetary Shock: Voyager, Helios, and IMP 8 Observations. J. Geophys. Res. 86, 6673–6684. doi:10.1029/JA086iA08p06673
Burton, R. K., McPherron, R. L., and Russell, C. T. (1975). An Empirical Relationship between Interplanetary Conditions and Dst. J. Geophys. Res. 80, 4204–4214. doi:10.1029/JA080i031p04204
Camporeale, E. (2019). The Challenge of Machine Learning in Space Weather: Nowcasting and Forecasting. Space Weather. 17, 1166–1207. doi:10.1029/2018SW002061
Cander, L. R., and Mihajlovic, S. J. (1998). Forecasting Ionospheric Structure during the Great Geomagnetic Storms. J. Geophys. Res. 103, 391–398. doi:10.1029/97JA02418
D’Amicis, R., Telloni, D., and Bruno, R. (2020). The Effect of Solar-Wind Turbulence on Magnetospheric Activity. Front. Phys. 8, 541. doi:10.3389/fphy.2020.604857
Dumbović, M., Devos, A., Vršnak, B., Sudar, D., Rodriguez, L., Ruždjak, D., et al. (2015). Geoeffectiveness of Coronal Mass Ejections in the SOHO Era. Sol. Phys. 290, 579–612. doi:10.1007/s11207-014-0613-8
Dungey, J. W. (1961). Interplanetary Magnetic Field and the Auroral Zones. Phys. Rev. Lett. 6, 47–48. doi:10.1103/PhysRevLett.6.47
Fairfield, D. H., and Cahill, L. J. (1966). Transition Region Magnetic Field and Polar Magnetic Disturbances. J. Geophys. Res. Space Phys. 71, 155–169. doi:10.1029/JZ071i001p00155
Forsyth, C., Watt, C. E. J., Mooney, M. K., Rae, I. J., Walton, S. D., and Horne, R. B. (2020). Forecasting GOES 15 >2 MeV Electron Fluxes from Solar Wind Data and Geomagnetic Indices. Space weather. 18, e02416. doi:10.1029/2019SW002416
Gonzalez, W. D., Joselyn, J. A., Kamide, Y., Kroehl, H. W., Rostoker, G., Tsurutani, B. T., et al. (1994). What Is a Geomagnetic Storm? J. Geophys. Res. Space Phys. 99, 5771–5792. doi:10.1029/93JA02867
Gonzalez, W. D., Tsurutani, B. T., and Clúa de Gonzalez, A. L. (1999). Interplanetary Origin of Geomagnetic Storms. Space Sci. Rev. 88, 529–562. doi:10.1023/A:1005160129098
Gosling, J. T., Bame, S. J., McComas, D. J., and Phillips, J. L. (1990). Coronal Mass Ejections and Large Geomagnetic Storms. Geophys. Res. Lett. 17, 901–904. doi:10.1029/GL017i007p00901
Gosling, J. T., Bame, S. J., McComas, D. J., Phillips, J. L., Scime, E. E., Pizzo, V. J., et al. (1994). A Forward-Reverse Shock Pair in the Solar Wind Driven by Over-expansion of a Coronal Mass Ejection: Ulysses Observations. Geophys. Res. Lett. 21, 237–240. doi:10.1029/94GL00001
Grappin, R., Frisch, U., Pouquet, A., and Leorat, J. (1982). Alfvenic Fluctuations as Asymptotic States of MHD Turbulence. Astron. Astrophys. 105, 6–14.
Iwai, K., Shiota, D., Tokumaru, M., Fujiki, K., Den, M., and Kubo, Y. (2021). Validation of Coronal Mass Ejection Arrival-Time Forecasts by Magnetohydrodynamic Simulations Based on Interplanetary Scintillation Observations. Earth, Planets Space 73, 9. doi:10.1186/s40623-020-01345-5
Klein, L. W., and Burlaga, L. F. (1982). Interplanetary Magnetic Clouds at 1 AU. J. Geophys. Res. Space Phys. 87, 613–624. doi:10.1029/JA087iA02p00613
Manoharan, P. K., Gopalswamy, N., Yashiro, S., Lara, A., Michalek, G., and Howard, R. A. (2004). Influence of Coronal Mass Ejection Interaction on Propagation of Interplanetary Shocks. J. Geophys. Res. Space Phys. 109, A06109. doi:10.1029/2003JA010300
Möstl, C., Amerstorfer, T., Palmerio, E., Isavnin, A., Farrugia, C. J., Lowder, C., et al. (2018). Forward Modeling of Coronal Mass Ejection Flux Ropes in the Inner Heliosphere with 3DCORE. Space Weather. 16, 216–229. doi:10.1002/2017SW001735
Odstrcil, D. (2003). Modeling 3-D Solar Wind Structure. Adv. Space Res. 32, 497–506. doi:10.1016/S0273-1177(03)00332-6
Pomoell, J., and Poedts, S. (2018). EUHFORIA: European Heliospheric Forecasting Information Asset. J. Space Weather. Space Clim. 8, A35. doi:10.1051/swsc/2018020
Russell, C. T., and McPherron, R. L. (1973). Semiannual Variation of Geomagnetic Activity. J. Geophys. Res. Space Phys. 78, 92. doi:10.1029/JA078i001p00092
Schwenn, R., dal Lago, A., Huttunen, E., and Gonzalez, W. D. (2005). The Association of Coronal Mass Ejections with Their Effects Near the Earth. Ann. Geophys. 23, 1033–1059. doi:10.5194/angeo-23-1033-2005
Telloni, D., Bruno, R., D’Amicis, R., Pietropaolo, E., and Carbone, V. (2012). Wavelet Analysis as a Tool to Localize Magnetic and Cross-Helicity Events in the Solar Wind. Astrophys. J. 751, 19. doi:10.1088/0004-637X/751/1/19
Telloni, D., Perri, S., Bruno, R., Carbone, V., and D’Amicis, R. (2013). An Analysis of Magnetohydrodynamic Invariants of Magnetic Fluctuations within Interplanetary Flux Ropes. Astrophys. J. 776, 3. doi:10.1088/0004-637X/776/1/3
Telloni, D., Antonucci, E., Bemporad, A., Bianchi, T., Bruno, R., Fineschi, S., et al. (2019). Detection of Coronal Mass Ejections at L1 and Forecast of Their Geoeffectiveness. Astrophys. J. 885, 120. doi:10.3847/1538-4357/ab48e9
Telloni, D., Carbone, F., Antonucci, E., Bruno, R., Grimani, C., Villante, U., et al. (2020). Study of the Influence of the Solar Wind Energy on the Geomagnetic Activity for Space Weather Science. Astrophys. J. 896, 149. doi:10.3847/1538-4357/ab91b9
Telloni, D., D’Amicis, R., Bruno, R., Perrone, D., Sorriso-Valvo, L., Raghav, A. N., et al. (2021). Alfvénicity-related Long Recovery Phases of Geomagnetic Storms: A Space Weather Perspective. Astrophys. J. 916, 64. doi:10.3847/1538-4357/ac071f
Tsurutani, B. T., Gonzalez, W. D., Gonzalez, A. L. C., Tang, F., Arballo, J. K., and Okada, M. (1995). Interplanetary Origin of Geomagnetic Activity in the Declining Phase of the Solar Cycle. J. Geophys. Res. Space Phys. 100, 21717–21734. doi:10.1029/95JA01476
Verbeke, C., Mays, M. L., Temmer, M., Bingham, S., Steenburgh, R., Dumbović, M., et al. (2019). Benchmarking CME Arrival Time and Impact: Progress on Metadata, Metrics, and Events. Space Weather. 17, 6–26. doi:10.1029/2018SW002046
Vourlidas, A. (2014). The Flux Rope Nature of Coronal Mass Ejections. Plasma Phys. Control. Fusion 56, 064001. doi:10.1088/0741-3335/56/6/064001
Vršnak, B., and Gopalswamy, N. (2002). Influence of the Aerodynamic Drag on the Motion of Interplanetary Ejecta. J. Geophys. Res. Space Phys. 107, 1019. doi:10.1029/2001JA000120
Vršnak, B., and Žic, T. (2007). Transit Times of Interplanetary Coronal Mass Ejections and the Solar Wind Speed. Astron. Astrophys. 472, 937–943. doi:10.1051/0004-6361:20077499
Vršnak, B., Žic, T., Vrbanec, D., Temmer, M., Rollett, T., Möstl, C., et al. (2013). Propagation of Interplanetary Coronal Mass Ejections: The Drag-Based Model. Sol. Phys. 285, 295–315. doi:10.1007/s11207-012-0035-4
Webb, D. F., and Howard, T. A. (2012). Coronal Mass Ejections: Observations. Living Rev. Sol. Phys. 9, 3. doi:10.12942/lrsp-2012-3
Yermolaev, Y. I., Yermolaev, M. Y., Zastenker, G. N., Zelenyi, L. M., Petrukovich, A. A., and Sauvaud, J. A. (2005). Statistical Studies of Geomagnetic Storm Dependencies on Solar and Interplanetary Events: a Review. Planet. Space Sci. 53, 189–196. doi:10.1016/j.pss.2004.09.044
Keywords: methods: statistical, solar-terrestrial relations, Sun: activity, Sun: coronal mass ejections (CMEs), solar wind, turbulence, interplanetary medium, magnetohydrodynamics (MHD)
Citation: Telloni D (2022) Statistical Methods Applied to Space Weather Science. Front. Astron. Space Sci. 9:865880. doi: 10.3389/fspas.2022.865880
Received: 30 January 2022; Accepted: 20 May 2022;
Published: 03 June 2022.
Edited by:
Bala Poduval, University of New Hampshire, United StatesReviewed by:
Munetoshi Tokumaru, Nagoya University, JapanRobert James Leamon, University of Maryland, United States
Copyright © 2022 Telloni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniele Telloni, ZGFuaWVsZS50ZWxsb25pQGluYWYuaXQ=
 Daniele Telloni
Daniele Telloni