Bulk Viscous Bianchi Type-V Cosmological Model in f(R, T) Theory of Gravity

This paper deals with the bulk viscous Bianchi type-V cosmological model with an exponential scale factor in Lyra geometry based on f(R, T) gravity, by considering a time dependent displacement field. To determine the nature and physical properties of the model, we considered Harko et al. (Harko et al., Phys. Rev. D, 2011, 84, 024020) [proposed the linear form f(R, T) = f₁(R) + f₂(T)], in which the barotropic equation of state for pressure, density, and bulk viscous pressure is proportional to energy density. The kinematical properties of the model are also discussed in the presence of bulk viscosity. Evolution of energy conditions is also studied and examined the behaviour of that in examined in order to explain the late-time cosmic acceleration.

1 Introduction

As evidenced by various observational data from Garnavich (Garnavich et al., 1998a; Garnavich et al., 1998b), Riess (Riess et al., 1998) and Perlmutter (Perlmutter et al., 1997; Perlmutter et al., 1999) the expansion of the universe is accelerating. The cause of this observed acceleration is still unknown, and the “dark energy” problem is commonly used to describe it. Two methods have been proposed to overcome this problem, one is to develop several dark energy candidates and the other is to modify Einstein’s theory of gravitation. It is very exclusively well known that modification of Einstein’s theory plays an important role in explaining the late time acceleration and negative pressure. Among these modifications of Einstein’s theories are Brans Dicke (BD) theory, f(R) gravity: Carroll (Carroll et al., 2004), Nojiri (Nojiri and Odintsov, 2007), Bertolami (Bertolami et al., 2007), Capozziello (Capozziello et al., 2008), Sotiriou (Sotiriou and Faraoni, 2010), Capozziello (Capozziello and Vignolo, 2010), Iosifidis (Iosifidis et al., 2019), Gogoi (Gogoi and Dev Goswami, 2020), f(T) gravity: Yang (Yang, 2011), Tamanini (Tamanini and Böhmer, 2012), Paliathanasis (Paliathanasis et al., 2016), Bamba (Bamba et al., 2017a), Ferraro (Ferraro and Guzmán, 2018), Bahamonde (Bahamonde et al., 2019), f(G) gravity: De Felice (De Felice and Tsujikawa, 2009), Abbas (Abbas et al., 2015), Bamba (Bamba et al., 2017b), Sharif (Sharif and Saba, 2018), and f (R, T) gravity: De Felice (De Felice et al., 2011), De Laurentis (De Laurentis and Lopez-Revelles, 2014), De Laurentis (De Laurentis et al., 2015), Odintsov (Odintsov et al., 2019), where R, T, and G indicate the scalar curvature, the torsion scalar, and the Gauss Bonnet scalar respectively. But in a recent cosmological model, f(R) gravity has become a more attractive theory to represent the behaviour of the expansion of the universe, known as f(R, T) gravity, where the matter Lagrangian is given by an arbitrary function of the Ricci scalar R and the trace of the energy momentum tensor T. Recently, Rao (Rao and Papa Rao, 2015), Kanakavalli (Kanakavalli et al., 2016), Sahoo (Sahoo et al., 2017), Nath (Nath and Sahu, 2019), and Sharma (Sharma et al., 2019), investigated the nature of the universe in f(R, T) gravity in different cosmological models in various space times. Very recently, Arora (Arora et al., 2021) discussed the late-time viscous cosmology in f(R, T) gravity considering a bulk viscous fluid with viscosity coefficient.

Bulk viscosity is particularly essential in current cosmology, because it plays a key role in the inflationary expansion. Misner (Misner, 1968) has mentioned that when neutrinos disconnect from the viscosity of the cosmic fluid, an effective process of entropy production may emerge during cosmic evolution. Barrow (Barrow, 1986) and Padmanabhan (Padmanabhan and Chitre, 1987) have pointed out that in the FRW space time, the presence of bulk viscosity causes inflationary solutions. Subsequently, Johri (Johri and Sudharsan, 1989)have studied the inflationary solutions in the presence of bulk viscosity in the Brans Dicke theory. The presence of bulk viscosity institutes a number of intriguing characteristics to the universe’s dynamics. It was once thought that neutrino viscosity may smooth out primordial anisotropies, resulting in the isotropic universe we see today. The big-bang singularity can also be avoided if bulk viscosity is present. A phenomenological process of particle production in a strong gravitational field can also be explained by bulk viscosity. A bulk viscous fluid can be used to represent the back-reaction consequences of string formation. The bulk viscosity cosmological models have been discussed, and the model’s nature has been discussed by Fabris (Fabris et al., 2006), Singh (Singh and Baghel, 2009), Yadav (Yadav and Yadav, 2011), Singh (Bali et al., 2012), Kiran (Kiran and Reddy, 2013), Mahanta (Mahanta, 2014), Rao (Bhaskara Rao et al., 2015), Tiwari (Tiwari and Tiwari, 2017), and Sahoo (Sahoo and Reddy, 2018). Very recently Goswami (Goswami et al., 2021) and Kotambkar (Kotambkar et al., 2021) have investigated the modeling of accelerating and the dynamical behaviours of Chaplygin gas, cosmological and gravitational “constants” with cosmic viscous fluid in different contexts.

The expansion of the universe, which is considered to be due to large scale recession of galaxies, was uknown during that period, and for that reason Einstein had to include the cosmological constant into the field equations when discussing cosmological solutions. Not only has the theory proved successful in describing gravitational phenomena, but it has also served as the foundation for cosmological models of the universe. Classical physics does not, however, describe gravity as the only force. Electromagnetic forces are also important, and they are not explained as geometric phenomena by general relativity. Many attempts to unify electromagnetic and gravitation have been made. Weyl proposed a modified Riemannian geometry theory to unify electromagnetic and gravitation in 1918. However, due to the non-integrability of length transfer, this hypothesis was later dismissed. By inserting a gauge function into the structureless manifold and removing the non-integrability of length transfer, G. Lyra (Lyra, 1951) introduced a new sort of alternative theory. Sen (Sen, 1957); Sen (Sen and Dunn, 1971) suggested a scalar-tensor theory of gravity based on this theory, which was an analogue of the Einstein field equations. Later, Halford (Halford, 1972)concluded that the constant displacement vector used in Lyra’s geometry acts as a cosmological constant in the typical general relativistic interpretation. Within observational constraints, the scalar-tensor theory based on Lyra’s geometry predicts the same result as the Einstein theory. Subsequently, Soleng (Soleng, 1987) looked into cosmological models based on Lyra geometry and discovered that the displacement field contains either a creation field equal to a specific vacuum field that can be regarded as a cosmological term when combined with a gauge vector. A lot of authors have looked into cosmological theories based on Lyra geometry as Pradhan (Pradhan and Vishwakarma, 2004), Singh (Singh, 2008), Singh (Singh and Kale, 2009), Ram (Ram et al., 2010), Adhav (Adhav, 2011), Kumari (Kumari et al., 2013), Singh (Singh and Rani, 2015), Maurya (Maurya and Zia, 2019), Ram (Ram et al., 2020), Hegazy (Hegazy, 2020), where they have investigated the different nature of the model in different cosmological models so far. Recently Brahma (Brahma and Dewri, 2021)has investigated the f(R, T) gravity for Bianchi type–V metric in Lyra geometry and to get the deterministic solution of the model one special form of Harko et al. (2011) is used with linearly varying deceleration parameter to investigate the myterious nature of the dark energy. Here, in this study we are interested in Bianchi type-v cosmological model, because it describes homogeneous and anisotropic universes with various scale factors along each spatial direction, which is a natural generalisation of the FRW model of the universe. The above exclusive analysis and investigation encourage us to study the Bianchi type V cosmological model with f(R, T) gravity in the presence of viscous fluid based on Lyra geometry.

2 Overview and the Field Equations of f(R, T) Gravity

Here we consider Bianchi type -V space time in the following form

$d{s}^2=-d{t}^2+A^{2}d{x}^2+e^{-2mx}\left(B^{2}d{y}^2+C^{2}d{z}^2\right)(1)$

where A, B, C are functions of cosmic time t and m is a constant.

The action of f(R, T) gravity, where we have obtained the various field equations and modification of f(R, T) gravity with observational constraints in Lyra geometry by Harko et al.(Harko et al., 2011) [Taking G = 1] as

$S=\frac{1}{16\pi }\int f\left(\tilde{R},T\right)\sqrt{-}g{d}^{4}x+\int L_m\sqrt{-}g{d}^{4}x(2)$

where

$\tilde{R}=R+3{\nabla }_i{\varphi }^i+\frac{3}{2}{\varphi }^i{\varphi }_i(3)$

In which $\tilde{R}$, T, and L_m respectively denote the function of Ricci scalar R, the trace of the stress tensor, and the Lagrangian density of matter, where the stress- energy tensor of the matter is defined as

$T_{ij}=-\frac{2}{\sqrt{-}g}\frac{\delta \sqrt{-}g{L}_m}{\delta g^{ij}}(4)$

such that its trace is given by T = g^ijT_ij

Consider that the matter Lagrangian L_m depends only on the metric tensor components g^ij and does not depend on its derivatives, thus it reduces to

$T_{ij}=g_{ij}{L}_m-2\frac{\partial L_m}{\partial g^{ij}}(5)$

Now by varying the action S in Eq. 2 with respect to metric tensor g_ij, the gravitational field equations of $f(\tilde{R},T)$ gravity are obtained as

$\begin{array}{cc}\hfill f_{\tilde{R}}\left(\tilde{R},T\right){\tilde{R}}_{ij}-\frac{1}{2}f\left(\tilde{R},T\right)g_{ij}+\left(g_{ij}{\nabla }^i{\nabla }_i-{\nabla }_i{\nabla }_j\right)f_{\tilde{R}}\left(\tilde{R},T\right)& \hfill \\ \hfill =-\frac{8\pi }{c^2}{T}_{ij}-f_T\left(\tilde{R},T\right)T_{ij}-f_T\left(\tilde{R},T\right){\mathrm{\Theta }}_{ij}\end{array}(6)$

where

${\mathrm{\Theta }}_{ij}=-2T_{ij}+g_{ij}{L}_m-2g^{lm}\frac{{\partial }^2{L}_m}{\partial g^{ij}\partial g^{lm}}(7)$

Here $f_{\tilde{R}}(\tilde{R},T)=\frac{\partial f(\tilde{R},T)}{\partial \tilde{R}}$, $f_T(\tilde{R},T)=\frac{\partial f(\tilde{R},T)}{\partial T}$, and ∇_i denote the covariant derivative.

If the matter is considered as a perfect fluid, then the stress energy tensor of the matter Lagrangian is given by

$T_{ij}=\left(\rho +\bar{p}\right)u_i{u}_j+\bar{p}{g}_{ij}(8)$

Here ρ denotes the energy density and uⁱ = (0, 0, 0, 1) is the four velocity vector in the co-moving co-ordinate system satisfying the condition u_iuⁱ = − 1 and uⁱ∇_ju_i = 0. Since there is no unique choice for matter Lagrangian, we assume a perfect fluid matter as $L_m=-\bar{p}$ and the trace of the total energy momentum tensor [Debnath (Debnath, 2019)] is given by $T=\rho -3\bar{p}$, so that Eq. 7 reduces as follows:

${\theta }_{ij}=-2T_{ij}-\bar{p}{g}_{ij}(9)$

As we know that the physical nature of the matter field depends on the metric tensor Θ_ij for the field equations of $f(\tilde{R},T)$ gravity. So among the three cases of Harko et al.(Harko et al., 2011), we can obtain so many theoretical results by the choice of different explicit forms of $f(\tilde{R},T)$ as

$f\left(\tilde{R},T\right)=\left\{\begin{array}{c}\tilde{R}+2f\left(T\right)\hfill \\ f_1\left(\tilde{R}\right)+f_2\left(T\right)\hfill \\ f_1\left(\tilde{R}\right)+f_2\left(\tilde{R}\right)f_3\left(T\right)\hfill \end{array}\right.(10)$

But, in this paper the second case is considered to describe the behaviour of the model in $f(\tilde{R},T)$ gravity as

$f\left(\tilde{R},T\right)=f_1\left(\tilde{R}\right)+f_2\left(T\right)(11)$

where $f(\tilde{R},T)$ is an arbitrary function of the trace of the stress tensor.

Now, using Eq. 11 in Eq. 6, we obtain

$\begin{array}{cc}\hfill f_1^{\prime }\left(\tilde{R},T\right){\tilde{R}}_{ij}-\frac{1}{2}{f}_1\left(\tilde{R}\right)g_{ij}+\left(g_{ij}{\nabla }^i{\nabla }_i-{\nabla }_i{\nabla }_j\right)f_1^{\prime }\left(\tilde{R}\right)& =-\frac{8\pi }{c^2}{T}_{ij}+f_2^{\prime }\left(T\right)T_{ij}\hfill \\ \hfill & +\left[f_2^{\prime }\left(T\right)\bar{p}+\frac{1}{2}{f}_2\left(T\right)\right]g_{ij}\hfill \end{array}(12)$

The field equations of $f(\tilde{R},T)$ gravity, for a perfect fluid matter source, by assuming $f_1=\mu \tilde{R}$ and f₂ = μT, where μ is taken as arbitrary constant and with this condition the above Eq. 12 reduces to

${\tilde{R}}_{ij}-\frac{1}{2}\tilde{R}{g}_{ij}=-\left(\frac{8\pi -\mu c^2}{c^2}\right)T_{ij}+\left[\bar{p}+\frac{1}{2}T\right]g_{ij}(13)$

Applying Eq. 3 in Eq. 13, we obtain the field equations in Lyra geometry [Maurya (Maurya, 2020)] as given by

$R_{ij}-\frac{1}{2}R{g}_{ij}+\frac{3}{2}{\varphi }_i{\varphi }_j-\frac{3}{4}{g}_{ij}{\varphi }_i{\varphi }^j=-h{T}_{ij}+\left[\bar{p}+\frac{1}{2}T\right]g_{ij}(14)$

Here the displacement vector field is ${\varphi }^i=\left(\mathrm{0,0,0},\beta (t)\right)$ and $h=\left(\frac{8\pi -\mu c^2}{\mu c^2}\right)$ is taken as unity.

For the metric (1), the Einstein field Equation 14 reduces to the form as

$\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\dot{B}\dot{C}}{BC}-\frac{m^2}{A^2}+\frac{3}{4}{\beta }^2=-\bar{p}+\left(\frac{\rho -\bar{p}}{2}\right)(15)$

$\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\dot{C}\dot{A}}{CA}-\frac{m^2}{A^2}+\frac{3}{4}{\beta }^2=-\bar{p}+\left(\frac{\rho -\bar{p}}{2}\right)(16)$

$\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{AB}-\frac{m^2}{A^2}+\frac{3}{4}{\beta }^2=-\bar{p}+\left(\frac{\rho -\bar{p}}{2}\right)(17)$

$\frac{\dot{A}\dot{B}}{AB}+\frac{\dot{B}\dot{C}}{BC}+\frac{\dot{C}\dot{A}}{CA}-\frac{3m^2}{A^2}-\frac{3}{4}{\beta }^2=\rho +\left(\frac{\rho -\bar{p}}{2}\right)(18)$

$\frac{\dot{B}}{B}+\frac{\dot{C}}{C}-2\frac{\dot{A}}{A}=0(19)$

3 Solutions of the Field Equations

The spatial volume (V) and the scale factor a(t) are given by

$V=a^3=\left(ABC\right)(20)$

The generalized Hubble’s parameter (H) and the scalar expansion (θ) are defined as

$H=\frac{\dot{a}}{a}=\left(H_1+H_2+H_3\right);\theta =3H(21)$

where $H_1=\frac{\dot{A}}{A}$, $H_2=\frac{\dot{B}}{B}$, $H_3=\frac{\dot{C}}{C}$ are the directional Hubble’s parameters in the directions of the X, Y, and Z axes respectively.

Integrating Eq. 19, we get

$A^2=k_{1}BC(22)$

where k₁ is an integrating constant and without loss of generality, the constant of integration k₁ can be chosen as unity as

$A^2=BC(23)$

In the field Equations 15–19, we found that there are five equations involving seven unknowns. As the field equations are highly non-linear differential equations, we need some other condition to complete the field equations such as.

• we consider the shear scalar (σ) is proportional to the expansion scalar (θ) [Collins et al. (Collins et al., 1980)]

$B=C^n(24)$

where n is a non zero constant.

• Let us consider the combined effect of the proper pressure and the bulk viscous pressure, for a barotropic fluid can be expressed as follows:

$\bar{p}=p-3\xi H=\epsilon \rho ;p={\epsilon }_0\rho (25)$

Such that ɛ = ɛ₀ − η(0 ≤ ɛ₀ ≤ 1) and ϵ, ɛ₀, and η are constant. The symbols ξ and p are respectively known as the coefficient of bulk viscosity and proper pressure of the model.

Let us consider a time dependent displacement field scale factor [ Pradhan et al. (Pradhan et al., 2006)] as given by

$a\left(t\right)=\alpha e^{{\alpha }_{1}t}(26)$

where α and α₁ are constants.

From Eqs 23, 24, 26, we get the metric potentials of the model which are

$A=\alpha e^{{\alpha }_{1}t},B={\left(\alpha e^{{\alpha }_{1}t}\right)}^{\frac{2n}{n+1}},C={\left(\alpha e^{{\alpha }_{1}t}\right)}^{\frac{2}{n+1}}(27)$

Then Eq. 1 reduces to

$d{s}^2=-d{t}^2+{\left(\alpha e^{{\alpha }_{1}t}\right)}^{2}d{x}^2+e^{-2mx}\left[{\left(\alpha e^{{\alpha }_{1}t}\right)}^{\frac{4n}{n+1}}d{y}^2+{\left(\alpha e^{{\alpha }_{1}t}\right)}^{\frac{4}{n+1}}d{z}^2\right](28)$

4 Physical Properties of the Model in f(R, T) Gravity

The Physical Parameters of the model are obtained as follows:

Spatial Volume:

$V=a^3\left(t\right)={\left(\alpha e^{{\alpha }_{1}t}\right)}^3(29)$

Hubble’s Parameter:

$H=\alpha {\alpha }_1(30)$

The Expansion Scalar:

$\theta =3\alpha {\alpha }_1(31)$

The Shear Scalar:

${\sigma }^2={\left(\frac{n-1}{n+1}\right)}^2{\left(\alpha {\alpha }_1\right)}^2(32)$

Anisotropy parameter:

$A_m=\frac{2}{3}{\left(\frac{n-1}{n+1}\right)}^2(33)$

Deceleration parameter:

$q=-1(34)$

Adding Eqs 15–17 and applying in Eq. 18, we have the energy density given by

$\rho =\frac{1}{2ϵ-1}\left[-6{\left(\alpha {\alpha }_1\right)}^2+\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}\right](35)$

Also the total pressure, proper pressure, the co-efficient of bulk viscosity and the displacement vector are given by

$\bar{p}=\frac{ϵ}{2ϵ-1}\left[-6{\left(\alpha {\alpha }_1\right)}^2+\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}\right](36)$

$p=\frac{{ϵ}_0}{2ϵ-1}\left[-6{\left(\alpha {\alpha }_1\right)}^2+\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}\right](37)$

$\xi =\frac{{ϵ}_0-ϵ}{3\left(2ϵ-1\right)\left(\alpha {\alpha }_1\right)}\left[-6{\left(\alpha {\alpha }_1\right)}^2+\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}\right](38)$

$\begin{array}{cc}\hfill \frac{3}{4}{\beta }^2& =-3{\left(\alpha {\alpha }_1\right)}^2-\frac{m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}+\frac{1-3ϵ}{2\left(2ϵ-1\right)}\left[-6{\left(\alpha {\alpha }_1\right)}^2+\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}\right]\hfill \\ \hfill & +{\left(\frac{n-1}{n+1}\right)}^2{\left(\alpha {\alpha }_1\right)}^2\hfill \end{array}(39)$

The Trace $(T=\rho -3\bar{p})$, function of Ricci-Scalar$(\tilde{R})$ and the $f(\tilde{R},T)$ gravity are given by

$T=\frac{1-3ϵ}{2ϵ-1}\left[-6{\left(\alpha {\alpha }_1\right)}^2+\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}\right](40)$

$\begin{array}{cc}\hfill \tilde{R}& =\left(\frac{ϵ}{1-2ϵ}\right)\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}-6\left(\frac{3ϵ-2}{2ϵ-1}\right)+\frac{18}{\sqrt{3}}\left(\alpha {\alpha }_1\right)Z_1\hfill \\ \hfill & +2\sqrt{3}{m}^2\left(\frac{8ϵ-3}{2ϵ-1}\right)\left(\frac{\alpha {\alpha }_1{e}^{{\alpha }_{1}t}}{{\left(\alpha {\alpha }_1{e}^{{\alpha }_{1}t}\right)}^3}\right)Z_2\hfill \end{array}(41)$

$\begin{array}{cc}\hfill \frac{1}{\mu }f\left(\tilde{R},T\right)& =\left(\frac{ϵ}{1-2ϵ}\right)\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}-6\left(\frac{3ϵ-2}{2ϵ-1}\right)+\frac{18}{\sqrt{3}}\left(\alpha {\alpha }_1\right)Z_1\hfill \\ \hfill & +2\sqrt{3}{m}^2\left(\frac{8ϵ-3}{2ϵ-1}\right)\left(\frac{\alpha {\alpha }_1{e}^{{\alpha }_{1}t}}{{\left(\alpha {\alpha }_1{e}^{{\alpha }_{1}t}\right)}^3}\right)Z_2\hfill \\ \hfill & +\frac{1-3ϵ}{2ϵ-1}\left[-6{\left(\alpha {\alpha }_1\right)}^2+\frac{4m^2}{{\left(\alpha e^{{\alpha }_{1}t}\right)}^2}\right]\hfill \end{array}(42)$

where $Z_1={\left[\frac{3ϵ}{2ϵ-1}{(\alpha {\alpha }_1)}^2+\frac{1-8ϵ}{2ϵ-1}\frac{m^2}{{\left(\alpha {\alpha }_1{e}^{{\alpha }_{1}t}\right)}^2}\right]}^{\frac{-1}{2}}$ and $Z_2={\left[\frac{3ϵ}{2ϵ-1}{(\alpha {\alpha }_1)}^2+\frac{1-8ϵ}{2ϵ-1}\frac{m^2}{{\left(\alpha {\alpha }_1{e}^{{\alpha }_{1}t}\right)}^2}\right]}^{\frac{1}{2}}$ are functions of cosmic time t.

From Eqs 28, 31, we obtain the statefinder parameters, which is defined as $r=\frac{\stackrel{⃛}{a}}{a{H}^3}$ and $s=\frac{r-1}{3(q-\frac{1}{2})}$, exactly gives the value 1 and 0 respectively.

Energy Conditions

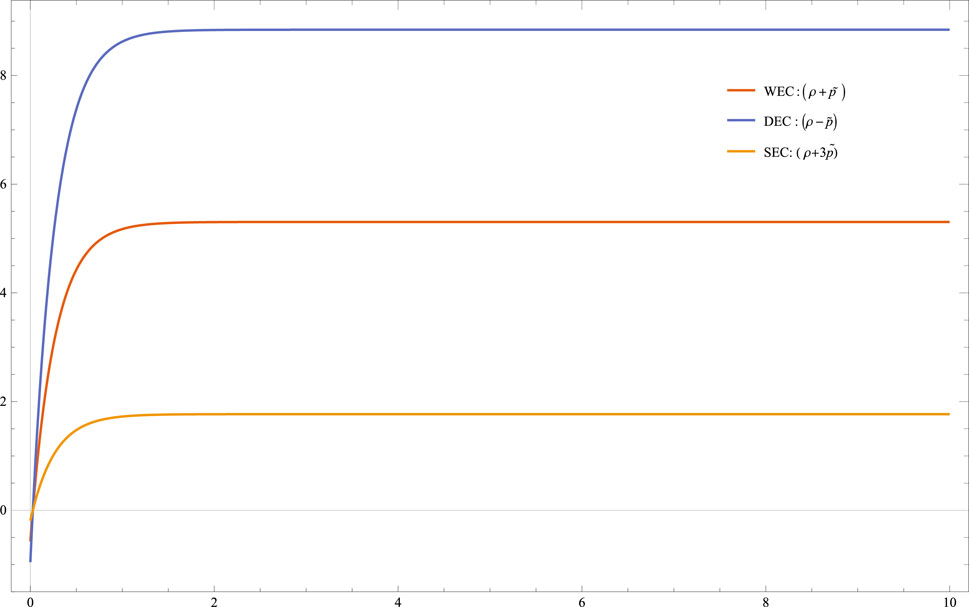
The energy conditions are constructed from the Raychaudhuri equation, which are very important tools to describe the behavior of the compatibility of timelike, lightlike, or spacelike curves and singularities. Very recently Alvarenga (Alvarenga et al., 2013), Moraes (Moraes and Sahoo, 2017), Zubair (Zubair et al., 2018), and Ahmed (Ahmed and Abbas, 2020) have tested the energy conditions in f (R, T) theory of gravity and to check the energy conditions for the present model, they defined the weak energy conditions (WECs), dominant energy conditions (DECs), and the strong energy conditions (SEC) as given by

1) ρ ≥ 0, ρ + p ≥ 0 2) ρ − p ≥ 0 (iii)ρ + 3p ≥ 0

To observe the absolute observational data, we have plotted the graphs for energy conditions in terms of ρ and $\bar{p}$, and we extensively observe from the graph that all the three energy conditions are satisfied in the present model.

5 Conclusion

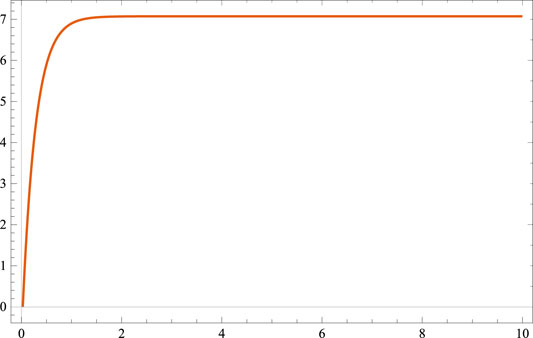
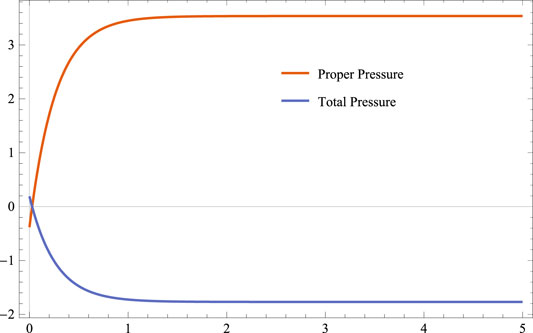
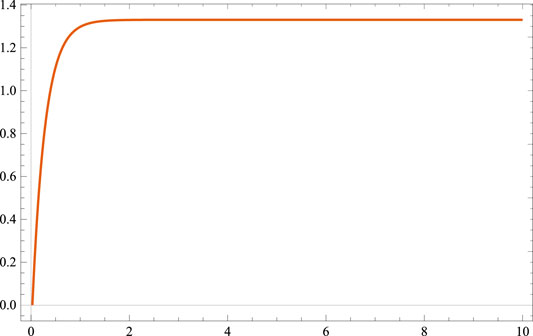
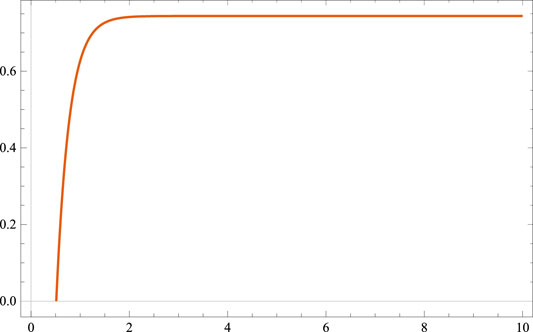
In this study, a completely spatially homogeneous and anisotropic Bianchi type-V cosmological model has been discussed in the presence of a bulk viscous fluid based on Lyra geometry, with an exponential form of scale factor. We employed a barotropic equation of state for pressure and energy density to determine the nature and deterministic solution of the highly non linear differential equation. Furthermore, we assumed that bulk viscous pressure is proportional to energy density [Naidu et al. (Naidu et al., 2013)]. As per recent observational data in combination with Baryonic Acoustic Oscillations (BAO), Cosmic Microwave Background (CMB), from Type Ia Supernova (SN Ia), the model found in this paper is in conformative. The model 28) found here is shearing, expanding, and anisotropic which is similar to [Zia (Zia et al., 2018), Tiwari (Tiwari et al., 2020), and Desikan (Desikan, 2020)]. At t = 0, we found that the model has no singularity. Subsequently, we can see from Eqs 30, 31 that the Hubble’s parameter (H) and the expansion scalar remain constant throughout the expansion, implying that model 28) represents a uniform expansion. It is evident from Eq. 29 that the volume (V) of the universe rises with cosmic time (t), and that as V approaches infinity, for t → ∞. We observed from Eq. 38 that the bulk viscosity coefficient increases with time and approaches infinity as t approaches infinity. The model’s energy density, total pressure, coefficient of bulk viscosity, and displacement vector all rise positively, but they all yield a constant value for t tending to infinity (Figures 1–4). The model predicts an accelerating phase of the universe for q = − 1, which is given by Eq. 34. In the current model of the universe, there is a dark energy due to negative pressure in the presence of bulk viscous fluid based on Lyra geometry with f (R, T) gravity, as shown in Figure 2. All the three energy conditions are satisfied as in Figure 5. The Trace and the Ricci scalar are always positive throughout the cosmic time t, and for t → ∞, it offers a constant value, as shown in Eqs 40, 41. Furthermore, r and s tend to 1 and 0 respectively, indicating that the current universe model approaches the ΛCDM model. There have been many works done by researchers in the area of Lyra geometry, but Lyra geometry with f(R, T) gravity is a very new concept and there is scope for the continuation of work.

FIGURE 1

FIGURE 1. Variation of density (ρ) vs. time (t).

FIGURE 2

FIGURE 2. Variation of total pressure $(\bar{p})$ and proper pressure (p) vs. time (t).

FIGURE 3

FIGURE 3. Variation of coefficient bulk viscosity (ξ) vs. time (t).

FIGURE 4

FIGURE 4. Variation of displacement vector (β²) vs. time (t).

FIGURE 5

FIGURE 5. Variation of strong energy condition vs. time (t).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, orclaim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbas, G., Momeni, D., Aamir Ali, M., Myrzakulov, R., and Qaisar, S. (2015). Anisotropic Compact Stars in F(G) Gravity. Astrophys. Space Sci. 357, 1–11. doi:10.1007/s10509-015-2392-6

CrossRef Full Text | Google Scholar

Adhav, K. S. (2011). LRS Bianchi Type-I Universe with Anisotropic Dark Energy in Lyra Geometry. Int. J. Astron. Astrophysics 01, 204–209. doi:10.4236/ijaa.2011.14026

CrossRef Full Text | Google Scholar

Ahmed, R., and Abbas, G. (2020). Non-adiabatic Gravitational Collapse in f(R,T) Gravity with Karmarkar Condition for Anisotropic Fluid. Mod. Phys. Lett. A. 35, 2050103. doi:10.1142/S0217732320501035

CrossRef Full Text | Google Scholar

Alvarenga, F. G., Houndjo, M. J. S., Monwanou, A. V., and Orou, J. B. C. (2013). Testing Some f(R,T) Gravity Models from Energy Conditions. Jmp 04, 130–139. doi:10.4236/jmp.2013.41019

CrossRef Full Text | Google Scholar

Arora, S., Bhattacharjee, S., and Sahoo, P. K. (2021). Late-time Viscous Cosmology in f(R, T) Gravity. New Astron. 82, 101452. doi:10.1016/j.newast.2020.101452

CrossRef Full Text | Google Scholar

Bahamonde, S., Flathmann, K., and Pfeifer, C. (2019). Photon Sphere and Perihelion Shift in Weak F(T) Gravity. Phys. Rev. D 100 (8), 084064. doi:10.1103/PhysRevD.100.084064

CrossRef Full Text | Google Scholar

Bali, R., Singh, P., and Singh, J. P. (2012). Bianchi Type V Viscous Fluid Cosmological Models in Presence of Decaying Vacuum Energy. Astrophys. Space Sci. 341, 701–706. doi:10.1007/s10509-012-1134-2

CrossRef Full Text | Google Scholar

Bamba, K., Ilyas, M., Bhatti, M. Z., and Yousaf, Z. (2017). Energy Conditions in Modified F(G) Gravity. Gen. Relativ. Gravit. 49, 1–17. doi:10.1007/s10714-017-2276-x

CrossRef Full Text | Google Scholar

Bamba, K., Odintsov, S. D., and Saridakis, E. N. (2017). Inflationary Cosmology in Unimodular F(T) Gravity. Mod. Phys. Lett. A. 32, 1750114. doi:10.1142/S0217732317501140

CrossRef Full Text | Google Scholar

Barrow, J. D. (1986). The deflationary universe: an instability of the de Sitter universe. Phys. Lett. B 180, 335–339. doi:10.1016/0370-2693(86)91198-6

CrossRef Full Text | Google Scholar

Bertolami, O., Böhmer, C. G., Harko, T., and Lobo, F. S. N. (2007). Extra Force inf(R)modified Theories of Gravity. Phys. Rev. D 75, 104016. doi:10.1103/PhysRevD.75.104016

CrossRef Full Text | Google Scholar

Bhaskara Rao, M. P. V. V., Reddy, D. R. K., and Sobhan Babu, K. (2015). Bianchi Type-V Bulk Viscous String Cosmological Model in a Self-Creation Theory of Gravitation. Astrophys. Space Sci. 359, 1–5. doi:10.1007/s10509-015-2501-6

CrossRef Full Text | Google Scholar

Brahma, B. P., and Dewri, M. (2021). Bianchi Type-V Modified f(R,T) Gravity Model in Lyra Geometry with Varying Deceleration Parameter. J. Math. Comput. Sci. 11, 1018–1028. doi:10.28919/jmcs/5281

CrossRef Full Text | Google Scholar

Capozziello, S., Cardone, V. F., and Salzano, V. (2008). Cosmography off(R)gravity. Phys. Rev. D 78, 063504. doi:10.1103/PhysRevD.78.063504

CrossRef Full Text | Google Scholar

Capozziello, S., and Vignolo, S. (2010). Metric-affine F(R)-gravity with Torsion: an Overview. Ann. Phys. 19 (3-5), 238–248. doi:10.1002/andp.201010420

CrossRef Full Text | Google Scholar

Carroll, S. M., Duvvuri, V., Trodden, M., and Turner, M. S. (2004). Is Cosmic Speed-Up Due to New Gravitational Physics? Phys. Rev. D 70, 043528. doi:10.1103/PhysRevD.70.043528

CrossRef Full Text | Google Scholar

Collins, C. B., Glass, E. N., and Wilkinson, D. A. (1980). Exact Spatially Homogeneous Cosmologies. Gen. Relat. Gravit. 12, 805–823. doi:10.1007/BF00763057

CrossRef Full Text | Google Scholar

De Felice, A., Suyama, T., and Tanaka, T. (2011). Stability of Schwarzschild-like Solutions inf(R,G)gravity Models. Phys. Rev. D 83 (10), 104035. doi:10.1103/PhysRevD.83.104035

CrossRef Full Text | Google Scholar

De Felice, A., and Tsujikawa, S. (2009). Construction of Cosmologically Viable Gravity Models. Phys. Lett. B 675, 1–8. doi:10.1016/j.physletb.2009.03.060

CrossRef Full Text | Google Scholar

De Laurentis, M., and Lopez-Revelles, A. J. (2014). Newtonian, Post-Newtonian and Parametrized Post-Newtonian Limits of f(R, G) Gravity. Int. J. Geom. Methods Mod. Phys. 11, 1450082. doi:10.1142/S0219887814500820

CrossRef Full Text | Google Scholar

De Laurentis, M., Paolella, M., and Capozziello, S. (2015). Cosmological Inflation in F(R,G) Gravity. Phys. Rev. D 91, 083531. doi:10.1103/PhysRevD.91.083531

CrossRef Full Text | Google Scholar

Debnath, P. S. (2019). Bulk Viscous Cosmological Model in f(R,T) Theory of Gravity. Int. J. Geom. Methods Mod. Phys. 16, 1950005. doi:10.1142/S0219887819500051

CrossRef Full Text | Google Scholar

Desikan, K. (2020). Cosmological Models in Lyra Geometry with Time-Varying Displacement Field. Afr. Rev. Phys. 15, 32.

Google Scholar

Fabris, J. C., Gonçalves, S. V. B., and Ribeiro, R. d. S. (2006). Bulk Viscosity Driving the Acceleration of the Universe. Gen. Relativ. Gravit. 38, 495–506. doi:10.1007/s10714-006-0236-y

CrossRef Full Text | Google Scholar

Ferraro, R., and Guzmán, M. J. (2018). Quest for the Extra Degree of freedom in F(T) Gravity. Phys. Rev. D 98, 124037. doi:10.1103/PhysRevD.98.124037

CrossRef Full Text | Google Scholar

Garnavich, P. M., Jha, S., Challis, P., Clocchiatti, A., Diercks, A., Filippenko, A. V., et al. (1998). Supernova Limits on the Cosmic Equation of State. Astrophysical J. 509, 74–79. doi:10.1086/306495

CrossRef Full Text | Google Scholar

Garnavich, P. M., Kirshner, R. P., Challis, P., Tonry, J., Gilliland, R. L., Smith, R. C., et al. (1998). Constraints on Cosmological Models from [ITAL]Hubble Space Telescope[/ITAL] Observations of High-[CLC][ITAL]z[/ITAL][/CLC] Supernovae. Astrophysical J. Lett. 493, L53–L57. doi:10.1086/311140

CrossRef Full Text | Google Scholar

Gogoi, D. J., and Dev Goswami, U. (2020). A New F(R) Gravity Model and Properties of Gravitational Waves in it. Eur. Phys. J. C 80, 1–21. doi:10.1140/epjc/s10052-020-08684-3

CrossRef Full Text | Google Scholar

Goswami, G. K., Yadav, A. K., Mishra, B., and Tripathy, S. K. (2021). Modeling of Accelerating Universe with Bulk Viscous Fluid in Bianchi V Space‐Time. Fortschr. Phys. 69 (6), 2100007. doi:10.1002/prop.202100007

CrossRef Full Text | Google Scholar

Halford, W. D. (1972). Scalar‐Tensor Theory of Gravitation in a Lyra Manifold. J. Math. Phys. 13 (11), 1699–1703. doi:10.1063/1.1665894

CrossRef Full Text | Google Scholar

Harko, T., Lobo, F. S. N., Nojiri, S. I., and Odintsov, S. D. (2011). f(R,T)gravity. Phys. Rev. D 84, 024020. doi:10.1103/PhysRevD.84.024020

CrossRef Full Text | Google Scholar

Hegazy, E. A. (2020). Bulk Viscous Bianchi Type I Cosmological Model in Lyra Geometry and in the General Theory of Relativity. Astrophys. Space Sci. 365, 1–8. doi:10.1007/s10509-020-03836-z

CrossRef Full Text | Google Scholar

Iosifidis, D., Petkou, A. C., and Tsagas, C. G. (2019). Torsion/nonmetricity Duality in F(R) Gravity. Gen. Relativ. Gravit. 51, 1–15. doi:10.1007/s10714-019-2539-9

CrossRef Full Text | Google Scholar

Johri, V., and Sudharsan, R. (1989). BD-FRW Cosmology with Bulk Viscosity. Aust. J. Phys. 42, 215–222. doi:10.1071/PH890215

CrossRef Full Text | Google Scholar

Kanakavalli, T., Rao, G. A., and Reddy, D. R. K. (2016). Bianchi Type V Scalar Field Cosmological Models in f(R, T) Theory of Gravity. Prespacetime J. 7, 1722–1728.

Google Scholar

Kiran, M., and Reddy, D. R. K. (2013). Non-existence of Bianchi Type-III Bulk Viscous String Cosmological Model in f(R,T) Gravity. Astrophys. Space Sci. 346, 521–524. doi:10.1007/s10509-013-1459-5

CrossRef Full Text | Google Scholar

Kotambkar, S., Kelkar, R. K., and Singh, G. P. (2021). Dynamical Behaviours of Chaplygin Gas, Cosmological and Gravitational 'constants' with Cosmic Viscous Fluid in Bianchi Type V Space-Time Geometry. J. Phys. Conf. Ser. 1913 (1), 012103. doi:10.1088/1742-6596/1913/1/012103

CrossRef Full Text | Google Scholar

Kumari, P., Singh, M. K., and Ram, S. (2013). Anisotropic Bianchi Type-III Bulk Viscous Fluid Universe in Lyra Geometry. Adv. Math. Phys. 2013, 1–5. doi:10.1155/2013/416294

CrossRef Full Text | Google Scholar

Lyra, G. (1951). über eine Modifikation der Riemannschen Geometrie. Math. Z. 54, 52–64. doi:10.1007/BF01175135

CrossRef Full Text | Google Scholar

Mahanta, K. L. (2014). Bulk Viscous Cosmological Models in f(R,T) Theory of Gravity. Astrophys. Space Sci. 353, 683–689. doi:10.1007/s10509-014-2040-6

CrossRef Full Text | Google Scholar

Maurya, D. C. (2020). Modified f(R,T) Cosmology with Observational Constraints in Lyra's Geometry. Int. J. Geom. Methods Mod. Phys. 17, 2050001. doi:10.1142/S0219887820500012

CrossRef Full Text | Google Scholar

Maurya, D. C., and Zia, R. (2019). Brans-Dicke Scalar Field Cosmological Model in Lyra's Geometry. Phys. Rev. D 100, 023503. doi:10.1103/PhysRevD.100.023503

CrossRef Full Text | Google Scholar

Misner, C. W. (1968). The Isotropy of the Universe. Astrophysical J. 151, 431. doi:10.1086/149448

CrossRef Full Text | Google Scholar

Moraes, P. H. R. S., and Sahoo, P. K. (2017). The Simplest Non-minimal Matter-Geometry Coupling in the f(R, T) Cosmology. Eur. Phys. J. C 77, 1–8. doi:10.1140/epjc/s10052-017-5062-8

CrossRef Full Text | Google Scholar

Naidu, R. L., Reddy, D. R. K., Ramprasad, T., and Ramana, K. V. (2013). Bianchi Type-V Bulk Viscous String Cosmological Model in f(R,T) Gravity. Astrophys Space Sci. 348, 247–252. doi:10.1007/s10509-013-1540-0

CrossRef Full Text | Google Scholar

Nath, A., and Sahu, S. K. (2019). LRS Bianchi Type V Perfect Fluid Cosmological Model in f(R, T) Theory. Can. J. Phys. 97, 443–449. doi:10.1139/cjp-2018-0061

CrossRef Full Text | Google Scholar

Nojiri, S. I., and Odintsov, S. D. (2007). eConf C0602061, 06. Int. J. Geom. Meth. Mod. Phys. 4 (115), 16.

Google Scholar

Odintsov, S. D., Oikonomou, V. K., and Banerjee, S. (2019). Dynamics of Inflation and Dark Energy from F(R,G) Gravity. Nucl. Phys. B 938, 935–956. doi:10.1016/j.nuclphysb.2018.07.013

CrossRef Full Text | Google Scholar

Padmanabhan, T., and Chitre, S. M. (1987). Viscous Universes. Phys. Lett. A. 120, 1–4. doi:10.1016/0375-9601(87)90104-6

CrossRef Full Text | Google Scholar

Paliathanasis, A., Barrow, J. D., and Leach, P. G. L. (2016). Cosmological Solutions off(T)gravity. Phys. Rev. D 94, 023525. doi:10.1103/PhysRevD.94.023525

CrossRef Full Text | Google Scholar

Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R. A., Nugent, P., Castro, P. G., et al. (1999). Measurements of Ω and Λ from 42 High‐Redshift Supernovae. Astrophysical J. 517, 565–586. doi:10.1086/307221

CrossRef Full Text | Google Scholar

Perlmutter, S., Gabi, S., Goldhaber, G., Goobar, A., Groom, D. E., Hook, I. M., et al. (1997). Measurements of the Cosmological Parameters Ω and Λ from the First Seven Supernovae Atz≥ 0.35. Astrophysical J. 483, 565–581. doi:10.1086/304265

CrossRef Full Text | Google Scholar

Pradhan, A., Shahi, J. P., and Singh, C. B. (2006). Cosmological Models of Universe with Variable Deceleration Parameter in Lyra's Manifold. Braz. J. Phys. 36, 1227–1231. doi:10.1590/S0103-97332006000700020

CrossRef Full Text | Google Scholar

Pradhan, A., and Vishwakarma, A. K. (2004). A New Class of LRS Bianchi Type-I Cosmological Models in Lyra Geometry. J. Geometry Phys. 49, 332–342. doi:10.1016/S0393-0440(03)00105-0

CrossRef Full Text | Google Scholar

Ram, S., Chandel, S., and Verma, M. K. (2020). Kantowski-Sachs Cosmological Model with Anisotropic Dark Energy in Lyra Geometry. Proc. Natl. Acad. Sci. India, Sect. A. Phys. Sci. 90, 109–114. doi:10.1007/s40010-018-0549-8

CrossRef Full Text | Google Scholar

Ram, S., Zeyauddin, M., and Singh, C. P. (2010). Anisotropic Bianchi Type V Perfect Fluid Cosmological Models in Lyra's Geometry. J. Geometry Phys. 60, 1671–1680. doi:10.1016/j.geomphys.2010.06.010

CrossRef Full Text | Google Scholar

Rao, V. U. M., and Papa Rao, D. C. (2015). Bianchi Type-V String Cosmological Models in f(R,T) Gravity. Astrophys. Space Sci. 357, 1–5. doi:10.1007/s10509-015-2242-6

CrossRef Full Text | Google Scholar

Riess, A. G., Filippenko, A. V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P. M., et al. (1998). Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 116, 1009–1038. doi:10.1086/300499

CrossRef Full Text | Google Scholar

Sahoo, P. K., Sahoo, P., and Bishi, B. K. (2017). Anisotropic Cosmological Models in f(R,T) Gravity with Variable Deceleration Parameter. Int. J. Geom. Methods Mod. Phys. 14 (06), 1750097. doi:10.1142/S0219887817500979

CrossRef Full Text | Google Scholar

Sahoo, P., and Reddy, R. (2018). LRS Bianchi Type-I Bulk Viscous Cosmological Models in f(R, T) Gravity. Astrophysics 61, 134–143. doi:10.1007/s10511-018-9522-0

CrossRef Full Text | Google Scholar

Sen, D. K. (1957). A Static Cosmological Model. Z. Physik 149, 311–323. doi:10.1007/BF01333146

CrossRef Full Text | Google Scholar

Sen, D. K., and Dunn, K. A. (1971). A Scalar‐Tensor Theory of Gravitation in a Modified Riemannian Manifold. J. Math. Phys. 12, 578–586. doi:10.1063/1.1665623

CrossRef Full Text | Google Scholar

Sharif, M., and Saba, S. (2018). Gravitational Decoupled Anisotropic Solutions in $$f({\mathcal {G}})$$ F ( G ) Gravity. Eur. Phys. J. C 78, 1–12. doi:10.1140/epjc/s10052-018-6406-8

CrossRef Full Text | Google Scholar

Sharma, U. K., Zia, R., Pradhan, A., and Beesham, A. (2019). Stability of LRS Bianchi Type-I Cosmological Models in f(R, T)-gravity. Res. Astron. Astrophys. 19, 055. doi:10.1088/1674–4527/19/4/5510.1088/1674-4527/19/4/55

CrossRef Full Text | Google Scholar

Singh, G. P., and Kale, A. Y. (2009). A New Class of Bianchi Type-I Cosmological Models in Lyra Geometry. Int. J. Theor. Phys. 48, 3049–3060. doi:10.1007/s10773-009-0100-4

CrossRef Full Text | Google Scholar

Singh, J. K. (2008). Exact Solutions of Some Cosmological Models in Lyra Geometry. Astrophys. Space Sci. 314, 361–365. doi:10.1007/s10509-008-9776-9

CrossRef Full Text | Google Scholar

Singh, J. K., and Rani, S. (2015). Bianchi Type-III Cosmological Models in Lyra's Geometry in the Presence of Massive Scalar Field. Int. J. Theor. Phys. 54, 545–560. doi:10.1007/s10773-014-2247-x

CrossRef Full Text | Google Scholar

Singh, J. P., and Baghel, P. S. (2009). Bianchi Type V Bulk Viscous Cosmological Models with Time Dependent Λ-term. Elect. J. Theor. Phys. 6, 85–9640.

Google Scholar

Soleng, H. H. (1987). Cosmologies Based on Lyra's Geometry. Gen. Relat. Gravit. 19, 1213–1216. doi:10.1007/BF00759100

CrossRef Full Text | Google Scholar

Sotiriou, T. P., and Faraoni, V. (2010). f(R)theories of Gravity. Rev. Mod. Phys. 82, 451–497. doi:10.1103/RevModPhys.82.451

CrossRef Full Text | Google Scholar

Tamanini, N., and Böhmer, C. G. (2012). Good and Bad Tetrads inf(T)gravity. Phys. Rev. D 86, 044009. doi:10.1103/PhysRevD.86.044009

CrossRef Full Text | Google Scholar

Tiwari, L. K., and Tiwari, R. K. (2017). Bianchi Type-V Cosmological Models with Viscous Fluid and Varying Λ. Prespacetime J. 8, 1509–1520.

Google Scholar

Tiwari, R. K., Sofuoğlu, D., and Dubey, V. K. (2020). Phase Transition of LRS Bianchi Type-I Cosmological Model in f(R,T) Gravity. Int. J. Geom. Methods Mod. Phys. 17, 2050187. doi:10.1142/S021988782050187X

CrossRef Full Text | Google Scholar

Yadav, V. K., and Yadav, L. (2011). Bianchi Type-III Bulk Viscous and Barotropic Perfect Fluid Cosmological Models in Lyra's Geometry. Int. J. Theor. Phys. 50, 1382–1394. doi:10.1007/s10773-010-0647-0

CrossRef Full Text | Google Scholar

Yang, R.-J. (2011). New Types of F(T) Gravity. Eur. Phys. J. C 71, 1–8. doi:10.1140/epjc/s10052-011-1797-9

CrossRef Full Text | Google Scholar

Zia, R., Maurya, D. C., and Pradhan, A. (2018). Transit Dark Energy String Cosmological Models with Perfect Fluid in F(R,T)-gravity. Int. J. Geom. Methods Mod. Phys. 15, 1850168. doi:10.1142/S0219887818501682

CrossRef Full Text | Google Scholar

Zubair, M., Azmat, H., and Noureen, I. (2018). Anisotropic Stellar Filaments Evolving under Expansion-free Condition in f(R,T) Gravity. Int. J. Mod. Phys. D 27 (04), 1850047. doi:10.1142/S0218271818500475

CrossRef Full Text | Google Scholar