A Study on Second Harmonic Excitation in Electron Beam–Plasma Instability

The electron beam–plasma interaction is a fundamental nonlinear plasma process that is frequently taking place in space and laboratory plasmas. Such an interaction is found to generate electromagnetic waves observed in space plasmas. Using the two-dimensional electromagnetic particle in cell simulations, we investigated the second harmonic excitation in the electron beam–plasma instability. Results showed that, first, the Langmuir waves are excited in the system; then at longer time scales, following the excitation of ion acoustic waves, the second harmonic electromagnetic waves are excited. We found that in the case of background pair plasmas, where the masses are the same, there is no signature of waves in the second harmonic, which is a direct verification of the three-wave coupling mechanism for the generation of electromagnetic waves in the second harmonic.

Introduction

The electron beam–plasma interaction is a fundamental nonlinear plasma process that is frequently taking place in space and laboratory plasmas. Such an interaction is found to generate electromagnetic waves observed in space plasmas (Lacombe et al., 1988; Brown et al., 1990; Gurnett et al., 1993; Stasiewicz et al., 1996; Kojima et al., 1997; Soucek et al., 2005; Sigsbee et al., 2010). Solar type II and type III radio bursts are also attributed to the electron beam–plasma instabilities (Willes et al., 1996; Li et al., 2005). So far, a large number of analytical (quasilinear/weak turbulence), simulational (PIC/Vlasov), experimental, and observational studies have investigated various aspects of this problem such as the effect of weak/strong equilibrium magnetic field, relativistic/warm/cold beam, and background non-uniform/modulated density (Gurnett et al., 1981; Pritchett and Dawson 1983; Hospodarsky et al., 1994; Omura et al., 1996; Muschietti et al., 1996; Umeda 2007; Silin et al., 2007; Yi et al., 2010; Baumgartel 2013).

The most important consequence of the beam–plasma interaction is the excitation and emission of electromagnetic waves in different frequencies. In fact, the emission of electromagnetic waves occurs at integer multiples of the local electron plasma frequency, nω_pe with ${\omega }_{pe}={(n_0{e}^2/m_e{ϵ}_0)}^{1/2}$. The exact mechanism for the generation of the second harmonic (n = 2) is yet under investigation, but the most probable and discussed one is thought to be a two-step process (Melrose, 1980; Cairns and Melrose, 1985). First, the excitation of backscattered Langmuir waves accompanied with ion acoustic waves through a parametric decay of large amplitude Langmuir waves. Second, the excitation of 2ω_pe electromagnetic waves followed the wave–wave coupling of forward and backward propagating Langmuir waves.

Therefore, the role of ion components of the plasma is important regarding the generation of the second harmonic. It is expected that the decay of long-lived solitons, being formed by amplitude modulation of Langmuir waves, is significantly affected by ion-related waves, in particular, ion acoustic waves. This parametric decay is necessary for second harmonic generation. The decay pattern and its duration are of special interest. Ion acoustic waves (IAWs) are the low-frequency longitudinal plasma density oscillations. In the oscillations, electrons and ions are propagating in the phase space. Ion acoustic waves can occur in an unmagnetized plasma or in a magnetized plasma parallel to the magnetic field, and in the long wavelength limit, the waves are dispersionless with ω = v_sk, where v_s is the so-called ion sound speed which depends on both the electron and ion temperatures. On the other hand, Langmuir waves or electron plasma waves are high-frequency longitudinal oscillations of electron species of the plasma around almost motionless ions. The propagation velocity of Langmuir waves depends on the wavelength. If the thermal motion of the electrons is ignored or the wavelength is very large, Langmuir waves reduce to the charge density which oscillates at the plasma frequency.

Therefore, it is of interest to investigate the evolution of the electron beam–plasma instability in the presence of ion species. In the presence of physical heavy ions, the excitation of ion acoustic waves would indeed take place at very late times on the order of a few thousand times of ω_pe. It is thought that the intensity of emission in the second harmonic depends on the ion-to-electron mass ratio since strong ion acoustic waves result in the effective backscattering of Langmuir waves. It is very important to verify by simulation that the three-wave coupling is the main working mechanism for the generation of electromagnetic waves in the second harmonic. The prerequisite for such a nonlinear wave–wave coupling is the existence of ion acoustic waves. We clearly showed that in the absence of ions, electromagnetic waves in the second harmonic are not generated. This finding is a direct verification of the three-wave coupling mechanism.

Most of electron–beam plasma interaction studies have assumed an equilibrium magnetic field in a specific direction. However, we omitted the equilibrium magnetic field as the main purpose here is to better understand the role of ion components on the generation of second harmonics and to verify the theoretical two-step process mechanism proposed for the electromagnetic emission in the second harmonic. Since the ions are magnetized in relatively strong magnetic fields compared to the electrons, our results might be applicable to the cases of weak magnetic fields.

To conduct this study, we have used 2D electromagnetic particle-in-cell simulations. In the absence of a strong equilibrium magnetic field, one-dimensional approximation for the beam–plasma interaction is not satisfactory, and at least 2D simulation is necessary to properly resolve instabilities. The study is structured as follows: the next section describes the model and simulation setup, while the results and discussion are presented in the third section which is followed by a brief summary.

Simulation Setup

Two-dimensional (2D3V) electromagnetic particle-in-cell simulations are carried out by using the EPOCH (Extendable PIC Open Collaboration) code, developed at the University of Warwick. It is a general purpose PIC code for modeling kinetic plasmas in one, two, or three spatial dimensions. The full set of Maxwell’s equations and the equation of motion for charged particles are solved in a self-consistent manner with the standard leapfrog algorithms, while the current density is computed with the charge conservation method for solving the continuity equation for charge.

The simulation box size in the xy plane is L_x = L_y = 538λ_D, with grid numbers N_x = N_y = 800, so the grid sizes are Δx = Δy = 0.67λ_D, where ${\lambda }_D={({ϵ}_0{K}_B{T}_e/n_0{e}^2)}^{1/2}$ is the electron Debye length. The time step is determined by the CFL condition as $\mathrm{\Delta }t=1.5\times 10^{-11}s=2.7\times 10^{-3}{\omega }_{pe}^{-1}$, which is sufficiently small to precisely detect the excited waves in the system.

Three kinds of species constitute the system: 1)—background plasma electrons with physical mass m_e, Maxwellian temperature T_e = 20 eV corresponding to the electron thermal velocity Vth_,e = 2.65 × 10⁶ m/s, and the initial uniform number density n₀ = 10¹³m⁻³; 2)—Plasma ions with mass, m_i = α m_e, where α is 0, 1, 100, and 1,000. The ion temperature is T_i = 0.25T_e = 5 eV, and its number density is n_i = n₀ + n_b = 1.01n₀, which satisfies the charge neutrality condition. 3)—Beam electrons with mass m_e. The Maxwellian beam temperature is T_b = T_e, and the non-relativistic drift velocity of beam along the y direction is V_d,b = 0.2 C = 22.6Vth_,e with the beam number density n_b = 0.01n₀. In order to preserve the initially zero current condition, the drift velocity of background electrons is V_d,e = n_bV_d,b/(n₀—n_b). Moreover, the number of macroparticles is 150 per grid per species. Due to the computational limitations, it was not possible to run the simulations with a larger number of particles or even with mass ratios much larger than those employed here. The plasma is initially free from any externally imposed magnetic or electric fields. Finally, for both fields and particles, the periodic boundary condition is imposed in the x and y directions. The aforementioned simulation parameters are similar to those considered by Sauer et al. (2019) and Yi et al. (2016).

Simulation Results and Discussion

The free energy provided by the kinetic energy of the warm beam triggers the instability in the plasma, and consequently, its energy decreases, as seen from Figure 1, which is normalized to the initial kinetic energy of plasma electrons, ${\sum }_{ix=1}^{N_x}{\sum }_{iy=1}^{N_y}{n}_e(ix,iy,t=0.){\tilde{E}}_{k,e}(ix,iy,t=0.)$ with ${\tilde{E}}_{k,e}(ix,iy,t=0.)$ as the mean kinetic energy of each electron at the position (ix, iy). The early time charge separation is totally determined by the background electrons (especially in the case of heavy ions), and as a result, the electric field is generated with an amplitude which grows exponentially in the quasilinear regime. In other words, the electrostatic Langmuir waves are excited which propagate mainly along the beam drift velocity with a phase speed greater than the thermal velocity of electrons.

FIGURE 1

FIGURE 1. Temporal evolution of beam kinetic energy.

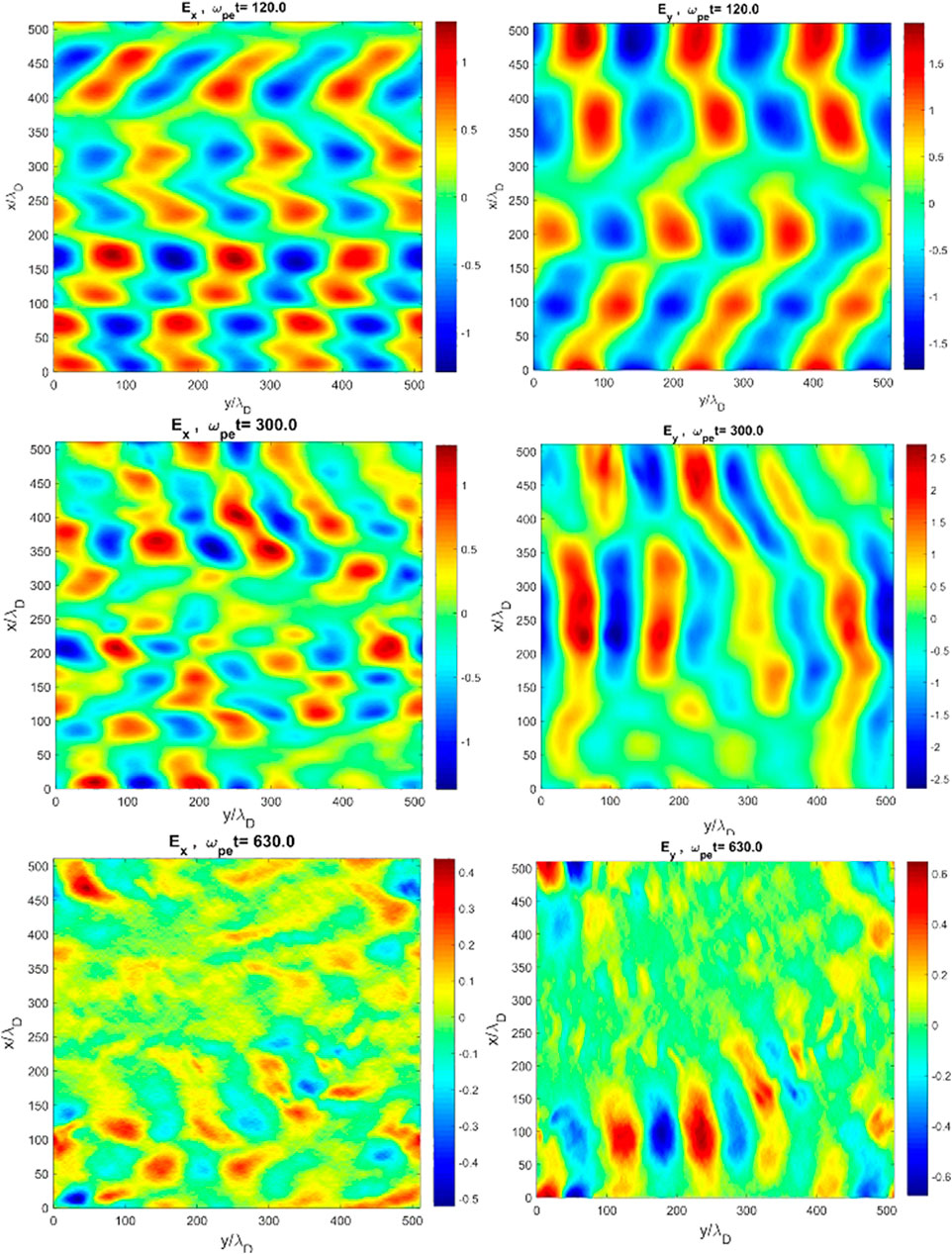
Figure 2 plots the E_x and E_y components of the electric field in the xy plane with m_i/m_e = 1,000 at times ω_pet = 120.0, 300.0, 630, which is normalized to m_eω_pev_th,e/e = 2.7 × 10³V/m. As seen, the non-uniform dipolar electric structures, which have been developed in both x and y directions at earlier times, are gradually destructed as the beam loses its free kinetic energy. In other words, as time goes on, instability develops to smaller wavenumbers (larger wavelengths). As these electrical structures develop, most of the low-energy population of beam electrons is trapped within the electric potential structures in a nonlinear process of the wave–particle interaction. These structures are called electron holes (or phase space holes). These non-uniform electric structures exist for longer time scales, while their non-uniformity increases in both directions in a way that the significant component of E_x grows due to the transverse instability in electron holes. The wavelength of quasilinear perturbations along the y direction at ω_pet ∼ 40 is λ/λ_D ∼ 150, which is in good agreement with that predicted by the theory as λ/λ_D ∼ 2πV_d,b/Vth_,e ∼ 2π × 6 × 107/2.65 × 106 = 142. This is almost the wavelength of the fastest growing mode. Using the temporal variation of electric energy, the growth rate at the quasilinear regime is found to be γ ∼ 0.14ω_pe, as predicted by the theory.

FIGURE 2

FIGURE 2. Plots of E_y and E_x in the xy plane at three different times (color online).

According to Figure 1, an almost abrupt decrease of the beam energy is observed at ω_pet ∼ 50, which is due to the satisfaction of the resonance condition by which the phase velocity of excited Langmuir waves is comparable to the beam drift velocity. Therefore, almost 30 percent of its energy is converted to the electric and kinetic energies of the plasma during a short time scale. The decrease in kinetic energy of beams is associated with the increase of kinetic (electron and ion), electric, and, up to small extent, the magnetic energy in the system. To be sure about the conservation of energy, total energy has been monitored continuously, which we found it a constant. The decrease of beam energy is associated with flattening of the low energy side of the initial Maxwellian distribution of beam electrons. Following the complementation of the flattening process and the significant decrease of the beam kinetic energy, the condition for Landau damping is satisfied in the system, and as a result, a strong interaction between beam electrons and Langmuir waves takes place. As the beam loses its energy sufficiently, then the interaction between beam electrons and plasma waves almost stops and beam’s energy becomes almost constant.

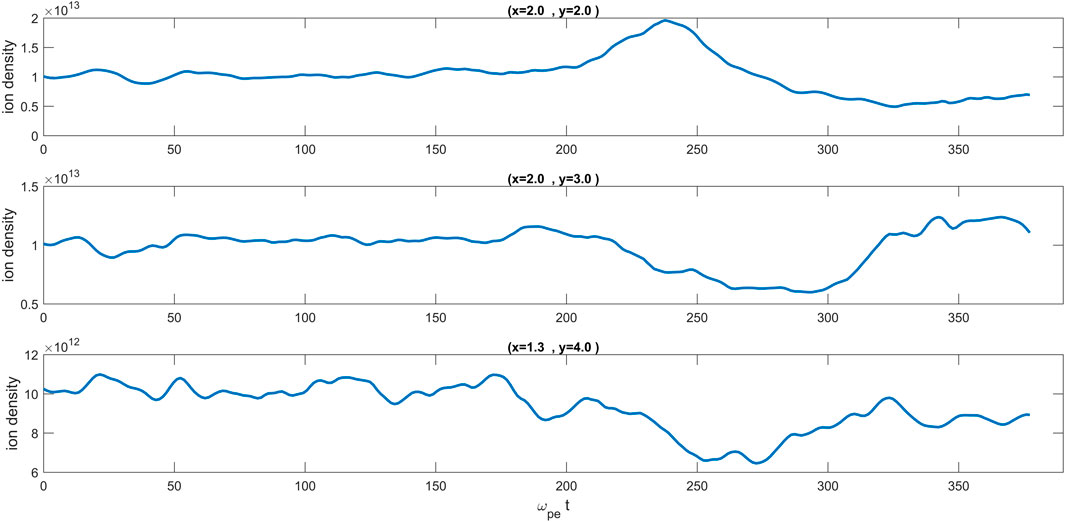
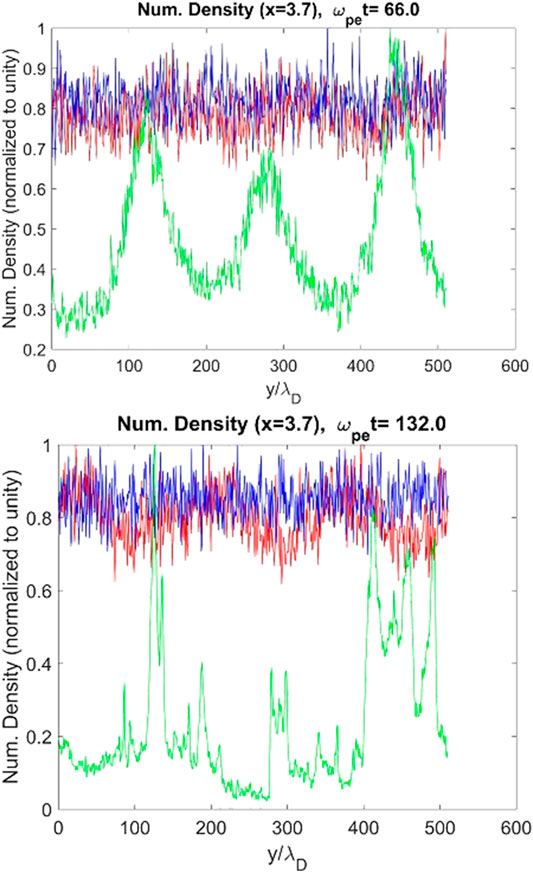
By sufficiently weakening the wave–particle interaction, when the amplitude of Langmuir waves is large enough, the ion acoustic waves are excited in the system with a growing amplitude. This is the phase in which the ion component of the plasma plays an important role in the dynamics of the system. Figure 3 presents the Figure 3 temporal variation of ion density at three locations. The time scale of the significant variation of ion density corresponds to the time scale of the electric energy decrease. The destruction of long-lived E_y structures is totally due to the excitation and growth of ion acoustic waves.

FIGURE 3

FIGURE 3. Temporal variation of the ion density at three locations.

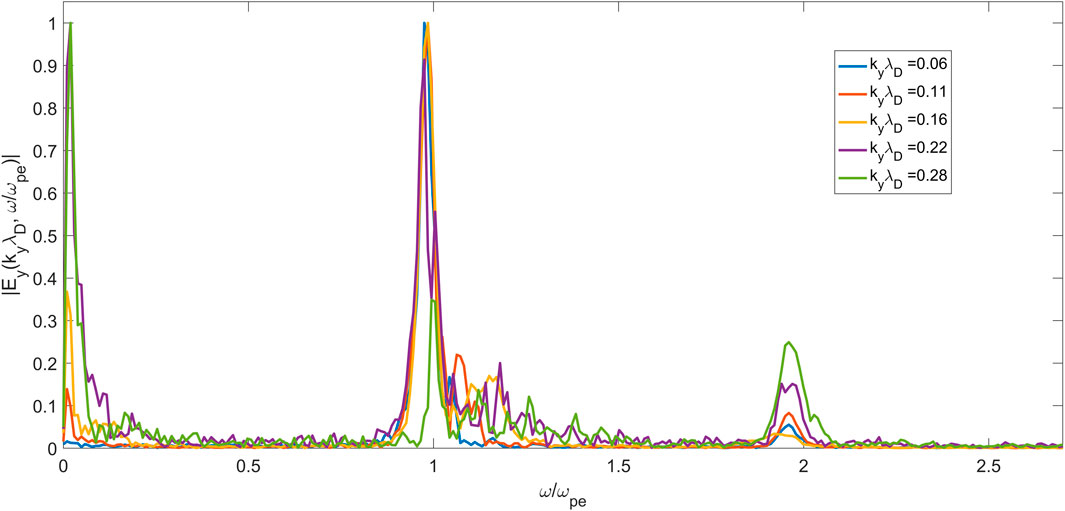
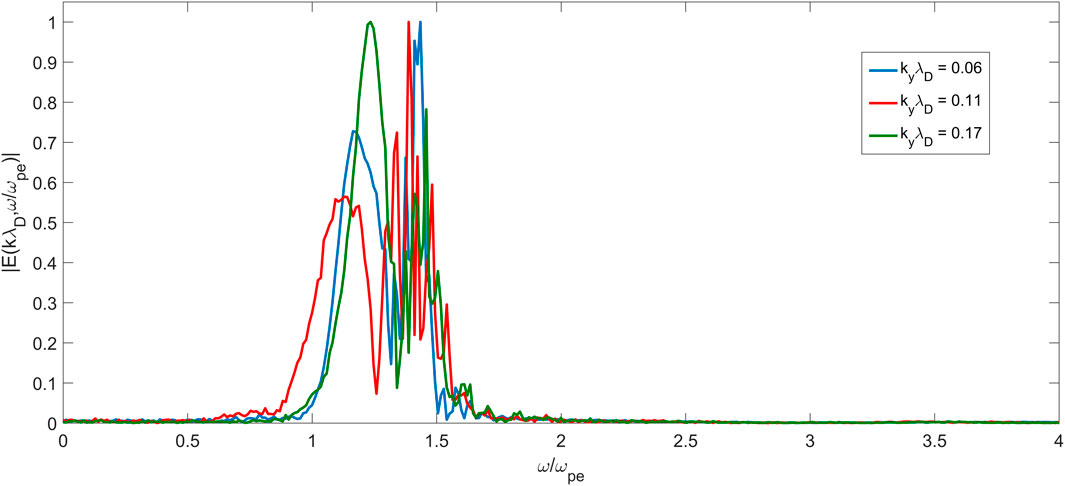
Figure 4 shows the dispersion diagram (ω/ω_pe, k_yλ_D) using the 2D spatial (x, y) and temporal fast Fourier transform (FFT) technique of E_y (x = 3.5, y). Figure 4 shows a strong excitation of Langmuir waves in the fundamental frequency, ω_pe, for k_yλ_D < 0.4 during 0 < ω_pet < 659. Moreover, the relatively weak second harmonic, 2ω_pe, of Langmuir waves has been excited. Also, the strong excitation of ion acoustic waves is observed at ω = ω_pi = 0.03ω_pe at 0.1 < k_yλ_D < 0.3. One can conclude that the generation of the second harmonic is basically caused by the presence of heavy ions, and therefore, in the absence of the ion component, second harmonics cannot be observed. This is the confirmation of the fact that the main mechanism for the generation of second harmonics is the scattering of Langmuir waves by ion acoustic waves. Figure 5 shows the dispersion diagram of E_y (x = 3.5, y) for the case of m_i/m_e = 1, for which there is no species heavier than electrons. As seen earlier, the second harmonic is not excited.

FIGURE 4

FIGURE 4. Dispersion diagram of E_y (x = 3.5, y) for m_i/m_e = 1,000 (color online).

FIGURE 5

FIGURE 5. Dispersion diagram of E_y (x = 3.5, y) for m_i/m_e = 1 (color online).

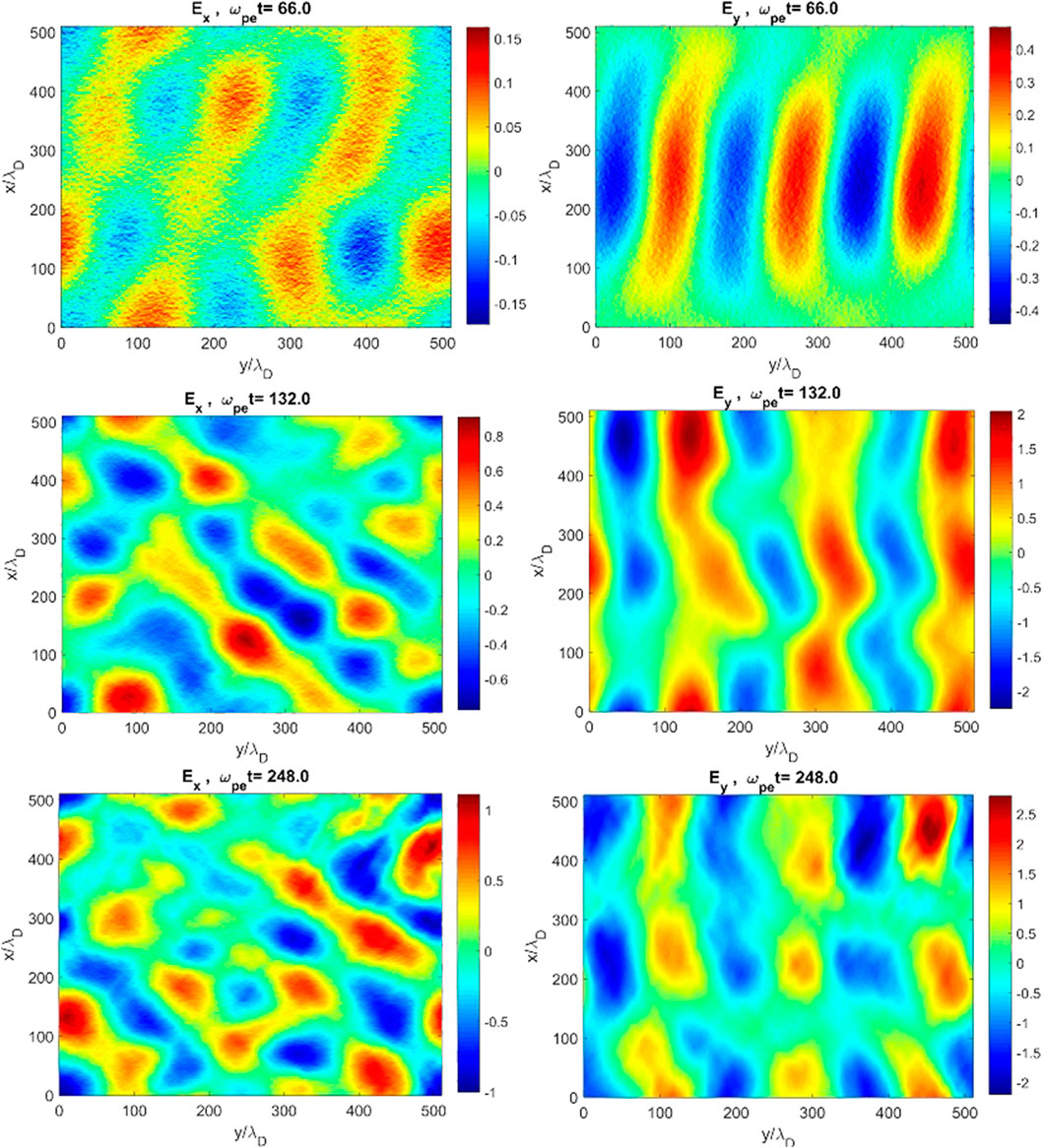
Furthermore, Figure 6 shows the E_x and E_y components of the electric structure with V_d,b = 0.35 C at times ω_pet = 66.0, 132.0, 248.0, which is normalized to m_eω_pev_th,e/e = 2.7 × 10³V/m. As seen, the non-uniform dipolar electric structures formed at earlier stages are gradually destructed as time instability develops. Also, the variation of three species number densities along the y direction is plotted in Figure 7 at times ω_pet = 66.0, 132.0. The yellow curve corresponds to the beam number density, which shows a strong variation along the “y” direction.

FIGURE 6

FIGURE 6. Plots of E_y and E_x in the xy plane at three different times (color online).

FIGURE 7

FIGURE 7. Variation of three species number densities along the y direction (color online).

Summary and Conclusion

We have performed 2D electromagnetic particle-in-cell simulations to investigate the second harmonic excitation in the electron beam–plasma instability. Temporal evolution of the kinetic energy of beam and electric energy for these cases shows that Langmuir waves in the electron plasma frequency are excited shortly. The amplitude of waves grows in the expense of beam energy decrement while the wave number moves toward smaller values. In other words, potential structures (or electron holes), being non-uniform in both directions, gradually merge to each other and form larger ones. In the quasilinear stage, the amplitude grows exponentially. Results show that parallel (with respect to the beam direction) cut of E_y is a bipolar structure. As the beam injects almost all of its free energy into the plasma, the electric energy saturates, and large amplitude solitons are stable for longer time durations. All stages of the instability are almost determined solely by the electron species as long as the IAWs are not excited.

As the amplitude of Langmuir wave solitons become sufficiently large, the IAWs are excited which in turn affects the effective scattering of Langmuir waves. Thus, the first step of the second harmonic generation is performed, and the coupling of forward- and backward-propagating Langmuir waves can produce the second harmonic. By performing spatial and temporal FFT of E_y, dispersion diagrams showed that the excitation of the second harmonic is obvious. Therefore, one can conclude that the presence of heavy ions results in the significant backscattering of the Langmuir waves, although very late. Consequently, the rate of the second step of wave–wave coupling is large enough to produce electromagnetic emission in the second harmonic. The presented results clearly confirm the proposed two-step wave–wave coupling mechanism for the generation of the second harmonic in the electron beam–plasma interaction. The prerequisite for a nonlinear wave–wave coupling is the existence of ion acoustic waves. We clearly showed that in the absence of ions, electromagnetic waves in the second harmonic are not generated. This finding is a direct verification of the three-wave coupling mechanism.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

MR: conducting the numerical simulations, visualizing the data, and preliminary writing. MS, MH, and AE: analyzing and interpretation of the data and writing and revising some parts of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are very thankful to the EPOCH code developing team for making the code accessible for our simulations.

References

Baumgärtel, K. (2013). A Linear Model for Amplitude Modulation of Langmuir Waves in Weak Electron-Beam Plasma Interaction. Ann. Geophys. 31, 31–38. doi:10.5194/angeo-31-31-2013

CrossRef Full Text | Google Scholar

Brown, J. C., Karlicky, M., MacKinnon, A. L., and Van den Oord, G. H. J. (1990). Beam Heating in Solar Flares - Electrons or Protons? ApJS 73, 343–348. doi:10.1086/191470

CrossRef Full Text | Google Scholar

Cairns, I. H., and Melrose, D. B. (1985). A Theory for the 2fpradiation Upstream of the Earth's bow Shock. J. Geophys. Res. 90, 6637–6640. doi:10.1029/ja090ia07p06637

CrossRef Full Text | Google Scholar

Gurnett, D. A., Hospodarsky, G. B., Kurth, W. S., Williams, D. J., and Bolton, S. J. (1993). Fine Structure of Langmuir Waves Produced by a Solar Electron Event. J. Geophys. Res. 98, 5631–5637. doi:10.1029/92ja02838

CrossRef Full Text | Google Scholar

Gurnett, D. A., Maggs, J. E., Gallagher, D. L., Kuhrt, W. S., and Scarf, F. L. (1981). Parametric Interaction and Spatial Collapse of Beam-Driven Langmuir Waves in the Solar Wind. J. Geophys. Res. 86, 833–8841. doi:10.1029/ja086ia10p08833

CrossRef Full Text | Google Scholar

Hospodarsky, G. B., Gurnett, D. A., Kurth, W. S., Kivelson, M. G., Strangeway, R. J., and Bolton, S. J. (1994). Fine Structure of Langmuir Waves Observed Upstream of the bow Shock at Venus. J. Geophys. Res. 99, 13363–13371. doi:10.1029/94ja00868

CrossRef Full Text | Google Scholar

Kojima, H., Furuya, H., Usui, H., and Matsumoto, H. (1997). Modulated Electron Plasma Waves Observed in the Tail Lobe: Geotail Waveform Observations. Geophys. Res. Lett. 24, 3049–3052. doi:10.1029/97gl03043

CrossRef Full Text | Google Scholar

Lacombe, C., Harvey, C. C., and Hoang, S. (1988). ISEE Observations of Radiation at Twice the Solar Wind Plasma Frequency. Ann. Geophys. 6 (1), 113–128.

Google Scholar

Li, B., Willes, A. J., Robinson, P. A., and Cairns, I. H. (2005). Second Harmonic Electromagnetic Emission via Beam-Driven Langmuir Waves. Phys. Plasmas 12, 012103. doi:10.1063/1.1812274

CrossRef Full Text | Google Scholar

Melrose, D. B. (1980). The Emission Mechanisms for Solar Radio Bursts. Space Sci. Rev. 26, 3–38. doi:10.1007/bf00212597

CrossRef Full Text | Google Scholar

Muschietti, L., Roth, I., and Ergun, R. E. (1996). On the Formation of Wave Packets in Planetary Foreshocks. J. Geophys. Res. 101, 15605–15613. doi:10.1029/96ja00926

CrossRef Full Text | Google Scholar

Omura, Y., Matsumoto, H., Miyake, T., and Kojima, H. (1996). Electron Beam Instabilities as Generation Mechanism of Electrostatic Solitary Waves in the Magnetotail. J. Geophys. Res. 101, 2685–2697. doi:10.1029/95ja03145

CrossRef Full Text | Google Scholar

Pritchett, P. L., and Dawson, J. M. (1983). Electromagnetic Radiation from Beam-Plasma Instabilities. Phys. Fluids 26, 1114. doi:10.1063/1.864222

CrossRef Full Text | Google Scholar

Sauer, K., Baumgärtel, K., Sydora, R., and Winterhalter, D. (2019). Parametric Decay of Beam‐Generated Langmuir Waves and Three‐Wave Interaction in Plateau Plasmas: Implications for Type III Radiation. J. Geophys. Res. Space Phys. 124, 68–89. doi:10.1029/2018ja025887

CrossRef Full Text | Google Scholar

Sigsbee, K., Kletznig, C. A., and Pickett, J. S. (2010). Characteristics of Langmuir Electric Field Waveforms and Power Spectra Exhibiting Nonlinear Behaviour in Erath’s Foreshock” J. Geophys. Res. 115, A10251. doi:10.1029/2009ja014948

CrossRef Full Text | Google Scholar

Silin, I., Sydora, R., and Sauer, K. (2007). Electron Beam-Plasma Interaction: Linear Theory and Vlasov-Poisson Simulations. Phys. Plasmas 14, 012106. doi:10.1063/1.2430518

CrossRef Full Text | Google Scholar

Soucek, J., Krasnoselskikh, V., Dudok deWit, T., Pickett, J., and Kletzing, C. (2005). Nonlinear Decay of Foreshock Langmuir Waves in the Presence of Plasma Inhomogeneities: Theory and Cluster Observations. J. Geophys. Res. 110, A08102. doi:10.1029/2004ja010977

CrossRef Full Text | Google Scholar

Stasiewicz, K., Holback, B., Krasnoselskikh, V., Boehm, M., Boström, R., and Kintner, P. M. (1996). Parametric Instabilities of Langmuir Waves Observed by Freja. J. Geophys. Res. 101, 21515–21525. doi:10.1029/96ja01747

CrossRef Full Text | Google Scholar

Umeda, T. (2007). Vlasov Simulation of Langmuir Wave Packets. Nonlin. Process. Geophys. 14, 671–679. doi:10.5194/npg-14-671-2007

CrossRef Full Text | Google Scholar

Willes, A. J., Robinson, P. A., and Melrose, D. B. (1996). Second Harmonic Electromagnetic Emission via Langmuir Wave Coalescence. Phys. Plasmas 3, 149–159. doi:10.1063/1.871841

CrossRef Full Text | Google Scholar

Yi, S., Rhee, T., Ryu, C-M., and Yoon, P. H. (2016). Simulation and Theory for Two-Dimensional Beam-Plasma Instability. Phys. Plasmas 17, 122318.

Google Scholar

Yi, S., Rhee, T., Ryu, C.-M., and Yoon, P. H. (2010). Simulation and Theory for Two-Dimensional Beam-Plasma Instability. Phys. Plasmas 17, 122318. doi:10.1063/1.3529359

CrossRef Full Text | Google Scholar