Coronal seismology by slow waves in non-adiabatic conditions

Slow magnetoacoustic waves represent an important tool for probing the solar coronal plasma. The majority of seismological methods with slow waves are based on a weakly non-adiabatic approach, which assumes the coronal energy transport has only weak effects on the wave dynamics. Despite it significantly simplifies the application of coronal seismology by slow waves, this assumption omits a number of important and confidently observed effects and thus puts strong limitations on the reliability of seismological estimations. We quantitatively assess the applicability of the weak thermal conduction theory to coronal seismology by slow waves. We numerically model the linear standing slow wave in a 1D coronal loop, with field-aligned thermal conduction κ_‖ as a free parameter and no restrictions on its efficiency. The time variations of the perturbed plasma parameters, obtained numerically with full conductivity, are treated as potential observables and analysed with the standard data processing techniques. The slow wave oscillation period is found to increase with κ_‖ by about 30%, indicating the corresponding modification in the effective wave speed, which is missing from the weak conduction theory. Phase shifts between plasma temperature and density perturbations are found to be well consistent with the approximate weakly conductive solution for all considered values of κ_‖. In contrast, the comparison of the numerically obtained ratio of temperature and density perturbation amplitudes with the weak theory revealed relative errors up to 30–40%. We use these parameters to measure the effective adiabatic index of the coronal plasma directly as the ratio of the effective slow wave speed to the standard sound speed and in the polytropic assumption, which is found to be justified in a weakly conductive regime only, with relative errors up to 14% otherwise. The damping of the initial perturbation is found to be of a non-exponential form during the first cycle of oscillation, which could be considered as an indirect signature of entropy waves in the corona, also not described by weak conduction theory. The performed analysis and obtained results offer a more robust scheme of coronal seismology by slow waves, with reasonable simplifications and without the loss of accuracy.

1 Introduction

The outermost layer of the solar atmosphere, the corona, consists of a fully ionised and strongly magnetised plasma, which is able to respond periodically or quasi-periodically to any impulsive perturbation. The interest in studying coronal waves and oscillations is connected with their possible role in the enigmatic coronal heating problem (Van Doorsselaere et al., 2020) and with a promising and sometimes unique opportunity to probe the coronal plasma parameters with the method of magnetohydrodynamic (MHD) seismology (Nakariakov and Kolotkov, 2020). In particular, fast magnetoacoustic wave modes, directly observed in the corona as e.g., kink oscillations of coronal loops or fast-propagating quasi-periodic wave trains, are extensively used for probing the coronal magnetic field strength and twist, density stratification, and cross-field fine structuring (see e.g., Nakariakov et al., 2021; Li et al., 2020; Shen et al., 2022, for the most recent comprehensive reviews). The slow mode of magnetoacoustic waves, which appear in standing (e.g., Wang et al., 2021), propagating (e.g., Banerjee et al., 2021), and sloshing (e.g., Nakariakov et al., 2019) forms, has in turn been found sensitive to both the magnetic and thermodynamic properties of the coronal plasma, which makes it a powerful seismological tool too.

The seismological applications of slow waves in the corona span from probing the absolute value of the magnetic field in active regions (e.g., Wang et al., 2007; Jess et al., 2016) and the magnetic field direction (Marsh et al., 2009) to estimating the effective adiabatic index of the coronal plasma (e.g., Van Doorsselaere et al., 2011; Wang et al., 2015; Krishna Prasad et al., 2018), its effective energy transport coefficients (Wang et al., 2015, 2018), multi-thermal nature of coronal loops (e.g., King et al., 2003; Krishna Prasad et al., 2017), and even properties of the coronal heating function (Reale et al., 2019; Kolotkov et al., 2020). Moreover, a similarity between the properties of the phenomenon of quasi-periodic pulsations, observed in solar and stellar flare lightcurves and attributed to the modulation of the flare emission by slow waves, allowed for revealing new solar-stellar analogies (Cho et al., 2016) and stimulated the development of the theory of slow waves in stellar coronal conditions (e.g., Reale et al., 2018; Lim et al., 2022).

The majority of seismological estimations with slow waves have been carried out under the assumption of weak non-adiabaticity of the coronal plasma, i.e., assuming the energy exchange and energy transfer processes (such as thermal conduction, compressive viscosity, optically thin radiation, etc.) are weak and slow in comparison with the oscillation period of a slow wave as its characteristic timescale. Under this assumption, the seismological analysis with slow waves gets substantially simplified. However, it cannot properly account for such important observable effects as rapid damping of slow waves, with the damping time being about the oscillation period (see e.g., Nakariakov et al., 2019, for the most recent multi-instrumental statistical survey), apparently linear scaling between the slow wave damping time and oscillation period (see e.g., Cho et al., 2016; Mandal et al., 2016), strong modification of a slow wave speed and effective adiabatic index of the corona (see e.g., Krishna Prasad et al., 2018, who detected the effective adiabatic index to vary from about 5/3 to 1), large phase shifts between the plasma temperature and density perturbed by slow waves (Kupriyanova et al., 2019), and yet undetected effects such as coupling of the slow and entropy wave modes (Zavershinskii et al., 2021). Furthermore, the transport coefficients of those non-adiabatic processes are often considered as free parameters in the corona, and their deviation from the classical values prescribed by Spitzer (1962) and Braginskii (1965) due to essentially dynamic and turbulent nature of the coronal plasma remains a subject to intensive studies. In particular, the parametric study of the dynamics of slow waves in coronal loops with suppressed field-aligned thermal conduction and of their diagnostic potential was performed recently by Wang and Ofman (2019). Likewise, the question of “anomalous transport” remains open in other astrophysical plasma environments too (see e.g., Muñoz et al., 2017, for the discussion of this topic in the Earth’s magnetospheric plasma context).

In this work, we delineate the applicability of a weak thermal conduction theory of slow waves to coronal seismology. For this, we numerically model the linear evolution of a standing slow oscillation in a hot coronal loop (alike those observed with the SUMER instrument onboard the SOHO spacecraft or in “hot” channels of SDO/AIA) with full conductivity, and compare the model outcomes to those obtained in a weakly conductive limit. In particular, we focus on the measurements of the phase shift and relative amplitude ratio between density and temperature perturbations and their use for probing the effective adiabatic index of the coronal plasma. The applicability of a polytropic assumption for estimating the effective adiabatic index is also discussed. The paper is structured as follows. In Section 2, we describe the numerical model and plasma loop parameters. In Section 3, we present the analysis of oscillatory variations of plasma loop density and temperature, caused by the standing slow wave, and the comparison of those in the numerical solution with full conductivity and in an approximate weakly conductive limit. The application of the obtained oscillation parameters to probing the effective adiabatic index of the coronal plasma, in the polytropic assumption and as ratio of the effective wave speed to the standard sound speed, is demonstrated in Section 4. The discussion of the obtained results and conclusions are summarised in Section 5.

2 Governing equations and modelling

We model the dynamics of a standing slow wave in a low-beta coronal plasma in the infinite magnetic field approximation (see Section 2.3 of Wang et al., 2021, and references therein), using the following set of linearised governing equations,

${\rho }_0\frac{\partial V_z}{\partial t}=-\frac{\partial p}{\partial z},(1)$

$\frac{\partial \rho }{\partial t}+{\rho }_0\frac{\partial V_z}{\partial z}=0,(2)$

$p=\frac{k_{\text{B}}}{m}\left({\rho }_{0}T+T_0\rho \right),(3)$

$\frac{\partial T}{\partial t}-\left(\gamma -1\right)\frac{T_0}{{\rho }_0}\frac{\partial \rho }{\partial t}=\frac{{\kappa }_{\Vert }}{{\rho }_0{C}_{\text{V}}}\frac{{\partial }^{2}T}{\partial z^2}.(4)$

In Eqs 1–4, the direction of the wave propagation along the z-axis is prescribed by the infinitely stiff (not perturbed by the wave) magnetic field; V_z, p, ρ, and T represent perturbations of the plasma velocity, pressure, density, and temperature, respectively; the subscripts “0” correspond to the values of those variables at t = 0; m, γ, and k_B are the mean particle mass, standard adiabatic index 5/3, and Boltzmann constant, respectively; C_V = (γ − 1)⁻¹ k_B/m is the standard specific heat capacity; and the coefficient of thermal conduction along the field κ_‖ is treated as a free parameter in this study. The effects of other non-ideal processes, such as compressive viscosity, optically thin radiation, heating, and the wave-induced misbalance between them, are omitted, with the field-aligned thermal conduction considered as the main wave damping mechanism (e.g., Ofman and Wang, 2002; De Moortel and Hood, 2003, 2004; Reale, 2016; Kolotkov et al., 2019).

The presence of a dissipative term on the right-hand side of energy Eq. 4 makes the model essentially non-adiabatic and may lead to the appearance of the phase shift Δφ between the temperature and density perturbations and modify the ratio of their instantaneous relative amplitudes A_T and A_ρ, respectively (see e.g., a series of works by Owen et al., 2009; Van Doorsselaere et al., 2011; Wang et al., 2015; Krishna Prasad et al., 2018; Prasad et al., 2022). In a weakly conductive limit, i.e., assuming the damping time by thermal conduction is much longer than the oscillation period and the wave speed remains equal to the standard sound speed $C_{\text{s}}=\sqrt{\gamma k_{\text{B}}{T}_0/m}$, the parameters Δφ and A_T/A_ρ have been previously derived as

$\tan \mathrm{\Delta }\phi \approx \frac{2\pi \left(\gamma -1\right){\kappa }_{\Vert }m}{k_{\text{B}}{C}_{\text{s}}^2{P}_0{\rho }_0},(5)$

$\frac{A_T}{A_{\rho }}\approx \left(\gamma -1\right)\cos \mathrm{\Delta }\phi ,(6)$

where P₀ = 2L/C_s is oscillation period in the ideal adiabatic case, with L being the loop length.

In this work, we solve Eqs 1–4 numerically in the mathematical environment Maple 2020.2, using the built-in function pdsolve. It implements a second order (in space and time) centred, implicit finite difference scheme¹, with timestep 0.02P₀ and spacestep 0.02λ (λ = 2L) providing the numerical accuracy up to 0.2% of the equilibrium plasma parameters during the first five oscillation cycles (estimated with the errorest keyword of the pdsolve command) for the initial perturbation amplitude of 10%. We do not apply the assumption of weak conductivity and vary the field-aligned thermal conduction coefficient κ_‖ from 0.01 to 10 of the standard Spitzer value ${\kappa }_{\text{Sp}}=10^{-11}{T}_0^{5/2}{\mathrm{W}\mathrm{m}}^{-1}{\mathrm{K}}^{-1}$. The considered interval of κ_‖ is motivated by previous observational findings. In particular, Wang et al. (2021) (see Section 8.1) demonstrated that to account for the coronal polytropic index measured by Van Doorsselaere et al. (2011), the thermal conductivity needs to be enhanced by an order of magnitude. The following values of the equilibrium plasma parameters are considered: ρ₀ = 3 × 10^–12 kg m⁻³ and T₀ = 6.3 MK (both uniform along the loop), L = 180 Mm, m = 0.6 × 1.67 × 10^–27 kg, typical for coronal loops hosting SUMER oscillations. We excite the fundamental harmonic of a standing slow wave by perturbing the plasma velocity with a harmonic function with maximum at z = 0 and the wavelength equal to double the loop length, λ = 2L, and apply rigid-wall boundary conditions at z = ±0.25λ mimicking the effective slow wave reflection from the transition region and dense chromosphere (e.g., Nakariakov et al., 2004). The form of the initial perturbation and an example of time variations of the plasma velocity, density, and temperature, obtained numerically for e.g. κ_‖ = 10κ_Sp, are shown in Figure 1. All oscillatory signals used in the further analysis are taken at z = 0.1λ.

FIGURE 1

FIGURE 1. Left: The form of the initial perturbation of the plasma velocity, V_z0=0.1C_s cos(2πz/λ), applied to the loop model described in Section 2. Right: Variations of the slow wave-perturbed plasma velocity, density, and temperature in red, blue, and green, measured at z =0.1λ and for κ_‖=10κ_Sp, normalised to C_s, ρ₀, and T₀, respectively. $C_{\text{s}}=\sqrt{\gamma k_{\text{B}}{T}_0/m}$ is the adiabatic sound speed; λ is the wavelength (prescribed by the loop length, L, as λ =2L); P₀ is the adiabatic acoustic oscillation period, 2L/C_s. The grey lines illustrate the numerical error estimate for the velocity perturbation.

3 Temperature/density phase shifts and amplitudes

We begin the analysis of the numerically modelled standing slow wave with obtaining the dependence of the oscillation period P on the thermal conduction coefficient κ_‖. It is estimated through the fast Fourier transform applied to the plasma velocity perturbations for several different values of κ_‖ (see e.g., the red line in Figure 1, right panel) and is presented in the left panel of Figure 2. As one can see, the oscillation period increases by about 30% with κ_‖, from the ideal adiabatic value P₀ determined by the standard sound speed C_s, to a new value in the isothermal regime (achieved for high κ_‖), determined by the isothermal sound speed $C_{\text{s}}/\sqrt{\gamma }$. Throughout this work, the loop length L (and therefore the wavelength λ) is kept constant. In other words, in the strongly conductive regime, the effective slow wave speed gets significantly modified, which leads to the corresponding modification in the wave travel time along the loop, i.e., the oscillation period. This empirical result is consistent with previous analytical estimations by e.g., Duckenfield et al. (2021).

FIGURE 2

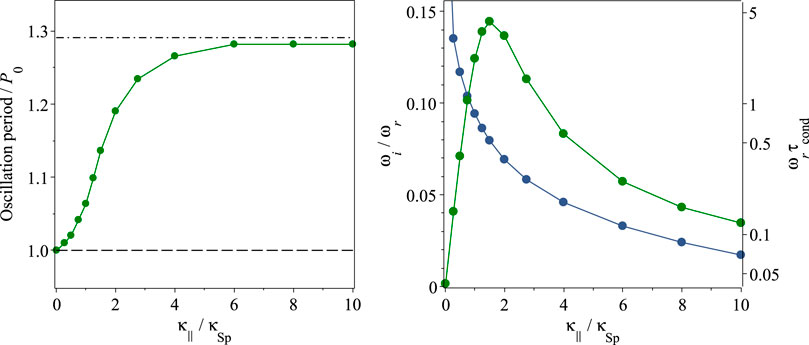
FIGURE 2. Left: Slow-wave oscillation period, P, estimated empirically via the fast Fourier transform of the numerical solution for the plasma velocity perturbation, vs. the coefficient of the field-aligned thermal conduction normalised to the standard Spitzer value. The horizontal dashed and dot-dashed lines show the period values in the ideal adiabatic and isothermal limits, obtained with the standard adiabatic and isothermal sound speeds, C_s and $C_{\text{s}}/\sqrt{\gamma }$, respectively. Right: Dependence of the ratio of the imaginary part ω_i =1/τ_D to the real part ω_r =2π/P of the slow-wave angular frequency ω on the field-aligned thermal conduction coefficient (green), with τ_D being the oscillation exponential damping time estimated empirically from the numerical solution. The dark blue line in the right panel shows the dimensionless parameter ω_rτ_cond, with ${\tau }_{\text{cond}}={\rho }_0{C}_{\text{V}}{\lambda }^2/{\kappa }_{\Vert }$ being the characteristic time scale of thermal conduction.

The phase shifts between density and temperature perturbations are estimated from our numerical solution through the cross-correlation analysis. More specifically, we obtain the time lag Δt for which the cross-correlation between density and temperature oscillations is the highest. With this, the phase shift Δφ is obtained as Δφ = (Δt/P) × 360° for each considered value of κ_‖, using the dependence of the oscillation period P on κ_‖ obtained above. Thus, the dependence of Δφ on κ_‖, revealed empirically, is shown in the left panel of Figure 3 in red. It is seen to vary from 0° in the ideal adiabatic case to about 80° in the strongly conductive regime with high κ_‖ (cf. Prasad et al., 2022).

FIGURE 3

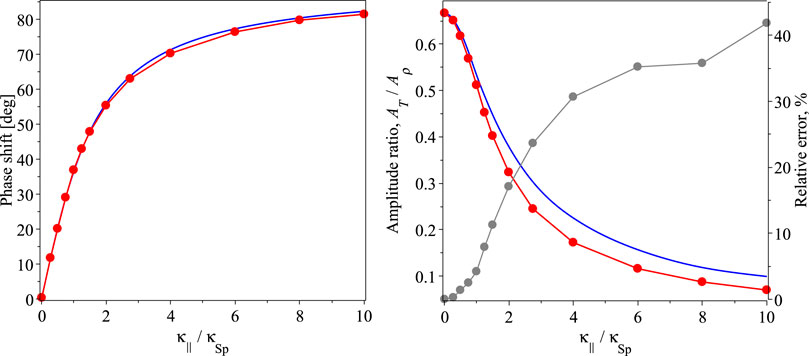
FIGURE 3. The phase shift (left) and relative amplitude ratio (right) between plasma temperature and density perturbations by the standing slow wave, obtained from the analysis of the numerical solution of Eqs 1–4 with full thermal conductivity as described in Section 3 (in red) and from the approximate analytical solutions Eqs 5–6 in a weakly conductive limit (in blue). The grey curve in the right panel shows the relative error between the estimations of the temperature and density relative amplitude ratio, shown in red and blue.

For estimating the ratio between temperature and density perturbation amplitudes, we obtain the instantaneous amplitudes A_T(t) and A_ρ(t) as oscillation envelopes by exponential fitting and with the use of the Hilbert transform (see Reale et al., 2019, for apparently the first use of the Hilbert transform for coronal seismology by slow waves). The edge effects of the Hilbert transform are mitigated by mirroring the signals with respect to the vertical axis and smoothing the resulting oscillation envelopes over a half of the oscillation period. The examples of A_T and A_ρ for κ_‖ = κ_Sp, obtained with the Hilbert transform and their best-fits by decaying exponential functions, are shown in the left panel of Figure 4. It shows, in particular, that actual temperature and density perturbation amplitudes do not obey the exponential law during the first cycle of oscillation, which we attribute to the simultaneous development and rapid decay of the entropy mode (Murawski et al., 2011; Zavershinskii et al., 2021). Thus, associating this mismatch with a possible signature of the slow wave coupling with entropy waves, the ratio A_T/A_ρ in slow waves is estimated via the exponentially decaying instantaneous amplitudes obtained by fitting (the right panel of Figure 4). More specifically, the red dashed lines in the right panel of Figure 4 show exponentially decaying A_T(t) vs. exponentially decaying A_ρ(t) for three different values of κ_‖. As the slow wave damping rate is the same in perturbations of all plasma parameters, the ratio of exponentially decaying A_T(t) and A_ρ(t) is independent of time. In other words, it may be characterised by the y-intercept of the red dashed lines shown in the right panel of Figure 4 (indeed, if A_T = const × A_ρ, then log(A_T) = log(const) + log(A_ρ)). The dependence of the obtained values of A_T/A_ρ on κ_‖ is shown in the right panel of Figure 3 in red. It varies from 2/3 (≡ γ − 1) in the ideal adiabatic regime to almost zero in the isothermal regime for high κ_‖, in which temperature gradients are effectively smoothed out by thermal conduction. We also note that the use of a non-exponential damping envelope may lead to underestimated values of A_T/A_ρ in slow waves.

FIGURE 4

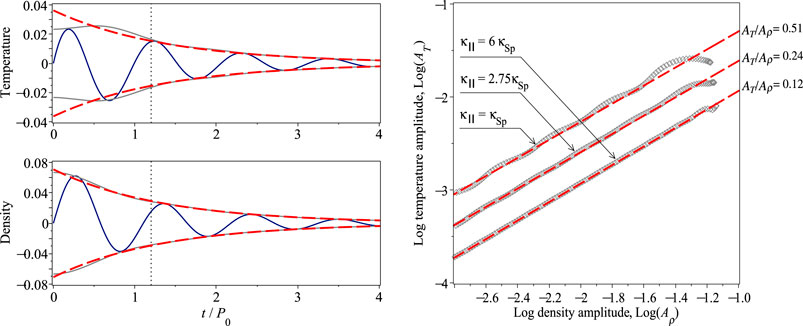
FIGURE 4. The time profiles of the temperature and density perturbations by a standing slow wave, obtained numerically from Eqs 1–4 at z =0.1λ, for κ_‖= κ_Sp, and normalised to T₀ and ρ₀, respectively (left). The envelopes of the temperature and density perturbations are obtained with the Hilbert transform (grey solid) and by exponential fitting (red dashed). The vertical dotted lines in the left panels indicate the apparent transition time from a non-exponential to exponential damping. The right panel shows examples of the amplitude ratios for several values of κ_‖ (shown in the inlet), estimated with the Hilbert transform (grey diamonds) and by exponential fitting (red dashed). Mind the logarithmic scale in the right panel.

In addition, this analysis allows us to estimate the conductive damping rate of standing slow waves and the characteristic thermal conduction time scale ${\tau }_{\text{cond}}={\rho }_0{C}_{\text{V}}{\lambda }^2/{\kappa }_{\Vert }$ for various values of the conduction coefficient κ_‖ (the right panel in Figure 2). For this, we consider the ratio of the imaginary part of the angular oscillation frequency ω_i (estimated as the reciprocal of the exponential damping time) to the real part ω_r = 2π/P. The obtained non-monotonic behaviour of ω_i/ω_r is consistent with the previous analytical estimations by e.g., De Moortel and Hood (2003), with the highest value of about 0.15, detected for κ_‖ ≈ 2κ_Sp, being consistent with the observed rapid damping of SUMER oscillations with quality factors (i.e., ratio of the oscillation damping time to period) of about unity (e.g., Nakariakov et al., 2019; Wang et al., 2021). The right panel of Figure 2 also shows the dimensionless parameter ω_rτ_cond that can be used for a quantitative discrimination between weak and strong conductive limits. Thus, ω_rτ_cond ≫ 1 and ω_i/ω_r ∝ 1/ω_rτ_cond in the weak limit, and ω_rτ_cond ≪ 1 and ω_i/ω_r ≈ ω_rτ_cond in the strong limit (see e.g., Krishna Prasad et al., 2014; Duckenfield et al., 2021). For κ_‖ ≈ 2κ_Sp consistent with observations, ω_rτ_cond is about 1 by an order of magnitude, so that neither of those limits is fully justified.

We now compare the dependences of Δφ and A_T/A_ρ on κ_‖ obtained from the analysis of our numerical solution to those prescribed by approximate solutions Eqs 5, 6, derived in a weakly conductive limit (see the red and blue lines in Figure 3). For both Δφ and A_T/A_ρ, the approximate and numerical solutions seem to perfectly agree for low values of κ_‖, i.e., in the weakly conductive regime. For higher κ_‖, the phase shifts Δφ, estimated in the fully conductive and weakly conductive regimes, remain well consistent with each other, with a relative error being below a few percent which is practically indistinguishable in observations. In contrast, the amplitude ratio A_T/A_ρ is found to differ significantly from its weakly conductive estimation for κ_‖ ≳ κ_Sp. The relative error of this offset is seen to be about 5% for κ_‖ = κ_Sp and reaches 30–40% for higher κ_‖.

4 Effective adiabatic index

In this section, we demonstrate the application of the obtained wave parameters to probing the effective adiabatic index of the coronal plasma, γ_eff, and assess the suitability of a commonly used polytropic assumption for it.

Following e.g., Wang et al. (2018) and Zavershinskii et al. (2019), we define γ_eff as a measure of the deviation of the observed phase speed V_p of slow waves affected by non-adiabatic effects (the field-aligned thermal conduction in our model) from the standard sound speed C_s, i.e.

${\gamma }_{\text{eff}}=\gamma {\left(\frac{V_{\text{p}}}{C_{\text{s}}}\right)}^2.(7)$

In the solar corona, the standard sound speed can be estimated as $C_{\text{s}}[\mathrm{k}\mathrm{m}/\mathrm{s}]\approx 152\sqrt{T_0[\mathrm{M}\mathrm{K}]}$. On the other hand, as the wavelength of the discussed standing slow wave is prescribed by the loop length and thus remains constant, we can use the dependence of the oscillation period P on κ_‖ obtained in Section 3 (see Figure 2) as a proxy (observable parameter) of the slow wave phase speed V_p. With this, the definition of γ_eff Eq. 7 can be re-written as

${\gamma }_{\text{eff}}=\gamma {\left(\frac{P_0}{P}\right)}^2,(8)$

with P₀ being the slow wave oscillation period in the ideal adiabatic case. The dependence of γ_eff estimated by Eq. 8 on the field-aligned thermal conduction coefficient κ_‖ is shown in the left panel of Figure 5 in red, using the dependence of the oscillation period P on κ_‖ shown in Figure 2. As expected, the obtained values of γ_eff decrease with κ_‖ from 5/3 to 1 in the ideal adiabatic and isothermal regimes, respectively.

FIGURE 5

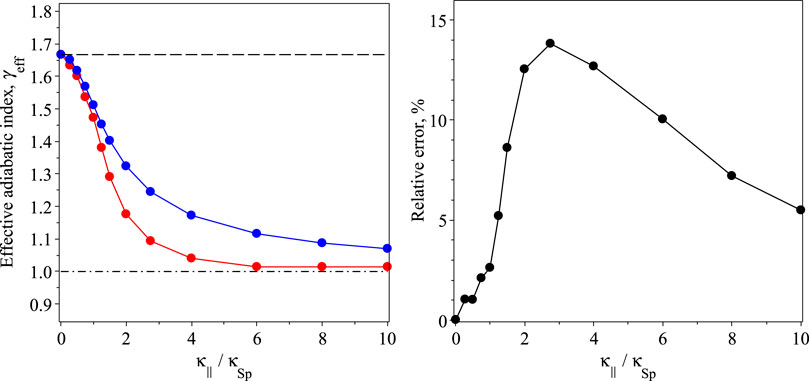
FIGURE 5. The dependence of the effective adiabatic index γ_eff of the coronal plasma on the field-aligned thermal conduction coefficient κ_‖ (left), estimated numerically as ratio of the effective slow wave speed to the standard sound speed (red), see Eqs 7, 8, and under the polytropic assumption (blue) with Eq. 9. The horizontal dashed and dot-dashed lines indicate the values of γ_eff in the ideal adiabatic case (5/3) for low κ_‖ and in the isothermal regime (1) for high κ_‖, respectively. The right panel shows the relative error between the estimations of γ_eff, shown in red and blue in the left panel.

In the polytropic assumption, i.e. assuming the plasma density and pressure perturbations to be connected through a power-law as $p\propto {\rho }^{{\gamma }_{\text{eff}}}$, γ_eff can be estimated through the ratio of the instantaneous relative amplitudes A_T and A_ρ of temperature and density perturbations (Van Doorsselaere et al., 2011) as

${\gamma }_{\text{eff}}\approx \frac{A_T}{A_{\rho }}+1.(9)$

Despite being not strictly consistent with the observed non-zero phase difference between temperature and density perturbations, this assumption is widely used for probing the effective adiabatic index of the corona with both standing (e.g., Wang et al., 2015; Reale et al., 2019) and propagating (e.g., Van Doorsselaere et al., 2011; Krishna Prasad et al., 2018) slow waves.

The dependence of γ_eff Eq. 9 on κ_‖, using A_T/A_ρ estimated empirically in Section 3 (the red line in Figure 3, right panel), is shown in the left panel on Figure 5 in blue. Its comparison with γ_eff Eq. 8, as ratio of the effective wave speed to the standard sound speed (i.e., ratio of the slow wave period in adiabatic case to the observed period), justifies the use of the polytropic assumption in a weakly conductive regime (for κ_‖ ≲ κ_Sp and γ_eff being between approximately 1.5 and 5/3) and reveals the relative errors (the right panel of Figure 5) comparable to those detected in observations for κ_‖ > κ_Sp, that reach the maximum of 14% for κ_‖ ≈ 3κ_Sp. Even in the isothermal regime with high κ_‖, the mismatch between γ_eff Eq. 8 and its polytropic approximation Eq. 9 remains above 5% (e.g., for κ_‖ = 6κ_Sp, γ_eff is about 1.0 by Eq. 8 and is about 1.1 by Eq. 9).

5 Discussion and conclusion

The applicability of a weakly non-adiabatic because of finite thermal conduction along the field and polytropic assumptions to coronal seismology with slow waves has been studied in this work. We numerically modelled a 1D evolution of the fundamental harmonic of a standing slow wave in a strongly magnetised coronal plasma loop, with the field-aligned thermal conduction as the dominant wave damping mechanism and the conduction coefficient κ_‖ as a free parameter. In the model, no restrictions on the effectiveness of thermal conduction were imposed. The time profiles of the plasma velocity, density, and temperature perturbations have been treated as effective observables to which the standard data analysis techniques, such as the fast Fourier transform and cross-correlation analysis, and more advanced Hilbert transform, were applied. The outcomes of this analysis have been compared to the approximate analytical solutions. The main results of this work can be summarised as:

• The finite thermal conductivity along the field modifies the effective speed of slow waves, which leads to the modification of the observed oscillation period by up to 30% from the value estimated in the ideal regime and used in the weakly conductive limit. Accounting for additional non-adiabatic effects, such as e.g., the wave-induced misbalance between coronal heating and cooling processes (Kolotkov et al., 2021), may make this modification even stronger.

• The dependences of the phase shift Δφ between the loop’s temperature and density perturbations on the thermal conductivity κ_‖, estimated in the strongly and weakly conductive cases, are well consistent with each other for both low and high values of κ_‖. The obtained ratio of temperature and density relative amplitudes A_T/A_ρ, in contrast, agrees with the weak conduction theory for κ_‖ ≲ κ_Sp only. For higher κ_‖, the mismatch can reach up to 30–40%, which clearly requires accounting for higher-order non-adiabatic effects.

• From the practical point of view, the previous finding allows one to reduce the analytical solutions for Δφ and A_T/A_ρ obtained with full conductivity (see e.g., Eqs. (51) and (52) in Wang et al., 2021), which are essentially coupled through two unknowns κ_‖ and γ_eff and therefore cannot be used independently, to Eq. 5 for Δφ and

$\frac{A_T}{A_{\rho }}=\frac{\left(\gamma -1\right)\cos \mathrm{\Delta }\phi }{1-2\pi \gamma d\chi \left(\gamma /{\gamma }_{\text{eff}}\right)},(10)$

where $d\equiv (\gamma -1){\kappa }_{\Vert }m/\gamma k_{\text{B}}{C}_{\text{s}}^2{P}_0{\rho }_0$, χ ≡ ω_i/ω_r, and γ_eff is given by Eq. 7. As such, Eqs 5 and 10 are de-coupled with respect to κ_‖ and γ_eff (the right-hand side of Eq. 5 has κ_‖ only), which would significantly simplify their future seismological applications without the loss of accuracy.

• The polytropic assumption Eq. 9 can be used for probing the effective adiabatic index of the coronal plasma, γ_eff, in the weakly conductive regime only, i.e., with κ_‖ ≲ κ_Sp and small deviations of γ_eff from the adiabatic value 5/3. For κ_‖ > κ_Sp or if γ_eff is deemed to differ from 5/3 by more than 10%, it should be estimated either as a ratio of the observed slow wave oscillation period (phase speed) to the period expected in the ideal adiabatic case (standard sound speed) or via the ratio of relative amplitudes A_T/A_ρ using Eq. 10. Otherwise, the relative errors may reach up to 14% (cf. 7% uncertainty in the estimation of γ_eff, detected by Krishna Prasad et al., 2018, for example).

• As an additional side result of this work, a non-exponential damping of slow waves during approximately the first cycle of oscillation was detected with the use of the Hilbert transform. Similarly to the transition time from a Gaussian to exponential damping of coronal kink oscillations by mode coupling with torsional Alfvén waves (e.g., Pascoe et al., 2017), the revealed non-exponential damping of slow waves can be used as an indirect signature of the entropy mode evolution with yet unexploited seismological potential. In particular, this non-exponential damping of slow waves is seen to be more pronounced in the perturbation of plasma temperature and for lower values of κ_‖ in our analysis, the reason for which is to be understood.

This work establishes an important ground for the application of the method of coronal seismology by slow waves in strongly non-adiabatic conditions. Moreover, the performed analysis can be readily generalised for additional non-adiabatic effects, such as compressive viscosity, optically thin radiation and enigmatic coronal heating, and used for validation of the corresponding theories (e.g., Prasad et al., 2022) without the need to deploy full-scale viscous 3D MHD simulations (e.g., Ofman and Wang, 2022) or dedicated MHD spectral codes (e.g., Claes et al., 2020).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DK is the sole author and is responsible for the entire content of this work.

Funding

The work was supported by the STFC Consolidated Grant ST/T000252/1.

Acknowledgments

The author is grateful to Dr Dmitrii Zavershinskii, Prof Valery Nakariakov, and members of the International Online Team “Effects of Coronal Heating/Cooling on MHD Waves” for inspiring discussions and comments.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://www.maplesoft.com/support/help/Maple/view.aspx?path=pdsolve/numeric.

References

Banerjee, D., Krishna Prasad, S., Pant, V., McLaughlin, J. A., Antolin, P., Magyar, N., et al. (2021). Magnetohydrodynamic waves in open coronal structures. Space Sci. Rev. 217, 76. doi:10.1007/s11214-021-00849-0

CrossRef Full Text | Google Scholar

Braginskii, S. I. (1965). Transport processes in a plasma. Rev. Plasma Phys. 1, 205.

Google Scholar

Cho, I. H., Cho, K. S., Nakariakov, V. M., Kim, S., and Kumar, P. (2016). Comparison of damped oscillations in solar and stellar X-ray flares. Astrophys. J. 830, 110. doi:10.3847/0004-637X/830/2/110

CrossRef Full Text | Google Scholar

Claes, N., De Jonghe, J., and Keppens, R. (2020). Legolas: A modern tool for magnetohydrodynamic spectroscopy. Astrophys. J. Suppl. Ser. 251, 25. doi:10.3847/1538-4365/abc5c4

CrossRef Full Text | Google Scholar

De Moortel, I., and Hood, A. W. (2003). The damping of slow MHD waves in solar coronal magnetic fields. Astron. Astrophys. 408, 755–765. doi:10.1051/0004-6361:20030984

CrossRef Full Text | Google Scholar

De Moortel, I., and Hood, A. W. (2004). The damping of slow MHD waves in solar coronal magnetic fields. II. The effect of gravitational stratification and field line divergence. Astron. Astrophys. 415, 705–715. doi:10.1051/0004-6361:20034233

CrossRef Full Text | Google Scholar

Duckenfield, T. J., Kolotkov, D. Y., and Nakariakov, V. M. (2021). The effect of the magnetic field on the damping of slow waves in the solar corona. Astron. Astrophys. 646, A155. doi:10.1051/0004-6361/202039791

CrossRef Full Text | Google Scholar

Jess, D. B., Reznikova, V. E., Ryans, R. S. I., Christian, D. J., Keys, P. H., Mathioudakis, M., et al. (2016). Solar coronal magnetic fields derived using seismology techniques applied to omnipresent sunspot waves. Nat. Phys. 12, 179–185. doi:10.1038/nphys3544

CrossRef Full Text | Google Scholar

King, D. B., Nakariakov, V. M., Deluca, E. E., Golub, L., and McClements, K. G. (2003). Propagating EUV disturbances in the Solar corona: Two-wavelength observations. Astron. Astrophys. 404, L1–L4. doi:10.1051/0004-6361:20030763

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Duckenfield, T. J., and Nakariakov, V. M. (2020). Seismological constraints on the solar coronal heating function. Astron. Astrophys. 644, A33. doi:10.1051/0004-6361/202039095

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Nakariakov, V. M., and Zavershinskii, D. I. (2019). Damping of slow magnetoacoustic oscillations by the misbalance between heating and cooling processes in the solar corona. Astron. Astrophys. 628, A133. doi:10.1051/0004-6361/201936072

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Zavershinskii, D. I., and Nakariakov, V. M. (2021). The solar corona as an active medium for magnetoacoustic waves. Plasma Phys. control. Fusion 63, 124008. doi:10.1088/1361-6587/ac36a5

CrossRef Full Text | Google Scholar

Krishna Prasad, S., Banerjee, D., and Van Doorsselaere, T. (2014). Frequency-dependent damping in propagating slow magneto-acoustic waves. Astrophys. J. 789, 118. doi:10.1088/0004-637X/789/2/118

CrossRef Full Text | Google Scholar

Krishna Prasad, S., Jess, D. B., Klimchuk, J. A., and Banerjee, D. (2017). Unravelling the components of a multi-thermal coronal loop using magnetohydrodynamic seismology. Astrophys. J. 834, 103. doi:10.3847/1538-4357/834/2/103

CrossRef Full Text | Google Scholar

Krishna Prasad, S., Raes, J. O., Van Doorsselaere, T., Magyar, N., and Jess, D. B. (2018). The polytropic index of solar coronal plasma in sunspot fan loops and its temperature dependence. Astrophys. J. 868, 149. doi:10.3847/1538-4357/aae9f5

CrossRef Full Text | Google Scholar

Kupriyanova, E. G., Kashapova, L. K., Van Doorsselaere, T., Chowdhury, P., Srivastava, A. K., and Moon, Y.-J. (2019). Quasi-periodic pulsations in a solar flare with an unusual phase shift. Mon. Not. R. Astron. Soc. 483, 5499–5507. doi:10.1093/mnras/sty3480

CrossRef Full Text | Google Scholar

Li, B., Antolin, P., Guo, M. Z., Kuznetsov, A. A., Pascoe, D. J., Van Doorsselaere, T., et al. (2020). Magnetohydrodynamic fast sausage waves in the solar corona. Space Sci. Rev. 216, 136. doi:10.1007/s11214-020-00761-z

CrossRef Full Text | Google Scholar

Lim, D., Nakariakov, V. M., and Moon, Y.-J. (2022). Slow magnetoacoustic oscillations in stellar coronal loops. Astrophys. J. 931, 63. doi:10.3847/1538-4357/ac69d8

CrossRef Full Text | Google Scholar

Mandal, S., Magyar, N., Yuan, D., Van Doorsselaere, T., and Banerjee, D. (2016). Forward modeling of propagating slow waves in coronal loops and their frequency-dependent damping. Astrophys. J. 820, 13. doi:10.3847/0004-637X/820/1/13

CrossRef Full Text | Google Scholar

Marsh, M. S., Walsh, R. W., and Plunkett, S. (2009). Three-dimensional coronal slow modes: Toward three-dimensional seismology. Astrophys. J. 697, 1674–1680. doi:10.1088/0004-637X/697/2/1674

CrossRef Full Text | Google Scholar

Muñoz, P. A., Büchner, J., and Kilian, P. (2017). Turbulent transport in 2D collisionless guide field reconnection. Phys. Plasmas 24, 022104. doi:10.1063/1.4975086

CrossRef Full Text | Google Scholar

Murawski, K., Zaqarashvili, T. V., and Nakariakov, V. M. (2011). Entropy mode at a magnetic null point as a possible tool for indirect observation of nanoflares in the solar corona. Astron. Astrophys. 533, A18. doi:10.1051/0004-6361/201116942

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Anfinogentov, S. A., Antolin, P., Jain, R., Kolotkov, D. Y., Kupriyanova, E. G., et al. (2021). Kink oscillations of coronal loops. Space Sci. Rev. 217, 73. doi:10.1007/s11214-021-00847-2

CrossRef Full Text | Google Scholar

Nakariakov, V. M., and Kolotkov, D. Y. (2020). Magnetohydrodynamic waves in the solar corona. Annu. Rev. Astron. Astrophys. 58, 441–481. doi:10.1146/annurev-astro-032320-042940

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Kosak, M. K., Kolotkov, D. Y., Anfinogentov, S. A., Kumar, P., and Moon, Y. J. (2019). Properties of slow magnetoacoustic oscillations of solar coronal loops by multi-instrumental observations. Astrophys. J. 874, L1. doi:10.3847/2041-8213/ab0c9f

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Tsiklauri, D., Kelly, A., Arber, T. D., and Aschwanden, M. J. (2004). Acoustic oscillations in solar and stellar flaring loops. Astron. Astrophys. 414, L25–L28. doi:10.1051/0004-6361:20031738

CrossRef Full Text | Google Scholar

Ofman, L., and Wang, T. (2022). Excitation and damping of slow magnetosonic waves in flaring hot coronal loops: Effects of compressive viscosity. Astrophys. J. 926, 64. doi:10.3847/1538-4357/ac4090

CrossRef Full Text | Google Scholar

Ofman, L., and Wang, T. (2002). Hot coronal loop oscillations observed by SUMER: Slow magnetosonic wave damping by thermal conduction. Astrophys. J. 580, L85–L88. doi:10.1086/345548

CrossRef Full Text | Google Scholar

Owen, N. R., De Moortel, I., and Hood, A. W. (2009). Forward modelling to determine the observational signatures of propagating slow waves for TRACE, SoHO/CDS, and Hinode/EIS. Astron. Astrophys. 494, 339–353. doi:10.1051/0004-6361:200810828

CrossRef Full Text | Google Scholar

Pascoe, D. J., Anfinogentov, S., Nisticò, G., Goddard, C. R., and Nakariakov, V. M. (2017). Coronal loop seismology using damping of standing kink oscillations by mode coupling. II. additional physical effects and Bayesian analysis. Astron. Astrophys. 600, A78. doi:10.1051/0004-6361/201629702

CrossRef Full Text | Google Scholar

Prasad, A., Srivastava, A. K., Wang, T., and Sangal, K. (2022). Role of non-ideal dissipation with heating-cooling misbalance on the phase shifts of standing slow magnetohydrodynamic waves. Sol. Phys. 297, 5. doi:10.1007/s11207-021-01940-z

CrossRef Full Text | Google Scholar

Reale, F., Lopez-Santiago, J., Flaccomio, E., Petralia, A., and Sciortino, S. (2018). X-ray flare oscillations track plasma sloshing along star-disk magnetic tubes in the orion star-forming region. Astrophys. J. 856, 51. doi:10.3847/1538-4357/aaaf1f

CrossRef Full Text | Google Scholar

Reale, F. (2016). Plasma sloshing in pulse-heated solar and stellar coronal loops. Astrophys. J. 826, L20. doi:10.3847/2041-8205/826/2/L20

CrossRef Full Text | Google Scholar

Reale, F., Testa, P., Petralia, A., and Kolotkov, D. Y. (2019). Large-amplitude quasiperiodic pulsations as evidence of impulsive heating in hot transient loop systems detected in the EUV with SDO/AIA. Astrophys. J. 884, 131. doi:10.3847/1538-4357/ab4270

CrossRef Full Text | Google Scholar

Shen, Y., Zhou, X., Duan, Y., Tang, Z., Zhou, C., and Tan, S. (2022). Coronal quasi-periodic fast-mode propagating wave trains. Sol. Phys. 297, 20. doi:10.1007/s11207-022-01953-2

CrossRef Full Text | Google Scholar

Spitzer, L. (1962). Physics of fully ionized gases. Am. J. Phys. 31, 891. doi:10.1119/1.1969155

CrossRef Full Text | Google Scholar

Van Doorsselaere, T., Srivastava, A. K., Antolin, P., Magyar, N., Vasheghani Farahani, S., Tian, H., et al. (2020). Coronal heating by MHD waves. Space Sci. Rev. 216, 140. doi:10.1007/s11214-020-00770-y

CrossRef Full Text | Google Scholar

Van Doorsselaere, T., Wardle, N., Del Zanna, G., Jansari, K., Verwichte, E., and Nakariakov, V. M. (2011). The first measurement of the adiabatic index in the solar corona using time-dependent spectroscopy of hinode/EIS observations. Astrophys. J. 727, L32. doi:10.1088/2041-8205/727/2/L32

CrossRef Full Text | Google Scholar

Wang, T., Innes, D. E., and Qiu, J. (2007). Determination of the coronal magnetic field from hot-loop oscillations observed by SUMER and SXT. Astrophys. J. 656, 598–609. doi:10.1086/510424

CrossRef Full Text | Google Scholar

Wang, T., and Ofman, L. (2019). Determination of transport coefficients by coronal seismology of flare-induced slow-mode waves: Numerical parametric study of a 1D loop model. Astrophys. J. 886, 2. doi:10.3847/1538-4357/ab478f

CrossRef Full Text | Google Scholar

Wang, T., Ofman, L., Sun, X., Provornikova, E., and Davila, J. M. (2015). Evidence of thermal conduction suppression in a solar flaring loop by coronal seismology of slow-mode waves. Astrophys. J. 811, L13. doi:10.1088/2041-8205/811/1/L13

CrossRef Full Text | Google Scholar

Wang, T., Ofman, L., Sun, X., Solanki, S. K., and Davila, J. M. (2018). Effect of transport coefficients on excitation of flare-induced standing slow-mode waves in coronal loops. Astrophys. J. 860, 107. doi:10.3847/1538-4357/aac38a

CrossRef Full Text | Google Scholar

Wang, T., Ofman, L., Yuan, D., Reale, F., Kolotkov, D. Y., and Srivastava, A. K. (2021). Slow-mode magnetoacoustic waves in coronal loops. Space Sci. Rev. 217, 34. doi:10.1007/s11214-021-00811-0

CrossRef Full Text | Google Scholar

Zavershinskii, D. I., Kolotkov, D. Y., Nakariakov, V. M., Molevich, N. E., and Ryashchikov, D. S. (2019). Formation of quasi-periodic slow magnetoacoustic wave trains by the heating/cooling misbalance. Phys. Plasmas 26, 082113. doi:10.1063/1.5115224

CrossRef Full Text | Google Scholar

Zavershinskii, D., Kolotkov, D., Riashchikov, D., and Molevich, N. (2021). Mixed properties of slow magnetoacoustic and entropy waves in a plasma with heating/cooling misbalance. Sol. Phys. 296, 96. doi:10.1007/s11207-021-01841-1

CrossRef Full Text | Google Scholar