Multispacecraft wave analysis of current sheet flapping motions in Earth’s magnetotail

In our work, for the first time, we conducted a comprehensive multispacecraft wave study of flapping current sheet oscillations in Earth’s magnetotail. Measurements taken from the Magnetospheric Multiscale (MMS) mission were analyzed for two flapping events with different morphologies of oscillation behavior: stationary-like and kink-like type. A comparison of the results calculated by the methods of phase difference, wave surveyor, and Multipoint Signal Resonator technique was carried out. For the first time, using observations, it was found that the energy distribution of wavy magnetic field contains complex multi-branch dispersion dependencies on $k_y$ and $k_z$. The phase velocities of propagation of flapping oscillations were estimated. The used methods complement each other, and their differences made it possible to assess the presence of non-linear wave packets during kink flapping and the azimuthal asymmetry of the current sheet profile.

Introduction

Flapping motions are wave-like oscillations of the current sheet (CS), and they often accompany explosive activity released in the geomagnetic tail (Sitnov et al., 2019). During such events, the magnetometers of the spacecraft (SC), which is located in the tail of Earth’s magnetosphere, register fluctuations of the $B_x$ component of the magnetic field around the zero value, which physically means multiple crossings of the current layer with bidirectional $B_x$ (by the x-component, we mean the x-th coordinate in the GSM system, i.e., the Earth–Sun direction). Mostly, such kink-like oscillations propagate azimuthally from the tail axis to the flanks of the magnetosphere at speeds up to hundreds of kilometers per second (Sergeev et al., 2004) and with spatial scales of disturbance of several Earth radii. The midnight region is mostly dominated by stationary oscillations (up–down, along z components in the GSM system) (Gao et al., 2018).

Flapping oscillations began to be studied more than half a century ago (Speiser and Ness, 1967), and since then, a sufficient number of quantitative methods have been developed to describe the processes in the current sheet. The minimum variance analysis and timing analysis (Harvey 1998; Sonnerup 1967) make it possible to estimate the phase speed of CS oscillations and its thickness $h$. These parameters often appear in models of CS instability, allowing us to make conclusions about the trigger of flapping oscillations. On the basis of the Harris model, single-spacecraft techniques were developed to determine the type of oscillations, direction, and speed of their propagation (Rong et al., 2015a). Such approaches are useful in the study of magnetospheric tails of other planetary systems, where multi-satellite missions are unavailable (Rong et al., 2015b; DiBraccio et al., 2017; Zhang et al., 2020).

Currently, the question of what is the contribution of flapping oscillations to the energy budget of the geomagnetic tail and what type of instability is responsible for flapping motions in one or another case remains open. Among the possible triggers are considered external—solar wind, interplanetary magnetic field and internal—ion–ion kink instability (Karimabadi et al., 2003), magnetic double-gradient instability (Erkaev et al., 2007), and reconnection (Zhang et al., 2020a).

Gao et al. (2018) conducted a statistical study of 79 flapping events and found that when approaching from the midnight sector to the flanks, the CS normal has larger angles with the z-axis, and stationary oscillations turn into kink-type oscillations; in fact, two motion types are a manifestation of the same wave propagation. In our work, for two specific events based on the data of the MMS mission, we will also determine the oscillation type and the phase speed of their propagation.

Dispersion analysis of such waves is absolutely important, which will make it possible to consider the trigger instability present. The main dispersive features of flapping oscillations have already been considered in the works of Richard et al. (2021) and Rong et al. (2018). In our work, we will apply a number of multispacecraft methods, which will allow us to quantitatively and qualitatively assess the contribution of various low-frequency modes to the general picture of flapping. In addition, the range of frequencies and wave vectors is significantly expanded compared to the works of Richard et al. (2021) and Rong et al. (2018). Consideration in stationary and moving coordinate systems, taking into account the Doppler shift, will make it possible to estimate which modes do not undergo this shift and are independent of fast plasma flows.

Multispacecraft methodology

Turbulent or wave-like fluctuations of plasma parameters during measurements onboard a SC have mixed manifestations of spatial and temporal variations due to the dynamics of the environment itself. Therefore, the distribution of such plasma disturbances in terms of frequency and spatial range plays the most important role in identifying their spectral properties, including spectral laws, dispersion branches, and turbulence features (Borovsky et al., 1997; Song and Russell, 1999; Kozak et al., 2018; Lin et al., 2022). A wide variety of methods are used to obtain an experimental $\omega -k$ picture: projection methods, k-filtering, the MUSIC algorithm (MUltiple SIGnal Classification, Schmidt, 1986), the MSR (Multipoint Signal Resonator) technique (Narita Y., 2011), the phase difference method (Balikhin, 1997), and the wave surveyor technique (Vogt. J, 2008). The spacecraft configuration allows for reliably recognizing fluctuations spatially at scale with wavelengths $\lambda \in \left[d,50d\right]$, where $d$ is the average inter-spacecraft separation distance (Sahraoui et al., 2010). The corresponding wavevector range is $k\in \left[2\pi /50d,2\pi /d\right]$. Larger values can be falsely interpreted through the aliasing wave effect, and values less than the specified range give more significant uncertainties (>10%) in determining the spectrum maximum (Sahraoui et al., 2010). This limitation is inherent to all multispacecraft dispersion techniques.

First, we describe the phase difference method (Beall et al., 1982; Balikhin 1997). It is used for measurements of two SC, or any two sensors, such as in seismology. The mathematical basis is the use of continuous wavelet transformation, which allows finding several wave modes at a fixed frequency with their power, and moreover, omits the assumptions about the planarity of waves and the small amplitude of wave packets (Dudok de Wit T., 2013).

For two scalar time series $b_{\alpha }=b_{\alpha }\left(t\right)$ and $b_{\beta }=b_{\beta }\left(t\right)$ from two SC separated in space by ${\overrightarrow{r}}_{\alpha \beta }={\overrightarrow{r}}_{\alpha }-{\overrightarrow{r}}_{\beta }$, the wavelet transformation $b_{\alpha }\left(\omega ,t\right)$, $b_{\beta }\left(\omega ,t\right)$ and the cross-wavelet spectrum $S_{\alpha \beta }\left(\omega ,t\right)$ with the phase difference ${\varphi }_{\alpha \beta }\left(\omega \right)$ were obtained as follows:

$\begin{array}{c}{S}_{\alpha \beta }\left(\omega ,t\right)=b_{\alpha }\left(\omega ,t\right)b_{\beta }^{*}\left(\omega ,t\right)=\left|S_{\alpha \beta }\left(\omega ,t\right)\right|e^{j{\varphi }_{\alpha \beta }\left(\omega ,t\right)}.\end{array}(1)$

Phase ${\varphi }_{\alpha \beta }$ allows finding the projected wave vector ${\overrightarrow{k}}_{\alpha \beta }$ in the direction ${\overrightarrow{r}}_{\alpha \beta }$ as a function of wave frequency:

${\overrightarrow{k}}_{\alpha \beta }\left(\omega ,t\right){\overrightarrow{r}}_{\alpha \beta }={\varphi }_{\alpha \beta }\left(\omega ,t\right).(2)$

Having found ${\overrightarrow{k}}_{\alpha \beta }\left(\omega ,t\right)$ for three independent SC pairs, a system of equations is solved to find the complete $\overrightarrow{k}\left(\omega ,t\right)$ (here, ${\widehat{V}}_{\alpha \beta }$ is a matrix formed from normalized vectors ${\overrightarrow{r}}_{\alpha \beta }$):

${\widehat{V}}_{\alpha \beta }\overrightarrow{k}\left(\omega ,t\right)={\overrightarrow{k}}_{\alpha \beta }\left(\omega ,t\right).(3)$

After that, the power spectrum is calculated as follows:

$P\left(\overrightarrow{k},\omega \right)=\frac{1}{4}{\displaystyle \sum }_t{S}_{\alpha \beta }\left(\omega ,t\right)\delta \left(\overrightarrow{k}\left(\omega ,t\right)-\overrightarrow{k}\right).(4)$

Alternatively, $\overrightarrow{k}\left(\omega ,t\right)$ can be obtained in another way: $\overrightarrow{k}\left(\omega ,t\right)=\omega \left(\overrightarrow{V}/V^2\right)$, where $\left(\overrightarrow{V}/V^2\right)$ is an inverse phase velocity vector from the system of equation $\widehat{R}\left(\overrightarrow{V}/V^2\right)=\overrightarrow{\tau }$, $\widehat{R}$ is a volumetric tensor, and $\overrightarrow{\tau }$ is weighted time delays formed from time differences ${\tau }_{\alpha \beta }$ from spacecraft pairs: ${\tau }_{\alpha \beta }=\left({\varphi }_{\alpha \beta }/\omega \right)$. This is the way we calculate phase difference spectra using the pyrfu package.

A fast method for finding dispersion patterns is the wave surveyor technique (Vogt, 2008; Kozak, 2019), which directly gives the functional dependence $\overrightarrow{k}\left(\omega \right)$ for dominant modes. The formula for finding dispersion distributions for a vector quantity of dimension $J$ ($J=3$) has the following form (Vogt, 2008):

$\overrightarrow{k}\left(\omega \right)={\left({\displaystyle \sum }_{\sigma =1}^S{\overrightarrow{r}}_{\sigma }{\overrightarrow{r}}_{\sigma }^T\right)}^{-1}{\displaystyle \sum }_{j=1}^J{\alpha }^j{\displaystyle \sum }_{\sigma =1}^S{\theta }_{\sigma }^j\left(\omega \right){\overrightarrow{r}}_{\sigma }(5)$

Here, ${\overrightarrow{r}}_{\sigma }$ denotes the position of the $\sigma$ spacecraft in the barycentric system and $S$ denotes the spacecraft total number.

Raising to the power of -1 means taking the inverse matrix or pseudo-inverse (for cases with S = 2,3). ${\theta }_{\sigma }^j\left(\omega \right)$ are the phases of the complex-valued eigenvector, ${\overrightarrow{c}}_1$, of the covariance matrix in the Fourier representation $\widehat{R}\left(\omega \right)$ corresponding to the largest eigenvalue, ${\gamma }_1$, from the set of all eigenvalues ${\gamma }_l,l=0,\dots ,L$. $L$ is the dimension of the matrix $\widehat{R}\left(\omega \right)$ for the j-th component of the analyzed vector. ${\alpha }^j$ is a multiplier, which essentially represents the weight of the j-th component for the normalized eigenvector ${\alpha }^j={\left|{\mathit{\prod }}^{\mathit{\hspace{0.17em}j}}{\overrightarrow{c}}_1\right|}^2$, where ${\mathit{\prod }}^{\mathit{\hspace{0.17em}j}}$ are the projection matrices:

${\mathit{\prod }}^{\mathit{\hspace{0.17em}j}}=\left(\begin{array}{ccc}{1}^{jT}& \cdots & 0^T\\ ⋮& \ddots & ⋮\\ 0^T& \cdots & 1^{jT}\end{array}\right),(6)$

where $1^{jT}=\left(0,\dots ,\stackrel{j-\mathit{t}\mathit{h}\mathit{p}\mathit{o}\mathit{s}\mathit{i}\mathit{t}\mathit{i}\mathit{o}\mathit{n}}{1},\dots ,0\right)$.

Here, $\widehat{R}\left(\omega \right)$ is the cross-spectral power matrix obtained from the product of the state vector $\overrightarrow{S}\left(\omega \right)$ by itself with Hermitian transposition:

$\widehat{R}\left(\omega \right)=〈\overrightarrow{S}\left(\omega \right){\overrightarrow{S}\left(\omega \right)}^H〉,(7)$

$\overrightarrow{S}\left(\omega \right)=\left(\begin{array}{c}\overrightarrow{b}\left(\omega ,{\overrightarrow{r}}_1\right)\\ \overrightarrow{b}\left(\omega ,{\overrightarrow{r}}_2\right)\\ \begin{array}{c}⋮\\ \overrightarrow{b}\left(\omega ,{\overrightarrow{r}}_L\right)\end{array}\end{array}\right).(8)$

The k-filtering method has become widely used in the geophysical field studies (Capon, 1969; Pinçon et al., 1998). Unlike the previous methods, with the help of k-filtering, the power spectrum $P=P\left(\overrightarrow{k},\omega \right)$ in the four-dimensional space $\left(\overrightarrow{k},\omega \right)$ is obtained as the output, which makes it possible to obtain several maxima of wave energy at their same frequency. However, as with all multispacecraft wave methods, information on wave properties cannot be established on scales smaller than inter-spacecraft distances due to the aliasing effect (in our case, this scale is $\approx 20$ km). Elements of this approach are used in the MSR technique discussed as follows.

The specificity of other methods based on the search for eigenvalues consists of the formation of additional matrices, which contain a vector of columns of eigenvectors and diagonal elements formed from eigenvalues (Pinçon et al., 1998; Narita 2012). In our work, we used one of these methods—the MSR technique—which has two significant advantages over other k-filtering methods, namely, in detecting waves with close wavelengths and in reducing background noise. The MSR technique is good for increasing the signal-to-noise ratio in power spectra compared to other methods but has the limitation of the finite number of wave modes that could be reconstructed from the signal.

The power spectrum according to the MSR method is calculated as follows (Narita, 2011):

${\widehat{P}}_{MSR}\left(\overrightarrow{k},\omega \right)=\frac{1}{P_{EM0}}{\widehat{P}}_{EM}\left(\overrightarrow{k},\omega \right){\widehat{P}}_{KF}\left(\overrightarrow{k},\omega \right).(9)$

The trace of the power matrix $tr\left({\widehat{P}}_{MSR}\left(\overrightarrow{k},\omega \right)\right)$ is the total power. Here, $P_{EM0}=\mathit{max}\left(P_{EM}\right)$ determines the normalization of the spectrum. Here, $P_{EM}$ is the spectrum obtained by the MUSIC (MUltiple SIGnal Classification) algorithm (Narita Y., 2012), ${\widehat{P}}_{KF}\left(\overrightarrow{k},\omega \right)$ denotes the Capon spectrum (projected approach) as follows:

${\widehat{P}}_{KF}\left(\overrightarrow{k},\omega \right)={\left[{\widehat{H}}^H\left(\overrightarrow{k}\right){\widehat{R}}^{-1}\left(\omega \right)\widehat{H}\left(\overrightarrow{k}\right)\right]}^{-1}.(10)$

Here, $\widehat{R}\left(\omega \right)$ is the cross-spectral power matrix defined previously. The position of the sensors is included in the steering matrix $\widehat{H}\left(\overrightarrow{k}\right)$, which includes a functional dependence on $\overrightarrow{k}$ (here, $\widehat{E}$ is a 3×3-unit matrix) given as follows:

$\widehat{H}\left(\overrightarrow{k}\right)=\left(\begin{array}{c}\widehat{E}\mathit{exp}\left(j\overrightarrow{k}\bullet {\overrightarrow{r}}_1\right)\\ \widehat{E}\mathit{exp}\left(j\overrightarrow{k}\bullet {\overrightarrow{r}}_2\right)\\ \begin{array}{c}⋮\\ \widehat{E}\mathit{exp}\left(j\overrightarrow{k}\bullet {\overrightarrow{r}}_L\right)\end{array}\end{array}\right).(11)$

Later in the paper, we will consider all spectra and dispersion patterns depending on the usual frequency in Hz and not on the angular frequency: $P\left(\overrightarrow{k},\omega \right)\to P\left(\overrightarrow{k},f\right)$.

Observations

Analysis the CS flapping oscillations in Earth’s magnetotail was performed using measurements from the four-spacecraft Magnetospheric Multiscale (MMS) mission. Magnetic field data have been given from fluxgate magnetometer (FGM) instruments (Russell et al., 2016) and particle moments from Fast Plasma Investigation (FPI) (Pollock et al., 2016). During 26 August 2020, the spacecraft registered CS flapping oscillations of the CS. MMS for these time intervals was located at points $\left[-\mathrm{26.1,9.2,1.7}\right]R\_E$ and $\left[-\mathrm{26.4,9.0,1.6}\right]R\_E$ GSM that is, in the evening sector of the middle magnetotail (Figure 1). The quality of tetrahedron formation is given as follows: TFQ = 0.875. The average inter-spacecraft separation distance in our case is $\approx 20$ km; so, the “robust” range of the wavevector domain covers ≈0.002 … 0.12 rad/km. In the period from 21:30 UTC to 23:30 UTC, two flapping motions of the CS were observed (Figure 2). The first event occurred in the interval 21:45:13–21:59:13 UTC and the second in 22:51:33–23:03:03 UTC. High-speed plasma flows moving tailward and earthward were observed with average values of $〈\overrightarrow{u}〉\approx \left[-\mathrm{211.1,31.8,2.6}\right]$ km/s and $〈\overrightarrow{u}〉\approx \left[\mathrm{155.7,19.5},-11.6\right]$ km/s, respectively. The beta parameter (ratio of kinetic to magnetic pressure) varies within two orders of magnitude $\approx 1\dots 100$ , which means the alternate SC localization in the high-beta plasma regions of the current sheet and middle-beta boundary layer.

FIGURE 1

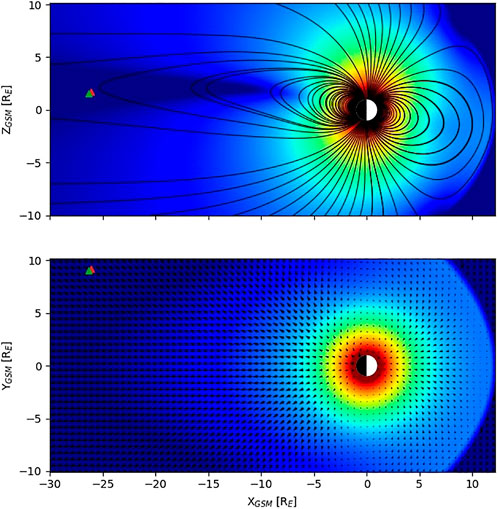
FIGURE 1. Position of MMS spacecraft during two flapping events on 2020/08/26 (red triangle indicates the location of the first event, and green indicates the location of the second event) in the XZ and XY GSM planes. The color gradation indicates the magnetic field magnitude (carried out with the SpacePy package).

FIGURE 2

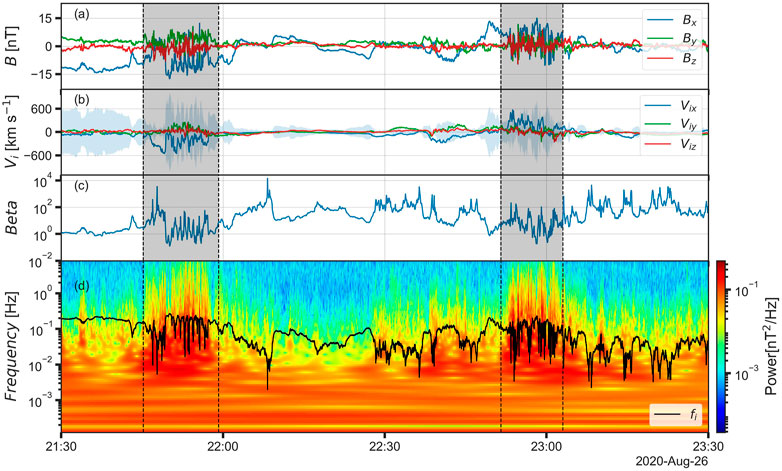
FIGURE 2. Flapping events 2020/08/26 (highlighted in gray) as observed by MMS. (A) Magnetic field. (B) Plasma flow velocity. The shadow shows local Alfven velocity calculated from FPI and resampled FGM MMS data. Plasma bulk velocities do not exceed the Alfven velocity almost throughout all flapping intervals. (C) β ion parameter. (D) Wavelet power spectrum of the magnetic field vector. The black line indicates proton gyrofrequency.

Results

For two flapping events, an analysis of the minimum variation (MVA) was applied to the magnetic field for the selected intervals, where a change in the sign of the $B_x$ component is observed; ${\Delta B}_x>0$ and subsequent ${\Delta B}_x<0$. To determine the type of flapping oscillations, we used the approach proposed by Rong Z. J. et al., 2015, by comparing the $\kappa$ parameter between adjacent intervals of the CS intersection (here, $\overrightarrow{n}$ denotes the minimum variance vector, i.e., the normal to the structure):

$\kappa =\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(n_y{\times n}_z\right)\times \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left({\mathit{\Delta }B}_x\right).(12)$

The first event shows the alternation of the κ parameter (+1, −1, +1...), which means a stationary type of flapping, that is, an up–down oscillation. For the second event $\kappa$, the parameter keeps its sign constancy, which means a kink type of flapping.

We calculated the phase difference spectra for each component of vector $\overrightarrow{B}$. Then, the obtained spectra were summed to analyze the power distribution for the vector quantity (Figure 3) (here, $j=x,y,z$) as follows:

$P\left(k_j,f\right)=P_{xx}\left(k_j,f\right)+P_{yy}\left(k_j,f\right)+P_{zz}\left(k_j,f\right).(13)$

FIGURE 3

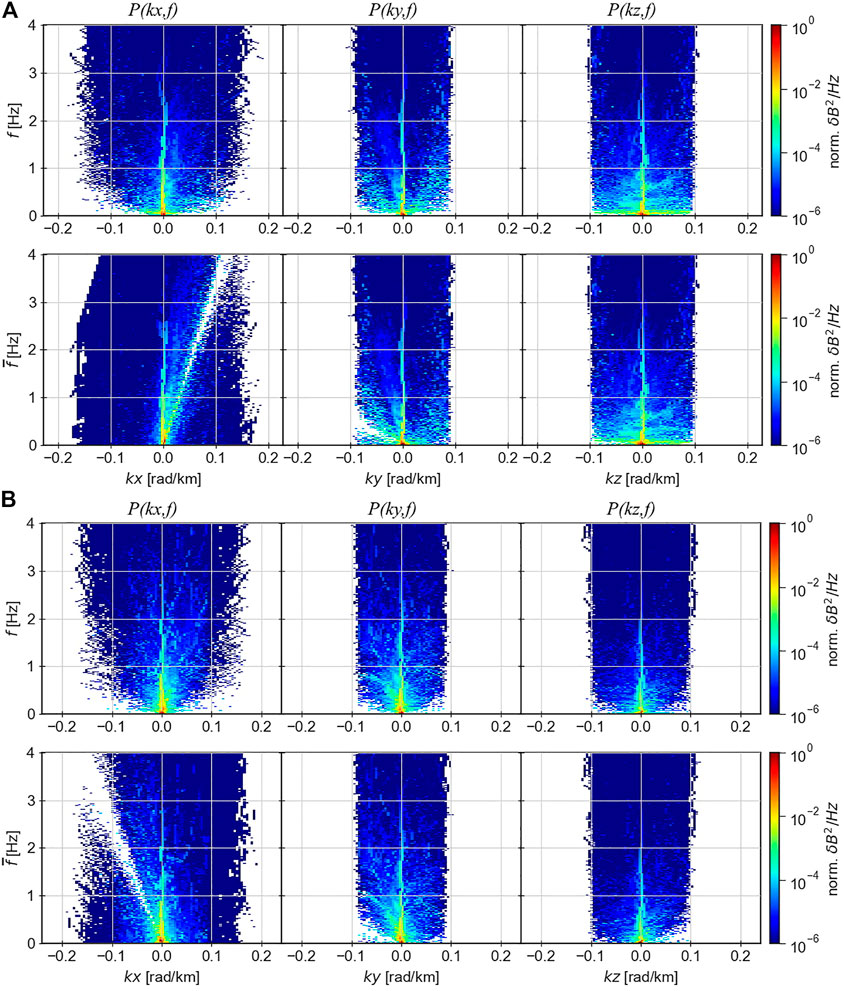
FIGURE 3. P (k,f) spectrum of the magnetic field vector for (A) the first event and (B) the second flapping event 2020/08/26. The spectra panels with $\overline{f}$ on the Y-axis are plotted taking into account the Doppler shift.

This makes it possible to correctly compare the results of this method with two others: the wave survey and the MSR method. The energy distribution was transferred to the plasma moving system using the Doppler correction ($\stackrel{\sim }{f}$ - frequency in the plasma rest frame) as follows:

$P\left(k_j,\stackrel{\sim }{f}\right)=P\left(\frac{k_j,f-k_j{〈\overrightarrow{u}〉}_j}{2\pi }\right).(14)$

The binning of frequencies is performed in a linear way, since it allows us to provide a Doppler shift for a specific value of $k_j$ in the simplest way. Since the flows mostly move along the X coordinate (earthward and tailward), when considering the wave processes in the plasma frame of reference, from Figure 3 we see that the $P\left(k_x,f\right)$ spectra undergo the largest Doppler shift compared to $P\left(k_x,f\right)$. For the first event, $P\left(k_z,\stackrel{\sim }{f}\right)$ demonstrates the presence of weak branches diverging from $k_z=0$ with an almost constant frequency. These oscillatory modes are dispersed, with phase velocity $v_{phz}\to 0$ as the wavelength ${\lambda }_z$ decreases ($v_{phz}=\left(\omega /k_z\sim {\lambda }_z\right)$ as $\omega \approx const$). The $P\left(k_y,\stackrel{\sim }{f}\right)$ spectrum clearly demonstrates the presence of at least three dispersionless branches with phase speeds along -Y: ${\upsilon }_{phy}\approx 0\left(km/s\right),{\upsilon }_{phy}\approx -55\left(km/s\right),{\upsilon }_{phy}\approx -340\left(km/s\right)$. That is, the propagation occurs from the flanks to the center, which determines the localization of the trigger not far from the location of the MMS further duskward. The $P\left(k_x,\stackrel{\sim }{f}\right)$ spectrum exhibits maxima near $\stackrel{\sim }{f}=-\left(k_x{〈\overrightarrow{u}〉}_x/2\pi \right)$; but, in addition, there is a weak branch with $v_{phx}\approx \left(580km/s\right)$, which is close to the maximum value of $u_x$ with the opposite sign ($u_x\approx -\left(580km/s\right)$). In fact, it may be a stationary structure along X that in the plasma rest moves in the +X direction in the spacecraft plasma frame moving tailward. A similar effect for the second event is also inherent for the $P\left(k_x,\stackrel{\sim }{f}\right)$ distribution but in a reverse direction. The $P\left(k_z,\stackrel{\sim }{f}\right)$ spectrum has a weaker feature compared to the first event, which could serve as a signature of the difference between a kink and stationary flapping (up–down motions along Z) types. The $P\left(k_y,\stackrel{\sim }{f}\right)$ spectrum clearly demonstrates the presence of a dispersionless wave mode with $v_{phy}\approx -\left(95km/s\right)$.

Let’s analyze the dispersion patterns constructed by the wave surveyor method (Figure 4). For the first event, one group of points is identical for the spectra obtained by the phase difference method. For the second event, we see some differences between the results of the two methods. This is due to the fact that the wave surveyor method is based on the Fourier transform, which allows viewing of the plane waves. Instead, phase difference spectra constructed from wavelet spectra can effectively identify the wave packets inherent to turbulent plasma. This is confirmed in the simple visual identification of the magnetic field time series—the second event contains a larger number of transient structures and intermittent patterns. However, the dispersion pattern $k_z\left(\stackrel{\sim }{f}\right)$ and the $P\left(k_z,\stackrel{\sim }{f}\right)$ spectrum have a commonly identified branch with a phase speed $v_{phz}\approx \left(45km/s\right)$. In addition, it can be seen that the $P\left(k_z,\stackrel{\sim }{f}\right)$ distribution is asymmetric relative to $k_z\approx 0$ in the low-frequency region, which may indicate the passage of magnetic wavy structures with asymmetric profiles elongated along + Y and steep along -Y in waveform relative to their centers. In this case, ${\Delta B}_z>0$ has a shorter time period than ${\Delta B}_z<0$. This effect is confirmed by the orientations of the normal according to the MVA results for the adjacent spans of the CS intersection.

FIGURE 4

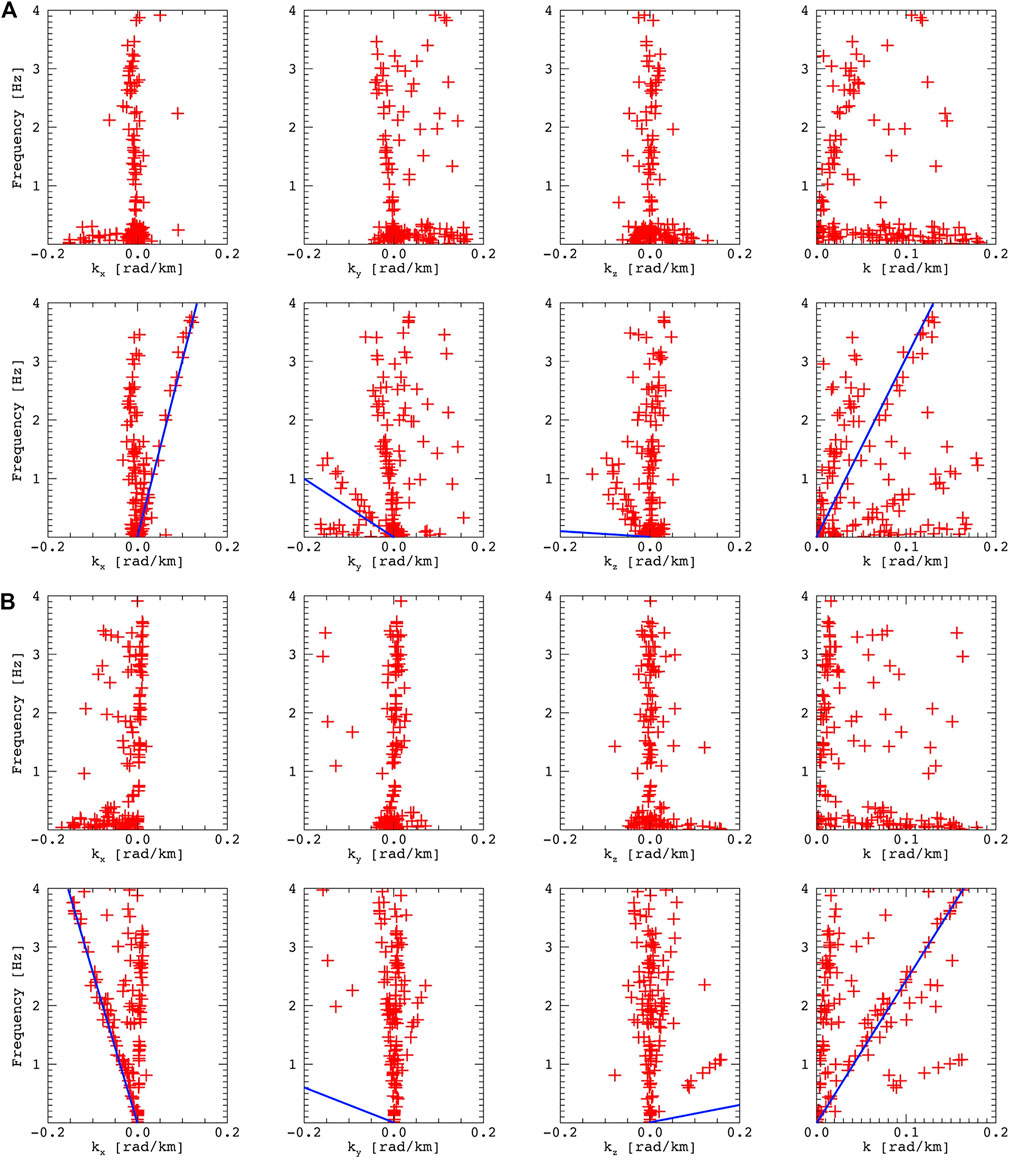
FIGURE 4. (A) f–k dispersion patterns of $\overrightarrow{\delta B}$ obtained by the wave surveyor method for the first event and (B) for the second flappingevent on 2020/08/26. The distributions with blue lines are plotted taking into account the Doppler shift.The blue straight lines indicate the zero frequency in the spacecraft reference system.

Spectra obtained using the MSR method are constructed for a separate set of three frequencies. The latter corresponds to the maxima of the wavelet power for the corresponding intervals. A set with the dominant frequencies of 0.02, 0.05, and 0.5 Hz was selected for the first flapping and 0.02, 0.046, and 0.5 Hz for the second. For a simplified visualization of the obtained 3D spectra $P\left(\overrightarrow{k},f_0\right)$, we made cuts in the $kx-ky$, $kx-kz$, and $ky-kz$ planes (Figure 5). When the frequency increases, the maxima of the distributions expand. The most complex energy distributions are observed for $ky-kz$. The distribution of $P\left({k_{y}k}_z,0.05Hz\right)$ for the first event shows a cross-shaped appearance, almost along the $ky-kz$ axes, which is consistent with the wave surveyor dispersion distributions. Analyzing the 3D distribution of spectra $P\left({k_{y}k}_z,0.5Hz\right)$ for two events, we see that the maximum for the second event occupies a much larger volume. This result is consistent with a closer grouping of points on the dispersion patterns $k_y\left(f\right)$ and $k_z\left(f\right)$ around $k_y=0$ and $k_z=0$, respectively. In general, the power spectrum has multi-branch distribution.

FIGURE 5

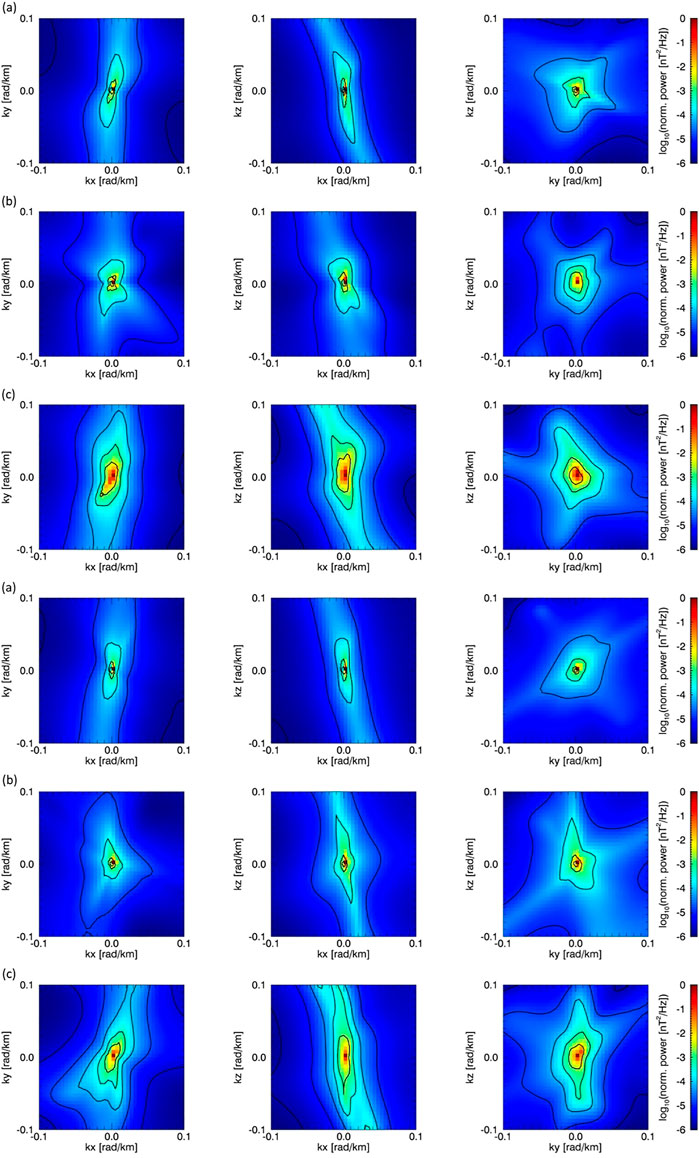
FIGURE 5. MSR 3D power spectra of $\overrightarrow{\delta B}$ in $kx-ky$, $kx-kz$, and $ky-kz$ planes for the dominant frequencies of the first flapping event [(1), 0.02 (A), 0.05 (B), and 0.5 (C) Hz from top to bottom] and the second flapping event [(2), 0.02 (A), 0.046 (B), and 0.5 (C) Hz from top to bottom] 2020/08/26.

Conclusion

We present, for the first time, a low-frequency multispacecraft wave analysis for two flapping oscillation events with high-speed plasma flows. It was found from magnetic polarity that two events of flapping oscillations differ in their type: the first event is characterized by up-and-down movements, and the second event demonstrates kink-type oscillations.

We found that the energy distribution of fluctuations of the magnetic field vector contains previously undetected complex multi-branch dispersion dependences on $k_y,k_z$, which significantly complements past dispersion studies of flapping oscillations. For the first event, the presence of several oscillatory modes was established, which spread azimuthally to the midnight sector with phase speeds ${\upsilon }_{phy}\approx 0\left(km/s\right),{\upsilon }_{phy}\approx -55\left(km/s\right),{\upsilon }_{phy}\approx -340\left(km/s\right)$. For the second event with kink-type oscillations, the presence of wave packets was established, which also spread along -Y with an estimated phase speed of $v_{phy}\approx -95\left(km/s\right)$.

The used methods complement each other, and their differences made it possible to assess the presence of non-linear wave packets when considering kink flapping and the asymmetry of the CS profile in the azimuthal direction (Burch et al., 2016).

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found at: https://lasp.colorado.edu/mms/sdc/public/about/browse/mms1/fgm/srvy/l2/2020/08/ https://lasp.colorado.edu/mms/sdc/public/about/browse/mms2/fgm/srvy/l2/2020/08/ https://lasp.colorado.edu/mms/sdc/public/about/browse/mms3/fgm/srvy/l2/2020/08/ https://lasp.colorado.edu/mms/sdc/public/about/browse/mms4/fgm/srvy/l2/2020/08/ https://lasp.colorado.edu/mms/sdc/public/about/browse/mms1/fpi/fast/l2/dis-moms/2020/08/.

Author contributions

LK proposed to conduct a comparative analysis of the results of specific multispacecraft methods. EK and RA made valuable suggestions about data visualization and text readability.

Funding

This work was supported by grant No. 97742 of the Volkswagen Foundation (VW-Stiftung) and the Royal Society International Exchanges Scheme 2021 IES\R1\211177, BF/30-2021. The work of Elena Kronberg was supported by the German Research Foundation (DFG) under number KR 4375/2-1 within SPP “Dynamic Earth.”

Acknowledgments

The data used in this work are publicly available at the MMS Science Data Center website https://lasp.colorado.edu/mms/sdc/. The phase difference method was performed using the pyrfu package, available at https://github.com/louis-richard/irfu-python.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Balikhin, M., Dudok de Wit, T., Alleyne, H. S. C. K., Woolliscroft, L. J. C., Walker, S. N., Krasnosel’skikh, V., et al. (1997). Experimental determination of the dispersion of waves observed upstream of a quasi-perpendicular shock. Geophys. Res. Lett. 24, 787–790. doi:10.1029/97gl00671

CrossRef Full Text | Google Scholar

Beall, J. M., Kim, Y. C., and Powers, E. J. (1982). Estimation of wavenumber and frequency spectra using fixed probe pairs. J. Appl. Phys. 53, 3933–3940. doi:10.1063/1.331279

CrossRef Full Text | Google Scholar

Borovsky, J., Elphic, R., Funsten, H., and Thomsen, M. (1997). The Earth's plasma sheet as a laboratory for flow turbulence in high-β MHD. J. Plasma Phys. 57 (1), 1–34. doi:10.1017/S0022377896005259

CrossRef Full Text | Google Scholar

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199 (1–4), 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Capon, J. (1969). High resolution frequency-wavenumber spectrum analysis. Proc. IEEE 57, 1408–1418. doi:10.1109/PROC.1969.7278

CrossRef Full Text | Google Scholar

DiBraccio, G. A., Dann, J., Espley, J. R., Gruesbeck, J. R., Soobiah, Y., Connerney, J. E. P., et al. (2017). MAVEN observations of tail current sheet flapping at Mars. J. Geophys. Res. Space Phys. 122, 4308–4324. doi:10.1002/2016JA023488

CrossRef Full Text | Google Scholar

Dudok de Wit, T., Alexandrova, O., Furno, I., Sorriso-Valvo, L., and Zimbardo, G. (2013). Methods for characterising microphysical processes in plasmas. Space Sci. Rev. 178, 665–693. doi:10.1007/s11214-013-9974-9

CrossRef Full Text | Google Scholar

Erkaev, N. V., Semenov, V. S., and Biernat, H. K. (2007). Magnetic double gradient instability and flapping waves in a current sheet. Phys. Rev. Lett. 99, 235003. doi:10.1103/PhysRevLett.99.235003

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, J. W., Rong, Z. J., Cai, Y. H., Lui, A. T. Y., Petrukovich, A. A., Shen, C., et al. (2018). The distribution of two flapping types of magnetotail current sheet: Implication for the flapping mechanism. J. Geophys. Res. Space Phys. 123, 7413–7423. doi:10.1029/2018JA025695

CrossRef Full Text | Google Scholar

Harvey, C. C. (1998). Spatial gradients and volumetric tensor, in Analysis methods for multi-spacecraft data. International Space Science Institute Scientific, 307–322. Bern, Switzerland.

Google Scholar

Karimabadi, H., Daughton, W., Pritchett, P. L., and Krauss-Varban, D. (2003). Ion-ion kink instability in the magnetotail: 1. Linear theory. J. Geophys. Res. 108 (A11), 1400. doi:10.1029/2003JA010026

CrossRef Full Text | Google Scholar

Kozak, L., Petrenko, B., Lui, A., Kronberg, E., Grigorenko, E., and Prokhorenkov, A. (2018). Turbulent processes in the Earth's magnetotail: Spectral and statistical research. Ann. Geophys. 36 (5), 1303–1318. doi:10.5194/angeo-36-1303-2018

CrossRef Full Text | Google Scholar

Kozak, L. V., Petrenko, B. A., Lui, A. T. Y., Kronberg, E. A., and Daly, P. W. (2021). Processes in the current disruption region: From turbulence to dispersion relation. J. Geophys. Res. Space Phys. 126, e2020JA028404. doi:10.1029/2020JA028404

CrossRef Full Text | Google Scholar

Lin, R., He, J., Zhu, X., Zhang, L., Duan, D., Sahraoui, F., et al. (2022). Power anisotropy, dispersion signature and turbulence diffusion region in the 3D wavenumber domain of space plasma turbulence. Astrophysical J. 939 (2), 121. doi:10.3847/1538-4357/ac8e07

CrossRef Full Text | Google Scholar

Narita, Y., Glassmeier, K. H., and Motschmann, U. (2011). High-resolution wave number spectrum using multi-point measurements in space – The multi-point signal resonator (MSR) technique. Ann. Geophys. 29 (2), 351–360. doi:10.5194/angeo-29-351-2011

CrossRef Full Text | Google Scholar

Narita, Y. (2012). Plasma turbulence in the solar system. Springer, Berlin, Germany. doi:10.1007/978-3-642-25667-7

CrossRef Full Text | Google Scholar

Pinçon, J. L., and Motschmann, U. (1998). Multi-spacecraft filtering: General framework, in Analysis methods for multi-spacecraft data. (ESA Publication), 65–78. Paris, France.

Google Scholar

Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast plasma investigation for magnetospheric multiscale. Space Sci. Rev. 199 (1–4), 331–406. doi:10.1007/s11214-016-0245-4

CrossRef Full Text | Google Scholar

Richard, L., Khotyaintsev, Y. V., Graham, D. B., Sitnov, M. I., Le Contel, O., and Lindqvist, P.-A. (2021). Observations of short-period ion-scale current sheet flapping. J. Geophys. Res. Space Phys. 126, e2021JA029152. doi:10.1029/2021JA029152

CrossRef Full Text | Google Scholar

Rong, Z. J., Barabash, S., Stenberg, G., Futaana, Y., Zhang, T. L., Wan, W. X., et al. (2015). Technique for diagnosing the flapping motion of magnetotail current sheets based on single-point magnetic field analysis. J. Geophys. Res. Space Phys. 120, 3462–3474. doi:10.1002/2014ja020973

CrossRef Full Text | Google Scholar

Rong, Z. J., Cai, Y. H., Gao, J. W., Lui, A. T. Y., Shen, C., Petrukovich, A. A., et al. (2018). Cluster observations of a dispersive flapping event of magnetotail current sheet. J. Geophys. Res. Space Phys. 123, 5571–5579. doi:10.1029/2018JA025196

CrossRef Full Text | Google Scholar

Rong, Z. J., Barabash, S., Stenberg, G., Futaana, Y., Zhang, T. L., Wan, W. X., et al. (2015). The flapping motion of the Venusian magnetotail: Venus Express observations. J. Geophys. Res. Space Phys. 120, 5593–5602. doi:10.1002/2015JA021317

CrossRef Full Text | Google Scholar

Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2016). The magnetospheric multiscale magnetometers. Space Sci. Rev. 199 (1–4), 189–256. doi:10.1007/s11214-014-0057-3

CrossRef Full Text | Google Scholar

Sahraoui, F., Belmont, G., Goldstein, M. L., and Rezeau, L. (2010). Limitations of multispacecraft data techniques in measuring wave number spectra of space plasma turbulence. J. Geophys. Res. Space Phys. 115 (A4). doi:10.1029/2009JA014724

CrossRef Full Text | Google Scholar

Schmidt, R. O. (1986). Multiple emitter location and signal parameter estimation. IEEE Trans. Ant. Prop. AP- 34, 276–280. doi:10.1109/tap.1986.1143830

CrossRef Full Text | Google Scholar

Sergeev, V., Runov, A., Baumjohann, W., Nakamura, R., Zhang, T. L., Balogh, A., et al. (2004). Transient, small-scale field-aligned currents in the plasma sheet boundary layer during storm time substorms. Geophys. Res. Lett. 31, 4841–4849. doi:10.1002/2016GL068768

PubMed Abstract | CrossRef Full Text | Google Scholar

Sitnov, M., Birn, J., Ferdousi, B., Gordeev, E., Khotyaintsev, Y., Merkin, V., et al. (2019). Explosive magnetotail activity. Space Sci. Rev. 215 (4), 31. doi:10.1007/s11214-019-0599-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, P., and Russell, C. (1999). Time series data analyses in space physics. Space Sci. Rev. 87, 387–463. doi:10.1023/A:1005035800454

CrossRef Full Text | Google Scholar

Sonnerup, B. Ö., and Cahill, L. J. (1967). Magnetopause structure and attitude from Explorer 12 observations. J. Geophys. Res. 72 (1), 171–183. doi:10.1029/jz072i001p00171

CrossRef Full Text | Google Scholar

Speiser, T. W., and Ness, N. F. (1967). The neutral sheet in the geomagnetic tail: Its motion, equivalent currents, and field line connection through it. J. Geophys. Res. 72, 131–141. doi:10.1029/JZ072i001p00131

CrossRef Full Text | Google Scholar

Vogt, J., Narita, Y., and Constantinescu, O. D. (2008). The wave surveyor technique for fast plasma wave detection in multi-spacecraft data. Ann. Geophys. 26, 1699–1710. doi:10.5194/angeo-26-1699-2008

CrossRef Full Text | Google Scholar

Zhang, C., Rong, Z. J., Gao, J. W., Zhong, J., Chai, L. H., Wei, Y., et al. (2020b). The flapping motion of mercury's magnetotail current sheet: MESSENGER observations. Geophys. Res. Lett. 47, e2019GL086011. doi:10.1029/2019GL086011

CrossRef Full Text | Google Scholar

Zhang, Y. C., Dai, L., Rong, Z. J., Wang, C., Rème, H., Dandouras, I., et al. (2020). Observation of the large-amplitude and fast-damped plasma sheet flapping triggered by reconnection-induced ballooning instability. J. Geophys. Res. Space Phys. 125, e2020JA028218. doi:10.1029/2020JA028218

CrossRef Full Text | Google Scholar