
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci. , 15 December 2022
Sec. Space Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.1062358
This article is part of the Research Topic The Future of Space Physics 2022 View all 66 articles
 Devin Huyghebaert1*
Devin Huyghebaert1* Daniel Billett2
Daniel Billett2 Alex Chartier3
Alex Chartier3 Jorge L. Chau4
Jorge L. Chau4 Glenn C. Hussey2
Glenn C. Hussey2 David L. Hysell5
David L. Hysell5 Magnus F. Ivarsen2
Magnus F. Ivarsen2 Rafael L. A. Mesquita3
Rafael L. A. Mesquita3 Enrique Rojas5
Enrique Rojas5 Juha Vierinen1
Juha Vierinen1 Matthew Young6
Matthew Young6The heating caused by ionospheric E-region plasma turbulence has documented global implications for the energy transfer from space into the terrestrial atmosphere. Traveling atmospheric disturbances, neutral wind motion, energy deposition rates, and ionospheric conductance have all been shown to be potentially affected by turbulent plasma heating. Therefore it is proposed to enhance and expand existing ionospheric radar capabilities and fund research into E-region plasma turbulence so that it is possible to more accurately quantify the solar-terrestrial energy budget and study phenomena related to E-region plasma turbulence. The proposed research funding includes the development of models to accurately predict and model the E-region plasma turbulence using particle-in-cell analysis, fluid-based analysis, and hybrid combinations of the two. This review provides an expanded and more detailed description of the past, present, and future of auroral E-region plasma turbulence research compared to the summary report submitted to the National Academy of Sciences Decadal Survey for Solar and Space Physics (Heliophysics) 2024–2033 (Huyghebaert et al., 2022a).
Recent research indicates E-region plasma turbulence plays a major role in regulating magnetosphere-ionosphere-atmosphere coupling and energy transfer processes (e.g., Oppenheim and Dimant, 2013; St-Maurice and Goodwin, 2021). Plasma turbulence in the auroral region has been shown to account for significant changes to the global auroral conductivity when incorporated into models (Liu et al., 2016; Wiltberger et al., 2017, see Figure 1). Changes to the conductivity can affect electron energy deposition from the magnetosphere (e.g., Ridley et al., 2004). The Heliophysics community must further investigate the causes and effects of E-region plasma turbulence if we are to understand global-scale phenomena that can be affected by high-latitude plasma heating (e.g. large-scale traveling ionospheric disturbances (Liu et al., 2018), thermospheric upwelling (Lu et al., 2016), ion upflow (Deng et al., 2011), magnetosphere-ionosphere (MI) wave coupling (Khazanov et al., 2018), etc.).
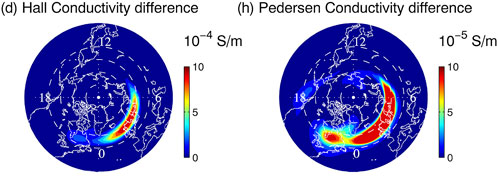
FIGURE 1. Modeled difference in the Hall and Pedersen conductivities at ∼ 112 km when plasma heating from E-region plasma turbulence is included compared to when it is excluded. The enhancement in Hall and Pedersen conductivities is on the order of 40%–80% and 26%–88% in the auroral oval, respectively. From Liu et al. (2016).
As a brief overview, it is expected that plasma turbulence heating in the auroral E-region ionosphere is responsible for the larger than expected heating rates of plasma during active geomagnetic events (e.g., Schlegel and St.-Maurice, 1981). When the ionospheric electric field in the E-region reaches ∼ 20 mV/m, electrons move with a differential velocity of approximately the ion-acoustic speed with respect to the ions at an altitude of ∼ 110 km. This creates plasma turbulence through the Farley-Buneman plasma instability mechanism (Buneman, 1963; Farley, 1963). As the electric field strength increases, so does the growth rate of the instability and the corresponding intensity of the plasma turbulence. The plasma turbulence causes an increase in the electron temperature of the plasma through anomalous heating effects (e.g., Schlegel and St.-Maurice, 1981; Fejer et al., 1986; Oppenheim and Dimant, 2013; St-Maurice and Goodwin, 2021).
Figure 2 shows both recent and previous incoherent scatter measurements from a study by St-Maurice and Goodwin (2021), where it provides examples of the amount of plasma heating that occurs during active ionospheric periods when the plasma flow speed reaches
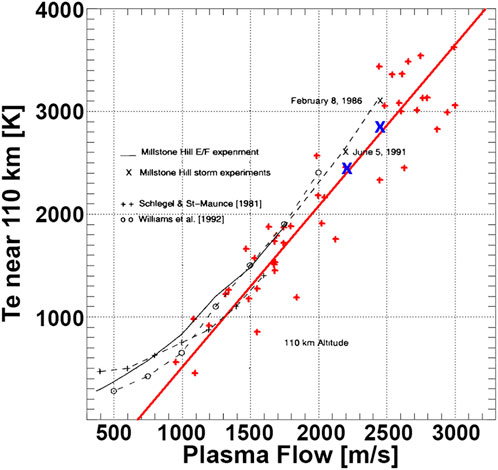
FIGURE 2. Electron temperature measured by incoherent scatter radars plotted against the E×B plasma drift. This electron temperature is greater than what is expected without anomalous turbulent plasma heating effects for the electric fields measured. From St-Maurice and Goodwin (2021).
The study Oppenheim and Dimant (2013) highlights the need to be able to model these complex turbulent systems to investigate and confirm that the hypotheses proposed are reasonable. It is also important to be able to model the turbulence both on small and large scales. The modeling can be accomplished with particle-in-cell (PIC) based models, magneto-hydrodynamic fluid based models, and through hybrid combinations of the two. The scalability of the models is important as it can allow the turbulence to be considered in global large scale electrodynamic models for accurate predictions of the energy exchange in solar-terrestrial interactions.
The E-region is important for the energy exchange as it is considered to be the boundary between the neutral atmosphere and space. Charged particles are able to travel along the magnetic field lines from higher altitudes in the magnetosphere and F-region and deposit their energy in the E-region. The E-region is located in a region where the neutral atmosphere and ionospheric plasma are highly coupled due to the atmospheric density and associated collisions between the neutral species and the ions and electrons. These collisions allow currents to flow across the magnetic field lines, thereby helping to “close” the magnetospheric current system. The collisions also result in transfers of energy from both the neutrals to the plasma, and the plasma to the neutrals. The collisions between neutrals and the ionospheric plasma can cause both the transfer and generation of heat, thereby potentially increasing the temperature of the neutral atmosphere. This has implications for the neutral density, as a higher neutral temperature will cause the atmosphere to expand. This results in higher neutral densities at higher altitudes, which can have implications for satellite drag. It follows that this coupling of the neutral and charged constituents in the E-region ionosphere is an important aspect to understand for E-region plasma turbulence studies.
To further investigate the E-region plasma turbulence, ionospheric coherent scatter radars can be used. Coherent scatter is measured by transmitting and receiving radio signals that scatter from plasma density fluctuations in the ionosphere. The scale size of the plasma density fluctuations that are scattered from are proportional to the radar signal wavelength, where for a monostatic system the scale size is half the wavelength of the signal. These small scale sizes, on the order of 1–5 m for VHF radars, are not resolved consistently over a relatively large field-of-view using other instruments such as optical imagers (scale-size based on resolution), and rockets (localized measurements). Ionospheric plasma turbulence is typically largest perpendicular to the geomagnetic field and is caused by plasma instabilities. The setup of E-region coherent scatter radars is therefore optimized for geomagnetically perpendicular measurements at altitudes of ∼ 110 km. From the characteristics of the scattered radio signal (e.g., Doppler shift, signal-to-noise ratio (SNR), spectral width), properties of the ionospheric plasma instabilities and associated turbulence can be determined. These measurements have been shown to related to the ionospheric electric field in the region, which is an additional aspect that can be utilized with E-region coherent scatter systems.
The current number of E-region coherent scatter radars at auroral latitudes is limited. There is no currently deployed multi-static, multi-frequency E-region coherent scatter radar with an overlapping field-of-view with an incoherent scatter radar, with the closest radar to matching these criteria being the Cornell Homer, Alaska VHF radar with the Poker Flat Incoherent Scatter Radar (PFISR) (Hysell et al., 2012). With the recent advances in computing capabilities and radio hardware for transmitting, receiving, and processing radar signals, the turbulent E-region ionosphere is able to be investigated in higher resolution than what was previously possible. This review highlights that there is an opportunity to expand the measurements and understanding of the undersampled E-region through: the deployment of new E-region coherent scatter radars, the adaptation of existing radar systems for E-region coherent scatter measurements, and the expansion of modeling efforts of the turbulent E-region plasma.
Due to the heating effects of E-region plasma turbulence, its potential role in Magnetosphere-Ionosphere (MI) coupling, and its influence on the neutral atmosphere, four science goals (SGs) are proposed to be researched with auroral E-region coherent scatter radars, incoherent scatter radars, and modeling efforts in the coming years.
• SG1. Understanding the generation mechanisms and ionospheric effects of E-region plasma turbulence
• SG2. Investigating neutral-charged atmosphere coupling and how E-region plasma turbulence is involved
• SG3. Deriving the ionospheric convection electric fields from E-region coherent scatter
• SG4. Analysis of the coupling between the magnetosphere, the E-region, and the F-region
Previous E-region coherent scatter radar measurements show different turbulence characteristics based on the look direction of the radar with respect to the assumed electron velocity (considered to be approximately the E×B drift at E-region altitudes). At radar observation directions parallel to E×B, the plasma turbulence is expected to have a phase speed of the plasma ion-acoustic speed from theory, and this is observed in the data. These measurements have been classified by previous researchers as “Type I” E-region coherent scatter spectra and are relatively well understood based on the Farley-Buneman instability mechanism. The other 3 “Types” of E-region coherent scatter spectra, labelled as “Type II”, “Type III”, and “Type IV”, are less well understood and are still under investigation. Examples of these different types are provided in Figure 3. Multiple publications are available reviewing the previous E-region coherent scatter radar measurements. These include reviews by Fejer and Kelley (1980); Haldoupis (1989); Sahr and Fejer (1996); Moorcroft (2002); Makarevich (2009); Hysell (2015); Chau and St.-Maurice (2016).
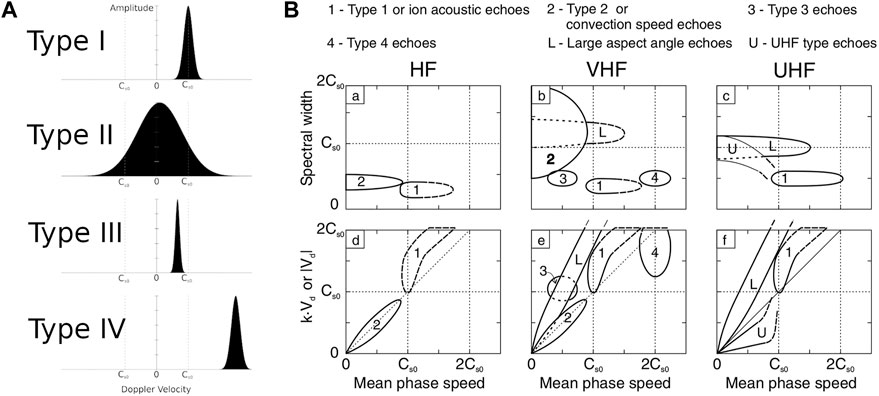
FIGURE 3. (A) Examples of spectra for the different types of E-region coherent scatter. Note that E-region coherent scatter can have both positive and negative Doppler shifts, where this figure highlights the Doppler speeds and spectral widths of observations. Cs0 is the ion-acoustic speed of the plasma. Figure adapted from Hussey (1995) (B) A general overview of the characteristics of E-region coherent scatter spectra measured with E-region coherent scatter radars at different frequencies before 2001. The figure is from Moorcroft (2002).
At radar look directions perpendicular to E×B, radar measurements with Doppler shifts close to 0 m/s and large spectral widths have been labelled as “Type II” spectra. In Figure 3 these are labelled as “Type II” in the left panel and with the number “2” in the right panel. The wide spectral width of Type II spectra means that a significant amount of energy goes into turbulence generation perpendicular to E×B (parallel to E). The “Type II” E-region coherent scatter spectra have multiple hypotheses as to why they are generated. One such explanation is that there are gradients in the plasma density that then create turbulence parallel to E, where this is known as the E-region gradient drift instability (e.g., Fejer and Kelley, 1980). There is also an expansion upon this idea, where large plasma density gradients generated by the Farley-Buneman instability generate turbulence perpendicular to the E×B direction through mode coupling (Hamza and St-Maurice, 1993). This implies that the Farley-Buneman instability is the primary instability mechanism, from which secondary turbulence is generated. How the turbulence varies based on radar look direction with respect to E×B can be measured with a multi-static E-region coherent scatter radar system. This would provide simultaneous measurements of the turbulence spectrum in the E-region from different directions, which has important implications for the understanding of secondary process turbulence generation.
There are also “Type III” and “Type IV” labelled E-region coherent spectra (see Figure 3). Both types of spectra have small spectral widths, corresponding to weak turbulence situations. This means that they likely do not contribute significantly to the turbulent heating in the E-region ionosphere, but they can provide insights into the turbulent processes occurring in the region. The Type III spectra have a Doppler velocity of approximately half the ion-acoustic speed, while the Type IV spectra have a Doppler velocity of approximately double the ion-acoustic speed.
Type III spectra have a few prevailing hypotheses on their origin. These include being generated as a result of large density gradients on small scales in the E-region (St.-Maurice et al., 1994), or from “modulated electron ohmic heating by waves” (MEOHW) (St.-Maurice and Chau, 2016). Both mechanisms require energetic charged particle precipitation to produce the weakly turbulent narrow spectra, making it difficult to distinguish which is the turbulence source of the spectra.
Type IV spectra also have hypotheses as to their origin, though the suggestion by St.-Maurice and Chau (2016) that the ion reference frame must be considered in the analysis due to the large phase velocity and small spectral width of the measurements provides a reasonable explanation. The other hypotheses include that there is a very large ion-acoustic speed due to enhanced electron temperatures in regions where Type IV measurements are made (Fejer et al., 1986), or that large plasma density gradients affect the differential electron and ion threshold speed required for positive Farley-Buneman instability growth (St.-Maurice et al., 1994).
If the differential ion and electron velocities become greater than the ion-acoustic speed at altitudes above 115 km, where the ions are beginning to have a significant velocity component in the E× B direction, Farley-Buneman instability turbulence will occur. Due to the differential velocity likely only being slightly greater than the ion-acoustic speed at these altitudes, this explains the narrow spectra corresponding to weak turbulence for Type IV measurements (St.-Maurice and Chau, 2016). The significance of the phase velocity of the plasma turbulence being in the ion reference-frame must be highlighted, where at the lower E-region altitudes the ion motion will be greatly affected by the neutral winds. The neutral winds will therefore change the required threshold electric field strength for Farley-Buneman instability turbulence to occur.
By combining fine-scale measurements made by E-region coherent scatter radars and incoherent scatter radars it will be possible to investigate and quantify the plasma heating occurring in regions of E-region plasma turbulence. The plasma turbulence can be mapped in 3D using interferometry information from coherent scatter systems, providing altitude information of the turbulent regions, in conjunction with altitude profiles of the ionospheric plasma from incoherent scatter radars. The Type II coherent scatter can also be investigated with a multi-static E-region coherent scatter radar system, providing details on how the properties of the plasma turbulence vary with direction with respect to the convection electric field. Furthermore, a multi-frequency radar would enable the small-scale turbulence spectrum to be investigated. The generation mechanisms of weakly turbulent plasma corresponding to Type III and Type IV spectra can also be investigated with joint E-region coherent scatter and incoherent scatter measurements. This would involve relating the characteristics of the E-region coherent scatter spectra at the different altitudes with the properties of the plasma at those altitudes derived from the incoherent scatter spectra (e.g., plasma temperature and ion velocity) in a common volume region.
In addition to the characteristics of the measured E-region plasma turbulence, the location of the turbulence with respect to other ionospheric phenomena, such as charged particle precipitation, is important to consider. In regions of particle precipitation and enhanced ionospheric plasma density there is a reduction in the occurrence of E-region coherent scatter measurements (e.g., Williams et al., 1999). The E-region coherent scatter is instead observed at the boundaries of these very enhanced plasma density regions. The reduction in E-region coherent scatter has been attributed to either a suprathermal electron population that suppresses plasma instability growth (Dimant et al., 2021), or a suppression of the electric field strength from enhanced conductivity due to higher plasma densities in the region (e.g., Maynard et al., 1973). The location of the plasma turbulence with respect to other ionospheric phenomena can provide information on the ionospheric characteristics in the region to aid in investigating the turbulence.
Changes in the ionosphere at E-region altitudes (e.g., in electron and ion temperatures or velocities) can have a considerable impact on the neutral atmosphere. Joule heating is deposited mostly in the E-region due to its high conductance (Huang et al., 2012), which in turn drives significant upwelling of the neutral density at E-region altitudes and beyond (Deng et al., 2011). Enhancements of the E-region ion-velocity, coupled to strong electric fields and the magnetosphere, also enhance neutral winds via ion-neutral collisions (Billett et al., 2020). These effects have serious implications for low-Earth-orbit satellites, as large and turbulence-scale E-region dynamics can cause significant drag effects, potentially leading to occurrences like the 2022 SpaceX satellite loss event (Hapgood et al., 2022).
The neutral atmosphere winds will also greatly affect the ion velocity in the E-region ionosphere. This can have implications for the electron velocity threshold for plasma turbulence to occur, as the plasma turbulence is expected to occur in the reference frame of the ions (e.g., St.-Maurice and Chau, 2016). By comparing the neutral wind motion with the phase speed of E-region coherent scatter radar measurements, it will be possible to determine the effects of the neutral atmosphere on plasma turbulence, and potentially derive the neutral wind motion from E-region coherent scatter measurements.
There have been previous comparisons between measurements from E-region coherent scatter systems measuring E-region plasma turbulence and incoherent scatter radars measuring the ionospheric plasma characteristics. Some joint experiments include the VHF Scandinavian Twin Auroral Radar Experiment (STARE) (Greenwald et al., 1978) and the Cornell University Portable Radar Interferometer (CUPRI) (e.g., Riggin et al., 1986) radars in conjunction with EISCAT incoherent scatter radars, and the Cornell Anchorage, Alaska E-region coherent scatter radar in conjunction with PFISR (Bahcivan et al., 2005). Many of the previous comparisons between the STARE and EISCAT systems focused on how the E-region coherent scatter Doppler velocity compared to the ion-acoustic speed. Some examples of this are provided in Nielsen and Schlegel (1983), Kofman and Nielsen (1990), and Nielsen et al. (2002). The coherent scatter was consistently found to have a Doppler velocity of approximately the ion-acoustic speed in the direction of the E×B drift. At measurements off the E×B direction but still perpendicular to the geomagnetic field, there was found to be a cosine dependence on the flow speed with respect to the measured Doppler velocity (Nielsen et al., 2002). This has been further studied to create an empirical formula for deriving the electric fields in the E-region ionosphere (e.g., Hysell et al., 2012). The results compared favorably with electric fields derived from measurements by PFISR.
Further work on deriving the ionospheric convection electric field from E-region coherent scatter has been performed by Rojas et al. (2018) to determine the validity of using the E-region coherent scatter measurements as a means to derive the ionospheric convection pattern. This work shows the potential for operational measurements of small-scale E-region electric fields during active conditions using a distributed network of E-region coherent scatter radars. Compared to Super Dual Auroral Radar Network (SuperDARN) HF radar determinations, ionospheric electric fields from VHF E-region coherent scatter radars will be improved by reducing location errors, and observing with higher range resolutions without concerns for multi-path propagation of the signal. This will allow for much finer scale detail of the ionospheric electric field in regions where E-region coherent scatter is measured. A network of E-region coherent scatter radars could then provide high-resolution electric field measurements, though the coverage would be more limited than that of the SuperDARN network due to less refraction of the radar signal and the systems measuring E-region coherent scatter rather than F-region coherent scatter (lower altitude and smaller region of perpendicular magnetic aspect condition).
There are links between the F-region ionosphere, the magnetosphere, and E-region plasma turbulence. High-energy particle precipitation in the nightside aurora directly impacts the ionosphere at E-region altitudes (Newell et al., 2009; Partamies et al., 2017). As an important consequence, high-energy precipitation causes significant enhancements in Pedersen conductance (Robinson et al., 2021), which in turn affects F-region irregularities with long field-aligned wavelengths (Ivarsen et al., 2021). In addition, high-energy particle precipitation deposits charge at E-region altitudes, causing modulations to the ionospheric electric field. Close scrutiny of E-region plasma turbulence in or around precipitation patches offers a way to study the coupling between E- and F-region plasma irregularities. The F-region irregularities can have very long field-aligned wavelengths, and these F-region irregularities with field-perpendicular wavelengths down to 1 km can efficiently map to the E-region (Ivarsen et al., 2021).
As mentioned in Section 1, E-region plasma turbulence causes conductivity enhancements through heating, while direct conductivity enhancements are also caused by high-energy precipitation. These two semi-independent drivers of Pedersen conductance affect the entire altitudinal stretch of the ionosphere through effective field-aligned transport. Investigations into E-region plasma turbulence, in conjunction with electric field, plasma density, or particle precipitation measurements, can offer key insights into the vertical coupling of the high-latitude ionosphere.
Alfvén waves constitute a subset of magneto-hydrodynamic (MHD) modes that deposit electromagnetic energy in the ionosphere (Lysak, 1991). Both Hall and Pedersen conductivities strongly modulate the degree to which Alfvén waves deposit energy by modulating the reflection coefficient of the region (Park et al., 2017; Ivarsen et al., 2020). The Hall and Pedersen conductivities peak at E-region altitudes (Kwak and Richmond, 2007), where Alfvén waves are commonly reflected. The study of precipitation-induced E-region plasma turbulence should then be a vital piece in a holistic investigation of the impact of Alfvén waves on the ionosphere.
Recent E-region coherent scatter radar studies by Hysell et al. (2012), Chau and St.-Maurice (2016), and Huyghebaert et al. (2019) show the progressing capabilities of radar systems to make accurate measurements of the E-region plasma turbulence volume over a large field-of-view. An example of E-region coherent scatter radar measurements from the recently deployed Ionospheric Continuous-wave E-region Bistatic Experimental Auroral Radar (ICEBEAR) in Canada at a center frequency of 49.5 MHz is provided in Figure 4. The top plot in Figure 4 shows how measured E-region coherent scatter spectra can change significantly with range, where this figure includes the full field-of-view for the range-Doppler measurements. The bottom plot depicts the coherent scatter if each range-Doppler bin were individually assigned an azimuth angle of arrival value. Even with this relatively straightforward analysis neglecting imaging of the coherent scatter, structure in both the location and Doppler shift of the E-region plasma density turbulence can be observed.
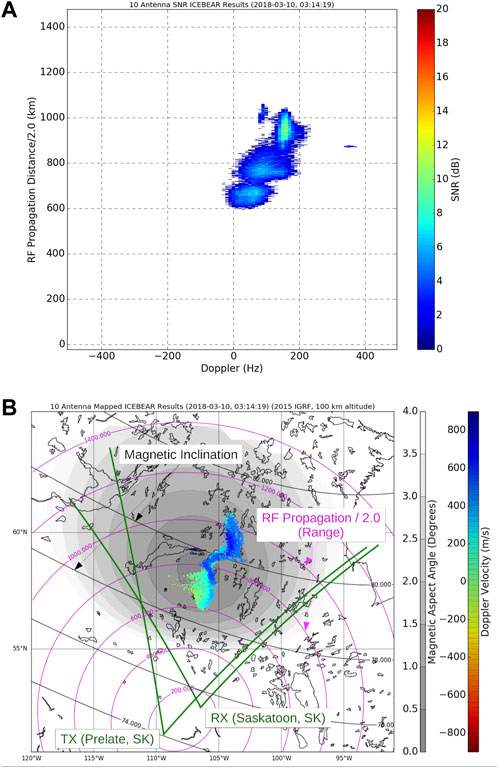
FIGURE 4. (A) The E-region coherent scatter spectra measured in the ICEBEAR radar field-of-view integrated over 5 s. To obtain the Doppler velocity, one can multiply the frequency by ∼ 3 m (approximate half wavelength for a 49.5 MHz radar transmit frequency) (B) The same measurements mapped to the radar field-of-view using the cross-spectra measurements from antennas in a linear interferometer configuration. Adapted from Figures in Huyghebaert et al. (2019).
It has been shown in Bahcivan et al. (2006) and Huyghebaert et al. (2021) that auroral E-region scatter can be imaged in the azimuthal plane of the radar. The turbulence in the E-region is a spread target that can span a large portion of the field-of-view and through interferometric techniques it is possible to image the coherent scatter to accurately re-create the plasma turbulence region. More recently, Lozinsky et al. (2022) has shown that it is also possible to obtain accurate altitude information of E-region coherent scatter with altitude resolution of the coherent scatter on the order of ∼ 1.5 km. This altitude information is important for putting the plasma instability mechanisms in context.
In addition to radars specifically designed for E-region coherent scatter studies, meteor radars and passive VHF receivers can be used to study E-region plasma turbulence. Some examples include the SIMONe meteor radar network (e.g., Huyghebaert et al., 2022b) and passive radars using FM radio transmitters as the signal source (e.g., Meyer and Sahr, 2004). By modifying and expanding the signal analysis capabilities of existing software-defined-radio (SDR) based systems, it is possible to further expand the coverage of E-region plasma turbulence measurements. SDR systems have the capability to record large bandwidths of raw voltage data, followed by post-recording processing on this data. This allows new processing pipelines to be implemented with the systems, for example to obtain E-region coherent scatter spectra measurements if the system is positioned in a suitable location. This can be used to expand the E-region coherent scatter measurement coverage over areas with many different radio systems, with measurements at different frequencies in the HF and VHF radio bands depending on the existing SDR system utilized.
It is therefore recommended to expand upon currently existing E-region coherent scatter radar systems and implement a more extensive network to fully investigate E-region plasma turbulence phenomena—preferably with field-of-views overlapping with complementary instrumentation, such as incoherent scatter radar systems (e.g., the Cornell Homer, Alaska VHF radar with PFISR, and a potential E-region coherent scatter radar with EISCAT 3D) and neutral wind measuring instruments (e.g., meteor radars, incoherent scatter radars, LIDARs, Fabry-Perot interferometers, and rocket ranges). By implementing modern SDR capabilities with E-region coherent scatter radar systems, such as MIMO interferometry, multi-directional measurements on the same frequency band, simultaneous multi-frequency operations, and phase coded CW transmissions, we will be able to fully investigate auroral E-region plasma turbulence and use the radars for continuous fine scale space weather monitoring (e.g., Science Goal 3).
There is also the possibility to use sub-auroral incoherent scatter radars to measure E-region coherent scatter, such as has been done previously with the Millstone Hill incoherent scatter radar located at MIT Haystack Observatory (e.g., St.-Maurice et al., 1989). Through careful experiment planning it is possible to simultaneously measure F-region incoherent scatter and E-region coherent scatter along the same geomagnetic L-shell at sub-auroral latitudes (e.g., Foster and Erickson, 2000). This allows simultaneous comparison between electric fields derived from F-region incoherent scatter radar spectra and the properties of E-region coherent scatter measurements at the same magnetic latitude. The use of radars at sub-auroral latitudes must also be considered for E-region plasma turbulence studies during active geomagnetic conditions.
Associated with the measurements of turbulence are the theoretical analyses and modeling required to understand and predict the E-region plasma turbulence effects on the global terrestrial atmospheric circulation, at both local and global scales. An example of the global models with E-region plasma turbulence heating effects has already been provided in Section 1, but the localized small-scale modeling of the instabilities occurring are also important.
Pure particle-in-cell (PIC) and hybrid PIC (fluid electrons and kinetic ions) have largely been the tools of choice for modelling systems that may trigger the Farley-Buneman instability, since ion Landau damping (a kinetic effect) suppresses growth of irregularities below roughly a meter, thereby preventing the growth rate from increasing as k2 without bound. Hybrid PIC simulations by Oppenheim et al. (1995) reported four principal results: First, that wave growth propagated at an angle offset from E0 ×B0, with the angle depending on the strength of the driving electric field. Second, that primary Farley-Buneman modes non-linearly coupled to modes propagating perpendicular to the local primary wavefronts. Third, that waves propagated at or above the acoustic speed but well below the speed predicted by linear theory. Fourth, that primary-wave phase velocities remained nearly constant in simulated radar scans. Oppenheim et al. (1996) added the conclusion that non-linear δE ×B0 motion dominates the behavior of saturated waves. Oppenheim (1996) showed that mode coupling not only leads to broad, turbulent spectra similar to that produced by the gradient drift instability even in the absence of a density gradient, but also moves energy from short to long wavelengths. Oppenheim and Otani (1996) further showed that a large-scale wave-driven current arises from the non-linear δE ×B0 motion of electrons within the density gradients of Farley-Buneman irregularities, and predicted that it should likewise form in the crests and troughs of gradient drift waves. Fully kinetic 2D PIC simulations presented by Oppenheim and Dimant (2004) describe the influence of ion thermal effects on the growth and saturation of Farley-Buneman irregularities. Much larger 2D PIC simulations (Oppenheim et al., 2008) clearly exhibited the inverse cascade of energy from meter-scale waves (in the growth stage) to the largest resolvable wavelength (in saturation), and the pioneering 3D PIC simulations of Oppenheim and Dimant (2013) revealed the importance of small but non-zero electric fields parallel to B0 in heating electrons, which leads to an anomalous conductivity that can have significant effects on magnetosphere-ionosphere coupling during geomagnetic storms.
An improved version of the Oppenheim et al. (1995) hybrid PIC simulation, described in Young et al. (2017), modelled alternating layers of high and low density in the plane perpendicular to the ambient magnetic field, vertically displaced by a sinusoidal perturbation spanning a few hundred kilometers in horizontal extent. Those simulations demonstrated simultaneous growth of the Farley-Buneman instability at a few meters and the gradient drift instability at tens of meters, as well as interaction of density perturbations originating from both instabilities. The simulated gradient drift instability developed everywhere that the plasma density gradient was parallel to the background electric field and the simulated Farley-Buneman instability developed only where the total electric field, which arose from the combined effects of the background electric field and the ambipolar electric field due to the density gradients, exceeded the threshold value of approximately 11 mV/m. While linear fluid theory readily explains the growth of simulated gradient drift turbulence, it does not as easily account for the isolated growth of meter-scale Farley-Buneman perturbations nor the interplay between density irregularities. The results of these simulations help explain the existence of mixed irregularity types in coherent-scatter radar spectra.
A second, related set of hybrid PIC simulations (Young et al., 2019) modelled a kilometer-scale density wave propagating perpendicular to the ambient electric field in the plane perpendicular to the ambient magnetic field. The simulation setup was designed to mimic the coherent-scatter radar observations at Jicamarca shown by Hysell et al. (2007). Simulation results showed meter-scale density irregularities propagating at approximately ±45° from horizontal in the trough and crest, respectively, increasing in amplitude with increasing altitude and for a higher amplitude kilometer-scale wave. Some results from this simulation are provided in Figure 5. The ambient electric field wave was oriented unfavorably, and its amplitude was too low, for directly driving the Farley-Buneman instability. However, the total electric field in the crests and troughs of the kilometer-scale wave exceeded the Farley-Buneman threshold, thereby triggering instability growth and propagation in the direction of the local Hall drift. As the simulation progressed, these meter-scale density irregularities led to additional plasma transport perpendicular to the direction of their own propagation (i.e., parallel and anti-parallel to the local Pedersen direction), similar to the anomalous transport demonstrated in Oppenheim and Dimant (2013). This anomalous transport produced an anomalous Pedersen conductivity (cf. Dimant and Oppenheim, 2011) that eventually reduced the local electric field to just above the Farley-Buneman threshold. In other words, the Farley-Buneman irregularities acted to short out the electric field that drove them. These simulations also showed that the same anomalous plasma Pedersen conductivity can produce flat-topped electric fields similar to those observed by Pfaff et al. (1987a), Pfaff et al. (1987b) and modelled in 1D by Oppenheim (1997).
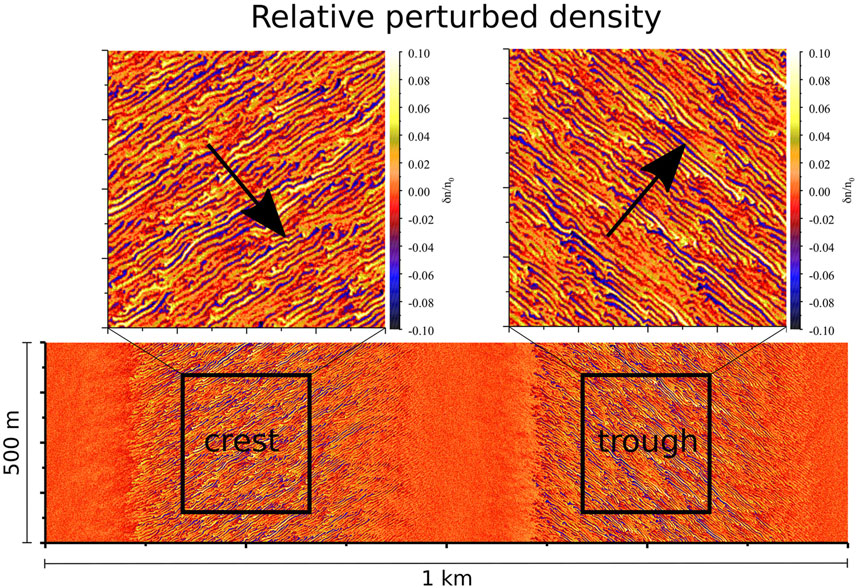
FIGURE 5. Relative perturbed plasma density during a hybrid PIC simulation initialized with an approximately 1-km wave propagating left to right. The ambient electric field points vertically and the ambient magnetic field points into the page. The large-scale wave structure has been filtered out in order to emphasize the small-scale irregularity structure; the initial maximum and minimum of the large-scale wave have been marked by “crest” and “trough”, respectively. Arrows in the top panels indicate the average local direction of irregularity propagation. Adapted from Young et al. (2019).
Fully kinetic 2D and 3D PIC simulations using the Oppenheim and Dimant (2013) simulator at three effective altitudes in the auroral E-Region ionosphere (Young et al., 2020) showed that the mean direction of Farley-Buneman irregularity flow was offset from E0 ×B0 at all altitudes due to a combination of thermal effects and the natural offset of the relative electron-ion flow, and that the deflection from E0 ×B0 increases from instability growth to saturation. Power spectra of density irregularities after instability saturation in the set of 3D simulation runs were nearly flat at the longest resolvable wavelengths, down to a few meters (near the wavelength of peak growth), at which point they all exhibited a power-law decrease into the noise level. The characteristics of 3D power spectra suggest that the saturation mechanism at work is independent of wavelength, and possibly of ion mean free path. Comparison of the set of 2D runs to the set of 3D runs further demonstrated that artificially restricting the Farley-Buneman instability to the plane perpendicular to B0 may yield misleading predictions of irregularity spectra during both growth and saturation stages.
These PIC models are therefore able to capture many of the observational characteristics of the Farley-Buneman instability and related plasma turbulence. Some areas for further study with PIC models include the modeling of the “Type III” E-region coherent scatter measurements, and an extension of the models to larger volumes of the ionosphere. This will allow the simultaneous simulation of both small-scale and large-scale processes in the E-region ionosphere, where large scale processes can commonly drive the smaller scales. Due to the computational complexity of the PIC models and the current difficulty in scaling the models to large data sets, there have also been efforts to investigate fluid-based dynamic models in parallel.
One drawback of the PIC approach is that the necessarily finite number of simulation particles—often implemented as “macro particles”, each representing millions of physical particles via a prescribed shape function for charge density—introduces numerical noise by virtue of the discrete nature of the simulation grid (Kovalev et al., 2008). presented an alternative approach, in which they modelled electrons as a continuous isothermal fluid and ions as a continuous distribution. The use of a fluid electron model is similar to the hybrid PIC approach, but the use of an ion distribution in place of ion macro particles avoids the numerical noise. Their simulations reproduced many characteristics of the Farley-Buneman instability, including non-linear instability saturation, an increase in the dominant wavelength in the saturated state, and wave turning from the E0 ×B0 direction. However, the model was only suited to simulations near the Farley-Buneman instability threshold. Subsequent simulations (Kovalev et al., 2009) improved on the previous results by accounting for electron thermal effects and more recent work by Rojas and Hysell (2021) presented significant advances to the numerical implementation of the hybrid continuous approach while reproducing Farley-Buneman irregularity growth, wave turning, saturation, and mode coupling.
Rojas Villalba et al. (2022) have proposed a five moment fluid model to simulate Farley–Buneman instabilities using similar parameters to Oppenheim et al. (2008). In order to attenuate the amplitude of larger wavemodes, the artificial viscosity operator proposed by Hassan et al. (2015) was used. Several features of the Farley–Buneman instability, were reproduced. However, a better qualitative correspondence was obtained when the artificial viscosity term was ignored (Figure 6). This suggests that the fully non-linear five moment system possess self–regularization properties despite the prediction of standard linear theory. Moreover, their numerical experiments show that instead of a simple cut–off, the growth rates peak at the dominant modes and then decay monotonically for larger wavemodes.
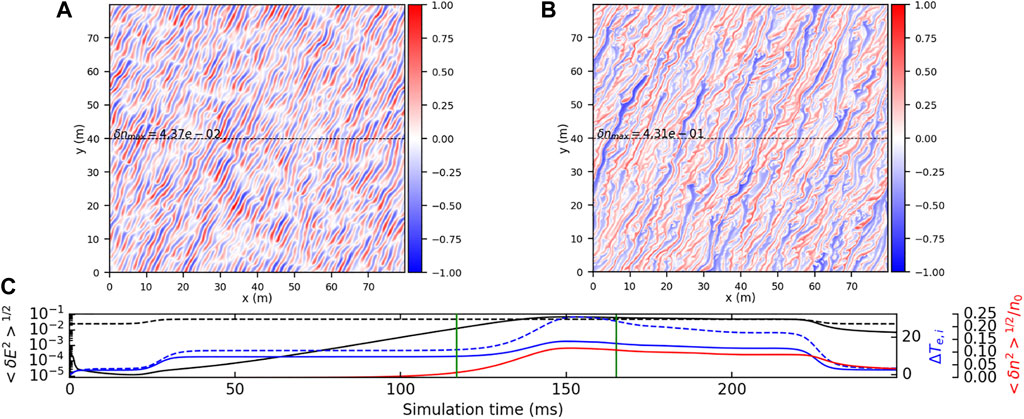
FIGURE 6. (A,B) Snapshots of normalized electron density perturbations taken at the mixing (left) and saturated (right) regimes. δnmax indicate the value of the maximum absolute perturbation (C) Various time series taken for diagnostic. The dashed black, continuous black, dashed blue, continuous blue, and continuous red lines correspond to the background electric field, perturbation electric field, average electron temperature, averaged ion temperature, and electron density root mean squared, respectively. The vertical green lines indicate the times of the snapshots of the top panels (left and right, respectively). The background electric field was switched on at 25 m and off at 225 m. Figure from Rojas Villalba et al. (2022).
Figure 6 shows the normalized electron density perturbations at the linear mixing and saturated regimes obtained with the model proposed by Rojas Villalba et al. (2022). The electron density, averaged temperatures, perturbation electric fields saturate in a similar way as in PIC simulations. Furthermore, the density structures of the saturated regime are very similar to those obtained by PIC models, including the wave turning effect not seen in other isothermal simulations. Even though there is good qualitative agreement between the Rojas Villalba et al. (2022) model and the PIC models, there are still some differences in the results. For example, both the electric field and density perturbation values are larger in the Rojas Villalba et al. (2022) model than the PIC models. This could be explained by the neglect of higher order thermal physics processes, such as Landau damping and diffusion.
In Figure 7 we see the corresponding phase velocities for k = 3 m−1 and for various flow angles. Notice that most of the waves are propagating with a phase speed lower than the convection speed predicted by linear theory and above the ion-acoustic speed. Furthermore, the empirical model relating Doppler spectra and local plasma parameters proposed by Bahcivan (2007) was fitted into the numerically estimated Doppler shift and spectral width, showing an excellent agreement.
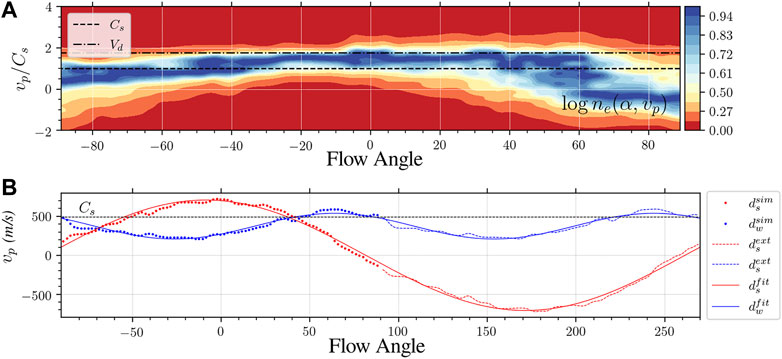
FIGURE 7. (A) The magnitude of the plasma density perturbations based on the phase velocity of the perturbations and the flow angle with respect to E×B for k = 3 m−1 (B) Empirical model determination of the Doppler spectra characteristics using the model proposed by Bahcivan (2007) compared with the Doppler spectra numerically determined from the fluid model of Rojas Villalba et al. (2022). In the figure, ‘sim’ refers to the simulated values, “ext” refers to extended values calculated from the simulation using the symmetry properties of the Fourier transform, and “fit” refers to values that were derived from an empirical model described in Rojas et al. (2018). Figure from Rojas Villalba et al. (2022).
A reason to use fluid models instead of PIC models is that fluid models can often scale much better to larger volumes. To further explore and improve current fluid models of Farley-Buneman instabilities, there are some efforts that should be focused on. These include working on an optimal Landau fluid closure for reproducing the Farley-Buneman plasma turbulence, expanding fluid models to couple them to gradient drift instabilities while extending the Farley-Buneman fluid model fully to 3D, and, using the fact that fluid models of Farley-Buneman instabilities are capable of capturing the main features at low grid resolutions, running large scale ionosphere simulations incorporating the fluid-based Farley-Buneman instability models.
The science goals presented can be studied through further analysis of existing E-region coherent scatter radar measurements, implementation of new E-region coherent scatter operating modes on existing systems, through the implementation of new E-region coherent scatter radars to utilize many of the modern radar techniques available, and through modeling of the E-region plasma turbulence. The radar techniques include MIMO interferometry, multi-static networks, CW coded signals, and simultaneous multi-frequency operations. These radar techniques have been shown to be feasible, though have yet to be simultaneously implemented on an E-region coherent scatter radar system. In addition to the hardware and signal processing, the modeling and research efforts are also required to place measurements into the context of MI coupling and the processes controlling the plasma turbulence generation.
As shown in Section 3.2, models of E-region plasma turbulence are continuously being advanced. The goal of these models is to be able to replicate the E-region coherent scatter measurements and the underlying plasma processes occurring. Once this is accomplished, the models can be incorporated into larger global models of solar-terrestrial interactions to accurately predict how changes in the terrestrial magnetosphere affect the E-region plasma and neutral atmosphere (e.g., Liu et al., 2016). The development of these models is ongoing, as the causes of the different E-region coherent scatter spectra are still being investigated (the investigation of this is covered in SG1).
The other science goals presented correspond to the coupling between the neutral atmosphere and E-region (SG2), the capability of E-region coherent scatter radars to make operational measurements of the ionospheric electric field (SG3), and the coupling of the E-region to both the F-region and higher altitude magnetosphere (SG4). The importance of the E-region ionosphere is emphasized by these science questions, as it is clearly a transition region between space and the terrestrial neutral atmosphere. Both electrodynamic and neutral forcing mechanisms can play a significant role in the processes that occur. This is why understanding the driving forces and effects of E-region turbulence is essential to understanding the transfer of energy in solar-terrestrial interactions.
The implementation and expansion of E-region coherent scatter systems to further investigate these science goals at this time is ideal, as the rising solar activity levels will result in more active ionospheric conditions—an essential aspect to measuring E-region coherent scatter. This will aid in accurately quantifying the energy input into the auroral zones from solar wind-magnetosphere-ionosphere interactions. The solar maximum is predicted to occur approximately halfway through 2025, 3 years away. This provides sufficient time to allocate resources for instruments and research corresponding to E-region plasma turbulence before the peak in solar activity. The cost of parts for a new E-region coherent scatter radar network with all the capabilities mentioned is on the order of 1 M USD, including operations for several years.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
DH is funded through a UiT The Arctic University of Norway contribution to the EISCAT_3D project funded by Research Council of Norway through research infrastructure grant 245683.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bahcivan, H., Hysell, D. L., Larsen, M. F., and Pfaff, R. F. (2005). The 30 MHz imaging radar observations of auroral irregularities during the JOULE campaign. J. Geophys. Res. 110, A05307. doi:10.1029/2004JA010975
Bahcivan, H., Hysell, D. L., Lummerzheim, D., Larsen, M. F., and Pfaff, R. F. (2006). Observations of colocated optical and radar aurora. J. Geophys. Res. 111, A12308. doi:10.1029/2006JA011923
Bahcivan, H. (2007). Plasma wave heating during extreme electric fields in the high-latitude E region. Geophys. Res. Lett. 34, L15106. doi:10.1029/2006GL029236
Billett, D. D., McWilliams, K. A., and Conde, M. G. (2020). Colocated observations of the E and F region thermosphere during a substorm. J. Geophys. Res. Space Phys. 125, e2020JA028165. doi:10.1029/2020ja028165
Buneman, O. (1963). Excitation of field aligned sound waves by electron streams. Phys. Rev. Lett. 10, 285–287. doi:10.1103/PhysRevLett.10.285
Chau, J. L., and St.-Maurice, J.-P. (2016). Unusual 5 m E region field-aligned irregularities observed from northern Germany during the magnetic storm of 17 March 2015. J. Geophys. Res. Space Phys. 121 (10), 316–340. doi:10.1002/2016JA023104
Deng, Y., Fuller-Rowell, T. J., Akmaev, R. A., and Ridley, A. J. (2011). Impact of the altitudinal Joule heating distribution on the thermosphere. J. Geophys. Res. 116, A05313. doi:10.1029/2010JA016019
Dimant, Y. S., Khazanov, G. V., and Oppenheim, M. M. (2021). Effects of electron precipitation on E-region instabilities: Theoretical analysis. JGR. Space Phys. 126, e2021JA029884. doi:10.1029/2021ja029884
Dimant, Y. S., and Milikh, G. M. (2003). Model of anomalous electron heating in the E region: 1. Basic theory. J. Geophys. Res. 108, 1350. doi:10.1029/2002JA009524
Dimant, Y. S., and Oppenheim, M. M. (2011). Magnetosphere-ionosphere coupling through E-region turbulence: 2. Anomalous conductivities and frictional heating. J. Geophys. Res. 116, A09304. doi:10.1029/2011JA016649
Farley, D. (1963). A plasma instability resulting in field-aligned irregularities in the ionosphere. J. Geophys. Res. 68, 6083–6097. doi:10.1029/jz068i022p06083
Fejer, B. G., and Kelley, M. C. (1980). Ionospheric irregularities. Rev. Geophys. 18, 401–454. doi:10.1029/RG018i002p00401
Fejer, B., Providakes, J., Farley, D., and Swartz, W. (1986). Auroral E region plasma waves and elevated electron temperatures. J. Geophys. Res. 91, 13583–13592. doi:10.1029/JA091iA12p13583
Foster, J. C., and Erickson, P. J. (2000). Simultaneous observations of E-region coherent backscatter and electric field amplitude at F-region heights with the Millstone Hill UHF Radar. Geophys. Res. Lett. 27, 3177–3180. doi:10.1029/2000GL000042
Greenwald, R. A., Weiss, W., Nielsen, E., and Thomson, N. R. (1978). Stare: A new radar auroral backscatter experiment in northern scandinavia. Radio Sci. 13, 1021–1039. doi:10.1029/RS013i006p01021
Haldoupis, C. (1989). A review on radio studies of auroral E-region ionospheric irregularities. Ann. Geophys. 121, 10316–10340.
Hamza, A. M., and St-Maurice, J. P. (1993). A turbulent theoretical framework for the study of current-driven E region irregularities at high latitudes: Basic derivation and application to gradient-free situations. J. Geophys. Res. 98, 11587–11599. doi:10.1029/92JA02836
Hapgood, M., Liu, H., and Lugaz, N. (2022). SpaceX—Sailing close to the space weather? Space weather. 20, e2022SW003074. doi:10.1029/2022sw003074
Hassan, E., Horton, W., Smolyakov, A. I., Hatch, D. R., and Litt, S. K. (2015). Multiscale equatorial electrojet turbulence: Baseline 2-D model. J. Geophys. Res. Space Phys. 120, 1460–1477. doi:10.1002/2014JA020387
Huang, Y., Richmond, A. D., Deng, Y., and Roble, R. (2012). Height distribution of Joule heating and its influence on the thermosphere. J. Geophys. Res. 117, A08334. doi:10.1029/2012JA017885
Hussey, G. (1995). The polarisation of 50 MHz auroral backscatter. Saskatoon, Canada: University of Saskatchewan. Ph.D. thesis.
Huyghebaert, D., Billett, D., Chartier, A., Chau, J. L., Hussey, G. C., Hysell, D. L., et al. (2022a). The future of auroral E-region plasma turbulence research. Bull. AAS press.
Huyghebaert, D., Clahsen, M., Chau, J. L., Renkwitz, T., Latteck, R., Johnsen, M. G., et al. (2022b). Multiple E-Region radar propagation modes measured by the VHF SIMONe Norway system during active ionospheric conditions. Front. Astron. Space Sci. 9. 886037. doi:10.3389/fspas.2022.886037
Huyghebaert, D., Hussey, G., Vierinen, J., McWilliams, K., and St-Maurice, J.-P. (2019). Icebear: An all-digital bistatic coded continuous-wave radar for studies of the E region of the ionosphere. Radio Sci. 54, 349–364. doi:10.1029/2018RS006747
Huyghebaert, D., McWilliams, K., Hussey, G., Galeschuk, D., Chau, J. L., and Vierinen, J. (2021). Determination of the azimuthal extent of coherent E-Region scatter using the ICEBEAR linear receiver array. Radio Sci. 56, e2020RS007191. doi:10.1029/2020RS007191
Hysell, D. L., Drexler, J., Shume, E. B., Chau, J. L., Scipion, D. E., Vlasov, M., et al. (2007). Combined radar observations of equatorial electrojet irregularities at Jicamarca. Ann. Geophys. 25, 457–473. doi:10.5194/angeo-25-457-2007
Hysell, D., Miceli, R., Munk, J., Hampton, D., Heinselman, C., Nicolls, M., et al. (2012). Comparing VHF coherent scatter from the radar aurora with incoherent scatter and all-sky auroral imagery. J. Geophys. Res. 117, A10313. doi:10.1029/2012JA018010
Hysell, D. (2015). The radar aurora. Washington, D.C., United States: American Geophysical Union AGU, 191–209. doi:10.1002/9781118978719.ch14
Ivarsen, M. F., Park, J., Kwak, Y.-S., Jin, Y., Knudsen, D. J., and Clausen, L. B. N. (2020). Observational evidence for the role of Hall conductance in Alfvén wave reflection. JGR. Space Phys. 125, e2020JA028119. doi:10.1029/2020ja028119
Ivarsen, M. F., St-Maurice, J.-P., Jin, Y., Park, J., Miloch, W., Spicher, A., et al. (2021). Steepening plasma density spectra in the ionosphere: The crucial role played by a strong E-region. JGR. Space Phys. 126, e2021JA029401. doi:10.1029/2021ja029401
Khazanov, G. V., Robinson, R. M., Zesta, E., Sibeck, D. G., Chu, M., and Grubbs, G. A. (2018). Impact of precipitating electrons and magnetosphere-ionosphere coupling processes on ionospheric conductance. Space weather. 16, 829–837. doi:10.1029/2018SW001837
Kofman, W., and Nielsen, E. (1990). STARE and EISCAT measurements: Evidence for the limitation of STARE Doppler velocity observations by the ion acoustic velocity. J. Geophys. Res. 95, 19131–19135. doi:10.1029/JA095iA11p19131
Kovalev, D. V., Smirnov, A. P., and Dimant, Y. S. (2008). Modeling of the farley-buneman instability in the E-region ionosphere: A new hybrid approach. Ann. Geophys. 26, 2853–2870. doi:10.5194/angeo-26-2853-2008
Kovalev, D. V., Smirnov, A. P., and Dimant, Y. S. (2009). Simulations of the nonlinear stage of Farley-Buneman instability with allowance for electron thermal effects. Plasma Phys. Rep. 35, 603–610. doi:10.1134/S1063780X09070095
Kwak, Y.-S., and Richmond, A. D. (2007). An analysis of the momentum forcing in the high-latitude lower thermosphere. J. Geophys. Res. 112, A01306. doi:10.1029/2006JA011910
Liu, J., Wang, W., Burns, A., Oppenheim, M., and Dimant, Y. (2018). Faster traveling atmosphere disturbances caused by polar ionosphere turbulence heating. J. Geophys. Res. Space Phys. 123, 2181–2191. doi:10.1002/2017JA024746
Liu, J., Wang, W., Oppenheim, M., Dimant, Y., Wiltberger, M., and Merkin, S. (2016). Anomalous electron heating effects on the E region ionosphere in TIEGCM. Geophys. Res. Lett. 43, 2351–2358. doi:10.1002/2016GL068010
Lozinsky, A., Hussey, G., McWilliams, K., Huyghebaert, D., and Galeschuk, D. (2022). ICEBEAR-3D: A low elevation imaging radar using a non-uniform coplanar receiver array for E region observations. Radio Sci. 57, e2021RS007358. doi:10.1029/2021rs007358
Lu, G., Richmond, A. D., Lühr, H., and Paxton, L. (2016). High-latitude energy input and its impact on the thermosphere. JGR. Space Phys. 121, 7108–7124. doi:10.1002/2015JA022294
Lysak, R. L. (1991). Feedback instability of the ionospheric resonant cavity. J. Geophys. Res. 96, 1553–1568. doi:10.1029/90JA02154
Makarevich, R. A. (2009). Coherent radar measurements of the Doppler velocity in the auroral E region. URSI Radio Sci. Bull. 2009, 33–46. doi:10.23919/URSIRSB.2009.7909539
Maynard, N. C., Bahnsen, A., Christophersen, P., Egeland, A., and Lundin, R. (1973). An example of anticorrelation of auroral particles and electric fields. J. Geophys. Res. 78, 3976–3980. doi:10.1029/JA078i019p03976
Meyer, M. G., and Sahr, J. D. (2004). Passive coherent scatter radar interferometer implementation, observations, and analysis. Radio Sci. 39, 1–10. doi:10.1029/2003RS002985
Moorcroft, D. R. (2002). Outstanding issues in the theory of radar aurora: Evidence from the frequency dependence of spectral characteristics. J. Geophys. Res. 107, 1301–SIA 13–19. doi:10.1029/2001JA009218
Newell, P. T., Liou, K., and Wilson, G. R. (2009). Polar cap particle precipitation and aurora: Review and commentary. J. Atmos. Solar-Terrestrial Phys. 71, 199–215. doi:10.1016/j.jastp.2008.11.004
Nielsen, E., del Pozo, C. F., and Williams, P. J. S. (2002). VHF coherent radar signals from the E region ionosphere and the relationship to electron drift velocity and ion acoustic velocity. J. Geophys. Res. 107, 1012. doi:10.1029/2001JA900111
Nielsen, E., and Schlegel, K. (1983). A first comparison of STARE and EISCAT electron drift velocity measurements. J. Geophys. Res. 88, 5745–5750. doi:10.1029/JA088iA07p05745
Oppenheim, M. (1996). A wave-driven nonlinear current in the E-region ionosphere. Geophys. Res. Lett. 23, 3333–3336. doi:10.1029/96GL03100
Oppenheim, M. (1997). Evidence and effects of a wave-driven nonlinear current in the equatorial electrojet. Ann. Geophys. 15, 899–907. doi:10.1007/s00585-997-0899-z
Oppenheim, M. M., Dimant, Y., and Dyrud, L. P. (2008). Large-scale simulations of 2-D fully kinetic Farley-Buneman turbulence. Ann. Geophys. 26, 543–553. doi:10.5194/angeo-26-543-2008
Oppenheim, M. M., and Dimant, Y. S. (2004). Ion thermal effects on E-region instabilities: 2D kinetic simulations. J. Atmos. Sol. Terr. Phys. 66, 1655–1668. doi:10.1016/j.jastp.2004.07.007
Oppenheim, M. M., and Dimant, Y. S. (2013). Kinetic simulations of 3-D Farley-Buneman turbulence and anomalous electron heating. J. Geophys. Res. Space Phys. 118, 1306–1318. doi:10.1002/jgra.50196
Oppenheim, M., Otani, N., and Ronchi, C. (1995). Hybrid simulations of the saturated Farley-Buneman instability in the ionosphere. Geophys. Res. Lett. 22, 353–356. doi:10.1029/94GL03277
Oppenheim, M., Otani, N., and Ronchi, C. (1996). Saturation of the Farley-Buneman instability via nonlinear electron E×B drifts. J. Geophys. Res. 101, 17273–17286. doi:10.1029/96JA01403
Oppenheim, M., and Otani, N. (1996). Spectral characteristics of the Farley-Buneman instability: Simulations versus observations. J. Geophys. Res. 101, 24573–24582. doi:10.1029/96JA02237
Park, J., Lühr, H., Knudsen, D. J., Burchill, J. K., and Kwak, Y.-S. (2017). Alfvén waves in the auroral region, their poynting flux, and reflection coefficient as estimated from Swarm observations. J. Geophys. Res. Space Phys. 122, 2345–2360. doi:10.1002/2016JA023527
Partamies, N., Whiter, D., Kadokura, A., Kauristie, K., Nesse Tyssøy, H., Massetti, S., et al. (2017). Occurrence and average behavior of pulsating aurora. J. Geophys. Res. Space Phys. 122, 5606–5618. doi:10.1002/2017JA024039
Pfaff, R. F., Kelley, M. C., Kudeki, E., Fejer, B. G., and Baker, K. D. (1987a). Electric field and plasma density measurements in the strongly driven daytime equatorial electrojet. 1 the unstable layer and gradient drift waves. J. Geophys. Res. 92, 13578–13596. doi:10.1029/JA092iA12p13578
Pfaff, R. F., Kelley, M. C., Kudeki, E., Fejer, B. G., and Baker, K. D. (1987b). Electric field and plasma density measurements in the strongly driven daytime equatorial electrojet. 2 Two-stream waves. J. Geophys. Res. 92, 13597–13612. doi:10.1029/JA092iA12p13597
Ridley, A. J., Gombosi, T. I., and DeZeeuw, D. L. (2004). Ionospheric control of the magnetosphere: Conductance. Ann. Geophys. 22, 567–584. doi:10.5194/angeo-22-567-2004
Riggin, D., Swartz, W. E., Providakes, J., and Farley, D. T. (1986). Radar studies of long-wavelength waves associated with mid-latitude sporadic E layers. J. Geophys. Res. 91, 8011–8024. doi:10.1029/JA091iA07p08011
Robinson, R. M., Zanetti, L., Anderson, B., Vines, S., and Gjerloev, J. (2021). Determination of auroral electrodynamic parameters from AMPERE field-aligned current measurements. Space weather. 19, e2020SW002677. doi:10.1029/2020sw002677
Robinson, T. (1986). Towards a self-consistent non-linear theory of radar auroral backscatter. J. Atmos. Terr. Phys. 48, 417–422. doi:10.1016/0021-9169(86)90118-2
Rojas, E. L., and Hysell, D. L. (2021). Hybrid plasma simulations of Farley buneman instabilities in the auroral E region. JGR. Space Phys. 126, e28379. doi:10.1029/2020JA028379
Rojas, E. L., Hysell, D. L., and Munk, J. (2018). Assessing ionospheric convection estimates from coherent scatter from the radio aurora. Radio Sci. 53, 1481–1491. doi:10.1029/2018RS006672
Rojas Villalba, E., Burns, K., and Hysell, D. (2022). Fluid models are probably capable to simulate Farley-Buneman instabilities. Earth Space Sci. Open Archive 9. doi:10.1002/essoar.10512168.2
Sahr, J. D., and Fejer, B. G. (1996). Auroral electrojet plasma irregularity theory and experiment: A critical review of present understanding and future directions. J. Geophys. Res. 101, 26893–26909. doi:10.1029/96JA02404
Schlegel, K., and St.-Maurice, J. P. (1981). Anomalous heating of the polar E region by unstable plasma waves 1. observations. J. Geophys. Res. 86, 1447–1452. doi:10.1029/JA086iA03p01447
St.-Maurice, J.-P., and Chau, J. L. (2016). A theoretical framework for the changing spectral properties of meter-scale Farley-Buneman waves between 90 and 125 km altitudes. J. Geophys. Res. Space Phys. 121 (10), 341–366. doi:10.1002/2016JA023105
St.-Maurice, J.-P., Foster, J., Holt, J., and del Pozo, C. (1989). First results on the observation of 440-MHz high-latitude coherent echoes from the E region with the Millstone Hill Radar. J. Geophys. Res. 94, 6771–6798. doi:10.1029/JA094iA06p06771
St-Maurice, J.-P., and Goodwin, L. (2021). Revisiting the behavior of the E-Region electron temperature during strong electric field events at high latitudes. JGR. Space Phys. 126, 2020JA028288. doi:10.1029/2020JA028288
St.-Maurice, J. P., Prikryl, P., Danskin, D. W., Hamza, A. M., Sofko, G. J., Koehler, J. A., et al. (1994). On the origin of narrow non-ion-acoustic coherent radar spectra in the high-latitude E region. J. Geophys. Res. 99, 6447–6474. doi:10.1029/93JA02353
Williams, P. J. S., Jones, B., Kustov, A. V., and Uspensky, M. V. (1999). The relationship between E region electron density and the power of auroral coherent echoes at 45 MHz. Radio Sci. 34, 449–457. doi:10.1029/1998RS900039
Wiltberger, M., Merkin, V., Zhang, B., Toffoletto, F., Oppenheim, M., Wang, W., et al. (2017). Effects of electrojet turbulence on a magnetosphere-ionosphere simulation of a geomagnetic storm. JGR. Space Phys. 122, 5008–5027. doi:10.1002/2016JA023700
Young, M. A., Oppenheim, M. M., and Dimant, Y. S. (2017). Hybrid simulations of coupled Farley-Buneman/gradient drift instabilities in the equatorial E region ionosphere. JGR. Space Phys. 122, 5768–5781. doi:10.1002/2017JA024161
Young, M. A., Oppenheim, M. M., and Dimant, Y. S. (2019). Simulations of secondary farley-buneman instability driven by a kilometer-scale primary wave: Anomalous transport and formation of flat-topped electric fields. JGR. Space Phys. 124, 734–748. doi:10.1029/2018JA026072
Keywords: ionosphere, E-region coherent scatter, E-region plasma turbulence, magnetosphere-ionosphere coupling, ionospheric conductance
Citation: Huyghebaert D, Billett D, Chartier A, Chau JL, Hussey GC, Hysell DL, Ivarsen MF, Mesquita RLA, Rojas E, Vierinen J and Young M (2022) The future of auroral E-region plasma turbulence research. Front. Astron. Space Sci. 9:1062358. doi: 10.3389/fspas.2022.1062358
Received: 05 October 2022; Accepted: 29 November 2022;
Published: 15 December 2022.
Edited by:
Sabrina Savage, Marshall Space Flight Center (NASA), United StatesReviewed by:
Chris Bard, Goddard Space Flight Center (NASA), United StatesCopyright © 2022 Huyghebaert, Billett, Chartier, Chau, Hussey, Hysell, Ivarsen, Mesquita, Rojas, Vierinen and Young. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Devin Huyghebaert, ZGV2aW4uci5odXlnaGViYWVydEB1aXQubm8=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.