- 1Department of Physics and Astronomy, Rice University, Houston, TX, United States
- 2Department of Physics, Center for Solar-Terrestrial Research, New Jersey Institute of Technology, Newark, NJ, United States
While the societal relevance of space physics drives most of the research in the field, this paper argues for the merit in addressing problems that are core to plasma physics, regardless of discipline or application to society. The geospace environment is a unique, naturally occurring laboratory that can be used for investigating basic plasma processes. Ground and satellite-based observations provide important data for understanding basic plasma processes such as transport, charge-neutral interactions, collisions, and turbulence. These are important topics in space physics, and we show how these topics are relevant to the broader plasma physics community. This paper recommends improved funding lines to examine fundamental plasma physics in the geospace environment. This can be accomplished by annual solicitation of the NASA ROSES B.3 Heliophysics Theory, Modeling, and Simulations (HTMS) program; consideration of plasma physics as relevant to all NASA proposals; and creating a pathway for high-risk research into fundamental science.
Introduction
The Earth’s magnetosphere-ionosphere system is home to numerous spacecraft that are critical to modern society. It is also a naturally occurring laboratory that can be exploited for investigating basic plasma processes. For example, studies of ionospheric scintillation are important for high-precision GPS use, but scintillation is also intimately linked with turbulence and plasma instabilities. Relativistic electrons pose an operational hazard to spacecraft, and studying their transport and diffusion is fundamentally the same as studying transport and confinement in a tokamak. Heliophysics research areas like ionospheric scintillation and radiation belt transport are readily funded due to their immediate and practical benefit to society, however, what is commonly overlooked is the fundamental science that can also be studied concurrently, particularly with regard to plasma physics. This paper argues for the merit in addressing problems that are core to plasma physics, regardless of discipline or application to society.
Modern heliophysics thrives due to its societal relevance, and accordingly the funding and research models are largely problem-driven. This creates a significant issue in that problem-driven research typically favors incremental and iterative science, proposing solutions that are slight improvements over previous studies. Proposals that go beyond this incremental model are often viewed as risky, since they aim to probe unknown regions of science and cannot guarantee success or feasibility. Our field needs both types of research programs to be successful. We must continue prioritizing operational solutions for problems in heliophysics, but we must also strive for a better understanding of the underlying plasma physics. It is inherently difficult to propose a low-risk research plan that will probe fundamental physics as a main goal, as this task is often left as a secondary goal, or even left to chance.
Current funding structures make it difficult to research these “fundamentals,” yet it is challenging to understand more “practical” geospace processes without truly understanding the fundamentals. We therefore need plasma physics to be a fundamental science topic within space physics, and to consider the upper atmosphere and magnetosphere as a unique type of active plasma laboratory. Furthermore, we advocate for continued regular solicitation of the NASA ROSES B.3 Heliophysics Theory, Modeling, and Simulations (HTMS) program since its goal is to “provide a complete chain of reasoning extending from the basic laws of nature to comparison with observation.”
In this white paper, we will provide a brief summary of just a few fundamental areas of research within plasma physics that are critical to heliophysics. The geospace laboratory provides ample data to study transport, charge-neutral interactions, collisions, turbulence, and more. Additionally, when applicable we will highlight knowledge outside of heliophysics that we need to tap into, and the invested interest from other communities into these space plasma related problems.
Plasma transport, confinement, and fusion
On 8 August 2021, the National Ignition Facility (NIF) at Lawrence Livermore National Laboratory achieved the most significant fusion milestone in decades—ignition (Abu-Shawareb et al., 2022; Kritcher et al., 2022; Zylstra et al., 2022). Ignition in a fusion plasma is where the energy produced by fusion reactions is high enough to create a positive feedback loop that heats the plasma and sustains fusion. Fusion achievements such as the milestone NIF experiment are benchmarked by how long a plasma is confined at a given density and temperature. In an inertial confinement system like NIF, the confinement time is limited by the onset of the Rayleigh-Taylor instability (Kilkenny et al., 1994)—the same instability responsible for spread-F in the ionosphere (Huba, 2022). In magnetic confinement fusion, which is viewed as the likely path towards viable energy plants, the main instabilities are the MHD kinking and ballooning modes (de Blank, 2006), which are observed by satellites in the Earth’s magnetotail (Panov et al., 2012).
Radiation belt physics can be thought of as a magnetic confinement problem—how long do energetic electrons stay trapped in the inner magnetosphere? The radiation belts are unique for providing a cold background plasma and an energetic population that acts as test particles. The individual trajectories of energetic particles can be simulated, leading to insights on radial diffusion, global losses, and wave-particle interactions (Elkington et al., 2002). In contrast to fusion plasmas, studies on radiation belt remediation seek artificial methods for depleting the radiation belts using either ground-based Very Low Frequency (3–30 kHz) waves (Carlsten et al., 2019) or neutral atom injection (Fletcher et al., 2020). In radiation belt physics and magnetic confinement systems the problems and methodology are the same, with both research areas seeking to understand the basic transport, diffusion, wave-particle interactions, and adiabatic invariants necessary for confining a hot plasma population.
Incoherent scatter (IS) radars provide data products that are heavily utilized in studies of the ionosphere. The core functionality of an IS radar is to transmit a radio wave from a large antenna and measure the Doppler spectrum that is Thomson scattered off the ionosphere. Historically, the field of Thomson scattering in a plasma was developed specifically for IS radars in the 1960s, but the field has evolved substantially due to fusion requiring measurements of >10 keV plasma temperatures. The importance of Thomson scattering in the near-relativistic limit is highlighted by Sheffield et al. (2011), which now serves as a foundational textbook for studies of IS radar theory and for Thomson scatter measurements of fusion plasmas. While the high energies in a fusion device have pushed the forefront of Thomson scatter theory, recent studies on IS theory have also advanced the field by showing need for analytic solutions for collisional physics (Goodwin et al., 2018; Longley et al., 2019), the coupling between different wave modes (Longley et al., 2020), and the importance of suprathermal distributions (Longley et al., 2021).
Partially ionized plasmas
The subfields of ionospheric physics and magnetospheric physics share similar historical origins, but diverged in methodology over time because of the high neutral density in the ionosphere. Global MHD codes are crucial workhorses for understanding the complex, large-scale dynamics of the magnetosphere during solar storms. In contrast, MHD has never been relied on for ionospheric studies since the presence of neutrals necessitates either two-fluid (ion and electron) or kinetic methods. For example, the Farley-Buneman instability in the E-region is a modified two-stream instability caused by neutrals dragging ions in a different direction than electrons and cannot be simulated with MHD. While the presence of neutrals has always been emphasized in ionospheric and chromospheric studies, the contribution of the geocorona to the cold plasma in the magnetosphere is starting to be understood (Borovsky et al., 2022).
Charge-neutral interactions are pervasive and fundamental in the ionosphere and can be exploited for remote sensing methods. Radar measurements of the high latitude E-region (NO + dominant) and lower ionosphere can be inverted to estimate the fluxes of precipitating energetic electrons (Semeter and Kamalabadi, 2005). 150 km echoes observed at low latitudes can be used to infer density contours at gaps in the echoes, and those gaps are observed to oscillate due to atmospheric gravity waves, providing a unique diagnostic into neutral forcing from lower altitudes (Longley et al., 2020; Reyes et al., 2020). Multi-static meteor radars are able to produce dynamic maps of neutral winds in the mesosphere (Chau et al., 2021). Meteor radar measurements require detailed modeling of how the plasma surrounding a meteor is created by neutral impacts (Dimant and Oppenheim, 2017a; Dimant and Oppenheim, 2017b), which has multiple parallels to laboratory plasma etching of semiconductors.
Partially ionized plasmas are heavily studied within geospace. This is a core focus of NSF funding for aeronomy and the Coupling Energetics and Dynamics of Atmospheric Regions (CEDAR) funding lines and workshops. NASA as well is invested in these important topics. For example, the upcoming Geospace Dynamics Constellation (GDC) mission will orbit in the F-region (the O+-O dominant region of the upper atmosphere). GDC is a constellation of spacecraft which will provide global multi-point in situ measurements within the ionosphere to examine the coupling between the magnetosphere and the ionosphere-thermosphere system, and the dissipation of energy due to this coupling. Additionally, NASA has approved the Dynamical Neutral Atmosphere-Ionosphere Coupling (DYNAMIC) mission, which allows the community to explore how the near-Earth space environment responds to lower atmospheric weather, and the role of wave processes in neutral-plasma coupling. Both these missions are a top-priority to the space physics community and will provide cutting-edge observations of ion-neutral coupling in the geospace laboratory.
O+-O collision cross section
Plasmas are commonly assumed to have a Maxwellian velocity distribution, implying an isotropic temperature. However, in the presence of strong electric fields (> 25 mV/m) the ion velocity distribution in the weakly-ionized, magnetized F-region ionosphere distorts, becoming more toroidal with more enhanced electric fields. This is the result of O+ and O collisions and Resonant Charge Exchange (RCE).
As the electric field increases in association with enhanced geomagnetic activity, the ion velocity distribution becomes distorted as it evolves from a Maxwellian shape into a toroidal shape. As the ion velocity distribution distorts from a Maxwellian shape to a toroidal shape, the width of the ion velocity distribution increases in both directions perpendicular to the magnetic field (in velocity space). Thus, the ion temperature becomes anisotropic, with the ion temperature perpendicular to the magnetic field being larger than the ion temperature parallel to the magnetic field. An example of this is seen in Figure 1 in the presence of a 150 mV/m electric field.
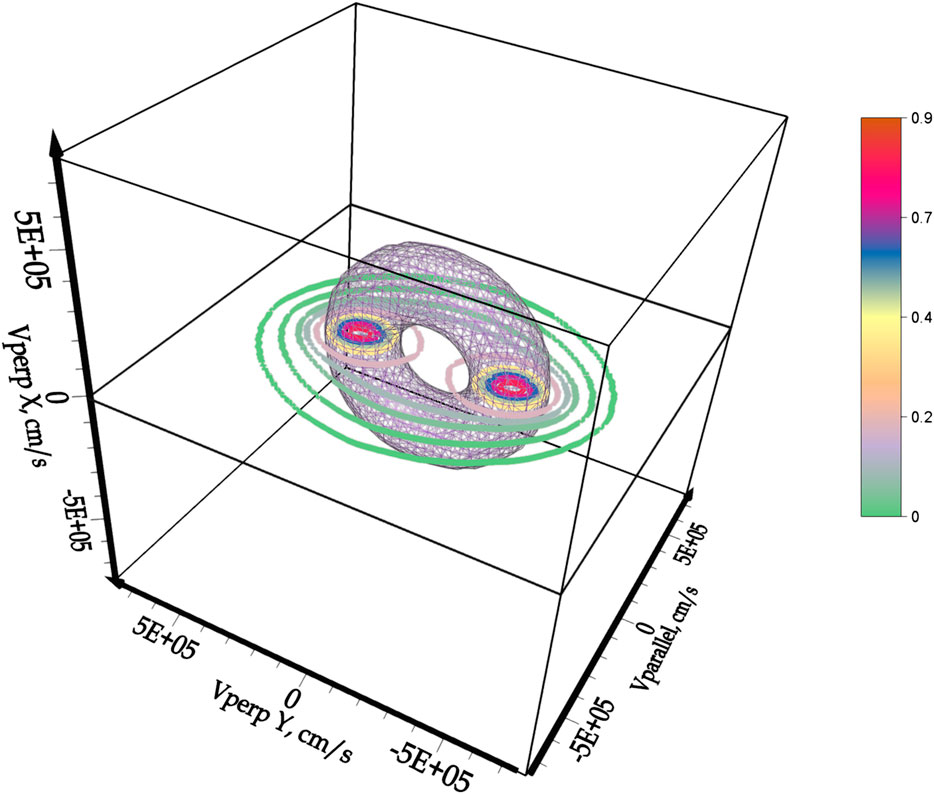
FIGURE 1. A distorted ion velocity distribution in the presence of O + -O collisions during a 150 mV/m electric field. The “Vperp X” and “Vperp Y” axes are perpendicular to the magnetic field, and the “Vparallel” axis is parallel to the magnetic field. The distribution is computed using the Monte-Carlo simulation from Winkler et al. (1992), but the figure is modified from Goodwin et al. (2018). The O+-O collision cross-section described in Knof et al. (1964) is used.
Although these distortions are well-documented (e.g., St.-Maurice and Schunk (1977)) and different estimates of this interaction have been developed (e.g., Knof et al., 1964; Pesnell et al., 1993), the cross-section between these species (and thus the momentum transfer collision frequency) is still not known with certainty. Laboratory estimates of the cross-sections contain many sources of error, and theoretical estimates involve detailed quantum mechanical calculations that are challenging to verify. One important source of error is that finding the O+-O collision cross-section in laboratory data requires extrapolating lower-energy laboratory data to higher energies. It is therefore common for ionospheric models and measurements to instead assume, in some manner, that the O+ velocity distribution is Maxwellian, or incorporate a constant (known as a “burnside factor”) multiplied by an approximated momentum transfer collision frequency.
In situ simultaneous measurements of collision frequency parameters can estimate the O+-O collision cross-section and resolve sources of errors in current laboratory-based or ground-based estimates. Upcoming missions, such as the GDC and DYNAMIC missions, can be utilized to provide information about ion-neutral coupling. However, of particular interest are the proposed Daedalus (Sarris et al., 2020) and Atmosphere-Space Transition Region Explorer (ASTRE) (Pfaff, 2022) mission concepts. These in situ dipper mission concepts in essence repeat laboratory measurements, but under actual ionospheric conditions from altitudes below 200 km in the E-region up to altitudes in the F-region. Daedalus and ASTRE will resolve ion temperature anisotropies by measuring the complete 3D ion distribution function and the atmospheric collision frequency profile, thereby providing relevant information on the O+-O cross-section and the effects of RCE.
Turbulence
Turbulence is the only problem in heliophysics with a $1,000,000 prize: all one has to do is prove smooth solutions exist for the Navier-Stokes equation. More realistically, the problem of turbulence in physics is to predict the onset and evolution of a turbulent flow. Solving turbulence will have a significant impact across all of heliophysics, but also a broad impact in other disciplines such as astrophysics, meteorology, oceanography, aeronautics, and engineering.
The geospace laboratory is ideal for studying turbulence due to how ubiquitous the phenomenon is, allowing for a wide array of ground and satellite-based experiments. For example, the Magnetospheric Multiscale (MMS) mission observed wave induced turbulence within the electron diffusion region of magnetic reconnection (Ergun et al., 2017). MMS has also observed turbulence in the flanks of the magnetopause driven by the Kelvin-Helmholtz instability (Hasegawa et al., 2020). Atmospheric radars can observe a different manifestation of the Kelvin-Helmholtz turbulence caused by shears in the neutral winds (Chau et al., 2020). Further, a wide range of turbulent plasma instabilities, such as Farley-Buneman, gradient-drift, and spread-F, can be observed in the ionosphere using ground-based radars, scintillation of radio signals, and rocket flights.
Some progress has been made on the theory of turbulence. Kolmogorov’s famous 5/3’s scaling law describes the energy cascade from large to small scales (Kolmogorov, 1941), however the scaling law does not address the onset of turbulence and has limitations for higher-order structure functions. In plasma physics, the onset of turbulence is often crudely predicted using linear instability analysis. Numerical models can simulate some of the features of turbulence, however, the multi-scale nature of turbulence creates a computational limit. For example, MHD models can simulate the large-scale structures of turbulent flow, but they cannot simultaneously and accurately simulate the micro-scale dissipation of energy. The important radiation belt processes of quasilinear theory and induced scattering are developed in the framework of weak turbulence, which describes the weak, nonlinear interaction of different wave modes.
A key feature of weak turbulence is that the system can still be Fourier-Laplace transformed and decomposed into a set of normal modes. In contrast, strong turbulence involves fluctuations with amplitudes on the order of the background motion, rendering the Fourier-Laplace transform meaningless. An analogy of this difference in a nonlinear system is shown in Figure 2, where the Fourier transforms of a double pendulum are shown. Standard plasma physics techniques rely heavily on linearizing and Fourier-Laplace transforming the governing plasma equations (i.e., Boltzmann or fluid equations), and are therefore ill-equipped to handle the problem of turbulence.
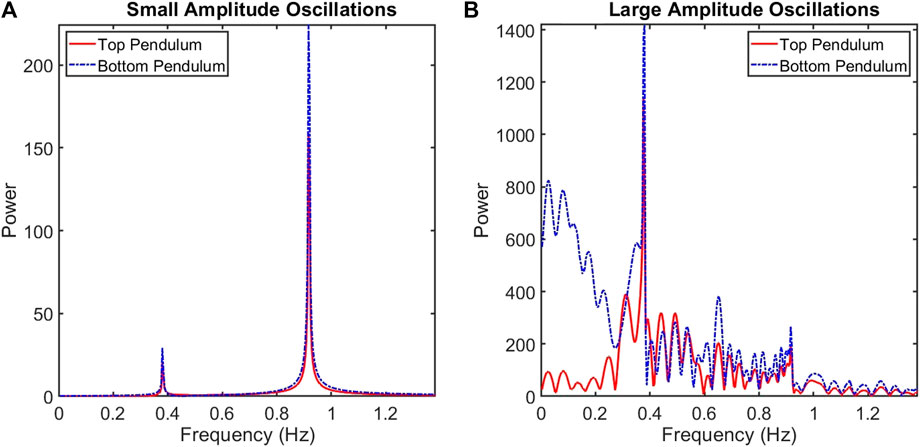
FIGURE 2. Fourier transforms of a double pendulum. Panel (A), small amplitude oscillations, and the resulting peaks (two normal modes) of the coupled oscillators. Panel (B), large amplitude oscillations governed by fully nonlinear equations and the resulting peaks (not normal modes) of the coupled oscillators. The Fourier analysis breaks down and offers no insight into the dynamics of the fully nonlinear system.
Most theoretical research in heliophysics is actually phenomenological, where existing theories are used to predict and interpret observations. Our current methods for plasma physics and fluid mechanics are not capable of describing the onset and evolution of turbulence, necessitating a completely new theoretical approach. This means the daunting task of developing new mathematical tools to deal with the nonlinear terms that break the applicability of the Fourier transform, and new insights into what measurable quantities need to be described analytically. Turbulence is a problem truly on the Frontier of theoretical physics and cannot be addressed with standard research proposals that are typically iterative, incremental, and low-risk. This raises a question underlying all of the fundamental plasma topics outlined in this paper: how can NASA funding support research into the core physics of geospace?
Summary
The space plasma communities are currently disjoint, despite a shared early history and overlapping curriculum and textbooks. Treating the geospace environment like a laboratory experiment allows researchers in all fields to broadly test their understanding of plasma physics. Furthermore, theoretical work on turbulence, instabilities, transport, charge-neutral interactions, collisions, and plasma diagnostics has direct applications between each field, with a high payoff for all of heliophysics.
This perspective paper recommends stable funding lines to study basic plasma physics within the geospace environment. The NASA B.3 Heliophysics Theory, Modeling, and Simulations (HTMS) program partially fulfills this, but this funding needs to be more consistently offered. Several topics of interest to the geospace community have been highlighted in this document, as well as their relevance to the broader plasma physics community. However, these topics alone do not fully encompass the synergy between space science and plasma physics (e.g., magnetic reconnection, beam physics, suprathermal velocity distributions). Therefore, we must consider plasma physics a fundamental science topic within space physics and relevant in all NASA solicitations.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
WL was funded by NASA grant #80NSSC21K1322. LG was funded by NJIT start-up funds.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abu-Shawareb, H., Acree, R., Adams, P., Adams, J., Addis, B., Aden, R., et al. (2022). Indirect drive ICF Collaboration)Lawson criterion for ignition exceeded in an inertial fusion experiment. Phys. Rev. Lett. 129, 075001. doi:10.1103/PhysRevLett.129.075001
Borovsky, J. E., Liu, J., Ilie, R., and Liemohn, M. W. (2022). Charge-Exchange byproduct cold protons in the Earth’s magnetosphere. Front. Astron. Space Sci. 8, 785305. doi:10.3389/fspas.2021.785305
Carlsten, B. E., Colestock, P. L., Cunningham, G. S., Delzanno, G. L., Dors, E. E., Holloway, M. A., et al. (2019). Radiation-belt remediation using space-based antennas and electron beams. IEEE Trans. Plasma Sci. 47 (5), 2045–2063. doi:10.1109/TPS.2019.2910829
Chau, J. L., Urco, J. M., Avsarkisov, V., Vierinen, J. P., Latteck, R., Hall, C. M., et al. (2020). Four-dimensional quantification of Kelvin-Helmholtz instabilities in the polar summer mesosphere using volumetric radar imaging. Geophys. Res. Lett. 47, e2019GL086081. doi:10.1029/2019GL086081
Chau, J. L., Urco, J. M., Vierinen, J., Harding, B. J., Clahsen, M., Pfeffer, N., et al. (2021). Multistatic specular meteor radar network in Peru: System description and initial results. Earth Space Sci. 8, e2020EA001293. doi:10.1029/2020EA001293
de Blank, H. J. (2006). MHD instabilities in tokamaks. Fusion Sci. Technol. 49 (2T), 118–130. doi:10.13182/FST06-A1111
Dimant, Y. S., and Oppenheim, M. M. (2017a). Formation of plasma around a small meteoroid: 1. Kinetic theory. J. Geophys. Res. Space Phys. 122, 4669–4696. doi:10.1002/2017JA023960
Dimant, Y. S., and Oppenheim, M. M. (2017b). Formation of plasma around a small meteoroid: 2. Implications for radar head echo. J. Geophys. Res. Space Phys. 122, 4697–4711. doi:10.1002/2017JA023963
Elkington, S. R., Hudson, M. K., Wiltberger, M. J., and Lyon, J. G. (2002). MHD/Particle simulations of radiation belt dynamics. J. Atmos. Sol. Terr. Phys. 64 (5-6), 607–615. doi:10.1016/S1364-6826(02)00018-4
Ergun, R. E., Chen, L. J., Wilder, F. D., Ahmadi, N., Eriksson, S., Usanova, M. E., et al. (2017). Drift waves, intense parallel electric fields, and turbulence associated with asymmetric magnetic reconnection at the magnetopause. Geophys. Res. Lett. 44, 2978–2986. doi:10.1002/2016GL072493
Fletcher, A. C., Crabtree, C., Huba, J., Ganguli, G., and Siefring, C. (2020). Early time evolution of turbulence in the space environment by neutral beam injection. JGR. Space Phys. 125, e2019JA027587. doi:10.1029/2019JA027587
Goodwin, L. V., Maurice, J. P. S., Akbari, H., and Spiteri, R. J. (2018). Incoherent scatter spectra based on Monte Carlo simulations of ion velocity distributions under strong ion frictional heating. Radio Sci. 53 (3), 269–287. doi:10.1002/2017rs006468
Hasegawa, H., Nakamura, T. K. M., Gershman, D. J., Nariyuki, Y., Viñas, A. F., Giles, B. L., et al. (2020). Generation of turbulence in Kelvin-Helmholtz vortices at the Earth's magnetopause: Magnetospheric Multiscale observations. J. Geophys. Res. Space Phys. 125, e2019JA027595. doi:10.1029/2019JA027595
Huba, J. D. (2022). Generalized Rayleigh-Taylor instability: Ion inertia, acceleration forces, and E region drivers. JGR. Space Phys. 127, e2022JA030474. doi:10.1029/2022JA030474
Kilkenny, J. D., Glendinning, S. G., Haan, S. W., Hammel, B. A., Lindl, J. D., Munro, D., et al. (1994). A review of the ablative stabilization of the Rayleigh–Taylor instability in regimes relevant to inertial confinement fusion. Phys. Plasmas 1, 1379–1389. doi:10.1063/1.870688
Knof, H., Mason, E. A., and Vanderslice, J. T. (1964). Interaction energies, charge exchange cross sections, and diffusion cross sections for N+–N and O+–O collisions. J. Chem. Phys. 40 (12), 3548–3553. doi:10.1063/1.1725050
Kolmogorov, A. N. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. 434, 9–Pft13. doi:10.1098/rspa.1991.0075
Kritcher, A. L., Zylstra, A. B., Callahan, D. A., Hurricane, O. A., Weber, C. R., Clark, D. S., et al. (2022). Design of an inertial fusion experiment exceeding the Lawson criterion for ignition. Phys. Rev. E 106, 025201. doi:10.1103/PhysRevE.106.025201
Longley, W. J., Oppenheim, M. M., and Dimant, Y. S. (2019). Nonlinear effects of electron-electron collisions on ISR temperature measurements. JGR. Space Phys. 124, 6313–6329. doi:10.1029/2019JA026753
Longley, W. J., Oppenheim, M. M., Pedatella, N. M., and Dimant, Y. S. (2020). The photoelectron-driven upper hybrid instability as the cause of 150-km echoes. Geophys. Res. Lett. 47, e2020GL087391. doi:10.1029/2020GL087391
Longley, W. J., Vierinen, J., Sulzer, M. P., Varney, R. H., Erickson, P. J., and Perillat, P. (2021). An explanation for Arecibo plasma line power striations. JGR. Space Phys. 126, e2020JA028734. doi:10.1029/2020JA028734
Panov, E. V., Sergeev, V. A., Pritchett, P. L., Coroniti, F. V., Nakamura, R., Baumjohann, W., et al. (2012). Observations of kinetic ballooning/interchange instability signatures in the magnetotail. Geophys. Res. Lett. 39, L08110. doi:10.1029/2012GL051668
Pesnell, W. D., Omidvar, K., and Hoegy, W. R. (1993). Momentum transfer collision frequency of O+‐O. Geophys. Res. Lett. 20 (13), 1343–1346. doi:10.1029/93gl01597
Pfaff, R. F. (2022). The atmosphere-space transition region explorer (ASTRE) - a low perigee satellite to investigate the coupling of the Earth’s upper atmosphere and magnetosphere, to be submitted to space science reviews.
Reyes, P. M., Kudeki, E., Lehmacher, G. A., Chau, J. L., and Milla, M. A. (2020). VIPIR and 50 MHz radar studies of gravity wave signatures in 150-km echoes observed at Jicamarca. J. Geophys. Res. Space Phys. 125, e2019JA027535. doi:10.1029/2019JA027535
Sarris, T. E., Talaat, E. R., Palmroth, M., Dandouras, I., Armandillo, E., Kervalishvili, G., et al. (2020). Daedalus: A low-flying spacecraft for in situ exploration of the lower thermosphere–ionosphere. Geosci. Instrum. Method. Data Syst. 9, 153–191. doi:10.5194/gi-9-153-2020
Semeter, J., and Kamalabadi, F. (2005). Determination of primary electron spectra from incoherent scatter radar measurements of the auroralEregion. Radio Sci. 40, RS2006. doi:10.1029/2004RS003042
Sheffield, J., Froula, D. H., Glenzer, S. H., and Luhmann, N. C. (2011). Plasma scattering of electromagnetic radiation: Theory and measurement techniques. Burlington, MA: Academic Press. doi:10.1016/B978-0-12-374877-5.00001-4
St.-Maurice, J. P., and Schunk, R. W. (1977). Auroral ion velocity distributions for a polarization collision model. Planet. Space Sci. 25 (3), 243–260. doi:10.1016/0032-0633(77)90135-0
Winkler, E., St-Maurice, J-P., and Barakat, A. R. (1992). Results from improved Monte Carlo calculations of auroral ion velocity distributions. J. Geophys. Res. 97 (A6), 8399–8423. doi:10.1029/91JA03104
Keywords: white paper, decadal survey, plasma physics, instabilities, turbulence, plasma transport, fusion, partially ionized plasmas
Citation: Longley WJ and Goodwin LV (2022) Geospace: The naturally occurring plasma laboratory. Front. Astron. Space Sci. 9:1060915. doi: 10.3389/fspas.2022.1060915
Received: 03 October 2022; Accepted: 21 October 2022;
Published: 04 November 2022.
Edited by:
Alexa Jean Halford, Goddard Space Flight Center (NASA), United StatesReviewed by:
Mourad Djebli, USTHB, AlgeriaCopyright © 2022 Longley and Goodwin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: William J. Longley, d2xvbmdsZXlAcmljZS5lZHU=
 William J. Longley
William J. Longley Lindsay V. Goodwin
Lindsay V. Goodwin