Flare quasi-periodic pulsation associated with recurrent jets

Quasi-periodic pulsations (QPPs), which carry time features and plasma characteristics of flare emissions, are frequently observed in light curves of solar/stellar flares. In this study, we investigated non-stationary QPPs associated with recurrent jets during an M1.2 flare on 2022 July 14. A quasi-period of $\sim 45\pm$10 s, determined by the wavelet transform technique, is simultaneously identified at wavelengths of soft/hard X-ray and microwave emissions, which are recorded by the Gravitational Wave High-Energy Electromagnetic Counterpart All-sky Monitor, Fermi and the Nobeyama Radio Polarimeters, respectively. A group of recurrent jets with an intermittent cadence of about 45 ± 10 s are found in the Atmospheric Imaging Assembly (AIA) image series at 304 Å, but they are 180 s earlier than the flare QPP. All observational facts suggest that the flare QPPs could be excited by recurrent jets, and they should be associated with non-thermal electrons that are periodically accelerated by a repeated energy release process, such as repetitive magnetic reconnection. Moreover, the same quasi-period is discovered at double footpoints connected by a hot flare loop in AIA 94 Å, and the phase speed is measured to be ∼1,420 km s⁻¹. Based on the differential emission measure, the average temperatures, number densities, and magnetic field strengths at the loop top and footpoint are estimated to be ∼7.7/6.7 MK, ∼7.5/3.6 × 10¹⁰ cm⁻³, and ∼143/99 G, respectively. Our measurements indicate that the 45-s QPP is probably modulated by the kink-mode wave of the flare loop.

1 Introduction

Quasi-periodic pulsations (QPPs) observed in solar/stellar flares usually appear as temporal intensity oscillations of electromagnetic radiation (see, Kupriyanova et al., 2020; Zimovets et al., 2021b, and references therein). They are frequently identified as a series of repetitive but irregular pulsations with anharmonic and symmetric triangular shapes, referring to non-stationary QPPs (e.g., Nakariakov et al., 2019). The observation of QPPs has been reported in flare time series over a broad range of wavelengths, ranging from radio/microwave emissions through ultraviolet (UV) and white light wavelengths to soft and hard X-ray (SXR/HXR) channels and even in the γ-ray emission (e.g., Nakariakov et al., 2010a; Tan et al., 2016; Li et al., 2017b; Milligan et al., 2017; Kashapova et al., 2021; Kolotkov et al., 2021; Lu et al., 2021; Zhang Q. et al., 2022; Doyle et al., 2022; Smith et al., 2022). Generally, a typical QPP should be at least three successive and complete pulsations. There is no reason to talk about the QPP behavior if there are only one or two pulsations, which might be just a coincidence, for instance, the similar time interval between successive pulsations occurred by chance (Nakariakov et al., 2019). The characteristic time of all pulsations in one QPP event is expected to be the same, which can be regarded as the period. However, the characteristic time of these pulsations could be varied, indicating the irregular nature of flare QPPs. Thus, they often show the variation of quasi-periods (e.g., Nakariakov et al., 2018). In observations, the quasi-periods of flare QPPs are found to vary from a fraction of seconds to a few dozens of minutes (Tan et al., 2010; Yuan et al., 2013; Ning, 2014; Mészárosová et al., 2016; Kolotkov et al., 2018; Hayes et al., 2020; Karlický et al., 2020; Hong et al., 2021; Bate et al., 2022).

It has been accepted that the quasi-periods of flare QPPs are often related to their generation mechanisms (Kupriyanova et al., 2020). The short-period (i.e., $<$1 s) QPPs, which are usually observed in radio/microwave emissions, are often driven by the dynamic interaction between plasma waves and energetic particles in complex magnetic structures (Nakariakov et al., 2018; Yu and Chen, 2019; Karlický et al., 2020). The flare QPPs with long periods in the order of seconds and minutes, which could detect in almost all wavelengths, are frequently interpreted in terms of magnetohydrodynamic (MHD) waves in slow modes (e.g., Wang et al., 2021), kink modes (e.g., Nakariakov et al., 2021), and sausage modes (e.g., Li B. et al., 2020). In such case, the flare QPPs with periods larger than 1 min could be associated with slow sausage waves (Sadeghi and Karami, 2019; Gao et al., 2021), global kink waves (Duckenfield et al., 2019; Gao et al., 2022), and slow magnetoacoustic waves (Wang, 2011; Ofman et al., 2012; Yuan et al., 2015; Prasad et al., 2022); while those with periods in the order of seconds are often explained as fast sausage or kink waves (Inglis and Nakariakov, 2009; Guo et al., 2021; Kashapova et al., 2021), depending on whether the plasma loop can be compressible or incompressible (Yuan and Van Doorsselaere, 2016; Nakariakov and Kolotkov, 2020). Those long-period QPPs might be also associated with the repetitive magnetic reconnection (Thurgood et al., 2019; Karampelas et al., 2022). The idea is that the released energy via intermittent magnetic reconnection is repeated, which can periodically accelerate non-thermal electrons. Thus, it is often used to explain the QPPs seen in the impulsive phase of solar flares (e.g., Yuan et al., 2019; Li et al., 2021). Moreover, this reconnection process could either be spontaneous such as “magnetic dripping” (e.g., Nakariakov et al., 2010b) and “magnetic tuning fork” (e.g., Takasao and Shibata, 2016), or it might be triggered by an external MHD wave (Foullon et al., 2005; Nakariakov et al., 2018).

Solar jets, which often show columnar and beam-like structures, are usually associated with solar flares, type III radio bursts, and filament eruptions (Shibata et al., 2007; Shen et al., 2011; Paraschiv et al., 2015; Raouafi et al., 2016). They can be observed everywhere on the Sun, such as active regions, quiet-Sun regions, and coronal holes (Brueckner and Bartoe, 1983; Shen, 2021). The recurrent jets, which always reveal ejected plasmas repeatedly and have the same base source (Tian et al., 2018; Lu et al., 2019), become a topic of particular interest because they could be associated with flare QPPs (Ning et al., 2022; Shi et al., 2022), fast-mode EUV waves, and quasi-periodic fast-propagating (QFP) magnetosonic waves (Shen et al., 2018d,a). The observed QFP waves often consist of multiple concentric and coherent wavefronts, termed as ‘QFP wave trains,’ and they are produced successively within periods of dozens of seconds or a few minutes near the epicenter of the accompanying flares (Shen et al., 2022b,a). Sometimes, the quasi-periods of QFP wave trains are quite similar to those of associated flare QPPs, implying that the two different phenomena might manifest the two different aspects of the same physical process, that is, the pulsed energy release via repeating magnetic reconnection (Liu et al., 2011; Shen and Liu, 2012; Shen et al., 2013, 2018b; Kolotkov et al., 2018; Zhou et al., 2022). On the other hand, some quasi-periods of QFP wave trains are completely unassociated with those of flare QPPs, indicating that the periodicity of QFP wave trains is diverse and could not be associated with flare QPPs (Shen et al., 2018c, 2019). Therefore, the relationship between flare QPPs and QFP wave trains still needs in-depth investigation (Shen et al., 2022b).

The observed QPPs could provide the time feature and plasma characteristic of flare emissions, which are helpful for diagnosing plasma properties on the Sun or Sun-like stars, especially at the flare location (Pugh et al., 2019; Zimovets I. V. et al., 2021). When considering that flare QPPs are modulated by MHD waves, they might potentially lead to coronal heating through dissipation of those waves (Reale et al., 2019; Van Doorsselaere et al., 2020; White and Verwichte, 2021; Li et al., 2022). Moreover, they can allow us to map coronal magnetic fields and estimate plasma parameters in the corona, named as ‘coronal seismology’ (e.g., Yang et al., 2020; Anfinogentov et al., 2022). In this study, we report multi-wavelength observations of the flare QPP associated with recurrent jets, and the flare QPP is also found at two opposite footpoints connected by a hot flare loop seen in AIA 94 Å images. Our measurements suggest that the flare QPP could be interpreted as a kink-mode MHD wave of the flare loop.

2 Observations

On 2022 July 14, a solar flare occurred in the active region NOAA 13058 (N15E81), which was close to the solar limb and erupted after a group of recurrent jets. It was simultaneously observed by several space-based telescopes, such as the Geostationary Operational Environmental Satellite X-ray Sensor (GOES/XRS; Hanser and Sellers, 1996), the Fermi Gamma-ray Burst Monitor (GBM; Meegan et al., 2009), the Gravitational Wave High-Energy Electromagnetic Counterpart All-sky Monitor (GECAM; Xiao et al., 2022), the Atmospheric Imaging Assembly (AIA; Lemen et al., 2012) and the Extreme Ultraviolet Variability Experiment (EVE; Woods et al., 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al., 2012), and the ground-based radio telescope, that is, the Nobeyama Radio Polarimeters (NoRP; Nakajima et al., 1985), as shown in Table 1; Figure 1. It should be pointed out that all light curves expected for GOES have been multiplied by a factor, so that they can be well displayed in a same window.

TABLE 1

TABLE 1. Observational instruments/telescopes used in this work.

FIGURE 1

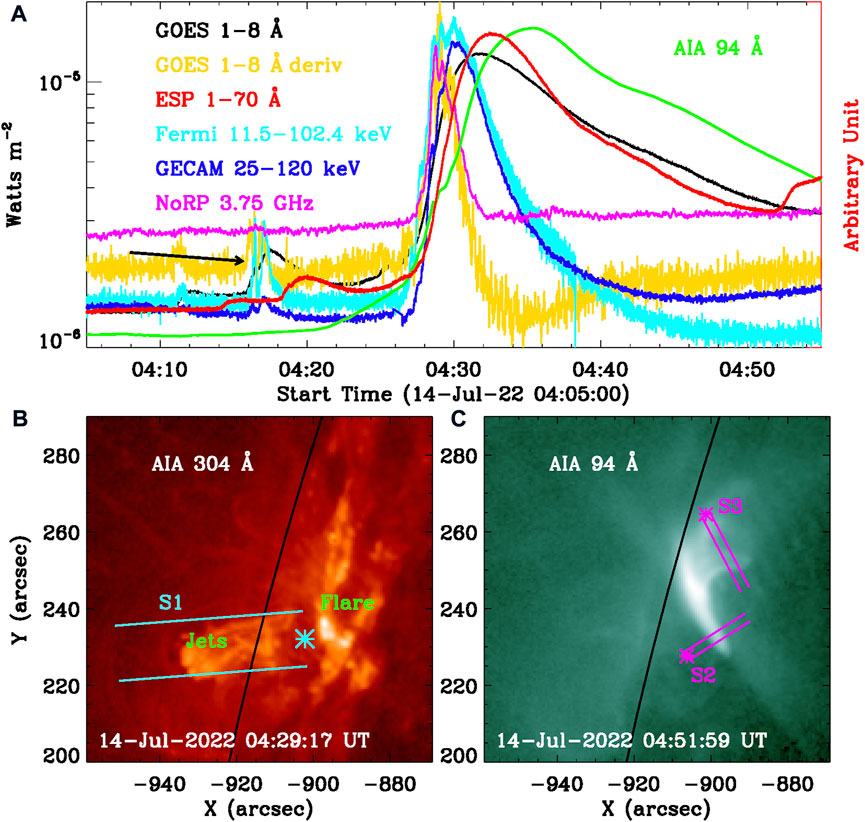
FIGURE 1. Overview of the solar flare on 2022 July 14. (A) Full-disk light curves from 04:05 UT to 04:55 UT recoded by GOES (black), EVE/ESP (red), Fermi/GBM (cyan), GECAM (blue), and NoRP (magenta). The local light curve in AIA 94 Å (green), which is integrated over the flare region in panel (C). (B,C) Snapshot with a FOV of 90”×90″ captured by SDO/AIA at wavelengths of 304 Å and 94 Å. Two cyan lines outline the slit (S1) that contains the solar jets, and the magenta lines mark two slits (S2 and S3) across double footpoints. The color symbols of ‘*’ indicate their beginning points, and the black curve represents the solar limb.

GOES/XRS (Hanser and Sellers, 1996; Loto’aniu et al., 2017) is used to monitor the full-disk solar irradiance at SXR channels with a time cadence of 1 s, particularly for monitoring the flare emission, as shown by the black line in Figure 1A. According to the GOES 1–8 Å flux, the solar flare was identified as an M1.2 class, it began at ∼04:22 UT, reached its maximum at about 04:31 UT, and stopped at ∼04:40 UT. The gold line shows the derivative flux at GOES 1–8 Å. The EUV SpectroPhotometer (ESP; Didkovsky et al., 2012) for SDO/EVE could also provide the SXR flux at 1–70 Å with a time cadence of 0.25 s, as indicated by the red line. The SXR light curves observed by GOES and ESP match well with each other, and they both show double peaks before the onset time of the M1.2 flare, that is, from 04:16 UT to 04:20 UT, as indicated by the black arrow. They might be a candidate for the flare precursor.

Fermi/GBM can provide the solar irradiance that is integrated over the whole Sun at both SXR and HXR channels. The temporal cadence is commonly 0.256 s, but it becomes 0.064 s automatically during solar flares (Meegan et al., 2009). Thus, we first interpolate them into a uniform temporal resolution of 0.256 s before analyzing and such a temporal resolution is sufficient to study the flare QPP with a quasi-period of tens of seconds (cf. Li et al., 2015; Ning, 2017). Figure 1A draws the Fermi/GBM light curve at 11.5–102.4 keV, as shown by the cyan curve, which is measured by the n5 detector. GECAM is designed to detect and localize high-energy transients, such as gamma-ray bursts and solar flares. It consists of 25 gamma-ray detectors (GRDs), which are used to detect the X-ray and γ-ray radiation (Xiao et al., 2022). Figure 1A shows the solar flux at 25–120 keV (blue) during the M1.2 flare with a uniform temporal cadence of 0.5 s, the GRD numbers and their averaged incident angles for each GRD used in this study are listed in Table 2. Both Fermi/GBM and GECAM/GRD light curves show double peaks between 04:16 UT and 04:20 UT, similar to what have been seen in SXR fluxes recorded by GOES/XRS and SDO/EVE/ESP.

TABLE 2

TABLE 2. List of GRD numbers and their angles used in this work.

The M1.2 flare was also observed by NoRP at the radio/microwave emission with a temporal cadence of 1 s, as shown by the magenta line in Figure 1A. It matches well with the GOES 1–8 Å derivative flux, indicating the Neupert effect during the M1.2 flare (cf. Neupert, 1968). The microwave flux also reveals several successive sub-peaks during the flare impulsive phase, similar to what was observed in the Fermi (cyan) and GECAM (blue) light curves, which could be regarded as QPPs. On the other hand, we do not see the small peak before the M1.2 flare in the NoRP light curve. So, it is impossible to determine a flare precursor here. Fortunately, SDO/AIA can provide full-disk spatial-resolved maps in seven EUV and two UV wavelength bands. The spatial scale for each AIA map is 0.6″ per pixel, and the temporal cadence is 12 s for EUV maps. Before analyzing, all the AIA maps have been preprocessed by ‘aia_prep.pro’ (Lemen et al., 2012). Figure 1 (B–C) presents AIA maps with a sub-field of about 90”×90” at 304 Å and 94 Å, respectively. A group of jets can be seen in the AIA 304 Å map (see also the animation. mp4), as outlined by two cyan lines. In order to cover the bulk of these jets as much as possible during their lifetime, we used a constant width of about 15″. The base of jets is close to one flare ribbon in AIA 304 Å maps. A post-flare loop can be seen in the AIA 94 Å map, and two pairs of magenta lines with a width of about 3″″ are used to outline double footpoints (or loop legs). Finally, the light curve at AIA 94 Å is integrated from the flare region, as indicated by the green line in Figure 1A. We cannot see the small peak during ∼04:16–04:20 UT before the flare onset. Thus, we can conclude that the small double peaks (indicated by the black arrow) in SXR/HXR channels are not identified as the flare precursor (e.g., Dudík et al., 2016; Benz et al., 2017; Yan et al., 2017; Li et al., 2018a, 2020b).

3 Results and discussions

3.1 Multi-wavelength observations of flare QPP

The small double peaks before the M1.2 flare seen in SXR/HXR fluxes cannot be regarded as the flare precursor, because they are not homologous with the flare source, as shown in Figure 1. Herein, only the successive sub-peaks seen in HXR and microwave emissions during the flare impulsive (i.e., ∼04:27–04:32 UT) are investigated in this study. Figure 2 presents HXR light curves at GECAM 25–120 keV (black), Fermi 11.5–26.6 keV (magenta), and 26.6–102.4 keV (cyan). They appear to be characterized by several small-amplitude sub-peaks superimposed on the large-amplitude pulse. These sub-peaks with small amplitudes are successive and could be regarded as QPPs, while the main pulse with the large amplitude can be regarded as a strong background trend. The vertical lines indicate seven sub-peaks from roughly 04:27:50 UT to about 04:32:20 UT, and the average duration is 45 s, corresponding to a quasi-period of 45 s. We also note that some sub-peaks might not be very clear in the raw light curve, largely due to their small amplitudes. Using a smooth window of 60 s (Nakariakov et al., 2010a; Yuan et al., 2011; Li et al., 2015; Li and Chen, 2022), the raw light curve is decomposed into two components: a rapidly varying component (QPP) and a slowly varying component (background). Thereby, the shorter-period oscillation (i.e, 45-s QPP) is enhanced, while the long-period background trend is suppressed (see Kupriyanova et al., 2010; Gruber et al., 2011; Auchère et al., 2016, for the discussion of this method). The overplotted blue dashed lines represent the slowly varying components, and the rapidly varying components are shown in panel (B). Obviously, the rapidly varying components are dominated by the QPP feature, that is, some repetitive but irregular pulsations, as marked by the vertical lines. They match well with the successive sub-peaks seen in the raw light curves, indicating that the smooth method only enhances the short-period oscillation, but does not change it. Therefore, these repetitive but irregular pulsations could be regarded as the signature of non-stationary QPPs (cf. Nakariakov et al., 2019), and they cannot be the artifact of smoothing (cf. Li et al., 2021). Here, the modulation depth of flare QPPs, which is regarded as the ratio between rapidly varying components and the maximum value of slowly varying components, is roughly equal to 10–25%. This result is consistent with previous findings for flare QPPs in HXR emissions (e.g., Nakariakov et al., 2010a; Li and Chen, 2022).

FIGURE 2

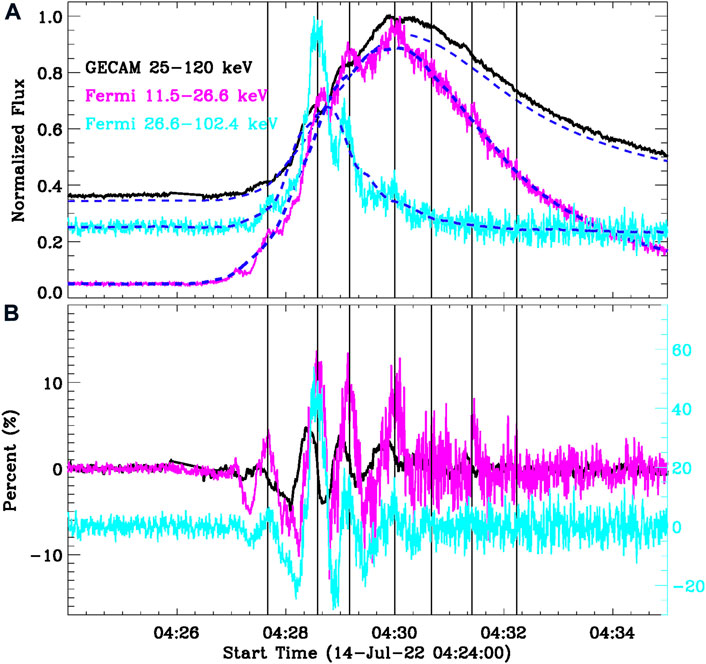
FIGURE 2. X-ray light curves of the M1.2 flare. (A) Normalized HXR/SXR fluxes recorded by GECAM (black) and Fermi/GBM (magenta and cyan), the overlaid dashed lines are their slowly varying components. (B) Corresponding rapidly varying components that are normalized to their maximum slow-varying components. The vertical lines indicate HXR peaks during the solar flare.

Next, the Morlet wavelet analysis method is applied to the rapidly varying components at Fermi 11.5–26.6 keV and GECAM 25–120 keV, as shown in Figure 3. Based on the Parseval’s theorem for wavelet analysis (Torrence and Compo, 1998), the wavelet power has been normalized, which could provide the conservation of total energy signals under the wavelet transform, and then obtain a distribution of the spectral power across wavelet periods. Panels (A1) and (B1) show the wavelet power spectra, and they both exhibit an enhanced power over a wide range in almost the same time interval from about 04:27:50 UT to 04:32:20 UT, indicating a flare QPP within large uncertainties. The bulk of the power spectrum (at the confidence level of 99%) is dominated by a quasi-period centered at ∼45 s. The dominant period of ∼45 s is confirmed by the global wavelet power spectrum, as shown in panels (A2) and (B2). From which, a significant peak at about 45 s is seen in the global wavelet power spectrum. On the other hand, the period uncertainty of ±10 s could be determined by the full width at the half-maximum value of the peak global power above the 99% confidence level (as performed by Yuan et al., 2011; Tian et al., 2016; Li et al., 2020c).

FIGURE 3

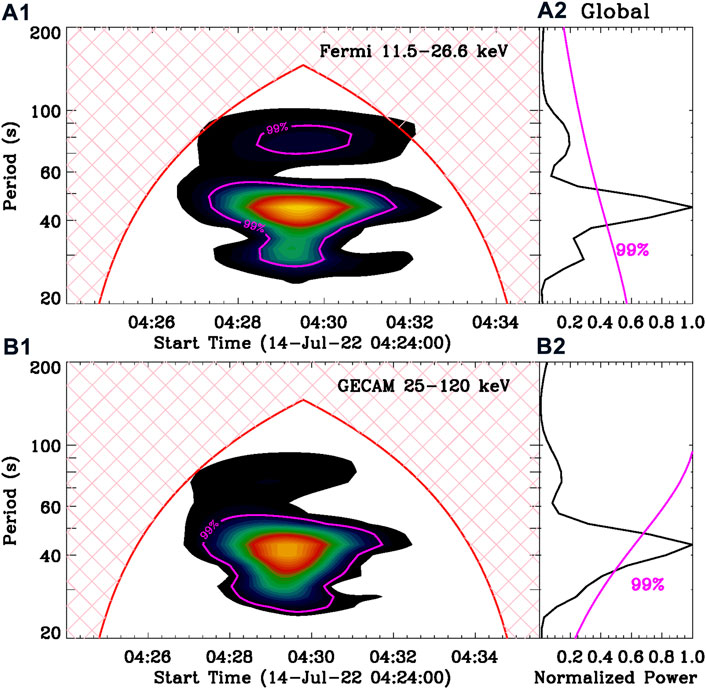
FIGURE 3. Wavelet analysis results of the rapidly varying components in Figure 2. (A1,A2) The wavelet power spectrum and global wavelet power at Fermi 11.5 − 26.6 keV. (B1,B2) The wavelet power spectrum and global wavelet power at GECAM 25 − 120 keV. The magenta lines indicate the significance level of 99%, and the red curve outline a confidence interval.

The flare QPP with a quasi-period of about 45 ± 10 s is seen in the HXR radiation observed by Fermi and GECAM. However, the Fermi flux at 11.5–26.6 keV might consist of SXR and HXR components. In order to know if the flare QPP could be found in the SXR emission, we then performed the Morlet wavelet analysis on SXR light curves at GOES 1–8 Å and ESP 1–70 Å, as shown in Figure 4. Panels (A1) and (B1) present the raw SXR light curves (black) and their slowly varying components (dashed blue) after applying a smooth window of 60 s. It should be pointed out that the slowly varying components have been multiplied by 0.95 to avoid overlap with the raw light curves (cf. Ning et al., 2022). Panels (A2) and (B2) plot the corresponding rapidly varying components, which are characterized by a series of successive pulsations. The modulation depth of SXR radiation is only about 0.4–0.6%, which is much smaller than that of HXR emissions. This is consistent with previous observations, for instance, the flare SXR emission often reveals the small-amplitude oscillation, while the HXR QPP usually has a large amplitude (e.g., Nakariakov et al., 2010a; Ning, 2017; Li et al., 2020d; Ning et al., 2022). Panels (A3) and (B3) show the Morlet wavelet power spectra of rapidly varying components. They both reveal an enhanced power at the period center of about 45 s over a time interval from roughly 04:27 UT to 04:31 UT, suggesting a dominant period of ∼45 s, similarly to what was observed in HXR QPPs.

FIGURE 4

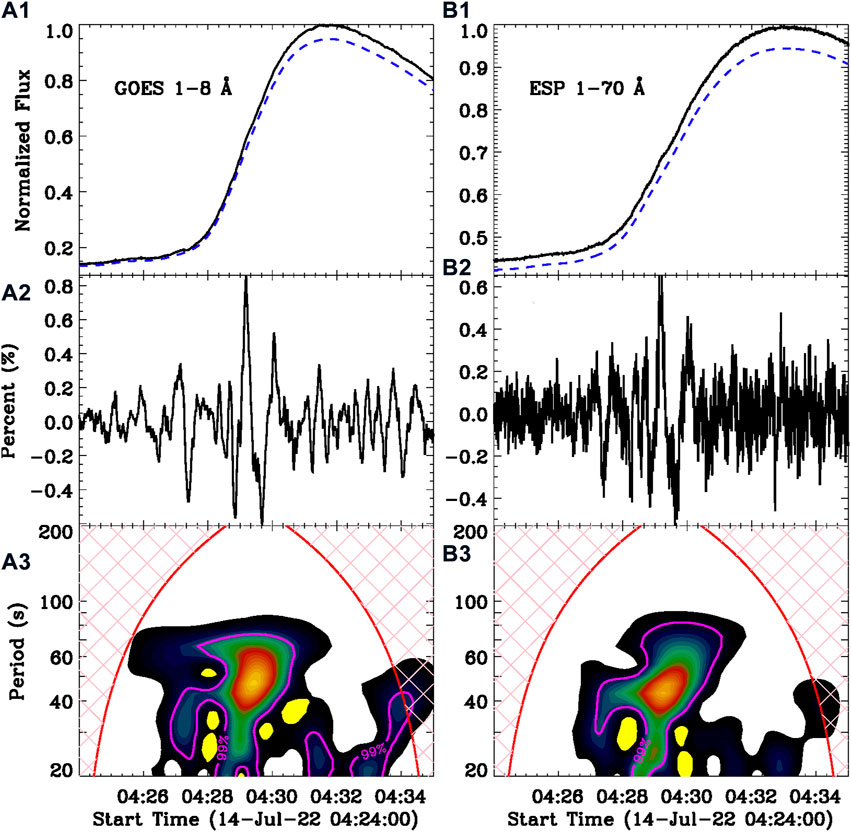
FIGURE 4. Morlet wavelet analysis results in SXR wavelengths. (A1,B1) Normalized SXR fluxes observed by GOES 1 − 8 Å and ESP 1 − 70 Å, the overlaid dashed lines are their slowly varying components, after multiplication by 0.95. (A2,B2) The corresponding rapidly varying components, which are normalized to their maximum slow-varying components. (A3,B3) Morlet wavelet power spectra of the rapidly varying components. The magenta lines indicate the significance level of 99%.

Figure 5 presents the Morlet wavelet analysis on radio fluxes at frequencies of NoRP 2 GHz (A1–A3) and 3.75 GHz (B1–B3). Using the same smooth window of 60 s, the raw light curves (black) are decomposed into slowly (dashed blue) and rapidly varying components (A2–B2). The modulation depth of radio QPPs is estimated to be about 1–2%, which is larger than that of SXR QPPs but is still smaller than that of HXR QPPs. We also note that only three or four successive pulsations appear in radio fluxes, which are less than those in HXR fluxes. On the other hand, the same quasi-period centered at ∼45 s is seen in the wavelet power spectrum, which agrees with the 45-s QPP observed by Fermi, GECAM, GOES, and EVE/ESP. The same quasi-period of 45 s is simultaneously detected in SXR, HXR, and microwave emissions during the impulsive phase of the M1.2 flare, suggesting that the 45-s QPP seen at multiple wavelengths should originate from the same process of energy release, that is, the repetitive magnetic reconnection.

FIGURE 5

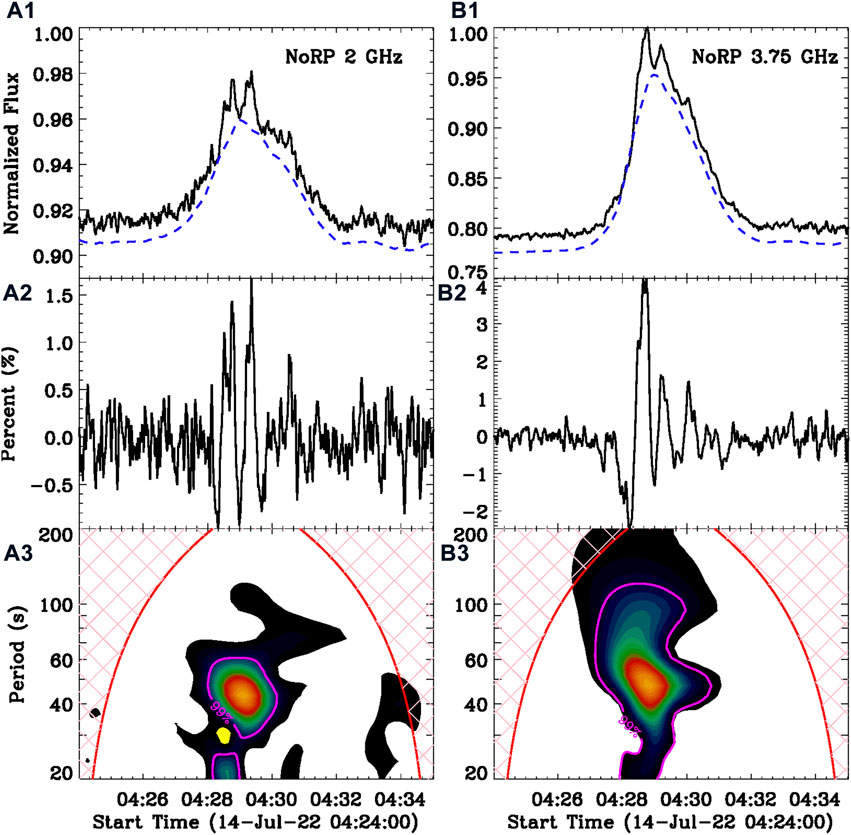
FIGURE 5. Similar to Figure 4, but the Morlet wavelet analysis is performed for radio fluxes at frequencies of NoRP 2 and 3.75 GHz.

The flare QPP could be observed at multiple wavelengths of HXR, SXR, and microwave emissions, suggesting that the 45-s QPP simultaneously appears in both the non-thermal and thermal emissions. In other words, the non-thermal and thermal processes could coexist during the M1.2 flare (e.g., Warmuth and Mann, 2016; Li et al., 2020c; Ning et al., 2022). The 45-s QPP observed in the thermal emission at SXR wavelengths may share the same origin as the QPP feature seen in the non-thermal emission at HXR and microwave channels. The M1.2 flare showed the Neupert effect (Figure 1), which is a plasma heating via energy releasing through electron beams (Neupert, 1968; Ning, 2008, 2009). The flare QPP observed at multiple wavelengths is most likely to be associated with the non-thermal process, that is, the periodically accelerated electron beams via the repetitive magnetic reconnection (e.g., Li et al., 2021; Karampelas et al., 2022). The idea is that the released energy via periodic reconnection could periodically accelerate electron beams, producing repetitive HXR and microwave pulsations in the solar corona. Meanwhile, the repeated SXR pulsations are periodically generated by plasma heating after magnetic reconnection (see Zimovets et al., 2021b, for a recent review).

3.2 Recurrent jets associated with flare QPP

Figure 1B and the animation. mp4 show a group of plasma ejections during the M1.2 flare. They manifest as collimated and beam-like structures in AIA 304 Å, which could be identified as “solar jets” (e.g., Shen, 2021). To look closely at the jet eruptions and periodicity, we draw the time–distance image along the slit of S1 that is made from the AIA 304 Å image series, as shown in Figure 6A. Here, the slit is selected to be a constant width of about 15″, and thus it can cover the bulk of jet bodies as much as possible. A series of solar jets can be seen in the time–distance image, and their apparent speed is estimated to be about 110–300 km s⁻¹, as indicated by the blue arrows. A total of nine jets are found during the time interval of about 450 s, and the average intermittent cadence is roughly equal to 50 s. Such intermittent cadence is quite close to the quasi-period of the flare QPP, implying that those jets occur periodically. Then the intensity variation integrated over two short cyan lines is overplotted, as shown by the cyan line. The intensity curve seems to reveal several sub-peaks corresponding to solar jets. However, it is hard to show a one-to-one correspondence, mainly due to the small-amplitude sub-peaks superimposed on the strong background emission. Therefore, the slowly (dashed green) and rapidly varying components are distinguished with the smooth window of 60 s, and the Morlet wavelet analysis is applied to the rapidly varying component. Panels (B) and (C) show the Morlet wavelet power spectrum and its global wavelet power spectrum. They both reveal a period centered at about 45 s, confirming that the recurrent jets are associated with flare QPPs. Moreover, the recurrent jets appear to start at about 04:24:50 UT, which are ∼180 s earlier than the flare QPPs. Our observation suggests that the flare QPPs could be excited by these recurrent jets.

FIGURE 6

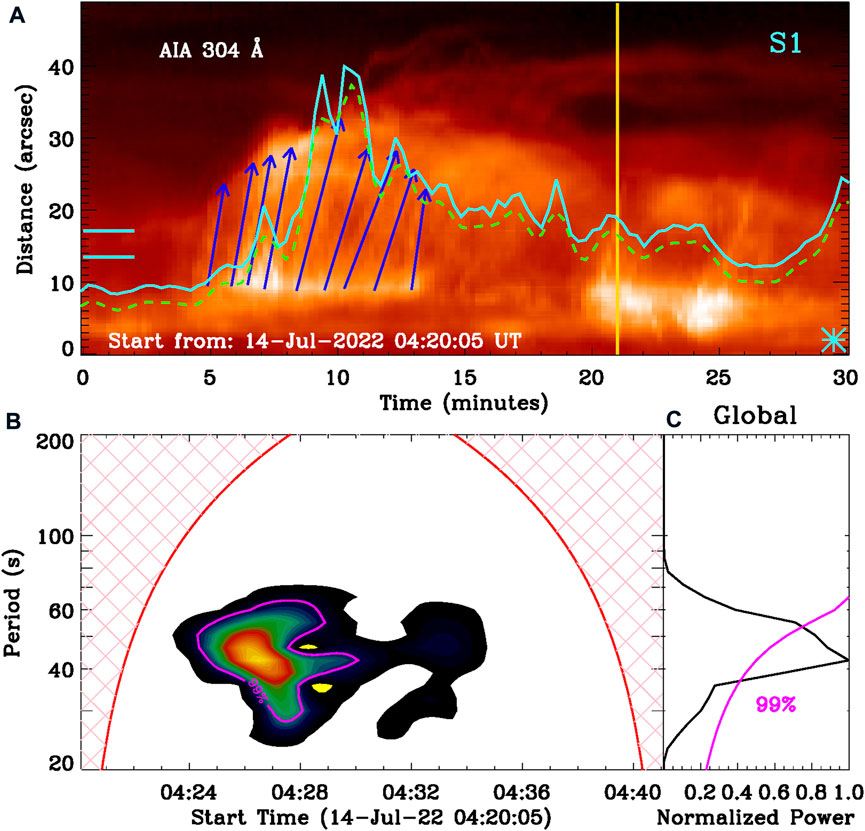
FIGURE 6. Solar jets observed by SDO/AIA 304 Å. (A) Time–distance diagram along S1 (Figure 1), the cyan symbol (*) marks the start point. The overlaid solid cyan curve is integrated from two short cyan lines on the left hand, and the green dashed curve represents its slowly varying component. The blue arrows mark the recurrent jets. The vertical gold line marks the stop time in panel (B). (B,C) Morlet wavelet power spectrum and global wavelet power. The magenta lines indicate the significance level of 99%.

Previous findings (e.g., Reid et al., 2012; Shen et al., 2012; Lu et al., 2019) found that solar jets were always accompanied by solar flares, coronal bright points, or filament eruptions. Recent observations also showed that solar jets triggered by a solar flare had repetitive and regular occurrences with a period of about 72 s, but they did not find the similar quasi-period between flare QPPs and recurrent jets (Ning et al., 2022). The same quasi-period of about 60 s was also discovered both in flare QPPs and recurrent jets, and they took place almost simultaneously (Shi et al., 2022). However, it is impossible to conclude that whether these recurrent jets have affected the flare QPPs or they are just the result of the flare QPPs (cf. Ning et al., 2022). In our study, a same quasi-period of 45 s is observed in both the flare QPPs and recurrent jets, and the onset time of these recurrent jets is ∼180 s earlier than the beginning of flare QPPs. Based on these observational facts, we may infer that the flare QPPs seen in the SXR/HXR and microwave emissions are probably excited by recurrent jets. The associated video (animation.mp4) shows that the eruption of the first jet is similar to a mini-filament-driven jet very much, indicating that the recurrent jets could be driven by the eruption of mini-filaments that is associated with magnetic reconnection (Sterling et al., 2020; Shen, 2021). Thus, both the recurrent jets and the accompanying flare QPPs could be associated with the magnetic reconnection that is modulated by same periodic processes.

3.3 Geometric and differential emission measure analysis

The flare QPP observed in SXR, HXR, and microwave emissions could be excited by a group of recurrent jets with the same intermittent cadence, and they are most likely to be associated with a non-thermal process, that is, electron beams periodically accelerated by the repetitive magnetic reconnection (e.g., Yuan et al., 2019; Li et al., 2021; Karampelas et al., 2022). In order to further know whether the quasi-period of 45 s is modulated by an external MHD wave (e.g., Foullon et al., 2005; Li et al., 2015; Nakariakov et al., 2018), or it is only a self-oscillating process (e.g., Nakariakov et al., 2010b; Takasao and Shibata, 2016), we perform the geometric and differential emission measure (DEM) analysis for the M1.2 flare, as shown in Figures 7, 8.

FIGURE 7

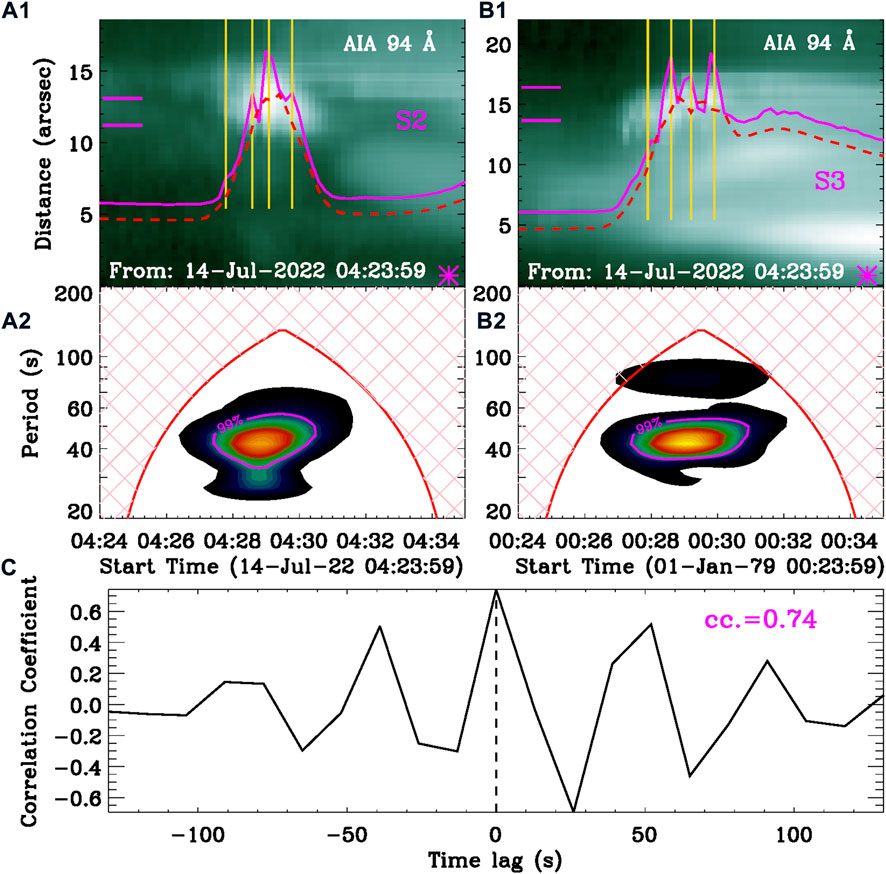
FIGURE 7. M1.2 flare observed by SDO/AIA 94 Å. (A1,B1) Time–distance diagrams along S1 and S2 (Figure 1), the magenta symbols (*) mark their start points. The overlaid solid magenta curves are integrated from two short magenta lines on the left hand, and the red dashed curves represent their slowly varying components. (A2,B2) Morlet wavelet power spectra of the corresponding rapidly varying components. The magenta lines indicate the significance level of 99%. (C) Correlation coefficients between two rapidly varying components as a function of the time lag, the vertical line mark the time lag at 0 s.

FIGURE 8

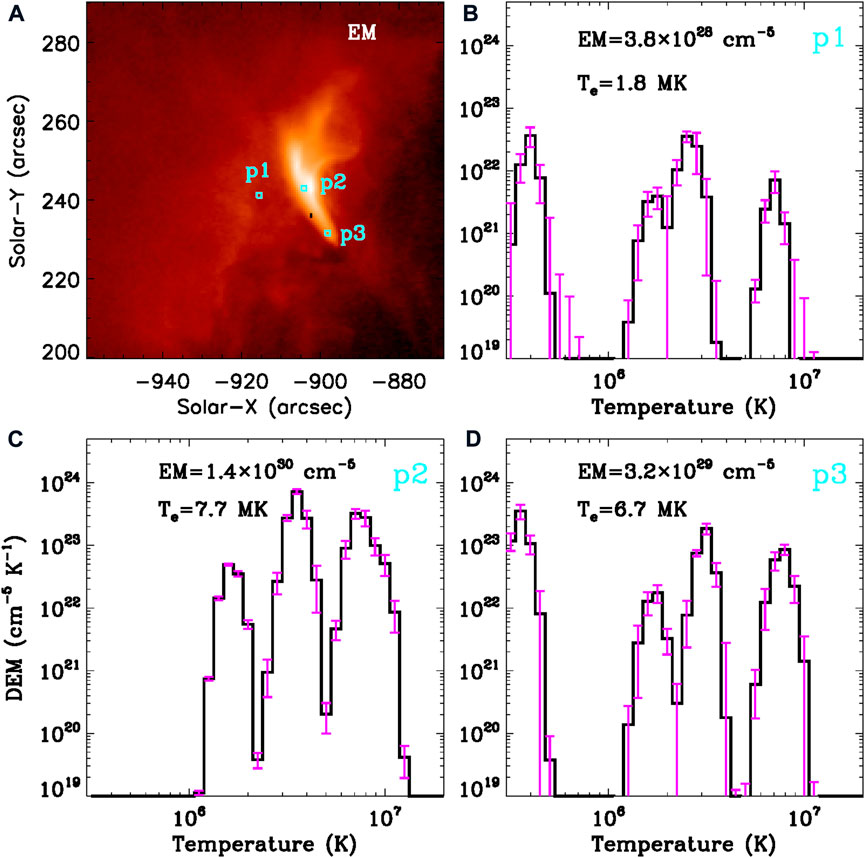
FIGURE 8. DEM analysis results of the M1.2 flare. (A) EM map integrated in the temperature range of 0.31 − 20 MK. Three cyan boxes outline the non-flare region (p1), loop-top region (p2), and footpoint (p3), respectively. (B–D) DEM profiles at the non-flare region, loop top, and footpoint. The EM and DEM-weighted average temperature (T_e) are also labeled in each panel.

Figures 7A1,B1 present time–distance diagrams at AIA 94 Å along two slits (S2 and S3) in Figure 1C, and the magenta symbols (‘*’) mark their start points. Here, the slits are selected to cross two opposite footpoints of the flare loop, but they do not cross the loop top. Because there are much more saturated pixels at the loop top than those at footpoints (see also the animation. mp4). In the two time–distance diagrams, it does not see any signatures of displacement oscillations that are perpendicular to loop legs. However, they appear clearly as signatures of brightness variations at double footpoints, as outlined by two short magenta lines. Thus, the normalized light curves at AIA 94 Å, which are integrated intensities between two short magenta lines, are overplotted in corresponding time–distance diagrams, as shown by the solid magenta curves. Similar to the microwave flux, at least four sub-peaks are found to superimpose on the background emission, as indicated by the gold vertical lines, which are less than those in HXR fluxes. They appear as non-stationary QPPs, for instance, each pulsation is mainly characterized by an anharmonic and triangular shape (e.g., Nakariakov et al., 2019). Using the same smooth window of 60 s, the slowly (dashed red) and rapidly varying components are distinguished from the raw light curves. Panels (A2–B2) show Morlet wavelet power spectra of the rapidly varying components at AIA 94 Å. They both reveal an enhanced power at the period center of about 45 s from around 04:27:50 UT to 04:30:05 UT, suggesting a dominant period of ∼45 s, similar to what was observed in SXR/HXR and microwave emissions. Panel (C) presents the cross-correlation analysis (e.g., Tian et al., 2016) between two rapidly varying components in AIA 94 Å at double footpoints, and the maximum correlation coefficient of 0.74 is seen at the time lag of 0 s, as indicated by the vertical line. This observational result suggests that the flare QPP at double footpoints is in phase.

Figure 8 shows the DEM analysis result. It is calculated from six EUV-wavelength observations measured by SDO/AIA. The DEM(T) distribution for each pixel is estimated by an improved sparse-inversion code (Cheung et al., 2015; Su Y. et al., 2018), and the DEM(T) uncertainty can be estimated from 100 Monte Carlo (MC) simulations, for instance, the three times of standard deviations of 100 MC simulations (3δ). Panel (A) presents the EM map integrated in the temperature range of 0.31–20 MK. Similar to the AIA 94 Å map, a post-flare loop can be seen in the EM map. Then, three small regions (cyan boxes) with a FOV of about 1.8”×1.8” are selected to display DEM profiles, and they are located in the non-flare region (or coronal background, p1), loop-top region (p2), and one footpoint (p3), respectively. Panels (B–D) draw DEM profiles as the function of temperature, and the error bars represent their uncertainties, that is, 3δ. The EM and DEM-weighted mean temperatures (T_e) are calculated in the temperature range between 0.31–20 MK, as labeled in each panel. It can be seen that both the EM and T_e at the loop top are higher than that at the footpoint, and thus the loop-top region is more saturated. The T_e is estimated to be ∼7.7 MK (C) at the loop top and ∼6.7 MK (D) at the footpoint, which is consistent with that the post-flare loop is most visible at AIA 94 Å (T ≈ 6.3 MK). At the non-flare region, the T_e is ∼1.8 MK (B), which is roughly equal to quiet coronal temperature.

3.4 MHD explanation and coronal seismology

Based on the AIA 94 Å map and EM map in Figures 1C, 8A, the distance between two footpoints of the flare loop is estimated to be ∼20.3 Mm, which leads to a loop length (L) of ∼31.9 Mm when assuming a semi-circular shape for the flare loop (cf. Tian et al., 2016; Gao et al., 2022; Li and Chen, 2022). Then under the assumption that the oscillation is associated with a standing wave, the phase speed (v_ph) can be determined by Eq. 1, for instance, twice the ratio of the loop length to the quasi-period (P), which is about 1,420 km s⁻¹.

$v_{\text{ph}}=\frac{2L}{P}.(1)$

The local sound speed in the flare loop can be estimated by using $v_{\text{s}}\approx 152\sqrt{T_{\text{e}}/\mathrm{M}\mathrm{K}}$ (cf. Nakariakov and Ofman, 2001; Kumar et al., 2015; Li et al., 2017a). The average temperatures at the loop top and footpoint are estimated to be 7.7 and 6.7 MK, which lead to the local sound speeds of ∼420 km s⁻¹ and ∼390 km s⁻¹, respectively. Obviously, the estimated phase speed of the flare loop is much faster than the local sound speeds at the loop top and footpoints. Therefore, the 45-s period observed in the M1.2 flare could not be modulated by the slow-mode wave in the flare loop (e.g., Wang et al., 2021), although the quasi-periods less than 1 min have been reported in flare QPPs and explained as standing slow-mode waves (e.g., Welsh et al., 2006; Cho et al., 2016).

The estimated phase speed is much slower than that requires for the global sausage-mode wave, that is, the speed in the range of $\sim 2400-$5,000 km s⁻¹ (e.g. Nakariakov et al., 2003; Melnikov et al., 2005; Tian et al., 2016). Moreover, the global sausage-mode wave is often found in the broader and denser plasma loop, and the necessary condition is given by Nakariakov et al. (2003) as in Eq. 2.

$\frac{n_{\text{i}}}{n_{\text{o}}}>{\left(\frac{L}{0.65w}\right)}^2.(2)$

Here, n_i and n_o are the number densities inside and outside of the flare loop (or non-flare region). w stands for the loop width and could be regarded as the full width at the half maximum of a Gaussian profile across the flare loop, which is about 2.5 Mm. Thus, the density contrast should be as high as 385 if the 45-s QPP is modulated by the global sausage-mode wave of the flare loop. The number density (n_i) inside the flare loop can be estimated by $\sqrt{\mathrm{E}\mathrm{M}/w}$, which are $\sim 7.5\times 10^{10}$ cm⁻³ at the loop top and $\sim 3.6\times 10^{10}$ cm⁻³ at the footpoint. At the non-flare region that has no plasma loops, the effective line-of-sight depth (i.e., w ≈ 4 × 10¹⁰ cm) is used to calculate the n_o (Zucca et al., 2014; Li et al., 2018b; Su W. et al., 2018), leading to $\sim 9.7\times 10^8$ cm⁻³. Then, the density contrast is in the range of $\sim 37-$77 from double footpoints to the loop top. Such a density contrast is rather low, compared to the necessary condition of the global sausage oscillation in flare loops (e.g., Nakariakov et al., 2003; Chen et al., 2015). Therefore, the quasi-period at about 45 s seen in the M1.2 flare is impossible to be modulated by the global sausage-mode wave of the flare loop.

In our study, the phase speed is quite close to the average speed of about 1,328 km s⁻¹ in a catalog of kink-mode oscillations (Nechaeva et al., 2019; Nakariakov et al., 2021), which are often identified as transverse oscillations of plasma loops (e.g., Nakariakov et al., 1999; Anfinogentov et al., 2015; Su W. et al., 2018; Li et al., 2020d; Tiwari et al., 2021). In the corona, kink oscillations are always compressive or weakly compressive in the long wavelength regime (Goossens et al., 2012; Nakariakov et al., 2021). On the other hand, they could be seen as the brightness variation or intensity disturbance if the loop displacement is not exactly perpendicular to the line-of-sight (Cooper et al., 2003; Tian et al., 2012; Wang et al., 2012; Zimovets and Nakariakov, 2015; Antolin et al., 2017; Li et al., 2018b). In such a case, the local Alfvén speed (v_A) could be determined by the phase speed (v_ph) and the density contrast (n_o/n_i), and the magnetic field strength (B) can be estimated by using the local Alfvén speed and mass density at the loop top and footpoints, as shown in Eqs (3), (4) (e.g., Yang et al., 2020; Zimovets I. V. et al., 2021; Zhang Q. M. et al., 2022; Tan, 2022).

$v_{\text{A}}=v_{\text{ph}}{\left(\frac{2}{1+n_{\text{o}}/n_{\text{i}}}\right)}^{-\frac{1}{2}}.(3)$

$B\approx v_{\text{A}}{\left({\mu }_{\text{0}}{n}_{\text{i}}{m}_{\text{p}}\tilde{\mu }\right)}^{\frac{1}{2}}.(4)$

Here, μ₀ and m_p stand for the magnetic permittivity of free space and the proton mass, n_i is the number density at the flare loop, and $\tilde{\mu }\approx 1.27$ represents the average molecular weight in the solar corona (e.g., Nakariakov and Ofman, 2001; Zhang et al., 2020). Then, the mass density (ρ_i) could be roughly equal to $n_{\text{i}}{m}_{\text{p}}\tilde{\mu }$. Herein, the Alfvén speed inside the oscillating loop is estimated to be about 1,010 km s⁻¹, leading to the magnetic field strength of about 99 G and 143 G at the footpoint and loop top, respectively. These strengths at the flare loop are consistent with previous estimations in solar flares (e.g., Qiu et al., 2009; Li et al., 2017a, 2018b; Zimovets I. et al., 2021). Our measurement and estimations support the idea that the quasi-period of 45 s in the M1.2 flare could be modulated by the kink-mode wave of a flare loop (Nakariakov et al., 2021).

4 Summary

Based on observations recorded by Fermi, GECAM, GOES, SDO/EVE, and NoRP, we investigated the non-stationary QPP at wavelengths of HXR, SXR, microwave, and EUV during the impulsive phase of an M1.2 flare on 2022 July 14. Combined with the imaging observation from SDO/AIA, the excitation and modulation of the flare QPP are discussed. Our conclusions are summarized as follows:

1) A quasi-period of $\sim 45\pm$10 s is simultaneously detected at Fermi 11.5–102.4 keV, GECAM 25–120 keV, GOES 1–8 Å, ESP 1–70 Å, NoRP, 2 and 3.75 GHz during the flare impulsive phase, that is, from about 04:27:50 UT to 04:32:20 UT. Our observations suggest the coexistence of non-thermal and thermal processes in the M1.2 flare, and the 45-s QPP at multiple wavelengths could share the same periodic process of energy release, such as the repetitive magnetic reconnection (e.g., Yuan et al., 2019; Li et al., 2021; Karampelas et al., 2022).

2) A group of recurrent jets with a periodicity of about $\sim 45\pm$10 is seen in the AIA 304 Å image series during ∼04:24:50–04:32:20 UT. The onset time of the flare QPP is 180 s later than that of recurrent jets, but they show the same quasi-period, indicating that the flare QPP is probably excited by recurrent jets. This observational result is different from previous findings, for instance, solar jets were always triggered by the flare eruption (Reid et al., 2012; Lu et al., 2019), or the periodicity of the solar flare and accompanied jets is different (e.g., Ning et al., 2022).

3) Because of the imaging observation from SDO/AIA at 94 Å, the quasi-period of $\sim 45\pm$10 s is also seen at two opposite footpoints of the flare loop. Also, the phase speed is estimated to be about 1,420 km s⁻¹. Our measurements imply that the 45-s period is most likely to be modulated by the kink-mode wave (cf. Nakariakov et al., 2010a; Nechaeva et al., 2019).

4) Based on the kink oscillation model, the Alfvén speed inside the flare loop is estimated to be ∼1,010 km s⁻¹. The magnetic field strengths are measured in the range of 99–143 G from the footpoint to the loop top, similar to what have been estimated in solar flares at the magnitude order of 100 G (e.g., Qiu et al., 2009; Li et al., 2018b; Zimovets I. et al., 2021).

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found here: https://fermi.gsfc.nasa.gov/ssc/data/ http://jsoc.stanford.edu/ajax/lookdata.html https://lasp.colorado.edu/home/eve/data/ https://solar.nro.nao.ac.jp/norp/index.html.

Author contributions

DL selected the topic, performed the main data analysis, led to discussions, and prepared the manuscript. FS contributed the SDO/AIA data analysis and joined to modify the manuscript. HZ, SX, LS, WP, and XL provided the GECAM data analysis. WC contributed to analyze the Fermi data. ZN joined to discuss the explanation of the flare QPP and recurrent jets.

Funding

This work was funded by the NSFC under grants 11973092, U1931138, 12073081, U1938102, as well as CAS Strategic Pioneer Program on Space Science, Grant No. XDA15052200 and XDA15320301. DL is also supported by the Surface Project of Jiangsu Province (BK20211402).

Acknowledgments

The authors would like to thank two anonymous referees for their inspiring and valuable comments. We thank the teams of Fermi, GECAM, GOES, SDO/AIA, SDO/EVE, and NoRP for their open data use policy. GECAM is a mission funded by the Chinese Academy of Sciences (CAS) under the Strategic Priority Research Program on Space Science. SDO is a mission of NASA’s Living With a Star Program (LWS). AIA and EVE data are courtesy of the NASA/SDO science teams. NoRP is operated by Solar Science Observatory, a branch of the National Astronomical Observatory of Japan, and their observing data are verified scientifically by the consortium for NoRP scientific operations.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.1032099/full#supplementary-material

References

Anfinogentov, S. A., Antolin, P., Inglis, A. R., Kolotkov, D., Kupriyanova, E. G., McLaughlin, J. A., et al. (2022). Novel data analysis techniques in coronal seismology. Space Sci. Rev. 218, 9. doi:10.1007/s11214-021-00869-w

CrossRef Full Text | Google Scholar

Anfinogentov, S. A., Nakariakov, V. M., and Nisticò, G. (2015). Decayless low-amplitude kink oscillations: A common phenomenon in the solar corona? Astron. Astrophys. 583, A136. doi:10.1051/0004-6361/201526195

CrossRef Full Text | Google Scholar

Antolin, P., De Moortel, I., Van Doorsselaere, T., and Yokoyama, T. (2017). Observational signatures of transverse magnetohydrodynamic waves and associated dynamic instabilities in coronal flux tubes. Astrophys. J. 836, 219. doi:10.3847/1538-4357/aa5eb2

CrossRef Full Text | Google Scholar

Auchère, F., Froment, C., Bocchialini, K., Buchlin, E., and Solomon, J. (2016). On the fourier and wavelet analysis of coronal time series. Astrophys. J. 825, 110. doi:10.3847/0004-637X/825/2/110

CrossRef Full Text | Google Scholar

Bate, W., Jess, D. B., Nakariakov, V. M., Grant, S. D. T., Jafarzadeh, S., Stangalini, M., et al. (2022). High-frequency waves in chromospheric spicules. Astrophys. J. 930, 129. doi:10.3847/1538-4357/ac5c53

CrossRef Full Text | Google Scholar

Benz, A. O., Battaglia, M., and Güdel, M. (2017). Observations of a radio-quiet solar preflare. Sol. Phys. 292, 151. doi:10.1007/s11207-017-1175-3

CrossRef Full Text | Google Scholar

Brueckner, G. E., and Bartoe, J. D. F. (1983). Observations of high-energy jets in the corona above the quiet sun, the heating of the corona, and the acceleration of the solar wind. Astrophys. J. 272, 329–348. doi:10.1086/161297

CrossRef Full Text | Google Scholar

Chen, S.-X., Li, B., Xia, L.-D., and Yu, H. (2015). Periods and damping rates of fast sausage oscillations in multishelled coronal loops. Sol. Phys. 290, 2231–2243. doi:10.1007/s11207-015-0751-7

CrossRef Full Text | Google Scholar

Cheung, M. C. M., Boerner, P., Schrijver, C. J., Testa, P., Chen, F., Peter, H., et al. (2015). Thermal diagnostics with the atmospheric imaging assembly on board the solar dynamics observatory: A validated method for differential emission measure inversions. Astrophys. J. 807, 143. doi:10.1088/0004-637X/807/2/143

CrossRef Full Text | Google Scholar

Cho, I. H., Cho, K. S., Nakariakov, V. M., Kim, S., and Kumar, P. (2016). Comparison of damped oscillations in solar and stellar X-ray flares. Astrophys. J. 830, 110. doi:10.3847/0004-637X/830/2/110

CrossRef Full Text | Google Scholar

Cooper, F. C., Nakariakov, V. M., and Tsiklauri, D. (2003). Line-of-sight effects on observability of kink and sausage modes in coronal structures with imaging telescopes. Astron. Astrophys. 397, 765–770. doi:10.1051/0004-6361:20021556

CrossRef Full Text | Google Scholar

Didkovsky, L., Judge, D., Wieman, S., Woods, T., and Jones, A. (2012). EUV SpectroPhotometer (ESP) in Extreme ultraviolet variability experiment (EVE): Algorithms and calibrations. Sol. Phys. 275, 179–205. doi:10.1007/s11207-009-9485-8

CrossRef Full Text | Google Scholar

Doyle, J. G., Irawati, P., Kolotkov, D. Y., Ramsay, G., Nhalil, N. V., Dhillon, V. S., et al. (2022). Doubling of minute-long quasi-periodic pulsations from super-flares on a low-mass star. Mon. Not. R. Astron. Soc. 514, 5178–5182. doi:10.1093/mnras/stac1695

CrossRef Full Text | Google Scholar

Duckenfield, T. J., Goddard, C. R., Pascoe, D. J., and Nakariakov, V. M. (2019). Observational signatures of the third harmonic in a decaying kink oscillation of a coronal loop. Astron. Astrophys. 632, A64. doi:10.1051/0004-6361/201936822

CrossRef Full Text | Google Scholar

Dudík, J., Polito, V., Janvier, M., Mulay, S. M., Karlický, M., Aulanier, G., et al. (2016). Slipping magnetic reconnection, chromospheric evaporation, implosion, and precursors in the 2014 september 10 X1.6-Class solar flare. Astrophys. J. 823, 41. doi:10.3847/0004-637X/823/1/41

CrossRef Full Text | Google Scholar

Foullon, C., Verwichte, E., Nakariakov, V. M., and Fletcher, L. (2005). X-ray quasi-periodic pulsations in solar flares as magnetohydrodynamic oscillations. Astron. Astrophys. 440, L59–L62. doi:10.1051/0004-6361:200500169

CrossRef Full Text | Google Scholar

Gao, Y., Li, F., Li, B., Cao, W., Song, Y., Tian, H., et al. (2021). Possible signature of sausage waves in photospheric bright points. Sol. Phys. 296, 184. doi:10.1007/s11207-021-01928-9

CrossRef Full Text | Google Scholar

Gao, Y., Tian, H., Van Doorsselaere, T., and Chen, Y. (2022). Decayless oscillations in solar coronal bright points. Astrophys. J. 930, 55. doi:10.3847/1538-4357/ac62cf

CrossRef Full Text | Google Scholar

Goossens, M., Andries, J., Soler, R., Van Doorsselaere, T., Arregui, I., and Terradas, J. (2012). Surface Alfvén waves in solar flux tubes. Astrophys. J. 753, 111. doi:10.1088/0004-637X/753/2/111

CrossRef Full Text | Google Scholar

Gruber, D., Lachowicz, P., Bissaldi, E., Briggs, M. S., Connaughton, V., Greiner, J., et al. (2011). Quasi-periodic pulsations in solar flares: New clues from theFermi Gamma-ray burst monitor. Astron. Astrophys. 533, A61. doi:10.1051/0004-6361/201117077

CrossRef Full Text | Google Scholar

Guo, M., Li, B., and Shi, M. (2021). Fast sausage oscillations in coronal loops with fine structures. Astrophys. J. Lett. 921, L17. doi:10.3847/2041-8213/ac30e3

CrossRef Full Text | Google Scholar

Hanser, F. A., and Sellers, F. B. (1996). “Design and calibration of the GOES-8 solar x-ray sensor: The XRS,” in GOES-8 and beyond. Editor E. R. Washwell, 2812, 344–352. of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. doi:10.1117/12.254082

CrossRef Full Text | Google Scholar

Hayes, L. A., Inglis, A. R., Christe, S., Dennis, B., and Gallagher, P. T. (2020). Statistical study of GOES X-ray quasi-periodic pulsations in solar flares. Astrophys. J. 895, 50. doi:10.3847/1538-4357/ab8d40

CrossRef Full Text | Google Scholar

Hong, Z., Li, D., Zhang, M., Tan, C., Ma, S., and Ji, H. (2021). Multi-wavelength observations of quasi-periodic pulsations in a solar flare. Sol. Phys. 296, 171. doi:10.1007/s11207-021-01922-1

CrossRef Full Text | Google Scholar

Inglis, A. R., and Nakariakov, V. M. (2009). A multi-periodic oscillatory event in a solar flare. Astron. Astrophys. 493, 259–266. doi:10.1051/0004-6361:200810473

CrossRef Full Text | Google Scholar

Karampelas, K., McLaughlin, J. A., Botha, G. J. J., and Régnier, S. (2022). The independence of oscillatory reconnection periodicity from the initial pulse. Astrophys. J. 933, 142. doi:10.3847/1538-4357/ac746a

CrossRef Full Text | Google Scholar

Karlický, M., Chen, B., Gary, D. E., Kašparová, J., and Rybák, J. (2020). Drifting pulsation structure at the very beginning of the 2017 september 10 limb flare. Astrophys. J. 889, 72. doi:10.3847/1538-4357/ab63d0

CrossRef Full Text | Google Scholar

Kashapova, L. K., Kolotkov, D. Y., Kupriyanova, E. G., Kudriavtseva, A. V., Tan, C., and Reid, H. A. S. (2021). Common origin of quasi-periodic pulsations in microwave and decimetric solar radio bursts. Sol. Phys. 296, 185. doi:10.1007/s11207-021-01934-x

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Nakariakov, V. M., Holt, R., and Kuznetsov, A. A. (2021). Multiwavelength quasi-periodic pulsations in a stellar superflare. Astrophys. J. Lett. 923, L33. doi:10.3847/2041-8213/ac432e

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Pugh, C. E., Broomhall, A.-M., and Nakariakov, V. M. (2018). Quasi-periodic pulsations in the most powerful solar flare of cycle 24. Astrophys. J. 858, L3. doi:10.3847/2041-8213/aabde9

CrossRef Full Text | Google Scholar

Kumar, P., Nakariakov, V. M., and Cho, K.-S. (2015). X-ray and EUV observations of simultaneous short and long period oscillations in hot coronal arcade loops. Astrophys. J. 804, 4. doi:10.1088/0004-637X/804/1/4

CrossRef Full Text | Google Scholar

Kupriyanova, E. G., Melnikov, V. F., Nakariakov, V. M., and Shibasaki, K. (2010). Types of microwave quasi-periodic pulsations in single flaring loops. Sol. Phys. 267, 329–342. doi:10.1007/s11207-010-9642-0

CrossRef Full Text | Google Scholar

Kupriyanova, E., Kolotkov, D., Nakariakov, V., and Kaufman, A. (2020). Quasi-periodic pulsations in solar and stellar flares. Review. Solar-Terrestrial Phys. 6, 3–23. doi:10.12737/stp-61202001

CrossRef Full Text | Google Scholar

Lemen, J. R., Title, A. M., Akin, D. J., Boerner, P. F., Chou, C., Drake, J. F., et al. (2012). The atmospheric imaging assembly (AIA) on the solar dynamics observatory (SDO). Sol. Phys. 275, 17–40. doi:10.1007/s11207-011-9776-8

CrossRef Full Text | Google Scholar

Li, B., Antolin, P., Guo, M. Z., Kuznetsov, A. A., Pascoe, D. J., Van Doorsselaere, T., et al. (2020a). Magnetohydrodynamic fast sausage waves in the solar corona. Space Sci. Rev. 216, 136. doi:10.1007/s11214-020-00761-z

CrossRef Full Text | Google Scholar

Li, D., and Chen, W. (2022). Quasi-periodic accelerations of energetic particles during a solar flare. Astrophys. J. Lett. 931, L28. doi:10.3847/2041-8213/ac6fd2

CrossRef Full Text | Google Scholar

Li, D., Feng, S., Su, W., and Huang, Y. (2020b). Preflare very long-periodic pulsations observed in Hα emission before the onset of a solar flare. Astron. Astrophys. 639, L5. doi:10.1051/0004-6361/202038398

CrossRef Full Text | Google Scholar

Li, D., Ge, M., Dominique, M., Zhao, H., Li, G., Li, X., et al. (2021). Detection of flare multiperiodic pulsations in mid-ultraviolet balmer continuum, lyα, hard X-ray, and radio emissions simultaneously. Astrophys. J. 921, 179. doi:10.3847/1538-4357/ac1c05

CrossRef Full Text | Google Scholar

Li, D., Kolotkov, D. Y., Nakariakov, V. M., Lu, L., and Ning, Z. J. (2020c). Quasi-periodic pulsations of gamma-ray emissions from a solar flare on 2017 september 6. Astrophys. J. 888, 53. doi:10.3847/1538-4357/ab5e86

CrossRef Full Text | Google Scholar

Li, D., Li, Y., Lu, L., Zhang, Q., Ning, Z., and Anfinogentov, S. (2020d). Observations of a quasi-periodic pulsation in the coronal loop and microwave flux during a solar preflare phase. Astrophys. J. Lett. 893, L17. doi:10.3847/2041-8213/ab830c

CrossRef Full Text | Google Scholar

Li, D., Li, Y., Su, W., Huang, Y., and Ning, Z. (2018a). Observations of electron-driven evaporation in a flare precursor. Astrophys. J. 854, 26. doi:10.3847/1538-4357/aaa9c0

CrossRef Full Text | Google Scholar

Li, D., Ning, Z. J., Huang, Y., Chen, N. H., Zhang, Q. M., Su, Y. N., et al. (2017a). Doppler shift oscillations from a hot line observed by IRIS. Astrophys. J. 849, 113. doi:10.3847/1538-4357/aa9073

CrossRef Full Text | Google Scholar

Li, D., Ning, Z. J., and Zhang, Q. M. (2015). Imaging and spectral observations of quasi-periodic pulsations in a solar flare. Astrophys. J. 807, 72. doi:10.1088/0004-637X/807/1/72

CrossRef Full Text | Google Scholar

Li, D., Xue, J., Yuan, D., and Ning, Z. (2022). Persistent fast kink magnetohydrodynamic waves detected in a quiescent prominence. Sci. China Phys. Mech. Astron. 65, 239611. doi:10.1007/s11433-021-1836-y

CrossRef Full Text | Google Scholar

Li, D., Yuan, D., Su, Y. N., Zhang, Q. M., Su, W., and Ning, Z. J. (2018b). Non-damping oscillations at flaring loops. Astron. Astrophys. 617, A86. doi:10.1051/0004-6361/201832991

CrossRef Full Text | Google Scholar

Li, D., Zhang, Q. M., Huang, Y., Ning, Z. J., and Su, Y. N. (2017b). Quasi-periodic pulsations with periods that change depending on whether the pulsations have thermal or nonthermal components. Astron. Astrophys. 597, L4. doi:10.1051/0004-6361/201629867

CrossRef Full Text | Google Scholar

Liu, W., Title, A. M., Zhao, J., Ofman, L., Schrijver, C. J., Aschwanden, M. J., et al. (2011). Direct imaging of quasi-periodic fast propagating waves of ˜2000 km s⁻¹ in the low solar corona by the solar dynamics observatory atmospheric imaging assembly. Astrophys. J. 736, L13. doi:10.1088/2041-8205/736/1/L13

CrossRef Full Text | Google Scholar

Loto’aniu, P., Rodriguez, J., Redmon, R., Machol, J., Kress, B., Seaton, D., et al. (2017). “Space weather monitoring with GOES-16: Instruments and data products,” in EGU general assembly conference abstracts. (Vienna, Austria: EGU General Assembly Conference Abstracts), 9663.

Google Scholar

Lu, L., Feng, L., Li, Y., Li, D., Ning, Z., and Gan, W. (2019). Spectroscopic and stereoscopic observations of the solar jets. Astrophys. J. 887, 154. doi:10.3847/1538-4357/ab530c

CrossRef Full Text | Google Scholar

Lu, L., Li, D., Ning, Z., Feng, L., and Gan, W. (2021). Quasi-periodic pulsations detected in ly α and nonthermal emissions during solar flares. Sol. Phys. 296, 130. doi:10.1007/s11207-021-01876-4

CrossRef Full Text | Google Scholar

Meegan, C., Lichti, G., Bhat, P. N., Bissaldi, E., Briggs, M. S., Connaughton, V., et al. (2009). THEFERMIGAMMA-RAY burst monitor. Astrophys. J. 702, 791–804. doi:10.1088/0004-637X/702/1/791

CrossRef Full Text | Google Scholar

Melnikov, V. F., Reznikova, V. E., Shibasaki, K., and Nakariakov, V. M. (2005). Spatially resolved microwave pulsations of a flare loop. Astron. Astrophys. 439, 727–736. doi:10.1051/0004-6361:20052774

CrossRef Full Text | Google Scholar

Mészárosová, H., Rybák, J., Kashapova, L., Gömöry, P., Tokhchukova, S., and Myshyakov, I. (2016). Broadband microwave sub-second pulsations in an expanding coronal loop of the 2011 August 10 flare. Astron. Astrophys. 593, A80. doi:10.1051/0004-6361/201528062

CrossRef Full Text | Google Scholar

Milligan, R. O., Fleck, B., Ireland, J., Fletcher, L., and Dennis, B. R. (2017). Detection of three-minute oscillations in full-disk lyα emission during a solar flare. Astrophys. J. 848, L8. doi:10.3847/2041-8213/aa8f3a

CrossRef Full Text | Google Scholar

Nakajima, H., Sekiguchi, H., Sawa, M., Kai, K., and Kawashima, S. (1985). The radiometer and polarimeters at 80, 35, and 17 GHz for solar observations at Nobeyama. Pub. Astron. Soc. Jpn. 37, 163–170.

Google Scholar

Nakariakov, V. M., Anfinogentov, S. A., Antolin, P., Jain, R., Kolotkov, D. Y., Kupriyanova, E. G., et al. (2021). Kink oscillations of coronal loops. Space Sci. Rev. 217, 73. doi:10.1007/s11214-021-00847-2

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Anfinogentov, S., Storozhenko, A. A., Kurochkin, E. A., Bogod, V. M., Sharykin, I. N., et al. (2018). Quasi-periodic pulsations in a solar microflare. Astrophys. J. 859, 154. doi:10.3847/1538-4357/aabfb9

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Foullon, C., Myagkova, I. N., and Inglis, A. R. (2010a). Quasi-periodic pulsations in the gamma-ray emission of a solar flare. Astrophys. J. 708, L47–L51. doi:10.1088/2041-8205/708/1/L47

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Inglis, A. R., Zimovets, I. V., Foullon, C., Verwichte, E., Sych, R., et al. (2010b). Oscillatory processes in solar flares. Plasma Phys. control. Fusion 52, 124009. doi:10.1088/0741-3335/52/12/124009

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Kolotkov, D. Y., Kupriyanova, E. G., Mehta, T., Pugh, C. E., Lee, D. H., et al. (2019). Non-stationary quasi-periodic pulsations in solar and stellar flares. Plasma Phys. control. Fusion 61–014024. doi:10.1088/1361-6587/aad97c

CrossRef Full Text | Google Scholar

Nakariakov, V. M., and Kolotkov, D. Y. (2020). Magnetohydrodynamic waves in the solar corona. Annu. Rev. Astron. Astrophys. 58, 441–481. doi:10.1146/annurev-astro-032320-042940

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Melnikov, V. F., and Reznikova, V. E. (2003). Global sausage modes of coronal loops. Astron. Astrophys. 412, L7–L10. doi:10.1051/0004-6361:20031660

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., and Davila, J. M. (1999). TRACE observation of damped coronal loop oscillations: Implications for coronal heating. Science 285, 862–864. doi:10.1126/science.285.5429.862

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakariakov, V. M., and Ofman, L. (2001). Determination of the coronal magnetic field by coronal loop oscillations. Astron. Astrophys. 372, L53–L56. doi:10.1051/0004-6361:20010607

CrossRef Full Text | Google Scholar

Nechaeva, A., Zimovets, I. V., Nakariakov, V. M., and Goddard, C. R. (2019). Catalog of decaying kink oscillations of coronal loops in the 24th solar cycle. Astrophys. J. Suppl. Ser. 241, 31. doi:10.3847/1538-4365/ab0e86

CrossRef Full Text | Google Scholar

Neupert, W. M. (1968). Comparison of solar X-ray line emission with microwave emission during flares. Astrophys. J. 153, L59. doi:10.1086/180220

CrossRef Full Text | Google Scholar

Ning, Z. (2014). Imaging observations of X-ray quasi-periodic oscillations at 3 - 6 keV in the 26 december 2002 solar flare. Sol. Phys. 289, 1239–1256. doi:10.1007/s11207-013-0405-6

CrossRef Full Text | Google Scholar

Ning, Z. (2017). One-minute quasi-periodic pulsations seen in a solar flare. Sol. Phys. 292, 11. doi:10.1007/s11207-016-1037-4

CrossRef Full Text | Google Scholar

Ning, Z. (2008). RHESSI observations of the Neupert effect in three solar flares. Sol. Phys. 248, 99–111. doi:10.1007/s11207-008-9124-9

CrossRef Full Text | Google Scholar

Ning, Z. (2009). The investigation of the Neupert effect in two solar flares. Sci. China Ser. G-Phys. Mech. Astron. 52, 1686–1690. doi:10.1007/s11433-009-0219-6

CrossRef Full Text | Google Scholar

Ning, Z., Wang, Y., Hong, Z., and Li, D. (2022). Detections of multi-periodic oscillations during a circular ribbon flare. Sol. Phys. 297, 2. doi:10.1007/s11207-021-01935-w

CrossRef Full Text | Google Scholar

Ofman, L., Wang, T. J., and Davila, J. M. (2012). Slow magnetosonic waves and fast flows in active region loops. Astrophys. J. 754, 111. doi:10.1088/0004-637X/754/2/111

CrossRef Full Text | Google Scholar

Paraschiv, A. R., Bemporad, A., and Sterling, A. C. (2015). Physical properties of solar polar jets. A statistical study with Hinode XRT data. Astron. Astrophys. 579, A96. doi:10.1051/0004-6361/201525671

CrossRef Full Text | Google Scholar

Pesnell, W. D., Thompson, B. J., and Chamberlin, P. C. (2012). The solar dynamics observatory (SDO). Sol. Phys. 275, 3–15. doi:10.1007/s11207-011-9841-3

CrossRef Full Text | Google Scholar

Prasad, A., Srivastava, A. K., Wang, T., and Sangal, K. (2022). Role of non-ideal dissipation with heating-cooling misbalance on the phase shifts of standing slow magnetohydrodynamic waves. Sol. Phys. 297, 5. doi:10.1007/s11207-021-01940-z

CrossRef Full Text | Google Scholar

Pugh, C. E., Broomhall, A. M., and Nakariakov, V. M. (2019). Scaling laws of quasi-periodic pulsations in solar flares. Astron. Astrophys. 624, A65. doi:10.1051/0004-6361/201834455

CrossRef Full Text | Google Scholar

Qiu, J., Gary, D. E., and Fleishman, G. D. (2009). Evaluating mean magnetic field in flare loops. Sol. Phys. 255, 107–118. doi:10.1007/s11207-009-9316-y

CrossRef Full Text | Google Scholar

Raouafi, N. E., Patsourakos, S., Pariat, E., Young, P. R., Sterling, A. C., Savcheva, A., et al. (2016). Solar coronal jets: Observations, theory, and modeling. Space Sci. Rev. 201, 1–53. doi:10.1007/s11214-016-0260-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Reale, F., Testa, P., Petralia, A., and Kolotkov, D. Y. (2019). Large-amplitude quasiperiodic pulsations as evidence of impulsive heating in hot transient loop systems detected in the EUV with SDO/AIA. Astrophys. J. 884, 131. doi:10.3847/1538-4357/ab4270

CrossRef Full Text | Google Scholar

Reid, H. A. S., Vilmer, N., Aulanier, G., and Pariat, E. (2012). X-ray and ultraviolet investigation into the magnetic connectivity of a solar flare. Astron. Astrophys. 547, A52. doi:10.1051/0004-6361/201219562

CrossRef Full Text | Google Scholar

Sadeghi, M., and Karami, K. (2019). The effect of weak magnetic twist on resonant absorption of slow sausage waves in magnetic flux tubes. Astrophys. J. 879, 121. doi:10.3847/1538-4357/ab24c4

CrossRef Full Text | Google Scholar

Shen, Y., Chen, P. F., Liu, Y. D., Shibata, K., Tang, Z., and Liu, Y. (2019). First unambiguous imaging of large-scale quasi-periodic extreme-ultraviolet wave or shock. Astrophys. J. 873, 22. doi:10.3847/1538-4357/ab01dd

CrossRef Full Text | Google Scholar

Shen, Y. D., Liu, Y., Su, J. T., Li, H., Zhang, X. F., Tian, Z. J., et al. (2013). Observations of a quasi-periodic, fast-propagating magnetosonic wave in multiple wavelengths and its interaction with other magnetic structures. Sol. Phys. 288, 585–602. doi:10.1007/s11207-013-0395-4

CrossRef Full Text | Google Scholar

Shen, Y., Liu, Y., Liu, Y. D., Su, J., Tang, Z., and Miao, Y. (2018a). Homologous large-amplitude nonlinear fast-mode magnetosonic waves driven by recurrent coronal jets. Astrophys. J. 861, 105. doi:10.3847/1538-4357/aac9be

CrossRef Full Text | Google Scholar

Shen, Y., and Liu, Y. (2012). Observational study of the quasi-periodic fast-propagating magnetosonic waves and the associated flare on 2011 may 30. Astrophys. J. 753, 53. doi:10.1088/0004-637X/753/1/53

CrossRef Full Text | Google Scholar

Shen, Y., Liu, Y., Song, T., and Tian, Z. (2018b). A quasi-periodic fast-propagating magnetosonic wave associated with the eruption of a magnetic flux rope. Astrophys. J. 853, 1. doi:10.3847/1538-4357/aaa3ff

CrossRef Full Text | Google Scholar

Shen, Y., Liu, Y., Su, J., and Deng, Y. (2012). On a coronal blowout jet: The first observation of a simultaneously produced bubble-like CME and a jet-like CME in a solar event. Astrophys. J. 745, 164. doi:10.1088/0004-637X/745/2/164

CrossRef Full Text | Google Scholar

Shen, Y., Liu, Y., Su, J., and Ibrahim, A. (2011). Kinematics and fine structure of an unwinding polar jet observed by the solar dynamic observatory/atmospheric imaging assembly. Astrophys. J. 735, L43. doi:10.1088/2041-8205/735/2/L43

CrossRef Full Text | Google Scholar

Shen, Y. (2021). Observation and modelling of solar jets. Proc. R. Soc. A 477, 20200217. doi:10.1098/rspa.2020.0217

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, Y., Song, T., and Liu, Y. (2018c). Dispersively formed quasi-periodic fast magnetosonic wavefronts due to the eruption of a nearby mini-filament. Mon. Not. Roy. Astron. Soc. 477, L6–L10. doi:10.1093/mnrasl/sly044

CrossRef Full Text | Google Scholar

Shen, Y., Tang, Z., Li, H., and Liu, Y. (2018d). Coronal EUV, QFP, and kink waves simultaneously launched during the course of jet-loop interaction. Mon. Not. Roy. Astron. Soc. 480, L63–L67. doi:10.1093/mnrasl/sly127

CrossRef Full Text | Google Scholar

Shen, Y., Yao, S., Tang, Z., Zhou, X., Qu, Z., Duan, Y., et al. (2022a). White-light QFP wave train and the associated failed breakout eruption. Astron. Astrophys. 665, A51. doi:10.1051/0004-6361/202243924

CrossRef Full Text | Google Scholar

Shen, Y., Zhou, X., Duan, Y., Tang, Z., Zhou, C., and Tan, S. (2022b). Coronal quasi-periodic fast-mode propagating wave trains. Sol. Phys. 297, 20. doi:10.1007/s11207-022-01953-2

CrossRef Full Text | Google Scholar

Shi, F., Li, D., and Ning, Z. (2022). One-minute quasi-periodic pulsations during an M-class solar flare. Universe 8, 104. doi:10.3390/universe8020104

CrossRef Full Text | Google Scholar

Shibata, K., Nakamura, T., Matsumoto, T., Otsuji, K., Okamoto, T. J., Nishizuka, N., et al. (2007). Chromospheric anemone jets as evidence of ubiquitous reconnection. Science 318, 1591–1594. doi:10.1126/science.1146708

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, C., Gordovskyy, M., and Browning, P. K. (2022). Pulsations of microwave emission from a solar flare in a twisted loop caused by intrinsic magnetohydrodynamic oscillations. Mon. Not. R. Astron. Soc. 511, 2880–2884. doi:10.1093/mnras/stac250

CrossRef Full Text | Google Scholar

Sterling, A. C., Moore, R. L., Samanta, T., and Yurchyshyn, V. (2020). Possible production of solar spicules by microfilament eruptions. Astrophys. J. 893, L45. doi:10.3847/2041-8213/ab86a5

CrossRef Full Text | Google Scholar

Su, W., Guo, Y., Erdélyi, R., Ning, Z. J., Ding, M. D., Cheng, X., et al. (2018a). Period increase and amplitude distribution of kink oscillation of coronal loop. Sci. Rep. 8, 4471. doi:10.1038/s41598-018-22796-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, Y., Veronig, A. M., Hannah, I. G., Cheung, M. C. M., Dennis, B. R., Holman, G. D., et al. (2018b). Determination of differential emission measure from solar Extreme ultraviolet images. Astrophys. J. 856, L17. doi:10.3847/2041-8213/aab436

CrossRef Full Text | Google Scholar

Takasao, S., and Shibata, K. (2016). Above-the-loop-top oscillation and quasi-periodic coronal wave generation in solar flares. Astrophys. J. 823, 150. doi:10.3847/0004-637X/823/2/150

CrossRef Full Text | Google Scholar

Tan, B. (2022). Diagnostic functions of solar coronal magnetic fields from radio observations. Res. Astron. Astrophys. 22, 072001. doi:10.1088/1674-4527/ac6f4b

CrossRef Full Text | Google Scholar

Tan, B., Yu, Z., Huang, J., Tan, C., and Zhang, Y. (2016). Very long-period pulsations before the onset of solar flares. Astrophys. J. 833, 206. doi:10.3847/1538-4357/833/2/206

CrossRef Full Text | Google Scholar

Tan, B., Zhang, Y., Tan, C., and Liu, Y. (2010). Microwave quasi-periodic pulsations in multi-timescales associated with a solar flare/CME event. Astrophys. J. 723, 25–39. doi:10.1088/0004-637X/723/1/25

CrossRef Full Text | Google Scholar

Thurgood, J. O., Pontin, D. I., and McLaughlin, J. A. (2019). On the periodicity of linear and nonlinear oscillatory reconnection. Astron. Astrophys. 621, A106. doi:10.1051/0004-6361/201834369

CrossRef Full Text | Google Scholar

Tian, H., McIntosh, S. W., Wang, T., Ofman, L., De Pontieu, B., Innes, D. E., et al. (2012). Persistent Doppler shift oscillations observed with hinode/EIS in the solar corona: Spectroscopic signatures of alfvénic waves and recurring upflows. Astrophys. J. 759, 144. doi:10.1088/0004-637X/759/2/144

CrossRef Full Text | Google Scholar

Tian, H., Young, P. R., Reeves, K. K., Wang, T., Antolin, P., Chen, B., et al. (2016). Global sausage oscillation of solar flare loops detected by the interface region imaging spectrograph. Astrophys. J. 823, L16. doi:10.3847/2041-8205/823/1/L16

CrossRef Full Text | Google Scholar

Tian, Z., Shen, Y., and Liu, Y. (2018). Formation and eruption of a double-decker filament triggered by micro-bursts and recurrent jets in the filament channel. New Astron. 65, 7–15. doi:10.1016/j.newast.2018.05.005

CrossRef Full Text | Google Scholar

Tiwari, A. K., Morton, R. J., and McLaughlin, J. A. (2021). A statistical study of propagating MHD kink waves in the quiescent corona. Astrophys. J. 919, 74. doi:10.3847/1538-4357/ac10c4

CrossRef Full Text | Google Scholar

Torrence, C., and Compo, G. P. (1998). A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78. doi:10.1175/1520-0477(1998)079¡0061:APGTWA¿2.0.CO;2

CrossRef Full Text | Google Scholar

Van Doorsselaere, T., Srivastava, A. K., Antolin, P., Magyar, N., Vasheghani Farahani, S., Tian, H., et al. (2020). Coronal heating by MHD waves. Space Sci. Rev. 216, 140. doi:10.1007/s11214-020-00770-y

CrossRef Full Text | Google Scholar

Wang, T., Ofman, L., Davila, J. M., and Su, Y. (2012). Growing transverse oscillations of a multistranded loop observed by SDO/AIA. Astrophys. J. 751, L27. doi:10.1088/2041-8205/751/2/L27

CrossRef Full Text | Google Scholar

Wang, T., Ofman, L., Yuan, D., Reale, F., Kolotkov, D. Y., and Srivastava, A. K. (2021). Slow-mode magnetoacoustic waves in coronal loops. Space Sci. Rev. 217, 34. doi:10.1007/s11214-021-00811-0

CrossRef Full Text | Google Scholar

Wang, T. (2011). Standing slow-mode waves in hot coronal loops: Observations, modeling, and coronal seismology. Space Sci. Rev. 158, 397–419. doi:10.1007/s11214-010-9716-1

CrossRef Full Text | Google Scholar

Warmuth, A., and Mann, G. (2016). Constraints on energy release in solar flares from RHESSI and GOES X-ray observations. I. Physical parameters and scalings. Astron. Astrophys. 588, A115. doi:10.1051/0004-6361/201527474

CrossRef Full Text | Google Scholar

Welsh, B. Y., Wheatley, J., Browne, S. E., Siegmund, O. H. W., Doyle, J. G., O’Shea, E., et al. (2006). GALEX high time-resolution ultraviolet observations of dMe flare events. Astron. Astrophys. 458, 921–930. doi:10.1051/0004-6361:20065304

CrossRef Full Text | Google Scholar

White, S. J., and Verwichte, E. (2021). Acoustic response to transverse oscillations in a solar coronal loop. Astron. Astrophys. 654, A33. doi:10.1051/0004-6361/202141515

CrossRef Full Text | Google Scholar

Woods, T. N., Eparvier, F. G., Hock, R., Jones, A. R., Woodraska, D., Judge, D., et al. (2012). Extreme ultraviolet variability experiment (EVE) on the solar dynamics observatory (SDO): Overview of science objectives, instrument design, data products, and model developments. Sol. Phys. 275, 115–143. doi:10.1007/s11207-009-9487-6

CrossRef Full Text | Google Scholar

Xiao, S., Liu, Y. Q., Peng, W. X., An, Z. H., Xiong, S. L., Tuo, Y. L., et al. (2022). On-ground and on-orbit time calibrations of GECAM. Mon. Not. R. Astron. Soc. 511, 964–971. doi:10.1093/mnras/stac085

CrossRef Full Text | Google Scholar

Yan, X. L., Jiang, C. W., Xue, Z. K., Wang, J. C., Priest, E. R., Yang, L. H., et al. (2017). The eruption of a small-scale emerging flux rope as the driver of an M-class flare and of a coronal mass ejection. Astrophys. J. 845, 18. doi:10.3847/1538-4357/aa7e29

CrossRef Full Text | Google Scholar

Yang, Z., Tian, H., Tomczyk, S., Morton, R., Bai, X., Samanta, T., et al. (2020). Mapping the magnetic field in the solar corona through magnetoseismology. Sci. China Technol. Sci. 63, 2357–2368. doi:10.1007/s11431-020-1706-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, S., and Chen, B. (2019). Possible detection of subsecond-period propagating magnetohydrodynamics waves in post-reconnection magnetic loops during a two-ribbon solar flare. Astrophys. J. 872, 71. doi:10.3847/1538-4357/aaff6d

CrossRef Full Text | Google Scholar

Yuan, D., Feng, S., Li, D., Ning, Z., and Tan, B. (2019). A compact source for quasi-periodic pulsation in an M-class solar flare. Astrophys. J. 886, L25. doi:10.3847/2041-8213/ab5648

CrossRef Full Text | Google Scholar

Yuan, D., Nakariakov, V. M., Chorley, N., and Foullon, C. (2011). Leakage of long-period oscillations from the chromosphere to the corona. Astron. Astrophys. 533, A116. doi:10.1051/0004-6361/201116933

CrossRef Full Text | Google Scholar

Yuan, D., Shen, Y., Liu, Y., Nakariakov, V. M., Tan, B., and Huang, J. (2013). Distinct propagating fast wave trains associated with flaring energy releases. Astron. Astrophys. 554, A144. doi:10.1051/0004-6361/201321435

CrossRef Full Text | Google Scholar

Yuan, D., Van Doorsselaere, T., Banerjee, D., and Antolin, P. (2015). Forward modeling of standing slow modes in flaring coronal loops. Astrophys. J. 807, 98. doi:10.1088/0004-637X/807/1/98

CrossRef Full Text | Google Scholar

Yuan, D., and Van Doorsselaere, T. (2016). Forward modeling of standing kink modes in coronal loops. I. Synthetic views. Astrophys. J. Suppl. Ser. 223, 23. doi:10.3847/0067-0049/223/2/23

CrossRef Full Text | Google Scholar

Zhang, Q., Li, C., Li, D., Qiu, Y., Zhang, Y., and Ni, Y. (2022a). First detection of transverse vertical oscillation during the expansion of coronal loops. arXiv e-printsarXiv:2209.00194.

Google Scholar

Zhang, Q. M., Chen, J. L., Li, S. T., Lu, L., and Li, D. (2022b). Transverse coronal-loop oscillations induced by the non-radial eruption of a magnetic flux rope. Sol. Phys. 297, 18. doi:10.1007/s11207-022-01952-3

CrossRef Full Text | Google Scholar

Zhang, Q. M., Dai, J., Xu, Z., Li, D., Lu, L., Tam, K. V., et al. (2020). Transverse coronal loop oscillations excited by homologous circular-ribbon flares. Astron. Astrophys. 638, A32. doi:10.1051/0004-6361/202038233

CrossRef Full Text | Google Scholar

Zhou, X., Shen, Y., Liu, Y. D., Hu, H., Su, J., Tang, Z., et al. (2022). Observations of a flare-ignited broad quasiperiodic fast-propagating wave train. Astrophys. J. Lett. 930, L5. doi:10.3847/2041-8213/ac651e

CrossRef Full Text | Google Scholar

Zimovets, I., Sharykin, I., and Myshyakov, I. (2021a). Quasi-periodic energy release in a three-ribbon solar flare. Sol. Phys. 296, 188. doi:10.1007/s11207-021-01936-9

CrossRef Full Text | Google Scholar

Zimovets, I. V., McLaughlin, J. A., Srivastava, A. K., Kolotkov, D. Y., Kuznetsov, A. A., Kupriyanova, E. G., et al. (2021b). Quasi-periodic pulsations in solar and stellar flares: A review of underpinning physical mechanisms and their predicted observational signatures. Space Sci. Rev. 217, 66. doi:10.1007/s11214-021-00840-9

CrossRef Full Text | Google Scholar

Zimovets, I. V., and Nakariakov, V. M. (2015). Excitation of kink oscillations of coronal loops: Statistical study. Astron. Astrophys. 577, A4. doi:10.1051/0004-6361/201424960

CrossRef Full Text | Google Scholar

Zucca, P., Carley, E. P., Bloomfield, D. S., and Gallagher, P. T. (2014). The formation heights of coronal shocks from 2D density and Alfvén speed maps. Astron. Astrophys. 564, A47. doi:10.1051/0004-6361/201322650

CrossRef Full Text | Google Scholar