The Generalized Uncertainty Principle and higher dimensions: Linking black holes and elementary particles

Black holes play an important role in linking microphysics with macrophysics, with those of the Planck mass (M_P ∼ 10⁻⁵ g) featuring in any theory of quantum gravity. In particular, the Compton-Schwarzschild correspondence posits a smooth transition between the Compton wavelength (R_C ∝ 1/M) below the Planck mass and the Schwarzschild radius (R_S ∝ M) above it. The duality between R_C and R_S implies a form of the Generalized Uncertainty Principle (GUP) and suggests that elementary particles may be sub-Planckian black holes. The simplest possibility is that the ADM mass has the form $M+\beta M_{\mathrm{P}}^2/M$ for some constant β and this model can be extended to charged and rotating black holes, clearly relevant to elementary particles. Another possibility is that sub-Planckian black holes may arise in loop quantum gravity and this explicitly links black holes and elementary particles. Higher dimensions may modify both proposals. If there are n extra dimensions, all with the same compactification scale, one expects R_S ∝ M^1/(1+n) below this scale but R_C depends on the form of the higher-dimensional wave-function. If it is spherically symmetric, then R_C ∝ M⁻¹, so duality is broken and the Planck mass is reduced, allowing the possibility of TeV quantum gravity. If the wave-function is pancaked in the extra dimensions, R_C ∝ M^−1/(1+n) and so duality is preserved but the Planck mass is unchanged.

1 Introduction

Whatever final theory amalgamates relativity theory and quantum mechanics, it is likely to involve two features: 1) what is termed the Black Hole Uncertainty Principle (BHUP) correspondence; and 2) the existence of extra dimensions on sufficiently small scales. Both features are expected to become important at the Planck length, R_P ∼ 10⁻³³ cm, and possibly on much larger scales. It is striking that black holes are involved in both these features and indeed there are many other ways in which these objects provide a link between macrophysics and microphysics (Carr, 2018).

As regards feature (1), the duality under the transformation $M\to M_{\mathrm{P}}^2/M$ between the Compton wavelength for a particle of mass M, R_C = ℏ/(Mc), and the Schwarzschild radius for a black hole of mass M, R_S = 2GM/c², suggests a unified Compton-Schwarzschild expression with a smooth minimum in the (M, R) plane. This implies that elementary particles may in some sense be sub-Planckian black holes. This proposal goes back to the 1970s, when it was motivated in the context of strong gravity theories.

As regards feature (2), if there are n extra spatial dimensions compactified on some scale R_E, then R_S scales as R^1/(1+n) for R < R_E, leading to the possibility of TeV quantum gravity and black hole production at accelerators if R_C scales as M⁻¹ for R < R_E. However, the higher-dimensional Compton wavelength depends on the form of the (3 + n)-dimensional wavefunction and in some circumstances one might expect R_C ∝ M^−1/(1+n) for R < R_E. This preserves the duality between R_C and R_S but TeV quantum gravity is precluded. Nevertheless, the extra dimensions could still have consequences for the detectability of black hole evaporations and the enhancement of pair-production at accelerators on scales below R_E.

The plan of this paper is as follows. Section 2 discusses the BHUP correspondence in general terms. Section 3 applies the correspondence to black holes in Loop Quantum Gravity (LQG), this being the first historical study of this kind. Section 4 then considers the simplest application of the BHUP correspondence: the‘M + 1/M’ Schwarzschild model and its extension to charged and rotating black holes. Higher-dimensional black holes are discussed in Section 5 and some concluding remarks about the connection between particles and black holes are made in Section 6.

2 The Black Hole Uncertainty Principle correspondence

A key feature of the microscopic domain is the (reduced) Compton wavelength for a particle of rest mass M, with the region R < R_C in the (M, R) diagram of Figure 1 being regarded as the “quantum domain”. A key feature of the macroscopic domain is the Schwarzschild radius for a body of mass M, with the region R < R_S being regarded as the “relativistic domain”. The Compton and Schwarzschild lines intersect at around the Planck scales,

$R_{\mathrm{P}}=\sqrt{\hslash G/c^3}\sim 10^{-33}\mathrm{c}\mathrm{m},M_{\mathrm{P}}=\sqrt{\hslash c/G}\sim 10^{-5}\mathrm{g},(1)$

and divide the (M, R) diagram into three regimes, which we label quantum, relativistic and classical. There are several other interesting lines in the figure. The vertical line M = M_P marks the division between elementary particles (M < M_P) and black holes (M > M_P), since the size of a black hole is usually required to be larger than the Compton wavelength associated with its mass. The horizontal line R = R_P is significant because quantum fluctuations in the metric should become important below this (Wheeler, 1955). Quantum gravity effects should also be important whenever the density exceeds the Planck value, ρ_P = c⁵/(G²ℏ) ∼ 10⁹⁴ g cm⁻³, corresponding to the sorts of curvature singularities associated with the big bang or the centres of black holes. This implies $R<R_{\mathrm{P}}{(M/M_{\mathrm{P}})}^{1/3}$, which is well above the R = R_P line for M ≫ M_P, so the shaded region specifies the ‘quantum gravity’ domain.

FIGURE 1

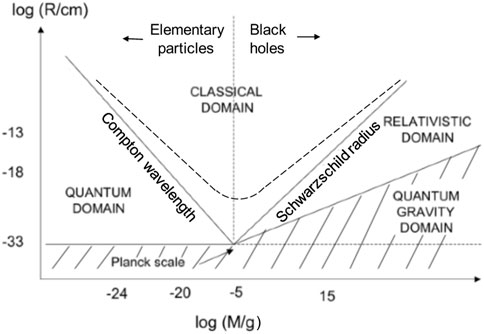
FIGURE 1. Division of (M, R) diagram into classical, quantum, relativistic and quantum gravity domains. The boundaries are specified by the Planck density, Compton wavelength and Schwarzschild radius. From Carr (2018).

The Compton and Schwarzschild lines transform into one another under the transformation $M\to M_{\mathrm{P}}^2/M$, which suggests some connection between elementary particles and black holes. This relates to what is termed “T-duality” in string theory and maps momentum-carrying states to winding states (Zwiebach, 2009). Although the Compton and Schwarzschild boundaries correspond to straight lines in the logarithmic plot of Figure 1, this form presumably breaks down near the Planck point due to quantum gravity effects. One might envisage two possibilities: either there is some form of critical point at the Planck scale, so that the separation between particles and black holes is maintained (Isi et al., 2013), or there is a smooth minimum, as indicated by the broken line in Figure 1, so that the Compton and Schwarzschild lines merge (Carr et al., 2016). Which alternative applies has important implications for the relationship between elementary particles and black holes.

One way of smoothing the transition between the Compton and Schwarzschild lines is to invoke some form of unified expression which asymptotes to the Compton wavelength and Schwarzschild radius in the appropriate regimes (Carr, 2015). The simplest such expression would be

$R_{\text{CS}}=\frac{\beta \hslash }{Mc}+\frac{2GM}{c^2},(2)$

where β is a dimensionless constant. In the super-Planckian regime, this becomes

$R_{\mathrm{S}}^{\prime }=\frac{2GM}{c^2}\left[1+\frac{\beta }{2}{\left(\frac{M_{\mathrm{P}}}{M}\right)}^2\right]\left(M\gg M_{\mathrm{P}}\right),(3)$

with the second term corresponding to a small correction to the usual Schwarzschild expression. In the sub-Planckian regime, it becomes

$R_{\mathrm{C}}^{\prime }=\frac{\beta \hslash }{Mc}\left[1+\frac{2}{\beta }{\left(\frac{M}{M_{\mathrm{P}}}\right)}^2\right]\left(M\ll M_{\mathrm{P}}\right),(4)$

with the second term corresponding to a small correction to the usual expression for the Compton wavelength. More generally, one might consider any unified expression $R_{\mathrm{C}}^{\prime }(M)\equiv R_{\mathrm{S}}^{\prime }(M)$ which has the asymptotic behaviour βℏ/(Mc) for M ≪ M_P and 2GM/c² for M ≫ M_P.

An expression of the form (3) arises in the quantum N-portrait model of Dvali et al. (Dvali et al., 2011), which regards a black hole as a weakly-coupled Bose-Einstein condensate of gravitons. From holographic considerations, the number of gravitons in the black hole is $N\approx M^2/M_{\mathrm{P}}^2$ and one can then argue that the black hole radius is (Frassino et al., 2016)

$R_{\text{CS}}\approx \frac{2GM}{c^2}\left(1+\frac{\beta }{2N}\right)\left(M>M_{\mathrm{P}}\right),(5)$

which is equivalent to Eq. 3. An expression of the form (4) also arises in the context of the Generalized Uncertainty Principle (GUP). This is because it can be argued that the Uncertainty Principle should be modified to the form (Adler, 2010)

$\mathit{\Delta }x=\frac{\hslash }{\mathit{\Delta }p}+\alpha \frac{R_{\mathrm{P}}^2\mathit{\Delta }p}{\hslash },(6)$

where α is a dimensionless constant. The first term represents the uncertainty in the position due to the momentum of the probing photon and leads to the usual expression for the Compton wavelength if one substitutes Δx → R and Δp → cM. The second term represents the gravitational effect of the probing photon and is much smaller than the first term for Δp ≪ cM_P. Variants of Eq. 6 are also motivated by string theory (Veneziano, 1986; Witten, 1996), non-commutative quantum mechanics (Gross and Mende, 1988; Amati et al., 1989; Yoneya, 1989; Konishi et al., 1990; Scardigli, 1999), general minimum length considerations (Maggiore, 1993a; Maggiore, 1993b; Maggiore, 1994), polymer corrections in the structure of spacetime in LQG (Ashtekar et al., 2003a; Hossain et al., 2010) and some approaches to quantum decoherence (Kay, 1998).

The GUP is usually restricted to the sub-Planckian domain (M < M_P). However, if we rewrite Eq. 6 using Δx → R and Δp → cM even in the super-Planckian regime, we obtain a revised Compton wavelength which applies for all M:

$R_{\text{CS}}=\frac{\hslash }{Mc}+\alpha \frac{GM}{c^2}.(7)$

This resembles Eq. 2 except that the constant is associated with the second term. This suggests that there is a different kind of positional uncertainty for an object larger than the Planck mass, related to the size of a black hole. This is not unreasonable since the usual Compton wavelength is below the Planck length here and also an outside observer cannot localize an object on a scale smaller than its Schwarzschild radius. This is termed the Black Hole Uncertainty Principle (BHUP) correspondence (Carr, 2015) or the Compton-Schwarzschild correspondence when discussing an interpretation in terms of extended de Broglie relations (Lake and Carr, 2015).

Strictly speaking, Eqs 2, 7 are consistent only if α = 2 and β = 1 but that would leave no free parameter at all. Therefore an interesting issue is whether one should associate the free constant in R_CS with the 1/M term, as in Eq. 2, or the M term, as in Eq. 7. Here we adopt the former approach, on the grounds that the expression for the Schwarschild radius is exact, whereas there is some ambiguity in the meaning of the Compton scale. However, for comparison with the GUP literature, we still need to identify an effective value of α and a simple rescaling of the relationship between Δx and R suggests α = 2/β. Another approach is to identify Δp with 1/M rather than M for M > M_P and Eq. 6 then equates α and β directly. One might even argue that Δp has the form (M + 1/M)⁻¹, in which case Δx ∼ 1/M and Δp ∼ M in the particle case (M < M_P) and Δx ∼ M and Δp ∼ 1/M in the black hole case (M > M_P). This would be consistent with the extended de Broglie relations (Hawking, 1974; Lake and Carr, 2015).

In the standard picture, one can calculate the black hole temperature from the Uncertainty Principle by identifying it with a multiple η of Δp. This gives (Hawking, 1974)

$kT=\eta c\mathit{\Delta }p=\frac{\eta \hslash c}{\mathit{\Delta }x}=\frac{\eta c^2{M}_{\mathrm{P}}^2}{2M},(8)$

which is precisely the Hawking temperature if we take η = 1/(4π). If one adopts the GUP but assumes the usual black hole size, one obtains the Adler form (Chen and Adler, 2003)

$kT=\frac{\eta M{c}^2}{\alpha }\left(1\pm \sqrt{1-\frac{\alpha M_{\mathrm{P}}^2}{M^2}}\right).(9)$

The negative sign gives a small perturbation to the standard Hawking temperature

$kT\approx \frac{\eta M_{\mathrm{P}}^2{c}^2}{2M}\left[1-\frac{\alpha M_{\mathrm{P}}^2}{4M^2}\right]\left(M\gg M_{\mathrm{P}}\right)(10)$

at large M. However, the solution becomes complex when M falls below $\sqrt{\alpha }{M}_{\mathrm{P}}$, corresponding to a minimum mass, and it then connects to the positive branch of Eq. 9. This form is indicated by the curve on the right of Figure 2.

FIGURE 2

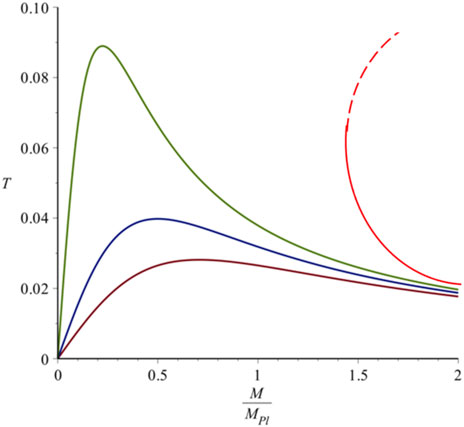
FIGURE 2. Hawking temperature (in Planck units) from Eq. 3 and surface gravity argument as a function of M/M_P for β = 1 (bottom), β = 0.5 (middle) and β = 0.1 (top). Also shown on the right is the Adler prediction. From Carr et al. (2016).

Eq. 9 is inconsistent with the BHUP correspondence since this also modifies the relationship between the black hole radius Δx and M. If we adopt Eq. 3 instead, then the surface gravity argument gives a temperature

$\begin{array}{cc}\hfill kT=& \frac{M_{\mathrm{P}}^2{c}^2}{4\pi M\left(2+\beta M_{\mathrm{P}}^2/M^2\right)}\hfill \\ \hfill & \approx \left\{\begin{array}{cc}\frac{M_{\mathrm{P}}^2{c}^2}{8\pi M}\left[1-\frac{\beta }{2}{\left(\frac{M_{\mathrm{P}}}{M}\right)}^2\right]\hfill & \left(M\gg M_{\mathrm{P}}\right)\hfill \\ \frac{M{c}^2}{4\pi \beta }\left[1-\frac{2}{\beta }{\left(\frac{M}{M_{\mathrm{P}}}\right)}^2\right]\hfill & \left(M\ll M_{\mathrm{P}}\right).\hfill \end{array}\right.\hfill \end{array}(11)$

This is plotted in Figure 2 and is very different from the Adler form. As M decreases, the temperature reaches a maximum of around T_P and then goes to zero as M → 0.

An important caveat is that Eq. 6 assumes that the two uncertainties add linearly. On the other hand, since they are independent, it might be more natural to assume that they add quadratically (Carr et al., 2011):

$\mathit{\Delta }x=\sqrt{{\left(\hslash /\mathit{\Delta }p\right)}^2+{\left(\alpha R_{\mathrm{P}}^2\mathit{\Delta }p/\hslash \right)}^2}.(12)$

We refer to Eqs 6, 12 as the linear and quadratic forms of the GEP, respectively. The latter corresponds to a unified expression

$R_{\text{CS}}=\sqrt{{\left(\beta \hslash /Mc\right)}^2+{\left(2GM/c^2\right)}^2},(13)$

where we have we have again introduced β. This leads to the approximations

$R_{\mathrm{S}}^{\prime }\approx \frac{2GM}{c^2}\left[1+\frac{{\beta }^2}{8}{\left(\frac{M_{\mathrm{P}}}{M}\right)}^4\right]\left(M\gg M_{\mathrm{P}}\right)(14)$

and

$R_{\mathrm{C}}^{\prime }\approx \frac{\beta \hslash }{Mc}\left[1+\frac{2}{{\beta }^2}{\left(\frac{M}{M_{\mathrm{P}}}\right)}^4\right]\left(M\ll M_{\mathrm{P}}\right).(15)$

These might be compared to the exact expressions in the linear case, given by Eqs 3, 4. As we now show, a model inspired by LQG permits the existence of a black hole whose horizon size has precisely the form (13).

3 Loop black holes

Loop Quantum Gravity is based on a canonical quantization of the Einstein equations, written in terms of the Ashtekar variables. One feature of this is that area is quantized, with its smallest possible value being

$A_{\text{min}}=4\pi \sqrt{3}\gamma R_{\mathrm{P}}^2,(16)$

where γ is the Immirzi parameter and of order 1. The quantity a_o ≡ A_min/8π, together with the dimensionless polymeric parameter δ, determines the deviation from classical theory.

One version of LQG, using the mini-superspace approximation, gives rise to cosmological solutions which resolve the initial singularity problem (Bojowald, 2001; Ashtekar et al., 2003b; Bojowald, 2005). Another version gives the loop black hole (LBH) solution (Modesto, 2010) and this replaces the singularity in the Schwarzschild solution with another asymptotically flat region. The metric depends only on the combined dimensionless parameter ɛ ≡ δγ, which must be small, and can be expressed as

$d{s}^2=-G\left(r\right)c^{2}d{t}^2+\frac{d{r}^2}{F\left(r\right)}+H\left(r\right)\left(d{\theta }^2+{\sin }^2\theta d{\varphi }^2\right)(17)$

with

$G\left(r\right)=\frac{\left(r-r_{+}\right)\left(r-r_{-}\right){\left(r+r_{\ast }\right)}^2}{r^4+a_o^2},F\left(r\right)=\frac{\left(r-r_{+}\right)\left(r-r_{-}\right)r^4}{{\left(r+r_{\ast }\right)}^2\left(r^4+a_o^2\right)}.(18)$

Here r₊ = 2GM/c² and r₋ = 2GMP²/c² are the outer and inner horizons, respectively, and $r_{\ast }\equiv \sqrt{r_{+}{r}_{-}}=2GMP/c^2$, where M is the black hole mass and

$P\equiv \frac{\sqrt{1+{\epsilon }^2}-1}{\sqrt{1+{\epsilon }^2}+1}\approx {\epsilon }^2/4\ll 1(19)$

is called the polymeric function. In the limit r → ∞ one has

$G\left(r\right)\to 1-\frac{2G\mathcal{M}}{c^{2}r}\left(1-{\epsilon }^2\right),F\left(r\right)\to 1-\frac{2G\mathcal{M}}{c^{2}r},(20)$

where $\mathcal{M}\equiv M{(1+P)}^2$ is the ADM mass (i.e. the mass measured as r → ∞). The function H(r) in Eq. 17 is not r² (as in the Schwarzschild case) but

$H\left(r\right)=r^2+\frac{a_o^2}{r^2}\Rightarrow R\equiv \sqrt{r^2+\frac{a_o^2}{r^2}}.(21)$

Here R is the physical radial coordinate, in the sense that the circumference function is 2πR. As r decreases from infinity to zero, R first decreases from infinity to a minimum value of $\sqrt{2a_0}$ at $r=\sqrt{a_0}$ and then increases again to infinity. In particular, the value of R associated with the outer event horizon is

$R_{\mathrm{S}}^{\prime }=\sqrt{{\left(\frac{2GM}{c^2}\right)}^2+{\left(\frac{a_o{c}^2}{2GM}\right)}^2}.(22)$

This corresponds to Eq. 13 if β = a_oc²/G. The important physical implication of Eq. 21 is that central singularity of the Schwarzschild solution is replaced with another asymptotic region, so the collapsing matter bounces and the black hole becomes part of a wormhole. The fact that a purely geometrical condition in LQG implies the quadratic version of the GUP suggests some deep connection between general relativity and quantum theory. The duality between the two asympotic spaces also suggests a link between elementary particles with M ≪ M_P and black holes with M ≫ M_P (Modesto and Premont-Schwarz, 2009), which is clearly relevant to the theme of this paper.

The temperature implied by the black hole’s surface gravity is

$T\propto \frac{GM}{R_{\mathrm{S}}^{\prime 2}}\propto \left\{\begin{array}{cc}{M}^{-1}\hfill & \left(M\gg M_{\mathrm{P}}\right)\hfill \\ M^3\hfill & \left(M\ll M_{\mathrm{P}}\right).\hfill \end{array}\right.(23)$

However, if one calculates the temperature using the GUP expression for Δp, one obtains

$kT\approx \left\{\begin{array}{cc}\frac{\eta \hslash c^3}{2GM}\left[1-\frac{{\beta }^2}{8}{\left(\frac{M_{\mathrm{P}}}{M}\right)}^4\right]\hfill & \left(M\gg M_{\mathrm{P}}\right)\hfill \\ \frac{\eta M{c}^2}{\beta }\left[1-\frac{2}{{\beta }^2}{\left(\frac{M}{M_{\mathrm{P}}}\right)}^4\right]\hfill & \left(M\ll M_{\mathrm{P}}\right).\hfill \end{array}\right.(24)$

This is similar to Eq. 11 but inconsistent with Eq. 23 in the sub-Planckian regime. The source of the discrepancy is that there are two asymptotic spaces—one on each side of the wormhole throat—and the temperature is different in these. Observer only detect radiation from the horizon on their side of the throat, so the inner horizon with respect to r = ∞ corresponds to the outer horizon with respect to r = 0 (Carr et al., 2011). For $M<\sqrt{\beta /2}{M}_{\mathrm{P}}$, T ∝ M³ in our space and T ∝ M in the other space, which explains the predictions of Eqs 23, 24. For $\sqrt{\beta /2}{M}_{\mathrm{P}}<M<P^{-2}\sqrt{\beta /2}{M}_{\mathrm{P}}$, T ∝ M⁻¹ in our space and T ∝ M in the other space. For $M>P^{-2}\sqrt{\beta /2}{M}_{\mathrm{P}}$, T ∝ M⁻¹ in our space and T ∝ M⁻³ in the other space.

4 Carr-Mureika-Nicolini approach

This section describes a particular interpretation of the linear version of the BHUP correspondence, described in my work with Mureika and Nicolini (Carr et al., 2016), in which the Arnowitt-Deser-Misner (ADM) mass is taken to be

$M_{\mathrm{A}\mathrm{D}\mathrm{M}}=M\left(1+\frac{\beta }{2}\frac{M_{\mathrm{P}}^2}{M^2}\right).(25)$

This is equivalent to Eq. 3 and we noted a possible connection with the energy-dependent metric in the “gravity’s rainbow” proposal (Magueijo and Smolin, 2004) and with the QFT renormalization of mass in the presence of stochastic metric fluctuations (Camacho, 2003). Putting ℏ = c = 1, the Schwarzschild radius for the modified metric is

$R_{\mathrm{S}}^{\prime }=\frac{2M_{\mathrm{A}\mathrm{D}\mathrm{M}}}{M_{\mathrm{P}}^2}\approx \left\{\begin{array}{cc}2M/M_{\mathrm{P}}^2\hfill & \left(M\gg M_{\mathrm{P}}\right)\hfill \\ \beta /M\hfill & \left(M\ll M_{\mathrm{P}}\right)\hfill \end{array}\right.(26)$

and the temperature is $kT=M_{\mathrm{P}}^2/(8\pi M_{\mathrm{A}\mathrm{D}\mathrm{M}})$, corresponding to Eq. 11. This is not the only black hole metric allowed by the GUP. This is illustrated by the discussion of LQG in Sec. 3 but there could be other relevant solutions in GR itself. However, Eq. 25 gives the simplest such solution.

The black hole luminosity in this model is $L={\xi }^{-1}{M}_{\mathrm{A}\mathrm{D}\mathrm{M}}^{-2}$ where $\xi \sim t_{\mathrm{P}}/M_{\mathrm{P}}^3$, so the mass loss rate decreases when M falls below M_P and the black hole never evaporates completely. There are two values of M for which the evaporation time (τ ∼ M/L) is comparable to the age of the Universe (t₀ ∼ 10¹⁷s). One is super-Planckian, $M_{\ast }\sim {(t_0/\xi )}^{1/3}\sim 10^{15}\mathrm{g}$, this being the standard expression for the mass of a PBH evaporating at the present epoch. The other is sub-Planckian, M_** ∼ β² (t_P/t₀)M_P ∼ 10⁻⁶⁵β² g, although the mass cannot actually reach this value at the present epoch because the black hole is cooler than the CMB temperature for M < M_CMB ∼ 10⁻³⁶β g. This leads to effectively stable relics of this mass.

It is interesting to consider observational constraints on the parameter β and these are discussed in Carr et al. (2022). Within the GUP context, these only arise in the microscopic domain and a variety of mechanical oscillator experiments imply α < 4 × 10⁴ (Pikovski et al., 2012; Bushev et al., 2019). A similar bound arises from the AURIGA gravitational bar detector (Marin et al., 2014). Since β = 2/α, both bounds corresponding to a lower limit β > 10^–4. Within the context of the BHUP correspondence, there are also constraints in the macroscopic domain from measuring the gravitational force between 100 mg masses with mm separation (Westphal et al., 2021) and these imply β < 10⁶. Clearly these limits still allow a wide range of values for β. One might also constrain β by observations on astrophysical scales but in this domain the effects of the Extended Uncertainty Principle, in which Δx Δp ∼ 1 + (δx)² rather than 1 + (δp)², becomes more relevant (Mureika, 2019).

Recently we have extended this work, together with Heather Mentzer, to charged and rotating black holes (Carr et al., 2020), since this is clearly relevant to elementary particles. The standard Reissner-Nordström (RN) already exhibits features of the GUP-modified Schwarzschild solution. This is because the RN metric has an outer (+) and inner (-) horizon at

$r_{\pm }=\frac{M}{M_{\mathrm{P}}^2}\left(1\pm \sqrt{1-\frac{{\alpha }_e{M}_{\mathrm{P}}^2{n}^2}{M^2}}\right)\approx \left\{\begin{array}{cc}\frac{2M}{M_{\mathrm{P}}^2}\left(1-\frac{\gamma M_{\mathrm{P}}^2}{M^2}\right)\hfill & \left(+\right)\hfill \\ \frac{2\gamma }{M}\left(1+\frac{\gamma M_{\mathrm{P}}^2}{M^2}\right)\hfill & \left(-\right)\hfill \end{array}\right.(27)$

where ne is the black hole charge, γ ≡ α_en²/4 with α_e ≈ 1/137 being the electric fine structure constant, and the last expression applies for a black hole which is far from extremal $(M\gg \sqrt{{\alpha }_e}n{M}_{\mathrm{P}})$. The form of the outer and inner horizons for different values of n are shown by the upper and lower parts of the solid curves in Figure 3, respectively. There are two asymptotic behaviors: the outer horizon correponds to Eq. 2 but with a negative value of β; the inner horizon resembles the Compton expression and it asymptotes to the Compton wavelength itself for n = 16, this being the integer part of $\sqrt{2/{\alpha }_e}$.

FIGURE 3

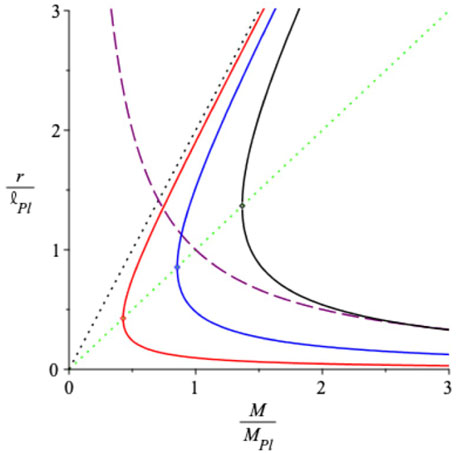
FIGURE 3. The solid curves show the outer and inner horizons for a standard RN black hole with n = 5, 11, 16 (left to right). For each n, the horizons meet at the extremal mass on the line $r=M/M_{\mathrm{P}}^2$ (green dotted) and are bounded from above by the Schwarzschild radius $r_{\mathrm{S}}=2M/M_{\mathrm{P}}^2$ (black dotted line). The Compton curve is shown by the dashed line and the inner horizon asymptotes to this for n = 16. Solutions with 11 < n < 16 penetrate the sub-Planckian RN regime. From Carr et al. (2020).

For each n, the two horizons merge on the line r = GM (lower dotted curve) at the minimum value of M. This corresponds to a sequence of “extremal” solutions (shown by the dots in Figure 3) with a spectrum of masses $\sqrt{{\alpha }_e}n{M}_{\mathrm{P}}$. For given n, there are no solutions with M less than this since these would correspond to naked singularities. In particular, n could be at most the integer part of $1/\sqrt{{\alpha }_e}$ (i.e. 11) for a Planck-mass black hole. As in the GUP case, the temperature of the RN solution reaches a maximum and then goes to zero as M tends to the limiting value $\sqrt{{\alpha }_e}n{M}_{\mathrm{P}}$. One might want to associate elementary particles only with extremal solutions (since they are stable) but these states all have masses in the range (0.1–1)M_P, which is too large. Also even extremal black holes may discharge through the Schwinger mechanism (Schwinger, 1951).

The (standard) Compton line intersects the outer black hole horizon, as required if one wants a smooth connection between particles and black holes, at the mass

$M=\frac{M_{\mathrm{P}}}{\sqrt{2-{\alpha }_e{n}^2}}\approx \frac{M_{\mathrm{P}}}{\sqrt{2-n^2/137}}.(28)$

(This is also termed the self-completeness condition (Isi et al., 2013).) For n = 0, the intersect is $M_{\mathrm{P}}/\sqrt{2}$ but it increases with n and tends to M_P as $n\to \sqrt{137}$ (middle curve). This implies a constraint n ≤ 11 on the charge of a self-complete RN black hole. The Compton line still intersects the inner horizon for $\sqrt{137}<n<\sqrt{274}$, but these solutions penetrate the r < R_P region.

One can extend this model to the GUP-modified RN solutions by replacing M with M_ADM given by Eq. 25. Providing $n<\sqrt{2\beta /{\alpha }_e}$ for fixed β, the outer horizon behaves as in the GUP-Schwarzschild case, with a continuous transition between the gravitational (r_CS ∝ M) and Compton (r_CS ∝ M⁻¹) scaling. Also, r₊ has a minimum and r₋ has a maximum at

$M=M_{\text{crit}}\equiv \sqrt{\beta /2}{M}_{\mathrm{P}},r_{\pm }=\left[\sqrt{2\beta }\pm \sqrt{2\beta -n^2{\alpha }_e}\right]R_{\mathrm{P}}.(29)$

This is indicated by the curves on the left of Figure 4. In principle, the particle-like black holes can have arbitrarily low mass in this case. However, it is unclear that these solutions are candidates for stable particles since none of them are extremal, this possibility arising only in the limit $n_{\mathit{max}}=\sqrt{2\beta /{\alpha }_e}$. For larger values of n, the form of the solutions changes, as indicated by the curves on the right of Figure 4. These represent super-Planckian black holes on the right (similar to the standard RN case with an extremal solution at the smallest value of M) and sub-Planckian particles on the left, with a mass gap in between. Equivalently, for a given value of n, there is a critical value of β = n²α_e/2 below which the solutions bifurcate and become separated by a mass gap.

FIGURE 4

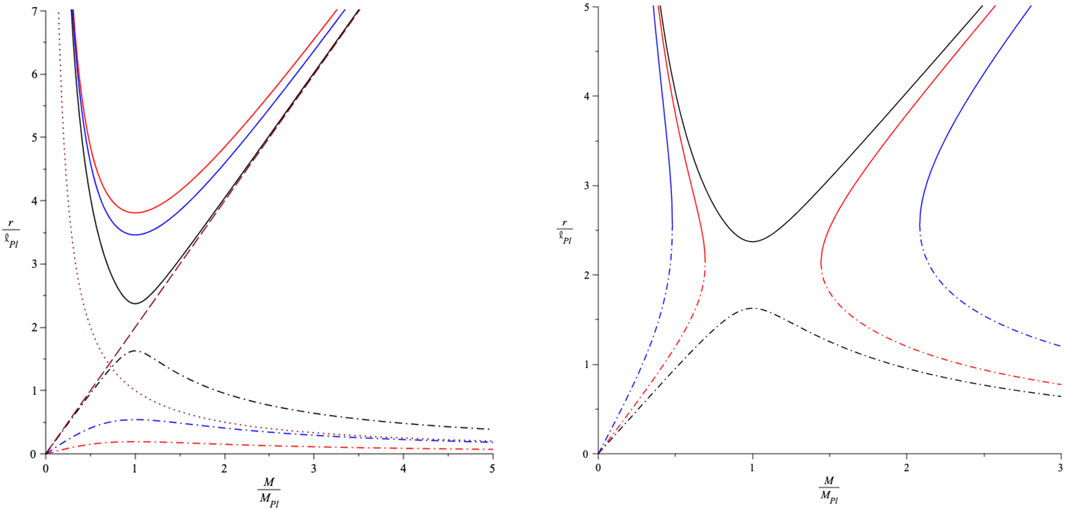
FIGURE 4. Outer (solid) and inner (dash-dot) horizon size for GUP-RN black hole with β = 2. Left: Outer (top) and inner (bottom) horizons for n = 10 (red), n = 16 (blue) and n = 23 (black). The dashed/dotted lines show the usual Schwarzschild/Compton scales. The inner horizon is nearly asymptotic to the Compton wavelength at large M for n = 16. There is a discontinuity when n reaches 23, this being close to an extremal solution. Right: Outer (top) and inner (bottom) horizons for n = 23 (black), n = 25 (blue) and n = 30 (black). The horizons in this case have a maximum value of M on the left and a minimum value on the right. There are no black holes between these values. From Carr et al. (2020).

The Kerr metric exhibits similar behaviour but there is a critical spin (nℏ) rather than a critical charge. The extremal case corresponds to the spectrum of masses $\sqrt{n}{M}_{\mathrm{P}}$, while the self-completeness condition corresponds to

$M=M_{\mathrm{P}}\sqrt{\frac{1+n^2}{2}}.(30)$

This allows all values of n, whereas n could not exceed $[1/\sqrt{{\alpha }_e}]=11$ in the RN case. In the GUP Kerr case, an expression similar to Eq. 29 still applies and there is a change in the form of the solutions for n > 2β.

5 Higher-dimensional black holes

The black hole boundary in Figure 1 assumes there are three spatial dimensions but many theories suggest that the dimensionality could increase on small scales. Although the extra dimensions are often assumed to be compactified on the Planck length, there are also models in which they are much larger. For example, the model of Arkani-Hamed et al. (1998) has n extra spatial dimensions, all compactified on the same scale R_E. If we assume that the standard expression for the Compton wavelength (R_C ∝ M⁻¹) still applies, then the masses with Compton and Schwarzschild scales R_E are

$M_{\mathrm{E}}\equiv \frac{\hslash }{c{R}_E}\simeq M_{\mathrm{P}}\frac{R_{\mathrm{P}}}{R_E},M_E^{\prime }\equiv \frac{c^2{R}_E}{G}\simeq M_{\mathrm{P}}\frac{R_E}{R_{\mathrm{P}}}.(31)$

For R < R_E, the gravitational potential generated by a mass M is

$V_{\text{grav}}=\frac{G_{D}M}{R^{1+n}},(32)$

where G_D is the higher-dimensional gravitational constant and D = 4 + n is the total number of spacetime dimensions. For R > R_E, one recovers the usual form, V_grav = GM/R with $G=G_D/R_E^n$. Thus the effective gravitational constants at large and small scales are different.

Eq. 32 implies that the usual expression for the Schwarzschild radius no longer applies for masses below $M_E^{\prime }$. If the black hole is assumed to be spherically symmetric in the higher-dimensional space, one has (Kanti, 2016)

$R_{\mathrm{S}}\simeq R_E{\left(\frac{M}{M_E^{\prime }}\right)}^{1/\left(n+1\right)}.(33)$

Therefore the slope of the black hole boundary in Figure 1 becomes shallower for $M<M_E^{\prime }$, as indicated in Figure 5A. The intersect with the Compton line then becomes

$R_{\mathrm{P}}^{\prime }\simeq {\left(R_{\mathrm{P}}^2{R}_E^n\right)}^{1/\left(2+n\right)},M_{\mathrm{P}}^{\prime }\simeq {\left(M_{\mathrm{P}}^2{M}_E^n\right)}^{1/\left(2+n\right)},(34)$

so $M_{\mathrm{P}}^{\prime }\ll M_{\mathrm{P}}$ and $R_{\mathrm{P}}^{\prime }\gg R_{\mathrm{P}}$ for R_E ≫ R_P.

FIGURE 5

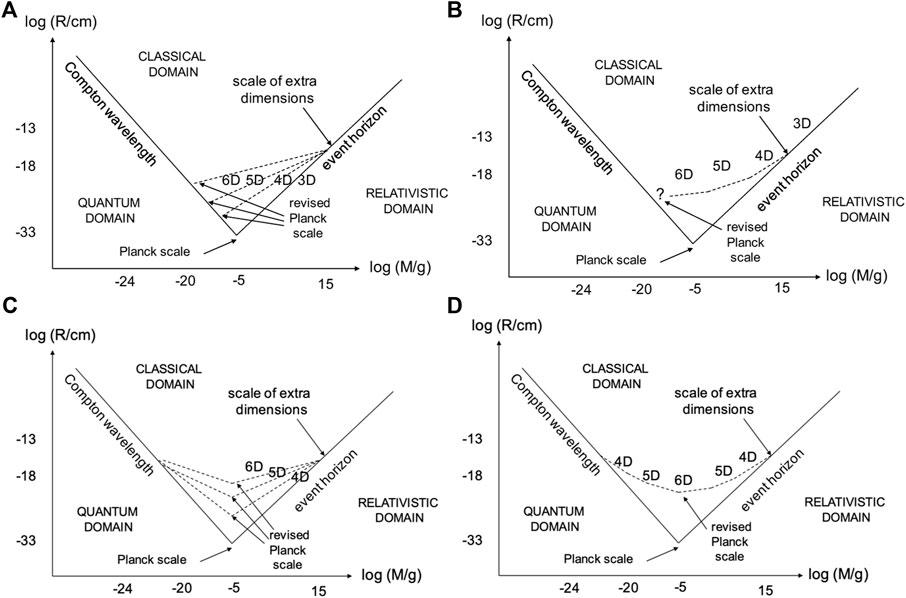
FIGURE 5. Modification of the Schwarzschild line and Planck scales in the (M, R) diagram for extra compact dimensions associated with (A) a single length scale or (B) a hierarchy of length scales (B) if the Compton scale preserves its usual form. (C) and (D) are the corresponding diagrams if the duality between the Compton and Schwarzschild expressions is preservd. From Lake and Carr (2019).

In principle, the lowering of the Planck mass could permit the possibility of TeV quantum gravity and the production of small black holes at the Large Hadron Collider (LHC), with their evaporation leaving a distinctive signature (Dimopoulos and Landsberg, 2001; Anchordoqui et al., 2002; Giddings and Thomas, 2002). If the accessible energy is E_max ≈ 10 TeV, then the extra dimensions can be probed for

$R_E>10^{-18+30/n}\mathrm{c}\mathrm{m}\simeq \left\{\begin{array}{cc}10^{12}\mathrm{c}\mathrm{m}\hfill & \left(n=1\right)\hfill \\ 10^{-3}\mathrm{c}\mathrm{m}\hfill & \left(n=2\right)\hfill \\ 10^{-14}\mathrm{c}\mathrm{m}\hfill & \left(n=7\right).\hfill \end{array}\right.(35)$

Clearly, n = 1 is excluded on empirical grounds but n = 2 is possible. One expects n = 7 in M-theory, so it is interesting that R_E must be of order a Fermi in this case. One could also consider a scenario with a hierarchy of compactification scales, R_i = α_i R_P with α₁ ≥ α₂ ≥…. ≥ α_n ≥ 1, such that the dimensionality progressively increases as one goes to smaller scales (Carr, 2013). This situation is represented in Figure 5B. There is still no evidence for the extra dimensions (ATLAS collaboration, 2016), which suggests that either they do not exist or they have a compactification scale R_E which is so small that $M_{\mathrm{P}}^{\prime }$ exceeds the energy attainable by the LHC

Another possible reason for the non-detection of accelerator black holes is that the M dependence of R_C is also affected by the extra dimensions. Lake and myself have argued that the effective Compton wavelength depends on the form of the (3 + n)-dimensional wavefunction (Lake and Carr, 2019). If this is spherically symmetric in all the dimensions, then one has R_C ∝ M⁻¹ (as usually assumed). However, if the wave function is pancaked in the extra dimensions and maximally asymmetric, then we find R_C ∝ M^−1/(1+n). This implies that the duality between the Compton wavelength and the Schwarzschild radius persists in the higher dimensional case but that there is no accelerator production of black holes. Thus the constraint on R_E given by Eq. 35 no longer applies. This scenario is illustrated in Figure 5C for extra dimensions compactified on a single length scale R_E and in Figure 5D for a hierarchy of length scales, when the extra dimensions help to smooth the minimum. The latter case resembles the smooth minimum in Figure 1, which suggests that higher dimensions might themselves underlie the BHUP correspondence.

The above discussion of higher-dimensional black holes has assumed that the simple power-law forms for R_S and R_C apply all the way to their intersect at the (modified) Planck scale. However, the BHUP correspondence suggests that they should be unified in some way, which would smooth the minima in Figure 5. This raises the issue of the form of the GUP and BHUP correspondence in the higher-dimensional case. If the Compton wavelength preserves its 3-dimensional form, one might expect the generalized Compton wavelength to become

$R_{\mathrm{C}}^{\prime }=\frac{\hslash }{Mc}\left[1+{\left(\frac{M}{M_{\mathrm{P}}^{\prime }}\right)}^{\left(n+2\right)/\left(n+1\right)}\right]\left(R<R_E\right),(36)$

so that $R_{\mathrm{C}}^{\prime }$ becomes $R_{\mathrm{S}}^{\prime }$ at large M. If duality between R_S and R_C is preserved in the higher-dimensional case, one might expect

$R_{\mathrm{C}}^{\prime }=R_{\ast }{\left(\frac{M_{\mathrm{P}}}{M}\right)}^{1/\left(1+n\right)}\left[1+{\left(\frac{M}{M_{\mathrm{P}}^{\prime }}\right)}^{2/\left(n+1\right)}\right]\left(R<R_E\right)(37)$

However, the literature on this gives different results (Koppel et al., 2017; Knipfer et al., 2019).

Finally, if we interpret the Compton wavelength as marking the boundary in the (M, R) diagram below which pair-production rates becomes significant, we might expect the presence of compact extra dimensions to affect pair-production rates at high energies. Specifically, pair-production above the energy scale M_Ec² ≡ ℏc/R_E, should be enhanced relative to the 3-dimensional case. Indeed, there is tentative evidence that this is a generic feature of higher-dimensional theories (He, 1999; Eboli et al., 2000).

6 Linking black holes and elementary particles

The suggestion that there could be a fundamental link between elementary particles and black holes goes back to the 1970s, when it was motivated in the context of strong gravity theories (Sivaram and Sinha, 1977). Various arguments supported this suggestion: 1) both hadrons and Kerr-Newman black holes are characterised by three parameters (M,J,Q); 2) both have a magnetic dipole moment and a gyromagnetic ratio of two but no electric dipole moment; 3) Regge trajectories and extreme Kerr solutions have the same relationship between angular momentum and mass (J ∼ M²); 4) when classical black holes interact, their surface area can never decrease, which is analogous to the increase in cross-sections found in hadron collisions.

Of course, elementary particles cannot be black holes with normal gravity, since their Compton wavelength is much larger than their Schwarschild radius, as illustrated in Figure 1. The early models therefore assumed that gravity becomes stronger by a factor of $G_F/G\sim {(M_{\mathrm{P}}/m_p)}^2\sim 10^{38}$ on the hadronic scale. This requires the existence of a massive spin-2 meson and corresponds to a short-range force. If the hadronic resonances are extremal black holes, their mass and spin should satisfy $G_F{m}_h^2=J$, corresponding to a Regge slope of (1Gev)⁻², and they should have a spectrum of masses M_n ∼ n^1/2 GeV (Oldershaw, 2010).

The current proposal—explored in more detail in work with Mureika and Nicolini (Carr et al., 2022)—is prompted by the Generalized Uncertainty Principle and the duality between the Compton and Schwarzschild expressions under the transformation $M\to M_{\mathrm{P}}^2/M$, so the context is somewhat different. Also elementary particles are regarded as sub-Planckian black holes under normal gravity rather conventional black holes under strong gravity However, there is a link with strong gravity because the force between two masses, while still obeying the inverse-square law, is much enhanced for $M<\sqrt{\beta }{M}_{\mathrm{P}}$.

Extending the BHUP correspondence to charged black holes adds important insights. Although the Reissner-Nordstrom itself has a nearly Planckian mass and therefore cannot represent an elementary particle, adding a GUP term introduces sub-Planckian solutions. This explains why the charge cannot exceed $\sqrt{2\beta /{\alpha }_e}\approx 1$ for β ∼ 10^–2, as observed for elementary particles. Similar considerations apply for spinning black holes. However, these solutions only correspond to extremal black holes if the mass is $\sqrt{\beta /2}{M}_P$, which is too large for an elementary particle (given the allowed range of β).

These considerations must be modified if there are extra dimensions on small scales. Although there is some uncertainty in the modifications to the GUP in this case, Figure 5 shows that the extra dimensions themselves smooth the Compton-Schwarzschild transition. Furthermore, the black hole mass may be shifted down towards the hadron scale, the effective strength of gravity being increased by the extra dimensions. However, the higher-dimensional analysis has not yet been extended to the charged and rotating black holes. Extra dimensions may also play an important role in amalgamating general relativity and quantum theory, with higher-dimensional relativity permitting a classical-type interpretation of some quantum anomalies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

This paper is the work of the author BC but also includes some review of earlier work done in collaboration with other authors.

Acknowledgments

I thank my collaborators in the work reported here: Matthew Lake, Heather Mentzner, Leonardo Modesto, Jonas Mureika, Piero Nicolini and Isabeau Prémont-Schwarz.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adler, R. J. (2010). Six easy roads to the Planck scale. Am. J. Phys. 78, 925–932. doi:10.1119/1.3439650

CrossRef Full Text | Google Scholar

Amati, D., Ciafaloni, M., and Veneziano, G. (1989). Phys. Lett. B 216, 41–47. doi:10.1016/0370-2693(89)91366-x

CrossRef Full Text

Anchordoqui, L. A., Feng, J. L., Goldberg, H., and Shapere, A. D. (2002). Black holes from cosmic rays: Probes of extra dimensions and new limits on TeV-scale gravity. Phys. Rev. D. 65, 124027. doi:10.1103/physrevd.65.124027

CrossRef Full Text | Google Scholar

Arkani-Hamed, N., Dimopoulos, S., and Dvali, G. (1998). The hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 428, 263.

Google Scholar

Ashtekar, A., Bojowald, M., and Lewandowski, J. (2003). Mathematical structure of loop quantum cosmology. Adv. Theor. Math. Phys. 7, 233–268. doi:10.4310/atmp.2003.v7.n2.a2

CrossRef Full Text | Google Scholar

Ashtekar, A., Fiarhurst, S., and Willis, J. L. (2003). Cl. Quant. Grav. 20, 1031.

CrossRef Full Text

Ashtekar, A., and Lewandowski, J. (2004). Background independent quantum gravity: A status report. Cl. Quantum Gravity 21, R53–R152. doi:10.1088/0264-9381/21/15/r01

CrossRef Full Text | Google Scholar

Atlas collaboration (2016). Search for new phenomena in different-flavour high-mass dilepton final states in pp collisions at 13 TeV with the ATLAS detector. Eur. Phys. J. C 76, 541.

Google Scholar

Bojowald, M. (2001). Absence of a singularity in loop quantum cosmology. Phys. Rev. Lett. 86, 5227–5230. doi:10.1103/physrevlett.86.5227

PubMed Abstract | CrossRef Full Text | Google Scholar

Bojowald, M. (2005). Loop quantum cosmology. Living Rev. Relativ. 8, 11. doi:10.12942/lrr-2005-11

PubMed Abstract | CrossRef Full Text | Google Scholar

Bushev, P. A., Bourhill, J., Goryachev, M., Kukharchyk, N., Ivanov, E., Galliou, S., et al. (2019). Testing the generalized uncertainty principle with macroscopic mechanical oscillators and pendulums. Phys. Rev. D. 100, 066020. doi:10.1103/physrevd.100.066020

CrossRef Full Text | Google Scholar

Camacho, A. (2003). Decoherence and bare mass induced by nonconformal metric fluctuations. Gen. Relativ. Gravit. 35, 319–325. doi:10.1023/a:1022349328278

CrossRef Full Text | Google Scholar

Carr, B. (2013). Black holes, the generalized uncertainty principle and higher dimensions. Mod. Phys. Lett. A 28, 1340011. doi:10.1142/s0217732313400117

CrossRef Full Text | Google Scholar

Carr, B. (2015). “The black hole uncertainty principle correspondence,” in 1st Karl Schwarzschild meeting on gravitational physics. Editors P. Nicolini, M. Kaminski, J. Mureika, and M. Bleicher (Berlin, Germany: Springer), 159–167. arXiv:1402:1427.

CrossRef Full Text | Google Scholar

Carr, B. (2018). “Quantum black holes as the link between microphysics and macrophysics,” in 2nd Karl Schwarzschild meeting on gravitational physics. Editors P. Nicolini, M. Kaminski, J. Mureika, and M. Bleicher (Berlin, Germany: Springer), 159–167. arXiv:1703.08655.

CrossRef Full Text | Google Scholar

Carr, B., Mureika, J., and Nicolini, P., (2022). In preparation.

Google Scholar

Carr, B., Mentzer, H., Mureika, J., and Nicolini, P. (2020). Self-complete and GUP-modified charged and spinning black holes. Eur. Phys. J. C 80, 1166. doi:10.1140/epjc/s10052-020-08706-0

CrossRef Full Text | Google Scholar

Carr, B., Modesto, L., and Premont-Schwarz, I. (2011). Generalized Uncertainty Principle and Self-dual Black Holes. arXiv: 1107.0708 [gr-qc].

Google Scholar

Carr, B., Mureika, J., and Nicolini, P. (2016). Sub-Planckian black holes and the generalized uncertainty principle. JHEP 07, 052.

Google Scholar

Chen, P., and Adler, R. J. (2003). Black hole remnants and dark matter. Nucl. Phys. B - Proc. Suppl. 124, 103–106. doi:10.1016/s0920-5632(03)02088-7

CrossRef Full Text | Google Scholar

Dimopoulos, S., and Landsberg, G. (2001). Black holes at the large hadron collider. Phys. Rev. Lett. 87, 161602. doi:10.1103/physrevlett.87.161602

PubMed Abstract | CrossRef Full Text | Google Scholar

Dvali, G., Folkerts, S., and Germani, C. (2011). Physics of trans-Planckian gravity. arXiv:1006.0984.

CrossRef Full Text | Google Scholar

Eboli, O. J. P., Han, T., Magro, M. B., and Mercadante, P. G. (2000). Diphoton signals for large extra dimensions at the Fermilab Tevatron and CERN LHC. Phys. Rev. D. D61, 094007. doi:10.1103/physrevd.61.094007

CrossRef Full Text | Google Scholar

Frassino, A. M., Koppel, S., and Nicolini, P. (2016). Geometric model of black hole quantum N-portrait, extradimensions and thermodynamics. Entropy 18, 181. doi:10.3390/e18050181

CrossRef Full Text | Google Scholar

Giddings, S., and Thomas, S. (2002). High energy colliders as black hole factories: The end of short distance physics. Phys. Rev. D. 65, 056010. doi:10.1103/physrevd.65.056010

CrossRef Full Text | Google Scholar

Gross, D. J., and Mende, P. F. (1988). String theory beyond the Planck scale. Nucl. Phys. B B303, 407–454. doi:10.1016/0550-3213(88)90390-2

CrossRef Full Text | Google Scholar

Hawking, S. W. (1974). Nature 248, 30–31. doi:10.1038/248030a0

CrossRef Full Text

He, X. G. (1999). Phys. Rev. D60, 115017.

Hossain, G. M., Husain, V., and Seahra, S. S. (2010). Nonsingular inflationary universe from polymer matter. Phys. Rev. D. 81, 024005. doi:10.1103/physrevd.81.024005

CrossRef Full Text | Google Scholar

Isi, M., Mureika, J., and Nicolini, P. (2013). Self-completeness and the generalized uncertainty principle. J. High. Energy Phys. 1311, 139. doi:10.1007/jhep11(2013)139

CrossRef Full Text | Google Scholar

Kanti, P. (2016). Black holes in theories with large extra dimensions: a review. Int. J. Mod. Phys. A 19, 4899–4951. doi:10.1142/s0217751x04018324

CrossRef Full Text | Google Scholar

Kay, B. S. (1998). Decoherence of macroscopic closed systems within Newtonian quantum gravity. Cl. Quantum Gravity 15, L89–L98. doi:10.1088/0264-9381/15/12/003

CrossRef Full Text | Google Scholar

Knipfer, M., Koppel, S., Mureika, J., and Nicolini, P. (2019). Generalized uncertainty principle and black holes in higher dimensional self-complete gravity. J. Cosmol. Astropart. Phys. 1908, 008. doi:10.1088/1475-7516/2019/08/008

CrossRef Full Text | Google Scholar

Konishi, K., Paffuti, G., and Proverpo, P. (1990). Minimum physical length and the generalized uncertainty principle in string theory. Phys. Lett. B 234, 276.

CrossRef Full Text | Google Scholar

Koppel, S., Knipfer, M., Isi, M., Mureika, J., and Nicolini, P. (2017). “2nd Karl Schwarzschild meeting on gravitational physics,” in Springer proceedings in Physics. Editors P. Nicolini, M. Kaminski, J. Mureika, and M. Bleicher (Berlin, Germany: Springer). arXiv:1703.05222.

Google Scholar

Lake, M. J., and Carr, B. (2015). The Compton-Schwarzschild correspondence from extended de Broglie relations. JHEP 1511, 105.

CrossRef Full Text | Google Scholar

Lake, M. J., and Carr, B. J. (2019). The Compton-Schwarzschild correspondence in higher dimensions. Int. J. Mod. Phys. D. 28, 1930001. doi:10.1142/s0218271819300015

CrossRef Full Text | Google Scholar

Maggiore, M. (1993). A generalized uncertainty principle in quantum gravity. Phys. Lett. B 304, 65–69. doi:10.1016/0370-2693(93)91401-8

CrossRef Full Text | Google Scholar

Maggiore, M. (1994). Quantum groups, gravity, and the generalized uncertainty principle. Phys. Rev. D. 49, 5182–5187. doi:10.1103/physrevd.49.5182

PubMed Abstract | CrossRef Full Text | Google Scholar

Maggiore, M. (1993). The algebraic structure of the generalized uncertainty principle. Phys. Lett. B 319, 83–86. doi:10.1016/0370-2693(93)90785-g

CrossRef Full Text | Google Scholar

Magueijo, J., and Smolin, L. (2004). Gravity's rainbow. Cl. Quantum Gravity 21, 1725–1736. doi:10.1088/0264-9381/21/7/001

CrossRef Full Text | Google Scholar

Marin, F., Marino, F., Bonaldi, M., Cerdonio, M., Conti, L., Falferi, P., et al. (2014). Investigation on Planck scale physics by the AURIGA gravitational bar detector. New J. Phys. 16, 085012. doi:10.1088/1367-2630/16/8/085012

CrossRef Full Text | Google Scholar

Modesto, L., and Premont-Schwarz, I. (2009). Self-dual black holes in loop quantum gravity: Theory and phenomenology. Phys. Rev. D. 80, 064041. doi:10.1103/physrevd.80.064041

CrossRef Full Text | Google Scholar

Modesto, L. (2010). Semiclassical loop quantum black hole. Int. J. Theor. Phys. 49, 1649–1683. doi:10.1007/s10773-010-0346-x

CrossRef Full Text | Google Scholar

Mureika, J. R. (2019). Extended uncertainty principle black holes. Phys. Lett. B 789, 88–92. doi:10.1016/j.physletb.2018.12.009

CrossRef Full Text | Google Scholar

Oldershaw, R. L. (2010). Hadrons as Kerr-Newman black holes. J. Cosmol. 6, 1361.

Google Scholar

Pikovski, I., Vanner, M. R., Aspelmeyer, M., Kim, M. S., and Brukner, C. (2012). Probing Planck-scale physics with quantum optics. Nat. Phys. 8, 393–397. doi:10.1038/nphys2262

CrossRef Full Text | Google Scholar

Rovelli, C. (2004). Quantum gravity. Cambridge: Cambridge University Press.

Google Scholar

Scardigli, F. (1999). Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment. Phys. Lett. B B452, 39–44. doi:10.1016/s0370-2693(99)00167-7

CrossRef Full Text | Google Scholar

Schwinger, J. (1951). On gauge invariance and vacuum polarization. Phys. Rev. 32, 664–679. doi:10.1103/physrev.82.664

CrossRef Full Text | Google Scholar

Sivaram, C., and Sinha, K. P. (1977). Strong gravity, black holes, and hadrons. Phys. Rev. D. 16, 1975–1978. doi:10.1103/physrevd.16.1975

CrossRef Full Text | Google Scholar

Veneziano, G. (1986). A stringy nature needs just two constants. Europhys. Lett. 2, 199–204. doi:10.1209/0295-5075/2/3/006

CrossRef Full Text | Google Scholar

Westphal, J. P. T., Hepach, H., and Aspelmeyer, M. (2021). Measurement of gravitational coupling between millimetre-sized masses. Nature 591, 225–228. doi:10.1038/s41586-021-03250-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Wheeler, J. A. (1955). Geons. Phys. Rev. 97, 511–536. doi:10.1103/physrev.97.511

CrossRef Full Text | Google Scholar

Witten, E. (1996). Reflections on the fate of spacetime. Phys. Today 49, 24. doi:10.1063/1.881493

CrossRef Full Text | Google Scholar

Yoneya, T. (1989). On the interpretation of minimal lengths in string theory. Mod. Phys. Lett. A 4, 1587–1595. doi:10.1142/s0217732389001817

CrossRef Full Text | Google Scholar

Zwiebach, B. (2009). A first course in string theory. Cambridge: Cambridge University Press.

Google Scholar