A review of instrument techniques to measure magnetospheric cold electrons and ions

A review of the instruments and techniques to directly measure the full distributions of the cold-ion and cold-electron populations in the magnetosphere is presented. Relatively few studies have focused on the cold plasma populations of the magnetosphere due to difficulties associated with obtaining measurements. The cold particle populations are defined here as those with total energy approximately <100 eV which is an energy range for which measurements are difficult (regardless of species), but which often make up the bulk of the plasma density. These populations have known and suspected impacts on the structure and dynamics of the magnetosphere but to date have not yet been measured adequately. The lack of accurate measurements cold ion and electron populations through the magnetosphere makes closure of these science questions extremely difficult if not impossible. Reaching closure will require innovations in plasma spectrometers and associated techniques required to obtain high-fidelity measurements of the cold ion and electron populations in the magnetosphere. This paper seeks to review the instruments and techniques that have been used to date and present possible options for future missions.

1 Introduction

Relatively few studies have focused on the cold electron and cold ion populations of the magnetosphere due to difficulties associated with obtaining measurements using instruments mounted on charged spacecraft. The cold particle populations are defined as those with total energy approximately <100 eV which is an energy range for which measurements are difficult (regardless of species), but which often make up the bulk of the plasma density. These populations have a number of known impacts on the structure and dynamics of the magnetosphere (Delzanno et al., 2021) but to date have not yet been measured extensively. In sunlight, spacecraft in the magnetosphere typically float from a few volts positive to several tens of volts positive (Thomsen, et al., 2007), preventing the bulk of the cold ion spectrum from reaching spacecraft instruments (Genestreti, et al., 2017). This effectively limits the energy measurement range to just the ion population with energy above the spacecraft potential. Simultaneously, sunlit spacecraft surfaces emit a constant flux of low-energy electrons (DeForest 1972) which contaminate or completely mask instrument measurements of ambient, low-energy magnetospheric electrons (Scime et al., 1994; Gershman, et al., 2017). These difficulties and subsequent scarcity of measurements have been well described in the literature (Andre and Cully 2012; Lee and Angelopoulos 2014; Haaland, et al., 2015; Delzanno, et al., 2021) leading to the colloquial term for low-energy magnetospheric ions as the “hidden populations” (Olsen 1982). This paper seeks to describe the instruments and techniques that have been used to date and present options for future missions.

There have been many theories, studies, and debates regarding the processes of magnetosphere-ionosphere coupling (MIC), currently focused on the location and driving conditions for magnetic reconnection and how the ionosphere regulates reconnection and convection (Lotko 2007; Welling, et al., 2015). An improved understanding of the complex plasma dynamics is needed to answer these long-standing mysteries and requires appropriate instrumentation for obtaining in-situ observations. Low-energy ions originating from the ionosphere dominate the magnetosphere 50%–70% of the time (Andre and Cully 2012). To accurately model the impact of various plasma sources on magnetospheric composition, distributed in-situ measurements of cold ion and cold electron populations are needed from the outflow regions through the magnetosphere. As described in detail by Delzanno et al. (2021), the primary sources of plasma in the Earth’s magnetosphere are attributed to ion and electron outflow at the low and high latitude ionosphere in addition to contributions from the solar wind. The outflow populations can get strongly energized as they journey through the magnetosphere and contribute to the warm plasma cloak, ring current and plasma sheet (C. R. Chappell 1982; Chappell et al., 2008).

Since the initial observations of heavy ions in the magnetosphere by Shelley et al. (1972), the dynamics leading to the ionospheric outflow of O⁺ ions and their impact on the evolution of the magnetosphere-ionosphere system have been the subject of numerous studies. At low latitudes, charged particles travel along closed field lines and create the cold (<eV) protons and electrons that make up the plasmasphere (Carpenter 1962; Lemaire, et al., 1998; Kotova 2007). Magnetospheric cold electron sources include outflow of low-energy photoelectrons from the sunlit upper atmosphere (Kitamura, et al., 2012). This creates a spatial separation between the light electrons and heavier ions resulting in the ambipolar electric field which aids in the acceleration of ions upwards in the polar wind (Khazanov et al., 1997; Haaland, et al., 2015; Glocer et al., 2017). The high latitude auroral outflow is composed of hydrogen and other heavy ions (O⁺, He⁺, N⁺, N₂⁺, and NO⁺) which flow from the high-latitude ionosphere along or near open magnetic field lines and into the low-pressure magnetosphere (Moore et al., 2005a; Ilie and Liehohn 2016). Outflow is commonly observed at high latitudes (Moore, et al., 1999a; Andre 2015) and is generally divided into three categories: 1) cold-temperature ion flows with energies of a few eV in which all ions acquire a bulk flow velocity such as the polar wind and auroral bulk O⁺ up-flow from the topside auroral and polar-cap ionosphere; 2) ions with suprathermal energies above the ionosphere (Eliasson, et al., 1994) or with higher energies at higher altitude (Möbius, et al., 1998) and 3) heated ion outflows in the cusp and auroral zone in which a fraction of the ions have been energized to much greater energies including transversely accelerated ions, upwelling ions, ion conics, and ion beams (Yau and Andre 1997; Welling, et al., 2015). The low-energy outflowing ions provide cold plasma filling to the plasmasphere (Welling, et al., 2015) and cold supersonic outflow to the inner magnetosphere and magnetotail such as from the polar wind (Su, et al., 1998; Engwall, et al., 2006a; Engwall, et al., 2009). A depiction of the ion outflow process as a function of ion energy category and destination as described by Yamauchi (2019) is shown in Figure 1. Consequently, the outflow flux of ions and electrons are highly dynamic and vary with the solar magnetospheric activity, including solar extreme ultra-violet (EUV) radiation, interplanetary magnetic fields, solar wind pressure, geomagnetic indices, precipitating electron fluxes and Poynting fluxes into the ionosphere (Yau, Shelley, et al., 1985; Barghouthi et al., 1998; Tam et al., 1998; Moore et al., 1999b; Barakat and Schunk 2001; Cully, et al., 2003; Strangeway, et al., 2005; Kitamura et al., 2011; Delzanno, et al., 2021).

FIGURE 1

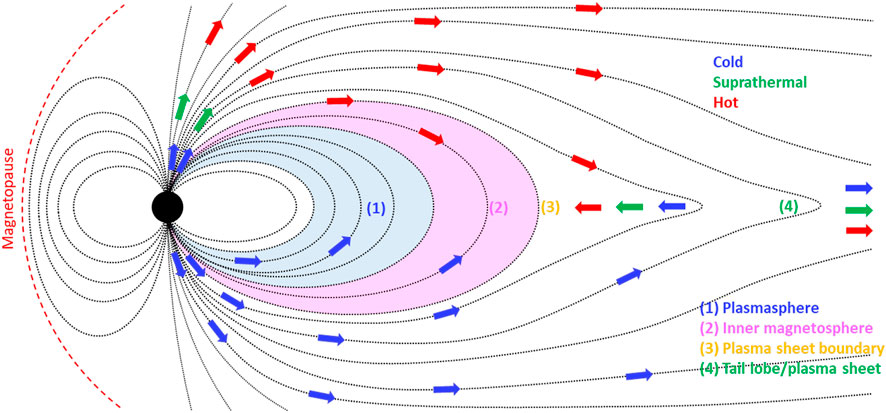
FIGURE 1. Schematic of the outflowing ions classified by energy and destination, recreated from Yamauchi (2019).

The solar wind is composed of predominantly hydrogen, alpha particles, and high charge-state heavy ions (Bame, Hundhausen, et al., 1968; Geiss et al., 1995; Zurbuchen et al., 2002). While not traditionally considered a source of cold ions or cold electrons, the solar wind does contribute significantly to the overall magnetospheric plasma populations. The solar wind protons and electrons travel outward at ∼400 km/s with temperature on the order of 10 eV (Feldman, et al., 1974; McComas et al., 1998). Upon crossing the bow shock the solar wind temperature in the magnetosheath increases to ∼20–60 eV for electrons and ∼100 eV–1 keV for ions on the dayside (Wang, et al., 2012; Delzanno, et al., 2021). As the magnetosheath plasma moves to the nightside the temperature decreases to ∼10–30 eV for electrons and ∼30–300 eV for ions (Wang, et al., 2012; Dimmock and Nykyri 2013). This results in a total energy of the magnetosheath ∼1 keV for ions while the electrons remain relatively cold (Delzanno, et al., 2021).

As a result of the ionospheric outflow and incident solar wind, the magnetospheric environment consists of multiple ion and electron populations with a broad range of energies, from sub-eV particles of the ionosphere to the relativistic energies of the radiation belts (Singh and Horowitz 1992; Zhao, et al., 2015; Genestreti, et al., 2017). Traditional ion mass spectrometer instruments are designed to detect the hot tenuous magnetospheric ion species and are typically not as effective at measuring cold, low energy (<100 eV) plasmas. This is due to the trade-off in the instrument design’s objective between having a large dynamic energy range from a few eV to tens of keV, versus focusing on low-energy sensitivity.

The amount of coupling of the solar wind to the Earth’s magnetosphere-ionosphere system is controlled by magnetic field-line reconnection between the solar wind and the magnetosphere, which is a function of local plasma parameters at the reconnection site (Cassak and Shay 2007; Borovsky et al., 2008; Borovsky et al., 2008). The magnetic field strength and mass density of the magnetospheric and magnetopause plasma populations at the magnetopause determine the reconnection rate between the solar wind and the magnetosphere. Ionospheric outflows, which can control the magnetospheric mass density, can have a direct role in controlling the dayside reconnection rate; therefore ionospheric outflows potentially have a significant role in controlling solar wind/magnetosphere coupling through mass loading (Borovsky et al., 2013; Fuselier et al., 2019a; Toledo-Redondo et al., 2021). Plasmaspheric plumes and the warm plasma cloak (whose energy spectrum partially overlaps with our definition of cold plasma) also affect solar wind/magnetospheric coupling during geomagnetically active times. Mass loading could also operate in the magnetotail although to what extent particles remains cold as they cross the tail remains an open question [see the discussion in Delzanno et al. (2021)].

The diverse magnetospheric particle populations are co-located and interact by means of plasma waves. For instance, acceleration and loss of radiation belt electrons is thought to be due to wave-particle interactions, with the relevant waves modulated by lower energy plasma particles (Summers et al., 2007; Reeves et al., 2009). In addition to mass loading and dayside magnetopause reconnection, the cold magnetospheric plasma impact the generation of whistler and electromagnetic ion cyclotron (EMIC) waves by the cyclotron instability (de Soria-Santacruz et al., 2013) and their subsequent propagation in the inhomogeneous magnetospheric plasma. The cold particle populations affect the frequencies and amplitudes of ultra-low-frequency (ULF) waves (Fraser, et al., 2005), whistler waves (Thorne 2010), whistler-mode hiss waves (Dunckel and Helliwell 1969; Russell et al., 1969; Bortnik et al., 2008; Hartley, et al., 2018), and EMIC waves (Blum et al., 2009; Chen et al., 2011; Blum and Breneman 2019), which control scattering and energization rates of the higher-energy populations, impacting the dynamics of the plasma sheet, ring current and radiation belts. Note also that accurate knowledge of the ion composition of the cold plasma in the magnetosphere is critical to determine the properties of EMIC waves. The mass density of cold ions also affects the magnetopause stability to Kelvin-Helmholtz waves and the transport of solar wind into the magnetosphere (Melander and Parks 1981; Hasegawa, et al., 2004).

To date, the majority of cold plasma research efforts have focused on the cold ion populations leaving a considerable gap in the understanding of cold electron populations in the magnetosphere. Cold electrons are considered to play an important role in wave-particle interactions such as chorus and hiss waves. Recent work by Roytershteyn and Delzanno (2021) suggests that the presence of cold electron population introduces coupling of the whistler modes to short-wavelength, oblique, electrostatic instabilities. This can subsequently lead to cold-electron heating and damping of the primary whistler waves. EMIC waves can also interact with cold electrons resulting in cold-electron heating (Zhou, et al., 2013; Yuan, et al., 2014). This mechanism is thought to be responsible for stable auroral arcs (Chandra et al., 1971; Chandra et al., 1972) through the enhancement of ionospheric electron temperature. A proposed mechanism for the subauroral heating is energy transfer from the ring current to magnetospheric electrons and the downward heat conduction into the ionosphere (Brace et al., 1967, Kozyra, et al., 1986, Khazanov et al., 1992).

The lack of accurate measurements of low-energy or “cold” ion and electron populations through the magnetosphere makes closure of these science questions extremely difficult if not impossible. Therefore, to significantly advance our understanding of magnetospheric plasma physics, the full phase-space densities of the cold plasma population must be thoroughly measured. This will require innovations in plasma spectrometers and associated techniques required to obtain high-fidelity measurements of the cold ion and electron populations in the magnetosphere.

2 Challenges related to magnetospheric cold ion and cold electron measurements

One of the primary challenges related to making cold ion and cold electron measurements in the magnetosphere is due to spacecraft charging. In sunlight, the spacecraft floating potential is typically a few volts or less in the plasmasphere and can be tens of volts or more in the tenuous outer magnetosphere (Thomsen, et al., 2007; Ferguson et al., 2015; Sarno-Smith, et al., 2016). The potential difference between the charged spacecraft and the ambient plasma will result in either an increase or decrease to the particle energy and total density measured by electrostatic analyzers depending on the charge of the incident particle. For example, ions impinging on negatively charged spacecraft surfaces will be accelerated and experience an increase in measured energy, while electrons will experience a decrease in measured energy. When the polarity of the spacecraft potential and the particle charge are the same, the resulting electrostatic repulsion results in truncation of the energy distributions at low energies and the resulting loss in density. A number of studies have examined the deleterious effects of spacecraft charging on charged particle measurements when comparing particle trajectories measured at the spacecraft with the actual particle distributions in the ambient plasma (Sojka et al., 1984, W. C; Knudsen 1966; Parker and Whipple 1970; Toledo-Redondo et al., 2019).

Measurements of low-energy electrons present additional challenges due to a combination of spacecraft charging effects and the presence of photoelectrons continuously emitted from sunlit spacecraft surfaces (DeForest 1972). The photoelectron population is emitted at ∼ eV energy and can contaminate the low-energy channels of instruments measuring ionospheric and magnetospheric electrons (Mozer, et al., 2017). Secondary electrons emitted by impact of high energy ambient electrons and ions create similar problems. Spacecraft with positive potentials accelerate both ambient low-energy electrons and photoelectrons alike into detector apertures resulting in an indiscernible measured distribution. The difficulty associated with deconvolving the two electron distributions has led to a lack of observations and understanding of the cold-electron impact in the magnetosphere (Gershman, et al., 2017).

2.1 Spacecraft charging

Any object immersed in a plasma builds up a charge by collecting ambient particles (electrons and ions) and by emitting photoelectrons and secondary electrons. The accumulated charge generates an electric potential with respect to the ambient plasma. Then, the generated electric field alters the dynamics of the particles in the spacecraft vicinity, creating all sort of challenging problems for the interpretation of in-situ measurements.

As described by Purvis et al. (1984); Garrett and Whittlesey (2012), the total current to the spacecraft, I_T, can be determined from

$I_T\left({\Phi }_{SC}\right)=I_e\left({\Phi }_{SC}\right)+I_i\left({\Phi }_{SC}\right)+I_{se}\left({\Phi }_{SC}\right)+I_{si}\left({\Phi }_{SC}\right)+I_{ph}\left({\Phi }_{SC}\right),(1)$

where ${\Phi }_{SC}$ is the surface potential relative to space, I_e is the current due to incident electrons, I_i is the incident ion current, I_se and I_si are the secondary emitted electron currents due to incident electrons and ions, and I_ph is the photoelectron current. At equilibrium, the total current absorbed by the spacecraft is zero (I_T (${\Phi }_{SC}$) = 0, floating condition). The voltage with respect to the ambient plasma (infinity) at which the current is balanced is known as the spacecraft floating potential ${\Phi }_{SC}$. Depending on the ambient plasma conditions and material parameters, spacecraft can float positively or negatively with respect to infinity.

For simplicity, the spacecraft charging dependence with ambient plasma conditions and material parameters can be illustrated with the Orbital-Motion-Limited (OML) theory (Mott-Smith and Langmuir 1926), by approximating the spacecraft as a conducting sphere of radius $r_{sc}$. Assuming Maxwellian distributions for the particle populations, the electron current collected by a sphere is given by

$I_e=-e4\pi r_{SC}^2{n}_e\sqrt{\frac{e{T}_e}{2\pi m_e}}\mathit{exp}\left(\frac{{\mathrm{e}\Phi }_{SC}}{k_B{T}_e}\right),{\Phi }_{SC}<0,(2)$

and

$I_e=-e4\pi r_{SC}^2{n}_e\sqrt{\frac{{eT}_e}{2\pi m_e}}\left(1+\frac{{\mathrm{e}\Phi }_{SC}}{{k_{B}T}_e}\right),{\Phi }_{SC}\ge 0.(3)$

For the ion current,

$I_i=e4\pi r_{SC}^2{n}_i\sqrt{\frac{{eT}_i}{2\pi m_i}}\left(1-\frac{{\mathrm{e}\Phi }_{SC}}{{k_{B}T}_i}\right),{\Phi }_{SC}\le 0,(4)$

and

$I_i=e4\pi r_{SC}^2{n}_i\sqrt{\frac{e{T}_i}{2\pi m_i}}\mathit{exp}\left(-\frac{{\mathrm{e}\Phi }_{SC}}{k_B{T}_i}\right),{\Phi }_{SC}>0.(5)$

OML theory is an appropriate approximation when the electron Debye length (${\lambda }_{De}$) is larger than the radius of the spacecraft (thick sheath approximation), which is typically the case for magnetospheric plasma conditions. Typical values of ${\lambda }_{De}$ range from meters to kilometers while typical spacecraft dimensions are a few meters. Moreover, the effect of the Earth’s magnetic field in the current collection is not accounted for in this approximation justified by assuming that the gyroradius is larger than the spacecraft dimensions which is typically the case in the Earth’s magnetosphere. We note that if any of these two approximations are not satisfied, the use of the unmagnetized OML theory presented here is not appropriate to estimate the current collected by the spacecraft. Alternatively, the thin sheath approximation (Conde 2011) and/or alternative analytic models that accounts for magnetic field effects in the particle collection (Laframboise 1976) can be used depending on the specific plasma conditions.

The photoelectron current is given by

$I_{ph}=\mathcal{A}4\pi r_{SC}^2{J}_{ph},{\Phi }_{SC}<0,(6)$

and

$I_{ph}=\mathcal{A}4\pi r_{SC}^2{J}_{ph}\left(1+\frac{{\mathrm{e}\Phi }_{SC}}{{k_{B}T}_{ph}}\right)\mathit{exp}\left(-\frac{{\mathrm{e}\Phi }_{SC}}{{k_{B}T}_{ph}}\right),{\Phi }_{SC}>0.(7)$

In Eq. 7 the point source approximation is used along with a single Maxwellian distribution to describe photoemission (Grard 1973). Note that the source point approximation is better suited to characterize photoemission when the size of the body is smaller than photoelectron Debye length. On the other hand, photoemission is better described with the planar source approximation [also given in Grard (1973)] when the size of the body is larger than shielding distance for the photoelectrons as shown in Nakagawa et al. (2000). For completeness, the current due to the secondary electron (Shukla and Mamun 2015) emission is given by

$I_{se}=e\frac{8{\pi }^2{r}_{sc}^2}{m_e^2}{\int }_0^{\infty }E{\delta }_{se}\left(E\right)f_{se}\left(E-{\mathrm{e}\Phi }_{SC}\right)dE,{\Phi }_{SC}<0(8)$

and

$I_{se}=e\frac{8{\pi }^2{r}_{sc}^2}{m_e^2}\mathit{exp}\left(-\frac{{\mathrm{e}\Phi }_{SC}}{{k_{B}T}_{se}}\right)\left(1+\frac{{\mathrm{e}\Phi }_{SC}}{{k_{B}T}_{se}}\right){\int }_0^{\infty }E{\delta }_{se}\left(E\right)f_{se}\left(E-{\mathrm{e}\Phi }_{SC}\right)dE,{\Phi }_{SC}>0(9)$

Where the secondary emission yield ${\delta }_{se}$, characterized by the maximum yield ${\delta }_m$ and energy at maximum yield $E_m$, is given by the Sternglass formula (Bruining 2016)

${\delta }_{se}\left(E\right)=\frac{7.4{\delta }_{m}E}{E_m}\mathit{exp}\left(-2\sqrt{\frac{E}{E_m}}\right)(10)$

while

$f_{se}\left(E-{\mathrm{e}\Phi }_{SC}\right)=n_e{\left(\frac{m_e}{2\pi k_B{T}_e}\right)}^{3/2}\mathit{exp}\left(-\frac{E-{\mathrm{e}\Phi }_{SC}}{{k_{B}T}_e}\right)(11)$

is the distribution function of the incident electrons. Note that different functional forms of the secondary emission yield ${\delta }_{se}$ can be found in the literature (see for example Whipple, 1981) given the different experimental setups and assumptions taken in the derivation of these theoretical models.

Here, $e$ is the elementary charge, $k_B$ is the Boltzmann constant, $m_{\alpha }$, $n_{\alpha }$, $T_{\alpha }$ are the mass, density and temperature of the plasma species, respectively. For photoelectron emission, $T_{ph}$ and $J_{ph}$ are the temperature and current density of the photoelectrons, respectively, while $\mathcal{A}$ is the fraction of the spacecraft illuminated area relative to the total surface area. $T_{se}$ is the temperature of the secondary electron emitted while E is the kinetic energy.

The current balance which determines the floating potential of a spacecraft immersed in a plasma is given by the environmental plasma conditions and the spacecraft material parameters. The OML equations above can be used to illustrate two different charging regimes in the Earth space environment: dayside ionosphere and dayside magnetosphere. Plasma densities in the ionosphere range between 1 $\times$ 10⁵ cm⁻³ and 1 $\times$ 10⁶ cm⁻³ on the dayside and 1 $\times$ 10³ cm⁻³ and 1 $\times$ 10⁴ cm⁻³ on the nightside. The plasma temperature is of the order of a fraction of eV while the predominant ion species is Oxygen. For example, let us consider a perfectly conducting spherical spacecraft of 1 m radius, immersed in the dayside ionospheric singly ionized plasma with $m_{\alpha }$ = 16 amu, $n_{\alpha }$ = 1 $\times$ 10⁵ cm⁻³, $T_{\alpha }$ = 0.5 eV, and with material parameters given by $T_{ph}$ = 2 eV, $J_{ph}$ = 40 μA/m² and $\mathcal{A}=0.3$. The spacecraft charges negatively to −3 V with respect to the ambient plasma. On the other hand, in the Earth’s magnetosphere, the plasma density is several orders of magnitude lower than in the ionosphere, while Hydrogen dominates the ion plasma composition. Under dayside magnetospheric plasma conditions given by $m_{\alpha }$ = 1 amu, $n_{\alpha }$ = 1 $3.5$ cm⁻³, $T_{\alpha }$ = 0.5 eV, and considering the same material parameters as in the previous example, $T_{ph}$ = 2 eV, $J_{ph}$ = 40 μA/m² and $\mathcal{A}=0.3$, the spherical spacecraft charges positively to 4.2 V with respect to the ambient plasma.

If the spacecraft is negatively charged, ions are attracted by the spacecraft and tend to reach the particle detector and be measured. This is the case for instance for the LANL MPA detectors mounted on the LANL-GEO spacecraft (Bame et al., 1993; Denton, et al., 2015). In this scenario, the energy resolution of the instrument becomes important, as well as correcting for the acceleration of the particles due to the electric field generated around the spacecraft (Lavraud et al., 2006). In a positively-charged spacecraft, however, incoming cold ions with energies below the spacecraft potential are repelled by the electric field near the spacecraft. As a result, the full distribution of the cold ions can not be measured (Olsen 1982). Panel A in Figure 3 (Olsen, 1982) illustrate the problem of cold ion measurements perfectly. The SCATHA data show that when the spacecraft potential is ∼10 V cold ions cannot reach the particle detector. However, when the spacecraft potential drops to ∼1–2 V (∼6 UT), part of the cold ion distribution is measured. This has been known for decades and has led to the term “hidden magnetosphere” as a reference to the elusive cold ions with energies below the spacecraft potential. The tail of the partially measured ion distribution can be extrapolated to estimate moments of the distribution (Genestreti, et al., 2017). The downside of using this approach, however, is that plasma parameter estimates may come with significant uncertainties when the spacecraft potential is much larger than the mean energy of the cold ions. This situation is similar for negatively-charged spacecraft and cold electrons. Indeed, this is why spacecraft charging is one of the main obstacles for cold-plasma measurements.

2.2 Photoelectron contamination

Cold electron measurements in the Earth’s magnetosphere are more difficult than cold ion measurements. A negatively charged spacecraft repels cold electrons and, depending on the mean cold electron energy compared to the spacecraft potential, the cold electron distribution may be measured only partially or, in the case of a strongly negatively charged spacecraft, not at all. In cases where the mean cold electron energy and the spacecraft potential are comparable, the extrapolation from the tail of the distribution can be used, similarly to what has been done for ions (Genestreti, et al., 2017). When the spacecraft is charged positively, which usually occurs for satellites in sunlight and in low density plasma conditions, cold electron measurements should in principle be possible, in the sense that ambient cold electrons can reach the particle detectors. In practice, however, spacecraft-generated photoelectrons are attracted back to the spacecraft and their flux can overwhelm the flux of the ambient cold electrons. Figure 2B shows an example of photoelectron contamination from a spectrogram for SCATHA data from 19 October 1979 (Olsen, 1982). Between 21 and 22 UTC (local midnight), a high flux of the low-energy photoelectrons is observed by the particle detector completely masking any signal of an ambient cold electron population.

FIGURE 2

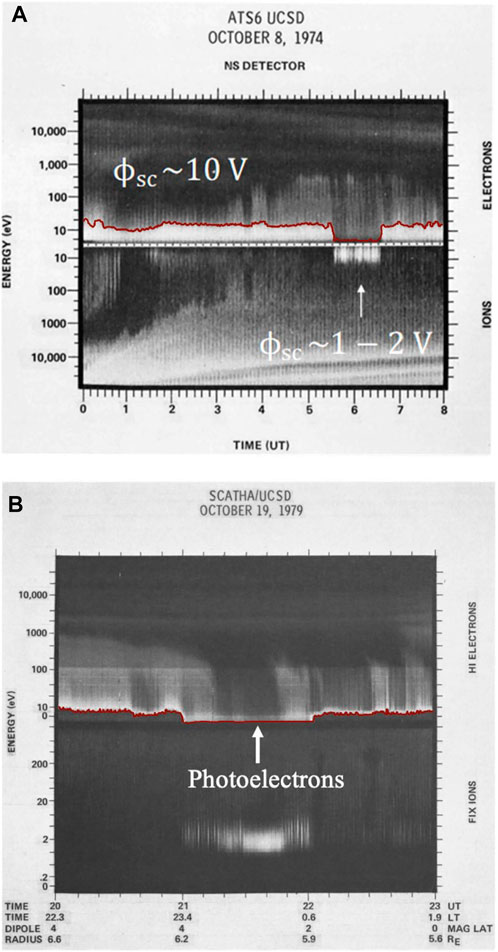
FIGURE 2. From (Olsen 1982) (A) ATS six measurements in the plasma sheet in eclipse, (B) SCATHA Hi electron data where photoelectron fluxes are detected.

To further illustrate the issue of photoelectron contamination, Figure 4 shows kinetic simulation results of the response of a particle detector in magnetospheric plasma conditions modeled with the Curvilinear Particle-in-Cell code (CPIC) (Meierbachtol, et al., 2017). Specifically, the ambient plasma consists of electrons and protons modeled by a Maxwellian distribution function with density equal to 13.50 cm⁻³ and electron (ion) temperature equal to 0.5 (0.35) eV. The spacecraft mimics the geometry of the Van Allen Probes spacecraft (Figure 3 right). The photoemission current density is J_ph = 100 μA/m² while the photoelectron temperature is 2 eV. Only the top part of the spacecraft is illuminated by UV sunlight and emits photoelectrons. In this example, the detector is mounted on the sun-illuminated, top part of the spacecraft, as can be seen in the right panel in Figure 4. Under these conditions, the spacecraft and the particle detector are floating at 4.7 V with respect to the ambient plasma. For a positively charged spacecraft, the full distribution of the cold electrons can indeed be measured by a particle detector as shown in the bottom left panel in Figure 3 (blue histogram), where the contribution of the photoelectrons and ambient electrons can be easily distinguished in the simulations. However, the problem of characterizing the ambient electrons from the photoelectrons reaching the particle detector at the same time becomes evident. Because the energy of the spacecraft-emitted electrons is comparable to that of the ambient cold electrons (generally a few ∼ eV, 2 eV in this case), it can be very difficult to distinguish between the two species in the detector signal, as can be seen in the top left panel of Figure 3, where the total signal is plotted and the photoelectron flux is overwhelming the ambient electron flux. In fact, in low density ambient plasma conditions (less than ∼10 cm⁻³), the particle detector signal is typically dominated by photoelectrons since materials used for space applications have photoelectron current densities of the order of 10–40 μA/m² (measured in the lab, (Grard 1973), and <100 μA/m² when estimated from spacecraft data (Nakagawa, et al., 2000; Scudder et al., 2000). As such, near the particle detector the photoelectron density can be two or three orders of magnitude larger than that of the ambient cold-electrons, as illustrated in the bottom right panel of Figure 3 (orange histogram). Additionally, the studies by Nakagawa et al. (2000); Scudder et al. (2000); Thiebault et al. (2006) suggest that the emission of low energy electrons by spacecraft materials in real space conditions is more complicated than what has been reported in laboratory studies, where photoemission is typically characterized by a single Maxwellian energy distribution. These studies report higher values for the current density compared to those estimated in the lab, <∼100 μA/m², as well as materials emitting photoelectrons with more complex spectra that can be characterized by multiple Maxwellians with different temperatures. As such, the tendency of photoelectrons to “blind” the particle measurements and the complexity of photoelectron spectra make it extremely hard to extract accurate information on the ambient cold electrons from particle measurements in nominal sunlight conditions. To date, this problem remains unsolved and it is the major reason why we know very little about cold electrons in the Earth magnetosphere.

FIGURE 3

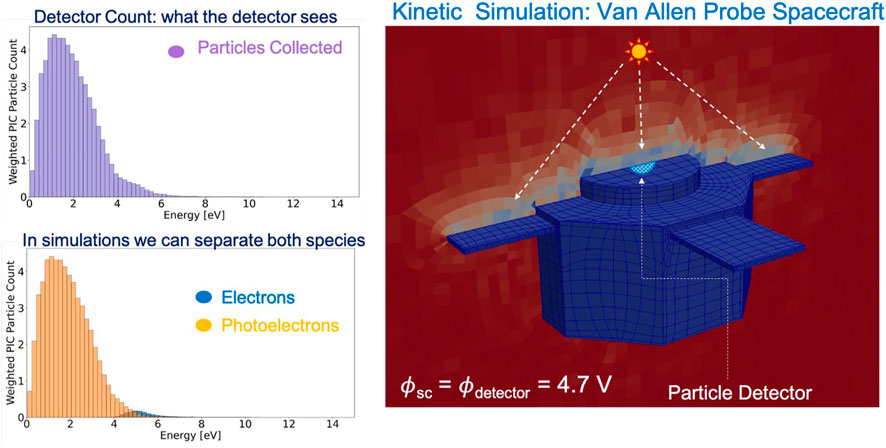
FIGURE 3. Kinetic simulation result: photoelectron blinding the signal of a particle detector mounted on a Van Allen Probe type spacecraft. Plasma parameters used in the simulation: $\mathit{n}$ = 13.5 cm⁻³, ${\mathit{T}}_{\mathit{e}}=\mathbf{0.5}\mathit{e}\mathit{V}$ ${\mathit{T}}_{\mathit{i}}$ = 0.35 eV, ${\mathit{T}}_{\mathit{p}\mathit{h}}=$ 2 eV and ${\mathit{J}}_{\mathit{p}\mathit{h}}$ = 100 μA/m².

FIGURE 4

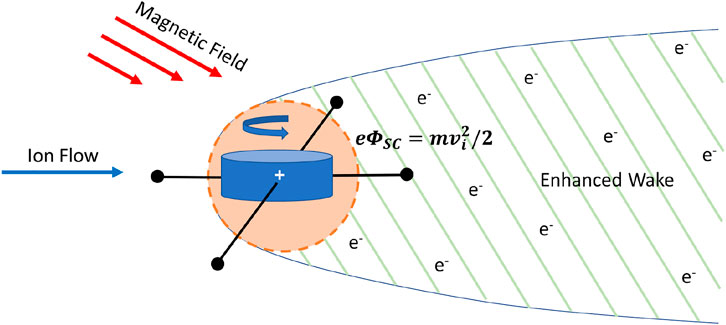
FIGURE 4. Schematic of the enhanced wake behind a positively charged spacecraft. The dashed circle illustrates the equipotential of the spacecraft electrostatic field where $\mathit{e}{\mathit{\Phi }}_{\mathit{S}\mathit{C}}=\mathit{m}{\mathit{v}}_{\mathit{i}}^{\mathbf{2}}/\mathbf{2}$.

3 In-situ ion measurements

Multiple instruments have made partial measurements of the cold ion populations in the magnetosphere with the difficulties discussed in Section 2. Traditional ion mass spectrometer instruments are designed to detect the hot tenuous magnetospheric ion species and are typically not as effective at measuring cold low-energy (<100 eV) plasmas. This is due to the trade-off in instrument design between having a large dynamic energy range from a few eV to tens of keV, versus focusing on low-energy sensitivity. Traditionally, space plasma instruments have focused on measuring large dynamic ranges due to limited spacecraft resources and mission opportunities.

An overview of ion mass spectrometers is captured (see Table 1) by briefly reviewing ion composition studies of the terrestrial magnetosphere by the Hot Plasma Composition Analyzers (HPCA) (Young, Burch, et al., 2016), the Helium, Oxygen, Proton, and Electron (HOPE) (Funsten, et al., 2013) mass spectrometer, the Cluster Ion Spectrometry (CIS) Experiment (Reme, et al., 1997), and the Retarding Ion Mass Spectrometer (RIMS) (Chappell, et al., 1981). These ion composition instruments and subsequent observations have provided the steppingstone for some of the most exciting magnetospheric science discoveries of the modern space science era. For example, the data from these instruments have been used to characterize the equatorial plasma environment and ion composition (Fernandes, et al., 2017; Yue, et al., 2018), evolution of the ring current during geomagnetic storms (Zhao, et al., 2015), initial observations of the “oxygen plasma torus” (Chappell 1982), magnetospheric ion influence on magnetic reconnection at the duskside and dayside magnetopause (Fuselier et al., 2016; Fuselier et al., 2019b), and the confirmation that wave-particle interactions can play a key role in acceleration within the radiation belts (Thorne 2010; Turner, et al., 2014; Baker 2021). These examples are a very limited sampling of the literature and by no means an exhaustive discussion of the total scientific advancements enabled by these instruments. For context, the Cluster mission alone has generated more than 2,587 refereed publications and 142 PhD/thesis (Escoubet, et al., 2020). However, while the HOPE, CIS/CODIF, and HCPA ion mass spectrometers have provided invaluable insights into the plasma source and transport within the terrestrial magnetosphere, these instruments have only made limited observations of the cold ions which often constitute the bulk of the magnetospheric plasma density.

TABLE 1

TABLE 1. Performance specifications for representative state-of-the-art mass spectrometers.

The difficulties associated with measuring low-energy magnetospheric ions have been addressed with limited success, i.e., measurements of partial distributions and limited time-series data sets, by earlier missions through the use of active spacecraft control (Riedler, et al., 1997; Torkar, et al., 2016) and electrostatic biasing of entrance apertures (Chappell, et al., 1981) or the entire instrument (Knudsen, et al., 2015). These active spacecraft potential controls reduced the spacecraft potential, but did not reduce the potential to zero for all measurements, resulting in portions of the distributions unmeasured.

The RIMS instrument on-board the Dynamics Explorer 1 (DE-1) mission has provided some of the earliest and most robust observations of the cold ion populations in the magnetosphere to date. The sensor design utilized a front aperture capable of being commanded to any of four values as a bias for a non-zero spacecraft potential (Chappell, et al., 1981). This bias created an electrostatic potential to steer low-energy ions through the spacecraft potential sheath to the detector aperture. The sensor had the ability to resolve H⁺, He⁺, O⁺, and O⁺⁺ within a narrow energy range of 0–50 eV. This allowed for the initial observations of the O⁺ torus, warm plasma cloak, thermal composition of the plasmapause, and the ionospheric outflow or polar wind (Chappell, et al., 1981, C. R; Chappell 1982, C. R; Chappell 1988, Chappell et al., 2008). However, due to a lack of spacecraft potential measurements the ion densities derived from the RIMS observations have considerable uncertainties. Initial density values were arrived at through an iterative method involving estimating the spacecraft potential as a function of geocentric distance and the electron density profile (Persoon et al., 1983), applying the spacecraft potential estimates to an empirical relation (Comfort et al., 1988), comparing to modeled total density (Ho and Horwitz 1993), and iterating until the spacecraft potential and density converged (Ho and Horwitz 1994). The temperatures obtained from the instrument measurements consist of a high degree of uncertainty due to the energy spacing of the RPA steps being larger than the thermal energies (Ho and Horwitz 1994). The temperature is also derived using a thin sheath approximation for the spacecraft potential sheath (Comfort et al., 1985) which has been shown to introduce significant error (W. C. Knudsen 1966; Parker and Whipple 1970; Sojka et al., 1984; Marchand et al., 2010; Lavraud and Larson 2016). Lastly, the radial retarding potential analyzer (RPA) head of the RIMS failed, limiting the DE-1 data set (Ho and Horwitz 1994). Although there are some limitations of the RIMS instrument, it has provided a wealth of data and contributed to our understanding of the ionosphere-magnetosphere system and provided a crucial steppingstone for cold ion and cold electron observations in the magnetosphere.

A statistical study of the spacecraft potential on Van Allen Probes demonstrated that the satellites charged to between 0 and 10 V for much of the mission (Sarno-Smith, et al., 2016; Denton, et al., 2017). Consequently, the low-energy portion of the magnetospheric cold ion population has not been measured by the HOPE instrument due to the positive spacecraft potential. The CIS/CODIF instrument demonstrated the ability to measure ∼0–25 eV ions (O⁺, H⁺, He⁺) while emitting indium ions to control the spacecraft potential (Reme, et al., 1997; Riedler, et al., 1997). However, while the active spacecraft control used for Cluster and the Magnetospheric Multiscale (MMS) missions (Burch, et al., 2016) does reduce the spacecraft potential it does not eliminate it. The potential is reduced to ∼1–2 V, thus leaving a portion of the cold ion energy distribution unobserved. ∼1 The Thermal Ion Dynamics Experiment (TIDE) on POLAR was designed to measure the low-energy polar winds at very high altitudes. The TIDE ion mass spectrometer was used in combination with the Plasma Source Instrument (PSI) to measure to overcome the effects of spacecraft potential on low-energy ion measurements (Moore et al., 1997). The PSI could actively control the spacecraft potential using emitted xenon ions to reduce the spacecraft potential to 1.8–2.2 V (Su, et al., 1998), resulting in a portion of the cold ion population remaining unmeasured. Unfortunately, TIDE lost its mass resolution capability in 1996, then returning total ion results. A critical distinction must also be made regarding the capabilities of the instruments listed in Table 1. The HOPE sensor is the only instrument that was designed to be insensitive to energetic particle contamination background counts as a result of penetrating radiation and capable of making measurements throughout the inner magnetosphere. The HOPE data were also used to estimate the temperature of plasmaspheric ions using novel techniques required to extract the low-energy values while correcting for charged spacecraft moving through the ambient plasma (Genestreti, et al., 2017).

While these methods have allowed for limited measurements of low-energy ions, there were also impacts to the measured distributions as a result of the non-uniform sheath near the spacecraft (Scime et al., 1994; Marchand et al., 2010). These effects can be mitigated by operating the plasma instrument outside of the spacecraft sheath, at least for conditions when the local plasma Debye length is not too large, thus minimizing ion trajectory distortions due to asymmetric spacecraft potential sheaths. As has been done for ionospheric missions, this requires either a low-resource instrument or an engineering solution to mount a larger instrument to a boom. Several thermal ion and electron instruments have been successfully developed as low-resource payloads for sounding rocket missions (Frederick-Frost, et al., 2007; Fernandes et al., 2016; Fraunberger, et al., 2020) even utilizing aperture biasing techniques to accelerate target populations in the presence of spacecraft potential (Cohen, et al., 2016). As opposed to driving the spacecraft potential to near 0 V relative to the plasma potential, as done with ion beams or plasma contactors (Torkar et al., 2016), an alternate method of making these low-energy measurements would be to actively bias the spacecraft potential to focus on either cold ions or cold electrons. A sufficient negative potential will enable transport of low-energy ions to detector apertures and thus be observed. This is the case of the LANL-GEO spacecraft, which tend to charge negatively (Thomsen et al., 2013). Conversely, a large positive potential will enable low-energy electrons to be distinguishable from contaminating photoelectrons as discussed in Section 5.

More recently, the Swarm (Friis-Christensen, et al., 2008) and Magnetospheric Multiscale (Burch, et al., 2016) missions have utilized computational methods to assess spacecraft charging effects with to analyze and develop correction relations for instrument data interpretation (Marchand et al., 2010; Barrie, et al., 2019). Importantly, these studies have demonstrated that thicker plasma sheaths tend to induce more distortions in particle trajectories. Therefore, spacecraft sheath effects are most pronounced in the low density, high temperature plasmas of the magnetosphere and are less pronounced in the high density, low temperature plasmas of the ionosphere (Marchand et al., 2010). Additionally, both Marchand et al. (2010) and Barrie et al. (2019) observed that spacecraft geometry, most notably spacecraft booms, produce asymmetrical spacecraft sheaths which cause additional trajectory perturbations. These previous studies have demonstrated the clear need for spacecraft charging corrections for all low-energy particle measurements intended for operation in the ionosphere to magnetosphere.

It is well established that our understanding of the terrestrial magnetosphere can be significantly advanced by flying suitable ion mass spectrometers. Ion mass spectrometers need to be designed for the appropriate energy range, be able to mitigate the effects of penetrating radiation, and have sufficient mass resolution to resolve at a minimum (O⁺, H⁺, He⁺, N⁺). If not operated in conjunction with active spacecraft potential control, it would be beneficial for the instrument to be mounted on a biasable panel or of such low-resource constraints as to enable mounting on a boom outside of the spacecraft sheath. While the instruments described here and listed in Table 1 are advanced in both design and capability at the time of their build, the measurement sensitivity comes at a high cost that precludes them from missions operating under ever increasing fiscal constraints or for implementation as science payloads of large constellations required for ubiquitous multi-point space plasma measurements. Specifically, the ion mass spectrometers listed in Table 1 come with such high monetary costs that they cannot be used in large constellations without incurring an exorbitant mission cost.

3.1 Wake measurements

Engwall et al. (2009) have developed and validated a novel method to measure some properties of the cold ion populations using two different electric field measurements. This was demonstrated using the Electric Fields and Waves (EFW) (Gustafsson, et al., 1997) and the Electron Drift Instrument (EDI) (Paschmann, et al., 1997) payloads on-board the Cluster satellites. Positively charged spacecraft traveling through the magnetosphere develop an electron-rich environment in their wake due to the surrounding potential structure (Andre and Cully 2012). An enhanced wake forms if the bulk ion flow energy mv_i²/2 exceeds the thermal energy KT_i but remains lower than the spacecraft potential, as shown below

${KT}_i<\frac{{mv}_i^2}{2}<{e\Phi }_{SC}.(12)$

As the wake becomes broader and increases in length, i.e., enhanced due to the positive spacecraft potential, the electron-rich volume develops a local wake field between the spacecraft and ambient plasma environment that can be measured by the EFW (Engwall et al., 2006b; Eriksson, et al., 2006). The EDI payloads measure the drift of artificial high-energy (keV) electrons that gyrate back to the spacecraft along the geophysical magnetic field. Since these electrons have gyroradii, on the order of kilometers, and the enhanced wake length scale is on the order of 100 km, the EDI measurements are not significantly affected by the enhanced wake (Eriksson, et al., 2006; André, et al., 2021). The wake electric field is then given by

$E^W=E^{EFW}-E^{EDI},(13)$

from which the flow velocity of the cold ions in the enhanced wake could be obtained. The derivation of the ion flow velocity calculation is described in detail by Engwall et al. (2009). A schematic of the enhanced wake is shown in Figure 4. With this method, Andre and Cully (2012) demonstrated that the cold ions are present in the magnetosphere 50%–70% of the time but were not detectable by standard, body-mounted particle instruments due to the ions’ very low energy. Limitations of the wake method include: 1) inability to distinguish between ion species and charge state, 2) measurement is not possible during active spacecraft potential control, since it removes the wake signature, 3) sufficiently strong magnetic fields must be present to enable EDI measurements, 4) the wake must not be completely perpendicular to the spin plane, 5) the technique does not work with cold ions coexisting with hot plasma, as the energetic ions will fill the wake and cancel the electric field, and 6) this technique provides bulk property observations and does not measure particle distributions (Engwall et al., 2009). Additionally, the wake technique is more sensitive to lighter ions which due to their higher mobility tend to dominate the ion density throughout the enhanced wake (Haaland, et al., 2015).

4 In-situ electron measurements

While the cold plasma populations of the magnetosphere have been termed a “hidden population”, the cold electron populations have received even less attention when compared to the cold ion populations. This can largely be attributed to the challenges associated with the contaminating photoelectrons in combination with the effects of spacecraft charging. An overview of state-of-the-art plasma spectrometers for measuring electron populations in the magnetosphere is briefly presented in Table 2. These spectrometers are based on conventional spherical electrostatic analyzer (ESA) designs and have provided observations of electron energy spectra data in the magnetosphere to advance our understanding of Whistler anisotropy instabilities as the source of banded chorus (Fu, et al., 2014), the contribution of precipitating electrons to pulsating aurora (Miyosh, et al., 2015), and spacecraft charging effects (Thomsen et al., 2013; Sarno-Smith, et al., 2016). Again, these are but a few of the many scientific discoveries enabled by the electron spectrometers described in this section.

TABLE 2

TABLE 2. Performance specifications for representative state-of-the-art electron spectrometers.

While the instruments in Table 2 have provided invaluable insights regarding the electron populations within the terrestrial magnetosphere, these instruments have made extremely limited observations of the cold electrons which often constitute the bulk of the magnetospheric plasma density. This is due in part to the effects of spacecraft potential but predominantly due to the difficulties associated with contamination of low-energy channels due to photoelectrons. The effects of spacecraft potential on the three-dimensional measurements of electron distributions in the solar wind were observed in the electron spectrometer data aboard the Ulysses spacecraft. It was observed that the electron distributions varied with the look angle of the instrument prompting the development of a correction factor to recover more gyrotropic distributions (Scime et al., 1994). The same effect is observed in the Solar Wind Electron Proton Alpha Monitor (SWEPAM) data which are subsequently corrected for spacecraft potential prior to dissemination to the broader space physics community (Koning, et al., 2006; Skoug, et al., 2006). It is important to note that the SWEPAM electron (SWEPAM-E) spectrometer is one of three nearly identical instruments flown, in chronological order, on the Ulysses (Bame et al., 1992), Advanced Composition Explorer (ACE) (McComas et al., 1998), and Genesis missions (Barraclough, et al., 2003). The initial observations of the Ulysses low-energy electron measurements near the spacecraft potential were identified as contaminated with photoelectrons (Bame et al., 1992) and subsequently the Genesis instrument avoided photoelectron contamination by setting the minimum measurable energy band at 61 eV (Barraclough, et al., 2003). The Los Alamos National Laboratory (LANL) Magnetospheric Plasma Analyzer (MPA) was also subject to background counts caused by photoelectrons believed to be created on nearby spacecraft surfaces within the instrument field-of-view (McComas et al., 1993). Further LANL/MPA observations concluded that the relatively high count rates at electron energies below 20 eV were caused by photoelectron contamination (McComas et al., 1993). The Plasma Electron And Current Experiment (PEACE) electron spectrometers (Johnstone, et al., 1997), on-board the Cluster satellites, also demonstrate that low-energy electron measurements (particularly below the spacecraft potential) are contaminated by photoelectrons and secondaries originating at the spacecraft (Chaston, et al., 2005). The Cluster satellites used active spacecraft potential control to reduce the potential to a few volts. However, the low-energy electron population below the controlled spacecraft potential could still not be differentiated from the contaminating background counts (Szita, et al., 2001).

More recent instruments include the HOPE on board the Van Allen Probes and the ESAs on board the Time History of Events and Macroscale Interactions during Substorms (THEMIS) and MMS satellites. The HOPE electron data go down to only 15 eV due to photoelectron contamination at the lowest energies (Goldstein et al., 2014). Note, the HOPE instrument is the only design capable of measuring the TOF of negatively charged particles, thus it can simultaneously measure electron and negative ion populations. During the in-flight calibration of the THEMIS ESA, the cold electron data with energies ∼ eΦ_SC were avoided due to the difficulty associated with separating the photoelectron and cold electron populations (McFadden, et al., 2008). The THEMIS ESA data with spacecraft potential and contaminating photoelectron population are shown in Figure 5 (Walsh, et al., 2020). The Dual Electron Spectrometers (DES), designed for electron measurements to support the Fast Plasma Investigation (FPI) on-board the MMS satellites (C. Pollock, et al., 2016), have also been shown to be susceptible to photoelectron contamination. Therefore, the DES plasma moments are determined by excluding the electron energy ranges below the spacecraft potential (Gershman, et al., 2017).

FIGURE 5

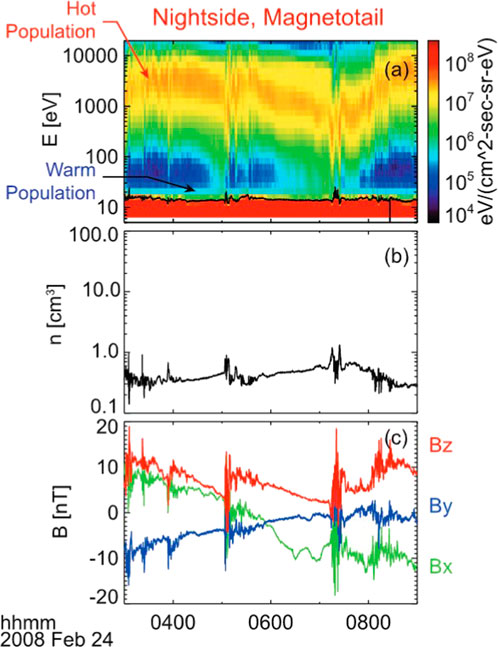
FIGURE 5. THEMIS D observations through the nightside magnetosphere of (A) electron energy spectra, (B) electron number density, and (C) magnetic field measurements in GSM coordinates. The spacecraft potential of ∼10 V is indicated by the black line (Walsh, et al., 2020).

In summary, cold electron measurements have been severely hindered by the inability to resolve ambient magnetospheric electrons from photoelectrons and this holds back our full understanding of the magnetosphere. Indeed, cold electrons play an important role in a variety of critical magnetospheric processes, including setting the ambipolar electric field and taking part in heating processes that drives some of the ionospheric outflow, controlling aspects of wave-particle interactions and magnetosphere-ionosphere coupling (such as the structuring of the pulsating aurora) (Delzanno, et al., 2021). The following section will discuss viable techniques to allow for the measurement of the elusive cold electron population within the magnetosphere.

5 Techniques to measure cold plasmas in the magnetosphere

As discussed in Sections 3 and Section 4, there have been limited successes at measuring the cold ion populations but there are essentially no measurements of cold electrons. Outside of ionospheric sounding rocket missions and POLAR, there has yet to be a large magnetospheric spacecraft mission dedicated to measuring the source of both the low energy electron and ion particle populations robustly.

While there are challenges to making measurements of the cold magnetospheric ions and electrons, a number of viable techniques exist for cold ions that have been conducted for sounding rocket missions such as 1) mounting a low-resource (mass and volume) instrument on a boom (L. Brace 1998, C. J; Pollock, et al., 1996), and 2) biasing the electrostatic plasma spectrometer mounted to a boom or plate thus allowing for differential biasing of the instrument and/or spacecraft (Chappell, et al., 1981, C. J; Pollock, et al., 1996). Measuring cold ion bulk properties through the properties of the wake of the spacecraft (Engwall et al., 2009) has also been performed successfully, but this technique does not yield the full energy distributions.

5.1 Active spacecraft potential control for cold electron measurements

Based on the experience gained from past missions (Section 4) and assuming that the detector cannot be mounted on booms due to mass restrictions, a promising idea to enable robust cold-electron measurements by a particle detector, i.e. measuring the full distribution of the ambient low-energy electrons, is to use an electron beam to control the spacecraft potential. This concept of active spacecraft control is similar to the use of plasma contactors (Comfort, et al., 1998) used to make cold ion measurements. By using an electron beam, on the other hand, the spacecraft is biased positively with respect to the ambient plasma with the objective of mitigating/removing the photoelectron contamination in the detector signal to enable robust cold electron measurements. This concept idea has been demonstrated with kinetic simulations, shown in Figure 6, where the response of a particle detector mounted on a Van-Allen-Probes-type spacecraft (Mauk, et al., 2012) is again simulated using the first-principles model CPIC. The local plasma parameters and the spacecraft photoelectron properties are the same as those used for the results presented in Figure 3. In Figure 6, the whole spacecraft (including the detector) is biased to 30 V with respect to the ambient plasma. In this simulation the authors do not include an actual electron beam emitted by the spacecraft. Rather, we assume that the effects of the emission of a suitable electron beam are to charge the whole spacecraft to 30 V. By biasing the entire spacecraft to a sufficiently positive voltage, the cold ambient electrons are attracted and accelerated towards the particle detector. The photoelectrons generated at the spacecraft, on the other hand, are attracted back to the spacecraft due to the strong electric field near the spacecraft with the same energy at which these were born. In other words, in this configuration, photoelectrons do not experiment any acceleration due to the spacecraft potential control, only the cold background electrons do. This can be seen in the histograms in the top left panel and bottom left panel of Figure 6. Here, if the detector is in shade, as shown in the right panel of Figure 6, fewer photoelectrons will be able to reach it and the photoelectron particle count in the detector will be reduced drastically. Note that the few photoelectrons that reached the detector are some of those born with sufficient energy to overcome the spacecraft potential, or/and those that are born with oblique trajectories with respect to the spacecraft surface at which these are generated. Non-etheless, by restoring the photoelectrons trajectories using active spacecraft control, and by positioning the particle detector away from the surfaces where photoelectron are generated, enables a robust way to clearly separate both species in the detector signal.

FIGURE 6

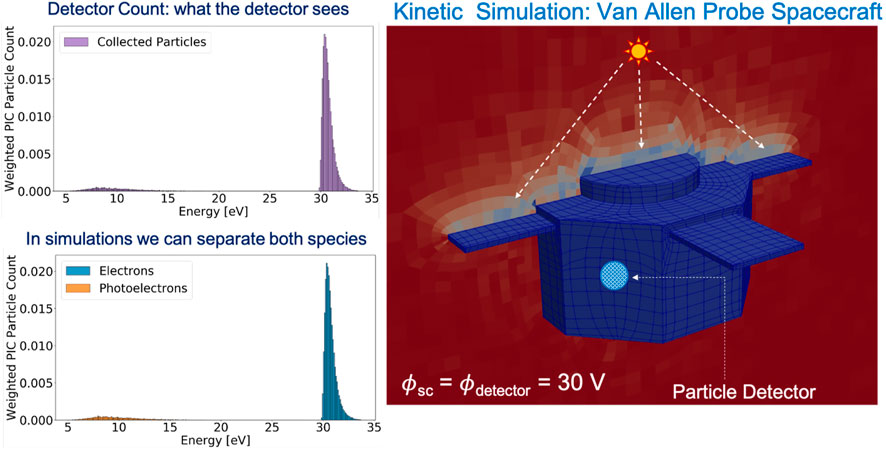
FIGURE 6. Kinetic simulation result: active spacecraft control enables cold-electron measurements. Cold-electron and photoelectron populations are clearly separated in detector signal as shown in the top-left panel and confirmed in the bottom-left panel. Simulation inputs: $\mathit{n}=$ 13.5 cm⁻³, ${\mathit{T}}_{\mathit{e}}=\mathbf{0.5}\mathit{e}\mathit{V}$ ${\mathit{T}}_{\mathit{i}}$ = 0.35 eV, ${\mathit{T}}_{\mathit{p}\mathit{h}}=$ 2 eV and ${\mathit{J}}_{\mathit{p}\mathit{h}}$ = 100 μA/m².

These results indicate that the full distribution of the magnetospheric cold particle populations, electrons and ions, can be measured using active spacecraft potential control and instrument biasing, respectively. However, by using these approaches, the effect of the electric field on the dynamics of the particles measured by the detector is enhanced drastically and are to be accounted for in the computation of the moments of the particle distributions. The parameters of the unperturbed plasma can be estimated using the Liouville theorem where the particle count measured by the detector (affected by the spacecraft electric field) is related to the distribution function of the unperturbed ambient plasma (Lavraud and Larson 2016). The caveat is that in this approximation, the sheath electric field depends on the geometry of the spacecraft, whether planar or spherical, and should be accounted for. Error estimation in the moments of the distribution due to dependence of the sheath electric field with spacecraft geometry is non-trivial. However, one way to estimate these is using kinetic simulations such as the ones presented in this paper. As for the uncertainties due to statistical errors, these can be computed as a covariance matrix using the approach presented in (Gershman, 2015). This approach is particularly useful for complex distribution functions and/or high order moments. For low-order moments, e. g, density, the uncertainty can simply scale as $\sim 1/\sqrt{\sum N}$ where N in the number of counts when a Maxwellian-Boltzmann distribution is assumed.

5.2 Low-resource instruments

Recent years have witnessed a tremendous growth in satellite constellations for scientific (Escoubet et al., 1997; Angelopoulos 2008; Burch, et al., 2016), commercial (Radtke et al., 2017; McDowell 2020), and government applications (Tournear 2020). Readily identifiable challenges with implementing a large or even mega-constellation of small satellites or CubeSats for scientific missions are: 1) the platforms need to be sophisticated enough that they can support quality sensors and subsystems while operating in the required space environments and 2) the sensors need to be reduced in size, weight, volume, and cost while still having the ability to make the appropriate measurements. The first topic includes the platform ability to support mission requirements such as power generation, pointing accuracy of attitude dynamics and control systems (ADCS), along with the ability to survive and operate in the natural space radiation environment. The survivability issue is a difficult task as the mass and volume constraints of these vehicles present considerable challenges in terms of supporting radiation shielding. However, engineering solutions such as appropriate electronics part selection, spot shielding, and software techniques to mitigate single-event-effects (SEUs) offer attractive engineering solutions for CubeSat missions targeting environments beyond low-Earth orbit (Klesh, et al., 2018; Blum et al., 2020; Maldonado et al., 2022).

As the space physics community has developed a growing interest in the benefits of CubeSat missions, with their ability to provide multiple spatial and temporal measurements at a reduced cost, there has been an increased focus on the development of miniaturized instruments. Historically, instrument design has been guided by the philosophy of “build to performance”. However, the current fiscal environment of ever dwindling budgets coupled with expanding CubeSat opportunities has revitalized the demand for low-resource instruments that can yield relevant science return (Funsten and McComas 1998; Young 1998; MacDonald et al., 2009; Fernandes et al., 2019). This interest, combined with advances in microelectromechanical systems (MEMS) have enabled the rapid increase in the number of miniaturized plasma analyzers with flight heritage (Maldonado, et al., 2019; Maldonado, et al., 2020a). Examples include retarding potential analyzers (RPA) (Fanelli, et al., 2015), laminated electrostatic analyzers (Maldonado, et al., 2020b; Maldonado et al., 2020c), ion mass spectrometers (Nordholt, et al., 2003; Kepko, et al., 2017; Ogasawara, et al., 2020), and traditional spherical analyzers (MacDonald et al., 2006).

These low-resource instruments have the potential to be mounted to booms outside of the spacecraft potential sheath. As has been done on sounding rockets, it would be advantageous to use a low-resource ion mass spectrometer or plasma spectrometer to enable the instrument to be mounted to a boom and biased or swept, positive or negative depending on the target population of interest, thus mitigating the effects of spacecraft potential and enabling greatly improved cold magnetospheric plasma measurements. Alternatively, a low-resource or traditional plasma spectrometer can be mounted to a biasable plate which can be differentially biased with respect to the spacecraft potential. This bias can be set to a sufficiently large positive or negative voltage thus creating a pathway for cold ions through the spacecraft potential sheath to the detector aperture. Additionally, a large constellation of CubeSats equipped with plasma spectrometers have the potential to provide multi-point simultaneous in-situ low energy measurements of ionospheric outflow and cold magnetospheric plasma. These data would enable closure of important science questions regarding the source of magnetospheric plasma, magnetosphere-ionosphere coupling, mass loading of the magnetosphere, magnetic reconnection, and with wave-particle interactions (Zurbuchen and Gershman 2016). The challenge remains for low-resource instruments operating within the deep inner magnetosphere to mitigate the effects penetrating radiation which can potentially obscure observations of low-energy ions and electrons (Denton, et al., 2017).

5.3 Other techniques

Due to the inherent difficulties associated with direct measurement of the low-energy ion and electron populations, alternative methods have been implemented to aid in indirect measurements beyond the wake technique (Walsh, et al., 2020). These additional methods include using the spacecraft potential to derive electron density (Escoubet, et al., 1997b; Pedersen, et al., 2008; Andriopoulou, et al., 2016) and standing Alfvén waves (Chi and Russell 2005; Takahashi, et al., 2014) along with limiting observations to periods when the bulk flow exceeds the spacecraft velocity (Lee and Angelopoulos 2014). As an example of the latter, the low-energy ion observations made using the Orbiting Geophysical Observatory 5 (OGO 5) ion spectrometer relied on the spacecraft velocity to raise the relative energy of cold ions past the potential barrier (Harris et al., 1970; Serbu and Maier 1970).

Remote sensing techniques such as radio tomography and EUV imaging have the potential to advance our understanding of global and regional scale phenomena pertaining to ionospheric outflow, erosion and refilling of the plasmasphere, along with subsequent redistribution of mass through the magnetosphere (Malaspina, et al., 2022). The radio tomography technique utilizes space-based radio receivers and transmitters to measure total electron content along line of sight between receiver-transmitter pairs which can then be used to produce two-dimensional images of plasma density (Ergun, et al., 2000). The EUV imaging technique utilizes optical cameras to detect resonantly-scattered emissions to capture light and heavy ion population densities for observations of global and mesoscale refilling dynamics (Sandel, et al., 2000).

While bulk parameters or densities can be obtained using remote and indirect measurements or even spacecraft potential, the full distributions of the cold ion and cold electron populations are required to close science questions related to the microphysics of individual flux tubes such as ion trapping, heating, and transport (Goldstein et al., 2021).

6 Conclusion

In-situ cold ion and cold electron measurements are key to understand the dynamics of the Earth magnetosphere. There are two main challenges to overcome to achieve the measuring of the full particle distribution of the cold plasma populations in the magnetosphere: spacecraft potential and contamination of low-energy spacecraft-generated electrons in the particle detector.

Cold ion and electron measurements are both affected by the sheath electric field on and surrounding the spacecraft which alters the trajectories of the particle measured by a detector. Depending on the polarity at which the spacecraft charges with respect to the ambient plasma, which depends on the environment and spacecraft materials, some plasma species will be attracted and some other repelled. For the repelled species, depending on the mean energy compared to the spacecraft potential, the particle distribution will be partially measured. In this case the full distribution can be approximated by extrapolating from the measured, truncated distribution. This approach, however, could yield large uncertainties in the parameter estimation. As for the attracted species, the problem comes from accounting for the acceleration that measured particles experiment inside the spacecraft sheath. It is mandatory to correct for the spacecraft potential effect on the particle counts to accurately estimate the plasma moments that characterize the unperturbed magnetospheric cold plasma. Given the complex spacecraft geometries on which the structure of the sheath depends, this is a challenging task.

On the other hand, the contamination of low-energy spacecraft-generated electrons only affects the cold electron measurements. Because the cold electrons and the spacecraft-generated electrons can have similar energies (a few eV), it is very difficult to distinguish one species from the other in the detector particle count. Moreover, the density of the spacecraft-generated electrons can be orders of magnitude larger than the density of magnetospheric cold electrons resulting in a complete masking of the ambient electron signal. This is the main reason why cold electron measurements of the lowest energies have not been accomplished yet.

Fortunately, there are promising techniques to enable robust cold ion and cold electron measurements in the Earth’s magnetosphere. Those discussed herein include, active spacecraft potential control, biasing of aperture surfaces, and low-resource instruments mounted to booms. Each of these methods have been demonstrated sparsely in space and some have been supported by numerical simulations. One possibility to measure the full ion distribution is to use differential biasing of the detector and mounting face to a sufficiently negative voltage with respect to the ambient plasma. This will eliminate any potential barrier due to the spacecraft sheath, giving free access for the cold ions to reach the detector. As for the cold electron measurements, this can be achieved by active spacecraft potential control realized by an electron beam. By biasing the entire spacecraft to sufficiently positive voltage, the spacecraft-generated electrons are clearly differentiated from the ambient cold electron signal in the detector count. Note that although these approaches (differential biasing for ions and active spacecraft potential control for electrons) enable robust measurement of the full particle distributions, the effect of the spacecraft sheath in the particle counts still needs to be corrected in order to compute accurate ambient plasma parameters.

In a complex system of interconnected parts like the Earth’s magnetosphere, a lack of understanding of one part of the system (the cold electron and ion populations) is disabling. Hence, until cold electron and cold ion measurements are obtained robustly with every mission, the magnetospheric plasma environment cannot be completely understood.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was funded through the Los Alamos National Laboratory (LANL) Laboratory Directed Research and Development–Exploratory Research (LDRD-ER) Project Number 20220453ER. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (DOE) (Contract No. 89233218CNA000001).

Acknowledgments

The research conducted at Los Alamos National Laboratory was under the auspices of the Department of Energy.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andre, M. (2015). Previously hidden low-energy ions: A better map of near-earth space and the terrestrial mass balance. Phys. Scr. 90, 128005. doi:10.1088/0031-8949/90/12/128005

CrossRef Full Text | Google Scholar

Andre, M., and Cully, C. M. (2012). Low-energy ions: A previously hidden solar system particle population. Geophys. Res. Lett. 39, L03101. doi:10.1029/2011GL050242

CrossRef Full Text | Google Scholar

André, M., Eriksson, A. I., Khotyaintsev, Y. V., and Toledo-Redondo, S. (2021). The spacecraft wake: Interference with electric field observations and a possibility to detect cold ions. J. Geophys. Res. Space Phys. 126, e2021JA029493. doi:10.1029/2021JA029493

CrossRef Full Text | Google Scholar

Andriopoulou, M., Nakamura, R., Torkar, K., Baumjohann, W., Torbert, R. B., Lindqvist, P.-A., et al. (2016). Study of the spacecraft potential under active control and plasma density estimates during the MMS commissioning phase. Geophys. Res. Lett. 43, 4858–4864. doi:10.1002/2016GL068529

CrossRef Full Text | Google Scholar

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141, 5–34. doi:10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Baker, D. N. (2021). Wave–particle interaction effects in the Van Allen belts. Earth, Planets, Space 73, 189. doi:10.1186/s40623-021-01508-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Bame, S. J., Hundhausen, A. J., Asbridge, J. R., and Strong, I. B. (1968). Solar wind ion composition. Phys. Rev. Lett. 20 (8), 393–395. doi:10.1103/PhysRevLett.20.393

CrossRef Full Text | Google Scholar

Bame, S. J., McComas, D. J., Barraclough, B. L., Phillips, J. L., Sofaly, K. J., Chavez, J. C., et al. (1992). The Ulysses solar wind plasma experiment. Astronomy Astrophysics Suppl. Ser. 92, 237–265.

Google Scholar

Bame, S. J., McComas, D. J., Thomsen, M. F., Barraclough, B. L., Elphic, R. C., Glore, J. P., et al. (1993). Magnetospheric plasma analyzer for spacecraft with constrained resources. Rev. Sci. Instrum. 64, 1026–1033. doi:10.1063/1.1144173

CrossRef Full Text | Google Scholar

Barakat, A., and Schunk, R. (2001). Effects of wave-particle interactions on the dynamic behavior of the generalized polar wind. J. Atmos. Solar-Terrestrial Phys. 63, 75–83. doi:10.1016/S1364-6826(00)00106-1

CrossRef Full Text | Google Scholar

Barghouthi, I. A., Barakat, A. R., and Persoon, A. M. (1998). The effects of altitude-dependent wave particle interactions on the polar wind plasma. Astrophysics Space Sci. 259, 117–140. doi:10.1023/A:1001569207346

CrossRef Full Text | Google Scholar

Barraclough, B. L., Dors, E. E., Abeyta, R. A., Alexander, J. F., Ameduri, F. P., Baldonado, J. R., et al. (2003). The plasma ion and electron instruments for the Genesis mission. Space Sci. Rev. 105, 627–660. doi:10.1023/A:1024426112422

CrossRef Full Text | Google Scholar

Barrie, A. C., Cipriani, F., Escoubet, C. P., Toledo-Redondo, S., Nakamura, R., Torkar, K., et al. (2019). Characterizing spacecraft potential effects on measured particle trajectories. Phys. Plasma 26, 103504. doi:10.1063/1.5119344

CrossRef Full Text | Google Scholar

Blum, L. W., and Breneman, A. W. (2019). “Observations of radiation belt losses due to cyclotron wave-particle interactions,” in The dynamic loss of earth's radiation belts. Editors A. N. Jaynes, and M. E. Usanova (Amsterdam, Netherlands: Elsevier), 49–98. doi:10.1016/B978-0-12-813371-2.00003-2

CrossRef Full Text | Google Scholar

Blum, L. W., Kepko, L., Turner, D., Gabrielse, C., Jaynes, A., Kanekal, S., et al. (2020). “The GTOSat CubeSat: Scientific objectives and instrumentation proceedings volume 11389,” in Micro- and nanotechnology sensors, systems, and applications XII (Washington, United States: SPIE).

Google Scholar

Blum, L. W., MacDonald, E. A., Gary, S. P., Thomsen, M. F., and Spence, H. E. (2009). Ion observations from geosynchronous orbit as a proxy for ion cyclotron wave growth during storm times. J. Geophys. Res. Space Phys. 114, A10214. doi:10.1029/2009JA014396

CrossRef Full Text | Google Scholar

Borovsky, J. E., Denton, M. H., Denton, R. E., Jordanova, V. K., and Krall, J. (2013). Estimating the effects of ionospheric plasma on solar wind/magnetosphere coupling via mass loading of dayside reconnection: Ion-plasma-sheet oxygen, plasmaspheric drainage plumes, and the plasma cloak. J. Geophys. Res. Space Phys. 118, 5695–5719. doi:10.1002/jgra.50527

CrossRef Full Text | Google Scholar

Borovsky, J. E., Hesse, M., Birn, J., and Kuznetsova, M. M. (2008). What determines the reconnection rate at the dayside magnetosphere? J. Geophys. Res. 113, A07210. doi:10.1029/2007JA012645

CrossRef Full Text | Google Scholar

Bortnik, J., Thorne, R. M., and Meredith, N. P. (2008). The unexpected origin of plasmaspheric hiss from discrete chorus emissions. Nature 452, 62–66. doi:10.1038/nature06741

PubMed Abstract | CrossRef Full Text | Google Scholar

Brace, L. H. (1998). Langmuir probe measurements in the ionosphere. Geophys. Monograph-American Geophys. Union 102, 23–26.

Google Scholar

Brace, L. H., Reddy, B. M., and Mayr, H. G. (1967). Global behavior of the ionosphere at 1000-kilometer altitude. J. Geophys. Res. 72, 265–283. doi:10.1029/JZ072i001p00265

CrossRef Full Text | Google Scholar

Bruining, H. (2016). Physics and applications of secondary electron emission. London: Pergamon Science Series: Electronics and Waves—a Series of Monographs.

Google Scholar

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Carpenter, D. L. (1962). Electron-density variations in the magnetosphere deduced from whistler data. J. Geophys. Res. 67, 3345–3360. doi:10.1029/JZ067i009p03345

CrossRef Full Text | Google Scholar

Cassak, P. A., and Shay, M. A. (2007). Scaling of asymmetric magnetic reconnection: General theory and collisional simulations. Phys. Plasmas 14, 102114. doi:10.1063/1.2795630

CrossRef Full Text | Google Scholar

Chandra, S., Maier, E. J., and Stubbe, P. (1972). The upper atmosphere as aregulator of subauroral red arcs. Planet. Space Sci. 20 (4), 461–472. doi:10.1016/0032-0633(72)90078-5

CrossRef Full Text | Google Scholar

Chandra, S., Maier, E. J., Troy, B. E., and Narasinga Rao, B. C. (1971). Subauroral red arcs and associated ionospheric phenomena. J. Geophys. Res. 76, 920–925. doi:10.1029/JA076i004p00920

CrossRef Full Text | Google Scholar

Chappell, C. R., Fields, S., Baugher, C., Hoffman, J., Hanson, W., Wright, W., et al. (1981). The retarding ion mass spectrometer on dynamics Explorer-A. United States: Marshall Space Flight Center, 447. NASA-TM-82418.

Google Scholar

Chappell, C. R., Huddleston, M. M., Moore, T. E., Giles, B. L., and Delcourt, D. C. (2008). Observations of the warm plasma cloak and an explanationof its formation in the magnetosphere. J. Geophys. Res. 113, A09206. doi:10.1029/2007ja012945

CrossRef Full Text | Google Scholar

Chappell, C. R. (1982). Initial observations of thermal plasma composition and energetics from Dynamics Explorer-1. Geophys. Res. Lett. 9, 929–932. doi:10.1029/gl009i009p00929

CrossRef Full Text | Google Scholar

Chappell, C. R. (1988). The terrestrial plasma source' A new perspective in solar-terrestrial processes from dynamics explorer. Rev. Geophys. 26, 229–248. doi:10.1029/RG026i002p00229

CrossRef Full Text | Google Scholar

Chaston, C. C., Peticolas, L. M., Carlson, C. W., McFadden, J. P., Mozer, F., Wilber, M., et al. (2005). Energy deposition by Alfvén waves into the dayside auroral oval: Cluster and FAST observations. J. Geophys. Res. Space Phys. 110 (A2), A02211. doi:10.1029/2004JA010483

CrossRef Full Text | Google Scholar

Chen, L., Thorne, R. M., and Bortnik, J. (2011). The controlling effect of ion temperature on EMIC wave excitation and scattering. Geophys. Res. Lett. 38, L16109. doi:10.1029/2011GL048653

CrossRef Full Text | Google Scholar

Chi, P. J., and Russell, C. T. (2005). Travel-time magnetoseismology: Magnetospheric sounding by timing the tremors in space. Geophys. Res. Lett. 32, L18108. doi:10.1029/2005GL023441

CrossRef Full Text | Google Scholar

Cohen, I. J., Widholm, M., Lessard, M. R., Riley, P., Heavisides, J., Moen, J. I., et al. (2016). Rocket-borne measurements of electron temperature and density with the Electron Retarding Potential Analyzer instrument. J. Geophys. Res. Space Phys. 121, 6774–6782. doi:10.1002/2016JA022562

CrossRef Full Text | Google Scholar

Comfort, R. H., Craven, P. D., Gallagher, D. L., West, R. L., and Chappell, C. R. (1988). Spacecraft potential dependence on plasma density from GEOS-2 and DE-1 measurements. Eos, Trans. Am. Geophys. Union 69, 448.

Google Scholar

Comfort, R. H., Moore, T. E., Craven, P. D., Pollock, C. J., Mozer, F. S., and Williamson, W. S. (1998). Spacecraft potential control by the plasma source instrument on the POLAR satellite. J. Spacecr. Rockets 35 (6), 845–849. doi:10.2514/2.7586

CrossRef Full Text | Google Scholar

Comfort, R. H., Waite, J. H., and Chappell, C. R. (1985). Thermal ion temperatures from the retarding ion mass spectrometer on DE 1. J. Geophys. Res. 90 (A4), 3475–3486. doi:10.1029/JA090iA04p03475

CrossRef Full Text | Google Scholar

Cully, C. M., Donovan, E. F., Yau, A. W., and Arkos, G. G. (2003). Akebono/Suprathermal Mass Spectrometer observations of low-energy ion outflow: Dependence on magnetic activity and solar wind conditions. J. Geophys. Res. Space Phys. 108, 1093. doi:10.1029/2001JA009200

CrossRef Full Text | Google Scholar

de Soria-Santacruz, M., Spasojevic, M., and Chen, L. (2013). EMIC waves growth and guiding in the presence of cold plasma density irregularities. Geophys. Res. Lett. 40, 1940–1944. doi:10.1002/grl.50484

CrossRef Full Text | Google Scholar

DeForest, S. E. (1972). Spacecraft charging at synchronous orbit. J. Geophys. Res. 77 (4), 651–659. doi:10.1029/JA077i004p00651

CrossRef Full Text | Google Scholar

Delzanno, G. L., Henderson, M. G., Borovsky, J. E., Lira, P. A. R., Roytershteyn, V., and Welling, D. T. (2021). The impact of cold electrons and cold ions in magnetospheric physics. J. Atmos. Solar-Terrestrial Phys. 220, 105599. doi:10.1016/j.jastp.2021.105599

CrossRef Full Text | Google Scholar

Denton, M. H., Reeves, G. D., Larsen, B. A., Friedel, R. H. W., Thomsen, M. F., Ffernandes, P. A., et al. (2017). On the origin of low-energyelectrons in the inner magnetosphere:Fluxes and pitch-angle distributions. J. Geophys. Res. Space Phys. 122, 1789–1802. doi:10.1002/2016JA023648

CrossRef Full Text | Google Scholar

Denton, M. H., Thomsen, M. F., Jordanova, V. K., Henderson, M. G., Borovsky, J. E., Denton, J. S., et al. (2015). An empirical model of electron and ion fluxes derived from observations at geosynchronous orbit. Space weather. 13 (4), 233–249. doi:10.1002/2015sw001168

CrossRef Full Text | Google Scholar

Dimmock, A. P., and Nykyri, K. (2013). The statistical mapping of magnetosheath plasma properties based on THEMIS measurements in the magnetosheath interplanetary medium reference frame. J. Geophys. Res. Space Phys. 118, 4963–4976. doi:10.1002/jgra.50465

CrossRef Full Text | Google Scholar

Dunckel, N., and Helliwell, R. A. (1969). Whistler-mode emissions on the OGO 1 satellite. J. Geophys. Res. 74, 6371–6385. doi:10.1029/JA074i026p06371

CrossRef Full Text | Google Scholar

Eliasson, L., Andre, M., Eriksson, A., Norqvist, P., Norberg, O., Lundin, R., et al. (1994). Freja observations of heating and precipitation of positive ions. Geophys. Res. Lett. 21, 1911–1914. doi:10.1029/94GL01067

CrossRef Full Text | Google Scholar

Engwall, E., Eriksson, A. I., Andre, M., Dandouras, I., Paschmann, G., Quinn, J., et al. (2006a). Low-energy (order 10 eV) ion flow in the magnetotail lobes inferred from spacecraft wake observations. Geophys. Res. Lett. 33, L06110. doi:10.1029/2005GL025179

CrossRef Full Text | Google Scholar

Engwall, E., Eriksson, A. I., Cully, C. M., Andre, M., Puhl-Quinn, P. A., Vaith, H., et al. (2009). Survey of cold ionospheric outflows in the magnetotail. Ann. Geophys. 27, 3185–3201. doi:10.5194/angeo-27-3185-2009

CrossRef Full Text | Google Scholar

Engwall, E., Eriksson, A. I., and Forest, J. (2006b). Wake formation behind positively charged spacecraft in flowing tenuous plasmas. Phys. Plasmas 13, 062904. doi:10.1063/1.2199207

CrossRef Full Text | Google Scholar

Ergun, R. E., Larson, D. E., Phan, T., Taylor, D., Bale, S., Carlson, C. W., et al. (2000). Feasibility of a multisatellite investigation of the Earth’s magnetosphere with radio tomography. J. Geophys. Res. 105, 361–373. doi:10.1029/1999JA900170

CrossRef Full Text | Google Scholar

Eriksson, A. I., Andre, M., Klecker, B., Laakso, H., Lindqvist, P.-A., Mozer, F., et al. (2006). Electric field measurements on cluster: Comparing the double-probe and electron drift techniques. Ann. Geophys. 24, 275–289. doi:10.5194/angeo-24-275-2006

CrossRef Full Text | Google Scholar

Escoubet, C. P., Pedersen, A., Schmidt, R., and A Lindqvist, P. (1997b). Density in the magnetosphere inferred from ISEE 1 spacecraft potential. J. Geophys. Res. 102 (A8), 17595595609. doi:10.1029/97JA00290

CrossRef Full Text | Google Scholar

Escoubet, C. P., Schmidt, R., and Goldstein, M. L. (1997). “Cluster - science and mission overview,” in The cluster and phoenix missions. Schmidt. Editors C. P. Escoubet, and C. T. Russell, (Dordrecht: Springer), 11–32. doi:10.1007/978-94-011-5666-0_1

CrossRef Full Text | Google Scholar

Escoubet, P., Masson, A., Laakso, H., and Goldstein, M. L. (2020). “Cluster mission's recent highlights at dayside boundaries,” in Dayside magnetosphere interactions. Editors Q. Zong, P. Escoubet, D. Sibeck, G. Le, and H. Zhang (Hoboken, NJ: AGU Monograph Series, John Wiley & Sons), 99–115. doi:10.1002/9781119509592.ch6

CrossRef Full Text | Google Scholar

Fanelli, L., Noel, S., Earle, G. D., Fish, C., Davidson, R. L., Robertson, R. V., et al. (2015). A versatile retarding potential analyzer for nano-satellite platforms. Rev. Sci. Instrum. 86, 124501. doi:10.1063/1.4937622

PubMed Abstract | CrossRef Full Text | Google Scholar

Feldman, W. C., Asbridge, J. R., Bame, S. J., and Montgomery, M. D. (1974). Interpenetrating solar wind streams. Rev. Geophys. Space Phys. 12 (4), 715–723. doi:10.1029/rg012i004p00715

CrossRef Full Text | Google Scholar

Ferguson, D. C., Hilmer, R. V., and Davis, V. A. (2015). Best geosynchronous Earth orbit daytime spacecraft charging index. J. Spacecr. Rockets 52 (2), 526–543. doi:10.2514/1.A32959

CrossRef Full Text | Google Scholar

Fernandes, P. A., Funsten, H. O., E> Dors, E., Larsen, R. W., Harper, B. A., MacDonald, E. A., et al. (2019). Low-resource technique for measurement of H+ and O+ in the terrestrial magnetosphere. J. Geophys. Res.:Space Phys. 124, 9137–9153. doi:10.1029/2019JA027138

CrossRef Full Text | Google Scholar

Fernandes, P. A., Larsen, B. A., Thomsen, M. F., Skoug, R. M., Reeves, G. D., Denton, M. H., et al. (2017). The plasma environment inside geostationary orbit: A van allen probes HOPE survey. J. Geophys. Res. 122, 9207–9227. doi:10.1002/2017JA024160

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernandes, P. A., Lynch, K. A., Zettergren, M., Hampton, D. L., Bekkeng, T. A., Cohen, I. J., et al. (2016). Measuring the seeds of ion outflow: Auroral sounding rocket observations of low-altitude ion heating and circulation. J. Geophys. Res. Space Phys. 121, 1587–1607. doi:10.1002/2015JA021536

CrossRef Full Text | Google Scholar

Fraser, B. J., Horwitz, J. L., Slavin, J. A., Dents, Z. C., and Mann, I. R. (2005). Heavy ion mass loading of the geomagnetic field near the plasmapause and ULF wave implications. J. Gephys. Res. 32, L04102. doi:10.1029/2004GL021315

CrossRef Full Text | Google Scholar

Fraunberger, M., Lynch, K. A., Clayton, R., Roberts, T. M., Hysell, D., Lessard, M., et al. (2020). Auroral ionospheric plasma flow extraction using subsonic retarding potential analyzers. Rev. Sci. Instrum. 91, 094503. doi:10.1063/1.5144498

PubMed Abstract | CrossRef Full Text | Google Scholar

Frederick-Frost, K. M., Lynch, K. A., Kintner, P. M., Klatt, E., Lorentzen, D., Moen, J., et al. (2007). Sersio: Svalbard EISCAT rocket study of ion outflows. J. Geophys. Res. 112, A08307. doi:10.1029/2006JA011942

CrossRef Full Text | Google Scholar

Friis-Christensen, E., Luhr, H., Knudsen, D., and Haagmans, R. (2008). Swarm - an Earth observation mission investigating geospace. Adv. Space Res. 41 (1), 210–216. doi:10.1016/j.asr.2006.10.008

CrossRef Full Text | Google Scholar

Fu, X., Cowee, M. H., Reinhard, R. H., Friedel, H., Funsten, H. O., Peter Gary, S. P., et al. (2014). Whistler anisotropy instabilities as the source of banded chorus: Van Allen Probes observations and particle-in-cell simulations. J. Geophys. Res. Space Phys. 119 (10), 8288–8298. doi:10.1002/2014JA020364

PubMed Abstract | CrossRef Full Text | Google Scholar

Funsten, H. O., and McComas, D. J. (1998). “Limited resource plasma analyzers:Miniaturization concepts,” in Measurement techniques in space plasmas: Particles. Editors R. F. Pfaff, J. E. Borovsky, and D. T. Young (Washington, DC: AGU Monograph Series), 157–167.

Google Scholar

Funsten, H. O., Skoug, R. M., Guthrie, A. A., MacDonald, E. A., Baldonado, J. R., Harper, R. W., et al. (2013). Helium, oxygen, proton, and electron (HOPE) mass spectrometer for the radiation belt storm probes mission. Space. Sci. Rev. 179, 423–484. doi:10.1007/s11214-013-9968-7

CrossRef Full Text | Google Scholar

Fuselier, S. A., Burch, J. L., Cassak, P. A., Goldstein, J., Gomez, R. G., Goodrich, K., et al. (2016). Magnetospheric ion influence on magnetic reconnection at the duskside magnetopause. Geophys. Res. Lett. 43, 1435–1442. doi:10.1002/2015GL067358

CrossRef Full Text | Google Scholar

Fuselier, S. A., Mukherjee, J., Denton, M. H., Petrinec, S. M., Trattner, K. J., Toledo-Redondo, S., et al. (2019b). High-density O+in Earth's outer magnetosphere and its effect on dayside magnetopause magnetic reconnection. J. Geophys. Res. Space Phys. 124 (10), 10257–10269. doi:10.1029/2019JA027396

CrossRef Full Text | Google Scholar

Fuselier, S. A., Trattner, K. J., Petrinec, S. M., Denton, M. H., Toledo-Redondo, S., André, M., et al. (2019a). Mass loading the Earth's dayside magnetopause boundary layer and its effect on magnetic reconnection. Geophys. Res. Lett. 46, 6204–6213. doi:10.1029/2019GL082384

CrossRef Full Text | Google Scholar

Garrett, H. B., and Whittlesey, A. C. (2012). Guide to mitigating spacecraft charging effects. Hoboken, NJ: Wiley.

Google Scholar

Geiss, J., Gloeckler, G., and von Steiger, R. (1995). Origin of the solar wind from composition data. Space Sci. Rev. 72, 49–60. doi:10.1007/BF00768753

CrossRef Full Text | Google Scholar

Genestreti, K. J., Goldstein, J., Corley, G. D., Farner, W., Kistler, L. M., Larsen, B. A., et al. (2017). Temperature of the plasmasphere from van allen probes HOPE. J. Geophys. Res. Space Phys. 122, 310–323. doi:10.1002/2016JA023047

CrossRef Full Text | Google Scholar

Gershman, D. J., Avanov, L. A., Boardsen, S. A., Dorelli, J. C., Gliese, U., Barrie, A. C., et al. (2017). Spacecraft and instrument photoelectrons measured by the dual electron spectrometers on MMS. J. Geophys. Res. Space Phys. 122, 11548–11558. doi:10.1002/2017JA024518

CrossRef Full Text | Google Scholar

Glocer, A., Khazanov, G., and Liemohn, M. (2017). Photoelectrons in the quiet polar wind. J. Geophys. Res. 122, 6708–6726. doi:10.1002/2017JA024177

CrossRef Full Text | Google Scholar

Goldstein, J., De Pascuale, S., Kletzing, C., Kurth, W., Genestri, K. J., Skoug, R. M., et al. (2014). Simulation of van allen probes plasmapause encounters. J. Geophys. Res. Space Phys. 119, 7464–7484. doi:10.1002/2014JA020252

CrossRef Full Text | Google Scholar

Goldstein, J., Molymeux, D. L., and Reeves, G. (2021). Core-plasma refilling and erosion: Science justification." heliophysics 2050 white papers. NASA Heliophysics Division.

Google Scholar

Grard, R. J. (1973). Properties of the satellite photoelectron sheath derived from photoemission laboratory measurements. J. Geophys. Res. 78 (16), 2885–2906. doi:10.1029/JA078i016p02885

CrossRef Full Text | Google Scholar

Gustafsson, G., Bostrom, R., Holback, B., Holmgren, G., Lundgren, A., Stasiewicz, K., et al. (1997). The electric field and wave experiment for the cluster mission. Space Sci. Rev. 79, 137–156. doi:10.1023/A:1004975108657

CrossRef Full Text | Google Scholar

Haaland, S., Eriksson, A., André, M., Maes, L., Baddeley, L., Barakat, A., et al. (2015). Estimation of cold plasma outflow during geomagnetic storms. J. Geophys. Res. Space Phys. 120, 639. doi:10.1002/2015JA021810

CrossRef Full Text | Google Scholar

Harris, K., Sharp, G., and Chappell, C. R. (1970). Observations of the plasmapause from OGO 5. J. Geophys. Res. 116, 219–224. doi:10.1029/JA075i001p00219

CrossRef Full Text | Google Scholar

Hartley, D. P., Kletzing, C. A., Santolík, O., Chen, L., and Horne, R. B. (2018). Statistical properties of plasmaspheric hiss from van allen probes observations. J. Geophys. Res. Space Phys. 123, 2605–2619. doi:10.1002/2017JA024593

CrossRef Full Text | Google Scholar

Hasegawa, H., Fujimoto, M., Phan, T.-D., Reme, H., Balogh, A., Dunlop, M. W., et al. (2004). Transport of solar wind into Earth's magnetosphere through rolled-up Kelvin–Helmholtz vortices. Nature 430, 755–758. doi:10.1038/nature02799

PubMed Abstract | CrossRef Full Text | Google Scholar

Ho, C. W., Horwitz, J. L., and Moore, T. E. (1994). DE1 observations of polar O⁺stream bulk parameters and comparison with a model of the centrifugally-accelerated polar wind. Geophys. Res. Lett. 21 (23), 2459–2462. doi:10.1029/94GL02340

CrossRef Full Text | Google Scholar

Ho, C. W., and Horwitz, J. L. (1993). Warm O+ polar wind and the DE-1 polar cap electron density profile. Geophys. Res. Lett. 20, 1715–1717. doi:10.1029/93GL01980

CrossRef Full Text | Google Scholar

Ilie, R., and Liehohn, M. W. (2016). The outflow of ionospheric nitrogen ions: A possible tracer for the altitude-dependent transport and energization processes of ionospheric plasma. J. Geophys. Res. Space Phys. 121, 9250–9255. doi:10.1002/2015JA022162

CrossRef Full Text | Google Scholar

Johnstone, A. D., Burge, S., Carter, P. J., Coates, A. J., Coker, A. J., Fazakerley, A. N., et al. (1997). “Peace: A plasma electron and current experiment,”. Editors C. P. Escoubet, C. T. Russell, and R. Schmidt (Dordrecht: Springer), 79, 351–398. doi:10.1007/978-94-011-5666-0_13Clust. Phoenix Missions

CrossRef Full Text | Google Scholar

Kepko, L., Clagett, C., Santos, L., Azimi, B., Berry, D., Chai, T., et al. (2017.Dellingr: NASA goddard space flight center's first 6U spacecraft, Proceedings of the 31st AIAA/USU Small Satellite Conference, Logan, UT, August 5–10: Utah State University .

Google Scholar

Khazanov, G. V., Liemohn, M. W., and Moore, T. E. (1997). Photoelectron effects on the self-consistent potential in the collisionless polar wind. J. Geophys. Res. 102, 7509–7521. doi:10.1029/96JA03343

CrossRef Full Text | Google Scholar

Khazanov, G. V., Nagy, A. F., Gombosi, T. I., Koen, M. A., and Cariglia, S. J. (1992). Analytic description of the electron temperature behavior in the upper ionosphere and plasmasphere. Geophys. Res. Lett. 19, 1915–1918. doi:10.1029/92GL01940

CrossRef Full Text | Google Scholar

Kitamura, N., Ogawa, Y., Nishimura, Y., Terada, N., Ono, T., Shinbori, A., et al. (2011). Solar zenith angle dependence of plasma density and temperature in the polar cap ionosphere and low altitude magnetosphere during geomagnetically quiet periods at solar maximum. J. Geophys. Res. Space Phys. 116, A08227. doi:10.1029/2011JA016631

CrossRef Full Text | Google Scholar

Kitamura, N., Seki, K., Nishimura, Y., Terada, N., Ono, T., Hori, T., et al. (2012). Photoelectron flows in the polar wind during geomagnetically quiet periods. J. Geophys. Res. Space Phys. 117, A07214. doi:10.1029/2011JA017459

CrossRef Full Text | Google Scholar

Klesh, A., Clement, B., Colley, C., Essmiller, J., Forgette, D., Krajewski, J., et al. (2018).MarCO: Early operations of the first CubeSats to mars. 32nd Annual AIAA/USU Conference on Small Satellites. 4th – 9th August 2018, Utah, USA (Logan, UT: AIAA/USU), 1–6 .

Google Scholar

Knudsen, D. J., Burchill, J. K., Cameron, T. G., Enno, G. A., Howarth, A., and Yau, A. W. (2015). The CASSIOPE/e-POP suprathermal electron imager (SEI). Space. Sci. Rev. 189, 65–78. doi:10.1007/s11214-015-0151-1

CrossRef Full Text | Google Scholar

Knudsen, W. C. (1966). Evaluation and demonstration of the use of retarding potential analyzers for measuring several ionospheric quantities. J. Geophys. Res. 71 (19), 4669–4678. doi:10.1029/JZ071i019p04669

CrossRef Full Text | Google Scholar

Koning, C. A., Gosling, J. T., Skoug, R. M., and Steinberg, J. T. (2006). Widths of suprathermal pitch angle distributions during solar electron bursts: ACE observations. J. Geophys. Res. 111, A04101. doi:10.1029/2005ja011326

CrossRef Full Text | Google Scholar

Kotova, G. A. (2007). The Earth's plasmasphere: State of studies (a review). Geomagnetism Aeronomy 47, 409–422. doi:10.1134/S0016793207040019

CrossRef Full Text | Google Scholar

Kozyra, J. U., Brace, L. H., Cravens, T. E., and Nagy, A. F. (1986). A statistical study of the subauroral electron temperature enhancement using Dynamics Explorer 2 Langmuir probe observations. J. Geophys. Res. 91 (11), 11270280–11270311. doi:10.1029/JA091iA10p11270

CrossRef Full Text | Google Scholar

Lavraud, B., and Larson, D. E. (2016). Correcting moments of in situ particle distribution functions for spacecraft electrostatic charging. J. Geophys. Res. Space Phys. 121 (9), 8462–8474. doi:10.1002/2016JA022591

CrossRef Full Text | Google Scholar

Lavraud, B., Thomsen, M. F., Borovsky, J. E., Denton, M. H., and Pulkkinen, T. I. (2006). Magnetosphere preconditioning under northward IMF: Evidence from the study of coronal mass ejection and corotating interaction region geoeffectiveness. J. Geophys. Res. Space Phys. 111, A09208. doi:10.1029/2005JA011566

CrossRef Full Text | Google Scholar

Lee, J. H., and Angelopoulos, V. (2014). On the presence and properties of cold ions near Earth’s equatorial magnetosphere. J. Geophys. Res. Space Phys. 119, 1749–1770. doi:10.1002/2013JA019305

CrossRef Full Text | Google Scholar

Lemaire, J. F., Gringauz, K. I., Carpenter, D. L., and Bassolo, V. (1998). The earth's plasmasphere. The earth's plasmasphere. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/CBO9780511600098

CrossRef Full Text | Google Scholar

Lotko, W. (2007). The magnetosphere-ionosphere system from the perspective of plasma circulation: A tutorial. J. Atmos. Sol.-Terr. Phys. 69, 191–211. doi:10.1016/j.jastp.2006.08.011

CrossRef Full Text | Google Scholar

MacDonald, E. A., Funsten, H. O., Dors, E. E., Thomsen, M. F., Janzen, P. H., Skoug, R. M., et al. (2009). AIP, 168–172. doi:10.1063/1.3169283New magnetospheric ion composition measurement techniques, Procedings of the AIP Conference Proceedings, 27–28 February 2021, Krishnagiri, India

CrossRef Full Text | Google Scholar

MacDonald, E. A., Lynch, K. A., Widholm, M., Arnoldy, R., Kintner, P. M., Klatt, E. M., et al. (2006). In situ measurement of thermal electrons on the SIERRA nightside auroral sounding rocket. J. Geophys. Res. 111, A12310. doi:10.1029/2005JA011493

CrossRef Full Text | Google Scholar

Malaspina, D., Ergun, R., Goldstein, J., Spittler, C., Andersson, L., Borovsky, J., et al. (2022). Plasma imaging, LOcal measurement, and tomographic experiment (pilot): A mission concept for transformational multi-scale observations of mass and energy flow dynamics in Earth’s magnetosphere. Front. Astron. Space Sci. 9, 910730. doi:10.3389/fspas.2022.910730

CrossRef Full Text | Google Scholar

Maldonado, C. A., Cress, R., Gresham, P., Armstrong, J. L., Wilson, G., Reisenfeld, D., et al. (2020c). Space radiation dosimetry using the integrated Miniaturized Electrostatic Analyzer - reflight (iMESA-R). Space Weather.

Google Scholar

Maldonado, C. A., Deming, J., Mosley, B. N., Morgan, K. S., McGlown, J., Nelson, A., et al. (2022). The experiment for space radiation analysis: A 12U CubeSat to explore the earth's radiation belts, Proceedings of the IEEE Aerospace Conference. 9-16 March 2002: Big SkyIEEE, 1–15.

CrossRef Full Text | Google Scholar

Maldonado, C. A., Eyler, Z., Pierce, B., Matson, L., Neal, P., Richards, H., et al. (2020b). A laminated energetic electrostatic analyzer for 0-5 keV charged particles. Rev. Sci. Instrum. 91 (1), 013303. doi:10.1063/1.5123395

PubMed Abstract | CrossRef Full Text | Google Scholar

Maldonado, C. A., Reisenfeld, D., Fernandes, P., Larsen, B., Wilson, G., Balthazor, R. L., et al. (2020a). The effects of spacecraft potential on ionospheric ion measurements. J. Spacecr. Rockets 58, 1704–1713. (submitted). doi:10.2514/1.a34995

CrossRef Full Text | Google Scholar

Maldonado, C., McHarg, M., Balthazor, R., and Osiander, R. (2019). “Undergraduate research and science mission opportunities with microtechnology enabled particle detectors,” in Micro- and nanotechnology sensors, systems, and applications XI (Washington, United States: SPIE), 109820I. doi:10.1117/12.2519128

CrossRef Full Text | Google Scholar

Marchand, R., Burchill, J. K., and Knudsen, D. J. (2010). Modelling electrostatic sheath effects on Swarm electric field instrument measurements. Space Sci. Rev. 156, 73–87. doi:10.1007/s11214-010-9735-y

CrossRef Full Text | Google Scholar

Mauk, B. H., Fox, N. J., Kanekal, S. G., Kessel, R. L., Sibeck, D. G., and Ukhorskiy, A. (2012). Science objectives and rationale for the radiation belt storm probes mission. Space Sci. Rev. 179, 3–27. doi:10.1007/s11214-012-9908-y

CrossRef Full Text | Google Scholar

McComas, D. J., Bame, S. J., Barker, P., Feldman, W. C., Phillips, J. L., Griffee, J. W., et al. (1998). Solar wind electron proton alpha monitor (SWEPAM) for the advanced composition explorer. Space Sci. Rev. 86, 563–612. doi:10.1023/a:1005040232597

CrossRef Full Text | Google Scholar

McComas, D. J., Bame, S. J., Barraclough, B. L., Donart, J. R., Elphic, R. C., Gosling, J. T., et al. (1993). Magnetospheric plasma analyzer: Initial three-spacecraft observations from geosynchronous orbit. J. Geophys. Res. 98, 13453–13465. doi:10.1029/93JA00726

CrossRef Full Text | Google Scholar

McDowell, J. C. (2020). The low Earth orbit satellite population and impacts of the SpaceX starlink constellation. Astrohpysical J. Lett. 892 (2), L36–L10. doi:10.3847/2041-8213/ab8016

CrossRef Full Text | Google Scholar

McFadden, J. P., Carlson, C. W., Larson, D., Ludlam, M., Abiad, R., Elliot, B., et al. (2008). The THEMIS ESA plasma instrument and in-flight calibration. Space Sci. Rev. 141, 277–302. doi:10.1007/s11214-008-9440-2

CrossRef Full Text | Google Scholar

Meierbachtol, C. S., Svyatskiy, D., Delzanno, G. L., Vernon, L. J., and Moulton, J. D. (2017). An electrostatic particle-in-cell code on multi-block structured meshes. J. Comput. Phys. 350, 796–823. doi:10.1016/j.jcp.2017.09.016

CrossRef Full Text | Google Scholar

Melander, B. G., and Parks, G. K. (1981). The effects of cold plasma on the kelvin-helmholtz instability. J. Geophys. Res. 86 (A6), 4697–4707. doi:10.1029/JA086iA06p04697

CrossRef Full Text | Google Scholar

Miyosh, Y., Oyama, S., Saito, S., Kurita, S., Fujiwara, H., Kataoka, R., et al. (2015). Energeticelectron precipitation associated withpulsating aurora: EISCAT and van AllenProbe observations. J. Geophys. Res. Space Phys. 120, 2754–2766. doi:10.1002/2014JA020690

CrossRef Full Text | Google Scholar

Möbius, E., Tang, L., Kistler, L. M., Popecki, M., Lund, E. J., Klumpar, D., et al. (1998). Species dependent energies in upward directed ion beams over auroral arcs as observed with FAST TEAMS. Geophys. Res. Lett. 25, 2029–2032. doi:10.1029/98GL00381

CrossRef Full Text | Google Scholar

Moore, T. E., Chappell, C. R., Chandler, M. O., Craven, P. D., Giles, B. L., Pollock, C. J., et al. (1997). High-altitude observations of the polar wind. Science 277, 349–351. doi:10.1126/science.277.5324.349

CrossRef Full Text | Google Scholar

Moore, T. E., Chappell, C. R., Chandler, M. O., Fields, S. A., Pollock, C. J., Reasoner, D. L., et al. (1995). The thermal ion dynamics experiment and plasma source instrument. Space Sci. Rev. 71, 409–458. doi:10.1007/bf00751337

CrossRef Full Text | Google Scholar

Moore, T. E., Fok, M.-C., Chandler, M. O., Chappell, C. R., Christon, S. P., Delcourt, D. C., et al. (2005). Plasma sheet and (nonstorm) ring current formation from solar and polar wind sources. J. Geophys. Res. 110. doi:10.1029/2004JA010563

CrossRef Full Text | Google Scholar

Moore, T. E., Lundin, R., Alcayde, D., Andre, M., Ganguli, S. B., Temerin, M., et al. (1999b). Source processes in the high-latitute ionosphere. Space Sci. Rev. 88, 7–84. doi:10.1023/A:1005299616446

CrossRef Full Text | Google Scholar

Moore, T. E., Peterson, W. K., Russell, C. T., Chandler, M. O., Collier, M. R., Collin, H. L., et al. (1999a). Ionospheric mass ejection in response to a CME. Geophys. Res. Lett. 26, 2339–2342. doi:10.1029/1999GL900456

CrossRef Full Text | Google Scholar

Mott-Smith, H. M., and Langmuir, I. (1926). The theory of collectors in gaseous discharges. Phys. Rev. 28 (4), 727–763. doi:10.1103/PhysRev.28.727

CrossRef Full Text | Google Scholar

Mozer, F. S., Agapitov, O. A., Angelopoulos, V., Hull, A., Larson, D., Lejosne, S., et al. (2017). Extremelyfield-aligned cool electrons inthe dayside outer magnetosphere. Geophys. Res. Lett. 44, 44–51. doi:10.1002/2016GL072054

CrossRef Full Text | Google Scholar

Nakagawa, T., Ishii, T., Tsuruda, K., Hayakawa, H., and Mukai, T. (2000). Net current density of photoelectrons emitted from the surface of the GEOTAIL spacecraft. Earth, planets space 52 (4), 283–292. doi:10.1186/bf03351637

CrossRef Full Text | Google Scholar

Nordholt, J. E., Reisenfeld, D. B., Wiens, R. C., Gary, S. P., Crary, F., Delapp, D. M., et al. (2003). Deep Space 1 encounter with Comet 19P/Borrelly: Ion compositionmeasurements by the PEPE mass spectrometer. Geophys. Res. Lett. 30 (9), 1465. doi:10.1029/2002GL016840

CrossRef Full Text | Google Scholar

Ogasawara, K., George, D. E., Goldstein, J., Hwang, K.-J., Nishimura, Y., Ruggles, D. A., et al. (2020). 3DI: A novel ion composition and three-dimensional velocity analyzer for the topside ionosphere. Sci. Rep. 10 (1), 7967–8013. doi:10.1038/s41598-020-64407-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Olsen, R. C. (1982). The hidden ion population of the magnetosphere. J. Geophys. Res. 87 (A5), 3481. doi:10.1029/JA087iA05p03481

CrossRef Full Text | Google Scholar

Parker, L. W., and Whipple, E. C. (1970). Theory of spacecraft sheath structure, potential, and velocity effects on ion measurements by traps and mass spectrometers. J. Geophys. Res. 75 (25), 4720–4733. doi:10.1029/JA075i025p04720

CrossRef Full Text | Google Scholar

Paschmann, G., Melzner, F., Frenzel, R., Vaith, H., Parigger, P., Pagel, U., et al. (1997). The electron drift instrument for cluster. Space Sci. Rev. 79, 233–269. doi:10.1023/A:1004917512774

CrossRef Full Text | Google Scholar

Pedersen, A., Lybekk, B., André, M., Eriksson, A., Masson, A., Mozer, F. S., et al. (2008). Electron density estimations derived from spacecraft potential measurements on Cluster in tenuous plasma regions. J. Geophys. Res. 113, A07S33. doi:10.1029/2007JA012636

CrossRef Full Text | Google Scholar

Persoon, A. M., Gurnett, D. A., and Shawhan, S. D. (1983). Polar cap electron densities from DE 1 plasma wave observations. J. Geophys. Res. 88, 10123–10136. doi:10.1029/ja088ia12p10123

CrossRef Full Text | Google Scholar

Pollock, C. J., Moore, T. E., Adrian, M. L., Kintner, P. M., and Arnoldy, R. L. (1996). Scifer - cleft region thermal electron distribution functions. Geophys. Res. Lett. 23 (14), 1881–1884. doi:10.1029/96GL01486

CrossRef Full Text | Google Scholar

Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast plasma investigation for magnetospheric Multiscale. Space Sci. Rev. 199, 331–406. doi:10.1007/s11214-016-0245-4

CrossRef Full Text | Google Scholar

Purvis, C. K., Garret, H. B., Whittlesey, A. C., and Stevens, N. J. (1984). Design guidelines for assessing and controlling spacecraft charging effects. United States: NASA. TP-2361.

Google Scholar

Radtke, J., Kebschull, C., and Stoll, E. (2017). Interactions of the space debris environment with mega constellations—using the example of the OneWeb constellation. Acta Astronaut. 131, 55–68. doi:10.1016/j.actaastro.2016.11.021

CrossRef Full Text | Google Scholar

Reeves, G. D., Chan, A. A., and Rodger, C. (2009). New directions for radiation belt research. Space weather. 7, S07004. doi:10.1029/2008sw000436

CrossRef Full Text | Google Scholar

Reme, H., Bosqued, J. M., Sauvaud, J. A., Cros, A., Dandouras, J., Aoustin, C., et al. (1997). The cluster ion Spectrometry (CIS) experiment. Space. Sci. Rev. 79, 303–350. doi:10.1023/a:1004929816409

CrossRef Full Text | Google Scholar

Riedler, W., Torkar, K., Rudenauer, F., Fehringer, M., Pedersen, A., Schmidt, R., et al. (1997). Active spacecraft potential control, in the cluster and phoenix missions. Space. Sci. Rev. 79, 271–302. doi:10.1023/A:1004921614592

CrossRef Full Text | Google Scholar

Roytershteyn, V., and Delzanno, G. L. (2021). Nonlinear coupling of whistler waves to oblique electrostatic turbulence enabled by cold plasma. Phys. Plasmas 28, 042903. doi:10.1063/5.0041838

CrossRef Full Text | Google Scholar

Russell, C. T., Holzer, R. E., and Smith, E. J. (1969). OGO 3 observations of ELF noise in the magnetosphere: 1. Spatial extent and frequency of occurrence. J. Geophys. Res. 74 (3), 755–777. doi:10.1029/JA074i003p00755

CrossRef Full Text | Google Scholar

Sandel, B. R., Broadfoot, A. L., Curtis, C. C., King, R. A., Stone, T. C., Hill, R. H., et al. (2000). “The extreme ultraviolet imager investigation for the image mission,” in The image mission. Editor J. L. Burch (Dordrecht: Springer), 197–242. doi:10.1007/978-94-011-4233-5_7

CrossRef Full Text | Google Scholar

Sarno-Smith, L. K., Larsen, B. A., Skoug, R. M., Liemohn, M. W., Breneman, A., Wygant, J. R., et al. (2016). Spacecraft surface charging within geosynchronous orbit observed by the Van Allen Probes. Space weather. 14, 151–164. doi:10.1002/2015SW001345

PubMed Abstract | CrossRef Full Text | Google Scholar

Scime, E. E., Phillips, J. L., and Bame, S. J. (1994). Effects of spacecraft potential on three-dimensional electron measurements in the solar wind. J. Geophys. Res. 99, 14769–14814. doi:10.1029/94JA00489

CrossRef Full Text | Google Scholar

Scudder, J. D., Cao, X., and Mozer, F. S. (2000). Photoemission current-spacecraft voltage relation: Key to routine, quantitative low-energy plasma measurements. J. Geophys. Res. Space Phys. 105 (A9), 21281–21294. doi:10.1029/1999ja900423

CrossRef Full Text | Google Scholar

Serbu, G., and Maier, E. (1970). Observations from OGO 5 of the thermal ion density and temperature within the magnetosphere. J. Geophys. Res. 75 (31), 6102–6113. doi:10.1029/JA075i031p06102

CrossRef Full Text | Google Scholar

Shelley, E. G., Johnson, R. G., and Sharp, R. D. (1972). Satellite observations of energetic heavy ions during a geomagnetic storm. J. Geophys. Res. 77, 6104–6110. doi:10.1029/JA077i031p06104

CrossRef Full Text | Google Scholar

Shukla, P. K., and Mamun, A. A. (2015). Introduction to dusty plasma physics. Florida, United States: CRC Press. doi:10.1201/9781420034103

CrossRef Full Text | Google Scholar

Singh, N., and Horowitz, J. L. (1992). Plasmasphere refilling: Recent observations and modeling. J. Geophys. Res. 97, 1049–1079. doi:10.1029/91JA02602

CrossRef Full Text | Google Scholar

Skoug, R. M., Gosling, J. T., McComas, D. J., Smith, C. W., and Hu, Q. (2006). Suprathermal electron 90° pitch angle depletions at reverse shocks in the solar wind. J. Geophys. Res. 111, A01101. doi:10.1029/2005ja011316

CrossRef Full Text | Google Scholar

Sojka, J. J., Wrenn, G. L., and Johnson, J. F. E. (1984). Pitch angle properties of magnetospheric thermal protons and satellite sheath interference in their observation. J. Geophys. Res. 89, 9801–9811. doi:10.1029/JA089iA11p09801

CrossRef Full Text | Google Scholar

Strangeway, R. J., Ergun, R. E., Su, Y.-J., Carlson, C. W., and Elphic, R. C. (2005). Factors controlling ionospheric outflows as observed at intermediate altitudes. J. Geophys. Res. Space Phys. 110, A03221. doi:10.1029/2004JA010829

CrossRef Full Text | Google Scholar

Su, Y. J., Horowitz, J. L., Moore, T. E., Giles, B. L., Chandler, M. O., Craven, P. D., et al. (1998). Polar wind survey with the thermal ion dynamics experiment/plasma source instrument suite aboard POLAR. J. Geophys. Res. 103, 29305–29337. doi:10.1029/98JA02662

CrossRef Full Text | Google Scholar

Summers, D., Ni, B., and Meredith, N. P. (2007). Timescales for radiation belt electron acceleration and loss due to resonant wave-particle interactions: 2. Evaluation for VLF chorus, ELF hiss, and electromagnetic ion cyclotron waves. J. Geophys. Res. 112, A04207. doi:10.1029/2006JA011993

CrossRef Full Text | Google Scholar

Szita, S., Fazakerley, A. N., Carter, P. J., James, A. M., Travnicek, P., Watson, G., et al. (2001). Cluster PEACE observations of electrons of spacecraft origin. Ann. Geophys. 19, 1721–1730. doi:10.5194/angeo-19-1721-2001

CrossRef Full Text | Google Scholar

Takahashi, K., Denton, R. E., Hirahara, M., Min, K., Ohtani, S., and Sanchez, E. (2014). Solar cycle variation of plasma mass density in the outer magnetosphere: Magnetoseismic analysis of toroidal standing Alfvén waves detected by Geotail. J. Geophys. Res. Space Phys. 119, 8338–8356. doi:10.1002/2014JA020274

CrossRef Full Text | Google Scholar

Tam, S. W. Y., Yasseen, F., and Chang, T. (1998). Further development in theory/data closure of the photoelectron-driven polar wind and day-night transition of the outflow. Ann. Geophys. 16, 948–968. doi:10.1007/s00585-998-0948-2

CrossRef Full Text | Google Scholar

Thiebault, B., Hilgers, A., Masson, A., Escoubet, C. P., and Laakso, H. (2006). Simulation of the Cluster-spacecraft floating probe potential. IEEE Trans. Plasma Sci. 34 (5), 2078–2083. doi:10.1109/TPS.2006.883407

CrossRef Full Text | Google Scholar

Thomsen, M. F., Denton, M. H., Lauvraud, B., and Bodeau, M. (2007). Statistics of plasma fluxes at geosynchronous orbit over more than a full solar cycle. Space weather. 5, S03004. doi:10.1029/2006SW000257

CrossRef Full Text | Google Scholar

Thomsen, M. F., Henderson, M. G., and Jordanova, V. (2013). Statistical properties of the surface-charging environment at geosynchronous orbit. Space weather. 11, 237–244. doi:10.1002/swe.20049

CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation belt dynamics: The importance of wave-particle interactions. Geophys. Res. Lett. 37, L22107. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar

Toledo-Redondo, S., André, M., Aunai, N., Chappell, C. R., Dargent, J., Fuselier, S. A., et al. (2021). Impacts of ionospheric ions on magnetic reconnection and Earth's magnetosphere dynamics. Rev. Geophys. 59 (3). doi:10.1029/2020RG000707

CrossRef Full Text | Google Scholar

Toledo-Redondo, S., Lavraud, B., Fuselier, S. A., André, M., Khotyaintsev, Y. V., Nakamura, N., et al. (2019). Electrostatic spacecraft potential structure and WakeFormation effects for characterization of cold IonBeams in the earth's magnetosphere. J. Geophys. Space Phys. 124 (10), 10048–10062. doi:10.1029/2019JA027145

CrossRef Full Text | Google Scholar

Torkar, K., Nakamura, R., Tajmar, M., Scharlemann, C., Jeszenszky, H., Laky, G., et al. (2016). Active spacecraft potential control investigation. Space. Sci. Rev. 199, 515–544. doi:10.1007/s11214-014-0049-3

CrossRef Full Text | Google Scholar

Tournear, D. (2020). “Future directions: Delivering capabilities,” in Proceedings of the Small Satellite Conference, SSC20-IV-02, Logan, UT, August 5-10, 2023 (AIAA/USU), 1–13.

Google Scholar

Turner, D. L., Angelopoulos, V., Li, W., Bortnik, J., Ni, B., Ma, Q., et al. (2014). Competingsource and loss mechanisms due to wave-particle interactions in Earth’s outer radiation belt during the 30 September to 3 October 2012 geomagnetic storm. J. Geophys. Res. Space Phys. 119, 1960–1979. doi:10.1002/2014JA019770

CrossRef Full Text | Google Scholar

Walsh, B. M., Hull, A. J., Agapitov, O., Mozer, F. S., and Li, H. (2020). A census of magnetospheric electrons from several eV to 30 keV. J. Geophys. Res. Space Phys. 125, e2019JA02757. doi:10.1029/2019JA027577

CrossRef Full Text | Google Scholar

Wang, C.-P., Gkioulidou, M., Lyons, L. R., and Angelopoulos, V. (2012). Spatial distributions of the ion to electron temperature ratio in the magnetosheath and plasma sheet. J. Geophys. Res. Space Phys. 117, A08215. doi:10.1029/2012JA017658

CrossRef Full Text | Google Scholar

Welling, D. T., Andre, M., Dandouras, I., Delcourt, D., Fazakerley, A., Fontaine, D., et al. (2015). The Earth: Plasma sources, losses, and transport processes. Space Sci. Rev. 192, 145–208. doi:10.1007/s11214-015-0187-2

CrossRef Full Text | Google Scholar

Yamauchi, M. (2019). Terrestrial ion escape and relevant circulation in space. Ann. Geophys. 37, 1197–1222. doi:10.5194/angeo-37-1197-2019

CrossRef Full Text | Google Scholar

Yau, A. W., and Andre, M. (1997). Sources of ion outflow in the high latitude ionosphere. Space Sci. Rev. 80, 1–25. doi:10.1023/A:1004947203046

CrossRef Full Text | Google Scholar

Yau, A. W., Shelley, E. G., Peterson, W. K., and Lenchyshyn, L. (1985). Energetic auroral and polar ion outflow at DE 1 altitudes: Magnitude, composition, magnetic activity dependence, and long-term variations. J. Geophys. Res. Space Phys. 90, 8417–8432. doi:10.1029/JA090iA09p08417

CrossRef Full Text | Google Scholar

Young, D. T., Burch, J. L., Gomez, R. G., De Los Santos, A., Miller, G. P., Wilson IV, P., et al. (2016). Hot plasma composition analyzer for the magnetospheric multiscale mission. Space. Sci. Rev. 199, 407–470. doi:10.1007/s11214-014-0119-6

CrossRef Full Text | Google Scholar

Young, D. T. (1998). “Space plasma particle instrumentation and the new paradigm: Faster, cheaper, better,” in Measurement techniques in space plasmas: Particles. Editors R. F. Pfaff, J. E. Borovsky, and D. T. Young (D.C., United States: American Geophysical Union), 102, 1–16.

Google Scholar

Yuan, Z., Xiong, Y., Huang, S., Deng, X., Pang, Y., Zhou, M., et al. (2014). Cold electron heating by EMIC waves in the plasmaspheric plume with observations of the Cluster satellite. Geophys. Res. Lett. 41, 1830–1837. doi:10.1002/2014GL059241

CrossRef Full Text | Google Scholar

Yue, C., Bortnik, J., LiMa, W. Q., Gkioulidou, M., Reeves, G. D., Wang, C.-P., et al. (2018). The composition of plasmainside geostationary orbit based on VanAllen Probes observations. J. ofGeophysical Res. Space Phys. 123, 6478–6493. doi:10.1029/2018JA025344

CrossRef Full Text | Google Scholar

Zhao, H., Li, X., Baker, D. N., Fennell, J. F., Blake, J. B., Larsen, B. A., et al. (2015). The evolution of ring current ion energy density and energy content during geomagnetic storms based on Van Allen Probes measurements. J. Geophys. Res. Space Phys. 120, 7493–7511. doi:10.1002/2015JA021533

CrossRef Full Text | Google Scholar

Zhou, Q., Xiao, F., Yang, C., He, Y., and Tang, L. (2013). Observation and modeling of magnetospheric cold electron heating by electromagnetic ion cyclotron waves. J. Geophys. Res. Space Phys. 118, 6907–6914. doi:10.1002/2013JA019263

CrossRef Full Text | Google Scholar

Zurbuchen, T. H., Fisk, L. A., Gloeckler, G., and von Steiger, R. (2002). The solar wind composition throughout the solar cycle: A continuum of dynamic states. Geophys. Res. Lett. 29 (9), 66-1–66-4. doi:10.1029/2001GL013946

CrossRef Full Text | Google Scholar

Zurbuchen, T. H., and Gershman, D. J. (2016). Innovations in plasma sensors. J. Geophys. Res. Space Phys. 121, 2891–2901. doi:10.1002/2016JA022493

CrossRef Full Text | Google Scholar