
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
PERSPECTIVE article
Front. Astron. Space Sci. , 19 January 2022
Sec. Astrochemistry
Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.814384
This article is part of the Research Topic Horizons in Astronomy and Astrophysics View all 6 articles
The investigation of reaction mechanisms in the interstellar medium requires the evaluation of reaction rates and branching ratios, which can be effectively obtained in the framework of the ab-initio transition state/master equation formalism. However, the reliability of this approach relies on the computation of accurate reaction enthalpies and activation energies for all the paths characterizing the potential energy surface under investigation. Two effective yet reliable parameter-free model chemistries are introduced to obtain accurate energies of all stationary points, with structural determination performed using double-hybrid density functionals. After their validation, these model chemistries have been employed to analyze the competition between hydrogen abstraction and addition/elimination in the reaction between the CN radical and ethylene or methanimine. The energetics has then been complemented by a kinetic study. The results provide new information about important reactive channels operative in different regions of the interstellar medium and in the atmospheres of exoplanets. These further extend the recent general addition/elimination mechanism for the formation of “complex imines” from the reaction of methanimine with a small radical species.
For many years, the interstellar medium (ISM) was believed to be a highly inhospitable place to host organic molecules, in particular those with a prebiotic character. This thought, however, changed about 80 years ago with the identification of optical absorption lines of CN and CH (Swings and Rosenfeld, 1937). Later on, the discovery of the hydroxyl radical in the radio absorption spectrum of Cassiopeia A (Weinreb et al., 1963) together with the detection, in 1968, of ammonia by Townes and co-workers toward the center of our galaxy via its inversion transitions (Townes, 2006), witnessed the birth of astrochemistry. Since then, about 250 molecules have been detected in the ISM or circumstellar shells and nearly 70 molecules have been observed in extragalactic sources (McGuire, 2018; Müller, 2021).
Most of our understanding about the composition of the interstellar medium and planetary atmospheres comes from spectroscopic observations, with rotational spectroscopy playing a pivotal role, also owing to the unprecedented resolution and sensitivity of modern interferometric observatories such as the Atacama Large Millimeter/submillimeter Array (ALMA). Among the species unequivocally detected in the ISM, the so-called “interstellar complex organic molecules” [iCOMS; (Herbst and van Dishoeck, 2009)] and, in particular, those with a strong prebiotic character, have attracted a great interest as they can represent the bridge between the matter in the Universe and living entities. In this respect, two alternative theories have been suggested for the emergence of life on Earth: the endogenous synthesis and the exogenous delivery (Figure 1). In the former, prebiotic molecules were synthesized directly on our planet starting from simple, inorganic precursors (e.g., NH3, HCN, H2CO), water and some energy source. In the alternative theory, prebiotic matter is postulated to have come from space on asteroids, comets and meteorites. To prove the reliability of this latter theory, it is crucial, on the one side, to have a complete census of the molecules populating the ISM and, on the other side, to understand how they could have been synthesized in the harsh interstellar conditions. Indeed, the ISM is characterized by extremely low temperatures and density together with energetic and ionizing radiation. As stressed by Figure 1, the molecular complexity is strongly related to the stage of the life circle of a star.
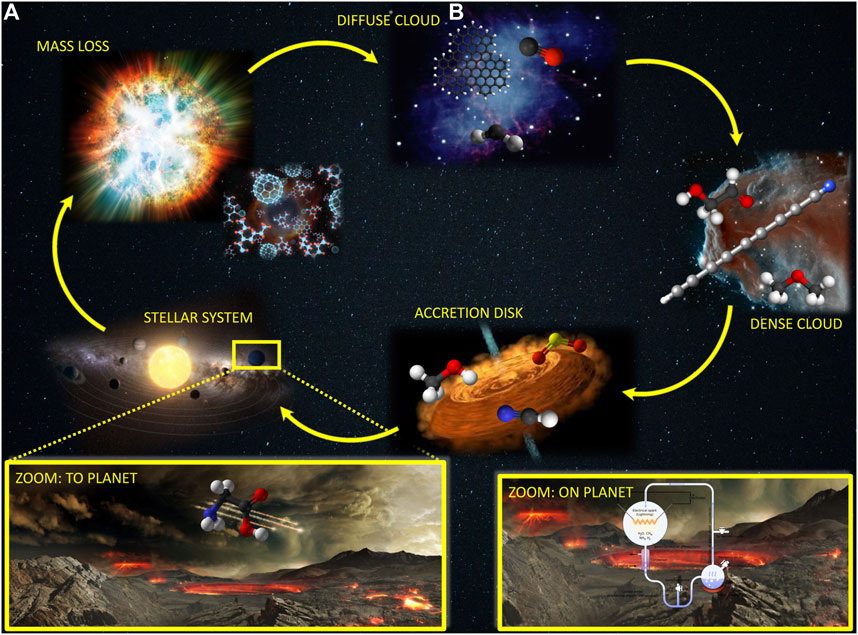
FIGURE 1. Life circle of a star and the corresponding molecular complexity. In the insets: The delivery of pre-biological molecules to Earth (A) and their synthesis in the early Earth (B).
Interstellar synthesis can occur according to two paradigms that conceive reactions taking place in the gas phase or on the surface of icy dust particles, with the focus of the present paper being on the first alternative. For modeling the complex network of elementary reactions occurring in astronomical objects, a large number of physical-chemical parameters (activation energies, reaction enthalpies and barriers, rate constants, …) is required. However, only a small fraction of the elementary reactions has been characterized in laboratory experiments under conditions mimicking the real ones, a major issue being the difficulty to reproduce the extreme interstellar environments. For this reason, accurate state-of-the-art computational approaches play a fundamental role in studying unstable species and analyzing feasible reaction mechanisms (Karton et al., 2006; Zheng et al., 2009; Puzzarini and Barone, 2020; Puzzarini et al., 2020; García de la Concepción et al., 2021b). In several cases, static correlation, non-adiabatic contributions, and/or quantum dynamical effects must be taken in consideration. However, an accurate description of single-reference adiabatic processes in the framework of transition state theory, also including tunneling, represents a mandatory prerequisite for any further improvement. On these grounds, in the present contribution, we present our recent efforts devoted to the development of effective yet reliable parameter-free model chemistries (Alessandrini et al., 2020; Barone et al., 2021) for the accurate computation of reactive potential energy surfaces. The paradigmatic case of radical additions to unsaturated targets will be considered as an application.
As suggested by Figure 1, the matter in the ISM is not uniformly distributed, but instead it is concentrated in clumps and filaments, the so-called interstellar clouds. From a molecular complexity point of view, molecular clouds (denoted as dense clouds in Figure 1) are those of interest. Their temperature is on average 10 K (with the exception of hot core regions where the temperature can reach 200 K) and the density ranges from 102 to 107 particles/cm3. These conditions put severe constraints on the reactivity taking place in the gas phase: except for cases where tunneling plays a dominant role [thus implying that hydrogen transfer is the rate determining step; Vazart et al. (2016); Blázquez et al. (2019); Ocaña et al. (2019); García de la Concepción et al. (2021a)], the entire reaction mechanism should occur at energy lower than that of the reactants, which implies submerged barriers. Therefore, only reactions with at least one reactive species (radical or ion) can occur, with their reaction rate being strongly dependent on the barrier heights. As a consequence, the energetics needs to be evaluated at high accuracy, with any potential error source being recovered at the best possible level.
The prerequisite of any accurate kinetic study is the characterization of all the stationary points (minima and transition states) of the reactive potential energy surface (PES) ruling the process under investigation. This step is conveniently performed using hybrid or double-hybrid density functionals that incorporate empirical dispersion corrections by means of the so-called D3 model combined with Becke-Johnson damping [D3BJ; (Grimme et al., 2010; Grimme, 2011)]. A preliminary investigation employing suitable hybrid density functionals [in our approach, B3LYP (Lee et al., 1988; Becke, 1993) or PW6B95 (Zhao and Truhlar, 2005)] in conjunction with (partially) augmented double-zeta basis sets [preferably jul-cc-pVDZ (Papajak et al., 2011)] is usually sufficient. Next, both geometries and energies are refined at a higher level. Concerning geometries, double-hybrid functionals in conjunction with (partially) augmented triple-zeta basis sets usually represent a remarkable compromise between accuracy and computational cost. In this connection, the B2PLYP-D3/maug-cc-pVTZ model (Grimme, 2006; Papajak et al., 2009) employed in our earlier studies has recently been replaced by the rev-DSD-PBEP86 functional (Santra et al., 2019) in conjunction with the jun-cc-pVTZ (Papajak et al., 2011) basis set (such a functional-basis combination is shortly denoted as rev-DSD in the following), which usually delivers improved results (with respect to the former) for transition states and non-covalent complexes without reducing the accuracy of other parameters. When more accurate geometries are sought (especially in connection with spectroscopic properties or inter-molecular distances of pre-reactive complexes), more accurate quantum-chemical approaches (vide infra) or a “LEGO bricks” approach can be employed (Ceselin et al., 2021; Melli et al., 2021).
The methodology presented in this work focuses on the energetics and implies that geometries are optimized using a double-hybrid density functional as explained above. The first model chemistry we address is the so-called ‘jun-Cheap’ scheme (Alessandrini et al., 2020; Lupi et al., 2021), which employs rev-DSD optimized geometries. While interested readers are referred to the specific literature for a complete account, here we briefly mention that it is based on the coupled-cluster (CC) singles, doubles and perturbative triples method [CCSD(T); (Raghavachari et al., 1989)] in conjunction with the jun-cc-pVTZ basis set [this implies that jun-cc-pV(T+d)Z is used for atoms of third period; (Papajak et al., 2011)]. To improve the fc-CCSD(T)/jun-cc-pVTZ level of theory, with fc standing for the frozen-core approximation, the extrapolation to the complete basis set limit (CBS) is performed and the core-valence correlation (CV) correction added. To reduce the computational cost of these two latter contributions, they are evaluated using Møller-Plesset perturbation theory to the second order [MP2; (Møller and Plesset, 1934)]. Within any ‘cheap’ scheme, as well tested in the literature (Lupi et al., 2020b; Alessandrini et al., 2021; Lupi et al., 2021), the MP2 energy is extrapolated using the n−3 formula proposed by Helgaker and coworkers (Helgaker et al., 1997). Overall, the jun-Cheap energy is given by the following expression:
where the first term on the right-hand side is the energy at the fc-CCSD(T)/jun-cc-pVTZ level. The second term is the contribution due to the MP2 extrapolation to the CBS limit, obtained –within the fc approximation– as follows:
where n = 4 (i.e., jun-cc-pVQZ and n-1 stands for jun-cc-pVTZ). Finally, the ΔE(MP2/CV) term is computed as energy difference between MP2 calculations correlating all electrons and within the fc approximation, both in the cc-p(w)CVTZ basis set (Woon and Dunning Jr., 1995; Peterson and Dunning Jr., 2002).
An alternative model (hereafter referred to as the jun-F12 scheme) replaces the conventional CCSD(T) method with its explicitly-correlated CCSD(T)-F12 counterpart (Knizia et al., 2009), still in conjunction with the jun-cc-pVTZ basis set. While the extrapolation to the CBS limit is avoided (because of the fast convergence of F12 methods), the CV correction is incorporated at the MP2-F12 level (Werner et al., 2007) employing the cc-p(w)CVTZ basis set (Woon and Dunning Jr., 1995; Peterson and Dunning Jr., 2002). In all CCSD(T)-F12 computations, the F12b approximation (Feller and Peterson, 2013) is employed, while the default approximation (3C with EBC) is used for MP2-F12. It has to be noted that a full F12 treatment of triple excitations is not yet available in commercial codes; thus, their contribution is essentially the same as in conventional CCSD(T).
To benchmark the performance of the two model chemistries introduced above, reference electronic energies are obtained by means of the so-called HEAT-like (HL) scheme, closely resembling the original HEAT methodology proposed by Stanton and co-workers (Tajti et al., 2004; Bomble et al., 2006; Harding et al., 2008; Lupi et al., 2020b), and entirely based on the CC ansatz. In this benchmark, the HL composite scheme is built on top of geometries optimized at the jun-Cheap level:
As evident from the formula above, HF and CCSD(T) correlation energies are extrapolated separately (differently from the jun-Cheap scheme). In particular, the HF CBS limit is estimated by using Feller exponential formula (Feller, 1992):
This is a three-point extrapolation expression used in conjunction with triple- quadruple-, and quintuple-zeta basis sets. Instead, the CBS limit of the CCSD(T) correlation energy is obtained using the two-point n−3 formula (see above, the discussion made for the jun-Cheap scheme) in combination with triple- and quadruple-zeta basis sets. The CV term is computed at the CCSD(T) level as energy difference, as described above. Higher-order terms in the CC expansion are also incorporated. These are the corrections due to the full treatment of triples, ΔEfT, and the perturbative treatment of quadruples, ΔEpQ, which are computed, within the fc approximation, as energy differences between CCSDT (Noga and Bartlett, 1987; Scuseria and Schaefer, 1988; Watts and Bartlett, 1990) and CCSD(T) and between CCSDT(Q) (Bomble et al., 2005; Kállay and Gauss, 2008) and CCSDT calculations employing the cc-pVTZ and cc-pVDZ basis sets, respectively. The last two terms are the diagonal Born-Oppenheimer correction, ΔEDBOC (Sellers and Pulay, 1984; Handy et al., 1986; Handy and Lee, 1996; Kutzelnigg, 1997), and the scalar relativistic contribution, ΔErel (Cowan and Griffin, 1976; Martin, 1983), which are computed at the HF-SCF/aug-cc-pVDZ and CCSD(T)/aug-cc-pCVDZ levels, respectively. If required, the effect of spin-orbit coupling is added to the electronic energies, mainly relying on the available experimental data (Moore, 1949).
A term not included in Eq. 3 is the zero-point energy (ZPE) correction. Within the harmonic approximation, this requires the evaluation of harmonic vibrational frequencies, which are computed at the same level of theory employed in the structural determinations. Indeed, this type of calculations is needed to check the nature of the stationary point under consideration, and in particular, for discriminating between minima and transition states. In this work, harmonic force-filed computations have been carried out at the rev-DSD level exploiting analytical second derivatives (Biczysko et al., 2010). The ZPE term can be improved by incorporating anharmonic corrections, which can be computed using hybrid or double-hybrid functionals within the generalized second-order vibrational perturbation theory [GVPT2; (Barone, 2005; Barone et al., 2014; Frisch et al., 2016)].
As far as technical details are concerned, all DFT, MP2 and single-point energy CCSD(T) computations are performed using the Gaussian program package (Frisch et al., 2016), while the CFOUR program (Stanton et al., 2016) is employed whenever geometry optimizations at the CCSD(T) level are needed as well as for relativistic and diagonal Born-Oppenheimer corrections. For explicitly-correlated calculations, the MOLPRO program (Werner et al., 2020) is used. Finally, CCSDT and CCSDT(Q) energy evaluations require the MRCC program (Kállay et al., 2018).
Global and channel-specific rate constants are computed solving the multi-well one-dimensional master equation using the chemically significant eigenvalues (CSEs) method within the Rice-Ramsperger-Kassel-Marcus (RRKM) approximation (Georgievskii et al., 2013). The collisional energy transfer probability is described using the exponential down model (Tardy and Rabinovitch, 1966) with a temperature dependent ΔEdown of 260 × (T/298)0.875 cm−1 in an argon gas bath. The ratio between the specific rate constant for each reaction product and the overall rate constant accounting for all products leads to the reaction branching ratios.
For channels ruled by a distinct saddle point, rate coefficients are determined using conventional transition state theory (TST) within the rigid-rotor harmonic-oscillator (RRHO) approximation (Fernández-Ramos et al., 2006), also incorporating tunneling and non-classical reflection effects by means of the Eckart model (Eckart, 1930). Instead, rate constants for barrierless elementary reactions (usually, the entrance channels) are evaluated employing the phase space theory [PST; (Hunter et al., 1993; Skouteris et al., 2018)] within the RRHO approximation. The isotropic attractive potential Veff entering the PST is described by a
To model the temperature dependence, the rate constants are evaluated at different temperatures and fitted using the three-parameter modified Arrhenius equation proposed by Kooij (Kooij, 1893; Laidler, 1996):
where A, n, and Ea are the fitting parameters, and R is the universal gas constant.
All kinetic computations presented in this manuscript have been performed with the MESS code (Georgievskii et al., 2013).
As mentioned above, reactions in the ISM require a reactive species, which is often an open-shell molecule. Unfortunately, these are challenging species and the presence of large spin contamination from higher spin states can strongly distort the reactive PESs described using unrestricted (U) methods (Sosa and Schlegel, 1986). For this reason, all the steps of the jun-Cheap and jun-F12 composite schemes are based on a spin-restricted treatment. It is well-known that the problem of spin contamination is strongly mitigated for DFT methods and this is especially true for double-hybrid density functionals due to an effective error compensation between the opposite deviations of UHF and UMP2 contributions (Menon and Radom, 2008). While DFT energies are not used in the present manuscript, spin contamination could affect the quality of rev-DSD gradients (used in geometry optimizations) and Hessians (for ZPE evaluations), whose restricted open-shell analytical implementation is still lacking. A systematic check of the spin contamination has shown that its effect is negligible for the systems considered in the following.
As a first benchmark, we focus our attention on the electronic energy contributions to reaction and activation energies employing as references the very accurate results of the well-known DBH24 database (Karton et al., 2008; Zheng et al., 2009), which contains results from state-of-the-art quantum-chemical approaches (estimated accuracy: 0.1–0.2 kJ/mol) for a statistically representative set of heavy atom transfer (NH), nucleophilic substitution (NS), unimolecular and association (UA) and hydrogen transfer (HT) reactions. Table 1 collects the reaction energies obtained at different levels. It is quite apparent that both the jun-F12 and jun-Cheap schemes fulfill the target of sub-chemical accuracy without the need of any empirical parameter. Furthermore, owing to the inclusion of the CV correlation contribution, the accuracy of the results for molecules containing third-row atoms is comparable to that of the first- and second-row-atom counterparts.
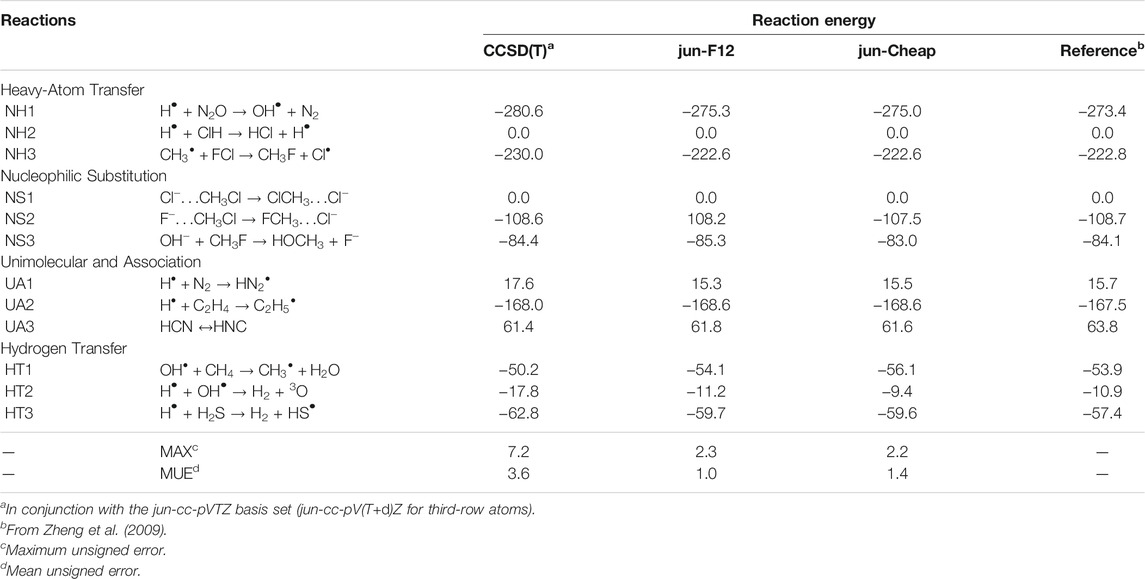
TABLE 1. Computed reaction energies for NH, NS, UA, and HT reactions from the DBH24/08 database at different levels of theory. All values are in kJ/mol.
From the inspection of Table 1 and, in particular, from the comparison of the first (fc-CCSD(T)/jun-cc-pVTZ) and the third (jun-Cheap) column, it is noted that the rather inexpensive MP2 estimate of the CBS and CV contributions reduces to about one third the deviation from the reference values. Moving from the jun-Cheap scheme to the jun-F12 model leads to a lowering of the mean unsigned error (MUE), while the maximum unsigned error (MAX) remains nearly unchanged. These results indicate that either the inclusion of an explicit correlation treatment or the extrapolation to the CBS limit at the MP2 level for conventional methods offer reliable routes for obtaining accurate reaction energies without any significant computational increase with respect to the underlying CCSD(T) step. In particular, already for reactions involving two non-hydrogen atoms, jun-Cheap computations require no more than twice the computer time of the CCSD(T) step. The effectiveness of the jun-Cheap model steeply increases with the dimension of the target system because of the favorable scaling of MP2, which can be further enhanced by the resolution of identity and other acceleration techniques. In the same vein, inclusion of explicit correlation through the F12 ansatz increases by 20–30% the computer time with respect to the standard CCSD(T) model employing the same basis set.
In Table 2, the energy barriers for the same DBH24 set as above, obtained at different levels of theory, are reported. It is remarkable that the errors associated to both the jun-F12 and jun-Cheap approaches only slightly increase with respect to those of the corresponding reaction energies, with MUEs of 1.2 and 1.5 kJ/mol and MAXs of 3.8 and 3.3 kJ/mol, respectively. This outcome paves the route toward the systematic use of the jun-F12 and jun-Cheap schemes in place of the widely used CCSD(T)/cc-pVTZ model with a remarkable increase of the accuracy, but without any significant increase of the computational cost. Furthermore, it has to be noted that the results are much improved with respect to those delivered by well-known (and largely employed) parametrized model chemistries such as CBS-QB3 (Montgomery et al., 1999) and G4 (Curtiss et al., 2007), whose MUEs are around 2.5 kJ/mol (Zheng et al., 2009). To put things in a wider perspective, we mention that the MUEs and MAXs of jun-F12 and jun-Cheap are close to those obtained employing larger basis sets, which in turn imply computational costs that might not be affordable for large systems. In detail, the MUE and MAX for CCSD(T)/aug-cc-pVQZ and CCSD(T)-F12/aug-cc-pVQZ are 1.2 and 4.1 kJ/mol and 1.1 and 2.5 kJ/mol, respectively (Zhang and Valeev, 2012).
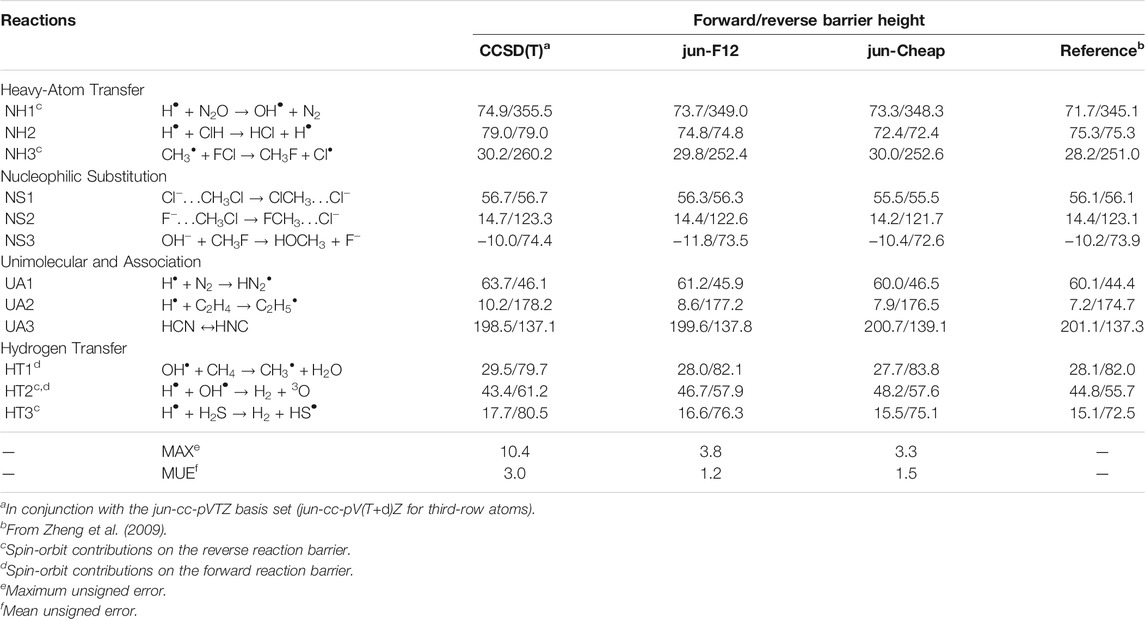
TABLE 2. Computed equilibrium barrier heights for NH, NS, UA and HT reactions from the DBH24/08 database at different levels of theory. All values are in kJ/mol.
Together with the accuracy of the electronic energies, also the quality of the geometrical structures employed in their evaluation can play a role in the final results (Puzzarini and Barone, 2018; Lupi et al., 2020b). The numerical evidence of this aspect has been investigated for the specific case of a radical attack to neutral molecules considering three extraction (Ex) and three addition (Add) reactions. The results are collected in Table 3. A re-optimization of the rev-DSD geometries at the jun-Cheap level has been performed. This slightly affects the energetic results, with differences within 0.6 kJ/mol, as evident in the ΔGeom column of Table 3. Therefore, rev-DSD structures can be safely employed in the evaluation of the energetics ruling astrochemical reactions.

TABLE 3. Computed equilibrium barrier heights for prototypical extraction and addition reactions: different contributions on top of the jun-Cheap approach. All values are in kJ/mol.
Another important issue to address is the effect of improved quantum-chemical treatments on the energetics and, for our discussion, we again resort to the “Ex” and “Add” reactions of Table 3. We note that the replacement of MP2 by CCSD(T) in both the extrapolation to the CBS limit and the evaluation of core-valence correlation (ΔCBS-CV) leads to very small discrepancies. The column ΔHL of Table 3 collects the differences arising from the incorporation of higher-order contributions in the coupled-cluster expansion (full treatment of triples and perturbative inclusion of quadruples) as well as the diagonal Born-Oppenheimer and relativistic corrections. As often noted in the literature (Puzzarini and Barone, 2020; Puzzarini et al., 2020), the sum of these contributions leads to a small corrective term, which is generally well within 1 kJ/mol. Overall, these results indicate that the jun-Cheap scheme is robust and very accurate, and that its improvement requires expensive calculations (and, often, it is not worth it). Furthermore, all the other contributions discussed above should be considered together because none of them plays a dominant role and all of them are rather small.
As already mentioned, electronic energies need to be corrected for the ZPE contributions in order to obtain the data to be used in the subsequent kinetic study. In Table 3 harmonic and anharmonic ZPE contributions to prototypical extraction and addition reactions are compared. As expected, these corrections are relevant, indeed ranging from a few kJ/mol to contributions as large as 19 kJ/mol. However it is noted that one can resort to harmonic ZPEs because the corresponding anharmonic corrections are well within 1 kJ/mol and can thus be safely neglected whenever –as in the present case– kJ/mol accuracy is sought.
However, further details on the vibrational frequencies determining ZPE corrections and also thermal effects (the latter via the vibrational partition functions) are deserved. At the harmonic level, several benchmark studies have shown that hybrid and, especially, double-hybrid functionals deliver quite reliable results, provided that empirical scaling factors (that should be different for ZPE and vibrational partition function) are employed (Kesharwani et al., 2015). Empirical parameters can be avoided by resorting to GVPT2 for small amplitude motions (Barone, 2005) together with a separate treatment of individual large amplitude motions, if any (Ayala and Schlegel, 1998). As an example of the accuracy reachable, a recent benchmark study for a database of 21 closed-shell molecules for which accurate reference values are available led to average errors of 0.2 kJ/mol and 0.2 cal/(mol K) for ZPE corrections and entropies, respectively (Barone et al., 2021). Experimental data are available only for a limited number of open-shell species, but the 10 small radicals investigated in Barone et al. (2021) suggest that a comparable accuracy can be obtained.
As a last comment, we address the impact of the level of theory on the computed reaction rates. To illustrate this, we consider the rate of the H• + CO reaction in the 50–4000 K temperature range, evaluated employing the CBS-QB3, jun-Cheap, jun-F12 and HEAT-like models. The results are graphically shown in Figure 2. From the inspection of this figure, the non-Arrhenius behavior of the reaction is apparent and the limits of the CBS-QB3 model at low temperatures (i.e., those of interest for astrochemical studies) are evident. Instead, the jun-Cheap, jun-F12 and HEAT-like results are very similar to each other in the whole temperature range and are similar to such an extent that only the jun-Cheap data are depicted in Figure 2, the jun-F12 and HEAT-like curves being indistinguishable from the jun-Cheap one at the scale of the figure. Finally, it is interesting to note that they are also in quantitative agreement with the available experimental data (Vichietti et al., 2020).
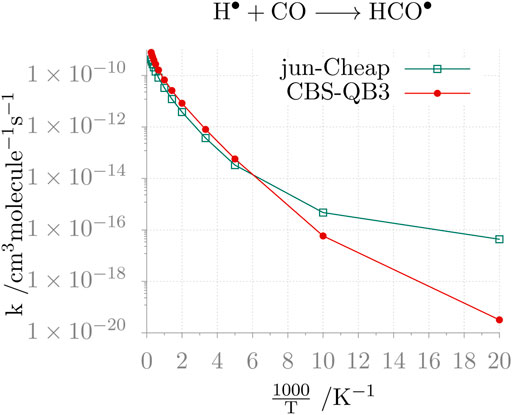
FIGURE 2. Temperature-dependence of the H• + CO reaction rate constant calculated at the jun-Cheap and CBS-QB3 levels.
The results discussed above give full support to the reliability of the jun-Cheap and jun-F12 computational models for studying reactions of astrochemical interest. Since the explicit correlation route (jun-F12) surely deserves further investigations, in the following we retain the jun-Cheap model. One of its advantages is that it can be accessed using a large panel of available computer codes.
Among the iCOMs, the species containing the -C ≡N moiety have a strong prebiotic character because they represent key intermediates toward the formation of biomolecule building blocks such as aminoacids and nucleobases. A large number of cyanides have been detected in the ISM (McGuire, 2018; Müller, 2021), and it has been demonstrated that they can be formed not only by reactions on dust-grain surfaces (Lovas et al., 2006; Krim et al., 2019), but also directly in the gas phase (Vazart et al., 2015; Tonolo et al., 2020; Lupi et al., 2020a). In the following, we focus on two specific cyano-compounds: acrylonitrile and cyanomethanimine. As it will be shown, they can be obtained by a general addition/elimination mechanism following the attack of the CN radical to the isoelectronic ethylene and methanimine molecules, respectively.
Figure 3 shows the stationary points ruling the addition of CN to ethylene. As far as the reaction mechanism is concerned, hydrogen abstraction could be in principle competitive with addition/elimination (Bowman et al., 2020). Both mechanisms start with the formation of the very stable intermediate 1 (Figure 3) and then proceed toward products through a number of steps. However, the transition state ruling hydrogen abstraction (leading to vinyl radical and HCN) lies above the reactants; therefore, this channel is closed in the ISM conditions and not shown in Figure 3. The only open channel leads to acrylonitrile (AN) and atomic hydrogen by either a one- or a two-step mechanism, with the former route being favored at low temperatures.
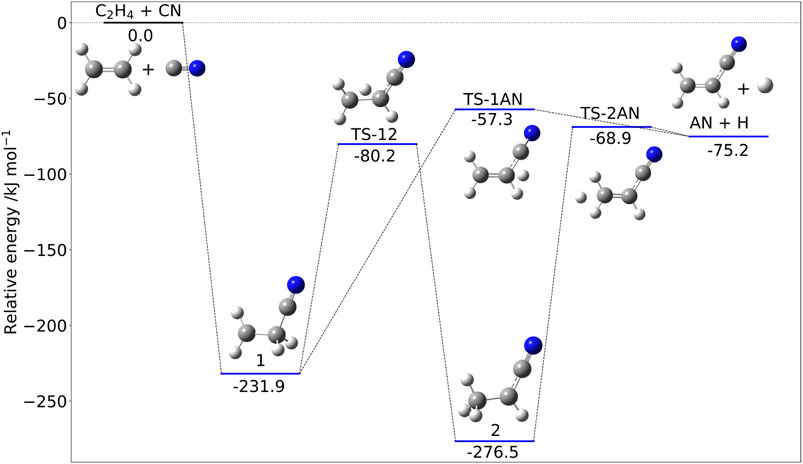
FIGURE 3. The C2H4 + CN reactive PES: Structures and relative jun-Cheap electronic energies (kJ/mol) of the stationary points ruling the addition/elimination channel.
The temperature dependence of the resulting rate constant is shown in Figure 4. It is apparent that, in the 30–300 K range, the rate coefficient varies a little (from 4×10−10 to 5.9 ×10−10 cm3molec−1 s−1) and follows the expected Arrhenius behavior. Furthermore, different electronic structure methods provide comparable results, as seen in the figure for the jun-Cheap and CBS-QB3 models.
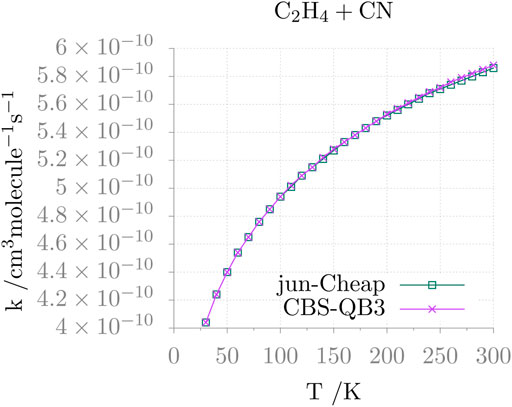
FIGURE 4. Rate constant as a function of the temperature (k(T)) for the C2H4 + CN addition reaction.
This reaction has been investigated with a variety of experimental techniques (Sims et al., 1993; Balucani et al., 2000; Leonori et al., 2012), which demonstrated that the reaction is very fast, approaching the gas-kinetics limit, also at very low temperatures and that the main reaction channel is the one leading to AN via an addition/elimination mechanism (Balucani et al., 2000). The computed reaction rate at low temperatures is in quantitative agreement with the experimental results by Sims et al. (1993). However, the experimental temperature dependence shows a rather surprising non-Arrhenius behavior, which leads, at room temperature, to a disagreement by a factor of 2 or more. While further investigations of this aspect is surely warranted [for instance, additional reaction channels should become open when increasing the temperature, as suggested by Leonori et al. (2012)], only the low-temperature region is of interest for astrochemical studies and, furthermore, a factor of 2 error on computed reaction rates is usually more than acceptable.
The situation is more involved for methanimine because of the presence of two possible attack sites: the C-atom and N-atom of CH2NH. Analogously to the C2H4 + CN reaction, the contribution of the abstration reaction is negligible, with test computations indicating that the corresponding rate constant is at least one order of magnitude smaller than that of the addition-elimination route. The addition/elimination mechanism is depicted in Figure 5, with the relative energies being computed at the jun-Cheap level. The comparison of these results with those recently obtained using an HEAT-like approach (Puzzarini and Barone, 2020) confirms the accuracy of the jun-Cheap model. The intermediate obtained upon attack to the N-side, 1N, is slightly more stable than those from the C-side attack, i.e., 1Z and 1E. However, the reaction channels originating from 1N are ruled by transition states significantly less stable (albeit submerged) than those issuing from 1Z or 1E.
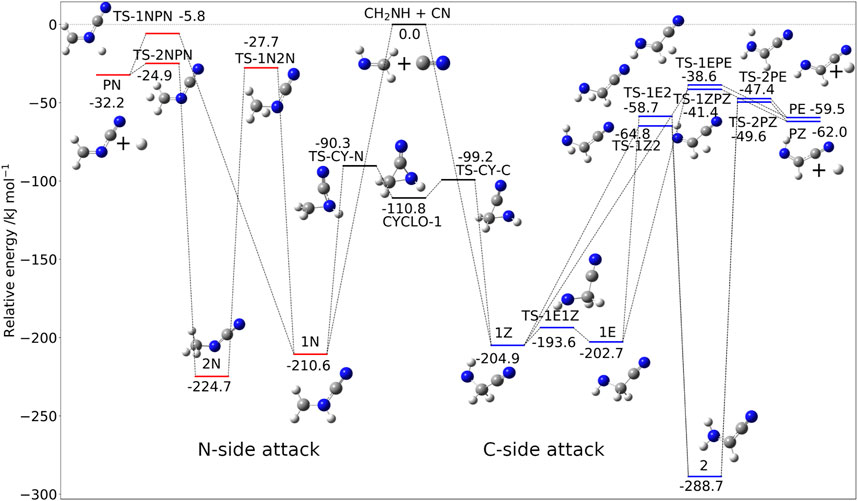
FIGURE 5. The CH2NH + CN reactive PES: Structures and relative jun-Cheap electronic energies (kJ/mol) of the stationary points ruling the addition/elimination channel.
Concerning the attack at the C-side, starting from the very stable 1Z (or 1E) pre-reactive complex, direct loss of a hydrogen atom, leading directly to the Z (or E) isomer of C-cyanomethanimine (C-CMIM), involves an exit barrier of 163.5 (or 164.1) kJ/mol. On the other hand, the stabilizing CN moiety on the carbon atom can promote hydrogen migration, which can lead to localize the unpaired electron on this atom. This migration is ruled by the transition state TS-1Z2 (TS-1E2 for the E form of C-CMIM) lying 140.1 kJ/mol above 1Z (144.0 kJ/mol above 1E for the E-route) and leads to 2, the most stable intermediate of the whole PES. Next, loss of hydrogen again leads to the Z (or E) form of C-CMIM and atomic hydrogen (denoted as PZ and PE in Figure 5) through the submerged transition state TS-2PZ (TS-2PE) lying about 49.6 kJ/mol (47.4 kJ/mol for the E route) below the reactants. As mentioned above, attack of the CN radical at the N-side of methanimine produces the very stable 1N intermediate from which two different paths can be followed in analogy with what is found for the C-side attack. While 1N is more stable than both 1Z and 1E, all the other stationary points of the N-side route are less stable than the C-route counterparts. The final product, i.e., N-cyanomethanimine (N-CMIM) + H (denoted as PN in Figure 5), is less stable than the products of the C-side attacks (PE or PZ) by about 30 kJ/mol.
Moving from thermochemistry to kinetics, the comparison between the jun-Cheap and CBS-QB3 rate constants and their temperature dependence is depicted in Figure 6 for the N-attack and in Figure 7 for the C-attack. From the inspection of these two figures, it is evident that the rate constant for the channel leading to N-CMIM is one order of magnitude smaller than those for the formation of the Z/E forms of C-CMIM. We also note that the discrepancies between jun-Cheap and CBS-QB3 results are significant (about a factor of 3–4). Focusing on the C-side attack, the prevalence of the PZ product over PE is due to the slightly lower energy barriers ruling the former path, with back-dissociation to reactants being always negligible. The overall rate constant for the formation of cyanomethanimine shows an increase with the temperature, which is accompanied by an increasing deviation from the Arrhenius behavior. At temperatures below 300 K, the value of the overall rate constant is determined by the faster one-step channel ruled by the TS-1ZPZ (TS-1EPE) transition state, while at higher temperatures the two-step mechanism starts to give non-negligible contributions.
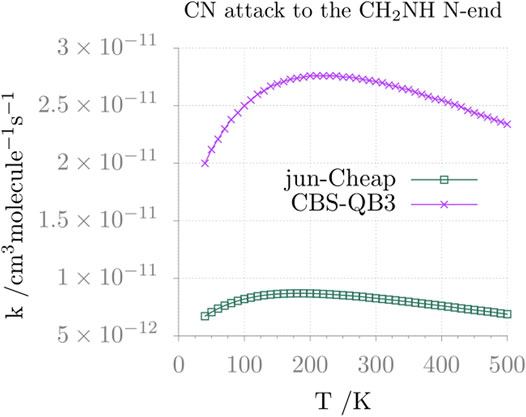
FIGURE 6. Reaction rate constant (and its temperature dependence) for the formation of N-cyanomethanimine (N-CMIM) upon CN attack at the N-side of methanimine.
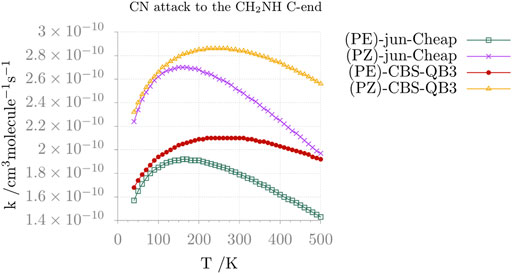
FIGURE 7. Reaction rate constants (and their temperature dependence) for the formation of Z and E C-CMIM upon CN attack at the C-side of methanimine.
The computed branching ratio (0.42/0.58) for the E and Z isomers at 150 K [the estimated temperature of G+0.693 where both isomers have been recently detected (Rivilla et al., 2018)] is much lower than the value of the abundance ratio derived from astronomical observations (which is about 6). While the observed ratio is close to that computed from a thermodynamic estimate based on the relative stability of the E and Z isomers (5.5), a fully satisfactory explanation of this puzzle requires the investigation of all possible destruction pathways for CMIM isomers and/or the demonstration that the thermodynamic equilibrium can be effectively established between the two isomers, even at low temperatures. Concerning the first issue, previous studies showed that all dissociation processes (also considering the cyclization to azirin-2-imine) require too much energy to occur in the ISM (Vazart et al., 2015). As regards the second issue, a recent study (García de la Concepción et al., 2021a) demonstrated that a multidimensional small curvature treatment of quantum-tunneling effects provides quite large (and nearly constant) inter-conversion rates, these being in the order of 10–11 sec−1 at temperatures between 10 and 150 K. Above the latter temperature, the contribution of tunneling becomes negligible with respect to thermal activation and the rate follows an Arrhenius behavior. The abundance ratio obtained when accounting for tunneling (6.0) is actually close to the value suggested by observations and to that computed from the thermodynamic equilibrium [provided that accurate energetics is used; see Puzzarini and Barone (2020)]. The situation being different for deuterated species for which the contribution of tunneling is always negligible, their astronomical observations would be of great interest and great help.
In this paper we have proposed and validated two parameter-free quantum-chemical models for the accurate study of the energetics underlying gas-phase formation routes in the interstellar medium for processes not showing strong multireference or non-adiabatic features. Comparison with state-of-the-art results for a number of model systems have convincingly shown that, starting from CCSD(T)/jun-cc-pVTZ energies evaluated on top of rev-DSD geometries, it is possible to reach kJ/mol accuracy following two different effective routes. The first alternative (jun-Cheap scheme) envisages the incorporation of two corrective terms, the CV correlation contribution and the extrapolation to the CBS limit, evaluated at the inexpensive MP2 level. The second option (jun-F12 model) employs the F12 ansatz to include explicit correlation, thus avoiding the extrapolation to the CBS limit, but still incorporating the CV correction. Next, it has been shown that accurate zero-point energies and thermal contributions can be effectively evaluated by the same rev-DSD model employed for geometry optimizations.
In the second part, the jun-Cheap scheme has been applied in the framework of the master equation/ab-initio transition state model to study the competition between abstraction and addition/elimination mechanisms in the reaction of the CN radical with ethylene and methanimine. The reaction rates obtained for these reactive systems are among the most accurate currently available (the most accurate for the C2H4 + CN system) and allow giving further support to a general model recently proposed for the formation of more complex imines in the interstellar medium (Lupi et al., 2020a).
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
This work has been supported by MIUR (Grant Number 2017A4XRCA) and by the Italian Space Agency (ASI; “Life in Space” project, N. 2019-3-U.0).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The SMART@SNS Laboratory is acknowledged for providing high-performance computing facilities.
Alessandrini, S., Barone, V., and Puzzarini, C. (2020). Extension of the "Cheap" Composite Approach to Noncovalent Interactions: The Jun-ChS Scheme. J. Chem. Theor. Comput. 16, 988–1006. doi:10.1021/acs.jctc.9b01037
Alessandrini, S., Tonolo, F., and Puzzarini, C. (2021). In Search of Phosphorus in Astronomical Environments: The Reaction between the CP Radical (X2Σ+) and Methanimine. J. Chem. Phys. 154, 054306. doi:10.1063/5.0038072
Ayala, P. Y., and Schlegel, H. B. (1998). Identification and Treatment of Internal Rotation in normal Mode Vibrational Analysis. J. Chem. Phys. 108, 2314–2325. doi:10.1063/1.475616
Balucani, N., Asvany, O., Chang, A. H. H., Lin, S. H., Lee, Y. T., Kaiser, R. I., et al. (2000). Crossed Beam Reaction of Cyano Radicals with Hydrocarbon Molecules. III. Chemical Dynamics of Vinylcyanide (C2H3CN;X1A′) Formation from Reaction of CN(X2Σ+) with Ethylene, C2H4(X1Ag). J. Chem. Phys. 113, 8643–8655. doi:10.1063/1.1289529
Barone, V. (2005). Anharmonic Vibrational Properties by a Fully Automated Second-Order Perturbative Approach. J. Chem. Phys. 122, 014108. doi:10.1063/1.1824881
Barone, V., Biczysko, M., and Bloino, J. (2014). Fully Anharmonic IR and Raman Spectra of Medium-Size Molecular Systems: Accuracy and Interpretation. Phys. Chem. Chem. Phys. 16, 1759–1787. doi:10.1039/c3cp53413h
Barone, V., Lupi, J., Salta, Z., and Tasinato, N. (2021). Development and Validation of a Parameter-free Model Chemistry for the Computation of Reliable Reaction Rates. J. Chem. Theor. Comput. 17, 4913–4928. doi:10.1021/acs.jctc.1c00406
Becke, A. D. (1993). Density‐functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 98, 5648–5652. doi:10.1063/1.464913
Biczysko, M., Panek, P., Scalmani, G., Bloino, J., and Barone, V. (2010). Harmonic and Anharmonic Vibrational Frequency Calculations with the Double-Hybrid B2PLYP Method: Analytic Second Derivatives and Benchmark Studies. J. Chem. Theor. Comput. 6, 2115–2125. doi:10.1021/ct100212p
Blázquez, S., González, D., García-Sáez, A., Antiñolo, M., Bergeat, A., Caralp, F., et al. (2019). Experimental and Theoretical Investigation on the OH + CH3C(O)CH3 Reaction at Interstellar Temperatures (T = 11.7-64.4 K). ACS Earth Space Chem. 3, 1873–1883. doi:10.1021/acsearthspacechem.9b00144
Bomble, Y. J., Stanton, J. F., Kállay, M., and Gauss, J. (2005). Coupled-cluster Methods Including Noniterative Corrections for Quadruple Excitations. J. Chem. Phys. 123, 054101. doi:10.1063/1.1950567
Bomble, Y. J., Vázquez, J., Kállay, M., Michauk, C., Szalay, P. G., Császár, A. G., et al. (2006). High-accuracy Extrapolated Ab Initio Thermochemistry. II. Minor Improvements to the Protocol and a Vital Simplification. J. Chem. Phys. 125, 064108. doi:10.1063/1.2206789
Bowman, M. C., Burke, A. D., Turney, J. M., and Schaefer, H. F. (2020). Conclusive Determination of Ethynyl Radical Hydrogen Abstraction Energetics and Kinetics*. Mol. Phys. 118, e1769214. doi:10.1080/00268976.2020.1769214
Ceselin, G., Barone, V., and Tasinato, N. (2021). Accurate Biomolecular Structures by the Nano-LEGO Approach: Pick the Bricks and Build Your Geometry. J. Chem. Theor. Comput. 17, 7290–7311. doi:10.1021/acs.jctc.1c00788
Cowan, R. D., and Griffin, D. C. (1976). Approximate Relativistic Corrections to Atomic Radial Wave Functions*. J. Opt. Soc. Am. 66, 1010. doi:10.1364/josa.66.001010
Curtiss, L. A., Redfern, P. C., and Raghavachari, K. (2007). Gaussian-4 Theory. J. Chem. Phys. 126, 084108. doi:10.1063/1.2436888
Eckart, C. (1930). The Penetration of a Potential Barrier by Electrons. Phys. Rev. 35, 1303–1309. doi:10.1103/physrev.35.1303
Feller, D. (1992). Application of Systematic Sequences of Wave Functions to the Water Dimer. J. Chem. Phys. 96, 6104–6114. doi:10.1063/1.462652
Feller, D., and Peterson, K. A. (2013). An Expanded Calibration Study of the Explicitly Correlated CCSD(T)-F12b Method Using Large Basis Set Standard CCSD(T) Atomization Energies. J. Chem. Phys. 139, 084110. doi:10.1063/1.4819125
Fernandez-Ramos, A., Miller, J. A., Klippenstein, S. J., and Truhlar, D. G. (2006). Modeling the Kinetics of Bimolecular Reactions. Chem. Rev. 106, 4518–4584. doi:10.1021/cr050205w
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16 Revision C.01. Wallingford CT: Gaussian Inc.
García de la Concepción, J., Jiménez-Serra, I., Corchado, J. C., Rivilla, V. M., and Martín-Pintado, J. (2021a). The Origin of the E/Z Isomer Ratio of Imines in the Interstellar Medium. Astrophys. J. Lett. 912, L6. doi:10.3847/2041-8213/abf650
García de la Concepción, J., Puzzarini, C., Barone, V., Jiménez-Serra, I., and Roncero, O. (2021b). Formation of Phosphorus Monoxide (PO) in the Interstellar Medium: Insights from Quantum-Chemical and Kinetic Calculations. Astrophys. J. Lett. 922, 169. doi:10.3847/1538-4357/ac1e94
Georgievskii, Y., Miller, J. A., Burke, M. P., and Klippenstein, S. J. (2013). Reformulation and Solution of the Master Equation for Multiple-Well Chemical Reactions. J. Phys. Chem. A. 117, 12146–12154. doi:10.1021/jp4060704
Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344
Grimme, S. (2011). Density Functional Theory with London Dispersion Corrections. Wires Comput. Mol. Sci. 1, 211–228. doi:10.1002/wcms.30
Grimme, S. (2006). Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys. 124, 034108. doi:10.1063/1.2148954
Handy, N. C., and Lee, A. M. (1996). The Adiabatic Approximation. Chem. Phys. Lett. 252, 425–430. doi:10.1016/0009-2614(96)00171-6
Handy, N. C., Yamaguchi, Y., and Schaefer, H. F. (1986). The diagonal Correction to the Born-Oppenheimer Approximation: Its Effect on the Singlet-Triplet Splitting of CH2 and Other Molecular Effects. J. Chem. Phys. 84, 4481–4484. doi:10.1063/1.450020
Harding, M. E., Vázquez, J., Ruscic, B., Wilson, A. K., Gauss, J., and Stanton, J. F. (2008). High-accuracy Extrapolated Ab Initio Thermochemistry. III. Additional Improvements and Overview. J. Chem. Phys. 128, 114111. doi:10.1063/1.2835612
Helgaker, T., Klopper, W., Koch, H., and Noga, J. (1997). Basis-set Convergence of Correlated Calculations on Water. J. Chem. Phys. 106, 9639–9646. doi:10.1063/1.473863
Herbst, E., and van Dishoeck, E. F. (2009). Complex Organic Interstellar Molecules. Annu. Rev. Astron. Astrophys. 47, 427–480. doi:10.1146/annurev-astro-082708-101654
Hunter, M., Reid, S. A., Robie, D. C., and Reisler, H. (1993). The Monoenergetic Unimolecular Reaction of Expansion‐cooled NO2: NO Product State Distributions at Excess Energies 0-3000 Cm−1. J. Chem. Phys. 99, 1093–1108. doi:10.1063/1.465408
Kállay, M., and Gauss, J. (2008). Approximate Treatment of Higher Excitations in Coupled-Cluster Theory. II. Extension to General Single-Determinant Reference Functions and Improved Approaches for the Canonical Hartree–Fock Case. J. Chem. Phys. 129, 144101. doi:10.1063/1.2988052
Kállay, M., Nagy, P. R., Rolik, Z., Mester, D., Samu, G., Csontos, J., et al. (2018). MRCC, a Quantum Chemical Program Suite. For the current version, see http://www.mrcc.hu.
Karton, A., Rabinovich, E., Martin, J. M. L., and Ruscic, B. (2006). W4 Theory for Computational Thermochemistry: In Pursuit of Confident Sub-kJ/mol Predictions. J. Chem. Phys. 125, 144108. doi:10.1063/1.2348881
Karton, A., Tarnopolsky, A., Lamère, J.-F., Schatz, G. C., and Martin, J. M. L. (2008). Highly Accurate First-Principles Benchmark Data Sets for the Parametrization and Validation of Density Functional and Other Approximate Methods. Derivation of a Robust, Generally Applicable, Double-Hybrid Functional for Thermochemistry and Thermochemical Kinetics. J. Phys. Chem. A. 112, 12868–12886. doi:10.1021/jp801805p
Kesharwani, M. K., Brauer, B., and Martin, J. M. L. (2015). Frequency and Zero-point Vibrational Energy Scale Factors for Double-Hybrid Density Functionals (And Other Selected Methods): Can Anharmonic Force fields Be Avoided. J. Phys. Chem. A. 119, 1701–1714. doi:10.1021/jp508422u
Knizia, G., Adler, T. B., and Werner, H.-J. (2009). Simplified CCSD(T)-F12 Methods: Theory and Benchmarks. J. Chem. Phys. 130, 054104. doi:10.1063/1.3054300
Kooij, D. M. (1893). Über die Zersetzung des gasförmigen Phosphorwasserstoffs. Zeitschr. Phys. Chem. 12U, 155–161. doi:10.1515/zpch-1893-1214
Krim, L., Guillemin, J.-C., and Woon, D. E. (2019). Formation of Methyl Ketenimine (CH3CH = C = NH) and Ethylcyanide (CH3CH2C≡N) Isomers through Successive Hydrogenations of Acrylonitrile (CH2 = CH − C≡N) under Interstellar Conditions: The Role of CH3C°H − C≡N Radical in the Activation of the Cyano Group Chemistry. MNRAS 485, 5210–5220. doi:10.1093/mnras/stz698
Kutzelnigg, W. (1997). The Adiabatic Approximation I. The Physical Background of the Born-Handy Ansatz. Mol. Phys. 90, 909–916. doi:10.1080/00268979709482675
Laidler, K. J. (1996). A Glossary of Terms Used in Chemical Kinetics, Including Reaction Dynamics (Iupac Recommendations 1996). Pure Appl. Chem. 68, 149–192. doi:10.1351/pac199668010149
Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 37, 785–789. doi:10.1103/physrevb.37.785
Leonori, F., Petrucci, R., Wang, X., Casavecchia, P., and Balucani, N. (2012). A Crossed Beam Study of the Reaction CN+C2H4 at a High Collision Energy: The Opening of a New Reaction Channel. Chem. Phys. Lett. 553, 1–5. doi:10.1016/j.cplett.2012.09.070
Lovas, F. J., Hollis, J. M., Remijan, A. J., and Jewell, P. R. (2006). Detection of Ketenimine (CH 2 CNH) in Sagittarius B2(N) Hot Cores. ApJ 645, L137–L140. doi:10.1086/506324
Lupi, J., Alessandrini, S., Puzzarini, C., and Barone, V. (2021). junChS and junChS-F12 Models: Parameter-free Efficient yet Accurate Composite Schemes for Energies and Structures of Noncovalent Complexes. J. Chem. Theor. Comput. 17, 6974–6992. doi:10.1021/acs.jctc.1c00869
Lupi, J., Puzzarini, C., and Barone, V. (2020a). Methanimine as a Key Precursor of Imines in the Interstellar Medium: The Case of Propargylimine. ApJ 903, L35. doi:10.3847/2041-8213/abc25c
Lupi, J., Puzzarini, C., Cavallotti, C., and Barone, V. (2020b). State-of-the-Art Quantum Chemistry Meets Variable Reaction Coordinate Transition State Theory to Solve the Puzzling Case of the H2S + Cl System. J. Chem. Theor. Comput. 16, 5090–5104. doi:10.1021/acs.jctc.0c00354
Martin, R. L. (1983). All-electron Relativistic Calculations on Silver Hydride. An Investigation of the Cowan-Griffin Operator in a Molecular Species. J. Phys. Chem. 87, 750–754. doi:10.1021/j100228a012
McGuire, B. A. (2018). 2018 Census of Interstellar, Circumstellar, Extragalactic, Protoplanetary Disk, and Exoplanetary Molecules. ApJS 239, 17. doi:10.3847/1538-4365/aae5d2
Melli, A., Tonolo, F., Barone, V., and Puzzarini, C. (2021). Extending the Applicability of the Semi-experimental Approach by Means of "Template Molecule" and "Linear Regression" Models on Top of DFT Computations. J. Phys. Chem. A. 125, 9904–9916. doi:10.1021/acs.jpca.1c07828
Menon, A. S., and Radom, L. (2008). Consequences of Spin Contamination in Unrestricted Calculations on Open-Shell Species: Effect of Hartree−Fock and Møller−Plesset Contributions in Hybrid and Double-Hybrid Density Functional Theory Approaches. J. Phys. Chem. A. 112, 13225–13230. doi:10.1021/jp803064k
Møller, C., and Plesset, M. S. (1934). Note on an Approximation Treatment for many-electron Systems. Phys. Rev. 46, 618–622.
Montgomery, J. A., Frisch, M. J., Ochterski, J. W., and Petersson, G. A. (1999). A Complete Basis Set Model Chemistry. VI. Use of Density Functional Geometries and Frequencies. J. Chem. Phys. 110, 2822–2827. doi:10.1063/1.477924
[Dataset] Müller, H. S. P. e. (2021). The Cologne Database for Molecular Spectroscopy: Molecules in Space. Available at: https://cdms.astro.uni-koeln.de/classic/molecules.
Noga, J., and Bartlett, R. J. (1987). The Full CCSDT Model for Molecular Electronic Structure. J. Chem. Phys. 86, 7041–7050. doi:10.1063/1.452353
Ocaña, A. J., Blázquez, S., Potapov, A., Ballestreros, B., Canosa, A., Antiñolo, M., et al. (2019). Gas-phase Reactivity of CH3OH toward Oh at Interstellar Temperatures (11.7-177.5 K): Experimental and Theoretical Study. Phys. Chem. Chem. Phys. 21, 6942–6957. doi:10.1039/c9cp00439d
Papajak, E., Leverentz, H. R., Zheng, J., and Truhlar, D. G. (2009). Efficient Diffuse Basis Sets: Cc-pVxZ+ and Maug-Cc-pVxZ. J. Chem. Theor. Comput. 5, 1197–1202. doi:10.1021/ct800575z
Papajak, E., Zheng, J., Xu, X., Leverentz, H. R., and Truhlar, D. G. (2011). Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theor. Comput. 7, 3027–3034. doi:10.1021/ct200106a
Peterson, K. A., and Dunning, T. H. (2002). Accurate Correlation Consistent Basis Sets for Molecular Core-Valence Correlation Effects: The Second Row Atoms Al-Ar, and the First Row Atoms B-Ne Revisited. J. Chem. Phys. 117, 10548–10560. doi:10.1063/1.1520138
Puzzarini, C., and Barone, V. (2018). Diving for Accurate Structures in the Ocean of Molecular Systems with the Help of Spectroscopy and Quantum Chemistry. Acc. Chem. Res. 51, 548–556. doi:10.1021/acs.accounts.7b00603
Puzzarini, C., and Barone, V. (2020). The Challenging Playground of Astrochemistry: an Integrated Rotational Spectroscopy - Quantum Chemistry Strategy. Phys. Chem. Chem. Phys. 22, 6507–6523. doi:10.1039/d0cp00561d
Puzzarini, C., Salta, Z., Tasinato, N., Lupi, J., Cavallotti, C., and Barone, V. (2020). A Twist on the Reaction of the CN Radical with Methylamine in the Interstellar Medium: New Hints from a State-Of-The-Art Quantum-Chemical Study. MNRAS 496, 4298–4310. doi:10.1093/mnras/staa1652
Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A Fifth-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 157, 479–483. doi:10.1016/s0009-2614(89)87395-6
Rivilla, V. M., Martín-Pintado, J., Jiménez-Serra, I., Zeng, S., Martín, S., Armijos-Abendaño, J., et al. (2018). Abundant Z-Cyanomethanimine in the Interstellar Medium: Paving the Way to the Synthesis of Adenine. MNRAS 483, L114–L119. doi:10.1093/mnrasl/sly228
Santra, G., Sylvetsky, N., and Martin, J. M. L. (2019). Minimally Empirical Double-Hybrid Functionals Trained against the GMTKN55 Database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A. 123, 5129–5143. doi:10.1021/acs.jpca.9b03157
Scuseria, G. E., and Schaefer, H. F. (1988). A New Implementation of the Full CCSDT Model for Molecular Electronic Structure. Chem. Phys. Lett. 152, 382–386. doi:10.1016/0009-2614(88)80110-6
Sellers, H., and Pulay, P. (1984). The Adiabatic Correction to Molecular Potential Surfaces in the SCF Approximation. Chem. Phys. Lett. 103, 463–465. doi:10.1016/0009-2614(84)85277-x
Sims, I. R., Queffelec, J.-L., Travers, D., Rowe, B. R., Herbert, L. B., Karthäuser, J., et al. (1993). Rate Constants for the Reactions of CN with Hydrocarbons at Low and Ultra-low Temperatures. Chem. Phys. Lett. 211, 461–468. doi:10.1016/0009-2614(93)87091-g
Skouteris, D., Balucani, N., Ceccarelli, C., Vazart, F., Puzzarini, C., Barone, V., et al. (2018). The Genealogical Tree of Ethanol: Gas-phase Formation of Glycolaldehyde, Acetic Acid, and Formic Acid. ApJ 854, 135. doi:10.3847/1538-4357/aaa41e
Sosa, C., and Bernhard Schlegel, H. (1986). Ab Initio calculations on the Barrier Height for the Hydrogen Addition to Ethylene and Formaldehyde. The Importance of Spin Projection. Int. J. Quan. Chem. 29, 1001–1015. doi:10.1002/qua.560290435
Stanton, J. F., Gauss, J., Harding, M. E., and Szalay, P. G. (2016). CFOUR. A Quantum Chemical Program Package. With contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, F. Engel, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, F. Lipparini, D. Matthews, T. Metzroth, L. A. Mück, D. P. O’Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de.
Swings, P., and Rosenfeld, L. (1937). Considerations Regarding Interstellar Molecules. ApJ 86, 483–486. doi:10.1086/143880
Tajti, A., Szalay, P. G., Császár, A. G., Kállay, M., Gauss, J., Valeev, E. F., et al. (2004). HEAT: High Accuracy Extrapolatedab Initiothermochemistry. J. Chem. Phys. 121, 11599–11613. doi:10.1063/1.1811608
Tardy, D. C., and Rabinovitch, B. S. (1966). Collisional Energy Transfer. Thermal Unimolecular Systems in the Low‐Pressure Region. J. Chem. Phys. 45, 3720–3730. doi:10.1063/1.1727392
Tonolo, F., Lupi, J., Puzzarini, C., and Barone, V. (2020). The Quest for a Plausible Formation Route of Formyl Cyanide in the Interstellar Medium: a State-Of-The-Art Quantum-Chemical and Kinetic Approach. ApJ 900, 85. doi:10.3847/1538-4357/aba628
Townes, C. H. (2006). The Discovery of Interstellar Water Vapor and Ammonia at the Hat Creek Radio Observatory. Astronomical Society of the Pacific Conference Series, Berkeley, California, September 9–10, 2005. Editors D. C. Backer, J. M. Moran, and J. L. Turner. San Francisco: Revealing the Molecular Universe: One Antenna is Never Enough 356, 81.
Vazart, F., Calderini, D., Puzzarini, C., Skouteris, D., and Barone, V. (2016). State-of-the-Art Thermochemical and Kinetic Computations for Astrochemical Complex Organic Molecules: Formamide Formation in Cold Interstellar Clouds as a Case Study. J. Chem. Theor. Comput. 12, 5385–5397. doi:10.1021/acs.jctc.6b00379
Vazart, F., Latouche, C., Skouteris, D., Balucani, N., and Barone, V. (2015). Cyanomethanimine Isomers in Cold Interstellar Clouds: Insights from Electronic Structure and Kinetic Calculations. ApJ 810, 111. doi:10.1088/0004-637x/810/2/111
Vichietti, R. M., Machado, F. B. C., and Haiduke, R. L. A. (2020). Accurate Rate Constants for the Forward and Reverse H + CO ↔ HCO Reactions at the High-Pressure Limit. ACS Omega 5, 23975–23982. doi:10.1021/acsomega.0c03267
Watts, J. D., and Bartlett, R. J. (1990). The Coupled‐cluster Single, Double, and Triple Excitation Model for Open‐shell Single Reference Functions. J. Chem. Phys. 93, 6104–6105. doi:10.1063/1.459002
Weinreb, S., Barrett, A. H., Meeks, M. L., and Henry, J. C. (1963). Radio Observations of OH in the Interstellar Medium. Nature 200, 829–831. doi:10.1038/200829a0
Werner, H.-J., Adler, T. B., and Manby, F. R. (2007). General Orbital Invariant MP2-F12 Theory. J. Chem. Phys. 126, 164102. doi:10.1063/1.2712434
Werner, H.-J., Knowles, P. J., Manby, F. R., Black, J. A., Doll, K., Hesselmann, A., et al. (2020). The Molpro Quantum Chemistry Package. J. Chem. Phys. 152, 144107. doi:10.1063/5.0005081
Woon, D. E., and Dunning, T. H. (1995). Gaussian Basis Sets for Use in Correlated Molecular Calculations. V. Core‐valence Basis Sets for boron through Neon. J. Chem. Phys. 103, 4572–4585. doi:10.1063/1.470645
Zhang, J., and Valeev, E. F. (2012). Prediction of Reaction Barriers and Thermochemical Properties with Explicitly Correlated Coupled-Cluster Methods: a Basis Set Assessment. J. Chem. Theor. Comput. 8, 3175–3186. doi:10.1021/ct3005547
Zhao, Y., and Truhlar, D. G. (2005). Design of Density Functionals that Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions. J. Phys. Chem. A. 109, 5656–5667. doi:10.1021/jp050536c
Keywords: complex organic molecules, formation mechanisms, reaction rates, quantum-chemical composite schemes, radical additions, interstellar medium
Citation: Barone V and Puzzarini C (2022) Toward Accurate Formation Routes of Complex Organic Molecules in the Interstellar Medium: The Paradigmatic Cases of Acrylonitrile and Cyanomethanimine. Front. Astron. Space Sci. 8:814384. doi: 10.3389/fspas.2021.814384
Received: 13 November 2021; Accepted: 21 December 2021;
Published: 19 January 2022.
Edited by:
Majdi Hochlaf, Université Paris Est Marne la Vallée, FranceReviewed by:
André Canosa, UMR6251 Institut de Physique de Rennes (IPR), FranceCopyright © 2022 Barone and Puzzarini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vincenzo Barone, dmluY2Vuem8uYmFyb25lQHNucy5pdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.