Diffusive Plasma Transport by the Magnetopause Kelvin-Helmholtz Instability During Southward IMF

At the Earth’s low-latitude magnetopause, the Kelvin-Helmholtz (KH) waves, which are driven by the super-Alfvénic velocity shear across the magnetopause, have been frequently observed during periods of northward interplanetary-magnetic-field (IMF) and believed to contribute to efficiently transporting the solar wind plasmas into the magnetosphere. On the other hand, during southward IMF periods, the signatures of the KH waves are much less frequently observed and how the KH waves contribute to the solar wind transport has not been well explored. Recently, the Magnetospheric Multiscale (MMS) mission successfully detected signatures of the KH waves near the dusk-flank of the magnetopause during southward IMF. In this study, we analyzed a series of two- and three-dimensional fully kinetic simulations modeling this MMS event. The results show that a turbulent evolution of the lower-hybrid drift instability (LHDI) near the low-density (magnetospheric) side of the edge layer of the KH waves rapidly disturbs the structure of the layer and causes an effective transport of plasmas across the layer. The obtained transport rate is comparable to or even larger than that predicted for the northward IMF. These results indicate that the diffusive solar wind transport induced by the KH waves may be active at the flank-to-tail magnetopause during southward IMF.

Introduction

The Kelvin-Helmholtz instability (KHI) becomes unstable when the plasma shear flow is super-Alfvénic with respect to the Alfvén speed based on the magnetic field component parallel to the shear flow (Chandrasekhar, 1961). At the Earth’s low-latitude magnetopause, this condition is easily satisfied when the interplanetary-magnetic-field (IMF) is strongly northward or southward. Indeed, clear signatures of surface waves and flow vortices, which could be generated by the KHI, have been frequently observed around the magnetopause during periods of strongly northward IMF (e.g., Sckopke et al., 1981; Kokubun et al., 1994; Kivelson and Chen, 1995; Fairfield et al., 2000; Slinker et al., 2003; Hasegawa et al., 2004; Hasegawa et al., 2006; Foullon et al., 2008; Kavosi and Raeder, 2015; Moore et al., 2016). High-time-resolution fields and plasma data collected by the recently-launched Magnetospheric Multiscale (MMS) mission (Burch et al., 2016) further demonstrated the evolution of small-scale processes within the observed KH waves and vortices, such as the vortex-induced reconnection (VIR), during strong northward IMF (Eriksson et al., 2016a; Eriksson et al., 2016b; Li et al., 2016; Vernisse et al., 2016; Stawarz et al., 2016; Tang et al., 2018; Hasegawa et al., 2020; Hwang et al., 2020; Kieokaew et al., 2020). 2-D and 3-D fully kinetic simulations of these northward IMF MMS events showed that the VIR can cause very efficient solar wind transport into the magnetosphere along the low-latitude magnetopause (e.g., Nakamura et al., 2017a; Nakamura et al., 2017b, Nakamura et al., 2020, Nakamura, 2021). Given that the simulated VIR signatures are reasonably consistent with many of the observation signatures, these studies indicated that the KHI and subsequent occurrence of the VIR would indeed contribute to efficient solar wind transport across the magnetopause during northward IMF.

On the other hand, the signatures of the magnetopause KH waves and vortices have been much less frequently observed during southward IMF (Kavosi and Raeder, 2015). Hwang et al. (2011) reported a Cluster observation event of non-linear KH vortices during a strong southward IMF period. In this Cluster event, observed plasma and field variations were irregular and temporally intermittent, indicating that the structure of the KH vortices was being distorted during this event. More recently, Blasl et al. (2022) (hereafter referred to as B22) reported the first MMS observation of the KH waves during southward IMF. In this MMS event, the observed surface waves, which can be interpreted as being formed by the KHI, also consisted of the intermittent and irregular variations as seen in the above Cluster event. Although clear VIR signatures as reported for the northward IMF were not found in this southward IMF event, the high-time-resolution MMS measurements detected small-scale fluctuations, which can be interpreted as being generated by the lower-hybrid drift instability (LHDI), near the edge of the surface waves (B22).

To investigate this southward IMF MMS event in more detail, in Nakamura et al. (2022) (hereafter referred to as N22), we performed a series of 2-D and 3-D fully kinetic simulations with parameters matched to this event. The simulation results are consistent with the observations in terms of both large-scale surface wave signatures and small-scale LHDI fluctuations. The simulations also demonstrated that reconnection locally occurs within the LHDI turbulence, but does not develop at the larger-scale that coherently changes the connectivity of the magnetic field lines on the two sides across the magnetopause, as seen in the simulations of the VIR for the above northward IMF cases. The simulations further demonstrated that the primary KH waves induce the secondary Rayleigh-Taylor instability (RTI) at the surface bent by the KHI. The RTI forms high-density arms penetrating into the low-density (magnetospheric) side. This arm penetration quickly distorts the primary KH wave structures and produces intermittent and irregular variations of the surface waves, leading to a reduction in the observational probability of the primary KH waves. Interestingly, this RTI-related reduction of the observational probability of the KH waves proceeds faster than the VIR-related reduction in the aforementioned northward IMF cases, indicating that the secondary RTI may be a key process that makes it more difficult to detect the KH waves during southward IMF (see B22 and N22 for more details of these initial results of this MMS event).

Based on these previous studies, in this paper, we revisited the 2-D and 3-D simulations of the southward IMF MMS event shown in B22 and N22, with a special focus on the mass and energy transfer process caused by the LHDI turbulence and additional, microscopic magnetic reconnection induced within the turbulence. The obtained mixing and transport rates are comparable to or even larger than the ones previously obtained in the northward IMF cases, indicating that the KHI and the resulting LHDI turbulence may actively contribute to the solar wind transport into the Earth’s magnetosphere during southward IMF.

Methods

We analyze the simulations that were initially presented by N22, which model the southward IMF MMS event introduced in B22. The simulations were performed on MareNostrum, using the fully kinetic particle-in-cell code VPIC (Bowers et al., 2008; Bowers et al., 2009). The x, y and z coordinates in the simulations correspond to the directions along the velocity shear (∼the magnetosheath flow), the boundary normal (∼magnetosheath-to-magnetosphere), and the out-of-the-vortex-plane (∼south-to-north), respectively. The initial density, magnetic field and bulk velocities across the magnetopause are set to the values obtained from the observations near the KH vortex-like interval 15:33-15:35 UT (see B22 for more details of this interval). Denoting the magnetosheath and magnetospheric sides as 1 and 2, respectively, we first selected the parameters on the two sides from the observations, as n₁₀/n₂₀ = 8.0, (B_x10,B_z10)=(0.17B₀, -B₀), (B_x20,B_z20)=(0.17B₀, B₀), U_x10 = V₀/2, and U_x20 = -V₀/2, where n₁₀ = 8cm⁻³, B₀ = 12nT, |V₀| = 290 km/s = 3.0V_A (V_A: Alfvén speed based on n₀ = n₁₀ and B₀). Note that the system is set to be in the frame with half the velocity of the magnetosheath flow. We then set the initial components by connecting these values using a tanh(y/L₀) function (Nakamura and Daughton, 2014), where L₀ = 1.5d_i is the initial half thickness of the shear layer and d_i = c/ω_pi is the ion inertial length based on n₀. To satisfy the force balance, the temperatures for the magnetospheric components are set to be higher than the magnetosheath components, where the ion-to-electron temperature ratio is fixed as T_i0/T_e0 = 5.0. The initial plasma beta on the magnetosheath side is β₁ = 1.5, the ratio between the electron plasma frequency and the gyrofrequency is ω_pe/Ω_e = 2.0 and the ion-to-electron mass ratio is m_i/m_e = 100. The system is periodic in x (and in z for 3-D), and y boundaries are modeled as perfect conductors for the fields and reflecting for the particles. Further details of the initial setup are given in N22.

In this paper, we will show a 3-D and a corresponding 2-D run, whose system sizes are L_x × L_y × L_z = 15d_i × 30d_i × 10.4d_i = 864 × 1728 × 600 cells with a total of 3.6 × 10¹¹ particles for 3-D, and L_xxL_y = 15d_ix30d_i = 864 × 1728 cells with a total of 6.0 × 10⁹ particles for 2-D. To investigate the effects of the in-plane magnetic field, we will also show an additional 2-D run in which the in-plane field (B_x) is initially set to be zero.

Results

Overviews

Figure 1 shows the time evolutions of the electron mixing measure F_e=(n_e1-n_e2)/(n_e1+n_e2) for the three runs. The simulation time is normalized by α⁻¹ = λ_KH/V₀ which is the time unit for the growth phase of the KHI (Nakamura et al., 2013). In the non-linear growth phase of the primary KHI (t > 4α⁻¹), the high-density vortex arm penetrates deep into the low-density (upper) side for all runs. As shown in N22, this is because the ion current in the direction nearly parallel to the shear flow, which is associated with the anti-parallel (south-north) magnetic field across the boundary, is bent by the primary KHI and drives the secondary RTI growing in the boundary normal (y) direction from the high-density to low-density sides. See N22 for the details of the evolution of the secondary RTI. As also shown in N22, the density jump across the edge of the primary KH wave and vortex further causes the LHDI, resulting in small-scale field and plasma fluctuations on the low-density side of the edge layer. Note that the LHDI-induced fluctuations are seen in the 3-D run and the 2-D run without initial in-plane fields (see left and right panels in Figure 1) but not seen in the 2-D run that has initial in-plane fields (see middle panels in Figure 1). This is because the in-plane field, which is locally compressed and enhanced along the edge of the surface wave (see white curves in Figure 1), prevents the small-scale fluctuations from growing in the 2-D run. For the 3-D run, a similar enhancement of the in-plane field is seen but the LHDI can still grow obliquely in the direction nearly perpendicular to the magnetic field. See N22 for the details of the onset conditions of the LHDI and the related linear analysis based on a dispersion relation solver in the fully kinetic regime (Umeda and Nakamura, 2018). As a result of the LHDI turbulence, plasmas near the edge layer are mixed and the layer is diffused (compare Figures 1D,H,L). In this paper, we will further investigate how the LHDI turbulence diffuses the layer and causes the mass and energy transfer across the layer.

FIGURE 1

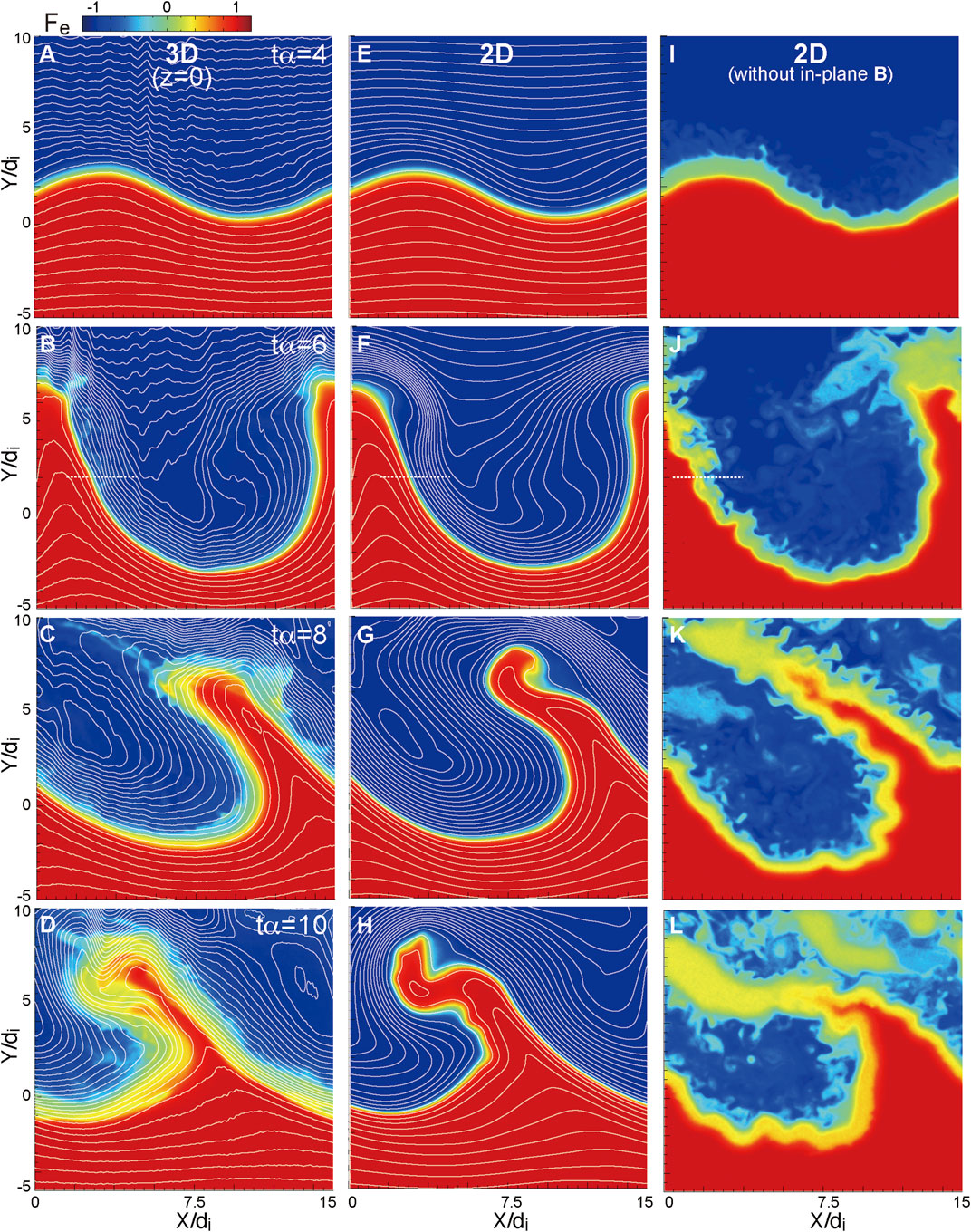
FIGURE 1. Time evolution of the mixing measure F_e=(n_e1-n_e2)/(n_e1+n_e2) in the x-y plane (z = 0 for the 3-D run) for the 3-D (A–D), the corresponding 2-D (E–H), and 2-D without initial in-plane fields (I–L) runs. The white curves for the 3-D and corresponding 2-D runs show the surfaces of the z-component of the vector potential, which corresponds to the in-plane magnetic field lines in 2-D.

The first three panels from the top in Figure 2 shows the electron density, the perpendicular and parallel components of the electric field at t = 6α⁻¹ for all three runs. We see the strong fluctuations caused by the LHDI near the vortex edge mainly in the density and perpendicular electric field (see panels in the first and second rows from the top). Note that in addition to the small-scale fluctuations of the LHDI, a pair of negative-positive electric field layer is seen for all runs near the edge of the vortex, whose half thickness is less than the ion gyro-radius (∼ion inertial length) (see panels in the second row from the top). The LHDI-induced fluctuations and the polarized field are seen mainly in the perpendicular component of the electric field, and we see no significant enhancement of the parallel electric field in the 2-D runs (see Figures 2G,K). On the other hand, for the 3-D run, we see some small-scale negative and positive peaks even in the parallel electric field within the LHDI turbulence (see Figure 2C). This is caused by local, microscopic magnetic reconnection as partially shown in N22.

FIGURE 2

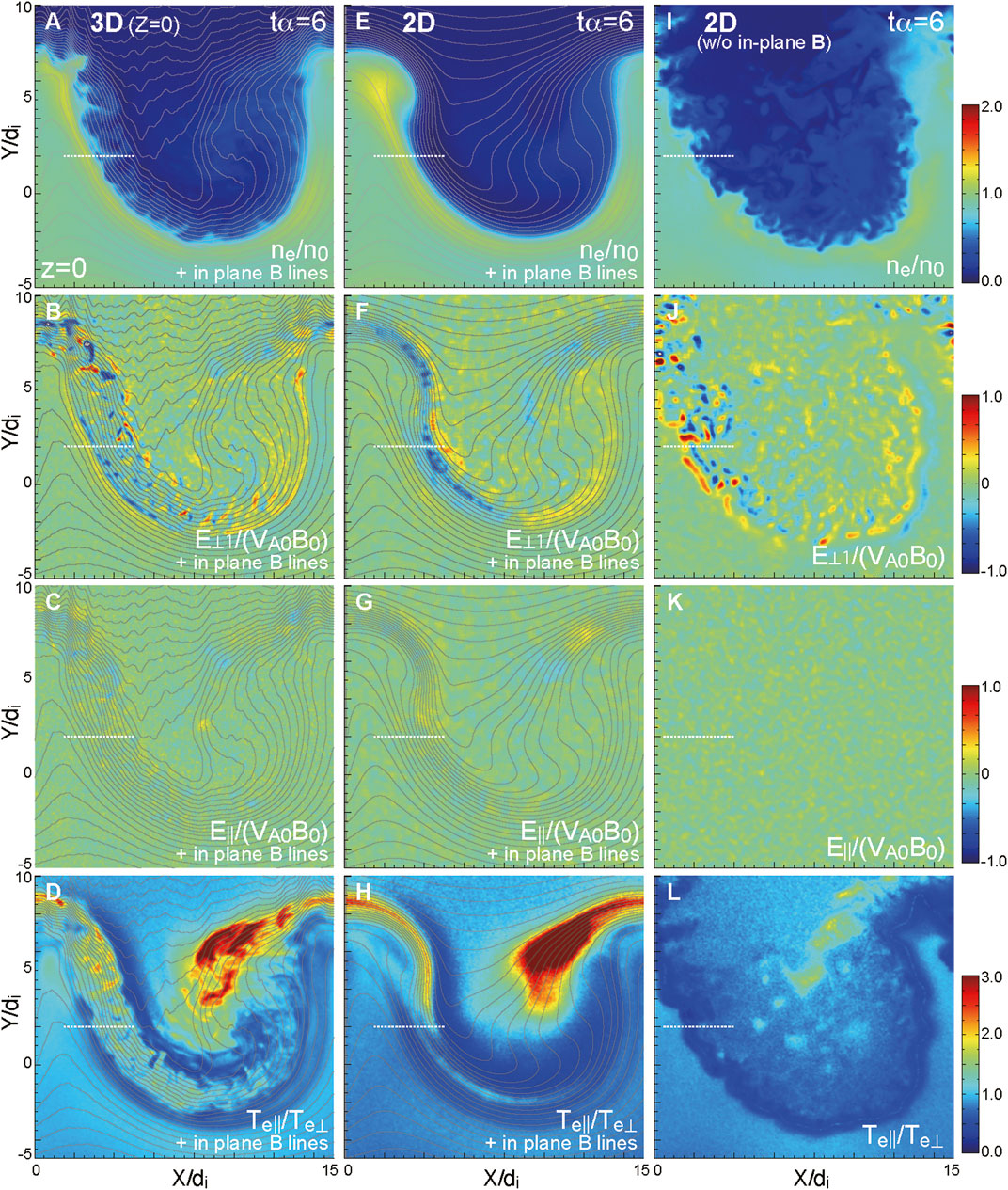
FIGURE 2. Color contours in the x-y plane (z = 0 for the 3-D run) of n_e, the perpendicular and parallel components of E, and the ratio of the parallel and perpendicular electron temperatures $T_{e\parallel }/T_{e\perp }$ at t = 6α⁻¹ for the 3-D (A–D), the corresponding 2-D (E–H), and 2-D without initial in-plane fields (I–L) runs. The gray curves for the 3-D and corresponding 2-D runs show the surfaces of the z-component of the vector potential.

The bottom panels in Figure 2 show $T_{e\parallel }/T_{e\perp }$. We here focus on the edge layer of the vortex including the region near the horizontal white dashed lines, where the strong fluctuations of the LHDI are produced as seen in Figures 2B,J. Note that the region near the head of the vortex arm, where the strong parallel anisotropy is produced by the adiabatic heating with concentrated magnetic field lines, are not our focus. Past kinetic studies showed that the LHDI heats electrons in the perpendicular direction (e.g., Daughton, 2004), and we indeed see the perpendicular temperature anisotropy widely within the LHDI turbulence for the 2-D run without in-plane field (Figure 2L). However, for the 3-D run in which the LHDI turbulence also appears near the vortex edge, a wide band of parallel anisotropy develops within the turbulence (Figure 2D). This additional electron heating in the parallel direction can arise from the parallel electric field associated with reconnection as hinted in Figure 2C. Similar parallel electron heating processes were seen in past kinetic studies of reconnection accompanied by the LHDI turbulence (e.g., Shinohara and Hoshino, 1999; Li et al., 2016).

Mass and Energy Transfer

The top panels in Figure 3 show a cut of crossing of the edge of the vortex arm (along the horizontal dashed lines in Figure 2) at t = 6α⁻¹ of B_z, U_ix, and n_e for all three runs. As seen in Figures 3A,E (i.e., the cases with the LHDI turbulence), the initially sharp density and magnetic gradients are diffused by the LHDI turbulence, forming humps that contain mixed plasmas on the low-density side of the boundary layer. As seen in Figure 4A, which shows the time evolution of the thickness of the mixing region, the expanding speed of this mixing region d(L_mix)/dt in the cases with the LHDI turbulence (red and blue curves) is nearly a quarter of the velocity shear (∼V₀/4), which is comparable to the rotating plasma flow speed within the vortex layer. That is, the time-scale in which the mixing region expands within the vortex layer in this run is comparable to the evolution time-scale of the primary KH vortex. Interestingly, this expanding speed of the mixing region is comparable to or even slightly faster than that in a 3-D run of the northward IMF event (Nakamura et al., 2017a; Nakamura et al., 2017b), in which the LHDI does not occur and the mixing is caused by the vortex-induced reconnection (VIR) across the magnetopause (black dashed curve in Figure 4A). This quick expansion of the mixing region in the present runs with the LHDI turbulence leads to a large mass flux across the mixing surface F_m and a large diffusion coefficient D_diff estimated from the Fick’s law F_m/D_diff = d(m_en_e)/dx ∼ m_en₀/L_mix (red and blue curves in Figures 4B,C), both of which are comparable to the ones for the 3-D run of the northward IMF event (black dashed curve). Note that there is no significant difference in these mixing measures between the two cases with the LHDI turbulence (red versus blue curves in Figure 4), indicating that microscopic reconnection, which appears only in the 3-D case, does not play a significant role in the plasma transport across the magnetopause.

FIGURE 3

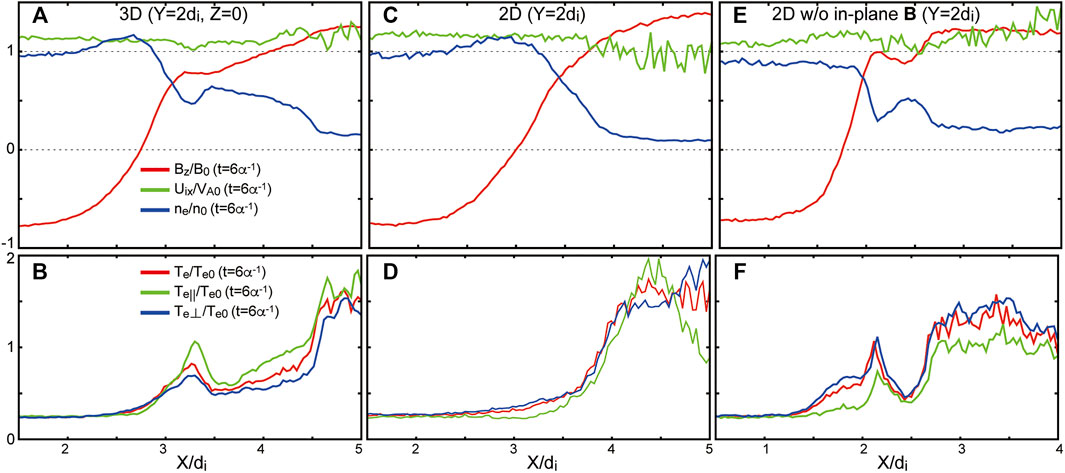
FIGURE 3. Quantities of the same three runs at t = 6α⁻¹ along the dashed lines marked in Figure 2 (the same lines in panels of the second row from the top in Figure 1). The top panels show the out-of-plane magnetic field (B_z), the x-component of the ion bulk velocity (U_ix), and the electron density (n_e). The bottom panels show the total, parallel and perpendicular temperatures of electrons ($T_e$, $T_{e\parallel }$, and $T_{e\perp }$).

FIGURE 4

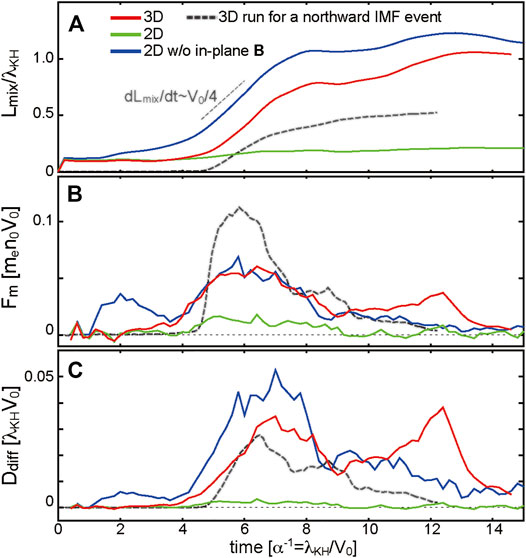
FIGURE 4. Time evolution of (A) the y-averaged thickness L_mix of the mixing region defined using |F_e|<0.99, (B) the electron mass flux F_m across the mixing surfaces defined as |F_e| = 0.99 and (C) the diffusion coefficient D_diff estimated from the Fick’s law F_m/D_diff = d(m_en_e)/dx ∼ m_en₀/L_mix, for the three runs and the 3-D run of the September 8 2015 event employed in Nakamura (2021) (black dashed curves), in which the KH waves were observed during northward IMF. Red, green and blue curves in Figure 4 are the same ones shown in Figure 9B in N22.

The expansion of the mixing region on the low-density side of the edge layer also plays a role in preventing the plasma in the low-density region from entering the high-density region and inhibiting the development of a larger-scale reconnection across the magnetopause current layer (i.e., between the high- and low-density sides). In Figure 3C (2-D), U_ix in the low-density region (x > 4), which corresponds to the flow component in the direction nearly perpendicular to the vortex edge, is smaller than that in the high-density region (x < 3), indicating the compression of the layer. In contrast, in Figure 3A (3-D), U_ix in the low-density side within the mixing region (x > 3.5) is not smaller than that in the high-density region (x < 2.5), indicating that the inflowing flux is diffused by the turbulence. As shown in N22, the global reconnection rate measured from the inflowing flux across the mixing surfaces (Figure 8 in N22) indeed suggested that reconnection occurs almost only within the mixing region on the low-density side and does not directly couple the two sides.

The bottom panels in Figure 3 use the same cut as the top panels but show the electron temperature components. The perpendicular and parallel temperatures are nearly identical near the edge layer of the vortex in the 2-D run with initial in-plane field (middle panels), while the perpendicular anisotropy caused by the LHDI turbulence is seen near the edge layer in the 2-D run without initial in-plane field (right panels). On the other hand, for the 3-D run, the parallel anisotropy is seen near the edge layer (left panels). The anisotropy is enhanced especially in the low-density side of the layer, where the layer is diffused as seen in the density profile in Figure 3A, and this enhancement is likely due to reconnection within the LHDI turbulence (discussed in Overviews Section). A similar parallel anisotropy is seen in the MMS observation of the present southward IMF event (see Figure 10 in B22), suggesting that the parallel electron heating within the LHDI turbulence as seen in the present 3-D simulation may occur in this MMS event.

Summary and Discussions

In this paper, we analyzed data from 2-D and 3-D fully kinetic simulations designed for an MMS observation event of the KH waves at the dusk-flank magnetopause during southward IMF, with a special focus on quantifying the mass and energy transfer efficiency. The results showed that the LHDI and the resulting small-scale field and plasma fluctuations strongly diffuse the edge layer of the primary KH vortex and cause efficient plasma mixing within the vortex. We find that the mixing measures, such as the diffusion coefficient D_diff, are comparable to those obtained in the previous 3-D simulation of the KH waves during northward IMF (Nakamura et al., 2017b). Here, considering the observed values of the primary KH wavekength λ_KH ∼ 4 × 10⁴ km and the velocity shear amplitude V₀∼290 km/s (see B22 for the estimation of λ_KH and V₀ in the observations), the estimated D_diff∼(0.01-0.02)λ_KHV₀ corresponds to (1-4)×10¹¹ m²/s, which is comparable to that in the northward IMF simulation (∼1 × 10¹¹ m²/s). This D_diff value is more than one order of magnitude larger than past predictions for the formation of the low-latitude boundary layer (LLBL) where plasmas are mixed across the magnetopause (Sonnerup 1980; Nykyri and Otto, 2001; Wing et al., 2006; Nakamura and Daughton, 2014). The 3-D simulation further demonstrates the parallel electron anisotropy within the diffused turbulent layer. Given that both the mixing and the parallel electron anisotropy are typical observational features of the LLBL (e.g., Nakamura, 2021 and references therein), this current work strongly suggests that the KH waves and the subsequent LHDI turbulence, where microscopic reconnection potentially takes place, may play an important role in the mass and energy transfer across the low-latitude magnetopause even during southward IMF.

Past simulation studies under northward IMF conditions suggested that the VIR across the edge layer of the KH vortex causes effective plasma mixing and transport across the layer (e.g., Nakamura and Daughton, 2014; Nakamura et al., 2017b). In comparison, the present simulation under a southward IMF condition shows that the diffusion of the edge layer by the LHDI turbulence prevents the VIR from fully developing across the layer. Instead, microscopic reconnection occurs within the turbulence on the lower-density (magnetospheric) side of the edge layer. This process does not significantly affect the mass transport across the layer, but leads to the parallel electron heating within the turbulence. This local, microscopic reconnection process may also change the magnetic field topology near the turbulent layer and lead to a global transport (leak) of the mixed plasma within the turbulence across the flank-to-tail magnetopause. Although the other dayside processes, such as the dayside low-latitude reconnection and the associated flux transfer events (FTEs), have been considered as primary processes that globally transport the solar wind plasmas into the magnetosphere during southward IMF (Fuselier, 2021 and references therein), investigating how the KHI-driven LHDI turbulence, as seen in the present simulation, contribute to the solar wind transport and affect (and/or be affected by) the other processes remains important to understand the global solar wind transport system during southward IMF.

This LHDI turbulence was not seen in the previous northward IMF case (Nakamura et al., 2017a; Nakamura et al., 2017b; Nakamura, 2021), probably due to the lower density ratio across the magnetopause (n₁/n₂ = 3.3) than that in the present southward IMF case (n₁/n₂ = 8). Since the pre-existing boundary layer formed by reconnection at the high-latitude magnetopause, which frequently occurs during northward IMF, can easily reduce the density ratio during northward IMF (Hasegawa et al., 2009; Nakamura et al., 2017b), the KHI-induced LHDI turbulence as seen in the present simulations may be more active during southward IMF. Nevertheless, of course, the LHDI turbulence would occur even during northward IMF as long as the instability conditions for the LHDI are satisfied. Indeed, the enhanced LHD waves were observed within the KH waves in an MMS observation event during northward IMF (Tang et al., 2018). A systematic study of the LHDI effects on the magnetopause KH waves under different IMF and other background conditions would also be an important next step to achieve a comprehensive understanding of the diffusive processes at the Earth’s magnetopause.

Data Availability Statement

The simulation data shown in this paper are made available upon request by the corresponding author.

Author Contributions

TN conducted the analyses of the diagnostics and wrote the paper. KB supported the diagnostics from the spacecraft observations. All listed authors discussed the simulation results.

Funding

This work was supported by the Austrian Research Fund (FWF): P32175-N27. Y-HL and SAP are grateful for support from grants NSF-DoE 1902867 and NASA MMS 80NSSC18K0289.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

For the simulations analyzed in this paper, we acknowledge PRACE for awarding us access to MareNostrum at Barcelona Supercomputing Center (BSC), Spain. A part of the simulation data was analyzed with resources at the Space Research Institute of Austrian Academy of Sciences.

References

Blasl, K. A., Nakamura, T. K. M., Plaschke, F., Nakamura, R., Hasegawa, H., Stawarz, J. E., et al. (2022). Multi-Scale Observations of the Magnetopause Kelvin-Helmholtz Waves during Southward IM. Phys. Plasmas 29, 012101. doi:10.1063/5.0067370

CrossRef Full Text | Google Scholar

Bowers, K. J., Albright, B. J., Yin, L., Bergen, B., and Kwan, T. J. T. (2008). Ultrahigh Performance Three-Dimensional Electromagnetic Relativistic Kinetic Plasma Simulation. Phys. Plasmas 15, 055703. doi:10.1063/1.2840133

CrossRef Full Text | Google Scholar

Bowers, K. J., Albright, B. J., Yin, L., Daughton, W., Roytershteyn, V., Bergen, B., et al. (2009). Advances in Petascale Kinetic Plasma Simulation with VPIC and Roadrunner. J. Phys. Conf. Ser. 180, 012055. doi:10.1088/1742-6596/180/1/012055

CrossRef Full Text | Google Scholar

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1961). Hydrodynamic and Hydromagnetic Stability. New York: Oxford University Press.

Google Scholar

Daughton, W., Lapenta, G., and Ricci, P. (2004). Nonlinear Evolution of the Lower-Hybrid Drift Instability in a Current Sheet. Phys. Rev. Lett. 93 (10), 105004. doi:10.1103/PhysRevLett.93.105004

PubMed Abstract | CrossRef Full Text | Google Scholar

Eriksson, S., Wilder, F. D., Ergun, R. E., Schwartz, S. J., Cassak, P. A., Burch, J. L., et al. (2016b). Magnetospheric Multiscale Observations of the Electron Diffusion Region of Large Guide Field Magnetic Reconnection. Phys. Rev. Lett. 117, 015001. doi:10.1103/PhysRevLett.117.015001

PubMed Abstract | CrossRef Full Text | Google Scholar

Eriksson, S., Lavraud, B., Wilder, F. D., Stawarz, J. E., Giles, B. L., Burch, J. L., et al. (2016a). Magnetospheric Multiscale Observations of Magnetic Reconnection Associated with Kelvin-Helmholtz Waves. Geophys. Res. Lett. 43, 5606–5615. doi:10.1002/2016GL068783

CrossRef Full Text | Google Scholar

Fairfield, D. H., Otto, A., Mukai, T., Kokubun, S., Lepping, R. P., Steinberg, J. T., et al. (2000). Geotail Observations of the Kelvin-Helmholtz Instability at the Equatorial Magnetotail Boundary for Parallel Northward fields. J. Geophys. Res. 105, 21159–21173. doi:10.1029/1999JA000316

CrossRef Full Text | Google Scholar

Foullon, C., Farrugia, C. J., Fazakerley, A. N., Owen, C. J., Gratton, F. T., and Torbert, R. B. (2008). Evolution of Kelvin-Helmholtz Activity on the Dusk Flank Magnetopause. J. Geophys. Res. 113. doi:10.1029/2008JA013175

CrossRef Full Text | Google Scholar

Fuselier, S. A. (2021). “Dayside Magnetopause Processes,” in Magnetospheres in the Solar SystemEditors R. Maggiolo, N. André, H. Hasegawa, D. T. Welling, Y. Zhang, and L. J. Paxton (Hoboken: Wiley). doi:10.1002/9781119815624.ch10

CrossRef Full Text | Google Scholar

Hasegawa, H., Fujimoto, M., Phan, T.-D., Rème, H., Balogh, A., Dunlop, M. W., et al. (2004). Transport of Solar Wind into Earth's Magnetosphere through Rolled-Up Kelvin-Helmholtz Vortices. Nature 430, 755–758. doi:10.1038/nature02799

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasegawa, H., Fujimoto, M., Takagi, K., Saito, Y., Mukai, T., and Rème, H. (2006). Single-spacecraft Detection of Rolled-Up Kelvin-Helmholtz Vortices at the Flank Magnetopause. J. Geophys. Res. 111, A09203. doi:10.1029/2006JA011728

CrossRef Full Text | Google Scholar

Hasegawa, H., Nakamura, T. K. M., Gershman, D. J., Nariyuki, Y., Viñas, A. F., Giles, B. L., et al. (2020). Generation of Turbulence in Kelvin‐Helmholtz Vortices at the Earth's Magnetopause: Magnetospheric Multiscale Observations. J. Geophys. Res. Space Phys. 125, e2019JA027595. doi:10.1029/2019JA027595

CrossRef Full Text | Google Scholar

Hasegawa, H., Retinò, A., Vaivads, A., Khotyaintsev, Y., André, M., Nakamura, T. K. M., et al. (2009). Kelvin-Helmholtz Waves at the Earth's Magnetopause: Multiscale Development and Associated Reconnection. J. Geophys. Res. 114, A12207. doi:10.1029/2009JA014042

CrossRef Full Text | Google Scholar

Hwang, K.-J., Kuznetsova, M. M., Sahraoui, F., Goldstein, M. L., Lee, E., and Parks, G. K. (2011). Kelvin-Helmholtz Waves under Southward Interplanetary Magnetic Field. J. Geophys. Res. 116, A08210. doi:10.1029/2011JA016596

CrossRef Full Text | Google Scholar

Hwang, K. J., Dokgo, K., Choi, E., Burch, J. L., Sibeck, D. G., Giles, B. L., et al. (2020). Magnetic Reconnection inside a Flux Rope Induced by Kelvin‐Helmholtz Vortices. J. Geophys. Res. Space Phys. 125, e2019JA027665. doi:10.1029/2019JA027665

PubMed Abstract | CrossRef Full Text | Google Scholar

Kavosi, S., and Raeder, J. (2015). Ubiquity of Kelvin-Helmholtz Waves at Earth's Magnetopause. Nat. Commun. 6, 7019. doi:10.1038/ncomms8019

PubMed Abstract | CrossRef Full Text | Google Scholar

Kieokaew, R., Lavraud, B., Foullon, C., Toledo‐Redondo, S., Fargette, N., Hwang, K. J., et al. (2020). Magnetic Reconnection inside a Flux Transfer Event‐Like Structure in Magnetopause Kelvin‐Helmholtz Waves. J. Geophys. Res. Space Phys. 125, e2019JA027527. doi:10.1029/2019JA027527

CrossRef Full Text | Google Scholar

Kivelson, M. G., and Chen, S.-H. (1995). “The Magnetopause: Surface Waves and Instabilities and Their Possible Dynamic Consequences,” in Physics of the Magnetopause (Washington, DC: AGU), 90, 257.

Google Scholar

Kokubun, S., Kawano, H., Nakamura, M., Yamamoto, T., Tsuruda, K., Hayakawa, H., et al. (1994). Quasi-periodic Oscillations of the Magnetopause during Northward Sheath Magnetic Field. Geophys. Res. Lett. 21, 2883–2886. doi:10.1029/94gl02103

CrossRef Full Text | Google Scholar

Li, W., André, M., Khotyaintsev, Y. V., Vaivads, A., Graham, D. B., Toledo‐Redondo, S., et al. (2016). Kinetic Evidence of Magnetic Reconnection Due to Kelvin‐Helmholtz Waves. Geophys. Res. Lett. 43, 5635–5643. doi:10.1002/2016GL069192

CrossRef Full Text | Google Scholar

Moore, T. W., Nykyri, K., and Dimmock, A. P. (2016). Cross-scale Energy Transport in Space Plasmas. Nat. Phys 12, 1164–1169. doi:10.1038/nphys3869

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., and Daughton, W. (2014). Turbulent Plasma Transport across the Earth's Low‐latitude Boundary Layer. Geophys. Res. Lett. 41, 8704–8712. doi:10.1002/2014GL061952

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Blasl, K. A., Hasegawa, H., Umeda, T., Liu, Y. -H., Peery, S. A., et al. (2022). Multi-Scale Evolution of Kelvin-Helmholtz Waves at the Earth’s Magnetopause during Southward IMF Periods. Phys. Plasmas29, 012901. doi:10.1063/5.0067391

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Daughton, W., Karimabadi, H., and Eriksson, S. (2013). Three-dimensional Dynamics of Vortex-Induced Reconnection and Comparison with THEMIS Observations. J. Geophys. Res. Space Phys. 118, 5742–5757. doi:10.1002/jgra.50547

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Eriksson, S., Hasegawa, H., Zenitani, S., Li, W. Y., Genestreti, K. J., et al. (2017b). Mass and Energy Transfer across the Earth's Magnetopause Caused by Vortex‐Induced Reconnection. J. Geophys. Res. Space Phys. 122, 11505–11522. doi:10.1002/2017JA024346

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Hasegawa, H., Daughton, W., Eriksson, S., Li, W. Y., and Nakamura, R. (2017a). Turbulent Mass Transfer Caused by Vortex Induced Reconnection in Collisionless Magnetospheric Plasmas. Nat. Commun. 8, 1582. doi:10.1038/s41467-017-01579-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Stawarz, J. E., Hasegawa, H., Narita, Y., Franci, L., Wilder, F. D., et al. (2020). Effects of Fluctuating Magnetic Field on the Growth of the Kelvin‐Helmholtz Instability at the Earth's Magnetopause. J. Geophys. Res. Space Phys. 125, e2019JA027515. doi:10.1029/2019ja027515

CrossRef Full Text | Google Scholar

Nakamura, T. K. M. (2021). “The Earth's Low‐Latitude Boundary Layer,” in Magnetospheres in the Solar System. Editors R. Maggiolo, N. André, H. Hasegawa, D. T. Welling, Y. Zhang, and L. J. Paxton (Hoboken: Wiley), 177–191. doi:10.1002/9781119815624.ch12

CrossRef Full Text | Google Scholar

Nykyri, K., and Otto, A. (2001). Plasma Transport at the Magnetospheric Boundary Due to Reconnection in Kelvin-Helmholtz Vortices. Geophys. Res. Lett. 28 (18), 3565–3568. doi:10.1029/2001GL013239

CrossRef Full Text | Google Scholar

Sckopke, N., Paschmann, G., Haerendel, G., Sonnerup, B. U. Ö., Bame, S. J., Forbes, T. G., et al. (1981). Structure of the Low-Latitude Boundary Layer. J. Geophys. Res. 86, 2099–2110. doi:10.1029/ja086ia04p02099

CrossRef Full Text | Google Scholar

Shinohara, I., and Hoshino, M. (1999). Electron Heating Process of the Lower Hybrid Drift Instability. Adv. Space Res. 24, 43–46. doi:10.1016/S0273-1177(99)00420-2

CrossRef Full Text | Google Scholar

Slinker, S. P., Fedder, J. A., Sibeck, D. G., Lyon, J. G., Frank, L. A., and Mukai, T. (2003). Simulation of Magnetopause Oscillations Observed January 9, 1996. Geophys. Res. Lett. 30 (11), 1569. doi:10.1029/2003gl017063

CrossRef Full Text | Google Scholar

Sonnerup, B. U. Ö. (1980). Theory of the Low-Latitude Boundary Layer. J. Geophys. Res. 85, 2017–2026. doi:10.1029/JA085iA05p02017

CrossRef Full Text | Google Scholar

Stawarz, J. E., Eriksson, S., Wilder, F. D., Ergun, R. E., Schwartz, S. J., Pouquet, A., et al. (2016). Observations of Turbulence in a Kelvin-Helmholtz Event on 8 September 2015 by the Magnetospheric Multiscale mission. J. Geophys. Res. Space Phys. 121 (11), 021–111. doi:10.1002/2016JA023458

CrossRef Full Text | Google Scholar

Tang, B., Li, W., Wang, C., Dai, L., Khotyaintsev, Y., Lindqvist, P.-A., et al. (2018). Magnetic Depression and Electron Transport in an Ion-Scale Flux Rope Associated with Kelvin-Helmholtz Waves. Ann. Geophys. 36, 879–889. doi:10.5194/angeo-36-879-2018

CrossRef Full Text | Google Scholar

Umeda, T., and Nakamura, T. K. M. (2018). Electromagnetic Linear Dispersion Relation for Plasma with a Drift across Magnetic Field Revisited. Phys. Plasmas 25, 102109. doi:10.1063/1.5050542

CrossRef Full Text | Google Scholar

Vernisse, Y., Lavraud, B., Eriksson, S., Gershman, D. J., Dorelli, J., Pollock, C., et al. (2016). Signatures of Complex Magnetic Topologies from Multiple Reconnection Sites Induced by Kelvin‐Helmholtz Instability. J. Geophys. Res. Space Phys. 121, 9926–9939. doi:10.1002/2016JA023051

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., and Fujimoto, M. (2006). Timescale for the Formation of the Cold-Dense Plasma Sheet: A Case Study. Geophys. Res. Lett. 33, L23106. doi:10.1029/2006GL027110

CrossRef Full Text | Google Scholar