PIC Simulations of Excited Waves in the Plasmoid Instability

Fragmentation of an elongated current sheet into many reconnection X-points, and therefore multiple plasmoids, occurs frequently in the solar corona. This speeds up the release of solar magnetic energy in the form of thermal and kinetic energy. Moreover, due to the presence of multiple reconnection X-points, the particle acceleration is more efficient in terms of the number of accelerated particles. This type of instability called “plasmoid instability” is accompanied with the excitation of some electrostatic/electromagnetic waves. We carried out 2D particle-in-cell simulations of this instability in the collisionless regime, with the presence of non-uniform magnetic guide field to investigate the nature of excited waves. It is shown that the nature and properties of waves excited inside and outside the current sheet are different. While the outside perturbations are transient, the inside ones are long-lived, and are directly affected by the plasmoid instability process.

1 Introduction

Magnetic reconnection is a fundamental phenomenon in highly conductive magnetized plasmas such as space and astrophysical plasmas in which the magnetic energy is abruptly released and converted to the heating and kinetic energies as well as the acceleration of particles. Magnetic reconnection takes place in narrow regions where the frozen-in-flow constraint breaks down. As a result the field lines cut and reconnect to each other continuously and the large scale topology of magnetic field lines changes significantly (Priest and Forbes 2000; Birn and Priest 2007; Yamada et al., 2010; Gonzalez and Parker 2016).

Large solar flares are the most powerful explosions in the Solar System releasing enormous amount of energy in a few minutes due to the reconnection process in their current sheet. How current sheets are formed in the corona is a long-standing problem. It is now widely accepted that large-scale photospheric motions lead to the formation of coronal current sheets (Galsgaard and Nordlund 1996; Gudiksen and Nordlund 2005). In large systems such as those found in solar flares, the formation of highly elongated current sheets in coronal magnetic fields would result in extremely low reconnection rates, which fail to account for the observed fast energy release rates. However, such current sheets are stressed by complex photospheric motions and/or eruptive motion of magnetic structures such as flux ropes (external perturbations), and therefore, are naturally subject to a violent plasma instability leading to the breakup, fragmentation and formation of multiple current sheets (secondary islands or plasmoids) instead of just one monolithic current layer with reconnection occurring at multiple X-points (Loureiro et al., 2007; Cargill et al., 2012).

The detailed theory of the plasmoid instability has already been investigated. According to the linear analytical theory of this scenario, a current sheet with a high length-to-width ratio, is not subject to slow well–known Sweet–Parker reconnection mechanism, but it is inherently unstable to the formation of plasmoids on very short timescales. It is therefore clear that for sufficiently large systems, plasmoid-dominated reconnection layers are inevitable. Plasmoid formation and magnetic reconnection are thus inextricably linked and further progress in understanding reconnection in realistic systems necessarily requires a theory that takes the plasmoid dynamics into account.

Some studies have reported the observation of plasmoid structures in the solar atmosphere (Bárta et al., 2011; Liu et al., 2013). Formation of such plasmoids (magnetic islands or helical flux ropes in 3D) gives rise to the tremendous increase in the reconnection rate and the magnitude of the reconnection electric field. Fragmentation of such a current sheet into smaller structures may offer a more promising way forward, providing not only multiple accelerator sites, but also the presence of micro-scale turbulence to both confine the particles to the vicinity of the accelerators and provide secondary acceleration.

Plasmoid chains are highly dynamic configurations and grow fast by coalescence of smaller plasmoids (Bhattacharjee et al., 1983; Daughton et al., 2009; Intrator et al., 2009; Karimabadi et al., 2011). The kinetic perspective of plasmoid chain formation and evolution has been investigated through particle-in-cell simulation by Markidis et al. (2012). Also, Drake et al. (2006) has studied the formation of secondary islands and shown that the presence or absence of an out-of-plane magnetic field (guide field) has a major effect on the long-term behavior of magnetic reconnection.

Kumar et al. (2019) reported observation of the formation and evolution of multiple small plasmoids with bidirectional flows associated with fast reconnection in 3D breakout current sheets in the solar corona. They demonstrated the existence and importance of plasmoids during fast reconnection in a fully 3D magnetic configuration. Liu et al. (2013) showed that the main sites of particle acceleration and plasma heating are in the reconnection outflow regions, rather than the reconnection site itself.

Furthermore, Zhou et al. (2012) studied the structure of electric field inside a secondary island in the diffusion region using particle-in-cell (PIC) simulation without initial guide field. They depicted the electric field component diagrams at a particular time and showed that intense in-plane electric fields, which point toward the center of the island, form inside the secondary island and the magnitudes of the in-plane electric fields inside the island are much larger than those outside the island in the surrounding diffusion region. Also, they found electric dipole structure by the electric field components.

Fan et al. (2016) compared the structure of primary and secondary magnetic islands through particle-in-cell simulation and discussed about the values of different components of the electric field in different parts of the primary and secondary islands. Also, they concluded that the out-of-plane magnetic field can be enhanced in the center of both the primary and secondary islands. According to their results, the magnitude of the electric field components in the o-points is greater than the X-points.

On the other hand, Chen et al. (2012) studied in-plane electric fields in secondary and primary islands by PIC simulations, and compared with spacecraft measurements from the Earth’s magnetotail. They found that in-plane electric field components are locally peaked around the secondary island cores.

In another work, Fu et al. (2018) by examining the structure of out-of-plane electric field with different guide field coefficients at a specific time in the X-point of magnetic reconnection concluded that the guide field coefficient higher than a specific value will cause the Hall electric field to be replaced by a tripolar electric field. Wan et al. (2008) investigated the time-evolution of the electric field component perpendicular to the reconnection plane at the X-point and showed that the energetic electrons were accelerated by the perpendicular component of electric field. They stated that the perpendicular component of the electric field has a monopolar structure in the early times and a bipolar structure in later times. Egedal et al. (2012) used two-dimensional kinetic simulation without guide field and showed that during reconnection, powerful energization of electrons by magnetic-field-aligned parallel electric field can occur over spatial scales that exceed previous theories and simulations. Also, the fine magnetic structure of plasmoids generated during reconnection in the presence of guide field was addressed by Karimabadi et al. (1999).

Study of spatial and temporal variation of the electric field in the plasmoid-dominated reconnection (plasmoid instability) is important because it can be the direct agent of charged particle acceleration to relativistic energies in space and astrophysical plasmas especially in the solar corona. Most of the related analytical and numerical works have considered the issue of magnetic reconnection in an X-point or a Sweet-Parker layer. Moreover, the effect of non-uniform guide field with varying-amplitude on the electric field has got less attention. Therefore, it is of interest for us to study the spatial and temporal variation of different components of the electric field during the collisionless plasmoid instability with the presence of non-uniform weak and medium guide fields. To understand the nature of disturbances in the electric field components, their respective dispersion diagrams are obtained and analyzed. To do so, we employ two-dimensional particle-in-cell simulations. The paper is organized as follows: The next section describes the simulation set-up which is followed by presentation and examination of the results in Section 3. Summary and conclusion is given in Section 4.

2 Simulation SET-UP

The initial magnetic field is a combination of a reconnection plane xy component and the out-of-plane guide field in the form $\mathbf{B}=B_0\tanh ((y-L_y/2)/\delta ){\widehat{e}}_x+b_{z0}sech((y-L_y/2)/\delta ){\widehat{e}}_z$. Here, B₀ and b_z0 are the amplitudes of initial magnetic field and the guide field, respectively. L_y is the simulation box size in the y direction and δ is the half-width of the initial current sheet. In order to facilitate the onset of collisionless magnetic reconnection in the center of simulation box, (x = L_x/2, y = L_y/2), a divergence-free small perturbation ${\mathbf{b}}_p=b_{px}{\widehat{e}}_x+b_{py}{\widehat{e}}_y$ is added to the initial magnetic field:

$b_{px}=b_{px0}\exp \left(-\frac{{\left(x-L_x/2\right)}^2}{\left(L_y^2/2\right)}\right)\cos \left(\pi y/L_y\right),$

$b_{py}=b_{py0}\frac{\left(x-L_x/2\right)}{\left(L_y/2\right)}\exp \left(-\frac{{\left(x-L_x/2\right)}^2}{\left(L_y^2/2\right)}\right)\sin \left(\pi y/L_y\right).(1)$

The total magnetic field is embedded in a collisionless hydrogen plasma with the reduced mass ratio m_i/m_e = 100, and the uniform temperature of electron and ion species are set to be T_e = 200 eV and T_i = 0.25T_e = 50 eV. The use of non-physical mass ratio due to the computational limitations has been considered in some relevant reconnection works. Considering the nature of modes discussed below, taking into account the physical mass ratio for hydrogen plasma will not result in the generation of new kind of waves, but will result in the very late excitation of ion-related modes. Moreover, the initial density of both species is n_i = n_e = n₀ sech² ((y − L_y/2)/δ) where n₀ = 1013 m⁻³. Therefore, the electron plasma frequency with considering n₀ is ω_pe = 0.18 GHz. Collision between all particles are neglected in the simulations. The mostly used approximation of collisionless plasma is an initial assumption based on the fact that our study considers a dilute (low-density) region of the solar corona where it is believed that the average Coulomb collision frequency between particles is less than the electron plasma frequency.

Two-dimensional (2D3V) electromagnetic particle-in-cell simulations are carried out by using the EPOCH (Extendable PIC Open Collaboration) code, developed at the University of Warwick. The size of the simulation domain is L_x = L_y = 18.5 d_i with d_i = c/ω_pi as the ion inertial skin-depth. Also, the number of grid points are N_x × N_y = 1,000 × 1,000, so the spatial resolution is Δx = Δy = 0.02 d_i. Time step being determined by the CFL condition is △t = 6.12 × 10^{–10 s} which is sufficiently small to precisely detect the excited waves in the system. We employ 100 particles per species per cell. Due to the computational limitations, it was not possible to run the simulations with larger number of particles. However, we were able to run only one simulation with physical mass ration m_i/m_e = 1836, Nx × Ny = 1,500, ×, 1,500 and 500 particles per species per cell for the case b_z0 = 0.3B₀ by using the High Performance Computing facility of the Sharif University of Technology (Tehran-Iran) but found no significant differences in the dispersion diagrams. This result makes us more confident about our results presented here. Having taken the solar corona parameters, we set B₀ = 0.001T, b_z0 = 0.3, 0.5, 0.7B₀, b_px0 = π/2 b_py0 = 0.15 B₀ and δ = d_i. Furthermore, for both fields and particles, the periodic and conducting boundary conditions are applied in the x and y directions, respectively.

3 Simulation Results

As mentioned, the initial magnetic field has a guide field component which depends on ‘y’ direction as b_z = b_z0 sech ((y − L_y/2)/δ). Its amplitude is set to be b_z0 = 0.3, 0.5, 0.7B₀, (b_z0 < B₀) in three distinct simulation Runs A, B and C, respectively. The only difference between three Runs is the value of b_z0. For Run A (weak guide field), Figure 1 plots perpendicular component of the electric current density, J_z, superimposed on the magnetic field lines at times tω_pe = 50, 250, 500, 750, 1,000, 1,500. The last time is equal to t = 8.4 μs. J_z is normalized to B₀/μ₀δ. Figure 1 illustrates how the plasmoid instability develops in the system; Initially, collisionless reconnection is triggered at the X-point near the center of the current sheet, (x = y = L_x/2). Then, following the fast elongation of reconnection layer at early times, some secondary X-points are formed (linear stage), which as instability evolves, the generated magnetic islands grow in size and coalesce with each other, forming larger islands with sizes even greater than the initial current sheet. Merging of islands continues until the saturation regime is reached. In other words, at this nonlinear stage, the current sheet is fragmented considerably and a fully nonlinear plasmoid instability has been set up in the system, where all main quantities such as perturbed electric/magnetic fields are completely nonlinear. Such a drastic fragmentation of current sheet at longer times changes the topological and dynamical structure of the simulation region. According to Figure 1, the electric current density inside magnetic islands (O-points) are relatively larger than X-points as the magnetic field gradients are stronger there.

FIGURE 1

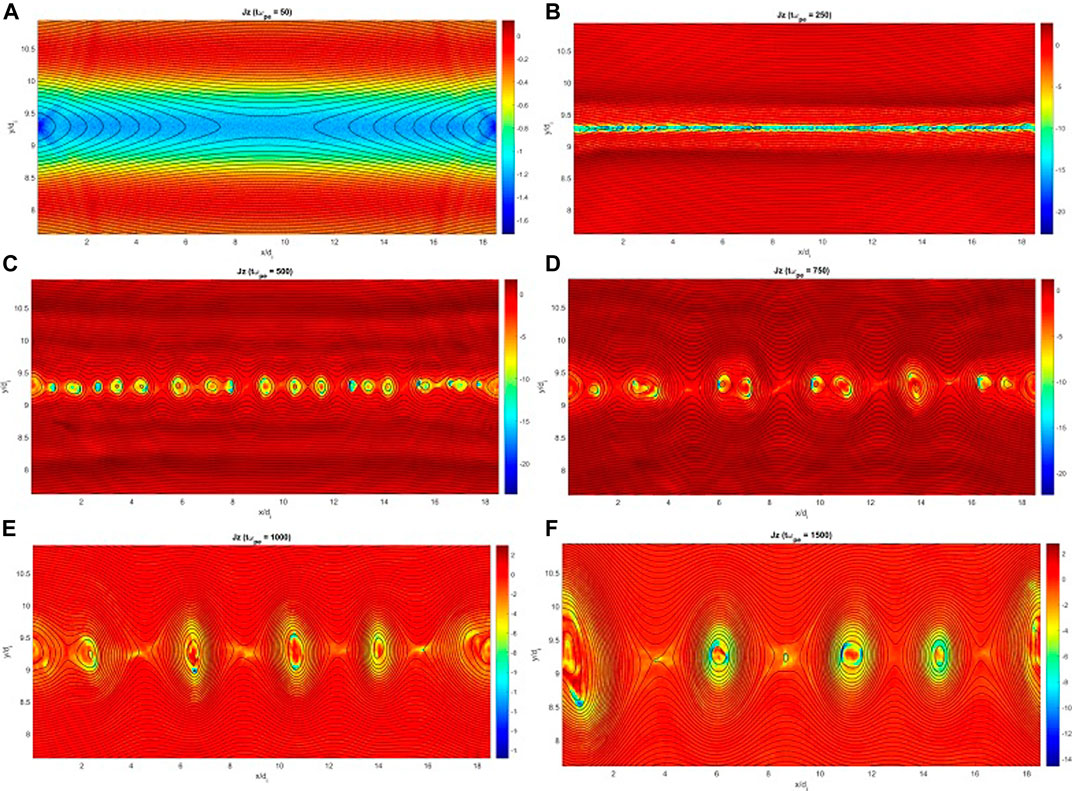
FIGURE 1. Perpendicular component of the electric current density J_z being superimposed by the magnetic field lines at times: tω_pe = 50 (A), 250 (B), 500 (C). 750 (D), 1,000 (E), 1,500 (F).

Now, it would be of interest to look at the way that the different components of electric field evolve during the growth of plasmoid instability in our system. Since, the electric field is responsible for acceleration of charged particles, therefore understanding its evolution in space and time is important.

Figures 2, 3 show the E_x and E_y components of the electric field on the reconnection-plane, xy, at tω_pe = 50, 250, 500, 750, 1,000, 1,500. Electric field is normalized to B₀c, where c is the speed of light. According to Figures 2, 3, two distinct types of disturbances can be distinguished.

1) There exist field perturbations originating very early at a few tω_pe from the current sheet and propagate perpendicularly away from the current sheet along the y axis. Theses disturbances are mainly y-dependent. As time passes, the growth of an instability along the x axis, makes the structure of disturbances non-uniform along the x axis too, which means that the wave-number vector has at least both components k_x, k_y. Meanwhile, both the amplitude and the dominant wave-length decrease in time. In other words, k_x and k_y shift to larger values. At tω_pe = 50 the maximums of E_x and E_y are 15 and 18 kV/m, respectively, which decrease almost five times at tω_pe = 1,500. The amplitude of initial magnetic field B₀ determines how large the electric field would be. To see this point, a Run (not reported here) with 10 times weaker magnetic field B₀ = 10⁻⁴T was done which showed that the maximum of electric field reduces down to below 1kV/m at tω_pe = 50.

FIGURE 2

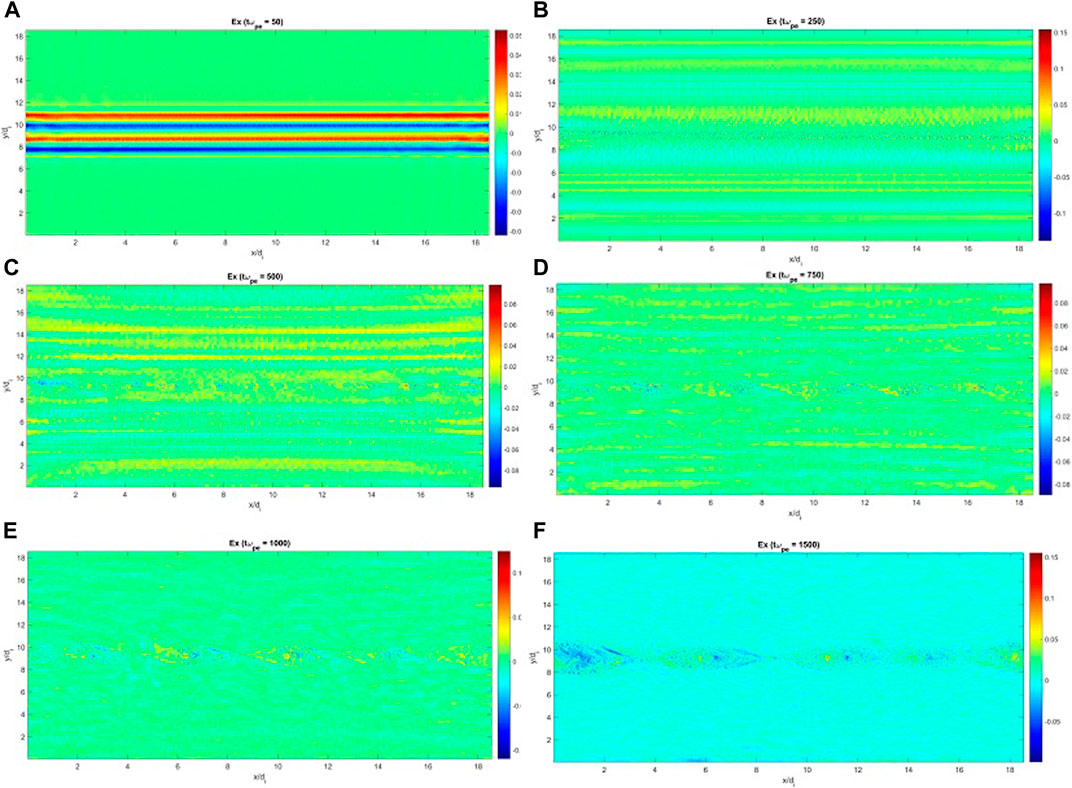
FIGURE 2. E_x component of the electric field at times: tω_pe = 50 (A), 250 (B), 500 (C). 750 (D), 1,000 (E), 1,500 (F) with b_z0 = 0.3B₀.

FIGURE 3

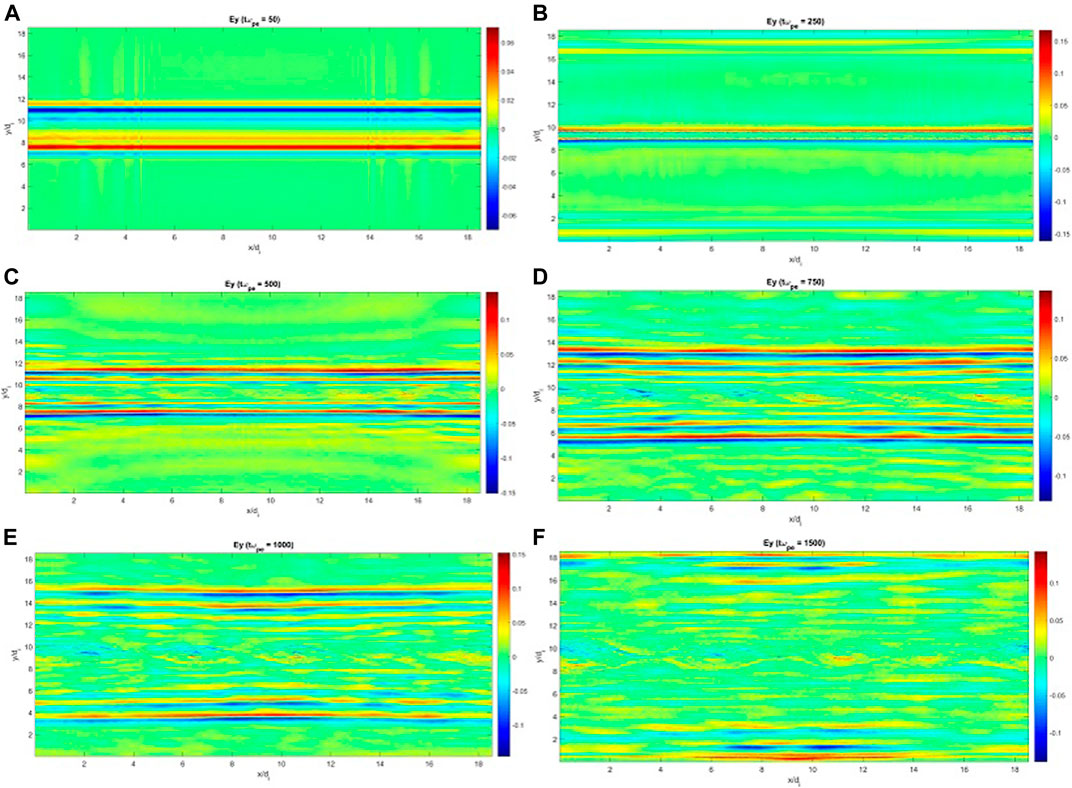
FIGURE 3. E_y component of the electric field at times: tω_pe = 50 (A), 250 (B), 500 (C). 750 (D), 1,000 (E), 1,500 (F) with b_z0 = 0.3B₀.

A similar pattern of disturbances are also observed for B_x and B_y components of the perturbed magnetic field. The nature of these oscillations, either electrostatic/electromagnetic, will be discussed below by implementing spatial and temporal Fourier analysis. It should be noted that, such types of disturbances appear for Runs B and C for which the amplitude of guide field is larger (medium guide field). It can be said that, the nature of these disturbances are indeed independent from the formation and evolution of plasmoid instability taking place initially inside the current sheet, although, these disturbances can be affected later by the nonlinear stage of the plasmoid instability. These disturbances are transient waves that propagate away from the current sheet with a large group velocity (see below) and are gradually damped. In particular, the wave-like perturbed electric field in the xy plane is less effective in accelerating charged particles compared to the same role that can be played by almost DC electric field generated during the magnetic reconnection and consequent plasmoid instability. So, at longer time scales the transient part of the electric field becomes ignorable.

2) As the reconnection is triggered, electric field is generated inside the current sheet and the subsequent transition of reconnection into the plasmoid instability is accompanied with the amplitude growth of different components of the electric field at there. According to Figures 2, 3, as the plasmoid instability evolves and develops in time, its associated electric field grows too and its components become larger. At longer times tω_pe > 1,000, the electric field perturbations inside the current sheet are predominant over the electric field disturbances of transient waves outside the current sheet. The in-plane electric field within magnetic islands closer to the O-points and also around separatracies are considerably stronger than the X-point regions. Additionally, E_x and E_y show a dipole field structures inside magnetic islands (see Figure 2G and Figure3G). To put it another way, inside magnetic islands, the electric field vector rotates around the O-points, and the electric field reverses its direction over the separatracies (see Figure 4). The maximums of E_x and E_y inside the islands at tω_pe = 1,500 are 45 and 30 kV/m, respectively. Generally speaking, the electric field supported by reconnection and subsequent plasmoid instability lasts for much longer times and are relatively larger and hence, as long as the particle acceleration is concerned, more attention should be paid to that compared to the electric field disturbances generated by transient waves.

FIGURE 4

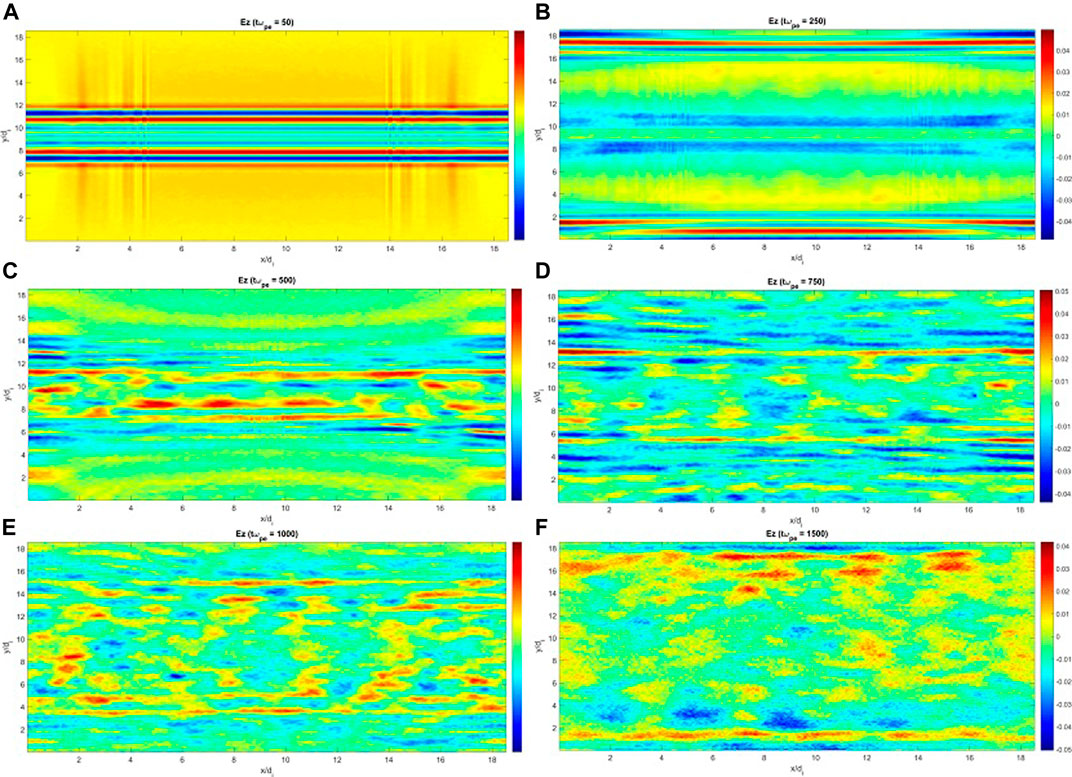
FIGURE 4. E_z component of the electric field at times: tω_pe = 50 (A), 250 (B), 500 (C). 750 (D), 1,000 (E), 1,500 (F) with b_z0 = 0.3B₀.

In the scenario of particle acceleration perpendicular to the reconnection plane, the role of out-of-plane electric field, E_z, generated by reconnection, is essential. Figure 5 plots E_z at the same times as before. Obviously, the previously described transient disturbances, have also been observed here. The disturbances, although, are uniform in the x direction, but as time increases, they become non-uniform structures in both directions since k_x component of unstable waves becomes comparable to k_y. Unlike the E_x, E_y plots, disturbances there exist and dominate especially close to the y axis boundaries even at longer times. Presumably, an electromagnetic mode supporting E_z is still propagating in the system. The maximum of E_z at tω_pe = 1,500 is 12 kV/m which is smaller than the maximums of E_x and E_y at that time. Note that, as the plasmoid instability proceeds, the E_z inside the current sheet does not show a simple specific pattern that can be examined visually. Therefore, let us do spatial (2D) and temporal Fourier analysis of different components of electric and magnetic fields in order to understand the nature of above-described disturbances.

FIGURE 5

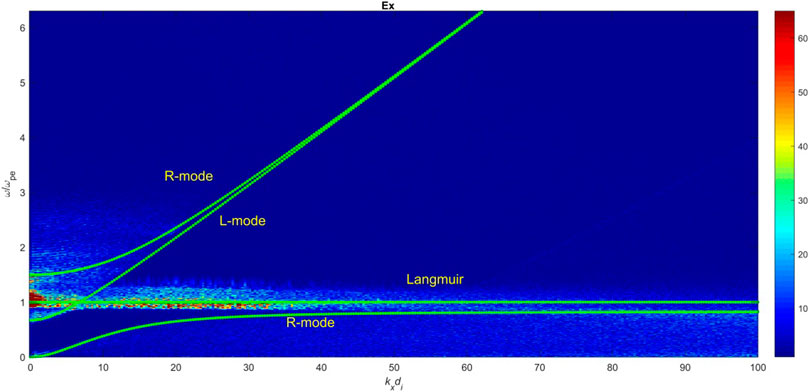
FIGURE 5. Dispersion diagram of Ex (x/d_i (0: 18.5), y/d_i = 13). Dotted lines indicate the theoretical parallel propagating modes along the initial magnetic field.

Figures 5, 6 depict the Fourier analysis of Ex (x/d_i (0 : 18.5), y/d_i = 13) and B_x (x/d_i (0 : 18.5), y/d_i = 13) along the initial magnetic field direction, x axis, in the time interval tω_pe = (0, −, 1,500) in terms of ω/ω_pe and k_xd_i. Here, the dotted lines indicate the theoretical parallel propagating modes along the initial magnetic field for the case ω_pe/ω_ce ∼ 1.20, >, 1, and help us to identify easily the nature of modes in our dispersion diagram. According to these graphs, both electromagnetic Right-hand (R) and Left-hand (L) polarized modes accompanied with electron Langmuir wave are excited. The existence of E_y, E_z components perpendicular to B₀ and also E_x parallel to B₀ are required for R/L and Langmuir modes, respectively. All three components are present in our results. Fourier analysis at early times shows that theses modes are indeed excited very early before the transition of simple reconnection into the plasmoid instability. These modes explain the nature of transient disturbances outside the current sheet described above. Based on our parameters, the theoretical cutoff frequency for L and R modes are 0.67ω_pe and 1.50ω_pe, respectively, which are in agreement with the obtained dispersion diagrams and respective cutoffs. Furthermore, according to the shown dispersion diagram the resonance frequency of R-mode (slow branch) is ω_res = ∼ 0.80ω_pe which agrees with the theoretical resonance frequency based on our parameters ω_ce = 0.83ω_pe. The dominant wave-numbers for R and L modes are small (k_xd_i < 2), however, the electrostatic Langmuir mode is excited over a wide range of wave-number (k_xd_i < 35) with the frequency ω ∼ ω_pe as expected.

FIGURE 6

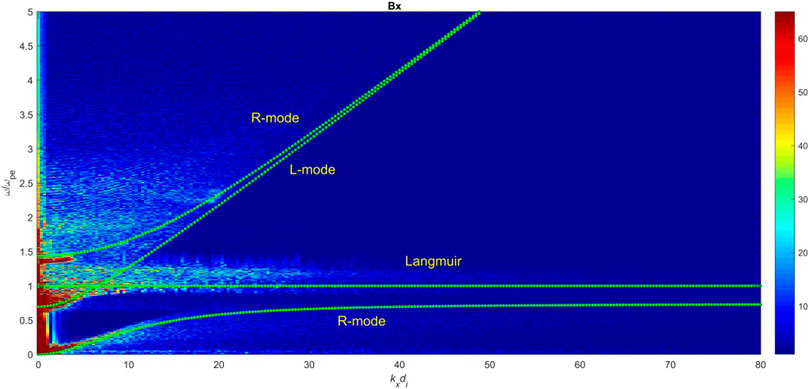
FIGURE 6. Dispersion diagram of Bx (x/d_i (0: 18.5), y/d_i = 13). Dotted lines indicate the theoretical parallel propagating modes along the initial magnetic field.

Similarly, the Fourier analysis of Ey (x/d_i = 9.3, y/d_i (0 : 18.5)) perpendicular to the initial magnetic field, during tω_pe = (0, −, 1,500) in terms of ω/ω_pe and k_yd_i is done. Here, only the X-mode (extraordinary mode) accompanied with magnetosonic wave are excited. The cutoffs of X-mode are the same as R and L mode cutoffs. The dispersion relation of magnetosonic wave perpendicular to the magnetic field line reduces to $\omega =k_y\sqrt{C_s^2+V_A^2}$ with the sound speed $C_s=\sqrt{(K{T}_e+\gamma K{T}_i)/m_i}\sim 7\times 10^{5}m/s$, and the Alfvén velocity $V_A=B_0/\sqrt{{\mu }_0{n}_i{m}_i}\sim 3\times 10^{7}m/s$. Since $V_A^2\gg C_s^2$, the dispersion relation takes the form ω ∼ k_yV_A, i. e, ω/ω_pe = 0.01 (k_yd_i). Taking into account the slope of the theoretical dispersion relation, 0.010, we can conclude that the respective mode is the magnetosonic waves propagating perpendicular to the magnetic field. Additionally, it seems that at very small frequencies ω/ω_pe < 1, ion-sound wave with a frequency on the order of ω_pi = 0.1ω_pe is excited. The corresponding theoretical dispensation relation is ω = k_yC_s, i. e, ω/ω_pe = 0.000 2 (k_yd_i), and the dispersion diagram of the ion-sound wave has a very small group velocity.

4 Summary and Conclusion

In this study, 2D PIC simulation was carried out to investigate the spatial and temporal variation of electric field generated during the collisionless magnetic reconnection which later transits into the plasmoid instability. The initial magnetic field is a Harris sheet superimposed by a non-uniform guide field. The input parameters are applicable for the solar corona, in the region where ω_pe > ω_ce is justified. Three Runs were done with three different amplitudes of guide field, all three smaller than the amplitude of initial magnetic field (i.e., weak and medium guide field). For all cases, the onset of collisionless magnetic reconnection in an specified X-point is fast. By setting appropriately a large L_x/δ ratio, the reconnection, consequently, proceeds into the well-known plasmoid instability in which the current sheet is fragmented by formation of multiple secondary X-points/magnetic islands. The results showed that as the amplitude of guide field increases, the growth rate of either magnetic reconnection in the initial X-point and the plasmoid instability decreases. This can be inferred from the slope of temporal variation of magnetic field energy. The growth rate of reconnection at $\sim 50<t{\omega }_{pe}<\sim 200$ decreases almost half as the guide field amplitude increases from 0.3B₀–0.7B₀. The results show that when a secondary X-point emerges, then the rate of magnetic energy release increases momentarily, and subsequently the electric field energy increases. Therefore, the decrement or increment trend of magnetic and electric energy during the linear and nonlinear stages of the plasmoid instability is not monoslope.

As the reconnection is triggered, some electrostatic/electromagnetic waves are excited and propagate perpendicularly away from the current sheet while they are uniform in the magnetic field direction, x. Later, some waves are excited along the magnetic field direction and hence the k_x and k_y components of wavenumber vector become comparable. Signature of these waves are observed in all components of the electric and magnetic fields. The dispersion diagrams of field components revealed that the X-mode propagates perpendicular to the magnetic field, while the R- and L-modes are the predominant modes parallel to the magnetic field. The electrostatic Langmuir and ion related slow magnetosonic modes are also excited on both propagation directions. Parallel and Perpendicular to the magnetic field, magnetosonic mode is reduced to the ion-sound and the Alfvén modes respectively. We found that these waves are transient modes and the corresponding amplitudes of the waves decrease in time and eventually become ignorable compared to the electric field generated later by the plasmoid instability which lasts for longer times. It should be noted that, the modes excited outside the current sheet, are present even with the open boundary condition applied for y axis. Following the growth of plasmoid instability and the later transition into the nonlinear stage, the associated electric field becomes stronger inside the magnetic islands and also around the separatracies compared to other places, and as time goes on, the amplitude of electric field increases. The strong electric field at longer times is favorable for accelerating charged particles to highly relativistic energies. It is worthy of note that, even in the absence of initial perturbations for magnetic field (b_p×0 = b_py0 = 0.), above discussed waves are still excited near the current sheet and propagate towards up and down boundaries away from the current sheet. This means that the excitation of these disturbances are physical.

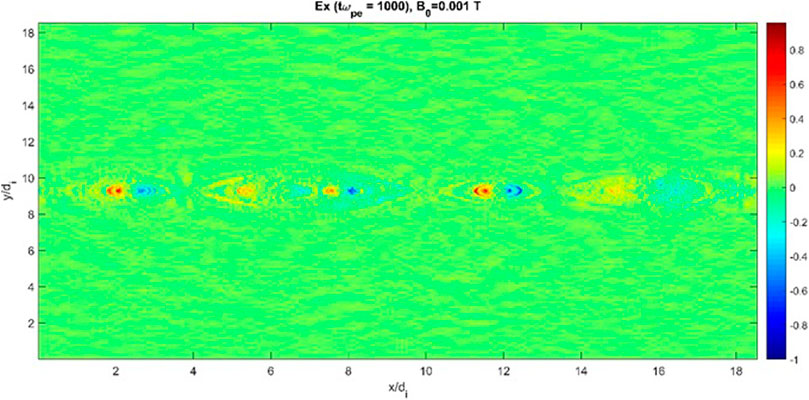
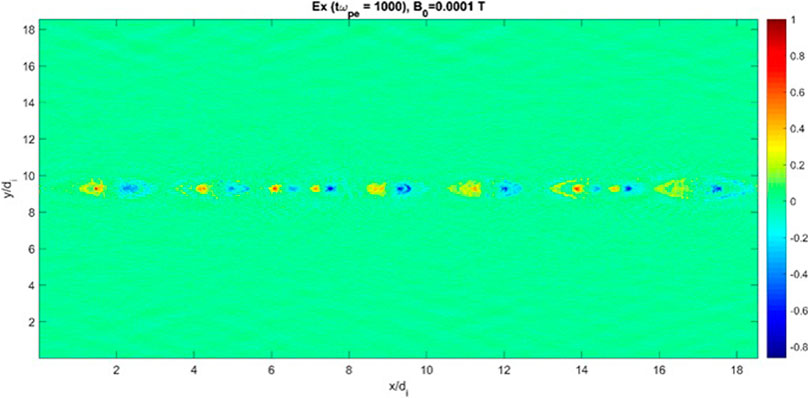
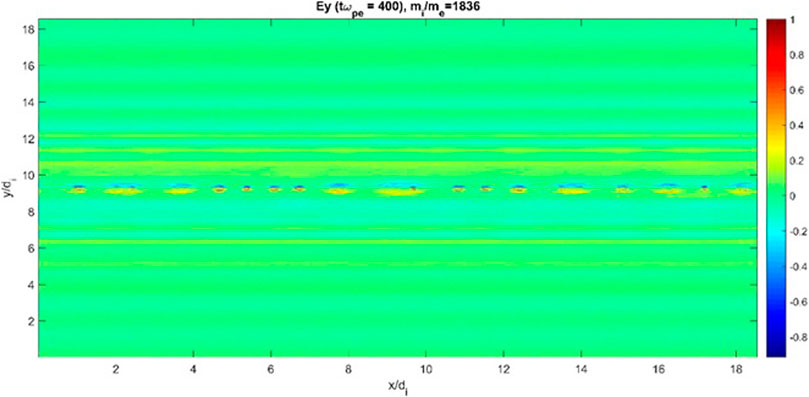
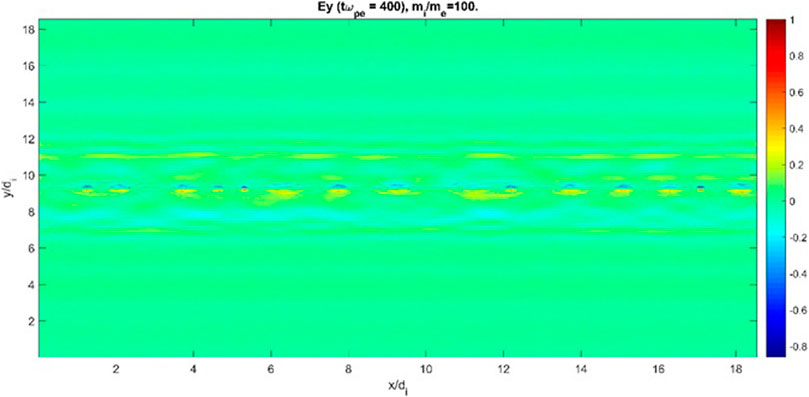
We note that the above-mentioned waves are excited even with a weaker equilibrium magnetic field and with a realistic ion-to-electron mass ratio, m_i/m_e = 1836. Figures 7, 8 show the xy plot of E_x at tω_pe = 1,000 for two cases B₀ = 0.001T and B₀ = 0.000 1T, respectively. For these runs, no initial perturbation for magnetic field is assumed b_p×0 = b_py0 = 0. As seen, even in the case of weaker equilibrium magnetic field, the same kind of disturbances (waves) are excited. The apparent difference as expected is that in the case of 10-times weaker magnetic field, the growth rate of instability is relatively smaller compared to the case of stronger magnetic field. On the other hand, Figures 9, 10 plot E_y at tω_pe = 200 for m_i/m_e = 1836 and 100, respectively. Comparing these figures, we did not find any significant difference. Such a conclusion was also found for other electric field component, E_x.

FIGURE 7

FIGURE 7. E_x plot at time tω_pe = 1,000 for B₀ = 0.001T.

FIGURE 8

FIGURE 8. E_x plot at time tω_pe = 1,000 for B₀ = 0.000 1T.

FIGURE 9

FIGURE 9. E_y plot at time tω_pe = 400 for m_i/m_e = 1836.

FIGURE 10

FIGURE 10. E_y plot at time tω_pe = 400 for m_i/m_e = 100.

Considering our input parameters, the time scale of fast growth of plasmoid instability in our simulations is on the order of a few μs. However, for larger guide fields, the growth rate is relatively smaller. In other words, for a reconnection with a weak guide field, transition to the plasmoid instability occurs faster and the generation of multiple secondary X-points and the size-growth of magnetic islands take place in shorter time scales. Since the X-points are the places where the magnetic energy is released due to the reconnection process, then the fast generation of such null-points in many number, results in the faster reduction of magnetic energy and so the faster increase of electric energy. Furthermore, during the plasmoid instability the out-of-plane electric field is generated which based on our parameters is on the order of a few KV/m. Such a strong electric field, although spatially localized around X-points, is the most suitable candidate for accelerating charged particles perpendicular to the reconnection plane. Studying the particle trajectory and acceleration in the presence of different components of the electric and magnetic field is our next work to do. The effect of reconnection-plane electric fields and also the different amplitude guide field on the acceleration scenario will be considered.

It was shown that the nature and properties of waves excited inside and outside the current sheet are different. While the outside perturbations are transient, the inside ones are long-lived, and are directly affected by the plasmoid instability process. FFT technique was used to clarify the nature of waves. This study has discussed in detail, the effect of non-uniform guide field on the spatial and temporal evolution of plasmoid instability. As a final point to make, according to the presented results, the electric field components located on the reconnection plane can play an important role in particle acceleration problem since their amplitude during the plasmoid instability is as large as of the out-of-plane component. In previously published literatures, the attention is mostly paid to the out-of-plane component of the electric field. Our study provides a prerequisite basis for the study of particle acceleration which is our future work to do.

The last point to mention is that while our study is 2D, the 3D PIC simulation of plasmoid instability is difficult to do for us due to the computational cost limitations. The point we can mention here is that unlike standard 2D depictions of reconnection and plasmoid formation, it seems that the 3D simulation would show a highly complex structure that has considerable winding of field lines. Additionally, the simulated plasmoid (or flux rope in 3D) does not move only to the right/left boundaries uniformly away from the X-points, but rather it can has asymmetric motion in the direction of third dimension. This results in a skewed plasmoid (flux rope) structure which requires more exact but expensive simulations either in MHD or Kinetic (PIC).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

MP: Doing the PIC simulations, visualizing the data and preliminary writing MH: Analyzing the data and writing and revising some part of manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to the EPOCH code developing team that allowed us to use the code for simulations.

References

Bárta, M., Büchner, J., Karlický, M., and Kotrč, P. (2011). Spontaneous Current-Layer Fragmentation and Cascading Reconnection in Solar Flares: II. Relation to observations 730, 47. doi:10.1088/0004-637X/737/1/24

CrossRef Full Text | Google Scholar

Bhattacharjee, A., Brunel, F., and Tajima, T. (1983). Magnetic Reconnection Driven by the Coalescence Instability. Phys. Fluids 26, 3332. doi:10.1063/1.864070

CrossRef Full Text | Google Scholar

Birn, J., and Priest, E. (2007). Reconnection of Magnetic Fields: Magnetohydrodynamic and Collisionless Theory and Observations. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Cargill, P. J., Vlahos, L., Baumann, G., Drake, J. F., and Nordlund, A. (2012). Current Fragmentation and Particle Acceleration in Solar Flares. Space Sci. Rev. 173, 223–245. doi:10.1007/s11214-012-9888-y

CrossRef Full Text | Google Scholar

Chen, L.-J., Daughton, W., Bhattacharjee, A., Torbert, R. B., Roytershteyn, V., and Bessho, N. (2012). In-plane Electric fields in Magnetic Islands during Collisionless Magnetic Reconnection. Phys. Plasmas 19, 112902. doi:10.1063/1.4767645

CrossRef Full Text | Google Scholar

Daughton, W., Roytershteyn, V., Albright, B. J., Karimabadi, H., Yin, L., and Bowers, K. J. (2009). Role of Electron Physics in the Development of Turbulent Magnetic Reconnection in Collisionless Plasmas. Phys. Rev. Lett. 103, 065004. doi:10.1103/physrevlett.103.065004

PubMed Abstract | CrossRef Full Text | Google Scholar

Drake, J. F., Swisdak, M., Schoeffler, K. M., Rogers, B. N., and Kobayashi, S. (2006). Formation of Secondary Islands during Magnetic Reconnection. Geophys. Res. Lett. 33, L13105. doi:10.1029/2006gl025957

CrossRef Full Text | Google Scholar

Egedal, J., Daughton, W., and Le, A. (2012). Large-scale Electron Acceleration by Parallel Electric fields during Magnetic Reconnection. Nat. Phys. 8, 321–324. doi:10.1038/nphys2249

CrossRef Full Text | Google Scholar

Fan, F., Huang, C., Lu, Q., Xie, J., and Wang, S. (2016). The Structures of Magnetic Islands Formed during Collisionless Magnetic Reconnections in a Force-free Current Sheet. Phys. Plasmas 23, 112106. doi:10.1063/1.4967286

CrossRef Full Text | Google Scholar

Fu, S., Huang, S., Zhou, M., Ni, B., and Deng, X. (2018). Tripolar Electric Field Structure in Guide Field Magnetic Reconnection. Ann. Geophys. 36, 373–379. doi:10.5194/angeo-36-373-2018

CrossRef Full Text | Google Scholar

Galsgaard, K., and Nordlund, A. (1996). Heating and Activity of the Solar corona: 1. Boundary Shearing of an Initially Homogeneous Magnetic Field. J. Geophys. Res. 101, 13445–13460. doi:10.1029/96ja00428

CrossRef Full Text | Google Scholar

Gonzalez, W., and Parker, E. (2016). Magnetic Reconnection Concepts and Applications. Berlin/Heidelberg, Germany: Springer.

Google Scholar

Gudiksen, B. V., and Nordlund, A. (2005). An Ab Initio Approach to the Solar Coronal Heating Problem. ApJ 618, 1020–1030. doi:10.1086/426063

CrossRef Full Text | Google Scholar

Intrator, T. P., Sun, X., Lapenta, G., Dorf, L., and Furno, I. (2009). Experimental Onset Threshold and Magnetic Pressure Pile-Up for 3D Reconnection. Nat. Phys. 5, 521–526. doi:10.1038/nphys1300

CrossRef Full Text | Google Scholar

Karimabadi, H., Dorelli, J., Roytershteyn, V., Daughton, W., and Chacón, L. (2011). Flux Pileup in Collisionless Magnetic Reconnection: Bursty Interaction of Large Flux Ropes. Phys. Rev. Lett. 107, 025002. doi:10.1103/PhysRevLett.107.025002

PubMed Abstract | CrossRef Full Text | Google Scholar

Karimabadi, H., Krauss-Varban, D., Omidi, N., and Vu, H. X. (1999). Magnetic Structure of the Reconnection Layer and Core Field Generation in Plasmoids. J. Geophys. Res. 104, 12313–12326. doi:10.1029/1999ja900089

CrossRef Full Text | Google Scholar

Kumar, P., Karpen, J. T., Antiochos, S. K., Wyper, P. F., and Devore, C. R. (2019). First Detection of Plasmoids from Breakout Reconnection on the Sun. ApJ 885, L15. doi:10.3847/2041-8213/ab45f9

CrossRef Full Text | Google Scholar

Liu, W., Chen, Q., and Petrosian, V. (2013). Plasmoid Ejections and Loop Contractions in an Eruptive M7.7 Solar Flare: Evidence of Particle Acceleration and Heating in Magnetic Reconnection Outflows. ApJ 767, 168. doi:10.1088/0004-637x/767/2/168

CrossRef Full Text | Google Scholar

Loureiro, N. F., Schekochihin, A. A., and Cowley, S. C. (2007). Instability of Current Sheets and Formation of Plasmoid Chains. Phys. Plasmas 14, 100703. doi:10.1063/1.2783986

CrossRef Full Text | Google Scholar

Markidis, S., Henri, P., Lapenta, G., Divin, A., Goldman, M. V., Newman, D., et al. (2012). Collisionless Magnetic Reconnection in a Plasmoid Chain. Nonlin. Process. Geophys. 19, 145–153. doi:10.5194/npg-19-145-2012

CrossRef Full Text | Google Scholar

Priest, E., and Forbes, T. (2000). Magnetic Reconnection: MHD Theory and Applications. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Wan, W., Lapenta, G., Delzanno, G. L., and Egedal, J. (2008). Electron Acceleration during Guide Field Magnetic Reconnection. Phys. Plasmas 15, 032903. doi:10.1063/1.2876465

CrossRef Full Text | Google Scholar

Yamada, M., Kulsrud, R., and Ji, H. (2010). Magnetic Reconnection. Rev. Mod. Phys. 82, 603–664. doi:10.1103/revmodphys.82.603

CrossRef Full Text | Google Scholar

Zhou, M., Deng, X. H., and Huang, S. Y. (2012). Electric Field Structure inside the Secondary Island in the Reconnection Diffusion Region. Phys. Plasmas 19, 042902. doi:10.1063/1.3700194

CrossRef Full Text | Google Scholar