- 1University of Alaska Fairbanks, Fairbanks, AK, United States
- 2Embry-Riddle Aeronautical University, Daytona Beach, FL, United States
- 3Andrews University, Berrien Springs, MI, United States
The flow shear-driven Kelvin-Helmholtz (KH) instability is ubiquitous in planetary magnetospheres. At Earth these surface waves are important along the dawn and dusk flanks of the magnetopause boundary while at Jupiter and Saturn the entire dayside magnetopause boundary can exhibit KH activity due to corotational flows in the magnetosphere. Kelvin-Helmholtz waves can be a major ingredient in the so-called viscous-like interaction with the solar wind. In this paper, we review the KH instability from the perspective of hybrid (kinetic ions, fluid electrons) simulations. Many of the simulations are based on parameters typically found at Saturn’s magnetopause boundary, but the results can be generally applied to any KH-unstable situation. The focus of the discussion is on the ion kinetic scale and implications for mass, momentum, and energy transport at the magnetopause boundary.
1 Introduction
From the perspective of hydrodynamics, any flow shear with a deformed interface develops pressure gradients following from the Bernoulli principle. A positive feedback yields further deformation leading to the Kelvin-Helmholtz (KH) instability where the boundary interface can be rolled up into a vortex structure. The planetary magnetopause boundary is a prime example of a potentially KH-unstable interface, provided that there is sufficient kinetic energy in the flow to overcome magnetic tension forces. Thus, the KH instability has generated considerable attention as a mechanism for facilitating a viscous-like interaction of the solar wind with planetary magnetospheres (review by Johnson et al. (2014) and references therein).
While magnetopause boundary processes garner much of the attention, it should be noted that a discontinuous flow shear with sufficient kinetic energy density to overcome magnetic tension will be KH unstable (Chandrasekhar, 1961). For the simple case of an incompressible plasma with a discontinuous flow shear, the condition for KH instability is
where v denotes velocity, ρ is the mass density, B is the magnetic field, k is the wave vector, and the indices refer to the two regions across the shear flow boundary. The corresponding linear growth rate of the wave is given by
where αi = ρi/(ρ1 + ρ2). Further refinements were made by Miura and Pritchett (1982) by considering compressibility, demonstrating that for finite half width, Lo, of the initial shear flow layer, the growth rates will be a function of the magnetosonic Mach number with most unstable modes occurring when the wavelength is comparable to the width of the shear layer, or 2kLo ∼ 1.
The flow shear on the dawn and dusk flanks of the terrestrial magnetopause boundary are inherently KH unstable, leading to global-scale KH vortices advecting down the magnetotail (Figure 1). In the broader context of planetary magnetospheres, KH waves are ubiquitous and are thought to play an even more important role at the giant planet magnetospheres where the viscous-like processes are thought to play a critical role in the solar wind interaction (Delamere and Bagenal, 2010). Figure 2, from a multifluid Lyon-Fedder-Mobarry simulation of Jupiter’s magnetosphere, shows KH waves on the dayside magnetpause boundary due to internal corotational flows (Zhang et al., 2018). It should be noted that KH waves are not found exclusively at the magnetopause boundary. For example, secondary KH instabilities could occur at the boundaries of injection channels associated with, e.g., tail reconnection events.
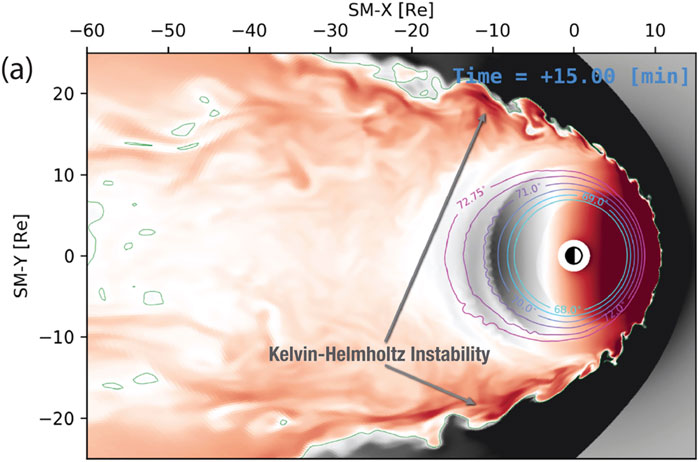
FIGURE 1. GAMERA simulation of Earth’s magnetosphere (Sorathia et al., 2020). The color depicts the residual magnetic field (with the dipole subtracted).
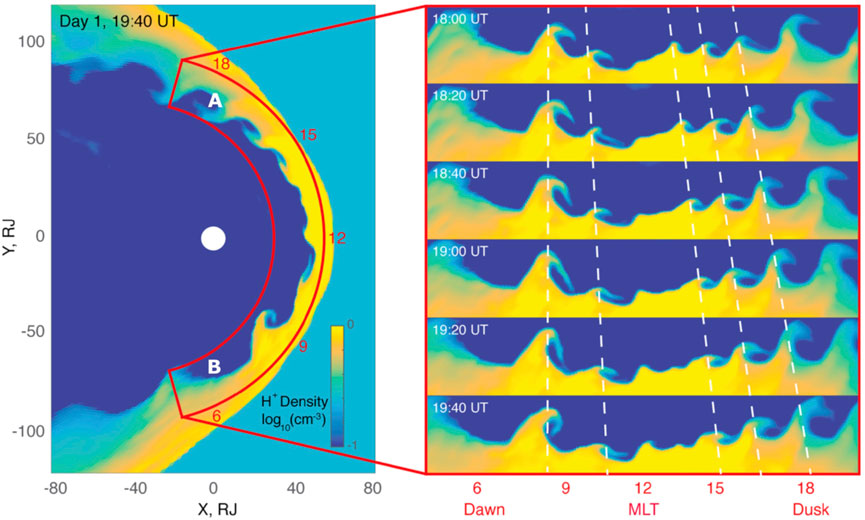
FIGURE 2. Multifluid Lyon-Fedder-Mobarry simulation of Jupiter’s magnetosphere showing KH waves on the dayside magnetopause boundary due to internal corotational flows (Zhang et al., 2018).
The KH instability is rife with kinetic-scale physics. In fact, KH vortices could be considered as a microcosm for kinetic-scale plasma physics. This papers explores the wealth of KH-related plasma processes with specific application to planetary magnetospheres. While the goal is to explore implications for the terrestrial magnetosphere, numerous examples from the giant planet magnetospheres will be discussed to further understand the kinetic aspects of the KH instability. Specifically, we discuss KH growth characteristics, magnetic field topology, heavy ion effects, momentum transport, particle transport, energy tranport and heating, and electron energization due to parallel electric fields associated with driven KH reconnection.
2 Hybrid Simulations
The basis of our discussion will be hybrid (kinetic ions, fluid electrons) simulations of the KH instability (Delamere et al., 2011; Delamere et al., 2018; Delamere et al., 2021). Hybrid simulations push ions according to the Lorentz force equation using the Boris (1970) method. The electric and magnetic fields are ordered on a Yee grid to facilitate the correct field topology for curl operations (Yee, 1966) and to guarantee a divergence-free magnetic field. The magnetic field is updated with Faraday’s law using a second-order, predictor-corrector method. The electric field is determined from the electron momentum equation (massless electrons) that contains an ion-electron collision term and an electron pressure term. The electron fluid is assumed to be isothermal in time and space for numerical simplicity. Ampere’s law is used to calculate the electron bulk flow used in the electric field calculation.
With the addition of the electron pressure term, the hybrid simulation is capable of modeling kinetic Alfvén waves (KAW). The dispersion relation for the KAW is
where ρi is the ion Larmor radius, vA is the Alfvén speed. At ion inertial scales, KAW modes capture Alfvén and ion-ion hybrid resonances of the fast magnetosonic/whistler branch. In addition, mode conversion of the compressional fast mode waves to KAW will be captured in hybrid simulations (Lin et al., 2010; Lin et al., 2012).
To elucidate the ion kinetic effects, the simulations have been typically conducted for plasma β ∼ 1 where both ion inertial and gyroradius effects are important. By expressing the plasma β as the ratio of thermal pressure to magnetic field pressure, it can be shown that
All simulations are based on typical conditions for Saturn’s magnetopause boundary. The magnetospheric (corotational) flows are in the +x direction, the +z is normal to the magnetopause boundary from magnetosheath to magnetosphere, and +y is the direction of the magnetic field. Protons are used by default and admixtures of heavy ions (where relevant) were added to the magnetospheric side of the boundary. The typical density is 0.4 cm−3 with an ion inertial length of 360 km. The magnetic field was of the order of 5 nT with a small (e.g., 2%) in-plane component included in the x direction. The velocity shear was of the form
3 KH Growth Characteristics
The fastest growing wavelength of KH modes is typically at the ion kinetic scale. Boundaries in space plasma can be comparable to the ion inertial length (e.g., magnetopause boundary); therefore, the wavelength of fastest growing wavelength will be of the order of 4πλi. Compared to magnetospheric scales, this is surprisingly small, i.e., a small fraction of the planet’s radius. The slower growing, larger-scale modes can subsume the small-scale modes leading to an apparent inverse cascade. Eventually the KH waves can reach global scale with average KH wavelengths ∼ 5 RE on the flanks of Earth’s magnetopause boundary (Otto and Fairfield, 2000).
In this paper we consider very simple configurations that promote an inverse cascade. But it is important to note that, e.g., density inhomogeneity can lead to secondary Rayleigh-Taylor instability that can disrupt vortex formation (Matsumoto and Hoshino, 2004). Faganello et al. (2008) showed that in the case where the magnetic field is strictly perpendicular to the flow, density inhomogeneity can lead to both inverse and direct cascades dominating the dynamics, though when an in-plane magnetic field component is added, the secondary instabilities can be stabilized (Cowee et al., 2010; Tenerani et al., 2010). For magnetospheric systems, the high latitude region is typically KH stable and the inverse cascade stops with the vortex scale is comparable to the height of the unstable region (Takagi et al., 2006).
One of the challenges for global-scale simulations is resolving the thin magnetopause boundary. With insufficient resolution and/or excessive numerical diffusion, the fastest growing mode could approach global-scale and the growth rates could be slower than the solar wind advection time scale, prohibiting the onset of KH waves. By using higher order numerics, the Lyon-Fedder-Mobarry model (and later incarnation as the Grid Agnostic MHD for Extended Research Applications or GAMERA simulation (Zhang et al., 2019)) has generated KH modes in both terrestrial (Merkin et al., 2013) and giant magnetosphere simulations (Zhang et al., 2018). Figure 1 shows a terrestrial GAMERA simulation with the KH waves reaching global-scale on the dawn and dusk flanks (Sorathia et al., 2020). Despite the success of global-scale simulations to model the KH instability, a three-dimensional, meso-scale simulation is required to capture the kinetic-scale processes to understand the interaction between the spectrum of modes that can be present. Typically, a meso-scale (few planetary radii) simulation will capture the inverse cascade and saturate at the m = 1 mode that is fixed by the spatial domain.
Figure 3 illustrates the inverse cascade from a two-dimensional hybrid simulation (Delamere et al., 2011). The cascade from an m = 20 (short wavelength) mode is apparent, with final state of the system in the m = 1 mode (longest wavelength supported by the simulation domain). An unresolved issue is the extent to which the slower-growing, smaller-m modes grow independently and subsume the larger m modes, or whether there is a true inverse cascade in which information is transferred from one scale to another. In section 8 we note that in the presence of heavy ions, the protons can separately exhibit a forward cascade while the heavy ions participate in an inverse cascade. This is a topic for more detailed investigation in future studies.
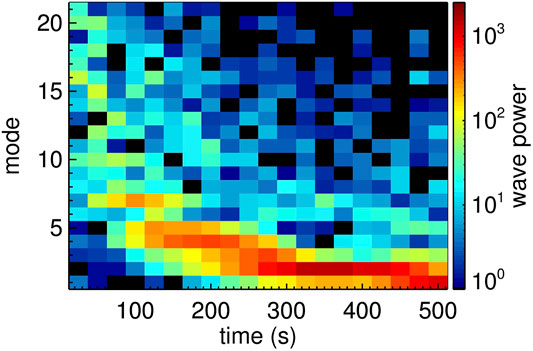
FIGURE 3. Growth of KH, showing inverse cascade (Delamere et al., 2011).
4 Magnetic Field Topology
Magnetic reconnection plays a critical role in the Kelvin-Helmholtz instability and requires a three dimensional treatment. We start with a discussion of strong guide field reconnection. The standard two-dimensional model (e.g., Sweet and Parker and/or Petschek) of a simple current sheet formed by strictly anti-parallel magnetic fields is misleading because these models neglect the more likely existence of a guide magnetic field in the ignorable, out-of-plane direction (Figure 4). Magnetic flux conservation in the two-dimensional configuration requires a constant out-of-plane electric field. But note that in the presence of an out-of-plane guide field, the electric field has a parallel component to the magnetic field in a small region of space near the X-line. Schindler et al. (1988) showed that magnetic reconnection occurs if and only if the integral of the parallel electric field is nonzero on a measurable set of field lines in the diffusion region. The parallel potential also gives the rate of reconnected flux (Hesse and Schindler, 1988).
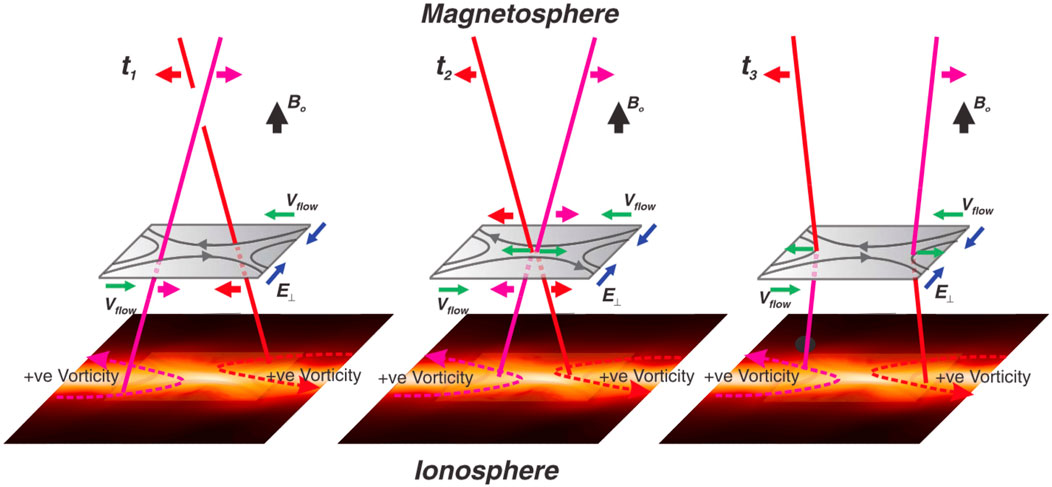
FIGURE 4. Schematic of extreme guide field reconnection and its relation to discrete auroral arc structure (Chaston et al., 2015). Reconnection involves the horizontal magnetic field components.
Auroral acceleration in planetary magnetospheres occurs close to the planet on (highly) dipolar magnetic field lines. Extreme guide field reconnection can operate in this case and Seyler (1990) and Otto and Birk (1993) have suggested that thin, discrete aurora arcs are governed by magnetic reconnection with small magnetic shear. Chaston et al. (2015) recently presented the first experimental evidence of the role of extreme guide field reconnection in the auroral acceleration region. Figure 4 summarizes the time sequence of the auroral reconnection process where red and magenta field lines reconnect, giving rise to islands of vorticity in thin auroral arcs (Chaston et al., 2015). Similar reconnection processes are expected to occur in KH vortices.
The magnetic field structure associated with KH vortices leads to intense currents due to the twisting of the magnetic field. The net result is driven reconnection which can lead to magnetic field line threading of the magnetopause boundary. In two-dimensions, the vortex structure can be defined by magnetic barriers. Figure 5 shows the magnitude of the in-plane component 1 of the magnetic field in a 2-D hybrid simulation. As the surface wave develops, magnetic flux accumulates along the spine and vortex boundary. In the limiting case,
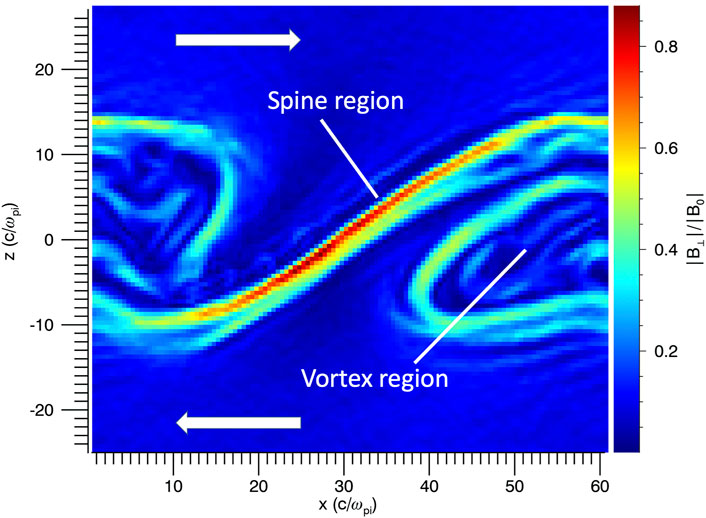
FIGURE 5. Structure of a KH vortex as illustrated with the magnitude of the in-plane magnetic field. The spine region connects adjacent vortices and is a barrier to flow due to the accumulation of magnetic flux.
While a simple 2-D picture of KH illustrates general KH properties, many interesting aspects are revealed in three dimensions. When the antiparallel components of the magnetic field in the presence of flow shear are considered in a 2-D plane, KH and reconnection are mutually exclusive. If the flow shear is sub-Alfvénic, spontaneous reconnection can operate (and KH is stabilized), while if the flow is super-Alfvénic, KH is destabilized and spontaneous reconnection is suppressed as information transport along the magnetic field is truncated (La Belle-Hamer et al., 1995; Faganello et al., 2010). We note that during the KH growth, driven reconnection can occur as current layers are pinched during vortex rollup with a rate that is independent of prescribed mechanism (Knoll and Chacón, 2002; Nakamura and Fujimoto, 2006). In three dimensions, on the other hand, KH and reconnection can interact. Ma et al. (2014a) showed that for an initial KH driver, reconnection can be triggered along the spine region as the current layer thins and intensifies. On the other hand, Ma et al. (2014b) showed that reconnection flows for a preexisting current layer at the magnetopause boundary can trigger the KH instability. Ultimately, the twisting of the magnetic field can lead to strong guide field reconnection in pairs of reconnection sites (Otto, 2007; Faganello et al., 2012, 2014). Ma et al. (2017) showed that a KH-active magnetopause boundary, the reconnection sites form in the midlatitudes and asynchronous reconnection can lead to open flux generation. The double reconnection process can also effectively transport plasma across the magnetopause boundary.
During the non-linear rollup of KH vortices, multiple current sheets (and associated magnetic barriers and/or filaments) are folded together. Therefore, a transect of the vortex region yields a highly variable magnetic field with many bipolar signatures, typically in component pairs. Delamere et al. (2013) used these bipolar signatures to identify potential KH active regions near Saturn’s magnetopause boundary, though any vortical flow associated with, e.g., radial transport can produce similar bipolar signatures (Stauffer et al., 2019).
In three-dimensional hybrid simulations, the complexity of the magnetic field topology is further enhanced during the inverse cascade. A key aspect of hybrid simulations is that the finite particle statistics provide the “stochastic” seed for surface wave formation. The phase of the surface wave at a given point along the magnetic field is therefore random. Provided that the simulation domain along the unperturbed magnetic field is sufficiently long (e.g., perpendicular to parallel spatial scale proportional to the Alfvén Mach number of the flow shear), then the phase of the surface waves can be a function of distance along the magnetic field. In other words, the system supports k∥∼ k⊥ where k⊥ is the KH wavenumber of the fastest growing mode. As a result, twisted nodes form between out-of-phase surface waves, promoting strong guide field reconnection. At each stage of the inverse cascade, twisted node formation promotes reconnection. As a result, multiple reconnection sites can be identified on an instantaneous field line trace, adding further complexity to the magnetic field topology.
Figure 6 shows field line tracing from a 3-D hybrid simulation. The image slices and field line color show the magnitude of the parallel electric field,
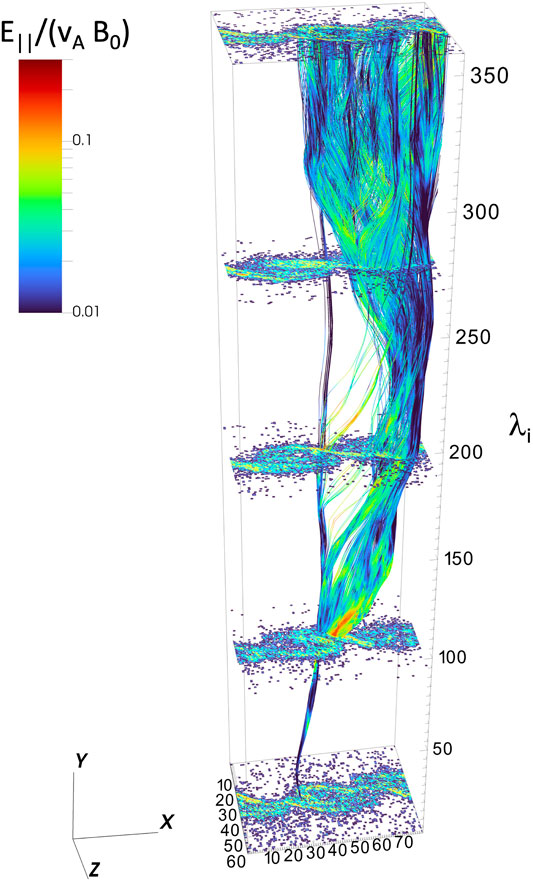
FIGURE 6. Magnetic field line traces through KH active regions in a 3-D hybrid simulation. The magnitude of the parallel electric field (E∥/(vAB0) is indicated in color. Spatial units are in ion inertial length (λi).
5 Momentum Transport
Momentum transport at the magnetopause boundary occurs as a result of the KH instability. The classic Chapman-Ferraro magnetopause boundary is the idealized case where the normal component of the magnetic field is zero and
Assuming an initial pressure balanced configuration, an estimate of the momentum transfer rates will be made by considering the steady flux conservative form of the momentum equation, i.e.,
This equation will be integrated over any arbitrary volume and rewritten as a surface integral using the divergence theorem (i.e.,
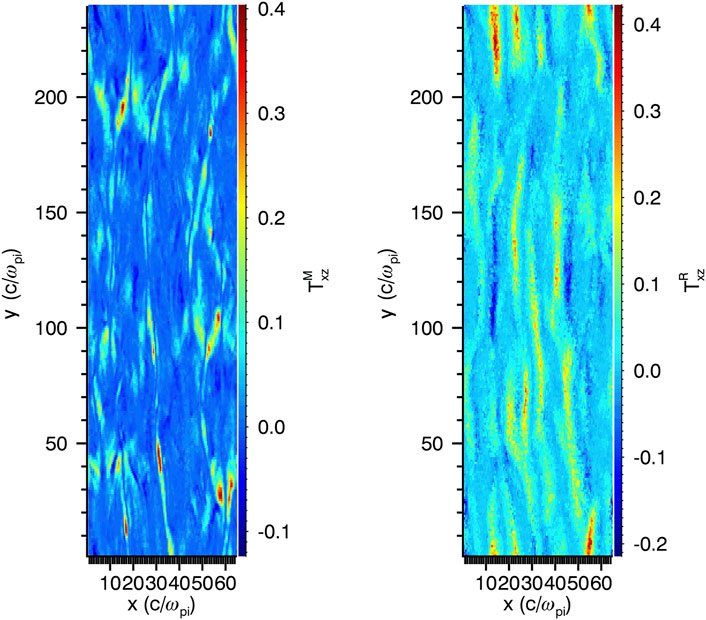
FIGURE 7. Maxwell and Reynolds stresses (normalized) at the magnetopause boundary in a 3-D hybrid simulation.
Delamere et al. (2018) estimated the flow reduction in Saturn’s dawnside magnetosheath due to Maxwell (TM) and Reynolds stresses (TR) from 3-D hybrid simulations. Figure 7 shows the midplane of the simulation (i.e., magnetopause boundary) for both TM and TR where the color scale indicates relative momentum fluxes. The upper limit for combined stress is roughly 4 × 10–13 N/m2 and this yields a flow reduction that is consistent with observations (Burkholder et al., 2019). Again, it should be emphasized that significant magnetic field line threading of the magnetopause boundary occurs and in general the Maxwell stresses (
6 Particle Transport
There are two mechanisms that facilitate mass transport. In the magnetohydrodynamic limit, magnetic reconnection is required, involving the flow-aligned components in both 2-D and 3-D cases (Fadanelli et al., 2018; Sisti et al., 2019). Hybrid simulations, on the other hand, show both magnetic reconnection operating as well as diffusive transport due to large gyroradius effects and wave-particle interactions (Johnson and Cheng, 1997; Chen, 1999; Chaston et al., 2009). In a 2-D comparison of MHD + test particles vs. hybrid simulations with periodic boundary conditions, Ma et al. (2019) showed that both simulations produced similar transport rates, but that particle mixing by finite gyroradius is the dominant process in the hybrid simulations. The derived diffusion coefficients are typically
Hybrid simulations allow for a simple calculation of the diffusion coefficient. Initially, the particles are labeled as either magnetospheric or magnetosheath particles. During the evolution of the KH instability, the ions are mixed on the grid with fully mixed grid cells containing 50% of both populations, or a mixing of 0.5. The width of the mixed cell region is Lmix (t) where values above, e.g., 0.1 are considered mixed. The diffusion coefficient is D (t) = dLmix (t)2/dt. Figure 8 compares mixing/diffusion in 2-D and 3-D hybrid simulations. In both cases the mixing is very strong in the KH active region, but the 3-D simulations tend to produce a narrower diffused region (boundary layer) due to the magnetic tension generated by out-of-phase surface waves during the inverse cascade. Presumably when the KH modes reach global scale and periodic boundary conditions are no longer valid, the system will evolve with coherent vortical structure as seen in the global simulations.
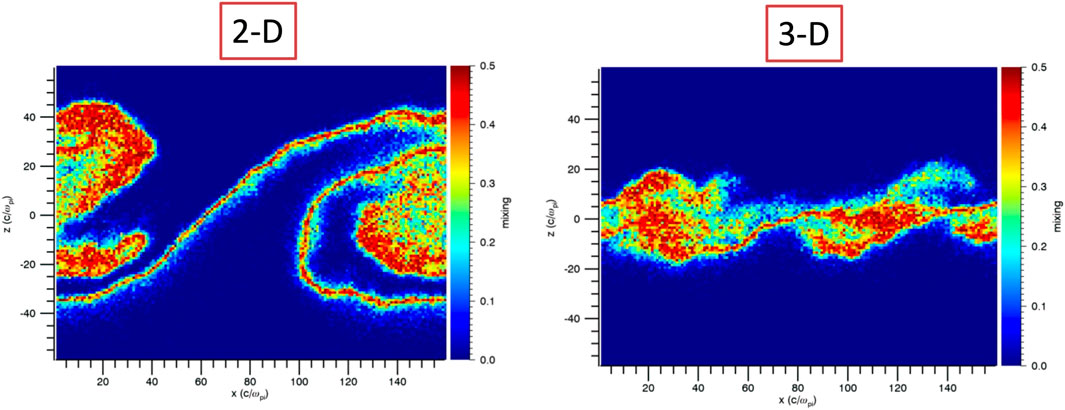
FIGURE 8. Comparison of 2D and 3D hybrid simulations. The 2-D result shows a coherent m = 1 vortex structure while the 3-D case does not exhibit a coherent rolled up structure and at the same time appears as an m = 2 mode.
Boundary layer formation can occur rapidly when growth rates exceed the solar wind/magnetospheric advection time. For an initial boundary width of the order of the ion inertial length, the growth rates can exceed γ = 0.01 s−1, or a growth time scale of minutes (Delamere et al., 2011). Eventually the boundary layer will thin such that the onset of KH waves is episodic. Burkholder et al. (2019) found an occurrence frequency
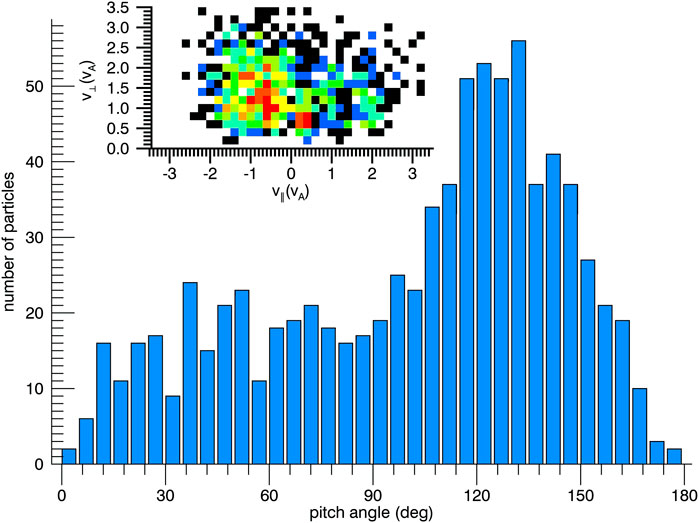
As a preliminary test of KH-related transport of energetic ions, we conducted a proton-only, 3-D hybrid simulation that contained a small population (e.g., 1% of total mass density) of energetic protons (4vth) on the magnetospheric side of the flow shear boundary. During the growth of the KH waves, these particles were found to be transported across the boundary (i.e., to regions dominated by magnetosheath plasma). The velocity distribution was often peaked well away from 90° pitch angle. Figure 9 shows an example of such a streaming distribution with a peak near 130°, similar to the distributions reported by Sergis et al. (2013). We note that streaming distributions have also been measured by the magnetospheric multiscale mission at Earth. Vernisse et al. (2016) suggested that the streaming particles were generated by reconnection induced by KH instabilities. The Themis and Cluster missions have also observed streaming ion distributions far away from the vortex location (Bavassano Cattaneo et al., 2010; Faganello et al., 2014).
Figure 10 shows a sample field line trace taken through the KH active region. The top to bottom is the ion pitch angle distribution of the superthermal magnetospheric ions, the ion mixing, the normalized x component of flow, the normalized perpendicular magnetic field perturbations, the parallel electric field, and the integrated parallel electric field (field-aligned potential). In this example, the magnetic field samples a wide range of mixing values, plasma flows. We note that the pitch angle distribution is often not peaked near 90° as would be expected for an unperturbed Maxwellian distribution. The modification of the distribution function as a function of energy is a topic for future study; however, initial studies suggest that transport can be facilitated and/or modulated by KH activity.
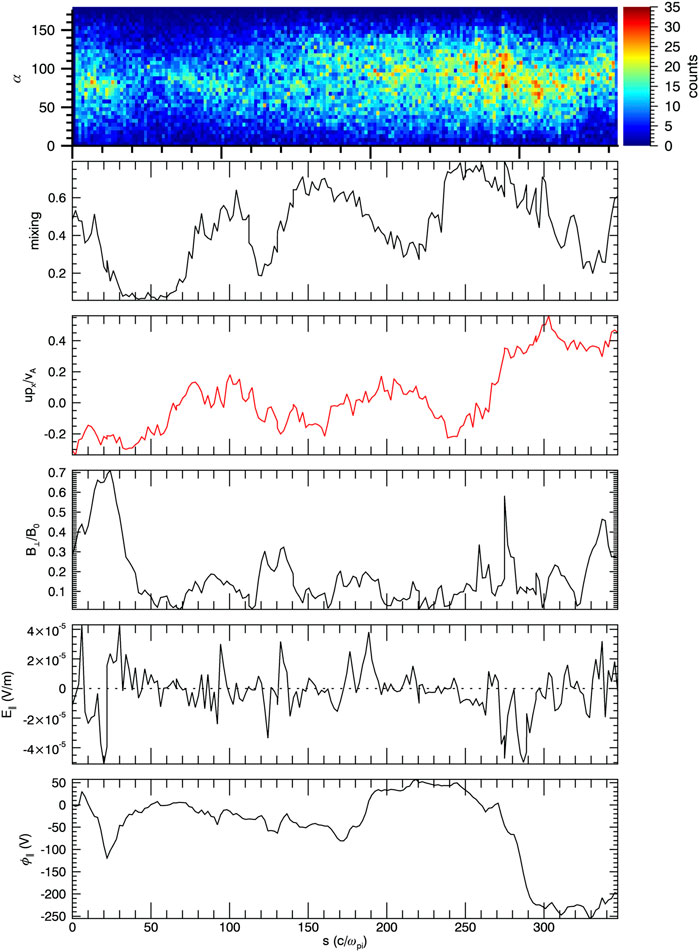
FIGURE 10. Magnetic field line trace through KH active region in hybrid simulation, showing various properties. From top to bottom is “superthermal” ions, plasma mixing, plasma flow, in-plane magnetic field normalized to the background magnetic field, parallel electric field, and field-aligned potential.
7 Energy Transport and Heating
KH waves radiate compressional modes into the magnetospheric cavity. Pu and Kivelson (1983) and Delamere et al. (2011) showed that roughly 1% of the incident solar wind power can be radiated into the magnetosphere. As a result, magnetospheric resonant cavity modes can be excited and/or plasma heating can occur. The empirical estimate for the plasma heating rate at Saturn is 30–400 GW (Bagenal and Delamere, 2011), which compares favorably with Poynting flux in generated in hybrid simulations multiplied by the expected KH-active area of the dayside magnetopause boundary (Delamere et al., 2011). The internal energy transport via the magnetosonic fast mode can be comparable to or even shorter than the solar wind advection time past the magnetosphere (e.g., hours for the giant magnetospheres); therefore, prompt KH modulation of magnetospheric processes should be expected. Though, the details of energy flow partitioning in the magnetospheric system remains unresolved.
Within the KH vortex, on the other hand, significant plasma heating can be expected based on models for the non-linear interaction between counter-propagating Alfvén waves (Burkholder et al., 2020a). Delamere et al. (2021) examined the heating in 3-D KH simulations and found that indeed the ion heating is consistent with the turbulent heating mechanism (Saur, 2004). Assuming a turbulent spectrum of magnetic field fluctuations (δB⊥), the heating rate density for the kinetic Alfvén wave (KAW) is
where ρ is the mass density and ρi is the thermal ion gyroradius. Figure 11 shows the heating rate density for a 3-D hybrid simulation, showing the localization of regions with significant heating. The contours show the magnitude of the in-plane magnetic field. Future studies should investigate, in detail, the interaction of ions with kinetic Alfvén waves to fully understand the heating process.
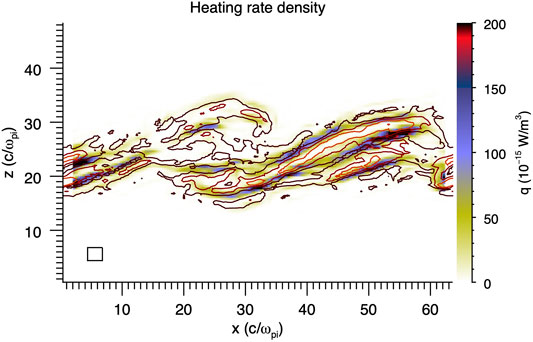
FIGURE 11. Turbulent heating rate density (Delamere et al., 2021). Contours indicate the magnitude of the in-plane magnetic field.
8 Heavy Ion Effects
Magnetospheric plasmas are rarely homogeneous and often contain multiple ion species. At Earth, ionospheric outflow can introduce heavy ions into the system (i.e., O+) (Welling et al., 2015). Bouhram et al. (2005) showed that heavy ions are the dominant contributor to the mass density 30% of the time on the dusk flank and 5% of the time on the dawn flank. In the giant planet magnetospheres, heavy ions are sourced from the moons and play a significant role in magnetospheric dynamics. Magnetospheric heavy ions can also modify the growth rates of the KH instability and at kinetic-scale can significantly modify the structure of the KH modes. (Delamere et al., 2011) showed, using 2-D hybrid simulations, that: 1) growth rates tend to increase when protons (magnetosheath) are separated from the heavies (magnetosphere); 2) growth rates tend to decrease with equal mixtures of protons and heavies; and 3) decrease when only heavy ions are present on both sides of the boundary. In the latter case, it was suggested that inhibited growth was due to suppression of wavelengths less than the ion inertial length. The dawn/dusk asymmetry of heavy ions at Earth could have implications for KH-related plasma transport.
In the limiting case of magnetospheric heavy ions separated from the magnetosheath protons, the initial onset of the KH modes is distinctly different. Figure 12 shows the results from a 2-D hybrid simulation during the onset of the KH instability for parameters based on Saturn’s magnetopause boundary environment (i.e., heavy ions = 17 AMU for water group ions). The top region is the magnetosheath containing protons and the bottom region is the magnetosphere containing heavy ions. From left to right and top to bottom the figure shows 1) the magnetic field pressure, 2) plasma pressure, 3) total ion mass density, 4) proton density, 5) heavy ion density, and 6) normalized local entropy. Perhaps the most striking result is the absence of heavy ions in the magnetosheath. The onset of an m ∼ 6–7 mode is clearly present, but the heavy ions do not participate in the fluid-scale wave motion because the wavelengths of the m > 6 modes are less than the heavy ion inertial length (e.g., cannot generate the compressional magnetosonic fast mode). Thus, the heavies cannot participate in the wave motion. On the other hand, the protons are affected by the surface wave and move in the vortical flows. The appearance of protons on the magnetospheric side of the boundary is not balanced by heavy ions in the sheath, leaving voids in plasma pressure. The local entropy (p/ργ) increases because of the apparent dominance of the inverse relation with plasma mass density (ρ). In terms of long-term wave evolution, the heavy ions exhibited the expected inverse cascade while the protons showed a forward cascade, saturating at m = 5 (Figure 13). These simulations are highly idealized but illustrate the potential importance of heavy ions in modifying the KH structure at kinetic scale. Future studies should examine the transfer entropy from conditional mutual information theory to further understand these forward and inverse cascades.
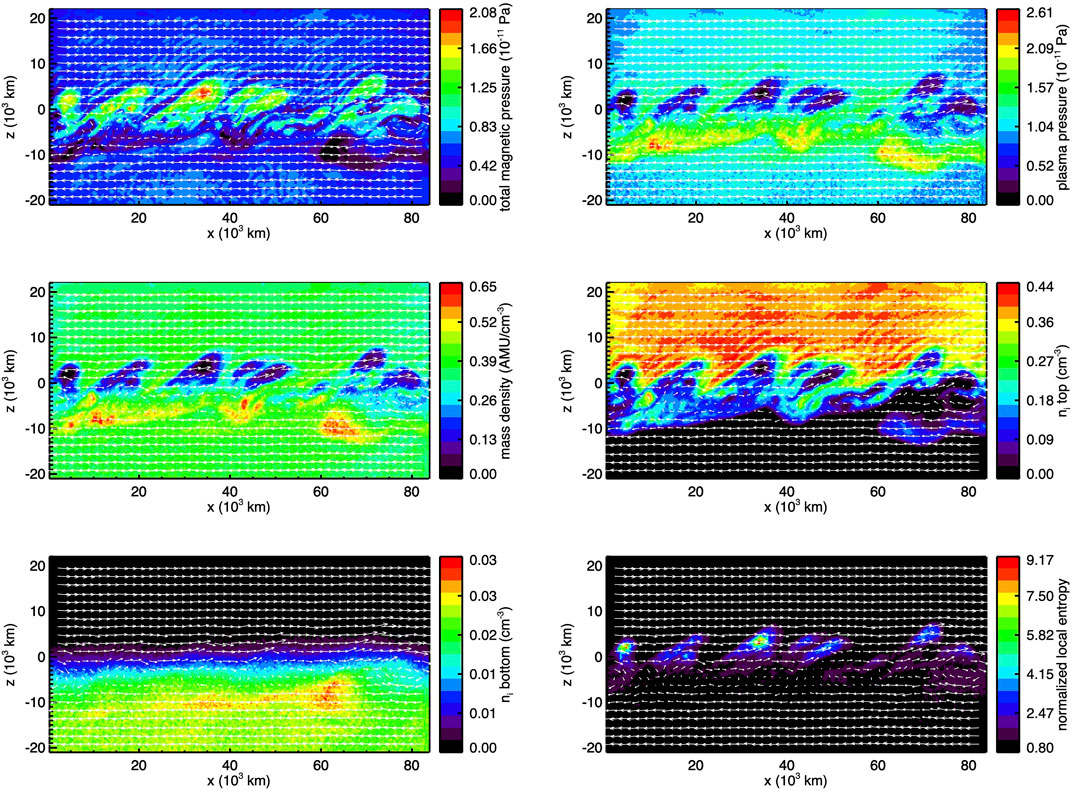
FIGURE 12. KH waves with heavy ions. The protons are initialized in the top half and the heavies (17 amu) in the bottom half of the domain. From top to bottom and left to right: total magnetic pressure, plasma pressure, mass density, ion density for the top region (protons), ion density for the bottom region (heavies), normalized local entropy.
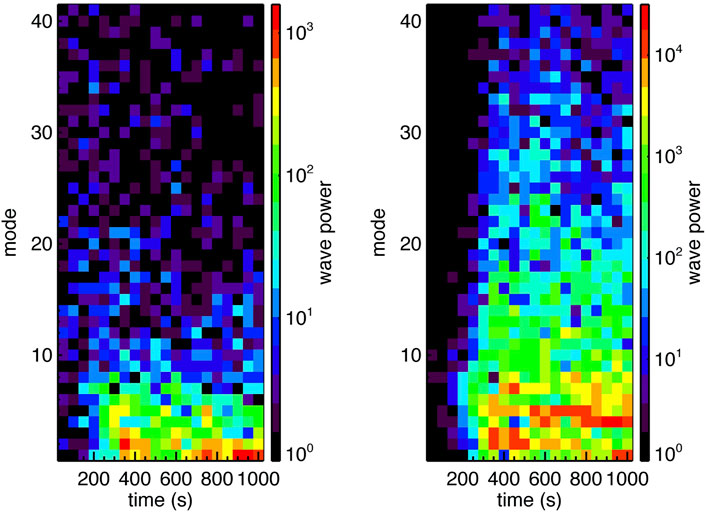
FIGURE 13. KH wave mode cascade with heavy ions for the simulation shown in Figure 12. The heavy ions exhibit an inverse cascade to m = 1 while the protons show a forward cascade to m ∼ 5.
In a 2-D study of density asymmetry with heavy ions, Meier (2012) found that mixing was reduced by increasing the mass density across the magnetopause boundary. The heavy magnetospheric ion (16 amu) fraction was fixed at 25% (with a mixture of protons) while magnetosheath to magnetosphere number density ratio was varied between 2 and 8 (the corresponding mass density ratio varied between 0.5 and 2). Pressure balance was achieved by modifying the magnetospheric proton temperature accordingly. In addition to reduced mixing (presumably due to large gyroradius effects in the non-linear rollup phase), the vortices developed on the low density (magnetospheric) side of the boundary. Thus, the density asymmetry may expedite the formation of mixed boundary layers in the giant magnetosphere as these asymmetric density conditions are often found at Jupiter and Saturn.
Heavy ions can affect mass transport at the magnetopause due to wave-particle interactions. While we have not explicitly investigated these effects in KH hybrid simulations, we note that transport coefficients can be derived following standard methods from the drift-kinetic or the gyrokinetic equation (Johnson and Cheng, 1997; Chen, 1999; Chaston et al., 2009). In particular, some of the dominant mechanisms include contributions from Landau damping, magnetic field gradient drift, and transit time damping associated with KAW-related magnetic bottles. The presence of heavy ions affects the diffusion coefficients in two ways. First, increased ion mass leads to larger parallel electric fields. This effect is necessary because the ion polarization drift is larger for heavy ions, leading to increased charge separation and thus the parallel electric field required to maintain quasineutrality. Similarly, the ion density fluctuations associated with the polarization drift enhances the magnetic field compressions (particularly in a high β plasma), enhancing the transit time damping. Second, the heavy ions reduce the Alfvén speed which increases the fraction of resonant particles in the wave-particle interaction. Future studies should compare hybrid simulation results with theoretical expectations for the effects on heavy ions on transport.
9 Electron Energization
While electron kinetic effects cannot be addressed directly in hybrid simulations, it is possible to study the effects of parallel electric fields using electron test particle simulations. The parallel electric fields have been evaluated in both Rayleigh-Taylor (Stauffer et al., 2019) and KH simulations and are found to be independent of the specified resistivity. Estimates for the magnitude of the parallel electric fields (Section 4) based on local conditions in the simulations show that the reconnection rates approach or exceed 0.1, consistent with expectation for driven fast reconnection.
Using an ensemble of field line traces (i.e., similar to Figure 6), we conducted electron test particle simulations for parallel motion, i.e.,
We initialized a 20 eV Maxwellian distribution on the field line ensemble. Figure 14 shows the phase space (v∥ vs. y) at a snapshot in time for a sample field line, showing field-aligned streaming (acceleration) as well as trapped populations. Assuming that the evolution of the non-linear KH vortex modifies the parallel electric field configuration in time, we conducted an ensemble average to determine the likely steady state electron velocity distribution. For Saturn-like conditions, the final distribution was consistent with a 120 eV Maxwellian. Curiously, this is consistent with the thermal electron temperature in Saturn’s outer magnetosphere (Neupane, 2021), but further study would be required to understand how internal radial transport could affect the thermal electron temperature. Figure 15 shows the initial distribution (red) with a 20 eV Maxwellian fit and the final distribution (blue) with a 120 eV Maxwellian fit. A snapshot of any given field line would likely reveal bidirectional electron beams. Such beams are commonly observed in KH active regions of the terrestrial magnetopause boundary (Burkholder et al., 2020b). Nykyri et al. (2021) suggested that, among other mechanisms, magnetic reconnection could be a candidate for explaining the
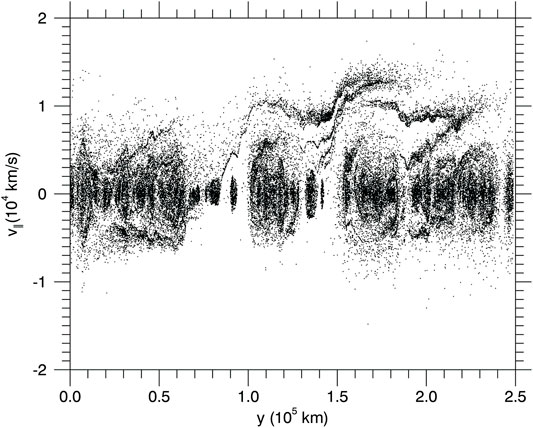
FIGURE 14. Electron test particle simulations using the sample magnetic field line trace. The distribution in Figure 15 is an ensemble average of many sample field lines taken from the KH active region.
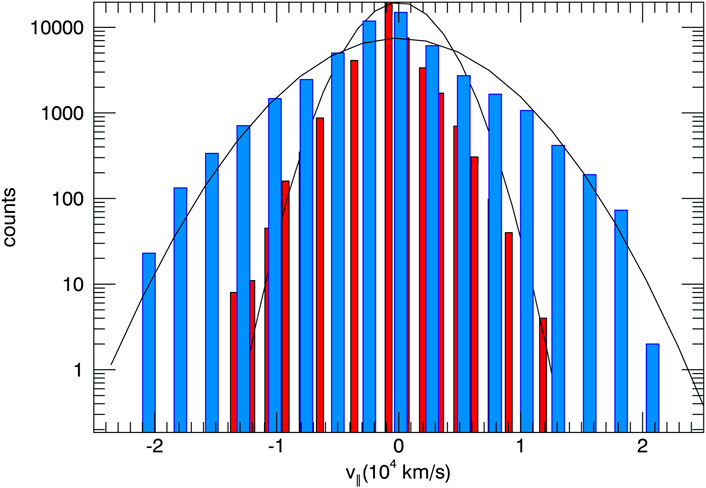
FIGURE 15. The parallel velocity distribution from electron test particle simulations. Red is the initial 20 eV distribution. Blue is the ∼120 eV ensemble-averaged distribution.
10 Conclusion
Considerable progress has been made with regard to ion kinetic-scale processes associated with the Kelvin-Helmholtz instability. Here we summarize the key advances in understanding and on directions for future studies.
• The growth of KH modes in our simulations can be described as a inverse cascade. For typical magnetopause boundary thickness (few ion inertial lengths), the fastest growing modes are relatively small scale (less than planetary radii) and, under certain conditions, could evolve to global scales (few planetary radii) as the structures advect down the tail flanks.
• The inverse cascade results in smaller scale structures being subsumed by larger scale structure, resulting in complex magnetic field topologies with a patchy network of strong guide field reconnection sites.
• Maxwell stresses associated with magnetic field line threading of the magnetopause boundary lead to substantial momentum transport and contribute to viscous-like tangential drag at the boundary.
• Plasma transport is facilitated by the patchy network of reconnection sites and diffusive transport is possible due, in part, to finite gyroradius effects. Energetic particles can be transported across the boundary with a strong field-aligned component to the velocity distribution.
• Turbulent magnetic field spectra can lead to substantial ion heating rates due to the non-linear interaction between counter propagating Alfvén waves. Future work should focus on the heating mechanism due to the interaction between particles and the kinetic Alfvén waves (Johnson and Cheng, 2001).
• Heavy ions can alter the growth rates, transport rates, and modify ion kinetic-scale structure due to competing ion scales during KH wave evolution. In the limiting case, heavy ions contained entirely on, e.g., the magnetospheric side of the boundary will be unaffected by KH wavelengths less than the heavy ion inertial length.
• Bidirectional electron beams can be expected from the parallel electric fields associated with the strong guide field reconnection.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
PD contributed to all aspects of this article. Author NB provided the field line tracing analysis. XM contributed to the general discussion of the interaction between reconnection of KH modes in three dimensions. JJ contributed to the analysis of heavy ion effects and turbulent heating.
Funding
The authors acknowledge support from NASA grants 80NSSC20K1279 and 80NSSC19K0822.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Most 2-D simulations include an initial (but small) magnetic field component in the plane of the KH wave vector.
References
Bagenal, F., and Delamere, P. A. (2011). Flow of Mass and Energy in the Magnetospheres of Jupiter and Saturn. J. Geophys. Res. 116, A05209. doi:10.1029/2010JA016294
Bavassano Cattaneo, M. B., Marcucci, M. F., Bogdanova, Y. V., Rème, H., Dandouras, I., Kistler, L. M., et al. (2010). Global Reconnection Topology as Inferred from Plasma Observations inside Kelvin-Helmholtz Vortices. Ann. Geophys. 28, 893–906. doi:10.5194/angeo-28-893-2010
Boris, J. (1970). The Acceleration Calculation from a Scalar Potential. Plasma Physics LaboratoryPrinceton University. MATT-152.
Bouhram, M., Klecker, B., Paschmann, G., Haaland, S., Hasegawa, H., Blagau, A., et al. (2005). Survey of Energetic O+ Ions Near the Dayside Mid-latitude Magnetopause with Cluster. Ann. Geophys. 23, 1281–1294. doi:10.5194/angeo-23-1281-2005
Burkholder, B., Delamere, P. A., Ma, X., Thomsen, M. F., Wilson, R. J., and Bagenal, F. (2017). Local Time Asymmetry of Saturn's Magnetosheath Flows. Geophys. Res. Lett. 44, 5877–5883. doi:10.1002/2017GL073031
Burkholder, B. L., Delamere, P. A., Johnson, J. R., and Ng, C. S. (2020a). Identifying Active Kelvin-Helmholtz Vortices on Saturn's Magnetopause Boundary. Geophys. Res. Lett. 47, e84206. doi:10.1029/2019GL084206
Burkholder, B. L., Delamere, P. A., Johnson, J. R., and Ng, C. S. (2019). Identifying Active Kelvin-Helmholtz Vortices on Saturn’s Magnetopause Boundary, submitted to Geophys. Res. Lett.
Burkholder, B. L., Nykyri, K., Ma, X., Rice, R., Fuselier, S. A., Trattner, K. J., et al. (2020b). Magnetospheric Multiscale Observation of an Electron Diffusion Region at High Latitudes. Geophys. Res. Lett. 47, e87268. doi:10.1029/2020GL087268
Chaston, C. C., Johnson, J. R., Wilber, M., Acuna, M., Goldstein, M. L., and Reme, H. (2009). Kinetic Alfvén Wave Turbulence and Transport through a Reconnection Diffusion Region. Phys. Rev. Lett. 102, 015001. doi:10.1103/PhysRevLett.102.015001
Chaston, C. C. (2015). Magnetic Reconnection in the Auroral Acceleration Region. Geophys. Res. Lett. 42, 1646–1653. doi:10.1002/2015GL063164
Chen, L. (1999). Theory of Plasma Transport Induced by Low-Frequency Hydromagnetic Waves. J. Geophys. Res. 104, 2421–2427. doi:10.1029/1998JA900051
Cowee, M. M., Winske, D., and Gary, S. P. (2010). Hybrid Simulations of Plasma Transport by Kelvin-Helmholtz Instability at the Magnetopause: Density Variations and Magnetic Shear. J. Geophys. Res. 115. doi:10.1029/2009JA015011
Cowee, M. M., Winske, D., and Gary, S. P. (2009). Two-dimensional Hybrid Simulations of Superdiffusion at the Magnetopause Driven by Kelvin-Helmholtz Instability. J. Geophys. Res. 114. doi:10.1029/2009JA014222
Delamere, P. A., and Bagenal, F. (2010). Solar Wind Interaction with Jupiter's Magnetosphere. J. Geophys. Res. 115, a–n. doi:10.1029/2010JA015347
Delamere, P. A., Burkholder, B., and Ma, X. (2018). Three‐Dimensional Hybrid Simulation of Viscous‐Like Processes at Saturn's Magnetopause Boundary. Geophys. Res. Lett. 45, 7901–7908. doi:10.1029/2018GL078922
Delamere, P. A., Ng, C. S., Damiano, P. A., Neupane, B. R., Johnson, J. R., Burkholder, B., et al. (2021). Kelvin-Helmholtz‐Related Turbulent Heating at Saturn's Magnetopause Boundary. J. Geophys. Res. Space Phys. 126, e28479. doi:10.1029/2020JA028479
Delamere, P. A., Wilson, R. J., Eriksson, S., and Bagenal, F. (2013). Magnetic Signatures of Kelvin-Helmholtz Vortices on Saturn's Magnetopause: Global Survey. J. Geophys. Res. Space Phys. 118, 393–404. doi:10.1029/2012ja018197
Delamere, P. A., Wilson, R. J., and Masters, A. (2011). Kelvin-Helmholtz Instability at Saturn's Magnetopause: Hybrid Simulations. J. Geophys. Res. 116, a–n. doi:10.1029/2011JA016724
Fadanelli, S., Faganello, M., Califano, F., Cerri, S. S., Pegoraro, F., and Lavraud, B. (2018). North‐South Asymmetric Kelvin‐Helmholtz Instability and Induced Reconnection at the Earth's Magnetospheric Flanks. J. Geophys. Res. Space Phys. 123, 9340–9356. doi:10.1029/2018JA025626
Faganello, M., Califano, F., Pegoraro, F., and Andreussi, T. (2012). Double Mid-latitude Dynamical Reconnection at the Magnetopause: An Efficient Mechanism Allowing Solar Wind to Enter the Earth's Magnetosphere. Epl 100, 69001. doi:10.1209/0295-5075/100/69001
Faganello, M., Califano, F., and Pegoraro, F. (2008). Competing Mechanisms of Plasma Transport in Inhomogeneous Configurations with Velocity Shear: The Solar-Wind Interaction with Earth's Magnetosphere. Phys. Rev. Lett. 100, 015001. doi:10.1103/PhysRevLett.100.015001
Faganello, M., Califano, F., Pegoraro, F., and Retinò, A. (2014). Kelvin-Helmholtz Vortices and Double Mid-latitude Reconnection at the Earth's Magnetopause: Comparison between Observations and Simulations. Epl 107, 19001. doi:10.1209/0295-5075/107/19001
Faganello, M., Pegoraro, F., Califano, F., and Marradi, L. (2010). Collisionless Magnetic Reconnection in the Presence of a Sheared Velocity Field. Phys. Plasmas 17, 062102. doi:10.1063/1.3430640
Hesse, M., and Schindler, K. (1988). A Theoretical Foundation of General Magnetic Reconnection. J. Geophys. Res. 93, 5559–5567. doi:10.1029/JA093iA06p05559
Johnson, J. R., and Cheng, C. Z. (1997). Kinetic Alfvén Waves and Plasma Transport at the Magnetopause. Geophys. Res. Lett. 24, 1423–1426. doi:10.1029/97GL01333
Johnson, J. R., and Cheng, C. Z. (2001). Stochastic Ion Heating at the Magnetopause Due to Kinetic Alfvã©n Waves. Geophys. Res. Lett. 28, 4421–4424. doi:10.1029/2001GL013509
Johnson, J. R., Wing, S., and Delamere, P. A. (2014). Kelvin Helmholtz Instability in Planetary Magnetospheres. Space Sci. Rev. 184, 1–31. doi:10.1007/s11214-014-0085-z
Kane Yee, K. (1966). Numerical Solution of Initial Boundary Value Problems Involving maxwell's Equations in Isotropic media. IEEE Trans. Antennas Propagat. 14, 302–307. doi:10.1109/TAP.1966.1138693
Knoll, D. A., and Chacón, L. (2002). Magnetic Reconnection in the Two-Dimensional Kelvin-Helmholtz Instability. Phys. Rev. Lett. 88, 215003. doi:10.1103/PhysRevLett.88.215003
La Belle-Hamer, A. L., Otto, A., and Lee, L. C. (1995). Magnetic Reconnection in the Presence of Sheared Flow and Density Asymmetry: Applications to the Earth's Magnetopause. J. Geophys. Res. 100, 11875–11890. doi:10.1029/94JA0096910.1029/95ja00969
Lin, Y., Johnson, J. R., and Wang, X. (2012). Three-Dimensional Mode Conversion Associated with Kinetic Alfvén Waves. Phys. Rev. Lett. 109. doi:10.1103/PhysRevLett.109.125003
Lin, Y., Johnson, J. R., and Wang, X. Y. (2010). Hybrid Simulation of Mode Conversion at the Magnetopause. J. Geophys. Res. 115, a–n. doi:10.1029/2009JA014524
Ma, X., Delamere, P. A., Nykyri, K., Burkholder, B., Neupane, B., and Rice, R. C. (2019). Comparison between Fluid Simulation with Test Particles and Hybrid Simulation for the Kelvin‐Helmholtz Instability. J. Geophys. Res. Space Phys. 124, 6654–6668. doi:10.1029/2019JA026890
Ma, X., Delamere, P., Otto, A., and Burkholder, B. (2017). Plasma Transport Driven by the Three‐Dimensional Kelvin‐Helmholtz Instability. J. Geophys. Res. Space Phys. 122 (10), 10,382–10,395. doi:10.1002/2017JA024394
Ma, X., Otto, A., and Delamere, P. A. (2014a). Interaction of Magnetic Reconnection and Kelvin-Helmholtz Modes for Large Magnetic Shear: 1. Kelvin-Helmholtz Trigger. J. Geophys. Res. Space Phys. 119, 781–797. doi:10.1002/2013JA019224
Ma, X., Otto, A., and Delamere, P. A. (2014b). Interaction of Magnetic Reconnection and Kelvin-Helmholtz Modes for Large Magnetic Shear: 2. Reconnection Trigger. J. Geophys. Res. Space Phys. 119, 808–820. doi:10.1002/2013JA019225
Matsumoto, Y., and Hoshino, M. (2004). Onset of Turbulence Induced by a Kelvin-Helmholtz Vortex. Geophys. Res. Lett. 31, 2807. doi:10.1029/2003GL018195
Mauk, B. H., Cohen, I. J., Haggerty, D. K., Hospodarsky, G. B., Connerney, J. E. P., Anderson, B. J., et al. (2019). Investigation of Mass‐/Charge‐Dependent Escape of Energetic Ions across the Magnetopauses of Earth and Jupiter. J. Geophys. Res. Space Phys. 124, 5539–5567. doi:10.1029/2019JA026626
Meier, M. (2012). ProQuest Dissertations And Theses; Thesis (Ph.D.). Dissertation Abstracts International (Boulder, CO: University of Colorado) 74–05 (E), Section: B, 156.
Merkin, V. G., Lyon, J. G., and Claudepierre, S. G. (2013). Kelvin-Helmholtz Instability of the Magnetospheric Boundary in a Three-Dimensional Global MHD Simulation during Northward IMF Conditions. J. Geophys. Res. Space Phys. 118, 5478–5496. doi:10.1002/jgra.50520
Miura, A. (1984). Anomalous Transport by Magnetohydrodynamic Kelvin-Helmholtz Instabilities in the Solar Wind-Magnetosphere Interaction. J. Geophys. Res. 89, 801. doi:10.1029/ja089ia02p00801
Miura, A., and Pritchett, P. L. (1982). Nonlocal Stability Analysis of the MHD Kelvin-Helmholtz Instability in a Compressible Plasma. J. Geophys. Res. 87, 7431–7444. doi:10.1029/JA087iA09p07431
Nakamura, T. K. M., and Fujimoto, M. (2006). Magnetic Reconnection within MHD-Scale Kelvin-Helmholtz Vortices Triggered by Electron Inertial Effects. Adv. Space Res. 37, 522–526. Boundary Layers, Waves and Non-Linear Dynamical Processes. doi:10.1016/j.asr.2005.01.057
Neupane, B. R. (2021). Plasma Transport and Magnetic Flux Circulation in Saturn’s Magnetosphere. Fairbanks, AK: Ph.D. thesis, University of Alaska Fairbanks.
Nykyri, K., Ma, X., Burkholder, B., Rice, R., Johnson, J. R., Kim, E. K., et al. (2021). MMS Observations of the Multiscale Wave Structures and Parallel Electron Heating in the Vicinity of the Southern Exterior Cusp. J. Geophys. Res. Space Phys. 126, e27698. doi:10.1029/2019JA027698
Nykyri, K., and Otto, A. (2001). Plasma Transport at the Magnetospheric Boundary Due to Reconnection in Kelvin-Helmholtz Vortices. Geophys. Res. Lett. 28, 3565–3568. doi:10.1029/2001GL013239
Otto, A., and Birk, G. T. (1993). Formation of Thin Auroral Arcs by Current Striation. Geophys. Res. Lett. 20, 2833–2836. doi:10.1029/93gl02492
Otto, A., and Fairfield, D. H. (2000). Kelvin-helmholtz Instability at the Magnetotail Boundary: MHD Simulation and Comparison with Geotail Observations. J. Geophys. Res. 105, 175. doi:10.1029/1999ja000312
Otto, A. (2007). Plasma Entry and Kelvin-Helmholtz Modes at the Flanks of the Magnetosphere. American Geophysical Union, Fall Meeting 2007, December 2007. abstract id.SM11B-07.
Pu, Z.-Y., and Kivelson, M. G. (1983). Kelvin-Helmholtz Instability at the Magnetopause: Energy Flux into the Magnetosphere. J. Geophys. Res. 88, 853–862. doi:10.1029/JA088iA02p00853
Saur, J. (2004). Turbulent Heating of Jupiter's Middle Magnetosphere. ApJ 602, L137–L140. doi:10.1086/382588
Schindler, K., Hesse, M., and Birn, J. (1988). General Magnetic Reconnection, Parallel Electric fields, and Helicity. J. Geophys. Res. 93, 5547–5557. doi:10.1029/JA093iA06p05547
Sergis, N., Jackman, C. M., Masters, A., Krimigis, S. M., Thomsen, M. F., Hamilton, D. C., et al. (2013). Particle and Magnetic Field Properties of the Saturnian Magnetosheath: Presence and Upstream Escape of Hot Magnetospheric Plasma. J. Geophys. Res. Space Phys. 118, 1620–1634. doi:10.1002/jgra.50164
Seyler, C. E. (1990). A Mathematical Model of the Structure and Evolution of Small-Scale Discrete Auroral Arcs. J. Geophys. Res. 95, 17199–17215. doi:10.1029/JA095iA10p17199
Sisti, M., Faganello, M., Califano, F., and Lavraud, B. (2019). Satellite Data‐Based 3‐D Simulation of Kelvin‐Helmholtz Instability and Induced Magnetic Reconnection at the Earth's Magnetopause. Geophys. Res. Lett. 46, 11597–11605. doi:10.1029/2019GL083282
Sorathia, K. A., Merkin, V. G., Panov, E. V., Zhang, B., Lyon, J. G., Garretson, J., et al. (2020). Ballooning‐Interchange Instability in the Near‐Earth Plasma Sheet and Auroral Beads: Global Magnetospheric Modeling at the Limit of the MHD Approximation. Geophys. Res. Lett. 47, e88227. doi:10.1029/2020GL088227
Stauffer, B. H., Delamere, P. A., Ma, X., Neupane, B. R., and Burkholder, B. L. (2019). Hybrid Simulations of Magnetodisc Transport Driven by the Rayleigh‐Taylor Instability. J. Geophys. Res. Space Phys. 124, 5107–5120. doi:10.1029/2018JA026420
Takagi, K., Hashimoto, C., Hasegawa, H., Fujimoto, M., and TanDokoro, R. (2006). Kelvin-helmholtz Instability in a Magnetotail Flank-like Geometry: Three-Dimensional Mhd Simulations. J. Geophys. Res. 111. doi:10.1029/2006JA011631
Tenerani, A., Faganello, M., Califano, F., and Pegoraro, F. (2010). Nonlinear Vortex Dynamics in an Inhomogeneous Magnetized Plasma with a Sheared Velocity Field. Plasma Phys. Control Fusion 53, 015003. doi:10.1088/0741-3335/53/1/015003
Vernisse, Y., Lavraud, B., Eriksson, S., Gershman, D. J., Dorelli, J., Pollock, C., et al. (2016). Signatures of Complex Magnetic Topologies from Multiple Reconnection Sites Induced by Kelvin‐Helmholtz Instability. J. Geophys. Res. Space Phys. 121, 9926–9939. doi:10.1002/2016JA023051
Welling, D. T., André, M., Dandouras, I., Delcourt, D., Fazakerley, A., Fontaine, D., et al. (2015). The Earth: Plasma Sources, Losses, and Transport Processes. Space Sci. Rev. 192, 145–208. doi:10.1007/s11214-015-0187-2
Zhang, B., Delamere, P. A., Ma, X., Burkholder, B., Wiltberger, M., Lyon, J. G., et al. (2018). Asymmetric Kelvin-Helmholtz Instability at Jupiter's Magnetopause Boundary: Implications for Corotation-Dominated Systems. Geophys. Res. Lett. 45, 56–63. doi:10.1002/2017GL076315
Keywords: kelvin-helmholtz, hybrid simulations, transport, ion kinetic scale, heavy ions, turbulence, heating
Citation: Delamere PA, Barnes NP, Ma X and Johnson JR (2021) The Kelvin-Helmholtz Instability From the Perspective of Hybrid Simulations. Front. Astron. Space Sci. 8:801824. doi: 10.3389/fspas.2021.801824
Received: 25 October 2021; Accepted: 03 November 2021;
Published: 13 December 2021.
Edited by:
Takuma Nakamura, Austrian Academy of Sciences (OeAW), AustriaReviewed by:
Matteo Faganello, UMR7345 Physique des interactions ioniques et moléculaires (P2IM), FranceMisa Cowee, Los Alamos National Laboratory (DOE), United States
Copyright © 2021 Delamere , Barnes , Ma and Johnson . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: P. A. Delamere , cGFkZWxhbWVyZUBhbGFza2EuZWR1
 P. A. Delamere
P. A. Delamere  N. P. Barnes
N. P. Barnes  X. Ma
X. Ma  J. R. Johnson
J. R. Johnson