
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci., 13 January 2022
Sec. Extragalactic Astronomy
Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.785092
Giant radio galaxies are arguably the least understood of jetted active galactic nuclei (AGN). We propose that radio galaxies are the product of large mergers that do not involve radio galaxies or radio quasars, such as in merging spiral galaxies, while giant radio galaxies emerge from a merger involving a parent that in the not-too-distant past harbored a radio galaxy. Predictions following from this are an upper limit to the number fraction of giant radio galaxies to radio galaxies, lower average redshift for giant radio galaxies, a higher incidence of high excitation for giant radio galaxies compared with radio galaxies, and lower average prograde black hole spin values for giant radio galaxies compared to radio galaxies and to bright radio quiet quasars.
Jets associated with accretion is a phenomenon that is observed across the mass scale, from objects less than about a solar mass, to billions of solar masses, with jet lengths ranging from about an astronomical unit to a few million parsecs. Giant radio galaxies (GRGs) are defined as jetted AGN with jet lengths that exceed 0.7 Mpc. Such objects have been observed to reach lengths up to about 4.7 Mpc (Machalski et al., 2008) and lifetimes on the order of 108 years (Hunik and Jamrozy 2016; Cantwell et al., 2020).
GRGs appear to have the same general properties as radio galaxies (RGs) (Kuzmicz and Jamrozy 2012; Dabhade et al., 2020a; Dabhade et al., 2020b) except for their larger jet lengths. Although detections have been steadily increasing (Willis et al., 1974; Cotter et al., 1999; Lara et al., 2001; Schoenmakers et al., 2001; Dabhade et al., 2017), LoFAR has allowed for the recent discovery of hundreds of GRGs (Dabhade et al., 2020a; Dabhade et al., 2020b) with a density per square degree of 0.55 while Bruggen (2021) report a density of 1.7 per square degree using the Evolutionary Map of the Universe survey. Additional evidence that the density of GRGs may be larger comes from Delhaize et al., 2021 using the MIGHTEE survey. Are GRGs old systems that have grown over time due to prolonged accretion periods or are they more recently triggered events? Are the environments of GRGs less dense, such that GRG jets can thrive there, or is there evidence for GRGs in dense environments as well? In Dabhade et al. (2020b), i.e. the SAGAN-1 paper, for example, there are 60 GRGs from the NRAO VLA Sky Survey hosted by the brightest cluster galaxy, which is the center of the galaxy cluster and therefore in dense environments. In terms of the presence of emission lines in their optical spectra or excitation class, do GRGs tend to have prominent emission lines that make high excitation or are they weak in emission lines and thus of low excitation class? These questions have yet to be answered definitively.
In this work we apply the gap paradigm for black hole accretion and jet formation to shed light and make predictions on GRGs. The term refers to the importance of the space between the disk inner edge and the black hole in determining both the radiative efficiency of the disk and the morphology of the jet. We will show how to understand that excitation class is distributed differently in GRGs compared to RGs and that GRGs are the result of merger re-triggered retrograde accreting black holes, implying their black holes are larger than their parent RG due to the merger and additional accretion phase. This introduces constraints on the relative mass of black holes in GRGs compared to RGs. Because jet power depends on black hole mass, and since accretion will double or triple the mass, a merger that doubles the black hole mass will produce a black hole that is 4–6 times the mass of the original RG black hole as a result of accretion. And since jet power can be proportional to the square of black hole mass theoretically (Blandford and Znajek 1977), have a more complicated form due to the gap region (Garofalo et al., 2010), or observationally seem to be a little less steep such as a power of 1.4 (Heinz and Sunyaev 2003), GRGs are expected in the model to produce jet powers in the range of a few tens of times that of the parent RG. As we will describe, however, the effect that jets have on their immediate environments depends on the ability to transfer jet energy to the gas in the large FRII (Fanaroff and Riley type II) radio lobes that in turn affects star formation and ultimately the state of accretion in radio galaxies. While FRII jets have a more immediate star formation enhancing ability that is then thwarted as FRI jets come into play (Singh et al., 2021a; Singh et al., 2021b), on larger scales the FRII jet instantiates a change in the accretion state. The focus in this paper is on the feedback that leads to a change in accretion state. Owing to the large sizes of GRGs and because of a past high excitation FRII, or radio quasar, phase (of no more than 107 years for RGs while no more than 109 years for GRGs), much of this physics is delayed, and this slower evolution has consequences for the heating of the gas in the GRG and its effect on future accretion. It is here that we see how large sizes of GRGs allows for differences with RGs despite the same underlying physical processes. While our focus in this work is on excitation class, and the effect of FRII star formation enhancement is not, it should be noted that the initial star formation rate depends on the merging galaxies. In RGs, both could provide ample amounts of cold gas while in GRGs one parent is likely to be an evolved RG which may no longer be forming stars. This will lead to an understanding of different excitation class distributions in the two populations and to an upper limit in the number ratio of GRGs to RGs.
In The Gap Paradigm we introduce the model; in Giant Radio Galaxies we apply it to GRGs, produce basic constraints, and discuss predictions; and, in Future Work and Summary suggest future extensions of the ideas. We then summarize.
By considering counterrotation between an accretion disk and a black hole, Garofalo et al. (2010) produced a scale-invariant model for accreting compact objects that has since been applied to observations of active galaxies and black hole and neutron star X-ray binaries, spanning 10 orders of magnitude in mass. The majority of mergers do not trigger retrograde accretion around black holes in the model because of the instability of such configurations. The fraction of accreting black holes that form stable counterrotating configurations is given by
where jd and jh are the angular momenta of the disk and black hole, respectively (King et al., 2005). A quantitative estimate of this is carried out by Garofalo et al. (2020b) and is captured in Figure 1, showing that below a threshold black hole mass value, retrograde accretion fails to form. Retrograde accretion is as stable as prograde accretion for very massive black holes as illustrated by the blue curve approaching 0.5 at the right end of Figure 1. The gap region is determined by the stability of circular orbits which depends on black hole spin and disk orientation. For high black hole spin and counterrotation, the innermost stable circular orbit is located near nine gravitational radii while it approaches 1.23 gravitational radii for high spin and corotation between disk and black hole.
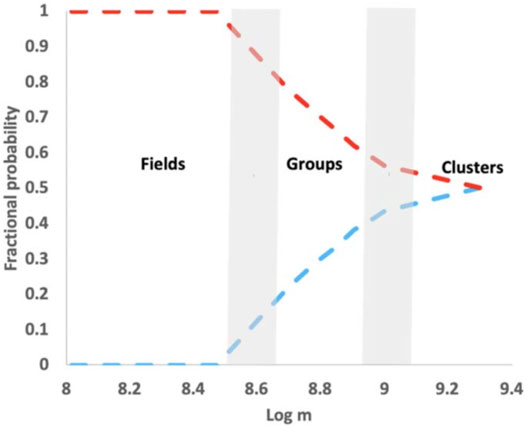
FIGURE 1. The radio loud/radio quiet dichotomy in the gap paradigm (Garofalo et al., 2020a). As the mass of the black hole increases beyond a threshold value, retrograde accretion becomes more stable. The y axis represents the chance that in a merger, the disk will settle into counterrotation around the black hole. The area under the blue curve gives the fraction of radio loud AGN. The area under the red curve gives the fraction of radio quiet AGN. The x axis is the mass of the black hole in solar masses.
One parameter that determines the impact of jets in these counterrotating black hole systems is the mass of the black hole, with more massive black holes producing stronger jets that more strongly couple to their environments. We illustrate this in Figure 2 where a radiatively efficient accretion disk (shown in blue) feeds a black hole in counterrotation. The FRII jet (in red) heats the galactic/intergalactic medium gas which flows back toward the center (e.g. Antonuccio-Delogu and Silk 2010), eventually settling into an advection dominated flow (ADAF) around the black hole. The effectiveness and swiftness of this change depends on the black hole mass. If this process is less effective, the change may not occur at all and the disk does not evolve to an ADAF (Figure 3) but remain in its radiatively efficient cold state. If the feedback is effective, the accretion state does evolve into a hot ADAF flow, and we get a difference as seen in the upper panel of Figure 4. Both Figures 3, 4 describe the evolution of a system with an originally counterrotating disk around a high spinning black hole, the conditions which maximize the Blandford and Znajek (1977) and Blandford and Payne (1982) effects, which constitute the foundation behind jet formation in the model. Because retrograde disk configurations spin black holes down to zero spin and continued accretion spins them up into the prograde regime, the different panels show how the jet, disk, and excitation class evolve as a function of the black hole spin, and thus in time. The difference between the lower panels in Figures 3, 4 is the black hole mass, with Figure 3 black holes on average less massive than those in Figure 4 by an order of magnitude (in groups the black hole ranges from 108 to 1010 solar masses while in the densest environments the range is 109 to 1011 solar masses). Figure 3 systems also tend to prefer isolated environments while those of Figure 4 prefer groups. While difficult to pin down precisely, we estimate that Figure 3 black holes occupy a range of a few 107 to a few 109 solar masses. Hence, their jets tend to be weaker and less effective in heating the gas. In addition to changing the accretion state, effective jet-gas coupling can also expand galaxies, which is why FRI radio galaxies tend to be larger than FRII HERGs in terms of their host galaxy size and not the overall radio end-to-end sizes (Mangalam et al., 2009). In Figure 6 we show the time evolution of originally retrograde accreting black holes triggered by mergers in the densest environments, where jet feedback tends to be most effective. This allows for such environments to experience a more rapid change in accretion state on average. While all three types of systems described in Figures 3, 4, 6, evolve from retrograde to prograde due to the effects of accretion, the timescales for such evolution varies in a quantifiable way. Figure 3 black holes are characterized by the weakest feedback on average, which means the accretion disk remains unaltered and gas therefore continues to settle in a thin, radiatively efficient, disk. When radiatively efficient disks have inner edges that are close enough to the black hole (i.e. those whose spins are above ∼0.7 in prograde configuration), jets become suppressed (Neilsen et al., 2009; Garofalo et al., 2010; Ponti et al., 2012). But as the feedback increases for more massive black holes, the disk transitions away from thin and radiatively efficient, and becomes an ADAF (upper panel of Figure 4 and in Figure 6). Such systems cannot suppress jets. Because such systems dominate in denser environments, we see why giant FRI radio galaxies tend to be found in the densest environments. The scenarios briefly described above have been fleshed out in the literature over the past decade. Because FRII jets are observed in GRGs, our model prescribes counterrotation for such systems as well, and since such systems are one possible product of mergers, GRGs must be the result of an additional merger leading to counterrotation in the central engine. In the next Section we apply the gap paradigm to GRGs.
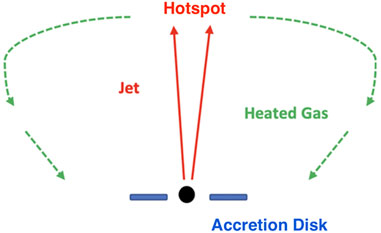
FIGURE 2. A high excitation FRII jetted counterrotating accreting black hole transferring its jet energy to the gas that eventually may alter the accretion mode. The point of this image is to capture the idea that this type of feedback is constrained by the time it takes for the jet to reach the hotspot, and then flow back in toward the central region as per the green arrows (Antonuccio-Delogu and Silk 2010). The order of magnitude increase in the timescale for GRGs means that unlike in RGs, the high excitation state lasts longer. Hence, giant FRII HERGs or giant radio quasars (GRQs) are comparably more common among GRGs than FRII HERGs or radio quasars (RQs) are among RGs. This is a model prediction.
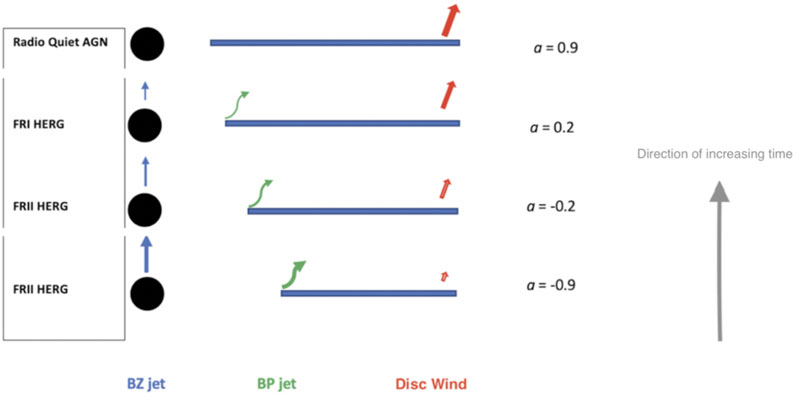
FIGURE 3. Time evolution of originally retrograde accreting black holes with relatively smaller black hole mass in the range 107–109 solar masses. Radio morphology and excitation class in left column. Blandford-Znajek jet in blue. Blandford-Payne jet in green. Radiative disk wind in red. Arrow length represents magnitude. Black hole spin and disk orientation in right column with negative values representing counterrotation. Time evolution is upward from bottom panel. While the BZ and BP jets are maximized for large gap region, the opposite is true for the disc wind because less gravitational potential energy exists for large gap regions.
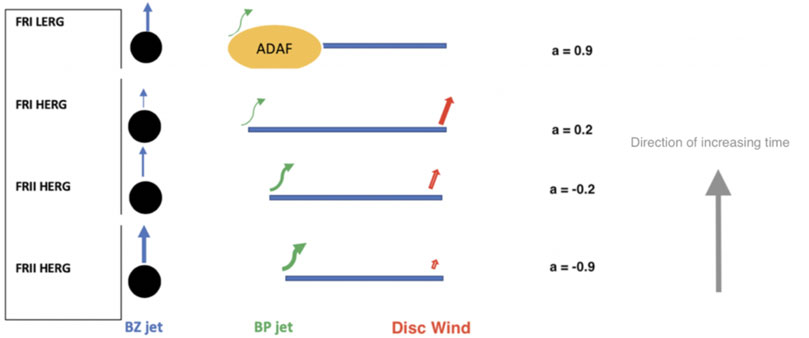
FIGURE 4. Same as in Figure 3 with the exception that these black holes are an order of magnitude more massive which means their range is 108–1010 solar masses which makes their FRII jets more effective, leading to accretion changes at later times as seen in the upper panel. The disk does not remain thin but evolves as a result of jet feedback into a hot advective dominated accretion flow (ADAF) as shown in yellow.
In the context of the gap paradigm where FRII jets are the result of counterrotation between black hole and accretion disk, the observation that GRGs have FRII jets implies counterrotation. Hence, we make the simple assumption that a GRG is the result of a merger between an RG and another galaxy, but such that this system also leads to a counterrotating disk around a spinning black hole. This, of course, means that there is another FRII jetted phase that further expands galaxy and jet size. Hence, in this model, RGs—or objects that were RGs in the not-too-distant past - can be GRG ancestors in the sense that at least one of the GRG parents was an RG. Quantitative conclusions emerge from this which we now discuss.
Because of the RG merger, the GRG will have a black hole mass that is less than an order of magnitude greater than the mass of the black hole in the parent RG. In SAGAN-1 (Dabhade. 2020b) it has been shown that RGs and GRGs have similar black hole mass distribution. Because the differences in black hole mass between Figures 4 and 6 objects is about an order of magnitude, GRGs would not have significant jet power difference with RGs given the large range in black hole mass that is measured for RGs. If Figures 3, 4, 6 black holes range from 107 to 1011 solar masses, then the GRGs that form from these RGs would have a similar range. This is compatible with observations. As a result, the observed order of magnitude larger extent for the jets in GRGs would have to be attributed to differences in environment and/or duty cycle. Whereas the environment of the original RG involves abundant cold gas flow into the nucleus following a merger between, say, two spiral galaxies (Barnes and Hernquist 1991), the environment of a GRG would result from the merger of the end product of an RG—which could be a low excitation FRI radio galaxy (as in the top panel of Figure 4 or Figure 6) or what remains once the accretion fuel is depleted—and, say, a spiral galaxy. This type of merger would likely generate comparatively less cold gas in its nucleus, and the jet might be expected to have a weaker work surface and the black hole a lower accretion rate. While the spiral galaxy could supply the system with sufficient cold gas to be a star forming system, the star formation rates of GRGs would tend to be lower than in systems where both parent galaxies provide abundant cold gas, i.e. FRII HERGs/radio quasars. In short, the idea that one of the GRG parents was a late state RG, has consequences for the star formation rates in GRGs compared to that in RGs.
The larger scale in GRGs implies a transition time for the accretion state to change (as described in Figure 2) that is an order of magnitude longer than in RGs. The gas that is heated by the lobe in FRII jets as shown in Figure 2, requires more time to flow back toward the black hole from the hot spot and this means black hole spin changes more than in the average RG case. The hot gas is required to travel on the order of an Mpc as opposed to hundreds of Kpc for RGs. If RGs can accomplish this within a time greater than 4 × 106 years, GRGs will require at least 4 × 107 years. The 4 × 106 year time scale is the shortest time for the change in the accretion state and occurs in the densest environments (Figure 6 second panel from bottom). In Figure 4 we see an ADAF accretion phase by the time the black hole has reached a prograde spin of 0.9. At the Eddington accretion limit, the timescale to reach this spin value from the original retrograde spin of 0.9 is about 100 million years (Kim et al., 2016). The order of magnitude increase in timescale for this process in GRGs means that low excitation GRGs will experience a characteristic time to reach these FRI ADAF phases of about 1 billion years. Hence, the model makes the simple prediction that GRGs will experience longer high excitation states compared to RGs and therefore that the number ratio of FRII HERGs/radio quasars NRQ to radio galaxies NRG must be smaller than that of giant radio quasars NGRQ to giant radio galaxies NGRG, i.e.
It is important to appreciate that our use of the label quasar implies high excitation. The increased time for high excitation states appears not merely due to the increased backflow timescale associated with the process described in Figure 2, but also due to the likelihood that the amount of cold gas in newly triggered GRQs will be less than in newly triggered RQs, such that the Eddington accretion rates in the former are smaller, i.e. that
Because of the radiatively efficient nature assumed for the post-merger GRQ, the additional constraint below also must be satisfied, where (dm/dt)Edd is the Eddington-limited accretion rate,
In Figure 5 we show the results of a study of the redshift distribution of the number of high and low excitation radio galaxies from LOFAR-Bootes (Williams, 2018). They find high excitation dominates at higher redshift (1.5 < z < 2) while that is reversed at lower redshift (0.01 < z < 0.5). Hence, there is a redshift dependence to NH/NL, where NH is the number of HERGs and NL is the number of LERGs. In terms of the total numbers, however, they get (see Williams, 2018 Table 1).
An additional prediction or consequence of the model is that NGRG/NRG has an upper limit which is the square of the merger rate R divided by the merger rate itself, which is simply the merger rate. GRGs that are the result of N > 2 mergers will be fewer than those resulting from N = 2 mergers. This has been estimated from
where <Tobs> is the average observation timescale, fp is the observed pair fraction and Cmerge is the fraction of observed pairs that actually merge. Over a wide range in redshift this has been evaluated between 2 and 6% per billion years (O’Leary et al., 2021). Hence, if we give the GRG the last 5 billion years to form, we get
and smaller if we allow less time. It is also clear that our model predicts that the average redshift of GRGs must be lower than that for RGs.
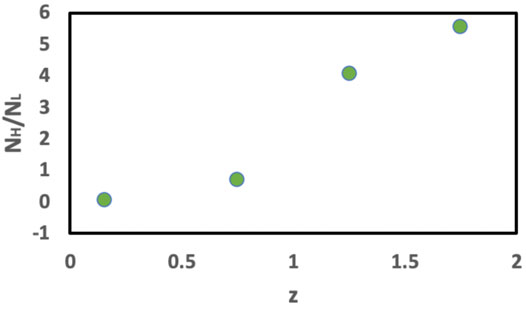
FIGURE 5. Ratio of the numbers of high excitation radio galaxies and number of low excitation radio galaxies as a function of redshift from LOFAR-Bootes (from Williams, 2018 Table 1).

TABLE 1. Data from Williams, 2018 plus the ratio of HERGs to LERGs.
It is also interesting to note that very powerful RGs in the model with sufficient fuel could evolve over billions of years at slow rates as shown in Figure 6, as a result of their rapid transition to low accretion rates. Such systems differ compared to Figures 3, 4 black holes in that their FRII jets instantiate the most rapid evolution of the accretion disk. These Figure 6 systems could grow to large sizes that compete with GRGs (e.g. M87). To the extent that Figure 6 RGs produce Mpc scale jets, they would amount to low excitation FRI GRGs and they could be compared with GRQs that are observed to have larger jet extensions. In short, there are considerations here that allow one to understand why FRIIs may be larger than FRIs in GRGs while the opposite is true in RGs. The FRII GRGs that are larger have not yet evolved into their FRI states.
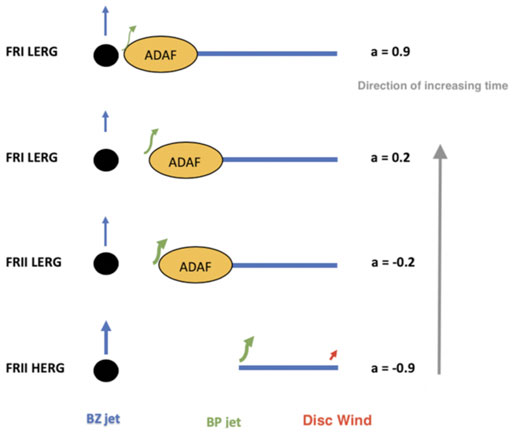
FIGURE 6. Same as in Figures 3, 4 but for originally counterrotating disks around the most massive black holes (109–1011 solar masses). Such systems produce the most effective FRII jets which couple jet energy to the environment ensuring a rapid transition of the accretion state to an ADAF. This is shown in the second to bottom panel with an ADAF already replacing the thin disk when the black hole is still in the retrograde configuration. This implies a timescale for this transition of only a few million years.
We have applied our time evolution paradigm for black hole accretion and jet formation to the giant radio galaxy phenomenon to generate subtle yet clear differences with respect to radio galaxies. Although we have illustrated the time evolution using the cartoons of Figures 3, 4, 6, the assumption that thin disks accrete at the Eddington limit places quantitative time constraints on both the RG and the GRG phenomenon. This is because ADAF accretion states emerge when the accretion rate is 10−2 the Eddington accretion rate and drops further toward 10−5 or 10−6 that rate by the time the system is in the mid prograde black hole spin regime. A number of predictions emerge. Figures 3, 4, 6 differ in terms of black hole mass spanning an average range of two orders of magnitude. The different evolutionary paths that result from different black hole masses have been applied recently to understand many aspects of radio galaxies and quasars, and, in particular, to environmental differences. Because bigger black holes live in larger dark matter halos, there are predictions about where different types of radio galaxies live in terms of environment richness. As one sees directly from Figures 3, 4, 6, radio galaxies with FRI morphology and low excitation will tend to distribute themselves in richer environments as more such states appear in Figure 4 and especially 6. In terms of giant radio galaxies, Figures 3, 4, 6 predict that rich environments should also be home to giant radio galaxies with the most massive black holes. Because transition times are slowed for giant radio galaxies, FRIIs linger longer in general and should therefore show an enhancement in their relative numbers compared to radio galaxies. We have seen this in this work. But while RGs with FRII jets will on average prefer less rich environments as recently shown in the literature from our model perspective (Garofalo et al., 2018; Garofalo et al., 2020b), GRGs with FRII jets will, as a result of longer transition times, tend to distribute themselves more in richer environments. Evidence for this is emerging but while this can be seen in the simple figures of this paper, tighter theoretical constraints are possible.
Figure 3 objects offer additional insights into possible alternative evolution of GRGs. Such black holes are the least effective in altering their accretion state, so they remain in radiatively efficient cold mode which relatively rapidly consumes the fuel. Although we have not focused on this type of time evolution here, such systems evolve into radio quiet quasars due to the phenomenon of jet suppression, which is connected to the strong disk wind as illustrated in that figure’s upper panel with no jet arrows. For GRGs that follow this path, there must be large galaxies that once harbored an Mpc scale jet that has died away and can possibly be observed at low radio frequencies (less than ∼300 MHz) owing to their steep spectrum nature. Observers may find more ways to explore possible observational signatures of this idea using deeper observations with existing observatories like LOFAR and uGMRT and upcoming SKA. Note that Figure 3 explains why GRQs cannot simply evolve from long-living RQs in the model (Komberg and Pashchenko 2009).
The model also makes a clear prediction that FRI jets live in the future of FRII states and given the possibility of lower accretion rates in GRGs compared to RGs, such FRI jet states could be order billions of years in the future of the FRII jet. It takes order 108 years to spin a black hole up to high prograde spin from zero spin at the Eddington limit. And since ADAF states accrete at rates below 1% the Eddington limit, this is the reason for such time scales. This would be true of systems that manage to instantiate the conditions that lead to FRI jet formation (paths shown in Figures 4, 6 but not Figure 3). The possibility that FRI GRGs could appear at such late times compared to many FRII GRGs, should show up in redshift differences over large samples. These are all quantitatively rooted statements.
Finally, because RG black holes take billions of years to reach high prograde spin values due to their low excitation accretion, and because GRGs are formed form a parent RG, GRG black holes are even less likely to reach their high prograde spin values. As a result, the model predicts that GRGs are limited on average to intermediate spin values (similar to M87). Although we have not focused on this here, Figure 3 allows us to understand that GRG black holes have spins that are considerably lower than radio quiet quasars whose spins are highest. The simplicity of the model is deceptive, and its predictive potential is surely not exhausted by this work.
The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author.
The author confirms being the sole contributor of this work and has approved it for publication.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
I thank Pratik Dabhade for detailed discussion and for specific contributions to the draft such as in explaining how to detect the extinct FRI radio galaxy, Francois Combes for stimulating conversation, and the referee for improving the manuscript.
Antonuccio-Delogu, V., and Silk, J. (2010). Active Galactic Nuclei Activity: Self-Regulation from Backflow. MNRAS 405, 1303.
Blandford, R. D., and Payne, D. G. (1982). Hydromagnetic Flows from Accretion Discs and the Production of Radio Jets. Monthly Notices R. Astronomical Soc. 199, 883–903. doi:10.1093/mnras/199.4.883
Blandford, R. D., and Znajek, R. L. (1977). Electromagnetic Extraction of Energy from Kerr Black Holes. Monthly Notices R. Astronomical Soc. 179, 433–456. doi:10.1093/mnras/179.3.433
Bruggen, M., Reiprich, T. H., Bulbul, E., Koribalski, B. S., Andernach, H., Rudnick, L., et al. (2021). Radio Observations of the Merging Galaxy Cluster System Abell 3391-Abell 3395★. Astron. Astrophys. 647, A3.
Cotter, G., Rawlings, S., and Saunders, R. (1996). Spectrophotometry of a Sample of 7C Giant Radio Sources. Monthly Notices R. Astronomical Soc. 281, 1081–1093. MNRAS. doi:10.1093/mnras/281.3.1081
Dabhade, P., Röttgering, H. J. A., Bagch, J., Shimwell, T. W., Hardcastle, M. J., Sankhyayan, S., et al. (2020a). Giant Radio Galaxies in the LOFAR Two-Metre Sky Survey.I.Radio and Environmental PropertiesAstron. Astrophys. 635, A5.
Dabhade, P., Mahato, M., Bagchi, J., Saikia, D. J., Combes, F., Sankhyayan, S., et al. (2020b). Search and Analysis of Giant Radio Galaxies with Associated Nuclei (SAGAN).I. New Sample and Multiwavelength Studies. Astron. Astrophys. 642, A153.
Dabhade, P., Gaikwad, M., Bagchi, J., Pandey-Pommier, M., Sankhyayan, S., and Raychaudhury, S. (2017). Discovery of Giant Radio Galaxies from NVSS: Radio and Infrared Properties. MNRAS 469, 2886–2906. doi:10.1093/mnras/stx860
Delhaize, J., Heywood, I., Prescott, M., Jarvis, M. J., Delvecchio, I., Whittam, I. H., et al. (2021). MIGHTEE: Are Giant Radio Galaxies More Common Than We Thought?. MNRAS 501, 3833.
Garofalo, D., Evans, D. A., and Sambruna, R. M. (2010). Signatures of Black Hole Spin in Galaxy Evolution. ApJ 699, 975–L54. doi:10.1088/0004-637x/699/1/l52
Garofalo, D., Joshi, R., Yang, X., Singh, C. B., North, M., and Hopkins, M. (2020b). A Unified Framework for X-Shaped Radio Galaxies. ApJ 889, 91. doi:10.3847/1538-4357/ab64e3
Garofalo, D., North, M., Belga, L., and Waddell, K. (2020a). Why Radio Quiet Quasars Are Preferred over Radio Loud Quasars Regardless of Environment and Redshift. ApJ 890, 144. doi:10.3847/1538-4357/ab6f70
King, A. R., Lubow, S. H., Ogilvie, G. I., and Pringle, J. E. (2005). MNRAS, 363, 49Komberg, B.V & Pashchenko, I.N. ARep 53, 1086.
Kuzmicz, A., and Jamrozy, M. (2012). Optical and Radio Properties of Giant Radio Quasars. MNRAS 426, 851.
Lara, L., Cotton, W. D., Feretti, L., Giovannini, G., Marcaide, J. M., Márquez, I., et al. (2001). A New Sample of Large Angular Size Radio Galaxies. Astron. Astrophys. 370, 409–425. doi:10.1051/0004-6361:20010254
Mangalam, A., Gopal-Krishna, P. J., and Wiita, P. J. (2009). The Changing Interstellar Medium of Massive Elliptical Galaxies and Cosmic Evolution of Radio Galaxies and Quasars. MNRAS 397, 2216–2224. doi:10.1111/j.1365-2966.2009.15183.x
Neilsen, J., and Lee, J. C. (2009). Accretion Disk Winds as the Jet Suppression Mechanism in the Microquasar GRS 1915+105. Nature 458, 481–484. doi:10.1038/nature07680
O’Leary, J. A., Moster, B. P., Naab, T., and Somerville, R. S. (2021). EMERGE: Empirical Predictions of Galaxy Merger Rates Since z ∼ 6. MNRAS 501, 3215.
Ponti, G., Fender, R. P., Begelman, M. C., Dunn, R. J. H., Neilsen, J., and Coriat, M. (2012). Ubiquitous Equatorial Accretion Disk Winds in Black Hole Soft States. MNRAS 422, L11.
Schoenmakers, A. P., de Bruyn, A. G., Röttgering, H. J. A., and van der Laan, H. (2001). A New Sample of Giant Radio Galaxies from the WENSS Survey. Astron. Astrophys. 374, 861–870. doi:10.1051/0004-6361:20010746
Singh, C. B., Kulasiri, N., North, M., and Garofalo, D. (2021b). The Black Hole-Star Formation Connection Over Cosmic Time. PASP 133, 104101.
Singh, C., Garofalo, D., and Lang, B. (2021a). Powerful Jets from Radiatively Efficient Disks, a Decades-Old Unresolved Problem in High Energy Astrophysics. Galaxies 9, 10. doi:10.3390/galaxies9010010
Williams, W. L. (2018). LOFAR-Bootes: Properties of High-and Low-Excitation Radio Galaxies at 0.5 < z < 2.0. MNRAS 475, 3429.
Keywords: radio galaxies, active—galaxies, jets - accretion, accretion disks - radio continuum, black holes
Citation: Garofalo D (2022) The Origin and Evolution of Giant Radio Galaxies. Front. Astron. Space Sci. 8:785092. doi: 10.3389/fspas.2021.785092
Received: 28 September 2021; Accepted: 23 December 2021;
Published: 13 January 2022.
Edited by:
Paola Marziani, Osservatorio Astronomico di Padova (INAF), ItalyReviewed by:
Marco Berton, European Southern Observatory, ChileCopyright © 2022 Garofalo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Garofalo, ZGdhcm9mYWxAa2VubmVzYXcuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.