Evolution of Hot and Dense Stellar Interiors: The Role of the Weak Interaction Processes

The evolution of the hot and dense interior of massive stars has aroused the intense interest of researchers the last more than three decades. In this article, the role of the semi-leptonic weak interaction processes of leptons (involving neutrinos) with nucleons and nuclei in the late stages of stellar evolution, as well as in the relevant terrestrial neutrino detection experiments, is reviewed. Such processes play crucial role for the massive stars’ evolution in the final stages of their life, and specifically in the core-collapse supernova leading to the supernova explosion phenomenon. We start by mainly focusing on the neutrino producing charged-lepton capture, like the electron-capture and the muon-capture on nuclei and, then, we discuss the neutrino absorbing reactions which are essential in the neutrino-driven explosive nucleo-synthesis. These processes are also significant in many ongoing and planned worldwide underground sensitive experiments aiming to detect astrophysical neutrinos which rely on the interactions of neutrinos with the bound nucleons inside atomic nuclei.

1 Introduction

It is well known that stars are born out of the gravitational collapse of cool and dense molecular clouds when they collapse into smaller regions which finally contract to form stellar cores, the proto-stars (Bethe, 1990; Phillips, 2013; Giannaka, 2015; Woosley, 2019). Due to the contraction of proto-stars, the central temperature increases up to the point where nuclear reactions start by firstly converting hydrogen into helium in the core and this way the star enters the stage of the main sequence (Fuller et al., 1982; Bethe, 1990; Suzuki et al., 2006; Phillips, 2013; Balasi et al., 2015). Subsequently, the interior of evolved high mass stars develop layers (fusion shells) like an onion where the outer shell drops fuel to the lower shell while heavier and heavier nuclear isotopes are being synthesized as we move towards the center of the star (Gastaldo et al., 2017; Woosley, 2019; Cantiello et al., 2021).

During the evolution of the massive stars (M ≥ 8M_{solar}, with M_{solar} being the Sun’s mass), specifically during the late stages of their life (Fuller et al., 1982; Bethe, 1990; Oda et al., 1994), a great number of thermonuclear reactions and among them weak interaction processes on nucleons and nuclei like the charged-lepton capture, the neutrino production and neutrino absorption, the β-decay modes and others, play key role. In addition, other charge-changing semi-leptonic processes (the elementary β-decay reactions, the elementary semi-leptonic ν-nucleon reactions, etc.,) play also significant role in core-collapse supernova (SN) (Langanke and Martinez-Pinedo, 1998; Langanke and Martínez-Pinedo, 1999). In this review we are going to pay special attention on the main conclusions of the state-of-the-art approaches related to the structure and evolution of the hot and dense stellar interior, focusing on those reactions taking place in the presence of nuclei as well as in the plethora of terrestrial astrophysical neutrino detection experiments.

In general, the semileptonic weak interactions in nuclei are of great interest for many physical reasons. At first, the accurate knowledge of the above mentioned processes determines to a large extent the evolution of massive stars, especially in their pre-supernova, their core-collapse supernova (CCSN) and their explosion phase (Fischer et al., 2020; Nagakura and Hotokezaka, 2021). Thus, the better the cross sections we know for these semi-leptonic processes the better the description of successful stars’ explosions is coming out of the various SN scenarios and relevant algorithms (explosion codes) (Langanke et al., 2001; Langanke et al., 2003; Langanke and Martínez-Pinedo, 2003; Titus et al., 2017). Nowadays, this knowledge needs to be extended so as to include as great as possible number of nuclear isotopes and number of different semi-leptonic electro-weak processes (Titus et al., 2017). Furthermore, various theoretical ideas related to the fundamental theory of the weak interactions between the involved nuclei with leptons, may be tested through terrestrial experiments aiming to investigate the nuclear and particle physics of these processes (Langanke et al., 2003; Bollig et al., 2017; Sieverding et al., 2019). In addition, once the fundamental nature of the weak interactions is fully understood, this can be used for testing the theoretical ideas on new nuclear excited states not being accessible by the electromagnetic interactions (O'Connell et al., 1972; Donnelly and Walecka, 1976; Donnelly and Peccei, 1979).

Moreover, from a nuclear theory viewpoint, it is important to note that the semi-leptonic weak processes are studied with the same methods employed for electron-nucleus scattering (for example, using the Donnelly-Walecka multipole decomposition and constructing the nuclear states within the context of the shell models, RPA, QRPA, etc.,) because there is a close analogy between these two classes of processes and because the electromagnetic interaction plays a similar role to that of the weak interactions (Donnelly and Peccei, 1979; Kosmas and Oset, 1996; Ejiri et al., 2019). Due to the fact that, the matrix elements of the vector current component of the operators are identical in the electromagnetic electron scattering and the weak interactions (conserved-vector-current, CVC theory), these operators represent half of the overall independent operators needed to describe the weak processes (Chasioti and Kosmas, 2009; Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b; Tsakstara and Kosmas, 2012). Furthermore, electron scattering data offer reliable tests for the calculated nuclear wave functions in order to acquire confidence on predictions relevant to the weak processes which in many cases, helps to eliminate nuclear physics uncertainties. In addition, the semi-leptonic weak reactions are, in principle, richer sources of information on nuclear structure because of the axial vector spin dependent operators of the interaction between the leptons and the target nucleus (Ejiri et al., 2019; Papoulias et al., 2019).

Regarding the ν-nucleus reactions, it is worth mentioning the challenges of the neutral current (NC) neutrino–nucleus scattering of which the measurements rely on a different signal to that of the charged current (CC) ν-nucleus reactions (Donnelly and Peccei, 1979; Kosmas and Oset, 1996). From these two different neutrino–nucleus reaction channels, the charged-current reaction in which the parent nucleus changes charge and the daughter one appears, in general, in an excited (final) state, has been firstly measured long ago. The neutral current channel has only recently been measured for the first time (forty three years after its first theoretical prediction), in the COHERENT experiment at ORNL, United States (Akimov et al., 2017). Today, the operating or planned worldwide neutral current “coherent elastic neutrino-nucleus scattering (CEvNS) experiments” are based on precise measurements of the nuclear-recoil and among their highest priorities are the investigation of the neutrino properties, the fundamental ν-matter weak interactions, etc., (Papoulias and Kosmas, 2018; Papoulias et al., 2020). The planned advances in the precision of these experiments require a commensurate effort in the understanding and modeling of the nuclear physics aspects of these interactions, which are incorporated as a particle model in neutrino physics and play important role in interpreting the respective experimental results (Akimov et al., 2017; Papoulias and Kosmas, 2018; Papoulias et al., 2020).

In core-collapse supernova simulations, precise description of neutrino processes deep into the hot and dense matter is required. In this review, we summarize the main conclusions extracted from the studies aiming to estimate the rates of charged-current weak processes involving electrons, muons and their anti-particles inside the massive stars’ matter (Suzuki et al., 2006; Suzuki et al., 2011; Suzuki and Kajino, 2013; Suzuki et al., 2018). The neutrino processes inside the hot and dense stellar medium are important in many aspects of core-collapse supernovae and, in particular for the explosion mechanism and the explosive neutrino nucleo-synthesis leading to the creation of the heavy elements (heavy nuclear isotopes) (Langanke and Martinez-Pinedo, 1998; Kajino et al., 2014). The multi-dimensional (2-D, 3-D, 4-D) simulations of successful explosions of core-collapse supernovae have shown that the neutrino-driven mechanism and the neutrino transport in hot and dense proto–neutron stars must necessarily be accurately described which means that the cross sections and event rates of the relevant reactions are appreciably important (Giannaka and Kosmas, 2013; Suzuki and Kajino, 2013; Giannaka and Kosmas, 2015b; Suzuki et al., 2018).

As is well known, in general, the gravitational collapse plays a vital role in the structural formation of the Universe, and in the death of massive stars through the gravitational collapse and the subsequent supernova explosions that are spectacular and very complex astrophysical events. Further, under the extreme conditions of the hot and dense interior of massive stars, all four known forces of nature are involved. Thus, the presence of the strong gravitational field determines the dynamics of the astrophysical plasma while the weak interactions govern the energy and lepton number loss of the system through the transport of neutrinos from high-opacity regions to the free-streaming ones (Langanke and Wiescher, 2001; Woosley et al., 2002). Electromagnetic and strong interactions determine the thermodynamic properties, while nuclear and weak interactions modify the stellar gas composition. Focusing on the stellar weak interaction processes we are interested in the present article, in recent years there has been much progress in describing these processes towards many directions involving their intimate connection with the stellar evolution phenomena. In a single article, however, one can hardly cover all interesting aspects of the massive star’s evolution and their death through the gravitational collapse followed by the supernova explosion related to the semi-leptonic weak interaction processes (Langanke and Wiescher, 2001).

For the above reason, in the present review we will focus on some selected topics (chosen according to our preference) mostly related to the role of the stellar weak interaction processes taken place in the presence of nuclei (Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b; Tsakstara and Kosmas, 2012; Giannaka and Kosmas, 2015a; Giannaka and Kosmas, 2015b). For the benefit of the reader, however, we mention some relevant topics like for example: 1) The neutrino absorption on nucleons, which is crucial for the supernova explosion mechanism and the explosive nucleosynthesis. 2) The elementary pair-production processes which are important for neutron star cooling. 3) The production mechanisms of muon and tau neutrinos in the late stages of collapse (because of their current interest, we will discuss in Section 7 their detection by Earth bound detectors through the production of muons or tau particles). 4) The neutrino–lepton scattering (as neutrino–muon scattering) (Bollig et al., 2017). On the other hand, we consider as purely astrophysical aspects the following: 1) the current progress occurred in astrophysical models and the treatment of the related uncertainties in each of these models in connection to the relevant experimental data, 2) phenomena related to the supernova dynamics, 3) the shock acceleration phases and the neutrino-spectra formation, etc., which are, of course, important and crucial for massive stars’ evolution, but they fall out of the scope of the special Volume and the Research Topic of the Journal for which the present review has been written.

The article is organized as follows. At first (Section 2), we review the general evolution of the massive stars as well as that of their main burning stages (H, He, C, Ne, O, … ). Next (in Section 3), we recapitulate the relevant formalism used for the semi-leptonic processes. Then, the muon capture (in Section 4), the electron capture (in Section 5) and the neutrino-nucleus reactions (in Section 6) under laboratory and stellar conditions are discussed. While the results presented for the muon capture rates (in Section 4) are based on a mean value of the muon-nucleus overlap integrals, we discuss here the accurate muon wave functions calculated by our group recently. Next (Section 7), we review the role of the aforementioned semi-leptonic processes in Earth neutrino detectors and, finally (Section 8), we summarize the main research addressed in this article and we discuss next generation investigations.

2 Stellar Evolution and the Role of the Weak Interaction Processes

In this section, we summarize briefly the main conclusions of the state-of-the-art approaches related to the structure and evolution of the hot and dense stellar interior focusing on the relevance of the weak interaction processes with the stellar dynamics and stellar evolution. The latter includes the way that stars change with time, although on human time-scale most stars (those being in the main sequence stage) do not show at all changes and this holds for millions of years. In general, the evolution of a star, is strongly determined by its mass (M) during the long lasting main sequence phase of its life and is expected to lead in a wide variety of outcomes (Fuller et al., 1982; Bethe, 1990; Phillips, 2013; Woosley, 2019). Thus, the gravitational contraction of stars is, in general, balanced from the nuclear fusion reactions taking place in their interior and lead to the development of a sequence of burning shells which from outer to inner are the H-burning, the He-, the C-, the Ne-, the O- and finally the Si-burning shell (the cycle of contraction, heating, ignition of another nuclear fuel is repeated several times from the outer to the inner layer).

As mentioned above, massive stars go through six burning stages [see e.g., (Langanke and Wiescher, 2001)]: H, He, C, Ne, O, and Si burning with the lifetimes of these stages to be: H- and He-burning stages last for roughly 10⁶⁻⁷ y and 10⁵⁻⁶ y, respectively, while the lifetime for the other phases is much shorter (due to neutrino losses dominating energy losses over radiation from C burning onward). Therefore C-, Ne-, O-, and Si-burning phases last about 10²⁻³ y, 1 y, 1 y, and 10⁻² y, respectively. During these stages, the mass density ρ and temperature T of the star’s core increase gradually and, at the end of Si-burning core, reach values up to ρ = 10⁹gcm⁻³ and up to T = 10⁹ K, respectively. Under the latter conditions, the bidirectional nuclear reactions reach the equilibrium, a situation known as nuclear statistical equilibrium (NSE). Then, the nuclear composition is described through the three variables: T, ρ and proton-to-nucleon ratio Y_e (Langanke and Wiescher, 2001; Woosley et al., 2002).

During the NSE phase, the nuclear fusion reactions cannot release energy anymore, which implies that the important thermonuclear pressure that balances the gravitational contraction is canceled. In more detail, at this stage the star’s core (known as Fe-core) is mainly made of Fe-group nuclei, produced by the Si-burning shell, namely nuclei in the Fe-Ni nuclear mass region which are favored under the core values of ρ and T mentioned above, while Y_e is a bit smaller than Y_e = 0.5. But, since Fe cannot be burned to heavier elements (this reaction requires energy to proceed and does not generate energy), the star finally runs out of fuel and collapses under its own gravity. The neutrinos generated at this phase interact with matter mainly via neutral-current coherent scattering on nucleons and nuclei (the rate is large so that their diffusion time-scale is longer than the collapse time-scale). Moreover, the electrons of the core inside such an environment form a degenerate relativistic gas that can balance the gravitational contraction only if the stellar mass is below the known Chandrasekhar mass limit $M_{Ch}=1.44{(Y_e)}^2{M}_{\left\{\mathrm{solar}\right\}}$. If this limit is exceeded (due to the e-capture and the Si-burning that modify the Y_e), the electron gas cannot stabilize the core any more and the star collapses.

Furthermore, during the early phase of the collapse, the neutrinos produced by the e⁻-capture process can leave the star unhindered carrying away energy that constitutes an effective cooling mechanism which keeps the entropy and core-temperature at low levels (for low entropy heavy nuclei exist during the entire collapse phase) (Langanke and Wiescher, 2001; Woosley et al., 2002). The situation changes when the collapse reaches densities of the order of ρ = 10¹²gcm⁻³. Then, due to the neutral current coherent neutrino-nucleus scattering mentioned above (the diffusion time-scale is longer than the collapse time of the core), neutrinos are effectively trapped in the core. At neutrino trapping (ρ = 10¹²gcm⁻³), the values of Y_e are significantly lower, while at higher densities the total lepton fraction Y_lep becomes constant (the trapped neutrinos increase the total lepton fraction in the core) but the Y_e still decreases. We note that during neutrino trapping, the continuous e⁻-capture reduces the electron abundance. Due to this crucial role of the electron capture in determining the dynamics of the core collapse of massive stars for core densities in the range 10⁹gcm⁻³ ≤ ρ ≤ 10¹²gcm⁻³, in this article we discuss in detail this process (see Section 5). We mention however that, despite the progress achieved in recent years in the determination of stellar e⁻-capture rates, further improvements are certainly required at least in specific regions of the periodic table (Langanke et al., 2021).

As mentioned before, the star’s life depends primarily on the star’s mass M at birth. Thus, stars with M⪅8M_{solar} proceed mainly through H- and He-burning. As they lose significant mass by stellar winds, at the end of He burning their masses are not sufficient to ignite further burning stages. Their life ends as White Dwarfs, that are compact objects with a mass limit M ≤ 1.44M_{solar}, i.e., Chandrasekhar mass, stabilized by electron degeneracy pressure (Hirschi et al., 2004; Jones et al., 2016; Langanke et al., 2021). The so called intermediate-mass stars (8⪅M⪅11M_{solar}) follow in-between fate and collapse into a neutron star or are ending in a thermonuclear runaway which disrupts most of the core (Langanke and Wiescher, 2001; Woosley et al., 2002). Simulations of such stars are quite sensitive to astrophysical uncertainties like convective mixing or mass loss rates (Hirschi et al., 2004; Jones et al., 2016; Langanke et al., 2021). Most of the mass loss of stars takes place during H- and He-burning phases (mainly for red giant stars). On the other hand, the major nuclear uncertainty, related to electron capture on ²⁰Ne, has recently been removed as this rate is now known experimentally at the relevant astrophysical conditions (Langanke et al., 2021). Finally, stars with M⪆11M_{solar} develop a core at the end of each burning phase which exceeds the Chandrasekhar mass, so that they can ignite the full cycle of hydrostatic burning and end their lives as core-collapse supernovae, leaving either neutron stars or black holes as remnants (Langanke and Wiescher, 2001; Woosley et al., 2002).

3 Formalism for Model Calculations on Semi-Leptonic Weak Processes

Usually, the event rates (total cross sections) calculations of the semi-leptonic processes (electron capture, muon-capture, neutrino induced reactions, beta decay modes, etc.,) start from the corresponding differential cross sections which, within the context of the Donnelly-Walecka multipole decomposition method, are obtained by the expression (O'Connell et al., 1972; Donnelly and Walecka, 1976; Donnelly and Peccei, 1979).

$\begin{array}{cc}\hfill \frac{d{\sigma }_{ec}}{d\mathrm{\Omega }}& =\frac{G_F^2{\cos }^2{\theta }_c}{2\pi }\frac{F(Z,E_e)}{(2J_i+1)}\left\{\sum _{J\ge 1}\mathcal{W}(E_e,E_{\nu })\left\{[(1-(\widehat{\nu }\cdot \widehat{\mathbf{q}})(\widehat{\mathit{\beta }}\cdot \widehat{\mathbf{q}}))]\right.\right.\left[|\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{mag}\Vert J_i\rangle {|}^2\right.\hfill \\ \hfill +& \left.|\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{el}\Vert J_i\rangle {|}^2\right]\left.-2\widehat{\mathbf{q}}\cdot (\widehat{\nu }-\widehat{\mathit{\beta }})Re\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{mag}\Vert J_i\rangle \langle J_f\Vert {\widehat{\mathcal{T}}}_J^{el}\Vert J_i\rangle \ast \right\}\hfill \\ \hfill +& \sum _{J\ge 0}\mathcal{W}(E_e,E_{\nu })\left\{(1+\widehat{\nu }\cdot \widehat{\mathit{\beta }})|\langle J_f\Vert {\widehat{\mathcal{M}}}_J\Vert J_i\rangle {|}^2+\left(1-\widehat{\nu }\cdot \widehat{\mathit{\beta }}+2(\widehat{\mathit{\beta }}\cdot \widehat{\mathbf{q}})|\langle J_f\Vert {\widehat{\mathcal{L}}}_J\Vert J_i\rangle {|}^2\right.\right.\hfill \\ \hfill -& 2\left.\left.\widehat{\mathbf{q}}\cdot (\widehat{\nu }+\widehat{\mathit{\beta }})Re\langle J_f\Vert {\widehat{\mathcal{L}}}_J\Vert J_i\rangle \langle J_f\Vert {\widehat{\mathcal{M}}}_J\Vert J_i\rangle \ast \right\}\right\}\hfill \end{array}(1)$

(G_F and θ_c stand for Fermi constant and the known Cabibbo angle of the weak interactions) where $\mathcal{W}(E_e,E_{\nu })=E_{\nu }^2/(1+E_{\nu }/M_T)$, takes into consideration the nuclear recoil (M_T is the mass of the target nucleus) (Niu et al., 2011), while F(Z, E_e) denotes the well known Fermi function (Langanke et al., 2003; Langanke and Martínez-Pinedo, 2003). We note that, this kind of calculations do not take into account possible modifications due to the final state interaction of the outgoing lepton like those applied in electron scattering where the effective momentum approximation may significantly improve this effect (Aste and Jourdan, 2004).

The nuclear matrix elements between the initial state $\left|J_i\right.⟩$ and a final state $\left|J_f\right.⟩$ refer to the Coulomb ${\widehat{\mathcal{M}}}_{JM}$, longitudinal ${\widehat{\mathcal{L}}}_{JM}$, transverse electric ${\widehat{\mathcal{T}}}_{JM}^{el}$ and transverse magnetic ${\widehat{\mathcal{T}}}_{JM}^{mag}$ multipole operators [see Ref. (Giannaka and Kosmas, 2015a)]. Also, $\widehat{q}$, $\widehat{\nu }$ are the unit vectors of the momentum transfer q, the outgoing-particle momentum and $\widehat{\mathit{\beta }}$ = k/E_e with k being the corresponding 3-momentum of the incoming particle (Donnelly and Peccei, 1979). For the evaluation of the wave functions $\left|J_i\right.⟩$ and $\left|J_f\right.⟩$ required for the reaction rates of semi-leptonic nuclear processes, up to now various microscopic models have been used which are briefly summarized as follows. The independent particle model (Fuller et al., 1982), the shell model for light s-d shell nuclei (Oda et al., 1994; Suzuki et al., 2006; Suzuki et al., 2018), the large scale shell model (Langanke and Martı́nez-Pinedo, 2000), the ordinary random phase approximation (RPA) (Nabi et al., 2007a; Nabi et al., 2007b; Nabi, 2011; Nabi and Riaz, 2019), the continuum RPA (CRPA) (Kolbe et al., 1997), the relativistic RPA (Paar et al., 2009; Niu et al., 2011; Fantina et al., 2012), the quasi-particle RPA (QRPA) (Chasioti and Kosmas, 2009; Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b; Tsakstara and Kosmas, 2012; Giannaka and Kosmas, 2015a; Giannaka and Kosmas, 2015b), the deformed QRPA (Sarriguren et al., 2001), the thermal QRPA (Dzhioev et al., 2020), and others (Hix et al., 2003). Each of these methods has advantages and disadvantages. We mention that, several of the above calculations are comprehensive. What is, however, worth noting at this point is the fact that the available results cover still a small portion of the input required in Supernova evolution codes (mostly those referred to the e-capture and ν-nucleus process designed to predict the SN explosions and multi-messenger signatures of many important astrophysical phenomena) (Titus et al., 2017). Furthermore, in the majority of the above studies, a number of simplifying assumptions (zero momentum transfer to the target nucleus, forward scattering angles of the outgoing particles, employment of schematic nucleon-nucleon interaction, etc.,) have been made (Ejiri et al., 2019). Under these assumptions, several authors found that the Gammow-Teller operators, ${\mathrm{G}\mathrm{T}}^{\pm }={\sum }_j{\tau }_j^{\pm }\sigma (j)$ with ΔT = 1, ΔL = 0, ΔJ^π = 1⁺, dominate the cross sections of several semi-leptonic processes. Even though these methods are still reliable and the results obtained interesting, some important details are missing and also some computations need to be further improved (Chasioti and Kosmas, 2009; Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b).

In the following sections, we will summarize briefly some muon-capture, e⁻-capture and neutrino-nucleus reactions cross sections obtained within the framework of a refined version of the proton-neutron QRPA (p-n QRPA) (Giannaka and Kosmas, 2013; Giannaka and Kosmas, 2015b; Giannaka and Kosmas, 2015a), but, for the sake of completeness we will also discuss the comparison of these QRPA results with some of those computed within the context of other methods as mentioned above. The p-n QRPA method offers a reliable construction of the ground state $\left|i\right.⟩$ and all the accessible final states $\left|f\right.⟩$ of the daughter nuclei entering the calculations of Eq. 1 for single charge-exchange nuclear reactions (Kosmas et al., 1994; Kosmas and Oset, 1996; Kosmas et al., 1997a). The method is tested through the reproducibility of: 1) nuclear ground state properties, 2) various electron scattering data, 3) experimental muon capture rates (Giannaka and Kosmas, 2015a), 4) beta-decay rates, etc. The corresponding QRPA predictions, may come out of state-by-state calculations of exclusive, partial and total rate transition matrix elements (Donnelly and Peccei, 1979; Kosmas et al., 1997b; Eramzhyan et al., 1998; Kolbe et al., 2000; Kosmas et al., 2001; Zinner et al., 2006). The use of the p-n QRPA with rich model space and adopting as realistic nucleon-nucleon interaction the Bonn C-D potential leads to reliable agreement with experimental data. This high confidence level encouraged its use to find muon-capture rates, electron capture cross sections in various nuclear isotopes (Giannaka and Kosmas, 2015a) and also neutrino nucleus neutral current reaction (Chasioti and Kosmas, 2009; Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b; Tsakstara and Kosmas, 2012; Papoulias and Kosmas, 2018).

4 The Muon Capture on Nuclei

In the stellar interior, but also in current experimental research, several well known processes involving muons and muonic neutrinos take place on nuclei as: 1) The conventional bound muon capture by the nucleus (A,Z), with A denoting the mass- and Z the atomic-number of the parent nucleus. Most important channels are: a) the ordinary muon-capture, represented by the reactions

${\mu }_b^{-}+\left(A,Z\right)\to {\nu }_{\mu }+{\left(A,Z-1\right)}^{\ast },(2)$

(the asterisk * stands for “excited state” of the daughter nucleus), b) the muon-decay-in-orbit (MDIO): ${\mu }_b^{-}\to {\nu }_{\mu }+e^{-}+{\tilde{\nu }}_e$, and c) the radiative muon capture: ${\mu }_b^{-}+(A,Z)\to {\nu }_{\mu }+{(A,Z-1)}^{\ast }+\gamma$. 2) The exotic neutrinoless capture of a bound muon $({\mu }_b^{-})$, known as muon-electron conversion: ${\mu }_b^{-}+(A,Z)\to e^{-}+{(A,Z)}^{\ast }$, as well as the known as muon-positron conversion: ${\mu }_b^{-}+(A,Z)\to e^{+}+{(A,Z-2)}^{\ast }$. 3) Reactions producing muons through muonic neutrino absorption by nuclei inside the stellar environment or at the terrestrial nuclear detectors (see Section 6 and Section 7). Below we will discuss briefly some recent results obtained for the process of Eq. 2 in connection with terrestrial relevant experiments.

An exclusive capture rate, Λ_i→f, of the process (2), for a transition from the initial $\left|i\right.⟩$ to a final $\left|f\right.⟩$ state of the muonic atom (in laboratory conditions), takes the form (Giannaka and Kosmas, 2015a).

${\mathrm{\Lambda }}_{i\to f}=\frac{2G^2{E}_f^2}{2J_i+1}{W}_f\left[\left|\right.\langle J_f\Vert {\mathrm{\Phi }}_{\mu }\left({\widehat{\mathcal{M}}}_J-{\widehat{\mathcal{L}}}_J\right)\Vert J_i\rangle {\left|\right.}^2+\left|\right.|\langle J_f\Vert {\mathrm{\Phi }}_{\mu }\left({\widehat{\mathcal{T}}}_J^{el}-{\widehat{\mathcal{T}}}_J^{magn}\right)\Vert J_i\rangle |{\left|\right.}^2\right],(3)$

where Φ_μ(r) represents the exact bound muon wave function (for the ground state of the muon-nucleus system, the muonic atom). From the latter expression exact muon-capture rates, by using a realistic bound-muon wave function through solving numerically the Schroedinger (Kosmas and Lagaris, 2002) or Dirac (Tsoulos et al., 2019) equations, may be obtained (Jokiniemi et al., 2021). Multipole muon-capture transition rates, referred to a given multipolarity ${\mathrm{\Lambda }}_{J^{\pi }}$, but also total muon capture rates, have been recently obtained by various research groups (Giannaka and Kosmas, 2015a). The evaluation of partial and total rates of such muonic processes was mostly realized by employing approximate wave functions for the bound muons in nuclei (Kosmas and Oset, 1996; Giannaka and Kosmas, 2015a; Giannaka and Kosmas, 2015b).

In Figures 1, 2 we show some multipole transition rates for the ⁴⁸Ti, ⁵⁶Fe, ⁶⁶Zn and ⁹⁰Zr isotopes obtained within the context of the pn QRPA. Such calculations indicate the dominance of J^π = 1⁻ and 1⁺ multipolarities in the studied nuclear isotopes. Moreover, individual contribution of Polar-vector, Axial-vector and the overlap part into the total muon-capture rate have also been obtained (Giannaka and Kosmas, 2015a). Furthermore, in Table 1, the total muon capture rates obtained by using the pn-QRPA for the light nuclei ²⁸Si and ³²S (with the free nucleon coupling constant g_A = 1.262), and for the medium weight nuclei ⁴⁸Ti,⁵⁶Fe,⁶⁶Zn and ⁹⁰Zr (with g_A = 1.135), are compared with the available experimental data as well as with the theoretical rates of Ref. (Zinner et al., 2006). For additional results the reader is referred to Ref. (Giannaka and Kosmas, 2015a; Giannaka and Kosmas, 2015b).

FIGURE 1

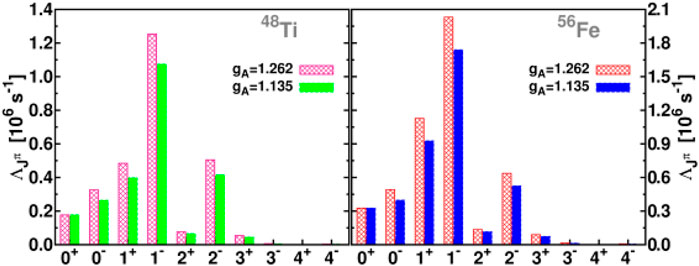
FIGURE 1. Contribution of multipole transition rates ${\mathrm{\Lambda }}_{J^{\pi }}$ (up to J^π = 4^±) into the total muon capture rate for the ⁴⁸Ti and ⁵⁶Fe isotopes with inclusion (filled histograms) and without inclusion (double dashed histogramms) of the g_A quenching effect. The dominance of J^π = 1⁻ and 1⁺ multipolarities is obvious for all nuclei.

FIGURE 2

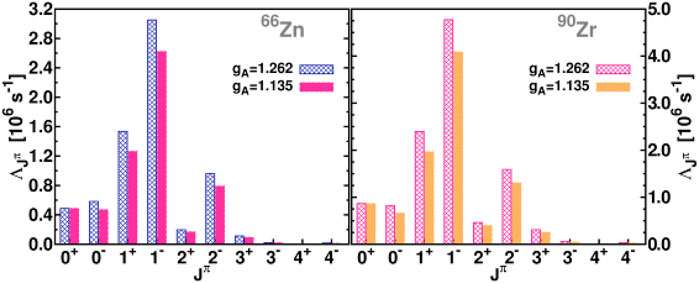
FIGURE 2. Same as in Figure 1 but here the muon capture rate refers to the ⁶⁶Z_n and ⁹⁰Zr isotopes.

TABLE 1

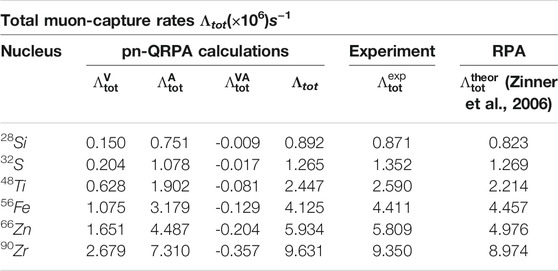
TABLE 1. Individual contribution of Polar-vector, Axial-vector and Overlap part into the total muon-capture rate. Also, the total muon capture rates obtained by using the pn-QRPA with 1) the quenched value of g_A = 1.135, for the medium-weight nuclei ⁴⁸Ti,⁵⁶Fe,⁶⁶Zn and ⁹⁰Zr and 2) the free nucleon coupling constant g_A = 1.262, for the light nuclei ²⁸Si and ³²S, are compared with the available experimental data and with the theoretical total rates of Ref. (Zinner et al., 2006).

The nuclear method used offers the possibility of estimating separately the individual contributions to the total and partial rates of the polar-vector and axial-vector components of the weak-interaction Hamiltonian for each accessible final state of the daughter nucleus. One of our main goals is to provide a reliable description of the charge-changing transitions matrix elements entering the description of other similar semileptonic nuclear processes like the charged-current (muonic) neutrino-nucleus reactions, the electron capture on nuclei, the single β^±-decay modes, etc., which play important role in currently interesting laboratory and astrophysical applications like the neutrino detection through lepton-nucleus interaction probes and neutrino nucleo-synthesis (Kolbe et al., 2003). Such results can also be useful in various ongoing muon capture experiments at Paul Scherrer Institute (PSI), at Fermilab, at Japan Proton Accelerator Research Complex (JPARC), and at the Research Center for Nuclear Physics (RCNP), Osaka University (Hashim et al., 2018; Ejiri, 2019; Hashim and Ejiri, 2021).

Recently, various sensitive experiments take advantage of the powerful muon beams produced in the above well-known muon factories for standard and nonstandard muon physics probes (Marketin et al., 2009; Cook et al., 2017; Hashim et al., 2018; Jokiniemi et al., 2019; Hashim and Ejiri, 2021). Among the standard-model probes, those involving muon capture on nuclei, specifically those emitting X-rays and/or several particles (p, n, α, etc.) after μ-capture (which are important for understanding the rates and spectra of these particles) are intensively investigated (Hashim et al., 2018; Hashim and Ejiri, 2021). For example, at PSI researchers are interested in experiments based on the emission of charged particles from the nuclei muonic atoms of Al, Si, and Ti or neutron emission following muon capture from Fe, Ca, Si, and Al (Hashim et al., 2018; Hashim and Ejiri, 2021). Also very recently, in the highly intense facilities of Muon Science Innovation Commission (MuSIC) at RCNP, nuclear muon capture reactions on Mo, Pb, etc., are planned to study nuclear weak responses for neutrino reactions, etc., (Hashim et al., 2018; Jokiniemi et al., 2019; Hashim and Ejiri, 2021; Jokiniemi et al., 2021). For such experiments, it is important to know the ordinary muon capture rates to the final (excited) states of the daughter nucleus, before proceeding to event rates of emitted X-rays or particles through de-excitation processes (Cook et al., 2017; Hashim and Ejiri, 2021).

4.1 Accurate Calculation of Muon-Nucleus Overlap Integrals Entering Muonic Reactions

The evaluation of reliable predictions in μ⁻-capture and e⁻-capture required for various physical observables (Giannaka and Kosmas, 2015b; Giannaka et al., 2021), must be based on accurate muon and electron wave functions [coming out of solutions of the Schroedinger (Kosmas and Lagaris, 2002) and Dirac (Giannaka et al., 2021) equations] obtained through the application of advanced algorithms (Kosmas and Vlachos, 2010; Kosmas and Leyendecker, 2015; Kosmas and Vlachos, 2016; Kosmas and Leyendecker, 2018). Recently, for the solution of the Dirac equations a fast algorithm has been derived by our group within the neural networks and stochastic optimization techniques (Giannaka et al., 2021).

Three intelligent independent algorithms, namely the Genetic algorithms, the Particle Swarm Optimization and the Simulated Annealing method (Kosmas and Vlachos, 2012) each of them with individual advantages, have been incorporated in the same numerical method (Giannaka et al., 2021). Its use is favored from intuitive, theoretical and practical arguments, since appropriate multi-parametric expressions representing the radial Dirac wave functions i.e., its small (bottom) and large (top) components for a bound muon orbiting around complex nuclear system, are optimized. These parameters reflect those of the assumed feed-forward artificial neural network (Kosmas and Lagaris, 2002), applied to obtain the ground state wave function describing a muon-nucleus system (muonic atom). From a computational point of view, the training in this method is performed by using the DiracSolver software package that proved to be both convenient and efficient (Tsoulos et al., 2019) and offers the possibility to be effectively applied in other atomic, nuclear and molecular systems. Among the interesting applications of the DiracSolver algorithm are the calculations of the up (large) and bottom (small) components of the radial wave functions for bound leptons in the Coulomb field of nuclei (atoms) as, electron (e⁻), muon (μ⁻) and tau (τ⁻), in the field of complex nuclei (Tsoulos et al., 2019; Jokiniemi et al., 2021).

In the Dirac Hamiltonian, the potential energy V(r) describing the extended nuclear Coulomb field, created by the nuclear charge density distribution ρ(r), is calculated as (Kosmas and Lagaris, 2002; Tsoulos et al., 2019).

$V\left(\mathbf{r}\right)=-e^2\int \frac{\rho \left({\mathbf{r}}^{\prime }\right)}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}{d}^3{\mathbf{r}}^{\prime },(4)$

where the (finite size) nuclear charge density ρ(r) is taken from electron scattering experimental data (De Vries et al., 1987). For the chosen nuclear systems (assuming spherically symmetric charge distributions) the radial charge density entering Eq. 4 is described by two-parameter Fermi distributions extracted from model-independent analysis of electron scattering data (De Vries et al., 1987). It should be also noted that, for the Dirac solutions, in addition, to the above potential V(r), the rather significant vacuum polarization correction, described by an effective potential V_vp [see e.g., Ref. (Kosmas and Lagaris, 2002)] is also considered.

Detailed calculations of the known muon-nucleus overlap integrals, entering the partial and total rates of the ordinary muon capture discussed above, could be obtained through the accurate muon wave functions Φ_μ(r) inserted in Eq. 3 (Jokiniemi et al., 2021). In ref. Giannaka et al. (2021) specifically, we concentrate on the prominent nuclear systems ²⁸Si and ⁶⁴Zn isotopes. By using such wave functions, one may perform accurate muon capture rate calculations for currently interesting nuclear isotopes (e.g., ²⁸Si, ³²S, ⁴⁸Ti, ⁵⁶Fe, ⁶⁶Zn and ⁹⁰Zr studied previously by using a mean value of the ground state muon wave functions) (Giannaka and Kosmas, 2015a). The reader is also referred to the recent works by Jokiniemi et al. (2021) for recent similar accurate calculations.

Before closing this Section, we should stress that current Earth bound detectors of high energy supernova neutrinos (e.g., muonic neutrinos, see Section 7.1) are based on signals created through charged-current reactions taking place with the detector materials (involving the ν_μ-nucleus reaction). The latter processes are particle conjugate reactions of the lepton-nucleus capture including the μ⁻-capture on nuclei which is, for this reason extensively discussed in the present article and is studied by many authors, see, e.g., Ref. (Kolbe et al., 2000; Kosmas et al., 2001; Zinner et al., 2006; Giannaka and Kosmas, 2015a; Jokiniemi et al., 2021) and references therein. The production of the aforementioned high energy supernova neutrinos (which are mostly the heavy flavor neutrinos ν_μ, ν_τ and their anti-particles) are closely related to processes taking place in the late stages of core-collapse SN and also the muonization process (see below) (Bollig et al., 2017; Fischer et al., 2020).

4.2 Muons Inside Core-Collapse Supernovae Environment

In the stellar interior, free muons (μ⁻) may be produced through the particle conjugate processes of Eq. 2 taking place when the temperature is high enough or the matter-density in the stellar interior is high enough so that the chemical potential difference of nucleons, λ_n − λ_p, or the interaction potential difference, U_n − U_p, reach the muon rest mass (m_μ = 105.6 MeV). In such cases, the muonization occurs in the stellar interior mainly through the semi-leptonic processes (Bollig et al., 2017; Fischer et al., 2020).

${\nu }_{\mu }+n\to {\mu }^{-}+p$

${\nu }_{\mu }+\left(A,Z\right)\to {\mu }^{-}+\left(A,Z+1\right)$

The latter semi-leptonic nuclear processes always dominate at high neutrino energies E_ν due to larger nuclear matrix elements. The charged current reactions of nucleons and nuclei with the high energy leptons (muon anti-neutrinos, ${\tilde{\nu }}_{\mu }$, and muon neutrinos, ν_μ, as well as the negative muon μ⁻, and the positive muon μ⁺) are crucial. Reaction rates of all the relevant weak processes which involve μ⁻ or ν_μ are required as input in the numerical simulations for the description of muonization mechanism inside the hot and dense stellar interior (Bollig et al., 2017; Fischer et al., 2020).

Recent calculations (Fischer et al., 2020) for the semileptonic reactions involving the μ⁻ with large energy-momenta transfer concluded that the pseudoscalar coupling term in the hadronic weak current (normally this is neglected for ν_e reactions), is as important as the weak magnetism. On the other hand, the effects of nucleon form factors become significant as the energy-momenta transfer increases and they must be considered rather equally important as the weak magnetism and the pseudoscalar corrections.

5 The Electron Capture on Nuclei

The process of bound-electron capture by a nucleus (analogous to the ordinary muon capture), called also orbital (ordinary) electron capture, is represented by the reaction (Giannaka and Kosmas, 2015b).

$e_b^{-}+\left(A,Z\right)\to \left(A,Z-1\right)\ast +{\nu }_e,(5)$

($e_b^{-}$ denotes a bound electron). In the latter process, the daughter nucleus appears at a definite energy level while, in general, the outgoing neutrino may carry off a portion of the available energy in process (5). Because process 5) is a charge-changing one (charge transfer occurs from the parent to the daughter nucleus), it is possible that, part of the available energy may escape as a γ-ray photon, so that only the remaining energy is carried away by the neutrino. This means that transitions to intermediate states, giving a continuous energy spectrum, are allowed. As a result, the maximum possible energy of the emitted γ-ray photon corresponds to the case in which the neutrino carries a very small (approximately zero) energy equal to the energy of its production. Consequently, the maximum endpoint energy of the above γ-ray which is measured experimentally, is equal to the energy available in the orbital electron capture process. This, for example, in the case of ⁵⁹Ni is E_γ = 1.065 MeV, in ⁶⁵Zn it is E_γ = 1.114 MeV, and in ⁶⁰Co it is E_γ = 1.320 MeV. Thus, the maximum neutrino energy E_ν is rather low (lower than E_e ≤ 3 m_e ≈ 1.5 MeV).

The ordinary electron capture differs from the stellar electron capture which takes place under the conditions of the stellar environment, i.e., core densities between 10⁹ g cm⁻³ ≤ ρ ≤ 10¹² g cm⁻³ and temperatures 10⁹ ≤ T ≤ 10¹² K (Nabi et al., 2007a; Nabi et al., 2007b; Nabi, 2011; Giannaka and Kosmas, 2015b; Nabi and Riaz, 2019). This process is crucial for the dynamics of the core collapse of massive stars and it is more interesting in nuclear astrophysics. In the hot and dense stellar environment, electrons (e⁻) have total energy E_e⪅30, − , 50 MeV, so the relevant nuclear calculations of the cross sections of process 5) in order to be translated to stellar cross sections through the folding procedure must have E_e up to this energy region (see below) (Giannaka and Kosmas, 2015b).

Within the J-projected multipole decomposition formalism of Donnelly-Walecka, the differential cross section of electron capture on nuclei under laboratory conditions takes the form

$\begin{array}{cc}\hfill \frac{d{\sigma }_{ec}}{d\mathrm{\Omega }}& =\frac{G_F^{2}co{s}^2{\theta }_c}{2\pi }\frac{F(Z,E_e)}{(2J_i+1)}\cdot \left\{\sum _{J\ge 1}\mathcal{W}(E_e,E_{\nu })\left\{[1-\alpha cos\mathrm{\Phi }+bsi{n}^2\mathrm{\Phi }]\left[|\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{mag}\Vert J_i\rangle {|}^2\right.\right.\right.\hfill \\ \hfill +& \left.\left.|\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{el}\Vert J_i\rangle {|}^2\right]-\left[\frac{({\epsilon }_i+{\epsilon }_f)}{q}(1-\alpha cos\mathrm{\Phi })-d\right]2Re\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{mag}\Vert J_i\rangle \langle J_f\Vert {\widehat{\mathcal{T}}}_J^{el}\Vert J_i\rangle *\right\}\hfill \\ \hfill +& \sum _{J\ge 0}\mathcal{W}(E_e,E_{\nu })\left\{(1+\alpha cos\mathrm{\Phi })|\langle J_f\Vert {\widehat{\mathcal{M}}}_J\Vert J_i\rangle {|}^2+(1+\alpha cos\mathrm{\Phi }-2bsi{n}^2\mathrm{\Phi })|\langle J_f\Vert {\widehat{\mathcal{L}}}_J\Vert J_i\rangle {|}^2\right.\hfill \\ \hfill -& \left.\left.\left[\frac{\omega }{q}(1+\alpha cos\mathrm{\Phi })+d\right]2Re\langle J_f\Vert {\widehat{\mathcal{L}}}_J\Vert J_i\rangle \langle J_f\Vert {\widehat{\mathcal{M}}}_J\Vert J_i\rangle \ast \right\}\right\}\hfill \end{array}(6)$

The latter expression is consistent with Eq. 1. The kinematical parameters α, b, d are given e.g., in Chasioti and Kosmas (2009). In the above equation, Φ represents the scattering angle (for forward scattering, used by many authors, Φ = 0) while ω_if = E_f − E_i denotes the excitation energy of the daughter nucleus. The energy E_ν of the outgoing neutrino in the reaction (5), due to energy conservation, is written as

$E_{\nu }=E_e-Q-{\omega }_{if},(7)$

where Q is the known Q-value determined from the experimental masses of the parent (M_i) and the daughter (M_f) nuclei as Q = M_f − M_i (Dean et al., 1998).

Based on Eq. 6 one may perform state-by-state calculations on the electron capture differential cross sections with respect to the excitation energy dσ/dω defined by

$\begin{array}{ccc}\hfill {\left[\frac{d\sigma }{d\omega }\right]}_{J_f^{\pi }}& \equiv \hfill & \int \frac{d{\sigma }_{ec}}{d\mathrm{\Omega }}d\mathrm{\Omega }\hfill \\ \hfill & =\hfill & \frac{G_F^{2}co{s}^2{\theta }_c}{2\pi }\frac{F(Z,E_e)}{(2J_i+1)}\cdot \left\{\int d\mathrm{\Omega }\mathcal{W}(E_e,E_{\nu })\left\{[1-\alpha cos\mathrm{\Phi }+bsi{n}^2\mathrm{\Phi }]\left[|\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{mag}\Vert J_i\rangle {|}^2\right.\right.\right.\hfill \\ \hfill & +\hfill & \left.|\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{el}\Vert J_i\rangle {|}^2\right]-\left[\frac{({\epsilon }_i+{\epsilon }_f)}{q}(1-\alpha cos\mathrm{\Phi })-d\right]2Re\langle J_f\Vert {\widehat{\mathcal{T}}}_J^{mag}\Vert J_i\rangle \langle J_f\Vert {\widehat{\mathcal{T}}}_J^{el}\Vert J_i\rangle \ast \hfill \\ \hfill & +\hfill & (1+\alpha cos\mathrm{\Phi })|\langle J_f\Vert {\widehat{\mathcal{M}}}_J\Vert J_i\rangle {|}^2+(1+\alpha cos\mathrm{\Phi }-2bsi{n}^2\mathrm{\Phi })|\langle J_f\Vert {\widehat{\mathcal{L}}}_J\Vert J_i\rangle {|}^2\hfill \\ \hfill & -\hfill & \left.\left.\left[\frac{\omega }{q}(1+\alpha cos\mathrm{\Phi })+d\right]2Re\langle J_f\Vert {\widehat{\mathcal{L}}}_J\Vert J_i\rangle \langle J_f\Vert {\widehat{\mathcal{M}}}_J\Vert J_i\rangle \ast \right\}\right\}\hfill \end{array}(8)$

(J ≡ J^π). By evaluating the exclusive e⁻-capture cross sections of Eq. 8 for all multipolarities (usually it’s enough for J^π ≤ 5^±), for the interior of core-collapse supernova we consider incident electron energies E_e ≤ 50.0 MeV, other authors consider E_e energies up to E_e = 30 MeV (Fantina et al., 2012; Dzhioev et al., 2020). In Eq. 8 the transition matrix elements are considered to be between the ground state $\left|J_i\right.⟩=\left|i\right.⟩\equiv \left|0_{g.s.}^{+}\right.⟩$ for a spherical target nucleus and an excited state $\left|J_f^{\pi }\right.⟩\equiv \left|f\right.⟩$ of the resulting odd-odd nucleus. The cross sections as functions of the incident electron energy E_e are evaluated after integrating numerically Eq. 6 over angles for each specific final state $\left|J_f^{\pi }\right.⟩$.

In the pn-QRPA code employed in Giannaka and Kosmas (2015b), Giannaka (2015), the excitations of the daughter nucleus appear as sets of multipole states and provide the possibility to calculate the contribution to the total cross sections of each multipole set of states separately. The dependence of the differential cross sections on the excitation energy ω through the entire pn-QRPA spectrum of the daughter nucleus may be illustrated (by using a special code which rearranges all possible excitations with the corresponding cross sections) in ascending order of the respective excitation energy ω_if [see Ref. (Tsakstara and Kosmas, 2011b; Tsakstara and Kosmas, 2011a)]. In Table 2, we list some representative results for the total e⁻-capture cross sections in ⁶⁶Z_n (corresponding to electron energy E_e = 25MeV). The percentages of each low-spin multipolarity into the total e⁻-capture cross section evaluated with the p-n QRPA code, are also tabulated in this table. It is worth mentioning that, in calculating the original total electron capture cross sections, the use of a quenched value of the static axial-vector coupling constant g_A is necessary, for the renormalization of the transition matrix elements (Wildenthal, 1984; Zinner et al., 2006; Marketin et al., 2009). The coupling constant g_A enters the axial-vector form factors, F_A(q²), and in the QRPA calculations the free nucleon value of g_A = 1.262 is multiplied by a factor of about 0.8 (Wildenthal, 1984; Häusser et al., 1991; Zinner et al., 2006; Marketin et al., 2009).

TABLE 2

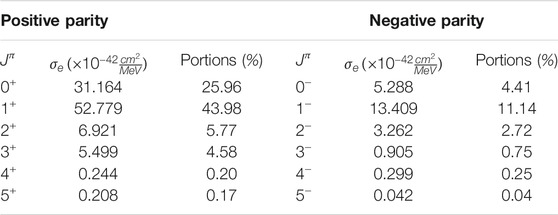
TABLE 2. Total e⁻-capture cross sections (in 10⁻⁴² MeV⁻¹ cm²) for E_e = 25MeV in ⁶⁶Z_n. The percentage of each multipolarity into the total e⁻-capture cross section, evaluated with our pn-QRPA code, are also tabulated here.

5.1 e-Capture Cross Sections in Stellar Environment

In astrophysical environment, where the finite temperature T and the matter density ϱ effects can’t be ignored (the initial nucleus is at finite temperature), the initial nuclear state must be a weighted sum over an appropriate energy distribution. Assuming that this distribution is of a Maxwell-Boltzmann type for the initial state $\left|i\right.⟩$ (Dean et al., 1998; Langanke and Martı́nez-Pinedo, 2000), the total e⁻-capture cross section is given by the expression (Paar et al., 2009).

$\begin{array}{ccc}\hfill \sigma \left(E_e,T\right)& =\hfill & \frac{G_F^2{\cos }^2{\theta }_c}{2\pi }\sum _{i}F\left(Z,E_e\right)\frac{\left(2J_i+1\right)e^{-E_i/\left(kT\right)}}{G\left(Z,A,T\right)}\hfill \\ \hfill & \times \hfill & \sum _{f,J}{\left(E_e-Q+E_i-E_f\right)}^2\frac{|⟨i|{\widehat{O}}_J|f⟩{|}^2}{\left(2J_i+1\right)}\hfill \end{array}(9)$

with G(Z, A, T) the corresponding partition function (Paar et al., 2009) and O_J denoting any of the multipole tensor operators [see Appendix of Ref. (Giannaka and Kosmas, 2015b)]. In other words, the sum over initial states in Eq. 9 denotes a thermal average of the initial energy levels. We should stress that, the first summation in Eq. 9 includes as initial states, in addition to the ground state $\left|i\right.⟩$ of the parent nucleus, also some low-lying excited states. This is because in the interior of stars the parent nucleus appears in excited states that follow Boltzmann distributions. Such studies have been taking into consideration in Paar et al. (2009), Fantina et al. (2012) and references therein. For example, ⁴⁸T, ⁵⁶Fe and ⁶⁶Zn have 2⁺ states below one MeV and their contributions can be large at high densities and temperatures.

Then, one may calculate the partial rate contributions of some specific individual multipolarities J^π by summing over the exclusive contributions of the multipole J^π states as

$\begin{array}{ccc}\hfill {\left[\frac{d\sigma }{d\omega }\right]}_{J^{\pi }}^{stel}\left(E_e,T,\omega \right)& =\hfill & \sum _f{\left[\frac{d\sigma }{d\omega }\right]}_{J_f^{\pi }}^{stel}\left(E_e,T,\omega \right)\hfill \\ \hfill & =\hfill & \frac{G_F^2{\cos }^2{\theta }_c}{2\pi }\sum _{i}F\left(Z,E_e\right)\frac{\left(2J_i+1\right)e^{-E_i/\left(kT\right)}}{G\left(Z,A,T\right)}\hfill \\ \hfill & \times \hfill & \sum _f{\left(E_e-Q+E_i-E_f\right)}^2\frac{|⟨i|{\widehat{O}}_J|J_f^{\pi }⟩{|}^2}{\left(2J_i+1\right)}\hfill \end{array}(10)$

As an example, in Figure 3 we illustrate the electron capture cross sections for the ⁶⁶Zn parent nucleus, being inside stellar environment with temperature T = 0.5 MeV (high temperature). They have been obtained by assuming that the incident electrons follow the Fermi-Dirac energy distribution.

FIGURE 3

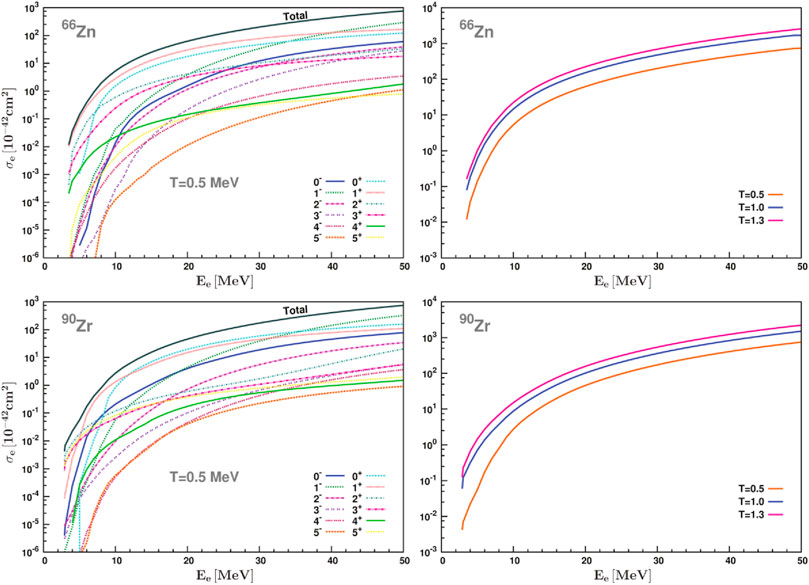
FIGURE 3. Electron-capture cross sections for the ⁶⁶Zn and ⁹⁰Zr parent nuclei at high temperature (T = 0.5 MeV) in stellar environment obtained by assuming Fermi-Dirac distribution for the incident electrons. The total cross sections and the dominant individual multipole channels (J^π ≤ 5^±) are demonstrated as functions of the incident electron energy E_e. Moreover, the right panels show the temperature dependence of the stellar cross sections for these nuclei. As can be seen, the cross sections increase doesn’t follow the stellar Temperature increase and a saturation of the cross sections is expected to occur at higher Temperatures (about at T = 1.5–1.8 MeV) (Giannaka, 2015).

We, furthermore, mention that in the central core of the stellar environment, the e⁻ (or positron e⁺) spectrum is well described by the known Fermi-Dirac distribution function parametrized with the stellar temperature T and the chemical potential of the electron μ_e as (Juodagalvis et al., 2005).

$S_{e,p}=\frac{1}{1+\mathit{exp}\left[\left(E_e-{\mu }_{e,p}\right)/\left(k_{B}T\right)\right]}.(11)$

The positron chemical potential is simply μ_p = − μ_e, while the Firmi-Dirac distribution for the e⁺ spectrum results from Eq. 11 by replacing μ_e with μ_p. In addition, at core collapse supernova, the neutrinos released through the weak interaction processes that take place in the presence of nuclei (mostly with 45 ≤ A ≤ 65) can escape (there is no-blocking of neutrinos in the phase space), i.e., S_ν ≈ 0.

In the above case, the connection of the matter density ϱ with the important quantity Y_e, i.e., the electron to baryon ratio, and the electron (positron) chemical potential μ_e (μ_p) is written as

$\varrho Y_e=\frac{1}{{\pi }^2{N}_A}{\left(\frac{m_{e}c}{\hslash }\right)}^3{\int }_0^{\propto }\left(S_e-S_p\right)p^{2}dp(12)$

S_e (S_p) is the electron’s (positron’s) distribution function, respectively, and N_A is the well known Avogadro number. Furthermore, $p=\sqrt{w^2-1}$ represents the electron (positron) momentum, with w being the corresponding total energy (rest mass plus kinetic energy), both in units of m_ec². Eq. 12, is an important expression and may provide the Y_e for a given matter density ρ at the point in question inside the stars’ core.

6 Neutrino–Nucleus Reactions in Stellar Environment

The charged-current neutrino absorption by nucleons and nuclei and the neutral current neutrino-nucleus scattering, represented by the reactions.

${\nu }_{\ell }+\left(A,Z\right)\to {\ell }^{-}+\left(A,Z+1\right),(13)$

${\nu }_{\ell }+\left(A,Z\right)\to {\nu }_{\ell }+{\left(A,Z\right)}^{\ast }(14)$

(with ℓ = e, μ, τ), are significant semileptonic processes occurring inside stellar environment. Their cross sections and event rates are crucial and important for the description of the stars’ evolution. In general, the calculations of charged-current ν-nucleus reaction cross sections, for processes involving μ⁻ and μ⁺ (or ν_μ and ${\tilde{\nu }}_{\mu }$), require full relativistic treatment where the Dirac muon wave functions are employed (Giannaka et al., 2021). On the other hand, as in any semi-leptonic reaction, the hadronic weak current (including weak magnetism and pseudoscalar terms as well as weak form factor effects) must be accurately treated (Kosmas and Oset, 1996; Chasioti and Kosmas, 2009; Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b; Tsakstara and Kosmas, 2012). The muonic semi-leptonic processes dominate at E_ν ≥ 110 MeV and play essential role in μ⁻ production as well as in the known muonization process shortly after supernova core bounce. The impact of the various weak processes, and especially of the muonic reactions, was studied with emphasis by considering the specific conditions (with densities ρ > 10¹³g cm⁻³) encountered in proto-neutron star $\approx 0.4$ s after the core-bounce (Dzhioev et al., 2020).

Nowadays, neutrinos generated in astrophysical sources (supernova explosion, interior of Sun and Earth, etc.,) are key-role particles in studying the structure and evolution of the star’s interior, the thermonuclear reactions taking place inside star’s, neutrino-driven mechanisms of core-collapse of massive stars, etc. The relevant observations, in conjunction with theoretical and phenomenological modeling offer further insight in deepening our knowledge on the fundamental interactions and the nuclear weak responses. Original neutrino-nucleus cross sections obtained with realistic nuclear structure calculations, e.g., using the QRPA method (Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b), through the application of the convolution procedure by adapting specific spectral distributions describing supernova neutrino energy spectra, provide simulated signals of the detector responses expected to be recorded by terrestrial ν-detection experiments (Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b; Tsakstara and Kosmas, 2012).

Such convoluted cross sections, like the double-differential, d²σ(ω)/dω, the single differential, dσ(ω)/dω, and the total, σ_tot, cross sections reflect the neutrino signals generated at the chosen nuclear isotopes in terrestrial detectors due to neutrinos emanating from specific ν-sources. Results like, for example, those of Refs. (Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b) demonstrate clearly the weak responses to pronounced low-spin multipoles (1⁻, 1⁺1, 2⁺, 0⁺, 2⁻, etc.,) generated by supernova neutrino spectra in a specific detector medium. They show rich responses in the energy range 20, − , 30 ≤ E_x ≤ 100, − , 120 MeV, which is relevant for low- and intermediate-energy supernova neutrinos, and also for neutral-current neutrino-nucleus scattering processes.

Moreover, reliable descriptions of the responses of various nuclear isotopes (Fe, Zn, Ge, Mo, Te, and others) provide precious information for the understanding of the isospin and spin-isospin nuclear responses for supernova physics, neutrino physics, the fundamental weak interactions, and specifically the SN dynamics and explosive neutrino-nucleosynthesis. Pursuing theoretical neutrino scattering calculations, at low and intermediate energies, is important in unraveling unknown properties of neutrinos and in understanding deeply their role in a plethora of open neutrino physics issues (Kosmas and Oset, 1996; Chasioti and Kosmas, 2009; Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b).

6.1 Neutrino Induced Nucleosynthesis

Inside the hot interior of massive stars, the neutrinos created through the various semi-leptonic processes mentioned above, may subsequently induce reactions leading to nucleo-synthesis of various (radioactive) isotopes as well as to the synthesis of new elements (Suzuki et al., 2006; Cheoun et al., 2012). As the interior of an evolved high mass star has layers (fusion shells) heavier and heavier nuclear isotopes are being synthesized as we move towards the center of the star (see Section 2) (Kolbe et al., 2003; Sieverding et al., 2018). Moreover, it is known that a set of important nuclides are produced by the neutrinos created during supernova explosions. The latter may create abundant nuclei in the outer stellar shells contributing this way to the synthesis of elements with dominant galactic abundances. Such nuclides produced in significant portion by neutrino nucleosynthesis are the: ⁷Li, ¹¹B, ¹⁵N, ¹⁹F, ¹³⁸La, ¹⁸⁰Ta, and the radionuclides ²²Na and ²⁶Al (Sieverding et al., 2018).

In general, stellar neutrinos may induce nuclear reactions that contribute to the synthesis of new elements (ν-process). Several important processes of this type have been studied (Sieverding et al., 2019), as the ¹²C(ν,ν′p)¹¹B and ²⁰Ne(ν,ν′p)¹⁹F reactions which produce the quite abundant ¹⁹F and ²⁰Ne nucleides. These reactions are mainly induced by the ν_x neutrinos, with x = μ, τ, which have larger average energies than ν_e and ${\tilde{\nu }}_e$ neutrinos (Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b). Furthermore, from detailed stellar evolution investigation, researchers concluded that the rare odd-odd heavy nuclides ¹³⁸La and ¹⁸⁰Ta are mainly products of the charged-current reactions ¹³⁸Ba${({\nu }_e,e^{-})}^{138}$ La and ¹⁸⁰Hf${({\nu }_e,e^{-})}^{180}$Ta and that the ν-process is rather sensitive to the spectra and luminosity of ν_e and ν_x neutrinos (note that these neutrinos have not been observed in the SN 1987a) (Suzuki et al., 2006; Cheoun et al., 2012).

6.2 Neutrino Spectra in Core Collapse Supernovae

The energy-spectra of neutrinos emanating from core-collapse SN resembles to the two-parameter Fermi-Dirac distribution (or to the two-parameter Power-Law distribution). They are of quasi-thermal shape, on peak pattern, which seems to be reliable for most of the SN phases (Langanke and Wiescher, 2001; Tsakstara and Kosmas, 2011a; Tsakstara and Kosmas, 2011b). As has been pointed out, the neutrino shock acceleration, which may create the non-thermal shape in the neutrino spectrum occurs in the early post-bounce phase (this argument is also supported by recent CCSN simulations). The main conclusions regarding the energy-spectra of such neutrinos may be summarized as follows. The neutrino shock acceleration is strongly ν-flavour dependent, so the heavy neutrinos ν_τ and ${\tilde{\nu }}_{\tau }$ may acquire energy up to about 200 MeV, while ν_μ and ${\tilde{\nu }}_{\mu }$ have similar spectra but up to about 120 MeV where a sharp cut-off appears. The spectra for ν_e and ${\tilde{\nu }}_e$ appear to be of quasi-thermal shape.

Recent studies of the neutrino spectra in massive stars core collapse supernovae have shown that the outcome of the neutrino emission (and, in particular, its time-dependence) is a combined result of the neutrino-induced reactions and the effect of the shock wave. The competition of these two effects depends sensitively on the radial position into the star at which the nucleo-synthesis reactions occur (Sieverding et al., 2018). In the latter work, the neutrino emission from the core of a collapsing star is considered as including the three major distinguishable phases. Such a discussion here goes beyond the scope of the present article and the reader is referred to Ref. (Langanke and Wiescher, 2001) for more details.

The detection of the high energy ν_μ and ν_τ neutrinos through charged-current reactions will be a clear evidence that neutrinos undergo flavour conversions which implies that, the neutrino shock acceleration offers the possibility of muon productions in Earth detectors. If muons would be observed in these detectors, this will be a precious information to put constraints on the neutrino oscillation parameters, which will open up the need this issue to be investigated in the future (Dzhioev et al., 2020; Nagakura and Hotokezaka, 2021). We should mention that, although up to now we haven’t taken into account the neutral-current reactions of neutrinos with the detectors, in reality, they may play important role for the data analysis (Papoulias and Kosmas, 2018). Since these reactions are sensitive to all ν-flavours, by combining the NC data with those of the CC reactions, we may extract constraints on relevant transition probabilities from each heavy neutrino-flavour to the other species. We also note that, it is expected the rapid drop off of neutrino distribution at E_ν ≈ 100 − 120 MeV to be more pronounced in neutral current reactions than that of the charged current, which would be a rather direct indication for the disappearance of ν_μ and ${\tilde{\nu }}_{\mu }$ around the energy of the core-collapse SN ν-source.

From the above discussion, one may conclude that, the survival probabilities of all neutrino-flavours constitute important quantities that may be inserted in various neutrino oscillation models. We must also remark that, in measuring the quite small event rates of the above high energy neutrinos, despite the fact that the neutrino shock acceleration increases them by a few orders of magnitude, the detection statistics on each detector will be rather poor. Hence, it will be crucial to combine the observed data of each neutrino detector in order to obtain reliable analyses of the high energy ν_μ and ν_τ neutrinos. The joint analysis will enable us to look for flavour-dependent features in the core-collapse SN neutrinos and put stringent constraints on the model parameters of neutrino oscillations in the future (Dzhioev et al., 2020; Nagakura and Hotokezaka, 2021).

7 The Role of Semi-Leptonic Processes in Terrestrial Detectors

A great class of Earth detectors aiming to detect cosmic neutrinos, are based on the charge-changing neutrino-nucleus reactions (13). In the other class of terrestrial detectors, aiming to detect neutrinos through the neutral current ν-nucleus scattering (14), the measured signal is the recoil energy of the nuclear-target isotope (detector medium). We mention that, some cosmic neutrino detectors on Earth are based on the scattering of neutrinos with the electrons or muons of the detector. Before closing this article, we consider of great interest to concentrate on the heavy neutrino detection in terrestrial ν-detectors proposed very recently focusing specifically on the muon production in extremely sensitive terrestrial experiments (Dzhioev et al., 2020; Nagakura and Hotokezaka, 2021).

7.1 Muon Production in Earth Detectors

In the operating and designed to operate at the Earth neutrino detectors, like the Super-Kamiokande (SK), the Hyper-Kamiokande (HK) and others, the muons (μ⁻ or μ⁺) can be created from the supernova ν_μ and ${\tilde{\nu }}_{\mu }$ neutrinos if they carry energies larger than the muon’s rest mass M_μ, i.e., $E_{\nu }>M_{\mu }\left(E_{\nu }\right.$ should exceed M_μ by at least the detector’s threshold energy E_thresh). The detector signal may come out of charged current reactions taking place with the detector materials which are particle conjugate reactions of the muon capture on nuclei studied by many authors [see, e.g., Ref. (Giannaka and Kosmas, 2015a) and references therein]. As is well known, core-collapse SN neutrinos provide precious information to study various neutrino phenomena (neutrino properties, neutrino oscillation, etc.). The event rates on each detector, could be estimated on the bases of various scenarios of the neutrino shock acceleration, and the necessary conditions to observe a given number of events, relevant to charged-current reactions with ν_μ and ${\tilde{\nu }}_{\mu }$ in the early post-bounce phase (Nagakura and Hotokezaka, 2021). The expected number of events is small (less than 1 for all detectors), indicating that the muon production may not happen in this case. It should be noted, however, that there remains a possibility to detect them, in particular for Hyper-Kamiokande (HK) detector, by taking into account uncertainties of the parameters and the neutrino cross-sections.

Recent estimations have shown that, the possibilities for muons to be produced in terrestrial detectors, like the Super-Kamiokande (SK), HK, DUNE, JUNO etc., through core-collapse SN (CCSN) neutrino, is rather high if these neutrinos are created during the late post-bounce phase for failed CCSN (Nagakura and Hotokezaka, 2021). For example, these authors found that, about 10 muons may be produced in HK (few of them having energy E_ν ≈ 150 MeV). The muons created from such high energy neutrinos have large enough kinetic energy to produce observable signal by emitting Cherenkov lights in the HK detector. Furthermore, muon production may also occur in SK, but the detectability depends on other factors (e.g., the distance to the CCSN source is an important factor). We mention that, the charged current reaction ν −¹⁶O, with the Oxygen of the water molecule, play dominant role for the muon productions in Water Cherenkov detectors.

As mentioned above, the distance to the CCSN source is an important parameter when discussing the detectability of the heavy flavor neutrinos. For example, the muon productions in DUNE and JUNO detectors seem to be unlikely if the CCSN distance is smaller than 10 kpc. However, the efficiency of neutrino shock acceleration depends on the mass accretion rate in the late post-bounce hence, ν_μ-detectability through muon productions. Furthermore detailed studies should be made with more quantitative arguments and statistical improvements regarding neutrino cross-sections with heavy nuclear detectors (Nagakura and Hotokezaka, 2021). In the early post-bounce phase, the muon production requires that the CCSN is located nearby about 5 kpc (for HK) and about 3 kpc (for SK). For other detectors the supernova should be very nearby, about 1 kpc (for DUNE) and about 0.5 kpc (for JUNO). In the late phase for failed CCSN, on the other hand, the threshold distance is increased by a factor of about 4 than that in the early phase, indicating muon productions likely occur in HK for all Galactic failed CCSN.

8 Summary and Outlook

In this article, at first we review the role of the semi-leptonic weak interaction processes that involve leptons and nuclei in the late stages of stellar evolution, i.e., inside the hot and dense stellar environment. Then, we review the role of these processes in the relevant neutrino detection experiments that operate or have been planned to operate in the near future at the Earth (underground, under ice, and under sea water). Such processes are of key role in the massive stars’ evolution and specifically in the final stages of their life, i.e., the pre-supernova and the core-collapse supernova leading to the SN explosion phenomenon. We also focus on the neutrino producing charged-lepton capture, like the electron-capture and the muon-capture on nuclei, and, then, we discuss the neutrino absorbing reactions which are essential in the neutrino-driven explosive nucleo-synthesis. These processes are also significant in many ongoing and planned worldwide sensitive experiments aiming to detect astrophysical neutrinos which rely on the interactions of neutrinos with the bound nucleons inside atomic nuclei.

Such astrophysical neutrino signals provide a precious information on deciphering the inner dynamics of CCSN, from which researchers may extract important constraints on the neutrino oscillation parameters. In core-collapse supernova, the key-particle players are the heavy neutrinos, ν_μ with energies above 110 MeV and ν_τ neutrinos with energies up to about $\approx 200$ MeV (in water Cherencov detectors). The neutrino energy, as suggested recently, is acquired through the known shock acceleration mechanism. Researches estimated that this effect occurs in the early post-bounce phase (about 50 ms after bounce) for all massive stellar collapse experiencing core bounce and would reoccur in the late phase (about 100 ms after bounce) for failed core-collapse supernovae. Due to the fact that the SN distance is crucial for the detectability of Galactic core-collapse SN, the event rate is not far from the sensitivity of operating detectors like the Hyper-Kamiokande, the Super-Kamiokande, the DUNE, and the JUNO, which offers new possibilities to detect high energy neutrinos by terrestrial detectors.

Author Contributions

Software, writing–original draft preparation and visualization (OK), software, project administration and writing–original draft preparation (IT), conceptualization, methodology, supervision, project administration and funding acquisition (TK), writing–original draft preparation and formal analysis (PG).

Funding

This research is co-financed by Greece and the European Union (European Social Fund-ESF) through the Operational Programme “Human Resources Development, Education and Lifelong Learning 2014–2020” in the context of the project MIS-5047635. This review article was supported by the Special Account for Research Funds (Research Committee) of the University of Ioannina. OK acknowledges gratefully the support of the Engineering and Physical Sciences Research Council (EPSRC), UK, via grand EP/N026136/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akimov, D., Albert, J. B., An, P., Awe, C., Barbeau, P. S., Becker, B., et al. (2017). Observation of Coherent Elastic Neutrino-Nucleus Scattering. Science. 357, 1123–1126. doi:10.1126/science.aao0990

PubMed Abstract | CrossRef Full Text | Google Scholar

Aste, A., and Jourdan, J. (2004). Improved Effective Momentum Approximation for Quasielastic ( e , e ′) Scattering off Highly Charged Nuclei. Europhys. Lett. 67, 753–759. doi:10.1209/epl/i2004-10113-x

CrossRef Full Text | Google Scholar

Balasi, K. G., Langanke, K., and Martínez-Pinedo, G. (2015). Neutrino-Nucleus Reactions and Their Role for Supernova Dynamics and Nucleosynthesis. Prog. Part. Nucl. Phys. 85, 33–81. doi:10.1016/j.ppnp.2015.08.001

CrossRef Full Text | Google Scholar

Bethe, H. A. (1990). Supernova Mechanisms. Rev. Mod. Phys. 62, 801–866. doi:10.1103/RevModPhys.62.801

CrossRef Full Text | Google Scholar

Bollig, R., Janka, H.-T., Lohs, A., Martínez-Pinedo, G., Horowitz, C. J., and Melson, T. (2017). Muon Creation in Supernova Matter Facilitates Neutrino-Driven Explosions. Phys. Rev. Lett. 119, 242702. doi:10.1103/PhysRevLett.119.242702

PubMed Abstract | CrossRef Full Text | Google Scholar

Cantiello, M., Jermyn, A. S., and Lin, D. N. C. (2021). Stellar Evolution in AGN Disks. ApJ. 910, 94. doi:10.3847/1538-4357/abdf4f

CrossRef Full Text | Google Scholar

Chasioti, V. C., and Kosmas, T. S. (2009). A Unified Formalism for the Basic Nuclear Matrix Elements in Semi-Leptonic Processes. Nucl. Phys. A. 829, 234–252. doi:10.1016/j.nuclphysa.2009.08.009

CrossRef Full Text | Google Scholar

Cheoun, M.-K., Ha, E., Hayakawa, T., Chiba, S., Nakamura, K., Kajino, T., et al. (2012). Neutrino Induced Reactions Forν-Process Nucleosynthesis of92Nb and98Tc. Phys. Rev. C. 85, 065807. doi:10.1103/PhysRevC.85.065807

CrossRef Full Text | Google Scholar

Cook, S., D’Arcy, R., Edmonds, A., Fukuda, M., Hatanaka, K., Hino, Y., et al. (2017). Delivering the World's Most Intense Muon Beam. Phys. Rev. Accel. Beams. 20, 030101. doi:10.1103/PhysRevAccelBeams.20.030101

CrossRef Full Text | Google Scholar

De Vries, H., De Jager, C. W., and De Vries, C. (1987). Nuclear Charge-Density-Distribution Parameters From Elastic Electron Scattering. At. Data Nucl. Data Tables. 36, 495–536. doi:10.1016/0092-640x(87)90013-1

CrossRef Full Text | Google Scholar

Dean, D. J., Langanke, K., Chatterjee, L., Radha, P. B., and Strayer, M. R. (1998). Electron Capture on Iron Group Nuclei. Phys. Rev. C. 58, 536–544. doi:10.1103/PhysRevC.58.536

CrossRef Full Text | Google Scholar

Donnelly, T. W., and Peccei, R. D. (1979). Neutral Current Effects in Nuclei. Phys. Rep. 50, 1–85. doi:10.1016/0370-1573(79)90010-3

CrossRef Full Text | Google Scholar

Donnelly, T. W., and Walecka, J. D. (1976). Semi-Leptonic Weak and Electromagnetic Interactions With Nuclei: Isoelastic Processes. Nucl. Phys. A. 274, 368–412. doi:10.1016/0375-9474(76)90209-8

CrossRef Full Text | Google Scholar

Dzhioev, A. A., Langanke, K., Martínez-Pinedo, G., Vdovin, A. I., and Stoyanov, C. (2020). Unblocking of Stellar Electron Capture for Neutron-Rich N=50 Nuclei at Finite Temperature. Phys. Rev. C. 101, 025805. doi:10.1103/PhysRevC.101.025805

CrossRef Full Text | Google Scholar

Ejiri, H. (2019). Nuclear Matrix Elements for β and ββ Decays and Quenching of the Weak Coupling gA in QRPA. Front. Phys. 7, 30. doi:10.3389/fphy.2019.00030

CrossRef Full Text | Google Scholar

Ejiri, H., Suhonen, J., and Zuber, K. (2019). Neutrino-Nuclear Responses for Astro-Neutrinos, Single Beta Decays and Double Beta Decays. Phys. Rep. 797, 1–102. doi:10.1016/j.physrep.2018.12.001

CrossRef Full Text | Google Scholar

Eramzhyan, R. A., Kuz'min, V. A., and Tetereva, T. V. (1998). Calculations of Ordinary and Radiative Muon Capture on 58,60,62Ni. Nucl. Phys. A. 642, 428–448. doi:10.1016/S0375-9474(98)00541-7

CrossRef Full Text | Google Scholar

Fantina, A. F., Khan, E., Colò, G., Paar, N., and Vretenar, D. (2012). Stellar Electron-Capture Rates on Nuclei Based on a Microscopic Skyrme Functional. Phys. Rev. C. 86, 035805. doi:10.1103/PhysRevC.86.035805

CrossRef Full Text | Google Scholar

Fischer, T., Guo, G., Martínez-Pinedo, G., Liebendörfer, M., and Mezzacappa, A. (2020). Muonization of Supernova Matter. Phys. Rev. D. 102, 123001. doi:10.1103/PhysRevD.102.123001

CrossRef Full Text | Google Scholar

Fuller, G. M., Fowler, W. A., and Newman, M. J. (1982). Stellar Weak Interaction Rates for Intermediate-Mass Nuclei. II - A = 21 to A = 60. ApJ. 252, 715–740. doi:10.1086/159597

CrossRef Full Text | Google Scholar

Gastaldo, L., Blaum, K., Chrysalidis, K., Day Goodacre, T., Domula, A., Door, M., et al. (2017). The Electron Capture in 163Ho Experiment - ECHo. Eur. Phys. J. Spec. Top. 226, 1623–1694. doi:10.1140/epjst/e2017-70071-y

CrossRef Full Text | Google Scholar

Giannaka, P. G., Kosmas, O., Tsoulos, I., and Kosmas, T. S. (2021). Exploiting Dirac Equations Solution for Exact Integral Calculations in Processes of Muonic Atoms. J. Phys. Conf. Ser. 1730, 012140. doi:10.1088/1742-6596/1730/1/012140

CrossRef Full Text | Google Scholar

Giannaka, P. G., and Kosmas, T. S. (2015a). Detailed Description of Exclusive Muon Capture Rates Using Realistic Two-Body Forces. Phys. Rev. C. 92, 014606. doi:10.1103/PhysRevC.92.014606

CrossRef Full Text | Google Scholar

Giannaka, P. G., and Kosmas, T. S. (2015b). Electron Capture Cross Sections for Stellar Nucleosynthesis. Adv. High Energ. Phys. 2015, 1–11. doi:10.1155/2015/398796

CrossRef Full Text | Google Scholar

Giannaka, P. G., and Kosmas, T. S. (2013). Electron-capture and its Role to Explosive Neutrino-Nucleosynthesis. J. Phys. Conf. Ser. 410, 012124. doi:10.1088/1742-6596/410/1/012124

CrossRef Full Text | Google Scholar

Giannaka, P. (2015). Stellar and Explosive Nucleosynthesis Producing and Induced by Neutrinos. Ioannina: Ioannina University Press. doi:10.12681/eadd/39690

CrossRef Full Text | Google Scholar

Hashim, I. H., and Ejiri, H. (2021). Ordinary Muon Capture for Double Beta Decay and Anti-Neutrino Nuclear Responses. Front. Astron. Space Sci. 8, 82. doi:10.3389/fspas.2021.666383

CrossRef Full Text | Google Scholar

Hashim, I. H., Ejiri, H., Shima, T., Takahisa, K., Sato, A., Kuno, Y., et al. (2018). Muon Capture Reaction on Mo100 to Study the Nuclear Response for Double- β Decay and Neutrinos of Astrophysics Origin. Phys. Rev. C. 97, 014617. doi:10.1103/PhysRevC.97.014617

CrossRef Full Text | Google Scholar

Häusser, O., Vetterli, M. C., Fergerson, R. W., Glashausser, C., Jeppesen, R. G., Smith, R. D., et al. (1991). Nuclear Response in theFe54(p→,p→') Reaction at 290 MeV. Phys. Rev. C. 43, 230–249. doi:10.1103/physrevc.43.230

CrossRef Full Text | Google Scholar

Hirschi, R., Meynet, G., and Maeder, A. (2004). Stellar Evolution With Rotation. A&A. 425, 649–670. doi:10.1051/0004-6361:20041095

CrossRef Full Text | Google Scholar

Hix, W. R., Messer, O. E. B., Mezzacappa, A., Liebendörfer, M., Sampaio, J., Langanke, K., et al. (2003). Consequences of Nuclear Electron Capture in Core Collapse Supernovae. Phys. Rev. Lett. 91, 201102. doi:10.1103/PhysRevLett.91.201102

PubMed Abstract | CrossRef Full Text | Google Scholar

Jokiniemi, L., Suhonen, J., Ejiri, H., and Hashim, I. H. (2019). Pinning Down the Strength Function for Ordinary Muon Capture on 100mo. Phys. Lett. B. 794, 143–147. doi:10.1016/j.physletb.2019.05.037

CrossRef Full Text | Google Scholar

Jokiniemi, L., Suhonen, J., and Kotila, J. (2021). Comparative Analysis of Nuclear Matrix Elements of 0νβ+β+ Decay and Muon Capture in 106Cd. Front. Phys. 9, 142. doi:10.3389/fphy.2021.652536

CrossRef Full Text | Google Scholar

Jones, S., Röpke, F. K., Pakmor, R., Seitenzahl, I. R., Ohlmann, S. T., and Edelmann, P. V. F. (2016). Do electron-Capture Supernovae Make Neutron Stars? A&A. 593, A72. doi:10.1051/0004-6361/201628321

CrossRef Full Text | Google Scholar

Juodagalvis, A., Langanke, K., Martínez-Pinedo, G., Hix, W. R., Dean, D. J., and Sampaio, J. M. (2005). Neutral-Current Neutrino-Nucleus Cross Sections for Nuclei. Nucl. Phys. A. 747, 87–108. doi:10.1016/j.nuclphysa.2004.09.005

CrossRef Full Text | Google Scholar

Kajino, T., Mathews, G. J., and Hayakawa, T. (2014). Neutrinos in Core-Collapse Supernovae and Nucleosynthesis. J. Phys. G: Nucl. Part. Phys. 41, 044007. doi:10.1088/0954-3899/41/4/044007

CrossRef Full Text | Google Scholar

Kolbe, E., Langanke, K., Martínez-Pinedo, G., and Vogel, P. (2003). Neutrino-Nucleus Reactions and Nuclear Structure. J. Phys. G: Nucl. Part. Phys. 29, 2569–2596. doi:10.1088/0954-3899/29/11/010

CrossRef Full Text | Google Scholar

Kolbe, E., Langanke, K., and Vogel, P. (1997). Comparison of Continuum Random Phase Approximation and the Elementary Particle Model for the Inclusive Muon Neutrino Reaction on 12C. Nucl. Phys. A. 613, 382–396. doi:10.1016/S0375-9474(96)00417-4

CrossRef Full Text | Google Scholar

Kolbe, E., Langanke, K., and Vogel, P. (2000). Muon Capture on Nuclei WithN>Z,random Phase Approximation, and In-Medium Value of the Axial-Vector Coupling Constant. Phys. Rev. C. 62, 055502. doi:10.1103/PhysRevC.62.055502

CrossRef Full Text | Google Scholar

Kosmas, O., and Leyendecker, S. (2015). Family of Higher Order Exponential Variational Integrators for Split Potential Systems. J. Phys. Conf. Ser. 574, 012002. doi:10.1088/1742-6596/574/1/012002

CrossRef Full Text | Google Scholar

Kosmas, O., and Leyendecker, S. (2018). Variational Integrators for Orbital Problems Using Frequency Estimation. Adv. Comput. Math. 45, 1–21. doi:10.1007/s10444-018-9603-y

CrossRef Full Text | Google Scholar

Kosmas, O. T., and Vlachos, D. S. (2010). Phase-Fitted Discrete Lagrangian Integrators. Computer Phys. Commun. 181, 562–568. doi:10.1016/j.cpc.2009.11.005

CrossRef Full Text | Google Scholar

Kosmas, O. T., and Vlachos, D. S. (2012). Simulated Annealing for Optimal Ship Routing. Comput. Operations Res. 39, 576–581. doi:10.1016/j.cor.2011.05.010

CrossRef Full Text | Google Scholar

Kosmas, O., and Vlachos, D. S. (2016). A Space-Time Geodesic Approach for Phase Fitted Variational Integrators. J. Phys. Conf. Ser. 738, 012133. doi:10.1088/1742-6596/738/1/012133

CrossRef Full Text | Google Scholar

Kosmas, T., Faessler, A., Šimkovic, F., and Vergados, J. (1997a). State-by-State Calculations for All Channels of the Exotic (μ-,e-) Conversion Process. Phys. Rev. C. 56, 526–534. doi:10.1103/physrevc.56.526

CrossRef Full Text | Google Scholar

Kosmas, T. S., Faessler, A., and Vergados, J. D. (1997b). The New Limits of the Neutrinoless , Conversion Branching Ratio. J. Phys. G: Nucl. Part. Phys. 23, 693–703. doi:10.1088/0954-3899/23/6/008

CrossRef Full Text | Google Scholar

Kosmas, T. S., Kovalenko, S., and Schmidt, I. (2001). B-Quark Mediated Neutrinoless μ−-e− Conversion in Presence of R-Parity Violation. Phys. Lett. B. 519, 78–82. doi:10.1016/s0370-2693(01)01096-6

CrossRef Full Text | Google Scholar

Kosmas, T. S., and Lagaris, I. E. (2002). On the Muon Nucleus Integrals Entering the Neutrinoless e Conversion Rates. J. Phys. G: Nucl. Part. Phys. 28, 2907–2920. doi:10.1088/0954-3899/28/12/302

CrossRef Full Text | Google Scholar

Kosmas, T. S., and Oset, E. (1996). Charged Current Neutrino-Nucleus Reaction Cross Sections at Intermediate Energies. Phys. Rev. C. 53, 1409–1415. doi:10.1103/PhysRevC.53.1409

PubMed Abstract | CrossRef Full Text | Google Scholar

Kosmas, T. S., Vergados, J. D., Civitarese, O., and Faessler, A. (1994). Study of the Muon Number Violating (μ−, e− Conversion in a Nucleus by Using Quasi-Particle RPA. Nucl. Phys. A. 570, 637–656. doi:10.1016/0375-9474(94)90077-9

CrossRef Full Text | Google Scholar

Langanke, K., Kolbe, E., and Dean, D. J. (2001). Unblocking of the Gamow-Teller Strength in Stellar Electron Capture on Neutron-Rich Germanium Isotopes. Phys. Rev. C. 63, 032801. doi:10.1103/PhysRevC.63.032801

CrossRef Full Text | Google Scholar

Langanke, K., and Martínez-Pinedo, G. (2003). Nuclear Weak-Interaction Processes in Stars. Rev. Mod. Phys. 75, 819–862. doi:10.1103/RevModPhys.75.819

CrossRef Full Text | Google Scholar

Langanke, K., Martínez-Pinedo, G., Sampaio, J. M., Dean, D. J., Hix, W. R., Messer, O. E. B., et al. (2003). Electron Capture Rates on Nuclei and Implications for Stellar Core Collapse. Phys. Rev. Lett. 90, 241102. doi:10.1103/PhysRevLett.90.241102

PubMed Abstract | CrossRef Full Text | Google Scholar

Langanke, K., and Martinez-Pinedo, G. (1998). Supernova Electron Capture Rates for 55co and 56ni. Phys. Lett. B. 436, 19–24. doi:10.1016/S0370-2693(98)00892-2

CrossRef Full Text | Google Scholar

Langanke, K., and Martínez-Pinedo, G. (1999). Supernova Electron Capture Rates on Odd-Odd Nuclei. Phys. Lett. B. 453, 187–193. doi:10.1016/S0370-2693(99)00363-9

CrossRef Full Text | Google Scholar

Langanke, K., and Martínez-Pinedo, G. (2000). Shell-model Calculations of Stellar Weak Interaction Rates: II. Weak Rates for Nuclei in the Mass Range in Supernovae Environments. Nucl. Phys. A. 673, 481–508. doi:10.1016/s0375-9474(00)00131-7

CrossRef Full Text | Google Scholar

Langanke, K., Martínez-Pinedo, G., and Zegers, R. G. T. (2021). Electron Capture in Stars. Rep. Prog. Phys. 84, 066301. doi:10.1088/1361-6633/abf207

CrossRef Full Text | Google Scholar

Langanke, K., and Wiescher, M. (2001). Nuclear Reactions and Stellar Processes. Rep. Prog. Phys. 64, 1657–1701. doi:10.1088/0034-4885/64/12/202

CrossRef Full Text | Google Scholar

Marketin, T., Paar, N., Nikšić, T., and Vretenar, D. (2009). Relativistic Quasiparticle Random-Phase Approximation Calculation of Total Muon Capture Rates. Phys. Rev. C. 79, 054323. doi:10.1103/PhysRevC.79.054323

CrossRef Full Text | Google Scholar

Nabi, J.-U. (2011). Ground and Excited States Gamow-Teller Strength Distributions of Iron Isotopes and Associated Capture Rates for Core-Collapse Simulations. Astrophys Space Sci. 331, 537–554. doi:10.1007/s10509-010-0477-9

CrossRef Full Text | Google Scholar

Nabi, J.-U., Rahman, M.-U., and Sajjad, M. (2007a). Electron and Positron Capture Rates on 55Co in Stellar Matter. Braz. J. Phys. 37, 1238–1245. doi:10.1590/s0103-97332007000800009

CrossRef Full Text | Google Scholar

Nabi, J.-U., Sajjad, M., and Rahman, G. I. K. (2007b). Electron Capture Rates on Titanium Isotopes in Stellar. Acta Physica Polonica B 38, 3203–3223. arXiv: [nucl-th] 1108.053.

Google Scholar

Nabi, J.-U., and Riaz, M. (2019). Electron Capture Cross Sections and Nuclear Partition Functions for Fp-Shell Nuclei. J. Phys. G: Nucl. Part. Phys. 46, 085201. doi:10.1088/1361-6471/ab2347

CrossRef Full Text | Google Scholar

Nagakura, H., and Hotokezaka, K. (2021). Non-Thermal Neutrinos Created by Shock Acceleration in Successful and Failed Core-Collapse Supernova. Monthly Notices R. Astronomical Soc. 502, 89–107. doi:10.1093/mnras/stab040

CrossRef Full Text | Google Scholar

Niu, Y. F., Paar, N., Vretenar, D., and Meng, J. (2011). Stellar Electron-Capture Rates Calculated With the Finite-Temperature Relativistic Random-Phase Approximation. Phys. Rev. C. 83, 045807. doi:10.1103/PhysRevC.83.045807

CrossRef Full Text | Google Scholar

O'Connell, J. S., Donnelly, T. W., and Walecka, J. D. (1972). Semileptonic Weak Interactions With C12. Phys. Rev. C. 6, 719–733. doi:10.1103/physrevc.6.719

CrossRef Full Text | Google Scholar

Oda, T., Hino, M., Muto, K., Takahara, M., and Sato, K. (1994). Rate Tables for the Weak Processes of Sd-Shell Nuclei in Stellar Matter. At. Data Nucl. Data Tables. 56, 231–403. doi:10.1006/adnd.1994.1007

CrossRef Full Text | Google Scholar

Paar, N., Colò, G., Khan, E., and Vretenar, D. (2009). Calculation of Stellar Electron-Capture Cross Sections on Nuclei Based on Microscopic Skyrme Functionals. Phys. Rev. C. 80, 055801. doi:10.1103/PhysRevC.80.055801

CrossRef Full Text | Google Scholar

Papoulias, D. K., and Kosmas, T. S. (2018). COHERENT Constraints to Conventional and Exotic Neutrino Physics. Phys. Rev. D. 97, 033003. doi:10.1103/PhysRevD.97.033003

CrossRef Full Text | Google Scholar

Papoulias, D. K., Kosmas, T. S., and Kuno, Y. (2019). Recent Probes of Standard and Non-Standard Neutrino Physics With Nuclei. Front. Phys. 7, 191. doi:10.3389/fphy.2019.00191

CrossRef Full Text | Google Scholar

Papoulias, D. K., Kosmas, T. S., Sahu, R., Kota, V. K. B., and Hota, M. (2020). Constraining Nuclear Physics Parameters With Current and Future COHERENT Data. Phys. Lett. B. 800, 135133. doi:10.1016/j.physletb.2019.135133

CrossRef Full Text | Google Scholar

Phillips, A. C. (2013). The Physics of Stars. John Wiley & Sons.

Google Scholar

Sarriguren, P., Moya de Guerra, E., and Escuderos, A. (2001). βdecay in Odd-Aand Even-Even Proton-Rich Kr Isotopes. Phys. Rev. C. 64, 064306. doi:10.1103/PhysRevC.64.064306

CrossRef Full Text | Google Scholar

Sieverding, A., Huther, L., Martínez-Pinedo, G., Langanke, K., and Heger, A. (2018). Neutrino Nucleosynthesis in Core-Collapse Supernova Explosions. J. Phys. Conf. Ser. 940, 012054. doi:10.1088/1742-6596/940/1/012054

CrossRef Full Text | Google Scholar

Sieverding, A., Langanke, K., Martínez-Pinedo, G., Bollig, R., Janka, H.-T., and Heger, A. (2019). The ν-Process With Fully Time-Dependent Supernova Neutrino Emission Spectra. ApJ. 876, 151. doi:10.3847/1538-4357/ab17e2

CrossRef Full Text | Google Scholar

Suzuki, T., Chiba, S., Yoshida, T., Kajino, T., and Otsuka, T. (2006). Neutrino-Nucleus Reactions Based on New Shell Model Hamiltonians. Phys. Rev. C. 74, 034307. doi:10.1103/PhysRevC.74.034307

CrossRef Full Text | Google Scholar

Suzuki, T., Chiba, S., Yoshida, T., Takahashi, K., and Umeda, H. (2018). Neutrino-Nucleus Reactions on O16 Based on New Shell-Model Hamiltonians. Phys. Rev. C. 98, 034613. doi:10.1103/PhysRevC.98.034613

CrossRef Full Text | Google Scholar

Suzuki, T., Honma, M., Mao, H., Otsuka, T., and Kajino, T. (2011). Evaluation of Electron Capture Reaction Rates in Ni Isotopes in Stellar Environments. Phys. Rev. C. 83, 044619. doi:10.1103/PhysRevC.83.044619

CrossRef Full Text | Google Scholar

Suzuki, T., and Kajino, T. (2013). Element Synthesis in the Supernova Environment and Neutrino Oscillations. J. Phys. G: Nucl. Part. Phys. 40, 083101. doi:10.1088/0954-3899/40/8/083101

CrossRef Full Text | Google Scholar

Titus, R., Sullivan, C., Zegers, R. G. T., Brown, B. A., and Gao, B. (2017). Impact of Electron-Captures on Nuclei nearN= 50 on Core-Collapse Supernovae. J. Phys. G: Nucl. Part. Phys. 45, 014004. doi:10.1088/1361-6471/aa98c1

CrossRef Full Text | Google Scholar

Tsakstara, V., and Kosmas, T. S. (2011a). Analyzing Astrophysical Neutrino Signals Using Realistic Nuclear Structure Calculations and the Convolution Procedure. Phys. Rev. C. 84, 064620. doi:10.1103/PhysRevC.84.064620

CrossRef Full Text | Google Scholar

Tsakstara, V., and Kosmas, T. S. (2011b). Low-energy Neutral-Current Neutrino Scattering onTe128,130isotopes. Phys. Rev. C. 83, 054612. doi:10.1103/PhysRevC.83.054612

CrossRef Full Text | Google Scholar

Tsakstara, V., and Kosmas, T. S. (2012). Nuclear Responses of64,66Zn Isotopes to Supernova Neutrinos. Phys. Rev. C. 86, 044618. doi:10.1103/PhysRevC.86.044618

CrossRef Full Text | Google Scholar

Tsoulos, I. G., Kosmas, O. T., and Stavrou, V. N. (2019). Diracsolver: A Tool for Solving the Dirac Equation. Computer Phys. Commun. 236, 237–243. doi:10.1016/j.cpc.2018.10.010

CrossRef Full Text | Google Scholar

Wildenthal, B. H. (1984). Empirical Strengths of Spin Operators in Nuclei. Prog. Part. Nucl. Phys. 11, 5–51. doi:10.1016/0146-6410(84)90011-5

CrossRef Full Text | Google Scholar

Woosley, S. E., Heger, A., and Weaver, T. A. (2002). The Evolution and Explosion of Massive Stars. Rev. Mod. Phys. 74, 1015–1071. doi:10.1103/RevModPhys.74.1015

CrossRef Full Text | Google Scholar

Woosley, S. E. (2019). The Evolution of Massive Helium Stars, Including Mass Loss. ApJ. 878, 49. doi:10.3847/1538-4357/ab1b41

CrossRef Full Text | Google Scholar

Zinner, N. T., Langanke, K., and Vogel, P. (2006). Muon Capture on Nuclei: Random Phase Approximation Evaluation Versus Data for6⩽Z⩽94nuclei. Phys. Rev. C. 74, 024326. doi:10.1103/PhysRevC.74.024326

CrossRef Full Text | Google Scholar