
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci., 04 October 2021
Sec. Space Physics
Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.745927
This article is part of the Research TopicCoupled Feedback Mechanisms in the Magnetosphere-Ionosphere SystemView all 25 articles
 Lunjin Chen1*
Lunjin Chen1* Xiao-Jia Zhang2
Xiao-Jia Zhang2 Anton Artemyev2,3
Anton Artemyev2,3 Liheng Zheng1
Liheng Zheng1 Zhiyang Xia1
Zhiyang Xia1 Aaron W. Breneman4
Aaron W. Breneman4 Richard B. Horne5
Richard B. Horne5Microbursts, short-lived but intense electron precipitation observed by low-Earth-orbiting satellites, may contribute significantly to the losses of energetic electrons in the outer radiation belt. Their origin is likely due to whistler mode chorus waves, as evidenced by a strong overlap in spatial correlation of the two. Despite previous efforts on modeling bursty electron precipitation induced by chorus waves, most, if not all, rely on the assumption that chorus waves are ducted along the field line with zero wave normal angle. Such ducting is limited to cases when fine-scale plasma density irregularities are present. In contrast, chorus waves propagate in a nonducted way in plasmas with smoothly varying density, allowing wave normals to gradually refract away from the magnetic field line. In this study, the interaction of ducted and nonducted chorus waves with energetic electrons is investigated using test particle simulation. Substantial differences in electron transport are found between the two different scenarios, and resultant electron precipitation patterns are compared. Such a comparison is valuable for interpreting low Earth-orbiting satellite observations of electron flux variation in response to the interaction with magnetospheric chorus waves.
Microbursts are impulsive (typically lasting a few tenths of a second) precipitation of energetic electrons (∼30 keV to >1 MeV) from the magnetosphere into the atmosphere. They have been detected indirectly through X-ray counts on balloons (e.g., Anderson and Milton, 1964; Parks et al., 1979; Millan, 2011), and directly through particle detectors onboard rockets (e.g., Lampton, 1967) and low-Earth-orbiting satellites (e.g., Imhof et al., 1992; Douma et al., 2017). Their existence at <100 keV energies has been known for decades, and at higher energies is known only relatively recently. It has been suggested that microburst precipitation into the upper atmosphere may play an important role in radiation belt electron losses (Lorentzen et al., 2001; O’Brien et al., 2004; Millan and Thorne, 2007; Breneman et al., 2017). Recently, bouncing packets in an apparent form of microbursts have been reported by Shumko et al. (2018), suggesting a mixture of precipitating and trapped fluxes in the observation of microbursts (Chen et al., 2020). Blake and O’Brien (2016) discovered that microbursts might not just be temporal bursts of precipitation but may sometimes be very narrow curtain structures of precipitation.
Whistler-mode chorus waves in the Earth’s magnetosphere have received great attention because of their dual role in energizing electrons and precipitating them into the lower atmosphere (Horne et al., 2003; Katoh and Omura, 2007; Ni et al., 2011; Reeves et al., 2013; Thorne et al., 2013). Whistler mode waves originate around the magnetic equator, often with nearly field-aligned propagation (e.g., LeDocq et al., 1998; Lauben et al., 2002; Santolík et al., 2005; Li et al., 2009) and they are excited by energetic electrons with anisotropic velocity distribution injected from the magnetotail (e.g., Kennel and Petschek, 1966; Tsurutani and Smith, 1974). Chorus waves often exhibit unique time-frequency spectrograms consisting of discrete rising (or sometimes falling) tones (e.g., Burtis and Helliwell, 1969; Burton and Holzer, 1974; Li et al., 2011a). Numerical theory and simulation studies have demonstrated that nonlinear resonant interactions with a coherent whistler mode wave leads to electron phase trapping, resulting in wave frequency chirping when the background magnetic field is inhomogeneous (Omura and Matsumoto, 1982; Nunn et al., 1997; Katoh and Omura, 2006; Omura and Summers, 2006; Omura et al., 2009; Tao, 2014; Gao et al., 2016). Chorus waves typically occur in the frequency range 0.1–0.8 fce (fce is the equatorial electron cyclotron frequency), often separated into distinct lower and upper bands with a wave power gap near fce/2 (e.g., Tsurutani and Smith, 1974; Li et al., 2016a). Statistically, the duration of individual chorus element spectra varies from 0.1 to 1 s, with peak occurrence at ∼0.4 s at dayside and ∼0.12 s at nightside (Teng et al., 2017). The spatial scales of individual chorus waves have been unavailable until recently when wave measurements over multiple nearby satellites are present. The estimate of the transverse spatial scale, based on individual event studies, ranges from 7–100 km at L ∼4.5 (Santolík and Gurnett, 2003), ∼500 km at L ∼ 4.7 (Shumko et al., 2018), 600–800 km at L ∼ 6 (Agapitov et al., 2017), to ∼3,000 km in the outer magnetosphere (L ∼ 10) (Agapitov et al., 2010). The statistical analysis based on 11-years THEMIS wave measurement shows the transverse scale is mostly in the range of ∼250–800 km over 2 < L < 10 (Agapitov O. et al., 2018), which is consistent with Shen et al. (2019) results from Van Allen Probes and THEMIS, where the averaged transverse size is ∼315 km over 5 < L < 6. These new observational features more thoroughly characterize the temporal and spatial scales of these individual elements, allowing for better modeling of the interaction of chorus waves with energetic electrons.
Whistler-mode chorus waves in the Earth’s magnetosphere are suggested to be the primary drivers of relativistic microbursts, creating them by resonant scattering into the loss cone. This association comes from numerous observational and theoretical studies that focus on spatial (L, MLT) (Oliven and Gurnett, 1968; Lam et al., 2010) and temporal similarities (e.g., Lorentzen et al., 2001; Kersten et al., 2011), as well as plausibility of scattering mechanism (to name a few, Chang and Inan, 1983; Rosenberg et al., 1990; Saito et al., 2012; Chen et al., 2020). Statistically, whistler-mode chorus waves are a potential driver of relativistic microbursts (Douma et al., 2017) and the majority of microbursts are shown to have sizes consistent with the sizes of chorus waves (Shumko et al., 2020). Previous simulation with self-consistent chorus waves (Hikishima et al., 2010) has demonstrated a one-to-one correspondence between microbursts of precipitating electrons and chorus elements. Due to finite transverse scale, individual chorus element will illuminate an area of electron precipitation in the lower atmosphere. Statistically, electron microburst size distribution ranges from 2 to 100 km (Shumko et al., 2020), which is consistent with the size estimate for individual microbursts (Blake et al., 1996; Crew et al., 2016; Shumko et al., 2018), and most occurrences are over a few tens of km, which is about 200 km in size when mapped to the magnetic equator. Such size is comparable to the size of chorus wave packets mentioned above.
The most intense chorus waves are typically confined to within 10–20° of their source near the magnetic equator (e.g., Meredith et al., 2012; Agapitov et al., 2013), while relativistic microbursts (>100 keV) are observed at much higher latitudes (Breneman et al., 2017). Therefore, chorus wave properties at higher latitudes are critically important for modeling microbursts. Depending on wave propagation, the chorus wave intensity off the equator will differ. In the presence of fine-scale density irregularities, chorus waves can be ducted along the field line, with much less attenuated wave intensity away from the equator when compared with the nonducted case in a medium with smoothly varying plasma density. A schematic picture of ducted and nonducted propagation is shown in Figure 1. There exists a number of studies on microburst modeling due to the ducted waves (e.g., Hikishima et al., 2010; Saito et al., 2012; Chen et al., 2020), while few focus on the case of nonducted chorus waves. Colpitts et al. (2020) recently showed the first direct observations of individual chorus elements propagating from the equatorial source to higher latitudes, and confirmed with ray tracing that the waves propagated in the nonducted mode. As nonducted chorus waves propagate away from the equator, three important physical processes occur when compared with ducted waves. First, waves experience refraction in the inhomogeneous magnetosphere with wave normal becoming increasingly oblique along the propagation path (e.g., Chen et al., 2013a; Lu et al., 2019; Colpitts et al., 2020). Therefore, oblique whistler-mode mode waves propagate not only along, but also across magnetic field lines. This means that chorus waves at a given field line at high latitude may originate from a different field line at the equator, and thus chorus wave modeling requires the knowledge of their transverse sizes at the equator. Unlike ducted chorus waves, nonducted chorus waves may induce electron precipitation over a broader range of field lines than the range at the equator. Second, chorus waves experience Landau damping as their wave normal angles increase, which will limit the wave intensity at middle latitudes, and high latitudes if accessible (e.g., Chen et al., 2013b; Watt et al., 2013; Colpitts et al., 2020). Third, multiple-harmonics resonances (whose resonance condition is ω−kzvz = nΩ/γ with n being an integer) become effective, when waves becomes oblique and field polarization becomes elliptical (instead of circular), while only the principal resonance (n = −1) is effective for ducted waves. Here ω and kz are wave angular frequency and parallel component of the wavenumber vector respectively, vz, Ω and γ are electron parallel velocity, non-relativistic gyrofrequency and Lorentz factor respectively. Thus for northward propagation (as shown in Figure 1), nonducted chorus waves could induce electron precipitation in the northern hemisphere (through the resonances with, e.g., n = 0 and +1) and the southern hemisphere (through the resonance with n = −1) while ducted chorus waves could only induce precipitation in the southern hemisphere (through the resonance with n = −1). The three physics processes are important for modeling relativistic microbursts due to nonducted chorus waves with oblique wave normal angles (e.g., Artemyev et al., 2016).
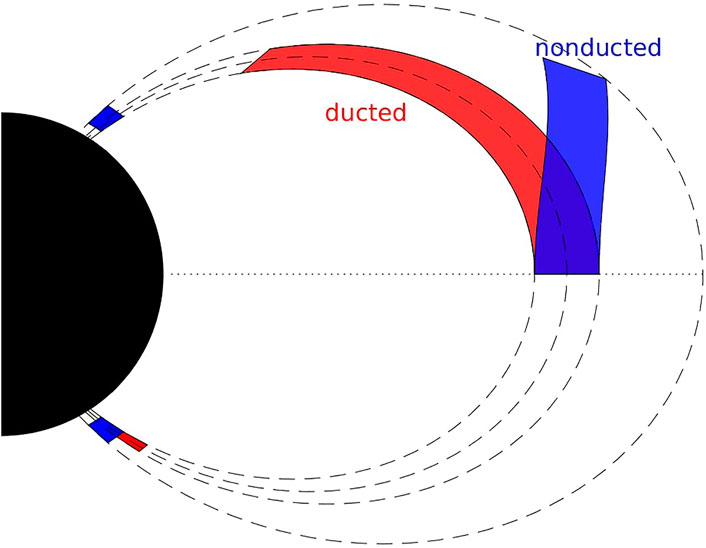
FIGURE 1. Schematic illumination regions of electron precipitation due to interaction with ducted (shaded by red color) and nonducted (shaded by blue color) chorus waves that propagate northward. Dashed lines denotes the dipole magnetic field lines. The schematic diagram is not scaled. Ducted chorus waves here only induce electron precipitation in the southern hemisphere while nonducted chorus waves induce electron precipitation in both hemispheres.
In this study, a nonducted chorus wave model is developed as an extension of the ducted chorus wave model (Chen et al., 2020). We will look into the characteristics of electron precipitation due to a nonducted chorus element seen by virtual LEO satellites, which will be compared with that due to a ducted chorus element. In addition to temporal structures, spatial structures of microburst due to the nonducted chorus element will be revealed.
The dynamics of electrons in a dipole magnetic field with prescribed chorus wave fields is modeled by the following test particle equations along a dipole field line with a given L value (Chen et al., 2020):
where B is the background dipole magnetic field strength, nonrelativistic electron gyrofrequency
Eqs. 1–4 are integrated over a time scale of several electron bounce periods (on the order of 1 s), which is sufficient to describe the interaction between chorus waves and electron gyromotion and to model electron precipitation induced by the chorus waves. Therefore it is safe to neglect drift motion of electrons across magnetic field lines. That is, electrons are trapped by the same field line (with constant L and magnetic local time). Hereafter, we investigate the effect of a single chorus element, either ducted or nonducted, on electron dynamics, and therefore the subscript j and the summation over j will be dropped. For the equations above, gyrophase-averaging on the wave force is not performed, and nonlinear wave particle interaction is included (as the wave phase ϕ depends on z). When test particles reach the atmospheric loss boundary, which is set to an altitude of 100 km, they are considered as lost (precipitated into the upper atmosphere) and no longer traced afterward.
To solve the test particle Eqs. 1–4 and examine the effect of chorus waves, either ducted or nonducted, on the dynamics of particles at a given field line, it is necessary to find a solution of chorus wave field along that field line (that is, for a given L value in the case of dipole magnetic field). The solution should describe wave phase ϕ and wave amplitude as a function of z and t.
The derivatives of ϕ(r, t) provide definition of wave angular frequency ω and wave normal vector k through:
Given ω(r, t) and k (r, t), the two equations above can be solved for ϕ(r, t).
ϕ(r, t) can be conveniently rewritten in terms of the guiding center location rc as
where ϕ(rc, t) is the wave phase at the guiding center rc along the field line and the second term on the right denotes the wave phase variation experienced due to the test particle’s gyromotion. Oscillatory gyro-radius vector rg⊥, defined as r−rc, can be written as
Initially, test particles are launched at a given L with Ng (= 120) different gyrophases of equal spacing Δθg = 2π/Ng, Nb(= 120) bounce phases of equal spacing Δϕb = 2π/Nb, NE (=51) energies of equal logarithmic spacing Δ ln E from 50 keV to 1 MeV, and
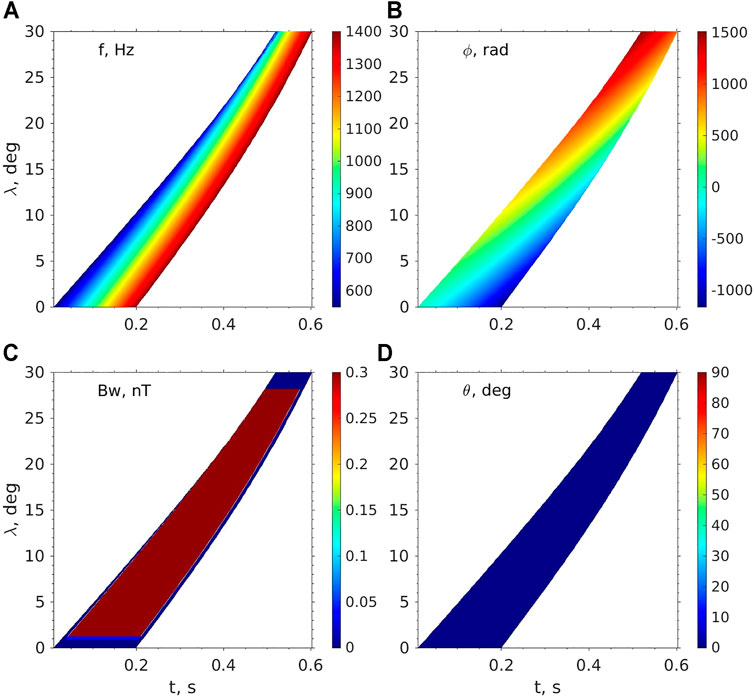
FIGURE 2. Solution of a ducted chorus element along a dipole magnetic field at L = 5.5. (A) wave frequency f(B) wave phase ϕ, (C) wave magnetic amplitude Bw, and (D) wave normal angle θ as a function of time t and magnetic latitude λ.
Ducted chorus waves are guided along a field line, say Lc, by keeping wavevector parallel or antiparallel to the field line. During ducted propagation, chorus waves follow:
where the first equation describes the constraint of parallel propagation, the second equation describes the local dispersion relation D, which adopts one for whistler mode in the cold plasma at the location z, and the third and fourth equations state the conservation of wave frequency and wave amplitude along the propagation path. The parallel component of group velocity vgz = − (∂D/∂kz)/(∂D/∂ω). These equations, assuming parallel propagation, have been widely used for chorus wave modeling (e.g., Furuya et al., 2008; Tao et al., 2012; Chen et al., 2020). For such “ideally” ducted propagation (k⊥ = 0), it is implicitly assumed that there exists a density duct with density gradients that perfectly overcome wave refraction due to magnetic field inhomogeneity. This implicit assumption places a constraint on the density gradients of the duct, whose solution, fortunately, is not required for modeling the ideally ducted propagation. For a more realistic ducted propagation (a non-ideal case, e.g., Liu et al., 2021), wave normal direction would experience oscillation near the parallel direction and so do ducted ray paths.
Let ω0(t) be the prescribed chorus wave frequency-time profile in the equatorial source region. Then the one-sided boundary condition at the equator can be provided as
For the calculation of the dispersion relation (D in Eq. 9), background plasma density is required. We adopt the modified diffusive equilibrium density model (Bortnik et al., 2011). The same initial condition ω0(t) as Chen et al. (2020) is used, with the wave frequency f rising from 550 to 1,400 Hz over an interval of 0.2 s. The solution of wave frequency and wave phase is shown in Figures 3A,B. At λ = 0, wave frequency chirps over a duration of 0.2 s, while as λ increases, the wave duration becomes shorter due to frequency dispersion. In Figure 3B, wave phase ϕ increases with λ and decreases with t, as shown by Eqs. 13, 14. The wave normal angle θ is zero, as expected (Figure 3D).
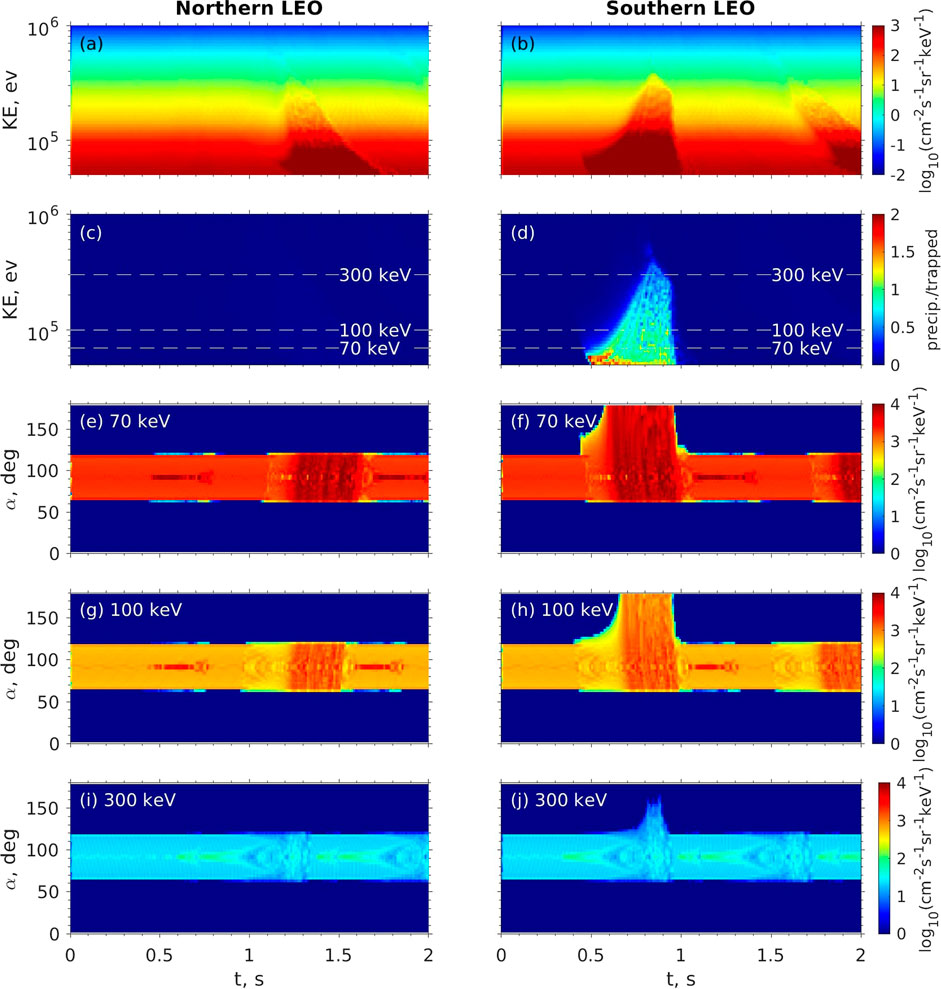
FIGURE 3. Modeled electron fluxes at virtual northern (left column) and southern (right column) LEO satellites due to the presence of the ducted wave shown in Figure 3. (A, B) omni-directional differential flux over the energy range from 50 keV to 1 MeV. (C, D) the ratio of precipitating and trapped electron fluxes over the energy range from 50 keV to 1 MeV. Local pitch angle distribution of electron fluxes at three selected electron kinetic energies (E, F) 70 keV, (G, H) 100 keV and (I, J) 300 keV. The three energies are also marked by the horizontal white dashed lines in panels c-d.
To represent a chorus element of a flexible amplitude, the initial amplitude profile is implemented as Aw0 (f, λ) = Aw,maxG ( f; f1, f2, δf1, δf2), where λ is magnetic latitude and Aw,max is the maximum wave amplitude. The function G has a Gaussian-like profile with a flat-top and four control parameters (x1, x2, δx1, δx2). Specifically, G (x; x1, x2, δx1, δx2) is defined as
Figure 3C shows the solution for the ducted chorus wave amplitude. The wave amplitude Bw is nearly constant in the z−t regime of the chorus wave field, expect the lower and higher latitude boundaries due to the introduced latitude-dependence term G (λ; λ1, λ2, δλ1, δλ2) and the lower and higher time boundaries due to the frequency-dependence term G (f; f1, f2, δf1, δf2). The introduction of the latitude-dependence term mimics the chorus growth near the equator and ensures the test particles are launched before the chorus wave field perturbation occurs, and the test particles, if not reaching the atmospheric loss boundary, are terminated after the chorus wave field perturbation ends. By doing so, the effect of chorus wave field perturbation on electron flux can be evaluated.
Figure 2 shows modeled electron distribution at two virtual LEO satellites, which are placed at northern and southern foot points of L = 5.5 at 500 km altitude. The electrons accessing these locations are reorganized to obtain the full velocity distribution as a function of t at the two locations, respectively. The distribution is then used to calculate derived quantities, such as omni-directional differential flux, precipitating flux (the averaged flux over the solid angle within the loss cone), and trapped flux (the averaged flux over the solid angle beyond the loss cone). Figures 2A,B shows the omni-directional differential flux at the two, northern and southern, LEO satellite locations. One can see flux enhancement with energy from 50 up to 400 keV. The flux enhancement first appears 0.5–1 s at the southern location (Figure 2B), then over 1.2–1.7 s at the northern location (Figure 2A), and then again near 1.7 s at the southern location (Figure 2B). Such a series have been identified previously (e.g., Chen et al., 2020) as bouncing microburst packet. The initial flux enhancement is caused by cyclotron resonance of southward moving electrons with a northward propagating chorus element, which leads to a net transport towards smaller pitch angle. To resonate with the northward propagating chorus wave, electrons must be counter-moving to the south in order to satisfy the Doppler-shifted resonance condition with n = −1. Such initial flux enhancement occurs for both precipitating flux and trapped flux near 0.5–1 s in the southern hemisphere (Figure 2D). The subsequent flux enhancements, which corresponds to enhanced trapped flux only (Figures 2C,D), is caused by bounce motions of the enhanced trapped flux in the initial flux enhancement (See more detailed explanation on electron bouncing packets in Chen et al. (2020)). The ratio of precipitating to trapped flux is only significant in the southern location during the initial enhancement. The ratio decreases for higher energy, from as high as 2 at 50 keV, near 1 at 100 keV, and to a fraction near 300 keV (Figure 2D). The ratio exceeding unity at the low energy demonstrates nondiffusive transport in pitch angle, as a signature of nonlinear wave-particle interaction (Chen et al., 2020). Figures 2E–J shows the pitch angle distribution of electron unidirectional different flux at 70 keV, 100 and 300 keV. One can see full loss cone distribution (at electron energy, e.g., 70 keV in Figure 2F and 100 keV in 3 h) when the ratio of precipitating to trapped flux is 1 and above while partial loss cone corresponds to the case with the ratio being a fraction (at electron energy, e.g., 300 keV in Figure 2J). As expected, the ratio is zero for a completely empty loss cone. The simultaneous enhancement of trapped flux and precipitating flux (Figures 2F,H,J) is caused by the induced transport from the larger αeq into the loss cone. Although short-lived, the chorus element can produce the permanent change to trapped electron distribution via bouncing packets, in addition to impulsive precipitation.
An extension is made from the ducted chorus wave case to the case allowing nonducted propagation of chorus waves across magnetic field lines. Nonducted propagation is modeled by solving the following ray tracing equations (e.g., Horne, 1989):
where D (k, ω, r) = 0 is the local dispersion relation, the right-handed side of the first equation is the general definition of the wave group velocity vg, and the fourth equation for wave amplitude Aw takes into account wave attenuation as a result of Landau damping due to the suprathermal electron population during oblique propagation. The suprathermal electron model used is based on THEMIS statistical observations of electron distribution over the energy range from ∼0.1 to 26 keV (see detail in Section 3 of Chen et al., 2013a). The ray tracing HOTRAY code (Horne, 1989) is used to calculate the nonducted propagation paths of whistler mode waves in a smoothly-varying plasma, and to evaluate the path integrated gain, which represents the relative change of wave amplitude. The ray tracing method assumes that the spatial scales of the medium, notably the plasma density and magnetic field, are large compared to the wavelength, and that their spatial gradients remain continuous. Like Section 3, the diffusive equilibrium density model (Bortnik et al., 2011) is used.
Say a ray with frequency ω0 is launched at a source location r0 and initial wave vector k0 at time t0. The ray is labeled by the set of initial parameters (ω0, t0, r0, k0), subject to two constraints. First, the launch time t0 depends on ω0 according to the prescribed chorus frequency-time profile at the source location r0. Second, the local dispersion relation is satisfied initially, D (k0, ω0, r0) = 0. The ray tracing equations are solved numerically; the solution can be obtained: ω = ω0, and symbolically r = r (t; ω0, t0, r0, k0), k = k (t; ω0, t0, r0, k0), and Aw = Aw (t; ω0, t0, r0, k0), subject to the constraint D (k, ω, r) = 0.
It should be noted that the solution of r = r (t; ω0, t0, r0, k0) provides characteristic curves (ray paths) for the following two equations for ω and Aw
The two equations are equivalent to Eqs. 17, 18, with the directive derivative
where ϕ0 = ϕ0 (t0, r0) is the initial phase at r0 and at t = t0. The solution of Aw can be written in an alternative fashion as
where Aw0 = Aw0 (t0, r0) is the initial amplitude at r0 and at t = t0.
For 3D space in r, the initial conditions Aw0 and ϕ0 over a 2D spatial area (spanned by r0) of the wave source are needed as input. For a simpler case of 2D propagation on the meridian plane at a fixed local time, the initial conditions over a 1D curve (spanned by r0) of the wave source are needed. Hereafter we will limit the nonducted propagation on a meridian plane. Let us consider a chorus element at the equator at magnetic local time (MLT) of 6 h with wave amplitude peak at a L-shell value of Lc = 5.5 and a Gaussian width of δL = 0.05 RE (corresponding to 320 km). The chosen location is consistent with the location of the microburst occurrence rate peak during geomagnetic active conditions (Douma et al., 2017) and the choice of the δL value is consistent with the mean spatial width of chorus wave elements (Shen et al., 2019). The source wave amplitude Aw0 ( f, L0) = Aw,max × G ( f; f1, f2, δf1, δf2) × G (L0; Lc, Lc, δL, δL). Without the loss of generality, the initial wave phase ϕ0 is set to 0. To ensure sufficient chorus rays, we use 51 launch locations with L0 from 5.25 to 5.75 in the spacing of 0.01 and 81 frequencies f from 600 to 1,400 Hz with spacing of 10 Hz. In total, 4,131 ray paths (characteristic curves) are traced. ϕ, Aw, and k along those paths are interpolated to reconstruct the corresponding 3D distributions in time t and position r (on the meridian plane), which are then fed into the test particle Eqs. 1–4.
Figure 4 shows examples of three rays launched at the equator on different field lines. As the rays propagate away from the equator, wave normals refract outward due to the dipole magnetic field (Figure 4C), i.e., k⊥ is pointed outward during wave propagation. Whether whistler-mode ray paths bend outward or inward depends on perpendicular wave group velocity (vg⊥) direction (e.g., Smith et al., 1960), which depends on wave frequency and wave normal angle. For ω > Ω/2, vg⊥ is always anti-parallel to k⊥ and thus is pointed inward. For ω < Ω/2, when the wave normal angle is smaller (larger) than the Gendrin angle, the vg⊥ direction is parallel (anti-parallel) with k⊥, which corresponds to outward (inward) bending of ray paths. Therefore, ray paths of the lower band chorus waves with initially parallel wave normal at the equator generally bend outward and toward larger L (as shown in Figures 4A–D). As wave normal increases, so does Landau damping. At the latitude of 20°, wave normal angles reach above 50° and path-integrated gain reaches below −20 dB. The same features can be also seen in the solution of nonducted chorus wave amplitude and wave normal angles as shown in Figure 5. In addition, chorus wave intensity is maximized at L = 5.5 near the equator, as chorus wave propagates outward, wave intensity peak is weakened and shifts toward higher latitude with more oblique wave normal angles. During wave propagation away from the equator, the nonducted chorus wave can extend to a higher L-shell, beyond the transverse range at the equator, and consequently is capable of interacting with electrons over a larger L range than the ducted chorus wave. However, due to Landau damping, the nonducted chorus wave intensity is mostly confined over λ < 20° and L < 5.8. It is also noted that the chorus wave above λ ∼ 10° is available only beyond L = 5.5 because of the outward propagation of wave energy and the limited chorus transverse size, while the chorus wave is confined near the equator near L ∼ 5.5. Bottom panels of Figure 5 show the corresponding solution for wave frequency. One can see frequency chirping evolve as chorus waves propagate away from the equator.
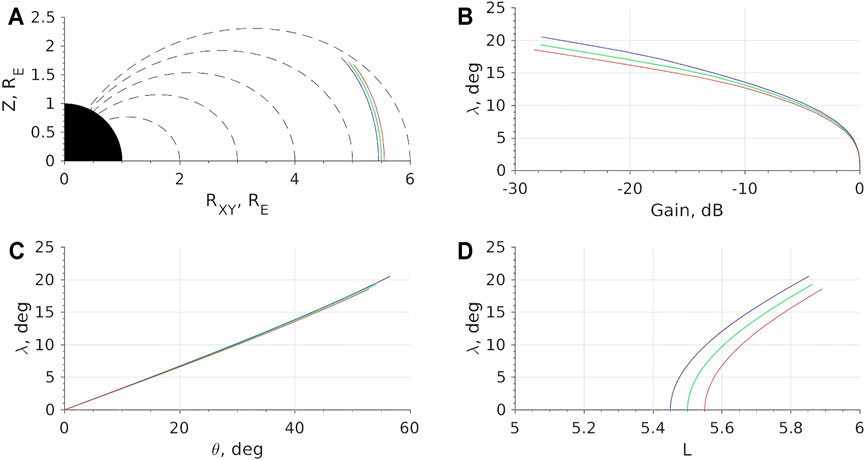
FIGURE 4. Examples of ray tracing simulation for rays with 700 Hz. (A) ray paths of rays launched at the equator with initial L = 4.45 (blue), 5.5 (green) and 5.55 (red). (B) wave gain, (C) wave normal angle and (D) L-shell as a function of magnetic latitude λ.
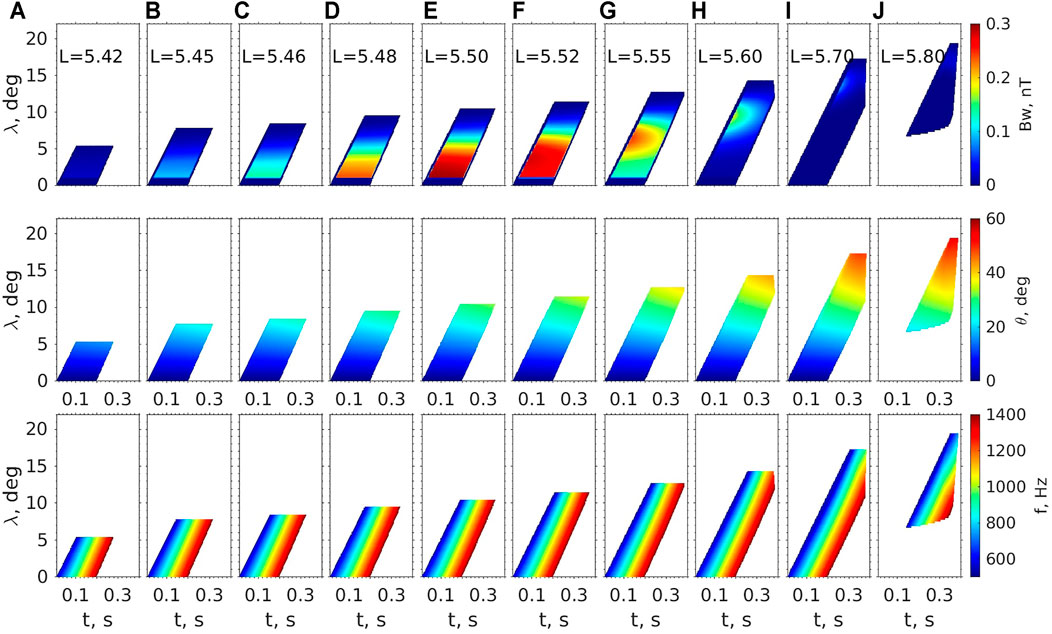
FIGURE 5. Solution of nonducted chorus elements, wave amplitude Bw(top panels), wave normal angles (middle panels), and wave frequency (bottom panels) as a function of t and λ, along selected field lines with L values from 5.42 to 5.80 (A–J).
Figure 6 shows the response of electron omni-directional fluxes at the two LEO satellite locations along different L values (represented by different columns). Due to the tendency of outward propagation of nonducted chorus waves, the responses are asymmetric with respect to the central location Lc of the equatorial chorus wave source, with more pronounced flux enhancement over a broader energy range outside Lc than inside Lc. The chorus waves are capable of inducing electron responses at the southern footpoints over a L range from 5.45 to 5.7, a factor of 5 greater than the transverse size δL (= 0.05) of the equatorial chorus waves. The perturbation of the omni-directional flux is hardly visible in the northern footpoints. The corresponding ratios of precipitating to trapped electron fluxes are shown in Figure 7. The ratios at the southern footpoints can be on the order of 1 over the energy range of 50–70 keV over the L range from 5.45 to 5.6. For higher energy range, the ratios becomes smaller and the corresponding L range becomes narrower. Such enhancement in electron precipitation at the southern hemisphere is induced by the principal cyclotron resonance (n = −1) with the chorus waves. At the northern footpoints, the enhanced electron precipitating-to-trapped flux ratios are on the order of 0.01–0.1 at the outer L-shell with L > 5.5, which was caused by anomalous cyclotron resonance with n = +1 (requiring northward moving electrons). The anomalous cyclotron resonance requires significant wave intensity at oblique angles, and therefore favors the outer L shells. These ratios are lower than those associated with the n = −1 resonance because the intensity of the oblique waves is less than that of the equatorial waves. Figure 8 shows pitch angle distribution of electron fluxes at a selected energy 70 keV. One can see partial and full loss cone (over the local pitch angle range from 118° to 180°) at the southern footpoints over the L range where chorus wave intensity remains strong, while at the northern footpoints, the loss cone in the pitch angle range below 62° is only slightly filled. The comparison of those pitch angle distributions is consistent with the precipitating-to-trapped flux ratio values shown in Figure 7.
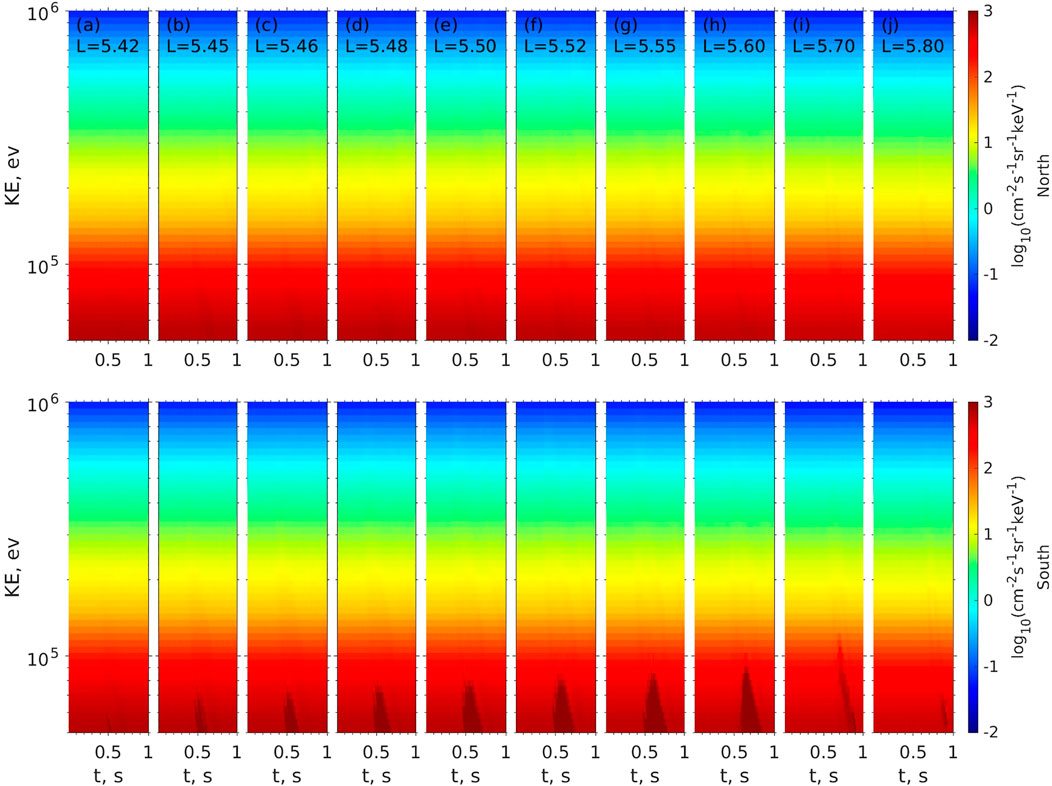
FIGURE 6. Modeled electron fluxes at virtual northern (top panels) and southern (bottom panels) LEO satellites due to the presence of the nonducted wave shown in Figure 5 at selected field lines with L values from 5.42 to 5.80 (A–J).
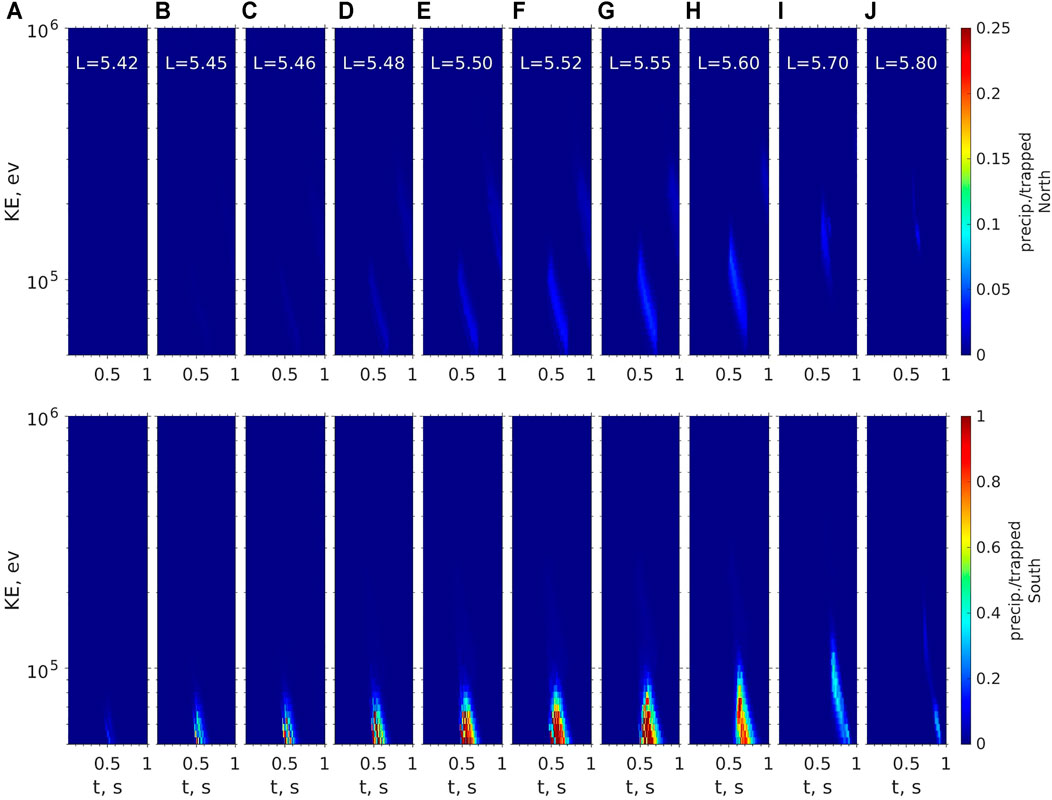
FIGURE 7. Modeled ratio of precipitating to trapped electron fluxes at virtual northern (top panels) and southern (bottom panels) LEO satellites due to the presence of the nonducted wave shown in Figure 5 at selected field lines with L values from 5.42 to 5.80 (A–J).
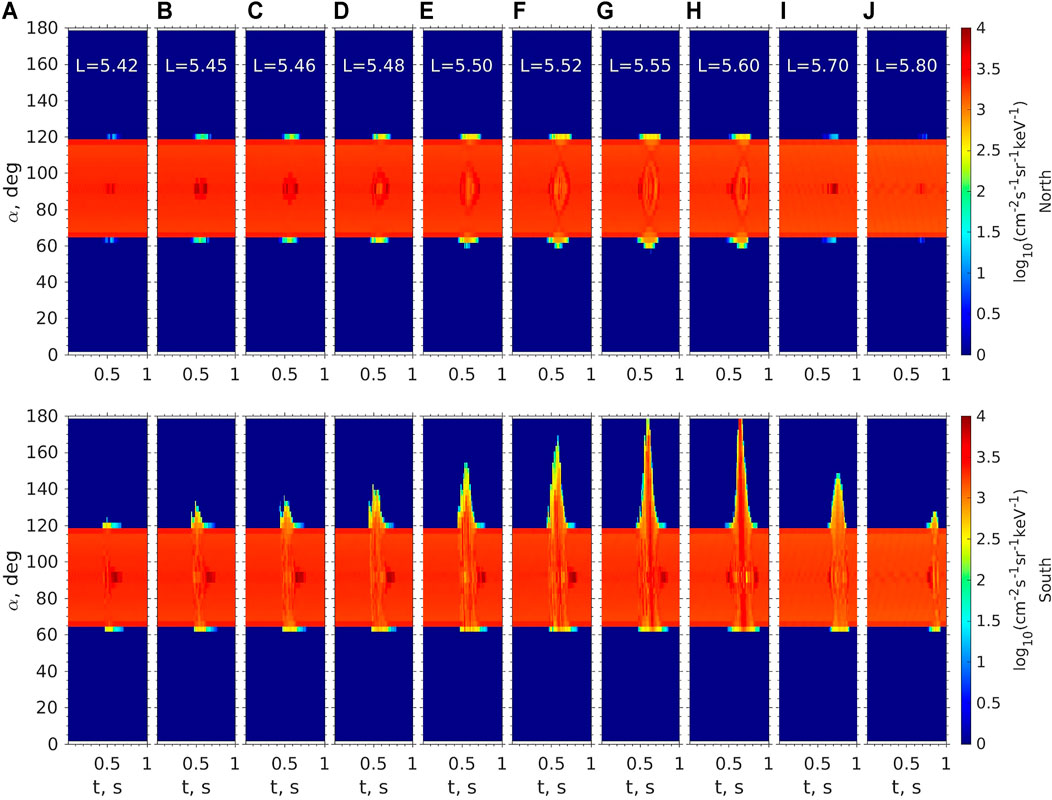
FIGURE 8. Modeled pitch angle distribution of electron fluxes for a fixed energy 70 keV at virtual northern (top panels) and southern (bottom panels) LEO satellites due to the presence of the nonducted wave shown in Figure 5 at selected field lines with L values from 5.42 to 5.80 (A–J).
The following four points are worth-noting when making comparison between ducted chorus waves and nonducted chorus waves. First, ducted chorus waves are capable of reaching higher latitude than nonducted chorus waves, and therefore are capable of inducing the electron precipitation at higher energy. Second, nonducted chorus waves can spread wave energy toward outer L-shell and becomes more oblique, Therefore, the electron precipitation, although at lower energy, will be induced over a spatial region a factor of several larger than the size of source chorus waves at the equator. Third, because of obliqueness, nonducted chorus waves introduce additional anomalous cyclotron resonance, as well as many higher order resonances that are generally less effective in electron scattering for moderately oblique waves (e.g., Shprits and Ni, 2009). The degree of outward propagation and wave obliqueness depends on the strength of Landau damping, which increases with L and Kp index and which is greater at nightside than dayside (Chen et al., 2013b). For a strong Landau damping case (such as nightside), one may expect more confinement of chorus waves at the equator, narrower L-shell spreading, less anomalous cyclotron resonance effect, and electron precipitation at lower energy. On the other hand, for a weak Landau damping case (such as morning side), one may expect more wave energy at higher latitudes, and spreaded wave intensity over a broader L range, electron precipitation at higher energy, and more significant anomalous cyclotron resonance effect. One can see the effects of the reduced Landau damping by comparing Figure 7 with Supplementary Figure S2 of Supplementary Material, where the Landau damping rate γL is halved. Fourth, for a given energy, nonducted chorus waves tend to introduce a narrower microburst duration compared with the ducted waves. That is because nonducted chorus waves at any given frequency only retain wave energy at a given L over a latitudinal range much narrower than the ducted waves along the same field. This reason also explains the difference in the energy dispersion of electron microbursts due to the ducted (Figure 2B) and nonducted chorus waves (Figure 6).
We model electron flux response (including trapped and precipitating electrons) due to ducted and nonducted chorus elements and make comparison of the induced electron precipitation between the two cases. Our principal conclusions are summarized as follows:
• A dynamic model of nonducted chorus propagation is developed. In comparison with ducted chorus, nonducted chorus tends to be more confined near the equator, with wave energy decaying and propagating outward while propagating away from the equator.
• A numerical model of electron flux variation to nonducted chorus elements is developed. Such a model is valuable when interpreting the cause of microburst flux and predicting electron flux variation at a virtual observation.
• Distinct electron precipitation patterns due to the nonducted chorus waves are identified. Comparing with ducted chorus waves, nonducted waves tend to produce electron microbursts at lower energy, over a shorter duration, and over a broader L-shell region, and can trigger different resonance mechanisms (in additional to the principal resonance with n = −1).
There exist three factors that affect nonducted wave propagation and wave intensity. First, Landau damping shows strong dependence on L and MLT and Kp (Chen et al., 2012). Severe Landau damping limits the chorus wave intensity at high latitude and reduces the obliqueness of chorus waves. Second, wave propagation depends on the background plasma density variation, such as strong density gradient near the plasmapause. Third, the transverse size δL of equatorial chorus waves is another important factor. For a larger size, the off-equatorial chorus waves can obtain higher intensity. One can see the effects of increased δL by comparing Figure 7 with Supplementary Figure S3 of Supplementary Material, where δL is doubled.
Our study is limited to the case of nonducted propagation on the meridian plane here. Whistler waves have been shown to be confined near a meridian plane except there exists strong azimuthal density gradient such as near the plasmapause or near the plume region. When needed for those cases, our model is capable of extending to a more general three spatial-dimension case. The presented comparison of microburst characteristics due to ducted and nonducted chorus waves will be valuable when interpreting the LEO observation of microburst structures. Our model is capable of revealing both temporal and spatial structures of induced electron precipitation.
The Landau damping can be significantly reduced by field-aligned electron beams or plateaus (see Ma et al., 2017) that are frequently observed around chorus generation regions (probably as an ionospheric response to electron precipitation by whistler waves, see Nishimura et al. (2015); Artemyev and Mourenas (2020)). Such reduced damping is associated with observations of very oblique chorus waves around the equatorial plane (e.g., Agapitov et al., 2016; Li et al., 2016b) and at middle latitudes Agapitov et al. (2013). The presented model results suggest that very oblique wave generation and propagation without significant damping also may generate microburst precipitation. Further simulations and model comparison with low-altitude spacecraft measurements will be required to reveal relative contributions of electron losses by different chorus wave modes (ducted waves, nonducted moderately and strongly oblique waves) for different electron energy ranges and geomagnetic conditions. To assess overall contribution of chorus waves to the radiation belt losses, relative occurrences of different chorus wave modes should be quantified separately, which is left for future exploration.
Finally, the development of nonducted chorus wave model, which is based on the solution of ray tracing, can be applied to model other coherent plasma waves, such as whistler waves due to lightning activities and from ground transmitter signals. The wave model allows flexible input on initial wave properties, and therefore is ideal for modeling a specific event with constraint by the observation. The general test particle equations can be used for modeling the effect of nonlinear wave particle interaction over a time scale of bounce periods. Results of such short-term simulation can be generalized for a long-term evolution due to nonlinear wave-particle interaction, by including test particle results into the modified Fokker-Planck equation describing phase trapping as a probabilistic process through the Green function approach (e.g., Omura et al., 2015), nonlocal transport operator (e.g., Artemyev et al., 2018), or the Markov chain method (e.g., Zheng et al., 2019).
No observational data were used in this study. Figure data are available at https://doi.org/10.5281/zenodo.5123390.
LC proposed the research idea, ran the simulation, and wrote the article. XZ and AA improved the idea and provided consultation on the interaction with ducted and nonducted chorus waves. LZ and ZX assisted with 1D and 2D chorus wave models. AB provided consultation on electron microbursts. RH developed the HOTRAY code and instructed its usage. All authors reviewed the article.
This work at UTD was supported by the NASA grants 80NSSC18K1224, 80NSSC19K0282, 80NSSC19K0283, 80NSSC21K0728, and 80NSSC21K1320. XZ and AA were supported by NSF grant 1914594. RH was supported by NERC Highlight Topic Grant NE/P01738X/1 (Rad-Sat) and NERC grant NE/V00249X/1 (Sat-Risk).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.745927/full#supplementary-material
Agapitov, O., Artemyev, A., Krasnoselskikh, V., Khotyaintsev, Y. V., Mourenas, D., Breuillard, H., et al. (2013). Statistics of Whistler Mode Waves in the Outer Radiation belt: Cluster STAFF‐SA Measurements. J. Geophys. Res. Space Phys. 118, 3407–3420. doi:10.1002/jgra.50312
Agapitov, O., Blum, L. W., Mozer, F. S., Bonnell, J. W., and Wygant, J. (2017). Chorus Whistler Wave Source Scales as Determined from Multipoint Van allen Probe Measurements. Geophys. Res. Lett. 44, 2634–2642. doi:10.1002/2017GL072701
Agapitov, O., Krasnoselskikh, V., Zaliznyak, Y., Angelopoulos, V., Le Contel, O., and Rolland, G. (2010). Chorus Source Region Localization in the Earth's Outer Magnetosphere Using THEMIS Measurements. Ann. Geophys. 28, 1377–1386. doi:10.5194/angeo-28-1377-2010
Agapitov, O., Mourenas, D., Artemyev, A., Mozer, F. S., Bonnell, J. W., Angelopoulos, V., et al. (2018a). Spatial Extent and Temporal Correlation of Chorus and Hiss: Statistical Results from Multipoint Themis Observations. J. Geophys. Res. Space Phys. 123, 8317–8330. doi:10.1029/2018JA025725
Agapitov, O. V., Mourenas, D., Artemyev, A. V., and Mozer, F. S. (2016). Exclusion Principle for Very Oblique and Parallel Lower Band Chorus Waves. Geophys. Res. Lett. 43, 112–120. doi:10.1002/2016GL071250
Agapitov, O. V., Mourenas, D., Artemyev, A. V., Mozer, F. S., Hospodarsky, G., Bonnell, J., et al. (2018b). Synthetic Empirical Chorus Wave Model from Combined Van allen Probes and Cluster Statistics. J. Geophys. Res. Space Phys. 123, 297–314. doi:10.1002/2017ja024843
Anderson, K. A., and Milton, D. W. (1964). Balloon Observations of X Rays in the Auroral Zone: 3. High Time Resolution Studies. J. Geophys. Res. 69, 4457–4479. doi:10.1029/JZ069i021p04457
Artemyev, A., Agapitov, O., Mourenas, D., Krasnoselskikh, V., Shastun, V., and Mozer, F. (2016). Oblique Whistler-Mode Waves in the Earth's Inner Magnetosphere: Energy Distribution, Origins, and Role in Radiation Belt Dynamics. Space Sci. Rev. 200, 261–355. doi:10.1007/s11214-016-0252-5
Artemyev, A. V., and Mourenas, D. (2020). On Whistler Mode Wave Relation to Electron Field‐Aligned Plateau Populations. J. Geophys. Res. Space Phys. 125, e27735. doi:10.1029/2019JA027735
Artemyev, A. V., Neishtadt, A. I., Vasiliev, A. A., and Mourenas, D. (2018). Long-term Evolution of Electron Distribution Function Due to Nonlinear Resonant Interaction with Whistler Mode Waves. J. Plasma Phys. 84, 905840206. doi:10.1017/S0022377818000260
Blake, J. B., Looper, M. D., Baker, D. N., Nakamura, R., Klecker, B., and Hovestadt, D. (1996). New High Temporal and Spatial Resolution Measurements by Sampex of the Precipitation of Relativistic Electrons. Adv. Space Res. 18, 171–186. doi:10.1016/0273-1177(95)00969-8
Blake, J. B., and O’Brien, T. P. (2016). Observations of Small‐scale Latitudinal Structure in Energetic Electron Precipitation. J. Geophys. Res. Space Phys. 121, 3031–3035. doi:10.1002/2015JA021815
Bortnik, J., Chen, L., Li, W., Thorne, R. M., and Horne, R. B. (2011). Modeling the Evolution of Chorus Waves into Plasmaspheric Hiss. J. Geophys. Res. 116, a–n. doi:10.1029/2011JA016499
Breneman, A. W., Crew, A., Sample, J., Klumpar, D., Johnson, A., Agapitov, O., et al. (2017). Observations Directly Linking Relativistic Electron Microbursts to Whistler Mode Chorus: Van allen Probes and Firebird Ii. Geophys. Res. Lett. 44, 11,265–11,272. doi:10.1002/2017GL075001
Burtis, W. J., and Helliwell, R. A. (1969). Banded Chorus-A New Type of VLF Radiation Observed in the Magnetosphere by OGO 1 and OGO 3. J. Geophys. Res. 74, 3002–3010. doi:10.1029/JA074i011p03002
Burton, R. K., and Holzer, R. E. (1974). The Origin and Propagation of Chorus in the Outer Magnetosphere. J. Geophys. Res. 79, 1014–1023. doi:10.1029/ja079i007p01014
Chang, H. C., and Inan, U. S. (1983). A Theoretical Model Study of Observed Correlations between Whistler Mode Waves and Energetic Electron Precipitation Events in the Magnetosphere. J. Geophys. Res. 88, 10053–10064. doi:10.1029/ja088ia12p10053
Chen, L., Bortnik, J., Li, W., Thorne, R. M., and Horne, R. B. (2012). Modeling the Properties of Plasmaspheric Hiss: 1. Dependence on Chorus Wave Emission. J. Geophys. Res. 117, 1. doi:10.1029/2011JA017201
Chen, L., Breneman, A. W., Xia, Z., and Zhang, X.-j. (2020). Modeling of Bouncing Electron Microbursts Induced by Ducted Chorus Waves. Geophys. Res. Lett. 47, e2020GL089400. doi:10.1029/2020GL089400
Chen, L., Thorne, R. M., Li, W., and Bortnik, J. (2013a). Modeling the Wave normal Distribution of Chorus Waves. J. Geophys. Res. Space Phys. 118, 1074–1088. doi:10.1029/2012ja018343
Chen, L., Thorne, R. M., Shprits, Y., and Ni, B. (2013b). An Improved Dispersion Relation for Parallel Propagating Electromagnetic Waves in Warm Plasmas: Application to Electron Scattering. J. Geophys. Res. Space Phys. 118, 2185–2195. doi:10.1002/jgra.50260
Colpitts, C., Miyoshi, Y., Kasahara, Y., Delzanno, G. L., Wygant, J. R., Cattell, C. A., et al. (2020). First Direct Observations of Propagation of Discrete Chorus Elements from the Equatorial Source to Higher Latitudes, Using the Van allen Probes and Arase Satellites. J. Geophys. Res. Space Phys. 125, e2020JA028315. doi:10.1029/2020JA028315
Crew, A. B., Spence, H. E., Blake, J. B., Klumpar, D. M., Larsen, B. A., O'Brien, T. P., et al. (2016). First Multipoint In Situ Observations of Electron Microbursts: Initial Results from the Nsf Firebird Ii mission. J. Geophys. Res. Space Phys. 121, 5272–5283. doi:10.1002/2016JA022485
Douma, E., Rodger, C. J., Blum, L. W., and Clilverd, M. A. (2017). Occurrence Characteristics of Relativistic Electron Microbursts from Sampex Observations. J. Geophys. Res. Space Phys. 122, 8096–8107. doi:10.1002/2017JA024067
Furuya, N., Omura, Y., and Summers, D. (2008). Relativistic Turning Acceleration of Radiation belt Electrons by Whistler Mode Chorus. J. Geophys. Res. 113. doi:10.1029/2007ja012478
Gao, X., Mourenas, D., Li, W., Artemyev, A. V., Lu, Q., Tao, X., et al. (2016). Observational Evidence of Generation Mechanisms for Very Oblique Lower Band Chorus Using Themis Waveform Data. J. Geophys. Res. Space Phys. 121, 6732–6748. doi:10.1002/2016JA022915
Hikishima, M., Omura, Y., and Summers, D. (2010). Microburst Precipitation of Energetic Electrons Associated with Chorus Wave Generation. Geophys. Res. Lett. 37, a–n. doi:10.1029/2010GL042678
Horne, R. B., Glauert, S. A., and Thorne, R. M. (2003). Resonant Diffusion of Radiation belt Electrons by Whistler-Mode Chorus. Geophys. Res. Lett. 30, 1. doi:10.1029/2003gl016963
Horne, R. B. (1989). Path-integrated Growth of Electrostatic Waves: The Generation of Terrestrial Myriametric Radiation. J. Geophys. Res. 94, 895–909. doi:10.1029/ja094ia07p08895
Imhof, W. L., Voss, H. D., Mobilia, J., Datlowe, D. W., Gaines, E. E., McGlennon, J. P., et al. (1992). Relativistic Electron Microbursts. J. Geophys. Res. 97, 13829–13837. doi:10.1029/92JA01138
Katoh, Y., and Omura, Y. (2007). Relativistic Particle Acceleration in the Process of Whistler-Mode Chorus Wave Generation. Geophys. Res. Lett. 34, 1. doi:10.1029/2007gl031335
Katoh, Y., and Omura, Y. (2006). Simulation Study on Nonlinear Frequency Shift of Narrow Band Whistler-Mode Waves in a Homogeneous Magnetic Field. Earth Planet. Sp 58, 1219–1225. doi:10.1186/BF03352013
Kennel, C. F., and Petschek, H. E. (1966). Limit on Stably Trapped Particle Fluxes. J. Geophys. Res. 71, 1–28. doi:10.1029/jz071i001p00001
Kersten, K., Cattell, C. A., Breneman, A., Goetz, K., Kellogg, P. J., Wygant, J. R., et al. (2011). Observation of Relativistic Electron Microbursts in Conjunction with Intense Radiation belt Whistler-Mode Waves. Geophys. Res. Lett. 38, 1. doi:10.1029/2011gl046810
Lam, M. M., Horne, R. B., Meredith, N. P., Glauert, S. A., Moffat-Griffin, T., and Green, J. C. (2010). Origin of Energetic Electron Precipitation >30 Kev into the Atmosphere. J. Geophys. Res. 115, a–n. doi:10.1029/2009JA014619
Lampton, M. (1967). Daytime Observations of Energetic Auroral-Zone Electrons. J. Geophys. Res. 72, 5817–5823. doi:10.1029/JZ072i023p05817
Lauben, D. S., Inan, U. S., Bell, T. F., and Gurnett, D. A. (2002). Source Characteristics of ELF/VLF Chorus. J. Geophys. Res. 107, 1429. doi:10.1029/2000ja003019
LeDocq, M. J., Gurnett, D. A., and Hospodarsky, G. B. (1998). Chorus Source Locations from VLF Poynting Flux Measurements with the Polar Spacecraft. Geophys. Res. Lett. 25, 4063–4066. doi:10.1029/1998GL900071
Li, W., Mourenas, D., Artemyev, A. V., Bortnik, J., Thorne, R. M., Kletzing, C. A., et al. (2016a). Unraveling the Excitation Mechanisms of Highly Oblique Lower Band Chorus Waves. Geophys. Res. Lett. 43, 8867–8875. doi:10.1002/2016gl070386
Li, W., Santolik, O., Bortnik, J., Thorne, R. M., Kletzing, C. A., Kurth, W. S., et al. (2016b). New Chorus Wave Properties Near the Equator from Van allen Probes Wave Observations. Geophys. Res. Lett. 43, 4725–4735. doi:10.1002/2016GL068780
Li, W., Thorne, R. M., Angelopoulos, V., Bortnik, J., Cully, C. M., Ni, B., et al. (2009). Global Distribution of Whistler-Mode Chorus Waves Observed on the THEMIS Spacecraft. Geophys. Res. Lett. 36, L09104. doi:10.1029/2009GL037595
Li, W., Thorne, R. M., Bortnik, J., Shprits, Y. Y., Nishimura, Y., Angelopoulos, V., et al. (2011a). Typical Properties of Rising and Falling Tone Chorus Waves. Geophys. Res. Lett. 38, a–n. doi:10.1029/2011GL047925
Liu, X., Gu, W., Xia, Z., Chen, L., and Horne, R. B. (2021). Frequency‐Dependent Modulation of Whistler‐Mode Waves by Density Irregularities during the Recovery Phase of a Geomagnetic Storm. Geophys. Res. Lett. 48, e2021GL093095. doi:10.1029/2021GL093095
Lorentzen, K. R., Blake, J. B., Inan, U. S., and Bortnik, J. (2001). Observations of Relativistic Electron Microbursts in Association with VLF Chorus. J. Geophys. Res. 106, 6017–6027. doi:10.1029/2000JA003018
Lu, Q., Ke, Y., Wang, X., Liu, K., Gao, X., Chen, L., et al. (2019). Two‐Dimensional gcPIC Simulation of Rising‐Tone Chorus Waves in a Dipole Magnetic Field. J. Geophys. Res. Space Phys. 124, 4157–4167. doi:10.1029/2019JA026586
Ma, Q., Artemyev, A. V., Mourenas, D., Li, W., Thorne, R. M., Kletzing, C. A., et al. (2017). Very Oblique Whistler Mode Propagation in the Radiation Belts: Effects of Hot Plasma and Landau Damping. Geophys. Res. Lett. 44, 057–066. doi:10.1002/2017GL075892
Meredith, N. P., Horne, R. B., Sicard-Piet, A., Boscher, D., Yearby, K. H., Li, W., et al. (2012). Global Model of Lower Band and Upper Band Chorus from Multiple Satellite Observations. J. Geophys. Res. 117, A10225. doi:10.1029/2012ja017978
Millan, R. M., and Thorne, R. M. (2007). Review of Radiation belt Relativistic Electron Losses. J. Atmos. Solar-Terrestrial Phys. 69, 362–377. doi:10.1016/j.jastp.2006.06.019
Millan, R. M. (2011). Understanding Relativistic Electron Losses with Barrel. J. Atmos. Solar-Terrestrial Phys. 73, 1425–1434. doi:10.1016/j.jastp.2011.01.006
Ni, B., Thorne, R. M., Shprits, Y. Y., Orlova, K. G., and Meredith, N. P. (2011). Chorus-driven Resonant Scattering of Diffuse Auroral Electrons in Nondipolar Magnetic fields. J. Geophys. Res. 116, a–n. doi:10.1029/2011JA016453
Nishimura, Y., Bortnik, J., Li, W., Liang, J., Thorne, R. M., Angelopoulos, V., et al. (2015). Chorus Intensity Modulation Driven by Time‐varying Field‐aligned Low‐energy Plasma. J. Geophys. Res. Space Phys. 120, 7433–7446. doi:10.1002/2015JA021330
Nunn, D., Omura, Y., Matsumoto, H., Nagano, I., and Yagitani, S. (1997). The Numerical Simulation of Vlf Chorus and Discrete Emissions Observed on the Geotail Satellite Using a Vlasov Code. J. Geophys. Res. 102, 27083–27097. doi:10.1029/97JA02518
O’Brien, T. P., Looper, M. D., and Blake, J. B. (2004). Quantification of Relativistic Electron Microburst Losses during the Gem Storms. Geophys. Res. Lett. 31, 1. doi:10.1029/2003GL018621
Oliven, M. N., and Gurnett, D. A. (1968). Microburst Phenomena: 3. An Association between Microbursts and Vlf Chorus. J. Geophys. Res. 73, 2355–2362. doi:10.1029/JA073i007p02355
Omura, Y., Hikishima, M., Katoh, Y., Summers, D., and Yagitani, S. (2009). Nonlinear Mechanisms of Lower-Band and Upper-Band Vlf Chorus Emissions in the Magnetosphere. J. Geophys. Res. Space Phys. 114, 1. doi:10.1029/2009ja014206
Omura, Y., and Matsumoto, H. (1982). Computer Simulations of Basic Processes of Coherent Whistler Wave-Particle Interactions in the Magnetosphere. J. Geophys. Res. 87, 4435–4444. doi:10.1029/ja087ia06p04435
Omura, Y., Miyashita, Y., Yoshikawa, M., Summers, D., Hikishima, M., Ebihara, Y., et al. (2015). Formation Process of Relativistic Electron Flux through Interaction with Chorus Emissions in the Earth's Inner Magnetosphere. J. Geophys. Res. Space Phys. 120, 9545–9562. doi:10.1002/2015JA021563
Omura, Y., and Summers, D. (2006). Dynamics of High-Energy Electrons Interacting with Whistler Mode Chorus Emissions in the Magnetosphere. J. Geophys. Res. 111, 1. doi:10.1029/2006JA011600
Parks, G. K., Gurgiolo, C., and West, R. (1979). Relativistic Electron Precipitation. Geophys. Res. Lett. 6, 393–396. doi:10.1029/GL006i005p00393
Reeves, G. D., Spence, H. E., Henderson, M. G., Morley, S. K., Friedel, R. H. W., Funsten, H. O., et al. (2013). Electron Acceleration in the Heart of the Van allen Radiation Belts. Science 341, 991–994. doi:10.1126/science.1237743
Rosenberg, T. J., Wei, R., Detrick, D. L., and Inan, U. S. (1990). Observations and Modeling of Wave-Induced Microburst Electron Precipitation. J. Geophys. Res. 95, 6467–6475. doi:10.1029/JA095iA05p06467
Saito, S., Miyoshi, Y., and Seki, K. (2012). Relativistic Electron Microbursts Associated with Whistler Chorus Rising Tone Elements: Gemsis-Rbw Simulations. J. Geophys. Res. 117, a–n. doi:10.1029/2012JA018020
Santolík, O., Gurnett, D. A., Pickett, J. S., Parrot, M., and Cornilleau-Wehrlin, N. (2005). Central Position of the Source Region of Storm-Time Chorus. Planet. Space Sci. 53, 299–305. doi:10.1016/j.pss.2004.09.056
Santolík, O., and Gurnett, D. A. (2003). Transverse Dimensions of Chorus in the Source Region. Geophys. Res. Lett. 30. doi:10.1029/2002GL016178
Shen, X. C., Li, W., Ma, Q., Agapitov, O., and Nishimura, Y. (2019). Statistical Analysis of Transverse Size of Lower Band Chorus Waves Using Simultaneous Multisatellite Observations. Geophys. Res. Lett. 46, 5725–5734. doi:10.1029/2019gl083118
Shprits, Y. Y., and Ni, B. (2009). Dependence of the Quasi-Linear Scattering Rates on the Wave normal Distribution of Chorus Waves. J. Geophys. Res. 114, a–n. doi:10.1029/2009JA014223
Shumko, M., Johnson, A. T., Sample, J. G., Griffith, B. A., Turner, D. L., O'Brien, T. P., et al. (2020). Electron Microburst Size Distribution Derived with Aerocube-6. J. Geophys. Res. Space Phys. 125, e2019JA027651. doi:10.1029/2019JA027651
Shumko, M., Sample, J., Johnson, A., Blake, B., Crew, A., Spence, H., et al. (2018). Microburst Scale Size Derived from Multiple Bounces of a Microburst Simultaneously Observed with the Firebird-Ii Cubesats. Geophys. Res. Lett. 45, 8811–8818. doi:10.1029/2018gl078925
Smith, R. L., Helliwell, R. A., and Yabroff, I. W. (1960). A Theory of Trapping of Whistlers in Field-Aligned Columns of Enhanced Ionization. J. Geophys. Res. 65, 815–823. doi:10.1029/JZ065i003p00815
Tao, X. (2014). A Numerical Study of Chorus Generation and the Related Variation of Wave Intensity Using the Dawn Code. J. Geophys. Res. Space Phys. 119, 3362–3372. doi:10.1002/2014JA019820
Tao, X., and Bortnik, J. (2010). Nonlinear Interactions between Relativistic Radiation belt Electrons and Oblique Whistler Mode Waves. Nonlin. Process. Geophys. 17, 599–604. doi:10.5194/npg-17-599-2010
Tao, X., Bortnik, J., Thorne, R. M., Albert, J. M., and Li, W. (2012). Effects of Amplitude Modulation on Nonlinear Interactions between Electrons and Chorus Waves. Geophys. Res. Lett. 39, a–n. doi:10.1029/2012GL051202
Teng, S., Tao, X., Xie, Y., Zonca, F., Chen, L., Fang, W. B., et al. (2017). Analysis of the Duration of Rising Tone Chorus Elements. Geophys. Res. Lett. 44, 074–082. doi:10.1002/2017GL075824
Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid Local Acceleration of Relativistic Radiation-belt Electrons by Magnetospheric Chorus. Nature 504, 411–414. doi:10.1038/nature12889
Tsurutani, B. T., and Smith, E. J. (1974). Postmidnight Chorus: A Substorm Phenomenon. J. Geophys. Res. 79, 118–127. doi:10.1029/JA079i001p00118
Tyler, E., Breneman, A., Cattell, C., Wygant, J., Thaller, S., and Malaspina, D. (2019). Statistical Distribution of Whistler Mode Waves in the Radiation Belts with Large Magnetic Field Amplitudes and Comparison to Large Electric Field Amplitudes. J. Geophys. Res. Space Phys. 124, 6541–6552. doi:10.1029/2019JA026913
Watt, C. E. J., Degeling, A. W., and Rankin, R. (2013). Constructing the Frequency and Wave normal Distribution of Whistler-Mode Wave Power. J. Geophys. Res. Space Phys. 118, 1984–1991. doi:10.1002/jgra.50231
Zhang, X.-J., Thorne, R., Artemyev, A., Mourenas, D., Angelopoulos, V., Bortnik, J., et al. (2018). Properties of Intense Field-Aligned Lower-Band Chorus Waves: Implications for Nonlinear Wave-Particle Interactions. J. Geophys. Res. Space Phys. 123, 5379–5393. doi:10.1029/2018JA025390
Keywords: chorus, microbursts, radiation belts, precipitation, wave-particle interaction
Citation: Chen L, Zhang X-J, Artemyev A, Zheng L, Xia Z, Breneman AW and Horne RB (2021) Electron Microbursts Induced by Nonducted Chorus Waves. Front. Astron. Space Sci. 8:745927. doi: 10.3389/fspas.2021.745927
Received: 22 July 2021; Accepted: 13 September 2021;
Published: 04 October 2021.
Edited by:
Jean-Francois Ripoll, CEA DAM Île-de-France, FranceReviewed by:
Chris Colpitts, University of Minnesota Twin Cities, United StatesCopyright © 2021 Chen, Zhang, Artemyev, Zheng, Xia, Breneman and Horne. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lunjin Chen, bHVuamluLmNoZW5AZ21haWwuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.