Tunneling of Hydrogen and Deuterium Atoms on Interstellar Ices (Ih and ASW)

Model calculations are performed to investigate the kinetic isotope effect of hydrogen and deuterium atom diffusion on hexagonal ice and amorphous solid water. Comparisons with experimental results by Kuwahata et al. (Phys. Rev. Lett., Sep. 2015, 115 (13), 133201) at 10 K are made. The experimentally derived kinetic isotope effect on amorphous solid water is reproduced by transition state theory. The experimentally found kinetic isotope effect on hexagonal ice is much larger than on amorphous solid water and is not reproduced by transition state theory. Additional calculations using model potentials are made for the hexagonal ice, but the experimental kinetic isotope effect is not fully reproduced. A strong influence of temperature is observed in the calculations. The influence of tunnelling is discussed in detail and related to the experiments. The calculations fully support the claims by the Kuwahata et al. (Phys. Rev. Lett., Sep. 2015, 115 (13), 133201) that on amorphous solid water the diffusion is predominantly by thermal hopping while on the polycrystalline ice tunnelling diffusion contributes significantly.

1 Introduction

H₂ is the most common molecule in the interstellar medium. Its formation is assumed to occur on grains as the gas phase formation is too slow to explain its abundance. In diffuse clouds the grains are bare and they are usually classified as silicates or carbonaceous (Wakelam et al., 2017). In dense interstellar clouds on the other hand the grains are often covered by a mantle of ice, which may contain for instance H₂O, H₂CO, N₂, O₂, CO, CO₂, H₂O₂, NH₃, CH₄ and CH₃OH (Tielens and Hagen 1982; Gibb et al., 2000). The ice is expected to primarily be in the form of amorphous solid water (ASW) or polycrystalline ice (PCI).

The process of forming H₂ on an icy grain surface is believed to involve hydrogen atom physisorption followed by diffusion such that another hydrogen atom is encountered whereby the two atoms can react and form a hydrogen molecule. Large amounts of energy is released as H₂ forms, which together with the weak interaction of the hydrogen molecule with the surface makes it plausible that it quickly desorbs and ends up in the gas phase. The process just described is essentially an example of how heterogeneous catalysis works. The hydrogen atoms on the grain surface do however not have to come from the gas phase. It is also possible that hydrogen atoms form in the bulk of the ice due to photodissociation. It should also be mentioned that if there is a hydrogen atom on the surface it could be hit directly by a hydrogen atom approaching from the gas phase, which is the Eley-Rideal mechanism. This mechanism is not so likely for a grain with low coverage of H atoms.

Much experimental effort has gone into investigating the diffusion of hydrogen and deuterium atoms on ASW and PCI at temperatures at and around 10 K (Manicò et al., 2001; Hornekær et al., 2003; Perets et al., 2005; Amiaud et al., 2007; Matar et al., 2008; Watanabe et al., 2010; Hama et al., 2012; Kuwahata et al., 2015). The diffusion is found to be much faster on PCI than on ASW. Recent work of Kuwahata et al. (2015) studies the diffusion of D and H atoms on both PCI and ASW. The authors find that the kinetic isotope effect (KIE) for diffusion of H atoms compared to D atoms is larger on PCI than on ASW. They also find that the KIE is larger for their larger fluxes of atoms towards the surfaces than for lower fluxes. Kuwahata et al. (2015) interpret their results as being due to a larger contribution of tunnelling to the diffusion rate on PCI than on ASW. For ASW they find that thermal hopping dominates although tunnelling diffusion may also partly contribute.

There has also been a substantial amount of theoretically based work on absorption diffusion on grains in the context of astrochemistry (Gould and Salpeter, 1963; Williams, 1968; Augason, 1970; Hollenbach and Salpeter, 1970; Hollenbach and Salpeter, 1971; Lee, 1972; Watson and Salpeter, 1972; Jura, 1975; Goodman, 1978; Smoluchowski, 1979, 1981, 1983; Pirronello et al., 1997a, 1997b, 1999; Katz et al., 1999; Karssemeijer et al., 2014; Senevirathne et al., 2017; Fredon and Cuppen 2018). Important for H₂ formation on a surface is that the residence time of the adsorbed species is long enough that the adsorbed hydrogen atoms have time to diffuse on the surface before desorbing. In early model calculations, using two types of adsorption sites (i.e. weak and strong adsorption sites), by Hollenbach and Salpeter (1970,1971) the tunneling was efficient enough to allow the adsorbed hydrogen atoms to diffuse over most of the grain surface before desorbing. Pirronello et al. (1997a, 1997b, 1999) measured hydrogen formation on olivine and carbonaceous substrates and found much lower hydrogen atom mobility and H₂ formation rate than Hollenbach and Salpeter and pointed to the temperature dependence of this rate. The experimental results were also modelled by Katz et al. (1999). Smoluchowski (1981, 1983) noticed based on quantum mechanical calculations that adsorbed hydrogen atoms would on an amorphous quickly get trapped in the deep sites, which lowered the H₂ production efficiency by orders of magnitude compared to Hollenbach and Salpeter’s.

In the present work we theoretically study the kinetic isotope effect between deuterium and protium (i.e. the common hydrogen isotope) atom diffusion by estimating the transition rates of H and D atoms hopping between adjacent local minima on the grain surface. This is done by employing simple models that are intended to represent the hexagonal ice and the amorphous solid water. In this way we obtain kinetic isotope effects for the transition rates and thereby also for the diffusion rates. We aim to offer some insight as to why Kuwahata et al. (2015) found larger values on hexagonal ice (I_h) than on ASW.

In calculating the KIE’s, we will begin by using harmonic transition state theory. First we apply it in completely classical form and thereafter with quantized partition functions. We will also consider a simple Wigner tunnelling correction to the transition state theory (TST) rate constant. As far as ASW is concerned, TST turns out to suffice to reproduce the experimentally derived KIE. For I_h, however, the TST derived KIE is not compatible with the experimental result. For I_h we will therefore pay more attention to tunnelling as it may be enhanced due to its more regular structure than in the ASW case. For this purpose we will treat the physisorbed hydrogen atom as moving in a double well model. First we will treat the double well as isolated and thereafter as weakly interacting with the ice lattice. Finally we will employ a band model by Kehr (1997), where we assume that the I_h is perfectly periodic over large distances.

The paper is structured such that this Introduction is followed by a brief description in Section 2 of the experiments of Kuwahata et al. (2015). Then in Section 3 the ice model that is used for the present calculations is introduced. Thereafter calculations and results are presented in Section 4 (ASW) and Section 5 (I_h). Section 6 contains a discussion and conclusions.

2 Experimental Background

Our calculations are inspired by the experimental work of Kuwahata et al. (2015) on H and D atom diffusion on PCI and ASW. Their work was performed at (or close to) 10 K. In the experimental work H (or D) atoms are deposited on a PCI (or ASW) surface, at varying fluxes. During deposition, atoms are photodesorbed by weak laser radiation and then detected by time-delayed resonance enhanced multi-photon ionization (REMPI). The time-delay between the laser pulses was varied and the H/D REMPI intensity ratios were summed over the delay-time. In this way KIE’s for the diffusion rate could be determined. This was done by assuming that the REMPI signal due to H (D) atoms depend on how many of the H (D) atoms were desorbed from the surface by the weak desorption laser, which in turn would depend on how many H (D) atoms had already disappeared by forming H₂ (D₂) due to diffusion on the surface.

The experiments were repeated for a range of deposition fluxes. The idea behind this is that at low flux, the surface coverage of atoms will be low and the atoms will be far apart. As they diffuse they are likely to encounter irregularities or defects in the ice surfaces. Therefore Kuwahata et al. (2015) suggest that thermal diffusion will be rate limiting. For high flux on the other hand the atoms will encounter each other after shorter travel. For the I_h this could mean that a more periodic surface is encountered, supposedly allowing enhanced tunnelling. In the Discussion we will return to this.

By reading from Figure 2 in Kuwahata et al. (2015) the following results are found. Their measurements on PCI give at high flux a KIE of 120 and accounting for their error bars the KIE is in the range 65–175. Their corresponding results for ASW give a KIE of 16 and accounting for error bars the KIE is in the range 10–25. The KIE is taken to be the ratio of the rate for the lighter isotope to that for the heavier one. At lower fluxes the KIE’s were smaller than at large fluxes, both for ASW and for PCI. Kuwahata et al. (2015) conclude that for PCI the much faster surface diffusion of the H atoms than the D atoms at high flux cannot be explained by classical thermal hopping. They also note that their work is the first experimental evidence of quantum-tunnelling diffusion on a PCI surface. For the ASW surface they conclude that tunnelling diffusion may partly contribute, but the diffusion is predominantly thermal hopping given the smaller KIE than that observed on PCI.

We end this section by noticing that the experimentally determined KIE represents the KIE of the diffusion constants for H and D, which may be related to hopping rates between potential minima as follows. The diffusion constant D on a surface can be obtained from the relationship

$D=\frac{<r^2>}{4t_{diff}},(1)$

where < r² > is the average distance that an atom/molecule diffuses on the surface in time t_diff, which is the sum of the individual hopping times, t_i, between potential minima on the surface (that occur in the total time t_diff). Since t_i = 1/k_i where k_i is the rate constant for a jump between two minima we can write

$D=\frac{<r^2>}{4{\mathrm{\Sigma }}_i\frac{1}{k_i}}.(2)$

If all k_i are increased by the same factor, we see that in that case D increases by the same factor. This motivates that we below assume that a certain KIE in the hopping rates between minima will be reflected in the same KIE in the diffusion constants.¹

3 Ice Model

For the purpose of the present paper we will need thermal rate constants for H and D atoms hopping between adjacent wells on ice surfaces. Here we will treat the underlying ice as frozen and thus the hydrogen atom is the only moving species, thereby making the problem three-dimensional. This is the same model as was used by Senevirathne et al. (2017). In deriving parameters for the models to be described below we use the interaction potential of Andersson et al. (2006), noticing the minor corrections described in Senevirathne et al. (2017). We note that since the ice is treated as frozen, self-trapping will not occur.

Our main interest is in studying the difference in hopping rates between H and D on ASW and I_h. ASW can be expected to have a larger spread in barrier heights than I_h (Senevirathne et al., 2017). On the other hand, typical pathways for diffusion likely avoid the highest barriers. This would make the barriers that are actually passed differ less in height than would otherwise be the case (Senevirathne et al., 2017).

Here we will pick out a single well and transition state from an I_h surface and base all of our calculations on that. The I_h surface was obtained by Andersson et al. (2006) by taking snapshots from molecular dynamics simulations. We choose a well that can reasonably well characterize H and D atom hopping for both our ASW and I_h calculations. Thus, possible differences that we find in hopping rates between ASW and I_h jumps should thus be related to how we treat effects of symmetry and periodicity of the I_h lattice, which are absent in ASW. Some relevant data regarding the potential well and transition state can be found in Table1.

TABLE 1

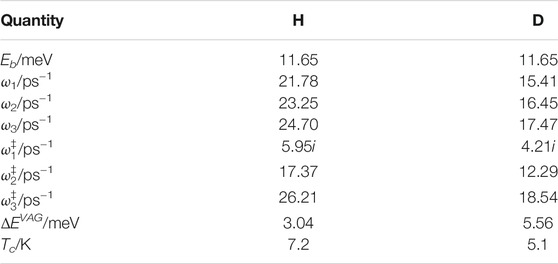
TABLE 1. Data relating to the potential employed for protium (¹H = H) and deuterium (D) atom motion on ice. E_b is the classical barrier height, the various ω′s are harmonic angular frequencies, ‡ indicates transition state, ΔE^VAG is the vibrationally adiabatic ground state barrier height and T_c is the cross-over temperature (Hänggi et al., 1990).

4 Transition State Theory Calculations for ASW

In this section we will investigate what transition state theory (TST) tells us about the H to D diffusion rate ratios on ASW and I_h. We assume that the diffusion rates are proportional to the rate constants for hopping between adjacent minima on the ice surfaces, see motivation at the end of Section 2. Our interest will thus be in finding the thermal rate constants for such hops by applying TST. In general we assume the underlying ice surfaces to be frozen such that only the physisorbed H (D) atoms move.

In TST the rate constant may be written:

$k\left(T\right)=\frac{k_{B}T}{h}\frac{Q^{‡}}{Q^R}{e}^{-E_b/k_{B}T},(3)$

where k_B is the Boltzmann constant, T is the temperature in Kelvin, h is the Planck constant, Q^‡ is the partition function at the transition state (with the imaginary frequency vibration excluded), Q^R is the reactant partition function and E_b is the barrier height on the potential energy surface.

If we evaluate the partition functions classically and assume uncoupled harmonic oscillators we get a contribution k_BT/ℏω_i from each vibrational mode i. Considering other approximations involved we may as well set the deuterium mass to be twice that of protium. In a fully classical TST calculation of the KIE, most factors will then cancel out, resulting in a KIE of $\sqrt{2}\approx 1.4$. This value is independent of temperature, as long as the temperature is high enough to motivate a classical treatment. This is however often not the case, and certainly not in the present case. Our result for the KIE is also independent of the number of harmonic oscillators that are included. Thus, for this case we do not need to assume the atoms in the ice to be frozen (ignoring self-trapping).

Let us now take TST a step further by evaluating the partition functions quantum mechanically, again assuming uncoupled harmonic oscillators and let us set the reference level for each individual oscillator to be its zero point energy (ZPE) level rather than the bottom of the potential well. Accounting for this the TST rate constant may be expressed as

$k\left(T\right)=\frac{k_{B}T}{h}\frac{Q_{ZPE}^{‡}}{Q_{ZPE}^R}{e}^{-\mathrm{\Delta }{E}^{VAG}/k_{B}T},(4)$

where the partition functions are evaluated with the ZPE level as reference and ΔE^VAG is the vibrationally adiabatic ground state barrier height

$\mathrm{\Delta }{E}^{VAG}=E_b+\sum _{i=2}^3\hslash {\omega }_i^{‡}/2-\sum _{i=1}^3\hslash {\omega }_i/2,(5)$

where ℏ is the reduced Planck constant.

The smallest real vibrational angular frequency involved in the evaluation of k(T) is 12.3 ps⁻¹ (Table1), which is one of the deuterium frequencies at the transition state. This individual oscillator gives a contribution to the partition function of ≈1.0001 (with the ZPE level as reference) when evaluated at 10 K, which will be the most interesting temperature as there we have experiments to compare with. All other individual oscillator contributions to the overall partition functions will be smaller (closer to unity), and we can thus approximate them all as essentially being unity. From Table 1 we find that ΔE^VAG = 3.04 meV for H and 5.56 meV for D. This gives a difference in VAG barrier height of 2.52 meV between the isotopes, which yields (using Eq. (4)) a KIE of 18.6 at 10 K.

For illustrative purposes we now perform the TST calculation for a one-dimensional case. Then $Q_{ZPE}^{‡}=1$ and in addition $Q_{ZPE}^R=1$ at low temperature. We also obtain

$\mathrm{\Delta }{E}_H^{VAG}=E_b-\frac{\hslash {\omega }_{1,H}}{2},(6)$

and

$\mathrm{\Delta }{E}_D^{VAG}=E_b-\frac{\hslash {\omega }_{1,D}}{2},(7)$

where ω_1,H = 21.8 ps⁻¹ is the relevant angular frequency for the hydrogen atom and other notation should be intuitive. Again taking the deuterium mass to be twice that of protium we find

$\mathrm{\Delta }{E}_D^{VAG}-\mathrm{\Delta }{E}_H^{VAG}=\frac{\hslash {\omega }_{1,H}}{2}\left(1-1/\sqrt{2}\right).(8)$

Using this to evalute the KIE [using Eq. (4)] at 10 K we find that it becomes 11.4. This result is independent of the choice of potential beyond the values used for ω_1,H and ω_1,D.

The difference between the KIE of 11.4 and the classical value of 1.4 may be viewed as resulting from the quantum mechanical zero point energy. We would typically see this as the effective barrier height to reaction becoming lower when the ZPE is accounted for and this effect is obviously larger for H than for D and thereof the increase in KIE compared to the classical case. The further change to find a KIE of 18.6 when treating three vibrational motions for the reactant, rather than a single one, is related to the additional changes in zero point energies.

The simple evaluation that we have just performed accounts harmonically for quantum effects in all degrees of freedom. For the reaction coordinate we are however lacking dynamic tunnelling through the barrier, which results from the wave function never decreasing to zero within the barrier. Since the cross over temperature (Hänggi et al., 1990) T_c = 7.2 and 5.1 K for H and D respectively, tunnelling is however not expected to be dominant at 10 K. A simple Wigner tunnelling correction (Wigner, 1932) would however give an increase in rate constant with a factor of 1.86 for H and 1.43 for D at 10 K (using imaginary angular frequencies from Table 1). This would increase the KIE to 24. We should also point out that reflection from the barrier (or recrossing classically) is not accounted for in TST, which would act to reduce the rate constants for H and D and more for H than D, so as to oppose the effect of tunnelling on the KIE.

The simple calculations just described give KIE’s that agree with the experimental results for ASW where the KIE is in the range 10–25 for high flux. While this may be a coincidence, it still suggests that there is some realism to the calculations, particularly as we have noticed that the calculated KIEs do not explicitly depend on the barrier height. The KIE results obtained by TST are summarized in Table 2. We consider these results final for ASW but not for I_h where we need to consider the effect of tunnelling in more detail. In the next section we focus on the tunnelling aspects for hexagonal ice.

TABLE 2

TABLE 2. Experimental and theoretical kinetic isotope effects obtained for ASW at 10 K using various forms of harmonic TST as described in the text.

5 Models and Calculations on I_h

The discussion above regarding TST estimation of the KIE for ASW applies just as well to hexagonal ice and calculations would give exactly the same result for the same potential. Kuwahata et al. (2015) however observed a substantial increase in KIE for I_h compared to ASW. This difference must result from the differences between potential energy landscapes. Here we will investigate some effects of symmetry and periodicity on the potential energy surface for the hexagonal ice, but otherwise let the single well be the same as used for ASW.

Three simple models from the literature will be briefly described in the context of H and D atom transitions between adjacent minima on hexagonal ice. The reader is reminded that in all cases the underlying ice is treated as frozen and thus the hydrogen atom is the only moving species, thereby making the problem three-dimensional.

5.1 Isolated Double Wells

Let us first gain some understanding of the KIE by modelling the transition on I_h as a transition from one well to the other in a symmetric double well potential. A symmetric double well is only a suitable model if the adjacent potential minima are equally deep. This model is useful for an ideal hexagonal crystalline surface, but not for ASW where the wells are of clearly different depths.

We begin with the particle localized in the left hand side well and calculate the time it takes for it to move to the right hand side well. Assume that we begin with a particle described by a superposition Ψ(t = 0) of equal weights of the lowest symmetric (ψ_s) and antisymmetric (ψ_a) eigenstates of the double well with energy eigenvalues E_s and E_a respectively. We write

$\mathrm{\Psi }\left(t=0\right)=\frac{1}{\sqrt{2}}\left({\psi }_s\left(t=0\right)+{\psi }_a\left(t=0\right)\right),(9)$

and let this correspond to the particle being localized in the left well at t = 0.

Since ψ_s and ψ_a are eigenstates we have that

${\psi }_s\left(t\right)=e^{-i\widehat{H}t/\hslash }{\psi }_s\left(t=0\right)=e^{-i{E}_{s}t/\hslash }{\psi }_s\left(t=0\right),(10)$

and similarly

${\psi }_a\left(t\right)=e^{-i\widehat{H}t/\hslash }{\psi }_a\left(t=0\right)=e^{-i{E}_{a}t/\hslash }{\psi }_a\left(t=0\right).(11)$

We want to know the first time when the particle has become localized in the right hand side well, i.e. when

$\mathrm{\Psi }\left(t\right)=\frac{1}{\sqrt{2}}\left({\psi }_s\left(t=0\right)-{\psi }_a\left(t=0\right)\right).(12)$

Thus, we search for the first time t = τ when E_at/ℏ = E_st/ℏ + π, which gives

$\tau =\frac{\pi \hslash }{\mathrm{\Delta }{E}_{as}}(13)$

where ΔE_as = E_a − E_s.

The time τ is the time it takes to move between the two wells. If left alone, i. e undisturbed in the double well, the particle would continue to oscillate back and forth between the two wells forever. Thus, the double well model can only lead to a diffusive motion if something disturbs the particle after each hop. Such a disturbance could come from the lattice motion that realistically takes place. We will return to this below.

Let us now apply the isolated double well model to describe tunnelling of an H atom between two adjacent wells on the hexagonal ice. We therefore create a one-dimensional effective potential along the reaction path between representative adjacent minima. Using this effective potential we will then calculate the quantum motion.

We consider the jumps to occur between adjacent hexagons on I_h. Since the actual geometries are taken from the surface obtained by Andersson et al. (2006) by taking snapshots from molecular dynamics simulations, the surface is not perfectly periodic. Here we will however treat the two adjacent sites such that they together form a symmetric double well.

Looking at the actual jumps that occur on our model surface we find that the separations between the centres of the adjacent hexagonal sites are all roughly the same and close to 4.5 Å, so we use this value. In order to illustrate the KIE we choose the same transition as in the previous section with the classical barrier height 11.65 meV. In the reactant well of the considered transition, the motion of the H atom gives rise to three vibrational frequencies. The numerical values of the angular frequencies are 21.8, 23.2 and 24.7 (ps)⁻¹ in the harmonic approximation, Table 1. We take the smallest frequency to correspond to the reaction coordinate.

Next we calculate harmonically the zero point energy from the two frequencies that are orthogonal to the reaction coordinate at the minimum and add it to the classical potential. By similarly adding the zero point energy for the two real frequencies at the saddle point (17.4 and 26.2 (ps)⁻¹), an effective barrier height of 10.22 meV is obtained. Note here that this is not the VAG barrier height, as the zero point energy of one of the reactant vibrations has not been included. For this particular transition the VAG barrier height is 3.04 meV, Table 1. The reason for not including the reactant zero point energy of the motion assumed to correspond to the reaction coordinate is that this degree of freedom will be treated quantum dynamically and therefore the corresponding zero point energy will be included in that way.

We now have enough information (effective barrier height and distance between minima) to uniquely set the parameters E₀ and C in the symmetric double well potential

$V\left(x\right)=E_0\left(C{x}^4-x^2\right)(14)$

which we will use to describe the H atom tunnelling. We obtain E₀ = 4.1556 × 10^–5 Hartree/bohr² and C = 0.0276571492 bohr⁻². Given this double well potential we can work out the energy eigenvalues. We have used the Numerov method (Press, 1988) to do this and find the separation between the two lowest eigenvalues to be ΔE_as = 0.501 cm⁻¹ for the H atom.

Following the same procedure as above but for deuterium instead of protium we find that the same transition now gives an effective barrier height of 10.64 meV and a tunnelling splitting ΔE_as = 0.024 cm⁻¹. This is a factor of about 20 lower than for H and thus the rate for moving between wells would also be about a factor 20 lower than for the H atom.

The isolated double well described above gives rise to a motion where the particle in it oscillates back and forth between the individual wells. This is not a diffusive motion. If somehow this oscillation was disturbed and the particle instead coupled to and underwent transition into yet another well, and so on, perhaps a diffusive motion could result. At first sight this would suggest a KIE of about 20 since the H atoms moves about a factor 20 faster than the D atom. In the next subsection we will take a closer look at a case where the double well is not isolated but interacts weakly with the surrounding lattice. We also note that the KIE obtained by Kuwahata et al. (2015) for high fluxes is about a factor of six larger than the value of 20 just hinted at for an isolated double well.

5.2 Double Wells With Lattice Interaction

The double well description given above makes a number of assumptions. One is that the ice is rigid. The interaction potential between the adsorbate and the double well is therefore constant over time. We may view this as the double well being isolated form the rest of the lattice. In reality the ice lattice is not rigid and the interaction of the adsorbate with any lattice site therefore fluctuates over time. Let us therefore now allow for a weak interaction between the double well and the remaining lattice. Then a perturbation treatment is reasonable.

The perturbation can be anything that affects the motion of the particle from one well to the other. In the present case it is the vibrations of the lattice that perturbs this motion. For perturbation theory to hold, the perturbation should only have a small effect on the motion, not a drastic effect. To find the hopping rate between adjacent sites we follow a proceudre used for instance by Sundell and Wahnström (2004) in the context of hydrogen diffusion on a copper surface. We can then use the expression (Kua et al., 2001; Sundell and Wahnström, 2004),

${\mathrm{\Gamma }}_0=\frac{2\pi {\mathrm{\Delta }}_0^2}{{\hslash }^2{\omega }_1}.(15)$

Here Γ₀ is the hopping rate between the two wells (starting conditions as in Eq. (9)) and Δ₀ is a tunnelling matrix element calculated as half the energy splitting between the lowest even and odd states in the double well. ω₁ is the lowest vibrational excitation energy in the double well, which we using Eq. (14) evaluate harmonically to be

${\omega }_1=2\sqrt{E_0/m},(16)$

where m here is set to be the mass of H or D. This gives ω₁ = 12.5 (ps)⁻¹ for H and 9.0 (ps)⁻¹ for D.

The expression in Eq. (15) represents transitions involving only the lowest pair of states (one symmetric and one antisymmetric) and the results are that Γ₀ = 1.1 × 10⁹ s⁻¹ for H and Γ₀ = 3.7 × 10⁶ s⁻¹ for D, which gives a kinetic isotope effect of about 300. This value is thus larger than the experimentally determined KIE (Kuwahata et al., 2015).

In the previous paragraphs we looked at tunnelling by starting in a superposition with equal weights of the two lowest eigenstates of the symmetric double well. Let us next look at what happens if we instead were to start with a superposition with equal weights of the two states in the second lowest pair of states, using the same perturbation treatment as above. In this case we obtain Γ₁, which for H turns out to be 6.3 × 10¹¹ s⁻¹ and for D it is 1.4 × 10¹⁰ s⁻¹. This yields a KIE of 40–50.

At a finite temperature, the eigenstates of the double well would be populated according to a Boltzmann distribution (normalized to unity). We can therefore obtain the KIE for various temperatures by averaging the rate constants for the various states according to the thermal population of these states. Table 3 exemplifies results that can be obtained by doing this up to 25 K. From the table it can again be seen that the calculated KIE is very sensitive to the temperature and that it shows a minimum close to 15 K. Note that the table has been obtained using only the two lowest pairs of eigenstates (i.e. four states), which gives a high temperature limiting value of 44 for the KIE. In reality still higher eigenstates become populated as the temperature is raised. The double well with its infinite walls however can not be used to describe the actual lattice potential as the thermal energy comes close to the well depth. As mentioned before, the eigenstates of the double well have been obtained numerically exactly (thus not in the harmonic approximation).

TABLE 3

TABLE 3. KIE for a symmetric double well with a weak coupling to its environment. The potential parameters are the same as for the isolated double well. A Boltzmann weighting was performed assuming two energy levels, one at the energetic middle of the lowest pair of eigenstates of the isolated double well and one at the middle of the second lowest pair of states (with equal populations within each of the pairs).

5.3 The Kehr Model

A freely moving atom would have a thermal de Broglie wave length of

${\lambda }_{th}=\frac{\hslash }{\sqrt{m{k}_{B}T/2\pi }},(17)$

where m is atomic mass. At 10 K this expression evaluates to give ${\lambda }_{th}=5.5\mathring{A}$ for H and 3.9 $\mathring{A}$ for D. As the atom approaches the surface and interacts with it, it will localize. Still, it will be of interest to see what a band model would suggest for the KIE. We therefore assume the hexagonal ice to have a perfectly periodic potential, with the same well depth and distances as above. The eigenstates will then extend over the full length of the periodic potential.

We will employ a band model described by Kehr (1997). To obtain the tunneling splitting Kehr assumes that a one-dimensional potential may be written

$V\left(x\right)=\frac{1}{2}{V}_0\cos \left(2\pi x/l\right).(18)$

We set l = 4.5 Å and V₀ = 10.22 meV for H and 10.64 meV for D, as above. This thus implies that we consider the ice as frozen and harmonically account for the hydrogen vibrations orthogonal to the tunnelling direction.

The angular frequency along the reaction coordinate is for the potential in Eq. (18)

${\omega }_1=\frac{2\pi }{l}\sqrt{V_0/\left(2m\right)},(19)$

which evaluates to 9.78 (ps)⁻¹ for H and 7.05 (ps)⁻¹ for D.

Kehr finds the tunnelling splitting from

$\mathrm{\Delta }=8\frac{{\hslash }^2}{2m{l}^2}{\left(\frac{2m{l}^2{V}_0}{{\hslash }^2}\right)}^{3/4}\exp \left[-\frac{2}{\pi }{\left(\frac{2m{l}^2{V}_0}{{\hslash }^2}\right)}^{\frac{1}{2}}\right],(20)$

In obtaining this equation it is assumed that V₀ ≫ ℏω₁.

Calculating a hopping rate as in Eq. (15) using Δ from Eq. (20) and ω₁ from Eq. (19) gives 3.0, ×, 10⁹ s⁻¹ for H and 1.1 × 10⁷ s⁻¹ for D, which yields a KIE of about 270. We may also note that if we had evaluated the Kehr model in 1D instead of 3D, i.e. using V₀ = 11.65 meV for both H and D, the KIE would have been about 280.

For the H atom the band width according to Eq. (20) is 0.045 meV. The band width is related to how localized H atom states in the (adjacent) wells couple to each other, again resulting from the localized state wave functions overlapping each other and thus giving an energy splitting. This band width is much smaller than the thermal energy at 10 K, which is k_BT = 0.86 meV. Thus, due to thermal motion, and additionally for a real ice also due to proton disorder in an otherwise perfectly hexagonal ice structure (Fletcher 1992; Buch et al., 2008), it is clear that the band model presented by Kehr (1997) is not realistic for the present case. This would also agree with the fact that in deriving it an assumption is that V₀ ≫ ℏω₁. This is not valid for the present case where for H this ratio is 1.6 and for D it is 2.3.

6 Discussion and Conclusions

As mentioned the present work has been inspired by the experimental work of Kuwahata et al. (2015) at 10 K, where they for instance state that tunnelling diffusion may occur for a short distance within each single crystal, whereas it should be highly suppressed for long-distance diffusion. This statement is fully supported by our results obtained using the Kehr model (Kehr 1997), described in Sec. 5.3. We find that the model is not applicable at 10 K, which supports that coherent tunnelling over several wells is not likely to happen.

We next discuss tunnelling over short distances on crystalline ice. The isolated symmetric double well model described in Sec. 5.1 represents an idealized case where we can numerically exactly calculate the time for a transition from one well to the other. For protium this time is 3.3 × 10^–11 s (for deuterium the corresponding time is 6.9, ×, 10^–10 s), assuming that we begin in a superposition of the two lowest eigenstates. If we start from a superposition of the next pair of vibrational eigenstates this time decreases markedly to become 2.8 × 10^–12 s (1.2 × 10^–10 s for D).

For a diffusion process to occur, the hydrogen atom must spend much longer time in a well waiting to jump to another, than the time that the actual jump takes. Otherwise the jumps may be correlated and not correspond to a diffusion process. The transition times mentioned in the previous paragraph correspond to the time the transition takes for a symmetric double well potential. In reality self-trapping and coupling to the thermal motion of the lattice would cause the transition time to be longer as we would have to wait for the lattice to thermally end up in a geometry that would correspond to a symmetric double well potential, thereby allowing fast tunnelling. In this way a diffusion process can occur.

In our supposedly most realistic model of the ones employed, a symmetric double well (DW) interacts weakly with the lattice. In this model we have approximately accounted for the interaction with the lattice vibrations, but not for self-trapping (or electron drag, should that matter). For this case, from the transition rates, we obtain lifetimes for how long time it takes for half of the population to move from one well to the other, i.e. the half-life. For protium the half-lives are 6.2 × 10^–10 s, 4.8 × 10^–10 s and 2.3 × 10^–11 s at 0 K, 10 and 25 K respectively. For TST the half-lives are 1.1 × 10^–10 and 9.7 × 10^–12 at 10 and 25 K respectively, while at 0 K the half-life goes to infinity. These half-lives, together with the tunnelling times for the isolated DW, suggest that at these temperatures the H atoms predominantly move by diffusion on the surface. As the temperature is further increased, however, a more fluid-like motion rather than a diffusive motion becomes more and more important (as does desorption).

The DW model accounts for tunnelling through the barrier while TST, without tunnelling correction, accounts for transitions above the barrier. Summing these two contributions up should thus roughly give us the total rate constant for transition from one well to the next. In Figure 1 this is illustrated for protium. We notice that k (T) approaches a constant value as T decreases. This can be seen to be due to the rate becoming limited by tunnelling from the lowest pair of eigenstates in the double well. This happens just above 7 K, which agrees with the cross over temperature being 7.2 K.² As the temperature increases above 7 K, TST makes the dominant contribution to the thermal rate constant, indicating that over-barrier jumps dominate.

FIGURE 1

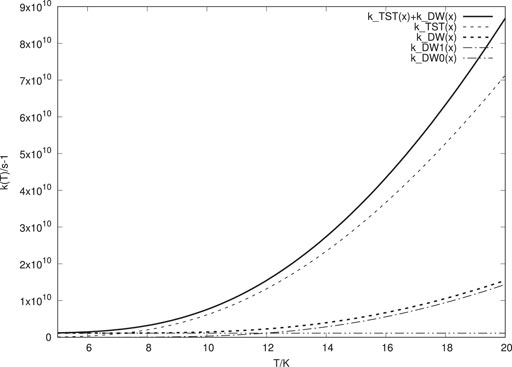
FIGURE 1. Thermal rate constants for H atom transitions between wells. “k-TST (x)” is the TST rate constant. “k-DW(x)” is the tunnelling rate constant for the double well with lattice interaction. “k-DW0 (x)” is the contribution to “k-DW (x)” from the lowest pair of eigenstates, while “k-DW1 (x)” is the contribution from the next pair of eigenstates. “k-TST(x)+k-DW (x)” is the total rate constant obtained as a sum of “k-TST (x)” and “k-DW (x)”.

In Figure 2, k (T) for deuterium is shown. As can be expected, in this case TST contributes even more than what tunnelling does in comparison to the H atom case. From the total rate constants for H and D transitions, we can obtain values for the KIE for various temperatures as illustrated in Figure 3. We notice that the KIE obtained is extremely sensitive to the temperature. At 10 K the calculated KIE is much lower (about a factor of six) than the experimentally estimated value. At 7 K, however, the calculated value has increased to coincide with the experimental value.

FIGURE 2

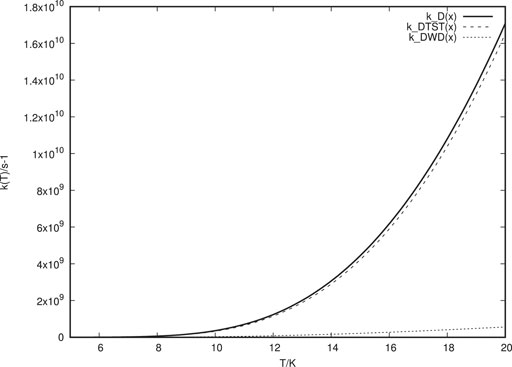
FIGURE 2. Thermal rate constants for D atom transitions between wells. “k-DTST (x)” is the TST rate constant. “k-DWD (x)” is the tunnelling rate constant for the double well with lattice interaction. “k-D(x)” is the total rate constant obtained as a sum of “k-DTST (x)” and “k-DWD (x)”.

FIGURE 3

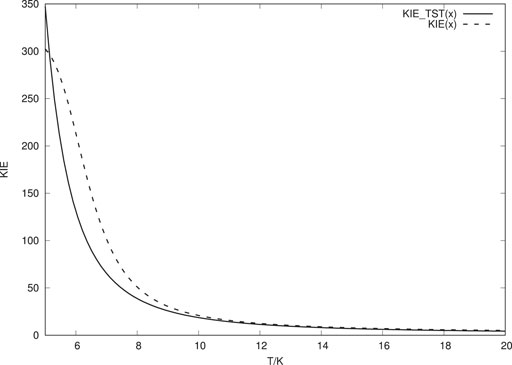
FIGURE 3. KIE as a function of temperature. “KIE (x)” shows the total KIE, while “KIE-TST” shows the KIE obtained from the TST contribution to the total hop rate.

In Figure 3 we also show the KIE that is obtained from the TST analyses only, i.e. over the barrier transitions. Since the vibrational partition functions are very close to unity (ZPE level as reference), this KIE is determined by the difference in VAG barrier height. Even if the classical potential barrier height is in error, this does not affect the KIE calculated by TST, beyond changes in vibrational frequencies. The TST contribution is thus likely less sensitive to the potential than what the tunneling contribution is. For the ASW, we expect much smaller tunnelling contribution than for the crystalline ice. We note that for the ASW, the TST KIE agrees with the experimentally derived KIE.

One explanation for the fact that we cannot reproduce the experimentally derived KIE on I_h could be that the height and/or shape of the employed potential is inaccurate. The calculated KIE for ASW hinges on the difference in TST rate constants for H and D, which in turn hinges on the difference in ΔE^VAG, which hinges on the vibrational frequencies and only indirectly on the barrier height itself. The tunnelling contribution to the KIE, which is more important for I_h, depends strongly on the barrier height and width. In addition, in the present double well calculations the KIE depends on at which temperature contributions from the excited pair of eigenstates kick in noticeably. If the energy level of the second pair of eigenstates is raised, its contribution, which lowers the KIE, decreases at a given temperature and thus the KIE will increase at a given temperature. In order to reproduce the experimentally deduced KIEs, the tunnelling contribution would need to be larger. This suggests that an increase in barrier height and/or width, which would increase the KIE for I_h much more than for ASW, would lead to better agreement with the experimental results.

The work on model potentials presented here has been aimed at giving basic insights into, and qualitative understanding of, the kinetic isotope effects observed by Kuwahata et al. (2015). Clearly, for quantitative results, other calculations using accurately determined potentials rather than the model potentials employed here would be useful. It should also be kept in mind that even the fairly smooth I_h surface does in reality show disorder even at short range, so that a single well with a single barrier height and no self-trapping will not capture all aspects of the adsorbate-ice interaction.

In conclusion we have found that transition state theory explains the experimentally found kinetic isotope effect on ASW. This supports the conclusion of Kuwahata et al. (2015) that for the ASW surface diffusion is predominantly thermal hopping rather than tunnelling. On the other hand, transition state theory does not explain the larger kinetic isotope effect on PCI. Our calculations indicate that a substantial tunneling contribution is required to explain the KIE on Ih. This agrees with the conclusion of Kuwahata et al. (2015). Further, Kuwahata et al. (2015) indicate that diffusion by tunnelling is temperature independent. From Figure 1 we see that this agrees with the present calculations up to say 10 K for H atom tunnelling, but for higher temperatures the tunnelling rate becomes more and more dependent on temperature. For the D atom, the transition from temperature independent to temperature dependent tunnelling occurs at a slightly lower temperature than for the H atom.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work has in part been funded by the European Community FP7-ITNMarie-Curie Programme (LASSIE 366 project, grant agreement no. 238258) and the Swedish Research Council through grant 2020-05293.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author would like to thank Bethmini Senevirathne for providing the classical barrier height and the vibrational frequencies used.

Footnotes

¹For a regular lattice where all k_i are the same, the diffusion constant is sometimes calculated as D = l²k_i/4, where l is the lattice spacing (Kua et al., 2001).

²We note that the tunnelling splitting between the two lowest eigenstates of the isolated double well is 0.5 cm⁻¹ (or 0.7 K). Thus, roughly equal population of these two states is less probable at really low temperatures

References

Al-Halabi, A., and van Dishoeck, E. F. (2007). Hydrogen Adsorption and Diffusion on Amorphous Solid Water Ice. Monthly Notices R. Astronomical Soc. 382, 1648–1656. doi:10.1111/j.1365-2966.2007.12415.x

CrossRef Full Text | Google Scholar

Amiaud, L., Dulieu, F., Fillion, J.-H., Momeni, A., and Lemaire, J. L. (2007). Interaction of Atomic and Molecular Deuterium with a Nonporous Amorphous Water Ice Surface between 8 and 30K. J. Chem. Phys. 127, 144709. doi:10.1063/1.2746323

CrossRef Full Text | Google Scholar

Andersson, S., Al-Halabi, A., Kroes, G.-J., and van Dishoeck, E. F. (2006). Molecular-dynamics Study of Photodissociation of Water in Crystalline and Amorphous Ices. J. Chem. Phys. 124 (6), 064715. doi:10.1063/1.2162901

CrossRef Full Text | Google Scholar

Augason, G. C. (1970). The Formation of Interstellar Molecular Hydrogen by Physical Adsorption on Grains. ApJ 162, 463. doi:10.1086/150679

CrossRef Full Text | Google Scholar

Buch, V., Groenzin, H., Li, I., Shultz, M. J., and Tosatti, E. (2008). Proton Order in the Ice crystal Surface. Proc. Natl. Acad. Sci. 105, 5969–5974. doi:10.1073/pnas.0710129105

PubMed Abstract | CrossRef Full Text | Google Scholar

Fletcher, N. H. (1992). Reconstruction of Ice crystal Surfaces at Low Temperatures. Philosophical Mag. B 66, 109–115. doi:10.1080/13642819208221298

CrossRef Full Text | Google Scholar

Fredon, A., and Cuppen, H. M. (2018). Molecular Dynamics Simulations of Energy Dissipation and Non-thermal Diffusion on Amorphous Solid Water. Phys. Chem. Chem. Phys. 20, 5569–5577. doi:10.1039/c7cp06136f

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibb, E. L., Whittet, D. C. B., Schutte, W. A., Boogert, A. C. A., Chiar, J. E., Ehrenfreund, P., et al. (2000). An Inventory of Interstellar Ices toward the Embedded Protostar W33A. ApJ 536, 347–356. doi:10.1086/308940

CrossRef Full Text | Google Scholar

Goodman, F. O. (1978). Formation of Hydrogen Molecules on Interstellar Grain Surfaces. ApJ 226, 87–94. doi:10.1086/156588

CrossRef Full Text | Google Scholar

Gould, R. J., and Salpeter, E. E. (1963). The Interstellar Abundance of the Hydrogen Molecule. I. Basic Processes. ApJ 138, 393. doi:10.1086/147654

CrossRef Full Text | Google Scholar

Hama, T., Kuwahata, K., Watanabe, N., Kouchi, A., Kimura, Y., Chigai, T., et al. (2012). The Mechanism of Surface Diffusion of H and D Atoms on Amorphous Solid Water: Existence of Various Potential Sites. ApJ 757, 185. doi:10.1088/0004-637x/757/2/185

CrossRef Full Text | Google Scholar

Hänggi, P., Talkner, P., and Borkovec, M. (1990). Reaction-rate Theory: Fifty Years after Kramers. Rev. Mod. Phys. 62, 251–341. doi:10.1103/revmodphys.62.251

CrossRef Full Text | Google Scholar

Hollenbach, D., and Salpeter, E. E. (1970). Surface Adsorption of Light Gas Atoms. J. Chem. Phys. 53, 79–86. doi:10.1063/1.1673836

CrossRef Full Text | Google Scholar

Hollenbach, D., and Salpeter, E. E. (1971). Surface Recombination of Hydrogen Molecules. ApJ 163, 155. doi:10.1086/150754

CrossRef Full Text | Google Scholar

Hornekaer, L., Baurichter, A., Petrunin, V. V., Field, D., and Luntz, A. C. (2003). Importance of Surface Morphology in Interstellar H2 Formation. Science 302, 1943–1946. doi:10.1126/science.1090820

PubMed Abstract | CrossRef Full Text | Google Scholar

Jura, M. (1975). Interstellar Clouds Containing Optically Thin H2. ApJ 197, 575–580. doi:10.1086/153545 ,

CrossRef Full Text | Google Scholar

Karssemeijer, L. J., de Wijs, G. A., and Cuppen, H. M. (2014). Interactions of Adsorbed CO2 on Water Ice at Low Temperatures. Phys. Chem. Chem. Phys. 16, 15630–15639. doi:10.1039/c4cp01622j

PubMed Abstract | CrossRef Full Text | Google Scholar

Katz, N., Furman, I., Biham, O., Pirronello, V., and Vidali, G. (1999). Molecular Hydrogen Formation on Astrophysically Relevant Surfaces. ApJ 522, 155–164. doi:10.1086/307642

CrossRef Full Text | Google Scholar

Kehr, K. W. (1997). in Hydrogen in Metals I: Basic Properties, Vol. 28 of Topics in Applied Physics. Editor H. Wipf (Berlin: Springer-Verlag). Chap. 2.

Google Scholar

Kua, J., Lauhon, L. J., Ho, W., and Goddard, W. A. (2001). Direct Comparisons of Rates for Low Temperature Diffusion of Hydrogen and Deuterium on Cu(001) from Quantum Mechanical Calculations and Scanning Tunneling Microscopy Experiments. J. Chem. Phys. 115, 5620–5624. doi:10.1063/1.1396815

CrossRef Full Text | Google Scholar

Kuwahata, K., Hama, T., Kouchi, A., and Watanabe, N. (2015). Signatures of Quantum-Tunneling Diffusion of Hydrogen Atoms on Water Ice at 10 K. Phys. Rev. Lett. 115 (13), 133201. doi:10.1103/physrevlett.115.133201

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T. J. (1972). Formation of Interstellar Molecular Hydrogen. Nat. Phys. Sci. 237, 99–100. doi:10.1038/physci237099a0

CrossRef Full Text | Google Scholar

Manicò, G., Ragunì, G., Pirronello, V., Roser, J. E., and Vidali, G. (2001). Laboratory Measurements of Molecular Hydrogen Formation on Amorphous Water Ice. ApJL 548, L253–L256. doi:10.1086/319116

CrossRef Full Text | Google Scholar

Matar, E., Congiu, E., Dulieu, F., Momeni, A., and Lemaire, J. L. (2008). Mobility of D Atoms on Porous Amorphous Water Ice Surfaces under Interstellar Conditions. A&A 492, L17–L20. doi:10.1051/0004-6361:200810434

CrossRef Full Text | Google Scholar

Perets, H. B., Biham, O., Manicó, G., Pirronello, V., Roser, J., Swords, S., et al. (2005). Molecular Hydrogen Formation on Ice under Interstellar Conditions. ApJ 627, 850–860. doi:10.1086/430435

CrossRef Full Text | Google Scholar

Pirronello, V., Biham, O., Liu, C., Shen, L., and Vidali, G. (1997a). Efficiency of Molecular Hydrogen Formation on Silicates. ApJ 483, L131–L134. doi:10.1086/310746

CrossRef Full Text | Google Scholar

Pirronello, V., Liu, C., Roser, J. E., and Vidali, G. (1999). Measurements of Molecular Hydrogen Formation on Carbonaceous Grains. A& A 344, 681–686.

Google Scholar

Pirronello, V., Liu, C., Shen, L., and Vidali, G. (1997b). Laboratory Synthesis of Molecular Hydrogen on Surfaces of Astrophysical Interest. ApJ 475, L69–L72. doi:10.1086/310464

CrossRef Full Text | Google Scholar

Press, W. H. (1988). Numerical Recipes C Diskette V1.3.

Google Scholar

Senevirathne, B., Andersson, S., Dulieu, F., and Nyman, G. (2017). Hydrogen Atom Mobility, Kinetic Isotope Effects and Tunneling on Interstellar Ices (I and ASW). Mol. Astrophysics 6, 59–69. doi:10.1016/j.molap.2017.01.005

CrossRef Full Text | Google Scholar

Smoluchowski, R. (1983). Adsorption and Mobility on Amorphous Surfaces. Application to Astrophysical Problems. J. Phys. Chem. 87, 4229–4233. doi:10.1021/j100244a050

CrossRef Full Text | Google Scholar

Smoluchowski, R. (1979). Formation of H2 on Amorphous Ice Grains and Their Importance for Planetary Atmospheres. Astrophys Space Sci. 65, 29–38. doi:10.1007/bf00643487

CrossRef Full Text | Google Scholar

Smoluchowski, R. (1981). Rate of H2 Formation on Amorphous Grains. Astrophys Space Sci. 75, 353–363. doi:10.1007/bf00648648

CrossRef Full Text | Google Scholar

Sundell, P. G., and Wahnström, G. (2004). Quantum Motion of Hydrogen on Cu(001) Using First-Principles Calculations. Phys. Rev. B 70, 081403. doi:10.1103/physrevb.70.081403

CrossRef Full Text | Google Scholar

Tielens, A. G. G. M., and Hagen, W. (1982). Model Calculations of the Molecular Composition of Interstellar Grain, Aug. 2005. Mantles Astron. Astrophys.The Phys. Chem. Interstellar Medium 114, 225–260.

Google Scholar

Wakelam, V., Bron, E., Cazaux, S., Dulieu, F., Gry, C., Guillard, P., et al. (2017). H 2 Formation on Interstellar Dust Grains: The Viewpoints of Theory, Experiments, Models and Observations. Mol. Astrophysics 9, 1–36. doi:10.1016/j.molap.2017.11.001

CrossRef Full Text | Google Scholar

Watanabe, N., Kimura, Y., Kouchi, A., Chigai, T., Hama, T., and Pirronello, V. (2010). Direct Measurements of Hydrogen Atom Diffusion and the Spin Temperature of Nascent H 2 Molecule on Amorphous Solid Water. ApJ 714, L233–L237. doi:10.1088/2041-8205/714/2/l233

CrossRef Full Text | Google Scholar

Watson, W. D., and Salpeter, E. E. (1972). Molecule Formation on Interstellar Grains. ApJ 174, 321. doi:10.1086/151492

CrossRef Full Text | Google Scholar

Wigner, E. (1932). Über das Überschreiten von Potentialschwellen bei chemischen Reaktionen. Z. ür Physikalische Chem. B 19B, 203–216. doi:10.1515/zpch-1932-1920

CrossRef Full Text | Google Scholar

Williams, D. A. (1968). Physical Adsorption Processes on Interstellar Graphite Grains. ApJ 151, 935. doi:10.1086/149494

CrossRef Full Text | Google Scholar