- 1Department of Physics and Astronomy, Louisiana State University, Baton Rouge, LA, Unites States
- 2Department of Physics, National Institute of Technology Karnataka, Surathkal, India
Anomalies in the cosmic microwave background (CMB) refer to features that have been observed, mostly at large angular scales, and which show some tension with the statistical predictions of the standard ΛCDM model. In this work, we focus our attention on power suppression, dipolar modulation, a preference for odd parity, and the tension in the lensing parameter AL. Though the statistical significance of each individual anomaly is inconclusive, collectively they are significant, and could indicate new physics beyond the ΛCDM model. In this article, we present a brief, but pedagogical introduction to CMB anomalies and propose a common origin in the context of loop quantum cosmology.
I Introduction
Observations of the cosmic microwave background (CMB) by the Planck satellite have revealed that the ΛCDM model together with the inflationary scenario checks nearly all the right boxes (Aghanim, 2018a; Akrami, 2018; Aghanim, 2020)—in the sense that it provides a detailed fit to the CMB spectrum based on a few free parameters (Aghanim, 2018a; Aghanim, 2019). The nearly scale-invariant power spectrum predicted by slow-roll inflation has been confirmed with a significance of more than 7σ (Aghanim, 2018b; Akrami, 2018). Further, observations are consistent with the near Gaussian nature of the primordial perturbations predicted by slow-roll inflation (Akrami, 2020).
But in spite of this success, several open questions remain. A prominent one concerns the past incompleteness of the inflationary scenario. As it is well known, general relativity, on which the inflationary scenario rests, breaks down as we approach the Planck regime. Loop quantum cosmology (LQC) uses the principles of loop quantum gravity to address this issue (Bojowald, 2001; Ashtekar et al., 2003; Mena Marugan, 2010; Ashtekar and Singh, 2011; Banerjee et al., 2012; Agullo et al., 2014; Agullo et al., 2017a). In LQC, the big bang singularity is replaced by a bounce (Ashtekar et al., 2006a; Ashtekar et al., 2006b; Ashtekar et al., 2007; Szulc, 2007; Szulc et al., 2007; Bentivegna and Pawlowski, 2008; Martin-Benito et al., 2008; Ashtekar and Wilson-Ewing, 2009a; Ashtekar and Wilson-Ewing, 2009b; Garay et al., 2010; Wilson-Ewing, 2010; Pawlowski and Ashtekar, 2012) which is triggered by quantum gravitational effects. This bounce by itself is not able to generate the primordial perturbations though, and it must be complemented with another mechanism. A natural strategy is to maintain the inflationary phase in the post-bounce era. In such a scenario, the goal of the bounce is, in addition to overcoming the difficulties arising from classical general relativity, to bring the Universe to an inflationary phase. Interestingly, although the inflationary phase is responsible for the primordial perturbations, certain features from the pre-inflationary bounce may survive if the inflationary era is not too long, and be imprinted in the CMB. Numerous studies have examined the way the bounce predicted by LQC modifies the primordial power spectra of scalar and tensor perturbations (Bojowald et al., 2009; Bojowald and Calcagni, 2011; Agullo et al., 2012; Agullo et al., 2013a; Agullo et al., 2013b; Fernández-Méndez et al., 2013; Fernández-Méndez et al.,2014; Agullo and Morris, 2015; Barrau et al., 2015; de Blas and Olmedo, 2016; Martínez and Olmedo, 2016; Ashtekar and Gupt, 2017; Agullo et al., 2017b; Castelló Gomar et al., 2017; Zhu et al., 2017; Agullo, 2018; Agullo et al., 2020a; Agullo et al., 2020b; Li et al., 2020a; Li et al., 2020b; Ashtekar et al., 2020; Navascués et al., 2020; Navascués and Mena Marugán, 2020; Martín-Benito et al., 2021) and the non-Gaussianity (Agullo, 2015; Agullo et al., 2018; Zhu et al., 2018; Sreenath et al., 2019) at large angular scales, and showed that at smaller scales in the CMB the predictions are indistinguishable from those of standard inflation with Bunch-Davies initial conditions. Hence, if at all early Universe scenarios such as LQC were to leave any imprints on the CMB, they would be expected at the longest observable scales, or equivalently, at the lowest angular multipoles.
It is for this reason that certain puzzling signatures which have been recently observed at large angular scales in the CMB become relevant (Akrami et al., 2019). These signatures, generically known as CMB anomalies, are features that are in conflict with the almost scale invariance predicted by inflation, or with the statistical isotropy and homogeneity assumed in the ΛCDM. In more detail, the anomalies observed by Planck include a lack of two-point correlations at large angular scales, a dipolar asymmetry, a preference for odd parity, alignment of low multipoles, a cold spot, etc. In addition, the Planck analysis has also found a preference for a larger value of the lensing parameter (Aghanim, 2018b) than it is expected. Some of these anomalies were already observed by the WMAP satellite and even by COBE. Hence, the consensus is that these signals are not due to unaccounted systematics. Put it simply, there is no debate about the fact that these are real features in the CMB [see e.g., (Schwarz et al., 2016)]. However, the statistical significance with which these features depart from the predictions of the ΛCDM model is, though non-negligible, inconclusive, and the debate is rather whether any of these features are significant enough to require the introduction of new physics. Recall that the ΛCDM only makes statistical predictions, and therefore none of these features are actually incompatible with ΛCDM. But if we accept the ΛCDM model, the observed features imply that we live in an uncommon realization of the underlying probability distribution. Another possibility is that some or all these features are signatures of new physics, and they are in fact expected signals in a suitable extension of the ΛCDM theory.
In recent work (Agullo et al., 2021a; Agullo et al., 2021b) we proposed that a cosmic bounce before inflation naturally changes the primordial probability distribution in such a way that, in a statistical sense, the observed features are not anomalous. The core of the idea is that a cosmic bounce generates strong correlations (non-Gaussianities) between the longest modes we observe in the sky and longer, super-horizon modes. We cannot observe directly these correlations since some of the modes involved have wave-lengths larger than the Hubble radius today. But these correlations produce indirect effects in observable modes, which can account for the observed anomalies. The goal of this article is to apply the general ideas introduced in (Agullo et al., 2021a; Agullo et al., 2021b) to LQC. We will also take the opportunity to provide a succinct and pedagogical introduction to CMB anomalies and the phenomenon of non-Gaussian modulation, addressed to the quantum cosmology community. See (Agullo and Morris, 2015; de Blas and Olmedo, 2016; Ashtekar and Gupt, 2017; Agullo et al., 2020a; Ashtekar et al., 2020; Agullo et al., 2020b) for other ideas to account for some of the features observed in the CMB within LQC. In particular, the companion article (Ashtekar et al., 2021) in this special issue, provides an interesting set of complementary ideas and perspectives on the way LQC can account for the CMB anomalies.
The plan of this article is as follows. In the next section, we discuss the basic principles behind quantifying temperature anisotropy and discuss the implications of statistical homogeneity and isotropy for CMB anisotropies. Then, we describe some of the anomalies observed by the Planck satellite, which point to a violation of the underlying assumption of statistical homogeneity and isotropy. In section III, we describe the mechanism behind the phenomenon of non-Gaussian modulation. In section IV, we provide a quick description of the evolution of perturbations in LQC and discuss the power spectrum and bispectrum generated therein. We then apply non-Gaussian modulation to LQC in section V and present our results. In this section, we describe how the presence of non-Gaussian modulation in LQC makes these anomalous features more likely to occur, in a way that they are no longer anomalous. Finally, in section VI, we conclude with a discussion of our results, its short comings, and future directions.
II Introduction to CMB Anomalies
The temperature
where in the last equality we have decomposed the function
The ΛCDM model predicts only the statistical properties of the temperature map
In other words, homogeneity and isotropy imply that all information contained in the second moments can be codified in the m-independent coefficients Cℓ, for ℓ = 1, 2, 3, …. Cℓ is known as the angular power spectrum.
The equivalent statement in angular space is that the second moments of
If the assumptions of statistical homogeneity and isotropy break down, then the simple characterization of the two-point correlations in terms of the simple quantity Cℓ or C(θ) becomes insufficient, and one would have to work with the full covariance matrix of aℓm or
The angular power spectrum Cℓ is measured by averaging the data from satellites. But, what is the correct notion of average? Ideally, one would like to have different realizations of the probability distribution (that is, different universes) and take averages on them, which is closer to the way averages are measured in quantum systems. Another possibility is to take averages over the CMB temperature map observed from different locations in the Universe. The ergodic theorem relates both averages. Unfortunately, none of these two strategies is available at the practical level. Rather, what is done in practice is to take advantage of the m-independence of the power spectrum Cℓ, and obtain it by averaging over its value obtained from individual m’s (we actually observe
Cosmic variance is an intrinsic limitation of cosmological observations, and cannot be overcome by building more precise instruments. Therefore, in making predictions for Cℓ or C(θ), one needs to keep in mind this inherent uncertainty.
We now discuss the anomalous features that have been observed in CMB. The Planck team has carried out several tests to check the statistical isotropy of the CMB (Ade, 2014; Ade, 2016a; Akrami et al., 2019). The CMB is a spherical shell of radiation, which captures a spherical sample of the density perturbations at the time of decoupling in the early Universe. Hence, deviations from isotropy in the CMB sphere will signal deviation from statistical homogeneity or isotropy in the early Universe. Since, as emphasized above, the predictions from the ΛCDM model are statistical, a key aspect of the analysis is to quantify the statistical significance of any observed departure from the theory. In statistical parlance, this is known as hypothesis testing, wherein a null hypothesis, which in this case is the ΛCDM model, is compared with observations. The departure from the null hypothesis is often quantified in terms of the so called p-value. Given a null hypothesis, the p-value is the probability with which a certain phenomenon can occur. If the p-value of an observed feature is zero, the null hypothesis is automatically considered as incorrect. A very small value of the p-value, would rather rule out the hypothesis with a statistical significance given by 1 − p. The concept is visually illustrated in Figure 1: the p-value corresponds to the area of the shaded region.
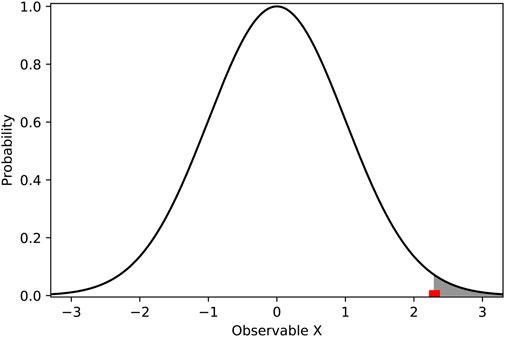
FIGURE 1. Illustration of the concept of p-value. The figure shows the probability distribution of a certain observable X according to the null hypothesis in black. The value of X that is actually observed is shown in red. Although the expected value of X is zero, the observation is not incompatible with the theoretical prediction, given the statistical character of the later. The shaded area gives us the p-value of the observed value of X. As it is evident from the figure, a smaller p-value implies a larger departure from the null hypothesis.
In order to quantify an anomaly, the first step is to choose an observable of interest, which will serve as the indicator of the anomaly. Rather than analytically deriving the probability distribution of the chosen observable out of the theory, a task that may be difficult for some observables, in practice it is often more convenient to estimate the p-value numerically. This can be done by simulating a large number of random realizations of the CMB temperature map from the probability distribution of the ΛCDM model—using the best fit for the free parameters—and computing the p-value of the chosen observable from them. This is the way the Planck collaboration has evaluated the p-value of the anomalies discussed below (Ade, 2014; Ade, 2016b). For example, if only five simulations out of a thousand lead to a value of an observable which is at least as extreme as the observed value, they would report a p-value of 0.005 for that observation, or equivalently 0.5%. The anomalies considered in this article have p-value ≤ 1% (Schwarz et al., 2016). In the remaining part of this section, we briefly describe the anomalies that we consider in this article.
A Power Suppression
Data from the satellites COBE (Hinshaw et al., 1996), WMAP (Bennett et al., 2003) and Planck (Akrami et al., 2019), have consistently found a lack of two-point correlations at low multipoles, or at large angular scales, compared to what is expected in the ΛCDM model. Visually, this lack of correlations is evident in the real space two-point correlation function C(θ), shown in the right panel of Figure 2: for angles larger than 60°, the two-point function is surprisingly low. The WMAP team had come up with an appropriate observable to quantify this lack of power (Spergel et al., 2003). It is defined by
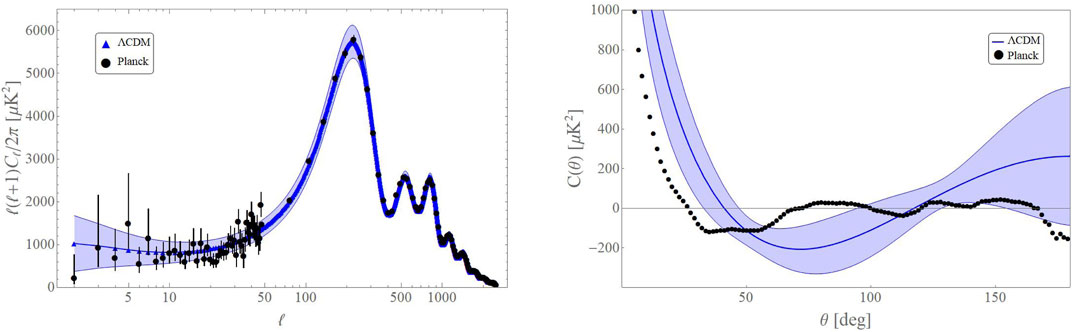
FIGURE 2. The TT power spectrum in the multipole (A) and angular space (B) generated in the standard model corresponding to the best fit parameters provided by Planck. The blue shaded region indicates the uncertainty due to cosmic variance. The black dots with error bars are the data from Planck. Note that the observed quadrupole is quite low compared to the prediction from the standard model, although it is compatible with the prediction within 1σ when we account for cosmic variance. The lack of power at large angular scales is more evident in the angular power spectrum, where the power is considerably low for angular scales greater than 60°. Furthermore, the amplitude of the predicted power is larger than the observed one by more than 1σ for the largest angular scales and for angles between ≈60° and 80°.
Its physical meaning is obvious: it captures the total amount of correlations squared (to avoid cancellations between positive and negative values of C(θ)) in angles θ > 60°. The ΛCDM model predicts S1/2 ≈ 42000 μK4, while the Planck satellite has reported a measured value1 of S1/2 = 1,209.2 μK4 (Akrami et al., 2019), which corresponds to a p-value less than 1% [≤0.5% according to (SchwarzSchwarz et al., 2016)]. Put in simpler terms, this p-value tells us that if we were able to observe one thousand universes ruled out by the ΛCDM model, only about a handful will show such a low value of S1/2.
B Dipolar Modulation Anomaly
A second important anomaly that has been also observed by multiple satellites, is the presence of a dipolar modulation of the entire CMB signal (Akrami et al., 2019). This dipole should not be confused with the multipole ℓ = 1. Rather, the anomaly makes reference to correlations between multipoles ℓ and ℓ + 1, which can be explained by a modulation of dipolar character, as we further discuss below.
Such modulation was first modeled mathematically in (Gordon et al., 2005), by adding a simple dipole to the temperature map as follows
where
The Planck team has carried out a likelihood analysis of such modulation of the CMB, and arrived at constraints on the amplitude and direction of the dipolar modulation in different bins of multipoles ℓ. Surprisingly, the analysis has revealed a non-zero amplitude of the dipolar modulation only for low multipoles, in the bin ℓ ∈ [2, 64]. The amplitude reported in this bin is A1 ≈ 0.07 (Ade, 2016a), and the significance of the detection is greater than 3σ. This reveals, not only a significant deviation of the ΛCDM model, but also that the dipolar modulation is scale-dependent, since it only appears for low multipoles. Therefore, the simple model (Eq. 2.6) is insufficient to account for the observed modulation. Finding a mechanism to generate a scale-dependent dipolar modulation, without introducing other undesired effects, has challenged the imagination of theorists during the last decade (Dai et al., 2013).
C Parity Anomaly
Observations from both WMAP and Planck have found a preference for odd parity two-point correlations, as opposed to the predictions of the standard ΛCDM model, which predicts that the primordial perturbations generated in our Universe are parity neutral. The parity of the primordial perturbations can be studied by analyzing the multipoles in the range [2, 50], known as the Sachs-Wolfe plateau. This range of multipoles corresponds to long wavelength perturbations which entered the horizon in the recent past, and hence have been relatively unmodified by late time physics. The asymmetry in the parity can be quantified using the estimator
where D±(ℓmax) quantify the sum of power contained in even (+) or odd (−) multipoles, up to ℓmax. More specifically, D±(ℓmax) are defined as
where the + or − signs on the right refer to the fact that we include only even or odd multipoles in the sum, respectively, and
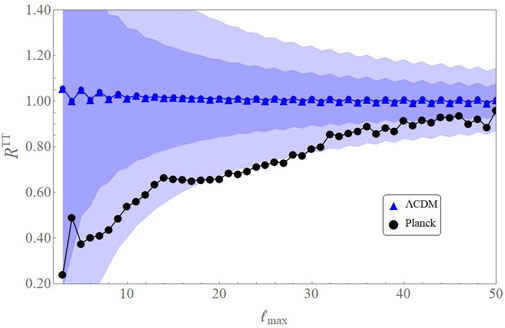
FIGURE 3. RTT(ℓmax) generated in the standard model (blue) along with 2σ shaded contours arising from cosmic variance. Black points are the observations by Planck. The observed value of RTT(ℓmax) for most points is lower than the predictions of the standard model by more than 1σ.
D Lensing Amplitude Anomaly
The cosmic microwave background radiation undergoes lensing by the intervening distribution of matter, as it propagates from the surface of last scattering to us. An important observable in the CMB, in addition to temperature and polarization, is the lensing potential. From the CMB maps, Planck has reconstructed the lensing potential and computed its power spectrum (Aghanim, 2018b). The effect of lensing is the smoothing of CMB power spectrum at small angular scales. The amount of smoothing observed in the CMB angular power spectrum should be consistent with the smoothing derived from the power spectrum of the lensing potential. In order to check this consistency, (Aghanim, 2018a), considered a test-parameter, known as the lensing parameter AL, that multiplies the lensing power spectrum. Theoretically, the value of lensing parameter should be AL = 1, and in fact Planck assumes this value during the process of parameter estimation. However, if AL is left as a free parameter, along with the six parameters of the ΛCDM model, in the Markov Chain Monte Carlo (MCMC) analysis, one finds that AL = 1.243 ± 0.096 for PlanckTT + lowE data, which is more than 2σ away from one. If the reconstructed lensing data is also used, along with Planck EE and TE data, then the lensing parameter is consistent with 1 within 2σ.
A key feature of the anomalies discussed above, except perhaps for the lensing anomaly, is that they appear clearly associated with the largest angular scales we can observe. This suggests a common origin in primordial physics for these diverse set of anomalies. The next section introduces a proposal for a mechanism that can provide such common origin, namely the phenomenon of non-Gaussian modulation. Together with the scale dependence introduced by the quantum bounce of LQC, this mechanism constitutes a promising candidate for the origin of the anomalies we have just described.
III Non-Gaussian Modulation
Temperature anisotropies in the CMB are a consequence of the evolution of photons and other constituents of the Universe in a perturbed spacetime. Since the observed anisotropies are small,
Primordial perturbations are random variables with zero mean and a variance characterized by the two-point correlations discussed in the previous section. We will show that one consequence of the coupling between super-horizon and sub-horizon wavelengths is to modify the two-point correlation functions (Schmidt and Hui, 2013; Agullo, 2015; Adhikari et al., 2016). Though the mean value of the primordial perturbations is not modified, the variance is, in such a way that certain features in the CMB are more likely to be observed than in the absence of non-Gaussian correlations, and consequently they should not be considered as anomalous. In this section, we will describe the essential features of the mechanism of non-Gaussian modulation. We will split the discussion in two parts: in the first one, we will discuss the modulation of the primordial power spectrum due to non-Gaussian correlations with a spectator mode, and in the second part, we describe the effect of such a modulation on the CMB TT angular power spectrum.
A Non-Gaussian Modulation of Primordial Perturbations
We are interested in computing the two-point correlation function of the curvature perturbation
A convenient and general way to model the effects of non-Gaussian correlations, is to write the curvature perturbations at a given time t in terms of a Gaussian field
The convolution in the integral is the Fourier transform of a quadratic combination of
Statistical isotropy and homogeneity implies that the function
and
The dimensionless power spectrum is defined as
Our goal is to compute the two-point function of
In order to evaluate the impact of the spectator modes
where the trailing dots indicate terms that are higher order in non-Gaussianity, and will be subdominant.
It is interesting to note the following facts about the above expression. First of all, non-Gaussianity leads to a modulation of the primordial power spectrum, and the strength of modulation depends on both the size and shape of
B Non-Gaussian Modulation of CMB
The primordial perturbations
where Δℓ(k) are the CMB temperature transfer functions, which encode the post-inflationary evolution of the perturbations from the re-entry of perturbations into the horizon during late radiation domination till today. From this equation, one can compute the covariance matrix
which is obtained from the two-point functions of the curvature perturbations given in (Eq. 3.5). Upon expanding fNL in terms of Legendre polynomials,
The above expression consists of two terms. The first term is the usual temperature power spectrum that is diagonal in ℓ and m. The second term arises from the non-Gaussian modulation and, as before, introduces non-diagonal terms.
These coefficients are known as bipolar spherical harmonic (BipoSH) coefficients (Hajian and Souradeep, 2003; Joshi et al., 2010). As we shall see, the BipoSH coefficients provide a convenient way to organize the effects of the non-Gaussian modulation.
The Clebsch-Gordan coefficients present in the above expressions enforce certain properties on the BipoSH coefficients. In particular, Clebsch-Gordan coefficients
i. L = 0, then ℓ1 = ℓ2
ii. L = 1, then |ℓ1 − ℓ2| = 1
iii. L = 2, then |ℓ1 − ℓ2| = 0, 2, etc.
Thus, a non-zero value of
Two remarks are in order now.
i. The strength of non-Gaussian modulation is dictated by the size of fNL(k1, q, μ). But it is the dependence of fNL on μ, the cosine of the angle between
ii.
where
These are the typical values that the BipoSH coefficients are expected to take in the sky. If these values are large, the effects they entail should be expected in the CMB or, more precisely, they would have a large p-value and should not be considered anomalous.
IV Loop Quantum Cosmology
LQC describes the spacetime geometry in the quantum language of loop quantum gravity. As discussed before, we consider in this paper an early Universe sourced by a scalar field, which drives the Universe to an inflationary phase after the bounce. The bounce introduces a new physical scale to the problem, which can be defined either from the value of the energy density or from the Ricci scalar at the bounce. Perturbations, both scalar and tensor, are sensitive to this new scale, and their propagation across the bounce amplifies them, for the same reason that propagation across the inflationary phase does. As a consequence, perturbations reach the onset of inflation in an excited and non-Gaussian state, rather than the Bunch-Davies vacuum commonly postulated. These excitations lead to a strongly scale-dependent power spectrum and bispectrum of primordial perturbations. In this section, we will briefly review some of the essential features of perturbations generated in LQC, and in the next section we will describe how these features can account for the anomalous signals observed in the CMB. For further details, see (Ashtekar et al., 2006b; Agullo et al., 2012; Agullo et al., 2013a; Agullo et al., 2013b; Agullo and Morris, 2015; Agullo, 2018).
A Background Dynamics and Free Evolution of Perturbations
Consider a spatially flat Friedmann-Lemaitre-Robertson-Walker spacetime. We shall describe the perturbations following the dressed metric approach. This approach has been discussed in (Agullo et al., 2012; Agullo et al., 2013a; Agullo et al., 2013b; Agullo and Morris, 2015; Agullo et al., 2018) [for a recent review, see (Agullo et al., 2017a)] and we refer the reader to these references for details omitted here. For the purpose of this article, it suffices to say that we consider perturbations as test fields propagating on the background described by the effective equations of LQC (Taveras, 2008; Ashtekar and Singh, 2011; Agullo et al., 2017a). The essential features of perturbations generated in LQC can be summarized using Figure 4. The left panel of this figure plots
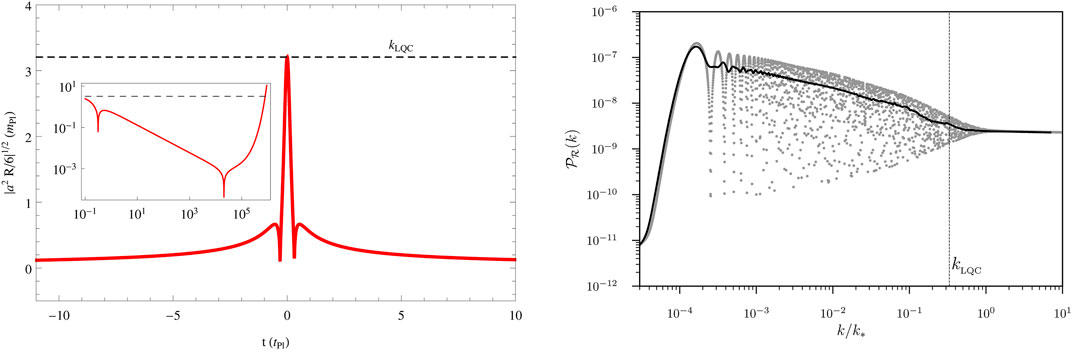
FIGURE 4. Left: Evolution of the Ricci scalar in LQC. This plot corresponds to a solution of the effective equations with 71 e-folds of expansion between the bounce and the end of inflation. Right: Primordial power spectrum of perturbations starting in an adiabatic initial state before the bounce in LQC. The gray dots correspond to numerically-obtained data for individual values of k, while the continuous black line is the average of the grey dots. This plot is obtained for the background geometry showed in the left panel.
B Generation of Primordial Non-gaussianity
The dressed metric approach was extended beyond linear perturbation theory in (Agullo, 2018), and we provide here a short summary. Primordial curvature perturbations whose wavenumbers are comparable to or smaller than kLQC not only get excited, as described above, but also become non-Gaussian as they cross the bounce. The non-Gaussianity thus generated is further enhanced as the perturbations cross the horizon during inflation. Equal-time three-point functions are computed using time dependent perturbation theory, generalizing the pioneering calculations in (Maldacena, 2003) to bouncing geometries:
where
The strong oscillatory character of the non-Gaussianity generated in LQC, makes it computationally difficult to obtain an exact evaluation of (Eq. 3.10). For this reason, in this work, rather than working with the exact numerically-evaluated non-Gaussianity, we shall work with an analytical approximation derived in (Agullo, 2018)
where α = 0.647,
V Results
In this section, we shall put the previous results together and compute the root mean square value of the BipoSH coefficients generated in LQC from (Eq. 3.10). We will show that the BipoSH coefficients generated in this model are non-zero and have the appropriate magnitude and scale dependence as demanded by observations.
A Monopolar Modulation–Power Suppression
We first consider the monopolar term (L = 0). The properties of the Clebsch-Gordan coefficients for L = 0 impose the constraints ℓ = ℓ′ and m = − m′. Therefore, the monopolar modulation introduces an isotropic shift in the value of Cℓ, although the shift can be different for different values of ℓ. More concretely, the modulated power spectrum
Note that
where
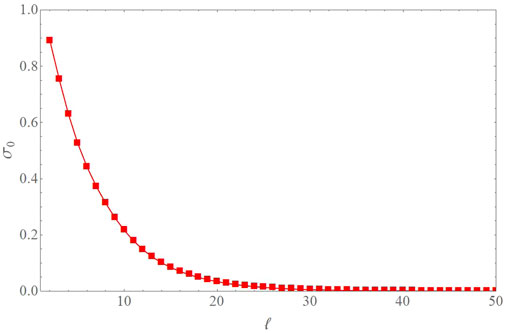
FIGURE 5. Root-mean-square of the monopolar modulation σ0(ℓ) generated in LQC. Note the dependence of σ0 on ℓ. The scale dependence introduced by the bounce in LQC makes the effects of the modulation significant only for ℓ ≲ 30.
We will assume that the probability distribution for the modulation is well approximated by a Gaussian, and hence completely characterized by σ0(ℓ). This is a reasonable approximation, since the deviations are expected to be of second order in non-Gaussianity, and therefore very small. With this probability distribution for the monopolar modulation, we can now investigate the connection with the power suppression observed in the CMB. In particular, we want to answer the following question: what is the p-value given the observed value of S1/2? We obtain that the probability to find S1/2 ≤ 1,209.2 once the non-Gaussian modulation is taken into account is approximately 16%. This is equivalent to saying that the observed suppression is around one standard deviation from the mean. Figure 6 shows the form of the T-T power spectrum for a simulation for which the monopolar modulation produces S1/2 in agreement with observation, along with the 1σ confidence contour arising from cosmic variance. For comparison, we provide the corresponding quantities arising from the standard model, as well as data from Planck (Aghanim, 2019).
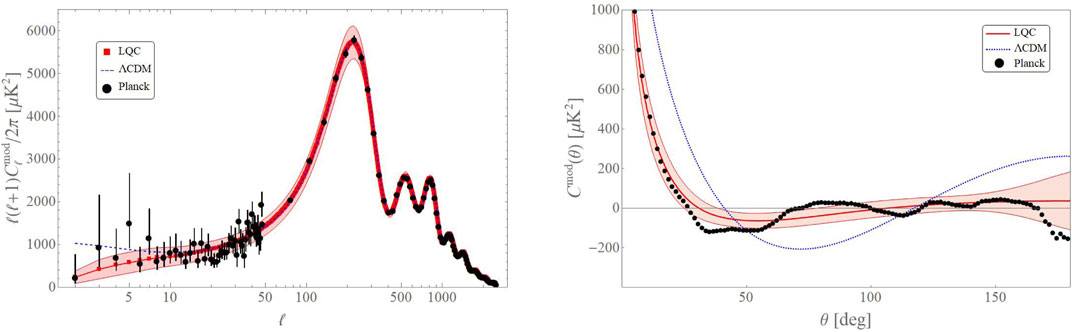
FIGURE 6. Form of the modulated power spectrum for a typical value of the suppression. The figure shows that the monopolar modulation can account for the suppression of power at multipoles lower than ℓ ≈ 30 (A). In the (B), we also see that the suppression translates to a very low real space power spectrum C(θ) for θ ≥ 60°. The shaded region shows cosmic variance, and the black dots data from Planck.
These results show that, in presence of the LQC bounce occurring before inflation, a power suppression as the one we observe in the CMB should not be considered anomalous. It is important to emphasize the precise sense in which the suppression is explained: not because the theory predicts that we should observe a suppression in the CMB, but rather because the probability of observing such a suppression is much larger than in the standard ΛCDM model with Bunch-Davies initial conditions. In this sense, the resolution of the anomaly has precisely the same character as its origin: probabilistic.
An important check is to confirm that the non-Gaussian effects are not large enough to jeopardize the validity of the perturbative expansion on which the calculations rest. This question was explored in detail in Ref. (Agullo, 2018), confirming that, in LQC, perturbation theory does not break down when non-Gaussianity is included. Regarding the non-Gaussian modulation discussed in this paper, we find that the correction to the unmodulated angular power spectrum is not small, and it is in fact a significant fraction of the final result, particularly for the smallest multipoles. The relative contribution is, however, smaller than one in all our calculations. In quantitative terms, the relative contribution of the non-Gaussian modulation is of order
B Dipolar Modulation
Next, we discuss the effects of the L = 1, dipolar modulation, induced by the BipoSH coefficients,
is called a form factor. The m1M(ℓ) defined above can take three values corresponding to M = −1, 0, +1, and in general, they depend on ℓ. From them, the amplitude of the dipolar modulation is defined as
Hence, from the value of the root-mean-square of
where we have used the modulated (i.e., suppressed)
The result for A1(ℓ) is plotted in Figure 7. We find that the dipolar modulation is strongly scale-dependent, as a consequence of the scale-dependent nature of the non-Gaussianity. Although Planck observations for A1(ℓ) are limited, in the sense that only its mean value in the range ℓ ∈ [2, 64] is reported, the order of magnitude and scale dependence agree with our results.
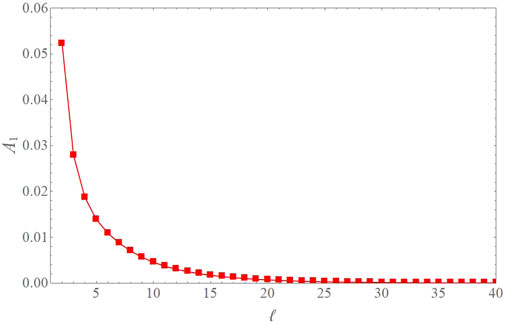
FIGURE 7. The dipole amplitude A1(ℓ) generated in LQC. Planck reports a value of A1 ≈ 0.07 in the multipole bin ℓ ∈ [2, 64].
We have also checked that higher order multipolar modulations, L = 2, 4, … have amplitudes significantly smaller than the dipolar one (Agullo et al., 2018), and therefore additional modulations are not expected in the CMB according to LQC, in agreement with observations. Hence, interestingly, the form of fNL(k1, k2, μ) derived from LQC produces a hierarchy in the amplitude of the modulations which is dominated by a monopole, and a smaller dipole.
C Parity and Lensing Anomalies
In this subsection we briefly discuss the results for the parity and lensing anomalies. As discussed in previous sections, the statistical evidence for these two features is weaker than the power suppression and the dipolar anomaly. Nevertheless, it is interesting to see what the predictions of LQC are.
We find that the monopolar modulation induces also a preference for odd parity multipoles ℓ, in agreement with observations. After inspection, this fact is not surprising, and it is a consequence of the simple fact that, in a power suppressed angular power spectrum, the sum of
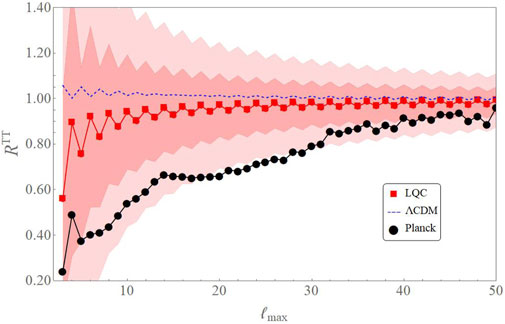
FIGURE 8. RTT(ℓmax) for the modulated spectrum generated in LQC (solid red). RTT(ℓmax) predicted in LQC shows a preference for odd parity for low multipoles, unlike the one in the standard model (dashed, blue).
Yet another effect of the power suppression caused by the monopolar modulation is the alleviation of the lensing tension. The relation between a power suppression and the lensing anomaly was discussed in (Ashtekar et al., 2020), also in the context of LQC, and our analysis confirms the relation. The value of AL is obtained from data by performing MCMC simulations involving the standard six free parameters, together with the lensing amplitude AL. We repeat the analysis with the modified probability distribution obtained from LQC, using TT + lowE data (Aghanim, 2019), and find that the marginalized mean value of the lensing parameter is AL = 1.20 ± 0.092. This value is 3.5% smaller than the result obtained from ΛCDM. This is a modest change. However, as shown in Figure 9, the joint probability distribution of τ-AL, with τ the optical depth, shows that the value of AL = 1 is within 2 standard deviations, and it is in this sense that the anomaly is alleviated. It should also be noted, however, that the marginalized mean value of the χ2 statistic, which is a measure of the difference between the predictions of the model and the data, scaled suitably by the expected error (Barlow, 1989), is larger for the modulated model by Δχ2 = 5.29. This lower value of the lensing parameter AL can be explained due to the slightly larger value of τ. This is because a larger value of τ implies a slightly larger value of the scalar amplitude As, which in turn leads to a smaller value of AL (Ashtekar et al., 2020).
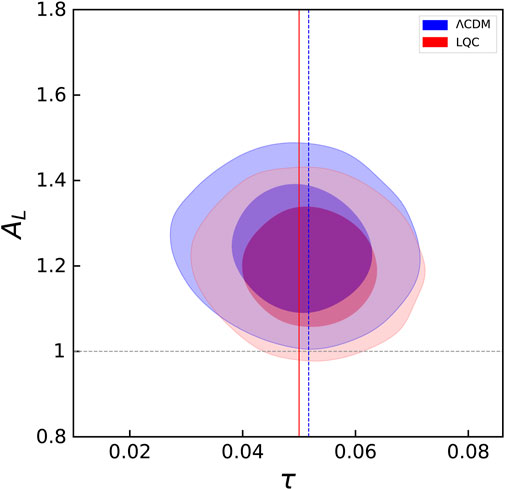
FIGURE 9. Marginalised joint probability distribution of τ and AL obtained from MCMC simulation for the standard model and modulated LQC. As we can see, AL = 1 lies within the 2σ contour for the modulated model, thus bringing the lensing parameter closer to one.
VI Discussion
The success of any theory seeking to describe the unknown rests on two criteria: it should be consistent with known facts and at the same time be able to make new predictions. Loop quantum cosmology, as an effort to extend the ΛCDM model to the Planck regime, has met the first criterion since, when combined with inflation, it is able to overcome the limitations of general relativity and to produce a nearly scale-invariant power spectrum and bispectrum for almost all scales in the CMB. As far as the second aspect is concerned, LQC predicts that, if we consider adiabatic initial conditions for perturbations before the bounce, the primordial power spectrum and bispectrum deviate from scale invariance at wavenumbers k ≲ kLQC. The question is whether these features occur at scales that are observable today. If this is the case, then we may keep the hope to use observations to confirm some of the predictions of LQC, and to further refine the theory. It is with this second aspect in mind that we investigate the link between the enhanced and scale-dependent perturbations generated in LQC and the CMB anomalies.
CMB anomalies, as we discussed in section II, include several features that have been observed, mostly at large angular scales in the CMB. The genuineness of these features is not under dispute. However, if considered individually, the p-values of these features are not small enough to unambiguously establish a statistically significant departure from the standard model. In other words, the possibility that some of these features appear in the CMB in a Universe governed by the standard ΛCDM model is not negligible. However, the fact that all these seemingly distinct features occur together in our Universe imply that we either live in a rare realization of the probability distribution of the ΛCDM model, or that new physics is needed. In this paper, we have explored the second possibility in the context of LQC.
In this scenario, the cosmic bounce modifies the initial state of the Universe from which inflation and the ΛCDM model take over. The most relevant aspect comes from the fact that the bounce generates strong correlations between the longest wavelengths we can observe in the CMB and longer, super-horizon perturbations. These correlations, although cannot be observed directly in the CMB—because they involve at least one super-horizon mode—bias the form of the observed power spectrum. This bias translates in a higher probability for certain features to be realized in our CMB. We find it interesting that such an effect can simultaneously produce a suppression and a dipolar modulation in the sky, both compatible with observations. These two features were thought to be unrelated, and LQC provides a common origin for both of them. It is important to keep in mind that the origin of the anomalies is probabilistic, and the way LQC can account for them is by modifying the probability distribution. For instance, the dipole asymmetry does not arise in LQC as the result of breaking isotropy at the fundamental level, but rather because in a non-Gaussian Universe the size of the anisotropies expected to be found by a typical observer are larger than in a Gaussian theory.
In our calculation we have adjusted a free parameter in LQC, which controls the amount of expansion accumulated from the bounce to the end of inflation. The statement is, therefore, that there exist a value of this parameter for which the observed anomalies can originate from LQC (this value is ≈71 e-folds, and it includes the expansion during both the inflationary and the pre-inflationary epochs). Our calculations also involve some approximations and limitations, and in particular we have not been able to account precisely for the effects of the oscillations in the bispectrum. It would be desirable to investigate the way these oscillations convolve with the power spectrum and transfer functions in order to understand their effect on CMB. Furthermore, the data quantifying the anomalies is limited, as it is based on simple estimators such as S1/2 and the binned value of the dipolar amplitude A1(ℓ). Additional data, for instance coming from tensor modes, would allow a more precise comparison of our ideas with observations. But in spite of these limitations, we find remarkable that the bounce of LQC can produce effects in the CMB which are in good consonance with the observed anomalies, regarding both the order of magnitude of the amplitudes as well as their scale dependence. The possibility that the observed features are informing us about the Planck era of the cosmos is mind-blowing, and certainly deserves further attention. Our contribution should be considered as a first step in this direction.
Finally, in this work we have assumed adiabatic initial conditions for the scalar perturbations before the bounce, wherein the unmodulated primordial power spectrum generated in LQC is enhanced at super-horizon scales. There has been a proposal in LQC (Ashtekar and Gupt, 2017; Ashtekar et al., 2020) for different initial conditions, which leads to a suppressed power spectrum even before considering the non-Gaussian modulation. It would be interesting to combine both sets of ideas and compute the effect of non-Gaussian modulation in that model.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work is supported by the NSF CAREER grant PHY-1552603, and by the Hearne Institute for Theoretical Physics. This paper is based on observations obtained from Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We have benefited from discussions with A. Ashtekar, B. Bolliet, B. Gupt, J. Olmedo, J. Pullin, and P. Singh. We also thank the referees for constructive and useful comments on the first version of this article. This research was conducted with high performance computing resources provided by Louisiana State University (http://www.hpc.lsu.edu).
Footnotes
1The value of S1/2 varies a bit depending on the choice of map and the mask used.
2Strong non-linearities are important at late times in the Universe during structure formation, but not to explain the CMB.
References
Ade, P. A. R. (2014). (Planck), “Planck 2013 Results. XXIII. Isotropy and Statistics of the CMB,” Astron. Astrophys 571, A23.
Ade, P. A. R. (2016b). Planck 2015 Results. XII. Full Focal Plane Simulations,” Astron. Astrophys 594, A12.
Ade, P. A. R. (2016a). (Planck), “Planck 2015 Results. XVI. Isotropy and Statistics of the CMB,” Astron. Astrophys 594, A16.
Adhikari, S., Shandera, S., and Erickcek, A. L. (2016). Large-scale Anomalies in the Cosmic Microwave Background as Signatures of Non-gaussianity. Phys. Rev. D93 023524. arXiv:1508.06489. doi:10.1103/physrevd.93.023524
Aghanim, N., (2019). Planck 2018 Results. V. CMB Power Spectra and Likelihoods. Astron. Astrophys 641, A5.
Aghanim, N., (2020). “Planck 2018 Results. I. Overview and the Cosmological Legacy of Planck,” Astron. Astrophys 641, A1.
Agullo, I., Ashtekar, A., and Nelson, W. (2012). Quantum Gravity Extension of the Inflationary Scenario. Phys. Rev. Lett. 109, 251301. doi:10.1103/physrevlett.109.251301
Agullo, I., Ashtekar, A., and Nelson, W. (2013b). The Pre-inflationary Dynamics of Loop Quantum Cosmology: Confronting Quantum Gravity with Observations. Class. Quan. Grav. 30, 085014. doi:10.1088/0264-9381/30/8/085014
Agullo, I., and Corichi, A. (2014). “Loop Quantum Cosmology,”in Springer Handbook of Spacetime Editors A. Ashtekar, and V. Petkov (Berlin, Heidelberg: Springer), 809–839. doi:10.1007/978-3-642-41992-8_39
Agullo, I., Kranas, D., and Sreenath, V. (2021a). Anomalies in the CMB from a Cosmic Bounce. Gen. Relativ Gravit. 53, 17. doi:10.1007/s10714-020-02778-9
Agullo, I., Kranas, D., and Sreenath, V. (2021b). Large Scale Anomalies in the CMB and Non-gaussianity in Bouncing Cosmologies. Class. Quan. Grav. 38, 065010. doi:10.1088/1361-6382/abc521
Agullo, I., and Morris, N. A. (2015). Detailed Analysis of the Predictions of Loop Quantum Cosmology for the Primordial Power Spectra. Phys. Rev. D 92, 124040. doi:10.1103/physrevd.92.124040
Agullo, I., Olmedo, J., and Sreenath, V. (2020a). Predictions for the Cosmic Microwave Background from an Anisotropic Quantum Bounce. Phys. Rev. Lett. 124, 251301. doi:10.1103/physrevlett.124.251301
Agullo, I. (2018). Primordial Power Spectrum from the Dapor-Liegener Model of Loop Quantum Cosmology. Gen. Relativ Gravit. 50, 91. doi:10.1007/s10714-018-2413-1
Agullo, I., and Singh, P. (2017). “Loop Quantum Cosmology,” in Loop Quan. Gravity: First 30 Years Editors Abhay. Ashtekar, and Jorge. Pullin (WSP), 183–240. doi:10.1142/9789813220003_0007
Agullo, Ivan., Ashtekar, Abhay., and Gupt, Brajesh. (2017). Phenomenology with Fluctuating Quantum Geometries in Loop Quantum Cosmology. Class. Quant. Grav. 34 074003. arXiv:1611.09810. doi:10.1088/1361-6382/aa60ec
Agullo, I., Ashtekar, A., and Nelson, W. (2013a). Extension of the Quantum Theory of Cosmological Perturbations to the Planck Era. Phys. Rev. D 87, 043507. doi:10.1103/physrevd.87.043507
Agullo, I., Bolliet, B., and Sreenath, V. (2018). Non-Gaussianity in Loop Quantum Cosmology. Phys. Rev. D97 066021. arXiv:1712.08148. doi:10.1103/physrevd.97.066021
Agullo, I. (2015). Loop Quantum Cosmology, Non-gaussianity, and CMB Power Asymmetry. Phys. Rev. D92 064038. arXiv:1507.04703. doi:10.1103/physrevd.92.064038
Agullo, I., Nelson, W., and Ashtekar, A. (2015). Preferred Instantaneous Vacuum for Linear Scalar fields in Cosmological Space-Times. Phys. Rev. D 91, 064051. doi:10.1103/physrevd.91.064051
Agullo, I., Olmedo, J., and Sreenath, V. (2020b). Observational Consequences of Bianchi I Spacetimes in Loop Quantum Cosmology. Phys. Rev. D 102 (043523). arXiv:2006.01883. doi:10.1103/physrevd.102.043523
Akrami, Y., (2020). (Planck), “Planck 2018 Results. IX. Constraints on Primordial Non-gaussianity. Astron. Astrophys 641, A9.
Ashtekar, A., Gupt, B., Jeong, D., and Sreenath, V. (2020). Alleviating the Tension in the Cosmic Microwave Background Using Planck-Scale Physics. Phys. Rev. Lett. 125, 051302. arXiv:2001.11689. doi:10.1103/PhysRevLett.125.051302
Ashtekar, A., Pawlowski, T., and Singh, P. (2006b). Quantum Nature of the Big Bang. Phys. Rev. Lett. 96, 141301.
Ashtekar, A., Gupt, B., and Sreenath, V. (2021). Cosmic Tango between the Very Small and the Very Large: Addressing CMB Anomalies through Loop Quantum Cosmology. Front. Astron. Space Sci. 8, 76. doi:10.3389/fspas.2021.685288
Ashtekar, A., and Gupt, B. (2017). “Quantum Gravity in the Sky: Interplay between Fundamental Theory and Observations. Class. Quant. Grav. 34 014002. doi:10.1088/1361-6382/34/1/014002
Ashtekar, A., Pawlowski, T., Singh, P., and Vandersloot, K. (2007). Loop Quantum Cosmology K=1 FRW Modelsp. hys. Rev. D 75, 024035. doi:10.1103/physrevd.75.024035
Ashtekar, A., and Wilson-Ewing, E. (2009a). Loop Quantum Cosmology of Bianchi I Models. Phys. Rev. D 79, 083535. doi:10.1103/physrevd.79.083535
Ashtekar, A., Bojowald, M., and Lewandowski, J. (2003). Mathematical Structure of Loop Quantum Cosmology. Adv. Theor. Math. Phys. 7, 233–268. doi:10.4310/atmp.2003.v7.n2.a2
Ashtekar, A., Pawlowski, T., and Singh, P. (2006a). Quantum Nature of the Big Bang. Phys. Rev. Lett. 96, 141301.
Ashtekar, A., and Singh, P. (2011). Loop Quantum Cosmology: a Status Report. Class. Quan. Grav. 28, 213001. doi:10.1088/0264-9381/28/21/213001
Ashtekar, A., and Wilson-Ewing, E. (2009b). Loop Quantum Cosmology of Bianchi Type II Models. Phys. Rev. D 80, 123532. doi:10.1103/physrevd.80.123532
Banerjee, K., Calcagni, G., and Martin-Benito, M. (2012). Introduction to Loop Quantum Cosmology. SIGMA 8, 016. doi:10.3842/sigma.2012.016
Barlow, R. (1989). Statistics : A Guide to the Use of Statistical Methods in the Physical Sciences. West Sussex, England: Wiley.
Barrau, A., Bojowald, M., Calcagni, G., Grain, J., and Kagan, M. (2015). Anomaly-free Cosmological Perturbations in Effective Canonical Quantum gravityJCAP. J. Cosmol. Astropart. Phys. 2015, 051. doi:10.1088/1475-7516/2015/05/051
Bennett, C. L., Halpern, M., Hinshaw, G., Jarosik, N., Kogut, A., Limon, M., et al. (2003). First‐Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results. Astrophys J. Suppl. S 148, 1–27. doi:10.1086/377253
Bentivegna, E., and Pawlowski, T. (2008). Anti-de Sitter Universe Dynamics in Loop Quantum Cosmology. Phys. Rev. D 77, 124025. doi:10.1103/physrevd.77.124025
Bojowald, M. (2001). Absence of a Singularity in Loop Quantum Cosmology. Phys. Rev. Lett. 86, 5227–5230. doi:10.1103/physrevlett.86.5227
Bojowald, M., and Calcagni, G. (2011). Inflationary Observables in Loop Quantum Cosmology. JCAP 032. doi:10.1088/1475-7516/2011/03/032
Bojowald, M., Mortuza Hossain, G., Kagan, M., and Shankaranarayanan, S. (2009). Gauge Invariant Cosmological Perturbation Equations with Corrections from Loop Quantum Gravity. Phys. Rev. D 7982, 043505109903. doi:10.1103/physrevd.79.043505
Bonga, B., and Gupt, B. (2016b). Phenomenological Investigation of a Quantum Gravity Extension of Inflation with the Starobinsky Potential. Phys. Rev.D93, 063513. doi:10.1103/physrevd.93.063513
Bonga, B., and Gupt, B. (2016a). Inflation with the Starobinsky Potential in Loop Quantum Cosmology. Gen. Relativ Gravit. 48, 71. arXiv:1510.00680. doi:10.1007/s10714-016-2071-0
Castelló Gomar, L., Mena Marugán, G. A., Martín de Blas, D., and Olmedo, J. (2017). Hybrid Loop Quantum Cosmology and Predictions for the Cosmic Microwave Background. Phys. Rev. D 96, 103528. doi:10.1103/physrevd.96.103528
Dai, L., Jeong, D., Kamionkowski, M., and Chluba, J. (2013). The Pesky Power Asymmetry. Phys. Rev. D 87, 123005. doi:10.1103/physrevd.87.123005
de Blas, D. M., and Olmedo, J. (2016). Primordial Power Spectra for Scalar Perturbations in Loop Quantum Cosmology. J. Cosmol. Astropart. Phys. 2016, 029. arXiv:1601.01716. doi:10.1088/1475-7516/2016/06/029
Elizaga Navascués, B., Marugán, G. A. M., and Thiemann, T. (2019). Hamiltonian Diagonalization in Hybrid Quantum Cosmology. Class. Quan. Grav. 36, 185010. arXiv:1903.05695. doi:10.1088/1361-6382/ab32af
Fernández-Méndez, M., Mena Marugán, G. A., and Olmedo, J. (2013). Hybrid Quantization of an Inflationary Model: The Flat Case. Phys. Rev. D 88, 044013. doi:10.1103/physrevd.88.044013
Fixsen, D. J. (2009). “The temperature cosmic microwave background,” Astrophysical J. 707, 916920. doi:10.1088/0004-637x/707/2/916
Mena Marugan, G. A. (2010). Loop Quantum Cosmology: A Cosmological Theory with a view. J. Phys. Conf. Ser. 314, 012012. doi:10.1088/1742-6596/314/1/012012
Garay, L. J., Martin-Benito, M., and Mena Marugan, G. A. (2010). Inhomogeneous Loop Quantum Cosmology: Hybrid Quantization of the Gowdy Model. Phys. Rev. D 82 044048. doi:10.1103/physrevd.82.044048
Gordon, C., Hu, W., Huterer, D., and Crawford, T. (2005). Spontaneous Isotropy Breaking: A Mechanism for Cmb Multipole Alignments. Phys. Rev. D 72, 10. doi:10.1103/physrevd.72.103002
Hajian, A., and Souradeep, T. (2003). Measuring the Statistical Isotropy of the Cosmic Microwave Background Anisotropy. ApJ 597, L5–L8. doi:10.1086/379757
Hinshaw, G., Banday, A. J., Bennett, C. L., Górski, K. M., Kogut, A., Lineweaver, C. H., et al. (1996). Two-Point Correlations in the [ITAL]COBE[/ITAL] DMR Four-Year Anisotropy Maps. Astrophys. J. 464, L25–L28. doi:10.1086/310076
Jeong, D., and Kamionkowski, M. (2012). Clustering Fossils from the Early Universe. Phys. Rev. Lett. 108, 251301. doi:10.1103/physrevlett.108.251301
Joshi, N., S.Jhingan, , Souradeep, T., and Hajian, A. (2010). Bipolar Harmonic Encoding of CMB Correlation Patterns. Phys. Rev. D81, 083012. doi:10.1103/physrevd.81.083012
Li, B.-F., Olmedo, J., Singh, P., and Wang, A. (2020b). Primordial Scalar Power Spectrum from the Hybrid Approach in Loop Cosmologies. Phys. Rev. D 102, 126025. doi:10.1103/physrevd.102.126025
Li, B-F., Singh, P., and Wang, A. (2020a). Primordial Power Spectrum from the Dressed Metric Approach in Loop Cosmologies. Phys. Rev. D 101 086004. doi:10.1103/physrevd.101.086004
Maldacena, J. (2003). Non-gaussian Features of Primordial Fluctuations in Single Field Inflationary Models. J. High Energ. Phys. 2003, 013. doi:10.1088/1126-6708/2003/05/013
Martin-Benito, M., Garay, L. J., and . Mena Marugan, G. A. (2008). Hybrid Quantum Gowdy Cosmology: Combining Loop and Fock Quantizations. Phys. Rev. D 78 083516. doi:10.1103/physrevd.78.083516
Martín-Benito, M., Neves, R. B., and Olmedo, J. (2021). States of Low Energy in Bouncing Inflationary Scenarios in Loop Quantum Cosmology. Phys. Rev. D 103 123524. doi:10.1103/PhysRevD.103.123524
Martínez, F. B., and Olmedo, J. (2016). Primordial Tensor Modes of the Early UniversearXiv:1605.04293. Phys. Rev. D 93, 124008. doi:10.1103/physrevd.93.124008
Fernández-Méndez, M., Mena Marugán, G. A., and Olmedo, J. (2014). Effective Dynamics of Scalar Perturbations in a Flat Friedmann-Robertson-Walker Spacetime in Loop Quantum Cosmology. Phys. Rev. D 89, 044041. doi:10.1103/physrevd.89.044041
Navascués, B. E., Mena Marugán, G. A., and Prado, S. (2020). Non-oscillating Power Spectra in Loop Quantum Cosmology. Class Quant. Grav. 38, 035001. doi:10.1088/1361-6382/abc6bb
Pawlowski, T., and Ashtekar, A. (2012). Positive Cosmological Constant in Loop Quantum Cosmology. Phys. Rev. D 85 064001.
Schmidt, F., and Hui, L. (2013). Cosmic Microwave Background Power Asymmetry from Non-gaussian Modulation. Phys. Rev. Lett. 110, 011301. doi:10.1103/PhysRevLett.110.011301
Schmidt, F., and Kamionkowski, M. (2010). Halo Clustering with Nonlocal Non-gaussianity. Phys. Rev. D 82, 103002. doi:10.1103/physrevd.82.103002
SchwarzSchwarz, D. J., CopiCopi, C. J., Huterer, D., and Starkman, G. D. (2016). CMB Anomalies after Planck. Class. Quan. Grav. 33, 184001. doi:10.1088/0264-9381/33/18/184001
Spergel, D. N., Verde, L., Peiris, H. V., Komatsu, E., Nolta, M. R., Bennett, C. L., et al. (2003). First‐Year Wilkinson Microwave Anisotropy Probe ( WMAP ) Observations: Determination of Cosmological Parameters. Astrophys J. Suppl. S 148, 175–194. doi:10.1086/377226
Sreenath, V., Agullo, I., and Bolliet, B. (2019). Computation of Non-gaussianity in Loop Quantum Cosmology.” in Fifteenth Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories, Rome, Italy.
Szulc, Ł. (2007). An Open FRW Model in Loop Quantum Cosmology. Class. Quan. Grav. 24, 6191–6200. doi:10.1088/0264-9381/24/24/003
Szulc, Ł., Kamiński, W., and Lewandowski, J. (2007). Closed Friedmann-Robertson-Walker Model in Loop Quantum Cosmology. Class. Quan. Grav. 24, 2621–2635. doi:10.1088/0264-9381/24/10/008
Taveras, V. (2008). Corrections to the Friedmann Equations from LQG for a Universe with a Free Scalar Field. Phys. Rev. D78, 064072. doi:10.1103/PhysRevD.78.064072
Wilson-Ewing, E. (2010). Loop Quantum Cosmology of Bianchi Type IX Models. Phys. Rev. D 82, 043508. doi:10.1103/physrevd.82.043508
Zhu, T., Wang, A., Cleaver, Gd., Kirsten, Ks., and Sheng, Q. (2017). Pre-inflationary Universe in Loop Quantum Cosmology. Phys. Rev. D96, 083520. arXiv:1705.07544. doi:10.1103/physrevd.96.083520
Keywords: cosmic microwave background, loop quantum cosmology, anomalies, early universe, quantum cosmology
Citation: Agullo I, Kranas D and Sreenath V (2021) Anomalies in the Cosmic Microwave Background and Their Non-Gaussian Origin in Loop Quantum Cosmology. Front. Astron. Space Sci. 8:703845. doi: 10.3389/fspas.2021.703845
Received: 30 April 2021; Accepted: 21 July 2021;
Published: 18 August 2021.
Edited by:
Francesca Vidotto, Western University, CanadaReviewed by:
Susanne Schander, Perimeter Institute for Theoretical Physics, CanadaHerman J. Mosquera Cuesta, Departamento Administrativo Nacional de Ciencia, Tecnologia e Innovacion, Colciencias, Colombia
Copyright © 2021 Agullo, Kranas and Sreenath. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ivan Agullo, YWd1bGxvQGxzdS5lZHU=
 Ivan Agullo
Ivan Agullo Dimitrios Kranas
Dimitrios Kranas V. Sreenath
V. Sreenath