
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci. , 24 June 2021
Sec. Cosmology
Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.701417
This article is part of the Research Topic Loop Quantum Cosmology View all 12 articles
In this paper, we first provide a brief review of the effective dynamics of two recently well-studied models of modified loop quantum cosmologies (mLQCs), which arise from different regularizations of the Hamiltonian constraint and show the robustness of a generic resolution of the big bang singularity, replaced by a quantum bounce due to non-perturbative Planck scale effects. As in loop quantum cosmology (LQC), in these modified models the slow-roll inflation happens generically. We consider the cosmological perturbations following the dressed and hybrid approaches and clarify some subtle issues regarding the ambiguity of the extension of the effective potential of the scalar perturbations across the quantum bounce, and the choice of initial conditions. Both of the modified regularizations yield primordial power spectra that are consistent with current observations for the Starobinsky potential within the framework of either the dressed or the hybrid approach. But differences in primordial power spectra are identified among the mLQCs and LQC. In addition, for mLQC-I, striking differences arise between the dressed and hybrid approaches in the infrared and oscillatory regimes. While the differences between the two modified models can be attributed to differences in the Planck scale physics, the permissible choices of the initial conditions and the differences between the two perturbation approaches have been reported for the first time. All these differences, due to either the different regularizations or the different perturbation approaches in principle can be observed in terms of non-Gaussianities.
Despite offering a solution to several fundamental and conceptual problems of the standard big bang cosmology, including the flatness, horizon, and exotic-relic problems, the cosmic inflation in the early Universe also provides a mechanism to produce density perturbations and primordial gravitational waves (PGWs) (Starobinsky, 1980; Guth, 1981; Sato, 1981; Kodama and Sasaki, 1984; Mukhanov et al., 1992; Malik, 2001; Dodelson, 2003; Mukhanov, 2005; Weinberg, 2008; Malik and Wands, 2009; Senatore, 2017). The latter arise from quantum fluctuations of spacetimes and produce not only a temperature anisotropy, but also polarizations in the cosmic microwave background (CMB), a smoking gun of PGWs. However, the inflationary paradigm is incomplete without the knowledge of key elements from quantum gravity. First, it is well-known that the cosmic inflation is sensitive to the ultraviolet (UV) physics, and its successes are tightly contingent on the understanding of this UV physics (Brandenberger, 1999; Martin and Brandenberger, 2001; Niemeyer and Parentani, 2001; Bergstorm and Danielsson, 2002; Niemeyer and Parentani, 2002; Niemeyer and Parentani, 2003; Easther et al., 2005; McAllister and Silverstein, 2007; Joras and Marozzi, 2009; Ashoorioon et al., 2011; Jackson and Schalm, 2012; Kiefer and Krämer, 2012; Brandenberger and Martin, 2013; Burgess et al., 2013; Chernoff and Tye, 2014; Krauss and Wilczek, 2014; Woodard, 2014; Baumann and McAllister, 2015; Cicoli, 2016; Silverstein, 2016). In particular, if the inflationary phase lasts somewhat longer than the minimal period required to solve the above mentioned problems, the length scales we observe today will originate from modes that are smaller than the Planck length during inflation (Brandenberger, 1999; Martin and Brandenberger, 2001; Niemeyer and Parentani, 2001; Bergstorm and Danielsson, 2002; Niemeyer and Parentani, 2002; Niemeyer and Parentani, 2003; Easther et al., 2005; Joras and Marozzi, 2009; Ashoorioon et al., 2011; Jackson and Schalm, 2012; Brandenberger and Martin, 2013). Then, the treatment of the underlying quantum field theory on a classical spacetime becomes questionable, as now the quantum geometric effects are expected to be large, and the space and time cannot be treated classically any more. This is often referred to as the trans-Planckian problem of cosmological fluctuations1.
The second problem of the inflationary paradigm is more severe. It is well known that inflationary spacetimes are past-incomplete because of the big bang singularity (Borde and Vilenkin, 1994; Borde et al., 2003), with which it is not clear how to impose the initial conditions. This problem gets aggravated for low energy inflation in spatially-closed models which are slightly favored by current observations where the Universe encounters a big crunch singularity and lasts only for a few Planck seconds (Linde, 2014; Linde, 2018).
Another problematic feature of inflation is that one often ignores the pre-inflationary dynamics and sets the Bunch-Davies (BD) vacuum in a very early time. But, it is not clear how such a vacuum state can be realized dynamically in the framework of quantum cosmology (McAllister and Silverstein, 2007; Burgess et al., 2013; Chernoff and Tye, 2014; Baumann and McAllister, 2015; Cicoli, 2016; Silverstein, 2016), considering the fact that a pre-inflationary phase always exists between the Plank and inflation scales, which are about
In particular, when applying the techniques of loop quantum gravity (LQG) to homogeneous and isotropic Universe, namely loop quantum cosmology (LQC) (Ashtekar and Singh, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017), it was shown that, purely due to quantum geometric effects, the big bang singularity is generically resolved and replaced by a quantum bounce at which the spacetime curvature becomes Planckian (Ashtekar et al., 2006; Ashtekar et al., 2006; Ashtekar et al., 2010). The robustness of the singularity resolution has been shown for a variety of isotropic and anisotropic spacetimes (Giesel et al., 2020). Interestingly, there exists a reliable effective spacetime description, which has been used to confirm a generic resolution of all strong curvature singularities (Singh, 2009; Singh, 2014). Various phenomenological implications have been studied using this effective spacetime description, whose validity has been verified for isotropic and anisotropic spacetimes (Diener et al., 2014; Diener et al., 2014; Agullo et al., 2017; Diener et al., 2017; Singh, 2018). For low energy inflation models with a positive spatial curvature, the singularity resolution and a successful onset of inflation for classically inadmissible initial conditions have been demonstrated (Dupuy and Singh, 2020; Gordon et al., 2021; Motaharfar and Singh, 2021).
In the last couple of years, several approaches have been proposed, in order to address the impacts of the quantum geometry on the primordial power spectra. These include the approaches of the deformed algebra (Bojowald et al., 2008; Cailleteau et al., 2012; Cailleteau et al., 2012), dressed metric (Agullo et al., 2012; Agullo et al., 2013; Agullo et al., 2013), and hybrid (Fernández-Méndez et al., 2012; Fernández-Méndez et al., 2013; Castelló Gomar et al., 2014; Gomar et al., 2015; Martínez and Olmedo, 2016) [For a recent discussion about similar ideas in anisotropic Bianchi I LQC spacetimes see Refs. (Gupt and Singh, 2012; Gupt and Singh, 2013; Agullo et al., 2020; Agullo et al., 2020) and references therein.]. In particular, the last two approaches have been widely studied and found that they are all consistent with current cosmological observations (Agullo and Morris, 2015; Bonga and Gupt, 2016; Bonga and Gupt, 2016; de Blas and Olmedo, 2016; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017; Castelló Gomar et al., 2017; Zhu et al., 2017; Zhu et al., 2017; Agullo et al., 2018; Elizaga Navascués et al., 2018; Navascues et al., 2018; Wu et al., 2018; Zhu et al., 2018). In addition, within the framework of the dressed metric approach recently it has been also shown that some anomalies from the CMB data (Akrami and Planck collaboration, 2020; Akrami and Planck collaboration, 2020; Schwarz et al., 2016) can be reconciled purely due to the quantum geometric effects (Ashtekar et al., 2020; Agullo et al., 2021; Agullo et al., 2021; Ashtekar et al., 2021).
In addition to the standard LQC, in which the Lorentzian term of the classical Hamiltonian constraint is first expressed in terms of the Euclidean term in the spatially flat Friedmann-Lemaître-Robertson-Walker (FLRW) Universe, and then only the quantization of the Euclidean term is considered, the robustness of the singularity resolution with respect to different quantizations of the classical Hamiltonian constraint in the symmetry reduced spacetimes have been extensively studied. Two notable examples are the so-called modified LQC-I (mLQC-I) and modified LQC-II (mLQC-II) models, which were first proposed by Yang, Ding and Ma more than a decade ago (Yang et al., 2009). In a recent study, Dapor and Liegener (DL) (Dapor and Liegener, 2018a; Dapor and Liegener, 2018b) obtained the expectation values of the Hamiltonian operator in LQG using complexifier coherent states (Thiemann, 2001a; Thiemann and Winkler, 2001b; Thiemann, 2006), adapted to the spatially flat FLRW Universe. Using the non-graph changing regularization of the Hamiltonian advocated by Thiemann (Thiemann, 1998a; Thiemann, 1998b; Giesel and Thiemann, 2007), DL obtained an effective Hamiltonian constraint, which, to the leading order, agrees with the mLQC-I model first obtained in (Yang et al., 2009). Sometimes, this model has also been referred to as the DL model or Thiemann regularized LQC. Strictly speaking, when constructing loops in (Dapor and Liegener, 2018a) DL treated the edge length μ as a free parameter, but in (Yang et al., 2009) it was considered as a specific triad dependent function, the so-called
In the two modified LQC models, mLQC-I and mLQC-II, since different regularizations of the Lorentzian term were used, the resulting equations become the fourth-order and non-singular quantum difference equations, instead of the second-order difference ones obtained in LQC. In these two models the big bang singularity is also generically resolved and replaced by a quantum bounce. In addition, the inflationary phase can naturally take place with a very high probability (Li et al., 2018a; Li et al., 2018b; Saini and Singh, 2019a; Saini and Singh, 2019b; Li et al., 2019). In addition, the dynamics in LQC and mLQC-II is qualitatively similar in the whole evolution of the Universe, while the one in mLQC-I becomes significantly different from LQC (as well as mLQC-II) in the contracting phase, in which an emergent quasi de Sitter space is present. This implies that the contracting phase in mLQC-I is purely a quantum regime without any classical limit2.
An important question now is what are the effects of these models and approaches on the CMB observations. The answer to this question requires the knowledge of how the quantum fluctuations propagate on a quantum spacetime in LQC and modified loop cosmological models. In particular, in the framework of the dressed metric approach the power spectra of the cosmological perturbations for both mLQC-I and mLQC-II models were investigated (Li et al., 2020c). In the same framework but restricted only to the mLQC-I model, the power spectra of the cosmological perturbations were studied in (Agullo, 2018). More recently, the hybrid approach was applied to mLQC-I (García-Quismondo and Mena Marugán, 2019; Castelló Gomar et al., 2020; García-Quismondo and Mena Marugán, 2020), for which the time-dependent mass of the perturbations was studied in detail (García-Quismondo et al., 2020). The primordial scalar power spectra obtained in the three models, LQC, mLQC-I and mLQC-II, were also investigated in the hybrid approach (Li et al., 2020a), and found that the relative differences in the amplitudes of the power spectra among the three models could be as large as
In this brief review, we shall focus mainly on the states that are sharply peaked along the classical trajectories, so that the description of the “effective” dynamics of the Universe becomes available (Ashtekar and Singh, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017), and the questions raised recently in (Kamiński et al., 2020) are avoided. This includes the studies of the “effective” dynamics of the homogeneous and isotropic mLQC-I and mLQC-II models, and their cosmological perturbations in the framework of the dressed metric and hybrid approaches. We shall first clarify the issue regarding the ambiguities in the extension of the effective potential for the scalar perturbations across the quantum bounce, and then pay particular attention to the differences among the three models, LQC, mLQC-I and mLQC-II, and possible observational signals. It is important to note that initial conditions are another subtle and important issue not only in LQC but also in mLQCs. This includes two parts: 1) when to impose the initial conditions, and 2) which kind of initial conditions one can impose consistently. To clarify this issue, we discuss it at length by showing the (generalized) comoving Hubble radius in each model and in each of the dressed and hybrid approaches. From this analysis, one can see clearly what initial conditions can and cannot be imposed at a chosen initial time.
The outline of this brief overview is as follows. In Sec. 2 we consider the effective dynamics of mLQC-I and mLQC-II, and discuss some universal features of their dynamics such as the resolution of big bang singularity. In addition, in this section we also show that for states such that the evolution of the homogeneous Universe was dominated initially at the bounce by the kinetic energy of the inflaton, that is,
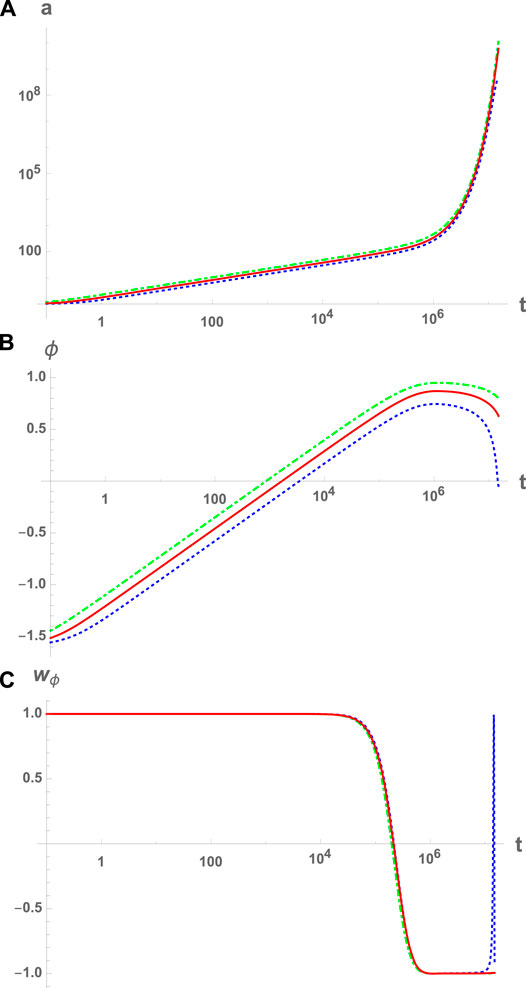
FIGURE 1. The evolution of the scale factor
In Sec. 3, the cosmological perturbations of mLQC-I and mLQC-II are studied. We discuss initial conditions and the subtle issue of the ambiguity in the choice of the variables
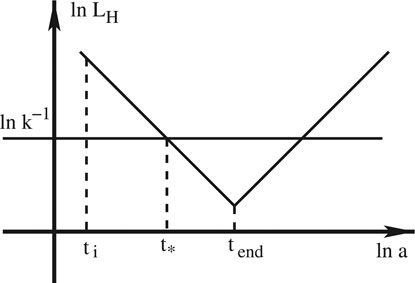
FIGURE 2. The evolution of the comoving Hubble radius
In Sec. 4, the cosmological perturbations of mLQC-I and mLQC-II are studied within the hybrid approach, and the subtleties of the initial conditions are shown in Figures 8–10, where Figures 8, 9 are respectively for the quadratic and Starobinsky potentials in mLQC-I, while Figure 10 is for the Starobinsky potential in mLQC-II. The case with the quadratic potential in mLQC-II is similar to that of mLQC-I, given by Figure 8. From these figures it is clear that imposing the initial conditions now becomes a more delicate issue, and sensitively depends on the potential
The review is concluded in Sec. 5, in which we summarize the main conclusions and point out some open questions for future studies.
To facilitate our following discussions, let us first briefly review the standard process of quantization carried out in LQC, from which one can see clearly the similarities and differences among the three models, LQC, mLQC-I and mLQC-II.
The key idea of LQC is to use the fundamental variables and quantization techniques of LQG to cosmological spacetimes, by taking advantage of the simplifications that arise from the symmetries of these spacetimes. In the spatially-flat FLRW spacetime,
there exists only one degree of freedom, the scale factor
In full GR, the gravitational phase space consists of the connection
where
The physical triad and cotriad are given by
Then, the gravitational part of the Hamiltonian is a sum of the Euclidean and Lorentzian terms,
where, with the choice
where
Upon quantization, ambiguities can arise due to different treatments of the Euclidean and Lorentzian terms in the Hamiltonian constraint. In particular, LQC takes the advantage that in the spatially-flat FLRW Universe the Lorentzian part is proportional to the Euclidean part,
so that, when coupled to a massless scalar field, the classical Hamiltonian can be rewritten as (Ashtekar et al., 2003; Ashtekar et al., 2006)
where
The elementary operators in the standard LQC are the triads5p and elements of the holonomies given by
with
where
Then, the equation satisfied by selecting the physical states
where
This is the main result of LQC (Ashtekar et al., 2006), which shows that: 1) It is a second order quantum difference equation with uniform discreteness in volume, rather than a simple differential equation, a direct consequence of the discrete nature of loop quantum geometry. 2) It provides the evolution of the quantum cosmological wavefunction
For the states sharply peaked around a classical solution, we can obtain “effective” Friedmann and Raychaudhuri (FR) equations, by using the geometric quantum mechanics in terms of the expectation values of the operators
which take the same forms as their classical ones, but all the quantities now represent their expectation values,
which can also be expressed in terms of v and b via the relations
where
and
For a scalar field ϕ with its potential
Then, from Eq. 2.16 we find that
In the rest of this review, we shall consider only the states that are sharply peaked around a classical solution, so the above “effective” descriptions are valid, and the questions raised recently in (Kamiński et al., 2020) are avoided.
As mentioned in the introduction, an important open issue in LQC is its connection with LQG (Brunnemann and Fleischhack, 2007; Engle, 2007; Brunnemann and Koslowski, 2011). In particular, in LQC the spacetime symmetry is first imposed (in the classical level), before the quantization process is carried out. However, it is well-known that this is different from the general process of LQG (Ashtekar and Lewandowski, 2004; Thiemann, 2007; Rovelli, 2008; Bojowald, 2011; Gambini and Pullin, 2011; Ashtekar and Pullin, 2017), and as a result, different Hamiltonian constraints could be resulted, hence resulting in different Planck scale physics. Though the question of ambiguities in obtaining the Hamiltonian in LQG is still open, based on some rigorous proposals by Thiemann (Thiemann, 1998a; Thiemann, 1998b; Giesel and Thiemann, 2007), various attempts have been carried out, in order to obtain deeper insights into the question.
One of the first attempts to understand this issue was made in (Dapor and Liegener, 2018a), in which the Euclidean and Lorentzian terms given by Eqs 2.5, 2.6 are treated differently, by closely following the actual construction of LQG. To be more specific, in the full theory (Ashtekar and Lewandowski, 2004; Thiemann, 2007; Rovelli, 2008; Bojowald, 2011; Gambini and Pullin, 2011; Ashtekar and Pullin, 2017), the extrinsic curvature in the Lorentzian term (2.6) can be expressed in terms of the connection and the volume as
which once substituted back into Eq. 2.6 lead to an expression of
Hence, the Hamilton’s equations take the form,
where P represents the pressure defined in Eq. 2.20. Once the matter Hamiltonian
It has been shown in detail that the big bang singularity is generically replaced by a quantum bounce when the energy reaches its maximum
and the Universe is asymmetric with respect to the bounce, in contrast to LQC.
To write Eqs 2.26–2.28 in terms of
where
As
These are exactly the FR equations in GR for an ordinary matter field coupled with a positive cosmological constant
Finally, we want to emphasize that the minimal energy density of this branch, for which the Hubble rate vanishes, turns out to be negative which can be shown as
In the post-bounce phase (
from which we obtain
Therefore, regardless of the matter content, the super-inflation (starting at the bounce) will always end at
for which we have
In the classical limit
whereby the standard relativistic cosmology is recovered.
It is remarkable to note that in the pre-bounce phase the limit
In LQG, the fundamental variables for the gravitational sector are the su (2) Ashtekar-Barbero connection
in the Lorentzian term (2.6). Then, the following effective Hamiltonian is resulted (Yang et al., 2009),
from which we find that the corresponding Hamilton’s equations are given by,
It can be shown that the corresponding (modified) FR equations now read (Li et al., 2018b),
where
which is different from the critical density
In addition, similar to the other two cases, now the bounce is accompanied by a phase of super-inflation, i.e.,
For
When
which are identical to those given in GR. Therefore, in this model, the classical limit is obtained in both pre- and post-bounce when the energy density ρ is much lower than the critical one
To study further the evolution of the Universe, it is necessary to specify the matter content
The effective quantum dynamics of LQC, mLQC-I, and mLQC-II were studied in detail recently in (Li et al., 2018b) for a single scalar field with various potentials, including the chaotic inflation, Starobinsky inflation, fractional monodromy inflation, non-minimal Higgs inflation, and inflation with an exponential potential, by using dynamical system analysis. It was found that, while several features of LQC were shared by the mLQC-I and mLQC-II models, others belong to particular models. In particular, in the pre-bounce phase, the qualitative dynamics of LQC and mLQC-II are quite similar, but are strikingly different from that of mLQC-I. In all the three models, the non-perturbative quantum gravitational effects always result in a non-singular post-bounce phase, in which a short period of super-inflation always exists right after the bounce, and is succeeded by the conventional inflation. The latter is an attractor in the phase space for all the three models.
Moreover, similar to LQC (Zhu et al., 2017; Zhu et al., 2017)6, for the initially kinetic energy dominated conditions,
it was found that the evolution of the Universe before the reheating is universal. In particular, in the post-bounce phase (between the quantum bounce and the reheating), the evolution can be uniquely divided into three phases: bouncing, transition and slow-roll inflation, as shown in Figure 1 for the Starobinsky potential,
For other potentials, similar results can be obtained, as long as at the bounce the evolution of the Universe is dominated by the kinetic energy of the inflaton
In each of these three phases, the evolutions of
for mLQC-I model, where the parameters A, B, C and D are fixed through numerical simulations. It was found that the best fitting is provided by (Li et al., 2019),
For the mLQC-II model, during the bouncing phase
but now with,
In the transition and slow-roll inflationary phases, the functions
For the initially potential energy dominated cases,
it was found that such universalities are lost. In particular, for the Starobinsky potential, the potential energy dominated bounce cannot give rise to any period of inflation for both mLQC-I and mLQC-II models, quite similar to what happens in LQC (Bonga and Gupt, 2016; Bonga and Gupt, 2016).
To consider the probability of the slow-roll inflation in the modified LQC models, let us start with the phase space
However, after taking the effective Hamiltonian constraint into account,
where
On the other hand, the phase space
For any given matter field that satisfies the weak energy condition (Hawking and Ellis, 1973), we have
where
On the other hand, from Eqs 2.25, 2.43 we find that
Inserting this expression into Eq. 2.59, we find that the pulled-back symplectic structure
from which we find that the Liouville measure
Note that
so that the 2D phase space
where
Once the probability is properly defined, we can calculate it in different models of the modified LQCs. In LQC (Ashtekar and Sloan, 2011a; Ashtekar and Sloan, 2011b), the calculations were carried out for the quadratic potential. In order to compare the results obtained in different models, let us consider the same potential. Then, for the mLQC-I model it was found that (Li et al., 2019)
so that the probability for the desired slow-roll not to happen is,
where
In mLQC-II, following a similar analysis, it can be shown that the probability for the desired slow-roll not to happen is (Li et al., 2019),
Note that in LQC the probability for the desired slow roll inflation not to occur is (Ashtekar and Sloan, 2011a; Ashtekar and Sloan, 2011b),
which is smaller than that for mLQC-I and slightly larger than the one for mLQC-II. However, it is clear that the desired slow-roll inflation is very likely to occur in all the models, including the two modified LQC ones.
As mentioned above, in the literature there exist several approaches to investigate the inhomogeneities of the Universe. Such approaches can be generalized to the modified LQC models, including mLQC-I and mLQC-II. In this section we shall focus ourselves on cosmological perturbations in the framework of mLQCs following the dressed metric approach (Agullo et al., 2012; Agullo et al., 2013; Agullo et al., 2013), while in the next section we will be following the hybrid approach (Fernández-Méndez et al., 2012; Fernández-Méndez et al., 2013; Castelló Gomar et al., 2014; Gomar et al., 2015; Martínez and Olmedo, 2016). We shall restrict ourselves to the effective dynamics, as we did with the homogeneous background in the last section. Such investigations in general include two parts: 1) the initial conditions; and 2) the dynamical evolutions of perturbations. In the framework of effective dynamics, the latter is a second-order ordinary differential equation in the momentum space, so in principle once the initial conditions are given, it uniquely determines the cosmological (scalar and tensor) perturbations.
However, the initial conditions are a subtle issue, which is true not only in LQC but also in mLQCs. This is mainly because that in general there does not exist a preferred initial time and state for a quantum field in an arbitrarily curved space-time (Birrell and Davies, 1982; Wald, 1994; Mukhanov and Winitzki, 2007; Parker and Toms, 2009). If the Universe is sufficiently smooth and its evolution is sufficiently slow, so that the characteristic scale of perturbations is much larger than the wavelengths of all the relevant modes, a well justified initial state can be defined: the BD vacuum. This is precisely the initial state commonly adopted in GR at the beginning of the slow-roll inflation, in which all the relevant perturbation modes are well inside the comoving Hubble radius (Baumann, 2009) [cf. Figure 2].
However, in LQC/mLQCs, especially near the bounce, the evolution of the background is far from “slow,” and its geometry is also far from the de Sitter. In particular, for the perturbations during the bouncing phase, the wavelengths could be larger, equal, or smaller than the corresponding characteristic scale, as it can be seen, for example, from Figure 5. Thus, it is in general impossible to assume that the Universe is in the BD vacuum state at the bounce (Agullo et al., 2013; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017; Zhu et al., 2017; Zhu et al., 2017). Therefore, in the following let us first elaborate in more details about the subtle issues regarding the initial conditions.
The initial conditions for cosmological perturbations in fact consists of two parts: when and which? However, both questions are related to each other. In LQC literature, for cosmological perturbations, two different moments have been chosen so far in the dressed and hybrid approaches: 1) the remote past in the contracting phase (Li et al., 2020c) and 2) the bounce (Agullo et al., 2013; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017). To see which conditions we need to impose at a given moment, let us first recall how to impose the initial conditions in GR, in which the scalar perturbations are governed by the equation,
where k denotes the comoving wave number, and
where
If we further require the vacuum to be the minimum energy state, a unique solution exists, which is given by
which is often referred to as the BD vacuum (Baumann, 2009).
Consider the de Sitter space as the background, we have
where
It is clear that on scales much smaller than the comoving Hubble radius (
Note that if the initial time
However, on the scales much larger than the comoving Hubble radius (
As shown in Figure 2, if the initial time
In modified LQC models, the mode function
where
One of the main reasons to choose the remote past in the contracting phase as the initial time for perturbations is that at such time either the background is well described by the de Sitter space (mLQC-I) or the expansion factor
On the other hand, if the initial time is chosen to be at the bounce, cautions must be taken on what initial conditions can be imposed consistently. In particular, if at this moment some modes are inside the comoving Hubble radius and others are not, it is clear that in this case imposing the BD vacuum at the bounce will lead to inconsistencies. In addition, there also exist the cases in which particle creation in the contracting phase is not negligible, then it is unclear how a BD vacuum can be imposed at the bounce, after the Universe is contracting for such a long time before the bounce. Thus, in these cases other initial conditions need to be considered, such as the fourth-order adiabatic vacuum (Agullo et al., 2013; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017; Zhu et al., 2017; Zhu et al., 2017).
With the above in mind, in the following we turn to consider power spectra of the cosmological perturbations.
Since the evolutions of the effective dynamics of the homogeneous backgrounds for mLQC-I and mLQC-II are different, in this subsection let us first consider the case of mLQC-I and then mLQC-II. To compare the results with those obtained in LQC, at the end of this subsection, we also discuss the LQC case.
For mLQC-I, the power spectrum of the cosmological scalar perturbations was first studied in (Agullo, 2018) for the quadratic
where
It should be noted that, when generalizing the classical expression of the function
where
with the choice of the lapse function
where “-” corresponds to
where
It should be noted that in (Agullo, 2018) only the function
In addition,
and
Another choice was introduced in (Li et al., 2020c), which was motivated from the following considerations. The functions
to replace
it behaves precisely as a step function, so that
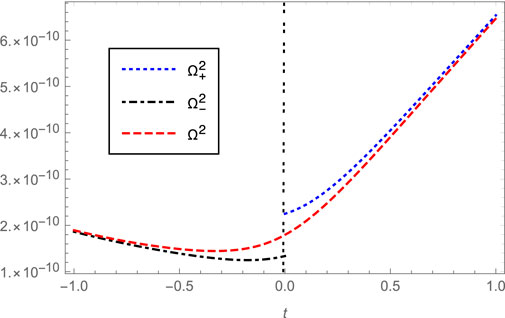
FIGURE 3. The potential terms
In addition to the above choices, motivated by the hybrid approach (Fernández-Méndez et al., 2012; Fernández-Méndez et al., 2013; Castelló Gomar et al., 2014; Gomar et al., 2015; Martínez and Olmedo, 2016), the following replacements for
where
Such obtained
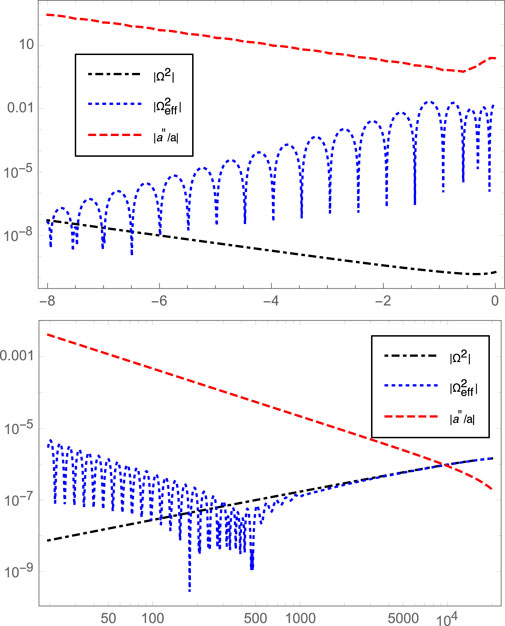
FIGURE 4. The potential terms
To study the effects of the curvature term, let us first introduce the quantity,
which is much larger than other two terms
From Figure 4 we can also see that the difference between
However, the power spectra obtained from
With the clarification of the ambiguities caused by the quantum mechanical generalization of the function
In mLQC-I, the evolution of the effective (quantum) homogeneous Universe is asymmetric with respect to the bounce (Dapor and Liegener, 2018a; Li et al., 2018a; Li et al., 2018b; Li et al., 2019). In particular, before the bounce (
where
where
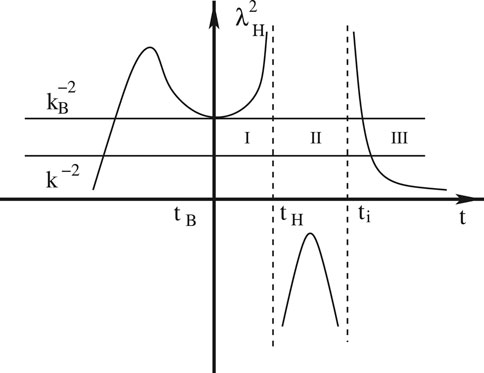
FIGURE 5. Schematic plot of
for which Eq. 3.9 has the exact solutions given by Eq. 3.6. Therefore, at sufficient early times, choosing
With the exact solution (3.7) as the initial conditions imposed at the moment
It should be noted that if the initial conditions are imposed at the bounce, from Figure 5 we can see clearly that some modes are inside the comoving Hubble radius, and some are not. In addition, in the neighborhood of the bounce, the background is far from de Sitter. So, it is impossible to impose either the BD vacuum or the de Sitter state at the bounce. In this case, one of the choices of the initial conditions is the fourth-order adiabatic vacuum, similar to that in LQC (Agullo et al., 2013; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017; Zhu et al., 2017; Zhu et al., 2017).
In mLQC-II, the evolution of the effective homogeneous Universe is different from that of mLQC-I. In particular, it is symmetric with respect to the bounce and in the initially kinetic energy dominated case at the bounce the solutions can be well approximated by Eq. 2.56 in the bouncing phase (Li et al., 2018b; Li et al., 2019), similar to that of LQC (Ashtekar and Singh, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017).
When considering the cosmological perturbations, similar ambiguities in the choices of
which behaves also like a step function across the bounce and picks up the right sign in both contracting and expanding phases, so it smoothly connects
On the other hand,
but now with
Such obtained
that is, the curvature term
To see how to impose the initial conditions, let us introduce the quantity
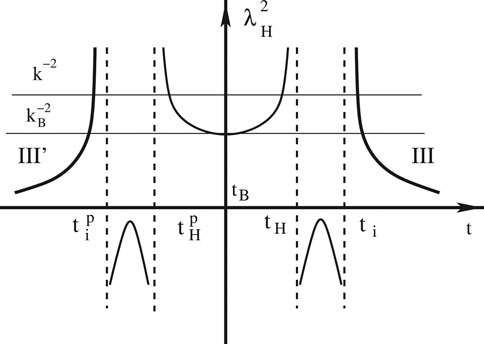
FIGURE 6. Schematic plot of
Certainly, one can choose different initial conditions. In particular, the fourth-order adiabatic vacuum was chosen even in the contracting phase in (Li et al., 2020c). With such a choice, the power spectra from
To consider the effects of the ambiguities in the choice of
while
As shown explicitly, the term
during the bouncing phase
As a result, the initial states of the linear perturbations can be either imposed in the contracting phase at a moment
To compare the results obtained from the three different models, in (Li et al., 2020c) the fourth-order adiabatic vacuum was chosen even in the contracting phase for LQC. Here, we cite some of the results in Figure 7. In particular, it was found that the relative difference in the amplitudes of the power spectra of the scalar perturbations due to the choice of
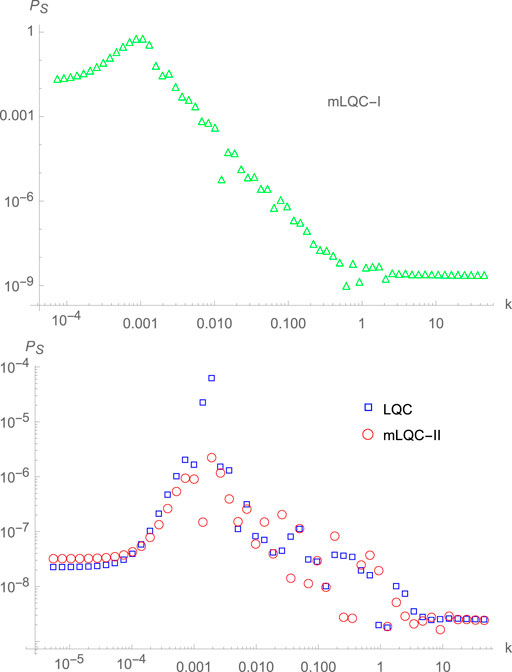
FIGURE 7. The figure shows the results of the scalar power spectra from three models presented in (Li et al., 2020c) when the potential term is given by
However, comparing the power spectra obtained from the three different models, even with the same choice of
For the tensor perturbations, the potential term
As in the previous section, in this section we also consider the three different models, LQC, mLQC-I, and mLQC-II, but now in the hybrid approach, and pay particular attention to the differences of the power spectra among these models. Since the scalar perturbations are the most relevant ones in the current CMB observations, in the following we shall mainly focus on them, and such studies can be easily extended to the tensor perturbations.
Power spectra of the cosmological scalar and tensor perturbations for the effective Hamilton in mLQC-I were recently studied in the hybrid approach (Fernández-Méndez et al., 2013; Castelló Gomar et al., 2014; Gomar et al., 2015). In particular, the mode function
where
which is the effective mass of the scalar mode, with
Note that in (Li et al. 2020a), instead of
in Eq. 4.2, where
This is the case referred to as prescription A in (García-Quismondo et al., 2020).
The other possibility is obtained by the replacement of Eqs 3.34, 3.35, which was referred to as Prescription B (García-Quismondo et al., 2020), and showed that the two prescriptions lead to almost the same results. So, in the rest of this section we restrict ourselves only to prescription A.
Then, for the case in which the evolution of the homogeneous Universe was dominated by kinetic energy at the bounce,
it was shown that the effective mass is always positive at the bounce (García-Quismondo et al., 2020). In fact, near the bounce we have (Wu et al., 2018),
Note that in writing the above expression, we have used the fact that during the bouncing phase we have
where
For the case that satisfies the condition (4.6) initially at the bounce, we find that
has similar behavior in the post-bounce phases for the case in which the evolution of the homogeneous Universe was dominated by kinetic energy at the bounce, but has different behaviors in the pre-bounce phases, depending specifically on the potentials considered.
In Figures 8, 9 we show the comoving Hubble radius for the quadratic and Starobinsky potentials, respectively. From these figures it is clear that for
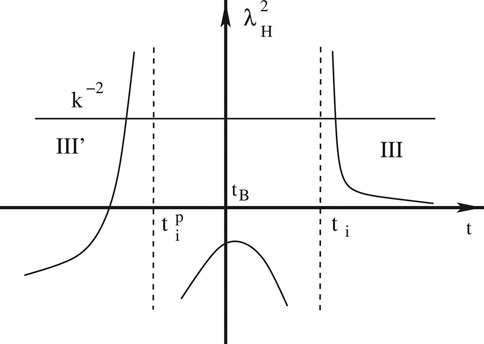
FIGURE 8. Schematic plot of
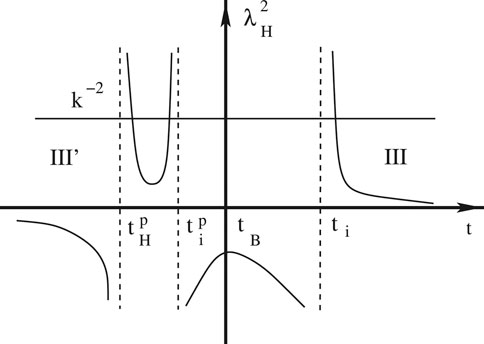
FIGURE 9. Schematic plot of
Similar to LQC, the homogeneous Universe of mLQC-II is symmetric with respect to the bounce, and is well described by the analytical solutions given by Eqs 2.56, 2.57 for the states that are dominated by kinetic energy at the bounce.
In this model, the cosmological perturbations are also given by Eqs 4.1–4.3 but now with the replacement (Li et al., 2020a),
where
In this case, it can be shown that the effective mass defined by Eq. 4.2 is always positive in the neighborhood of the bounce, but far from the bounce, the properties of
In Figure 10, we plot
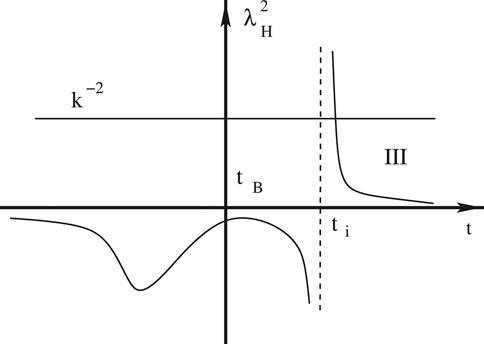
FIGURE 10. Schematic plot of
Moreover, as
The evolution of the homogeneous Universe of standard LQC model is also symmetric with respect to the bounce, and is well described by the analytical solutions given in (Zhu et al., 2017; Zhu et al., 2017) for the states that are dominated by kinetic energy at the bounce.
In this model, the cosmological perturbations are also given by Eqs 4.1.3.–.Eqs 4.4.3 but now with the replacement (Li et al., 2020a),
where
In this case, it can be shown that the effective mass defined by Eq. 4.2 is always positive for the states that are dominated by kinetic energy at the bounce (Navascues et al., 2018; Wu et al., 2018), and the quantity
As it can be seen that one of the preferred moments to impose the initial conditions for the cosmological perturbations in all these three models is a moment in the contracting phase
The nth-order adiabatic vacuum conditions can be obtained as follows: Let us first consider the solution,
Then, inserting it into (4.1), one can find an iterative equation for
Here
In addition, the power spectrum is normally evaluated at the end of inflation, at which all the relevant modes are well outside the Hubble horizon [cf. Figure 2].
It should be also noted that the above formula is only applicable to the case where
In addition, in the following only the Starobinsky potential given in Eq. 3.24 will be considered, as it represents one of the most favorable models by current observations (Bennett et al., 1996; Banday et al., 1996; Komatsu et al., 2011; Larson et al., 2011; Ade and PLANCK Collaboration, 2016; Aghanim and PLANCK Collaboration, 2020). Let us turn to consider the power spectrum of the scalar perturbations in each of the three models. Similar results can be also obtained for the tensor perturbations. In particular, it was found that the scalar power spectra in these three models can be still divided into three distinctive regimes: the infrared, oscillatory and UV, as shown in Figure 11.
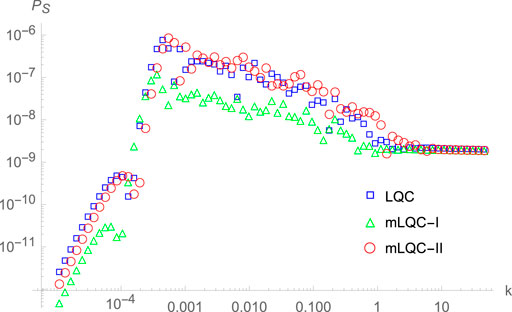
FIGURE 11. The primordial power spectra of the cosmological scalar perturbations in the hybrid approach with the Starobinsky potential, respectively, for LQC, mLQC-I, and mLQC-II. The mass of the inflaton field is set to
In the infrared and oscillatory regimes, the relative difference between LQC and mLQC-I can be as large as
However, it is interesting to note that in the infrared and oscillatory regimes, the power spectrum in mLQC-I is suppressed in comparison with that of LQC, which has been found only in the hybrid approach. As a matter of fact, in the dressed metric approach, the power spectrum in mLQC-I is largely amplified in the infrared regime, and its magnitude is of the Planck scale as depicted in Figure 7 (Agullo, 2018; Li et al., 2020c). The main reason might root in the distinctive behavior of the effective masses in the two approaches, as shown explicitly in Figures 5, 8.
On the other hand, the difference of the power spectra between LQC and mLQC-II is smaller than that between LQC and mLQC-I. In particular, in the infrared regime, it is about
To summarize, in the hybrid approach the maximum relative differences of the power spectra among these three different models always happen in the infrared and oscillatory regimes, while in the UV regime, the differences reduce to no larger than
In the past 2 decades, LQC has been studied extensively, and several remarkable features have been found (Ashtekar and Singh, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017), including the generic resolution of the big bang singularity (replaced by a quantum bounce) in the Planckian scale, the slow-roll inflation as an attractor in the post-bounce evolution of the Universe, and the scale-invariant power spectra of the cosmological perturbations, which are consistent with the current CMB observations. Even more interestingly, it was shown recently that some anomalies from the CMB data (Akrami and Planck collaboration, 2020; Akrami and Planck collaboration, 2020; Schwarz et al., 2016) can be reconciled purely due to the quantum geometric effects in the framework of LQC (Ashtekar et al., 2020; Agullo et al., 2021; Agullo et al., 2021; Ashtekar et al., 2021).
Despite of all these achievements, LQC is still plagued with some ambiguities in the quantization procedure. In particular, its connection with LQG is still not established (Brunnemann and Fleischhack, 2007; Engle, 2007; Brunnemann and Koslowski, 2011), and the quantization procedure used in LQC owing to symmetry reduction before quantization can result in different Hamiltonian constraints than the one of LQG.
Motivated by the above considerations, recently various modified LQC models have been proposed, see, for example (Alesci and Cianfrani, 2013; Alesci and Cianfrani, 2015; Alesci et al., 2017; Oriti, 2017; Oriti et al., 2017; Wilson-Ewing, 2017; Engle and Vilensky, 2018; Gerhardt et al., 2018; Wilson-Ewing, 2018; Baytas et al., 2019; Engle and Vilensky, 2019; Neuser et al., 2019; Olmedo and Alesci, 2019; Schander and Thiemann, 2019; Schander and Thiemann, 2019; Han and Liu, 2020a; Han and Liu, 2020b; Giesel et al., 2020; Giesel et al., 2020; Han et al., 2020; Li et al., 2020b), and references therein. In this brief review, we have restricted ourselves only to mLQC-I and mLQC-II (Yang et al., 2009; Dapor and Liegener, 2018a; Dapor and Liegener, 2018b), as they are the ones that have been extensively studied in the literature not only the dynamics of the homogeneous Universe (Li et al., 2018a; Li et al., 2018b; Saini and Singh, 2019a; Saini and Singh, 2019b; García-Quismondo and Mena Marugán, 2019; Li et al., 2019; García-Quismondo and Mena Marugán, 2020), but also the cosmological perturbations (Agullo, 2018; Castelló Gomar et al., 2020; García-Quismondo et al., 2020; Li et al., 2020a; Li et al., 2020b).
In these two modified LQC models, it was found that the resolution of the big bang singularity is also generic (Li et al., 2018a; Li et al., 2018b; Saini and Singh, 2019a; Saini and Singh, 2019b; Li et al., 2019). This is closely related to the fact that the area operator in LQG has a minimal but nonzero eigenvalue (Ashtekar and Lewandowski, 2004; Thiemann, 2007; Rovelli, 2008; Ashtekar and Singh, 2011; Bojowald, 2011; Gambini and Pullin, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017; Ashtekar and Pullin, 2017), quite similar to the eigenvalue of the ground state of the energy operator of a simple harmonic oscillator in quantum mechanics. This deep connection also shows that the resolution of the big bang singularity is purely due to the quantum geometric effects. In addition, similar to LQC, the slow-roll inflation also occurs generically in both mLQC-I and mLQC-II (Li et al., 2019). In particular, when the inflaton has a quadratic potential,
When dealing with perturbations, another ambiguity rises in the replacement of the momentum conjugate
However, the interactions between the infrared and UV modes appearing in non-Gaussianities might provide an excellent window to observe such effects. This was initially done in LQC (Agullo et al., 2018; Wu et al., 2018; Zhu et al., 2018), and lately generalized to bouncing cosmologies (Agullo et al., 2021; Agullo et al., 2021). It should be noted that in (Agullo et al., 2021; Agullo et al., 2021), the expansion factor
where b and n are two free parameters. For example, for LQC we have
Moreover, initial conditions are another subtle and important issue not only in LQC but also in mLQCs. As a matter of fact, the initial conditions consist of two parts: the initial time, and the initial conditions. Different choices of the initial times lead to different choices of the initial conditions, or vice versa. To clarify these issues, in Sections 3, 4 we have discussed it at length by showing the (generalized) comoving Hubble radius in each model as well as in each of the two approaches, dressed metric and hybrid. From these analyses, we have shown clearly which initial conditions can and cannot be imposed at a given initial time.
In addition, when the Universe changes from contraction to expansion at the bounce, particle and entropy creations are expected to be very large, and it is crucial to keep such creations under control, so that the basic assumptions of the models are valid, including the one that the cosmological perturbations are small and can be treated as test fields propagating on the quantum homogeneous background, as assumed in both the dressed metric and hybrid approaches.
Yet, different initial conditions also affect the amplitudes and shapes of the primordial power spectra, and it would be very interesting to investigate the consistency of such obtained spectra with current observations, in particular the possible explanations to the anomalies found in the CMB data (Akrami and Planck collaboration, 2020; Akrami and Planck collaboration, 2020; Schwarz et al., 2016), and the naturalness of such initial conditions.
On the other hand, bouncing cosmologies, as an alternative to the cosmic inflation paradigm, have been extensively studied in the literature, see, for example (Wand, 1999; Brandenberger and Peter, 2017), and references therein. However, in such classical bounces, exotic matter fields are required in order to keep the bounce open. This in turn raises the question of instabilities of the models. On the other hand, quantum bounces found in LQC/mLQCs are purely due to the quantum geometric effects, and the instability problem is automatically out of the question. So, it would be very interesting to study bouncing cosmologies in the framework of LQC/mLQCs. The first step in this direction has already been taken (Li et al., 2020b), and more detailed and extensive analyses are still needed.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
BL and PS are supported by NSF grant PHY-1454832. BL is also partially supported by the National Natural Science Foundation of China (NNSFC) with the Grants No. 12005186.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We are grateful to Robert Brandenberger and David Wands for valuable comments on the manuscript and helpful discussions. We thank Javier Olmedo and Tao Zhu for various discussions related to works presented in this manuscript.
1It has been conjectured using models in string theory that the trans-Planckian problem might never arise (Bedroya and Vafa, 2020), which results on severe constraints on various cosmological models [See (Bedroya et al., 2020; Brandenberger, 2021) for more details].
2A similar contracting branch is found in certain anisotropic models in the standard regularization of LQC [see for e.g., (Dadhich et al., 2015)].
3It should be noted that anisotropies rise during the contracting phase and generically dominate the earliest stages of the post-bounce of the homogeneous Universe (Gupt and Singh, 2012; Gupt and Singh, 2013; Agullo et al., 2020; Agullo et al., 2020). So, cautions must be taken, when imposing initial conditions at the bounce.
4To be distinguished from the BD vacuum described by Eq. 3.4 we refer to the state described by Eq. 3.7 as the de Sitter state. The difference between them is due to the term
5For a modification of LQC based on using gauge-covariant fluxes, see (Liegener and Singh, 2019; Liegener and Singh, 2020).
6In LQC, this universality was first found for the quadratic and Starobinsky potentials (Zhu et al., 2017; Zhu et al., 2017) [see also (Bhardwaj et al., 2019)], and later was shown that they are also true for other potentials, including the power-law potentials (Shahalam et al., 2017; Shahalam, 2018), α-attractor potentials (Shahalam et al., 2018; Shahalam et al., 2020), Monodromy potentials (Sharma et al., 2018), warm inflation (Xiao and Wang, 2020), Tachyonic inflation (Xiao, 2019) and even in Brans-Dicke LQC (Jin et al., 2019; Sharma et al., 2019).
7It is interesting to note that Eq. 2.61 holds not only in mLQC-I, but also in LQC and mLQC-II.
8In the framework of LQC, such effects were also studied in (Agullo et al., 2013; Zhu et al., 2017; Zhu et al., 2017; Navascues et al., 2018; Li et al., 2020). In particular, in (Agullo et al., 2018; Li et al., 2020; Agullo et al., 2021; Agullo et al., 2021) the function
Abazajian, K. N. (2015). Inflation Physics from the Cosmic Microwave Background and Large Scale Structure. Astropart. Phys. 63, 55.
Ade, P.PLANCK Collaboration (2016). Planck 2015 Results. XX. Constraints on Inflation. A&A 594, A20.
Aghanim, N.PLANCK Collaboration (2020). Planck 2018 Results. X. Constraints on Inflation. A&A 641, A10.
Agullo, I., Ashtekar, A., and Gupt, B. (2017). Phenomenology with Fluctuating Quantum Geometries in Loop Quantum Cosmology. Class. Quan. Grav. 34, 074003. doi:10.1088/1361-6382/aa60ec
Agullo, I., Ashtekar, A., and Nelson, W. (2013). Extension of the Quantum Theory of Cosmological Perturbations to the Planck Era. Phys. Rev. D87, 043507.
Agullo, I., Ashtekar, A., and Nelson, W. (2012). Quantum Gravity Extension of the Inflationary Scenario. Phys. Rev. Lett. 109, 251301. doi:10.1103/physrevlett.109.251301
Agullo, I., Ashtekar, A., and Nelson, W. (2013). The Pre-inflationary Dynamics of Loop Quantum Cosmology: Confronting Quantum Gravity with Observations. Class. Quan. Grav. 30, 085014. doi:10.1088/0264-9381/30/8/085014
Agullo, I., Bolliet, B., and Sreenath, V. (2018). Non-Gaussianity in Loop Quantum Cosmology. Phys. Rev. D97, 066021.
Agullo, I., Kranas, D., and Sreenath, V. (2021). Anomalies in the CMB from a Cosmic Bounce. Gen. Relativ Gravit. 53, 17. doi:10.1007/s10714-020-02778-9
Agullo, I., Kranas, D., and Sreenath, V. (2021). Large Scale Anomalies in the CMB and Non-gaussianity in Bouncing Cosmologies. Class. Quan. Grav. 38, 065010. doi:10.1088/1361-6382/abc521
Agullo, I., and Morris, N. A. (2015). Detailed Analysis of the Predictions of Loop Quantum Cosmology for the Primordial Power Spectra. Phys. Rev. D 92, 124040. doi:10.1103/physrevd.92.124040
Agullo, I., Olmedo, J., and Sreenath, V. (2020). Observational Consequences of Bianchi I Spacetimes in Loop Quantum Cosmology. Phys. Rev. D102, 043523.
Agullo, I., Olmedo, J., and Sreenath, V. (2020). Predictions for the Cosmic Microwave Background from an Anisotropic Quantum Bounce. Phys. Rev. Lett. 124, 251301. doi:10.1103/physrevlett.124.251301
Agullo, I. (2018). Primordial Power Spectrum from the Dapor-Liegener Model of Loop Quantum Cosmology. Gen. Relativ Gravit. 50, 91. doi:10.1007/s10714-018-2413-1
Agullo, I., and Singh, P. (2017). “Loop Quantum Cosmology,” in Loop Quantum Gravity: The First 30 Years. Editors A. Ashtekar, and J. Pullin (Singapore: Wald Scientific).
Akrami, Y.Planck collaboration (2020). Planck 2018 Results. I. Overview and the Cosmological Legacy of Planck. A&A 641, A1.
Akrami, Y.Planck collaboration (2020). Planck 2018 Results. VII. Isotropy and Statistics of the CMB. A&A 641, A7.
Alesci, E., Botta, G., Cianfrani, F., and Liberati, S. (2017). Cosmological Singularity Resolution from Quantum Gravity: the Emergent-Bouncing Universe. Phys. Rev. D96, 046008.
Alesci, E., and Cianfrani, F. (2015). Quantum Reduced Loop Gravity: a Realistic Universe. Phys. Rev. D92, 084065.
Alesci, E., and Cianfrani, F. (2013). Quantum-Reduced Loop Gravity: Cosmology. Phys. Rev. D87, 083521.
Ashoorioon, A., Chialva, D., and Danielsson, U. (2011). Effects of Nonlinear Dispersion Relations on Non-gaussianities. J. Cosmol. Astropart. Phys. 2011, 034. doi:10.1088/1475-7516/2011/06/034
Ashtekar, A., Gupt, B., Jeong, D., and Sreenath, V. (2020). Alleviating the Tension in the Cosmic Microwave Background Using Planck-Scale Physics. Phys. Rev. Lett. 125, 051302. doi:10.1103/PhysRevLett.125.051302
Ashtekar, A., Pawlowski, T., and Singh, P. (2006). Quantum Nature of the Big Bang. Phys. Rev. Lett. 96, 141301. doi:10.1103/PhysRevLett.96.141301
Ashtekar, A., and Barrau, A. (2015). Loop Quantum Cosmology: From Pre-inflationary Dynamics to Observations. Class. Quan. Grav. 32, 234001. doi:10.1088/0264-9381/32/23/234001
Ashtekar, A., Bojowald, M., and Lewandowski, J. (2003). Mathematical Structure of Loop Quantum Cosmology. Adv. Theor. Math. Phys. 7, 233–268. doi:10.4310/atmp.2003.v7.n2.a2
Ashtekar, A., Corichi, A., and Singh, P. (2010). Robustness of Key Features of Loop Quantum Cosmology. Phys. Rev. D77, 024046.
Ashtekar, A., and Gupt, B. (2017). Initial Conditions for Cosmological Perturbations. Class. Quan. Grav. 34, 035004. doi:10.1088/1361-6382/aa52d4
Ashtekar, A., Gupt, B., Jeong, D., and Sreenath, V. (2021). Cosmic Tango between the Very Small and the Very Large: Addressing CMB Anomalies through Loop Quantum Cosmology. arXiv:2103.14568.
Ashtekar, A., and Gupt, B. (2017). Quantum Gravity in the Sky: Interplay between Fundamental Theory and Observations. Class. Quan. Grav. 34, 014002. doi:10.1088/1361-6382/34/1/014002
Ashtekar, A., and Lewandowski, J. (2004). Background Independent Quantum Gravity: A Status Report. Class. Quan. Grav. 21, R53–R152. doi:10.1088/0264-9381/21/15/r01
Ashtekar, A., Pawlowski, T., and Singh, P. (2006). Quantum Nature of the Big Bang: An Analytical and Numerical Investigation. Phys. Rev. D 73, 124038. doi:10.1103/physrevd.73.124038
Ashtekar, A., and Pullin, J. (2017). Loop Quantum Gravity - the First 30 Years. Singapore: World Scientific.
Ashtekar, A., and Singh, P. (2011). Loop Quantum Cosmology: a Status Report. Class. Quan. Grav. 28, 213001. doi:10.1088/0264-9381/28/21/213001
Ashtekar, A., and Sloan, D. (2011a). Probability of Inflation in Loop Quantum Cosmology. Gen. Relativ. Gravit. 43, 3619–3655. doi:10.1007/s10714-011-1246-y
Ashtekar, A., and Sloan, D. (2011b). Loop Quantum Cosmology and Slow Roll Inflation. Phys. Lett. B 694, 108.
Assanioussi, M., Dapor, A., Liegener, K., and Pawłowski, T. (2018). Emergent de Sitter epoch of the quantum Cosmos from Loop Quantum Cosmology. Phys. Rev. Lett. 121, 081303. doi:10.1103/PhysRevLett.121.081303
Assanioussi, M., Dapor, A., Liegener, K., and Pawlowski, T. (2019b). Challenges in Recovering a Consistent Cosmology from the Effective Dynamics of Loop Quantum Gravity. Phys. Rev. D100, 106016.
Assanioussi, M., Dapor, A., Liegener, K., and Pawlowski, T. (2019a). Emergent de Sitter epoch of the loop quantum cosmos: A detailed analysis. Phys. Rev. D100, 084003.
Banday, K. M. A. J., Bennett, C. L., Hinshaw, G., Kogut, A., Smoot, G. F., and Wright, E. L. (1996). Power Spectrum of Primordial Inhomogeneity Determined from the FOUR-Year [ITAL]COBE[/ITAL] DMR Sky Maps. ibid 464, L11–L15. doi:10.1086/310077
Baumann, D., and McAllister, L. (2015). Inflation and String Theory. Cambridge: Cambridge Monographs on Mathematical Physics, Cambridge University Press.
Baytas, B., Bojowald, M., and Crowe, S. (2019). Equivalence of Models in Loop Quantum Cosmology and Group Field Theory. Universe 5, 41.
Becker, K., Becker, M., and Schwarz, J. H. (2007). String Theory and M-Theory. Cambridge: Cambridge University Press.
Bedic, S., and Vereshchagin, G. (2019). Probability of Inflation in Loop Quantum Cosmology. Phys. Rev. D99 (4), 043512.
Bedroya, A., Brandenberger, R., Loverde, M., and Vafa, C. (2020). Trans-Planckian Censorship and Inflationary Cosmology. Phys. Rev. D 101, 103502. doi:10.1103/physrevd.101.103502
Bedroya, A., and Vafa, C. (2020). Trans-Planckian Censorship and the Swampland. J. High Energ. Phys. 2020, 123. doi:10.1007/jhep09(2020)123
Bennett, C. L., Banday, A. J., Górski, K. M., Hinshaw, G., Jackson, P., Keegstra, P., et al. (1996). Four-Year [ITAL]COBE[/ITAL] DMR Cosmic Microwave Background Observations: Maps and Basic Results. Astrophys. J. 464, L1–L4. doi:10.1086/310075
Bergstorm, L., and Danielsson, U. H. (2002). Can MAP and Planck Map Planck Physics? J. High Energ. Phys. 12, 038.
Bhardwaj, A., Copeland, E. J., and Louko, J. (2019). Inflation in Loop Quantum Cosmology. Phys. Rev. D99, 063520.
Birrell, N. D., and Davies, P. C. W. (1982). Quantum fields in Curved Space. Cambridge: Cambridge University Press.
Bojowald, M. (2011). Canonical Gravity and Applications: Cosmology, Black Holes, and Quantum Gravity. Cambridge: Cambridge University Press.
Bojowald, M., Hossain, G. M., Kagan, M., and Shankaranarayanan, S. (2008). Anomaly freedom in Perturbative Loop Quantum Gravity. Phys. Rev. D78, 063547.
Bojowald, M. (2015). Quantum Cosmology: a Review. Rep. Prog. Phys. 78, 023901. doi:10.1088/0034-4885/78/2/023901
Bonga, B., and Gupt, B. (2016). Inflation with the Starobinsky Potential in Loop Quantum Cosmology. Gen. Relativ. Grav. 48, 1. doi:10.1007/s10714-016-2071-0
Bonga, B., and Gupt, B. (2016). Phenomenological Investigation of a Quantum Gravity Extension of Inflation with the Starobinsky Potential. Phys. Rev. D93, 063513.
Borde, A., Guth, A. H., and Vilenkin, A. (2003). Inflationary Spacetimes Are Incomplete in Past Directions. Phys. Rev. Lett. 90, 151301. doi:10.1103/physrevlett.90.151301
Borde, A., and Vilenkin, A. (1994). Eternal Inflation and the Initial Singularity. Phys. Rev. Lett. 72, 3305–3308. doi:10.1103/physrevlett.72.3305
Brandenberger, R. H., and Martin, J. (2013). Trans-Planckian Issues for Inflationary Cosmology. Class. Quan. Grav. 30, 113001. doi:10.1088/0264-9381/30/11/113001
Brandenberger, R., and Peter, P. (2017). Bouncing Cosmologies: Progress and Problems. Found. Phys. 47, 797–850. doi:10.1007/s10701-016-0057-0
Brandenberger, R. (2021). Trans-Planckian Censorship Conjecture and Early Universe Cosmology. arXiv:2102.09641.
Brunnemann, J., and Fleischhack, C. (2007). On the Configuration Spaces of Homogeneous Loop Quantum Cosmology and Loop Quantum Gravity. arXiv:0709.1621.
Brunnemann, J., and Koslowski, T. A. (2011). Symmetry Reduction of Loop Quantum Gravity. Class. Quan. Grav. 28, 245014. doi:10.1088/0264-9381/28/24/245014
Burgess, C. P., Cicoli, M., and Quevedo, F. (2013). String Inflation after Planck 2013. J. Cosmol. Astropart. Phys. 2013, 003. doi:10.1088/1475-7516/2013/11/003
Cailleteau, T., Barrau, A., Grain, J., and Vidotto, F. (2012). Consistency of Holonomy-Corrected Scalar, Vector and Tensor Perturbations in Loop Quantum Cosmology. Phys. Rev. D86, 087301.
Cailleteau, T., Mielczarek, J., Barrau, A., and Grain, J. (2012). Anomaly-free Scalar Perturbations with Holonomy Corrections in Loop Quantum Cosmology. Class. Quan. Grav. 29, 095010. doi:10.1088/0264-9381/29/9/095010
Carlip, S. (2003). Quantum Gravity in 2+1 Dimensions. Cambridge: Cambridge Monographs on Mathematical Physics, Cambridge University Press.
Castelló Gomar, L., Fernández-Méndez, M., Mena Marugan, G. A., and Olmedo, J. (2014). Cosmological Perturbations in Hybrid Loop Quantum Cosmology: Mukhanov-Sasaki Variables. Phys. Rev. D90, 064015.
Castelló Gomar, L., García-Quismondo, A., and Mena Marugán, G. A. (2020). Primordial Perturbations in the Dapor-Liegener Model of Hybrid Loop Quantum Cosmology. Phys. Rev. D102, 083524.
Castelló Gomar, L., Mena Marugán, G. A., Martín de Blas, D., and Olmedo, J. (2017). Hybrid Loop Quantum Cosmology and Predictions for the Cosmic Microwave Background. Phys. Rev. D 96, 103528. doi:10.1103/physrevd.96.103528
Chen, L., and Zhu, J.-Y. (2015). Loop Quantum Cosmology: The Horizon Problem and the Probability of Inflation. Phys. Rev. D92, 084063.
Corichi, A., and Karami, A. (2011). Measure Problem in Slow Roll Inflation and Loop Quantum Cosmology. Phys. Rev. D 83, 104006. doi:10.1103/physrevd.83.104006
Corichi, A., and Singh, P. (2008). Is Loop Quantization in Cosmology Unique? Phys. Rev. D78, 024034.
Corichi, A., and Sloan, D. (2014). Inflationary Attractors and Their Measures. Class. Quan. Grav. 31, 062001. doi:10.1088/0264-9381/31/6/062001
Craig, D. A., and Singh, P. (2013). Consistent Probabilities in Loop Quantum Cosmology. Class. Quan. Grav. 30, 205008. doi:10.1088/0264-9381/30/20/205008
Dadhich, N., Joe, A., and Singh, P. (2015). Emergence of the Product of Constant Curvature Spaces in Loop Quantum Cosmology. Class. Quan. Grav. 32, 185006. doi:10.1088/0264-9381/32/18/185006
Dapor, A., and Liegener, K. (2018b). Cosmological Coherent State Expectation Values in Loop Quantum Gravity I. Isotropic Kinematics. Class. Quan. Grav. 35, 135011. doi:10.1088/1361-6382/aac4ba
Dapor, A., and Liegener, K. (2018a). Cosmological Effective Hamiltonian from Full Loop Quantum Gravity Dynamics. Phys. Lett. B 785, 506–510. doi:10.1016/j.physletb.2018.09.005
de Blas, D. M., and Olmedo, J. (2016). Primordial Power Spectra for Scalar Perturbations in Loop Quantum Cosmology. J. Cosmol. Astropart. Phys. 2016, 029. doi:10.1088/1475-7516/2016/06/029
Diener, P., Gupt, B., Megevand, M., and Singh, P. (2014). Numerical Evolution of Squeezed and Non-gaussian States in Loop Quantum Cosmology. Class. Quan. Grav. 31, 165006. doi:10.1088/0264-9381/31/16/165006
Diener, P., Gupt, B., and Singh, P. (2014). Numerical Simulations of a Loop Quantum cosmos: Robustness of the Quantum Bounce and the Validity of Effective Dynamics. Class. Quan. Grav. 31, 105015. doi:10.1088/0264-9381/31/10/105015
Diener, P., Joe, A., Megevand, M., and Singh, P. (2017). Numerical Simulations of Loop Quantum Bianchi-I Spacetimes. Class. Quan. Grav. 34, 094004. doi:10.1088/1361-6382/aa68b5
Dupuy, J. L., and Singh, P. (2020). Hysteresis and Beats in Loop Quantum Cosmology. Phys. Rev. D101, 086016.
Easther, R., Kinney, W. H., and Peiris, H. (2005). Observing Trans-planckian Signatures in the Cosmic Microwave Background. J. Cosmol. Astropart. Phys. 2005, 009. doi:10.1088/1475-7516/2005/05/009
Elizaga Navascués, B., Martín de Blas, D., and Mena Marugán, G. (2018). The Vacuum State of Primordial Fluctuations in Hybrid Loop Quantum Cosmology. Universe 4, 98. doi:10.3390/universe4100098
Engle, J. (2007). Relating Loop Quantum Cosmology to Loop Quantum Gravity: Symmetric Sectors and Embeddings. Class. Quan. Grav. 24, 5777–5802. doi:10.1088/0264-9381/24/23/004
Engle, J., and Vilensky, I. (2018). Deriving Loop Quantum Cosmology Dynamics from Diffeomorphism Invariance. Phys. Rev. D98, 023505.
Engle, J., and Vilensky, I. (2019). Uniqueness of Minimal Loop Quantum Cosmology Dynamics. Phys. Rev. D 100, 121901. doi:10.1103/physrevd.100.121901
Fernández-Méndez, M., Mena Marugán, G. A., and Olmedo, J. (2013). Hybrid Quantization of an Inflationary Model: The Flat Case. Phys. Rev. D88, 044013.
Fernández-Méndez, M., Mena Marugán, G. A., and Olmedo, J. (2012). Hybrid Quantization of an Inflationary Universe. Phys. Rev. D86, 024003.
Gambini, R., and Pullin, J. (2011). A First Course in Loop Quantum Gravity. Oxford: Oxford University Press.
García-Quismondo, A., and Mena Marugán, G. A. (2020). Dapor-Liegener Formalism of Loop Quantum Cosmology for Bianchi I Spacetimes. Phys. Rev. D101, 023520.
García-Quismondo, A., and Mena Marugán, G. A. (2019). Martin-Benito-Mena Marugan-Olmedo Prescription for the Dapor-Liegener Model of Loop Quantum Cosmology. Phys. Rev. D99, 083505.
García-Quismondo, A., Mena Marugán, G. A., and Pérez, G. S. (2020). The Time-dependent Mass of Cosmological Perturbations in Loop Quantum Cosmology: Dapor-Liegener Regularization. Class. Quan. Grav. 37, 195003. doi:10.1088/1361-6382/abac6d
Gerhardt, F., Oriti, D., and Wilson-Ewing, E. (2018). The Separate Universe Framework in Group Field Theory Condensate Cosmology. Phys. Rev. D98, 066011.
Giesel, K., Li, B.-F., and Singh, P. (2020). Revisiting the Bardeen and Mukhanov-Sasaki Equations in the Brown-Kuchar and Gaussian Dust Models. arXiv:2012.14443.
Giesel, K., Li, B.-F., and Singh, P. (2020). Towards a Reduced Phase Space Quantization in Loop Quantum Cosmology with an Inflationary Potential. Phys. Rev. D 102, 126024. doi:10.1103/physrevd.102.126024
Giesel, K., and Thiemann, T. (2007). Algebraic Quantum Gravity (AQG): I. Conceptual Setup. Class. Quan. Grav. 24, 2465–2497. doi:10.1088/0264-9381/24/10/003
Gomar, L. C., Martín-Benito, M., and Marugán, G. A. M. (2015). Gauge-invariant Perturbations in Hybrid Quantum Cosmology. J. Cosmol. Astropart. Phys. 2015, 045. doi:10.1088/1475-7516/2015/06/045
Gordon, L., Li, B.-F., and Singh, P. (2021). Quantum Gravitational Onset of Starobinsky Inflation in a Closed Universe. Phys. Rev. D103, 046016.
Green, M. B., Schwarz, J. H., and Witten, E. (1999). Superstring Theory: Vol.1 & 2. Cambridge: Cambridge Monographs on Mathematical Physics, Cambridge University Press.
Gupt, B., and Singh, P. (2013). A Quantum Gravitational Inflationary Scenario in Bianchi-I Spacetime. Class. Quan. Grav. 30, 145013. doi:10.1088/0264-9381/30/14/145013
Gupt, B., and Singh, P. (2012). Quantum Gravitational Kasner Transitions in Bianchi-I Spacetime. Phys. Rev. D86, 024034.
Guth, A. H. (1981). Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 23, 347–356. doi:10.1103/physrevd.23.347
Han, M., Li, H., and Liu, H. (2020). Manifestly Gauge-Invariant Cosmological Perturbation Theory from Full Loop Quantum Gravity. arXiv:2005.00883.
Han, M., and Liu, H. (2020a). Effective Dynamics from Coherent State Path Integral of Full Loop Quantum Gravity. Phys. Rev. D101, 046003.
Han, M., and Liu, H. (2020b). Semiclassical Limit of New Path Integral Formulation from Reduced Phase Space Loop Quantum Gravity. Phys. Rev. D102, 024083.
Hawking, S. W., and Ellis, G. F. R. (1973). The Large Scale Structure of Spacetime. Cambridge: Cambridge University Press.
Jackson, M. G., and Schalm, K. (2012). Model Independent Signatures of New Physics in the Inflationary Power Spectrum. Phys. Rev. Lett. 108, 111301. doi:10.1103/physrevlett.108.111301
Jin, W.-J., Ma, Y.-G., and Zhu, T. (2019). Pre-inflationary Dynamics of Starobinsky Inflation and its Generalization in Loop Quantum Brans-Dicke Cosmology. JCAP 02, 010.
Johson, C. V. (2003). D-Branes, Cambridge Monographs on Mathematical Physics. Cambridge: Cambridge University Press.
Joras, A. E., and Marozzi, G. (2009). Trans-Planckian Physics from a Nonlinear Dispersion Relation. Phys. Rev. D79, 023514.
Kamiński, W., Kolanowski, M., and Lewandowski, J. (2020). Dressed Metric Predictions Revisited. Class. Quan. Grav 37, 095001. doi:10.1088/1361-6382/ab7ee0
Kiefer, C., and Krämer, M. (2012). Quantum Gravitational Contributions to the Cosmic Microwave Background Anisotropy Spectrum. Phys. Rev. Lett. 108, 021301. doi:10.1103/PhysRevLett.108.021301
Kodama, H., and Sasaki, M. (1984). Cosmological Perturbation Theory. Prog. Theor. Phys. Suppl. 78, 1–166. doi:10.1143/ptps.78.1
Komatsu, E., Smith, K. M., Dunkley, J., Bennett, C. L., Gold, B., Hinshaw, G., et al. WMAP Collaboration (2011). Seven-year Wilkinson Microwave Anisotropy Probe ( Wmap ) Observations: Cosmological Interpretation. ApJS 192, 18. doi:10.1088/0067-0049/192/2/18
Krauss, L. M., and Wilczek, F. (2014). Using Cosmology to Establish the Quantization of Gravity. Phys. Rev. D89, 047501.
Larson, D., Dunkley, J., Hinshaw, G., Komatsu, E., Nolta, M. R., Bennett, C. L., et al. WMAP Collaboration (2011). Seven-year Wilkinson Microwave Anisotropy Probe ( Wmap ) Observations: Power Spectra and Wmap -Derived Parameters. ApJS 192, 16. doi:10.1088/0067-0049/192/2/16
Li, B.-F., Olmedo, J., Singh, P., and Wang, A. (2020a). Primordial Scalar Power Spectrum from the Hybrid Approach in Loop Cosmologies. Phys. Rev. D 102, 126025. doi:10.1103/physrevd.102.126025
Li, B.-F., Saini, S., and Singh, P. (2020b). Primordial Power Spectrum from a Matter-Ekpyrotic Bounce Scenario in Loop Quantum Cosmology. arXiv:2012.10462.
Li, B.-F., Singh, P., and Wang, A. (2019). Genericness of Pre-inflationary Dynamics and Probability of the Desired Slow-Roll Inflation in Modified Loop Quantum Cosmologies. Phys. Rev. D100, 063513.
Li, B.-F., Singh, P., and Wang, A. (2020c). Primordial Power Spectrum from the Dressed Metric Approach in Loop Cosmologies. Phys. Rev. D100, 086004.
Li, B.-F., Singh, P., and Wang, A. (2018b). Qualitative Dynamics and Inflationary Attractors in Loop Cosmology. Phys. Rev. D98, 066016.
Li, B.-F., Singh, P., and Wang, A. (2018a). Towards Cosmological Dynamics from Loop Quantum Gravity. Phys. Rev. D97, 084029.
Liegener, K., and Singh, P. (2020). Gauge-invariant Bounce from Loop Quantum Gravity. Class. Quan. Grav. 37, 085015. doi:10.1088/1361-6382/ab7962
Liegener, K., and Singh, P. (2019). New Loop Quantum Cosmology Modifications from Gauge-Covariant Fluxes. Phys. Rev. D 100, 124048. doi:10.1103/physrevd.100.124048
Liegener, K., and Singh, P. (2019). Some Physical Implications of Regularization Ambiguities in SU(2) Gauge-Invariant Loop Quantum Cosmology. Phys. Rev. D 100, 124049. doi:10.1103/physrevd.100.124049
Linde, A. (2018). On the Problem of Initial Conditions for Inflation. Found. Phys. 48, 1246–1260. doi:10.1007/s10701-018-0177-9
Linsefors, L., and Barrau, A. (2013). Duration of Inflation and Conditions at the Bounce as a Prediction of Effective Isotropic Loop Quantum Cosmology. Phys. Rev. D 87, 123509. doi:10.1103/physrevd.87.123509
Malik, K. A. (2001). Cosmological Perturbations in an Inflationary Universe. arXiv:astro-ph/0101563.
Malik, K. A., and Wands, D. (2009). Cosmological Perturbations. Phys. Rep. 475, 1–51. doi:10.1016/j.physrep.2009.03.001
Martin, J., and Brandenberger, R. H. (2001). Trans-Planckian Problem of Inflationary Cosmology. Phys. Rev. D 63, 123501. doi:10.1103/physrevd.63.123501
Martínez, F. B., and Olmedo, J. (2016). Primordial Tensor Modes of the Early Universe. Phys. Rev. D 93, 124008. doi:10.1103/physrevd.93.124008
McAllister, L., and Silverstein, E. (2007). String Cosmology: A Review. Gen. Relativ. Grav. 40, 565.
Meissner, K. A. (2004). Black-hole Entropy in Loop Quantum Gravity. Class. Quan. Grav. 21, 5245–5251. doi:10.1088/0264-9381/21/22/015
Mena Marugán, G. A., Olmedo, J., and Pawlowski, T. (2011). Prescriptions in Loop Quantum Cosmology: A Comparative Analysis. Phys. Rev. D 84, 064012. doi:10.1103/physrevd.84.064012
Motaharfar, M., and Singh, P. (2021). On the Role of Dissipative Effects in the Quantum Gravitational Onset of Warm Starobinsky Inflation in a Closed Universe. arXiv:gr-qc/2102.09578.
Mukhanov, V., Feldman, H. A., and Brandenberger, R. H. (1992). Theory of Cosmological Perturbations. Phys. Rep. 215, 203–333. doi:10.1016/0370-1573(92)90044-z
Mukhanov, V. F., and Winitzki, S. (2007). Introduction to Quantum Effects in Gravity. Cambridge: Cambridge University Press.
Navascues, B. E., de Blas, D. M., and Marugan, G. A. M. (2018). Time-dependent Mass of Cosmological Perturbations in the Hybrid and Dressed Metric Approaches to Loop Quantum Cosmology. Phys. Rev. D97, 043523.
Neuser, J., Schander, S., and Thiemann, T. (2019). Quantum Cosmological Backreactions II: Purely Homogeneous Quantum Cosmology. arXiv:1906.08185.
Niemeyer, J. C., and Parentani, R. (2002). Corley-Jacobson Dispersion Relation and Trans-planckian Inflation. Phys. Rev. D65, 103514.
Niemeyer, J. C., and Parentani, R. (2003). Dependence of the Spectra of Fluctuations in Inflationary Cosmology on Trans-planckian Physics. Phys. Rev. D68, 063513.
Niemeyer, J. C., and Parentani, R. (2001). Trans-Planckian Dispersion Relation and Scale Invariance of Inflationary Perturbations. Phys. Rev. D64, 101301(R).
Olmedo, J., and Alesci, E. (2019). Power Spectrum of Primordial Perturbations for an Emergent Universe in Quantum Reduced Loop Gravity. J. Cosmol. Astropart. Phys. 2019, 030. doi:10.1088/1475-7516/2019/04/030
Oriti, D., Sindoni, L., and Wilson-Ewing, E. (2017). Bouncing Cosmologies from Quantum Gravity Condensates. Class. Quan. Grav. 34, 04LT01. doi:10.1088/1361-6382/aa549a
Oriti, D. (2017). The Universe as a Quantum Gravity Condensate. Comptes Rendus Physique 18, 235–245. doi:10.1016/j.crhy.2017.02.003
Parker, L., and Toms, D. (2009). Quantum Field Theory in Curved Spacetime: Quantized Fields and Gravity. Cambridge: Cambridge University Press.
Saini, S., and Singh, P. (2019a). Generic Absence of strong Singularities and Geodesic Completeness in Modified Loop Quantum Cosmologies. Class. Quan. Grav. 36, 105014. doi:10.1088/1361-6382/ab1274
Saini, S., and Singh, P. (2019b). Von Neumann Stability of Modified Loop Quantum Cosmologies. Class. Quan. Grav. 36, 105010. doi:10.1088/1361-6382/ab1608
Sato, K. (1981). First-order Phase Transition of a Vacuum and the Expansion of the Universe. Monthly Notices R. Astronomical Soc. 195, 467–479. doi:10.1093/mnras/195.3.467
Schander, S., and Thiemann, T. (2019). Quantum Cosmological Backreactions I: Cosmological Space Adiabatic Perturbation Theory. arXiv:1906.08166.
Schander, S., and Thiemann, T. (2019). Quantum Cosmological Backreactions III: Deparametrised Quantum Cosmological Perturbation Theory. arXiv:1906.08194.
Schwarz, D. J., Copi, C. J., Huterer, D., and Starkman, G. D. (2016). CMB Anomalies after Planck. Class. Quan. Grav. 33, 184001. doi:10.1088/0264-9381/33/18/184001
Senatore, L. (2017). “Lectures on Inflation,” in New Frontiers in Fields and Strings, Proceedings of the 2015 Theoretical Advanced Study Institute in Elementary Particle Physics, Boulder, Colorado, 1 - 26 June 2015. Editors J. Polchinski, P. Vieira, and O. DeWolfe (Singapore: World Scientific), 447–543.
Shahalam, M., Al Ajmi, M., Myrzakulov, R., and Wang, A. (2020). Revisiting Pre-inflationary Universe of Family of α -attractor in Loop Quantum Cosmology. Class. Quan. Grav. 37, 195026. doi:10.1088/1361-6382/aba486
Shahalam, M. (2018). Preinflationary Dynamics of Power-Law Potential in Loop Quantum Cosmology †. Universe 4, 87. doi:10.3390/universe4080087
Shahalam, M., Sami, M., and Wang, A. (2018). Pre-inflationary Dynamics of α-attractor in Loop Quantum Cosmology. Phys. Rev. D98, 043524.
Shahalam, M., Sharma, M., Wu, Q., and Wang, A. (2017). Preinflationary Dynamics in Loop Quantum Cosmology: Power-Law Potentials. Phys. Rev. D 96, 123533. doi:10.1103/physrevd.96.123533
Sharma, M., Shahalam, M., Wu, Q., and Wang, A. (2018). Preinflationary Dynamics in Loop Quantum Cosmology: Monodromy Potential. J. Cosmol. Astropart. Phys. 2018, 003. doi:10.1088/1475-7516/2018/11/003
Sharma, M., Zhu, T., and Wang, A. (2019). Background Dynamics of Pre-inflationary Scenario in Brans-Dicke Loop Quantum Cosmology. Commun. Theor. Phys. 71, 1205. doi:10.1088/0253-6102/71/10/1205
Silverstein, E. (2016). TASI Lectures on Cosmological Observables and String Theory. arXiv:1606.03640.
Singh, P. (2009). Are Loop Quantum cosmos Never Singular? Class. Quan. Grav. 26, 125005. doi:10.1088/0264-9381/26/12/125005
Singh, P. (2018). Glimpses of Space-Time beyond the Singularities Using Supercomputers. Comput. Sci. Eng. 20, 26–38. doi:10.1109/mcse.2018.042781324
Singh, P. (2014). Loop Quantum Cosmology and the Fate of Cosmological Singularities. Bull. Astron. Soc. India 42, 121.
Singh, P., Vandersloot, K., and Vereshchagin, G. V. (2006). Non-singular Bouncing Universes in Loop Quantum Cosmology. Phys. Rev. D74, 043510.
Starobinsky, A. A. (1980). A New Type of Isotropic Cosmological Models without Singularity. Phys. Lett. B 91, 99–102. doi:10.1016/0370-2693(80)90670-x
Thiemann, T. (2006). Complexifier Coherent States for Quantum General Relativity. Class. Quan. Grav. 23, 2063–2117. doi:10.1088/0264-9381/23/6/013
Thiemann, T. (2001a). Gauge Field Theory Coherent States (GCS): I. General Properties. Class. Quan. Grav. 18, 2025–2064. doi:10.1088/0264-9381/18/11/304
Thiemann, T. (2007). Modern Canonical Quantum General Relativity. Cambridge: Cambridge University Press.
Thiemann, T. (1998a). Quantum Spin Dynamics (QSD). Class. Quan. Grav. 15, 839–873. doi:10.1088/0264-9381/15/4/011
Thiemann, T. (1998b). Quantum Spin Dynamics (QSD): II. The Kernel of the Wheeler - DeWitt Constraint Operator. Class. Quan. Grav. 15, 875–905. doi:10.1088/0264-9381/15/4/012
Thiemann, T., and Winkler, O. (2001b). Gauge Field Theory Coherent States (GCS): II. Peakedness Properties. Class. Quan. Grav. 18, 2561–2636. doi:10.1088/0264-9381/18/14/301
Wald, R. M. (1994). Quantum Field Theory Om Curved Spacetime and Black Hole Thermodynamics. Chicago: The University of Chicago Press.
Weinberg, S. (1980). in General Relativity, an Einstein Centenary Survey. Editors S. W. Hawking, and W. Israel (Cambridge: Cambridge University Press).
Wilson-Ewing, E. (2017). Testing Loop Quantum Cosmology. Comptes Rendus Physique 18, 207–225. doi:10.1016/j.crhy.2017.02.004
Wilson-Ewing, E. (2018). The Loop Quantum Cosmology Bounce as a Kasner Transition. Class. Quan. Grav. 35, 065005. doi:10.1088/1361-6382/aaab8b
Wu, Q., Zhu, T., and Wang, A. (2018). Nonadiabatic Evolution of Primordial Perturbations and Non-gaussinity in Hybrid Approach of Loop Quantum Cosmology. Phys. Rev. D 98, 103528. doi:10.1103/physrevd.98.103528
Xiao, K. (2020). Tachyon Field in Loop Cosmology. Phys. Lett. B 811, 135859. doi:10.1016/j.physletb.2020.135859
Xiao, K. (2019). Tachyonic Inflation in Loop Quantum Cosmology. Eur. Phys. J. C 79, 1019. doi:10.1140/epjc/s10052-019-7538-1
Xiao, K., and Wang, S.-Q. (2020). Pre-inflation Dynamical Behavior of Warm Inflation in Loop Quantum Cosmology. Mod. Phys. Lett. A. 35, 2050293. doi:10.1142/s0217732320502934
Yang, J., Ding, Y., and Ma, Y. (2009). Alternative Quantization of the Hamiltonian in Loop Quantum Cosmology. Phys. Lett. B 682, 1–7. doi:10.1016/j.physletb.2009.10.072
Zhu, T., Wang, A., Kirsten, K., Cleaver, G., and Sheng, Q. (2017). Pre-inflationary Universe in Loop Quantum Cosmology. Phys. Rev. D96, 083520.
Zhu, T., Wang, A., Kirsten, K., Cleaver, G., and Sheng, Q. (2018). Primoridial Non-gaussianity and Power Asymmetry with Quantum Gravitational Effects in Loop Quantum Cosmology. Phys. Rev. D97, 043501.
Keywords: modified loop quantum cosmology, initial conditions, cosmic microwave background, power spectrum, big bang singularity resolution
Citation: Li B-F, Singh P and Wang A (2021) Phenomenological Implications of Modified Loop Cosmologies: An Overview. Front. Astron. Space Sci. 8:701417. doi: 10.3389/fspas.2021.701417
Received: 27 April 2021; Accepted: 02 June 2021;
Published: 24 June 2021.
Edited by:
Guillermo A. Mena Marugán, Instituto de Estructura de la Materia (IEM), SpainReviewed by:
Esteban Mato, Universidad de la República, UruguayCopyright © 2021 Li, Singh and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anzhong Wang, anzhong_wang@baylor.edu
†These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.