- 1Dipartimento di Fisica, Università di Pisa, Pisa, Italy
- 2Arnold Sommerfeld Center for Theoretical Physics, Ludwig-Maximilians-Universität München, München, Germany
- 3Istituto Nazionale di Fisica Nucleare sez. Pisa, Pisa, Italy
- 4Arnold Sommerfeld Center for Theoretical Physics, Ludwig-Maximilians-Universität München, München, Germany
We analyze the size and evolution of quantum fluctuations of cosmologically relevant geometric observables, in the context of the effective relational cosmological dynamics of GFT models of quantum gravity. We consider the fluctuations of the matter clock observables, to test the validity of the relational evolution picture itself. Next, we compute quantum fluctuations of the universe volume and of other operators characterizing its evolution (number operator for the fundamental GFT quanta, effective Hamiltonian and scalar field momentum). In particular, we focus on the late (clock) time regime, where the dynamics is compatible with a flat FRW universe, and on the very early phase near the quantum bounce produced by the fundamental quantum gravity dynamics.
1 Introduction
Three closely related challenges have to be overcome by fundamental quantum gravity approaches, especially those based on discrete or otherwise non-geometric, non-spatiotemporal entities, in order to make contact with General Relativity and observed gravitational physics, based on effective (quantum) field theory. The first is the continuum limit/approximation leading from the fundanental entities and their quantum dynamics to an effective continuum description of spacetime and geometry, with matter fields living on it (Oriti et al., 2017). This requires a mixture of renormalization analysis of the fundamental quantum dynamics and of coarse-graining of its states and observables. The second is a classical limit/approximation of the sector of the theory corresponding to (would-be) spacetime and geometry, to show that indeed an effective classical dynamics compatible with General Relativity and observations emerges, once in the continuum description (Oriti et al., 2017). The third is a definition of suitable observables that can, on the one hand, give a physical meaning to both continuum and classical approximations in terms of spacetime geometry and gravity, and, on the other hand, allow to make contact with phenomenology (Marchetti and Oriti, 2021). In particular, suitable observables are needed to recast the dynamics of the quantum gravity system, in the same continuum and classical approximations, at least, in more customary local evolutionary terms, i.e. in the form of evolution of local quantities with respect to some notion of time (Giddings et al., 2006; Tambornino, 2012). This, in fact, is the language of effective field theory used in gravitational and high energy physics. The first two challenges are standard in any quantum many-body system, but are made more difficult in the quantum gravity context by the necessary background (and spacetime) independence of the fundamental theory, which requires adapting non-trivially standard renormalization, coarse-graining and classical approximation techniques. The same background independence, closely related at the formal level to the diffeomorphism invariance of General Relativity (Giulini, 2007), makes the third challenge a peculiar difficulty in quantum gravity. Locality or temporal evolution cannot be defined with respect to any manifold point or direction and generic configurations (classical and even less quantum) of the gravitational field (or what replaces it at the fundamental level) do not single out any such notions either. Beside special situations (e.g. in the presence of asymptotic boundaries) local and temporal geometric observables can be understood as relational quantities, i.e. defined as a relation between geometry and other dynamical matter degrees of freedom, that provide a notion of local regions and temporal direction when used as physical reference frames. In other words, and restricting to the issue of time (Isham, 1992; Kuchař, 2011), the relational perspective holds that the absence of preferred, external or background notions of time in generally relativistic quantum theories does not mean that there is no quantum evolution, but only that evolution should be defined with respect to internal, physical degrees of freedom (Höhn et al., 1912; Tambornino, 2012).
From the perspective of “Quantum General Relativity” theories (Rovelli, 2004; Thiemann, 2007), in which the fundamental entities remain (quantized) continuum fields, the relational strategy to define evolution boils down to either the selection of a relational clock at the classical level, in terms of which the remaining subsystem is canonically quantized (“tempus ante quantum” (Isham, 1992; Anderson, 2012)) or the definition of an appropriate clock-neutral quantization (e.g., Dirac quantization) and the representation of classical complete (i.e., relational) observables (Rovelli, 2002; Dittrich, 2006; Dittrich, 2007; Tambornino, 2012) on the physical Hilbert space resulting from such quantization (“tempus post quantum” (Isham, 1992; Anderson, 2012)). Of course, while the first approach (deparametrization) is technically easier, when possible, the second one is in principle preferable because manifestly “clock covariant,” since it treats all the quantum degrees of freedom on the same footing, thus allowing in principle to switch from one relational clock to another (see (Bojowald et al., 2011a; Bojowald et al., 2011b; Hoehn et al., 2011; Hoehn and Vanrietvelde, 2018) for more details).
In “emergent quantum gravity” theories, in which the fundamental degrees of freedom are pre-geometric and non-spatiotemporal, and not identified with (quantized) continuum fields, the situation has an additional layer of complications (Marchetti and Oriti, 2021). Any kind of continuum notion in such theories is expected to emerge in a proto-geometric phase of the theory from the collective behavior of the fundamental entities, i.e. only at an effective and approximate level. Among such continuum notions there is any notion of relational dynamics, as we understand it from the generally relativistic perspective.
In the tensorial group field theory formalism (TGFT) for quantum gravity (see (Krajewski, 2011; Oriti, 2011; Carrozza, 2016; Gielen and Sindoni, 2016) for general introductions), comprising random tensor models, tensorial field theories and group field theories (closely related to canonical loop quantum gravity, and providing a reformulation of lattice gravity path integrals and spin foam models), we are in this last emergent spacetime situation (Oriti, 1807).
The issue of the continuum limit is tackled adapting standard renormalization group (Carrozza, 2016) and statistical methods for quantum field theories, leading also to several results concerning the critical behavior of a variety of models. In the more quantum geometric group field theory (GFT) models (Magnen et al., 2009; Baratin et al., 2014; Ben Geloun et al., 2016; Carrozza et al., 2017; Carrozza and Lahoche, 2017; Geloun et al., 2018) (see also (Finocchiaro and Oriti, 2004) and references therein), one can take advantage of the group theoretic data and of their discrete geometric interpretation to give tentative physical meaning to suitable quantum states and to specific regimes of approximation of their quantum dynamics (Oriti et al., 2015). Specifically, the hydrodynamic regime of models of 4d quantum geometry admits a cosmological interpretation and has been analyzed in some detail for simple condensate states (Gielen et al., 2014; Gielen and Sindoni, 2016; Oriti et al., 2016). The corresponding effective dynamics has been recast in terms of cosmological observables both via the relational strategy and by a deparametrization with respect to the added matter degrees of freedom (Gielen and Sindoni, 2016; Oriti et al., 2016; Oriti, 2017; Pithis and Sakellariadou, 2019; Wilson-Ewing, 2019; Marchetti and Oriti, 2021). Among many results (Gielen and Menéndez-Pidal, 2005; Gielen, 2014; Pithis et al., 2016; Pithis and Sakellariadou, 2017; Adjei et al., 2018; Gielen and Polaczek, 2020), the correct classical limit in terms of a flat FRW universe has been obtained rather generically for large expectation values of the volume operator at late relational (clock) times (Oriti et al., 2016; Gielen and Polaczek, 2020; Marchetti and Oriti, 2021), and the big bang singularity is resolved, with a similar degree of generality (Oriti et al., 2016; Gielen and Polaczek, 2020), and replaced with a quantum bounce. In addition, the fundamental quantum gravity interactions seem to be able produce (at least for some regime of parameters) an accelerated cosmological expansion, possibly long-lasting, without introducing additional matter (e.g. inflaton) fields (de Cesare et al., 2016).
The above results have been obtained looking at the expectation values of interesting cosmological observables in (the simplest) GFT condensate states. A careful analysis of quantum fluctuations of the same observables is then important to test the validity of the hydrodynamic description in terms of expectation values, in particular in the large volume limit when one expects classical GR to be valid, but also close to the big bounce regime where one expects them to be strong but still controllable if the bouncing scenario is to be trustable at all. Moreover, the relational evolution relies on the chosen physical (matter) degrees of freedom to behave nicely enough to serve as a good clock, and this would not be the case if subject to strong quantum fluctuations. This analysis of quantum fluctuations is what we perform in this paper.
The precise context in which we perform the analysis is that of the effective relational dynamics framework developed in (Marchetti and Oriti, 2021).
This construction is motivated by the argued usefulness and conceptual importance of effective approaches to relational dynamics (Bojowald et al., 2009; Bojowald and Tsobanjan, 2009; Bojowald et al., 2011a; Bojowald et al., 2011b; Bojowald, 2012), and it was suggested a general framework in which the latter is realized in a “tempus post quantum” approach, but only at a proto-geometric level, i.e. after some suitable coarse graining, the one provided by the GFT hydrodynamic approximation (or its improvements).
Besides its conceptual motivations, this effective relational framework improves on previous relational constructions in GFT cosmology providing a mathematically more solid definition of relational observables, allowing the explicit computation of quantum fluctuations, which will be one the main objectives of the present work.
This improved effective relational dynamics was obtained by the use of “Coherent Peaked States” (CPSs), in which the fundamental GFT quanta collectively (and only effectively) reproduce the classical notion of a spacelike slice of a spacetime foliation labeled by a massless scalar field clock. For this effective foliation to be meaningful quantum flctuations of the clock observables should be small enough (e.g. in the sense of relative variances). When this is the case, the relevant physics is captured by averaged relational dynamics equations for the other observables of cosmological interest, like the universe volume or the matter energy density or the effective Hamiltonian. The purpose of this paper is to explore under which conditions this averaged relational dynamics is meaningful and captures the relevant physics, checking quantum fluctuation for both clock observables and cosmological, geometric ones.
2 Effective Relational Framework for GFT Condensate Cosmology
The GFT condensate cosmology framework is based on three main ingredients (see e.g. (Gielen and Sindoni, 2016) for a review):
1. The identification of appropriate states which admit an interpretation in terms of (homogeneous and isotropic) cosmological 3-geometries;
2. The construction of an appropriate relational framework allowing to describe e.g. the (averaged) geometric quantities (in the homogeneous and isotropic case, the volume operator) as a function of a matter field (usually a minimally coupled massless scalar field);
3. The extraction of a mean field dynamics from the quantum equations of motion of the microscopic GFT theory, which in turn determines the relational evolution of the aforementioned (averaged) volume operator.
In this section, we will review the concrete realization of the first two steps and of the first part of the third step (i.e. the extraction of a mean field dynamics), in order to prepare the ground for the calculation of expectation values, first, and the quantum fluctuations of geometric observables of cosmological interest. More precisely, the first step will be reviewed in Section 2.1, while the second and the first part of the third one will be discussed in Sections 2.2, Sections 2.3, respectively. The second part of the last step, which requires the detailed computations of expectation values performed in Section 4.1, will be instead discussed in Section 4.2.
2.1 The Kinematic Structure of GFT Condensate Cosmology
In the Group Field Theory (GFT) formalism (Krajewski, 2011; Oriti, 2011; Carrozza, 2016; Gielen and Sindoni, 2016), one aims at a microscopic description of spacetime in terms of simplicial building blocks (Reisenberger and Rovelli, 2001). The behavior of the fundamental “atoms” that spacetime has dissolved into is described by a (in general, complex) field
Indeed, in this case, the fundamental quanta of the field, assuming it satisfies the “closure” condition
2.1.1 The GFT Fock Space
The Fock space of such “atoms of space” can be constructed in terms of the field operators
together with a vacuum state
GFT “
are then constructed from the matrix elements
Coupling to a Massless Scalar Field
Following (Marchetti and Oriti, 2021; Oriti et al., 2016), a scalar field is minimally coupled to the discrete quantum geometric data, with the purpose of using it as a relational clock at the level of GFT hydrodynamics. This is done by adding to the GFT field and action the degree of freedom associated to a scalar field in such a way that the GFT partition function, once expanded perturbatively around the Fock vacuum, can be identified with the (discrete) path-integral of a model of simplicial gravity minimally coupled with a free massless scalar field (or, equivalently, with the corresponding spin-foam model)1 (Oriti et al., 2016). Therefore, the field operator changes as follows:
meaning that the one-particle Hilbert space is now enlarged to
and that operators (Eq. 2) in the second quantization picture now involve integrals over the possible values of the massless scalar field (Oriti et al., 2016; Marchetti and Oriti, 2021).
2.1.2 GFT Condensate Cosmology: Kinematics
The Fock space construction described above proves technically very useful in order to address the problem of extraction of continuum physics from GFTs. In particular, in previous works (Gielen, 2014; Oriti et al., 2016), this was exploited to build quantum states that, in appropriate limits, can be interpreted as continuum and homogeneous 3-geometries, thus paving the way to cosmological applications of GFTs. Such states are characterized by a single collective wavefunction, defined over the space of geometries associated to a single tetrahedron or, equivalently (when some additional symmetry conditions are imposed on the wavefunction) over the minisuperspace of homogeneous geometries (Gielen, 2014). For such condensate states then, classical homogeneity is lifted at the quantum level by imposing ‘wavefunction homogeneity’. Among the many possible condensate states (characterized by different “gluing” of the fundamental GFT quanta one to another) satisfying the above wavefunction homogeneity, most of the attention was directed toward the simplest GFT coherent states, i.e.,
where
They satisfy the important property
i.e., they are eigenstates of the annihilation operator.
In order to make contact with cosmological geometries, one typically also imposes isotropy on the wave function, requiring the associated tetrahedra to be equilateral. This results in the following condensate wavefunction (Oriti et al., 2016)
where
and where
2.2 Effective Relational Dynamics Framework and its Implementation in GFT Condensate Cosmology
In (Marchetti and Oriti, 2021), a procedure for extracting an effective relational dynamics framework was proposed for the cosmological context, when one is interested in describing the evolution of some geometric operators with respect of some scalar matter degree of freedom. Since our analysis of quantum fluctuations will take place within such effective relational framework, let us summarize how it is obtained and under which conditions it is expected to be meaningful. In the following, we will analyze also the limits of validity of such conditions.
2.2.1 Effective Relational Evolution of Geometric Observables with Respect to Scalar Matter Degrees of Freedom
The fundamental observables one is interested in are: a “scalar field operator”
at least locally and far enough from singular turning points of the scalar field clock4. In order to interpret this evolution as truly relational with respect to the scalar field used as a clock, all the moments of
This equality was investigated in (Marchetti and Oriti, 2021) in the context of GFT cosmology, and we will discuss it further below.
A further condition that is necessary in order to interpret Eq. 8a as a truly relational dynamics involves the smallness of the quantum fluctuations on the matter clock. In (Marchetti and Oriti, 2021), this was imposed by requiring the relative variance of
where the relative variance on
This is of course formally correct only when one is assuming that the expectation value of
Let us also notice, that, strictly speaking, one would have to require that all the moments of the scalar field operator higher than the first one are much smaller than one in order to guarantee a negligible impact of quantum fluctuations of the clock on the relational framework. However, one also expects that, being the system fundamentally a many-body system (for which the second condition in (Eq. 9) is satisfied), moments higher than the second one get also suppressed in the large N limit which we will be mainly interested in, forming a hierarchy of less and less important quantum effects (typically, in many-body systems, relative moments of order n are suppressed by
2.2.2 Implementation in GFT Condensate Cosmology: CPSs
The strategy to realize the above framework in the context of GFT condensate cosmology in (Marchetti and Oriti, 2021) made use of Coherent Peaked States (CPSs). These states are constructed so that they can provide, under appropriate approximations, “bona fide” leaves of a relational χ-foliation of spacetime. Given the proto-geometric nature of the states (Eq. 5) the idea is to look for a subclass of them characterized by a given value of the relational clock, say
where
where
In order for the average clock value to be really meaningful in defining a relational evolution, it is necessary for the width ϵ of the peaking function to be small,
For more remarks and comments on this particular class of states we refer to (Marchetti and Oriti, 2021).
2.3 Reduced Wavefunction Dynamics and Solutions
Since the relational approach discussed in the previous section is by its very nature effective and approximate, following (Marchetti and Oriti, 2021) we will only extract an effective mean field dynamics from the full quantum equations of motion. In other words, we will only consider the imposition of the quantum equations of motion averaged on the states that we consider to be relevant for an effective relational description of the cosmological system:
where
For cosmological applications, there are typically two assumptions that are done on the GFT action. The first is that the classical field symmetries of the action of a minimally coupled massless scalar field (invariance under shift and reflection) are respected by the GFT action as well. This greatly simplifies the form of the interaction and kinetic terms, which read (Oriti et al., 2016; Marchetti and Oriti, 2021)
The details about the EPRL model are encoded in the specific form of the kinetic and interaction kernels
The second assumption usually made in cosmological applications, however, is that one is interested in a “mescocopic regime” where these interactions are assumed to be negligible (though see (Pithis et al., 2016; Pithis and Sakellariadou, 2017), for some phenomenological studies including interactions). Under these two assumptions and imposing isotropy on the condensate wavefunction (see Section 2.1.2), the above quantum equations of motion reduce to two equations for the modulus
where
Here,
where the constants
The most general solution can be written as
Of course we can find some relations between the constants
Thus our solution becomes
where we have chosen only the positive solution because
where we have defined
The solution is now only parametrized by
For the following discussion, it will be useful to derive some bounds on the modulus of the derivatives of
Then, denoting
In the following sections we will discuss in more detail under which conditions the above states indeed implement a notion of relational dynamics, as defined in Section 2.2.1.
3 Averages and Fluctuations: Generalities
In this section we compute expectation values of relevant operators in the effective relational GFT cosmology framework (i.e., the number operator
We express these expectation values and relative variances in terms of the modulus of the reduced wavefunction only, possibly using Eq. 14b in order to trade any dependency on the phase of the reduced wavefunction for its modulus. In Section 4, instead, we use the explicit solution (Eq. 19a, Eq. 19b) to considerably simplify the equations obtained in the following two subsections.
3.1 Expectation Value of Relevant Operators
First, let us compute the expectation value of the relevant operators, whose definitions are reviewed below.
Number and Volume Operators
The simple case of the number operator allows us to discuss the prototypical computation that we are going to perform frequently in the following. Its definition is (Oriti, 2017; Marchetti and Oriti, 2021)
Its expectation value on a isotropic CPS is therefore given by
In order to evaluate this quantity, one can expand the function
By normalizing
giving zero, instead, for odd powers. In conclusion, one finds
Similar computations hold for the volume operator, counting the volume contributions of all tetrahedra in a given GFT state and defined as (Oriti et al., 2016; Marchetti and Oriti, 2021)
in terms of matrix elements
where
In particular, when higher order derivatives can be neglected, we notice that we can write
for the expectation value of the number and of the volume operator. We will see in Section 4.1 that this will be indeed the case when these quantities are evaluated on solutions of the dynamical equations and under some fairly general conditions on the parameters characterizing the dynamics.
Momentum and Hamiltonian Operator
Similar results hold for the scalar field momentum and the hamiltonian operators. The effective7 Hamiltonian operator
Such an operator generates by construction translations with respect to
Defining
By definition of
so that, in conclusion we obtain, for
The situation for the momentum operator is similar. By definition
and one has
From this explicit form, we notice that the evaluation of both the expectation value of
Now, in the approximation
Massless Scalar Field Operator
The massless scalar field operator is defined as (Oriti et al., 2016; Marchetti and Oriti, 2021)
so its expectation value on an isotropic CPS is given by
Notice, however, that this operator is extensive (with respect to the GFT number of quanta, thus indirectly with respect to the universe volume), so it can not be directly related (not even in expectation value) to an intensive quantity such as the massless scalar field. This identification, however, can be meaningful for the rescaled operator
The evaluation of
As a result of the integration one obtains
The first terms in squared brackets are the same that appear in the expectation value of the number operator. The second terms in square brackets are new. And these terms are in fact crucial: when they are not negligible, the expectation value
More precisely, in the most general case, by defining
we see that this leads to an expectation value of the “intrinsic” massless scalar field operator of the form
and when the second term satisfies
Given that the reason why we can not take the limit
3.2 Relative Variances
According to the requirements specified in Section 2.2.1, it is fundamental to check the behavior of clock quantum fluctuations in order to understand whether the relational framework is truly realized at an effective level.
Having done that, this analysis should be extended to all the relevant geometric operators in terms of which we write the emergent cosmological dynamics; this is true in particular for the volume operator, whose averaged dynamics was shown in (Marchetti and Oriti, 2021) to reproduce, “at late times” and under some additional assumptions, a Friedmann dynamics. In order for this “late time regime” to be truly interpreted as a classical one, quantum fluctuations of the volume operator (and possibly also of the other physically interesting operators) should be negligible.
We now proceed to study the behavior of these fluctuations, limiting ourselves here only to relative variances. The explicit computations of these quantum fluctuations can be found in Supplementary Appendix A.
Number Operator
As before, we start from the number operator. Its relative variance can be easily found to be
thus decreasing as the number of atoms of space increases, as expected. When the lowest order saddle point approximation is justified, one can write the above expression as
Volume Operator
For the volume operator the computations are similar. One finds
If one can neglect higher order derivatives, then
Hamiltonian Operator
The relative variance of the Hamiltonian operator, instead, is given by
which is under control in the regime
Momentum Operator
Next, we discuss the variance of the momentum operator. The computations are a little more involved, but under the assumption that
From the explicit form of
• In the formal limit
• By taking the limit8
Massless Scalar Field Operator
Finally, we discuss the variance of the massless scalar field operator. Its quantum fluctuations are given by
which, once divided by (Eq. 34) squared, gives the relative variance of
The prefactor on the right-hand-side is by assumption large, but it can be suppressed by the factor
So, already from this example we can deduce that, in the limit of arbitrarily large N, the only point which has to formally be excluded from the analysis because clock fluctuations become too large is
4 Averages and Fluctuations: Explicit Evaluation
Having obtained the expectation values and the relative variances of relevant operators in the effective relation GFT cosmology frameowork in terms of the modulus of the reduced wavefunction (and possibily of its derivatives), we can now further simplify the obtained expressions by means of Eq. 19b.
4.1 Expectation Values
The explicit evaluation of the expectation values of operators, as shown above, involves an infinite number of derivatives of the modulus of the reduced wavefunction. However, it is interesting to notice that
since
under our working assumption
we see that terms with
the first equation above also determining the expectation values of
Similarly, the natural hierarchy of derivatives obtained from Eqs. 43, 42 is present also in the sum over n in Eq. 35. For the same reasons as above, therefore, we can write
so that
However, determining whether these higher derivative terms become important in the expectation values of operators like
As we have already mentioned, the smallness of the factor
Whether this condition is actually satisfied, though, drastically depends on the properties of the solution
this interpretation is allowed. Following the same steps of (Eq. 41), we see that the above condition is satisfied as long as
where
1. First, since
condition (Eq. 46) is actually satisfied. Notice also that since
2. Second, notice that if all the
More generally, instead, the value of
Of course, the desired condition (Eq. 46) is satisfied for
so, while in the first case the condition
for all js, then we can write
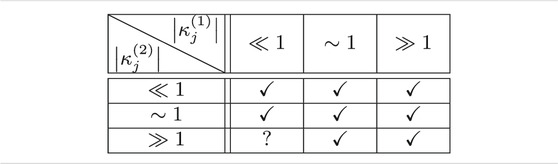
TABLE 1. Validity of the condition (Eq. 46) depending on the scales
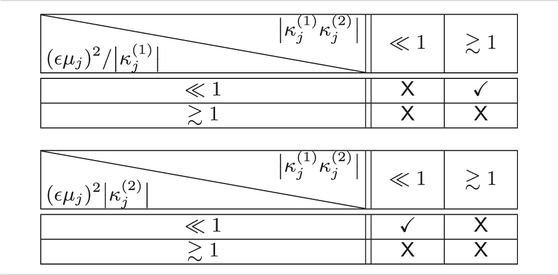
TABLE 2. Validity of the condition (Eq. 46) depending on the scales
4.2 Fluctuations
The arguments exposed above can be used straightforwardly to compute relative variances of operators.
Number, Hamiltonian and Volume
For the relative variances of the number, Hamiltonian and volume operators, we have
Momentum
For the momentum operator, given that we require
As a result, we finally have
Now, we recall that in order to have an identification between the first moments of the Hamiltonian and the momentum operator one needs to have either
So, we see that the first term of the relative variance behaves as
Also, let us notice that
where
Let us estimate how large is the last term in square brackets. Since
since, for each
Thus, generally speaking, we have
and the right-hand-side is of course positive because
we see that in this limit we can approximately write
so that the relative variance becomes
Massless Scalar Field
Instead, about the relative variance of the massless scalar field operator, we have
Let us make two remarks about this quantity:
1. First, in order for (Eq. 40) to be non-negative, we need to impose that
Contrarily to what happens for the momentum operator, this is actually a feature that we must impose “by hand” on our solutions. We will assume it to be true from now on.
2. Second, the divergence in the above variance at the point
The scaling of all the relative variances (Eq. 48e, 48a, 48b, 48d) is essentially determined by
4.2.1 Large Number of GFT Quanta
We will first consider the case of large number of GFT quanta,
1. There exists at least one of the
2. All the
While for the number and the Hamiltonian operators variances are smaller than one by assumption, for the momentum, the volume and the massless scalar field operator, the situation is more complicated, so it is useful to discuss them by distinguishing between the two cases above.
First Case
When at least one of the
which is certainly satisfied for a large class of initial conditions, given the large value of the right-hand-side. For instance, notice that for
Also, notice that when
where
On the other hand, let us consider the situation in which
again neglecting unimportant factors 2. It is interesting to notice that, depending on how large the factor
1.When
2.When instead
thus leading to a small relative variance of the massless scalar field operator but to the impossibility of identifying
Second Case
The arguments exposed in the first case about the variances of all the operators besides the volume operator (which after all just made reference to N, which is still
where
where the last approximate equality has been obtained by an explicit fit. Notice that, since
which are however not particularly helpful in extracting tighter bounds. As a conclusion, by defining
fluctuations on the volume operator are certainly large, while when
the relative volume variance is certainly negligible. This is of course the case when all the
4.2.2 Number of GFT quanta of order of or smaller than one
When the number of GFT quanta is
In such a case, therefore, not only we expect the CPSs not to define a notion of relational dynamics, but we expect averaged results not to capture all the relevant physics of the system. Hence, we will leave the study of this specific regime to some future work.
5 Effective Relational Dynamics: the Impact of Quantum Effects
Let us now recapitulate our results and draw some conclusions from them.
In order for the cosmological CPS construction to fit in an effective relational framework, a certain number of conditions, proposed in (Marchetti and Oriti, 2021) and reviewed in Section 2.2.1, should be satisfied. Here, we summarize in which regimes they are satisfied, ensuring the reliability of the cosmological evolution obtained in (Marchetti and Oriti, 2021), with its classical Friedmann-like late times dynamics and singularity resolution into a bounce.
As mentioned in Section 2.2.1, variances are not in general enough to characterize the properties of operators in a fully quantum regime (see also Section 4.2.2), except when there is a clear hierarchy among operator moments, with the higher ones being suppressed by higher powers of the number of quanta. If we try to quantify quantum fluctuations in terms of relative variances, as we will mostly do here, we must be careful not to assume that certain features characterizing the behavior of relative variances are true also for higher moments, since in certain regimes, variances may be indeed small but higher moments become relevant. Still, as we have mentioned, we do expect that there exists a regime in which the aforementioned hierarchy among moments is indeed present: it is the case in which the number of GFT quanta is large.
While in mesoscopic regimes it is not possible to determine under which conditions the hydrodynamic and the effective relational approximations are satisfied only by studying relative variances, large variances can however be taken as a clear evidence that one, or possibly both the above approximations are not adequate.
5.1 Quantum Effects in the Effective Relational CPS Dynamics
First, therefore, let us discuss the form that the conditions in II B 1 take in the CPS cosmology framework, focusing on the volume operator. Then Eq. 8a is satisfied by the CPS construction (Marchetti and Oriti, 2021) provided that.
1. The Expectation Value of the (Intrinsic) Massless Scalar Field Operator Is
We have already mentioned that in general this is not exactly the case, essentially because we can not take the limit
Also, in order to interpret the evolution generated by
A similar situation happens for the relative variance. Indeed, again in the large N regime,
On the other hand, let us notice that imposing the equality between (48a) and (48d) for smaller N, and so for mesoscopic intermediate regimes, would impose another constraint on the initial conditions, requiring that all the
Next, according to the general discussion in (Marchetti and Oriti, 2021) and in Subsection II B 1, one has to be sure that the clock variable is not “too quantum,” which, in our framework can be phrased as the requirement that.
2. Relative Quantum Fluctuations of
As usual, we can get some information about the behavior of clock quantum fluctuations from the form of
Conditions 1 and 2 are the two necessary conditions that need to be satisfied in order to qualify the framework constructed so far as a truly relational one.
Further, the evolution of the expectation value of the volume operator is a good enough characterization of the universe evolution (in the homogeneous and isotropic context) if.
3. Quantum Fluctuations (Encoded in Moments Higher than the First One) of the Volume Operator are Negligible
Also for this operator, as in the massless scalar field case, the existence of a hierarchy of moments is in general far from being trivial, since the relative variance is already strictly dependent on the possible spin cut-off scale.
However, even when satisfying condition 3, the resulting system might be highly non-classical, depending on the value of quantum fluctuations for the remaining operators
4. Quantum Fluctuations (Encoded in Moments Higher than the First One) of all the Relevant Operators (N, χ, Π, H, V) are Negligible.
Therefore, in order for a classical relational regime to be realized at late enough times in the CPS framework, both conditions 5.1 (together with the identification of the moments of H and Π) and 4 should be satisfied. In particular, large variances of any of these operators actually signal a breakdown of the hydrodynamic approximation underlying Eq. 13.
5.2 Effective Relational Volume Dynamics with CPSs
In light of the above conditions it is interesting to examine the relational evolution of the average of the volume operator, since, in GFT cosmology, it is at this level that the comparison with the Friedmann dynamics is usually performed. We will review this below, in Section 5.2.1, emphasizing two main regimes of its evolution: a possible bounce and a Friedmann-like late evolution. In Section 5.2.2, instead, we will draw some general conclusions on the relationality and classicality of these two phases in light of the results obtained in the previous sections.
5.2.1 General Properties of the Volume Evolution
Let us start from the general expression (Eq. 26)
We see that
where
Since
Bounce
The bounce happens at a relational time
Friedmann Regime
When
which are indeed the flat space (
5.2.2 Effective Relational Volume Dynamics with CPS: The Impact of Quantum Effects
Let us now characterize better these two phases of the evolution of the average volume in terms of their relationality and quantumness.
Friedmann Dynamics and Classical Regime
The Friedmann regime is selected by the condition
As the parameter
Statement 1: For the chosen approximation of the underlying GFT dynamics, a classical regime in which the volume evolution with respect to
Bounce
The situation concerning the bounce is much more complicated, essentially because it is not an asymptotic regime, and thus the value of initial conditions turns out to be important. It is less obvious whether the bounce can be interpreted as a relational dynamics result, or if the averaged evolution is overwhelmed by quantum fluctuations, thus making us question also the validity of the hydrodynamic approximation in (Eq. 13).
In general, it might happen that both the conditions 1 and 2 are not satisfied. For instance, this is the case if the bounce happens at
with arbitrarily large values of
On the other hand, there are regimes in which a bounce can satisfy all the conditions from 5.1 to 5.1. For instance, let us consider the case in which all the
The relevant quantities for a simplified two-spin scenario like the one described above with
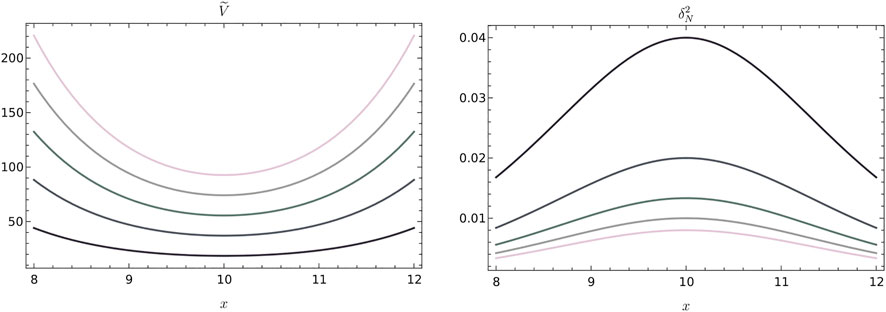
FIGURE 1. Plots of the dimensionless volume operator
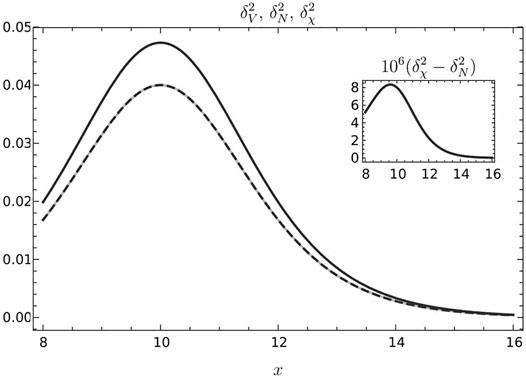
FIGURE 2. Plot of
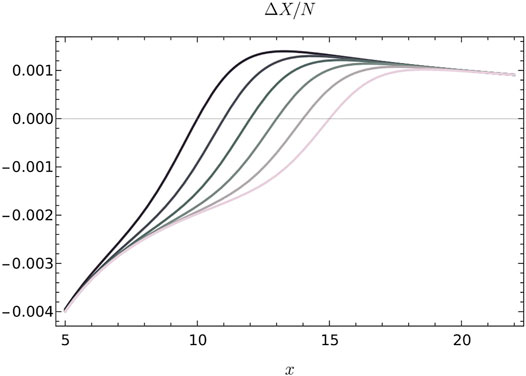
FIGURE 3. Plot of
In general, therefore, we can draw the following conclusion:
Statement 2:The bouncing scenario is not a universal feature of the model, meaning that it is not realized under arbitrary choices of the initial conditions. However, if i) there exists at least one
5.2.3 An Example: Single Spin Condensate
As an explicit and fairly simple (though possibly very physically relevant (Gielen, 2016)) example of the arguments exposed above, let us consider the case in which only one spin among those in J is excited, say
where
where we have imposed the condition
Let us study in detail under which conditions a resolution of the initial singularity into a bouncing universe, assuming that indeed quantum effects are effectively encoded into relative variances (so that we can neglect the impact on the system of moments of relevant operators higher than the second one). From Eqs. 52, 53, we deduce that a bounce with a non-zero value of the (average) volume happens only when
Before proceeding with further considerations, it is interesting to remark that the single spin case mirrors the situation appearing in Loop Quantum Cosmology (LQC) (Bojowald, 2008; Ashtekar and Singh, 2011), where one considers a LQG fundamental state corresponding to a graph constructed out of a large number of nodes and links with the latter being associated all to the same spin. This similarity can be also observed in fluctuations. Indeed, from the above equation we see that in this case the quantity governing quantum fluctuations is exactly the average number of particles, with variances suppressed as
Going back to Eq. 54, we see that, in order for the bounce to have any hope of being classical, we also need to require
What is left to check are the values of
So, we conclude that for each
Since the first term is always much smaller than 1 under our assumptions, the relative variance of the massless scalar field operator is negligible as long as
Notice that the assumption of
the singularity is indeed replaced by a bounce (again assuming
To sum up, a classical bounce that can be understood within the effective relational framework discussed above and in (Marchetti and Oriti, 2021), can be obtained in this single spin case for instance by requiring that.
1.
2. Conditions (Eq. 55) are satisfied, the first of which guarantees that the expectation value of the volume operator reaches a non-zero minimum before bouncing, and the second of which guarantees small relative variances of the operators
3. Assuming that
Under these assumptions, the relational time elapsed from the bounce would be
where we have assumed the term
where the last line is just the result of a crude estimate obtained from
6 Conclusion
We have analyzed the size and evolution of quantum fluctuations of cosmologically relevant geometric observables (in the homogeneous and isotropic case), in the context of the effective relational cosmological dynamics of quantum geometric GFT models of quantum gravity. We considered first of all the fluctuations of the matter clock observables, to test the validity of the relational evolution picture itself. Next, we studied quantum fluctuations of the universe volume and of other operators characterizing its evolution, like the number operator for the fundamental GFT quanta, the effective Hamiltonian and the scalar field momentum (which is expected to contribute to the matter density). In particular, we focused on the late (clock) time regime (see Statement 1, Section 5.2.2), where the dynamics of volume expectatation value is compatible with a flat FRW universe, and on the very early phase near the quantum bounce. We found that the relative quantum fluctuations of all observables are generically suppressed at late times, thus confirming the good classical relativistic limit of the effective QG dynamics. Near the bounce, corresponding to a mesoscopic regime in which the average number of fundamental GFT quanta can not be arbitrarily large, the situation is much more delicate (see Statement 2, Section 5.2.2). Depending on the specific choice of parameters in the fundamental dynamics and in the quantum condensate states, relational evolution as implemented by the CPSs strategy may remain consistent or become unreliable, due to fluctuations of the clock itself and to possible issues with “synchronization” of the fundamental GFT quanta. Even when the relational evolution picture remains valid, quantum fluctuations of the geometric observables may become large, depending again on the precise values of the various parameters. When this happens, this could signal simply a highly quantum regime, but one that is still describable within the hydrodynamic approximation in which the effective cosmological dynamics has been obtained; or it could be interpreted as a signal of a breakdown of the same hydrodynamic approximation, calling for a more refined approximation of the underlying quantum gravity dynamics of the universe.
The analysis will have now to be extended to the case in which GFT interactions are not negligible. We expect such interactions to be most relevant at late clock times and largish universe volume (i.e. largish GFT condensate densities) (Oriti et al., 2016; Marchetti and Oriti, 2021), thus it is unclear whether they should be expected to modify much the behavior of quantum fluctuations, since the are suppressed in the same regime. However, GFT interactions also modify the underlying dynamics of the volume itself, possibly causing a recollapsing phase (de Cesare et al., 2016), thus they may as well enhance quantum fluctuations in such cases. Another important extension would be of course the inclusion of anisotropies (de Cesare et al., 2018), but this is something we need to control much better already at the level of expectation values of geometric observables, in order to be confident about the resulting physical picture. Finally, quantum fluctuations should be considered in parallel with thermal fluctuations, which we can now compute as well using the recently developed thermofield double formalism for GFTs (Assanioussi and Kotecha, 2003; Kotecha and Oriti, 2018; Assanioussi and Kotecha, 2020).
Thus, much more work is called for. It is clear, however, that we now have a solid context to tackle cosmological physics from within full quantum gravity, also for what concerns quantum fluctuations. While we move toward the analysis of cosmological perturbations (Gielen and Oriti, 2018; Gielen, 2019) and the associated quantum gravity phenomenology, these results will help to control better the viability of the picture of the evolution universe we are going to obtain.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
Financial support from the Deutsche Forschunggemeinschaft (DFG) is gratefully acknowledged. LM thanks the University of Pisa and the INFN (section of Pisa) for financial support, and the Ludwig-Maximilians-Universität Munich for the hospitality.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.683649/full#supplementary-material
Footnotes
1This procedure can in fact be seen as a discrete version of what would be done in a 3rd quantized framework for quantum gravity; indeed, GFT models (like matrix models for 2d gravity) are a discrete realization of the 3rd quantization idea (Gielen and Oriti, 2011).
2For instance, in a cosmological context in which one is interested only to homogeneous and isotropic geometries, the volume operator is expected to capture all the geometric properties of the system. In this case, therefore, one only includes this volume operator among the geometric observables of interest.
3In this sense, the operators
4The above equation is however expected to hold globally if the clock is a minimally coupled massless scalar field, which is going to be the only case we will consider here.
5For instance, a reduced wavefunction (whose modulus is) behaving as
6It is interesting to notice that the above equation is equivalent to the equation of motion of a conformal particle (de Alfaro et al., 1976) with a harmonic potential, which is a system characterized by a conformal symmetry. Since there are some interesting examples of systems whose dynamics can be can be mapped into a Friedmann one exactly in virtue of their conformal symmetry, (see e.g. (Lidsey, 1802; Ben Achour and Livine, 2019)), the above equation alone would already suggest a connection between the effective mean field dynamics discussed here and a cosmological one.
7We remark that this is an “effective” operator since its construction is always subject to a prior choice of appropriate states; in this case, CPSs (see (Marchetti and Oriti, 2021) for a more detailed discussion).
8As we have mentioned above, the result above was obtained using the condition
9Notice that under this assumption, which seems natural given the smallness of ϵ required by the CPS construction, the details of the underlying GFT model become effectively unimportant for the derivation of the results discussed below.
10We will formally assume that the set J is finite, either because there is an explicit cut-off
11While a formal proof would be needed that similar results extend to even higher moments, it seems likely that this is the case.
12Here we are assuming
13See (Oriti et al., 2016; Marchetti and Oriti, 2021) for a comparison with LQG effective bouncing dynamics and (Battefeld and Peter, 2015) for a review of bouncing models.
14Let us also mention, however, that another important role is played by the assumption
15Indeed, under these assumptions expectation values and variances of
16Notice that the requirements (ii) and (iii) correspond to conditions from 1 to 3 being satisfied. The first two of them qualify the framework as relational, while the third one guarantees that the expectation value of the volume operator captures in a satisfactory way the relational evolution of the homogeneous and isotropic geometry.
17If
References
Adjei, E., Gielen, S., and Wieland, W. (2018). Cosmological Evolution as Squeezing: a Toy Model for Group Field Cosmology. Class. Quan. Grav. 35, 105016. doi:10.1088/1361-6382/aaba11
Ashtekar, A., Bombelli, L., and Corichi, A. (2005). Semiclassical States for Constrained Systems. Phys. Rev. D 72, 025008. doi:10.1103/physrevd.72.025008
Ashtekar, A., and Lewandowski, J. (2004). Background Independent Quantum Gravity: A Status Report. Class. Quan. Grav. 21, R53–R152. doi:10.1088/0264-9381/21/15/r01
Ashtekar, A., and Singh, P. (2011). Loop Quantum Cosmology: A Status Report. Class. Quan. Grav. 28, 213001. doi:10.1088/0264-9381/28/21/213001
Assanioussi, M., and Kotecha, I. (2003). Thermal Quantum Gravity Condensates in Group Field Theory Cosmology, 01097.
Assanioussi, M., and Kotecha, I. (2020). Thermal Representations in Group Field Theory: Squeezed Vacua and Quantum Gravity Condensates. J. High Energ. Phys. 2020, 173. doi:10.1007/jhep02(2020)173
Baratin, A., Carrozza, S., Oriti, D., Ryan, J., and Smerlak, M. (2014). Melonic Phase Transition in Group Field Theory. Lett. Math. Phys. 104, 1003–1017. doi:10.1007/s11005-014-0699-9
Baratin, A., and Oriti, D. (2012). Group Field Theory and Simplicial Gravity Path Integrals: A Model for Holst-Plebanski Gravity. Phys. Rev. D 85, 044003. doi:10.1103/physrevd.85.044003
Battefeld, D., and Peter, P. (2015). A Critical Review of Classical Bouncing Cosmologies. Phys. Rep. 571, 1–66. doi:10.1016/j.physrep.2014.12.004
Ben Geloun, J., Martini, R., and Oriti, D. (2016). Functional Renormalisation Group Analysis of Tensorial Group Field Theories on. Phys. Rev. D 94, 024017. doi:10.1103/physrevd.94.024017
Bojowald, M., Höhn, P. A., and Tsobanjan, A. (2011). An Effective Approach to the Problem of Time. Class. Quan. Grav. 28, 035006. doi:10.1088/0264-9381/28/3/035006
Bojowald, M., Höhn, P. A., and Tsobanjan, A. (2011). Effective Approach to the Problem of Time: General Features and Examples. Phys. Rev. D 83, 125023. doi:10.1103/physrevd.83.125023
Bojowald, M. (2012). Quantum Cosmology: Effective Theory. Class. Quan. Grav. 29, 213001. doi:10.1088/0264-9381/29/21/213001
Bojowald, M., Sandhofer, B., Skirzewski, A., and Tsobanjan, A. (2009). Effective Constraints for Quantum Systems. Rev. Math. Phys. 21 (111), 0804. doi:10.1142/s0129055x09003591
Bojowald, M., and Tsobanjan, A. (2009). Effective Constraints for Relativistic Quantum Systems. Phys. Rev. D 80, 125008. doi:10.1103/physrevd.80.125008
Carrozza, S., and Lahoche, V. (2017). Asymptotic Safety in Three-Dimensional SU(2) Group Field Theory: Evidence in the Local Potential Approximation. Class. Quan. Grav. 34, 115004. doi:10.1088/1361-6382/aa6d90
Carrozza, S., Lahoche, V., and Oriti, D. (2017). Renormalizable Group Field Theory beyond Melonic Diagrams: an Example in Rank Four. Phys. Rev. D 96, 066007. doi:10.1103/physrevd.96.066007
de Alfaro, V., Fubini, S., and Furlan, G. (1976). Conformal Invariance in Quantum Mechanics. Nuov. Cim. A 34, 569–612. doi:10.1007/bf02785666
de Cesare, M. (2019). Limiting Curvature Mimetic Gravity for Group Field Theory Condensates. Phys. Rev. D 99, 063505. doi:10.1103/physrevd.99.063505
de Cesare, M., Oriti, D., Pithis, A. G. A., and Sakellariadou, M. (2018). Dynamics of Anisotropies Close to a Cosmological Bounce in Quantum Gravity. Class. Quan. Grav. 35, 015014. doi:10.1088/1361-6382/aa986a
de Cesare, M., Pithis, A. G. A., and Sakellariadou, M. (2016). Cosmological Implications of Interacting Group Field Theory Models: Cyclic Universe and Accelerated Expansion. Phys. Rev. D94, 064051.
Dittrich, B. (2006). Partial and Complete Observables for Canonical General Relativity. Class. Quan. Grav. 23, 6155–6184. doi:10.1088/0264-9381/23/22/006
Dittrich, B. (2007). Partial and Complete Observables for Hamiltonian Constrained Systems. Gen. Relativ Gravit. 39, 1891–1927. doi:10.1007/s10714-007-0495-2
Oriti, D. (2017). “Group Field Theory and Loop Quantum Gravity,” in Loop Quantum Gravity: The First 30 Years. Editor A. Ashtekar, and J. Pullin (WSP). 125–151. doi:10.1142/9789813220003_0005
Finocchiaro, M., and Oriti, D. (2004). Renormalization of Group Field Theories for Quantum Gravity: New Scaling Results and Some Suggestions, 07361.
Geloun, J. B., Koslowski, T. A., Oriti, D., and Pereira, A. D. (2018). Functional Renormalization Group Analysis of Rank-3 Tensorial Group Field Theory: The Full Quartic Invariant Truncation. Phys. Rev. D 97, 126018. doi:10.1103/physrevd.97.126018
Giddings, S. B., Marolf, D., and Hartle, J. B. (2006). Observables in Effective Gravity. Phys. Rev. D 74, 064018. doi:10.1103/physrevd.74.064018
Gielen, S. (2016). Emergence of a Low Spin Phase in Group Field Theory Condensates. Class. Quan. Grav. 33, 224002. doi:10.1088/0264-9381/33/22/224002
Gielen, S. (2019). Inhomogeneous Universe from Group Field Theory Condensate. J. Cosmol. Astropart. Phys. 2019, 013. doi:10.1088/1475-7516/2019/02/013
Gielen, S., and Oriti, D. (2018). Cosmological Perturbations from Full Quantum Gravity. Phys. Rev. D 98, 106019. doi:10.1103/physrevd.98.106019
Gielen, S., and Oriti, D. (2011). “Discrete and Continuum Third Quantization of Gravity,” in Quantum Field Theory and Gravity: Conceptual and Mathematical Advances in the Search for a Unified Framework, 2, 1102.
Gielen, S., and Oriti, D. (2014). Quantum Cosmology from Quantum Gravity Condensates: Cosmological Variables and Lattice-Refined Dynamics. New J. Phys. 16, 123004. doi:10.1088/1367-2630/16/12/123004
Gielen, S., Oriti, D., and Sindoni, L. (2014). Homogeneous Cosmologies as Group Field Theory Condensates. JHEP 06, 013.
Gielen, S., and Polaczek, A. (2020). Generalised Effective Cosmology from Group Field Theory. Class. Quan. Grav. 37, 165004. doi:10.1088/1361-6382/ab8f67
Gielen, S. (2014). Quantum Cosmology of (Loop) Quantum Gravity Condensates: An Example. Class. Quan. Grav. 31, 155009. doi:10.1088/0264-9381/31/15/155009
Gielen, S., and Sindoni, L. (2016). Quantum Cosmology from Group Field Theory Condensates: a Review. SIGMA 12, 082.
Giulini, D. (2007). Remarks on the Notions of General Covariance and Background Independence. Lect. Notes Phys. 721, 105–120. doi:10.1007/978-3-540-71117-9_6
Hoehn, P. A., Kubalova, E., and Tsobanjan, A. (2011). Effective Relational Dynamics of a Nonintegrable Cosmological Model. Phys. Rev. D - Particles, Fields, Gravitation Cosmology 86.
Höhn, P. A., Smith, A. R., and Lock, M. P. (1912). The Trinity of Relational Quantum Dynamics, 00033.
Isham, C. J. (1992). “Canonical Quantum Gravity and the Problem of Time,” in Integrable Systems, Quantum Groups, and Quantum Field Theories (Springer), 157.
Kotecha, I., and Oriti, D. (2018). Statistical Equilibrium in Quantum Gravity: Gibbs States in Group Field Theory. New J. Phys. 20, 073009. doi:10.1088/1367-2630/aacbbd
Li, Y., Oriti, D., and Zhang, M. (2017). Group Field Theory for Quantum Gravity Minimally Coupled to a Scalar Field. Class. Quan. Grav. 34, 195001. doi:10.1088/1361-6382/aa85d2
Lidsey, J. E. (1802). Inflationary Cosmology. Diffeomorphism Group of the Line and Virasoro Coadjoint Orbits, 09186.
Magnen, J., Noui, K., Rivasseau, V., and Smerlak, M. (2009). Scaling Behavior of Three-Dimensional Group Field Theory. Class. Quan. Grav. 26, 185012. doi:10.1088/0264-9381/26/18/185012
Marchetti, L., and Oriti, D. (2021). Effective Relational Cosmological Dynamics from Quantum Gravity. JHEP 05, 025.
Oriti, D. (2016). Group Field Theory as the Second Quantization of Loop Quantum Gravity. Class. Quan. Grav. 33, 085005. doi:10.1088/0264-9381/33/8/085005
Oriti, D., Pranzetti, D., Ryan, J. P., and Sindoni, L. (2015). Generalized Quantum Gravity Condensates for Homogeneous Geometries and Cosmology. Class. Quan. Grav. 32, 235016. doi:10.1088/0264-9381/32/23/235016
Oriti, D., Sindoni, L., and Wilson-Ewing, E. (2016). Emergent Friedmann Dynamics with a Quantum Bounce from Quantum Gravity Condensates. Class. Quan. Grav. 33, 224001. doi:10.1088/0264-9381/33/22/224001
Oriti, D. (2011). “The Microscopic Dynamics of Quantum Space as a Group Field Theory,” in Foundations of Space and Time: Reflections on Quantum Gravity, 257–320.
Oriti, D. (2017). The Universe as a Quantum Gravity Condensate. Comptes Rendus Physique 18, 235–245. doi:10.1016/j.crhy.2017.02.003
Pithis, A. G. A., and Sakellariadou, M. (2019). Group Field Theory Condensate Cosmology: An Appetizer. Universe 5, 147. doi:10.3390/universe5060147
Pithis, A. G. A., and Sakellariadou, M. (2017). Relational Evolution of Effectively Interacting Group Field Theory Quantum Gravity Condensates. Phys. Rev. D 95, 064004. doi:10.1103/physrevd.95.064004
Pithis, A. G., Sakellariadou, M., and Tomov, P. (2016). Impact of Nonlinear Effective Interactions on Group Field Theory Quantum Gravity Condensates. Phys. Rev. D 94, 064056. doi:10.1103/physrevd.94.064056
Reisenberger, M. P., and Rovelli, C. (2001). Spacetime as a Feynman Diagram: the Connection Formulation. Class. Quan. Grav. 18, 121–140. doi:10.1088/0264-9381/18/1/308
Rovelli, C. (2004). “Quantum Gravity,” in Cambridge Monographs on Mathematical Physics (Cambridge, UK: Cambridge University Press). doi:10.1017/CBO9780511755804
Rovelli, C., and Wilson-Ewing, E. (2014). Why Are the Effective Equations of Loop Quantum Cosmology So Accurate? Phys. Rev. D 90, 023538. doi:10.1103/physrevd.90.023538
Thiemann, T. (2007). “Modern Canonical Quantum General Relativity,” in Cambridge Monographs on Mathematical Physics (Cambridge University Press). doi:10.1017/CBO9780511755682
Keywords: quantum gravity, cosmology: theory, loop quantum cosmology, group field theory, emergent spacetime, relational dynamics
Citation: Marchetti L and Oriti D (2021) Quantum Fluctuations in the Effective Relational GFT Cosmology. Front. Astron. Space Sci. 8:683649. doi: 10.3389/fspas.2021.683649
Received: 21 March 2021; Accepted: 14 June 2021;
Published: 26 July 2021.
Edited by:
Guillermo A. Mena Marugán, Instituto de Estructura de la Materia, SpainReviewed by:
Etera Livine, Université de Lyon, FranceHerman J. Mosquera Cuesta, Departamento Administrativo Nacional de Ciencia, Tecnologia e Innovacion, Colciencias, Colombia
Hanno Sahlmann, Friedrich Alexander University Erlangen-Nuremberg, Germany
Copyright © 2021 Marchetti and Oriti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: D. Oriti, ZGFuaWVsZS5vcml0aUBwaHlzaWsubG11LmRl
 L. Marchetti
L. Marchetti D. Oriti
D. Oriti