Abstract
Spin- excitations of nuclei are important for describing neutrino reactions in supernovae or in neutrino detectors since they are allowed transitions mediated by neutral current neutrino interactions. The spin- excitation strength distributions in self-conjugate nuclei were studied by proton inelastic scattering at forward angles for each of isovector and isoscalar excitations as reported in H. Matsubara et al., Phys. Rev. Lett. 115, 102501 (2015). The experiment was carried out at the Research Center for Nuclear Physics, Osaka University, employing a proton beam at 295 MeV and the high-resolution spectrometer Grand Raiden. The measured cross-section of each excited state was converted to the squared nuclear matrix elements of spin- transitions by applying a unit cross-section method. Comparison with predictions by a shell-model has revealed that isoscalar spin- strengths are not quenched from the prediction although isovector spin- strengths are quenched similarly with Gamow-Teller strengths in charged-current reactions. This finding hints at an important origin of the quenching of the strength relevant to neutrino scattering, that is, the proton-neutron spin-spin correlation in the ground state of the target nucleus. In this manuscript we present the details of the unit cross-section method used in the data analysis and discuss the consistency between the quenching of the isoscalar magnetic moments and that of the isoscalar spin-M1 strengths.
1 Introduction
Response of nuclei to incoming neutrinos is categorized into two types of reactions: charged-current (CC) and neutral-current (NC). Gamow-Teller (GT) transition of nuclei belongs to the CC neutrino reaction, while the isovector (IV) spin magnetic-dipole () transition to NC. The GT (, and ) transitions are analogous to the IV spin- (, and ) transitions under isospin symmetry. Relevant transition rates are predicted by theoretical models such as the shell-model. The experimentally observed transition rates are, however, quenched compared to the model predictions by employing bare transition operators. Quenching is a basic property of nuclear structure and influences the neutrino reaction rates in astrophysical processes and terrestrial neutrino detectors. The nuclear spin responses and their quenching have strong effects on the mean free path of neutrinos in dense nuclear matter, the size of the neutrino sphere formed in the center of a core-collapsing star, and the cooling process of proton-neutron stars.
The quenching has been extensively studied for the GT transitions. The GT transition strength contained in the GT giant resonances studied by reactions was found to be ∼60% of the prediction by the Ikeda-Fujii-Fujita sum-rule () consistently for a large variety of nuclei. Two mechanisms were presented to explain GT quenching in the context of the mixing of higher-order configurations with the fundamental one-particle-one-hole nature of the GT excitation. One is the -hole mixing originating from the quark degree of freedom. The other is the two-particle-two-hole as well as the higher-order particle-hole excitations within the nucleonic degree of freedom. Detailed study of the GT strength distribution embedded in the continuum located above the GT giant resonance revealed that the major part of quenching is caused by mixing in the nucleonic degree of freedom (). The observed GT transition strengths studied by beta-decay are also quenched from shell-model predictions using the bare g-factor. Recent ab initio calculations using the chiral effective field theory () indicated that quenching was resolved by introducing two-body currents and nuclear many-body correlations. Quenching in the analogous spin- transitions was studied by proton inelastic scattering (; ). The result was unclear due to the poor quality of the experimental data and to the ambiguity of the transition matrix element relying on the reaction calculation. This problem has been overcome by the achievement of a high-precision measurement () using high-resolution proton scattering at forward scattering angles including zero degrees that reported the quenching of the nuclear matrix elements for the IV spin- transitions, similar to the analogous GT transitions, but no-quenching for the isoscalar (IS) spin-. Exhaustion of the sum-rule of the spin- strengths is relevant to the spin susceptibility of asymmetric nuclear matter, its response to the strong magnetic field in magnetars, and possible phase-transition of nuclear medium in a neutron star to the ferromagnetic state.
The experimental work gave new insight, by the use of the non-energy-weighted sum-rule, that the underlying quenching mechanism is embedded in the ground state property as spin-spin correlation of neutron(n)-proton(p) pairs. The expectation value of the correlation in the ground state is equivalent to the difference of the quenching of nuclear matrix elements between the IS and IV spin- transitions. Thus, the quenching of the IS and IV spin- transitions needs to be described simultaneously and mutually-consistently. The details are described in Section 5.4.
The n-p correlation in the nuclear ground state is one of the recent topics in nuclear physics. The short range correlation as well as the tensor correlation are considered to be the origin of the neutron-proton correlation and are relevant to the IS spin-triplet n-p pairing. The high-momentum nature of the correlation has been studied by the knockout reaction by electron scattering (; ; ) or by high-momentum transfer reaction by using scattering (; ). In both cases, dominant contribution of the n-p pairs is reported rather than the identical pairs, n-n or p-p, to the high-momentum component in the ground state.
In a different approach, the spin-aligned IS n-p coupling of the valence particles around the Fermi surface was studied from a level structure determined by gamma spectroscopy (). It is interesting to observe how those n-p paring components and the IS spin-triplet n-p pairing are related to the n-p spin-spin correlation in the ground state.
In the work of , IS and IV spin- excitation strength distributions were individually determined by a high-resolution proton inelastic scattering experiment at zero degrees and forward angles for self-conjugate even-even nuclei from 12C to 36Ar. The squared nuclear matrix element of each transition was extracted from the observed differential cross-section by using the unit cross-section method. The summed strength up to the excitation energy of 16 MeV was compared with the prediction by a shell-model for the discussion of quenching of the IS and IV transitions. In this article we describe in greater detail the unit cross-section method in the data analysis. Also, the observed no-quenching of the IS spin-M1 transitions is compared with the historical knowledge of the quenching of the IS magnetic moment. The difference of IS and IV quenching is discussed in terms of the n-p spin-spin correlation in the ground state.
In Section 2, formalism is presented for discussion of the nuclear matrix elements of the IS and IV spin- transitions, the IS and IV magnetic moments of the nuclear ground state, sum-rules, and the n-p spin-spin correlation function. The experimental methods and the data analysis are described in Section 3. The nuclear matrix elements are determined from the experimental data by using the unit cross-section method as described in Section 4. The quenching of the IS and IV spin- nuclear matrix elements, IS magnetic moment, and the n-p spin-spin correlation are discussed in Section 5. Summary and prospects are given in Section 6.
2 Formalism
2.1 Nuclear Magnetic Moment
The operator for magnetic dipole moments and transitions consists of an orbital part () and a spin part ().where is the nuclear magneton, is the Pauli spin matrix, the operator is the third component of the isospin operator acting on the k-th nucleon and its eigen value is +1 for neutrons (ν) and −1 for protons (π). The gyromagnetic factors (g-factors) of , , , and are taken as , , , and , where the g-factors in the free space, , , , and , are employed. The suffixes of IS and IV denote isoscalar and isovector, respectively. Thus, a magnetic moment is expressed aswhere denotes an initial state. Here, magnetic moments can be divided into IS and IV parts by corresponding analogous magnetic moments in mirror nuclei () asrespectively, where is a magnetic moment in the case of . Because total spin has a relation , the following can be obtainedwhere and (). Applying the above relation to IS magnetic moment , one getswhere we denote the function as according to , and it will be discussed in Section 5.3.
2.2 M1 Transition Strength
The reduced transition probability (transition strength) for excitation is written aswhere denotes a final state in a transition. Following the convention of Edmonds (; ), the reduced nuclear matrix element in spin from an initial state to a final state is defined aswhere denotes , , , and . Expressing corresponding analogous transitions in mirror nuclei () as , IS and IV parts of a transition strength can be written using (; ) or using the reduced matrix elements asrespectively. If only spin parts are extracted as IS and IV spin- transition strengths, they are expressed asrespectively.
Here, we focus on an IS part, . Because total angular momentum operator () gives a good quantum number, taking a ground state as , is proportional to but is orthogonal to any other eigenstates. Thus, the following restriction (; ) can be obtained
Since the above restriction leads to , the right-hand side of Eq. 10 is rewritten as
2.3 Squared Nuclear Matrix Element
Nuclear excitation with is an transition. When nuclear excitation at low momentum transfer is considered, spin-parts of the transition are probed due to the local nature of the nucleon-nucleon () interaction (). Thus, the excitation by () reaction at forward angles is spin- transition. Since spin- transition is not probed by electromagnetic interaction but by nuclear interaction, its transition strength does not relate to g-factors. Therefore, transition strengths of IS and IV spin-M1 transitions from the ground state to an excited state are expressed by squared nuclear matrix element (SNME) asrespectively. The factor is unity for a 0+ ground state.
2.4 Relation to Gamow-Teller Excitation
Next, reduced nuclear matrix element and transition strength in GT excitation are defined asrespectively, where . Applying the Wigner-Eckart theorem in the isospin space, transition strengths of GT and IV spin- excitations are obtained asrespectively, where and are reduced nuclear matrix elements in spin and isospin expressed asrespectively. Because is realized under the assumption of isospin symmetry, the following relationship between and can be obtained as
Here, it should be noted that the isospin symmetry is reasonably assumed within the accuracy of the data in the present study although the meson exchange current contribution can be different between an IV transition measured by electron scattering and the analogous GT transition by charge-exchange reaction (; ).
2.5 Total Spin Correlation in Ground State
For the discussion of total spin correlation in a ground state (), the difference between the sums of the IS and IV spin- SNMEs integrated up to the excitation energy of , , is defined as
With the proton (neutron) total spin operator defined asthe sum is taken for all the protons (neutron).When a ground state is , the IS and IV spin- nuclear matrix elements are represented byrespectively, where denotes the ground state. In the limit of , the completeness of the final state, , yields
Here the expectation values of the left side of the equations are taken for the 0+ ground state. We then derivewhich represents the expectation value of the proton-neutron spin-spin correlation in the ground state.
3 Experiment
In this section we briefly describe the experimental method and the assignment of the spin-M1 excitations. Details can be found in former publications (; ; ).
3.1 Measurement of the (p,p’) Reactions
The experiment was performed at the cyclotron facility of the Research Center for Nuclear Physics (RCNP), Osaka University. A proton beam was accelerated by a cascade of two cyclotrons to Ep = 295 MeV. The beam was transported to the West-South (WS) beam line (), where a high-dispersion on target was created. An excitation-energy resolution of 18 keV (FWHM) was achieved by applying dispersion matching (; ; ) between the WS beam line and the Grand Raiden (GR) spectrometer (). The scattered protons by the target were momentum-analyzed and were detected by two sets of multi-wire drift-chambers and two plastic scintillation counters at the focal plane by GR spectrometer. A scattering angle range of 0–14° was covered by placing the GR spectrometer at 0, 2.5, 4.5, 6, 8, 10, 12, and 14°. The details of the experimental technique are described in Ref. (; ).
Self-conjugate even-even nuclei, 12C, 24Mg, 28Si, 32S and 36Ar, were used as the target. Areal densities of 1.0–2.5 mg/cm2 were prepared for 12C, 24Mg, and 28Si. Magnesium and argon targets were isotopically enriched to 100%, while the others were in natural abundance. The 32S target was kept at the liquid nitrogen temperature for preventing sublimation due to heat by charged particle irradiation () with an areal density of 15 mg/cm2. The 36Ar target was kept at 1.0 atm in a gas cell at room temperature () sealed by aramid foils with a thickness of 6 μm on one side.
3.2 Assignment of Spin-M1 Excitations
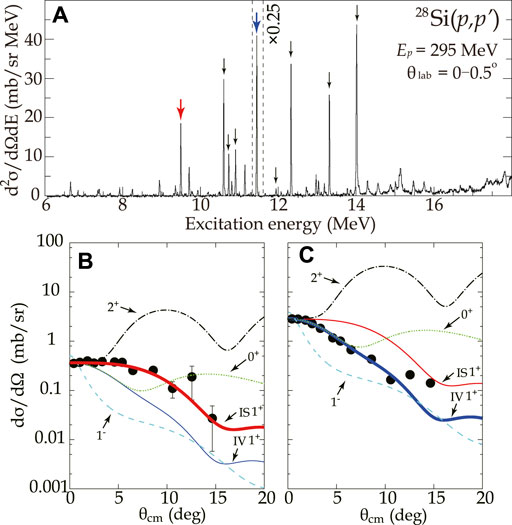
Figure 1A shows an excitation energy spectrum of the 28Si() reaction at a scattering angle of 0.0–0.5°. The excited states below Ex = 16 MeV are well isolated from the others. Excited state with a spin-parity of 1+ state was identified by comparing the shape of the measured angular distribution of the differential cross-section with Distorted-Wave Impulse Approximation (DWIA) calculations by using the code DWBA07 (). One-body transition densities were obtained by shell-model calculations with the code Nushell@MSU () and the USD interactions (). No sizable difference in the angular distribution was observed depending on the choice of the effective interaction from USD, USDA, or USDB (; ). The effective NN interaction parametrized at 325 MeV was used after conversion to a beam energy of 295 MeV as indicated in (; ). Optical potential parameters were determined by fitting the angular distribution of the differential cross-section of the elastic scattering measured in the same experiment (). Harmonic oscillator parameters were taken from a global analysis ().
FIGURE 1
The measured angular distributions of the differential cross-section for the excited states at Ex = 9.495 (1+: T = 0) and 11.447 MeV (1+: T = 1) in 28Si are shown in Figures 1B,C, respectively, by the solid circles. They are compared with the predictions of the DWIA calculation shown by the curves for Jπ = 0+, 1−, and 2+, and for each of the IS and IV 1+ transitions. The predicted cross-sections are normalized to the experimental data at the smallest measured angle. The angular distribution of the IS 1+ excitation is predicted to be flatter than the IV 1+ excitation at the forward angles smaller than 5° due to the relatively stronger contribution of the exchange tensor component compared to the central component in the effective NN interaction (; ). Thus, the measured angular distribution allowed determination of the transferred isospin, ΔT = 0 (IS) or 1 (IV), for the 1+ transitions.
The IS and IV 1+ excited states were assigned from the observed discrete excited states by the following method. First the angular distribution of the differential cross-sections for each of the observed discrete excited states was deduced from the data analysis. The excited states were selected according to the angular distribution below 5° for those having an almost flat distribution as a signature of an IS 1+ state or a quickly dropping distribution of an IV 1+ state as shown in Figures 1B,C, respectively. Second, the most appropriate assignment was chosen from IS 1+, IV 1+, 0+, 1−, and 2+ distributions by comparing the angular distribution up to 14° with the theoretical predictions. Third, the assignment for the IS or IV 1+ states with a reduced χ2 value close to unity was taken as confident and that for the rests as less confident. The confident assignments of the IS and IV 1+ states were in good agreement for the conditions studied by electron scattering (; ; ; ; ). The high energy-resolution measurement allowed us to observe several new states including the less-confident assignments as shown in Section 5.1.
4 Unit Cross-Section Method
4.1 Definition
4.1.1 Unit Cross-Section
The differential cross-section of the 1+ excitations by proton inelastic scattering at 0° is considered to be approximately proportional to SNME in the intermediate energy region of 100–400 MeV. Unit cross-sections (UCSs), and , are introduced in analogy to the study of Gamow-Teller excitations by reactions (; ). The differential cross-section at 0° is written aswhere T stands for IS or IV. is the operator, or , for IS or IV transitions, respectively. is the kinematic factor that accounts for dependence on the momentum transfer (q) and the excitation energy (), and was determined by the DWIA calculation as explained in Section 4.1.2. The target mass (A) dependence of UCSs is parameterized as ()where and are the normalization and mass-dependence parameters. The mass-dependence parameter essentially originates from the distortion effect of the reaction that is common between the IS and IV transitions. Thus we assume = , which is held within an accuracy of 5% in DWIA calculations. Details will be discussed in Section 4.4.2.
4.1.2 Kinematic Factor
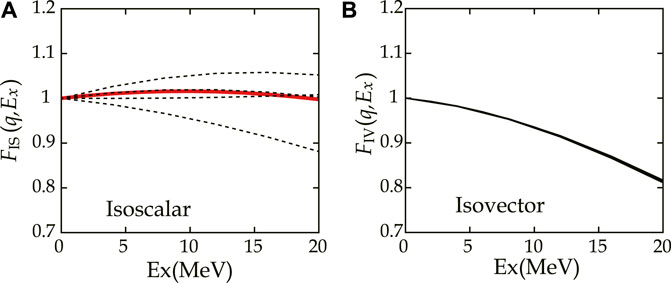
The kinematic factors and were determined by DWIA calculation using the USD interaction as shown in Figure 2 as a case of 28Si, where only OBTDs above the experimental detection limit were employed. The distributions were obtained from a ratio of differential cross-section at 0° at to that at . As seen in Figure 2B, IV distributions of the kinematic factor overlap. Since the result suggests that does not depend on wavefunction, was expressed as a smooth function of and A by fitting. As shown in Figure 2A, however, IS distributions of the kinematic factor depend on wavefunction as they do not overlap. Because the result suggests that cannot be expressed as a function of owing to dependence of wavefunction, was simply assumed in order to cover the variation of wavefunctions below MeV.
FIGURE 2
4.2 Derivation From Experiment
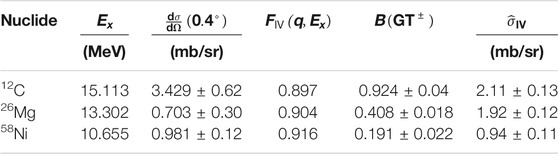
4.2.1 Cases of 12-Carbon, 26-Magnesium, 58-Nickel
Isovector UCSs of 12C, 26Mg, and 58Ni were obtained using the data summarized in Table 1 by assuming isospin symmetry. The differential cross-section of () reaction at MeV at scattering angles 0.4° was taken from , where 0.4° is the most forward angle by selecting scattering angles between 0.0 and 0.5°. The cross-section was extrapolated to MeV using .
TABLE 1
| Nuclide | |||||
|---|---|---|---|---|---|
| (MeV) | (mb/sr) | (mb/sr) | |||
| 12C | 15.113 | 3.429 ± 0.62 | 0.897 | 0.924 ± 0.04 | 2.11 ± 0.13 |
| 26Mg | 13.302 | 0.703 ± 0.30 | 0.904 | 0.408 ± 0.018 | 1.92 ± 0.12 |
| 58Ni | 10.655 | 0.981 ± 0.12 | 0.916 | 0.191 ± 0.022 | 0.94 ± 0.11 |
Data used for obtaining IV UCSs.
Log -value of β-decay and (3He, t) data (; ; ; ; ) were used to obtain GT strength (B(GT±)) from ground state to an excited state corresponding to the () cross-section under the isospin symmetry. After B(GT±) was converted to IV spin- SNME following Eqs. 13, 24, was obtained. Here, the () data () were also employed for the calibration of B(GT−) in 58Ni.
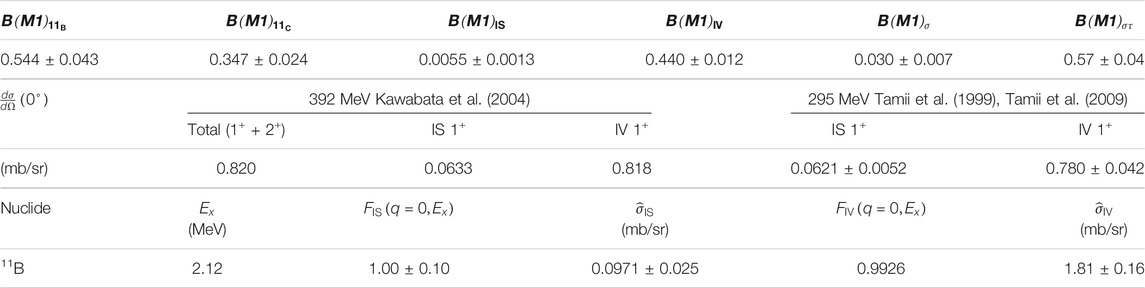
4.2.2 Case of 11-Boron
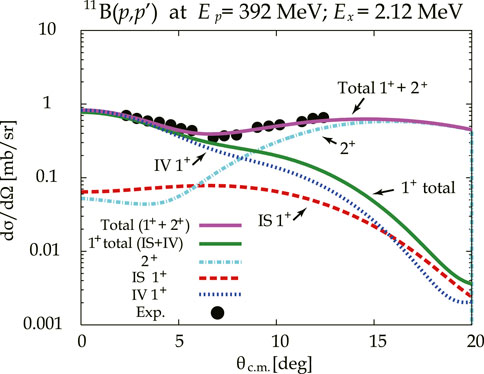
The γ-decay widths of the mirror states in 11B and 11C from the first excited states (), corresponding to and , respectively, were employed to obtain and following Eqs. 10, 11. Then, and were obtained from and (; ) using Eqs. 15, 24, respectively. Finally, IS and IV spin- SNMEs in the case of were obtained using Eqs. 12, 13, respectively.
The differential cross-section data of the 11B() reaction at MeV and at MeV was taken from . The angular distribution of the differential cross-section was decomposed into IS 1+, IV 1+, and 2+ transitions using the DWIA calculation, where an incoherent (a coherent) sum was assumed between 1+ and 2+ (IS 1+ and IV 1+) excitations. The OBTDs based on CKPOT interaction (), the effective interaction derived at 325 MeV (; ), and the global optical potential parameters () were employed in this calculation. The OBTDs were normalized to reproduce the experimental values of IS and IV SNMEs, and () in IS 1+, IV 1+, and 2+ excitations, respectively. Because the normalized OBTDs did not reproduce the experimental angular distribution of the differential cross-section, additional normalization factors of 1.1 and 1.3 were applied to the 1+ and 2+ excitations, respectively, as shown in Figure 3. The differential cross-section data of total, IS 1+, and IV 1+ at MeV and at 0° were decomposed as summarized in Table 2, where the experimental uncertainty was assumed to be negligible because the error bars were invisible in . Here, choice of an interaction with OBTDs did not change the final result because differences among CKPOT, SFO (), and MK3w () interactions in the model spaces of p, , and , respectively, were within 0.5%. Next, the cross-section data at MeV were converted to those at MeV by making use of a ratio of the 12C() reaction at 0° to the states and 15.11 MeV known as IS 1+ and IV 1+ excitations, respectively, where the experimental data were taken from , . Thus, the data of 11B() excitation to MeV at MeV and at 0° were obtained.
FIGURE 3
TABLE 2
| 0.544 ± 0.043 | 0.347 ± 0.024 | 0.0055 ± 0.0013 | 0.440 ± 0.012 | 0.030 ± 0.007 | 0.57 ± 0.04 |
| 392 MeV | 295 MeV , | ||||
| Total (1+ + 2+) | IS 1+ | IV 1+ | IS 1+ | IV 1+ | |
| (mb/sr) | 0.820 | 0.0633 | 0.818 | 0.0621 ± 0.0052 | 0.780 ± 0.042 |
| Nuclide | |||||
| (MeV) | (mb/sr) | (mb/sr) | |||
| 11B | 2.12 | 1.00 ± 0.10 | 0.0971 ± 0.025 | 0.9926 | 1.81 ± 0.16 |
Data used for obtaining UCSs of 11B. The upper table is expressed in unit of .
Combining the SNMEs with the differential cross-section after correction of , IS and IV UCSs in the case of 11B were obtained as summarized in Table 2. Here, does not include uncertainty owing to .
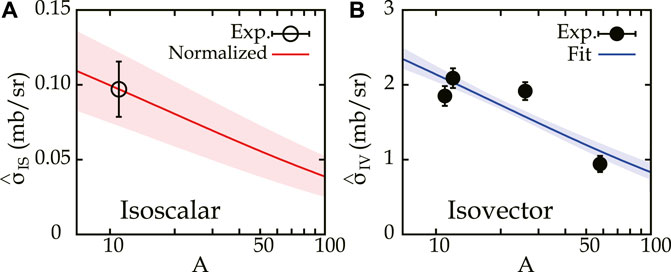
4.3 Results of Unit Cross-Section
The experimentally obtained IS and IV UCSs were plotted as a function of the mass number in Figures 4A,B, respectively. The mass dependence of the IV UCS data was fitted with the functional form of Eq. 33 having free parameters of and . The result is shown by the solid line in Figure 4B with the one-sigma uncertainty band. The IS normalization parameter, , was determined from the data at A = 11. The IS slope parameter, , was taken to be the same as as discussed in Section 4.4.2. The IS uncertainty band includes contribution of 10% from the (Section 4.1.2). The obtained parameters are summarized in Table 3.
FIGURE 4
TABLE 3
| (mb/sr) | (mb/sr) | |
|---|---|---|
| 0.226 ± 0.043 | 4.85 ± 0.82 | 0.38 ± 0.06 |
Empirically determined UCS parameters from the fit shown in Figure 4.
4.4 Model Study
4.4.1 Proportionality of Squared Nuclear Matrix Elements to the Differential Cross-Section
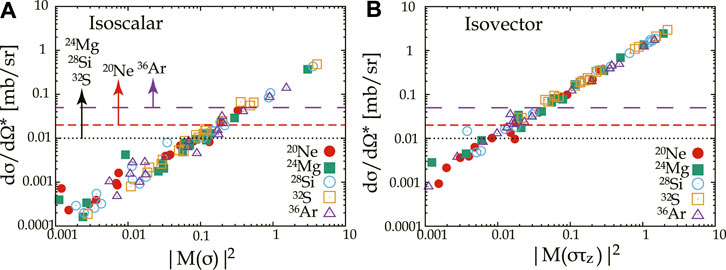
Validity of the application of the UCS method has been theoretically examined by the use of shell-model target wave functions as USD interaction and DWIA calculation. Since and were calculated using the code Nushell@MSU (), SNMEs were obtained from the relations in Eqs. 12, 13. Each differential cross-section at and at MeV was calculated using corresponding OBTD of the USD interaction. Here the following correction for mass dependence to be normalized to was applied aswhere is the corrected cross-section and 0.38 comes from determined in Table 3. As shown in Figure 5, good linearity was seen especially above the experimental detection limit shown by the lines for each target nucleus.
FIGURE 5
4.4.2 Distortion Effect
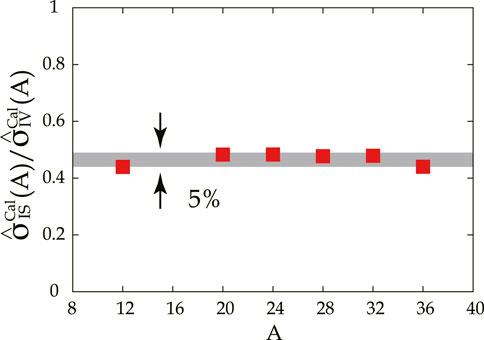
The mass-dependence term in Eq. 32, , essentially originates from the distortion effect that is common between the IS and IV transitions. A slope for each nucleus in Figure 5 corresponds to UCSs theoretically obtained, where the weighting sum within the experimental detection limit was taken. Those ratios of IS to IV UCSs for each nucleus are plotted as a function of mass number in Figure 6, where the suffix of “cal” indicates that the value of UCS is obtained from the calculation. The result for 12C is added in Figure 6. The SFO interaction (), which is applicable to the p-shell nuclei, is used instead of the USD interaction. The results suggest that the assumption is supported, as the ratios are constant within 5%.
FIGURE 6
5 Results and Discussion
5.1 Strength Distribution
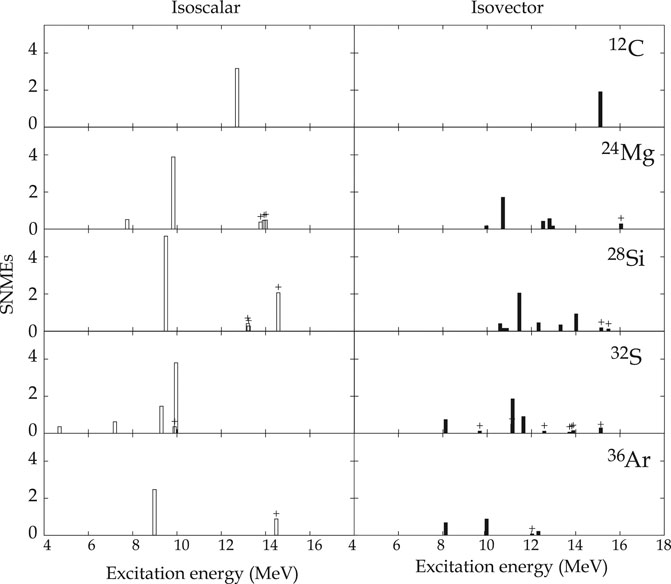
The SNMEs of the transitions to the excited states assigned as (IS) or (IV) 1+ states were determined by using Eq. 32 from the measured differential cross-section at 0°. The results are plotted in Figure 7 , where the figure was taken from with addition of the 12C data. The strengths of 12C were observed to be centered to single state, which was consistent with previous work (). For 24Mg, 28Si, 32S, and 36Ar, we identified 1–4 (4–8) states in each target nucleus corresponding to the IS (IV) spin- transitions.
FIGURE 7
Additionally, 1–3 (1–7) states were assigned as IS (IV) spin- transitions with less confidence, and they are marked with ”+.” We reassigned 1–6 states as 0+, which were claimed as 1+ in previous studies (; ).
5.2 Quenching of Squared Nuclear Matrix Elements of Isoscalar and Isovector Spin-M1 Transitions
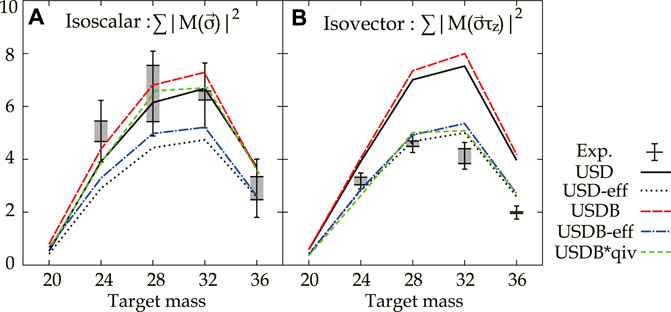
The integrated values of the SNMEs up to MeV were plotted as a function of the target mass in Figure 8 for each of the IS (left panel) and IV (right panel) transitions. Error bars show the full experimental uncertainties, while gray bands show the partial uncertainties originating from the less-confident spin-parity assignment of the transitions (see Section 5.1). Predicted SNMEs by shell-model calculation employing USD interaction () integrated up to 16 MeV is shown by solid lines. Altering the effective interaction to USDA or USDB (; ) gave only a small change in the prediction (<10%), as shown in Figure 8 for USDB (dashed line). It has been found that the measured values are significantly smaller than the model prediction for the integrated IV SNMEs, while the values are consistent with the model prediction of the integrated IS SNMEs within the experimental uncertainties. We defined the quenching factor as the ratio of the experimentally observed SNMEs integrated up to the experimental limit of 16 MeV to the theoretical predictions integrated to the same excitation energy. The numbers are 1.01(9) and 0.61(6), compared with predictions by the shell model using the USD interaction for the IS and IV spin- transitions, respectively, when the averages of the measured nuclei are used.
FIGURE 8
The observed quenching factor of the IV spin- transitions is similar to the study of the quenching of the Gamow Teller transitions that is analogous to the IV spin- transitions in terms of isospin symmetry (). Quenching of the reduced transition probability is, in a conventional prescription, implemented by modification of the g-factors () that is multiplied to the SNMEs to obtain . Here, we applied the same empirical quenching factor as used in the modification of g-factors to the SNMEs calculated by the shell model. The results are shown by the dotted lines (USDBeff) in Figure 8. The empirical quenching factors are similar between IS and IV transitions. SNMEs of the IV spin- transitions with the empirical quenching factor turned out to be compatible with the data.
In contrast, description of the IS transitions became worse by introducing the empirical quenching factor. The present result shows that the widely-used effective g-factors lead to an over-quenching of the IS spin component of the transition in the -shell. It should be noted that the observed strength of the 1+ excited state at 10.23 MeV in 48Ca by scattering is more consistent with electron scattering data when no quenching is assumed for the IS part of the transition strength (; ). A recent theoretical work (; ) reported that both the IS and IV SNMEs can be reproduced (short dashed line) by enhancing the IS spin-triplet pairing matrices by a factor of 1.1 in addition to applying the empirical quenching factor to the IV spin- operator but not the IS spin- operator (USDB*qiv). Note that in () the USDB*qiv result for the IS spin- excitations is not shown, but it is the same as USDB*. The theoretical work implies that the present description of the shell model using USD interactions and the empirical quenching factors may have room to be improved in the IS spin-triplet interaction channel and in the IS quenching factor.
5.3 Isoscalar Magnetic Moments
In this section, we discuss how the new finding of quenching of the IS and IV spin- SNMEs is understood in relation to the IS and IV magnetic moment studied in the past. The magnetic moment is described by the diagonal component of the nuclear matrix element with the relevant operator while the transitions correspond to the off-diagonal components as described in Section 2.
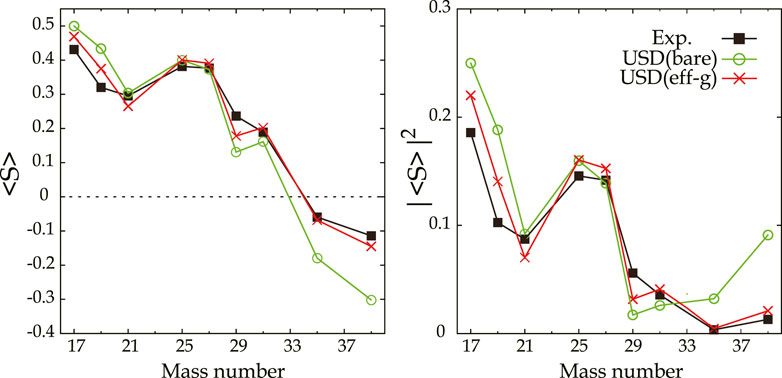
The experimental data are plotted in the left panel of Figure 9, and the squared values in the right panel. The values calculated by the shell model with the effective IS g-factors (; ) using the USD interaction are indicated by open circles and crosses for the bare and effective g factors, respectively. The results show clear discrepancies between the experimental data and the prediction with the bare g-factor, corresponding to the quenching, in the edge regions of the sd-shell (A = 17–19 and 35–39) close to the magic numbers of A = 16 and 40. The difference is, however, not obvious in the mid-shell region (A = 21–31). The discrepancies in the edge regions are reduced by introduction of the effective IS g-factors. The IS magnetic moments in the mid-shell region are reasonably reproduced without introducing the effective IS g-factors, which is consistent with our finding of no quenching of the IS spin- SNMEs.
FIGURE 9
5.4 Proton-Neutron Spin-Spin Correlation in the Ground State
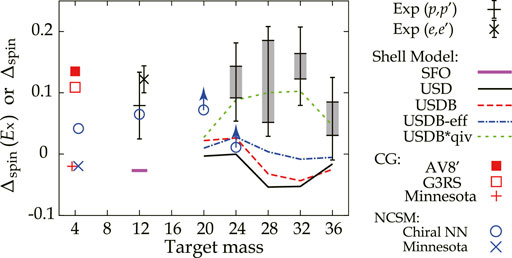
Figure 10 shows the data summed up to =16 MeV by the solid bars. Electron scattering data () is plotted at A = 12 by the black cross mark with the error bar, which is consistent with the proton scattering data within experimental uncertainty. It is interesting to note that all the experimental data show positive numbers. The values at A = 4 predicted by Correlated Gaussian (CG) method (), an ab initio approach, are plotted for each of the interactions of AV8’ (red solid square), G3RS (red open square) and Minnesota (red plus). The predictions by the No-Core Shell-Model (NCSM) () are plotted for chiral () (blue open circle) and Minnesota (blue cross) interactions. Both predictions using the Minnesota interaction are consistent with each other and are slightly negative. The Minnesota interaction does not contain tensor interactions. It is illuminating to see that the predictions are positive when more realistic interactions are used: AV8’ () and G3RS () interactions for the CG method and chiral interaction () for NCSM. The shell model predictions of at A = 12 with SFO interaction (solid horizontal line) and A = 20–36 with USD interaction are slightly negative or close to zero, which is significantly smaller than the experimental data of . The trend of the USDB interaction (dashed line) is similar. The predicted values increase a little but are still much smaller than the experimental results when the IS and IV effective quenching factors determined in the study of the g-factors () are applied to the SNME predicted by the shell model (dot-dashed line). The situation is similar for the other studies of effective g-factors (; ; ). The experimental data are reproduced when IS spin-triple pairing matrices are enhanced by a factor of 1.1, and only the IV part of SNME is quenched by effective quenching factors (dotted line) ().
FIGURE 10
NCSM with the chiral interaction predicts values for () and (), as indicated by the open blue circles in Figure 10. Here, defines the maximal allowed harmonic-oscillator excitation energy above the unperturbed ground state (), hence representing a measure of the model space. Variation of the values depending on shows a clear trend toward positive when increases: −0.007, 0.028, and 0.072 for = 0, 2 and 4 for and −0.018 and 0.011 for =0 and 2 for 24Mg, respectively. Although the values are not converged yet, they are taken as a lower limit in the plot (expressed by arrows). The increase of with increasing implies that mixing of higher-lying orbits is important for reproducing the values.
The observed positive value implies that deuteron-like correlated pairs are formed in the ground state of the target nuclei. Note that takes a value of 1/4 for the IS pair like a deuteron, −3/4 for the IV pair, and zero for uncorrelated pairs. Thus the IS pairs are favored over the IV pairs. It would be interesting to see how values are predicated by ab initio calculations () that reproduce the GT transition strengths studied by beta-decay without a quenching factor by introducing the contribution from the two-body current and many-body correlations. The finding would have relevance to the observed pair dominance in the correlated pairs with high relative momentum in nuclei observed by electron scattering (; ; ) or by reactions (; ). The electron scattering data probe all the components of the correlated pairs due to the high incident energy of the electrons without limitation placed on the excitation energy of the residual nucleus after knockout of a correlated pair. In contrast, the data would be relevant to the pairs at around the Fermi surface of the target nucleus since the excitation energy of the residual nucleus is limited in the region of several MeV. The present experimental data of are also limited to 16 MeV and thus are considered to be sensitive to the spin-spin correlation in the pairs at around the Fermi surface. The spin-aligned IS coupling of the valence particles in 92Pd was studied from the level structure determined by gamma spectroscopy (), which also indicates the effect of IS pairs at around the Fermi surface. It would be interesting to extend the study of to higher-excitation energies to observe how the spin-spin correlation changes in deeper single particle orbits.
6 Summary
In summary, spin- excitation in nuclei is important for the study of NC neutrino reactions in astrophysical phenomena and in neutrino detectors. Quenching of the IS and IV spin- SNMEs for sd-shell nuclei has been studied by high energy-resolution measurement of proton inelastic scattering up to the excitation energy of 16 MeV. No quenching of the IS spin- SNMEs has been observed in the measured nuclei, while the IV spin- SNMEs are quenched by an amount comparable with the analogous GT transitions. Consistency with the study of the IS and IV magnetic moment in the same mass region has been discussed. It has been shown by applying the sum rule values that the difference of the IS and IV spin- SNMEs is relevant to the spin-spin correlation in the ground state. Thus, quenching of the IS and IV spin- SNMEs needs to be described in a mutually consistent manner by theoretical models. The spin-spin correlation would have a relevance to the correlated pair with high relative momentum studied by electron scattering and reactions as well as to the spin-aligned IS coupling. It would be of interest to extend the present study to higher excitation energies and to mass and isotope dependencies. For example, decomposition of the spin-M1 strength in the continuum might be applicable by the multipole decomposition analysis of the angular distribution in combination with an isoscalar probe like deuteron scattering or with a pure isovector probe like . It is worth considering the measurement of reactions for studying each of the IS and IV spin-flip excitations of the target nucleus by tagging the IS and IV 1+ states of the ejectile with the coincidence detection of the α or γ emission. Also a measurement in inverse kinematics with an active target based on a time projection chamber would be able to extend the study to larger masses than 40 by employing radioactive secondary beams.
We note that a theoretical work () appeared during the review process of this article. That study reported that the positive values, referred as in their paper, were not reproduced by Hamiltonian for all the possible parameter values describing neutrons and protons interacting in a single-l shell through a surface delta interaction. Theoretical interpretation of the positive values is still an open question.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the JSPS International Training Program (ITP) and was partially supported by JSPS (No. 14740154, and 25105509).
Acknowledgments
The authors gratefully acknowledge the collaborators of the E249 and E299 experiments at the RCNP. They are indebted to the RCNP cyclotron staff for providing us with the excellent beam. We are grateful to Sagawa, Nakada, and Ichimura for valuable discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with one of the authors AT.
References
1
AlburgerD. E.NathanA. M. (1978). Beta-Ray Branching and Half-Lives of 12B and 12N. Phys. Rev. C17, 280–286. 10.1103/PhysRevC.17.280
2
AnantaramanN.BrownB. A.CrawleyG. M.GalonskyA.DjalaliC.MartyN.et al (1984). Observation of Quenching in Isoscalar and Isovector 0+ → 1+ Transitions in Si28(p,p′). Phys. Rev. Lett.52, 1409–1412. 10.1103/PhysRevLett.52.1409
3
AndersonB. D.ChittrakarnT.BaldwinA. R.LeboC.MadeyR.TandyP. C.et al (1987). Gamow-Teller and M1 Strength in the 32S(p,n)32Cl Reaction at 135 Mev. Phys. Rev. C. Nucl. Phys.36, 2195–2205. 10.1103/physrevc.36.2195
4
ArimaA.ShimizuK.BentzW.HyugaH. (1987). Nuclear Magnetic Properties and Gamow-Teller Transitions. Adv. Nucl. Phys.18, 1–106.
5
BendelW. L.FaggL. W.NumrichS. K.JonesE. C.KaiserH. F. (1971). Excitation of by 180 Electron Scattering. Phys. Rev. C3, 1821–1827. 10.1103/PhysRevC.3.1821
6
BernabéuJ.EricsonT.HernándezE.RosJ. (1992). Effects of the Axial Isoscalar Neutral-Current for Solar Neutrino Detection. Nucl. Phys. B378, 131–149. 10.1016/0550-3213(92)90006-W
7
BirkhanJ.MatsubaraH.von Neumann-CoselP.PietrallaN.PonomarevV. Y.RichterA.et al (2016). Electromagnetic M 1 Transition Strengths from Inelastic Proton Scattering: The Cases of ca 48 and pb 208. Phys. Rev. C93, 041302. 10.1103/PhysRevC.93.041302
8
BrownB.RaeW. (2014). The Shell-Model Code Nushellx@msu. Nucl. Data Sheets120, 115–118. 10.1016/j.nds.2014.07.022
9
BrownB.WildenthalB. (1987). Empirically Optimum m1 Operator for sd-Shell Nuclei. Nucl. Phys. A474, 290–306. 10.1016/0375-9474(87)90619-1
10
BrownB. A.RichterW. A. (2006). New “usd” Hamiltonians for the sd Shell. Phys. Rev. C74, 034315. 10.1103/PhysRevC.74.034315
11
BrownB. A.WildenthalB. H. (1983). Corrections to the Free-Nucleon Values of the Single-Particle Matrix Elements of the m1 and Gamow-Teller Operators, From a Comparison of Shell-Model Predictions With -Shell Data. Phys. Rev. C28, 2397–2413. 10.1103/PhysRevC.28.2397
12
CederwallB.MoradiF. G.BäckT.JohnsonA.BlomqvistJ.ClémentE.et al (2011). Evidence for a Spin-Aligned Neutron–Proton Paired Phase From the Level Structure of 92 pd. Nature469, 68–71. 10.1038/nature09644
13
CohenS.KurathD. (1965). Effective Interactions for the 1p Shell. Nucl. Phys.73, 1–24. 10.1016/0029-5582(65)90148-3
14
CooperE. D.HamaS.ClarkB. C. (2009). Global Dirac Optical Potential from Helium to lead. Phys. Rev. C80, 034605. 10.1103/PhysRevC.80.034605
15
CrawleyG. M.DjalaliC.MartyN.MorletM.WillisA.AnantaramanN.et al (1989). Isovector and Isoscalar Spin-Flip Excitations in Even-Even s-d Shell Nuclei Excited by Inelastic Proton Scattering. Phys. Rev. C39, 311–323. 10.1103/PhysRevC.39.311
16
EdmondsA. (1960). Angular Momentum in Quantum Mechanics. Princeton, NJ: Princeton University Press.
17
EntemD. R.MachleidtR. (2003). Accurate Charge-Dependent Nucleon-Nucleon Potential at Fourth Order of Chiral Perturbation Theory. Phys. Rev. C68, 041001. 10.1103/PhysRevC.68.041001
18
FirestoneR. (1996). Table of Isotopes. 8th Edn. New York: John Wiley & Sons.
19
FoltzC. W.SoberD. I.FaggL. W.GräfH. D.RichterA.SpamerE.et al (1994). Electroexcitation of Low-Multipolarity Magnetic Transitions in 36Ar and 38Ar. Phys. Rev. C49, 1359–1371. 10.1103/PhysRevC.49.1359
20
FraneyM. A.LoveW. G. (1985). Nucleon-Nucleon t-Matrix Interaction for Scattering at Intermediate Energies. Phys. Rev. C31, 488–498. 10.1103/PhysRevC.31.488
21
FujitaH.FujitaY.AdachiT.BacherA. D.BergG. P. A.BlackT.et al (2007). Isospin Structure of States in 58Ni and 58Cu Studied by 58Ni(p, p′) and 58Ni(3He,t)58Cu Measurements. Phys. Rev. C75, 034310. 10.1103/PhysRevC.75.034310
22
FujitaH.FujitaY.BergG.BacherA.FosterC.HaraK.et al (2002). Realization of Matching Conditions for High-Resolution Spectrometers. Nucl. Instr. Methods Phys. Res. A: Acc. Spectr. Detect. Assoc. Equip.484, 17–26. 10.1016/S0168-9002(01)01970-2
23
FujitaY.BrownB. A.EjiriH.KatoriK.MizutoriS.UenoH. (2000). Separation of Isoscalar, Isovector, Orbital, and Spin Contributions in Transitions in Mirror Nuclei. Phys. Rev. C62, 044314. 10.1103/PhysRevC.62.044314
24
FujitaY.FujitaH.AdachiT.BergG. P. A.CaurierE.FujimuraH.et al (2002). Gamow-Teller Transitions From 58Ni to Discrete States of 58Cu - The Study of Isospin Symmetry in Atomic Nuclei. Eur. Phys. J. A.13, 411–418. 10.1140/epja/iepja1344
25
FujitaY.HatanakaK.BergG.HosonoK.MatsuokaN.MorinobuS.et al (1997). Matching of a Beam Line and a Spectrometer New Beam Line Project at rcnp. Nucl. Instr. Methods Phys. Res. B: Beam Inter. Mater. Atoms126, 274–278. 10.1016/S0168-583X(96)01008-7
26
FujitaY.RubioB.GelletlyW. (2011). Spin-Isospin Excitations Probed by Strong, Weak and Electro-Magnetic Interactions. Prog. Part. Nucl. Phys.66, 549–606. 10.1016/j.ppnp.2011.01.056
27
FujiwaraM.AkimuneH.DaitoI.FujimuraH.FujitaY.HatanakaK.et al (1999). Magnetic Spectrometer Grand Raiden. Nucl. Instr. Methods Phys. Res. A422, 484–488. 10.1016/S0168-9002(98)01009-2
28
GysbersP.HagenG.HoltJ.JansenG. R.MorrisT. D.NavrátilP.et al (2019). Discrepancy Between Experimental and Theoretical β-Decay Rates Resolved From First Principles. Nat. Phys.15, 428–431. 10.1038/s41567-019-0450-7
29
HenO.MillerG. A.PiasetzkyE.WeinsteinL. B. (2017). Nucleon-Nucleon Correlations, Short-Lived Excitations, and the Quarks Within. Rev. Mod. Phys.89, 045002. 10.1103/RevModPhys.89.045002
30
HenO.SargsianM.WeinsteinL. B.PiasetzkyE.HakobyanH.HiginbothamD. W.et al (2014). Momentum Sharing in Imbalanced Fermi Systems. Science346, 614–617. 10.1126/science.1256785
31
HofmannF.von Neumann-CoselP.NeumeyerF.RangacharyuluC.ReitzB.RichterA.et al (2002). Magnetic Dipole Transitions in 32S From Electron Scattering at 180. Phys. Rev. C65, 024311. 10.1103/PhysRevC.65.024311
32
IchimuraM.SakaiH.WakasaT. (2006). Spin-Isospin Responses via (p,n) and (n,p) Reactions. Prog. Part. Nucl. Phys.56, 446–531. 10.1016/j.ppnp.2005.09.001
33
IkedaK.FujiiS.FujitaJ. (1963). The (p,n) Reactions and Beta Decays. Phys. Lett.3, 271–272. 10.1016/0031-9163(63)90255-5
34
IsackerP. V.MacchiavelliA. (2021). Neutron-proton Spin-Spin Correlations in the Ground States of Nuclei. Eur. Phys. J.57, 178. 10.1140/epja/s10050-021-00489-6
35
KawabataT.AkimuneH.FujimuraH.FujitaH.FujitaY.FujiwaraM.et al (2004). Isovector and Isoscalar Spin-Flip Strengths in 11B. Phys. Rev. C70, 034318. 10.1103/PhysRevC.70.034318
36
KirsonM. W. (2007). Oscillator Parameters in Nuclei. Nucl. Phys. A781, 350–362. 10.1016/j.nuclphysa.2006.10.077
37
LoveW. G.FraneyM. A. (1981). Effective Nucleon-Nucleon Interaction for Scattering at Intermediate Energies. Phys. Rev. C24, 1073–1094. 10.1103/PhysRevC.24.1073
38
LüttgeC.Neumann-CoselPv.NeumeyerF.RangacharyuluC.RichterA.SchriederG.et al (1996). Isovector m1 Transitions in and the Role of Meson Exchange Currents. Phys. Rev. C53, 127–130. 10.1103/PhysRevC.53.127
39
MathyM.BirkhanJ.MatsubaraH.von Neumann-CoselP.PietrallaN.PonomarevV. Y.et al (2017). Search for Weak m 1 Transitions in ca 48 With Inelastic Proton Scattering. Phys. Rev. C95, 054316. 10.1103/PhysRevC.95.054316
40
MatsubaraH. (2010). Isoscalar and isovector spin-M1 transitions from the even-even, N = Z nuclei across the sd-shell region. PhD thesis. Toyonaka: Osaka University.
41
MatsubaraH.SakaguchiH.KishiT.TamiiA. (2009). Self-supporting Elemental Sulfur Target for Charged Particle Irradiation. Nucl. Instr. Methods Phys. Res. B267, 3682–3687. 10.1016/j.nimb.2009.09.002
42
MatsubaraH.TamiiA.NakadaH.AdachiT.CarterJ.DozonoM.et al (2015). Nonquenched Isoscalar Spin- Excitations in -Shell Nuclei. Phys. Rev. Lett.115, 102501. 10.1103/PhysRevLett.115.102501
43
MatsubaraH.TamiiA.ShimizuY.SudaK.TameshigeY.ZenihiroJ. (2012). Wide-Window Gas Target System for High Resolution experiment with Magnetic Spectrometer. Nucl. Instr. Methods Phys. Res. A678, 122–129. 10.1016/j.nima.2012.03.005
44
OngH.TanihataI.TamiiA.MyoT.OgataK.FukudaM.et al (2013). Probing Effect of Tensor Interactions in 16o via (p,d) Reaction. Phys. Lett. B725, 277–281. 10.1016/j.physletb.2013.07.038
45
PetrovichF.LoveW. (1981). The Scattering of Elementary Probes From Nuclei at Medium Energy: A New Look at the Nucleus. Nucl. Phys. A354, 499–534. 10.1016/0375-9474(81)90613-8
46
PudlinerB. S.PandharipandeV. R.CarlsonJ.PieperS. C.WiringaR. B. (1997). Quantum Monte Carlo Calculations of Nuclei With A <= 7. Phys. Rev. C56, 1720–1750. 10.1103/PhysRevC.56.1720
47
RaynalJ. (2007). Computer Code dwba07. Report No. NEA-1209/008.
48
RichterA.WeissA.HaüsserO.BrownB. A. (1990). New Evidence for Meson-Exchange-Current Enhancement of Isovector M1 Strength. Phys. Rev. Lett.65, 2519–2522. 10.1103/PhysRevLett.65.2519
49
RichterW. A.MkhizeS.BrownB. A. (2008). sd-Shell Observables for the usda and usdb Hamiltonians. Phys. Rev. C78–064302. 10.1103/PhysRevC.78.064302
50
RothR.NeffT.FeldmeierH. (2010). Nuclear Structure in the Framework of the Unitary Correlation Operator Method. Prog. Part. Nucl. Phys.65, 50–93. 10.1016/j.ppnp.2010.02.003
51
SagawaH.SuzukiT. (2018). Isoscalar and Isovector Spin Response in -Shell Nuclei. Phys. Rev. C97, 054333. 10.1103/PhysRevC.97.054333
52
SagawaH.SuzukiT.SasanoM. (2016). Effect of Isoscalar Spin-Triplet Pairings on Spin-Isospin Responses in s d-Shell Nuclei. Phys. Rev. C94, 041303. 10.1103/PhysRevC.94.041303
53
SasanoM.SakaiH.YakoK.WakasaT.AsajiS.FujitaK.et al (2009). Gamow-teller Unit Cross Sections of the Reaction at 198 and 297 mev on Medium-Heavy Nuclei. Phys. Rev. C79, 024602. 10.1103/PhysRevC.79.024602
54
SubediR.ShneorR.MonaghanP.AndersonB.AniolK.AnnandJ.et al (2008). Probing Cold Dense Nuclear Matter. Science320, 1476–1478. 10.1126/science.1156675
55
SuzukiT.FujimotoR.OtsukaT. (2003). Gamow-Teller Transitions and Magnetic Properties of Nuclei and Shell Evolution. Phys. Rev. C67, 044302. 10.1103/PhysRevC.67.044302
56
SuzukiY.HoriuchiW.OrabiM.AraiK. (2008). Global-vector Representation of the Angular Motion of Few-Particle Systems ii. Few-Body Syst.42. 10.1007/s00601-008-0200-3
57
TaddeucciT.GouldingC.CareyT.ByrdR.GoodmanC.GaardeC.et al (1987). The (p,n) Reaction as a Probe of Beta Decay Strength. Nucl. Phys. A469, 125–172. 10.1016/0375-9474(87)90089-3
58
TaddeucciT. N.ByrdR. C.CareyT. A.CiskowskiD. E.FosterC. C.GaardeC.et al (1990). Gamow-teller Transition Strengths from the 11B(p,nc) Reaction in the Energy Range 160–795 mev. Phys. Rev. C42, 935–946. 10.1103/PhysRevC.42.935
59
TamagakiR. (1968). Potential Models of Nuclear Forces at Small Distances. Prog. Theor. Phys.39, 91–107. 10.1143/PTP.39.91
60
TamiiA.AkimuneH.DaitoI.FujitaY.FujiwaraM.HatanakaK.et al (1999). Polarization Transfer Observables for Proton Inelastic Scattering from 12c at 0. Phys. Lett. B459, 61–66. 10.1016/S0370-2693(99)00654-1
61
TamiiA.FujitaY.MatsubaraH.AdachiT.CarterJ.DozonoM.et al (2009). Measurement of High Energy Resolution Inelastic Proton Scattering at and Close to Zero Degrees. Nucl. Instrum.Methods Phys. Res. Sect. A.605, 326–338. 10.1016/j.nima.2009.03.248
62
TerashimaS.YuL.OngH. J.TanihataI.AdachiS.AoiN.et al (2018). Dominance of Tensor Correlations in High-Momentum Nucleon Pairs Studied by Reaction. Phys. Rev. Lett.121, 242501. 10.1103/PhysRevLett.121.242501
63
TownerI.KhannaF. (1983). Corrections to the Single-Particle m1 and Gamow-Teller Matrix Elements. Nucl. Phys. A399, 334–364. 10.1016/0375-9474(83)90252-X
64
TownerI. (1987). Quenching of Spin Matrix Elements in Nuclei. Phys. Rep.155, 263–377. 10.1016/0370-1573(87)90138-4
65
von Neumann-CoselP.TamiiA. (2019). Electric and Magnetic Dipole Modes in High-Resolution Inelastic Proton Scattering at 0. Eur. Phys. J. A55. 10.1140/epja/i2019-12781-7
66
von Neumann-CoselP.GräfH. D.KrämerU.RichterA.SpamerE. (2000). Electroexcitation of Isoscalar and Isovector Magnetic Dipole Transitions in 12c and Isospin Mixing. Nucl. Phys. A6693–13. 10.1016/S0375-9474(99)00564-3
67
WakasaT.HatanakaK.FujitaY.BergG.FujimuraH.FujitaH.et al (2002). High Resolution Beam Line for the Grand Raiden Spectrometer. Nucl. Instr. Methods Phys. Res. A482, 79–93. 10.1016/S0168-9002(01)01686-2
68
WarburtonE. K.MillenerD. J. (1989). Structure of 17C and 17N. Phys. Rev. C39, 1120–1129. 10.1103/PhysRevC.39.1120
69
ZegersR. G. T.AkimuneH.AustinS. M.BazinD.van der BergA. M.BergG. P. A.et al (2006). The (t,3He) and (3He,t) Reactions as Probes of Gamow-Teller Strength. Phys. Rev. C74, 024309. 10.1103/PhysRevC.74.024309
Summary
Keywords
Sd-shell nuclei, shell-model calculation, proton inelastic scattering, spin-M1 transition, GT-transition
Citation
Matsubara H and Tamii A (2021) Quenching of Isovector and Isoscalar Spin-M1 Excitation Strengths in N = Z Nuclei. Front. Astron. Space Sci. 8:667058. doi: 10.3389/fspas.2021.667058
Received
11 February 2021
Accepted
14 June 2021
Published
14 July 2021
Volume
8 - 2021
Edited by
Francesco Cappuzzello, University of Catania, Italy
Reviewed by
Marco Martini, Institut Polytechnique des Sciences Avancées, France
Zhenbin Wu, University of Illinois at Chicago, United States
Updates
Copyright
© 2021 Matsubara and Tamii.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hiroaki Matsubara, mats.hiroaki@gmail.com
This article was submitted to High-Energy and Astroparticle Physics, a section of the journal Frontiers in Astronomy and Space Sciences
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.