Asteroseismology of Close Binary Stars: Tides and Mass Transfer

Guo, Zhao

doi:10.3389/fspas.2021.663026

REVIEW article

Front. Astron. Space Sci., 14 May 2021

Sec. Stellar and Solar Physics

Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.663026

This article is part of the Research Topic Asteroseismology in the Kepler Era View all 11 articles

Asteroseismology of Close Binary Stars: Tides and Mass Transfer

$\nZhao Guo$ Zhao Guo^*

Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge, United Kingdom

The study of stellar oscillations allows us to infer the properties of stellar interiors. Meanwhile, fundamental parameters such as mass and radius can be obtained by studying stars in binary systems. The synergy between binarity and asteroseismology can constrain the parameter space of stellar properties and facilitate the asteroseismic inference. On the other hand, binarity also introduces additional complexities such tides and mass transfer. From an observational perspective, we briefly review the recent advances in the study of tidal effects on stellar oscillations, focusing on upper main sequence stars (F-, A-, or OB- type). The effect can be roughly divided into two categories. The first one concerns the tidally excited oscillations (TEOs) in eccentric binaries where TEOs are mostly due to resonances between dynamical tides and gravity modes of the star. TEOs appear as orbital-harmonic oscillations on top of the eccentric ellipsoidal light curve variations (the “heartbeat” feature). The second category is regarding the self-excited oscillations perturbed by static tides in circularized and synchronized close binaries. It includes the tidal deformation of the propagation cavity and its effect on eigenfrequencies, eigenfunctions, and the pulsation alignment. We list binary systems that show these two types of tidal effect and summarize the orbital and pulsation observables. We also discuss the theoretical approaches used to model these tidal oscillations and relevant complications such as non-linear mode coupling and resonance locking. Further information can be extracted from the observations of these oscillations which will improve our understanding of tides. We also discuss the effect of mass transfer, the extreme result of tides, on stellar oscillations. We bring to the readers' attention: (1) oscillating stars undergoing mass accretion (A-, F-, and OB type pulsators and white dwarfs), for which the pulsation properties may be changed significantly by accretion; (2) post-mass transfer pulsators, which have undergone a stable or unstable Roche-Lobe overflow. These pulsators have great potential in probing detailed physical processes in stellar interiors and mass transfer, as well as in studying the binary star populations.

1. Introduction

Stars tend to reside in binary or multiple systems, especially for those of early-type (Raghavan et al., 2010; Moe and Di Stefano, 2017). The intermediate and massive stars also possess a stably stratified radiative envelope which facilitates the propagation of gravity waves. When forming global normal modes, these gravity (g) modes can be observed in photometry or spectroscopcy and be used to study the stellar interiors. Thanks to the recent space telescopes, significant advances have been made in asteroseismology (Aerts et al., 2010; Bowman, 2020) including, e.g., the self-excited g-mode pulsators such as the F or A type γ Dor stars (Van Reeth et al., 2016; Li et al., 2020b) and the Slowly Pulsating B-stars (SPB) (Pápics et al., 2017). In binary stars, tidal forcing from the companion star naturally falls into the low-frequency (inertial and gravity mode) regime¹, with characteristic periods on the order of days. The tidally excited oscillations are crucial for the orbital evolution of binaries (Zahn, 1975, 1977; Ogilvie, 2014). It requires precise (generally <10⁻⁴ magnitude), long, and continuous observations to detect the direct effect of tides on stellar oscillations. We are witnessing a huge amount of evidence of tidal effects on stellar oscillations, including both the tidally excited modes and perturbed modes.

The effect of tides can be classified into two categories. First, the non-wavelike, equilibrium tide regime, where the tidal effect is a global static deformation (Remus et al., 2012). The shape can be approximated as a spheroid or, more generally, as the Roche model, which is frequently used in the modeling of binary star light curves (Wilson and Devinney, 1971; Prša and Zwitter, 2005; Sepinsky et al., 2007). Second, in the wave-like, dynamical tide regime, the harmonic tidal forcing induces gravity waves in the radiative envelope and inertial waves in the convective core. If the waves suffer from less damping and manifest themselves as temperature variations on the stellar surface, they can be observed and studied.

Observationally, we discuss two classes of pulsating binaries. The first is pulsating eccentric binaries, i.e., the heartbeat stars (HBs). HBs are eccentric binary systems showing the eccentric ellipsoidal variations (the “heartbeat,” sometimes similar to the electrocardiogram) near the periastron passage. Figure 1 shows the typical light curves of three HBs observed by Kepler from low to high inclinations. The heartbeat feature stems from the ellipsoidal variation (mainly from the temperature and geometric perturbations due to tidal deformation) and the reflection effect (mutual heating). Doppler boosting also contributes to the feature but to a much lesser degree (Loeb and Gaudi, 2003; van Kerkwijk et al., 2010; Hambleton et al., 2016). The prototype of HB is KOI-54, which consists of two A-type main-sequence stars in a face-on, very eccentric orbit (Welsh et al., 2011). Later compilations of HBs include Thompson et al. (2012) and Kirk et al. (2016). The spectroscopic follow-up studies include Smullen and Kobulnicky (2015), Shporer et al. (2016), Kjurkchieva et al. (2016), and Dimitrov et al. (2017). Detailed studies of individual systems have been performed (see below). Some HBs show tidally excited oscillations (TEOs) on top of the heartbeat feature, i.e., additional g-mode oscillations induced by the dynamical tide.

FIGURE 1

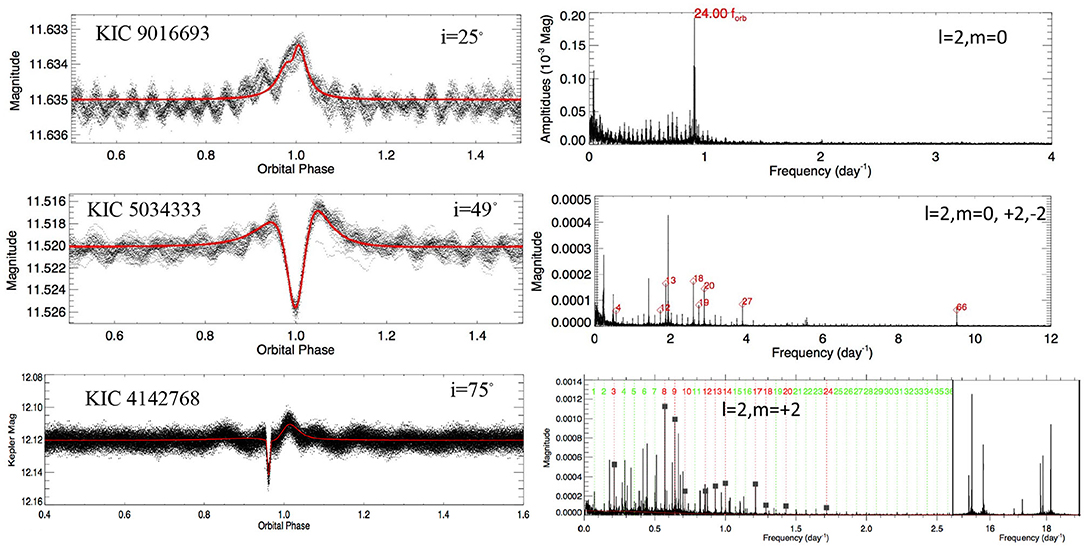
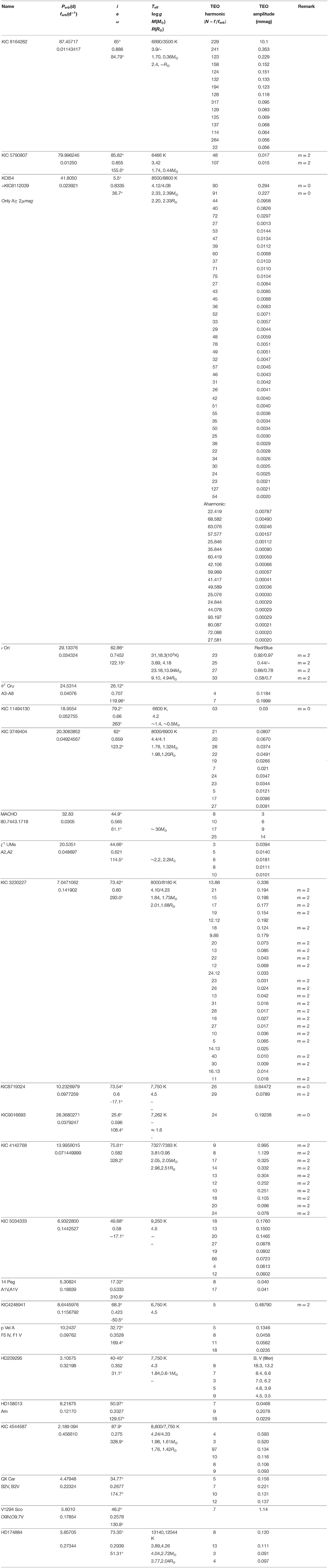
Figure 1. (Left) Kepler Light curves of three heartbeat binaries with TEOs, from low to high orbital inclinations (i). In particular, KIC 4142768 has an eclipse near the periastron (phase = 1.0). (Right) Fourier spectrum of the light curves after removing the equilibrium tide contribution (red lines in left panels). The TEOs (red symbols or gray squares) are labeled by their orbital harmonic number (N) in red, and their tentative mode identification (l and m) are also shown. In the lower panel, intrinsic self-excited oscillations (γ Dor g-modes in the frequency range f < 2 d⁻¹ and δ Scuti p-modes in f > 15 d⁻¹) are also present. Imperfect equilibrium-tide removal also generates a series of consecutive low-amplitude peaks, most notably in the upper and middle panels (see text). Adopted from Guo et al. (2019, 2020).

The other class is circularized and synchronized close binaries with self-excited oscillations. For example, the A or F-type, pressure(p)-mode pulsating stars of δ Scuti type (Breger, 1979; Rodŕıguez et al., 2000) have been frequently found in close binaries. Some systems show p-modes perturbed by static tides. The manifestation can be seen in the perturbed eigenfrequencies and pulsational alignment (tidal splittings) and the modified eigenfunctions (e.g., flux may be non-uniformly distributed on the stellar surface).

Lastly, in section 4, we also discuss the extreme case of tides: mass transfer, and its effect on stellar oscillations. Particular attention is paid to the mode excitation and the binary-channel formation of pulsating stars via mass transfer.

2. Eccentric Binaries With Tidally Excited Oscillations (TEOs)

The HBs depict the upper envelope of the classical orbital period-eccentricity diagram (Shporer et al., 2016). The relatively short period (mostly P ≲ 50 d) and high eccentricity (e ≳ 0.2) indicate an on-going strong tidal evolution (Dong et al., 2013). Zimmerman et al. (2017) showed that about 20 HBs have a surface rotation period ≈ 1.5 times longer than the pseudo-synchronous rotation period (Hut, 1981). Some heartbeat stars are actually in a hierarchical system. For example, high-resolution spectroscopy reveals a third spectral component in KIC 3230227 (Guo et al., 2017a; Lampens, 2017²). The high eccentricity (e = 0.89) and spin-orbit misalignment of the heartbeat binary KIC 8164262 (Hambleton et al., 2018) suggest that it is probably formed via the Kozai-Lidov mechanism (Kozai, 1962; Lidov, 1962; Naoz, 2016), a possible formation channel for some HBs. It is quite possible that many HBs have a hidden tertiary companion (Anderson et al., 2017).

The heartbeat signature can be present in the light curve irrespective of the spectral type. We will not discuss HBs with red giant components (Nicholls and Wood, 2012; Gaulme et al., 2013, 2014; Beck et al., 2014; Kuszlewicz et al., 2019) but focus on HBs with A- F- and OB-type stars. These stars possess radiative envelopes which facilitate the observability of tidally excited oscillations.

Observationally, we subtract the contribution from the equilibrium tide (the heartbeat feature, red lines in Figure 1) before studying the oscillations in the Fourier domain (Figure 1, right panel). TEOs represent the dynamical tidal response of the star to the companion, mostly manifest as exact orbital-harmonic frequencies (except for non-linear TEOs, see section 2.2 below). In the right panels of Figure 1, the peaks labeled with red numbers or gray squares are orbital-harmonic TEOs. Very-low-inclination HBs usually show l = 2, m = 0 TEOs while near-edge-on HBs tend to show l = 2, m = 2 TEOs. Tentative mode identification (l and m) of TEOs are labeled in Figure 1. The amplitude and frequency range (orbital harmonic number N) of TEOs can be predicted from theory and these expectations can be used to distinguish from the aliases resulting from imperfect equilibrium-tide light curve removal and other artifacts generated in the data reduction (e.g., frequency peaks without labels in the Fourier spectra of the upper and middle panels of Figure 1). An estimate can be made to the largest possible amplitude of these aliases and thus they can usually be distinguished from real TEOs. Note that the Fourier spectrum can also contain self-excited oscillations (e.g., γ Dor type g-modes and δ Scuti p-modes in KIC 4142768, lower panel of Figure 1). Furthermore, modulations from the stellar spin also introduce frequency peaks at the rotation frequency and its harmonics.

We compile a list of 22 heartbeat binaries with TEOs:

OB- type: HD 177863 (Willems and Aerts, 2002); ι Ori (Pablo et al., 2017); MACHO80.7443.1718 (Jayasinghe et al., 2019); QX Car and V1294 Sco (Kołaczek-Szymański et al., 2020); two possible candidates: η Car (Richardson et al., 2018); R81 (Tubbesing et al., 2002).

A-F- type: HD209295 (Handler et al., 2002); KOI-54 (Welsh et al., 2011); KIC 3230227 (Guo et al., 2017a); KIC 4142768 (Guo et al., 2019); KIC 9016693, KIC 8719324 and KIC 4248941, KIC 5034333 (Guo et al., 2020); KIC 11494130 and KIC 5790807 (Cheng et al., 2020), KIC 4544587 (Hambleton et al., 2013); KIC 3749404 (Hambleton et al., 2016), KIC 8164262 (Fuller et al., 2017; Hambleton et al., 2018); p Vel, θ¹ Cru, η¹ UMa, HD158013 and 14 Peg (Kołaczek-Szymański et al., 2020).

This list is of course incomplete. Kirk et al. (2016) included 24 HBs with TEOs, which is about 15% of all heartbeat binaries in the Kepler eclipsing catalog. Only ten systems are included here since TEOs in the rest have not been studied in detail. Table 1 contains the stellar, orbital and oscillation parameters of 22 heartbeat binaries (A detailed online version can be found at: http://www.astro.gsu.edu/~guo/tides_review_table.pdf).

TABLE 1

Table 1. Heartbeat binaries with Tidally Excited Oscillations.

2.1. Tidally Excited Oscillations (TEOs) in Heartbeat Stars

We briefly describe the general physical picture of tidally excited waves in early-type stars. Early seminal studies used asymptotic approximations of gravity waves (Zahn, 1975, 1977; Goldreich and Nicholson, 1989), and it was extended to include the effect of rotation (Mathis, 2009). Later numerical calculations include the effect of non-adiabaticity and rotation (Savonije et al., 1995; Papaloizou and Savonije, 1997; Savonije and Papaloizou, 1997). Dedicated calculations (Witte and Savonije, 1999a,b) on massive stars studied the binary evolution and the intricate effects such as resonance locking. Other studies implemented the mode decomposition approach (Alexander, 1987; Lai et al., 1993; Lai, 1997; Schenk et al., 2002; Fuller, 2017).

Intermediate and massive stars possess a convective core and radiative envelope. In binaries containing these stars, internal gravity waves (IGW) are generated by the tidal potential (also by the convective motion in the core) at the radiative-convective boundary and propagate outward (Goldreich and Nicholson, 1989; Lecoanet and Quataert, 2013; Rogers et al., 2013; Edelmann et al., 2019; Lecoanet et al., 2019; Horst et al., 2020). They suffer from linear damping due to radiative diffusion (Press, 1981; Garcia Lopez and Spruit, 1991; Zahn et al., 1997). The low-frequency, short-wavelength waves are damped strongly and behave like traveling waves (Ratnasingam et al., 2019). Higher-frequency waves can be reflected at the outer turning points and interfere constructively to form global normal modes (Prat et al., 2016).

Most of the observed prominent TEOs in HBs are standing waves, suffering from less damping. When the TEO amplitudes surpass the parametric instability threshold, the TEOs begin to suffer from non-linear mode coupling and transfer energy to daughter modes or multiple pairs of daughter modes (Weinberg et al., 2012; Yu et al., 2020). The daughter modes may again become unstable and couple with grand-daughter modes. In general, a mode coupling network can be formed. Observationally, this can be seen as mode triplets or multiplets satisfying the resonance conditions. This weakly-nonlinear regime will be discussed in the next section.

The amplitudes of the tidally excited gravity waves, when propagating to the near-surface layers with smaller densities, increase significantly. If the waves become significantly non-linear (the multiplication of the radial wavenumber and radial displacement k_rξ_r ≳ 1), they overturn the stratification and break (Su et al., 2020). Thus, they deposit their energy (tidal heating) and angular momentum (tidal synchronization), and turn into small-scale turbulence. Thus, the surface layers are synchronized first and a differential rotation profile may be produced (Goldreich and Nicholson, 1989), although the hydromagnetic effects tend to smooth out differential rotation (Rüdiger et al., 2015; Townsend et al., 2018). Critical layers where the Doppler-shifted wave frequency approaches zero, may form and move inward (Alvan et al., 2013). The subsequent gravity waves cannot pass the critical layer and waves dissipate strongly. Observationally, single upper main-sequence stars tend to have a nearly uniform rotation profile in the radiative envelope, inferred from asteroseismology (Bowman, 2020; Aerts, 2021)³. The g-mode pulsating γ Dor stars (spectral type A-F-) in close binaries with P_orb ≤ 10 d show a convective-core-boundary rotation period that is similar to the orbital period, suggesting that the tidal synchronization has already reached the deep interior (Guo et al., 2019; Li et al., 2020a; Saio, 2020). Nevertheless, Kallinger et al. (2017) found a Slowly Pulsating B-star in a triple system that appears to show a faster-rotating surface layer, which may fall into the Goldreich and Nicholson's outside-in synchronization scenario.

Since the TEOs are direct manifestation of dynamical tides, they are crucial for our understanding of the above physical processes. First, we show some general properties of the TEOs in heartbeat stars.

The overall strength of the tidal response of star 1 due to star 2 is determined by the tidal parameter ϵ_l:

\begin{array}{l} ϵ_{l} = (\frac{M_{2}}{M_{1}}) {(\frac{R_{1}}{D_{p e r i}})}^{l + 1} & (1) \end{array}

where D_peri = a(1 − e). Since $\frac{R_{1}}{D_{p e r i}} ≪ 1$ , it is usually sufficient to consider the dominant l = 2 component.

Thus, to have a larger tidal amplitude, one could (1) make the mass ratio M₂/M₁⁴ larger (i.e., close to 1.0); (2) make the stellar radius R₁ bigger; (3) have a smaller periastron distance D_peri. And indeed, observationally: (1) many heartbeat stars have a mass ratio close to unity⁵; (2) lots of heartbeat stars with tidally excited oscillations are slightly evolved main-sequence stars (e.g., KIC 4142768 has a primary star with M = 2.05M_⊙, R = 2.96R_⊙, Guo et al., 2019); (3) heartbeat binaries have a high eccentricity (≈ 0.2−0.9) and short periastron distance. The D_peri of 19 HBs in Shporer et al. (2016) ranges from 0.05 to 0.1AU, and the corresponding tidal parameter ϵ₂ values are ≈ 10⁻³.

The observed TEOs correspond to the frequencies of stellar g-modes with radial orders from ≈ 10 to a few tens. For example, the primary star in KIC 3230227 (M = 1.84M_⊙, R = 2.01R_⊙, Guo et al., 2017a) shows orbital-harmonic oscillations corresponding to l = 2, m = 2 g modes, with radial order n_g ~ 10−30; KOI 54 (M = 2.05M_⊙, R = 2.33R_⊙, O'Leary and Burkart, 2014) shows TEOs that mostly have l = 2, m = 0, corresponding to radial order n_g ~ 10−50. The slightly evolved primary in KIC4142768 (Guo et al., 2017a) shows TEOs that are in agreement with n_g ≈ 30 − 70 g modes.

In Figure 2, we stack the observed TEOs in 22 heartbeat binaries together, with decreasing orbital eccentricities from the top to the bottom. These Fourier spectra show that the TEOs generally have oscillation frequencies <~5 d⁻¹. They mostly correspond to orbital harmonics N from 4 to 40, although in some special cases the N can reach much larger values (N ~ 300 in KIC 8164262). The TEO amplitudes can be as large as > 10 milli-mag although the majority are lower than 0.5 milli-mag (right panel in Figure 2).

FIGURE 2

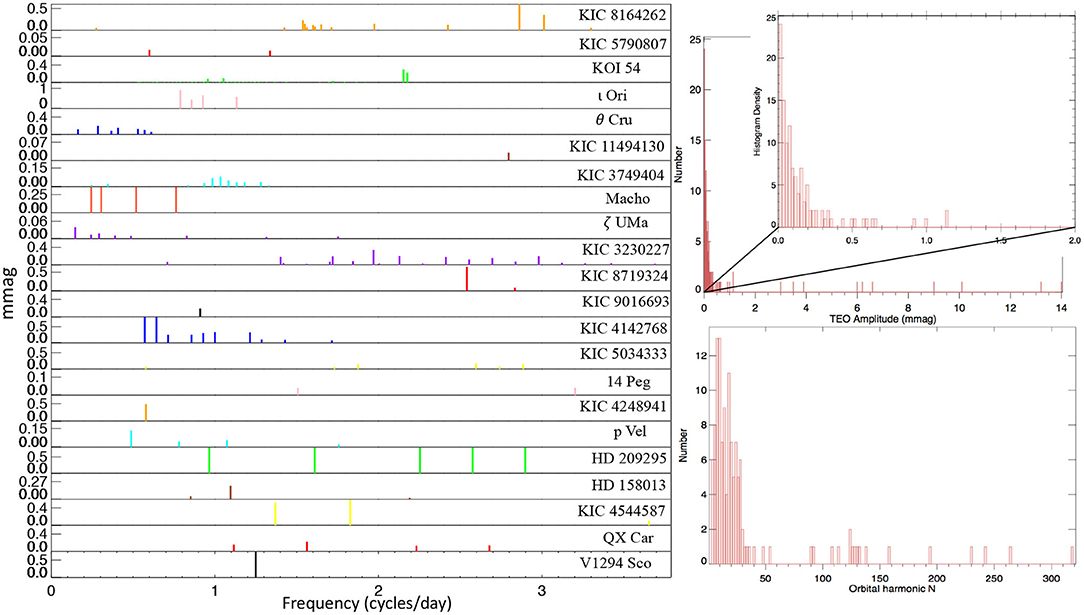
Figure 2. Fourier amplitude spectrum of all 22 heartbeat binaries with TEOs. The TEO amplitudes are shown in mmag. The inset plots show the TEO amplitude histogram (upper) and the orbital harmonic N histogram (lower).

In general, most of the observed TEOs are likely (linearly) excited by the dynamical tide (exact orbital-harmonic frequencies (Nf_orb, see next section for nonlinear non-harmonic TEOs), with the stellar response dominated by the closest frequency g-mode. But which orbital harmonics N are favorably excited? Following Burkart et al. (2012), the favorable range of orbital harmonics depends essentially on the multiplication of Q_nl and X_lm (see immediately later in this paragraph for the definitions). First, not all g-modes couple with the tidal potential equally. The weights are described by the tidal overlap integral Q_nl, which peaks around the dynamical frequency of the star. Q_nl decreases toward lower frequencies since higher order g-modes have shorter wavelength and cannot couple well spatially with the tidal potential. Secondly, stars in eccentric orbits experience a series of forcing frequencies (Nf_orb, with |N| < ∞) which are weighted by the eccentricity-dependent Hansen coefficient X_lm. X_{l = 2, m = 2} peaks at the periastron-passage frequency and decreases toward larger N; X_{l = 2, m = 0} monotonically decreases as N increases (Willems, 2003, Figures 1, 2; Fuller, 2017, Figure 3). Thus, the favored range of orbital harmonics N is between the peaks of Q_nl and X_lm (Burkart et al., 2012, Figures 2, 3).

In Figure 3, we show the observed TEO amplitudes (in magnitude variation Δmag or luminosity variation ΔL/L, related by ΔL/L ≈ 1.086Δmag) as a function of the orbital harmonic number (N) in four HBs KIC4142768, KIC3230227, ι Ori and KOI-54 (gray squares, circles, red squares, and red crosses, respectively). These observed TEOs should be compared with the theoretical amplitudes for m = 2, m = 2, m = 2, m = 0 modes (blue diamonds, open diamonds, blue circles, and open triangles, respectively, same ordering as above). It can be seen that the observed TEO range (between the two vertical lines) matches well with the theoretical expectations (the “bump” formed by background symbols. For ι Ori, the theoretical TEO amplitudes of m = 0 modes (cyan open circles) are below the detection limit and much lower than observed TEOs (m = 2). For KOI-54, the Δmag from the temperature effect (Δmag_T; upper) and geometrical effect (Δmag_G; lower) are distinguished. Note that the observed magnitude variations are primarily due to the temperature perturbations (slightly overestimated in Fuller and Lai, 2012).

FIGURE 3

Figure 3. The amplitude of TEOs in magnitude variation (Δmag) or relative luminosity variation (ΔL/L) as a function of orbital harmonic (N) for four heartbeat binaries. The observed TEOs are indicated by the gray squares (upper left, KIC 4142768), open circles (upper right, KIC 3230227), red squares (lower left, ι Ori), and red crosses (lower right, KOI-54). The theoretical TEO amplitudes are shown as blue diamonds (upper left, m = 2 modes), open diamonds (upper right, m = 2 modes), blue/cyan circles (lower left, m = 2/m = 0 modes), and open triangles/filled circles (lower right, m = 0/m = 2 modes, respectively). The two vertical lines in each panel show the lower and upper frequency limits of the observed TEOs.

However, to model the TEO amplitudes individually, one needs to consider the Lorentzian term Δ_nlmN (a term describing the resonances, see Equation 13, Burkart et al., 2012), which depends sensitively on the frequency detuning, i.e., the closeness of a certain forcing frequency (Nf_orb) to the nearest eigenmode frequency. Unfortunately, even a change of 0.001M_⊙ in stellar models can significantly change the detuning parameter, thus the Lorentzian term. A better way is to treat the detuning parameter as a random variable, which is uniformly distributed between its minimum value (= 0, perfect resonance) and maximum values (half of the adjacent g-mode spacing). In this way, a credible interval can be calculated for the Lorentzian term and thus the observed TEO amplitude (Fuller, 2017). For example, the 95% credible interval (±2σ) of theoretical TEO amplitude for KIC 4142768 is shown as the shaded region in the upper left panel of Figure 3.

TEO phases, measured with respect to the periastron, deserve a particular discussion. We expect most observed TEOs are standing waves and nearly adiabatic, and their phases are close to the adiabatic expectations which are essentially only a function of ω (argument of periastron) and m (Burkart et al., 2012; Guo et al., 2020). In Figure 4, we show the observed TEO phases (symbols) and the theoretical adiabatic phases (vertical lines) for five HBs. As expected, low inclination HBs tend to show m = 0 modes (top two systems), and intermediate/high inclination HBs usually present both m = 0 and m = 2 modes. The low-frequency TEOs experience more radiative damping, and they can be distinguished by their relatively large phase offset from adiabatic phases (O'Leary and Burkart, 2014, Figure 4; Guo et al., 2019, Figure 7). Weakly non-linear TEOs that experience non-linear mode coupling also show deviations from the adiabatic phases. It is possible that TEOs locked in resonance with the orbit still have relatively large frequency detuning compared with the mode damping rate, and thus they do not show arbitrary phases as in the perfect-resonance case.

FIGURE 4

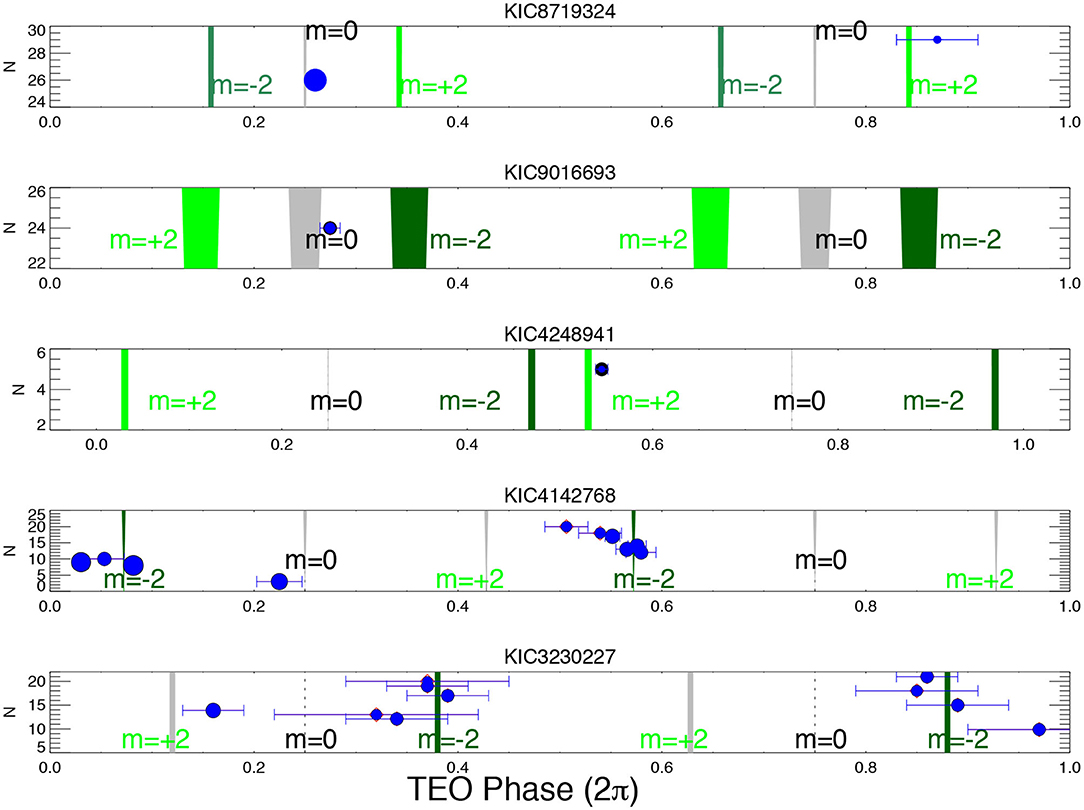
Figure 4. Observed TEO phases (symbols) as a function of orbital harmonics (N) for five heartbeat binary systems. The theoretical phases in the adiabatic approximation are indicated by vertical lines, with the azimuthal number m = 0, or ±2 labeled. Adopted from Guo et al. (2017a, 2020).

To summarize, the tidal response to a forcing frequency (Nf_orb) is a summation of the mode eigenfunctions weighted by the mode amplitude A_nlmN ∝ ϵ_lQ_nlX_lmΔ_nlmN (Burkart et al., 2012; Fuller, 2017). Roughly speaking, ϵ_l determines the overall strength, Q_nlX_lm controls the range of excited orbital harmonics N, and Δ_nlmN sets the detailed amplitude of each TEO. TEO phases are primarily determined by the orbital orientation. Most observed TEOs in HBs are chance resonances (i.e., random frequency detuning) with g-modes and can be modeled by the above theoretical framework. In fact, the aforementioned statistical approach is good for finding TEOs larger than expectation. These TEOs may be locked in resonance with the orbit and require a different modeling approach (see section 2.3).

2.2. Weakly Non-linear TEOs: Mode Coupling

Modes near resonances can non-linearly interact and observationally, this can generate combination frequencies in the form of mf_a ± nf_b, with m and n being integers. Resonance mode couplings have been observed and studied in free oscillations for B-type pulsators (Degroote et al., 2009), δ Scuti pulsators (Breger and Montgomery, 2014; Bowman et al., 2016) as well as compact pulsators (Zong et al., 2016a,b) and other types of variables. Theoretical studies include, e.g., Dziembowski and Krolikowska (1985), Van Hoolst (1994), and Buchler et al. (1997).

In the context of tidal oscillations, a striking feature in the observed TEOs is that some of them are not orbital harmonics. And the anharmonic frequencies can pair up and sum to an orbital harmonic (f_a + f_b ≈ Nf_orb). This can be explained by the non-linear resonance mode coupling.

When the tidally excited oscillations surpass the linear regime and become weakly non-linear, the oscillation mode can suffer from parametric instability (Schenk et al., 2002; Arras et al., 2003), which is the leading-order non-linear effect (Weinberg et al., 2012). In the dominant three-mode resonance coupling scenario (f_A = f_a + f_b), the parent mode A is resonantly excited by a linear dynamical tide (an orbital harmonic Nf_orb); and when its amplitude exceeds the three-mode instability threshold, it can transfer energy to two daughter modes (a, b). In Figure 5, we show different mode coupling patterns. The upper left is the aforementioned basic three-mode coupling. The mode-coupling triplet (A, a, b) can also couple to other mode triplets, either by sharing the parent (lower left) or sharing a daughter mode (upper middle panel). Multiple mode-triplets can also couple together (lower middle panel). In KIC 3230227, we find that two mode-coupling triplets share one daughter mode. And the resonance conditions for the two mode triplets are labeled in Figure 5: f_A(22) = f_a(9.88) + f_b(12.12) and f_B(26) = f_d(13.88) + f_b(12.12), where all frequencies are in units of the orbital frequency. In KOI-54, it is found that the 91st orbital harmonic resonantly excites an eigenmode very close to it, and this parent mode has at least four pairs of daughter modes. Some of the pairs even share daughters (O'Leary and Burkart, 2014). Furthermore, third-order mode coupling is also evidenced (the rightmost panel in Figure 5).

FIGURE 5

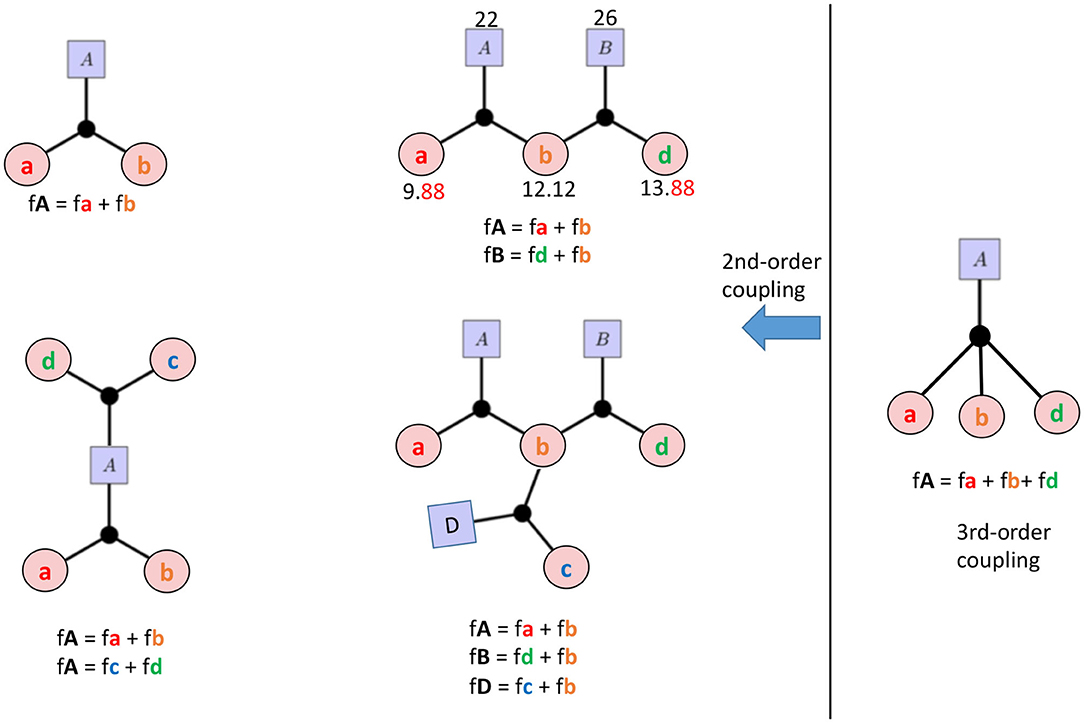
Figure 5. The patterns of multi-mode coupling observed in TEOs. Capital letters (A, B, D) represent parent modes and lowercase letters (a, b, c, d) correspond to daughter modes. The left four cases are second-order coupling and the right is a third-order coupling. For the upper middle pattern, we use the observed TEOs in KIC3230227 and label the TEO frequencies (f_A, f_B, f_a, f_b, f_d) in units of the orbital frequency Ω_orb.

Observationally, these non-linear coupled TEOs can offer us lots of information beyond the linear theory. Firstly, the selection rules (relating the modes' l and m, Dziembowski, 1982) in mode coupling can help to identify the daughter modes (O'Leary and Burkart, 2014; Guo, 2020). If we have a large number of these mode triplets, since the linearly driven parent modes can be identified from phases, we may be able to discern the g-mode period spacings among the daughter modes and possibly among the close-to-resonance parent modes. The asymptotic period spacing pattern has been routinely found in self-excited g-modes in γ Dor stars and SPB stars, but not in tidally excited modes. Secondly, parent modes that suffer from mode-coupling instability should be close to the eigenmode frequency (although they do not necessarily have a larger amplitude than the daughter modes). Together with the anharmonic daughter modes, these mode frequencies provide a list of eigenmodes that can be compared with stellar models. This kind of tidal asteroseismology can thus be performed. After the preliminary effort by Burkart et al. (2012), we are still waiting for its first concrete application in a real star. Thirdly, the observed parent mode amplitude can be compared to the mode-coupling threshold. This helps to determine the nature of coupling. For KOI-54, O'Leary and Burkart (2014) showed that five-mode coupling can decrease the threshold amplitude of parametric instability (i.e., smaller than three-mode coupling threshold). This explains the observed parent-mode amplitude being much smaller than the three-mode instability threshold. In fact, Weinberg et al. (2012) showed that, if the parent mode couples to N daughter-mode pairs, the threshold amplitude can decrease by a factor of N. Fourthly, the mode coupling systems can have different behavior (Wersinger et al., 1980; Wu and Goldreich, 2001), depending on the frequency detuning (the difference between the parent-mode frequency f_A and the resonant linear tide at Nf_orb ≈ f_A, and also between the parent-mode frequency and the daughter-mode frequency sum f_a + f_b) and the daughter-mode damping rates. Guo (2020) showed that the observed stable amplitudes/phases of the parent and daughter modes in KIC3230227 indicate the five-mode-coupling system has settled into an equilibrium state, and this agrees with the theoretical mode damping rates. The mode-coupling systems can show limit cycles (Moskalik, 1985) and observables such as cycle period can help to constrain mode parameters (e.g., damping rates). In ZZ Ceti (DAV) type pulsating white dwarfs, it is in fact limit cycles that explain the observed outbursts in the light curves (Luan and Goldreich, 2018). Non-linear mode coupling is believed to be the dominant amplitude limitation mechanism in many types of pulsators such as δ Scuti (Dziembowski and Krolikowska, 1985; Dziembowski et al., 1988) and SPB stars (Lee, 2012). The same limitation mechanism applies to the tidally excited g modes. Unfortunately, relevant studies in this direction are rare.

2.3. Resonance Locking

When the evolution of a mode frequency is in pace with that of the forcing frequency (i.e., their time derivatives are the same), the oscillation mode can be locked into resonance with the orbit. This resonance locking phenomenon can have significant consequences on the orbital evolution of not only stellar binaries, but also satellites of gaseous giant planets (Fuller et al., 2016; Lainey et al., 2020). In the context of heartbeat stars, it can have several observational implications. Firstly, the mode in resonance locking has a larger-than-expected amplitude (i.e., compared to the amplitude from the aforementioned statistical approach). This has been demonstrated for the dominant oscillation mode in the primary star of KIC 8164262 (Fuller et al., 2017; Hambleton et al., 2018). The mode in resonance locking has an orbital harmonic of N = 229 and is likely an m = 1 mode in this misaligned binary. Cheng et al. (2020) found that the oscillation at 53rd orbital harmonic is a possible candidate for resonance locking in KIC 11494130. Resonance locking can significantly enhance the tidal dissipation and orbital evolution (e.g., see Figure 3 in Witte and Savonije, 1999b for a 10M_⊙ + 1.4M_⊙ binary). For KIC 8164262, Fuller et al. (2017) estimated that the tidal quality factor Q′ is reduced from ≈ 2 × 10⁷ to ≈ 5 × 10⁴ due to the mode in resonance locking. Secondly, it remains to be seen observationally whether the TEOs in resonance locking suffer more from the (weakly) non-linear mode coupling and strong non-linear damping. In fact, the dominant TEO in KOI-54 at 91 times of orbital frequency has multiple daughter pairs, although the resonance-locking nature of this l = 2, m = 0 mode is still under debate. An examination of the resonantly-locked TEO amplitude and phase is desirable. Resonance locking depends on the evolutionary speed of the oscillation mode due to stellar evolution, and thus it is sensitive to the stellar age. A study of the resonance-locking condition spanning from ZAMS to TAMS, and for different orbital parameters would be very useful. The orbital harmonic N of a resonantly locked mode as a limited range and a predictable amplitude, allow for inference about whether resonance locking is occurring (Fuller and Lai, 2012; Burkart et al., 2014; Fuller, 2017).

3. Circular Binaries With Tidally Perturbed Modes

In the circularized and synchronized close binaries, tides do not dynamically excite oscillation modes but rather perturb the propagation cavity and pulsation alignment. The effects of equilibrium tides on stellar oscillations include:

(a) perturbed eigenfrequencies (tidal splitting):

The study of oscillations of tidally distorted polytropes can date back to early work by Chandrasekhar (1969). Other works using polytrope models include Saio (1981), Horedt (2004), Reyniers and Smeyers (2003), and also Roxburgh (unpublished). These works use the perturbative method and concentrate on the perturbing effect on eigenfrequencies. Preece et al. (2019) implemented a different method to calculate the oscillation frequencies of a tidally distorted sub-dwarf B star. It involves performing the surface-averaging of local oscillation frequencies calculated from the local density profile.

Observational work includes Balona (2018), in which he applied the above perturbative theory to KIC 4142768⁶. Tidally perturbed oscillations have been found in U Gru (Bowman et al., 2019b), V453 Cyg (Southworth et al., 2020), VV Ori (Southworth et al., 2021), and RS Cha (Steindl et al., 2021). These are mostly close, nearly circular and synchronous, Algol-like binary systems with self-excited oscillations. In addition, tidally perturbed gravity modes (tidal splittings) have been found in the SPB star π⁵ Orionis (Jerzykiewicz et al., 2020), and this 3.7-day-binary also shows ellipsoidal variations⁷.

(b) perturbed eigenfunctions and pulsation alignment.

Recently, tidally tilted binaries have been found which show modulated oscillation amplitude and phase (similar to the oblique roAp pulsators, Kurtz, 1982). The pulsation axis is almost aligned with the tidal axis, and thus pulsation frequencies have side-lobes separated by the orbital frequencies. The first system HD74423, was found by Handler et al. (2020) and was termed a “single-sided pulsator.” Subsequent discoveries include CO Cam by Kurtz et al. (2020) and TIC 63328020 by Rappaport et al. (2021). Fuller et al. (2020) used the more general operator-perturbation method in Dahlen and Tromp (1998) and modeled the stellar response to the static tides by decomposing it into free-oscillation eigenfunctions. Thus, they obtained not only tidally perturbed eigenfrequencies, but also eigenfunctions. It is found that modes can be trapped at the pole, equator, or some intermediate latitude. The amplitude/phase modulation can be modeled and thus be used to as a mode identification method. Springer and Shaviv (2013) studied the propagation and damping of high-frequency acoustic waves in a Roche-lobe filling star.

The above tidal perturbation effect due to equilibrium tide should also work in the case of eccentric orbits, maybe in a different fashion since the tidal deformation is quite different at different orbital phases. In fact, in the eccentric binary KIC 4544587 (Hambleton et al., 2013), in addition to the orbital harmonic g-modes excited by the dynamical tide, p-modes separated by orbital frequency are also present. These modes are interpreted as tidally perturbed p modes. It would be interesting to re-examine this system and study the equilibrium tidal effect on the self-excited oscillations.

4. Oscillating Close Binaries With Mass transfer

4.1. Mass-Accreting Pulsators

In the strong-tide regime when a star fills its Roche lobe, tides induce mass transfer. Depending on the adjustment of the stellar radius and the Roche-lobe radius, the mass transfer can be in the form of stable or unstable Roche-lobe overflow (RLOF) (Vanbeveren and De Loore, 1994; Soberman et al., 1997). Mass transfer affects the evolution of the binary orbit (Dosopoulou and Kalogera, 2016a,b). But the asteroseismic consequences of accretion have not been studied. How does the mixing process modify the excitation of heat-driven pulsations? The κ-mechanism excitation occurs at the near-surface layer where the opacity due to the hydrogen/helium or iron-group elements ionization zones have a local maximum (Unno et al., 1989, chapter 5). In addition, another necessary condition for the driving is that the local thermal timescale has to be comparable to the oscillation period (Pamyatnykh, 1999). Even without material mixing, the accretion may drive the star out of thermal equilibrium, and this may also change the geometric depth of the ionization zone and thus the pulsation excitation and frequencies. If mixing (e.g., thermohaline mixing when a negative chemical composition gradient is present) does happen (Stancliffe and Glebbeek, 2008), the change of composition also needs to be taken into account.

Observationally, many mass-accreting stars do show pulsations. The Oscillating Algol (oEA) systems are a class of δ Scuti/γ Dor pulsators in Algol-type binaries with mass accretion (Mkrtichian et al., 2004, 2020). The companion is usually a low-mass star filling or nearly-filling its Roche lobe, depending on whether the mass transfer process is finished or not. To name a few, AS Eri (Mkrtichian et al., 2004), KIC 4739791 (Lee et al., 2016), KIC 8553788 (Liakos, 2018), V392 Orionis (Hong et al., 2019), KIC 10736223 (Cheng et al., 2020). Guo and Li (2019) found the period spacing pattern of dipole g modes in mass-accreting γ Dor star in KIC 9592855. A comparison with theoretical g-mode period spacings suggests that the mass of this primary star is lower than previously reported. Streamer et al. (2018) did detailed binary star evolution modeling and calculate the pulsation properties of the mass-accreting δ Scuti primary (≈ 2.2M_⊙) in TT Hor. They managed to match the observed oscillation frequencies and found a likely evolutionary history for the δ Scuti pulsator. It was initially a 1.3M_⊙ star and accreted about 0.9M_⊙ from the companion. Accretion-driven variability in oEA binaries has been studied (Mkrtichian et al., 2018) and the Fourier spectrum of accreting δ Scuti pulsators can change during the outburst. Although some of these variabilities may be attributed to the variation of mass transfer rate, the pulsation changes also contribute to the variability. A significant number of Agol-type eclipsing binaries have δ Scuti pulsating components and it seems that many of them show very high-frequency p-modes (~60 d⁻¹), which is a signature of youth and probably the result of rejuvenation from RLOF (Dray and Tout, 2007).

Previous works on how mass-transfer modifies stellar oscillations are scarce. Note that numerous oscillations of mass-accreting white dwarfs (WD) in Cataclysmic Variables (CVs) have been discovered (Mukadam et al., 2007, 2011). Arras et al. (2006) studied the g-mode pulsational instabilities of accreting WDs in CVs. He found that an envelope of solar-like composition (accreted material) on top of the pure-hydrogen layer of the WD can change the edge of the instability strip significantly. During the accretion, outbursts can heat the WD, bringing it out of the instability strip. Similar work to the pulsational instability of other types of opacity-driven pulsators would be interesting.

4.2. Post-mass Transfer Pulsating Binaries

Post-mass transfer binaries with a δ Scuti pulsating component have been discovered, including KIC 10661783 (Southworth et al., 2011; Lehmann et al., 2013), KIC 8262223 (Guo et al., 2017c), and the aforementioned TIC 63328020 (Rappaport et al., 2021). The previous-mass-gainer δ Scuti star in KIC 8262223 pulsates at about 60 d⁻¹, suggesting that the system only just finished the mass transfer, i.e., the effect of rejuvenation is still present. In contrast, KIC 10661783 pulsates at much lower frequencies (15 d⁻¹). This is likely due to the fact that it has finished the mass transfer long ago and the δ Scuti pulsator is already evolved. Similarly, post-mass transfer γ Dor and SPB-type pulsating binaries have also been identified (Matson et al., 2015; Guo et al., 2017b). It is quite clear that δ Scuti and γ Dor type pulsations are not suppressed in close binaries. This is in contrast with red giants in binaries, in which solar-like oscillations seem to be suppressed by binarity, probably due to the enhanced magnetic activity. The majority of the aforementioned binary can be formed in the formation channel of EL CVn binaries⁸ (Maxted et al., 2013, 2014). The formation involves the evolution of two low-mass stars with stable RLOF and mass reversal (Chen et al., 2017). In Figure 6, we show typical evolutionary tracks of an EL CVn type binary. Staring with two low-mass stars (M₁ = 1.35, M₂ = 1.15M_⊙), the mass gainer can evolve to a δ Scuti/γ Dor pulsator (M = 1.72M_⊙) or even an SPB star with slightly changed initial conditions. The mass donor can become a pre-ELM WD (extremely low-mass white dwarf precursor) pulsator (M ≲ 0.2M_⊙) with p, or g-mode pulsations (Maxted et al., 2013; Gianninas et al., 2016; Istrate et al., 2016), and possibly later on the WD cooling track, become a g-mode pulsating helium WD. These five types of post-mass transfer pulsators have been marked in Figure 6 as ellipses.

FIGURE 6

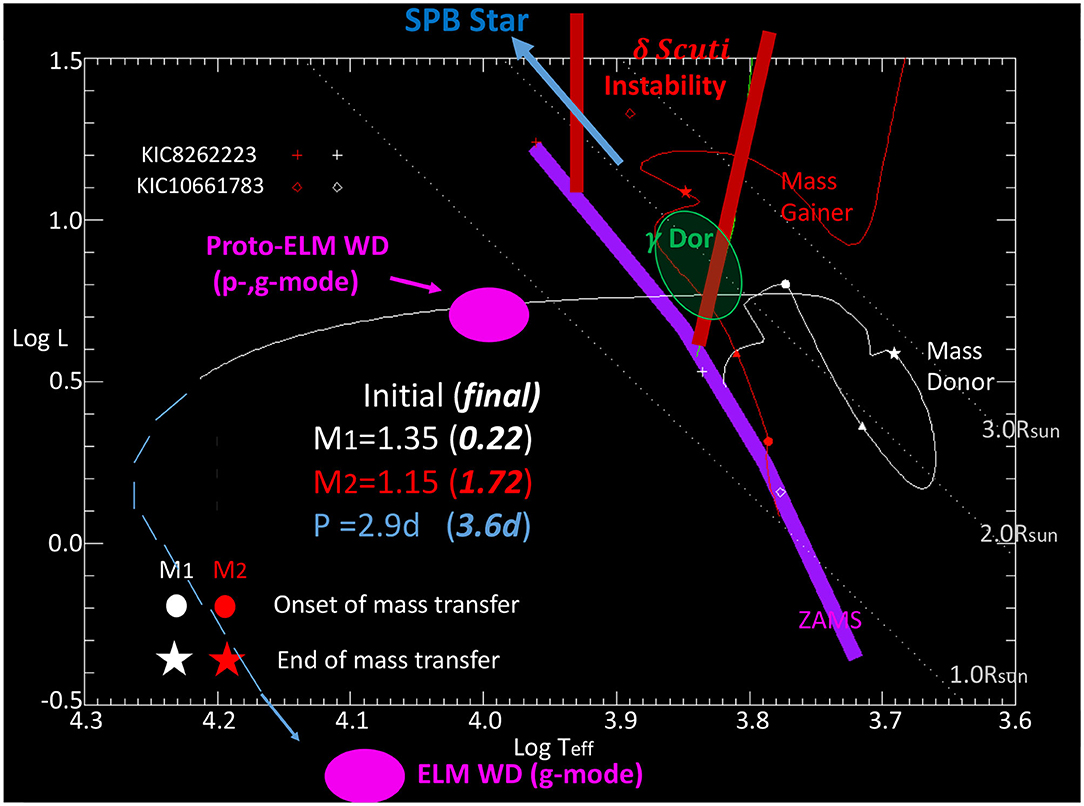
Figure 6. Typical evolutionary tracks for the formation an EL CVn type binary via stable RLOF mass transfer. This binary channel can generate 5 type of pulsating stars: Slowly Pulsating B-stars (SPB), δ Scuti stars (indicated by the red instability strip edges), γ Dor pulsators (green ellipses), Pre-ELM white dwarf, and He white dwarf pulsator (purple ellipses).

Post-mass transfer RR Lyrae and Cepheid pulsators have been found by Pietrzyński et al. (2012) and Pilecki et al. (2017), respectively. Gautschy and Saio (2017) studied the binary evolution channel to form anomalous Cepheids via RLOF and merger-like evolution. Similar work by Karczmarek et al. (2017) found stars crossing the classical instability strip of RR Lyrae and Cepheids via the binary channel. The formation of recently-discovered Blue Large-Amplitude Pulsators (BLAP) also involves binary evolution with mass transfer (Pietrukowicz et al., 2017). Recently, Byrne and Jeffery (2020) studied the non-adiabatic pulsational properties by using the post-mass-transfer stellar models. We also know sub-dwarf B-stars (sdB) and blue stragglers can be formed by mass-transfer or merger (Han et al., 2002, 2003). The list of post-mass transfer pulsators can go on and on. Binary channels can generate all kinds of exotic binary systems (de Loore and Doom, 1992; Hurley et al., 2002; Eggleton, 2006). It can also generate new types of pulsating stars and also contaminate the existing pulsators (Jeffery and Saio, 2016). Pulsational analysis of post-mass transfer systems is still the frontier of asteroseismology, and it holds great promise to improve our understanding on stellar structure and evolution.

5. Discussion and Future Prospects

Detailed analysis of existing Kepler HBs needs to be done on a one-by-one basis. There are also tidal oscillations in binaries that are not identified yet in Kepler data. Gaulme and Guzik (2019) identified KIC 11572363 as an HB with TEOs. They also find some other “tidal pulsators,” and most of them have circular orbits with self-excited modes, probably perturbed by tides. Sekaran et al. (2020) compiled 95 g-mode pulsators in eclipsing binaries. The sample may contain tidally perturbed modes or tidally excited modes. More tidally excited or perturbed oscillations can be obtained from the on-going surveys such as TESS (Ricker et al., 2015), KELT (Pepper et al., 2007), etc.

Willems and Aerts (2002) modeled the radial velocity (RV) variation from tides in an eccentric binary HD177863 with a B-type star component. Arras et al. (2012) predicted the tidally induced RV amplitude in exoplanet hosts. For heartbeat binaries, it was already noted by Welsh et al. (2011) that the radial velocity variations Δv_r in KOI-54 show significant non-Gaussian RV residuals after removing the Keplerian orbit. The RV variations due to the equilibrium tide and dynamical tide can be calculated and compared with observations (Bunting and Terquem, 2021). Massive stars can show periastron activities, including non-Keplerian RV variations and line-profile variations (Koenigsberger et al., 2012; Richardson et al., 2017; Koenigsberger and Schmutz, 2020). It is worth a modeling effort although other effects (e.g., stellar wind and magnetic field) are also important in these hot stars. Other types of observation can also reveal the signature of tides, e.g., line profile variations from high-resolution spectroscopy, and spectro-polarimetric observations. In particular, multi-color observations of stellar oscillations are going to gain importance as more space surveys are underway.

The potential of tidal asteroseismology in constraining stellar parameters has not been exploited yet. Fuller et al. (2017) experimented with KIC 8164262 and found small amounts of convective core overshoot and diffusive mixing can yield better agreement with observed TEO amplitude. The convective boundary criterion adopted can also be important (Chernov, 2017). A detailed analysis would involve scanning the large multi-dimensional parameter space. Actually, Burkart et al. (2012) did preliminary asteroseismic modeling of the TEOs in KOI-54 by varying the stellar masses and radii, assuming fixed metallicity and the rotation period. They found that the TEO amplitude sensitively depends on the stellar models, and to match with observations requires a fined-tuned degree of resonance which is very difficult to capture in a grid of stellar models. Even a small difference in stellar models can significantly change the degree of resonance and thus the TEO amplitude. Their final adopted models have Fourier spectra semi-quantitatively consistent with the observations, although they also find that there are many local minima which can produce comparably good fits. Other factors also make tidal seismic modeling challenging, e.g., weak non-linearity of TEOs can set in and detailed mode-coupling calculations may involve many mode-coupling networks (Essick and Weinberg, 2016; Yu et al., 2020).

Convective motion in the core can excite internal gravity waves (Lecoanet and Quataert, 2013; Rogers et al., 2013; Edelmann et al., 2019; Lecoanet et al., 2019). This has have been observed as the low-frequency power excess of OB stars by Bowman et al. (2019a, 2020) (Other interpretation also exists, e.g., arising from the subsurface convection zone, Cantiello et al., 2021). Similarly, tidally excited internal gravity/gravito-inertial waves are also expected to be present in the observed Fourier spectra. It would be interesting to do a similar study of the low-frequency background of the Fourier spectrum and check if there is evidence of tidal origin.

The Rossby (r) modes and inertial modes constitute the very low-frequency part of the tidal response. Global r-modes have been discovered (Van Reeth et al., 2016; Saio et al., 2018; Saio, 2019) in many single γ Dor stars, B-type stars, eclipsing binaries including HBs, and white dwarfs in Cataclysmic Variables. Although r-modes can be heat-driven, the observations seem to favor a mechanical origin since most discoveries are related to fast-rotating systems. Theoretically, tidally excited r-modes can also be present in rotating early-type stars (e.g., see Witte and Savonije, 1999b, Figure 2 for a 10M_⊙ example), although an observational confirmation is still awaiting. Recently, indirect evidence of pure inertial modes in the convective core has been discovered from their coupling effect with the dipole g-modes in the radiative envelope of γ Dor stars (Ouazzani et al., 2020; Saio et al., 2021). Observationally, this is inferred from the unexpected dips in the g-mode period spacing pattern which requires computations beyond the traditional approximation for rotation. Pure inertial waves can be induced by tides, similar to the inertial waves in the convective envelope of solar-type stars (Ogilvie and Lin, 2007). Again, the confirmation of theory awaits future observations.

In addition to the tidally excited oscillation, self-excited oscillations may also affect the orbital evolution. In the “inverse-tide” scenario (Fuller, 2021), angular momentum can be transferred from the self-excited modes to the orbit, and this may explain some of the very-slowly rotating convective cores discovered in γ Dor binaries (Guo and Li, 2019; Li et al., 2020a).

Studies on the tidal perturbative effect on the mode properties are still at an early stage, e.g., oscillations of tidally distorted stars are generally limited to simplified stellar models. Also some important factors have not been included. For example, detailed calculations in Fuller et al. (2020) only considered the effect of static tidal distortion on the mode eigenfrequencies and eigenfunctions and ignored the effect of Coriolis force. Close binaries with circular/synchronized orbits are easier to follow up observationally. Their oscillation properties are only studied on a one-by-one basis. Observationally, photometric and spectroscopic surveys are starting to offer a large sample of binary stars. The potential of these stars in constraining the tidal theory is still yet to be fully exploited (Justesen and Albrecht, 2021). With a large sample of various of binaries with pulsations and better theoretical understanding on mode properties, we may begin to perform the binary population synthesis with stellar oscillations included. The studies of stellar oscillations in binaries are, and will continue, revolutionizing the field of stellar astrophysics.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by STFC (grant ST/T00049X/1).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the referees for the pertinent comments and suggestions. ZG is in debt to Gordon Ogilvie for the thorough reading of this article and his enlightening comments, to Phil Arras, Nevin Weinberg, Rich Townsend, and Meng Sun for illuminating discussions on tides. Jim Fuller kindly grants us permission to use his plots in Figure 2. We acknowledge the usage of Kepler data by NASA.

Footnotes

1. ^In some rare cases, pressure modes can also be tidally excited, e.g., in the central red giant star of the triple system HD181068 (Fuller et al., 2013).

2. ^Presented as a poster at the KASOC conference.

3. ^Asteroseismology of pre-Kepler β Cephei stars (since none were observed by Kepler) have a large range in their inferred interior rotation profiles.

4. ^Usually defined so that M₂ ≤ M₁.

5. ^(if the two components can be resolved in the spectra).

6. ^Although the method is valid, this system is found to be an eccentric binary with TEOs and the application is thus questionable.

7. ^Some of these systems may be slightly out of synchronization, and dynamical tides can also be viable in asynchronous rotating stars in circular orbits.

8. ^EL CVn binary is a type of binary consisting of an F-,A-type dwarf and a low-mass helium white dwarf precursor.

References

Aerts, C. (2021). Probing the interior physics of stars through asteroseismology. Rev. Modern Phys. 93:015001. doi: 10.1103/RevModPhys.93.015001