Do Impulsive Solar-Energetic-Electron (SEE) Events Drive High-Voltage Charging Events on the Nightside of the Moon?

When the Earth’s moon is in the supersonic solar wind, the darkside of the Moon and the lunar plasma wake can be very dangerous charging environments. In the absence of photoelectron emission (dark) and in the absence of cool plasma (wake), the emission or collection of charge to reduce electrical potentials is difficult. Unique extreme charging events may occur during impulsive solar-energetic-electron (SEE) events when the lunar wake is dominated by relativistic electrons, with the potential to charge and differentially charge objects on and above the lunar surface to very-high negative electrical potentials. In this report the geometry of the magnetic connections from the Sun to the lunar nightside are explored; these magnetic connections are the pathways for SEEs from the Sun. Rudimentary charging calculations for objects in the relativistic-electron environment of the lunar wake are performed. To enable these charging calculations, secondary-electron yields for impacts by relativistic electrons are derived. Needed lunar electrical-grounding precautions for SEE events are discussed. Calls are made 1) for future dynamic simulations of the plasma wake in the presence of time-varying SEE-event relativistic electrons and time-varying solar-wind magnetic-field orientations and 2) for future charging calculations in the relativistic-electron wake environment and on the darkside lunar surface.

Introduction

This report concerns the electrical charging on the dark side of the Moon and in the lunar wake during impulsive solar energetic electron (SEE) events when there are significant fluxes of relativistic (100’s of keV) electrons in the environment.

The electrical charging of an object in the space environment is a balance of all electron and ion currents to and from the object. In sunlight very large photoelectron fluxes off an object often dominate this current balance, keeping the potentials of objects in sunlight to within a few photoelectron temperatures (a few eV) with respect to the potential at infinity. On the nightside surface of the Moon, in shadowed lunar craters, or for objects in eclipse in orbit around the Moon this is not the case. In eclipse, the fluxes of ambient electrons to the object tend to dominate the current balance, with the electrical potential of objects reaching negative potentials associated with the temperatures of the ambient electrons. When the ambient electrons have energies of ∼keV, the emission of secondary electrons associated with the keV-electron impacts on the object reduces the effectiveness of the electron flux and lowers the potentials of the objects; however, as analyzed in Appendix 1, for very-high-energy electrons (100’s of keV) the secondary-electron yields are low (Bruining, 1954; Schultz and Pomerantz, 1963; Suszcynsky and Borovsky, 1991; Xie et al., 2009) and secondary-electron emission no longer reduces the charging.

At 1 AU there are occasional solar-energetic-electron events related to activations on the Sun (Reames, 1999; Kahler, 2007). Solar-energetic-electron events can be impulsive (lasting an hour or less) or gradual (lasting a day or so): impulsive events are associated with solar x-ray flares (e.g. Kallenrode and Svestka, 1994) and gradual events have been associated with coronal mass ejections from the Sun (Stolpovskii et al., 1998). Strong solar energetic electron events (>300 keV) occur about 20 times per year (Wang et al., 2012), with concentrations around solar maximum, but with several events per year throughout the other phases of the solar cycle. The survey by Dresing et al. (2020) also found on average about 20 events per year at 1 AU that had electrons with energies >150 keV. SEE events may or may not be accompanied by multi-MeV protons in the solar wind (Kallenrode et al., 1992), which occur during “solar-energetic-particle” (SEP) events. Posner (2007) pointed out that the flux of solar energetic electrons is often a ∼1-h precursor of the flux of solar energetic protons.

Lunar surface charging has been examined by the Lunar Prospector experiments during SEP events (Halekas et al., 2007; Halekas et al., 2009) where indications of potentials of up to 4.5 kV were found between the nightside lunar surface and the Lunar Prospector spacecraft 100-km above the lunar nightside. SEP events can also lead to deep dielectric charging of the lunar regolith on the nightside or in shadowed craters (Jordan et al., 2015; Jordan et al., 2017).

Electrostatic charging is of great concern for objects and astronauts on the lunar surface (Halekas et al., 2007; Jackson et al., 2011; Zimmerman et al., 2012; Chou et a., 2019; Rhodes et al., 2020; Wang and Huang, 2020) and for objects in space (Rosen, 1976; Reagan et al., 1983; Fennell et al., 2001; Koons et al., 2006; Roeder and Fennell, 2009; Delzanno et al., 2013), and dust-charging phenomena on the lunar surface are of great interest (Borisov and Mall, 2006; Pines et al., 2011; Borisov and Zakharov, 2015; Rakesh Chandran et al., 2017). When the Moon is in the solar wind upstream from the bow shock, objects on the nightside lunar surface are in a plasma void produced by the plasma wake of the Moon in the supersonic solar-wind flow (Ogilvie et al., 1996; Farrell et al., 1998; Halekas et al., 2005; Zhang et al., 2014; Xu et al., 2019). Several studies (E.g. Knott, 1973; Halekas et al., 2002; Zimmerman et al., 2012; Rakesh Chandran et al., 2017) point out that objects on the nightside lunar surface or in the lunar plasma wake will undergo strong electrical charging. This note points out that during impulsive solar electron events objects on the lunar surface or in the wake can undergo extreme electrical charging with respect to the solar wind outside of the plasma wake. This note explores the electrical charging of objects on the nightside lunar surface and in the lunar wake when SEE events occur to lay out future problems that must be solved 1) to determine the nature of the charging and 2) to protect objects on the lunar surface and in lunar orbit.

This manuscript is organized as follows. In Geometry of the Environment the magnetic connection of the solar wind to the nightside of the Moon is examined for 216 SEE events. In High-Voltage Charging rudimentary calculations of the charging of objects in the lunar wake during SEE events are performed and in Charging across the Sunlight Terminator the charging across the lunar terminator during SEE events is examined. In Electrical Grounding the electrical grounding of objects on the lunar surface is discussed and in Needed Future Calculations calculations and simulations needed in the future are outlined. In Appendix 1 empirical expressions for the secondary-electron yield from oxidized-aluminum and silicon-dioxide surfaces are derived for relativistic-electron impact and in Appendix 2 an expression is derived for the effective relativistic-electron collection area of a charged sphere.

Geometry of the Environment

In Figure 1 the lunar orbit (red dashed curve) is sketched around the Earth (light blue) along with a Fairfield-Greenstadt bow shock model (Fairfield, 1971; Greenstadt et al., 1990) (Eqs. 1a,b of Greenstadt (1990)) plotted in blue. Also indicated in green in Figure 1 is the orientation of the interplanetary magnetic field (IMF) projected into the ecliptic plane during the first hour of each of 216 strong impulsive SEE events observed near the Earth by the WIND spacecraft. The 216 events are those with maximum electron energies above 300 keV in the catalog of Table 1 of Wang et al. (2012). The magnetic-field orientation is determined from the Magnetic Field Instrument (MFI) (Lepping et al., 1995) on board the WIND spacecraft. The right-handed GSE X,Y,Z reference frame is indicated in the sketch. In Figure 1, with the Sun to the right, the Earth-facing side of the Moon will be in darkness much of the time that the Moon is on the sunward side of the bow shock in the supersonic solar wind (Properties of the electron strahl and the solar-wind plasma at Earth during these 216 SEE events are further analyzed in Borovsky (2021)).

FIGURE 1

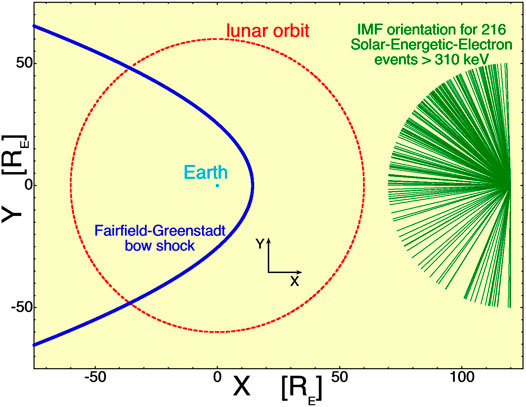
FIGURE 1. A depiction of the lunar orbit (red dashed) relative to the Earth (light blue) and the Earth’s bow shock (blue solid). Indicated in green is the orientation of the solar wind magnetic field at the onsets of 216 strong solar-energetic-electron events. The orientation of the GSE coordinate system is also indicated.

Figure 2 depicts the Moon (with its nightside shaded in gray) in the presence of a nominal 45^o Parker-spiral magnetic-field orientation. The orientation of the GSE X,Y,Z coordinate system is indicated in the figure, with the Sun-Moon line sketched in green. The sketch is drawn without accounting for any distortion of the solar-wind magnetic field by the Moon or by the Moon’s plasma wake (e.g. Taylor et al., 1968; Owen et al., 1996). Red arrows indicate the direction of a field-aligned flux of energetic electrons from the Sun, but note that often during solar-energetic-electron events the observed relativistic solar electrons at 1 AU are isotropic and will hit the Moon from both directions along the magnetic-field lines (e.g. Lario et al., 2016; Gomez-Herrero et al., 2017; Dresing et al., 2018). In a typical ∼5-nT magnetic-field strength for the solar wind, 100-keV electrons have gyroradii of ∼220 km and 500-keV electrons have gyroradii of ∼580 km, both of which are small compared with the 3476-km diameter of the Moon. Figure 2 depicts how far past the daylight terminator the surface of the Moon is magnetically connected to the Sun in a Parker-spiral-oriented magnetic field. However, instantaneously the magnetic-field of the Sun varies substantially about the Parker-spiral direction in both the ecliptic and the out-of-plane (north-south) senses (Borovsky, 2010). For the case sketched in Figure 2 where the field is in the ecliptic plane, if the angle between the solar-wind magnetic-field orientation and the Sun-Moon line is ϕ (labeled in green in Figure 2), then the direct magnetic connection of the Sun to the dark surface extends back from the terminator about ϕ degrees of lunar longitude into the darkness. When the solar-wind magnetic field has a Parker-spiral orientation, the midnight-to-dawn sector of the Moon’s dark surface will have direct magnetic connection to the Sun.

FIGURE 2

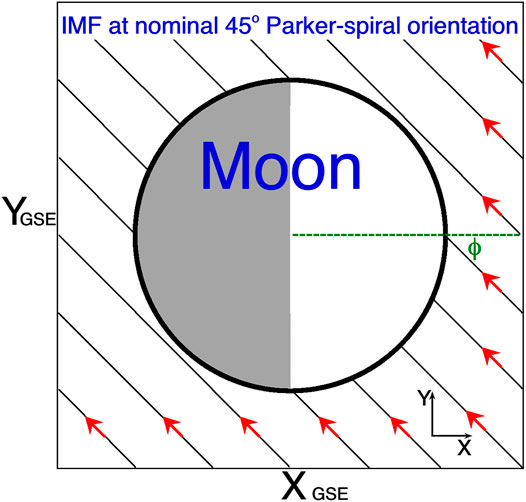
FIGURE 2. A sketch of the Moon and its darkside (shaded) in the presence of a nominal θ = 45^o Parker-spiral-oriented magnetic field. The Sun-Moon line is indicated as the green dashed line.

The magnetic-field orientations in the first hour of each of the 216 solar-energetic-electron events are examined in Figure 3 (The orientations were drawn in green in Figure 1.) For the energetic-electron events Figure 3A plots (solid black curve) the distribution of the angle ϕ that the projection of the magnetic field into the ecliptic plane makes with the Sun-Moon line: ϕ = 0 is alignment with the Sun-Moon line and the Parker spiral lies at ϕ = + 28^o to ϕ = + 53^o for a typical range of solar wind speeds (300–750 km/s). For values of ϕ that are negative, the magnetic field is considered to have an “ortho-Parker-spiral” or “ortho-gardenhose” orientation (cf. Lockwood et al., 2019). The 216 field orientations are concentrated around the Parker-spiral direction, and in fact the distribution strongly resembles the typical distribution of field orientations in the solar wind (Borovsky, 2010); this typical distribution is plotted in Figure 3A as the red dashed curve, which is the distribution of 380,458 1 h values of the field orientation at Earth in the years 1963–2020 obtained from the OMNI2 data set (King and Papitashvili, 2005). Figure 3A indicates that the midnight to dawn sector of the dark side surface of the Moon will most often be magnetically connected to the Sun, but a fair amount of the time the dawnside will be directly connected instead. In Figure 3B the angle θ between the solar-wind magnetic-field line and the Sun-Moon line is binned (solid black curve) for the 216 solar-energetic-electron events, accounting for all three components of the magnetic-field orientation. The mean value of θ is 55^o and the median value is 53^o; hence the direct magnetic connection to the Sun will tend to extend to about 55^o past the sunlight terminator. Note that when there is a strong north-south component to the magnetic field the magnetic connection to the Sun will extend into the lunar nightside over on of the polar regions. The dashed red curve in Figure 3B is the distribution of 380,458 hourly magnetic-field orientations from the OMNI2 data set: considering the weak statistics of the 216 energetic-electron events, the distribution of the field orientations for the energetic-electron events shows no outstanding difference from the typical distribution of values.

FIGURE 3

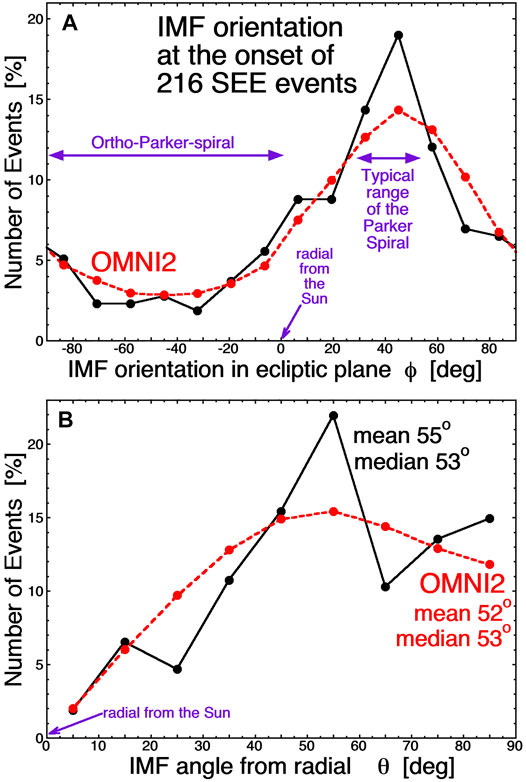
FIGURE 3. The orientation of the solar-wind magnetic field at the onset of 216 strong solar-energetic-electron events is binned (black solid) and compared with 380,458 hourly values of the solar-wind magnetic field from the OMNI2 1963-2020 data set (red dashed). (A) is the orientation of the projection of the magnetic field into the ecliptic plane and (B) is the angle of the field line from the Moon-Sun line.

Note that the orientation of the interplanetary magnetic field changes rapidly with time. Examining statistics similar to those in Figure 1 of Borovsky (2020), the magnetic-field direction in the solar wind at Earth changes by an average of 8.4^o every minute, and large (∼90^o) changes in the field direction in timescales of 2–3 s are common as the Earth passes through the heliospheric magnetic structure. As a result, during a single solar-energetic-electron event the magnetic-field orientation of the solar wind will vary substantially and various dark-side-surface regions of the Moon will be intermittently directly connected to the Sun. Note that when there are sudden strong changes in the direction of the interplanetary magnetic field, there can also be sudden changes in the flux of energetic electrons (e.g. Gosling et al., 2004a; Gosling et al., 2004b; Tan and Reames, 2016), with the change in field direction representing a change in the magnetic-field connection back to the Sun (Gosling et al., 2004a; Gosling et al., 2004b; Borovsky, 2021).

Charging Issues

For the nightside surface of the Moon in the plasma void created by the Moon’s plasma wake in the supersonic solar wind, and for objects on or above that surface, the environment during a solar-energetic-electron event can be severe for charging. The energetic-electron fluxes are time varying and the magnetic connections of objects on the lunar surface to the Sun and to the anti-sunward solar wind are rapidly time varying. There are a number of dynamic lunar charging issues associated with solar-energetic-electron events.

High-Voltage Charging

During impulsive SEE events in the absence of solar energetic protons, portions of the negatively-charged lunar wake will be dominated by the population of SEE electrons. The nightside surface of the Moon, objects upon the nightside surface, and objects in the lunar wake will charge to negative potentials with respect to the distant solar wind that are large enough to prevent the flux of solar energetic electrons from reaching the surface. Secondary-electron emission from electron impact is small at energies of 100’s of keV or more (cf. Appendix 1), so secondary electrons will not be effective in reducing the charging flux of the solar energetic electrons. With electron energies of 500 keV and higher, negative potentials of 500 kV and higher would be possible with sufficient time and sufficient electron flux. Objects with different sizes, with different shapes, and with different surface materials will have different temporal charging profiles as the electron fluxes change, resulting in differential charging at high Voltages.

Calculations of charging for objects well above the charged lunar surface are simpler than charging calculations for objects on the charged lunar surface. For two spherical objects, one with a radius r = 1 cm and one with r = 1000 cm, rudimentary charging calculations in the lunar wake are shown in Figure 4. Plotted is the potential ϕ of the object with respect to infinity as a function of time. The objects are in baths of electrons comprised of two populations: a population of solar energetic electrons and a population of solar-wind strahl electrons. The calculations ignore 1) the possible presence of solar-energetic-proton fluxes (e.g. Mewalt et al., 2005; Cliver and Ling, 2007; Cane et al., 2010), 2) cycloidal protons reflected from dayside crustal magnetic anomalies (e.g. Richmond and Hood, 2008; Halekas et al., 2010; Nishino et al., 2015), and 3) ions and electrons from the Earth’s foreshock (e.g. Nishino et al., 2017). The calculations also ignore photoelectron emission produced by Earthshine on the objects. For the solar-energetic-electron population the fluxes as a function of electron kinetic energy E of Figure 2 of Dresing et al. (2020) are used: those differential fluxes F are

$\mathrm{F=26}\mathrm{.4}{\mathrm{E}}_{\mathrm{Me}\mathrm{V}}^{\mathrm{-2}\mathrm{.18}}\mathrm{c}{\mathrm{m}}^{\mathrm{-2}}{\mathrm{s}}^{\mathrm{-1}}\mathrm{s}{\mathrm{t}}^{\mathrm{-1}}\mathrm{Me}{\mathrm{V}}^{\mathrm{-1}}\mathrm{for\; 2\; keV<E<114\; keV}(\mathrm{1a})$

$\mathrm{F = 1}\mathrm{.02}{\mathrm{E}}_{\mathrm{Me}\mathrm{V}}^{\mathrm{-3}\mathrm{.68}}c{m}^{-2}{\mathrm{s}}^{\mathrm{-1}}\mathrm{s}{\mathrm{t}}^{\mathrm{-1}}\mathrm{Me}{\mathrm{V}}^{\mathrm{-1}}\mathrm{for\; 114\; keV<E<1}\mathrm{.5\; MeV}(\mathrm{1b})$

where E_MeV is the electron kinetic energy in units of MeV. For the strahl population the reduced distribution f (e.g. Shevchenko and Galinsky (2010)) is taken as

$\text{f}\left(\text{E}\right)=\left\{{\text{n}}_{\text{strahl}}{\text{/log}}_{\text{e}}{(\text{E}}_{\text{max}}{\text{/E}}_{\text{min}})\right\}{\mathrm{E}}^{-1}\text{for}{\text{E}}_{\text{min}}<\text{E}<{\text{E}}_{\text{max}}(2)$

with a strahl number density n_strahl = 0.25 cm⁻³ and with E_min = 20 eV and E_max = 3000 eV. The potential ϕ of the object is taken to be ϕ = Q/r, where Q is the charge collected on the object as a function of time. Debye shielding of the 1/r potential outside the sphere is negligible in this electron gas: for the strahl population (n_strahl = 0.25 cm⁻³ and T_strahl ∼ 1 keV, where T_strahl is a characteristic energy spread of the strahl) the Debye length is λ_De ∼ 5 × 10⁴ cm and for the SEE population (n ∼ 4 × 10⁻⁵ cm⁻³) and T ∼ 50 keV dominated by the population below the 0.114 MeV break) the Debye length is λ_De ∼ 3 × 10⁷ cm. In collecting electron flux, angular-momentum orbital effects are accounted for as negative electrons approach the negatively charged object with potential ϕ_o resulting in a reduction of the collection area from πr2 of the object to an effective collection area

$\mathrm{\sigma =\pi }{\mathrm{r}}^{\mathrm{2}}\left(\mathrm{1-2\gamma }{\mathrm{\Phi }}_{\mathrm{o}}{\left({\mathrm{\gamma }}^{\mathrm{2}}\mathrm{-1}\right)}^{\mathrm{-1}}\mathrm{+}{\mathrm{\Phi }}_{\mathrm{o}}^{\mathrm{2}}{\left({\mathrm{\gamma }}^{\mathrm{2}}\mathrm{-1}\right)}^{\mathrm{-1}}\right)(3)$

where Φo = |eϕ_o/mc²| is the dimensionless potential of the sphere, γ = (1-(v_o/c)²)^−1/2 is the relativistic factor, v_o is the velocity of the electron far from the sphere, e is the electron charge, and m is the electron mass. Expression Eq. 3) is derived in Appendix 2. For non-relativistic electrons, expression Eq. 3) reduces to πr2 (1+(eϕ/E_o)) where ϕ (negative) is the potential of the object and E_o is the kinetic energy of the electron at infinity (cf. Eq. (7) of Borovsky (1986)). The collection cross section is plotted in Figure 5 as a function of the initial electron kinetic energy for six values of the potential of a sphere (Note that for illustration purposes the electron kinetic energies and the sphere potentials in Figure 5 extend well above the upper limits for SEE events.) As can be seen in the plot, electrons with kinetic energies < −eϕ cannot reach the sphere and σ → πr2 for electron kinetic energies much larger than the potential of the sphere. Magnetization effects in the electron orbits are unimportant for the electron collection by r = 1 cm and r = 1000 cm spheres: in a 5-nT solar-wind magnetic field the gyroradius of a 1 keV electron is 21 km and that of a 1 MeV electron is 590 km. In these example calculations electron collection is only on one side of the object πr2: for isotropic SEE events the collection will be on all sides of the object 4πr2 and the charging rate will be four times faster than these calculations. In collecting the electron charge, the emission of secondary electrons from the electron impacts is accounted for. The secondary-electron yields used are those plotted in Figure 6A appropriate for an oxidized-aluminum surface, derived in Appendix 1. The energy downshift E_o-|ϕ| of electrons hitting the surface caused by the negative potential ϕ of the object is accounted for in the calculation of the secondary electron yield from the ambient electron populations. However the angle at which the electron strikes the object surface is not accounted for: for all electrons hitting the object the normal-incidence secondary-electron yield Y (expressions (A1) and (A2)) is used.

FIGURE 4

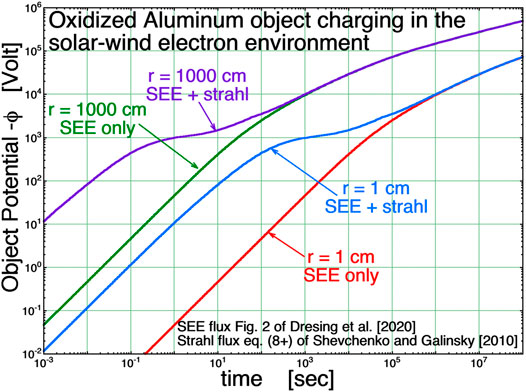
FIGURE 4. Rudimentary charging calculations for spherical objects in a bath of energetic electrons using a measured distribution of solar energetic electrons at 1 AU.

FIGURE 5

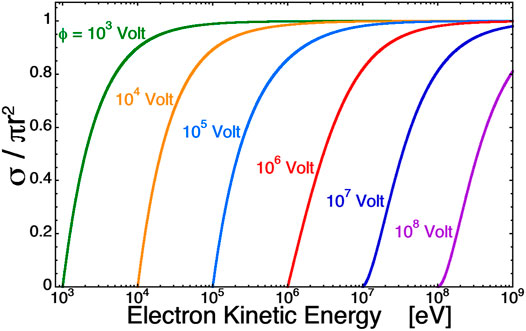
FIGURE 5. The reduction of collection area of a negatively-charged sphere (vertical axis) as a function of electron kinetic energy (horizontal axis) and as a function of the potential of the sphere (colored curves).

FIGURE 6

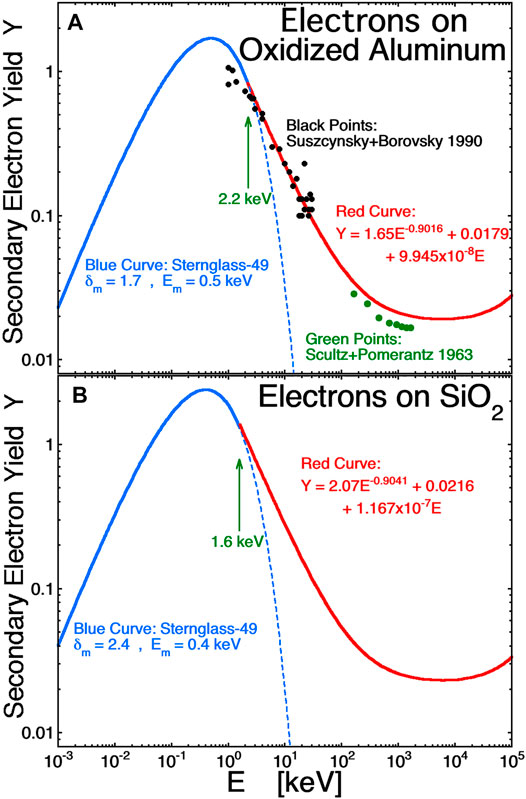
FIGURE 6. Theoretical secondary-electron yield curves for relativistic electrons hitting (A) aluminum oxide and (B) SiO₂.

In Figure 4 potential on the sphere ϕ(t) = Q(t)/r as a function of time is calculated by numerically integrating the current I(t) to the sphere

$\mathrm{Q}\left(\mathrm{t}\right)\mathrm{=}{\displaystyle {\int }_{\mathrm{0}}^{\mathrm{t}}\mathrm{I}\left(\mathrm{t}\right)\mathrm{dt}}(\mathrm{4a})$

$\mathrm{I}\left(\mathrm{\phi }\right)\mathrm{=-e}{\displaystyle {\int }_{\mathrm{-\phi }}^{\mathrm{Emax}}\mathrm{F}\left(\mathrm{E}\right)\mathrm{\sigma }\left(\mathrm{\phi ,E}\right)\left\{\mathrm{1-Y}\left(\mathrm{E+\phi }\right)\right\}\mathrm{dE}}(\mathrm{4b})$

where ϕ is negative in expressions (Eqs. 4a,b), -e is the charge of an electron, and Y (E+ϕ) indicates that the secondary-electron yield Y is a function of the downshifted electron kinetic energy E+ϕ. Looking at the green and red curves in Figure 4 that represent the charging in the presence of only the SEE population, one can see that different sized objects charge at different rates and that there will be potential differences between objects of different sizes. There will also be potential differences between objects of different shapes and with different surface properties. The green curve in Figure 4 indicates that, in the SEE flux of Figure 2 of Dresing et al. (2020) (expressions (Eqs. 1a,b)), a 1000 cm object will charge to 10⁵ V in about 10⁵ s ≈ 28 h. These are slow timescales, however SEE fluxes at 1 AU can be one or two orders of magnitude higher than the fluxes of expressions (Eqs. 1a,b) and so the charging times can be one or two orders of magnitude faster. This puts charging times to high voltage in the range of minutes, certainly within the lifetime of an SSE event. For various sized and shaped objects, differential Voltages of the magnitude of |ϕ| can be expected.

Objects of larger radius will charge up more rapidly. This is the case for the Moon itself with a radius of 3476 km. However, for the case of the darkside of the Moon with the hot-electron Debye length being a non-negligible fraction of the wake size, a full temporal sheath model of the lunar wake must be calculated to look at the rudimentary temporal charging evolution the lunar surface with respect to the solar wind outside of the wake.

In the wake of the Moon it is unlikely that low-energy strahl electrons will be present if solar energetic electrons are present, owing to the fact that the solar energetic electrons will drive the region to a large negative potential which the strahl electrons are incapable of entering. However, it is interesting to see (purple and blue curves of Figure 4) that the strahl electrons would not significantly change the charging time to reach high potentials.

Note for future charging calculations that the electron spectra in Figure 2 of Dresing et al. (2020) is the time-integrated spectra of an SEE event at 1 AU: for actual SEE events there is a systematic time evolution of the electron spectra at 1 AU that must be used in the calculation. And along with the time evolution, there are temporal fluctuations in the intensity of the SEE electrons owing to the fine-scale spatial structure of the magnetic field in the solar wind (Gosling et al., 2004a; Gosling et al., 2004b; Tan and Reames, 2016; Borovsky, 2021).

Charging Across the Sunlight Terminator

Owing to the fact that the solar-wind velocity vector is not aligned with the Sun-Moon line, the lunar plasma wake is not aligned with the Sun-Moon line. 1) The solar-wind velocity vector is time dependent with Y (dusk-dawn) and Z (north-south) velocity components that are often 50 km/s or more; the solar-wind vector velocity varies by ±5^o with time (cf. Borovsky 2012; Borovsky, 2018). 2) The solar-wind flow to the Moon is aberrated duskward by 30 km/s owing to the motion of the Earth-Moon system around the Sun. 3) The average flow of th solar wind at 1 AU is not exactly radial, but has on average a ∼10 km/s duskward offset from radial (Nemecek et al., 2020). Particularly on the duskside (owing to the aberration and the non-radial mean flow), the sunlight terminator can be in the plasma void of the lunar plasma wake, even accounting for the angle of the Mach cone of the solar-wind plasma filling the wake.

If the terminator is in the plasma void during an impulsive solar-energetic-electron event, then the lunar soil on the dark side of the terminator could be charged to 100’s of kV negative while the soil on the sunlit side of the terminator is charged to a few V positive owing to the copious emission of low-energy photoelectrons. With the Debye lengths of solar-wind suprathermal electrons being λ_De ∼ 1 km and the Debye lengths of the SEE population being λ_De ∼ 300 km (cf. Section High-Voltage Charging), the lunar surface at the terminator in the wake could be many solar-wind Debye lengths away from the solar-wind plasma but less than one SEE Debye length away from the solar-wind plasma outside of the wake.

Earlier works (Farrell et al., 2010; Zimmermann et al., 2012) have suggested that large-scale topographic structures near the terminator or in the polar region can be electrically complex, creating mini-wakes that obstruct the solar wind flow. In the leeward sides, an electron cloud can be formed, deprived of ions, which drives the surface potential to large negative values (∼−100 V). Since the electron current to the surface is unbalanced, Farrell et al. (2010) have suggested that negatively-charged dust particles could then be mobilized to produce a remediating current. This idea is supported by Lunar Ejecta and Meteorite (LEAM) observations from the Apollo 17 mission (Berg et al., 1976). Farrell et al. (2010) have also analyzed the charging of objects in these shadowed craters, showing that small objects with secondary-emission properties that are very different from the lunar regolith can differentially charge by tens of Volts. Similar considerations are applicable to the extreme charging cases treated in this paper, where it is however expected that dust mobilization or differential charging of objects would be stronger. Note that mobilized dust is potentially a serious concern for human lunar operations because of its tendency to stick to surfaces and several methods to clean surfaces from accumulated dust are being pursued (Afshar-Mohajer et al., 2015).

Discussion

During solar-energetic-electron events there is a potential for very high Voltage charging on the lunar surface and in the lunar wake.

Electrical Grounding

Thought must be given to provide a grounding of objects on the lunar surface to prevent electrical discharges. Grounding of objects on the Moon may be difficult since the conductivity of lunar soil is so poor. For examples, Strangway et al. (1972) report electrical conductivity values 10⁻¹⁴–10⁻¹⁵ siemens/m and Olhoeft et al. (1974) report conductivity values of 10⁻¹⁴–10⁻¹⁰ siemens/m, with the conductivity being lower at cooler temperatures such as occur on the night side of the Moon, particularly the midnight-to-dawn sector of the lunar surface where sunlight has been absent for seven or more days. The conductivity values of the lunar soil are similar to the values for glass, which are 10⁻¹⁰–10⁻¹⁷ siemens/m (cf. Table 10.26 of Cardarelli (2018)). The lunar-soil electrical conductivity is seven or more orders of magnitude less than the conductivities of Earth soil, which tends to be in the range 10⁻³–10⁻² siemens/m (cf. Figures 5, 6 and Table 28-1 of ITT (1977)). The interior lunar electrical conductivity is in the range of 10⁻⁴–10⁻³ siemens/m (Sonett 1975; Vanyan, 1980), with a higher-conductivity lunar core (Hood et al., 1982).

Of course, in such an insulating environment, one can ask: If a charged object were to discharge, to what would it discharge? Wise precautions would be 1) to electrically connect nearby objects together to prevent discharges between objects, 2) to ensure that the outer surfaces of objects placed on the lunar surface are conducting to avoid differential surface charging, and 3) to be cautious if an astronaut exits from the inside of a structure (a Faraday cage) to the outside of the structure.

Needed Future Calculations

Solutions to the lunar-wake problem need to be performed for a variety of relativistic-electron properties (energy spectrum, maximum energy, number density, anisotropy) and for a variety of solar-wind magnetic-field orientations. Full two-dimensional and three-dimensional time-dependent simulations for the plasma wake with relativistic electrons will be eventually needed. The plasma refilling of the wake is driven by ambipolar electric fields set up by the high mobility of solar wind electrons, with the ambipolar field strength (and potential) related to the electron temperature of the solar-wind plasma. When there are multiple electron populations present, the ambipolar driving of the ions is controlled by the temperature of the hotter population of electrons (cf. Diaw and Mora, 2013; Kiefer et al., 2013; Bennaceur-Doumaz et al., 2015). Ambipolar electric fields set up by a relativistic-electron population with 100-keV temperatures can result in proton acceleration to 1000’s of km/s from the edge of a plasma (e.g. Figures 1A, 3, and 7 of Tan and Borovsky, 1986). During a solar-energetic-electron event, the energetic-electron temperature can be in the 100’s of keV and the plasma refilling of the wake may be governed by that electron population, changing the geometry of the plasma wake.

Following the wake calculations, more-sophisticated object-charging calculations in the wake environment are needed. Additional physics that needs to be added to those future object-charging calculations are processes that can limit the potential of an object. One such process mentioned in High-Voltage Charging is photoelectron emission caused by Earthshine on the object in the eclipse of the Moon. Another process is field electron emission into vacuum (Fowler and Nordheim, 1928; Lau et al., 1994), which becomes important as electric fields near the object surface approach strengths of 10⁷ V/cm (Cooray, 2003). Charged objects of smaller size (e.g. an isolated dust grain) are more susceptible to field emission and field emission is particularly effective for sharp protuberances from an object where the electric field becomes concentrated (e.g. a needle cathode (Fukuyama et al., 2009)).

Calculations and simulations of the charging of objects on the lunar surface for a variety of magnetic-field orientations and relativistic-electron populations are critically needed. These calculations and simulations would use the results of wake calculations as boundary conditions. A complication to the emission of secondary electrons by insulating materials is small-scale differential charging on the surface, which can cause secondary electrons emitted from more-negative regions of the surface to be collected by more-positive regions instead of escaping to infinity. This electrical trapping of secondaries can reduce the overall secondary-electron yield of a surface (Olsen et al., 1981; Ura, 1998; Maekawa et al., 2007; Thomsen et al., 2013). One should anticipate that this collection effect will be stronger if the surface is comprised spatially of different materials, such as a soil of different grains with different compositions. See Richterova et al. (2012), Richterova et al. (2016), Yu et al. (2015), and Mishra and Bhardwaj (2020) for other secondary-electron-emission complications.

The dynamic effects of rapid temporal variations of the energetic-electron energy distribution function and of the magnetic-field orientation of the solar wind (cf. Gosling et al., 2004a; Gosling et al., 2004b; Borovsky, 2021) need to be investigated for the dynamics of the wake and the dynamics of charging and differential charging at the lunar surface. An interesting analysis will be the passage of a strong solar-wind current sheet (a directional discontinuity) and its effect on the high-Voltage lunar wake driven by relativistic electrons. Across a strong current sheet, the magnetic-field direction can change by 90^o or more. Typical thicknesses of solar-wind current sheets are ∼1000 km (e.g. Siscoe et al., 1968; Vasquez et al., 2007) but some strong current sheets are considerably thinner (See, for example, Figure 4D of Borovsky and Burkholder (2020) where an oblique-oriented current sheet is advected past the WIND spacecraft in 1 s with a solar-wind speed of 450 km/s: an analysis accounting for the sheet orientation finds the sheet was 270 km thick.). These transitions of the solar-wind plasma and magnetic field, which occur several times per hour, have spatial scales much smaller than the Moon and its wake.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JB and GD both initiated this project, both performed plasma calculations, and both composed the manuscript.

Funding

JEB was supported at the Space Science Institute by the NSF SHINE program via grant AGS-1723416, by the NASA Heliophysics Guest Investigator Program via award NNX17AB71G, by the NSF GEM Program via grant AGS-2027569, and by the NASA Heliophysics LWS program via award NNX16AB75G. GLD was supported by the Laboratory Directed Research and Development program at Los Alamos National Laboratory (LANL) under project 20200276ER. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (DOE) (Contract No. 89233218CNA000001).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix 1

Secondary-Electron Yields for Relativistic SEE Electrons and High-Energy SEP Ions

Secondary-electron yields have been rarely measured for relativistic-electron impacts (e.g. Pomerantz et al., 1960; Schultz and Pomerantz, 1963; Checkik et al., 1994). Here we will construct yield-versus-energy curves at high electron energies using the Sternglass-57 theory of secondary emission (Sternglass, 1957) based on the Coulomb-collisional energy deposition of the energetic electrons in the material of a target (see also Sect. 6.1 of Bruining (1954)).

The Sternglass-1957 theory for secondary-electron emission by fast electrons assumes that there is a layer of the material near the surface (typically 100-Å or so thick) wherein electrons from the target material that are dislodged from their orbitals by Coulomb scattering have a chance to diffuse to the surface and escape as secondary electrons. The larger the number of electrons freed in this layer, the larger the secondary-electron yield. The number of electrons freed per unit pathlength of the fast primary electron passing through the target material is proportional to the collision stopping power dE/dx of the fast electron through the material. Note that for relativistic electrons, the “total” stopping power dE/dx is comprised of the sum of the collisional stopping power (which frees electrons) and the radiative (bremstralung) stopping power (which does not free electrons). Only the collisional stopping power is relevant for the production of secondary electrons. To construct the yield Y curves in Figure 6, a fit with the shape of the high-energy collisional dE/dx curve is matched onto a low-energy secondary-electron-yield curve. In Figure 6A, the oxidized-aluminum stopping-power curve is a fit to the collisional stopping data in the Page-89 table of Berger and Seltzer (1982) for electrons in aluminum that is matched onto a low-energy “Sternglass-49 formula” (Sternglass, 1949) for the normal-incidence secondary-electron yield Y (number of secondary electrons emitted for each incident primary electron)

$\text{Y}=7.4{\mathrm{\delta }}_{\text{max}}(\text{E}/{\text{E}}_{\text{max}})\text{exp}(-2{(\text{E}/{\text{E}}_{\text{max}})}^{1/2})(\mathrm{A1})$

with δ_max = 1.7 and E_max = 0.5 keV, where E is in keV in expression (A1). Normal-incidence secondary electron measurements for electrons with energies >1 keV on oxidized aluminum in Table 2 of Suszcynsky et al. (1990) (black points) are used to guide the matching of the curves. Above 2.5 keV the high energy curve is

$\text{Y}=1.65{\text{E}}^{-0.9016}+0.0179+9.94\times {10}^{-8}\text{E}(\mathrm{A2})$

where E is in keV. In creating this yield curve, a modification to the Sternglass-57 theory that accounts for secondary electrons created by the exit of backscattered primary electrons (Suszcynsky and Borovsky, 1992) was not implemented: at relativistic energies the backscatter of electrons from a target no longer occurs. The green points in Figure 6A are measured secondary-electron yields for oxidized aluminum from Figure 6 of Schultz and Pomerantz (1963). The theoretical curve and the measurement points are close, but note that the secondary-electron yield of oxidized-aluminum targets vary from target to target according to the alloy of the aluminum and the aging of the surface (cf. Borovsky et al., 1988). When the primary electron strikes the target at an angle θ from normal, the pathlenth through the critical surface layer increases by a factor 1/cos(θ) and so the energy deposited in the layer increases by the factor 1/cos(θ) and the secondary-electron yield increases by the factor 1/cos(θ) from the normal-incidence value.

As a proxy for lunar soil (e.g. Heiken, 1975), SiO₂ is used. In Figure 6B, the stopping-power curve that is a fit to the collisional stopping data in the Page-145 table of Berger and Seltzer (1982) for electrons in SiO₂ is fitted onto a “Sternglass-49 formula” with δ_max = 2.4 and E_max = 0.4 keV (cf. Figure 2 of Suszcynsky et al. (1992) and see also Richterova et al. (2007)). Above 1.6 keV the high-energy yield curve is.

$\text{Y}=2.07{\text{E}}^{-0.9041}+0.0216+1.17\times {10}^{-7}\text{E}(\mathrm{A3})$

where E is in keV. At low energies the yield curve of Figure 6B is similar to those of lunar soil samples (e.g. Horanyi et al., 1998; Dukes and Baragiola, 2013).

Note that the measured secondary-electron yields for energetic protons (appropriate to SEP energies) (Borovsky et al., 1988) follow the dE/dx law rather than the Sternglass-49 formula, as do the measured yields for high-energy heavy ions (Borovsky and Barraclough, 1989) and for high-charge-state heavy ions (Borovsky and Suszcynsky, 1991). These secondary-electron yields for high-energy electrons and ions are much larger than predicted by a Sternglass (1949) formula, rather they follow the Sternglass (1957) theory.

Appendix 2

Relativistic Collection Area of a Sphere

For a flux of relativistic electrons moving toward a negatively charged sphere, the cross section for the collection of electrons is

$\sigma =\pi {\text{b}}_{\text{o}}^2(\mathrm{A1})$

where b_o is the impact parameter of an electron that strikes the charged sphere with a grazing incidence. For an electron, the relativistic Hamiltonian H is conserved, where H = (p²+m²c²)^1/2 + eϕ. In spherical coordinates the momentum pp of the electron can be written p² = p_r² + p_θ² with p_θ = J/r, where J is the (conserved) angular momentum of the electron J = b_op_o, with p_o being the momentum of the electron far from the sphere (r→∞). Thus, (e.g. Newton, 1982)

$\text{H}=\text{c}{({\text{p}}_{\text{r}}^2+{\text{m}}^2{\text{c}}^2+{\text{b}}_{\text{o}}^2{\text{p}}_{\text{o}}^2/{\text{r}}_2)}^{1/2}+\text{e}\varphi (\mathrm{A2})$

Far from the sphere H = c (p_o² + m²c²)^1/2 and when the electron is grazing the charged sphere (p_r=0) the Hamiltonian is H = c (m²c² + b_o²p_o²/r_o²)^1/2 + eϕ_o, where r_o is the radius of the sphere and ϕ_o is the potential of the sphere. Conservation of H can be written

${({\text{p}}_{\text{o}}^2+{\text{m}}^2{\text{c}}^2)}^{1/2}={({\text{m}}^2{\text{c}}^2+{\text{b}}_{\text{o}}^2{\text{p}}_{\text{o}}^2/{\text{r}}_{\text{o}}^2)}^{1/2}+\text{e}{\mathrm{\varphi }}_{\mathrm{o}}/c(\mathrm{A3})$

Subtracting eϕ_o/c from both sides of expression (A3), squaring, and solving for b_o² yields

${\text{b}}_{\text{o}}^2={\text{r}}_{\text{o}}^2[1-(2\text{e}{\varphi }_{\text{o}}/{\text{cp}}_{\text{o}}){(1+({\text{m}}^2{\text{c}}^2/{\text{p}}_{\text{o}}^2))}^{1/2}+{\text{e}}^2{\mathrm{\varphi }}_{\mathrm{o}}^{\mathrm{2}}/{\text{c}}^2{\text{p}}_{\text{o}}^2]$

Writing p_o = γmv_o = (γ²-1)^1/2mc where γ = (1 - v_o²/c²)^-1/2 is the relativistic factor far from the sphere and defining Φ_o = eϕ_o/mc², this becomes

${\text{b}}_{\text{o}}^2={\text{r}}_{\text{o}}^2[1-2{\Phi }_{\mathrm{o}}\mathrm{\gamma }{({\mathrm{\gamma }}^2-1)}^{-1}+{\Phi }_o^2{({\mathrm{\gamma }}^2-1)}^{-1}](\mathrm{A4})$

With expression (A4), the cross-sectional area (expression (A1)) becomes

$\sigma =\pi {\text{r}}_{\text{o}}^2[1-2{\Phi }_{\text{o}}\gamma {({\gamma }^2-1)}^{-1}+{\Phi }_{\text{o}}^2{({\gamma }^2-1)}^{-1}](\mathrm{A5})$

For electrons repelled by a negatively charged sphere, both e and ϕ_o are taken to be negative quantities so that Φ_o is positive.

References

Afshar-Mohajer, N., Wu, C.-Y., Curtis, J. S., and Gaier, J. R. (2015). Review of Dust Transport and Mitigation Technologies in Lunar and Martian Atmospheres. Adv. Space Res. 56, 1222–1241. doi:10.1016/j.asr.2015.06.007

CrossRef Full Text | Google Scholar

Bennaceur-Doumaz, D., Bara, D., and Djebli, M. (2015). Self-similar Two-Electron Temperature Plasma Expansion into Vacuum. Laser Part. Beams 33, 723–730. doi:10.1017/s0263034615000877

CrossRef Full Text | Google Scholar

Berg, O. E., Wolf, H., and Rhee, J. (1976). “2.2.4 Lunar Soil Movement Registered by the Apollo 17 Cosmic Dust Experiment, Int. Astronomical Union Colloquium,” in Interplanetary Dust and Zodiacal Light, Editors H. Elsasser, and H. Fectig, Berlin: Springer 31, 233–237. doi:10.1017/s0252921100051757

CrossRef Full Text | Google Scholar

Berger, M. J., and Seltzer, S. M. (1982). Stopping powers and Ranges of Electrons and Positrons. Washington, DC: NBSIR 82-2550. National Bureau of Standards.

CrossRef Full Text

Borisov, N., and Mall, U. (2006). Charging and Motion of Dust Grains Near the Terminator of the Moon. Planet. Space Sci. 54, 572–580. doi:10.1016/j.pss.2006.01.005

CrossRef Full Text | Google Scholar

Borisov, N., and Zakharov, A. (2015). The Influence of the Surface Conductivity on the Local Electric fields and the Motion of Charged Dust Grains on the Moon. Planet. Space Sci. 117, 295–302. doi:10.1016/j.pss.2015.07.001

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Barraclough, B. L. (1989). High- Velocity Ionic Projectiles Interacting with Metals: Models and Measurements of Secondary-Electron Yields from Gold and Aluminum Targets Struck by 13.5-31.5 MeV 7Li and 9-63 MeV 12C. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 36, 377–394. doi:10.1016/0168-583x(89)90341-8

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Burkholder, B. L. (2020). On the Fourier Contribution of strong Current Sheets to the High-Frequency Magnetic Power Spectral Density of the Solar Wind. J. Geophys. Res. 125, e2019JA027307. doi:10.1029/2019ja027307

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2021). Exploring the Properties of the Electron Strahl at 1 AU as an Indicator of the Quality of the Magnetic Connection between the Earth and the Sun. Front. Astron. Space Sci. 8, 646443. doi:10.3389/fspas.2021.646443

CrossRef Full Text | Google Scholar

Borovsky, J. E., McComas, D. J., and Barraclough, B. L. (1988). The Secondary-Electron Yield Measured for 5-24 MeV Protons on Aluminum-Oxide and Gold Targets. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 30, 191–195. doi:10.1016/0168-583x(88)90116-4

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2010). On the Variations of the Solar Wind Magnetic Field about the Parker Spiral Direction. J. Geophys. Res. 115, ja015040. doi:10.1029/2009ja015040

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Suszcynsky, D. M. (1991). Experimental Investigation of Thez2scaling Law of Fast-Ion-Produced Secondary-Electron Emission. Phys. Rev. A. 43, 1416–1432. doi:10.1103/physreva.43.1416

PubMed Abstract | CrossRef Full Text | Google Scholar

Borovsky, J. E. (2012). The Effect of Sudden Wind Shear on the Earth's Magnetosphere: Statistics of Wind Shear Events and CCMC Simulations of Magnetotail Disconnections. J. Geophys. Res. 117, ja017623 doi:10.1029/2012ja017623

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2020). The Plasma and Magnetic-Field Structure of the Solar Wind at Inertial-Range Scale Sizes Discerned from Statistical Examinations of the Time-Series Measurements. Front. Astron. Space Sci. 7, 20. doi:10.3389/fspas.2020.00020

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2018). The Spatial Structure of the Oncoming Solar Wind at Earth and the Shortcomings of a Solar-Wind Monitor at L1. J. Atmos. Solar-Terrestrial Phys. 177, 2–11. doi:10.1016/j.jastp.2017.03.014

CrossRef Full Text | Google Scholar

Borovsky, J. E. (1986). The Theory of Langmuir Probes in strong Electrostatic Potential Structures. Phys. Fluids 29, 718. doi:10.1063/1.865925

CrossRef Full Text | Google Scholar

Bruining, H. (1954). Physics and Applications of Secondary Electron Emission. New York: Pergamon.

Cane, H. V., Richardson, I. G., and von Rosenvinge, T. T. (2010). A Study of Solar Energetic Particle Events of 1997-2006: Their Composition and Associations. J. Geophys. Res. 115, ja014848. doi:10.1029/2009ja014848

CrossRef Full Text | Google Scholar

Cardarelli, F. (2018). Materials Handbook. 3rd Edition. Cham, Switzerland: Springer Nature.

Chandran, S. B. R., Rajesh, S. R., Abraham, A., Renuka, G., and Venugopal, C. (2017). SEP Events and Wake Region Lunar Dust Charging with Grain Radii. Adv. Space Res. 59, 483–489. doi:10.1016/j.asr.2016.09.027

CrossRef Full Text | Google Scholar

Chechik, R., Breskin, A., Aclander, H., Comforti, E., and Gibrekhterman, A. (1994). Secondary Electron Emission from Thin CsI Films Induced by Relativistic Electrons. Nucl. Instr. Methods Phys. Res. Section A: Acc. Spectrometers, Detectors Associated Equipment 342, 458–465. doi:10.1016/0168-9002(94)90272-0

CrossRef Full Text | Google Scholar

Chou, K., Wang, A., Yu, W., and Wang, J. (2019). Laboratory Experiments on Dusty Spacesuit Charging and Arcing in Plasma. IEEE Trans. Plasma Sci. 47, 3898–3904. doi:10.1109/tps.2019.2922243

CrossRef Full Text | Google Scholar

Cliver, E. W., and Ling, A. G. (2007). Electrons and Protons in Solar Energetic Particle Events. ApJ 658, 1349–1356. doi:10.1086/511737

CrossRef Full Text | Google Scholar

Cooray, V. (2003). The Lightning Flash. Sect. 3.6.4. London: The Institution of Engineering and Technology.

Delzanno, G. L., Camporeale, E., Moulton, J. D., Borovsky, J. E., MacDonald, E. A., and Thomsen, M. F. (2013). CPIC: A Curvilinear Particle-In-Cell Code for Plasma-Material Interaction Studies. IEEE Trans. Plasma Sci. 41, 3577–3587. doi:10.1109/tps.2013.2290060

CrossRef Full Text | Google Scholar

Diaw, A., and Mora, P. (2013). Expansion of a Plasma into Vacuum with a Bi-maxwellian Electron Distribution Function. EPJ Web of Conferences 59, 17009. doi:10.1051/epjconf/20135917009

CrossRef Full Text | Google Scholar

Dresing, N., Effenberger, F., Gómez-Herrero, R., Heber, B., Klassen, A., Kollhoff, A., et al. (2020). Statistical Results for Solar Energetic Electron Spectra Observed over 12 Yr with STEREO/SEPT. ApJ 889, 143. doi:10.3847/1538-4357/ab64e5

CrossRef Full Text | Google Scholar

Dresing, N., Gómez-Herrero, R., Heber, B., Klassen, A., Temmer, M., and Veronig, A. (2018). Long-lasting Injection of Solar Energetic Electrons into the Heliosphere. Astronomy & Astrophysics 613, A21. doi:10.1051/0004-6361/201731573

CrossRef Full Text | Google Scholar

Dukes, C. A., and Baragiola, R. A. (2013). Secondary Electron Emission from Lunar Soil: Yields, Energy Distributions, and Charging Effects. Planet. Space Sci. 89, 36–41. doi:10.1016/j.pss.2013.04.011

CrossRef Full Text | Google Scholar

Fairfield, D. H. (1971). Average and Unusual Locations of the Earth's Magnetopause and bow Shock. J. Geophys. Res. 76, 6700–6716. doi:10.1029/ja076i028p06700

CrossRef Full Text | Google Scholar

Farrell, W. M., Kaiser, M. L., Steinberg, J. T., and Bale, S. D. (1998). A Simple Simulation of a Plasma Void: Applications to Wind Observations of the Lunar Wake. J. Geophys. Res. 103, 23653–23660. doi:10.1029/97ja03717

CrossRef Full Text | Google Scholar

Farrell, W. M., Stubbs, T. J., Halekas, J. S., Killen, R. M., Delory, G. T., Collier, M. R., et al. (2010). Anticipated Electrical Environment within Permanently Shadowed Lunar Craters. J. Geophys. Res. 115, E03004. doi:10.1029/2009je003464

CrossRef Full Text | Google Scholar

Fennell, J. F., Koons, H. C., Roeder, J. L., and Blake, J. B. (2001). Spacecraft Charging: Observations and Relationship to Satellite Anomalies. Noordwijk, Netherlands: ESA Special Publications SP, European Space Agency Publication Division, 476, 279.

Fowler, R. H., and Nordheim, L. (1928). Electron Emission in Intense Electric fields. Proc. Roy. Soc. Lond. A119, 173.

Google Scholar

Fukuyama, C., Murakami, K., Abo, S., Wakaya, F., Takai, M., et al. (2009). Field Enhanced Surface Treatment of Needle-Shaped TiO[sub 2] Cathode for Improvement in Field Emission. J. Vac. Sci. Technol. B 27, 775. doi:10.1116/1.3070652

CrossRef Full Text | Google Scholar

Gómez-Herrero, R., Dresing, N., Klassen, A., Temmer, M., Veronig, A., et al. (2017). Sunward-propagating Solar Energetic Electrons inside Multiple Interplanetary Flux Ropes. ApJ 840, 85. doi:10.3847/1538-4357/aa6c5c

CrossRef Full Text | Google Scholar

Gosling, J. T., de Koning, C. A., Skoug, R. M., Steinberg, J. T., and McComas, D. J. (2004a). Dispersionless Modulations in Low-Energy Solar Electron Bursts and Discontinuous Changes in the Solar Wind Electron Strahl. J. Geophys. Res. 109, A05102. doi:10.1029/2003ja010338

CrossRef Full Text | Google Scholar

Gosling, J. T., Skoug, R. M., McComas, D. J., and Mazur, J. E. (2004b). Correlated Dispersionless Structure in Suprathermal Electrons and Solar Energetic Ions in the Solar Wind. ApJ 614, 412–419. doi:10.1086/423368

CrossRef Full Text | Google Scholar

Greenstadt, E. W., Traver, D. P., Coroniti, F. V., Smith, E. J., and Slavin, J. A. (1990). Observations of the Flank of Earth's bow Shock to −110 REby ISEE 3/ICE. Geophys. Res. Lett. 17, 753–756. doi:10.1029/gl017i006p00753

CrossRef Full Text | Google Scholar

Halekas, J. S., Bale, S. D., Mitchell, D. L., and Lin, R. P. (2005). Electrons and Magnetic fields in the Lunar Plasma Wake. J. Geophys. Res. 110, A07222. doi:10.1029/2004ja010991

CrossRef Full Text | Google Scholar

Halekas, J. S., Delory, G. T., Brain, D. A., Lin, R. P., Fillingim, M. O., Lee, C. O., et al. (2007). Extreme Lunar Surface Charging during Solar Energetic Particle Events. Geophys. Res. Lett. 34, L02111. doi:10.1029/2006gl028517

CrossRef Full Text | Google Scholar

Halekas, J. S., Delory, G. T., Lin, R. P., Stubbs, T. J., and Farrell, W. M. (2009). Lunar Surface Charging during Solar Energetic Particle Events: Measurement and Prediction. J. Geophys. Res. 114, ja014113. doi:10.1029/2009ja014113

CrossRef Full Text | Google Scholar

Halekas, J. S., Lillis, R. J., Lin, R. P., Manga, M., Purucker, M. E., and Carley, R. A. (2010). How strong Are Lunar Crustal Magnetic fields at the Surface? Considerations from a Reexamination of the Electron Reflectometry Technique. J. Geophys. Res. 115, E03006. doi:10.1029/2009je003516

CrossRef Full Text | Google Scholar

Halekas, J. S., Mitchell, D. L., Lin, R. P., Hood, L. L., Acuna, M. H., and Binder, A. B. (2002). Evidence for Negative Charging of the Lunar Surface in Shadow. Geophys. Res. Lett. 29, 1435. doi:10.1029/2001gl014428

CrossRef Full Text | Google Scholar

Heiken, G. (1975). Petrology of Lunar Soils. Rev. Geophys. 13, 567. doi:10.1029/rg013i004p00567

CrossRef Full Text | Google Scholar

Hood, L. L., Herbert, F., and Sonett, C. P. (1982). The Deep Lunar Electrical Conductivity Profile: Structural and thermal Inferences. J. Geophys. Res. 87, 5311–5326. doi:10.1029/jb087ib07p05311

CrossRef Full Text | Google Scholar

Horonyi, M., Walch, B., Robertson, S., and Alexander, D. (1998). Electostatic Charging Properties of Apollo 17 Lunar Dust. J. Geophys. Res. 103, 8575.

Google Scholar

ITT International Telephone and Telegraph Corporation (1977). Reference Data For Radio Engineers. Indianapolis, Indiana: Howard Sams and Co.

Jackson, T. L., Farrell, W. M., Killen, R. M., Delory, G. T., Halekas, J. S., and Stubbs, T. J. (2011). Discharging of Roving Objects in the Lunar Polar Regions. J. Spacecraft Rockets 48, 700–704. doi:10.2514/1.51897

CrossRef Full Text | Google Scholar

Jordan, A. P., Stubbs, T. J., Wilson, J. K., Schwadron, N. A., Spance, H. E., and Joyce, C. J. (2015). Deep Dielectric Charging of Regolith within the Moon’s Permanently Shadowed Regions. J. Geophys. Res. Planets 119, 1806–1821. doi:10.1002/2014JE004648

CrossRef Full Text | Google Scholar

Jordan, A. P., Stubbs, T. J., Wilson, J. K., Schwadron, N. A., and Spence, H. E. (2017). The Rate of Dielectric Breakdown Weathering of Lunar Regolith in Permanently Shadowed Regions. Icarus 283, 352–358. doi:10.1016/j.icarus.2016.08.027

CrossRef Full Text | Google Scholar

Kahler, S. W. (2007). Solar Sources of Heliospheric Energetic Electron Events-Shocks or Flares? Space Sci. Rev. 129, 359–390. doi:10.1007/s11214-007-9143-0

CrossRef Full Text | Google Scholar

Kallenrode, M.-B., Cliver, E. W., and Wibberenz, G. (1992). Composition and Azimuthal Spread of Solar Energetic Particles from Impulsive and Gradual Flares. ApJ 391, 370. doi:10.1086/171352

CrossRef Full Text | Google Scholar

Kallenrode, M.-B., and Švestka, Z. (1994). The Participation of Nuclei in Type-III-Related Electron Streams. Sol. Phys. 155, 121–148. doi:10.1007/bf00670735

CrossRef Full Text | Google Scholar

Kiefer, T., Schlegel, T., and Kaluza, M. C. (2013). Plasma Expansion into Vacuum Assuming a Steplike Electron Energy Distribution. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 87, 043110. doi:10.1103/PhysRevE.87.043110

PubMed Abstract | CrossRef Full Text | Google Scholar

King, J. H., and Papitashvili, N. E. (2005). Solar Wind Spatial Scales in and Comparisons of Hourly Wind and ACE Plasma and Magnetic Field Data. J. Geophys. Res. 110, 2104. doi:10.1029/2004ja010649

CrossRef Full Text | Google Scholar

Knott, K. (1973). Electrostatic Charging of the Lunar Surface and Possible Consequences. J. Geophys. Res. 78, 3172–3175. doi:10.1029/ja078i016p03172

CrossRef Full Text | Google Scholar

Koons, H., Mazur, J., Lopatin, A., Pitchford, D., bogorad, A., and Herschitz, R. (2006). Spatial and Temporal Correlation of Spacecraft Surface Charging in Geosynchronous Orbit. J. Spacecraft Rockets 43, 178–185. doi:10.2514/1.10805

CrossRef Full Text | Google Scholar

Lario, D., Kwon, R.-Y., Vourlidas, A., Raouafi, N. E., Haggerty, D. K., Ho, G. C., et al. (2016). Longitudinal Properties of a Widespread Solar Energetic Particle Event on 2014 February 25: Evolution of the Associated CME Shock. ApJ 819, 72. doi:10.3847/0004-637x/819/1/72

CrossRef Full Text | Google Scholar

Lau, Y. Y., Liu, Y., and Parker, R. K. (1994). Electron Emission: From the Fowler-Nordheim Relation to the Child-Langmuir Law. Phys. Plasmas 1, 2082–2085. doi:10.1063/1.870603

CrossRef Full Text | Google Scholar

Lepping, R. P., Acũna, M. H., Burlaga, L. F., Farrell, W. M., Slavin, J. A., Schatten, K. H., et al. (1995). The WIND Magnetic Field Investigation. Space Sci. Rev. 71, 207–229. doi:10.1007/bf00751330

CrossRef Full Text | Google Scholar

Lockwood, M., Owens, M. J., and Macneil, A. (2019). On the Origin of Ortho-Gardenhose Heliospheric Flux. Solar Phys. 294, 85. doi:10.1007/s11207-019-1478-7

CrossRef Full Text | Google Scholar

Maekawa, T., Tanaka, H., and Kotera, M. (2007). “Collection Field Dependence of Charging-Up of Insulators in Low Voltage Scanning Electron Microscope”, in Microprocesses And Technology 2007 Digest Of Papers. Editor H. Arimoto (Tokyo, Japan: Japan Society Applied Physics), 74–75. doi:10.1109/imnc.2007.4456111

CrossRef Full Text | Google Scholar

Mewalt, R. A., Cohen, C. M. S., Labrador, A. W., Leske, R. A., Mason, G. M., Desai, M. I., et al. (2005). Proton, Helium, and Electron Spectra during the Large Solar Particle Events of October-November 2003. J. Geophys. Res. 110, A09S18. doi:10.1029/2005JA011038

CrossRef Full Text | Google Scholar

Mishra, S. K., and Bhardwaj, A. (2020). Electrostatic Charging of Permanently Shadowed Craters on the Moon. Mon. Not. R. Astron. Soc. 496, L80–L84. doi:10.1093/mnrasl/slaa082

CrossRef Full Text | Google Scholar

Nemecek, Z., Durovcova, T., Safrankova, J., Richardson, J. D., Simunek, J., and Stevens, M. L. (2020). Non radial Solar Wind Propagation through the Heliosphere. Astrophys. J. Lett. 897, L39. doi:10.3847/2041-8213/ab9ff7

CrossRef Full Text | Google Scholar

Newton, R. G. (1982). Scattering Theory of Waves and Particles. Berlin: Sringer-Verlag. doi:10.1007/978-3-642-88128-2

CrossRef Full Text

Nishino, M. N., Harada, Y., Saito, Y., Tsunakawa, H., Takahashi, F., Yokota, S., et al. (2017). Kaguya Observations of the Lunar Wake in the Terrestrial Foreshock: Surface Potential Change by bow-shock Reflected Ions. Icarus 293, 45–51. doi:10.1016/j.icarus.2017.04.005

CrossRef Full Text | Google Scholar

Nishino, M. N., Saito, Y., Tsunakawa, H., Takahashi, F., Fujimoto, M., Harada, Y., et al. (2015). Electrons on Closed Field Lines of Lunar Crustal fields in the Solar Wind Wake. Icarus 250, 238–248. doi:10.1016/j.icarus.2014.12.007

CrossRef Full Text | Google Scholar

Ogilvie, K. W., Steinberg, J. T., Fitzenreiter, R. J., Owen, C. J., Lazarus, A. J., Farrell, W. M., et al. (1996). Observations of the Lunar Plasma Wake from the WIND Spacecraft on December 27, 1994. Geophys. Res. Lett. 23, 1255–1258. doi:10.1029/96gl01069

CrossRef Full Text | Google Scholar

Olhoeft, G. R., Frisillo, A. L., and Strangway, D. W. (1974). Electrical Properties of Lunar Soil Sample 1530138. J. Geophys. Res. 79, 1599–1604. doi:10.1029/jb079i011p01599

CrossRef Full Text | Google Scholar

Olsen, R. C., McIlwain, C. E., and Whipple, E. C. (1981). Observations of Differential Charging Effects on ATS 6. J. Geophys. Res. 86, 6089. doi:10.1029/ja086ia08p06809

CrossRef Full Text | Google Scholar

Owen, C. J., Lepping, R. P., Ogilvie, K. W., Slavin, J. A., Farrell, W. M., and Byrnes, J. B. (1996). The Lunar Wake at 6.8 RL: WIND Magnetic Field Observations. Geophys. Res. Lett. 23, 1263–1266. doi:10.1029/96gl01354

CrossRef Full Text | Google Scholar

Pines, V., Zlatkowski, M., and Chait, A. (2011). Lofted Charged Dust Distribution above the Moon Surface. Planet. Space Sci. 59, 1795–1803. doi:10.1016/j.pss.2011.01.013

CrossRef Full Text | Google Scholar

Pomerantz, M. A., Shatas, R. A., and Schieve, W. C. (1960). Secondary Electron Emission of MgO Crystals Bombarded by Relativistic Electrons. J. Appl. Phys. 31, 2038. doi:10.1063/1.1735491

CrossRef Full Text | Google Scholar

Posner, A. (2007). Up to 1-hour Forecasting of Radiation Hazards from Solar Energetic Ion Events with Relativistic Electrons. Space Weather 5, 268. doi:10.1029/2006sw000268

CrossRef Full Text | Google Scholar

Reagan, J. B., Meyerott, R. E., Gaines, E. E., Nightingale, R. W., Filbert, P. C., and Imhof, W. L. (1983). Space Charging Currents and Their Effects on Spacecraft Systems. IEEE Trans. Elect. Insul. 18, 354–365. doi:10.1109/tei.1983.298625

CrossRef Full Text | Google Scholar

Reames, D. V. (1999). Particle Acceleration at the Sun and in the Heliosphere. Space Sci. Rev. 90, 413–491. doi:10.1023/a:1005105831781

CrossRef Full Text | Google Scholar

Rhodes, D. J., Farrell, W. M., and McLain, J. L. (2020). Tribocharging and Electrical Grounding of a Drill in Shadowed Regions of the Moon. Adv. Space Res. 66, 753–759. doi:10.1016/j.asr.2020.05.005

CrossRef Full Text | Google Scholar

Richmond, N. C., and Hood, L. L. (2008). A Preliminary Global Map of the Vector Lunar Crustal Magnetic Field Based on Lunar Prospector Magnetometer Data. J. Geophys. Res. 113, E02010. doi:10.1029/2007je002933

CrossRef Full Text | Google Scholar

Richterova, I., Nemecek, Z., Pavlu, J., Safrankova, J., and Vaverka, J. (2016). Secondary Emission from Clusters Composed of Spherical Grains. IEEE Trans. Plasma Sci. 44, 505–511. doi:10.1109/tps.2015.2509238

CrossRef Full Text | Google Scholar

Richterová, I., Němeček, Z., Beránek, M., Šafránková, J., and Pavlů, J. (2012). Secondary Emission from Non-spherical Dust Grains with Rough Surfaces: Application to Lunar Dust. ApJ 761, 108. doi:10.1088/0004-637x/761/2/108

CrossRef Full Text | Google Scholar

Richterova, I., Pavlu, J., Nemecek, Z., Safrankova, J., and Beranek, M. (2007). Secondary Emission from Glass Grains: Comparison of the Model and experiment. IEEE Trans. Plasma Sci. 35, 286–291. doi:10.1109/tps.2007.892131

CrossRef Full Text | Google Scholar

Roeder, J. L., and Fennell, J. F. (2009). Differential Charging of Satellite Surface Materials. IEEE Trans. Plasma Sci. 37, 281–289. doi:10.1109/tps.2008.2004765

CrossRef Full Text | Google Scholar

Rosen, A. (1976). Spacecraft Charging: Environment-Induced Anomalies. J. Spacecraft Rockets 13, 129–136. doi:10.2514/3.57073

CrossRef Full Text | Google Scholar

Schultz, A. A., and Pomerantz, M. A. (1963). Secondary Electron Emission Produced by Relativistic Primary Electrons. Phys. Rev. 130, 2135–2141. doi:10.1103/physrev.130.2135

CrossRef Full Text | Google Scholar

Shevchenko, V. I., and Galinsky, V. L. (2010). Stability of the Strahl Electron Distribution Function and its Dynamics. Nonlin. Process. Geophys. 17, 593–597. doi:10.5194/npg-17-593-2010

CrossRef Full Text | Google Scholar

Siscoe, G. L., Davis, L., Coleman, P. J., Smith, E. J., and Jones, D. E. (1968). Power Spectra and Discontinuities of the Interplanetary Magnetic Field: Mariner 4. J. Geophys. Res. 73, 61–82. doi:10.1029/ja073i001p00061

CrossRef Full Text | Google Scholar

Sonett, C. P. (1975). Solar-wind Induction and Lunar Conductivity. Phys. Earth Planet. Interiors 10, 313–322. doi:10.1016/0031-9201(75)90057-6

CrossRef Full Text | Google Scholar

Srangway, D. W., Chapman, W. B., Olhoeft, G. R., and Carnes, J. (1972). Electrical Properties of Lunar Soil Dependence on Frequency, Temperature, and Moisture. Earth Planet. Sci. Lett. 16, 275. doi:10.1016/0012-821X(72)90203-8

CrossRef Full Text | Google Scholar

Sternglass, E. J. (1949). An Interpretation of Secondary Electron Emission Data for Homogeneous Solids. Phys. Rev. 76, 189.

Google Scholar

Sternglass, E. J. (1957). Theory of Secondary Electron Emission by High-Speed Ions. Phys. Rev. 108, 1–12. doi:10.1103/physrev.108.1

CrossRef Full Text | Google Scholar

Stolpovskii, V. G., Daibog, E. I., Kahler, S. W., and Erdos, G. (1998). CME-driven Shocks as a Possible Source of the Electron Component in SEP-Events. Adv. Space Res. 21 (4), 543–546. doi:10.1016/s0273-1177(97)00959-9

CrossRef Full Text | Google Scholar

Suszcynsky, D. M., Borovsky, J. E., and Barraclough, B. L. (1990). Secondary-Electron Yield Measurements From Metals Impacted By High-Velocity Ions, Electrons, and Molecules, LA-11915-MS. Los Alamos, New Mexico, USA: Los Alamos National Laboratory.

Suszcynsky, D. M., Borovsky, J. E., and Goertz, C. K. (1992). Secondary Electron Yields of Solar System Ices. J. Geophys. Res. 97, 2611. doi:10.1029/91je02944

CrossRef Full Text | Google Scholar

Suszcynsky, D. M., and Borovsky, J. E. (1992). Modified Sternglass Theory for the Emission of Secondary Electrons by Fast-Electron Impact. Phys. Rev. A. 45, 6424–6428. doi:10.1103/physreva.45.6424

PubMed Abstract | CrossRef Full Text | Google Scholar

Suszcynsky, D. M., and Borovsky, J. E. (1991). Secondary-electron Emission from Metals Impacted by High-Velocity Particles: Molecular-Effect Deviations from a Single-Particle Picture. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 53, 255–266. doi:10.1016/0168-583x(91)95611-g

CrossRef Full Text | Google Scholar

Tan, L. C., and Reames, D. V. (2016). Dropout of Directional Electron Intensities in Large Solar Energetic Particle Events. ApJ 816, 93. doi:10.3847/0004-637x/816/2/93

CrossRef Full Text | Google Scholar

Tan, T.-H., and Borovsky, J. E. (1986). Spherically Symmetric High-Velocity Plasma Expansions into Background Gases. J. Plasma Phys. 35, 239–256. doi:10.1017/s0022377800011302

CrossRef Full Text | Google Scholar

Taylor, H. E., Behannon, K. W., and Ness, N. F. (1968). Measurements of the Perturbed-Interplanetary Magnetic Field in the Lunar Wake. J. Geophys. Res. 73, 6723–6735. doi:10.1029/ja073i021p06723

CrossRef Full Text | Google Scholar

Thomsen, M. F., Henderson, M. G., and Jordanova, V. K. (2013). Statistical Properties of the Surface-Charging Environment at Geosynchronous Orbit. Space Weather 11, 237–244. doi:10.1002/swe.20049

CrossRef Full Text | Google Scholar

Ura, K. (1998). Contrast Mechanism of Negatively Charged Insulators in Scanning Electron Microscope. J. Electron Microsc. 47, 143–147. doi:10.1093/oxfordjournals.jmicro.a023571

CrossRef Full Text | Google Scholar

Vanyan, L. L. (1980). The Electrical Conductivity of the Moon. Geophys. Surv. 4, 173–185. doi:10.1007/bf01452965

CrossRef Full Text | Google Scholar

Vasquez, B. J., Abramenko, V. I., Haggerty, D. K., and Smith, C. W. (2007). Numerous Small Magnetic Field Discontinuities of Bartels Rotation 2286 and the Potential Role of Alfvénic Turbulence. J. Geophys. Res. 112, ja012504. doi:10.1029/2007ja012504

CrossRef Full Text | Google Scholar

Wang, J., and Huang, Z. (2020). Dust Effects of Spacesuit Charging/arcing: Implications for Astronaut Safety on Lunar Surface. Houston, Texas: Lunar Planetary Institute, The Impact of Lunar Dust on Human Exploration, 5019.

Wang, L., Lin, R. P., Krucker, S., and Mason, G. M. (2012). A Statistical Study of Solar Electron Events over One Solar Cycle. ApJ 759, 69. doi:10.1088/0004-637x/759/1/69

CrossRef Full Text | Google Scholar

Xie, A.-G., Li, C.-Q., Wang, T.-B., and Pei, Y.-J. (2009). The Formulas for the Secondary Electron Yield at High Incident Electron Energy from Gold and Aluminum. Mod. Phys. Lett. B 23, 2331–2338. doi:10.1142/s0217984909020503

CrossRef Full Text | Google Scholar

Xu, S., Poppe, A. R., Halekas, J. S., Mitchell, D. L., McFadden, J. P., and Harada, Y. (2019). Mapping the Lunar Wake Potential Structure with ARTEMIS Data. J. Geophys. Res. Space Phys. 124, 3360–3377. doi:10.1029/2019ja026536

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, W., Wang, J., and Chou, K. (2015). Laboratory Measurement of Lunar Regolith Simulant Surface Charging in a Localized Plasma Wake. IEEE Trans. Plasma Sci. 43, 4175–4181. doi:10.1109/tps.2015.2492551

CrossRef Full Text | Google Scholar

Zhang, H., Khurana, K. K., Kivelson, M. G., Angelopoulos, V., Wan, W. X., Liu, L. B., et al. (2014). Three-dimensional Lunar Wake Reconstructed from ARTEMIS Data. J. Geophys. Res. Space Phys. 119, 5220–5243. doi:10.1002/2014ja020111

CrossRef Full Text | Google Scholar

Zimmerman, M. I., Jackson, T. L., Farrell, W. M., and Stubbs, T. J. (2012). Plasma Wake Simulations and Object Charging in a Shadowed Lunar Crater during a Solar Storm. J. Geophys. Res. 117, E00K03. doi:10.1029/2012je004094

CrossRef Full Text | Google Scholar