
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci. , 05 March 2021
Sec. Space Physics
Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.646443
This article is part of the Research Topic Magnetic connectivity of the Earth and planetary environments to the Sun in Space Weather studies View all 9 articles
In this report some properties of the electron strahl at 1 AU are examined to assess the strahl at 272 eV as an indicator of the quality of the magnetic connection of the near-Earth solar wind to the Sun. The absence of a strahl has been taken to represent either a lack of magnetic connection to the corona or the strahl not surviving to 1 AU owing to scattering. Solar-energetic-electron (SEE) events can be used as indicators of good magnetic connection: examination of 216 impulsive SEE events finds that they are all characterized by strong strahls. The strahl intensity at 1 AU is statistically examined for various types of solar-wind plasma: it is found that the strahl is characteristically weak in sector-reversal-region plasma. In sector-reversal-region plasma and other slow wind, temporal changes in the strahl intensity at 1 AU are examined with 64 s resolution measurements and the statistical relationships of strahl changes to simultaneous plasma-property changes are established. The strahl-intensity changes are co-located with current sheets (directional discontinuities) with strong changes in the magnetic-field direction. The strahl-intensity changes at 1 AU are positively correlated with changes in the proton specific entropy, the proton temperature, and the magnetic-field strength; the strahl-intensity changes are anti-correlated with changes in the proton number density, the angle of the magnetic field with respect to the Parker-spiral direction, and the alpha-to-proton number-density ratio. Reductions in the strahl intensity are not consistent with expectations for a simple model of whistler-turbulence scattering. Reductions in the strahl intensity are mildly consistent with expectations for Coulomb scattering, however the strongest-observed plasma-change correlations are unrelated to Coulomb scattering and whistler scattering. The implications of the strahl-intensity-change analysis are that the change in the magnetic-field direction at a strahl change represents a change in the magnetic connection to the corona, resulting in a different strahl intensity and different plasma properties. An outstanding question is: Does an absence of an electron strahl represent a magnetic disconnection from the Sun or a poor strahl source in some region of the corona?
Knowing the magnetic connectivity between the Earth and the Sun is desirable for several reasons: e.g., 1) to gain a global understanding of the heliospheric magnetic structure, (e.g. McComas et al., 1989; Crooker et al., 2002; Crooker and Pagel, 2008; Crooker and Owens, 2012; Lockwood, 2013; Viall and Borovsky, 2020), 2) for understanding solar energetic particle (proton and electron) events and particle transport (Mazur et al., 2000; Chollet and Giacalone, 2011; Trenchi et al., 2013), and 3) for assessing the likelihood that Earth will or will not undergo an energetic-particle event.
One promising method to assess the magnetic connectivity between the near-Earth solar wind and the Sun is to interpret observations of the electron strahl in the near-Earth solar wind. The electron strahl is a beam of magnetic-field-aligned electrons originating from the solar corona that propagate away from the Sun (Feldman et al., 1976; Pilipp et al., 1987; Maksimovic et al., 2005). A robust strahl is a signature of a good magnetic connection to the Sun; an absence of a strahl has been historically interpreted as an indication of either 1) no magnetic connection to the Sun (McComas et al., 1989; Gosling et al., 2005) or 2) a strahl that does not survive from the Sun to the observer (Pagel et al., 2005a; Crooker and Pagel, 2008; Chollet et al., 2010).
In the present study the intensity of the electron strahl at 272 eV is measured. Lin and Kahler (1992) examined a number of events that were judged to be magnetic-disconnection events by an absence of a low-energy strahl and found the presence of higher-energy (2 keV–8.5 keV) strahls, calling into question whether the absence of a lower-energy strahl is an indication of a magnetic disconnection from the Sun. However, Gosling et al., (2005) examined cases of reconnection-exhause magnetic disconnections and found that electron-halo intermixing could give the impression of a higher-energy strahl, even though those magnetic-field lines were definitely disconnected from the Sun (See also the analysis of Crooker and Pagel (2008).).
At a distance of 1 AU from the Sun, the intensity of the electron strahl varies on multiple timescales, with sudden jumps in strahl intensity that are observed to be co-located with strong current sheets (magnetic directional discontinuities) (Gosling et al., 2004a; Borovsky, 2020a,b). Hence, temporal jumps in the strahl intensity are associated with sudden changes in the magnetic-field orientation.
This report explores some properties of the electron strahl that impact the ability to assess the magnetic connection between Earth and the Sun using observations of the strahl in the near-Earth solar wind. In The Electron Strahl and the Types of Solar Wind Plasma the relationship of the strahl intensity to the type of solar-wind plasma is investigated. In Impulsive SEE Events, the Electron Strahl, and the Type of Plasma the intensity of the electron strahl at 1 AU is examined during impulsive solar-energetic-electron (SEE) events, which are times when there must be a good magnetic connection between the Earth and the Sun. In Strahl Analysis sudden changes in the intensity of the electron strahl at 1 AU are statistically examined in relation to sudden changes in other plasma parameters and the statistical results are discussed in relation to ideas about strahl destruction by Coloumb scattering and whistler-turbulence scattering are tested. Discussion: Interpretation of Strahl-Intensity Changes, Assessing the Sun-Earth Connection, and the Future contains discussions of 1) the interpretations of strahl-intensity changes, 2) an assessment of the ability to determine the Sun-Earth magnetic connection, and 3) suggestions for future research.
Various types of solar-wind plasma are emitted into the heliosphere from various types of regions on the rotating Sun. These various types of plasma have systematically differing parameters at 1 AU, (e.g. proton specific entropy, speed, heavy-ion charge-state ratios, Alfven velocity, etc.), which allows the solar wind to be categorized into the various types of plasmas (cf. Neugebauer et al., 2003, 2016; Reisenfeld et al., 2003; Zhao et al., 2009; Xu and Borovsky, 2015; Camporeale et al., 2017; Veselovsky et al., 2018; Li et al., 2020; Amaya et al., 2020; Heidrich-Meisner et al., 2020; Bloch et al., 2020). One characteristic difference between the various types of plasma at 1 AU is the intensity of the electron strahl (Borovsky, 2018). In Figure 1 the hourly averaged intensity of the electron strahl as measured by the SWEPAM instrument (McComas et al., 1998) on the ACE spacecraft at L1 upstream of the Earth is binned for the four types of solar-wind plasma in the Xu and Borovsky (2015) plasma-categorization scheme. I272 is the base-10 logarithm of the phase-space density f272 (in units of s2cm−5) of the electron strahl in the dominant (parallel-to-B or antiparallel-to-B) direction at an energy of 272 eV, as measured by ACE SWEPAM (See Borovsky. (2017) for a discussion of the creation of an hourly averaged index of I272.). In Figure 1 the gray dashed curve is the occurrence distribution of the hourly averaged strahl intensity I272 for all data in the years 1998–2013. The other four curves in Figure 1 are the occurrence distributions of hourly averaged strahl intensity in four types of solar-wind plasma: coronal-hole-origin plasma (red), streamer-belt-origin plasma (green), sector-reversal-region plasma (purple), and ejecta (blue). Ejecta plasma (blue) has a systematically more-intense strahl and sector-reversal-region plasma (purple) has a systematically weaker strahl, with coronal-hole-origin plasma (red) and streamer-belt-origin plasma (green) have more-typical values of the strahl intensity.
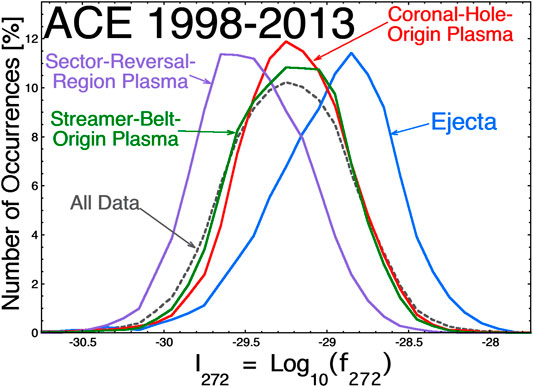
FIGURE 1. For the years 1998–2013, the occurrence distributions of hourly averaged values of the strahl intensity at Earth separated into four categories of solar-wind plasma.
Because of the robust strahl intensities in Figure 1, (e.g. greater than ∼ -29.75), it can be assumed that coronal-hole-origin, streamer-belt-origin, and ejecta plasmas at 1 AU are, in general, well connected magnetically to the Sun. This can’t be assumed for sector-reversal-region plasmas, which has a range of strahl intensities in Figure 1 that can be quite weak, (e.g. less than -29.75). Two sources of sector-reversal-region plasma are discussed in the literature. The first is disconnection of magnetic field caused by reconnection between open flux on either side of a streamer stalk (Wang et al., 1999; Sanchez-Diaz et al., 2019; Lavraud et al., 2020), resulting in the emission of blobs of plasma in the streamer-stalk region. Disconnections will certainly result in a decreased strahl intensity. The second source is interchange reconnection between open field lines and closed loops of streamers (Wang et al., 2000; Crooker et al., 2004; Rouillard et al., 2020). Individual interchange reconnection events, which change the magnetic connection into loops of different heights and electron temperatures, will almost certainly result in a change in the strahl intensity. Sector-reversal-region plasma contains such features as streamer-stalk blobs and puffs (Wang et al., 2000; Bemporad et al., 2005; Sheeley et al., 2009; Rouillard et al., 2010; Sheeley and Rouillard, 2010; Foullon et al., 2011) and periodic density structures (Viall et al., 2010; Viall and Vourlidas, 2015) that are of interest for their impact on Earth (Kepko and Spence, 2003; Viall et al., 2009; Kepko and Viall, 2019). These plasma structures in the sector-reversal-region plasma can be associated with magnetic disconnections from the Sun (Wang et al., 1999; Kepko et al., 2016). There are also reconnection-disconnection events in the vicinity of the heliospheric current sheet in the sector-reversal-region plasma, (e.g. Gosling et al., 2005; Lavraud et al., 2009, 2020; Sanchez-Diaz et al., 2019). Based on the weaker strahl, streamer-belt-origin plasma is the most likely solar-wind type to be poorly connected to the Sun.
Another possible indicator of magnetic connection to the Sun is whether or not the magnetic-field in a plasma has a Parker-spiral orientation. Plasma that is steadily emitted from a spot on the Sun will have an approximately Parker-spiral oriented magnetic field (Parker, 1958; Fisk, 2001; Georgieva et al., 2005); plasma that is impulsively emitted, which can include magnetic disconnections, need not have a Parker-spiral-oriented magnetic field. Even for steadily emitted solar wind, there can be underwinding, (e.g. Gosling and Skoug, 2002; Murphy et al., 2002; Riley and Gosling, 2007) or overwinding, (e.g. Smith and Bieber, 1991; Bruno and Bavassano, 1997) of the Parker spiral caused by large-scale compressions and rarefactions, and there are always large fluctuations of the magnetic-field direction about the Parker-spiral direction (Ness and Wilcox, 1966; Forsyth et al., 1996; Burlaga and Ness, 1997; Borovsky, 2010). In Figure 2 the hourly averaged angle between the magnetic-field-line orientation in the solar wind at Earth and the Parker-spiral direction is binned, with the Parker-spiral direction calculated every hour using the hourly averaged speed of the solar wind (This field-line orientation does not account for the sign of B nor does it consider the sign of B relative to the toward or away sector structure.) The OMNI data set (King and Papitashvili, 2005) for the years 1963–2013 was used. In Figure 2 the distribution of coronal-hole-origin values (red curve) is the most Parker-spiral aligned and the distribution of sector-reversal-region values (purple curve) is the least Parker-spiral aligned. Note that owing to fluctuations in the direction of the magnetic field about the mean Parker-spiral direction, the instantaneous magnetic-field direction (and the hourly averaged field direction) is rarely exactly Parker-spiral aligned (Borovsky, 2010). The facts 1) that the magnetic field is less-Parker-spiral oriented in sector-reversal-region plasma and 2) that the strahl intensity is less intense in sector-reversal-region plasma enforce the notion that the strahl intensity and the field orientation can be indicators of good or poor magnetic connection to the Sun. As will be seen in Strahl Analysis, the strahl intensity and the angle of the magnetic field from the Parker spiral are weakly anti-correlated in the solar wind at 1 AU.
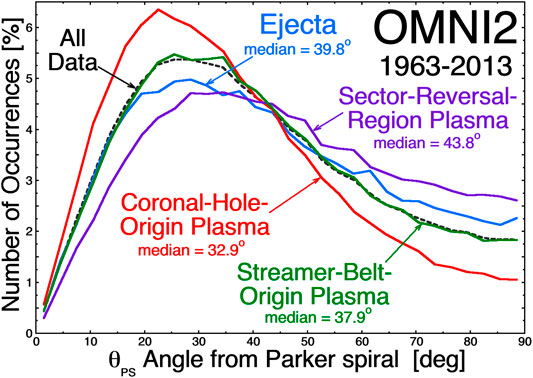
FIGURE 2. For the years 1963–2013, the occurrence distributions at Earth of the hourly averaged angle θPS of the solar-wind magnetic-field orientation with respect to the Parker-spiral direction are plotted for four types of solar-wind plasma (colors) and for all data from 1963 to 2015 (black dashed curve).
Impulsive solar energetic electron (SEE) events at 1 AU are associated with solar x-ray flares, (e.g. Kallenrode and Svestka, 1994; Cliver and Ling, 2007) or near-Sun events (Li et al., 2013) and electrons accelerated near the Sun traveling along the solar-wind magnetic field out to a measuring spacecraft at 1 AU. If one can assume that impulsive SEE events are good indicators of magnetic connectivity to the Sun, then examining the strahl intensity during the early times in impulsive SEE events vs. the strahl intensity when SEE events are not seen could be a test of the viability of using the strahl intensity as a gauge of magnetic connectivity to the Sun. Good connectivity to the Sun may be a valid assumption for impusive SEE events (cf. Figure 2.3b of Reames (1999)) or it might not be a valid assumption (cf. Figure 6 of Wibberenz and Cane (2006)).
Assuming SEE events are well connected to the Sun at early times, to explore other conditions of good magnetic connection 216 impulsive SEE events from the near-Earth catalog of Wang et al., (2012) are used: specifically, the 216 events in the catalog that had peak electron kinetic energies of 310 keV or higher.
In Figure 3 the distribution of the 216 SEE events vs. time is plotted as the red bars, along with the monthly sunspot number (blue) and the daily averaged F10.7 flux (green). As could be expected, since the SEE events are associated with solar flares, the occurrence of the SEE events is concentrated during solar maximum.
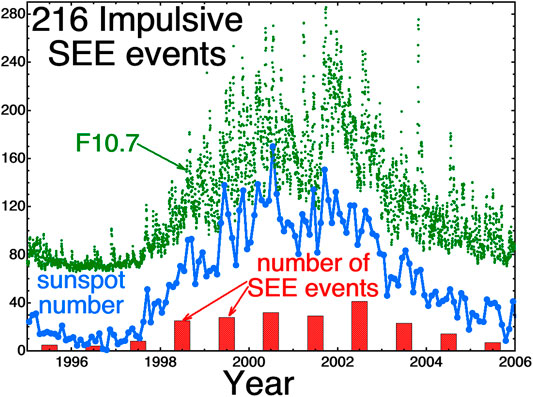
FIGURE 3. For 216 impulsive SEE events from the Wang et al., (2012) catalog, the number of events per year is plotted as the red bars. Also plotted is the monthly sunspot number (blue) and the daily averaged value of F10.7 (green).
In Figure 4 the occurrence distribution of electron-strahl intensities at Earth during the 216 SEE events is plotted as the red curve using hourly averaged values of the strahl intensities from ACE SWEPAM. The black dashed curve plots the distribution of strahl intensities for the years 1998–2013 and the blue curve plots the distribution for the solar-maximum interval 1998–2004 (which is also plotted in Figure 1). Hence, it is probably not the case that there are SEE events at Earth that are missed because the Earth was not magnetically connected to the Sun: it would appear that the Earth tends to have good magnetic connections during solar maximum. As can be seen in Figure 4 the strahl intensities for the 216 SEE events are robust in comparison with the black distribution for all times during the years 1998–2013. One might think that the electron strahl should be intense when solar energetic electrons are present because they are two energies out of the same electron distribution function, but that is not the case: the strahl is a representation of the coronal electron temperature (Bercic et al., 2020; Boldyrev et al., 2020) and the solar energetic electrons are produced by specific temporal acceleration processes (Kallenrode and Svestka, 1994; Cliver and Ling, 2007; Li et al., 2013). Also, for the early times of impulsive SSE events, the 272 eV electrons of the observed strahl at 1 AU left the Sun more than 4.3 h before the flare occurred.
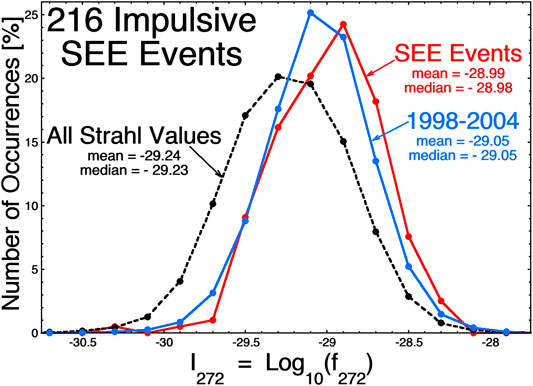
FIGURE 4. For the 216 impulsive SEE events, the distribution of strahl intensities is plotted (red curve). Also plotted is the occurrence distribution of hourly averaged strahl intensities in the 1998–2004 solar maximum (blue curve) and for the years 1998–2013 (black dashed curve).
Using the Xu and Borovsky (2015) categorization scheme, the type of solar-wind plasma that the Earth is in when each of the 216 SEE events were seen is binned as the red bars in Figure 5; also binned is the plasma categorization for the 1998–2004 solar maximum interval (blue bars, right) and for the entire 1963–2017 OMNI2 solar-wind data base (black bars, left). With poor statistics having divided the 216 SEE events into four bins, the occurrence distribution of plasma types for the 216 SEE events (red) is not inconsistent with the occurrence distribution of plasma types for solar maximum (blue): the SEE occurrence distribution is a little higher on ejecta and a little lower on coronal-hole-origin plasma.
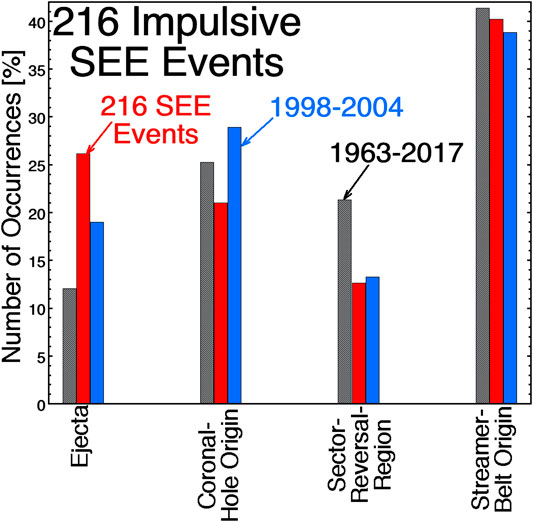
FIGURE 5. The occurrence distribution of the type of solar-wind plasma that the Earth is in when 216 impulsive SEE events occurred is plotted as the red bars (middle). The occurrence distributions of the type of solar-wind plasma the Earth is in are also plotted for the solar-maximum years 1998–2004 (blue, right) and for the years 1963–2017 (black, left).
Magnetic disconnections from the Sun have been indicated by heat-flux dropouts (an absence of an electron strahl), although it has been argued that not all heat-flux dropouts are magnetic disconnections (cf. Lin and Kahler, 1992; Pagel et al., 2005a; Crooker and Pagel, 2008; Chollet et al., 2010). It is of interest to interpret whether the presence or absence of an electron strahl at 1 AU indicates the presence or absence of a magnetic connection to the Sun, or whether the absence of a strahl is caused by the scattering of the strahl between the Sun and 1 AU. To inform this, sudden changes in the intensity of the electron strahl at 1 AU are examined and compared with other simultaneous changes to determine whether the strahl-intensity changes at 1 AU might be associated with changes in the amount of strahl scattering. In the present study the focus of the strahl-change analysis will be on sector-reversal-region plasma with its generally weak strahl intensity; changes of strahl intensity in fast solar wind, (i.e. coronal-hole-origin plasma), (e.g. Hammond et al., 1996; Pagel et al., 2005b; Louarn et al., 2009; Borovsky, 2016) where the strahl intensity stays robust (cf. Figure 1), indicating always a magnetic connection to the corona, are not examined since those variations may not provide information about magnetic disconnections (A future study of the strahl-intensity changes in the coronal-hole-origin solar wind could, however, provide additional information about how to interpret strahl changes.)
Using the 64-sec-resolution ACE plasma SWEPAM and magnetic-field MAG (Smith et al., 1998) data at L1, two examples of strahl changes appear in Figures 6 and 7. The first change, in Figure 6, was a sudden decrease in the strahl intensity at ACE at 1:24 UT on April 4 (Day 94) of 2005. In the top panel the strahl phase space density f272 at 272 eV is plotted in red, the phase-space density in the opposite direction (anti-strahl) is plotted in blue, and the electron phase-space density at 272 eV perpendicular to the magnetic-field direction is plotted in green. The drop in strahl intensity by a factor of about two is denoted by the vertical black dashed line. In the middle panel of Figure 6 a number of plasma parameters are plotted: the proton number density np (green), the proton temperature Tp (purple), the proton specific entropy Sp = Tp/np2/3 (red), the alpha-to-proton number-density ratio α/p (orange), and magnetic-field strength Bmag (blue). Note that simultaneously for this drop in the strahl intensity there is a drop in the proton specific entropy Sp and a drop in the proton temperature Tp. In the bottom panel of Figure 6 some information about the direction of the solar-wind magnetic field is plotted: Δθ (red) is the angular change in the magnetic-field direction every 64 s, θPS 3-D (green) is the angle between the magnetic field and the Parker-spiral direction, and θPS eq (blue) is the angle between the equatorial projection of the magnetic field and the Parker-spiral direction. A large value of Δθ is an indication of a crossing of a strong current sheet: as can be seen in the plot of Δθ, there is a strong current sheet co-located with the change in the strahl intensity (See also Borovsky (2020a) for a statistical study of the co-locations of strahl-intensity changes with strong current sheets.). Note in the bottom panel of Figure 6 that as the strahl intensity decreases, the two calculated angles θPS indicate that the solar-wind magnetic field makes a transition from Parker-spiral aligned to not-Parker-spiral aligned.
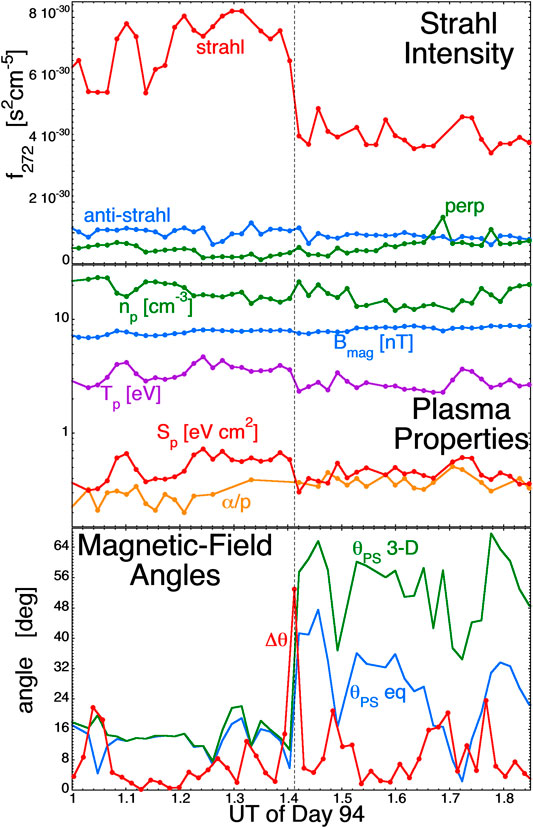
FIGURE 6. An example of a sudden decrease in the strahl intensity (marked by the vertical dashed line) on April 5, 2005.51 min of 64-s-resolution measurements by the instruments on ACE at L1 are plotted. The quantities plotted are described in the text.
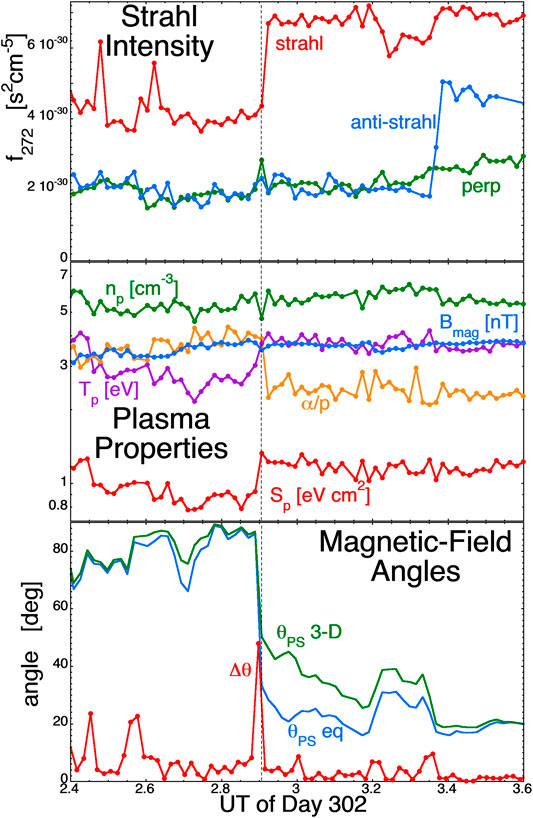
FIGURE 7. An example of a sudden increase in the strahl intensity (marked by the vertical dashed line) on October 29, 2005.72 min of 64-s-resolution measurements by the instruments on ACE at L1 are plotted. The quantities plotted are described in the text.
Figure 7 is similar to Figure 6, where an increase in the strahl intensity occurs in the top panel of Figure 7 at 2:54 UT on October 29 (Day 302) of 2005. That increase is marked by a vertical black dashed line. In the middle panel of Figure 7 the increase in the strahl intensity is accompanied by an increase the proton temperature Tp (purple) and the proton specific entropy Sp (red) and by a decrease in the alpha-to-proton number-density ratio α/p (orange). The bottom panel of Figure 7 indicates the presence of a strong current sheet at the location of the strahl change (the red Δθ curve) and the solar-wind magnetic field makes a transition from a non-Parker-spiral orientation to a more-Parker-spiral orientation.
Two causes of scattering for the electron strahl that have been well explored in the literature are Coulomb scattering (Scudder and Olbert, 1979; Lemons and Feldman, 1983; Boldyrev et al., 2020) and scattering by whistler waves (Gary et al., 1975; Saito and Gary, 2007; Viñas et al., 2010). The different mechanisms can cause scattering of the strahl at different electron energies. The rate of fast-electron angular scattering by Coulomb collisions SCoulomb is proportional to the background number density n of the plasma (cf. eq. (6.4.10) of Krall and Trivelpiece (1973) or Sect. 3 of Tang et al., (2018)), written SCoulomb ∝ n. For strahl angular scattering by whistler turbulence with a fixed amplitude, modeling indicates that the scattering rate is approximately proportional to B3/n times a weak power n/B2, resulting approximately in Swhistler ∝ B2/n1/2 (cf. eq. (B4) of Steinacker and Miller (1992), eq. (8) of Pierrard et al., (2011), or Sect. 3 of Tang et al., (2018)). For angular scattering by kinetic-Alfven-wave turbulence, eq. (30) of Boldyrev and Horiates. (2019) gives SkineticAlfven ∝ n.
Using the 64-sec-resolution ACE plasma SWEPAM and magnetic-field MAG data for the year 2005, 528 strong changes in the intensity of the electron strahl at 1 AU were analyzed: 282 of those 528 strahl changes occurred when the solar-wind plasma was categorized as sector-reversal-region plasma and 246 of the strahl changes occurred in wind with vsw < 460 km/s that was categorized as either ejecta or streamer-belt-origin plasma. This list of jumps collected in 2005 is by no means exhaustive. Only 528 jumps were collected owing to the restrictions 1) that the jumps must occur in sector-reversal-region plasma or in the slow wind surrounding sector-reversal-region plasma, 2) a jump must represent an increase or a decrease in the strahl intensity that is a change in the intensity of about 50% or greater in the timescale of 1 or two data points, 3) that there must be a clear persistence in the strahl intensity for a few minutes both before and after the jump, and 4) there must be strahl and plasma measurements free of nearby data dropouts. This latter restriction was the strongest because validated ACE SWEPAM proton-plasma measurements are typically absent when the solar-wind speed goes very low, as it tends to do in sector-reversal-region plasma. The statistical analysis of the 528 strahl-intensity changes from the year 2005 is summarized in Table 1 and graphically represented in Figure 8.
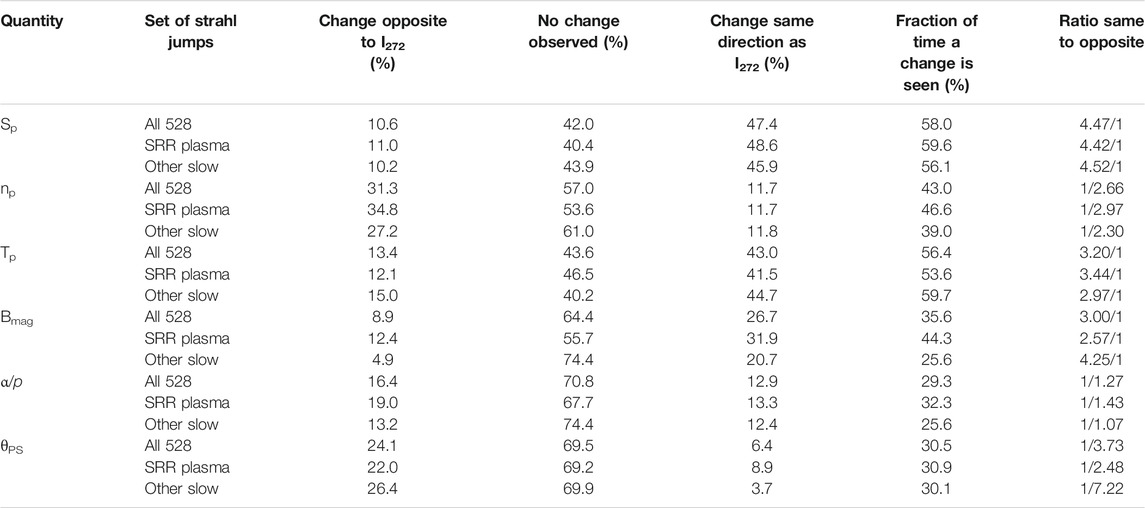
TABLE 1. The statistical connection of strahl-intensity changes to changes in other plasma parameters in the year 2005.
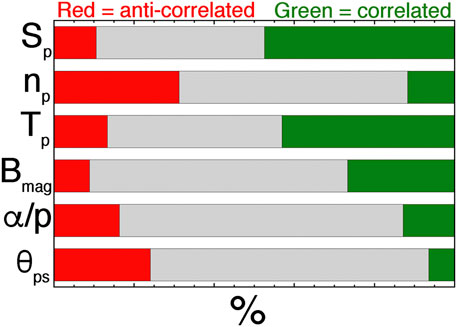
FIGURE 8. For all 528 strahl-intensity changes examined, this is a graphic representation of the data of Table 1 showing the frequency that a variable change was the same sign as the strahl-intensity change (green) and the frequency that a variable change was the opposite sign to the strahl-intensity change (red). Gray represents the per cent of the 528 strahl-intensity changes wherein no substantial change in the other variable was observed.
For the strong changes in the intensity of the electron strahl, attention was paid to the sign of simultaneous changes in the magnetic-field strength Bmag, the proton number density np, the proton temperature Tp, the proton specific entropy Sp = Tp/np2/3, the alpha-to-proton number-density ratio α/p, and the change in the angle θPS between the magnetic-field orientation and the Parker-spiral direction. A change in each of the parameters was only recorded 1) if the parameter exhibited a simultaneous shift (jump) in its magnitude and 2) if the shift change was larger than the fluctuation levels of that parameter prior to and after the change. A change in θPS was only recorded if the field direction strongly changed from an orientation that would definitely be categorized as Parker-spiral-oriented to an orientation that would definitely be categorized as not-Parker-spiral-oriented (a positive change) or if the direction strongly changed from definitely not-Parker-spiral-oriented to definitely Parker-spiral-oriented (a negative change) (These are typically angular changes by greater than 45o). For all 528 changes in the strahl intensity, the statistics of simultaneous changes in those other quantities are collected into Table 1. The first three data columns of Table 1 contain the fraction of time that the change was in the same direction as the strahl-intensity change, (i.e. both simultaneously increasing or both simultaneously decreasing), the fraction of time that the changes were in the opposite directions, and the fraction of time that there was a change in the strahl intensity but no change in the other quantity that was larger than the noise level in the measurements. Each set of three rows in Table 1 represents the statistics for all of the 528 strahl changes, the statistics for the 282 strahl changes in sector-reversal-region plasma, and the statistics for the 246 strahl changes in other slow solar-wind types. Note for each variable that the statistical numbers in Table 1 are similar for each of the three rows: the similarity in the statistics of the 282 sector-reversal-region plasma strahl changes and of the 246 other strahl changes indicates that the statistical results are robust since similar values are obtained for two independent sets of events. For “All 528” rows of Table 1, the first three columns are graphically represented in Figure 8, with green corresponding to changes of the same sign (correlation), red corresponding to changes of the opposite sign (anti-correlation), and gray representing no clear changes observed. The second from the last column of Table 1 is the fraction of strahl-change events that had observed changes in the other quantity of interest. In Table 1 the strongest connections with strahl-intensity changes are for the variables Sp and Tp, with 58% and 56% of the strahl changes being accompanied by changes in these two variables, respectively. Note that only 35.6% of the strahl changes have Bmag changes accompanying them; further, since the Bmag measurements in the ACE 64-sec data set have very low noise, it is easier to find a Bmag change if it occurs than it is with the other plasma variables. Still only 35.6% of the strahl-intensity changes had Bmag changes: hence the connection of Bmag changes to strahl changes is considerably weaker than the connection of other plasma variables to strahl changes. Note also that changes in the angle θPS between the magnetic-field orientation and the Parker-spiral direction are only counted as nonzero if the angle change is very strong, (e.g. going between a very low angle to something greater than 45o or vice versa); hence, in reality the connection of strahl-intensity changes to the transition between Parker-spiral aligned and not Parker-spiral aligned is probably greater than the ∼31o recorded in Table 1.
The final column of Table 1 contains the ratio of the number of changes that were of the same sign as the strahl-intensity change to the number of changes that were of the opposite sign as the strahl-intensity change. Changes in the strahl-intensity were positively correlated with changes in Sp, Tp, and Bmag and changes in the strahl intensity were anti-correlated with changes in np, α/p, and θPS. The strongest connections to the strahl change were for Sp and Tp. For all of the 528 strahl changes, Sp changes that were of the same sign as the strahl-intensity changes were 4.47 times as likely to be found as Sp changes that were of the opposite sign as the strahl change. Hence, same-sign changes are greatly preferred. For Tp that ratio in Table 1 is 3.20 to 1. Bmag changes were 3.0 times as likely to be of the same sign of the strahl-intensity changes than to be of the opposite sign, but Bmag changes were only observed for 35.6% of the strahl changes.
Overall, changes in the alpha-to-proton number-density ratio α/p are poorly connected to strahl-intensity changes, with only 29.3% of the strahl changes having clearly identified changes in α/p, and the number of changes of α/p that were of the same sign as the strahl changes was about equal to the number of α/p changes that were of the opposite sign.
For changes in the strahl intensity caused by changes in the amount of whistler-turbulence scattering of the strahl (with the strength of the scattering going approximately as Swhistler ∝ B2/n1/2), one would expect the strahl intensity to increase when Bmag decreases and/or when np increases: however, Table 1 indicates that the opposite tends to occur for both Bmag and np.
For changes in the strahl intensity caused by changes in the amount of Coulomb scattering or in the amount of kinetic-Alfven-wave turbulence scattering (with SCoulomb ∝ n and with SkineticAlfven ∝ n), one would expect the strahl intensity to increase when the number density np decreases, which is seen in Table 1 strahl-change association between the strahl intensity and np. However, np changes are only seen for 43.0% of the strahl-intensity changes and the changes with Tp and with Sp are stronger than the changes with np. Table 1 yields weak support for strahl scattering by Coulomb collisions or by kinetic Alfven waves.
In the associations of Table 1 there is modest support for the notion that transfers from Parker-spiral-oriented plasma to non-Parker-spiral-oriented plasma result in a decrease in the intensity of the strahl, and that transfers from non-Parker-spiral-oriented plasma to Parker-spiral-oriented plasma result in an increase in the intensity of the strahl.
Note that the relations between changes in the strahl intensity at 1 AU and changes in the plasma properties at 1 AU are examined via Table 1 and interpretations are made; however, the changes across these same strahl-intensity boundaries closer to the Sun than 1 AU may differ in nature from the changes observed at 1 AU across the boundaries.
Further information about the strahl intensity is provided by Tables 2 and 3, which contain the Pearson linear correlation coefficients between the hourly averages of the logarithm of the strahl intensity I272 = Log10 (f272) at Earth and hourly averages of various solar-wind parameters at Earth. The correlations of I272 with solar-wind parameters listed in Tables 2 and 3 are also graphically represented in Figure 9. Tables 2 and 3 also provide information about the intercorrelations among the solar-wind variables. Note that the logarithms of some variables are used in the correlations: for some variables (e.g. np, Sp, Tp, and Bmag) this keeps outlier values from strongly affecting the correlation coefficients and other variables are ratios (e.g. C6+/C4+, C6+/C5+, O7+/O6+, and Fe/O) and using the logarithm of the ratio gives more weight in the correlations to extremely small values of the ratio; in other words, the logarithms of these variables are closer to Gaussian distributed. Table 2 pertains to all solar-wind data and Table 3 pertains to times when the solar wind is categorized as sector-reversal-region plasma. The strahl-correlation information of Tables 2 and 3 is related to, but not exactly the same as, the information in Table 1. The information of Table 1 addresses the question: when the strahl-intensity changes, does a particular plasma quantity X make a change in the same direction? The information of Tables 2 and 3 addresses the question: how well can the value of I272 be predicted if there is a knowledge of the value of the plasma quantity X? Tables 2 and 3 also address the question: are large values of X related to large values of I272 and are small values of X related to small values of I272? Tables 2 and 3 utilize hourly averaged values of the electron strahl from ACE SWEPAM, hourly averaged values of the solar-wind plasma and field parameters from OMNI2, and hourly averaged heavy-ion measurements from ACE SWICS (Gloeckler et al., 1998) (the “1.1” version of the SWICS data set). The strahl values in the years 1998–2013 are used. In Tables 2 and 3 δBvec is the rms amplitude of the vector magnetic-field fluctuations in each hour of data and δBvec/Bmag is the amplitude of the wiggle angle (in radians) of the solar-wind magnetic-field vector during each hour. In Tables 2 and 3 the angle θPS between the magnetic-field direction and the Parker-spiral direction is calculated two ways: 1) the direction of the equatorial projection of the magnetic field from the Parker-spiral direction and 2) the full 3-D direction of the field with respect to the Parker-spiral direction. The latter includes the Bz (or Bn) component of the field. For the sake of correlation coefficients it does not matter, but the logarithms are base-10 logarithms. The statistical noise in the correlation coefficients of Tables 2 and 3 is very low. For N points correlated, the statistical noise level on the correlation coefficient is 2/(N+1)1/2 (Beyer, 1966; Bendat and Piersol, 1971). In Table 2 there are N = 127,130 data points for I272 yielding a statistical noise level of ±0.006 for the correlation coefficients and in Table 3 there are N = 25,569 data points for I272 yielding a statistical noise level of ±0.013 for the correlation coefficients.
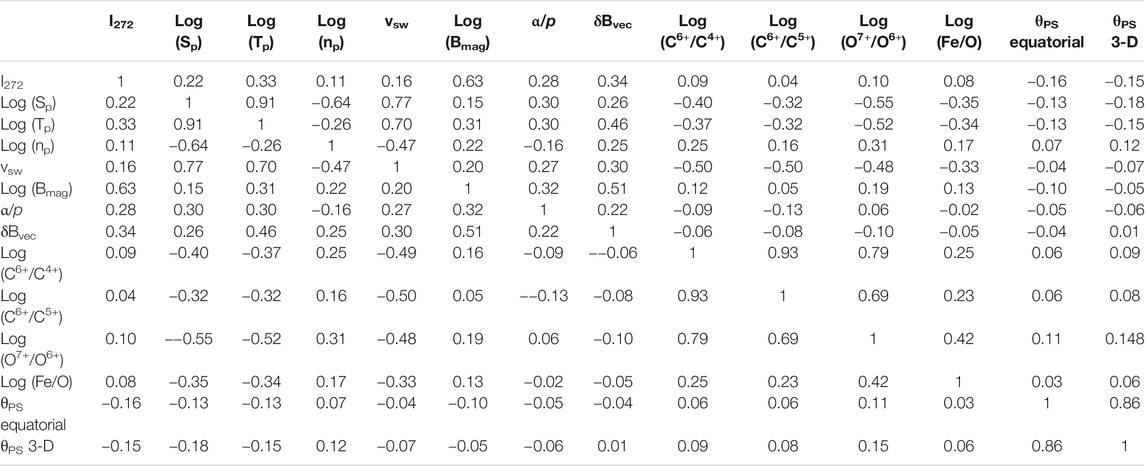
TABLE 2. For all solar-wind data, the Pearson linear correlation coefficients between hourly averaged solar-wind parameters including the strahl intensity I272 = Log10 (f272).
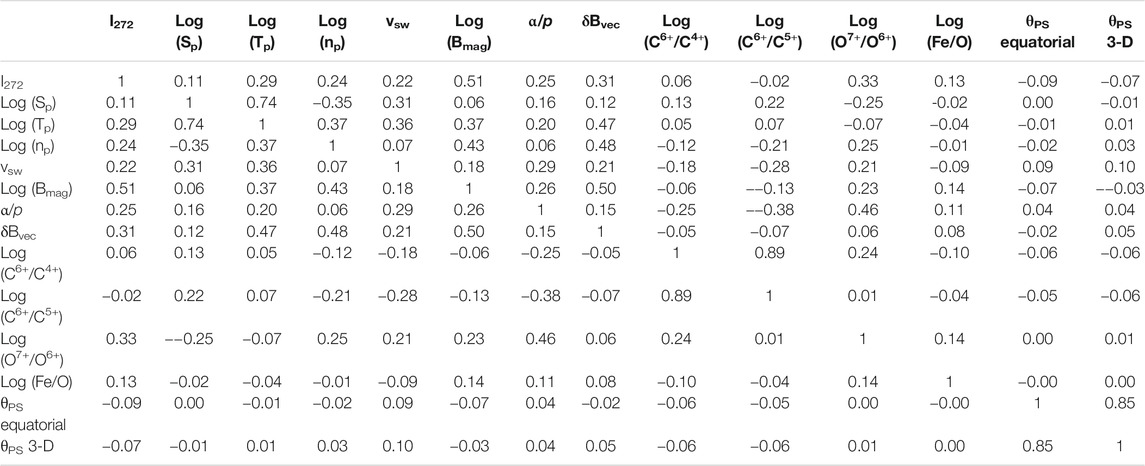
TABLE 3. For sector-reversal-region plasma, the Pearson linear correlation coefficients between hourly averaged solar-wind parameters including the strahl intensity I272 = Log10 (f272).
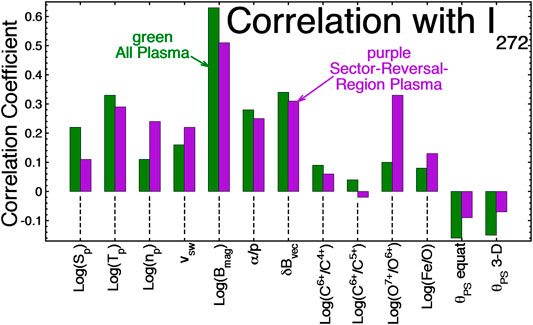
FIGURE 9. The Pearson linear correlation coefficients between I272 and the various solar-wind parameters of Tables 2 and 3 are plotted. The green bars are for all solar-wind data (Table 2) and the purple bars are for sector-reversal-region plasma (Table 3).
Between the all-solar-wind Table 2 and the sector-reversal-region-plasma Table 3 there are often substantial variations of the correlation coefficients between solar-wind variables. In the all-solar-wind correlations of Table 2, many of the correlations and anti-correlations are set up 1) by large-scale compressions and rarefactions of the solar-wind plasma owing to large variations in the solar-wind speed and 2) by solar-rotation-driven sequential switching between plasma types that have systematic differences in their parameters (cf. Borovsky, 2018). In the sector-reversal-region plasma correlations of Table 3, neither of those two mechanisms operate since 1) the range of sector-reversal-region-plasma velocities is quite limited and 2) there is only one type of solar-wind plasma. In general, since the data used in Table 3 is a subset of the data used in Table 2, and since that subset is chosen by restricting the range of some of the solar-wind parameters, the correlation coefficients in Table 3 are expected to be of a lower magnitude than the coefficients in Table 2. Noticeable correlations with I272 that are actually higher in the sector-reversal-region-plasma Table 3 than in the all-wind Table 2 are the correlations of I272 with Log (np), with vsw, and with Log (O7+/O6+) (see also Figure 9).
In Table 3 the strongest correlations of I272 are with Log (Bmag). If the field-aligned flux of the electron strahl is conserved, then a positive correlation between I272 and Bmag is expected, (e.g. in Tables 1–3 and Figure 9); this is very clearly seen in CIR compressions and trailing-edge rarefactions where the magnetic-field lines are squeezed together or expanded apart and the strahl-intensity pattern tracks the magnetic-field-strength pattern (Crooker et al., 2010; Borovsky, 2016). The next strongest I272 correlations in Table 3 are with Log (07+/O6+), δBvec, and Log (Tp) (with δBvec being strongly correlated with Bmag). Comparing the I272 correlations of Table 3 with the strahl-change findings of Table 1, the correlations of Table 3 support the positive correlations of strahl-intensity changes with changes in Sp, Tp, and Bmag and the correlations of Table 3 support the anti-correlations of strahl-intensity changes with changes in θPS. The positive correlations of I272 with np and α/p in Table 3 are counter to Table 1 findings of anti-correlations between changes in the strahl intensity and changes in np and α/p. Of course, in using the correlations of Table 3 as support or not support of the strahl-change trends of Table 1, it must be realized that the factors that drive the large-scale correlation with strahl intensity (Table 3) may not be the same factors that drive the sudden ∼50% strahl-intensity changes of Table 1.
Being aware that different mechanisms can act on different energy electrons in the strahl, examining 272 eV strahl-intensity changes in sector-reversal-region plasma and other slow solar wind (Table 1) found that increases or decreases of the strahl intensity are positively correlated with Sp, Tp, and Bmag increases or decreases and that strahl-intensity increases or decreases are anti-correlated with np, θPS, and α/p increases or decreases. Relevant to the Bmag and α/p anti-correlations, note that 1) most (64.4%) strahl-intensity changes do not show Bmag changes and 2) the association of α/p changes with strahl changes is weak.
The results of the 272 eV strahl-change analysis are inconsistent with a constant-amplitude model for whistler-turbulence scattering of the strahl as the reason for the strahl-intensity changes; for whistler scattering the changes in the strahl intensity should be correlated with np changes and anti-correlated with Bmag changes and the opposite correlations are observed. The 272 eV strahl-change analysis weakly supports Coulomb scattering and/or kinetic-Alfven-wave scattering as the cause of strahl-intensity changes; the support is only weak because the expected strahl-intensity-change anti-correlation with np is not the strongest association with strahl changes (Further, Table 3 solar-wind correlations show that the strahl intensity positively correlates with np.). The strongest connection of strahl-intensity changes is with changes in Tp and Sp, which are not involved in the Coulomb-scatting, whistler-scattering, or kinetic-Alfven-wave scattering scenarios.
The strongest associations with strahl-intensity changes are the positive correlations with changes in Sp and Tp (Table 1). The factors that govern the values of Sp and Tp in the solar wind are not well understood. The value of the proton specific entropy Sp of the solar wind at 1 AU is a strong indicator of the plasma type (cf. Figure 3 of Xu and Borovsky (2015)). Excluding ejecta plasma, the proton temperature Tp of the solar wind at 1 AU is strongly associated with vsw (cf. Figure 1 of Lopez and Freeman (1986), Figure 12 of Borovsky and Steinberg (2006), Figures. 4 and 5 of Elliott et al., (2012)). The proton specific entropy Sp is also strongly positively correlated with vsw (cf. Tables 2 and 3).
In the slower solar wind (such as sector-reversal-region plasma) it is well known that the observed solar-wind velocity vsw systematically increases with distance from the Sun beyond 0.3 AU (Schwenn et al., 1981; Arya and Freeman, 1991): this could be the result of a hot-electron-driven interplanetary ambipolar electric potential accelerating the solar-wind protons away from the Sun (Jockers, 1970; Lemaire, 2010; Pierrard, 2012; Borovsky and Gary, 2014). The strahl-change (Table 1) and strahl-correlation (Table 3) data indicates that weaker sector-reversal-region-plasma strahls are related to weaker proton temperatures and weaker proton specific entropies and the correlation data indicates that weaker strahls are associated with slower solar wind at 1 AU. These correlations could be consistent with weaker electron-driven interplanetary electric field owing to poor magnetic connection to the corona or to connections that produce poor strahl. Note however that the correlation coefficients in Table 3 are weak, indicating that strahl intensity is not the dominant driver of the proton values.
In the all-solar-wind data set (Table 2) Sp is strongly anti-correlated with the heavy-ion charge state ratios C6+/C4+, C6+/C5+, and O7+/O6+, but in sector-reversal-region plasma (Table 3) these correlations become complicated with Sp being anti-correlated with C6+/C4+ and C6+/C5+ and positively correlated with O7+/O6+. The oxygen-charge-state relation to the carbon-charge states differs in sector-reversal-region plasma (and ejecta) from its relation in coronal-hole-origin plasma and streamer-belt-origin plasma (cf. Figures. 10 and 12 of Xu and Borovsky (2015) and Figure 1 of Zhao et al., (2016)); Xu and Borovsky (2015) speculated that this carbon-oxygen charge-state relation is an indicator of impulsive vs. steady emission of plasma from the corona, with sector-reversal-region plasma being impulsive at times.
The strahl-change analysis also finds an anti-correlation between changes in the strahl intensity and changes in the angle θPS of the magnetic field from the Parker-spiral direction: this is consistent with stronger strahl in Parker-spiral plasma (continuously emitted with open magnetic flux from the corona) vs. non-Parker-spiral plasma (impulsively emitted, perhaps with magnetic disconnections). There may, however, be magnetic-pathlength differences between Parker-spiral fields and non-Parker-spiral fields that might also be playing a role in the 1-AU strahl intensity.
Examining the sudden changes in the intensity of the electron strahl at 1 AU accompanied by sudden changes in the magnetic-field direction, Gosling et al., (2004A,B) speculated that abrupt changes in the strahl intensity are the manifestations of abrupt changes in the mapping of the solar-wind magnetic field back to the corona. In the strahl-change statistics of Table 1, strong changes in the field direction from Parker-spiral oriented to non-Parker-spiral oriented could account for ∼25% of the strahl changes. This change in connection to the corona is also supported by the plasma-property changes found to accompany strahl-intensity changes (Table 1) (However in Table 1 the weakest connection of strahl change is with α/p, which should change with magnetic connection to the corona.) Further, this change-in-magnetic-connection picture is supported by the above-the-corona MHD simulations of Burkholder et al., (2019) where current sheets in the plasma represent topological changes in the magnetic mapping back to the photosphere.
Sector-reversal-region plasma at 1 AU is characterized by a wide range of low strahl intensities and by sudden changes in the strahl intensity. Analysis of the strahl-intensity changes at 1 AU imply that the changes in the strahl intensity are caused by changes in the magnetic connection to the corona. When the strahl-intensities change to low values a question is: Which low values represent a lack of magnetic connection to the Sun and which low values are caused by something else? A related question is: Why is the strahl intensity so low if it is still magnetically connected to the corona?
Analysis of strahl intensity during impulsive SEE events was used to test the idea that strahl presence or absence could be used to assess the magnetic connection to the Sun. This test was based on the assumption that SEE events at Earth can only occur when the Earth is well connected magnetically to the Sun. The SEE test was not helpful in making the assessment: SEE event occur during solar maximum and the analysis found that the strahl is almost always strong during solar maximum.
To assess the quality of the magnetic connection between the near-Earth solar wind and the Sun, three tools have been explored: 1) using the strahl intensity, 2) using the orientation θPS of the solar-wind magnetic field with respect to the Parker-spiral direction, and 3) using the type of solar-wind plasma. Using the strahl intensity is the most promising, although questions remain when the strahl intensity at 1 AU is low: 1) is the magnetic field disconnected from the Sun, 2) is the magnetic field connected to a region of the corona that is producing poor strahl, or 3) has the strahl been destroyed between the Sun and 1 AU? Using the magnetic-field orientation θPS, along with an observation of the strahl intensity, provides more indication of whether or not the magnetic field is disconnected from the Sun. Using the plasma categorization “sector-reversal-region plasma” (with the categorization made using only proton measurements and the magnetic-field strength (Xu and Borovsky, 2015)) gives an indication of generally weak and intermittent strahl and the probability of an in-general poor or intermittent magnetic connection to the Sun.
Five suggestions are given for future research, mostly focused on the changes in strahl-intensity. 1) An examination is needed of the connection between strahl-intensity changes and the heavy-ion charge-state ratios of the solar-wind plasma. Such information is important in determining the nature of the change in the magnetic connection into the corona that may be occurring when there is a change in the strahl intensity and a change in the magnetic-field orientation. Such an examination has been recently enabled by the heavy-ion measurements onboard Solar Orbiter with ≤30-s time resolution (Owen et al., 2020), measurements that are an order of magnitude faster than on previous solar-wind missions. 2) Examination of strahl changes on spacecraft closer to the Sun is important for a better determination of the interpretation of strahl-intensity changes. An analysis with Parker Solar Probe in particular will be helpful, especially after a substantial data base is collected. 3) Often at 1 AU a sudden change is seen in the intensity of the anti-strahl: this change can be simultaneous with a change in the strahl or it can occur without a change in the strahl (An example of this can be seen at 3.37 UT in the blue curve the top panel of Figure 7.) A statistical examination of anti-strahl intensity changes might provide insight into the physics of strahl changes. It is also a method of exploring the magnetic topology beyond 1 AU. 4) The connection of strahl-intensity changes to whistler scattering made in the present study are based on a model of whistler scattering in the heliosphere that does not account for factors that could control the whistler-turbulence amplitude in the solar wind. Improvements in the prediction of the solar-wind parameters that control the amplitude of whistler turbulence in the solar wind and the resulting electron scattering are needed for an improved assessment of the role of whistlers in the observed strahl-intensity changes. 5) Another possible reason why a strahl may not be detected at 1 AU is because of plasma-wave instabilities that may have disrupted the strahl, (e.g. Gary and Saito, 2007; Kuzichev et al., 2019; Lopez et al., 2019; Vasko et al., 2019; Versharen et al., 2019; Jeong et al., 2020; Micera et al., 2020). Parameterization of instability thresholds is needed and then a matching of strahl-change locations with plasma-parameter changes is needed to test the instability possibility.
Publicly available datasets were analyzed in this study. This data can be found here: http://www.srl.caltech.edu/ace/ASC/.
The author confirms being the sole contributor of this work and has approved it for publication.
This work was supported by the NSF SHINE program via grant AGS-1723416, by the NASA Heliophysics Guest Investigator Program via award NNX17AB71G, by the NSF GEM Program via grant AGS-2027569, and by the NASA Heliophysics LWS program via award NNX16AB75G.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author thanks Stas Boldyrev, Ed Cliver, Larry Kepko, Ruth Skoug, John Steinberg, Nikki Vial for help and helpful conversations.
Amaya, J., Dupus, R., Innocenti, M. E., and Lapenta, G. (2020). Visualizing and interpreting unsupervised solar wind classifications. Front. Astron. Space Sci. 7, 553207. doi:10.3389/fspas.2020.553207
Arya, S., and Freeman, J. W. (1991). Estimates of solar wind velocity gradients between 0.3 and 1 AU based on velocity probability distributions from Helios 1 at perihelion and aphelion. J. Geophys. Res. 96, 14183. doi:10.1029/91ja01135
Bemporad, A., Sterling, A. C., Moore, R. L., and Poletto, G. (2005). A new variety of coronal mass ejection: streamer puffs from compact ejective flares. Astrophys. J. 635, L189. doi:10.1086/499625
Bendat, J. S., and Piersol, A. G. (1971). Random data: analysis and measurement procedures. New York, NY, United States: John Wiley, Sect. 4.8.1.
Bercic, L., Larson, D., Whittlesey, P., Maksimovic, M., Badman, S. T., Landi, S., et al. (2020). Coronal electron temperature inferred from the strahl electrons in the inner heliosphere: Parker Solar Probe and Helios observations. Astrophys. J. 892, 88. doi:10.3847/1538-4357/ab7b7a
Beyer, W. H. (1966). Handbook of Tables for Probability and statistics. Sect. IX. Cleveland, OH, United States: Chemical Rubber Company.
Bloch, T., Watt, C., Owens, M., McInnes, L., and Macneil, A. R. (2020). Data-driven classification of coronal hole and streamer belt solar wind. Solar Phys. 295, 41. doi:10.1007/s11207-020-01609-z
Boldyrev, S., Forest, C., and Egedal, J. (2020). Electron temperature of the solar wind. Proc. Natl. Acad. Sci. United States 117, 9232. doi:10.1073/pnas.1917905117
Boldyrev, S., and Horaites, K. (2019). Kinetic theory of the electron strahl in the solar wind. MNRAS 489, 3412. doi:10.1093/mnras/stz2378
Borovsky, J. E. (2010). On the variations of the solar wind magnetic field about the Parker spiral direction. J. Geophys. Res. 115, A09101. doi:10.1029/2009ja015040
Borovsky, J. E. (2016). The plasma structure of coronal hole solar wind: origins and evolution. J. Geophys. Res. 121, 5055. doi:10.1002/2016ja022686
Borovsky, J. E. (2017). Time-integral correlations of multiple variables with the relativistic-electron flux at geosynchronous orbit: the strong roles of the substorm-injected electrons and the ion plasma sheet. J. Geophys. Res. 122, 11961. doi:10.1002/2017ja024476
Borovsky, J. E. (2018). On the origin of the intercorrelations between solar-wind variables. J. Geophys. Res. 123, 20. doi:10.1002/2017ja024650
Borovsky, J. E. (2020a). The magnetic structure of the solar wind: ionic composition and the electron strahl. Geophys. Res. Lett. 47, e2019GL084586. doi:10.1029/2019gl084586
Borovsky, J. E. (2020b). Plasma and magnetic-field structure of the solar wind at inertial-range scale sizes discerned from statistical examinations of the time-series measurements. Front. Astron. Space Sci. 7, 20. doi:10.3389/fspas.2020.00020
Borovsky, J. E., and Gary, S. P. (2014). How important are the alpha-proton relative drift and the electron heat flux for the proton heating of the solar wind in the inner heliosphere?. J. Geophys. Res. 119, 5210. doi:10.1002/2014ja019758
Borovsky, J. E., and Steinberg, J. T. (2006). The freestream turbulence effect in solar-wind/magnetosphere coupling: analysis through the solar cycle and for various types of solar wind. Geophys. Monog. Ser. 167, 59. doi:10.1029/167gm07
Bruno, R., and Bavassano, B. (1997). On the winding of the IMF spiral for slow and fast wind within the inner heliosphere. Geophys. Res. Lett. 24, 2267. doi:10.1029/97gl02183
Burkholder, B. L., Otto, A., Delamere, P. A., and Borovsky, J. E. (2019). Magnetic connectivity in the corona as a source of structure in the solar wind. J. Geophys. Res. 124, 32. doi:10.1029/2018ja026132
Burlaga, L. F., and Ness, N. F. (1997). Global patterns of heliospheric magnetic field polarities and elevation angles: 1990 through 1995. J. Geophys. Res. 102, 19731. doi:10.1029/97ja01568
Camporeale, E., Care, A., and Borovsky, J. E. (2017). Classification of solar wind with machine learning. J. Geophys. Res. 122, 10910. doi:10.1002/2017ja024383
Chollet, E. E., and Giacalone, J. (2011). Evidence of confinement of solar-energetic particles to interplanetary magnetic field lines. Astrophys. J. 728, 64. doi:10.1088/0004-637x/728/1/64
Chollet, E., Skoug, R., Steinberg, J., Crooker, N., and Giacalone, J. (2010). Reconnection and disconnection: observations of suprathermal electron heat flux dropouts. AIP Conf. Proc. 1216, 600. doi:10.1063/1.3395937
Cliver, E. W., and Ling, A. G. (2007). Electrons and protons in solar energetic particle events. Astrophys. J. 658, 1349. doi:10.1086/511737
Crooker, N. U., Gosling, J. T., and Kahler, S. W. (2002). Reducing heliospheric magnetic flux from coronal mass ejections without disconnection. J. Geophys. Res. 107, 1028. doi:10.1029/2001ja000236
Crooker, N. U., Huang, C.-L., Lamassa, S. M., Larson, D. E., Kahler, S. W., and Spence, H. E. (2004). Heliospheric plasma sheets. J. Geophys. Res. 109, A03107. doi:10.1029/2003ja010170
Crooker, N. U., and Owens, M. J. (2012). Interchange reconnection: remote sensing of solar signature and role in heliospheric magnetic flux budget. Space Sci. Rev. 172, 201. doi:10.1007/s11214-011-9748-1
Crooker, N. U., and Pagel, C. (2008). Residual strahls in solar wind electron dropouts: signatures of magnetic connection to the Sun, disconnection, or interchange reconnection? J. Geophys. Res. 113, A02106. doi:10.1029/2007ja012421
Elliott, H. A., Henney, C. J., McComas, D. J., Smith, C. W., and Vasquez, B. J. (2012). Temporal and radial variation of the solar wind temperature-speed relationship. J. Geophys. Res. 117, A09102. doi:10.1029/2011ja017125
Feldman, W. C., Asbridge, J. R., Bame, S. J., Gary, S. P., Montgomery, M. D., and Zink, S. M. (1976). Evidence for the regulation of solar wind heat flux at 1 AU. J. Geophys. Res. 81, 5207. doi:10.1029/ja081i028p05207
Fisk, L. A. (2001). On the global structure of the heliospheric magnetic field. J. Geophys. Res. 106, 15849. doi:10.1029/2000ja000117
Forsyth, R. J., Balogh, A., Smith, E. J., Erdös, G., and McComas, D. J. (1996). The underlying Parker spiral structure in the Ulysses magnetic field observations, 1990-1994. J. Geophys. Res. 101, 395. doi:10.1029/95ja02977
Foullon, C., Lavraud, B., Luhmann, J. G., Farrugia, C. J., Retino, A., Simunac, K. D. C., et al. (2011). Plasmoid releases in the heliospheric current sheet and associated coronal hole boundary layer evolution. Astrophys. J. 737, 16. doi:10.1088/0004-637x/737/1/16
Gary, S. P., Feldman, W. C., Forslund, D. W., and Montgomery, M. D. (1975). Electron heat flux instabilities in the solar wind. Geophys. Res. Lett. 2, 79–82. doi:10.1029/gl002i003p00079
Gary, S. P., and Saito, S. (2007). Broadening of solar wind strahl pitch-angles by the electron/electron instability: particle-in-cell simulations. Geophys. Res. Lett. 34, L14111. doi:10.1029/2007gl030039
Georgieva, K., Kirov, B., Javaraiah, J., and Krasteva, R. (2005). Solar rotation and solar wind-magnetosphere coupling. Planet. Space Sci. 53, 197. doi:10.1016/j.pss.2004.09.045
Gloeckler, G., Cain, J., Ipavich, F. M., Tums, E. O., Bedini, P., Fisk, L. A., et al. (1998). Investigation of the composition of solar and interstellar matter using solar wind and pickup ion measurements with SWICS and SWIMS on the ACE spacecraft. Space Sci. Rev. 86, 497. doi:10.1007/978-94-011-4762-0_18
Gosling, J. T., de Koning, C. A., Skoug, R. M., Steinberg, J. T., and McComas, D. J. (2004a). Dispersionless modulations in low-energy solar electron bursts and discontinuous changes in the solar wind electron strahl. J. Geophys. Res. 109, A05102. doi:10.1029/2003ja010338
Gosling, J. T., Skoug, R. M., McComas, D. J., and Mazur, J. E. (2004b). Correlated dispersionless structure in suprathermal electrons and solar energetic ions in the solar wind. Astrophys. J. 614, 412. doi:10.1086/423368
Gosling, J. T., Skoug, R. M., McComas, D. J., and Smith, C. W. (2005). Magnetic disconnection from the Sun: observations of a reconnection exhaust in the solar wind at the heliospheric current sheet. Geophys. Res. Lett. 32, L05105. doi:10.1029/2005gl022406
Gosling, J. T., and Skoug, R. M. (2002). On the origin of radial magnetic fields in the heliosphere. J. Geophys. Res. 107, 1327. doi:10.1029/2002ja009434
Hammond, C. M., Feldman, W. C., McComas, D. J., Phillips, J. L., and Forsyth, R. J. (1996). Variation of electron-strahl width in the high-speed solar wind: ulysses observations. Aston. Astrophys. 316, 350–354.
Heidrich-Meisner, V., Berger, L., and Wimmer-Schweingruber, R. F. (2020). Proton-proton collisional age to order solar wind types. Astron. Astrophys. 636, A103. doi:10.1051/0004-6361/201937378
Jeong, S.-Y., Verscharen, D., Wicks, R. T., and Fazakerley, A. N. (2020). A quasi-linear diffusion model for resonant wave-particle instability in homogeneous plasma. Astrophys. J. 902, 128. doi:10.3847/1538-4357/abb099
Kallenrode, M.-B., and Švestka, Z. (1994). The participation of nuclei in type-III-related electron streams. Sol. Phys. 155, 121. doi:10.1007/bf00670735
Kepko, L., and Spence, H. E. (2003). Observations of discrete, global magnetospheric oscillations directly driven by solar wind density variations. J. Geophys. Res. 108, 1257. doi:10.1029/2002ja009676
Kepko, L., Viall, N. M., Antiochos, S. K., Lepri, S. T., Kasper, J. C., and Weberg, M. (2016). Implications of L1 observations for slow solar wind formation by solar reconnection. Geophys. Res. Lett. 43, 4089. doi:10.1002/2016gl068607
Kepko, L., and Viall, N. M. (2019). The source, significance, and magnetospheric impact of periodic density structures within stream interaction regions. J. Geophys. Res. 124, 2019JA026962. doi:10.1029/2019ja026962
King, J. H., and Papitashvili, N. E. (2005). Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. 110, 2104. doi:10.1029/2004ja010649
Krall, N. A., and Trivelpiece, A. W. (1973). Principles of plasma physics. New York, NY, United States: McGraw-Hill.
Kuzichev, I. V., Vasko, I. Y., Soto-Chavez, A. R., Tong, Y., Artemyev, A. V., Bale, S. D., et al. (2019). Nonlinear evolution of the whistler heat flux instability. Astrophys. J. 882, 81. doi:10.3847/1538-4357/ab3290
Lavraud, B., Fargette, N., Reville, V., Szabo, A., Huang, J., Ruillard, A. P., et al. (2020). The heliospheric current sheet and plasma sheet during Parker Solar Probe’s first orbit. Astrophys. J. Lett. 894, L19. doi:10.3847/2041-8213/ab8d2d
Lavraud, B., Gosling, J. T., Rouillard, A. P., Fedorov, A., Opitz, A., Sauvaud, J.-A., et al. (2009). Observations of a complex solar wind reconnection exhaust from spacecraft separated by over 1800 RE. Sol. Phys. 256, 379. doi:10.1007/s11207-009-9341-x
Lemaire, J. (2010). Half a century of kinetic solar wind models. AIP Conf. Proc. 1216, 8. doi:10.1063/1.3395971
Lemons, D. S., and Feldman, W. C. (1983). Collisional modification to the exospheric theory of solar wind halo electron pitch angle distributions. J. Geophys. Res. 88, 6881. doi:10.1029/ja088ia09p06881
Li, C., Sun, L. P., Wang, X. Y., and Dai, Y. (2013). Coronal magnetic topology and the production of solar impulsive energetic electrons. Astron. Astrophys. 556, L2. doi:10.1051/0004-6361/201322072
Li, H., Wang, C., Tu, C., and Xu, F. (2020). Machine learning approach for solar wind categorization. Earth Space Sci. 7, e2019EA000997. doi:10.1029/2019ea000997
Lin, R. P., and Kahler, S. W. (1992). Interplanetary magnetic field connection to the Sun during electron heat flux dropouts in the solar wind. J. Geophys. Res. 97, 8203. doi:10.1029/92ja00230
Lockwood, M. (2013). Reconstruction and prediction of variations in the open solar magnetic flux and interplanetary conditions. Living Rev. Solar Phys. 10, 4. doi:10.12942/lrsp-2013-4
Lopez, R. E., and Freeman, J. W. (1986). Solar wind proton temperature-velocity relationship. J. Geophys. Res. 91, 1701. doi:10.1029/ja091ia02p01701
Louarn, P., Diéval, C., Génot, V., Lavraud, B., Opitz, A., Fedorov, A., et al. (2009). On the temporal variability of the “strahl” and its relationship with solar wind characteristics: STEREO SWEA observations. Sol. Phys. 259, 311–321. doi:10.1007/s11207-009-9402-1
Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., Issautier, K., Scime, E. E., Littleton, J. E., et al. (2005). Radial evolution of the electron distribution functions in the fast solar wind between 0.3 and 1.5 AU. J. Geophys. Res. 110, A09104. doi:10.1029/2005ja011119
Mazur, J. E., Mason, G. M., Dwyer, J. R., Giacalone, J., Jokipii, J. R., and Stone, E. C. (2000). Interplanetary magnetic field line mixing deduced from impulsive solar flare particles. Astrophys. J. 532, L79. doi:10.1086/312561
McComas, D. J., Bame, S. J., Barker, P., Feldman, W. C., Phillips, J. L., Riley, P., et al. (1998). Solar wind electron proton alpha monitor (SWEPAM) for the advanced composition explorer. Space Sci. Rev. 86, 563. doi:10.1007/978-94-011-4762-0_20
McComas, D. J., Gosling, J. T., Phillips, J. L., Bame, S. J., Luhmann, J. G., and Smith, E. J. (1989). Electron heat flux dropouts in the solar wind: evidence for interplanetary magnetic field reconnection?. J. Geophys. Res. 94, 6907. doi:10.1029/ja094ia06p06907
Micera, A., Zhukov, A. N., López, R. A., Innocenti, M. E., Lazar, M., Boella, E., et al. (2020). Particle-in-cell simulation of whistler heat-flux instabilities in the solar wind: heat-flux regulation and electron halo formation. Astrophys. J. Lett. 903, L23. doi:10.3847/2041-8213/abc0e8
Murphy, N., Smith, E. J., and Schwadron, N. A. (2002). Strongly underwound magnetic fields in co-rotating rarefaction regions: observations and implications. Geophys. Res. Lett. 29, 2066. doi:10.1029/2002gl015164
Ness, N. F., and Wilcox, J. M. (1966). Extension of the photospheric magnetic field into interplanetary space. Astrophys. J. 143, 23. doi:10.1086/148473
Neugebauer, M., Reisenfeld, D., and Richardson, I. G. (2016). Comparison of algorithms for determination of solar wind regimes. J. Geophys. Res. 121, 8215. doi:10.1002/2016ja023142
Neugebauer, M., Steinberg, J. T., Tokar, R. L., Barraclough, B. L., Dors, E. E., Wiens, R. C., et al. (2003). Genesis on-board determination of the solar wind flow regime. Space Sci. Rev. 105, 661. doi:10.1023/a:1024478129261
Owen, C. J., Bruno, R., Livi, S., Louarn, P., and Al Janabi, K. (2020). The solar orbiter solar wind analyzer (SWA) suite. Astron. Astrophys. 642, A16. doi:10.1051/0004-6361/201937259
Pagel, C., Crooker, N. U., and Larson, D. E. (2005a). Assessing electron heat flux dropouts as signatures of magnetic field line disconnection from the sun. Geophys. Res. Lett. 32, L14105. doi:10.1029/2005gl023043
Pagel, C., Crooker, N. U., Larson, D. E., Kahler, S. W., and Owen, M. J. (2005b). Understanding electron heat flux signatures in the solar wind. J. Geophys. Res. 110, A01103. doi:10.1029/2004ja010767
Parker, E. N. (1958). Dynamics of the interplanetary gas and magnetic fields. Astrophys. J. 128, 664. doi:10.1086/146579
Pierrard, V., Lazar, M., and Schlickeiser, R. (2011). Evolution of the electron distribution function in the whistler wave turbulence of the solar wind. Sol. Phys. 269, 421. doi:10.1007/s11207-010-9700-7
Pierrard, V. (2012). Solar wind electron transport: interplanetary electric field and heat conduction. Space Sci. Rev. 172, 315. doi:10.1007/s11214-011-9743-6
Pilipp, W. G., Miggenrieder, H., Montgomery, M. D., Mühlhäuser, K.-H., Rosenbauer, H., and Schwenn, R. (1987). Characteristics of electron velocity distribution functions in the solar wind derived from the Helios Plasma experiment. J. Geophys. Res. 92, 1075. doi:10.1029/ja092ia02p01075
Reames, D. V. (1999). Particle acceleration at the Sun and in the heliosphere. Space Sci. Rev. 90, 413. doi:10.1023/a:1005105831781
Reisenfeld, D. B., Steinberg, J. T., Barraclough, B. L., Dors, E. E., Weins, R. C., Neugebauer, M., et al. (2003). Comparison of the Genesis solar wind regime algorithm results with solar wind composition observed by ACE. AIP Conf. Proc. 679, 632. doi:10.1063/1.1618674
Riley, P., and Gosling, J. T. (2007). On the origin of near-radial magnetic fields in the heliosphere: numerical simulations. J. Geophys. Res. 112, A06115. doi:10.1029/2006ja012210
Rouillard, A. P., Davies, J. A., Lavraud, B., Forsyth, R. J., Savani, N. P., Bewsher, D., et al. (2010). Intermittent release of transients in the slow solar wind: 1. Remote sensing observations. J. Geophys. Res. 115, A04103. doi:10.1029/2009ja014471
Rouillard, A. P., Kouloumvakos, A., Vourlidas, A., Kasper, J., Bale, S., Raouafi, N.-E., et al. (2020). Relating streamer flows to density and magnetic structures at the parker solar robe. Astrophys. J. Suppl. Ser. 246, 37. doi:10.3847/1538-4365/ab579a
Saito, S., and Gary, S. P. (2007). All whistlers are not created equally: scattering of strahl electrons in the solar wind via particle-in-cell simulations. Geophys. Res. Lett. 34, L01102. doi:10.1029/2006gl028173
Sanchez-Diaz, E., Rouillard, A. P., Lavraud, B., Kilpua, E., and Davies, J. A. (2019). In Situ measurements of the variable slow solar wind near sector boundaries. Astrophys. J. 882, 51. doi:10.3847/1538-4357/ab341c
Schwenn, R., Muhlhauser, K.-H., Marsch, E., and Rosenbauer, H. (1981). Two states of the solar wind at the time of solar activity minimum II. Radial gradients of plasma parameters in fast and slow streams. Solar wind four, MPAE-W-100-81-31. Lindau, Germany: Max Planck Institut fur Aeronomie. 126.
Scudder, J. D., and Olbert, S. (1979). A theory of local and global processes which affect solar wind electrons, 1. The origin of typical 1 AU velocity distribution functions-Steady state theory. J. Geophys. Res. 84, 2755. doi:10.1029/ja084ia06p02755
Sheeley, N. R., Lee, D. D.-H., Casto, K. P., Wang, Y.-M., and Rich, N. B. (2009). The structure of streamer blobs. ApJ 694, 1471. doi:10.1088/0004-637x/694/2/1471
Sheeley, N. R., and Rouillard, A. P. (2010). Tracking streamer blobs into the heliosphere. ApJ 715, 300. doi:10.1088/0004-637x/715/1/300
Smith, C. W., and Bieber, J. W. (1991). Solar cycle variation of the interplanetary magnetic field spiral. Astrophys. J. 370, 435. doi:10.1086/169830
Smith, C. W., Acuna, M. H., Burlaga, L. F., L’Heureux, J., Ness, N. F., and Scheifele, J. (1998). The ACE magnetic fields experiment. Space Sci. Rev. 86, 611. doi:10.1023/a:1005092216668
Steinacker, J., and Miller, J. A. (1992). Stochastic gyroresonant electron acceleration in a low-beta plasma. I - interaction with parallel transverse cold plasma waves. Astrophys. J. 393, 764. doi:10.1086/171544
Tang, B., Zank, G. P., and Kolobov, V. (2018). Numerical modeling of electron transport in solar wind: effects of whistler turbulence and Coulomb collisions. J. Phys. Conf. Ser. 1100, 012025. doi:10.1088/1742-6596/1100/1/012025
Trenchi, L., Bruno, R., Telloni, D., D’amicis, R., Marcucci, M. F., Zurbuchen, T. H., et al. (2013). Solar energetic particle modulations associated with coherent magnetic structures. Astrophys. J. 770, 11. doi:10.1088/0004-637x/770/1/11
Versharen, D., Chandran, B. D. G., Jeong, S.-Y., Salem, C. S., Pulupa, M. P., and Bale, S. D. (2019). Self-induced scattering of strahl electrons in the solar wind. Astrophys. J. 886, 136. doi:10.3847/1538-4357/ab4c30
Veselovsky, I. S., Lukashenko, A. T., and Kaportseva, K. B. (2018). Classification scheme for solar wind. Phys. Atom. Nuclei 81, 766. doi:10.1134/s1063778818050186
Viall, N. M., and Borovsky, J. E. (2020). Nine outstanding questions of solar wind physics. J. Geophys. Res. 125, e2018JA026005. doi:10.1029/2018ja026005
Viall, N. M., Kepko, L., and Spence, H. E. (2009). Relative occurrence rates and connection of discrete frequency oscillations in the solar wind density and dayside magnetosphere. J. Geophys. Res. 114, A01201. doi:10.1029/2008ja013334
Viall, N. M., Spence, H. E., Vourlidas, A., and Howard, R. (2010). Examining periodic solar‐wind density structures observed in the SECCHI Heliospheric imagers. Sol. Phys. 267, 175. doi:10.1007/s11207-010-9633-1
Viall, N. M., and Vourlidas, A. (2015). Periodic density structures and the origin of the slow solar wind. Astrophys. J. 807, 176. doi:10.1088/0004-637x/807/2/176
Viñas, A. F., Gurgiolo, C., Nieves-Chinchilla, T., Gary, S. P., and Goldstein, M. L. (2010). Whistler waves driven by anisotropic strahl velocity distributions: cluster observations. AIP Conf. Proc. 1216, 265. doi:10.1063/1.3395852
Wang, Y.-M., Sheeley, N. R., Howard, R. A., Rich, N. B., and Lamy, P. L. (1999). Streamer disconnection events observed with the LASCO coronagraph. Geophys. Res. Lett. 26, 1349. doi:10.1029/1999gl900177
Wang, Y.-M., Sheeley, N. R., Socker, D. G., Howard, R. A., and Rich, N. B. (2000). The dynamical nature of coronal streamers. J. Geophys. Res. 105, 25113. doi:10.1029/2000ja000149
Wang, L., Lin, R. P., Krucker, S., and Mason, G. M. (2012). A statistical study of solar electron events over one solar cycle. Astrophys. J. 759, 69. doi:10.1088/0004-637x/759/1/69
Wibberenz, G., and Cane, H. V. (2006). Multi‐spacecraft observations of solar flare particles in the inner heliosphere. Astrophys. J. 650, 1199. doi:10.1086/506598
Xu, F., and Borovsky, J. E. (2015). A new four-plasma categorization scheme for the solar wind. J. Geophys. Res. 120, 70. doi:10.1002/2014ja020412
Zhao, L., Zurbuchen, T. H., and Fisk, L. A. (2009). Global distribution of the solar wind during solar cycle 23: ACE observations. Geophys. Res. Lett. 36, L14104. doi:10.1029/2009gl039181
Keywords: solar wind, heliosphere, corona, strahl, space weather
Citation: Borovsky JE (2021) Exploring the Properties of the Electron Strahl at 1 AU as an Indicator of the Quality of the Magnetic Connection Between the Earth and the Sun. Front. Astron. Space Sci. 8:646443. doi: 10.3389/fspas.2021.646443
Received: 26 December 2020; Accepted: 29 January 2021;
Published: 05 March 2021.
Edited by:
Daniele Telloni, National Institute of Astrophysics (INAF), ItalyReviewed by:
Daniel Verscharen, University College London, United KingdomCopyright © 2021 Borovsky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph E. Borovsky, amJvcm92c2t5QHNwYWNlc2NpZW5jZS5vcmc=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.