
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci. , 04 May 2021
Sec. Astrochemistry
Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.641067
This article is part of the Research Topic Theoretical Characterization of Astrophysical Species View all 8 articles
The thionitroxyl radical (H2NS) isomers are characterized using advanced ab initio methodologies. Computations are done using standard and explicitly correlated coupled cluster, CASSCF and MRCI approaches in conjunction with large basis sets, extrapolated to the complete basis set (CBS) limit. The lowest electronic states of different isomers are mapped along the stretching coordinates, thereby confirming the existence of the four already known ground state structures, namely H2NS, H2SN, cis-HNSH and trans-HNSH. Also, it is shown that only the lowest electronic excited states are stable, whereas the upper electronic states may undergo unimolecular decomposition processes forming H + HNS/HSN or the HN + SH or N + H2S or S + NH2 fragments. These data allow an assignment of the deep blue glow observed after reactions between “active nitrogen” and H2S at the beginning of the XXth century. For stable species, a set of accurate structural and spectroscopic parameters are provided. Since small nitrogen-sulfur molecular species are of astrophysical relevance, this work may help for identifying the thionitroxyl radical isomers in astrophysical media and in the laboratory.
To date, several molecular species containing H, N and S atoms are identified in astrophysical media. These include the Galactic center cloud Sgr B2, cold dark clouds, R Andromedae, circumstellar envelopes of evolved stars, regions of massive star formation, planetary atmospheres, brown dwarfs, stellar atmospheres, and comae (Espin, 1890; Neugebauer et al., 1965; Wöhl, 1971; Gottlieb et al., 1975; Meyer and Roth, 1991; van Dishoeck et al., 1993; Wagenblast et al., 1993; McGonagle et al., 1994; McGonagle and Irvine, 1997; Irvine et al., 2000; Yamamura et al., 2000; Ziurys, 2006; Phuong et al., 2018). The list of identified species contains the NS, SH, NH, and NH2 radicals as well as the H2S molecule. Other species are also very likely to be present there, such as HSN/HNS and their ions (Ben Yaghlane et al., 2014; Ajili et al., 2016; Trabelsi et al., 2016). In these media, these molecules and the H, N, and S atoms may undergo complex chemistry that may lead to the formation of larger molecular species, already detected or possibly present. All of them are closely related to the molecule investigated here, i.e., the thionitroxyl radical (H2NS), since they may be involved in its formation or fragmentation.
At the beginning of the XXth century, Strutt, Fowler and Vaidya (Strutt and Fowler, 1912; Strutt, 1913; Fowler and Vaidya, 1931) investigated the reactions of “active nitrogen” with hydrogen sulfide (i.e., N + H2S) producing NS + H2. They suggested that these products are formed by decomposition of an N.H2S tetratomic intermediate. These findings were confirmed in 1960 by Westbury and Winkler (1960) who studied the kinetics of such processes in the 85–440°C temperature range. A deep blue glow was observed in the reaction flame, attributed a priori to the N.H2S long-lived intermediate. In the literature, no solid confirmation of this assignment is found.
In the laboratory, two isomers of the thionitroxyl radical (namely HNSH and H2SN) and their positively- and negatively-charged ions were detected in 1994 by a combination of collisional activation and neutralization-reionization mass spectrometry, complemented by theoretical computations based on Möller-Plesset (MP2 and MP4) approaches (Nguyen et al., 1994). These computations showed that the most stable [H,H,N,S] species corresponds to H2NS (C2v symmetry) and not to the already detected HNSH and H2SN isomers. In 1998, the most stable [H,H,N,S] form was observed by Habara et al. (1998) using source-modulation and Fourier-transform microwave spectrometers. These authors recorded the rotational spectral lines of the X2B1 electronic ground state of the H2NS and D2NS radicals in the 150–390 GHz region. They provided accurate equilibrium (re) and zero-point average structures (rz), and estimated the 6 fundamental vibrational modes (ν1−6). Theoretically, earlier works revealed the existence of four stable isomers with molecular formula H2NS, namely H2NS (C2v symmetry), trans-HNSH, cis-HNSH and H2SN (Cs symmetry). In 2010, Pereira et al. (2010) used the CCSD/6-311++G(d,p) technique to study the 1NH + 2SH → cis-2HNSH → trans-2HNSH → 2H2NS → 2NS → + H2 reactive channels. The H2NS species are found to be intermediates in these reactions. Although this work is performed at a relatively high computational level, it does not provide structural parameters for the four H2NS isomers with the accuracy required for their detection in the laboratory and in astrophysical surveys. In addition, it does not consider the H + HNS/HSN reactive channels, which are likely to be involved in the formation of the NS radical in the interstellar clouds, since its formation cannot be fully explained by the electron capture and following fragmentation of the protonated NS. The deduced abundances of NS differ by several orders of magnitude from the measured ones in interstellar dark clouds (Millar et al., 1991; McGonagle et al., 1994; Irvine et al., 2000). The involvement of large H-, N- and S-containing molecules is not invoked. However, these compounds may play key roles in these processes, as intermediates. In this context, H2NS species are most likely present, as stable molecules or intermediates, in the astrophysical media mentioned and should be considered in the chemical models for the study of their physicochemical properties. Nevertheless, the main limitation of the identification of such compounds is the lack of spectroscopic data. The present work provides a set of structural, vibrational and electronic parameters for the [H,H,N,S] molecular species. It should help for their identification in astrophysical media and in the laboratory. We also show that these tetratomics undergo spin-orbit-induced predissociation and photodissociation upon absorbing UV-Vis light. These restrain the astrophysical environments where they can be formed and detected.
We started our computations by mapping the lowest doublet potential energy surface (PES) of the [H,H,N,S] molecular system to locate the stationary points (both minimal-energy and transition state structures). These geometry optimizations were done without symmetry constraints (i.e., in the C1 point group), using the partially spin restricted coupled cluster (CC) method with a perturbative treatment of triple excitations [RCCSD(T)] (Hampel et al., 1992; Deegan and Knowles, 1994; Knowles et al., 2000) as well as the explicitly correlated version of this method [RCCSD(T)-F12] (Adler et al., 2007; Werner et al., 2007; Knizia and Werner, 2008; Knizia et al., 2009) and complete active space self-consistent field (CASSCF) (Knowles and Werner, 1985; Werner and Knowles, 1985) approaches as implemented in the MOLPRO suite of programs (Werner et al., 2015). The use of CC approaches is justified by the mono configurational nature of the wavefunctions of H2NS ground state species close to equilibrium as certified by the T1 and D1 diagnostics close to 0.02 and 0.06 in Coupled Clusters computations and by the dominance of a unique configuration in their CASSCF wavefunctions (weight > 0.95). In CASSCF, the active space is formed by the whole set of valence orbitals, in which all the possible valence electron excitations are considered. For the RCCSD(T) and CASSCF computations, we used the aug-cc-pV(X+d)Z (X = D, T, Q) basis sets for sulfur and the aug-cc-pVXZ (X = D, T, Q) for hydrogen and nitrogen atoms (Kendall and Dunning, 1992; Woon and Dunning, 1993; Dunning et al., 2001). The use of tight d functions for sulfur improves the quality of the results, as established in the benchmark computations presented in Refs (BenYaghlane et al., 2013; Ben Yaghlane et al., 2014; Trabelsi et al., 2018), since it allows for a better description of the electron density of this polarizable atom and can provide accurate descriptions of the electronic structures of its compounds. In the RCCSD(T)-F12 calculations, the cc-pVXZ-F12 (X = D, T, Q) basis sets (Peterson et al., 2008) together with the corresponding auxiliary basis sets and density-fitting functions, as implemented in MOLPRO (Klopper, 2001; Weigend, 2002; Hättig, 2005), were used. These optimizations are followed by frequency computations to establish the nature of the stationary points, either minima or saddle points. Subsequently, we extrapolated the geometrical values and energetics to the CBS limit using the two-parameter equation: A = B + C/X3, in conjunction with a least square procedure, where A is the extrapolated quantity, X is the cardinal number of the basis set and B and C are fitting parameters (Helgaker et al., 1997). For the RCCSD(T)/CBS and RCCSD(T)-F12/CBS geometrical parameters, we evaluated the core-valence correlation corrections at the RCCSD(T)/cc-pCVTZ and RCCSD(T)-F12/cc-pCVTZ-F12 levels, respectively. Within a given level, this was achieved by taking the difference between the optimized geometrical parameters obtained from a calculation where all the electrons are correlated and a calculation where the core electrons are kept frozen.
The PESs of the low-lying electronic states of the H2NS species were mapped along the stretching and out-of-plane torsion coordinates with the remaining internal coordinates fixed at their respective equilibrium ground state values. These computations were carried out with the CASSCF approach followed by the internally contracted multi-reference configuration interaction (MRCI) method (Werner and Knowles, 1988; Shamasundar et al., 2011), where the H, N, and S atoms were described with the aug-cc-pV(5+d)Z basis set. In the MRCI procedure, all single and double electron excitations from the configurations of the CASSCF wavefunction having a CI coefficient larger than 0.005 were performed. The resulting MRCI wavefunctions are composed of ~1.7 × 107 contracted (~1 × 109 uncontracted) configurations per Cs symmetry. Furthermore, we optimized the equilibrium geometries of the long-lived and stable electronic excited states at the CASSCF/aug-cc-pV(X+d)Z (X= T, Q, 5, CBS) level. The minimal-energy nature of these structures is indicated by all positive frequencies.
For the thionitroxyl molecule, as established in the literature, our computations confirm the existence of only four stable forms in the ground state PES. Unlike H2SN, which is located in the lowest 2A′ PES, H2NS, cis-HNSH and trans-HNSH are found in the lowest 2A″ PES. These equilibrium structures are displayed in Figure 1. For each of them Figure 2 displays the corresponding singly occupied molecular orbital (SOMO), the next-to-SOMO (SOMO-1) and the lowest unoccupied molecular orbital (LUMO) as computed at the CASSCF/aug-cc-pVTZ level. This figure shows that the SOMOs of H2NS, cis-HNSH and trans-HNSH are π* orbitals, while the SOMO-1s are of σ type. All these orbitals are mainly located on the NS bond. Whereas, the SOMO-1 and the SOMO of H2SN correspond to π orbitals mainly located on the nitrogen atom. For all species, the LUMOs are σ* SN bonds.
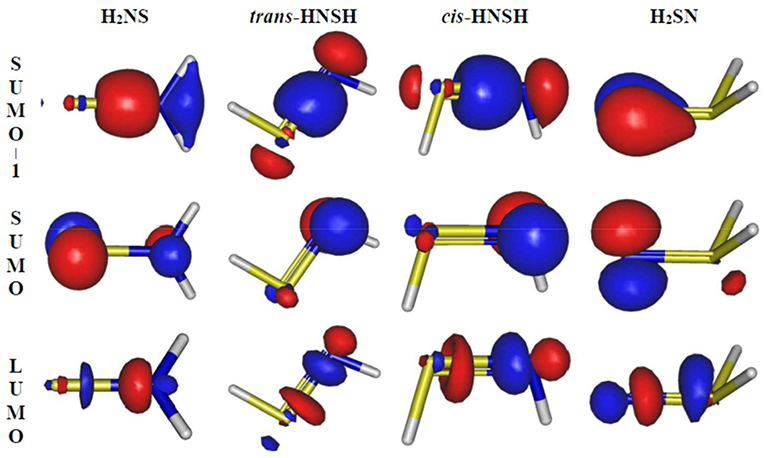
Figure 2. Outermost molecular orbitals (SOMO-1, SOMO and LUMO) of the molecular species of interest obtained at the CASSCF/aug-cc-pVTZ. The isovalue is 0.13 a.u.
Figures 3–6 present one-dimensional cuts of the 6D-PESs of the doublet and quartet electronic states of H2NS, cis-HNSH, trans-HNSH and H2SN along the stretching coordinates, with the remaining internal coordinates kept fixed at their ground state values. We give also the evolution along the out-of-plane / torsion angle. These potentials are computed at the CASSCF/MRCI/aug-cc-pV(5+d)Z level of theory. In these cuts, energies are given with respect to the H2NS ground state energy at equilibrium. These potentials correlate adiabatically to the HNS/HSN + H or NH + HS or NH2 + S or H2S + N dissociation limits at internuclear separations. Table 1 lists the electronic states of H2NS species located in the 0–6.5 eV internal energy range and gives also their CASSCF/MRCI/aug-cc-pV(5+d)Z vertical electronic excitation energies and dominant electronic configurations, as quoted at the equilibrium geometry of the corresponding electronic state.
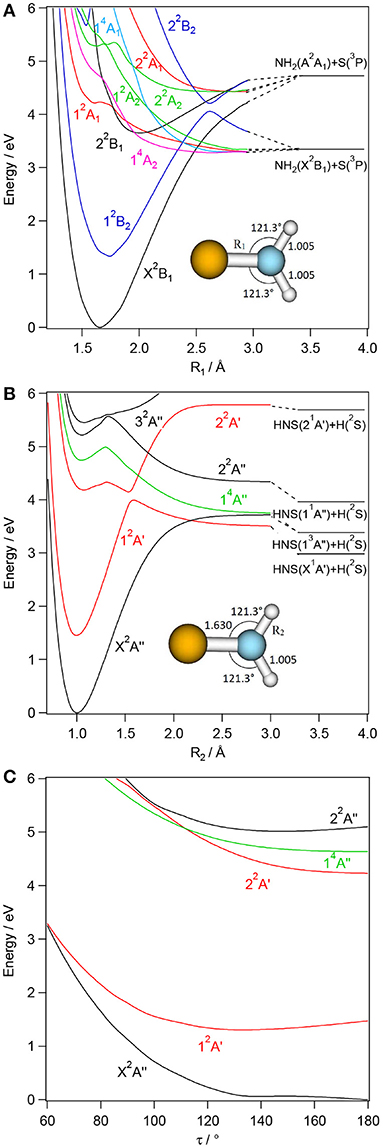
Figure 3. CASSCF/MRCI/aug-cc-pV(5+d)Z one-dimensional cuts of the 6D-PESs of the low-lying electronic states of H2NS along the NS (R1, A) and NH (R2, B) stretching and τ out-of-plane (C) coordinates. The remaining internal coordinates are kept fixed at their values in the H2NS(X2B1) state i.e. R3= 1.630 Å, R2=R3= 1.005 Å, θ1 = θ2= 121.3° and τ= 180° (for planar configuration). The H + HNS/HSN and NH2 + S asymptotes are located using the data in Supplementary Tables 8, 9 and (Xin et al., 2003; Trabelsi et al., 2015)1.
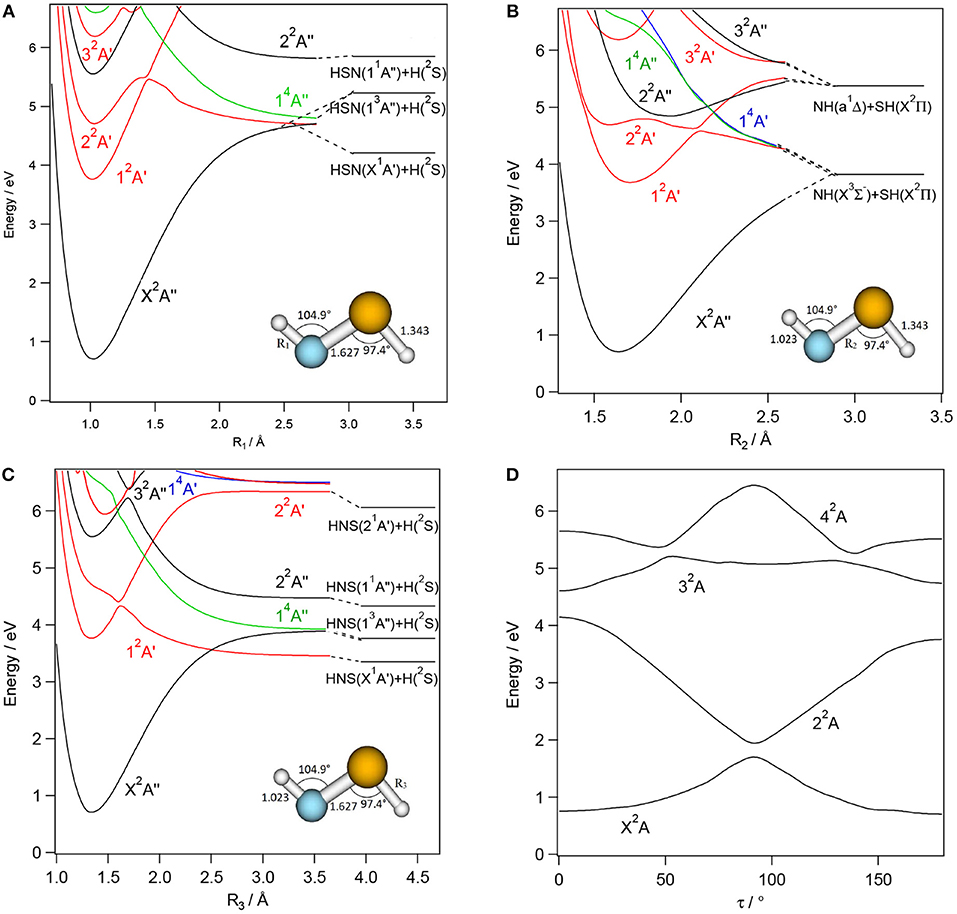
Figure 4. CASSCF/MRCI/aug-cc-pV(5+d)Z one-dimensional cuts of the 6D-PESs of the low lying electronic states of trans-HNSH along the SH (R1, A), NS (R2, B), and NH (R3, C) stretching and τ torsion, (D) coordinates. The remaining internal coordinates are kept fixed at their values in the trans-HNSH(X2A″) state i.e., R1= 1.023 Å, R2= 1.627 Å, R3= 1.343 Å, θ1= 104.9° θ2= 97.4°, and τ= 180°. The H + HNS/HSN, NH + SH asymptotes are located using the data in Supplementary Tables 8, 9 and (Trabelsi et al., 2015)1. The reference energy is that of H2NS(X2B1) at equilibrium.
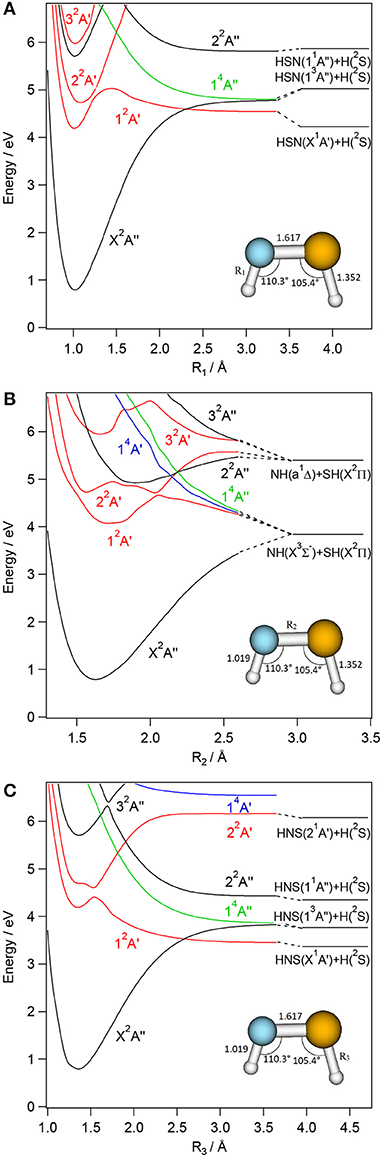
Figure 5. CASSCF/MRCI/aug-cc-pV(5+d)Z one-dimensional cuts of the 6D-PESs of the low lying electronic states of cis-HNSH along the SH (R1, A), NS (R2, B) and NH (R3, C) stretching coordinates. The remaining internal coordinates are kept fixed at their values in the cis-HNSH(X2A″) state i.e., R1= 1.019 Å, R2= 1.617 Å; R3= 1.352 Å, θ1= 110.3°, θ2= 105.4°, and τ=0°. The H + HNS/HSN, NH + SH asymptotes are located using the data in Supplementary Tables 8, 9 and (Trabelsi et al., 2015)1. The reference energy is that of H2NS(X2B1) at equilibrium.
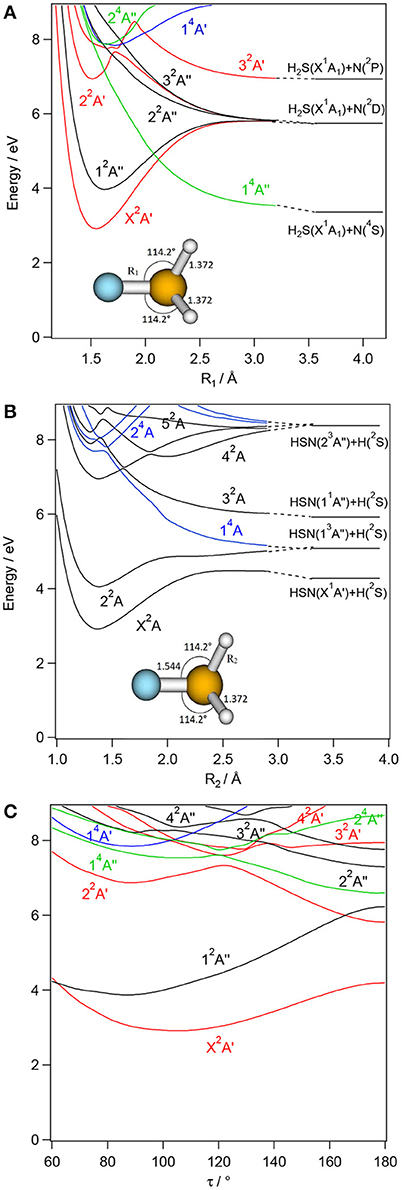
Figure 6. CASSCF/MRCI/aug-cc-pV(5+d)Z one dimensional cuts of the 6D-PESs of the low lying electronic states of H2SN along the NS (R1, A) and NH (R2, B) stretching coordinates and τ torsion, (C) coordinate. The remaining internal coordinates are kept fixed at their values in the H2SN(X2A′) state i.e., R1= 1.544 Å, R2=R3= 1.372 Å, θ1 = θ2= 114.2°, and τ=104.1°. The H + HNS/HSN and H2S + N asymptotes are located using the data in Supplementary Tables 6, 7 and (Trabelsi et al., 2015)1. The reference energy is that of H2NS(X2B1) at equilibrium.
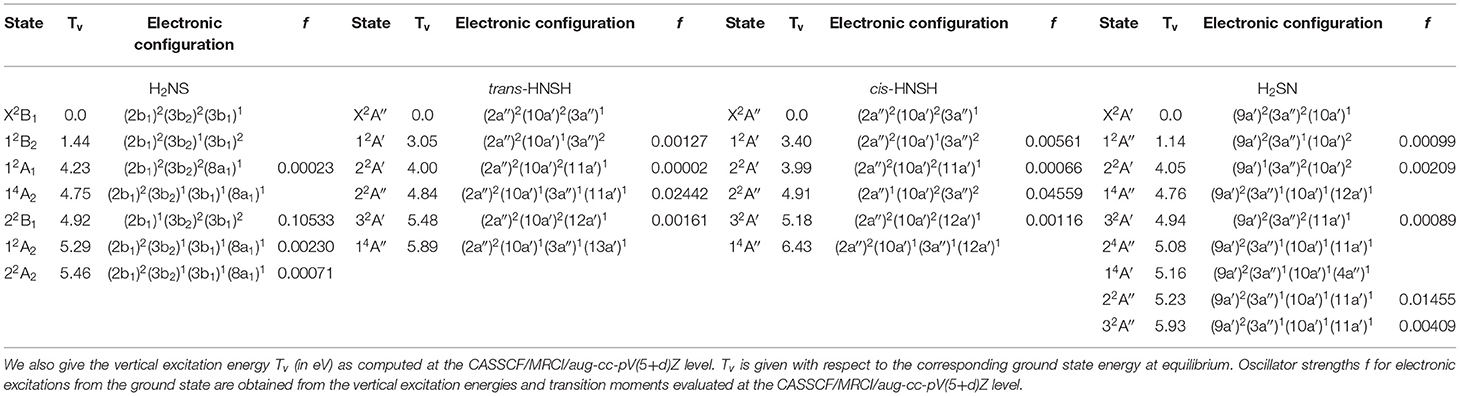
Table 1. Dominant electronic configurations of the lowest-lying electronic states of H2NS, cis- and trans-HNSH and H2SN at the corresponding ground state equilibrium geometry.
For each [H,H,N,S] isomer, Figures 3–6 reveal that the two lowest electronic states have deep potential wells along the stretching coordinates. Besides, the ground electronic states are well-separated from the upper ones in the molecular region and free from interactions that could lead to mixing of their wavefunctions. Therefore, these electronic states are monoconfigurational in nature and can be accurately described by the monoconfigurational post-Hartree-Fock methods used in the present investigation (cf. infra).
Table 1 shows that the first excited states are obtained upon SOMO-1 → SOMO electron promotion. In the Franck-Condon region accessed from the corresponding ground states, the first excited states correspond to 12B2, 12A′, 12A′, and 12A″ space symmetry species for H2NS, cis-HNSH, trans-HNSH, and H2SN, respectively. They are located at 1.15 – 1.5 eV for H2NS(12B2) and H2SN(12A″) and at 3–3.4 eV for cis-HNSH(12A′) and trans-HNSH(12A′) with respect to their corresponding electronic ground state. At equilibrium, they possess non-planar configurations with Cs symmetry for H2NS and H2SN and C1 symmetry for HNSH. For cis-HNSH and trans-HNSH a unique minimum is found in the 22A state PES, whereas both cis and trans forms exist in the ground state potential. Moreover, the lowest electronic excited states interact with the other states for non-planar configurations. For instance, Figure 4 shows that the local minimum in the HNSH excited PES is due to an avoided crossing between the lowest doublets at τ ~100°. In this region the wavefunctions of both states are mixed and acquire multiconfigurational character. Such states should be investigated using multi configurational approaches (cf. infra).
For the low-lying doublet excited states of Table 1, we calculated the oscillator strengths from the vertical excitation energies and transition moments evaluated at the CASSCF/MRCI/aug-cc-pV(5+d)Z level. The calculated values show that rather intense transitions are expected from the X2B1 to the 22B1 state of H2NS and from the ground to the 22A″ states of trans-HNSH, cis- HNSH and H2SN. The other transitions range from very weak to moderately weak.
In the Franck-Condon region accessed from the corresponding electronic ground states, the upper electronic states of H2NS, trans-HNSH, cis- HNSH and H2SN are located above 4 eV. They correspond to electron excitations from the occupied inner valence MOs to the LUMO and LUMO+1 unoccupied MOs. The shapes of the resulting potentials are far from the standard Morse-like ones, since most of them are repulsive at large distances. Local minima can also exist at short distances and for non-planar configurations. Moreover, there is a high density of electronic states, which favors the mixing of their wavefunctions by vibronic and spin-orbit couplings. For instance, the quartets are crossing the doublets at intermediate R distances where spin-orbit conversion may occur. At these distances, the quartets are mostly repulsive and lead to fragmentations. For instance, the lowest quartet is crossing the electronic excited doublets at different nuclear geometries, where spin-orbit-induced predissociations may happen. At large internuclear separations, the reactions evolve along the repulsive part of this quartet state, which correlates adiabatically to lower dissociation limits. This is the case indeed for H2NS, where a crossing between the H2NS(22A′) and the H2NS(14A″) states occurs at NH ~1.6 Å (Figure 3). For this doublet, we note also an avoided crossing with the 12A′ state at NH ~1.5 Å (Figure 3), where vibronic coupling may occur. Interestingly this avoided crossing is responsible for the double well-shape of H2NS(22A′) and cis-HNSH(22A′) along the SN distance. Also, the cuts of the PESs show that the second electronic excited state presents a flat potential along the torsion/out-of-plane coordinate resulting in a planar structure for H2NS, whereas two minima can be seen for HNSH (cis and trans) and for H2SN (C2v and Cs). In all cuts displayed in Figures 3–6, the potential of such state has generally an odd shape, which may favor intramolecular isomerizations converting H2NS into HNSH and H2SN, and vice versa.
For the investigation of the structure and vibrational spectroscopy of [H,H,N,S] in their electronic ground states, we used monoconfigurational approaches since their electronic wavefunctions, as discussed above, can be dominantly described by a unique configuration close to equilibrium. Thus, we characterized the stable forms of this molecular system in the ground state PES at the RCCSD(T)/aug-cc-pV(X+d)Z (X=D, T, Q) and RCCSD(T)-F12/cc-pVXZ-F12 (X=D, T, Q) levels of theory. Supplementary Tables 1–4 report the corresponding optimized geometrical parameters, harmonic frequencies and total energies for the minimal structures and Supplementary Table 5 those of the transition states. These tables show that the computed bond distances present slight variations by increasing the size of the basis set, where a systematic shortening of the bond distances is noticed because of the refined description of the electron correlation with the larger basis sets. Besides, variations in the bond angles are almost negligible upon changing the basis set.
We give in Table 2 the data after CBS extrapolation, together with their comparison to previous works. Computations confirm the existence of the already predicted H2NS, trans-HNSH, cis-HNSH, and H2SN forms and the transition states connecting them. The nature of these stationary points was carefully checked by harmonic frequency analysis, as given in Supplementary Tables 1–5. No other isomers were located. The relative energies confirm the previously established order: H2NS followed by trans-HNSH, cis-HNSH and H2SN. Table 2 shows also that all these compounds have relatively large dipole moments (1.1 < μe <3.7 debye). Therefore, these molecular species are susceptible to be observed by high-resolution rotational spectroscopy techniques in the laboratory and by radioastronomy. To-date, only H2NS (X2B1) was identified by Habara et al. (1998) using a source-modulation microwave spectrometer and a Fourier-transform microwave spectrometer. These authors deduced an accurate equilibrium molecular structure: RNS = R1 = 1.6398 Å, RNH = R3 = R2 = 1.0055 Å and in-plane angle θ1 = θ2 = 120.5°. Our RCCSD(T)/CBS and RCCSD(T)-F12/CBS values compare well with this experimental geometry, with deviations of less than 0.6%. As expected, the less accurate previous calculations lead to larger deviations. For the other not yet detected isomers, we expect a similar accuracy. From the RCCSD(T)/CBS and RCCSD(T)-F12/CBS optimized geometries, we deduced the equilibrium rotational constants (Ae, Be, Ce), to which we added the respective vibrational and centrifugal distortion corrections computed at the RMP2/aug-cc-pV(Q+d)Z level, within the VPT2 approach. Hence, at the RCCSD(T)/CBS level, the corrected (A0, B0, C0) rotational constants of Table 2 are straightforwardly obtained from the following equation:
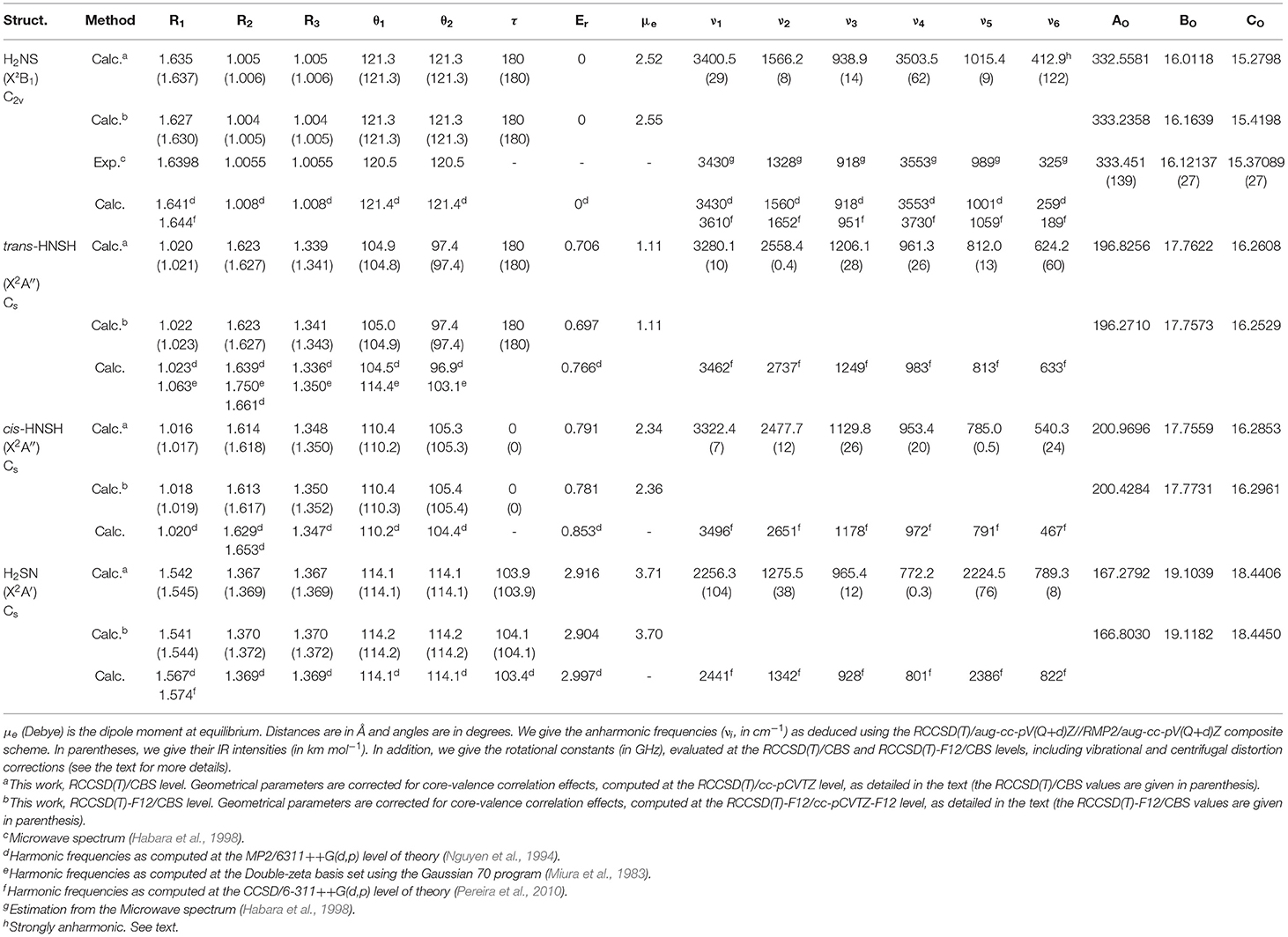
Table 2. Optimized equilibrium geometries and relative energies (Er, eV) of [H,H,N,S] isomers as computed at the RCCSD(T)/CBS and CCSD(T)-F12/CBS levels of theory.
B0(RCCSD(T)/CBS) = Be(RCCSD(T)/CBS) + B0(RMP2/aug-cc-pV(Q+d)Z) – Be(RMP2/aug-cc-pV(Q+d)Z)
and similarly for A0(RCCSD(T)/CBS), C0(RCCSD(T)/CBS), A0(RCCSD(T)-F12/CBS), B0(RCCSD(T)-F12/CBS), and C0(RCCSD(T)-F12/CBS). Table 2 shows that we have good agreement with the experimental data by Habara et al. (1998).
Table 2 lists the anharmonic frequencies of the fundamental modes (νi), which have been evaluated using the RCCSD(T)/aug-cc-pV(Q+d)Z//RMP2/aug-cc-pV(Q+d)Z composite scheme described in Hochlaf et al., 2015). Here, νi is equal to ωi + Δνi, where ωi is the RCCSD(T)/aug-cc-pV(Q+d)Z harmonic frequency of the i-th mode, and Δνi is the corresponding RMP2/aug-cc-pV(Q+d)Z anharmonic correction (Supplementary Table 6) as determined using second-order vibrational perturbation theory (VPT2) (Mills, 1972; Aliev and Watson, 1985), as implemented in GAUSSIAN. The validity of such procedure was widely discussed in (Carbonnière et al., 2005; McKean et al., 2008; Temelso and Shields, 2011; Zen et al., 2012). Briefly, it allows to predict accurate and fully ab initio anharmonic vibrational frequencies at a low computational cost.
For H2NS(X2B1), we compute ν1 = 3400.5, ν2 = 1566.2, ν3 = 938.9, ν4 = 3503.5, ν5 = 1015.4 and ν6 = 412.9 (all values in cm−1). These fundamentals are of a1 symmetry for ν1-ν3, b2 symmetry for ν4-ν5 and b1 symmetry for ν6 (out-of-plane mode). They compare favorably with the values by Habara et al. (1998) for the following modes: ν1 (= 3430 cm−1), ν3 (= 918 cm−1), ν4 (= 3553 cm−1) and ν5 (= 989 cm−1), while the comparison is less satisfactory for ν2 (= 1328 cm−1) and ν6 (= 325 cm−1). Also, we found that the ν6 mode is strongly anharmonic, with inverted anharmonicity. This is related to the flatness of the PES along this normal coordinate. VPT2 treatment is not enough for deducing the ν6 frequency. Instead, a full variational treatment in a 6D-PES is needed, which is beyond the scope of the present work.
For cis-HNSH and trans-HNSH, ν1 through ν5 are of a′ symmetry, and ν6 is of a″ symmetry, while for H2SN ν1 through ν4 are of a′ symmetry, and ν5 and ν6 are of a″ symmetry. Table 2 lists their fundamentals. Moreover, Table 2 lists the respective IR intensities, which show that all the possible modes are potentially detectable in the IR spectra.
Supplementary Figure 1 and Supplementary Table 5 give the optimized transition states (TS1-TS4) geometries, harmonic frequencies and total energies as calculated at the RCCSD(T)/aug-cc-pV(X+d)Z and RCCSD(T)-F12/cc-pVXZ (X=D,T,Q, CBS) levels. TS1 connects cis-HNSH and trans-HNSH. The corresponding isomerization barrier is computed to be 0.88 eV at the RCCSD(T)/CBS level. TS2 connects trans-HNSH and H2NS. It is located at 1.84 eV above trans-HNSH. TS3 and TS4 are transition states along the H2NS and H2SN → H2 + NS production channels, respectively. The energy barrier for H2NS → TS3 is relatively large (> 3 eV) and that of H2SN → H2 + NS is about 1 eV. The relative energies and the structures of these transition states are close and consistent with the data obtained by Pereira et al. (2010) using the CCSD/6-311++G(d,p) approach. The interconversion processes through these transition states may compete with the photophysical processes discussed in Section Photochemistry.
Table 3 lists the CASSCF/CBS optimized geometrical and spectroscopic parameters of the first electronic excited state for each isomer. The full set of data is given in Supplementary Table 7. Here, only three structures are found since cis- and trans-HNSH have the same excited state for non-planar HNSH arrangement. The comparison of the bond distances in H2NS(X2B1) and H2NS(12A′) reveals that the SN distance is lengthened upon electronic excitation, since the outermost electron is promoted from a bonding MO (SOMO-1) to an antibonding MO (SOMO), as illustrated in Figure 2. On the contrary, the NH bonds are only slightly affected. This is also the case for H2SN, whereas no variations are seen for the HNSH species.
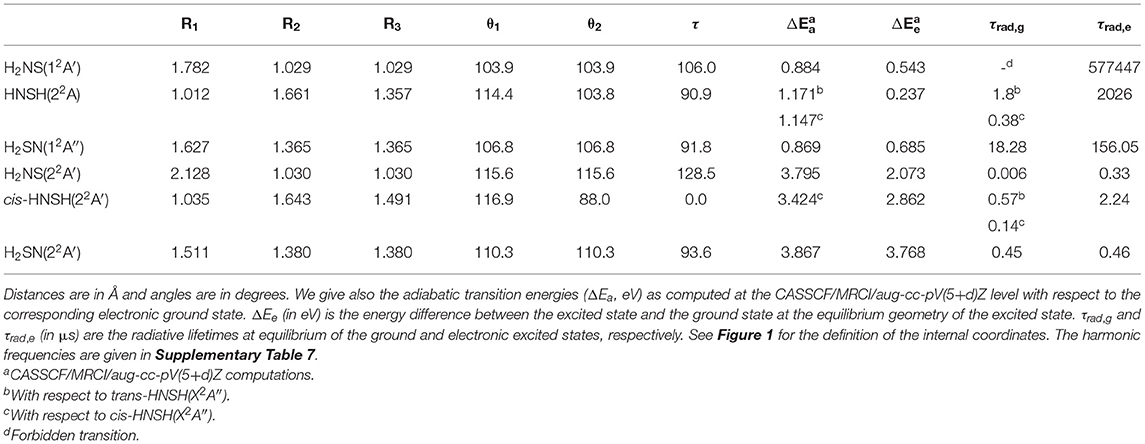
Table 3. CASSCF/CBS optimized equilibrium geometries of [H,H,N,S] isomers in their lowest electronic excited states.
For the calculated electronic state of each isomer, we evaluated the radiative lifetime (τrad) using the formula
1/τrad = Σi 1/τi,rad, where τi,rad (= 6.07706 /(|Re,i|2 (ΔEa,i)3) in μs) is the radiative lifetime populating the lower doublet states. Here, |Re,i| (in debye) is the transition moment between the upper and the lower states as computed at the CASSCF/aug-cc-pV(5+d)Z level, and ΔEa,i (in eV) is the corresponding CASSCF/MRCI/aug-cc-pV(5+d)Z adiabatic excitation energy.
Radiative lifetime computations were carried out at the ground state (τrad,g) and excited state (τrad,e) equilibrium geometries. The results are summarized in Table 3. This table shows that the calculated lifetimes are at least of several hundred ns, i.e., long enough to allow these electronic states to emit if populated.
In order, to understand the thermodynamic aspects of the different dissociation processes taking place in [H,H,N,S] species or their formation from simple fragments, we give in Figure 7 the fragmentation energies to form diatomic + diatomic and atomic + triatomic entities, which are computed using:
or
where E(D), E(AB), E(CD), E(ABC) and E(ABCD) are the total energies of the D, AB, CD, ABC and ABCD entities. The ZPEs are their zero-point vibrational energies.
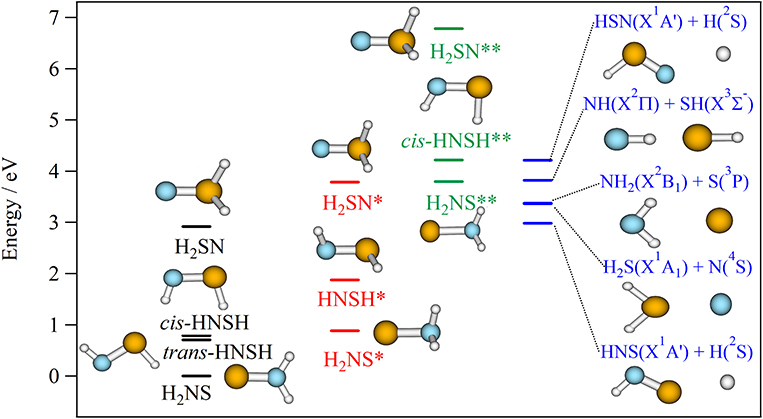
Figure 7. (R)CCSD(T)/CBS fragmentation energies (in eV) of H2NS, trans-HNSH, cis- HNSH and H2SN forming HNS/HSN + H; NH2 + S, H2S + N and NH2 + SH. These energies are given with respect to the H2NS ground state at equilibrium. Molecular species denoted by * and ** are electronically excited species in the first and second excited states, respectively (Table 3). All molecular species are taken at their equilibrium structure as optimized at the respective theoretical level. The ZPE correction is also included. See Supplementary Tables 8, 9 for more details.
Figure 7 shows that the electronic ground state of each isomer is located below the lowest dissociation limit, i.e., HNS(X2A′)+H(2S). Therefore, all the calculated species are expected to be stable with respect to dissociation. All bimolecular reactions may lead to their formation. This is also the case for the first excited states of H2NS and HNSH (denoted as H2NS* and HNSH* in Figure 7). Such compounds are also expected to be long-lived. Table 3, which gives their radiative lifetimes, confirm such assumptions. Indeed, we compute lifetimes of several hundreds of ns for H2NS* and HNSH*. On the other hand, the lifetime of the first electronic excited state of H2SN (labeled H2SN*) may be reduced by spin-orbit-induced predissociation to populate the SN bond breaking channels HNS(X2A′)+H(2S), NH2(X2B1)+S(3P) or H2S(X1A1)+N(4S). Figure 6 shows that the latter process is plausible since the H2SN*(12A″) is crossed by the repulsive 14A″ state which leads directly to these fragments. Figure 7 shows also that the second electronic excited states of all species are located above the lowest dissociation limit. Their lifetimes should be reduced by predissociation phenomena via the couplings with the quartet manifolds. Nevertheless, Table 3 shows that their radiative lifetimes are long enough to fluoresce whenever populated. For the upper electronic states (> 4 eV), they are located in energy above the lowest dissociation limit. They may undergo unimolecular decomposition processes forming H+HNS/HNS, H2+NS or NH+SH. A multi-step mechanism along the PESs of their doublet states is expected, where the wavepackets on these PESs evolve until reaching the regions of conical intersections or avoided crossings. The electronic de-excitation of the H2NS, trans-HNSH, cis- HNSH and H2SN molecules may occur via emission of light or more likely by radiationless internal conversion processes. The lowest states are thus populated. Alternatively, a conversion to the quartet manifold takes place at the doublet-quartet crossings, followed by dissociation.
In their pioneering work on “active nitrogen,” Strutt, Fowler and Vaidya (Strutt and Fowler, 1912; Strutt, 1913; Fowler and Vaidya, 1931) and later on Westbury and Winkler (Westbury and Winkler, 1960) showed that the reactions of “active nitrogen” with hydrogen sulfide occurring in a flame are associated with a deep blue glow that appeared to fill the entire upper half of the reaction vessel. This light emission was interpreted as emanating from the N.H2S tetratomic intermediate. Computations show that the bimolecular reactive collisions, in the presence of a third party to absorb the excess energy, should lead to the formation of [H,H,N,S] tetratomics in their electronic ground states as established by Pereira et al. (2010) for the 1NH + 2SH → cis-2HNSH → trans-2HNSH → 2H2NS → 2NS + H2 reactive channels. Also the [H,H,N,S] tetratomics can be formed in their first electronic excited states, which are long-lived enough to emit light in the IR domain (hν <1.2 eV, Table 3). Nevertheless, such light was not observed in the experiment most likely because it was not possible to measure it at the beginning of the XXth century. Table 3 shows also that the second electronic excited state of [H,H,N,S] species can be a suitable candidate to explain the deep blue glow. Indeed the H2SN(X2A′) ← H2SN(22A′) transition has an energy of ~3.8 eV. As mentioned above the PES of this electronic state is flat, so intramolecular isomerization to form the other isomers is possible. At least, we may obtain the cis-HNSH (22A′) species, which is long lived enough to emit light with hν ~ 2.8 eV i.e., close to the ~2.7 eV experimentally observed deep blue glow. Thus, our work establishes that the less stable forms HSNH and H2SN are responsible for the flame color. Figure 6 shows that the upper state can be populated after collisions between N(2D) or N(2P) with H2S, which means that the N atom is not in its electronic ground state (4S). Accordingly, the so-called “active nitrogen” corresponds to electronically excited nitrogen atoms that might be formed in the flame. The reactions evolve on the PESs of the electronic excited states of doublet spin multiplicity.
Using advanced ab initio methodologies, we mapped the PESs of the lowest electronic states of the [H,H,N,S] molecular species. Thence, we characterized the stable forms in the ground and two lowest electronic states. For the ground states, we confirm the existence of the four already known isomers. Since the corresponding experimental data are estimates, we suggest that the IR spectra of these compounds should be measured again for a definitive conclusion. On the excited potentials, the H2NS, HNSH and H2SN forms were identified for the first time. Also, we used these potentials to examine the unimolecular decomposition processes undergone by the H2NS, HNSH and H2SN species and the bimolecular reactions processes between H and HNS/HSN, NH + SH and H2S + N. The findings relative to the latter process were used to confirm the observation of H2SN fluorescent as an intermediate during the reactions between “active nitrogen” and H2S, known since the beginning of the XXth century. Our data should help in identifying [H,H,N,S] molecular compounds in the laboratory as well as in astrophysical and environmental media.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
MJ and SB performed computations. RF and RL discussed the results and wrote the paper. MH designed research and conducted computations and wrote the paper. All authors contributed to the article and approved the submitted version.
MJ thanks the Tunisian Ministry for High Education and Research for a fellowship for the preparation of this work. RF and MH acknowledge financial support from the Swedish Research Council (Sweden). This work was also supported by the CNRS program Physique et Chimie du Milieu Interstellaire (PCMI) co-funded by the Centre National d'Etudes Spatiales (CNES).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This study was undertaken while MH was Waernska Guest Professor at University of Gothenburg (Sweden). The support of this Guest Professorship is hereby gratefully acknowledged. Some of the computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at Chalmers Centre for Computational Science and Engineering (C3SE) partially funded by the Swedish Research Council through grant agreement no. 2018-05973.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.641067/full#supplementary-material
Adler, T. B., Knizia, G., and Werner, H.-J. (2007). A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 127:221106. doi: 10.1063/1.2817618
Ajili, Y., Ben Abdallah, D., Mogren Al-Mogren, M., Francisco, J. S., and Hochlaf, M. (2016). Rotational (de-)excitation of HNS by He: Three-dimensional potential energy surface and collision rate coefficients. Mon. Not. R. Astron. Soc. 458, 1581–1589. doi: 10.1093/mnras/stw371
Aliev, M. R., and Watson, J. K. G. (1985). Molecular Spectroscopy: Modern Research, Vol. III, edited by K. N. Rao. New York, NY: Academic Press.
Ben Yaghlane, S., Jaidane, N.-E., Cotton, C. E., Francisco, J. S., Mogren Al Mogren, M., Linguerri, R., and Hochlaf, M. (2014). Theoretical spectroscopic investigations of HNSq and HSNq (q = 0,+1,-1) in the gas phase. J. Chem. Phys. 140:244309. doi: 10.1063/1.4883915
BenYaghlane, S., Cotton, C. E., Francisco, J. S., Linguerri, R., and Hochlaf, M. (2013). Ab initio structural and spectroscopic study of HPSx and HSPx (x = 0,+1,−1) in the gas phase. J. Chem. Phys. 139:174313. doi: 10.1063/1.4827520
Carbonnière, P., Lucca, T., Pouchan, C., Rega, N., and Barone, V. (2005). Vibrational computations beyond the harmonic approximation: performances of the B3LYP density functional for semirigid molecules. J. Comput. Chem. 26, 384–388. doi: 10.1002/jcc.20170
Deegan, M. J. O., and Knowles, P. J. (1994). Perturbative corrections to account for triple excitations in closed and open shell coupled cluster theories. Chem. Phys. Lett. 227, 321–326. doi: 10.1016/0009-2614(94)00815-9
Dunning, T. H., Peterson, K. A., and Wilson, A. K. (2001). Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited. J. Chem. Phys. 114, 9244–9253. doi: 10.1063/1.1367373
Espin, T. E. (1890). Über helle linien im spectrum von R andromedae. Astronomische Nachrichten 123:31. doi: 10.1002/asna.18901230106
Fowler, A., and Vaidya, W. H. (1931). The spectrum of the flame of carbon disulphide. Proc. Roy. Soc. A 132, 310–330. doi: 10.1098/rspa.1931.0103
Gottlieb, C. A., Ball, J. A., Gottlieb, E. W., Lada, C. J., and Penfield, H. (1975). Detection of interstellar nitrogen sulfide. Astrophys. J. 200, L147–L149. doi: 10.1086/181918
Habara, H. S., and Yamamoto Saito, S. (1998). Microwave spectrum and molecular structure of the H2NS radical. J. Chem. Phys. 109, 2700–2707. doi: 10.1063/1.476876
Hampel, C., Peterson, K., and Werner, H.-J. (1992). A comparison of the efficiency and accuracy of the quadratic configuration interaction (QCISD), coupled cluster (CCSD), and Brueckner coupled cluster (BCCD) methods. Chem. Phys. Lett. 190, 1–12. doi: 10.1016/0009-2614(92)86093-W
Hättig, C. (2005). Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core–valence and quintuple-ζ basis sets for H to Ar and QZVPP basis sets for Li to Kr. Phys. Chem. Chem. Phys. 7, 59–66. doi: 10.1039/B415208E
Helgaker, T., Klopper, W., Koch, H., and Noga, J. (1997). Basis-set convergence of correlated calculations on water. J. Chem. Phys. 106, 9639–9646. doi: 10.1063/1.473863
Hochlaf, M., Puzzarini, C., and Senent, M. L. (2015). Towards the computations of accurate spectroscopic parameters and vibrational spectra for organic compounds. Mol. Phys. 113, 1661–1673. doi: 10.1080/00268976.2014.1003986
Irvine, W. M., Senay, M., Lovell, A. J., Matthews, H. E., McGonagle, D., and Meier, R. (2000). Detection of nitrogen sulfide in Comet Hale-Bopp. Icarus 143, 412–414. doi: 10.1006/icar.1999.6281
Kendall, R. A., Dunning, T. H. Jr., and Harrison, R. J. (1992). Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 96, 6796–6806. doi: 10.1063/1.462569
Klopper, W. (2001). Highly accurate coupled-cluster singlet and triplet pair energies from explicitly correlated calculations in comparison with extrapolation techniques. Mol. Phys. 99, 481–507. doi: 10.1080/00268970010017315
Knizia, G., Adler, T. B., and Werner, H.-J. (2009). Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 130:054104. doi: 10.1063/1.3054300
Knizia, G., and Werner, H.-J. (2008). Explicitly correlated RMP2 for high-spin open-shell reference states. J. Chem. Phys. 128:154103. doi: 10.1063/1.2889388
Knowles, P. J., Hampel, C., and Werner, H.-J. (2000). Coupled cluster theory for high spin, open shell reference wave functions. J. Chem. Phys. 99, 5219–5227. doi: 10.1063/1.465990
Knowles, P. J., and Werner, H.-J. (1985). An efficient second-order MC SCF method for long configuration expansions. Chem. Phys. Lett. 115, 259–267. doi: 10.1016/0009-2614(85)80025-7
McGonagle, D., and Irvine, W. M. (1997). Nitrogen sulfide in giant molecular clouds. Astrophys. J. 477, 711–721. doi: 10.1086/303749
McGonagle, D., Irvine, W. M., and Ohishi, M. (1994). Nitrogen sulfide in quiescent dark clouds. Astrophys. J. 422, 621–625. doi: 10.1086/173755
McKean, D. C., Craig, N. C., and Law, M. M. (2008). Vibrational Anharmonicity and Harmonic Force Fields for Dichloromethane from Quantum-Chemical Calculations. J. Phys. Chem. A 112, 10006–10016. doi: 10.1021/jp803881c
Meyer, D. M., and Roth, K. C. (1991). Discovery of interstellar NH. Astrophys. J. Letters 376:L49–L52. doi: 10.1086/186100
Millar, T. J., Herbst, E., and Charnley, S. B. (1991). The formation of oxygen-containing organic molecules in the Orion compact ridge. Astrophys. J. 369, 147–156. doi: 10.1086/169745
Mills, I. M. (1972). Molecular Spectroscopy: Modern Research, edited by K.N. Rao and C.W. Mathews. New York, NY: Academic Press.
Miura, Y., Asada, H., Klnoshita, M., and Ohta, K. (1983). Electron spin resonance study of N-Alkyl-N-(a1kylthio)aminyl Radicals. J. Phys. Chem. 87, 3450–4555. doi: 10.1021/j100241a020
Neugebauer, G., Martz, D. E., and Leighton, R. B. (1965). Observations of extremely cool stars. Astrophys. J. 142, 399–401. doi: 10.1086/148300
Nguyen, M. T., Vanquickenborne, L. G., and Flammang, R. (1994). The thionitroxyl free radical (H2NS) and its ionic counterparts (H2NS+ and H2NS−): a theoretical and experimental study. J. Chem. Phys. 101, 4885–4892. doi: 10.1063/1.467410
Pereira, P. S. S., Macedo, L. G. M., and Pimentel, A. S. (2010). New insight into the formation of nitrogen sulfide: a quantum chemical study. J. Phys. Chem. A 114, 509–515. doi: 10.1021/jp907384d
Peterson, K. A., Adler, T. B., and Werner, H.-J. (2008). Systematically convergent basis sets for explicitly correlated wavefunctions: the atoms H, He, B–Ne, and Al–Ar. J. Chem. Phys. 128:084102. doi: 10.1063/1.2831537
Phuong, N. T., Chapillon, E., Majumdar, L., Dutrey, A., Guilloteau, S., Piétu, V., et al. (2018). First detection of H2S in a protoplanetary disk. The dense GG Tauri A ring. A&A 616:6. doi: 10.1051/0004-6361/201833766
Shamasundar, K. R., Knizia, G., and Werner, H.-J. (2011). A new internally contracted multi-reference configuration interaction method. J. Chem. Phys. 135:054101. doi: 10.1063/1.3609809
Strutt, R. J. (1913). An active modification of nitrogen, produced by the electric discharge.—V. Proc. Roy. Soc. A 88, 539–549. doi: 10.1098/rspa.1913.0049
Strutt, R. J., and Fowler, A. (1912). Spectroscopic investigations in connection with the active modification of nitrogen. II—Spectra of elements and compounds excited by the nitrogen. Proc. Roy. Soc. (London) A 86, 105–117. doi: 10.1098/rspa.1912.0005
Temelso, B., and Shields, G. C. (2011). The role of anharmonicity in hydrogen-bonded systems: the case of water clusters. J. Chem. Theory Comput. 7, 2804–2817. doi: 10.1021/ct2003308
Trabelsi, T., Ben Yaghlane, S., Mogren Al Mogren, M., Francisco, J. S., and Hochlaf, M. (2016). HNS+ and HSN+ cations: electronic states, spin-rovibronic spectroscopy with planetary and biological implications. J. Chem. Phys. 145:084307. doi: 10.1063/1.4961313
Trabelsi, T., Linguerri, R., Ben Yaghlane, S., Jaidane, N.-E., Mogren Al-Mogren, M., Francisco, J. S., and Hochlaf, M. (2015). On the role of HNS and HSN as light-sensitive NO-donors for delivery in biological media. J. Chem. Phys. 143:134301. doi: 10.1063/1.4932084
Trabelsi, T., Mogren Al-Mogren, M., Hochlaf, M., and Francisco, J. S. (2018). Mechanistic study of the photoexcitation, photoconversion, and photodissociation of CS2. J. Chem. Phys. 149:064304. doi: 10.1063/1.5040141
van Dishoeck, E. F., Jansen, D. J., Schilke, P., and Phillips, T. G. (1993). Detection of the Interstellar NH2 Radical. Astrophys. J. Letters, 416: L83–L86. doi: 10.1086/187076
Wagenblast, R., Williams, D. A., Millar, T. J., and Nejad, L. A. M. (1993). On the origin of NH in diffuse interstellar clouds. Mon. Not. R. Astron. Soc. 260, 420–424. doi: 10.1093/mnras/260.2.420
Weigend, F. (2002). A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 4, 4285–4291. doi: 10.1039/b204199p
Werner, H.-J., and Knowles, P. J. (1985). A second order multiconfiguration SCF procedure with optimum convergence. J. Chem. Phys. 82, 5053–5063. doi: 10.1063/1.448627
Werner, H.-J., and Knowles, P. J. (1988). An efficient internally contracted multiconfiguration–reference configuration interaction method. J. Chem. Phys. 89, 5803–5814. doi: 10.1063/1.455556
Werner, H. J., Adler, T. B., and Manby, F. R. (2007). General orbital invariant MP2-F12 theory. J. Chem. Phys. 126:164102. doi: 10.1063/1.2712434
Werner, H. J.Knowles, J., et al. (2015). MOLPRO version 2015 is a package of ab initio programs. University of Cardiff Chemistry Consultants (UC3): Cardiff, Wales, UK. Available online at: http://www.molpro.net
Westbury, R. A., and Winkler, C. A. (1960). The reactions of active nitrogen with hydrogen sulfide and carbon disulfide. Can. J. Chem. 38, 334–342. doi: 10.1139/v60-049
Woon, D. E., and Dunning, T. H. Jr. (1993). Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 98, 1358–1371. doi: 10.1063/1.464303
Xin, J., Fan, H., Ionescu, I., Annesley, C., and Reid, S. A. (2003). Fluorescence excitation spectroscopy of the A2A1 - X2B1 system of jet-cooled NH2 in the region 2900–4300Å. J. Mol. Spectrosc. 219, 37–44. doi: 10.1016/S0022-2852(03)00008-0
Yamamura, S. T., Kawaguchi, K., and Ridgway, S. T. (2000). Identification of SH v=1 Ro-vibrational Lines in R Andromedae. Astrophys. J. 528, L33–L36. doi: 10.1086/312420
Zen, A., Zhelyazov, D., and Guidoni, L. (2012). Optimized structure and vibrational properties by error affected potential energy surfaces. J. Chem. Theory Comput. 8, 4204–4215. doi: 10.1021/ct300576n
Keywords: ab intio calculations, electronic state calculations, nitrogen sulfur compounds, vibrational spectroscopy, equilibrium structure
Citation: Jarraya M, Ben Yaghlane S, Feifel R, Linguerri R and Hochlaf M (2021) Thionitroxyl Radical (H2NS) Isomers: Structures, Vibrational Spectroscopy, Electronic States and Photochemistry. Front. Astron. Space Sci. 8:641067. doi: 10.3389/fspas.2021.641067
Received: 13 December 2020; Accepted: 23 March 2021;
Published: 04 May 2021.
Edited by:
Ryan C. Fortenberry, University of Mississippi, United StatesReviewed by:
Tarek Trabelsi, University of Pennsylvania, United StatesCopyright © 2021 Jarraya, Ben Yaghlane, Feifel, Linguerri and Hochlaf. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Majdi Hochlaf, aG9jaGxhZkB1bml2LW1sdi5mcg==; orcid.org/0000-0002-4737-7978
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.