Computational Infrared Spectroscopy of 958 Phosphorus-Bearing Molecules

Phosphine is now well-established as a biosignature, which has risen to prominence with its recent tentative detection on Venus. To follow up this discovery and related future exoplanet biosignature detections, it is important to spectroscopically detect the presence of phosphorus-bearing atmospheric molecules that could be involved in the chemical networks producing, destroying or reacting with phosphine. We start by enumerating phosphorus-bearing molecules (P-molecules) that could potentially be detected spectroscopically in planetary atmospheres and collecting all available spectral data. Gaseous P-molecules are rare, with speciation information scarce. Very few molecules have high accuracy spectral data from experiment or theory; instead, the best current spectral data was obtained using a high-throughput computational algorithm, RASCALL, relying on functional group theory to efficiently produce approximate spectral data for arbitrary molecules based on their component functional groups. Here, we present a high-throughput approach utilizing established computational quantum chemistry methods (CQC) to produce a database of approximate infrared spectra for 958 P-molecules. These data are of interest for astronomy and astrochemistry (importantly identifying potential ambiguities in molecular assignments), improving RASCALL's underlying data, big data spectral analysis and future machine learning applications. However, this data will probably not be sufficiently accurate for secure experimental detections of specific molecules within complex gaseous mixtures in laboratory or astronomy settings. We chose the strongly performing harmonic ωB97X-D/def2-SVPD model chemistry for all molecules and test the more sophisticated and time-consuming GVPT2 anharmonic model chemistry for 250 smaller molecules. Limitations to our automated approach, particularly for the less robust GVPT2 method, are considered along with pathways to future improvements. Our CQC calculations significantly improve on existing RASCALL data by providing quantitative intensities, new data in the fingerprint region (crucial for molecular identification) and higher frequency regions (overtones, combination bands), and improved data for fundamental transitions based on the specific chemical environment. As the spectroscopy of most P-molecules have never been studied outside RASCALL and this approach, the new data in this paper is the most accurate spectral data available for most P-molecules and represent a significant advance in the understanding of the spectroscopic behavior of these molecules.

1. Introduction

Phosphine (PH₃) is currently a strong biosignature candidate as there are few, if any, non-biological formation pathways of phosphine for terrestrial planets (Sousa-Silva et al., 2020). A tentative discovery of phosphine in the cloud decks of Venus was recently reported, with predicted abundances on the order of ppb (Greaves et al., 2020)¹ that cannot be explained by non-biological sources (Bains et al., 2020). To investigate the presence and formation mechanisms of phosphine on Venus, and to interpret future observations of planetary atmospheres, we must improve our understanding of the chemical networks that may include phosphine. A crucial tool in this process is the ability to detect phosphorus-bearing molecules (P-molecules) that can provide clues to the formation pathways of phosphine, and provide insight into the mechanisms of a possible phosphine-producing biosphere. Gaseous P-molecules can be remotely detected using spectroscopy, but currently very limited spectral data is available for these molecules.

A more in-depth understanding of planetary environments through the interpretation of both archival and future observational data, will require spectral data on all relevant atmospheric molecules. To follow-up potential phosphine detections in Venus and exoplanets will similarly require in-depth analyses of the wider context of these atmospheres, which in turn relies on our ability to detect the P-molecules that participate in the chemical networks where phosphine is present. Thus, discussions and explorations in this paper pioneer key processes and considerations by which an initial biosignature detection can be followed up, and as a by-product identify a wide variety of opportunities and challenges in the field of spectral detection of unknown chemistry (whether geochemical, photochemical or biochemical) that will be crucial for upcoming explorations of exoplanetary atmospheres.

P-molecules are particularly interesting in astrobiology due to the phosphorus's ability to create complex organic molecules with unique functionality. Phosphorus plays a universally vital role in cellular metabolism (ATP), storage of genetic information (RNA/DNA), formation of cell membranes (Phosolipids) and in cell regulation (phosphate buffer). Phosphorus, in the form of phosphates (${\text{PO}}_4^{3-}$), plays an essential role in carbon chemistry as it: (1) maintains constant negative charge in biochemical conditions; (2) most phosphates (especially polyphosphates) are thermodynamically unstable and have multiple energetic intermediates that can enable polyphosphates like ATP to act as rechargeable batteries in nearly all cellular metabolism; and (3) it works as an efficient pH buffer with free phosphate in cellular plasma regulating acidity (Pasek, 2014). Phosphorus is present in all life on Earth (Cockell et al., 2016) and is expected to be central to life elsewhere. Therefore, understanding the abundance and chemical form of phosphorus on other planets will play an important role in the search for life beyond Earth (Elser, 2003; Hinkel et al., 2020).

Understanding the spectroscopy of P-molecules has value beyond the search for biosignatures in planetary atmospheres. Although phosphorus is a relatively scarce element, P-molecules are ubiquitously found throughout the galaxy: various P-molecules participate in the convective and chemical cycles of gas giants and are expected to behave similarly in cool stars (e.g., Larson et al., 1977; Tokunaga et al., 1980; Weisstein and Serabyn, 1996; Visscher et al., 2006); phosphine and five other P-molecules have been detected in circumstellar regions (Turner and Bally, 1987; Ziurys, 1987; Guélin et al., 1990; Agúndez et al., 2007, 2014b; Tenenbaum et al., 2007; Halfen et al., 2008); and also comets with a significant phosphorus content are expected to have P-molecules in their coma (Crovisier et al., 2004; Kissel et al., 2004; Maciá, 2005; Agúndez et al., 2014a).

Despite its relevance for both astronomy and Earth sciences, the rich chemistry of atmospheric phosphorous species is understudied, partially because of the paucity of spectral data for these molecules. Lack of suitable spectral data seriously hinders atmospheric characterizations. Obviously, if there is no spectral data on a molecule suitable for use in astronomy, the spectroscopic detection of the molecule can never be confirmed. Incorrect assignments are also a strong possibility, particularly with the limited low resolution data that is commonly available from exoplanet observations; it is all too easy to incorrectly assign a spectral signature when the reference data is not sufficiently comprehensive. As an example, the recent confirmation of water on the Moon (Honniball et al., 2020; Schorghofer and Williams, 2020) relied on a less ambiguous spectral signature at 6 μm—the H-O-H bend region—rather than earlier detections at 3 μm—the O-H stretch region—which could have easily been any molecule with an alcohol (-OH) functional group, such as methanol.

Production of high-quality rovibrational or rovibronic spectral data is extremely time-consuming even for small molecules, usually requiring a combined theoretical-experimental approach to achieve accurate frequency and intensity predictions that are reliable across a large spectral region. For a thorough description of the current theoretical approaches including strengths and limitations, see Tennyson et al. (2016a) for diatomic rovibronic spectroscopy and Tennyson (2016) for polyatomics. Experimentally, typical laboratory challenges are exacerbated for P-molecules due to safety concerns around many phosphorous-containing molecules and the difficulty in obtaining or synthesizing pure samples. This research effort is only reasonable for a relatively small number of molecules, targeted for their importance in known or proposed chemical processes.

An alternative is to use high-throughput methods to produce spectral data for hundreds to thousands of molecules. These procedures can be used to identify groups of molecules difficult to distinguish, screen molecules with strong transitions and provide a database for alternative potential assignments of observed spectral features. High-throughput methodologies often must compromise accuracy for coverage. Nonetheless, they allow for a statistical and pattern-focused analysis of atmospheric and molecular spectra that is mostly out of reach to traditional spectral databases. Sousa-Silva et al. (2019) pioneered this data generation by producing approximate spectral data for more than 16,000 molecules using a functional-group driven approach called RASCALL that relies primarily on organic chemistry. In this paper, we develop a complementary approach, called CQC, using automated approaches with standard computational quantum chemistry (hence CQC) methods to produce spectral data for more than 900 P-molecules over a wider spectral range than RASCALL data.

This paper focuses on infrared spectroscopy of gas-phase P-molecules and is organized as follows: section 2 presents an extensive literature synthesis of potentially volatile P-molecules that could be spectroscopically observed in planetary atmospheres. Section 3 collates and discusses the key existing sources of infrared spectral data for P-molecules along with presenting and analysing our new results for 958 molecules obtained with computational quantum chemistry (CQC). Section 4 considers the diverse uses of our new large spectral CQC dataset, discusses the interplay of spectroscopic detections with reaction network and kinetic modeling, and reflects on the interdisciplinary approach adopted in this paper. Finally, in section 5 we conclude with a summary of the key contributions of this paper.

The scope of this paper is deliberately broad. We aim to identify critical research sub-projects for future detailed analysis, whilst simultaneously (and as importantly) identifying sub-projects with less impact potential. To achieve this broad perspective, we directed interdisciplinary expertise to the specific problem of P-molecule atmospheric speciation and spectroscopy. Significant insights to the problem were contributed from computational quantum chemistry, astronomy, atmospheric chemistry, kinetics and reaction network modeling, experimental spectroscopy, machine learning, geology, and origin of life research disciplines.

2. Potentially Volatile Phosphorus-Bearing Molecules

In this section, we tackle the challenging problem of enumerating and prioritizing the phosphorus-bearing molecules (P-molecules) that could be spectroscopically observed in planetary atmospheres. There are two main approaches to this problem:

• a targeted approach, developed in sub-section 2.1, that iteratively builds up a list of molecules based on known or proposed chemistry in planetary atmospheres including Jupiter, Earth, and Venus;

• a reaction-agnostic approach, developed in sub-section 2.2, that simply enumerates all molecules that fulfill certain criteria.

2.1. Targeted Approach

Our goal in this section is to identify target P-molecules that may be detectable in planetary atmospheres, including species that are predicted to be important for understanding the phosphorus chemistry on Venus. Table 1 details the small number of atmospheric P-molecules that have been explicitly considered.

TABLE 1

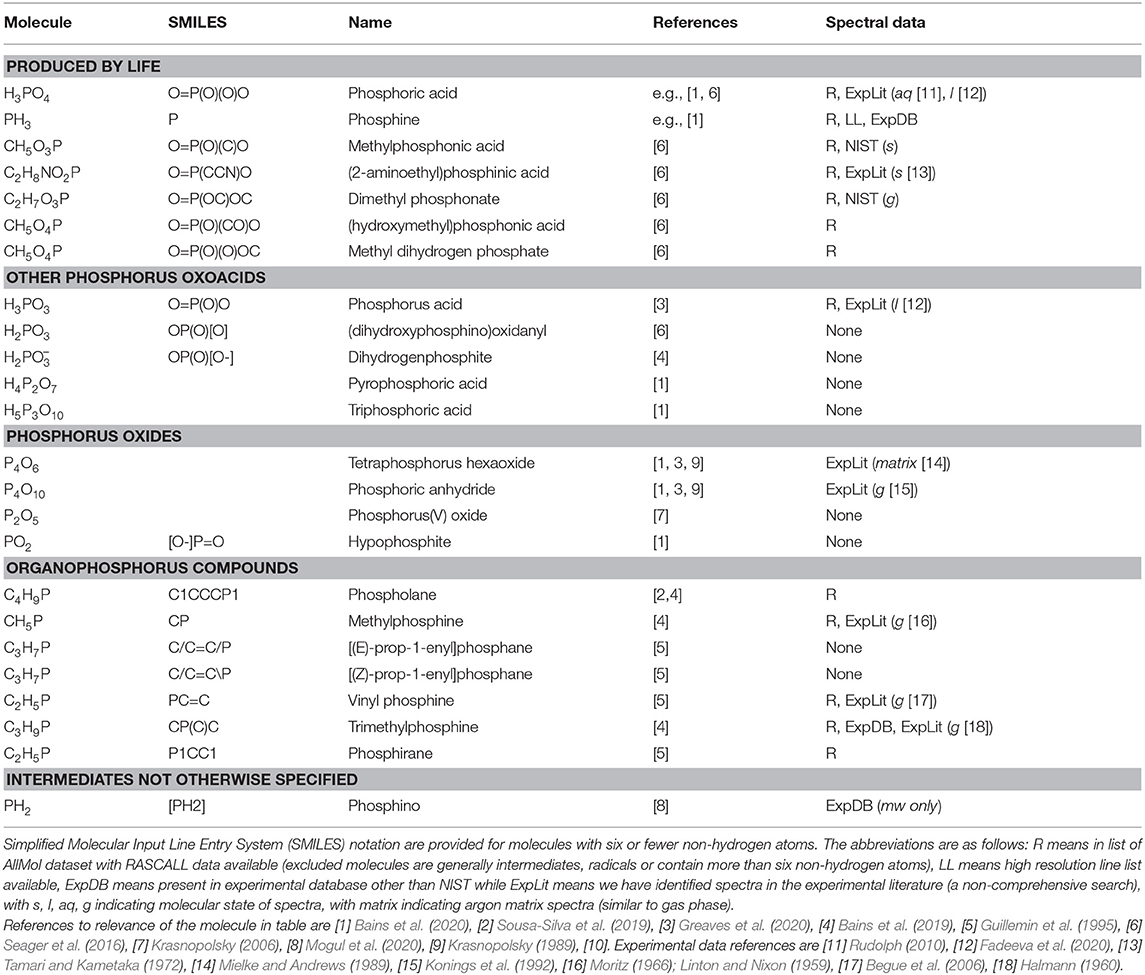
Table 1. Non-diatomic potentially gaseous phosphorus-bearing molecules identified in the literature (ref column) as relevant to terrestrial atmospheres.

Let us first clarify important terminology and phosphorus chemistry concepts. ${\text{PO}}_4^{3-}$ is the most oxidized form of phosphorus, with a phosphorus oxidation state of +5, and is generally present in the atmosphere as phosphoric acid, H₃PO₄. Other forms of phosphorus are considered to be reduced phosphorus, with PH₃ being the most reduced form of phosphorus (oxidation state of −3), but not thermodynamically favored at temperatures below 800 K with low hydrogen-pressure (Visscher et al., 2006) or in oxidizing environments like modern Earth where it reacts rapidly with OH^• and O^• radicals. Therefore, the dominant forms of phosphorous on a planet will depend on the planet's (bio)geochemical cycles, as well as whether the atmosphere contains reduced (e.g., H₂, CO) or oxidized gases (e.g., O₂, H₂O, CO₂).

Phosphorus compounds are generally categorized as organic (containing carbon) or inorganic (do not contain carbon). Only some of the P-molecules in the atmosphere are volatile, for example large quantities of inorganic phosphorous are dispersed into the atmosphere as coarse solid particles (aerosols) from dusts or combustion sources (Mahowald et al., 2008). Inorganic (poly)phosphates and several organic atmospheric phosphorous compounds are soluble in water and thus bioavailable. Additionally, plant activity can emit complex biogenic P-molecules that aggregate as coarse aerosols, which are insoluble and only transport and deposit organic phosphorous locally, rather than globally (Tipping et al., 2014).

2.1.1. P-molecules in Hydrogen-Rich Reducing Gas Giants, e.g., Jupiter, Saturn

In the reducing environments of Jupiter and Saturn, the most abundant P-molecule is phosphine (PH₃). Though phosphine is not the most thermodynamically favorable form of phosphorus at temperatures of the atmosphere, phosphine formed in the hot deep layers is brought to the top of the atmosphere through convection. In modeling this phenomena and seeking to understand the phosphorus chemistry of gas giants, Barshay and Lewis (1978), Fegley and Lodders (1994), and Borunov et al. (1995) considered the abundances of PH₃, PH₂, PH, P₄O₆, P₄O₇, P₄O₈, P₄O₉, P₄O₁₀, PS, P₂, P, PO, PO₂, PF, PC, PCl, PN, P₄, and P₃; with many of these compounds having very low modeled abundances. P₄O₆ and P₄O₁₀ are particularly notable as they arise often in the literature considering P-molecules and gas-phase chemistry due to their stability, despite their large molecular weight. P₄O₆ has a boiling point of 173.1°C, while P₄O₁₀ sublimes at 360°C. These properties imply the vapor pressure and thus gaseous abundance of both compounds may be appreciable, especially in higher temperature environments. It has also been hypothesized that alkyl phosphines, i.e., PR₁R₂R₃, may be formed in hydrogen-rich environment from the photolysis of PH₃ in the presence of hydrocarbons (Guillemin et al., 1995, 1997).

2.1.2. P-molecules Expected on Earth

The speciation of phosphorus in the Earth's atmosphere is quite different than gas giants. Earth's atmosphere is an oxidizing environment and therefore the reduced species PH₃ is associated solely with biological and industrial activity (Sousa-Silva et al., 2020). Instead, phosphates (${\text{PO}}_4^{3-}$) are most common, with H₃PO₄ assumed as the dominant species and the only P-molecule with gas-phase kinetic data (Bains et al., 2020). In the context of this paper, the most notable aspect about phosphorus on Earth is the almost complete absence of gas phase P-molecules. Most descriptions of Earth's phosphorus cycle (e.g., Schlesinger and Bernhardt, 2020) completely ignore any atmospheric involvement of P-molecules, and focus instead on the much more numerous and biologically critical processes by which phosphorus moves through the lithosphere, hydrosphere, and biosphere.

The atmospheric impact of P-molecules can usually be neglected because most P-molecules either have low volatility (such as P₄O₁₀) and quickly “rain out” into the hydrosphere, or are highly reactive and are destroyed in Earth's oxidizing atmosphere. Consequently, few P-molecules are the subject of study in the Earth's atmosphere, and no P-molecules are included explicitly in the two most chemically comprehensive Earth atmospheric models, the Master Chemical Mechanism (Rickard and Young, 2005) and GEOS-chem (The International GEOS-Chem User Community, 2019).

For the phosphorus that does cycle into the Earth's atmosphere, the conditions are so oxidizing that atmospheric budgets have total atmospheric phosphorus (primarily from dust or biogenic aerosols) as generally being oxidized to ${\text{PO}}_4^{3-}$ and deposited into the Earth's oceans (Mahowald et al., 2008). Atmospheric deposition and biological fixation of phosphorus is typically considered negligible in comparison to total phosphorus, and subsequently ignored in terrestrial phosphorus budgets (Zhang et al., 2019).

Experimentally, the speciation of atmospheric phosphorus on Earth is still poorly understood; typical analytical techniques destroy speciation information (Morton et al., 2003), such as acidification of samples to pH 1 in spectrophotometry (Mahowald et al., 2008). Contemporary techniques are able to distinguish between soluble/insoluble phosphorous and inorganic/organic phosphorous (Violaki et al., 2018), but an exact chemical inventory of these species has not been made. Recently, there has been recognition of plant emissions, such as phosphate esters, i.e., P(OR₁)(OR₂)(OR₃), in contributing to atmospheric volatile organic phosphorus, not just to coarse biogenic aerosols (Li et al., 2020); but the overall impact of atmospheric organic phosphorous is not widely recognized yet.

A perhaps surprising source of information on potential gaseous P-molecules in atmospheres comes from the origin of life literature. Phosphorus is considered an essential component of life, yet dominant phosphorus sources (notably apatite) are only slightly soluble, raising the question of how phosphorus was introduced into the hydrosphere in sufficient quantities to enable life to emerge on Earth (e.g., Yamagata et al., 1991; Schwartz, 2006). Studies into the solution to this phosphorus problem—usually volcanoes, lightning, and meteorites—lead to consideration of some gas-phase P-molecules. For example, Yamagata et al. (1991) discussed the volatilization of P₄O₁₀ from high temperature apatite in volcanoes; P₄O₁₀ can then be hydrolysed to form phosphates, such as H₃PO₄. Schwartz (2006) considers the production of phosphite ${\text{PO}}_3^{3-}$ and phosphorus acid H₃PO₃ by lightning in volcanoes. Ritson et al. (2020) also proposed that water can react with meteorite mineral to produce organophosphates by reacting with the phosphide species (containing P³⁻) from meteorite mineral enstatite chondrites to produce P-molecules with various oxidation states that are then fully oxidized through photochemical reactions to the bioavailable ${\text{PO}}_4^{3-}$ form. Ablation of cosmic particles can produce phosphorus gases, such as PO₂ that then dissociates to PO (Carrillo-Sánchez et al., 2020).

2.1.3. P-molecules Expected on Venus

In the observable upper and middle atmosphere, Venus is an oxidizing environment due to the high concentration of sulfuric acid—a strong oxidizing agent—and the high production rate of oxidizing radicals through photolysis (Bierson and Zhang, 2020). Therefore, H₃PO₄ is predicted to be the most dominant P-containing species in the upper atmosphere (Glindemann et al., 2003), with some phosphate in the form of dehydration products, e.g., H₄P₂O₇, H₅P₃O₁₀ (Bains et al., 2020). H₃PO₃ concentration is predicted to be negligible, at tens of milligrams across the whole atmosphere (Bains et al., 2020). In the lower Venusian atmosphere, P₄O₆ is thermodynamically favored and dominates the chemistry of P-molecules at this altitude (Krasnopolsky, 1989), while P₄O₁₀ is disfavored.

Overall, similar geological processes are likely to occur in Venus as on Earth as the bulk composition for both planets is expected to be similar (Treiman, 2009; Shellnutt, 2013). Some differences are expected due to the differing atmospheric composition (far less O₂, more CO₂, and more sulfuric acid) (Johnson and de Oliveira, 2019), lack of plate tectonics on Venus (Nimmo and McKenzie, 1998), the higher ground temperature (Taylor et al., 2018), and lack of water oceans (Taylor et al., 2018) on Venus. The effect of these differences on the atmospheric speciation of P-molecules is unexplored.

2.1.4. P-molecules From Life on Earth

Life can produce a much richer range of molecular species than geological processes and has the potential to influence the sources and sinks of molecules to drastically impact the atmospheric composition, e.g., enabling 21% oxygen on Earth. P-molecule species produced by life (Seager et al., 2016) include CH₅O₃P, C₂H₈NO₂P, two structural isomers of CH₅O₄P, H₃PO₄, and of most recent interest, phosphine (PH₃).

As reviewed by Sousa-Silva et al. (2020), on Earth, atmospheric PH₃ is associated exclusively with life, either through anthropogenic sources (e.g., agriculture), or through its production in anaerobic ecosystems (e.g., lake sediments, marshlands), but has very low abundance (ppt/ppq locally at sites of anaerobic activity). The largest sink for PH₃ on the Earth is destruction by OH^• (Glindemann et al., 2005), causing a very short PH₃ lifetime measured in hours (Sousa-Silva et al., 2020).

Despite phosphine being present in a range of environments—almost exclusively anoxic—the exact basis and mechanism for phosphine formation in nature is not well-understood. Early work has reported the production of phosphine from mixed bacterial cultures (mixed acid and butyric acid bacteria) in the laboratory (Jenkins et al., 2000). Pasek et al. (2014) proposed that phosphite [H₂PO₃]^{− 2} and hypophosphite [H₂PO₂]⁻ are first produced through microbial metabolism, and these compounds are then converted to phosphine by other mechanisms. Bains et al. (2019) suggested that, in some environments, it is a combination of phosphate-reducing bacteria and the coupling with phosphite metabolism that results in phosphine release. Several very recent studies are beginning to provide more informed insights into the potential roles of specific microorganisms and pathways in phosphine production. For example, Fan et al. (2020a) indicated that the production of acetic acid via the tricarboxylic acid cycle promoted the production of phosphine. Most recently it was found that the phosphine production was enhanced when the hydrogen levels were increased (Fan et al., 2020b). The authors suggested that phosphine production was promoted with hydrogen as an electron donor (i.e., H₂${\text{PO}}_4^{-}$ + H⁺ + 4H₂ → PH₃ + 4H₂O), and it was concluded that both reducing power and excess electrons are necessary prerequisites for the production of phosphine. The activity of the enzyme dehydrogenase was shown to be positively correlated with phosphine production (Fan et al., 2020b), suggesting that this enzyme's function in producing electrons and reducing agents contributes to phosphine generation. Furthermore, co-factors, such as NADH and riboflavin vitamins were suggested to be key in phosphine production (Bains et al., 2019; Fan et al., 2020b). Given the limited studies and the debate surrounding the exact pathways and the diverse microorganisms potentially involved in phosphine production, significantly more work is needed in this area on the biological basis for phosphine production.

2.1.5. P-Molecules Potentially Involved in Phosphine Production on Venus

Recently, phosphine has risen to prominence due to its potential as a strong biosignature (with few non-biological sources on temperate planets) and tentative detection on Venus. We refer to the very detailed previous publications for known and proposed geochemical and photochemical networks of phosphine production in exoplanets (Sousa-Silva et al., 2020) as well as an in-depth consideration on Venus (Bains et al., 2020).

For this paper, we are interested in enumerating the P-molecules identified in these papers as part of the reaction network involving phosphine. The photochemical network proposed by Bains et al. (2020) for PH₃ formation involves many other P-molecules in a radical reaction network: H₄PO₄, H₂PO₃, HPO₃, HPO₂, HPO, PO₂, PO, PH, and PH₂, several of which will be transient intermediates.

2.1.6. Discussion of Targeted Approach

The targeted approach followed in this section helped identify molecules of particular interest that are not obvious to non-specialists, such as P₄O₁₀, as well as identifying challenges to remote detection, such as the relative low volatility of many P-molecules. This approach has the ability to synthesize relevant interdisciplinary knowledge across sub-fields and enhance the common understanding of the scope, context and limitations of existing disciplinary expertise.

Overall, there is a paucity of modeling work on the atmospheric speciation, kinetics and reaction networks of P-molecules. Though we can identify some species likely to be important, this poor understanding means that it is desirable to consider a much broader range of potential volatile P-molecules, as described in the next section, in order to detect the P-molecules present in a given atmosphere and facilitate the elucidation of atmospheric phosphorus reaction networks. This broad perspective will be particularly critical for characterizing diverse exoplanet atmospheres.

2.2. Reaction-Agnostic Approach

The search for extra-terrestrial life currently relies on the detection of biosignature gases, i.e., gases produced by life that accumulate in the atmosphere and could be detected remotely (Schwieterman et al., 2018). A molecule's suitability as a biosignature is impacted by multiple factors (e.g., the host planet's atmospheric chemistry and geology) and so any selection criteria are necessarily broad. There is an unavoidable Earth-centric bias in the search for life in the universe; nonetheless, it is laudable to attempt to approach the search for biosignatures on exoplanets as agnostically as possible. With that in mind, Seager et al. (2016) proposed a list of more than 16,000 molecules (hereafter AllMol list) that may be associated with life and are likely to be volatile in the atmosphere of potentially habitable exoplanets.

The AllMol list contains molecules with up to six non-hydrogen atoms that are expected to be volatile and stable at Earth's standard temperature and pressure (STP). Volatile molecules were estimated as those with boiling points below 150°C, as most molecules with boiling points above this temperature are likely to be non-volatile. Stability was interpreted as molecules being able to remain as pure entities under STP conditions and not reacting readily with water. The cutoff of molecules with up to six non-hydrogen atoms was chosen as it implies volatility for a substantial fraction of molecules, including several molecules that are currently studied as biosignature gases.

The AllMol list contains 2,130 P-molecules made of the elements C, N, O, F, S, Cl, Se, Br, and I. However, for our quantum chemistry studies, we have excluded molecules containing the elements Se, Br, and I, as they posed additional computational difficulties that were not worth addressing given the rarity of these elements (see section 3.3.4). For completeness, we have included the water-reactive PCl₃ and PF₃ molecules in our calculations due to their relevance in organophosphorus chemistry, thus leading to a working list containing 962 P-molecules.

Figure 1 presents the distribution of the molecules present in the full 2,130 P-molecules list and our working list with 962 molecules, considering the total number of atoms (left) and the total number of non-hydrogen atoms (right). For both lists, most molecules have between 9 to 14 total atoms and five to six non-hydrogen atoms.

FIGURE 1

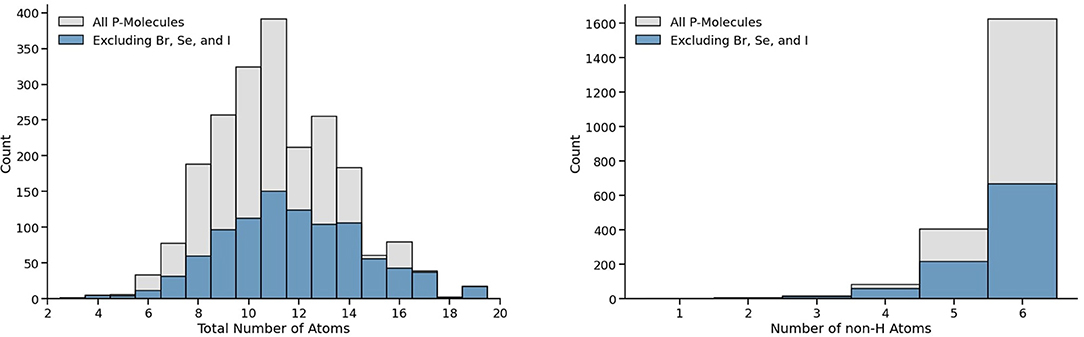
Figure 1. Distribution of AllMol list's 2,130 P-molecules as a function of total number atoms and non-hydrogen atoms are shown to the left and right top plots, respectively. The total distribution is displayed in gray, with those in blue corresponding to molecules that do not contain Br, Se, and I; our working list of 962 molecules.

For further insight into our working list, Figure 2 shows the count of elemental composition and various combinations of elements, and the number of atoms in each combination of elements. Carbon and Hydrogen are the most abundant elements in P-molecules overall, but there are actually more C_aH_bP_cCl_d than C_aH_bP_c molecules. Almost all our working molecule set contained carbon, i.e., were organic; only 20 molecules were inorganic.

FIGURE 2

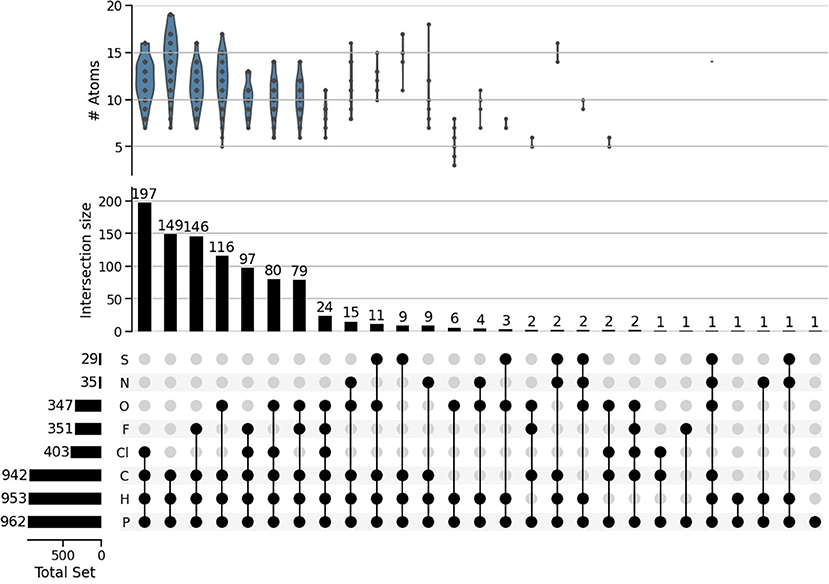
Figure 2. Distribution of elements within our subset of 962 P-molecules. The horizontal histogram on the left details the number of molecules that contain the corresponding element to the right. The dots create sets of elements that form various molecules, with the counts of those sets shown in the histogram above. For example the first column contains 197 molecules that are made up of only Cl, C, H, and P. The plot above the histogram details the distribution of molecules' size, given by total number of atoms in each set of elements.

Another useful categorization is to consider the bonds to the phosphorus atom within our working set of 962 P-molecules; broadly speaking, this determines the class of the compound. These statistics are detailed in Table 2. The dominant class were organophosphines (602/962) in which the phosphorus atom was bonded only to carbon or hydrogen. Phosphorus-oxygen single or double bonds were the other key phosphorus bond types, with 203 molecules with P=O only, 61 with P-O only, and 73 with both P=O and P-O bonds. A small number of compounds have P-S, P=S, and/or P-N bonds. Only 42 compounds had no P-C bonds at all.

TABLE 2

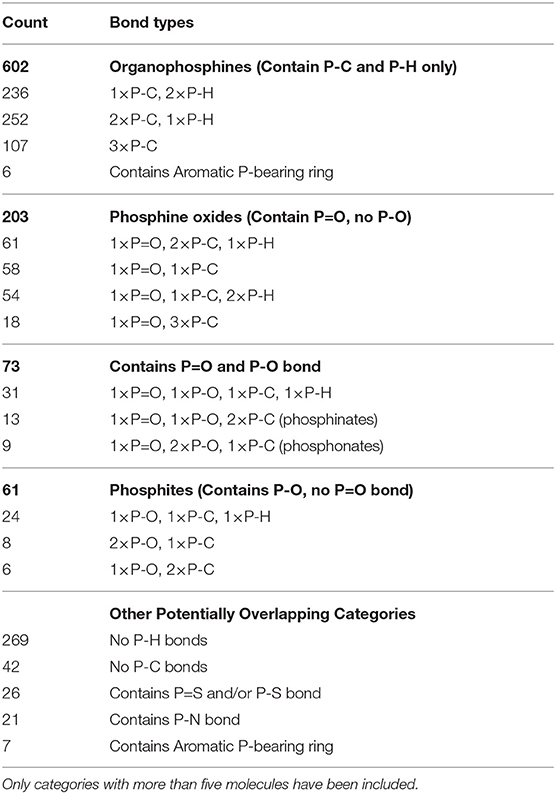
Table 2. Categorization of P-molecules within our 962 working set according to the phosphorus bonds in the molecule.

Despite the large number of molecules considered, the constraints imposed when constructing AllMol exclude many molecules considered in our targeted approach, especially large phosphate oxides, such as P₄O₁₀ and radicals, such as the diatomics PN, PC, PO, and PH. Therefore, there is surprisingly little overlap between our targeted molecule set and our working list of 962 P-molecules. This small overlap probably occurs due to the sparsity of gas-phase P-molecules in Earth-conditions and would not be expected for many other elements.

3. Infrared Spectroscopy

Infrared (IR) spectroscopy is currently the technique of choice for future searches of extrasolar biosignatures in planetary atmospheres (Schwieterman et al., 2018). The successful identification of molecules requires available reference spectroscopic data. Therefore, in this section we consider pre-existing experimentally-derived data, RASCALL-generated data based on functional group decomposition, and the newly generated CQC spectral data based on computational quantum chemistry (CQC) calculations for the P-molecules considered.

3.1. Existing Experimentally-Derived Data

The infrared spectral data available for P-molecules are relatively sparse, especially in the gas-phase. There are three main sources of data: (1) line lists of spectral positions and intensities, (2) experimental databases usually containing only un-digitized image spectra (often in liquid phase), and (3) individual papers. Of these, only line lists provide astronomers with accessible data in a format suitable for molecule detection.

Extensive line lists containing spectral line positions and intensities in the infrared spectral regions are available for 11 P-molecules. These data are generated individually for each molecule by combining the best available experimental data and ab intio CQC calculations, with the latter particularly necessary for dipole moments. There are two broad methodological approaches: the variational approach solving the nuclear motion Schrödinger equation on an explicit potential energy surface, and the empirical approach where model Hamiltonian constants are used. Specifically, line list data is available in the centralized ExoMol database (Tennyson et al., 2016b, 2020; Wang et al., 2020) in a standardized format for the following P-molecules: using the ExoMol variational approach (Tennyson, 2016; Tennyson et al., 2016a) for PH₃ (Sousa-Silva et al., 2015), PF₃ (Mant et al., 2020), PN (Yorke et al., 2014), PH (Langleben et al., 2019), PO and PS (both in Prajapat et al., 2017), cis−P₂H₂ and trans−P₂H₂ (both in Owens and Yurchenko, 2019) and using the MoLLIST empirical approach (Bernath, 2020) for CP (Ram et al., 2014). Alternative line list data for phosphine are also available in various sources, e.g., HITRAN (Gordon et al., 2017), TheoRETs (Nikitin et al., 2009, 2014), and GEISA (Jacquinet-Husson et al., 2016).

Experimental infrared spectral absorption cross-sections have been collated mainly by national institutes, such as the USA National Institute for Standards and Technology (NIST, Chu et al., 2020) and the Japanese National Institute of Advanced Industrial Science and Technology (AIST³). NIST's extensive database of spectral data contains cross-sections with a wide range of accuracy, resolution, and instrumental set-ups. For hundreds of molecules, NIST is the only source of spectral data, and as such mistakes can go unnoticed for many years [e.g., liquid state spectra mislabeled as gas phase, incorrectly assigned spectra or vibrational modes (Sousa-Silva et al., 2019)]. AIST's Spectral Database for Organic Compounds has a useful feature to sort by molecular weight as a proxy for volatility as well as a helpful ability to search by spectral features in a given spectral range. For the P-molecules considered here we have identified two [C₂H₇O₃P (O=P(OC)OC), CH₅O₃P (O=P(O)(C)O)]⁴ matches in the NIST database, and three [C₂H₇O₂P (O=P(O)(C)C), CH₆NO₃P (O=P(O)(CN)O), C₃H₈ClOP (O=P(CCl)(C)C)] in AIST.

Often when infrared data cannot be found in databases or linelists, they may still be found in individual papers. However, in the absence of a centralized database, identifying and processing data for individual molecules is time-consuming due to the diverse literature and poor data digitization. For some target P-molecules, we performed a non-exhaustive literature search for experimental data. Usually, the spectral data was contained solely in figures, and digitization software would be needed. Papers containing experimental infrared data from the twentieth century, when a large body of these papers were written, often suffer from problems of saturation (concentration too high for linear absorption), low resolution, and insufficient detail to obtain absorption cross-sections. These problems can result in intensities that are inconsistent with lower pressure measurements, the fine structure being obscured, and difficulty assessing the abundance of the molecule being identified. In the case of more transient molecules generated by pyrolysis, photolysis or in situ reaction, the target species may be produced in a mixture of gases, its' partial pressure unknown and the spectra affected by bands from other species present. Thus, experimental data can be used for visual identification of molecules but is generally unsuitable for use by astronomers.

Data useful for astronomical purposes can be obtained by measurements of the gaseous, low-pressure, infrared spectra of molecules at the very low temperatures achievable in a jet expansion (representing the interstellar medium) and room temperature (representing temperate potentially habitable planets). This data should be produced at high resolution in the full mid-infrared range and distributed in digitized format either as a spectra or as individual line identifications. Typically, we would expect the difficulty of the experiment to depend primarily on the ease of acquiring a pure gaseous sample of a molecule. Stable molecules with a high vapor pressure that can be bought from commercial chemical companies would usually be measurable in low-resolution in a day though high resolution scans would take a few weeks, especially if data is taken for multiple temperatures. Unstable molecules or those not commercial available would require more extensive synthesis.

3.2. Predicted Spectra From Functional Group Decomposition: RASCALL

RASCALL was the first approach to address the large deficiencies in infrared spectral reference data for atmospheric molecules by mass data production using computational approaches. The RASCALL program produces spectral data stored in the RASCALL database; a living document constantly updated (Sousa-Silva et al., 2019). Currently, the database contains spectral data for 15,477 out of the 16,368 AllMol molecules, with a total of 201,985 fundamental frequencies. The RASCALL database contains spectral data for 1,992 P-molecules with 44 different functional groups, only four of which specifically consider P atoms [namely P−H bend and stretch, P=O stretch, and (O=)PO−H stretch].

Figure 3 illustrates the functional groups frequency distribution across the RASCALL data, highlighting those frequencies corresponding to P-molecules. The P-H stretch and bends are the most ubiquitious P-molecule-specific functional group, with significant numbers of P=O stretches. Of particular interest is the sparsity surrounding the P-H stretch functional group at 2,360 cm⁻¹. This region could represent an interesting signal to look at when searching for molecules with the P-H functional group. The main contaminant will be CO₂ which has a strong absorption peak at 2,350 cm⁻¹ that, in high abundances and at low resolution, can obfuscate the spectral feature from the P-H stretch. However, this CO₂ spectral band is usually much more narrow than that caused by P-H stretch, allowing for multiple strong transitions in the wings of the P-H band to be detectable (e.g., as is the case between PH₃ and CO₂), especially when the P-H stretch frequency is shifted slightly in different environments. The figure also shows that the majority of functional groups in the data set are shared by molecules with and without phosphorus, with the most prominent one corresponding to the C-H stretch near 3,000 cm⁻¹.

FIGURE 3

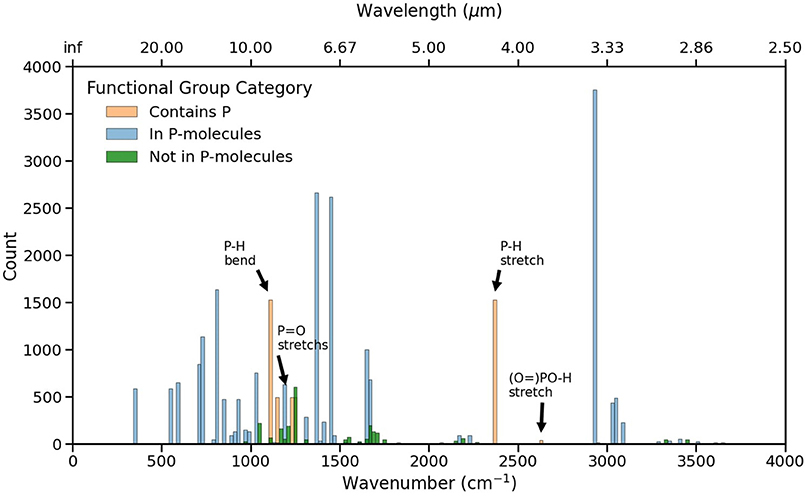
Figure 3. Frequency distribution for all functional groups within RASCALL. The blue bars correspond to the functional groups present in all 1992 P-molecules in RASCALL that do not involve P and the orange bars are functional groups containing P. The green bars correspond to functional groups that are not included in any of the P-molecules present in RASCALL. Data bins of 20 cm⁻¹ has been selected for visibility.

RASCALL is a computational method that does not utilize quantum chemistry but relies on structural chemistry, especially on functional group theory, to efficiently produce approximate molecular spectral data for arbitrary molecules (Sousa-Silva et al., 2019). As functional groups account for characteristic spectral features, RASCALL estimates the contribution of each functional group present in a given molecule to generate a first approximation to the molecule's vibrational spectrum. The spectrum given by RASCALL is composed of the approximate vibrational frequencies of the molecule's most common functional groups together with the qualitative intensity for each frequency. The functional group database contains more than 100 functional groups and is also a living document, updated as new spectrally active functional groups are identified.

RASCALL is an extremely quick and powerful approach, but the functional group approach has some inherent limitations. Most notably, the approximate spectra predicted by RASCALL are based on identified functional groups without taking into account their neighboring atoms and bonds. This functional group approach makes it nearly impossible to predict the non-localized vibrational modes in the fingerprint spectral region from 500 to 1,450 cm⁻¹, and restricts the accuracy of local mode predictions in diverse environments.

Ongoing RASCALL updates will expand functional group definitions to help address this weakness. For example, consider the O-H stretch region near 3,600 cm⁻¹ in Figure 3, where there are few spectral features in our data. As the spectral behavior of the O-H stretch strongly depend upon the remaining atoms and bonds in the molecule, and consequently vary widely between molecules, RASCALL does not consider it a single functional group. Instead, RASCALL uses a categorization criteria based on different O-H sub-groups that must be considered individually to provide more realistic O-H stretch frequencies. Currently, the RASCALL database has categorized only a small portion of the O-H variants and those affecting P-molecules have not been included yet.

RASCALL currently only provides qualitative intensities ranging from 1 to 3, representing weak to strong absorption, respectively; this is an area of active method development.

3.3. Large-Scale Computational Quantum Chemistry Data Generation: CQC Approach

3.3.1. Method

An alternative to the RASCALL approach is to use standard computational quantum chemistry (CQC) approaches to directly solve the Schrodinger equation (within a given approximation) and predict vibrational frequencies and intensities of input molecules. Our goal here is to develop the first version of the harmonic CQC-H1 procedure: a high-throughput, largely automated, reliable approach that can be used for hundreds to thousands of molecules by taking as input the molecule's Simplified Molecular Input Line Entry System (SMILES) notation to produce computationally-derived infrared spectra.

Initial molecular geometries for all 962 P-molecules were obtained from SMILES codes through a Python script utilizing the RDKit (RDK, 2000), ChemML (Haghighatlari et al., 2020), and ChemCoord (Weser, 2017) libraries.

Harmonic frequency and intensity calculations for our CQC-H1 approach were performed under the standard double-harmonic approximation utilizing the ωB97X-D hybrid functional (Chai and Head-Gordon, 2008; Alipour and Fallahzadeh, 2016) together with the augmented def2-SVPD basis set (Weigend and Ahlrichs, 2005; Rappoport and Furche, 2010). This model chemistry combination (i.e., hybrid functional/double-zeta basis set augmented with diffuse functions) was chosen as it reproduces reliable dipole moments (Zapata and McKemmish, 2020), a key component for vibrational intensities, and ωB97X-D represents a good general purpose hybrid density functional (Goerigk and Mehta, 2019). Harmonic frequencies were also scaled using a multiplicative scaling factor of 0.9542 (Kesharwani et al., 2015). All calculations were performed with the Gaussian 16 quantum chemistry package (Frisch et al., 2016).

The initial geometries for all 962 P-molecules were optimized using a tight convergence criteria (maximum force and maximum displacement smaller than 1.5 × 10⁻⁵ Hartree/Bohr and 6.0 × 10⁻⁵ Å, respectively) and an ultrafine integration grid (99 radial shells and 590 angular points per shell). For ~50 molecules, the jobs did not converge to a minima with the automated approach and needed manual intervention, most commonly recomputing an input geometry in Avogadro (Hanwell et al., 2012). Four molecules were excluded from our analysis due to geometry convergence problems (see sub-section 3.3.4), leading to a total of 958 P-molecules considered in our CQC-H1 approach.

3.3.2. Results

Figure 4 presents the frequency distribution of the scaled CQC-H1 harmonic frequencies compared to the RASCALL data, considering the 868 molecules with data available from both sources; incorporating CQC-H1 data from all 958 molecules (total of 28,152 frequencies) produces a similar frequency distribution. The fundamentals bands predicted by the harmonic calculations are predominantly found in the region below 500 cm⁻¹, within 600–1,400 cm⁻¹ (the fingerprint spectral region) and in the 2,900–3,100 cm⁻¹ domain characterized mostly by the C-H stretches. Like the RASCALL data, our calculated harmonic data also exhibits a small number of signals between 2,000 and 2,700 cm⁻¹, apart from the signals around 2,360 cm⁻¹, corresponding to the P-H stretch signal.

FIGURE 4

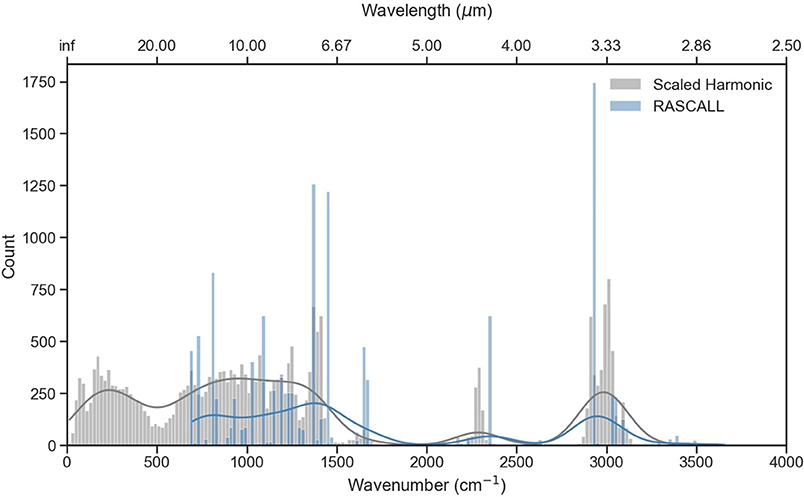
Figure 4. Frequency distribution across the RASCALL (blue) and the ωB97X-D/def2-SVPD scaled harmonic calculations (gray) data for 868 molecules. A bin width of 20 cm⁻¹ has been selected for visibility. The solid line on top of the histograms represents an estimate of the probability distribution for the data.

Figure 4 highlights how the CQC-H1 approach, unlike RASCALL, can differentiate the frequencies at which functional groups absorb based on the specific chemical environment surrounding that functional group. For example, RASCALL places all C-H stretches at a particular frequency value (prominent blue bar at 2,923 cm⁻¹), whereas the scaled harmonic calculations for this functional group result in frequencies that are spread over a larger frequency window. The figure also demonstrates the capability of the quantum chemistry calculations to provide data in the fingerprint region of the spectrum (500–1,450 cm⁻¹), as all normal modes are computed (by comparison, RASCALL only predicts around 45% of the normal modes). Calculation of normal mode frequencies in the fingerprint region poses a fundamental and probably insoluble challenge to the RASCALL approach, as these fingerprint modes involve motion of large portions of the molecule rather than the movement of isolated functional groups.

Figure 5 shows a logarithmic scale count of the intensity distribution for the harmonic calculations. The count of molecules decreases exponentially with larger intensity values, with a median intensity of 7.5 km/mol.

FIGURE 5

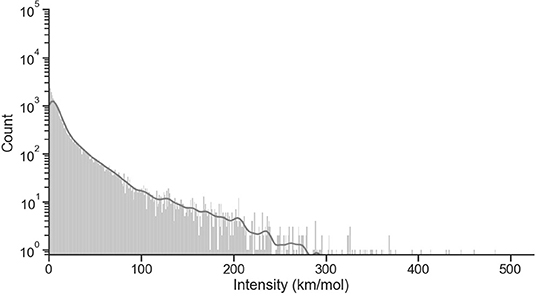
Figure 5. Distribution of intensities for scaled harmonic (958 molecules, 28,152 frequencies). A bin width of 1 km/mol has been selected for visibility. The solid line on top of the histogram represents an estimate of the probability distribution for the data.

To further illuminate the differences in spectral predictions, Figure 6 compares the RASCALL and CQC-H1 vibrational spectra for a selection of P-molecules relevant to planetary bodies, and Figure 7 does the same with P-molecules formed through biotic processes (see Table 1). The SMILES code for each molecule as well as the maximum intensities for the harmonic data is shown in the figure and indicates the vertical scaling of the data.

FIGURE 6

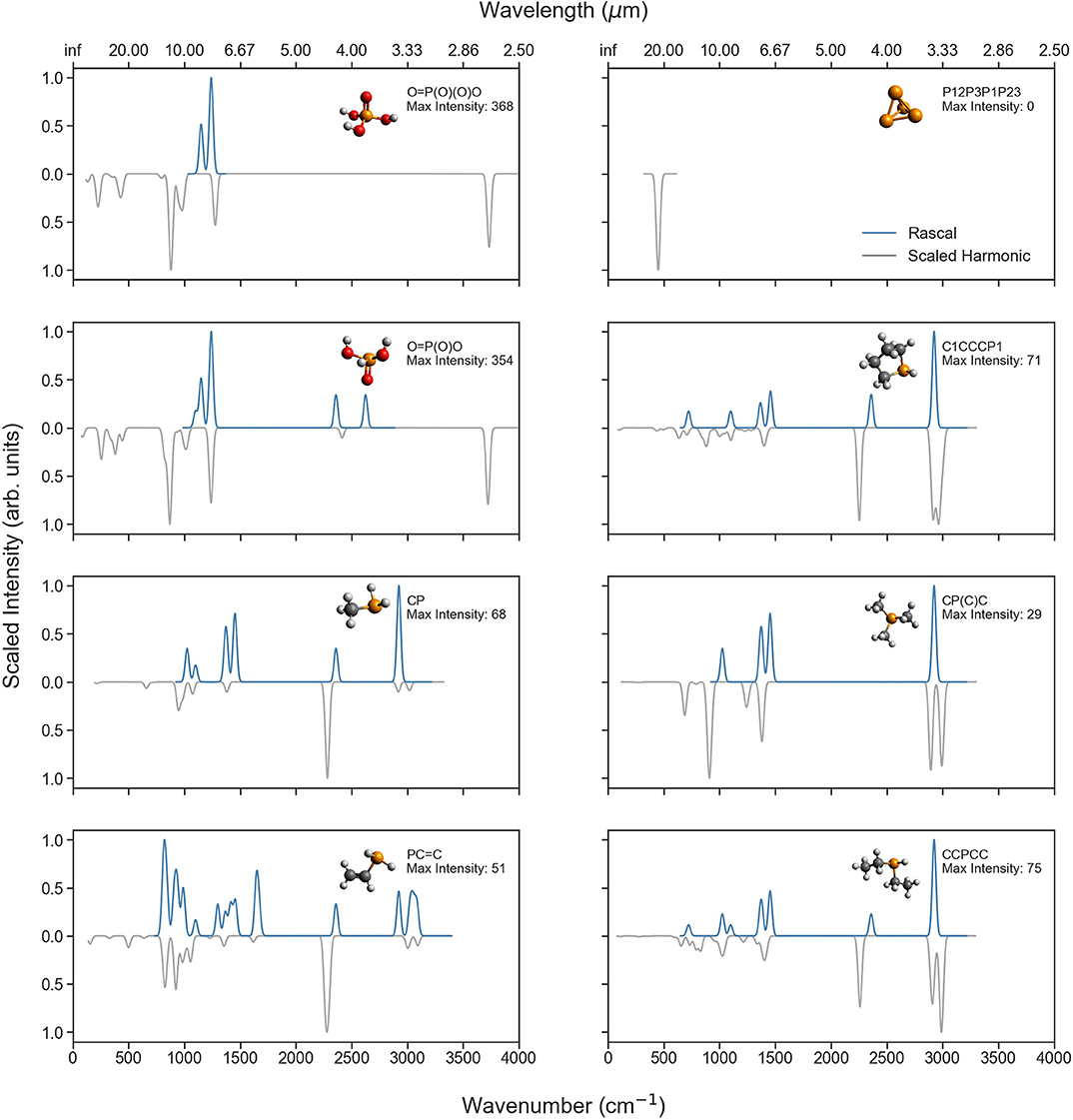
Figure 6. Comparison of the RASCALL (blue) and scaled harmonic (gray) quantum chemistry data available for eight of the P-molecules mentioned in Table 1. The SMILES code is presented for each molecule as well as the largest values for the predicted intensities (km/mol) with the harmonic calculations.

FIGURE 7

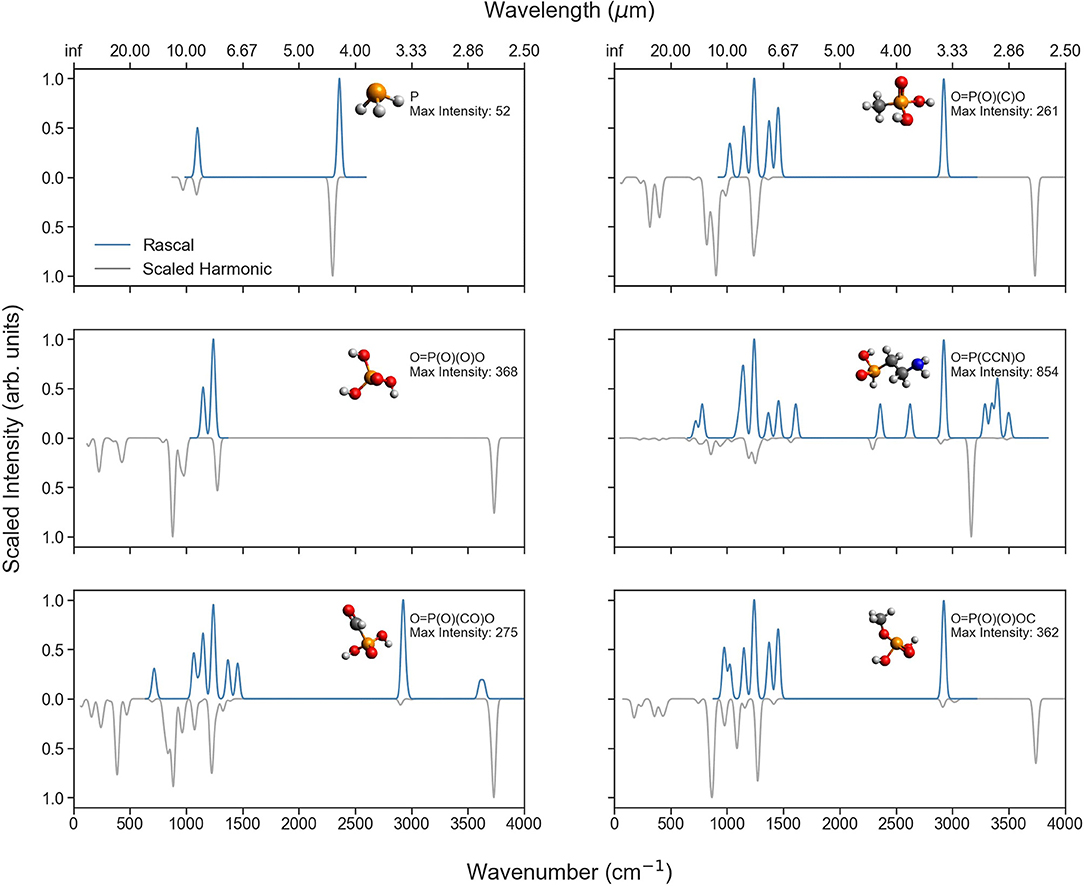
Figure 7. Comparison of the RASCALL (blue) and scaled harmonic (gray) quantum chemistry data for six P-molecules produced by life (according to the AllMol list). The SMILES code is presented for each molecule as well as the largest values for the predicted intensities (km/mol) with the harmonic calculations.

Across the molecules presented in these two figures, different degrees of agreement can be observed between RASCALL and the CQC-H1 data. Overall, for most molecules there is clear semi-quantitative agreement in the location of peaks across both sources of data, while RASCALL often overestimates the intensity of weak bands, especially around 3,000 cm⁻¹. As an example, the RASCALL spectrum for methylphosphonic acid [O=P(O)(C)O top right of Figure 7] shows a high intensity peak for the C-H stretch with nothing shown in the harmonic CQC-H1 data as the band intensity is significantly low, highlighting the limitations in RASCALL's intensity approximations. Regarding the band positions, several of the subplots in both figures show a shift of more the 20 cm⁻¹ in the RASCALL data corresponding to the P-H stretch (around 2,360 cm⁻¹). This likely arises from inadequacies in the P-H frequency data in RASCALL and could be easily corrected with an update using our new P-molecule CQC-H1 data. These figures also provide further evidence of the current deficiencies in the treatment of O-H stretches in RASCALL.

Figure 8 reports the vibrational spectra for two P-molecules for which both theoretical and experimental data from NIST is available. The top figure shows an overall fair agreement between the different sources of data, especially in the C-H stretch region where both the NIST and scaled harmonic CQC-H1 data are very alike. In the fingerprint domain (500–1,450 cm⁻¹), the agreement is somewhat less obvious, but still a qualitative similarity is found between the NIST and CQC-H1 data. RASCALL, as previously stated, performs less accurately in this area. On the other hand, there is poorer agreement in the bottom figure as the data collected from NIST corresponds to the solid-phase spectrum for methylphosphonic acid [O=P(O)(C)O] as gas-phase spectrum is not available (or at least not easily accessible). We can see that RASCALL only provides data for the C-H stretches, disregarding the O-H stretches present in the molecule. Though the scaled harmonic calculations do supply frequencies for both the C-H and O-H stretches, the calculated intensities for the C-H stretches are significantly lower and they are therefore overshadowed by the other frequencies. In the fingerprint region, the agreement between the experimental and scaled harmonic data is somewhat better, with the scaled harmonic frequencies being slightly off and missing some bands. This discrepancy could be due to anomalous frequencies or hydrogen bonding manifesting in the solid-phase spectrum. A gas-phase spectrum would be preferred for a more meaningful comparison.

FIGURE 8

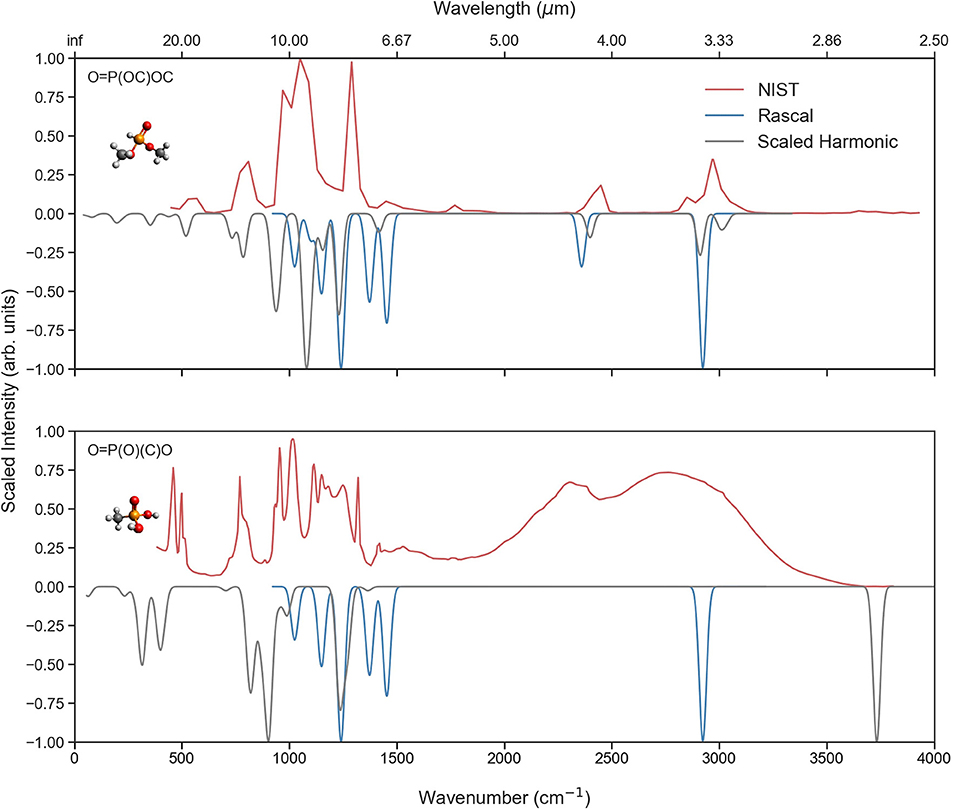
Figure 8. A comparison of the RASCALL (blue), quantum chemistry (gray) and experimental (red) data for two P-molecules for which experimental data is available. The figure also presents the SMILES code for each molecule.

Something particularly important to highlight from this analysis is that among all the 958 P-molecules considered in our study, we could only find easily accessible reference spectroscopic data for the two molecules illustrated in Figure 8, justifying the necessity of supplemental sources of reference data.

3.3.3. Consideration of Anharmonic Vibrational Treatment

Further improvements to our harmonic CQC-H1 approach may be achievable by performing the calculations with the more expensive and complete Generalized Vibrational Second-order Perturbation Theory (GVPT2) approximation (Barone, 2005; Puzzarini et al., 2019); an anharmonic method that allows the calculation of overtones and combination bands along with the fundamental frequencies. We tested this approach (hereafter named as CQC-A1) by calculating anharmonic frequencies and intensities for 250 smaller molecules in our dataset, finding significant issues.

Specifically, substantial deviations were found between the scaled harmonic (CQC-H1) and anharmonic (CQC-A1) fundamental frequencies across the molecules tested. These deviations were predominately observed in two cases: (1) low-frequency transitions with small force constants, where differences of up to a factor of 50 between the scaled harmonic and anharmonic frequencies were found; and (2) the P-H stretch frequencies, where the anharmonic frequencies are 200–700 cm⁻¹ or higher over the scaled harmonic ones. The first issue is well-known for large amplitude vibrations (LAMs) and is an inherent limitation of perturbative approaches, while the second issue is far more concerning and can be traced back to deficiencies in the density functional to compute higher-order derivatives of the potential energy, as recently noted by Barone et al. (2020).

The theoretical foundations, technical specifications and analysis of our anharmonic results are provided in Appendix A, including a discussion of these two key failures and their likely causes.

For the purposes of the main article's objectives, we can conclude that (1) anharmonic GVPT2 calculations are not yet suitable for automated high-throughput calculations due to the prevalence of unexpected anomalous unreliable results and (2) to establish the best anharmonic treatment will require careful testing against experimental frequencies and some criteria that identifies when calculations are unreliable.

3.3.4. Challenges, Limitations, and Future Directions

The calculation of vibrational spectra for all P-molecules has various challenges and limitations that are worth discussing.

Our automated approach for obtaining molecular geometries is generally successful, but some issues and limitations were found with its performance. First, as the current version of the libraries used in our automated script for initial geometries does not support the optimization of molecules containing Se, these molecules were excluded from our final data set. Second, the generated geometries often optimized to saddle-points (indicated by one or more imaginary frequencies) and needed to be manually corrected. As a matter of fact, one of the C₄H₇P isomers (CC#CPC) had to be removed from our working set due to the prevalence of imaginary frequencies in the calculation despite testing the available options to deal with this problematic; future work will attempt to automate this process to enable high throughput calculations. Finally, for three molecules [namely C₂H₄FO₂P (O=P1(O)C(F)C1), C₃H₄ClOP (O=PCC=CCl), and C₂H₅O₂P (O=P1(O)CC1)], the geometry optimization procedure led to their decomposition in the final state, due to their inherent instability. These molecules were identified through their anomalous vibrational partition functions that were calculated for a future application, but could have easily been missed.

Perhaps the most significant limitation of our current method is that only one conformer, as calculated by our automated approach, was considered. However, other conformers may certainly have lower energies than the ones used in our calculations. This limitation will be addressed in the future by consideration of multiple conformers generated by an automated semi-empirical conformational search followed by DFT optimizations. Data for the low energy conformers will be presented concurrently in the database alongside their relative energies to enable a Boltzmann-weighted summation of their contributions at the target temperature to be used in spectral predictions.

In this study, we have only considered one model chemistry (ωB97X-D/def2-SVPD); however, the level of theory (e.g., density functional approximation), basis set, vibrational treatment, and software package can be easily modified within the same analysis framework as new software capabilities and better benchmarking results become available. Indeed, beyond the anharmonic approach discussed above, we are also very interested to explore a hybrid approach, where harmonic calculations are performed at a very high level of theory [usually corresponding to CCSD(T) or B2PLYP calculations with larger basis sets] and the calculated frequencies and intensities are then corrected by means of GVPT2 anharmonic calculations performed at a computationally less-demanding method (e.g., hybrid functionals coupled with double-zeta basis sets) (Biczysko et al., 2010, 2018; Barone et al., 2014). The method has shown to provide reliable results for small to medium-sized molecules at reasonable computational times (though significantly longer than the current method), and will be considered for future work.

Our analysis has not included isotopes because the non-dominant isotope has abundances below 4.5% in all cases except for chlorine. Nevertheless, expansion to isotopes is straightforward in Gaussian and will be considered in future work.

Ideally, the calculated spectra should incorporate the true rotational profiles associated with the vibrational bands. The necessary band-by-band A, B, and C rotational constants and dipole moments in the principal molecular axis are given within the Gaussian output file. An automated method for the generation of rotational spectra and rotational envelopes for each vibrational band from calculated rotational constants and dipole moment components will be considered in a future publication.

3.4. Synergies Between RASCALL and CQC Data

RASCALL and our CQC approach are symbiotic methods. RASCALL supplies preliminary data on any arbitrary molecule, providing guidance and helping to prioritize theoretical calculations. Conversely, CQC data can easily contribute to the refining, expanding, and improving the functional group data that are the primary input for the creation of RASCALL data. For example, a major limitation of RASCALL is the reliance on good data for the prediction of the spectral behavior of different functional groups. In RASCALL 1.0 (Sousa-Silva et al., 2019), these data are generated from experimental spectra and/or theoretically extrapolating from existing functional group data. Future updates to the RASCALL database can use a small number of CQC calculations to parameterize these functional group data; specifically, infrared spectra can be computed for a representative series of molecules containing a functional group, with the average predicted vibrational frequencies and intensities extracted for the functional-group related vibrations (as identified most robustly through consideration of the vibrational eigenvectors). In this way, a relatively small number of high level CQC calculations can be used to parameterize RASCALL. Subsequently, RASCALL can predict vibrational spectra for very large molecules beyond the reach of traditional CQC methods, a key future application of this approach.

4. Discussion

In this section, we discuss a few important aspects of this research, including: the diverse potential uses of these data; how the spectroscopic data work alongside the kinetic and reaction network data to enable better understanding of remote gaseous environments; and a brief discussion of the advantages and challenges of our interdisciplinary approach for biosignature detection follow-up.

4.1. Data Utilization

Our data predicts semi-quantitative spectral intensities for most of the P-molecules studied for the first time, essential information to assess detectability in remote environments. Molecules with strong transition intensities can be far more easily detected than those with weaker transitions. For instance, on Earth, the very strong infrared absorption of CO₂, which, at over 0.041% of the atmosphere, dominates associated spectroscopy and majorly influences global temperatures, while O₂ at 21% atmospheric concentration does not absorb infrared light due to selection rules and only has very weak (forbidden) visible transitions. The data in this paper provides sufficiently accurate intensity predictions to both rank molecular detectability and place good thresholds on the minimum observable abundance of molecules in a given environment.

Accuracy requirements for frequencies are much more demanding and certainly our CQC results, as expected, do not reach spectroscopic accuracy, unlike some molecule-specific line list approaches. Thorough error analysis is beyond the scope of this paper but is certainly a worthwhile future pursuit. For the CQC-H1 harmonic data, we estimate our errors as 38 cm⁻¹ based on the root-mean-squared error of the scaling factor of the ωB97X-D/def2-SVPD model chemistry from Kesharwani et al. (2015) which was calculated for 119 experimental frequencies of 30 molecules, similar to other model chemistries with hybrid functionals and augmented double-zeta basis sets. RASCALL errors are expected to be larger but this needs to be verified by comparison to experimentally-measured frequencies.

Despite being unsuitable for definitive molecular identification in complex gaseous mixtures, such as remote atmospheres, our frequency information provides useful information for remote characterization of gaseous environments, such as planets. First, our data can be used to categorize molecules into groups that may be difficult to disambiguate with observational data at certain resolutions and spectral windows. Second, our data can help assess the difficulty of detecting a molecule or class of molecules and identify optimal spectral windows by considering the specific molecule amongst possible contaminants. For example, the major contaminant to the P-H peak prevalent in our P-molecules is the CO₂ infrared absorption, which can then be closely considered as discussed above. Finally, the scope and accuracy of our data is still enough to both comprehensively build up and selectively constrain a pool of molecular candidates that may be responsible for a particular signal.

The value of this is evident when considering the detection of phosphine on Venus and subsequent debate about whether the single observed microwave line possibly arose from a different molecule. According to the data available to the involved astronomers, the only possible contender for the signal was the nearby absorber, SO₂, which could be ruled out. However, while the available data did cover the molecules that are likely to be most abundant in that context, it was limited in coverage; the data we produce as part of this work could support a much more comprehensive investigation for similar detections in the infrared region.

Another key use of this data is the assignment of experimental spectra. For example, computational quantum chemistry calculations have been used previously to correct misassignments in P-molecule infrared spectroscopy (Robertson and McNaughton, 2003; McNaughton and Robertson, 2006). The CQC approach can be useful to aid molecule identification for experiments with complex molecular mixtures formed, for example, by a discharge or as reaction products.

Finally, the generation of a large molecular dataset is worth consideration within the context of machine learning (ML). Certainly, the last few years have witnessed a delayed but definitive permeation of techniques and approaches from the latest wave of artificial-intelligence research, i.e., deep learning, into chemistry (Butler et al., 2018; Tkatchenko, 2020), and more broadly, the physical sciences (Carleo et al., 2019). This influence has extended to the production of infrared spectra, with, for example, one study considering the hybridization of ML and molecular-dynamics simulations (Gastegger et al., 2017). More recently, VPT2 calculations have been mixed with data generated by neural networks to explore anharmonic corrections to vibrational frequencies (Lam et al., 2020). However, ML is more traditionally used in processing pre-produced data, and indeed, ML models can be trained on a variety of relations present in the dataset within this work. Certain coding packages support such an approach, for example, the Python-based DeepChem (Ramsundar et al., 2019), which wraps around RDKit (RDK, 2000) to convert molecular SMILES codes into hashed extended-connectivity fingerprints (Rogers and Hahn, 2010); these breakdowns of molecular structure are useful as input feature vectors for ML models. Consequently, it is possible to efficiently learn how combinations of molecular substructures influence infrared frequencies and intensities; RASCALL is based on a similar principle derived from domain knowledge in organic chemistry that functional groups determine infrared frequencies and approximate intensities. It is likely that ML can improve on the RASCALL dataset by providing updated functional group information extrapolated from CQC data. As a related example, Kovács et al. (2020) recently explored ML for predicting infrared spectra for polycyclic aromatic hydrocarbons based on a NASA Ames dataset of more than 3,000 spectra. Given that ML benefits from the statistical power provided by big data, the high-throughput nature of our CQC results is particularly valuable in fueling the performance of future ML models.

4.2. Molecules in Reaction Network Modeling

Important species in reaction networks might be difficult to detect remotely as they have low concentrations, e.g., the important OH radical in Earth's atmosphere is mostly detected with in situ measurements (Piccioni et al., 2008; Stone et al., 2012). Therefore, the spectroscopic measurements need to be combined with a chemistry-based reaction network model that contains reaction rates for all molecules in the atmospheric system. For observable species, if the observed abundance is very different from the predicted abundance this could be due to incorrect model predictions, misinterpreted data, or could indicate unusual chemistry that warrants further investigation (e.g., the detection of phosphine on Venus).

To help readers understand the strengths and limitations of existing approaches in reaction network modeling and kinetics rate predictions, we provide appendices with brief summaries of the current approaches in these fields. Appendix B provides an overview of reaction network modeling, which is important to contextualize the sources and sinks of volatile molecules. Appendix B focuses on approaches to modeling the Earth's atmosphere and references some introductory texts on the more limited reaction network modeling of exoplanets. Appendix C introduces the fundamentals of theoretical kinetics calculations, which can be used to supplement rate constants whenever they are missing from reaction networks. Popular codes for performing theoretical kinetics calculations are also referenced in Appendix C.

The application of reaction networks and kinetics modeling is considered below for the specific situation of the potential for atmospheric formation of phosphine on Venus.

4.2.1. Constraining Models Involving Phosphine on Venus

The preceding sections of this paper present spectra for a wide array of P-molecules that could feed into PH₃ formation in the Venusian atmosphere. Ultimately, if PH₃ were being formed from volatile P-molecules and not through a geological process, these P-molecules must decompose into single-phosphorus molecules that can be successively reduced to PH₃. To understand this process and elucidate potential abiotic pathways to PH₃, we ideally want spectroscopic measurement of the Venusian atmospheric concentrations of these PH₃-precursor P-molecules which could greatly constraint the Venus atmospheric models. The high-throughput spectra in this paper are a first step toward these future spectroscopic measurements.

The thick cloud layers in Venus's atmosphere around 48–70 km prevent significant solar radiation from penetrating to the lower Venusian atmosphere (Titov et al., 2007; Bains et al., 2020). The atmospheres within and above the cloud deck, however, do receive significant solar radiation (Titov et al., 2007). Thus, this middle Venusian atmosphere, like Earth, is largely driven by reactions with radical species formed through photochemistry (Prinn and Fegley, 1987). A photochemical network approach can therefore be used to simulate the composition of the middle atmospheres of Venus, which typically has temperatures of 200–350 K (Ando et al., 2020). This approach is considered Bains et al. (2020) when modeling the production and destruction of phosphine in Venus.

However, the atmospheric processes of Venus are far less studied than for Earth and considerable data is missing. Even in modeling the most abundant species in the middle and lower atmospheres of Venus (SO_x, CO_x, Cl^•/HCl), Bierson and Zhang (2020) note that ~40% of their reaction rates used have no experimental measurements, and those that are measured are only upper limits, or for a single temperature. This statistic reveals much is unknown about the reaction rates of core Venusian atmospheric processes, especially minor cycles like phosphorus reactions.

Bierson and Zhang (2020) highlight which rates contained in their Venus atmospheric model are of highest priority for experimental measurement or ab initio prediction. The photochemical model of PH₃ formation by Bains et al. (2020) presents similar crucial reactions that can be considered a priority in terms of: spectroscopic detection of these species (or their precursors), lab-based measurement of key reaction rates with radicals, or ab initio calculations. These are radical-mediated reactions that could generate the direct precursors of PH₃, as shown in Scheme 1.

SCHEME 1

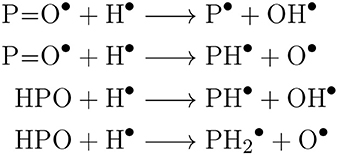
Scheme 1. Proposed, network limiting, reactions of P-molecules in the model of photochemical PH 3 production by Bains et al.

The spectroscopic detection and quantification of any of the intermediates shown in Scheme 1 would greatly help constrain photochemical models of PH₃ formation. High quality line lists are available for PO from ExoMol (Prajapat et al., 2017). However, spectroscopic signatures of molecules in Scheme 1, such as the P−H stretch, P=O stretch, and P−H bending modes, are common to multiple P-molecules (see Figure 3). Therefore, a moiety-based approach to predict spectra, like RASCALL, will yield false positives, and the CQC spectra presented in this paper provide an improvement for the identification of these intermediates. In the absence of spectroscopically determined abundances of these P-molecules, reaction network modeling must be used.

The reactions in Scheme 1 generate immediate PH₃-precursors and are the presumed bottle-necks in the photochemical reaction pathway. These key reactions also lack any reaction rate data. Instead, surrogate rate data from equivalent nitrogen-containing species undergoing the equivalent reaction are used (Bains et al., 2020). However, the nitrogen surrogate reaction energies differ by ~50–60 kJ/mol from calculated energies of the actual phosphorous compounds (Chase, 1998; Bains et al., 2020). In theoretical kinetics calculations each 10 kJ/mol difference in activation energy can alter calculated reaction rates by an order of magnitude. Therefore, the use of nitrogen surrogates could lead to misestimation of rates by several orders of magnitude, with implications on the importance of Scheme 1 reactions as network bottlenecks.

Therefore, rate data crucially needs to be determined for the true phosphorous compounds in Scheme 1, either experimentally or with ab initio calculations. The instability of HPO and PO^• limits the availability of lab-based kinetics studies (Douglas et al., 2020), but their chemistry can be calculated with high-level quantum chemical methods since only 2–3 atoms are involved. Highly accurate composite ab intio methods can calculate energies of these small systems to kJ/mol, or even sub-kJ/mol, accuracy (Tajti et al., 2004; Karton et al., 2006; Karton, 2016). After accurate calculation of the geometries and energies of these reactions, the theoretical kinetics methods outlined in Appendix B could be used to calculate reaction rates. In fact, many molecules in the atmospheric reaction networks are likely to be transient and hard to detect, so theory may provide the most viable route to good estimates of their reaction rates.

4.3. Initial Interdisciplinary Survey Approach to Biosignature Followup

Astrobiology and the related study of the chemistry of planetary atmospheres are such a diverse fields that no single person can be an expert on all aspects. Instead, interdisciplinary collaborative approaches are essential.

Establishing productive interdisciplinary collaborations is rewarding but challenging, and proved essential in this pilot to appreciate diverse aspects of biosignature follow-ups. We found that astronomers, geologists, origin of life researchers, experimental spectroscopists, computational spectroscopy theorists and data scientists all had significant core knowledge—sometimes trivial in their field but unknown to others and useful in combination. Identifying and refining the salient contributions of each sub-discipline—often not what was originally anticipated—and placing it within the context of this work required time and frequent communication, aided by modern technology tools. As a concrete example, the scarcity of gaseous P-molecules and the relative lack of knowledge on P-molecule speciation in Earth's atmosphere was surprising to many authors. Unexpectedly, most key knowledge on gas-phase P-molecules came not from modern atmospheric chemistry modeling, but from origin of life research. Atmospheric chemistry expertise instead was crucial in highlighting an under-appreciated limitation of spectroscopy in remote characterization of atmospheres; crucially important intermediates and radicals may be unobservable remotely as their reactivity makes their atmospheric lifetime extremely short and prevents atmospheric buildup to observable concentrations.

5. Conclusions

The key new data presented in this paper is the calculated infrared spectra of 958 phosphorus-bearing molecules (P-molecules), which represents the best available data for almost all of these molecules. These data can be useful to highlight ambiguities in molecular detection in remote atmospheres and thus prevent misassignments of spectral features while suggesting potential assignments for a given spectral signal. These data also provide sufficiently reliable intensities of different spectral features between molecules to enable evaluation of the limits of detectability for different molecules.

These data were produced with a high-throughput mostly automated methodology using computational quantum chemistry (CQC) with the ωB97X-D/def2-SVPD model chemistry used to calculate harmonic frequencies and intensities (CQC-H1) for all 958 P-molecules. Compared to the previously available RASCALL spectral data which was produced based on the frequencies of functional groups within individual molecules, these new CQC data introduce for the first time quantitatively accurate predicted intensities and frequencies data for vibrations within the fingerprint spectral region (~500–1,450 cm⁻¹) that involve large molecular motions as well as improved frequency predictions for higher frequency modes through consideration of detailed chemical environmental effects. Though further improvements to our CQC-H1 approach may be obtained by performing the calculations with anharmonic methodologies like GVPT2, we identified some challenges and limitations, particularly for anharmonic prediction of modes with low force constants, and highlighted future opportunities for methodology improvements, noting that modifications of the quantum chemistry procedure are trivial to implement within our framework. We also note the recurrence of the sporadic large errors in GVPT2 ωB97X-D calculations (first noted by Barone et al., 2020), which seemed to affect mostly P-H stretches for a significant number of molecules. Future work to determine an appropriate functional for anharmonic calculation is warranted as these calculations are the only data source for accurate frequencies and intensities for overtone and combination bands, which provides a more complete picture of molecular opacity and may help distinguish between some molecules.

The other key contribution of this paper is the demonstration of significant advantages with an interdisciplinary approach to follow-up of biosignature detection. Phosphine and P-molecules are certainly of broad interest astrophysically in gas giants and as potential biosignatures, but the immediate impetus for this paper was the tentative detection of PH₃ in the clouds of Venus with extraordinary high abundance (Bains et al., 2020). An important aspect of investigating this detection is to look for other gaseous P-molecules that could be sources or sinks of phosphine in Venus and can provide insights into the possible atmospheric network that allows for the accumulation of phosphine. To identify the molecules of interest, we used two approaches; the targeted approach consolidating known or predicted chemistry to identify gas-phase P-molecules of particular interest for characterization of remote planetary atmospheres, and the reaction agnostic approach which instead considered all potentially volatile stable P-molecules with six or fewer non-hydrogen atoms. We conclude that, given the low volatility of many P-molecules and the relative poor understanding of gaseous phosphorus chemistry, a more reaction-agnostic comprehensive search for volatile molecules is probably the most suitable path forward for P-molecules.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

LM conceived, designed, and managed the project. MG, EC, LJ, FL, A-MS, and JZ collated the pre-existing data. JZ, LM, PK, and JO'S developed the CQC approach. JZ applied CQC to produce novel vibrational spectra. A-MS and JZ produced the figures. JZ, A-MS, EC, FL, and JO'S analyzed the data. CM, ER, and CT provided the expert knowledge and feedback to assist with analysis. JZ, LM, CS-S, KR, BB, LJ, DK, GS, LS, and BT provided the expert knowledge and wrote the significant sections of the paper. All authors reviewed the literature and wrote, edited, or provided the feedback on sections of the paper. All authors reviewed and approved the final manuscript.

Funding

KR was supported from a grant by the Australian Research Council (DP160101792).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer JP declared a past co-authorship with one of the authors CS-S to the handling editor.

Acknowledgments

The authors thank to Maria Cunningham, Maria Paula Pérez-Peña, and Max Litherland for their enthusiastic participation in the hackathon that started this project.

LM would also like to thank her awesome colleagues for the writing groups and active encouragement that fast-tracked this paper to submission in the difficult 2020 year.

This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI Australia), an NCRIS enabled capability supported by the Australian Government.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.639068/full#supplementary-material

The supplementary data consists of:

• A read.me file explaining the full supplementary information contents;

• A csv file listing all molecules considered with relevant information (e.g., SMILES code, boiling point);

• A csv file with tabulated frequencies (cm⁻¹) and intensities (km mole⁻¹) including the empirical formula and SMILES code for each molecule, the mode to which the frequency and intensity belongs to, and the mode kind (i.e., fundamental, scaled fundamental, overtone, or combination band);

• A csv file containing the force constants for fundamental frequencies for the 250 molecules with GVPT2 anharmonic data available;

• A zip file with individual folders for each molecules named by molecular formulae and SMILES codes. Within each folder there is all RASCALL, CQC-H1, and where available CQC-A1 quantum chemistry data for the molecule, along with the raw Gaussian output files and links to all other known spectral data sources.

Footnotes

1. ^We note that the discovery of phosphine on Venus is preliminary. Independent analyses of the data are ongoing and the unambiguous detection of phosphine on Venus will require follow-up observations.

2. ^Note there are differing naming conventions with ${\text{HPO}}_3^{2-}$ also often known as phosphite.

3. ^SDBSWeb : https://sdbs.db.aist.go.jp (National Institute of Advanced Industrial Science and Technology, date of access).

4. ^Notation in parenthesis corresponds to the SMILES code for each molecule.

References

Agúndez, M., Biver, N., Santos-Sanz, P., Bockelée-Morvan, D., and Moreno, R. (2014a). Molecular observations of comets c/2012 s1 (ison) and c/2013 r1 (lovejoy): Hnc/hcn ratios and upper limits to ph3. Astron. Astrophys. 564:L2. doi: 10.1051/0004-6361/201423639

CrossRef Full Text | Google Scholar

Agúndez, M., Cernicharo, J., Decin, L., Encrenaz, P., and Teyssier, D. (2014b). Confirmation of circumstellar phosphine. Astrophys. J. Lett. 790:L27. doi: 10.1088/2041-8205/790/2/L27

CrossRef Full Text | Google Scholar

Agúndez, M., Cernicharo, J., and Guélin, M. (2007). Discovery of phosphaethyne (HCP) in space: phosphorus chemistry in circumstellar envelopes. Astrophys. J. Lett. 662:L91. doi: 10.1086/519561

CrossRef Full Text | Google Scholar

Alipour, M., and Fallahzadeh, P. (2016). First principles optimally tuned range-separated density functional theory for prediction of phosphorus-hydrogen spin-spin coupling constants. Phys. Chem. Chem. Phys. 18, 18431–18440. doi: 10.1039/C6CP02648F

PubMed Abstract | CrossRef Full Text | Google Scholar

Ando, H., Imamura, T., Tellmann, S., Pätzold, M., Häusler, B., Sugimoto, N., et al. (2020). Thermal structure of the venusian atmosphere from the sub-cloud region to the mesosphere as observed by radio occultation. Sci. Rep. 10:3448. doi: 10.1038/s41598-020-59278-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Bains, W., Jurand Petkowski, J., Sousa-Silva, C., and Seager, S. (2019). Trivalent phosphorus and phosphines as components of biochemistry in anoxic environments. Astrobiology 19, 885–902. doi: 10.1089/ast.2018.1958

PubMed Abstract | CrossRef Full Text | Google Scholar

Bains, W., Petkowski, J. J., Seager, S., Ranjan, S., Sousa-Silva, C., Rimmer, P. B., et al. (2020). Phosphine on venus cannot be explained by conventional processes. arXiv [Preprint] arXiv: 2009.06499.

Google Scholar

Barone, V. (2005). Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 122, 1–10. doi: 10.1063/1.1824881

PubMed Abstract | CrossRef Full Text | Google Scholar

Barone, V., Biczysko, M., and Bloino, J. (2014). Fully anharmonic IR and Raman spectra of medium-size molecular systems: accuracy and interpretation. Phys. Chem. Chem. Phys. 16, 1759–1787. doi: 10.1039/C3CP53413H

PubMed Abstract | CrossRef Full Text | Google Scholar

Barone, V., Ceselin, G., Fusè, M., and Tasinato, N. (2020). Accuracy meets interpretability for computational spectroscopy by means of hybrid and double-hybrid functionals. Front. Chem. 8:584203. doi: 10.3389/fchem.2020.584203

PubMed Abstract | CrossRef Full Text | Google Scholar

Barshay, S. S., and Lewis, J. S. (1978). Chemical structure of the deep atmosphere of Jupiter. Icarus 33, 593–611. doi: 10.1016/0019-1035(78)90192-6

CrossRef Full Text | Google Scholar

Begue, D., Benidar, A., and Pouchan, C. (2006). The vibrational spectra of vinylphosphine revisited: Infrared and theoretical studies from CCSD(T) and DFT anharmonic potential. Chem. Phys. Lett. 430, 215–220. doi: 10.1016/j.cplett.2006.08.129

CrossRef Full Text | Google Scholar

Bernath, P. F. (2020). MoLLIST: molecular line lists, intensities and spectra. J. Quant. Spectrosc. Radiat. Transf. 240:106687. doi: 10.1016/j.jqsrt.2019.106687

CrossRef Full Text | Google Scholar

Biczysko, M., Bloino, J., and Puzzarini, C. (2018). Computational challenges in astrochemistry. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8, 1–38. doi: 10.1002/wcms.1349

CrossRef Full Text | Google Scholar

Biczysko, M., Panek, P., Scalmani, G., Bloino, J., and Barone, V. (2010). Harmonic and anharmonic vibrational frequency calculations with the double-hybrid B2PLYP method: analytic second derivatives and benchmark studies. J. Chem. Theory Comput. 6, 2115–2125. doi: 10.1021/ct100212p

PubMed Abstract | CrossRef Full Text | Google Scholar

Bierson, C. J., and Zhang, X. (2020). Chemical cycling in the venusian atmosphere: a full photochemical model from the surface to 110 km. J. Geophys. Res. 125:e2019JE006159. doi: 10.1029/2019JE006159

CrossRef Full Text | Google Scholar

Borunov, S., Dorofeeva, V., Khodakovsky, I., Drossart, P., Lellouch, E., and Encrenaz, T. (1995). Phosphorus chemistry in the atmosphere of Jupiter: a reassessment. Icarus 113, 460–464. doi: 10.1006/icar.1995.1036

CrossRef Full Text | Google Scholar

Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O., and Walsh, A. (2018). Machine learning for molecular and materials science. Nature 559, 547–555. doi: 10.1038/s41586-018-0337-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Carleo, G., Cirac, I., Cranmer, K., Daudet, L., Schuld, M., Tishby, N., et al. (2019). Machine learning and the physical sciences. Rev. Mod. Phys. 91:045002. doi: 10.1103/RevModPhys.91.045002

CrossRef Full Text | Google Scholar

Carrillo-Sánchez, J. D., Bones, D. L., Douglas, K. M., Flynn, G. J., Wirick, S., Fegley, B., et al. (2020). Injection of meteoric phosphorus into planetary atmospheres. Planet. Space Sci. 187:104926. doi: 10.1016/j.pss.2020.104926

CrossRef Full Text | Google Scholar

Chai, J. D., and Head-Gordon, M. (2008). Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 128:084106. doi: 10.1063/1.2834918

PubMed Abstract | CrossRef Full Text | Google Scholar

Chase, M. J. (1998). Journal of Physical and Chemical Reference Data.

Google Scholar

Chu, P. M., Guenther, F. R., Rhoderick, G. C., and Lafferty, W. J. (2020). Qunatitative Infrared Database, Volume 69 of NIST Chemistry WebBook. Gaithersburg, MD: National Institute of Standards and Technology. NIST Standard Reference Database Number 69.

Google Scholar

Cockell, C. S., Bush, T., Bryce, C., Direito, S., Fox-Powell, M., Harrison, J. P., et al. (2016). Habitability: a review. Astrobiology 16, 89–117. doi: 10.1089/ast.2015.1295

CrossRef Full Text | Google Scholar

Crovisier, J., Bockelée-Morvan, D., Colom, P., Biver, N., Despois, D., and Lis, D. (2004). The composition of ices in comet c/1995 O1 (hale-bopp) from radio spectroscopy-further results and upper limits on undetected species. Astron. Astrophys. 418, 1141–1157. doi: 10.1051/0004-6361:20035688

CrossRef Full Text | Google Scholar

Douglas, K. M., Blitz, M. A., Mangan, T. P., Western, C. M., and Plane, J. M. C. (2020). Kinetic study of the reactions PO + O2 and PO2 + O3 and spectroscopy of the po radical. J. Phys. Chem. A 124, 7911–7926. doi: 10.1021/acs.jpca.0c06106

PubMed Abstract | CrossRef Full Text | Google Scholar

Elser, J. J. (2003). Biological stoichiometry: a theoretical framework connecting ecosystem ecology, evolution, and biochemistry for application in astrobiology. Int. J. Astrobiol. 2:185. doi: 10.1017/S1473550403001563

CrossRef Full Text | Google Scholar

Fadeeva, Y. A., Fedorova, I. V., Krestyaninov, M. A., and Safonova, L. P. (2020). Structural characterization of H3PO3 and H3PO4 acids solutions in DMF: spectral analysis and CPMD simulation. J. Mol. Liq. 300:112342. doi: 10.1016/j.molliq.2019.112342

CrossRef Full Text | Google Scholar

Fan, Y., Lv, M., Niu, X., Ma, J., and Song, Q. (2020a). Evidence and mechanism of biological formation of phosphine from the perspective of the tricarboxylic acid cycle. Int. Biodeterior. Biodegrad. 146:104791. doi: 10.1016/j.ibiod.2019.104791

CrossRef Full Text | Google Scholar

Fan, Y., Niu, X., Zhang, D., Lin, Z., Fu, M., and Zhou, S. (2020b). Analysis of the characteristics of phosphine production by anaerobic digestion based on microbial community dynamics, metabolic pathways, and isolation of the phosphate-reducing strain. Chemosphere 262:128213. doi: 10.1016/j.chemosphere.2020.128213

PubMed Abstract | CrossRef Full Text | Google Scholar

Fegley Bruce, J., and Lodders, K. (1994). Chemical models of the deep atmospheres of Jupiter and Saturn. Icarus 110, 117–154. doi: 10.1006/icar.1994.1111

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16 Revision C.01. Wallingford, CT: Gaussian Inc.

Google Scholar

Gastegger, M., Behler, J., and Marquetand, P. (2017). Machine learning molecular dynamics for the simulation of infrared spectra. Chem. Sci. 8, 6924–6935. doi: 10.1039/C7SC02267K

PubMed Abstract | CrossRef Full Text | Google Scholar

Glindemann, D., Edwards, M., and Kuschk, P. (2003). Phosphine gas in the upper troposphere. Atmos. Environ. 37, 2429–2433. doi: 10.1016/S1352-2310(03)00202-4

CrossRef Full Text | Google Scholar

Glindemann, D., Edwards, M., Liu, J., and Kuschk, P. (2005). Phosphine in soils, sludges, biogases and atmospheric implications—a review. Ecol. Eng. 24, 457–463. doi: 10.1016/j.ecoleng.2005.01.002

CrossRef Full Text | Google Scholar

Goerigk, L., and Mehta, N. (2019). A trip to the density functional theory zoo: warnings and recommendations for the user. Aust. J. Chem. 72, 563–573. doi: 10.1071/CH19023

CrossRef Full Text | Google Scholar

Gordon, I. E., Rothman, L. S., Hill, C., Kochanov, R. V., Tan, Y., Bernath, P. F., et al. (2017). The HITRAN 2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 203, 3–69. doi: 10.1016/j.jqsrt.2017.06.038

CrossRef Full Text | Google Scholar

Greaves, J. S., Richards, A. M., Bains, W., Rimmer, P. B., Sagawa, H., Clements, D. L., et al. (2020). Phosphine gas in the cloud decks of venus. Nat. Astron. 1–10. doi: 10.1038/s41550-020-1174-4

CrossRef Full Text | Google Scholar

Guélin, M., Cernicharo, J., Paubert, G., and Turner, B. (1990). Free CP in IRC+ 10216. Astron. Astrophys. 230, L9–L11.

Google Scholar

Guillemin, J. C., Janati, T., and Lassalle, L. (1995). Photolysis of phosphine in the presence of acetylene and propyne, gas mixtures of planetary interest. Adv. Space Res. 16, 85–92. doi: 10.1016/0273-1177(95)00196-L

PubMed Abstract | CrossRef Full Text | Google Scholar

Guillemin, J. C., Le Serre, S., and Lassalle, L. (1997). Regioselectivity of the photochemical addition of phosphine to unsaturated hydrocarbons in the atmospheres of Jupiter and Saturn. Adv. Space Res. 19, 1093–1102. doi: 10.1016/S0273-1177(97)00358-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Haghighatlari, M., Vishwakarma, G., Altarawy, D., Subramanian, R., Kota, B. U., Sonpal, A., et al. (2020). ChemML: A machine learning and informatics program package for the analysis, mining, and modeling of chemical and materials data. Wiley Interdiscip. Rev. Comput. Mol. Sci. 10, 1–10. doi: 10.1002/wcms.1458

CrossRef Full Text | Google Scholar

Halfen, D., Clouthier, D., and Ziurys, L. M. (2008). Detection of the CCP radical (x2πr) in IRC+ 10216: a new interstellar phosphorus-containing species. Astrophys. J. Lett. 677:L101. doi: 10.1086/588024

CrossRef Full Text | Google Scholar

Halmann, M. (1960). Infrared absorption of trimethylphosphine. Spectrochim. Acta A Mol. Biomol. Spectrosc. 16, 407–412. doi: 10.1016/0371-1951(60)80034-3

CrossRef Full Text | Google Scholar

Hanwell, M. D., Curtis, D. E., Lonie, D. C., Vandermeersch, T., Zurek, E., and Hutchison, G. R. (2012). Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 4, 1–17. doi: 10.1186/1758-2946-4-17

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinkel, N. R., Hartnett, H. E., and Young, P. A. (2020). The influence of stellar phosphorus on our understanding of exoplanets and astrobiology. Astrophys. J. Lett. 900:L38. doi: 10.3847/2041-8213/abb3cb

CrossRef Full Text | Google Scholar

Honniball, C. I., Lucey, P. G., Li, S., Shenoy, S., Orlando, T. M., Hibbitts, C. A., et al. (2020). Molecular water detected on the sunlit Moon by SOFIA. Nat. Astron. 5, 121–127. doi: 10.1038/s41550-020-01222-x

CrossRef Full Text | Google Scholar

Jacquinet-Husson, N., Armante, R., Scott, N. A., Chédin, A., Crépeau, L., Boutammine, C., et al. (2016). The 2015 edition of the GEISA spectroscopic database. J. Mol. Spectrosc. 327, 31–72. doi: 10.1016/j.jms.2016.06.007

CrossRef Full Text | Google Scholar

Jenkins, R. O., Morris, T. A., Craig, P. J., Ritchie, A. W., and Ostah, N. (2000). Phosphine generation by mixed-and monoseptic-cultures of anaerobic bacteria. Sci. Total Environ. 250, 73–81. doi: 10.1016/S0048-9697(00)00368-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, N. M., and de Oliveira, M. R. (2019). Venus atmospheric composition in situ data: a compilation. Earth Space Sci. 6, 1299–1318. doi: 10.1029/2018EA000536

CrossRef Full Text | Google Scholar

Karton, A. (2016). A computational chemist's guide to accurate thermochemistry for organic molecules. Wiley Interdiscip. Rev. Comput. Mol. Sci. 6, 292–310. doi: 10.1002/wcms.1249

CrossRef Full Text | Google Scholar

Karton, A., Rabinovich, E., Martin, J. M. L., and Ruscic, B. (2006). W4 theory for computational thermochemistry: in pursuit of confident sub-kJ/mol predictions. J. Chem. Phys. 125:144108. doi: 10.1063/1.2348881

PubMed Abstract | CrossRef Full Text | Google Scholar

Kesharwani, M. K., Brauer, B., and Martin, J. M. (2015). Frequency and zero-point vibrational energy scale factors for double-hybrid density functionals (and other selected methods): Can anharmonic force fields be avoided? J. Phys. Chem. A 119, 1701–1714. doi: 10.1021/jp508422u

PubMed Abstract | CrossRef Full Text | Google Scholar

Kissel, J., Krueger, F., Silén, J., and Clark, B. (2004). The cometary and interstellar dust analyzer at comet 81p/wild 2. Science 304, 1774–1776. doi: 10.1126/science.1098836

PubMed Abstract | CrossRef Full Text | Google Scholar

Konings, R. J., Cordfunke, E. H., and Booij, A. S. (1992). The infrared spectra of gaseous P4O10, As4O6, and As4O10. J. Mol. Spectrosc. 152, 29–37. doi: 10.1016/0022-2852(92)90113-3

CrossRef Full Text | Google Scholar

Kovács, P., Zhu, X., Carrete, J., Madsen, G. K., and Wang, Z. (2020). Machine-learning prediction of infrared spectra of interstellar polycyclic aromatic hydrocarbons. Astrophys. J. 902:100. doi: 10.3847/1538-4357/abb5b6

CrossRef Full Text | Google Scholar

Krasnopolsky, V. A. (1989). Vega mission results and chemical composition of Venusian clouds. Icarus 80, 202–210. doi: 10.1016/0019-1035(89)90168-1

CrossRef Full Text | Google Scholar

Krasnopolsky, V. A. (2006). Chemical composition of Venus atmosphere and clouds: some unsolved problems. Planet. Space Sci. 54, 1352–1359. doi: 10.1016/j.pss.2006.04.019

CrossRef Full Text | Google Scholar

Lam, J., Abdul-Al, S., and Allouche, A. R. (2020). Combining quantum mechanics and machine-learning calculations for anharmonic corrections to vibrational frequencies. J. Chem. Theory Comput. 16, 1681–1689. doi: 10.1021/acs.jctc.9b00964

PubMed Abstract | CrossRef Full Text | Google Scholar

Langleben, J., Yurchenko, S. N., and Tennyson, J. (2019). ExoMol line list XXXIV: a rovibrational line list for phosphinidene (PH) in its X³Σ⁻ and a¹Δ electronic states. Mon. Notices R. Astron. Soc. 488:2332. doi: 10.1093/mnras/stz1856

CrossRef Full Text | Google Scholar

Larson, H., Treffers, R., and Fink, U. (1977). Phosphine in jupiter's atmosphere-the evidence from high-altitude observations at 5 micrometers. Astrophys. J. 211, 972–979. doi: 10.1086/155009

CrossRef Full Text | Google Scholar

Li, W., Li, B., Tao, S., Ciais, P., Piao, S., and Shen, G. (2020). Missed atmospheric organic phosphorus emitted by terrestrial plants, part 2: experiment of volatile phosphorus. Environ. Pollut. 258:113728. doi: 10.1016/j.envpol.2019.113728

PubMed Abstract | CrossRef Full Text | Google Scholar

Linton, H. R., and Nixon, E. R. (1959). Infrared spectra of methyl and silyl phosphines. Spectrochim. Acta A Mol. Biomol. Spectrosc. 15, 146–155. doi: 10.1016/S0371-1951(59)80300-3

CrossRef Full Text | Google Scholar

Maciá, E. (2005). The role of phosphorus in chemical evolution. Chem. Soc. Rev. 34, 691–701. doi: 10.1039/b416855k

CrossRef Full Text | Google Scholar

Mahowald, N., Jickells, T. D., Baker, A. R., Artaxo, P., Benitez-Nelson, C. R., and Bergametti, G. (2008). Global distribution of atmospheric phosphorus sources, concentrations and deposition rates, and anthropogenic impacts. Glob. Biogeochem. Cycles 22:GB4026. doi: 10.1029/2008GB003240

CrossRef Full Text | Google Scholar

Mant, B. P., Chubb, K. L., Yachmenev, A., Tennyson, J., and Yurchenko, S. N. (2020). The infrared spectrum of PF₃ and analysis of rotational energy clustering effect. Mol. Phys. 118:e1581951. doi: 10.1080/00268976.2019.1581951

CrossRef Full Text | Google Scholar

McNaughton, D., and Robertson, E. G. (2006). Comment on gas phase infrared spectrum and ab initio calculations of phosphorus (iii) thiocyanide, spcn. Spectrochim. Acta A Mol. Biomol. Spectrosc. 65, 1000–1002. doi: 10.1016/j.saa.2006.01.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Mielke, Z., and Andrews, L. (1989). Infrared spectra of phosphorus oxides (P4O6, P4O7, P4O8, P4O9 and P4O10) in solid argon. J. Phys. Chem. 93, 2971–2976. doi: 10.1021/j100345a024

CrossRef Full Text | Google Scholar

Mogul, R., Limaye, S. S., Way, M. J., and Cordova, J. A. (2020). Is phosphine in the mass spectra from Venus' clouds? Nat. Astron.

Google Scholar

Moritz, A. G. (1966). The PH and PD stretching bands of CH3PH2, CH3PHD and CH3PD2. Spectrochim. Acta A Mol. Biomol. Spectrosc. 22, 1015–1020. doi: 10.1016/0371-1951(66)80190-X

CrossRef Full Text | Google Scholar

Morton, S. C., Glindemann, D., and Edwards, M. A. (2003). Phosphates, phosphites, and phosphides in environmental samples. Environ. Sci. Technol. 37, 1169–1174. doi: 10.1021/es020738b

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikitin, A. V., Holka, F., Tyuterev, V. G., and Fremont, J. (2009). Vibration energy levels of the PH3, PH2D, and PHD2 molecules calculated from high order potential energy surface. J. Chem. Phys. 130:244312. doi: 10.1063/1.3156311

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikitin, A. V., Rey, M., and Tyuterev, V. G. (2014). High order dipole moment surfaces of PH3 and ab initio intensity predictions in the Octad range. J. Mol. Spectrosc. 305, 40–47. doi: 10.1016/j.jms.2014.09.010

CrossRef Full Text | Google Scholar

Nimmo, F., and McKenzie, D. (1998). Volcanism and tectonics on venus. Annu. Rev. Earth Planet. Sci. 26, 23–51. doi: 10.1146/annurev.earth.26.1.23

PubMed Abstract | CrossRef Full Text | Google Scholar

Owens, A., and Yurchenko, S. N. (2019). Theoretical rotation-vibration spectroscopy of cis- and trans-diphosphene (P₂H₂) and the deuterated species P₂HD. J. Phys. Chem. 150:194308. doi: 10.1063/1.5092767

PubMed Abstract | CrossRef Full Text | Google Scholar

Pasek, M. (2014). “Role of phosphorus in prebiotic chemistry,” in Astrobiology: An Evolutionary Approach, ed V. M. Kolb (Boca Raton, FL: CRC press), 257–270.

Google Scholar

Pasek, M. A., Sampson, J. M., and Atlas, Z. (2014). Redox chemistry in the phosphorus biogeochemical cycle. Proc. Natl. Acad. Sci. U.S.A. 111, 15468–15473. doi: 10.1073/pnas.1408134111

PubMed Abstract | CrossRef Full Text | Google Scholar

Piccioni, G., Drossart, P., Zasova, L., Migliorini, A., Gérard, J. C., Mills, F. P., et al. (2008). First detection of hydroxyl in the atmosphere of venus. Astron. Astrophys. 483, L29–L33. doi: 10.1051/0004-6361:200809761

CrossRef Full Text | Google Scholar

Prajapat, L., Jagoda, P., Lodi, L., Gorman, M. N., Yurchenko, S. N., and Tennyson, J. (2017). Exomol molecular line lists–XXIII. Spectra of PO and PS. Mon. Notices R. Astron. Soc. 472, 3648–3658. doi: 10.1093/mnras/stx2229

CrossRef Full Text | Google Scholar

Prinn, R. G., and Fegley, B. (1987). The atmospheres of venus, earth, and mars: a critical comparison. Annu. Rev. Earth Planet. Sci. 15, 171–212. doi: 10.1146/annurev.ea.15.050187.001131

CrossRef Full Text | Google Scholar

Puzzarini, C., Bloino, J., Tasinato, N., and Barone, V. (2019). Accuracy and interpretability: the devil and the holy grail. New routes across old boundaries in computational spectroscopy. Chem. Rev. 119, 8131–8191. doi: 10.1021/acs.chemrev.9b00007

PubMed Abstract | CrossRef Full Text | Google Scholar

Ram, R., Brooke, J., Western, C., and Bernath, P. (2014). Einstein a-values and oscillator strengths of the a2π-x2σ+ system of CP. J. Quant. Spectrosc. Radiat. Transf. 138, 107–115. doi: 10.1016/j.jqsrt.2014.01.030

CrossRef Full Text | Google Scholar

Ramsundar, B., Eastman, P., Walters, P., Pande, V., Leswing, K., and Wu, Z. (2019). Deep Learning for the Life Sciences. O'Reilly Media. Available online at: https://www.amazon.com/Deep-Learning-Life-Sciences-Microscopy/dp/1492039837

Google Scholar

Rappoport, D., and Furche, F. (2010). Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 133:134105. doi: 10.1063/1.3484283

PubMed Abstract | CrossRef Full Text | Google Scholar

RDK (2000). RDKit: Open-Source Cheminformatics.

Google Scholar

Rickard, A., and Young, J. (2005). The Master Chemical Mechanism (MCM) v3.2.

Google Scholar

Ritson, D. J., Mojzsis, S. J., and Sutherland, J. D. (2020). Supply of phosphate to early Earth by photogeochemistry after meteoritic weathering. Nat. Geosci. 13, 344–348. doi: 10.1038/s41561-020-0556-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Robertson, E. G., and McNaughton, D. (2003). Ir spectroscopy of op-x and derivatives: mistaken identity on a large scale. J. Phys. Chem. A 107, 642–650. doi: 10.1021/jp021302l

CrossRef Full Text | Google Scholar

Rogers, D., and Hahn, M. (2010). Extended-connectivity fingerprints. J. Chem. Inf. Model. 50, 742–754. doi: 10.1021/ci100050t

CrossRef Full Text | Google Scholar

Rudolph, W. W. (2010). Raman- and infrared-spectroscopic investigations of dilute aqueous phosphoric acid solutions. Dalton Trans. 39, 9642–9653. doi: 10.1039/c0dt00417k

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlesinger, W. H., and Bernhardt, E. S. (2020). “Chapter 12–the global cycles of nitrogen, phosphorus and potassium,” in Biogeochemistry, 4th Edn., eds W. H. Schlesinger and E. S. Bernhardt (London, UK: Academic Press), 483–508. doi: 10.1016/B978-0-12-814608-8.00012-8

CrossRef Full Text | Google Scholar

Schorghofer, N., and Williams, J. P. (2020). Mapping of ice storage processes on the moon with time-dependent temperatures. Planet. Sci. J. 1:54. doi: 10.3847/PSJ/abb6ff

CrossRef Full Text | Google Scholar

Schwartz, A. W. (2006). Phosphorus in prebiotic chemistry. Philos. Trans. R. Soc. Lond. B Biol. Sci. 361, 1743–1749. doi: 10.1098/rstb.2006.1901

CrossRef Full Text | Google Scholar

Schwieterman, E. W., Kiang, N. Y., Parenteau, M. N., Harman, C. E., DasSarma, S., Fisher, T. M., et al. (2018). Exoplanet biosignatures: a review of remotely detectable signs of life. Astrobiology 18, 663–708. doi: 10.1089/ast.2017.1729

PubMed Abstract | CrossRef Full Text | Google Scholar

Seager, S., Bains, W., and Petkowski, J. J. (2016). Toward a list of molecules as potential biosignature gases for the search for life on exoplanets and applications to terrestrial biochemistry. Astrobiology 16, 465–485. doi: 10.1089/ast.2015.1404

PubMed Abstract | CrossRef Full Text | Google Scholar

Shellnutt, J. G. (2013). Petrological modeling of basaltic rocks from venus: a case for the presence of silicic rocks. J. Geophys. Res. Planets 118, 1350–1364. doi: 10.1002/jgre.20094

CrossRef Full Text | Google Scholar

Sousa-Silva, C., Al-Refaie, A. F., Tennyson, J., and Yurchenko, S. N. (2015). ExoMol line lists–VII. The rotation-vibration spectrum of phosphine up to 1500 K. Mon. Notices R. Astron. Soc. 446, 2337–2347. doi: 10.1093/mnras/stu2246

CrossRef Full Text | Google Scholar

Sousa-Silva, C., Petkowski, J. J., and Seager, S. (2019). Molecular simulations for the spectroscopic detection of atmospheric gases. Phys. Chem. Chem. Phys. 21, 18970–18987. doi: 10.1039/C8CP07057A

PubMed Abstract | CrossRef Full Text | Google Scholar

Sousa-Silva, C., Seager, S., Ranjan, S., Petkowski, J., Zhan, Z., Hu, R., et al. (2020). Phosphine as a biosignature gas in exoplanet atmospheres. Astrobiology 20, 235–268. doi: 10.1089/ast.2018.1954

PubMed Abstract | CrossRef Full Text | Google Scholar

Stone, D., Whalley, L. K., and Heard, D. E. (2012). Tropospheric OH and HO2 radicals: field measurements and model comparisons. Chem. Soc. Rev. 41:6348. doi: 10.1039/c2cs35140d

PubMed Abstract | CrossRef Full Text | Google Scholar

Tajti, A., Szalay, P. G., Császár, A. G., Kállay, M., Gauss, J., and Valeev, E. F. (2004). HEAT: high accuracy extrapolated ab initio thermochemistry. J. Phys. Chem. 121, 11599–11613. doi: 10.1063/1.1811608

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamari, M., and Kametaka, M. (1972). Isolation and identification of ciliatine (2-aminoethylphosphonic acid) from phospholipids of the oyster, crassostrea gigas. Agric. Biol. Chem. 36, 1147–1152. doi: 10.1080/00021369.1972.10860383

CrossRef Full Text | Google Scholar

Taylor, F. W., Svedhem, H., and Head, J. W. (2018). Venus: the atmosphere, climate, surface, interior and near-space environment of an earth-like planet. Space Sci. Rev. 214, 1–36. doi: 10.1007/s11214-018-0467-8

CrossRef Full Text | Google Scholar

Tenenbaum, E., Woolf, N., and Ziurys, L. M. (2007). Identification of phosphorus monoxide (x2πr) in vy canis majoris: detection of the first po bond in space. Astrophys. J. Lett. 666:L29. doi: 10.1086/521361

CrossRef Full Text | Google Scholar

Tennyson, J. (2016). Perspective: accurate ro-vibrational calculations on small molecules. J. Chem. Phys. 145:120901. doi: 10.1063/1.4962907

PubMed Abstract | CrossRef Full Text | Google Scholar

Tennyson, J., Lodi, L., McKemmish, L. K., and Yurchenko, S. N. (2016a). The ab initio calculation of spectra of open shell diatomic molecules. J. Phys. B 49:102001. doi: 10.1088/0953-4075/49/10/102001

CrossRef Full Text | Google Scholar

Tennyson, J., Yurchenko, S. N., Al-Refaie, A. F., Barton, E. J., Chubb, K. L., Coles, P. A., et al. (2016b). The ExoMol database: molecular line lists for exoplanet and other hot atmospheres. J. Mol. Spectrosc. 327, 73–94. doi: 10.1016/j.jms.2016.05.002

CrossRef Full Text | Google Scholar

Tennyson, J., Yurchenko, S. N., Al-Refaie, A. F., Clark, V. H. J., Chubb, K. L., Conway, E. K., et al. (2020). The 2020 release of the ExoMol database: molecular line lists for exoplanet and other hot atmospheres. J. Quant. Spectrosc. Radiat. Transf. 255:107228. doi: 10.1016/j.jqsrt.2020.107228

CrossRef Full Text | Google Scholar

The International GEOS-Chem User Community (2019). GEOS-Chem 12.6.1.

Google Scholar

Tipping, E., Benham, S., Boyle, J. F., Crow, P., Davies, J., Fischer, U., et al. (2014). Atmospheric deposition of phosphorus to land and freshwater. Environ. Sci. Process. Impacts 16, 1608–1617. doi: 10.1039/C3EM00641G

PubMed Abstract | CrossRef Full Text | Google Scholar

Titov, D. V., Bullock, M. A., Crisp, D., Renno, N. O., Taylor, F. W., and Zasova, L. V. (2007). “Radiation in the atmosphere of Venus,” in Geophysical Monograph Series, eds L. W. Esposito, E. R. Stofan, and T. E. Cravens (Washington, DC: American Geophysical Union), 121–138. doi: 10.1029/176GM08

CrossRef Full Text | Google Scholar

Tkatchenko, A. (2020). Machine learning for chemical discovery. Nat. Commun. 11:4125. doi: 10.1038/s41467-020-17844-8

CrossRef Full Text | Google Scholar

Tokunaga, A., Dinerstein, H., Lester, D., and Rank, D. (1980). The phosphine abundance on saturn derived from new 10-micrometer spectra. Icarus 42, 79–85. doi: 10.1016/0019-1035(80)90245-6

CrossRef Full Text | Google Scholar

Treiman, A. H. (2009). Venus-bulk and Mantle compositions: are Venus and Earth really twins? LPICo 1470, 47–48.

Google Scholar

Turner, B., and Bally, J. (1987). Detection of interstellar pn-the first identified phosphorus compound in the interstellar medium. Astrophys. J. 321, L75–L79. doi: 10.1086/185009

CrossRef Full Text | Google Scholar

Violaki, K., Bourrin, F., Aubert, D., Kouvarakis, G., Delsaut, N., and Mihalopoulos, N. (2018). Organic phosphorus in atmospheric deposition over the Mediterranean Sea: an important missing piece of the phosphorus cycle. Prog. Oceanogr. 163:50–58. doi: 10.1016/j.pocean.2017.07.009

CrossRef Full Text | Google Scholar

Visscher, C., Lodders, K., and Fegley, B. Jr. (2006). Atmospheric chemistry in giant planets, brown dwarfs, and low-mass dwarf stars. II. Sulfur and phosphorus. Astrophys. J. 648:1181. doi: 10.1086/506245

CrossRef Full Text | Google Scholar

Wang, Y., Tennyson, J., and Yurchenko, S. N. (2020). Empirical line lists in the ExoMol database. Atoms 8:7. doi: 10.3390/atoms8010007

CrossRef Full Text | Google Scholar

Weigend, F., and Ahlrichs, R. (2005). Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy. Phys. Chem. Chem. Phys. 7:3297. doi: 10.1039/b508541a

PubMed Abstract | CrossRef Full Text | Google Scholar

Weisstein, E. W., and Serabyn, E. (1996). Submillimeter line search in jupiter and saturn. Icarus 123, 23–36. doi: 10.1006/icar.1996.0139

CrossRef Full Text | Google Scholar

Weser, O. (2017). An efficient and general library for the definition and use of internal coordinates in large molecular systems (Ph.D. thesis), Georg August Universität Göttingen, Göttingen, Germany.

Google Scholar

Yamagata, Y., Watanabe, H., Saitoh, M., and Namba, T. (1991). Volcanic production of polyphosphates and its relevance to prebiotic evolution. Nature 352, 516–519. doi: 10.1038/352516a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Yorke, L., Yurchenko, S. N., Lodi, L., and Tennyson, J. (2014). ExoMol line lists VI: a high temperature line list for phosphorus nitride. Mon. Notices R. Astron. Soc. 445, 1383–1391. doi: 10.1093/mnras/stu1854

CrossRef Full Text | Google Scholar

Zapata, J. C., and McKemmish, L. K. (2020). Computation of dipole moments: a recommendation on the choice of the basis set and the level of theory. J. Phys. Chem. A 124, 7538–7548. doi: 10.1021/acs.jpca.0c06736

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, W., Li, H., and Li, Y. (2019). Spatio-temporal dynamics of nitrogen and phosphorus input budgets in a global hotspot of anthropogenic inputs. Sci. Total Environ. 656, 1108–1120. doi: 10.1016/j.scitotenv.2018.11.450

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziurys, L. M. (1987). Detection of interstellar PN-the first phosphorus-bearing species observed in molecular clouds. Astrophys. J. 321, L81–L85. doi: 10.1086/185010

PubMed Abstract | CrossRef Full Text | Google Scholar