- 1Aryabhatta Research Institute of Observational Sciences, Nainital, India
- 2Instituto de Astrofisíca de Canarias, Tenerife, Spain
- 3Departamento de Astrofisíca, Universidad de La Laguna, Tenerife, Spain
- 4Indian Institute of Astrophysics, Bangalore, India
- 5Harish-Chandra Research Institute, Allahabad, India
- 6Center of Excellence in Space Sciences, IISER, Kolkata, India
- 7NASA Goddard Space Flight Center, Greenbelt, MD, United States
Coronal Mass Ejections (CMEs) are highly dynamic events originating in the solar atmosphere, that show a wide range of kinematic properties and are the major drivers of the space weather. The angular width of the CMEs is a crucial parameter in the study of their kinematics. The fact that whether slow and fast CMEs (as based on their relative speed to the average solar wind speed) are associated with different processes at the location of their ejection is still debatable. Thus, in this study, we investigate their angular width to understand the differences between the slow and fast CMEs. We study the width distribution of slow and fast CMEs and find that they follow different power law distributions, with a power law indices (α) of –1.1 and –3.7 for fast and slow CMEs respectively. To reduce the projection effects, we further restrict our analysis to only limb events as derived from manual catalog and we find similar results. We then associate the slow and fast CMEs to their source regions, and classified the sources as Active Regions (ARs) and Prominence Eruptions. We find that slow and fast CMEs coming from ARs and PEs, also follow different power laws in their width distributions. This clearly hints toward a possibility that different mechanisms might be involved in the width expansion of slow and fast CMEs coming from different sources.These results are also crucial from the space weather perspective since the width of the CME is an important factor in that aspect.
1 Introduction
Coronal mass ejections (CMEs) consist of plasma and magnetic field that are expelled from the solar atmosphere into the heliosphere at speeds which can range from 100 to 3,000 km s−1 (Gopalswamy, 2004; Gopalswamy, 2010; Manoharan and Mujiber Rahman, 2011; Yashiro et al., 2004; Manoharan and Mujiber Rahman, 2011; Webb and Howard, 2012). They appear as bright, white-light features moving outward in the coronagraph field of view (FOV) (Hundhausen et al., 1984; Schwenn, 1996). Though, early observations of CMEs date back to 1970s (Hansen et al., 1971), it is Tousey (1973) who first observed CMEs in the coronagraph images (see recent review by Gopalswamy (2016), on the history of CMEs). Since the launch of the Large Angle and Spectrometric Coronagraph (LASCO) (Brueckner et al., 1995) on the Solar and Heliospheric Observatory (SOHO) and Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI) (Howard et al., 2008) on the Solar Terrestrial Relation Observatory (STEREO), CMEs are being routinely monitored.
CMEs are the major drivers of space weather, as they are capable of producing shock waves and interplanetary disturbances (Gosling et al., 1991; Gosling, 1993), where the height of formation of the shock wave can often be estimated from the radio observations (Gopalswamy et al., 2013). Recently, Vourlidas et al. (2020) have outlined the role of radio observations of CMEs during different stages of the CME eruption and its subsequent propagation in the heliosphere. Thus it is important to understand the kinematics of CMEs. CMEs during their radial propagation, have been known to follow a three phase kinematic profile (Zhang et al., 2001; Zhang and Dere, 2006; Webb and Howard, 2012). During their propagation, they interact with the ambient solar wind and experience a drag, which leads to a decreasing or constant speed in the later stages of their propagation (Webb and Howard, 2012). This average solar wind speed reportedly divides the CMEs into slow and fast (Gopalswamy et al., 2000). CMEs are also known to be associated with active regions and eruptive prominences (Subramanian and Dere, 2001; Webb and Howard, 2012). These two classes of source regions of CMEs tend to associate CMEs to two distinct classes (MacQueen and Fisher, 1983). Sheeley et al. (1999) used the data from LASCO and confirmed this classification by suggesting that there are two dynamical classes of CMEs, which are gradual and impulsive CMEs. The former are slower and are preferentially associated with eruptive prominences, whereas, the latter CMEs are faster and are mostly associated with flares and active regions. So, it seems that these two classes of source regions of CMEs also tend to segregate CMEs into being gradual or impulsive events. The most intriguing question in this context is whether there are two physically different processes that are involved in the launch of these slow and fast CMEs or whether they belong to a dynamical continuum with a single unified process, the answer to which is still not clear (also see Webb and Howard, 2012).
Apart from their radial propagation, CMEs are also known to exhibit lateral expansion that leads to an increase in their angular width as they propagate outwards (Kay et al., 2015; Cremades et al., 2020; Majumdar et al., 2020) and that it is the Lorentz force at their source region that is closely responsible for translating and expanding them (Subramanian et al., 2014). In this regard, Zhao et al. (2017) reported on the importance of the angular width of a CME, in determining whether the corresponding interplanetary CME and the preceding shock will reach Earth. Lugaz et al. (2017a) reported on the importance of studying the expansion in slow CMEs on their ability to drive shocks. The width of the CME also sheds light on the source region of the CME it is coming from. Moore et al. (2007) showed that the strength of the magnetic field of the source region flare arcade producing a CME can be estimated from the final angular width of the CME and the angular width of the flare arcade. Recently Majumdar et al. (2020) connected 3D profiles of width evolution to the 3D acceleration profiles of slow and fast CMEs and found that the vanishing of the initial impulsive acceleration phase and the ceasing of width expansion phase both tend to occur in a height range of 2.5–3 Rʘ, thus showing the observational evidence of the height of impact of Lorentz force on CME kinematics. So, it is evident that the width of a CME is an essential ingredient in the understanding of their kinematics, and is also an important parameter for the consideration of their space weather impact. Furthermore, since the width largely influences the kinematics of CMEs, it is still not known whether we observe any differences in the angular width distribution of slow and fast CMEs originating from different source regions.
It has also been reported that the width distribution of CMEs follow a power law (Yashiro et al., 2006; Robbrecht et al., 2009; D’Huys et al., 2014). A study of the statistical distribution of a physical parameter sheds light on the underlying physics of it, and a presence of power law in the distribution of a quantity indicates the presence of Self-Organized Criticality (Bak et al., 1987). The presence of power laws, and hence Self-Organized Criticality (SOC) in nature have become evident in the last few years in many different areas and astrophysical phenomena (Aschwanden et al., 2018, and references therein). The presence of power laws in solar astrophysics, in the global energetics of solar flares, has also been reported by Aschwanden (2016). Thus, a study of the distribution of the angular width of CMEs should provide important clues in understanding the physical mechanisms responsible for expanding the CMEs. Recently, Bidhu et al. (2017) studied the distribution of width of CMEs during the maximum phase of solar cycle 23 and 24. Meng et al. (2014) studied the distribution of CME width and its comparison with the phase of sunspot number in solar cycle 23. Inspite of these studies, whether the slow and fast CMEs follow different width distributions or whether there is any imprint of the source regions on the width distribution of these slow and fast CMEs, is still not properly understood. Thus it is worth looking at the width distribution of slow and fast CMEs and also if there is any imprint of the source region of these two dynamical classes on their width distribution.
Motivated by the above findings and the deficit in our understanding of these slow and fast CMEs, we in this work study the width distribution of slow and fast CMEs that occurred during different phases of cycle 23 and 24. We outline the data sources and the working method in Section 2, followed by our results in Section 3. Finally, we outline our main conclusions from this work in Section 4.
2 Data and Method
2.1 Data Source
We use the data from CDAW catalog for the analysis presented in this paper. The CDAW catalog lists the properties of CMEs detected manually (Yashiro et al., 2004; Gopalswamy et al., 2009) in SOHO/LASCO images. The work on source region identification and segregation is done with the images taken by Atmospheric Imaging Assembly (AIA) on-board Solar Dynamics Observatory (SDO) (Lemen et al., 2011) and the Extreme Ultraviolet Imager (EUVI) on-board STEREO (for details, refer to Section 2.4).
2.2 Event Selection
We have selected the CMEs from the CDAW catalog that have occurred during different phases of solar cycle 23 and 24. For the analysis presented in this work, we first remove the “very poor” CMEs from the CDAW catalog. Wang and Colaninno (2014) reported that the detection of “very poor” CMEs are based on the discretion of manual operators, we discard such CMEs in order to remove any bias from our analysis. It should be noted that some of the “very poor” CMEs may be the real CMEs but we remove them from the analysis because there are large errors in the measurement of the properties of such CMEs. Furthermore, we impose a lower threshold of 30° on CME width to remove narrow CMEs. Yashiro et al. (2008) and Gopalswamy et al. (2010) have reported that there exists a discrepancy in the detection of the number of CMEs with width
2.3 Segregation of CMEs Into Slow and Fast
After shortlisting the CMEs based on the above selection criteria, we segregate the CMEs as slow and fast based on their speeds. CMEs are usually classified as slow and fast relative to the speed of the solar wind. The slow solar wind typically has speeds less than 400 km s−1 while the fast solar wind has speeds greater 400 km s−1 (see, Schwenn, 2006). Therefore, 400 km s−1 can be taken as the average solar wind speed for a long term statistical study. We classify CMEs with speeds less than 300 km s−1 as slow CMEs and those with speeds greater than 500 km s−1 as fast CMEs. We consider CMEs with speeds between 300 km s−1 and 500 km s−1 as intermediate CMEs, as they cannot be strictly categorized as either slow or fast CMEs because of uncertainties in speed measurements. It is worth noting at this point that the speeds of CMEs listed in the CDAW catalog are the speeds with which the leading edge of a CME propagates. Table 1 lists the number of fast and slow CMEs in the CDAW catalog.
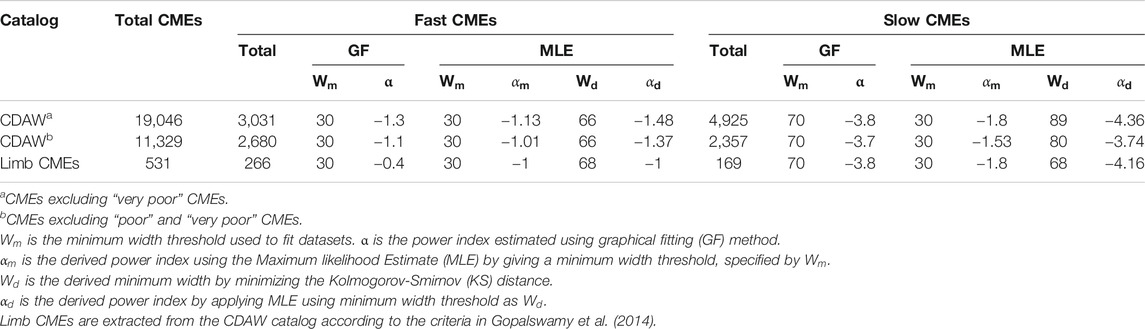
TABLE 1. Power–law indices of width distribution of fast and slow CMEs obtained using two different methods.
2.4 Segregation of the Slow and Fast CMEs on the Basis of Their Source Region
After segregating the CMEs as slow and fast, we search their source regions on the solar disk. For this we included a total of 1,064 events that occurred during 2000–2002, 2008, 2009, and also from 2012 to 2014, which covers the maxima of cycle 23, the minima of cycle 24 and the maxima of cycle 24. Here, we have followed a similar method as reported in Majumdar et al. (2020) and using the JHelioviewer software (Muller et al., 2009; Müller et al., 2017) to back-project the CMEs onto the solar disk. We further segregated the identified source regions of the CMEs into two broad categories, namely 1) Active Regions(ARs) and 2) Prominence Eruptions(PEs). We define them as follows:
Active Regions(ARs) (refer Figure 1) are prime features making up only a small fraction of the total surface area of the Sun, but harboring most of the solar activity (Webb and Howard, 2012). These being areas of strong magnetic field, are predominantly hotter and denser than the background coronal plasma, producing bright emission in the soft X-ray and extreme ultraviolet regions. In order to identify ARs, we look into the images taken by 1) the Extreme Ultraviolet Imaging Telescope (EIT; Delaboudinière et al., 1995) (195 Å) onboard SOHO, 2) Atmospheric Imaging Assembly (AIA; Lemen et al., 2011) (171 Å, 193 Å) onboard SDO, and also 3) the Extreme Ultraviolet Imager (EUVI; Wuelser et al., 2004) (171 Å, 195 Å) onboard STEREO SECCHI. We also detect the ARs by the Active Region numbers provided by the National Oceanic and Atmospheric Administration (NOAA) as supplied by Space Weather Event Knowledgebase (SWEK) using Jhelioviewer1 (Müller et al., 2017).

FIGURE 1. (Left) Active regions (ARs) as observed in the corona on May 03, 2012. The image is taken by AIA 171 Å. The ARs (pointed out in the figure by circular marks with AR written on them), are identified as bright regions, being hotter and denser than the background coronal plasma, showing strong magnetic activity (Right) Prominence Eruptions (PEs, enclosed in green box) as observed in the corona on April 04, 2012. This image is taken by AIA 304 Å. The dark strands of plasma as seen projected against the disk of the sun are filaments (at a position angle of 40° and 300° in this image), whereas the same object is termed as a prominence when observed at the solar limb (at a position angle of 235° in this image).
Prominences (refer Figure 1) are cool dense material (8000 K) embedded in the hotter corona, observed as an emission feature when seen at the solar limb, and an absorption feature when seen projected against the background hotter corona (termed as filament) (Gilbert et al., 2000). We classify an eruption as a prominence eruption if we see a strong radial component of motion away from the solar surface where all or some of the prominence material is seen to escape the gravitational field of the Sun. For a filament eruption (we include these in the same category with prominence eruption) we either looked for tangential motion across the solar surface with a subsequent eruption, or simply by observing any disappearance of the filament in the subsequent images with a transient coronal manifestation following it (also refer Webb and Hundhausen (1987)). It is also important to note that, there can be possibilities of failed eruptions (Joshi et al., 2013a), CME-jet interactions (Duan et al., 2019; Solanki et al., 2020), and CME-CME interactions (Joshi et al., 2013b; Lugaz et al., 2017b) which can influence the kinematic properties. Furthermore, CMEs are also observed to be associated with coronal jets, minifilaments, etc (Liu et al., 2015; Duan et al., 2019; Solanki et al., 2019). It is also not properly understood whether such CMEs can be categorized as the active region eruptions and prominence eruptions or classified as a different category. Thus, in the present work, we exclude such events. Furthermore, CMEs are also related to the active region filaments, however, due to the lack of comparable statistics with the other two classes (ARs and PEs), we have excluded such events from our analysis. To detect PEs, we look into the images taken by, 1) EIT 195 Å, 304 Å, 2) AIA 304 Å, and 3) EUVI 304 Å. Finally, it should be borne in mind that kinematic properties of CMEs largely depend on the overlying field strength and decay index (Xu et al., 2012; Joshi et al., 2013a). In this work we do not consider these effects into account.
For a spatial association (see Gilbert et al., 2000; Majumdar et al., 2020) between a source region and a subsequent CME, we require that the latitude of the source region to be around
For a temporal association we consider source region to erupt or show radially outward movement in the above latitude window in a time interval of at least 30 min before the first appearance of the leading front in the LASCO C2 field of view.
3 Data Analysis and Results
3.1 Width Distribution of CMEs
Recently, it has been reported that the CMEs evolve non self-similarly in the inner corona (see Cremades et al., 2020; Majumdar et al., 2020). In the CDAW catalog, the width of a CME is defined as the maximum angle subtended by a CME on the center of the Sun when the CME enters the LASCO C3 field of view (FOV) where the width appears to approach a constant value (Gopalswamy, 2004). To investigate the width distribution of CMEs during solar cycle 23 and 24, we fit a power law to it as follows:
where N is the number of CMEs with width W, α is the power-law exponent, and C a constant. In Figure 2 we plot the histogram (left panel) of the width distribution and the width distribution in log scale (right panel) with the power law fit for all CMEs excluding the “very poor” events as mentioned in the CDAW catalog. It is worth noting that after removing “very poor” CMEs from our analysis, we believe that we have reduced the bias introduced by manual operators, respectively. We find a power law index of −1.9. In order to understand the goodness of fit we perform the Kolmogorov Smirnov (KS) test where the KS distance (see Clauset et al., 2007) which is defined as the maximum distance between the empirical distribution function of the sample and cumulative distribution function of the assumed expression, is minimum for the distribution which fits the data best with a corresponding high p-value that gives the probability confidence. Here we find the KS distance and p-value as 0.13 and 0.99. It is worth noting from Figure 2, that the width distribution is not fitted well by a single power law. This serves as a motivation for us to investigate power laws segregating fast and slow CMEs. Since we aim to understand the width distribution of slow and fast CMEs, we next remove the intermediate events from our study sample, as such events are neither fast nor slow (refer section 3.2). We again study the width distribution of all events except the “very poor” and the intermediate events (Figure 3). We find that after removing the intermediate events, we still get the same power law index of −1.9 with the KS distance and p-value to be the almost same. Thus we ensure that there is no bias introduced in the estimation of the power law index of widths distribution by rejecting the intermediate events from our sample. The graphical fitting (GF) of the data points used above is not the best method to estimate the power-law, especially when number of data points is small (D’Huys et al., 2016). Therefore, we also use maximum likelihood estimate (MLE) fitting method to derive the power-law index, α. Using MLE, we get the power law index to be −1.6 which again remains the same for CMEs with or without the intermediate events.
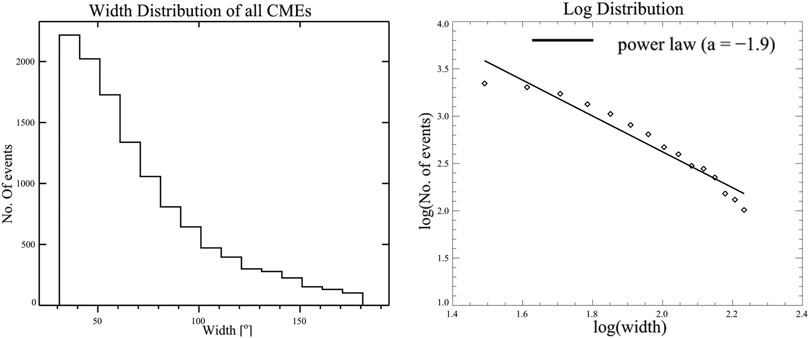
FIGURE 2. Width distribution of all CMEs (excluding “very poor” events) during solar cycle 23 and 24 using the CDAW catalog. The black line corresponds to a power law fit to the width distribution where α is the power law index.
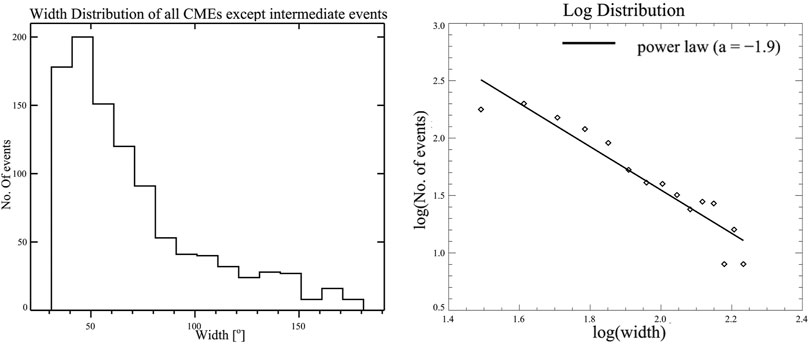
FIGURE 3. Width distribution of CMEs (excluding the intermediate and “very poor” events) during solar cycle 23 and 24 using the CDAW catalog. The black line corresponds to a power law fit to the width distribution where α is the power law index.
Now that we have ensured that the exclusion of the intermediate events does not affect our study, we try to understand now if the slow and fast CMEs follow different power laws in their width distribution.
3.2 Width Distribution of Slow and Fast CMEs
In this section we study the width distribution of slow and fast CMEs separately. We use the same power law distribution as mentioned in Eq. 2. Figure 4A shows the histograms of the width distribution of fast (black line) and slow (blue line) CMEs using CDAW catalog after excluding the “very poor” CMEs and the intermediate CMEs. Figure 4B, shows the width distributions in log scale. Black and blue lines represent the best fit power-laws obtained for the fast and slow CMEs, respectively using least square fitting method. We estimate α as −1.3 and −3.8 for fast and slow CMEs respectively. Thus we find that the slow and fast CMEs follow different power laws in their width distribution, but to get a better confidence on our result, we again perform power law fitting by MLE.
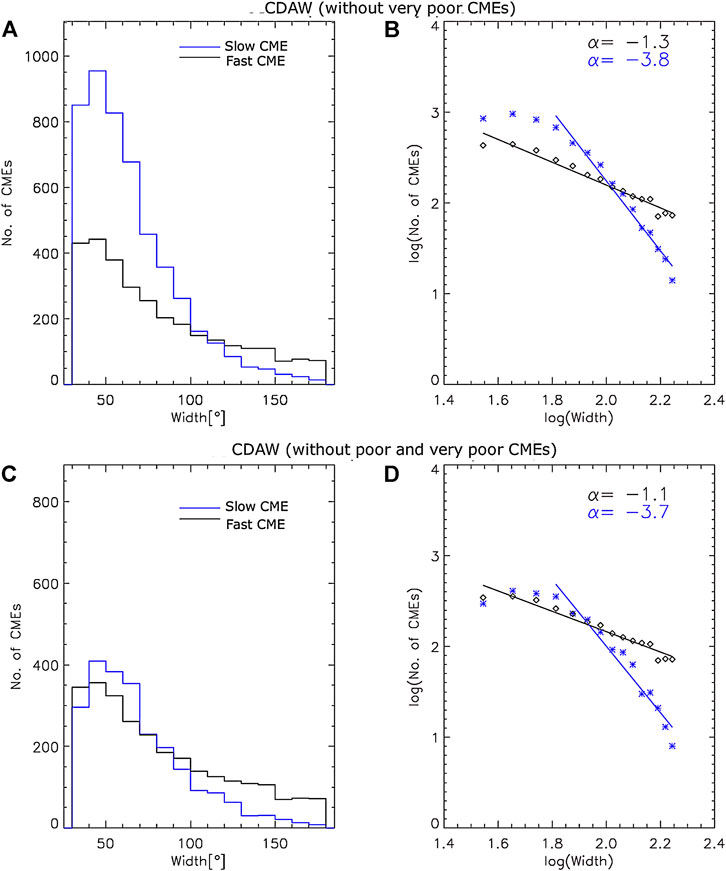
FIGURE 4. (A): Width distribution and, (B): log distribution of width for slow and fast CMEs using CDAW catalog after excluding “very poor” CMEs. The best fit straight line to the data points of fast CMEs is overplotted in black. The best fit straight line to the data points (except first three points) of slow CMEs is overplotted in blue. (C) and (D) are the same as (A) and (B) but excluding “poor” and “very poor” CMEs from the CDAW catalog.
It should be noted that the number of slow CMEs in CDAW catalog with widths less than 70° flattens. This could partially be due to the observational limitations of C2 coronagraph or human subjectivity or both. The minimum width for the graphical fitting is decided by visually inspecting the distribution and choosing the width beyond which the distribution is supposedly following a power-law. Thus, we fit the tail of the width distribution of slow CMEs with a power-law. Later, we used MLE to derive the minimum width beyond which the distribution is best represented by the power law.
We performed MLE fitting in two different ways. First we set the minimum width value,
We also remove the CMEs labeled as “poor” in the CDAW catalog to study their effects on the width distribution. We find that removal of both “poor” and “very poor” CMEs has little effect on the width distribution and power-law indices (see, Figures 4C,D and Table 1) of slow and fast CMEs. The speeds listed in the CDAW catalog are the projected speeds in the plane of sky measured at a fixed position angle. Therefore, applying a speed threshold uniformly to all CMEs introduces projection effects. In order to reduce projection effects, we also estimate the power-law for fast and slow limb CMEs in solar cycles 23 and 24. First we plot CMEs with all velocities whose widths fall between 30 and 180° (top panel of Figure 5). We estimate the power index of −1.5 and −1.19 using the GF and MLE methods for the minimum width threshold of 30°. Then, we segregate fast and slow CMEs and estimate the power indices using the GF (bottom panel of Figure 5) and MLE methods (see Table 1). We find that the power indices for fast and slow limb CMEs are different from each other; they are different from the power index of non–limb fast and slow CMEs. One of the reasons for this discrepancy is the small number of slow and fast limb CMEs. From Table 1, we note that the fast and slow limb CMEs are 10–20 times less than fast and slow CMEs when non-limb events are also considered. To evaluate the goodness of fit we again estimate the KS distance. The KS distances for fast limb CMEs and all fast CMEs are 0.09 and 0.01, respectively. The critical values of KS distances with 99% of confidence limit for fast limb CMEs and all fast CMEs are 0.1 and 0.03, respectively. Smaller the KS distance, better is the fit. Similarly, KS distances for slow limb CMES and all slow CMEs are 0.04 and 0.02, respectively. Further, critical KS distance at 99% of confidence limit for slow limb CMEs and all slow CMEs are 0.13 and 0.03, respectively.Thus the power indices corresponding to the limb CMEs differ from that of non-limb cases. We want to emphasize that the slow CME power-law is steeper than that of the fast CMEs in both cases, although the values may differ. However, the limb CME values may be closer to reality because of minimal projection effects. It should be noted that the results are consistent with the speed–width relation as reported in Gopalswamy et al. (2014); where authors have reported wider CMEs tend to propagate faster than narrow CMEs. Also, we note that the KS distance of fast CMEs without “very poor” and intermediate events is of an order of magnitude better than KS distance estimated by fitting a single power law to all CMEs. This demonstrates that fast and slow CMEs are better represented by different power-laws than fast and slow CMEs combined.
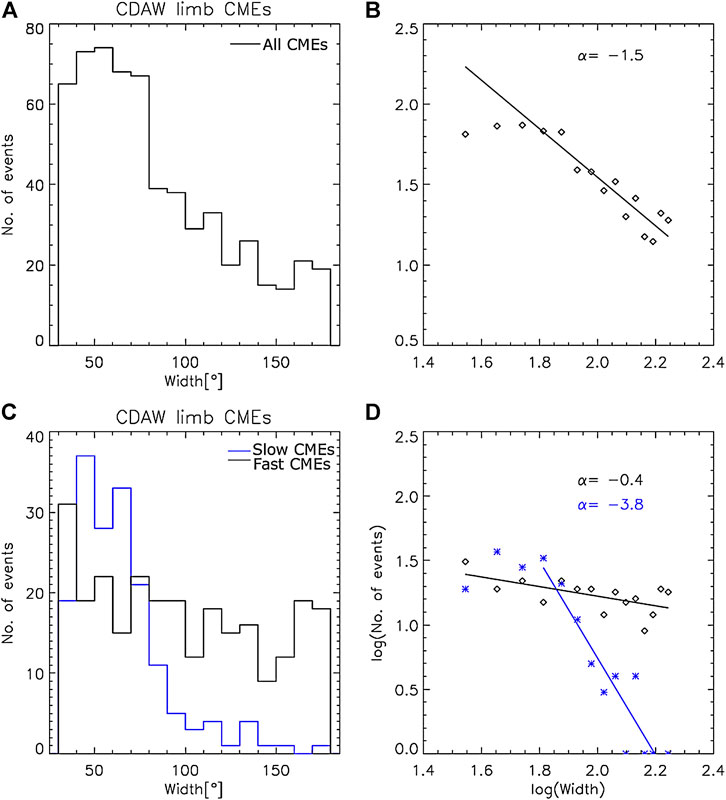
FIGURE 5. (A): Width distribution for all limb CMEs extracted from CDAW catalog without velocity thresholding. (B) is the log-distribution of limb CMEs. (C) and (D): Width distribution of slow and fast limb CMEs extracted from CDAW catalog.
3.3 Width Distribution of Slow and Fast CMEs Coming from ARs and PEs
In previous sections, we note that the slow and fast CMEs follow different power laws. This lights on the fact that may be the slow and fast CMEs have different physics involved in the mechanism that leads to their expansion and hence their widths. Since Lorentz force is responsible for propelling and expanding a CME (refer Section 1), we expect to see its imprint in the width distribution of slow and fast CMEs originating from different source regions.
The entries in Table 2 have been computed by taking events from different phases of cycle 23 and 24 as mentioned in Section 2.4. After segregating the source regions, their width distribution is studied separately. Here we use a similar power-law fitting to the width distribution of CMEs coming from the two source regions. We do power-law fitting by graphical fitting and also by MLE to estimate power-law indices.

TABLE 2. Power-law indices of width distribution of fast and slow CMEs from different source regions obtained using two different methods.
Figures 6, 7 show the width distribution of slow and fast CMEs originating from ARs and PEs, and plotted alongside it are the power-law fit (in black). We get α as −1.29 and −3.43 for fast CMEs coming from ARs and PEs with a KS distance of 0.13 (p-value 0.99) and 0.22 (p-value 0.86) respectively. Thus we see that indeed the width distribution of fast CMEs have different power indices for CMEs originating from ARs and PEs. In the case of slow CMEs we get α as −3.20 and −3.53 for CMEs from ARs and PEs with a KS distance of 0.14 (p-value 0.99) and 0.21 (p-value 0.86) respectively. Thus for slow CMEs too the power indices are slightly different for CMEs from ARS and PEs. Again, GF is not the best method to estimate the power-law since the number of data points is small here, by using MLE fitting, we get α as −1.23 and −2.00 for fast CMEs coming from ARs and PEs respectively, whereas for slow CMEs we get α as −1.91 and −2.08 for CMEs from ARs and PEs keeping
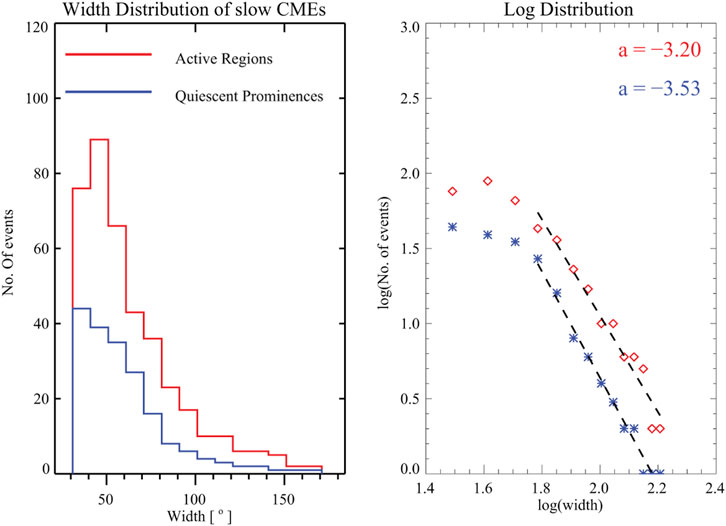
FIGURE 6. (Left) Width distribution of slow CMEs from different source regions, with their widths taken from the CDAW catalog. (Right) power-law fitting of the width distribution. The black line is the power-law fit to the data.
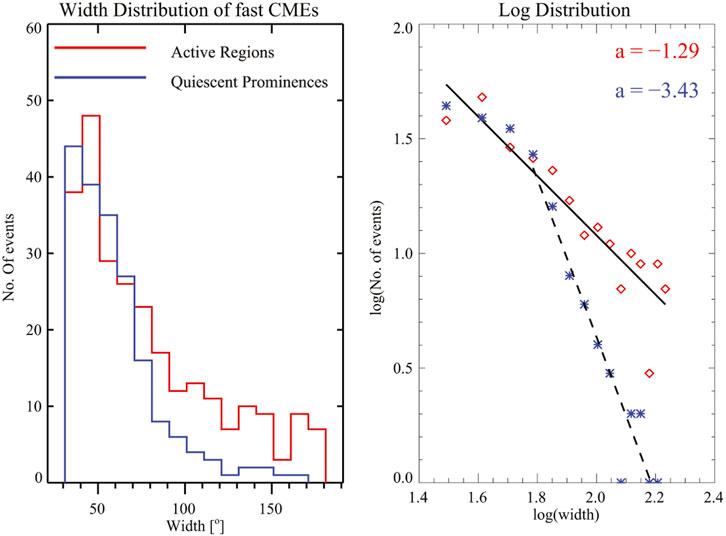
FIGURE 7. (Left) Width distribution of fast CMEs from different source regions, with their widths taken from the CDAW catalog. (Right) power-law fitting of the width distribution. The black line is the power-law fit to the data.
Thus the fact that slow and fast CMEs from ARs and PEs following different power laws in their width distribution vividly points toward a possibly different mechanism that leads to the width expansion of these CMEs and hence demands a more deeper understanding of the same. It should be noted that a few studies Zuccarello et al. (2014); Seaton et al. (2011); O’Kane et al. (2019) have tried to explore the possible mechanims of the CMEs but these studies are confined to isolated cases of CMEs. Also, a few statistical studies on large number of CMEs suggested that there may be different classes of CMEs with different driving mechanisms (Cyr et al., 1999; Subramanian and Dere, 2001; Moon et al., 2002).
From Figures 6, 7 we also note that in case of the fast CMEs, effect of change in source region is more pronounced unlike the case for slow events. The limit of the field strength in the source region could be the physical reason for the strength of field in ARs, which in turn determines the available energy to power the eruptions, whereas in case of the CMEs from PEs, the magnetic structure in the periphery of the ejection site controls the chances of ejection and eventually the observed kinematic properties of the ejected material (Gopalswamy, 2017). So, possibly a different mechanism governs the width expansion of CMEs coming from ARs and PEs, irrespective of them being slow or fast.
4 Summary and Conclusion
In this work, we study the width distribution of CMEs that occurred during different phases of solar cycle 23 and 24. The CMEs were then segregated into slow (
1. CMEs excluding ‘very poor’ events from the CDAW catalog tend to follow a power law in their width distribution with a power law index of −1.9 (Figure 2). Using MLE, we find the power law index to be −1.6. This power law index remains unchanged on the exclusion of the intermediate events from our sample set (Figure 3). Thus the intermediate events do not affect our results and thus we removed them from our sample set, as they cannot be strictly considered either slow or fast. Using GF method, we note that a single power law is unable to explain the observed distribution.
2. We find different power indices for the width distribution of fast and slow CMEs (see Table 1). To reduce the projection effects from our results, we study the width distribution of slow and fast limb CMEs, and we found that they follow different power laws and the results remain unchanged. However, the absolute value of power indices are not the same as compared to limb and non limb CMEs which may be due to poor statistics, as demonstrated by KS test. Since both fast and slow limb and non-limb CMEs follow different power-laws in width distribution, we believe that slow and fast CMEs may have different energy sources and generation mechanisms.
3. We study the width distribution of slow and fast CMEs coming from different source regions (ARs and PEs), and find that the power law indices are different for CMEs coming from ARs and PEs (refer Table 2). Furthermore, CMEs coming from PEs tend to follow a steeper power law irrespective of their speeds. Also, we find that slow CMEs tend to follow a steeper power law than fast CMEs, irrespective of the source region they are coming from. This clearly hints toward a possibly different mechanism for width expansion of these CMEs.
Thus we find from this study that apart from their speeds, slow and fast CMEs are also distinctly different in terms of the distribution of their angular width in each case. We believe that this study will help in a better understanding of the mechanism of width expansion of slow and fast CMEs coming from different source regions, and in establishing the width of a CME as a crucial parameter in the study of kinematics of CMEs and their ejection mechanisms. Extending this work on a larger sample of CMEs using de-projection methods will further help in better confirmation of our conclusions.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: CDAW Catalogue.
Author Contributions
VP planned the study and performed initial analysis. SM, RP generated source region catalog. VP and SM wrote manuscript. AC performed analysis on the limb events. VP, SM, DB, and NG interpreted the results. All authors took part in the discussion.
Funding
VP was further supported by the GOA-2015-014 (KU Leuven) and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 724326). VP is supported by the Spanish Ministerio de Ciencia, Innovación y Universidades through project PGC2018-102108-B-I00 and FEDER funds.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank referees for their comments which has improved the presentation. The authors thank IAC and IIA for providing the required computational facilities for doing this work. We also thank Mr. Bibhuti Kumar Jha for his useful comments during the work.
Footnotes
1https://www.jhelioviewer.org/
References
Aschwanden, M. J. (2016). Global Energetics of Solar Flares. IV. Coronal Mass Ejection Energetics. Astrophys. J. 831, 105. doi:10.3847/0004-637X/831/1/105
Aschwanden, M. J., Scholkmann, F., Béthune, W., Schmutz, W., Abramenko, V., Cheung, M. C. M., et al. (2018). Order Out of Randomness: Self-Organization Processes in Astrophysics. Space Sci. Rev. 214, 55. doi:10.1007/s11214-018-0489-2
Bak, P., Tang, C., and Wiesenfeld, K. (1987). Self-organized Criticality: An Explanation of the 1/f Noise. Phys. Rev. Lett. 59, 381–384. doi:10.1103/PhysRevLett.59.381
Bidhu, S., Iren, S., and Benjamin, D. (2017). Cme Speed and Angular Width Distributions during 23 and 24 Solar Cycle Maximum. J. Space Explor. 6, 122. doi:10.1007/s11214-019-0605-y
Brueckner, G. E., Howard, R. A., Koomen, M. J., Korendyke, C. M., Michels, D. J., Moses, J. D., et al. (1995). The Large Angle Spectroscopic Coronagraph (LASCO). Solar Phys. 162, 357–402. doi:10.1007/BF00733434
Clauset, A., Rohilla Shalizi, C., and Newman, M. E. J. (2007). Power-Law Distributions in Empirical Data. SIAM Rev. 51, 661–703. 10.1137/070710111
Cremades, H., Iglesias, F. A., and Merenda, L. A. (2020). Asymmetric Expansion of Coronal Mass Ejections in the Low Corona. Astron. Astrophys. 635, A100. doi:10.1051/0004-6361/201936664
Cyr, St. O. C., Burkepile, J. T., Hundhausen, A. J., and Lecinski, A. R. (1999). A Comparison of Ground-Based and Spacecraft Observations of Coronal Mass Ejections from 1980–1989. J. Geophys. Res. 104, 12493–12506. doi:10.1029/1999JA900045
Delaboudinière, J.-P., Artzner, G. E., Brunaud, J., Gabriel, A. H., Hochedez, J. F., Millier, F., et al. (1995). EIT: Extreme-Ultraviolet Imaging Telescope for the SOHO Mission. Solar Phys. 162, 291–312. doi:10.1007/BF00733432
D’Huys, E., Berghmans, D., Seaton, D. B., and Poedts, S. (2016). The Effect of Limited Sample Sizes on the Accuracy of the Estimated Scaling Parameter for Power-Law-Distributed Solar Data. Solar Phys. 291, 1561–1576. doi:10.1007/s11207-016-0910-5
D’Huys, E., Seaton, D. B., Poedts, S., and Berghmans, D. (2014). Observational Characteristics of Coronal Mass Ejections without Low-Coronal Signatures. Astrophys. J. 795, 49. doi:10.1088/0004-637X/795/1/49
Duan, Y., Shen, Y., Chen, H., and Liang, H. (2019). The Birth of a Jet-Driven Twin CME and its Deflection from Remote Magnetic Fields. Astrophys. J. 881, 132. doi:10.3847/1538-4357/ab32e9
Gilbert, H. R., Holzer, T. E., Burkepile, J. T., and Hundhausen, A. J. (2000). Active and Eruptive Prominences and Their Relationship to Coronal Mass Ejections. Astrophysical J. 537, 503–515. doi:10.1086/309030
Gopalswamy, N. (2004). “A Global Picture of CMEs in the Inner Heliosphere,” in The Sun and the Heliosphere as an Integrated System. Editors G. Poletto, and S. T. Suess (Dordrecht, The Netherlands: Astrophysics and Space Science Library), vol. 317, 201. doi:10.1007/978-1-4020-2666-9˙8
Gopalswamy, N. (2010). “Corona Mass Ejections: A Summary of Recent Results,” in 20th National Solar Physics Meeting. Editor I. Dorotovic (Papradno, Slovakia: Proceedings of the 20th National Solar Physics Meeting), 108–130.
Gopalswamy, N. (2017). Extreme Solar Eruptions and Their Space Weather Consequences. arXiv:1709.03165.
Gopalswamy, N. (2016). History and Development of Coronal Mass Ejections as a Key Player in Solar Terrestrial Relationship. Geosci. Lett. 3, 8. doi:10.1186/s40562-016-0039-2
Gopalswamy, N., Akiyama, S., Yashiro, S., and Mäkelä, P. (2010). Coronal Mass Ejections from Sunspot and Non-Sunspot Regions. Astrophys. Space Sci. Proc. 19, 289–307. doi:10.1007/978-3-642-02859-5˙24
Gopalswamy, N., Akiyama, S., Yashiro, S., Xie, H., Mäkelä, P., and Michalek, G. (2014). Anomalous Expansion of Coronal Mass Ejections during Solar Cycle 24 and its Space Weather Implications. Geophys. Res. Lett. 41, 2673–2680. doi:10.1002/2014GL059858
Gopalswamy, N., Lara, A., Lepping, R. P., Kaiser, M. L., Berdichevsky, D., and Cyr, St. O. C. (2000). Interplanetary Acceleration of Coronal Mass Ejections. Geophys. Res. Lett. 27, 145–148. doi:10.1029/1999GL003639
Gopalswamy, N., Xie, H., Mäkelä, P., Yashiro, S., Akiyama, S., Uddin, W., et al. (2013). Height of Shock Formation in the Solar Corona Inferred from Observations of Type II Radio Bursts and Coronal Mass Ejections. Adv. Space Res. 51, 1981–1989. doi:10.1016/j.asr.2013.01.006
Gopalswamy, N., Yashiro, S., Michalek, G., Stenborg, G., Vourlidas, A., Freeland, S., et al. (2009). The SOHO/LASCO CME Catalog. Earth Moon Planets 104, 295–313. doi:10.1007/s11038-008-9282-7
Gosling, J. T. (1993). The Solar Flare Myth. J. Geophys. Res. 98, 18937–18950. doi:10.1029/93JA01896
Gosling, J. T., McComas, D. J., Phillips, J. L., and Bame, S. J. (1991). Geomagnetic Activity Associated with Earth Passage of Interplanetary Shock Disturbances and Coronal Mass Ejections. J. Geophys. Res. 96, 7831–7839. doi:10.1029/91JA00316
Hansen, R. T., Garcia, C. J., Grognard, R. J.-M., and Sheridan, K. V. (1971). A Coronal Disturbance Observed Simultaneously with a White-Light Corona-Meter and the 80 MHz Culgoora Radioheliograph. Proc. Astron. Soc. Aust. 2, 57.
Howard, R. A., Moses, J. D., Vourlidas, A., Newmark, J. S., Socker, D. G., Plunkett, S. P., et al. (2008). Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI). Space Sci. Rev. 136, 67–115. doi:10.1007/s11214-008-9341-4
Hundhausen, A. J., Sawyer, C. B., House, L., Illing, R. M. E., and Wagner, W. J. (1984). Coronal Mass Ejections Observed during the Solar Maximum Mission - Latitude Distribution and Rate of Occurrence. J. Geophys. Res. 89, 2639–2646. doi:10.1029/JA089iA05p02639
Joshi, N. C., Srivastava, A. K., Filippov, B., Uddin, W., Kayshap, P., and Chandra, R. (2013a). A Study of a Failed Coronal Mass Ejection Core Associated with an Asymmetric Filament Eruption. Astrophys. J. 771, 65. doi:10.1088/0004-637X/771/1/65
Joshi, N. C., Uddin, W., Srivastava, A. K., Chandra, R., Gopalswamy, N., Manoharan, P. K., et al. (2013b). A Multiwavelength Study of Eruptive Events on January 23, 2012 Associated with a Major Solar Energetic Particle Event. Adv. Space Res. 52, 1–14. doi:10.1016/j.asr.2013.03.009
Kay, C., Opher, M., and Evans, R. M. (2015). Global Trends of CME Deflections Based on CME and Solar Parameters. Astrophys. J. 805, 168. doi:10.1088/0004-637x/805/2/168
Lemen, J., Title, A., Boerner, P., Chou, C., Drake, J., Duncan, D., et al. (2011). The Atmospheric Imaging Assembly (Aia) on the Solar Dynamics Observatory (Sdo). Solar Phys. 275, 17–40. doi:10.1007/s11207-011-9776-8
Liu, J., Wang, Y., Shen, C., Liu, K., Pan, Z., and Wang, S. (2015). A Solar Coronal Jet Event Triggers a Coronal Mass Ejection. Astrophys. J. 813, 115. doi:10.1088/0004-637X/813/2/115
Lugaz, N., Farrugia, C. J., Winslow, R. M., Small, C. R., Manion, T., and Savani, N. P. (2017a). Importance of CME Radial Expansion on the Ability of Slow CMEs to Drive Shocks. Astrophys. J. 848, 75. doi:10.3847/1538-4357/aa8ef9
Lugaz, N., Temmer, M., Wang, Y., and Farrugia, C. J. (2017b). The Interaction of Successive Coronal Mass Ejections: A Review. Solar Phys. 292, 64. doi:10.1007/s11207-017-1091-6
MacQueen, R. M., and Fisher, R. R. (1983). The Kinematics of Solar Inner Coronal Transients. Solar Phys. 89, 89–102. doi:10.1007/BF00211955
Majumdar, S., Pant, V., Patel, R., and Banerjee, D. (2020). Connecting 3D Evolution of Coronal Mass Ejections to Their Source Regions. Astrophys. J. 899, 6. doi:10.3847/1538-4357/aba1f2
Manoharan, P. K., and Mujiber Rahman, A. (2011). Coronal Mass Ejections– Propagation Time and Associated Internal Energy. J. Atmos. Solar-Terr. Phys. 73, 671–677. doi:10.1016/j.jastp.2011.01.017
Meng, W.-J., Le, G.-M., Lin, Z.-X., Zhang, Y., and Yang, X.-X. (2014). Distribution of CMEs with Different Angular Widths and Comparison with the Phase of Sunspot Number in the 23rd Solar Cycle. Chin. Astron. Astrophys. 38, 85–91. doi:10.1016/j.chinastron.2014.01.008
Moon, Y. J., Choe, G. S., Wang, H., Park, Y. D., Gopalswamy, N., Yang, G., et al. (2002). A Statistical Study of Two Classes of Coronal Mass Ejections. Astrophys. J. 581, 694–702. doi:10.1086/344088
Moore, R. L., Sterling, A. C., and Suess, S. T. (2007). The Width of a Solar Coronal Mass Ejection and the Source of the Driving Magnetic Explosion: A Test of the Standard Scenario for CME Production. Astrophys. J. 668, 1221–1231. doi:10.1086/521215
Muller, D., Fleck, B., Dimitoglou, G., Caplins, B. W., Amadigwe, D. E., García Ortiz, J. P., et al. (2009). JHelioviewer: Visualizing Large Sets of Solar Images Using JPEG 2000. Comput. Sci. Eng. 11, 38–47. doi:10.1109/MCSE.2009.142
Müller, D., Nicula, B., Felix, S., Verstringe, F., Bourgoignie, B., Csillaghy, A., et al. (2017). JHelioviewer. Time-dependent 3D Visualisation of Solar and Heliospheric Data. Astron. Astrophys. 606, A10. doi:10.1051/0004-6361/201730893
O’Kane, J., Green, L., Long, D. M., and Reid, H. (2019). Stealth Coronal Mass Ejections from Active Regions. Astrophys. J. 882, 85. doi:10.3847/1538-4357/ab371b
Robbrecht, E., Berghmans, D., and Van der Linden, R. A. M. (2009). Automated LASCO CME Catalog for Solar Cycle 23: Are CMEs Scale Invariant?. Astrophys. J. 691, 1222–1234. doi:10.1088/0004-637X/691/2/1222
Schwenn, R. (1996). An Essay on Terminology, Myths and Known Facts: Solar Transient - Flare - CME - Driver Gas - Piston - BDE - Magnetic Cloud - Shock Wave - Geomagnetic Storm. Astrophys. Space Sci. 243, 187–193. doi:10.1007/BF00644053
Schwenn, R. (2006). Space Weather: The Solar Perspective. Living Rev. Solar Phys. 3, 2. doi:10.12942/lrsp-2006-2
Seaton, D. B., Mierla, M., Berghmans, D., Zhukov, A. N., and Dolla, L. (2011). SWAP-SECCHI Observations of a Mass-Loading Type Solar Eruption. Astrophys. J. Lett. 727, L10. doi:10.1088/2041-8205/727/1/L10
Sheeley, N. R., Walters, J. H., Wang, Y. M., and Howard, R. A. (1999). Continuous Tracking of Coronal Outflows: Two Kinds of Coronal Mass Ejections. J. Geophys. Res. 104, 24739–24768. doi:10.1029/1999JA900308
Solanki, R., Srivastava, A. K., and Dwivedi, B. N. (2020). CME Productive and Non-productive Recurring Jets Near an Active Region AR11176. Solar Phys. 295, 27. doi:10.1007/s11207-020-1594-4
Solanki, R., Srivastava, A. K., Rao, Y. K., and Dwivedi, B. N. (2019). Twin CME Launched by a Blowout Jet Originated from the Eruption of a Quiet-Sun Mini-Filament. Solar Phys. 294, 68. doi:10.1007/s11207-019-1453-3
Subramanian, P., Arunbabu, K. P., Vourlidas, A., and Mauriya, A. (2014). Self-Similar Expansion of Solar Coronal Mass Ejections: Implications for Lorentz Self-Force Driving. Astrophys. J. 790, 125. doi:10.1088/0004-637x/790/2/125
Subramanian, P., and Dere, K. P. (2001). Source Regions of Coronal Mass Ejections. Astrophys. J. 561, 372–395. doi:10.1086/323213
Tousey, R. (1973). “The Solar Corona,” in Space Research Conference. Editors M. J. Rycroft, and S. K. Runcorn, vol. 2, 713–730.
Vourlidas, A., Carley, E. P., and Vilmer, N. (2020). Radio Observations of Coronal Mass Ejections: Space Weather Aspects. Front. Astron. Space Sci. 7, 43. doi:10.3389/fspas.2020.00043
Wang, Y.-M., and Colaninno, R. (2014). Is Solar Cycle 24 Producing More Coronal Mass Ejections Than Cycle 23? Astrophys. J. Lett. 784, L27. doi:10.1088/2041-8205/784/2/L27
Webb, D. F., and Howard, T. A. (2012). Coronal Mass Ejections: Observations. Living Rev. Solar Phys. 9, 3. doi:10.12942/lrsp-2012-3
Webb, D. F., and Hundhausen, A. J. (1987). Activity Associated with the Solar Origin of Coronal Mass Ejections. Solar Phys. 108, 383–401. doi:10.1007/BF00214170
Wuelser, J.-P., Lemen, J. R., Tarbell, T. D., Wolfson, C. J., Cannon, J. C., Carpenter, B. A., et al. (2004). “EUVI: the STEREO-SECCHI Extreme Ultraviolet Imager,” in Telescopes and Instrumentation for Solar Astrophysics. Editors S. Fineschi, and M. A. Gummin (Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series), vol. 5171, 111–122. doi:10.1117/12.506877
Xu, Y., Liu, C., Jing, J., and Wang, H. (2012). On the Relationship between the Coronal Magnetic Decay Index and Coronal Mass Ejection Speed. Astrophys. J. 761, 52. doi:10.1088/0004-637X/761/1/52
Yashiro, S., Akiyama, S., Gopalswamy, N., and Howard, R. A. (2006). Different Power-Law Indices in the Frequency Distributions of Flares with and without Coronal Mass Ejections. Astrophys. J. Lett. 650, L143–L146. doi:10.1086/508876
Yashiro, S., Gopalswamy, N., Michalek, G., Cyr, St. O. C., Plunkett, S. P., Rich, N. B., et al. (2004). A Catalog of White Light Coronal Mass Ejections Observed by the SOHO Spacecraft. J. Geophys. Res. (Space Phys.) 109, A07105. doi:10.1029/2003JA010282
Yashiro, S., Gopalswamy, N., Michalek, G., and Howard, R. A. (2003). Properties of Narrow Coronal Mass Ejections Observed with LASCO. Adv. Space Res. 32, 2631–2635. doi:10.1016/j.asr.2003.03.018
Yashiro, S., Michalek, G., and Gopalswamy, N. (2008). A Comparison of Coronal Mass Ejections Identified by Manual and Automatic Methods. Ann. Geophys. 26, 3103–3112. doi:10.5194/angeo-26-3103-2008
Zhang, J., and Dere, K. P. (2006). A Statistical Study of Main and Residual Accelerations of Coronal Mass Ejections. Astrophys. J. 649, 1100–1109. doi:10.1086/506903
Zhang, J., Dere, K. P., Howard, R. A., Kundu, M. R., and White, S. M. (2001). On the Temporal Relationship between Coronal Mass Ejections and Flares. Astrophys. J. 559, 452–462. doi:10.1086/322405
Zhao, X. H., Feng, X. S., Feng, H. Q., and Li, Z. (2017). Correlation between Angular Widths of CMEs and Characteristics of Their Source Regions. Astrophys. J. 849, 79. doi:10.3847/1538-4357/aa8e49
Keywords: coronal mass ejections, corona, kinematics, space weather, solar cycle
Citation: Pant V, Majumdar S, Patel R, Chauhan A, Banerjee D and Gopalswamy N (2021) Investigating Width Distribution of Slow and Fast CMEs in Solar Cycles 23 and 24. Front. Astron. Space Sci. 8:634358. doi: 10.3389/fspas.2021.634358
Received: 27 November 2020; Accepted: 26 April 2021;
Published: 13 May 2021.
Edited by:
Nandita Srivastava, Physical Research Laboratory, IndiaReviewed by:
Jiajia Liu, Queen’s University Belfast, United KingdomAbhishek Kumar Srivastava, Indian Institute of Technology (BHU), India
Copyright © 2021 Pant, Majumdar, Patel, Chauhan, Banerjee and Gopalswamy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: V. Pant, dmFpYmhhdi5wYW50QGFyaWVzLnJlcy5pbg==
 V. Pant
V. Pant S. Majumdar4
S. Majumdar4 R. Patel
R. Patel A. Chauhan
A. Chauhan D. Banerjee
D. Banerjee