An Auroral Alfvén Wave Cascade

Folding, kinking, curling and vortical optical forms are distinctive features of most bright auroral displays. These forms are symptomatic of non-linear forcing of the plasma above auroral arcs resulting from the intensification of electrical currents and Alfvén waves along high-latitude geomagnetic field-lines during periods of disturbed space weather. Electrons accelerated to energies sufficient to carry these currents impact the atmosphere and drive visible emission with spatial structure and dynamics that replicate the morphology and time evolution of the plasma region where the acceleration occurs. Movies of active auroral displays, particularly when combined with conjugate in-situ fields and plasma measurements, therefore capture the physics of a driven, non-linearly evolving space plasma system. Here a perspective emphasizing the utility of combining in-situ measurements through the auroral acceleration region with high time and spatial resolution auroral imaging for the study of space plasma turbulence is presented. It is demonstrated how this special capacity reveals the operation of a cascade of vortical flows and currents through the auroral acceleration region regulated by the physics of Alfvén waves similar to that thought to operate in the Solar wind.

Introduction

Earth’s discrete aurora is a consequence of the closure of geomagnetic field-aligned electric currents through the ionosphere and propagating Alfvén waves. The concentration of Earthward field-aligned current from a magnetospheric source due to the convergence of the geomagnetic field requires electron acceleration (Knight, 1973). The region where this acceleration occurs is known as the auroral acceleration region (Paschmann et al., 2003). Qualitatively, this region is bound at low altitudes by the topside ionosphere, below which densities rapidly increase, and at high altitudes by the capacity of hot ambient electrons to carry the current with little or no acceleration. Observations show that the auroral acceleration region extends from >2,000 to ∼10,000km in altitude depending on local time, season and solar activity (Karlsson, 2012).

The auroral acceleration region is host to a variety of non-linear processes including the formation of double layers and phase space holes (Ergun et al., 2004) as well as meso-scale plasma instabilities (Selyer and Wu, 2001) that shape the evolving form of auroral displays. These processes decouple magnetospheric convection from the ionosphere through the formation of parallel electric fields. An outer-scale for the operation of these dynamics can be defined by considering the relationship between the cross-field potential in the magnetospheric generator region and that in the ionosphere. Observations above discrete aurora suggest that the field-aligned current ($J_{\parallel }$) and the potential $\varphi$ along an auroral the field-line can be modeled by the current voltage relation $J_{\parallel I}=K\left({\varphi }_M-{\varphi }_I\right)$ (Lyons, 1981) where the $M$ and $I$ subscripts refer to locations in the magnetosphere and ionosphere respectively. Here, $K={\displaystyle \int \sigma dz}$ is the conductance along the geomagnetic field and $\sigma$ the local conductivity. On the other hand, Ohm’s law at the ionosphere provides $J_{\parallel I}={\displaystyle {\sum }_P{\nabla }_{\perp I}^2{\varphi }_I}$ where ${\Sigma }_P$ is the height integrated ionospheric Pedersen conductivity and $\nabla \cdot J=0$ is used to replace the horizontal current, $J_{\perp i}$ with $J_{\parallel I}$. Equating $J_{\parallel I}$ from the current voltage relation with that from Ohm’s law provides,

${\varphi }_M=\left(1-{\lambda }_{MI}^2\lambda {\nabla }_{\perp I}^2\right){\varphi }_I(1)$

after Lysak and Song (1996) where ${\lambda }_{MI}={\left({\Sigma }_P/K\right)}^{1/2}$ is the magnetosphere-ionosphere coupling scale length. Typically, λ_MI = 50–100 km at 100 km altitude. It is apparent from Eq. 1 that for gradient scale-lengths less than ${\lambda }_{MI}$ the majority of the cross-field potential of the generator will not map to the ionosphere but instead will appear along the geomagnetic field above the ionosphere in the form of parallel electric fields. The altitude range over which these parallel fields exist is the auroral acceleration region.

For time varying potential structures or Alfvén waves the same procedure can be performed by replacing the current voltage relation with the cold plasma wave impedance relationship (Stasiewicz et al., 2000),

$E_{\perp }=b_{\perp }{V}_A\sqrt{1+k_{\perp }^2{\lambda }_e^2}(2)$

and using Ampere’s law with $E_{\perp }\approx -{\nabla }_{\perp }{\varphi }_{\perp }$, to provide the result,

${\varphi }_M\ge {\mu }_o{\Sigma }_P\sqrt{V_{AM}{V}_{AI}}\left(1+k_{\perp M}^2{\lambda }_{eM}^2\right){\varphi }_I(3)$

Here, ${\lambda }_{eM}$ and $k_{\perp M}^2$ are the electron inertial length and perpendicular wavenumber in the magnetosphere, and the wave is mapped along the geomagnetic field to the ionosphere using the WKB approximation. Reflection of incoming Alfvén wave Poynting flux from inhomogeneities, particularly at the base of the acceleration region (Chaston, 2006), means that the WKB estimate provides an upper limit for the magnitude of ${\varphi }_I$ relative to ${\varphi }_M$ - hence the inequality in Eq. 3. Here, it has also been assumed that $n_M/n_I\ll B_{\mathrm{0M}}/B_{\mathrm{0I}}$ so we can take $k_{\perp I}^2{\lambda }_{eI}^2\to 0$ (n is the plasma density and B₀ is the geomagnetic field strength). For an acceleration region at 1 Earth radius above the surface and densities of the order of 1 and 10⁵ cm⁻³ in the acceleration region and ionosphere respectively, one finds ${\varphi }_I/{\varphi }_M<1$ for a weakly conducting ionosphere (${\Sigma }_P=1 mho$) but more typically ${\varphi }_I/{\varphi }_M\ll 1$ above auroral arcs where the conductivity is large and the transverse scales are often of the order of acceleration region ${\lambda }_e$ (Borovsky, 1993).

For the interpretation of auroral imagery the large size of ${\varphi }_M$, relative to ${\varphi }_I$, has the significant implication that fast transverse motions in auroral luminosity on scales less than ${\lambda }_{MI}$ more likely correspond to structured $E\times B$ flows in the magnetosphere than flows in the ionosphere. These flows advect acceleration structures whose motion is projected onto the ionosphere/upper atmosphere by the precipitating accelerated electrons that such structures drive. The guiding center of these electrons follow ballistic trajectories below the acceleration region subject to the conservation of the first adiabatic invariant along the geomagnetic field before depositing their energy in the upper atmosphere. These trajectories are largely independent of the plasma dynamics operating below the acceleration region and through the topside ionosphere except via coupling/feedback on the acceleration region fields (Lysak, 1990) that drive them Earthward. While the low altitude dynamics may have a turbulent character (Kintner and Seyler, 1985; Pécseli, 2015) this turbulence is not the topic of this “Perspective” article. This distinction is supported by the fact that observed ionospheric electric fields in and around auroral arcs (e.g., Vondrak, 1981) are insufficient to account for the rapid motions of optical features in the aurora; while in contrast, the electric fields observed in-situ, in and around regions of auroral electron acceleration have magnitudes and orientations consistent with these motions (Hallinan, 1981). Consequently, the motion of optical elements within regions of luminosity provide the capacity to image flows and electric fields in the acceleration region (Hallinan, 1981). This capacity is augmented by the fact that auroral luminosity for the most commonly observed lines in bright discrete aurora is proportional to the energy flux of field-aligned precipitating electrons (Rees and Jones, 1973). This relationship has been demonstrated via simulation and observations specifically for Alfven wave accelerated electron distributions (Chaston et al., 2003). The motion and intensity of bright discrete auroral forms can therefore be considered projections of the plasma dynamics and field-line integrated dissipation through the auroral acceleration region.

In the following we draw on previously reported observations to present a perspective on the relationship between the spectral scaling of field structures through the acceleration region and the motions of optical elements within auroral forms. The consistency of the spectral scaling observed in-situ with that observed via auroral imaging supports the connection of $E\times B$ drifts through the acceleration region to small-scale auroral motions and provides evidence for the operation of a turbulence-like Alfvén wave cascade above bright dynamic auroral arcs.

The Turbulent Alfvénic Aurora

Figure 1 shows spectrograms of the spectral energy density in electric and magnetic fields through the auroral acceleration region as derived from statistics reported from the FAST mission (Chaston et al., 2008). FAST had the unique capacity to measure the electric field at several points in the spacecraft spin plane allowing unambiguous measurement of $k_{\perp }$ ($k_x$ in Figure 1). Under the assumption that at each spacecraft frame frequency this measurement applies to both the magnetic and electric fields, the $k$-spectra in $b_{\perp }$ ($b_y$ in Figure1A) and $E_{\perp }$ ($E_x$ in Figure1B) were derived. The measurements shown in Figure 1, apply specifically to what is termed the “Alfvénic” aurora. The “Alfvénic” aurora is characterized by electric and magnetic field variations that obey the local Alfvénic impedance relation of Eq. 2, as shown in Figure 1C where the finite gyro-radius term is included. In the example shown here, the Alfvénic nature of the fields extends over the range ${10}^{-4}\mathrm{\lesssim }{k}_{\perp }\mathrm{\lesssim }{10}^{-1}{\mathrm{m}}^{-1}$ or scales from ∼60 km, representative of ${\lambda }_{MI}$, down to 10 s of meters, encompassing ${\lambda }_e$ and even reaching ion gyro-radii (${\rho }_i$). Significantly, over the range from ${10}^{-4}\mathrm{\lesssim }{k}_{\perp }\mathrm{\lesssim }{10}^{-2}{\mathrm{m}}^{-1}$ there exists a distinct power-law scaling where the energy density of the fluctuation varies as $b_{\perp }^2/\Delta k_{\perp }\propto k_{\perp }^{-7/3}$. These relationships along with an analysis of structure functions motivated Chaston et al. (2008) to suggest the operation of a Kolmogorov-like turbulent cascade above “Alfvenic” aurora much in the manner of critically balanced cascades postulated by Goldreich and Sridhar (1997) and more recently by Howes et al. (2008) in the Solar wind. The operation of such a cascade above dynamic aurora was first proposed by Seyler (1990) based on 3-D fluid-kinetic simulations.

FIGURE 1

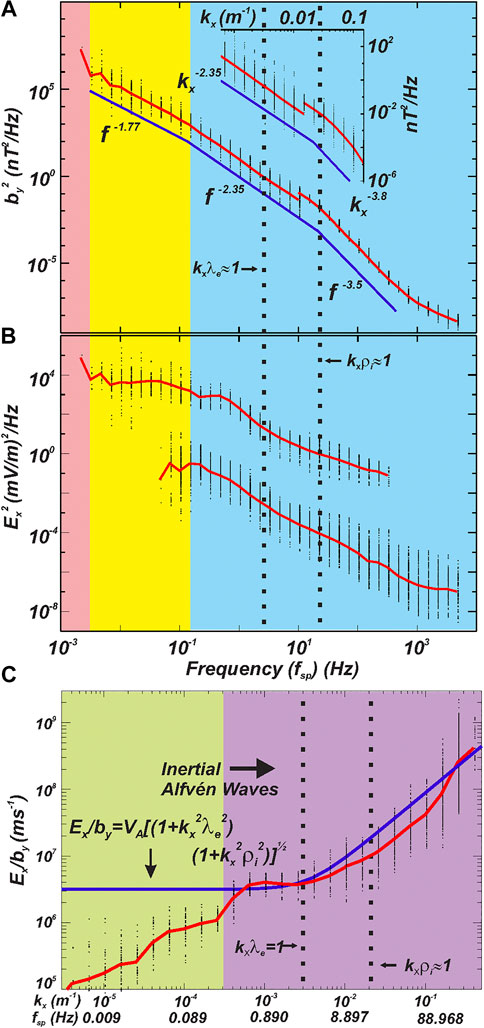
FIGURE 1. Spectral statistics above “Alfvenic” aurora. (A) Average spectral energy density in magnetic field variations ($b_Y$) perpendicular to the geomagnetic field as a function of frequency ($f_{sp}$) measured in the spacecraft frame. The inset plot shows the same result but as a function of the wavenumber measured perpendicular to the geomagnetic field ($k_x$). The offset in these curves at ∼10 Hz is due to the transition from fluxgate to search coil magnetometer measurements. The later are recorded only during intervals of enhanced auroral activity where spectral energy densities are larger leading to the offset. (B) Average spectral energy density in electric field variations ($E_x$) perpendicular to both the geomagnetic field and the magnetic field variations shown in part (A). The two curves shown correspond to measurements made in survey and burst instrument modes with the burst mode data downshifted by 4 orders of magnitude for visibility. The black bars are composed of points representing individual measurements in each frequency bin. (C) Observed average value (red) of the ratio $E_x/b_y$ as a function of perpendicular wavenumber ($k_x$) and $f_{sp}$. The blue line shows the ratio given by the dispersion relation for inertial Alfvén waves based on locally observed parameters [Modified from Chaston et al. (2008)].

Indeed, the measurements shown in Figure 1 bear remarkable similarity to those reported in turbulent Alfvénic fields on kinetic scales in the solar wind. In the work of Bale et al., (2005), for example, spectral energy densities with a Kolmogorov $b_{\perp }^2/\Delta k_{\perp }\propto k_{\perp }^{-5/3}$ dependency are observed on scales larger than Alfvén wave dispersive scale lengths, while within the dispersive range (i.e. $k_{\perp }{\rho }_i\mathrm{\gtrsim }1$) a scaling close to $b_{\perp }^2/\Delta k_{\perp }\propto k_{\perp }^{-7/3}$ is found. While this is much like that shown in Figure 1 an important difference, is that above aurorae, $\beta <m_e/m_i$ where $\beta$ is plasma beta and $m_e$ and $m_i$ are respectively the electron and ion masses. Under these circumstances the largest dispersive scale length for Alfvén waves is ${\lambda }_e$ rather than ${\rho }_i$. As a consequence, while the turbulent fields on kinetic scales in the solar wind are sometimes described as kinetic Alfvén waves, in the auroral acceleration region a more appropriate description is that of inertial Alfvén waves (Stasiewicz et al., 2000). Here, the reflection of magnetospherically driven Earthward propagating waves off the ionosphere naturally provides the counter-propagation required to facilitate the cross-scale cascade. The study of the operation and consequences of this cascade process above aurorae has the special advantage that its operation is manifest in visible emissions that can be imaged.

Imaging an Alfvénic Cascade

The Reimei spacecraft (Sakanoi et al., 2003) provided conjugate measurements of accelerated electrons and high temporal/spatial resolution imaging of evolving auroral luminosity. Example measurements of a rapidly evolving “Alfvénic” auroral arc are shown in Figure 2. This identification is based on the relatively flat electron spectra shown in Figure 2A as opposed to the clear mono-energetic peak or inverted-V attributed to “quasi-static” discrete aurora. The snapshots in Figure 2B-F show luminosity over a 66 by 66 km field of view (FOV) at 110 km altitude and ∼670 nm on a logarithmic scale. Note that this prompt emission is a consequence of energetic electron precipitation (Lanchester et al., 2009; Frey et al., 2010). A bright feature with evolving vortical forms at the upper edge of the region of luminosity can be identified in each snapshot. This feature moves upward through the FOV with the location of the magnetic foot-point of the spacecraft on each image shown by the white box. This allows identification of the electron spectrogram in Figure 2A driving the luminosity at that location. Following this bright “arc” is a region of swirling variations in luminosity corresponding to larger vortical features. These snapshots are at a cadence of 0.6 s or every fifth frame retuned by the Reimei camera.

FIGURE 2

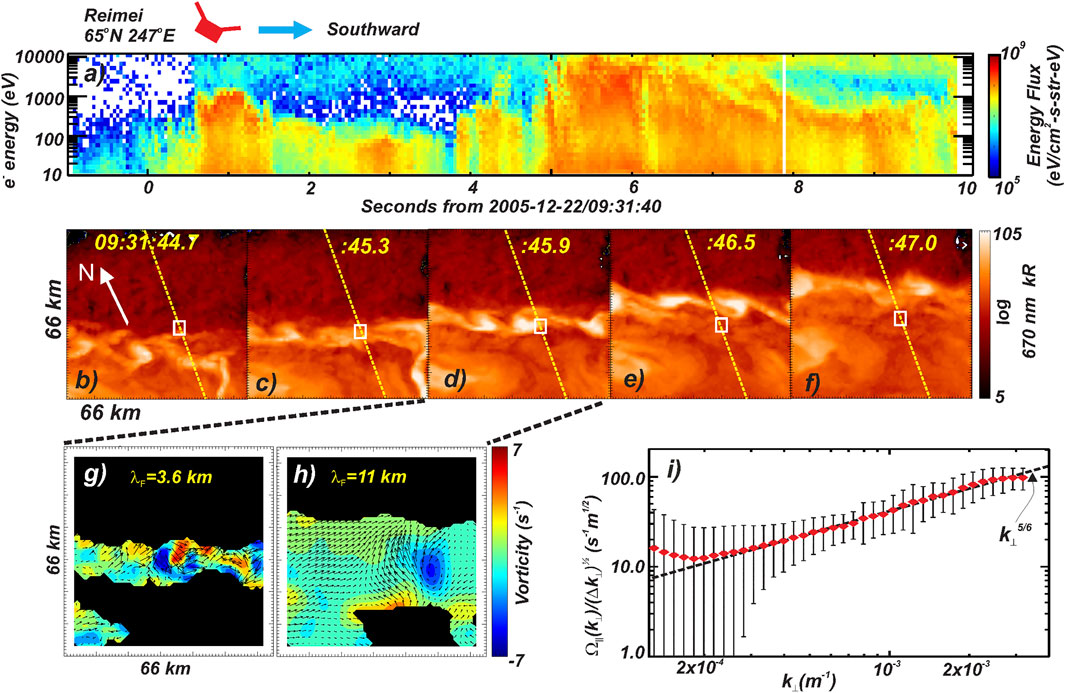
FIGURE 2. Reimei spacecraft measurements above an “Alfvenic” auroral arc. (A) Omni-directional electron energy spectrogram. (B–F) Snapshots at ∼670 nm of the evolving luminosity. Yellow trace shows the trajectory of the spacecraft mapped onto each image with the white box indicating the spacecraft magnetic foot-point at the snapshot time. (G–H) Optical vorticity measurements derived from cross-spectral analysis between snapshot d and the next frame capture (not shown) at the scales indicated. Arrows show optical flow direction and relative speed. (I) Vorticity spectrum derived from the full resolution measurements over the time-range comprising the sequence (B–F). Red dots show the log normal average in each $k_{\perp }$ bin while the error bars show 1 standard deviation.

By cross-correlating the consecutive images at full resolution it is possible to measure the velocity field of the features observed in regions of luminosity. At the time of these observations the camera looked along the geomagnetic field nearly normal to the Earth’s surface so that the velocities observed are perpendicular to $B_0$, The cross-correlation is performed using a wavelet approach as described in Chaston et al. (2010). This technique allows the decomposition of the optical motions as a function of scale subject to a cross-spectral correlation factor that allows the removal of noise. The analysis is performed on the 2-D spatial derivative of the luminosity on scales defined by the wavelet used. Results from this analysis using Paul wavelets (Torrence and Compo, 1998) applied to the central snapshot shown in Figures 2D, and the snapshot 0.12 s later (not shown) for scales of 3.6 and 11 km are presented in Figures 2G,H. Here the arrows indicate the direction and magnitude of the velocity at half resolution while the color scale shows the vorticity (${\Omega }_{\parallel }=\nabla \times v_{\perp }$) derived by finite differencing the velocity field measurements. $B_0$ is into the page with blue showing clockwise rotation about $B_0$ while red is anticlockwise. If these flows correspond to $E\times B$ drifts, then blue corresponds to converging electric fields, or negative space charge for electrostatic fields. The regions in black in each frame indicate those regions where a reliable determination could not be found.

Figure 2G shows there is considerable structure in the vorticity on small scales distributed over the width of the bright “arc”. As indicated by the arrows these features arise from fast motions of the order of 20 km/s composed of both shears and rotational flows. Nested regions of positive and negative vorticity are observed representing structured electric fields on kilometer scales. On larger scales the flow is smoother and a prominent peak in negative vorticity or clockwise rotation can be identified in the center right portion of Figure 2H. Performing the same analysis for subsequent image pairs shows rapid temporal variations in the small-scale vorticity with these features advected in the larger scale flow. Compiling statistics over the whole image sequence shown in Figures 2B–F provides the spectrum presented in Figure 2I. Here, each point represents the average of the distribution in vorticity at each scale normalized by the bandwidth occupied by each spectral bin in $k$-space. The error bars shown correspond to the standard deviation. The spectrum is well described by a power law varying as ${\Omega }_{\parallel }\left(k_{\perp }\right)/\Delta k_{\perp }^{1/2}\propto k_{\perp }^{5/6}$ over the range $2\times {10}^{-4}\mathrm{\lesssim }{k}_{\perp }<3\times {10}^{-3}$ where $k_{\perp }=2\pi /{\lambda }_F$ and ${\lambda }_F$ is the Fourier wavelength of the wavelet (Torrence and Compo, 1998).

Discussion and Conclusion

The in-situ measurements and auroral imagery presented above suggest the operation of a turbulent cascade of inertial Alfvén waves in the auroral acceleration region. Over a range of scales extending from ∼60 km down to 10 s of meters perpendicular to $B_0$ the relationship between the electric and magnetic fields is that expected from a broad $k$-spectrum of Alfvén waves. This range comprises physical length scales extending from ${\lambda }_{MI}$, down to less than ${\lambda }_e$ in the acceleration region. The spectral scaling of the magnetic field over the wavenumber subrange from ${10}^{-4}\mathrm{\lesssim }{k}_{\perp }\mathrm{\lesssim }{10}^{-2}{\mathrm{m}}^{-1}$ is well described by the power law, $b_{\perp }^2/\Delta k_{\perp }\propto k_{\perp }^{-7/3}$ while the imaged optical vorticity, within the same range, scales as ${\Omega }_{\parallel }\left(k_{\perp }\right)/\Delta k_{\perp }^{1/2}\propto k_{\perp }^{5/6}$. A direct comparison between the in-situ fields measurements and imaged vorticity measurements requires conjugate measurements, however these spectral results are statistical in nature and both pertain to “Alfvénic” aurora. This allows a test to determine if the motions observed in the luminosity are statistically consistent with those expected of flows in the measured in-situ electromagnetic fields, and moreover, if the spectral trends observed reflect those expected from a turbulent cascade of Alfvén waves.

In inertial Alfvén waves the plasma moves at the $E\times B$ drift speed so that the eddy turnover time is $\tau \sim 1/k_{\perp }{v}_{\perp }=B_0/b_{\perp }{k}_{\perp }{V}_A\sqrt{1+k_{\perp }^2{\lambda }_e^2}$ where based on the result shown in Figure 1C we use $E_{\perp }=b_{\perp }{V}_A\sqrt{1+k_{\perp }^2{\lambda }_e^2}$ (Eq. 2). On the other hand, the energy transport rate through the cascade is $\epsilon \left(k\right)=H\left(k\right)/\tau \left(k\right)$, So taking $H= b_{\perp }^2/2{\mu }_o$ and substituting for $\tau$ provides $\epsilon \left(k\right)=b_{\perp }^3{k}_{\perp }{V}_A\sqrt{1+k_{\perp }^2{\lambda }_e^2}/2{\mu }_o{B}_0$. Noting that in classical turbulence, $\epsilon \left(k\right)$ is invariant with scale (Frisch, 1995) one finds after rearranging,

$b_{\perp }^2/d{k}_{\perp }\propto k^{-5/3} {\left(1+k_{\perp }^2{\lambda }_e^2\right)}^{-1/3}(4)$

which for $k_{\perp }{\lambda }_e>1$ provides $b_{\perp }^2/d{k}_{\perp }\propto k^{-7/3}$ as observed. On the other hand, defining the vorticity as ${\Omega }_{\parallel }=\nabla \times v_{\perp }$ and again using $E_{\perp }=b_{\perp }{V}_A\sqrt{1+k_{\perp }^2{\lambda }_e^2}$ with $b_{\perp }^2/d{k}_{\perp }\propto k^{-7/3}$ provides,

${\Omega }_{\parallel }\left(k_{\perp }\right)/d{k}_{\perp }^{1/2}\propto k_{\perp }^{-1/6}\sqrt{1+k_{\perp }^2{\lambda }_e^2}(5)$

which in the limit $k_{\perp }{\lambda }_e>1$ returns ${\Omega }_{\parallel }\left(k_{\perp }\right)/d{k}_{\perp }^{1/2}\propto k_{\perp }^{5/6}$ as derived from the imagery. Eq. 4 and Eq. 5 provide an internally consistent description of the observed spectral scaling in the fields and optical vorticity for $k_{\perp }{\lambda }_e>1$ based on the constancy of energy transport across scales through a cascade of Alfvén waves. The same scalings are returned by 3-D fluid-kinetic simulations of auroral structures (Chaston et al., 2011)

While this model may describe the large wavenumber portion of the spectrum, Figures 1A and 2I respectively show that the $b_{\perp }^2/d{k}_{\perp }\propto k_{\perp }^{-7/3}$ and ${\Omega }_{\parallel }\left(k_{\perp }\right)/d{k}_{\perp }^{1/2}\propto k_{\perp }^{5/6}$ scalings extend to $k_{\perp }{\lambda }_e\mathrm{\lesssim }1$. Consequently, there is additional physics operating at large scales or small $k_{\perp }{\lambda }_e$. A clue as to the nature of this physics is provided by the fact that the lower limit of the range over which this scaling prevails is qualitatively consistent with the M-I coupling scale length which depends on the effective field-line conductivity. If we define $\sigma =\frac{1}{{\mu }_o{\lambda }_e^2\nu }$, where $\nu$ is an anomalous collision frequency, the impedance relationship for the inertial Alfvén wave becomes (Lysak and Carlson, 1981),

$E_{\perp }=b_{\perp }{V}_A\sqrt{1+k_{\perp }^2{\lambda }_e^2\left(1+i\nu /\omega \right)}(6)$

Where $\omega$ is the wave frequency. Re-deriving Eq. 4 and Eq. 5 using Eq. 6 shows that the expression under the radical in both cases is replaced by that in Eq. 6. Since $\omega \ll {\Omega }_i$, $\nu$ can be quite small relative to ${\Omega }_i$ while still providing $\left|k_{\perp }^2{\lambda }_e^2\left(1+i\nu /\omega \right)\right|>1$ even if $k_{\perp }{\lambda }_e\mathrm{\lesssim }1$. Under these circumstances the observed scaling relations, $b_{\perp }^2/d{k}_{\perp }\propto k_{\perp }^{-7/3}$ and ${\Omega }_{\parallel }\left(k_{\perp }\right)/d{k}_{\perp }^{1/2}\propto k_{\perp }^{5/6}$, will be retained in the Alfvén wave model on scales larger than several inertial lengths.

An estimate for the value of $\nu$, independent of that required to account for the observed spectral scaling, is not currently available and the physics it represents goes beyond the scope of this article. It may however, be a consequence of localized irregularities in phase space (Ergun et al., 1998) or non-local kinetic effects (Rankin et al., 1999) intrinsic to current closure in Alfvén waves for finite electron temperatures in the converging geomagnetic field. In either case, the requirement for finite field-line conductance on large scales parameterized here in terms of $\nu$, highlights the importance of electron kinetics in defining the cross-scale cascade observed in “Alfvénic” aurora.

Finally, an analysis similar to that above has been performed to examine the scale dependency of variations in auroral luminosity (Chaston, 2015), albeit within an “inverted-V” or “quasi-static” auroral arc with a different scaling in $b_{\perp }^2/d{k}_{\perp }$. That analysis showed that the integrated dissipation through the acceleration region predicted by the Alfvén wave cascade model reproduces the observed scale dependency of luminosity, and, similar to those results derived above, requires an effective field-line conductivity to reproduce the observed scaling at small $k_{\perp }{\lambda }_e$. Given that this dissipation should reduce the spectral index of the energy cascade it is surprising how well the observed $k$-spectra in $b_{\perp }^2/d{k}_{\perp }$ replicates the predicted spectral-scaling from the Kolmogorov-like treatment developed above. This result suggests that either the energy transport rate across scales is sufficiently rapid that the losses through dissipation are relatively small, or that the dissipation on scales less than ${\lambda }_{MI}$ is such that the effect is uniform across the observed range. This a topic requiring further investigation. Nonetheless, the fact that the observed statistics describing the spectral scaling in $k$-space of the magnetic energy density, vorticity and luminosity can all be derived from the assumption of a constant cross-scale energy transport rate is evidence that a turbulent cascade operates above “Alfvénic” aurora.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: the JAXA website https://darts.isas.jaxa.jp/stp/reimei/ and the FAST data repository at https://cdaweb.gsfc.nasa.gov/index.html.

Author Contributions

CC performed the analysis/interpretation in this report and is solely responsible for the results described.

Funding

This research was supported by NASA grant NNX17AI55G.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

CC thanks the FAST and Reimei teams for the providing the calibrated measurements used in this research.

References

Bale, S. D., Kellogg, P. J., Mozer, F. S., Horbury, T. S., and Reme, H. (2005). Measurement of the electric fluctuation spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 94, 215002. doi:10.1103/PhysRevLett.94.215002

PubMed Abstract | CrossRef Full Text | Google Scholar

Borovsky, J. E. (1993). Auroral arc thicknesses as predicted by various theories. J. Geophys. Res. 98 (A4), 6101–6138. doi:10.1029/92JA02242

CrossRef Full Text | Google Scholar

Chaston, C. C., Peticolas, L. M., Bonnell, J. W., Carlson, C. W., Ergun, R. E., and McFadden, J. P. (2003). The width and brightness of auroral arcs driven by inertial Alfvén waves. J. Geophys. Res. 108, 1091. doi:10.1029/2001ja007537

CrossRef Full Text | Google Scholar

Chaston, C. C., Salem, C., Bonnell, J. W., Carlson, C. W., Ergun, R. E., Strangeway, R. J., et al. (2008). The turbulent Alfvénic aurora. Phys. Rev. Lett. 100, 175003. doi:10.1103/PhysRevLett.100.175003

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaston, C. C. (2015). “Inverted-V auroral arcs and Alfvén waves,” in Auroral dynamics and space weather. Editors Y. Zhang, and L. J. Paxton (Hoboken, NJ: John Wiley & Sons). doi:10.1002/9781118978719.ch3

CrossRef Full Text | Google Scholar

Chaston, C. C., Seki, K., Sakanoi, T., Asamura, K., Hirahara, M., and Carlson, C. W. (2011). Cross-scale coupling in the auroral acceleration region. Geophys. Res. Lett. 38, L20101. doi:10.1029/2011GL049185

CrossRef Full Text | Google Scholar

Chaston, C. C., Seki, K., Sakanoi, T., Asamura, K., and Hirahara, M. (2010). Motion of aurorae. Geophys. Res. Lett. 37, L08104. doi:10.1029/2009GL042117

CrossRef Full Text | Google Scholar

Chaston, C. C. (2006). ULF waves and auroral electrons. Geophys. Monogr. Ser., 169, 239. doi:10.1029/169GM16

CrossRef Full Text | Google Scholar

Ergun, R. E., Carlson, C. W., McFadden, J. P., Mozer, F. S., Delory, G. T., Peria, W., et al. (1998). FAST satellite observations of large-amplitude solitary structures. Geophys. Res. Lett. 25, 2041.

Ergun, R. E., Andersson, L., Main, D., Su, Y.‐J., Newman, D. L., Goldman, M. V., et al. (2004). Auroral particle acceleration by strong double layers: the upward current region. J. Geophys. Res. 109, A12220. doi:10.1029/2004JA010545

CrossRef Full Text | Google Scholar

Frey, H. U., Amm, O., Chaston, C. C., Fu, S., Haerendel, G., Juusola, L., et al. (2010). Small and meso-scale properties of a substorm onset auroral arc. J. Geophys. Res. 115, A10209. doi:10.1029/2010JA015537

CrossRef Full Text | Google Scholar

Frisch, U. (1995). Turbulence: the legacy of A. N. Kolmogorov. Cambridge, England: Cambridge University Press.

Goldreich, P., and Sridhar, S. (1997). Magnetohydrodynamic turbulence revisited. Astrophys. J. 485, 680–688. doi:10.1086/304442

CrossRef Full Text | Google Scholar

Hallinan, T. J. (1981). “The distribution of vorticity in auroral arcs,” in Physics of auroral arc formation, Geophys. Monogr. Ser. Editors S.‐I. Akasofu, and J. R. Kan (Washington, DC: AGU), Vol. 25, 42. doi:10.1029/GM025p0042

CrossRef Full Text | Google Scholar

Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E., and Schekochihin, A. A. (2008). A model of turbulence in magnetized plasmas: implications for the dissipation range in the solar wind. J. Geophys. Res. 113, A05103. doi:10.1029/2007JA012665

CrossRef Full Text | Google Scholar

Karlsson, T. (2012). “The acceleration region of stable auroral arcs,” in Auroral phenomenology and magnetospheric processes: Earth and other planets, Geophysical Monograph, 197. Editors A. Keiling, E. Donovan, F. Bagenal, and T. Karlsson (Washington, DC: AGU). doi:10.1029/2011GM001179

CrossRef Full Text | Google Scholar

Kintner, P. M., and Seyler, C. E. (1985). The status of observations and theory of high latitude ionospheric and magnetospheric plasma turbulence. Space Sci. Rev. 41, 91–12. doi:10.1007/bf00241347

CrossRef Full Text | Google Scholar

Knight, S. (1973). Parallel electric fields. Planet. Space Sci. 21, 741–750. doi:10.1016/0032-0633(73)90093-7

CrossRef Full Text | Google Scholar

Lanchester, B. S., Ashrafi, M., and Ivchenko, N. (2009). Simultaneous imaging of aurora on small scale in OI (777.4 nm) and N21P to estimate energy and flux of precipitation. Ann. Geophys. 27, 2881–2891. doi:10.5194/angeo-27-2881-2009

CrossRef Full Text | Google Scholar

Lyons, L. R. (1981). “The field aligned current versus electric potential relation and auroral electrodynamics,” in Physics of auroral arc formation, Geophys. Monogr. Ser. Editors S.‐I. Akasofu, and J. R. Kan (Washington, DC: AGU), Vol. 25, 252.

Google Scholar

Lysak, R. L., and Carlson, C. W. (1981). The effect of microscopic turbulence on magnetosphere-ionosphere coupling. Geophys. Res. Lett. 8, 269–272. doi:10.1029/gl008i003p00269

CrossRef Full Text | Google Scholar

Lysak, R. L. (1990). Electrodynamic coupling of the magnetosphere and ionosphere. Space Sci. Rev. 52, 33. doi:10.1007/BF00704239

CrossRef Full Text | Google Scholar

Lysak, R. L., and Song, Y. (1996). Coupling of Kelvin-Helmholtz and current sheet instabilities to the ionosphere: a dynamic theory of auroral spirals. J. Geophys. Res. 101, 15411–15422. doi:10.1029/96JA00521

CrossRef Full Text | Google Scholar

G. Paschmann, S. Haaland, and R. Treumann (Editors) (2003). Auroral plasma physics. Dodrecht, Netherlands: Kluwer Academic.

Pécseli, H. L. (2015). Spectral properties of electrostatic drift wave turbulence in the laboratory and the ionosphere. Ann. Geophys. 33, 875–900. doi:10.5194/angeo-33-875-2015

CrossRef Full Text | Google Scholar

Rankin, R., Samson, J. C., and Tikhonchuk, V. T. (1999). Parallel electric fields in dispersive shear Alfvén waves in the dipolar magnetosphere. Geophys. Res. Lett. 26, 3601. doi:10.1029/1999gl010715

CrossRef Full Text | Google Scholar

Rees, M. H., and Jones, R. A. (1973). Time dependent studies of the aurora-II. Spectroscopic morphology. Planet. Space Sci. 21, 1213. doi:10.1016/0032-0633(73)90207-9

CrossRef Full Text | Google Scholar

Sakanoi, T., Okano, S., Obuchi, Y., Kobayashi, T., Ejiri, M., Asamura, K., et al. (2003). Development of the multi-spectral auroral camera onboard the INDEX satellite. Adv. Space Res. 32, 379–384. doi:10.1016/s0273-1177(03)90276-6

CrossRef Full Text | Google Scholar

Seyler, C. E. (1990). A mathematical model of the structure and evolution of small-scale discrete auroral arcs. J. Geophys. Res. 95 (A10), 17199–17215. doi:10.1029/JA095iA10p17199

CrossRef Full Text | Google Scholar

Seyler, C. E., and Wu, K. (2001). Instability at the electron inertial scale. J. Geophys. Res. 106, 21623–21644. doi:10.1029/2000JA000410

CrossRef Full Text | Google Scholar

Stasiewicz, K., Bellan, P., Chaston, C., Kletzing, C., Lysak, R., Maggs, J., et al. (2000). Small scale Alfvénic structure in the aurora. Space Sci. Rev. 92, 423–533. doi:10.1023/a:1005207202143

CrossRef Full Text | Google Scholar

Torrence, C., and Compo, G. P. (1998). A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78. doi:10.1175/1520-0477(1998)079<0061:apgtwa>2.0.co;2

CrossRef Full Text | Google Scholar

Vondrak, R. R. (1981). “Chatanika radar measurements of the electrical properties of auroral arcs,” in Physics of auroral arc formation. Editors S.‐I. Akasofu, and J. Kan doi:10.1029/GM025p0185

CrossRef Full Text | Google Scholar