Massive Star Modeling and Nucleosynthesis

After a brief introduction to stellar modeling, the main lines of massive star evolution are reviewed, with a focus on the nuclear reactions from which the star gets the needed energy to counterbalance its gravity. The different burning phases are described, as well as the structural impact they have on the star. Some general effects on stellar evolution of uncertainties in the reaction rates are presented, with more precise examples taken from the uncertainties of the ¹²C(α, γ)¹⁶O reaction and the sensitivity of the s-process on many rates. The changes in the evolution of massive stars brought by low or zero metallicity are reviewed. The impact of convection, rotation, mass loss, and binarity on massive star evolution is reviewed, with a focus on the effect they have on the global nucleosynthetic products of the stars.

1. Introduction to stellar modeling

Massive stars are key drivers of the evolution of the Universe, through the chemical and kinetic imprint they impose on their surrounding. Their intense luminosity makes them dominant contributors to the spectra of galaxies, and tracers of star formation in the early Universe. However, as they are much rarer than low- or intermediate-mass stars, it has for a long time been impossible to have statistically significant observations of massive stars, and our understanding relied mainly on stellar models. Since a couple of decades, large surveys (either dedicated to massive stars or wide enough to include a significant number of them) are starting to fill this gap and provide observational constraints that highlight the strengths and weaknesses of our massive stars models. In parallel, the improvement of computational facilities makes it possible to study some physical processes (like convection) from first principles in hydrodynamical simulations. While a full evolution of the entire star for its complete lifetime is not possible in 3D, the hydrodynamical simulations can provide precious recipes for 1D secular evolution modeling. This review intends to summarize the safe grounds and challenges of massive star evolution modeling and nucleosynthesis, with a focus on the role played by the reaction rates of importance in the modeling.

The evolution of stars is a long and desperate struggle against gravity. Thanks to their gaseous nature, they resist most of their lifetime by adjusting on a thermal structure that provides the pressure needed to exactly counterbalance the gravitational pull, and settle on what is called hydrostatic equilibrium, where the pressure gradient exactly compensate for the gravity:

$\begin{array}{ll}\frac{\text{d}P}{\text{d}r}=-g\rho & (1)\end{array}$

with P the pressure (gas and radiation), r the internal radius, $g=-\frac{G{M}_r}{r^2}$ the local gravity at radius r with internal mass M_r, and ρ the density.

This equation is the first of the four equations of the internal structure of stars, developed by Sir Eddington in his series of papers about the constitution of stars (Eddington, 1916, 1917, 1918). To fully describe a stellar structure, we need three other equations: the mass continuity

$\begin{array}{ll}\frac{\text{d}M}{\text{d}r}=4\pi r^2\rho ,& (2)\end{array}$

the conservation of energy

$\begin{array}{ll}\frac{\text{d}L}{\text{d}r}=4\pi r^2\rho \left(ϵ+{ϵ}_{\text{grav}}\right),& (3)\end{array}$

with L the local luminosity, ϵ the energy generated inside the star through nuclear burning, and ϵ_grav the gravitational energy, and finally an expression for the radiative transfer

$\begin{array}{ll}\frac{\text{d}T}{\text{d}r}=-\frac{3\kappa \rho }{ac{T}^3}\frac{L_r}{4\pi r^2}& (4)\end{array}$

with T the temperature, κ the opacity of the gas, and a and c the constants of radiation and light speed respectively. In this equation, we need to define the opacity of the stellar matter κ. This is usually done through data tables provided by large opacity projects such as OPAL¹ or the OP² projects.

To close this set of equations, we need an equation of state (EOS) linking P, T, and ρ in an expression like

$\begin{array}{ll}\Delta ln\rho =\alpha \Delta lnP-\delta \Delta lnT-\phi \Delta ln\mu .& (5)\end{array}$

where the dependence of ρ on the gradient of chemical composition Δlnμ has been added. If we combine Equations (1) and (2), we obtain that $\Delta lnP=\frac{4}{3}\Delta ln\rho$, and with Equation (5) we have:

$\begin{array}{ll}\Delta lnT=\left(\frac{4\alpha -3}{3\delta }\right)\Delta ln\rho .& (6)\end{array}$

In this general expression for the hydrostatic equilibrium, all the subtleties of the physics are hidden in the values for α, δ, and φ. For example, in the case of a perfect gas ($P=\frac{\rho }{\mu m_{\mathrm{\text{H}}}}kT$, with k the Boltzmann's constant and m_H the hydrogen mass), we have α = δ = φ = 1. Neglecting the gradient of composition, Equation 6 becomes $\Delta lnT=\frac{1}{3}\Delta ln\rho$, which gives the 1/3 slope of the evolution of stars in a diagram of T as a function of ρ (Figure 1). In this region of the diagram, if there is an increase in energy, which drives an increase in temperature, the pressure will react to it and restore the equilibrium. In contrast, for a degenerate non-relativistic gas we have α = 3/5 and δ = 0. The annihilation of δ has for consequence that the evolution of T is no longer linked to that of P or ρ. Instead of having a stable nuclear reactor (for which any increase in T is compensated by a readjustment of P that restores the equilibrium), the star enters an unstable regime where nuclear deflagration is possible. Of course, stars are not just composed of gas, and the radiation contributes to the total pressure: $P_{\mathrm{\text{tot}}}=\frac{\rho }{\mu m_{\mathrm{\text{H}}}}kT+\frac{1}{3}a{T}^4$. The more massive the star, the stronger the radiation component becomes.

FIGURE 1

Figure 1. T vs. ρ diagram showing the different regimes of the state of matter.

While most of the time we observe only the surface of stars, their fate depends almost uniquely on what happens deep in their cores. We saw that the center of a star evolves more or less on a slope of 1/3 in the T vs. ρ diagram. But sooner or later, it will hit the limit between perfect gas and degenerate gas, which has a slope 2/3. The phase at which this limit is attained defines the type of a star. Low-mass stars become degenerate at the end of core H burning; intermediate-mass stars reach it after core He burning; massive stars are able to go through all fusion phases before entering too much into the degenerate zone. The exact masses at which the transitions occur depend on the input physics of the models, but roughly, below 2 M_⊙ we have low-mass stars, between 2 and 10 M_⊙ we have intermediate-mass stars, and above 10 M_⊙ we have massive stars (Siess, 2008; Jones et al., 2013).

To solve the equation of the conservation of energy, Equation (3), we need to determine the energy generated inside the star (ϵ). The nuclear reaction rates providing this energy are usually included in stellar evolution codes either through analytical expressions based on T and ρ, or through tables of the rates as a function of the temperature. In many cases, several determinations of a given reaction rates have been performed, and sometime large uncertainties remain. The consequences of these uncertainties will be presented in section 3.

2. Massive stars evolution and nucleosynthesis

2.1. Main Sequence

Like all types of stars, massive stars start their nuclear journey with H fusion. Like intermediate-mass stars, they do so dominantly through the CNO cycle, which has a much steeper dependence on temperature than the pp-chains:

${ϵ}_{pp}\left(T\right)={ϵ}_{pp}\left(T_0\right){\left(\frac{T}{T_0}\right)}^4$

${ϵ}_{\text{CNO}}\left(T\right)={ϵ}_{\text{CNO}}\left(T_0\right){\left(\frac{T}{T_0}\right)}^{17}$

The CNO cycle dominates upon pp-chains when T ≳ 20 MK. The transition from a pp-chain dominated H burning to a CNO-cycle dominated H burning marks the limit between the typical low-mass stars structure (with a radiative core and a convective envelope) and the intermediate-mass and massive stars structure (having a convective core and a radiative envelope).

Details of the nuclear reactions occurring inside the stars can be found in Iliadis (2007), we will just summarize the main ones here. The principle of the CNO cycle is to produce He from H using C, N, and O as catalysts, through a cycle of reactions (CNO1):

${}^{12}{(p,\gamma )}^{13}\text{N}{({\beta }^{+}\nu )}^{13}\text{C}{(p,\gamma )}^{14}\text{N}{(p,\gamma )}^{15}\text{O}{({\beta }^{+}\nu )}^{15}\text{N}{(p,\alpha )}^{12}\text{C}.$

At the end of this chain, the ¹²C atom used at the beginning of the chain is released along with the α particle, which is why we called it a catalyst. While α-decay is the dominant channel for the proton capture by ¹⁵N, the γ-decay channel can occur and leads to a secondary cycle (CNO2):

${}^{14}\text{N}{(p,\gamma )}^{15}\text{O}{({\beta }^{+}\nu )}^{15}\text{N}{(p,\gamma )}^{16}\text{O}{(p,\gamma )}^{17}\text{F}{({\beta }^{+}\nu )}^{17}\text{O}{(p,\alpha )}^{14}\text{N}.$

The same branching between (p, α) and (p, γ) channels occurs for the proton capture on ¹⁷O, leading to a tertiary cycle (CNO3):

${}^{17}\text{O}{(p,\gamma )}^{18}\text{F}{({\beta }^{+}\nu )}^{18}\text{O}{(p,\alpha )}^{15}\text{N.}$

Generally, the (p, α) channel is a thousand times more probable than the (p, γ) one, favoring CNO1 over CNO2, and CNO2 over CNO3. The slowest reaction of the complete CNO cycle is ¹⁴N(p, γ)¹⁵O (with a timescale of around 10⁸ yrs), which results in an accumulation of ¹⁴N in zones where H-burning has left its imprint. Note however that the sum C+N+O remains mostly unchanged in those layers during H burning.

When the temperature is high enough, the H burning into He can occur through two other cycles: the Ne-Na and Mg-Al cycles. Though the reaction rates for these cycles are subject to large uncertainties, they are supposed to play a role in the anti-correlation between O and Na observed in multiple populations of globular clusters (Gratton et al., 2004, and references therein). Also the synthesis of ²⁶Al in H-burning with T > 35 − 40 MK makes it a tracer of the formation of massive stars in the Galaxy (Prantzos and Diehl, 1996).

When H becomes depleted in the core, the burning starts moving outwards, to the border of the contracting core. This translates at the surface by a hook in the Hertzsprung-Russell (HR) diagram, the star moving toward a higher effective temperature (see the red dot on the black track of Figure 4). When H is completely depleted, the core stops producing any energy, and the star is sustained only by the H-burning shell.

Below the shell, the core contracts rapidly, while the envelope expands. The reason for this “mirror” behavior across the shell is debated since the 70s (see the Appendix of Sugimoto and Fujimoto, 2000, for a historical review of the proposed mechanisms). A simple and somehow intuitive explanation can be found in Padmanabhan (2001). At this moment of the evolution, the typical timescale becomes of the order of or shorter than the Kelvin-Helmholtz timescale $\left({\tau }_{\mathrm{\text{KH}}}=\frac{G{M}^2}{RL}\right)$. In that case, both the conservation of energy (Ω + U = constant) and the virial theorem (Ω + 2U = 0) must hold, with Ω and U the potential and internal energy respectively. The only way of achieving this is to conserve both Ω and U separately. If we have most of the mass in the core compared to that in the envelope, M_c ≫ M_env, we can express the potential energy as:

$|\Omega |\approx \frac{G{M}_{\text{c}}^2}{R_{\text{c}}}+\frac{G{M}_{\text{c}}{M}_{\text{env}}}{R_{\star }}\approx \text{constant}$

with R_c and R_⋆ the radius of the core and the star respectively. Since the location of the shell is more or less constant, we can consider M_c and M_env to be constant, and hence we have:

$-\frac{G{M}_{\text{c}}^2}{R_{\text{c}}^2}\frac{d{R}_{\text{c}}}{dt}-\frac{G{M}_{\text{c}}{M}_{\text{env}}}{R_{\star }^2}\frac{d{R}_{\star }}{dt}=0$

$\to \frac{d{R}_{\star }}{d{R}_{\text{c}}}\approx -\left(\frac{M_{\text{c}}}{M_{\text{env}}}\right){\left(\frac{R_{\star }}{R_{\text{c}}}\right)}^2$

which means that the core contraction implies the envelope's expansion. Note that a more detailed description of this mirror behavior invokes the thermal equilibrium inside the H-burning shell (Sugimoto and Fujimoto, 2000), and the evolution of the entropy in the envelope (Hekker et al., 2020).

Eventually, the star evolves rapidly to low Teff, crossing the HR diagram and becoming a red supergiant (RSG). Its luminosity increases while its core contracts until it reaches the temperature of He fusion.

2.2. Helium Burning

Helium is fused through a three-particles reaction, the so-called 3α reaction. It is actually a two-steps reaction, with first the formation of unstable ⁸Be by the fusion of two α particles. The lifetime of ⁸Be is 6.7 × 10⁻¹⁷ s. In a second step, ¹²C is produced through the reaction ⁸Be(α, γ). The probability that the unstable ⁸Be captures another α before its own α-disintegration is increased by a resonance level in the ¹²C atom. The resonant level has been predicted by Hoyle (1954) on considerations based on the observed abundances of ¹²C. The 3α reaction is extremely sensitive in temperature:

${ϵ}_{3\alpha }\left(T\right)={ϵ}_{3\alpha }\left(T_0\right){\left(\frac{T}{T_0}\right)}^{41}$

During He burning, carbon is built up, but when the temperature is hot enough, the reaction ¹²C(α, γ)¹⁶O consumes part of the carbon. The more massive the star, the more efficiently C is converted into O, so the ratio C/O left at the end of He burning decreases for more massive stars. This ratio, together with the mass of the CO core left after central He burning, plays a key role in the compactness of the stellar core, and hence in its ability to explode or not (Chieffi and Limongi, 2020). Though ¹²C(α, γ)¹⁶O is one of the key reactions in stellar evolution, its rate is still uncertain and subject to numerous studies in the literature (see section 3).

Two other reactions contribute to the destruction of He nuclei, ¹⁶O(α, γ)²⁰Ne and ²⁰Ne(α, γ)²⁴Mg. Below T = 0.3 GK, however, these reactions are only negligible compared to 3α and ¹²C(α, γ)¹⁶O. Stellar He burning is thus the main astrophysical site for the synthesis of oxygen in the Universe. Figure 2 (top left) shows the abundances profiles at the end of central He burning.

FIGURE 2

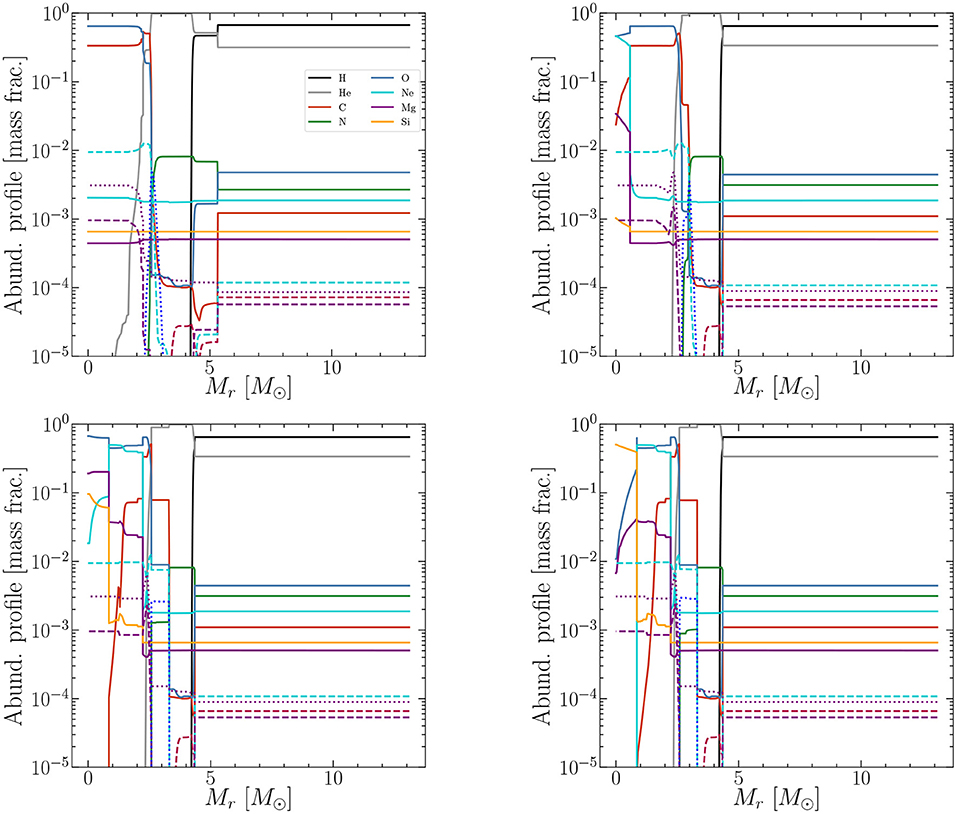
Figure 2. Abundances profiles at the end of He burning (top left), C burning (top right), Ne burning (bottom left), and O burning (bottom right). The precise temporal locations are marked by gray arrows in Figure 3. The species shown are indicated with their colors in the legend on the top left panel. Solid lines are used for the main isotopes (¹H, ⁴He, ¹²C, ¹⁴N, ¹⁶O, ²⁰Ne, ²⁴Mg, and ²⁸Si). For some species, other isotopes are shown with the corresponding colors but dashed (¹³C, ¹⁵N, ¹⁷O, ²²Ne, and ²⁵Mg) or dotted lines (¹⁸O and ²⁶Mg).

Helium burning is also an important site for nucleosynthesis beyond the iron peak and the slow neutron-capture process (s-process). Indeed, when the nitrogen produced by the CNO cycle diffuses into a He-burning zone, it will be rapidly converted into ²²Ne through the chain of reactions ¹⁴N(α,γ)¹⁸F(β⁺ν)¹⁸O(α,γ)²²Ne. This ²²Ne can then react further with an α through ²²Ne(α, n)²⁵Mg, producing a neutron. Though it is in some way self-poisoning, since the ²⁵Mg is a neutron eater through the reaction ²⁵Mg(n,γ)²⁶Mg, the ²²Ne(α, n)²⁵Mg reaction is a neutron source for the so-called “weak s-process,” building up nuclei up to strontium (Raiteri et al., 1991a,b; Kaeppeler et al., 1994; Käppeler et al., 2011; Frischknecht et al., 2016). It is considered that massive stars undergoing this s-process during He burning are the main producers of ³⁶S, ³⁷Cl, ⁴⁰Ar, and ⁴⁰K in the Universe (Woosley et al., 2002). The ²²Ne(α, n)²⁵Mg reaction enters in direct competition with the ²²Ne(α,γ)²⁶Mg. The preferred channel for ²²Ne destruction depend strongly on the ratio of these two reactions, and hence the strength of s-process elements creation (Pignatari et al., 2010), but large uncertainties remain for these two reactions (see section 3).

2.3. Advanced Phases

At the end of He burning, the star is sustained by two burning shells (H and He) while its core contracts until it reaches a temperature that is high enough for the fusion of carbon.

2.3.1. Carbon Burning

The fusion of two ¹²C nuclei forms a ²⁴Mg atom that is highly excited. The excess energy (~ 14 MeV) is more easily removed by the ejection of a light massive particle (p, n, α) than a photon. So the main channels for carbon fusion are ¹²C(¹²C,α)²⁰Ne, ¹²C(¹²C,p)²³Na, ¹²C(¹²C,n)²³Mg, with a global sensitivity in temperature that is relatively moderate:

${ϵ}_{\text{C}}\left(T\right)={ϵ}_{\text{C}}\left(T_0\right){\left(\frac{T}{T_0}\right)}^{28}$

The α and p channels have almost the same probability to occur. Secondary reactions like ²³Na(p,α)²⁰Ne and ¹⁶O(α,γ)²⁰Ne also take place, however the oxygen destruction is weak. At the end of central C burning, the core is mainly composed of ¹⁶O, ²⁰Ne, and ²³Na.

After C exhaustion in the core, the C burning proceeds in a succession of convective shells appearing and disappearing. If the CO core mass left after central He burning is smaller than 3M_⊙, the star has to wait for the disappearance of the second C convective shell before its core becomes massive enough to start central Ne burning (see Figure 3), while if M_CO is larger, Ne burning can occur rapidly after C exhaustion (Chieffi and Limongi, 2020). The transition mass lies somewhere between 15 and 20 M_⊙, the precise value depending strongly on the physics of the models.

FIGURE 3

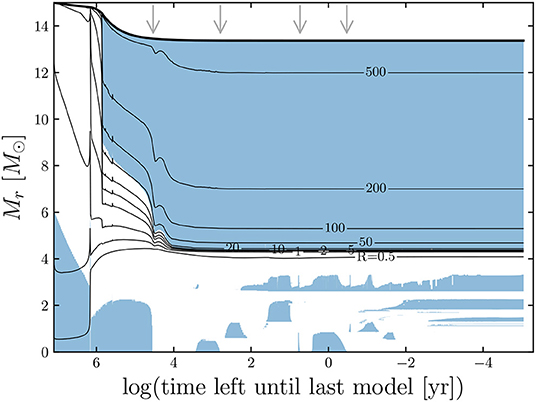
Figure 3. Kippenhahn diagram of a 15M_⊙ model at solar metallicity, computed until the end of central O burning. The blue shaded regions are convective. Iso-radii are over-plotted (in solar radius units). The gray arrows mark the temporal location of the abundances profiles of Figure 2.

The less massive of massive stars (M < 30 M_⊙) have a quite efficient s-process in the C-burning shells, creating nuclei with A = 60 − 90 (Käppeler et al., 2011). Above M = 30 M_⊙, most of the ²²Ne is consumed at the end of He burning, but below that mass, a significant amount of ²²Ne may survive (see however Talwar et al., 2016). The reaction ²²Ne(α, n)²⁵Mg can be reactivated during shell C burning thanks to α particles released via ¹²C(¹²C,α)²⁰Ne. During shell C burning, the temperature is a factor of 3-4 higher than during core He burning, the density is higher by a factor of 100, and the cross section of the ²²Ne(α, n)²⁵Mg reaction is much higher. Though the neutron exposure is short, the high neutron density (a factor of 1000 higher than during He burning) helps building neutron-rich isotopes (The et al., 2007). In contrast with core C burning, the s-process elements produced in the C-burning shell are easily ejected during the supernova, and are not destroyed by photo-disintegration reactions during core O and Si burning. They will be affected by the explosive event at the end of the stellar evolution but not dramatically destroyed (Rauscher et al., 2002).

2.3.2. Beyond Carbon

Though oxygen is next in line in terms of atomic mass, its greater stability imposes extremely high temperatures (T > 1 GK) to be able to burn, a temperature regime higher than the one in which photo-disintegration reactions can take place and halt the core contraction. The neon atoms present in the core can thus be photo-disintegrated through ²⁰Ne(γ,α)¹⁶O. Neon can also react with an α particle and build magnesium through the reaction ²⁰Ne(α,γ)²⁴Mg. Some silicon is further produced by ²⁴Mg(α,γ)²⁸Si. Neon burning is extremely sensitive in temperature:

${ϵ}_{\text{Ne}}\left(T\right)={ϵ}_{\text{Ne}}\left(T_0\right){\left(\frac{T}{T_0}\right)}^{49}$

At the end of Ne burning, the core (composed mainly of ¹⁶O, ²⁴Mg, and ²⁸Si) contracts again, reaching 2 GK and is at last able to burn oxygen. As in the case of C burning and the resulting ²⁴Mg atom, the sulfur atom created through ¹⁶O(¹⁶O,γ)³²S is highly excited, with many overlapping compounds levels. The excess energy (~ 16.5 MeV) is most efficiently removed by the emission of a light massive particle. The channels for oxygen fusion are mainly p-, α-, and n-emitting reactions: ¹⁶O(¹⁶O,p)³¹P, ¹⁶O(¹⁶O,α)²⁸Si, and ¹⁶O(¹⁶O,n)³¹S, but two-particles emissions are also quite probable: ¹⁶O(¹⁶O,2p)³⁰Si and ¹⁶O(¹⁶O,2α)²⁴Mg. The temperature sensitivity of O burning is less acute than that of Ne burning:

${ϵ}_{\text{O}}\left(T\right)={ϵ}_{\text{O}}\left(T_0\right){\left(\frac{T}{T_0}\right)}^{34}$

The cross-section determination at the energy of the Gamow peak at a typical T = 2.2 GK is subject to large variations according to different authors and analysis techniques. The branching ratio between the different O-burning channels is still widely unknown. Both uncertainties result in the rates for O burning being know only up to a factor of 3.

The ³¹P produced can further interact with a proton with two possible disintegration channels: ³¹P(p,γ)³²S or ³¹P(p,α)²⁸Si. The ³²S can further be transformed into ³⁶Ar through ³²S(α,p)³⁵Cl(p,γ)³⁶Ar.

At the end of O burning, the core of the star mainly consists in ²⁸Si and ³²S. Silicon has a too large Coulomb barrier to be able to fuse with itself, so at that stage of the evolution, the star gets its energy mainly from photo-disintegration reactions, followed by captures of the light particles released. Ascending and descending chains of reactions take place, reaching an equilibrium flow in some sub-domains of nuclei, as for instance the domain A = 25 − 40 or A = 46 − 64. Though the two domains are linked with much less active reaction rates, slowly the nuclei of the iron peak (A > 40) are accumulating, while the abundance of the lighter nuclei decreases. Around the iron peak, electron captures start taking place [⁵³Mn(e⁻,ν)⁵³Cr, ⁵⁴Fe(e⁻,ν)⁵⁴Mn, ⁵⁵Fe(e⁻,ν)⁵⁵Mn, ⁵⁵Co(e⁻,ν)⁵⁵Fe, ⁵⁶Co(e⁻,ν)⁵⁶Fe], adding a significant contribution from the weak interactions to thermal neutrino emission (see section 2.3.3).

The sensitivity in temperature of the network of reactions involved in silicon burning is high:

${ϵ}_{\text{Si}}\left(T\right)={ϵ}_{\text{Si}}\left(T_0\right){\left(\frac{T}{T_0}\right)}^{47}$

An interesting feature for stellar evolution modeling is that since equilibrium flows are rapidly attained, the precise rates of the nuclear reactions do not really matter. We only need to compute their equilibrium ratios, that depends mainly on atomic masses and binding energies.

At the end of Si burning, the whole network of nuclei reaches equilibrium, from proton to iron-peak elements. This is known as the nuclear statistical equilibrium. Only the weak interactions cannot get to equilibrium, because the neutrinos are escaping the star, preventing the reverse reaction to occur. During the bulk of Si burning, these weak interactions induce a neutron excess $\eta =\sum _i\frac{N_n,i-N_p,i}{A_i}{X}_i>0$³. The neutron excess influences the relative abundances of isotopes. A large neutron excess favors neutron-rich isotopes, playing a role as important as the binding energies themselves: for a given η, the nuclides having an individual neutron excess (N − Z)/A ≃ η will be the most abundant.

2.3.3. General Remarks

Shell burning episodes usually occur in conditions that are hotter and denser than the conditions prevailing in the core of the corresponding burning. This makes the nucleosynthetic results of shell burning slightly different from core burning.

From the end of central He burning onwards, there is a disconnect between the core and the envelope, because the timescales of evolution start to have orders of magnitude of difference. This disconnect implies that the surface of the star cannot translate the internal evolution anymore, and doesn't evolve (in an HR diagram, for example). While the envelope is still living on the Kelvin-Helmholtz timescale:

$\begin{array}{ll}{\tau }_{\text{KH}}=\frac{G{M}^2}{R{L}_{\gamma }}& (7)\end{array}$

(with obvious meanings for the variables G, M, and R, and L_γ the photon luminosity of the star), the core lives on the nuclear timescale, contraction plus burning time:

${\tau }_{\text{contr}}+{\tau }_{12}=\frac{\frac{1}{2}\Delta \Omega +E_{12}{M}_{\text{core}}}{L_{\nu }}$

(with ΔΩ the potential energy released by contraction, E₁₂ the energy production by C burning, M_core the mass of the core where the burning takes place, and L_ν the neutrino luminosity).

Both expressions involve the luminosity of the star, but in the nuclear timescale of advanced phases, it is the neutrino luminosity that plays the major role, being orders of magnitudes higher than the photon luminosity. The neutrino loss is not related to the nuclear reactions, which globally do not involve neutrinos. Actually, when the temperature reaches 10⁹ K, neutrinos can be produced by three different mechanisms (Beaudet et al., 1967): electron-positron pair annihilation ($e^{-}{e}^{+}\to \nu \bar{\nu }$), photo-production ($\gamma e^{\pm }\to \nu \bar{\nu }{e}^{\pm }$), or plasmon decay (plasmon $\to \nu \bar{\nu }$). Once created, neutrinos escape freely from the star, taking away a large part of the energy produced by the nuclear burning (Woosley and Janka, 2005). This high energy loss accelerates the pace of the evolution, as can be seen from Table 1, which presents the lifetimes in the different burning phases of a 25M_⊙ stellar model (Hirschi et al., 2004). In contrast, the modeling itself takes longer and longer, so while we started on the main sequence with a computation that was a factor of 50 billions times more rapid than the true evolution, we finish the modeling of a star 10 times slower than nature.

TABLE 1

Table 1. Lifetimes in the different nuclear burning phases for non-rotating and rotating stellar models of 25M_⊙ (from Hirschi et al., 2004 A&A, 425, 649, reproduced with permission ©ESO).

2.4. Explosion

Once it is composed of iron-peak elements, the core cannot extract energy from nuclear reactions and hence collapses. Depending on its mass, it will form a neutron star or a black hole (Woosley et al., 2002).

The mechanism leading from collapse to explosion is very complex and a full description is out of the scope of this review. The reader is referred to the reviews by Janka (2012) or Müller et al. (2016) for a detailed description. I will just summarize here the general picture drawn by supernova simulations.

The core collapses in the free-fall timescale, reaching quickly supra-nuclear densities, which makes it rebounce, creating a shock. The shock moves slightly outwards, but stalls, being insufficient to reverse the velocity field of the in-falling matter, and becoming an accretion shock. The neutronization of the core generates a strong neutrino flux that is trapped by the density of the in-falling matter around the shock (neutrino-sphere). The neutrinos energy heats this region, creating a negative entropy gradient which drives convection in the standing shock region, transferring heat to the stellar matter. Early 1D supernova simulations have identified a critical neutrino luminosity that is needed to be able to power an explosion (Burrows and Goshy, 1993; Müller and Janka, 1995). Multi-D simulations show that a breaking of spherical symmetry brought by convective movements can reduce the critical neutrino luminosity. A large-scale hydrodynamical instability, the so-called standing accretion shock instability (SASI, see Foglizzo, 2002; Scheck et al., 2004; Buras et al., 2006; Burrows et al., 2006) induces advective acoustic cycles and increases the non-sphericity even more. When rotation is taken into account, the centrifugal force helps the breaking of spherical symmetry (Nakamura et al., 2014), but the neutron star that is formed has a larger radius and is cooler, so the neutrino luminosity is lower (Marek and Janka, 2009; Summa et al., 2018), which could prevent a successful explosion. When the rotation is fast, it presents an angle-dependent neutrino emission, and sustains violent SASI spiraling that increase the volume where heat can be transferred from the neutrino to the matter, particularly in the equatorial plane (Nakamura et al., 2014; Summa et al., 2018). When magnetic fields are added to the simulations, the magnetic pressure creates a polar expansion and stimulates also spiral SASI movements, favoring the explosion (Kuroda et al., 2020).

Note that the perfect supernova simulation, including all needed ingredients with an exquisite treatment in full 3D with a perfect resolution of all time- and space-scales at play is yet to come. It is a very active field of research that benefits highly from any improvement in computational power and/or numerical solver. Also, improvements in the progenitor stellar models with which the supernova simulations are fed, especially in what concerns convection (see section 5.1), might give fundamental ingredients to the simulations (Müller et al., 2016). From an observational point of view, it is not clear whether a star that is still very massive at the end of its evolution is able to explode as a supernova or will just collapse directly into a black hole. The lack of identified massive progenitors for SN type Ibc, and the maximal mass of type II events progenitors (Maund and Smartt, 2005; Maund et al., 2005; Crockett et al., 2008; Smartt et al., 2009) suggests that above M_ini ≃ 25 − 30 M_⊙, the collapse cannot be reversed and a black hole is formed without any SN (Allan et al., 2020) or with a failed SN. The debate is still not settled to date (see for example Smartt et al., 2009; Yoon et al., 2012; Kochanek, 2014; Suzuki and Maeda, 2018; Farrell et al., 2020).

In special mass domains, there are two other mechanisms that have been identified as the cause of the supernova explosion. In the low-mass end of massive stars (M < = 10M_⊙), carbon ignites in degenerate conditions, by an off-center flame that reaches progressively the center (Nomoto, 1984; Garćıa-Berro et al., 1997; Siess, 2007). At the end of carbon burning, the core is a degenerate mixture of O, Ne, and some Mg, supported by the pressure of electron degeneracy. Electron-captures on ²⁴Mg followed by that on ²⁰Ne (Eldridge and Tout, 2004; Jones et al., 2013) removes a source of pressure, driving an electron-capture core-collapse supernova (EC-SN). The occurrence of an EC-SN depends on several stellar parameters: the mass of the ONe core at the end of C burning, the growth rate of the core, but also the mass-loss rate, since an efficient mass loss can halt the growth of the core (Poelarends et al., 2008).

At the other end of the mass domain lies the region of pair-instability supernovae (PISN). When the central temperature is of the order of 1-2 GK, the photons energy is of the same order of magnitude as the rest mass energy of an electron-positron pair. We saw in section 1 that massive stars are dominated by radiation pressure. If the conditions for pair creation are met (for CO core masses M_CO between 30 and 135 M_⊙ Woosley et al., 2002), photons are removed from the pressure support of the star, destabilizing the hydrostatic equilibrium by lowering the adiabatic index $\frac{\partial lnP}{\partial ln\rho }{|}_{\mathrm{\text{ad}}}$ below 4/3 (Barkat et al., 1967; Rakavy and Shaviv, 1967). If a sufficiently large part of the star lies in this region, the core collapses, triggering violent oxygen burning that disrupts the star entirely, leaving no remnant at all (Ober et al., 1983; El Eid and Langer, 1986; Woosley et al., 2002). For M_CO between 30 and 60 M_⊙, a more regular supernova can be triggered by pulsational pair-instability (PPISN, Chatzopoulos and Wheeler, 2012; Chen et al., 2014; Woosley, 2017; Leung et al., 2019; Marchant et al., 2019). For CO cores larger than 140 M_⊙, the oxygen burning is not powerful enough to reverse the collapse, and a black hole (BH) is formed (Woosley et al., 2002). The PISN or PPISN are supposed to occur more frequently at low metallicity because the low radiative mass loss allows the star to have a larger core (see section 4). In a time when the observation of gravitational waves starts giving access to the mass of BH formed in the early Universe (Abbott et al., 2016a,b, 2017), the existence of PISN predicts a gap in the possible mass of observed BH (Heger et al., 2003; Belczynski et al., 2016; Woosley, 2019) that can now be confronted to observations. Recently, the detection of GW190521 implying the merger of two BHs, one of which having a mass inside the mass gap predicted (85M_⊙, Abbott et al., 2020), has stirred the pot of stellar modeling and presented a real challenge to theory. One of the proposed explanations is of direct interest in this review since it highlights the role the ¹²C(α, γ)¹⁶O reaction rate plays in shaping the fate of massive stars (Costa et al., 2020, see also section 3).

But let us go back to the more standard supernovae and turn to the explosive yields. Once exploded, depending on the envelope composition, the supernova will be characterized as type II (H and He rich), type Ib (H deficient), or type Ic (H and He deficient). During the explosion, the shock wave passes through the star, and the high temperature of the shock triggers nuclear burning. The type of burning and nucleosynthetic result depends almost uniquely on the temperature reached in a specific layer, whatever the initial composition. The iron-peak elements and silicon expelled during a core-collapse supernova come from the silicon and oxygen shells reprocessed by the explosive front with temperatures of the order of 4-5 GK, not from the core itself that ends up locked inside the remnant. To date, most of the explosive yields are determined from 1D stellar supernova progenitors in which either a piston is applied, or a thermal bomb. The mass cut (above which matter is expelled in the explosion) does not come naturally from such simulations and has to be fixed arbitrarily. Often the amount of nickel ejected is used to set the mass cut (Limongi and Chieffi, 2003; Umeda and Nomoto, 2008). The nucleosynthesis is then computed by simulating the passage of the shock wave: the maximum temperature and density are often determined within the radiation-dominated shock approximation (Weaver and Woosley, 1980; Arnett, 1996; Chieffi and Limongi, 2002; Woosley et al., 2002). In this framework, the shock temperature is a function of the energy released and the radius of the layer: $T_{\mathrm{\text{shock}}}={\left(\frac{4}{3\pi a}\right)}^{1/4}{E}_{\mathrm{\text{expl}}}^{1/4}{r}^{-3/4}$, and the density during the shock is obtained by multiplying the pre-shock density by a factor of between 4 (mild shock) and 7 (strong shock). The density and temperature evolve then in the hydrodynamical timescale of an adiabatic expansion at the escape velocity $V_{\mathrm{\text{esc}}}=\sqrt{\frac{2GM}{r}}$: $\rho \left(t\right)={\rho }_{\mathrm{\text{shock}}}{e}^{t/{\tau }_{\mathrm{\text{HD}}}}$ with ${\tau }_{\mathrm{\text{HD}}}={\left(\frac{1}{\rho }\frac{\partial \rho }{\partial t}\right)}^{-1}=\frac{R}{3V_{\mathrm{\text{esc}}}}=\frac{446}{\sqrt{\rho }}$, and T ∝ ρ^γ−1, with γ the adiabatic index. An example of pre-SN vs. post-SN yields is presented in Rauscher et al. (2002, Figure 7). Iron-peak elements are massively produced during the explosion, while the light elements up to Al and the s-process elements are not drastically modified by the explosion (except for a few isotopes).

While piston- or bomb-triggered explosions give a fairly appropriate result for the nucleosynthesis of the intermediate or outer layers of the stars, the very innermost layers' nucleosynthesis is sensitive to the electron fraction Y_e = < Z/A>, which depends strongly on the neutrino or antineutrino captures by protons and neutrons (Curtis et al., 2019). A careful treatment of neutrino transport is needed, and the effects of asymmetries could be significant on the nucleosynthetic budget (Pruet et al., 2005). Given the complexity of multi-D core-collapse simulations, and the necessity to wait for the delayed explosion to deploy, only a few attempts to derived nucleosynthetic yields from multi-D simulations of iron-core collapse supernovae have been performed. The simulations themselves are conducted with a limited chemical network (mainly H and the α elements, plus a tracer of the neutron-rich species, see Wongwathanarat et al., 2015), so a detailed nucleosynthesis needs to be post-processed (Pruet et al., 2005; Harris et al., 2017; Yoshida et al., 2017; Eichler et al., 2018; Wanajo et al., 2018).

3. Effects of nuclear rates uncertainties

Most nuclear reaction rates are determined in laboratory experiments, with conditions that are very far from stellar conditions. Different methods are then applied to extrapolate those rates down to the much lower energies of stellar burnings, but in many of them, large uncertainties remain. A very difficult problem the extrapolations meet is the possibility to miss a low-energy resonance that would significantly change the reaction rates. Many reaction rates still suffer from a lack of robust determination, but it would be beyond the scope of this paper to review them all. I will just present here some general trends and the examples of the ¹²C(α, γ)¹⁶O reaction, and the reactions affecting the s-process.

Depending whether the uncertainty touches a reaction that is a main energy producer for the star, or only a marginal reaction, the effects of varying the rates have very different outcomes. Of course, the first effect we expect concerns simply the nucleosynthetic products: a stronger (weaker) rate will produce more (less) child nuclides, and reduce more (less) efficiently the abundance of the parent nuclides. Varying reaction rates that do not count strongly in the energy budget of the star usually results in just this nucleosynthetic outcome. In that case, differences in physical assumptions in the models (rotation, overshoot value) have a much stronger effect than a change in the rate itself (see for instance Siess et al., 2004, about the ¹³C(α,n)¹⁶O reaction).

However, if the reaction is a dominant energy source for the star, the outcome is much more complicated than the naive picture of “increased rates = increased production of child nuclides.” Stars are self-gravitating systems that adapt their structure to get the energy needed to sustain their gravity. A stronger (weaker) rate can make the burning to take place in lower (higher) T and ρ conditions, modifying strongly the stellar structure. In some cases, the global nucleosynthetic budget will not be that much affected because the structural compensations will be sufficient to keep a similar nucleosynthetic outcome, but in other cases, the structural changes will lead to modifications of the full evolutionary path, with strong consequences on the nucleosynthetic result at large.

The ¹²C(α, γ)¹⁶O reaction is a good example of a reaction that is of paramount importance for massive stars, by playing a role on the C/O ratio at the end of He burning. Though it is a key reaction for massive star evolution, shaping the future path to the supernova, it is still not determined robustly, and the successive attempts (Caughlan et al., 1985; Caughlan and Fowler, 1988; Angulo et al., 1999; Kunz et al., 2002; Katsuma, 2008; deBoer et al., 2017; Holt et al., 2019) show very different behaviors as a function of the temperature (see Figure 1 from El Eid et al., 2009). As in increasingly massive stars, a stronger rate leaves the core deprived in C, inducing a shorter C-burning timescale (Tur et al., 2007). Since C burning is the longer of the advanced burning phases, it is the one that allows the largest energy loss through neutrinos escape. A shorter C-burning phase helps the star to keep a higher entropy, to have a larger migration of the C-burning shell, and hence to end up with a larger O and Si core, affecting its explodability. In that line, let us mention that variations in the ¹²C(α, γ)¹⁶O reaction can affect the possibility of a low-metallicity star to end up as pair-instability supernova or not and modify the limiting masses for PISN (Takahashi, 2018; Costa et al., 2020; Farmer et al., 2020).

A good example of an energetically marginal reaction network which suffers from many uncertainties is the s-process. These uncertainties are either direct (concerning the neutron-producing reaction) or indirect (concerning reactions not directly linked to the s-process but that set the stage for it in the structure of the star). The main neutron producer for the weak s-process, the ²²Ne(α, n)²⁵Mg reaction is still uncertain to about a factor of 2. More complicated for stellar evolution, the competing reaction ²²Ne(α,γ)²⁶Mg is also very uncertain, particularly concerning the strength of low-energy resonances (Kaeppeler et al., 1994; Rauscher et al., 2002; Karakas et al., 2006; Talwar et al., 2016). These uncertainties affect the relative efficiency of these two competing α captures on neon, in particular at temperatures typical of He burning. As mentioned above, some reactions affecting the structure of the star can also modify the result of the s-process. The uncertainties flawing the determination of the ¹²C(α, γ)¹⁶O reaction play a role in the nucleosynthetic results of the weak s-process (Tur et al., 2007, 2009; deBoer et al., 2017) since the ²²Ne(α, n)²⁵Mg reaction becomes more efficient at the end of He burning, when the ¹²C(α, γ)¹⁶O reaction starts competing on the α capture (Pignatari et al., 2010). The 3α rates are better constrained, but even a variation at the level of 10% (Austin, 2005) plays a significant role since this rate is directly confronted to the ¹²C(α, γ)¹⁶O rate in determining the conditions for C burning, affecting the s-process products (Tur et al., 2007, 2010). Variations in the ¹²C(α, γ)¹⁶O rates have an impact on the shell C-burning s-process production as well (El Eid et al., 2004; The et al., 2007; deBoer et al., 2017), because the C/O ratio at the end of He burning determines the future structure of the shell C burning (number and thickness of the shells). During carbon burning, the carbon fusion reaction is also the subject of debate because low-energy resonances are complicated to determine (Gasques et al., 2007; Tumino et al., 2018; Fruet et al., 2020; Tan et al., 2020). Again, by changing the condition of T and ρ at which carbon burning occurs, a variation in the carbon fusion rate modifies the width of the core and subsequent shells and affects the s-process yields (Gasques et al., 2007; Bennett et al., 2012).

4. Effect of metallicity

Except for the extreme case of Z = 0, lowering the metallicity does not modify the burning phases and the reactions themselves, but it changes the conditions in which they take place. When there is less C available, the CNO cycle is weaker and the star has to contract further in order to get enough energy to counterbalance its gravity. This effect, along with the fact that the star has a more transparent envelope, makes low-Z stars hotter and more compact.

A variation in metallicity changes slightly the conditions in which hydrogen burns, but mostly it changes the maximal amount of helium at the end of H burning. This has an impact on the He core size (Woosley and Weaver, 1995). However, after that, the nucleosynthesis of heavy elements depends almost exclusively on the mass of the core (whatever the initial mass), and not on metallicity itself.

When no metals at all are present, the star cannot halt its initial contraction until the core is marginally hot enough to fuse He. The carbon produced through 3α is immediately used to start the CNO cycle. The limit in metallicity for this behavior is around Z = 10⁻⁸. Figure 4 shows the HR diagram for 9M_⊙ models at decreasing metallicity. We see clearly in the track of the Z = 0 model (green line) that the evolution on the main sequence starts while the star is still contracting (blueward evolution). When the CNO cycle is ignited, the contraction is halted and the evolution proceeds redwards as normal (a filled black dot marks this turn on the track). The time needed to produce enough carbon is longer for less massive stars, and gets ever shorter for more massive stars. Between 20 and 25 M_⊙, the CNO cycle starts directly on the ZAMS (Siess et al., 2002; Ekström et al., 2008; Murphy et al., 2021) and no main sequence "knee" is visible anymore. At the end of H burning, the zero-metallicity stars (or zero-like) have a hot enough core to enter into He burning very smoothly, without the usual strong contraction. As a result, He is burnt in a very blue location of the HR diagram. Another consequence is that the H-burning shell is not hotter than the MS core, in contrast with what we saw previously, so the shell is powered only by the pp-chains reactions.

FIGURE 4

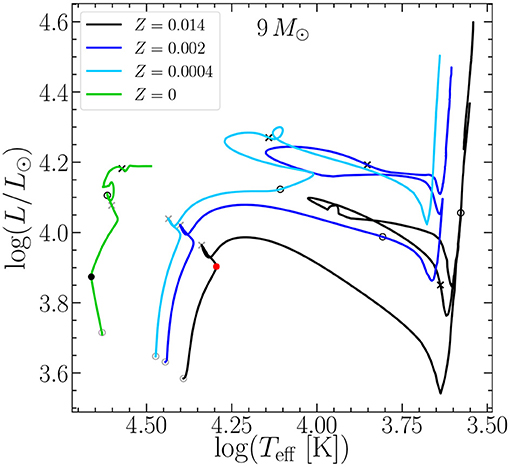
Figure 4. HR diagram for 9M_⊙ models at different metallicities: Z = 0.014 (Ekström et al., 2012), Z = 0.002 (Georgy et al., 2013a), Z = 0.0004 (Groh et al., 2019), and Z = 0 (Murphy et al., 2021). The beginning and end of fusion phases are marked with a circle and a cross respectively (gray: H burning; black: He burning). The red dot on the black track marks the hook described in section 2.1. The filled black dot on the green track marks the point where the CNO cycle is ignited in the Z = 0 model as described in section 4.

An important feature found in low-metallicity stars is the interactions between H- and He-burning zones (shell or core Woosley and Weaver, 1995; Hirschi, 2007; Ekström et al., 2008; Heger and Woosley, 2010; Ritter et al., 2018b). We will see in section 5.1 that connections between burning shells is a common feature during the advanced phases, but a low metallicity favors the connection between H and He shells in earlier phases of the evolution. The carbon brought from the He-burning region into the H-burning shell boosts the CNO cycle in the shell, producing a significant amount of nitrogen (called primary because it is directly produced from newly synthesized carbon, Truran and Cameron, 1971; Edmunds and Pagel, 1978). In non-rotating models, this feature is found in a restricted mass domain, between 25 and 35M_⊙ (Chieffi and Limongi, 2004; Heger and Woosley, 2010; Limongi and Chieffi, 2012), but in more recent models, Clarkson and Herwig (2021) find it to happen in a much larger mass domain (15 − 140 M_⊙) and for all sorts of convection treatments. Rotating models have also been found to show these burning zones interactions in the full range of masses through rotational mixing (Hirschi, 2007; Ekström et al., 2008; Frischknecht et al., 2012, 2016; Choplin et al., 2017b). Choplin et al. (2017a) have evoked a late mixing of this type to reproduce the puzzling ¹²C/¹³C and C/N in some carbon-enriched extremely metal-poor stars. The chemical connection between the two burning zones allows some nitrogen to diffuse back into the He-burning region, building Ne and producing neutrons that can be used for s-process (Pignatari et al., 2008; Frischknecht et al., 2016), as we saw in section 2.2. Another important impact a shell CNO-boost can have when it occurs during core He burning is the reduction of the size of the CO core.

By drastically reducing the radiative mass loss (see section 5.3), a low or zero metallicity helps the stars keep most of their mass until the end of the evolution. This influences the type of explosive event that will end the star's evolution. Low-metallicity stars can have very high mass at the time of explosion, but they also have very large CO cores. In this case, they are good candidates for pair-instability supernovae (Woosley et al., 2002), as we saw in section 2.4.

5. Important processes in massive star evolution

Some processes play an important role in stellar evolution and have to be considered when modeling stars. They can have repercussions on the nucleosynthetic budget of the star.

5.1. Convection

A very basic ingredient of stellar evolution is the treatment of convection. Being a multi-dimensional (multi-D) process because of its turbulent nature, it is impossible to model it from first principles in one-dimensional (1D) evolution codes.

The implementation of convection in stellar codes follows two steps. The first one is to identify the convective or radiative nature of the layer. There are two different criteria assessing the stability to convection: the Schwarzschild or the Ledoux criteria. The Schwarzschild criterion (Schwarzschild, 1958) states that a stellar layer is unstable to convection if the radiative thermal gradient is larger than the adiabatic thermal gradient:

$\frac{3}{16\pi acG}\frac{\kappa LP}{M{T}^4}={\nabla }_{\text{rad}}>{\nabla }_{\text{ad}}=\frac{P\delta }{C_P\rho T}$

with $a=\frac{4\sigma }{c}$ the radiation constant (where σ is the Stefan-Boltzmann constant), κ the opacity, $\delta =-\frac{\mathrm{\text{d}}ln\rho }{\mathrm{\text{d}}lnT}$ (see Equation 5), C_P the specific heat at constant pressure, and obvious meanings for c, G, L, M, P, T, and ρ. The Ledoux criterion (Ledoux, 1947) adds a dependence on the gradient of chemical composition: ${\nabla }_{\mathrm{\text{rad}}}>{\nabla }_{\mathrm{\text{ad}}}+\frac{\phi }{\delta }{\nabla }_{\mu }$ (with φ and δ as in Equation (5). Care must be taken in the way this is done because the definition of the border as the place where ∇_ad = ∇_rad is valid only from within the convective zone (Gabriel et al., 2014). During the main sequence, both definitions lead to similar convective core size in massive stars, but after the main sequence, using one or the other leads to important changes in the way the star crosses the HR diagram, in the surface chemical enrichment amplitude (Georgy et al., 2014), and in the final He core mass (Hirschi et al., 2004).

The second step concerns the definition of the temperature stratification and the chemical mixing in convective zones. In the deep interior of stars, convection can be considered adiabatic, and the mixing is usually considered instantaneous, except during the very late stages of evolution when the nuclear timescale becomes shorter than the convective timescale. At the surface, however, these considerations are no more valid, and the most used framework is the mixing length theory (MLT Vitense, 1953; Böhm-Vitense, 1958). Note that more sophisticated and non-local theories have been proposed (Shaviv and Salpeter, 1973; Roxburgh, 1978; Kuhfuss, 1986; Langer, 1986; Canuto, 1992, 2011a,b,c,d,e; Xiong et al., 1997; Deng et al., 2006; Gabriel and Belkacem, 2018), but none of them are used routinely in stellar evolution codes. The MLT considers that the convective cell travels a fixed distance before being dissipated. This distance, the mixing length, is taken as a multiple of the pressure height scale: ℓ = α_MLTH_P, with $H_P=-\frac{dr}{dP}P$, and α_MLT a free parameter needing to be calibrated. The calibration is usually done on the Sun, and the value inferred is then used in all stellar models, although there is no reason for it to be a constant and indeed some works show a dependence on the stellar parameters or the metallicity (Magic et al., 2015; Song et al., 2020). Varying the value for α_MLT has also been shown to impact the light curve and spectral evolution of type II supernova (SN) models (Dessart et al., 2013).

A confrontation of the characteristics of models computed with this definition for the convective boundary with observations shows that it leads to too small cores (see for example Maeder and Mermilliod, 1981; Aerts et al., 2003; Aerts, 2008; Moravveji et al., 2015; Claret and Torres, 2016; Deheuvels et al., 2016), which gave rise to the notion of overshoot: the convective movement does not stop where the acceleration stops, and the convective cell overshoots into the radiative layer where it is braked and stopped after a certain distance. Stellar models include overshoot in different ways, the most commonly used being either penetrative or diffusive overshoot. In the penetrative scheme, the border of the convective region is displaced by a distance that is a fraction of the pressure scale height d_ov = α_ovH_P (Shaviv and Salpeter, 1973; Maeder, 1975). In the diffusive scheme, an extra mixing is applied at the border of the convective zone with an exponentially-decaying diffusive coefficient $D_{\mathrm{\text{ov}}}=D_{0}exp\left(2\frac{r-r0}{f_{\mathrm{\text{ov}}}{H}_P}\right)$ with r₀ the location of the boundary, and D₀ a reference diffusion coefficient, often taken as D_MLT (Herwig et al., 1997, based on hydro simulations by Freytag et al. 1996). In any case, the overshoot implementation includes at least one free parameter (α_ov or f_ov in the two examples above) that needs to be calibrated. The two more used methods are either the width of the main sequence in an HR diagram (Herwig, 2000; Bressan et al., 2012; Ekström et al., 2012; Choi et al., 2016), or the velocity drop at the end of the main sequence (Brott et al., 2011a). More recently, it has been proposed to calibrate the overshoot on binary stars systems (Tkachenko et al., 2020). Some studies indicate that there could be a dependence of the overshoot with the mass of the star (see for example Castro et al., 2014; Claret and Torres, 2016), and so using a fixed value would lead either to overestimate the overshoot in the lower mass domain, or to underestimate it in the higher mass domain. In any case, a calibration is only valid for the models on which it was determined, since the differences in the input physics of the different stellar evolution codes have repercussions on the determination of the border of the convective zones. Note that since the work of Denissenkov et al. (2013), the term convective boundary mixing (CBM) is starting to take over the old term of overshoot, since it covers all sorts of hydrodynamical instabilities resulting in mixing.

Multi-D hydro simulations are essential in this field to improve the way convection is implemented in 1D stellar evolution codes. In the last 15 years or so, there has been a number of simulations exploring different convection regimes: cool stars envelopes (Freytag and Höfner, 2008; Chiavassa et al., 2009; Magic et al., 2013; Viallet et al., 2013), He-burning shells (Herwig et al., 2006; Woodward et al., 2015), or advanced-phases burning shells like C-burning shell (Cristini et al., 2017), O-burning shell (Meakin and Arnett, 2007; Müller et al., 2016; Jones et al., 2017), or Si-burning shell (Couch et al., 2015), and very recently, ZAMS convective cores (Higl et al., 2021). These simulations show that indeed, there is a mixing at the boundary of the convective zone, mainly due to plumes, gravity waves, or the turn-over of the convective eddies (Herwig et al., 2006; Meakin and Arnett, 2007; Jones et al., 2017; Arnett et al., 2019; Edelmann et al., 2019). Jones et al. (2017) calibrated the f_ov, or f_CBM parameter of the exponentially-decaying diffusive coefficient implementation of CBM on an O-burning shell, finding a value of f_CBM = 0.03. Higl et al. (2021) find that the value for f_CBM should increase with mass, well in line with the results of Claret and Torres (2016). Many simulations show that the bottom CBM occurs in a narrower region than the top CBM. The challenge is now to translate the multi-D results into relations between quantities that are followed in 1D models. A 3-to-1D procedure is proposed by Arnett et al. (2015), who apply a Reynolds-average Navier-Stokes treatment (Meakin and Arnett, 2007; Viallet et al., 2013) to the simulation results. In the advanced-phases shell simulations, the border of the convective zones has been shown to evolve in space and time following a turbulent entrainment that can be parametrized by the bulk Richardson number Ri_B (Meakin and Arnett, 2007; Garcia and Mellado, 2014; Müller et al., 2016; Cristini et al., 2017, 2019): $V_{\mathrm{\text{ent}}}/V_{\mathrm{\text{conv}}}=A{\mathrm{\text{Ri}}}_B^{-n}$, where V_ent is the entrainment velocity, V_conv is the convection velocity, and A and n are parameters expressing the efficiency of the entrainment. The bulk Richardson number expresses the ratio between the stabilization potential of the boundary and the turbulent kinetic energy: ${\mathrm{\text{Ri}}}_B=\frac{\Delta B\ell }{V_{\mathrm{\text{conv}}}^2}$ with ℓ the length scale for the turbulent motion, and $\Delta B={\int }_{r_1}^{r_2}{N}^{2}dr$ the buoyancy jump across the boundary expressed in term of the buoyancy frequency (or Brunt-Väisälä frequency) $N^2=\frac{g}{H_P}\left[\delta \left({\nabla }_{\mathrm{\text{ad}}}-\nabla \right)+\phi {\nabla }_{\mu }\right]$. A first implementation in a 1D stellar evolution code has been performed by Staritsin (2013), which computed models of 16 and a 24 M_⊙. The efficiency parameters were taken to be n = 1, in agreement with the 3D results, and A ≃ 4 · 10⁻⁴ calibrated on asteroseismic results (Briquet et al., 2011). They find that the extent of the mixed region above the convection-unstable one is decreasing with time, reducing the amount of newly synthesized He with respect to the classical overshoot implementation. This reduction of the core size in turn reduces the luminosity increase of the model during the main sequence. Recently, Scott et al. (2021) presented a grid of models, with mass ranging between 1.5 and 60 M_⊙, computed with the entrainment law and compared them to similar models computed with a penetrative overshoot. They find that the entrainment CBM scheme leads to a natural increase of the mixed region with mass, improving agreement with the observational constraints derived by Castro et al. (2014). In contrast with Staritsin (2013), they obtain an entrained mass that increases with time. This difference is due to the difference in the implementation: Staritsin (2013) scales the instantaneous entrained distance with the Richardson number (d_ent = V_entΔt), while Scott et al. (2021), following Cristini et al. (2019), scale the mass entrainment rate (Ṁ_ent) with Ri_B, building a cumulative entrainment. Note that while the cumulative implementation reproduces the trend seen in the hydro simulation, it is not clear how the secular evolution differs from the evolution on a dynamical timescale probed by 3D modeling. Moreover, Higl et al. (2021) tried to calibrate A and n in 2D modeling of ZAMS convective cores of intermediate-mass models, but failed in finding a satisfactory solution through the whole mass range (1.3 to 3.5M_⊙), an indication that more stellar parameters might be necessary to adjust the entrainment law. They suggest that it could scale not only with Ri_B but also with the Peclet number.

Viallet et al. (2015) suggest that different convection regimes (and hence different overshoot schemes) should be used depending on the conditions in which the convection takes place and the importance of radiation. Where the radiation plays an important role, it reduces the efficiency of convection. They recommend to use the diffusive scheme on convective envelopes, while in the deep interior, penetrative overshoot seems more adequate in the phases when the star is cooled by photons, and entrainment should be used in advanced phases when the cooling is due to neutrinos.

The hydro simulations have also revealed the excitation of internal gravity waves (IGW) by the convective eddies and plumes penetration in the radiative zone above. Rogers et al. (2013) and more recently Edelmann et al. (2019) have computed in 2D and 3D respectively the IGW spectrum and amplitude expected in a star with a convective core and a radiative envelope. Space asteroseismology has detected a low-frequency stochastic variability in O- and B-type stars (Blomme et al., 2011; Buysschaert et al., 2015; Aerts et al., 2018; Bowman et al., 2019a,b). This signal has been attributed to IGW generated by the convective core (Bowman et al., 2019b), or sub-surface convective zones (Blomme et al., 2011; Lecoanet et al., 2019). If the ability of IGW to transport angular momentum inside radiative envelopes is confirmed, it would make them good candidates to explain strong angular momentum transport in some observed intermediate-mass or massive stars (Aerts et al., 2017, 2019), or even the strange case of the counter-rotating envelope observed for the late B-type star KIC 10526294 (Triana et al., 2015).

An important feature seen in the advanced phases of both 1D and multi-D models is the merger of the O-burning shell with the Ne shell above, or even the C-burning shell (Rauscher et al., 2002; Woosley et al., 2002; Tur et al., 2007; Andrassy et al., 2020; Yadav et al., 2020). According to Collins et al. (2018), it happens commonly in SN progenitors models between 16 and 26 M_⊙, very shortly prior to the collapse. Of course, the amplitude of this phenomenon is strongly related to the CBM efficiency (Davis et al., 2019) and to the spatial resolution (Farmer et al., 2016), but the fact that it also appears in 3D modeling tells us that it is a process we have to account for. Ritter et al. (2018a) show that it is responsible for overproductions of P, Cl, K, and Sc that could reconcile the nucleosynthetic predictions with the observations of odd-Z elements in the Galaxy. Similarly, the merger of the Si-burning shell up to the C-burning shell drives an overproduction of Cr (Côté et al., 2020). By changing the compactness, shell mergers can also impact the explodability of the models (Davis et al., 2019), and build asymmetries that can help revive the shock and increase the amplitude of the SASI instability (Andrassy et al., 2020; Yadav et al., 2020).

5.2. Rotation

A spinning star is affected by rotation in two different ways. First, the centrifugal force helps it counterbalance its own gravity. This has an effect on the hydrostatic equilibrium the star is settling on, making it behave like a slightly lower-mass non-rotating star. In an HR diagram, this translates into a slight shift toward lower Teff and L at the very beginning of the evolution. The centrifugal force increases also the mass loss experienced by the star, the gravitational pull being slightly lower. The star shape is not spherical anymore but oblate, with an equatorial radius larger than the polar one. In the framework of the Roche model, where the gravitational potential is approximated by $\frac{G{M}_r}{r}$ (with M_r the mass coordinate at the internal radius r), we can express the oblateness as a function of the ratio of the centrifugal force to the gravity at the equator: $\frac{R_{\mathrm{\text{eq}}}}{R_{\mathrm{\text{pol}}}}=1+\frac{1}{2}\frac{a_{\mathrm{\text{cen}}}}{g_{\mathrm{\text{eq}}}}=1+\frac{1}{2}\frac{{\Omega }^2{R}_{\mathrm{\text{eq}}}^3}{GM}$. When the star is rotating at the critical limit, we have a_cen = g_eq, and hence the maximal oblateness corresponds to $R_{\mathrm{\text{eq}}}=\frac{3}{2}{R}_{\mathrm{\text{pol}}}$. In this case, the outer layers of the star are no longer bound to it and can be lost through a mechanical mass loss (Georgy et al., 2013b).

The second effect is actually the more important for the whole evolution of the star: internal mixing. Rotation induces several instabilities, the first one being the meridional circulation (Eddington, 1925; Vogt, 1925; Sweet, 1950; Zahn, 1992; Maeder and Zahn, 1998). The oblateness of the star prevents it to be both in hydrostatic and thermal equilibrium at the same time. This impossibility drives a large scale circulation inside the star, which transports angular momentum and chemicals by an advecto-diffusive mixing (Zahn, 1992; Maeder and Zahn, 1998). Moreover, if the star does not rotate like a rigid body, the differential rotation induces a shear mixing that diffuses both angular momentum and chemicals through the star. The transport of angular momentum can thus be written as:

$\begin{array}{ll}\rho \frac{\partial }{\partial t}{\left(r^2\bar{\Omega }\right)}_{M_r}=\frac{1}{5r^2}\frac{\partial }{\partial r}\left(\rho r^4\bar{\Omega }U\left(r\right)\right)+\frac{1}{r^2}\frac{\partial }{\partial r}\left(\rho D_{\Omega }{r}^4\frac{\partial \bar{\Omega }}{\partial r}\right)& (8)\end{array}$

with $\bar{\Omega }$ the mean angular velocity at radius r, U(r) the radial component of the meridional circulation, and D_Ω the diffusion coefficient corresponding to the various diffusive processes transporting Ω, like shear mixing or convection.

In the case of chemicals, it has been shown by Chaboyer and Zahn (1992) that despite the advective nature of meridional flows, the net effect on the chemical mixing can be satisfactorily approximated by a diffusive-only process. The changes in chemical composition in a layer of the stellar interior can be expressed as:

$\rho \frac{\text{d}{X}_i}{\text{d}t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(\rho r^{2}D\frac{\partial X_i}{\partial r}\right)+{\left(\frac{\text{d}{X}_i}{\text{d}t}\right)}_{\text{nucl}}$

with ρ the density in the layer, X_i the mass fraction abundance of species i in the layer, r the internal radius at that layer, D the diffusion coefficient taking into account all the diffusive processes included (D = D_conv + D_shear + D_{eff, U}, where “conv” is for convection, and “eff,U” is for the meridional circulation effective diffusive process), and ${\left(\frac{\mathrm{\text{d}}{X}_i}{\mathrm{\text{d}}t}\right)}_{\mathrm{\text{nucl}}}$ expresses the change in composition due to the nuclear reactions in the layer.

Figure 5 shows evolutionary tracks in the HRD for the 9 M_⊙ models of Georgy et al. (2013b) at solar metallicity. For increasing initial rotation Ωini/Ωcrit⁴, the tracks start on lower Teff and L, the gravitation of the star being partially lifted by the centrifugal force. Over the course of the main sequence, the mixing effects start dominating over the hydrostatic one, so the convective H-burning core recedes more slowly and hence the tracks are getting more luminous (without a net change in Teff). For really rapid rotation (Ωini/Ωcrit ≥ 0.6), the hydrostatic effects start playing again an important role and though the cores are still larger, L decreases slightly. The luminosity difference between rotating and non-rotating models remains throughout the whole further evolution. Roughly summarized, the rotating star begins its life behaving like a lower-mass star because of the hydrostatic effect of rotation, and ends its life behaving like a higher-mass star because of the rotational mixing.

FIGURE 5

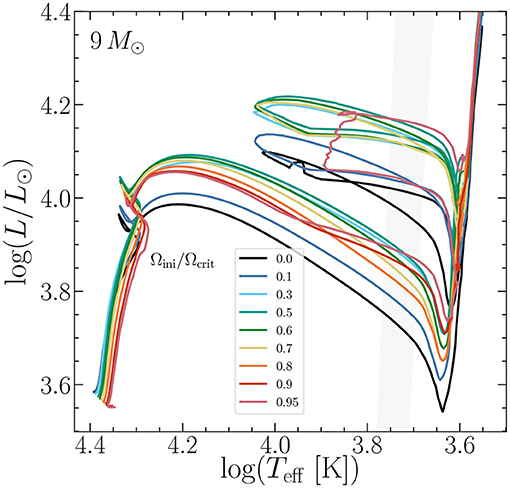
Figure 5. Hertzsprung-Russell diagram for 9 M_⊙ models with increasing rotation (models from Georgy et al., 2013b).

Concerning the stellar nucleosynthesis, the increase of the core makes the central burnings to occur in a hotter and slightly less dense environment. Central H burning is longer because the core is being replenished with fresh H by mixing (see Table 1). In contrast, central He burning is generally shorter, mostly because of the higher luminosity induced by the larger core. Many features of the behavior of massive stars in advanced phases depend on the mass of the CO core left by He burning, as for example the ability to ignite carbon or not, off-center or at the center, convectively or radiatively. Rotation lowers the different limiting masses for these features. The mass of the core also defines almost uniquely the final luminosity of the star just before the supernova explosion (Farrell et al., 2020). The link between the core mass and the initial mass can differ strongly whether rotation is taken into account or not, and of course depending on the treatment of convection or the inclusion of overshooting (see section 5.1), so it is not straightforward to link the luminosity of a SN progenitor to its initial mass. Another important quantity for the advanced-phases behavior is the C/O ratio at the end of He burning (Chieffi and Limongi, 2020). By increasing the central temperature, rotation helps the star build more oxygen at the expense of carbon, so the C/O ratio is lower in rotating models.

Rotational mixing also chemically connects different regions inside the star. This can have profound effects on the nucleosynthesis. Rotating stars are good producers of primary nitrogen, because ¹²C and ¹⁶O produced in the core are diffused upwards into the H-burning shell, and then immediately processed into ¹⁴N through the CNO cycle. This ¹⁴N can diffuse back into the He-burning core and be further transformed into ²²Ne by two successive α captures (Meynet and Maeder, 2002a,b; Hirschi, 2007). As seen above, the reaction ²²Ne(α,n)²⁵Mg is a neutron producer that plays an important role in the s-process nucleosynthesis, and rotation is able to increase the s-process elements production as well as to shift the peak to heavier elements (Pignatari et al., 2008; Chiappini et al., 2011; Frischknecht et al., 2016).

More generally, by modifying the chemical structure of the star, rotation modifies the path it will follow, for example in an HR diagram. Generally, rotation favors a redward evolution (Meynet and Maeder, 2002a), but rapid rotation can mix so strongly the star that it follows a quasi chemically-homogeneous blueward evolution (CHE, see Maeder, 1987; Langer, 1992). This is more easily the case at low metallicity (Szécsi et al., 2015; Choi et al., 2016) since the compactness of the star makes the mixing time shorter (${\tau }_{\mathrm{\text{mix}}}\simeq \frac{R^2}{D}$, with D the mixing coefficient, see Maeder and Meynet, 2001).

The implementation of the effects of rotation in 1D stellar evolution codes suffers from a native problem: the non-1D nature of rotation by definition. Stellar codes implement those effects in very different ways, and unsurprisingly, their results are widely different. Even when the same code uses different implementation of the same advecto-diffusive scheme for the transport of angular momentum, the results show large variations (Meynet et al., 2013). When different codes are compared, the picture becomes even more blurred because not only the rotation implementation is different, but some basic scheme of resolution and the treatment of convection also are different. Martins and Palacios (2013) have performed a comparison of stellar tracks coming from published grids (Bertelli et al., 2008; Brott et al., 2011a; Ekström et al., 2012; Chieffi and Limongi, 2013, without any attempt to benchmark the physical ingredients and parametrization) and added models computed with two other codes, STAREVOL (Siess et al., 1997; Decressin et al., 2009) and MESA (Paxton et al., 2011, 2013). Without rotation, large differences appear, the main culprit being the treatment of convection, as shown also in Jones et al. (2015). The divergence occurs principally after the main sequence. When rotation is switched on, the divergence in the HR diagram between codes is larger on the main sequence, and starts sooner, but is slightly reduced in the post main sequence, probably thanks to mixing effects that reduce the dispersion in luminosity (see Figure 7 in Martins and Palacios, 2013).

The physics of rotation has been partially tested in multi-D hydro simulations. Simulations focussing on the shear mixing (Prat and Lignières, 2013, 2014; Prat et al., 2016) have shown a good agreement with the 1D prescription of Zahn (1992). Edelmann et al. (2017) have shown that 2D models are unstable to the dynamical shear (triggered in the zones where the gradient of Ω is very steep) in the locations predicted by 1D models. In this work, the profile of Ω is affected during about 150 min in both 2D and 1D models. In the 2D model, the instability stops in the previously unstable layer, while in the 1D model the shear mixing is still active, but with such a low diffusion coefficient that it would not be seen in the 2D model due to the hydro timescale. The instability in both models propagates to neighboring layers (much quicker in the 1D than in the 2D model), until the stability is restored. Since the hydro simulation does not include any evolution process impacting the structure (contraction/expansion or energy production/loss), the Ω profile cannot evolve further. The resulting mixing on the chemicals is much stronger in the 2D model, but occurs on a much shorter timescale than the usual evolutionary timescale of 1D models. The net effect, if confirmed by 3D models, could point to the need to apply a lower diffusion coefficient, or a stronger one but on a larger region of the model. The diffusive effect of erasing the Ω gradient is expected to reinforce the advective part of the meridional circulation, that will tend to build it again. Unfortunately, the spatial and temporal resolutions needed to model the meridional circulation are still out of reach of hydro simulations, so only the diffusive part of the net transport of angular momentum can be explored with this tool.

The best observational constraints we can hope for come from surface enrichments, and from asteroseismology. However, they are not at the same level of accuracy concerning the process under scrutiny. Surface enrichments probe the mixing of chemicals, which might be the result of different processes (rotation, but also convection, IGW, magnetic fields, binary tides,.) while asteroseismology probes precisely the transport of angular momentum inside the star. On the nucleosynthesis side, the CNO cycle is expected to shift the chemical balance of the elements toward nitrogen, depleting carbon and oxygen. The nucleosynthetic behavior is clearly framed theoretically in a diagram of N/C vs. N/O with the two following assumptions (Maeder et al., 2014; Martins et al., 2015a):

1. in the lower mass domain, we can consider that only the first CN cycle is really active, so the oxygen content remains the same and only carbon is transformed into nitrogen. In that case, we have that dC = -dN (in numbers), so $\mathrm{\text{d}}\left(\frac{\mathrm{\text{N}}}{\mathrm{\text{C}}}\right)=\frac{\mathrm{\text{dN}}}{\mathrm{\text{C}}}\left(1+\frac{\mathrm{\text{N}}}{\mathrm{\text{C}}}\right)$, while $\mathrm{\text{d}}\left(\frac{\mathrm{\text{N}}}{\mathrm{\text{O}}}\right)=\frac{\mathrm{\text{dN}}}{\mathrm{\text{O}}}$. In the N/C vs. N/O diagram, this case draws a curve $\frac{\mathrm{\text{d}}log\left(\mathrm{\text{N/C}}\right)}{\mathrm{\text{d}}log\left(\mathrm{\text{N/O}}\right)}=1+\frac{\mathrm{\text{N}}}{\mathrm{\text{C}}}$;

2. in the higher mass domain, carbon is immediately put to equilibrium by the CN cycle and stays constant, so we have that $\mathrm{\text{d}}\left(\frac{\mathrm{\text{N}}}{\mathrm{\text{C}}}\right)=\frac{\mathrm{\text{dN}}}{\mathrm{\text{C}}}$, while oxygen is converted into nitrogen and dO = -dN, so $\mathrm{\text{d}}\left(\frac{\mathrm{\text{N}}}{\mathrm{\text{O}}}\right)=\frac{\mathrm{\text{dN}}}{\mathrm{\text{O}}}\left(1+\frac{\mathrm{\text{N}}}{\mathrm{\text{O}}}\right)$. In the N/C vs. N/O diagram, this case draws a curve $\frac{\mathrm{\text{d}}log\left(\mathrm{\text{N/C}}\right)}{\mathrm{\text{d}}log\left(\mathrm{\text{N/O}}\right)}=\frac{1}{\left(1+\mathrm{\text{N/O}}\right)}$.

This N/C vs. N/O diagram constitutes a kind of sanity check for the abundances observed at the surface of stars, that should lie somewhere between the two limiting lines described above, whatever the source or the physics of surface enrichment (mixing, mass loss, internal gravity waves, .). If there is a source of mixing, like rotation, or if mass loss removes a large enough part of the envelope of the star, one expects the nucleosynthetic products to be brought up to the surface of stars and they will populate different parts of this diagram, but always between the two limiting lines. Nitrogen enrichments are thus used as tracers of mixing.

When rotational mixing is to be tested, a plot of N enrichment vs. surface velocity (the so-called Hunter diagram, after Hunter et al., 2009), or variations of it (Maeder et al., 2009; Brott et al., 2011b; Aerts et al., 2014; Martins et al., 2017) are considered. In the work of Brott et al. (2011b), 60% of the observed stars are located in parts of this diagram where evolutionary models predict they would. The 40% that are off can be regrouped in two categories: the slow rotators showing strong enrichments, and the unenriched rapid rotators. This result has led to a strong challenge of rotational mixing. The problem with this approach (that we could summarize as “rapid rotators should be enriched, slow rotators should not”) is that the surface enrichment of a star is not simply a function of its rotational velocity. It has been shown to be a complex function of mass, age, rotation rate, metallicity, and multiplicity (Maeder et al., 2009). When a heterogeneous sample of stars are confronted to models in such a diagram, it is difficult to draw firm conclusions about whether rotational mixing is effective or not. Moreover, depending on the angular momentum transport efficiency (mild core-envelope coupling leading to differential rotation, or strong coupling leading to solid-body rotation), the same data can give different answers. Martins et al. (2015a) show that in a given sample of 74 observed O-type stars, 80–90% are consistent with the predictions of the two different mild-coupling sets of models (Ekström et al., 2012; Chieffi and Limongi, 2013), while the strong-coupling set of models (Brott et al., 2011a) can only account for 50% of the sample. The differences are linked to both the enrichment process and the surface velocity evolution. The strong-coupling models experience a strong and rapid N enrichment which then remains constant, and the surface velocity is maintained almost constant through the main sequence because of the solid-body rotation. The mild-coupling models have a more progressive enrichment, and the surface velocity changes through the main sequence under the influence of structural modifications (radius inflation) and angular momentum budget (transport from the contracting core, removal by stellar winds). In such models, the strongest enrichments can be associated with only moderate or even slow rotation velocities (Martins et al., 2017), matching the observations. In the work of Aerts et al. (2014) on 68 massive stars, a strong correlation of N enrichment with Teff, and also with the acoustic mode frequency is found, but no clear correlation with the rotational frequency: they find a slightly higher than average enrichment for the most rapid rotators, and a larger and larger dispersion for decreasing rotational frequencies. Actually this behavior is qualitatively compatible with what is expected by mild-coupling models from such an heterogeneous sample, ranging from 5 to 40 M_⊙ in very different evolutionary status. The large dispersion of the N enrichment of the slower rotators may arise from a group formed from truly slower rotators (with moderate or no enrichment) mixed with previously rapid rotators that are highly enriched but braked. However, this work points to the need to explore the effects of IGW in the transport of angular momentum and species in massive stellar models and to study their interaction with rotation. The very detailed work by Markova et al. (2018) on 53 Galactic O stars points to the fact that the efficiency of rotational mixing might need to be revised downwards for the mild-coupling models (in line with the 2D result of Edelmann et al., 2017), or upwards for the strong-coupling models. This last trend is echoed in the work by Dufton et al. (2018) on 54 B-type stars in the LMC with low projected rotational velocities. While 75–80% of the observed stars follow the models predictions, the fraction of N-enriched apparently slow rotators is too high to be explained by rapidly-rotating stars being seen pole-on. This fraction is however compatible with the fraction of stars found to have a significant enough surface magnetic field to be detected by the MiMes survey (7% of B-type stars, see Wade et al., 2014). Magnetic fields leading to simultaneously the braking-down of the star's rotational velocity and a strong N enrichment (Meynet et al., 2011) is hence proposed by the authors as a possible solution for these stars, along with stellar mergers (see section 5.4). Binaries interactions can only partly explain the result for the very strong N enrichment of ON stars (Martins et al., 2015b), so these peculiar stars still present a puzzle for stellar models.

The treatment of rotation leading to a mild coupling, that seems to be the best fit for the bulk of the surface enrichments of main-sequence massive stars, implies a differential rotation inside the models. Asteroseismology is able to probe stellar interiors and give informations on the rotational profile inside the stars. Unfortunately, to date, only a handful of β Cephei stars (main sequence stars with masses between 7 and 20 M_⊙) have been analyzed by asteroseismic techniques allowing to probe their internal rotation profile. On the seven stars observed, only three have yielded a clear detection of the core-to-envelope rotation ratio: ν Eri (Pamyatnykh et al., 2004; Dziembowski and Pamyatnykh, 2008), V836 Cen (also known as HD 129929, Aerts et al., 2003; Dupret et al., 2004), and 12 Lac (Dziembowski and Pamyatnykh, 2008). The first two are compatible with differential rotation (with Ω_core/Ω_env > 1.) For 12 Lac the answer depends on the model used to fit the asteroseismic data, one model being compatible with a flat profile (Ω_core/Ω_env = 1) and the other with a differential rotation (Ω_core/Ω_env ~ 5). For one other star, V2052 Oph (Briquet et al., 2012), the presence of a magnetic field have lead to the conclusion that the star should have a flat profile. The fifth one for which an analysis of the rotation profile has been intended, θ Oph (Briquet et al., 2007; Walczak et al., 2019) is a member of a triple system, with an SPB tertiary (Slowly Pulsating B-type star) contributing significantly to the light of the primary. Both analyses are compatible with rigid rotation in the envelope. While the overall picture of these analyses would advocate a 50%-50% fraction of differentially and rigidly rotating β Cephei stars, this sample is way too small to give us firm answers about the rotation profiles in massive stars, and only when statistically-significant large asteroseismic surveys will have yielded their results will we be able to assess whether the same problem of angular momentum occurs in massive stars as in low-mass stars. We might not have to wait too long: Labadie-Bartz et al. (2020) have identify 86 new β Cephei stars and 97 candidates from the KELT project (Kilodegree Extremely Little Telescope exoplanet survey) that will be included in the target list of TESS (Transiting Exoplanet Survey Satellite).

Low-mass stars modeling have undergone a revolution when asteroseismic results have started to reveal the stellar interiors that where impossible to probe before. An important result brought by the unprecedented precision and wealth of data yielded by the satellites CoRoT and Kepler is the need for an additional transport mechanism inside the radiative zone of low-mass stars in order to explain the rotation profile of red giants and sub-giants (Beck et al., 2012; Eggenberger et al., 2012; Deheuvels et al., 2014). The asteroseismic analyses show that there is a stronger coupling between the contracting core and the expanding envelope after the main sequence. This additional transport could also extract some angular momentum from the core and reconcile the predictions of the models with the measurements of the core rotation of white dwarfs (Suijs et al., 2008; Fuller et al., 2019). The physical mechanism is not yet understood, but some characterization of its behavior with evolutionary status or mass have been performed (Cantiello et al., 2014; Spada et al., 2016; Eggenberger et al., 2017, 2019a). The proposed solution of a modified Tayler-Spruit magnetic dynamo (Fuller et al., 2019) has been shown to be unable to reproduce the observations of both red giants and sub-giants (Eggenberger et al., 2019b; den Hartogh et al., 2020). Explorations of the role of IGW (see section 5.1) in the angular momentum transport in red giants and sub-giants have shown that they are not efficient enough to solve the problem, though they could play a role (Fuller et al., 2014; Pinçon et al., 2017).

Would the same additional mechanism be needed in massive stars? It has been shown that the cores of supernova progenitors were rotating too fast to explain the spin rate of young neutron stars (Suijs et al., 2008), suggesting the need for a stronger core-envelope coupling during the nuclear lifetime of the stars. This conclusion rests on the assumption that there is conservation of angular momentum between the collapsing star and the resulting neutron star after the explosion. However, as we saw in section 2.4, the explosion mechanism involves large-scale convective instabilities, and it has been shown that SASI sloshing or spiral movements can redistribute the angular momentum of the progenitor and alter the amount that is enclosed in the neutron star (Blondin and Mezzacappa, 2007; Wongwathanarat et al., 2010, 2013; Kazeroni et al., 2017). In section 5.1, we saw that convective penetration generates IGW in the radiative zone above. These IGW have been shown to be able to modify significantly the spin of the pre-SN core during the very late stages of nuclear burning (Fuller et al., 2015). These late-time alterations suggest that the spin rates of young pulsars might not be good constraints on the angular momentum transport during the evolution of massive stars. In any case, solid-body rotation is disfavored by surface enrichment observations of main sequence stars so far, so if confirmed by large-scale asteroseismic campaigns, the strong coupling mechanism should be effective only in the advanced phases of the evolution.

5.3. Mass Loss

Massive stars experience mass loss throughout their life, either as a thin and fast main-sequence wind, a thick and slow RSG wind, or a thick and very fast WR wind uncovering the stellar core. Luminous blue variables (LBVs) shed mass in episodic dramatic bursts, sometimes close to disruption. The fate of massive stars depends strongly on the mass loss they experience (Vanbeveren et al., 1998a,b; Meynet et al., 2015), and so does the type of supernova they will make (Georgy, 2012).

Mass loss is not explicitly modeled in 1D stellar evolution codes. Modelers rely on prescriptions to implement this very important process. Some prescriptions are empirical or semi-empirical, others are theoretical. The most common description of stellar mass loss is the radiatively-driven wind theory (Lucy and Solomon, 1970), with the CAK formalism from Castor et al. (1975). However, this driving seems to fail to describe the winds of advanced phases stars like RSG or WR. RSG winds show variations of more than 2 orders of magnitude for a given luminosity (van Loon et al., 2005; Mauron and Josselin, 2011). This scatter could come from the analysis being performed on field stars of mixed ages and masses: the relation between mass loss and luminosity seems much more straightforward when stars in clusters are observed (Beasor and Davies, 2016, 2018). Very recently, Kee et al. (2021) have proposed a relation between RSG mass loss and strong atmospheric turbulence. Beside a more or less steady wind, RSGs seem to undergo episodic mass-loss events, linked in one way or the other to dust production (van Loon et al., 2005), like we recently witnessed in the case of Betelgeuse (Levesque and Massey, 2020). Our difficulty as modelers is that we cannot include these particular events in the stellar modeling, hence we need to use averaged rates accounting for the total mass-loss budget of a star, steady and episodic flows altogether. WR winds also deviate from the pure CAK theory as they show a strong dependence on the Eddington factor ${\Gamma }_{\mathrm{\text{Edd}}}=\frac{\kappa L}{4\pi cGM}$, which seems to play a major role as the driver of the WR mass loss (Vink, 2006; Gräfener et al., 2011; Vink et al., 2011; Bestenlehner et al., 2014).

For a given location in the HR diagram, some overlapping prescriptions give very different results. Generally, observations give different mass-loss rates depending on the diagnostic line used. This has been pointing toward a problem of clumping in the wind (Najarro et al., 2011; Šurlan et al., 2013; Rauw et al., 2015). While accounting for clumping tends to reduce the mass loss inferred, the inclusion of light leakage (porosity) compensates in some cases this reduction (Oskinova et al., 2007; Sundqvist et al., 2014).

Beside the problem of clumping and porosity, low-luminosity late O-type dwarf stars present what has been called the "weak-wind problem": below a luminosity of log(L/L_⊙) ≃ 5.2, their observed mass-loss rates are orders of magnitude lower than predicted by theoretical mass-loss prescriptions (Martins et al., 2005; Marcolino et al., 2009; Najarro et al., 2011; Oskinova et al., 2011; Muijres et al., 2012). Recently, de Almeida et al. (2019) have shown that late O giants (luminosity class III) show the same trend as the dwarf (luminosity class V). The reason for this downshift in mass-loss rates below a given luminosity is still debated. Oskinova (2016) propose that most of the late O stars winds are in the hot gas phase, and hence accessible only through X-rays diagnostics. More recently Vilhu and Kallman (2019) have proposed that the weak-wind problem could be linked to a velocity porosity (vorocity, Owocki, 2014) in the wind stratification.

Although mass loss concerns the surface of a star, it can have some deep repercussions and actually modify the nucleosynthetic yields. If the mass loss during the main sequence is high, it has time to modify the structure of the star and its core mass, changing the conditions for nucleosynthesis in the subsequent advanced phases. If the mass loss in the advanced phases is high, it can remove parts of the star that will no longer be available for nucleosynthesis (hydrostatic shell burning or explosive nucleosynthesis) and hence change the yields. In the extreme case of WR stars, the He-burning phase ends with a star that is reduced to its naked core. The core cannot increase anymore since the H-burning shell was stripped off, and it can only decrease even more since mass loss can still remove some mass during the latest phases.

The radiative mass loss is dependent on the metallicity of the star (Ṁ ∝ Z^0.85), since metals offer the largest number of electron transitions. Note that the Z exponent is not firmly determined yet (Mokiem et al., 2007). Low-metallicity stars retain more mass and angular momentum than their high-Z counterparts. They are more prone to reach the critical velocity and lose mass mechanically in a decretion disk (Owocki, 2004; Krtička et al., 2011; Georgy et al., 2013b; Granada et al., 2013). This mechanism is thought to be the driver of the Be phenomenon: B-type stars presenting H_α emission lines that are supposed to come from a disk around the (more or less) rapidly rotating star (Secchi, 1866; Struve, 1931; Dachs et al., 1986). Rapidly-rotating low-metallicity massive stars are also supposed to be the progenitors of long soft GRBs (Yoon et al., 2006).

5.4. Binarity

Binarity is a game-changer for stellar evolution. It populates region of the HR diagram that single star populations cannot reach, and strongly changes the expected spectral outputs (Eldridge and Stanway, 2020). Most massive stars are born in multiple systems (Sana et al., 2008, 2009; Moe and Di Stefano, 2017). While single stars grids of models have to deal with a parameter space essentially of three parameters (mass, chemical composition, and rotation rate), binaries open a huge combination of mass ratios and separations. The distribution of orbital periods favors close binary systems and a uniform distribution of mass ratios (Sana et al., 2012; Moe and Di Stefano, 2017), which means that interactions between the components are very common. Analyses of spectral populations of external galaxies need to take the effect of binarity into account (Eldridge et al., 2008; Eldridge and Stanway, 2009, 2020).

Concerning the effects binarity has on stellar evolution, I refer the reader to the review by Langer (2012) for a detailed description. I will only summarize them here. The most basic modifications brought by binarity are linked to rotation and mass loss.

5.4.1. Rotation

A star in a binary system will tend to synchronize its spin to the orbital period, and this process will trigger tidal mixing (Zahn, 1977, 2008), dissipating the excess kinetic energy. The torque exerted at the surface is larger for large angular velocity differences (Ω − ω, with Ω the star's angular velocity and ω the orbital angular velocity), and for small separations a. According to Zahn (1977, 2008), the time needed to achieve synchronization is:

$\begin{array}{l}\frac{1}{t_{\text{sync}}}=-\frac{d}{dt}|\frac{2\left(\Omega -\omega \right)}{\omega }{|}^{-5/3}\\ =5·2^{5/3}{\left(\frac{GM}{R^3}\right)}^{1/2}\frac{M{R}^2}{I}{q}^2{\left(1+q\right)}^{5/6}{E}_2{\left(\frac{R}{a}\right)}^{17/2}\end{array}$

where $q=\frac{m}{M}$ is the ratio of the companion mass over the star's mass, I the inertia, and E₂ a parameter describing the coupling between the tidal potential and the gravity mode dissipating it in the radiative envelope of massive stars. We see that there is a strong dependence on the ratio between the star's radius and the semi-major axis $\frac{R}{a}$. It is expected that the binary components will synchronize before the orbit achieves circularization, so the time for circularization can be expressed supposing Ω = ω, as:

$\frac{1}{t_{\text{circ}}}=\frac{dlne}{dt}=\frac{21}{2}{\left(\frac{GM}{R^3}\right)}^{1/2}q{\left(1+q\right)}^{11/6}{E}_2{\left(\frac{R}{a}\right)}^{21/2}$

with e the eccentricity.

The internal tides increase the rotational mixing experienced by the star, magnifying the effects described in section 5.2. The strong mixing can in some cases keep the star extremely compact through quasi CHE, preventing the filling of its Roche lobe and the mass transfer that it would trigger (Song et al., 2016).

5.4.2. Mass Transfer

Binary components can either shed or receive mass through the filling of the Roche lobe, which radius can be approximated as $R_{\mathrm{\text{L}}}=a\frac{0.49q^{2/3}}{0.6q^{2/3}+ln\left(1+q^{1/3}\right)}$ (Eggleton, 1983). Their are three different cases of mass transfer episodes:

• case A when the mass transfer occurs while the primary is still on the main sequence. This requires very close binaries at birth;

• case B when the mass transfer occurs after the primary has left the main sequence;

• case C when it occurs after central He burning.

The component that is the donor experiences a strong mass and angular-momentum loss, while the receiver gains both mass and angular momentum, but the efficiency of the transfer on the gainer is usually limited either by the thermal response to the accretion (Ṁ_g ≤ M_g/τ_KH, with τ_KH as Equation 7, see Eldridge et al., 2008), or by the maximal amount of angular momentum the star can absorb before reaching the critical limit (Langer, 2012). It is not clear how the non-accreted mass is removed, maybe in the form of a circum-binary disk that will be later erased by radiation (Vanbeveren et al., 1998b; Langer, 2012). In case the angular-momentum criterion is used to modulate the accretion on the receiver, the efficiency of the accretion changes with time, early accretion episodes (case A) being more efficient than later ones. If the mass donor has experienced rotational mixing or evolutionary dredge-ups, the matter that is accreted by the mass gainer has a more heavy molecular weight than its own envelope. Some thermohaline mixing is then expected (Cox and Giuli, 1968; Kippenhahn et al., 1980; Bitzaraki et al., 2003).

Since the more massive stars evolve quicker than the less massive ones, it is usually the more massive (primary) component that starts shedding mass on the secondary, sometimes losing enough mass to invert the mass ratio, like in Algol-type systems. The evolution of the orbit of the binary depends critically on the mass ratio between the mass donor star and the mass gainer q = M_d/M_g (Siess et al., 2013):

$\begin{array}{ll}\frac{ȧ}{a}=2\frac{{\stackrel{\bullet }{J}}_{\text{orb}}}{J_{\text{orb}}}-2\left(\frac{{Ṁ}_{\text{d}}}{M_{\text{d}}}+\frac{{Ṁ}_{\text{g}}}{M_{\text{g}}}\right)+\frac{{Ṁ}_{\text{d}}+{Ṁ}_{\text{g}}}{M_{\text{d}}+M_{\text{g}}}+\frac{2eė}{1-e^2}& (9)\end{array}$

In the simple case of conservative mass transfer, we have ${\stackrel{\bullet }{J}}_{\mathrm{\text{orb}}}=0$, Ṁ_g = − Ṁ_d, and if we suppose the orbit to be circularized, we can rewrite Equation (9) as:

$\frac{ȧ}{a}=2\left(q-1\right)\frac{\stackrel{\bullet }{M_{\text{d}}}}{M_{\text{d}}}$

As long as the mass donor remains the more massive component (q > 1), the orbital separation tends to shrink (ȧ/a < 0 because the donor loses mass and hence $\stackrel{\bullet }{M_{\mathrm{\text{d}}}}<0$). When the mass ratio gets inverted and the mass gainer becomes more massive than the donor (q < 1), the separation increases (ȧ/a > 0), a minimum separation being reached when M_g = M_d.

It is usually considered that donors with a radiative envelope (as it is the case in case A mass transfer for massive stars) experience stable mass transfer because the radiative envelope settles on a smaller radius after the mass transfer. In contrast, convective envelopes tend to readjust to the same radius after the initial mass transfer, or even to expand, while the Roche lobe radius has decreased, so the mass transfer evolves into an unstable kind of runaway (Paczyński and Sienkiewicz, 1972). Note however that it has been shown that this is a too simplified picture, and that the adjustment of the envelope depends strongly on the donor's radius and the mass ratio (Podsiadlowski et al., 2002; Woods and Ivanova, 2011; Passy et al., 2012b; Pavlovskii et al., 2017). If an unstable mass transfer occurs, it is supposed to end in what is called a common-envelope (CE) phase. When this happens, the two components are dragged into a spiraling-in process, in which orbital energy is released (Livio, 1989). This energy might be sufficient to unbind the envelope, leaving a very tight system where the donor has become a naked core. It is not clear at all how the CE phase should be treated in binary models. Multi-D numerical simulations seem to indicate that it is difficult to really unbind the whole envelope (Ricker and Taam, 2008, 2012; Passy et al., 2012a; Ohlmann et al., 2016). In case the released orbital energy is not sufficient, the outcome is the merger of the two components, forming a rejuvenated rapidly-rotating single star (Schneider et al., 2019, 2020).

Mass transfer can alter the size of the core of the donor if it happens before the end of core He burning. Since the core mass defines the nucleosynthesis conditions of the advanced phases, it can have repercussions on the stellar yields. However, it has been shown that this effect is moderate when models of galactic chemical evolution include binaries (De Donder and Vanbeveren, 2002).

6. Discussion and perspectives

Stellar models are advanced numerical experiments, needing to describe a very complex physical object. They will be as good as the physics processes they include, and the way those processes are implemented. We saw that the most important processes for massive stars evolution are highly multi-dimensional, and are a challenge to implement in 1D stellar evolution codes. They come with all sorts of free parameters that need to be calibrated. One never knows whether the calibration will hold when they explore different mass or metallicity domains than the ones the calibration was performed on. These calibrations make the models to be only descriptive, their predictive nature is extremely uncertain.

Could we imagine that the twenty-first century stellar models would be fully 3D models, computed from birth to collapse with the high resolution needed to capture in a consistent way the complexity of turbulence and transport processes? Large state-of-the-art hydro simulations have 1536³ cells, and the computation of just 1000 seconds of carbon shell burning requires 10 million CPU-hours. The computation of a full star during its whole life on 1000 billions CPUs would last for 10 Gyr! So we are bound to 1D stellar models, and we need to take them into the 21st century.

The way to go comes from combining large-scale surveys (for statistical relevance), asteroseismic observations (for constraints on the internal conditions), and multi-D simulations (for constraints on the physical processes from first principles). With these strong observational constraints, and with recipes developed from hydro simulations, we can hope to improve the modeling of stars and lead them to a point where they can become predictive one day.

Hydro simulations have started to yield valuable recipes for convection, but they are still lacking for early phases like H or He burning. The long timescales involved and the necessity to include radiative transport are still a difficult hurdle to overcome. The 3D simulations have shown that convective penetration generates IGW that are able to transport both angular momentum and chemicals. Their implementation in massive stars modeling still needs to be attempted. Also the physics of rotation is still elapsing a complete ab initio 3D modeling. A few simulations of the complex but crucial phase of common envelope in binaries have been performed. More are needed before we will be able to derive prescriptions that can be used in 1D models or in population synthesis.

Dedicated simulations of the winds of hot stars are now coming with results that are much more in agreement with the observations (Sundqvist et al., 2019; Björklund et al., 2020). They need to be implemented in stellar evolution codes so that we can assess the changes they bring to the outcomes of stellar modeling.

On the observation side, constraints can be difficult to interpret, because of the high fraction of massive stars that are in binary systems and that have their evolution modified by binary interactions (Sana et al., 2012; de Mink et al., 2014). It has been proposed that the best single stars could be binaries with orbital separations wide enough for the components not to have been interacting strongly (de Mink et al., 2011). However, the high rate of hierarchical multiplicity in massive stars (Duchêne and Kraus, 2013; Moe and Di Stefano, 2017) does complicate the picture, since a wide binary could be composed of one or two close binary systems. Hierarchical multiplicity has been shown to affect strongly the evolution (Toonen et al., 2016).

On the asteroseismology side, the satellites CoRoT and Kepler have shown that extremely valuable informations can be retrieved with this technique. TESS has started harvesting very promising results, and PLATO will have extended observation durations. Unfortunately, both missions have large pixel sizes that are not suitable for crowded regions. There is a need for missions dedicated to high-resolution asteroseismic campaigns, like the HAYDN project (Miglio et al., 2019).

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author thanks Raphael Hirschi, Cyril Georgy, Patrick Eggenberger, and Georges Meynet for fruitful discussions. She is grateful to the referees who helped improving significantly this review. She acknowledges the STAREX grant from the ERC Horizon 2020 research and innovation programme (grant agreement No. 833925), and the COST Action ChETEC (CA 16117) supported by COST (European Cooperation in Science and Technology).

Footnotes

1. ^https://opalopacity.llnl.gov

2. ^http://opacities.osc.edu

3. ^η = 0 if the matter is made of species with A = 2Z.

4. ^Ω_crit is the critical angular momentum at which the centrifugal force counterbalances gravity.

References

Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016a). GW151226: observation of gravitational waves from a 22-solar-mass binary black hole coalescence. Phys. Rev. Lett. 116:241103. doi: 10.1103/PhysRevLett.116.241103

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016b). Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116:061102. doi: 10.1103/PhysRevLett.116.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017). GW170104: observation of a 50-solar-mass binary black hole coalescence at redshift 0.2. Phys. Rev. Lett. 118:221101. doi: 10.1103/PhysRevLett.118.221101

PubMed Abstract | CrossRef Full Text

Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., Adams, C., et al. (2020). Properties and astrophysical implications of the 150 M_⊙ binary black hole merger GW190521. Astrophys. J. Lett. 900:L13. doi: 10.3847/2041-8213/aba493

CrossRef Full Text | Google Scholar

Aerts, C. (2008). “Core overshoot and nonrigid internal rotation of massive stars: current status from asteroseismology,” in IAU Symposium, Vol. 250, eds F. Bresolin, P. A. Crowther, and J. Puls, 237.

Aerts, C., Bowman, D. M., Símon-Díaz, S., Buysschaert, B., Johnston, C., Moravveji, E., et al. (2018). K2 photometry and HERMES spectroscopy of the blue supergiant ρ Leo: rotational wind modulation and low-frequency waves. Mon. Not. R. Astron. Soc. 476:1234. doi: 10.1093/mnras/sty308

CrossRef Full Text | Google Scholar

Aerts, C., Mathis, S., and Rogers, T. M. (2019). Angular momentum transport in stellar interiors. Annu. Rev. Astron. Astrophys. 57:35. doi: 10.1146/annurev-astro-091918-104359

CrossRef Full Text | Google Scholar

Aerts, C., Molenberghs, G., Kenward, M. G., and Neiner, C. (2014). The surface nitrogen abundance of a massive star in relation to its oscillations, rotation, and magnetic field. Astrophys. J. 781:88. doi: 10.1088/0004-637X/781/2/88

CrossRef Full Text | Google Scholar

Aerts, C., Thoul, A., Daszyńska, J., Scuflaire, R., Waelkens, C., Dupret, M. A., et al. (2003). Asteroseismology of HD 129929: core overshooting and nonrigid rotation. Science 300:1926. doi: 10.1126/science.1084993

PubMed Abstract | CrossRef Full Text | Google Scholar

Aerts, C., Van Reeth, T., and Tkachenko, A. (2017). The interior angular momentum of core hydrogen burning stars from gravity-mode oscillations. Astrophys. J. Lett. 847:L7. doi: 10.3847/2041-8213/aa8a62

CrossRef Full Text | Google Scholar

Allan, A. P., Groh, J. H., Mehner, A., Smith, N., Boian, I., Farrell, E. J., et al. (2020). The possible disappearance of a massive star in the low-metallicity galaxy PHL 293B. Mon. Not. R. Astron. Soc. 496:1902. doi: 10.1093/mnras/staa1629

CrossRef Full Text | Google Scholar

Andrassy, R., Herwig, F., Woodward, P., and Ritter, C. (2020). 3D hydrodynamic simulations of C ingestion into a convective O shell. Mon. Not. R. Astron. Soc. 491:972. doi: 10.1093/mnras/stz2952

CrossRef Full Text | Google Scholar

Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 656:3.

Google Scholar

Arnett, D. (1996). Supernovae and Nucleosynthesis: An Investigation of the History of Matter from the Big Bang to the Present. Princeton University Press.

Google Scholar

Arnett, W. D., Meakin, C., Hirschi, R., Cristini, A., Georgy, C., Campbell, S., et al. (2019). 3D Simulations and MLT. I. Renzini's Critique. Astrophys. J. 882:18. doi: 10.3847/1538-4357/ab21d9

CrossRef Full Text | Google Scholar

Arnett, W. D., Meakin, C., Viallet, M., Campbell, S. W., Lattanzio, J. C., and Mocák, M. (2015). Beyond mixing-length theory: a step toward 321D. Astrophys. J. 809:30. doi: 10.1088/0004-637X/809/1/30

CrossRef Full Text | Google Scholar

Austin, S. M. (2005). Making carbon in stars. Nucl. Phys. A 758:375. doi: 10.1016/j.nuclphysa.2005.05.178

CrossRef Full Text | Google Scholar

Barkat, Z., Rakavy, G., and Sack, N. (1967). Dynamics of supernova explosion resulting from pair formation. Phys. Rev. Lett. 18:379. doi: 10.1103/PhysRevLett.18.379

CrossRef Full Text | Google Scholar

Beasor, E. R., and Davies, B. (2016). The evolution of red supergiants to supernova in NGC 2100. Mon. Not. R. Astron. Soc. 463:1269. doi: 10.1093/mnras/stw2054

CrossRef Full Text | Google Scholar

Beasor, E. R., and Davies, B. (2018). The evolution of red supergiant mass-loss rates. Mon. Not. R. Astron. Soc. 475:55. doi: 10.1093/mnras/stx3174

CrossRef Full Text | Google Scholar

Beaudet, G., Petrosian, V., and Salpeter, E. E. (1967). Energy losses due to neutrino processes. Astrophys. J. 150:979.

Google Scholar

Beck, P. G., Montalban, J., Kallinger, T., De Ridder, J., Aerts, C., García, R. A., et al. (2012). Fast core rotation in red-giant stars as revealed by gravity-dominated mixed modes. Nature 481, 55–57. doi: 10.1038/nature10612

PubMed Abstract | CrossRef Full Text | Google Scholar

Belczynski, K., Heger, A., Gladysz, W., Ruiter, A. J., Woosley, S., Wiktorowicz, G., et al. (2016). The effect of pair-instability mass loss on black-hole mergers. Astron. Astrophys. 594:A97. doi: 10.1051/0004-6361/201628980

CrossRef Full Text | Google Scholar

Bennett, M. E., Hirschi, R., Pignatari, M., Diehl, S., Fryer, C., Herwig, F., et al. (2012). The effect of ¹²C +¹²C rate uncertainties on the evolution and nucleosynthesis of massive stars. Mon. Not. R. Astron. Soc. 420:3047. doi: 10.1111/j.1365-2966.2012.20193.x

CrossRef Full Text | Google Scholar

Bertelli, G., Girardi, L., Marigo, P., and Nasi, E. (2008). Scaled solar tracks and isochrones in a large region of the Z-Y plane. I. From the ZAMS to the TP-AGB end for 0.15-2.5 M_⊙ stars. Astron. Astrophys. 484:815. doi: 10.1051/0004-6361:20079165

CrossRef Full Text | Google Scholar

Bestenlehner, J. M., Gräfener, G., Vink, J. S., Najarro, F., de Koter, A., Sana, H., et al. (2014). The VLT-FLAMES Tarantula Survey. XVII. Physical and wind properties of massive stars at the top of the main sequence. Astron. Astrophys. 570:A38. doi: 10.1051/0004-6361/201423643

CrossRef Full Text | Google Scholar

Bitzaraki, O. M., Tout, C. A., and Rovithis-Livaniou, H. (2003). Thermohaline-mixing – binary evolution. New Astron. 8:23. doi: 10.1016/S1384-1076(02)00199-9

CrossRef Full Text | Google Scholar

Björklund, R., Sundqvist, J. O., Puls, J., and Najarro, F. (2020). New predictions for radiation-driven, steady-state mass-loss and wind-momentum from hot, massive stars II. A grid of O-type stars in the Galaxy and the Magellanic Clouds. arXiv preprints arXiv:2008.06066. doi: 10.1051/0004-6361/202038384

CrossRef Full Text | Google Scholar

Blomme, R., Mahy, L., Catala, C., Cuypers, J., Gosset, E., Godart, M., et al. (2011). Variability in the CoRoT photometry of three hot O-type stars. HD 46223, HD 46150, and HD 46966. Astron. Astrophys. 533:A4. doi: 10.1051/0004-6361/201116949

CrossRef Full Text | Google Scholar

Blondin, J. M., and Mezzacappa, A. (2007). Pulsar spins from an instability in the accretion shock of supernovae. Nature 445:58. doi: 10.1038/nature05428

PubMed Abstract | CrossRef Full Text | Google Scholar

Böhm-Vitense, E. (1958). Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. ZA 46:108.

Google Scholar

Bowman, D. M., Aerts, C., Johnston, C., Pedersen, M. G., Rogers, T. M., Edelmann, P. V. F., et al. (2019a). Photometric detection of internal gravity waves in upper main-sequence stars. I. Methodology and application to CoRoT targets. Astron. Astrophys. 621:A135. doi: 10.1051/0004-6361/201833662

CrossRef Full Text | Google Scholar

Bowman, D. M., Burssens, S., Pedersen, M. G., Johnston, C., Aerts, C., Buysschaert, B., Michielsen, M., et al. (2019b). Low-frequency gravity waves in blue supergiants revealed by high-precision space photometry. Nat. Astron. 3:760. doi: 10.1038/s41550-019-0768-1

CrossRef Full Text | Google Scholar

Bressan, A., Marigo, P., Girardi, L., Salasnich, B., Dal Cero, C., Rubele, S., et al. (2012). PARSEC: stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 427:127. doi: 10.1111/j.1365-2966.2012.21948.x

CrossRef Full Text | Google Scholar

Briquet, M., Aerts, C., Baglin, A., Nieva, M. F., Degroote, P., Przybilla, N., et al. (2011). An asteroseismic study of the O9V star HD 46202 from CoRoT space-based photometry. Astron. Astrophys. 527:A112. doi: 10.1051/0004-6361/201015690

CrossRef Full Text | Google Scholar

Briquet, M., Morel, T., Thoul, A., Scuflaire, R., Miglio, A., Montalbán, J., et al. (2007). An asteroseismic study of the β Cephei star θ Ophiuchi: constraints on global stellar parameters and core overshooting. Mon. Not. R. Astron. Soc. 381:1482. doi: 10.1111/j.1365-2966.2007.12142.x

CrossRef Full Text | Google Scholar

Briquet, M., Neiner, C., Aerts, C., Morel, T., Mathis, S., Reese, D. R., et al. (2012). Multisite spectroscopic seismic study of the β Cep star V2052 Ophiuchi: inhibition of mixing by its magnetic field. Mon. Not. R. Astron. Soc. 427:483. doi: 10.1111/j.1365-2966.2012.21933.x

CrossRef Full Text | Google Scholar

Brott, I., de Mink, S. E., Cantiello, M., Langer, N., de Koter, A., Evans, C. J., et al. (2011a). Rotating massive main-sequence stars. I. Grids of evolutionary models and isochrones. Astron. Astrophys. 530:A115. doi: 10.1051/0004-6361/201016113

CrossRef Full Text | Google Scholar

Brott, I., Evans, C. J., Hunter, I., de Koter, A., Langer, N., Dufton, P. L., et al. (2011b). Rotating massive main-sequence stars. II. Simulating a population of LMC early B-type stars as a test of rotational mixing. Astron. Astrophys. 530:A116. doi: 10.1051/0004-6361/201016114

CrossRef Full Text | Google Scholar

Buras, R., Rampp, M., Janka, H. T., and Kifonidis, K. (2006). Two-dimensional hydrodynamic core-collapse supernova simulations with spectral neutrino transport. I. Numerical method and results for a 15 M⊙ star. Astron. Astrophys. 447:1049. doi: 10.1051/0004-6361:20053783

CrossRef Full Text | Google Scholar

Burrows, A., and Goshy, J. (1993). A theory of supernova explosions. Astrophys. J. Lett. 416:L75.

Google Scholar

Burrows, A., Livne, E., Dessart, L., Ott, C. D., and Murphy, J. (2006). A new mechanism for core-collapse supernova explosions. Astrophys. J. 640:878. doi: 10.1086/500174

CrossRef Full Text | Google Scholar

Buysschaert, B., Aerts, C., Bloemen, S., Debosscher, J., Neiner, C., Briquet, M., et al. (2015). Kepler's first view of O-star variability: K2 data of five O stars in Campaign 0 as a proof of concept for O-star asteroseismology. Mon. Not. R. Astron. Soc. 453:89. doi: 10.1093/mnras/stv1572

CrossRef Full Text | Google Scholar

Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., and Paxton, B. (2014). Angular momentum transport within evolved low-mass stars. Astrophys. J. 788:93. doi: 10.1088/0004-637X/788/1/93

CrossRef Full Text | Google Scholar

Canuto, V. M. (1992). Turbulent convection with overshooting: reynolds stress approach. Astrophys. J. 392:218.

Google Scholar

Canuto, V. M. (2011a). Stellar mixing. I. Formalism. Astron. Astrophys. 528:A76. doi: 10.1051/0004-6361/201014447

CrossRef Full Text | Google Scholar

Canuto, V. M. (2011b). Stellar mixing. II. Double diffusion processes. Astron. Astrophys. 528:A77. doi: 10.1051/0004-6361/201014448

CrossRef Full Text | Google Scholar

Canuto, V. M. (2011c). Stellar mixing. III. The case of a passive tracer. Astron. Astrophys. 528:A78. doi: 10.1051/0004-6361/201015372

CrossRef Full Text | Google Scholar

Canuto, V. M. (2011d). Stellar Mixing. IV. The angular momentum problem. Astron. Astrophys. 528:A79. doi: 10.1051/0004-6361/201014449

CrossRef Full Text | Google Scholar

Canuto, V. M. (2011e). Stellar mixing. V. Overshooting. Astron. Astrophys. 528:A80. doi: 10.1051/0004-6361/201014450

CrossRef Full Text | Google Scholar

Castor, J. I., Abbott, D. C., and Klein, R. I. (1975). Radiation-driven winds in of stars. Astrophys. J. 195:157.

Google Scholar

Castro, N., Fossati, L., Langer, N., Simón-Díaz, S., Schneider, F. R. N., and Izzard, R. G. (2014). The spectroscopic Hertzsprung-Russell diagram of Galactic massive stars. Astron. Astrophys. 570:L13. doi: 10.1051/0004-6361/201425028

CrossRef Full Text | Google Scholar

Caughlan, G. R., and Fowler, W. A. (1988). Thermonuclear reaction rates V. Atom. Data Nucl. Data Tables 40:283.

Google Scholar

Caughlan, G. R., Fowler, W. A., Harris, M. J., and Zimmerman, B. A. (1985). Tables of thermonuclear reaction rates for low-mass nuclei (1 &le Z < = 14). Atom. Data Nucl. Data Tables 32:197.

Google Scholar

Chaboyer, B., and Zahn, J.-P. (1992). Effect of horizontal turbulent diffusion on transport by meridional circulation. Astron. Astrophys. 253:173.

Google Scholar

Chatzopoulos, E., and Wheeler, J. C. (2012). Effects of rotation on the minimum mass of primordial progenitors of pair-instability supernovae. Astrophys. J. 748:42. doi: 10.1088/0004-637X/748/1/42

CrossRef Full Text | Google Scholar

Chen, K.-J., Woosley, S., Heger, A., Almgren, A., and Whalen, D. J. (2014). Two-dimensional simulations of pulsational pair-instability supernovae. Astrophys. J. 792:28. doi: 10.1088/0004-637X/792/1/28

CrossRef Full Text | Google Scholar

Chiappini, C., Frischknecht, U., Meynet, G., Hirschi, R., Barbuy, B., Pignatari, M., et al. (2011). Imprints of fast-rotating massive stars in the Galactic Bulge. Nature 472:454. doi: 10.1038/nature10000

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiavassa, A., Plez, B., Josselin, E., and Freytag, B. (2009). Radiative hydrodynamics simulations of red supergiant stars. I. interpretation of interferometric observations. Astron. Astrophys. 506:1351. doi: 10.1051/0004-6361/200911780

CrossRef Full Text | Google Scholar

Chieffi, A., and Limongi, M. (2002). The explosive yields produced by the first generation of core collapse supernovae and the chemical composition of extremely metal poor stars. Astrophys. J. 577:281. doi: 10.1086/342170

CrossRef Full Text | Google Scholar

Chieffi, A., and Limongi, M. (2004). Explosive yields of massive stars from Z = 0 to Z = Z_⊙. Astrophys. J. 608:405. doi: 10.1086/392523

CrossRef Full Text | Google Scholar

Chieffi, A., and Limongi, M. (2013). Pre-supernova evolution of rotating solar metallicity stars in the mass range 13-120 M _⊙ and their explosive yields. Astrophys. J. 764:21. doi: 10.1088/0004-637X/764/1/21

CrossRef Full Text | Google Scholar

Chieffi, A., and Limongi, M. (2020). The presupernova core mass - radius relation of massive stars: understanding its formation and evolution. Astrophys. J. 890:43. doi: 10.3847/1538-4357/ab6739

CrossRef Full Text | Google Scholar

Choi, J., Dotter, A., Conroy, C., Cantiello, M., Paxton, B., and Johnson, B. D. (2016). Mesa isochrones and stellar tracks (MIST). I. Solar-scaled models. Astrophys. J. 823:102. doi: 10.3847/0004-637X/823/2/102

CrossRef Full Text | Google Scholar

Choplin, A., Ekström, S., Meynet, G., Maeder, A., Georgy, C., and Hirschi, R. (2017a). Pre-supernova mixing in CEMP-no source stars. Astron. Astrophys. 605:A63. doi: 10.1051/0004-6361/201630182

CrossRef Full Text | Google Scholar

Choplin, A., Hirschi, R., Meynet, G., and Ekström, S. (2017b). Are some CEMP-s stars the daughters of spinstars? Astron. Astrophys. 607:L3. doi: 10.1051/0004-6361/201731948

CrossRef Full Text | Google Scholar

Claret, A., and Torres, G. (2016). The dependence of convective core overshooting on stellar mass. Astron. Astrophys. 592:A15. doi: 10.1051/0004-6361/201628779

CrossRef Full Text | Google Scholar

Clarkson, O., and Herwig, F. (2021). Convective H-He interactions in massive population III stellar evolution models. Mon. Not. R. Astron. Soc. 500:2685. doi: 10.1093/mnras/staa3328

CrossRef Full Text | Google Scholar

Collins, C., Müller, B., and Heger, A. (2018). Properties of convective oxygen and silicon burning shells in supernova progenitors. Mon. Not. R. Astron. Soc. 473:1695. doi: 10.1093/mnras/stx2470

CrossRef Full Text | Google Scholar

Costa, G., Bressan, A., Mapelli, M., Marigo, P., Iorio, G., and Spera, M. (2020). Formation of GW190521 from stellar evolution: the impact of the hydrogen-rich envelope, dredge-up and ¹²C(α, γ)¹⁶O rate on the pair-instability black hole mass gap. arXiv preprints arXiv:2010.02242. doi: 10.1093/mnras/staa3916

CrossRef Full Text | Google Scholar

Côté, B., Jones, S., Herwig, F., and Pignatari, M. (2020). Chromium nucleosynthesis and silicon-carbon shell mergers in massive stars. Astrophys. J. 892:57. doi: 10.3847/1538-4357/ab77ac

CrossRef Full Text | Google Scholar

Couch, S. M., Chatzopoulos, E., Arnett, W. D., and Timmes, F. X. (2015). The three-dimensional evolution to core collapse of a massive star. Astrophys. J. Lett. 808:L21. doi: 10.1088/2041-8205/808/1/L21

CrossRef Full Text | Google Scholar

Cox, J. P., and Giuli, R. T. (1968). Principles of stellar structure. New York, NY: Gordon & Breach.

Google Scholar

Cristini, A., Hirschi, R., Meakin, C., Arnett, D., Georgy, C., and Walkington, I. (2019). Dependence of convective boundary mixing on boundary properties and turbulence strength. Mon. Not. R. Astron. Soc. 484:4645. doi: 10.1093/mnras/stz312

CrossRef Full Text | Google Scholar

Cristini, A., Meakin, C., Hirschi, R., Arnett, D., Georgy, C., Viallet, M., et al. (2017). 3D hydrodynamic simulations of carbon burning in massive stars. Mon. Not. R. Astron. Soc. 471, 279–300. doi: 10.1093/mnras/stx1535

CrossRef Full Text | Google Scholar

Crockett, R. M., Eldridge, J. J., Smartt, S. J., Pastorello, A., Gal-Yam, A., Fox, D. B., et al. (2008). The type IIb SN 2008ax: the nature of the progenitor. Mon. Not. R. Astron. Soc. 391:L5. doi: 10.1111/j.1745-3933.2008.00540.x

CrossRef Full Text | Google Scholar

Curtis, S., Ebinger, K., Fröhlich, C., Hempel, M., Perego, A., Liebendörfer, M., et al. (2019). PUSHing core-collapse supernovae to explosions in spherical symmetry. III. Nucleosynthesis yields. Astrophys. J. 870:2. doi: 10.3847/1538-4357/aae7d2

CrossRef Full Text | Google Scholar

Dachs, J., Hanuschik, R., Kaiser, D., and Rohe, D. (1986). Geometry of rotating envelopes around Be stars derived from comparative analysis of H-alpha emission line profiles. Astron. Astrophys. 159:276.

Google Scholar

Davis, A., Jones, S., and Herwig, F. (2019). Convective boundary mixing in a post-He core burning massive star model. Mon. Not. R. Astron. Soc. 484:3921. doi: 10.1093/mnras/sty3415

CrossRef Full Text | Google Scholar

de Almeida, E. S. G., Marcolino, W. L. F., Bouret, J. C., and Pereira, C. B. (2019). Probing the weak wind phenomenon in Galactic O-type giants. Astron. Astrophys. 628:A36. doi: 10.1051/0004-6361/201834266

CrossRef Full Text | Google Scholar

De Donder, E., and Vanbeveren, D. (2002). The chemical evolution of the solar neighbourhood: the effect of binaries. New Astron. 7:55. doi: 10.1016/S1384-1076(01)00090-2

CrossRef Full Text | Google Scholar

de Mink, S. E., Langer, N., and Izzard, R. G. (2011). Binaries are the best single stars. Bull. Soc. R. Sci. Liege 80:543.

Google Scholar

de Mink, S. E., Sana, H., Langer, N., Izzard, R. G., and Schneider, F. R. N. (2014). The incidence of stellar mergers and mass gainers among massive stars. Astrophys. J. 782:7. doi: 10.1088/0004-637X/782/1/7

CrossRef Full Text | Google Scholar

deBoer, R. J., Görres, J., Wiescher, M., Azuma, R. E., Best, A., Brune, C. R., et al. (2017). The ¹²C(α, γ )¹⁶O reaction and its implications for stellar helium burning. Rev. Mod. Phys. 89:035007. doi: 10.1103/RevModPhys.89.035007

CrossRef Full Text | Google Scholar

Decressin, T., Mathis, S., Palacios, A., Siess, L., Talon, S., Charbonnel, C., et al. (2009). Diagnoses to unravel secular hydrodynamical processes in rotating main sequence stars. Astron. Astrophys. 495:271. doi: 10.1051/0004-6361:200810665

CrossRef Full Text | Google Scholar

Deheuvels, S., Brandão, I., Silva Aguirre, V., Ballot, J., Michel, E., Cunha, M. S., et al. (2016). Measuring the extent of convective cores in low-mass stars using Kepler data: toward a calibration of core overshooting. Astron. Astrophys. 589:A93. doi: 10.1051/0004-6361/201527967

CrossRef Full Text | Google Scholar

Deheuvels, S., Doğan, G., Goupil, M. J., Appourchaux, T., Benomar, O., Bruntt, H., et al. (2014). Seismic constraints on the radial dependence of the internal rotation profiles of six Kepler subgiants and young red giants. Astron. Astrophys. 564:A27. doi: 10.1051/0004-6361/201322779

CrossRef Full Text | Google Scholar

den Hartogh, J. W., Eggenberger, P., and Deheuvels, S. (2020). Asteroseismology of evolved stars to constrain the internal transport of angular momentum. III. Using the rotation rates of intermediate-mass stars to test the Fuller-formalism. Astron. Astrophys. 634:L16. doi: 10.1051/0004-6361/202037568

CrossRef Full Text | Google Scholar

Deng, L., Xiong, D. R., and Chan, K. L. (2006). An anisotropic nonlocal convection theory. Astrophys. J., 643:426. doi: 10.1086/502707

CrossRef Full Text | Google Scholar

Denissenkov, P. A., Herwig, F., Bildsten, L., and Paxton, B. (2013). MESA models of classical nova outbursts: the multicycle evolution and effects of convective boundary mixing. Astrophys. J. 762:8. doi: 10.1088/0004-637X/762/1/8

CrossRef Full Text | Google Scholar

Dessart, L., Hillier, D. J., Waldman, R., and Livne, E. (2013). Type II-Plateau supernova radiation: dependences on progenitor and explosion properties. Mon. Not. R. Astron. Soc. 433:1745. doi: 10.1093/mnras/stt861

CrossRef Full Text | Google Scholar

Duchêne, G., and Kraus, A. (2013). Stellar multiplicity. Annu. Rev. Astron. Astrophys. 51, 269–310. doi: 10.1146/annurev-astro-081710-102602

CrossRef Full Text | Google Scholar

Dufton, P. L., Thompson, A., Crowther, P. A., Evans, C. J., Schneider, F. R. N., de Koter, A., et al. (2018). The VLT-FLAMES Tarantula Survey. XXVIII. Nitrogen abundances for apparently single dwarf and giant B-type stars with small projected rotational velocities. Astron. Astrophys. 615:A101. doi: 10.1051/0004-6361/201732440

CrossRef Full Text | Google Scholar

Dupret, M.-A., Thoul, A., Scuflaire, R., Daszyńska-Daszkiewicz, J., Aerts, C., Bourge, P.-O., et al. (2004). Asteroseismology of the β Cep star HD 129929. II. Seismic constraints on core overshooting, internal rotation and stellar parameters. Astron. Astrophys. 415:251. doi: 10.1051/0004-6361:20034143

PubMed Abstract | CrossRef Full Text | Google Scholar

Dziembowski, W. A., and Pamyatnykh, A. A. (2008). The two hybrid B-type pulsators: ν Eridani and 12 Lacertae. Mon. Not. R. Astron. Soc. 385:2061. doi: 10.1111/j.1365-2966.2008.12964.x

CrossRef Full Text | Google Scholar

Eddington, A. S. (1916). On the radiative equilibrium of the stars. Mon. Not. R. Astron. Soc. 77:16.

Google Scholar

Eddington, A. S. (1917). On the radiative equilibrium of the stars. Mon. Not. R. Astron. Soc. 77:596.

Google Scholar

Eddington, A. S. (1918). On the conditions in the interior of a star. Astrophys. J. 48:205.

Google Scholar

Eddington, A. S. (1925). Circulating currents in rotating stars. Observatory 48:73.

Google Scholar

Edelmann, P. V. F., Ratnasingam, R. P., Pedersen, M. G., Bowman, D. M., Prat, V., and Rogers, T. M. (2019). Three-dimensional Simulations of Massive Stars. I. Wave Generation and Propagation. Astrophys. J. 876:4. doi: 10.3847/1538-4357/ab12df

CrossRef Full Text | Google Scholar

Edelmann, P. V. F., Röpke, F. K., Hirschi, R., Georgy, C., and Jones, S. (2017). Testing a one-dimensional prescription of dynamical shear mixing with a two-dimensional hydrodynamic simulation. Astron. Astrophys. 604:A25. doi: 10.1051/0004-6361/201629873

CrossRef Full Text | Google Scholar

Edmunds, M. G., and Pagel, B. E. J. (1978). Nitrogen synthesis and the “age” of galaxies. Mon. Not. R. Astron. Soc. 185, 77–80.

Google Scholar

Eggenberger, P., Deheuvels, S., Miglio, A., Ekström, S., Georgy, C., Meynet, G., et al. (2019a). Asteroseismology of evolved stars to constrain the internal transport of angular momentum. I. Efficiency of transport during the subgiant phase. Astron. Astrophys. 621:A66. doi: 10.1051/0004-6361/201833447

CrossRef Full Text | Google Scholar

Eggenberger, P., den Hartogh, J. W., Buldgen, G., Meynet, G., Salmon, S. J. A. J., and Deheuvels, S. (2019b). Asteroseismology of evolved stars to constrain the internal transport of angular momentum. II. Test of a revised prescription for transport by the Tayler instability. Astron. Astrophys. 631:L6. doi: 10.1051/0004-6361/201936348

CrossRef Full Text | Google Scholar

Eggenberger, P., Lagarde, N., Miglio, A., Montalbán, J., Ekström, S., Georgy, C., et al. (2017). Constraining the efficiency of angular momentum transport with asteroseismology of red giants: the effect of stellar mass. Astron. Astrophys. 599:A18. doi: 10.1051/0004-6361/201629459

CrossRef Full Text | Google Scholar

Eggenberger, P., Montalbán, J., and Miglio, A. (2012). Angular momentum transport in stellar interiors constrained by rotational splittings of mixed modes in red giants. Astron. Astrophys. 544:L4. doi: 10.1051/0004-6361/201219729

CrossRef Full Text | Google Scholar

Eggleton, P. P. (1983). Approximations to the radii of Roche lobes. Astrophys. J. 268:368.

Google Scholar

Eichler, M., Nakamura, K., Takiwaki, T., Kuroda, T., Kotake, K., Hempel, M., et al. (2018). Nucleosynthesis in 2D core-collapse supernovae of 11.2 and 17.0 M_⊙ progenitors: implications for Mo and Ru production. J. Phys. G Nucl. Phys. 45:014001. doi: 10.1088/1361-6471/aa8891

CrossRef Full Text | Google Scholar

Ekström, S., Georgy, C., Eggenberger, P., Meynet, G., Mowlavi, N., Wyttenbach, A., et al. (2012). Grids of stellar models with rotation. I. Models from 0.8 to 120 M_⊙ at solar metallicity (Z = 0.014). Astron. Astrophys. 537:A146. doi: 10.1051/0004-6361/201117751

CrossRef Full Text | Google Scholar

Ekström, S., Meynet, G., Chiappini, C., Hirschi, R., and Maeder, A. (2008). Effects of rotation on the evolution of primordial stars. Astron. Astrophys. 489:685. doi: 10.1051/0004-6361:200809633

CrossRef Full Text | Google Scholar

El Eid, M. F., and Langer, N. (1986). The evolution of very luminous stars. II. Pair creation supernova in massive Wolf-Rayet stars. Astron. Astrophys. 167:274.

Google Scholar

El Eid, M. F. Meyer, B. S. and The L. S. (2004). Evolution of massive stars up to the end of central oxygen burning. Astrophys. J. 611:452. doi: 10.1086/422162

CrossRef Full Text | Google Scholar

El Eid, M. F. The, L. S. and Meyer B. S. (2009). Massive stars: input physics and stellar models. Space Sci. Rev. 147, 1–29. doi: 10.1007/s11214-009-9517-6

CrossRef Full Text | Google Scholar

Eldridge, J. J., Izzard, R. G., and Tout, C. A. (2008). The effect of massive binaries on stellar populations and supernova progenitors. Mon. Not. R. Astron. Soc. 384:1109. doi: 10.1111/j.1365-2966.2007.12738.x

CrossRef Full Text | Google Scholar

Eldridge, J. J., and Stanway, E. R. (2009). Spectral population synthesis including massive binaries. Mon. Not. R. Astron. Soc. 400:1019. doi: 10.1111/j.1365-2966.2009.15514.x

CrossRef Full Text | Google Scholar

Eldridge, J. J., and Stanway, E. R. (2020). Population and spectral synthesis: it doesn't work without binaries. arXiv preprints arXiv:2005.11883.

Google Scholar

Eldridge, J. J., and Tout, C. A. (2004). The progenitors of core-collapse supernovae. Mon. Not. R. Astron. Soc. 353:87. doi: 10.1111/j.1365-2966.2004.08041.x

CrossRef Full Text | Google Scholar

Farmer, R., Fields, C. E., Petermann, I., Dessart, L., Cantiello, M., Paxton, B., et al. (2016). On variations of pre-supernova model properties. Astrophys. J. Suppl. 227:22. doi: 10.3847/1538-4365/227/2/22

CrossRef Full Text | Google Scholar

Farmer, R., Renzo, M., de Mink, S., Fishbach, M., and Justham, S. (2020). Constraints from gravitational wave detections of binary black hole mergers on the ¹²C(α, γ)¹⁶O rate. arXiv preprints arXiv:2006.06678. doi: 10.3847/2041-8213/abbadd

CrossRef Full Text | Google Scholar

Farrell, E. J., Groh, J. H., Meynet, G., and Eldridge, J. J. (2020). The uncertain masses of progenitors of core-collapse supernovae and direct-collapse black holes. Mon. Not. R. Astron. Soc. 494:L53. doi: 10.1093/mnrasl/slaa035

CrossRef Full Text | Google Scholar

Foglizzo, T. (2002). Non-radial instabilities of isothermal Bondi accretion with a shock: vortical-acoustic cycle vs. post-shock acceleration. Astron. Astrophys. 392:353. doi: 10.1051/0004-6361:20020912

CrossRef Full Text | Google Scholar

Freytag, B., and Höfner, S. (2008). Three-dimensional simulations of the atmosphere of an AGB star. Astron. Astrophys. 483:571. doi: 10.1051/0004-6361:20078096

CrossRef Full Text | Google Scholar

Freytag, B., Ludwig, H. G., and Steffen, M. (1996). Hydrodynamical models of stellar convection. The role of overshoot in DA white dwarfs, A-type stars, and the Sun. Astron. Astrophys. 313:497.

Google Scholar

Frischknecht, U., Hirschi, R., Pignatari, M., Maeder, A., Meynet, G., Chiappini, C., et al. (2016). s-process production in rotating massive stars at solar and low metallicities. Mon. Not. R. Astron. Soc. 456:1803. doi: 10.1093/mnras/stv2723

CrossRef Full Text | Google Scholar

Frischknecht, U., Hirschi, R., and Thielemann, F.-K. (2012). Non-standard s-process in low metallicity massive rotating stars. Astron. Astrophys. 538:L2. doi: 10.1051/0004-6361/201117794

CrossRef Full Text | Google Scholar

Fruet, G., Courtin, S., Heine, M., Jenkins, D. G., Adsley, P., Brown, A., et al. (2020). Advances in the direct study of carbon burning in massive stars. Phys. Rev. Lett. 124:192701. doi: 10.1103/PhysRevLett.124.192701

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuller, J., Cantiello, M., Lecoanet, D., and Quataert, E. (2015). The spin rate of pre-collapse stellar cores: wave-driven angular momentum transport in massive stars. Astrophys. J. 810:101. doi: 10.1088/0004-637X/810/2/101

CrossRef Full Text | Google Scholar

Fuller, J., Lecoanet, D., Cantiello, M., and Brown, B. (2014). Angular momentum transport via internal gravity waves in evolving stars. Astrophys. J. 796:17. doi: 10.1088/0004-637X/796/1/17

CrossRef Full Text | Google Scholar

Fuller, J., Piro, A. L., and Jermyn, A. S. (2019). Slowing the spins of stellar cores. Mon. Not. R. Astron. Soc. 485:3661. doi: 10.1093/mnras/stz514

CrossRef Full Text | Google Scholar

Gabriel, M., and Belkacem, K. (2018). A non-local mixing-length theory able to compute core overshooting. Astron. Astrophys. 612:A21. doi: 10.1051/0004-6361/201731835

CrossRef Full Text | Google Scholar

Gabriel, M., Noels, A., Montalbán, J., and Miglio, A. (2014). Proper use of Schwarzschild Ledoux criteria in stellar evolution computations. Astron. Astrophys. 569:A63. doi: 10.1051/0004-6361/201423442

CrossRef Full Text | Google Scholar

Garcia, J. R., and Mellado, J. P. (2014). The two-Layer structure of the entrainment zone in the convective boundary layer. J. Atmos. Sci. 71:1935. doi: 10.1175/JAS-D-13-0148.1

CrossRef Full Text | Google Scholar

García-Berro, E., Ritossa, C., and Iben Icko, J. (1997). On the evolution of stars that form electron-degenerate cores processed by carbon burning. III. The inward propagation of a carbon-burning flame and other properties of a 9 M_⊙ model star. Astrophys. J. 485:765.

Google Scholar

Gasques, L. R., Brown, E. F., Chieffi, A., Jiang, C. L., Limongi, M., Rolfs, C., et al. (2007). Implications of low-energy fusion hindrance on stellar burning and nucleosynthesis. Phys. Rev. C 76:035802. doi: 10.1103/PhysRevC.76.035802

CrossRef Full Text | Google Scholar

Georgy, C. (2012). Yellow supergiants as supernova progenitors: an indication of strong mass loss for red supergiants? Astron. Astrophys. 538:L8. doi: 10.1051/0004-6361/201118372

CrossRef Full Text | Google Scholar

Georgy, C., Ekström, S., Eggenberger, P., Meynet, G., Haemmerlé, L., Maeder, A., et al. (2013a). Grids of stellar models with rotation. III. Models from 0.8 to 120 M_⊙ at a metallicity Z = 0.002. Astron. Astrophys. 558:A103. doi: 10.1051/0004-6361/201322178

CrossRef Full Text | Google Scholar

Georgy, C., Ekström, S., Granada, A., Meynet, G., Mowlavi, N., Eggenberger, P., et al. (2013b). Populations of rotating stars. I. Models from 1.7 to 15 M_⊙ at Z = 0.014, 0.006, and 0.002 with Ω/Ω_crit between 0 and 1. Astron. Astrophys. 553:A24. doi: 10.1051/0004-6361/201220558

CrossRef Full Text | Google Scholar

Georgy, C., Saio, H., and Meynet, G. (2014). The puzzle of the CNO abundances of α Cygni variables resolved by the Ledoux criterion. Mon. Not. R. Astron. Soc. 439:L6. doi: 10.1093/mnrasl/slt165

CrossRef Full Text | Google Scholar

Gräfener, G., Vink, J. S., de Koter, A., and Langer, N. (2011). The Eddington factor as the key to understand the winds of the most massive stars. Evidence for a Γ-dependence of Wolf-Rayet type mass loss. Astron. Astrophys. 535:A56. doi: 10.1051/0004-6361/201116701

CrossRef Full Text | Google Scholar

Granada, A., Ekström, S., Georgy, C., Krtička, J., Owocki, S., Meynet, G., et al. (2013). Populations of rotating stars. II. Rapid rotators and their link to Be-type stars. Astron. Astrophys. 553:A25. doi: 10.1051/0004-6361/201220559

CrossRef Full Text | Google Scholar

Gratton, R., Sneden, C., and Carretta, E. (2004). Abundance variations within globular clusters. Annu. Rev. Astron. Astrophys. 42:385. doi: 10.1146/annurev.astro.42.053102.133945

CrossRef Full Text | Google Scholar

Groh, J. H., Ekström, S., Georgy, C., Meynet, G., Choplin, A., Eggenberger, P., et al. (2019). Grids of stellar models with rotation. IV. Models from 1.7 to 120 M_⊙ at a metallicity Z = 0.0004. Astron. Astrophys. 627:A24. doi: 10.1051/0004-6361/201833720

CrossRef Full Text | Google Scholar

Harris, J. A., Hix, W. R., Chertkow, M. A., Lee, C. T., Lentz, E. J., and Messer, O. E. B. (2017). Implications for post-processing nucleosynthesis of core-collapse supernova models with Lagrangian particles. Astrophys. J. 843:2. doi: 10.3847/1538-4357/aa76de

CrossRef Full Text | Google Scholar

Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., and Hartmann, D. H. (2003). How massive single stars end their life. Astrophys. J. 591:288. doi: 10.1086/375341

CrossRef Full Text | Google Scholar

Heger, A., and Woosley, S. E. (2010). Nucleosynthesis and evolution of massive metal-free stars. Astrophys. J. 724, 341–373. doi: 10.1088/0004-637X/724/1/341

CrossRef Full Text | Google Scholar

Hekker, S., Angelou, G. C., Elsworth, Y., and Basu, S. (2020). Mirror principle and the red-giant bump: the battle of entropy in low-mass stars. Mon. Not. R. Astron. Soc. 492:5940. doi: 10.1093/mnras/staa176

CrossRef Full Text | Google Scholar

Herwig, F. (2000). The evolution of AGB stars with convective overshoot. Astron. Astrophys. 360:952.

Google Scholar

Herwig, F., Bloecker, T., Schoenberner, D., and El Eid, M. (1997). Stellar evolution of low and intermediate-mass stars. IV. Hydrodynamically-based overshoot and nucleosynthesis in AGB stars. Astron. Astrophys. 324:L81.

Google Scholar

Herwig, F., Freytag, B., Hueckstaedt, R. M., and Timmes, F. X. (2006). Hydrodynamic simulations of He shell flash convection. Astrophys. J. 642, 1057–1074. doi: 10.1086/501119

CrossRef Full Text | Google Scholar

Higl, J., Müller, E., and Weiss, A. (2021). Calibrating core overshooting parameters with two-dimensional hydrodynamical simulations. Astron. Astrophys. 646:A133. doi: 10.1051/0004-6361/202039532

CrossRef Full Text | Google Scholar

Hirschi, R. (2007). Very low-metallicity massive stars: pre-SN evolution models and primary nitrogen production. Astron. Astrophys. 461:571. doi: 10.1051/0004-6361:20065356

CrossRef Full Text | Google Scholar

Hirschi, R., Meynet, G., and Maeder, A. (2004). Stellar evolution with rotation. XII. Pre-supernova models. Astron. Astrophys. 425:649. doi: 10.1051/0004-6361:20041095

CrossRef Full Text | Google Scholar

Holt, R. J., Filippone, B. W., and Pieper, S. C. (2019). Impact of ¹⁶O(γ, α )¹²C measurements on the ¹²C(α, γ )¹⁶O astrophysical reaction rate. Phys. Rev. C 99(5):055802. doi: 10.1103/PhysRevC.99.055802

CrossRef Full Text | Google Scholar

Hoyle, F. (1954). On nuclear reactions occuring in very hot STARS.I. The synthesis of elements from carbon to nickel. Astrophys. J. Suppl. 1:121.

Google Scholar

Hunter, I., Brott, I., Langer, N., Lennon, D. J., Dufton, P. L., Howarth, I. D., et al. (2009). The VLT-FLAMES survey of massive stars: constraints on stellar evolution from the chemical compositions of rapidly rotating Galactic and Magellanic Cloud B-type stars. Astron. Astrophys. 496:841. doi: 10.1051/0004-6361/200809925

CrossRef Full Text | Google Scholar

Iliadis, C. (2007). Nuclear Physics of Stars. Wiley-VCH.

PubMed Abstract | Google Scholar

Janka, H.-T. (2012). Explosion mechanisms of core-collapse supernovae. Annu. Rev. Nucl. Part. Sci. 62:407. doi: 10.1146/annurev-nucl-102711-094901

CrossRef Full Text | Google Scholar

Jones, S., Andrassy, R., Sandalski, S., Davis, A., Woodward, P., and Herwig, F. (2017). Idealized hydrodynamic simulations of turbulent oxygen-burning shell convection in 4π geometry. Mon. Not. R. Astron. Soc. 465, 2991–3010. doi: 10.1093/mnras/stw2783

CrossRef Full Text | Google Scholar

Jones, S., Hirschi, R., Nomoto, K., Fischer, T., Timmes, F. X., Herwig, F., et al. (2013). Advanced burning stages and fate of 8-10 M_⊙ stars. Astrophys. J. 772:150. doi: 10.1088/0004-637X/772/2/150

CrossRef Full Text | Google Scholar

Jones, S., Hirschi, R., Pignatari, M., Heger, A., Georgy, C., Nishimura, N., et al. (2015). Code dependencies of pre-supernova evolution and nucleosynthesis in massive stars: evolution to the end of core helium burning. Mon. Not. R. Astron. Soc. 447, 3115–3129. doi: 10.1093/mnras/stu2657

CrossRef Full Text | Google Scholar

Kaeppeler, F., Wiescher, M., Giesen, U., Goerres, J., Baraffe, I., El Eid, M., et al. (1994). Reaction rates for 18O(alpha, gamma) 22Ne, 22Ne(alpha, gamma) 26Mg, and 22Ne( alpha, n) 25Mg in stellar helium burning and s-Process nucleosynthesis in massive stars. Astrophys. J. 437:396.

Google Scholar

Käppeler, F., Gallino, R., Bisterzo, S., and Aoki, W. (2011). The s process: nuclear physics, stellar models, and observations. Rev. Mod. Phys. 83, 157–194. doi: 10.1103/RevModPhys.83.157

CrossRef Full Text | Google Scholar

Karakas, A. I., Lugaro, M. A., Wiescher, M., Görres, J., and Ugalde, C. (2006). The uncertainties in the ²²Ne+α-capture reaction rates and the production of the heavy magnesium isotopes in asymptotic giant branch stars of intermediate mass. Astrophys. J. 643:471. doi: 10.1086/502793

CrossRef Full Text | Google Scholar

Katsuma, M. (2008). Low-energy cross sections in the ¹²C(α,γ)¹⁶O reaction. Phys. Rev. C 78:034606. doi: 10.1103/PhysRevC.78.034606

CrossRef Full Text | Google Scholar

Kazeroni, R., Guilet, J., and Foglizzo, T. (2017). Are pulsars spun up or down by SASI spiral modes? Mon. Not. R. Astron. Soc. 471, 914–925. doi: 10.1093/mnras/stx1566

CrossRef Full Text | Google Scholar

Kee, N. D., Sundqvist, J. O., Decin, L., de Koter, A., and Sana, H. (2021). Analytic, dust-independent mass-loss rates for red supergiant winds initiated by turbulent pressure. Astron. Astrophys. 646:A180. doi: 10.1051/0004-6361/202039224

CrossRef Full Text | Google Scholar

Kippenhahn, R., Ruschenplatt, G., and Thomas, H. C. (1980). The time scale of thermohaline mixing in stars. Astron. Astrophys. 91:175.

Google Scholar

Kochanek, C. S. (2014). Failed supernovae explain the compact remnant mass function. Astrophys. J. 785:28. doi: 10.1088/0004-637X/785/1/28

CrossRef Full Text | Google Scholar

Krtička, J., Owocki, S. P., and Meynet, G. (2011). Mass and angular momentum loss via decretion disks. Astron. Astrophys. 527:A84. doi: 10.1051/0004-6361/201015951

CrossRef Full Text | Google Scholar

Kuhfuss, R. (1986). A model for time-dependent turbulent convection. Astron. Astrophys. 160, 116–120.

Google Scholar

Kunz, R., Fey, M., Jaeger, M., Mayer, A., Hammer, J. W., Staudt, G., et al. (2002). Astrophysical reaction rate of 12C(α, γ)16O. Astrophys. J. 567:643. doi: 10.1086/338384

CrossRef Full Text | Google Scholar

Kuroda, T., Arcones, A., Takiwaki, T., and Kotake, K. (2020). Magnetorotational explosion of a massive star supported by neutrino heating in general relativistic three-dimensional simulations. Astrophys. J. 896:102. doi: 10.3847/1538-4357/ab9308

CrossRef Full Text | Google Scholar

Labadie-Bartz, J., Handler, G., Pepper, J., Balona, L., Cat, P. D., Stevens, D. J., et al. (2020). New beta cephei stars from the KELT project. Astron. J. 160:32. doi: 10.3847/1538-3881/ab952c

CrossRef Full Text | Google Scholar

Langer, N. (1986). Non-local treatment of convection and overshooting from stellar convective cores. Astron. Astrophys. 164:45.

Google Scholar

Langer, N. (1992). Helium enrichment in massive early type stars. Astron. Astrophys. 265, L17–L20.

Google Scholar

Langer, N. (2012). Presupernova evolution of massive single and binary stars. Annu. Rev. Astron. Astrophys. 50:107. doi: 10.1146/annurev-astro-081811-125534

CrossRef Full Text | Google Scholar

Lecoanet, D., Cantiello, M., Quataert, E., Couston, L.-A., Burns, K. J., Pope, B. J. S., et al. (2019). Low-frequency variability in massive stars: core generation or surface phenomenon? Astrophys. J. Lett. 886:L15. doi: 10.3847/2041-8213/ab5446

CrossRef Full Text | Google Scholar

Ledoux, P. (1947). Stellar models with convection and with discontinuity of the mean molecular weight. Astrophys. J. 105:305. doi: 10.1086/144905

CrossRef Full Text | Google Scholar

Leung, S.-C., Nomoto, K., and Blinnikov, S. (2019). Pulsational pair-instability Supernovae. I. Pre-collapse evolution and pulsational mass ejection. Astrophys. J. 887:72. doi: 10.3847/1538-4357/ab4fe5

CrossRef Full Text | Google Scholar

Levesque, E. M., and Massey, P. (2020). Betelgeuse just is not that cool: effective temperature alone cannot explain the recent dimming of betelgeuse. Astrophys. J. Lett. 891:L37. doi: 10.3847/2041-8213/ab7935

CrossRef Full Text | Google Scholar

Limongi, M., and Chieffi, A. (2003). Evolution, explosion, and nucleosynthesis of core-collapse supernovae. Astrophys. J. 592:404. doi: 10.1086/375703

CrossRef Full Text | Google Scholar

Limongi, M., and Chieffi, A. (2012). Presupernova evolution and explosive nucleosynthesis of zero metal massive stars. Astrophys. J. Suppl. 199:38. doi: 10.1088/0067-0049/199/2/38

CrossRef Full Text | Google Scholar

Livio, M. (1989). Common envelope evolution of binary stars. Space Sci. Rev. 50:299.

Google Scholar

Lucy, L. B., and Solomon, P. M. (1970). Mass loss by hot stars. Astrophys. J. 159:879.

Google Scholar

Maeder, A. (1975). Stellar evolution III: the overshooting from convective cores. Astron. Astrophys. 40:303.

Google Scholar

Maeder, A. (1987). Evidences for a bifurcation in massive star evolution. The ON-blue stragglers. Astron. Astrophys. 178:159.

Google Scholar

Maeder, A., and Mermilliod, J. C. (1981). The extent of mixing in stellar interiors: evolutionary models and tests based on the HR diagrams of 34 open clusters. Astron. Astrophys., 93:136.

Google Scholar

Maeder, A., and Meynet, G. (2001). Stellar evolution with rotation. VII. Low metallicity models and the blue to red supergiant ratio in the SMC. Astron. Astrophys. 373:555. doi: 10.1051/0004-6361:20010596

CrossRef Full Text | Google Scholar

Maeder, A., Meynet, G., Ekström, S., and Georgy, C. (2009). Modeling massive stars with rotation: the case of Nitrogen enrichments. Coast 158:72. doi: 10.1553/cia158

CrossRef Full Text | Google Scholar

Maeder, A., Przybilla, N., Nieva, M.-F., Georgy, C., Meynet, G., Ekström, S., et al. (2014). Evolution of surface CNO abundances in massive stars. Astron. Astrophys. 565:A39. doi: 10.1051/0004-6361/201220602

CrossRef Full Text | Google Scholar

Maeder, A., and Zahn, J.-P. (1998). Stellar evolution with rotation. III. Meridional circulation with MU -gradients and non-stationarity. Astron. Astrophys. 334:1000.

Google Scholar

Magic, Z., Collet, R., Asplund, M., Trampedach, R., Hayek, W., Chiavassa, A., et al. (2013). The Stagger-grid: a grid of 3D stellar atmosphere models. I. Methods and general properties. Astron. Astrophys. 557:A26. doi: 10.1051/0004-6361/201321274

CrossRef Full Text | Google Scholar

Magic, Z., Weiss, A., and Asplund, M. (2015). The Stagger-grid: a grid of 3D stellar atmosphere models. III. The relation to mixing length convection theory. Astron. Astrophys. 573:A89. doi: 10.1051/0004-6361/201423760

CrossRef Full Text | Google Scholar

Marchant, P., Renzo, M., Farmer, R., Pappas, K. M. W., Taam, R. E., de Mink, S. E., et al. (2019). Pulsational pair-instability supernovae in very Close binaries. Astrophys. J. 882:36. doi: 10.3847/1538-4357/ab3426

CrossRef Full Text | Google Scholar

Marcolino, W. L. F., Bouret, J. C., Martins, F., Hillier, D. J., Lanz, T., and Escolano, C. (2009). Analysis of Galactic late-type O dwarfs: more constraints on the weak wind problem. Astron. Astrophys. 498:837. doi: 10.1051/0004-6361/200811289

CrossRef Full Text | Google Scholar

Marek, A., and Janka, H.-T. (2009). Delayed neutrino-driven supernova explosions aided by the standing accretion-shock instability. Astrophys. J. 694:664. doi: 10.1088/0004-637X/694/1/664

CrossRef Full Text | Google Scholar

Markova, N., Puls, J., and Langer, N. (2018). Spectroscopic and physical parameters of Galactic O-type stars. III. Mass discrepancy and rotational mixing. Astron. Astrophys. 613:A12. doi: 10.1051/0004-6361/201731361

CrossRef Full Text | Google Scholar

Martins, F., Hervé, A., Bouret, J. C., Marcolino, W., Wade, G. A., Neiner, C., et al. (2015a). The MiMeS survey of magnetism in massive stars: CNO surface abundances of Galactic O stars. Astron. Astrophys. 575:A34. doi: 10.1051/0004-6361/201425173

CrossRef Full Text | Google Scholar

Martins, F., and Palacios, A. (2013). A comparison of evolutionary tracks for single Galactic massive stars. Astron. Astrophys. 560:A16. doi: 10.1051/0004-6361/201322480

CrossRef Full Text | Google Scholar

Martins, F., Schaerer, D., Hillier, D. J., Meynadier, F., Heydari-Malayeri, M., and Walborn, N. R. (2005). On stars with weak winds: the Galactic case. Astron. Astrophys. 441:735. doi: 10.1051/0004-6361:20052927

CrossRef Full Text | Google Scholar

Martins, F., Simón-Díaz, S., Barbá, R. H., Gamen, R. C., and Ekström, S. (2017). A study of the effect of rotational mixing on massive stars evolution: surface abundances of Galactic O7-8 giant stars. Astron. Astrophys. 599:A30. doi: 10.1051/0004-6361/201629548

CrossRef Full Text | Google Scholar

Martins, F., Simón-Díaz, S., Palacios, A., Howarth, I., Georgy, C., Walborn, N. R., et al. (2015b). Surface abundances of ON stars. Astron. Astrophys. 578:A109. doi: 10.1051/0004-6361/201526130

CrossRef Full Text | Google Scholar

Maund, J. R., and Smartt, S. J. (2005). Hubble Space Telescope imaging of the progenitor sites of six nearby core-collapse supernovae. Mon. Not. R. Astron. Soc. 360:288. doi: 10.1111/j.1365-2966.2005.09034.x

CrossRef Full Text | Google Scholar

Maund, J. R., Smartt, S. J., and Schweizer, F. (2005). Luminosity and mass limits for the progenitor of the type Ic supernova 2004gt in NGC 4038. Astrophys. J. Lett. 630:L33. doi: 10.1086/491620

CrossRef Full Text | Google Scholar

Mauron, N., and Josselin, E. (2011). The mass-loss rates of red supergiants and the de Jager prescription. Astron. Astrophys. 526:A156. doi: 10.1051/0004-6361/201013993

CrossRef Full Text | Google Scholar

Meakin, C. A., and Arnett, D. (2007). Turbulent convection in stellar interiors. I. Hydrodynamic simulation. Astrophys. J. 667:448. doi: 10.1086/520318

CrossRef Full Text | Google Scholar

Meynet, G., Chomienne, V., Ekström, S., Georgy, C., Granada, A., Groh, J., et al. (2015). Impact of mass-loss on the evolution and pre-supernova properties of red supergiants. Astron. Astrophys. 575:A60. doi: 10.1051/0004-6361/201424671

CrossRef Full Text | Google Scholar

Meynet, G., Eggenberger, P., and Maeder, A. (2011). Massive star models with magnetic braking. Astron. Astrophys. 525:L11. doi: 10.1051/0004-6361/201016017

CrossRef Full Text | Google Scholar

Meynet, G., Ekström, S., Maeder, A., Eggenberger, P., Saio, H., Chomienne, V., et al. (2013). “Models of rotating massive stars: impacts of various prescriptions,” in Studying Stellar Rotation and Convection, volume 865 of Lecture Notes in Physics, eds M. Goupil, K. Belkacem, C. Neiner, F. Lignières, and J. J. Green (Berlin; Heidelberg), 3.

Google Scholar

Meynet, G., and Maeder, A. (2002a). Stellar evolution with rotation. VIII. Models at Z = 10⁻⁵ and CNO yields for early galactic evolution. Astron. Astrophys. 390:561. doi: 10.1051/0004-6361:20020755

CrossRef Full Text | Google Scholar

Meynet, G., and Maeder, A. (2002b). The origin of primary nitrogen in galaxies. Astron. Astrophys. 381:L25. doi: 10.1051/0004-6361:20011554

CrossRef Full Text | Google Scholar

Miglio, A., Girardi, L., Grundahl, F., Mosser, B., Bastian, N., Bragaglia, A., et al. (2019). HAYDN – High-precision AsteroseismologY of DeNse stellar fields (ESA Voyage 2050 White Paper). arXiv preprints arXiv:1908.05129.

Google Scholar

Moe, M., and Di Stefano, R. (2017). Mind your Ps and Qs: the interrelation between period (P) and mass-ratio (Q) distributions of binary stars. Astrophys. J. Suppl. Ser. 230:15. doi: 10.3847/1538-4365/aa6fb6

CrossRef Full Text | Google Scholar

Mokiem, M. R., de Koter, A., Vink, J. S., Puls, J., Evans, C. J., Smartt, S. J., et al. (2007). The empirical metallicity dependence of the mass-loss rate of O- and early B-type stars. Astron. Astrophys. 473:603. doi: 10.1051/0004-6361:20077545

CrossRef Full Text | Google Scholar

Moravveji, E., Aerts, C., Pápics, P. I., Triana, S. A., and Vandoren, B. (2015). Tight asteroseismic constraints on core overshooting and diffusive mixing in the slowly rotating pulsating B8.3V star KIC 10526294. Astron. Astrophys. 580:A27. doi: 10.1051/0004-6361/201425290

CrossRef Full Text | Google Scholar

Muijres, L. E., Vink, J. S., de Koter, A., Müller, P. E., and Langer, N. (2012). Predictions for mass-loss rates and terminal wind velocities of massive O-type stars. Astron. Astrophys. 537:A37. doi: 10.1051/0004-6361/201015818

CrossRef Full Text | Google Scholar

Müller, B., Viallet, M., Heger, A., and Janka, H.-T. (2016). The last minutes of oxygen shell burning in a massive star. Astrophys. J. 833:124. doi: 10.3847/1538-4357/833/1/124

CrossRef Full Text | Google Scholar

Müller, E., and Janka, H. T. (1995). “Convection in type-II supernovae:the first second,” in Seventeeth Texas Symposium on Relativistic Astrophysics and Cosmology, Vol. 759, eds H. Böhringer, G. E. Morfill, and J. E. Trümper, 368.

Google Scholar

Murphy, L. J., Groh, J. H., Ekström, S., Meynet, G., Pezzotti, C., Georgy, C., et al. (2021). Grids of stellar models with rotation - V. Models from 1.7 to 120 M_⊙ at zero metallicity. Mon. Not. R. Astron. Soc. 501:2745. doi: 10.1093/mnras/staa3803

CrossRef Full Text | Google Scholar

Najarro, F., Hanson, M. M., and Puls, J. (2011). L-band spectroscopy of Galactic OB-stars. Astron. Astrophys. 535:A32. doi: 10.1051/0004-6361/201016003

CrossRef Full Text | Google Scholar

Nakamura, K., Kuroda, T., Takiwaki, T., and Kotake, K. (2014). Impacts of rotation on three-dimensional hydrodynamics of core-collapse supernovae. Astrophys. J. 793:45. doi: 10.1088/0004-637X/793/1/45

CrossRef Full Text | Google Scholar

Nomoto, K. (1984). “Type-II supernovae from 8-10 solar mass progenitors,” in Stellar Nucleosynthesis. Proceedings of the 3rd. Workshop of the Advanced School of Astronomy of the Ettore Majorana Centre for Scientific Culture, eds C. Chiosi and A. Renzini (Dordrecht), 239.

Google Scholar

Ober, W. W., El Eid, M. F., and Fricke, K. J. (1983). Evolution of massive pregalactic stars - Part Two - nucleosynthesis in pair creation supernovae and pregalactic enrichment. Astron. Astrophys. 119:61.

Google Scholar

Ohlmann, S. T., Röpke, F. K., Pakmor, R., and Springel, V. (2016). Hydrodynamic moving-mesh simulations of the common envelope phase in binary stellar systems. Astrophys. J. Lett. 816:L9. doi: 10.3847/2041-8205/816/1/L9

CrossRef Full Text | Google Scholar

Oskinova, L. M. (2016). X-ray diagnostics of massive star winds. Adv. Space Res. 58:739. doi: 10.1016/j.asr.2016.06.030

CrossRef Full Text | Google Scholar

Oskinova, L. M., Hamann, W. R., and Feldmeier, A. (2007). Neglecting the porosity of hot-star winds can lead to underestimating mass-loss rates. Astron. Astrophys. 476:1331. doi: 10.1051/0004-6361:20066377

CrossRef Full Text | Google Scholar

Oskinova, L. M., Todt, H., Ignace, R., Brown, J. C., Cassinelli, J. P., and Hamann, W. R. (2011). Early magnetic B-type stars: X-ray emission and wind properties. Mon. Not. R. Astron. Soc. 416:1456. doi: 10.1111/j.1365-2966.2011.19143.x

CrossRef Full Text | Google Scholar

Owocki, S. (2014). Theory of winds from hot, luminous massive stars. arXiv preprints arXiv:1409.2084.

Google Scholar

Owocki, S. P. (2004). “Rotation and mass ejection: the launching of Be-star disks (invited review),” in Stellar Rotation, volume 215 of IAU Symposium, eds A. Maeder and P. Eenens (San Francisco, CA), 515.

Google Scholar

Paczyński, B., and Sienkiewicz, R. (1972). Evolution of close binaries VIII. Mass exchange on the dynamical time scale. Acta Astron. 22:73.

Google Scholar

Padmanabhan, T. (2001). Theoretical Astrophysics, Volume 2: Stars and Stellar Systems. Cambridge University Press.

Google Scholar

Pamyatnykh, A. A., Handler, G., and Dziembowski, W. A. (2004). Asteroseismology of the β Cephei star ν Eridani: interpretation and applications of the oscillation spectrum. Mon. Not. R. Astron. Soc. 350:1022. doi: 10.1111/j.1365-2966.2004.07721.x

CrossRef Full Text | Google Scholar

Passy, J.-C., De Marco, O., Fryer, C. L., Herwig, F., Diehl, S., Oishi, J. S., et al. (2012a). Simulating the common envelope phase of a red giant using smoothed-particle hydrodynamics and uniform-grid codes. Astrophys. J. 744:52. doi: 10.1088/0004-637X/744/1/52

CrossRef Full Text | Google Scholar

Passy, J.-C., Herwig, F., and Paxton, B. (2012b). The response of giant stars to dynamical-timescale mass loss. Astrophys. J. 760:90. doi: 10.1088/0004-637X/760/1/90

CrossRef Full Text | Google Scholar

Pavlovskii, K., Ivanova, N., Belczynski, K., and Van, K. X. (2017). Stability of mass transfer from massive giants: double black hole binary formation and ultraluminous X-ray sources. Mon. Not. R. Astron. Soc. 465:2092. doi: 10.1093/mnras/stw2786

CrossRef Full Text | Google Scholar

Paxton, B., Bildsten, L., Dotter, A., Herwig, F., Lesaffre, P., and Timmes, F. (2011). Modules for experiments in stellar astrophysics (MESA). Astrophys. J. Suppl. 192:3. doi: 10.1088/0067-0049/192/1/3

PubMed Abstract | CrossRef Full Text | Google Scholar

Paxton, B., Cantiello, M., Arras, P., Bildsten, L., Brown, E. F., Dotter, A., et al. (2013). Modules for experiments in stellar astrophysics (MESA): planets, oscillations, rotation, and massive stars. Astrophys. J. Suppl. 208:4. doi: 10.1088/0067-0049/208/1/4

CrossRef Full Text | Google Scholar

Pignatari, M., Gallino, R., Heil, M., Wiescher, M., Käppeler, F., Herwig, F., et al. (2010). The Weak s-process in massive stars and its dependence on the neutron capture cross sections. Astrophys. J. 710:1557. doi: 10.1088/0004-637X/710/2/1557

CrossRef Full Text | Google Scholar

Pignatari, M., Gallino, R., Meynet, G., Hirschi, R., Herwig, F., and Wiescher, M. (2008). The s-process in massive stars at low metallicity: the effect of primary ¹⁴N from fast rotating stars. Astrophys. J. Lett. 687:L95. doi: 10.1086/593350

CrossRef Full Text | Google Scholar

Pinçon, C., Belkacem, K., Goupil, M. J., and Marques, J. P. (2017). Can plume-induced internal gravity waves regulate the core rotation of subgiant stars? Astron. Astrophys. 605:A31. doi: 10.1051/0004-6361/201730998

CrossRef Full Text | Google Scholar

Podsiadlowski, P., Rappaport, S., and Pfahl, E. D. (2002). Evolutionary sequences for low- and intermediate-mass X-ray binaries. Astrophys. J. 565:1107. doi: 10.1086/324686

CrossRef Full Text | Google Scholar

Poelarends, A. J. T., Herwig, F., Langer, N., and Heger, A. (2008). The supernova channel of super-AGB stars. Astrophys. J. 675:614. doi: 10.1086/520872

CrossRef Full Text | Google Scholar

Prantzos, N., and Diehl, R. (1996). Radioactive 26Al in the galaxy: observations versus theory. Phys. Rep. 267:1.

Google Scholar

Prat, V., Guilet, J., Viallet, M., and Müller, E. (2016). Shear mixing in stellar radiative zones. II. Robustness of numerical simulations. Astron. Astrophys. 592:A59. doi: 10.1051/0004-6361/201527946

CrossRef Full Text | Google Scholar

Prat, V., and Lignières, F. (2013). Turbulent transport in radiative zones of stars. Astron. Astrophys. 551:L3. doi: 10.1051/0004-6361/201220577

CrossRef Full Text | Google Scholar

Prat, V., and Lignières, F. (2014). Shear mixing in stellar radiative zones. I. Effect of thermal diffusion and chemical stratification. Astron. Astrophys. 566:A110. doi: 10.1051/0004-6361/201423655

CrossRef Full Text | Google Scholar

Pruet, J., Woosley, S. E., Buras, R., Janka, H. T., and Hoffman, R. D. (2005). Nucleosynthesis in the hot convective bubble in core-collapse supernovae. Astrophys. J. 623, 325–336. doi: 10.1086/428281

CrossRef Full Text | Google Scholar

Raiteri, C. M., Busso, M., Gallino, R., and Picchio, G. (1991a). S-process nucleosynthesis in massive stars and the weak component. II. Carbon burning and galactic enrichment. Astrophys. J. 371:665.

Google Scholar

Raiteri, C. M., Busso, M., Gallino, R., Picchio, G., and Pulone, L. (1991b). S-Process nucleosynthesis in massive stars and the weak component. I. Evolution and neutron captures in a 25 M_sun star. Astrophys. J. 367:228.

Google Scholar

Rakavy, G., and Shaviv, G. (1967). Instabilities in highly evolved stellar models. Astrophys. J. 148:803.

Google Scholar

Rauscher, T., Heger, A., Hoffman, R. D., and Woosley, S. E. (2002). Nucleosynthesis in massive stars with improved nuclear and stellar physics. Astrophys. J. 576:323. doi: 10.1086/341728

CrossRef Full Text | Google Scholar

Rauw, G., Hervé, A., Nazé, Y., González-Pérez, J. N., Hempelmann, A., Mittag, M., et al. (2015). Simultaneous X-ray and optical spectroscopy of the Oef supergiant λ Cephei. Astron. Astrophys. 580:A59. doi: 10.1051/0004-6361/201526057

CrossRef Full Text | Google Scholar

Ricker, P. M., and Taam, R. E. (2008). The interaction of stellar objects within a common envelope. Astrophys. J. Lett. 672:L41. doi: 10.1086/526343

CrossRef Full Text | Google Scholar

Ricker, P. M., and Taam, R. E. (2012). An AMR study of the common-envelope phase of binary evolution. Astrophys. J. 746:74. doi: 10.1088/0004-637X/746/1/74

CrossRef Full Text | Google Scholar

Ritter, C., Andrassy, R., Côté, B., Herwig, F., Woodward, P. R., Pignatari, M., et al. (2018a). Convective-reactive nucleosynthesis of K, Sc, Cl and p-process isotopes in O-C shell mergers. Mon. Not. R. Astron. Soc. 474:L1. doi: 10.1093/mnrasl/slx126

CrossRef Full Text | Google Scholar

Ritter, C., Herwig, F., Jones, S., Pignatari, M., Fryer, C., and Hirschi, R. (2018b). NuGrid stellar data set - II. Stellar yields from H to Bi for stellar models with M_ZAMS = 1-25 M_⊙ and Z = 0.0001-0.02. Mon. Not. R. Astron. Soc. 480:538. doi: 10.1093/mnras/sty1729

CrossRef Full Text | Google Scholar

Rogers, T. M., Lin, D. N. C., McElwaine, J. N., and Lau, H. H. B. (2013). Internal gravity waves in massive stars: angular momentum transport. Astrophys. J. 772:21. doi: 10.1088/0004-637X/772/1/21

CrossRef Full Text | Google Scholar

Roxburgh, I. W. (1978). Convection and stellar structure. Astron. Astrophys. 65:281.

Google Scholar

Sana, H., de Mink, S. E., de Koter, A., Langer, N., Evans, C. J., Gieles, M., et al. (2012). Binary interaction dominates the evolution of massive stars. Science, 337:444. doi: 10.1126/science.1223344

PubMed Abstract | CrossRef Full Text | Google Scholar

Sana, H., Gosset, E., and Evans, C. J. (2009). The massive star binary fraction in young open clusters - II. NGC6611 (Eagle Nebula). Mon. Not. R. Astron. Soc. 400:1479. doi: 10.1111/j.1365-2966.2009.15545.x

CrossRef Full Text | Google Scholar

Sana, H., Gosset, E., Nazé, Y., Rauw, G., and Linder, N. (2008). The massive star binary fraction in young open clusters - I. NGC 6231 revisited. Mon. Not. R. Astron. Soc. 386:447. doi: 10.1111/j.1365-2966.2008.13037.x

CrossRef Full Text | Google Scholar

Scheck, L., Plewa, T., Janka, H. T., Kifonidis, K., and Müller, E. (2004). Pulsar recoil by large-scale anisotropies in supernova explosions. Phys. Rev. Lett. 92:011103. doi: 10.1103/PhysRevLett.92.011103

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneider, F. R. N., Ohlmann, S. T., Podsiadlowski, P., Röpke, F. K., Balbus, S. A., Pakmor, R., et al. (2019). Stellar mergers as the origin of magnetic massive stars. Nature 574, 211. doi: 10.1038/s41586-019-1621-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneider, F. R. N., Ohlmann, S. T., Podsiadlowski, P., Röpke, F. K., Balbus, S. A., and Pakmor, R. (2020). Long-term evolution of a magnetic massive merger product. Mon. Not. R. Astron. Soc. 495, 2796–2812. doi: 10.1093/mnras/staa1326

CrossRef Full Text | Google Scholar

Schwarzschild, M. (1958). Structure and Evolution of the Stars. Princeton University Press.

Google Scholar

Scott, L. J. A., Hirschi, R., Georgy, C., Arnett, W. D., Meakin, C., Kaiser, E. A., et al. (2021). Convective core entrainment in 1D main sequence stellar models. Mon. Not. R. Astron. Soc. arXiv:2103.06196. doi: 10.1093/mnras/stab752

CrossRef Full Text | Google Scholar

Secchi, A. (1866). Schreiben des Herrn Prof. Secchi, Directors der Sternwarte des Collegio Romano, an den Herausgeber. Astron. Nachrichten 68:63.

Google Scholar

Shaviv, G., and Salpeter, E. E. (1973). Convective overshooting in stellar interior models. Astrophys. J. 184, 191–200.

Google Scholar

Siess, L. (2007). Evolution of massive AGB stars. II. model properties at non-solar metallicity and the fate of Super-AGB stars. Astron. Astrophys. 476:893. doi: 10.1051/0004-6361:20078132

CrossRef Full Text | Google Scholar

Siess, L. (2008). “Structural and chemical evolution of low- and intermediate-mass stars„” in Stellar Nucleosynthesis 50 Years After B²FH, Vol. 32 of EAS Publications Series, eds C. Charbonnel and J.-P. Zahn, 131.

Google Scholar

Siess, L., Forestini, M., and Dougados, C. (1997). Synthetic Hertzsprung-Russell diagrams of open clusters. Astron. Astrophys. 324:556.

Google Scholar

Siess, L., Goriely, S., and Langer, N. (2004). Nucleosynthesis of s-elements in rotating AGB stars. Astron. Astrophys. 415:1089. doi: 10.1051/0004-6361:20034281

CrossRef Full Text | Google Scholar

Siess, L., Izzard, R. G., Davis, P. J., and Deschamps, R. (2013). BINSTAR: a new binary stellar evolution code. Tidal interactions. Astron. Astrophys. 550:A100. doi: 10.1051/0004-6361/201220327

CrossRef Full Text | Google Scholar

Siess, L., Livio, M., and Lattanzio, J. (2002). Structure, evolution, and nucleosynthesis of primordial stars. Astrophys. J. 570:329. doi: 10.1086/339733

CrossRef Full Text | Google Scholar

Smartt, S. J., Eldridge, J. J., Crockett, R. M., and Maund, J. R. (2009). The death of massive stars - I. Observational constraints on the progenitors of Type II-P supernovae. Mon. Not. R. Astron. Soc. 395:1409. doi: 10.1111/j.1365-2966.2009.14506.x

CrossRef Full Text | Google Scholar

Song, H. F., Meynet, G., Maeder, A., Ekström, S., and Eggenberger, P. (2016). Massive star evolution in close binaries. Conditions for homogeneous chemical evolution. Astron. Astrophys. 585:A120. doi: 10.1051/0004-6361/201526074

CrossRef Full Text | Google Scholar

Song, N., Alexeeva, S., Sitnova, T., Wang, L., Grupp, F., and Zhao, G. (2020). Impact of the convective mixing-length parameter α on stellar metallicity. Astron. Astrophys. 635:A176. doi: 10.1051/0004-6361/201937110

CrossRef Full Text | Google Scholar

Spada, F., Gellert, M., Arlt, R., and Deheuvels, S. (2016). Angular momentum transport efficiency in post-main sequence low-mass stars. Astron. Astrophys. 589:A23. doi: 10.1051/0004-6361/201527591

CrossRef Full Text | Google Scholar

Staritsin, E. I. (2013). Turbulent entrainment at the boundaries of the convective cores of main-sequence stars. Astron. Rep. 57, 380–390. doi: 10.1134/S1063772913050089

CrossRef Full Text | Google Scholar

Struve, O. (1931). On the origin of bright lines in spectra of stars of class B. Astrophys. J. 73:94.

Google Scholar

Sugimoto, D., and Fujimoto, M. Y. (2000). Why stars become red giants. Astrophys. J. 538:837. doi: 10.1086/309150

CrossRef Full Text | Google Scholar

Suijs, M. P. L., Langer, N., Poelarends, A.-J., Yoon, S.-C., Heger, A., and Herwig, F. (2008). White dwarf spins from low-mass stellar evolution models. Astron. Astrophys. 481:L87. doi: 10.1051/0004-6361:200809411

CrossRef Full Text | Google Scholar

Summa, A., Janka, H.-T., Melson, T., and Marek, A. (2018). Rotation-supported neutrino-driven supernova explosions in three dimensions and the critical luminosity condition. Astrophys. J. 852:28. doi: 10.3847/1538-4357/aa9ce8

CrossRef Full Text | Google Scholar

Sundqvist, J. O., Björklund, R., Puls, J., and Najarro, F. (2019). New predictions for radiation-driven, steady-state mass-loss and wind-momentum from hot, massive stars. I. Method and first results. Astron. Astrophys. 632:A126. doi: 10.1051/0004-6361/201936580

CrossRef Full Text | Google Scholar

Sundqvist, J. O., Puls, J., and Owocki, S. P. (2014). Mass loss from inhomogeneous hot star winds. III. An effective-opacity formalism for line radiative transfer in accelerating, clumped two-component media, and first results on theory and diagnostics. Astron. Astrophys. 568:A59. doi: 10.1051/0004-6361/201423570

CrossRef Full Text | Google Scholar

Šurlan, B., Hamann, W. R., Aret, A., Kubát, J., Oskinova, L. M., and Torres, A. F. (2013). Macroclumping as solution of the discrepancy between Hα and P v mass loss diagnostics for O-type stars. Astron. Astrophys. 559:A130. doi: 10.1051/0004-6361/201322390

CrossRef Full Text | Google Scholar

Suzuki, A., and Maeda, K. (2018). Constraining the final fates of massive stars by oxygen and iron enrichment history in the galaxy. Astrophys. J. 852:101. doi: 10.3847/1538-4357/aaa024

CrossRef Full Text | Google Scholar

Sweet, P. A. (1950). The importance of rotation in stellar evolution. Mon. Not. R. Astron. Soc. 110:548.

Google Scholar

Szécsi, D., Langer, N., Yoon, S.-C., Sanyal, D., de Mink, S., Evans, C. J., et al. (2015). Low-metallicity massive single stars with rotation. Evolutionary models applicable to I Zwicky 18. Astron. Astrophys. 581:A15. doi: 10.1051/0004-6361/201526617

CrossRef Full Text | Google Scholar

Takahashi, K. (2018). The low detection rate of pair-instability supernovae and the effect of the core carbon fraction. Astrophys. J. 863:153. doi: 10.3847/1538-4357/aad2d2

CrossRef Full Text | Google Scholar

Talwar, R., Adachi, T., Berg, G. P. A., Bin, L., Bisterzo, S., Couder, M., et al. (2016). Probing astrophysically important states in the ²⁶Mg nucleus to study neutron sources for the s process. Phys. Rev. C 93:055803. doi: 10.1103/PhysRevC.93.055803

CrossRef Full Text | Google Scholar

Tan, W. P., Boeltzig, A., Dulal, C., deBoer, R. J., Frentz, B., Henderson, S., et al. (2020). New measurement of C 12 +C 12 fusion reaction at astrophysical energies. Phys. Rev. Lett. 124:192702. doi: 10.1103/PhysRevLett.124.192702

PubMed Abstract | CrossRef Full Text | Google Scholar

The L.-S. El Eid M. F. Meyer B. S. (2007). s-Process nucleosynthesis in advanced burning phases of massive stars. Astrophys. J. 655:1058. doi: 10.1086/509753

CrossRef Full Text | Google Scholar

Tkachenko, A., Pavlovski, K., Johnston, C., Pedersen, M. G., Michielsen, M., Bowman, D. M., et al. (2020). The mass discrepancy in intermediate- and high-mass eclipsing binaries: The need for higher convective core masses. Astron. Astrophys. 637:A60. doi: 10.1051/0004-6361/202037452

CrossRef Full Text | Google Scholar

Toonen, S., Hamers, A., and Portegies Zwart, S. (2016). The evolution of hierarchical triple star-systems. Comput. Astrophys. Cosmol. 3:6. doi: 10.1186/s40668-016-0019-0

CrossRef Full Text | Google Scholar

Triana, S. A., Moravveji, E., Pápics, P. I., Aerts, C., Kawaler, S. D., and Christensen-Dalsgaard, J. (2015). The internal rotation profile of the B-type star KIC 10526294 from frequency inversion of its dipole gravity modes. Astrophys. J. 810:16. doi: 10.1088/0004-637X/810/1/16

CrossRef Full Text | Google Scholar

Truran, J. W., and Cameron, A. G. W. (1971). Evolutionary models of nucleosynthesis in the galaxy. Astrophys. Space Sci. 14:179. doi: 10.1007/BF00649203

CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., La Cognata, M., Cherubini, S., Guardo, G. L., Gulino, M., et al. (2018). An increase in the ¹²C + ¹²C fusion rate from resonances at astrophysical energies. Nature 557:687. doi: 10.1038/s41586-018-0149-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Tur, C., Heger, A., and Austin, S. M. (2007). On the sensitivity of massive star nucleosynthesis and evolution to solar abundances and to uncertainties in helium-burning reaction rates. Astrophys. J. 671:821. doi: 10.1086/523095

CrossRef Full Text | Google Scholar

Tur, C., Heger, A., and Austin, S. M. (2009). Dependence of s-process nucleosynthesis in massive stars on triple-alpha and 12C(alpha,gamma)16O reaction rate uncertainties. Astrophys. J. 702:1068. doi: 10.1088/0004-637X/702/2/1068

CrossRef Full Text | Google Scholar

Tur, C., Heger, A., and Austin, S. M. (2010). Production of 26Al, 44Ti, and 60Fe in core-collapse supernovae: sensitivity to the rates of the triple alpha and 12C(alpha,gamma)16O reactions. Astrophys. J. 718:357. doi: 10.1088/0004-637X/718/1/357

CrossRef Full Text | Google Scholar

Umeda, H., and Nomoto, K. (2008). How much 56Ni can be produced in core-collapse supernovae? Evolution and explosions of 30-100 Msol stars. Astrophys. J. 673:1014. doi: 10.1086/524767

CrossRef Full Text | Google Scholar

van Loon, J. T., Cioni, M.-R. L., Zijlstra, A. A., and Loup, C. (2005). An empirical formula for the mass-loss rates of dust-enshrouded red supergiants and oxygen-rich Asymptotic Giant Branch stars. Astron. Astrophys. 438:273. doi: 10.1051/0004-6361:20042555

CrossRef Full Text | Google Scholar

Vanbeveren, D., De Donder, E., Van Bever, J., Van Rensbergen, W., and De Loore, C. (1998a). The WR and O-type star population predicted by massive star evolutionary synthesis. New Astron. 3:443. doi: 10.1016/S1384-1076(98)00020-7

CrossRef Full Text | Google Scholar

Vanbeveren, D., De Loore, C., and Van Rensbergen, W. (1998b). Massive stars. Astron. Astrophys. Rev. 9:63.

Google Scholar

Viallet, M., Meakin, C., Arnett, D., and Mocák, M. (2013). Turbulent convection in stellar interiors. III. Mean-field analysis and stratification effects. Astrophys. J. 769:1. doi: 10.1088/0004-637X/769/1/1

CrossRef Full Text | Google Scholar

Viallet, M., Meakin, C., Prat, V., and Arnett, D. (2015). Toward a consistent use of overshooting parametrizations in 1D stellar evolution codes. Astron. Astrophys. 580:A61. doi: 10.1051/0004-6361/201526294

CrossRef Full Text | Google Scholar

Vilhu, O., and Kallman, T. R. (2019). Models for weak wind and momentum problems in the winds of hot stars. arXiv preprints arXiv:1906.05581.

Google Scholar

Vink, J. S. (2006). “Massive star feedback – from the first stars to the present,” in Stellar Evolution at Low Metallicity: Mass Loss, Explosions, Cosmology, volume 353 of Astronomical Society of the Pacific Conference Series, eds H. J. G. L. M. Lamers, N. Langer, T. Nugis, and K. Annuk, 113.

Google Scholar

Vink, J. S., Muijres, L. E., Anthonisse, B., de Koter, A., Gräfener, G., and Langer, N. (2011). Wind modelling of very massive stars up to 300 solar masses. Astron. Astrophys. 531:A132. doi: 10.1051/0004-6361/201116614

CrossRef Full Text | Google Scholar

Vitense, E. (1953). Die Wasserstoffkonvektionszone der Sonne. Mit 11 Textabbildungen. ZA 32:135.

Google Scholar

Vogt, H. (1925). Zum Strahlungsgleichgewicht der Sterne. Astron. Nachrichten 223:229.

Google Scholar

Wade, G. A., Grunhut, J., Alecian, E., Neiner, C., Aurière, M., Bohlender, D. A., et al. (2014). “The magnetic characteristics of Galactic OB stars from the MiMeS survey of magnetism in massive stars,” in IAU Symposium, Vol. 302, 265.

Google Scholar

Walczak, P., Daszyńska-Daszkiewicz, J., Pigulski, A., Pamyatnykh, A., Moffat, A. F. J., Handler, G., et al. (2019). Seismic modelling of early B-type pulsators observed by BRITE - I. θ Ophiuchi. Mon. Not. R. Astron. Soc. 485:3544. doi: 10.1093/mnras/stz639

CrossRef Full Text | Google Scholar

Wanajo, S., Müller, B., Janka, H.-T., and Heger, A. (2018). Nucleosynthesis in the innermost ejecta of neutrino-driven supernova explosions in two dimensions. Astrophys. J. 852:40. doi: 10.3847/1538-4357/aa9d97

CrossRef Full Text | Google Scholar

Weaver, T. A., and Woosley, S. E. (1980). “Evolution and explosion of massive stars,” in Ninth Texas Symposium on Relativistic Astrophysics, Vol. 336, 335.

Google Scholar

Wongwathanarat, A., Janka, H.-T., and Müller, E. (2010). Hydrodynamical neutron star kicks in three dimensions. Astrophys. J. Lett. 725:L106. doi: 10.1088/2041-8205/725/1/L106

CrossRef Full Text | Google Scholar

Wongwathanarat, A., Janka, H. T., and Müller, E. (2013). Three-dimensional neutrino-driven supernovae: neutron star kicks, spins, and asymmetric ejection of nucleosynthesis products. Astron. Astrophys. 552:A126. doi: 10.1051/0004-6361/201220636

CrossRef Full Text | Google Scholar

Wongwathanarat, A., Müller, E., and Janka, H. T. (2015). Three-dimensional simulations of core-collapse supernovae: from shock revival to shock breakout. Astron. Astrophys. 577:A48. doi: 10.1051/0004-6361/201425025

CrossRef Full Text | Google Scholar

Woods, T. E., and Ivanova, N. (2011). Can we trust models for adiabatic mass loss? Astrophys. J. Lett. 739:L48. doi: 10.1088/2041-8205/739/2/L48

CrossRef Full Text | Google Scholar

Woodward, P. R., Herwig, F., and Lin, P.-H. (2015). Hydrodynamic simulations of H entrainment at the top of He-shell flash convection. Astrophys. J. 798:49. doi: 10.1088/0004-637X/798/1/49

CrossRef Full Text | Google Scholar

Woosley, S., and Janka, T. (2005). The physics of core-collapse supernovae. Nat. Phys. 1, 147–154. doi: 10.1038/nphys172

CrossRef Full Text | Google Scholar

Woosley, S. E. (2017). Pulsational pair-instability supernovae. Astrophys. J. 836:244. doi: 10.3847/1538-4357/836/2/244

PubMed Abstract | CrossRef Full Text | Google Scholar

Woosley, S. E. (2019). The evolution of massive helium stars, including mass loss. Astrophys. J. 878:49. doi: 10.3847/1538-4357/ab1b41

CrossRef Full Text | Google Scholar

Woosley, S. E., Heger, A., and Weaver, T. A. (2002). The evolution and explosion of massive stars. Rev. Mod. Phys. 74:1015. doi: 10.1103/RevModPhys.74.1015

CrossRef Full Text | Google Scholar

Woosley, S. E., and Weaver, T. A. (1995). The evolution and explosion of massive stars. II. Explosive hydrodynamics and nucleosynthesis. Astrophys. J. Suppl. 101:181.

Google Scholar

Xiong, D. R., Cheng, Q. L., and Deng, L. (1997). Nonlocal time-dependent convection theory. Astrophys. J. Suppl. 108:529.

Google Scholar

Yadav, N., Müller, B., Janka, H. T., Melson, T., and Heger, A. (2020). Large-scale mixing in a violent oxygen-neon shell merger prior to a core-collapse supernova. Astrophys. J. 890:94. doi: 10.3847/1538-4357/ab66bb

CrossRef Full Text | Google Scholar

Yoon, S., Langer, N., and Norman, C. (2006). Single star progenitors of long gamma-ray bursts. I. Model grids and redshift dependent GRB rate. Astron. Astrophys. 460:199. doi: 10.1051/0004-6361:20065912

CrossRef Full Text | Google Scholar

Yoon, S.-C., Gräfener, G., Vink, J. S., Kozyreva, A., and Izzard, R. G. (2012). On the nature and detectability of Type Ib/c supernova progenitors. Astron. Astrophys. 544:L11. doi: 10.1051/0004-6361/201219790

CrossRef Full Text | Google Scholar

Yoshida, T., Suwa, Y., Umeda, H., Shibata, M., and Takahashi, K. (2017). Explosive nucleosynthesis of ultra-stripped Type Ic supernovae: application to light trans-iron elements. Mon. Not. R. Astron. Soc. 471:4275. doi: 10.1093/mnras/stx1738

CrossRef Full Text | Google Scholar

Zahn, J.-P. (1977). Tidal friction in close binary stars. Astron. Astrophys. 57:383–394.

Google Scholar

Zahn, J.-P. (1992). Circulation and turbulence in rotating stars. Astron. Astrophys. 265:115.

Google Scholar

Zahn, J.-P. (2008). “Tidal dissipation in binary systems,” in EAS Publications Series, Vol. 29, eds M.-J. Goupil and J.-P. Zahn, 67–90.

Google Scholar