Anharmonic Vibrational Frequencies and Spectroscopic Constants for the Detection of Ethynol in Space

The ethynol (HCCOH) molecule has recently been shown to be present in simulated astrochemical ices possibly linking it to molecular building blocks for interstellar complex organic molecules like amino acids. The proposed reaction mechanism suggests the simultaneous formation of both ketene and ethynol from mixed carbon monoxide/water ice in simulated interstellar conditions. Rigorous anharmonic spectral data within both the IR and microwave regions are needed for possible detection of ethynol in the interstellar medium. This study provides the first such data for this molecule from high-level quantum chemical computations where experiment is currently lacking. Ethynol has a $B_{eff}$ comparable to, but distinct from acetonitrile at 9,652.1 MHz and three notable infrared features with two in the hydride stretching-regions and the C–C stretch at 2,212.8 cm⁻¹. The ketene isomer has already been detected in the interstellar medium, and the possible detection of ethynol made possible by this work may lead to a deeper understanding of the proposed ice formation mechanism involving both species and how this relates to the molecular origins of life.

1 Introduction

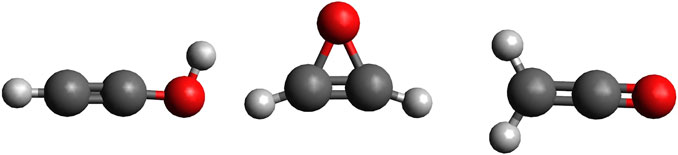
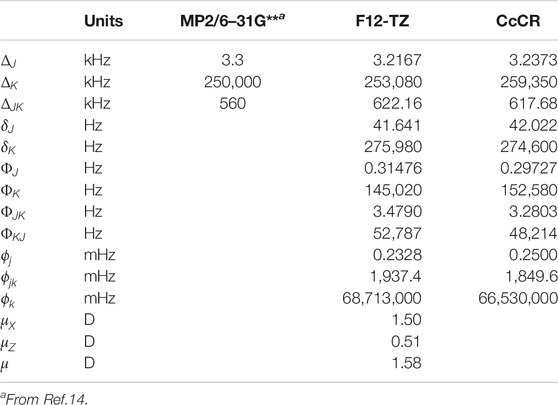
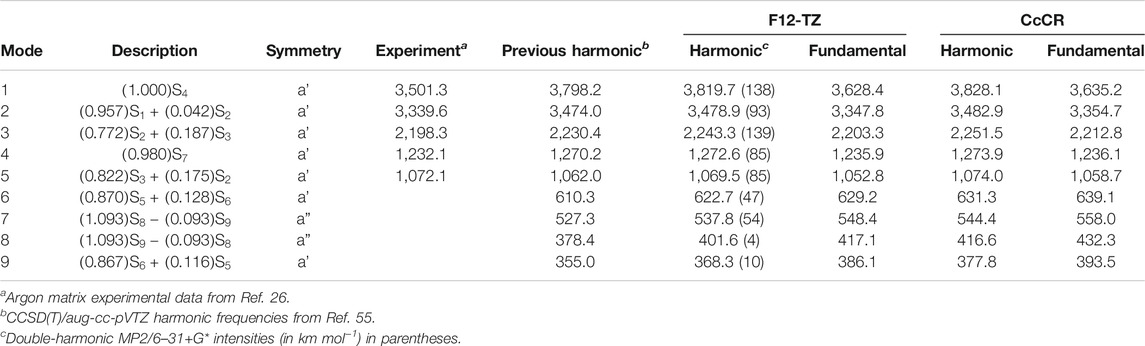
Structural isomers of complex organic molecules (COMs) are telling of the chemical and physical traits of interstellar environments and are useful testers of molecular cloud chemical models (Turner et al., 2020). Therefore, the ability to accurately recognize the abundance of COM building blocks in interstellar environments is critical for the prediction of interstellar chemical pathways. Two promising reactants to form larger COMs are ethynol (Zasimov et al., 2019), also known as hydroxyacetylene, and ketene, both members of the C₂H₂O isomer family. Ketene has a carbon=carbon double bond as well as a carbon=oxygen double bond. Ethynol has a carbon–carbon triple bond and an accompanying hydroxyl group. Previous ab initio computations have shown ethynol to lie 150.9 kJ/mol above the more stable ketene (Tanaka and Yoshimine, 1980). A third C₂H₂O isomer, oxirene, is suspected to be a possible intermediate structure facilitating some isomerization between the more stable structures of ethynol and ketene (Turner et al., 2020). Visual representation of these three molecules can be seen in Figure 1. Of these three molecules, only ketene and its ketenyl radical have been observed in the interstellar medium (ISM) with the former first detected toward Sgr B2 (Turner, 1977). However, the downhill pathway for the formation of ethynol from the same starting materials as ketene implies that it should have non-negligible abundance. Furthermore, detection of ethynol giving the ketene/ethynol pair would imply that mixed CO/H₂O ices could be the provenance of both molecules including the known ketene molecule.

FIGURE 1

FIGURE 1. From left to right: ethynol, oxirene, and ketene.

In addition to ice experiments, part of the previous work by Turner et al. (2020) explored quantum chemical reaction schemes at the coupled cluster singles, doubles, and perturbative triples [CCSD(T)] level beginning with dicarbon monoxide in the presence of free hydrogen and found barrier free pathways producing both ketene and ethynol. The ketenyl radical is an intermediate along this pathway. The addition of hydrogen to the carbon of the ketenyl radical is strongly preferred and leads to the formation of ketene. The addition of hydrogen to the oxygen of the radical is feasible, however extremely disfavored, and leads to the formation of ethynol. This barrier free pathway was then tested experimentally and resulted in the first identification of ethynol in interstellar ice analogs (Turner et al., 2020). Preceding work has also experimentally shown the reversible conversion of ketene into ethynol via photolysis in an argon matrix (Hochstrasser and Wirz, 1990). However, energy must be put into the system for this conversion to take place. Regardless, considering these reaction pathways and that ketene and the ketenyl radical have been previously observed in the ISM, ethynol is likely present in detectable quantities as even tautomers that are less stable than HCCOH compared to their global minima are known to persist in the ISM if their barriers to rearrangement are high enough (Dommen et al., 1987). Before it can be detected, however, highly-accurate anharmonic vibrational frequencies and/or rotational spectroscopic data for ethynol must be produced in order to provide the necessary reference data for comparison to any subsequent experiments or observations. This is the primary objective of the current work.

An early theoretical study on the rotational and vibrational characteristics of ethynol was carried out by DeFrees and McLean (1982). Using Hartree-Fock and a 3–21G basis set, they obtained harmonic vibrational frequencies that they suggested could be scaled by a previously-derived empirical factor (Pople et al., 1981) to obtain values comparable to experiment. They further computed CISD+Q/DZ+P equilibrium rotational constants and accompanying scaling factors derived from the experimental rotational constants of HNCO and HN₃ (DeFrees et al., 1982). Later work on ethynol offered rotational constants at the third-order Møller-Plesset perturbation theory (MP3) level with a 6–31G** basis set (Brown et al., 1985). The MP3 values were then scaled using factors obtained from experimental ketene data, yielding constants that were in good agreement with those computed by DeFrees and McLean (Brown et al., 1985).

Later theoretical work by Dommen et al. (1987) produced vibrational frequencies based on an MP2/6–31G** harmonic force field, with the force constants scaled based on empirical corrections from similar computations on methanol and acetylene (Dommen et al., 1987). Dommen et al. (1987) also questioned the proposed multiplicative scaling scheme of DeFrees and McLean, instead suggesting that the equilibrium rotational constants should be divided by the scaling factors (Dommen et al., 1987). The scaled vibrational frequencies and re-scaled rotational constants presented by Dommen and coworkers are the most accurate theoretical data currently available for ethynol, revealing the need for new, high-level computational data. In the meantime, some progress has been made on the experimental characterization of ethynol, with five of its vibrational frequencies observed in an argon matrix in 1989 (Hochstrasser and Wirz, 1989). More recently, its ground-state C rotational constant was detected at 9553 MHz in 2019 (Martin-Drumel et al., 2019). The authors therein also report scaled CCSD(T)/cc-pVQZ principle rotational constants for comparison (Martin-Drumel et al., 2019). In spite of these previous computational results, more rigorous theoretical treatment is necessary to complement further experimental and observational work in the gas phase.

The current approach to obtaining high-level, theoretical vibrational frequencies is via a fourth-order Taylor series expansion to the internuclear potential with composite CCSD(T) energies making considerations for complete basis set extrapolation, core electron correlation, and scalar relativity (Huang and Lee, 2008; Huang and Lee, 2009; Huang et al., 2011). Such a scheme is referred to as “CcCR”. The rigor of this method makes it very attractive, with it producing vibrational frequencies within 1.0 cm⁻¹ of gas-phase experimental values in many cases (Huang and Lee, 2008; Huang and Lee, 2009; Huang et al., 2011; Fortenberry et al., 2012b; Huang et al., 2013; Fortenberry et al., 2014; Zhao et al., 2014; Fortenberry et al., 2015; Kitchens and Fortenberry, 2016; Bizzocchi et al., 2017; Fortenberry, 2017). However, its high computational cost makes this method less viable as molecules become larger and more complex. For this reason, a less complete but commensurately less computationally demanding method utilizing explicit correlation with a triple-ζ basis set is used as a point of comparison (Huang et al., 2010; Agbaglo et al., 2019; Agbaglo and Fortenberry, 2019a; Agbaglo and Fortenberry, 2019b), as it typically provides vibrational frequencies to within 7.0 cm⁻¹ of gas-phase experimental values. The rotational constants, on the other hand, still require the more expensive composite approach in order to provide high-accuracy values (Agbaglo et al., 2019; Agbaglo and Fortenberry, 2019a; Agbaglo and Fortenberry, 2019b).

Cheaper methods do exist for determining relatively accurate rotational constants, such as the procedures outlined by Lee and McCarthy (2020). However, even in the best case outlined therein of the MP2/cc-pVQZ B rotational constants, the average deviation from experiment is 0.65%, while the performance of CcCR relative to experiment for the B and C rotational constants was recently shown to be 0.12% (Gardner et al., 2020), albeit for a much smaller selection of molecules. Additionally, the rotational constants from the CcCR methodology come at virtually no additional cost with the fundamental vibrational frequencies, making even marginal accuracy gains in these constants worth the increased computational demand when anharmonic frequencies are desired.

Both the aforementioned CcCR and explicitly correlated procedures are utilized within the current work to produce accurate vibrational frequencies for ethynol. By using the high-level anharmonic vibrational frequencies proposed in the current work, the search for interstellar ethynol may continue with more clarity in the regions in which ketene has been previously detected such as Sgr B2 (Turner, 1977); Orion KL (Johansson et al., 1984); and TMC-1 (Matthews and Sears, 1986).

2 Computational Details

Optimized geometries, dipole moments, and harmonic frequencies are computed using the MOLPRO 2015.1 software package (Werner et al., 2015) with canonical CCSD(T) and CCSD(T) within the F12 explicitly correlated construction [CCSD(T)-F12b] (Raghavachari et al., 1989; Crawford and Schaefer, 2000; Adler et al., 2007; Shavitt and Bartlett, 2009). As mentioned above, anharmonic frequencies are produced by a fourth-order Taylor series expansion of the internuclear portion of the Watson A-Reduced Hamiltonian referred to as a quartic force field (QFF). Two QFFs are utilized. The CCSD(T)-F12/cc-pVTZ-F12 version (Adler et al., 2007; Peterson et al., 2008; Yousaf and Peterson, 2008; Knizia et al., 2009) will be referred to as the F12-TZ QFF. The second QFF is the composite approach mentioned previously. This methodology is defined as the CcCR QFF since it includes complete basis set extrapolation (“C”) using a three-point formula from aug-cc-pVTZ, aug-cc-pVQZ, and aug-cc-pV5Z basis sets (Martin and Lee, 1996); core electron correlation (“cC”) using the Martin-Taylor (MT) core correlating basis set (Martin and Taylor, 1994); and scalar relativity (“R”) using Douglas-Kroll basis sets (Douglas and Kroll, 1974; de Jong et al., 2001). Recent results show that the F12-TZ QFF produces comparable anharmonic data to the CcCR QFF but with significantly lower computational costs (Agbaglo and Fortenberry, 2019a).

For both QFFs, an optimized reference geometry is required. For the F12-TZ QFF, this optimization is carried out at the CCSD(T)-F12/cc-pVTZ-F12 level. For the CcCR QFF, structural optimizations are determined at the canonical CCSD(T) level using the aug-cc-pV5Z basis set (Dunning, 1989; Kendall et al., 1992; Peterson and Dunning, 1995) as well as the MT core correlating basis set (Martin and Taylor, 1994). The difference in the bond lengths and angles between the CCSD(T)/MT computations with and without the core correction is then added to the respective variables within the optimized CCSD(T)/aug-cc-pV5Z geometry in order to correct for core correlation.

From the previously discussed reference geometries, displacements of 0.005 Å for bond lengths, 0.005 radians for bond angles, and 0.005 unitless displacements of LINX/LINY coordinates (Fortenberry et al., 2012b), which are necessary for the near-prolate structure of ethynol, are used to generate a QFF of 3,161 points using the following coordinate system:

$S_1=\text{r}(\text{H}-\text{C})(1)$

$S_2=\text{r}(\text{C}-\text{C})(2)$

$S_3=\text{r}(\text{C}-\text{O})(3)$

$S_4=\text{r}(\text{O}-\text{H})(4)$

$S_5=\text{LINX}\left(\text{H}-\text{C}-\text{C}\right)(5)$

$S_6=\angle \left(\text{C}-\text{C}-\text{O}\right)(6)$

$S_7=\angle \left(\text{C}-\text{O}-\text{H}\right)(7)$

$S_8=\text{LINY}\left(\text{H}-\text{C}-\text{C}-\text{O}\right)(8)$

$S_9=\tau \left(\text{C}-\text{C}-\text{O}-\text{H}\right)(9)$

From this coordinate system, single point energies are computed for the composite method using the definition described above. The F12-TZ method only relies on CCSD(T)-F12/cc-pVTZ-F12. Once the single point energies are computed for both of the QFFs, they are fit using a least squares procedure with a sum of squared residuals less than $3\times {10}^{-16}$ a.u.² for both CcCR and F12-TZ. Next, the force constants’ simple internal coordinates are converted into Cartesian coordinates using the INTDER program (Allen, 2005). These Cartesian coordinates are then fed into the SPECTRO program (Gaw et al., 1991) in which rotational, rovibrational, and vibrational perturbation theory at second order (VPT2) (Mills, 1972; Watson, 1977; Papousek and Aliev, 1982) are used to obtain the fundamental vibrational frequencies and spectroscopic constants. The CcCR force constants themselves are available in Supplementary Table S1 of the Supplementary Material.

Combinations of ${\nu }_5$ and ${\nu }_3$, ${\nu }_6$ and ${\nu }_5$, ${\nu }_7$ and ${\nu }_5$ are considered as type 1 Fermi resonances. Combinations of ${\nu }_5$, ${\nu }_3$, and ${\nu }_2$ are treated as type 2 Fermi resonances as well as combinations of ${\nu }_5$, ${\nu }_4$, and ${\nu }_3$. Polyads of the Fermi resonances are also handled. Finally, Coriolis resonances are included, with the combinations of ${\nu }_7$ and ${\nu }_6$, ${\nu }_9$ and ${\nu }_7$, ${\nu }_9$ and ${\nu }_8$ all resulting in A-type Coriolis resonances.

3 Results and Discussion

3.1 Structure and Rotational Spectroscopic Constants

The optimized structures at both the F12-TZ and CcCR levels are given in Table 1. The optimized bond lengths computed at both levels of theory agree to within 0.02 Å when compared to one another and previous computations at the MP2/6–31G** level of theory (Dommen et al., 1987). The quartic and sextic A-reduced Hamiltonian spectroscopic constants of ethynol are given in Table 2 alongside dipole moments. Ethynol’s vibrationally-excited rotational constants are provided in Table 1 in the same order as the fundamental vibrational frequencies. Due to ethynol’s considerable dipole moment of 1.58 D, as shown in Table 2, its rotational transitions should be easily observable via rovibrational spectroscopy.

TABLE 1

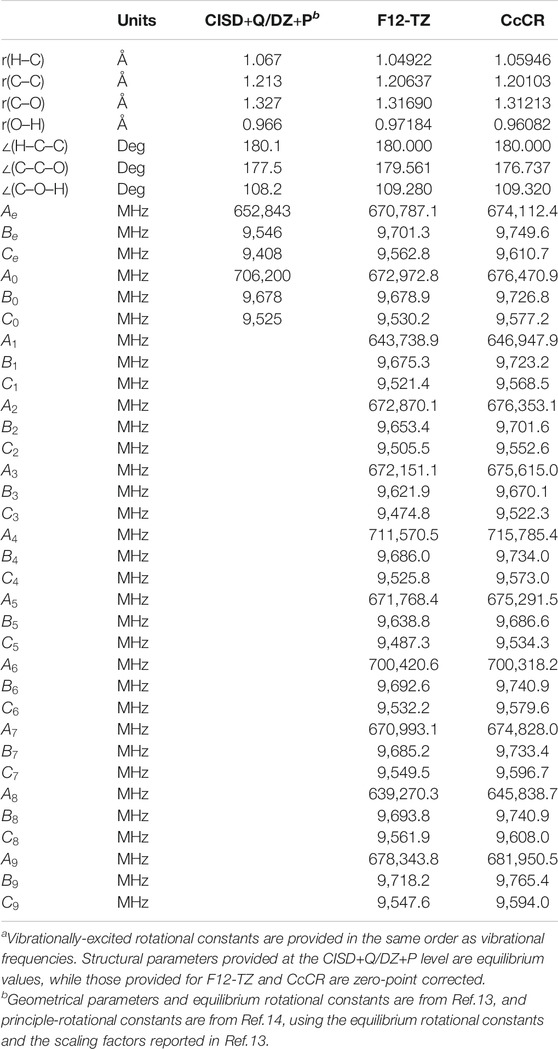
TABLE 1. Structural data and rotational constants for HCCOH.^a

TABLE 2

TABLE 2. Quartic and sextic spectroscopic constants.

A useful point of comparison for ethynol’s equilibrium rotational constants would be with those of acetonitrile. Acetonitrile is a prolate molecule that compares nicely to ethynol’s near-prolate structure and has a nearly equivalent molecular weight to that of ethynol. As seen in Table 1, ethynol has CcCR $B_0$ and $C_0$ values of 9726.8 and 9576.9 MHz, respectively. Previous work has shown CcCR rotational constants to be accurate within 20 MHz of experimental values for closed shell molecules (Gardner et al., 2020). Acetonitrile has equivalent $B_0$ and $C_0$ values of 6,200.9 MHz (Herzberg, 1966). As expected, ethynol has $B_0$ and $C_0$ values higher than those of acetonitrile due to its near-prolate, as opposed to fully prolate, nature. These similarities will make acetonitrile a useful sign-post for the observation of ethynol in the ISM, but, because acetonitrile has a larger dipole moment (3.92 D), observed rotational modes of ethynol will have considerably lower intensity than those of acetonitrile.

3.2 Vibrational Frequencies

Vibrational frequencies for ethynol are given at the F12-TZ and CcCR levels of theory alongside experimental values in Table 3. F12-TZ and CcCR anharmonic frequencies compare well to each other, with a mean absolute error of less than 8 cm⁻¹ between the two methods. Although gas-phase experimental data are currently unavailable for ethynol, argon matrix experimental data (Hochstrasser and Wirz, 1989) correlates in expected fashion with theoretical values presented in this work. Namely, all but ${\nu }_5$ are shifted to the red in the matrix results, in line with the typical behavior of a matrix (Anderson and Ogden, 1969). Of the nine vibrational frequencies present in ethynol, only the five most intense have experimental data. The others are too weak to be observed. This is corroborated by MP2 intensities presented alongside F12-TZ harmonic frequencies in Table 3, which are seen to drastically drop off after ${\nu }_5$.

TABLE 3

TABLE 3. Vibrational frequencies (in cm⁻¹) of ethynol.

Of ethynol’s vibrational frequencies, ${\nu }_1$, ${\nu }_2$, and ${\nu }_3$ have the three brightest intensities. These modes are described in Table 3 using the coordinate system established in the Computational Details section and are attributed to the O–H, C–H, and C–C stretching modes, respectively. Comparison of ethynol’s anharmonic frequencies to known values of similar structures in the gas-phase may be useful in aiding the vibrational assignment of ethynol in the ISM. The CcCR ${\nu }_3$, corresponding to the C–C stretching mode, occurs at 2,212.8 cm⁻¹ or 4.519 μm and is the brightest vibrational mode present in ethynol, making it a critical resource for the future assignment of ethynol in the ISM. The C–N triple bond stretch present in acetonitrile, a molecule of, again, similar structure and weight to ethynol that is known to be present in the ISM (Solomon et al., 1971), is observed at 2,267 cm⁻¹ or 4.411 μm in gas-phase experiment (Shimanouchi, 1972). The reported CcCR frequency for ${\nu }_3$ is redshifted 0.108 μm from the experimental acetonitrile C–N stretch. This redshifting is to be expected as ethynol is a slightly more massive system.

With only a slightly lower intensity than ${\nu }_3$, the CcCR ${\nu }_1$ is observed at 3,635.2 cm⁻¹ or 2.751 μm. As ${\nu }_1$ is attributed to the O–H stretch of ethynol, a reasonable mode to compare as an analog is the O–H stretch present in methanol, which is well known in the ISM (Ball et al., 1970). This methanol stretching mode is observed in gas-phase experiment at 3,681 cm⁻¹ (Shimanouchi, 1972) or 2.717 μm. When comparing ${\nu }_1$ to this stretching mode in methanol, the CcCR ${\nu }_1$ exhibits a redshift of 0.034 μm away from methanol’s stretching mode.

Of the three brightest vibrational frequencies present in ethynol, ${\nu }_2$, observed at 3,354.7 cm⁻¹ or 2.980 μm, is considerably dimmer than ${\nu }_1$ and ${\nu }_3$ but still has potential to serve as a useful indicator in future detection. As ${\nu }_2$ is attributed to the C–H stretching mode of ethynol, a practical mode for comparison would be that of the C–H stretching mode of the ethynyl radical, which has also been previously observed in the ISM (Tucker et al., 1974). This gas-phase stretching mode is observed at 3,298.85 cm⁻¹ or 3.031 μm (Stephens et al., 1988). Similar to ${\nu }_1$ and ${\nu }_3$, ${\nu }_2$ is shifted by 0.051 μm when compared to the C–H stretch present in the ethynyl radical.

Positive anharmonicities are present for ${\nu }_6$–${\nu }_9$ in Table 3. These positive anharmonicities range from 6.5 to 17.8 cm⁻¹ when examining ${\nu }_6$ and ${\nu }_9$, respectively. This behavior in the anharmonicities arises due to the nearly linear nature of the H–C–C–O backbone present in ethynol and has been documented previously in molecules of similar near-prolate construction (Fortenberry et al., 2012a; Fortenberry et al., 2012b; Fortenberry et al., 2013).

The high intensity stretching modes ${\nu }_1$–${\nu }_5$ are observed in the region of previously identified peaks (Peeters et al., 2004). However, the ${\nu }_1$–${\nu }_5$ frequencies occur in regions not typically attributed to polycyclic aromatic hydrocarbons or dust, thus making these regions less well confined in terms of potential molecular provenance. Although far from conclusive, ethynol’s distinct vibrational peaks combined with their high intensities show promise for IR spectroscopy identifying the molecule in the ISM. Additionally, its notable dipole moment is encouraging for rotational observation, thus providing even more avenues of detection.

4 Conclusion

Considering that ethynol has already been shown to form in interstellar ice analogs and that the related ketene molecule (Turner et al., 2020) is known to be present in the ISM, the high-level vibrational and rotational data provided here may lead to the detection of ethynol in various astrophysical regions, especially those where ketene and its dehydrogenated radical are known to exist. Detection of ethynol through rotational spectroscopy should be possible due to its 1.58 D dipole moment. Further, detection is also feasible via mid-IR spectroscopy due to the bright nature of vibrational frequencies ${\nu }_1$–${\nu }_3$, leading to multiple spectral regions for detection. Once ethynol has been detected in the ISM, investigation of relative populations of ethynol compared to ketene within certain regions will increase understanding of the recently proposed mechanism by Turner et al. (2020). This knowledge may then further augment models exploring COM formation in the ISM and help the collective understanding of how small molecules like ethynol and ketene relate to the molecular origins of life in the ISM.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JD and BW performed the computations. JD wrote the draft. JD, BW, and RF edited the manuscript. RF provided conceptualization, oversight, methodology, and provision of funds.

Funding

Additional funding provided by the Barry Goldwater Foundation. Funds from NASA and the NSF supported the student workers and provided much of the computational power utilized in this work. Open access publication fees are provided by the University of Mississippi.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

RF acknowledges support from NSF Grant OIA-1757220, NASA Grant NNX17AH15G, and the University of Mississippi for the provision of startup funds. JD recognizes support from the Goldwater Foundation. Additionally, the authors would like to thank Ralf I. Kaiser of the University of Hawaii for useful discussions related to the development of this manuscript and for initiating the research collaboration that led to the work reported herein.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2020.626407/full#supplementary-material.

References

Adler, T. B., Knizia, G., and Werner, H. J. (2007). A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 127, 221106. doi:10.1063/1.2817618

PubMed Abstract | CrossRef Full Text | Google Scholar

Agbaglo, D., and Fortenberry, R. C. (2019a). The performance of explicitly correlated methods for the computation of anharmonic vibrational frequencies. Int. J. Quant. Chem. 119, e25899. doi:10.1002/qua.25899

CrossRef Full Text | Google Scholar

Agbaglo, D., and Fortenberry, R. C. (2019b). The performance of explicitly correlated wavefunctions [CCSD(T)-F12b] in the computation of anharmonic vibrational frequencies. Chem. Phys. Lett. 734, 136720. doi:10.1016/j.cplett.2019.136720

CrossRef Full Text | Google Scholar

Agbaglo, D., Lee, T. J., Thackston, R., and Fortenberry, R. C. (2019). A small molecule with PAH vibrational properties and a detectable rotational spectrum: ?-(C)C₃H₂, cyclopropenylidenyl carbene. Astrophys. J. 871, 236. doi:10.3847/1538-4357/aaf85a

CrossRef Full Text | Google Scholar

Allen, W. D.coworkers (2005). Is a general program written by W. D. Allen and coworkers, which performs vibrational analysis and higher-order non-linear transformations. Athens, Georgia; Center for Computational Quantum Chemistry.

Google Scholar

Anderson, J. S., and Ogden, J. S. (1969). Matrix isolation studies of group-iv oxides. i. infrared spectra and structures of sio, sio, and sio. J. Chem. Phys. 51, 4189. doi:10.1063/1.1671778

CrossRef Full Text | Google Scholar

Ball, J. A., Gottlieb, C. A., Lilley, A. E., and Radford, H. E. (1970). Detection of methyl alcohol in Sagittarius. Astrophys. J. Lett. 162, L203. doi:10.1086/180654

CrossRef Full Text | Google Scholar

Bizzocchi, L., Lattanzi, V., Laas, J., Spezzano, S., Giuliano, B. M., Prudenzano, D., et al. (2017). Accurate sub-millimetre rest frequencies for HOCO and DOCO ions. Astron. Astrophys. 602, A34. doi:10.1051/0004-6361/201730638

CrossRef Full Text | Google Scholar

Brown, R. D., Rice, E. H. N., and Rodler, M. (1985). Ab Initio studies of the structures and force fields of ketenimine and related molecules. Chem. Phys. 99, 347–356. doi:10.1016/0301-0104(85)80175-0

CrossRef Full Text | Google Scholar

Crawford, T. D., and Schaefer, H. F. (2000). “An introduction to coupled cluster theory for computational chemists,” in Reviews in computational chemistry. Editors K. B. Lipkowitz, and D. B. Boyd (New York: Wiley), Vol. 14, 33–136.

Google Scholar

de Jong, W. A., Harrison, R. J., and Dixon, D. A. (2001). Parallel Douglas-Kroll energy and gradients in nwchem: estimating scalar relativistic effects using douglas-kroll contracted basis sets. J. Chem. Phys. 114, 48–53. doi:10.1063/1.1329891

CrossRef Full Text | Google Scholar

DeFrees, D. J., Loew, G. H., and McLean, A. D. (1982). The rotational spectra of hoco, hocn, hn, and hnco from quantum mechanical calculations. Astrophys. J. 254, 405–411. doi:10.1086/159745

CrossRef Full Text | Google Scholar

DeFrees, D. J., and McLean, A. D. (1982). Rotational and vibrational spectra of ethynol from quantum-mechanical calculations. J. Phys. Chem. 86, 2835–2837. doi:10.1021/j100212a006

CrossRef Full Text | Google Scholar

Dommen, J., Rodler, M., and Ha, T.-K. (1987). Vibrational spectrum of ethynol: ab initio calculation and matrix isolation studies. Chem. Phys. 117, 65–72. doi:10.1016/0301-0104(87)80097-6

CrossRef Full Text | Google Scholar

Douglas, M., and Kroll, N. (1974). Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 82, 89–155. doi:10.1016/0003-4916(74)90333-9

CrossRef Full Text | Google Scholar

Dunning, T. H. (1989). Gaussian basis sets for use in correlated molecular calculations. i. the atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Francisco, J. S., Crawford, T. D., and Lee, T. J. (2012a). Fundamental vibrational frequencies and spectroscopic constants of HOCS+, HSCO+, and isotopologues via quartic force fields. J. Phys. Chem. 116, 9582–9590. doi:10.1021/jp3073206

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Francisco, J. S., Crawford, T. D., and Lee, T. J. (2012b). Quartic force field predictions of the fundamental vibrational frequencies and spectroscopic constants of the cations HOCO+ and DOCO+. J. Chem. Phys. 136, 234309. doi:10.1063/1.4729309

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Schwenke, D. W., and Lee, T. J. (2014). Limited rotational and rovibrational line lists computed with highly accurate quartic force fields and ab initio dipole surfaces. Spectrochim. Acta Mol. Biomol. Spectrosc. 119, 76–83. doi:10.1016/j.saa.2013.03.092

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Crawford, T. D., and Lee, T. J. (2013). High-accuracy quartic force field calculations for the spectroscopic constants and vibrational frequencies of ?-CH: a possible link to lines observed in the horsehead nebula pdr. Astrophys. J. 772, 39. doi:10.1088/0004-637x/772/1/39

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Lee, T. J., and Müller, H. S. P. (2015). Excited vibrational level rotational constants for SiC: a sensitive molecular diagnostic for astrophysical conditions. Molec. Astrophys. 1, 13–19. doi:10.1016/j.molap.2015.07.001

CrossRef Full Text | Google Scholar

Fortenberry, R. C. (2017). Rovibrational characterization of the proton-bound, noble gas complexes: ArHNe, ArHAr, and NeHNe. ACS Earth Space Chem. 1, 60–69. doi:10.1021/acsearthspacechem.7b00003

CrossRef Full Text | Google Scholar

Gardner, M. B., Westbrook, B. R., Fortenberry, R., and Lee, T. J. (2020). Highly-accurate quartic force fields for the prediction of anharmonic rotational constants and fundamental vibrational frequencies. Spectrochim. Acta A Mol. Biomol. Spectrosc. [Epub ahead of print]. doi:10.1016/j.saa.2020.119184

CrossRef Full Text | Google Scholar

Gaw, J. F., Willets, A., Green, W. H., and Handy, N. C. (1991). “SPECTRO: a program for the derivation of spectrscopic constants from provided quartic force fields and cubic dipole fields,” in Advances in molecular vibrations and collision dynamics. Editors J. M. Bowman, and M. A. Ratner (Greenwich, Connecticut: JAI Press, Inc.), 170–185.

Google Scholar

Herzberg, G. (1966). Electronic spectra and electronic structure of polyatomic molecules. New York: Van Nostrand).

Google Scholar

Hochstrasser, R., and Wirz, J. (1989). Ethynol: photochemical generation in an argon matrix, ir spectrum, and photoisomerization to ketene. Angew. Chem. Int. Ed. 28, 181–183. doi:10.1002/anie.198901811

CrossRef Full Text | Google Scholar

Hochstrasser, R., and Wirz, J. (1990). Reversible photoisomerization of ketene to ethynol. Angew. Chem. Int. Ed. 29, 411–413. doi:10.1002/anie.199004111

CrossRef Full Text | Google Scholar

Huang, X., and Lee, T. J. (2008). A procedure for computing accurate ab initio quartic force fields: application to HO2+ and H2O. J. Chem. Phys. 129, 044312. doi:10.1063/1.2957488

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X., Taylor, P. R., and Lee, T. J. (2011). Highly accurate quartic force fields, vibrational frequencies, and spectroscopic constants for cyclic and linear C3H3(+). J. Phys. Chem. 115, 5005–5016. doi:10.1021/jp2019704

CrossRef Full Text | Google Scholar

Huang, X., Fortenberry, R. C., and Lee, T. J. (2013). Spectroscopic constants and vibrational frequencies for l-CH and isotopologues from highly-accurate quartic force fields: the detection of l-CH in the Horsehead Nebula PDR questioned. Astrophys. J. Lett. 768, 25. doi:10.1088/2041-8205/768/2/l25

CrossRef Full Text | Google Scholar

Huang, X., and Lee, T. J. (2009). Accurate quartic force fields for NH and CCH and rovibrational spectroscopic constants for their isotopologs. J. Chem. Phys. 131, 104301. doi:10.1063/1.3212560

CrossRef Full Text | Google Scholar

Huang, X., Valeev, E. F., and Lee, T. J. (2010). Comparison of one-particle basis set extrapolation to explicitly correlated methods for the calculation of accurate quartic force fields, vibrational frequencies, and spectroscopic constants: application to HO, NH, NO, and CH. J. Chem. Phys. 133, 244108. doi:10.1063/1.3506341

PubMed Abstract | CrossRef Full Text | Google Scholar

Johansson, L. E., Andersson, C., Ellder, J., Friberg, P., Hjalmarson, A., Hoglund, B., et al. (1984). Spectral scan of orion A and IRC+10216 from 72 to 91 GHz. Astron. Astrophys. 130, 227–256

PubMed Abstract | Google Scholar

Kitchens, M. J. R., and Fortenberry, R. C. (2016). The rovibrational nature of closed-shell third-row triatomics: HOX and HXO, X = Si, P, S, and Cl. Chem. Phys. 472, 119–127. doi:10.1016/j.chemphys.2016.03.018

CrossRef Full Text | Google Scholar

Knizia, G., Adler, T. B., and Werner, H. J. (2009). Simplified CCSD(T)-F12 methods: theory and benchmarks. J. Chem. Phys. 130, 054104. doi:10.1063/1.3054300

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, K. L. K., and McCarthy, M. (2020). Bayesian analysis of theoretical rotational constants from low-cost electronic structure methods. J. Phys. Chem. 124, 898–910. doi:10.1021/acs.jpca.9b09982

CrossRef Full Text | Google Scholar

Martin, J. M. L., and Lee, T. J. (1996). The atomization energy and proton affinity of NH. an calibration study. Chem. Phys. Lett. 258, 136–143. doi:10.1016/0009-2614(96)00658-6

CrossRef Full Text | Google Scholar

Martin, J. M. L., and Taylor, P. R. (1994). Basis set convergence for geometry and harmonic frequencies. are h functions enough?. Chem. Phys. Lett. 225, 473–479. doi:10.1016/0009-2614(94)87114-0

CrossRef Full Text | Google Scholar

Martin-Drumel, M.-A., Lee, K. L. K., Pirali, O., Guillemin, J.-C., and McCarthy, M. C. (2019). “Investigating isomers of astrophysical molecules by rotational spectroscopy: the case of [CHO] compounds,” in International symposium on molecular spectroscopy. [Dataset].

CrossRef Full Text | Google Scholar

Matthews, H. E., and Sears, T. J. (1986). Interstellar molecular line searches at 1.5 centimeters. Astrophys. J. 300, 766. doi:10.1086/163852

CrossRef Full Text | Google Scholar

Mills, I. M. (1972). “Vibration-rotation structure in asymmetric- and symmetric-top molecules,” in Molecular spectroscopy–modern research. Editors K. N. Rao, and C. W. Mathews (New York: Academic Press), 115–140.

CrossRef Full Text | Google Scholar

Papousek, D., and Aliev, M. R. (1982). Molecular vibration-rotation spectra. Amsterdam: Elsevier.

Google Scholar

Peeters, E., Allamandola, L. J., Hudgins, D. M., Hony, S., and Tielens, A. G. G. M. (2004). “The unidentified infrared features after ISO,” in Astrophysics of dust, ASP conference series. Editors A. N. Witt, G. C. Clayton, and B. T. Draine (San Francisco, CA: Astronomical Society of the Pacific), 309.

Google Scholar

Peterson, K. A., Adler, T. B., and Werner, H. J. (2008). Systematically convergent basis sets for explicitly correlated wavefunctions: the atoms H, He, B-Ne, and Al-Ar. J. Chem. Phys. 128, 084102. doi:10.1063/1.2831537

PubMed Abstract | CrossRef Full Text | Google Scholar

Peterson, K. A., and Dunning, T. H. (1995). Benchmark calculations with correlated molecular wave functions. vii. binding energy and structure of the hf dimer. J. Chem. Phys. 102, 2032–2041. doi:10.1063/1.468725

CrossRef Full Text | Google Scholar

Pople, J. A., Schlegel, H. B., Krishnan, R., DeFrees, D. J., Binkley, J. S., Frisch, M. J., et al. (1981). Molecular orbital studies of vibrational frequencies. Int. J. Quant. Chem. 15, 269–278

Google Scholar

Raghavachari, K., Trucks, G. W., Pople, J. A., and Replogle, E. (1989). Highly correlated systems: structure, binding energy and harmonic vibrational frequencies of ozone. Chem. Phys. Lett. 158, 207–212. doi:10.1016/0009-2614(89)87322-1

CrossRef Full Text | Google Scholar

Rydbeck, R. A., Dunning, T. H., and Harrison, R. J. (1992). Electron affinities of the first-row atoms revisited. systematic basis sets and wave functions. J. Chem. Phys. 96, 6796–6806. doi:10.1063/1.462569

CrossRef Full Text | Google Scholar

Shavitt, I., and Bartlett, R. J. (2009). Many-body methods in chemistry and physics: MBPT and coupled-cluster theory. Cambridge: Cambridge University Press.

CrossRef Full Text | Google Scholar

Shimanouchi, T. (1972). Tables of molecular vibrational frequencies. 39th Edn. Washington, DC: National Standards Reference Data System, Vol. 1.

Google Scholar

Solomon, P. M., Jefferts, K. B., Penzias, A. A., and Wilson, R. W. (1971). Detection of millimeter emission lines from interstellar methyl cyanide. Astrophys. J. Lett. 168, L107. doi:10.1086/180794

CrossRef Full Text | Google Scholar

Stephens, J., Yan, W.-B., Richnow, M. L., Solka, H., and Curl, R. (1988). Infrared kinetic spectroscopy of CH and CD. J. Mol. Struct. 190, 41–60. doi:10.1016/0022-2860(88)80269-2

CrossRef Full Text | Google Scholar

Tanaka, K., and Yoshimine, M. (1980). An ab initio study on ketene, hydroxyacetylene, formylmethylene, oxirene, and their rearrangement paths. J. Am. Chem. Soc. 102, 7655–7662. doi:10.1021/ja00546a006

CrossRef Full Text | Google Scholar

Tucker, K. D., Kutner, M. L., and Thaddeus, P. (1974). The ethynyl radical C2H–A new interstellar molecule. Astrophys. J. 193, L115–L119. doi:10.1086/181646

CrossRef Full Text | Google Scholar

Turner, A. M., Koutsogiannis, A. S., Kleimeier, N. F., Bergantini, A., Zhu, C., Fortenberry, R. C., et al. (2020). An experimental and theoretical investigation into the formation of ketene (HCCO) and ethynol (HCCOH) in interstellar analog ices. Astrophys. J. 896, 88. doi:3847/1538-4357/ab8dbc

CrossRef Full Text | Google Scholar

Turner, B. E. (1977). Microwave detection of interstellar ketene. Astrophys. J. Lett. 213, L75–L79. doi:10.1086/182413

CrossRef Full Text | Google Scholar

Watson, J. K. G. (1977). “Aspects of quartic and sextic centrifugal effects on rotational energy levels,” in Vibrational spectra and structure. Editor J. R. During (Amsterdam: Elsevier), 1–89.

Google Scholar

Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., Schütz, M., Celani, P., et al. (2015). Molpro, version 2015.1, a package of programs. Available at: http://www.molpro.net (Accessed February 22, 2015)

Google Scholar

Yousaf, K. E., and Peterson, K. A. (2008). Optimized auxiliary basis sets for explicitly correlated methods. J. Chem. Phys. 129, 184108. doi:10.1063/1.3009271

PubMed Abstract | CrossRef Full Text | Google Scholar

Zasimov, P. V., Ryazantsev, S. V., Tyurin, D. A., and Feldman, V. I. (2019). Radiation-induced chemistry in the CH–HO system at cryogenic temperatures: a matrix isolation study. Mon. Not. Roy. Astron. Soc. 491, 5140–5150. doi:10.1093/mnras/stz3228

CrossRef Full Text | Google Scholar

Zhao, D., Doney, K. D., and Linnartz, H. (2014). Laboratory gas-phase detection of the cyclopropenyl cation (c-C 3 H 3 + ). Astrophys. J. Lett. 791, L28. doi:10.1088/2041-8205/791/2/l28

CrossRef Full Text | Google Scholar