Langmuir Turbulence in the Auroral Ionosphere: Origins and Effects

Theory and observations of Langmuir waves and turbulence induced in the auroral ionosphere by electron beams of magnetospheric-origin are reviewed. The theoretical discussions include a brief description of the electrostatic dispersion relation, excitation of Langmuir waves by electron beams, and the stability of beam distributions. The theory of Langmuir turbulence—including the parametric decay instability and wave collapse—is also briefly discussed. The main focus of the review, however, is on the observations of Langmuir waves and turbulence in the ionosphere by in-situ and ground-based sensors. A summary of five decades of in-situ wave and particle observations is presented and combined with a collection of more recent results from ground-based instruments. The ground-based observations include signatures of Langmuir turbulence in the form of coherent echoes in incoherent scatter radar measurements; signatures of electron beams in the form of auroral morphologies recorded by high-speed, high-resolution optical imagers; and electromagnetic emissions received on the ground at high latitudes. Uniting the various observations obtained by the vastly different sensors is shown to provide further insight into the micro-scale processes that occur in the ionosphere. Also discussed in this review is the potential of the ground-based sensors to provide a broader spatial and temporal context for single-point in-situ measurements of such processes.

1 Introduction

The Earth’s auroral ionosphere is characterized by the presence of intense particle precipitation from the magnetosphere. The large amount of energy deposited by accelerated electrons and ions in this region induces a range of multi-scale processes that ultimately shape the plasma dynamics at high latitudes. In the same region, collision-less interactions of the streaming electrons with the background plasma leads to the appearance of micro-scale phenomena—which, although they have smaller effects on large-scale plasma dynamics, are extremely rich in physics. Excitation of Langmuir waves by electron beams is an example of such processes.

With typical amplitudes of tens to hundreds of mV/m, Langmuir waves are among the strongest electrostatic waves in the auroral ionosphere (e.g., McFadden et al., 1986; Kintner et al., 1995). The waves are known to be very common and are detected on nearly every auroral zone pass in which precipitating electrons are observed (Kintner et al., 1995). A large body of observational works from satellites such as Freja (Lundin et al., 1994), FAST (Pfaff et al., 2001), as well as sounding rockets have uncovered an extremely wide range of processes associated with the waves. These include nonlinear wave-wave interactions, linear mode conversions, modifications of electron distributions by the waves, etc. Explaining such observational features has inspired intense research over the past several decades.

While the large body of theoretical, numerical, and experimental works on Langmuir waves in space plasmas have significantly advanced our understanding of these processes on the fundamental level, certain observational features from ground-based sensors at high latitudes have emerged in the past several years that deserve further attention. For example, Langmuir caviton formation and collapse induced by natural electron beams—as one of the most discussed feature of Langmuir turbulence—has been consistently absent in measurements by in-situ instruments in the ionosphere. Nevertheless, in the past decade or two, incoherent scatter radars at high latitudes have commonly detected echoes from the auroral ionosphere that include signatures of Langmuir collapse (e.g., Akbari et al., 2012; Isham et al., 2012). Furthermore, despite their large amplitudes and their abundance in the auroral plasma, possible effects of Langmuir waves on the local plasma dynamics have remained largely unaddressed by the in-situ observations. This is partly due to sparsity and limitations of single-point measurements by rockets and satellites. Such limitations, however, do not apply to volumetric measurements by stationary ground-based instruments. Under favored situations signatures of Langmuir turbulence could appear and last for several minutes in radar’s field-of-view over an extended altitude range, allowing to identify any modification of the ionosphere by the micro-scale processes.

In what follows, we briefly discuss the various regimes of beam-plasma interactions under which Langmuir waves grow. We then provide a brief description of the theory of Langmuir turbulence. This is followed by a review of five decades of in-situ observations of Langmuir waves in the ionosphere as well as more recent results from a collection of ground-based incoherent scatter radars, high-resolution auroral imagers, and electromagnetic receivers. The wide range of observations summarized allows us to review the topic of Langmuir waves in the auroral ionosphere and discuss a number of open questions. By uniting the various observations, one goal of this work is to introduce the potential of the ground-based instruments to provide a broader spatial and temporal context for single-point in-situ measurements of micro-scale processes.

Although the review is meant to be comprehensive, it only includes the basic concepts. Many details and discussions from the literature are not repeated here—for which, readers are routinely guided to the referenced original papers. Furthermore, this review only includes studies related to Langmuir waves produced naturally by electron beams in space plasmas and does not cover laboratory studies, results observed during injection of artificial electron beams in the ionosphere (a review provided by Mishin (2019)), or Langmuir turbulence induced in ionospheric modification experiments.

2 General Description of Beam-Plasma Interactions and Langmuir Turbulence

2.1 Beam-Plasma Interactions

2.1.1 Plasma Dispersion Relation

In a plasma consisting of a background population f_e(ν) and an electron beam f_b(ν), electrostatic plasma oscillations and their growth rates can be obtained by solving the dispersion relation (Clemmow, 2018):

$\epsilon =1+{\displaystyle \sum }_s{\chi }_s\left(\mathit{k},\omega \right)=0(1)$

Here, ${\chi }_s\left(\mathit{k},\omega \right)$ is the susceptibility for species‘s’—which includes a core electron population ‘e’, background ions ‘i’, and beam electrons ‘b’—and is given by:

${\chi }_s\left(\mathit{k},\omega \right)=\frac{{\omega }_s^2}{k^2}{{\displaystyle \int }}^{\text{}}{\mathrm{d}}^{3}v{\displaystyle \sum }_{n=-\infty }^{\infty }{J}_n^2\left(\frac{k_{\perp }{v}_{\perp }}{{\Omega }_s}\right)\times \frac{\left[k_{\parallel }\left(\partial f_s/\partial v_{\parallel }\right)+\left(n{\Omega }_s/k_{\perp }{v}_{\perp }\right)k_{\perp }\left(\partial f_s/\partial v_{\perp }\right)\right]}{\omega -n{\Omega }_s-k_{\parallel }{v}_{\parallel }}(2)$

In this equation, ω is the wave frequency, k is the wave vector, ${\omega }_s$ and ${\Omega }_s$ are the plasma and cyclotron frequencies of species‘s’, J_n is the Bessel function of the first kind of order n, and the subscript $\parallel$ and $\perp$ indicate the directions parallel and perpendicular to the magnetic field B, respectively.

The dispersion relation 1 needs to be solved for a real wave vector k, and a complex frequency $\omega ={\omega }_R+j\gamma$, where γ is the growth/damping rate at $\omega ={\omega }_R$. In the limit ${\omega }_R\gg \gamma$, Taylor expansion of $\epsilon \equiv {\epsilon }_R+j{\epsilon }_I$ about ${\omega }_R$ leads to the following descriptions for the wave modes and their growth rates, respectively: ${\epsilon }_R=0$ and $\gamma =-{\epsilon }_I/{\left(\partial {\epsilon }_R/\partial {\omega }_R\right)}_{{\omega }_R}$. Focusing on high-frequency waves (and thus ignoring ion dynamics), the dispersion relation ${\epsilon }_R=0$ describes several electrostatic modes—including the upper-hybrid, Langmuir, and the electrostatic whistler—that can be amplified in the presence of an electron beam. A detailed discussion on amplification of the electrostatic modes by auroral electron beams is given by Kaufmann et al. (1978).

In the auroral ionosphere, Eq. 1 should ideally include an additional term for the secondary or the scattered electrons which dominate the electron distribution function in the suprathermal energy range from a few eV to several keV. As will be discussed later in this review, the suprathermal electrons can introduce additional Landau damping for plasma waves and consequently affect the collisionless interaction of an electron beam with the ionospheric plasma (Lotko and Maggs, 1979; Mishin and Telegin, 1986; Newman et al., 1994c, b). Such effects of the suprathermal electrons, however, are ignored for the moment but will be discussed in Section 2.2 in the context of beam-generated Langmuir turbulence.

Considering the complexity of the dispersion relation given by Eq. 1, the analytical approach to investigate beam-plasma interactions often requires some level of approximation. For wave vector $\mathit{k}$ strictly parallel to B (i.e., ${\mathit{k}}_{\perp }=0$), the arguments of the Bessel functions $J_n$ in Eq. 2 vanish and only the $n=0$ term contributes to the sum over n. In this limit, the unmagnetized susceptibility reduces to

${\chi }_s\left(k,\omega \right)=\frac{{\omega }_s^2}{k^2}{{\displaystyle \int }}^{\text{}}\mathrm{d}{v}_{\parallel }\frac{k_{\parallel }\left(\partial F_s/\partial v_{\parallel }\right)}{\omega -k_{\parallel }{v}_{\parallel }}(3)$

where $F_s\left(v_{\parallel }\right)$ is the reduced distribution function

$F_s\left(v_{\parallel }\right)={{\displaystyle \int }}^{\text{}}{\mathrm{d}}^2{v}_{\perp }{f}_s\left(\mathit{v}\right).(4)$

When there is no ambiguity regarding the use of a 1D model, the notation is often simplified by making the following substitutions: $F_s\to f_s$; $k_{\parallel }\to k$; and $v_{\parallel }\to v$. After further limiting consideration to the case of two electron populations (background electrons designated by $s\to e$ and beam electrons designated by $s\to b$), with ions forming an immobile neutralizing background (i.e., ${\chi }_i=0$), the dispersion relation reduces to the familiar form (Stix, 1962):

$1+\frac{{\omega }_e^2}{k^2}{{{\displaystyle \int }}^{\text{}}}_{-\infty }^{\infty }\mathrm{d}v\frac{k\left(\partial f_e/\partial v\right)}{\omega -kv}+\frac{{\omega }_b^2}{k^2}{{{\displaystyle \int }}^{\text{}}}_{-\infty }^{\infty }\mathrm{d}v\frac{k\left(\partial f_b/\partial v\right)}{\omega -kv}=0(5)$

Although the $k_{\perp }\to 0$ limit assumes the presence of a non-zero magnetic field, the 1D susceptibility is valid even in the limit $\left|\mathbf{B}\right|\to 0$. In the unmagnetized case, the product $k_{\parallel }\left(\partial F_s/\partial v_{\parallel }\right)$ can be replaced by $\mathit{k}\cdot {\nabla }_v{F}_s\left(\mathit{v}\right)$, where the reduced distribution $F_s$ is now understood as being the integral over velocities perpendicular to k rather than perpendicular to B as in the magnetized case. The above substitution, in which k can point in an arbitrary direction, leads directly to the general 2D and 3D dispersion in the unmagnetized limit.

From the linear stability analysis of Eq. 5 it is found that the details of beam-plasma instability and the characteristics of the growing waves highly depend on the parameters of the beam (i.e., beam number density $n_b$, beam velocity $v_b$, and beam velocity spread $\text{Δ}{v}_b$) and the background plasma (O’neil and Malmberg, 1968; Peter Gary, 1985). Specifically, for relatively dense, cold, and fast electron beams such that $P={\left(n_b/n_0\right)}^{1/3}\left(v_b/\Delta v_b\right)>6$, the instability is fluid (also called ‘reactive’) and arises as a growing wave bunches the beam electrons at certain points of its oscillation in space to produce an electric field, which then enhances the modulation of the beam particle (e.g., Cairns, 1989; Cairns and Nishikawa, 1989). The fastest-growing modes, in this case, occur on the ‘beam mode’ with the dispersion relation $\omega \approx v_{b}k$. The beam mode is not a normal mode of plasma and appears in a beam-plasma system due to the contribution of ${\chi }_b$ to the real part of the dielectric function ${\epsilon }_R$. The term ‘reactive’ refers to the fact that the interactions are dominated by the real (or reactive) component of ${\epsilon }_R$ which also contributes to growth rates. The reactive instability is often saturated by trapping of beam electrons in potential wells of the self-generated electrostatic waves or via an increase in the thermal spread of the beam (Cairns and Nishikawa, 1989; Klimas, 1990). The interaction of the electron beam with the background plasma is then passed onto the kinetic domain (Nishikawa and Cairns, 1991; Dum and Nishikawa, 1994). Observational features associated with the instability in space plasmas when $P>6$ include electrostatic oscillations with frequencies below and above the local plasma frequency in planetary foreshocks (e.g., Etcheto and Faucheux, 1984; Fuselier et al., 1985; Cairns, 1989).

In contrast to the reactive limit, for relatively weak, warm, and slow electron beams such that $P<1$, the instability is kinetic (Cairns, 1989). In this case, modification of the real part of the dispersion relation 1 by ${\chi }_b$ is small and the solutions of the dispersion relation are close to the normal modes of the plasma. The beam primarily modifies the imaginary (resistive) component of the dielectric function and as such the instability is sometimes referred to as ‘resistive’. In this regime, the fastest-growing waves occur on the Langmuir dispersion relation with $\omega \ge {\omega }_p$ and grow due to inverse Landau damping associated with a positive slope in the one-dimensional (reduced) electron distribution function. The growth rate is given by Shapiro and Shevchenko (1988):

$\gamma =\frac{\pi {\omega }_e^2}{2n_0{k}^2}{\omega }_L\frac{\partial }{\partial v}{\left(f_e+f_b\right)}_{\omega /k}(6)$

where $n_0$ is the background plasma density and ${\omega }_L$ is the wave frequency. It is in this kinetic regime where unstable Langmuir waves grow to high intensities and result in Langmuir turbulence.

Numerical investigation of the dispersion relation for conditions in between the two limits above is discussed in the literature (Cairns, 1989; Dum, 1989). It is shown that by increasing P from below 1 to above 6, a smooth transition occurs in the shape of the dispersion curve, the frequency of the fastest-growing waves, and the kinetic versus reactive nature of the instability. Here, we do not further discuss the reactive regime of the beam-plasma instability since the ionospheric observations that are subject of this review fall well into the kinetic domain.

While the use of Eq. 5 greatly simplifies the analytical approach, it also eliminates a considerable amount of physics. Specifically, the one-dimensional unmagnetized description ignores the presence of several wave modes—such as the electrostatic whistler, upper-hybrid, and the electron Bernstein modes—which are described by the general electrostatic dispersion relation and are commonly observed in the auroral ionosphere. This reduction is evident in Eq. 2 where the assumption of $k_{\perp }=0$ leads to $J_n\left(\frac{k_{\perp }{v}_{\perp }}{{\text{Ω}}_s}\right)=0$ for $n\ne 0$. With respect to the growth rates, the term associated with $n=0$ becomes equivalent to the growth rate given by Eq. 6 and is referred to as the ‘Landau resonance’. The $n>0$ terms are referred to as the ‘cyclotron resonances’—which are often responsible for amplification of oblique waves with $k_{\perp }\gg k_{\parallel }$—whereas, the $n<0$ terms are sometimes referred to as the ‘anomalous Doppler resonances’. For further discussions of the growth of various wave modes and their competition for the free energy provided by auroral electron beams readers are referred to Kaufmann et al. (1978); McFadden et al. (1986); Ergun et al. (1993); Dum and Nishikawa (1994); Muschietti et al. (1997).

2.1.2 Saturation of the Bump-on-Tail Instability

In a uniform plasma, and in the absence of nonlinear wave-wave interactions, saturation of the bum-on-tail instability is due to quasi-linear beam flattening. In this process, the waves that are in resonance with the positive slope of the beam grow to large intensities, to the point that they react back on the distribution function, converting the positive slope into a plateau. Figure 1, from Krafft et al. (2015), shows an example from a one-dimensional simulation of beam-plasma instability in the solar wind, where quasi-linear relaxation of a 2 keV electron beam is described. Saturation of the bump-on-tail instability by quasi-linear beam flattening occurs on time scales of the order of ${\tau }_{ql}\sim \left(n_0/n_b\right){\omega }_e^{-1}$ (Davidson, 1972; Papadopoulos, 1975). The time scale is several milliseconds for the plasma parameters at about 1000 km and in the order of tens of millisecond for the plasma parameters at 300 km. Electron distribution measurements with instruments onboard sounding rockets and satellites have shown that the phase-space distribution of energetic electrons in the keV energy range—i.e., the so-called ‘inverted V’ electron beams—often consist of a plateau rather than a positive slope at the F region altitudes (e.g., Kaufmann et al., 1978), implying that the electron distributions have already stabilized by quasi-linear diffusion by the time the beams reach to ionospheric altitudes.

FIGURE 1

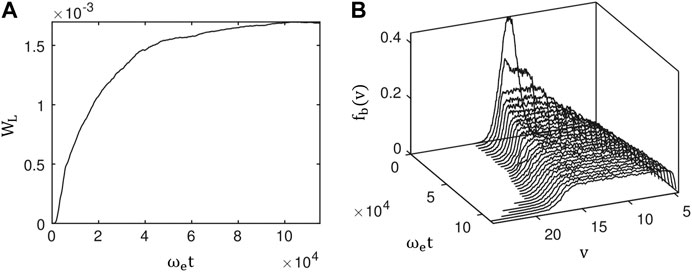
FIGURE 1. Adapted from Krafft et al. (2015): Results from one-dimensional simulations describing quasi-linear relaxation of an electron beam. (A) Time variation of the normalized energy density of beam-generated Langmuir waves (W_L). And, (B) evolution of the beam distribution in velocity space (v) as a function of time. Here, v is in the unit of electron thermal velocity defined as $V_{e,th}=\sqrt{k_B{T}_e/m_e}$. The simulation corresponds to choices of $n_0=5\times {10}^6{\mathrm{m}}^{-3}$, $T_e=20\mathrm{eV}$, $n_b/n_0=5\times {10}^{-5}$ and $v_b=2\mathrm{keV}$, comparable to observations in the solar wind.

Despite the relatively short timescales (equivalently, short distances) on which quasi-linear beam flattening occurs, Langmuir waves have been commonly observed in the solar wind and in the ionosphere far from the generation point of the source electron beams. Several scenarios have been proposed to resolve this contradiction. One scenario involves velocity dispersion, whereby faster beam electrons continuously precede the slower ones, momentarily reproducing a positive slope which is then quickly flattened (e.g., Lin et al., 1981; McFadden et al., 1986). The constant formation and flattening of the positive slope leads to a marginally unstable distribution which can travel to long distances. Another scenario involves nonlinear wave-wave interactions that are not included in the quasi-linear theory. In this scenario, the beam-resonant unstable waves undergo a parametric instability by which their energy quickly transfers to waves that are not in resonance with the beam and, thus, not in direct energy exchange. The beam-resonant waves, therefore, remain at a lower energy level and are less effective in altering the beam distribution (Papadopoulos and Coffey, 1974; Galeev, 1975; Galeev et al., 1977b; Muschietti and Dum, 1991; Goldman et al., 1996). Whether or not the beam flattening is significantly limited by the nonlinear wave-wave interactions depends on the timescales on which the two processes occur. Numerical simulations have demonstrated that for the parameters of the auroral ionosphere, ∼1000 km, the parametric decay of Langmuir waves and wave-particle interactions occur on similar timescales and as such both are important in determining the evolution of a beam-plasma system (Sanbonmatsu et al., 1997, 2001).

The presence of spatial and temporal variations in electron beams and background plasma can also significantly affect the growth of electrostatic waves and, consequently, the evolution of a beam distribution. Several examples include 1) propagation of the beam-resonant waves out of the region where the beam exists—for example, oblique propagation of waves outside of an auroral arc (Maggs, 1976, 1978; Maggs and Lotko, 1981); 2) change in the phase velocity of the enhanced waves due to the presence of background density gradient (e.g., Akbari et al., 2013); and 3) temporal variations within the beam and the background plasma that alter the growth rate as a function of time and space. Accounting for the random spatiotemporal variations of the beam and the background plasma has led to the development of the so-called Stochastic Growth Theory (SGT) (Robinson, 1995; Cairns and Robinson, 1997; Cairns et al., 2000; Cairns and Menietti, 2001). At the heart of this theory is a particle distribution that is and remains close to time- and space-averaged marginal stability but includes stochastic fluctuations—due to variations in the beam and background plasma—that cause linear wave growth at random times and locations. This theory provides an intrinsic explanation for certain observational features of Langmuir waves in space plasmas such as the burstiness of the wave fields and their observations far from the source region of the unstable distribution. One prediction of SGT is that the amplitude of the observed waves should follow a log-normal distribution. This prediction has been verified experimentally for several Langmuir wave observations in the solar wind (Cairns et al., 2000), in planetary foreshocks (Cairns and Robinson, 1997), as well as the Earth’s topside ionosphere (Samara et al., 2008).

Other processes that may contribute to the stability of electron beams and their interactions with background plasma involve electron-neutral collisions (e.g., Volokitin and Mishin, 1979). Theoretical calculations show that for electron-neutral collision frequencies, ${\nu }_e$, greater than a threshold (${\nu }_e>\pi {\omega }_e{n}_b/n_0$), the increased linear collisional damping can stop the plateau formation and preserve the positive slope. Above a threshold, electron-neutral collisions may also influence the transfer of turbulence energy to dissipative scales by wave collapse (this will be further discussed in the next section), leading to an increased level of wave energy compared to the collisionless case (e.g., Volokitin and Mishin, 1979). Such collisional effects may manifest in the E region of the auroral ionosphere where the exponential increase in the neutral density causes a rapid transition from collisionless to collisional turbulence. It has been proposed that this transition can lead to the appearance of a thin layer in altitude, called the plasma turbulence layer (PTL), in which wave energy is elevated (e.g., Mishin and Telegin, 1989). The dissipation of wave energy in the turbulence layer has been proposed to explain thin layers of enhanced electron temperature and density (e.g, Swider and Narcisi, 1977; Wahlund et al., 1989; Schlesier et al., 1997), as well as auroral luminosity (i.e., the so-called ‘Enhanced Aurora’) (e.g., Stenbaek-Nielsen and Hallinan, 1979; Dziubenko et al., 1980; Mishin et al., 1981; Hallinan et al., 1985) commonly observed by ground-based incoherent scatter radars and optical instruments at high latitudes.

2.2 Langmuir Turbulence

Langmuir turbulence is a result of nonlinear coupling between Langmuir waves and ion density perturbations. In plasmas, the refractive index is a function of plasma density, with a lower density corresponding to a higher refractive index. An existing density depression, therefore, forms a region of higher refractive index, which tends to concentrate the distribution of wave energy inside. On the other hand, a nonuniform distribution of Langmuir energy acts to push the plasma toward the area of weaker field strength (i.e., outside of the cavity) via the Ponderomotive force ${\mathit{F}}_P=-\frac{q^2}{4\pi {\omega }_e^2}\nabla |\mathit{E}{|}^2$. As a result of this positive feedback, instabilities emerge that lead to strong responses in electric fields and density perturbations which are referred to as Langmuir turbulence. Langmuir turbulence includes the phenomena of linear parametric instabilities, as well as the completely nonlinear phenomenon of caviton formation and wave collapse. It is known to occur in a variety of space and astrophysical plasmas—including pulsar magnetospheres (Asseo and Porzio, 2006), lower solar corona (Nulsen et al., 2007), the solar wind (e.g., Thejappa et al., 2012a, b; Graham et al., 2012; Graham and Cairns, 2014), planetary foreshocks (e.g., Robinson and Newman, 1991; Thiessen and Kellogg, 1993), and the Earth’s ionosphere (e.g., Akbari et al., 2012; Isham et al., 2012)—as well as laboratory laser-plasma (e.g., Kline et al., 2006) and beam-plasma experiments (e.g., Wong and Quon, 1975).

Langmuir turbulence is often modeled by numerical integration of a set of coupled, nonlinear, partial differential equations known as the Zakharov equations (e.g., Newman et al., 1994b; Robinson, 1997; Guio and Forme, 2006). The Zakharov equations for an unmagnetized plasma in multiple dimensions can be expressed as:

$\nabla \cdot \left(j\frac{\partial }{\partial t}+j{\nu }_e\times +\frac{3}{2}{\omega }_e{\lambda }_D^2{\nabla }^2\right)\mathit{E}=\frac{{\omega }_e}{2n_0}\nabla \cdot \left(\delta n\mathit{E}\right)(7)$

$\left(\frac{{\partial }^2}{\partial t^2}+2{\nu }_i\times \frac{\partial }{\partial t}-C_s^2{\nabla }^2\right)\delta n=\frac{1}{16\pi m_i}{\nabla }^2{\left|\mathit{E}\right|}^2(8)$

Here, $\mathit{E}$ is the slowly varying envelope of the high-frequency electrostatic wave field, and $\delta n$ is the quasineutral plasma density fluctuations. ${\nu }_e$ and ${\nu }_i$ are damping coefficients for Langmuir and ion-acoustic waves. The coefficients are wavenumber-dependent and are implemented by incorporating the convolution product operator $\times$. Also, ${\lambda }_D$, $C_s$, and, $m_i$ are the Debye length, ion sound velocity, and ion mass, respectively. In order to account for thermal spontaneous emission of Langmuir and ion-acoustic waves, stochastic complex source terms may also be added to the right-hand side of the two equations (e.g., Guio and Forme, 2006). Electron beams are often accounted for by including their wavenumber-dependent inverse Landau damping in the damping coefficient ${\nu }_e$. More generally, both the damping and dispersion of Langmuir waves can depend on the direction of k due to anisotropy of the plasma. For example, in (Newman et al., 1994b), the Laplacian operator ${\nabla }^2$ in Eq. 7 is replaced by a generalized dispersion operator $D^2$ that includes magnetic corrections to the dispersion relation. The Zakharov equations can be understood in the light of the description provided in the previous paragraph and by noting that 1) the Fourier transform of the expressions in parentheses on the left side of the equations represent the linear dispersion relation of the Langmuir and ion-acoustic waves; 2) the term on the right side of Eq. 8 represents the Ponderomotive force which couples the ion dynamics to Langmuir field; and 3) that the right side of Eq. 7 represents the non-uniform plasma density—i.e., the variations of the refractive index.

The standard description of beam-induced Langmuir turbulence in one dimension is as follows (Robinson, 1997): in the kinetic domain of the beam-plasma instability, Langmuir waves with phase velocities in the vicinity of the positive slope of the distribution function (i.e., $k_L\sim {\omega }_e/v_b$) experience a linear exponential growth according to Eq. 6. Provided that $k_L>k^{\ast }/2$ and $W<k{\lambda }_D{\left(m_e/m_i\right)}^{1/2}$ (i.e., region I in Figure 3 of Robinson, 1997)—where, $W=\frac{{\epsilon }_0{E}_L^2}{4n_0{k}_B{T}_e}$ is the ratio of the Langmuir electric field energy density to the plasma kinetic energy density, $k^{\ast }=\frac{2}{3{\lambda }_D}{\left(\gamma m_e/m_i\right)}^{1/2}$, ${\lambda }_D$ is the Debye length and $\gamma =1+3T_i/T_e$—and for sufficiently large wave amplitudes, the nonlinear transfer rate of energy into a daughter mode will exceed its damping rate and the waves become unstable to the parametric decay instability (PDI). Subsequently, the energy quickly transfers from the beam-resonant Langmuir waves to a daughter Langmuir wave with a wavenumber $k_{L^{\prime }}\approx -k_L+k^{\text{*}}$ and an ion acoustic wave at $k_s\approx 2k_L-k^{\text{*}}$. The change of sign of $k_{L^{\prime }}$ with respect to $k_L$ for $\left|k_L\right|>\left|k^{\ast }\right|$ indicates that the daughter wave propagates in the direction opposite to that of the original wave. Provided that there is enough input energy to the system, the daughter wave becomes unstable, producing its own set of product waves, transferring energy to yet smaller wavenumbers. A cascade of parametric decay instabilities then could be initiated which ultimately leads to the concentration of energy in the low wavenumber part of the spectrum. Results from a one-dimensional simulation illustrating the energy transfer from an electron beam to beam-resonant Langmuir waves at $k\sim 8m^{-1}$ and subsequently to a broad spectrum of waves is shown in Figure 2.

FIGURE 2

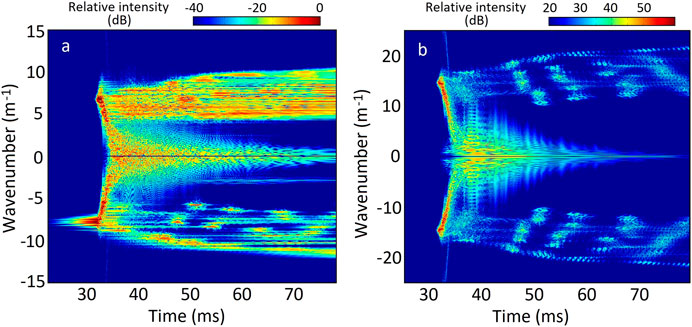
FIGURE 2. Adapted from Akbari et al. (2016): Results from a one-dimensional simulation of Langmuir turbulence induced in the nightside F region auroral plasma with a 125 eV electron beam. The left and right panels show the evolution of the electric field and ion density perturbations, respectively, as a function of time and wavenumber. A cascade of parametric decay instabilities is seen after t ∼32 ms following an exponential amplification of beam-resonant Langmuir waves at $k\sim 8{\mathrm{m}}^{-1}$. Other parameters of the electron beam are $n_b/n_0=6\times {10}^{-6}$ and $\text{Δ}{v}_b/v_b=0.3$.

In multiple spatial dimensions, the above description of a cascade of parametric decays is slightly altered since the participating waves are now allowed to obtain wave vectors in arbitrary directions—that is, as long as the wave vector matching condition ${\mathit{k}}_{\mathit{L}}={\mathit{k}}_{{\mathit{L}}^{\prime }}+{\mathit{k}}_{\mathit{s}}$ is satisfied. In two or three dimensions, therefore, the parametric decay instability may result in product waves that spread over broad arc-like features in k-space while transferring energy to lower wavenumbers. An example of a cascade of PDIs in two spatial dimensions is shown in Figure 5 of Robinson (1997).

In the absence of significant linear damping (collision and Landau damping), dissipation of the concentrated energy at small wavenumbers is achieved by the nonlinear process of caviton formation and collapse. The process is as follows: at $k<k^{\ast }/2$, the long-wavelength, relatively uniform Langmuir waves become unstable to the modulational instability by which a wave packet breaks-up into a train of smaller-scale modulations (see Figure 10 of Goldman, 1984). The modulational instability leads to the formation of plasma density cavities of the same scale in which Langmuir waves are trapped. If the intensity of a Langmuir packet is higher than a threshold ($E_c\left(L\right)\ge \sqrt{\frac{170n_0{k}_B{T}_e{V}_s}{{\epsilon }_0{V}_{e,th}}}\sqrt{\frac{{\lambda }_D}{L}}$, where $V_{e,th}={\left(k_B{T}_e/m_e\right)}^{1/2}$ and $V_s={\left(\gamma m_e/m_i\right)}^{1/2}{V}_{e,th}$ are the electron thermal velocity and the ion sound speed, respectively) (Cairns and Robinson, 1995), collapse initiates—i.e., the Ponderomotive force of the high-frequency field progressively pushes the plasma out of the corresponding density well, further deepening and narrowing the cavity, intensifying the trapped electric field inside. At very small scales (tens of Debye lengths), the collapsing wave packet experiences strong transit-time damping (Robinson, 1997, and references therein), which dissipates the electric field, releasing the energy in the form of accelerated electrons (e.g., Newman et al., 1990; Wang et al., 1996). The density cavity, now unsupported by Ponderomotive force, slowly relaxes in place (in the case of significant ion-acoustic damping) or breaks up into ion sound pulses that propagate in either direction (in the case of small ion-acoustic damping) (Doolen et al., 1985; Russell et al., 1988).

The relevance of the modulational instability at $k<k^{\text{*}}/2$ in the above description has been discussed by various works (Robinson, 1997, and references therein). Specifically, it has been argued that in a broadband turbulence produced by successive parametric decays, the modulational instability is likely stable (see Sec. III.C of Robinson, 1997). Collapse is instead expected to occur via the alternate ‘nucleation’ mechanism. This mechanism relies on the fact that, in the presence of density fluctuations, localized Langmuir eigenmodes exist in the form of trapped standing waves in density depressions (e.g., McAdams et al., 2000). The trapped waves may accumulate energy from the background turbulence, for example via three-wave decays, and undergo collapse. An example from a one-dimensional simulation is presented in Figure 3 where an ion density cavity undergoes nucleation and collapse. Here, collapse is seen at the initial stage of the time development of the feature at x ∼32.2 m, during which the cavity steepens and the pushed-aside plasma density propagates to the sides in the form of two ion sound pulses. After the dissipation stage, the density cavity relaxes in place, gradually becoming shallower. This is a consequence of the large ion damping rate chosen in this simulation ($T_e/T_i=3$) that is suitable for the F region auroral plasma. What remains of the density cavity may later re-nucleate energy, initiating another cycle of nucleation-collapse-dissipation (Doolen et al., 1985; Russell et al., 1988). A fully developed Langmuir turbulence in this picture simultaneously consists of linear Langmuir and ion-acoustic waves along with collapsing cavitons in the turbulence region.

FIGURE 3

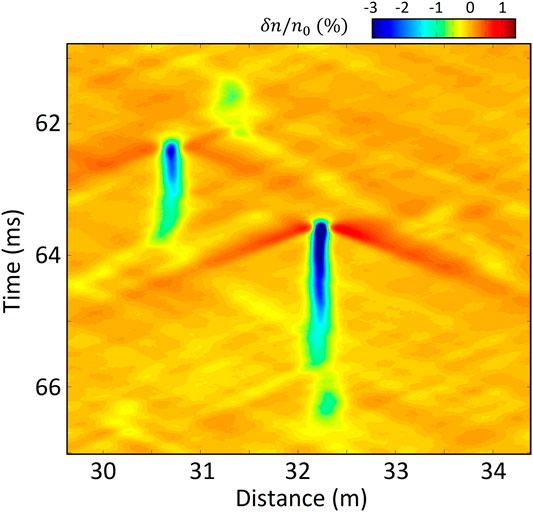
FIGURE 3. Adapted from Akbari et al. (2016): Results from a one-dimensional simulation of Langmuir turbulence in the nightside F region auroral plasma. Normalized ion density fluctuations are shown in real space as a function of time. The feature located in the center of the plot illustrates a cycle of nucleation–collapse–dissipation.

The picture described above is the standard description of Langmuir turbulence that applies to unmagnetized or weakly magnetized plasmas (${\omega }_e>{\text{Ω}}_e$). Several modifications to the description above are discussed in the literature. First, in the presence of a moderate magnetic field (${\text{Ω}}_e>{\omega }_e$)—applicable to environments such as the lower solar corona and the topside F region of the ionosphere—the topological changes to the Langmuir dispersion relation due to the magnetic field suppress self-focusing of wave energy in density cavities. In such environments, therefore, wave collapse is not possible (Newman et al., 1994a). On the other hand, the altered Langmuir dispersion relation allows the three-wave decay to directly transfer energy to larger wavenumbers where dissipation via Landau damping is significant. This is in contrast to the unmagnetized case where the kinematics of the parametric decay only allows energy transfer to lower wavenumbers.

It has been pointed out recently (Layden et al., 2013; Cairns and Layden, 2018) that the modification of the Langmuir dispersion relation to the generalized forms (Willes and Cairns, 2000) of the Langmuir-z mode for weakly magnetized plasmas (${\omega }_e>{\text{Ω}}_e$) and that of the Langmuir-whistler mode for strongly/moderately magnetized plasmas (${\text{Ω}}_e>{\omega }_e$) may also affect the standard description of Langmuir turbulence. Specifically, the deviation of the dispersion relation from that of the electrostatic Langmuir curve at small wavenumbers allows the parametric decay instability to be kinematically viable even for $k<k^{\text{*}}/2$. This is, again, contrary to the unmagnetized case and may potentially affect wave collapse due to the competition between the parametric decay instability and the modulational instability at small wavenumbers.

Another important consideration for Langmuir turbulence in the auroral plasma is the presence of the secondary and the scattered electrons which dominate the electron distribution function in the suprathermal energy range from a few eV to several keV (Mishin and Telegin, 1986). These electrons substantially enhance Landau damping of Langmuir waves at intermediate wavenumbers, causing the cascade of parametric decays to truncate. This, in turn, prevents the accumulation of energy at low wavenumbers, disabling wave collapse even when ${\omega }_e>{\text{Ω}}_e$ (Newman et al., 1994c, c). Furthermore, the damping enhances as the angle between k and B increases. Another effect of the suprathermal electrons is, therefore, to confine the turbulence to within ∼10° from the magnetic field direction. This is consistent with various observations by in-situ and ground-based sensors.

The above description of Langmuir turbulence, which is mainly developed based on the Zakharov equations, are limited to interactions of Langmuir and ion-acoustic waves and does not include the direct excitation of waves on the lower hybrid/whistler branch by the beam or the parametric decay of Langmuir waves into such wave modes (Stasiewicz et al., 1996; Bonnell et al., 1997; Lizunov et al., 2001; Singh et al., 2001). The electrostatic Zakharov equations also exclude the well-known parametric decay instabilities involving the first and second harmonics of the electromagnetic radiation near the local plasma frequency (e.g., Li et al., 2005a; Li et al., 2005b).

As we wrap up the theoretical discussions, we note that Langmuir turbulence—as would result from nonlinear interactions of warm, tenuous electron beams with background plasma—has also been investigated within the framework of the plasma weak turbulence theory (e.g., Ziebell et al., 2001; Yoon, 2006; Ziebell et al., 2008; Yoon et al., 2012b, and references therein). One advantage of the weak turbulence formalism is that it combines quasi-linear diffusion and wave kinetic equations and, as such, self-consistently describes the evolution of electron beams along with wave-wave interactions and wave-particle scattering effects. The weak turbulence framework has been extensively employed to investigate the generation of Langmuir waves in the solar wind, their conversion to electromagnetic emission near the plasma frequency and its harmonics, as well as their role in the generation of energetic tails in electron distribution functions (e.g., Yoon et al., 2005; Gaelzer et al., 2008; Yoon et al., 2012a; Ziebell et al., 2015; Lee et al., 2019). The weak turbulence theory properly describes three-wave interactions, such as the parametric decay instability, however, does not describe coherent phenomena such as caviton collapse or modulational instabilities. A detailed description of the equations of the weak turbulence theory is beyond the scope of this work; we instead refer the readers to the references mentioned above.

3 Observations of Langmuir Waves/Turbulence in the Ionosphere

3.1 In-situ Observations

In-situ observations of particles and fields by instruments onboard satellites and sounding rockets have played a major role in establishing that Langmuir waves are common in the high-latitude plasma environment and identifying their features and consequences. There have been many comparable in-situ observations of upper-hybrid waves, including similar physical effects as those reported for Langmuir waves, but this review concentrates on the modes with nearly parallel wave vectors.

Early spacecraft traversing the auroral zone included wave receivers that detected signals around the local plasma frequency (Gregory, 1969, and references therein). Bauer and Stone (1968), for example, combined many of these observations to estimate the electron density profile far into the topside. The Porcupine series of rockets launched in 1977 from Esrange, Sweden, detected Langmuir waves with amplitudes few to tens of mV/m in subsecond bursts both in the natural auroral environment and trapped in an artificial barium cloud (Carlson et al., 1987). Another 1977 rocket launch from Churchill, Manitoba, detected narrow-band signals near 2.3 MHz, tentatively identified as Langmuir waves, with estimated amplitudes 50 mV/m, occurring in bursts of approximately 100 ms duration, and correlated with energetic electrons beams (Kellogg et al., 1978). The bursty nature of auroral Langmuir waves and their correlation with magnetospheric-origin electron beams have been subsequently confirmed by many in-situ observations (e.g., Boehm, 1987; Kintner et al., 1995; LaBelle et al., 2010).

McFadden et al. (1986), for example, analyzed data from a 1982 rocket launched to over 600 km from Cape Perry, Canada, observing small amplitude (few mV/m) bursty Langmuir waves associated with ∼1.5 keV inverted V electron beams and others associated with broadband lower energy electrons below 375 eV. Through detailed consideration of the stability of measured electron distributions, they concluded that the primary source of energy for the waves was the positive slope in the parallel component of the electron distribution function. They also argued that the small amplitudes of the observed waves required processes to limit wave growth, such as propagation on a density gradient that could result in shifting the waves out of resonance with the beam. Significantly larger amplitude Langmuir wave bursts, up to and exceeding 800 mV/m, were later observed in many experiments (e.g., Boehm, 1987; Ergun et al., 1991a; Kintner et al., 1995; Kletzing et al., 2005; Samara et al., 2008; LaBelle et al., 2010); which also showed that Langmuir waves were more common at altitude above 600 km. In contrast to the small-amplitude waves, the large ∼V/m amplitude events require a mechanism to keep Langmuir waves in resonance longer, such as wave reflection or trapping discussed by Boehm (1987), or larger growth rates provided by electron beams.

Repeated in-situ observations (e.g., Kletzing et al., 2016) have shown that large-amplitude Langmuir waves in the ionosphere are often observed in conjunction with bursts of broadband (with energies from tens to thousands of eV), field-aligned electrons that are accelerated by the parallel electric field of inertial Alfvén waves (e.g., Kletzing and Hu, 2001). One characteristic of the field-aligned electron bursts is their velocity dispersion, by which the faster, higher energy electrons are observed first, followed by the slower electrons. The free energy for Langmuir waves is attributed to such modulations in the electron flux which lead to the appearance of a transient positive slope in the one-dimensional electron distribution function (McFadden et al., 1986). As was described in Section 2.1, the appearance of the transient positive slope, and thus the amplitude of the resulting waves, is determined by the competition between quasi-linear beam flattening, nonlinear parametric instabilities of Langmuir waves, and variations in the electron flux which can occur on similar timescales at ionospheric altitudes. Large-amplitude Langmuir waves in the ionosphere are often not associated with intense, energetic (keV) inverted V electron beams. Such beams, however, could be unstable in oblique directions and give rise to electrostatic whistler and upper-hybrid waves (Maggs, 1976; Kaufmann et al., 1978; Maggs, 1978; Lotko and Maggs, 1981; Maggs and Lotko, 1981; Gough et al., 1990).

3.1.1 Spectral and Temporal Characteristics of Langmuir Waves

A wealth of information on various linear and nonlinear processes involving Langmuir waves and electromagnetic emissions associated with them can be obtained by a careful investigation of their spectral and temporal features. Data from the AUREOL/ARCAD-3 satellite at 400-2000 km, for example, showed evidence of frequency structure associated with auroral Langmuir waves (Beghin et al., 1989). This data set also established the ubiquity of the phenomenon, with occurrence rates up to 80$\text{\%}$ on the dayside and 60$\text{\%}$ on the nightside. Wave structures extended above the plasma frequency when ${\omega }_e>{\text{Ω}}_e$ and extended below the plasma frequency when ${\omega }_e<{\text{Ω}}_e$. McAdams and LaBelle (1999) made continuous measurements of the waveform up to 5 MHz on a sounding rocket PHAZE-2 launched to 945 km into the nightside aurora from Alaska, revealing detailed frequency structure of the Langmuir waves. As found by Beghin et al. (1989), the structure depended on the value of ${\omega }_e/{\text{Ω}}_e$. For the ‘underdense’ case (${\omega }_e<{\text{Ω}}_e$), emissions appear in the form of relatively long-lasting monochromatic, banded structures below ${\omega }_e$, often punctuated by intense waves where the wave frequency matches local plasma frequency (McAdams et al., 1999). These were interpreted as mode conversion of Langmuir wave bursts into whistler waves that propagate long distances particularly as their frequency becomes well below local ${\omega }_e$ away from the source. The banded structure arises because the causative Langmuir waves consist of short-duration bursts. For the ‘overdense’ case (${\omega }_e>{\text{Ω}}_e$), short-duration frequency-drifting signals called “chirps” were detected just above ${\omega }_e$ in association with electron density irregularities with scales sizes meters to a kilometer. The chirps have bandwidths of 300–600 Hz, amplitudes of $\sim$0.7 mV/m, and last about tens of ms. They often appear in pairs or multiplets.

Figure 4 (from McAdams and LaBelle, 1999) shows spectral data of Langmuir waves measured in the overdense nightside aurora with the PHAZE-2 sounding rocket. The top panel shows Langmuir waves at and above the plasma frequency, that is identified by the lower cutoff descending from 2.2 to 1.7 MHz. The structured Langmuir waves are associated with density enhancements of around 1 km spatial scale believed to be caused by electron impact ionization from the same electron beam which generates the waves. Lower panels B–E show expanded views of the Langmuir wave fine structure, consisting of multiplet structures “chirps”.

FIGURE 4

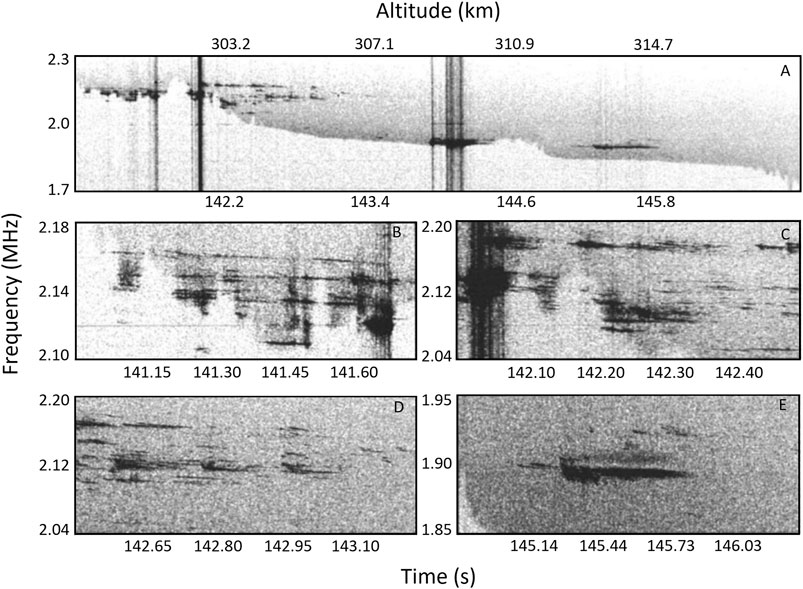
FIGURE 4. Adapted from McAdams and LaBelle (1999): Spectrograms of electric field measured with a 30-cm double-probe antenna at ∼310 km altitude with the PHAZE-2 sounding rocket. Top panel: overview spectrogram showing Langmuir emissions at and just above the plasma frequency, associated with density structures. Bottom panels: zoomed-in spectrograms showing the detailed structure of the Langmuir waves.

McAdams et al. (2000) put forth a model of the HF “chirp” emissions as quasi-trapped eigenmodes in a field-aligned density depletion. Observed frequency spacings of the “chirps” (0.1–1.4 kHz) and observed density cavity sizes and depths agreed with predictions of the linear theory of the waves in the depletions using equivalent of WKB approximation. The model also correctly predicts that the modes are evenly spaced, as well as the number of modes predicted for a given density cavity. Yoon and LaBelle (2005) extend the model to a wider class of density irregularities. These observations motivated the analysis discovering analogous eigenmodes of Langmuir waves observed by STEREO spacecraft in the solar wind (Ergun et al., 2008). Samara and LaBelle (2006) review observations of “chirp” features on three different rocket experiments, showing a greater variety of “chirp” frequency variations (upward as well as downward) and a typical 3-km distance scale of decay of amplitudes of escaping chirps as a function of distance from their sources.

Another, clearly noticeable, characteristic of Langmuir waves is their amplitude modulation at very low frequencies (VLF), typically between 1 and 60 kHz. Boehm (1987), for example, reported up to 100% modulations in Langmuir wave amplitudes suggesting nonlinear wave-wave interactions. Such amplitude modulations of Langmuir waves have since been confirmed in many experiments and have resulted in several possible explanations. The proposed mechanisms include beating between Langmuir waves of different frequencies (Newman et al., 1994b; Burinskaya et al., 2003; LaBelle et al., 2010); nonlinear wave-wave interaction involving low-frequency waves such as ion-acoustic, lower hybrid, or ion Bernstein waves (Ergun et al., 1991a; Stasiewicz et al., 1996; Bonnell et al., 1997; Khotyaintsev et al., 2001; Lizunov et al., 2001; Singh et al., 2001), as well as purely kinetic processes where electron motions are affected by the electrostatic potential of the generated waves (Muschietti et al., 1995, 1996; Akimoto et al., 1996; Umeda, 2006).

An example of such modulations is presented in Figure 5 (adapted from LaBelle et al., 2010) which shows Langmuir waves measured in the dayside aurora with the TRICE sounding rocket. Here, panel a shows a spectrogram from an 11-s interval covering a 200 kHz band centered on the plasma frequency which is near 500 kHz. This panel illustrates the bursty nature of the Langmuir waves. Panel b shows a spectrogram of a relatively long individual burst lasting nearly 200 ms. The upper bound of the waves rises and then falls during the burst, interpreted as evidence of a plasma density enhancement in which the Langmuir waves are trapped. Panel c shows a selected spectrum, at the time of the vertical white dashed line in panel b, showing that the Langmuir waves consist of a forest of spectral peaks spanning about 40 kHz. The coherence and duration of the peaks can be inferred from the spectrogram. Panel d shows waveform data during a 2-ms interval illustrating envelope modulations with amplitudes approaching 100%, typical of auroral Langmuir wave observations.

FIGURE 5

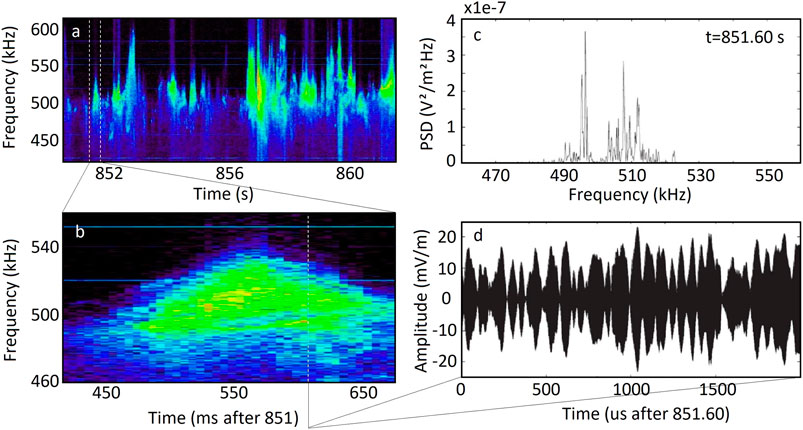
FIGURE 5. Adapted from LaBelle et al. (2010): Langmuir wave electric fields measured with a 30-cm double-probe antenna at 967–894 km with the TRICE sounding rocket launched from Andoya, Norway on December 10, 2007. Left panels: overview spectrogram showing Langmuir wave bursts (top), and zoomed-in spectrogram showing Langmuir wave structure (bottom). Right panels: selected spectrum showing a forest of peaks at and below $f_p$(top), and time series waveform showing typical Langmuir wave modulations.

Bonnell et al. (1997) present a statistical study of several hundred modulated Langmuir wave bursts observed with the Freja satellite at 1400-1700 km and the Scifer sounding rocket launched from Norway to 1450 km in the cusp. They find modulation frequencies from 1 kHz, an instrumental lower limit, to 60 kHz. They demonstrate that parametric decay into oblique Langmuir waves and whistler/lower hybrid waves is kinematically possible and could account for modulation frequencies above 7 kHz. They, furthermore, suggest that below 7 kHz, modulations require involvement of ion sound waves. In none of the preceding studies, however, is the low-frequency daughter wave observed. Stasiewicz et al. (1996), in contrast, shows case studies of Langmuir wave-wave interactions observed with the Freja satellite, in which the low-frequency wave is detected. In some cases, the presence of the low-frequency wave are interpreted as parametric decay of Langmuir waves into lower hybrid waves and in other cases as wave coalescence involving pre-existing lower hybrid waves. Khotyaintsev et al. (2001) and Lizunov et al. (2001) provide support for this mechanism. LaBelle et al. (2010) studies 41 Langmuir bursts out of 1000 estimated to occur during the TRICE rocket experiment launched to 1146 km from Norway into the cusp. They confirm modulation frequencies ranging to above 50 kHz but also find about 10% of events have modulation frequencies below 1 kHz, near the limit of detectability in bursts lasting tens of ms. They suggest interference of independently generated Langmuir wave modes as the source of the modulations. This is based on the statistical distribution of electric fields in the waves, which at the low field end exhibits a power-law spectrum. Li et al. (2010) show that such a distribution is expected for a superposition of random modes. Burinskaya et al. (2003) also suggest wave beating as the source of structure in 1–40 mV/m Langmuir waves detected at 2–3.5 Earth radii at high latitudes by the INTERBALL spacecraft. In contrast, Boehm (1987) originally rejected superposition of independent modes as being too improbable requiring too similar amplitudes to produce nearly 100% modulations.

3.1.2 Polarization

Polarization is another aspect of in-situ observations of Langmuir waves. Although, partly because of the large data rates involved, relatively few instruments have measured multiple components of the wave electric fields. McFadden et al. (1986) using measurements of two components of electric field were able to ascertain that the parallel field dominated, possibly by a factor of three or more, in the low amplitude Langmuir waves they measured. The TRICE sounding rocket launched into the cusp from Norway obtained, via small baseline antennas, snapshots of three components of electric field of waveforms at Langmuir wave frequencies. Dombrowski et al. (2012) found that the nature of the observed modulated Langmuir waves, in which the modulation nulls and peaks were not aligned between all three electric field components, could only be explained by mixing of different polarizations of waves, including both linear and elliptically polarized modes. Colpitts and LaBelle (2008) used statistics of the spin dependence of Langmuir wave detection with a single spinning electric field antenna, combined with Monte Carlo simulations, to probe the polarization of observed Langmuir waves.

3.1.3 Wave-Particle Correlators

The relationship of auroral Langmuir waves to the causative electron distribution, subject of linear theory tested by McFadden et al. (1986) and Beghin et al. (1989), has been investigated more deeply using large geometric factor particle instruments and/or wave-particle correlators. Such instruments are designed to sort detected electrons according to the phase of simultaneously measured Langmuir waves, thereby probing the detailed wave-particle interaction. Early versions of this type of experiment detected various levels (5–30%) of modulations of 4–7 keV electrons at megahertz frequencies, in some cases simultaneous with detections of positive slopes in the electron distribution functions (Spiger et al., 1976; Gough and Urban, 1983; Gough et al., 1990).

Ergun et al. (1991b), using a wave-particle correlator that sorted electrons according to the quadrant of the Langmuir wave phase, detected electron bunching at the few percent level in the fields of ∼100 mV/m, ∼100 ms Langmuir wave bursts, establishing the resonant energy, hence obtaining the parallel wavelength of 15 m. Ergun et al. (1991b) followed up by determining that the electron bunching was in 0 or 180 phase with the electric field, implying wave growth or damping. Simulations suggested that growth/in-phase bunching should be followed by trapping/quadrature bunching, but the latter was not observed, perhaps due to stationarity issues, finite size of the wave packet, or insufficient energy resolution as suggested by Kletzing and Muschietti (2006), who showed that the trapping signature is bimodal in energy and hence requires higher energy resolution to detect. Kletzing et al. (2005, 2016) developed a wave-particle correlator that sorted electrons into sixteen phase bins locked to the Langmuir wave phase. The instruments were flown on two sounding rockets (RACE and Charm-2) launched into the nightside aurora from Alaska and found evidence of electron bunching where the phase relation indicated trapping of electrons in wave fields, in contrast to the result of Ergun et al. (1991b).

Figure 6 adapted from Kletzing et al. (2017) shows an expanded view of 120 ms of data from the CHARM-2 rocket flight. The top panel shows a 0–1 MHz spectrogram where a monochromatic Langmuir wave emission slightly above 400 kHz is observed. The middle panel shows a spectrogram of downgoing electrons where a time-dispersed signature at energies below 500 eV is present. The bottom panel show outputs of the wave-particle correlator for several energies of electrons within the time-dispersed electron flux feature, with Langmuir wave phase bin on the vertical axis and color scale representing standard deviation. The latter is a measure of the degree of electron bunching. Significant correlation is observed in many of the energy channels. The phase bunching is positive near a phase of 180 or 0 degrees relative to the electric potential, indicating reactive phase bunching where electrons are trapped in the wave field.

FIGURE 6

FIGURE 6. Adapted from Kletzing et al. (2017): Langmuir wave electric field, particle, and wave-particle correlator data measured near 725 km altitude with the CHARM-2 sounding rocket. Top panel: electric field spectrogram showing extremely monochromatic Langmuir waves slightly above 400 kHz. Middle panel: energy flux spectrogram of downgoing electrons showing broadband dispersed feature below 500 eV coincident with the Langmuir waves. Bottom panel: the output of the wave-particle correlator showing significant bunching of 385 eV downgoing electrons in the field of the wave at 10:00:01.66 UT, evidenced by count rates significantly above or below expected values in most of the sixteen phase bins.

Dombrowski et al. (2019) analyzed 57 Langmuir wave bursts from the CHARM-2 rocket flight, in which significant correlations were detected between electrons and Langmuir wave phases. In their observations, signatures of energy exchange slightly dominated over those of particle trapping. Moreover, they observed that at times when the electron beam flux was increasing with time, the phase of the electron bunching indicated energy transfer from the electron beam to the waves, and at times when the beam electron flux was decreasing, the reverse. Test particle simulations showed that short term enhancements in the growth or damping of the Langmuir waves due to time-of-flight effects on the electron distribution could plausibly explain the observations.

3.1.4 Non-thermal Features of the Electron Distribution Function as Signatures of Langmuir Turbulence

Among important signatures of Langmuir turbulence are non-thermal features of the electron distribution function in the form of energetic tails and accelerated suprathermal populations. The non-thermal features are the consequences of nonlinear stabilization of a beam-plasma system and are produced as the parametric instabilities spread the wave energy in k-space from $k_L\sim {\omega }_e/v_b$ to lower and higher wavenumbers. The common observations of electron velocity distributions with energetic tails at energies above a beam in the solar wind (e.g., Ergun et al., 1998; Fitzenreiter et al., 1998), for example, are reproduced in Langmuir turbulence simulations based on the weak turbulence theory. Here the tail formation is associated with the dissipation of wave energy that is transferred to smaller wavenumbers by the parametric decay and scattering processes (Yoon et al., 2005, 2006; Ryu et al., 2007). This mechanism is shown to be able to produce both symmetric and asymmetric energetic tails (Gaelzer et al., 2008; Yoon et al., 2012a).

Suprathermal electron populations at intermediate energies—between thermal electrons and an energetic beam—with fluxes larger than those predicted from collisional interaction of the beam with the neutral atmosphere, are also commonly observed by in-situ instruments in the auroral ionosphere (e.g, Arnoldy and Choy, 1973; Reasoner and Chappell, 1973; Bryant et al., 1978; Fung and Hoffman, 1988; Ogasawara et al., 2017). An explanation based on collisionless beam-plasma interactions has been provided for such observations. In this scenario, modulational instability transfers the energy from beam-resonant waves to higher wavenumbers (i.e., lower phase velocities), making energy exchange possible between the electrostatic waves and the electrons on the tail of the background population (Papadopoulos and Coffey, 1974; Matthews et al., 1976).

Acceleration of electrons to suprathermal energies is also a well-known process associated with the dissipation of collapsing cavitons (e.g., Galeev et al., 1977a; Newman et al., 1990; Wang et al., 1996). In this case, efficient energy exchange could occur as electrons pass through the intense wave packets that are localized in density cavities. Electron acceleration occurs provided that the phase of a Langmuir oscillation during the energy exchange is such that it leads to a net energy gain for the particle. Generation of a suprathermal tail by Langmuir turbulence consisting of collapsing cavitons is an important outcome in the ionospheric modification (heating) experiments. In these experiments, high-power, high-frequency (HF) electromagnetic waves, that is injected into the bottom-side F region, artificially induce Langmuir turbulence, heating the plasma and accelerating electrons (e.g., DuBois et al., 1990, 1993; Isham et al., 1999; Mishin et al., 2004). Collisional interaction of the accelerated electrons with neutral species then produces enhanced ionization and artificial aurora that are detectable with ground-based incoherent scatter radars and optical instruments (e.g., Carlson et al., 1982; Bernhardt et al., 1989; Mishin et al., 2004; Pedersen et al., 2010; Mishin and Pedersen, 2011; Eliasson et al., 2012).

3.2 Ground-Based Observations

Over the past decade or two, a type of anomalous non-thermal echo from the F region auroral ionosphere has been detected by various incoherent scatter radars (ISRs) (e.g., Strømme et al., 2005; Ekeberg et al., 2010; Akbari et al., 2012; Isham et al., 2012; Schlatter et al., 2014; Akbari et al., 2016). The echoes are often characterized by simultaneous enhancement of spectral peaks in the ISR spectrum that are associated with ion-acoustic and Langmuir waves. They, therefore, indicate the occurrence of naturally produced Langmuir turbulence within the plasma volume illuminated by the radar pulse.

A detailed description of the incoherent scatter radar theory will not be provided here. The following brief description is, however, necessary to provide a proper context for the results presented in this section. For a detailed description of the ISR theory, readers are referred to a review by Akbari et al. (2017) which focuses on Langmuir wave observations by incoherent scatter radars and their numerous applications in ionospheric studies. The fundamental measurement of an incoherent scatter radar is the ISR spectrum. The ISR spectrum is directly related to the frequency spectrum of plasma density fluctuations at a single spatial Fourier component (wavenumber). It is, therefore, related to a cut through the electrostatic dispersion surface along a single wave vector $\mathit{k}={\mathit{k}}_{\text{detection}}$, where ${\mathit{k}}_{\text{detection}}$ is determined by the radar’s geometry and operating frequency. The electrostatic solutions of the plasma dispersion relation—such as the ion-acoustic and Langmuir waves—then appear in the ISR spectrum as spectral peaks at frequency offsets that satisfy the relevant dispersion relations for the specific k. Example simulated ISR spectra associated with a thermal plasma are shown in the top panels of Figure 7 (from Isham et al., 2012). The spectra include two resonance lines associated with up- and down-going (more accurately, propagating away and toward the radar) ion-acoustic waves which are closely located in the vicinity of zero Doppler frequency (see top row, middle panel in Figure 7) and two resonance lines associated with up- and down-going Langmuir waves with offset Doppler frequencies of about −f_e and +f_e, respectively. In the presence of a beam-generated Langmuir turbulence (shown in other panels of Figure 7) the resonance lines may be significantly enhanced due to amplification of ion-acoustic and Langmuir waves, and additional features, associated with caviton formation and collapse, may appear in the spectra. The latter signatures may appear in the form of a central peak at zero Doppler and a broadened or additional spectral peaks in the vicinity of ±f_e.

FIGURE 7

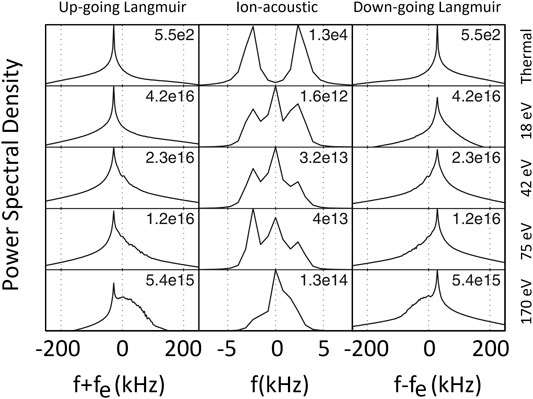
FIGURE 7. Adapted from Isham et al. (2012): Results from a one-dimensional simulation with plasma parameters of the auroral F region. The spectra of up and down-going Langmuir and ion-acoustic waves are calculated for a wavelength of about 0.67 m ($k\approx 9.4{\mathrm{m}}^{-1}$), approximately matching the Bragg backscatter condition of the European Incoherent Scatter Scientific Association (EISCAT) 224-MHz radar located near Tromsø, Norway. Modification of the spectra due to Langmuir turbulence produced by downward-going beams of electrons at beam energies of 18, 42, 75, and 170 eV are shown. The appearance of the zero-frequency peak in the ion-acoustic channel and the broadened spectral peaks associated with Langmuir waves are signatures of caviton formation and wave collapse. $\text{Δ}{v}_b/v_b=0.3$ and $n_b/n_0=2\times {10}^{-5}$ are adopted for the beams. The parameters result in $P\approx 0.09$, corresponding to the kinetic regime of beam-plasma instability. The numbers at the top right section of each panel indicate the peak value of each spectrum.

Figure 8, from Isham et al. (2012), shows example ISR data, obtained by the European Incoherent Scatter Scientific Association (EISCAT) 224-MHz radar on November 11, 1999, for a single radar beam in $\mathbf{B}\parallel$ direction. Shown are the total scattered power associated with Langmuir and ion-acoustic waves—i.e., the area under the power spectral density features—as a function of altitude and time. Several distinct sources of scattering can be identified. The dark background in the ion-acoustic channel is backscatter from thermal-level ion-acoustic waves. The repeated 10-s-long enhancements seen in all three channels at about 225 and 125 km before and after 18:18:30, respectively, are experimental features irrelevant to our discussions. The intense features occurring between 18:18:30 and 18:20:30 UT near 300 km and at 18:23:30 UT near 250 km are backscatter signals associated with amplified Langmuir and ion-acoustic waves which indicate the occurrence of parametric decay instability in the local plasma. Echoes similar to those detected by the 224-MHz EISCAT VHF radar, at the detecting wavenumber $\left|\mathit{k}\right|\sim 9.4{\mathrm{m}}^{-1}$, have also been commonly observed by other radars, including the 500-MHz EISCAT Svalbard radar at $\left|\mathit{k}\right|\sim 21{\mathrm{m}}^{-1}$ (e.g., Strømme et al., 2005; Ekeberg et al., 2010; Schlatter et al., 2014), the 931-MHz EISCAT UHF radar at $\left|\mathit{k}\right|\sim 39{\mathrm{m}}^{-1}$ (e.g., Schlatter et al., 2013), and the 450-MHz Poker Flat Incoherent Scatter Radar (PFISR) at $\left|\mathit{k}\right|\sim 19{\mathrm{m}}^{-1}$ (e.g., Akbari et al., 2012; Michell et al., 2014). For the rest of this manuscript, such coherent echoes are referred to as ‘Langmuir turbulence echoes’ or ‘LT echoes’. In addition to the simultaneous amplification of ion-acoustic and Langmuir waves, many observations, commonly include important spectral details (not shown here) such as additional peaks in the ISR spectra at zero Doppler frequency and in the vicinity of the local plasma frequency (Akbari et al., 2012; Isham et al., 2012; Schlatter et al., 2013, 2014; Akbari et al., 2016), similar to the simulation results shown in Figure 7 when electron beams are included. Such spectral features are signatures of Langmuir wave collapse which involve stationary (thus, resulting in a zero Doppler shift) ion density cavities in which Langmuir waves are trapped. These experimental features are considered as the first conclusive evidence of naturally induced Langmuir collapse anywhere in space plasmas.

FIGURE 8

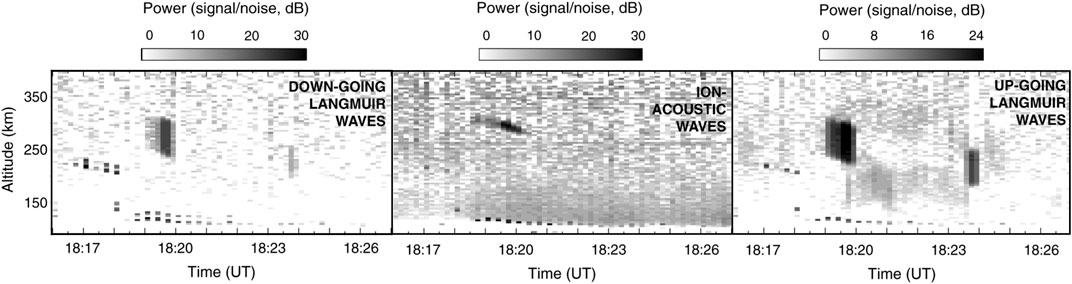
FIGURE 8. Adapted from Isham et al. (2012): Range-Time-Intensity plot of received power associated with ion-acoustic (middle) and down- and up-going Langmuir waves (left and right, respectively) obtained by the EISCAT 224-MHz radar on November 11, 1999. The simultaneous amplification of ion-acoustic and Langmuir waves is a signature of Langmuir turbulence.

ISR experimental features very similar to those shown in Figures 7 and 8 are also commonly obtained in ionospheric modification experiments, where Langmuir turbulence and wave collapse are artificially induced in the ionosphere by the injection of powerful high frequency electromagnetic waves (e.g., DuBois et al., 1990, 1993; Isham et al., 1999). A difference between the results discussed in this review and those from ionospheric heating experiments is the source of the free energy for the turbulence—which for the case of natural turbulence, is thought be the magnetosphere-origin electron beams.

Correlating LT echoes with optical images of the aurora reveals that natural Langmuir turbulence underlying radar echoes may occur on the edge of auroral arcs and just outside of regions of energetic electron precipitation (Akbari et al., 2013). Two examples are shown in Figures 9A,B—here, the optical images are recorded when LT echoes appear in the field of view of the Poker Flat incoherent scatter radar, represented by the white circles. Analysis of high-speed ground-based auroral imagery often indicates the presence of dispersive-scale Alfvén waves at the time of LT echoes, suggesting a relationship between the two. The signatures of dispersive-scale Alfvén waves are seen in Figures 9A,B in the form of small-scale structures of the auroral arcs (Semeter and Blixt, 2006; Semeter et al., 2008). Association of LT echoes with auroral forms is further studied by Michell and Samara (2013) and Michell et al. (2014), where correlation with active arcs consisting of small-scale features similar to those shown in Figures 9A,B is found. Some radar studies, furthermore, find a correlation between coherent echoes and high-energy flux of precipitating electrons which produce enhanced E region ionization (e.g., Dahlgren et al., 2017). In Figure 9, the auroral morphology shown in panel c is different than those in the left two panels. At the time of this image, the radar detected a type of coherent echo known as the Naturally Enhanced Ion Acoustic Line. This will be further discussed in the following. For more discussions on Figure 9 and the detected radar echoes see the original referenced work.

FIGURE 9

FIGURE 9. Adapted from Semeter et al. (2008) and Akbari et al. (2012): Auroral morphologies recorded by a high-speed, high-resolution optical imager when coherent echoes appeared in the Poker Flat incoherent scatter radar’s field of view (represented by the white circles) on March 23, 2007. The auroral arcs in panels a and b consist of small-scale features, thought to be associated with dispersive-scale Alfvén waves, and are recorded at times when the radar detected LT echoes. The auroral morphology in panel c is different than those in panels (A) and (B). At the time of this image, the radar detected a type of coherent echo known as the Naturally Enhanced Ion Acoustic Line.

The radar echoes underlying the natural Langmuir turbulence are primarily observed in radar beam directions parallel to the magnetic field. They are often observed in thin layers (thickness of $<$10 km) at or close to the F region peak between 200 and 300 km and are occasionally accompanied by a secondary layer some tens of km below the main layer (e.g. Akbari et al., 2013; Michell et al., 2014; Schlatter et al., 2014). Such localization of the turbulence in multiple thin layers is very intriguing and requires an explanation. The duration of the echoes is typically only a few seconds in radar’s field-of-view but events lasting as long as several minutes have been observed. In an apparent contradiction to the explanation of the radar signatures in terms of Langmuir turbulence, often a one-to-one correlation between enhanced echoes associated with amplified Langmuir and ion-acoustic waves is not observed. In Figure 8, for example, the enhanced signals associated with Langmuir waves between 18:23:30 and 18:24:00 are not accompanied by an enhancement in the middle panel. A statistical study by Schlatter et al. (2014), using a dataset collected by the 500-MHz European Incoherent Scatter Svalbard Radar, shows that only about 25% of ion-acoustic echoes are accompanied by Langmuir echoes (provided that the frequency of the Langmuir waves fall within the pass-band of the receive channels). The lack of one-to-one correlation between enhanced ion-acoustic and Langmuir waves, however, may arise from the wavenumber matching requirement for detecting wave activities by radars, combined with the fact that ion-acoustic and Langmuir waves involved in a parametric decay instability have different wavenumbers—all of which may not satisfy $k_{\text{wave}}=k_{\text{detection}}$. Schlatter et al. (2014), furthermore, find a maximum occurrence rate of ∼0.09% for LT echoes at 21 Magnetic Local Time (MLT). The occurrence rate is shown to increase with geomagnetic activity to ∼0.6% for the Kelvin (K) index of 5. This maximum detection rate is small compared to the detection rate of Langmuir waves by in-situ instruments and is most likely due to the strict detection criteria of radars.

Based on experimental evidence that Langmuir turbulence echoes appear at altitudes where the vertical background plasma density gradient is minimal—i.e., at the peak of the F region and the valley between the E and F regions—a potential explanation for the localization of the turbulence in thin layers has been described by Akbari et al. (2013). They argue that, while destabilizing features of electron beams may exist on a given field line over an extended altitude range, propagation of waves in a vertical plasma density gradient, which leads to a change in their phase velocity, could drive the waves out of resonance with electron beams, limiting wave growth. Given the group velocity of Langmuir waves and the parameters of the auroral ionosphere, waves could fall out of resonance within tens of milliseconds. This is comparable to the timescales of quasi-linear beam flattening and those of nonlinear wave-wave interactions in the F region. Outside of the turbulence layer, therefore, the amplitude of Langmuir waves likely remains small. When the plasma density gradient is negligible, Langmuir waves may grow to large amplitudes and produce a broadband turbulence that is detectable by incoherent scatter radars. A similar mechanism, based on variations of the background density gradient, has been considered in the auroral E region to explain thin layers of enhanced ionospheric response during electron precipitation events (Voronkov and Mishin, 1993; Mishin and Khazanov, 2006).

Propagation of Langmuir waves in density gradient outside of the turbulence layers can eventually lead to linear mode conversion of the waves into electromagnetic radiation. LaBelle (2011) proposed a scenario where Langmuir waves driven in the topside ionosphere by low-energy electron beams of a few hundred eV, propagate downward to regions of higher plasma density and linearly convert to radiation when they cross the dispersion relation of the LO-mode at small wavenumber. This scenario is proposed as an underlying generation mechanism for the “medium frequency burst (MF burst)”—an impulsive, broadband emission at 1.3–4.5 MHz often detected via ground-based electromagnetic receivers at the onset of substorms (Weatherwax et al., 1994; LaBelle, 2011; Broughton et al., 2014). Interestingly, LT echoes and medium frequency bursts have simultaneously been detected by the Poker Flat incoherent scatter radar and electromagnetic receivers located in Alaska. An example, obtained on April 5, 2012, is shown in Figure 10. Figure 10A presents a Range–Time–Intensity plot of the received power in the ion line channel where coherent echoes are observed during three intervals, marked by orange bars, at 250–400 km. Here, the intermittent enhanced power below 200 km is due to increased E region ionization by energetic electron precipitation. Figure 10B shows spectrogram of natural electromagnetic emissions recorded at Toolik Lake, AK at the time of the radar data. Four types of EM emissions occur sporadically during the one-hour interval. The emissions include 2f_c and 3f_c auroral roars, which are narrowband emissions near 2.9 and 4.0 MHz presumed to result from upper-hybrid waves; auroral Hiss at frequencies below 1 MHz; and four occurrences of auroral MF burst, exceeding 2 min duration and spanning approximately 2.9–3.3 MHz. Two of the three radar echoes detected with the PFISR, centered at 8:49 and 9:03 UT, coincide with two of the four MF burst events. However, considering the vastly different conditions under which Langmuir turbulence and MF Burst are detected, the correlation between the two phenomena is difficult to establish. Conversion of Langmuir waves to LO-mode waves through the window for parallel propagation at $f=f_e$ may also explain narrowband signals, perhaps related to MF-burst, observed occasionally at South Pole Station (Broughton et al., 2014). Ground-based studies provide some support for this mechanism (e.g., Broughton et al., 2012; Burnett and LaBelle, 2020), but it has yet to be confirmed with in-situ data.

FIGURE 10

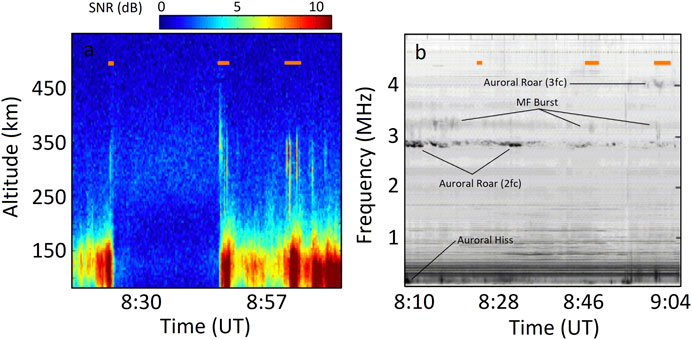
FIGURE 10. Adapted from Akbari et al. (2013): Correlation of Langmuir turbulence echoes and MF Burst. (A) Range–Time–Intensity plot of received power in the ion line channel from the Poker Flat incoherent scatter radar, showing the occurrence of coherent echoes in three intervals on April 5, 2012. (B) Spectrogram of natural electromagnetic emissions recorded at Toolik Lake, AK. For aiding the comparison, the locations of the LT echoes are marked on the two panels with orange bars.

It was discussed in this section that a collection of ground-based observations from incoherent scatter radars, high-speed, high-resolution auroral imagers, and electromagnetic receivers have the potential to uncover a range of complex micro-scale plasma processes that occur in the ionosphere—topics that have historically been investigated via in-situ measurements. In the discussion section below, we combine the understandings from the in-situ and ground-based observations and discuss several open questions regarding the origin and effects of Langmuir turbulence in the ionosphere.

4 Discussion of Several Open Questions

Observations of Langmuir turbulence with in-situ instruments and incoherent scatter radars are in many cases complementary. This is due to the widely different natures of the measurement techniques. The most important differences arise from the fact that radars only sense a single spatial Fourier component of the plasma density fluctuations. Wave activities at different scales, regardless of their intensity, remain undetectable to the radar. This is a strong contrast to in-situ measurements where attention is often focused on the strongest temporal/spectral components of the measured signal. The inherent sensitivity of radars to wavenumber allows to precisely determine the phase velocity, $v_{\varphi }=\omega /k_{\text{detection}}$, of the detected waves and thus the energy of the Landau resonant electrons $E=\frac{1}{2}{m}_e{v}_{\varphi }^2$. Such calculations generally indicate that Langmuir waves underlying LT echoes are in direct energy exchange with low energy electrons in the range ∼5–20 eV. Langmuir waves generated by a more energetic electron beam would obtain wavenumbers smaller than $k_{\text{detection}}$—from which the energy is expected to transfer to yet smaller wavenumber via parametric decay, bypassing detection by radars. The detection of turbulence by incoherent scatter radars would then require a mechanism to transfer the energy to larger wavenumbers—perhaps via Langmuir collapse.

The apparent inconsistency between the common detection of signatures of collapse in radar data and the lack of such observations in in-situ measurements may have its roots in the altitude of various observations. Radar echoes are consistently observed in the vicinity of the F region peak where the local plasma frequency is often a factor of 2–3 greater than the electron gyro-frequency of ${\Omega }_e\approx 1.5$ MHz. At higher altitudes, the domain of many in-situ observations, plasma frequency could drop to below the electron gyrofrequency, where collapse is inhibited by the altered topology of the Langmuir dispersion relation. The effect of the enhanced damping introduced by the suprathermal electrons exits at both the altitudes of the radar observations and in-situ measurements. The enhanced damping could truncate the cascade of parametric decays, preventing the transfer of energy to $k\approx 0$ where collapse may initiate via the modulational instability. This, however, may be a secondary issue since as was discussed in Section 2.2, modulational instability at small wavenumbers is not the only path to collapse. Nucleation in density cavities and direct wave collapse of sufficiently intense Langmuir waves (for which W > (kλ_D)²) (Nicholson and Goldman, 1978) can still lead to wave collapse at larger wavenumbers.

Another curious aspect of Langmuir wave observations in the auroral ionosphere is the near-complete absence of harmonic wave detection at multiples of plasma frequency. An exception to this is the study of Boehm (1987) where they detected short (∼1 s) intervals of waves near 2f_e in the presence of Langmuir waves when 2f_e matched the cyclotron frequency. They found the observations to be consistent with second harmonic generation in the upper-hybrid mode just above f_c. Electrostatic or electromagnetic harmonic waves at multiples of f_e are commonly observed during intense Langmuir wave events in type III radio burst source regions as well as in planetary foreshocks (e.g., Kellogg et al., 2010; Malaspina et al., 2010, and references therein). A diverse range of mechanisms has been proposed to explain the harmonic fields. These include electromagnetic emission by coalesce of oppositely-directed Langmuir waves (e.g., Cairns and Melrose, 1985; Cairns, 1987), electrostatic Langmuir wave harmonic generation (e.g., Klimas, 1983; Gaelzer et al., 2003; Umeda et al., 2003; Yoon et al., 2003), electromagnetic emission from collapsing cavitons (Galeev and Krasnoselskikh, 1976; Goldman et al., 1980; Akimoto et al., 1988), antenna radiation (Papadopoulos and Freund, 1978; Malaspina et al., 2013), electron trapping (Kellogg et al., 2010), and wave rectification in spacecraft’s plasma sheath (Boehm et al., 1994; Graham et al., 2014).

With respect to the source of free energy for Langmuir turbulence in the ionosphere, in-situ measurements have shown that intense Langmuir waves are often associated with dispersive, field-aligned electron bursts that are accelerated by inertial Alfvén waves. On the other hand, conjugate measurements by radars and high-resolution optical imagers have shown that LT echoes are associated with dynamic small-scale auroral structures likely related to dispersive-scale Alfvén waves (see Figures 9A,B). Results from one-dimensional Zakharov simulations suggest that the measured ISR spectra are best reproduced numerically when the modeled electron beams extend a positive slope to energies as low as 5 eV, such that ion-acoustic waves are induced by parametric decays at wavenumbers greater than $k_{\text{detection}}$ (Akbari et al., 2015). Such low energy components of an electron beam, however, would likely be significantly modified by collisions at altitudes of some radar observations between 180 and 300 km. This leads to a speculation that perhaps an unstable feature of the electron distribution function which eventually gives rise to LT echoes is produced locally at ionospheric heights in response to electron precipitation (Akbari et al., 2015). Such a speculation, however, is not backed with concrete evidence. The source of the free energy for the turbulence, thus, remains unknown.

As a result of several decades of experimental, theoretical, and numerical investigations, various aspects of Langmuir wave observations in the ionosphere—including their evolution into turbulence and their interactions with the streaming and the background electrons—are now reasonably understood. Less understood, however, are the possible consequences of the micro-scale processes for the ionosphere on a larger scale. Often mentioned in the literature, is the role of Langmuir waves in the energy exchange chain, in which a part of energy carried by energetic electrons become available to the background particles via excitation of Langmuir waves, their decay into other wave modes, and the subsequent damping (e.g., Beghin et al., 1989; Kintner et al., 1995; Stasiewicz et al., 1996; Lizunov et al., 2001; Singh et al., 2001). The applicability of these scenarios to the plasma of the F region ionosphere is open to investigation thanks to the spatiotemporal context that is provided by ground-based instruments.

Examination of several events where enhanced Langmuir and ion-acoustic signatures continuously persist in radar’s field of view for several minutes reveals that the bulk of the ionospheric plasma in the vicinity of the turbulence layers, is not significantly affected by the turbulence—that is, no significant change in the background electron temperature, ion temperature, or bulk plasma drift at altitudes above the layers are observed. It is, however, not clear whether the lack of ionospheric response is due to the nature of the instabilities, the energetics of the process, or a limited spatial extent over which they exist. Conjugate auroral imagery at the time of echoes indicates that similar optical morphologies observed on the magnetic field lines probed by the radar often exists over a wider spatial extent in field-perpendicular directions. This, however, does not necessarily imply that the turbulence is active over the same spatial extents. Answering this question would ideally require in-situ measurements from within the turbulence layers.

An ionospheric phenomenon that is potentially relevant to the discussions above is the so-called ‘Naturally Enhanced Ion Acoustic Lines (NEIALs)’. NEIAL—a well-known terminology in the incoherent scatter radar community—refers to the sudden intensification of the ion-acoustic peaks in the ISR spectrum. At high-latitudes, NEIALs are often detected along the magnetic field lines over an extended altitude range (several hundred km). An example is shown in the left panels of Figure 11 where received backscatter power in the ion line channel is shown for three radar beam directions within two degrees from $\parallel \mathbf{B}$. The streaks with power >10 dB are all NEIALs. Similar to the low-frequency components of the Langmuir turbulence echoes, NEIALs are manifestations of large-amplitude ion-acoustic waves. The two types of echoes, however, are easily distinguished given the different altitudinal and spectral features they pose (see for example Michell et al. (2014).) Several mechanisms have been proposed to explain the occurrence of NEIALs—each of which remains plausible. These include the electron-ion streaming instability (Foster et al., 1988), ion-ion streaming instability (Wahlund et al., 1992a), ion cyclotron waves (Bahcivan and Cosgrove, 2008), as well as the parametric decay of beam-generated Langmuir waves (Forme, 1993). The plausibility of a number of these mechanisms is discussed in a review by Sedgemore-Schulthess and Maurice (2001).

FIGURE 11

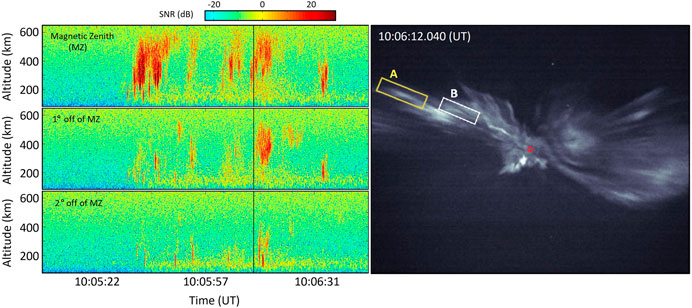
FIGURE 11. Adapted from Dahlgren et al. (2013) and Akbari and Semeter (2014): Naturally Enhanced Ion Acoustic Lines and conjugate auroral features. The left panels show the Range–Time–Intensity plots of received power in the ion line channel for three radar beams during a period when a substorm expansion crossed through the PFISR beam configuration. Mentioned in parentheses are angles with respect to the magnetic-zenith. The right panel shows an image captured by a high-speed, high-resolution imager at 10:06:12.040 UT, marked by the vertical line in the left panels. Example optical features identified as ‘A’ and ‘B’ show flaming motion in the radial direction with respect to the red circle which marks the location of the magnetic zenith over Poker Flat, AK. A video of a sequence of optical images are available from Dahlgren et al. (2013).

Despite the fact that enhanced Langmuir waves are generally not detected in conjunction with NEIALs (potentially, due to the different wavenumbers of Langmuir and ion-acoustic waves involved in a parametric decay), the plausibility of the latter mechanism has been demonstrated by several theoretical and numerical works (Forme, 1999; Kontar and Pécseli, 2005; Guio and Forme, 2006; Sullivan et al., 2008; Pavan et al., 2010; Diaz et al., 2011; Ziebell et al., 2011; Diaz et al., 2012). An evidence suggesting a connection between Langmuir waves and NEIALs comes from conjugate optical and radar observations. Such observations have shown that NEIALs are detected in association with aurora that contains large fluxes of low energy electrons as well as optical features often referred to as the “flaming” aurora (Blixt et al., 2005; Dahlgren et al., 2013; Michell et al., 2014). An example of the latter is shown in the right panel of Figure 11. The flaming aurora—the apparent upward motion of localized auroral features along the magnetic field lines—is the optical manifestation of field-aligned dispersive electron bursts where a flux of high energy electrons reach the ionosphere first, depositing energy at lower altitudes, followed by less energetic electrons which increasingly deposit energy at higher altitudes. As discussed in the previous section, field-aligned electron bursts are linked to large-amplitude Langmuir waves and their nonlinear evolution in the auroral ionosphere. In Figure 11A, significant variations in the backscatter power are observed from beam to beam. The echoes at higher altitudes (>250 km) in the magnetic zenith beam (top panel) are less pronounced at 1° offset and almost completely disappear at 2° offset. This is consistent with a generation mechanism based on parametric decay of Langmuir waves—which has been shown, theoretical and experimentally, to be confined within small angles from the magnetic field direction.

One significance of NEIALs is their relation with strong modification of the bulk ionospheric plasma. NEIALs are often observed along with significant electron temperature enhancements, up to 8000 K, and upward motion of cold ions with velocities in excess of 0.5 km/s (Wahlund et al., 1992b; Forme et al., 1995; Forme and Fontaine, 1999; Ogawa et al., 2000). It has been suggested that the enhanced electron heating and the ion up-flow may be direct consequences of the turbulence (e.g., Wahlund et al., 1993; Forme et al., 1993). NEIALs are, therefore, reminders that the micro-scale processes that are discussed in this review may have larger-scale effects on the bulk ionospheric plasma. Regardless of such effects, however, the extremely rich range of plasma processes that are involved—which are relevant to observations in many space and astrophysical plasmas far from Earth, including planetary foreshocks (e.g., Robinson and Newman, 1991; Thiessen and Kellogg, 1993), the solar wind (e.g., Thejappa et al., 2012a, b; Graham et al., 2012; Graham and Cairns, 2014), the lower solar corona (e.g., Nulsen et al., 2007), and pulsar magnetospheres (e.g., Asseo and Porzio, 2006)—themselves, underline their importance and justify and call for more focused investigations.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

HA is supported by the NASA Postdoctoral Program (NPP) administrated by USRA. Work at Dartmouth College was supported by NASA Grant NNX17AF92G and sub-award W000726838 to NASA Grant NNX15AL08G.

References

Akbari, H., Bhatt, A., La Hoz, C., and Semeter, J. L. (2017). Incoherent scatter plasma lines: observations and applications. Space Sci. Rev. 212, 249–294. doi:10.1007/s11214-017-0355-7

CrossRef Full Text | Google Scholar

Akbari, H., Guio, P., Hirsch, M. A., and Semeter, J. L. (2016). Zakharov simulations of beam-induced turbulence in the auroral ionosphere. J. Geophys. Res. Space Phys. 121, 4811–4825. doi:10.1002/2016ja022605

CrossRef Full Text | Google Scholar

Akbari, H., Semeter, J., Dahlgren, H., Diaz, M., Zettergren, M., Strømme, A., et al. (2012). Anomalous isr echoes preceding auroral breakup: evidence for strong Langmuir turbulence. Geophys. Res. Lett. 39. doi:10.1029/2011gl050288

CrossRef Full Text | Google Scholar

Akbari, H., and Semeter, J. L. (2014). Aspect angle dependence of naturally enhanced ion acoustic lines. J. Geophys. Res. Space Phys. 119, 5909–5917. doi:10.1002/2014ja019835

CrossRef Full Text | Google Scholar

Akbari, H., Semeter, J. L., Hirsch, M. A., Guio, P., and Nicolls, M. J. (2015). Evidence for generation of unstable suprathermal electron population in the auroral f region. Geophys. Res. Lett. 42, 185–192. doi:10.1002/2014gl062598

CrossRef Full Text | Google Scholar

Akbari, H., Semeter, J. L., Nicolls, M. J., Broughton, M., and LaBelle, J. W. (2013). Localization of auroral Langmuir turbulence in thin layers. J. Geophys. Res. Space Phys. 118, 3576–3583. doi:10.1002/jgra.50314

CrossRef Full Text | Google Scholar

Akimoto, K., Omura, Y., and Matsumoto, H. (1996). Rapid generation of Langmuir wave packets during electron beam-plasma instabilities. Phys. Plasmas 3, 2559–2563. doi:10.1063/1.871963

CrossRef Full Text | Google Scholar

Akimoto, K., Rowland, H. L., and Papadopoulos, K. (1988). Electromagnetic radiation from strong Langmuir turbulence. Phys. Fluids 31, 2185–2189. doi:10.1063/1.866618

CrossRef Full Text | Google Scholar

Arnoldy, R. L., and Choy, L. W. (1973). Auroral electrons of energy less than 1 kev observed at rocket altitudes. J. Geophys. Res. 78, 2187–2200. doi:10.1029/ja078i013p02187

CrossRef Full Text | Google Scholar

Asseo, E., and Porzio, A. (2006). Strong Langmuir turbulence in a pulsar emission region: statistical analysis. Month. Notices R. Astronom. Soc. 369, 1469–1490. doi:10.1111/j.1365-2966.2006.10386.x

CrossRef Full Text | Google Scholar

Bahcivan, H., and Cosgrove, R. (2008). Enhanced ion acoustic lines due to strong ion cyclotron wave fields. Ann. Geophys. 26, 2081–2095. doi:10.5194/angeo-26-2081-2008

CrossRef Full Text | Google Scholar

Bauer, S. J., and Stone, R. G. (1968). Satellite observations of radio noise in the magnetosphere. Nature 218, 1145. doi:10.1038/2181145a0

CrossRef Full Text | Google Scholar

Beghin, C., Rauch, J. L., and Bosqued, J. M. (1989). Electrostatic plasma waves and hf auroral hiss generated at low altitude. J. Geophys. Res. 94, 1359–1378. doi:10.1029/ja094ia02p01359

CrossRef Full Text | Google Scholar

Bernhardt, P. A., Tepley, C. A., and Duncan, L. M. (1989). Airglow enhancements associated with plasma cavities formed during ionospheric heating experiments. J. Geophys. Res. 94, 9071–9092. doi:10.1029/ja094ia07p09071

CrossRef Full Text | Google Scholar

Blixt, E., Grydeland, T., Ivchenko, N., Hagfors, T., La Hoz, C., Lanchester, B., et al. (2005). Dynamic rayed aurora and enhanced ion-acoustic radar echoes. Berlin: Springer.

Boehm, M. H., Carlson, C. W., McFadden, J. P., Clemmons, J. H., Ergun, R. E., and Mozer, F. S. (1994). Wave rectification in plasma sheaths surrounding electric field antennas. J. Geophys. Res. 99, 21361–21374. doi:10.1029/94ja01766

CrossRef Full Text | Google Scholar

Boehm, M. H. (1987). Waves and static electric fields in the auroral acceleration region. Ph.D. thesis. Berkeley: University of California.

Google Scholar

Bonnell, J., Kintner, P., Wahlund, J.-E., and Holtet, J. A. (1997). Modulated Langmuir waves: observations from freja and scifer. J. Geophys. Res. 102, 17233–17240. doi:10.1029/97ja01499

CrossRef Full Text | Google Scholar

Broughton, M. C., LaBelle, J., Roberg-Clark, G. T., McCready, M., and Bunch, N. L. (2012). Experimental tests of a topside generation mechanism for auroral medium frequency radio emissions. J. Geophys. Res. 117, 33. doi:10.1029/2012JA018034

CrossRef Full Text | Google Scholar

Broughton, M. C., LaBelle, J., and Yoon, P. H. (2014). A new natural radio emission observed at South Pole Station. J. Geophys. Res. Space Phys. 119, 566. doi:10.1002/2013JA019467

CrossRef Full Text | Google Scholar

Bryant, D. A., Hall, D. S., and Lepine, D. R. (1978). Electron acceleration in an array of auroral arcs. Planet. Space Sci. 26, 81–92. doi:10.1016/0032-0633(78)90039-9

CrossRef Full Text | Google Scholar

Burinskaya, T. M., Rusanov, A. A., Rauch, J. L., Miles, A., Mogilevsky, M. M., Trotignon, J. G., et al. (2003). Small-scale bursts of Langmuir waves in the polar cap. Adv. Space Res. 31, 1247–1252. doi:10.1016/s0273-1177(02)00937-7

CrossRef Full Text | Google Scholar

Cairns, I. H. (1989). Electrostatic wave generation above and below the plasma frequency by electron beams. Phys. Fluids B: Plasma Phys. 1, 204–213. doi:10.1063/1.859088

CrossRef Full Text | Google Scholar

Cairns, I. H., and Layden, A. (2018). Kinematics of electrostatic 3-wave decay of generalized Langmuir waves in magnetized plasmas. Phys. Plasmas 25, 082309. doi:10.1063/1.5037300

CrossRef Full Text | Google Scholar

Cairns, I. H., and Melrose, D. B. (1985). A theory for the 2fpradiation upstream of the Earth's bow shock. J. Geophys. Res. 90, 6637–6640. doi:10.1029/ja090ia07p06637

CrossRef Full Text | Google Scholar

Cairns, I. H., and Menietti, J. D. (2001). Stochastic growth of waves over Earth's polar cap. J. Geophys. Res. 106, 29515–29529. doi:10.1029/2000ja000422

CrossRef Full Text | Google Scholar

Cairns, I. H., and Nishikawa, K.-I. (1989). Simulations relevant to the beam instability in the foreshock. J. Geophys. Res. 94, 79–88. doi:10.1029/ja094ia01p00079

CrossRef Full Text | Google Scholar

Cairns, I. H., Robinson, P. A., and Anderson, R. R. (2000). Thermal and driven stochastic growth of Langmuir waves in the solar wind and Earth's foreshock. Geophys. Res. Lett. 27, 61–64. doi:10.1029/1999gl010717

CrossRef Full Text | Google Scholar

Cairns, I. H., and Robinson, P. A. (1997). First test of stochastic growth theory for Langmuir waves in Earth’s foreshock. Geophys. Res. Lett. 24, 369–372. doi:10.1029/97gl00084

CrossRef Full Text | Google Scholar

Cairns, I. H., and Robinson, P. A. (1995). Inconsistency of ulysses millisecond Langmuir spikes with wave collapse in type iii radio sources. Geophys. Res. Lett. 22, 3437–3440. doi:10.1029/95gl03513

CrossRef Full Text | Google Scholar

Cairns, I. H. (1987). Second harmonic plasma emission involving ion sound waves. J. Plasma Phys. 38, 179–198. doi:10.1017/s0022377800012502

CrossRef Full Text | Google Scholar

Carlson, C., Ergun, R. E., Mallinckrodt, A. J., and Haerendel, G. (1987). Observations of intense electron bernstein wave emissions in an auroral plasma. Unpublished manuscript

Carlson, H. C., Wickwar, V. B., and Mantas, G. P. (1982). Observations of fluxes of suprathermal electrons accelerated by hf excited instabilities. J. Atmos. Terrestrial Phys. 44, 1089–1100. doi:10.1016/0021-9169(82)90020-4

CrossRef Full Text | Google Scholar

Clemmow, P. C. (2018). Electrodynamics of particles and plasmas. Boca Raton: CRC Press.

Colpitts, C. A., and LaBelle, J. (2008). Mode identification of whistler mode, Z-mode, and Langmuir/Upper Hybrid mode waves observed in an auroral sounding rocket experiment. J. Geophys. Res. 113, 27. doi:10.1029/2007JA012325

CrossRef Full Text | Google Scholar

Dahlgren, H., Schlatter, N. M., Ivchenko, N., Roth, L., and Karlsson, A. (2017). Relation of anomalous f region radar echoes in the high-latitude ionosphere to auroral precipitation. Ann. Geophys. 35, 475–479. doi:10.5194/angeo-35-475-2017

CrossRef Full Text | Google Scholar

Dahlgren, H., Semeter, J. L., Marshall, R. A., and Zettergren, M. (2013). The optical manifestation of dispersive field-aligned bursts in auroral breakup arcs. J. Geophys. Res. Space Phys. 118, 4572–4582. doi:10.1002/jgra.50415

CrossRef Full Text | Google Scholar

Davidson, R. C. (1969). Nonlinear plasma theory. New York: Academic Press.

Diaz, M., Oppenheim, M., Semeter, J., and Zettergren, M. (2011). Particle-in-cell simulation of incoherent scatter radar spectral distortions related to beam-plasma interactions in the auroral ionosphere. J. Geophys. Res. Space Phys. 116, 39–43. doi:10.1029/2010ja016096

CrossRef Full Text | Google Scholar

Diaz, M., Zettergren, M., Semeter, J., and Oppenheim, M. (2012). Plasma parameter analysis of the Langmuir decay process via particle-in-cell simulations. Annales Geophysicae 30, 1169. doi:10.5194/angeo-30-1169-2012

CrossRef Full Text | Google Scholar

Dombrowski, M., LaBelle, J., Rowland, D., Pfaff, R., and Kletzing, C. (2012). Interpretation of vector electric field measurements of bursty Langmuir waves in the cusp. J. Geophys. Res. Space Phys. 117, 1173. doi:10.1029/2012ja017741

CrossRef Full Text | Google Scholar

Dombrowski, M. P., LaBelle, J., Kletzing, C. A., Bounds, S. R., Cairns, I. H., and Kaeppler, S. R. (2019). Statistical study of electron bunching in auroral Langmuir waves. J. Geophys. Res. Space Phys. 124, 5956. doi:10.1029/2018JA026262

CrossRef Full Text | Google Scholar

Doolen, G. D., DuBois, D. F., and Rose, H. A. (1985). Nucleation of cavitons in strong Langmuir turbulence. Phys. Rev. Lett. 54, 804. doi:10.1103/physrevlett.54.804

PubMed Abstract | CrossRef Full Text | Google Scholar

DuBois, D. F., Hansen, A., Rose, H. A., and Russell, D. (1993). Excitation of strong Langmuir turbulence in the ionosphere: comparison of theory and observations. Phys. Fluids B: Plasma Phys. 5, 2616–2622. doi:10.1063/1.860699

CrossRef Full Text | Google Scholar

DuBois, D. F., Rose, H. A., and Russell, D. (1990). Excitation of strong Langmuir turbulence in plasmas near critical density: application to hf heating of the ionosphere. J. Geophys. Res. 95, 21221–21272. doi:10.1029/ja095ia12p21221

CrossRef Full Text | Google Scholar

Dum, C. T., and Nishikawa, K. I. (1994). Two‐dimensional simulation studies of the electron beam‐plasma instability. Phys. Plasmas 1, 1821–1826. doi:10.1063/1.870636

CrossRef Full Text | Google Scholar

Dum, C. T. (1989). Transition in the dispersive properties of beam-plasma and two-stream instabilities. J. Geophys. Res. 94, 2429–2442. doi:10.1029/ja094ia03p02429

CrossRef Full Text | Google Scholar

Dziubenko, N., Ivchenko, V., Milinevskii, G., and Mishin, E. (1980). Influence of plasma collective effects on the structure of the aurora borealis streamers. Soviet J. Exp. Theor. Phys. Lett. 31, 607–610.

Google Scholar

Ekeberg, J., Wannberg, G., Eliasson, L., and Stasiewicz, K. (2010). Ion-acoustic solitary waves and spectrally uniform scattering cross section enhancements. Annales Geophysicae 28, 1299–1306. doi:10.5194/angeo-28-1299-2010

CrossRef Full Text | Google Scholar

Eliasson, B., Shao, X., Milikh, G., Mishin, E. V., and Papadopoulos, K. (2012). Numerical modeling of artificial ionospheric layers driven by high-power hf heating. J. Geophys. Res. Space Phys. 117, 67. doi:10.1029/2012ja018105

CrossRef Full Text | Google Scholar

Ergun, R. E., Carlson, C. W., McFadden, J. P., Clemmons, J. H., and Boehm, M. H. (1991a). Evidence of a transverse Langmuir modulational instability in a space plasma. Geophys. Res. Lett. 18, 1177–1180. doi:10.1029/91gl01563

CrossRef Full Text | Google Scholar

Ergun, R. E., Carlson, C. W., McFadden, J. P., Clemmons, J. H., and Boehm, M. H. (1991b). Langmuir wave growth and electron bunching: results from a wave-particle correlator. J. Geophys. Res. 96, 225–238. doi:10.1029/90ja01596

CrossRef Full Text | Google Scholar

Ergun, R. E., Delory, G. T., Klementis, E., Carlson, C. W., McFadden, J. P., Roth, I., et al. (1993). Vlf wave growth from dispersive bursts of field-aligned electron fluxes. J. Geophys. Res. 98, 3777–3787. doi:10.1029/92ja02193

CrossRef Full Text | Google Scholar

Ergun, R. E., Larson, D., Lin, R. P., McFadden, J. P., Carlson, C. W., Anderson, K. A., et al. (1998). WindSpacecraft observations of solar impulsive electron events associated with solar type III radio bursts. ApJ 503, 435. doi:10.1086/305954

CrossRef Full Text | Google Scholar

Ergun, R., Malaspina, D., Cairns, I. H., Goldman, M., Newman, D., Robinson, P., et al. (2008). Eigenmode structure in solar-wind Langmuir waves. Phys. Rev. Lett. 101, 051101. doi:10.1103/physrevlett.101.051101

PubMed Abstract | CrossRef Full Text | Google Scholar

Etcheto, J., and Faucheux, M. (1984). Detailed study of electron plasma waves upstream of the Earth's bow shock. J. Geophys. Res. 89, 6631–6653. doi:10.1029/ja089ia08p06631

CrossRef Full Text | Google Scholar

Fitzenreiter, R. J., Ogilvie, K. W., Chornay, D. J., and Keller, J. (1998). Observations of electron velocity distribution functions in the solar wind by the wind spacecraft: high angular resolution strahl measurements. Geophys. Res. Lett. 25, 249–252. doi:10.1029/97gl03703

CrossRef Full Text | Google Scholar

Forme, F., and Fontaine, D. (1999). Enhanced ion acoustic fluctuations and ion outflows. Annales Geophysicae 17, 182–189. doi:10.1007/s00585-999-0182-6

CrossRef Full Text | Google Scholar

Forme, F. (1999). Parametric decay of beam-driven Langmuir wave and enhanced ion-acoustic fluctuations in the ionosphere: a weak turbulence approach. Annales Geophysicae 17, 1172–1181. doi:10.1007/s00585-999-1172-4

CrossRef Full Text | Google Scholar

Forme, F. R. E. (1993). A new interpretation on the origin of enhanced ion acoustic fluctuations in the upper ionosphere. Geophys. Res. Lett. 20, 2347–2350. doi:10.1029/93gl02490

CrossRef Full Text | Google Scholar

Forme, F. R. E., Fontaine, D., and Wahlund, J. E. (1995). Two different types of enhanced ion acoustic fluctuations observed in the upper ionosphere. J. Geophys. Res. 100, 14625–14636. doi:10.1029/94ja01093

CrossRef Full Text | Google Scholar

Forme, F. R. E., Wahlund, J.-E., Opgenoorth, H. J., Persson, M. A. L., and Mishin, E. V. (1993). Effects of current driven instabilities on the ion and electron temperatures in the topside ionosphere. J. Atmos. terrestrial Phys. 55, 647–666. doi:10.1016/0021-9169(93)90011-m

CrossRef Full Text | Google Scholar

Foster, J. C., Del Pozo, C., Groves, K., and St. Maurice, J.-P. (1988). Radar observations of the onset of current driven instabilities in the topside ionosphere. Geophys. Res. Lett. 15, 160–163. doi:10.1029/gl015i002p00160

CrossRef Full Text | Google Scholar

Fung, S. F., and Hoffman, R. A. (1988). On the spectrum of the secondary auroral electrons. J. Geophys. Res. 93, 2715–2724. doi:10.1029/ja093ia04p02715

CrossRef Full Text | Google Scholar

Fuselier, S. A., Gurnett, D. A., and Fitzenreiter, R. J. (1985). The downshift of electron plasma oscillations in the electron foreshock region. J. Geophys. Res. 90, 3935–3946. doi:10.1029/ja090ia05p03935

CrossRef Full Text | Google Scholar

Gaelzer, R., Yoon, P. H., Umeda, T., Omura, Y., and Matsumoto, H. (2003). Harmonic Langmuir waves. ii. turbulence spectrum. Phys. Plasmas 10, 373–381. doi:10.1063/1.1537239

CrossRef Full Text | Google Scholar

Gaelzer, R., Ziebell, L. F., Viñas, A. F., Yoon, P. H., and Ryu, C. M. (2008). Asymmetric solar wind electron superthermal distributions. ApJ 677, 676. doi:10.1086/527430

CrossRef Full Text | Google Scholar

Galeev, A., and Krasnoselskikh, V. (1976). Strong Langmuir turbulence in the earth’s magnetosphere as a source of kilometer radio emission. Soviet J. Exp. Theor. Phys. Lett. 24, 515–517.

Google Scholar

Galeev, A. (1975). Plasma turbulence in the magnetosphere with special regard to plasma heating. Physics of the hot plasma in the magnetosphere. Berlin: Springer, 251–270.

CrossRef Full Text

Galeev, A., Sagdeev, R., Shapiro, V., and Shevchenko, V. (1977a). Langmuir turbulence and dissipation of high frequency energy. Soviet J. Exp. Theor. Phys. 73, 1352–1369.

Google Scholar

Galeev, A., Sagdeev, R., Shapiro, V., and Shevchenko, V. (1977b). Relaxation of high-current electron beams and the modulational instability. Soviet J. Exp. Theor. Phys. 45, 266–271.

Google Scholar

Goldman, M. V., Newman, D. L., Wang, J. G., and Muschietti, L. (1996). Langmuir turbulence in space plasmas. Phys. Scr., T63, 28. doi:10.1088/0031-8949/1996/t63/003

CrossRef Full Text | Google Scholar

Goldman, M. V., Reiter, G. F., and Nicholson, D. R. (1980). Radiation from a strongly turbulent plasma: application to electron beam-excited solar emissions. Phys. Fluids 23, 388–401. doi:10.1063/1.862982

CrossRef Full Text | Google Scholar

Goldman, M. V. (1984). Strong turbulence of plasma waves. Rev. Mod. Phys. 56, 709. doi:10.1103/revmodphys.56.709

CrossRef Full Text | Google Scholar

Gough, M. P., Christiansen, P. J., and Wilhelm, K. (1990). Auroral beam-plasma interactions: particle correlator investigations. J. Geophys. Res. 95, 12287–12294. doi:10.1029/ja095ia08p12287

CrossRef Full Text | Google Scholar

Gough, M. P., and Urban, A. (1983). Auroral beam/plasma interaction observed directly. Planet. Space Sci. 31, 875.

Google Scholar

Graham, D. B., and Cairns, I. H. (2014). Dynamical evidence for nonlinear Langmuir wave processes in type iii solar radio bursts. J. Geophys. Res. Space Phys. 119, 2430–2457. doi:10.1002/2013ja019425

CrossRef Full Text | Google Scholar

Graham, D. B., Cairns, I. H., Malaspina, D. M., and Ergun, R. E. (2012). Evidence against the oscillating two-stream instability and spatial collapse of Langmuir waves in solar type iii radio bursts. ApJ 753, L18. doi:10.1088/2041-8205/753/1/l18

CrossRef Full Text | Google Scholar

Graham, D. B., Cairns, I. H., and Malaspina, D. M. (2014). Harmonic waves and sheath rectification in type iii solar radio bursts. J. Geophys. Res. Space Phys. 119, 723–741. doi:10.1002/2013ja019317

CrossRef Full Text | Google Scholar

Gregory, P. C. (1969). Radio emission from auroral electrons. Nature 221, 350. doi:10.1038/221350a0

CrossRef Full Text | Google Scholar

Guio, P., and Forme, F. (2006). Zakharov simulations of Langmuir turbulence: effects on the ion-acoustic waves in incoherent scattering. Phys. Plasmas 13, 122902. doi:10.1063/1.2402145

CrossRef Full Text | Google Scholar

Hallinan, T. J., Stenbaek-Nielsen, H. C., and Deehr, C. S. (1985). Enhanced aurora. J. Geophys. Res. 90, 8461–8475. doi:10.1029/ja090ia09p08461

CrossRef Full Text | Google Scholar

Isham, B., La Hoz, C., Rietveld, M. T., Hagfors, T., and Leyser, T. B. (1999). Cavitating Langmuir turbulence observed during high-latitude ionospheric wave interaction experiments. Phys. Rev. Lett. 83, 2576. doi:10.1103/physrevlett.83.2576

CrossRef Full Text | Google Scholar

Isham, B., Rietveld, M., Guio, P., Forme, F., Grydeland, T., and Mjølhus, E. (2012). Cavitating Langmuir turbulence in the terrestrial aurora. Phys. Rev. Lett. 108, 105003. doi:10.1103/physrevlett.108.105003

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaufmann, R. L., Dusenbery, P. B., and Thomas, B. J. (1978). Stability of the auroral plasma: parallel and perpendicular propagation of electrostatic waves. J. Geophys. Res. 83, 5663–5669. doi:10.1029/ja083ia12p05663

CrossRef Full Text | Google Scholar

Kellogg, P. J., Goetz, K., and Monson, S. (2010). Harmonics of Langmuir waves in the earth’s foreshock. J. Geophys. Res. Space Phys. 115, 63. doi:10.1029/2009ja014635

CrossRef Full Text | Google Scholar

Kellogg, P. J., Monson, S. J., and Whalen, B. A. (1978). Rocket observation of high frequency waves over a strong aurora. Geophys. Res. Lett. 5, 47. doi:10.1029/gl005i001p00047

CrossRef Full Text | Google Scholar

Khotyaintsev, Y., Lizunov, G., and Stasiewicz, K. (2001). Langmuir wave structures registered by freja: analysis and modeling. Adv. Space Res. 28, 1649–1654. doi:10.1016/s0273-1177(01)00485-9

CrossRef Full Text | Google Scholar

Kintner, P. M., Bonnell, J., Powell, S., Wahlund, J.-E., and Holback, B. (1995). First results from the freja hf snapshot receiver. Geophys. Res. Lett. 22, 287–290. doi:10.1029/94gl02549

CrossRef Full Text | Google Scholar

Kletzing, C. A., and Hu, S. (2001). Alfvén wave generated electron time dispersion. Geophys. Res. Lett. 28, 693–696. doi:10.1029/2000gl012179

CrossRef Full Text | Google Scholar

Kletzing, C. A., LaBelle, J., Bounds, S. R., Dolan, J., Kaeppler, S. R., and Dombrowski, M. (2017). Phase sorting wave‐particle correlator. J. Geophys. Res. Space Phys. 122, 2069–2078. doi:10.1002/2016ja023334

CrossRef Full Text | Google Scholar

Kletzing, C. A., LaBelle, J., Bounds, S. R., Dolan, J., Kaeppler, S. R., and Dombrowski, M. (2017). Phase sorting wave‐particle correlator. J. Geophys. Res. Space Phys. 122, 2069. doi:10.1002/2016JA023334

CrossRef Full Text | Google Scholar

Kletzing, C., Bounds, S., LaBelle, J., and Samara, M. (2005). Observation of the reactive component of Langmuir wave phase-bunched electrons. Geophys. Res. Lett. 32, 112. doi:10.1029/2004gl021175

CrossRef Full Text | Google Scholar

Kletzing, C., and Muschietti, L. (2006). Phase correlation of electrons and Langmuir waves. Geospace electromagnetic waves and radiation. Berlin: Springer, 313–337.

Klimas, A. J. (1983). A mechanism for plasma waves at the harmonics of the plasma frequency in the electron foreshock boundary. J. Geophys. Res. 88, 9081–9091. doi:10.1029/ja088ia11p09081

CrossRef Full Text | Google Scholar

Klimas, A. J. (1990). Trapping saturation of the bump-on-tail instability and electrostatic harmonic excitation in Earth's foreshock. J. Geophys. Res. 95, 14905–14924. doi:10.1029/ja095ia09p14905

CrossRef Full Text | Google Scholar

Kline, J., Montgomery, D., Yin, L., DuBois, D., Albright, B., Bezzerides, B., et al. (2006). Different k λ d regimes for nonlinear effects on Langmuir waves. Phys. Plasmas 13, 055906. doi:10.1063/1.2178777

CrossRef Full Text | Google Scholar

Kontar, E., and Pécseli, H. (2005). Nonlinear wave interactions as a model for naturally enhanced ion acoustic lines in the ionosphere. Geophys. Res. Lett. 32. doi:10.1029/2004gl022182

CrossRef Full Text | Google Scholar

Krafft, C., Volokitin, A. S., and Krasnoselskikh, V. V. (2015). Langmuir wave decay in inhomogeneous solar wind plasmas: simulation results. ApJ 809, 176. doi:10.1088/0004-637x/809/2/176

CrossRef Full Text | Google Scholar

LaBelle, J. (2011). An explanation for the fine structure of mf burst emissions. Geophys. Res. Lett. 38, 114. doi:10.1029/2010gl046218

CrossRef Full Text | Google Scholar

LaBelle, J., Cairns, I. H., and Kletzing, C. (2010). Electric field statistics and modulation characteristics of bursty Langmuir waves observed in the cusp. J. Geophys. Res. Space Phys. 115, 139. doi:10.1029/2010ja015277

CrossRef Full Text | Google Scholar

Layden, A., Cairns, I. H., Li, B., and Robinson, P. (2013). Electrostatic decay in a weakly magnetized plasma. Phys. Rev. Lett. 110, 185001. doi:10.1103/physrevlett.110.185001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S.-Y., Ziebell, L. F., Yoon, P. H., Gaelzer, R., and Lee, E. S. (2019). Particle-in-cell and weak turbulence simulations of plasma emission. ApJ 871, 74. doi:10.3847/1538-4357/aaf476

CrossRef Full Text | Google Scholar

Lefeuvre, A. C., and LaBelle, J. (2020). Estimating polar cap density and medium-frequency burst source heights using 2fce roar radio emissions. J. Geophys. Res. Space Phys. 125, e2020JA028166. doi:10.1029/2020ja028166

CrossRef Full Text | Google Scholar

Li, B., Cairns, I. H., Robinson, P., LaBelle, J., and Kletzing, C. (2010). Waveform and envelope field statistics for waves with stochastically driven amplitudes. Phys. Plasmas 17, 032110. doi:10.1063/1.3353092

CrossRef Full Text | Google Scholar

Li, B., Willes, A. J., Robinson, P. A., and Cairns, I. H. (2005a). Dynamics of fundamental electromagnetic emission via beam-driven Langmuir waves. Phys. Plasmas 12, 052324. doi:10.1063/1.1906214

CrossRef Full Text | Google Scholar

Li, B., Willes, A. J., Robinson, P. A., and Cairns, I. H. (2005b). Second harmonic electromagnetic emission via beam-driven Langmuir waves. Phys. Plasmas 12, 012103. doi:10.1063/1.1812274

CrossRef Full Text | Google Scholar

Lin, R. P., Potter, D. W., Gurnett, D. A., and Scarf, F. L. (1981). Energetic electrons and plasma waves associated with a solar type iii radio burst. ApJ 251, 364–373. doi:10.1086/159471

CrossRef Full Text | Google Scholar

Lizunov, G. V., Khotyaintsev, Y., and Stasiewicz, K. (2001). Parametric decay to lower hybrid waves as a source of modulated Langmuir waves in the topside ionosphere. J. Geophys. Res. 106, 24755–24763. doi:10.1029/2001ja900074

CrossRef Full Text | Google Scholar

Lotko, W., and Maggs, J. E. (1981). Amplification of electrostatic noise in cyclotron resonance with an adiabatic auroral beam. J. Geophys. Res. 86, 3449–3458. doi:10.1029/ja086ia05p03449

CrossRef Full Text | Google Scholar

Lotko, W., and Maggs, J. E. (1979). Damping of electrostatic noise by warm auroral electrons. Planet. Space Sci. 27, 1491–1506. doi:10.1016/0032-0633(79)90095-3

CrossRef Full Text | Google Scholar

Lundin, R., Haerendel, G., and Grahn, S. (1994). The freja project. Geophys. Res. Lett. 21, 1823–1826. doi:10.1029/94gl01424

CrossRef Full Text | Google Scholar

Maggs, J. E. (1976). Coherent generation of vlf hiss. J. Geophys. Res. 81, 1707–1724. doi:10.1029/ja081i010p01707

CrossRef Full Text | Google Scholar

Maggs, J. E. (1978). Electrostatic noise generated by the auroral electron beam. J. Geophys. Res. 83, 3173–3188. doi:10.1029/ja083ia07p03173

CrossRef Full Text | Google Scholar

Maggs, J. E., and Lotko, W. (1981). Altitude dependent model of the auroral beam and beam-generated electrostatic noise. J. Geophys. Res. 86, 3439–3447. doi:10.1029/ja086ia05p03439

CrossRef Full Text | Google Scholar

Malaspina, D. M., Cairns, I. H., and Ergun, R. E. (2010). The 2fp radiation from localized Langmuir waves. J. Geophys. Res. Space Phys. 115, 339. doi:10.1029/2009ja014609

CrossRef Full Text | Google Scholar

Malaspina, D. M., Graham, D. B., Ergun, R. E., and Cairns, I. H. (2013). Langmuir wave harmonics due to driven nonlinear currents. J. Geophys. Res. Space Phys. 118, 6880–6888. doi:10.1002/2013ja019309

CrossRef Full Text | Google Scholar

Matthews, D. L., Pongratz, M., and Papadopoulos, K. (1976). Nonlinear production of suprathermal tails in auroral electrons. J. Geophys. Res. 81, 123–129. doi:10.1029/ja081i001p00123

CrossRef Full Text | Google Scholar

McAdams, K. L., Ergun, R. E., and LaBelle, J. (2000). Hf chirps: eigenmode trapping in density depletions. Geophys. Res. Lett. 27, 321–324. doi:10.1029/1999gl003655

CrossRef Full Text | Google Scholar

McAdams, K. L., and LaBelle, J. (1999). Narrowband structure in hf waves above the electron plasma frequency in the auroral ionosphere. Geophys. Res. Lett. 26, 1825–1828. doi:10.1029/1999gl900428

CrossRef Full Text | Google Scholar

McAdams, K. L., LaBelle, J., Trimpi, M. L., Kintner, P. M., and Arnoldy, R. A. (1999). Rocket observations of banded structure in waves near the Langmuir frequency in the auroral ionosphere. J. Geophys. Res. 104, 28109–28122. doi:10.1029/1999ja900379

CrossRef Full Text | Google Scholar

McFadden, J. P., Carlson, C. W., and Boehm, M. H. (1986). High-frequency waves generated by auroral electrons. J. Geophys. Res. 91, 12079–12088. doi:10.1029/ja091ia11p12079

CrossRef Full Text | Google Scholar

Michell, R. G., Grydeland, T., and Samara, M. (2014). Characteristics of poker flat incoherent scatter radar (pfisr) naturally enhanced ion-acoustic lines (neials) in relation to auroral forms. Ann. Geophys. 32, 1333–1347. doi:10.5194/angeo-32-1333-2014

CrossRef Full Text | Google Scholar

Michell, R. G., and Samara, M. (2013). Observability of neials with the sondrestrom and poker flat incoherent scatter radars. J. Atmos. Solar-Terrestrial Phys. 105-106, 299–307. doi:10.1016/j.jastp.2012.12.008

CrossRef Full Text | Google Scholar

Mishin, E., Burke, W., and Pedersen, T. (2004). On the onset of hf-induced airglow at haarp. J. Geophys. Res. Space Phys. 109, 112. doi:10.1029/2003ja010205

CrossRef Full Text | Google Scholar

Mishin, E., and Khazanov, G. (2006). Tether-induced airglow: collisionless effects. Geophys. Res. Lett. 33, 127. doi:10.1029/2006gl026220

CrossRef Full Text | Google Scholar

Mishin, E., and Pedersen, T. (2011). Ionizing wave via high-power hf acceleration. Geophys. Res. Lett. 38, 139. doi:10.1029/2010gl046045

CrossRef Full Text | Google Scholar

Mishin, E., and Telegin, V. (1989). Effects of plasma turbulence on auroras. Geomagn. Aeron 29, 1–13.

Google Scholar

Mishin, E., and Telegin, V. (1986). Spectrum of suprathermal electrons in the auroral plasma. Plasma Phys. Rep. 12, 509–510.

Google Scholar

Mishin, E. V. (2019). Artificial aurora experiments and application to natural aurora. Front. Astron. Space Sci. 6, 14. doi:10.3389/fspas.2019.00014

CrossRef Full Text | Google Scholar

Mishin, E. V., Ivchenko, V. N., and Milinevskii, G. P. (1981). Fine structure of artificial auroral rays. Adv. Space Res. 1, 163–165. doi:10.1016/0273-1177(81)90286-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Muschietti, L., and Dum, C. T. (1991). Nonlinear wave scattering and electron beam relaxation. Phys. Fluids B: Plasma Phys. 3, 1968–1982. doi:10.1063/1.859665

CrossRef Full Text | Google Scholar

Muschietti, L., Roth, I., and Delory, G. (1997). Oblique turbulence driven by field-aligned electron fluxes in the auroral ionosphere. J. Geophys. Res. 102, 27217–27226. doi:10.1029/97ja02532

CrossRef Full Text | Google Scholar

Muschietti, L., Roth, I., and Ergun, R. E. (1995). Kinetic localization of beam-driven Langmuir waves. J. Geophys. Res. 100, 17481–17490. doi:10.1029/95ja00595

CrossRef Full Text | Google Scholar

Muschietti, L., Roth, I., and Ergun, R. E. (1996). On the formation of wave packets in planetary foreshocks. J. Geophys. Res. 101, 15605–15613. doi:10.1029/96ja00926

CrossRef Full Text | Google Scholar

Newman, D. L., Goldman, M. V., Ergun, R. E., and Boehm, M. H. (1994c). Langmuir turbulence in the auroral ionosphere: 1. linear theory. J. Geophys. Res. 99, 6367–6376. doi:10.1029/93ja03182

CrossRef Full Text | Google Scholar

Newman, D. L., Goldman, M. V., and Ergun, R. E. (1994a). Langmuir turbulence in moderately magnetized space plasmas*. Phys. Plasmas 1, 1691–1699. doi:10.1063/1.870672

CrossRef Full Text | Google Scholar

Newman, D. L., Goldman, M. V., and Ergun, R. E. (1994b). Langmuir turbulence in the auroral ionosphere: 2. nonlinear theory and simulations. J. Geophys. Res. 99, 6377–6391. doi:10.1029/93ja03183

CrossRef Full Text | Google Scholar

Newman, D. L., Winglee, R. M., Robinson, P. A., Glanz, J., and Goldman, M. V. (1990). Simulation of the collapse and dissipation of Langmuir wave packets. Phys. Fluids B: Plasma Phys. 2, 2600–2622. doi:10.1063/1.859385

CrossRef Full Text | Google Scholar

Nicholson, D. R., and Goldman, M. V. (1978). Cascade and collapse of Langmuir waves in two dimensions. Phys. Fluids 21, 1766–1776. doi:10.1063/1.862093

CrossRef Full Text | Google Scholar

Nishikawa, K.-I., and Cairns, I. H. (1991). Simulation of the nonlinear evolution of electron plasma waves. J. Geophys. Res. 96, 19343–19351. doi:10.1029/91ja01738

CrossRef Full Text | Google Scholar

Nulsen, A., Cairns, I. H., and Robinson, P. (2007). Field distributions and shapes of Langmuir wave packets observed by ulysses in an interplanetary type iii burst source region. J. Geophys. Res. Space Phys. 112. doi:10.1029/2006ja011873

CrossRef Full Text | Google Scholar

Ogasawara, K., Livadiotis, G., Grubbs, G. A., Jahn, J.-M., Michell, R., Samara, M., et al. (2017). Properties of suprathermal electrons associated with discrete auroral arcs. Geophys. Res. Lett. 44, 3475–3484. doi:10.1002/2017gl072715

CrossRef Full Text | Google Scholar

O’neil, T., and Malmberg, J. (1968). Transition of the dispersion roots from beam-type to landau-type solutions. Phys. Fluids 11, 1754–1760.

Google Scholar

Papadopoulos, K., and Coffey, T. (1974). Nonthermal features of the auroral plasma due to precipitating electrons. J. Geophys. Res. 79, 674–677. doi:10.1029/ja079i004p00674

CrossRef Full Text | Google Scholar

Papadopoulos, K., and Freund, H. P. (1978). Solitons and second harmonic radiation in type iii bursts. Geophys. Res. Lett. 5, 881–884. doi:10.1029/gl005i010p00881

CrossRef Full Text | Google Scholar

Papadopoulos, K. (1975). Nonlinear stabilization of beam plasma interactions by parametric effects. Phys. Fluids 18, 1769–1777. doi:10.1063/1.861096

CrossRef Full Text | Google Scholar

Park, P. H., Rhee, T., and Ryu, C.-M. (2005). Self-consistent generation of superthermal electrons by beam-plasma interaction. Phys. Rev. Lett. 95, 215003. doi:10.1103/physrevlett.95.215003

PubMed Abstract | CrossRef Full Text | Google Scholar

Pavan, J., Ziebell, L., Yoon, P., and Gaelzer, R. (2010). Ionospheric ion-acoustic enhancements by turbulent counterstreaming electron beam-plasma interaction. J. Geophys. Res. Space Phys. 115, 237. doi:10.1029/2009ja014448

CrossRef Full Text | Google Scholar

Pedersen, T., Gustavsson, B., Mishin, E., Kendall, E., Mills, T., Carlson, H., et al. (2010). Creation of artificial ionospheric layers using high-power hf waves. Geophys. Res. Lett. 37, 119. doi:10.1029/2009gl041895

CrossRef Full Text | Google Scholar

Peter Gary, S. (1985). Electrostatic instabilities in plasmas with two electron components. J. Geophys. Res. 90, 8213–8221. doi:10.1029/ja090ia09p08213

CrossRef Full Text | Google Scholar

Pfaff, R., Carlson, C., Watzin, J., Everett, D., and Gruner, T. (2001). An overview of the fast auroral snapshot (fast) satellite. The FAST mission. Berlin: Springer, 1–32.

CrossRef Full Text

Reasoner, D. L., and Chappell, C. R. (1973). Twin payload observations of incident and backscattered auroral electrons. J. Geophys. Res. 78, 2176–2186. doi:10.1029/ja078i013p02176

CrossRef Full Text | Google Scholar

Robinson, P. A., and Newman, D. L. (1991). Strong plasma turbulence in the Earth's electron foreshock. J. Geophys. Res. 96, 17733–17749. doi:10.1029/91ja01734

CrossRef Full Text | Google Scholar

Robinson, P. A. (1997). Nonlinear wave collapse and strong turbulence. Rev. Mod. Phys. 69, 507. doi:10.1103/revmodphys.69.507

CrossRef Full Text | Google Scholar

Robinson, P. A. (1995). Stochastic wave growth. Phys. Plasmas 2, 1466–1479. doi:10.1063/1.871362

CrossRef Full Text | Google Scholar

Russell, D., DuBois, D. F., and Rose, H. A. (1988). Nucleation in two-dimensional Langmuir turbulence. Phys. Rev. Lett. 60, 581. doi:10.1103/physrevlett.60.581

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryu, C.-M., Rhee, T., Umeda, T., Yoon, P. H., and Omura, Y. (2007). Turbulent acceleration of superthermal electrons. Phys. Plasmas 14, 100701. doi:10.1063/1.2779282

CrossRef Full Text | Google Scholar

Samara, M., LaBelle, J., and Cairns, I. (2008). Statistics of auroral Langmuir waves. Annales Geophysicae. 26, 3885–3895. doi:10.5194/angeo-26-3885-2008

CrossRef Full Text | Google Scholar

Samara, M., and LaBelle, J. (2006). Structured waves near the plasma frequency observed in three auroral rocket flights. Ann. Geophys. 24, 2911. doi:10.5194/angeo-24-2911-2006

CrossRef Full Text | Google Scholar

Sanbonmatsu, K. Y., Doxas, I., Goldman, M. V., and Newman, D. L. (1997). Non-markovian electron diffusion in the auroral ionosphere at high Langmuir-wave intensities. Geophys. Res. Lett. 24, 807–810. doi:10.1029/97gl00669

CrossRef Full Text | Google Scholar

Sanbonmatsu, K. Y., Newman, D. L., and Goldman, M. V. (2001). Quasi-linear zakharov simulations of Langmuir turbulence at rocket altitudes in the auroral ionosphere. J. Geophys. Res. 106, 10519–10535. doi:10.1029/2000ja000270

CrossRef Full Text | Google Scholar

Schlatter, N. M., Ivchenko, N., and Häggström, I. (2014). On the relation of Langmuir turbulence radar signatures to auroral conditions. J. Geophys. Res. Space Phys. 119, 8499–8511. doi:10.1002/2013ja019457

CrossRef Full Text | Google Scholar

Schlatter, N. M., Ivchenko, N., Sergienko, T., Gustavsson, B. J., and Brändström, B. (2013). Enhanced eiscat uhf backscatter during high-energy auroral electron precipitation. Copernicus 31, 1681–1687. doi:10.5194/angeo-31-1681-2013

CrossRef Full Text | Google Scholar

Schlesier, A., Mishin, E., and Schlegel, K. (1997). “Non-collisional” ionization and temperature layers in the auroral E/F1layer: EISCAT observations. Geophys. Res. Lett. 24, 1407–1410. doi:10.1029/97gl01178

CrossRef Full Text | Google Scholar

Sedgemore-Schulthess, F., and St. Maurice, J.-P. (2001). Naturally enhanced ion-acoustic spectra and their interpretation. Surv. Geophys. 22, 55–92. doi:10.1023/a:1010691026863

CrossRef Full Text | Google Scholar

Semeter, J., and Blixt, E. (2006). Evidence for alfvén wave dispersion identified in high-resolution auroral imagery. Geophys. Res. Lett. 33, 121. doi:10.1029/2006gl026274

CrossRef Full Text | Google Scholar

Semeter, J., Zettergren, M., Diaz, M., and Mende, S. (2008). Wave dispersion and the discrete aurora: new constraints derived from high-speed imagery. J. Geophys. Res. Space Phys. 113, 211. doi:10.1029/2008ja013122

CrossRef Full Text | Google Scholar

Shapiro, V., and Shevchenko, V. (1988). Astrophysical plasma turbulence. i. Sov. Sci. Rev. Sect. E 6, 425–546.

Google Scholar

Sharber, Y., Fujii, R., Buchert, S. C., Nozawa, S., Watanabe, S., and Van Eyken, A. P. (2000). Simultaneous eiscat svalbard and vhf radar observations of ion upflows at different aspect angles. Geophys. Res. Lett. 27, 81–84. doi:10.1029/1999gl010665

CrossRef Full Text | Google Scholar

Singh, N., Loo, S. M., Wells, B. E., and Lakhina, G. S. (2001). Evolution of electron beam generated waves resulting in transverse ion heating and filamentation of the plasma. J. Geophys. Res. 106, 21165–21181. doi:10.1029/2000ja000335

CrossRef Full Text | Google Scholar

Spiger, R. J., Murphree, J. S., Anderson, H. R., and Loewenstein, R. F. (1976). Modulation of auroral electron fluxes in the frequency range 50 khz to 10 mhz. J. Geophys. Res. 81, 1269–1278. doi:10.1029/ja081i007p01269

CrossRef Full Text | Google Scholar

Stasiewicz, K., Holback, B., Krasnoselskikh, V., Boehm, M., Boström, R., and Kintner, P. M. (1996). Parametric instabilities of Langmuir waves observed by freja. J. Geophys. Res. 101, 21515–21525. doi:10.1029/96ja01747

CrossRef Full Text | Google Scholar

Stenbaek-Nielsen, H. C., and Hallinan, T. J. (1979). Pulsating auroras: evidence for noncollisional thermalization of precipitating electrons. J. Geophys. Res. 84, 3257–3271. doi:10.1029/ja084ia07p03257

CrossRef Full Text | Google Scholar

Stix, T. H. (1962). The theory of plasma waves. New York City, NY: McGraw-Hill.

Strømme, A., Belyey, V., Grydeland, T., La Hoz, C., Løvhaug, U., and Isham, B. (2005). Evidence of naturally occurring wave-wave interactions in the polar ionosphere and its relation to naturally enhanced ion acoustic lines. Geophys. Res. Lett. 32.

Google Scholar

Sullivan, J. M., Lockwood, M., Lanchester, B. S., Kontar, E. P., Ivchenko, N., Dahlgren, H., et al. (2008). An optical study of multiple neial events driven by low energy electron precipitation. Ann. Geophys. 26, 2435–2447. doi:10.5194/angeo-26-2435-2008

CrossRef Full Text | Google Scholar

Swider, W., and Narcisi, R. S. (1977). Auroral e-region: ion composition and nitric oxide. Planet. Space Sci. 25, 103–116. doi:10.1016/0032-0633(77)90014-9

CrossRef Full Text | Google Scholar

Thejappa, G., MacDowall, R., and Bergamo, M. (2012a). In situ detection of strong Langmuir turbulence processes in solar type iii radio bursts. J. Geophys. Res. Space Phys. 117, 267. doi:10.1029/2012ja017695

CrossRef Full Text | Google Scholar

Thejappa, G., MacDowall, R. J., Bergamo, M., and Papadopoulos, K. (2012b). Evidence for the oscillating two stream instability and spatial collapse of Langmuir waves in a solar type iii radio burst. ApJ 747, L1. doi:10.1088/2041-8205/747/1/l1

CrossRef Full Text | Google Scholar

Thiessen, J. P., and Kellogg, P. J. (1993). Langmuir wave decay and collapse in the jovian foreshock. Planet. Space Sci. 41, 823–832. doi:10.1016/0032-0633(93)90089-k

CrossRef Full Text | Google Scholar

Umeda, T., Omura, Y., Yoon, P. H., Gaelzer, R., and Matsumoto, H. (2003). Harmonic Langmuir waves. iii. vlasov simulation. Phys. Plasmas 10, 382–391. doi:10.1063/1.1537240

CrossRef Full Text | Google Scholar

Umeda, T. (2006). Vlasov simulation of amplitude-modulated Langmuir waves. Phys. Plasmas 13, 092304. doi:10.1063/1.2348088

CrossRef Full Text | Google Scholar

Volokitin, A., and Mishin, E. (1979). Relaxation of an electron beam in a plasma with infrequent collisions. Soviet J. Plasma Phys. 5, 654–656.

Google Scholar

Voronkov, I., and Mishin, Y. (1993). Quasilinear regime of Langmuir turbulence in the auroral e region of the ionosphere. Geomagn. Aeronom. C/C Geomagn. Aeronom. 33, 350.

Google Scholar

Wahlund, J.-E., Forme, F. R. E., Opgenoorth, H. J., Persson, M. A. L., Mishin, E. V., and Volokitin, A. S. (1992a). Scattering of electromagnetic waves from a plasma: enhanced ion acoustic fluctuations due to ion-ion two-stream instabilities. Geophys. Res. Lett. 19, 1919–1922. doi:10.1029/92gl02101

CrossRef Full Text | Google Scholar

Wahlund, J.-E., Opgenoorth, H. J., Forme, F. R. E., Persson, M. A. L., Häggström, I., and Lilensten, J. (1993). Electron energization in the topside auroral ionosphere: on the importance of ion-acoustic turbulence. J. Atmos. terrestrial Phys. 55, 623–645. doi:10.1016/0021-9169(93)90010-v

CrossRef Full Text | Google Scholar

Wahlund, J.-E., Opgenoorth, H. J., Häggström, I., Winser, K. J., and Jones, G. O. L. (1992b). Eiscat observations of topside ionospheric ion outflows during auroral activity: Revisited. J. Geophys. Res. 97, 3019–3037. doi:10.1029/91ja02438

CrossRef Full Text | Google Scholar

Wahlund, J.-E., Opgenoorth, H. J., and Rothwell, P. (1989). Observations of thin auroral ionization layers by eiscat in connection with pulsating aurora. J. Geophys. Res. 94, 17223–17233. doi:10.1029/ja094ia12p17223

CrossRef Full Text | Google Scholar

Wang, J. G., Payne, G. L., DuBois, D. F., and Rose, H. A. (1996). Comparison of zakharov simulation and open boundary vlasov simulation of strong Langmuir turbulence. Phys. Plasmas 3, 111–121. doi:10.1063/1.871837

CrossRef Full Text | Google Scholar

Weatherwax, A. T., LaBelle, J., and Trimpi, M. L. (1994). A new type of auroral radio emission observed at medium frequencies (∼1,350–3,700 kHz) using ground-based receivers. Geophys. Res. Lett. 21, 2753–2756. doi:10.1029/94gl02512

CrossRef Full Text | Google Scholar

Willes, A. J., and Cairns, I. H. (2000). Generalized Langmuir waves in magnetized kinetic plasmas. Phys. Plasmas 7, 3167–3180. doi:10.1063/1.874180

CrossRef Full Text | Google Scholar

Wong, A. Y., and Quon, B. H. (1975). Spatial collapse of beam-driven plasma waves. Phys. Rev. Lett. 34, 1499. doi:10.1103/physrevlett.34.1499

CrossRef Full Text | Google Scholar

Yoon, P. H., Gaelzer, R., Umeda, T., Omura, Y., and Matsumoto, H. (2003). Harmonic Langmuir waves. i. nonlinear dispersion relation. Phys. Plasmas 10, 364–372. doi:10.1063/1.1537238

CrossRef Full Text | Google Scholar

Yoon, P. H., Hong, J., Kim, S., Lee, J., Lee, J., Park, J., et al. (2012a). Asymmetric solar wind electron distributions. ApJ 755, 112. doi:10.1088/0004-637x/755/2/112

CrossRef Full Text | Google Scholar

Yoon, P. H., and LaBelle, J. (2005). Discrete Langmuir waves in density structure. J. Geophys. Res. 110, 39–47. doi:10.1029/2005JA011186

CrossRef Full Text | Google Scholar

Yoon, P. H., Rhee, T., and Ryu, C.-M. (2006). Self-consistent formation of electron κ distribution: 1. theory. J. Geophys. Res. Space Phys. 111, 233. doi:10.1029/2006ja011681

CrossRef Full Text | Google Scholar

Yoon, P. H. (2006). Statistical theory of electromagnetic weak turbulence. Phys. Plasmas 13, 022302. doi:10.1063/1.2167587

CrossRef Full Text | Google Scholar

Yoon, P. H., Ziebell, L. F., Gaelzer, R., and Pavan, J. (2012b). Electromagnetic weak turbulence theory revisited. Phys. Plasmas 19, 102303. doi:10.1063/1.4757224

CrossRef Full Text | Google Scholar

Ziebell, L. F., Gaelzer, R., and Yoon, P. H. (2001). Nonlinear development of weak beam-plasma instability. Phys. Plasmas 8, 3982–3995. doi:10.1063/1.1389863

CrossRef Full Text | Google Scholar

Ziebell, L. F., Yoon, P. H., Petruzzellis, L. T., Gaelzer, R., and Pavan, J. (2015). Plasma emission by nonlinear electromagnetic processes. ApJ 806, 237. doi:10.1088/0004-637x/806/2/237

CrossRef Full Text | Google Scholar

Ziebell, L., Gaelzer, R., Pavan, J., and Yoon, P. (2008). Two-dimensional nonlinear dynamics of beam–plasma instability. Plasma Phys. Control. Fusion 50, 085011. doi:10.1088/0741-3335/50/8/085011

CrossRef Full Text | Google Scholar

Ziebell, L., Yoon, P., Pavan, J., and Gaelzer, R. (2011). Ion-acoustic enhancements generated by beam-plasma instability in an auroral cavity. J. Geophys. Res. Space Phys. 116, 111. doi:10.1029/2010ja016147

CrossRef Full Text | Google Scholar