Anna Wawrzaszek
Marius Echim- 1Centrum Badań Kosmicznych, Polska Akademia Nauk, Warsaw, Poland
- 2The Royal Belgian Institute for Space Aeronomy, Brussels, Belgium
- 3Institute of Space Science, Măgurele, Romania
Intermittency, an important property of astrophysical plasma turbulence, is studied extensively during last decades from in-situ measurements of the solar wind plasma and magnetic field in the ecliptic plane and at higher latitudes, and heliocentric distances between 0.3 and 5 Astronomical Units. In this paper, we review the main findings on intermittency derived from investigation of solar wind turbulence for the inertial range of scales. It turns out that our current knowledge on the evolution of intermittency in the heliosphere is based on two missions, Helios two and Ulysses. We discuss the importance of data selection methodologies and applications for heliospheric spacecraft, the different data analysis techniques (the anomalous scaling of the structure function, the non-Gaussianity of the probability distribution functions, the local intermittency measure estimated from a wavelet representation and the multifractal spectrum). Studies show that Alvénic solar wind is less intermittent but reveals increase with the radial distance. Moreover, intermittency is stronger for the magnetic than for velocity fluctuations and is considered to be responsible for the increase with the radial distance of the anisotropy of magnetic fluctuations. The intermittency of fast solar wind at solar minimum decreases with latitude. Finally, the level of intermittency in the solar wind depends on solar cycle phase, reflecting the changes of the state of solar wind and suggesting that the deeper study of origin of fast and slow wind can further improve our understanding of the intermittency.
1. Introduction
The solar wind is considered as natural laboratory to study turbulence of astrophysical plasmas (Bruno and Carbone, 2013, and references therein). Indeed, solar wind Reynolds number is quite large and the spectral properties of magnetic field and plasma velocity fluctuations show power law behavior (Coleman and Paul, 1968; Goldstein et al., 1995; Tu and Marsch, 1995; Biskamp, 2003; Bruno and Carbone, 2013), similar to neutral fluids turbulence. The solar wind power spectral density reveals the existence of an inertial range of scales, where the energy is transferred nonlinearly from larger to smaller scales. The power law exponent,
One of the open-question is related to the structure of solar wind turbulence, more specifically, on how irregular is the transfer of energy between scales. The irregularity of the energy transfer rate (see, e.g., Marsch et al., 1996; Horbury et al., 1997) leads to the phenomenon of intermittency (from Latin intermitere, to interrupt). This type of irregularity represents a violation of the fundamental hypothesis adopted to derive the classical model of Kolmogorov turbulence and is generally described as a deviation from the perfect self-similarity (Frisch, 1995, ch. 8). Indeed, while in the classical model of turbulence the energy is transferred by nonlinear structures (e.g. vortices) that fully occupy the space at all scales and which are characterized by a constant, scale-independent energy transfer rate, in intermittent turbulence the energy is transferred non-uniformly, by processes whose transfer rate is scale and spatially dependent. The phenomenon of intermittency can be defined as the property of the plasma structures carying the turbulent fluctuations (e.g., eddies, Alfvén vortices) to break down heterogeneously at smaller and smaller scales, i.e. they become scattered in time and/or space (Biskamp, 2003, ch. 7). In solar wind turbulence, intermittency can be detected at scales pertaining to the inertial range, orders of magnitude away from dissipative scales, which is a significant difference between hydrodynamic and MHD turbulence (Frisch, 1995; Biskamp, 2003; Bruno, 2019). Intermittency in solar wind turbulence was first identified by Burlaga, 1991. Since then, it has been widely studied and documented using data from many missions: Voyager (Burlaga, 1991; Burlaga, 1995; Burlaga et al., 1993), Helios (e.g., Marsch and Liu, 1993; Marsch and Tu, 1994; Marsch et al., 1996; Sorriso-Valvo et al., 1999; Veltri and Mangeney, 1999; Sorriso-Valvo et al., 2001; Bruno et al., 2003), Ulysses (e.g., Horbury et al., 1996; Tu et al., 1996; Horbury et al., 1997; Pagel and Balogh, 2001; Pagel and Balogh, 2003; Yordanova et al., 2009; Wawrzaszek et al., 2015, Wawrzaszek et al., 2019), Advanced Composition Explorer and WIND (Hnat et al., 2003; Vörös et al., 2006; Szczepaniak and Macek, 2008; Greco et al., 2009; Salem et al., 2009; Wan et al., 2011), and recently also from Parker Solar Probe (e.g., Alberti et al., 2020; Chhiber et al., 2020; Perrone et al., 2020).
Intermittency can be revealed by several complementary data analysis methodologies. Most of the analysis methods focus on higher-order moments of fluctuations probabilities in order to reveal their scale dependence and a departure from self-similarity expected for intermittent fluctuations (e.g., Frisch, 1995).
(1) A first class of methods estimate intermittency from the anomalous scaling of the Structure Functions (SF) and its deviation from self-similarity quantified by fitting different intermittency models (e.g., Meneveau and Sreenivasan, 1987; Burlaga, 1991; Carbone, 1993; Marsch and Liu, 1993; She and Leveque, 1994; Burlaga, 1995; Horbury et al., 1997).
(2) Another approach evaluates intermittency from the non-Gaussian features of Probability Distribution Functions (PDF) of the solar wind fluctuation (Marsch and Tu, 1994), e.g. by comparison/fitting with Castaing distributions (Castaing et al., 1990; Sorriso-Valvo et al., 1999; Sorriso-Valvo et al., 2001; Pagel and Balogh, 2003; Yang and Tam, 2010) or from the evaluation of the fourth order moment (kurtosis, Flatness Factor) (e.g., Bruno et al., 2003; Yordanova et al., 2009).
(3) A third methodology adopted to evaluate intermittency is based on the so-called Local Intermittency Measure (LIM) computed from the normalized squared module of wavelet coefficients calculated for an incremental measure of the signal, similar to the one used to estimate the PDFs (Farge, 1992; Veltri and Mangeney, 1999; Bruno et al., 2001).
(4) Finally, a fourth approach is based on calculation of the multifractal spectrum of an incremental measure (e.g., Marsch et al., 1996; Burlaga and Ness, 2010; Wawrzaszek and Macek, 2010; Macek et al., 2014; Wawrzaszek et al., 2015).
More details and exhaustive description of each method applied for intermittency can be found in recent reviews like, e.g., Salem et al. (2009), Bruno and Carbone (2013), Matthaeus et al. (2015), Bruno (2019).
Due to the relatively reduced time resolution of most of solar wind data, the methods mentioned above were applied to study intermittency of the inertial range turbulence (e.g., Burlaga, 1991; Marsch and Liu, 1993; Tu et al., 1996; Sorriso-Valvo et al., 1999; Bruno et al., 2003; Wawrzaszek et al., 2015; Wawrzaszek et al., 2019). In this review, we summarize the observations of MHD intermittency in the solar wind, and discuss how intermittency changes with the type of solar wind (fast vs. slow), the radial distance, the heliolatitude, and solar cycle. We also emphasize the importance of using robust data selection algorithms, the impact of various reference systems and how the interpretation of results depends on the characteristics of the different data analysis methods. The study of intermittency in the MHD range of scales is crucial and complementary to investigation of kinetic scales reported recently by (e.g., Perri et al., 2012; Wan et al., 2012; Sorriso-Valvo et al., 2017).
2. Solar WIND Intermittency versus Radial Distance and Heliolatitude
2.1. Radial Evolution of Intermittency in the Ecliptic
The first study of intermittency for different solar wind conditions and for a range of heliocentric distances in the ecliptic plane is due to Marsch and Liu (1993), who investigated Helios two observations of fast and slow streams (bulk velocity and Alfvén velocity) at two heliocentric distances (0.3 and 1 AU), for scales between 40.5 s and 24 h. Their analysis was based on the structure function approach and found that intermittency is stronger for the small scales, while the fast solar wind reveals generally less intermittent nature than slow wind. It was also shown that the intermittency level in the ecliptic increases with the increasing heliocentric distance for fast wind streams and was suggested that solar wind turbulence results from a mixture of waves, advected sheets and eddies.
Tu et al. (1996) considered 5 cases of Helios two data and detected magnetic intermittency in the range of scales between 81 and 2,500 s. From estimation of the anomalous scaling of structure function they showed that the intermittency in the fast solar wind is relatively stable, but it varies significantly in the slow wind. However, a clear radial evolution trend was not found.
Sorriso-Valvo et al. (1999) analyzed fluctuations of the solar wind at time scales from 81 s to 1 day from four months of Helios two data recorded in 1976 when the heliocentric distance varied from 1 AU to 0.29 AU. They studied intermittency with the Castaing distribution approach and found that the magnetic field intensity presents higher level of intermittency than the bulk speed for fast and slow wind. No significant differences were found between slow and fast wind. Sorriso-Valvo et al. (1999) considered compressive phenomena to be at the origin of the slow solar wind intermittency.
Bruno et al. (1999) investigated the effects of intermittency on anisotropy (defined as the ratio between the total power perpendicular to the minimum variance direction and the power along this direction) for three heliospheric distances, 0.3, 0.7, and 0.9 AU, from magnetic and velocity data provided by Helios 2. It is shown that there is a link between the radial evolution of intermittency and anisotropy. Indeed, it is demonstrated, aided by the computation of the Local Intermittency Measure (LIM), that the increase of magnetic anisotropy with radial distance is mainly due to radial evolution of magnetic intermittency. However, the intermittency of the velocity field does not alter significantly the radial trend of velocity anisotropy.
Bruno et al. (2003) focused on the radial behavior of intermittency in the ecliptic determined from the fourth-order moment (or flatness) of PDFs computed for the compressive and vector fluctuations of the magnetic field and plasma velocity, measured by Helios two at 0.3, 0.7 and 0.9 AU. While previous analyses were based on data representation in the Solar Ecliptic (SE) reference systems (Marsch and Liu, 1993; Tu et al., 1996; Sorriso-Valvo et al., 1999), Bruno et al. (2003) used a Mean Field (MF) reference system (see Appendix D.2 of Bruno and Carbone, 2013). In MF reference frame one component,
Yang and Tam (2010) analyzed 39 time intervals of fast solar wind data provided by Helios 1 and 2 at radial distances between 0.3 and 1 AU. From a conditioned flatness analysis and the fitting of Castaing distribution, these authors confirmed that fast solar wind magnetic intermittency increases with larger distance from the Sun. The increase of intermittency with distance in the ecliptic plane was confirmed for two parameters of the fast solar wind (velocity and magnetic field).
Bruno et al. (2014a) considered also the radial evolution of intermittency of density fluctuations in fast solar wind as observed by Helios 2 between 0.3 and 0.9 AU. It is shown that, in contrast to observations for velocity and magnetic field, the density fluctuations show a stronger intermittent character at short heliocentric distances and the level of density intermittency decreases with the distance from the Sun.
Recent analysis of Parker Solar Probe (PSP) data measured during the first two orbits, when slow solar wind dominated, provide insight on intermittency at rather close distances from the Sun. Some studies focused on data measured at 0.17 AU and on the identification coherent structures (Bandyopadhyay et al., 2020; Chhiber et al., 2020), various types of intermittent events like current sheets, vortex-like structures or wave packets (Perrone et al., 2020). Alberti et al. (2020) analyzed magnetic field components measured by PSP at different locations (between 0.17 and 0.7 AU). Authors reveled statistical global self-similar scaling at radial distances below 0.4 AU and scaling properties typical for intermittent turbulence above 0.4 AU. They suggested that around 0.4 AU there is a transition region in which intermittency appears and the scaling in the inertial range changes (Chen et al., 2020).
2.2. Radial Dependence of Intermittency Outside the Ecliptic
In the ecliptic plane, the solar wind turbulence is driven by velocity shears, parametric decay, and the interaction between Alfvénic modes with convected structures (Bruno and Carbone, 2013). Thanks to Ulysses measurements, the radial dependence of the intermittent turbulence can be investigated outside the ecliptic plane. It is found that at higher latitudes solar wind turbulence shows different properties compared to the equatorial regions (Ruzmaikin et al., 1995; Bavassano et al., 2000, Bavassano et al., 2001). The radial evolution of turbulence in the polar wind is less rapid (e.g., Horbury et al., 1996; Bruno and Trenchi, 2014), what seems to have also influence on the level of magnetic intermittency (e.g., Ruzmaikin et al., 1995; Horbury and Balogh, 2001; Pagel and Balogh, 2002, Pagel and Balogh, 2003; Yordanova et al., 2009).
An analysis of structure function scaling (Pagel and Balogh, 2001) at solar minimum (1994–1995), radial distances between 1.3 and 2.4 AU and heliolatitudes between −80° to +80°, revealed the evolution of intermittency outside the ecliptic. A high level of intermittency was found for a range of scales between 10 and 300 s in the fast solar wind; however, the data in the slow wind were much more variable and difficult to interpret. Nevertheless, it was shown that the transverse magnetic components have a comparable level of intermittency, while the radial component is slightly less intermittent.
Pagel and Balogh (2002) confirmed the radial trends at solar minimum (1994–1995) and maximum (2000–2001) and also found, contrary to previous studies, that the slow solar wind presents a level of intermittency comparable to the fast wind. It is worth to add that authors used wind speed as the criterion to discriminate between two states of solar wind. Bruno and Carbone (2013) suggested that this discrepancy results mainly from the representation of data in the RTN reference system instead of the Mean Field frame.
Pagel and Balogh (2003) analyzed 28 cases of polar coronal fast wind measured during solar minimum (1994–1996) and fitted the PDFs of magnetic field fluctuations with the Castaing distribution, for time scales between 40 and 200 s. Their results showed that intermittency, or non-Gaussianity, of the magnetic field fluctuations increases with the radial distance in the range 1.4–4.1 AU and is stronger for transverse than for radial component. It is suggested that the increase of intermittency with the radial distance is the effect of the increase of the scale range of the inertial range sustained by the radial expansion of the solar wind.
Yordanova et al. (2009) analyzed 21 time intervals without CMEs and, based on kinetic parameters and ions (oxygen) charge states, considered four states of the solar wind, 1) pure fast, 2) fast streams, 3) pure slow, 4) slow streams, from Ulysses data recorded between 1992 and 1997. The results indicated that only pure fast wind (4 cases) show clear trends for radial evolution of the intermittency with the heliocentric distance, between 1.5 AU and 3.0 AU and at heliolatitudes between 50° and 80°. Yordanova et al. (2009) concluded also that pure slow wind measured at 5.1–5.4 AU and at latitudes narrowed to <20° presents the most intermittent state.
Wawrzaszek et al. (2015) studied the radial dependence of magnetic field intermittency as observed by Ulysses during two solar minima (1997–1998, 2007–2008) and one maximum (1999–2001), between 1.4 and 5.4 AU and a heliolatitudes ranging between −80° and +70°. To avoid the problem of mixing of different states of the solar wind, these authors applied a multi-parametric procedure based on several solar wind variables to select data and discriminate between slow and fast wind. Additionally, interplanetary transients like shocks and CMEs have been excluded from the analysis. Thus, they found 98 time intervals of slow (43 time intervals) and fast solar wind (55 time intervals). Wawrzaszek et al. (2015) applied the multifractal formalism to investigate intermittency and limited their analyses to the compressional component. More precisely, they determined multifractal spectra and Δ, the degree of multifractality, as a quantative descriptor of the intermittency level. This study suggests that the level of intermittency decreases with distance in contrast to the previous analyses based on statistical description (Pagel and Balogh, 2003; Yordanova et al., 2009). However, during the identification of the multifractal scaling, authors included also scales less than 16 s, what could have an impact on the results. Nevertheless, the collection of data used by Wawrzaszek et al. (2015) is the largest in terms of number of time intervals and total data (more than 17,000 h), among all studies devoted to intermittency based on Ulysses data.
Wawrzaszek et al. (2019) extended their study by using a larger number of time intervals (126) at solar minima (1997–1998, 2007–2008) and solar maximum (1999–2001). The multifractal analysis were applied for the all magnetic field components in the MHD range of scales (larger than 16 s). Additionally, the authors investigated intermittency of the parallel and perpendicular component in the Mean Field reference system, used previously by Bruno et al. (2003) for Helios two data. Wawrzaszek et al. (2019) confirmed the decrease of intermittency with the radial distance, for all components of the magnetic field, regardless the reference system, RTN or Mean Field. However, the rate of decrease of the intermittency with the distance from the Sun, was influenced by the range of the analyzed scales; smaller scales less than 16 s caused a slowdown of this decrease, interpreted as the influence of compressibility processes that strengthen the phenomenon of intermittency (Alexandrova et al., 2008). In general, Wawrzaszek et al. (2019) reminded the idea that the intermittency in MHD range have solar origin (Pagel and Balogh, 2002; Wawrzaszek et al., 2015) and suggested that the strength of various solar wind drivers like fast and slow streams, shocks interaction, pressure balanced, incompressible current sheets and interplanetary shocks (Veltri and Mangeney, 1999) diminishes with the distance from the Sun leading to a decrease of intermittency. On the other hand, Greco et al. (2012) performing numerical simulation and data analysis from the ecliptic suggested that intermittency is formed in the solar wind through active in-situ dynamics. In the light of this suggestion solar wind beyond ecliptic seems to be insufficiently active turbulent medium, the coherent character of advected structures can be somehow reduced with the increase of radial distance.
2.3. Latitudinal Dependence and Solar Cycle Effect
Another possible source for the differences observed between radial variation trends provided by different methodologies can be the mixing of different heliolatitudes in the same dataset. The solar cycle phase can also play a role. In Table 1 we provide a summary of datasets analyzed in the papers discussed above.
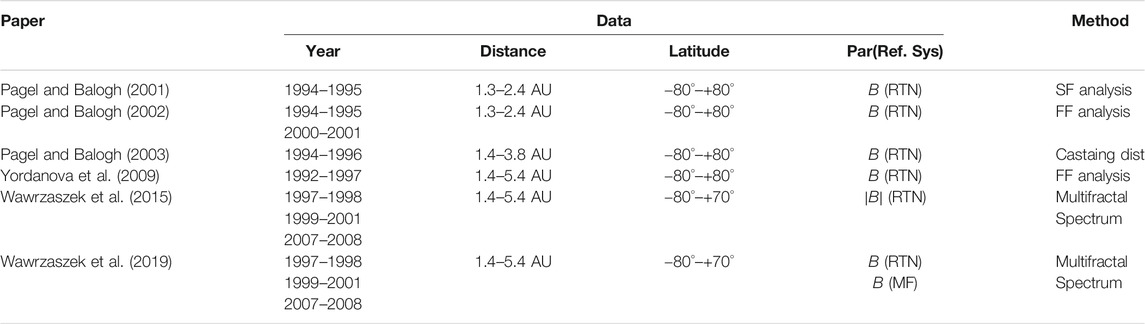
TABLE 1. Selected papers devoted to the analysis of intermittency in the solar wind beyond the ecliptic plane by using Ulysses measurements.
Pagel and Balogh (2002) compared two Ulysses fast-latitude scans at solar minimum and maximum, and did not reveal any latitudinal dependence of intermittency (Wawrzaszek et al., 2015; Wawrzaszek et al., 2019). showed that the fast solar wind at solar minimum exhibit a decrease of intermittency as the latitude increases; the smallest values of intermittency were found near solar poles. An example form Wawrzaszek et al. (2019) is shown in the composite Figure 1, where left/right panels refer to the fast/slow solar wind. Color in Figure 1 denotes the values Δ, the degree of multifractality as an intermittency measure. Figure 1 presents results for the radial component BR (in RTN reference system, panels A and B) and component
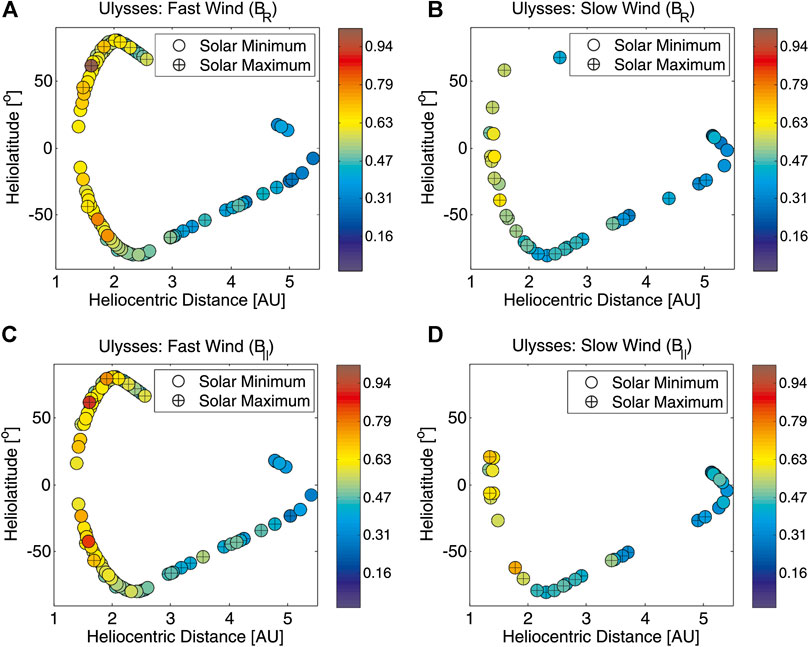
FIGURE 1. Map of the degree of multifractality as a level of intermittency determined for fast (left panel) and slow (right panel) solar wind during solar minima (1997–1998, 2007–2008) and solar maximum (1999–2001), correspondingly. Color denotes the level of multifractality (intermittency) calculated for the radial components BR (in RTN reference system, (A,B)) and component
The solar cycle trends need more discussion. Indeed, on the one hand trends in the radial dependence of intermittency in the ecliptic were derived from Helios 1 and 2 data recorded during solar cycle 21, between 1974 and 1981. On the other hand, the first, second and third orbit of Ulysses data captured the solar wind properties during cycles 22 and 23, revealing also differences in the state of the solar wind (McComas et al., 2008).
The analysis of solar wind data from each solar cycle confirmed the presence of intermittency, virtually at all radial distances and both at solar minimum and solar maximum (Pagel and Balogh, 2001; Pagel and Balogh, 2002; Pagel and Balogh, 2003; Wawrzaszek et al., 2015, Wawrzaszek et al., 2019). Pagel and Balogh (2002) suggested intermittency varies less with the solar cycle phase than with the type of wind. Analysis of Ulysses data for the years 1992–1997 (Yordanova et al., 2009) and results obtained for the solar minimum (1997–1998) (Wawrzaszek et al., 2015; Wawrzaszek et al., 2019) showed that intermittency is stronger for slow solar wind than for the fast wind. This is in agreement with research performed in the ecliptic (Marsch and Liu, 1993; Bruno et al., 2003). However, the study by (Wawrzaszek et al., 2015; Wawrzaszek et al., 2019) based on data recorded at solar maximum (1999–2001) and minimum (2007–2008) reveals cases when the slow solar wind shows a lower level of intermittency than the fast solar wind. Similar conclusions were given by Pagel and Balogh, (2002), who analyzed data from the same solar maximum and found a high level of intermittency in the fast coronal hole solar wind and a varying and lower level in the slow wind. However, one should note that most of the slow solar wind cases considered in (Pagel and Balogh, 2002; Wawrzaszek et al., 2015, 2019) pertained to solar cycle 23 characterized by specific properties (e.g., McComas et al., 2008; D’Amicis et al., 2011). In particular, the slow wind observed at maximum of solar cycle 23 (the year 2001) showed a degree of Alfvénicity comparable or even higher than for the fast wind observed at the minimum of the same cycle (2007) as discussed by D’Amicis et al. (2011). Moreover, a new type of Alfvénic slow wind is believed to show having some characteristics common to the fast wind (D’Amicis and Bruno, 2015; D’Amicis et al., 2018). Very interesting are recent observations of PSP performed during minimum of solar cycle no. 24, which confirmed the existence of the slow solar wind with high Alfvénicity and its intermittent character (Bandyopadhyay et al., 2020; Chhiber et al., 2020; Perrone et al., 2020).
Finally it is worth to stress that at solar maximum the statistics of slow wind intervals is rather poor (compare cases in Figure 1B, D marked by circles with a cross for maximum and empty circles for minimum). At solar maximum intermittency spans a larger domain of values, as a confirmation of the complex nature of the solar wind during strong activity of the Sun.
3. Summary and Perspective
In this review we discuss recent findings on solar wind inertial range intermittency observed over a large range of heliocentric distances and latitudes, for different levels of solar activity.
Intermittency is a real and omnipresent characteristic of solar wind turbulence, detected for fluctuations of solar wind magnetic field and plasma parameters (velocity, density), for fast and slow types of wind. The main source of intermittency are magnetic non-Alfvénic coherent structures involved in the radial evolution of solar wind turbulence, different than filaments or vortices observed in neutral fluid turbulence (Bruno and Carbone, 2013; Bruno, 2019). The most intermittent events identified in the inertial range of scales are parallel shocks, slow mode shocks, or tangential discontinuities/current sheets (Veltri and Mangeney, 1999; Bruno et al., 2001; Borovsky, 2008) or planar sheets in MHD flows (Bruno, 2019). Data from Helios and Ulysses show different trends for the radial evolution of intermittency in fast and slow winds. While in the inner heliosphere, in the equatorial plane and at radial distances less than 1 AU intermittency tends to increase with distance, this tendency is reversed outside the ecliptic and for larger radial distances. It is argued that decreasing of intermittency with large radial distances is the result of the interplay between coherent, intermittent structures convected by the wind and propagating Alfvén fluctuations, which tend to reduce intermittency. Examples of solar wind data for which Alfvénic fluctuations are less dominant, are generally more intermittent but do not show a clear radial evolution. Nevertheless, intermittency in the Alfvénic solar wind increases with heliocentric distance. Moreover, data indicate intermittent properties of fast polar wind show a symmetry in the two hemispheres. The fast solar wind at solar minimum exhibits a decrease of intermittency as the latitude increases. However, this trend is less clear at solar maximum, when intermittency values are more scattered. The level of intermittency in the solar wind is solar cycle-dependent, reflecting the changes of the state of solar wind and suggesting that the origin of fast and slow wind is important for the subsequent structure of turbulent transfer of energy within the heliosphere.
Although the studies discussed above provide evidence on the existence of a radial evolution of intermittency beyond the ecliptic plane, it is difficult to define a universal trend and to indicate how intermittency changes with the radial distance for all types of wind, and all phases of the solar cycle. On the one hand, different methodologies capture different aspects of intermittency (Sorriso-Valvo et al., 2017). The multifractal analysis emphasizes the role of the higher-order moments, and collect the measure of intermittency from an estimation of large (positive moments) and small (negative moments) concentrations of measure. The structure function and the flatness approaches are based on positive moments only. On the other hand, the mathematical formalism of the multifractal scalings does not lend itself to a interpretation in terms of coherent structures (Wan et al., 2011). It is certain that the multifractal approach and the analysis based on the structure function, PDFs and their moments capture complementary characteristics of the same phenomenon, the irregular structure of the energy transfer in astrophysical plasma turbulence. Further studies are expected to illuminate more the intricate relationship between the insight provided by these higher order analyses and the impact on understanding solar wind and astrophysical intermittency.
Nevertheless, some additional analyses should still be performed to better understand solar wind turbulence and intermittent dynamics at MHD scales. As we tried to underline in this short review, a large part of the studies devoted to intermittency are based on a relatively small number of samples selected by different methods, making it difficult to interpret and compare results. Moreover, most often only a subset of plasma or magnetic field measurements were analyzed, and due to the limitations of in-situ interplanetary data, similar scaling ranges are seldom considered by different approaches. Therefore, a complementary analysis of intermittency with various descriptors estimated for the same large datasets is still needed. One of the simplest ways to achieve such a goal seems to be using analysis tools designed to perform automatic analysis of large collections of space measurements, in-situ or simulations (e.g., Teodorescu and Echim, 2020). Moreover, significant advances in data selection procedures allow to identify more than the two basic states of the solar wind, fast and slow, as discussed by (Landi et al., 2012; Xu and Borovsky, 2015; Camporeale et al., 2017). Such categorization procedures will likely provide further refinement of data analysis and allow for a deeper analysis of solar wind intermittency and its relationship with the various states of solar wind. A continuation of detailed studies of the relationship between solar wind anisotropy and intermittency and of the dependence on the solar wind conditions is also needed. It would allow for new comparisons between turbulence properties revealed by in-situ data analysis and the results of numerical simulations and improve our understanding of physical processes like dynamic alignment, critical balance and intermittency. Additionally, a better understanding of the formation, stability and dynamics of solar wind discontinuities can help understanding the origin of intermittency (Borovsky, 2008; Greco et al., 2008; Greco et al., 2009).
Finally, there is a need to advance the understanding of the couplings between the inertial range structure of turbulence and intermittency and the phenomena taking place at smaller, kinetic scales (e.g., Bruno et al., 2014b), for example their influence on field-particle interaction (e.g., Chen et al., 2019; Sorriso-Valvo et al., 2019). As Bruno (2019) reviewed recently, most studies focus now on the analysis of intermittent events at small, kinetic scales as the key to understanding the dissipation mechanisms in the collisionless solar wind plasma. This topic, due to the lack of adequate plasma observations was mainly explored by using plasma numerical simulations. Recently, thanks to new missions like Magnetospheric Multiscale Mission, Parker Solar Probe or Solar Orbiter, new opportunities are opened for the scientific community to analyze the intermittent nature of solar wind turbulence at much smaller scales and in new regions of the heliosphere (at closer distances from the Sun and during new solar cycles). This opens up new research options and makes upcoming years very exciting for the heliospheric community.
Author Contributions
AW and ME planned, outlined, researched, and wrote the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
ME acknowledge support from the Belgian Solar Terrestrial Center of Excellence (STCE) and the Romanian Government UEFISCDI PCCDI Project VESS and Program Nucleu LAPLAS.
References
Alberti, T., Laurenza, M., Consolini, G., Milillo, A., Marcucci, M. F., Carbone, V., et al. (2020). On the scaling properties of magnetic-field fluctuations through the inner heliosphere. Astrophys. J. 902, 84. doi:10.3847/1538-4357/abb3d2
Alexandrova, O., Carbone, V., Veltri, P., and Sorriso-Valvo, L. (2008). Small-scale energy cascade of the solar wind turbulence. Astrophys. J. 674, 1153–1157. doi:10.1086/524056
Bandyopadhyay, R., Matthaeus, W. H., Parashar, T. N., Chhiber, R., Ruffolo, D., Goldstein, M. L., et al. (2020). Observations of energetic-particle population enhancements along intermittent structures near the sun from the parker solar probe. Astrophys. J. Suppl. 246, 61. doi:10.3847/1538-4365/ab6220
Bavassano, B., Pietropaolo, E., and Bruno, R. (2000). On the evolution of outward and inward Alfvénic fluctuations in the polar wind. J. Geophys. Res. 105, 15959–15964. doi:10.1029/1999JA000276
Bavassano, B., Pietropaolo, E., and Bruno, R. (2001). Radial evolution of outward and inward alfvénic fluctuations in the solar wind: a comparison between equatorial and polar observations by ulysses. J. Geophys. Res. 106, 10659–10668. doi:10.1029/2000JA000453
Belcher, J. W., and Davis, L. (1971). Large-amplitude alfven waves in the interplanetary medium, 2. J. Geophys. Res. 76, 3534–3563. doi:10.1029/JA076i016p03534
Biskamp, D. (2003). Magnetohydrodynamic turbulence. Plasma Phys. Contr. Fusion 45, 1827. doi:10.1088/0741-3335/45/9/701
Borovsky, J. E. (2008). Flux tube texture of the solar wind: strands of the magnetic carpet at 1 au? J. Geophys. Res. 113, A08110. doi:10.1029/2007JA012684
Bruno, R., Bavassano, B., Pietropaolo, E., Carbone, V., and Veltri, P. (1999). Effects of intermittency on interplanetary velocity and magnetic field fluctuations anisotropy. Geophys. Res. Lett. 26, 3185–3188. doi:10.1029/1999GL010668
Bruno, R., Carbone, V., Sorriso-Valvo, L., and Bavassano, B. (2003). Radial evolution of solar wind intermittency in the inner heliosphere. J. Geophys. Res. 108, 1130. doi:10.1029/2002JA009615
Bruno, R., and Carbone, V. (2013). The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10, 2. doi:10.12942/lrsp-2013-2
Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., and Bavassano, B. (2001). Identifying intermittency events in the solar wind. Planet. Space Sci. 49, 1201–1210. doi:10.1016/S0032-0633(01)00061-7
Bruno, R. (2019). Intermittency in solar wind turbulence from fluid to kinetic scales. Earth Space Sci. 6, 656–672. doi:10.1029/2018EA000535
Bruno, R., Telloni, D., Primavera, L., Pietropaolo, E., D’Amicis, R., Sorriso-Valvo, L., et al. (2014a). Radial evolution of the intermittency of density fluctuations in the fast solar wind. Astrophys. J. 786, 53. doi:10.1088/0004-637x/786/1/53
Bruno, R., and Trenchi, L. (2014). Radial dependence of the frequency break between fluid and kinetic scales in the solar wind fluctuations. Astrophys. J. 787, L24. doi:10.1088/2041-8205/787/2/l24
Bruno, R., Trenchi, L., and Telloni, D. (2014b). Spectral slope variation at proton scales from fast to slow solar wind. Astrophys. J. 793, L15. doi:10.1088/2041-8205/793/1/l15
Burlaga, L. F. (1991). Intermittent turbulence in the solar wind. J. Geophys. Res. 96, 5847–5851. doi:10.1029/91JA00087
Burlaga, L. F., and Ness, N. F. (2010). Sectors and large-scale magnetic field strength fluctuations in the heliosheath near 110 au: voyager 1, 2009. Astrophys. J. 725, 1306. doi:10.1088/0004-637X/725/1/1306
Burlaga, L. F., Perko, J., and Pirraglia, J. (1993). Cosmic-ray modulation, merged interaction regions, and multifractals. Astrophys. J. 407, 347–358. doi:10.1086/172517
Burlaga, L. (1995). Interplanetary mganetohydrodynamics. 1st Edn. New York, NY: Oxford University Press, 272.
Camporeale, E., Carè, A., and Borovsky, J. E. (2017). Classification of solar wind with machine learning. J. Geophys. Res. 122 (10), 910–920. doi:10.1002/2017JA024383
Carbone, V. (1993). Cascade model for intermittency in fully developed magnetohydrodynamic turbulence. Phys. Rev. Lett. 71, 1546–1548. doi:10.1103/PhysRevLett.71.1546
Castaing, B., Gagne, Y., and Hopfinger, E. (1990). Velocity probability density functions of high Reynolds number turbulence. Phys. Nonlinear Phenom. 46, 177–200. doi:10.1016/0167-2789(90)90035-N
Chen, C. H. K., Bale, S. D., Bonnell, J. W., Borovikov, D., Bowen, T. A., Burgess, D., et al. (2020). The evolution and role of solar wind turbulence in the inner heliosphere. Astrophys. J. Suppl. 246, 53. doi:10.3847/1538-4365/ab60a3
Chen, C., Klein, K., and Howes, G. (2019). Evidence for electron Landau damping in space plasma turbulence. Nat. Commun. 10, 740. doi:10.1038/s41467-019-08435-3
Chhiber, R., Goldstein, M. L., Maruca, B. A., Chasapis, A., Matthaeus, W. H., Ruffolo, D., et al. (2020). Clustering of intermittent magnetic and flow structures near parker solar probe’s first perihelion—a partial-variance-of-increments analysis. Astrophys. J. Suppl. 246, 31. doi:10.3847/1538-4365/ab53d2
Coleman, J., and Paul, J. (1968). Turbulence, viscosity, and dissipation in the solar-wind plasma. Astrophys. J. 153, 371. doi:10.1086/149674
D’Amicis, R., Bruno, R., and Bavassano, B. (2011). Response of the geomagnetic activity to solar wind turbulence during solar cycle 23. J. Atmos. Sol. Terr. Phys. 73, 653–657. doi:10.1016/j.jastp.2011.01.012
D’Amicis, R., and Bruno, R. (2015). On the origin of highly Alfvénic slow solar wind. Astrophys. J. 805, 84. doi:10.1088/0004-637x/805/1/84
D’Amicis, R., Consolini, G., Bavassano, B., and Bruno, R. (2012). Conditioned analysis of high-latitude solar wind intermittency. Astrophys. J. 755, 63. doi:10.1088/0004-637x/755/1/63
D’Amicis, R., Matteini, L., and Bruno, R. (2018). On the slow solar wind with high Alfvénicity: from composition and microphysics to spectral properties. Mon. Not. Roy. Astron. Soc. 483, 4665–4677. doi:10.1093/mnras/sty3329
Farge, M. (1992). Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 24, 395–458. doi:10.1146/annurev.fl.24.010192.002143
Frisch, U. (1995). Turbulence. The legacy of A. N. Kolmogorov. Cambridge, United Kingdom: Cambridge University Press, 296.
Gazis, P. R. (1996). Solar cycle variation in the heliosphere. Rev. Geophys. 34, 379–402. doi:10.1029/96RG00892
Gerick, F., Saur, J., and von Papen, M. (2017). The uncertainty of local background magnetic field orientation in anisotropic plasma turbulence. Astrophys. J. 843, 5. doi:10.3847/1538-4357/aa767c
Goldstein, M. L., Roberts, D. A., and Matthaeus, W. H. (1995). Magnetohydrodynamic turbulence in the solar wind. Annu. Rev. Astron. Astrophys. 33, 283–326. doi:10.1146/annurev.aa.33.090195.001435
Greco, A., Chuychai, P., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2008). Intermittent mhd structures and classical discontinuities. Geophys. Res. Lett. 35, L19111. doi:10.1029/2008GL035454
Greco, A., Matthaeus, W. H., D’Amicis, R., Servidio, S., and Dmitruk, P. (2012). Evidence for nonlinear development of magnetohydrodynamic scale intermittency in the inner heliosphere. Astrophys. J. 749, 105. doi:10.1088/0004-637x/749/2/105
Greco, A., Matthaeus, W. H., Servidio, S., Chuychai, P., and Dmitruk, P. (2009). Statistical analysis of discontinuities in solar wind ACE data and comparison with intermittent MHD turbulence. Astrophys. J. 691, L111–L114. doi:10.1088/0004-637x/691/2/l111
Hnat, B., Chapman, S. C., and Rowlands, G. (2003). Intermittency, scaling, and the fokker-planck approach to fluctuations of the solar wind bulk plasma parameters as seen by the wind spacecraft. Phys. Rev. E–Stat. Nonlinear Soft Matter Phys. 67, 056404. doi:10.1103/PhysRevE.67.056404
Horbury, T., Balogh, A., Forsyth, R., and Smith, E. (1997). Ulysses observations of intermittent heliospheric turbulence. Adv. Space Res. 19, 847–850. doi:10.1016/S0273-1177(97)00290-1
Horbury, T. S., Forman, M., and Oughton, S. (2008). Anisotropic scaling of magnetohydrodynamic turbulence. Phys. Rev. Lett. 101, 175005. doi:10.1103/PhysRevLett.101.175005
Horbury, T. S., and Balogh, A. (2001). Evolution of magnetic field fluctuations in high-speed solar wind streams: ulysses and helios observations. J. Geophys. Res. 106, 15929–15940. doi:10.1029/2000JA000108
Horbury, T. S., Balogh, A., Forsyth, R. J., and Smith, E. J. (1996). The rate of turbulent evolution over the Sun’s poles. Astron. Astrophys. 316, 333–341.
Khotyaintsev, A., and Macek, W. M. (2008). Asymmetric multifractal model for solar wind intermittent turbulence. Nonlinear Process Geophys. 15, 615–620. doi:10.5194/npg-15-615-2008
Kolmogorov, A. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Akademiia Nauk SSSR Doklady 30, 301–305.
Lacombe, C., Alexandrova, O., and Matteini, L. (2017). Anisotropies of the magnetic field fluctuations at kinetic scales in the solar wind: cluster observations. Astrophys. J. 848, 13. doi:1538-4357/aa8c06
Landi, E., Alexander, R. L., Gruesbeck, J. R., Gilbert, J. A., Lepri, S. T., Manchester, W. B., et al. (2012). Carbon ionization stages as a diagnostic of the solar wind. Astrophys. J. 744, 100, doi:10.1088/0004-637X/744/2/100
Macek, W. M., Wawrzaszek, A., and Burlaga, L. F. (2014). Multifractal structures detected by voyager 1 at the heliospheric boundaries. Astrophys. J. Lett. 793, L30, doi:10.1088/2041-8205/793/2/L30
Macek, W. M., Wawrzaszek, A., Kucharuk, B., and Sibeck, D. G. (2017). Intermittent anisotropic turbulence detected by THEMIS in the magnetosheath. Astrophys. J. 851, L42. doi:10.3847/2041-8213/aa9ed4
Marsch, E., and Liu, S. (1993). Structure functions and intermittency of velocity fluctuations in the inner solar wind. Ann. Geophys. 11, 227–238.
Marsch, E., Tu, C.-Y., and Rosenbauer, H. (1996). Multifractal scaling of the kinetic energy flux in solar wind turbulence. Ann. Geophys. 14, 259–269. doi:10.1007/s00585-996-0259-4
Marsch, E., and Tu, C. Y. (1994). Non-Gaussian probability distributions of solar wind fluctuations. Ann. Geophys. 12, 1127–1138. doi:10.1007/s00585-994-1127-8
Matthaeus, W. H., Wan, M., Servidio, S., Greco, A., Osman, K. T., Oughton, S., et al. (2015). Intermittency, nonlinear dynamics and dissipation in the solar wind and astrophysical plasmas. Philos Trans A Math Phys Eng Sci 373, 20140154. doi:10.1098/rsta.2014.0154
McComas, D. J., Ebert, R. W., Elliott, H. A., Goldstein, B. E., Gosling, J. T., Schwadron, N. A., et al. (2008). Weaker solar wind from the polar coronal holes and the whole sun. Geophys. Res. Lett. 35, L18103. doi:10.1029/2008GL034896
Meneveau, C., and Sreenivasan, K. R. (1987). Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 59, 1424–1427. doi:10.1103/PhysRevLett.59.1424
Pagel, C., and Balogh, A. (2001). A study of magnetic fluctuations and their anomalous scaling in the solar wind: the Ulysses fast-latitude scan. Nonlinear Process Geophys. 8, 313–330. doi:10.5194/npg-8-313-2001
Pagel, C., and Balogh, A. (2002). Intermittency in the solar wind: a comparison between solar minimum and maximum using ulysses data. J. Geophys. Res.: Space Physics 107, SSH 6. doi:10.1029/2002JA009331
Pagel, C., and Balogh, A. (2003). Radial dependence of intermittency in the fast polar solar wind magnetic field using ulysses. J. Geophys. Res. 108, SSH 2. doi:10.1029/2002JA009498
Perri, S., Goldstein, M. L., Dorelli, J. C., and Sahraoui, F. (2012). Detection of small-scale structures in the dissipation regime of solar-wind turbulence. Phys. Rev. Lett. 109, 191101. doi:10.1103/PhysRevLett.109.191101
Perrone, D., Bruno, R., D’Amicis, R., Telloni, D., De Marco, R., Stangalini, M., et al. (2020). Coherent events at ion scales in the inner Heliosphere: arker Solar Probe observations during the first Encounter. Preprint repository name [Preprint]. Available at: arXiv:2010.02578 (Accessed October 06, 2020).
Podesta, J. J. (2017). How to define the mean square amplitude of solar wind fluctuations with respect to the local mean magnetic field. J. Geophys. Res.: Space Physics 122 (11), 835–844. doi:10.1002/2017JA023864
Ruzmaikin, A. A., Feynman, J., Goldstein, B. E., Smith, E. J., and Balogh, A. (1995). Intermittent turbulence in solar wind from the south polar hole. J. Geophys. Res. 100, 3395–3403. doi:10.1029/94JA02808
Salem, C., Mangeney, A., Bale, S. D., and Veltri, P. (2009). Solar wind Magnetohydrodynamics turbulence: anomalous scaling and role of intermittency. Astrophys. J. 702, 537–553. doi:10.1088/0004-637x/702/1/537
She, Z. S., and Leveque, E. (1994). Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72, 336–339. doi:10.1103/PhysRevLett.72.336
Sorriso-Valvo, L., Catapano, F., Retinò, A., Le Contel, O., Perrone, D., Roberts, O. W., et al. (2019). Turbulence-driven ion beams in the magnetospheric kelvin-helmholtz instability. Phys. Rev. Lett. 122, 035102. doi:10.1103/PhysRevLett.122.035102
Sorriso-Valvo, L., Carbone, F., Leonardis, E., Chen, C. H., Safrankova, J., and Nemecek, Z. (2017). Multifractal analysis of high resolution solar wind proton density measurements. Adv. Space Res. 59, 1642–1651. doi:10.1016/j.asr.2016.12.024
Sorriso-Valvo, L., Carbone, V., Giuliani, P., Veltri, P., Bruno, R., Antoni, V., et al. (2001). Intermittency in plasma turbulence. Planet. Space Sci. 49, 1193–1200. doi:10.1016/S0032-0633(01)00060-5
Sorriso-Valvo, L., Carbone, V., Veltri, P., Consolini, G., and Bruno, R. (1999). Intermittency in the solar wind turbulence through probability distribution functions of fluctuations. Geophys. Res. Lett. 26, 1801–1804. doi:10.1029/1999GL900270
Teodorescu, E., and Echim, M. (2020). Open-source software analysis tool to investigate space plasma turbulence and nonlinear dynamics (odyn). Earth Space Sci. 7, e2019EA001004. doi:10.1029/2019EA001004
Tu, C.-Y., Marsch, E., and Rosenbauer, H. (1996). An extended structure-function model and its application to the analysis of solar wind intermittency properties. Ann. Geophys. 14, 270–285. doi:10.1007/s00585-996-0270-9
Tu, C. Y., and Marsch, E. (1995). Magnetohydrodynamic structures waves and turbulence in the solar wind - observations and theories. Space Sci. Rev. 73, 1–210. doi:10.1007/BF00748891
Vörös, Z., Leubner, M. P., and Baumjohann, W. (2006). Cross-scale coupling-induced intermittency near interplanetary shocks. J. Geophys. Res. 111, A02102. doi:10.1029/2005JA011479
Veltri, P., and Mangeney, A. (1999). “Scaling laws and intermittent structures in solar wind MHD turbulence,” in American institute of physics conference series, Editors. S. R. Habbal, R. Esser, J. V. Hollweg, and P. A. Isenberg (New York : American Institute of Physics Conference Series), Vol. 471, 543–546.
Wan, M., Osman, K. T., Matthaeus, W. H., and Oughton, S. (2011). Investigation of intermittency in magnetohydrodynamics and solar wind turbulence: scale-dependent kurtosis. Astrophys. J. 744, 171. doi:10.1088/0004-637x/744/2/171
Wan, M., Matthaeus, W. H., Karimabadi, H., Roytershteyn, V., Shay, M., Wu, P., et al. (2012). Intermittent dissipation at kinetic scales in collisionless plasma turbulence. Phys. Rev. Lett. 109, 195001. doi:10.1103/PhysRevLett.109.195001
Wawrzaszek, A., Echim, M., and Bruno, R. (2019). Multifractal analysis of heliospheric magnetic field fluctuations observed by ulysses. Astrophys. J. 876, 153. doi:10.3847/1538-4357/ab1750
Wawrzaszek, A., Echim, M., Macek, W. M., and Bruno, R. (2015). Evolution of intermittency in the slow and fast solar wind beyond the ecliptic plane. Astrophys. J. Lett. 814, L19. doi:10.1088/2041-8205/814/2/L19
Wawrzaszek, A., and Macek, W. M. (2010). Observation of the multifractal spectrum in solar wind turbulence by ulysses at high latitudes. J. Geophys. Res. 115, A07104. doi:10.1029/2009JA015176
Wicks, R. T., Horbury, T. S., Chen, C. H. K., and Schekochihin, A. A. (2010). Power and spectral index anisotropy of the entire inertial range of turbulence in the fast solar wind. Mon. Not. Roy. Astron. Soc. Lett. 407, L31–L35. doi:10.1111/j.1745-3933.2010.00898.x
Xu, F., and Borovsky, J. E. (2015). A new four-plasma categorization scheme for the solar wind. J. Geophys. Res. 120, 70–100. doi:10.1002/2014JA020412
Yang, Y.-H., and Tam, S. W. (2010). Intermittency analysis and spatial dependence of magnetic field disturbances in the fast solar wind. J. Atmos. Sol. Terr. Phys. 72, 97–108. doi:10.1016/j.jastp.2009.10.013
Keywords: solar wind, turbulence, intermittency, plasma, Interplanetary medium, solar cycle
Citation: Wawrzaszek A and Echim M (2021) On the Variation of Intermittency of Fast and Slow Solar Wind With Radial Distance, Heliospheric Latitude, and Solar Cycle. Front. Astron. Space Sci. 7:617113. doi: 10.3389/fspas.2020.617113
Received: 14 October 2020; Accepted: 10 November 2020;
Published: 13 January 2021.
Edited by:
Joseph Eric Borovsky, Space Science Institute, United StatesReviewed by:
Luca Sorriso-Valvo, Institute for Space Physics (Uppsala), SwedenAntonella Greco Università della Calabria, Italy
Copyright © 2021 Wawrzaszek and Echim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anna Wawrzaszek, anna.wawrzaszek@cbk.waw.pl