- 1NASA Goddard Space Flight Center, Heliophysics Science Division, Greenbelt, MD, United States
- 2Space Science Institute, Boulder, CO, United States
Recent time series observations of electric fields within collisionless shocks have shown that the fluctuating, electrostatic fields can be in excess of one hundred times that of the quasi-static electric fields. That is, the largest amplitude electric fields occur at high frequencies, not low. In contrast, many if not most kinetic simulations show the opposite, where the quasi-static electric fields dominate, unless they are specifically tailored to examine small-scale instabilities. Further, the shock ramp thickness is often observed to fall between the electron and ion scales while many simulations tend to produce ramp thicknesses at least at or above ion scales. This raises numerous questions about the role of small-scale instabilities and about the ability to directly compare simulations with observations.
1 Introduction
Collisionless shock waves are an ubiquitous phenomenon in heliospheric and astrophysical plasmas. They most often manifest as a nonlinearly steepened fast magnetosonic-whistler wave that has reached a stable balance between steepening and some form of irreversible energy dissipation. If a balance is reached, a stationary shock ramp is formed. The shock ramp is the part of shock transition region between upstream and downstream with an abrupt, discontinuity-like change in number density (nS where s is the particle species), pressure1, quasi-static2 magnetic field magnitude vector (Bo), and bulk flow velocity (Vbulk). The thickness of this ramp is thought to depend upon macroscopic shock parameters like the fast mode Mach number (Mf), shock normal angle,
The term collisionless derives from the fact that the shock ramp thickness ranges from several electron inertial lengths3 to an ion inertial length with the majority below ∼35
The topic of interest for this study is electric fields in observations and simulations, so we will limit the discussion to wave-particle interactions and macroscopic quasi-static field effects. Further, given that the primary discrepancy between simulations and observations lies in the lack of large amplitude, high frequency electrostatic waves in the former, we will limit the discussion to high frequency electrostatic waves. Note that some PIC simulations do generate the electrostatic waves of interest but the simulations are often tailored to generate the modes (e.g., isolated simulation mimicking shock foot region) by artificially injecting known free energy sources (e.g., initialize with two counter-streaming beams). Therefore, all of the modes listed in the following discussion have been generated in PIC simulations (Dyrud and Oppenheim, 2006; Matsukiyo and Scholer, 2006; Matsukiyo and Scholer, 2012; Muschietti and Lembège, 2017; Saito et al., 2017). However, as will be shown, parameters like the wavelengths and amplitudes tend to differ from those in observations, sometimes significantly.
Recent work using time series electric field data has shown that the common electrostatic wave modes near collisionless shocks include lower hybrid waves (LHWs), ion acoustic waves (IAWs), electrostatic solitary waves (ESWs), waves radiated by the electron cyclotron drift instability (ECDI), and Langmuir waves (Filbert and Kellogg, 1979; Mellott and Greenstadt, 1988; Kellogg, 2003; Wilson et al., 2007; Pulupa and Bale, 2008; Walker et al., 2008; Wilson et al., 2010; Breneman et al., 2013; Wilson et al., 2014a; Wilson et al., 2014b; Chen et al., 2018; Goodrich et al., 2018; Goodrich et al., 2019). The properties of these modes are summarized in Table 1 and discussed in detail below.
Electrostatic LHWs have been theorized to play a critical role in collisionless shock dynamics for decades (Papadopoulos, 1985; Tidman and Krall, 1971; Wu et al., 1984) but observations of their electrostatic form have been limited (Mellott and Greenstadt, 1988; Walker et al., 2008; Wygant et al., 1987). They are present in spacecraft observations at frequencies, in the spacecraft frame, near the local lower hybrid resonance frequency4. They are linearly polarized nearly perpendicular to Bo with
Electrostatic IAWs have been observed in the solar wind and near collisionless shocks for over 40 years (Fredricks et al., 1968; Fredricks et al., 1970a; Gurnett and Anderson, 1977; Gurnett et al., 1979; Kurth et al., 1979). They present in spacecraft observations at frequencies, in the spacecraft frame, above the proton plasma frequency6 (due to the Doppler effect), typically in the ∼1–10 kHz range in the solar wind near 1 AU. They are observed as linearly polarized (mostly parallel to Bo but sometimes at small oblique angles), modulated sine waves with bursty wave envelopes lasting 10 s of ms (Wilson et al., 2007; Wilson et al., 2010; Wilson et al., 2014a; Wilson et al., 2014b). They have been shown to have wavelengths on the order of a few to several Debye lengths7, or 10–100 s of meters near 1 AU (Fuselier and Gurnett, 1984; Breneman et al., 2013; Goodrich et al., 2018; Goodrich et al., 2019). They are thought to be driven unstable by the free energy in currents (Biskamp et al., 1972; Lemons and Gary, 1978), temperature gradients (Allan and Sanderson, 1974), electron heat flux (Dum et al., 1980; Henchen et al., 2019), or ion/ion streaming instabilities (Auer et al., 1971; Akimoto and Winske, 1985; Akimoto et al., 1985b; Goodrich et al., 2019) or they can result from a nonlinear wave-wave process (Cairns and Robinson, 1992; Dyrud and Oppenheim, 2006; Kellogg et al., 2013; Saito et al., 2017). These modes are important for collisionless shock dynamics because they can stochastically accelerate thermal electrons (parallel to Bo) generating self-similar velocity distribution functions (VDFs) or the so called “flattop” distributions (Vedenov, 1963; Sagdeev, 1966; Dum et al., 1974; Dum, 1975; Dyrud and Oppenheim, 2006). They are also capable of stochastically accelerating the high energy tail of the ion VDF (parallel to Bo) (Dum et al., 1974). Note that the generation of the flattop has recently been interpreted as evidence of inelastic collisions (Wilson et al., 2019a; Wilson et al., 2019b; Wilson et al., 2020).
ESWs present in spacecraft observations as short duration (few ms), bipolar electric field pulses parallel to Bo and monopolar perpendicular (Behlke et al., 2004; Wilson et al., 2007; Wilson et al., 2010; Wilson et al., 2014b). They tend to be on Debye scales and are thought to be BGK phase space holes (Ergun et al., 1998; Cattell et al., 2005; Franz et al., 2005; Vasko et al., 2018). ESWs can be driven unstable by electron beams (Ergun et al., 1998; Cattell et al., 2005; Franz et al., 2005), ion beams (Vasko et al., 2018), modified two-stream instability (MTSI) (Matsukiyo and Scholer, 2006), or the produce of high frequency wave decay (Singh et al., 2000). Until recently, it was thought all ESWs outside the auroral acceleration region were electron holes. However, work by (Vasko et al., 2018) and (Wang et al., 2020) suggest that many of the ESWs in the terrestrial bow shock are not only ion holes, they do not propagate exactly along Bo as was previously thought. ESWs are important in collisionless shock dynamics because they can trap incident electrons (Dyrud and Oppenheim, 2006; Lu et al., 2008) or ions (Vasko et al., 2018; Wang et al., 2020), depending on the type of hole. They have also been shown to dramatically heat ions (Ergun et al., 1998), and/or couple to (or directly cause) the growth of IAWs (Dyrud and Oppenheim, 2006), whistler mode waves (Singh et al., 2001; Lu et al., 2008; Goldman et al., 2014), LHWs (Singh et al., 2000).
The ECDI is driven by the free energy in the relative drift between the incident electrons and shock-reflected ions (Forslund et al., 1970; Forslund et al., 1971; Lampe et al., 1972; Matsukiyo and Scholer, 2006; Muschietti and Lembège, 2013). They also range from Debye to electron thermal gyroradius scales (Breneman et al., 2013) and present in spacecraft observations as mixtures of Doppler-shifted IAWs and electron Bernstein modes. The polarization of these modes can be confusing, presenting as shaped like a tadpole or tear drop, with one part of the “tadpole” nearly parallel to Bo (i.e., IAW part) and the other nearly orthogonal (i.e., the Bernstein mode part) (Wilson et al., 2010; Breneman et al., 2013; Wilson et al., 2014b; Goodrich et al., 2018). This results from the coupling between two modes that are normally orthogonal to each other in their electric field oscillations. ECDI-driven modes are important for collisionless shocks because they can resonantly interact with the bulk of the ion VDF, generate a suprathermal tail on the ion VDF, and strongly heat the electrons perpendicular to Bo (Forslund et al., 1970; Forslund et al., 1972; Lampe et al., 1972; Muschietti and Lembège, 2013).
Langmuir waves have been observed upstream of collisionless shocks for decades (Gurnett and Anderson, 1977; Filbert and Kellogg, 1979; Kellogg et al., 1992; Cairns, 1994; Bale et al., 1998; Bale et al., 1999; Malaspina et al., 2009; Soucek et al., 2009; Krasnoselskikh et al., 2011). These waves have
In summary, the most commonly observed electrostatic wave modes near collisionless shocks are IAWs, ESWs, ECDI-driven modes, and Langmuir waves. Electrostatic LHWs are less commonly observed, which may be due to instrumental effects as many electric field instruments (Bonnell et al., 2008; Bougeret et al., 2008; Cully et al., 2008) have been designed with gain roll-offs at ∼1–10 Hz (low- or high-pass filters), which happens to be the typical value of flh in the solar wind near 1 AU. It may also be that electrostatic LHWs are just less commonly generated or damp very quickly in collisionless shocks. Langmuir waves tend to occur upstream of the shock in regions filled with shock reflected electron beams (Cairns, 1994; Bale et al., 1999; Wilson et al., 2007; Pulupa et al., 2010). Although they can be common in the upstream, they tend to be much less so in the ramp and immediate downstream region. Therefore, the remaining discussion will focus on the most commonly observed Debye-scale, electrostatic modes: IAWs, ESWs, and ECDI-driven modes. These three modes are observed in and around both quasi-parallel and quasi-perpendicular shocks. The only macroscopic shock parameters on which they appear to depend are the shock density compression ratio and Mf [e.g., Wilson et al., 2007; Wilson et al., 2014a; Wilson et al., 2014b]. The ECDI-driven modes tend not to be observed for Mf
2 Historical Context
2.1 Spacecraft Observations
Early spacecraft electric field observers had very limited resources, compared to modern day, in memory, computational power, and spacecraft telemetry. As such, the common practice was to perform onboard computations to generate Fourier spectra for predefined frequency ranges (Fredricks et al., 1968; Fredricks et al., 1970a; Fredricks et al., 1970b; Rodriguez and Gurnett, 1975). These Fourier spectra are spectral intensity data averaged over fixed time and frequency intervals, which has been more recently shown to significantly underestimate the instantaneous wave amplitude (Tsurutani et al., 2009). The underestimation led to some confusion in multiple areas of research because the estimated wave amplitudes from the spectra were too small to noticeably impact the dynamics of the system in question.
For instance, for decades the radiation belt community had relied upon such dynamic spectra and came to conclusion that the whistler mode waves (e.g., chorus and hiss) were typically in the
Similar issues arose in observations of collisionless shock waves. The early work using dynamic spectra data found electrostatic waves with spacecraft frame frequencies, fsc, greater than a few hundred hertz to have amplitudes of, at most, a few 10s of mV/m but typically smaller in the few mV/m range (Fredricks et al., 1970b; Rodriguez and Gurnett, 1975). Numerous theoretical studies had suggested that small-scale, high frequency waves were an important dissipation mechanism to regulate the nonlinear steepening of collisionless shock waves (Sagdeev, 1966; Tidman and Krall, 1971; Papadopoulos, 1985). However, such small amplitude electric field observations raised doubts about the ability of the high frequency modes to supply sufficient dissipation to maintain a stable shock.
The first published example (of which the authors are aware) of a time series electric field component observed by a spacecraft within a collisionless shock was presented in Wygant et al. (1987) observed by the ISEE-1 probe. The observation was one of the first pieces of evidence that the dynamic spectra plots were not fully capturing the electric field dynamics because the data showed electric fields up to nearly ∼100 mV/m. Later work using the Wind spacecraft found ESWs in the terrestrial bow shock with amplitudes in excess of ∼100 mV/m (Bale et al., 1998; Bale et al., 2002). A few bow shock crossings were observed with the Polar spacecraft, which found nonlinear, electrostatic IAWs within the shock with amplitudes up to ∼80 mV/m (Hull et al., 2006). The picture starting to emerge was that high frequency, electrostatic waves were common and large amplitude in collisionless shocks. Note that the occurrence rate of electrostatic waves was already implied by studies using dynamic spectra data, but not such large amplitude.
Wilson et al. (2007) examined waveform capture data of electrostatic waves above the proton cyclotron frequency, fpp, from the Wind spacecraft finding a positive correlation between peak wave amplitude and shock strength, i.e., stronger shocks had larger amplitude waves. They also observed that ion acoustic waves were the dominant electrostatic mode within the shock ramp. Shortly after, a study (Wilson et al., 2010) of a supercritical shock showed evidence of waves radiated by the ECDI. Since then, a series of papers using MMS (Chen et al., 2018; Goodrich et al., 2018; Goodrich et al., 2019), STEREO (Breneman et al., 2013), THEMIS (Wilson et al., 2014a; Wilson et al., 2014b), and Wind (Breneman et al., 2013) have examined these electrostatic waves in collisionless shocks.
While the discussion has almost exclusively focused on fluctuating electric fields,
Prior to the launch of MMS, there were several studies that attempted to measure the cross shock electric field but each suffered from inaccuracies or under resolved electric field measurements which kept the issue of its magnitude in doubt (Dimmock et al., 2011; Dimmock et al., 2012; Wilson et al., 2014a; Wilson et al., 2014b). The launch of MMS allowed researchers, for the first time, to probe Eo with sufficient cadence and accuracy to properly measure the cross shock electric field in an interplanetary shock (Cohen et al., 2019). Note that the Eo measured in this study peaked at
The current picture from observations is summarized in the following. In the studies where the quasi-static electric field could be reliably measured (Cohen et al., 2019) or approximated from measurements (Wilson et al., 2014a; Wilson et al., 2014b; Goodrich et al., 2018; Goodrich et al., 2019), the findings were that
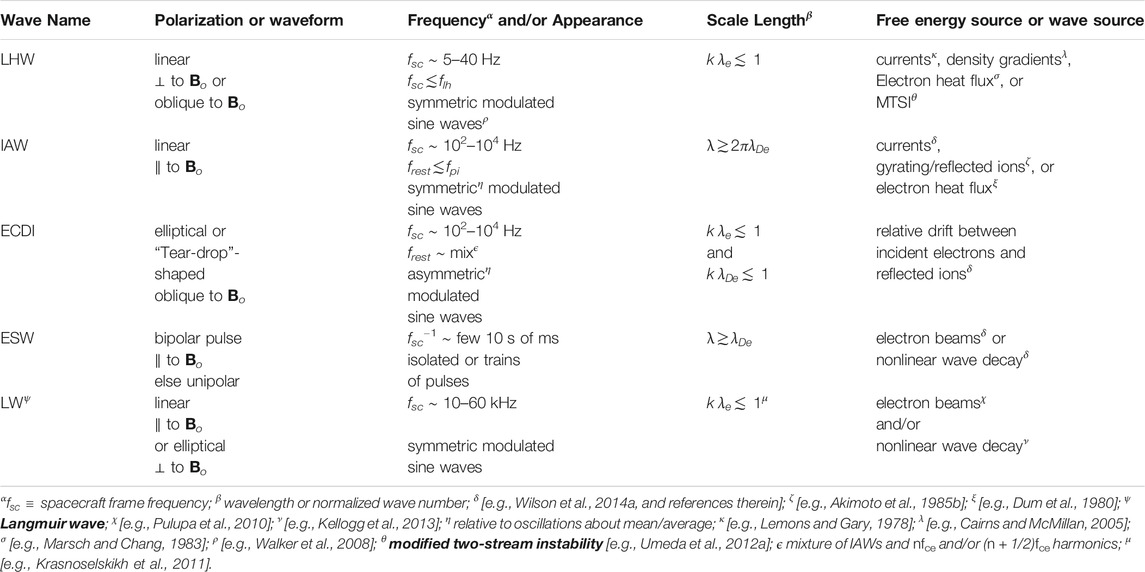
Figure 1 shows seven waveform captures observed by the Wind spacecraft’s WAVES instrument (Bougeret et al., 1995) while passing through the quasi-perpendicular terrestrial bow shock. The first column shows the x-antenna electric field (
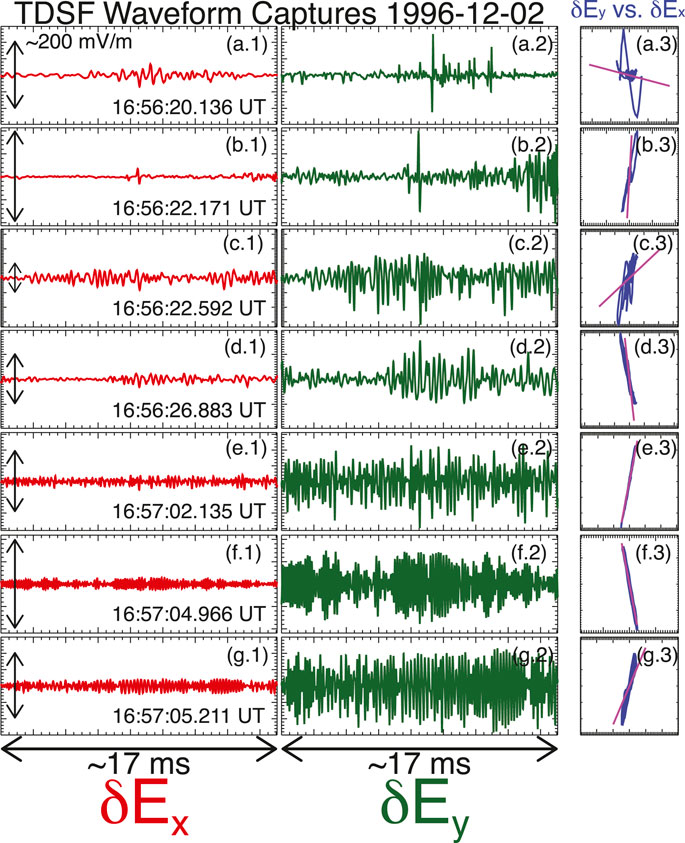
FIGURE 1. Example of six waveform captures observed by Wind while crossing the Earth’s quasi-perpendicular bow shock on 1996-12-02. Each row corresponds to, by column, the X vs time, Y vs time, and Y vs X hodogram (in instrument coordinates) from the Wind/WAVES time domain sampler (TDS) instrument (Bougeret et al., 1995). Each waveform capture/snapshot is ∼17 ms in duration. The quasi-static magnetic field projection is shown as the magenta line in hodograms (Adapted from Figure 3.6 in Wilson (2010).
2.2 Kinetic Simulations
Kinetic simulations of shocks are challenging due to the need to resolve global structure of the shock (generally associated with
Early kinetic particle-in-cell (PIC) simulations were much more limited by computational constraints than those performed today. A common approach to scaling the problem in order reduce the computational load is to consider one- or two-dimensional problems and to reduce ratios of the ion-to-electron mass,
Some of the first two-dimensional PIC simulations using realistic
Despite all of the progress made since the early full PIC simulations, there still remains two striking discrepancies between observations and many simulations: the amplitude and wavelength at which the strongest electric fields are observed and inconsistencies in the thickness of the shock ramp. The second issue is more obvious from cursory examinations of simulation results, so we will discuss it first. As previously discussed, observations consistently show that the shock ramp thickness, Lsh, tends to satisfy 5 <
Note that the thickness of the magnetic ramp of a collisionless shock is not significantly affected by the presence of corrugation/ripples (Johlander et al., 2016) other than the temporal dependence that can occur during reformation (Mazelle et al., 2010). The spatial extent of the entire transition region can indeed be increased by such oscillations but the magnetic gradient scale length does not appear to be significantly affected. The biggest limiation to determining the shock ramp thickness in data is time resolution. More recent spacecraft like THEMIS (Angelopoulos, 2008) and MMS (Burch et al., 2016) have, for instance, fluxgate magnetometers that return 3-vector components 128 times every second, which is more than sufficient to resolve the bow shock ramp. The bow shock moves slower in the spacecraft frame than interplanetary shocks, so time resolution is more of a constraint for examining the shock ramp thickness of interplanetary shocks. Even so, the 128 sps of the THEMIS and MMS fluxgate magnetometers is still sufficient for most interplanetary shocks.
As previously discussed, observations consistently show
It is worth noting the severe computational costs of using fully realistic plasma parameters. The separation of spatial scales satisfies
3 Example Observations Versus Simulations
In this section we will present two example observations made by the THEMIS (Angelopoulos, 2008) and MMS (Burch et al., 2016) missions to further illustrate the difference in magnitude between
Figure 2 shows a direct comparison between
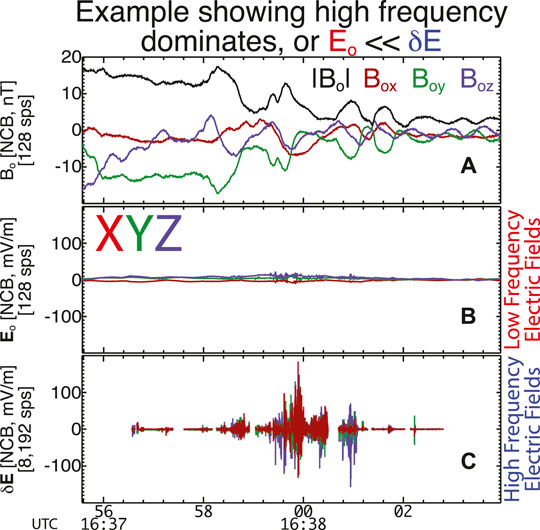
FIGURE 2. An example terrestrial bow shock crossing observed by THEMIS-C on 2009-09-05. Panel (A) shows the magnetic field magnitude (black) and three normal incidence frame coordinate basis (NCB) (Scudder et al., 1986a) components vs time at 128 samples/second (sps) observed by the fluxgate magnetometer (Auster et al., 2008). Panel (B) shows the DC-coupled electric field at 128 sps observed by EFI (Bonnell et al., 2008; Cully et al., 2008). Panel (C) shows the AC-coupled electric field at 8,192 sps observed by EFI. Note that Panels (B,C) share the same vertical axis range for direct comparison (Adapted from Figure I:2 in Wilson et al. (2014a)).
Figure 3 provides another example directly comparing
FIGURE 3. An example terrestrial bow shock crossing observed by MMS3 and MMS4 on 2019-01-30. Panels (A,D) show the magnetic field magnitude (black) vs time at 128 sps observed by the fluxgate magnetometer (Russell et al., 2016). Panels (B,E) show the DC-coupled electric field components at 128 sps observed by the electric field instrument (Ergun et al., 2016; Lindqvist et al., 2016). Panels (C,F) show the AC-coupled electric field at 8,192 sps. Note that Panels (B,C,E) share the same vertical axis range for direct comparison.
As a practical list of reference values, we present one-variable statistics of solar wind parameters from the same data set as in Wilson et al. (2018) and all interplanetary (IP) shocks in the Harvard Smithsonian’s Center for Astrophysics Wind shock database14. The following will show parameters as
1.10
1.15
36.6
79.6
22.2
where Ushn is the upstream average flow speed in the shock rest frame and Vshn is the upstream average shock speed in the spacecraft frame. Note that the values of Mf, MA, and Ushn will all be, on average, larger for most bow shocks in the interplanetary medium. These values are only meant to serve as a statistical baseline for reference. For example, the 11 bow shock crossings in Wilson et al. (2014a); Wilson et al. (2014b) satisfied 3.1
80.2
0.04
17.2
371
1,579
21.9
1.03
32.5
1.12
50.5
4.74
where fcs is the cyclotron frequency of species s, fps is the plasma frequency of species s,
176
131 ≲
8,000
0.34
92.4
4.79
43.1
0.53
where
Figure 4 shows example one-dimensional cuts at three different time steps taken from a PIC simulation. The simulation parameters are as follows:
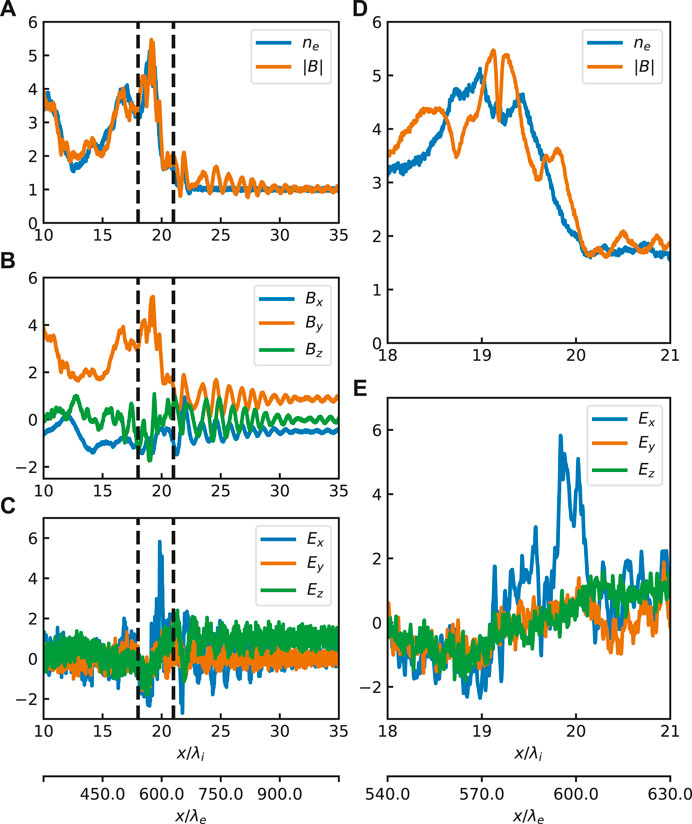
FIGURE 4. An example taken from a PIC simulation with the shock normal along the x-direction. Each plot shows a 1D cut through the middle of 2D simulation domain. Panel (A) shows the magnetic field magnitude, B (orange), and the electron number density, ne (blue), vs. spatial position x. Panels (B,C) show the components of magnetic field (B) and the electric field (E). Panels (D,E) show a zoomed region of panels (A,C) respectively. The boundaries of the zoomed region are indicated by vertical dashed lines in panels (A–C). All fields are measured in the simulation frame, where the shock moves in the positive x direction with the speed of ∼2 VA.
One can see that the largest values of
4 Discussion
We have presented examples illustrating that spacecraft observations of collisionless shocks consistently show
Further, many simulations still generate shock ramps satisfying
Another potential issue that was not explicitly discussed in detail is that of the separation between
The origins of the discrepancy between the observation that
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://cdaweb.gsfc.nasa.gov.
Author Contributions
LW wrote most of the content and generated all the observational data figures presented herein. L-JC provided critical contributions to the bridge between observations and simulations. VR provided critical contributions to simulation techniques and limitations induced by the variation of different normalized parameters.
Funding
The work was supported by the International Space Science Institute’s (ISSI) International Teams program. LW was partially supported by Wind MO&DA grants and a Heliophysics Innovation Fund (HIF) grant. Contributions of VR were supported by NASA grant 80NSSC18K1649. Computational resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank B. Lembège, R. A. Treumann, M. Hesse, J. TenBarge, and J. Juno for useful discussions of kinetic simulations.
Footnotes
1Ps = nskBTs, where Ts is the temperature of species s.
2Note we use the term quasi-static instead of background here since electromagnetic fluctuations near shocks in the solar wind can have amplitudes larger than the surrounding mean. That is, quasi-static refers to the lowest frequency response of an instrument, for practical purposes, but one can think of it as the effective background field.
3
4
5There are two modes radiated by the MTSI at collisionless shocks, both of which are very obliquely propagating and have real frequencies near or below flh. The two free energy sources for the MTSIs are between incident electrons and reflected ions and incident electrons and incident ions.
6
7
8Ec has typical values satisfying ∼0.1–3 mV/m in the solar wind near Earth. In contrast, the waves shown in Figure 1 have
9Note that the data is taken in the ecliptic plane to within ∼1° and the fraction of the local Bo in this plane exceeds 89% for all events except the first two rows.
10The size of the problem may significantly exceed
11Note that
12Note that similar current densities have been found using multi-spacecraft techniques (Hull et al., 2020) supporting the results in Wilson III et al. (2014a) and Wilson III et al. (2014b).
13Note that Qo in this context is not the quasi-static terms in quasi-linear or linear theory but that from the DC-coupled measurements. Further,
14https://www.cfa.harvard.edu/shocks/wi_data/.
15Note that none of these are Doppler-shifted.
References
Akimoto, K., and Winske, D. (1985). Ion-acoustic-like waves excited by the reflected ions at the earth’s bow shock. J. Geophys. Res. 90, 12095. doi:10.1029/JA090iA12p12095
Akimoto, K., Papadopoulos, K., and Winske, D. (1985b). Ion-acoustic instabilities driven by an ion velocity ring. J. Plasma Phys. 34, 467–479. doi:10.1017/S0022377800003019
Akimoto, K., Papadopoulos, K., and Winske, D. (1985a). Lower-hybrid instabilities driven by an ion velocity ring. J. Plasma Phys. 34, 445–465. doi:10.1017/S0022377800003007
Allan, W., and Sanderson, J. J. (1974). Temperature gradient drive ion acoustic instability. Plasma Phys. 16, 753–767. doi:10.1088/0032-1028/16/8/005
Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141, 5–34. doi:10.1007/s11214-008-9336-1
Auer, P. L., Kilb, R. W., and Crevier, W. F. (1971). Thermalization in the earth’s bow shock. J. Geophys. Res. 76, 2927–2939. doi:10.1029/JA076i013p02927
Auster, H. U., Glassmeier, K. H., Magnes, W., Aydogar, O., Baumjohann, W., Constantinescu, D., et al. (2008). The THEMIS fluxgate magnetometer. Space Sci. Rev. 141, 235–264. doi:10.1007/s11214-008-9365-9
Bale, S. D., Goetz, K., Harvey, P. R., Turin, P., Bonnell, J. W., Dudok de Wit, T., et al. (2016). The FIELDS instrument suite for solar probe plus. Measuring the coronal plasma and magnetic field, plasma waves and turbulence, and radio signatures of solar transients. Space Sci. Rev. 204, 49–82. doi:10.1007/s11214-016-0244-5
Bale, S. D., Hull, A., Larson, D. E., Lin, R. P., Muschietti, L., Kellogg, P. J., et al. (2002). Electrostatic turbulence and debye-scale structures associated with electron thermalization at collisionless shocks. Astrophys. J. 575, L25–L28. doi:10.1086/342609
Bale, S. D., Kellogg, P. J., Goetz, K., and Monson, S. J. (1998). Transverse z-mode waves in the terrestrial electron foreshock. Geophys. Res. Lett. 25, 9–12. doi:10.1029/97GL03493
Bale, S. D., Reiner, M. J., Bougeret, J. L., Kaiser, M. L., Krucker, S., Larson, D. E., et al. (1999). The source region of an interplanetary type II radio burst. Geophys. Res. Lett. 26, 1573–1576. doi:10.1029/1999GL900293
Behlke, R., André, M., Bale, S. D., Pickett, J. S., Cattell, C. A., Lucek, E. A., et al. (2004). Solitary structures associated with short large-amplitude magnetic structures (SLAMS) upstream of the Earth’s quasi-parallel bow shock. Geophys. Res. Lett. 31, 16805. doi:10.1029/2004GL019524
Biskamp, D., von Hagenow, K. U., and Welter, H. (1972). Computer studies of current-driven ion-sound turbulence in three dimensions. Phys. Lett. 39, 351–352. doi:10.1016/0375-9601(72)90090-4
Bonnell, J. W., Mozer, F. S., Delory, G. T., Hull, A. J., Ergun, R. E., Cully, C. M., et al. (2008). The electric field instrument (EFI) for THEMIS. Space Sci. Rev. 141, 303–341. doi:10.1007/s11214-008-9469-2
Bougeret, J. L., Goetz, K., Kaiser, M. L., Bale, S. D., Kellogg, P. J., Maksimovic, M., et al. (2008). S/WAVES: the radio and plasma wave investigation on the STEREO mission. Space Sci. Rev. 136, 487–528. doi:10.1007/s11214-007-9298-8
Bougeret, J. L., Kaiser, M. L., Kellogg, P. J., Manning, R., Goetz, K., Monson, S. J., et al. (1995). Waves: the radio and plasma wave investigation on the wind spacecraft. Space Sci. Rev. 71, 231–263. doi:10.1007/BF00751331
Breneman, A., Cattell, C., Kersten, K., Paradise, A., Schreiner, S., Kellogg, P. J., et al. (2013). STEREO and Wind observations of intense cyclotron harmonic waves at the Earth’s bow shock and inside the magnetosheath. J. Geophys. Res. 118, 7654–7664. doi:10.1002/2013JA019372
Breneman, A., Cattell, C., Wygant, J., Kersten, K., Wilson, L. B., Dai, L., et al. (2012). Explaining polarization reversals in STEREO wave data. J. Geophys. Res. 117, A04317. doi:10.1029/2011JA017425
Breneman, A., Cattell, C., Wygant, J., Kersten, K., Wilson, L. B., Schreiner, S., et al. (2011). Large-amplitude transmitter-associated and lightning-associated whistler waves in the Earth’s inner plasmasphere at L
Burch, J. L., Moor, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9
Cairns, I. H. (1994). Fine structure in plasma waves and radiation near the plasma frequency in Earth’s foreshock. J. Geophys. Res. 99, 23505. doi:10.1029/94JA01997
Cairns, I. H., and McMillan, B. F. (2005). Electron acceleration by lower hybrid waves in magnetic reconnection regions. Phys. Plasmas. 12, 102110. doi:10.1063/1.2080567
Cairns, I. H., and Robinson, P. A. (1992). Theory for low-frequency modulated Langmuir wave packets. Geophys. Res. Lett. 19, 2187–2190. doi:10.1029/92GL02632
Cattell, C., Dombeck, J., Wygant, J., Drake, J. F., Swisdak, M., Goldstein, M. L., et al. (2005). Cluster observations of electron holes in association with magnetotail reconnection and comparison to simulations. J. Geophys. Res. 110, A01211. doi:10.1029/2004JA010519
Cattell, C., Wygant, J. R., Goetz, K., Kersten, K., Kellogg, P. J., von Rosenvinge, T., et al. (2008). Discovery of very large amplitude whistler-mode waves in Earth’s radiation belts. Geophys. Res. Lett. 35, L01105. doi:10.1029/2007GL032009
Chen, L. J., Wang, S., Wilson, L. B., Schwartz, S. J., Gershman, D. J., Bessho, N., et al. (2018). Electron bulk acceleration and thermalization at Earth’s quasi-perpendicular bow shock. Phys. Rev. Lett. 120, 225101. doi:10.1103/PhysRevLett.120.225101
Cohen, I. J., Schwartz, S. J., Goodrich, K. A., Ahmadi, N., Ergun, R. E., Fuselier, S. A., et al. (2019). High-resolution measurements of the cross-shock potential, ion reflection, and electron heating at an interplanetary shock by MMS. J. Geophys. Res. 124, 3961–3978. doi:10.1029/2018JA026197
Comişel, H., Scholer, M., Soucek, J., and Matsukiyo, S. (2011). Non-stationarity of the quasi-perpendicular bow shock: comparison between cluster observations and simulations. Ann. Geophys. 29, 263–274. doi:10.5194/angeo-29-263-2011
Coroniti, F. V. (1970). Dissipation discontinuities in hydromagnetic shock waves. J. Plasma Phys. 4, 265–282. doi:10.1017/S0022377800004992
Cully, C. M., Ergun, R. E., Stevens, K., Nammari, A., and Westfall, J. (2008). The THEMIS digital fields board. Space Sci. Rev. 141, 343–355. doi:10.1007/s11214-008-9417-1
Decker, G., and Robson, A. E. (1972). Instability of the whistler structure of oblique hydromagnetic shocks. Phys. Rev. Lett. 29, 1071–1073. doi:10.1103/PhysRevLett.29.1071
Dimmock, A. P., Balikhin, M. A., and Hobara, Y. (2011). Comparison of three methods for the estimation of cross-shock electric potential using Cluster data. Ann. Geophys. 29, 815–822. doi:10.5194/angeo-29-815-2011
Dimmock, A. P., Balikhin, M. A., Krasnoselskikh, V. V., Walker, S. N., Bale, S. D., and Hobara, Y. (2012). A statistical study of the cross-shock electric potential at low Mach number, quasi-perpendicular bow shock crossings using cluster data. J. Geophys. Res. 117, A02210. doi:10.1029/2011JA017089
Dum, C. T. (1975). Strong-turbulence theory and the transition from Landau to collisional damping. Phys. Rev. Lett. 35, 947–950. doi:10.1103/PhysRevLett.35.947
Dum, C. T., Chodura, R., and Biskamp, D. (1974). Turbulent heating and quenching of the ion sound instability. Phys. Rev. Lett. 32, 1231–1234. doi:10.1103/PhysRevLett.32.1231
Dum, C. T., Marsch, E., and Pilipp, W. (1980). Determination of wave growth from measured distribution functions and transport theory. J. Plasma Phys. 23, 91–113. doi:10.1017/S0022377800022170
Dyrud, L. P., and Oppenheim, M. M. (2006). Electron holes, ion waves, and anomalous resistivity in space plasmas. J. Geophys. Res. 111, A01302. doi:10.1029/2004JA010482
Edmiston, J. P., and Kennel, C. F. (1984). A parametric survey of the first critical Mach number for a fast MHD shock. J. Plasma Phys. 32, 429–441. doi:10.1017/S002237780000218X
Ergun, R. E., Carlson, C. W., McFadden, J. P., Mozer, F. S., Muschietti, L., Roth, I., et al. (1998). Debye-scale plasma structures associated with magnetic-field-aligned electric fields. Phys. Rev. Lett. 81, 826–829. doi:10.1103/PhysRevLett.81.826
Ergun, R. E., Malaspina, D. M., Bale, S. D., McFadden, J. P., Larson, D. E., Mozer, F. S., et al. (2010). Spacecraft charging and ion wake formation in the near-Sun environment. Phys. Plasmas. 17, 072903. doi:10.1063/1.3457484
Ergun, R. E., Tucker, S., Westfall, J., Goodrich, K. A., Malaspina, D. M., Summers, D., et al. The axial double probe and fields signal processing for the MMS mission. Space Sci. Rev. 199, (2016). 167–188. doi:10.1007/s11214-014-0115-x
Filbert, P. C., and Kellogg, P. J. (1979). Electrostatic noise at the plasma frequency beyond the earth’s bow shock. J. Geophys. Res. 84, 1369–1381. doi:10.1029/JA084iA04p01369
Forslund, D., Morse, R., Nielson, C., and Fu, J. (1972). Electron cyclotron drift instability and turbulence. Phys. Fluids. 15, 1303–1318. doi:10.1063/1.1694082
Forslund, D. W., Morse, R. L., and Nielson, C. W. Electron cyclotron drift instability. Phys. Rev. Lett. 25, (1970). 1266–1270. doi:10.1103/PhysRevLett.25.1266
Forslund, D. W., Morse, R. L., and Nielson, C. W. (1971). Nonlinear electron-cyclotron drift instability and turbulence. Phys. Rev. Lett. 27, 1424–1428. doi:10.1103/PhysRevLett.27.1424
Franz, J. R., Kintner, P. M., Pickett, J. S., and Chen, L. J. (2005). Properties of small-amplitude electron phase-space holes observed by Polar. J. Geophys. Res. 110, A09212. doi:10.1029/2005JA011095
Fredricks, R. W., Coroniti, F. V., Kennel, C. F., and Scarf, F. L. (1970a). Fast time-resolved spectra of electrostatic turbulence in the earth’s bow shock. Phys. Rev. Lett. 24, 994–998. doi:10.1103/PhysRevLett.24.994
Fredricks, R. W., Crook, G. M., Kennel, C. F., Green, I. M., Scarf, F. L., Coleman, P. J., et al. (1970b). OGO 5 observations of electrostatic turbulence in bow shock magnetic structures. J. Geophys. Res. 75, 3751–3768. doi:10.1029/JA075i019p03751
Fredricks, R. W., Kennel, C. F., Scarf, F. L., Crook, G. M., and Green, I. M. (1968). Detection of electric-field turbulence in the earth’s bow shock. Phys. Rev. Lett. 21, 1761–1764. doi:10.1103/PhysRevLett.21.1761
Fuselier, S. A., and Gurnett, D. A. (1984). Short wavelength ion waves upstream of the earth’s bow shock. J. Geophys. Res. 89, 91–103. doi:10.1029/JA089iA01p00091
Galeev, A. A. (1976). “Collisionless shocks,” in Physics of solar planetary environments; Proceedings of the International Symposium on Solar-Terrestrial Physics, Boulder, CO, June 7–18, 1976. Vol. 1. (A77-44201 20-88). Editor D. J. Williams (Washington, D.C.: American Geophysical Union). 464–490.
Galeev, A. A., and Karpman, V. I. (1963). Turbulence theory of a weakly nonequilibrium low-density plasma and structure of shock waves. Sov. Phys.–JETP. 17, 403–409.
Gary, S. P. (1981). Microinstabilities upstream of the earth’s bow shock – a brief review. J. Geophys. Res. 86, 4331–4336. doi:10.1029/JA086iA06p04331
Gladd, N. T. (1976). The lower hybrid drift instability and the modified two stream instability in high density theta pinch environments. Plasma Phys. 18, 27–40. doi:10.1088/0032-1028/18/1/002
Goldman, M. V., Newman, D. L., Lapenta, G., Andersson, L., Gosling, J. T., Eriksson, S., et al. (2014). Čerenkov emission of quasiparallel whistlers by fast electron phase-space holes during magnetic reconnection. Phys. Rev. Lett. 112, 145002. doi:10.1103/PhysRevLett.112.145002
Goodrich, K. A., Ergun, R. E., Schwartz, S. J., Wilson, L. B., Johlander, A., Newman, D., et al. (2019). Impulsively reflected ions: a plausibile mechanism for ion acoustic wave growth in collisionless shocks. J. Geophys. Res. 124, 1855–1865. doi:10.1029/2018JA026436
Goodrich, K. A., Ergun, R. E., Schwartz, S. J., Wilson, L. B., Newman, D., Wilder, F. D., et al. (2018). MMS observations of electrostatic waves in an oblique shock crossing. J. Geophys. Res. 123, 9430–9442. doi:10.1029/2018JA025830
Gurnett, D. A., and Anderson, R. R. (1977). Plasma wave electric fields in the solar wind - initial results from HELIOS 1. J. Geophys. Res. 82, 632–650. doi:10.1029/JA082i004p00632
Gurnett, D. A., Neubauer, F. M., and Schwenn, R. (1979). Plasma wave turbulence associated with an interplanetary shock. J. Geophys. Res. 84, 541–552. doi:10.1029/JA084iA02p00541
Henchen, R. J., Sherlock, M., Rozmus, W., Katz, J., Masson-Laborde, P. E., Cao, D., et al. (2019). Measuring heat flux from collective Thomson scattering with non-Maxwellian distribution functions. Phys. Plasmas. 26, 032104. doi:10.1063/1.5086753
Hobara, Y., Balikhin, M., Krasnoselskikh, V., Gedalin, M., and Yamagishi, H. (2010). Statistical study of the quasi-perpendicular shock ramp widths. J. Geophys. Res. 115, 11106. doi:10.1029/2010JA015659
Hoshino, M., and Shimada, N. (2002). Nonthermal electrons at high Mach number shocks: electron shock surfing acceleration. Astrophys. J. 572, 880–887. doi:10.1086/340454
Hull, A. J., and Scudder, J. D. (2000). Model for the partition of temperature between electrons and ions across collisionless, fast mode shocks. J. Geophys. Res. 105, 27323–27342. doi:10.1029/2000JA900105
Hull, A. J., Larson, D. E., Wilber, M., Scudder, J. D., Mozer, F. S., Russell, C. T., et al. (2006). Large-amplitude electrostatic waves associated with magnetic ramp substructure at Earth’s bow shock. Geophys. Res. Lett. 33, 15104. doi:10.1029/2005GL025564
Hull, A. J., Muschietti, L., Le Contel, O., Dorelli, J. C., and Lind, P. A. (2020). MMS observations of intense whistler waves within earth’s supercritical bow shock: source mechanism and impact on shock structure and plasma transport. J. Geophys. Res. 125, e27290. doi:10.1029/2019JA027290
Johlander, A., Schwartz, S. J., Vaivads, A., Khotyaintsev, Y. V., Gingell, I., Peng, I. B., et al. (2016). Rippled quasiperpendicular shock observed by the magnetospheric multiscale spacecraft. Phys. Rev. Lett. 117, 165101. doi:10.1103/PhysRevLett.117.165101
Kellogg, P. J. (2003). Langmuir waves associated with collisionless shocks; a review. Planet. Space Sci. 51, 681–691. doi:10.1016/j.pss.2003.05.001
Kellogg, P. J., Cattell, C. A., Goetz, K., Monson, S. J., and Wilson, L. B. (2010). Electron trapping and charge transport by large amplitude whistlers. Geophys. Res. Lett. 37, L20106. doi:10.1029/2010GL044845
Kellogg, P. J., Cattell, C. A., Goetz, K., Monson, S. J., and Wilson, L. B. (2011). Large amplitude whistlers in the magnetosphere observed with wind-waves. J. Geophys. Res. 116, A09224. doi:10.1029/2010JA015919
Kellogg, P. J., Goetz, K., Howard, R. L., and Monson, S. J. (1992). Evidence for Langmuir wave collapse in the interplanetary plasma. Geophys. Res. Lett. 19, 1303–1306. doi:10.1029/92GL01016
Kellogg, P. J., Goetz, K., Monson, S. J., and Opitz, A. (2013). Observations of transverse Z mode and parametric decay in the solar wind. J. Geophys. Res. 118, 4766–4775. doi:10.1002/jgra.50443
Kennel, C. F. (1987). Critical Mach numbers in classical magnetohydrodynamics. J. Geophys. Res. 92, 13427–13437. doi:10.1029/JA092iA12p13427
Kennel, C. F., Edmiston, J. P., and Hada, T. (1985). “A quarter century of collisionless shock research,” in Collisionless shocks in the heliosphere: a tutorial review. Geophysics monograph series. Editors R. G. Stone, and B. T. Tsurutani (Washington, D.C.: AGU), Vol. 34, 1–36. doi:10.1029/GM034p0001
Kersten, K., Cattell, C. A., Breneman, A., Goetz, K., Kellogg, P. J., Wygant, J. R., et al. (2011). Observation of relativistic electron microbursts in conjunction with intense radiation belt whistler-mode waves. Geophys. Res. Lett. 38, L08107. doi:10.1029/2011GL046810
Krasnoselskikh, V. V., Dudok de Wit, T., and Bale, S. D. (2011). Determining the wavelength of Langmuir wave packets at the Earth’s bow shock. Ann. Geophys. 29, (2011). 613–617. doi:10.5194/angeo-29-613-2011
Krasnoselskikh, V. V., Lembège, B., Savoini, P., and Lobzin, V. V. (2002). Nonstationarity of strong collisionless quasiperpendicular shocks: theory and full particle numerical simulations. Phys. Plasmas. 9, 1192–1209. doi:10.1063/1.1457465
Kurth, W. S., Gurnett, D. A., and Scarf, F. L. (1979). High-resolution spectrograms of ion acoustic waves in the solar wind. J. Geophys. Res. 84, 3413–3419. doi:10.1029/JA084iA07p03413
Lampe, M., Manheimer, W. M., McBride, J. B., Orens, J. H., Papadopoulos, K., Shanny, R., et al. (1972). Theory and simulation of the beam cyclotron instability. Phys. Fluids. 15, 662–675. doi:10.1063/1.1693961
Lavraud, B., and Larson, D. E. (2016). Correcting moments of in situ particle distribution functions for spacecraft electrostatic charging. J. Geophys. Res. 121, 8462–8474. doi:10.1002/2016JA022591
Lembège, B., Savoini, P., Hellinger, P., and Trávníček, P. M. (2009). Nonstationarity of a two-dimensional perpendicular shock: competing mechanisms. J. Geophys. Res. 114, A03217. doi:10.1029/2008JA013618
Lemons, D. S., and Gary, S. P. Current-driven instabilities in a laminar perpendicular shock. J. Geophys. Res. 83, (1978). 1625–1632. doi:10.1029/JA083iA04p01625
Lemons, D. S., and Gary, S. P. (1977). Electromagnetic effects on the modified two-stream instability. J. Geophys. Res. 82, 2337–2342. doi:10.1029/JA082i016p02337
Lindqvist, P. A., Olsson, G., Torbert, R. B., King, B., Granoff, M., Rau, D., et al. (2016). The spin-plane double probe electric field instrument for MMS. Space Sci. Rev. 199, 137–165. doi:10.1007/s11214-014-0116-9
Lu, Q. M., Lembège, B., Tao, J. B., and Wang, S. (2008). Perpendicular electric field in two-dimensional electron phase-holes: a parameter study. J. Geophys. Res. 113, A11219. doi:10.1029/2008JA013693
Malaspina, D. M., and Ergun, R. E. (2008). Observations of three-dimensional Langmuir wave structure. J. Geophys. Res. 113, A12108. doi:10.1029/2008JA013656
Malaspina, D. M., Li, B., Cairns, I. H., Robinson, P. A., Kuncic, Z., and Ergun, R. E. Terrestrial foreshock Langmuir waves: STEREO observations, theoretical modeling, and quasi-linear simulations. J. Geophys. Res. 114, (2009). A12101. doi:10.1029/2009JA014493
Marsch, E., and Chang, T. Electromagnetic lower hybrid waves in the solar wind. J. Geophys. Res. 88, (1983). 6869–6880. doi:10.1029/JA088iA09p06869
Matsukiyo, S., and Matsumoto, Y. (2015). Electron acceleration at a high beta and low Mach number rippled shock. J. Phys. Conf. 642, 012017. doi:10.1088/1742-6596/642/1/012017
Matsukiyo, S., and Scholer, M. (2012). Dynamics of energetic electrons in nonstationary quasi-perpendicular shocks. J. Geophys. Res. 117, A11105. doi:10.1029/2012JA017986
Matsukiyo, S., and Scholer, M. (2006). On microinstabilities in the foot of high Mach number perpendicular shocks. J. Geophys. Res. 111, A06104. doi:10.1029/2005JA011409
Mazelle, C., Lembège, B., Morgenthaler, A., Meziane, K., Horbury, T. S., Génot, V., et al. (2010). Self-reformation of the quasi-perpendicular shock: CLUSTER observations. Proc. 12th Intl. Solar Wind Conf. 1216, 471–474. doi:10.1063/1.3395905
Mellott, M. M., and Greenstadt, E. W. (1988). Plasma waves in the range of the lower hybrid frequency – ISEE 1 and 2 observations at the earth’s bow shock. J. Geophys. Res. 93, 9695–9708. doi:10.1029/JA093iA09p09695
Mitchell, J. J., and Schwartz, S. J. (2014). Isothermal magnetosheath electrons due to nonlocal electron cross talk. J. Geophys. Res. 119, 1080–1093. doi:10.1002/2013JA019211
Mitchell, J. J., and Schwartz, S. J. Nonlocal electron heating at the Earth’s bow shock and the role of the magnetically tangent point. J. Geophys. Res. 118, (2013). 7566–7575. doi:10.1002/2013JA019226
Morton, K. W. (1964). Finite amplitude compression waves in a collision-free plasma. Phys. Fluids. 7, 1800–1815. doi:10.1063/1.2746780
Muschietti, L., and Lembège, B. (2013). Microturbulence in the electron cyclotron frequency range at perpendicular supercritical shocks. J. Geophys. Res. 118, 2267–2285. doi:10.1002/jgra.50224
Muschietti, L., and Lembège, B. (2017). Two-stream instabilities from the lower-hybrid frequency to the electron cyclotron frequency: application to the front of quasi-perpendicular shocks. Ann. Geophys. 35, 1093–1112. doi:10.5194/angeo-35-1093-2017
Papadopoulos, K. (1985). “Microinstabilities and anomalous transport,” in Collisionless shocks in the heliosphere: a tutorial review. Geophysics Monograph Series. Editors R. G. Stone, and B. T. Tsurutani (Washington, DC: AGU), Vol. 34, 59–90. doi:10.1029/GM034p0059
Papadopoulos, K., and Palmadesso, P. (1976). Excitation of lower hybrid waves in a plasma by electron beams. Phys. Fluids. 19, 605. doi:10.1063/1.861501
Pulupa, M., and Bale, S. D. (2008). Structure on interplanetary shock fronts: type II radio burst source regions. Astrophys. J. 676, 1330–1337. doi:10.1086/526405
Pulupa, M. P., Bale, S. D., and Kasper, J. C. (2010). Langmuir waves upstream of interplanetary shocks: dependence on shock and plasma parameters. J. Geophys. Res. 115, A04106. doi:10.1029/2009JA014680
Pulupa, M. P., Bale, S. D., Salem, C., and Horaites, K. (2014). Spin-modulated spacecraft floating potential: observations and effects on electron moments. J. Geophys. Res. 119, 647–657. doi:10.1002/2013JA019359
Rodriguez, P., and Gurnett, D. A. (1975). Electrostatic and electromagnetic turbulence associated with the earth’s bow shock. J. Geophys. Res. 80, 19–31. doi:10.1029/JA080i001p00019
Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2016). The magnetospheric multiscale magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/s11214-014-0057-3
Sagdeev, R. Z. (1966). Cooperative phenomena and shock waves in collisionless plasmas. Rev. Plasma Phys. 4, 23.
Saito, S., Nariyuki, Y., and Umeda, T. (2017). Generation of intermittent ion acoustic waves in whistler-mode turbulence. Phys. Plasmas. 24, 072304. doi:10.1063/1.4990443
Santolík, O., Gurnett, D. A., Pickett, J. S., Parrot, M., and Cornilleau-Wehrlin, N. (2003). Spatio-temporal structure of storm-time chorus. J. Geophys. Res. 108, 1278. doi:10.1029/2002JA009791
Savoini, P., and Lembège, B. (2015). Production of nongyrotropic and gyrotropic backstreaming ion distributions in the quasi-perpendicular ion foreshock region. J. Geophys. Res. 120, 7154–7171. doi:10.1002/2015JA021018
Scholer, M., and Burgess, D. (2006). Transition scale at quasiperpendicular collisionless shocks: full particle electromagnetic simulations. Phys. Plasmas. 13, 062101. doi:10.1063/1.2207126
Scholer, M., and Burgess, D. (2007). Whistler waves, core ion heating, and nonstationarity in oblique collisionless shocks. Phys. Plasmas. 14, 072103. doi:10.1063/1.2748391
Scholer, M., and Matsukiyo, S. (2004). Nonstationarity of quasi-perpendicular shocks: a comparison of full particle simulations with different ion to electron mass ratio. Ann. Geophys. 22, 2345–2353. doi:10.5194/angeo-22-2345-2004
Schwartz, S. J., Thomsen, M. F., Bame, S. J., and Stansberry, J. (1988). Electron heating and the potential jump across fast mode shocks. J. Geophys. Res. 93, 12923–12931. doi:10.1029/JA093iA11p12923
Scime, E. E., Bame, S. J., Feldman, W. C., Gary, S. P., Phillips, J. L., and Balogh, A. (1994b). Regulation of the solar wind electron heat flux from 1 to 5 AU: ULYSSES observations. J. Geophys. Res. 99, 23401–23410. doi:10.1029/94JA02068
Scime, E. E., Phillips, J. L., and Bame, S. J. (1994a). Effects of spacecraft potential on three-dimensional electron measurements in the solar wind. J. Geophys. Res. 99, 14769–14776. doi:10.1029/94JA00489
Scudder, J. D., Aggson, T. L., Mangeney, A., Lacombe, C., and Harvey, C. C. (1986a). The resolved layer of a collisionless, high beta, supercritical, quasi-perpendicular shock wave. I–rankine-Hugoniot geometry, currents, and stationarity. J. Geophys. Res. 91, 11019–11052. doi:10.1029/JA091iA10p11019
Scudder, J. D., Aggson, T. L., Mangeney, A., Lacombe, C., and Harvey, C. C. (1986b). The resolved layer of a collisionless, high beta, supercritical, quasi-perpendicular shock wave. II - dissipative fluid electrodynamics. J. Geophys. Res. 91, 11053–11073. doi:10.1029/JA091iA10p11053
Scudder, J. D., Cao, X., and Mozer, F. S. (2000). Photoemission current-spacecraft voltage relation: key to routine, quantitative low-energy plasma measurements. J. Geophys. Res. 105, 21281–21294. doi:10.1029/1999JA900423
Scudder, J. D., Mangeney, A., Lacombe, C., Harvey, C. C., and Wu, C. S. (1986c). The resolved layer of a collisionless, high beta, supercritical, quasi-perpendicular shock wave. III – Vlasov electrodynamics. J. Geophys. Res. 91, 11075–11097. doi:10.1029/JA091iA10p11075
Singh, N., Loo, S. M., Wells, B. E., and Deverapalli, C. (2000). Three-dimensional structure of electron holes driven by an electron beam. Geophys. Res. Lett. 27, 2469–2472. doi:10.1029/2000GL003766
Singh, N., Loo, S. M., and Wells, B. E. (2001). Electron hole as an antenna radiating plasma waves. Geophys. Res. Lett. 28, 1371–1374. doi:10.1029/2000GL012652
Soucek, J., Santolík, O., Dudok de Wit, T., and Pickett, J. S. (2009). Cluster multispacecraft measurement of spatial scales of foreshock Langmuir waves. J. Geophys. Res. 114, A02213. doi:10.1029/2008JA013770
Stringer, T. E. (1963). Low-frequency waves in an unbounded plasma. J. Nuclear Energy. 5, 89–107. doi:10.1088/0368-3281/5/2/304
Tidman, D. A., and Krall, N. A. (1971). Shock waves in collisionless plasmas. New York, NY: John Wiley & Sons.
Tidman, D. A., and Northrop, T. G. (1968). Emission of plasma waves by the Earth’s bow shock. J. Geophys. Res. 73, 1543–1553. doi:10.1029/JA073i005p01543
Tsurutani, B. T., Verkhoglyadova, O. P., Lakhina, G. S., and Yagitani, S. (2009). Properties of dayside outer zone chorus during HILDCAA events: loss of energetic electrons. J. Geophys. Res. 114, A03207. doi:10.1029/2008JA013353
Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R. (2014). Dynamics and microinstabilities at perpendicular collisionless shock: a comparison of large-scale two-dimensional full particle simulations with different ion to electron mass ratio. Phys. Plasmas. 21, 022102. doi:10.1063/1.4863836
Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R. (2012b). Microinstabilities at perpendicular collisionless shocks: a comparison of full particle simulations with different ion to electron mass ratio. Phys. Plasmas. 19, 042109. doi:10.1063/1.3703319
Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R. (2012a). Modified two-stream instability at perpendicular collisionless shocks: full particle simulations. J. Geophys. Res. 117, A03206. doi:10.1029/2011JA017182
Umeda, T., Yamao, M., and Yamazaki, R. (2011). Cross-scale coupling at a perpendicular collisionless shock. Planet. Space Sci. 59, 449–455. doi:10.1016/j.pss.2010.01.007
Umeda, T., Yamazaki, R., Ohira, Y., Ishizaka, N., Kakuchi, S., Kuramitsu, Y., et al. (2019). Full particle-in-cell simulation of the interaction between two plasmas for laboratory experiments on the generation of magnetized collisionless shocks with high-power lasers. Phys. Plasmas. 26, 032303. doi:10.1063/1.5079906
Vasko, I. Y., Mozer, F. S., Krasnoselskikh, V. V., Artemyev, A. V., Agapitov, O. V., Bale, S. D., et al. (2018). Solitary waves across supercritical quasi-perpendicular shocks. Geophys. Res. Lett. 45, 5809–5817. doi:10.1029/2018GL077835
Vedenov, A. A. (1963). Quasi-linear plasma theory (theory of a weakly turbulent plasma). J. Nucl. Energy. 5, 169–186. doi:10.1088/0368-3281/5/3/305
Walker, S. N., Balikhin, M. A., Alleyne, H. S. C. K., Hobara, Y., André, M., and Dunlop, M. W. (2008). Lower hybrid waves at the shock front: a reassessment. Ann. Geophys. 26, 699–707. doi:10.5194/angeo-26-699-2008
Wang, R., Vasko, I. Y., Mozer, F. S., Bale, S. D., Artemyev, A. V., Bonnell, J. W., et al. (2020). Electrostatic turbulence and debye-scale structures in collisionless shocks. Astrophys. J. Lett. 889, L9. doi:10.3847/2041-8213/ab6582
Wilson, L. B. (2010). The microphysics of collisionless shocks. PhD thesis, University of Minnesota. Publication Number: AAT 3426498; ISBN: 9781124274577; Minneapolis, MN: Advisor: Cynthia Cattell.
Wilson, L. B., Cattell, C., Kellogg, P. J., Goetz, K., Kersten, K., Hanson, L., et al. (2007). Waves in interplanetary shocks: a wind/WAVES study. Phys. Rev. Lett. 99, 041101. doi:10.1103/PhysRevLett.99.041101
Wilson, L. B., Cattell, C. A., Kellogg, P. J., Goetz, K., Kersten, K., Kasper, J. C., et al. (2010). Large-amplitude electrostatic waves observed at a supercritical interplanetary shock. J. Geophys. Res. 115, A12104. doi:10.1029/2010JA015332
Wilson, L. B., Cattell, C. A., Kellogg, P. J., Wygant, J. R., Goetz, K., Breneman, A., et al. (2011). The properties of large amplitude whistler mode waves in the magnetosphere: propagation and relationship with geomagnetic activity. Geophys. Res. Lett. 38, L17107. doi:10.1029/2011GL048671
Wilson, L. B., Chen, L. J., Wang, S., Schwartz, S. J., Turner, D. L., Stevens, M. L., et al. (2019a). Electron energy partition across interplanetary shocks: II. Statistics. Astrophys. J. 245. doi:10.3847/1538-4365/ab5445
Wilson, L. B., Chen, L. J., Wang, S., Schwartz, S. J., Turner, D. L., Stevens, M. L., et al. (2020). Electron energy partition across interplanetary shocks: III. Analysis. Astrophys. J. 893. doi:10.3847/1538-4357/ab7d39
Wilson, L. B., Chen, L. J., Wang, S., Schwartz, S. J., Turner, D. L., Stevens, M. L., et al. (2019b). Electron energy partition across interplanetary shocks: I. Methodology and data product. Astrophys. J. 243. doi:10.3847/1538-4365/ab22bd
Wilson, L. B., Koval, A., Sibeck, D. G., Szabo, A., Cattell, C. A., Kasper, J. C., et al. (2013). Shocklets, SLAMS, and field-aligned ion beams in the terrestrial foreshock. J. Geophys. Res. 118, 957–966. doi:10.1029/2012JA018186
Wilson, L. B., Koval, A., Szabo, A., Breneman, A., Cattell, C. A., Goetz, K., et al. (2012). Observations of electromagnetic whistler precursors at supercritical interplanetary shocks. Geophys. Res. Lett. 39, L08109. doi:10.1029/2012GL051581
Wilson, L. B., Koval, A., Szabo, A., Stevens, M. L., Kasper, J. C., Cattell, C. A., et al. (2017). Revisiting the structure of low Mach number, low beta, quasi-perpendicular shocks. J. Geophys. Res. 122, 9115–9133. doi:10.1002/2017JA024352
Wilson, L. B., Sibeck, D. G., Breneman, A. W., Le Contel, O., Cully, C., Turner, D. L., et al. (2014a). Quantified energy dissipation rates in the terrestrial bow shock: 1. Analysis techniques and methodology. J. Geophys. Res. 119, 6455–6474. doi:10.1002/2014JA019929
Wilson, L. B., Sibeck, D. G., Breneman, A. W., Le Contel, O., Cully, C., Turner, D. L., et al. (2014b). Quantified energy dissipation rates in the terrestrial bow shock: 2. Waves and dissipation. J. Geophys. Res. 119, 6475–6495. doi:10.1002/2014JA019930
Wilson, L. B., Sibeck, D. G., Turner, D. L., Osmane, A., Caprioli, D., and Angelopoulos, V. (2016). Relativistic electrons produced by foreshock disturbances observed upstream of the Earth’s bow shock. Phys. Rev. Lett. 117, 215101. doi:10.1103/PhysRevLett.117.215101
Wilson, L. B., Stevens, M. L., Kasper, J. C., Klein, K. G., Maruca, B., Bale, S. D., et al. (2018). The Statistical Properties of Solar Wind Temperature Parameters Near 1 au. Astrophys. J. Suppl. 236, 41. doi:10.3847/1538-4365/aab71c
Wu, C. S., Winske, D., Papadopoulos, K., Zhou, Y. M., Tsai, S. T., and Guo, S. C. (1983). A kinetic cross-field streaming instability. Phys. Fluids. 26, 1259–1267. doi:10.1063/1.864285
Wu, C. S., Winske, D., Tanaka, M., Papadopoulos, K., Akimoto, K., Goodrich, C. C., et al. (1984). Microinstabilities associated with a high Mach number, perpendicular bow shock. Space Sci. Rev. 37, 63–109. doi:10.1007/BF00213958
Wygant, J. R., Bensadoun, M., and Mozer, F. S. (1987). Electric field measurements at subcritical, oblique bow shock crossings. J. Geophys. Res. 92, 11109–11121. doi:10.1029/JA092iA10p11109
Wygant, J. R., Bonnell, J. W., Goetz, K., Ergun, R. E., Mozer, F. S., Bale, S. D., et al. (2013). The electric field and waves instruments on the radiation belt storm probes mission. Space Sci. Rev. 179, 183–220. doi:10.1007/s11214-013-0013-7
Yang, Z., Lu, Q., Gao, X., H, C., Yang, H., Liu, Y., et al. (2013). Magnetic ramp scale at supercritical perpendicular collisionless shocks: full particle electromagnetic simulations. Phys. Plasmas. 20, 092116. doi:10.1063/1.4821825
Keywords: PIC simulation, electric field measurement, kinetic instabilities, collisionless shock, energy dissipation
Citation: Wilson LB, Chen L-J and Roytershteyn V (2021) The Discrepancy Between Simulation and Observation of Electric Fields in Collisionless Shocks. Front. Astron. Space Sci. 7:592634. doi: 10.3389/fspas.2020.592634
Received: 07 August 2020; Accepted: 02 November 2020;
Published: 25 January 2021.
Edited by:
Luca Sorriso-Valvo, National Research Council, ItalyReviewed by:
Silvia Perri, University of Calabria, ItalyQuanming Lu, University of Science and Technology of China, China
Copyright © 2021 Wilson III, Chen and Roytershteyn. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lynn B. Wilson III, bHlubi5iLndpbHNvbkBuYXNhLmdvdg==
 Lynn B. Wilson
Lynn B. Wilson  Li-Jen Chen1
Li-Jen Chen1