- Center for Space Plasma Physics, Space Science Institute, Boulder, CO, United States
As a test of the action of MHD turbulence in the solar wind, the compression of the heliospheric magnetic structure at 1AU by 109 interplanetary shocks is examined. In the magnetic structure the orientations of solar-wind strong current sheets are statistically examined vs. time in the downstream plasmas after shock compression. If the current sheets of the solar wind are features of an active MHD turbulence, they should be destroyed and remade with isotropic orientations on the timescale of an eddy-turnover time. If the current-sheet orientations remain anisotropic after the shock compression, it is an indication that the current sheets of the solar wind are not created by MHD turbulence. This statistical analysis finds no evolution of the current-sheet orientations after the solar wind is compressed by the shocks, implying a non-turbulent origin of the current sheets. A possibility is that the heliospheric magnetic structure at 1 AU is fossil structure from the solar corona.
1. Introduction
The magnetic structure of the solar wind in the inner heliosphere is dominated by strong current sheets (directional discontinuities) (e.g., Burlaga and Ness, 1969; Vasquez et al., 2007; Li, 2008; D'Amicis et al., 2012). Statistical examinations of the spacings and orientations of the solar-wind current sheets lead to a picture of a spaghetti-like network of flux tubes forming the magnetic structure of the heliosphere (Mariani et al., 1973, 1983; Borovsky, 2008a, 2010; Greco et al., 2009; Arnold et al., 2013; Ruffolo et al., 2013). Depictions of this structure appear in Figure 3 of McCracken and Ness (1966), Figure 6 or Bartley et al. (1966), Figures 1 and 9 of Michel (1967), Figure 5 of Bruno et al. (2001), Figure 1a of Borovsky (2008a), Figure 22 of Borovsky (2010), and Figure 7 of Bruno (2019).
An outstanding question concerns the origin of the heliospheric magnetic structure (Neugebauer and Giacalone, 2010, 2015; Li and Qin, 2011; Owens et al., 2011; Tu et al., 2016; Borovsky, 2020a; Viall and Borovsky, 2020): Is the observed magnetic structure created in situ in the heliosphere or is it fossil structure from the solar coronal? A strong argument for the in situ creation of the heliospheric magnetic structure focuses on MHD turbulence: simulations of MHD turbulence exhibit strong current sheets that are created and destroyed by the action of the turbulence (Zimbardo et al., 2004; Greco et al., 2009; Zhdankin et al., 2012). Among the arguments that there is an active MHD turbulence operating in the inner heliosphere are: (1) a matching of the magnetic and velocity Fourier spectra of the solar wind (with an inertial-range, a high-frequency breakpoint, and a low-frequency breakpoint) to the spectra expected for MHD turbulence (e.g., Goldstein et al., 1995; Tu and Marsch, 1995; Podesta, 2010; Carbone, 2012; Bruno and Carbone, 2016); (2) third-order-moment analysis of the solar-wind fluctuations indicating an energy cascade operating in the solar wind (Sorriso-Valvo et al., 2007; MacBride et al., 2008; Stawarz et al., 2010; Podesta, 2011); and (3) the solar-wind plasma having an extremely high Reynolds number for its flow structures (Borovsky and Gary, 2009). Some of the arguments against an active MHD turbulence operating in the inner heliosphere are: (1) the absence of turbulent mixing in the slow solar wind (Borovsky, 2012); (2) the absence of discernable time-evolution of the magnetic fluctuations of the fast solar wind (Borovsky, 2020b); (3) the lack of discernable isotropization of the magnetic structure in coroating-interaction-region compressions and trailing-edge rarefactions (Borovsky and Denton, 2016); (4) the strong current sheets of the solar wind being co-located with ion-composition boundaries, which can only be formed in the corona (Borovsky, 2020c); (5) the strong current sheets of the solar wind being co-located with electron-strahl-intensity boundaries, implying that the current sheets are coherent all the way back to the corona (Borovsky, 2020c); (6) the co-location of strong current sheets with intensity boundaries of solar energetic particles, again implying a coherence of the flux tubes back to near-Sun region (Trenchi et al., 2013a,b); (7) the survival of some inertial-range-sized solar-wind structures from the corona to the Earth (Viall and Vourlidas, 2015; Kepko and Viall, 2019). The absence of turbulent mixing (Paul et al., 2003; Borovsky, 2012) means (a) an absence of evidence for the action of turbulent stretching and folding reducing (macromixing) the sizes of plasma chunks as the solar wind advects from 0.3 to 1 AU and (b) an absence of homogenization of plasma properties (micromixing) as the solar wind advects from 0.3 to 1 AU. The absence of time evolution of the structure (Borovsky, 2020b) come from the fact that in the Alfvenic fast solar wind a reference frame can be found that moves outward from the Sun with the magnetic structure; in this frame all flow velocities are parallel to the local magnetic field and, to within measurement error, v⊥ is everywhere zero. With v⊥ = 0 everywhere in the frame of the magnetic structure, there is no time evolution to the propagating structure [cf. Sect. 7.2 and Figure 7.1 of Parker (1979)]. The strong current sheets of the solar wind also could be created in situ by the steeping of Alfvén waves propagating outward from the Sun (Malara et al., 1996; Tsurutani and Ho, 1999; Vasquez and Hollweg, 1999; Kellogg and Horbury, 2005) or by mirror-mode instabilities (Russell et al., 2008, 2009; Yao et al., 2013).
Typically, the normals of the strong current sheets of the solar wind are oriented quasi-isotropically perpendicular to the Parker-spiral direction (Borovsky, 2008a; Borovsky and Denton, 2016). If the current sheets were created by MHD turbulence, one would expect the current-sheet orientations to be approximately isotropic about a mean-field direction. Interplanetary shocks compress the plasma and magnetic-field structure of the solar wind in a non-isotropic fashion. A test of in situ creation by turbulence is to examine the compression of the magnetic structure by interplanetary shocks and then see if the current sheets re-isotropize downstream of the shocks as they are newly re-created in situ. If the current-sheet orientations isotropize with time (distance) downstream from the shock, they are likely created in situ: if they do no isotropize they are likely fossil from the Sun.
The existence of “planar magnetic structures” downstream from coronal-mass-ejection-driven interplanetary shocks is well known (Neugebauer et al., 1993; Jones et al., 1999; Kataoka et al., 2005; Savani et al., 2011; Palmiero et al., 2016; Shaikh et al., 2018, 2019). These planar magnetic structures are characterized by multiple sudden changes in the direction of the solar-wind magnetic field wherein the changing field vector remains parallel to a single plane (Nakagawa et al., 1989). The planar magnetic structures are characterized by slabs of magnetized plasma separated by co-planar tangential discontinuities (strong current sheets) (Nakagawa et al., 1989, 2000; Jones et al., 1999), as envisioned in Figure 8 of Nakagawa et al. (1989). Planar magnetic structures are associated with compressions of the solar-wind plasma (Neugebauer et al., 1993; Crooker et al., 1996; Intriligator et al., 2008). To get sufficient compression for planar magnetic structures to be observable in the downstream plasma, an interplanetary shock needs to have a Mach number of about 2 or greater (cf. Kataoka et al., 2005; Savani et al., 2011). Quasi-parallel shocks do not efficiently create planar magnetic structures in the downstream plasma (Jones et al., 2002; Savani et al., 2011), although a complication is that the shock-normal angle θBn between the solar-wind magnetic field and the plane of the shock is to a degree local owing to the upstream magnetic structure of the solar wind. This is depicted in Figure 1, where the shocking of a single magnetic flux tube in the spaghetti structure of the solar wind is sketched; the spatial meandering of the flux tube in the upstream plasma leads to different portions of the flux tube having different shock-normal angles θBn and the differing θBn values result in different amounts of magnetic compression for the different portions of the flux tubes (Tidman and Krall, 1971; Kennell, 1994). Portions of the flux tube that were quasi-perpendicular are compressed and flattened in the downstream plasma and portions of the flux tube that were quasi-parallel are not magnetically compressed. Hence, the downstream plasma will have a mixture of compression strengths.
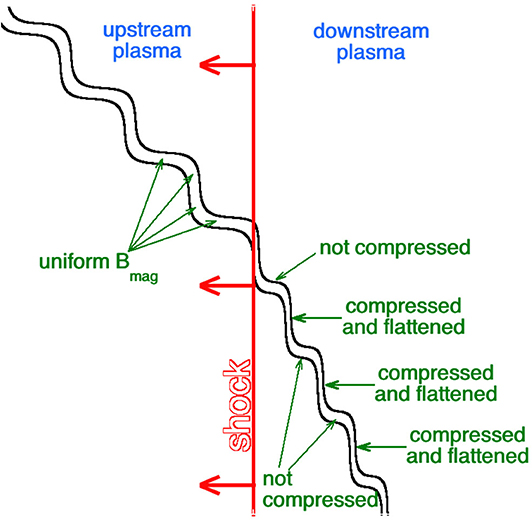
Figure 1. The shocking of one flux tube in the spaghetti structure of the heliosphere is sketched, with the variable shock normal angle resulting in different amounts of magnetic compression.
Planar magnetic structures are also seen in the compression regions of corotating interaction regions (Crooker et al., 1996; Clack et al., 2000; Jones and Balogh, 2000; Shaikh et al., 2020), where they have been described as flattened magnetic noodles (cf. Figure 6 of Crooker et al., 1996). Corotating interaction region compressions are particularly efficient at flattening the magnetic structure of the solar wind because the compressions are oriented transverse to the Parker-spiral direction, and so the compression is quasi-perpendicular to the magnetic-field vector. Borovsky and Denton (2016) have used the observed statistical orientations of the noodle (flux-tube) walls as a measure of the amount of solar-wind compression in corotating interaction regions and as a measure of the amount of solar-wind rarefaction in the trailing edges of high-speed streams.
2. The Interplanetary Shocks and the Plasma Analysis
In this study the evolution of compressed magnetic structure is studied downstream of 109 strong-compression forward interplanetary shocks observed with the WIND spacecraft at 1 AU. These 109 shocks are cataloged in Table 1 of Borovsky (2020d). The shocks were chosen to have density compression rations of ~2 of more. For each of the 109 forward shocks, the driver for each shock was assessed by examining the temporal profile of the solar-wind speed vsw, the magnetic-field strength Bmag, the proton temperature Tp in comparison with the solar-wind speed, the orientation of the magnetic field, the fluctuation level of the magnetic field, the presence or absence of a bi-directional electron strahl, and the presence of magnetic sector reversals. Only 7 of the 107 shocks were consistent with the shock being driven by the interaction of a high-speed stream with slower plasma [shock numbers 7, 11, 26, 35, 38, 42, and 105 in Table 1 of Borovsky (2020d)]; 100 shocks were not consistent with this. Of the 100 shocks, 42 had drivers that were identifiable as coronal mass ejections and 58 had drivers that were not seen or that could not be clearly identified as a coronal mass ejection. In many of the cases, the driver gas may have missed the WIND spacecraft.
The evolution of the compressed magnetic structure downstream of the 109 strong forward shocks is studied using the 3-s time-resolution MFI magnetic-field measurements (Lepping et al., 1995) onboard the WIND spacecraft at 1 AU. The positions of the WIND spacecraft relative to the Earth for the 109 shock crossings can be seen in Figure 1 of Borovsky (2020d). In Figure 2 the superposed epoch averages of the plasma and magnetic-field properties for the 109 shocks are plotted showing 6 h upstream and 6 h downstream with the zero epoch (t = 0) being the crossing time of each shock. The plasma properties are measured with the 3-s time-resoluton 3DP instrument (Lin et al., 1995) onboard WIND. Figure 2a plots the GSE X component of the solar-wind velocity -vx and Figure 2b plots the magnetic-field strength Bmag, the number density n, the proton Alfvén speed vA, the proton temperature Tp, and the proton specific entropy Sp = Tp/n2/3 [A change in the specific entropy is an indication of non-adiabatic heating or cooling: a requirement of a “shock” is that the specific entropy is higher downstream than it is upstream (Kennell, 1994)]. All of these quantities increase going from upstream of the shocks (left) to downstream of the shocks (right). Note in the downstream region in Figure 2b that the values of the number density n (red curve) and the magnetic-field strength Bmag (green curve) do not change appreciably with time in the downstream plasma: this indicates that there is compression of the plasma at the shock, but not much additional compression of the plasma between the shock and the coronal-mass-ejection driver gas [This is the same case as the compression of solar-wind plasma at the Earth's bow shock without additional compression in the sheath between the shock and the magnetosphere (cf. Figure 4 of Borovsky (2008b) for a variety of shock Mach numbers)].
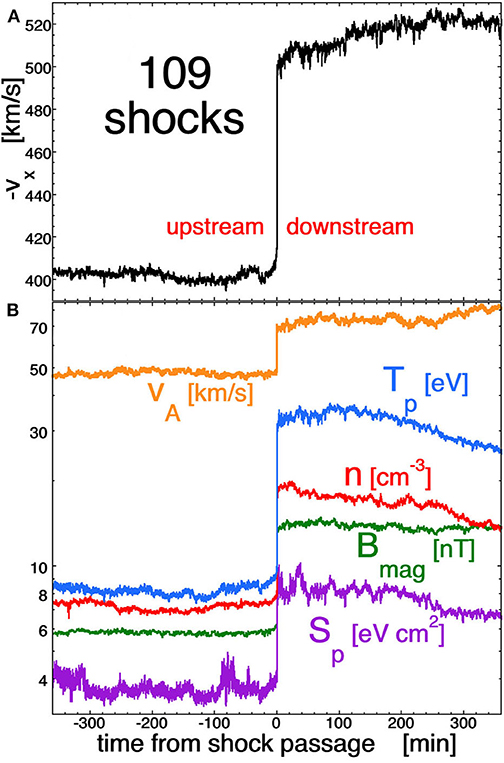
Figure 2. A superposed epoch average of the plasma and magnetic-field properties of the 109 forward interplanetary shocks measured with 3-s time resolution by the WIND spacecraft. In panel (A) vx (GSE) of the solar wind is plotted. In panel (B) the magnetic-field strength (green), number density (red), Alfvén speed (orange), proton temperature (blue), and proton specific entropy Sp = Tp/n2/3 (purple) are plotted.
The analysis of current sheets in the downstream plasma will be restricted to the time interval 0–6 h after the shock encounter to avoid driver gas, which tends to reach the spacecraft a fraction of a day after the shock (Russell and Mulligan, 2002; Oh et al., 2007; Kilpua et al., 2017); analyzing 41 forward shocks, Kilpua et al. (2013) found the time from the shock to the driver to range from 3.1 to 28.1 h with a mean value of 9.8 h. The time intervals upstream and downstream within 0.5 h of the shocks will be avoided in most of the statistical analyses to avoid foreshock and shock effects.
For locating strong current sheets in the WIND MFI data set, the criterion is used that the change in the magnetic-field direction across the current sheet must be >30° in 18s. The statistical results do not qualitatively change if a weaker (<30°) or a stronger (more than 30°) criterion is chosen. If a stronger criterion is chosen, fewer current sheets are collected and the statistics are poorer. For the 109 interplanetary shocks, 11,465 strong current sheets are collected in the intervals between 6 h prior to the shock until 6 h after the shock.
In single-spacecraft measurements of the magnetic-field vector of the solar wind, the orientation of strong current sheets is obtained using “cross-product method” where the field vector temporally changes from B1 to B2 in crossing the current sheet and the normal to the sheet is in the direction B1 × B2 (Burlaga and Ness, 1969; Knetter et al., 2004; Borovsky, 2008a). Plasma compression has been measured for corotating interaction regions by examining the change in the statistics of the current-sheet orientations (e.g., Borovsky and Denton, 2016); because corotating-interaction-region compressions are perpendicular to the Parker-spiral direction, there are straightforward expectations for the statistical change in the orientations of the current sheets vs. the amount of compression. Interplanetary shocks, however, propagate through the solar wind at a variety of directions and the expected changes in the orientations of the current sheets depend on the shock direction relative to the mean-field direction. A superior method to measure compression from interplanetary shocks is to statistically examine the angular change Δα in the current-sheet orientations from one current sheet to the next. Flattening of the magnetic structure by compression will statistically reduce the angular-change values between the normal of one current sheet and the next current sheet, regardless of the direction of the compression.
This study assumes that the strong current sheets downstream of the shocks forming part of the downstream magnetic structure are strong current sheets that were upstream of the shock forming part of the upstream magnetic structure. That assumption worked well when examining the asymmetry of current-sheet orientations when the solar wind was slowly compressed or rarefied in corotating interaction regions or high-speed-stream trailing-edge rarefactions (cf. Borovsky and Denton, 2016) and where the current-sheet did not appear to isotropize with time. For the 109 shocks, the frequency of passage of strong current sheets is higher in the downstream plasma than it is in the upstream plasma: this increase is caused by a combination of (1) the current sheets being closer together in the compressed downstream plasma, (2) the solar wind speed being faster in the downstream plasma, hence advecting structure past a spacecraft faster, and (3) a reduction of the magnetic-shear angles across current sheets in the compressed plasma. (1) and (2) act to increase the rate of passage of current sheets past a spacecraft, but (3) reduces the number of current sheets identified with the use of a fixed shear-angle criterion. If it were the case that the strong current sheets downstream of the shock were not current sheets upstream of the shock, the conclusion of the study would be the same, that the current sheets in the downstream plasma are not part of an active turbulence.
3. Results
For the 11,465 strong current sheets, the angle between one current-sheet normal and the next current-sheet normal (the “change in orientation”) Δα is plotted as the black points in Figure 3a as a function of the time from the shock crossing that the current sheet is crossed. In Figure 3b a 300-point running average of the black points in Figure 3a is plotted (black) and in Figure 3c a 300-point running median of the black points is plotted (black). As can be seen in Figures 3b,c the average of Δα and the median value of Δα both drop strongly going from the uncompressed upstream plasma (left) to the compressed downstream plasma (right). Also shown in Figure 3b are the mean values ± standard deviations for equally spaced half-hour bins (blue) and in Figure 3c the 25th (blue) and 75th (red) percentiles for half-hour bins: these values also drop going from upstream to downstream. In the 30–300 min range upstream the mean value of Δα is 35.5° and the median value of Δα is 29.9°. Note that in the uncompressed upstream plasma the current sheets are not randomly oriented, which would result in an average Δα value of 57.3° (1 radian). The current sheets are the walls of flux tubes and the flux tubes are aligned, generally, along the Parker-spiral direction with a spread in flux-tube orientations of ~35° about the Parker-spiral direction [cf. Figure 18 of Borovsky (2010)]. In the uncompressed solar wind the current-sheet normals are statistically quasi-isotropic perpendicuar to the Parker-spiral direction [cf. Figure 7d of Borovsky (2008a)], indicating that the tubes may be “cylindrical-like” in cross section, but with flattened walls owing to the tubes pressing against each other. If the flux tubes were all of the same size, one might expect a hexagonal packing. With different diameters of the flux tubes, this pressing will result in a Voronoi-like pattern of current sheets, as depicted in Figure 2 of Borovsky (2018). Note also that in crossing a flux tube, the orientations of the two walls are not independent. In the 30–300 min range downstream the mean value of Δα is 29.6° and the median value is 22.5°: this is a reduction of the mean value of Δα of 5.9° from upstream to downstream and a reduction of the median value of Δα of 7.4° from upstream to downstream. Note in the downstream plasma in Figures 3b,c that the mean and median values of Δα do not appear to be evolving with time back to the values they had in the upstream plasma: this is an indication that the current sheets are not re-isotropizing in the downstream plasma after the magnetic structure is compressed by the shock.
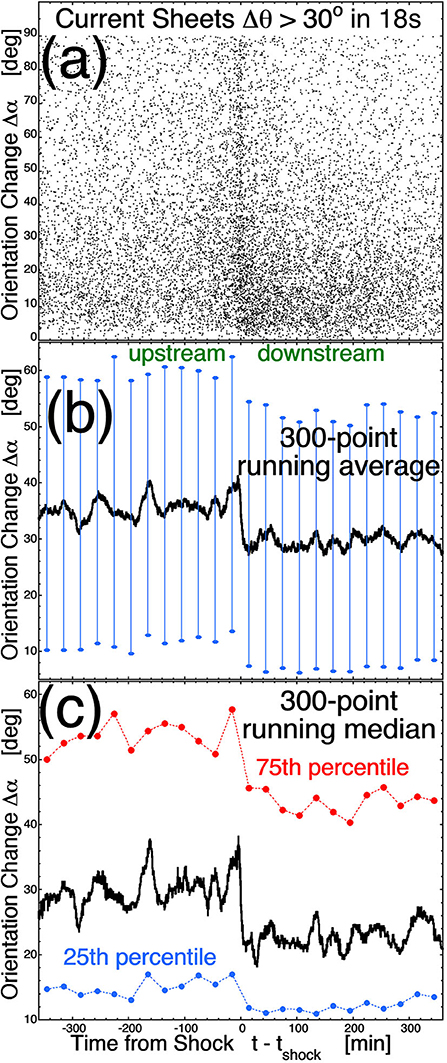
Figure 3. For 11,465 current sheets from the 109 interplanetary shocks, (a) the angle Δα between one current-sheet normal and the next current-sheet normal is plotted as a function of the time at which the sheet is seen by WIND relative to the shock-crossing time. (b) A 300-point running average of the 11,465 Δα values is plotted (black), ± one standard deviation (blue). (c) A 300-point running median (red) of the 11,465 Δα values, the 75th percentile (red) and the 25th percentile (blue).
After the interplanetary shock passes the WIND spacecraft, with increasing time the spacecraft samples downstream plasma that has been in a compressed state for a longer time. Each element of the downstream plasma had been shock-compressed for a time considerably greater than the time between the observation and the shock crossing. Using the methodology of Pitna et al. (2016), Borovsky (2020d) provided an estimate for the strong-compression shocks of the duration of time τage since the plasma was shocked: τage ~ 5.5(t-tshock), where t is the time that the spacecraft samples the element of downstream plasma and tshock is the time that the spacecraft crossed the shock. Hence an element of plasma that is seen 1 h after the shock crossing had been shocked ~5.5 h earlier than the spacecraft measured it. In Figure 4, the running average and running median of the Δα values of Figure 3b are replotted using the τage ~ 5.5(t-tshock) conversion into the time τage since the observed plasma was shock-compressed (With this modified time axis the values of Δα are plotted in the upstream plasma merely for reference). Figure 4 estimates that the Δα are not statistically evolving in the downstream plasma even 30 h or so after the solar-wind plasma is compressed by the shock.
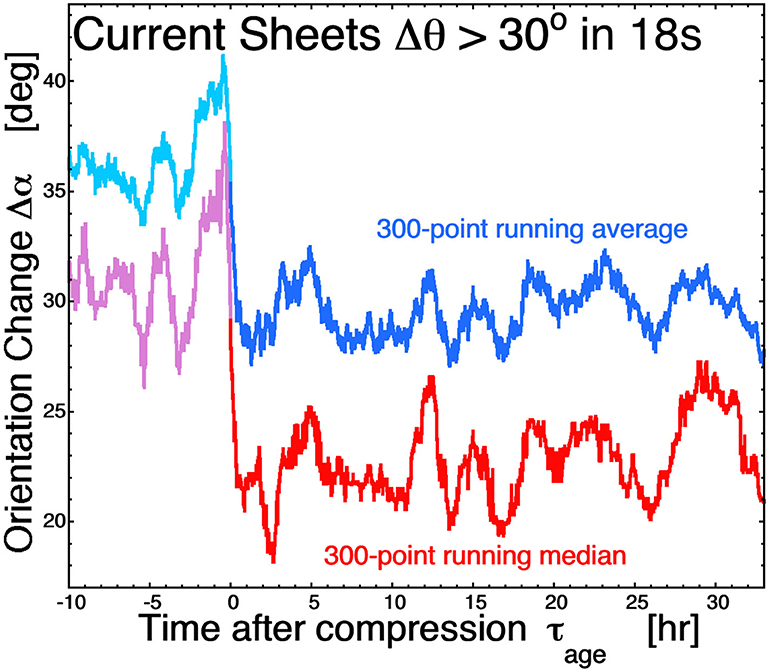
Figure 4. The curves of Figure 3b are replotted as a function of the time since each element of plasma was shock-compressed.
In Figure 5 the individual Δα values from Figure 3a are binned to form distribution functions. Plotted in rainbow colors are the 1 h-wide distributions of points downstream of the shocks, starting 30 min downstream to avoid effects near the shock. Plotted as the black dashed curve in Figure 5 is a 4 h-wide distribution of the Δα values upstream of the shock, starting 30 min upstream to avoid foreshock effects. As can be seen, the distribution of Δα values does not show any systematic evolution with time in the downstream plasma, from near the shock (red distribution) to elements of plasma that are observed ~30 h after compression by the shock (purple distribution). Like Figures 3b, 4, 5 shows no evidence that the current sheets of the solar-wind magnetic structure are becoming isotropic with time after they are made anisotropic by shock compression.
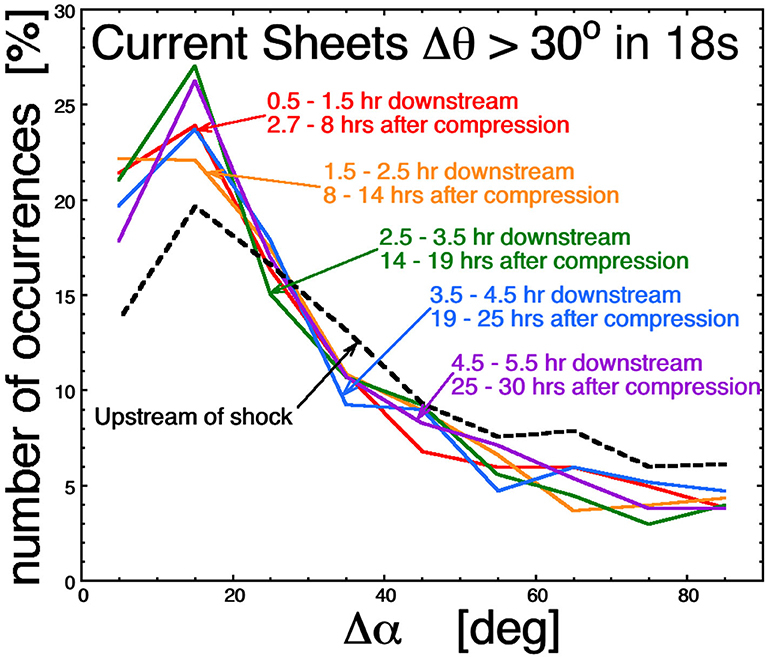
Figure 5. The distributions of change angles Δα are plotted at different times in the downstream plasmas (colors) and compared with the distribution of Δα values in the upstream plasmas (black).
In Table 1 of Borovsky (2020d) 104 of the 109 interplanetary shocks were categorized [using the Xu and Borovsky (2015) plasma-categorization scheme] according to the type of solar-wind plasma that is being shocked. The scheme categorizes the solar wind into four plasma types: coronal-hole-origin plasma, streamer-belt-origin plasma, sector-reversal-region plasma, and ejecta. Coronal-hole-origin plasma and streamer-belt-origin plasma both tend to be homogeneous plasmas with Parker-spiral-oriented magnetic fields and with prominent Alfvénic fluctuations. Sector-reversal-region plasma and ejecta both tend to be inhomogeneous plasmas with non-Parker-spiral magnetic-field orientations and with prominent non-Alfvénic fluctuations. The statistical results are independent of the type of solar-wind plasma being shocked. This is shown in Figure 6, where the mean and median values of Δα upstream and downstream of the shocks are plotted separately for Alfvénic upstream plasma (coronal-hole-origin plasma and streamer-belt-origin plasma, red curves) and for non-Alfvénic upstream plasma (sector-reversal-region plasma and ejecta, green curves).
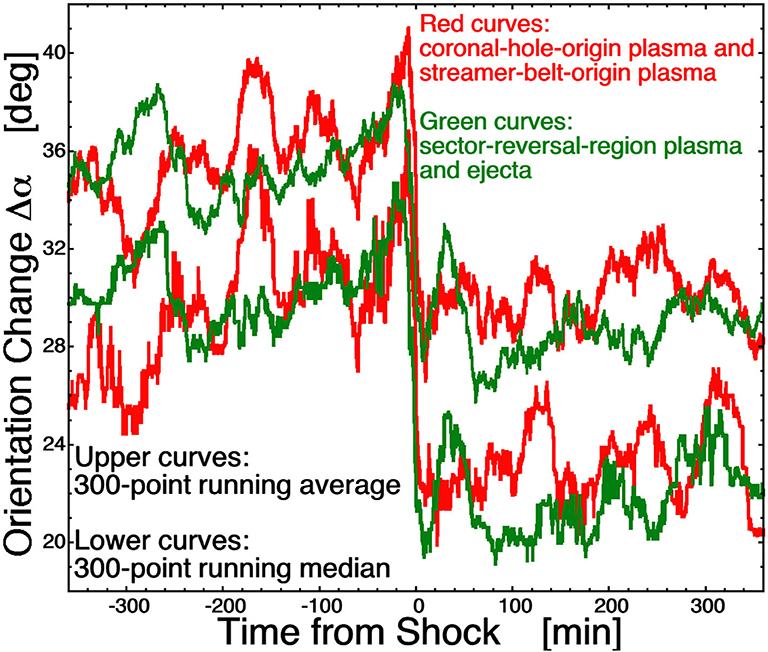
Figure 6. 300-point running averages (upper curves) and 300-point running medians (lower curves) are plotted for 57 shocks that are propagating through coronal-hole-origin plasma or streamer-belt-origin plasma (red curves) and for 47 shocks that are propagating through sector-reversal-region plasma or ejecta (green curves).
4. Conclusions
The analyses of Figures 3, 4, 5, 6 find no obvious indication that the current sheets of the compressed plasma downstream of interplanetary shocks are isotropizing with time. The analysis looks at a timescale of about 30 h after compression by shocks.
Neglecting cross-helicity effects associated with imbalanced Alfvénic fluctuations (e.g., Dobrowolny et al., 1980; Podesta, 2011), one expects the current sheets in turbulence to be destroyed and remade on a non-linear (eddy turnover) timescale τnl ≈ Leddy/δv, where Leddy is a large-eddy spatial scale and δv is the amplitude of the turbulence at the large-eddy scale. The large-eddy scale can be estimated from a correlation time or from the low-frequency breakpoint in the magnetic power spectral density. Taking the timescale of the low-frequency breakpoint in the upstream plasma to be 103−104 s (e.g., Horbury et al., 1996; Bruno et al., 2019) and a solar-wind speed of 400 km/s (cf. the upstream region of Figure 2a) yields Leddy ~ 4 × –105-4 × –106 km. Taking δv ~ vA/2 ~ 25 km/s yields τnl ~ 4–44 h in the upstream solar-wind plasma. Shock compressing the upstream plasma decreases Leddy and increases δv, and so τnl < 4–44 h in the downstream plasma. Further, the downstream plasma is systematically less Alfvénic than the upstream plasma (Borovsky, 2020d) so the lengthening of τnl by cross-helicity effects is not as applicable downstream. In an MHD-turbulence simulation based on solar-wind parameters at 1 AU, Yang et al. (2017) examined the birth-to-death lifetimes of 228 current sheets; analyzing the distribution of lifetimes in Figure 9 of Yang et al. (2017) finds the median lifetime to be ~1.5 h and the average lifetime to be ~1.9 h.
The analyses finds no indication that the current sheets of the compressed downstream plasma are isotropizing with time, up to a time of about 30 h after compression by shocks, which is estimated to be about 1–11 non-linear times and which is about 15 times longer than the ~1.9-h median lifetime of the current sheets estimated by Yang et al. (2017). If the strong current sheets of the solar wind are features of an active MHD turbulence, one would expect the current sheets to be destroyed and remade in an isotropic fashion: no evidence is found for this process in the present study. This finding agrees with an earlier analysis (Borovsky and Denton, 2016) wherein the anisotropy of solar wind current sheets in the compression regions of corotating interaction regions and in the rarefaction regions of the trailing edges of high-speed streams: that analysis found no indication of current sheets isotropizing in the 10's of hours after the solar-wind plasma is compressed or rarefacted. This may support the idea that the heliospheric magnetic structure at 1 AU and its current sheets are largely fossil structure from the solar corona (e.g., Michel, 1967; Borovsky, 2008a; Huang et al., 2014; Burkholder et al., 2019; Eselevich, 2019) or remnants of a near-Sun turbulence that ceased to be active (e.g., Dobrowolny et al., 1980; Telloni et al., 2016).
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found at: https://cdaweb.gsfc.nasa.gov.
Author Contributions
JB planned, outlined, researched, and drafted the manuscript.
Funding
This work was supported by the NASA Heliophysics Guest Investigator Program via award NNX17AB71G, by the NSF SHINE program via grant AGS-1723416, by the NASA Heliophysics LWS program via award NNX16AB75G, and by the NSF GEM Program via grant AGS-2027569. All WIND data sets utilized are available at the NASA Space Physics Data Facility https://cdaweb.gsfc.nasa.gov.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Arnold, L., Li, G., Li, X., and Yan, Y. (2013). Observation of flux-tube crossings in the solar wind. Astrophys. J. 766, 1–6. doi: 10.1088/0004-637X/766/1/2
Bartley, W. C., Bakata, R. P., McCracken, K. G., and Rao, Y. R. (1966). Anisotropic cosmic radiation fluxes of solar origin. J. Geophys. Res. 71, 3297–3304. doi: 10.1029/JZ071i013p03297
Borovsky, J. E. (2008a). The flux-tube texture of the solar wind: strands of the magnetic carpet at 1 AU? J. Geophys. Res. 113, 1–25. doi: 10.1029/2007JA012684
Borovsky, J. E. (2008b). The rudiments of a theory of solar-wind/magnetosphere coupling derived from first principles. J. Geophys. Res. 113, 1–14. doi: 10.1029/2007JA012646
Borovsky, J. E. (2010). On the variations of the solar-wind magnetic field about the Parker-spiral direction. J. Geophys. Res. 115, 1–33. doi: 10.1029/2009JA015040
Borovsky, J. E. (2012). Looking for evidence of mixing in the solar wind from 0.31 to 0.98 AU. J. Geophys. Res. 117, 1–11. doi: 10.1029/2012JA017525
Borovsky, J. E. (2018). The spatial structure of the oncoming solar wind at Earth. J. Atmos. Solar-Terr. Phys. 177, 2–11. doi: 10.1016/j.jastp.2017.03.014
Borovsky, J. E. (2020a). The Plasma and magnetic-field structure of the solar wind at inertial-range scale sizes discerned from statistical examinations of the time-series measurements. Front. Astron. Space Sci. 7:20. doi: 10.3389/fspas.2020.00020
Borovsky, J. E. (2020b). On the motion of the heliospheric magnetic structure through the solar wind plasma. J. Geophys. Res. 125, 1–14. doi: 10.1029/2019JA027377
Borovsky, J. E. (2020c). The magnetic structure of the solar wind: ionic composition and the electron strahl. Geophys. Res. Lett. 47, 1–8. doi: 10.1029/2019GL084586
Borovsky, J. E. (2020d). A statistical analysis of the fluctuations in the upstream and downstream plasmas of 109 strong-compression interplanetary shocks at 1 AU. J. Geophys. Res. 125, 1–27. doi: 10.1029/2019JA027518
Borovsky, J. E., and Denton, M. H. (2016). The trailing edges of high-speed streams at 1 AU. J. Geophys. Res. 121, 6107–6140. doi: 10.1002/2016JA022863
Borovsky, J. E., and Gary, S. P. (2009). On viscosity and the Reynolds number of MHD turbulence in collisionless plasmas: coulomb collisions, landau damping, and bohm diffusion. Phys. Plasmas 16, 1–22. doi: 10.1063/1.3155134
Bruno, R. (2019). Intermittency in solar wind turbulence from fluid to kinetic scales. Earth Space Sci. 6, 656–672. doi: 10.1029/2018EA000535
Bruno, R., and Carbone, V. (2016). Turbulence in the solar wind. Lect. Notes Phys. 928, 1–267. doi: 10.1007/978-3-319-43440-7
Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., and Bavassano, B. (2001). Identifying intermittency events in the solar wind. Planet. Space Sci. 49, 1201–1210. doi: 10.1016/S0032-0633(01)00061-7
Bruno, R., Telloni, D., Sorriso-Valvo, L., Marino, R., De Marco, R., and D'Amicis, R. (2019). The low-frequency break observed in the slow solar wind magnetic spectra. Astron. Astrophys. 627, 1–7. doi: 10.1051/0004-6361/201935841
Burkholder, B. L., Otto, A., Delamere, P. A., and Borovsky, J. E. (2019). Magnetic connectivity in the corona as a source of structure in the solar wind. J. Geophys. Res. 124, 32–49. doi: 10.1029/2018JA026132
Burlaga, L. F., and Ness, N. F. (1969). Tangential discontinuities in the solar wind. Solar Phys. 9, 467–477. doi: 10.1007/BF02391672
Carbone, V. (2012). Scalings, cascade and intermittency in solar wind turbulence. Space Sci. Rev. 172, 343–360. doi: 10.1007/s11214-012-9907-z
Clack, D., Forsyth, R. J., and Dunlop, M. W. (2000). Ulysses observations of the magnetic field structure within CIRs. Geophys. Res. Lett. 27, 625–628. doi: 10.1029/1999GL010764
Crooker, N. U., Burton, M., Phillips, J. L., Smith, E. J., and Balogh, A. (1996). Heliospheric plasma sheets as small-scale transients. J. Geophys. Res. 101, 2467–2474. doi: 10.1029/95JA03148
D'Amicis, R., Consolini, G., Bavassano, B., and Bruno, R. (2012). Conditioned analysis of high-latitude solar wind intermittency. Astrophys. J. 755, 1–7. doi: 10.1088/0004-637X/755/1/63
Dobrowolny, M., Mangeney, A., and Veltri, P. (1980). Fully developed anisotropic turbulence in interplanetary space. Phys. Rev. Lett. 45, 144–147. doi: 10.1103/PhysRevLett.45.144
Eselevich, V. G. (2019). Diamagnetic structures as a basis of quasi-stationary slow solar wind. Solar-Terr. Phys. 5, 29–41. doi: 10.12737/stp-53201904
Goldstein, M. L., Roberts, D. A., and Matthaeus, W. H. (1995). Magnetohydrodynamic turbulence in the solar wind. Ann. Rev. Astron. Astrophys. 33, 283–325. doi: 10.1146/annurev.aa.33.090195.001435
Greco, A., Matthaeus, W. H., Servidio, S., Chuychai, P., and Dmitruk, P. (2009). Statistical analysis of discontinuities in solar wind ACE data and comparison with intermittent MHD turbulence. Astrophys. J. 691, L111–L114. doi: 10.1088/0004-637X/691/2/L111
Horbury, T. S., Balogh, A., Forsyth, R. J., and Smith, E. J. (1996). The rate of turbulent evolution over the Sun's poles. Astron. Astrophys. 316, 333–341.
Huang, C., Yan, Y., Li, G., Deng, Y., and Tan, B. (2014). Tracking back the solar wind to its photospheric footpoints from Wind observations – a statistical study. Solar Phys. 289, 3109–3119. doi: 10.1007/s11207-014-0508-8
Intriligator, D. S., Rees, A., and Horbury, T. S. (2008). First analysis of planar magnetic structures associated with the halloween 2003 events from the earth to voyager 1 at 93 AU. J. Geophys. Res. 113, 1–13. doi: 10.1029/2007JA012699
Jones, G. H., and Balogh, A. (2000). Context and heliographic dependence of heliospheric planar magnetic structures. J. Geophys. Res. 105, 12713–12724. doi: 10.1029/2000JA900003
Jones, G. H., Balogh, A., and Horbury, T. S. (1999). Observations of heliospheric planar and offset-planar magnetic structure. Geophys. Res. Lett. 26, 13–16. doi: 10.1029/1998GL900258
Jones, G. H., Rees, A., Balogh, A., and Forsyth, R. J. (2002). The draping of heliospheric magnetic fields upstream of coronal mass ejecta. Geophys. Res. Lett. 29, 1–4. doi: 10.1029/2001GL014110
Kataoka, R., Watari, S., Shimada, N., Simazu, H., and Marubashi, K. (2005). Downstream structures of interplanetary fast shocks associated with coronal mass ejections. Geophys. Res. Lett. 32, 1–5. doi: 10.1029/2005GL022777
Kellogg, P. J., and Horbury, T. S. (2005). Rapid density fluctuations in the solar wind. Ann. Geophys. 23, 3765–3773. doi: 10.5194/angeo-23-3765-2005
Kennell, C. F. (1994). The magnetohydrodyanic Rankine-Hugoniot relations. AIP Conf. Proc. 314, 180–227. doi: 10.1063/1.46750
Kepko, L., and Viall, N. M. (2019). The source, significance, and magnetospheric impact of periodic density structures within stream interaction regions. J. Geophys. Res. 124, 1–22. doi: 10.1029/2019JA026962
Kilpua, E., Koskinen, H. E. J., and Pulkkinen, T. I. (2017). Coronal mass ejections and their sheath regions in interplanetary space. Living Rev. Solar Phys. 14, 1–83. doi: 10.1007/s41116-017-0009-6
Kilpua, E. K. J., Hietala, H., Koskinen, H. E. J., Fontaine, D., and Ture, L. (2013). Magnetic field and dynamic pressure ULF fluctuations in coronal-mass-ejection-driven sheath regions. Ann. Geophys. 31, 1559–1567. doi: 10.5194/angeo-31-1559-2013
Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2004). Four-point discontinuity observations using cluster magnetic field data: a statistical survey. J. Geophys. Res. 109, 1–12. doi: 10.1029/2003JA010099
Lepping, R. P., Acuna, M. H., Burlaga, L. F., Farrell, W. M., Slavin, J. A., Schatten, K. H., et al. (1995). The WIND magnetic field investigation. Space Sci. Rev. 71, 207–229. doi: 10.1007/BF00751330
Li, G. (2008). Flux tubes in the fast and slow solar wind. AIP Conf. Proc. 932, 26–31. doi: 10.1063/1.2778941
Lin, R. P., Anderson, K. A., Ashford, S., Carlson, C., Curtis, D., Ergun, R., et al. (1995). A three-dimensional plasma and energetic particle investigation for the WIND spacecraft. Space Sci. Rev. 71, 125–153. doi: 10.1007/BF00751328
MacBride, B. T., Smith, C. W., and Forman, M. A. (2008). The turbulent cascade at 1 AU: energy transfer and the third-order scaling for MHD. Astrophys. J. 679, 1644–1660. doi: 10.1086/529575
Malara, F., Primavera, L., and Veltri, P. (1996). Compressive fluctuations generated by time evolution of alfvénic perturbations in the solar wind current sheet. J. Geophys. Res. 101, 21597–21617. doi: 10.1029/96JA01637
Mariani, F., Bavassano, B., and Villante, U. (1983). A statistical study of MHD discontinuities in the inner solar system: helios 1 and 2. Solar Phys. 83, 349–365. doi: 10.1007/BF00148285
Mariani, F. B., Bavassano, U., Villante, and, Ness, N. F. (1973). Variations of the occurrence rate of discontinuities in the interplanetary magnetic field. J. Geophys. Res. 78, 8011–8022. doi: 10.1029/JA078i034p08011
McCracken, K. G., and Ness, N. F. (1966). The collimation of cosmic rays by the interplanetary magnetic field. J. Geophys. Res. 71, 3315–3318. doi: 10.1029/JZ071i013p03315
Michel, F. C. (1967). Model of solar wind structure. J. Geophys. Res. 72, 1917–1932. doi: 10.1029/JZ072i007p01917
Nakagawa, T., Kokubun, S., and Mukai, T. (2000). Plasma velocity in interplanetary magnetic structures. Adv. Space Res. 26, 811–814. doi: 10.1016/S0273-1177(00)00011-9
Nakagawa, T., Nishida, A., and Saito, T. (1989). Planar magnetic structures in the solar wind. J. Geophys. Res. 94, 11761–11775. doi: 10.1029/JA094iA09p11761
Neugebauer, M., Clay, D. R., and Gosling, J. T. (1993). The origins of planar magnetic structures in the solar wind. J. Geophys. Res. 98, 9383–9389. doi: 10.1029/93JA00216
Neugebauer, M., and Giacalone, J. (2010). Progress in the study of interplanetary discontinuities. AIP Conf. Proc. 1216, 194–197. doi: 10.1063/1.3395834
Neugebauer, M., and Giacalone, J. (2015). Energetic particles, tangential discontinuities, and solar flux tubes. J. Geophys. Res. 120, 8281–8287. doi: 10.1002/2015JA021632
Oh, S. Y., Yi, Y., and Kim, K. H. (2007). Solar cycle variation of the interplanetary forward shock drivers observed at 1 AU. Solar Phys. 245, 391–410. doi: 10.1007/s11207-007-9042-2
Owens, M. J., Wicks, R. T., and Horbury, T. S. (2011). Magnetic discontinuities in the near-Earth solar wind: evidence of in-transit turbulence or remnants of coronal structure? Solar Phys. 269, 411–420. doi: 10.1007/s11207-010-9695-0
Palmiero, E., Kilpua, E. K. J., and Savani, N. P. (2016). Planar magnetic structures in coronal mass ejection-driven sheath regions. Ann. Geophys. 34, 313–322. doi: 10.5194/angeo-34-313-2016
Paul, E. L., Atiemo-Obeng, V. A., and Kresta, S. M. (2003). Handbook of Industrial Mixing. Hoboken, NJ: Wiley-Interscience. doi: 10.1002/0471451452
Pitna, A., Safrankova, J., Nemecek, Z., Goncharov, O., Nemec, F., Prech, L., et al. (2016). Density fluctuations upstream and downstream of interplanetary shocks. Astrophys. J. 819, 1–9. doi: 10.3847/0004-637X/819/1/41
Podesta, J. J. (2010). Solar wind turbulence: advances in observation and theory. Adv. Plasma Astrophys. Proc. IAU Symp. 274, 295–301. doi: 10.1017/S1743921311007162
Podesta, J. J. (2011). On the energy cascade rate of solar wind turbulence in high cross helicity flows. J. Geophys. Res. 116, 1–10. doi: 10.1029/2010JA016306
Ruffolo, D., Seripienlert, A., Tooprakai, P., Chychai, P., and Matthaeus, W. H. (2013). Squeezing of particle distributions by expanding magnetic turbulence and space weather variability. Astrophys. J. 779, 1–6. doi: 10.1088/0004-637X/779/1/74
Russell, C. T., Blanco-Cano, X., Jian, L. K., and Luhmann, J. G. (2009). Mirror-mode storms: STEREO observations of protracted generation of small amplitude waves. Geophys. Res. Lett. 36, 1–4. doi: 10.1029/2008GL037113
Russell, C. T., Jian, L. K., Luhmann, J. G., Zhang, T. L., Neubauer, F. M., Skoug, R. M., et al. (2008). Mirror mode waves: messengers from the coronal heating region. Geophys. Res. Lett. 35, 1–4. doi: 10.1029/2008GL034096
Russell, C. T., and Mulligan, T. (2002). On the magnetosheath thicknesses of interplanetary coronal mass ejections. Planet. Space Sci. 50, 527–534. doi: 10.1016/S0032-0633(02)00031-4
Savani, N. P., Owens, M. J., Rouillard, A. P., Forsyth, R. J., Kusano, K., Shiota, D., et al. (2011). Evolution of corornal mass ejection morphology with increasing heliocentric distance. II. In situ observations. Astrophys. J. 732, 1–11. doi: 10.1088/0004-637X/732/2/117
Shaikh, Z. I., Raghav, A. N., and Vichare, G. (2019). Coexistence of a planar magnetic structure and an alfvén wave in the shock-sheath of an interplanetary coronal mass ejection. Mon. Not. Roy. Astron. Soc. 490, 1638–1643. doi: 10.1093/mnras/stz2743
Shaikh, Z. I., Raghav, A. N., and Vichare, G. (2020). Evolution of planar magnetic structure within the stream interaction region and its connection with a recurrent forbush decrease. Mon. Not. Roy. Astron. Soc. 494, 5075–5080. doi: 10.1093/mnras/staa1039
Shaikh, Z. I., Raghav, A. N., Vichare, G., Bhaskar, A., and Mishra, W. (2018). The identification of planar magnetic structure within the ICME shock sheath and its influence on galactic cosmic-ray flux. Astrophys. J. 866, 1–9. doi: 10.3847/1538-4357/aae1b1
Sorriso-Valvo, L., Marino, R., Carbone, V., Noullez, A., Lepreti, F., Veltri, P., et al. (2007). Observation of inertial energy cascade in interplanetary space. Phys. Rev. Lett. 99, 1–4. doi: 10.1103/PhysRevLett.99.115001
Stawarz, J. E., Smith, C. W., Vasaquez, B. J., Forman, M. A., and MacBride, B. T. (2010). The turbulent cascade for high cross-helicity states at 1 AU. Astrophys. J. 713, 920–934. doi: 10.1088/0004-637X/713/2/920
Telloni, D., Perri, S., Carbone, V., and Bruno, R. (2016). Selective decay and dynamic alignment in the MHD turbulence: the role of the rugged invariants. AIP Conf. Proc. 1720, 1–4. doi: 10.1063/1.4943826
Tidman, D. A., and Krall, N. A. (1971). Shock Waves in Collisionless Plasmas Sect. 1.6. New York, NY: Wiley-Interscience.
Trenchi, L., Bruno, R., D'Amicis, R., Marcucci, M. F., and Telloni, E. (2013b). Observation of IMF coherent structures and their relationship to SEP dropout events. Ann. Geophys. 31, 1333–1341. doi: 10.5194/angeo-31-1333-2013
Trenchi, L., Bruno, R., Telloni, D., D'Amicis, R., Marcucci, M. F., Zurbuchen, T. H., et al. (2013a). Solar energetic particle modulation associated with coherent magnetic structures. Astrophys. J. 770, 1–4. doi: 10.1088/0004-637X/770/1/11
Tsurutani, B. T., and Ho, C. M. (1999). A review of discontinuities and alfvén waves in interplanetary space: ULYSSES results, Rev. Geophys. 37, 517–541. doi: 10.1029/1999RG900010
Tu, C. Y., and Marsch, E. (1995). MHD structures, waves and turbulence in the solar wind. Space Sci. Rev. 73, 1–210. doi: 10.1007/BF00748891
Tu, C. Y., Wang, X., He, J., Marsch, E., and Wang, L. (2016). Two cases of convecting structure in the slow solar wind turbulence. AIP Conf. Proc. 1720, 1–4. doi: 10.1063/1.4943828
Vasquez, B. J., and Hollweg, J. V. (1999). Formation of pressure-balanced structures and fast waves from nonlinear alfvén waves. J. Geophys. Res. 104, 4681–4696. doi: 10.1029/1998JA900090
Vasquez, B. J., Smith, C. W., Hamilton, K., MacBride, B. T., and Leamon, R. J. (2007). Evaluation of the turbulent energy cascade rates from the upper inertial range in the solar wind at 1 AU. J. Geophys. Res. 112, 1–19. doi: 10.1029/2007JA012305
Viall, N. M., and Borovsky, J. E. (2020). Nine outstanding questions of solar wind physics. J. Geophys. Res. 125, 1–35. doi: 10.1029/2018JA026005
Viall, N. M., and Vourlidas, A. (2015). Periodic density structures and the origin of the slow solar wind. Astrophys. J. 807, 1–13. doi: 10.1088/0004-637X/807/2/176
Xu, F., and Borovsky, J. E. (2015). A new 4-plasma categorization scheme for the solar wind. J. Geophys. Res. 120, 70–100. doi: 10.1002/2014JA020412
Yang, L., Zhang, L., He, J., Tu, C., Li, S., Wang, X., et al. (2017). Formation and properties of tangential discontinuities in three-dimensional compressive MHD turbulence. Astrophys. J. 851, 1–9. doi: 10.3847/1538-4357/aa9993
Yao, S., He, J. S., Tu, C. Y., Wang, L. H., and Marsch, E. (2013). Small-scale pressure-balanced structures driven by mirror-mode waves in the solar wind. Astrophys. J. 776, 1–7. doi: 10.1088/0004-637X/776/2/94
Zhdankin, V., Boldyrev, S., Mason, J., and Perez, J. C. (2012). Magnetic discontinuities in magnetohydrodynamic turbulence and in the solar wind. Phys. Rev. Lett. 108, 1–5. doi: 10.1103/PhysRevLett.108.175004
Keywords: solar wind, turbulence, heliosphere, coherent structure, current sheets, solar corona
Citation: Borovsky JE (2020) The Compression of the Heliospheric Magnetic Structure by Interplanetary Shocks: Is the Structure at 1 AU a Manifestation of Solar-Wind Turbulence or Is It Fossil Structure From the Sun? Front. Astron. Space Sci. 7:582564. doi: 10.3389/fspas.2020.582564
Received: 12 July 2020; Accepted: 17 August 2020;
Published: 29 September 2020.
Edited by:
Luca Sorriso-Valvo, National Research Council, ItalyReviewed by:
Chen Shi, UCLA Department of Earth, Planetary, and Space Sciences, United StatesAlexei V. Dmitriev, Lomonosov Moscow State University, Russia
Copyright © 2020 Borovsky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph E. Borovsky, amJvcm92c2t5QHNwYWNlc2NpZW5jZS5vcmc=
 Joseph E. Borovsky
Joseph E. Borovsky