Asteroseismology of High-Mass Stars: New Insights of Stellar Interiors With Space Telescopes

Massive stars are important metal factories in the Universe. They have short and energetic lives, and many of them inevitably explode as a supernova and become a neutron star or black hole. In turn, the formation, evolution and explosive deaths of massive stars impact the surrounding interstellar medium and shape the evolution of their host galaxies. Yet the chemical and dynamical evolution of a massive star, including the chemical yield of the ultimate supernova and the remnant mass of the compact object, strongly depend on the interior physics of the progenitor star. We currently lack empirically calibrated prescriptions for various physical processes at work within massive stars, but this is now being remedied by asteroseismology. The study of stellar structure and evolution using stellar oscillations—asteroseismology—has undergone a revolution in the last two decades thanks to high-precision time series photometry from space telescopes. In particular, the long-term light curves provided by the MOST, CoRoT, BRITE, Kepler/K2, and TESS missions provided invaluable data sets in terms of photometric precision, duration and frequency resolution to successfully apply asteroseismology to massive stars and probe their interior physics. The observation and subsequent modeling of stellar pulsations in massive stars has revealed key missing ingredients in stellar structure and evolution models of these stars. Thus, asteroseismology has opened a new window into calibrating stellar physics within a highly degenerate part of the Hertzsprung–Russell diagram. In this review, I provide a historical overview of the progress made using ground-based and early space missions, and discuss more recent advances and breakthroughs in our understanding of massive star interiors by means of asteroseismology with modern space telescopes.

1. Introduction

Stars are the essential building blocks of planetary systems, stellar clusters and galaxies. The lives and energetic deaths of massive stars, i.e., those with birth masses larger than ~8 times that of the Sun (8 M_⊙)—play a pivotal role in shaping the Universe (Maeder and Meynet, 2000; Maeder, 2009; Kippenhahn et al., 2012; Langer, 2012). Massive stars were amongst the first stars in our Universe (Bromm and Larson, 2004; Bromm et al., 2009), and are progenitors of core-collapse supernovae and gamma-ray bursts (Heger et al., 2003; Smartt, 2009; Tanvir et al., 2009; Modjaz et al., 2019). The properties of massive stars allow them to be observed at large distances (see e.g., Stark, 2016), hence allow us to study the early epochs of the Universe including the re-ionization of the Universe and the formation of the first galaxies (Bromm and Larson, 2004; Robertson et al., 2010).

Massive stars typically form in dense, cold and large molecular clouds with one of the important signatures of massive star formation being giant filament structures and powerful bi-polar outflows when they are embedded in such dense clouds—see the recent review by Rosen et al. (2020). After the formation phase, massive stars enter the so-called main sequence phase of stellar evolution, which is defined by the onset of hydrogen fusion in the core via the CNO cycle whilst maintaining hydrostatic equilibrium. The length of the main sequence is governed by the nuclear time scale, with more massive stars having shorter main sequence life times. During their lives, massive stars produce intense radiation fields from their high luminosities and experience line-driven winds, which together play major roles in the shaping of their environment (Kippenhahn et al., 2012; Langer, 2012). The majority of massive stars experience an explosive death as a supernova, which provides mechanical and chemical feedback to the interstellar environment (Mac Low and Klessen, 2004; de Rossi et al., 2010; Hopkins et al., 2014; Crowther et al., 2016; Stark, 2016) and can trigger a new generation of stars and planets. The exotic compact remnants of massive star evolution are neutron stars and black holes, with the latter being end products for many of the higher-mass progenitor stars. These remnants facilitate important tests of Einstein's theory of General Relativity and the study of the Universe using gravitational waves when they coalesce (Abbott et al., 2016, 2019). Hence, understanding the evolution of massive stars and their roles as supernovae and gravitational-wave progenitors represent fundamental questions in astronomy (Smartt, 2009; Langer, 2012). It is especially important to understand massive star evolution since there is a strong dependence of a supernova's chemical yield and the mass of the remnant on the interior physics of the progenitor star (Hirschi et al., 2005; Nomoto et al., 2006; Langer, 2012; Stark, 2016), and because of the large diversity in observed supernovae light curves (Dessart and Hillier, 2019).

Despite the importance of massive stars in our Universe, their physics is not yet fully understood. There are still many questions spanning all evolutionary phases, and specifically how their formation, evolution and inevitable deaths differ to those of the more common intermediate- and low-mass stars (Langer, 2012). A major shortcoming of current stellar evolution models is that they contain large theoretical uncertainties for massive stars, which is evident already during the earliest phases of stellar evolution including the main sequence. Consequently these uncertainties propagate and strongly impact the post-main sequence stage of stellar evolution (Maeder and Meynet, 2000; Ekström et al., 2012; Chieffi and Limongi, 2013). Hence the power of models for predicting if a massive star will explode as a supernova, the corresponding chemical yield and the mass of the compact remnant are limited by the accuracy of models reproducing the observed properties of stars prior to them exploding as supernovae.

Since massive stars have convective cores and radiative envelopes during the main sequence, the physics and numerical implementation of convection and convective-boundary mixing is crucial in determining their core masses and subsequent evolution (Gabriel et al., 2014; Georgy et al., 2014; Paxton et al., 2018, 2019). The mixing profile at the interface of convective and radiative regions, and the mixing profile within the envelope directly impact the amount of hydrogen available for nuclear burning. With more internal mixing, a massive star experiences a longer main sequence and produces a larger helium core mass at the end of the main sequence since fresh hydrogen from the envelope is readily supplied to the convective core (Miglio et al., 2008b; Kippenhahn et al., 2012; Pedersen et al., 2018; Michielsen et al., 2019). In the case of single, slowly rotating and non-magnetic massive stars, it is the internal mixing profile and helium core mass that dictates the evolution beyond the main sequence and determines the ultimate end state. However, probing the physical processes beneath the opaque surfaces of massive stars is practically impossible using standard methods and techniques in astronomy, such as spectroscopy.

Rotation plays a major role among massive stars, specifically because rotationally induced mixing is expected within their interiors (Zahn, 1992; Maeder and Meynet, 2000). Yet prescriptions for such mixing profiles are currently assumed in models and controlled by numerous free parameters that have yet to be empirically calibrated. This represents a large source of uncertainty within theoretical evolution models when estimating the masses and ages of high-mass stars (see e.g., Aerts, 2020 and Serenelli et al., 2020 for recent detailed reviews). The combined influence of various rotation rates, different metallicity regimes and mass loss through stellar winds also introduce strong degeneracies within evolutionary models of massive stars (Maeder and Meynet, 2000; Georgy et al., 2011, 2013; Ekström et al., 2012; Chieffi and Limongi, 2013; Groh et al., 2019). Furthermore, based on dedicated studies, such as MiMeS (Wade et al., 2016), the BOB campaign (Morel et al., 2015), and the BRITE spectropolarimetric survey (Neiner et al., 2017), ~10% of massive stars are inferred to host a large-scale magnetic field with polar field strengths that range from ~100 G up to a few kG. The degeneracies within evolutionary models are also more complex when dealing with the presence of magnetic fields in massive stars (Alecian et al., 2014; Shultz et al., 2018; Keszthelyi et al., 2019, 2020).

It is known that many massive stars are members of multiple systems, which interact over the course of their lifetimes, so theoretical uncertainties are further compounded by the effects of binarity and mass transfer (Podsiadlowski et al., 1992; Sana et al., 2012; de Mink et al., 2013; Duchêne and Kraus, 2013; Moe and Di Stefano, 2017). However, despite the complexities associated with rotation, metallicity, mass loss and magnetic fields, massive stars in multiple systems have proven extremely useful in probing and mitigating model parameter uncertainties (Guinan et al., 2000; Hilditch et al., 2005; Torres et al., 2010; Tkachenko et al., 2014, 2016; Almeida et al., 2015; Abdul-Masih et al., 2019; Johnston et al., 2019; Mahy et al., 2020a,b). This is primarily because binary studies have the potential to provide masses and radii from the stars' relative orbital motion around a common center of mass. Moreover, accurate, absolute and model-independent masses and radii are achievable in the case of eclipsing binary systems (see e.g., Southworth et al., 2020 and Tkachenko et al., 2020) owing to the ability to simultaneously model spectroscopic radial velocities together with the eclipse depths in the light curve of a binary system.

To truly maximize the predictive power of evolutionary models for massive stars, it is essential to calibrate their physical prescriptions and parameters using stringent observational constraints on stellar interiors. One of the most successful and novel methodologies for this is called asteroseismology, which uses the resonant oscillation frequencies of stars to probe their structure—see the research monograph by Aerts et al. (2010). Until recently, most observational studies of massive stars have focused on the determination of global and/or average properties of these stars, such as the effective temperature and surface gravity derived from spectroscopy being used to estimate masses and ages. On the other hand, the recent space photometry revolution has truly brought asteroseismology to the forefront of astronomy as a means to calibrate stellar evolution theory across the Hertzsprung–Russell (HR) diagram (Chaplin and Miglio, 2013; Hekker and Christensen-Dalsgaard, 2017; García and Ballot, 2019; Aerts, 2020).

In this review, I discuss the progress that has been made in constraining the interiors of massive stars by means of asteroseismology and the space photometry revolution made possible thanks to modern space missions. In section 2, I provide a brief overview of asteroseismology, its methodology, and the types of pulsating massive stars it can be applied to. In section 3, an overview of the space telescopes that have led to the space photometry revolution is described. In section 4, I discuss the recent advances in massive star interiors made by means of asteroseismology, and section 5 describes the state-of-the-art of variability studies in some of the most massive stars. I finish by discussing the current challenges and future prospects for asteroseismology of high-mass stars in section 6.

2. Asteroseismology

A powerful method for probing and constraining the physics of stellar interiors is asteroseismology, which uses stellar oscillations to probe the physics of stellar structure (Aerts et al., 2010). The pulsation modes of stars are standing waves exhibiting nodes and anti-nodes and are described by spherical harmonics. In the case of non-rotating and non-magnetic stars, the wavefunctions of stellar pulsations are separable into the radial and angular directions. The radial parts of the wavefunction solutions are characterized by the radial order n. Whereas, the angular dependence is characterized by the angular degree ℓ (number of surface nodes), and the azimuthal order m (where |m| is the number of surface nodes that are lines of longitude). The simplest example of a pulsation mode is a radial mode for which {ℓ, m} = 0 such that the surface of a star expands and contracts during a pulsation cycle. More complex examples of pulsation modes include non-radial modes (i.e., ℓ > 0), for which the indices ℓ and m define the surface geometry of the oscillation. As an example, the axisymmetric dipole mode (i.e., {ℓ, m} = {1, 0}) has the stellar equator as a node. Thus, the northern and southern hemispheres of a star expand and contract in anti-phase with one another.

Although they have a common structure comprising a convective core and a radiative envelope during the main sequence, there are different types of pulsations that can be excited in massive stars. In general, however, the excitation mechanism of pulsation modes has been shown to be the heat-engine mechanism operating in the local maximum of the Rosseland mean opacity caused by iron-group elements—the so-called Z-bump (Dziembowski and Pamyatnykh, 1993; Dziembowski et al., 1993; Gautschy and Saio, 1993; Pamyatnykh, 1999; Miglio et al., 2007). This κ-mechanism gives rise to pulsation modes with properties and excitation physics which depend on the host star's mass, age and chemical composition. There are two main types of pulsation modes excited by the κ-mechanism in massive stars, which are defined based on their respective restoring force: pressure (p) modes and gravity (g) modes.

2.1. Pressure Modes

Pressure (p) modes are standing waves for which the pressure force acts as a restoring force (Aerts et al., 2010). Typically, p modes have high frequencies (i.e., pulsation periods of order several hours in massive stars), can be radial or non-radial and are mostly sensitive to the radiative envelopes of massive stars. For radial p modes, the entire interior of the star acts as a pulsation cavity, with the center of a star being a node and its surface an anti-node. In the cases of non-radial p modes, the depth of the pulsation cavity from the surface is determined by the local adiabatic sound speed c(r). A non-radial pulsation mode encounters an increasing c(r) when traveling inward from the stellar surface, which causes it to travel faster and be refracted. The depth a non-radial p mode can reach is called its turning radius, r_t, which is proportional to $\sqrt{\ell (\ell +1)}$ and defined outwards from the center of the star (Aerts et al., 2010). Thus, higher degree p modes have smaller pulsation cavities that are more sensitive to the stellar surface. The power of asteroseismology is that each pulsation has a cavity defined by a star's structure, such that each pulsation mode can be used as a direct probe of the physical processes at work within its cavity.

If the radial orders of p modes are sufficiently large such that the modes satisfy n ≫ ℓ, which is called the asymptotic regime, the pulsations are approximately equally-spaced in frequency (Tassoul, 1980). Deviations from a constant frequency spacing are possible, and become more prevalent for more evolved stars. During the main sequence phase of evolution the radius of a massive star increases and the core contracts, which drives the g- and p-mode pulsation cavities closer to one another as a result of an increasing Brunt-Väisälä frequency (Aerts et al., 2010). Consequently, this can cause a form of pulsation mode interaction called avoided crossings, in which p and g modes can exchange character whilst retaining their identities if their frequencies approach one another (Osaki, 1975). In more evolved cases, such as post-main sequence stars, the evanescent region between the p- and g-mode cavities inside massive stars decreases. This can allow p and g modes to couple with each other and form mixed modes, which are modes with the character of a p mode in the envelope and the character of a g mode in the deep interior (Aerts et al., 2010). The regularities of asymptotic p modes in the amplitude spectra of low- and intermediate-mass stars has greatly simplified the issue of mode identification and facilitated asteroseismology for low-mass stars (see e.g., Chaplin and Miglio, 2013; Hekker and Christensen-Dalsgaard, 2017; García and Ballot, 2019), but are rarely observed in massive stars (see e.g., Belkacem et al., 2010; Degroote et al., 2010b). Such high-radial order p modes are generally not expected for massive stars owing to the excitation physics of the κ-mechanism being inefficient in driving such modes in massive stars (Dziembowski and Pamyatnykh, 1993; Dziembowski et al., 1993; Gautschy and Saio, 1993; Pamyatnykh, 1999; Miglio et al., 2007).

In the presence of rotation the frequency degeneracy of non-radial pulsation modes with respect to m is lifted, which serves as a unique method of mode identification in certain pulsating stars. The simplest case is for stars that rotate (very) slowly and rigidly, i.e., with a uniform interior rotation angular frequency Ω—such that the splitting of non-radial pulsation frequency, ω_nℓm, is given by

$\begin{array}{ll}{\omega }_{n\ell m}={\omega }_{n\ell }+m(1-C_{n\ell })\Omega ,& (1)\end{array}$

where C_nℓ is the Ledoux constant which sets the size of the splitting due to the Coriolis force. In this idealized example, the result of Equation (1) produces a multiplet of pulsation frequencies separated by the stellar rotation frequency in the amplitude spectrum for p modes of high radial order or high-angular degree since C_nℓ ≃ 0 in such cases (Aerts et al., 2010). An example of rotationally-split quadrupole p modes is shown in Figure 1, using the example of KIC 11145123 originally discovered by Kurtz et al. (2014). The amplitude spectrum of the resultant quintuplet split by rotation shown in Figure 1 uses both 1 and 4-years light curves to emphasize the significant improvement in the resolving power of longer light curves for asteroseismic studies of rotation. Therefore, if the rotation rate is sufficiently slow, p-mode multiplets serve as a means of determining the interior rotation rates of stellar envelopes using an almost model-independent methodology.

FIGURE 1

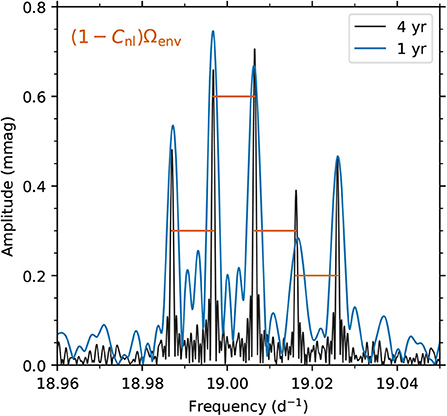
Figure 1. Example of rotational splitting of quadrupole p modes into a quintuplet using both 1 and 4-years light curves of the star KIC 11145123 (Kurtz et al., 2014). Horizontal red lines correspond to the rotational splitting value of the modes.

Beyond the first-order perturbative approach for including the Coriolis force in slow and rigid rotators given in Equation (1), second- and third-order perturbative formalisms have been discussed by, for example, Dziembowski and Goode (1992), Daszyńska-Daszkiewicz et al. (2002), and Suárez et al. (2010). As described by Suárez et al. (2010), it is important to note that the first-order perturbative treatment of the Coriolis force applied to p modes is only applicable for stars with rotation velocities below ~15% of their critical breakup velocity, with faster rotating stars requiring more complex formalisms.

2.2. Gravity Modes

Gravity (g) modes are standing waves for which buoyancy (i.e., gravity) acts as a restoring force (Aerts et al., 2010). Typically, g modes have low frequencies, can only be non-radial and are mostly sensitive to the deep interiors of massive stars near their convective cores. In the asymptotic regime, g modes are equally spaced in period (Tassoul, 1980), and exhibit a characteristic period Π₀. In the case of a non-rotating and chemically-homogeneous star, Π₀ can be calculated from the individual g-mode periods, P_{n, ℓ}, given by

$\begin{array}{ll}{P}_{n\ell }=\frac{{\Pi }_0}{\sqrt{\ell (\ell +1)}}(\left|n\right|+\alpha ),& (2)\end{array}$

in which α is a phase term independent of the mode degree, ℓ, and

$\begin{array}{ll}{\Pi }_0=2{\pi }^2{\left({\displaystyle {\int }_{r_1}^{r_2}}N(r)\frac{\text{dr}}{r}\right)}^{-1},& (3)\end{array}$

where r₁ and r₂ are the inner and outer boundaries of the g-mode pulsation cavity, and N(r) is its Brunt-Väisälä frequency. Thus, Equation (2) defines a constant spacing in period for g modes of the same angular degree, ℓ, and consecutive radial order, n. Equation (3) demonstrates that the characteristic period, Π₀, is largely determined by the Brunt-Väisälä frequency, N(r), which has a strong dependence on the mass of the convective core, and hence the mass and age of a star (Miglio et al., 2008a).

2.2.1. Interior Rotation

Since all massive stars rotate to some extent, the Coriolis force is also a dominant restoring force for g modes. Therefore, it is more appropriate to describe massive stars having gravito-inertial modes, for which both the Coriolis force and buoyancy are important. This is particularly true for pulsation modes with frequencies in the co-rotating frame below twice the rotation frequency (see Aerts et al., 2019a). As discussed in detail by Bouabid et al. (2013), the period spacing increases with period in the co-rotating frame for prograde modes, and decreases in the inertial frame. This is because in the co-rotating frame the effective ℓ(ℓ + 1) (cf. Equation 2) for prograde sectoral modes decreases with rotation due to the effect of Coriolis force. Whereas, in the inertial frame an increasing period spacing is caused by the frequency increase (i.e., period decrease) due to the effect of advection |m|Ω. Therefore, for rotating stars as viewed in the inertial frame by an observer, one expects a decreasing period spacing for prograde g modes and an increasing period spacing for retrograde g modes.

Consequently, a powerful diagnostic in interpreting the oscillation spectrum of a rotating star pulsating in g modes is its period spacing pattern, which is defined as the period differences, ΔP, of consecutive radial order (n) gravity modes of the same angular degree (ℓ) and azimuthal order (m) as a function of the pulsation mode period, P. An example of an observed period spacing pattern for a series of prograde dipole g modes in the star KIC 3459297 (Pápics et al., 2017) is shown in Figure 2, in which a fit to the g-mode period spacing pattern reveals the near-core rotation rate—see Van Reeth et al. (2016), Ouazzani et al. (2017), and Pápics et al. (2017) for the application of this technique. Under the asymptotic approximation, g modes in a non-rotating, chemically homogenous star are equally spaced in period (cf. Equation 2), yet rotation and a chemical gradient left behind from nuclear burning within a receding convective core introduce perturbations in the form of a tilt and dips, respectively (Miglio et al., 2008a; Bouabid et al., 2013). Higher rotation rates induce a larger tilt with the gradient being negative for prograde modes and positive for retrograde modes in the inertial frame.

FIGURE 2

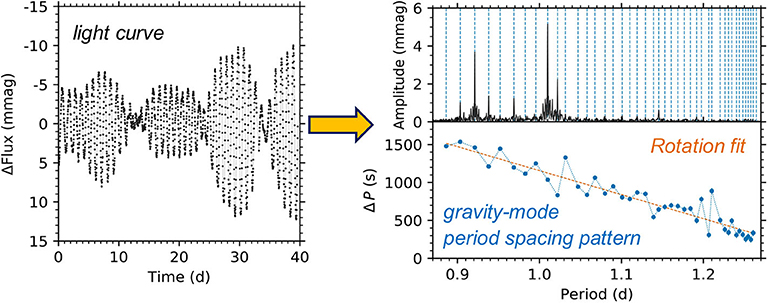
Figure 2. Schematic of the methodology of constraining interior rotation using g modes. (Left) Light curve of the Slowly Pulsating B (SPB) star KIC 3459297 pulsating in low-frequency g modes (cf. Pápics et al., 2017). (Right) Amplitude spectrum and period-spacing pattern of the prograde g-mode pulsations in the light curve are shown as the top and bottom panels, respectively. Pápics et al. (2017) determined f_rot = 0.63 ± 0.04 d⁻¹ from the g-mode period spacing pattern for KIC 3459297.

The commonly-used and mathematically appropriate approach to including rotation in the numerical computation of pulsation mode frequencies is the use of the Traditional Approximation for Rotation (TAR; Eckart, 1960; Lee and Saio, 1987a,b; Bildsten et al., 1996; Townsend, 2003b). Such a treatment of the Coriolis force is necessary for g-mode pulsators if 2Ω/ω ≳ 1 (Aerts et al., 2018). This is because high-radial order g modes in moderately and rapidly-rotating stars are in the gravito-inertial regime (Aerts et al., 2019a). Within the formalism of the TAR, the horizontal component of the rotation vector is ignored, which is a reasonable assumption for gravito-inertial modes in main sequence stars given that the Lagrangian displacement vector is predominantly horizontal. The differential equations for non-radial pulsations in rotating stars are almost equivalent to those of non-rotating stars (using the Cowling approximation) if ℓ(ℓ + 1) is replaced by the eigenvalue of the Laplace tidal equation, λ. Hence, the mathematical framework of the TAR allows the asymptotic approximation to be used for high-radial g modes in rotating stars (see Lee and Saio, 1997, Townsend, 2003b and Townsend, 2003a). Today, the TAR has been used to probe the impact of rotation on g-mode period spacing patterns both theoretically (e.g., Bouabid et al., 2013) and observationally (e.g., Van Reeth et al., 2016), and has been extended by Mathis (2009) and Mathis and Prat (2019) to take into account differential rotation and the slight deformation of stars, respectively. The TAR is implemented within the state-of-the-art pulsation code GYRE (Townsend and Teitler, 2013; Townsend et al., 2018) and has been used by various observational studies to probe (differential) rotation inside g-mode pulsators (Van Reeth et al., 2016, 2018). We refer the reader to Aerts (2020) for a detailed discussion of the TAR and its application to pulsating stars.

2.2.2. Interior Mixing

Since massive stars have convective cores and radiative envelopes during the main sequence, the physics of convection and convective-boundary mixing is crucial in determining their core masses and evolution (Kippenhahn et al., 2012). The mixing profile at the interface of convective and radiative regions, and the mixing profile within the envelope directly impact the amount of hydrogen available for nuclear burning. Mixing at the boundary of convective regions, such as near the convective core in a main sequence star, is typically implemented as overshooting in numerical codes and expressed in terms of the local pressure scale height (Freytag et al., 1996; Herwig, 2000). This is predicated on the non-zero inertia of convective bubbles at a convective boundary causing them to overshoot into a radiative layer. In massive stars, the overshooting of the convective core (also known as convective-boundary mixing) entrains hydrogen from the envelope into the core resulting in a longer main sequence lifetime and a larger helium core mass (Pedersen et al., 2018; Michielsen et al., 2019). This has a direct impact on the characteristic g-mode period, Π₀, of main-sequence stars with convective cores (Mombarg et al., 2019).

A non-zero amount of convective core overshooting is necessary when interpreting pulsations in massive stars using 1D stellar evolution codes (Dupret et al., 2004; Briquet et al., 2007; Daszyńska-Daszkiewicz et al., 2013b). Yet, the amount and shape of convective-boundary mixing remains largely unconstrained for such stars. Two examples of typical shapes of convective-boundary mixing profiles currently implemented in evolution codes include a step overshoot and an exponential overshoot (see e.g., Herwig, 2000; Paxton et al., 2015). Typically, these two prescriptions in the shape of convective core overshooting are referred to as α_ov and f_ov, respectively, in the literature and differ approximately by a factor of 10–12 (Moravveji et al., 2015). However, it is only recently that asteroseismology has demonstrated the potential to discriminate them in observations using g-mode period spacing patterns (Moravveji et al., 2015, 2016; Pedersen et al., 2018). Moreover, there is considerable ongoing work using 3D hydrodynamical simulations (Augustson and Mathis, 2019) and g-mode pulsations to probe the temperature gradient within an overshooting layer and ascertain if it is adiabatic, radiative, or intermediate between the two (Michielsen et al., 2019).

In addition to the need for convective-boundary mixing in massive stars, the origin of mixing within their radiative envelopes is also unconstrained within evolutionary models. Direct evidence for needing increased envelope mixing comes from enhanced surface nitrogen abundances in massive stars (Hunter et al., 2009; Brott et al., 2011). Since nitrogen is a by-product of the CNO cycle of nuclear fusion in a massive star (Kippenhahn et al., 2012), an efficient mixing mechanism in the stellar envelope must bring it to the surface. Rotationally-induced mixing has been proposed as a possible mechanism (Maeder and Meynet, 2000), but it is currently unable to explain observed surface nitrogen abundances in slowly-rotating massive stars in the Milky Way and low-metallicity Large Magellanic Cloud (LMC) galaxies (Hunter et al., 2008; Brott et al., 2011). Nor can rotational mixing fully explain surface abundances in massive overcontact systems (Abdul-Masih et al., 2019, 2020). Furthermore, there was no statistically-significant relationship between the observed rotation and surface nitrogen abundance in a sample of galactic massive stars studied by Aerts et al. (2014). In fact, the only robust correlation with surface nitrogen abundance in the sample was the dominant pulsation frequency (Aerts et al., 2014), which suggests that pulsations play a significant role in determining the mixing properties within the interiors of massive stars.

2.2.3. Period Spacing Patterns as Probes of Interior Rotation and Mixing

As previously illustrated in Figure 2, an observed g-mode period spacing pattern provides direct insight of the interior rotation rate of a star. Such patterns also allow the amount of interior mixing in terms of both convective core overshooting and envelope mixing to be determined. Since massive stars have a receding core whilst on the main sequence, they develop a chemical gradient in the near-core region as they evolve. Gravity modes are particularly sensitive to this molecular weight (μ) gradient and in the absence of large amounts of internal mixing this leads to mode trapping (Aerts, 2020). Thus, the g modes get trapped which leads to “dips” in the g-mode period spacing pattern on top of the overall “tilt” caused by rotation (cf. Figure 2).

An illustration of the effect of different amounts of interior mixing and rotation on the g-mode period spacing patterns of prograde dipole modes in a 12 M_⊙ star about halfway through the main sequence is shown in Figure 3. In the left column of Figure 3, the effect of increasing the amount of envelope mixing (denoted by D_mix) is shown going from top to bottom. Whereas, in the right column, the effect of increasing the amount of convective core overshooting (denoted by f_ov) is shown from top to bottom. Such values of D_mix and f_ov represent the range of values typically found by asteroseismic studies of stars with convective cores. Clearly, even for moderate values of envelope mixing (i.e., $D_{\text{mix}}\simeq 10^4$ cm² s⁻¹), the presence of dips in the g-mode period spacing pattern are strongly diminished, as shown in the bottom-left panel of Figure 3. Thus, the observed presence of strong dips in g-mode period spacing patterns already places an upper limit on the amount of envelope mixing possible in such stars. In all panels of Figure 3, three different rotation rates are shown in green, blue and red, demonstrating the significant affect of rotation for g modes, which correspond approximately to rotation frequencies of 0.0, 0.1, and 0.2 d⁻¹, respectively. The effect of rotation was calculated assuming rigid rotation using the TAR implemented in the GYRE pulsation code (Townsend and Teitler, 2013; Townsend et al., 2018).

FIGURE 3

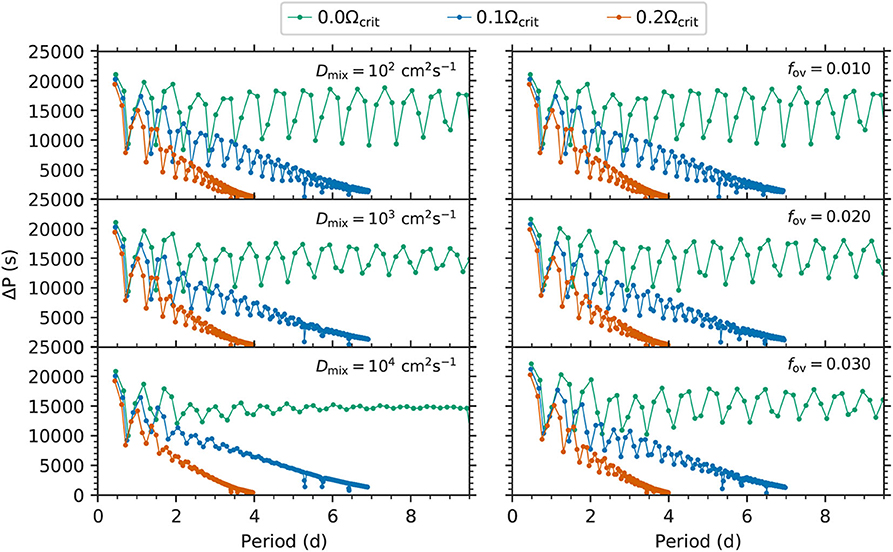
Figure 3. Theoretical g-mode period spacing patterns for prograde dipole modes of a 12 M_⊙ star about halfway through the main sequence (i.e., X_c = 0.4). The left and right columns are for different envelope mixing (D_mix) in cm² s⁻¹, and exponential convective-boundary mixing (f_ov) expressed in local pressure scale heights, respectively, calculated using the MESA stellar evolution code (Paxton et al., 2019). For each panel, three different rotation rates expressed as a fraction of the critical rotation rate, Ω_crit, calculated using the Traditional Approximation for Rotation (TAR) using the GYRE pulsation code (Townsend and Teitler, 2013) are shown.

Yet, it is possible that only some, or even none, of the pulsation modes shown in Figure 3 are observed in massive stars, since the excitation of a given pulsation mode depends on stellar parameters, including mass, age, metallicity. The example using a 12 M_⊙ shown in Figure 3 does not include any predictions of mode excitation. Nevertheless, Figure 3 serves as a schematic example of similar behavior for any main sequence star born with a convective core. In summary, the morphology of an observed g-mode period spacing pattern facilitates mode identification and offers a direct measurement of the near-core rotation and chemical mixing within a star. In practice, asteroseismology of g modes requires long-term and high-precision time series (space) photometry to extract g-mode period spacing patterns. These patterns consequently allows one to measure the interior rotation and constrain the envelope mixing of the host star, and the corresponding characteristic g-mode period, Π₀, which places constraints on its mass and age. From a large and multi-dimensional grid of stellar structure models covering the possible values of mass, age, and interior mixing parameterized by f_ov and D_mix, a quantitative comparison of observed and theoretical g-mode period spacing patterns facilitates asteroseismology to derive the interior properties of massive stars (Aerts et al., 2018).

2.3. Instability Domains of High-Mass Stars

The common interior structures of massive stars includes a convective core and radiative envelope, with pulsations in these stars being driven by the κ-mechanism operating within the local opacity enhancements caused by the Z-bump associated with iron-peak elements in their near-surface layers (Dziembowski and Pamyatnykh, 1993; Dziembowski et al., 1993; Gautschy and Saio, 1993; Pamyatnykh, 1999; Miglio et al., 2007). The depth of the Z-bump at T ≃ 200,000 K depends on the effective temperature of the star and in turn defines an upper and lower temperature boundary for the instability region of the κ-mechanism in the HR diagram, which are sometimes referred to the blue and red edges of an instability region, respectively. In addition to the mass, radius and effective temperature of a star, which define its thermal structure, the metallicity and choice of opacity table in models are also important parameters (Dziembowski and Pamyatnykh, 2008; Paxton et al., 2015; Walczak et al., 2015; Daszyńska-Daszkiewicz et al., 2017). Since the κ-mechanism operates in the Z-bump, it requires a sufficiently-large opacity enhancement to block radiation and excite coherent pulsation modes. This is supported by theoretical models of pulsation excitation, and observations which indicate a dearth of massive pulsators in low-metallicity environments, such as the LMC galaxy with Z ≃ 0.5 Z_⊙ (see e.g., Salmon et al., 2012).

Furthermore, rotation plays an important role in defining the instability regions of massive stars. From an observational perspective, moderate and fast rotation distorts the spherical symmetry of a star. This has significant implications for the spectroscopic determination of atmospheric parameters, such as the effective temperature and surface gravity, as these parameters are significantly affected by gravity darkening (von Zeipel, 1924; Townsend et al., 2004; Espinosa Lara and Rieutord, 2011). From a more theoretical perspective, the distorted spherical symmetry of rapidly-rotating stars impacts the applicability of using 1D models, and because phenomena associated with rapid rotation, such as rotationally-induced mixing, can significantly influence evolutionary tracks in the HR diagram (Maeder and Meynet, 2000; Maeder, 2009; Lovekin, 2020). Moreover, as discussed in section 2.2.1, the Coriolis force perturbs the pulsation frequencies of a rotating star and consequently also the expected parameter range of instability regions in the HR diagram (Townsend, 2005; Bouabid et al., 2013; Szewczuk and Daszyńska-Daszkiewicz, 2017).

The calculation of instability regions for stars requires non-adiabatic calculations, and specifically the calculation of a pulsation mode's growth rate (Unno et al., 1989; Aerts et al., 2010). Following the laws of thermodynamics, heat-driven pulsation modes require that heat is gained in phase with compression during a pulsation cycle. A non-adiabatic pulsation calculation yields a mode's eigenfrequency, and its imaginary component yields the growth rate. For heat-driven modes excited by the κ-mechanism, the growth rate is a positive quantity for modes that are effectively excited and negative for modes that are damped (Unno et al., 1989; Aerts et al., 2010). The instability regions of pulsations in massive stars for different masses, ages, metallicities, and rotation rates can be readily calculated for early-type stars by means of stellar structure and evolution codes, such as MESA (Paxton et al., 2011, 2013, 2015, 2018, 2019), when coupled to non-adiabatic stellar pulsation codes, such as GYRE (Townsend and Teitler, 2013; Townsend et al., 2018). We refer the reader to Moravveji (2016), Godart et al. (2017), and Szewczuk and Daszyńska-Daszkiewicz (2017) for instability regions of main-sequence massive stars calculated with and without rotation, and to Daszyńska-Daszkiewicz et al. (2013a) and Ostrowski and Daszyńska-Daszkiewicz (2015) for instability calculations for post-main sequence massive stars.

Amongst the early-type stars, there are two main groups of stars that pulsate in coherent pulsation modes excited by the κ-mechanism: the β Cephei (β Cep) stars and the Slowly Pulsating B (SPB) stars, which together span the approximate mass range from 3 to 25 M_⊙. Although not traditionally classified as a distinct pulsator group amongst massive stars, the pulsating Be stars are also discussed in this section for completeness. Pulsations in more evolved and/or more massive stars have also been detected, such as those in periodically variable supergiant (PVSG) stars (Aerts et al., 2010). However, they are not included here since there are currently very few asteroseismic studies of these objects. The reader is referred to Saio et al. (2006) and Ostrowski et al. (2017) for insightful work on the variability of such stars.

2.3.1. β Cephei Stars

The β Cephei (β Cep) stars are Population I stars with spectral types ranging from late O to early B on the main sequence, and have birth masses larger than some 8 M_⊙ and up to 25 M_⊙. They pulsate in low-radial order g and p modes excited by the κ-mechanism operating in the Z-bump (Dziembowski and Pamyatnykh, 1993), and have pulsation periods that range between about 2 and 8 h (Stankov and Handler, 2005; Pigulski and Pojmański, 2008a,b; Aerts et al., 2010). Most β Cep stars are dwarf stars, making them likely main sequence stars, although a significant fraction are giants or supergiants. Our understanding of the driving of low-radial order g modes in high-mass β Cep stars remains somewhat elusive (Handler et al., 2004, 2017; Aerts et al., 2004a), since a substantial overabundance of iron and nickel in the Z-bump is typically needed for the κ-mechanism to be efficient at exciting g modes in such stars (Pamyatnykh et al., 2004; Moravveji, 2016; Daszyńska-Daszkiewicz et al., 2017). Moreover, in addition to the mode excitation by the κ-mechanism, β Cep stars have been shown to exhibit non-linear mode excitation (Degroote et al., 2009) and stochastically-excited pulsation modes (Belkacem et al., 2009, 2010; Degroote et al., 2010b), which demonstrate that multiple pulsation driving mechanisms exist in these stars.

2.3.2. Slowly Pulsating B Stars

The Slowly Pulsating B (SPB) stars are the lower-mass counterparts of the β Cep stars, with the original definition of this type of variable star made by Waelkens (1991) although individual examples of SPB stars were known previously (e.g., 53 Persei; Smith and McCall, 1978). The SPB stars are Population I stars with spectral types that range from B3 to B9 on the main sequence, thus they have birth masses between ~3 and 8 M_⊙ (Aerts et al., 2010). They pulsate in high-radial order and predominantly prograde dipole g modes excited by the κ-mechanism operating in the Z-bump (Dziembowski et al., 1993; Gautschy and Saio, 1993) and have pulsation periods that range between a few days and several hours (Waelkens et al., 1998b; Aerts et al., 1999b; De Cat and Aerts, 2002).

2.3.3. Pulsating Be Stars

A subset of ~20% of non-supergiant massive stars are classified as Be stars (Porter and Rivinius, 2003). This group comprises stars that have shown Balmer lines in emission on at least one occasion, since such emission lines are known to be transient (Zorec and Briot, 1997; Neiner et al., 2011; Rivinius et al., 2013). The Be stars are rapid rotators with circumstellar decretion disks, and their near-critical rotation rates are thought to be related to their evolutionary history. More specifically, Be stars may have accreted mass from a companion or are the result of a stellar merger, which is supported by the relative rarity of Be stars with main-sequence companions (Bodensteiner et al., 2020). Many Be stars show evidence of pulsations and experience outbursts of material thought to be driven by pulsations (Rivinius et al., 2003; Huat et al., 2009; Kurtz et al., 2015). The pulsational behavior of Be stars is quite diverse, with such stars showing coherent g modes and stochastically excited gravito-interial waves, with the amplitude of their pulsations being connected to whether the star is mid-outburst or in quiescence (Kambe et al., 1993; Porter and Rivinius, 2003; Neiner et al., 2009, 2012b; Baade et al., 2016). Given the diverse variability seen in Be stars, it remains unclear if a single excitation mechanism is unanimously responsible for exciting pulsations in Be stars, with their fast rotation being their main common characteristic (Porter and Rivinius, 2003; Townsend et al., 2004).

3. The Space Photometry Revolution

The successful application of asteroseismology requires long-term, continuous and high-precision time series data to resolve individual pulsation mode frequencies, and perform unambiguous mode identification. As discussed in sections 2.1 and 2.2.3, mode identification using the continuous photometry provided by space telescopes can be readily achieved using rotationally-split modes and period spacing patterns, respectively. However, prior to space telescope missions different techniques were more common. Nevertheless, once mode identification has been achieved, a quantitative comparison of observed pulsation mode frequencies and those predicted by theoretical models in addition to atmospheric constraints, such as the effective temperature and metallicity from spectroscopy reveals the physics that best represents the observed star—a fitting process known as forward seismic modeling (Aerts et al., 2018).

3.1. Prior to Space Telescopes

Prior to the near-continuous photometry provided by space telescopes, pulsation modes in massive stars were identified by means high-resolution and high-cadence spectroscopic and/or photometric time series data assembled using ground-based telescopes (e.g., Smith, 1977; Waelkens, 1991; De Cat et al., 2005). In the early days of massive star asteroseismology, mode identification via spectroscopic line profile variations (LPVs) targeted the silicon triplet at 4,560 Å in slowly-rotating β Cep stars (Gies and Kullavanijaya, 1988; Aerts et al., 1992, 1994a,b; Aerts and Waelkens, 1993; Telting and Schrijvers, 1997; Telting et al., 1997; Uytterhoeven et al., 2004, 2005), whereas for SPB stars the silicon doublet at 4,130 Å was also useful (Aerts et al., 1999a; Aerts and De Cat, 2003). A spectral resolving power of at least 50,000 and a very high signal-to-noise being preferable. In fast rotating B stars, such as Be stars, these silicon multiplets can be blended and one must target isolated lines, such as the helium I 6,678 Å line (e.g., Balona and Kambe, 1999; Balona et al., 1999; Maintz et al., 2003; Štefl et al., 2003). Balmer lines are not suitable for LPV studies as they are less sensitive to the radial and non-radial velocities of pulsations since they are dominated by intrinsic (i.e., Stark) broadening. For a complete discussion of mode identification using spectroscopic time series, we refer the reader to Aerts et al. (2010).

An alternative and complementary methodology to using LPVs in the identification of pulsation modes in massive stars is to use amplitude ratios from multi-color photometry. Originally devised by Watson (1988) and Heynderickx et al. (1994), this approach was particularly effective when applied to β Cep stars owing to their relatively high amplitude and short-period pulsations. We refer the reader to Shobbrook et al. (2006), Handler et al. (2012) and Handler et al. (2017) for examples of this technique. The analysis of ground-based photometry and/or spectroscopy has been successful in demonstrating the importance of constraining parameters, such as convective core overshooting, rotation and metallicity in massive star evolution (Aerts et al., 2003; Handler et al., 2004, 2006; Briquet et al., 2007; Daszyńska-Daszkiewicz et al., 2013b; Szewczuk and Daszyńska-Daszkiewicz, 2015).

3.2. Early Space Missions

When the era of space telescopes dawned, the revolution of asteroseismology for stars across the HR diagram truly began. Space telescopes not only provide long-term and near-continuous observations of multiple stars simultaneously, but the typical precision of space-based photometry is at least two orders of magnitude better than what is possible from the ground. Such early space missions, which were not designed for asteroseismic surveys but nonetheless were extremely useful, included the Hipparcos mission (van Leeuwen et al., 1997), which discovered hundreds of pulsating B stars (Waelkens et al., 1998a; Aerts et al., 2006c; Lefèvre et al., 2009). The drastically improved time series data allowed low-amplitude pulsation modes to be detected in stars previously believed to be constant, and yielded precise pulsation frequencies in multi-periodic pulsators that are dominated by complex beating patterns (Koen and Eyer, 2002).

The first space telescope dedicated to asteroseismology was the MOST mission, which was launched in 2003 (Walker et al., 2003). The MOST spacecraft may have been a small telescope, but it detected pulsations in a wide variety of different types of variable stars. Among the massive stars, MOST studied SPB, β Cep, and Be stars (Walker et al., 2005; Aerts et al., 2006a,b; Saio et al., 2007a,b; Cameron et al., 2008), including rare instances of β Cep stars in eclipsing binary systems (Desmet et al., 2009a,c). Simultaneous MOST photometry and ground-based spectroscopy proved vital in understanding and modeling the first massive star exhibiting hybrid p- and g-mode behavior, γ Peg (Handler et al., 2009; Walczak et al., 2013). Furthermore, MOST detected pulsations in blue supergiants, such as Rigel (Saio et al., 2006; Moravveji et al., 2012), and interestingly it also detected pulsations in some Wolf-Rayet stars (Lefèvre et al., 2005; Moffat et al., 2008a) but the absence of pulsations in others (Moffat et al., 2008b). Although the time series photometry assembled by the MOST mission was limited in length, it served as a valuable proof-of-concept exercise demonstrating the power of massive star asteroseismology using space telescopes compared to facilities on the ground.

The next major milestone in the space photometry revolution was the French-led CoRoT mission launched in 2006 (Auvergne et al., 2009). The CoRoT spacecraft was a combined planet hunting and asteroseismology focused mission, which delivered short-cadence (i.e., 32 s) time series photometry for different fields of view across the sky for up to 150 days (Baglin et al., 2009). Over the mission duration, CoRoT contributed a wealth of information concerning variability in massive stars, with some aspects remaining unchallenged in quality and impact more than a decade later. The CoRoT fields of view were optimized to contain hundreds of candidate pulsating B stars (Degroote et al., 2009), which included β Cep, SPB, and Be stars (Degroote et al., 2009; Aerts et al., 2011, 2019b; Briquet et al., 2011; Pápics et al., 2011; Neiner et al., 2012b; Degroote, 2013). The mission was a great success for massive star variability studies, with CoRoT detecting regular frequency spacings in the O8.5 V star HD 46149 (Degroote et al., 2010b), and providing firm confirmation that massive stars can pulsate in both p- and g-mode frequencies (Degroote et al., 2012). Furthermore, CoRoT led to the first discovery of deviations from a constant period spacing in the B3 V star HD 50230 (Degroote et al., 2010a). In addition to high-precision asteroseismology of targeted β Cep stars (Aerts et al., 2011, 2019a), CoRoT also discovered stochastic variability caused by pulsations in massive star photospheres. This includes stochastic non-radial pulsations in B stars (Belkacem et al., 2009; Neiner et al., 2012b) and stochastic low-frequency variability in the three O stars HD 46223, HD 46150, and HD 46966 (Blomme et al., 2011; Bowman et al., 2019a).

Of all the space photometry missions available for asteroseismology, the BRITE-constellation of nanosatellites is ranked amongst the highest for providing excellent asteroseismic returns considering its budget and etendue (Weiss et al., 2014; Pablo et al., 2016). The constellation of nanosatellites from the collaboration of Austria, Poland, and Canada, was originally launched in 2013 and have provided long-term time series photometry of some of the brightest stars in the sky. This includes β Cep, SPB and Be stars (Baade et al., 2016; Pigulski et al., 2016; Daszyńska-Daszkiewicz et al., 2017; Handler et al., 2017; Walczak et al., 2019), but also pulsating stars in multiple systems (Kallinger et al., 2017; Pablo et al., 2017, 2019) and stochastic variability in O supergiants and Wolf-Rayet stars (Buysschaert et al., 2017b; Ramiaramanantsoa et al., 2018a,b, 2019). The multi-color and long-term photometry of BRITE and its observing strategy are naturally complementary to combing BRITE data with simultaneous ground-based photometry and/or spectroscopy (e.g., Handler et al., 2017).

3.3. The Kepler and K2 Missions

Perhaps the most famous of all space telescopes providing time series photometry, the Kepler space telescope was launched in 2009 and had a primary goal of finding Earth-like planets orbiting Sun-like stars (Borucki et al., 2010; Koch et al., 2010). Although by the end of the nominal Kepler mission, the 4-years light curves of more than 200,000 stars proved invaluable for asteroseismology as well as exoplanet studies. Massive stars (>8 M_⊙) were purposefully avoided by the Kepler mission since they are bright and typically saturated the CCDs, although dozens of SPB stars and rotationally-variable B stars were discovered (McNamara et al., 2012; Balona et al., 2015). Since the end of the nominal 4-years Kepler mission, the extremely high precision light curves have been used to discover and analyse rotationally-split modes and period spacing patterns of prograde dipole g modes in dozens of SPB stars (Pápics et al., 2014, 2015, 2017). Such asteroseismic studies have revealed the interior rotation rates, convective core overshooting and mixing in main-sequence B stars (Moravveji et al., 2015, 2016; Szewczuk and Daszyńska-Daszkiewicz, 2018). Despite massive stars not being included in the Kepler field of view, ingenious techniques to extract the light curves of nearby massive stars have been successful (Pope et al., 2016, 2019a), which includes the scattered-light variability of the O9.5 Iab star HD 188209 (Aerts et al., 2017).

After ~4 years the Kepler spacecraft lost a second vital reaction wheel, which meant that the field of view could not be maintained without a significant expenditure of fuel. A new mission, K2: Kepler's second light, was devised by NASA, which consisted of 80-days campaigns pointing in the direction of the ecliptic (Howell et al., 2014). Since the K2 campaign fields included young star-forming regions, a plethora of massive stars were available to study using K2 light curves. The first proof-of-concept of O-star asteroseismology was demonstrated by Buysschaert et al. (2015), which acted as an important demonstration of the feasibility of massive star asteroseismology with space photometry. The K2 mission allowed the rotation, pulsation, and binary properties of the seven sisters of the Pleiades to be studied in detail for the first time thanks to its long time base and high precision (White et al., 2017). Since the end of the K2 mission in 2018, these high-precision data have revealed dozens of previously unknown β Cep and SPB stars (Pope et al., 2016, 2019b; Burssens et al., 2019) and ubiquitous stochastic low-frequency variability in the photospheres of massive stars (Bowman et al., 2019b).

3.4. The TESS Mission

The ongoing Transiting Exoplanet Survey Satellite (TESS; Ricker et al., 2015) is currently providing high-precision and short cadence (i.e., 2 min) observations for hundreds of thousands of stars across the sky. Each ecliptic hemisphere (|b| > 6°) is divided into 13 sectors which are each observed for up to 28 days. However, there is overlap of the observational sectors near the ecliptic poles, such that stars within the TESS continuous viewing zones (CVZ) have uninterrupted light curves spanning 1 year. Such an observing strategy is optimized to find transiting exoplanets orbiting bright stars across the sky, but TESS data are also extremely valuable for massive star asteroseismology. Amongst the earliest studies of massive star variability as viewed by TESS are those by Handler et al. (2019), Bowman et al. (2019b) and Pedersen et al. (2019) in which the diverse variability of massive stars is demonstrated using a total sample of more than 200 massive stars. The study by Handler et al. (2019) considers one of the first β Cep stars observed by the TESS mission, which revealed it to be multi-periodic and subsequent asteroseismic modeling indicated it was a runaway star because of its inferred age.

Since the first 13 sectors of TESS data in the southern ecliptic hemisphere have become available, Burssens et al. (2020) have completed a census of massive star variability using TESS data, and coupled this to high-resolution spectroscopy from the IACOB (Simón-Díaz et al., 2011, 2015; Simón-Díaz and Herrero, 2014) and OWN (Barbá et al., 2010, 2014, 2017) surveys. This allowed them to place more than 100 pulsating massive stars in the spectroscopic HR diagram. A summary of the variability catalog by Burssens et al. (2020) is shown in the spectroscopic HR diagram in Figure 4, in which the observed stars are shown as green circles overlaid on top of evolutionary tracks (gray lines) and theoretical instability regions for p and g modes (blue and red hatched regions, respectively), which were calculated using the MESA evolution code (Paxton et al., 2019) and the GYRE pulsation code (Townsend and Teitler, 2013). Although there is general agreement between the observed location of pulsating stars and the predicted instability regions, the study by Burssens et al. (2020) clearly demonstrates that our understanding of the variability mechanisms in massive stars is far from complete given the overall distribution of stars within the HR diagram.

FIGURE 4

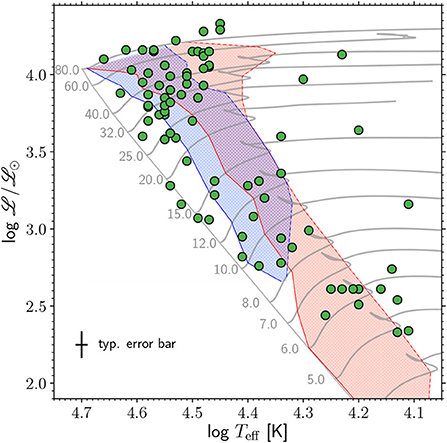
Figure 4. Spectroscopic HR diagram of the pulsating massive stars observed by TESS in its sectors 1–13, which have spectroscopic parameters derived by high-resolution spectroscopy, are shown as green circles. Note that the ordinate axis shows spectroscopic luminosity such that ${L}:=T_{\text{eff}}^4/g$ (Langer and Kudritzki, 2014). Red and blue hatched regions denote the theoretical instability regions of g and p modes, respectively, for main sequence stars. Non-rotating evolutionary tracks at solar metallicity (in units of M_⊙) are shown as solid gray lines, and a typical spectroscopic error bar is shown in the bottom-left corner. Figure adapted from Burssens et al. (2020), their Figure 3.

4. Empirical Constraints on Massive Star Interiors

In the previous section, it was described how early asteroseismic studies of massive star interiors were predominantly based on ground-based campaigns. The acquisition of these necessary data was painstakingly complex and required substantial dedication from all those involved, since it is non-trivial to collect and analyse such fragmented time series. However, despite the complications some aspects of these ground-based studies remain unrivaled to this day owing to the carefully-selected sample of stars and the relative exclusion of massive stars in later space missions. In particular, there remain only a handful of truly massive stars that have been undergone forward seismic modeling. In this section, some important case studies of pulsating massive stars that have studied using asteroseismology are presented. In particular the range of parameters that have been obtained via forward seismic modeling, where available, are summarized in Table 1, but we refer the reader to the individual studies for full details.

TABLE 1

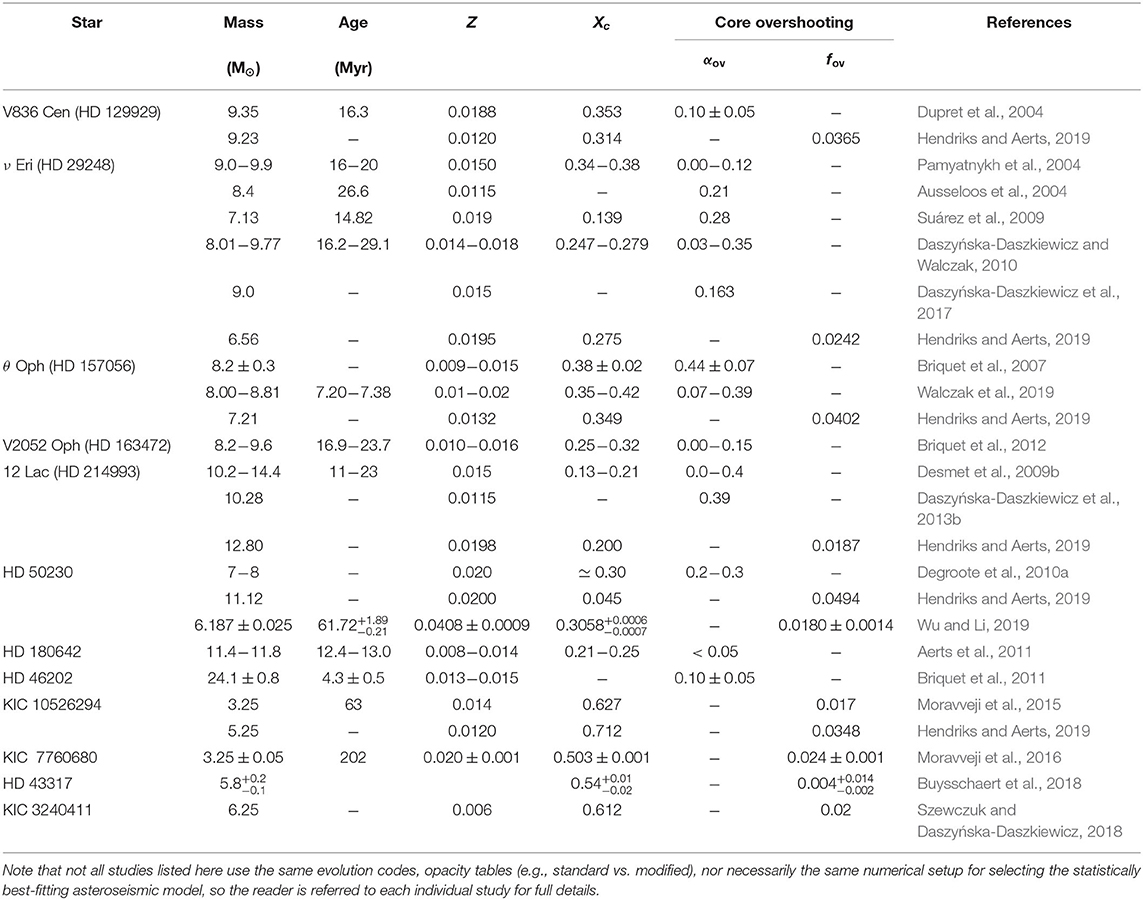
Table 1. Best-fitting parameters of high-mass stars derived from forward seismic modeling of pulsations discussed in this review.

4.1. Ground-Based Studies

The first detailed study of the interior of a massive star using asteroseismology is arguably that of the slowly-rotating B3 V star V836 Cen (HD 129929) (Aerts et al., 2003, 2004b; Dupret et al., 2004). The analysis of the extensive ground-based data set consisting of multicolor Geneva photometry and high-resolution spectroscopy revealed HD 129929 to be a multiperiodic β Cep star pulsating in low-radial order g and p modes (Aerts et al., 2003, 2004b). The rotationally-split multiplets in HD 129929 yielded a non-rigid interior rotation rate where the near-core region was determined to be rotating a factor of ~4 times faster than the envelope. This was the first measurement of the interior rotation rate of a main-sequence star. Subsequent forward seismic modeling allowed the best-fitting mass, age, metallicity, core hydrogen mass fraction, and convective core overshooting to be determined (Dupret et al., 2004), which are provided in Table 1.

An important example of extensive ground-based multicolor photometry and spectroscopy being used to probe the interior of a β Cep star is that of B2 III star ν Eri (HD 29248) (Handler and Aerts, 2002; Ausseloos et al., 2004; De Ridder et al., 2004; Handler et al., 2004; Pamyatnykh et al., 2004; Aerts et al., 2004a; Jerzykiewicz et al., 2005; Suárez et al., 2009; Daszyńska-Daszkiewicz and Walczak, 2010). At the time, and arguably still true today, ν Eri represents one of the best studied β Cep stars owing to the substantial data set having been assembled for the star. The spectroscopic and frequency analyses of this slowly-rotating (v sin i ≲ 20 km s⁻¹) star revealed rotationally-split low-radial order dipole g and p modes, and possibly high-radial order g modes (Handler et al., 2004; Aerts et al., 2004a). Forward seismic modeling of ν Eri was unable to find a satisfactory theoretical model unless an iron enhancement throughout the star, and in particular in the Z-bump, was included in the models to explain the mode excitation (Ausseloos et al., 2004; Pamyatnykh et al., 2004). The best-fitting parameters of ν Eri yielded a non-rigid interior rotation rate of ~3–5 times faster in the near-core region compared to the envelope, although this is quite uncertain given the asymmetry of the small number of rotationally-split modes available (Ausseloos et al., 2004; Pamyatnykh et al., 2004). Later, Dziembowski and Pamyatnykh (2008), Suárez et al. (2009), and Daszyńska-Daszkiewicz and Walczak (2010) revisited the modeling of ν Eri and investigated its interior rotation, overshooting and mode excitation properties based on different opacity tables, specifically focusing on the relative abundance of iron in the Z-bump. In particular, these asteroseismic modeling studies were able to produce a better fit to the observed pulsation mode frequencies using larger overshooting values and an enhancement of iron in the Z-bump, albeit at the expense of not necessarily re-producing the inferred location of the star in the HR diagram. The best-fitting parameters from these studies are provided in Table 1, although the variance in the parameters can be understood as arising from the different metallicities and opacity tables being used.

A similarly famous β Cep star is 12 Lac (B1.5 III; HD 214993), which is comparable in mass to ν Eri although it is somewhat more rapidly rotating with a projected rotational velocity of 30 ≲ v sin i ≲ 40 km s⁻¹ (Gies and Lambert, 1992; Abt et al., 2002). However, producing a satisfactory asteroseismic model for 12 Lac has been difficult owing to inconsistencies between observed and theoretically-predicted mode identifications, the consequential impact on the inferred interior rotation profile, and stellar opacity data being unable to explain the excitation of all observed pulsation mode frequencies (Aerts, 1996; Dziembowski and Jerzykiewicz, 1999; Handler et al., 2006; Dziembowski and Pamyatnykh, 2008; Desmet et al., 2009b). Despite these difficulties, Dziembowski and Pamyatnykh (2008) conclude based on the then-available observations of 12 Lac that it also exhibits an interior rotation rate of ~4–5 times faster in the near-core region compared to the envelope. Desmet et al. (2009b) were able to constrain the parameters of 12 Lac, but the most advanced study of 12 Lac to date was performed by Daszyńska-Daszkiewicz et al. (2013b), who performed mode identification, asteroseismic modeling and studied how rotation, metallicity and opacity data significantly affect the modeling results.

The slowly-rotating (v sin i ≃ 30 km s⁻¹) β Cep star θ Oph (B2 IV; HD 157056) was also subject to intense photometric campaigns to detect, extract and identify its variability (Briquet et al., 2005; Handler et al., 2005; Daszyńska-Daszkiewicz and Walczak, 2009). The frequency spectrum of θ Oph resembled that of V836 Cen in that it also contained a single radial mode and a handful of low-radial order rotationally-split multiplets, although one difference is that θ Oph is known to be a multiple system (Briquet et al., 2005). However, contrary to previous examples of β Cep stars discussed in this section, forward seismic modeling of θ Oph by Briquet et al. (2007) revealed an approximately rigid interior rotation rate and a significantly larger amount of convective core overshooting with the best-fitting model yielding α_ov = 0.44 ± 0.07. Such a high value of convective core overshooting is rare in the context of modern asteroseismology of stars with convective cores (Aerts et al., 2019a), but does highlight the trend that stellar models typically underestimate the mass of the convective cores in high-mass main-sequence stars.

A final example case study of forward seismic modeling of a slowly-rotating β Cep star based on ground-based data is the B2 IV/V star V2052 Oph (HD 163472; Briquet et al., 2012). The importance of V2052 Oph in this context is that it is a known magnetic star (Neiner et al., 2003, 2012a). A large-scale magnetic field is thought to suppress the near-core mixing caused by convective core overshooting in massive stars. The data set of V2052 Oph assembled and analyzed by Briquet et al. (2012) included more than 1300 spectra from 10 different telescopes around the world, and the resultant frequency spectrum of included a radial mode and two prograde non-radial modes identified by means of spectroscopy. Forward seismic modeling of these identified pulsation modes yielded a relatively fast rotation rate with v_eq ≃ 75 km s⁻¹, and only a small amount of convective core overshooting with α_ov ∈ [0.00, 0.15], which was concluded to be low because of the star's magnetic field (Briquet et al., 2012).

4.2. Space-Based Studies

Early space missions, such as MOST (Walker et al., 2003) have targeted massive stars for the purposes of asteroseismology. However, in this review we focus on selected case studies from the BRITE, CoRoT and Kepler missions. This is because of their high photometric precision and their long observational base lines (Auvergne et al., 2009; Baglin et al., 2009; Borucki et al., 2010; Koch et al., 2010; Weiss et al., 2014), which are necessary for successful forward seismic modeling.

The CoRoT mission provided near-continuous light curves up to 150 days in length at a cadence of 32 s, which at the time was a major revolution for asteroseismology. Early important results from the mission included the seismic modeling of the β Cep star HD 180642 (Aerts et al., 2011), and detection of the g-mode period spacing pattern in the B3 III SPB star HD 50230 (Degroote et al., 2010a). Such a g-mode period spacing pattern was a huge step forward in asteroseismology, as such patterns enable mode identification and allow interior rotation and mixing to be measured directly. Subsequent modeling of HD 50230 revealed it to be a mid-main sequence star with a mass of ~7 M_⊙, and convective core overshooting of 0.2 ≤ α_ov ≤ 0.3 (Degroote et al., 2010a). Later, Degroote et al. (2012) discovered that HD 50230 is a wide-binary system, and confirmed its ultra-slow rotation rate of v_eq ≃ 10 km s⁻¹ using spectroscopy, although they concluded that this does not impact the aforementioned g-mode period spacing pattern. More recently, Wu and Li (2019) have revisited the analysis of HD 50230 and conclude it to be a metal-rich hybrid pulsator with a modest amount of convective core overshooting.

Not long after the early studies by Degroote et al. (2010a) and Aerts et al. (2011), another important result for massive star asteroseismology from the CoRoT mission was made based on the O9 V star HD 46202 (Briquet et al., 2011). Spectroscopy of HD 46202 confirmed its literature spectral type and yielded a projected surface rotation rate of v sin i ≃25 km s⁻¹ and an effective temperature of T_eff = 34,100 ± 600 K, which makes it amongst the hottest β Cep pulsators known (Briquet et al., 2011). Several radial and non-radial pulsation modes were identified using the CoRoT photometry of HD 46202. Forward seismic modeling of these identified modes yielded a precise mass and age for this massive pulsator, confirming it as the most massive modeled β Cep star to date. A significant amount of convective core overshooting was required to fit the observed pulsation frequencies and the best-fitting asteroseismic parameters from Briquet et al. (2011) are provided in Table 1.

A third pivotal study of a massive star using asteroseismology from CoRoT data is the magnetic and fast-rotating B3.5 V star HD 43317 (Pápics et al., 2012; Briquet et al., 2013; Buysschaert et al., 2017a, 2018). This star was originally studied by Pápics et al. (2012) using the 150-d CoRoT light curve and it was concluded to exhibit g and p modes based on its frequency spectrum, since it appeared to have independent pulsation modes in both high and low frequency regimes. High-resolution spectroscopy confirmed HD 43317 as an early-type star with an effective temperature of T_eff = 17,350 ± 750 K, and as a fast rotator with a projected surface rotational velocity of v sin i = 115 ± 9 km s⁻¹ (Pápics et al., 2012). Later, HD 43317 was detected to host a large-scale magnetic field with a polar field strength of ~1.3 kG (Briquet et al., 2013; Buysschaert et al., 2017a). After revisiting the light curve with the knowledge of how such fast rotation perturbs the frequencies of g-mode pulsations in B stars (see e.g., Kurtz et al., 2015), Buysschaert et al. (2018) extracted all significant pulsation mode frequencies and performed forward seismic modeling of HD 43317 and determined its fundamental parameters, which are provided in Table 1. The small amount of convective core overshooting in the rapidly-rotating and magnetic star HD 43317 led Buysschaert et al. (2018) to a similar conclusion to that of Briquet et al. (2011) for the β Cep star V2052 Oph (cf. 4.1): the presence of a large-scale magnetic field is a plausible cause for the suppression of additional mixing (i.e., overshooting) in the near-core region.

As discussed in section 3.3, during the life time of the Kepler space mission, massive stars were avoided as targets in the field of view. Hence, whereas much of the asteroseismic inference of massive stars based on ground-based data were focused on β Cep stars, more recent asteroseismic results based on the 4-years light curves of the Kepler telescope are typically derived from SPB stars (Aerts et al., 2019a). Although not all SPB stars are “massive” stars, they do share a common interior structure whilst on the main sequence, so their discussion is relevant as part of this review.

Amongst the early days of Kepler asteroseismology, two SPB stars were identified as high priority targets: KIC 10526294 and KIC 7760680. A long series of rotationally-split g modes in the B8.3 V star KIC 10526294 allowed Pápics et al. (2014) to determine a near-core rotation period of ~188 days. Later, Moravveji et al. (2015) performed the first in-depth asteroseismic modeling of this main-sequence B star, from which it was concluded that a modest amount of exponential diffusive overshooting (i.e., f_ov) fit the Kepler data significantly better than when using the step overshooting prescription (i.e., α_ov). Furthermore, a small but non-negligible amount of additional envelope mixing (D_mix ≃ 100 cm² s⁻¹) was needed despite KIC 10526294 being an ultra-slow rotator (Moravveji et al., 2015). The best-fitting asteroseismic modeling parameters, including the measured overshooting of 0.017 ≤ f_ov ≤ 0.018, are included in Table 1. The exquisite Kepler data allowed Triana et al. (2015) to compute a near-rigid interior rotation profile through an asteroseismic inversion. Interestingly, at the 1-σ confidence level, the inversion by Triana et al. (2015) confirmed the ultra-slow rotation rate, but revealed that KIC 10526294 had a counter-rotating envelope compared to that of its core. Similar conclusions in terms of a non-negligible amount of convective core overshooting and envelope mixing were also reached for the B8 V SPB star KIC 7760680 based on the period spacing pattern of prograde dipole g modes by Moravveji et al. (2016). However, it should be noted that the uncertainties obtained by Moravveji et al. (2015) and Moravveji et al. (2016) are typically quoted as the step size within the computed grid of evolution models and may be unrealistically small, because they ignore degeneracies amongst the model parameters (see Aerts et al., 2018). There has been substantial development in the correct way to treat parameter correlations and degeneracies for asteroseismology of g-mode pulsators by moving away from the often-used χ² merit function and toward the use of the Mahalanobis distance which includes heteroscedasticity. We refer the reader to Aerts et al. (2018) for further details.

At somewhat higher masses, Szewczuk and Daszyńska-Daszkiewicz (2018) performed forward seismic modeling of the SPB star KIC 3240411 using its axisymmetric (m = 0) period spacing pattern extracted from Kepler data. KIC 3240411 was found to be a relatively young star near the zero-age main sequence with the upper limit on its convective core overshooting being f_ov ≤ 0.030. The best-fitting model parameters (i.e., model #2 in Table 2 of Szewczuk and Daszyńska-Daszkiewicz, 2018) are included in Table 1. Importantly, Szewczuk and Daszyńska-Daszkiewicz (2018) also studied the effect of rotation and opacity data within their modeling for the purposes of explaining mode excitation of high-radial order g modes in such stars. This is because the excitation of such a large number and radial order range for high-radial order g modes remains somewhat difficult to explain from a theoretical perspective.

Recently, the nanosatellites of the BRITE-constellation mission have been targeting pulsating massive stars with the aim of performing forward seismic modeling of the detected pulsation mode frequencies. Notable examples of the importance of the contribution of the BRITE mission in this aspect include ν Eri (Daszyńska-Daszkiewicz et al., 2017) and θ Oph (Walczak et al., 2019). The BRITE data marked the first time that these famous β Cep stars were observed from space, thus the first time an asteroseismic analysis of them benefitted from having near-continuous, short-cadence and long-term monitoring. Handler et al. (2017) discovered new g-mode pulsations in ν Eri using BRITE data, and Daszyńska-Daszkiewicz et al. (2017) used the extracted pulsation mode frequencies to perform forward seismic modeling. Daszyńska-Daszkiewicz et al. (2017) determined optimum parameters for ν Eri and emphasized the improvement of using modified opacity tables to explain all the observed pulsation mode frequencies. Moreover, the modified opacity data increases the efficiency of convection within the Z-bump, an effect also predicted when increasing the metallicity of the star (Cantiello et al., 2009) or increasing the rotation (Maeder et al., 2008). In the analysis of θ Oph using BRITE data, Walczak et al. (2019) discovered several g modes. From their forward seismic modeling, similar conclusions made by Daszyńska-Daszkiewicz et al. (2017) for ν Eri were made. Specifically that an increase in the mean opacity within the Z-bump is needed to explain all pulsation mode frequencies in θ Oph (Walczak et al., 2019). However, since θ Oph is a triple system with ~ 8.5 and ~ 5.5 M_⊙ primary and tertiary components, respectively, it was difficult to ascertain the origin of the g-mode frequencies (Walczak et al., 2019).

Recently, a new method of performing forward seismic modeling by means of a machine learning was developed by Hendriks and Aerts (2019). The authors trained a deep neural network using more than 62 million pulsation mode frequencies, which were calculated from a vast grid of stellar models covering main sequence intermediate- and high-mass stars spanning from 2 to 20 M_⊙. Optimum models were selected using a genetic algorithm making such an automated pipeline extremely quick compared to more conventional forward seismic modeling techniques. Hendriks and Aerts (2019) test their methodology using several well-studied massive stars to benchmark the accuracy of their technique and good agreement is found overall. However, as discussed in detail by Hendriks and Aerts (2019), the modeling results based on their deep neural network depend on the choice of hyperparameters, which affect the ability to find the global minimum in the solution space. In Table 1 the model parameters resulting from the optimized tuning of these hyperparameters are provided (cf. gray points), but such values are claimed to be an “optimal starting point” for further complex modeling. We refer the reader to Hendriks and Aerts (2019) for full details.

Asteroseismology using Kepler data has also been applied to hundreds of intermediate-mass stars covering masses between ~1 and 8 M_⊙, rotation rates up to 80% of critical, and evolutionary stages spanning from the main sequence through to the red giant branch. More specifically, g-mode period spacings have also been used to probe interior rotation in hundreds of intermediate-mass main-sequence stars, which are more commonly known as γ Dor stars (Van Reeth et al., 2015a,b, 2016, 2018; Ouazzani et al., 2017, 2019; Li et al., 2019a,b, 2020). An important conclusion from these works is that current angular momentum transport theory is erroneous by more than an order of magnitude (Aerts et al., 2019a). The situation is less clear for massive stars owing to the much smaller sample size currently available, but significant progress has already been made in recent years because of ground- and space-based data sets and asteroseismology.

The pioneering asteroseismic studies of massive stars using ground- and space-based data sets clearly demonstrate the importance of constraining the interior properties of massive stars and the effectiveness of using g-mode period spacing patterns in SPB stars and low-radial order g and p modes for β Cep stars. Thanks to the ongoing TESS mission (Ricker et al., 2015), the asteroseismic sample of pulsating massive stars has increased in size by at least two orders of magnitude (Pedersen et al., 2019; Burssens et al., 2020). Thus, detailed forward seismic modeling of many high-mass TESS targets are expected in the not-so-distant future. We refer the reader to Handler et al. (2019) for the first modeling study of a β Cep star using TESS data. Despite the relatively small sample size so far compared to intermediate-mass stars, asteroseismic studies of massive stars have demonstrated the need to include improved prescriptions for convective core overshooting and envelope mixing given that current evolution models underestimate the core masses of massive stars and consequently also their main-sequence lifetimes.

4.3. Implications of Mixing for the Post-Main Sequence

The majority of asteroseismic studies of massive stars have been of main sequence stars. Of course, based on evolutionary time scales, stars spend more than 90% of their lives in this phase (Kippenhahn et al., 2012). However, pulsating post-main sequence massive stars do exist (Saio et al., 2006; Aerts et al., 2010), and to truly understand their interior physics requires us to first understand the interiors of main-sequence stars. For example, the interplay of different mixing processes can cause some post-main sequence massive stars to undergo blue loops in the HR diagram. However, the exact nature of why some massive stars undergo blue loops and others do not remains unknown (Langer, 2012), especially given the differences in the physics and numerics in various stellar evolution codes (e.g., Martins and Palacios, 2013). It is known, however, that convection, mixing and mass loss all play significant roles in determining if stars undergo blue loops in the HR diagram and their pulsational properties (Georgy, 2012; Saio et al., 2013; Georgy et al., 2014; Wagle et al., 2019). To demonstrate how the difference in the amount of the mixing at the boundary of a convective core within a massive main-sequence star drastically impacts its post-main sequence evolution, evolutionary tracks calculated with the MESA stellar evolution code (Paxton et al., 2011, 2013, 2015, 2018, 2019; r11554) for initial masses of 12- and 13.5-M_⊙ and two moderate values for their convective core-overshooting value using the diffusive exponential prescription (i.e., f_ov) are shown in Figure 5. The evolutionary tracks shown in Figure 5 use initial hydrogen and metal mass fractions of X = 0.71 and Z = 0.02, respectively, OP opacity tables (Seaton, 2005), and the chemical mixture of Nieva and Przybilla (2012) and Przybilla et al. (2013) for cosmic B stars. As illustrated in Figure 5, only one of the four evolution tracks contains a blue loop in the post-main sequence stage of evolution.

FIGURE 5

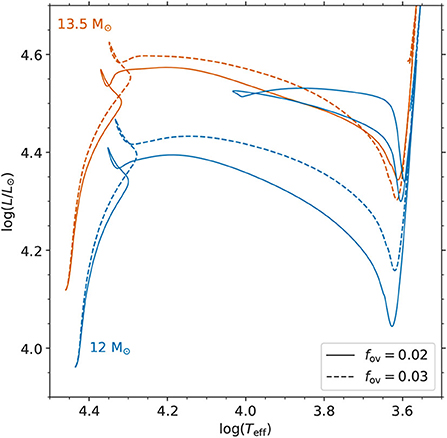
Figure 5. HR diagram containing non-rotating evolutionary tracks starting from the zero-age main-sequence for stars of initial masses of 12- and 13.5-M_⊙ calculated using the MESA stellar evolution code (Paxton et al., 2019), using two different values for the diffusive exponential convective core-overshooting value (f_ov), which are expressed in pressure scale heights. With increased mixing in the near-core region, a massive star has a longer main-sequence lifetime and produces a larger convective core mass at the terminal age main-sequence. The increased core mass and interior mixing during the main sequence phase of evolution also impacts the post-main sequence evolution of a massive star, including whether it performs a “blue loop,” which is demonstrated by the evolutionary track of the 12-M_⊙ star with f_ov = 0.02.

Currently, there exists a knowledge gap concerning the interiors of blue supergiants yet to be filled by asteroseismology. This is primarily because until recently few pulsating blue supergiants had been found within the Hertzsprung gap in the HR diagram (Bowman et al., 2019b), despite theoretical models predicting such stars should pulsate (Saio et al., 2013; Daszyńska-Daszkiewicz et al., 2013a; Ostrowski and Daszyńska-Daszkiewicz, 2015). Asteroseismology of post-main sequence massive stars represents a major future goal for the community, especially since g-mode period spacing patterns and the presence of radial p modes have the capability to distinguish shell-hydrogen burning and core-helium burning massive stars (Saio et al., 2013; Bowman et al., 2019b). Furthermore, when coupled to spectroscopic surface abundances of core-processed material (e.g., C, N, and O), convection and mixing in massive stars can be significantly improved within stellar evolution codes, which has important consequences for stars that eventually explode as a supernova (e.g., Saio et al., 1988; Georgy et al., 2014; Wagle et al., 2019). In particular, the helium core masses of post-main sequence massive stars represent a critical deliverable to the wider astronomical community as it is a fundamental parameter for predicting the chemical properties of supernovae (Smartt, 2009; Langer, 2012).

5. Diverse Photometric Variability in Massive Stars

A recent discovery made using the CoRoT, K2, and TESS missions was that the vast majority of early-type stars have significant low-frequency variability in photometry (Bowman et al., 2019a,b). Such stochastic variability is not predicted from the κ-mechanism, but is expected from convectively-driven internal gravity waves (IGWs) excited by core convection (Rogers et al., 2013; Rogers, 2015; Edelmann et al., 2019; Horst et al., 2020). 2D and 3D hydrodynamical simulations predict that IGWs reach the surface with significant amplitudes and provide detectable perturbations in temperature and velocity (Edelmann et al., 2019), and that IGWs are also extremely efficient at transporting angular momentum and chemical elements (Rogers, 2015; Rogers and McElwaine, 2017). A snapshot of a 3D simulation of IGWs propagating within a 3-M_⊙ main-sequence star from Edelmann et al. (2019) is shown in Figure 6.

FIGURE 6

Figure 6. Snapshot of a non-rotating 3D numerical simulation of gravity waves excited by core convection inside a main-sequence massive star, with a white-blue color scale indicating temperature fluctuations. Simulation courtesy of Edelmann et al. (2019).

The morphology of the low-frequency variability in more than 160 massive stars was found to be similar across a large range of masses and ages for both metal-rich galactic and metal-poor LMC stars (Bowman et al., 2019b). The insensitivity of the stochastic variability to a star's metallicity together with the fact that evolutionary timescales predicted most stars were likely on the main sequence was concluded as strong evidence that the observed stochastic variability is likely caused by IGWs excited by core convection (Bowman et al., 2019b). More recently, Bowman et al. (2020) demonstrated that the morphology of the IGWs in the frequency spectrum probes the evolutionary properties of the star, such as mass and radius. Furthermore, the amplitudes of IGWs in photometry were found to correlate with the macroturbulent broadening in the spectral lines of dozens of massive stars observed by the TESS mission (Bowman et al., 2020), with macroturbulence also having been associated with pulsations (Aerts et al., 2009; Simón-Díaz et al., 2010, 2017). Thus, mixing and angular momentum transport caused by IGWs are important to take into account when studying massive star evolution (Aerts et al., 2019a), and are currently not implemented in most stellar evolution codes.

There are currently four known excitation mechanisms that can trigger variability in early-type stars: (i) coherent p and g modes excited by the κ-mechanism (Dziembowski et al., 1993; Gautschy and Saio, 1993; Szewczuk and Daszyńska-Daszkiewicz, 2017); (ii) IGWs generated by turbulent core convection (Edelmann et al., 2019); (iii) IGWs generated by thin sub-surface convection zones (Cantiello et al., 2009); and (iv) waves generated from tides in binary systems (Fuller, 2017). Whereas, essentially all of the asteroseismic results discussed in section 4 are based on heat-driven modes, the other variability mechanisms in massive stars remain somewhat under-utilized despite having great probing power of stellar interiors. In the future, it is expected that binary asteroseismology in particular is going to play a more substantial role in providing excellent constraints of massive star interiors because recent space telescopes, such as BRITE and TESS are providing the necessary high-quality time-series observations (see e.g., Jerzykiewicz et al., 2020 and Southworth et al., 2020).

6. Conclusions and Future Prospects

Our knowledge of the interior physics of massive stars has historically been based on a handful of asteroseismic studies using time series data obtained with ground-based telescopes. Such data sets are notoriously limited by their poor duty cycles which complicates mode identification (Aerts et al., 2003; Ausseloos et al., 2004; Dupret et al., 2004; Handler et al., 2004; Pamyatnykh et al., 2004; Briquet et al., 2007, 2012; Desmet et al., 2009b; Daszyńska-Daszkiewicz et al., 2013b, 2017). These initial asteroseismic studies, however, provided the first evidence of the interior rotation profiles of massive stars and that evolutionary models of such stars lacked calibrated prescriptions for interior processes, such as convective core overshooting. Consequently standard evolutionary models typically underestimate the mass of convective cores and hence the main sequence lifetimes of massive stars. Furthermore, ground-based studies yielded the first measurements of the interior rotation rates of main sequence stars (Aerts et al., 2003), with both rigid and non-rigid rotation rates being inferred for a handful of β Cep stars (Aerts et al., 2003; Ausseloos et al., 2004; Pamyatnykh et al., 2004; Briquet et al., 2007). More recently, the MOST (Walker et al., 2003), CoRoT (Auvergne et al., 2009), Kepler/K2 (Borucki et al., 2010; Howell et al., 2014), and the ongoing BRITE-Constellation (Weiss et al., 2014) missions have advanced asteroseismic studies beyond measuring only the masses, ages and metallicities of massive stars. More advanced forward seismic modeling techniques and improved observations have constrained both macroscopic and microscopic physical processes and mechanisms inside stars, such as the amount and shape of mixing in their radiative envelopes (Moravveji et al., 2015, 2016; Buysschaert et al., 2018; Szewczuk and Daszyńska-Daszkiewicz, 2018; Walczak et al., 2019) and angular momentum transport as a function of stellar evolution (Aerts et al., 2019a).

Today, thanks to the ongoing TESS mission (Ricker et al., 2015), there is huge asteroseismic potential for massive stars as we are no longer limited by the biases of having a small sample of pulsating massive stars. The long-term and high-photometric precision provided by space telescopes is unrivaled by ground-based telescopes, and the sample of massive stars has expanded to hundreds of stars because of the all-sky TESS mission (Pedersen et al., 2019; Burssens et al., 2020). Crucially, TESS is observing massive stars which span a large range in mass and age, but also massive stars in different metallicity regimes. This is because the southern CVZ of TESS includes the LMC galaxy, which allows pulsation excitation models to be tested for metal-rich and metal-poor stars (Bowman et al., 2019b). TESS also offers the opportunity to revisit “old friends” in terms of previously studied massive stars with high-precision photometry, which is particularly useful to probe the long-term stability in pulsation mode amplitudes and frequencies in relatively short-lived stars (e.g., Neilson and Ignace, 2015). The diverse variability of massive stars, which includes both coherent pulsation modes excited by the κ-mechanism and IGWs excited by core convection (Pedersen et al., 2019; Bowman et al., 2019b; Burssens et al., 2020), enables asteroseismology for a sample of massive stars larger by two orders of magnitude compared to any that came before.

The important future goals of asteroseismic studies based on the large and diverse TESS data set include constraining the helium core masses, near-core and envelope mixing processes, interior rotation profiles and angular momentum transport mechanisms inside massive stars. Insight of the physics in the near-core region of stars above ~8 M_⊙ is currently lacking compared to intermediate- and low-mass stars (Aerts et al., 2019a). Moreover, HD 46202 remains the only massive star above 15 M_⊙ to have undergone forward seismic modeling (Briquet et al., 2011). In turn TESS data combined with high-resolution spectroscopy and asteroseismology will mitigate the currently large uncertainties in stellar evolution theory and lead to constraining why only some massive stars undergo blue loops during the post-main sequence phase of evolution (e.g., Bowman et al., 2019b), and improved predictions of supernovae chemical yields and remnant masses. The future is very bright for massive stars, and the goal to calibrate stellar structure and evolution models of massive stars using asteroseismology is now within reach.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

DB gratefully acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 670519: MAMSIE), and a senior post-doctoral fellowship from the Research Foundation Flanders (FWO) with grant agreement No. 1286521N. The Kepler, K2 and TESS data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST) at the Space Telescope Science Institute (STScI), which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support to MAST for these data is provided by the NASA Office of Space Science via grant NAG5-7584 and by other grants and contracts. Funding for the Kepler/K2 mission was provided by NASA's Science Mission Directorate. Funding for the TESS mission was provided by the NASA Explorer Program. Funding for the TESS Asteroseismic Science Operations Centre is provided by the Danish National Research Foundation (Grant agreement no.: DNRF106), ESA PRODEX (PEA 4000119301) and Stellar Astrophysics Centre (SAC) at Aarhus University. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France; the SAO/NASA Astrophysics Data System; and the VizieR catalog access tool, CDS, Strasbourg, France.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

DB was grateful to S. Burssens who graciously re-produced Figure 4 and to P. V. F. Edelmann who made Figure 6. DB was grateful to the reviewers and Prof. C. Aerts for constructive feedback. DB was also grateful to the MESA and GYRE developers, in particular B. Paxton and R. H. D. Townsend, for continually supporting the development of state-of-the-art and open-source tools for modeling massive stars. This research has made use of the PYTHON library for publication quality graphics (MATPLOTLIB; Hunter 2007) and Numpy (van der Walt et al., 2011).

References

Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016). Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116:061102. doi: 10.1103/PhysRevLett.116.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2019). GWTC-1: a gravitational-wave transient catalog of compact binary mergers observed by LIGO and virgo during the first and second observing runs. Phys. Rev. X 9:031040. doi: 10.1103/PhysRevX.9.031040

CrossRef Full Text | Google Scholar

Abdul-Masih, M., Sana, H., Conroy, K. E., Sundqvist, J., Prša, A., Kochoska, A., et al. (2020). Spectroscopic patch model for massive stars using PHOEBE II and FASTWIND. Astron. Astrophys. 636:A59. doi: 10.1051/0004-6361/201937341

CrossRef Full Text | Google Scholar

Abdul-Masih, M., Sana, H., Sundqvist, J., Mahy, L., Menon, A., Almeida, L. A., et al. (2019). Clues on the origin and evolution of massive contact binaries: atmosphere analysis of VFTS 352. Astrophys. J. 880:115. doi: 10.3847/1538-4357/ab24d4

CrossRef Full Text | Google Scholar

Abt, H. A., Levato, H., and Grosso, M. (2002). Rotational velocities of B stars. Astrophys. J. 573, 359–365. doi: 10.1086/340590

CrossRef Full Text | Google Scholar

Aerts, C. (1996). Mode identification of pulsating stars from line-profile variations with the moment method: a more accurate discriminant. Astron. Astrophys. 314, 115–122.

Google Scholar

Aerts, C. (2020). Probing the interior physics of stars through asteroseismology. arXiv[Preprint].arXiv:1912.12300.

Google Scholar

Aerts, C., Briquet, M., Degroote, P., Thoul, A., and van Hoolst, T. (2011). Seismic modelling of the β Cephei star HD 180642 (V1449 Aquilae). Astron. Astrophys. 534:A98. doi: 10.1051/0004-6361/201117629

CrossRef Full Text | Google Scholar

Aerts, C., Christensen-Dalsgaard, J., and Kurtz, D. W. (2010). Asteroseismology. Berlin: Springer.

Google Scholar

Aerts, C., De Boeck, I., Malfait, K., and De Cat, P. (1999a). HD 42927 and HD 126341: two pulsating B stars surrounded by circumstellar dust. Astron. Astrophys. 347, 524–531.

Google Scholar

Aerts, C., and De Cat, P. (2003). β Cep stars from a spectroscopic point of view. Space Sci. Rev. 105, 453–492. doi: 10.1023/A:1023983704925

CrossRef Full Text | Google Scholar

Aerts, C., De Cat, P., Handler, G., Heiter, U., Balona, L. A., Krzesinski, J., et al. (2004a). Asteroseismology of the β Cephei star ν Eridani - II. Spectroscopic observations and pulsational frequency analysis. Mon. Not. R. Astron. Soc. 347, 463–470. doi: 10.1111/j.1365-2966.2004.07215.x

CrossRef Full Text | Google Scholar

Aerts, C., De Cat, P., Kuschnig, R., Matthews, J. M., Guenther, D. B., Moffat, A. F. J., et al. (2006a). Discovery of the new slowly pulsating B star HD 163830 (B5 II/III) from MOST space-based photometry. Astrophys. J. Letters 642, L165–L168. doi: 10.1086/504634

CrossRef Full Text | Google Scholar

Aerts, C., De Cat, P., Peeters, E., Decin, L., De Ridder, J., Kolenberg, K., et al. (1999b). Selection of a sample of bright southern Slowly Pulsating B Stars for long-term photometric and spectroscopic monitoring. Astron. Astrophys. 343, 872–882.

Google Scholar

Aerts, C., de Pauw, M., and Waelkens, C. (1992). Mode identification of pulsating stars from line profile variations with the moment method. An example : the beta Cephei star delta Ceti. Astron. Astrophys. 266, 294–306.

Google Scholar

Aerts, C., Marchenko, S. V., Matthews, J. M., Kuschnig, R., Guenther, D. B., Moffat, A. F. J., et al. (2006b). δ Ceti is not monoperiodic: seismic modeling of a β Cephei star from MOST space-based photometry. Astrophys. J. 642, 470–477. doi: 10.1086/500800

CrossRef Full Text | Google Scholar

Aerts, C., Mathias, P., Gillet, D., and Waelkens, C. (1994a). Multiperiodicity and pulsation characteristics of β Cephei. Astron. Astrophys. 286, 109–120.

Google Scholar

Aerts, C., Mathis, S., and Rogers, T. M. (2019a). Angular momentum transport in stellar interiors. Ann. Rev. Astron. Astrophys. 57, 35–78. doi: 10.1146/annurev-astro-091918-104359

CrossRef Full Text | Google Scholar

Aerts, C., Molenberghs, G., Kenward, M. G., and Neiner, C. (2014). The surface nitrogen abundance of a massive star in relation to its oscillations, rotation, and magnetic field. Astrophys. J. 781:88. doi: 10.1088/0004-637X/781/2/88

CrossRef Full Text | Google Scholar

Aerts, C., Molenberghs, G., Michielsen, M., Pedersen, M. G., Björklund, R., Johnston, C., et al. (2018). Forward asteroseismic modeling of stars with a convective core from gravity-mode oscillations: parameter estimation and stellar model selection. Astrophys. J. Supp. Ser. 237:15. doi: 10.3847/1538-4365/aaccfb

CrossRef Full Text | Google Scholar

Aerts, C., Pedersen, M. G., Vermeyen, E., Hendriks, L., Johnston, C., Tkachenko, A., et al. (2019b). Combined asteroseismology, spectroscopy, and astrometry of the CoRoT B2V target HD 170580. Astron. Astrophys. 624:A75. doi: 10.1051/0004-6361/201834762

CrossRef Full Text | Google Scholar

Aerts, C., Puls, J., Godart, M., and Dupret, M.-A. (2009). Collective pulsational velocity broadening due to gravity modes as a physical explanation for macroturbulence in hot massive stars. Astron. Astrophys. 508, 409–419. doi: 10.1051/0004-6361/200810471

CrossRef Full Text | Google Scholar

Aerts, C., Símon-Díaz, S., Bloemen, S., Debosscher, J., Pápics, P. I., Bryson, S., et al. (2017). Kepler sheds new and unprecedented light on the variability of a blue supergiant: gravity waves in the O9.5Iab star HD 188209. Astron. Astrophys. 602:A32. doi: 10.1051/0004-6361/201730571

CrossRef Full Text | Google Scholar

Aerts, C., Thoul, A., Daszyńska, J., Scuflaire, R., Waelkens, C., Dupret, M. A., et al. (2003). Asteroseismology of HD 129929: core overshooting and nonrigid rotation. Science 300, 1926–1928. doi: 10.1126/science.1084993

PubMed Abstract | CrossRef Full Text | Google Scholar

Aerts, C., and Waelkens, C. (1993). Line profile variations of rotating, pulsating stars. Astron. Astrophys. 273, 135–146.

Google Scholar

Aerts, C., Waelkens, C., Daszyńska-Daszkiewicz, J., Dupret, M.-A., Thoul, A., Scuflaire, R., et al. (2004b). Asteroseismology of the β Cep star HD 129929. I. Observations, oscillation frequencies and stellar parameters. Astron. Astrophys. 415, 241–249. doi: 10.1051/0004-6361:20034142

CrossRef Full Text | Google Scholar

Aerts, C., Waelkens, C., De Cat, P., Kolenberg, K., Kestens, E., Grenon, M., et al. (2006c). Pulsating B stars discovered by HIPPARCOS. J. Am. Assoc. Var. Star Observ. 35:58.

Google Scholar

Aerts, C., Waelkens, C., and de Pauw, M. (1994b). Mode identification with the moment method in four multiperiodic β Cephei stars: KK Velorum, ν Eri, β CMa, and V348 Normae. Astron. Astrophys. 286, 136–148.

Google Scholar

Alecian, E., Kochukhov, O., Petit, V., Grunhut, J., Landstreet, J., Oksala, M. E., et al. (2014). Discovery of new magnetic early-B stars within the MiMeS HARPSpol survey. Astron. Astrophys. 567:A28. doi: 10.1051/0004-6361/201323286

CrossRef Full Text | Google Scholar

Almeida, L. A., Sana, H., de Mink, S. E., Tramper, F., Soszyński, I., Langer, N., et al. (2015). Discovery of the massive overcontact binary VFTS352: evidence for enhanced internal mixing. Astrophys. J. 812:102. doi: 10.1088/0004-637X/812/2/102

CrossRef Full Text | Google Scholar

Augustson, K. C., and Mathis, S. (2019). A model of rotating convection in stellar and planetary interiors. I. Convective Penetration. Astrophys. J. 874:83. doi: 10.3847/1538-4357/ab0b3d

CrossRef Full Text | Google Scholar

Ausseloos, M., Scuflaire, R., Thoul, A., and Aerts, C. (2004). Asteroseismology of the β Cephei star ν Eridani: massive exploration of standard and non-standard stellar models to fit the oscillation data. Mon. Not. R. Astron. Soc. 355, 352–358. doi: 10.1111/j.1365-2966.2004.08320.x

CrossRef Full Text | Google Scholar

Auvergne, M., Bodin, P., Boisnard, L., Buey, J.-T., Chaintreuil, S., Epstein, G., et al. (2009). The CoRoT satellite in flight: description and performance. Astron. Astrophys. 506, 411–424. doi: 10.1051/0004-6361/200810860

CrossRef Full Text | Google Scholar

Baade, D., Rivinius, T., Pigulski, A., Carciofi, A. C., Martayan, C., Moffat, A. F. J., et al. (2016). Short-term variability and mass loss in Be stars. I. BRITE satellite photometry of η and μ Centauri. Astron. Astrophys. 588:A56. doi: 10.1051/0004-6361/201528026

CrossRef Full Text | Google Scholar

Baglin, A., Auvergne, M., Barge, P., Deleuil, M., Michel, E., and CoRoT Exoplanet Science Team (2009). “CoRoT: description of the mission and early results,” In Transiting Planets, Vol. 253 of IAU Symposium, eds F. Pont, D. Sasselov, and M. J. Holman, 71–81. doi: 10.1017/S1743921308026252

CrossRef Full Text | Google Scholar

Balona, L. A., Aerts, C., and Štefl, S. (1999). Simultaneous photometry and spectroscopy of the Be star 28 (omega) CMa–II. Line profile modelling. Mon. Not. R. Astron. Soc. 305, 519–526. doi: 10.1046/j.1365-8711.1999.02386.x

CrossRef Full Text | Google Scholar

Balona, L. A., Baran, A. S., Daszyńska-Daszkiewicz, J., and De Cat, P. (2015). Analysis of Kepler B stars: rotational modulation and Maia variables. Mon. Not. R. Astron. Soc. 451, 1445–1459. doi: 10.1093/mnras/stv1017

CrossRef Full Text | Google Scholar

Balona, L. A., and Kambe, E. (1999). On the moving subfeatures in the Be star ζ OPH. Mon. Not. R. Astron. Soc. 308, 1117–1125. doi: 10.1046/j.1365-8711.1999.02770.x

CrossRef Full Text | Google Scholar

Barbá, R., Gamen, R., Arias, J. I., Morrell, N., Walborn, N. R., Maíz Apellániz, J., et al. (2014). “OWN survey: results after seven years of high-resolution spectroscopic monitoring of Southern O and WN stars,” in Revista Mexicana de Astronomia y Astrofisica Conference Series. Vol. 44 of Revista Mexicana de Astronomia y Astrofisica Conference Series, 148–148.

Google Scholar

Barbá, R. H., Gamen, R., Arias, J. I., Morrell, N., Maíz Apellániz, J., Alfaro, E., et al. (2010). “Spectroscopic survey of galactic O and WN stars. OWN survey: new binaries and trapezium-like systems,” in Revista Mexicana de Astronomia y Astrofisica Conference Series. Vol. 38 of Revista Mexicana de Astronomia y Astrofisica Conference Series, 30–32.

Google Scholar

Barbá, R. H., Gamen, R., Arias, J. I., and Morrell, N. I. (2017). “OWN survey: a spectroscopic monitoring of Southern Galactic O and WN-type stars,” in The Lives and Death-Throes of Massive Stars, Vol. 329 of IAU Symposium, eds. J. J. Eldridge, J. C. Bray, L. A. S. McClelland, and L. Xiao, 89–96. doi: 10.1017/S1743921317003258

CrossRef Full Text | Google Scholar

Belkacem, K., Dupret, M. A., and Noels, A. (2010). Solar-like oscillations in massive main-sequence stars. I. Asteroseismic signatures of the driving and damping regions. Astron. Astrophys. 510:A6. doi: 10.1051/0004-6361/200913221

CrossRef Full Text | Google Scholar

Belkacem, K., Samadi, R., Goupil, M.-J., Lefèvre, L., Baudin, F., Deheuvels, S., et al. (2009). Solar-like oscillations in a massive star. Science 324:1540. doi: 10.1126/science.1171913

PubMed Abstract | CrossRef Full Text | Google Scholar

Bildsten, L., Ushomirsky, G., and Cutler, C. (1996). Ocean g-modes on rotating neutron stars. Astrophys. J. 460:827. doi: 10.1086/177012

CrossRef Full Text

Blomme, R., Mahy, L., Catala, C., Cuypers, J., Gosset, E., Godart, M., et al. (2011). Variability in the CoRoT photometry of three hot O-type stars. HD 46223, HD 46150, and HD 46966. Astron. Astrophys. 533:A4. doi: 10.1051/0004-6361/201116949

CrossRef Full Text | Google Scholar

Bodensteiner, J., Shenar, T., and Sana, H. (2020). Investigating the lack of main-sequence companions to massive Be stars. arXiv 641, A42. doi: 10.1051/0004-6361/202037640

CrossRef Full Text | Google Scholar

Borucki, W. J., Koch, D., Basri, G., Batalha, N., Brown, T., Caldwell, D., et al. (2010). Kepler planet-detection mission: introduction and first results. Science 327:977. doi: 10.1126/science.1185402

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouabid, M.-P., Dupret, M.-A., Salmon, S., Montalbán, J., Miglio, A., and Noels, A. (2013). Effects of the Coriolis force on high-order g modes in γ Doradus stars. Mon. Not. R. Astron. Soc. 429, 2500–2514. doi: 10.1093/mnras/sts517

CrossRef Full Text | Google Scholar

Bowman, D. M., Aerts, C., Johnston, C., Pedersen, M. G., Rogers, T. M., Edelmann, P. V. F., et al. (2019a). Photometric detection of internal gravity waves in upper main-sequence stars. I. Methodology and application to CoRoT targets. Astron. Astrophys. 621:A135. doi: 10.1051/0004-6361/201833662

CrossRef Full Text | Google Scholar

Bowman, D. M., Burssens, S., Pedersen, M. G., Johnston, C., Aerts, C., Buysschaert, B., et al. (2019b). Low-frequency gravity waves in blue supergiants revealed by high-precision space photometry. Nat. Astron. 3, 760–765. doi: 10.1038/s41550-019-0768-1

CrossRef Full Text | Google Scholar

Bowman, D. M., Burssens, S., Simón-Díaz, S., Edelmann, P. V. F., Rogers, T. M., Horst, L., et al. (2020). Photometric detection of internal gravity waves in upper main-sequence stars. II. Combined TESS photometry and high-resolution spectroscopy. Astron. Astrophys. 640:A36. doi: 10.1051/0004-6361/202038224

CrossRef Full Text | Google Scholar

Briquet, M., Aerts, C., Baglin, A., Nieva, M. F., Degroote, P., Przybilla, N., et al. (2011). An asteroseismic study of the O9V star HD 46202 from CoRoT space-based photometry. Astron. Astrophys. 527:A112. doi: 10.1051/0004-6361/201015690

CrossRef Full Text | Google Scholar

Briquet, M., Lefever, K., Uytterhoeven, K., and Aerts, C. (2005). An asteroseismic study of the β Cephei star θ Ophiuchi: spectroscopic results. Mon. Not. R. Astron. Soc. 362, 619–625. doi: 10.1111/j.1365-2966.2005.09287.x

CrossRef Full Text | Google Scholar

Briquet, M., Morel, T., Thoul, A., Scuflaire, R., Miglio, A., Montalbán, J., et al. (2007). An asteroseismic study of the β Cephei star θ Ophiuchi: constraints on global stellar parameters and core overshooting. Mon. Not. R. Astron. Soc. 381, 1482–1488. doi: 10.1111/j.1365-2966.2007.12142.x

CrossRef Full Text | Google Scholar

Briquet, M., Neiner, C., Aerts, C., Morel, T., Mathis, S., Reese, D. R., et al. (2012). Multisite spectroscopic seismic study of the β Cep star V2052 Ophiuchi: inhibition of mixing by its magnetic field. Mon. Not. R. Astron. Soc. 427, 483–493. doi: 10.1111/j.1365-2966.2012.21933.x

CrossRef Full Text | Google Scholar

Briquet, M., Neiner, C., Leroy, B., Pápics, P. I., and MiMeS Collaboration (2013). Discovery of a magnetic field in the CoRoT hybrid B-type pulsator HD 43317. Astron. Astrophys. 557:L16. doi: 10.1051/0004-6361/201321779

CrossRef Full Text | Google Scholar

Bromm, V., and Larson, R. B. (2004). The first stars. Ann. Rev. Astron. Astrophys. 42, 79–118. doi: 10.1146/annurev.astro.42.053102.134034

CrossRef Full Text | Google Scholar

Bromm, V., Yoshida, N., Hernquist, L., and McKee, C. F. (2009). The formation of the first stars and galaxies. Nature 459, 49–54. doi: 10.1038/nature07990

PubMed Abstract | CrossRef Full Text | Google Scholar

Brott, I., Evans, C. J., Hunter, I., de Koter, A., Langer, N., Dufton, P. L., et al. (2011). Rotating massive main-sequence stars. II. Simulating a population of LMC early B-type stars as a test of rotational mixing. Astron. Astrophys. 530:A116. doi: 10.1051/0004-6361/201016114

CrossRef Full Text | Google Scholar

Burssens, S., Bowman, D. M., Aerts, C., Pedersen, M. G., Moravveji, E., and Buysschaert, B. (2019). New β Cep pulsators discovered with K2 space photometry. Mon. Not. R. Astron. Soc. 489, 1304–1320. doi: 10.1093/mnras/stz2165

CrossRef Full Text | Google Scholar

Burssens, S., Simón-Díaz, S., Bowman, D. M., Holgado, G., Michielsen, M., de Burgos, A., et al. (2020). Variability of OB stars from TESS southern Sectors 1-13 and high-resolution IACOB and OWN spectroscopy. Astron. Astrophys. 639:A81. doi: 10.1051/0004-6361/202037700

CrossRef Full Text | Google Scholar

Buysschaert, B., Aerts, C., Bloemen, S., Debosscher, J., Neiner, C., Briquet, M., et al. (2015). Kepler's first view of O-star variability: K2 data of five O stars in Campaign 0 as a proof of concept for O-star asteroseismology. Mon. Not. R. Astron. Soc. 453, 89–100. doi: 10.1093/mnras/stv1572

CrossRef Full Text | Google Scholar

Buysschaert, B., Aerts, C., Bowman, D. M., Johnston, C., Van Reeth, T., Pedersen, M. G., et al. (2018). Forward seismic modeling of the pulsating magnetic B-type star HD 43317. Astron. Astrophys. 616:A148. doi: 10.1051/0004-6361/201832642

CrossRef Full Text | Google Scholar

Buysschaert, B., Neiner, C., Briquet, M., and Aerts, C. (2017a). Magnetic characterization of the SPB/β Cep hybrid pulsator HD 43317. Astron. Astrophys. 605:A104. doi: 10.1051/0004-6361/201731012

CrossRef Full Text | Google Scholar

Buysschaert, B., Neiner, C., Richardson, N. D., Ramiaramanantsoa, T., David-Uraz, A., Pablo, H., et al. (2017b). Studying the photometric and spectroscopic variability of the magnetic hot supergiant ζ Orionis Aa. Astron. Astrophys. 602:A91. doi: 10.1051/0004-6361/201630318

CrossRef Full Text | Google Scholar

Cameron, C., Saio, H., Kuschnig, R., Walker, G. A. H., Matthews, J. M., Guenther, D. B., et al. (2008). MOST detects SPBe pulsations in HD 127756 and HD 217543: asteroseismic rotation rates independent of v sin i. Astrophys. J. 685, 489–507. doi: 10.1086/590369

CrossRef Full Text | Google Scholar

Cantiello, M., Langer, N., Brott, I., de Koter, A., Shore, S. N., Vink, J. S., et al. (2009). Sub-surface convection zones in hot massive stars and their observable consequences. Astron. Astrophys. 499, 279–290. doi: 10.1051/0004-6361/200911643

CrossRef Full Text | Google Scholar

Chaplin, W. J., and Miglio, A. (2013). Asteroseismology of solar-type and red-giant stars. Ann. Rev. Astron. Astrophys. 51, 353–392. doi: 10.1146/annurev-astro-082812-140938

CrossRef Full Text | Google Scholar

Chieffi, A., and Limongi, M. (2013). Pre-supernova evolution of rotating solar metallicity stars in the mass range 13-120 M _⊙ and their explosive yields. Astrophys. J. 764:21. doi: 10.1088/0004-637X/764/1/21

CrossRef Full Text | Google Scholar

Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., Maíz Apellániz, J., Schneider, F. R. N., Walborn, N. R., et al. (2016). The R136 star cluster dissected with Hubble Space Telescope/STIS. I. Far-ultraviolet spectroscopic census and the origin of He II λ1640 in young star clusters. Mon. Not. R. Astron. Soc. 458, 624–659. doi: 10.1093/mnras/stw273

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., Dziembowski, W. A., Pamyatnykh, A. A., and Goupil, M. J. (2002). Photometric amplitudes and phases of nonradial oscillation in rotating stars. Astron. Astrophys. 392, 151–159. doi: 10.1051/0004-6361:20020911

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., Ostrowski, J., and Pamyatnykh, A. A. (2013a). Pulsational instability in B-type supergiant stars. Mon. Not. R. Astron. Soc. 432, 3153–3160. doi: 10.1093/mnras/stt670

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., Pamyatnykh, A. A., Walczak, P., Colgan, J., Fontes, C. J., and Kilcrease, D. P. (2017). Interpretation of the BRITE oscillation data of the hybrid pulsator ν Eridani: a call for the modification of stellar opacities. Mon. Not. R. Astron. Soc. 466, 2284–2293. doi: 10.1093/mnras/stw3315

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., Szewczuk, W., and Walczak, P. (2013b). The β Cep/SPB star 12 Lacertae: extended mode identification and complex seismic modelling. Mon. Not. R. Astron. Soc. 431, 3396–3407. doi: 10.1093/mnras/stt418

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., and Walczak, P. (2009). Constraints on opacities from complex asteroseismology of B-type pulsators: the β Cephei star θ Ophiuchi. Mon. Not. R. Astron. Soc. 398, 1961–1969. doi: 10.1111/j.1365-2966.2009.15229.x

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., and Walczak, P. (2010). Complex asteroseismology of the β Cep/slowly pulsating B-type pulsator ν Eridani: constraints on opacities. Mon. Not. R. Astron. Soc. 403, 496–504. doi: 10.1111/j.1365-2966.2009.16141.x

CrossRef Full Text | Google Scholar

De Cat, P., and Aerts, C. (2002). A study of bright southern slowly pulsating B stars. II. The intrinsic frequencies. Astron. Astrophys. 393, 965–981. doi: 10.1051/0004-6361:20021068

CrossRef Full Text | Google Scholar

De Cat, P., Briquet, M., Daszyńska-Daszkiewicz, J., Dupret, M. A., De Ridder, J., Scuflaire, R., et al. (2005). A study of bright southern slowly pulsating B stars. III. Mode identification for singly-periodic targets in spectroscopy. Astron. Astrophys. 432, 1013–1024. doi: 10.1051/0004-6361:20042103

CrossRef Full Text | Google Scholar

de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., and de Koter, A. (2013). The Rotation Rates of Massive Stars: The Role of Binary Interaction through Tides, Mass Transfer, and Mergers. Astrophys. J. 764:166. doi: 10.1088/0004-637X/764/2/166

CrossRef Full Text | Google Scholar

De Ridder, J., Telting, J. H., Balona, L. A., Handler, G., Briquet, M., Daszyńska-Daszkiewicz, J., et al. (2004). Asteroseismology of the β Cephei star ν Eridani–III. Extended frequency analysis and mode identification. Mon. Not. R. Astron. Soc. 351, 324–332. doi: 10.1111/j.1365-2966.2004.07791.x

CrossRef Full Text | Google Scholar

de Rossi, M. E., Tissera, P. B., and Pedrosa, S. E. (2010). Impact of supernova feedback on the Tully-Fisher relation. Astron. Astrophys. 519:A89. doi: 10.1051/0004-6361/201014058

CrossRef Full Text | Google Scholar

Degroote, P. (2013). Chaos in large-amplitude pulsators: application to the β Cep star HD 180642. Mon. Not. R. Astron. Soc. 431, 2554–2559. doi: 10.1093/mnras/stt350

CrossRef Full Text | Google Scholar

Degroote, P., Aerts, C., Baglin, A., Miglio, A., Briquet, M., Noels, A., et al. (2010a). Deviations from a uniform period spacing of gravity modes in a massive star. Nature 464, 259–261. doi: 10.1038/nature08864

PubMed Abstract | CrossRef Full Text | Google Scholar

Degroote, P., Aerts, C., Michel, E., Briquet, M., Pápics, P. I., Amado, P., et al. (2012). The CoRoT B-type binary HD 50230: a prototypical hybrid pulsator with g-mode period and p-mode frequency spacings. Astron. Astrophys. 542:A88. doi: 10.1051/0004-6361/201118548

CrossRef Full Text | Google Scholar

Degroote, P., Briquet, M., Auvergne, M., Simón-Díaz, S., Aerts, C., Noels, A., et al. (2010b). Detection of frequency spacings in the young O-type binary HD 46149 from CoRoT photometry. Astron. Astrophys. 519:A38. doi: 10.1051/0004-6361/201014543

CrossRef Full Text | Google Scholar

Degroote, P., Briquet, M., Catala, C., Uytterhoeven, K., Lefever, K., Morel, T., et al. (2009). Evidence for nonlinear resonant mode coupling in the β Cephei star HD 180642 (V1449 Aquilae) from CoRoT photometry. Astron. Astrophys. 506, 111–123. doi: 10.1051/0004-6361/200911782

CrossRef Full Text | Google Scholar

Desmet, M., Aerts, C., Matthews, J. M., Cameron, C., Kuschnig, R., Walker, G. A. H., et al. (2009a). “MOST reveals spica as an eclipsing binary,” inn American Institute of Physics Conference Series, Vol. 1170 of American Institute of Physics Conference Series, eds. J. A. Guzik and P. A. Bradley, 376–378. doi: 10.1063/1.3246517

CrossRef Full Text | Google Scholar

Desmet, M., Briquet, M., Thoul, A., Zima, W., De Cat, P., Handler, G., et al. (2009b). An asteroseismic study of the β Cephei star 12 Lacertae: multisite spectroscopic observations, mode identification and seismic modelling. Mon. Not. R. Astron. Soc. 396, 1460–1472. doi: 10.1111/j.1365-2966.2009.14790.x

CrossRef Full Text | Google Scholar

Desmet, M., Walker, G., Yang, S., Bohlender, D., Briquet, M., Østensen, R. H., et al. (2009c). Simultaneous MOST photometry and high-resolution spectroscopy of Spica, a binary system with a massive beta Cephei star component. Commun. Asteroseismol. 158:303. doi: 10.1063/1.3246517

CrossRef Full Text | Google Scholar

Dessart, L., and Hillier, D. J. (2019). Supernovae from blue supergiant progenitors: What a mess! Astron. Astrophys. 622:A70. doi: 10.1051/0004-6361/201833966

CrossRef Full Text | Google Scholar

Duchêne, G., and Kraus, A. (2013). Stellar multiplicity. Ann. Rev. Astron. Astrophys. 51, 269–310. doi: 10.1146/annurev-astro-081710-102602

CrossRef Full Text | Google Scholar

Dupret, M.-A., Thoul, A., Scuflaire, R., Daszyńska-Daszkiewicz, J., Aerts, C., Bourge, P.-O., et al. (2004). Asteroseismology of the β Cep star HD 129929. II. Seismic constraints on core overshooting, internal rotation and stellar parameters. Astron. Astrophys. 415, 251–257. doi: 10.1051/0004-6361:20034143

CrossRef Full Text | Google Scholar

Dziembowski, W. A., and Goode, P. R. (1992). Effects of differential rotation on stellar oscillations—a second-order theory. Astrophys. J. 394, 670–687. doi: 10.1086/171621

CrossRef Full Text | Google Scholar

Dziembowski, W. A., and Jerzykiewicz, M. (1999). Asteroseismology of the beta Cephei stars. II. 12 (DD) Lacertae. Astron. Astrophys. 341, 480–486.

Google Scholar

Dziembowski, W. A., Moskalik, P., and Pamyatnykh, A. A. (1993). The opacity mechanism in B-type stars–part two–excitation of high-order G-modes in main sequence stars. Mon. Not. R. Astron. Soc. 265:588.

Google Scholar

Dziembowski, W. A., and Pamyatnykh, A. A. (1993). The opacity mechanism in B-type stars. I–unstable modes in beta Cephei star models. Mon. Not. R. Astron. Soc. 262, 204–212.

Google Scholar

Dziembowski, W. A., and Pamyatnykh, A. A. (2008). The two hybrid B-type pulsators: ν Eridani and 12 Lacertae. Mon. Not. R. Astron. Soc. 385, 2061–2068. doi: 10.1111/j.1365-2966.2008.12964.x

CrossRef Full Text | Google Scholar

Eckart, C. (1960). Variation principles of hydrodynamics. Phys. Fluids 3, 421–427. doi: 10.1063/1.1706053

CrossRef Full Text | Google Scholar

Edelmann, P. V. F., Ratnasingam, R. P., Pedersen, M. G., Bowman, D. M., Prat, V., and Rogers, T. M. (2019). Three-dimensional simulations of massive stars. I. Wave generation and propagation. Astrophys. J. 876:4. doi: 10.3847/1538-4357/ab12df

CrossRef Full Text | Google Scholar

Ekström, S., Georgy, C., Eggenberger, P., Meynet, G., Mowlavi, N., Wyttenbach, A., et al. (2012). Grids of stellar models with rotation. I. Models from 0.8 to 120 M_⊙ at solar metallicity (Z = 0.014). Astron. Astrophys. 537:A146. doi: 10.1051/0004-6361/201117751

CrossRef Full Text | Google Scholar

Espinosa Lara, F., and Rieutord, M. (2011). Gravity darkening in rotating stars. Astron. Astrophys. 533:A43. doi: 10.1051/0004-6361/201117252

CrossRef Full Text | Google Scholar

Freytag, B., Ludwig, H. G., and Steffen, M. (1996). Hydrodynamical models of stellar convection. The role of overshoot in DA white dwarfs, A-type stars, and the Sun. Astron. Astrophys. 313, 497–516.

Google Scholar

Fuller, J. (2017). Heartbeat stars, tidally excited oscillations and resonance locking. Mon. Not. R. Astron. Soc. 472, 1538–1564. doi: 10.1093/mnras/stx2135

CrossRef Full Text | Google Scholar

Gabriel, M., Noels, A., Montalbán, J., and Miglio, A. (2014). Proper use of Schwarzschild Ledoux criteria in stellar evolution computations. Astron. Astrophys. 569:A63. doi: 10.1051/0004-6361/201423442

CrossRef Full Text | Google Scholar

García, R. A., and Ballot, J. (2019). Asteroseismology of solar-type stars. Liv. Rev. Sol. Phys. 16:4. doi: 10.1007/s41116-019-0020-1

CrossRef Full Text | Google Scholar

Gautschy, A., and Saio, H. (1993). On non-radial oscillations of B-type stars. Mon. Not. R. Astron. Soc. 262, 213–219. doi: 10.1093/mnras/262.1.213

CrossRef Full Text | Google Scholar

Georgy, C. (2012). Yellow supergiants as supernova progenitors: an indication of strong mass loss for red supergiants? Astron. Astrophys. 538:L8. doi: 10.1051/0004-6361/201118372

CrossRef Full Text | Google Scholar

Georgy, C., Ekström, S., Eggenberger, P., Meynet, G., Haemmerlé, L., Maeder, A., et al. (2013). Grids of stellar models with rotation. III. Models from 0.8 to 120 M_⊙ at a metallicity Z = 0.002. Astron. Astrophys. 558:A103. doi: 10.1051/0004-6361/201322178

CrossRef Full Text | Google Scholar

Georgy, C., Meynet, G., and Maeder, A. (2011). Effects of anisotropic winds on massive star evolution. Astron. Astrophys. 527:A52. doi: 10.1051/0004-6361/200913797

CrossRef Full Text | Google Scholar

Georgy, C., Saio, H., and Meynet, G. (2014). The puzzle of the CNO abundances of α Cygni variables resolved by the Ledoux criterion. Mon. Not. R. Astron. Soc. 439, L6–L10. doi: 10.1093/mnrasl/slt165

CrossRef Full Text | Google Scholar

Gies, D. R., and Kullavanijaya, A. (1988). The line profile variations of epsilon Persei. I. Evidence for multimode nonradial Pulsations. Astrophys. J. 326:813. doi: 10.1086/166140

CrossRef Full Text | Google Scholar

Gies, D. R., and Lambert, D. L. (1992). Carbon, nitrogen, and oxygen abundances in early B-type stars. Astrophys. J. 387:673. doi: 10.1086/171116

CrossRef Full Text | Google Scholar

Godart, M., Simón-Díaz, S., Herrero, A., Dupret, M. A., Grötsch-Noels, A., Salmon, S. J. A. J., et al. (2017). The IACOB project. IV. New predictions for high-degree non-radial mode instability domains in massive stars and their connection with macroturbulent broadening. Astron. Astrophys. 597:A23. doi: 10.1051/0004-6361/201628856

CrossRef Full Text | Google Scholar

Groh, J. H., Ekström, S., Georgy, C., Meynet, G., Choplin, A., Eggenberger, P., et al. (2019). Grids of stellar models with rotation. IV. Models from 1.7 to 120 M_⊙ at a metallicity Z = 0.0004. Astron. Astrophys. 627:A24. doi: 10.1051/0004-6361/201833720

CrossRef Full Text | Google Scholar

Guinan, E. F., Ribas, I., Fitzpatrick, E. L., Giménez, Á., Jordi, C., McCook, G. P., et al. (2000). Eclipsing binaries as astrophysical laboratories: internal structure, core convection, and evolution of the B-star components of V380 Cygni. Astrophys. J. 544, 409–422. doi: 10.1086/317211

CrossRef Full Text | Google Scholar

Handler, G., and Aerts, C. (2002). A five-month multitechnique, multisite campaign on the Beta Cephei star Nu Eridani. Commun. Asteroseismol. 142, 20–24.

Google Scholar

Handler, G., Jerzykiewicz, M., Rodríguez, E., Uytterhoeven, K., Amado, P. J., Dorokhova, T. N., et al. (2006). Asteroseismology of the β Cephei star 12 (DD) Lacertae: photometric observations, pulsational frequency analysis and mode identification. Mon. Not. R. Astron. Soc. 365, 327–338. doi: 10.1111/j.1365-2966.2005.09728.x

CrossRef Full Text | Google Scholar

Handler, G., Matthews, J. M., Eaton, J. A., Daszyńska-Daszkiewicz, J., Kuschnig, R., Lehmann, H., et al. (2009). Asteroseismology of hybrid pulsators made possible: simultaneous MOST space photometry and ground-based spectroscopy of γ peg. Astrophys. J. Letters 698, L56–L59. doi: 10.1088/0004-637X/698/1/L56

CrossRef Full Text | Google Scholar

Handler, G., Pigulski, A., Daszyńska-Daszkiewicz, J., Irrgang, A., Kilkenny, D., Guo, Z., et al. (2019). Asteroseismology of massive stars with the TESS mission: the runaway β Cep pulsator PHL 346 = HN Aqr. Astrophys. J. Letters 873:L4. doi: 10.3847/2041-8213/ab095f

CrossRef Full Text | Google Scholar

Handler, G., Rybicka, M., Popowicz, A., Pigulski, A., Kuschnig, R., Zocłońska, E., et al. (2017). Combining BRITE and ground-based photometry for the β Cephei star ν Eridani: impact on photometric pulsation mode identification and detection of several g modes. Mon. Not. R. Astron. Soc. 464, 2249–2258. doi: 10.1093/mnras/stw2518

CrossRef Full Text | Google Scholar

Handler, G., Shobbrook, R. R., Jerzykiewicz, M., Krisciunas, K., Tshenye, T., Rodríguez, E., et al. (2004). Asteroseismology of the β Cephei star ν Eridani–I. Photometric observations and pulsational frequency analysis. Mon. Not. R. Astron. Soc. 347, 454–462. doi: 10.1111/j.1365-2966.2004.07214.x

CrossRef Full Text | Google Scholar

Handler, G., Shobbrook, R. R., and Mokgwetsi, T. (2005). An asteroseismic study of the β Cephei star θ Ophiuchi: photometric results. Mon. Not. R. Astron. Soc. 362, 612–618. doi: 10.1111/j.1365-2966.2005.09341.x

CrossRef Full Text | Google Scholar

Handler, G., Shobbrook, R. R., Uytterhoeven, K., Briquet, M., Neiner, C., Tshenye, T., et al. (2012). A multisite photometric study of two unusual β Cep stars: the magnetic V2052 Oph and the massive rapid rotator V986 Oph. Mon. Not. R. Astron. Soc. 424, 2380–2391. doi: 10.1111/j.1365-2966.2012.21414.x

CrossRef Full Text | Google Scholar

Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., and Hartmann, D. H. (2003). How Massive Single Stars End Their Life. Astrophys. J. 591, 288–300. doi: 10.1086/375341

CrossRef Full Text | Google Scholar

Hekker, S., and Christensen-Dalsgaard, J. (2017). Giant star seismology. Astron. Astrophys. Rev. 25:1. doi: 10.1007/s00159-017-0101-x

CrossRef Full Text | Google Scholar

Hendriks, L., and Aerts, C. (2019). Deep learning applied to the asteroseismic modeling of stars with coherent oscillation modes. Public. Astronom. Soc. Pac. 131:108001. doi: 10.1088/1538-3873/aaeeec

CrossRef Full Text | Google Scholar

Herwig, F. (2000). The evolution of AGB stars with convective overshoot. Astron. Astrophys. 360, 952–968.

Google Scholar

Heynderickx, D., Waelkens, C., and Smeyers, P. (1994). A photometric study of β Cephei stars. II. Determination of the degrees L of pulsation modes. Astron. Astrophys. Sup. Ser. 105, 447–480.

Google Scholar

Hilditch, R. W., Howarth, I. D., and Harries, T. J. (2005). Forty eclipsing binaries in the small magellanic cloud: fundamental parameters and cloud distance. Mon. Not. R. Astron. Soc. 357, 304–324. doi: 10.1111/j.1365-2966.2005.08653.x

CrossRef Full Text | Google Scholar

Hirschi, R., Meynet, G., and Maeder, A. (2005). Stellar evolution with rotation. XIII. Predicted GRB rates at various Z. arXiv 443, 581–591. doi: 10.1051/0004-6361:20053329

CrossRef Full Text | Google Scholar

Hopkins, P. F., Kereš, D., Oñorbe, J., Faucher-Giguère, C.-A., Quataert, E., Murray, N., et al. (2014). Galaxies on FIRE (feedback in realistic environments): stellar feedback explains cosmologically inefficient star formation. Mon. Not. R. Astron. Soc. 445, 581–603. doi: 10.1093/mnras/stu1738

CrossRef Full Text | Google Scholar

Horst, L., Edelmann, P. V. F., Andrássy, R., Röpke, F. K., Bowman, D. M., Aerts, C., et al. (2020). Fully compressible simulations of waves and core convection in main-sequence stars. Astron. Astrophys. 641:A18. doi: 10.1051/0004-6361/202037531

CrossRef Full Text | Google Scholar

Howell, S. B., Sobeck, C., Haas, M., Still, M., Barclay, T., Mullally, F., et al. (2014). The K2 mission: characterization and early results. Public. Astronom. Soc. Pac. 126, 398–408. doi: 10.1086/676406

CrossRef Full Text | Google Scholar

Huat, A. L., Hubert, A. M., Baudin, F., Floquet, M., Neiner, C., Frémat, Y., et al. (2009). The B0.5IVe CoRoT target HD 49330. I. Photometric analysis from CoRoT data. Astron. Astrophys. 506, 95–101. doi: 10.1051/0004-6361/200911928

CrossRef Full Text | Google Scholar

Hunter, I., Brott, I., Langer, N., Lennon, D. J., Dufton, P. L., Howarth, I. D., et al. (2009). The VLT-FLAMES survey of massive stars: constraints on stellar evolution from the chemical compositions of rapidly rotating Galactic and Magellanic Cloud B-type stars. Astron. Astrophys. 496, 841–853. doi: 10.1051/0004-6361/200809925

CrossRef Full Text | Google Scholar

Hunter, I., Brott, I., Lennon, D. J., Langer, N., Dufton, P. L., Trundle, C., et al. (2008). The VLT FLAMES survey of massive stars: rotation and nitrogen enrichment as the key to understanding massive star evolution. Astrophys. J. Letters 676:L29. doi: 10.1086/587436

CrossRef Full Text | Google Scholar

Hunter, J. D. (2007). Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 9, 90-95. doi: 10.1109/MCSE.2007.55

CrossRef Full Text | Google Scholar

Jerzykiewicz, M., Handler, G., Shobbrook, R. R., Pigulski, A., Medupe, R., Mokgwetsi, T., et al. (2005). Asteroseismology of the β Cephei star ν Eridani–IV. The 2003–2004 multisite photometric campaign and the combined 2002–2004 data. Mon. Not. R. Astron. Soc. 360, 619–630. doi: 10.1111/j.1365-2966.2005.09088.x

CrossRef Full Text | Google Scholar

Jerzykiewicz, M., Pigulski, A., Handler, G., Moffat, A. F. J., Popowicz, A., Wade, G. A., et al. (2020). BRITE-constellation photometry of π⁵ orionis, an ellipsoidal SPB variable. Mon. Not. R. Astron. Soc. 496, 2391–2401. doi: 10.1093/mnras/staa1665

CrossRef Full Text | Google Scholar

Johnston, C., Pavlovski, K., and Tkachenko, A. (2019). Modelling of the B-type binaries CW Cephei and U Ophiuchi. A critical view on dynamical masses, core boundary mixing, and core mass. Astron. Astrophys. 628:A25. doi: 10.1051/0004-6361/201935235

CrossRef Full Text | Google Scholar

Kallinger, T., Weiss, W. W., Beck, P. G., Pigulski, A., Kuschnig, R., Tkachenko, A., et al. (2017). Triple system HD 201433 with a SPB star component seen by BRITE–constellation: pulsation, differential rotation, and angular momentum transfer. Astron. Astrophys. 603:A13. doi: 10.1051/0004-6361/201730625

CrossRef Full Text | Google Scholar

Kambe, E., Ando, H., and Hirata, R. (1993). Short-term line-profile variations and episodic mass loss in the Be star dzeta Ophiuchi. Astron. Astrophys. 273, 435–450.

Google Scholar

Keszthelyi, Z., Meynet, G., Georgy, C., Wade, G. A., Petit, V., and David-Uraz, A. (2019). The effects of surface fossil magnetic fields on massive star evolution: I. Magnetic field evolution, mass-loss quenching, and magnetic braking. Mon. Not. R. Astron. Soc. 485, 5843–5860. doi: 10.1093/mnras/stz772

CrossRef Full Text | Google Scholar

Keszthelyi, Z., Meynet, G., Shultz, M. E., David-Uraz, A., ud-Doula, A., Townsend, R. H. D., et al. (2020). The effects of surface fossil magnetic fields on massive star evolution - II. Implementation of magnetic braking in MESA and implications for the evolution of surface rotation in OB stars. Mon. Not. R. Astron. Soc. 493, 518–535. doi: 10.1093/mnras/staa237

CrossRef Full Text | Google Scholar

Kippenhahn, R., Weigert, A., and Weiss, A. (2012). Stellar Structure and Evolution. Berlin: Springer. doi: 10.1007/978-3-642-30304-3

CrossRef Full Text | Google Scholar

Koch, D. G., Borucki, W. J., Basri, G., Batalha, N. M., Brown, T. M., Caldwell, D., et al. (2010). Kepler mission design, realized photometric performance, and early science. Astrophys. J. Letters 713:L79. doi: 10.1088/2041-8205/713/2/L79

CrossRef Full Text | Google Scholar

Koen, C., and Eyer, L. (2002). New periodic variables from the Hipparcos epoch photometry. Mon. Not. R. Astron. Soc. 331, 45–59. doi: 10.1046/j.1365-8711.2002.05150.x

CrossRef Full Text | Google Scholar

Kurtz, D. W., Saio, H., Takata, M., Shibahashi, H., Murphy, S. J., and Sekii, T. (2014). Asteroseismic measurement of surface-to-core rotation in a main-sequence A star, KIC 11145123. Mon. Not. R. Astron. Soc. 444, 102–116. doi: 10.1093/mnras/stu1329

CrossRef Full Text | Google Scholar

Kurtz, D. W., Shibahashi, H., Murphy, S. J., Bedding, T. R., and Bowman, D. M. (2015). A unifying explanation of complex frequency spectra of γ Dor, SPB and Be stars: combination frequencies and highly non-sinusoidal light curves. Mon. Not. R. Astron. Soc. 450, 3015–3029. doi: 10.1093/mnras/stv868

CrossRef Full Text | Google Scholar

Langer, N. (2012). Presupernova evolution of massive single and binary stars. Ann. Rev. Astron. Astrophys. 50, 107–164. doi: 10.1146/annurev-astro-081811-125534

CrossRef Full Text | Google Scholar

Langer, N., and Kudritzki, R. P. (2014). The spectroscopic Hertzsprung-Russell diagram. Astron. Astrophys. 564:A52. doi: 10.1051/0004-6361/201423374

CrossRef Full Text | Google Scholar

Lee, U., and Saio, H. (1987a). Low-frequency oscillations of uniformly rotating stars. Mon. Not. R. Astron. Soc. 224, 513–526. doi: 10.1093/mnras/224.3.513

CrossRef Full Text | Google Scholar

Lee, U., and Saio, H. (1987b). Non-adiabatic analysis of low-frequency oscillations of uniformly rotating stars. Mon. Not. R. Astron. Soc. 225, 643–651. doi: 10.1093/mnras/225.3.643

CrossRef Full Text | Google Scholar

Lee, U., and Saio, H. (1997). Low-frequency nonradial oscillations in rotating stars. I. Angular dependence. Astrophys. J. 491, 839–845. doi: 10.1086/304980

CrossRef Full Text | Google Scholar

Lefèvre, L., Marchenko, S. V., Moffat, A. F. J., and Acker, A. (2009). A systematic study of variability among OB-stars based on HIPPARCOS photometry. Astron. Astrophys. 507, 1141–1201. doi: 10.1051/0004-6361/200912304

CrossRef Full Text | Google Scholar

Lefèvre, L., Marchenko, S. V., Moffat, A. F. J., Chené, A. N., Smith, S. R., St-Louis, N., et al. (2005). Oscillations in the massive Wolf-Rayet star WR 123 with the MOST satellite. Astrophys. J. Letters 634, L109–L112. doi: 10.1086/498393

CrossRef Full Text | Google Scholar

Li, G., Bedding, T. R., Murphy, S. J., Van Reeth, T., Antoci, V., and Ouazzani, R.-M. (2019a). Period spacings of γ Doradus pulsators in the Kepler field: detection methods and application to 22 slow rotators. Mon. Not. R. Astron. Soc. 482, 1757–1785. doi: 10.1093/mnras/sty2743

CrossRef Full Text | Google Scholar

Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., and Antoci, V. (2019b). Period spacings of γ Doradus pulsators in the Kepler field: Rossby and gravity modes in 82 stars. Mon. Not. R. Astron. Soc. 487, 782–800. doi: 10.1093/mnras/stz1171

CrossRef Full Text | Google Scholar

Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., Antoci, V., Ouazzani, R.-M., et al. (2020). Gravity-mode period spacings and near-core rotation rates of 611 γ Doradus stars with Kepler. Mon. Not. R. Astron. Soc. 491, 3586–3605. doi: 10.1093/mnras/stz2906

CrossRef Full Text | Google Scholar

Lovekin, C. C. (2020). Challenges in 2D stellar modelling. Front. Astron. Space Sci. 6:77. doi: 10.3389/fspas.2019.00077

CrossRef Full Text | Google Scholar

Mac Low, M.-M., and Klessen, R. S. (2004). Control of star formation by supersonic turbulence. Rev. Mod. Phys. 76, 125–194. doi: 10.1103/RevModPhys.76.125

CrossRef Full Text | Google Scholar

Maeder, A. (2009). Physics, Formation and Evolution of Rotating Stars. Berlin: Springer.

Google Scholar

Maeder, A., Georgy, C., and Meynet, G. (2008). Convective envelopes in rotating OB stars. Astron. Astrophys. 479, L37–L40. doi: 10.1051/0004-6361:20079007

CrossRef Full Text | Google Scholar

Maeder, A., and Meynet, G. (2000). The evolution of rotating stars. Ann. Rev. Astron. Astrophys. 38, 143–190. doi: 10.1146/annurev.astro.38.1.143

CrossRef Full Text | Google Scholar

Mahy, L., Almeida, L. A., Sana, H., Clark, J. S., de Koter, A., de Mink, S. E., et al. (2020a). The Tarantula massive binary monitoring. IV. Double-lined photometric binaries. Astron. Astrophys. 634:A119. doi: 10.1051/0004-6361/201936152

CrossRef Full Text | Google Scholar

Mahy, L., Sana, H., Abdul-Masih, M., Almeida, L. A., Langer, N., Shenar, T., et al. (2020b). The Tarantula massive binary monitoring. III. Atmosphere analysis of double-lined spectroscopic systems. Astron. Astrophys. 634:A118. doi: 10.1051/0004-6361/201936151

CrossRef Full Text | Google Scholar

Maintz, M., Rivinius, T., Štefl, S., Baade, D., Wolf, B., and Townsend, R. H. D. (2003). Stellar and circumstellar activity of the Be star omega CMa. III. Multiline non-radial pulsation modeling. Astron. Astrophys. 411, 181–191. doi: 10.1051/0004-6361:20031375

CrossRef Full Text | Google Scholar

Martins, F., and Palacios, A. (2013). A comparison of evolutionary tracks for single Galactic massive stars. Astron. Astrophys. 560:A16. doi: 10.1051/0004-6361/201322480

CrossRef Full Text | Google Scholar

Mathis, S. (2009). Transport by gravito-inertial waves in differentially rotating stellar radiation zones. I–theoretical formulation. Astron. Astrophys. 506, 811–828. doi: 10.1051/0004-6361/200810544

CrossRef Full Text | Google Scholar

Mathis, S., and Prat, V. (2019). The traditional approximation of rotation, including the centrifugal acceleration for slightly deformed stars. Astron. Astrophys. 631:A26. doi: 10.1051/0004-6361/201935639

CrossRef Full Text | Google Scholar

McNamara, B. J., Jackiewicz, J., and McKeever, J. (2012). The classification of Kepler B-star variables. Astrom. J. 143:101. doi: 10.1088/0004-6256/143/4/101

CrossRef Full Text | Google Scholar

Michielsen, M., Pedersen, M. G., Augustson, K. C., Mathis, S., and Aerts, C. (2019). Probing the shape of the mixing profile and of the thermal structure at the convective core boundary through asteroseismology. Astron. Astrophys. 628:A76. doi: 10.1051/0004-6361/201935754

CrossRef Full Text | Google Scholar

Miglio, A., Montalbán, J., and Dupret, M.-A. (2007). Instability strips of slowly pulsating B stars and β Cephei stars: the effect of the updated OP opacities and of the metal mixture. Mon. Not. R. Astron. Soc. 375, L21–L25. doi: 10.1111/j.1745-3933.2006.00267.x

CrossRef Full Text | Google Scholar

Miglio, A., Montalbán, J., Eggenberger, P., and Noels, A. (2008a). Gravity modes and mixed modes as probes of stellar cores in main-sequence stars: from solar-like to β Cep stars. Astron. Nach. 329, 529–534. doi: 10.1002/asna.200710991

CrossRef Full Text | Google Scholar

Miglio, A., Montalbán, J., Noels, A., and Eggenberger, P. (2008b). Probing the properties of convective cores through g modes: high-order g modes in SPB and γ Doradus stars. Mon. Not. R. Astron. Soc. 386, 1487–1502. doi: 10.1111/j.1365-2966.2008.13112.x

CrossRef Full Text | Google Scholar

Modjaz, M., Gutiérrez, C. P., and Arcavi, I. (2019). New regimes in the observation of core-collapse supernovae. Nat. Astron. 3, 717–724. doi: 10.1038/s41550-019-0856-2

CrossRef Full Text | Google Scholar

Moe, M., and Di Stefano, R. (2017). Mind your Ps and Qs: the interrelation between period (P) and mass-ratio (Q) distributions of binary stars. Astrophys. J. Supp. Ser. 230:15. doi: 10.3847/1538-4365/aa6fb6

CrossRef Full Text | Google Scholar

Moffat, A. F. J., Marchenko, S. V., Lefèvre, L., Chené, A.-N., St-Louis, N., Zhilyaev, B. E., et al. (2008a). “Pulsations beneath the winds: unique precise photometry from MOST,” in Mass Loss from Stars and the Evolution of Stellar Clusters, Vol. 388 of Astronomical Society of the Pacific Conference Series, eds. A. de Koter, L. J. Smith, and L. B. F. M. Waters (Potsdam), 29.

Google Scholar

Moffat, A. F. J., Marchenko, S. V., Zhilyaev, B. E., Rowe, J. F., Muntean, V., Chené, A.-N., et al. (2008b). MOST finds no coherent oscillations in the hot carbon-rich Wolf-Rayet star HD 165763 (WR 111). Astrophys. J. Letters 679:L45. doi: 10.1086/589237

CrossRef Full Text | Google Scholar

Mombarg, J. S. G., Van Reeth, T., Pedersen, M. G., Molenberghs, G., Bowman, D. M., Johnston, C., et al. (2019). Asteroseismic masses, ages, and core properties of γ Doradus stars using gravito-inertial dipole modes and spectroscopy. Mon. Not. R. Astron. Soc. 485, 3248–3263. doi: 10.1093/mnras/stz501

CrossRef Full Text | Google Scholar

Moravveji, E. (2016). The impact of enhanced iron opacity on massive star pulsations: updated instability strips. Mon. Not. R. Astron. Soc. 455, L67–L71. doi: 10.1093/mnrasl/slv142

CrossRef Full Text | Google Scholar

Moravveji, E., Aerts, C., Pápics, P. I., Triana, S. A., and Vandoren, B. (2015). Tight asteroseismic constraints on core overshooting and diffusive mixing in the slowly rotating pulsating B8.3V star KIC 10526294. Astron. Astrophys. 580:A27. doi: 10.1051/0004-6361/201425290

CrossRef Full Text | Google Scholar

Moravveji, E., Guinan, E. F., Shultz, M., Williamson, M. H., and Moya, A. (2012). Asteroseismology of the nearby SN-II progenitor: Rigel. I. The MOST high-precision photometry and radial velocity monitoring. Astrophys. J. 747:108. doi: 10.1088/0004-637X/747/2/108

CrossRef Full Text | Google Scholar

Moravveji, E., Townsend, R. H. D., Aerts, C., and Mathis, S. (2016). Sub-inertial gravity modes in the B8V star KIC 7760680 reveal moderate core overshooting and low vertical diffusive mixing. Astrophys. J. 823:130. doi: 10.3847/0004-637X/823/2/130

CrossRef Full Text | Google Scholar

Morel, T., Castro, N., Fossati, L., Hubrig, S., Langer, N., Przybilla, N., et al. (2015). “The B fields in OB stars (BOB) survey,” in New Windows on Massive Stars, Vol. 307 of IAU Symposium, eds. G. Meynet, C. Georgy, J. Groh, and P. Stee (Geneva), 342–347. doi: 10.1017/S1743921314007054

CrossRef Full Text | Google Scholar

Neilson, H. R., and Ignace, R. (2015). Period change and stellar evolution of β Cephei stars. Astron. Astrophys. 584:A58. doi: 10.1051/0004-6361/201526836

CrossRef Full Text | Google Scholar

Neiner, C., Alecian, E., Briquet, M., Floquet, M., Frémat, Y., Martayan, C., et al. (2012a). Detecting and modelling the magnetic field of the β Cephei star V 2052 Ophiuchi. Astron. Astrophys. 537:A148. doi: 10.1051/0004-6361/201117941

CrossRef Full Text | Google Scholar

Neiner, C., de Batz, B., Cochard, F., Floquet, M., Mekkas, A., and Desnoux, V. (2011). The Be star spectra (beSS) Database. Astrom. J. 142:149. doi: 10.1088/0004-6256/142/5/149

CrossRef Full Text | Google Scholar

Neiner, C., Floquet, M., Samadi, R., Espinosa Lara, F., Frémat, Y., Mathis, S., et al. (2012b). Stochastic gravito-inertial modes discovered by CoRoT in the hot Be star HD 51452. Astron. Astrophys. 546:A47. doi: 10.1051/0004-6361/201219820

CrossRef Full Text | Google Scholar

Neiner, C., Gutiérrez-Soto, J., Baudin, F., de Batz, B., Frémat, Y., Huat, A. L., et al. (2009). The pulsations of the B5IVe star HD 181231 observed with CoRoT and ground-based spectroscopy. Astron. Astrophys. 506, 143–151. doi: 10.1051/0004-6361/200911971

CrossRef Full Text | Google Scholar

Neiner, C., Henrichs, H. F., Floquet, M., Frémat, Y., Preuss, O., Hubert, A. M., et al. (2003). Rotation, pulsations and magnetic field in < ASTROBJ>V 2052 Ophiuchi < /ASTROBJ>: a new He-strong star. Astron. Astrophys. 411, 565–579. doi: 10.1051/0004-6361:20031342

CrossRef Full Text | Google Scholar

Neiner, C., Wade, G. A., Marsden, S. C., and Blazère, A. (2017). “The BRITE spectropolarimetric program,” in Second BRITE-Constellation Science Conference: Small Satellites–Big Science, Proceedings of the Polish Astronomical Society Volume 5, Held 22–26 August, 2016 in Innsbruck, Austria (Warsaw: Polish Astronomical Society), 86–93.

Google Scholar

Nieva, M.-F., and Przybilla, N. (2012). Present-day cosmic abundances. A comprehensive study of nearby early B-type stars and implications for stellar and Galactic evolution and interstellar dust models. Astron. Astrophys. 539:A143. doi: 10.1051/0004-6361/201118158

CrossRef Full Text | Google Scholar

Nomoto, K., Tominaga, N., Umeda, H., Kobayashi, C., and Maeda, K. (2006). Nucleosynthesis yields of core-collapse supernovae and hypernovae, and galactic chemical evolution. Nucl. Phys. A 777, 424–458. doi: 10.1016/j.nuclphysa.2006.05.008

CrossRef Full Text | Google Scholar

Osaki, J. (1975). Nonradial oscillations of a 10 solar mass star in the main-sequence stage. Public. Astronom. Soc. Jpn. 27, 237–258.

Google Scholar

Ostrowski, J., and Daszyńska-Daszkiewicz, J. (2015). Pulsations in B-type supergiants with masses M <20 M_⊙ before and after core helium ignition. Mon. Not. R. Astron. Soc. 447, 2378–2386. doi: 10.1093/mnras/stu2605

CrossRef Full Text | Google Scholar

Ostrowski, J., Daszyńska-Daszkiewicz, J., and Cugier, H. (2017). Revising the evolutionary stage of HD 163899: the effects of convective overshooting and rotation. Astrophys. J. 835:290. doi: 10.3847/1538-4357/835/2/290

CrossRef Full Text | Google Scholar

Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., Bedding, T. R., Murphy, S. J., and Roxburgh, I. W. (2017). A new asteroseismic diagnostic for internal rotation in γ Doradus stars. Mon. Not. R. Astron. Soc. 465, 2294–2309. doi: 10.1093/mnras/stw2717

CrossRef Full Text | Google Scholar

Ouazzani, R. M., Marques, J. P., Goupil, M. J., Christophe, S., Antoci, V., Salmon, S. J. A. J., et al. (2019). γ Doradus stars as a test of angular momentum transport models. Astron. Astrophys. 626:A121. doi: 10.1051/0004-6361/201832607

CrossRef Full Text | Google Scholar

Pablo, H., Richardson, N. D., Fuller, J., Rowe, J., Moffat, A. F. J., Kuschnig, R., et al. (2017). The most massive heartbeat: an in-depth analysis of ı Orionis. Mon. Not. R. Astron. Soc. 467, 2494–2503. doi: 10.1093/mnras/stx207

CrossRef Full Text | Google Scholar

Pablo, H., Shultz, M., Fuller, J., Wade, G. A., Paunzen, E., Mathis, S., et al. (2019). ∈ Lupi: measuring the heartbeat of a doubly magnetic massive binary with BRITE constellation. Mon. Not. R. Astron. Soc. 488, 64–77. doi: 10.1093/mnras/stz1661

CrossRef Full Text | Google Scholar

Pablo, H., Whittaker, G. N., Popowicz, A., Mochnacki, S. M., Kuschnig, R., Grant, C. C., et al. (2016). The BRITE constellation nanosatellite mission: testing, commissioning, and operations. Public. Astronom. Soc. Pac. 128:125001. doi: 10.1088/1538-3873/128/970/125001

CrossRef Full Text | Google Scholar

Pamyatnykh, A. A. (1999). Pulsational instability domains in the upper main sequence. Astron. Nach. 49, 119–148.

Google Scholar

Pamyatnykh, A. A., Handler, G., and Dziembowski, W. A. (2004). Asteroseismology of the β Cephei star ν Eridani: interpretation and applications of the oscillation spectrum. Mon. Not. R. Astron. Soc. 350, 1022–1028. doi: 10.1111/j.1365-2966.2004.07721.x

CrossRef Full Text | Google Scholar

Pápics, P. I., Briquet, M., Auvergne, M., Aerts, C., Degroote, P., Niemczura, E., et al. (2011). CoRoT high-precision photometry of the B0.5 IV star HD 51756. Astron. Astrophys. 528:A123. doi: 10.1051/0004-6361/201016131

CrossRef Full Text | Google Scholar

Pápics, P. I., Briquet, M., Baglin, A., Poretti, E., Aerts, C., Degroote, P., et al. (2012). Gravito-inertial and pressure modes detected in the B3 IV CoRoT target HD 43317. Astron. Astrophys. 542:A55. doi: 10.1051/0004-6361/201218809

CrossRef Full Text | Google Scholar

Pápics, P. I., Moravveji, E., Aerts, C., Tkachenko, A., Triana, S. A., Bloemen, S., et al. (2014). KIC 10526294: a slowly rotating B star with rotationally split, quasi-equally spaced gravity modes. Astron. Astrophys. 570:A8. doi: 10.1051/0004-6361/201424094

CrossRef Full Text | Google Scholar

Pápics, P. I., Tkachenko, A., Aerts, C., Van Reeth, T., De Smedt, K., Hillen, M., et al. (2015). Asteroseismic fingerprints of rotation and mixing in the slowly pulsating B8 V star KIC 7760680. Astrophys. J. Letters 803:L25. doi: 10.1088/2041-8205/803/2/L25

CrossRef Full Text | Google Scholar

Pápics, P. I., Tkachenko, A., Van Reeth, T., Aerts, C., Moravveji, E., Van de Sande, M., et al. (2017). Signatures of internal rotation discovered in the Kepler data of five slowly pulsating B stars. Astron. Astrophys. 598:A74. doi: 10.1051/0004-6361/201629814

CrossRef Full Text | Google Scholar

Paxton, B., Bildsten, L., Dotter, A., Herwig, F., Lesaffre, P., and Timmes, F. (2011). Modules for experiments in stellar astrophysics (MESA). Astrophys. J. Supp. Ser. 192:3. doi: 10.1088/0067-0049/192/1/3

PubMed Abstract | CrossRef Full Text | Google Scholar

Paxton, B., Cantiello, M., Arras, P., Bildsten, L., Brown, E. F., Dotter, A., et al. (2013). Modules for experiments in stellar astrophysics (MESA): planets, oscillations, rotation, and massive stars. Astrophys. J. Supp. Ser. 208:4. doi: 10.1088/0067-0049/208/1/4

CrossRef Full Text | Google Scholar

Paxton, B., Marchant, P., Schwab, J., Bauer, E. B., Bildsten, L., Cantiello, M., et al. (2015). Modules for experiments in stellar astrophysics (MESA): binaries, pulsations, and explosions. Astrophys. J. Supp. Ser. 220:15. doi: 10.1088/0067-0049/220/1/15

CrossRef Full Text | Google Scholar

Paxton, B., Schwab, J., Bauer, E. B., Bildsten, L., Blinnikov, S., Duffell, P., et al. (2018). Modules for experiments in stellar astrophysics (MESA): convective boundaries, element diffusion, and massive star explosions. Astrophys. J. Supp. Ser. 234:34. doi: 10.3847/1538-4365/aaa5a8

CrossRef Full Text | Google Scholar

Paxton, B., Smolec, R., Schwab, J., Gautschy, A., Bildsten, L., Cantiello, M., et al. (2019). Modules for experiments in stellar astrophysics (MESA): pulsating variable stars, rotation, convective boundaries, and energy conservation. Astrophys. J. Supp. Ser. 243:10. doi: 10.3847/1538-4365/ab2241

CrossRef Full Text | Google Scholar

Pedersen, M. G., Aerts, C., Pápics, P. I., and Rogers, T. M. (2018). The shape of convective core overshooting from gravity-mode period spacings. Astron. Astrophys. 614:A128. doi: 10.1051/0004-6361/201732317

CrossRef Full Text | Google Scholar

Pedersen, M. G., Chowdhury, S., Johnston, C., Bowman, D. M., Aerts, C., Handler, G., et al. (2019). Diverse variability of O and B stars revealed from 2-minute Cadence light curves in sectors 1 and 2 of the TESS mission: selection of an asteroseismic sample. Astrophys. J. Letters 872:L9. doi: 10.3847/2041-8213/ab01e1

CrossRef Full Text | Google Scholar

Pigulski, A., Cugier, H., Popowicz, A., Kuschnig, R., Moffat, A. F. J., Rucinski, S. M., et al. (2016). Massive pulsating stars observed by BRITE-Constellation. I. The triple system β Centauri (Agena). Astron. Astrophys. 588:A55. doi: 10.1051/0004-6361/201527872

CrossRef Full Text | Google Scholar

Pigulski, A., and Pojmański, G. (2008a). β Cephei stars in the ASAS-3 data. I. Long-term variations of periods and amplitudes. Astron. Astrophys. 477, 907–915. doi: 10.1051/0004-6361:20078580

CrossRef Full Text | Google Scholar

Pigulski, A., and Pojmański, G. (2008b). β Cephei stars in the ASAS-3 data. II. 103 new β Cephei stars and a discussion of low-frequency modes. Astron. Astrophys. 477, 917–929. doi: 10.1051/0004-6361:20078581

CrossRef Full Text | Google Scholar

Podsiadlowski, P., Joss, P. C., and Hsu, J. J. L. (1992). Presupernova evolution in massive interacting binaries. Astrophys. J. 391:246. doi: 10.1086/171341

CrossRef Full Text | Google Scholar

Pope, B. J. S., Davies, G. R., Hawkins, K., White, T. R., Stokholm, A., Bieryla, A., et al. (2019a). The Kepler smear campaign: light curves for 102 very bright stars. Astrophys. J. Supp. Ser. 244:18. doi: 10.3847/1538-4365/ab2c04

CrossRef Full Text | Google Scholar

Pope, B. J. S., White, T. R., Farr, W. M., Yu, J., Greklek-McKeon, M., Huber, D., et al. (2019b). The K2 bright star survey. I. Methodology and data release. Astrophys. J. Supp. Ser. 245:8. doi: 10.3847/1538-4365/ab3d29

CrossRef Full Text | Google Scholar

Pope, B. J. S., White, T. R., Huber, D., Murphy, S. J., Bedding, T. R., Caldwell, D. A., et al. (2016). Photometry of very bright stars with Kepler and K2 smear data. Mon. Not. R. Astron. Soc. 455, L36–L40. doi: 10.1093/mnrasl/slv143

CrossRef Full Text | Google Scholar

Porter, J. M., and Rivinius, T. (2003). Classical Be stars. Public. Astronom. Soc. Pac. 115, 1153–1170. doi: 10.1086/378307

CrossRef Full Text | Google Scholar

Przybilla, N., Nieva, M. F., Irrgang, A., and Butler, K. (2013). “Hot stars and cosmic abundances,” in EAS Publications Series, Vol. 63 of EAS Publications Series, eds. G. Alecian, Y. Lebreton, O. Richard, and G. Vauclair, 13–23. doi: 10.1051/eas/1363002

CrossRef Full Text | Google Scholar

Ramiaramanantsoa, T., Ignace, R., Moffat, A. F. J., St-Louis, N., Shkolnik, E. L., Popowicz, A., et al. (2019). The chaotic wind of WR 40 as probed by BRITE. Mon. Not. R. Astron. Soc. 490, 5921–5930. doi: 10.1093/mnras/stz2895

CrossRef Full Text | Google Scholar

Ramiaramanantsoa, T., Moffat, A. F. J., Harmon, R., Ignace, R., St-Louis, N., Vanbeveren, D., et al. (2018a). BRITE-Constellation high-precision time-dependent photometry of the early O-type supergiant ζ Puppis unveils the photospheric drivers of its small- and large-scale wind structures. Mon. Not. R. Astron. Soc. 473, 5532–5569. doi: 10.1093/mnras/stx2671

CrossRef Full Text | Google Scholar

Ramiaramanantsoa, T., Ratnasingam, R., Shenar, T., Moffat, A. F. J., Rogers, T. M., Popowicz, A., et al. (2018b). A BRITE view on the massive O-type supergiant V973 Scorpii: hints towards internal gravity waves or sub-surface convection zones. Mon. Not. R. Astron. Soc. 480, 972–986. doi: 10.1093/mnras/sty1897

CrossRef Full Text | Google Scholar

Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., et al. (2015). Transiting exoplanet survey satellite (TESS). J. Astron. Telesc. Instrum. Syst. 1:014003. doi: 10.1117/1.JATIS.1.1.014003

PubMed Abstract | CrossRef Full Text | Google Scholar

Rivinius, T., Baade, D., and Štefl, S. (2003). Non-radially pulsating Be stars. Astron. Astrophys. 411, 229–247. doi: 10.1051/0004-6361:20031285

CrossRef Full Text | Google Scholar

Rivinius, T., Carciofi, A. C., and Martayan, C. (2013). Classical Be stars. Rapidly rotating B stars with viscous Keplerian decretion disks. Astron. Astrophys. Rev. 21:69. doi: 10.1007/s00159-013-0069-0

CrossRef Full Text | Google Scholar

Robertson, B. E., Ellis, R. S., Dunlop, J. S., McLure, R. J., and Stark, D. P. (2010). Early star-forming galaxies and the reionization of the universe. Nature 468, 49–55. doi: 10.1038/nature09527

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, T. M. (2015). On the differential rotation of massive main-sequence stars. Astrophys. J. Letters 815:L30. doi: 10.1088/2041-8205/815/2/L30

CrossRef Full Text | Google Scholar

Rogers, T. M., Lin, D. N. C., McElwaine, J. N., and Lau, H. H. B. (2013). Internal gravity waves in massive stars: angular momentum transport. Astrophys. J. 772:21. doi: 10.1088/0004-637X/772/1/21

CrossRef Full Text | Google Scholar

Rogers, T. M., and McElwaine, J. N. (2017). On the chemical mixing induced by internal gravity waves. Astrophys. J. Letters 848:L1. doi: 10.3847/2041-8213/aa8d13

CrossRef Full Text | Google Scholar

Rosen, A. L., Offner, S. S. R., Sadavoy, S. I., Bhandare, A., Vázquez-Semadeni, E., and Ginsburg, A. (2020). Zooming in on individual star formation: low- and high-mass stars. Space Sci. Rev. 216:62. doi: 10.1007/s11214-020-00688-5

CrossRef Full Text | Google Scholar

Saio, H., Cameron, C., Kuschnig, R., Walker, G. A. H., Matthews, J. M., Rowe, J. F., et al. (2007a). g-modes in the late-type Be star β CMi detected by the MOST satellite. Commun. Asteroseismol. 150:215. doi: 10.1553/cia150s215

CrossRef Full Text | Google Scholar

Saio, H., Cameron, C., Kuschnig, R., Walker, G. A. H., Matthews, J. M., Rowe, J. F., et al. (2007b). MOST detects g-modes in the late-type Be star β Canis Minoris (B8 Ve). Astrophys. J. 654, 544–550. doi: 10.1086/509315

CrossRef Full Text | Google Scholar

Saio, H., Georgy, C., and Meynet, G. (2013). Evolution of blue supergiants and α Cygni variables: puzzling CNO surface abundances. Mon. Not. R. Astron. Soc. 433, 1246–1257. doi: 10.1093/mnras/stt796

CrossRef Full Text | Google Scholar

Saio, H., Kato, M., and Nomoto, K. (1988). Why did the progenitor of SN 1987A undergo the blue-red-blue evolution? Astrophys. J. 331, 388–393. doi: 10.1086/166565

CrossRef Full Text | Google Scholar

Saio, H., Kuschnig, R., Gautschy, A., Cameron, C., Walker, G. A. H., Matthews, J. M., et al. (2006). MOST detects g- and p-modes in the B supergiant HD 163899 (B2 Ib/II). Astrophys. J. 650, 1111–1118. doi: 10.1086/507409

CrossRef Full Text | Google Scholar

Salmon, S., Montalbán, J., Morel, T., Miglio, A., Dupret, M.-A., and Noels, A. (2012). Testing the effects of opacity and the chemical mixture on the excitation of pulsations in B stars of the magellanic clouds. Mon. Not. R. Astron. Soc. 422, 3460–3474. doi: 10.1111/j.1365-2966.2012.20857.x

CrossRef Full Text | Google Scholar

Sana, H., de Mink, S. E., de Koter, A., Langer, N., Evans, C. J., Gieles, M., et al. (2012). Binary interaction dominates the evolution of massive stars. Science 337:444. doi: 10.1126/science.1223344

PubMed Abstract | CrossRef Full Text | Google Scholar

Seaton, M. J. (2005). Opacity project data on CD for mean opacities and radiative accelerations. Mon. Not. R. Astron. Soc. 362, L1–L3. doi: 10.1111/j.1365-2966.2005.00019.x

CrossRef Full Text | Google Scholar

Serenelli, A., Weiss, A., Aerts, C., Angelou, G. C., Baroch, D., Bastian, N., et al. (2020). Weighing stars from birth to death: mass determination methods across the HRD. arXiv[Preprint].arXiv:2006.10868.

Google Scholar

Shobbrook, R. R., Handler, G., Lorenz, D., and Mogorosi, D. (2006). Photometric studies of three multiperiodic β Cephei stars: β CMa, 15 CMa and KZ Mus. Mon. Not. R. Astron. Soc. 369, 171–181. doi: 10.1111/j.1365-2966.2006.10289.x

CrossRef Full Text | Google Scholar

Shultz, M. E., Wade, G. A., Rivinius, T., Neiner, C., Alecian, E., Bohlender, D., et al. (2018). The magnetic early B-type stars I: magnetometry and rotation. Mon. Not. R. Astron. Soc. 475, 5144–5178. doi: 10.1093/mnras/sty103

CrossRef Full Text | Google Scholar

Simón-Díaz, S., Castro, N., Garcia, M., Herrero, A., and Markova, N. (2011). The IACOB spectroscopic database of Northern Galactic OB stars. Bull. Soc. R. Sci. Liege 80, 514–518.

Google Scholar

Simón-Díaz, S., Godart, M., Castro, N., Herrero, A., Aerts, C., Puls, J., et al. (2017). The IACOB project. III. New observational clues to understand macroturbulent broadening in massive O- and B-type stars. Astron. Astrophys. 597:A22. doi: 10.1051/0004-6361/201628541

CrossRef Full Text | Google Scholar

Simón-Díaz, S., and Herrero, A. (2014). The IACOB project. I. Rotational velocities in northern Galactic O- and early B-type stars revisited. The impact of other sources of line-broadening. Astron. Astrophys. 562:A135. doi: 10.1051/0004-6361/201322758

CrossRef Full Text | Google Scholar

Simón-Díaz, S., Herrero, A., Uytterhoeven, K., Castro, N., Aerts, C., and Puls, J. (2010). Observational evidence for a correlation between macroturbulent broadening and line-profile variations in OB supergiants. Astrophys. J. Letters 720, L174–L178. doi: 10.1088/2041-8205/720/2/L174

CrossRef Full Text | Google Scholar

Simón-Díaz, S., Negueruela, I., Maíz Apellániz, J., Castro, N., Herrero, A., Garcia, M., et al. (2015). “The IACOB spectroscopic database: recent updates and first data release,” in Highlights of Spanish Astrophysics VIII, eds. A. J. Cenarro, F. Figueras, C. Hernández-Monteagudo, J. Trujillo Bueno, and L. Valdivielso (Teruel), 576–581.

Google Scholar

Smartt, S. J. (2009). Progenitors of core-collapse supernovae. Ann. Rev. Astron. Astrophys. 47, 63–106. doi: 10.1146/annurev-astro-082708-101737

CrossRef Full Text | Google Scholar

Smith, M. A. (1977). Nonradial pulsations in early to mid-B stars. Astrophys. J. 215, 574–583. doi: 10.1086/155391

CrossRef Full Text | Google Scholar

Smith, M. A., and McCall, M. L. (1978). Undulations of a B-type star: 53 Persei. Astrophys. J. 223, 221–233. doi: 10.1086/156253

CrossRef Full Text | Google Scholar

Southworth, J., Bowman, D. M., Tkachenko, A., and Pavlovski, K. (2020). Discovery of β Cep pulsations in the eclipsing binary V453 Cygni. Mon. Not. R. Astron. Soc. 497, L19–L23. doi: 10.1093/mnrasl/slaa091

CrossRef Full Text | Google Scholar

Stankov, A., and Handler, G. (2005). Catalog of Galactic β Cephei stars. Astrophys. J. Supp. Ser. 158, 193–216. doi: 10.1086/429408

CrossRef Full Text | Google Scholar

Stark, D. P. (2016). Galaxies in the first billion years after the big bang. Ann. Rev. Astron. Astrophys. 54, 761–803. doi: 10.1146/annurev-astro-081915-023417

PubMed Abstract | CrossRef Full Text | Google Scholar

Štefl, S., Baade, D., Rivinius, T., Stahl, O., Budovičová, A., Kaufer, A., et al. (2003). Stellar and circumstellar activity of the Be star omega CMa. II. Periodic line-profile variability. Astron. Astrophys. 411, 167–180. doi: 10.1051/0004-6361:20031179

CrossRef Full Text | Google Scholar

Suárez, J. C., Goupil, M. J., Reese, D. R., Samadi, R., Lignières, F., Rieutord, M., et al. (2010). On the interpretation of Echelle diagrams for solar-like oscillations effect of centrifugal distortion. Astrophys. J. 721, 537–546. doi: 10.1088/0004-637X/721/1/537

CrossRef Full Text | Google Scholar

Suárez, J. C., Moya, A., Amado, P. J., Martín-Ruiz, S., Rodríguez-López, C., and Garrido, R. (2009). Seismology of β Cephei stars: differentially rotating models for interpreting the oscillation spectrum of ν Eridani. Astrophys. J. 690, 1401–1411. doi: 10.1088/0004-637X/690/2/1401

CrossRef Full Text | Google Scholar

Szewczuk, W., and Daszyńska-Daszkiewicz, J. (2015). Seismic modelling of the rotating, slowly pulsating B-type star HD 21071. Mon. Not. R. Astron. Soc. 453, 277–286. doi: 10.1093/mnras/stv1589

CrossRef Full Text | Google Scholar

Szewczuk, W., and Daszyńska-Daszkiewicz, J. (2017). Domains of pulsational instability of low-frequency modes in rotating upper main sequence stars. Mon. Not. R. Astron. Soc. 469, 13–46. doi: 10.1093/mnras/stx738

CrossRef Full Text | Google Scholar

Szewczuk, W., and Daszyńska-Daszkiewicz, J. (2018). KIC 3240411–the hottest known SPB star with the asymptotic g-mode period spacing. Mon. Not. R. Astron. Soc. 478, 2243–2256. doi: 10.1093/mnras/sty1126

CrossRef Full Text | Google Scholar

Tanvir, N. R., Fox, D. B., Levan, A. J., Berger, E., Wiersema, K., Fynbo, J. P. U., et al. (2009). A γ-ray burst at a redshift of z~8.2. Nature 461, 1254–1257. doi: 10.1038/nature08459

PubMed Abstract | CrossRef Full Text | Google Scholar

Tassoul, M. (1980). Asymptotic approximations for stellar nonradial pulsations. Astrophys. J. Supp. Ser. 43, 469–490. doi: 10.1086/190678

CrossRef Full Text | Google Scholar

Telting, J. H., Aerts, C., and Mathias, P. (1997). A period analysis of the optical line variability of β Cephei: evidence for multi-mode pulsation and rotational modulation. Astron. Astrophys. 322, 493–506.

Google Scholar

Telting, J. H., and Schrijvers, C. (1997). Line-profile variations of non-radial adiabatic pulsations of rotating stars. II. The diagnostic value of amplitude and phase diagrams derived from time series of spectra. Astron. Astrophys. 317, 723–741.

Google Scholar

Tkachenko, A., Degroote, P., Aerts, C., Pavlovski, K., Southworth, J., Pápics, P. I., et al. (2014). The eccentric massive binary V380 Cyg: revised orbital elements and interpretation of the intrinsic variability of the primary component. Mon. Not. R. Astron. Soc. 438, 3093–3110. doi: 10.1093/mnras/stt2421

CrossRef Full Text | Google Scholar

Tkachenko, A., Matthews, J. M., Aerts, C., Pavlovski, K., Pápics, P. I., Zwintz, K., et al. (2016). Stellar modelling of Spica, a high-mass spectroscopic binary with a β Cep variable primary component. Mon. Not. R. Astron. Soc. 458, 1964–1976. doi: 10.1093/mnras/stw255

CrossRef Full Text | Google Scholar

Tkachenko, A., Pavlovski, K., Johnston, C., Pedersen, M. G., Michielsen, M., Bowman, D. M., et al. (2020). The mass discrepancy in intermediate- and high-mass eclipsing binaries: the need for higher convective core masses. Astron. Astrophys. 637:A60. doi: 10.1051/0004-6361/202037452

CrossRef Full Text | Google Scholar

Torres, G., Andersen, J., and Giménez, A. (2010). Accurate masses and radii of normal stars: modern results and applications. Astron. Astrophys. Rev. 18, 67–126. doi: 10.1007/s00159-009-0025-1

CrossRef Full Text | Google Scholar

Townsend, R. H. D. (2003a). A semi-analytical formula for the light variations due to low-frequency g modes in rotating stars. Mon. Not. R. Astron. Soc. 343, 125–136. doi: 10.1046/j.1365-8711.2003.06640.x

CrossRef Full Text | Google Scholar

Townsend, R. H. D. (2003b). Asymptotic expressions for the angular dependence of low-frequency pulsation modes in rotating stars. Mon. Not. R. Astron. Soc. 340, 1020–1030. doi: 10.1046/j.1365-8711.2003.06379.x

CrossRef Full Text | Google Scholar

Townsend, R. H. D. (2005). Influence of the Coriolis force on the instability of slowly pulsating B stars. Mon. Not. R. Astron. Soc. 360, 465–476. doi: 10.1111/j.1365-2966.2005.09002.x

CrossRef Full Text | Google Scholar

Townsend, R. H. D., Goldstein, J., and Zweibel, E. G. (2018). Angular momentum transport by heat-driven g-modes in slowly pulsating B stars. Mon. Not. R. Astron. Soc. 475, 879–893. doi: 10.1093/mnras/stx3142

CrossRef Full Text | Google Scholar

Townsend, R. H. D., Owocki, S. P., and Howarth, I. D. (2004). Be-star rotation: how close to critical? Mon. Not. R. Astron. Soc. 350, 189–195. doi: 10.1111/j.1365-2966.2004.07627.x

CrossRef Full Text | Google Scholar

Townsend, R. H. D., and Teitler, S. A. (2013). GYRE: an open-source stellar oscillation code based on a new Magnus Multiple Shooting scheme. Mon. Not. R. Astron. Soc. 435, 3406–3418. doi: 10.1093/mnras/stt1533

CrossRef Full Text | Google Scholar

Triana, S. A., Moravveji, E., Pápics, P. I., Aerts, C., Kawaler, S. D., and Christensen-Dalsgaard, J. (2015). The internal rotation profile of the B-type star KIC 10526294 from frequency inversion of its dipole gravity modes. Astrophys. J. 810:16. doi: 10.1088/0004-637X/810/1/16

CrossRef Full Text | Google Scholar

Unno, W., Osaki, Y., Ando, H., Saio, H., and Shibahashi, H. (1989). Nonradial Oscillations of Stars. Tokyo: University of Tokyo Press.

Google Scholar

Uytterhoeven, K., Briquet, M., Aerts, C., Telting, J. H., Harmanec, P., Lefever, K., et al. (2005). Disentangling component spectra of κ Scorpii, a spectroscopic binary with a pulsating primary. II. Interpretation of the line-profile variability. Astron. Astrophys. 432, 955–967. doi: 10.1051/0004-6361:20041444

CrossRef Full Text | Google Scholar

Uytterhoeven, K., Telting, J. H., Aerts, C., and Willems, B. (2004). Interpretation of the variability of the β Cephei star λ Scorpii. II. The line-profile diagnostics. Astron. Astrophys. 427, 593–605. doi: 10.1051/0004-6361:20041224

CrossRef Full Text | Google Scholar

van der Walt, S., Colbert, S. C., and Varoquaux, G. (2011). The NumPy Array: a structure for efficient numerical computation. Comput. Sci. Eng. 13, 22–30.

Google Scholar

van Leeuwen, F., Evans, D. W., Grenon, M., Grossmann, V., Mignard, F., and Perryman, M. A. C. (1997). The HIPPARCOS mission: photometric data. Astron. Astrophys. 323, L61–L64.

Google Scholar

Van Reeth, T., Mombarg, J. S. G., Mathis, S., Tkachenko, A., Fuller, J., Bowman, D. M., et al. (2018). Sensitivity of gravito-inertial modes to differential rotation in intermediate-mass main-sequence stars. Astron. Astrophys. 618:A24. doi: 10.1051/0004-6361/201832718

CrossRef Full Text | Google Scholar

Van Reeth, T., Tkachenko, A., and Aerts, C. (2016). Interior rotation of a sample of γ Doradus stars from ensemble modelling of their gravity-mode period spacings. Astron. Astrophys. 593:A120. doi: 10.1051/0004-6361/201628616

CrossRef Full Text | Google Scholar

Van Reeth, T., Tkachenko, A., Aerts, C., Pápics, P. I., Degroote, P., Debosscher, J., et al. (2015a). Detecting non-uniform period spacings in the Kepler photometry of γ Doradus stars: methodology and case studies. Astron. Astrophys. 574:A17. doi: 10.1051/0004-6361/201424585

CrossRef Full Text | Google Scholar

Van Reeth, T., Tkachenko, A., Aerts, C., Pápics, P. I., Triana, S. A., Zwintz, K., et al. (2015b). Gravity-mode period spacings as a seismic diagnostic for a sample of γ Doradus stars from Kepler space photometry and high-resolution ground-based spectroscopy. Astrophys. J. Supp. Ser. 218:27. doi: 10.1088/0067-0049/218/2/27

CrossRef Full Text | Google Scholar

von Zeipel, H. (1924). The radiative equilibrium of a rotating system of gaseous masses. Mon. Not. R. Astron. Soc. 84, 665–683. doi: 10.1093/mnras/84.9.665

CrossRef Full Text | Google Scholar

Wade, G. A., Neiner, C., Alecian, E., Grunhut, J. H., Petit, V., Batz, B. d., et al. (2016). The MiMeS survey of magnetism in massive stars: introduction and overview. Mon. Not. R. Astron. Soc. 456, 2–22. doi: 10.1093/mnras/stv2568

CrossRef Full Text | Google Scholar

Waelkens, C. (1991). Slowly pulsating B stars. Astron. Astrophys. 246, 453–468.

Google Scholar

Waelkens, C., Aerts, C., Grenon, M., and Eyer, L. (1998a). “Pulsating B stars discovered by HIPPARCOS,” in A Half Century of Stellar Pulsation Interpretation, Vol. 135 of Astronomical Society of the Pacific Conference Series, eds. P. A. Bradley and J. A. Guzik (Los Alamos, NM), 375.

Google Scholar

Waelkens, C., Aerts, C., Kestens, E., Grenon, M., and Eyer, L. (1998b). Study of an unbiased sample of B stars observed with Hipparcos: the discovery of a large amount of new slowly pulsating B stars. Astron. Astrophys. 330, 215–221.

Google Scholar

Wagle, G. A., Ray, A., Dev, A., and Raghu, A. (2019). Type IIP supernova progenitors and their explodability. I. Convective overshoot, blue loops, and surface composition. Astrophys. J. 886:27. doi: 10.3847/1538-4357/ab4a19

CrossRef Full Text | Google Scholar

Walczak, P., Daszyńska-Daszkiewicz, J., Pamyatnykh, A. A., and Zdravkov, T. (2013). The hybrid B-type pulsator γ Pegasi: mode identification and complex seismic modelling. Mon. Not. R. Astron. Soc. 432, 822–831. doi: 10.1093/mnras/stt492

CrossRef Full Text | Google Scholar

Walczak, P., Daszyńska-Daszkiewicz, J., Pigulski, A., Pamyatnykh, A., Moffat, A. F. J., Handler, G., et al. (2019). Seismic modelling of early B-type pulsators observed by BRITE–I. θ Ophiuchi. Mon. Not. R. Astron. Soc. 485, 3544–3557. doi: 10.1093/mnras/stz639

CrossRef Full Text | Google Scholar

Walczak, P., Fontes, C. J., Colgan, J., Kilcrease, D. P., and Guzik, J. A. (2015). Wider pulsation instability regions for β Cephei and SPB stars calculated using new Los Alamos opacities. Astron. Astrophys. 580:L9. doi: 10.1051/0004-6361/201526824

CrossRef Full Text | Google Scholar

Walker, G., Matthews, J., Kuschnig, R., Johnson, R., Rucinski, S., Pazder, J., et al. (2003). The MOST asteroseismology mission: ultraprecise photometry from space. Public. Astronom. Soc. Pac. 115, 1023–1035. doi: 10.1086/377358

CrossRef Full Text | Google Scholar

Walker, G. A. H., Kuschnig, R., Matthews, J. M., Cameron, C., Saio, H., Lee, U., et al. (2005). MOST detects g-modes in the Be star HD 163868. Astrophys. J. Letters 635, L77–L80. doi: 10.1086/499362

CrossRef Full Text | Google Scholar

Watson, R. D. (1988). Contributing factors to flux changes in nonradial stellar pulsations. Astrophys. Space Sci. 140, 255–290. doi: 10.1007/BF00638984

CrossRef Full Text | Google Scholar

Weiss, W. W., Rucinski, S. M., Moffat, A. F. J., Schwarzenberg-Czerny, A., Koudelka, O. F., Grant, C. C., et al. (2014). BRITE-constellation: nanosatellites for precision photometry of bright stars. Public. Astronom. Soc. Pac. 126:573. doi: 10.1086/677236

CrossRef Full Text | Google Scholar

White, T. R., Pope, B. J. S., Antoci, V., Pápics, P. I., Aerts, C., Gies, D. R., et al. (2017). Beyond the Kepler/K2 bright limit: variability in the seven brightest members of the Pleiades. Mon. Not. R. Astron. Soc. 471, 2882–2901. doi: 10.1093/mnras/stx1050

CrossRef Full Text | Google Scholar

Wu, T., and Li, Y. (2019). High-precision asteroseismology in a slowly pulsating B star: HD 50230. Astrophys. J. 881:86. doi: 10.3847/1538-4357/ab2ad8

CrossRef Full Text | Google Scholar

Zahn, J.-P. (1992). Circulation and turbulence in rotating stars. Astron. Astrophys. 265, 115–132.

Google Scholar

Zorec, J., and Briot, D. (1997). Critical study of the frequency of Be stars taking into account their outstanding characteristics. Astron. Astrophys. 318, 443–460.

Google Scholar