Incoherent Solar Radio Emission

Incoherent solar radio radiation comes from the free-free, gyroresonance, and gyrosynchrotron emission mechanisms. Free-free is primarily produced from Coulomb collisions between thermal electrons and ions. Gyroresonance and gyrosynchrotron result from the acceleration of low-energy electrons and mildly relativistic electrons, respectively, in the presence of a magnetic field. In the non-flaring Sun, free-free is the dominant emission mechanism with the exception of regions of strong magnetic fields which emit gyroresonance at microwaves. Due to its ubiquitous presence, free-free emission can be used to probe the non-flaring solar atmosphere above temperature minimum. Gyroresonance opacity depends strongly on the magnetic field strength and orientation; hence it provides a unique tool for the estimation of coronal magnetic fields. Gyrosynchrotron is the primary emission mechanism in flares at frequencies higher than 1–2 GHz and depends on the properties of both the magnetic field and the accelerated electrons, as well as the properties of the ambient plasma. In this paper we discuss in detail the above mechanisms and their diagnostic potential.

1. Introduction

The Sun produces radiation across virtually the entire electromagnetic spectrum. Radio frequencies offer valuable diagnostic potential because two of the natural frequencies of the atmosphere of the Sun, the electron plasma frequency and the electron gyrofrequency, belong to the radio band.

In the Sun there are no significant spectral lines, either in emission or absorption, from millimeter to meter wavelengths (but see Dravskikh and Dravskikh, 1988, for a possible detection); pressure broadening is so high that makes such lines undetectable. In the Sun the free electrons dominate the radio emission mechanisms. Solar radio emission is produced from electrons with either a thermal or a non-thermal distribution, and the emission can be either incoherent or coherent. In incoherent mechanisms, no back-reaction of the emission on the electron distribution is present, and the emitted photons show no phase association while their number is proportional to the number of electrons. In coherent mechanisms, all electrons exhibit acceleration in phase; they act together to generate photons that are in phase.

Coherent radiation due to wave-particle and wave-wave interactions plays an important role in transient phenomena at frequencies below 1–2 GHz. Coherent emission mechanisms are discussed elsewhere in this issue by Fleishman.

There are two classes of incoherent emission mechanisms that are important on the Sun: free-free (or bremsstrahlung) and gyromagnetic. At radio frequencies free-free emission is primarily produced from collisions between ions and thermal electrons and dominates the radio emission of the quiet Sun. Furthermore it contributes significantly to the radio emission of non-flaring active regions and of certain flares during their decay phase. Erupting prominences and coronal mass ejections (CMEs) may also produce free-free emission. Gyromagnetic radiation is produced from electrons that are accelerated in the presence of magnetic fields. It is called gyroresonance emission when it is produced by thermal electrons with energies that correspond to temperatures of the non-flaring corona (about 10⁶ K). Gyroresonance plays an important role in the emission above sunspots at microwaves. Gyromagnetic emission is called gyrosynchrotron when it is produced by mildly relativistic electrons having either non-thermal or thermal electron energy distributions. Gyrosynchrotron is the principle incoherent emission mechanism in flares.

There are several textbooks and review articles devoted to incoherent solar radio emission. The classical textbooks by Kundu (1965), Zheleznyakov (1970), and Krüger (1979) are valuable sources of information. More recent textbooks include the volume edited by Gary and Keller (2004), as well as Aschwanden's (Aschwanden, 2004) book on the solar corona. A historical account of solar radio astronomy together with recent developments has been given in the review by Pick and Vilmer (2008). A review about the radio emission of the quiet Sun has been published by Shibasaki et al. (2011) while reviews about gyroresonance have been provided by White and Kundu (1997) and Lee (2007). Transient incoherent solar radio emission has been discussed by Bastian et al. (1998) and Nindos et al. (2008). A more recent book about incoherent microwave emission from flaring loops has been written by Huang et al. (2018).

The structure of this paper is as follows. In section 2, we give a short introduction on radiative transfer and propagation of radio emission. In section 3, we discuss free-free emission, and in section 4 the different types of gyromagnetic emission are outlined briefly. Section 5 and section 6 are devoted to gyroresonance and gyrosynchrotron radiation, respectively. We present concluding remarks in section 7.

2. Radiative Transfer and Propagation of Radio Emission

2.1. Radiative Transfer Basics

Radiation is always intimately related to material through emission and absorption processes. When both emission and absorption are considered, the intensity, I_ν, inside a plasma slab of thickness dl changes by

$\begin{array}{ll}\frac{d{I}_{\nu }}{dl}=j_{\nu }\rho -k_{\nu }\rho I_{\nu }& (1)\end{array}$

where j_ν and k_ν are the emission and absorption coefficients, respectively, which are defined by

$\begin{array}{ll}d{I}_{\nu }=j_{\nu }\rho dl& (2)\end{array}$

and

$\begin{array}{ll}d{I}_{\nu }=-k_{\nu }\rho I_{\nu }dl& (3)\end{array}$

where ρ is the plasma density. The above discussion is only valid for thermal plasma radiation. For non-thermal electron distributions these formulas hold if ρ describes the concentration of non-thermal electrons.

It is convenient to discuss radiative transfer in terms of the optical depth, τ_ν, which is defined by:

$\begin{array}{ll}d{\tau }_{\nu }=-k_{\nu }\rho dl& (4)\end{array}$

Using the optical depth, Equation (1) becomes

$\begin{array}{ll}\frac{d{I}_{\nu }}{d{\tau }_{\nu }}=I_{\nu }-S_{\nu }& (5)\end{array}$

where S_ν = j_ν/k_ν is the source function. Equation (5) is called radiative transfer equation (RTE). Its typical solution (i.e., the intensity at the observer where τ_ν = 0) is

$\begin{array}{ll}{I}_{\nu }({\tau }_{\nu }=0)={\displaystyle {\int }_0^{\infty }}{S}_{\nu }{e}^{-t_{\nu }}d{t}_{\nu }& (6)\end{array}$

Therefore the intensity at the observer results from the contribution of all layers of a stellar atmosphere, with each layer contributing proportionally to its emissivity, attenuated by the absorption of the overlying layers, $e^{-t_{\nu }}$.

From the RTE, we obtain for a finite slab of constant source function:

$\begin{array}{ll}{I}_{\nu }=S_{\nu }(1-e^{-{\tau }_{\nu }})& (7)\end{array}$

In the optically thin case (i.e., transparent slab; τ_ν ≪ 1), Equation (7) yields

$\begin{array}{ll}{I}_{\nu }={\tau }_{\nu }{S}_{\nu }& (8)\end{array}$

while for the optically thick case (i.e., opaque slab; τ_ν ≫ 1), we obtain

$\begin{array}{ll}{I}_{\nu }=S_{\nu }& (9)\end{array}$

Thermal solar radio emission originates from local thermodynamic equilibrium (LTE) conditions (i.e., the temperature, T, does not change much with respect to the mean free path of photons and free electrons, and the anisotropy of the radiation field is small). In LTE, the emission and absorption coefficients are not independent, but the source function is equal to the Planck function. At radio frequencies the inequality hν/k_BT ≪ 1 holds, (k_B is the Boltzmann constant), and the Planckian simplifies to the Rayleigh-Jeans law. Then it is convenient to define a brightness temperature, T_b, as the equivalent temperature a black body would have in order to be as bright as the observed brightness:

$\begin{array}{ll}{I}_{\nu }=B_{\nu }(T_b)=\frac{2{\nu }^2}{c^2}{k}_B{T}_b& (10)\end{array}$

Similarly, we can define an effective temperature, T_eff:

$\begin{array}{ll}{S}_{\nu }=\frac{j_{\nu }}{k_{\nu }}=\frac{2{\nu }^2}{c^2}{k}_B{T}_{eff}& (11)\end{array}$

Using our definitions of brightness temperature and effective temperature the RTE can be expressed as:

$\begin{array}{ll}\frac{d{T}_b}{d{\tau }_{\nu }}=T_b-T_{eff}& (12)\end{array}$

Similar to Equation (5), for an homogeneous source, the solution is:

$\begin{array}{ll}{T}_b=T_{eff}(1-e^{-{\tau }_{\nu }}),& (13)\end{array}$

For the optically thin and optically thick cases, Equation (13) yields

$\begin{array}{ll}{T}_b={\tau }_{\nu }{T}_{eff}& (14)\end{array}$

and

$\begin{array}{ll}{T}_b=T_{eff}& (15)\end{array}$

respectively. When the emission is incoherent, T_eff is the kinetic temperature in the case of thermal emission or corresponds to the mean energy, E, of the emitting electrons (i.e., T_eff = E/k_B) when the emission is non-thermal. Therefore for an incoherent emission, T_b is limited by the mean energy of the radiating particles. Since the rest energy of the electron corresponds to $T_b=0.6\times 10^{10}$ K, we conclude that sources with $T_b\gg 10^{10}$ K cannot be due to incoherent emission from non-relativistic or mildly relativistic electrons. Incoherent emission by highly relativistic electrons is dominated by synchrotron emission (see section 4), which is limited to $T_b\le 10^{12}$ K by Compton scattering (Kellermann and Pauliny-Toth, 1969).

2.2. Propagation of Radio Emission

In most cases, the corona can be described as a cold magnetized plasma, and the magnetoionic theory (e.g., Melrose, 1980, volume 1, chapter 2) is used to study the propagating electromagnetic modes. These are the extraordinary (x-), ordinary (o-), z-, and whistler mode. Only the x- and o- mode waves can propagate from the source to the observer, whereas the z- and whistler mode waves cannot due to stopbands in the refractive index. For most applications in solar radiophysics, the propagation of the x- and o-mode waves can be described by either the quasi-longitudinal (QL) or the quasi-transverse (QT) approximation (propagation almost parallel and almost perpendicular to the magnetic field, respectively).

For observational purposes it is easier to describe radiation using the Stokes parameters I, Q, U, and V. Under conditions of QL propagation, we get Q = U = 0, and the x- and o-mode waves are circularly polarized in opposite senses. Thus we obtain V = I_x − I_o, and the polarization is circular having the sense of the dominant mode. In the case of QT propagation, we obtain Q = I_x − I_o and U = V = 0, and the polarization is linear. However, because the Faraday rotation in the corona is large, we can detect linear polarization only if we use receivers of much narrower bandwidth than those currently available. There is only one observation of linear polarization at microwaves from active regions; it was accomplished by Alissandrakis and Chiuderi-Drago (1994) who used a multichannel spectral line receiver of very small bandwidth.

Under the approximation of geometrical optics (not very low values for the magnetic field and electron density) when conditions change along the radiation path, the polarization of the x- and o-mode waves will change accordingly. Therefore when a transverse field region is crossed, the sense of polarization changes because of the change of the sign of the longitudinal magnetic field. This is valid when the coupling between the x- and o-mode waves is weak (i.e., they propagate independently). However, as both the coronal magnetic field and density decrease with height, the differences between the characteristics of the x- and o-mode waves decrease, and hence their mutual coupling increases. In the strong coupling regime, the waves are not independent and the polarization does not change along the path but attains a limiting value, even if a transverse field region is crossed (e.g., Cohen, 1960; Zheleznyakov, 1970). Therefore, data of circular polarization do not necessarily reflect the polarity of the magnetic field at the source of radiation (e.g., Alissandrakis and Preka-Papadema, 1984; Alissandrakis et al., 1993b; Shain et al., 2017).

The refractive index of the unmagnetized plasma is $n={\left[1-{({\nu }_p/\nu )}^2\right]}^{1/2}$ where ν_p is the electron plasma frequency. At low frequencies it can become much smaller than unity which could trigger refraction and total reflection effects. Total reflection of the radio waves will occur when ν = ν_p. Refraction modifies the ray paths and also decreases the brightness because the rays move away from regions of high density and the optical depth becomes less than unity (Alissandrakis, 1994). Generally, refraction is not important unless the optical depth between the region of total reflection and the observer is small. Its effect becomes more serious when large-scale density inhomogeneities are present in the corona and inner heliosphere (e.g., coronal holes, streamers, slow or fast solar wind streams). This can result in distorions and/or apparent position offsets of the radio sources (e.g., Duncan, 1979; Lecacheux et al., 1989). Ionospheric refraction can also significantly modify the apparent position of radio sources, sometimes more than several minutes of arc in the metric range (e.g., Mercier, 1996).

When small-scale inhomogeneities are present between the observer and the radio source, several scattering phenomena may take place. These include spectral and angular broadenings that cause frequency-dependent blurring in radio structures (e.g., Bastian, 1994) and decrease of the detected brightness temperature at low frequencies (Thejappa and MacDowall, 2008). Furthermore, anisotropic scattering displaces radio sources (Kontar et al., 2019).

3. Free-Free Emission

3.1. Emissivity and Absorption Coefficient

3.1.1. Electron-ion Free-Free Mechanism

From the middle chromosphere upward, the free-free emission (or bremsstrahlung) exclusively originates from electrons that are diverted in the Coulomb field of ambient ions because they are accelerated by the Coulomb force. The term “free-free” is due to the state of the electrons; they are free both before and after the interaction.

In the classical limit, the radiation of free accelerated charged particles is described by Larmor's formula:

$\begin{array}{ll}\frac{dP}{d\Omega }=\frac{q^2{a}^2}{4\pi c^2}{\text{sin}}^2\theta & (16)\end{array}$

where P is the power emitted within the solid angle dΩ by a particle of charge q, mass m, and acceleration a in the direction θ relative to the acceleration vector. The total radiated power is obtained after integration over solid angle:

$\begin{array}{ll}P=\frac{2q^2{a}^2}{3c^2}& (17)\end{array}$

Since a ∝ 1/m, the power is ∝ 1/m² and the proton radiation can be ignored because it is much smaller than that of electrons. This conclusion holds for all radio emission processes. Interaction between identical charges also does not produce much radiation because radiation power is proportional to the second derivative of the dipole moment of the system of charged particles, which does not change when two identical particles interact. Consequently, only electron-ion collisions are relevant, and significant radiation is produced by the electrons only.

In a binary encounter between an electron of speed v and an ion of charge Z, the electron deviates from its straight line path by an angle θ, which depends on its speed and the distance of the encounter, called impact parameter, b. In the corona there is a large number of particles inside the Debye sphere and hence the ratio of small-to-large angle encounters is ≈ λ_D/r_c, where λ_D is the Debye length and r_c is the impact parameter that produces a 90° deflection (e.g., see Raulin and Pacini, 2005). Consequently, small-angle collisions dominate and the path of an incoming electron is determined primarily by multiple interactions that yield small deflections, and therefore low energy (radio, that is) photons are produced. In large-angle encounters, high energy electrons may undergo large deflections that yield the emission of high energy (X-ray, that is) photons. Large-angle encounters become more important as we move to cooler and denser deeper layers of the solar atmosphere, because the size of the Debye sphere decreases.

The calculation of the emission from free-free interactions is given in detail by Rybicki and Lightman (1979); here, we only outline the procedure. Since we are interested in the radio emission, the small-angle approximation is appropriate for which the deflection of electrons can be neglected, and therefore we assume the motion takes place along a straight line where the electron and ion are separated by $r=\sqrt{b^2+v^2{t}^2}$. We further use the dipole approximation to obtain the net acceleration along the path, and therefore for a single collision an electron emits:

$\begin{array}{ll}\frac{dW(b)}{d\omega }=\frac{8Z^2{e}^6}{3\pi c^3{m}_e^2{v}^2{b}^2}\text{ for }b\ll v/\omega & (18)\end{array}$

(collisions at a given b lead to emission only at ω < ν/b). The total incoming flux of electrons with speed v is (n_ev)(2πbdb), where n_e is the electron number density. Then the free-free emissivity (i.e., emission per unit time, volume, and frequency) is:

$\begin{array}{ll}\frac{dW}{dtdVd\omega }=n_e{n}_{i}2\pi v{\displaystyle {\int }_{b_{min}}^{b_{max}}}\frac{dW(b)}{d\omega }bdb& (19)\end{array}$

where n_i is the ion number density. The limits of integration are determined by $b_{min}=4Z{e}^2/(\pi m_e{v}^2)$ corresponding to a 90° deflection, and b_max = v/ω, above which the emitted power is negligible. When we combine Equations (18) and (19), we obtain:

$\begin{array}{ll}\frac{dW}{dtdVd\omega }=\frac{16e^6{n}_e{n}_i{Z}^2}{3c^3{m}_e^{2}v}{\displaystyle {\int }_{b_{min}}^{b_{max}}}\frac{db}{b}=\frac{16e^6{n}_e{n}_i{Z}^2}{3c^3{m}_e^2\nu }\text{ln }\left(\frac{b_{max}}{b_{min}}\right)& (20)\end{array}$

Usually the above equation is written as

$\begin{array}{ll}\frac{dW}{dtdVd\omega }=\frac{16\pi e^6}{3^{3/2}{c}^3{m}_e^{2}v}{n}_e{n}_i{Z}^2{G}_{ff}(v,\omega )& (21)\end{array}$

where G_ff (ν, ω) is the Gaunt factor (Karzas and Latter, 1961).

The next step is to integrate Equation (21) over the velocity distribution of the electrons. In radio astronomy, a thermal distribution is used in most cases, and the calculation yields

$\begin{array}{ll}{\eta }_{\nu }=\frac{2^5\pi e^6}{3m_e{c}^3}{\left(\frac{2\pi }{3m_e{k}_B{T}_e}\right)}^{1/2}{n}_e{n}_i{Z}^2{G}_{ff}(T_e,\nu )& (22)\end{array}$

where the emissivity is now denoted by η_ν, and T_e is the electron temperature. The emissivity is proportional to the product of the electron number density with the ion number density. The decrease of emissivity with increasing temperature comes from the decrease of dW(b)/dω with increasing relative speed v of the electron-ion pairs (Equation 18).

Using the emissivity and the Rayleigh-Jeans law, $B_{\nu }(T_e)=2k_B{T}_e{\nu }^2/c^2$, we obtain the absorption coefficient:

$\begin{array}{ll}{k}_{\nu }=\frac{1}{3c}\sqrt{\frac{2\pi }{3}}{\left(\frac{{\nu }_p}{\nu }\right)}^2\frac{4\pi e^4{n}_e{n}_i{Z}^2}{m_e^{1/2}{(k_{B}T)}^{3/2}}{G}_{ff}(T_e,\nu )& (23)\end{array}$

which is also written as

$\begin{array}{l}{k}_{\nu }=\frac{9.78\times {10}^{-3}{n}_e{n}_i{Z}^2}{{\nu }^2{T}_e^{3/2}}\\ \times \{\begin{array}{ll}18.2+\text{ln }{T}_e^{3/2}-\text{ln }\nu \hfill & (T_e<2\times {10}^{5}K)\hfill \\ 24.5+\text{ln }{T}_e-\text{ln }\nu \hfill & (T_e>2\times {10}^{5}K)\hfill \end{array}& (24)\end{array}$

where two expressions for the Gaunt factor have been used for conditions relevant to the solar atmosphere (Dulk, 1985).

3.1.2. H⁻ Free-Free Mechanism

Free-free absorption can result not only from interactions between ions and free electrons but also from free-free transitions of electrons in the field of hydrogen atoms. The latter mechanism is often referred to as H⁻ absorption. Stallcop (1974) has provided analytical expressions for the H⁻ absorption coefficient, $k_{H^{-}}$, from which we obtain:

$\begin{array}{ll}{k}_{H^{-}}=1.2754\times 10^{-11}\frac{n_e{n}_H\sqrt{T}}{{\nu }^2}{e}^{-\zeta (2.065K)}& (25)\end{array}$

where n_H is the hydrogen density and

$\begin{array}{ll}K=2.517\times 10^{-3}\sqrt{T}& (26)\end{array}$

and

$\begin{array}{ll}\zeta (2.065K)=4.862K(1-0.2096K+0.0170K^2-0.00968K^3)& (27)\end{array}$

The contribution of H⁻ absorption becomes non-negligible at wavelengths shorter than about 1 mm, where radiation is formed in cooler layers. Alissandrakis et al. (2017) have estimated that at around electron temperature of 6,000 K, the H⁻ opacity is about 10% of the total opacity (see also Wedemeyer et al., 2016).

3.2. Polarization

With the above treatment we did not take into account the magnetic field and we also assumed that the index of refraction n is unity. If we relax these assumptions, we obtain equations which are more complicated than Equations (22) and (24). However, simplifications are often used (e.g., Kundu, 1965), which yield a simpler expression for the absorption coefficient:

$\begin{array}{ll}{k}_{\nu }=\xi \frac{n_e^2}{n{\nu }^2{T}_e^{3/2}}\frac{1}{{(\nu \pm {\nu }_{ce}|\text{cos }\theta |)}^2}& (28)\end{array}$

where ξ is a slowly varying function of T_e and n_e, ν_ce is the electron gyrofrequency, and θ the angle between the magnetic field and the line of sight. The plus sign in Equation (28) corresponds to the o-mode emission while the minus sign corresponds to the x-mode wave. Therefore the x- and o-mode opacities are slightly larger and smaller, respectively, than that of the unmagnetized situation. The radiation forms in regions where the temperature increases with height, and so does the brightness temperature. Consequently, we expect weak polarization in the sense of the x-mode.

For uniform thermal material and using Equation (28), we derive that the degree of circular polarization ρ_c of the optically thin free-free emission is:

$\begin{array}{ll}{\rho }_c=\frac{V}{I}=\frac{2{\nu }_{ce}\text{cos }\theta }{\nu }& (29)\end{array}$

where the longitudinal component of the magnetic field, B cos θ, is involved because ν_ce = eB/(2πm_ec). However, one should take into a count that the density and magnetic field are not constant along the line of sight, and that the emission should not necessarily be optically thin. However, in the weak field limit Grebinskij et al. (2000) and Gelfreikh (2004) have shown that one may nevertheless constrain the coronal magnetic field from spectrally resolved data of free-free radiation.

3.3. Observations of Free-Free Emission

At most frequencies and locations (exceptions include regions with strong coronal magnetic fields observed at microwaves, see section 5), the non-flaring Sun produces radio emission via the free-free mechanism. At low frequencies the corresponding emission is optically thick in the corona (though refraction may bring τ_ν below unity at metric wavelengths), while at higher frequencies there is a mixture of optically thick radiation from cool chromospheric plasmas together with contributions from hot coronal plasmas (can be either optically thin or thick) in active regions.

3.3.1. Spectrum

A model of the spectrum of the microwave brightness temperature of free-free emission is presented in the left column of Figure 1 (from Gary and Hurford, 1994). The calculation was performed for coronal conditions ($T_e\approx 1.5\times 10^6$ K, fully ionized H and 10% He) neglecting magnetic field and assuming that the index of refraction is 1. Then by using Equation (28) and the definition of optical depth, τ_ν, we obtain

$\begin{array}{ll}{\tau }_{\nu }\approx 0.2\frac{\int n_e^{2}dl}{{\nu }^2{T}_e^{3/2}}& (30)\end{array}$

The spectrum is flat where the emission is optically thick and the corresponding T_b is merely the electron temperature of the corona (see Equation 15). At high frequencies, the coronal radiation becomes optically thin and the brightness temperature decreases as $T_b\propto {\nu }^{-2}$ (see Equations 14 and 30). The brightness temperature spectrum we show in the right panel of Figure 1 comes from observations obtained with the Owens Valley Solar Array (OVSA) at 16 frequencies in the range 1.4–8 GHz (Gary and Hurford, 1987) and is consistent with the above interpretation. More recent observations by Saint-Hilaire et al. (2012) have confirmed the above results.

FIGURE 1

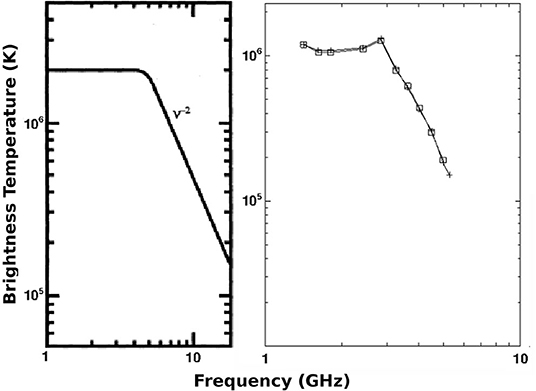
Figure 1. Left: Model of the microwave brightness temperature spectrum of free-free emission (adapted from Gary and Hurford, 1994). ©AAS. Reproduced with permission. Right: Brightness temperature spectrum of part of an active region, with crosses and boxes representing left-hand and right-hand circular polarization, respectively. The observations were obtained with the OVSA at 16 frequencies in the range 1.4–8 GHz (adapted from Gary and Hurford, 1987). ©AAS. Reproduced with permission.

Recently, Rodger and Labrosse (2018) and Rodger et al. (2019) have shown that the spectral gradient of millimeter free-free emission can be used for the diagnosis of the optical depth of either isothermal or multithermal material provided a correction is introduced to compensate for the change of the Gaunt factor over the observed frequency range.

There is a long tradition of comparisons of brightness temperature spectra of the free-free emission that span a wide range of frequencies (from sub-mm to microwaves) with either standard one-dimensional atmospheric models or with the computed radio brightness resulted from EUV observations. The reader is referred to the review by Shibasaki et al. (2011) and to the paper about the solar atmosphere written by Alissandrakis in this issue for a detailed discussion of the subject.

3.3.2. Imaging Observations of the Non-flaring Sun

The quiet Sun radio emission comes from the free-free mechanism. At frequencies ≳ 20 GHz the corona is optically thin everywhere and radio emission probes the chromosphere. The first high-resolution images of the quiet Sun in the millimeter range were obtained by White et al. (2006) and Loukitcheva et al. (2006) who used the Berkeley-Illinois-Maryland Association Array (BIMA) to obtain ~ 10^′′ resolution. With the advent of ALMA a new generation of high-resolution millimeter-wavelength images has been forming (e.g., Bastian et al., 2017; Shimojo et al., 2017a,b; Nindos et al., 2018; Yokoyama et al., 2018; Jafarzadeh et al., 2019; Loukitcheva et al., 2019; Molnar et al., 2019; Patsourakos et al., 2020; Wedemeyer et al., 2020) and an example is presented in Figure 2. The figure indicates that the chromospheric network, delineated in the AIA 1,600 Å image, is the dominant structure in the radio images. The AIA images of Figure 2 have been degraded to the resolution of the ALMA images hence the size of the network is similar in all three wavelengths. The chromospheric network is also visible at microwaves (Kundu et al., 1979; Gary and Zirin, 1988; Gary et al., 1990). Subsequent observations (e.g., Bastian et al., 1996; Benz et al., 1997; Krucker et al., 1997) confirmed that result.

FIGURE 2

Figure 2. The top row shows a composite (oriented in the south-east direction with respect to solar north) of seven 3 mm average ALMA images (each one computed from visibilities of duration 10 min) while the second and third rows show composites of AIA 1,600 and 304 Å average images for the same fields of view and time intervals as the ALMA images. The AIA images have been convolved with the ALMA beam (from Nindos et al., 2018). Reproduced with permission ©ESO.

In active regions, free-free emission is produced by the plage and coronal loops. At high microwave frequencies (ν > 3 GHz), the active region free-free emission is optically thin (for an example see the 17 GHz image of Figure 3); at such high frequencies the only regions of the non-flaring corona that are optically thick are those with strong magnetic fields (> 400 G) where gyroresonance opacity is significant. White (1999) points out that large active regions almost always contain optically thick regions at 1.5 GHz due to free-free opacity, but their free-free opacity is never optically thick at 5 GHz.

FIGURE 3

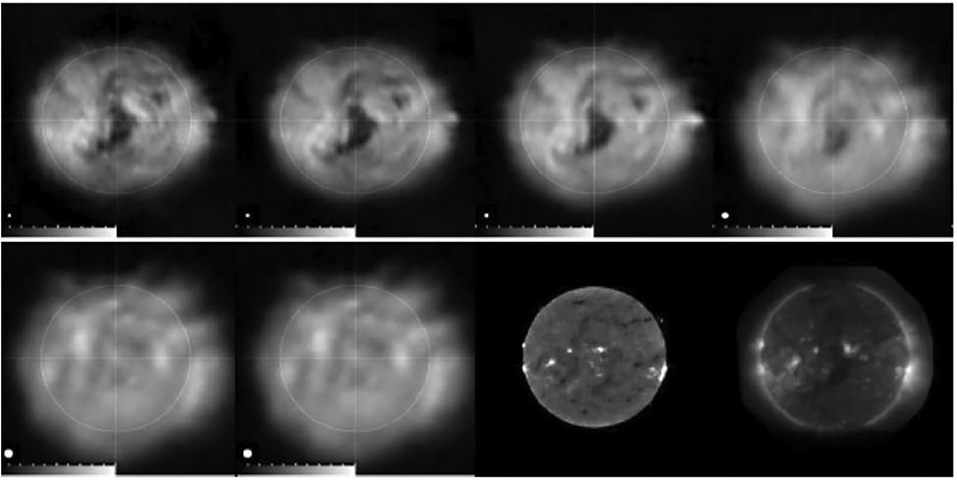
Figure 3. Solar images on 2004 June 27. From left to right and from top to bottom: NRH images obtained at 432, 410, 327, 236, 164, and 150 MHz, NoRH image at 17 GHz, and soft X-rays image obtained from the Solar X-Ray Imager (SXI) on board GOES12 (from Mercier and Chambe, 2009). ©AAS. Reproduced with permission.

The observed brightness temperature of the free-free emission may fall below the coronal electron temperature not only at microwaves, but also at metric wavelengths. The corresponding fall of the optical depth below unity at metric wavelengths is attributed to scattering and refraction effects (see section 2.2). Note, however, that the recent analysis of quiet Sun images obtained with the Low Frequency Array (LOFAR) in the range 25–79 MHz indicates the presence of higher brightness temperatures, of the order of 1 MK (Vocks et al., 2018).

Figure 3 (see also Mercier and Chambe, 2009, 2012) shows images of the Sun at 150–432 MHz obtained with the Nançay Radioheliograph (NRH). These frequencies probe altitudes from the upper transition region to the low corona. At the highest frequencies (327–432 MHz) the most prominent feature is a coronal hole that appears as a depression south of the disk center. Its contrast decreases at lower frequencies in agreement with previous (e.g., Lantos et al., 1987; Lantos and Alissandrakis, 1999) and more recent observations (Rahman et al., 2019). However, the dark-to-bright transition at low frequencies cannot be easily reproduced in model computations (Rahman et al., 2019). Furthermore McCauley et al. (2019) reported values up to 8% for the polarization of coronal holes.

Figure 3 also shows that the similarity of the soft X-ray image with the radio images decreases with frequency. This is not due to spatial resolution differences only. Apart from radio refraction effects, the optical depth of the radio emission is larger than that of the X-ray emission which is always optically thin. Consequently the radio images probe higher coronal layers and lower-lying structures that emit soft X-rays are obscured by dense overlying material. With similar arguments one can interpret the little resemblance between the NRH images and the Nobeyama Radioheliograph (NoRH) image at 17 GHz.

3.3.3. Imaging Observations of Flares and CMEs

The hot soft-X-ray-emitting coronal material that fills flaring loops is expected to produce optically thin free-free emission at millimeter wavelengths and in the decay phase of microwave flares (e.g., Kundu and Vlahos, 1982; Hanaoka, 1999). Thermal free-free emission has also been detected in weak transient brightenings observed at microwaves (White et al., 1995) and millimeter wavelengths (Nindos et al., 2020). For the sake of completeness we note that (i) non-thermal emissions have occasionally also been reported in the decay phase of flares (e.g., Kundu et al., 2001a, 2004a), and (ii) sub-THz emission may originate from optically thick and relatively hot free-free sources located at the chromospheric footpoints of flaring loops (Kontar et al., 2018; Morgachev et al., 2018, 2020).

CME material is also expected to radiate optically thin free-free emission. Ideally, one anticipates that the free-free-emitting structures will be similar to those appearing in coronagraphs because both are associated with multi-thermal plasmas and depend on the electron emission measure (radio frequencies) or column density (white-light data). But the free-free emission of CMEs should be weak because of their low densities and high temperatures (see Equation 30) and often obscured by stronger non-thermal emissions. The published reports on thermal free-free CME emissions at low frequencies are rare. The reader is referred to the articles by Sheridan et al. (1978) and Gopalswamy and Kundu (1992) for early detections with the extinct Culgoora Radioheliograph. Maia et al. (2000) imaged CME fronts at frequencies between 164 and 450 MHz. The radio source motions matched those of white-light CME fronts and their brightness temperature (~ 10⁴ K) implied thermal emission. However, their spectral characteristics and polarization were not consistent with such interpretation. Thermal emission from CMEs has also been reported at 109 MHz by Kathiravan et al. (2002) and Ramesh et al. (2003) (Gauribidanur Radioheliograph observations). The thermal free-free CME emission, when detected, can be used for the calculation of the CME mass. Such calculations provide results similar to those obtained from white-light data (Gopalswamy and Kundu, 1992).

Prominences can be observed not only in Hα but also in radio. The Hα emission strongly depends on the plasma temperature but since prominence material is dense (~ 10¹⁰ − 10¹¹ cm⁻³) and cool (~ 8, 000 K), it produces optically thick thermal free-free microwave emission (e.g., Gopalswamy and Hanaoka, 1998), which can be easily detected beyond the disk. But quiescent filaments, i.e., quiet prominence seen on the disk, are associated with brightness depressions in the microwave range (e.g., Chiuderi-Drago et al., 2001) and sometimes at decimeter-meter wavelengths (e.g., Marqué et al., 1999; Marqué, 2004). At microwaves, the angular resolution is not as good as in Hα but, thanks to the continuum nature of the free-free emission, the microwave data have the ability to probe the prominence material even at relatively high temperatures which is not always possible in Hα. From the radio data one can calculate the prominence mass (e.g., Gopalswamy and Hanaoka, 1998), but such estimates ignore possible downflows of plasma from the rising prominence. Several events of prominence eruptions at microwaves (see Figure 4 for an example) have been reported (e.g Hanaoka et al., 1994; Gopalswamy et al., 1996a, 2003; Hori, 2000; Uralov et al., 2002; Grechnev et al., 2006b; Alissandrakis et al., 2013; Fedotova et al., 2018; Huang et al., 2019). In most cases the eruptive prominence detected in radio eventually evolves into the core of the white-light CME.

FIGURE 4

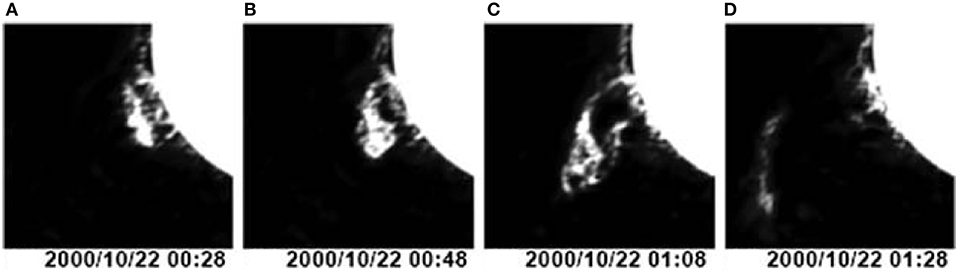
Figure 4. (A–D) 17-GHz images of an eruptive prominence obtained by the NoRH (from Gopalswamy et al., 2003). ©AAS. Reproduced with permission.

4. Types of Gyromagnetic Emission

Gyromagnetic emission is generated when free electrons are accelerated or/and change their velocity direction in a magnetic field due to the influence of the magnetic component of the Lorentz force (in solar plasmas, there are no macroscopic electric fields, except probably in current sheets). An electron with velocity components ν_∥ and ν_⊥ parallel and perpendicular to the magnetic field, respectively, will be accelerated perpendicular to both v_⊥ and B. Its acceleration, a, is:

$\begin{array}{ll}a={\omega }_{ce}{v}_{\perp }& (31)\end{array}$

where ω_ce is the electron gyrofrequency

$\begin{array}{ll}{\omega }_{ce}=\frac{eB}{m_{e}c}& (32)\end{array}$

For non-relativistic speeds, the total power emitted by the electron is provided by the Larmor formula (Equation 17) which yields:

$\begin{array}{ll}P=\frac{2e^2}{3c^2}{\omega }_{ce}^2{v}_{\perp }^2& (33)\end{array}$

This expression requires modification when the electron speed is not small compared to the speed of light, c. Then the power of the electron is given by the relativistic Larmor formula:

$\begin{array}{ll}P=\frac{2e^2}{3c^2}{\gamma }^2{\omega }_{ce}^2{v}_{\perp }^2& (34)\end{array}$

where γ is the Lorentz factor.

It is straightforward to prove that the total emitted power, P, is Lorentz invariant. However, its angular distribution dP/dΩ is not. In the electron rest frame, the radiated power per solid angle is given by Equation (16) and the radiation pattern is the classical dipole pattern which shows two lobes with power proportional to sin² θ. We assume that the relative velocity between the electron rest frame and the observer rest frame is along the x-axis, and we use spherical coordinates such that the angle θ is measured with respect to x-axis while the angle ϕ is the angle between the acceleration and the projection of the line from the charge to the observer onto the plane that is perpendicular to the velocity. Then for the emitted power per solid angle in the rest frame of the observer, the calculations give:

$\begin{array}{ll}\frac{dP}{d\Omega }=\frac{e^2{a}^2}{4\pi c^2}\frac{1}{{(1-\beta \text{cos }\theta )}^4}\left[1-\frac{{\text{sin}}^2\theta {\text{ cos}}^2\varphi }{{\gamma }^2{(1-\beta \text{ cos }\theta )}^2}\right]& (35)\end{array}$

where β = v/c. There is a strong dependence on the 1 − β cos θ factor in the denominator which dominates when θ → 0 and β → 1. In other words, the observer detects strong radiation in the forward direction with respect to the motion of the electron; this is called relativistic beaming. Therefore, in the relativistic case, we obtain strongly beamed emission along the direction of motion which, in turn, is perpendicular to the acceleration. The width of the beam where the emission is concentrated is 2/γ. This means that the signal detected by the observer appears more and more sharply pulsed as the energy of the electron increases. Beaming plays important role in the observed spectrum emitted by a single electron.

The above discussion is valid for an electron radiating in vacuo. In the presence of ambient plasma, we should take into account the influence of the index of refraction n on radiation. In that case, the width of the emission beam is θ = 2(1 − n²β²)^1/2. If n ≈ 1 we return to the vacuum case. But if n ≪ 1, then for the ultra-relativistic case (β ~ 1) we obtain $\theta =2{(1-n^2)}^{1/2}=2{\nu }_p/\nu$ for a cold plasma. Therefore at low frequencies, the medium quenches wave propagation and plasma effects dominate beaming effects. The decrease in beaming takes place because the electron cannot “catch up” to the wave it just emitted to reinforce it with yet another emission wave.

In the limit of non-relativistic speed (see left column of Figure 5), the electron gyrates with frequency equal to the classical gyrofrequency (Equation 32) which is independent of the speed. An observer will detect a sinusoidally varying electric field which has a period of 2π/ω_ce. In that case, the power spectrum is a single line (cyclotron line) at the gyrofrequency. When the electron energy increases, mild beaming is initiated and the observed temporal variation of the electric field becomes non-sinusoidal. In such circumstances, when the electron energy corresponds to quiescent solar coronal temperatures (~ 10⁶ K; see middle column of Figure 5), the power spectrum consists of lines at frequencies equal to small integer multiples (called harmonics) of the gyrofrequency. In that case, gyromagnetic emission is called gyroresonance emission. For a mildly relativistic electron (energy of a few tens of keV to a few MeV) there is even more beaming, and there is power in a wide frequency range at harmonics of the gyrofrequency from about 10 to 100. Now the lines exhibit Doppler broadening and start blending together. This type of gyromagnetic emission is called gyrosynchrotron emission. Finally, when the electron is highly relativistic (right column of Figure 5) the electric field's temporal variation becomes highly non-sinusoidal and there is power at a large number of harmonics, up to more than s ~ γ³, which overlap to yield continuum emission. The frequency $\nu ={\gamma }^3{\nu }_{ce}$ that corresponds to the maximum synchrotron emission of a single electron (see Figure 5) is sometimes referred to as the “characteristic frequency of synchrotron emission.”

FIGURE 5

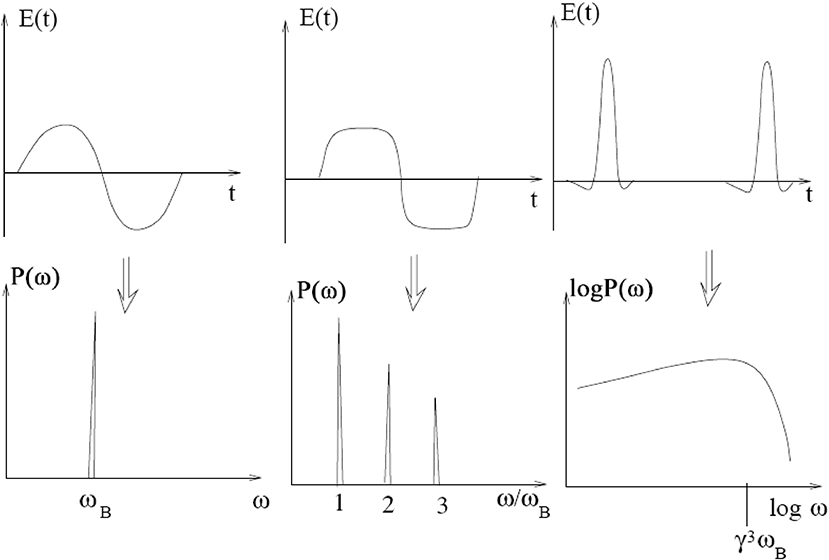
Figure 5. Top: Schematic time variability of the detected electric field that has been produced by a gyrating electron in the cases of small speed (left panel), thermal speed (middle panel) and relativistic speed (right panel). Bottom: Schematic power spectra resulted from the cases of the top row.

The above discussion is valid for a single electron in the presence of uniform magnetic field. However, in the corona, even along a single line of sight, the magnetic field is not uniform, but generally decreases with height. The non-uniformity of the field together with the spread of the distribution function of the electron energy tend to smear out the spectral lines into an, essentially, continuum emission.

Single expressions for the gyromagnetic emission and absorption coefficients that are valid for all electron energies are not available. Instead, expressions have been derived for separate electron energy regimes.

• At low, non-relativistic energies (γ − 1 ≪ 1), the electron velocity distribution in the corona is thermal and the resulting gyroresonance emission is the primary emission mechanism above sunspots with strong magnetic fields at microwaves.

• In the case of gyrosynchrotron emission from mildly relativistic electrons (γ − 1 ~ 1 − 5), both thermal and non-thermal electron energy distributions have been used. Gyrosynchrotron emission is the primary incoherent emission mechanism in solar flares.

• Synchrotron emission comes from ultra-relativistic (γ − 1 ≫ 1) electrons. It is well-known that synchrotron emission is relevant in neutron stars, and some extra-galactic sources. In the Sun, it is debated whether it may contribute to the impulsive submillimeter component of some flares (Trottet et al., 2008).

5. Gyroresonance Emission

5.1. Optical Depth

Gyroresonance opacity for electrons with a thermal energy distribution has been discussed in several textbooks (e.g., Zheleznyakov, 1970; Melrose, 1980). More recent detailed reviews about the physical mechanism and the properties of gyroresonance emission can be found in White and Kundu (1997) and Lee (2007). The gyroresonance absorption coefficient from non-Maxwellian quasi-steady-state electron distributions has been calculated by Fleishman and Kuznetsov (2014) but their predictions have not been tested against observations yet.

The absorption coefficient decreases quickly at frequencies not equal to the resonance frequencies

$\begin{array}{ll}\nu =s{\nu }_{ce}.& (36)\end{array}$

where s is the harmonic number. In units of the scale height of the magnetic field, L_B = B/|∇B|, the frequency width of the resonances is ~ v/c, where v is the speed of the emitting electron. In other words, when we observe at a fixed frequency, ν, gyroresonance opacity becomes appreciable only at those points along the line of sight where ν_ce = ν/s. Therefore, the magnetic field, electron density and temperature are almost constant across gyroresonance layers.

The exact expression for the optical depth τ of a gyroresonance layer has been provided by Zheleznyakov (1970) and will not be repeated here. The optical depth depends on many parameters but its most sensitive dependence is on the angle, θ, between the magnetic field and the line of sight.

In Figure 6, we show calculations (taken from White and Kundu, 1997) of the optical depth, at 5 GHz, of the second, third, and fourth gyroresonance coronal layers vs. the angle θ. In the figure, the strong dependence of gyroresonance optical depth on θ is evident and shows better at small angles where the opacity drops quickly in both modes. The second and third harmonics are optically thick at most intermediate angles in both x- and o-mode. The fourth harmonic is optically thin in both polarizations. Harmonics greater than the fourth have negligible opacity. Only o-mode emission is possible from the first harmonic, and this can happen if the local cyclotron frequency exceeds the local plasma frequency. The x-mode emission from the first harmonic does not propagate out into the corona because the reflecting point of the x wave is located higher in the corona (i.e., closer to the observer) than the s = 1 layer. At a given harmonic and angle, the o-mode opacity is about an order of magnitude smaller than x-mode opacity. For a given mode and angle, the transition from harmonic s to harmonic s+1 decreases the opacity by about two orders of magnitude.

FIGURE 6

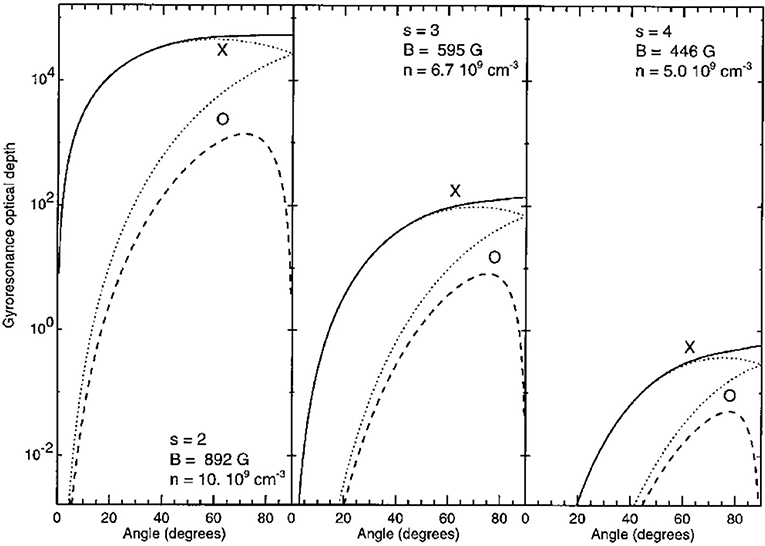
Figure 6. Integrated optical depth, at 5 GHz, of the second, third, and fourth gyroresonance layers (left, middle, and right panels, respectively) as a function of the angle between the magnetic field and the line of sight. The scale height of the magnetic field is 10⁹ cm, the electron temperature is 3 × 10⁶ K and the densities are denoted in the figure. The solid and dashed lines correspond to x- and o-mode exact calculations, respectively. The dotted lines show x- and o-mode approximate calculations (from White and Kundu, 1997). Reproduced with permission ©Springer Nature.

5.2. Structure of Gyroresonance Sources

The structure of gyroresonance sources is determined to a large extent by the number of harmonic layers that lie above the base of the transition region (TR). The magnetic field decreases with height and therefore higher harmonic layers are located above lower ones. In the case of magnetic field decreasing away from the center of a sunspot, the height of a given harmonic layer decreases with the distance from the center.

The brightness temperature of a given harmonic layer depends on the electron temperature at the height where it is located and on its optical depth. Let us consider the case of a symmetric sunspot. When the harmonic layer is optically thick, the brightness temperature will peak around the center of the spot. Away from the spot center, the electron temperature decreases, at first slowly and then fast as the harmonic layer reaches regions with higher gradient of electron temperature. Consequently, the source will have a flat top and sharp borders. When the source is away from disk center the maximum intensity is located toward the limb because the angle θ attains its highest values there. Furthermore, projection effects will result in a faster drop of the brightness temperature in the direction of the limb and a smoother drop toward disk center.

Due to the strong dependence of the gyroresonance opacity on the angle θ, a harmonic layer can become optically thick or thin at a given frequency and heliocentric distance, depending on the position within the source. The opacity is zero at θ = 0, thus there is always a region around θ = 0 where the harmonic layer is optically thin. This region can have considerable effects on the structure of the source: it shows up as a region of small intensity and it can result to a ring-shaped or a crescent-shaped harmonic. When the spot is at disk center, this zero-θ region is located at the center of the source, but as the source moves toward the limb, the zero-θ region is displaced. In the current-free case, where the field lines project radially on the photosphere, this displacement is toward the disk center. On the other hand, when the field is not potential, the twist of the field lines introduces an additional displacement in the direction perpendicular to the direction of the center. Thus a microwave source associated with a non-potential field will appear rotated with respect to a source associated with a potential field.

Since the opacity is significantly greater in the x-mode than in the o-mode, the same source may appear very different in the two modes, and therefore such differences will be prominent in the circular polarization maps. In general, the source is essentially unpolarized in regions where both modes are optically thick but circular polarization may go near the 100% level if the x-mode is optically thick and the o-mode is optically thin.

To illustrate the structure of microwave gyroresonance sources, we will present model computations of both the gyroresonance and free-free emission resulted from a dipole magnetic field. The magnetic moment of the dipole is 8 × 10³⁰ erg/G and is located vertically below the photospheric disk center at a depth of 2 × 10⁴ km. With these parameters, the value of the maximum field at the photosphere is 2,000 G.

For the computation of the x- and o-mode emissions, we also need to know the electron temperature, T_e, and density, n_e, in the TR and the low corona. We have used the same approach as in Alissandrakis et al. (1980): both the electron temperature and density change only with height; the temperature is determined by constant conductive flux, F_c, and the density by hydrostatic equilibrium. The model is specified by an $F_c=2\times 10^6$ erg cm⁻² s⁻¹ and a density of 10¹⁰ cm⁻³ at $T_e=10^5$ K; the 10⁵ K level is located at a height of 2000 km above the chromosphere. Below 10⁵ K and down to 2 × 10⁴ K, the temperature is determined by the model of Cheng and Moe (1977), while above 2.6 × 10⁶ K it is taken as constant. Models of gyroresonance emission can be found in several other publications (e.g., Zlotnik, 1968a,b; Gelfreikh and Lubyshev, 1979; Alissandrakis et al., 1980; Alissandrakis and Kundu, 1984; Holman and Kundu, 1985; Krüger et al., 1985; Hurford, 1986; Brosius and Holman, 1989; Lee et al., 1993, 1998, 1999; Gopalswamy et al., 1996b; Nindos et al., 1996, 2002; Vourlidas et al., 1997; Tun et al., 2011; Kaltman et al., 2012; Wang et al., 2015; Nita et al., 2018).

Figure 7 shows the x- and o-mode brightness temperature as a function of distance from the center of the model sunspot that results from the dipole field. Figure 8 shows the resulted I and V emission. The positions at which the harmonic layers cross the base of the TR are marked on the figures, so that the contribution of each harmonic can be identified. At the highest frequency, 11.2 GHz, only the fourth and third harmonic layers are above the base of the TR. Moreover, only the third has some contribution and this is at the x-mode only. Here we can clearly see the zero-θ region near the center of the source.

FIGURE 7

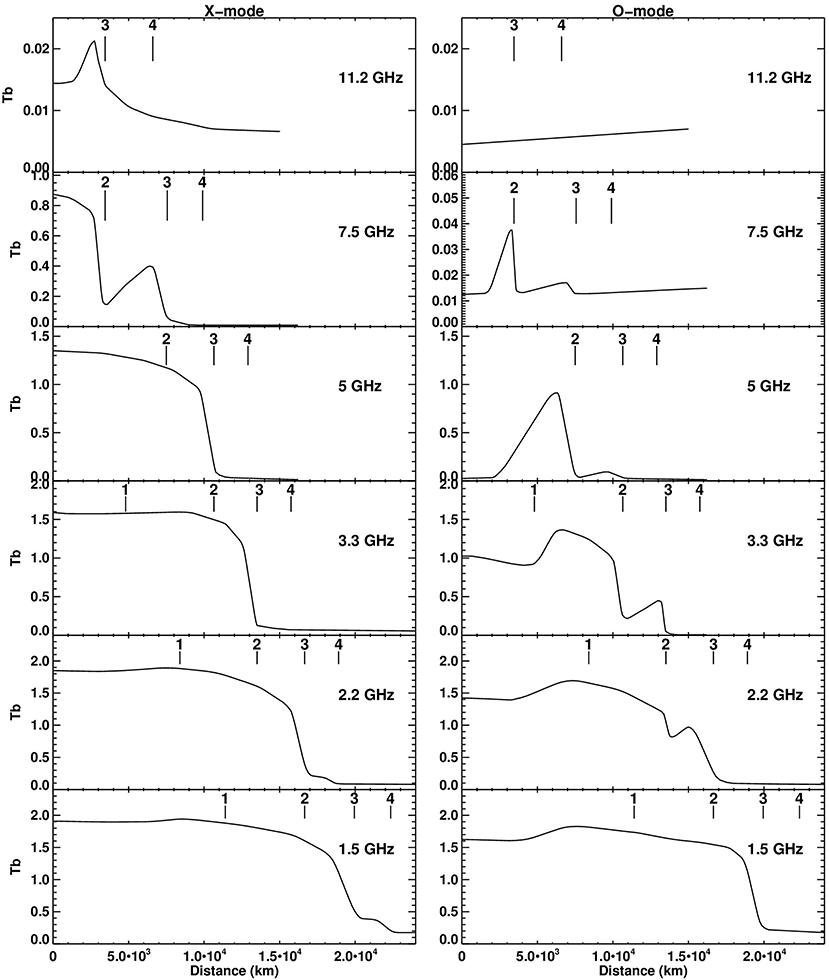
Figure 7. Brightness temperature (in units of million degrees Kelvin) of the x-mode (left) and o-mode (right) emission as a function of distance from the center of a dipole sunspot model at several frequencies (see text for details). The position at which the harmonic layers cross the base of the TR are marked with vertical straight lines.

FIGURE 8

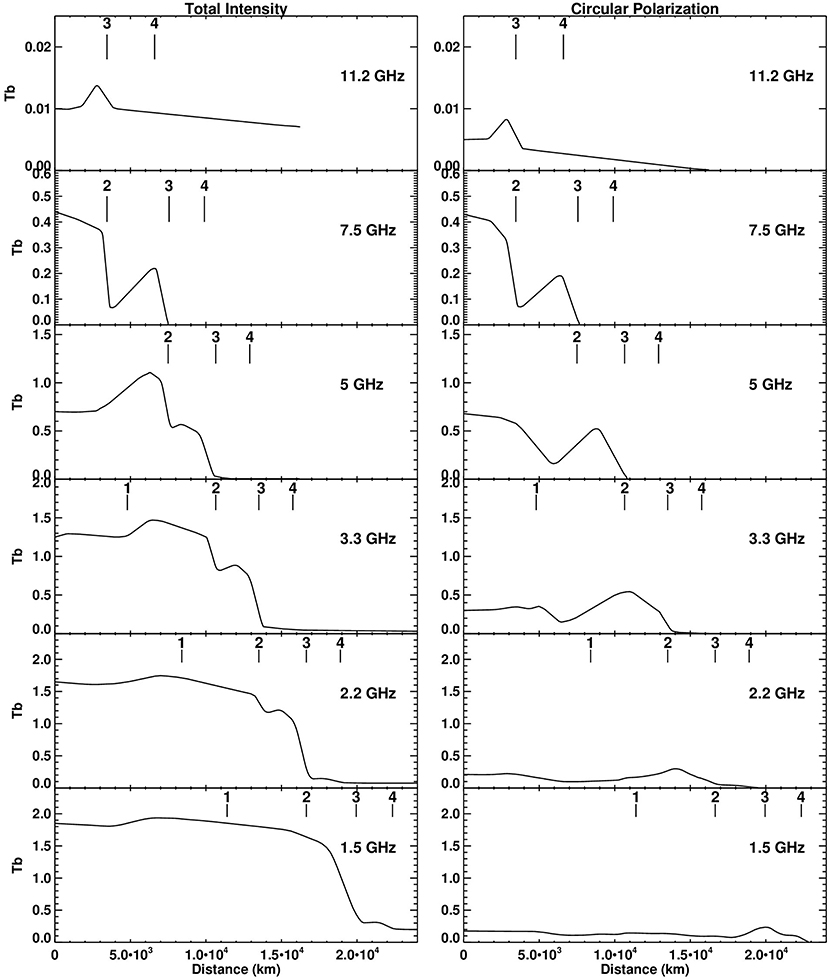
Figure 8. Brightness temperature (in units of million degrees Kelvin) in I (left) and V (right) as a function of distance from the center of the dipole sunspot model of Figure 7, calculated from the radio models of Figure 7.

The second harmonic shows up at 7.5 GHz, but it is optically thick only in the x-mode; the third harmonic has still a small optical depth and the source in the x-mode appears like a disk, surrounded by a ring. Both the disk and the ring have sharp borders, a consequence of the steep TR as noted above. The o-mode emission is very weak, which results in a circular polarization of almost 100%.

At 5 GHz the third harmonic becomes optically thick at the x-mode and the source has the shape of a disk. On the contrary this as well as the second harmonic show extended zero θ regions in the o-mode emission, which appears as a bright ring surrounded by a weaker one. The ring structure is also present in the total intensity while the circular polarization has a disk-ring structure. Contrary to the distribution at 7.5 GHz, the minimum in the polarization does not occur just outside of the second harmonic, but it is located at the region of maximum brightness of the ordinary emission.

At frequencies lower than 5 GHz, there is contribution from the first harmonic, as well. This has practically no effect on the x-mode (see the relevant comments in section 5.1), but it serves to fill the gap of the zero-θ region in the o-mode (the local cyclotron frequency was larger than the local plasma frequency, therefore o-mode emission from the first harmonic was possible). Thus the disk part of the circular polarization becomes progressively lower as the frequency decreases. The ring part is preserved still at 1.5 GHz due to the contribution of the fourth harmonic in the x-mode. In general, the circular polarization has a maximum around 5 GHz decreasing toward higher frequencies due to the decrease of the brightness temperature of both modes and toward lower frequencies due to the decrease of opacity difference of the modes. The brightness temperature in total intensity increases as the frequency decreases due to the increase of both the opacity and the height of the harmonic layers.

5.3. Observations of Gyroresonance Emission

The expected properties of gyroresonance sources discussed above, have been confirmed by both high spatial resolution observations at a few frequencies (e.g., Kundu et al., 1977; Alissandrakis et al., 1980; Alissandrakis and Kundu, 1982, 1984; Lang and Wilson, 1982; Kundu and Alissandrakis, 1984; Gopalswamy et al., 1996b; Nindos et al., 1996, 2002; Vourlidas and Bastian, 1996; Zlotnik et al., 1996; Vourlidas et al., 1997; Lee et al., 1998, 1999; Brosius and White, 2004, 2006; Tun et al., 2011; Nita et al., 2018) as well as multi-frequency spectral observations (e.g., Akhmedov et al., 1982; Alissandrakis et al., 1993a, 2019; Lee et al., 1993; Gary and Hurford, 1994; Tun et al., 2011; Kaltman et al., 2012; Stupishin et al., 2018).

5.3.1. Modeling of a Well-Observed Sunspot Source

An example of a well-observed gyroresonance source associated with a simple sunspot near disk center is provided in Figures 9, 10. Active region 4682 was observed with the RATAN-600 and the Very Large Array (VLA). The RATAN-600 observations provided one-dimensional scans of the Sun at several microwave frequencies, while the VLA provided high-resolution maps at 5 and 1.5 GHz. The flux density spectra of the sunspot source in R and L appear in Figure 9. In the same figure, we also present model flux density spectra in R and L (the magnetic polarity of the sunspot was negative and therefore the model o- and x-mode emissions correspond to R and L polarizations, respectively).

FIGURE 9

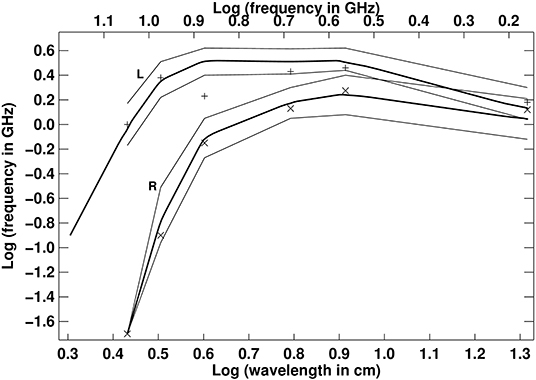
Figure 9. Model flux density spectra in L and R polarizations (x- and o-mode, respectively), computed from magnetic field extrapolations for the cases: (i) h₀ = 2, 000 km, $F_c=6\times 10^6$ erg cm⁻² s⁻¹, (thick lines), (ii) h₀ = 2, 000 km, $F_c=3\times 10^6$ erg cm⁻² s⁻¹, (iii) h₀ = 2, 000 km, $F_c=1.2\times 10^7$ erg cm⁻² s⁻¹. In case (i) the flux was computed at frequencies from 2 to 15 GHz while in cases (ii) and (iii) it was computed for 1.5, 3.7, 4.8, 7.5, 9.4, and 11.1 GHz. The observed flux density spectra in R (×) and L (+) are also given (from Nindos et al., 1996). Reproduced with permission ©Springer Nature.

FIGURE 10

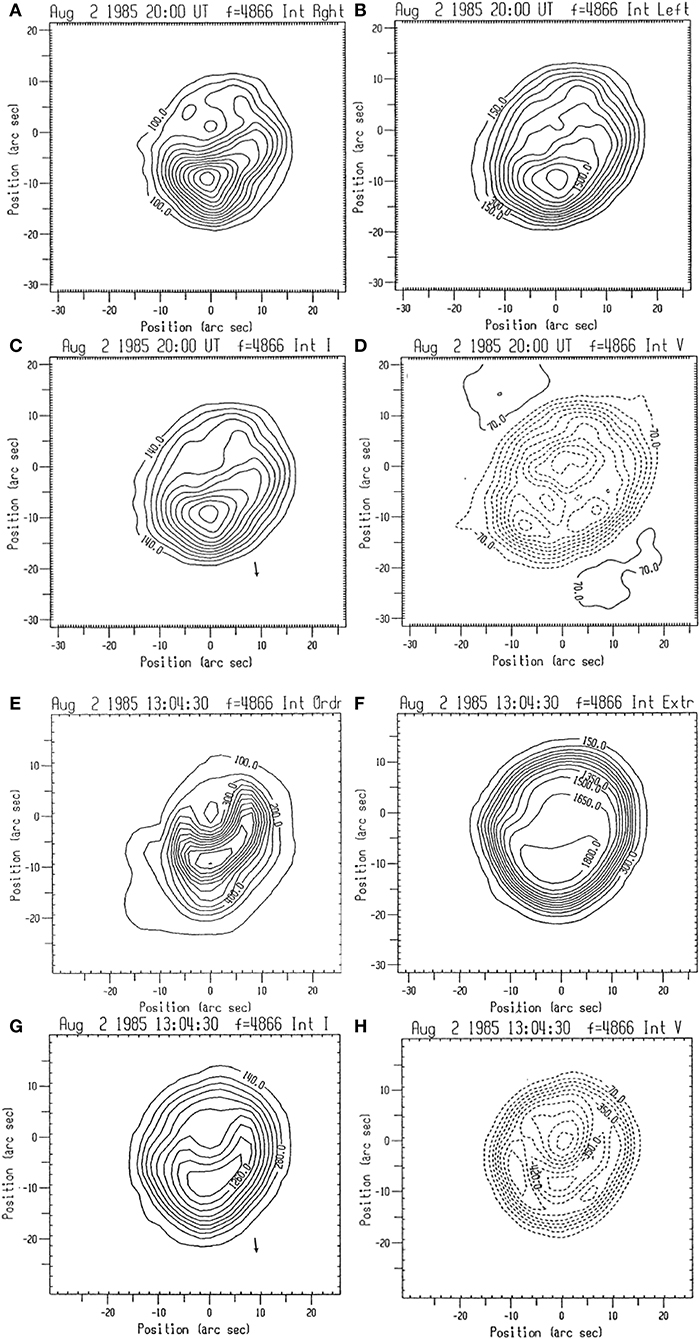
Figure 10. Maps of active region 4862 observed with the VLA at 5 GHz in Stokes I, V (C,D, respectively) and in R and L polarization (A,B, respectively). The contours are in brightness temperature steps of 1.4 × 10⁵, 0.7 × 10⁵, 1.5 × 10⁵, and 10⁵ K, respectively. Dashed contours indicate negative values. Panels (E,F) show models of active region 4862 at 5 GHz in R and L which were computed with α = −2.4 × 10⁻⁵ km⁻¹ and α = 2.4 × 10⁻⁵ km⁻¹, respectively. Panels (G,H) show model I and V maps, respectively, calculated from the models of panels (E,F). The arrow in panels (C,G) shows the direction of the limb (adapted from Nindos et al., 1996). Reproduced with permission ©Springer Nature.

The model we used was the same as the one described in section 5.2 with the exceptions that (i) the magnetic field was computed through extrapolations of the photospheric field provided by a vector magnetogram, and (ii) pressure data in the TR from O IV lines were available for part of the sunspot region. The comparison of the observed and computed flux density spectra allowed us to estimate the conductive flux, F_c and the height, h₀, of the base of the TR: we found $F_c=6\times 10^6$ erg cm⁻² s⁻¹ and h₀ = 2, 000 km.

Figure 9 shows that at 11.1 GHz there is weak o-mode emission and significant x-mode emission and the source is almost 100% polarized. Consequently, the third harmonic is located in the low TR. The x-mode model fluxes increase from 15 to 7.5 GHz (note that the RATAN 7.5 GHz L data were not reliable) and reach a maximum around 7.5 to 4.3 GHz, whereas the o-mode fluxes increase from 11.1 to 4.8 GHz and reach maximum around 3.7 GHz. At frequencies lower than ~ 3.7 GHz there is contribution to the emission from the plage. However, both the L and R fluxes decrease because the second and third harmonics have entered the upper part of the TR where the temperature gradient is not large and cannot compensate the effect of the ν² factor which is involved in the computation of the spatially integrated flux density spectra.

The above discussion indicates that the third harmonic enters the TR at ν ≥ 11.1 GHz and reaches the upper part of the TR at about 7.5 GHz. The corresponding frequencies for the second harmonic are about 9.4 and 4.8 GHz. The combination of these results yields a lower limit of 1,400 G and an upper limit of 1,800 G for the magnetic field strength at the base of the TR. In the upper TR and low corona the field is ~ 900 G.

In Figure 10 (top four panels), we present the 5 GHz VLA maps in I, V, R, and L. The I and R maps and to some extent the L map feature a crescent-shaped source which was rather asymmetric with larger brightness temperatures toward the south. There is also a region of weak intensity in the I and R maps, which is attributed to the zero-θ region; it does not appear exactly at the sunspot center but is displaced northward. The maxima of the I, R, and L maps show some clockwise rotation with respect to the limb direction. These features can be explained in the framework of non-potential magnetic fields (see the discussion in section 5.2). The V map indicates that there is little circular polarization where the total intensity is high. It also shows three distinct maxima: one is associated with the “zero-θ” region and the others occur west and east of the I maximum, in locations where only the third harmonic was in the corona.

In the bottom four panels of Figure 10 we present the best-fit models to the VLA observations. The models were calculated using the F_c and h₀ values deduced from the spectral modeling and allowing the force-free parameter, α, used for the magnetic field extrapolations to take different values for the x-mode and o-mode computations. This was consistent with the analysis of the vector magnetograms which revealed that α was not constant over the active region. The effect of pressure variations into the computed models was not important at 5 GHz, and this confirms that the magnetic field is the dominant contributor to the emission. A comparison of the observations and models of Figure 10 shows that the models reproduce key features of the microwave morphology: the zero-θ and crescent shape of the R and I maps, the clockwise rotation of the maximum intensity with respect to the limb derection, and the three local maxima of the V map.

5.3.2. Gyroresonance vs. Free-Free Emission

In active regions, at microwaves, gyroresonance opacity is competing with free-free opacity. Free-free emission is ubiquitous in the corona (see section 3.3) but whenever sunspot-associated microwave sources of coronal brightness temperature or/and high degree of circular polarization appear, they can be safely attributed to gyroresonance emission. In these cases, the sunspot's photospheric magnetic field should be strong enough to bring harmonic layers of the gyrofrequency above the base of the TR. On the other hand, microwave free-free emission is spatially extended, its brightness temperature is smaller (because it is optically thin) and its degree of polarization is small. This situation is illustrated in Figure 11 where the spatial scale of the 1.5 GHz emission is consistent with the spatial scale of the soft X-ray loops and the plage and comes primarily from free-free emission. Gyroresonance emission may have some contribution to the two bright sources of the 1.5 GHz image, but the rest of the 1.5 GHz emission (including the band of lower emission which is more or less orthogonal to the soft X-ray loops near the loop tops) should come exclusively from free-free emission. On the other hand, the 4.5 GHz image is radically different: it shows localized bright emission above the sunspot due to gyroresonance in the strong magnetic fields there. Note, however, that some weak free-free emission can be traced east of the sunspot source even at 4.5 GHz. Multi-frequency observations of active regions allowed Gary and Hurford (1987) to observe the change in emission mechanism from gyroresonance to predominantly free-free at about 3 GHz.

FIGURE 11

Figure 11. Images of an active region. Top left: soft X-ray image obtained by Yohkoh Soft X-ray Telescope (SXT). Top right: Hα image from Learmonth Observatory. Bottom left: 1.5 GHz VLA image in right circular polarization. Bottom right: 4.5 GHz VLA image in left circular polarization (image credit: S.M. White).

The highest frequencies where gyroresonance emission has been detected lie in the range of 15–17 GHz (e.g., Akhmedov et al., 1982; White et al., 1991; Alissandrakis et al., 1993a; Shibasaki et al., 1994; Nindos et al., 2000a; Vourlidas et al., 2006). At even higher frequencies, the results are not conclusive because only a few imaging observations have been reported. We note that an active-region 34-GHz emission has been modeled as purely free-free by Selhorst et al. (2008). At decimetric and metric wavelengths, we cannot trace any sunspot-associated sources because the free-free opacity is so high that all the emission comes from regions well above sunspots.

5.3.3. Gyroresonance as a Tool to Study Coronal Magnetic Fields

From Equation (36), we get that the magnetic field (in G) can be written as a function of the harmonic number and frequency of observations through

$\begin{array}{ll}B=357\frac{1}{s}\frac{\nu }{1\text{ GHz}}& (37)\end{array}$

and once we identify the harmonics which produce the emission, it is easy to constrain the field strength in the TR and low corona. This technique is especially powerful when multi-frequency data are available and was demonstrated in section 5.3.1 (see also e.g., Akhmedov et al., 1982; Alissandrakis et al., 1993a; Lee et al., 1993; Gary and Hurford, 1994; Korzhavin et al., 2010; Tun et al., 2011; Wang et al., 2015; Nita et al., 2018). When only a single frequency is available, we may identify the size of the region, at the base of the TR, in which the field strength exceeds the value that corresponds to the frequency of observations: at 15 GHz (e.g., White et al., 1991) and 17 GHz (e.g., Shibasaki et al., 1994; Nindos et al., 2000a; Vourlidas et al., 2006) field strengths of at least 1,800 and 2,000 G, respectively, have been measured. Details on the subject are given in this issue in the papers about coronal magnetic field measurements by Alissandrakis and Bastian.

6. Gyrosynchrotron Emission

6.1. General Remarks

Gyrosynchrotron emission may arise in quite diverse solar environments:

(1) Solar flares. Gyrosynchrotron radiation from electrons that gyrate in the magnetic field with energies of tens to hundreds of keV is the basic emission mechanism at microwaves. The literature is vast and selected references will be provided in sections 6.2–6.4, primarily for publications that link modeling of gyrosynchrotron emission with observations. Gyrosynchrotron radiation can also be detected at millimeter wavelengths and is produced by electrons with energies of more than 1 MeV (e.g., White and Kundu, 1992; Kundu et al., 1994; Silva et al., 1996; Raulin et al., 1999; Silva and Valio, 2016; Tsap et al., 2018).

(2) Weak transient brightenings, when observed at microwaves, may sometimes show emission consistent with the properties of gyrosynchrotron radiation (e.g., Gary et al., 1997; Krucker et al., 1997; Nindos et al., 1999; Kundu et al., 2006).

(3) Gyrosynchrotron emission has been detected in a small number of CMEs at decimetric and metric wavelengths (Bastian et al., 2001; Maia et al., 2007; Tun and Vourlidas, 2013; Bain et al., 2014; Carley et al., 2017; Mondal et al., 2019).

In what follows we will put emphasis on the microwave gyrosynchrotron emission from flares because it is a mature topic that has attracted most of the attention on the subject, and because it demonstrates nicely the properties of the gyrosynchrotron mechanism. More on gyrosynchrotron emission from CMEs can be found in this issue in the paper about radio CMEs by Vourlidas.

Both the free-free (e.g., Bastian et al., 2007) and gyroresonance (e.g., Preka-Papadema and Alissandrakis, 1988) emissions produced by ambient thermal electrons should be taken into account when discussing incoherent emission of microwave bursts. Compared to gyrosynchrotron, they both have negligible effects in the emission, but they are important because they may increase the optical depth in the chromosphere and the low corona.

Gyrosynchrotron emission can be produced by electrons with either a non-thermal or a thermal distribution; in the latter case (e.g., Gary and Hurford, 1989 and for more recent examples see Fleishman et al., 2015; Wang et al., 2017) they could be electrons heated due to the flare. Usually the emission is first computed for a single electron radiating in cold plasma (e.g., Ramaty, 1969, the “parent” of all modeling papers), while for the thermal case, Gershman (1960) considered small fluctuations in the thermal equilibrium of a magnetized plasma described by the linearized Vlasov equation. The resulting formulas for the emission and absorption coefficients for an ensemble of electrons involve integration over the distribution function and summation over harmonics.

Simplified expressions have been provided by Petrosian (1981) and Dulk and Marsh (1982). They have a limited range of validity but they are useful in some applications. The model of Petrosian (1981) is valid at harmonic numbers below 10. But it only deals with emissivity, which means that it can only be applied to high frequencies. Klein (1987) extended this model to the absorption coefficient. The agreement with Ramaty's numerical calculations was quite good, starting at low harmonic numbers. By construction Klein's model completely smears out the lines, and it is devised for an isotropic electron population. Furthermore, it does not provide handy formulas for analytical calculations.

The model by Dulk and Marsh (1982) is valid above the tenth harmonic of the gyrofrequency (consequently if the magnetic field is 500 G it cannot be used at frequencies lower than 15 GHz), for a spectral index δ of an isotropic power-law distribution of radiating electrons with 2 ≤ δ ≤ 7, and for angles θ between the magnetic field and the line of sight with θ ≥ 20°. At high harmonics (above the 50th), the synchrotron approximation can be used in cases where the effects of high energy cut-off can be neglected.

The flux spectrum is divided into an optically thick part (flux rises with frequency) and an optically thin part (flux falls with frequency). Spectral maximum corresponds to the frequency defined by τ_ν ~ 1, and usually occurs at low harmonics of the gyrofrequency. The optically thin component of the spectrum is mostly shaped by the energy distribution of the electrons. In the synchrotron approximation the spectral index α in the high-frequency part of the spectrum is

$\begin{array}{ll}\alpha =\frac{\delta -1}{2}& (38)\end{array}$

For mildly relativistic electrons, the approximation given by Dulk and Marsh (1982) is often used:

$\begin{array}{ll}\alpha =0.90\delta -1.22& (39)\end{array}$

A comparison of Equations (38) and (39) indicates that the emission decrease with frequency is steeper at mildly than at ultra relativistic energies. This is because a highly relativistic electron radiates over a broader frequency range than a mildly relativistic electron.

The optically thick part of the spectrum is influenced primarily by the effects of the ambient plasma and radiative transfer. For large ambient densities the refractive index reaches zero at low frequencies (see the discussion in section 4) and both the absorption and emission coefficients are suppressed. This leads to intensity suppression at low frequencies and the shift of the spectral maximum toward higher frequencies. This effect is known as the Razin effect (Razin, 1960; Klein, 1987; Belkora, 1997; Melnikov et al., 2008; Song et al., 2016; Fleishman et al., 2018). Furthermore, if the optical depth of the emitting electrons is larger than unity, as it often happens at low frequencies, the intensity spectrum falls below the emission coefficient spectrum. This is the self-absorption effect which makes gyrosynchrotron radiation to fall off steeply with decreasing frequency.

The x-mode is associated with higher emission coefficient than the o-mode while the inverse holds for the source function. Therefore, the sense of polarization corresponds to x-mode in an optically thin region and to o-mode in an optically thick region. The degree of polarization increases with the angle θ between the magnetic field and the line of sight.

For the above discussion we assumed that the pitch-angle (i.e., angle between the velocity of the electron and the magnetic field) distribution of the radiating electrons was isotropic. This can be achieved by collisions or by wave-particle interactions. But in a flaring loop there is little emission from electrons with small pitch angles, so the emissions produced by different electrons, some with large and some with small pitch angles, can be significantly different. Fleishman and Melnikov (2003b) and Fleishman and Melnikov (2003a) have discussed how pitch-angle anisotropies affect gyrosynchrotron emission. It is known (see Fleishman and Mel'nikov, 1998, and references therein) that when anisotropic pitch-angle distributions prevail, the absorption coefficient can become negative and coherent electron cyclotron maser emission is produced. In flares such emission has a typical timescale of the order of tens of milliseconds which is much shorter than that of gyrosynchrotron emission (order of tens of seconds). Therefore, these two types of emission can be distinguished from their different duration. Moreover, there are cases that although the pitch-angle anisotropy significantly reduces the absorption coefficient, the latter remains positive (Fleishman and Melnikov, 2003b).

Fleishman and Melnikov (2003b) and Fleishman and Melnikov (2003a) showed that the changes to the gyrosynchrotron spectrum due to pitch-angle anisotropy are larger for small values of the angle, θ, between the magnetic field and the line of sight (compare the two top panels of Figure 12). The degree of polarization increases as the anisotropy of the pitch-angle distribution becomes larger and may approach the 100% level in the optically thin limit (see middle row of Figure 12). A similar trend is registered for the spectral index of the optically thin part of the spectrum (see bottom row of Figure 12) when the angle θ is small.

FIGURE 12

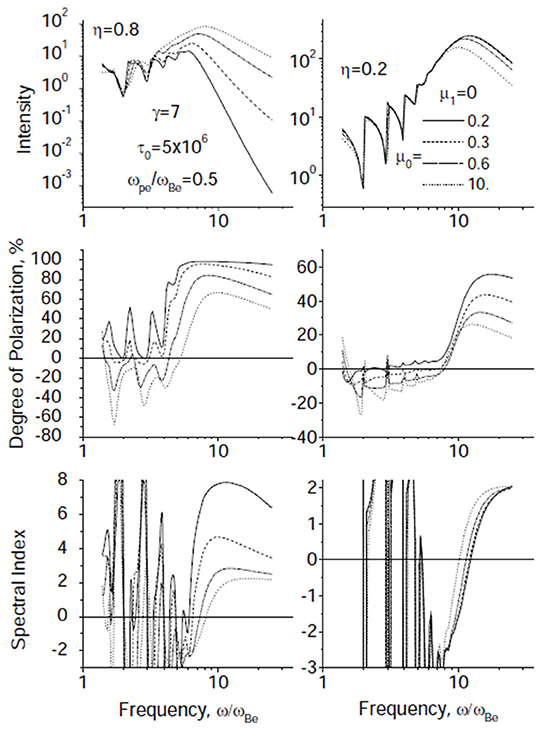
Figure 12. Gyrosynchrotron intensity, degree of polarization and spectral index as a function of frequency for various values of μ₀ in the Gaussian loss-cone type pitch-angle distribution $f\propto exp\left[-{\mu }^2/{\mu }_0^2\right]$. The computations presented in the left and right columns have been made for η = 0.8 and 0.2, respectively, where η is the cosine of the angle between the magnetic field and the line of sight (from Fleishman and Melnikov, 2003a). ©AAS. Reproduced with permission.

6.2. Gyrosynchrotron Emission From Model Flaring Loops

We will present calculations of the gyrosynchrotron emission in a model flaring loop to illustrate the properties of gyrosynchrotron radiation. The models have been published by Kuznetsov et al. (2011) and are based on the codes developed by Fleishman and Kuznetsov (2010). Similar models have been developed by Simões and Costa (2010) and Osborne and Simões (2019). The magnetic field of the model loop is produced by a dipole below the solar surface. The loop is located at the solar equator and its orientation is characterized by a heliographic longitude of 20° and an angle of 60° between the magnetic dipole and the equatorial plane. The height of the loop is 10^′′, its radius at the top is 2^′′, and the footpoint separation is 11.5^′′. The magnetic field strength at the footpoints and the top of the loop is 800 G and 75 G, respectively. The loop is filled with uniform ambient thermal plasma with a density of 10¹⁰ cm⁻³ and a temperature of 2 × 10⁷ K.

The energetic electrons have a power-law index of δ = 4 and low- and high-energy cutoffs of 100 keV and 10 MeV, respectively. The pitch-angle distribution can be either isotropic or a loss cone modeled by

$\begin{array}{ll}{g}_{\mu }~\{\begin{array}{cc}1,\hfill & \text{ for }|\mu |<{\mu }_c\hfill \\ \text{exp}\left[-\frac{{(|\mu |-{\mu }_c)}^2}{\Delta {\mu }^2}\right],& \text{for }|\mu |\ge {\mu }_c\hfill \end{array}\hfill & (40)\end{array}$

where μ_c = cos α_c, α_c is the boundary of the loss cone, and Δμ controls how sharp this boundary is. In the models of Figure 13, Δμ = 0.2. The spatial distribution of energetic electrons along the loop is given by

$\begin{array}{ll}{n}_e~\text{exp}\left[-{ϵ}^2{(\varphi -\pi /2)}^2\right]& (41)\end{array}$

where n_e is the number density, ϕ is the magnetic latitude, and ϵ is a dimensionless parameter controlling the degree of spatial inhomogeneity of n_e along the loop (for ϵ = 0 the distribution is homogeneous).

FIGURE 13

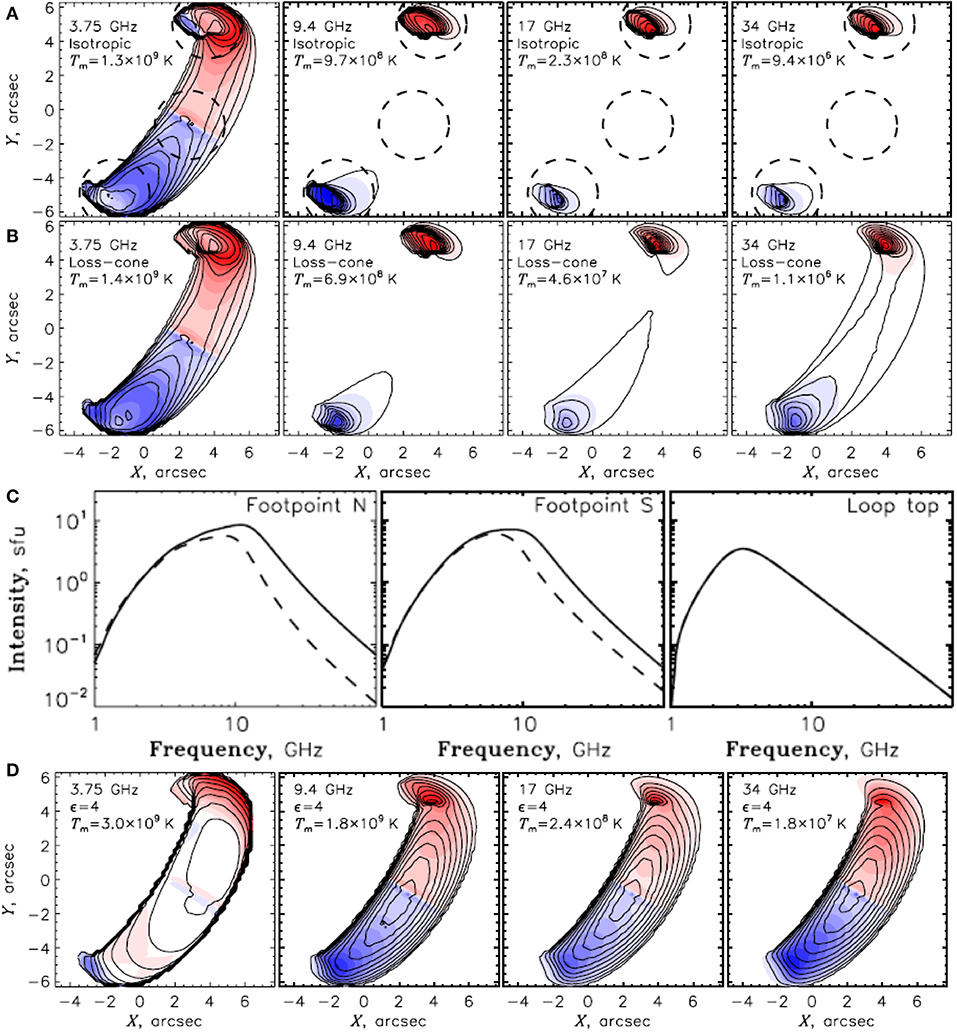
Figure 13. Brightness temperature maps of the gyrosynchrotron emission from a model loop for an isotropic electron pitch-angle distribution (A), and a loss-cone pitch-angle distribution (B). In both cases the density of the accelerated electrons is constant along the loop. (C) Flux density spectra of the northern footpoint source (left), southern footpoint source (middle) and loop top source (right) resulted from the models of rows (A,B) (solid lines and dashed lines, respectively). These spectra were computed in the areas defined by the dashed circles of row (A). (D) Same as row (B) but with an inhomogeneous spatial profile of the electron density along the loop. In rows (A,B,D), the contours denote intensities evenly distributed from zero to the maximum brightness temperature which is given in each panel. The red and blue colors denote the circular polarization (right and left sense, respectively). Adapted from Kuznetsov et al. (2011). ©AAS. Reproduced with permission.

The gyrosynchrotron emission from the model loop is shown in Figure 13 for the cases of (i) energetic electrons with isotropic pitch-angle distribution and constant number density, $n_e=3\times 10^6$ cm⁻³, along the loop, (ii) same as (i) but with a loss-cone pitch-angle distribution, and (iii) same as (ii) but with a spatially inhomogeneous energetic electron distribution which is controlled by ϵ = 4 and by a loop-top number density of 2.8×10⁸ cm⁻³. These parameters yield a footpoint number density equal to the number density used in cases (i) and (ii).

Let us have a closer look at the models with homogeneous and isotropic electron distribution (see Figure 13A). Similar models have been published by Preka-Papadema and Alissandrakis (1992), Bastian et al. (1998), Nindos et al. (2000b), Kundu et al. (2004b), Simões and Costa (2006), and Costa et al. (2013). At 3.75 GHz, the source is optically thick and traces out the spatial extent of magnetic volume accessible to energetic electrons. At 9.4–34 GHz, the emission is optically thin and shows compact sources associated with the footpoints of the loop.

This picture agrees well with the properties of gyrosynchrotron emission. The magnetic field is larger near the footpoints and smaller at the loop top. At a fixed frequency, the harmonic number varies from lower values at the footpoints to higher values at the loop top. The mean energy of the emitting electrons is proportional to the effective temperature, T_eff which in turn is (according to the simplified expressions by Dulk and Marsh, 1982) proportional to s^0.5+0.085δ. Therefore, higher energy electrons emit at the loop top, while lower energy electrons emit at the footpoints. In other words, the strong field near the footpoints favors the higher frequencies. Decreasing the observing frequency has approximately the same effect for the gyrosynchrotron emission as increasing the magnetic field. Consequently when the observing frequency decreases, we anticipate to obtain emission not only from the footpoints but also from a large part of the flaring loop.

In the models with homogeneous and isotropic electron distributions, changes to the model parameters have the following effects.

Magnetic field strength. A large magnetic field strength increases the opacity and therefore decreases the electron number density required to obtain the same optically thin flux. Furthermore it decreases the harmonic at which the electrons radiate at a given frequency. A larger field than that of the model is required to make the 9.4-34 GHz emissions optically thick and produce extended emission there.

Loop thickness. Changing the loop thickness increases the opacity proportionally, and that effect increases the optically thin flux without changing the optically thick flux significantly.

Electron number density. In the optically thin case, the optical depth increases with the column density of the energetic electrons. Changing the number density has little effect in the optically thick case, but it affects the frequency where the spectral maximum occurs.

Electron energy cutoffs. A decrease of the upper limit to the electron energies suppresses radiation at high frequencies which requires very energetic electrons if the magnetic field is not large. An increase of the lower energy cutoff does not affect much the high-frequency emission because the low energy electrons do not radiate at high frequencies, but it increases the mean energy of the electrons producing the 3.75 GHz optically thick emission and makes it stronger.

Viewing angle. The viewing angle changes when we change the orientation and location of the loop. In many cases, the changes affect the microwave morphology significantly, because the gyrosynchrotron mechanism depends strongly on the angle between the line of sight and the magnetic field.

When there is a homogeneous density profile of energetic electrons along the loop, the morphologies of the sources are similar in both the isotropic and the loss-cone pitch-angle distribution cases (compare Figures 13A,B). However, there are differences in intensity which show better in the spatially integrated spectra of row (c) of the figure: at the optically thin frequencies, the emission from the loss-cone distribution is lower than the emission from the isotropic electrons by a factor of ~ 2–6 (note also the differences in maximum brightness temperatures between the maps, at a given frequency, of Figures 13A,B). Furthermore, at 17 and 34 GHz, the emission from the anisotropic population is more evenly distributed along the loop than the emission from the isotropic population. On the other hand, at the optically thick frequencies the corresponding intensities are almost identical.

The interpretation of the above differences is as follows. The model loop is located relatively close to disk center, where the angle θ between the magnetic field and the line of sight is small near the footpoints, whereas near the loop top θ is large. When θ is small, the intensity at low frequencies is not sensitive to the pitch-angle anisotropy because the low-energy electrons contribute most of the emission. The beaming effect (see section 4) for a single low-energy electron is not large and therefore, the actual angular distribution is not so important for the low-frequency emission.

The beaming effect becomes more prominent as the energy of the emitting electrons increases, which results in the suppression of higher frequency emission from the loss-cone distribution when θ is small (we remind that close to the footpoints, the electrons with loss-cone distribution are concentrated around a pitch angle of 90° whereas the model field is almost parallel to the line of sight). When the distribution is anisotropic, this effect results in the decrease of the footpoint emission which makes the difference between the footpoint and looptop emission smaller than that of the isotropic distribution.

When θ is large (i.e., near the loop top), the loss-cone boundary, α_c, falls to ~ 20° and therefore the loss-cone distribution does not differ much from the isotropic one. Consequently, both distributions will produce very similar emissions.

The emission from electrons with loss-cone pitch-angle distribution and inhomogeneous spatial profile of the electron density along the loop (see Figure 13D) shows significant differences from the cases discussed so far. The emission at 9.4, 17, and 34 GHz is optically thin (the turnover frequency of the spectrum occurs at 7.6 GHz) but it peaks close to the loop top, and so does the emission at 3.75 GHz which is optically thick. This change is attributed to the larger concentration of energetic electrons at the loop top. Since the relative contribution of the electrons close to the footpoints decreases, the effect of the anisotropy discussed previously becomes less prominent.

Modeling of gyrosynchrotron emission has gone a long way from the pioneering publications by Klein and Trottet (1984) and Alissandrakis and Preka-Papadema (1984). In recent years it received a major boost with the development of the “GX_Simulator,” an interactive IDL application which implements the fitting scheme developed by Fleishman et al. (2009) and the code by Kuznetsov et al. (2011) and allows the user to produce spatially-resolved radio or X-ray spectra using realistic inputs for the magnetic field and the properties of both the energetic and ambient electrons (Nita et al., 2015). Results have appeared in several publications; some of them have already been cited while references for others will be provided below.

A final note about the determination of the magnetic field of flaring loops is in place here. The diagnostic strength of gyrosynchrotron, albeit significant, is not as straightforward as that of gyroresonance; for meaningful results one needs to combine observations (ideally spectroscopic imaging ones) with detailed modeling. In spite of all the complications, modeling of individual flares (e.g., Nindos et al., 2000b; Kundu et al., 2004a; Tzatzakis et al., 2008; Gary et al., 2013, 2018; Kuznetsov and Kontar, 2015; Fleishman et al., 2016b,c, 2018; Kuroda et al., 2018) showed that the magnetic field may lie from less than 200 G (loop top) to about 1700 G (footpoints). Probably the most spectacular result was obtained by Fleishman et al. (2020) who modeled spectroscopic imaging observations from Expanded OVSA (EOVSA) and found that the magnetic field decayed at a rate of about 5 G s⁻¹ for 2 min.

6.3. Observational Examples

Actual microwave observations of flares do not always show the simple loop configuration used in the models of section 6.2. First of all, in some cases the spatial structure of the emission may not be resolved in the radio maps. Furthermore, microwave sources may arise from pairs of interacting loops of widely differing scales (Hanaoka, 1997; Nishio et al., 1997; Grechnev et al., 2006a). Configurations involving more complex loop systems have also been revealed (e.g., Kundu et al., 1982, 2004a). Pre-eruptive flux rope configurations have also been imaged at microwaves (Wu et al., 2016; Chen et al., 2020) with their emission coming, at least partly, from the gyrosynchrotron mechanism.

The comparison between observations and models of the gyrosynchrotron emission becomes possible in events with single-loop morphology. As an example of such events, we consider a microwave flaring loop (Nindos et al., 2000b) observed by the VLA at 5 and 15 GHz (see Figure 14, top panel). Additional spectral data were obtained from the OVSA at several frequencies between 2 and 15 GHz; they revealed that the turnover frequency was 5.4 GHz. At 15 GHz, the emission was optically thin and was produced at the footpoints of the flaring loop, while the 5 GHz emission outlined the loop with most of it being optically thick with a maximum close to the loop top. In the middle and bottom panels of Figure 14, we compare the observations with computations of gyrosynchrotron emission from a model magnetic loop in order to diagnose the conditions in the flaring loop. The best fit to the data was reached with a model flaring loop with photospheric footpoint magnetic field of 870 G. The thickness of the model loop was much smaller than its footpoint separation. The energetic electrons were characterized by an energy spectral index of 3.7, number density of 7.9 × 10⁷ cm⁻³ as well as low- and high-energy cutoffs of 8 and 210 keV, respectively. In this model, the 5 GHz emission comes from low harmonics of the gyrofrequency (3-7), while the lack of electrons with energies higher than 210 keV was necessary to interpret the absence of emission from the loop top at 15 GHz. That model [which is consistent with the models presented in Figure 13A] reproduced well both the high-frequency part of the OVSA spectrum and the basic spatial structure of the VLA I maps (propagation effects, see section 2.2, affected the structure of the V maps, and therefore its comparison with the model was not straightforward).

FIGURE 14

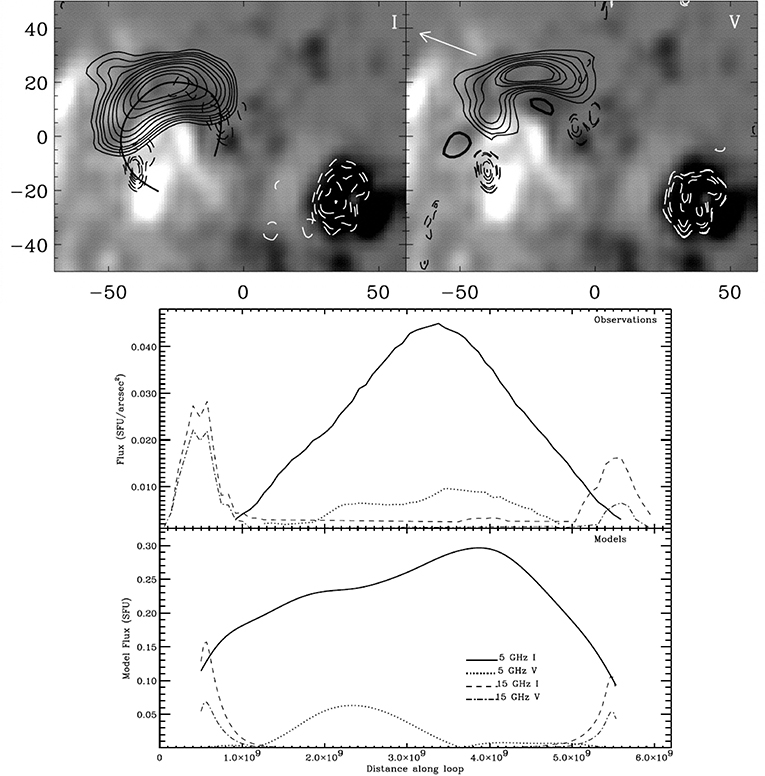
Figure 14. Top row: The 1992 July 1 flare. Contour plots of the flare radio emission maximum observed by the VLA. The gray-scale background is a photospheric magnetogram. The I maps are on the left, and the V maps on the right. The solid and dashed contours show 5 and 15 GHz emission, respectively. In the 5 GHz V map, the thick contours represent positive brightness temperatures. In both images the white contours show emission from the sunspot at 15 GHz. The arrow shows the direction of the limb. Middle row: One-dimensional profiles of the flare computed along the black curve of the top left panel. Bottom row: spatial profiles of the gyrosynchrotron models (see text for details) as a function of the distance along the loop. For comparison with the observations, the profiles have been computed after the models were convolved with the appropriate VLA beam. In both panels the absolute values of the V profiles are presented (adapted from Nindos et al., 2000b). ©AAS. Reproduced with permission.

Observations show that in several cases the electrons that produce gyrosynchrotron emission have often anisotropic and/or inhomogeneous distributions. Such examples are the limb events presented by Kundu et al. (2001b). These flares were imaged by the NoRH at 17 and 34 GHz, and the emission at both frequencies was extended and peaked close to the top of the loop. On the other hand, spectral data from the Nobeyama Polarimeter revealed that both the 17 and 34 GHz emissions were optically thin. A similar event was studied by White et al. (2002). Tzatzakis et al. (2008) found that 36% of the events of an extended database of single-loop limb flares observed by the NoRH showed optically thin emission with maximum close to the loop top. The morphology of these events is not consistent with the morphology of optically thin sources from homogeneous distributions of electrons.

Melnikov et al. (2002) found that optically thin sources with loop-top maxima can result from enhanced concentrations of accelerated electrons at the loop top due to the transverse pitch-angle anisotropy of the injected particles. When the pitch-angle distribution of the injected population is either beam-like (i.e., injection along magnetic field lines) or isotropic, the resulted microwave emission peaks above the footpoints. Melnikov et al. (2002) noted that another possible reason for the concentration of energetic electrons near the loop top is the enhanced losses of electrons close to the footpoints. This possibility may occur either from Coulomb collisions if in the lower part of the loop the plasma density is higher or from stronger turbulence there. Stepanov et al. (2007) reported that strong scattering of electrons by whistler waves can reproduce the evolution of collimated streams of non-thermal electrons observed by Yokoyama et al. (2002). Kuznetsov and Kontar (2015) observed an optically-thin loop-top source and argued that the strong concentration of electrons near the loop top reflected the localized particle injection process accompanied by trapping and scattering.

Other publications that report pitch-angle anisotropies of the electrons that emit gyrosynchrotron emission include Lee and Gary (2000), Lee et al. (2000), Fleishman et al. (2003); Fleishman (2006), Altyntsev et al. (2008, 2019), Tzatzakis et al. (2008), Reznikova et al. (2009), and Charikov et al. (2017). Generally speaking, when pitch-angle anisotropy is present it is not correct to derive the energy spectrum of the energetic electrons from the slope of the optically thin part of the gyrosynchrotron spectrum (see Fleishman and Melnikov, 2003a,b, and the discussion in section 6.1). Instead, one needs to resort to either forward fitting (e.g., Gary et al., 2013) or 3D modeling (e.g., Tzatzakis et al., 2008; Nita et al., 2015) in order to obtain meaninful electron diagnostics from the radio emission.

The study of the dynamics of flare microwave gyrosynchrotron emission can provide important information about the kinematics of accelerated electrons in flaring loops. For example, analysis of the dynamics of the spatial distribution of emission intensity, circular polarization and frequency spectrum allows one to determine the localization of the electron acceleration/injection region in a flare loop, as well as the type of electron pitch-angle distribution in different parts of the flare loop (e.g., Reznikova et al., 2009; Melnikov et al., 2012; Morgachev et al., 2015). Furthermore, the measured spectral dynamics of the microwave emission in the optically thin part of the spectrum may provide important information on the whistler turbulence in the flare loop (Filatov and Melnikov, 2017).

Imaging spectroscopy can provide additional information to the study of gyrosynchrotron emission and this is highlighted in Figure 15 (Gary et al., 2018) where imaging observations from the Expanded OVSA (EOVSA) of a partially occulted flare at 28 frequencies are presented. Figure 15a shows the diversity of source morphologies: as the frequency increases the marginally resolved cusp-like source at frequencies between 7.4 and 8.9 GHz gradually evolves toward a loop-like source while at frequencies below 5 GHz two additional sources appear (see Figure 15f), presumably associated with the footpoints of a larger loop. The spectral modeling presented in Figures 15b–e yields the magnetic field and spectral index of the electron energy distribution at the points marked in Figure 15f. This example shows that the combination of spatially resolved radio spectra with realistic modeling can provide detailed estimates of the dynamically evolving parameters in the flare configuration.

FIGURE 15

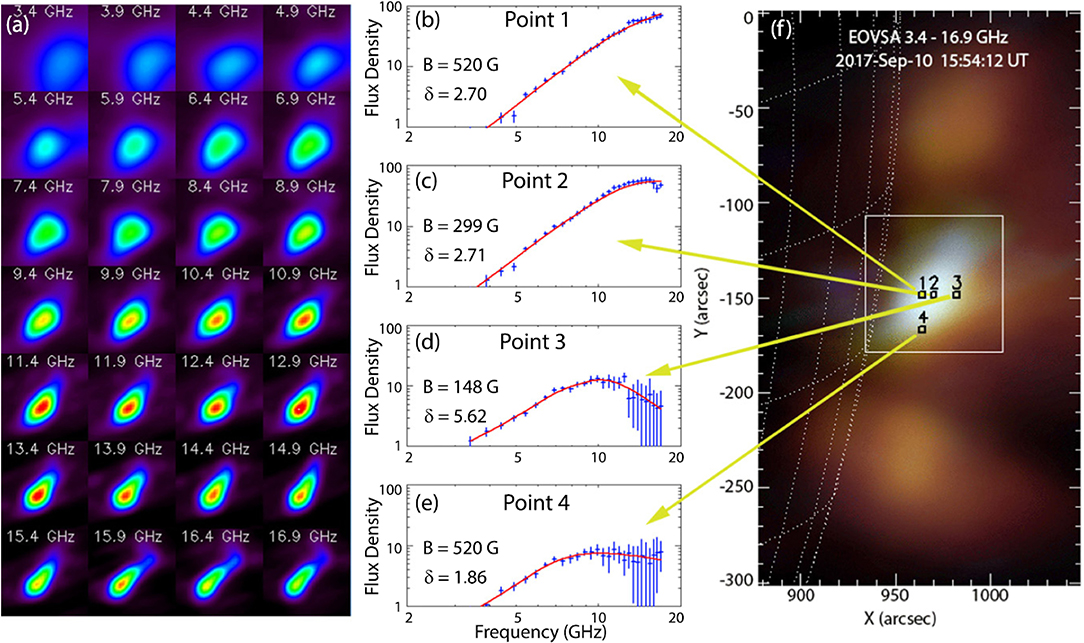
Figure 15. (a) Images of the microwave emission from a partially occulted limb flare obtained at 28 frequencies with EOVSA. The field of view of the images corresponds to the white box of panel (f). (b–e) Flux density spectra in those pixels of the images of panel (a) that correspond to points 1–4 of panel (f), together with model spectral fits (red lines). (f) True-color display of the EOVSA dataset after combining images at the 28 frequencies that are marked in panel (a). From Gary et al. (2018). ©AAS. Reproduced with permission.

6.4. Electron Acceleration and Transport

In sections 6.2 and 6.3, we discussed gyrosynchrotron emission primarily at a fixed time (presumably at the peak of the emission). However, flares are dynamic phenomena, and there is a large literature on the dynamics of flare microwave emission with emphasis on the processes of electron acceleration and transport. Details are given elsewhere in this issue, thus this topic will be only touched on here.

The study of the dynamics of flare microwave gyrosynchrotron emission can provide important information about the kinematics of accelerated electrons in flaring loops.

The combination of microwave and hard X-ray observations of flares with state-of-the-art 3D modeling provides a powerful diagnostic of accelerated electrons (e.g., Fleishman et al., 2016a; Kuroda et al., 2018). In the former study several flares were analyzed which, instead of showing the usual broad-band gyrosynchrotron emission produced by electrons trapped in flaring loops, they showed narrow-band gyrosynchrotron spectra (see also Fleishman et al., 2011, 2013). The relationship of these bursts with hard X-rays together with spectral modeling revealed that the trapped electron population was negligible and the radio emission originated directly from the acceleration sites which featured rather strong magnetic fields and densities. In the Kuroda et al. (2018) study the microwave and hard X-ray observations were successfully fitted with a broken power-law spectrum that reproduced the main characteristics of both emissions.

The most popular model for the study of electron transport during flares is the “direct precipitation/trap plus precipitation” (DP/TPP) model (see Bastian et al., 1998; Aschwanden, 2002, 2004; White et al., 2011, and references therein). Energetic electrons with small pitch angles traveling along appropriate magnetic field lines approach the chromosphere where they are stopped by its dense and cool material. Most of their energy heats the chromosphere, but a smaller fraction is emitted in hard X-rays through the non-thermal thick-target free-free mechanism. The coronal magnetic field traps electrons with large pitch angles inside the flaring loop where they emit gyrosynchrotron radiation. However, eventually they will be scattered into the loss cone under the influence of either Coulomb collisions or wave-particle interactions and will precipitate into the chromosphere emitting additional hard X-ray radiation.

Using the TPP scenario one can study the effect of Coulomb collisions on the energy of electrons (see Aschwanden, 2004, and references therein). The more energetic the electrons, the fewer collisions they undergo, and therefore the longer their lifetimes in the loop. In this way we can interpret the frequency-dependent delays among microwave maxima, the usual lag of microwave emission with respect to the hard X-ray emission, and the slower decay of microwaves than hard X-rays.

Microwave emissions from either directly precipitating electrons (Kundu et al., 2001c; Lee et al., 2002) or from electrons that have been efficiently scattered (Musset et al., 2018) have also been detected. The microwave emission from these populations does not have the same emissivity as the trapped electrons because their pitch-angle distributions are different. Hard X-rays do not come exclusively from precipitated electrons; of course the thick-target emission is more efficient, but trapped electrons also emit free-free radiation, and this has been used to interpret long-duration hard X-ray bursts (Vilmer et al., 1982; Bruggmann et al., 1994). On the other hand, microwave emission is also sensitive to the entire distribution of electrons (both trapped and DP components), but the trapped component will dominate the emission at a given frequency.

7. Concluding Remarks

Incoherent solar radio emission is provided by the free-free, gyroresonance, and gyrosynchrotron processes. Free-free radiation dominates the quiet Sun and non-flaring active region emissions with the exception of regions of strong fields above sunspots where gyroresonance emission is large at microwaves. Gyrosynchrotron is the most important incoherent mechanism in flares.

Free-free opacity favors cool, dense plasmas, but if the density is high enough then hot material can also produce bright radiation. Since free-free emission is ubiquitous in the Sun, it can be used to probe the non-flaring solar atmosphere above temperature minimum. For this task, the free-free emission has the advantage that it can be observed from the ground and that it is not sensitive to processes affected by ionization equilibrium which characterize the EUV and X-ray observations.

Gyroresonance opacity depends strongly on the magnetic field strength and orientation. The emission is generated in thin layers above the base of the TR that have practically constant magnetic field strength which is determined by the condition that the observing frequency is equal to low harmonics of the gyrofrequency. Coronal magnetic fields cannot be measured from the Zeeman effect; consequently multi-frequency microwave imaging observations of gyroresonance sources provide a unique tool for the determination of the three-dimensional structure of sunspot coronal magnetic field.

Unlike EUV and X-ray coronal emissions which are optically thin everywhere, coronal radio emission can become optically thick due to gyroresonance above regions of strong fields or due to free-free at low frequencies. This means that radio data may allow us to probe different layers in the solar atmosphere by observing at different frequencies. On the other hand, it is fair to say that radio images cannot reach the spatial resolution and crispness of the images obtained with some modern EUV instruments, for example the Atmospheric Imaging Assembly aboard Solar Dynamics Observatory.

Gyrosynchrotron radiation is emitted at microwaves and millimeter wavelengths from accelerated electrons of mildly relativistic energies (i.e., from a few tens of keV to a few MeV) as they move in the coronal magnetic field. Gyrosynchrotron provides powerful diagnostics of physical conditions in flaring sources, because it depends on the properties of both the magnetic field and the accelerated electrons, as well as the properties of the ambient plasma.

The diagnostic potential of the emission mechanisms discussed in this paper has not been fully exploited yet. The basic reason is that until relatively recently there was no instrument capable of performing imaging spectroscopy over a wide frequency range. However, things have been changing with the upgrade of both solar-dedicated (Owens Valley Solar Array, and Siberian Solar Radio Telescope, now named Expanded Owens Valley Solar Array and Siberian Radioheliograph, respectively) and general-purpose interferometers (Very Large Array) as well as the design of new interferometers, either solar-dedicated like the Chinese Mingantu Ultrawide Spectral Radioheliograph (MUSER) or for general astronomical use (e.g., LOFAR and ALMA) while “first light” from the Square Kilometre Array (SKA) is expected in the mid-2020s. The upgraded/new instrumentation combined with the continuous operation of other important facilities (e.g., Nançay Radioheliograph and RATAN-600) and the efforts on the modeling side promise exciting new results in the years to come.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank Dr. K.-L. Klein for his valuable comments on an earlier version of this manuscript. I also thank Prof. C.E. Alissandrakis for his valuable comments on the manuscript.

References

Akhmedov, S. B., Gelfreikh, G. B., Bogod, V. M., and Korzhavin, A. N. (1982). The measurement of magnetic fields in the solar atmosphere above sunspots using gyroresonance emission. Solar Phys. 79, 41–58. doi: 10.1007/BF00146972

CrossRef Full Text | Google Scholar

Alissandrakis, C. E. (1994). Radio observations of the quiet solar corona. Adv. Space Res. 14:81. doi: 10.1016/0273-1177(94)90167-8

CrossRef Full Text | Google Scholar

Alissandrakis, C. E., Bogod, V. M., Kaltman, T. I., Patsourakos, S., and Peterova, N. G. (2019). Modeling of the sunspot-associated microwave emission using a new method of DEM inversion. Solar Phys. 294:23. doi: 10.1007/s11207-019-1406-x

CrossRef Full Text | Google Scholar

Alissandrakis, C. E., and Chiuderi-Drago, F. (1994). Detection of linear polarization in the microwave emission of solar active regions. Astroph. J. Lett. 428, L73–L76. doi: 10.1086/187396

CrossRef Full Text | Google Scholar

Alissandrakis, C. E., Gelfreikh, G. B., Borovik, V. N., Korzhavin, A. N., Bogod, V. M., Nindos, A., et al. (1993a). Spectral observations of active region sources with RATAN-600 and WSRT. Astron. Astrophys. 270, 509–515.

Google Scholar

Alissandrakis, C. E., Kochanov, A. A., Patsourakos, S., Altyntsev, A. T., Lesovoi, S. V., and Lesovoya, N. N. (2013). Microwave and EUV observations of an erupting filament and associated flare and coronal mass ejections. Publ. Astron. Soc. Japan 65:8. doi: 10.1093/pasj/65.sp1.S8

CrossRef Full Text | Google Scholar

Alissandrakis, C. E., and Kundu, M. R. (1982). Observations of ring structure in a sunspot associated source at 6 centimeter wavelength. Astroph. J. Lett. 253, L49–L52. doi: 10.1086/183734

CrossRef Full Text | Google Scholar

Alissandrakis, C. E., and Kundu, M. R. (1984). Center-to-limb variation of a sunspot-associated microwave source. Astron. Astrophys. 139, 271–284.

Google Scholar

Alissandrakis, C. E., Kundu, M. R., and Lantos, P. (1980). A model for sunspot associated emission at 6 CM wavelength. Astron. Astrophys. 82, 30–40.

Google Scholar

Alissandrakis, C. E., Nindos, A., and Kundu, M. R. (1993b). Evidence for ordinary mode emission from microwave bursts. Solar Phys. 147, 343–358. doi: 10.1007/BF00690724

CrossRef Full Text | Google Scholar

Alissandrakis, C. E., Patsourakos, S., Nindos, A., and Bastian, T. S. (2017). Center-to-limb observations of the Sun with ALMA. Implications for solar atmospheric models. Astron. Astrophys. 605:A78. doi: 10.1051/0004-6361/201730953

CrossRef Full Text | Google Scholar

Alissandrakis, C. E., and Preka-Papadema, P. (1984). Microwave emission and polarization of a flaring loop. Astron. Astrophys. 139, 507–511.

Google Scholar

Altyntsev, A. T., Fleishman, G. D., Huang, G.-L., and Melnikov, V. F. (2008). A broadband microwave burst produced by electron beams. Astroph. J. 677, 1367–1377. doi: 10.1086/528841

CrossRef Full Text | Google Scholar

Altyntsev, A. T., Meshalkina, N. S., Lysenko, A. L., and Fleishman, G. D. (2019). Rapid variability in the SOL2011-08-04 flare: implications for electron acceleration. Astroph. J. 883:38. doi: 10.3847/1538-4357/ab3808

CrossRef Full Text | Google Scholar

Aschwanden, M. J. (2002). Particle acceleration and kinematics in solar flares. Space Sci. Rev. 101, 1–227. doi: 10.1007/978-94-017-2541-5

CrossRef Full Text | Google Scholar

Aschwanden, M. J. (2004). Physics of the Solar Corona. An Introduction. Berlin: Praxis Publishing Ltd.

Google Scholar

Bain, H. M., Krucker, S., Saint-Hilaire, P., and Raftery, C. L. (2014). Radio imaging of a type IVM radio burst on the 14th of August 2010. Astroph. J. 782:43. doi: 10.1088/0004-637X/782/1/43

CrossRef Full Text | Google Scholar

Bastian, T. S. (1994). Angular scattering of solar radio emission by coronal turbulence. Astroph. J. 426, 774–781. doi: 10.1086/174114

CrossRef Full Text | Google Scholar

Bastian, T. S., Benz, A. O., and Gary, D. E. (1998). Radio emission from solar flares. Ann. Rev. Astron. Astrophys. 36, 131–188. doi: 10.1146/annurev.astro.36.1.131

CrossRef Full Text | Google Scholar

Bastian, T. S., Chintzoglou, G., De Pontieu, B., Shimojo, M., Schmit, D., Leenaarts, J., et al. (2017). A first comparison of millimeter continuum and Mg II ultraviolet line emission from the solar chromosphere. Astroph. J. Lett. 845:L19. doi: 10.3847/2041-8213/aa844c

CrossRef Full Text | Google Scholar

Bastian, T. S., Dulk, G. A., and Leblanc, Y. (1996). High-resolution microwave observations of the quiet solar chromosphere. Astroph. J. 473:539. doi: 10.1086/178165

CrossRef Full Text | Google Scholar

Bastian, T. S., Fleishman, G. D., and Gary, D. E. (2007). Radio spectral evolution of an x-ray-poor impulsive solar flare: implications for plasma heating and electron acceleration. Astroph. J. 666, 1256–1267. doi: 10.1086/520106

CrossRef Full Text | Google Scholar

Bastian, T. S., Pick, M., Kerdraon, A., Maia, D., and Vourlidas, A. (2001). The coronal mass ejection of 1998 April 20: direct imaging at radio wavelengths. Astroph. J. Lett. 558, L65–L69. doi: 10.1086/323421

CrossRef Full Text | Google Scholar

Belkora, L. (1997). Time evolution of solar microwave bursts. Astroph. J. 481:532. doi: 10.1086/304052

CrossRef Full Text | Google Scholar

Benz, A. O., Krucker, S., Acton, L. W., and Bastian, T. S. (1997). Fine structure of the X-ray and radio emissions of the quiet solar corona. Astron. Astrophys. 320, 993–1000.

Google Scholar

Brosius, J. W., and Holman, G. D. (1989). The structure of the microwave emission from sunspot magnetic fields. Astroph. J. 342, 1172–1186. doi: 10.1086/167674

CrossRef Full Text | Google Scholar

Brosius, J. W., and White, S. M. (2004). Close association of an extreme-ultraviolet sunspot plume with depressions in the sunspot radio emission. Astroph. J. 601, 546–558. doi: 10.1086/380394

CrossRef Full Text | Google Scholar

Brosius, J. W., and White, S. M. (2006). Radio measurements of the height of strong coronal magnetic fields above sunspots at the solar limb. Astroph. J. Lett. 641, L69–L72. doi: 10.1086/503774

CrossRef Full Text | Google Scholar

Bruggmann, G., Vilmer, N., Klein, K.-L., and Kane, S. R. (1994). Electron trapping in evolving coronal structures during a large gradual hard X-ray/radio burst. Solar Phys. 149, 171–193. doi: 10.1007/BF00645188

CrossRef Full Text | Google Scholar

Carley, E. P., Vilmer, N., Simões, P. J. A., and Ó Fearraigh, B. (2017). Estimation of a coronal mass ejection magnetic field strength using radio observations of gyrosynchrotron radiation. Astron. Astrophys. 608:A137. doi: 10.1051/0004-6361/201731368

CrossRef Full Text | Google Scholar

Charikov, Y. E., Shabalin, A. N., and Kuznetsov, S. A. (2017). Modeling of physical processes by analysis of hard x-ray and microwave radiations in the solar flare of November 10, 2002. Geomagnet. Aeronomy 57, 1009–1017. doi: 10.1134/S0016793217080060

CrossRef Full Text | Google Scholar

Chen, B., Yu, S., Reeves, K. K., and Gary, D. E. (2020). Microwave spectral imaging of an erupting magnetic flux rope: implications for the standard solar flare model in three dimensions. Astroph. J. Lett. 895:L50. doi: 10.3847/2041-8213/ab901a

CrossRef Full Text | Google Scholar

Cheng, C.-C., and Moe, K. O. (1977). Emission measures and structure of the transition region of a sunspot from emission lines in the far ultraviolet. Solar Phys., 52, 327–335. doi: 10.1007/BF00149649

CrossRef Full Text | Google Scholar

Chiuderi-Drago, F., Alissandrakis, C. E., Bastian, T., Bocchialini, K., and Harrison, R. A. (2001). Joint EUV/radio observations of a solar filament. Solar Phys. 199, 115–132. doi: 10.1023/A:1010390726242

CrossRef Full Text | Google Scholar

Cohen, M. H. (1960). Magnetoionic mode coupling at high frequencies. Astroph. J. 131:664. doi: 10.1086/146878

CrossRef Full Text | Google Scholar

Costa, J. E. R., Simões, P. J. D. A., Pinto, T. S. N., and Melnikov, V. F. (2013). Solar burst analysis with 3D loop models. Publ. Astron. Soc. Japan 65:5. doi: 10.1093/pasj/65.sp1.S5

CrossRef Full Text | Google Scholar

Dravskikh, A. F., and Dravskikh, Z. V. (1988). Expected detection of the 2(2)P3/2-2(2)S1/2 hydrogen line in the radio emission spectrum of the quiet sun. Astron. Zh. 65, 199–202.

Google Scholar

Dulk, G. A. (1985). Radio emission from the sun and stars. Ann. Rev. Astron. Astrophys. 23, 169–224. doi: 10.1146/annurev.aa.23.090185.001125

CrossRef Full Text | Google Scholar

Dulk, G. A., and Marsh, K. A. (1982). Simplified expressions for the gyrosynchrotron radiation from mildly relativistic, nonthermal and thermal electrons. Astroph. J. 259, 350–358. doi: 10.1086/160171

CrossRef Full Text | Google Scholar

Duncan, R. A. (1979). Wave ducting of solar metre-wave radio emission as an explanation of fundamental/harmonic source coincidence and other anomalies. Solar Phys. 63, 389–398. doi: 10.1007/BF00174543

CrossRef Full Text | Google Scholar

Fedotova, A., Altyntsev, A., Kochanov, A., Lesovoi, S., and Meshalkina, N. (2018). Observation of eruptive events with the Siberian Radioheliograph. Solar Terrestrial Phys. 4, 13–19. doi: 10.12737/stp-43201802

CrossRef Full Text | Google Scholar

Filatov, L. V., and Melnikov, V. F. (2017). Influence of whistler turbulence on fast electron distribution and their microwave emissions in a flare loop. Geomagnet. Aeronomy 57, 1001–1008. doi: 10.1134/S0016793217080084

CrossRef Full Text | Google Scholar

Fleishman, G. D. (2006). “Radio emission from anisotropic electron distributions,” in Solar Physics with the Nobeyama Radioheliograph, ed K. Shibasaki (Nobeyama: NSRO Report 1), 51–62.

Google Scholar

Fleishman, G. D., Gary, D. E., Chen, B., Kuroda, N., Yu, S., and Nita, G. M. (2020). Decay of the coronal magnetic field can release sufficient energy to power a solar flare. Science 367, 278–280. doi: 10.1126/science.aax6874

PubMed Abstract | CrossRef Full Text | Google Scholar

Fleishman, G. D., Gary, D. E., and Nita, G. M. (2003). Decimetric spike bursts versus microwave continuum. Astroph. J. 593, 571–580. doi: 10.1086/376362

CrossRef Full Text | Google Scholar

Fleishman, G. D., Kontar, E. P., Nita, G. M., and Gary, D. E. (2011). A cold, tenuous solar flare: acceleration without heating. Astroph. J. Lett. 731:L19. doi: 10.1088/2041-8205/731/1/L19

CrossRef Full Text | Google Scholar

Fleishman, G. D., Kontar, E. P., Nita, G. M., and Gary, D. E. (2013). Probing dynamics of electron acceleration with radio and x-ray spectroscopy, imaging, and timing in the 2002 April 11 solar flare. Astroph. J. 768:190. doi: 10.1088/0004-637X/768/2/190

CrossRef Full Text | Google Scholar

Fleishman, G. D., and Kuznetsov, A. A. (2010). Fast gyrosynchrotron codes. Astroph. J. 721, 1127–1141. doi: 10.1088/0004-637X/721/2/1127

CrossRef Full Text | Google Scholar

Fleishman, G. D., and Kuznetsov, A. A. (2014). Theory of gyroresonance and free-free emissions from non-maxwellian quasi-steady-state electron distributions. Astroph. J. 781:77. doi: 10.1088/0004-637X/781/2/77

CrossRef Full Text | Google Scholar

Fleishman, G. D., Loukitcheva, M. A., Kopnina, V. Y., Nita, G. M., and Gary, D. E. (2018). The coronal volume of energetic particles in solar flares as revealed by microwave imaging. Astroph. J. 867:81. doi: 10.3847/1538-4357/aae0f6

CrossRef Full Text | Google Scholar

Fleishman, G. D., and Mel'nikov, V. F. (1998). REVIEWS OF TOPICAL PROBLEMS: millisecond solar radio spikes. Phys. Uspekhi 41, 1157–1189. doi: 10.1070/PU1998v041n12ABEH000510

CrossRef Full Text | Google Scholar

Fleishman, G. D., and Melnikov, V. F. (2003a). Gyrosynchrotron emission from anisotropic electron distributions. Astroph. J. 587, 823–835. doi: 10.1086/368252

CrossRef Full Text | Google Scholar

Fleishman, G. D., and Melnikov, V. F. (2003b). Optically thick gyrosynchrotron emission from anisotropic electron distributions. Astroph. J. 584, 1071–1083. doi: 10.1086/345849

CrossRef Full Text | Google Scholar

Fleishman, G. D., Nita, G. M., and Gary, D. E. (2009). Dynamic magnetography of solar flaring loops. Astroph. J. Lett. 698, L183–L187. doi: 10.1088/0004-637X/698/2/L183

CrossRef Full Text | Google Scholar

Fleishman, G. D., Nita, G. M., and Gary, D. E. (2015). Energy partitions and evolution in a purely thermal solar flare. Astroph. J. 802:122. doi: 10.1088/0004-637X/802/2/122

CrossRef Full Text | Google Scholar

Fleishman, G. D., Nita, G. M., Kontar, E. P., and Gary, D. E. (2016a). Narrowband gyrosynchrotron bursts: probing electron acceleration in solar flares. Astroph. J. 826:38. doi: 10.3847/0004-637X/826/1/38

CrossRef Full Text | Google Scholar

Fleishman, G. D., Pal'shin, V. D., Meshalkina, N., Lysenko, A. L., Kashapova, L. K., and Altyntsev, A. T. (2016b). A cold flare with delayed heating. Astroph. J. 822:71. doi: 10.3847/0004-637X/822/2/71

CrossRef Full Text | Google Scholar

Fleishman, G. D., Xu, Y., Nita, G. N., and Gary, D. E. (2016c). Validation of the coronal thick target source model. Astroph. J. 816:62. doi: 10.3847/0004-637X/816/2/62

CrossRef Full Text | Google Scholar

Gary, D. E., Chen, B., Dennis, B. R., Fleishman, G. D., Hurford, G. J., Krucker, S., et al. (2018). Microwave and hard x-ray observations of the 2017 September 10 solar limb flare. Astroph. J. 863:83. doi: 10.3847/1538-4357/aad0ef

CrossRef Full Text | Google Scholar

Gary, D. E., Fleishman, G. D., and Nita, G. M. (2013). Magnetography of solar flaring loops with microwave imaging spectropolarimetry. Solar Phys. 288, 549–565. doi: 10.1007/s11207-013-0299-3

CrossRef Full Text | Google Scholar

Gary, D. E., Hartl, M. D., and Shimizu, T. (1997). Nonthermal radio emission from solar soft x-ray transient brightenings. Astroph. J. 477:958. doi: 10.1086/303748

CrossRef Full Text | Google Scholar

Gary, D. E., and Hurford, G. J. (1987). Multifrequency observations of a solar active region during a partial eclipse. Astroph. J. 317, 522–533. doi: 10.1086/165296

CrossRef Full Text | Google Scholar

Gary, D. E., and Hurford, G. J. (1989). A simple solar microwave burst observed with high spectral resolution. Astroph. J. 339:1115. doi: 10.1086/167366

CrossRef Full Text | Google Scholar

Gary, D. E., and Hurford, G. J. (1994). Coronal temperature, density, and magnetic field maps of a solar active region using the Owens Valley Solar Array. Astroph. J. 420, 903–912. doi: 10.1086/173614

CrossRef Full Text | Google Scholar

Gary, D. E., and Keller, C. U. (eds.). (2004). “Solar and space weather radiophysics - current status and future developments,” in Astrophysics and Space Science Library (Berlin: Springer), 1–400. doi: 10.1007/1-4020-2814-8

CrossRef Full Text | Google Scholar

Gary, D. E., and Zirin, H. (1988). Microwave structure of the quiet sun. Astroph. J. 329, 991–1001. doi: 10.1086/166443

CrossRef Full Text | Google Scholar

Gary, D. E., Zirin, H., and Wang, H. (1990). Microwave structure of the quiet sun at 8.5 GHz. Astroph. J. 355, 321–328. doi: 10.1086/168766

CrossRef Full Text | Google Scholar

Gelfreikh, G. B. (2004). “Coronal magnetic field measurements through bremsstrahlung emission,” in Astrophysics and Space Science Library, eds D. E. Gary and C. U. Keller (Berlin: Springer), 115. doi: 10.1007/1-4020-2814-8_6

CrossRef Full Text | Google Scholar

Gelfreikh, G. B., and Lubyshev, B. I. (1979). Structure of local sources of the s-component of solar radio emission. Soviet Astron. 23:316.

Google Scholar

Gershman, B. N. (1960). Gyromagnetic resonance absorption of electromagnetic waves in a plasma. Zh. Eksperim. Teor. Fiz. 38:912.

Google Scholar

Gopalswamy, N., and Hanaoka, Y. (1998). Coronal dimming associated with a giant prominence eruption. Astroph. J. Lett. 498:L179. doi: 10.1086/311330

CrossRef Full Text | Google Scholar

Gopalswamy, N., and Kundu, M. R. (1992). Estimation of the mass of a coronal mass ejection from radio observations. Astroph. J. Lett. 390, L37–L39. doi: 10.1086/186366

CrossRef Full Text | Google Scholar

Gopalswamy, N., Kundu, M. R., Hanaoka, Y., Enome, S., Lemen, J. R., and Akioka, M. (1996a). Yohkoh/SXT observations of a coronal mass ejection near the solar surface. N. Astron. 1, 207–213. doi: 10.1016/S1384-1076(96)00016-4

CrossRef Full Text | Google Scholar

Gopalswamy, N., Raulin, J.-P., Kundu, M. R., Hildebrandt, J., Krüger, A., and Hofmann, A. (1996b). Observations and model calculations of sunspot ring structure at 8.46 GHz. Astron. Astrophys. 316, L25–L28.

Google Scholar

Gopalswamy, N., Shimojo, M., Lu, W., Yashiro, S., Shibasaki, K., and Howard, R. A. (2003). Prominence eruptions and coronal mass ejection: a statistical study using microwave observations. Astroph. J. 586, 562–578. doi: 10.1086/367614

CrossRef Full Text | Google Scholar

Grebinskij, A., Bogod, V., Gelfreikh, G., Urpo, S., Pohjolainen, S., and Shibasaki, K. (2000). Microwave tomography of solar magnetic fields. Astron. Astrophys. Suppl. 144, 169–180. doi: 10.1051/aas:2000202

CrossRef Full Text | Google Scholar

Grechnev, V. V., Kundu, M. R., and Nindos, A. (2006a). A study of accelerated electrons in solar flares using microwave and x-ray observations. Publ. Astron. Soc. Japan 58, 47–54. doi: 10.1093/pasj/58.1.47

CrossRef Full Text | Google Scholar

Grechnev, V. V., Uralov, A. M., Zandanov, V. G., Baranov, N. Y., and Shibasaki, K. (2006b). Observations of prominence eruptions with two radioheliographs, SSRT, and NoRH. Publ. Astron. Soc. Japan 58, 69–84. doi: 10.1093/pasj/58.1.69

CrossRef Full Text | Google Scholar

Hanaoka, Y. (1997). Double-loop configuration of solar flares. Solar Phys. 173, 319–346. doi: 10.1023/A:1004953003558

CrossRef Full Text | Google Scholar

Hanaoka, Y. (1999). “Long duration events observed with the Nobeyama radioheliograph,” in Proceedings of the Nobeyama Symposium, eds T. S. Bastian, N. Gopalswamy, and K. Shibasaki, 153–158.

Google Scholar

Hanaoka, Y., Kurokawa, H., Enome, S., Nakajima, H., Shibasaki, K., Nishio, M., et al. (1994). Simultaneous observations of a prominence eruption followed by a coronal arcade formation in radio, soft X-rays, and H(alpha). Publ. Astron. Soc. Japan 46, 205–216.

Google Scholar

Holman, G. D., and Kundu, M. R. (1985). The microwave structure of hot coronal loops. Astroph. J. 292, 291–296. doi: 10.1086/163159

CrossRef Full Text | Google Scholar

Hori, K. (2000). Origin of helical coronal disturbances from the sun. Astroph. J. 543, 1011–1015. doi: 10.1086/317162

CrossRef Full Text | Google Scholar

Huang, G., Melnikov, V. F., Ji, H., and Ning, Z. (2018). Solar Flare Loops: Observations and Interpretations. Berlin: Springer. doi: 10.1007/978-981-10-2869-4

CrossRef Full Text | Google Scholar

Huang, J., Tan, B., Masuda, S., Cheng, X., Bisoi, S. K., and Melnikov, V. (2019). Localized microwave and EUV bright structures in an eruptive prominence. Astroph. J. 874:176. doi: 10.3847/1538-4357/ab0e80

CrossRef Full Text | Google Scholar

Hurford, G. J. (1986). “High-spectral resolution solar microwave observations,” in Solar Flares and Coronal Physics Using P/OF as a Research Tool, eds E. Tandberg, R. M. Wilson, and R. M. Hudson (Washington, DC: NASA), 191–200.

Google Scholar

Jafarzadeh, S., Wedemeyer, S., Szydlarski, M., De Pontieu, B., Rezaei, R., and Carlsson, M. (2019). The solar chromosphere at millimetre and ultraviolet wavelengths. I. Radiation temperatures and a detailed comparison. Astron. Astrophys. 622:A150. doi: 10.1051/0004-6361/201834205

CrossRef Full Text | Google Scholar

Kaltman, T. I., Bogod, V. M., Stupishin, A. G., and Yasnov, L. V. (2012). The altitude structure of the coronal magnetic field of AR 10933. Astron. Rep. 56, 790–799. doi: 10.1134/S1063772912100022

CrossRef Full Text | Google Scholar

Karzas, W. J., and Latter, R. (1961). Electron radiative transitions in a Coulomb field. Astroph. J. Suppl. 6:167. doi: 10.1086/190063

CrossRef Full Text | Google Scholar

Kathiravan, C., Ramesh, R., and Subramanian, K. R. (2002). Metric radio observations and ray-tracing analysis of the onset phase of a solar eruptive event. Astroph. J. Lett. 567, L93–L95. doi: 10.1086/339801

CrossRef Full Text | Google Scholar

Kellermann, K. I., and Pauliny-Toth, I. I. K. (1969). The spectra of opaque radio sources. Astroph. J. Lett. 155:L71. doi: 10.1086/180305

CrossRef Full Text | Google Scholar

Klein, K.-L. (1987). Microwave radiation from a dense magneto-active plasma. Astron. Astrophys. 183, 341–350.

Google Scholar

Klein, K. L., and Trottet, G. (1984). Gyrosynchrotron radiation from a source with spatially varying field and density. Astron. Astrophys. 141, 67–76.

Google Scholar

Kontar, E. P., Chen, X., Chrysaphi, N., Jeffrey, N. L. S., Emslie, A. G., Krupar, V., et al. (2019). Anisotropic radio-wave scattering and the interpretation of solar radio emission observations. Astroph. J. 884:122. doi: 10.3847/1538-4357/ab40bb

CrossRef Full Text | Google Scholar

Kontar, E. P., Motorina, G. G., Jeffrey, N. L. S., Tsap, Y. T., Fleishman, G. D., and Stepanov, A. V. (2018). Frequency rising sub-THz emission from solar flare ribbons. Astron. Astrophys. 620:A95. doi: 10.1051/0004-6361/201834124

CrossRef Full Text | Google Scholar

Korzhavin, A. N., Opeikina, L. V., and Peterova, N. G. (2010). Transition region above sunspots inferred from microwave observations. Astrophys. Bull. 65, 60–74. doi: 10.1134/S1990341310010062

CrossRef Full Text | Google Scholar

Krucker, S., Benz, A. O., Bastian, T. S., and Acton, L. W. (1997). X-ray network flares of the quiet sun. Astroph. J. 488:499. doi: 10.1086/304686

CrossRef Full Text | Google Scholar

Krüger, A. (1979). Introduction to Solar Radio Astronomy and Radio Physics. Dordrecht: Reidel.

Google Scholar

Krüger, A., Hildebrandt, J., and Fuerstenberg, F. (1985). A working model of the solar S-component radio emission. Astron. Astrophys. 143, 72–76.

Google Scholar

Kundu, M. R. (1965). Solar Radio Astronomy. New York, NY: Interscience.

Google Scholar

Kundu, M. R., and Alissandrakis, C. E. (1984). Structure and polarization of active region microwave emission. Solar Phys. 94, 249–283. doi: 10.1007/BF00151317

CrossRef Full Text | Google Scholar

Kundu, M. R., Alissandrakis, C. E., Bregman, J. D., and Hin, A. C. (1977). 6 centimeter observations of solar active regions with 6 SEC resolution. Astroph. J. 213, 278–295. doi: 10.1086/155155

CrossRef Full Text | Google Scholar

Kundu, M. R., Garaimov, V. I., White, S. M., and Krucker, S. (2004a). Nobeyama Radioheliograph and RHESSI Observations of the X1.5 Flare of 2002 April 21. Astroph. J. 600, 1052–1060. doi: 10.1086/379876

CrossRef Full Text | Google Scholar

Kundu, M. R., Nindos, A., and Grechnev, V. V. (2004b). The configuration of simple short-duration solar microwave bursts. Astron. Astrophys. 420, 351–359. doi: 10.1051/0004-6361:20034461

CrossRef Full Text | Google Scholar

Kundu, M. R., Nindos, A., Vilmer, N., Klein, K. L., Shibata, K., and Ohyama, M. (2001a). Metric radio emission associated with x-ray plasmoid ejections. Astroph. J. 559, 443–451. doi: 10.1086/322301

CrossRef Full Text | Google Scholar

Kundu, M. R., Nindos, A., White, S. M., and Grechnev, V. V. (2001b). A multiwavelength study of three solar flares. Astroph. J. 557, 880–890. doi: 10.1086/321534

CrossRef Full Text | Google Scholar

Kundu, M. R., Rao, A. P., Erskine, F. T., and Bregman, J. D. (1979). High-resolution observations of the quiet sun at 6 centimeters using the Westerbork Synthesis Radio Telescope. Astroph. J. 234, 1122–1136. doi: 10.1086/157596

CrossRef Full Text | Google Scholar

Kundu, M. R., Schmahl, E. J., Grigis, P. C., Garaimov, V. I., and Shibasaki, K. (2006). Nobeyama radio heliograph observations of RHESSI microflares. Astron. Astrophys. 451, 691–707. doi: 10.1051/0004-6361:20053987

CrossRef Full Text | Google Scholar

Kundu, M. R., Schmahl, E. J., Vlahos, L., and Velusamy, T. (1982). Radio imaging of solar flares using the very large array - New insights into flare process. Astron. Astrophys. 108, 188–194.

Google Scholar

Kundu, M. R., and Vlahos, L. (1982). Solar microwave bursts - A review. Space Sci. Rev. 32, 405–462. doi: 10.1007/BF00177449

CrossRef Full Text | Google Scholar

Kundu, M. R., White, S. M., Gopalswamy, N., and Lim, J. (1994). Millimeter, microwave, hard X-ray, and soft X-ray observations of energetic electron populations in solar flares. Astroph. J. Suppl. 90, 599–610. doi: 10.1086/191881

CrossRef Full Text | Google Scholar

Kundu, M. R., White, S. M., Shibasaki, K., Sakurai, T., and Grechnev, V. V. (2001c). Spatial structure of simple spiky bursts at microwave/millimeter wavelengths. Astroph. J. 547, 1090–1099. doi: 10.1086/318422

CrossRef Full Text | Google Scholar

Kuroda, N., Gary, D. E., Wang, H., Fleishman, G. D., Nita, G. M., and Jing, J. (2018). Three-dimensional forward-fit modeling of the hard x-ray and microwave emissions of the 2015 June 22 M6.5 Flare. Astroph. J. 852:32. doi: 10.3847/1538-4357/aa9d98

CrossRef Full Text | Google Scholar

Kuznetsov, A. A., and Kontar, E. P. (2015). Spatially resolved energetic electron properties for the 21 May 2004 flare from radio observations and 3D simulations. Solar Phys. 290, 79–93. doi: 10.1007/s11207-014-0530-x

CrossRef Full Text | Google Scholar

Kuznetsov, A. A., Nita, G. M., and Fleishman, G. D. (2011). Three-dimensional simulations of gyrosynchrotron emission from mildly anisotropic nonuniform electron distributions in symmetric magnetic loops. Astroph. J. 742:87. doi: 10.1088/0004-637X/742/2/87

CrossRef Full Text | Google Scholar

Lang, K. R., and Wilson, R. F. (1982). Polarized horseshoes around sunspots at 6 centimeter wavelength. Solar Phys. 255, L111–L114. doi: 10.1086/183780

CrossRef Full Text | Google Scholar

Lantos, P., and Alissandrakis, C. E. (1999). Analysis of coronal emissions observed at meter wavelengths. Astron. Astrophys. 351, 373–381.

Google Scholar

Lantos, P., Alissandrakis, C. E., Gergely, T., and Kundu, M. R. (1987). Quiet sun and slowly varying component at meter and decameter wavelengths. Solar Phys. 112, 325–340. doi: 10.1007/BF00148787

CrossRef Full Text | Google Scholar

Lecacheux, A., Steinberg, J.-L., Hoang, S., and Dulk, G. A. (1989). Characteristics of type III bursts in the solar wind from simultaneous observations on board ISEE-3 and Voyager. Astron. Astrophys. 217, 237–250.

Google Scholar

Lee, J. (2007). Radio emissions from solar active regions. Space Sci. Rev. 133, 73–102. doi: 10.1007/s11214-007-9206-2

CrossRef Full Text | Google Scholar

Lee, J., and Gary, D. E. (2000). Solar microwave bursts and injection pitch-angle distribution of flare electrons. Astroph. J. 543, 457–471. doi: 10.1086/317080

CrossRef Full Text | Google Scholar

Lee, J., Gary, D. E., Qiu, J., and Gallagher, P. T. (2002). Electron transport during the 1999 August 20 flare inferred from microwave and hard x-ray observations. Astroph. J. 572, 609–625. doi: 10.1086/340311

CrossRef Full Text | Google Scholar

Lee, J., Gary, D. E., and Shibasaki, K. (2000). Magnetic trapping and electron injection in two contrasting solar microwave bursts. Astroph. J. 531, 1109–1120. doi: 10.1086/308511

CrossRef Full Text | Google Scholar

Lee, J., McClymont, A. N., Mikic, Z., White, S. M., and Kundu, M. R. (1998). Coronal currents, magnetic fields, and heating in a solar active region. Astroph. J. 501:853. doi: 10.1086/305851

CrossRef Full Text | Google Scholar

Lee, J., White, S. M., Kundu, M. R., Mikic, Z., and McClymont, A. N. (1999). A test for coronal magnetic field extrapolations. Astroph. J. 510, 413–421. doi: 10.1086/306556

CrossRef Full Text | Google Scholar

Lee, J. W., Hurford, G. J., and Gary, D. E. (1993). Microwave emission from a sunspot. I - Implications for the sunspot magnetic structure. Solar Phys. 144, 45–57. doi: 10.1007/BF00667981

CrossRef Full Text | Google Scholar

Loukitcheva, M., Solanki, S. K., and White, S. (2006). The dynamics of the solar chromosphere: comparison of model predictions with millimeter-interferometer observations. Astron. Astrophys. 456, 713–723. doi: 10.1051/0004-6361:20053171

CrossRef Full Text | Google Scholar

Loukitcheva, M. A., White, S. M., and Solanki, S. K. (2019). ALMA detection of dark chromospheric holes in the quiet sun. Astroph. J. Lett. 877:L26. doi: 10.3847/2041-8213/ab2191

CrossRef Full Text | Google Scholar

Maia, D., Pick, M., Vourlidas, A., and Howard, R. (2000). Development of coronal mass ejections: radio shock signatures. Astroph. J. Lett. 528, L49–L51. doi: 10.1086/312421

PubMed Abstract | CrossRef Full Text | Google Scholar

Maia, D. J. F., Gama, R., Mercier, C., Pick, M., Kerdraon, A., and Karlicky, M. (2007). The radio-coronal mass ejection event on 2001 April 15. Astroph. J. 660, 874–881. doi: 10.1086/508011

CrossRef Full Text | Google Scholar

Marqué, C. (2004). Radio metric observations of quiescent filament cavities. Astroph. J. 602, 1037–1050. doi: 10.1086/381085

CrossRef Full Text | Google Scholar

Marqué, C., Lantos, P., Delouis, J. M., and Alissandrakis, C. E. (1999). “Metric and decimetric observations of the quiet solar corona,” in 8th SOHO Workshop: Plasma Dynamics and Diagnostics in the Solar Transition Region and Corona, eds J.-C. Vial and B. Kaldeich-Schü (ESA Special Publication), 483.

Google Scholar

McCauley, P. I., Cairns, I. H., White, S. M., Mondal, S., Lenc, E., Morgan, J., et al. (2019). The low-frequency solar corona in circular polarization. Solar Phys. 294:106. doi: 10.1007/s11207-019-1502-y

CrossRef Full Text | Google Scholar

Melnikov, V. F., Gary, D. E., and Nita, G. M. (2008). Peak frequency dynamics in solar microwave bursts. Solar Phys. 253, 43–73. doi: 10.1007/s11207-008-9275-8

CrossRef Full Text | Google Scholar

Melnikov, V. F., Pyatakov, N. P., and Shibasaki, K. (2012). “Constraints for electron acceleration models in solar flares from microwave observations with high spatial resolution,” in Hinode-3: The 3rd Hinode Science Meeting, eds T. Sekii, T. Watanabe, and T. Sakurai, 321.

Google Scholar

Melnikov, V. F., Shibasaki, K., and Reznikova, V. E. (2002). Loop-top nonthermal microwave source in extended solar flaring loops. Astroph. J. Lett. 580, L185–L188. doi: 10.1086/345587

CrossRef Full Text | Google Scholar

Melrose, D. B. (1980). Plasma astrohysics. Nonthermal processes in diffuse magnetized plasmas - Vol.1: The emission, absorption and transfer of waves in plasmas; Vol.2: Astrophysical applications. New York, NY: Gordon and Breach.

Google Scholar

Mercier, C. (1996). Some characteristics of atmospheric gravity waves observed by radio-interferometry. Ann. Geoph. 14, 42–58. doi: 10.1007/s00585-996-0042-6

CrossRef Full Text | Google Scholar

Mercier, C., and Chambe, G. (2009). High dynamic range images of the solar corona between 150 and 450 MHz. Astroph. J. Lett. 700, L137–L140. doi: 10.1088/0004-637X/700/2/L137

CrossRef Full Text | Google Scholar

Mercier, C., and Chambe, G. (2012). Morphology of the quiet Sun between 150 and 450 MHz as observed with the Nançay radioheliograph. Astron. Astrophys. 540:A18. doi: 10.1051/0004-6361/201118163

CrossRef Full Text | Google Scholar

Molnar, M. E., Reardon, K. P., Chai, Y., Gary, D., Uitenbroek, H., Cauzzi, G., et al. (2019). Solar chromospheric temperature diagnostics: a joint ALMA-Hα analysis. Astroph. J. 881:99. doi: 10.3847/1538-4357/ab2ba3

CrossRef Full Text | Google Scholar

Mondal, S., Oberoi, D., and Vourlidas, A. (2019). Estimation of the physical parameters of a CME at high coronal heights using low frequency radio observations. arXiv preprint arXiv:1909.12041. doi: 10.3847/1538-4357/ab7fab

CrossRef Full Text | Google Scholar

Morgachev, A. S., Kuznetsov, S. A., Melnikov, V. F., and Simões, J. A. (2015). Modeling the distribution of circular polarization degree of microwave emission along the flare loops in event July 19, 2012. Geomagnet. Aeron. 55, 1118–1123. doi: 10.1134/S0016793215080228

CrossRef Full Text | Google Scholar

Morgachev, A. S., Tsap, Y. T., Smirnova, V. V., and Motorina, G. G. (2018). Simulation of subterahertz emission from the April 2, 2017 solar flare based on the multiwavelength observations. Geomagnet. Aeron. 58, 1113–1122. doi: 10.1134/S001679321808011X

CrossRef Full Text | Google Scholar

Morgachev, A. S., Tsap, Y. T., Smirnova, V. V., and Motorina, G. G. (2020). On the source of sub-terahertz radiation of the solar flare on April 2, 2017. Geomagnet. Aeron. 59, 1114–1120. doi: 10.1134/S0016793219080140

CrossRef Full Text | Google Scholar

Musset, S., Kontar, E. P., and Vilmer, N. (2018). Diffusive transport of energetic electrons in the solar corona: x-ray and radio diagnostics. Astron. Astrophys. 610:A6. doi: 10.1051/0004-6361/201731514

CrossRef Full Text | Google Scholar

Nindos, A., Alissandrakis, C. E., Bastian, T. S., Patsourakos, S., De Pontieu, B., Warren, H., et al. (2018). First high-resolution look at the quiet Sun with ALMA at 3mm. Astron. Astrophys. 619:L6. doi: 10.1051/0004-6361/201834113

CrossRef Full Text | Google Scholar

Nindos, A., Alissandrakis, C. E., Gelfreikh, G. B., Bogod, V. M., and Gontikakis, C. (2002). Spatially resolved microwave oscillations above a sunspot. Astron. Astrophys. 386, 658–673. doi: 10.1051/0004-6361:20020252

CrossRef Full Text | Google Scholar

Nindos, A., Alissandrakis, C. E., Gelfreikh, G. B., Kundu, M. R., Dere, K. P., Korzhavin, A. N., et al. (1996). A model for active region emission at centimeter wavelengths. Solar Phys. 166, 55–87. doi: 10.1007/BF00179356

CrossRef Full Text | Google Scholar

Nindos, A., Alissandrakis, C. E., Patsourakos, S., and Bastian, T. S. (2020). Transient brightenings in the quiet Sun detected by ALMA at 3 mm. Astron. Astrophys. 638:A62. doi: 10.1051/0004-6361/202037810

CrossRef Full Text | Google Scholar

Nindos, A., Aurass, H., Klein, K.-L., and Trottet, G. (2008). Radio emission of flares and coronal mass ejections. Invited review. Solar Phys. 253, 3–41. doi: 10.1007/s11207-008-9258-9

CrossRef Full Text | Google Scholar

Nindos, A., Kundu, M. R., and White, S. M. (1999). A study of microwave-selected coronal transient brightenings. Astroph. J. 513, 983–989. doi: 10.1086/306886

CrossRef Full Text | Google Scholar

Nindos, A., Kundu, M. R., White, S. M., Shibasaki, K., and Gopalswamy, N. (2000a). Soft x-ray and gyroresonance emission above sunspots. Astroph. J. Suppl. 130, 485–499. doi: 10.1086/317355

CrossRef Full Text | Google Scholar

Nindos, A., White, S. M., Kundu, M. R., and Gary, D. E. (2000b). Observations and models of a flaring loop. Astroph. J. 533, 1053–1062. doi: 10.1086/308705

CrossRef Full Text | Google Scholar

Nishio, M., Yaji, K., Kosugi, T., Nakajima, H., and Sakurai, T. (1997). Magnetic field configuration in impulsive solar flares inferred from coaligned microwave/x-ray images. Astroph. J., 489:976. doi: 10.1086/304793

CrossRef Full Text | Google Scholar

Nita, G. M., Fleishman, G. D., Kuznetsov, A. A., Kontar, E. P., and Gary, D. E. (2015). Three-dimensional radio and x-ray modeling and data analysis software: revealing flare complexity. Astroph. J. 799:236. doi: 10.1088/0004-637X/799/2/236

CrossRef Full Text | Google Scholar

Nita, G. M., Viall, N. M., Klimchuk, J. A., Loukitcheva, M. A., Gary, D. E., Kuznetsov, A. A., et al. (2018). Dressing the coronal magnetic extrapolations of active regions with a parameterized thermal structure. Astroph. J. 853:66. doi: 10.3847/1538-4357/aaa4bf

CrossRef Full Text | Google Scholar

Osborne, C. M. J., and Simões, P. J. A. (2019). Thyr: a volumetric ray-marching tool for simulating microwave emission. MNRAS 485, 3386–3397. doi: 10.1093/mnras/stz660

CrossRef Full Text | Google Scholar

Patsourakos, S., Alissandrakis, C. E., Nindos, A., and Bastian, T. S. (2020). Observations of solar chromospheric oscillations at 3 mm with ALMA. Astron. Astrophys. 634:A86. doi: 10.1051/0004-6361/201936618

CrossRef Full Text | Google Scholar

Petrosian, V. (1981). Synchrotron emissivity from mildly relativistic particles. Astroph. J. 251, 727–738. doi: 10.1086/159517

CrossRef Full Text | Google Scholar

Pick, M., and Vilmer, N. (2008). Sixty-five years of solar radioastronomy: flares, coronal mass ejections and Sun Earth connection. Astron. Astrophys. Rev. 16, 1–153. doi: 10.1007/s00159-008-0013-x

CrossRef Full Text | Google Scholar

Preka-Papadema, P., and Alissandrakis, C. E. (1988). Spatial and spectral structure of a solar flaring loop at centimeter wavelengths. Astron. Astrophys. 191, 365–373.

Google Scholar

Preka-Papadema, P., and Alissandrakis, C. E. (1992). Two-dimensional model maps of flaring loops at cm-wavelengths. Astron. Astrophys. 257, 307–314.

Google Scholar

Rahman, M. M., McCauley, P. I., and Cairns, I. H. (2019). On the relative brightness of coronal holes at low frequencies. Solar Phys. 294:7. doi: 10.1007/s11207-019-1396-8

CrossRef Full Text | Google Scholar

Ramaty, R. (1969). Gyrosynchrotron emission and absorption in a magnetoactive plasma. Astroph. J. 158:753. doi: 10.1086/150235

CrossRef Full Text | Google Scholar

Ramesh, R., Kathiravan, C., Narayanan, A. S., and Ebenezer, E. (2003). Metric observations of transient, quasi-periodic radio emission from the solar corona in association with a “halo” CME and an “EIT wave” event. Astron. Astrophys. 400, 753–758. doi: 10.1051/0004-6361:20030019

CrossRef Full Text | Google Scholar

Raulin, J.-P., and Pacini, A. A. (2005). Solar radio emissions. Adv. Space Res. 35, 739–754. doi: 10.1016/j.asr.2005.03.138

CrossRef Full Text | Google Scholar

Raulin, J.-P., White, S. M., Kundu, M. R., Silva, A. V. R., and Shibasaki, K. (1999). Multiple components in the millimeter emission of a solar flare. Astroph. J. 522, 547–558. doi: 10.1086/322974

CrossRef Full Text | Google Scholar

Razin, V. A. (1960). On the spectrum of nonthermal cosmic radio emission. Izv. Vys. Ucheb. Zav. Radiofiz. 3:584.

Reznikova, V. E., Melnikov, V. F., Shibasaki, K., Gorbikov, S. P., Pyatakov, N. P., Myagkova, I. N., et al. (2009). 2002 August 24 limb flare loop: dynamics of microwave brightness distribution. Astroph. J. 697, 735–746. doi: 10.1088/0004-637X/697/1/735

CrossRef Full Text | Google Scholar

Rodger, A. S., and Labrosse, N. (2018). Spectral gradient of the thermal millimetre continuum as a diagnostic for optical thickness in the solar atmosphere. Astron. Astrophys. 617:L6. doi: 10.1051/0004-6361/201833848

CrossRef Full Text | Google Scholar

Rodger, A. S., Labrosse, N., Wedemeyer, S., Szydlarski, M., Simões, P. J. A., and Fletcher, L. (2019). First spectral analysis of a solar plasma eruption using ALMA. Astroph. J. 875:163. doi: 10.3847/1538-4357/aafdfb

CrossRef Full Text | Google Scholar

Rybicki, G. B., and Lightman, A. P. (1979). Radiative Processes in Astrophysics. New York, NY: Wiley.

Google Scholar

Saint-Hilaire, P., Hurford, G. J., Keating, G., Bower, G. C., and Gutierrez-Kraybill, C. (2012). Allen telescope array multi-frequency observations of the sun. Solar Phys. 277, 431–445. doi: 10.1007/s11207-011-9906-3

CrossRef Full Text | Google Scholar

Selhorst, C. L., Silva-Válio, A., and Costa, J. E. R. (2008). Solar atmospheric model over a highly polarized 17 GHz active region. Astron. Astrophys. 488, 1079–1084. doi: 10.1051/0004-6361:20079217

CrossRef Full Text | Google Scholar

Shain, A. V., Melnikov, V. F., and Morgachev, A. S. (2017). The role of quasi-transverse propagation in observed polarization of flare loop microwave radiation. Geomagnet. Aeron. 57, 988–995. doi: 10.1134/S0016793217080217

CrossRef Full Text | Google Scholar

Sheridan, K. V., Jackson, B. V., McLear, D. J., and Dulk, G. A. (1978). Radio observations of a massive, slow moving ejection of coronal material. Proc. Astron. Soc. Australia 3, 249–250. doi: 10.1017/S1323358000015423

CrossRef Full Text | Google Scholar

Shibasaki, K., Alissandrakis, C. E., and Pohjolainen, S. (2011). Radio emission of the quiet sun and active regions (invited review). Solar Phys. 273, 309–337. doi: 10.1007/s11207-011-9788-4

CrossRef Full Text | Google Scholar

Shibasaki, K., Enome, S., Nakajima, H., Nishio, M., Takano, T., Hanaoka, Y., et al. (1994). A purely polarized S-component at 17 GHz. Publ. Astron. Soc. Japan 46, L17–L20.

Google Scholar

Shimojo, M., Bastian, T. S., Hales, A. S., White, S. M., Iwai, K., Hills, R. E., et al. (2017a). Observing the Sun with the Atacama Large Millimeter/submillimeter Array (ALMA): high-resolution interferometric imaging. Solar Phys. 292:87. doi: 10.1007/s11207-017-1095-2

CrossRef Full Text | Google Scholar

Shimojo, M., Hudson, H. S., White, S. M., Bastian, T. S., and Iwai, K. (2017b). The first ALMA observation of a solar plasmoid ejection from an x-ray bright point. Astroph. J. Lett. 841:L5. doi: 10.3847/2041-8213/aa70e3

CrossRef Full Text | Google Scholar

Silva, A. V. R., White, S. M., Lin, R. P., de Pater, I., Shibasaki, K., Hudson, H. S., et al. (1996). First images of a solar flare at millimeter wavelengths. Astroph. J. Lett. 458:L49. doi: 10.1086/309918

CrossRef Full Text | Google Scholar

Silva, D. F., and Valio, A. B. M. (2016). “Millimeter observation of solar flares with polarization,” in Astronomical Society of the Pacific Conference Series, 55.

Google Scholar

Simões, P. J. A., and Costa, J. E. R. (2006). Solar bursts gyrosynchrotron emission from three-dimensional sources. Astron. Astrophys. 453, 729–736. doi: 10.1051/0004-6361:20054665

CrossRef Full Text | Google Scholar

Simões, P. J. A., and Costa, J. E. R. (2010). Gyrosynchrotron emission from anisotropic pitch-angle distribution of electrons in 3-D solar flare sources. Solar Phys. 266, 109–121. doi: 10.1007/s11207-010-9596-2

CrossRef Full Text | Google Scholar

Song, Q. W., Nakajima, H., Huang, G. L., Tan, B. L., Huang, Y., and Wu, Z. (2016). Turnover frequency in solar microwave bursts with an extremely flat optically thin spectrum. Solar Phys. 291, 3619–3635. doi: 10.1007/s11207-016-1004-0

CrossRef Full Text | Google Scholar

Stallcop, J. R. (1974). Absorption of infrared radiation by electrons in the field of a neutral hydrogen atom - I. Astroph. J. 187, 179–184. doi: 10.1086/152607

CrossRef Full Text | Google Scholar

Stepanov, A. V., Yokoyama, T., Shibasaki, K., and Melnikov, V. F. (2007). Turbulent propagation of high-energy electrons in a solar coronal loop. Astron. Astrophys. 465, 613–619. doi: 10.1051/0004-6361:20066573

CrossRef Full Text | Google Scholar

Stupishin, A. G., Kaltman, T. I., Bogod, V. M., and Yasnov, L. V. (2018). Modeling of solar atmosphere parameters above sunspots using RATAN-600 microwave observations. Solar Phys. 293:13. doi: 10.1007/s11207-017-1228-7

CrossRef Full Text | Google Scholar

Thejappa, G., and MacDowall, R. J. (2008). Effects of scattering on radio emission from the quiet sun at low frequencies. Astroph. J. 676, 1338–1345. doi: 10.1086/528835

CrossRef Full Text | Google Scholar

Trottet, G., Krucker, S., Lüthi, T., and Magun, A. (2008). Radio Submillimeter and γ-Ray observations of the 2003 October 28 solar flare. Astroph. J. 678, 509–514. doi: 10.1086/528787

CrossRef Full Text | Google Scholar

Tsap, Y. T., Smirnova, V. V., Motorina, G. G., Morgachev, A. S., Kuznetsov, S. A., Nagnibeda, V. G., et al. (2018). Millimeter and x-ray emission from the 5 July 2012 solar flare. Solar Phys. 293:50. doi: 10.1007/s11207-018-1269-6

CrossRef Full Text | Google Scholar

Tun, S. D., Gary, D. E., and Georgoulis, M. K. (2011). Three-dimensional structure of a solar active region from spatially and spectrally resolved microwave observations. Astroph. J. 728:1. doi: 10.1088/0004-637X/728/1/1

CrossRef Full Text | Google Scholar

Tun, S. D., and Vourlidas, A. (2013). Derivation of the magnetic field in a coronal mass ejection core via multi-frequency radio imaging. Astroph. J. 766:130. doi: 10.1088/0004-637X/766/2/130

CrossRef Full Text | Google Scholar

Tzatzakis, V., Nindos, A., and Alissandrakis, C. E. (2008). A statistical study of microwave flare morphologies. Solar Phys. 253, 79–94. doi: 10.1007/s11207-008-9263-z

CrossRef Full Text | Google Scholar

Uralov, A. M., Lesovoi, S. V., Zandanov, V. G., and Grechnev, V. V. (2002). Dual-filament initiation of a coronal mass ejection: observations and model. Solar Phys. 208, 69–90. doi: 10.1023/A:1019610614255

CrossRef Full Text | Google Scholar

Vilmer, N., Kane, S. R., and Trottet, G. (1982). Impulsive and gradual hard X-ray sources in a solar flare. Astron. Astrophys. 108, 306–313.

Google Scholar

Vocks, C., Mann, G., Breitling, F., Bisi, M. M., Dabrowski, B., Fallows, R., et al. (2018). LOFAR observations of the quiet solar corona. Astron. Astrophys. 614:A54. doi: 10.1051/0004-6361/201630067

CrossRef Full Text | Google Scholar

Vourlidas, A., and Bastian, T. S. (1996). Multiband VLA observations of solar active regions: implications for the distribution of coronal plasma. Astroph. J. 466:1039. doi: 10.1086/177574

CrossRef Full Text | Google Scholar

Vourlidas, A., Bastian, T. S., and Aschwanden, M. J. (1997). The structure of the solar corona above sunspots as inferred from radio, x-ray, and magnetic field observations. Astroph. J. 489:403. doi: 10.1086/304769

CrossRef Full Text | Google Scholar

Vourlidas, A., Gary, D. E., and Shibasaki, K. (2006). Sunspot gyroresonance emission at 17 GHz: a statistical study. Publ. Astron. Soc. Japan 58, 11–20. doi: 10.1093/pasj/58.1.11

CrossRef Full Text | Google Scholar

Wang, H., Liu, C., Ahn, K., Xu, Y., Jing, J., Deng, N., et al. (2017). High-resolution observations of flare precursors in the low solar atmosphere. Nat. Astron. 1:0085. doi: 10.1038/s41550-017-0085

CrossRef Full Text | Google Scholar

Wang, Z., Gary, D. E., Fleishman, G. D., and White, S. M. (2015). Coronal magnetography of a simulated solar active region from microwave imaging spectropolarimetry. Astroph. J. 805:93. doi: 10.1088/0004-637X/805/2/93

CrossRef Full Text | Google Scholar

Wedemeyer, S., Bastian, T., Brajša, R., Hudson, H., Fleishman, G., Loukitcheva, M., et al. (2016). Solar science with the Atacama large millimeter/submillimeter Array-A new view of our sun. SSRv 200, 1–73. doi: 10.1007/s11214-015-0229-9

CrossRef Full Text | Google Scholar

Wedemeyer, S., Szydlarski, M., Jafarzadeh, S., Eklund, H., Guevara Gomez, J. C., Bastian, T., et al. (2020). The Sun at millimeter wavelengths. I. Introduction to ALMA Band 3 observations. Astron. Astrophys. 635:A71. doi: 10.1051/0004-6361/201937122

CrossRef Full Text | Google Scholar

White, S. M. (1999). Radio versus EUV/x-ray observations of the solar atmosphere. Solar Phys. 190, 309–330. doi: 10.1007/978-94-017-3429-5_20

CrossRef Full Text | Google Scholar

White, S. M., Benz, A. O., Christe, S., Fárník, F., Kundu, M. R., Mann, G., et al. (2011). The relationship between solar radio and hard x-ray emission. SSRv 159, 225–261. doi: 10.1007/s11214-010-9708-1

CrossRef Full Text | Google Scholar

White, S. M., and Kundu, M. R. (1992). Solar observations with a millimeter-wavelength array. Solar Phys. 141, 347–369. doi: 10.1007/BF00155185

CrossRef Full Text | Google Scholar

White, S. M., and Kundu, M. R. (1997). Radio observations of gyroresonance emission from coronal magnetic fields. Solar Phys. 174, 31–52.

Google Scholar

White, S. M., Kundu, M. R., Garaimov, V. I., Yokoyama, T., and Sato, J. (2002). The physical properties of a flaring loop. Astroph. J. 576, 505–518. doi: 10.1086/341621

CrossRef Full Text | Google Scholar

White, S. M., Kundu, M. R., and Gopalswamy, N. (1991). Strong magnetic fields and inhomogeneity in the solar corona. Astroph. J. Lett. 366, L43–L46. doi: 10.1086/185905

CrossRef Full Text | Google Scholar

White, S. M., Kundu, M. R., Shimizu, T., Shibasaki, K., and Enome, S. (1995). The radio properties of solar active region soft x-ray transient brightenings. Astroph. J. 450:435. doi: 10.1086/176153

CrossRef Full Text | Google Scholar

White, S. M., Loukitcheva, M., and Solanki, S. K. (2006). High-resolution millimeter-interferometer observations of the solar chromosphere. Astron. Astrophys. 456, 697–711. doi: 10.1051/0004-6361:20052854

CrossRef Full Text | Google Scholar

Wu, Z., Chen, Y., Huang, G., Nakajima, H., Song, H., Melnikov, V., et al. (2016). Microwave imaging of a hot flux rope structure during the pre-impulsive stage of an eruptive M7.7 solar flare. Astroph. J. Lett. 820:L29. doi: 10.3847/2041-8205/820/2/L29

CrossRef Full Text | Google Scholar

Yokoyama, T., Nakajima, H., Shibasaki, K., Melnikov, V. F., and Stepanov, A. V. (2002). Microwave observations of the rapid propagation of nonthermal sources in a solar flare by the nobeyama radioheliograph. Astroph. J. Lett. 576, L87–L90. doi: 10.1086/343098

CrossRef Full Text | Google Scholar

Yokoyama, T., Shimojo, M., Okamoto, T. J., and Iijima, H. (2018). ALMA observations of the solar chromosphere on the polar limb. Astroph. J. 863:96. doi: 10.3847/1538-4357/aad27e

CrossRef Full Text | Google Scholar

Zheleznyakov, V. V. (1970). Radio Emission of the Sun and Planets. Oxford: Pergamon Press.

Google Scholar

Zlotnik, E. Y. (1968a). The theory of the slowly changing component of solar radio emission. II. Soviet Astron. 12:464.

Google Scholar

Zlotnik, E. Y. (1968b). Theory of the slowly changing component of solar radio emission. I. Soviet Astron. 12:245.

Google Scholar

Zlotnik, E. Y., Kundu, M. R., and White, S. M. (1996). A model of the atmosphere above a sunspot from radio observations. Radiophys. Quant. Electron. 39, 255–267. doi: 10.1007/BF02144449

CrossRef Full Text | Google Scholar