
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci. , 28 August 2020
Sec. Stellar and Solar Physics
Volume 7 - 2020 | https://doi.org/10.3389/fspas.2020.00047
This article is part of the Research Topic Asteroseismology in the Kepler Era View all 11 articles
In the course of their evolution, white-dwarf stars go through at least one phase of variability in which the global pulsations they undergo allow astronomers to peer into their interiors, making it possible to shed light on their deep inner structure and evolutionary stage by means of asteroseismology. The study of pulsating white dwarfs has undergone substantial progress in the last decade, and this is largely thanks to the arrival of continuous observations of unprecedented quality from space, like those of the CoRoT, Kepler, and TESS missions. This, along with the advent of new detailed theoretical models and the development of improved asteroseismological techniques, has helped to unravel the internal chemical structure of many pulsating white dwarfs, and, at the same time, has posed new questions that challenge theoreticians. In particular, uninterrupted monitoring of white-dwarf stars for months has allowed discovering phenomena impossible to detect with ground-based observations, despite previous admirable efforts like the Whole Earth Telescope (WET). Here, we start by reviewing the essential properties of white-dwarf and pre-white dwarf stars and their pulsations, and then, we go through the different families of pulsating objects known to date. Finally, we review the most outstanding findings about pulsating white dwarfs and pre-white dwarfs made possible with the unprecedented-quality observations of the Kepler space telescope, although we envisage that future analyses of space data from this mission that still await examination, may reveal new secrets of these extremely interesting variable stars.
White-dwarf stars constitute the most common compact remnants of the evolution of stars with initial masses below ~ 10 − 11M⊙ (Woosley and Heger, 2015), including our Sun. Comprehensive accounts referring to the origin and evolution of white dwarfs can be found in the review articles of Fontaine et al. (2001) and Althaus et al. (2010). White dwarfs are extremely old objects, with typical ages in the range 1 − 10 Gyr (1 Gyr ≡109 yr). These stellar fossils are found in a range of masses of 0.15 ≲ M⋆/M⊙ ≲ 1.25, with an average value of M⋆/M⊙ ~ 0.60 (Tremblay et al., 2016), although for the majority of white dwarfs the mass lies between M⋆/M⊙ ~ 0.50 and M⋆/M⊙ ~ 0.70. Since they are characterized by planetary dimensions (R⋆ ~ 0.01R⊙), the matter inside is highly concentrated, with average densities of white dwarfs being in the order of g/cm3. Consequently, the prevailing equation of the state inside white dwarfs is that of a highly-degenerate Fermi gas (Chandrasekhar, 1939). Indeed, the hydrostatic equilibrium in the interior of a white dwarf is provided by the pressure of degenerate electrons counteracting the gravity force, thus avoiding the collapse of the star. In particular, electron degeneracy is responsible for a curious relationship between the stellar mass and radius: the more massive the white dwarf, the smaller its radius. The process of discovery of white dwarfs, starting from the observation of variations of the proper motion of Procyon and Sirius by Friedrich Wilhelm Bessel in 1844 (Bessel, 1844), was fascinating. The emergence of the quantum-mechanics theory toward the first quarter of the 20th century paved the way in explaining the existence of white dwarfs. An excellent historical account of the discovery of white dwarfs and the theoretical arguments that led to explaining the existence of these compact objects in nature is provided by Van Horn (2015).
Apart from the degenerate electrons, the interior of white dwarfs is composed by non-degenerate ions that store the thermal energy generated by previous nuclear burning—generally extinct in the white-dwarf stage. White dwarfs are found at a huge interval of effective temperatures (4, 000 ≲ Teff ≲ 200, 000 K) thus spanning seven orders of magnitude in luminosity, . Regarding their inner chemical composition, average-mass white dwarfs are characterized by cores likely made of 12C and 16O—the products of He burning—although ultra-massive white dwarfs (M⋆/M⊙ ≳ 1.0) could contain cores composed of 16O, 20Ne, and 24Mg as well, and the lowest-mass white dwarfs (low-mass and extremely low-mass white dwarfs, abbreviated as LM and ELM white dwarfs, respectively) could harbor cores made of 4He. In particular, ELM white dwarfs (M⋆/M⊙ ≲ 0.2) must be formed in interacting binary systems, otherwise they would be much older than the Universe. A description of the different formation channels of white dwarfs, either single- or binary-star evolution, can be found in the review articles of Althaus et al. (2010) and Córsico et al. (2019). Unlike other stages of stellar evolution, the white-dwarf phase is characterized by a relatively simple process of gradual cooling of the star, shining at the expense of the heat stored in its core during the prior evolutionary history. This process was first described in a simplified way by Mestel (1952). The cooling rate of white dwarfs depends on many factors: surface temperature, stellar mass, core chemical composition, surface chemical composition, etc. The surface chemical composition of white dwarfs defines the spectral type. Most white dwarfs (~ 80%) have atmospheres rich in 1H, and are called DA white dwarfs. About a ~ 15% of white dwarfs have atmospheres rich in 4He, and are denominated by DB and DO white dwarfs. The remaining population of white dwarfs (~ 5%) show atmospheres rich in 4He, 12C, and 16O (PG1159 stars)1, 12C and 4He (DQ white dwarfs), and metals without 1H or 4He present (DZ white dwarfs). There are also some exotic objects, such as SDSS J0922+2928 and SDSS J1102+2054, that exhibit O in their atmospheres (Gänsicke et al., 2010), SDSS J1240+6710 that has a nearly pure 16O atmosphere, diluted only by traces of 20Ne, 26Mg, and 28Si (Kepler et al., 2016a), and finally WD J0551+4135, that shows a mixed 1H and 12C atmosphere (Hollands et al., 2020). The origin of these unfamiliar objects is not yet known, but might involve stellar mergers. By virtue of the high densities and small radii of the white dwarfs, they are characterized by very high surface gravities, in the range of log g ~ 6 − 9 [cm/s2]. The extremely high gravities of white dwarfs force heavy elements to sink and light nuclear species to float on the white-dwarf surface. This effect, called gravitational settling, explains the purity of the atmospheres of DA and DB/DO white dwarfs. Any “impurity” observed in white dwarf atmospheres at intermediate temperatures—for instance, photospheric trace metals found in many white dwarfs—must be attributed either to accreted material (i.e., tidally disrupted planetesimals; see Koester et al., 2014), material floating on the surface due to radiative levitation, or material dredged up from the interior due to convection. The typical chemical structure of an average-mass DA white dwarf consists of a core composed of 12C and 16O—in unknown proportions—containing ~ 99% of the mass, surrounded by a 4He layer with a mass , it is in turn enclosed by a thin 1H envelope with a mass of . The thickness of the 1H and 4He mantles depends on the mass of the white dwarf. Despite the thinness of these layers, they play a fundamental role in the cooling rate (Wood, 1990).
The population of known white dwarfs has increased dramatically in recent years. Ground-based observations, principally with the spectral observations of the Sloan Digital Sky Survey (SDSS; York et al., 2000), have enlarged the number of known white dwarfs by a factor of 15 (Kleinman et al., 2013; Kepler et al., 2016b, 2019). Recently, Gentile Fusillo et al. (2019) presented a catalog of ~ 260, 000 high-confidence white-dwarf candidates selected from Gaia DR2.
White-dwarf research has relevant applications to various areas of modern astrophysics. A primary application of the analysis of white-dwarf properties, either individual or collective—like the mass distribution, core chemical composition, and cooling times—is to place constraints on the evolution of low-mass stars, including third dredge up and mass loss on the Asymptotic Giant Branch (AGB), the efficiency of extra-mixing during core He burning, and nuclear reaction rates (Kunz et al., 2002; Metcalfe, 2003; Straniero et al., 2003; Salaris et al., 2009; Fields et al., 2016).
By virtue of the large number of white dwarfs that are currently known, and thanks to the extreme longevity of these stars (they are among the oldest objects of the Galaxy), they are a key part in our understanding of the formation and evolution of stars, evolution of planetary systems, and the history of our Galaxy itself. For instance, since the existing population of white dwarfs holds a detailed account of the early star formation in the Galaxy, then accurate white-dwarf luminosity functions can be employed to deduce the age, structure, and evolution of the Galactic disk and the nearest open and globular clusters, through what is called cosmochronology (Fontaine et al., 2001; Bedin et al., 2009, 2015; García-Berro et al., 2010; Campos et al., 2013, 2016; García-Berro and Oswalt, 2016; Kilic et al., 2017).
From another perspective, since the majority of low-mass stars will evolve into white dwarfs, then most of the host stars of planetary systems will end their lives as white dwarfs. At present, many white dwarfs with planetary debris are currently being detected, and their study provides valuable information about the chemical composition of extra-solar planets (Gänsicke et al., 2012; Hollands et al., 2018). In particular, Gänsicke et al. (2019) have detected a white dwarf accreting material probably coming from a giant planet.
In a different context, white dwarfs are found in binary systems. This allows exploring the interactions among stars, and in particular, to study type Ia supernovae progenitors (Maoz et al., 2014). Indeed, since the mechanical properties of a white dwarf are described by a Fermi gas of degenerate electrons, there exist a limit mass—the Chandrasekhar mass, ~ 1.4M⊙—beyond which the structure of a white dwarf becomes unstable. Therefore, a 12C/16O-core white dwarf in a binary system that receives mass from its companion, can approach the Chandrasekhar mass and explode as a supernova.
Finally, another very important aspect of white dwarfs is that, due to the high density prevailing in their interiors, they are extremely useful as cosmic laboratories to study dense plasma physics and solid state physics (crystallization; Montgomery and Winget, 1999; Montgomery et al., 1999; Winget et al., 2009; Tremblay et al., 2019), and “exotic physics” (axions, neutrino magnetic dipole moment, variation of fundamental constants, etc; Isern et al., 1992, 2008, 2018; Córsico et al., 2001, 2012b, 2013, 2014; Miller Bertolami, 2014; Miller Bertolami et al., 2014).
An important characteristic of white dwarfs is that, along their evolution, all of them go through at least one phase of pulsational instability that converts white dwarfs into variable stars. As such, variable white dwarfs can be studied through asteroseismology, which allows for key information about the internal structure of pulsating stars to be extracted, through the study of their normal modes. In a sense, the global pulsations are something like “windows” that allow astronomers to “see” inside the stars (Cox, 1980; Unno et al., 1989; Aerts et al., 2010; Catelan and Smith, 2015). In the case of white dwarfs, the properties derived through asteroseismology for pulsating objects are likely valid for non-pulsating white dwarfs as well. On the other hand, this is a unique tool that makes it possible to delve inside the white dwarfs. Finally, and due to the fact that the equilibrium structures of white dwarfs are simple—by virtue of its degenerate nature—their pulsation properties are consequently simple and relatively easy to model to a meaningful precision. In particular, they can be treated within the context of the linear theory of stellar pulsations. These unique qualities explain why white-dwarf asteroseismology has, in recent years, become one of the most powerful tools to learn about their origin, evolution, and internal structure, complementing the traditional techniques of spectroscopy, photometry, and astrometry (Fontaine and Brassard, 2008; Winget and Kepler, 2008; Althaus et al., 2010; Córsico et al., 2019). As a matter of fact, white-dwarf asteroseismology has been a cornerstone of the field of asteroseismology (Brown and Gilliland, 1994). Below, we briefly describe the pulsational properties of white dwarfs along with their immediate precursors, the pre-white dwarfs, and the different classes of these compact pulsators known at the time of writing this review (March 2020).
Pulsations in white dwarfs manifest as brightness fluctuations in the optical, the ultraviolet (UV), and infrared (IR) regions of the electromagnetic spectrum, with amplitudes between 0.001 mmag and 0.4 mag. The variations are thought to be produced by changes in the surface temperature due to non-radial g modes (McGraw, 1979; Robinson et al., 1982) with low harmonic degree (ℓ = 1, 2) and low and intermediate radial order (k). In particular, Robinson et al. (1982) showed that during pulsations, the changes of the stellar radius are fairly small (), and that the variations in surface temperature (ΔTeff ~ 200 K) are the true cause of the variability of pulsating white dwarfs. Kepler (1984) investigated the effects of r-mode non-radial pulsations2 on the lightcurves and line profiles of a slowly rotating star, and concluded that the observed variations of the prototype H-rich pulsating white dwarf, G117−B15A, are not caused by r-mode pulsations, but are consistent with g-mode pulsations. By virtue of the high electron degeneracy in the core of white dwarfs, the g-mode critical frequency—the “buoyancy” or Brunt-Väisälä frequency—is very low at the core regions. This forces g modes to probe, in particular, the regions of the envelope (see, for instance Brassard et al., 1991), although some low radial-order modes are generally sensitive to the central regions. In the case of hot pre-white dwarfs like PG1159 stars, degeneracy is not as important, and g modes can propagate throughout the star, including the core regions (Kawaler et al., 1985; Córsico and Althaus, 2006). The first pulsating white dwarf ever detected, HL Tau 76, was discovered unexpectedly by Landolt (1968). Since then, an increasing number of pulsating white dwarfs have been detected, either through observations from Earth—mainly for candidates identified from SDSS—and recently as a result of uninterrupted observations of space missions, such as Kepler/K2 (Borucki et al., 2010; Howell et al., 2014). Prior to the era of observations from space, an important international collaborative tool called the Whole Earth Telescope (WET; Nather et al., 1990) was successfully used to observe pulsating white dwarfs and pre-white dwarfs for long intervals of time, without interruption. As a matter of fact, observations from this world-wide network of telescopes resulted in the most precise light curves ever obtained for any pulsating star at that time (see, for instance, Winget et al., 1991, 1994). The properties of the light curves of pulsating white dwarfs and pre-white dwarfs are varied, ranging from very simple and with low-amplitude variations (containing a single period) to complex and with high-amplitude fluctuations (usually harboring several periods). The first ones are usually associated with pulsating white dwarfs located at the hot edge of the specific instability domain, and the last ones are found generally for stars populating the cool boundary of that instability region—as the convection zone deepens, longer-period modes are excited. In the case of the complex lightcurves, that usually exhibit features of non-linearity, it is common to find harmonics and linear combinations of eigenfrequencies that are not related to real pulsation modes. Rather, they are likely connected with physical phenomena inherent to the outermost regions of the white dwarf, probably related to the outer convection zone. In the case of pulsating pre-white dwarfs, the effective temperatures are so high that these stars probably lack an extensive external convective zone. This may be the explanation for the fact that non-linearities are not detected in any pulsating hot pre-white dwarf star.
Currently, the number of known pulsating white dwarfs and pre-white dwarfs is about 350 (Córsico et al., 2019). They are distributed in six confirmed types, namely ZZ Ceti (or DAV) stars, GW Lib stars, V777 Her (or DBV) stars, GW Vir (or pulsating PG1159) stars, ELMV stars, and pre-ELMV stars. There are two additional claimed classes of pulsating white dwarfs, the hot DAV stars (Teff ~ 30, 000 K, 7.3 ≲ log g ≲ 7.8; Kurtz et al., 2008, 2013) and the DQV stars (Montgomery et al., 2008). Pulsational instabilities in hot DAVs were predicted on theoretical grounds by Shibahashi (2005, 2007); the actual existence of pulsations in these stars must be confirmed by additional observations. On the other hand, DQVs are hot DQ (C- and He-rich atmospheres) white dwarfs with surface parameters 19, 000 K ≲ Teff ≲ 22, 000 K and 8 ≲ log g ≲ 9. At present, there is a growing consensus that the variability of these objects could be due to other effects than global pulsations. The main characteristics of the confirmed classes of pulsating white dwarfs are listed in Table 1 and the location in the log Teff − log g is depicted in Figure 1 (details can be found in Córsico et al., 2019). In Table 1, the second column indicates the discovery year of the first star of each type and the number of detected objects at the time of writing this review, the third column corresponds to the range of effective temperatures at which they are found (instability domain), the fourth column shows the range of surface gravity, the fifth column indicates the range of periods detected, the sixth column is the range of amplitudes of the fluctuations in the light curves, and the seventh column shows the surface chemical composition. Pulsation periods usually span the interval ~ 100 − 1, 400 s; however PNNVs and ELMVs display longer periods, up to ~ 6, 300 s. In Figure 2 we show the periods detected in the different families of pulsating white dwarfs and pre-white dwarfs. Curiously, and due to the compactness of these objects, the periods of g modes in white dwarfs have magnitudes comparable to the values of the periods of p modes exhibited by non-degenerate pulsating stars, like the Sun.
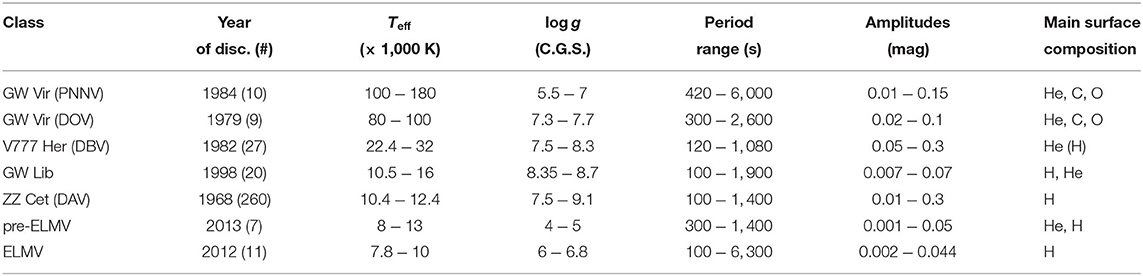
Table 1. Basic characteristics of the different types of pulsating white dwarfs and pre-white dwarfs, sorted by decreasing effective temperature.
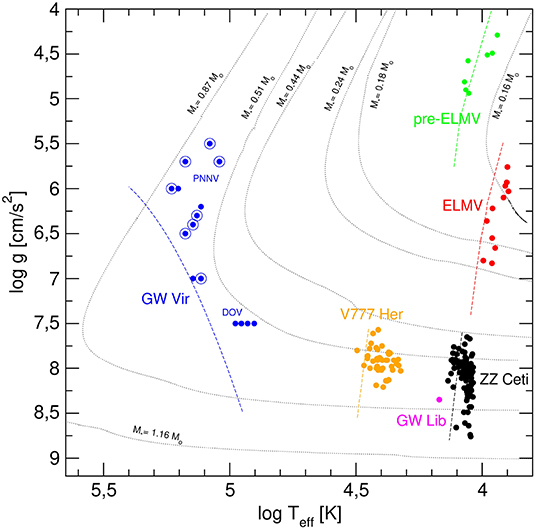
Figure 1. The families of confirmed pulsating white dwarf and pre-white dwarf stars (circles of different colors) in the log Teff − log g plane. This figure is an update of Figure 1 of Córsico et al. (2019). GW Vir stars indicated with blue circles surrounded by blue circumferences are PNNVs. Only the location of the prototypical object of GW Lib class, the star GW Librae, has been indicated (magenta dot). Two post-VLTP (Very Late Thermal Pulse) evolutionary tracks for H-deficient white dwarfs (0.51 and 0.87M⊙; Miller Bertolami and Althaus, 2006), four evolutionary tracks of low-mass He-core H-rich white dwarfs (0.16, 0.18, 0.24, and 0.44M⊙; Althaus et al., 2013), and one evolutionary track for ultra-massive H-rich white dwarfs (1.16M⊙; Camisassa et al., 2019) are included for reference. Dashed lines correspond to the location of the theoretical hot boundary of the different instabilities strips.
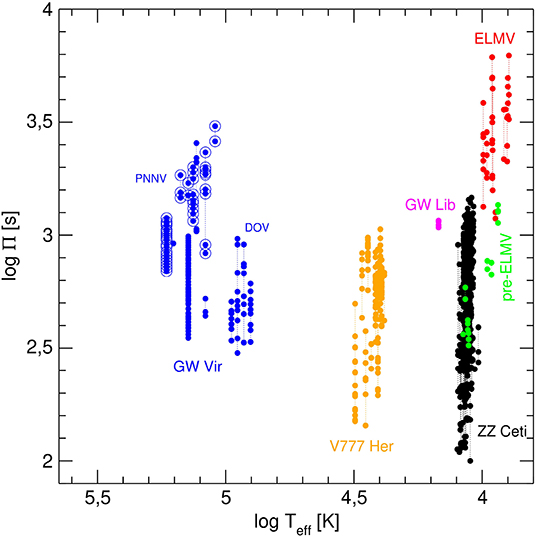
Figure 2. The logarithm of the observed periods in terms of the logarithm of the effective temperature corresponding to the different families of confirmed pulsating white dwarf and pre-white dwarf stars (circles of different colors; see Figure 1). This figure is an update of Figure 2 of Saio (2013).
Pulsations in white dwarfs are self-excited, in contrast to the stochastic pulsations, which are forced oscillations driven by turbulent convection in the Sun, the solar-like, and red giant pulsating stars. The cause of the pulsations in white dwarfs appears to be a mechanism that begins to act when the star cools down to an effective temperature at which the dominant nuclear species becomes partially ionized near the stellar surface (that is, when there is a coexistence of neutral and ionized atoms of the same chemical element; “partial ionization zone”). At the partial ionization zones, the opacity increases at the compression phase of the oscillations, and this excites global pulsations with periods that are of the same order of magnitude as the thermal timescale at the driving region. The κ − γ mechanism has been invoked to explain at least the onset of pulsations in all the categories of pulsating white dwarfs (see, for instance, Winget et al., 1982; Starrfield et al., 1984, for the case of the DAV and GW Vir stars, respectively). For DAVs and DBVs, the validity of the κ − γ mechanism has been questioned. Instead, it has been proposed that the so-called “convective driving” mechanism (Brickhill, 1991; Goldreich and Wu, 1999), that becomes efficient when the base of the outer convective zone sinks, is the responsible mode of driving. For GW Vir stars, which do not have surface convection zones as a result of their very-high effective temperatures, the κ − γ mechanism seems to be enough to destabilize high-order g-mode pulsations3. The proposed mechanisms are able to predict with decent precision the Teff of the blue (hot) edge of the instability strips. However, in general, all theories fail in terms of the predicted effective temperature of the red (cool) boundary, where white dwarfs quench their pulsations. This is discouraging, since even detailed calculations that take into account the interaction between convection and pulsations (Van Grootel et al., 2012) fail to reproduce the location of the red edges in the cases of DAVs and DBVs. Recently, Luan and Goldreich (2018) proposed a theoretical framework that accounts for the existence of the red edge of the DAV instability strip.
Therefore, the physical processes that excite and quench pulsations in white dwarfs are not fully understood. This happens, in general, for all the classes of pulsating stars, aside from white dwarfs. However, this does not prevent us from extracting information from the pulsation periods through adiabatic asteroseismological analyses alone. In the case of white dwarfs, these analyses are based on the forward approximation, in which the measured periods are compared with the periods calculated on a huge set of white-dwarf models to obtain a representative asteroseismological solution of the star under study. The theoretical models can be the result of detailed computations that take into account the complete evolutionary history of the white-dwarf progenitor, the approach adopted by the La Plata Group4 (see e.g., Córsico et al., 2008, 2012a), or instead, they can consist of static white-dwarf models with parameterized chemical composition profiles (see, for instance Giammichele et al., 2018). A variant of this last method is the use of evolutionary models with parameterized chemical profiles (see Bischoff-Kim et al., 2019). These approaches are complementary, among them (Córsico et al., 2019). In some cases, a large set of consecutive periods can be detected, and it is possible to make asteroseismological inferences of the stellar mass from the mean period of spacing. This is the case of several DBV and GW Vir stars.
The primary goal of the Kepler spacecraft was to detect transiting planets, discovering by the end of the mission a total of more than 4, 000 exoplanets (Thompson et al., 2018). As a byproduct of the planetary hunt, high-quality photometric data of variable stars was collected, allowing a rapid blooming of asteroseismology of many classes of pulsating stars, in particular solar-like and red giant pulsators. The initial survey of pulsating stars undertaken by the Kepler Asteroseismic Science Consortium (KASC) contained a total of 113 compact pulsator candidates (including subdwarfs and white dwarfs) which were checked for variability using Kepler short-cadence exposures. Unfortunately, none of the 17 white dwarfs contained in the sample turned out to be variable. In order not to miss the exceptional capacity of the Kepler mission, other candidate objects (not included in the initial survey; Østensen et al., 2011b) began to be monitored with Kepler. Fortunately, this search resulted in the first observations of pulsating white dwarfs by this space mission (Hermes et al., 2011; Østensen et al., 2011a; Greiss et al., 2014, 2015, 2016). Once it finished the nominal 4-years mission, the Kepler spacecraft lost two of its four reaction wheels (2013 May). The mission was then redirected to monitoring new fields along the ecliptic plane during uninterrupted time-intervals of ~ 90 days (Howell et al., 2014). This extended Kepler mission was renamed as K2 and operated from 2014 until the spacecraft ran out of fuel in 2018. The K2 mission provided an exceptional chance to extend space-based monitoring for a lot of new white dwarfs. This extended mission was cleverly exploited by astronomers, and, at the end, many pulsating white dwarfs were discovered and studied.
In the following sections, we summarize the main findings achieved in white-dwarf asteroseismology thanks to the observations of Kepler and K2. In particular, we focus on several detailed asteroseismological studies performed on pulsating white dwarfs observed by this space mission, and also on selected outstanding discoveries that have been the result of uninterrupted observations from space. As a result of the Kepler and K2 observations, 2 DBV and 29 DAV stars have been intensively studied, and the results of those analyses have been published. We have to add to this list three more DAV stars analyzed and published in a PhD Thesis (Bell, 2017). One of the DBV stars, KIC 8626021, has been the focus of intense modeling by several independent groups of asteroseismologists, thanks to which, its internal structure is known with unprecedented precision. In Table 2 we show the main characteristics of all the published pulsating white dwarfs observed with the Kepler spacecraft (in both the Kepler and K2 missions). The first column corresponds to the name of the star, the second column is the class of pulsating white dwarf, the third and fourth columns correspond to the effective temperature and surface gravity values, the fifth column is the stellar mass, the sixth column corresponds to the rotation period determined using the observed splittings of frequencies, the seventh column gives the phase of the space mission (Kepler or K2), and the last column shows the reference to the paper in which the pulsational analysis has been presented.
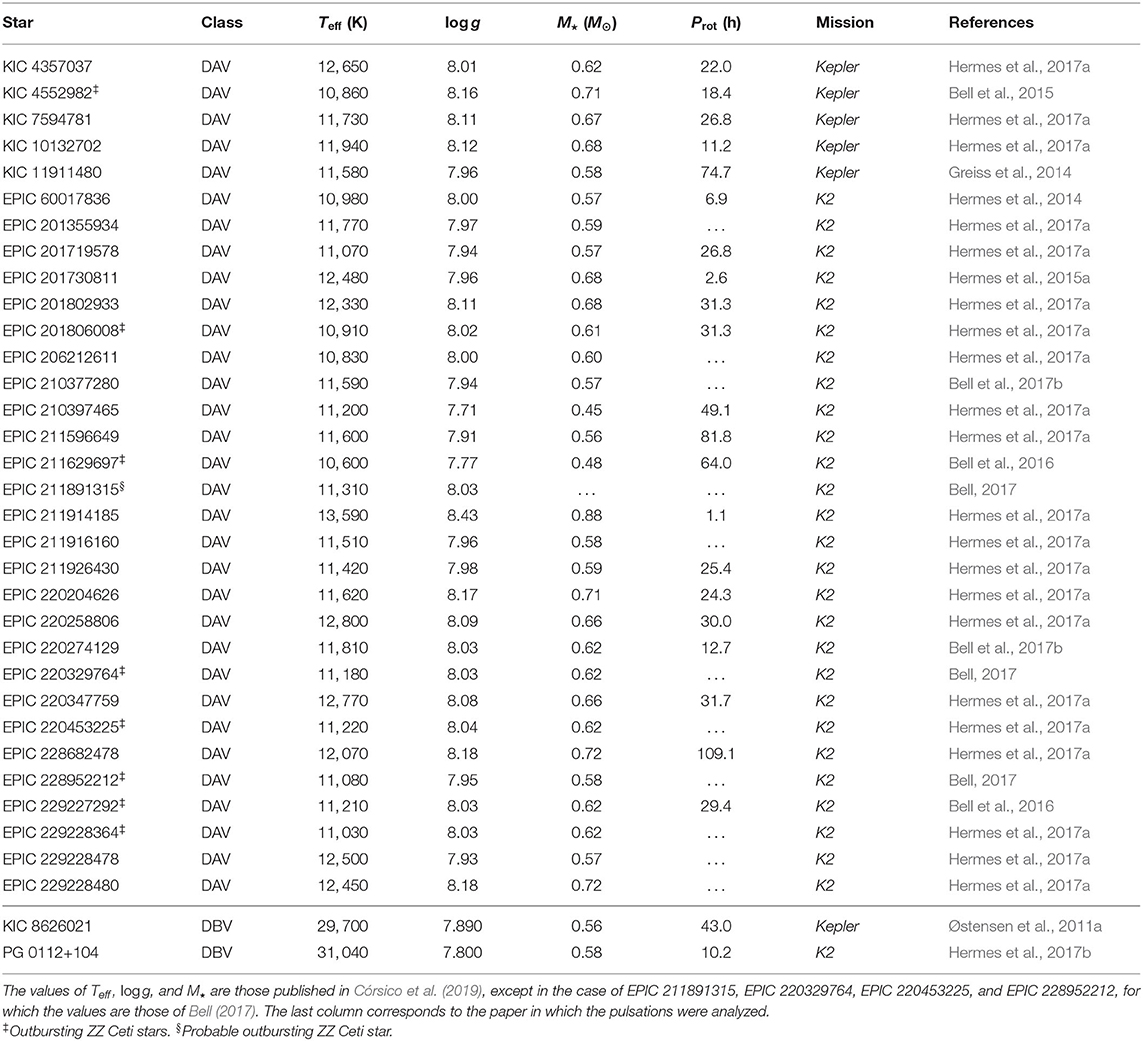
Table 2. All the published pulsating white-dwarf stars observed with the Kepler spacecraft (Kepler and K2 missions).
The findings reported from here to the end of the article are associated with results already published (up to early 2020). However, we emphasize that there is still a large amount of reduced data from the Kepler and K2 missions that have not yet been analyzed, and which could translate into future new discoveries about pulsating white-dwarf and pre-white-dwarf stars.
The DB white dwarf star GALEX J192904.6+444708 (Teff = 24, 900 ± 750 K and log g = 7.91 ± 0.07), identified with the name KIC 8626021 in the Kepler input catalog (also known as WD J1929+4447), was photometrically observed by Østensen et al. (2011a) to check for variability from the Earth. This star was part of a number of targets that had not been included in the original sample of 17 white dwarfs to be observed by Kepler. A 2-hr photometry run on this star clearly revealed the presence of variability with a period of 232 s and an additional period around 270 s. With ground-based photometry, the dataset was too short to perform any meaningful analysis on, but it clearly demonstrated the pulsational nature of KIC 8626021. After that, Østensen et al. (2011a) analyzed 1 month of short-cadence observations of this pulsating star by Kepler. The Fourier transform of the lightcurve is shown in the upper panel of Figure 3. The detected frequencies are depicted in the sub-panels, three of which show clear signals of triplet structures due to rotation. The periods detected appear to be associated to a sequence of ℓ = 1 g modes with low radial order values. The period spacing is close to 36 s, typical of DBV stars. On the basis of the frequency splitting (δν ~ 3.3 μHz) it is possible to infer an estimate of the rotational period of Prot ~ 1.7 days. By using the grids of model atmospheres of Koester (2010), Østensen et al. (2011a) determined Teff = 24, 900 ± 750 K and log g = 7.91 ± 0.07, placing the star in the middle of the DBV instability strip.
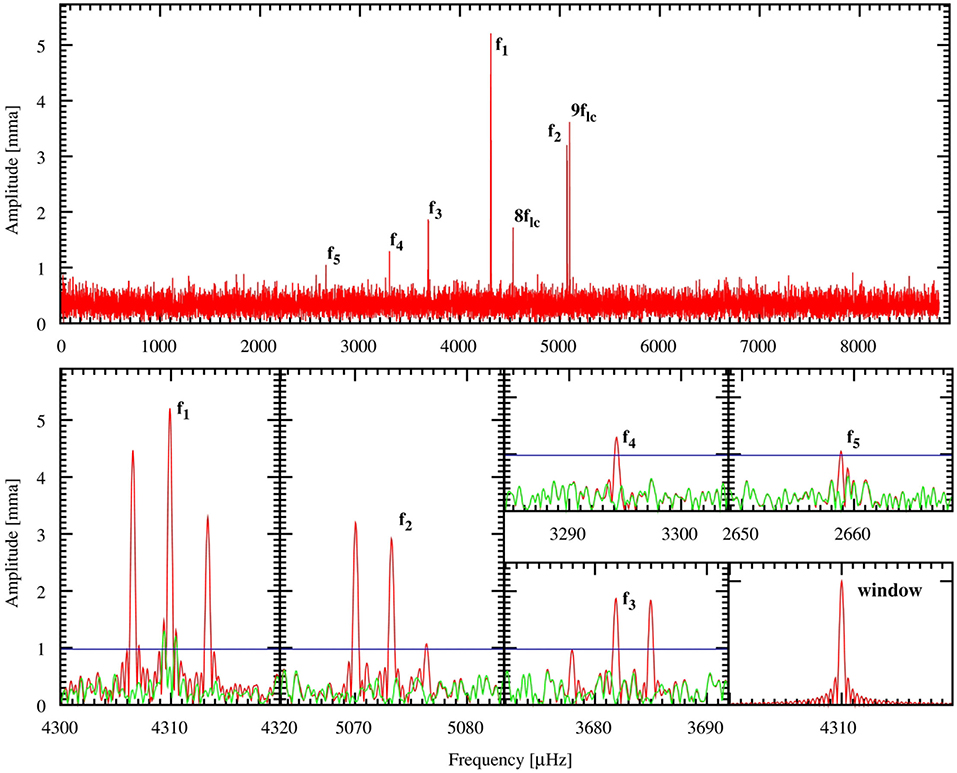
Figure 3. Fourier Transform of the Kepler lightcurve of the DBV star KIC 8626021 (upper panel) derived from Østensen et al. (2011a). The peaks labeled as 8flc and 9flc are two long-cadence artifacts. The real frequencies are labeled as f1 to f5. Lower panels: Zoomed-in views of the five frequencies, including the spectral window of the Kepler data set (final panel). Reproduced with permission from the AAS.
Shortly after the discovery of pulsations in KIC 8626021, the first detailed asteroseismological analysis of the star was performed by Bischoff-Kim and Østensen (2011). They presented an analysis based on the five-mode pulsation spectrum detected by Østensen et al. (2011a) with Kepler data. The observed pulsational characteristics of the star and the asteroseismic analysis strongly suggested that KIC 8626021 was actually hotter than indicated by model-atmosphere fits to the low signal-to-noise electromagnetic spectrum of the object. Indeed, Bischoff-Kim and Østensen (2011) employed a large set of evolutionary models of DB white dwarfs with parameterized chemical profiles, and took three different avenues to determine the effective temperature of KIC 8626021: (i) by means of an inspection of the observed pulsation spectrum, noting that only short-period g modes were present; (ii) employing the average separation between consecutive periods; and (iii) by carrying out asteroseismological period-to-period fits of the pulsation spectrum. All three approaches pointed to an effective temperature of Teff ~ 29, 200 K, in disagreement with the spectroscopic value derived by Østensen et al. (2011a) (Teff = 24, 900 K). If true, since hot DBVs are thought to lose a large portion of their internal energy through the emission of plasmon neutrinos (Winget et al., 2004), this star could be an extremely important target to place limits on the plasmon-neutrino emission rate. However, the measurement of a rate of period change requires extremely stable (over many years) oscillation modes, a condition that is not perfectly met by KIC 8626021 (see at the end of this section).
As a sanity check for this important result, an independent asteroseismological analysis was crucial at that time. This did not take long. Córsico et al. (2012a) carried out a second asteroseismological analysis, which was based on a set of fully evolutionary/pulsational DB white-dwarf models constructed with the LPCODE evolutionary code (Althaus et al., 2005) and the LP-PUL pulsation code (Córsico and Althaus, 2006). By considering the mean period spacing of KIC 8626021, Córsico et al. (2012a) found that the star should be substantially more massive than suggested by spectroscopy. From period-to-period fits these authors found an asteroseismological model characterized by an effective temperature much higher than the spectroscopic estimate, in agreement with the results of Bischoff-Kim and Østensen (2011). So, this analysis was the second piece of evidence that KIC 8626021 should be located near the blue edge of the DBV instability strip. A very interesting and exciting point is that the DB white-dwarf models used by both groups were completely different, particularly regarding the composition profiles (see Figure 4), but nonetheless, similar conclusions were reached regarding the effective temperature of the star.
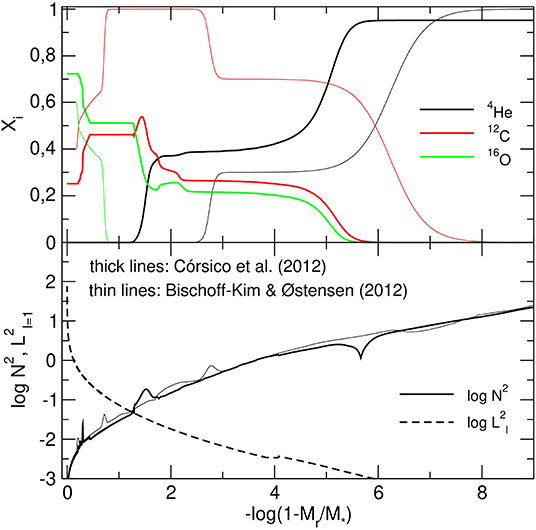
Figure 4. Internal chemical profiles (upper panel), and the logarithm of the squared Brunt-Väisälä and Lamb frequencies for ℓ = 1 (lower panel) corresponding to a template DB white-dwarf model of Córsico et al. (2012a) with a stellar mass of M⋆ = 0.565M⊙, an effective temperature Teff ~ 28, 400 K, and a He envelope mass of (thick lines). For comparison, we show, using thin lines, the chemical profiles and the Brunt-Väisälä frequency of the best-fit model for KIC 8626021 found by Bischoff-Kim and Østensen (2011).
A subsequent asteroseismological analysis of KIC 8626021 was carried out by Bischoff-Kim et al. (2014) on the basis of an augmented set of observed pulsation periods and DB white-dwarf evolutionary models with parameterized chemical profiles, like in Bischoff-Kim and Østensen (2011). The analysis of Bischoff-Kim et al. (2014) was better constrained by the employment of a set of seven independent periods for this star—instead of the five original periods—resulting from 2-years long observations of Kepler. By exploiting the presence of the various triplets and doublets, the authors were able to constrain the value of ℓ and m, something that simplified the period-to-period fit and reduced the assumptions at the outset. The resulting asteroseismological model for KIC 8626021 is characterized by a thin pure-He envelope [log(1 − MHe/M⋆ = −7.90)] and a high effective temperature (Teff = 29, 650 K). This last result confirmed that the star is near the blue edge of the DBV instability strip, in line with the previous analyses. Furthermore, a thin pure-helium layer constituted evidence that the hotter the DB model, the thinner the pure-He layer, supporting the theory that as a DB cools and He diffuses outward, the pure-He layer becomes thicker (see Bischoff-Kim et al., 2014, and references therein).
The most detailed asteroseismological analysis on KIC 8626021 was presented by Giammichele et al. (2018). These authors considered a set of eight periods from the analysis of Zong et al. (2016b). The additional period comes from the alternative interpretation that the structure in the 3.677 − 3.686 μHz range of the spectrum, identified previously as a triplet of frequencies, is actually a doublet, and then the third component is actually an independent mode. Giammichele et al. (2018) presented a new method for parameterizing the chemical profiles in the core of static white-dwarf models, based on Akima splines. They derived an asteroseismological model characterized by a 16O content and an extent of its core that clearly goes beyond the limits predicted by standard DB white dwarf models resulting from fully evolutionary computations. The asteroseismological model is characterized by Teff = 29, 968 ± 200 K and log g = 7.917 ± 0.009, which closely match the independent measurements obtained from spectroscopy by the same authors (Teff = 29, 360 ± 780 K and log g = 7.89 ± 0.05) using the DB white-dwarf model atmospheres of Bergeron et al. (2011). One point to note is that these results confirm the predictions of previous studies that this star is a hot DBV and is close to the blue edge of the V777 Her instability strip. On the other hand, with the new spectroscopic determination of Teff, the discrepancy between asteroseismology and spectroscopy is eliminated. But the most relevant conclusion of this work is that the star seems to have a 16O core (and thus a 16O content) much larger than what standard evolutionary calculations predict. The total 16O content of the white-dwarf core reaches 78.0 ± 4.2%, large in excess when compared with the expected value of around 64% for a standard evolutionary DB white-dwarf model of the same stellar mass. This result constitutes a challenge for the theory of white-dwarf formation and has aroused the interest of several research groups to try to explain how an object of these characteristics could be formed. For example, De Gerónimo et al. (2019) find that, within our current understanding of white-dwarf formation and evolution, it is difficult (if not impossible) to replicate the most relevant features of the chemical structure of KIC 08626021 derived with asteroseismology. Timmes et al. (2018) have drawn attention to the impact that neutrino emission—a physical ingredient ignored in the DB white-dwarf modeling on which the Giammichele et al. (2018) analysis is based—should have on the pulsation periods of KIC 08626021. In order to assess the effect of neutrino emission on the asteroseismological solution of Giammichele et al. (2018), Charpinet et al. (2019) have redone the analysis on this star by incorporating the effects of neutrino cooling, and basically find the same asteroseismological model for KIC 08626021 than in Giammichele et al. (2018). A summary of all the asteroseismological analyses carried out until now for KIC 08626021 are given in Table 3.
We close this section by noting an interesting phenomenon discovered thanks to the continuous observations of KIC 08626021 with Kepler. Zong et al. (2016b) have detected amplitude and frequency modulations of the components of the triplets of frequencies due to a rotation present in the pulsation spectrum of KIC 08626021. Similar secular changes of oscillation frequencies and amplitudes have been measured with the Kepler mission in the subdwarf B star KIC 10139564 by Zong et al. (2016a). Since these frequency and amplitude changes occur with timescales that are several orders of magnitude shorter than the cooling timescale of a DB white dwarf, these modulations of frequencies and amplitudes have nothing to do with any evolutionary effect, such as, e.g., neutrino cooling. Also, it is not expected that these modulations are provoked by orbiting companions around the star, since different timescales for the different triplets are involved. A clue to clarify this behavior could be a the possible interaction between the components of the rotationally split triplets, that is, the presence of non-linear resonant mode coupling (see, for details, Buchler et al., 1997). If true, this star could constitute an excellent opportunity to study non-linear effects in pulsating white dwarfs. Note that, unfortunately, the presence of frequency modulations can make the measurement of the evolutionary (cooling) rate of period change of KIC 08626021 unrealizable, thus hampering any possibility of placing constraints on the plasmon-neutrino emission rate.
Hermes et al. (2017b) presented a pulsational analysis of the already known DBV star PG 0112+104. With Teff ≳ 30, 000 K, this star is the hottest V777 Her star known, that defines the blue edge of the DBV instability strip. The star was analyzed on the basis of 78.7 days of nearly uninterrupted photometry from the Kepler space telescope—specifically the campaign eight of the K2 extended mission. Hermes et al. (2017b) discovered nine additional periods apart from the two periods that were already known from ground-based observations. The pulsation spectrum of this star includes clear patterns of rotational splittings from consecutive sequences of ℓ = 1 and ℓ = 2 modes. In addition, a surface rotational period of 10.17 h has been measured using an apparent spot modulation. To summarize, this hot star is a promising candidate to derive the dependence of rotational angular velocity with depth, that is, the differential rotation of the star, through asteroseismology. The estimation of the surface rotation independently from the spot would constitute a strong test for the asteroseismological analysis. On the other hand, as PG 0112+104 is such a hot DBV star, it constitutes an excellent laboratory for studying plasmon neutrino production if the rate of period change for any mode is measured. Since the pulsation frequencies in PG 0112+104 are extremely stable in phase, the secular change of the periods could be detected and measured with additional—ground- or space-based—observations.
Hermes et al. (2011) reported the discovery of the first identified DAV, WD J1916+3938 (Kepler ID 4552982), in the original field of the Kepler mission. This ZZ Ceti star was first identified through ground-based, time-series photometry. A follow-up spectroscopic analysis indicated that it is a DA white dwarf with Teff = 11, 129 ± 115 K and log g = 8.34 ± 0.06, situating it near the hot boundary of the ZZ Ceti instability domain. The object showed up to 0.5 % amplitude variability at several periods between 800 and 1,450 s (Bell et al., 2015). This star was submitted for Kepler short-cadence observations. These observations led to the unexpected discovery of a new phenomenon: outburst-like events in DAV stars with effective temperatures near the cool edge of the instability strip (Bell et al., 2015, see section 3.5 for details).
The second DAV in the Kepler field, KIC 11911480, was discovered by Greiss et al. (2014) using the Kepler-INT Survey (KIS; Greiss et al., 2012) to select white-dwarf candidates with color-colors diagrams. The variable nature of KIC 11911480 was confirmed using ground-based time series photometry. This star is close to the blue edge of the ZZ Ceti instability strip (Teff = 12, 160 ± 250 K and log g = 7.94 ± 0.10). The star was scrutinized for 6 months with the short-cadence mode of the Kepler telescope, and a total of six independent pulsation periods in the range 172.9 − 324.5 s—typical of the hot ZZ Ceti stars—were detected. A preliminary analysis indicated that the star is rotating with a period of ~ 3.5 days. Greiss et al. (2015) and Greiss et al. (2016) reported the pulsation properties of three additional DAV stars observed with Kepler: KIC 10132702 (Teff = 11048 ± 217 K, log g = 8.07 ± 0.08), KIC 04357037 (Teff = 11898 ± 200 K, log g = 8.03 ± 0.08), and KIC 07594781 (Teff = 12217 ± 1700 K, log g = 7.54 ± 0.22). Using the frequency spacing in the triplets and doublets, these authors estimated the rotation periods of these stars, obtaining values in the range of (0.9 − 3.2) days.
The first DAV star observed with the K2 mission was GD 1212 (Hermes et al., 2014). This star, which was already known to be pulsating (Gianninas et al., 2006), is a cool DAV with Teff = 10, 970 ± 170 K and log g = 8.03 ± 0.05, corresponding to a mass of 0.62 ± 0.03M⊙. K2 short-cadence observations revealed at least 19 independent pulsation modes, ranging from 828.2 to 1220.8 s, and at least 17 non-linear combination frequencies. This star also exhibits amplitude and frequency variations on timescales less than a week, reminiscent to the behavior detected by Zong et al. (2016b) in the DBV star KIC 08626021 (see at the end of section 3.1). This phenomenon makes a precise determination of the pulsation periods of GD 1,212 more complicated. Since this star is a cool ZZ Ceti, it would be expected to be characterized by high amplitudes. However, the independent modes detected, as well as the frequency combinations, show low amplitudes.
Another DAV star analyzed with the K2 mission is SDSS J113655.17+040952.6 (hereafter SDSS J1136+0409), the first known pulsating DA white-dwarf in a post-common envelope binary system with a main-sequence (dM) companion star (Pyrzas et al., 2015). The ZZ Ceti component has Teff = 12, 330 ± 260 K and M⋆ = 0.601 ± 0.036M⊙. Nearly 78 days of K2 observations allowed Hermes et al. (2015a) to detect seven independent pulsation modes, three of which are rotationally split multiplets compatible with a rotation period of 2.49 ± 0.53 h.
Usually, observations of pulsating white dwarfs with the Kepler space telescope have to be performed using the short-cadence mode of observations (1-min exposures) to sufficiently over-sample typical white-dwarf pulsation periods (3–20 min) for straightforward frequency measurement. However, Bell et al. (2017b) have demonstrated that it is possible to combine long-cadence K2 data (30 min exposures) with high-speed follow-up ground-based observations, to derive accurate oscillation frequencies to a precision of ~ 0.01 μHz. Using this approach, Bell et al. (2017b) have discovered two new ZZ Ceti variables from K2 long-cadence data: EPIC 210377280 and EPIC 220274129. For EPIC 220274129, Bell et al. (2017b) inferred a stellar rotation period of 12.7 ± 1.3 h.
The most complete and detailed study of ZZ Ceti stars observed with the Kepler space telescope has been presented by Hermes et al. (2017a). This monumental work, based on the observations of 27 ZZ Ceti stars collected with the nominal Kepler mission and mostly with the extended K2 mission, presents, in detail, the occurrence of outbursts in ZZ Ceti stars near the red edge of the DAV instability strip (see section 3.5), the discovery of a dichotomy of the widths of peaks in the Fourier spectrum (section 3.6), and a possible relationship between the rotation periods derived from frequency splittings for 20 of the 27 DAVs and their stellar mass (see section 3.7). In addition, Hermes et al. (2017a) have been able to characterize the DAV instability strip as observed by Kepler and K2. Indeed, they show how the different trends regarding the length of the excited periods and the amplitude of the modes evolve as the effective temperature decreases along the instability strip. In particular, Hermes et al. (2017a) find that the excited periods are short and with low amplitude near the blue edge of the instability domain, but then the excited periods grow (modes of larger radial orders are excited) and the amplitude also increases with decreasing Teff. Toward effective temperatures near the cool boundary of the instability strip, some ZZ Ceti show outbursts. Finally, at the red edge, the excited modes of DAVs are the longest-period pulsations with relatively small amplitude. Figure 5, which displays the Fourier spectrum of ZZ Ceti stars at different effective temperatures, dramatically illustrates the described trend.
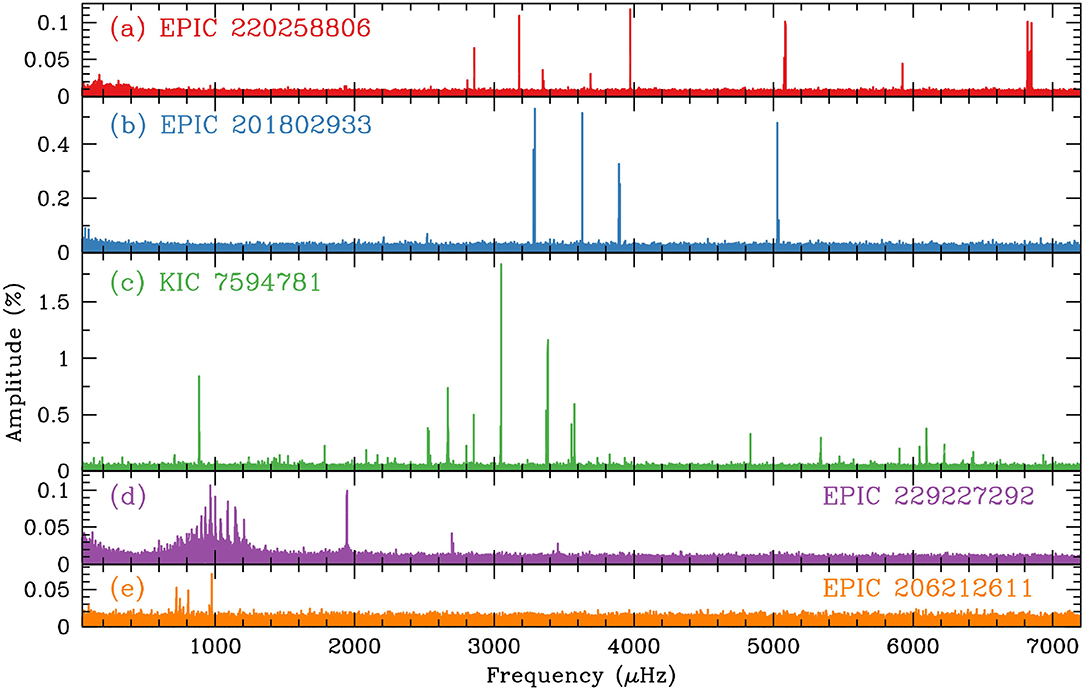
Figure 5. The Fourier Transform corresponding to five representative ZZ Ceti stars observed with K2, with decreasing Teff from the top to bottom panel (Hermes et al., 2017a). The figures highlight the different phases of DAV stars along the ZZ Ceti instability strip. Reproduced with permission from the AAS.
The Kepler spacecraft observations of ZZ Ceti stars led to the discovery of a energetic phenomenon never observed before from the ground in this type of quiet pulsating stars: outburst-like events (Bell et al., 2017a). So far, this constitutes one of the most transcendent discoveries (perhaps the most transcendent) in relation to pulsations in white dwarfs observed with Kepler. An important aspect of these events is that they repeat chaotically, with no fixed period of recurrence. The first outbursting DAV, KIC45529825, which is located near the red edge of the ZZ Ceti instability strip (Teff = 11, 129 ± 115 K, log = 8.34 ± 0.06), was observed during ~ 20 months with the nominal Kepler mission, yielding the longest pseudo-continuous light curve of a ZZ Ceti ever obtained (Bell et al., 2015). These observations allowed the detection of 20 pulsation modes with periodicities commonly observed in ZZ Ceti stars, along with 178 increments of brightness typical of outburst phenomena, with peaks of up to 17% above the quiescent level. The outbursts involve very energetic events (E ~ 1033 erg), with a mean recurrence period of about 2.7 days and 4–25 h of duration (Bell et al., 2015). The second outbursting star, the already known cool DAV PG 1149+057 (Teff = 11, 060 ± 170 K, log = 8.06 ± 0.05), was analyzed by Hermes et al. (2015b) with nearly continuous K2 observations for more than 78.8 days. This star shows outbursts with a typical recurrence time of ~ 8 days and 15 h of duration, and very large flux enhancements of up to 45% above the quiescent level. For this star, the outbursts have a measurable impact on the spectrum of g modes (in amplitude and frequency), demonstrating that outbursts are an intrinsic phenomenon of the (otherwise isolated) star. In Figure 6 we show the complete K2 light curve of PG 1149+057 (upper panel) and the Fourier Transforms for the case during and out of outburst (lower panels). At the time of writing this article, a total of eight outbursting (isolated) DAV stars have been discovered (Bell et al., 2016, 2017a), all of them populating the red edge of the ZZ Ceti instability strip (see Figure 12 of Córsico et al., 2019). This strongly suggests that outbursts could be related to the origin of the cool edge of the DAV instability domain, that is, the cessation of the g-mode pulsations (Bell et al., 2017a). A possible explanation for both the occurrence of outbursts and the origin of the cool edge of the ZZ Ceti instability strip, has been proposed by Luan and Goldreich (2018). It is connected with parametric instability through mode coupling of white-dwarf pulsations (Dziembowski, 1982; Wu and Goldreich, 2001; Luan and Goldreich, 2018).
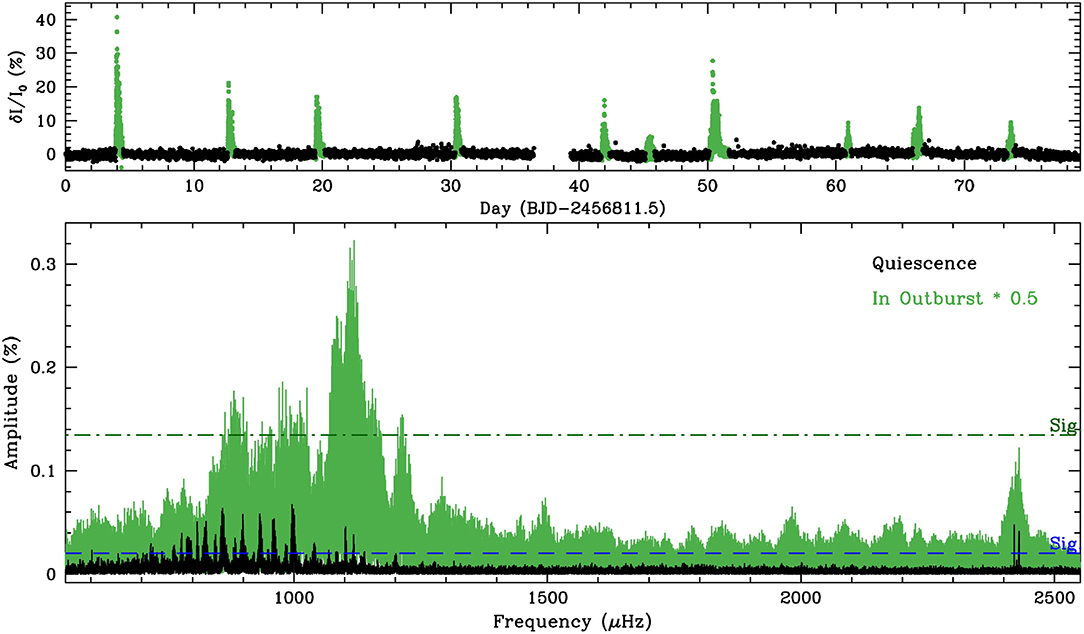
Figure 6. Upper panel: the complete K2 light curve of PG 1149+057 derived by Hermes et al. (2015b). The 10 outburst events are emphasized with green dots and the data in quiescence are marked with black dots. Bottom panel: the Fourier Transforms during and out of outburst (green and black). In both cases, pulsations have amplitudes larger than the corresponding significance thresholds, shown as dark green dashed–dotted and blue dashed lines. Note that normal-mode pulsations remain during the outbursts, but they have larger amplitudes and higher frequencies than in quiescence. Reproduced with permission from the AAS.
Another major observational result from the Kepler space telescope is the discovery by Hermes et al. (2017a) of a clear dichotomy of oscillation mode-line widths in the power spectrum of 27 DAVs observed from space. Indeed, g modes characterized by periods longer than roughly 800 s are generally incoherent (large line widths) over the length of observations, while g modes with periods ≲ 800 s are observed to be much more stable in phase and amplitude (smaller line width)6. We depict in Figure 7 (extracted from Hermes et al., 2017a) the half-width at half-maximum (HWHM) of all significant peaks (excluding any non-linear combination frequencies) in the power spectra of 27 DAVs observed through Kepler and K2. The dichotomy of mode-line widths could be intimately linked to the oscillation of the outer convection zone of a DA white dwarf during pulsations. Specifically, the oscillation out of and in the base of the convection zone would affect the radial eigenfunction of certain g modes—those that have the outer turning point of oscillation located precisely at the base of the convection zone (Montgomery et al., 2020). This mechanism may be relevant for the limitation of pulsation amplitudes in pulsating white dwarfs for modes with periods above a threshold period.
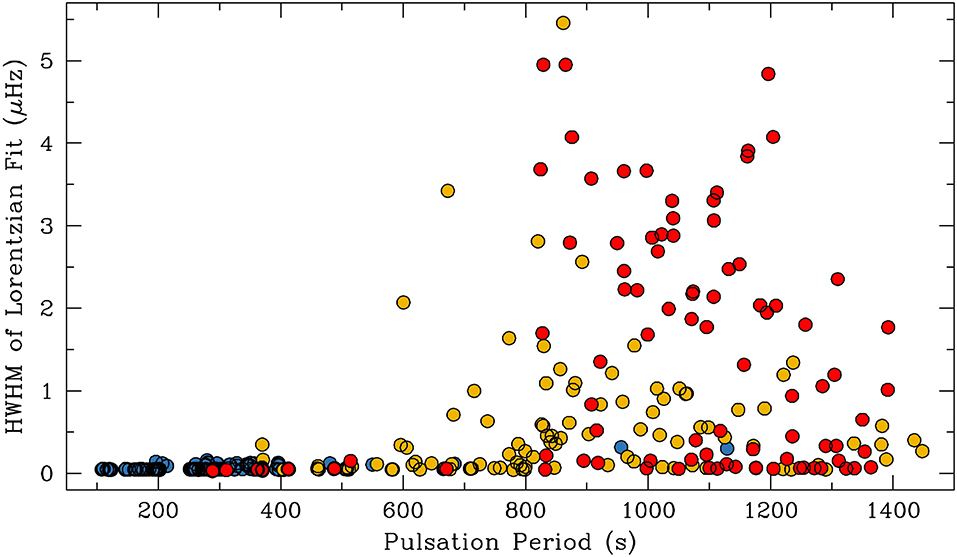
Figure 7. Half-width at half-maximum (HWHM) of Lorentzian functions fit to all significant peaks (corresponding to genuine eigenmodes) in the power spectra of 27 DAVs observed through K2 (Hermes et al., 2017a). Blue circles are for objects with weighted mean period (WMP) <600 s, gold with WMP >600 s, and red are those with outbursts. A clear increase in HWHM at ~800 s is present. Reproduced with permission from the AAS.
Hermes et al. (2017a) have also derived the rotation rates of 20 isolated DAVs observed with Kepler and K2 using rotational splittings, doubling the number of pulsating white dwarfs with measured rotation rates via asteroseismology7 (see Table 2 of this article and Table 10 of Córsico et al., 2019). The results indicate that the average rotation period is ~ 30 − 40 h, although ZZ Ceti stars that rotate faster (with periods of ~ 1 − 2 h) have also been found. There is some evidence of the existence of a correlation between high mass and fast rotation, an idea reinforced by the fastest rotation ever measured in an isolated white dwarf8, of 1.13 h, for the massive ZZ Ceti star SDSSJ0837+1856 (M⋆ = 0.87M⊙) by Hermes et al. (2017c), although more high-mass white dwarfs are necessary to confirm this trend. Hermes et al. (2017a) find that most isolated descendants of 1.7−3.0M⊙ ZAMS progenitors rotate at ~ 1.5 days, instead of minutes, which would be expected if the angular momentum of a 3.0M⊙ MS star with an initial rotation period of 10 h, were fully conserved (Kawaler, 2004). This fact strongly indicates that most internal angular momentum must be lost on the first-ascent giant branch.
In section 3.1 we described, in detail, the various asteroseismological analyses conducted to elucidate the internal structure of the Kepler DBV star KIC 8626021. Here, we briefly describe the asteroseismological analysis on ZZ Cetis observed with Kepler carried out by Romero et al. (2017). This analysis was based on evolutionary and pulsational white-dwarf models computed with the LPCODE and LP-PUL codes, adopting the La Plata Group's approach of white-dwarf asteroseismology (see at the end of section 2). Specifically, the first four published ZZ Ceti stars observed with the Kepler mission, that is, EPIC 60017836 (GD 1212), EPIC 201730811 (SDSS J113655.17+040952.6), KIC 11911480, and KIC 4552982, were studied. Currently, this remains the only detailed asteroseismological study of DAVs observed with the Kepler space telescope. A period-to-period fit analysis of the four target stars was carried out by employing a grid of full evolutionary models representative of C/O-core DA white-dwarf stars constructed with detailed and updated input physics. These models have consistent chemical profiles for both the core and the envelope for various stellar masses, particularly suitable for asteroseismological fits of ZZ Ceti stars. The chemical profiles of the models were computed considering the complete evolution of the progenitor stars from the ZAMS through the thermally pulsing and mass-loss phases on the asymptotic giant branch (AGB).
Apart from the observed periods, the analysis by Romero et al. (2017) incorporated the amplitude of the modes, rotational splitting multiplets, and period spacing data, as well as photometry and spectroscopy information. For each analyzed star, an asteroseismological model that closely reproduces observed properties, such as periods, stellar mass, and effective temperature was presented. In the particular case of KIC 11911480 and EPIC 201730811, the asteroseismological masses are similar to each other, although the H envelope for EPIC 201730811 (that is part of a binary system and likely went through a common envelope phase) is 10 times thinner than that for KIC 11911480. This result confirms what was discussed in Hermes et al. (2015a) on the basis of a preliminary asteroseismological analysis, that the H-layer mass of EPIC 201730811 is roughly . In the case of KIC 4552982, which is a red-edge ZZ Ceti star, the asteroseismological model has a very thin H envelope mass (), which could be related to the outburst nature of this star, as reported by Bell et al. (2015). Whether this is a common characteristic between all the outbursting DAVs or not is a very interesting topic that deserves further exploration. Finally, in the case of EPIC 60017836 (another red-edge DAV), an asteroseismological model was obtained with a stellar mass compatible with the atmospheric parameters from photometry combined with parallax and spectroscopy.
The Kepler space telescope—both the nominal Kepler mission and the extended mission K2—has been very successful in its search for extrasolar planets and has also meant a revolution in the area of asteroseismology for many classes of pulsating stars. In the particular case of pulsating white dwarfs, the numbers speak for themselves. In total, 2, 166 white dwarfs were observed by Kepler/K2. There were 81 DAVs observed by Kepler/K2, with 75 of them obtaining short cadence data. Of them, analyses of 32 DAVs have been published (29 stars analyzed in journals and three objects analyzed in a PhD Thesis; see Table 2). Thanks to Kepler/K2, the number of ZZ Ceti stars that have a rotation period measured with asteroseismology has increased by a factor of 2. Regarding DBVs, seven stars were observed, although the analysis of only two of them have been published to date. Finally, two unique GW Vir stars were observed, including the prototypical star PG 1159−035, but no results have been published yet.
The story of the Kepler mission and the pulsating white dwarf stars does not end here. There is an immense amount of data waiting to be analyzed, and this will likely lead to new discoveries in the near future. In turn, this will drive new asteroseismological analyses, in addition to those already published. Altogether, the Kepler space telescope has had a strong impact (and will continue to have) on the area of white-dwarf asteroseismology. This first step will be multiplied by current and future space missions, such as the Transiting Exoplanet Survey Satellite (TESS; Ricker et al., 2015), which is already in full operation and is providing the first results on pulsating white dwarfs (Bell et al., 2019; Althaus et al., 2020; Bognár et al., 2020), and other space missions that will become operational in the coming years, such as Cheops (Moya et al., 2018) and Plato (Piotto, 2018).
The author confirms being the sole contributor of this work and has approved it for publication.
Part of this work was supported by AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR, by the PIP 112-200801-00940 grant from CONICET, and by the grant G149 from the University of La Plata.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
I thank the referees for their valuable suggestions that improved the content and presentation of the paper. I warmly thank Leandro G. Althaus, Keaton J. Bell, and J. J. Hermes for being so kind to read the manuscript and suggest relevant changes that greatly improved its content. This research has made intensive use of the NASA Astrophysics Data System.
1. ^Strictly speaking, since these stars still have substantial nuclear burning, they should be considered pre-white dwarfs.
2. ^r modes are toroidal modes in presence of rotation (Papaloizou and Pringle, 1978).
3. ^There exist theoretical evidence of another mechanism that could excite global pulsations in white dwarfs and pre-white dwarfs, that is, the ϵ mechanism due to nuclear burning. This could be responsible for short-period g-mode pulsations in GW Vir stars (Córsico et al., 2009), ELMVs (Córsico and Althaus, 2014), ZZ Ceti stars coming from low-metalicity progenitors (Camisassa et al., 2016), and in very hot DA white dwarfs (Maeda and Shibahashi, 2014; Calcaferro et al., 2017). However, the predicted pulsations have not been detected, so far, in any case.
4. ^http://evolgroup.fcaglp.unlp.edu.ar/
5. ^This star was the first ZZ Ceti identified in the original Kepler mission field (Hermes et al., 2011, ; see section 3.3).
6. ^This phenomenon cannot be associated to stochastic mode driving, which for white dwarfs would excite pulsations with very short periods, of the order of ~ 1 s (Saio, 2013).
7. ^Note that rotation rates can sometimes also be measured from long-cadence data, as in Bell et al. (2017b).
8. ^Except for the magnetic DA white dwarf RE J0317-853, with an apparent period of ~725 s (Barstow et al., 1995), and SDSSJ125230.93?023417.72, which is the fastest-rotating apparently isolated white dwarf yet discovered, that rotates with a period of 317.278 ± 0.013 s (Reding et al., 2020).
Aerts, C., Christensen-Dalsgaard, J., and Kurtz, D. W. (2010). Asteroseismology. Dordrecht; Heidelberg; London; New York, NY: Springer.
Althaus, L. G., Córsico, A. H., Isern, J., and García-Berro, E. (2010). Evolutionary and pulsational properties of white dwarf stars. Astron. Astrophys. Rev. 18, 471–566. doi: 10.1007/s00159-010-0033-1
Althaus, L. G., Córsico, A. H., Uzundag, M., Vučković, M., Baran, A. S., Bell, K. J., et al. (2020). About the existence of warm H-rich pulsating white dwarfs. Astron. Astrophys. 633:A20. doi: 10.1051/0004-6361/201936346
Althaus, L. G., Miller Bertolami, M. M., and Córsico, A. H. (2013). New evolutionary sequences for extremely low-mass white dwarfs. Homogeneous mass and age determinations and asteroseismic prospects. Astron. Astrophys. 557:A19. doi: 10.1051/0004-6361/201321868
Althaus, L. G., Miller Bertolami, M. M., Córsico, A. H., García-Berro, E., and Gil-Pons, P. (2005). The formation of DA white dwarfs with thin hydrogen envelopes. Astron. Astrophys. 440, L1–L4. doi: 10.1051/0004-6361:200500159
Barstow, M. A., Jordan, S., O'Donoghue, D., Burleigh, M. R., Napiwotzki, R., and Harrop-Allin, M. K. (1995). RE J0317-853: the hottest known highly magnetic DA white dwarf. Mon. Not. R. Astron. Soc. 277, 971–985. doi: 10.1093/mnras/277.3.971
Bedin, L. R., Salaris, M., Anderson, J., Cassisi, S., Milone, A. P., Piotto, G., et al. (2015). Hubble space telescope observations of the Kepler-field cluster NGC 6819–I. The bottom of the white dwarf cooling sequence. Mon. Not. R. Astron. Soc. 448, 1779–1788. doi: 10.1093/mnras/stv069
Bedin, L. R., Salaris, M., Piotto, G., Anderson, J., King, I. R., and Cassisi, S. (2009). The end of the white dwarf cooling sequence in M4: an efficient approach. Astrophys. J. 697, 965–979. doi: 10.1088/0004-637X/697/2/965
Bell, K. J. (2017). Pulsational oddities at the extremes of the DA white dwarf instability strip (Ph.D. thesis), University of Texas, Austin, TX, United States.
Bell, K. J., Córsico, A. H., Bischoff-Kim, A., Althaus, L. G., Bradley, P. A., Calcaferro, L. M., et al. (2019). TESS first look at evolved compact pulsators. Asteroseismology of the pulsating helium-atmosphere white dwarf TIC 257459955. Astron. Astrophys. 632:A42. doi: 10.1051/0004-6361/201936340
Bell, K. J., Hermes, J. J., Bischoff-Kim, A., Moorhead, S., Montgomery, M. H., Østensen, R., et al. (2015). KIC 4552982: outbursts and asteroseismology from the Longest pseudo-continuous light curve of a ZZ Ceti. Astrophys. J. 809:14. doi: 10.1088/0004-637X/809/1/14
Bell, K. J., Hermes, J. J., Montgomery, M. H., Gentile Fusillo, N. P., Raddi, R., Gänsicke, B. T., et al. (2016). Outbursts in two new cool pulsating DA white dwarfs. Astrophys. J. 829:82. doi: 10.3847/0004-637X/829/2/82
Bell, K. J., Hermes, J. J., Montgomery, M. H., Winget, D. E., Gentile Fusillo, N. P., Raddi, R., et al. (2017a). “The first six outbursting cool DA white dwarf pulsators,” in 20th European White Dwarf Workshop, Volume 509 of Astronomical Society of the Pacific Conference Series, eds P. E. Tremblay, B. Gaensicke, and T. Marsh (San Francisco, CA), 303.
Bell, K. J., Hermes, J. J., Vanderbosch, Z., Montgomery, M. H., Winget, D. E., Dennihy, E., et al. (2017b). Destroying aliases from the ground and space: super-nyquist ZZ Cetis in K2 long cadence data. Astrophys. J. 851:24. doi: 10.3847/1538-4357/aa9702
Bergeron, P., Wesemael, F., Dufour, P., Beauchamp, A., Hunter, C., Saffer, R. A., et al. (2011). A comprehensive spectroscopic analysis of DB white dwarfs. Astrophys. J. 737:28. doi: 10.1088/0004-637X/737/1/28
Bessel, F. W. (1844). On the variations of the proper motions of Procyon and Sirius. Mon. Not. R. Astron. Soc. 6, 136–141. doi: 10.1093/mnras/6.11.136a
Bischoff-Kim, A., and Østensen, R. H. (2011). Asteroseismology of the Kepler field DBV white dwarf. It is a hot one. Astrophys. J. Lett. 742:L16. doi: 10.1088/2041-8205/742/1/L16
Bischoff-Kim, A., Østensen, R. H., Hermes, J. J., and Provencal, J. L. (2014). Seven-period asteroseismic fit of the Kepler DBV. Astrophys. J. 794:39. doi: 10.1088/0004-637X/794/1/39
Bischoff-Kim, A., Provencal, J. L., Bradley, P. A., Montgomery, M. H., Shipman, H. L., Harrold, S. T., et al. (2019). GD358: three decades of observations for the in-depth asteroseismology of a DBV star. Astrophys. J. 871:13. doi: 10.3847/1538-4357/aae2b1
Bognár, Z., Kawaler, S. D., Bell, K. J., Schrand t, C., Baran, A. S., Bradley, P. A., et al. (2020). TESS first look at evolved compact pulsators: known ZZ Ceti stars of the southern ecliptic hemisphere as seen by TESS. arXiv arXiv:2003.11481.
Borucki, W. J., Koch, D., Basri, G., Batalha, N., Brown, T., Caldwell, D., et al. (2010). Kepler planet-detection mission: introduction and first results. Science 327:977. doi: 10.1126/science.1185402
Brassard, P., Fontaine, G., Wesemael, F., Kawaler, S. D., and Tassoul, M. (1991). Adiabatic properties of pulsating DA white dwarfs. I–the treatment of the Brunt-Vaisala frequency and the region of period formation. Astrophys. J. 367, 601–611. doi: 10.1086/169655
Brickhill, A. J. (1991). The pulsations of ZZ Ceti stars. III–the driving mechanism. Mon. Not. R. Astron. Soc. 251, 673–680. doi: 10.1093/mnras/251.4.673
Brown, T. M., and Gilliland, R. L. (1994). Asteroseismology. ARA&A 32, 37–82. doi: 10.1146/annurev.aa.32.090194.000345
Buchler, J. R., Goupil, M. J., and Hansen, C. J. (1997). On the role of resonances in nonradial pulsators. Astron. Astrophys. 321, 159–176.
Calcaferro, L. M., Córsico, A. H., Camisassa, M. E., Althaus, L. G., and Shibahashi, H. (2017). “Pulsational instability of high-luminosity H-rich pre-white dwarf star,” in European Physical Journal Web of Conferences, Volume 152 of European Physical Journal Web of Conferences (Les Ulis), 06012.
Camisassa, M. E., Althaus, L. G., Córsico, A. H., De Gerónimo, F. C., Miller Bertolami, M. M., Novarino, M. L., et al. (2019). The evolution of ultra-massive white dwarfs. Astron. Astrophys. 625:A87. doi: 10.1051/0004-6361/201833822
Camisassa, M. E., Córsico, A. H., Althaus, L. G., and Shibahashi, H. (2016). Pulsations powered by hydrogen shell burning in white dwarfs. Astron. Astrophys. 595:A45. doi: 10.1051/0004-6361/201628857
Campos, F., Bergeron, P., Romero, A. D., Kepler, S. O., Ourique, G., Costa, J. E. S., et al. (2016). A comparative analysis of the observed white dwarf cooling sequence from globular clusters. Mon. Not. R. Astron. Soc. 456, 3729–3742. doi: 10.1093/mnras/stv2911
Campos, F., Kepler, S. O., Bonatto, C., and Ducati, J. R. (2013). Multichromatic colour-magnitude diagrams of the globular cluster NGC 6366. Mon. Not. R. Astron. Soc. 433, 243–250. doi: 10.1093/mnras/stt719
Chandrasekhar, S. (1939). An Introduction to the Study of Stellar Structure. Chicago, IL: University of Chicago Press.
Charpinet, S., Brassard, P., Giammichele, N., and Fontaine, G. (2019). Improved seismic model of the pulsating DB white dwarf KIC 08626021 corrected from the effects of neutrino cooling. Astron. Astrophys. 628:L2. doi: 10.1051/0004-6361/201935823
Córsico, A. H., and Althaus, L. G. (2006). Asteroseismic inferences on GW Virginis variable stars in the frame of new PG 1159 evolutionary models. Astron. Astrophys. 454, 863–881. doi: 10.1051/0004-6361:20054199
Córsico, A. H., and Althaus, L. G. (2014). Short-period G-mode pulsations in low-mass white dwarfs triggered by H-shell burning. Astrophys. J. Lett. 793:L17. doi: 10.1088/2041-8205/793/1/L17
Córsico, A. H., Althaus, L. G., García-Berro, E., and Romero, A. D. (2013). An independent constraint on the secular rate of variation of the gravitational constant from pulsating white dwarfs. J. Cosmol. Astropart. Phys. 2013:032. doi: 10.1088/1475-7516/2013/06/032
Córsico, A. H., Althaus, L. G., Kepler, S. O., Costa, J. E. S., and Miller Bertolami, M. M. (2008). Asteroseismological measurements on PG 1159-035, the prototype of the GW Virginis variable stars. Astron. Astrophys. 478, 869–881. doi: 10.1051/0004-6361:20078646
Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., and Bischoff-Kim, A. (2012a). Asteroseismology of the Kepler V777 Herculis variable white dwarf with fully evolutionary models. Astron. Astrophys. 541:A42. doi: 10.1051/0004-6361/201118736
Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., González Pérez, J. M., and Kepler, S. O. (2009). On the possible existence of short-period G-mode instabilities powered by nuclear-burning shells in post-asymptotic giant branch H-deficient (PG1159-type) stars. Astrophys. J. 701, 1008–1014. doi: 10.1088/0004-637X/701/2/1008
Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., and Kepler, S. O. (2019). Pulsating white dwarfs: new insights. Astron. Astrophys. Rev. 27:7. doi: 10.1007/s00159-019-0118-4
Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., Kepler, S. O., and García-Berro, E. (2014). Constraining the neutrino magnetic dipole moment from white dwarf pulsations. J. Cosmol. Astropart. Phys. 2014:054. doi: 10.1088/1475-7516/2014/08/054
Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., Romero, A. D., García-Berro, E., Isern, J., et al. (2012b). The rate of cooling of the pulsating white dwarf star G117-B15A: a new asteroseismological inference of the axion mass. Mon. Not. R. Astron. Soc. 424, 2792–2799. doi: 10.1111/j.1365-2966.2012.21401.x
Córsico, A. H., Benvenuto, O. G., Althaus, L. G., Isern, J., and García-Berro, E. (2001). The potential of the variable DA white dwarf G117-B15A as a tool for fundamental physics. Nature 6, 197–213. doi: 10.1016/S1384-1076(01)00055-0
De Gerónimo, F. C., Battich, T., Miller Bertolami, M. M., Althaus, L. G., and Córsico, A. H. (2019). On the recent parametric determination of an asteroseismological model for the DBV star KIC 08626021. Astron. Astrophys. 630:A100. doi: 10.1051/0004-6361/201834988
Dziembowski, W. (1982). Nonlinear mode coupling in oscillating stars. I–second order theory of the coherent mode coupling. Acta Astron. 32, 147–171.
Fields, C. E., Farmer, R., Petermann, I., Iliadis, C., and Timmes, F. X. (2016). Properties of carbon-oxygen white dwarfs from Monte Carlo stellar models. Astrophys. J. 823:46. doi: 10.3847/0004-637X/823/1/46
Fontaine, G., and Brassard, P. (2008). The pulsating white dwarf stars. Publ. ASP 120, 1043–1096. doi: 10.1086/592788
Fontaine, G., Brassard, P., and Bergeron, P. (2001). The potential of white dwarf cosmochronology. Publ. ASP 113, 409–435. doi: 10.1086/319535
Gänsicke, B. T., Koester, D., Farihi, J., Girven, J., Parsons, S. G., and Breedt, E. (2012). The chemical diversity of exo-terrestrial planetary debris around white dwarfs. Mon. Not. R. Astron. Soc. 424, 333–347. doi: 10.1111/j.1365-2966.2012.21201.x
Gänsicke, B. T., Koester, D., Girven, J., Marsh, T. R., and Steeghs, D. (2010). Two white dwarfs with oxygen-rich atmospheres. Science 327:188. doi: 10.1126/science.1180228
Gänsicke, B. T., Schreiber, M. R., Toloza, O., Fusillo, N. P. G., Koester, D., and Manser, C. J. (2019). Accretion of a giant planet onto a white dwarf star. Nature 576, 61–64. doi: 10.1038/s41586-019-1789-8
García-Berro, E., and Oswalt, T. D. (2016). The white dwarf luminosity function. New Astron. Rev. 72, 1–22. doi: 10.1016/j.newar.2016.08.001
García-Berro, E., Torres, S., Althaus, L. G., Renedo, I., Lorén-Aguilar, P., Córsico, A. H., et al. (2010). A white dwarf cooling age of 8Gyr for NGC 6791 from physical separation processes. Nature 465, 194–196. doi: 10.1038/nature09045
Gentile Fusillo, N. P., Tremblay, P.-E., Gänsicke, B. T., Manser, C. J., Cunningham, T., Cukanovaite, E., et al. (2019). A Gaia data release 2 catalogue of white dwarfs and a comparison with SDSS. Mon. Not. R. Astron. Soc. 482, 4570–4591. doi: 10.1093/mnras/sty3016
Giammichele, N., Charpinet, S., Fontaine, G., Brassard, P., Green, E. M., Van Grootel, V., et al. (2018). A large oxygen-dominated core from the seismic cartography of a pulsating white dwarf. Nature 554, 73–76. doi: 10.1038/nature25136
Gianninas, A., Bergeron, P., and Fontaine, G. (2006). Mapping the ZZ Ceti instability strip: discovery of six new pulsators. Astron. J. 132, 831–835. doi: 10.1086/506516
Goldreich, P., and Wu, Y. (1999). Gravity modes in ZZ Ceti stars. I. Quasi-adiabatic analysis of overstability. Astrophys. J. 511, 904–915. doi: 10.1086/306705
Greiss, S., Gänsicke, B. T., Hermes, J. J., Giammichele, N., Fontaine, G., Koester, D., et al. (2015). White Dwarfs in the Kepler Field–What's New? Volume 493 of Astronomical Society of the Pacific Conference Series, 169. San Francisco, CA: Astronomical Society of the Pacific.
Greiss, S., Gänsicke, B. T., Hermes, J. J., Steeghs, D., Koester, D., Ramsay, G., et al. (2014). KIC 11911480: the second ZZ Ceti in the Kepler field. Mon. Not. R. Astron. Soc. 438, 3086–3092. doi: 10.1093/mnras/stt2420
Greiss, S., Hermes, J. J., Gänsicke, B. T., Steeghs, D. T. H., Bell, K. J., Raddi, R., et al. (2016). The search for ZZ Ceti stars in the original Kepler mission. Mon. Not. R. Astron. Soc. 457, 2855–2863. doi: 10.1093/mnras/stw053
Greiss, S., Steeghs, D., Gänsicke, B. T., Martín, E. L., Groot, P. J., Irwin, M. J., et al. (2012). Initial data release of the Kepler-INT survey. Astron. J. 144:24. doi: 10.1088/0004-6256/144/1/24
Hermes, J. J., Charpinet, S., Barclay, T., Pakstiene, E., Mullally, F., Kawaler, S. D., et al. (2014). Precision asteroseismology of the pulsating white dwarf GD 1212 using a two-wheel-controlled Kepler spacecraft. Astrophys. J. 789:85. doi: 10.1088/0004-637X/789/1/85
Hermes, J. J., Gänsicke, B. T., Bischoff-Kim, A., Kawaler, S. D., Fuchs, J. T., Dunlap, B. H., et al. (2015a). Insights into internal effects of common-envelope evolution using the extended Kepler mission. Mon. Not. R. Astron. Soc. 451, 1701–1712. doi: 10.1093/mnras/stv1053
Hermes, J. J., Gänsicke, B. T., Kawaler, S. D., Greiss, S., Tremblay, P.-E., Gentile Fusillo, N. P., et al. (2017a). White dwarf rotation as a function of mass and a dichotomy of mode line widths: Kepler observations of 27 pulsating DA white dwarfs through K2 campaign 8. Astrophys. J. Suppl. 232:23. doi: 10.3847/1538-4365/aa8bb5
Hermes, J. J., Kawaler, S. D., Bischoff-Kim, A., Provencal, J. L., Dunlap, B. H., and Clemens, J. C. (2017b). A deep test of radial differential rotation in a helium-atmosphere white dwarf. I. Discovery of pulsations in PG 0112+104. Astrophys. J. 835:277. doi: 10.3847/1538-4357/835/2/277
Hermes, J. J., Kawaler, S. D., Romero, A. D., Kepler, S. O., Tremblay, P.-E., Bell, K. J., et al. (2017c). Evidence from K2 for rapid rotation in the descendant of an intermediate-mass star. Astrophys. J. Lett. 841:L2. doi: 10.3847/2041-8213/aa6ffc
Hermes, J. J., Montgomery, M. H., Bell, K. J., Chote, P., Gänsicke, B. T., Kawaler, S. D., et al. (2015b). A second case of outbursts in a pulsating white dwarf observed by Kepler. Astrophys. J. Lett. 810:L5. doi: 10.1088/2041-8205/810/1/L5
Hermes, J. J., Mullally, F., Østensen, R. H., Williams, K. A., Telting, J., Southworth, J., et al. (2011). Discovery of a ZZ Ceti in the Kepler mission field. Astrophys. J. Lett. 741:L16. doi: 10.1088/2041-8205/741/1/L16
Hollands, M. A., Gänsicke, B. T., and Koester, D. (2018). Cool DZ white dwarfs II: compositions and evolution of old remnant planetary systems. Mon. Not. R. Astron. Soc. 477, 93–111. doi: 10.1093/mnras/sty592
Hollands, M. A., Tremblay, P. E., Gänsicke, B. T., Camisassa, M. E., Koester, D., Aungwerojwit, A., et al. (2020). An ultra-massive white dwarf with a mixed hydrogen-carbon atmosphere as a likely merger remnant. Nat. Astron. 4, 663–669. doi: 10.1038/s41550-020-1028-0
Howell, S. B., Sobeck, C., Haas, M., Still, M., Barclay, T., Mullally, F., et al. (2014). The K2 mission: characterization and early results. Publ. ASP 126:398. doi: 10.1086/676406
Isern, J., García-Berro, E., Torres, S., and Catalán, S. (2008). Axions and the cooling of white dwarf stars. Astrophys. J. Lett. 682:L109. doi: 10.1086/591042
Isern, J., García-Berro, E., Torres, S., Cojocaru, R., and Catalán, S. (2018). Axions and the luminosity function of white dwarfs: the thin and thick discs, and the halo. Mon. Not. R. Astron. Soc. 478, 2569–2575. doi: 10.1093/mnras/sty1162
Isern, J., Hernanz, M., and Garcia-Berro, E. (1992). Axion cooling of white dwarfs. Astrophys. J. Lett. 392, L23–L25. doi: 10.1086/186416
Kawaler, S. D. (2004). “White dwarf rotation: observations and theory,” in Stellar Rotation, Volume 215 of IAU Symposium, eds A. Maeder and P. Eenens (Paris), 561.
Kawaler, S. D., Winget, D. E., and Hansen, C. J. (1985). Evolution of the pulsation properties of hot pre-white dwarf stars. Astrophys. J. 295, 547–560. doi: 10.1086/163398
Kepler, S. O. (1984). Light and line profile variations die to r-mode pusations with an application to the ZZ Ceti star G 117-B15A. Astrophys. J. 286, 314–327. doi: 10.1086/162601
Kepler, S. O., Koester, D., and Ourique, G. (2016a). A white dwarf with an oxygen atmosphere. Science 352, 67–69. doi: 10.1126/science.aad6705
Kepler, S. O., Pelisoli, I., Koester, D., Ourique, G., Romero, A. D., Reindl, N., et al. (2016b). New white dwarf and subdwarf stars in the Sloan Digital Sky Survey data release 12. Mon. Not. R. Astron. Soc. 455, 3413–3423. doi: 10.1093/mnras/stv2526
Kepler, S. O., Pelisoli, I., Koester, D., Reindl, N., Geier, S., Romero, A. D., et al. (2019). White dwarf and subdwarf stars in the Sloan Digital Sky Survey data release 14. Mon. Not. R. Astron. Soc. 486, 2169–2183. doi: 10.1093/mnras/stz960
Kilic, M., Munn, J. A., Harris, H. C., von Hippel, T., Liebert, J. W., Williams, K. A., et al. (2017). The ages of the thin disk, thick disk, and the halo from nearby white dwarfs. Astrophys. J. 837:162. doi: 10.3847/1538-4357/aa62a5
Kleinman, S. J., Kepler, S. O., Koester, D., Pelisoli, I., Peçanha, V., Nitta, A., et al. (2013). SDSS DR7 white dwarf catalog. Astrophys. J. Suppl. 204:5. doi: 10.1088/0067-0049/204/1/5
Koester, D., Gänsicke, B. T., and Farihi, J. (2014). The frequency of planetary debris around young white dwarfs. Astron. Astrophys. 566:A34. doi: 10.1051/0004-6361/201423691
Kunz, R., Fey, M., Jaeger, M., Mayer, A., Hammer, J. W., Staudt, G., et al. (2002). Astrophysical reaction rate of 12C(α, γ)16O. Astrophys. J. 567, 643–650. doi: 10.1086/338384
Kurtz, D. W., Shibahashi, H., Dhillon, V. S., Marsh, T. R., and Littlefair, S. P. (2008). A search for a new class of pulsating DA white dwarf stars in the DB gap. Mon. Not. R. Astron. Soc. 389, 1771–1779. doi: 10.1111/j.1365-2966.2008.13664.x
Kurtz, D. W., Shibahashi, H., Dhillon, V. S., Marsh, T. R., Littlefair, S. P., Copperwheat, et al. (2013). Hot DAVs: a probable new class of pulsating white dwarf stars. Mon. Not. R. Astron. Soc. 432, 1632–1639. doi: 10.1093/mnras/stt585
Luan, J., and Goldreich, P. (2018). DAVs: red edge and outbursts. Astrophys. J. 863:82. doi: 10.3847/1538-4357/aad0f4
Maeda, K., and Shibahashi, H. (2014). Pulsations of pre-white dwarfs with hydrogen-dominated atmospheres. Publ. ASJ 66:76. doi: 10.1093/pasj/psu051
Maoz, D., Mannucci, F., and Nelemans, G. (2014). Observational clues to the progenitors of type Ia supernovae. Annu. Rev. Astron. Astrophys. 52, 107–170. doi: 10.1146/annurev-astro-082812-141031
McGraw, J. T. (1979). The physical properties of the ZZ Ceti stars and their pulsations. Astrophys. J. 229, 203–211. doi: 10.1086/156946
Mestel, L. (1952). On the theory of white dwarf stars. I. The energy sources of white dwarfs. Mon. Not. R. Astron. Soc. 112:583. doi: 10.1093/mnras/112.6.583
Metcalfe, T. S. (2003). White dwarf asteroseismology and the 12C(α,γ)16O rate. Astrophys. J. Lett. 587, L43–L46. doi: 10.1086/375044
Miller Bertolami, M. M. (2014). Limits on the neutrino magnetic dipole moment from the luminosity function of hot white dwarfs. Astron. Astrophys. 562:A123. doi: 10.1051/0004-6361/201322641
Miller Bertolami, M. M., and Althaus, L. G. (2006). Full evolutionary models for PG 1159 stars. Implications for the helium-rich O(He) stars. Astron. Astrophys. 454, 845–854. doi: 10.1051/0004-6361:20054723
Miller Bertolami, M. M., Melendez, B. E., Althaus, L. G., and Isern, J. (2014). Revisiting the axion bounds from the galactic white dwarf luminosity function. J. Cosmol. Astropart. Phys. 2014:069. doi: 10.1088/1475-7516/2014/10/069
Montgomery, M. H., Hermes, J. J., Winget, D. E., Dunlap, B. H., and Bell, K. J. (2020). Limits on mode coherence in pulsating DA white dwarfs due to a nonstatic convection zone. Astrophys. J. 890:11. doi: 10.3847/1538-4357/ab6a0e
Montgomery, M. H., Klumpe, E. W., Winget, D. E., and Wood, M. A. (1999). Evolutionary calculations of phase separation in crystallizing white dwarf stars. Astrophys. J. 525, 482–491. doi: 10.1086/307871
Montgomery, M. H., Williams, K. A., Winget, D. E., Dufour, P., DeGennaro, S., and Liebert, J. (2008). SDSS J142625.71+575218.3: a prototype for a new class of variable white dwarf. Astrophys. J. Lett. 678:L51. doi: 10.1086/588286
Montgomery, M. H., and Winget, D. E. (1999). The effect of crystallization on the pulsations of white dwarf stars. Astrophys. J. 526, 976–990. doi: 10.1086/308044
Moya, A., Barceló Forteza, S., Bonfanti, A., Salmon, S. J. A. J., Van Grootel, V., and Barrado, D. (2018). Asteroseismic potential of CHEOPS. Astron. Astrophys. 620:A203. doi: 10.1051/0004-6361/201833772
Nather, R. E., Winget, D. E., Clemens, J. C., Hansen, C. J., and Hine, B. P. (1990). The whole earth telescope–a new astronomical instrument. Astrophys. J. 361, 309–317. doi: 10.1086/169196
Østensen, R. H., Bloemen, S., Vučković, M., Aerts, C., Oreiro, R., Kinemuchi, K., et al. (2011a). At last A V777 Her pulsator in the Kepler field. Astrophys. J. Lett. 736:L39. doi: 10.1088/2041-8205/736/2/L39
Østensen, R. H., Silvotti, R., Charpinet, S., Oreiro, R., Bloemen, S., Baran, A. S., et al. (2011b). First Kepler results on compact pulsators–VI. Targets in the final half of the survey phase. Mon. Not. R. Astron. Soc. 414, 2860–2870. doi: 10.1111/j.1365-2966.2011.18405.x
Papaloizou, J., and Pringle, J. E. (1978). Non-radial oscillations of rotating stars and their relevance to the short-period oscillations of cataclysmic variables. Mon. Not. R. Astron. Soc. 182, 423–442. doi: 10.1093/mnras/182.3.423
Piotto, G. (2018). “PLATO science: main goals and expected achievements,” in European Planetary Science Congress, EPSC2018–969 (Berlin).
Pyrzas, S., Gänsicke, B. T., Hermes, J. J., Copperwheat, C. M., Rebassa-Mansergas, A., Dhillon, V. S., et al. (2015). Discovery of ZZ Cetis in detached white dwarf plus main-sequence binaries. Mon. Not. R. Astron. Soc. 447, 691–697. doi: 10.1093/mnras/stu2412
Reding, J. S., Hermes, J. J., Vanderbosch, Z., Dennihy, E., Kaiser, B. C., Mace, C. B., et al. (2020). An isolated white dwarf with 317 s rotation and magnetic emission. Astrophys. J. 894:19. doi: 10.3847/1538-4357/ab8239
Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., et al. (2015). Transiting exoplanet survey satellite (TESS). J. Astron. Telesc. Instr. Syst. 1:014003. doi: 10.1117/1.JATIS.1.1.014003
Robinson, E. L., Kepler, S. O., and Nather, R. E. (1982). Multicolor variations of the ZZ Ceti stars. Astrophys. J. 259, 219–231. doi: 10.1086/160162
Romero, A. D., Córsico, A. H., Castanheira, B. G., De Gerónimo, F. C., Kepler, S. O., Koester, D., et al. (2017). Probing the structure of Kepler ZZ Ceti stars with full evolutionary models-based asteroseismology. Astrophys. J. 851:60. doi: 10.3847/1538-4357/aa9899
Saio, H. (2013). “Pulsations in white dwarfs: selected topics,” in European Physical Journal Web of Conferences, Volume 43 of European Physical Journal Web of Conferences (Les Ulis), 05005.
Salaris, M., Serenelli, A., Weiss, A., and Miller Bertolami, M. (2009). Semi-empirical white dwarf initial-final mass relationships: a thorough analysis of systematic uncertainties due to stellar evolution models. Astrophys. J. 692, 1013–1032. doi: 10.1088/0004-637X/692/2/1013
Shibahashi, H. (2005). “The DB gap and pulsations of white dwarfs,” in EAS Publications Series, Volume 17 of EAS Publications Series, eds G. Alecian, O. Richard, and S. Vauclair (Les Ulis), 143–148.
Shibahashi, H. (2007). “The DB gap and pulsations of white dwarfs,” in Unsolved Problems in Stellar Physics: A Conference in Honor of Douglas Gough, Volume 948 of American Institute of Physics Conference Series, eds R. J. Stancliffe, G. Houdek, R. G. Martin, and C. A. Tout (College Park, MD), 35–42.
Starrfield, S., Cox, A. N., Kidman, R. B., and Pesnell, W. D. (1984). Nonradial instability strips based on carbon and oxygen partial ionization in hot, evolved stars. Astrophys. J. 281, 800–810. doi: 10.1086/162158
Straniero, O., Domínguez, I., Imbriani, G., and Piersanti, L. (2003). The chemical composition of white dwarfs as a test of convective efficiency during core helium burning. Astrophys. J. 583, 878–884. doi: 10.1086/345427
Thompson, S. E., Coughlin, J. L., Hoffman, K., Mullally, F., Christiansen, J. L., Burke, C. J., et al. (2018). Planetary candidates observed by Kepler. VIII. A fully automated catalog with measured completeness and reliability based on data release 25. Astrophys. J. Suppl. 235:38. doi: 10.3847/1538-4365/aab4f9
Timmes, F. X., Townsend, R. H. D., Bauer, E. B., Thoul, A., Fields, C. E., and Wolf, W. M. (2018). The impact of white dwarf luminosity profiles on oscillation frequencies. Astrophys. J. Lett. 867:L30. doi: 10.3847/2041-8213/aae70f
Tremblay, P.-E., Fontaine, G., Fusillo, N. P. G., Dunlap, B. H., Gänsicke, B. T., Hollands, M. A., et al. (2019). Core crystallization and pile-up in the cooling sequence of evolving white dwarfs. Nature 565, 202–205. doi: 10.1038/s41586-018-0791-x
Tremblay, P. E., Cummings, J., Kalirai, J. S., Gänsicke, B. T., Gentile-Fusillo, N., and Raddi, R. (2016). The field white dwarf mass distribution. Mon. Not. R. Astron. Soc. 461, 2100–2114. doi: 10.1093/mnras/stw1447
Unno, W., Osaki, Y., Ando, H., Saio, H., and Shibahashi, H. (1989). Nonradial Oscillations of Stars. Tokyo: University of Tokyop Press.
Van Grootel, V., Dupret, M.-A., Fontaine, G., Brassard, P., Grigahcène, A., and Quirion, P.-O. (2012). The instability strip of ZZ Ceti white dwarfs. I. Introduction of time-dependent convection. Astron. Astrophys. 539:A87. doi: 10.1051/0004-6361/201118371
Van Horn, H. M. (2015). Unlocking the Secrets of White Dwarf Stars. Cham; Heidelberg; New York, NY; Dordrecht; London: Springer.
Winget, D. E., and Kepler, S. O. (2008). Pulsating white dwarf stars and precision asteroseismology. ARA&A 46, 157–199. doi: 10.1146/annurev.astro.46.060407.145250
Winget, D. E., Kepler, S. O., Campos, F., Montgomery, M. H., Girardi, L., Bergeron, P., et al. (2009). The physics of crystallization from globular cluster white dwarf stars in NGC 6397. Astrophys. J. Lett. 693, L6–L10. doi: 10.1088/0004-637X/693/1/L6
Winget, D. E., Nather, R. E., Clemens, J. C., Provencal, J., Kleinman, S. J., Bradley, P. A., et al. (1991). Asteroseismology of the DOV star PG 1159-035 with the whole earth telescope. Astrophys. J. 378, 326–346. doi: 10.1086/170434
Winget, D. E., Nather, R. E., Clemens, J. C., Provencal, J. L., Kleinman, S. J., Bradley, P. A., et al. (1994). Whole earth telescope observations of the DBV white dwarf GD 358. Astrophys. J. 430, 839–849. doi: 10.1086/174455
Winget, D. E., Sullivan, D. J., Metcalfe, T. S., Kawaler, S. D., and Montgomery, M. H. (2004). A strong test of electroweak theory using pulsating DB white dwarf stars as plasmon neutrino detectors. Astrophys. J. Lett. 602, L109–L112. doi: 10.1086/382591
Winget, D. E., van Horn, H. M., Tassoul, M., Fontaine, G., Hansen, C. J., and Carroll, B. W. (1982). Hydrogen-driving and the blue edge of compositionally stratified ZZ ceti star models. Astrophys. J. Lett. 252, L65–L68. doi: 10.1086/183721
Wood, M. A. (1990). Astero-archaeolgy reading the galactic history recorded in the white dwarf stars (Ph.D. thesis), Texas University, Austin, TX, United States.
Woosley, S. E., and Heger, A. (2015). The remarkable deaths of 9-11 solar mass stars. Astrophys. J. 810:34. doi: 10.1088/0004-637X/810/1/34
Wu, Y., and Goldreich, P. (2001). Gravity modes in ZZ Ceti stars. IV. Amplitude saturation by parametric instability. Astrophys. J. 546, 469–483. doi: 10.1086/318234
York, D. G., Adelman, J., Anderson, J. E. Jr., Anderson, S. F., Annis, J., Bahcall, N. A., et al. (2000). The Sloan Digital Sky Survey: technical summary. Astron. J. 120, 1579–1587. doi: 10.1086/301513
Zong, W., Charpinet, S., and Vauclair, G. (2016a). Signatures of nonlinear mode interactions in the pulsating hot B subdwarf star KIC 10139564. Astron. Astrophys. 594:A46. doi: 10.1051/0004-6361/201629132
Zong, W., Charpinet, S., Vauclair, G., Giammichele, N., and Van Grootel, V. (2016b). Amplitude and frequency variations of oscillation modes in the pulsating DB white dwarf star KIC 08626021. The likely signature of nonlinear resonant mode coupling. Astron. Astrophys. 585:A22. doi: 10.1051/0004-6361/201526300
Keywords: stellar evolution, white dwarf stars, stellar interiors, stellar oscillations, asteroseismology
Citation: Córsico AH (2020) White-Dwarf Asteroseismology With the Kepler Space Telescope. Front. Astron. Space Sci. 7:47. doi: 10.3389/fspas.2020.00047
Received: 13 April 2020; Accepted: 18 June 2020;
Published: 28 August 2020.
Edited by:
Anthony Eugene Lynas-Gray, University College London, United KingdomReviewed by:
J. J. Hermes, Boston University, United StatesCopyright © 2020 Córsico. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alejandro H. Córsico, YWNvcnNpY29AZmNhZ2xwLnVubHAuZWR1LmFy
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.