Gravitational Waves From Binary Black Hole Mergers: Modeling and Observations

Schmidt, Patricia

doi:10.3389/fspas.2020.00028

MINI REVIEW article

Front. Astron. Space Sci., 16 June 2020

Sec. Cosmology

Volume 7 - 2020 | https://doi.org/10.3389/fspas.2020.00028

This article is part of the Research Topic Gravitational Waves: A New Window to the Universe View all 9 articles

Gravitational Waves From Binary Black Hole Mergers: Modeling and Observations

$\nPatricia Schmidt$ Patricia Schmidt^*

School of Physics and Astronomy and Institute for Gravitational Wave Astronomy, University of Birmingham, Birmingham, United Kingdom

Only a few years after the first detection of gravitational waves from coalescing stellar-mass black holes, the field of gravitational-wave astronomy is now firmly established after the detection of several more. These discoveries have opened up a new window onto the universe, which allows us to probe gravity and astrophysics in some of the most extreme environments in the universe. The detection and, in particular, the subsequent inference of the binaries' properties rely heavily on theoretical models of the signals. In this review, we first discuss the techniques used to model the gravitational-wave signals from coalescing black holes, before we summarize the observations made to date. We conclude with a brief outlook onto the prospects for binary black hole observations in the future.

1. Introduction

The first detection of gravitational waves (GWs) from the coalescence of two stellar-mass black holes (BHs) in 2015 by the Advanced LIGO GW-detectors (Abbott et al., 2016d) marked the beginning of a new area: GW astronomy. Since then, more than ten binary black hole (BBH) mergers have been identified (Abbott et al., 2019c, 2020; Nitz et al., 2019a; Venumadhav et al., 2019a). First predicted in the 1910s by Einstein's General Theory of Relativity (GR) (Einstein, 1915, 1918), the hunt for these perturbations of spacetime itself spanned many decades and was ultimately enabled by tremendous technological and theoretical advances.

Stellar mass BBHs with a total mass between one and a few hundred solar masses, are prime GW sources for the currently operating ground-based interferometric GW detectors Advanced LIGO (Aasi et al., 2015) and Virgo (Acernese et al., 2015) as well the Japanese detector KAGRA (Akutsu et al., 2019), set to join the global GW detector network shortly. These detectors are sensitive to GWs with frequencies between 10 Hz to a few kHz. In order to detect GWs in lower frequency bands, such as from the collisions of supermassive black holes in the centers of galaxies, the Earth's seismic wall needs to be overcome, which will be achieved with space-based GW missions expected to commence operation in the next decade.

The observation of GWs from inspiralling BBHs provides us with a unique means to study black holes, allowing us to perform precision tests of GR in the high-curvature, strong-field regime and shedding light on the astrophysical origin and nature of entire populations of black holes.

Gravitational waves from BBHs carry characteristic information about the astrophysical properties of the BHs, such as their masses and spins. These properties can be inferred via Bayesian inference (Bayes, 1764) by using highly accurate general-relativistic waveform models, which describe the last stages of the gravitationally-driven BBH evolution: the inspiral, the merger and the ringdown of the remnant black hole. This allows us to constrain the mass and spin distributions of stellar-mass black holes, which has implications for their possible formation history, and put constraints on the rate of such merger events in the universe.

In this review, we will first summarize the current avenues of modeling GWs from binary black holes (section 2), then discuss the current status of observations (section 3), before concluding with a very brief outlook onto the future of BBH GW astronomy in section 4.

2. Modeling Binary Black Holes

Compact binaries, such as two black holes, on quasi-spherical orbits, lose orbital energy due to the emission of GWs, which causes their orbital separation to shrink until the two black holes plunge, merge and, in General Relativity, form a Kerr black hole. Intrinsically, a BBH is characterized by seven parameters: the mass ratio, q = m₁/m₂ ≥ 1, where m₁ ≥ m₂, and the two (dimensionless) spin angular momenta ${\vec{χ}}_{1}$ and ${\vec{χ}}_{2}$ . We note that the total mass M = m₁ + m₂ of the binary is not relevant intrinsically but determines the GW frequency in physical units and is therefore relevant for detection. Moreover, for astrophysical black holes one commonly assumes charge neutrality.

Two black holes in orbit undergo a purely gravitationally-driven evolution, which is characterized by three distinct stages: the inspiral, the merger and the ringdown of the remnant black holes. The emission of gravitational radiation causes the orbital separation to shrink. If the spin angular momenta of the two black holes are (anti-)parallel to the orbital angular momentum of the binary motion, the orbital motion is confined to a two-dimensional plane whose orientation is fixed in time. In this case, the emitted GW signal is the characteristic chirp signal, a wave with monotonically increasing amplitude and frequency until the merger is reached. An example of such a waveform is shown in Figure 1. The largest amount of radiation is emitted along the direction of the orbital angular momentum (O'Shaughnessy et al., 2011; Schmidt et al., 2011), and the signal is well-described by the dominant (quadrupole) harmonic, h₂₂.

FIGURE 1

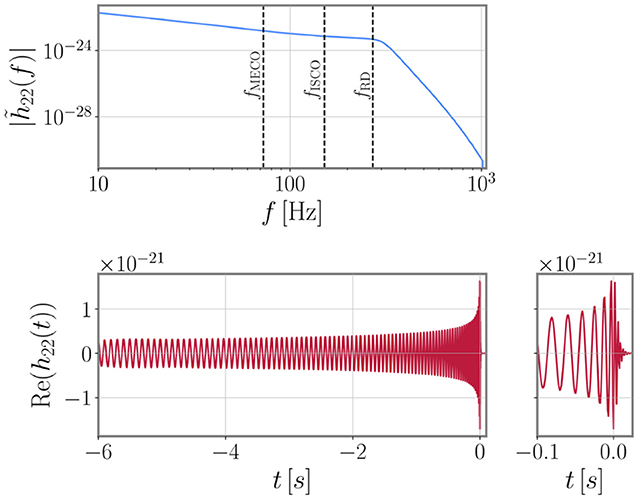
Figure 1. The gravitational waveform of a non-spinning 30 + 30M_⊙ binary black hole at a distance of 400 Mpc generated from the phenomenological waveform model IMRPhenomX (Pratten et al., 2020b). The top panel shows the frequency-domain GW strain starting at 10 Hz when viewed face-on. The vertical dashed lines indicate three characteristic frequencies: the frequency of the innermost stable circular orbit (f_ISCO), the minimal energy circular orbit (f_MECO) and the ringdown frequency (f_RD). The bottom panel shows the corresponding time-domain GW, where the smaller right panel shows a close-up of the last few inspiral cycles, the merger, and ringdown waveform.

Any misalignment between the spins and the orbital angular momentum, however, induces relativistic precession effects, which cause the orbital plane to change its spatial orientation as the binary evolves (Apostolatos et al., 1994; Kidder, 1995). This more complex dynamics is directly reflected into the emitted GW signal, which, depending on the relative orientation w.r.t. the observer, can show strong amplitude and phase modulations (Apostolatos et al., 1994; Kidder, 1995; Schmidt et al., 2012). Further, due to the time-dependent orientation of the binary, the quadrupole approximation may no longer be sufficient to describe the radiation and higher-order harmonic modes need to be taken into account.

Due to the lack of analytic solutions of the general relativistic two-body problem, the dynamics and the corresponding GW signal must be approximated using a variety of analytic and numerical techniques. During the inspiral stage, where the orbital separation between two black holes is much larger than their extent, the BHs can be treated as point particles and their motion as well as the GW signal can be described using the post-Newtonian (PN) formalism. At small separations, however, the PN approximation is no longer valid and the Einstein field equations must be solved numerically to obtain the late-time dynamics and GW signal. In GW data analysis applications, such as matched-filter searches (Allen et al., 2012; Usman et al., 2016; Messick et al., 2017; Nitz et al., 2017; Venumadhav et al., 2019b) and Bayesian inference (Veitch et al., 2015; Zackay et al., 2018; Biwer et al., 2019), semi-analytic models with a continuous dependence on the binary parameters are most commonly used. This requires the smooth connection between PN and numerical relativity results. We briefly summarize the main modeling strategies below.

2.1. Post-Newtonian Theory

The post-Newtonian (PN) formalism is an approximation to GR valid in the slow-motion, weak-field regime (see Blanchet, 2014 and references therein for an extensive review). It is well-suited for describing the motion of compact binaries and their GW emission in the inspiral regime. In PN theory, relativistic corrections to the Newtonian solution are incorporated systematically order-by-order in the expansion parameter ϵ = v²/c², where v is the orbital velocity and c the speed of light. The PN formalism starts to break down when the orbital velocity of the black holes becomes comparable to the speed of light, i.e., v ~ c. At this point, one requires numerical solutions to the Einstein field equations.

2.2. Numerical Relativity

Solving the general relativistic two-body problem in its full generality was considered the holy grail of numerical relativity (NR) for many decades. It is only possible since the breakthroughs in 2005 (Pretorius, 2005; Campanelli et al., 2006b; Baker et al., 2007) to simulate two merging black holes and obtain the GW signal emitted in the highly dynamical, non-linear merger regime. Since the initial breakthroughs, the simulations of BBHs have become a standard tool in GW astrophysics, with ever improving accuracy and also aided by faster compute cores. To date thousands of NR simulations across the BBH parameter space have been performed (Mroue et al., 2013; Husa et al., 2016; Jani et al., 2016; Boyle et al., 2019; Healy et al., 2019), but the sampling is still very sparse mainly due to the high computational cost. Moreover, large mass ratio (q ≥ 20) and high spin magnitudes ( $| {\vec{χ}}_{i} | \geq 0.9$ ) pose particularly challenging problems that are yet to be overcome.

Since the initial breakthrough in 2005, significant progress has been made: While the first successful simulations were those of equal-mass non-spinning BBHs spanning only the last few orbits, today simulations of aligned-spin as well as precessing quasi-circular binaries, eccentric-orbit binaries (Sperhake et al., 2008; Gold and Brügmann, 2013; Lewis et al., 2017; Hinder et al., 2018; Huerta et al., 2019; Ramos-Buades et al., 2020), and even evolutions that are long enough to reach into the early-inspiral regime (Szilágyi et al., 2015) are performed. Today, several codes based on different numerical techniques and formulations are capable of stably evolving BBHs and extracting their GW signal (Campanelli et al., 2006a; Scheel et al., 2006; Sperhake, 2007; Vaishnav et al., 2007; Brügmann et al., 2008; Loffler et al., 2012; Babiuc-Hamilton et al., 2019).

Numerical relativity does not only provide the waveform through merger but also for the ringdown. The quasi-normal mode spectrum emitted during this last stage of the binary evolution is analytically described by black hole perturbation theory (Teukolsky, 1973; Kokkotas and Schmidt, 1999). While the analytic prescription provides the mode frequencies and mode damping times (Berti et al., 2006), it does not provide the amplitude of the waves. Numerical relativity simulations, on the other hand, provide this crucial information, which, in combination, allows for the construction of parameter space fits (Kamaretsos et al., 2012; London et al., 2014).

The merger-ringdown waveforms obtained from NR are a key ingredient in the construction and verification of accurate waveform models used in GW data analysis. These applications, however, often require a continuous sampling across the parameter space, hence semi-analytic models or interpolants are paramount. In current analyses, waveforms from three families are most commonly employed: effective-one-body waveforms, phenomenological waveforms, and NR surrogates. While the first two paradigms model the complete inspiral-merger-ringdown (IMR) signal, NR-based surrogates are commonly restricted to a few GW cycles before the merger, the merger, and the ringdown.

2.3. Effective-One-Body

The effective-one-body (EOB) formalism combines information from the test particle limit as well PN results to obtain a complete description of the two-body dynamics as well as the IMR GW signal (Buonanno and Damour, 1999, 2000). It is based on a Hamiltonian map of the conservative dynamics of the two bodies to an effective one-body prescription, where a test particle with the reduced mass μ of the two-body system moves in an effective Kerr background spacetime characterized by the total mass M, the symmetric mass ratio η and the total spin $\vec{S}$ :

\begin{array}{l} H = M \sqrt{1 + 2 η (\frac{H_{eff}}{μ} - 1)} . & (1) \end{array}

The EOB prescription requires that the test particle limit reduces to the motion of a particle in a Kerr spacetime and that the EOB Hamiltonian reduces to the PN Hamiltonian in the weak-field, slow-motion limit. While the Hamiltonian encapsulates the inspiral dynamics, one additionally requires a prescription for the calculation of the GWs and the radiation reaction forces as well as a smooth transition to the ringdown of a perturbed black hole. The radiative degrees of freedom are described by factorized waveforms, which include a calibration to NR simulations. We note that the EOB formalism is inherently time-domain and requires solving a system of coupled ordinary differential equations, which makes the waveform generation rather costly.

The EOB waveform family includes highly accurate quadrupolar models for non-spinning and aligned-spin binaries (Bohé et al., 2017; Nagar et al., 2018), NR-calibrated extensions to higher-order harmonics (Cotesta et al., 2018; Nagar et al., 2020a,b), and extensions to precessing BBH (Pan et al., 2014; Ossokine et al., 2020). Recently, extensions to include eccentric motion have been presented (Cao and Han, 2017; Hinderer and Babak, 2017).

2.4. Phenomenological Waveforms

The phenomenological framework takes a different approach: The focus here is exclusively on modeling the IMR GW signal itself without providing equations of motions for the BH dynamics (Ajith et al., 2007). The aim is to provide a fast-to-evaluate, closed-form expression of the GW signal in the frequency domain by splitting the signal into an amplitude and a phase, assuming the following schematic form:

\begin{array}{l} \tilde{h} (f; \vec{λ}, \vec{θ}) = Ã (f; \vec{λ}) e^{i \tilde{Ψ} (f; \vec{θ})}, & (2) \end{array}

where $\vec{λ}$ are (phenomenological) parameters in the amplitude and $\vec{θ}$ in the phase respectively.

The amplitude and phase are modeled separately, where each part is subdivided into three regions: the inspiral (f_GW ≤ f_MECO, where MECO denotes the minimum-energy circular orbit), an intermediate region and the ringdown. The inspiral is modeled based on analytic PN information augmented with an artificial extension (pseudo PN terms), which are calibrated to analytic, e.g., EOB, results. The intermediate region, which governs the merger phase, is modeled as a polynomial, while the ringdown is well-described by a deformed Lorentzian. These latter two regions are calibrated to NR information. For further details see (Santamaría et al., 2010; Khan et al., 2016; Pratten et al., 2020b).

Phenomenological waveform model are constructed in the frequency domain, which makes them computationally fast to evaluate and hence particularly attractive for data analysis applications. We emphasize, however, that the validity range of any NR-calibrated waveform model depends strongly on the calibration region, which, due to the lack of NR simulations for q ≥ 10, is limited. The most recent waveform family, PhenomX (Garcia-Quiros et al., 2020; Pratten et al., 2020b), also includes extreme mass-ratio information which allows for a smooth evaluation up to q ≃ 1, 000 (Harms et al., 2016), although the accuracy of waveforms between 19 ≤ q ≤ 1, 000 cannot be assessed. The current Phenom waveform families include aligned-spin models with and without higher-order modes as well as precessing ones (Hannam et al., 2014; Khan et al., 2019; Pratten et al., 2020a). An example of the IMR waveform of an equal-mass non-spinning BBH in the both the frequency and the time domain is shown in Figure 1.

2.5. Numerical Relativity Surrogates

In recent years it has become possible to produce thousands of NR simulations for restricted parameter ranges. These relatively short waveforms can then directly be used to construct an NR-based interpolant, i.e., a surrogate model, across a (limited) volume of the binary parameter space (Field et al., 2014; Blackman et al., 2017; Varma et al., 2019a,b). Such NR-based surrogates are considered the most accurate merger models but due to their restrictions in length and parameter space coverage, their usage is currently limited.

2.6. Gravitational Self-Force

While moderate to high mass ratio NR simulations remain a challenge, and therefore limit the accuracy of NR-calibrated waveform models in this regime, in the extreme mass ratio limit (q ≥ 10⁴) and possibly even the intermediate mass ratio regime (q ~ 100), a perturbative approach, often referred to as gravitational self-force (GSF), can be used to obtain an accurate approximation (see Poisson et al., 2011; Barack and Pound, 2019 for detailed reviews). Recent progress has seen the first second-order calculations (Pound et al., 2020), which will be crucial in order to fulfill the waveform accuracy requirements for future ground- and space-based GW observations of intermediate and extreme mass ratio binary black holes (Berry et al., 2019).

3. Observations of Binary Black Holes

The first observation of GWs from a coalescing BBH by the Advanced LIGO – Virgo detector network, GW150914, in September 2015, marked the beginning of the GW discovery era. The LIGO Scientific and Virgo Collaborations have since announced a total of eleven confident detections of GWs from merging BBHs (Abbott et al., 2019c): GW150914 (Abbott et al., 2016d), GW151012 (Abbott et al., 2016b), GW151226 (Abbott et al., 2016c), GW170104 (Abbott et al., 2017a), GW170608 (Abbott et al., 2017b), GW170729, GW170809 (Abbott et al., 2019c), GW170814 (Abbott et al., 2017c), GW170818, GW170823 (Abbott et al., 2019c), and most recently GW190412 (Abbott et al., 2020). Moreover, several tens of BBH candidates have been identified in the currently ongoing third observing run (LIGO Scientific, Virgo Collaboration). Independent analyses of the publicly available GW strain data (LIGO Scientific Collaboration, Virgo Collaboration, 2018) have claimed the detection of additional eight binary black hole events (Nitz et al., 2019a; Venumadhav et al., 2019a; Zackay et al., 2019): Nitz et al. (2019a) reported GW170121, GW170304, GW170727, and GW151205; Venumadhav et al. (2019a) and Zackay et al. (2019) also reported GW170121, GW170304, GW170727 as well as GW151216, GW170202, GW170403 and GW170425. These observations allow us to put GR to the test in the strong-field regime (Abbott et al., 2016e, 2019d; Yunes et al., 2016), probe the astrophysics of black holes in previously unexplored mass regimes and shed light on the possible formation scenarios of black holes (Abbott et al., 2016a, 2019b).

The majority of GW events was identified via matched filtering (Sathyaprakash and Dhurandhar, 1991; Allen et al., 2012), the optimal method to extract GW signals from compact binary coalescences from noise, by comparing GR-based waveform models (see section 2) to the data. Very high-mass short-duration signals have also been identified by unmodeled searches (Klimenko et al., 2016), i.e, searches that do not rely on waveforms models but rather look for generic features.

The black hole binaries observed through GWs to date span a wide range of total masses from just under 20M_⊙ for GW170608 (Abbott et al., 2017b), to more than 100M_⊙ for GW151205 (Nitz et al., 2019a)¹ at the 90% credible level as shown in Figure 2. In particular, the heavier black holes have masses not previously seen in x-ray binaries (Corral-Santana et al., 2016), and they raise interesting questions regarding their possible formation process and history such as secondary mergers (Gerosa and Berti, 2017). So far, no black holes in either the lower mass gap between observed neutron star and BH masses (Özel et al., 2010; Farr et al., 2011), and the upper mass gap due to pair instability supernovae (Woosley, 2016; Marchant et al., 2018), have been identified. Further, most BBH observations are consistent with equal mass or marginally unequal mass binaries (Abbott et al., 2019c; Nitz et al., 2019a; Venumadhav et al., 2019a) but recently, the first BBH with an asymmetric mass ratio (q ~ 0.28) has been reported (Abbott et al., 2020).

FIGURE 2

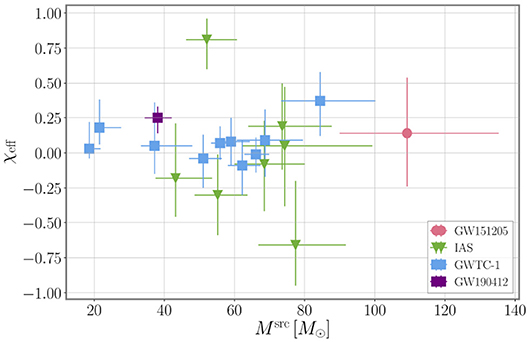
Figure 2. Inferred total source-frame masses and effective inspiral spin of BBH observations. The error bars indicate the 90% credible interval of the 1D posterior probability. Blue square markers: Ten BBH events from GWTC-1 (Abbott et al., 2019c); purple square marker: GW190412 (Abbott et al., 2020); green triangular markers: events from Zackay et al. (2019) and Venumadhav et al. (2019a); red round marker: event GW151205 from Nitz et al. (2019a). Posterior samples were obtained from LIGO Scientific Collaboration, Virgo Collaboration (2018), Nitz et al. (2019b), Venumadhav et al. (2019c), and Abbott et al. (2020). The conversion from detector-frame to source-frame masses assumes a flat ΛCDM cosmology (Ade et al., 2016).

Placing precise constraints on the spins of the black holes is more difficult with the best measured spin parameter being χ_eff, a mass-weighted linear combination of the dimensionless spin components along the orbital angular momentum direction $\hat{L}$ (Racine, 2008; Ajith et al., 2011),

\begin{array}{l} χ_{eff} = \frac{(m_{1} {\vec{χ}}_{1} + m_{2} {\vec{χ}}_{2}) \cdot \hat{L}}{m_{1} + m_{2}} . & (3) \end{array}

The majority of observations is consistent with χ_eff = 0 at the 90% credible level as shown in Figure 2, with the exceptions of: GW151226 (Abbott et al., 2016c), GW170729 (Abbott et al., 2019c), GW190412 (Abbott et al., 2020), GW151216, and GW170403 (Venumadhav et al., 2019b; Zackay et al., 2019). It should be noted, however, that the latter two events were analyzed under different spin prior assumptions. A recent re-analysis suggests that the χ_eff-values reported in Venumadhav et al. (2019b) and Zackay et al. (2019) for those two events may not be robust (Huang et al., 2018).

The individual black hole spin magnitudes are more difficult to constrain due to the strong dependence of the GW phase on χ_eff. However, a few observations find a net positive spin in the binary, implying that at least one of the two BHs must have a positive, non-zero spin angular momentum. Misalignment between the orbital angular momentum and the black holes spins induces relativistic precession, which is directly reflect into the GW signal (Apostolatos et al., 1994; Kidder, 1995). The observation of such precessional signatures is considered to be of key importance for distinguishing different BBH formation channels (Mandel and O'Shaughnessy, 2010; Rodriguez et al., 2016; Stevenson et al., 2017): BBHs formed in the field are expected to have predominantly aligned spins (Kalogera, 2000), while BBHs formed dynamically in dense environments are expected to have a more isotropic spin distribution (Rodriguez et al., 2016). In the GW observations made to date, spin misalignment remains unconstrained but it is anticipated that future observations will yield the first concrete measurements of precession.

Gravitational waves from merging black holes are a unique probe of GR in the strong-field high-curvature regime, and hence these observations can be used to test their consistency with the predictions from GR (Berti et al., 2015). Due to the absence of complete IMR waveforms derived in alternative theories of gravity², we cannot directly test the validity of GR by comparison against these other theories but can perform a variety of consistency tests. One possibility is to introduce ad hoc parameterized modifications to the GR waveforms, representing either modifications in the strong-field regime or the wave propagation (Yunes and Pretorius, 2009; Mirshekari et al., 2012; Agathos et al., 2014; Berti et al., 2018b; Abbott et al., 2019d). One can then determine to which degree the inferred values of these modifications agree with the values predicted by GR. For binaries where the complete IMR signal is observed, one can further test the consistency of the inferred final mass and spin of the remnant black hole with the parameters inferred from the low- and high-frequency regimes of the signal (Hughes and Menou, 2005; Ghosh et al., 2016a,b). A detector network with non co-aligned detectors allows us to investigate the presence of additional polarization states as predicted in some alternative metric theories of gravity (Eardley et al., 1973; Corda, 2009). Current observations show significant preference for purely tensor polarizations over purely scalar or vector polarizations respectively (Abbott et al., 2017c, 2019d). To date, all tests of GR using BBHs yield results that are consistent with GR. For current observations, the limits on deviations from GR are dominated by the statistical uncertainty due to the detector noise. Improved detector sensitivities will allow for these constraints to tighten but the impact of systematic modeling errors, such as the neglect of eccentricity (Moore and Yunes, 2020), must be carefully taken into account (Berti et al., 2015).

4. Outlook

The observation of GWs from coalescing black holes has opened a new window onto the electromagnetically dark universe. The observations to date have already revealed the existence of black holes in previously unexplored mass regimes and have allowed us to perform the first tests of GR in a novel regime. The next generation of ground-based facilities will be significantly more sensitive than current detectors (Punturo et al., 2010; Reitze et al., 2019), allowing for even tighter measurements of black hole masses and spins, and probing the existence of stellar mass black holes throughout the history of the universe. Moreover, future observations will enable us to perform black hole spectroscopy by measuring individual quasi-normal modes (Berti et al., 2006, 2018a), probe the Kerr nature of astrophysical black holes and constrain parameterized deviations from GR in the strong-field regime to unrivaled precision (Sathyaprakash et al., 2012). Recent progress has been made calculating gravitational waveforms in alternative theories of gravity, which will allow for concrete tests of predictions beyond all-violations encompassing parameterized tests as are performed at the moment.

The detection of hundreds of BBH will allow for the cross-correlations between the GW signals and galaxy catalogs will allow for an independent, precise measurement of Hubble constant H₀ (Abbott et al., 2019a), which can help shed light on the current tensions between early-time and late-time cosmological probes (Verde et al., 2019).

Furthermore, observing the mergers of BBHs throughout the history of the universe will allow us to probe fundamental physics at a range of energy scales (Barack et al., 2019; Barausse et al., 2020). Intermediate mass black holes, in particular, have the potential to provide us with important evidences as to what the nature of dark matter may be (Eda et al., 2015; Bertone et al., 2019).

Planned space-based missions such as LISA will see a fraction of stellar mass BBHs that will later be detected by ground-based observatories while they are still in the early inspiral stage, enabling multi-band GW astronomy and providing early-warnings to both GW and electromagnetic observatories (Sesana, 2016). This will allow us to pin-point telescopes and detect any coincident electromagnetic emission.

Gravitational-wave science has already delivered key insights into the nature and astrophysics of black holes and future observations will continue to nurture and improve our understanding of these fundamental objects in the universe.

Author Contributions

PS has written this review article on her own to the best of her knowledge, she has produced all figures herself from publicly available data and codes. The references are extensive but they are by no means exhaustive.

Funding

PS acknowledges Dutch Research Council (NWO) Veni Grant No. 680-47-460.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^We note that this event is considered marginal. The most significant high-mass BBH discovered to date is GW170729 (Abbott et al., 2019c).

2. ^Although recent progress has been made in simulating BBH mergers in alternative theories of gravity (Okounkova et al., 2019; Witek et al., 2019) and there is also ongoing effort in deriving inspiral waveforms (Sennett et al., 2016), which allow for concrete tests of alternative predictions beyond all-violations encompassing parameterized tests.

References

Aasi, J., Abbott, B. P., Abbott, R., Abbott, T., Abernathy, M. R., Ackley, K. et al. (2015). Advanced LIGO. Class. Quant. Grav. 32:074001.

Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016a). Astrophysical implications of the Binary Black-Hole Merger GW150914. Astrophys. J. Lett. 818:L22. doi: 10.3847/2041-8205/818/2/l22