
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci. , 30 April 2020
Sec. Space Physics
Volume 7 - 2020 | https://doi.org/10.3389/fspas.2020.00016
This article is part of the Research Topic Collisionless Shock Research: Current State and Perspectives View all 4 articles
We study the transport of energetic particles accelerated at three different shock events observed in the solar wind by the ACE spacecraft. We consider particle propagation for a quasi-parallel, an oblique, and a quasi-perpendicular shock. The transport regime is deduced from the shape of the energetic particle profiles upstream of the shock, and for these events the profiles are well-fitted by power-laws with slope β. This corresponds to a superdiffusive transport with the anomalous diffusion exponent α = 2−β when β <1, and to normal diffusion when β≥1. We checked the resonant turbulence level upstream of the shocks, finding that this is statistically constant, so that the transport regime is not expected to change with the shock distance. For the three shocks under study, particle transport upstream of the shock is mostly superdiffusive, although the superdiffusive character appears to diminish with the increase of the shock normal angle θBn. We discuss possible interpretations of these results.
Energetic particles of heliospheric origin as well cosmic rays of galactic origin are routinely observed in space plasmas. These particles (electrons, protons, ad heavier nuclei) are thought to be accelerated by solar flares, by coronal mass ejection-driven shocks, by interplanetary shocks, as well as by the blast wave generated by supernova explosions. Beside the acceleration mechanism itself, it is important to understand the transport regime that allows the energetic particles to propagate from the acceleration site to the observer position: this is important both for the prediction of solar energetic particle (SEP) events, which are of concern to space weather, and for a proper understanding of the acceleration mechanisms based on Fermi models (e.g., Blasi, 2013; Amato, 2014; Sioulas et al., 2020). However, in spite of many studies, the transport properties of energetic particles in the presence of magnetic turbulence remain a challenge. For instance, in the case of normal diffusion the transport parallel to the magnetic field can be characterized by the parallel mean free path λ∥, which is simply related to the parallel diffusion coefficient by , with v the particle speed. Yet, the estimates of λ∥ obtained by various methods do not always agree (Bieber et al., 1994; Reames, 1999; Giacalone, 2013), to the point that a large range of values of λ∥ is used in numerical simulations of solar energetic particle transport (Wang et al., 2014). On the other hand, the transport in the direction perpendicular to the magnetic field can be influenced by field line random walk (Matthaeus et al., 2003), by compound diffusion (Zimbardo, 2005; Webb et al., 2006; Shalchi, 2015), and by the hierarchical structure of magnetic fluctuations in fully developed turbulence (Lazarian and Yan, 2014), so that many different regimes, ranging from subdiffusion to superdiffusion, can be envisaged.
In this context, collisionless shocks, where energetic particles are thought to be accelerated, offer a tool to investigate energetic particle transport both in the heliosphere, thanks to in situ measurements, and in the interstellar medium, thanks to the remote observations of an extended precursor of accelerated electrons upstream of supernova remnant (SNR) blast waves (Morlino et al., 2010; Perri et al., 2016; Perri, 2018). Indeed, knowledge of the fact that the shock is the source of energetic particles and observations of their density profile, which is the result of the transport regime, allows to derive the main transport parameters. Basically, one can distinguish between normal diffusion, when , and superdiffusion, when the particle mean square displacement grows as 〈Δx2〉∝tα with α>1. Here, x is a coordinate perpendicular to the shock front. In the former case, the energetic particle profile upstream of the shock corresponds to an exponential decay with typical scale Ldiff and, under the assumptions of stationarity, time independence and statistical homogeneity of turbulence, one can obtain the diffusion coefficient in the direction perpendicular to the shock surface as , where is the upstream plasma velocity in the shock frame (e.g., Giacalone, 2012). Instead, downstream of the shock a flat energetic particle profile is predicted. In the latter case, i.e., superdiffusion, Perri and Zimbardo (2007, 2008) have shown that the energetic particle flux upstream of the shock decays as a power-law, with an exponent β related to the anomalous diffusion exponent by α = 2−β, with 0 ≤ β ≤ 1. Also, downstream of the shock a non-constant, decreasing energetic particle profile is predicted (Perri and Zimbardo, 2012b; Zimbardo and Perri, 2013; Prete et al., 2019). Analysis of a number of shocks, both in the heliosphere and upstream of SNR shocks, has shown that superdiffusive transport can indeed be the case (Perri and Zimbardo, 2009; Zimbardo et al., 2012; Perri et al., 2016; Perri, 2018).
Nevertheless, it is still unclear under what physical conditions (e.g., turbulence level and anisotropy, shock normal angle, particle energy, etc.) anomalous transport regimes emerges. To help clarifying this issue, here we study energetic particle transport for interplanetary shocks observed by the ACE spacecraft; for these, we investigate three shocks which are characterized by different values of the shock normal angle θBn, that is, we investigate a quasi-parallel shock, an oblique shock, and a quasi-perpendicular shock, and we compare the results. We have chosen these shocks among those listed by Giacalone (2012) because those shocks are selected from the ACE database with the criterion to be rather strong, in order to be able to efficiently accelerate particles. In particular, Giacalone (2012) selected shocks having at least a density compression ratio r > 2.5, and at least an Alfvenic Mach number MA > 3. We also took care to choose shock events with relatively smooth energetic particle profiles.
Space missions offer the possibility to measure directly in situ the electromagnetic fields, the plasma properties and the fluxes of energetic particles, thus representing a powerful tool to study shock acceleration and particle transport. However, one should remember that most theoretical models of shocks assume a one-dimensional, planar spatial structure, time independence of the whole structure, and a homogeneous and infinite environment. Actually, often these assumptions are not satisfied. For instance, shocks due to solar flares and coronal mass ejections are spheroidal, not planar; they are transient events and evolve with time and with solar distance; even the solar wind is unsteady and carries several structures embedded within itself; magnetic turbulence is ubiquitous in the solar wind, and the many spatial scales implied by turbulence can modify the magnetic field orientation far off the spacecraft, i.e., the observer-shock magnetic connection, in a way that is unpredictable. For all these reasons, particular care has to be used in analyzing spacecraft data and in comparing them with theoretical models. In this paper, we study three shocks observed by the Advanced Composition Explorer (ACE) spacecraft, which is located in the Lagrangian point L1. Data have been obtained from the CDAWeb service of NASA at https://cdaweb.gsfc.nasa.gov/index.html/ and from the University of New Hampshire ACE shock list at http://www.ssg.sr.unh.edu/mag/ace/ACElists/obs_list.html.
For energetic particles, we used data from the ACE/EPAM LEMS-30 instrument and we note that the energetic particle profiles in the LEMS-120 are very similar. The plasma data is from the ACE/SWEPAM instrument and the magnetic field data is from te ACE/MAG instrument. We selected three events in order to explore the variations with the shock normal angle θBn, i.e., a quasi-parallel shock (event of 23 April 2002), an oblique shock (event of 08 June 2000), and a quasi-perpendicular shock (event of 26 August 1998) (shock normal angles from http://www.ssg.sr.unh.edu/mag/ace/ACElists/obs_list.html). These events are characterized by relatively steady conditions both upstream and downstream of the shocks, and are observed at 1 AU, so that the planarity and the stationarity assumptions should be satisfied. They are also listed in the shocks analyzed by Giacalone (2012).
For this shock, the upstream shock normal angle is given by in the ACE shock list, so that this shock is quasi-parallel: this means that a fraction of the thermal plasma particles are reflected upstream of shock and propagate upwind to form the ion foreshock. Also energetic particles accelerated at the shock can easily propagate upstream by means of diffusion or superdiffusion parallel to the average magnetic field. Figure 1 shows, from top to bottom, the energetic particle fluxes measured by EPAM/LEMS-30 in the energy channels from 45–67 to 315–580 keV (see legend), the solar wind number density, the solar wind radial velocity Vsw, the magnitude of the magnetic field B, the angle ψ between the radial direction and the magnetic field, obtained from cosψ = Br/|B|, and the magnetic variances , normalized to the average magnetic field B0 calculated over the whole dataset, but upstream and downstream separately. The transport of energetic particles parallel to the average magnetic field depends on wave-particle interactions which can cause pitch-angle scattering (e.g., Kennel and Petschek, 1966; Veltri and Zimbardo, 1993a,b). Wave-particle interactions are most effective when the wavelength is close to the particle gyroradius. The variances in Figure 1 are computed on the time scales corresponding to the gyroradius ρp of protons having an energy corresponding the middle of the three energy channels 45–67, 115–193, and 315–580 keV, that is on time intervals Δt = ρp/Vsw (Perri and Zimbardo, 2012a). Such variances are indicative of the strength of resonant wave-particle interactions, and indeed they enter in the expression of the pitch angle scattering coefficient obtained by quasi-linear theory (Kennel and Petschek, 1966; Blasi, 2013; Amato, 2014).
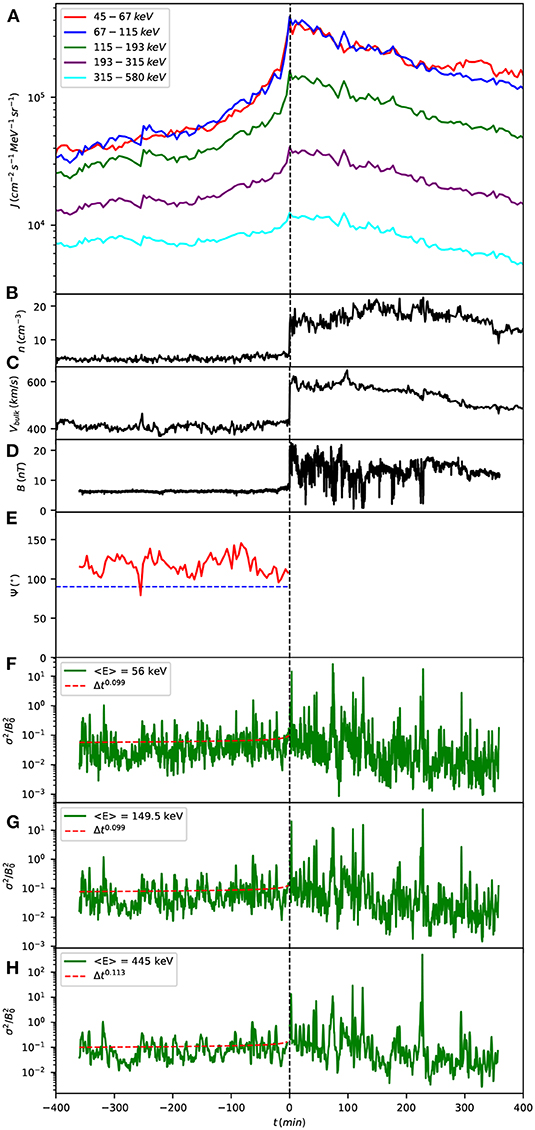
Figure 1. Measured quantities for the shock crossing observed by ACE on 23 April 2002. From top to bottom: (A) differential flux J of energetic particles measured by LEMS-30 in the energy channels from 45–67 to 315–580 keV, see colors in the legend; for this event only, the particle fluxes in the energy channel 45–67 keV of LEM-30 are not available, so we are showing the flux measured by LEMS-120. (B) Proton number density; (C) bulk velocity in the spacecraft frame; (D) magnetic field amplitude; (E) angle ψ between the magnetic field and the radial direction; (F,G,H) magnetic variances normalized to the average magnetic field B0, computed on the spatial scale corresponding to the proton gyroradius at the mean energies of three energy channels, as indicated (see text).
Inspection of the energetic particle fluxes in Figure 1 shows that the upstream decay is not exponential, but rather exhibits a long upstream tail which can be well described by a power-law decay: this suggests that transport is superdiffusive. In this connection, we notice that the normalized magnetic field variances (bottom panels of Figure 1) do not exhibit an increasing or decreasing trend with the shock distance, although short scale variations are present. Therefore, the relatively constant fluctuation levels imply that the transport properties should not change with the shock distance, so that the assumption of spatially independent diffusion coefficient is reasonable. Then, the upstream long precursor of particle fluxes has to be ascribed to the intrinsic scale-free properties of superdiffusive transport. A further indication of superdiffusive transport comes from the fact that the downstream energetic particle fluxes are not constant, as predicted by normal transport, but rather decrease downwind, after peaking at the shock time: this agrees with predictions of superdiffusive transport (Perri and Zimbardo, 2012b; Zimbardo and Perri, 2013; Prete et al., 2019).
For the above reasons we assume that this shock event, as well as the following two, is characterized by superdiffusive transport, and we study the upstream particle profiles by making power-law fits. In these fits, we consider the differential flux J measured at the spacecraft as a function of time to be proportional to Δt−β, where Δt = |t−tsh| is the time interval before the shock arrival. The differential flux is given in terms of the particle velocity distribution function f(r, v, t) as J = (v2/8πm)f(r, v, t) (Moraal, 2013). As explained above, several factors can influence the observed time profile of energetic particles: for instance, from Figure 1 we can see that when the direction of the average magnetic field is close to 90° to the radial direction, at around 260 min before the shock crossing, a marked decrease in J is observed in all the energy channels (except for the 45–67 keV flux, which for this event only is obtained from LEMS-120 since the data from LEMS-30 at 45–67 keV are not available). Clearly, this decrease is due to the increased length of the magnetic field line connecting the spacecraft and the advancing shock, which causes a decrease in the fluxes at the spacecraft. Conversely, when B is nearly radial, the magnetic field line connecting the shock and the observer is shorter and particle fluxes are larger. It is important to notice that while we can measure the change of direction of the magnetic field at the spacecraft, we cannot measure these changes along the connecting magnetic field lines but, also, we cannot exclude that these changes are present, just because of the magnetic turbulence which causes changes in B on many spatial scales. In addition, relevant levels of magnetic fluctuations at ultra-low-frequencies (ULFs) are due to ions backstreaming from the shock front and propagating upstream, as shown by both observations and numerical simulations (Hoppe et al., 1981; Otsuka et al., 2019; Lembége et al., 2020). Therefore, this may be one of the reasons for the small scale changes in the energetic particle fluxes which are frequently seen (other reasons may be found in the non smooth, corrugated structure of the shock surface and in time dependent, cyclic reformation Burgess, 1989; Neugebauer et al., 2006; Lobzin et al., 2007; Giacalone and Decker, 2010, although the latter changes would be on rather small time scales). For this reason, we make the energetic particle flux fits on temporal scales which arguably are larger than the magnetic turbulence correlation time; this is usually estimated to be on the order of 1–2 h at one AU, so we make the fits on 4 h, i.e., on 240 min. On the other hand, we avoid to make fits on scales much longer than this, in order to minimize the variations of the shock properties due to the solar wind expansion while the shocks are propagating radially outward and the possible explicit time variations of solar wind properties like density, bulk velocity, etc.
Figure 2 shows the power-law fits of the energetic particle fluxes for the shock crossing of 23 April 2002. The fits appear to be satisfactory and the slope β is given in each panel. These results, together with the statistical error of the fits, are summarized for this and for the other events in Table 1, together with some shock parameters. The values of β <1 imply a superdiffusive regimes with α>1 (Perri and Zimbardo, 2007, 2008), so we can say that for this shock the transport of energetic particles is clearly superdiffusive.
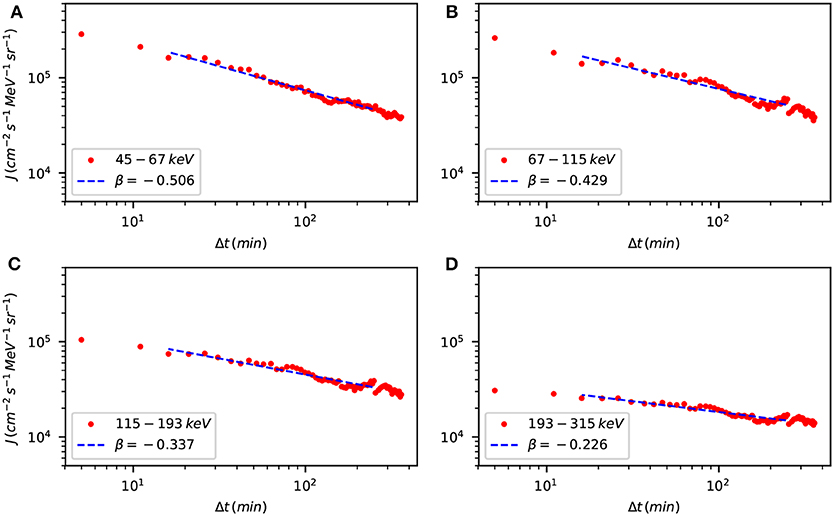
Figure 2. Power-law fits (dashed lines) of the energetic particle fluxes (red dots) in several energy channels, see legends, for the shock crossing of 23 April 2002. The exponent of power-law fit is indicated in legend. The panels correspond to the energy channels (A) 45–67 keV, (B) 67–115 keV, (C) 115–193, and (D) 193–315 keV.
For this shock, the upstream shock normal angle is given by in the ACE shock list, so that this shock could be considered quasi-perpendicular; however, is not very different from the limiting angle of which separates quasi-perpendicular from quasi-parallel shocks, and because of the fluctuations in the upstream magnetic field direction, it is possible the shock normal angle at the shock is frequently changing from larger to smaller than 45°, so that we prefer to classify this shock as oblique. One can imagine that there are times when reflected thermal plasma particles propagate upwind to form the ion foreshock, and times when they do not. Anyway, energetic particles accelerated at the shock can easily propagate upstream by means of diffusion or superdiffusion parallel to the average magnetic field, provided that they are fast enough to overcome the solar wind advection speed. Figure 3 shows, from top to bottom, the energetic particle fluxes and the other shock parameters (same format as Figure 1). This event exhibits a non-exponential profile of energetic particles and a nearly constant level of resonant magnetic fluctuations upstream of the shock, therefore we assume that transport is superdiffusive, too. We also point out a flattening of the energetic particle fluxes upstream of the shock at about 90–150 min before the shock crossing, which correlates well with a nearly-transverse-to-the-radial-direction (ψ~90°) solar wind magnetic field.
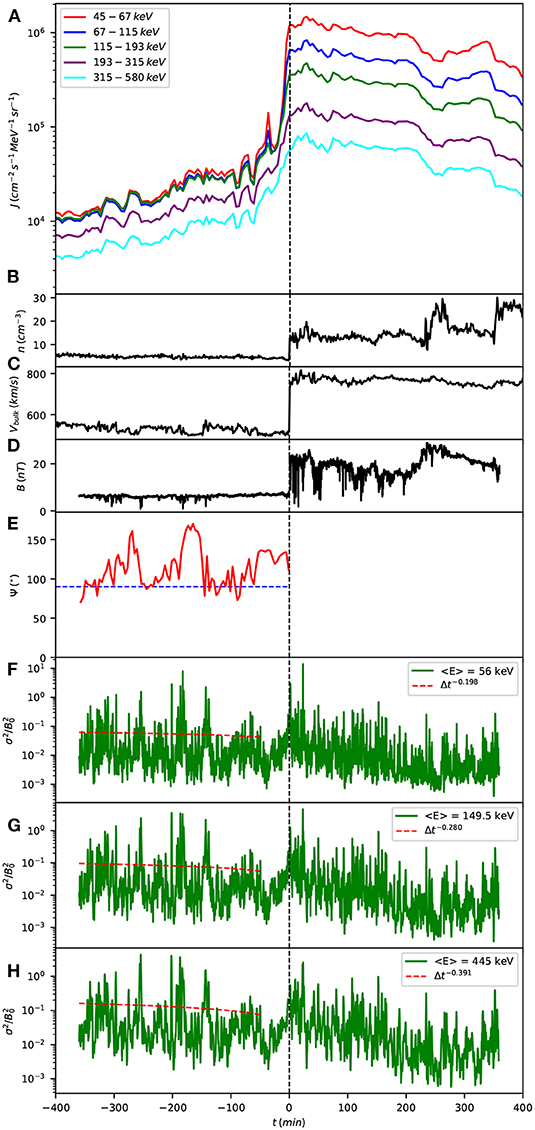
Figure 3. Same as Figure 1 but for the ACE shock crossing of 8 June 2000. The shock normal angle was .
Figure 4 shows the power-law fits of the energetic particle fluxes for this shock crossing, again showing β <1 (see also Table 1) and correspondingly superdiffusion. For this event, the exponent β depends very weakly on energy, at variance with the behavior found for the other two cases. Further analyses are needed to understand this finding.
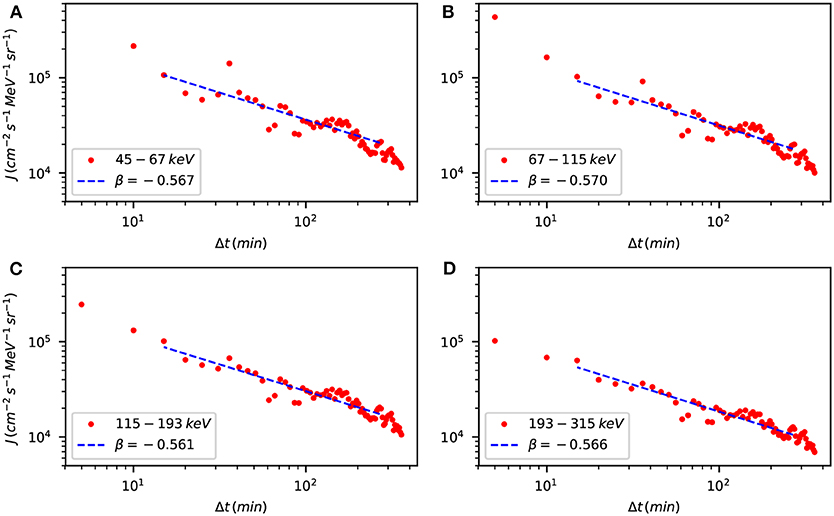
Figure 4. Power-law fits (dashed lines) of the energetic particle fluxes (red dots) in several energy channels, see legends, for the shock crossing of 8 June 2000. The exponent of power-law fit is indicated in each legend. The panels correspond to the energy channels (A) 45–67 keV, (B) 67–115 keV, (C) 115–193, and (D) 193–315 keV.
For this shock, the upstream shock normal angle is given by in the ACE shock list, so that this shock is quasi-perpendicular: this means that the thermal plasma particles which are reflected at the shock do not propagate upwind but rather re-enter the shock after gyrating in the upstream magnetic field. Conversely, energetic particles accelerated at the shock can still propagate upstream by means of diffusion or superdiffusion parallel to the average magnetic field. This is possible if the particle speed along the radial direction toward upstream is larger than the solar wind velocity in the shock frame : indeed, an energetic particle of speed v and pitch-angle cosine μ can propagate toward upstream if , otherwise the particle is convected downstream. Since we are considering particles with energies in the range 47–580 keV, the corresponding proton speeds are in the range 3,000–10,600 km/s so that a large number of accelerated particles can propagate upstream. Figure 5 shows, from top to bottom, the energetic particle fluxes and the other data (same format as Figure 1). This event, too, exhibits clearly non-exponential profiles of energetic particle fluxes and nearly constant level of upstream magnetic fluctuations. Farther upstream than about 130 min before the shock crossing, the energetic particle fluxes in the energy channels from 67–115 to 315–580 keV are nearly equal, a fact that is reminiscent of the properties of the shock events considered by Lario et al. (2018). Instead, nearly 40 min before the shock crossing a strong decrease is observed in all the energy channels: this decrease correlates well with the fact that in this time period the solar wind magnetic field was nearly transverse to the radial direction (see Figure 5E). As explained above, we make the profile fits on periods larger than that of typical local variations, in order to average out the changes in the magnetic field orientation.
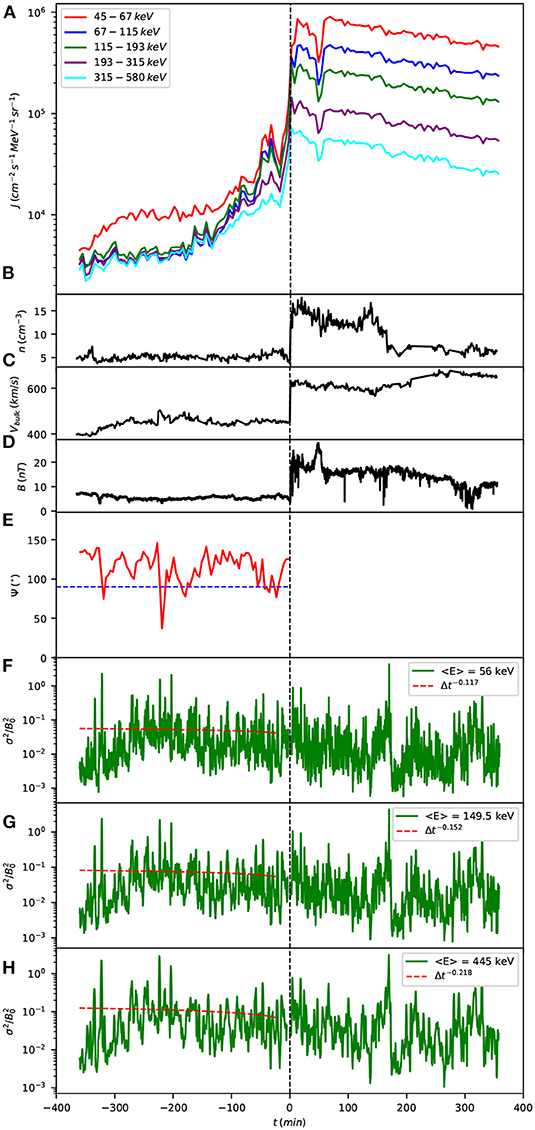
Figure 5. Same as Figure 1 but for the ACE shock crossing of 26 August 1998. The shock normal angle was .
Figure 6 shows the power-law fits of the energetic particle fluxes for this shock crossing. For this event, although the upstream flux decay is well fitted by a power-law, the exponent β≥1 for the energy channels from 45–67 to 115–193 keV, implying that transport is diffusive (normal) (see Perri and Zimbardo, 2008). Instead, for the 193–315 and the 315–580 keV channels β <1, implying superdiffusive transport. Further, we notice that similar to the quasi-parallel shock of 23 April 2002, the exponent β exhibits a tendency to decrease with the increase of energy, although some irregularity is also present in such a trend.
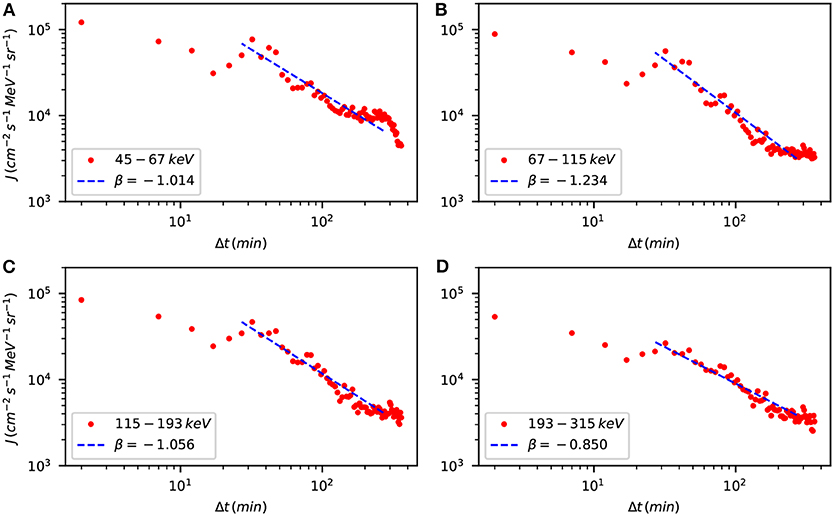
Figure 6. Power-law fits (dashed lines) of the measured energetic particle fluxes (red dots) in several energy channels, see legends, for the shock crossing of 26 August 1998. The exponent of power-law fit is indicated in each legend. The panels correspond to the energy channels (A) 45–67 keV, (B) 67–115 keV, (C) 115–193, and (D) 193–315 keV.
In this paper we have studied the transport of energetic particles accelerated at three different shock events observed in the solar wind by the ACE spacecraft at the Lagrangian point L1. The transport regime is deduced from the shape of the energetic particle profiles upstream of the shock, and for these events the profiles are well fitted by power-laws. This corresponds to a superdiffusive transport with the anomalous diffusion exponent α = 2−β when β <1, and to normal diffusion when β≥1. Therefore, the study of the energetic particle profile is an effective tool to unravel the transport properties.
We note that we have found superdiffusion for the quasi-parallel shock and the oblique shock, while for the quasi-perpendicular shock normal diffusion is found for the three lowest energy channels, and superdiffusion only for the two highest energy channels. From the values of β and α that we obtained and that are reported in Table 1, although there are some irregular variations, we can identify the following trends: (i) the larger the particle energy, the stronger is the superdiffusive behavior (larger α) (at least for the considered quasi-parallel and the quasi-perpendicular shocks); (ii) the larger the shock normal angle θBn, the weaker the superdiffusive behavior (smaller α), to the extent that normal diffusion is also found for the quasi-perpendicular shock.
Here, we tentatively propose some possible explanations for the trends (i) and (ii) outlined above. For (i), we can remember that in the case of normal diffusion, the diffusion coefficient is expected to grow with energy E. For instance, quasi-linear theory in the presence of a Kolmogorov spectrum of magnetic fluctuations predicts for non relativistic particles (e.g., Giacalone, 2012; Blasi, 2013). In the case of superdiffusive transport, we can see that the exponent of superdiffusion α grows with energy, rather than the anomalous diffusion coefficient. This finding suggests that the pitch-angle scattering due to magnetic fluctuations corresponds to a flatter probability distribution, the larger the particle energy (Perri and Zimbardo, 2012a; Perri et al., 2019), a suggestion which calls for theoretical investigations.
For (ii), we recall that a number of numerical studies of particle transport in the presence of magnetic turbulence find that transport parallel to the average magnetic field direction can be superdiffusive or normal, depending on parameters like the turbulence level and the turbulence anisotropy, while transport perpendicular to the average magnetic field can be either subdiffusive or normal (Zimbardo et al., 2006; Pommois et al., 2007; Shalchi and Kourakis, 2007). A recent study with a very extended turbulence spectrum also finds that parallel transport can be diffusive while perpendicular transport can be subdiffusive (Pucci et al., 2016). Then, we consider that the mean square displacement of particles in the direction x perpendicular to the shock surface can be expressed as (e.g., Perri and Zimbardo, 2015). Since parallel transport is usually faster than perpendicular transport, even in the diffusive cases (e.g., Giacalone and Jokipii, 1999), for small to intermediate values of θBn it is possible to find superdiffusion. Conversely, when θBn is close to 90° parallel transport is mostly along the shock surface and the propagation upstream of the shock relays on perpendicular transport, which may be normal diffusive or subdiffusive. Our results show that when going from a quasi-parallel shock to a quasi-perpendicular shock there is a gradual change in the transport regime from superdiffusive to normal, and this can be considered as an experimental validation of the numerical results on transport reported in Zimbardo et al. (2006), Pommois et al. (2007), and Shalchi and Kourakis (2007). Another effect which should be taken into account is the velocity filtering due the quasi-transverse magnetic field which can make more difficult for particles to propagate upstream. An energetic particle of speed v and pitch-angle cosine μ can propagate toward upstream if , otherwise the particle is convected downstream. For a fixed energy and assuming an isotropic pitch-angle distribution, the more θBn approaches 90°, the harder is for particles to propagate upstream. However, the larger v, the less stringent is this condition, resulting in an effective velocity filtering; apparently, this is also going to influence the transport regime, decreasing the value of the exponent β, so that an appropriate modeling is required here, too.
It is important to remark that, in all of the considered shocks, the level of magnetic fluctuations in resonance with particles having the energies under study do not appear to change with the upstream shock distance, see also the dashed red lines in Figures 1F–H, 3F–H, 5F–H. This means that there is not an effect of magnetic fluctuation amplification due to instabilities excited by the conterstreaming energetic particles, not even in the case of the quasi-parallel shock. These observations are at variance with the common belief that magnetic fluctuations are amplified upstream of the shock: while this can be true, and is sometimes observed, for stronger shocks which accelerate a larger number of particles, it is not true for the present events, irrespective of the shock normal angle. Therefore, particle pitch-angle scattering is provided solely by the magnetic turbulence normally present in the solar wind; this indicates that such turbulence is capable of inducing superdiffusive, multiple-scale transport in the direction parallel to the background magnetic field. We suggest that studies of SEP propagation aiming at space weather predictions should consider this possibility. We also notice that the sharp decrease in the intensity of energetic particles, which is observed for many shock crossing when going from downstream to upstream, cannot be ascribed to a locally enhanced level of magnetic fluctuations which would confine particles close to the shock, since such enhancement is not observed. We consider instead that this is due to the multi-scale character of superdiffusive transport (Perri et al., 2019), see for instance the energetic particle profiles obtained by Prete et al. (2019); indeed, superdiffusion is a transport regime due to the simultaneous presence of short and long free paths, with a power-law probability distribution of free path lengths: the long free paths contribute to the far upstream power-law decay of the energetic particle profiles, and the short free paths contribute to the steep decrease in the intensity just in front of the shock.
Finally, we notice that there are many shock events measured by spacecraft, so this is just an initial study about the influence of the shock normal angle on the transport properties of energetic particles. Therefore, at this moment our results cannot be considered to be general, even though we have analyzed three other events which show a similar behavior for the dependence of β on the shock normal angle and the energy (not shown). Indeed, each shock crossing event is different from the others, also because the differences in the levels and properties of upstream waves, which may include ultra low frequency waves and sometimes whistler waves. Thus, a much larger number of cases has to be studied in order to reach a comprehensive understanding of energetic particle transport upstream of shocks. Once the method of analysis has been established, a more systematic study will be carried out.
The datasets analyzed for this study can be found in the CDAWeb service of NASA at https://cdaweb.gsfc.nasa.gov/index.html/ and in the Advanced Composition Explorer (ACE) University of New Hampshire shock list at http://www.ssg.sr.unh.edu/mag/ace/ACElists/obs_list.html.
GZ wrote the manuscript. GP and SP carried out the data analysis. All authors participated in the research design and in the interpretation of the results.
This work has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 776262 (AIDA, www.aida-space.eu). The research by GP acknowledges POR Calabria FSE/FESR 2014-2020 for financial support.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We would like to thank D. Burgess, J. Giacalone, and D. Trotta for useful discussions.
Amato, E. (2014). The origin of galactic cosmic rays. Int. J. Modern Phys. D 23:1430013. doi: 10.1142/S0218271814300134
Bieber, J. W., Matthaeus, W. H., Smith, C. W., Wanner, W., Kallenrode, M.-B., and Wibberenz, G. (1994). Proton and electron mean free paths: the palmer consensus revisited. Astrophys. J. 420, 294–306. doi: 10.1086/173559
Blasi, P. (2013). The origin of galactic cosmic rays. Astron. Astrophys. Rev. 21:70. doi: 10.1007/s00159-013-0070-7
Burgess, D. (1989). Cyclic behavior at quasi-parallel collisionless shocks. Geophys. Res. Lett. 16, 345–348. doi: 10.1029/GL016i005p00345
Giacalone, J. (2012). Energetic charged particles associated with strong interplanetary shocks. Astrophys. J. 761:28. doi: 10.1088/0004-637X/761/1/28
Giacalone, J. (2013). Cosmic-ray transport and interaction with shocks. Space Sci. Rev. 176, 73–88. doi: 10.1007/s11214-011-9763-2
Giacalone, J., and Decker, R. (2010). The origin of low-energy anomalous cosmic rays at the solar-wind termination shock. Astrophys. J. 710, 91–96. doi: 10.1088/0004-637X/710/1/91
Giacalone, J., and Jokipii, J. (1999). The transport of cosmic rays across a turbulent magnetic field. Astrophys. J. 520, 204. doi: 10.1086/307452
Hoppe, M. M., Russell, C. T., Frank, L. A., Eastman, T. E., and Greenstadt, E. W. (1981). Upstream hydromagnetic waves and their association with backstreaming ion populations - ISEE 1 and 2 observations. J. Geophys. Res. 86, 4471–4492. doi: 10.1029/JA086iA06p04471
Kennel, C. F., and Petschek, H. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71, 1–28. doi: 10.1029/JZ071i001p00001
Lario, D., Berger, L., Wilson, L. B. I., Decker, R. B., Haggerty, D. K., Roelof, E. C., et al. (2018). “Flat proton spectra in large solar energetic particle events,” in The 17th Annual International Astrophysics Conference, Journal of Physics Conference Series, Vol. 1100 (Santa Fe, NM). doi: 10.1088/1742-6596/1100/1/012014
Lazarian, A., and Yan, H. (2014). Superdiffusion of cosmic rays: implications for cosmic ray acceleration. Astrophys. J. 784:38. doi: 10.1088/0004-637X/784/1/38
Lembége, B., Yang, Z., and Zank, G. P. (2020). Energy power spectra measured at an interplanetary shock by the New Horizon's SWAP experiment: 1D full particle simulations versus observations. Astrophys. J. 890, 1–8. doi: 10.3847/1538-4357/ab65c5
Lobzin, V. V., Krasnoselskikh, V. V., Bosqued, J.-M., Pinçon, J.-L., Schwartz, S. J., and Dunlop, M. (2007). Nonstationarity and reformation of high-Mach-number quasiperpendicular shocks: cluster observations. Geophys. Res. Lett. 34:L05107. doi: 10.1029/2006GL029095
Matthaeus, W., Qin, G., Bieber, J., and Zank, G. (2003). Nonlinear collisionless perpendicular diffusion of charged particles. Astrophys. J. Lett. 590:L53. doi: 10.1086/376613
Moraal, H. (2013). Cosmic-ray modulation equations. Space Sci. Rev. 176, 299–319. doi: 10.1007/s11214-011-9819-3
Morlino, G., Amato, E., Blasi, P., and Caprioli, D. (2010). Spatial structure of X-ray filaments in SN 1006. Mon. Notices R. Astron. Soc. 405, L21–L25. doi: 10.1111/j.1745-3933.2010.00851.x
Neugebauer, M., Giacalone, J., Chollet, E., and Lario, D. (2006). Variability of low-energy ion flux profiles on interplanetary shock fronts. J. Geophys. Res. 111:A12107. doi: 10.1029/2006JA011832
Otsuka, F., Matsukiyo, S., and Hada, T. (2019). PIC Simulation of a quasi-parallel collisionless shock: interaction between upstream waves and backstreaming ions. High Energy Dens. Phys. 33:100709. doi: 10.1016/j.hedp.2019.100709
Perri, S. (2018). Superdiffusion of relativistic electrons at supernova remnant shocks. Plasma Phys. Control. Fus. 60:014005. doi: 10.1088/1361-6587/aa8602
Perri, S., Amato, E., and Zimbardo, G. (2016). Transport of relativistic electrons at shocks in shell-type supernova remnants: diffusive and superdiffusive regimes. Astron. Astrophys. 596:A34. doi: 10.1051/0004-6361/201628767
Perri, S., Pucci, F., Malara, F., and Zimbardo, G. (2019). On the power-law distribution of pitch-angle scattering times in solar wind turbulence. Solar Phys. 294:34. doi: 10.1007/s11207-019-1421-y
Perri, S., and Zimbardo, G. (2007). Evidence of superdiffusive transport of electrons accelerated at interplanetary shocks. Astrophys. J. Lett. 671, L177–L180. doi: 10.1086/525523
Perri, S., and Zimbardo, G. (2008). Superdiffusive transport of electrons accelerated at corotating interaction regions. J. Geophys. Res. 113:A03107. doi: 10.1029/2007JA012695
Perri, S., and Zimbardo, G. (2009). Ion superdiffusion at the solar wind termination shock. Astrophys. J. Lett. 693, L118–L121. doi: 10.1088/0004-637X/693/2/L118
Perri, S., and Zimbardo, G. (2012a). Magnetic variances and pitch-angle scattering times upstream of interplanetary shocks. Astrophys. J. 754:8. doi: 10.1088/0004-637X/754/1/8
Perri, S., and Zimbardo, G. (2012b). Superdiffusive shock acceleration. Astrophys. J. 750:87. doi: 10.1088/0004-637X/750/2/87
Perri, S., and Zimbardo, G. (2015). Short acceleration times from superdiffusive shock acceleration in the heliosphere. Astrophys. J. 815:75. doi: 10.1088/0004-637X/815/1/75
Pommois, P., Zimbardo, G., and Veltri, P. (2007). Anomalous, non-Gaussian transport of charged particles in anisotropic magnetic turbulence. Phys. Plasmas 14:012311. doi: 10.1063/1.2434795
Prete, G., Perri, S., and Zimbardo, G. (2019). Influence of the transport regime on the energetic particle density profiles upstream and downstream of interplanetary shocks. Adv. Space Res. 63, 2659–2671. doi: 10.1016/j.asr.2019.01.002
Pucci, F., Malara, F., Perri, S., Zimbardo, G., Sorriso-Valvo, L., and Valentini, F. (2016). Energetic particle transport in the presence of magnetic turbulence: influence of spectral extension and intermittency. Mon. Notices R. Astron. Soc. 459, 3395–3406. doi: 10.1093/mnras/stw877
Reames, D. V. (1999). Particle acceleration at the sun and in the heliosphere. Space Sci. Rev. 90, 413–491. doi: 10.1023/A:1005105831781
Shalchi, A. (2015). Perpendicular diffusion of energetic particles in collisionless plasmas. Phys. Plasmas 22:010704. doi: 10.1063/1.4906359
Shalchi, A., and Kourakis, I. (2007). A new theory for perpendicular transport of cosmic rays. Astron. Astrophys. 470, 405–409. doi: 10.1051/0004-6361:20077260
Sioulas, N., Isliker, H., Vlahos, L., Koumtzis, A., and Pisokas, T. (2020). Superdiffusive stochastic Fermi acceleration in space and energy. Mon. Notices R. Acad. Soc. 491, 3860–3869. doi: 10.1093/mnras/stz3259
Veltri, P., and Zimbardo, G. (1993a). Electron-whistler interaction at the Earth's bow shock: 1. Whistler instability. J. Geophys. Res. 98, 13325–13334. doi: 10.1029/93JA00812
Veltri, P., and Zimbardo, G. (1993b). Electron-whistler interaction at the Earth's bow shock: 2. Electron pitch angle diffusion. J. Geophys. Res. 98, 13335–13346. doi: 10.1029/93JA01144
Wang, Y., Qin, G., Zhang, M., and Dalla, S. (2014). A numerical simulation of solar energetic particle dropouts during impulsive events. Astrophys. J. 789:157. doi: 10.1088/0004-637X/789/2/157
Webb, G., Zank, G., Kaghashvili, E. K., and Le Roux, J. (2006). Compound and perpendicular diffusion of cosmic rays and random walk of the field lines. I. parallel particle transport models. Astrophys. J. 651:211. doi: 10.1086/507415
Zimbardo, G. (2005). Anomalous particle diffusion and lévy random walk of magnetic field lines in three-dimensional solar wind turbulence. Plasma Phys. Control. Fus. 47:B755. doi: 10.1088/0741-3335/47/12B/S57
Zimbardo, G., and Perri, S. (2013). From lévy walks to superdiffusive shock acceleration. Astrophys. J. 778:35. doi: 10.1088/0004-637X/778/1/35
Zimbardo, G., Perri, S., Pommois, P., and Veltri, P. (2012). Anomalous particle transport in the heliosphere. Adv. Space Res. 49, 1633–1642. doi: 10.1016/j.asr.2011.10.022
Keywords: space plasmas, collisionless shocks, heliosphere, anomalous transport, energetic particles, superdiffusion
Citation: Zimbardo G, Prete G and Perri S (2020) Collisionless Shocks as a Diagnostic Tool for Understanding Energetic Particle Transport in Space Plasmas. Front. Astron. Space Sci. 7:16. doi: 10.3389/fspas.2020.00016
Received: 28 January 2020; Accepted: 03 April 2020;
Published: 30 April 2020.
Edited by:
Michael Gedalin, Ben-Gurion University of the Negev, IsraelReviewed by:
Zhongwei Yang, National Space Science Center (CAS), ChinaCopyright © 2020 Zimbardo, Prete and Perri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gaetano Zimbardo, Z2FldGFuby56aW1iYXJkb0BmaXMudW5pY2FsLml0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.