Cosmology With Quasars: Predictions for eROSITA From a Quasar Hubble Diagram

The effort for understanding the matter and energy content of the Universe and its evolution relies on different probes, such as cosmic background radiation, cluster lensing, supernovae. Yet, we are still far from grasping what dark matter is made of, and what the physical origin of dark energy is. Our group has developed a technique that makes use of the observed non-linear relation between the ultraviolet and the X-ray luminosity in quasars to provide an independent measurement of their distances, thus turning quasars into standardizable candles. This technique, at present, it is mostly based upon quasar samples with data from public catalogs both in the X-rays and in the optical/ultraviolet and extends the Hubble diagram of supernovae to a redshift range still poorly explored (z > 2). From the X-ray perspective, we are now on the eve of a major change, as the upcoming mission eROSITA is going to provide us with up to ~3 millions of active galactic nuclei across the entire sky. Here we present predictions for constraining cosmological parameters, such as the amount of dark matter (Ω_m), dark energy (Ω_Λ) and the evolution of the equation of state of dark energy (w) through the Hubble diagram of quasars, based on the 4-years eROSITA all-sky survey. Our simulations show that the eROSITA quasars, complemented by redshift and broad-band photometric information, will supply the largest quasar sample at z < 2, but with very few objects available for cosmology at higher redshifts that survives the cut for the Malmquist bias, as eROSITA will sample the brighter end of the X-ray luminosity function. The power of the quasar Hubble diagram for precision cosmology lies in the high-redshift regime, where quasars can be observed up to redshift ~7.5, essential to discriminate amongst different model extrapolations. Therefore, to be competitive for cosmology, the eROSITA quasar Hubble diagram must be complemented with the already available quasar samples and dedicated (deep) large programmes at redshift z > 3.

1. Introduction

The driving forces behind the present era of precision cosmology have been the detection of anisotropies in the cosmic microwave background (CMB; e.g., Smoot et al., 1992) and the discovery of the accelerated expansion of the Universe, based on the Hubble diagram (i.e., the distance modulus vs. redshift relation) of Type Ia supernovae (SNe Ia), the standard candles par excellence (e.g., Riess et al., 1998; Perlmutter et al., 1999). The currently accepted parameterization of our Universe is based on the so-called Λ Cold Dark Matter (ΛCDM) model, hinging upon the existence of cold dark matter and on the cosmological constant (Λ). The nucleosynthesis of primordial elements, the large-scale galaxy distribution, and gravitational lensing are some of the usual probes into the nature of dark matter, and into how this interacts with visible (baryonic) matter. Yet, we are still far from grasping what the real constituents of this invisible cosmic ingredient are. Moreover, both the physical origin and the properties of dark energy are still unknown, as the interpretation of Λ is plagued by the extreme degree of fine tuning required to obtain the right amount of dark energy observed today. Only the combination of multiple perspectives and of the optimal cosmological probes at different redshifts is the way forward to solve the dark matter and dark energy problems.

In the past years, our group has developed a technique that makes use of the observed non-linear relation between the optical/ultraviolet and the X-ray luminosity in quasars (e.g., Steffen et al., 2006; Just et al., 2007; Lusso et al., 2010; Lusso and Risaliti, 2016). In contrast to previous ideas of high stochasticity, this relation can be employed to standardize the emission of quasars (Risaliti and Lusso, 2015; Lusso et al., 2019). The methodology is complementary to the traditional resort to Type Ia SNe to estimate the cosmological parameters, yet it extends the Hubble diagram to a redshift range currently inaccessible to supernovae (z = 2−6). The tightness of the UV-to-X-ray relation across both a wide redshift (up to z ≃ 5 − 6) and luminosity range (see Lusso and Risaliti, 2016) must be the manifestation of a universal physical mechanism that governs the disc-corona synergy in the quasar engines, yet the details of the physical process originating this relation is still unknown (e.g., Lusso and Risaliti, 2017).

The main result of our work is that the distance modulus/redshift relation of quasars at z < 1.4 is in agreement with that of supernovae and with the concordance model (Risaliti and Lusso, 2015; Lusso et al., 2019). Yet, a deviation from the ΛCDM model emerges at higher redshift, with a statistical significance of 4σ. If we consider an evolution of the dark energy equation of state in form w(z) = w₀ + w_a × z/(1 + z), the data suggest that the dark energy density is increasing with time (Lusso et al., 2019; Risaliti and Lusso, 2019).

In order to build a quasar sample that can be utilized for cosmological purposes, both X-ray and optical/UV data are required to cover the rest-frame 2 keV and the 2,500 Å. At the time of writing, the most extended spectroscopic coverage in the optical/UV is provided by the Sloan Digital Sky Survey (Pâris et al., 2018), which supplies more than ~500,000 quasars with spectroscopic redshift up to z ~ 7. This sample needs to be cross-matched with the current X-ray catalogs, namely the Chandra CXC2.0¹ (Evans et al., 2010) and the 3XMM Data Release 8² (Rosen et al., 2016), which contain all the X-ray sources detected by the XMM-Newton and Chandra observatories that are publicly available in the archives. The number of quasars with a detection in both the UV and X-rays ranges from about a few thousands to ~13,000, respectively. Once our filtering criteria are applied to select blue quasars with low levels of UV reddening and X-ray absorption and the Malmquist bias is corrected (the interested reader should refer to Risaliti and Lusso, 2015, 2019; Lusso and Risaliti, 2016; Bisogni et al., 2017 for details on the sample selection), the final samples drastically reduce to <2,000 objects (~1,000 in the case of SDSS-CXC2.0, Bisogni et al., in preparation). Our leverage in building extended quasar samples for cosmology is thus entirely based upon archival data of pointed X-ray observations, which cover a very limited portion of the sky compared to SDSS, i.e., roughly 1,000 deg² for both 3XMM-DR8 and CXC2.0 compared to >14,000 deg² for SDSS.

We are now on the eve of the next major revolution in the field of X-ray astrophysics. The extended Roentgen Survey with an Imaging Telescope Array (eROSITA, Merloni et al., 2012; Predehl, 2012) is the flagship instrument of the Russian Spektrum-Roentgen-Gamma (SRG) mission, and it will represent the most powerful and versatile X-ray observatory of the next decade. In the first 4 years of scientific operations, eROSITA will perform 8 deep scans of the entire sky, one every 6 months. When completed, the survey will be ~20 times deeper than ROSAT at 0.5–2 keV, and it will provide the very first sensitive imaging of the whole sky in the hard band (2–10 keV). eROSITA will bring an improvement of over two orders of magnitude in the number of sources shining close to or above the break in the X-ray luminosity function (i.e., Figure 5.2.2 in Merloni et al., 2012). eROSITA's sky will be dominated by the active galactic nuclei (AGN) population, with ~3 million AGN expected by the end of the nominal 4-years all-sky survey at the sensitivity of $F_{0.5-2\text{keV}}\simeq 10^{-14}$ erg s⁻¹ cm⁻² and with a median redshift of z ~ 1.

In this work we discuss the potential of the 4-years eROSITA all-sky survey for constraining cosmological parameters, such as Ω_m, Ω_Λ and w, through the Hubble diagram of quasars.

2. The Simulated eROSITA Quasar Sample

The SDSS-DR14 quasar catalog contains 526,356 objects with 0.008 < z < 6.968. We first selected a clean quasar sample in the optical/UV based on the selection criteria discussed in depth in our previous works (Risaliti and Lusso, 2015, 2019; Lusso and Risaliti, 2016). The main goal of this first step is to obtain the intrinsic flux at the rest-frame 2,500 Å. We excluded all quasars flagged as broad absorption line (BAL, BI_CIV=0) and selected only the sources with a detection in all SDSS photometric bands, leading to a preliminary sample of 503,746 quasars. The SDSS-DR14 quasar catalog also provides us with multi-wavelength information from several surveys, from the radio (FIRST survey) to the UV (GALEX survey; see section 7 in Pâris et al., 2018). Thanks to this extended multi-band coverage, we built the spectral energy distributions (SEDs) that are then employed to compute the slope Γ₁ of a log(ν)−log(νFν) power law in the 0.3–1 μm (rest frame) range, and the analogous slope Γ₂ in the 0.3–0.145 μm range (rest frame). We assumed a standard SMC extinction law (Prevot et al., 1984, appropriate for unobscured quasars, Hopkins et al., 2004; Salvato et al., 2009) to estimate the Γ₁ − Γ₂ correlation as a function of extinction [parameterized by E (B–V)]. The Γ₁ − Γ₂ value that corresponds to zero extinction (E(B–V) = 0) is derived from the standard quasar SED of Richards et al. (2006, i.e., Γ₁ = 0.82, Γ₂ = 0.40). We then selected all objects within a circle centered at E(B–V) = 0 with a radius of 0.8 (i.e., E(B-V)<0.1). From the SED we also calculated the flux at the rest-frame 2,500 Å (F₂₅₀₀) and the one at 6 cm from the FIRST flux using a slope of −0.8, and we further excluded all the objects with F_{6 cm}/F₂₅₀₀ > 10. We also excluded all quasars in the sample defined as radio loud in the MIXR catalog (Mingo et al., 2016) within a matching radius of 2 arcsec. This leads to a final clean sample in the UV of 291,944 quasars, within a redshift interval 0.061 < z < 5.25 (〈z〉 ≃ 1.8).

Since eROSITA is expected to survey the entire X-ray sky down to a flux that well matches the SDSS quasar optical magnitudes, we forecast that almost all SDSS quasars will be detected by eROSITA (Menzel et al., 2016). We thus simulated an X-ray flux measurement for each object as follows.

We assumed the observed linear log F_{2 keV} − log F₂₅₀₀ relation, with a slope α = 0.6, a flat ΛCDM cosmology with H₀ = 70 km s⁻¹ Mpc⁻¹, Ω_m = 0.3 and Ω_Λ = 1 − Ω_m, and a dispersion in the F_{2 keV} − F₂₅₀₀ relation on the order of 0.1 dex. These values have been chosen to be representative of the mainstream models, although we know that the constraints on the cosmological parameters from observations in the local and in the early Universe are somewhat different (see section 4.1). We started from fluxes as they are cosmology independent, and we have demonstrated in our previous works that the log F_{2 keV} − log F₂₅₀₀ relation in narrow redshift bins displays the same slope (i.e., γ ≃ 0.6) across a wide redshift range (see Figure 8 in Risaliti and Lusso, 2019, Supplementary Material). Moreover, the main aim of our simulations is to quantify the expected uncertainties on the cosmological parameters rather than focus on the absolute values per se. As such, we defer possible extensions of these simulations to non-standard cosmological values and to a possible evolution of these parameters with redshift to future works.

As the eROSITA survey is flux limited, we also need to take into account the Malmquist bias (also known as the Eddington bias), which is a redshift dependent correction. We conservatively assumed an observed flux limit in the soft X-ray band of 3 × 10⁻¹⁴ erg s⁻¹ cm⁻², which will be reached after the first year of operations, and considered all the sources with an expected monochromatic flux at 2 keV that corresponds to about twice the value above, i.e., 5 × 10⁻³² erg s⁻¹ cm⁻² Hz⁻¹, assuming a photon index of 1.9. This selection leaves very few sources at redshift higher than 2. We obtain a final sample of ~11,000 quasars in the redshift range 0.061−2.850, with a mean redshift 〈z〉 ≃ 0.64, consistent with the predicted statistical properties based on the best available redshift-dependent AGN X-ray luminosity function (Kolodzig et al., 2013).

3. Results

The distance modulus-redshift relation of the eROSITA quasars is presented in Figure 1 with 1σ uncertainties. The error bars on the distance modulus values for the quasar sample are estimated by propagating the uncertainties on the slope γ, F_{2 keV} and F₂₅₀₀. We assumed typical uncertainties on the slope and F_{2 keV} of 0.02 and 20%, respectively. Uncertainties on F₂₅₀₀ are computed by propagating the magnitude uncertainties from the SEDs we compiled for each SDSS quasar in the catalog (see section 2 in Risaliti and Lusso, 2019, Supplementary Material). The red points are the mean (also with 1σ uncertainties) of the distance modulus in narrow redshift bins for quasars (shown for visualization purposes). Here we also show the SNe Ia sample from the Pantheon survey consisting of 1,048 objects ranging from 0.01 < z < 2.26 (Scolnic et al., 2018). The dashed magenta line shows the input flat ΛCDM cosmology with Ω_m = 0.3 and Ω_Λ = 0.7.

FIGURE 1

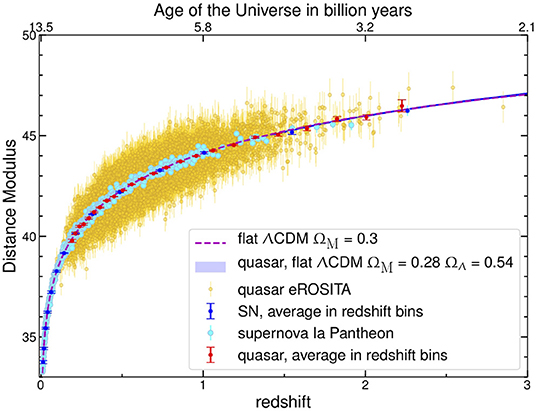
Figure 1. Hubble diagram of eROSITA quasars (~11,000, yellow points) and SNe Ia (Pantheon, cyan points) with 1σ uncertainties. Red points are the mean (also with 1σ uncertainties) of the distance modulus in narrow redshift bins for quasars only (shown for visualization purposes). The dashed magenta line shows a flat ΛCDM model fit with Ω_m = 0.3. The blue line is the best MCMC fit of the eROSITA quasars (with uncertainties) only for a ΛCDM cosmology where Ω_m and Ω_Λ are left free to vary (section 3).

We then fitted to this sample a ΛCDM model where Ω_m and Ω_Λ are left free to vary, and a model with a dark energy equation of state parameter w (assuming a flat Universe, wCDM). The results are shown in Figure 2, whilst a summary of the predictions on the cosmographic parameters from the analysis of the eROSITA quasar Hubble diagram is presented in Table 1. The confidence contours are at 68 and 95% levels and all the plotted uncertainties are statistical, computed from the marginalized posterior probability distributions. All the simulations have been performed through a standard fully Bayesian procedure by making use of the affine invariant Monte Carlo Markov Chain ensemble sampler (Foreman-Mackey et al., 2013). We adopted uniform priors on the cosmological parameters with 0 < Ω_m < 1.2 and 0 < Ω_Λ < 1.5 for the ΛCDM model, whilst we used 0 < Ω_m < 1.2 and −3 < w₀ < 1 for wCDM. The adopted likelihood also contains an intrinsic dispersion (δ) as a free parameter (see Risaliti and Lusso, 2019 for details). An additional free parameter is the cross-calibration (β′) between supernovae Ia and quasars. Overall we have four free parameters for both the ΛCDM (i.e., Ω_m, Ω_Λ, β′ and δ) and the flat wCDM (i.e., Ω_m, w₀, β′ and δ).

FIGURE 2

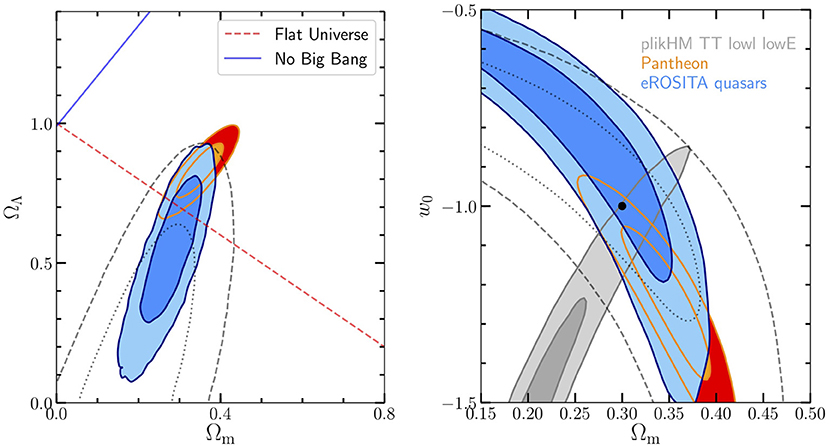
Figure 2. (Left) Confidence contours at 68 and 95% levels for the Ω_m and Ω_Λ cosmological parameters in the ΛCDM model, where both Ω_m and Ω_Λ are free to vary. All the plotted uncertainties are statistical. Orange/red contours: Pantheon. Blue/cyan: eROSITA simulated sample. (Right) Confidence contours at 68 and 95% levels for the Ω_m and w₀ cosmological parameters in the wCDM model. All the plotted uncertainties are statistical. Orange/red contours: Pantheon. Filled dark/light gray: Planck constraints from a Plik TT+lowl+lowE likelihood. Blue/cyan: eROSITA simulated sample. The dashed/dotted contours represent the constraints on the cosmological parameters of a mock eROSITA quasar sample of ~17,000 quasars assuming a dispersion in the L_{2 keV} − L₂₅₀₀ relation of 0.2 dex.

TABLE 1

Table 1. Prediction on the cosmographic parameters from the analysis of the eROSITA quasar Hubble diagram.

Our method governs the shape of the Hubble diagram, whilst to determine the absolute value of the distances we need an external calibrator to build the distance ladder (like Cepheids are for supernovae Ia).

As a consequence of the marginalization over the β′, our technique does not provide any direct constraint on the Hubble parameter, H₀. In the simulations, the value of H₀ used for the calibration with the supernovae Ia is thus assumed and then marginalized over β′. Considering a different value of H₀ would just modify the final cross-calibration with no change on the values of the best fit cosmological parameters and confidence intervals.

4. Discussion

The precision on Ω_m that can be achieved with the eROSITA quasars only is similar to that obtained today by supernovae Ia in the case Ω_m and Ω_Λ are fitted simultaneously (i.e., Ω_m = 0.35 ± 0.04, see Table 8 in Scolnic et al., 2018). The current accuracy on Ω_Λ from supernovae Ia is ~8%, whilst the precision on Ω_Λ from the simulated quasar Hubble diagram is on the order of ~30%. This is due to the much higher dispersion of the data in the quasar Hubble diagram with respect to Pantheon in the common redshift range. We also note that the assumed dispersion on the L_{2 keV} − L₂₅₀₀ relation is rather optimistic. In fact, we can obtain a dispersion of ~ 0.12 − 0.15 dex only when we consider pointed X-ray observations (see the Supplementary Material in Risaliti and Lusso, 2019), whilst the dispersion in the L_{2 keV} − L₂₅₀₀ relation that we can achieve at present is 0.2 − 0.24 dex. We also considered another mock quasar sample where we assume a dispersion of 0.2 dex, having similar statistics and redshift distribution to the one in Figure 1. The accuracy on Ω_m and Ω_Λ decreases to ~30 and ~40%, respectively. The precision on Ω_m is more affected by the increased dispersion in the L_{2 keV} − L₂₅₀₀ relation than the one on Ω_Λ. This is somewhat expected given the redshift distribution of the mock sample (see also Figure 5 in Kolodzig et al., 2013 for the statistical quasar sample predictions). The range of accuracy on w₀ for the best-case scenario and the more realistic one is shown in Figure 2 for a wCDM.

From our simulations one can conclude that, with the eROSITA quasars alone and the current observed dispersion in the L_{2 keV} − L₂₅₀₀ relation, it will be challenging to provide stringent constraints on the cosmological parameters. Nonetheless, the simulated quasar sample does not include the hundreds of quasars at redshift z > 2.5 that are already available from the public archives, which would not only improve the precision of the determination of both Ω_m and Ω_Λ, but will allow us to test with greater precision a possible evolution of the equation of state of dark energy with redshift w(z). In fact, the parameter Ω_m is partly degenerate with w_a in models with an evolving equation of state of the dark energy, w_zCDM.

Even with a dispersion on the L_{2 keV} − L₂₅₀₀ relation that matches the current ones (see Supplementary Figure 6 in Risaliti and Lusso, 2019), thanks to the much greater statistics at redshift lower than 2 offered by eROSITA, we will sample the knee of the Hubble diagram with several thousands of sources. The eROSITA sample combined to the high redshift quasars (in particular z > 3) from the archives will allow us to test models where the dark energy equation of state w is allowed to evolve with redshift.

4.1. On the Tension of the Hubble Parameter

It is clear from the left panel of Figure 2 that CMB data alone do not constrain the equation of state of dark energy, w, due to strong geometrical model degeneracies. Indeed, Planck data on their own (i.e., CMB+lensing) can only assess the equation of state with ~30% uncertainty: $w=-1.57_{-0.40}^{+0.50}$, whilst this measure becomes w = −1.04 ± 0.1 by considering a combination of Planck with Baryon Acoustic Oscillation (BAO, Aghanim et al., 2018, Planck collaboration). This value is consistent with the expected one for a cosmological constant in the standard ΛCDM model, but the comparison between the concordance cosmological parameters obtained from the different probes brings out some tensions. For example, the most recent results from Planck assuming the standard ΛCDM cosmology are in tension at the 4.4σ level with the direct measurement of the Hubble parameter (H₀, which measures the current expansion rate of the Universe) from Cepheids plus supernovae Ia (Riess et al., 2019), and at about 2.5σ with the matter density estimates from supernovae Ia (e.g., Rest et al., 2014) and with the Lyα BAO measurements (e.g., Font-Ribera et al., 2014; Delubac et al., 2015). Recently, results on H₀ (assuming a standard flat ΛCDM cosmology) from six multiple-imaged quasar systems through strong gravitational lensing have confirmed this tension at more than 5σ level with respect to Planck (H0LiCOW collaboration; Wong et al., 2019). Whilst the reason for these tensions can be partially alleviated by accounting for the systematics in the different data sets (e.g., dependence of the supernovae Ia luminosity on age, Kang et al., 2020), most of the discrepancy still remains unclear. In fact, within the ΛCDM framework, where w is assumed to be constant (w = −1) across the cosmic time, there should be no difference between the H₀ value measured locally and the one measured in the early Universe. These discrepancies can in fact be the indication of new physics beyond the standard ΛCDM cosmology.

Our technique does not provide constraints on H₀ since this parameter is degenerate with the absolute cross-calibration of the Hubble diagram. Nonetheless, if we could confirm with high accuracy that w indeed evolves with time (see Zhao et al., 2017; Lusso et al., 2019; Risaliti and Lusso, 2019), this will provide an independent, compelling proof that this tension is real. Reducing the measurement uncertainties on cosmological parameters has become the main goal of current and forthcoming cosmological projects, in order to either corroborate the standard model or find new physics beyond it (see also results from N-body simulations, e.g., Adamek et al., 2016). Only the combination of different approaches, supported by an increased data quality and sample statistics, is the way forward to solve the H₀ tension.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge financial contribution from the agreement ASI-INAF n.2017-14-H.O.

This work was initiated at the Aspen Center for Physics, which was supported by National Science Foundation grant PHY-1607611.

This research made use of Astropy a community-developed core Python package for Astronomy (Price-Whelan et al., 2018). This research made use of Matplotlib, a 2D graphics package used for Python (Hunter, 2007).

Footnotes

1. ^http://cxc.cfa.harvard.edu/csc2/

2. ^http://xmmssc.irap.omp.eu/Catalogue/3XMM-DR8/3XMM_DR8.html

References

Adamek, J., Daverio, D., Durrer, R., and Kunz, M. (2016). General relativity and cosmic structure formation. Nat. Phys. 12, 346–349. doi: 10.1038/nphys3673

CrossRef Full Text | Google Scholar

Aghanim, N., Akrami, Y., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., et al. (2018). Planck 2018 results. VI. Cosmological parameters. arXiv 1807.06209.

Google Scholar

Bisogni, S., Risaliti, G., and Lusso, E. (2017). A hubble diagram for quasars. Front. Astron. Space Sci. 4:68. doi: 10.3389/fspas.2017.00048

CrossRef Full Text | Google Scholar

Delubac, T., Bautista, J. E., Busca, N. G., Rich, J., Kirkby, D., Bailey, S., et al. (2015). Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 574:A59. doi: 10.1051/0004-6361/201423969

CrossRef Full Text | Google Scholar

Evans, I. N., Primini, F. A., Glotfelty, K. J., Anderson, C. S., Bonaventura, N. R., Chen, J. C., et al. (2010). The Chandra source catalog. Astrophys. J. Suppl. 189, 37–82. doi: 10.1088/0067-0049/189/1/37

CrossRef Full Text | Google Scholar

Font-Ribera, A., Kirkby, D., Busca, N., Miralda-Escudé, J., Ross, N. P., Slosar, A., et al. (2014). Quasar-Lyman α forest cross-correlation from BOSS DR11: Baryon acoustic oscillations. J. Cosmol. Astropart. Phys. 2014:027. doi: 10.1088/1475-7516/2014/05/027

CrossRef Full Text | Google Scholar

Foreman-Mackey, D., Hogg, D. W., Lang, D., and Goodman, J. (2013). EMCEE: the MCMC hammer. Publ. Astronom. Soc. Pac. 125, 306–312. doi: 10.1086/670067

CrossRef Full Text | Google Scholar

Hopkins, P. F., Strauss, M. A., Hall, P. B., Richards, G. T., Cooper, A. S., Schneider, D. P., et al. (2004). Dust reddening in sloan digital sky survey quasars. Astronom. J. 128, 1112–1123. doi: 10.1086/423291

CrossRef Full Text | Google Scholar

Hunter, J. D. (2007). Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 9, 90–95. doi: 10.1109/MCSE.2007.55

CrossRef Full Text | Google Scholar

Just, D. W., Brandt, W. N., Shemmer, O., Steffen, A. T., Schneider, D. P., Chartas, G., et al. (2007). The X-ray properties of the most luminous quasars from the sloan digital sky survey. Astrophys. J. 665, 1004–1022. doi: 10.1086/519990

CrossRef Full Text | Google Scholar

Kang, Y., Lee, Y.-W., Kim, Y.-L., Chung, C., and Ree, C. H. (2020). Early-type host galaxies of type Ia supernovae. II. Evidence for luminosity evolution in supernova cosmology. Astrophys. J. 889:8. doi: 10.3847/1538-4357/ab5afc

CrossRef Full Text | Google Scholar

Kolodzig, A., Gilfanov, M., Sunyaev, R., Sazonov, S., and Brusa, M. (2013). AGN and QSOs in the eROSITA all-sky survey. I. Statistical properties. Astron. Astrophys. 558:A89. doi: 10.1051/0004-6361/201220880

CrossRef Full Text | Google Scholar

Lusso, E., Comastri, A., Vignali, C., Zamorani, G., Brusa, M., Gilli, R., et al. (2010). The X-ray to optical-UV luminosity ratio of X-ray selected type 1 AGN in XMM-COSMOS. Astron. Astrophys. 512:A34. doi: 10.1051/0004-6361/200913298

CrossRef Full Text | Google Scholar

Lusso, E., Piedipalumbo, E., Risaliti, G., Paolillo, M., Bisogni, S., Nardini, E., et al. (2019). Tension with the flat ΛCDM model from a high-redshift Hubble diagram of supernovae, quasars, and gamma-ray bursts. Astron. Astrophys. 628:L4. doi: 10.1051/0004-6361/201936223

CrossRef Full Text | Google Scholar

Lusso, E., and Risaliti, G. (2016). The tight relation between X-ray and ultraviolet luminosity of quasars. Astrophys. J. 819:154. doi: 10.3847/0004-637X/819/2/154

CrossRef Full Text | Google Scholar

Lusso, E., and Risaliti, G. (2017). Quasars as standard candles. I. The physical relation between disc and coronal emission. Astron. Astrophys. 602:A79. doi: 10.1051/0004-6361/201630079

CrossRef Full Text | Google Scholar

Menzel, M.-L., Merloni, A., Georgakakis, A., Salvato, M., Aubourg, E., Brandt, W. N., et al. (2016). A spectroscopic survey of X-ray-selected AGNs in the northern XMM-XXL field. Monthly Notices R. Astronom. Soc. 457, 110–132. doi: 10.1093/mnras/stv2749

CrossRef Full Text | Google Scholar

Merloni, A., Predehl, P., Becker, W., Böhringer, H., Boller, T., Brunner, H., et al. (2012). eROSITA science book: mapping the structure of the energetic universe. arXiv 1209.3114.

Google Scholar

Mingo, B., Watson, M. G., Rosen, S. R., Hardcastle, M. J., Ruiz, A., Blain, A., et al. (2016). The MIXR sample: AGN activity versus star formation across the cross-correlation of WISE, 3XMM, and FIRST/NVSS. Monthly Notices R. Astronom. Soc. 462, 2631–2667. doi: 10.1093/mnras/stw1826

CrossRef Full Text | Google Scholar

Pâris, I., Petitjean, P., Aubourg, É., Myers, A. D., Streblyanska, A., Lyke, B. W., et al. (2018). The sloan digital sky survey quasar catalog: fourteenth data release. Astron. Astrophys. 613:A51. doi: 10.1051/0004-6361/201732445

CrossRef Full Text | Google Scholar

Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R. A., Nugent, P., Castro, P. G., et al. (1999). Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 517, 565–586. doi: 10.1086/307221

CrossRef Full Text | Google Scholar

Predehl, P. (2012). “eROSITA,” in Proceedings of SPIE, Volume 8443 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series (Amsterdam), 8443:84431R. doi: 10.1117/12.925843

CrossRef Full Text | Google Scholar

Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., and Rocca-Volmerange, B. (1984). The typical interstellar extinction in the small magellanic cloud. Astron. Astrophys. 132, 389–392.

Google Scholar

Price-Whelan, A. M., Sipőcz, B. M., Günther, H. M., Lim, P. L., Crawford, S. M., Conseil, S., et al. (2018). The astropy project: building an open-science project and status of the v2.0 core package. Astronom. J. 156:123. doi: 10.3847/1538-3881/aabc4f/meta

CrossRef Full Text | Google Scholar

Rest, A., Scolnic, D., Foley, R. J., Huber, M. E., Chornock, R., Narayan, G., et al. (2014). Cosmological constraints from measurements of type Ia supernovae discovered during the first 1.5 yr of the Pan-STARRS1 survey. Astrophys. J. 795:44. doi: 10.1088/0004-637X/795/1/44

CrossRef Full Text | Google Scholar

Richards, G. T., Strauss, M. A., Fan, X., Hall, P. B., Jester, S., Schneider, D. P., et al. (2006). The sloan digital sky survey quasar survey: quasar luminosity function from data release 3. Astronom. J. 131, 2766–2787. doi: 10.1086/503559

CrossRef Full Text | Google Scholar

Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., and Scolnic, D. (2019). Large magellanic cloud cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond ΛCDM. Astrophys. J. 876:85. doi: 10.3847/1538-4357/ab1422

CrossRef Full Text | Google Scholar

Riess, A. G., Filippenko, A. V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P. M., et al. (1998). Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astronom. J. 116, 1009–1038. doi: 10.1086/300499

CrossRef Full Text | Google Scholar

Risaliti, G., and Lusso, E. (2015). A Hubble diagram for quasars. Astrophys. J. 815:33. doi: 10.1088/0004-637X/815/1/33

CrossRef Full Text | Google Scholar

Risaliti, G., and Lusso, E. (2019). Cosmological constraints from the Hubble diagram of quasars at high redshifts. Nat. Astron. 3, 272–277. doi: 10.1038/s41550-018-0657-z

CrossRef Full Text | Google Scholar

Rosen, S. R., Webb, N. A., Watson, M. G., Ballet, J., Barret, D., Braito, V., et al. (2016). The XMM-Newton serendipitous survey. VII. The third XMM-Newton serendipitous source catalogue. Astron. Astrophys. 590:A1. doi: 10.1051/0004-6361/201526416

CrossRef Full Text | Google Scholar

Salvato, M., Hasinger, G., Ilbert, O., Zamorani, G., Brusa, M., Scoville, N. Z., et al. (2009). Photometric redshift and classification for the XMM-COSMOS sources. Astrophys. J. 690, 1250–1263. doi: 10.1088/0004-637X/690/2/1250

CrossRef Full Text | Google Scholar

Scolnic, D. M., Jones, D. O., Rest, A., Pan, Y. C., Chornock, R., Foley, R. J., et al. (2018). The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined pantheon sample. Astrophys. J. 859:101. doi: 10.3847/1538-4357/aab9bb

CrossRef Full Text | Google Scholar

Smoot, G. F., Bennett, C. L., Kogut, A., Wright, E. L., Aymon, J., Boggess, N. W., et al. (1992). Structure in the COBE differential microwave radiometer first-year maps. Astrophys. J. Lett. 396:L1. doi: 10.1086/186504

CrossRef Full Text | Google Scholar

Steffen, A. T., Strateva, I., Brandt, W. N., Alexander, D. M., Koekemoer, A. M., Lehmer, B. D., et al. (2006). The X-ray-to-optical properties of optically selected active galaxies over wide luminosity and redshift ranges. Astronom. J. 131, 2826–2842. doi: 10.1086/503627

CrossRef Full Text | Google Scholar

Wong, K. C., Suyu, S. H., Chen, G. C. F., Rusu, C. E., Millon, M., Sluse, D., et al. (2019). H0LiCOW XIII. A 2.4% measurement of H₀ from lensed quasars: 5.3σ tension between early and late-Universe probes. arXiv 1907.04869.

Google Scholar

Zhao, G.-B., Raveri, M., Pogosian, L., Wang, Y., Crittenden, R. G., Handley, W. J., et al. (2017). Dynamical dark energy in light of the latest observations. Nat. Astron. 1, 627–632. doi: 10.1038/s41550-017-0216-z

CrossRef Full Text | Google Scholar