Relativistic Particle Beams as a Resource to Solve Outstanding Problems in Space Physics

Sanchez, Ennio R.; Powis, Andrew T.; Kaganovich, Igor D.; Marshall, Robert; Porazik, Peter; Johnson, Jay; Greklek-Mckeon, Michael; Amin, Kailas S.; Shaw, David; Nicolls, Michael

doi:10.3389/fspas.2019.00071

REVIEW article

Front. Astron. Space Sci., 27 November 2019

Sec. Space Physics

Volume 6 - 2019 | https://doi.org/10.3389/fspas.2019.00071

This article is part of the Research Topic Active Experiments in Space: Past, Present, and Future View all 21 articles

Relativistic Particle Beams as a Resource to Solve Outstanding Problems in Space Physics

$\nEnnio R. Sanchez$ Ennio R. Sanchez¹^*

Andrew T. Powis²

Igor D. Kaganovich²

Robert Marshall³

Peter Porazik²^†

Jay Johnson²^†

Michael Greklek-Mckeon²^†

Kailas S. Amin²^†

David Shaw²^†

Michael Nicolls¹^†

¹SRI International, Menlo Park, CA, United States
²Princeton Plasma Physics Laboratory, Princeton, NJ, United States
³Ann and H. J. Smead Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO, United States

The Sun's connection with the Earth's magnetic field and atmosphere is carried out through the exchange of electromagnetic and mass flux and is regulated by a complex interconnection of processes. During space weather events, solar flares, or fast streams of solar atmosphere strongly disturb the Earth's environment. Often the electric currents that connect the different parts of the Sun-Earth system become unstable and explosively release the stored electromagnetic energy in one of the more dramatic expressions of space weather—the geomagnetic storm and substorm. Some aspects of the magnetosphere-ionosphere connection that generates auroral arcs during space weather events are well-known. However, several fundamental problems remain unsolved because of the lack of unambiguous identification of the magnetic field connection between the magnetosphere and the ionosphere. The correct mapping between different regions of the magnetosphere and their foot-points in the ionosphere, coupled with appropriate distributed measurements of plasma and fields in focused regions of the magnetosphere, is necessary to establish unambiguously that a given magnetospheric process is the generator of an observed arc. We present a new paradigm that should enable the resolution of the mapping ambiguities. The paradigm calls for the application of energetic electron beams as magnetic field tracers. The three most important problems for which the correct magnetic field mapping would provide closure to are the substorm growth phase arcs, the expansion phase onset arcs and the system of arcs that emerge from the magnetosphere-ionosphere connection during the development of the early substorm expansion phase phenomenon known as substorm current wedge (SCW). In this communication we describe how beam tracers, in combination with distributed measurements in the magnetosphere, can be used to disentangle the mechanisms that generate these critical substorm phenomena. Since the application of beams as tracers require demonstration that the beams can be injected into the loss cone, that the spacecraft potentials induced by the beam emission are manageable, and that sufficient electron flux reaches the atmosphere to be detectable by optical or radio means after the beam has propagated thousands of kilometers under competing effects of beam spread and constriction as well as effects of beam-induced instabilities, in this communication we review how these challenges are currently being addressed and discuss the next steps toward the realization of active experiments in space using relativistic electron beams.

Introduction

The Sun and the Earth are coupled in multiple ways. Heat coming from the Sun is the main energy source of Earth's weather. Solar ultraviolet emissions are the main source of the ionized layer of the Earth's upper atmosphere—the ionosphere. The particles and magnetic field emanated by the Sun flow over and merge with the Earth's magnetic field, reconfiguring it as well as the particle distributions trapped within. The Sun's interaction with the Earth's magnetic field, ionosphere and atmosphere leads to exchange of electromagnetic and mass flux which is regulated by a complex interconnection of processes (e.g., Vasyliunas, 1984; Lysak, 1990). Solar flares or fast streams of solar wind strongly disturb the Earth's surrounding environment known as the magnetosphere. Often during these events the electric currents that connect the different parts of the Earth's magnetosphere with the ionosphere become unstable and explosively release the stored electromagnetic and particle energy in one of the more dramatic expressions of space weather—geomagnetic storms and substorms (e.g., Gonzalez et al., 1994). These phenomena deposit large fluxes of energetic charged particles and electromagnetic energy into the atmosphere, driving the bright dynamic optical auroral displays. They also accelerate charged particles and inject them from regions deeper in the magnetotail into regions now thickly populated by commercial, scientific, and military spacecraft. The incident electromagnetic and particle fluxes can cause major ionospheric disturbances that impede communications and navigation during space weather events. The physical processes involved in substorms occur throughout the solar system and the universe: Substorms are observed on Saturn and Jupiter (Russell et al., 2000; Cowley et al., 2005; Mitchell et al., 2005; Kronberg et al., 2008) and the flares of energetic X-rays and gamma rays associated with such reconfigurations are observed routinely from our Sun and other stars (Masuda et al., 1994; Shibata, 1998).

Several fundamental questions about how the magnetosphere and the ionosphere are connected during storms and substorms remain unsolved. Understanding the connection is the most critical step toward understanding how the magnetosphere-ionosphere (M-I) system evolves from a stable to an unstable state. This will only be possible when we are able to unambiguously determine what processes and regions in the magnetosphere are linked to the aurora. This goal requires the ability to map the magnetic field lines that connect a given arc with its source region in the magnetosphere, and to measure the spatial and temporal evolution of the source region. The three most important questions for which the correct magnetic field mapping would provide closure to are: How are the substorm growth phase arcs generated, how are the expansion phase onset arcs generated and how does the system of arcs and electric currents known as substorm current wedge (SCW; e.g., McPherron et al., 1973; Pytte et al., 1976) emerge during the early substorm expansion phase.

The Substorm Growth Phase

Ever since Akasofu and Chapman coined the term substorm (Akasofu and Chapman, 1961) and Akasofu described the auroral phenomenology of substorms (Akasofu, 1964), observational and theoretical investigations have been carried with the objective of explaining substorm evolution. These investigations have revealed that before the explosive release of energy occurs, there is an interval where energy from the Sun is being deposited in the Earth's magnetosphere. This interval is commonly referred to as the growth phase. The growth phase of the substorm is characterized by forming of multiple arcs, which brighten and remain stable for ~1 h (Figure 1; e.g., Akasofu, 1964; Lyons et al., 2002; Partamies et al., 2015). At the end of the growth phase, the M-I system reaches a state that allows explosive release of energy into the ionosphere, referred to as expansion phase. The start of the expansion phase is commonly referred to as breakup or expansion onset. Substorm auroral onset is characterized by a brightening near the equatorial boundary of the auroral oval, frequently along pre-existing growth phase arc (Akasofu, 1964). There are multiple unanswered questions regarding growth phase arcs and their relationship to the onset arc. For instance, it is unclear what makes the breakup arc different from all the others, aside from the obvious phenomenological evidence of brightening. It is therefore unclear how the electromagnetic coupling between the ionosphere and the magnetosphere differs for both sets of arcs. Recent modeling efforts of growth phase arcs carried out with the Rice Convection Model show the formation of a thin arc that extends several hours in magnetic local time in the transition region during the late growth phase, generated by large-scale adiabatic convection under equilibrium conditions (Yang et al., 2013). The arc in the pre-midnight sector is associated with precipitating electrons along an azimuthally elongated sheet of region-1 sense (whereby current flows into the ionosphere on the post-midnight side of the sheet and out of the ionosphere on its pre-midnight side) field-aligned current (FAC) just poleward of the main region-2 FAC, which has a polarity opposite that of the region-1 (Figure 2). The newly formed FACs are produced by a redistribution of pressure in the inner magnetosphere generated by convection and azimuthal particle drifts. As the pressure redistribution continues, it concentrates Alfvén layers within progressively narrower L-shell range which maps to a narrower arc, thus forming what Yang et al. (2013) termed a “convection front.”

FIGURE 1

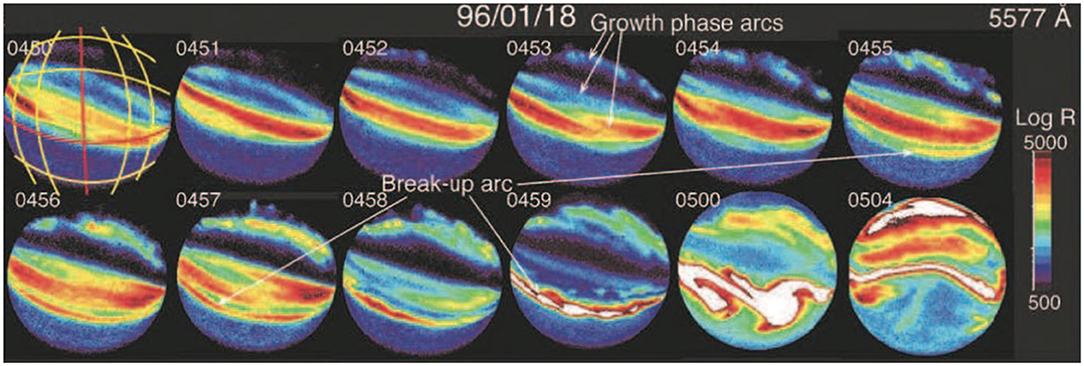
Figure 1. Auroral arcs observed with all-sky imagers in the 557.7 nm band between the last few minutes of growth phase of substorms and the first few minutes of expansion phase (Reproduced from Lyons et al., 2002). Emission is shown in units of Rayleighs.

FIGURE 2

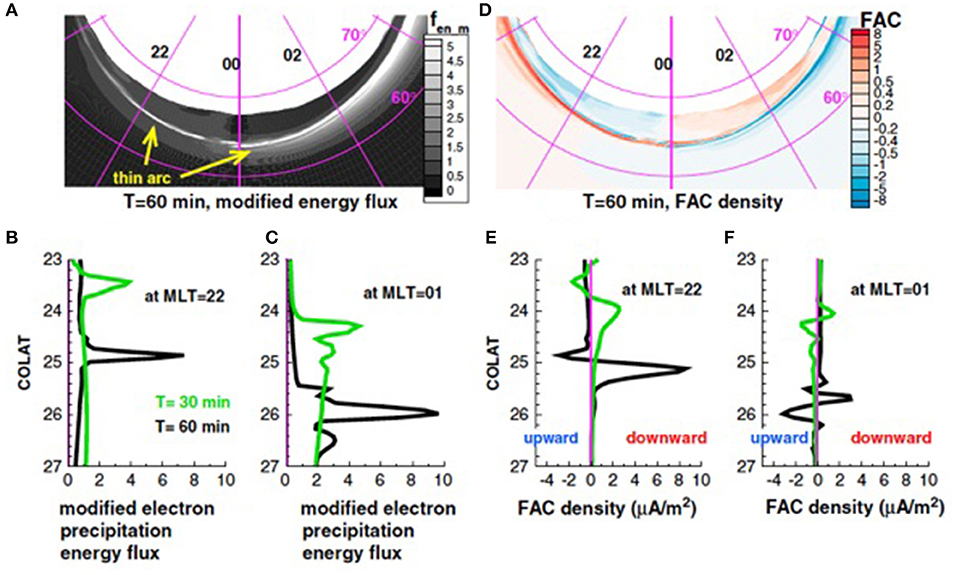
Figure 2. Ionospheric view of (A) modified precipitating energy flux in units of erg/cm²/s, (D) FAC density toward the end of growth phase in units of μA/m² (blue is out of the ionosphere). Latitudinal slices of (B,C) energy flux and (E,F) FAC density at MLT = 22 and MLT = 1 at two different times (Reproduced from Yang et al., 2013). The vertical axis COLAT denotes degrees away from the Earth's magnetic dipole axis.

Models' predictions for the growth phase electric current generators can be properly tested with an array of spacecraft in the nightside magnetosphere with the following attributes:

1) A main spacecraft emitting an electron beam to measure the unambiguous magnetic-field connection between the growth phase arcs observed with ground-based auroral cameras and the magnetospheric region where the beam was emitted from;

2) Three daughter spacecraft equidistant to the main spacecraft and to each other to enable measurement of plasma pressure and convection gradients in the radial and azimuthal directions. Variable radial separation of ~10–4,000 km among spacecraft will allow the in-situ testing of the growth phase models' predicted pressure gradients in the magnetospheric equator.

The Substorm Expansion Phase

At the end of the growth phase, the M-I system reaches a state that allows explosive release of energy into the ionosphere, referred to as expansion phase. The transition usually occurs along an east-west-aligned auroral arc with a characteristic thickness between a few km (e.g., Hull et al., 2016) and ~30 km (e.g., Knudsen et al., 2001), emerges in the growth phase ~10 min before, and undergoes a sudden increase in brightness and subsequent rapid expansion azimuthally and longitudinally (e.g., Lyons et al., 2002; Hull et al., 2016, and references therein). Substorm current formation and evolution beyond growth phase is a process that involves both electron acceleration from static potentials at high altitude and Alfvénic acceleration mechanisms (e.g., Keiling, 2009 and references therein). Several case studies suggest that, as one of the most equatorward arcs intensifies during the transition from growth to onset of substorms, the arc may also develop filamentation into smaller scales which show wave properties (e.g., Wygant et al., 2002; Mende et al., 2003; Lessard et al., 2011; Hull et al., 2016). The transition is argued to be consistent with the notion that small-scale or dispersive Alfvén waves may be generated from larger-scale Alfvén waves and/or destabilization of macroscale currents (e.g., Chaston et al., 2011 and references therein).

As the magnetosphere-ionosphere system evolves into substorm breakup onset the brightening arc usually develops discrete rays, also called “beads,” pulsating in a wave-like form along the arc (Donovan et al., 2006; Liang et al., 2008; Henderson, 2009; Rae et al., 2010; Kalmoni et al., 2015; Nishimura et al., 2016; Figure 3). Onset waves have received attention because their optical properties seem to match at least some of the properties, such as growth rate and frequency, expected for several near-Earth instabilities that have been proposed as triggers of substorm expansion onset. These include cross-field current instabilities (Lui et al., 1991), various forms of fluid, hybrid, and kinetic ballooning/interchange instabilities (Roux et al., 1991; Voronkov et al., 1997; Cheng, 2004; Saito et al., 2008; Pritchett and Coroniti, 2010) and electromagnetic ion cyclotron instability (Le Contel et al., 2000; Perraut et al., 2000). Optical measurements from ground-based all-sky cameras (Liang et al., 2008; Rae et al., 2010; Kalmoni et al., 2015; Nishimura et al., 2016) have shown that the optical wave properties (period between 18 and 23 s, azimuthal wavelengths between ~60 and ~100 km, growth rates ~0.04 s⁻¹ and duration of 1 to 1.5 min) are in best agreement with the kinetic ballooning instability (Pritchett and Coroniti, 2010, 2011, 2013). Kinetic instabilities are likely to play a role since the optical wavelengths map to cross-tail distances comparable to the ~2,000 km ion gyro-radius at 8 R_e, which is inside the region in the Earth's magnetotail between ~6 and 10 R_e, where the Earth's magnetic field often transitions between a quasi-dipolar geometry to a tail-like one. It is in the neighborhood of this region where the onset of substorms is widely acknowledged to occur (e.g., Petrukovich and Yahnin, 2006 and references therein). Models' predictions for the cross-tail wavelength, growth rate, and frequency of instabilities associated with bead development can be properly tested with an array of spacecraft in the nightside magnetosphere with the following attributes: (1) A main spacecraft emitting an electron beam to ensure the unambiguous magnetic-field connection between the beads observed with ground-based auroral cameras and the magnetospheric region where the beam was emitted from; (2) At least two daughter spacecraft separated azimuthally ~350–800 km to allow sufficient resolution to measure azimuthal variation of plasma density, pressure, and convection over the observed ~1,250–3,200 km range for beads' wavelength projected to the magnetospheric equator (Rae et al., 2010; Kalmoni et al., 2015; Nishimura et al., 2016). Similar variable radial separations among spacecraft will allow the necessary resolution of radial gradients. Field and plasma measurements with a 30 s cadence are desirable to test wave growth rates of ballooning and CFCI instabilities in the inner plasma sheet (Rae et al., 2010; Kalmoni et al., 2015; Nishimura et al., 2016).

FIGURE 3

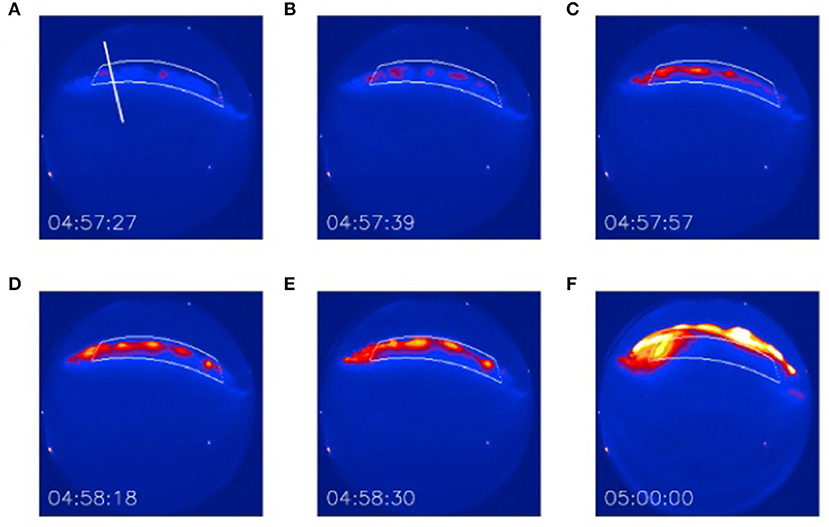
Figure 3. Auroral beads observed by an all-sky imager along an onset arc on 2 October, 2011 in arbitrary units of luminosity in the 557.7 nm emission band. Lines of geomagnetic latitude at 67.8° and 68.4° and geomagnetic longitude at −33.0° and −24.0° define the field of view of the images and show that the onset arc is aligned with constant geomagnetic latitude. The formation and evolution of the beads are observed with time (A–F). The white line in A shows the orientation perpendicular to the arc. After 04:58:30 UT (E) the aurora expands poleward out the box, as can be seen at a later time (F; Reproduced from Kalmoni et al., 2015).

Auroral and in-situ measurements in the magnetosphere suggest that a local decrease in entropy may in some instances influence the triggering of instabilities that cause the onset arcs (Figure 4). Observations indicate that a large fraction (~84%) of onsets are preceded by equatorward moving auroral forms (streamers; Nishimura et al., 2010; Xing et al., 2010; Lyons et al., 2011). The decrease in entropy may be caused by low-entropy flux tubes that are injected from the far tail reconnection and intrude into the transition region. In this framework, the streamers observed in the auroral region are assumed to be the low-altitude projection of the low-entropy flux tubes that are moving in the magnetosphere from their source, in reconnection sites farther than 10 R_E in the magnetotail, toward the near-Earth environment. The streamers show total field-aligned currents of a few tenths of MA, thicknesses of ~100–600 km, field-aligned current densities ranging from less than 1 μA/m² to more than 20 μA/m², and a potential drop of a few kV across the stream (Amm et al., 1999; Sergeev et al., 2004). Models of low-entropy earthward propagating flux tubes, sometimes termed “bubbles,” have produced similar Region-1/Region-2 current systems (e.g., Yang et al., 2012). Models' predictions for the rate of change of Hall and Pedersen conductance, horizontal currents, and FACs as well as for the energy flux of precipitating electrons produced by the arrival of bubbles into the inner magnetosphere would be properly tested with the array of spacecraft in the transition region of the nightside magnetosphere, measurements of convection, conductance and FACs in the ionosphere and, most importantly, a method to ensure that the region measured in the magnetosphere maps unambiguously to the region measured in the ionosphere. The azimuthal separation prescribed for testing the predictions of instability models would be sufficient to measure pressure gradients of ~1.5–2.5 nPa/km invoked in the entropy decrease models of onset arc. The same azimuthal spacecraft separation would also resolve the cross-tail structure of the incoming low-entropy flux tubes and, through the electron beam mapping, determine if the low-entropy flow channels measured in-situ actually correspond to auroral streamers observed by ground-based imager networks.

FIGURE 4

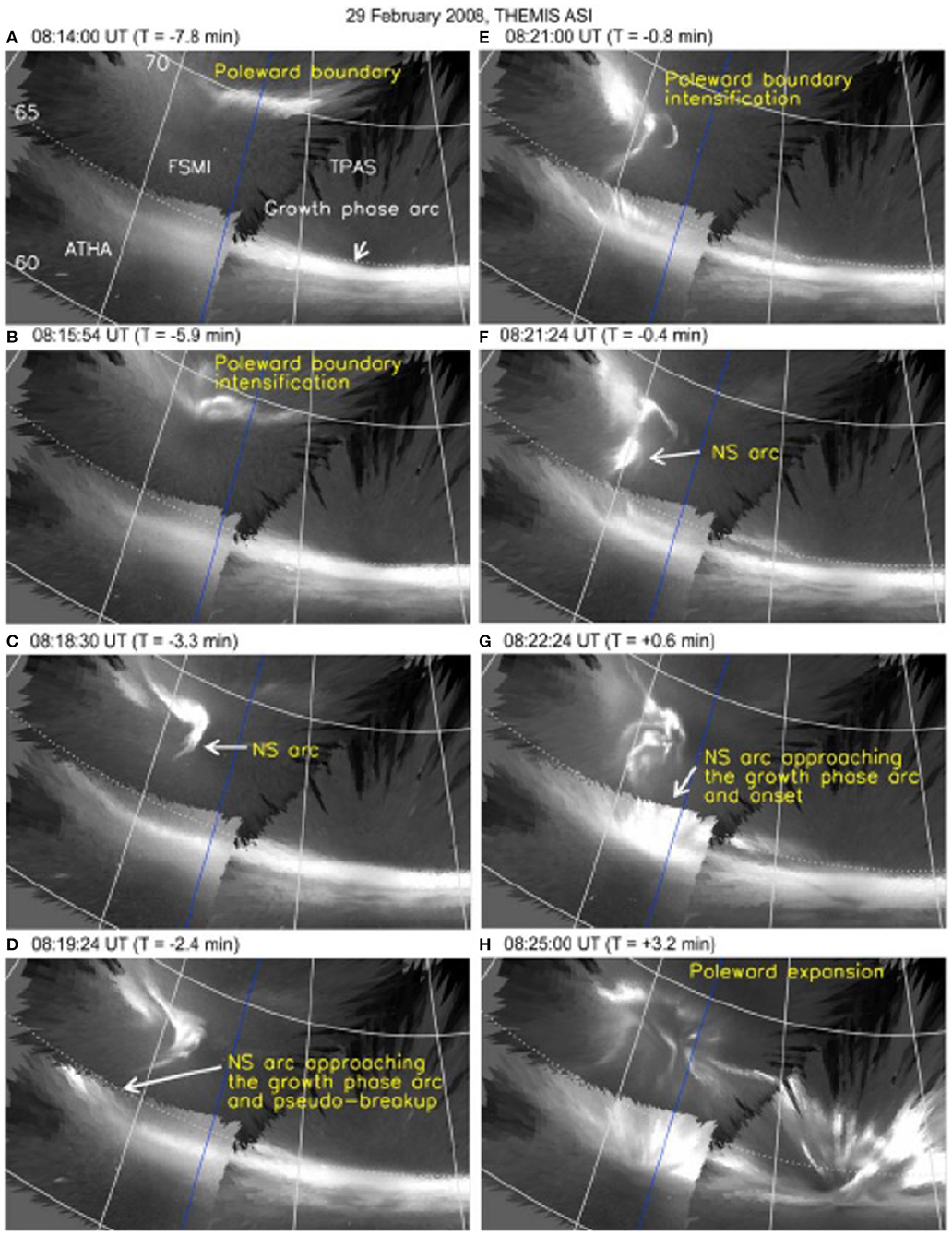
Figure 4. Auroral streamers advancing southward from their origin, the polar cap boundary, to the locus of susbtorm onset, the growth phase arc (Reproduced from Nishimura et al., 2010). Auroral streamers advancing southward from their origin, the polar cap boundary, to the locus of susbtorm onset, the growth phase arc (A–G). Onset occurred at 0821:48 UT and expansion is apparent at 0825:00 UT (H) (Reproduced from Nishimura et al., 2010).

The Substorm Current Wedge

Another crucial outstanding question of substorm development that will be answered with an unambiguous mapping between the magnetosphere and the ionosphere is how the near-Earth M-I coupled system evolves toward a large-scale SCW (McPherron et al., 1973). The SCW is part of a magnetosphere-ionosphere current system that forms during substorm expansion and comprises a current from space into the ionosphere at the eastern edge and out from the ionosphere into space at the western edge of the aurora.

Multiple MHD modeling efforts have related the transport of mass and magnetic flux from the tail to the near-Earth to explain the formation of the SCW (e.g., Birn and Hesse, 1991, 1996, 2005, 2013, 2014; Birn et al., 1999). However, the exact relationship between tail reconnection and near-Earth breakup onset remains to be elucidated. Models show that the SCW configuration that starts with a canonical current polarity (into the ionosphere in the eastern edge of the aurora, out of the ionosphere in the western edge) develops finer structure over the span of a few minutes. The actual SCW current system may actually contain more circuit elements than the standard traditional picture, because of the combined effect of dipolarization, azimuthal flow diversion, shear flows, and twisted/sheared magnetic field. Dipolarization is the process where magnetic geometry changes from tail-like to dipole-like as earthward convection transports magnetic flux from a reconnection site in the tail to near-Earth (Figure 5A). The magnetic shear between the dipole-like geometry inside the SCW and the tail-like geometry outside generates currents that flow into the ionosphere on the eastward edge of the SCW and out of the ionosphere on the westward edge, i.e., Region-1 polarity. As the flow is transported closer to Earth it gets diverted to the flanks by the increased magnetic pressure of the ambient dipole magnetic field resulting in rotation of the magnetic field away from the local meridian plane (Figure 5B) and field line twisting generated by earthward and azimuthal flow at the edges of the SCW (Figure 5C). The combined motion generates pairs of oppositely oriented field-aligned currents. The combination of all these effects produce a composite current system as shown in Figure 5D. The outermost (red) current system 1 represents the perturbed currents of the traditional SCW which flows into the ionosphere on the dawn side, flows westward in the ionosphere and flows back to the magnetosphere on the dusk side. The current system 2 (green) is formed by a diversion of radial perpendicular currents into a pair of currents with opposite polarity and closes in the north-south direction in the ionosphere. Current system 3 (blue) is a dusk-to-dawn current near the equatorial plane which is a consequence of the tailward propagation of the dipolarizing region and the associated reduction of the tail-aligned component of the magnetic field. Current system 4 (black) is confined to the equatorial plane and opens the possibility that the current system 2 may close azimuthally in the magnetosphere through current system 4 rather than radially. Models' predictions for the different FAC circuits would be properly tested with an array of spacecraft in the nightside magnetosphere with the following attributes: (1) An appropriate separation to discern particle pressure and flow gradients on the magnetospheric equator as well as spatio-temporal deformation of the magnetic field; (2) An electron beam that ensures the unambiguous identification of the ionospheric foot-point of the regions measured in the magnetosphere; and (3) Appropriate measurements FACs at and around the ionospheric foot-point of the different regions of the SCW. Azimuthally and radially separated measurements of particles and fields enabled by the spacecraft arrangement used for the substorm instability triggering problem would allow the calculation of magnetic-field-aligned currents generated by divergence of current in the magnetosphere and provide in-situ measurements of vorticity and pressure gradients that contribute to the complex system of currents in the substorm current wedge.

FIGURE 5

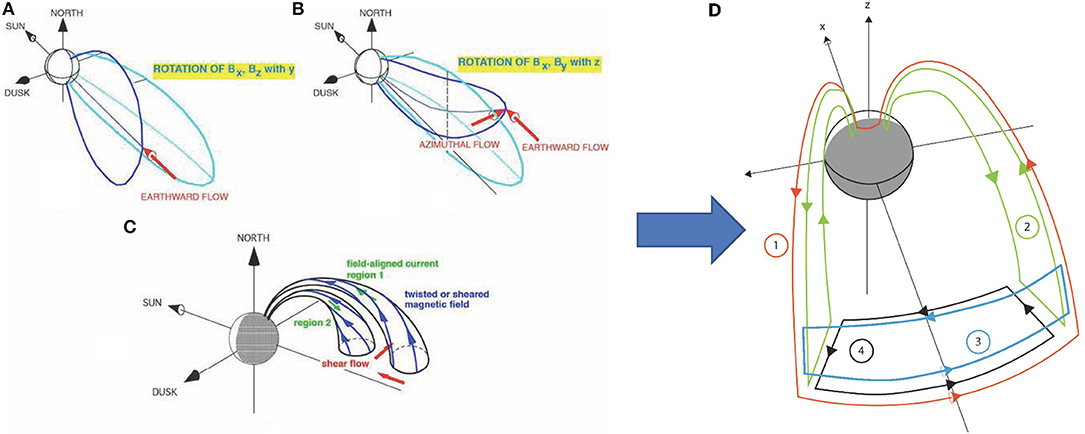
Figure 5. (A–C) Sources of the multi-component substorm current wedge (A,B are adapted from Amm et al., 2002; C is adapted from Birn and Hesse, 2013). (D) A schematic of the current loops associated with the SCW and inferred from MHD simulations of reconnection and field collapse (adapted from Birn et al., 1999; Kepko et al., 2015).

Electrons as Probes of the Magnetic Field

All the comparisons between observations and predictions for substorm growth, onset and current wedge theories have involved space and time histories of optical auroral features coupled with ad-hoc mappings between in-situ measurements in the magnetotail and the observed auroral forms. Various empirical and magnetohydrodynamic (MHD) modeling techniques have been used to approximate the instantaneous configuration of the magnetospheric magnetic field (e.g., Tsyganenko, 1989; Sergeev et al., 1993; Fedder et al., 1995; Kubyshkina et al., 1999; De Zeeuw et al., 2004; Toffoletto et al., 2004; Pembroke et al., 2012). Despite advances in field mapping, the uncertainties involved are still quite large. Difficulties arise due to dynamic phenomena, especially in the tail region, in the form of thin current sheets, magnetic flux ropes, non-adiabatic substorm and storm magnetic field reconfigurations, and high-speed flows (e.g., Donovan et al., 1992; Jordan et al., 1992; Peredo et al., 1993; Fairfield et al., 1994; Pulkkinen and Tsyganenko, 1996; Thomsen et al., 1996). At geosynchronous altitude, the statistical uncertainty in the mapping given by magnetic field models is ~±3° (e.g., Reeves et al., 1996). Up to 20% of the time-field models could be off by more than 5°. Non-adiabatic conditions also mean field lines will no longer be equipotential, making it hard to causally relate magnetospheric and ionospheric flows (e.g., Hesse et al., 1997). Recent efforts to couple models of ion drift physics in the inner magnetosphere to MHD models of the outer magnetosphere (De Zeeuw et al., 2004; Pembroke et al., 2012) reveal new structure and dynamics in the magnetotail; the same efforts underline inherent complexity in the magnetic-field topology. This communication describes how unambiguous magnetic field mapping can be achieved by firing a beam of high-energy electrons from the source region into the ionosphere. It also describes how the properties of the magnetosphere source region can be properly described by deploying a constellation of spacecraft in the vicinity of the spacecraft that fires the beam.

Multiple active experiments that include the injection of artificial energetic electron beams from sounding rockets to investigate magnetospheric structure and dynamics were conducted by a number of groups in the 1960s and 1970s (see Winckler, 1980, for a review). These experiments used keV electron beams and focused on tracing magnetic-field lines by injecting and detecting mirrored electrons; using beams as diagnostic tools to sense local electric and magnetic fields; and investigating wave-particle interactions, including the generation of electromagnetic radiation, the scattering of energetic electrons by waves, and general beam-plasma physics. The optical signature of electrons emitted from a rocket in the polar region of one hemisphere was detected in the conjugate ionosphere and in the hemisphere of origin after bouncing along field lines (Hallinan et al., 1978, 1990). Rocket experiments with electron beams, emitted at energies up to several-keV and currents up to 1–2 Amperes, were carried out in the 1980s and 1990s to explore the effects of these beams on the vehicle near-plasma environment and the upper and middle ionosphere (e.g., Mandell et al., 1990; Neubert et al., 1991; Neubert and Banks, 1992; Raitt et al., 1995). Shuttle/Spacelab electron beam experiments with similar energies and currents were carried out in the same time period to further measure and model the effects of beams (Neubert et al., 1986, 1995; Bush et al., 1987; Cai et al., 1987; Reeves et al., 1988, 1990; Burch et al., 1993). Beam effects studied under these experiments included beam-induced space charge, generation of artificial aurora, and generation of VLF waves by pulsed beams. In the late1990s and early 2000s some theoretical studies considered the applications and technical challenges associated with injection of relativistic electron beams into the space environment (e.g., Neubert et al., 1996; Krause, 1998; Krause et al., 1999; Gilchrist et al., 2001; Neubert and Gilchrist, 2002, 2004). Results from these studies indicate that relativistic beams should be far more stable than keV beams due to a combination of the higher relativistic electron mass, lower beam densities, and less pronounced spacecraft-charging effects, at least for injections from the ionosphere.

Compact linear accelerators are currently capable of generating beams with currents (≲100 mA), energies (1–10 MeV), pulse durations (μs), and duty cycles (~0.1%) that make them the best candidates for application to magnetic field mapping. Because of increased efficiency, high frequency, and high gradient technologies developed since the 1990s (Ruth et al., 1993; Wang, 2009; Dolgashev and Tantawi, 2010; Neilson et al., 2010; Tantawi and Neilson, 2012), compact linear accelerators can fit in a Mid Explorer class mission's size, mass, and power envelope. However, the realization of the proposition that beams of relativistic electrons can be used as magnetic field tracers require demonstration that the beam can be injected into the loss cone from magnetospheric altitudes, that the spacecraft potentials induced by the beam emission are manageable, and that sufficient electron flux reaches the atmosphere to be detectable by optical or radio means after the beam has propagated thousands of kilometers under competing effects of beam spread and constriction as well as effects of beam-induced instabilities.

In the next section we provide a review of the latest results of synergistic research carried out under the NSF INSPIRE program to address these challenges and discuss the next steps toward the realization of active experiments in space using relativistic electron beams.

Challenges with the Injection of Space-Based Beams

Plasma Response Time and Spacecraft Charge Control

Past electron beam experiments encountered issues with the injection of space-based beams due to rapid spacecraft charging, which influences beam fidelity and beam-plasma interactions (e.g., Cohen et al., 1980a,b; Gussenhoven et al., 1980). These issues led to studies of the fundamental processes associated with electron-beam-plasma interactions, including the formation of sheath regions of particle and field fluctuations, plasma-neutral gas interactions, wave-particle interactions, and non-linear phenomena (Neubert and Banks, 1992). Some of these issues are associated with charge and current neutralization: in a plasma, the axial field of an electron beam can effectively expel thermal electrons to become charge-neutralized (Humphries, 1990). SCATHA spacecraft experiments carried out in 1979 to investigate the effect of the interaction between the magnetospheric plasma and keV beam emission on spacecraft potential demonstrated that, for certain beam currents, the plasma can supply the return current required to keep the spacecraft potential below the beam energy so the beam can safely be emitted (Cohen et al., 1980a), but for higher beam currents most of the beam electrons return to the spacecraft (Gussenhoven et al., 1980) or even cause the failure of the spacecraft systems (Cohen et al., 1980b).

The ability of the plasma to respond to an injected beam of electrons depends on the plasma response time, which is driven by the plasma frequency (Humphries, 1990). Charging for single-pulse injections is expected to have a negligible effect on beam fidelity due to the low charge-accumulation build up (~ kV spacecraft potential) compared to the beam energy (~ MeV). The charging resulting from extended pulse emissions depends on the ability of the ambient plasma to supply the return current, given by the thermal current density. Neubert and Gilchrist (2002) have shown that spacecraft charging and beam-plasma interactions become significant for currents of ~100 A for ionospheric injections of 5 MeV beams, far larger than the expected electric current demands of space-based electron accelerators.

For injections from the magnetosphere, the effects of spacecraft charging on beam fidelity must be considered, but with flexible beam operations (beam energy, duty cycle, etc.), paradigms for stable injection are expected. Recent studies by Delzanno et al. (2015a,b) have demonstrated an operational paradigm where releasing a high-density neutral contactor plasma prior and during beam ejection leads to successful beam ejection. As such, several-MeV beams should be suitable for injections from the ionosphere and the magnetosphere.

Beam Injection Into the Loss Cone

To maximize the fraction of the relativistic electron beam entering the atmosphere, the beam must be injected into a geometrical region known as the loss cone. Beams injected outside the loss cone will bounce back to their source, due to the magnetic mirror force, before they reach the atmosphere. Standard calculation of the loss cone involves the conservation of the first adiabatic invariant (e.g., Rossi and Olbert, 1970). For sub-relativistic particles the calculation of the width of the loss cone is sufficiently accurate using the zeroth order term, μ⁽⁰⁾, of the adiabatic invariant corresponding to the cyclotron motion, μ, which is an asymptotic series in the small parameter ρ/L_B (Northrop, 1963) where ρ is the effective Larmor radius, defined by v/Ω_c, where v is the initial velocity of the particle (total, not just v_⊥), Ω_c is the cyclotron frequency of the particle |q_||B|/mc, q is the particle's charge; and m is its relativistic mass, given by m₀γ, where m₀ is the rest mass of the particle, and γ = 1/√1 – v²/c². The denominator, L_B, of the small parameter is the characteristic gradient length scale of the mangetic field $L_{B}^{- 1}$ = |∇ lnB|. For relativistic electrons Porazik et al. (2014) showed that higher-order terms of the magnetic moment invariant are necessary to correctly determine the mirror point of trapped energetic particles, and therefore the loss cone. Figure 6 (left) shows the pitch angles (δ) that would lead to precipitation for different azimuthal injection angles (λ) as a function of electron energy at 10 R_e. The electron is considered to be lost if its mirror point is at the radial distance of 1 R_e or less. For comparison, the dashed line shows the loss cone computed based on only the lowest-order term of the magnetic moment. The importance of higher-order terms is most dramatically reflected in the λ-dependence of the loss cone. As the energy of the electron increases, the λ-dependence becomes more pronounced, and eventually the loss cone becomes a closed contour with unique boundaries in both angles. The largest range of δ angles is always at λ = –90°, in the direction of electron drift, tangentially to the flux surface (for positive ions, the optimal value of λ would be +90°). Figure 6 (right) shows the loss cone for a 7-MeV electron initialized in the equatorial plane at different distances. As the distance increases the loss cone again becomes confined to a small region in phase space, with unique boundaries in both angles. The modified loss cone resulting from the inclusion of higher order terms is no longer entirely defined by the traditional pitch angle but also by the phase angle of the particle at the point of injection. The optimal orientation of the injection has a non-zero component perpendicular to the magnetic field line, and is in the plane tangential to the flux surface. The results show that injection-angle control is important and depends on location and beam energy. Also, as we will discuss in the next section, this theory is backed up by single-particle simulations, which do not rely on the assumption of conservation of the first adiabatic invariant.

FIGURE 6

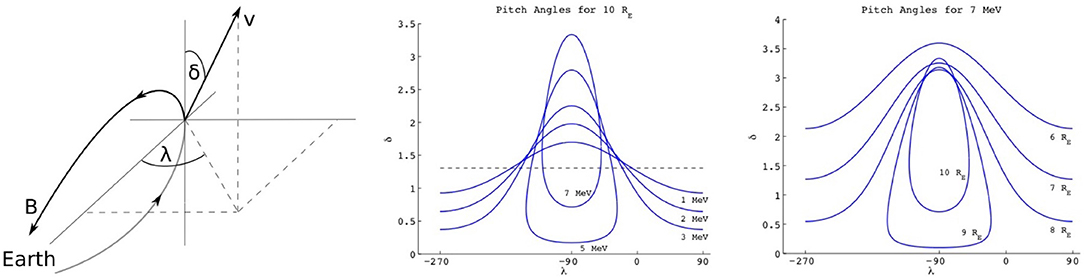
Figure 6. Geometry for injection of MeV electrons (Left). The angle δ is the traditional pitch angle, the azimuth λ denotes the angle away from the plane of the flux surface. Edges of loss cones for (Middle) an electron initialized from 10 Re at the equatorial plane of a dipole field for different energies and (Right) for a 7-MeV electron initialized from different distances at the equatorial plane of a dipole field. The black dashed line corresponds to the unmodified loss cone for injection from the equatorial plane (Adapted from Porazik et al., 2014).

The results of these studies are important in guiding the design considerations that determine the energy and pointing envelopes that ensure electrons trajectories' reaching the atmosphere when injection occurs in the magnetosphere. The fraction of the beam reaching the atmosphere will depend on the fraction of its phase space density lying inside the modified loss cone at injection. For instance, Figure 6 shows that a 7 MeV beam injected at −90° azimuth at 10 R_E must have a spread smaller than 2.6° to ensure precipitation into the atmosphere. Current accelerators can achieve spreads that are approximately an order of magnitude smaller than 2.6° thus enabling the entire particle flux to be inside the loss cone.

Using the physical parameters of a reference 1 MeV electron beam instrument, Powis et al. (2019) determine that an appropriate treatment for injection of relativistic particles in a dipolar field at the geomagnetic equator must include the first three terms in the expansion series for μ in order to capture small changes in δ and λ (Powis et al., 2019, Equation 12). As particles approach Earth, the most significant contribution to the magnetic moment is given by the zeroth order component because of the combined effect of a stronger magnetic field and a larger the perpendicular velocity. Relating the initial magnetic moment, μ⁽⁰⁾+ μ⁽¹⁾+ μ⁽²⁾, to the final magnetic moment, $μ_{\oplus}^{(0)}$ , gives a general relationship for the final cyclotron radius at impact for any particle injected from the equatorial plane along a dipole field line, as a function of injection radial distance from Earth, injection energy and injection angles λ and δ. For a particle injected directly along the field line δ = 0 and reference properties, 5.7% of the initial parallel kinetic energy is converted into perpendicular kinetic energy at impact, resulting in a cyclotron radius, r_c, of 21.8 m. Increasing the value of δ results in an increase of the beam radius at Earth's impact. Powis et al.'s calculations show, for instance, that increasing δ to 1° results in a final cyclotron radius of 60 m.

Beam Propagation

The electron beam produced by a radio-frequency (RF) linear accelerator is a concatenation of periodic pulses the smallest of which are picosecond length micro-pulses. Multiple micro-pulses are bunched together to form a mini-pulse, typically lasting several microseconds, and a group of mini-pulses constitute a macro-pulse. Multiple combinations of macro-pulse duration and repetition rate can be chosen according to science objectives, from sub-second to multiple seconds. To illustrate the propagation properties of the beam and to characterize its properties at the point where it comes in contact with the Earth's topside atmosphere we have used a set of illustrative beam parameters described in Powis et al. (2019).

One approach that we have adopted to describe the beam propagation assumes that the evolution of the mini-pulse's RMS radius, r_b, can be decoupled from the electrons' helical motion so, within the frame of the beam centroid the evolution of the mini-pulse distribution depends on the initial conditions, the self-generated electromagnetic forces, and the ambient magnetic field. Since the mini-pulse length remains much longer (~10³) than the beam's radius even at maximum expansion, the mini-pulse is modeled as an infinitely long beam. Under these circumstances the radius r_b can be considered as the envelope of the beam and the standard one-dimensional beam envelope equation is applied (Reiser, 2008),

\begin{array}{l} \frac{d^{2} r_{b}}{d S^{2}} = - k_{0}^{2} r_{b} + \frac{K}{r_{b}} + \frac{ϵ_{r}^{2}}{r_{b}^{3}} & (1) \end{array}

Where S is the arc length from its injection point to its current position, $ϵ_{r} = \frac{v_{⊥} r_{b}}{v_{0}}$ is the beam radial emittance, v₀ = βc, $k_{0} = \frac{q B (S)}{2 m c γ β}$ parametrizes the focusing due to the ambient magnetic field and $K = \frac{q I_{0}}{2 π ε_{0} m_{0} c^{3} β^{3} γ^{3}}$ is the perveance, which captures the influence of beam self-charge and self-magnetic field (Powis et al., 2019, and references therein).

The solution to Equation (1) produces an oscillating beam envelope that initially grows to a size greater than a hundred kilometers but progressively narrows as the beam propagates into stronger magnetic field when it approaches Earth (Figure 7). The final beam radius at Earth's topside atmosphere impact is 2.6 m.

FIGURE 7

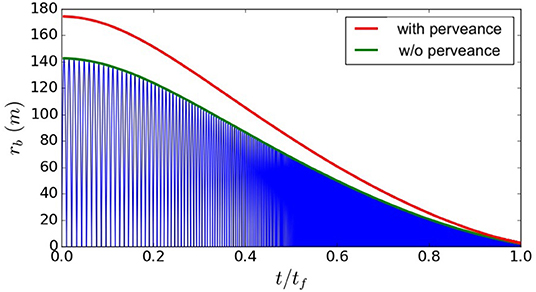
Figure 7. Solution to the envelope equations without beam perveance (blue lines). Extrema solutions with (red) and without perveance (green) for the reference beam conditions (Reproduced from Powis et al., 2019).

Equation (1) is also solved for the case without perveance (K = 0) to allow for comparison with ballistic simulations resulting from a single-particle propagation algorithm which does not incorporate the effects of space charge. The comparison is used to determine the appropriateness of ballistic simulations to describe the beam propagation. Parametric solutions for the envelope equation show that for the reference beam current of 1 mA, the final beam envelope radius is only weakly affected by beam perveance. This is due to the small magnitude of the average current and to the fact that, for relativistic beams, the self -generated magnetic field acts to cancel out a large fraction of the beam self-charge. This also demonstrates that despite self-forces being neglected, the use of single-particle simulations is suitable for modeling beams with similar properties to those of the reference values. Two other important properties are found. Firstly, increasing the initial beam energy results in a larger final radius since the increased electron momentum reduces the effectiveness of the applied magnetic field to focus the beam. Secondly, increasing beam current results in an increased final radius due to the increased current density at the point of emission. The larger the beam current, the less suitable ballistic simulations are for modeling the beam.

The properties of the cross-section density profile expected for a beam arriving to the topside atmosphere can be explored by applying the single particle algorithm to an ensemble of electrons from a mini-pulse injected from 10 R_e along a dipole field line using the physical parameters of the reference 1 MeV electron beam instrument described by Powis et al. (2019). The resulting density distribution (shown in Figure 8A) is ring-shaped rather than circular. The white dashed line shows the cyclotron radius r_c = 21.8 m expected for a 1 MeV electron at the topside ionosphere after having propagated along a dipolar field with a conserved first adiabatic invariant. The density distribution given by $n / n_{0} = exp ({(r - r_{c})}^{2} / 2 r_{b, f}^{2})$ (shown in Figure 8B) suggests that the beam radius at Earth's impact obtained from the simulation is 15% larger than 21.8 m. Cyclotron radius calculated at the topside ionosphere is expected to be the dominant parameter in determining the final beam spot size at the top of the atmosphere. There is less clear agreement between the simulated and predicted RMS beam envelope radius, as the simulation shows a larger envelope radius than the 2.2 m predicted by the envelope equation. Such discrepancy may be due to the effect of energy dependence of the ∇B and curvature drifts. Since the beam particles have an initial spread in energy, that spread translates into a smearing of the beam's final density distribution. The reason for the beam's ring shape can be explained by a combination of the following effects. Initially the envelope of the ensemble of electrons is expanding and contracting with the cyclotron frequency and in phase with the centroid motion of the entire beam rotating at r_c. Note that for the given beam parameters in the simulation, r_c > r_b. Since there is energy spread in the beam the cyclotron frequencies of particles will also have a spread due to small variations in the γ factor. As the beam propagates along the magnetic field line the particles will spread many periods in gyro-phase resulting in a beam density profile that evolves into a ring.

FIGURE 8

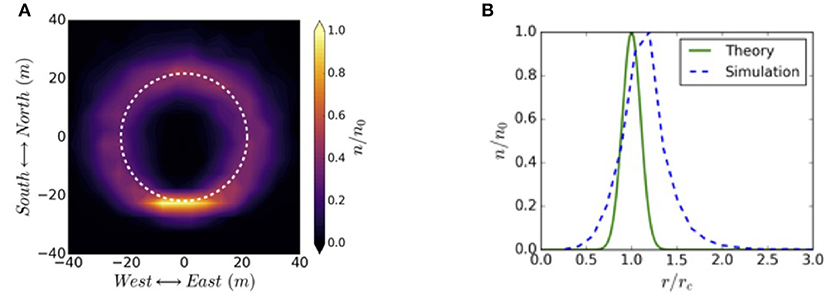
Figure 8. (A) Normalized electron density distribution at impact with the Earth. The dashed white line represents the cyclotron radius predicted theoretically. (B) Normalized radial electron distribution compared with theoretical prediction for the beam cyclotron radius and final beam envelope RMS radius (Reproduced from Powis et al., 2019).

We note that in Figure 8A density appears preferentially concentrated on a spot at the bottom of the ring when beam self-forces are not included. This occurs despite the expected decorrelation of particle gyro-orbit phase because a large number of particles remain closely correlated after traveling the length of the field line. Including self-forces (perveance) will in reality generate a more uniform density distribution around the ring.

An additional property of the cross-section density profile that must be considered for beams emitted from the magnetosphere into the atmosphere is the east-west spread of the beam caused by the spacecraft motion relative to the Earth's atmosphere. Simple Newtonian mechanics calculations show that the east-west elongation of the density distribution increases slightly, to ~72 m, for a 0.5-s burst of mini-pulses from a spacecraft orbiting at 10 R_e altitude (Figure 9). Other less pronounced effects, such as the gradient and curvature particle drifts, contribute to the elongation of the distribution as well.

FIGURE 9

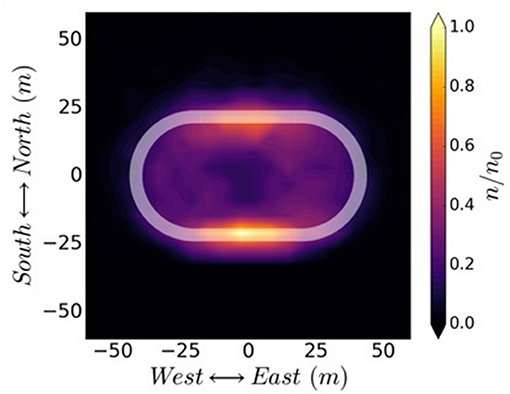
Figure 9. Normalized particle density distribution of a beam pulse at impact with the Earth's atmosphere in the case of a moving satellite (Reproduced from Powis et al., 2019).

The beam propagation calculations done in a dipolar field can be extended to a more realistic magnetic fields that are generated self-consistently by global MHD simulations such as BATS-R-US (Tóth, 2005). Beam injections from 5 R_e were simulated for varying magnetic field configurations experienced at different stages in the development of a geomagnetic storm in March 2015. The simulation provides a picture of the range of variation in the latitude of atmospheric foot-point of the beam as well as the size of the beam. The spread of ~10° on either side of the foot-point of geosynchronous altitude (Figure 10) shows the large variation in the geographical location of the beam's signature due to the significant changes in magnetic field topology induced by geomagnetic activity. Prediction of beam foot-point location as a function of geomagnetic activity level provides guidance on where ground-based imagers should be placed to ensure that the beam's optical signature would be captured.

FIGURE 10

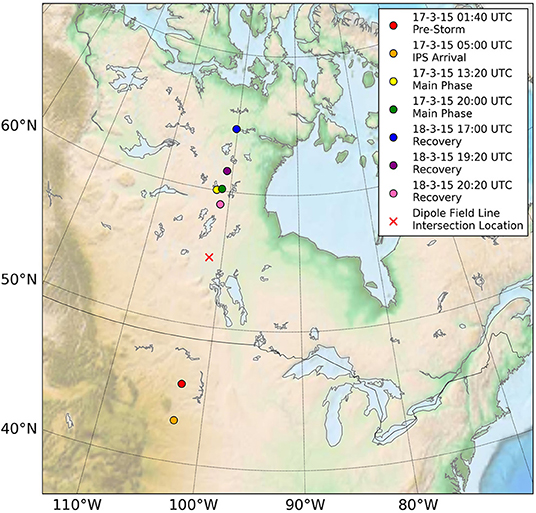
Figure 10. Impact locations of each beam emitted from x = −5R_E during various phases of the 2015 St. Patrick's Day magnetospheric storm (Reproduced from Powis et al., 2019).

Beam Detectability and Ground-Based Diagnostics

Neubert et al. (1996), Krause (1998), and Krause et al. (1999) demonstrated that relativistic beams injected from the ionosphere into the atmosphere below would produce significant electron-density enhancements, optical emissions, and measureable height-integrated X-ray fluxes.

Marshall et al. (2014) expanded on the work of Krause (1998) to calculate optical emissions observable from the ground, X-ray production and propagation and detectability from satellites and balloons, and backscattered electrons that could be observed from Low Earth Orbit (LEO). That study showed that optical signatures were likely detectable, X-ray fluxes were likely to be far too low from either LEO or balloon altitudes, and ionization could likely be measured form the ground using incoherent scatter radar. That study investigated a pulse of electrons with 0.05–1 Joules of total energy. Recent accelerator design efforts are targeting a beam total energy of 100–1,000 J, prompting a revisit to the calculations of Marshall et al. (2014).

In the new simulations (Marshall et al., this issue), the accelerator under consideration produces an output of 5 J of electrons at 1 MeV in each pulse (3.1 × 10¹³ electrons), with a pulse every 5 ms. A beam of 1 MeV electrons injected from a distance of 10 R_e was simulated by Porazik et al. (2014), who then propagated ballistically the beam to 300 km altitude and calculated the spatial, energy, and pitch angle distributions of the beam at that altitude. Those distributions are used as the input distributions to Marshall et al.'s Monte Carlo modeling. A 2-D histogram of the particle positions shows that the beam is distributed approximately as a Gaussian with a 1-sigma diameter of 311 m at 300 km altitude. The beam is extremely field-aligned, with a divergence of less than 1 degree, due to the careful choice of the firing direction in Porazik et al. (2014). However, simulations show that as long as the beam is inside the loss cone, the pitch angle distribution plays only a small role in the atmospheric signatures. For example, a beam with all electrons 60-degree pitch angle at 300 km altitude, just inside the loss cone, will have a similar energy deposition profile, but raised in altitude by 4 km.

The new simulation results show that the peak of the energy deposition from a sequence of 20 pulses spanning 100 ms and totaling 100 J, or a sequence of 200 pulses spanning 1 second and totaling 1 kJ, occurs slightly below 60 km altitude, in the atmospheric region known as the D-region, and that approximately 2.2% of the total injected energy is converted to N2 1P emissions, and 0.6% is converted to N+2 1N emissions. Using these parameters and considering an optical aperture of 50 mm diameter (a typical camera lens) with a field-of-view that is larger than the emitting region, and where one can expect 3.3 × 10³ photons to be collected by the instrument, Marshall et al. conclude that a PMT-based system can detect the emission produced by the beam with a signal-to-noise-ratio (SNR) of 25 when sampled at 100 Hz. For a 50 mm diameter lens wide field-of-view camera system an SNR of 10 is feasible when sampling at 10 Hz.

Marshall et al. also consider whether the electron density enhancement that would be produced by the beam in the D-region is detectable by radar. Their calculations show that the expected electron density enhancement after the 1-s train of pulses and the ~1-s recovery in the D-region for the 100 J (20 pulses in 100 ms) beam emission case. After 20 pulses, the peak electron density of 3.9 × 10⁹ cm⁻³ occurs at an altitude of 59 km. It also shows the SNR that an incoherent scatter radar (ISR) such as the Poker Flat ISR (PFISR) would measure and the expected relative error, dS/S. Although SNR < 1, detectability is actually determined after calculating the gain for a Lorentzian radar spectrum done by averaging radar pulses coherently (e.g., Farley, 1969). The relative error dS/S is then found by incoherently averaging all the sets of coherent averages embedded in the interval where the radar sampled the ambient electron density enhancement produced by the electron beam. The relative error for the example shown by Marshall et al. is dS/S = 0.27. A value of dS/S = 1 indicates that the signal is 1σ above zero SNR; dS/S = 0.33 indicates 3σ above zero SNR, and so forth. The analysis thus shows that ISRs operating standard beam codes (whose parameters were applied in the calculation of SNR and dS/S) are capable of detecting the beam pulse sequence of 1 kJ injected over 1 s. New radar beam codes that increase the coherent gain, combined with longer integration times and longer electron beam pulses, will decrease dS/S thus improving detectability. For example, a 50% increase in the number of averaging intervals would decrease dS/S to 0.22.

An important environmental consequence of the beam interaction with the atmosphere addressed by Marshall et al. is the possibility of adverse effects on the atmosphere. Energetic electron precipitation leads to enhancement of odd nitrogen (Rusch et al., 1981) and odd hydrogen (Solomon et al., 1982). These molecules are long-lived and, as they are transported downward into the stratosphere, can affect ozone concentration (e.g., Callis et al., 1991, 1996). Marshall et al. apply the Glukhov-Pasko-Inan (GPI) chemistry model (Glukhov et al., 1992; Lehtinen and Inan, 2009) and the Sodankylä Ion and Neutral Chemistry (SIC) model (Verronen et al., 2005; Turunen et al., 2009) to calculate the density increase in NOx, HOx and decrease in ozone due to the precipitation of the electron beam. The SIC model shows an increase in NOx density of only 0.5% from its background density and an increase in HOx of 0.4%. The ozone signature is negligible. These results show that active experiments with relativistic electron beams pulsed at short intervals can be used for magnetosphere-ionosphere research without causing significant adverse long-term effects in the atmosphere.

Additional Applications of Beam Experiments

Relativistic electron beams have multiple applications beyond the fundamental problems in space physics discussed so far. We briefly discuss two of them: Sprite triggering and beam-induced waves to precipitate radiation belt electrons through resonant pitch angle scattering.

Sprite Triggering

Enhanced conductivity channels above thunderstorm systems can lead to the modification of the atmospheric potential structure. The resulting electric fields may lead to atmospheric breakdown and discharge, known as sprite, especially at high altitudes, where the breakdown fields, E_k, are less than 100 mV/m (Banks et al., 1987, 1990; Neubert and Banks, 1992; Neubert et al., 1996). Neubert and Gilchrist (2004) suggested the possibility that the relativistic electron beam, upon its interaction with the atmosphere, could modify the conductivity enough to enhance the triggering of sprites at their typical triggering altitude of ~75 km (Stenbaek-Nielsen et al., 2010; Pasko et al., 2012). Marshall et al. investigate the possibility of triggering sprites with Mev-class beams by calculating the electric fields induced by the beam precipitation above a thunderstorm system using the 2-D quasi-electric (QES) field model of Kabirzadeh et al. (2015, 2017). These results show that after the discharge E > E_k within 1 km of the beam radius which is a condition expected favorable for sprite triggering, thus allowing for the possibility to conduct a carefully timed experiment to increase the high-altitude electric field to trigger sprites.

Wave-Particle Interactions and Loss of Electrons

The radiation belts are near-Earth magnetosphere regions populated by protons and electrons with energies from 100 keV to >15 MeV. Enhanced radiation-belt electron fluxes, which can be caused by geomagnetic storms or anthropogenic sources, are known to be damaging to space assets (Baker, 2001; Horne, 2003). Particles originating in the solar wind and the ionosphere are accelerated during geomagnetic storms through wave-particle interactions and radial transport and become trapped in the 1.5–5 R_e region (e.g., Horne et al., 2005; Shprits et al., 2008a,b and references therein). Some of these particles can be lost by precipitation into the atmosphere (Lorentzen et al., 2001a; Millan et al., 2002; Green et al., 2004; O'Brien et al., 2004; Bortnik et al., 2006; Millan and Thorne, 2007; Thorne et al., 2010). Theoretical work carried out in the 1960s and 1970s showed that wave-particle interactions can lead to pitch-angle scattering of electrons and their subsequent loss to the atmosphere (Kennel and Petschek, 1966; Thorne and Kennel, 1971). Violation of the first two adiabatic invariants can induce pitch-angle scattering (and potential loss to the atmosphere) and energy diffusion.

Elucidating how wave-particle interactions cause the radiation belts to lose electrons is important for mitigating space weather effects. Considerable research has investigated methods to control radiation belt populations using VLF-wave injection to precipitate these particles (e.g., Inan et al., 1984, 2003). However, challenges exist with methods for efficiently transmitting VLF waves to the space plasma.

Radiation-belt electrons in the 0.1–10 MeV range resonate with VLF whistler-mode waves of 0.1–10 kHz. The natural environment often contains waves in the VLF band, such as hiss, chorus, and lightning-generated whistlers. The source of hiss and the depletion and refilling rates of the radiation belts are topics of active research. Whistler mode chorus consists of discrete whistler mode emissions observed outside the plasmasphere in the frequency range of 0.1–1 fce (~100 Hz−5 kHz). Models of whistler-electron interaction suggest that whistler mode chorus waves are generated at the equator first, driving the pitch angle scattering of ~10 keV electrons, which can cause pulsating aurora (Lessard, 2012). Subsequently, the waves propagate to higher latitudes where pitch angle scattering of sub-relativistic (~few hundreds of keV) and relativistic electrons (~MeV) occurs. Whistler mode waves first resonate with electrons at tens of keV near the equator, and then with higher-energy electrons at higher latitudes (Lorentzen et al., 2001a; Horne and Thorne, 2003; Thorne et al., 2005). Therefore, precipitation of electrons across a wide energy range is expected. In most cases, whistler mode chorus is characterized by discrete elements called “risers,” which generally have rising-tone frequency-time spectra between ~0.1 and 0.8 fce, although falling tones can occur. Outside the plasmasphere, electron resonant energies for typical whistler-mode frequencies near 2 kHz are ~100 keV for interactions occurring at the equator. Scattering by whistler- mode chorus was suggested as the mechanism responsible for relativistic electron microbursts, since both are most often observed between 0300 and 1,500 magnetic local time (Lorentzen et al., 2001b).

Controlled electron injections at specified energies and pitch angles would enable detailed studies of wave-particle interactions and scattering. An injected beam of known particle energy and pitch angle can be used to target specific wave frequencies for growth or generation. The use of a modulated (via changes to pitch angle and energy), relativistic electron beam to excite VLF waves may be an efficient method to scatter enhanced radiation-belt electrons into the loss cone. Investigations of the dynamics, stability, and loss of artificially injected relativistic electron beams (Pritchett et al., 1989; Khazanov et al., 1999a,b, 2000) indicate that they could be powerful means for studying wave and collisional interactions. The application of electron beams to trigger waves that can scatter radiation belt electrons into the loss cone is an active area of research (see Delzanno et al., this issue).

Conclusion, Roadmap to the Application of Electron Beams

Active experiments with relativistic electron beams represent the most viable opportunity to finally bring closure to long-standing problems how the magnetosphere and the ionosphere connect to generate aurora, to transfer energy between the two domains, and to regulate the circulation of mass, momentum, and energy throughout the ionosphere-magnetosphere system. A spacecraft mission that measures in-situ particle density, pressure, convection, and electric current as well as radial and azimuthal gradients of these quantities with a distributed set of measurements will be able to quantify the source terms that drive the electromagnetic connection with the ionosphere. Accurate correspondence between magnetospheric processes or regions and their ionospheric foot-points can be achieved with beams of energetic electrons emitted in the magnetosphere under controlled conditions, propagating along magnetic-field lines in fractions of a second, and detected by an array of ground-based optical imagers, radars, riometers, or X-ray detectors through the optical, radio, and electron density imprints created in the atmosphere by the impact between the beam's electrons and the neutral particles in the atmosphere. Given the current state of compact-accelerator technology, development, and launch of a space-based energetic particle accelerator are only a few years away. The technology for relativistic linear electron accelerators will overcome the challenges encountered with previous efforts to trace magnetic-field lines with lower energy electron beams emitted from the magnetosphere.

The research results presented here demonstrate the feasibility of using relativistic electron beams that: (1). When emitted under appropriate conditions do not raise the spacecraft potential more than a few kV; (2). Can propagate along realistic field lines, when emitted inside a modified loss cone geometry applicable only to relativistic particles; (3). Can propagate into the topside ionosphere with sufficient flux to generate a perturbation in the middle atmosphere that is detectable on the ground with optical and radio instruments and such that does not produce a significant lasting adverse effect on the chemistry of the atmosphere.

These results are highly encouraging, and work continues to definitively demonstrate the validity of the beam emission concept as a viable active experiment tool for magnetosphere-ionosphere research applications. One of the areas of ongoing research is the determination of the stability properties of the beam as it travels along magnetic field lines from the region around 6–10 R_e in the night-side magnetosphere to the topside atmosphere. Simple linear analysis suggests that a beam propagating through the magnetosphere will be stable to two-stream instabilities (Galvez and Borovsky, 1988), and a beam propagating into the ionosphere will be stable to resistive hose, ion hose and filamentation instabilities (Gilchrist et al., 2001). Simulations that track the beam from its source in the magnetosphere to its contact with the topside ionosphere are currently being carried out to quantify the effects of beam-plasma interactions as the beam moves through magnetic field and density gradients. Initial particle-in-cell simulation results, supported by theoretical analysis, suggest no major effect of instabilities on the beam propagation (Kaganovich, private communication). Theory and simulation results will be reserved for a future publication.

Author Contributions

ES assembled the INSPIRE team and, as Principal Investigator of the project, he coordinated research activities to ensure their relevance in addressing solutions to compelling magnetospheric problems, contributed to calculations of MHD magnetic field used to guide MeV electrons' trajectories, contributed to calculations of detectability thresholds of atmospheric effects measured with radar, and contributed to definition of beam properties for science applications. PP developed the loss cone calculations for MeV electron beams and developed the ballistic code for electrons. AP extended ballistic code for magnetic fields inferred from MHD global models. IK contributed with PP, AP, JJ, and DS developing ballistic codes and trajectory visualization tools. RM applied Monte Carlo techniques to measure atmospheric effects of MeV electron precipitation. JJ, MG-M, and KA developed algorithms to infer electron propagation preperties in analytic magnetic field models. MN contributed to calculations of beam detection with radars and to definition of beam properties for science applications.

Funding

This research was funded by NSF's INSPIRE initiative through grant 1344303.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Akasofu, S.-I. (1964). The development of the auroral substorm. Planet. Space Sci. 12, 273–282. doi: 10.1016/0032-0633(64)90151-5