
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci., 07 February 2019
Sec. Space Physics
Volume 6 - 2019 | https://doi.org/10.3389/fspas.2019.00002
This article is part of the Research TopicActive Experiments in Space: Past, Present, and FutureView all 21 articles
Controlled experiments involving injection of 0.5 Hz–8 kHz electromagnetic waves into the Earth's magnetosphere have played an important role in discovering and elucidating wave-particle interactions in near-Earth space. Due to the significant engineering challenges of efficiently radiating in the ELF/VLF: 300 Hz–30 kHz band, few experiments have been able to provide sustained transmissions of sufficient power to excite observable effects for scientific studies. Two noteworthy facilities that were successful in generating a large database of pioneering and repeatable observations were the Siple Station Transmitter in Antarctica and the High Frequency Active Auroral Research Program (HAARP) facility in Alaska. Both facilities were able to excite Doppler shifted cyclotron resonance interactions leading to linear and non-linear wave amplification, triggering of free running emissions, and pitch angle scattering of energetic electrons. Amplified and triggered waves were primarily observed on the ground in the geomagnetic conjugate region after traversal of the magnetosphere along geomagnetic field aligned propagation paths or in the vicinity of the transmitter following two traversals of the magnetosphere. In several cases, spacecraft observations of the amplified and triggered signals were also made. The observations show the amplifying wave particle interaction to be dynamically sensitive to specific frequency and also specific frequency-time format of the transmitted wave. Transmission of multiple coherent waves closely spaced in frequency showed that the wave particle interaction requires a minimum level of coherency to enter the non-linear regime. Theory and numerical simulations point to cyclotron resonance with counter streaming particles in the 10–100 keV range as the dominant process. A key feature of the non-linear interaction is the phase-trapping of resonant particles by the wave that is believed to drive non-linear wave amplification and the triggering of free-running emissions. Observations and modeling of controlled wave injections have important implications for naturally occurring whistler mode emissions of hiss and chorus and the broader phenomena of radiation belt dynamics. A review of observational, theoretical, and numerical results is presented and suggestions for future studies are made.
Appreciation of the role of whistler mode waves in the near-Earth space environment predates the space age and began with the landmark publication by Storey (1953). Storey (1953) identified the plasma nature of the space around of the Earth (out to several Earth radii of altitude) as responsible for the phenomena of “whistling” atmospherics which were first observed on communications hardware during World War I. He described how lightning induced impulsive radiation in the ELF/VLF band (3 Hz–30 kHz) couples through the ionosphere, into the magnetosphere and experiences frequency dispersion due to propagation along the geomagnetic field line in a right hand circularly polarized mode below the electron cyclotron frequency and plasma frequency. This mode has since been called the whistler mode. The work of Storey (1953) was foundational in magnetospheric physics in that it not only established the magnetosphere as filled with significant densities of cold plasma, but also was the first to describe natural whistler wave emissions, known as hiss and chorus, subsequently identified to result from hot plasma instabilities. Today whistler mode waves of both terrestrial and magnetospheric origin are seen as key drivers in near-Earth space energy dynamics (Reeves et al., 2003; Bortnik and Thorne, 2007; Thorne, 2010). Despite several decades of research, whistler-mode wave particle interactions continue to be the subject of active investigations since the near-Earth space environment and its energy dynamics are of increasing economic and strategic importance. Recently there has been renewed interest in non-linear whistler mode phenomena and a consensus that the non-linear regime of wave-particle interactions needs to be quantified to achieve accurate prediction capabilities in global flux and energy models. Active whistler mode injection experiments, which are the topic of this review, have been the drivers of non-linear phenomena investigation and can play an important role in future efforts.
Almost a decade after Storey's results (Storey, 1953) were published, it was discovered that it is possible to actively trigger whistler mode emissions in the magnetosphere with controlled transmissions from VLF communication transmitters (Helliwell et al., 1964). A VLF receiver on board a ship USNS Eltanin in the magnetic conjugate region of the U.S. Navy NAA transmitter in Cutler, Maine observed amplification and triggering of new frequencies from the Morse code 14.7 kHz transmissions. The observed records revealed that the emissions were triggered almost exclusively by the 150 ms Morse dashes and only rarely by the 50 ms Morse dots (Helliwell et al., 1964; Helliwell, 1965, p. 297–298). This remarkable phenomenon was dubbed the “dot-dash anomaly” and sparked interest in dedicated transmissions at variable frequency for controlled experiments of magnetospheric wave particle interactions.
As illustrated in Figure 1, an hemisphere to hemisphere wave injection experiment turns the inner magnetosphere into a plasma chamber in which controlled whistler mode sources can be used as diagnostics of the condition of the plasma and for excitation of instabilities. In such experiments transmitted signals which have made one traverse through the magnetosphere and are observed in the magnetic conjugate region are known as “one hop echoes” and signals that have made two traverses and returned to the transmitter region are known as “two hop echoes.” Antarctica was initially seen as an optimal location for a VLF wave injection experiment where transmissions into the magnetosphere along geomagnetic field lines would be possible. The advantages of Antarctica included the lack of major sources of electromagnetic noise including man-made interference and thunderstorm activity, the established observations of natural VLF emissions, and the accessibility of the conjugate locations on landmasses in the northern hemisphere. Furthermore, the presence of thick ice sheets allowed for significant elevation of an horizontal antenna above the conducting surface of the Earth. An initial attempt of a transmitter near Byrd Station (80.02° S, 119.53° W, L~7.2) known at the Bryd Longwire was operated from 1966 to 1969 but yielded mixed results (Helliwell and Katsufrakis, 1974; Gibby, 2008). One reason that the Byrd Longwire was not able to excite signals that could be observed at the conjugate point was that it was located at a high L shell where geomagnetic field lines can be open and hemisphere to hemisphere ducting is unfavorable. Whistlers in Antarctica were typically observed to have propagated along paths near L~4.
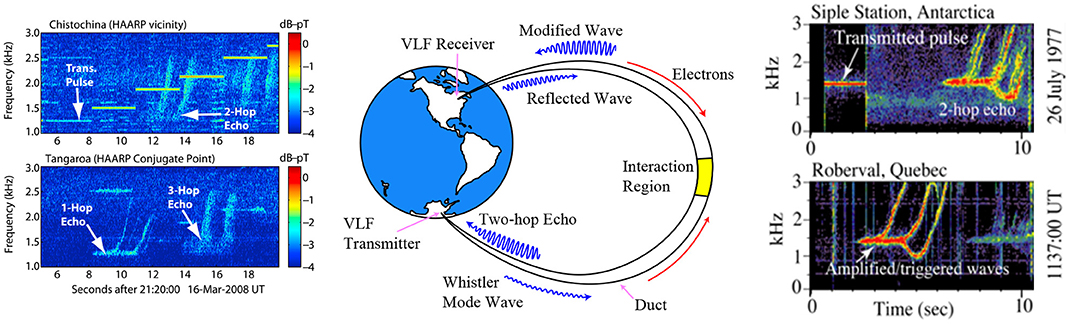
Figure 1. Propagation and amplification of whistler waves along ducted paths for fixed transmitter/receiver locations. Spectrograms of transmitted and received signals from HAARP (Left) and Siple (Right) transmitters are shown. Adapted from Figure 1 of Gołkowski et al. (2011).
In 1969 an effort was undertaken to find an ideal site in Antarctica for a VLF wave injection experiment and after an exhaustive search, a site was selected at 79.93° S, 84.25° W, 2381 km east of McMurdo Station. At L~4.3, the site, named Siple Station in honor of American Antarctic pioneer Paul Siple, offered access to high magnetic latitudes, the plasmapause, and natural VLF emissions. The magnetic conjugate point was located near the city of Roberval in Quebec, Canada, making establishment of a conjugate monitoring station straightforward. The initial installation, completed in 1973 used the 80 kW VLF transmitter from Byrd Station and a single 21.2 km horizontal antenna giving a resonant frequency of approximately 5 kHz. The installation received significant upgrades over the years with a 150 kW transmitter installed in 1979, the antenna lengthened to 42 km in 1983 and the addition of a second 42 km dipole in 1986. The 42 km crossed dipoles of the final installation were resonant at 2.5 kHz and could directly excite a right hand polarization that could propagate in the ionosphere and magnetosphere (Helliwell, 1988).
Analysis by Raghuram et al. (1974) showed that the antenna efficiency at Siple Station was on the order of 2–3%. The 2 km thick ice sheet was key in elevating the antenna above the conducting ground and mitigating detrimental image currents (Helliwell, 1988). This controlled science dedicated injection of several kW of power in the few kHz band continues to be unmatched to this day. The Siple experiment was very successful in producing observations of non-linear growth and triggering of whistler mode waves in the conjugate region and in the vicinity of the transmitter. The reception statistics show that the amplified and triggered signals were received in the conjugate region for ~25% of transmission cases for the 80 kW transmitter and over 50% for the 150 kW transmitter (Carpenter and Miller, 1976, 1983; Gibby, 2008; Li et al., 2015b). The observation occurrence was also optimized by following a procedure in which the transmission frequency and format was dynamically set and changed in response to observations of natural VLF emissions or excited echoes of transmitted signals (Gibby, 2008). In particular, transmissions within a few hundred Hz of a natural hiss band were observed to be favorable for triggering a magnetospheric response. This underlines both signal amplitude and specific frequency as important parameters in active magnetospheric whistler mode probing. Sometimes the band of frequencies over which growth occurs may be only a few hundred Hz wide (Helliwell, 1988). Signals from Siple Station were also observed on numerous spacecraft (Inan et al., 1977; Bell et al., 1981; Rastani et al., 1985). The signal amplitudes observed on the spacecraft varied from 0.01 to 0.5 pT with the strongest signals received outside the plasmapause and/or after crossing the magnetic equatorial plane. Amplitudes prior to crossing the magnetic equator were lower and in the range of 0.01 to 0.05 pT (Sonwalkar et al., 1984; Rastani et al., 1985; Sonwalkar and Inan, 1986).
The unique richness of the observations from Siple Station, which we describe in more detail in the subsequent section, motivated a wide range of theoretical studies of non-linear whistler mode wave particle interactions and the triggering of new emissions in the 1970s and 1980s (Sudan and Ott, 1971; Karpman et al., 1974, 1975; Nunn, 1974; Roux and Pellat, 1978; Vomvoridis and Denavit, 1979; Matsumoto et al., 1980). Other active experiments during this time yielded less data but confirmed the resulting effects of excited wave-particle interactions. Injection with temporary balloon transmitters (Dowden et al., 1978) or observations of pulsed VLF transmissions for maritime navigation (Tanaka et al., 1987) were also pursued. However, the former were limited by their temporary nature and the latter did not have favorable frequency and location to regularly excite the richer non-linear behavior.
Funding for Siple Station station ended in 1989 at which time the station was abandoned. A concise history of Siple Station operation can be found in Chapter 2 of the thesis by Gibby (2008); a more detailed history of experiments and operations during this period has been provided by Carpenter (2016). Data from the Siple Station experiment originally recorded on magnetic tape has been digitized and is the subject of continued investigations (Li et al., 2014, 2015a,b; Costabile et al., 2017)
The construction of the High Frequency Active Auroral Research Program (HAARP) ionospheric facility in Gakona, Alaska (62.4° N, 145.2°W) in the 1990s opened new opportunities for dedicated transmissions for magnetospheric wave injection. The main instrument of the facility is the ionospheric heater, which, upon its final completion, could radiate 3.6 MW in a wide band from 2.75 to 9 MHz, making it both the most powerful and versatile HF heater in the world. Unlike Siple Station which radiated ELF/VLF frequencies directly from a conventional antenna, the HAARP heater had the ability to generate ELF/VLF by modulating overhead natural ionospheric currents. The concept of using an ionospheric heating facility to generate ELF/VLF waves by modulating the ionospheric electrojet had been illustrated at the Tromsø facility in Norway during the 1980s (Stubbe et al., 1982) and also earlier in the Soviet Union (Getmantsev et al., 1974). However, it was initially not clear whether such a technique would be effective at HAARP since the latitude was lower than the Tromsø facility and the auroral electrojet was therefore expected to be less prominent. To the surprise of some, the first experiments of modulating the electrojet over HAARP were a huge success (Milikh et al., 1999). Even with the initial version of the heater with only 960 kW of power, ELF/VLF signals were clearly observed at a receiving station 36 km away and the facility proved effective in probing the magnetosphere (Inan et al., 2004).
The location of the HAARP ionospheric heating facility was determined by the availability of an existing military site that was originally intended to be an over-the horizon radar installation. One of the consequences of this location was that the magnetic conjugate point of the facility was in the southern Pacific Ocean about 1,000 km from the coast of New Zealand and 500 km from the nearest land of Campbell Island. An ambitious engineering effort was made to deploy autonomous receivers on buoy platforms (Cole et al., 2005) that would transmit recorded data via Iridium satellite modem. Shipborne VLF receivers were also used to make conjugate observations (Gołkowski et al., 2008; Carpenter, 2016, section 5.3). The two autonomous buoy receivers deployed did not operate as long as had been initially planned but both yielded observations of one hop and higher order echoes. Likewise, almost every ship borne observation during a HAARP campaign also yielded evidence of direct whistler mode triggering by the HAARP facility. When receivers were not available in the conjugate point, a network of receivers near the HAARP facility were used to observe two hop echoes (Golkowski, 2009).
Wave injection experiments at HAARP leveraged the experience gathered during Siple Station operations. Campaigns were typically run for 1–2 weeks with ~8 h of transmissions a day. The years 2007–2008 saw a large number of campaigns dedicated to wave injection studies. The magnetospheric response to the transmissions was monitored with local receivers, which would create spectrograms in near-real time and post to a website for viewing. Changes in transmission format could be made within a minute or two by communication with the facility operator. As with Siple Station, changing the transmission frequency and the frequency-time format would often have a significant effect on the presence and strength of magnetospheric echoes observed. HAARP ELF/VLF signals were regularly observed on the DEMETER spacecraft at 700 km altitude (Platino et al., 2006; Piddyachiy et al., 2008) and also by the CLUSTER spacecraft (Platino et al., 2004). HAARP induced one-hop echoes were observed on DEMETER in the conjugate point (Gołkowski et al., 2011). Additional relavent reports on HAARP wave injection include work by Golkowski et al. (2009) and Streltsov et al. (2010). A broader review of research efforts at HAARP additionally encapsulating HF wave interactions in the ionosphere has recently been compiled by Streltsov et al. (2018).
A key difference between the HAARP ELF/VLF transmissions and the Siple Station transmitter is total radiated power. As mentioned above, the Siple Station transmitter would radiate on the order of 1 kW or more of ELF/VLF power. The ELF/VLF generation capability of HAARP is variable as it depends on the overhead elecrojet current intensity and the lower ionosphere profile in a complicated way (Jin et al., 2011). The radiated ELF/VLF power is also harder to quantify and estimates using both ground and space observations range from from less than 1 W to a maximum of 200 W on rare select days of optimal conditions (Platino et al., 2006; Moore et al., 2007; Cohen et al., 2011; Cohen and Gołkowski, 2013). Despite its lower power, the HAARP facility had the advantage of greater transmission bandwidth over spans of up to 10 kHz and ability to synthesize complex transmissions.
The most characteristic repeatable feature of the observations and emblematic of the non-linear nature of the phenomena is the temporal growth in amplitude of a signal observed at a stationary receiver in the conjugate point that results from the transmission of a constant amplitude pulse. Examples of this canonical behavior from both the Siple and HAARP experiments are shown in Figures 2, 3 respectively. The growth phase typically lasts on the order of less than a second and subsequently the amplitude saturates. During the exponential growth phase the observed frequency remains within ~10−15 Hz of the transmitted frequency, but phase is also exponentially advancing. At saturation a free running emission commences. This free running emission typically increases in frequency and is called a riser. Frequency fallers that decrease in frequency and “hook” emissions that reverse in frequency change are also observed as shown in Figure 4. A remarkable feature of the free running emission is that even though it swings through a wide range of frequencies of several kHz, its instantaneous bandwidth is typically restricted to less than 10−15 Hz. The free running emissions triggered by injection experiments are identical to features of chorus waves observed on spacecraft and on the ground. A recent analysis of two hop echoes from the HAARP experiment concurrent with chorus risers has been presented by Hosseini et al. (2017) and illustrates how the frequency sweep rate of both types of emissions shows similar evolution.
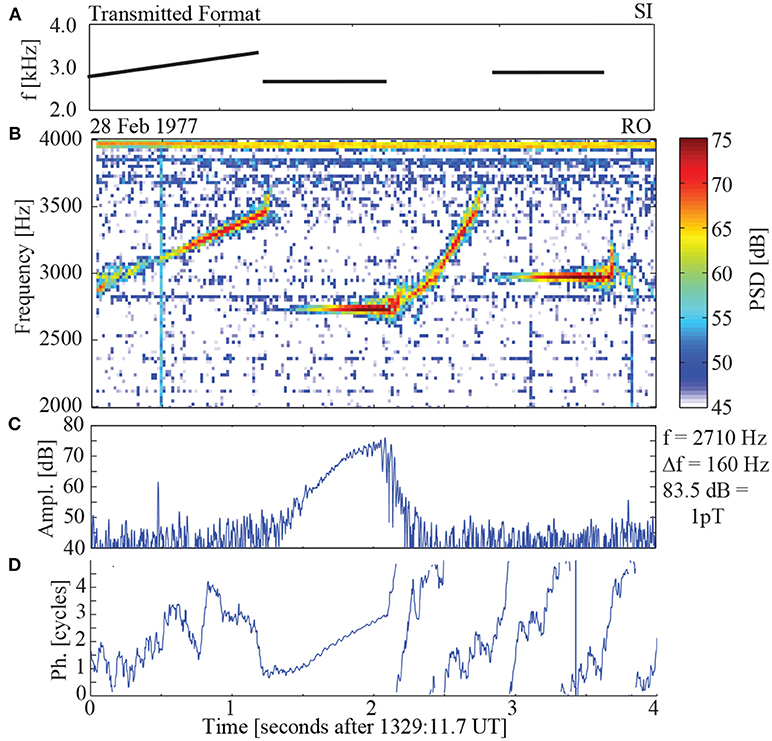
Figure 2. Growth and triggering characteristics of the instability from the Siple Station experiment seen in the transmission of 2.71 kHz pulse (A) The time frequency format transmitted from Siple Station. (B) The time-frequency spectrogram of the VLF data received at the conjugate point. (C) A narrowband amplitude plot, centered on 2.71 kHz, with a 160 Hz bandwidth. (D) The phase of the narrowband data in (C). Adapted from Figure 2.3 of Gibby (2008).
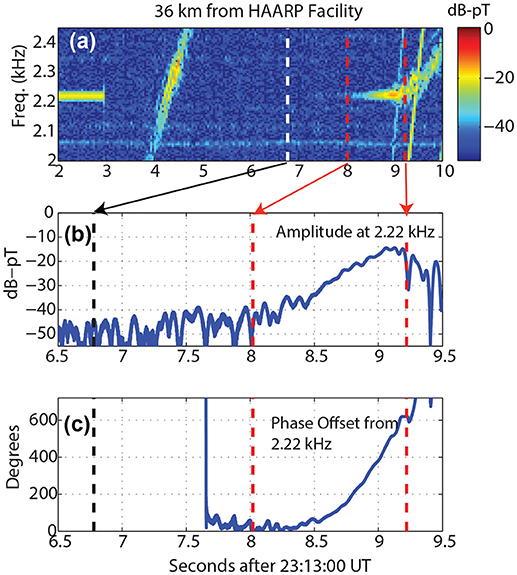
Figure 3. Received two hop echo with triggered emissions due to a monochromatic transmitted pulse from HAARP at 2.22 kHz. (a) Spectrogram of transmitted and received signal, (b) temporal increase in signal amplitude at the transmitted frequency. (c) Exponential phase advance that accompanies the temporal amplitude increase. Features of amplitude and phase dynamics simlar to those shown in Figure 2 for a one hop echo from the Siple Station experiment. The emission at 4 s in the record is from an earlier transmitted frequency-time ramp. Adapted from Figure 3 of Gołkowski et al. (2010).
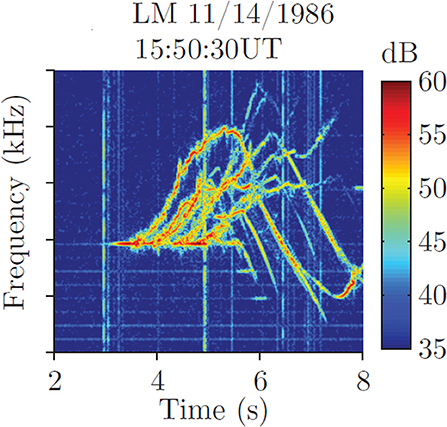
Figure 4. Complex triggered emissions observed at Lake Mistissini in response to Siple Station transmissions showing multiple risers and hooks. Adapted from Figure 2 of Li et al. (2015c).
Whether or not the triggered free running emission is a riser, faller, or hook is variable. Helliwell and Katsufrakis (1974) show clear change of fallers to risers when transmitted pulse duration is changed. Fallers are generated by short pulses up to 250 ms in duration and risers are generated by longer pulses 300–400 ms long. A more comprehensive statistical study of Siple Station observations by Li et al. (2015b) confirms that shorter pulses are more likely to trigger fallers while longer pulses trigger risers. The simplest theory of the free running emission frequency change is that it is created by counterstreaming energetic electrons that are initially in forced resonance with the wave and then exit the wave field and revert back to adiabatic motion. If those electrons retain an element of phase coherence after they exit the wave field they will radiate either a falling or rising emission depending on if the reversion to adiabatic motion takes place before or after the equator (toward lower or higher gyrofrequency). This model was put forth by Roux and Pellat (1978) and is enticing in its simple elegance. However, it is noted that electrons no longer under the influence of the wave will quickly mix in gyrophase and not radiate coherently, so the distance over which this mechanism radiates would have to be small. Other more complicated theories of risers vs. fallers have these emissions being radiated by particles remaining in forced resonance with the wave but on different sides of the equator (Nunn and Omura, 2012). In either case, the magnitude and position of wave amplitude spatial gradients along the field aligned propagation path is seen as a key parameter.
There is a threshold for excitation of the non-linear growth but is relatively low, on the order of a 1 W of ELF/VLF radiated power as evidenced by power stepping studies at Siple Station (Helliwell et al., 1980) and the fact that the HAARP facility was able to excite the phenomena at all given the power levels described above. In the Siple experiment, observations showing only linear growth of transmitted signals without the non-linear features were obtained (Paschal and Helliwell, 1984). For wave growth in the linear regime the echo of a transmitted single frequency constant amplitude pulse observed in the conjugate region does not show temporal amplitude change since each part of the pulse is amplified the same amount. Linear growth rates can be calculated directly from the anisotropy (see section 3.2) and flux of the energetic electron distribution (Kennel and Petschek, 1966). In the literature on Siple Station observations, linear growth is often described as “spatial” growth. Gołkowski et al. (2010) show that the exponential growth duration and also the final saturation amplitude are surprisingly similar even if the transmitted input amplitude is decreased by 13 dB. What is different in those cases is that for the weaker input the non-linear temporal growth phase occurs later and the free running emission triggered is a relatively steeper frequency riser and not a hook or faller as it is for the higher amplitude input (Gołkowski et al., 2010). The maximum saturation amplitude achieved is therefore a function of magnetospheric plasma and not the input signal amplitude. The time delay of the temporal growth and saturation can be understood as the lower input amplitude requiring more time to grow in the linear regime before the non-linear growth threshold is breached. This also means that the spatial gradients of wave amplitude along the interaction region would be in different places along the field line and thus the counterstreaming electron exiting the interaction region would exhibit different rates of gyrofrequency change when they revert back to adiabatic motion. This latter behavior can explain the riser vs. faller difference in features. In general, the non-linear temporal growth rates observed are in the range of 3 to 270 dB/s with a median growth rate of 68 dB/s (Li et al., 2015c). The observed peak echo amplitudes observed on the ground for the HAARP experiment were in the range of 0.01–1 pT. The simultaneous occurrence of both linear and non-linear wave growth makes it challenging to estimate the wave amplitude in the magnetospheric interaction region at a specific point in time and space (Gołkowski et al., 2008).
Other important features of the observations include suppression of growth by signals adjacent in frequency, the generation of sidebands, and entrainment. Two waves with a frequency spacing of ~5 Hz or less behave as a single wave and waves with frequency spacing greater than ~120 Hz generate independent magnetospheric responses. Between these values, the response is suppressed relative to the independent response, with minimum response at a frequency spacing of ~20 Hz. The suppression occurs almost instantaneously (in less than < 10 ms) and is up to 15 dB. This suppression has been explained as stemming from the disruption of the coherent nature of a single frequency signal. Experiments testing the limits of the coherence bandwidth for triggering were performed both at Siple Station and HAARP. At Siple Station hiss like signals of band limited noise were created by modulating the frequency of the carrier. It was found that rising emissions were triggered for bandwidths less than 60 Hz but not for bandwidth at 100 Hz or greater (Helliwell et al., 1986). At HAARP, synthetic band limited Gaussian noise of instantaneous bandwidth of 10, 30, and 100 Hz was modulated onto a ELF/VLF carrier frequency. When the instantaneous bandwidth was 30 Hz or below, magnetospheric amplification and triggering was observed, when it was 100 Hz no amplification was observed (Gołkowski et al., 2011). These results suggest that hiss emissions can trigger or evolve to discrete chorus like emissions but only if a minimum level of coherence or maximum bandwidth is achieved. In this context, observations made by Hosseini et al. (2017) show a band of hiss narrowing in bandwidth before the hiss emissions evolve to chorus emissions.
Entrainment is a multi-frequency interaction in which an injected signal captures a free running emission and controls its frequency (Helliwell and Katsufrakis, 1974; Gibby, 2008; Gołkowski et al., 2008). An example of free running emissions being successively entrained by a series of transmitted pulses decreasing and then increasing in frequency is shown in Figure 5. This phenomenon shows how the hot plasma distribution that is radiating the free running emission can be directly modified in a very deterministic manner. In a broader context, modification of the frequency content of chorus waves may be possible if controlled wave power can be injected at the appropriate place and time.
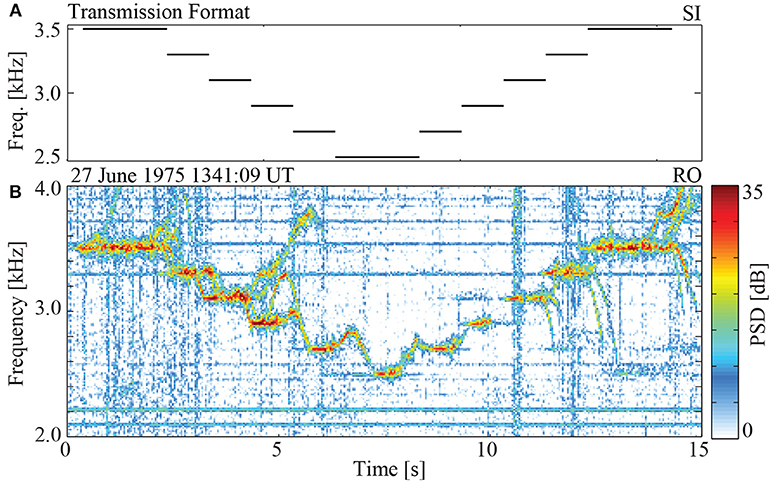
Figure 5. A case of entrainment from the Siple Station experiment received at Roberval on 27 June 1975 at 13:41:09 UT, in which a “stair-step” transmission from Siple starting at 3.5 kHz triggered a free-running plasma emission whose time-frequency characteristics are controlled by the subsequent constant frequency transmissions. (A) Time-frequency format transmitted by Siple. (B) Received signal at Roberval (magnetic conjugate point), showing characteristics of entrainment. Adapted from Figure 2.7 of Gibby (2008).
Sidebands occur when one or more quasi-constant frequency components appear within less than 100 Hz of a monochromatic input wave. The term sidebands originates from the overall similarity to modulated radio communications. Sidebands appear rarely and when the observed carrier wave is strong, but there is no simple relationship between carrier amplitude and sideband amplitude. Sideband amplitude may be symmetrical or asymmetrical about the carrier, and in the asymmetrical case it is usually the upper sideband that is stronger. Sideband amplitude is usually 10 dB or more below the carrier amplitude, but sometimes it can exceed the carrier amplitude (Park, 1981). Costabile et al. (2017) performed relative phase analysis of sidebands from the Siple experiment and discuss theories of sideband generation.
Both the Siple Station and HAARP experiments found that observations of magnetospheric echoes were most likely after 2–3 days of quieting geomagnetic conditions following a magnetospheric disturbance (Carpenter and Bao, 1983; Helliwell, 1988; Gołkowski et al., 2011; Li et al., 2015c). Although highly disturbed conditions and the associated free energy of high radiation belt fluxes can seem favorable for triggering of non-linear phenomena, the requirement for a stable ducted path for propagation of a ground injected signal to the equatorial interaction region appears to be a dominant factor. The latter condition is known to be associated with quieting conditions. For the Siple Station experiments the vast majority of signal receptions occurred when the transmitted frequency was between 0.2 and 0.5 of the equatorial gyrofrequency (~6 kHz for L = 4.2). For the HAARP experiment, the observed echoes were always below half the equatorial gyrofrequency (~3.8 kHz for L = 4.9). A common explanation put forth for very few observations above the equatorial half gyrofrequency has been that guiding of waves in density enhancement ducts is limited by this upper cuttoff (Smith, 1960) (in depletion ducts, propagation above the half the gyrofrequency is possible.) However, recent work suggests that for typical pitch angle anisotropy values found in the magnetosphere, linear growth also exhibits an upper frequency cutoff. For anisotropy values of 1, the cutoff is exactly at half the gyrofrequency (Hosseini et al., 2019). Additional theories posit that the observed half-gyrofrequency cutoff may be due to non-linear damping of longitudinal components due to quasi-parallel propagation (Omura et al., 2009; Yagitani et al., 2014).
The richness of the observations has caused a number of terms to be used to describe the phenomena and this can lead to confusion. In the literature describing Siple Station results the term “coherent wave instability”(CWI) is commonly used to emphasize that the injected wave needs to be phase coherent over a minimum temporal duration for the non-linear interaction to take place. This minimum duration requirement was also seen in the “dot-dash” anomaly of the early observations. The prominent stages of the single frequency excitation, namely temporal growth near the transmitted frequency followed by saturation, and a “free” running riser or faller are also often parsed with the terms “echo,” “triggering wave,” or “embryo emission” for the initial part (Dowden et al., 1978) and “triggered emission” for the latter free running component. On the other hand, theoretical publications by authors removed from the active experiments tend to use the term “VLF triggered emissions” to describe all the phenomena. Due to the common physics between wave injection results and natural chorus waves, a broader term of magnetospheric non-linear cyclotron growth is perhaps the most appropriate.
The fundamental physical environment of cyclotron wave-particle interactions in the magnetosphere is reasonably well-understood (Gendrin, 1975; Omura et al., 1991; Thorne, 2010). Specifically, in the region of the plasmasphere 2 < L < 6, the Earth's magnetic field retains an approximately dipole shape. Additionally, a population of low energy 1 eV < E < 10 eV but relatively dense 10 5,000cm−3 electrons permeate the background which results in a magnetized plasma environment. The plasmasphere thus supports the propagation of several plasma wave modes of which, as discussed previously, the whistler mode is of particular importance. Superimposed on the cold particles are the outer Van Allen radiation belts which consist of high energy electrons 1 keV < E < 100 keV that are trapped in a magnetic mirror configuration by the geomagnetic field (Walt, 2005). Since radiation belt electrons are forced into helical orbits by the background field, the particles can resonate with the circularly polarized whistler mode waves that are also propagating along the field line. Electrons that are counter streaming to the wave's propagation direction can undergo Doppler shifted cyclotron resonance, or gyro-resonance. That is, electrons that travel at the appropriate velocity will experience an approximately static wave electric field and significant energy exchange Inan (1977). This is referred to as the resonance velocity, vr and is given by
where the quantities ω and k correspond to the wave frequency and wavenumber respectively and are related by the whistler mode dispersion relation. The quantity γ is relativistic Lorentz factor and is important for ultra-relativistic particles (Omura et al., 2007). An important assumption in (1) is that the waves are assumed to propagate parallel to the magnetic field lines and all other wave modes are ignored. This is a reasonable assumption when assuming ducted propagation although some work may suggest the importance of additional wave modes as well (Bell and Ngo, 1990; Zhang et al., 1993). Recent work has shown that the results of parallel propagation are still applicable for small oblique angles of propagation (Nunn and Omura, 2015). Note, as per the convention of Omura et al. (2008), the waves propagate in the z-direction and the resonance velocity is thus negative for counter streaming electrons.
The mathematical basis of modeling wave-particle interactions is via the Vlasov-Maxwell system of equations. Specifically, the Vlasov equation (2) describes the evolution of the electron phase space density f(r, v) in a collision-free plasma.
Here, the quantities r and v correspond to the position and velocity coordinates of phase-space. Ew corresponds to be the wave electric field while B is the total magnetic field. The total magnetic field can be decomposed into B = Bw+B0 where Bw is the wave magnetic field while B0 represents the background geomagnetic field.
Maxwell's equations govern the evolution of the wave electric and magnetic fields and are given by (3-4),
The quantities Jh and Jc represents the currents due to the hot and cold plasma respectively.
Although the general theory of wave particle interactions is rather complex, analytical expressions can be derived under certain simplifying assumptions. Specifically, wave growth is typically separated into two regimes, (i) linear growth driven by temperature anisotropy and (ii) non-linear growth driven by phase-trapping of resonant particles. The two regimes are both important components of the whistler mode instability and are discussed in more detail in the following subsections.
When modeling the evolution of the electric and magnetic fields in a magneto-plasma, the wave equations can be simplified under the assumption of a narrowband modulating wavepacket. This is a reasonable assumption given the coherence of the signals observed in the data. Specifically, the expression for a circularly polarized whistler wave magnetic field propagating in the +z-direction is given by
where . The term ωt−∫kdz in the argument of the exponent corresponds to the phase variation of a monochromatic plane wave and can be thought of as a feature of the injected carrier wave. The quantity corresponds to the complex wavepacket that modulates the carrier whistler wave. Under the slowly-varying or narrowband assumption (Nunn, 1974) the evolution equations for the amplitude and phase of the modulating wavepacket is given by (6)-(7),
These narrowband wave equations describe the evolution of a wavepacket that is propagating at the group velocity of the whistler wave. Specifically, (6) shows that the wave amplitude is driven by the component of the resonant current that is parallel to the wave electric field JE. When JE is negative the wave will experience growth, otherwise the wave will be damped for positive JE. On the other hand, the wave phase (and hence frequency change) is driven by the component of the current that is anti-parallel to the wave magnetic field JB. The geometry that shows the wave fields, the resonant currents, and the particle velocity variables are delineated in Figure 6. The quantity JR represents the resonant current due to the hot plasma. (JE and JB are orthogonal components of JR) The variables v⊥ and ζ correspond to each particle's velocity perpendicular to B0 and the gyrophase angle respectively.
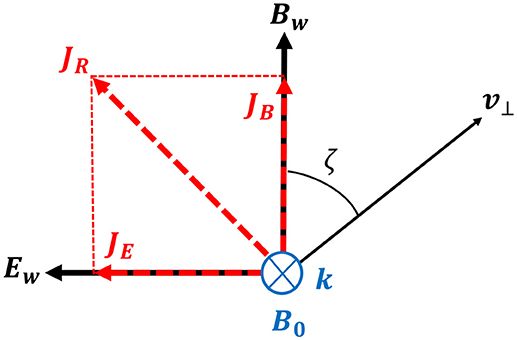
Figure 6. Geometry showing resonant currents and particle perpendicular velocity relative to the wave fields (Ew, Bw) and background geomagnetic field (B0).
Equations (6–7) have been derived independently by several authors (Karpman et al., 1974; Nunn, 1974; Rathmann et al., 1978; Omura and Matsumoto, 1982; Trakhtengerts, 1995) and are believed to adequately describe the wave fields for the whistler mode instability.
Under the assumption of small amplitude waves and small perturbations to the initial particle distribution, the Vlasov-Maxwell system can be linearized and a closed form expression can be derived accordingly (Kennel and Petschek, 1966). Following the method of Gołkowski and Gibby (2017), the resonant currents under the linearized assumption are given by (8, 9),
where γL is the well-known linear growth rate (Kennel and Petschek, 1966) and is given by the expression (10),
Nc represents the cold plasma density, while η and A correspond to the particle resonant flux and anisotropy respectively. As can be seen in (10), the sign of the linear growth rate is dictated by the value A. In the case of a Bi-Maxwellian velocity distribution, the expression for the anisotropy simplifies to
The quantities T⊥ and T∥ correspond to the electron temperatures in the directions that are perpendicular and parallel to geomagnetic field respectively. Thus, if the electron distribution has sufficient temperature anisotropy the radiation belt velocity distribution is unstable and whistler waves can be amplified. An interesting consequence of (8, 9) is that only JE is non-zero while JB is identically zero under the linearized model. Thus, linear theory predicts amplification and no frequency change of the injected whistler wave. However, observations as discussed in section 1 show frequency changes as defining features of the non-linear instability. As such, linear theory only describes the initial process of wave amplification and cannot be used to model the instability in its entirety.
Once the magnetic field of the wave becomes sufficiently large, linear theory does not adequately model the whistler mode instability. Accurately understanding the dynamics of resonant particles is required to correctly describe the non-linear aspect of the problem.
The dynamics of an energetic electron in a monochromatic whistler mode wave field is in general governed by the Lorentz force. Although several authors have analyzed the equations of motion with different approaches, this section will review the simplified equations that are generally accepted to be the most relevant. The equations of motion can be simplified by neglecting the transverse spatial motion of electrons and by only considering spatial variation along the field line coordinate, z. Additionally, by using a cylindrical coordinate system in velocity and only considering the dynamics of near-resonant particles (Omura et al., 1991), the equations of motion can be written as (12, 13),
Here, the variable θ = k(v∥−vr) represents a normalized change of the electron's parallel velocity from resonance. The quantity is known as the trapping frequency. The quantity S is called the collective inhomogeneity factor or the “S-parameter” and is given by
The S-parameter quantifies the effect of background inhomogeneity as well as the frequency sweep rate as observed by the particle (). It is worth noting that several authors have derived (12),(13), and (14) with different notation over the past several decades (Dysthe, 1971; Nunn, 1974; Matsumoto and Omura, 1981; Trakhtengerts and Rycroft, 2008). Differentiating (12) with respect to time and plugging into (13), results in a non-linear ordinary differential equation given by
Equation (15) represents a forced pendulum equation where the forcing term is proportional to S. For S = 0, (15) is identical to the conventional pendulum equation and the particle will oscillate around ζ = π at the trapping frequency ωtr in a manner similar to which a pendulum oscillates in a constant gravitational field. For values in the range −1 < S < 1, the central phase angle around which the particle oscillates is moved to ζ0 = −arcsin(S). For |S| > 1 particles are not trapped and do not remain in resonance with the wave. For a dipole geomagnetic field that is typically accurate in the plasmasphere and , S = 0 only at the magnetic equator. For a distorted geomagnetic field geometry so called “minimum B” pockets can occur off the equator and also enhance particle phase trapping even for low amplitude waves. In this context it is worth noting that chorus waves are observed to be primarily generated at the equator (Santolik and Gurnett, 2003) or in such minimum B pockets (Tsurutani and Smith, 1977).
Of particular importance is the formation of a wave-induced trap in phase-space (Omura et al., 2008). Figure 8 shows twelve test particle trajectories with trapped resonant particles (red) and untrapped resonant particles (black) for an assumed dipole geomagnetic field. All particles start with the same value of v∥ and v⊥ as well as the same initial position. The particles are uniformly distributed in gyrophase, and as shown in Figure 8, the untrapped particles are deflected when they come into resonance with the wave. On the other hand, the trapped particles are forced to stay in resonance with the wave over thousands of kilometers after which they are released from the trap. Whether or not a specific particle is trapped depends on the initial gyrophase angle when the particle goes into resonance with the wave. Phase-trapping of particles is believed to be a vital component of the non-linear instability (Dysthe, 1971; Matsumoto et al., 1980; Harid, 2015). Specifically, trapped particles deviate significantly from their adiabatic trajectories which in turn appreciably alter the distribution function.
The structure of the phase-space trap depends on location along the field line and Figure 7 shows the shape of the phase-space trap at several positions (for a monochromatic whistler mode wave). The variable ζ on the vertical axis is defined by and is essentially a normalized deviation of v∥ from resonance. The trapped trajectories correspond to closed curves in phase-space while the untrapped particles follow open curves. The trapped and untrapped electron populations are separated by a boundary known as a separatrix and are shown by the red contours. For a monochromatic signal, the phase-space trap can only exist in a narrow range around the magnetic equator after which the trap disintegrates and the mirror force dominates over the non-linear effects of the wave.
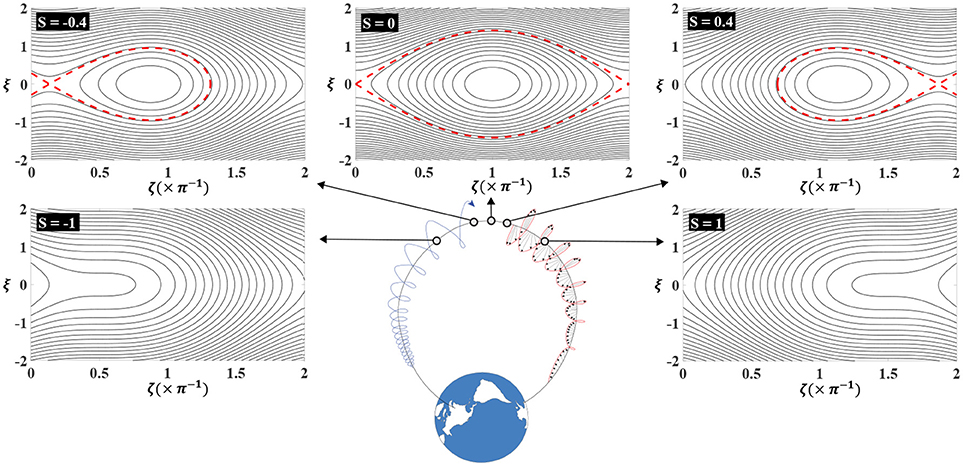
Figure 7. Local phase-space trajectories at different locations along the field line for a monochromatic and constant amplitude signal. The separatrix is shown by the red contours. A zero value on the vertical axis represents the resonance velocity given in Equation (1). The horizontal axis is gyrophase as defined in Figure 6.
Since trapped particles that are downstream of the wave are forced to remain in resonance for a long period of time, by virtue of Liouville's theorem the trapped particles drag the downstream value of the distribution function to locations that are upstream (Here upstream and downstream are defined relative to the wave propagation direction). Within a few trapping periods, the density inside the trap will be approximately constant (i.e phase-mixed) while the region outside the trap will be close to the unperturbed velocity distribution. As shown in Figure 8, electrons that are trapped downstream will start at high value of v∥ and follow the resonance velocity curve to a lower values of v∥ at the equator. Since the initial velocity distribution typically has a lower value at higher particle velocities, the density inside the trap at the equator will be much lower than the surrounding regions of phase-space. This results in what is known as an “electron hole” in phase-space.
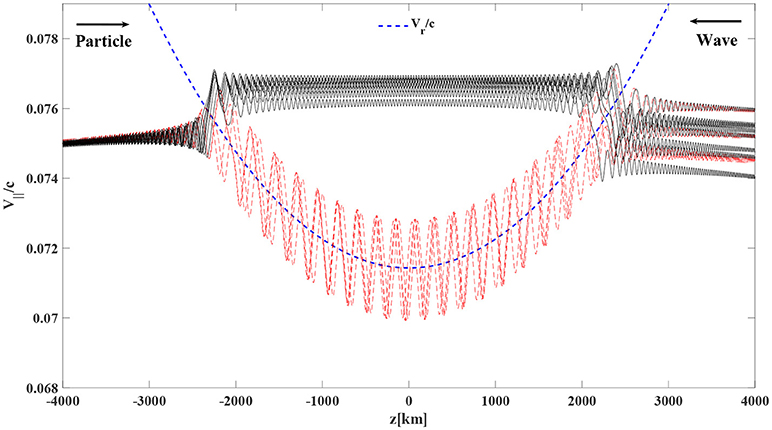
Figure 8. Trajectories of trapped (red) and untrapped (black) electrons with uniformly distributed initial gyro-phase. The wave is assumed to be constant amplitude and monochromatic.
By running test particle trajectories backwards in time and employing Liouville's theorem, the distribution function can be reconstructed in high resolution (Nunn, 2012; Harid et al., 2014a). Figure 9 clearly shows the electron hole in for three different locations along the field line (upstream, equator, and downstream of the wave) in the presence of a monochromatic and constant amplitude signal. As shown, the electron hole is well-defined and has an approximately constant density inside the phase-space trapping region. It is worth noting that for higher pitch angles or short pulses the opposite can occur and an “electron hill” can be formed as well (Hikishima and Omura, 2012; Nunn and Omura, 2012).
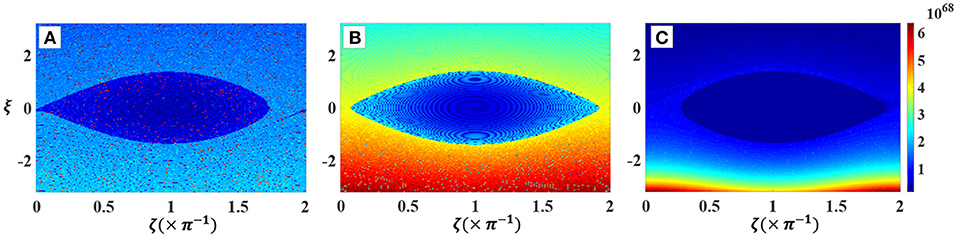
Figure 9. Formation of phase-space electron hole from test particle trajectories. (A) upstream location, (B) equator, and (C) downstream location relative to the wave propagation direction.
The formation of an approximately constant density across the phase-space trap allows for semi-analytical calculation of the resonant currents (Omura et al., 2008, 2009; Summers et al., 2012). Omura et al. (2009) and Cully et al. (2011) used such expressions along with further assumptions to estimate frequency sweep rates of chorus emissions. Costabile et al. (2017) used such expressions to investigate sideband formation. Although these simplifications have been validated against simulations (Katoh and Omura, 2016) and satellite observations (Cully et al., 2011) of chorus emissions, it does not entirely describe the complex dynamics of triggered VLF emissions. This is partly because triggered emissions are induced by a coherent seed wave while chorus waves are generated from amplification of background noise that is maximized at the equator (Foust, 2012). The formation of triggered waves, however, may occur at a point along the field line that is offset from the equator resulting in falling tones, hook like emissions, and other complex frequency-time relations (Smith and Nunn, 1998). Thus, the theoretical framework requires some extension to handle the rich variation that is observed in data (Helliwell, 1965; Li et al., 2015b).
Several theoretical features of the whistler instability, particularly the basis of amplification, has been well studied over the past several decades. However, many important features are yet to be properly understood from a theoretical point of view. These include complex variability of rising, falling, and hook-like emissions. The interaction between multiple waves that are closely spaced in frequency (and thus have overlapping traps), can lead to what is known as the coherence bandwidth effect and has not been considered in rigorous detail. Additionally features such as the entraining of one signal onto another has yet to be accurately described from fundamental physics. Effects of additional plasma modes or three dimensional aspects of the real physical scenario have often been neglected and some research suggests that there may be important physical phenomena that is yet to be captured (Omura and Matsumoto, 1987; Bell and Ngo, 1990; Ke et al., 2017). It is likely that theoretical insight will be gained via numerical simulations, especially in the current era of high performance computing paradigms.
The inherent non-linearity associated with non-linear whistler phenomena is largely analytically intractable and thus numerical simulations are the primary means of approaching the problem. From a theoretical point of view, the cyclotron instability can be modeled using the Vlasov-Maxwell system of equations. Although the problem is well-defined in theory, the multi-scale aspect of the problem requires care when developing self-consistent simulations. Specifically, the electron resonant velocity in the presence of a monochromatic wave varies significantly along the field line due to the spatial variation of the geomagnetically field. On the other hand, the size of the trap in phase-space () is much smaller than the typical values of the resonance velocity. Additionally, adiabatic motion of particles that are outside the phase-space trap cover a very large range of velocities due to the geomagnetic mirror geometry. Thus, the simulations must resolve the trap with enough detail to discern non-linear dynamics while the range of particle velocities must be large enough to encompass all the resonance velocities and adiabatic trajectories that constantly fall into resonance. These complications make simulations difficult and simplifying assumptions are often needed for computational feasibility at the expense of ignoring certain physical effects. For this reason, several computer models have been developed over the past five decades, each of which have various strengths and weaknesses. Although several authors have considered test particle dynamics in the presence of whistler mode waves (Inan, 1977; Albert, 2002; Tao et al., 2012; Albert et al., 2013), only models that self-consistently account for wave amplification are considered in this review. Reviewing the historical development of various numerical models helps provide a good understanding of the major contributions so far as well as the unanswered questions that are relevant for future work.
Self-consistent computer simulations of the non-linear whistler mode instability in the magnetosphere have been utilized extensively since the late 1960s. Only certain major works are described in this review to illustrate the historical progression of computational techniques. Thus, the ensuing discussion is by no means exhaustive and is meant to provide a high level view of simulation results over the past 50 years.
The earliest simulations can be traced back to Helliwell and Crystal (1973) where the authors considered radiation due to a monoenergetic stream of resonant sheets of phase-bunched electrons. Although the model predicted wave-growth, the important effect of the geomagnetic field inhomogeneity was ignored as well as the changing frequency of the wave. Additionally, the model did not consider a realistic initial electron distribution function which plays an important role in the wave-particle interactions process.Nunn (1974) developed a hybrid code where the cold particle population was modeled via a fluid equation while the resonant currents were assumed to be dominated by stably trapped particles and the wave equations were approximated under a narrowband assumption. Additionally, a phenomenological damping term was included to account for effects such as landau damping and leakage from a duct. The model did produce non-linear amplification and demonstrated the formation of currents due to resonant interactions, however, frequency change was not readily observed in the simulations. This was primarily due to the fact the range of particle velocities in the simulations were quite close to the local resonance velocity in the presence of a monochromatic wave-packet, thus velocities corresponding to resonance at new frequencies were inherently ignored. Denavit and Sudan (1975) utilized a full particle simulation where both the cold and hot plasma are modeled with a large number of macro-particles. Just as in Nunn (1974), the waves were treated with a narrowband assumption for computational simplicity. The authors showed that the model did produce non-linear amplification for an unstable plasma. Additionally elongation and frequency change of the wavepacket was observed due to phase correlations of detrapped resonant electrons.
The work of Denavit and Sudan (1975) was one of the first full-particle simulations of the whistler-mode instability. Similarly, Vomvoridis and Denavit (1980) applied the long-time scale (LTS) algorithm of Rathmann et al. (1978) to the wave-particle interactions problem. The model essentially tracked particle trajectories through time and the resonant currents were determined by giving the particles a finite size in a manner similar to Denavit and Sudan (1975). Unlike the Vlasov Hybrid Simulation (described below), no phase-space grid was required for the simulations. They found that the growth could be separated into a homogeneous component, inhomogeneous untrapped component, and an inhomogeneous trapped component. Although the model elucidated features of non-linear growth due to resonant wave-particle interactions, the simulated frequency change primarily showed temporal oscillations that were in part attributed to undersampling of the particle distribution. The code utilized a narrowband assumption for the wave envelope without any filtering which may have caused further difficulty in modeling free running emissions. Additionally, the code was highly susceptible to numerical noise and oscillations due to the undersampling problems associated with particle methods. Matsumoto et al. (1980) and Omura and Matsumoto (1985) also considered full particle simulations but with a homogeneous background magnetic field. The work clearly demonstrated non-linear growth, however, significant frequency changes was not observed which further highlighted the importance of a spatially varying geomagnetic field.
One of most impactful numerical models was the development VHS (Vlasov Hybrid Simulation) code by Nunn (1990). The code included the effects of trapped and untrapped resonant particles and relied on continuously tracking particle trajectories in time while interpolating to a phase-space grid with the aid of Liouville's Theorem. The resonant currents were then calculated by appropriately integrating over phase-space. The VHS code successfully reproduced several features of triggered VLF emissions including non-linear growth, rising frequency tones, falling tones, and hook-like signals. Although the code shed light on several aspects of free-running emissions, it required artificial filtering to ensure a well-defined frequency as well as the stability of the simulations. Additionally the narrowband assumption make it unsuitable for complex multi-frequency interactions or broadband signals. Even so, the VHS code has been successfully used to reproduce several features observed in data (Nunn et al., 1997, 2009; Smith and Nunn, 1998).
Increased computational power in the early 2000s permitted the design of higher resolution codes and renewed interest in modern simulations of the whistler mode instability. Specifically, the ability to use several million to even billions of grid points has become a practical reality with parallel computing paradigms and decreased memory costs. Additionally, simplified models with fewer grid points were capable of being run on a desktop computer within a few hours. Gibby et al. (2008) used a model similar to Nunn (1990) with a narrowband hybrid approach, however, the particle trajectories were not calculated continuously but were reset at every time step. This is known as a semi-Lagrangian method and typically results in a smoother interpolation of the particle distribution (Sonnendrücker et al., 1999). The model demonstrated saturation of coherent waves as well the beginning stages of frequency change. The window of particle velocities in the simulations were a relatively narrow sliver around resonance, thus large changes in frequency was not supported by the code. Harid et al. (2014b) also used a similar approach, however, a canonical resonant coordinate transformation was used to employ a finite difference scheme in phase-space. The number of grid points was an order of magnitude higher than used by Gibby et al. (2008) which provided high resolution features in phase-space. Specifically the clear formation of a density depletion in the phase-space trap was observed during the non-linear growth phase, which confirmed the long-standing hypothesis of the electron “phase-space hole” as a dominating feature of the wave-growth process (Omura et al., 2009).
Katoh and Omura (2006) developed the first modern hybrid-particle simulation where the cold plasma was treated as a fluid and the hot plasma was modeled with a PIC approach. The simulation used approximately 67 million particles and successfully produced rising tone triggered emissions. The distinguishing feature from previous work is that the initial distribution function was a Bi-Maxwellian where all particles (resonant and non-resonant alike) were taken into account. Additionally, the model did not utilize a narrowband assumption for the waves and Maxwell's equations were solved with a forth order finite difference time domain (FDTD) scheme. Thus, the code can in principle be used to model narrowband wave-particle interactions, multi-wave interactions, as well as broadband injected signals. The code was later successfully utilized to simulate the generation of naturally generated chorus and hiss waves (Katoh and Omura, 2008, 2016; Omura et al., 2009) which further demonstrated the robustness and utility of the hybrid-particle model.
Hikishima et al. (2009) utilized the first full particle simulation to successfully model chorus emissions. The code was then used to model triggered emissions by injecting a constant frequency signal at the equatorial region of the simulation (Hikishima et al., 2010). The model used approximately 150 million particles and successfully simulated triggered rising tone emissions along with the corresponding amplification of the seed and triggered waves. The large number of particles were required to overcome the noisy fluctuations associated with particle codes. The results also showed evidence of the generation of rising tone emissions at the back end of the seed signal, indicating both the importance of trapping as well as detrapping of resonant particles. Hikishima and Omura (2012) used the same particle code to run a parametric study by varying the injected wave amplitude. The authors found that either extremely small () or extremely large amplitudes () did not result in rising tone emissions, where B0 is the value of the background magnetic field strength at the equator. Additionally, in the range of amplitudes where triggered emissions were generated, a clear formation of a hole in phase-space was observed in the simulations. This code was the first to show the formation of an electron hole while employing a broadband particle simulation without simplifying assumptions.
The work of Katoh and Omura (2008) and Hikishima and Omura (2012) demonstrates the current state-of-the-art in modeling the whistler mode instability in the magnetosphere with controlled excitation. However, all the mentioned works so far have the inherent limitation of being one-dimensional in space and three dimensional in velocity. Additionally, the simulations all consider parallel propagation with only electromagnetic plasma waves so the electrostatic components have been neglected. Ke et al. (2017) was the first published work that employed a two dimensional hybrid-PIC code to simulate the generation of chorus emissions. The results showed that chorus waves are generated close to the magnetic equator and increase in wavenormal angle during propagation to higher latitudes. Although the code has not been utilized for excitation by injected waves, the physical mechanism behind triggered emissions and chorus waves are similar. Thus, the method used by Ke et al. (2017) is a powerful approach to model higher dimensional effects of controlled wave excitations.
A summary of several numerical models that have been developed for the whistler instability in the magnetosphere is shown in Table 1.
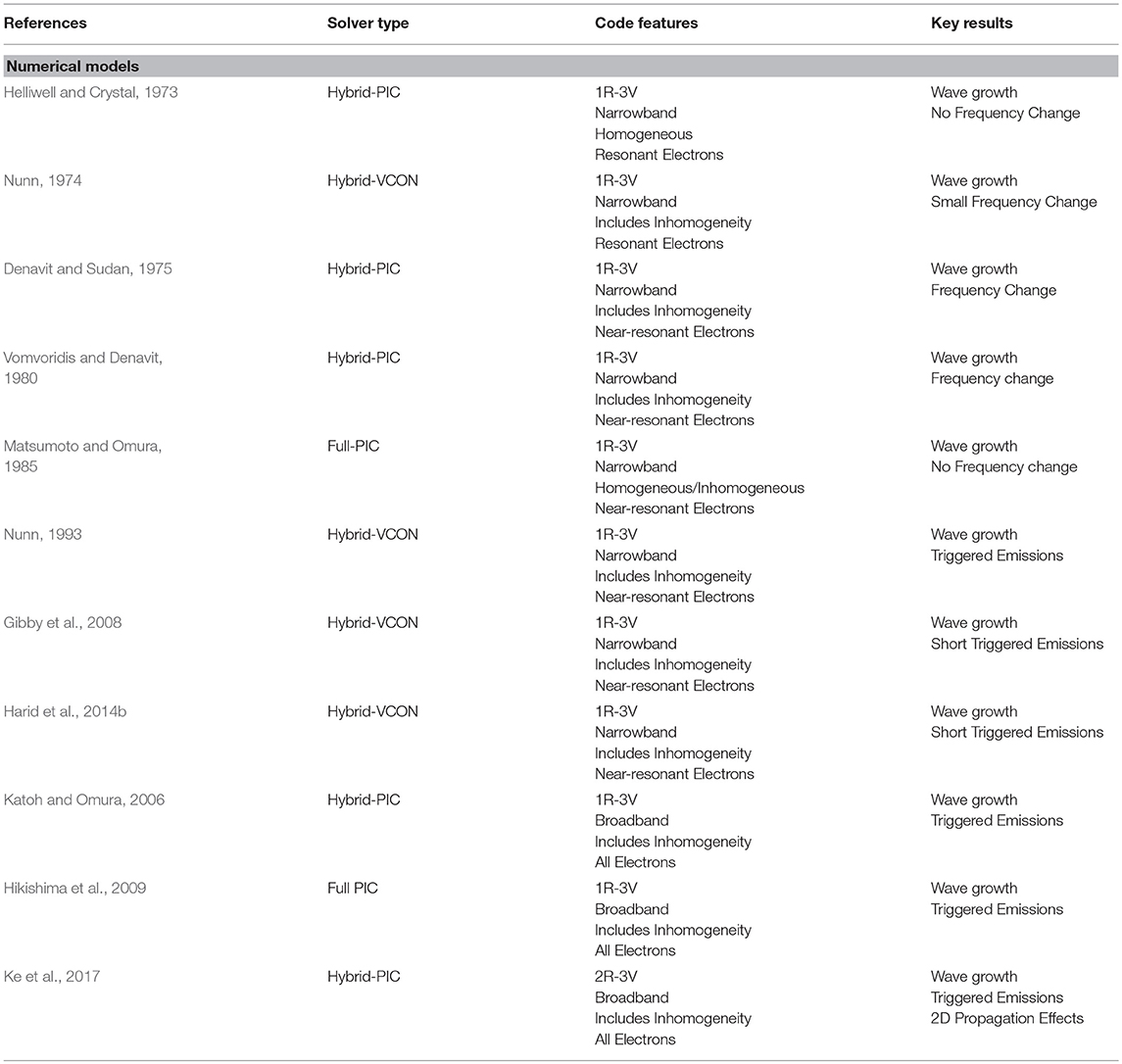
Table 1. Key self-consistent numerical codes used to simulate nonlinear cyclotron resonance and wave growth.
Given the several codes that have been successfully utilized over the past several decades, it is useful to categorize the various self-consistent models into general types. The most general simulation requires providing a numerical approximation to the Vlasov-Maxwell system of Equations (2),(3), and (4). This type of solution is typically referred to as a fully kinetic simulation. A fully kinetic simulation treats both the cold plasma and radiation belt particles via a Vlasov approach. However, since kinetic effects of cold plasma particles are effectively negligible, a common methodology is to consider a hybrid-kinetic approach. In hybrid methods, the cold electrons are treated as a fluid while the hot electron evolution is governed by the Vlasov equation. As far as solving the Vlasov equation for the hot plasma, most solvers can be lumped into two general categories, Vlasov continuous codes (VCON) or particle codes (PIC) (Filbet et al., 2001; Gutnic et al., 2004).
The distinguish feature of VCON codes is that they rely on creating a grid in phase-space and determining the value of the distribution function on these grid points. The generation of a phase-space grid is often referred to as an Eulerian method. The currents are then calculated by appropriately integrating over phase-space. There are several possible techniques that utilize a phase-space grid, however, the few methods that have been applied to the whistler-mode instability will be discussed.
The method employed by Nunn (1990) can be considered a semi-Eulerian or semi-Lagrangian method. For simplicity of presentation, we consider a two-dimensional phase-space (z, v), however the analysis naturally translates over to higher dimensions. In this technique, the initial distribution function f(z, v) is first initialized on a grid in phase-space of size Nz × Nv where each grid point has the coordinates (zn, vm) and volume ΔzΔv for n = 1, 2…Nz and m = 1, 2…Nv. Each cell on the grid can then be be thought of as a“super-particle” with density fnm = f(zn, vm) and thus charge Qnm = fnmΔzΔv. In order to track the evolution of the distribution function, each super-particle is tracked continuously in time (Lagrangian frame of reference). The value of the distribution function on the original grid points can then be determined via interpolation after which the current and charge densities can be computed via numerical integration. More generally, the distribution function can be thought of as having the functional form
where the summation index i is over all super-particles. The quantities Sv and Sz are shape functions and are an alternative means of expressing the interpolation process. The trajectory (zi(t), vi(t)) of the i-th particle is determined via the Lorentz force. The quantity wi represents the particle weight that comes from the initial distribution function. The current density is then computed via
Another popular semi-Lagrangian scheme follows a procedure similar to Gibby et al. (2008) and Gibby (2008) in which the particles are only traced backwards for one time step and are not tracked continuously in time. This may result in some artificial diffusion, however, the number of super-particles that are in a cell at any given time are always known, which reduces the computational cost relative to the method of Nunn (1990).
Another class of methods which has not been utilized significantly for non-linear wave-particle interactions modeling are fully Eulerian schemes (Sonnendrücker et al., 1999; Harid et al., 2014b). In this approach, the Vlasov equation is solved numerically as a PDE using a finite difference or finite volume formalism. The advantage of such a technique is that the simulations are relatively simple to code and the stability criteria are well understood. Nevertheless, the grid based Courant-Friedrichs-Lewy (CFL) condition can be quite stringent and a non-uniform grid is difficult to implement. However, such methods can be successfully utilized with appropriate curvilinear coordinate transformations (Harid, 2015).
All the aforementioned VCON methods have only been considered for the whistler instability by using the narrowband approximation of Maxwell's equations (6,7). An important extension of this work for future researchers would be to utilize a fully broadband formalism for the wave equations along with a VCON solver.
PIC codes, on the other hand, do not rely on a phase-space grid and continuously track the particle trajectories through time. Particle based techniques are thus often referred to as Lagrangian schemes. The currents are calculated by assuming a shape to the “super-particles” and accordingly interpolating to the spatial grid points where the wave fields need to be calculated. Mathematically, the distribution function in a PIC simulation can be written as
The expression in (18) is essentially the same as (16), with Sv(v − vi) = δ(v − vi). That is, the shape function in velocity space is modeled as a Dirac delta function. This subtle feature allows for a significant reduction in computational resources. The computational burden is relieved when computing the current and charge densities since the delta function makes the velocity integrals trivial. Specifically, the current density is given by
The lack of a velocity grid is a salient feature of PIC codes that is computationally desirable. However, although the computational cost of high-dimensional grid generation is removed, PIC simulations in turn suffer from numerical noise due to the random sampling of particles. For this reason, PIC codes often require millions of particles to reduce the artificial noise that is introduced (Birdsall and Langdon, 2004). Even so, current computational resources have permitted the use of PIC simulations to model the whistler mode instability. The works by Katoh and Omura (2008) and Hikishima and Omura (2012) demonstrate the clear utility of modern PIC simulations with a promising outlook for future computer experiments.
Over the past decades several numerical simulations have been utilized to clarify several aspects of wave-particle interactions in the magnetosphere. Even so, many observed phenomena have yet to be properly understood and certain physical assumptions used in current simulations may need to be relaxed. For instance, most models have primarily considered whistler mode interactions, yet electrostatic instabilities are believed to play an important role in the wave-particle interactions process (Omura et al., 2009). Particularly, the gap in chorus wave energy at frequencies around the half gyrofrequency may be in part due to Landau damping. The formation of an electron hole in phase-space inherently introduces non-zero space charge density that can drive quasi-electrostatic fields. Additionally saturation of whistler mode signals may also be due to mode conversion with electrostatic waves (Nunn, 1974). Effects known as wave-wave scattering involving interactions between electrostatic, electromagnetic, and quasi-electrostatic (lower hybrid) modes in the magnetosphere (Ganguli et al., 2010; Crabtree et al., 2012) are also yet to be explored with self consistent models.
An important simplification that is often used in simulation is ducted propagation. The waves are believed to be guided by field-aligned density irregularities that effectively force waves to propagate parallel to the geomagnetic field lines. However, additional spatial effects due to a finite sized guiding structure has not been explicitly considered in most modeling efforts. Since the ducts effectively act like a waveguide, they may also be responsible for exciting additional plasma modes via waveguide mode conversion. In the absence of ducts, higher dimensional effects may still be important as waves propagate away from the equator (Ke et al., 2017). Thus, including two and eventually three dimensional features in space would serve as an important contribution to magnetospheric research.
The ideal simulation would consider a full six-dimensional model of the particle distribution in phase-space while self-consistently modeling the wave evolution in all three spatial dimensions. Current state-of-the-art computational resources may still be inadequate to solve the general problem. However, incrementally introducing additional physics will help isolate and clarify the dominant physical phenomena behind non-linear wave-particle interactions in the magnetosphere.
Almost 30 years have past since the dismantling of Siple Station and there are currently no plans known to the authors to construct new facilities for radiation of ELF and low VLF waves with conventional multi-kilometer antennas. Future work on wave injection form the ground will therefore most likely take place at the HAARP facility. Although the management of the HAARP facility moved from the US Air Force to the University of Alaska in 2014, the facility continues to be used for active heating experiments. New formats can be designed and transmitted to validate numerical simulations that have greatly increased their capabilities in the last few years. Active experiments can serve not only to shed light on the fundamental theoretical process of non-linear cyclotron resonance and its dynamic evolution but also provide practical results for future strategic schemes of radiation belt mitigation (Inan et al., 2003). In the latter the key objective is pitch angle scattering, which strongly depends on wave amplitude. Therefore learning under what conditions what frequency-time formats can lead to the greatest amplification is a key question. Such investigations would build upon the identification of positive frequency-time ramps as being favorably amplified in a large number of past experiments. Another outstanding question in magnetospheric physics that active experiments are ripe to address is the relationship between natural hiss and chorus waves. In the past it has been proposed that either hiss creates chorus (Koons, 1981) or chorus is the source of hiss (Bortnik et al., 2008). Experiments can be performed to test whether hiss like signals can trigger chorus or how spectral changes of coherent injected signals can evolve to appear like hiss emissions. The already completed preliminary investigations of coherence bandwidth done at HAARP (Gołkowski et al., 2011) show that this is a fruitful line of investigation. The real-time interaction of the injected signals with present chorus and hiss emissions is also worthy of deeper investigation.
Wave injection and subsequent observation of whistler mode waves from the ground requires at least minimal guiding along the geomagnetic field from density irregularities or the plasmapause. The presence or absence of these structures has been shown to affect the occurrence of observations (Gołkowski et al., 2011). There have been efforts to use the HAARP facility to generate field aligned irregularities that could guide waves to the conjugate point (Milikh et al., 2008). At the same time, whether or not such efforts create structures that extend along the entire field line and can compete with processes in the natural environment has been called into question by other authors (Piddyachiy et al., 2011). More investigations in this area seem appropriate. For all of the studies proposed there is no question that a conjugate observation station for HAARP with a ELF/VLF receiver and other instruments would be extremely useful for wave injection experiments and also other investigations performed at HAARP.
One aspect of past studies that has only seen mixed results in the Siple and HAARP experiments is the detection of transmitter induced energetic electron precipitation from the magnetosphere. As discussed above, the interaction leading to amplification is a manifestation of the same fundamental process as pitch angle scattering. However, detection of energetic electron precipitation from the magnetosphere on the ground is challenging and often involves indirect methods. Direct one to one correlation between precipitation signatures and Siple Station transmissions has not been reported even though X-ray observations on balloon platforms have shown evidence of precipitation from individual chorus elements (Rosenberg et al., 1981). The recent work of the Balloon Array for Radiation belt Relativistic Electron Losses (BARREL) mission (Woodger et al., 2015) and FIREBIRD II cubesat (Breneman et al., 2017) have shown that ballon platforms and small satellites can be effective tools in observing energetic electron precipitation going forward. At HAARP an attempt was made to detect induced precipitation using VLF remote sensing and also the Poker Flat incoherent scatter radar (ISR) but did not lead to conclusive findings in the limited attempts that were made (Golkowski, 2009). Increasing ISR capability at the HAARP facility is seen as the best way to approach future induced precipitation studies. It is noted that evidence of direct precipitation induced from a VLF ground transmitter was reported in the SEEP experiment (Imhof et al., 1983; Inan et al., 1984). At the same time, more recent experiments with the NPM transmitter in Hawaii although initially interpreted as bearing evidence of precipitation were later shown to be more ambiguous (Graf et al., 2011). A thorough investigation of controlled precipitation using multiple detection methods ould have a broad impact on numerous efforts in the magnetospheric community.
The upcoming US Air Force Demonstration and Science Experiments (DSX) mission brings with it the exciting prospect of controlled radiation of waves directly in the magnetosphere (Scherbarth et al., 2009). Space based injection will have easier access to the non-linear wave-particle regime since the high losses from penetration of the ionosphere will be absent. Observationally, full disambiguation of the non-linear growth process would require multiple closely spaced satellites to observe transmissions along their propagation path. In this context closely spaced (< 200 km) spacecraft observations have been shown to be very fruitful for investigations of chorus wave properties (Santolik and Gurnett, 2003). Deploying such spacecraft for wave injection observations would be most effective if the spacecraft could be arranged to be along the same geomagnetic field line.
Controlled excitation of non-linear whistler mode wave particle interactions has a rich and fruitful history. Experimental activities and likewise the theoretical and computational efforts they have motivated have been a cornerstone of near-Earth space physics. The current times embody quickly improving computational tools and ever easier access to space with improved sensors and hardware capabilities. Conditions are thus favorable for active controlled experiments to yield new fundamental discoveries.
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
This work was supported by the National Science Foundation with awards AGS 1451210, PLR 1542608, and AGS 1254365 (CAREER) to the University of Colorado Denver.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Albert, J. (2002). Nonlinear interaction of outer zone electrons with VLF waves. Geophys. Res. Lett. 29, 116. doi: 10.1029/2001GL013941
Albert, J. M., Tao, X., and Bortnik, J. (2013). “Aspects of nonlinear wave-particle interactions,” in Dynamics of the Earth's Radiation Belts and Inner Magnetosphere, eds D. Summers, I. R. Mann, D. N. Baker, and M. Schulz, 255–264. doi: 10.1029/2012GM001324
Bell, T., and Ngo, H. (1990). Electrostatic lower hybrid waves excited by electromagnetic whistler mode waves scattering from planar magnetic-field-aligned plasma density irregularities. J. Geophys. Res. Space Phys. 95, 149–172.
Bell, T. F., Inan, U. S., and Helliwell, R. A. (1981). Nonducted coherent VLF waves and associated triggered emissions observed on the isee-1 satellite. J. Geophys. Res. Space Phys. 86, 4649–4670. doi: 10.1029/JA086iA06p04649
Birdsall, C. K., and Langdon, A. B. (2004). Plasma Physics via Computer Simulation. Boca Raton, FL: CRC Press.
Bortnik, J., and Thorne, R. (2007). The dual role of ELF/VLF chorus waves in the acceleration and precipitation of radiation belt electrons. J. Atmos. Solar Terres. Phys. 69, 378–386. doi: 10.1016/j.jastp.2006.05.030
Bortnik, J., Thorne, R. M., and Meredith, N. P. (2008). The unexpected origin of plasmaspheric hiss from discrete chorus emissions. Nature 452:62. doi: 10.1038/nature06741
Breneman, A., Crew, A., Sample, J., Klumpar, D., Johnson, A., Agapitov, O., et al. (2017). Observations directly linking relativistic electron microbursts to whistler mode chorus: Van allen probes and firebird ii. Geophys. Res. Lett. 44, 11265–11272. doi: 10.1002/2017GL075001
Carpenter, D., and Bao, Z. (1983). Occurrence properties of ducted whistler-mode signals from the new VLF transmitter at siple station, antarctica. J. Geophys. Res. Space Phys. 88, 7051–7057. doi: 10.1029/JA088iA09p07051
Carpenter, D., and Miller, T. (1976). Ducted magnetospheric propagation of signals from the siple, antarctica, VLF transmitter. J. Geophys. Res. 81, 2692–2700. doi: 10.1029/JA081i016p02692
Carpenter, D. L. (2016). Very Low Frequency Space Radio Research at Stanford 1950-1990: Discovery, Innovation, and Analysis, Supported by Field Work Extending from Antartica to Alaska. Lulu. com.
Carpenter, D. L., and Miller, T. (1983). Rare ground-based observations of siple VLF transmitter signals outside the plasmapause. J. Geophys. Res. Space Phys. 88, 10227–10232. doi: 10.1029/JA088iA12p10227
Cohen, M., and Gołkowski, M. (2013). 100 days of ELF/VLF generation via hf heating with haarp. J. Geophys. Res. Space Phys. 118, 6597–6607. doi: 10.1002/jgra.50558
Cohen, M. B., Inan, U., Piddyachiy, D., Lehtinen, N., and Gołkowski, M. (2011). Magnetospheric injection of ELF/VLF waves with modulated or steered hf heating of the lower ionosphere. J. Geophys. Res. Space Phys. 116. doi: 10.1029/2010JA016194
Cole, R., Reddell, N., Inan, U., Kery, S., Cappellini, J., Smit, P., et al. (2005). “From Alaska to the south pacific in one-hop,” in OCEANS, 2005. Proceedings of MTS/IEEE (Washington, DC: IEEE), 917–922.
Costabile, J. D., Gołkowski, M., and Wall, R. E. (2017). Modulation analysis of whistler mode sidebands in VLF-triggered emissions and implications for conditions of nonlinear growth. J. Geophys. Res. Space Phys. 122, 12505–12516. doi: 10.1002/2017JA024501
Crabtree, C., Rudakov, L., Ganguli, G., Mithaiwala, M., Galinsky, V., and Shevchenko, V. (2012). Weak turbulence in the magnetosphere: formation of whistler wave cavity by nonlinear scattering. Phys. Plasmas 19:032903. doi: 10.1063/1.3692092
Cully, C. M., Angelopoulos, V., Auster, U., Bonnell, J., and Le Contel, O. (2011). Observational evidence of the generation mechanism for rising-tone chorus. Geophys. Res. Lett. 38. doi: 10.1029/2010GL045793
Denavit, J., and Sudan, R. N. (1975). Effect of phase-correlated electrons on whistler wavepacket propagation. Phys. Fluids 18, 1533–1541. doi: 10.1063/1.861050
Dowden, R., McKay, A., Amon, L., Koons, H., and Dazey, M. (1978). Linear and nonlinear amplification in the magnetosphere during a 6.6-khz transmission. J. Geophys. Res. Space Phys. 83, 169–181. doi: 10.1029/JA083iA01p00169
Dysthe, K. (1971). Some studies of triggered whistler emissions. J. Geophys. Res. 76, 6915–6931. doi: 10.1029/JA076i028p06915
Filbet, F., Sonnendrücker, E., and Bertrand, P. (2001). Conservative numerical schemes for the vlasov equation. J. Comput. Phys. 172, 166–187. doi: 10.1006/jcph.2001.6818
Foust, F. (2012). Discontinuous Galerkin Modeling of Wave Propagation, Scattering, and Nonlinear Growth in Inhomogeneous Plasmas. PhD thesis, Stanford University.
Ganguli, G., Rudakov, L., Scales, W., Wang, J., and Mithaiwala, M. (2010). Three dimensional character of whistler turbulence. Phys. Plasmas, 17:052310. doi: 10.1063/1.3420245
Gendrin, R. (1975). Waves and wave-particle interactions in the magnetosphere: a review. Space Sci. Rev. 18, 145–200. doi: 10.1007/BF00172533
Getmantsev, G., Zuikov, N., Kotik, D., Mironenko, L., Mitiakov, N., Rapoport, V., et al. (1974). Combination frequencies in the interaction between high-power short-wave radiation and ionospheric plasma. ZhETF Pisma Redaktsiiu 20, 229–232.
Gibby, A., Inan, U. S., and Bell, T. F. (2008). Saturation effects in the VLF-triggered emission process. J. Geophys. Res. Space Phys. 113. doi: 10.1029/2008JA013233
Gibby, A. R. (2008). Saturation Effects in VLF Triggered Emissions. PhD thesis, Stanford University.
Golkowski, M. (2009). Magnetospheric Wave Injection by Modulated HF Heating of the Auroral Electrojet. PhD thesis.
Gołkowski, M., Cohen, M. B., Carpenter, D., and Inan, U. (2011). On the occurrence of ground observations of ELF/VLF magnetospheric amplification induced by the haarp facility. J. Geophys. Res. Space Phys. 116. doi: 10.1029/2010JA016261
Gołkowski, M., and Gibby, A. R. (2017). On the conditions for nonlinear growth in magnetospheric chorus and triggered emissions. Phys. Plasmas 24:092904. doi: 10.1063/1.4986225
Golkowski, M., Inan, U. S., and Cohen, M. B. (2009). Cross modulation of whistler mode and hf waves above the HAARP ionospheric heater. Geophys. Res. Lett. 36. doi: 10.1029/2009GL039669
Gołkowski, M., Inan, U. S., Cohen, M. B., and Gibby, A. (2010). Amplitude and phase of nonlinear magnetospheric wave growth excited by the HAARP HF heater. J. Geophys. Res. Space Phys. 115. doi: 10.1029/2009JA014610
Gołkowski, M., Inan, U. S., Gibby, A., and Cohen, M. B. (2008). Magnetospheric amplification and emission triggering by ELF/VLF waves injected by the 3.6 mw haarp ionospheric heater. J. Geophys. Res. Space Phys. 113. doi: 10.1029/2008JA013157
Graf, K., Inan, U., and Spasojevic, M. (2011). Transmitter-induced modulation of subionospheric VLF signals: Ionospheric heating rather than electron precipitation. J. Geophys. Res. Space Phys. 116:12313. doi: 10.1029/2011JA016996
Gutnic, M., Haefele, M., Paun, I., and Sonnendrücker, E. (2004). Vlasov simulations on an adaptive phase-space grid. Comput. Phys. Commun. 164, 214–219. doi: 10.1016/j.cpc.2004.06.073
Harid, V. (2015). Coherent Interactions Between Whistler Mode Waves and Energetic Electrons in the Earth's Radiation Belts. PhD thesis, Stanford University.
Harid, V., Gołkowski, M., Bell, T., and Inan, U. (2014a). Theoretical and numerical analysis of radiation belt electron precipitation by coherent whistler mode waves. J. Geophys. Res. Space Phys. 119, 4370–4388. doi: 10.1002/2014JA019809
Harid, V., Gołkowski, M., Bell, T., Li, J., and Inan, U. (2014b). Finite difference modeling of coherent wave amplification in the earth's radiation belts. Geophys. Res. Lett. 41, 8193–8200. doi: 10.1002/2014GL061787
Helliwell, R., Carpenter, D., Inan, U., and Katsufrakis, J. (1986). Generation of band-limited VLF noise using the siple transmitter: a model for magnetospheric hiss. J. Geophys. Res. Space Phys. 91, 4381–4392. doi: 10.1029/JA091iA04p04381
Helliwell, R., Carpenter, D., and Miller, T. (1980). Power threshold for growth of coherent VLF signals in the magnetosphere. J. Geophys. Res. Space Phys. 85, 3360–3366. doi: 10.1029/JA085iA07p03360
Helliwell, R., and Katsufrakis, J. (1974). VLF wave injection into the magnetosphere from siple station, antarctica. J. Geophys. Res. 79, 2511–2518. doi: 10.1029/JA079i016p02511
Helliwell, R., Katsufrakis, J., Trimpi, M., and Brice, N. (1964). Artificially stimulated very-low-frequency radiation from the ionosphere. J. Geophys. Res. 69, 2391–2394. doi: 10.1029/JZ069i011p02391
Helliwell, R. A. (1965). Whistlers and Related Ionospheric Phenomena, Vol 50. Stanford University Press, Stanford, CA.
Helliwell, R. A. (1988). VLF wave stimulation experiments in the magnetosphere from Siple Station, Antarctica. Rev. Geophys. 26, 551–578. doi: 10.1029/RG026i003p00551
Helliwell, R. A., and Crystal, T. L. (1973). A feedback model of cyclotron interaction between whistler-mode waves and energetic electrons in the magnetosphere. J. Geophys. Res. 78, 7357–7371. doi: 10.1029/JA078i031p07357
Hikishima, M., and Omura, Y. (2012). Particle simulations of whistler-mode rising-tone emissions triggered by waves with different amplitudes. J. Geophys. Res. Space Phys. 117:A04226. doi: 10.1029/2011JA017428
Hikishima, M., Omura, Y., and Summers, D. (2010). Self-consistent particle simulation of whistler mode triggered emissions. J. Geophys. Res. Space Phys. 115. doi: 10.1029/2010JA015860
Hikishima, M., Yagitani, S., Omura, Y., and Nagano, I. (2009). Full particle simulation of whistler-mode rising chorus emissions in the magnetosphere. J. Geophys. Res. Space Phys. 114:A01203. doi: 10.1029/2008JA013625
Hosseini, P., Gołkowski, M., and Harid, V. (2019). Remote sensing of radiation belt energetic electrons using lightning triggered upper band chorus. Geophys. Res. Lett. 46. doi: 10.1029/2018GL081391
Hosseini, P., Gołkowski, M., and Turner, D. L. (2017). Unique concurrent observations of whistler mode hiss, chorus, and triggered emissions. J. Geophys. Res. Space Phys. 122, 6271–6282. doi: 10.1002/2017JA024072
Imhof, W., Reagan, J., Voss, H., Gaines, E., Datlowe, D., Mobilia, J., Helliwell, R., Inan, U., Katsufrakis, J., and Joiner, R. (1983). The modulated precipitation of radiation belt electrons by controlled signals from VLF transmitters. Geophys. Res. Lett. 10, 615–618. doi: 10.1029/GL010i008p00615
Inan, U., Chang, H.-C., and Helliwell, R. (1984). Electron precipitation zones around major ground-based VLF signal sources. J. Geophys. Res. Space Phys. 89, 2891–2906. doi: 10.1029/JA089iA05p02891
Inan, U. S. (1977). Non-linear Gyroresonant Interactions of Energetic Particles and Coherent VLF Waves in the Magnetosphere. PhD thesis, Stanford University.
Inan, U. S., Bell, T. F., Bortnik, J., and Albert, J. (2003). Controlled precipitation of radiation belt electrons. J. Geophys. Res. Space Phys. 108. doi: 10.1029/2002JA009580
Inan, U. S., Bell, T. F., Carpenter, D., and Anderson, R. (1977). Explorer 45 and imp 6 observations in the magnetosphere of injected waves from the siple station VLF transmitter. J. Geophys. Res. 82, 1177–1187.
Inan, U. S., Gołkowski, M., Carpenter, D. L., Reddell, N., Moore, R., Bell, T., et al. (2004). Multi-hop whistler-mode ELF/VLF signals and triggered emissions excited by the HAARP HF heater. Geophys. Res. Lett. 31. doi: 10.1029/2004GL021647
Jin, G., Spasojevic, M., Cohen, M. B., Inan, U. S., and Lehtinen, N. G. (2011). The relationship between geophysical conditions and ELF amplitude in modulated heating experiments at haarp: modeling and experimental results. J. Geophys. Res. Space Phys. 116. doi: 10.1029/2011JA016664
Karpman, V., Istomin, J. N., and Shklyar, D. (1974). Nonlinear frequency shift and self-modulation of the quasi-monochromatic whistlers in the inhomogeneous plasma (magnetosphere). Planet. Space Sci. 22, 859–871. doi: 10.1016/0032-0633(74)90155-X
Karpman, V., Istomin, J. N., and Shklyar, D. (1975). Effects of nonlinear interaction of monochromatic waves with resonant particles in the inhomogeneous plasma. Phys. Script. 11, 278. doi: 10.1088/0031-8949/11/5/008
Katoh, Y., and Omura, Y. (2006). A study of generation mechanism of VLF triggered emission by self-consistent particle code. J. Geophys. Res. Space Phys. 111. doi: 10.1029/2006JA011704
Katoh, Y., and Omura, Y. (2008). Computer simulation of chorus wave generation in the earth's inner magnetosphere. Geophys. Res. Lett. 34. doi: 10.1029/2006GL028594
Katoh, Y., and Omura, Y. (2016). Electron hybrid code simulation of whistler-mode chorus generation with real parameters in the earth's inner magnetosphere. Earth Planets Space 68:192. doi: 10.1186/s40623-016-0568-0
Ke, Y., Gao, X., Lu, Q., Wang, X., and Wang, S. (2017). Generation of rising-tone chorus in a two-dimensional mirror field by using the general curvilinear pic code. J. Geophys. Res. Space Phys. 122, 8154–8165. doi: 10.1002/2017JA024178
Kennel, C. F., and Petschek, H. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71, 1–28.
Koons, H. C. (1981). The role of hiss in magnetospheric chorus emissions. J. Geophys. Res. Space Phys. 86, 6745–6754.
Li, J., Harid, V., Spasojevic, M., Gołkowski, M., and Inan, U. (2015a). Preferential amplification of rising versus falling frequency whistler mode signals. Geophys. Res. Lett. 42, 207–214. doi: 10.1002/2014GL062359
Li, J., Spasojevic, M., Harid, V., Cohen, M., Gołkowski, M., and Inan, U. (2014). Analysis of magnetospheric ELF/VLF wave amplification from the siple transmitter experiment. J. Geophys. Res. Space Phys. 119, 1837–1850. doi: 10.1002/2013JA019513
Li, J., Spasojevic, M., and Inan, U. (2015b). An empirical profile of VLF triggered emissions. J. Geophys. Res. Space Phys. 120, 6581–6595. doi: 10.1002/2015JA021444
Li, J., Spasojevic, M., and Inan, U. (2015c). Predicting conditions for the reception of one-hop signals from the siple transmitter experiment using the kp index. J. Geophys. Res. Space Phys. 120, 8440–8447. doi: 10.1002/2015JA021547
Matsumoto, H., Hashimoto, K., and Kimura, I. (1980). Dependence of coherent nonlinear whistler interaction on wave amplitude. J. Geophys. Res. Space Phys. 85, 644–652. doi: 10.1029/JA085iA02p00644
Matsumoto, H., and Omura, Y. (1981). Cluster and channel effect phase bunchings by whistler waves in the nonuniform geomagnetic field. J. Geophys. Res. Space Phys. 86, 779–791. doi: 10.1029/JA086iA02p00779
Matsumoto, H., and Omura, Y. (1985). Particle simulation of electromagnetic waves and its application to space plasmas. Comput. Simul. Space Plasmas 43. doi: 10.1007/978-94-009-5321-5_2
Milikh, G., Papadopoulos, K., McCarrick, M., and Preston, J. (1999). ELF emission generated by the HAARP HF-heater using varying frequency and polarization. Radiophys. Quantum Electron. 42, 639–646. doi: 10.1007/BF02676849
Milikh, G., Papadopoulos, K., Shroff, H., Chang, C., Wallace, T., Mishin, E., Parrot, M., and Berthelier, J.-J. (2008). Formation of artificial ionospheric ducts. Geophys. Res. Lett. 35:L17104. doi: 10.1029/2008GL034630
Moore, R., Inan, U. S., Bell, T. F., and Kennedy, E. (2007). ELF waves generated by modulated hf heating of the auroral electrojet and observed at a ground distance of 4400 km. J. Geophys. Res. Space Phys. 112. doi: 10.1029/2006JA012063
Nunn, D. (1974). A self-consistent theory of triggered VLF emissions. Planet. Space Sci. 22, 349–378. doi: 10.1016/0032-0633(74)90070-1
Nunn, D. (1990). The numerical simulation of VLF nonlinear wave-particle interactions in collision-free plasmas using the vlasov hybrid simulation technique. Comput. Phys. Commun. 60, 1–25. doi: 10.1016/0010-4655(90)90074-B
Nunn, D. (1993). A novel technique for the numerical simulation of hot collision-free plasma; vlasov hybrid simulation. J. Comput. Phys. 108, 180–196. doi: 10.1006/jcph.1993.1173
Nunn, D. (2012). Discussion at Special Workshop on Whistler Mode Waves at Stanford University. Palo Alto, CA.
Nunn, D., and Omura, Y. (2012). A computational and theoretical analysis of falling frequency VLF emissions. J. Geophys. Res. Space Phys. 117:A08228. doi: 10.1029/2012JA017557
Nunn, D., and Omura, Y. (2015). A computational and theoretical investigation of nonlinear wave-particle interactions in oblique whistlers. J. Geophys. Res. Space Phys. 120, 2890–2911. doi: 10.1002/2014JA020898
Nunn, D., Omura, Y., Matsumoto, H., Nagano, I., and Yagitani, S. (1997). The numerical simulation of VLF chorus and discrete emissions observed on the geotail satellite using a vlasov code. J. Geophys. Res. Space Phys. 102, 27083–27097.
Nunn, D., Santolik, O., Rycroft, M., and Trakhtengerts, V. (2009). On the numerical modelling of VLF chorus dynamical spectra. Ann. Geophys. 27:2341. doi: 10.5194/angeo-27-2341-2009
Omura, Y., Furuya, N., and Summers, D. (2007). Relativistic turning acceleration of resonant electrons by coherent whistler mode waves in a dipole magnetic field. J. Geophys. Res. Space Phys. 112:A06236. doi: 10.1029/2006JA012243
Omura, Y., Hikishima, M., Katoh, Y., Summers, D., and Yagitani, S. (2009). Nonlinear mechanisms of lower-band and upper-band VLF chorus emissions in the magnetosphere. J. Geophys. Res. Space Phys. 114. doi: 10.1029/2009JA014206
Omura, Y., Katoh, Y., and Summers, D. (2008). Theory and simulation of the generation of whistler-mode chorus. J. Geophys. Res. Space Phys. 113:A04223. doi: 10.1029/2007JA012622
Omura, Y., and Matsumoto, H. (1982). Computer simulations of basic processes of coherent whistler wave-particle interactions in the magnetosphere. J. Geophys. Res. Space Phys. 87, 4435–4444. doi: 10.1029/JA087iA06p04435
Omura, Y., and Matsumoto, H. (1985). Simulation study of frequency variations of VLF triggered emissions in a homogeneous field. J. Geomagnet. Geoelectr. 37, 829–837. doi: 10.5636/jgg.37.829
Omura, Y., and Matsumoto, H. (1987). Competing processes of whistler and electrostatic instabilities in the magnetosphere. J. Geophys. Res. Space Phys. 92, 8649–8659. doi: 10.1029/JA092iA08p08649
Omura, Y., Nunn, D., Matsumoto, H., and Rycroft, M. (1991). A review of observational, theoretical and numerical studies of VLF triggered emissions. J. Atmos. Terrest. Phys. 53, 351–368. doi: 10.1016/0021-9169(91)90031-2
Park, C. (1981). Generation of whistler-mode sidebands in the magnetosphere. J. Geophys. Res. Space Phys. 86, 2286–2294. doi: 10.1029/JA086iA04p02286
Paschal, E. W., and Helliwell, R. A. (1984). Phase measurements of whistler mode signals from the siple VLF transmitter. J. Geophys. Res. Space Phys. 89, 1667–1674. doi: 10.1029/JA089iA03p01667
Piddyachiy, D., Bell, T., Berthelier, J.-J., Inan, U., and Parrot, M. (2011). Demeter observations of the ionospheric trough over haarp in relation to hf heating experiments. J. Geophys. Res. Space Phys. 116:A06304. doi: 10.1029/2010JA016128
Piddyachiy, D., Inan, U. S., Bell, T. F., Lehtinen, N. G., and Parrot, M. (2008). Demeter observations of an intense upgoing column of ELF/VLF radiation excited by the HAARP HF heater. J. Geophys. Res. Space Phys. 113. doi: 10.1029/2008JA013208
Platino, M., Inan, U., Bell, T., Pickett, J., Kennedy, E., Trotignon, J., et al. (2004). Cluster observations of ELF/VLF signals generated by modulated heating of the lower ionosphere with the HAARP HF transmitter. in Ann. Geophys.22, 2643–2653. doi: 10.5194/angeo-22-2643-2004
Platino, M., Inan, U. S., Bell, T. F., Parrot, M., and Kennedy, E. (2006). Demeter observations of ELF waves injected with the HAARP HF transmitter. Geophys. Res. Lett. 33:L16101. doi: 10.1029/2006GL026462
Raghuram, R., Smith, R., and Bell, T. (1974). VLF Antarctic antenna: Impedance and efficiency. IEEE Trans. Antennas Propag. 22, 334–338. doi: 10.1109/TAP.1974.1140777
Rastani, K., Inan, U. S., and Helliwell, R. A. (1985). De 1 observations of siple transmitter signals and associated sidebands. J. Geophys. Res. Space Phys. 90, 4128–4140. doi: 10.1029/JA090iA05p04128
Rathmann, C., Vomvoridis, J., and Denavit, J. (1978). Long-time-scale simulation of resonant particle effects in langmuir and whistler waves. J. Comput. Phys. 26, 408–442. doi: 10.1016/0021-9991(78)90078-5
Reeves, G., McAdams, K., Friedel, R., and O'Brien, T. (2003). Acceleration and loss of relativistic electrons during geomagnetic storms. Geophys. Res. Lett. 30:1529. doi: 10.1029/2002GL016513
Rosenberg, T., Siren, J., Matthews, D., Marthinsen, K., Holtet, J., Egeland, A., et al. (1981). Conjugacy of electron microbursts and VLF chorus. J. Geophys. Res. Space Phys. 86, 5819–5832. doi: 10.1029/JA086iA07p05819
Roux, A., and Pellat, R. (1978). A theory of triggered emissions. J. Geophys. Res. 83. doi: 10.1029/JA083iA04p01433
Santolik, O., and Gurnett, D. (2003). Transverse dimensions of chorus in the source region. Geophys. Res. Lett. 30. doi: 10.1029/2002GL016178
Scherbarth, M., Smith, D., Adler, A., Stuart, J., and Ginet, G. (2009). “AFRL'S demonstration and science experiments (DSX) mission,” in Solar Physics and Space Weather Instrumentation III (San Diego, CA: International Society for Optics and Photonics).
Smith, A., and Nunn, D. (1998). Numerical simulation of VLF risers, fallers, and hooks observed in antarctica. J. Geophys. Res. Space Phys. 103, 6771–6784. doi: 10.1029/97JA03396
Smith, R. (1960). Theory of trapping of whistlers in field-aligned columns of enhanced ionization. J. Geophys. Res. 65:815. doi: 10.1029/JZ065i003p00815
Sonnendrücker, E., Roche, J., Bertrand, P., and Ghizzo, A. (1999). The semi-lagrangian method for the numerical resolution of the vlasov equation. J. Comput. Phys. 149, 201–220. doi: 10.1006/jcph.1998.6148
Sonwalkar, V. S., Bell, T. F., Helliwell, R. A., and Inan, U. S. (1984). Direct multiple path magnetospheric propagation: a fundamental property of nonducted VLF waves. J. Geophys. Res. Space Phys. 89, 2823–2830. doi: 10.1029/JA089iA05p02823
Sonwalkar, V. S., and Inan, U. (1986). Measurements of siple transmitter signals on the de 1 satellite: Wave normal direction and antenna effective length. J. Geophys. Res. Space Phys. 91, 154–164. doi: 10.1029/JA091iA01p00154
Storey, L. (1953). An investigation of whistling atmospherics. Philos. Trans. R. Soc. Lond. A 246, 113–141. doi: 10.1098/rsta.1953.0011
Streltsov, A., Berthelier, J.-J., Chernyshov, A., Frolov, V., Honary, F., Kosch, M., et al. (2018). Past, present and future of active radio frequency experiments in space. Space Sci. Rev. 214:118. doi: 10.1007/s11214-018-0549-7
Streltsov, A., Gołkowski, M., Inan, U., and Papadopoulos, K. (2010). Propagation of whistler mode waves with a modulated frequency in the magnetosphere. J. Geophys. Res. Space Phys. 115. doi: 10.1029/2009JA015155
Stubbe, P., Kopka, H., Rietveld, M., and Dowden, R. (1982). ELF and VLF wave generation by modulated hf heating of the current carrying lower ionosphere. J. Atmos. Terrest. Phys. 44, 1123–1135. doi: 10.1016/0021-9169(82)90023-X
Sudan, R., and Ott, E. (1971). Theory of triggered VLF emissions. J. Geophys. Res. 76, 4463–4476. doi: 10.1029/JA076i019p04463
Summers, D., Omura, Y., Miyashita, Y., and Lee, D.-H. (2012). Nonlinear spatiotemporal evolution of whistler mode chorus waves in earth's inner magnetosphere. J. Geophys. Res. Space Phys. 117:A09206. doi: 10.1029/2012JA017842
Tanaka, Y., Nishino, M., and Hayakawa, M. (1987). Conjugate measurements of VLF transmitter signals at middle latitude (l= 1.93). Planet. Space Sci. 35, 1053–1059. doi: 10.1016/0032-0633(87)90009-2
Tao, X., Bortnik, J., Albert, J. M., and Thorne, R. M. (2012). Comparison of bounce-averaged quasi-linear diffusion coefficients for parallel propagating whistler mode waves with test particle simulations. J. Geophys. Res. Space Phys. 117. doi: 10.1029/2012JA017931
Thorne, R. M. (2010). Radiation belt dynamics: the importance of wave-particle interactions. Geophys. Res. Lett. 37:L22107. doi: 10.1029/2010GL044990
Trakhtengerts, V. Y. (1995). Magnetosphere cyclotron maser: backward wave oscillator generation regime. J. Geophys. Res. Space Phys. 100, 17205–17210. doi: 10.1029/95JA00843
Trakhtengerts, V. Y., and Rycroft, M. J. (2008). Whistler and Alfven Mode Cyclotron Masers in Space. Cambridge: Cambridge University Press.
Tsurutani, B. T., and Smith, E. J. (1977). Two types of magnetospheric ELF chorus and their substorm dependences. J. Geophys. Res. 82, 5112–5128. doi: 10.1029/JA082i032p05112
Vomvoridis, J., and Denavit, J. (1979). Test particle correlation by a whistler wave in a nonuniform magnetic field. Phys. Fluids 22, 367–377. doi: 10.1063/1.862589
Vomvoridis, J. L., and Denavit, J. (1980). Nonlinear evolution of a monochromatic whistler wave in a nonuniform magnetic field. Phys. Fluids 23, 174–183. doi: 10.1063/1.862836
Walt, M. (2005). Introduction to Geomagnetically Trapped Radiation. Cambridge, UK: Cambridge University Press.
Woodger, L. A., Halford, A. J., Millan, R. M., McCarthy, M. P., Smith, D. M., Bowers, G. S., et al. (2015). A summary of the barrel campaigns: technique for studying electron precipitation. J. Geophys. Res. Space Phys. 120, 4922–4935. doi: 10.1002/2014JA020874
Yagitani, S., Habagishi, T., and Omura, Y. (2014). Geotail observation of upper band and lower band chorus elements in the outer magnetosphere. J. Geophys. Res. Space Phys. 119, 4694–4705. doi: 10.1002/2013JA019678
Keywords: whistler anisotropy instability, triggered emissions, whistler mode chorus waves, active experiments, HAARP facility, radiation belts, space weather
Citation: Gołkowski M, Harid V and Hosseini P (2019) Review of Controlled Excitation of Non-linear Wave-Particle Interactions in the Magnetosphere. Front. Astron. Space Sci. 6:2. doi: 10.3389/fspas.2019.00002
Received: 01 October 2018; Accepted: 15 January 2019;
Published: 07 February 2019.
Edited by:
Evgeny V. Mishin, Air Force Research Laboratory, United StatesReviewed by:
Arnaud Masson, European Space Astronomy Centre (ESAC), SpainCopyright © 2019 Gołkowski, Harid and Hosseini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mark Gołkowski, bWFyay5nb2xrb3dza2lAdWNkZW52ZXIuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.