
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci., 22 January 2019
Sec. High-Energy and Astroparticle Physics
Volume 5 - 2018 | https://doi.org/10.3389/fspas.2018.00050
This article is part of the Research TopicFrom the Fermi Scale to CosmologyView all 10 articles
 Javier Rubio*
Javier Rubio*The properties of the recently discovered Higgs boson together with the absence of new physics at collider experiments allows us to speculate about consistently extending the Standard Model of particle physics all the way up to the Planck scale. In this context, the Standard Model Higgs non-minimally coupled to gravity could be responsible for the symmetry properties of the Universe at large scales and for the generation of the primordial spectrum of curvature perturbations seeding structure formation. We overview the minimalistic Higgs inflation scenario, its predictions, open issues and extensions and discuss its interplay with the possible metastability of the Standard Model vacuum.
Inflation is nowadays a well-established paradigm (Starobinsky, 1980; Guth, 1981; Mukhanov and Chibisov, 1981; Albrecht and Steinhardt, 1982; Linde, 1982, 1983) able to explain the flatness, homogeneity and isotropy of the Universe and the generation of the primordial density fluctuations seeding structure formation (Hawking, 1982; Starobinsky, 1982; Sasaki, 1986; Mukhanov, 1988). In spite of the phenomenological success, the inflaton's nature remains unknown and its role could be played by any particle physics candidate able to imitate a slowly-moving scalar field in the very early Universe.
In spite of dedicated searches, the only outcome of the Large Hadron Collider (LHC) experiments till date is a scalar particle with mass (Aad et al., 2012; Chatrchyan et al., 2012; Tanabashi et al., 2018)
and properties similar to those of the Standard Model (SM) Higgs. The mass value (1.1) is certainly particular since it allows to extend the SM up to the Planck scale without leaving the perturbative regime (Shaposhnikov and Wetterich, 2010). The main limitation to this appealing scenario is the potential instability of the electroweak vacuum at high energies. Roughly speaking, the value of the Higgs self-coupling following from the SM renormalization group equations decreases with energy till a given scale and starts increasing thereafter. Whether it stays positive all the way up to the Planck scale, or turns negative at some intermediate scale μ0 depends, mainly, on the interplay between the Higgs mass mH and the top quark Yukawa coupling yt extracted from the reconstructed Monte-Carlo top mass in collider experiments (Butenschoen et al., 2016), cf. Figure 1. Neglecting the effect of gravitational corrections, the critical value separating the region of absolute stability from the metastability/instability1 regions is given by (Bezrukov and Shaposhnikov, 2015b)
with αs(mZ) the strong coupling constant at the Z boson mass. Within the present experimental and theoretical uncertainties (Bezrukov and Shaposhnikov, 2015b; Butenschoen et al., 2016; Espinosa et al., 2017), the SM is compatible with vacuum instability, metastability and absolute stability (Bezrukov et al., 2012; Degrassi et al., 2012; Buttazzo et al., 2013; Espinosa et al., 2015; Espinosa, 2016), with the separation among the different cases strongly depending on the ultraviolet completion of gravity (Branchina and Messina, 2013; Branchina et al., 2014, 2015), cf. Figure 2.
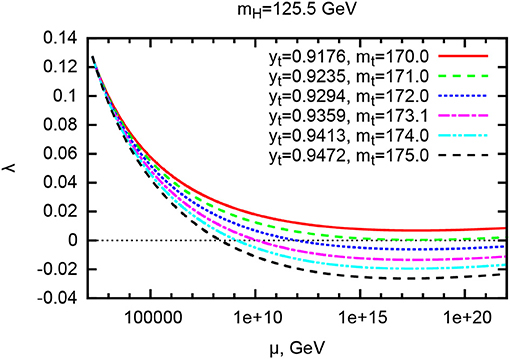
Figure 1. The running of the Higgs self-coupling following from the Standard Model renormalization group equations for several values of the top quark Yukawa coupling at the electroweak scale and a fixed Higgs boson mass mH = 125.5 GeV (Bezrukov et al., 2015).
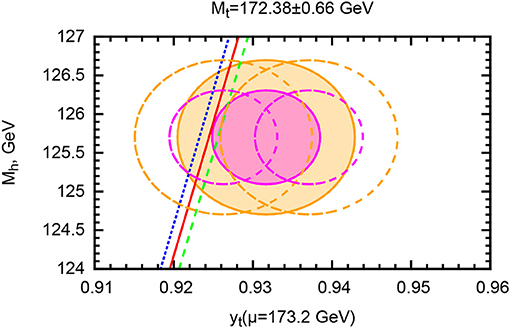
Figure 2. The SM stability and metastability regions for a renormalization point μ = 173.2 GeV in the scheme (Bezrukov and Shaposhnikov, 2015b). The solid red line corresponds to the critical top quark Yukawa coupling (1.2) leading to vacuum instability at a sub-Planckian energy scale μ0, with the dashed lines accounting for uncertainties associated with the strong coupling constant. To the left (right) of these diagonal lines, the SM vacuum is unstable (metastable). The filled elliptical contours account for the 1σ and 2σ experimental errors on the Higgs mass in Olive et al. (2014) and the CMS (Monte-Carlo) top quark mass in Collaboration (2014), namely mH = 125.7±0.4 GeV and mt = 172.38±0.10(stat)±0.66(syst)GeV (note that the current value of the Higgs mass is slightly lower Tanabashi et al., 2018). The additional empty contours illustrate the shifts associated with the theoretically ambiguous relation between the top quark Yukawa coupling and the (Monte-Carlo) top quark mass (cf. Bezrukov and Shaposhnikov, 2015b for details).
In the absence of physics beyond the SM, it is certainly tempting to identify the recently discovered Higgs boson with the inflaton condensate. Unfortunately, the Higgs self-interaction significantly exceeds the value λ ~ 10−13 leading to a sufficiently long inflationary period without generating an excessively large spectrum of primordial density perturbations (Linde, 1983). The situation is unchanged if one considers the renormalization group enhanced potential following from the extrapolation of the SM renormalization group equations to the inflationary scale (Isidori et al., 2008; Fairbairn et al., 2014; Hamada et al., 2014a). The simplest way out is to modify the Higgs field kinetic term in the large-field regime. In Higgs inflation2 this is done by including a direct coupling to the Ricci scalar R (Bezrukov and Shaposhnikov, 2008), namely3
with H the Higgs doublet and ξ a dimensionless constant to be fixed by observations. The inclusion of the non-minimal coupling (1.3) can be understood as an inevitable consequence of the quantization of the SM in a gravitational background, where this term is indeed required for the renormalization of the energy-momentum tensor (Callan et al., 1970; Birrell and Davies, 1984).
When written in the Einstein frame, the Higgs inflation scenario displays two distinct regimes. At low energies, it approximately coincides with the SM minimally coupled to gravity. At high energies, it becomes a chiral SM with no radial Higgs component (Dutta et al., 2008; Bezrukov and Shaposhnikov, 2009). In this latter regime, the effective Higgs potential becomes exponentially flat, allowing for inflation with the usual chaotic initial conditions. The associated predictions depend only on the number of e-folds of inflation, which is itself related to the duration of the heating stage. As the type and strength of the interactions among the Higgs field and other SM particles is experimentally known, the duration of this entropy production era can be computed in detail (Bezrukov et al., 2009a, 2011a; Garcia-Bellido et al., 2009; Repond and Rubio, 2016; Ema et al., 2017a), leading to precise inflationary predictions in perfect agreement with observations (Akrami et al., 2018).
The situation becomes more complicated when quantum corrections are included. The shape of the inflationary potential depends then on the values of the Higgs mass and top Yukawa coupling at the inflationary scale. In addition to the plateau already existing at tree-level (Bezrukov and Shaposhnikov, 2014; Enckell et al., 2016; Fumagalli and Postma, 2016; Fumagalli, 2017), the renormalization group enhanced potential can develop a quasi-inflection point along the inflationary trajectory (Allison, 2014; Bezrukov and Shaposhnikov, 2014; Hamada et al., 2014b; Bezrukov et al., 2015, 2018; Rubio, 2015; Enckell et al., 2016; Fumagalli and Postma, 2016; Rasanen and Wahlman, 2017) or a hilltop (Fumagalli and Postma, 2016; Rasanen and Wahlman, 2017; Enckell et al., 2018), with different cases giving rise to different predictions.
Although a precise measurement of the inflationary observables could be understood as an interesting consistency check between cosmological observations and particle physics experiments (Barvinsky et al., 2008, 2012; Espinosa et al., 2008; Bezrukov and Shaposhnikov, 2009; Bezrukov et al., 2009b, 2012; De Simone et al., 2009; Popa and Caramete, 2010; Salvio, 2013), the low- to high-energy connection is subject to unavoidable ambiguities related to the non-renormalizability of the model (Barbon and Espinosa, 2009; Burgess et al., 2009, 2010; Bezrukov et al., 2011b, 2015, 2018; George et al., 2014, 2016; Rubio, 2015; Enckell et al., 2016; Fumagalli and Postma, 2016). In particular, the finite parts of the counterterms needed to renormalize the tree-level action lead to localized jumps in the SM renormalization group equations when connected to the chiral phase of Higgs inflation. The strength of these jumps encodes the remnants of the ultraviolet completion and cannot be determined within effective field theory approach (Bezrukov et al., 2011b, 2015; Burgess et al., 2014). If the finite parts are significantly smaller than the associated coupling constants, Higgs inflation leads to a direct connection among the SM parameters measured at collider experiments and the large scale properties of the Universe, provided that the former do not give rise to vacuum instability. On the contrary, if the jumps in the coupling constants are large, the relation between high- and low-energy physics is lost, but Higgs inflation can surprisingly occur even if the electroweak vacuum is not completely stable (Bezrukov et al., 2015).
In this article we review the minimalistic Higgs inflation scenario, its predictions, open issues and extensions, and discuss its interplay with the potential metastability of the SM vacuum. The paper is organized as follows:
• The general framework is introduced in section 2. To illustrate the effect of non-minimal couplings, we consider an induced gravity scenario in which the effective Newton constant is completely determined by the Higgs vacuum expectation value. Having this toy model in mind, we reformulate Higgs inflation in the so-called Einstein frame in which the coupling to gravity is minimal and all non-linearities appear in the scalar sector of the theory. After emphasizing the pole structure of the Einstein-frame kinetic term and its role in the asymptotic flatness of the Higgs inflation potential, we compute the tree-level inflationary observables and discuss the decoupling properties of the SM degrees of freedom.
• The limitations of Higgs inflation as a fundamental theory are reviewed in section 3. In particular, we present a detailed derivation of the cutoff scales signaling the violation of perturbative unitarity in different scattering processes and advocate the interpretation of Higgs inflation as an effective field theory to be supplemented by an infinite set of higher dimensional operators. Afterwards, we adopt a self-consistent approach to Higgs inflation and formulate the set of assumptions leading to a controllable relation between low- and high-energy observables. Based on the resulting framework, we analyze the contribution of quantum corrections to the renormalization group enhanced potential and their impact on the inflationary observables. We finish this section by discussing the potential issues of Higgs inflation with the metastability of the SM vacuum.
• Some extensions and alternatives to the simplest Higgs inflation scenario are considered in section 4. In particular, we address the difference between the metric and Palatini formulations of the theory and its extension to a fully scale invariant framework (Shaposhnikov and Zenhausern, 2009; Blas et al., 2011; Garcia-Bellido et al., 2011, 2012; Bezrukov et al., 2013; Rubio and Shaposhnikov, 2014; Karananas and Rubio, 2016; Trashorras et al., 2016; Casas et al., 2017, 2018). The inflationary predictions in these models are put in one to one correspondence with the pole structure of the Einstein-frame kinetic term, allowing for an easy comparison with the results of the standard Higgs inflation scenario.
Overall, we intend to complement the existing monographs in the literature (Bezrukov, 2013; Bezrukov and Shaposhnikov, 2015a; Moss, 2015) by i) providing a further insight on the classical formulation of Higgs inflation and by ii) focusing on the uncertainties associated with the non-renormalizability of the theory and their impact on model building.
The inflationary paradigm is usually formulated in terms of conditions on the local flatness on an arbitrary potential, which can in principle contain a large number of extrema and slopes (Artymowski and Rubio, 2016). This flatness is usually related to the existence of some approximate shift-symmetry, which, for the purposes of Higgs inflation, is convenient to reformulate as a non-linear realization of approximate scale-invariance.
Let us start by considering an induced gravity scenario
involving a scalar field h, a vector field Bμ and a fermion field ψ, with interactions similar to those appearing in the SM of particle physics when written in the unitary gauge . The quantity stands for the standard Bμ kinetic term, which for simplicity we take to be Abelian. In this toy model, the effective Newton constant is induced by the scalar field expectation value,
In order for GN, eff to be well-behaved, the non-minimal coupling ξ is restricted to take positive values. This condition is equivalent to require the semi-positive definiteness of the scalar field kinetic term, as can be easily seen by performing a field redefinition h2 → h2/ξ.
An important property of the induced gravity action (2.1) is its invariance under scale transformations
Here α is an arbitrary constant, φ(x) compactly denotes the various fields in the model and Δφ's are their corresponding scaling dimensions. The consequences of this dilatation symmetry are more easily understood in a minimally-coupled frame displaying the standard Einstein-Hilbert term. This Einstein frame is achieved by a Weyl redefinition of the metric4
together with a Weyl rescaling of the vector and fermion fields,
After some trivial algebra we obtain an Einstein-frame action5
containing a non-canonical term for the Θ field. The coefficient of this kinetic term,
involves a quadratic pole at Θ = 0 and a constant
varying between zero at ξ = 0 and −1/6 when ξ → ∞. The Θ-field kinetic term can be made canonical by performing an additional field redefinition,
mapping the vicinity of the pole at Θ = 0 to ϕ → ∞. The resulting action
is invariant under shift transformations ϕ → ϕ+C, with C a constant. The exponential mapping in Equation (2.9) indicates that such translational symmetry is nothing else than the non-linear realization of the original scale invariance we started with in Equation (2.1) (Csaki et al., 2014). The Einstein-frame transition in Equation (2.4) is indeed equivalent to the spontaneous breaking of dilatations, since we implicitly required the field h to acquire a non-zero expectation value. The canonically normalized scalar field ϕ is the associated Goldstone boson and as such it is completely decoupled from the matter fields Bμ and ψ. The non-minimal coupling to gravity effectively replaces h by F∞ in all dimension-4 interactions involving conformal degrees of freedom. Note, however, that this decoupling statement does not apply to scale-invariant extensions including additional scalar fields (Kaiser, 2010; Garcia-Bellido et al., 2011; Bezrukov et al., 2013; Kaiser et al., 2013; Kaiser and Sfakianakis, 2014; Karananas and Rubio, 2016) or other non-conformal interactions such as R2 terms (Starobinsky, 1980; Gorbunov and Panin, 2011, 2012; Gorbunov and Tokareva, 2013).
Although the toy model presented above contains many of the key ingredients of Higgs inflation, it is not phenomenologically viable. In particular, the Einstein-frame potential is completely shift-symmetric and does not allow for inflation to end. On top of this limitation, the scalar field ϕ is completely decoupled from all conformal fields, excluding the possibility of entropy production and the eventual onset of a radiation-dominated era. All these phenomenological limitations are intrinsically related to the exact realization of scale invariance and as such they should be expected to disappear once a (sizable) dimensionfull parameter is included into the action. This is precisely what happens in Higgs inflation. The total Higgs inflation action (Bezrukov and Shaposhnikov, 2008)
contains two dimensionfull parameters: the reduced Planck GeV and the Higgs vacuum expectation value vEW ≃ 250 GeV responsible for the masses within the SM Lagrangian density SM. Among these two scales, the Planck mass is the most important one at the large field values relevant for inflation. To illustrate how the inclusion of MP modifies the results of the previous section, let us consider the graviscalar part of Equation (2.11) in the unitary gauge , namely
with
the usual SM symmetry-breaking potential. As in the induced gravity scenario, the inclusion of the non-minimal coupling to gravity changes the strength of the gravitational interaction and makes it dependent on the Higgs field,
In order for the graviton propagator to be well-defined at all h values, the non-minimal coupling ξ must be positive6. If ξ≠0, this requirement translates into a weakening of the effective Newton constant at increasing Higgs values. For non-minimal couplings in the range , this effect is important in the large-field regime , but completely negligible otherwise.
As we did in section 2.1, it is convenient to reformulate Equation (2.12) in the Einstein frame by performing a Weyl transformation gμν → Θgμν with
In the new frame, all the non-linearities associated with the non-minimal Higgs-gravity interaction are moved to the scalar sector of the theory,
which contains now a non-exactly flat potential
and a non-canonical kinetic sector resulting from the rescaling of the metric determinant and the non-homogeneous part of the Ricci scalar transformation. The kinetic function
shares some similarities with that in Equation (2.7). In particular, it contains two poles located respectively at Θ = 0 and Θ = 1. The first pole is an inflationary pole, like the one appearing in the induced gravity scenario. This pole leads to an enhanced friction for the Θ field around Θ = 0 and allows for inflation to happen even if the potential V(Θ) is not sufficiently flat. The second pole is a Minkowski pole around which the Weyl transformation equals one and the usual SM action is approximately recovered. To see this explicitly, we carry out an additional field redefinition 7,
to recast Equation (2.16) in terms of a canonically normalized scalar field ϕ. This differential equation admits an exact solution (Garcia-Bellido et al., 2009)
In terms of the original field h, we can distinguish two asymptotic regimes
separated by a critical value
The comparison between these approximate expressions and the exact field redefinition in Equation (2.20) is shown in Figure 3.
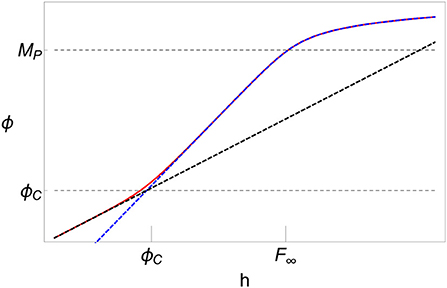
Figure 3. Comparison between the approximate expressions in Equation (2.21) (dashed black and blue lines) and the exact solution (2.20) (solid red). Below the critical scale ϕc, Higgs inflation coincides, up to highly suppressed corrections, with the SM minimally coupled to gravity. Above that scale, the Higgs field starts to decouple from the SM particles. The decoupling becomes efficient at a scale F∞, beyond which the model can be well approximated by a chiral SM with no radial Higgs component.
The large hierarchy between the transition scale ϕC and the electroweak scale allows us to identify in practice the vacuum expectation value vEW with ϕ = 0. In this limit, the Einstein-frame potential (2.17) can be rewriten as
with
At ϕ < ϕC we recover the usual Higgs potential (up to highly suppressed corrections, cf. section 3.1). At ϕ > ϕC the Einstein-frame potential becomes exponentially stretched and approaches the asymptotic value F∞ at . The presence of MP in Equation (2.11) modifies also the decoupling properties of the Higgs field as compared to those in the induced gravity scenario. In particular, the masses of the intermediate gauge bosons and fermions in the Einstein-frame8,
coincide with the SM masses in the small field regime (ϕ < ϕC) and evolve toward constant values proportional to F∞ in the large-field regime (). The transition to the Einstein-frame effectively replaces h by F(ϕ) in all (non-derivative) SM interactions. This behavior allows us to describe the Einstein-frame matter sector in terms of a chiral SM with vacuum expectation value F(ϕ) (Dutta et al., 2008; Bezrukov and Shaposhnikov, 2009).
The flattening of the Einstein-frame potential (2.23) due to the Θ = 0 pole allows for inflation with the usual slow-roll conditions even if the potential V(Θ) is not sufficiently flat. Let us compute the inflationary observables in the corresponding region ϕ > ϕC, where
The statistical information of the primordial curvature fluctuations generated by a single-field model like the one under consideration is mainly encoded in the two-point correlation functions of scalar and tensor perturbations, or equivalently in their Fourier transform, the power spectra. Following the standard approach (Mukhanov et al., 1992), we parameterize these spectra in an almost scale-invariant form,
and compute the inflationary observables
with
the first and second slow-roll parameters and the primes denoting derivatives with respect to ϕ. The quantities in (2.28) should be understood as evaluated at a field value ϕ* ≡ ϕ(N*), with
the e-fold number at which the reference scale k* in Equation (2.27) exits the horizon, i.e. k* = a*H*. Here,
stands for the field value at the end of inflation, which is defined, as usual, by the condition ϵ(ϕE)≡1. Equation (2.30) admits an exact inversion,
with −1 the lower branch of the Lambert function and
a rescaled number of e-folds. Inserting Equation (2.32) into (2.28) we get the following analytical expressions for the primordial scalar amplitude,
its spectral tilt,
and the tensor-to-scalar ratio
At large |a|N*, these predictions display an interesting attractor behavior, very similar to that appearing in α-attractor scenarios (Ferrara et al., 2013; Kallosh et al., 2013; Galante et al., 2015) (see also Artymowski and Rubio, 2016). Indeed, by taking into account the lower bound on the Lambert function (Chatzigeorgiou, 2016),
we can obtain the approximate expressions9
at . The free parameter |a| (or equivalently the non-minimal coupling ξ) can be fixed by combining Equation (2.34) with the normalization of the primordial spectrum at large scales (Akrami et al., 2018),
Doing this, we get a relation
among the non-minimal coupling ξ, the number of e-folds and the Higgs self-coupling λ.
The precise value of the number of e-folds in Equations (2.38), (2.40) depends on the whole post-inflationary expansion and, in particular, on the duration of the heating stage. As the strength of the interactions among the Higgs field and the SM particles is experimentally known, the entropy production following the end of inflation can be computed in detail (Bezrukov et al., 2009a; Garcia-Bellido et al., 2009; Repond and Rubio, 2016)10. The depletion of the Higgs-condensate is dominated by the non-perturbative production of massive intermediate gauge bosons, which, contrary to the SM fermions, can experience bosonic amplification. Once created, the W± and Z bosons can decay into lighter SM fermions with a decay probability proportional to the instantaneous expectation value of the Higgs field ϕ(t). The onset of the radiation-domination era is determined either by i) the time at which the Higgs amplitude approaches the critical value ϕC where the effective potential becomes quartic or by ii) the moment at which the energy density into relativistic fermions approaches that of the Higgs condensate; whatever happens first. The estimates in Garcia-Bellido et al. (2009), Bezrukov et al. (2009a), and Repond and Rubio (2016) provide a range
with the lower and upper bounds associated respectively with the cases i) and ii) above. For the upper limit of this narrow window, we have and we can rewrite Equation (2.40) as a relation between ξ and λ,
Note that a variation of the Higgs self-coupling in this equation can be compensated by a change of the a priori unknown non-minimal coupling to gravity. For the tree-level value λ~(1), the non-minimal coupling must be significantly larger than one, but still much smaller than the value leading to sizable modifications of the effective Newton constant at low energies. In this regime, the parameter |a| is very close to its maximum value 1/6. This effective limit simplifies considerably the expression for the critical scale ϕC separating the low- and high-energy regimes,
and collapses the inflationary predictions to the attractor values (Bezrukov and Shaposhnikov, 2008)
in very good agreement with the latest results of the Planck collaboration (Akrami et al., 2018). Note that, although computed in the Einstein frame, these predictions could have been alternatively obtained in the non-minimally coupled frame (2.12), provided a suitable redefinition of the slow-roll parameters in order to account for the Weyl factor relating the two frames (Makino and Sasaki, 1991; Fakir et al., 1992; Komatsu and Futamase, 1999; Flanagan, 2004; Tsujikawa and Gumjudpai, 2004; Koh, 2006; Chiba and Yamaguchi, 2008, 2013; Weenink and Prokopec, 2010; Postma and Volponi, 2014; Ren et al., 2014; Jarv et al., 2015a,b, 2017; Burns et al., 2016; Kuusk et al., 2016; Karam et al., 2017; Karamitsos and Pilaftsis, 2018a,b).
The presence of gravity makes Higgs inflation perturbatively non-renormalizable (Barbon and Espinosa, 2009; Burgess et al., 2009, 2010; Bezrukov et al., 2011b) and forbids its interpretation as an ultraviolet complete theory. The model should be therefore understood as an effective description valid up to a given cut-off scale Λ (Bezrukov et al., 2011b; George et al., 2016). This cutoff could either indicate the onset of a strongly coupled regime to be studied within the model by non-perturbative techniques (such as resummations, lattice simulations or functional renormalization studies) (Aydemir et al., 2012; Calmet and Casadio, 2014; Saltas, 2016; Escrivà and Germani, 2017) or the appearance of new degrees of freedom beyond the initially-assumed SM content (Giudice and Lee, 2011; Barbon et al., 2015).
A priori, the cutoff scale of Higgs inflation could coincide with the Planck scale, where gravitational effects should definitely taken into account. Although quite natural, the identification of these two energy scales may not be theoretically consistent, since other interactions could lead to violations of tree-level unitarity at a lower energy scale. An estimate11 of the cutoff scale can be obtained by expanding the fields around their background values, such that all kind of higher dimensional operators appear in the resulting action (Bezrukov et al., 2011b; Ferrara et al., 2011). The computation is technically simpler in the original frame (2.11). In order to illustrate the procedure let us consider the graviscalar sector in Equation (2.12). Expanding the fields around their background values ḡμν and ,
we obtain the following quadratic Lagrangian density for the perturbations γμν and δh
with denoting the trace of the metric excitations. For non-vanishing ξ, the last term in this equation mixes the trace of the metric perturbation with the scalar perturbation δh (Barvinsky et al., 2008, 2009; De Simone et al., 2009). To identify the different cutoff scales one must first diagonalize the kinetic terms. This can be done by performing a redefinition of the perturbations with
Once Equation (3.2) has been reduced to a diagonal form, we can proceed to read the cutoff scales. The easiest one to identify is that associated with purely gravitational interactions,
which coincides with the effective Planck scale in Equation (2.12). For scalar-graviton interactions, the leading-order higher-dimensional operator is , where
Although we have focused on the graviscalar sector of the theory, the lack of renormalizability associated with the non-minimal coupling to gravity permeates all SM sectors involving the Higgs field. One could study, for instance, the scattering of intermediate W± and Z bosons. Since we are working in the unitary gauge, it is sufficient to consider the longitudinal polarization. The modification of the Higgs kinetic term at large field values changes the delicate pattern of cancellations in the SM and leads to a tree-level unitarity violation at a scale
Note that the above scales depend on the background field . For small field values (), the cutoffs (3.5), (3.6) and (3.7) coincide with those obtained by naively expanding the theory around the electroweak scale, namely ΛP ≃ MP, (Barbon and Espinosa, 2009; Burgess et al., 2009, 2010; Hertzberg, 2010; Atkins and Calmet, 2011). At large field values, (), the suppression scale depends on the particular process under consideration. For the graviscalar cutoff ΛS grows quadratically till , where it becomes linear in and traces the dynamical Planck mass in that regime, . On the other hand, the gauge cutoff ΛG smoothly interpolates between ΛG ~ MP/ξ at and at . Note that all cutoffs scales become linear in at . This means that any operator Δ constructed out of them, the Higgs field and some Wilson coefficients cn approaches a scale-invariant form at large field values, namely
In what follows we will assume that the ultraviolet completion of the theory respects the original symmetries of the tree-level action, and in particular the approximate scale invariance of Equation (2.12) in the large-field regime and the associated shift-symmetry of its Einstein-frame formulation. This strong assumption forbids the generation of dangerous higher-dimensional operators that would completely spoil the predictivity of the model. In some sense, this requirement is not very different from the one implicitly assumed in other inflationary models involving trans-Planckian field displacements.
The minimal set of higher-dimensional operators to be included on top of the tree-level action is the one generated by the theory itself via radiative corrections (Bezrukov et al., 2011b, 2015). The cancellation of the loop divergences stemming from the original action requires the inclusion of an infinite set of counterterms with a very specific structure. As in any other non-renormalizable theory, the outcome of this subtraction procedure depends on the renormalization scheme, with different choices corresponding to different assumptions about the ultraviolet completion of the theory. Among the different subtractions setups, a dimensional regularization scheme involving a field-dependent subtraction point (Bezrukov and Shaposhnikov, 2009)
fits pretty well with the approximate scale-symmetry of Equation (2.11) at large-field values12. Given this frame and scheme, the minimal set of higher-dimensional operators generated by the theory can be computed in any Weyl-related frame provided that all fields and dimensionfull parameters are appropriately rescaled. The computation becomes particularly simple in the Einstein-frame, where the Weyl-rescaled renormalization point μ2Θ coincides with the standard field-independent prescription of renormalizable field theories, . A general counter-term in dimensional regularization contains a finite part δ and a divergent part in the form of a pole in ϵ = (4−d)/2, with d the dimension of spacetime. The coefficient of the pole is chosen to cancel the loop divergences stemming from the original action. Once this divergent part is removed, we are left with the finite contribution δ. The strength of this term encodes the remnants of a particular ultraviolet completion and cannot be determined within the effective field theory approach (Bezrukov et al., 2011b, 2015; Burgess et al., 2014). From a quantitative point of view, the most relevant δ terms are related to the Higgs and top-quark interactions. In the Einstein-frame at one loop, they take the form (Bezrukov et al., 2015)
where the primes denote again derivatives with respect to ϕ. Note that these operators differ, as expected, from those appearing in the tree-level action. This means that, while the contribution δλb can be removed by a self-coupling redefinition, the finite parts δλa, δya and δyb should be promoted to new couplings constants. Once the associated operators are added to the tree-level action, the re-evaluation of radiative corrections will generate additional contributions beyond the original one-loop result. These contributions come together with new finite parts that must be again promoted to novel couplings with their own renormalization group equations. The iteration of this scheme leads to a renormalized action including an infinite set of higher-dimensional operators constructed out of the function F and its derivatives. For small field values, the function F becomes approximately linear (F≈ϕ, F′ = 1) and one recovers the SM non-minimally coupled to gravity up to highly suppressed interactions. In this limit, the coefficients of the infinite set of counterterms can be eliminated by a redefinition of the low energy couplings, as happens in a renormalizable theory. When evolving toward the inflationary region, the function F becomes approximately constant (F∞ = F∞, F′ = 0) and some of the previously absorbed finite parts are dynamically subtracted. The unknown finite parts modify therefore the running of the SM couplings at the transition region , such that the SM masses at the electroweak scale cannot be unambiguously related to their inflationary counterparts without a precise knowledge of the ultraviolet completion (Hertzberg, 2012; Burgess et al., 2014; Bezrukov et al., 2015).
If the finite contributions are of the same order as the loops generating them, the tower of higher dimensional operators generated by radiative corrections can be truncated (Bezrukov et al., 2015). In this case, the effect of the 1-loop threshold corrections can be imitated by an effective change13 (Bezrukov et al., 2015)
with λ(μ) and yt(μ) given by the SM renormalization group equations. We emphasize, however, that the truncation of the renormalization group equations is not essential for most of the results presented below, since, within the self-consistent approach to Higgs inflation, the functional form of the effective action is almost insensitive to it (Bezrukov et al., 2011b, 2015, 2018).
To describe the impact of radiative corrections on the inflationary predictions, we will make use of the renormalization group enhanced potential. This is given by the one in Equation (2.26) but with the Higgs self-coupling λ replaced by its corresponding running value λ(ϕ),
Note that we are not promoting the non-minimal coupling ξ within F(ϕ) to a running coupling ξ(ϕ)—as done, for instance, in Ezquiaga et al. (2018)—but rather assuming it to be constant during inflation. This is indeed a reasonable approximation since the one-loop beta function determining the running of ξ (Yoon and Yoon, 1997; Bezrukov and Shaposhnikov, 2009),
is rather small for realistic values of the couplings constant at the inflationary scale, (Bezrukov et al., 2018; Masina, 2018) (see also Salvio, 2018).
Although, strictly speaking, the renormalization group enhanced potential is not gauge invariant, the gauge dependence is small during slow-roll inflation, especially in the presence of extrema (Cook et al., 2014; Espinosa et al., 2015, 2017). In the vicinity of the minimum of λ(ϕ), we can use the approximation (Bezrukov and Shaposhnikov, 2014)
with the parameters λ0, q and b depending on the inflationary values of the Einstein-frame Higgs and top quark masses, according to the fitting formulas (Bezrukov and Shaposhnikov, 2014)
with and in GeV. As seen in the last expression, the parameter b, standing for the derivative of the beta function for λ at the scale of inflation, is rather insensitive to the Higgs and top quark mass values at that scale and can be well-approximated by b≃2.3 × 10−5. The choice
with α = 0.6 optimizes the convergence of perturbation theory (Bezrukov and Shaposhnikov, 2009; Bezrukov et al., 2009b), while respecting the asymptotic symmetry of the tree-level action (2.12) and its non-linear shift-symmetric Einstein-frame realization. In the second equality, we have introduced an effective parameter κ to facilitate the numerical computation of the inflationary observables.
A simple inspection of Equations (3.12) and (3.14) allows us to distinguish three regimes:
i) Non-critical regime/Universal: If λ0 ≫ b/(16κ), the effective potential (3.12) is almost independent of the radiative logarithmic correction and can be well approximated by its tree-level form (2.26). Consequently, the inflationary observables retain their tree-level values (Bezrukov and Shaposhnikov, 2014; Enckell et al., 2016; Fumagalli and Postma, 2016; Bezrukov et al., 2018), cf. Figure 4.
ii) Critical regime: If λ0 ≳ b/(16κ), the first two derivatives of the potential are approximately zero, V′ ≃ V″ ≃ 0, leading to the appearance of a quasi-inflection point at
Qualitatively, the vast majority of inflationary e-folds in this scenario takes place in the vicinity of the inflection point ϕI, while the inflationary observables depend on the form of the potential as some value ϕ* > ϕI.
Given the small value of the Higgs self-coupling in this scenario, , the nonminimal coupling ξ can be significantly smaller than in the universal regime, ξ ~ (10), while still satisfying the normalization condition (2.39) (Allison, 2014; Bezrukov and Shaposhnikov, 2014; Hamada et al., 2014b, 2015). This drastic decrease of the non-minimal coupling alleviates the tree-level unitary problems discussed in section 3.1 by raising the cutoff scale.
For small ξ values, the tensor-to-scalar ratio can be rather large, r ~ (10−1) (Allison, 2014; Bezrukov and Shaposhnikov, 2014; Hamada et al., 2014b, 2015) (see also Masina, 2018). Note, however, that although CMB data seems to be consistent with the primordial power spectrum at large scales, the simple expansion in (2.27) cannot accurately describe its global behavior since the running of the spectral tilt αs ≡ dln ns/dln k and its scale dependence also become considerably large, cf. Figure 5.
The non-monotonic evolution of the slow-roll parameter ϵ in the vicinity of the inflection point leads to the enhancement of the spectrum of primordial density fluctuations at small and intermediate scales. It is important to notice at this point that the standard slow-roll condition may break down if the potential becomes extremely flat and the inertial contribution in the equation of motion for the inflation field is not negligible as compared with the Hubble friction (Garcia-Bellido and Ruiz Morales, 2017; Germani and Prokopec, 2017; Kannike et al., 2017). In this regime, even the classical treatment is compromised since stochastic effects can no longer be ignored (Starobinsky and Yokoyama, 1994; Vennin and Starobinsky, 2015; Pattison et al., 2017; Ezquiaga and Garcia-Bellido, 2018).
If we restrict ourselves to situation in which the slow-roll approximation is satisfied during the whole inflationary trajectory (Bezrukov et al., 2018)14, the height and width of the generated bump at fixed spectral tilt are correlated with the tensor-to-scalar ratio r, cf. Figure 4. Contrary to some claims in the literature (Ezquiaga et al., 2018), the maximum amplitude of the power-spectrum compatible with the 95% C.L Planck ns − r contours (Bezrukov et al., 2018) is well below the critical threshold needed for primordial black hole formation (Bird et al., 2016; Carr et al., 2016, 2017) (see however, Ezquiaga and Garcia-Bellido, 2018; Rasanen and Tomberg, 2018). This conclusion is unchanged if one considers the effect of non-instantaneous threshold corrections (Bezrukov et al., 2018), which could potentially affect the results given the numerical proximity of the inflection point (3.17) to the upper boundary of the transition region, .
iii) Hilltop regime: If λ≲b/(16κ) the potential develops a new minimum at large field values (Fumagalli, 2017; Rasanen and Wahlman, 2017). This minimum is separated from the electroweak minimum by a local maximum where hilltop inflation can take place (Boubekeur and Lyth, 2005; Barenboim et al., 2016). This scenario is highly sensitive to the initial conditions since the inflaton field must start on the electroweak vacuum side and close enough to the local maximum in order to support an extended inflationary epoch. On top of that, the fitting formulas in (3.15) may not be accurate enough for this case, since they are based on an optimization procedure around the λ(ϕ) minimum. The tensor-to-scalar ratio in this scenario differs also from the universal/non-critical Higgs inflation regime, but contrary to the critical case, it is decreased to 2 × 10−5 < r < 1 × 10−3, rather than increased (Fumagalli and Postma, 2016; Rasanen and Wahlman, 2017).
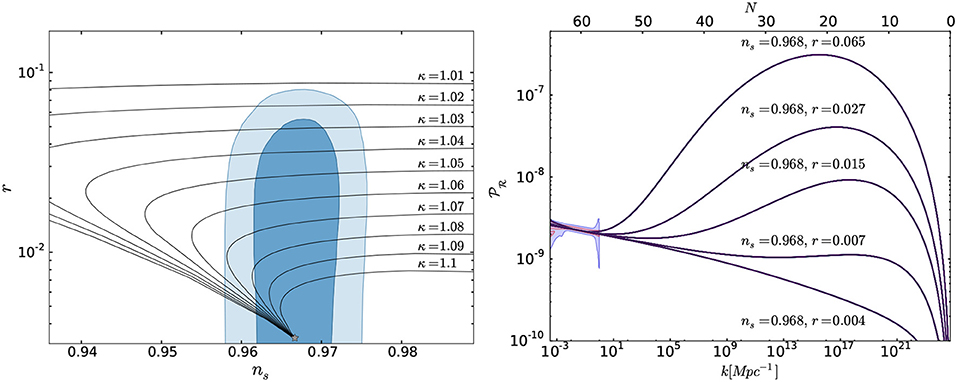
Figure 4. (Left) The tensor-to-scalar ratio r and the spectral tilt ns following from the effective potential (3.12) (Bezrukov et al., 2018). The non-minimal coupling ξ varies between 10 and 100 along the lines of constant κ, with larger values corresponding to smaller tensor-to-scalar ratios. The star in the lower part of the plot stands for the universal values in Equation (2.44). The blue contours indicate the latest 68 and 95% C.L. Planck constraints on the r-ns plane (Akrami et al., 2018). (Right) The power spectrum as a function of the number of e-folds before the end of inflation and the associated comoving scale κ in inverse megaparsecs (Bezrukov et al., 2018). The monotonic curve at the bottom of the plot corresponds to the universal/non-critical Higgs inflation scenario. The upper non-monotonic curves are associated with different realizations of the critical Higgs inflation scenario. The shaded regions stand for the latest 68 and 95% C.L. constraints provided by the Planck collaboration (Akrami et al., 2018).
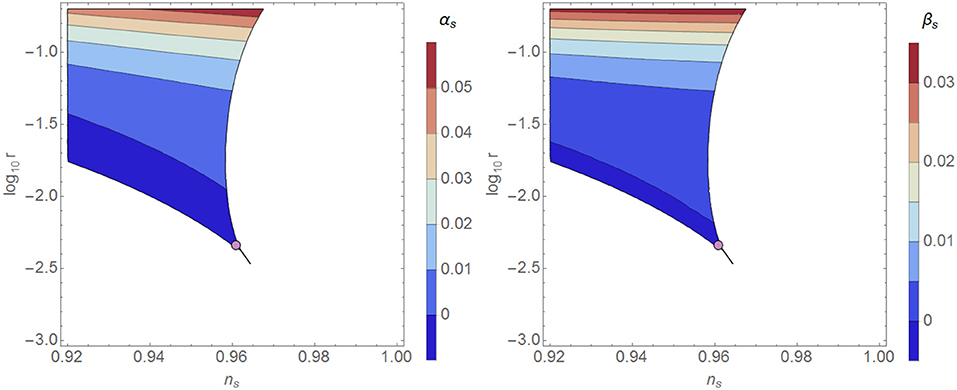
Figure 5. (Left) Spectral tilt running αs ≡ dln ns/dln k in critical Higgs inflation as a function of the tensor-to-scalar ratio r and the spectral-tilt ns (Rasanen and Wahlman, 2017). (Right) Scale dependence of the spectral-tilt in the same case (Rasanen and Wahlman, 2017). The purple dots indicate the universal/non-critical Higgs inflation regime. The boundaries on the right-hand side of the figures correspond to the constraint on the number of e-folds following the heating estimates in Garcia-Bellido et al. (2009), Bezrukov et al. (2009a), and Repond and Rubio (2016). For lower heating efficiencies, the boundaries move to the left, decreasing the spectral tilt but not significantly affecting the tensor-to-scalar ratio (Rasanen and Wahlman, 2017).
The qualitative classification of scenarios and predictions presented in the previous section depends on the inflationary values of the Higgs and top quark masses and holds independently of the value of their electroweak counterparts. In particular, any pair of couplings following from the SM renormalization group equations can be connected to a well-behaved pair of couplings in the chiral phase by a proper choice of the unknown threshold corrections. This applies also if the SM vacuum is not completely stable. Some examples of the 1-loop threshold correction δλa needed to restore the universal/non-critical Higgs inflation scenario beyond , and 1012 GeV are shown in Figure 6. For a detailed scan of the parameter space, see Enckell et al. (2016); Fumagalli and Postma (2016).
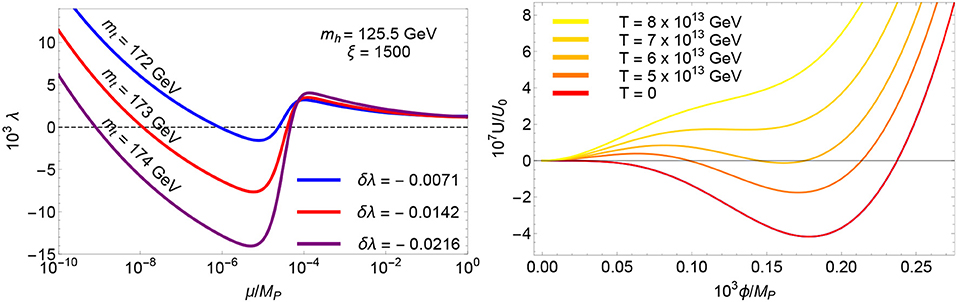
Figure 6. (Left) Illustrative values of the 1-loop threshold corrections needed to restore the asymptotic behavior of the universal Higgs inflation potential at large field values for electroweak SM pole masses leading to SM vacuum instability at , and 1012 GeV. (Right) Comparison between the potential following from the set of parameters leading to the red line in the previous plot and the thermally-corrected effective potential accounting for the backreaction effects of the decay products created during the heating stage. The normalization factor account for the typical energy density at the end of inflation.
The non-trivial interplay between vacuum stability and threshold corrections generates an additional minimum at large field values. Provided the usual chaotic initial conditions, the Higgs field will evolve in the trans-Planckian field regime, inflating the Universe while moving toward smaller field values. Since the new minimum is significantly wider and deeper than the electroweak one, it seems likely that the Higgs field will finish its post-inflationary evolution there. Note, however, that this conclusion is strongly dependent on the ratio of the Higgs energy density to the second minimum depth. If this ratio is large, the entropy production at the end of inflation may significantly modify the shape of the potential, triggering its stabilization and allowing the Higgs field to evolve toward the desired electroweak vacuum (Bezrukov et al., 2009a).
The one-loop finite temperature corrections to be added on top of the Einstein-frame renormalization group enhanced potential take the form (Linde, 1979)
with the plus and minus signs corresponding respectively to fermions and bosons and mB, F standing for the Einstein-frame masses in Equation (2.25). The most important contributions in Equation (3.18) are associated with the top quark and the electroweak bosons, with the corresponding coupling constants yt and g evaluated at μyt = 1.8T and μg = 7T, in order to minimize the radiative corrections (Kajantie et al., 1996).
A detailed analysis of the universal/non critical Higgs inflation scenario reveals that the temperature of the decay products generated during the heating stage exceeds generically the temperature at which the unwanted secondary vacuum at large field values disappears (Bezrukov et al., 2009a; Garcia-Bellido et al., 2009), see Figure 615. The stabilization becomes favored for increasing μ0 values16. and holds even if this scale is as low as 1010 GeV (Bezrukov et al., 2009a). The thermally-corrected potential enables the Higgs field to relax to the SM vacuum. After the heating stage, the temperature decreases as the Universe expands and the secondary minimum reappears, first as a local minimum and eventually as the global one. When that happens, the Higgs field is already trapped in the electroweak vacuum. Although the barrier separating the two minima prevents a direct decay, the Higgs field could still tunnel to the global minimum. The probability for this to happen is, however, very small and the lifetime of SM vacuum significantly exceeds the life of the Universe (Anderson, 1990; Arnold and Vokos, 1991; Espinosa and Quiros, 1995; Espinosa et al., 2008). Universal/non-critical Higgs inflation with a graceful exit can therefore take place for electroweak SM pole masses leading to vacuum metastability at energies below the inflationary scale (Bezrukov et al., 2009a).
The situation changes completely if one considers the critical Higgs inflation scenario. In this case, the energy of the Higgs condensate is comparable to the depth of the secondary minimum and symmetry restoration does not take place. Unless the initial conditions are extremely fine-tuned, the Higgs field will relax to the minimum of the potential at Planckian values, leading with it to the inevitably collapse of the Universe (Felder et al., 2002). The success of critical Higgs inflation requires therefore the absolute stability of the electroweak vacuum (Bezrukov et al., 2009a).
Many variations and extensions of Higgs inflation have been considered in the literature (see for instance Ben-Dayan and Einhorn, 2010; Lerner and McDonald, 2010, 2011; Arai et al., 2011; Giudice and Lee, 2011; Kamada et al., 2011, 2012; Einhorn and Jones, 2012; Greenwood et al., 2013; Kanemura et al., 2013; Steinwachs, 2013; Choudhury et al., 2014; He and Xianyu, 2014; Oda and Tomoyose, 2014a,b; Xianyu and He, 2014; Cai et al., 2015; Ellis et al., 2015, 2016; Kamada, 2015b; Lazarides and Pallis, 2015; Okada and Shafi, 2015; Calmet and Kuntz, 2016; Ge et al., 2016; Takahashi and Takahashi, 2016; van de Bruck and Longden, 2016; Ema, 2017; Ema et al., 2017b; Marian et al., 2017; Okada and Raut, 2017; Chen et al., 2018; He et al., 2018). In what follows we will restrict ourselves to those proposals that are more closely related to the minimalistic spirit of the original scenario. In particular, we will address a Palatini formulation of Higgs inflation and the embedding of the model to a fully scale invariant framework.
In the usual formulation of Higgs inflation presented in section 2.2, the action is minimized with respect to the metric. This procedure implicitly assumes the existence of a Levi-Civita connection depending on the metric tensor and the inclusion of a York-Hawking-Gibbons term ensuring the cancellation of a total derivative term with no-vanishing variation at the boundary (York, 1972; Gibbons and Hawking, 1977). One could alternatively consider a Palatini formulation of gravity in which the metric tensor and the connection are treated as independent variables and no additional boundary term is required to obtain the equations of motion (Ferraris et al., 1982). Roughly speaking, this formulation corresponds to assuming an ultraviolet completion involving different gravitational degrees of freedom.
Although the metric and Palatini formulations of General Relativity give rise to the same equations of motion (Ferraris et al., 1982), this is not true for scalar-tensor theories as Higgs inflation. To see this explicitly let us consider the Higgs inflation action in Equation (2.12) with and Γ a non-Levi-Civita connection17. Performing a Weyl rescaling of the metric gμν → Θgμν with Θ given by Equation (2.15) we obtain an Einstein-frame action
containing a potential (2.17) and a non-canonical kinetic term with
and
Note that the kinetic function (4.2) differs from that obtained in the metric formulation, see Equation (2.18). In particular, it does not contain the part associated with the non-homogeneous transformation of the Ricci scalar, since R = R(Γ) is now invariant under Weyl rescalings. For the purposes of inflation, this translates into a modification of the residue of the inflationary pole at Θ = 0 with respect to the metric case. While the metric value of |a| in Equation (2.18) is bounded from above [cf. Equation (2.8)], it can take positive arbitrary values in the Palatini formulation [cf. Equation (4.3)]. Performing a field redefinition
to canonically normalize the h-field kinetic term, we can rewrite the graviscalar action (4.1) at ϕ≫vEW as
with
The comparison of the latest expression with Equation (2.24) reveals some important differences between the metric and Palatini formulations. In both cases, the effective Einstein-frame potential smoothly interpolates between a low-energy quartic potential and an asymptotically flat potential at large field values. Note, however, that the transition in the Palatini case is rather direct and does not involve the quadratic piece appearing in the metric formulation. On top of that, the flatness of the asymptotic plateau is different in the two cases, due to the effective change in |a|. The Palatini dependence |a| = ξ has a strong impact on the inflationary observables. In the large-field regime they read
with
a rescaled number of e-folds and
the inflaton value at the end of inflation (ϵ(ϕend)≡1), with corresponding to the ξ → ∞ limit and to the end of inflation in a minimally coupled λϕ4 theory. A relation between the non-minimal coupling ξ, the self-coupling λ and the number of e-folds can be obtained by taking into account the amplitude of the observed power spectrum in Equation (2.39),
A simple inspection of Equation (4.7) reveals that the predicted tensor-to-scalar ratio in Palatini Higgs inflation is within the reach of current or future experiments (Matsumura et al., 2016) only if ξ≲10, which, assuming , requires a very small coupling λ≲10−9. For a discussion of unitarity violations in the Palatini formulation, see Bauer and Demir (2011).
The existence of robust predictions in (non-critical) Higgs inflation is intimately related to the emerging dilatation symmetry of its tree-level action at large field values. The uplifting of Higgs inflation to a completely scale-invariant setting was considered in Shaposhnikov and Zenhausern (2009), Garcia-Bellido et al. (2011), Blas et al. (2011), Bezrukov et al. (2013), Garcia-Bellido et al. (2012), Rubio and Shaposhnikov (2014), Trashorras et al. (2016), Karananas and Rubio (2016), Casas et al. (2017), and Casas et al. (2018). In the unitary gauge , the graviscalar sector of the Higgs-Dilaton model considered in these papers takes the form
with
a scale-invariant version of the SM symmetry-breaking potential and α, β positive dimensionless parameters. The existence of a well-defined gravitational interactions at all field values requires the non-minimal gravitational couplings to be positive-definite, i.e. ξh, ξχ > 0. In the absence of gravity, the ground state of Equation (4.11) is determined by the scale-invariant potential (4.12). For α ≠ 0 and β = 0, the vacuum manifold extends along the flat directions h0 = ± α χ0. Any solution with χ0 ≠ 0 breaks scale symmetry spontaneously and induces non-zero values for the effective Planck mass and the electroweak scale18. The relation between these highly hierarchical scales is set by fine-tuning . For this small value, the flat valleys in the potential U(h, χ) are essentially aligned and we can safely approximate α≃0 for all inflationary purposes.
To compare the inflationary predictions of this model with those of the standard Higgs-inflation scenario, let us perform a Weyl rescaling followed by a field redefinition (Casas et al., 2017)
with
After some algebra, we obtain a rather simple Einstein-frame action (Karananas and Rubio, 2016; Casas et al., 2017)
containing a potential
and a non-canonical, albeit diagonal, kinetic sector. The kinetic function for the Θ field,
contains two “inflationary" poles at Θ = 0 and Θ = c/|ā| and a “Minkowski” pole at Θ = 1, where the usual SM action is approximately recovered. As in the single field case, the “Minkowski” pole does not play a significant role during inflation and can be neglected for all practical purposes. Interestingly, the field-derivative space becomes in this limit a maximally symmetric hyperbolic manifold with Gaussian curvature a < 0 (Karananas and Rubio, 2016).
Inflation takes place in the vicinity of the inflationary poles. During this regime, the kinetic term of the Φ-field is effectively suppressed and the dilaton rapidly approaches a constant value Φ = Φ0 (Garcia-Bellido et al., 2011). This effective freezing is an immediate consequence of scale invariance. As in the single field case, the shift symmetry Φ → Φ+C in Equation (4.15) allows us to interpret Φ as the dilaton or Goldstone of dilatations. As first shown in Garcia-Bellido et al. (2011), the equation of motion for this field coincides with the scale-current conservation equation, effectively restricting the evolution to constant Φ ellipsoidal trajectories in the {h, χ} plane. Given this emergent single-field dynamics, no non-gaussianities nor isocurvature perturbations are significantly generated during inflation (Garcia-Bellido et al., 2011). If the Θ variable is dominated by the Higgs component (ξh ≫ ξχ), the spectral tilt and the tensor-to-scalar ratio take the compact form
with |a| ≃ 1/6 in order to satisfy the normalization condition (2.39). Note that these expressions rapidly converge to the Higgs inflation values (2.38) for 4cN* ≪ 1. For increasing c and fixed N*, the spectral tilt decreases linearly and the tensor-to-scalar ratio approaches zero.
Before the start of the LHC, it was widely believed that we would find a plethora of new particles and interactions that would reduce the Standard Model to a mere description of Nature at energies below the TeV scale. From a bottom-up perspective, new physics was typically advocated to cure the divergences associated with the potential growth of the Higgs self-coupling at high energies. The finding of a relatively light Higgs boson in the Large Hadron Collider concluded the quest of the Standard Model spectrum while demystifying the concept of naturalness and the role of fundamental scalar fields in particle physics and cosmology. The Standard Model is now a confirmed theory that could stay valid till the Planck scale and provide a solid theoretical basis for describing the early Universe.
The Higgs field itself could lead to inflation if a minimalistic coupling to the Ricci scalar is added to the Standard Model action. The value of this coupling can be fixed by the normalization of the spectrum of primordial density perturbations, leaving a theory with no free parameters at tree level. On top of that, the experimental knowledge of the Standard Model couplings reduces the usual uncertainties associated with the heating stage and allows us to obtain precise predictions in excellent agreement with observations. Note, however, the mere existence of gravity makes the theory non-renormalizable and forces its interpretation as an effective field theory. Even in a self-consistent approach to Higgs inflation, the finite parts of the counterterms needed to make the theory finite obscure the connection between low- and high-energy observables. If these unknown coefficients are small, Higgs inflation provides an appealing relation between the Standard Model parameters and the properties of the Universe at large scales. If they are large, this connection is lost but Higgs inflation can surprisingly take place even when the Standard Model vacuum is not completely stable.
The author confirms being the sole contributor of this work and has approved it for publication.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author acknowledges support from the Deutsche Forschungsgemeinschaft through the Open Access Publishing funding programme of the Baden-Württemberg Ministry of Science, Research and Arts and the Ruprecht-Karls-Universität Heidelberg as well as through the project TRR33 The Dark Universe. He thanks Guillem Domenech, Georgios Karananas and Martin Pauly for useful comments and suggestions on the manuscript.
1. ^The metastability region is defined as the parameter space leading to vacuum instability at energies below the Planck scale but with an electroweak vacuum lifetime longer than the age of the Universe.
2. ^An alternative possibility involving a derivative coupling among the Einstein tensor and the Higgs kinetic term was considered in Germani and Kehagias (2010b), Germani and Kehagias (2010a), and Fumagalli et al. (2018).
3. ^Prior to Bezrukov and Shaposhnikov (2008), the effect of non-minimal couplings had been extensively studied in the literature (see for instance Minkowski, 1977; Smolin, 1979; Zee, 1979; Spokoiny, 1984; Futamase and Maeda, 1989; Salopek et al., 1989; Fakir and Unruh, 1990a,b; Makino and Sasaki, 1991; Fakir et al., 1992; Cervantes-Cota and Dehnen, 1995a,b; Kaiser, 1995; Komatsu and Futamase, 1998), but never with the SM Higgs as the inflaton.
4. ^In spite of its extensive use in the literature, we avoid referring to point-wise rescalings of the metric as “conformal transformations.” For a comprehensive discussion on the differences between Weyl and conformal symmetries, see for instance Karananas and Monin (2016a,b).
5. ^In order to keep the notation as simple as possible, we will not introduce different notations for the quantities defined in different Weyl-related frames. In particular, the implicit Lorentz contractions in this article should be understood to be performed with the metric of the frame under consideration.
6. ^Models with negative ξ have been considered in the literature (Herranen et al., 2014; Kamada, 2015a; Figueroa et al., 2018). In this type of scenarios the gravitational instability at large field values can be avoided by replacing the quadratic coupling ξh2 by a designed function ξf(h) remaining smaller than during the whole field regime.
7. ^Note that all equations till this point hold even if the non-minimal coupling ξ is field-dependent (Ezquiaga et al., 2018; Masina, 2018).
8. ^Here we use a compact notation for the gauge boson couplings, namely g = g2 and g2cosθw for the B = W± and Z bosons respectively, with g1 and g2 the gauge couplings of the U(1)Y and SU(2)L SM groups and the weak mixing angle. The coupling y denotes a generic Yukawa coupling.
9. ^Note that the expressions contain rather than N*.
10. ^This allows, for instance, to distinguish Higgs inflation from R2 Starobinsky inflation (Starobinsky, 1980; Bezrukov and Gorbunov, 2012).
11. ^This procedure does not take into account possible cancellations among scattering diagrams, as those taking place, for instance, in models involving a singlet scalar field not minimally coupled to gravity (Hertzberg, 2010).
12. ^The use of other schemes such as Pauli-Villars regularization or standard dimensional regularization with field-independent subtraction point leads to dilatation-symmetry breaking and the consequent bending of the Higgs inflation plateau due to radiative corrections (see for instance Barvinsky et al., 2008, 2009, 2012; De Simone et al., 2009).
13. ^This replacement implicitly neglects the running of the finite parts δλa and δya in the transition region .
14. ^The onset of the slow-roll regime prior to the arrival of the field to the inflection point and its dependence on pre-inflationary conditions was studied in Salvio (2018), where a robust inflationary attractor was shown to exist.
15. ^A detailed scan of the parameter space assuming instantaneous conversion of the inflaton energy density into a thermal bath was performed in Enckell et al. (2016).
16. ^The larger μ0 is, the shallower and narrower the “wrong” minimum becomes, cf. Figure 6
17. ^For a recent generalization built from the Higgs, the metric and the connection and involving only up to two derivatives (see Rasanen, 2018).
18. ^Among the possible values of β in the presence of gravity, the case β = 0 seems also preferred (Allen and Folacci, 1987; Garcia-Bellido et al., 2011; Jalmuzna et al., 2011, see also Antoniadis et al., 1986, 2007; Tsamis and Woodard, 1993, 1995; Polyakov, 2010; Wetterich, 2017).
Aad, G., Abajyan, T., Abbott, B., Abdallah, J., Abdel Khalek, S., Abdelalim, A. A., et al. (2012). Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B716, 1–29. doi: 10.1016/j.physletb.2012.08.020
Akrami, Y., Arroja, F., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., et al. (2018). Planck 2018 results. X. Constraints on inflation. arXiv:1807.06211.
Albrecht, A., and Steinhardt, P. J. (1982). Cosmology for grand unified theories with radiatively induced symmetry breaking. Phys. Rev. Lett. 48, 1220–1223. doi: 10.1103/PhysRevLett.48.1220
Allen, B., and Folacci, A. (1987). The massless minimally coupled scalar field in De sitter space. Phys. Rev. D35:3771. doi: 10.1103/PhysRevD.35.3771
Allison, K. (2014). Higgs xi-inflation for the 125-126 GeV Higgs: a two-loop analysis. J. High Ener. Phys. 02:040. doi: 10.1007/JHEP02(2014)040
Anderson, G. W. (1990). New cosmological constraints on the Higgs Boson and top quark Masses. Phys. Lett. B243, 265–270. doi: 10.1016/0370-2693(90)90849-2
Antoniadis, I., Iliopoulos, J., and Tomaras, T. N. (1986). Quantum instability of De sitter space. Phys. Rev. Lett. 56:1319. doi: 10.1103/PhysRevLett.56.1319
Antoniadis, I., Mazur, P. O., and Mottola, E. (2007). Cosmological dark energy: prospects for a dynamical theory. New J. Phys. 9:11. doi: 10.1088/1367-2630/9/1/011
Arai, M., Kawai, S., and Okada, N. (2011). Higgs inflation in minimal supersymmetric SU(5) GUT. Phys. Rev. D84:123515. doi: 10.1103/PhysRevD.84.123515
Arnold, P. B., and Vokos, S. (1991). Instability of hot electroweak theory: bounds on m(H) and M(t). Phys. Rev. D44, 3620–3627. doi: 10.1103/PhysRevD.44.3620
Artymowski, M., and Rubio, J. (2016). Endlessly flat scalar potentials and α-attractors. Phys. Lett. B761, 111–114. doi: 10.1016/j.physletb.2016.08.024
Atkins, M., and Calmet, X. (2011). Remarks on higgs inflation. Phys. Lett. B697, 37–40. doi: 10.1016/j.physletb.2011.01.028
Aydemir, U., Anber, M. M., and Donoghue, J. F. (2012). Self-healing of unitarity in effective field theories and the onset of new physics. Phys. Rev. D86:014025. doi: 10.1103/PhysRevD.86.014025
Barbon, J. L. F., Casas, J. A., Elias-Miro, J., and Espinosa, J. R. (2015). Higgs inflation as a mirage. J. High Ener. Phys. 09:027. doi: 10.1007/JHEP09(2015)027
Barbon, J. L. F., and Espinosa, J. R. (2009). On the naturalness of higgs inflation. Phys. Rev. D79:081302. doi: 10.1103/PhysRevD.79.081302
Barenboim, G., Park, W.-I., and Kinney, W. H. (2016). Eternal hilltop inflation. J. Cosmol. Astropart. Phys. 1605:030. doi: 10.1088/1475-7516/2016/05/030
Barvinsky, A. O., Kamenshchik, A. Yu., Kiefer, C., Starobinsky, A. A., and Steinwachs, C. (2009). Asymptotic freedom in inflationary cosmology with a non-minimally coupled Higgs field. J. Cosmol. Astropart. Phys. 0912:003. doi: 10.1088/1475-7516/2009/12/003
Barvinsky, A. O., Kamenshchik, A. Yu., Kiefer, C., Starobinsky, A. A., and Steinwachs, C. F. (2012). Higgs boson, renormalization group, and naturalness in cosmology. Eur. Phys. J. C72:2219. doi: 10.1140/epjc/s10052-012-2219-3
Barvinsky, A. O., Kamenshchik, A. Yu., and Starobinsky, A. A. (2008). Inflation scenario via the Standard Model Higgs boson and LHC. J. Cosmol. Astropart. Phys. 0811:021. doi: 10.1088/1475-7516/2008/11/021
Bauer, F., and Demir, D. A. (2011). Higgs-palatini inflation and unitarity. Phys. Lett. B698, 425–429. doi: 10.1016/j.physletb.2011.03.042
Ben-Dayan, I., and Einhorn, M. B. (2010). Supergravity higgs inflation and shift symmetry in electroweak theory. J. Cosmol. Astropart. Phys. 1012:002. doi: 10.1088/1475-7516/2010/12/002
Bezrukov, F. (2013). The Higgs field as an inflaton. Class. Quant. Grav. 30:214001. doi: 10.1088/0264-9381/30/21/214001
Bezrukov, F., Gorbunov, D., and Shaposhnikov, M. (2009a). On initial conditions for the Hot Big Bang. J. Cosmol. Astropart. Phys. 0906:029. doi: 10.1088/1475-7516/2009/06/029
Bezrukov, F., Gorbunov, D., and Shaposhnikov, M. (2011a). Late and early time phenomenology of Higgs-dependent cutoff. J. Cosmol. Astropart. Phys. 1110:001. doi: 10.1088/1475-7516/2011/10/001
Bezrukov, F., Kalmykov, M. Yu., Kniehl, B. A., and Shaposhnikov, M. (2012). Higgs boson mass and new physics. J. High Ener. Phys., 10:140. doi: 10.1007/JHEP10(2012)140
Bezrukov, F., Karananas, G. K., Rubio, J., and Shaposhnikov, M. (2013). Higgs-Dilaton Cosmology: an effective field theory approach. Phys. Rev. D87:096001. doi: 10.1103/PhysRevD.87.096001
Bezrukov, F., Magnin, A., Shaposhnikov, M., and Sibiryakov, S. (2011b). Higgs inflation: consistency and generalisations. J. High Ener. Phys. 01:016. doi: 10.1007/JHEP01(2011)016
Bezrukov, F., Pauly, M., and Rubio, J. (2018). On the robustness of the primordial power spectrum in renormalized Higgs inflation. J. Cosmol. Astropart. Phys. 1802:40. doi: 10.1088/1475-7516/2018/02/040
Bezrukov, F., Rubio, J., and Shaposhnikov, M. (2015). Living beyond the edge: higgs inflation and vacuum metastability. Phys. Rev. D92:83512. doi: 10.1103/PhysRevD.92.083512
Bezrukov, F., and Shaposhnikov, M. (2009). Standard Model Higgs boson mass from inflation: Two loop analysis. J. High Ener. Phys. 7:89. doi: 10.1088/1126-6708/2009/07/089
Bezrukov, F., and Shaposhnikov, M. (2014). Higgs inflation at the critical point. Phys. Lett. B734, 249–254. doi: 10.1016/j.physletb.2014.05.074
Bezrukov, F., and Shaposhnikov, M. (2015a). Inflation, LHC and the Higgs boson. Comptes Rendus Physique 16, 994–1002. doi: 10.1016/j.crhy.2015.08.005
Bezrukov, F., and Shaposhnikov, M. (2015b). Why should we care about the top quark Yukawa coupling? J. Exp. Theor. Phys. 120, 335–343. doi: 10.1134/S1063776115030152
Bezrukov, F. L., and Gorbunov, D. S. (2012). Distinguishing between R2-inflation and Higgs-inflation. Phys. Lett. B713, 365–368. doi: 10.1016/j.physletb.2012.06.040
Bezrukov, F. L., Magnin, A., and Shaposhnikov, M. (2009b). Standard model higgs boson mass from inflation. Phys. Lett. B675, 88–92. doi: 10.1016/j.physletb.2009.03.035
Bezrukov, F. L., and Shaposhnikov, M. (2008). The standard model higgs boson as the inflaton. Phys. Lett. B659, 703–706. doi: 10.1016/j.physletb.2007.11.072
Bird, S., Cholis, I., Munoz, J. B., Ali-Haimoud, Y., Kamionkowski, M., Kovetz, E. D., et al. (2016). Did LIGO detect dark matter? Phys. Rev. Lett. 116:201301. doi: 10.1103/PhysRevLett.116.201301
Birrell, N. D., and Davies, P. C. W. (1984). Quantum Fields in Curved Space. Cambridge Monographs on Mathematical Physics. Cambridge: Cambridge University Press.
Blas, D., Shaposhnikov, M., and Zenhausern, D. (2011). Scale-invariant alternatives to general relativity. Phys. Rev. D84:044001. doi: 10.1103/PhysRevD.84.044001
Boubekeur, L., and Lyth, D. H. (2005). Hilltop inflation. J. Cosmol. Astropart. Phys. 0507:010. doi: 10.1088/1475-7516/2005/07/010
Branchina, V., and Messina, E. (2013). Stability, higgs boson mass and new physics. Phys. Rev. Lett. 111:241801. doi: 10.1103/PhysRevLett.111.241801
Branchina, V., Messina, E., and Platania, A. (2014). Top mass determination, Higgs inflation, and vacuum stability. J. High Ener. Phys. 09:182. doi: 10.1007/JHEP09(2014)182
Branchina, V., Messina, E., and Sher, M. (2015). Lifetime of the electroweak vacuum and sensitivity to Planck scale physics. Phys. Rev. D91:013003. doi: 10.1103/PhysRevD.91.013003
Burgess, C. P., Lee, H. M., and Trott, M. (2009). Power-counting and the validity of the classical approximation during inflation. J. High Ener. Phys. 09:103. doi: 10.1088/1126-6708/2009/09/103
Burgess, C. P., Lee, H. M., and Trott, M. (2010). Comment on higgs inflation and naturalness. J. High Ener. Phys. 07:007. doi: 10.1007/JHEP07(2010)007
Burgess, C. P., Patil, S. P., and Trott, M. (2014). On the predictiveness of single-field inflationary models. J. High Ener. Phys. 06:010. doi: 10.1007/JHEP06(2014)010
Burns, D., Karamitsos, S., and Pilaftsis, A. (2016). Frame-covariant formulation of inflation in scalar-curvature theories. Nucl. Phys. B907, 785–819. doi: 10.1016/j.nuclphysb.2016.04.036
Butenschoen, M., Dehnadi, B., Hoang, A. H., Mateu, V., Preisser, M., and Stewart, I. W. (2016). Top quark mass Calibration for Monte Carlo Event Generators. Phys. Rev. Lett. 117:232001. doi: 10.1103/PhysRevLett.117.232001
Buttazzo, D., Degrassi, G., Giardino, P. P., Giudice, G. F., Sala, F., Salvio, A., et al. (2013). Investigating the near-criticality of the Higgs boson. J. High Ener. Phys. 12:089. doi: 10.1007/JHEP12(2013)089
Cai, R.-G., Guo, Z.-K., and Wang, S.-J. (2015). Higgs inflation in Gauss-Bonnet braneworld. Phys. Rev. D92:063514. doi: 10.1103/PhysRevD.92.063514
Callan, C. G. Jr., Coleman, S. R., and Jackiw, R. (1970). A New improved energy - momentum tensor. Ann. Phys. 59, 42–73. doi: 10.1016/0003-4916(70)90394-5
Calmet, X., and Casadio, R. (2014). Self-healing of unitarity in Higgs inflation. Phys. Lett. B734, 17–20. doi: 10.1016/j.physletb.2014.05.008
Calmet, X., and Kuntz, I. (2016). Higgs Starobinsky Inflation. Eur. Phys. J. C76:289. doi: 10.1140/epjc/s10052-016-4136-3
Carr, B., Kuhnel, F., and Sandstad, M. (2016). Primordial black holes as dark matter. Phys. Rev. D94:083504. doi: 10.1103/PhysRevD.94.083504
Carr, B., Raidal, M., Tenkanen, T., Vaskonen, V., and Veermae, H. (2017). Primordial black hole constraints for extended mass functions. Phys. Rev. D96:023514. doi: 10.1103/PhysRevD.96.023514
Casas, S., Karananas, G. K., Pauly, M., and Rubio, J. (2018). Scale-invariant alternatives to general relativity. III. The inflation–dark-energy connection, arXiv:1811.05984.
Casas, S., Pauly, M., and Rubio, J. (2017). Higgs-dilaton cosmology: an inflation-dark-energy connection and forecasts for future galaxy surveys. Phys. Rev. D97:043520. doi: 10.1103/PhysRevD.97.043520
Cervantes-Cota, J. L., and Dehnen, H. (1995a). Induced gravity inflation in the standard model of particle physics. Nucl. Phys. B442, 391–412. doi: 10.1016/0550-3213(95)00128-X
Cervantes-Cota, J. L., and Dehnen, H. (1995b). Induced gravity inflation in the SU(5) GUT. Phys. Rev. D51, 395–404. doi: 10.1103/PhysRevD.51.395
Chatrchyan, S., Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adamm W,. Aguilo, E., et al. (2012). Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B716, 30–61. doi: 10.1016/j.physletb.2012.08.021
Chatzigeorgiou, I. (2016). Bounds on the lambert function and their application to the outage analysis of user cooperation. CoRR, abs/1601.04895.
Chen, H.-Y., Gogoladze, I., Hu, S., Li, T., and Wu, L. (2018) Natural Higgs Inflation, Gauge Coupling Unification, Neutrino Masses, arXiv:1805.00161.
Chiba, T., and Yamaguchi, M. (2008). Extended slow-roll conditions and rapid-roll conditions. J. Cosmol. Astropart. Phys. 0810:021. doi: 10.1088/1475-7516/2008/10/021
Chiba, T., and Yamaguchi, M. (2013). Conformal-frame (in)dependence of cosmological observations in scalar-tensor theory. J. Cosmol. Astropart. Phys. 1310:040. doi: 10.1088/1475-7516/2013/10/040
Choudhury, S., Chakraborty, T., and Pal, S. (2014). Higgs inflation from new Kähler potential. Nucl. Phys. B880, 155–174. doi: 10.1016/j.nuclphysb.2014.01.002
Collaboration, C. (2014) Combination of the CMS Top-quark Mass Measurements From Run 1 of the LHC, Report number CMS-PAS-TOP-14-015.
Cook, J. L., Krauss, L. M., Long, A. J., and Sabharwal, S. (2014). Is Higgs inflation ruled out? Phys. Rev. D89:103525. doi: 10.1103/PhysRevD.89.103525
Csaki, C., Kaloper, N., Serra, J., and Terning, J. (2014). Inflation from broken scale invariance. Phys. Rev. Lett. 113:161302. doi: 10.1103/PhysRevLett.113.161302
De Simone, A., Hertzberg, M. P., and Wilczek, F. (2009). Running inflation in the standard model. Phys. Lett. B678, 1–8. doi: 10.1016/j.physletb.2009.05.054
Degrassi, G., Di Vita, S., Elias-Miro, J., Espinosa, J. R., Giudice, G. F., Isidori, G., et al. (2012). Higgs mass and vacuum stability in the Standard Model at NNLO. J. High Ener. Phys. 08:098. doi: 10.1007/JHEP08(2012)098
Dutta, S., Hagiwara, K., Yan, Q.-S., and Yoshida, K. (2008). Constraints on the electroweak chiral Lagrangian from the precision data. Nucl. Phys. B790, 111–137. doi: 10.1016/j.nuclphysb.2007.08.017
Einhorn, M. B., and Jones, D. R. T. (2012). GUT scalar potentials for higgs inflation. J. Cosmol. Astropart. Phys. 1211:049. doi: 10.1088/1475-7516/2012/11/049
Ellis, J., He, H.-J., and Xianyu, Z.-Z. (2015). New Higgs Inflation in a No-Scale Supersymmetric SU(5) GUT. Phys. Rev. D91:021302. doi: 10.1103/PhysRevD.91.021302
Ellis, J., He, H.-J., and Xianyu, Z.-Z. (2016). Higgs inflation, reheating and gravitino production in no-scale supersymmetric GUTs. J. Cosmol. Astropart. Phys. 1608:068. doi: 10.1088/1475-7516/2016/08/068
Ema, Y. (2017). Higgs scalaron mixed inflation. Phys. Lett. B770, 403–411. doi: 10.1016/j.physletb.2017.04.060
Ema, Y., Jinno, R., Mukaida, K., and Nakayama, K. (2017a). Violent preheating in inflation with nonminimal coupling. J. Cosmol. Astropart. Phys. 1702:045. doi: 10.1088/1475-7516/2017/02/045
Ema, Y., Karciauskas, M., Lebedev, O., Rusak, S., and Zatta, M. (2017b) Higgs-Inflaton Mixing Vacuum Stability, arXiv:1711.10554.
Enckell, V.-M., Enqvist, K., and Nurmi, S. (2016). Observational signatures of Higgs inflation. J. Cosmol. Astropart. Phys. 1607:047. doi: 10.1088/1475-7516/2016/07/047
Enckell, V.-M., Enqvist, K., Rasanen, S., and Tomberg, E. (2018). Higgs inflation at the hilltop. J. Cosmol. Astropart. Phys. 1806:005. doi: 10.1088/1475-7516/2018/06/005
Escrivà, A., and Germani, C. (2017). Beyond dimensional analysis: Higgs and new Higgs inflations do not violate unitarity. Phys. Rev. D95:123526. doi: 10.1103/PhysRevD.95.123526
Espinosa, J. R. (2016). Implications of the top (and Higgs) mass for vacuum stability. PoS TOP2015:043. doi: 10.22323/1.257.0043
Espinosa, J. R., Garny, M., Konstandin, T., and Riotto, A. (2017). Gauge-independent scales related to the standard Model Vacuum Instability. Phys. Rev. D95:056004. doi: 10.1103/PhysRevD.95.056004
Espinosa, J. R., Giudice, G. F., Morgante, E., Riotto, A., Senatore, L., Strumia, A., et al. (2015). The cosmological Higgstory of the vacuum instability. J. High Ener. Phys. 09:174. doi: 10.1007/JHEP09(2015)174
Espinosa, J. R., Giudice, G. F., and Riotto, A. (2008). Cosmological implications of the Higgs mass measurement. J. Cosmol. Astropart. Phys. 0805:2. doi: 10.1088/1475-7516/2008/05/002
Espinosa, J. R., and Quiros, M. (1995). Improved metastability bounds on the standard model Higgs mass. Phys. Lett. B353, 257–266. doi: 10.1016/0370-2693(95)00572-3
Ezquiaga, J. M., and Garcia-Bellido, J. (2018). Quantum diffusion beyond slow-roll: implications for primordial black-hole production. J. Cosmol. Astropart. Phys. 1808:018. doi: 10.1088/1475-7516/2018/08/018
Ezquiaga, J. M., Garcia-Bellido, J., and Ruiz Morales, E. (2018). Primordial black hole production in critical higgs inflation. Phys. Lett. B776, 345–349. doi: 10.1016/j.physletb.2017.11.039
Fairbairn, M., Grothaus, P., and Hogan, R. (2014). The problem with false vacuum higgs inflation. J. Cosmol. Astropart. Phys. 1406:039. doi: 10.1088/1475-7516/2014/06/039
Fakir, R., Habib, S., and Unruh, W. (1992). Cosmological density perturbations with modified gravity. Astrophys. J. 394:396. doi: 10.1086/171591
Fakir, R., and Unruh, W. G. (1990a). Improvement on cosmological chaotic inflation through nonminimal coupling. Phys. Rev. D41, 1783–1791. doi: 10.1103/PhysRevD.41.1783
Fakir, R., and Unruh, W. G. (1990b). Induced gravity inflation. Phys. Rev. D41, 1792–1795. doi: 10.1103/PhysRevD.41.1792
Felder, G. N., Frolov, A. V., Kofman, L., and Linde, A. D. (2002). Cosmology with negative potentials. Phys. Rev. D66:023507. doi: 10.1103/PhysRevD.66.023507
Ferrara, S., Kallosh, R., Linde, A., Marrani, A., and Van Proeyen, A. (2011). Superconformal symmetry, NMSSM, and inflation. Phys. Rev. D83:025008. doi: 10.1103/PhysRevD.83.025008
Ferrara, S., Kallosh, R., Linde, A., and Porrati, M. (2013). Minimal supergravity models of inflation. Phys. Rev. D88:085038. doi: 10.1103/PhysRevD.88.085038
Ferraris, M., Francaviglia, M., and Reina, C. (1982). Variational formulation of general relativity from 1915 to 1925 Palatini's method discovered by Einstein in 1925. Gen. Relat. Gravit. 14, 243–254. doi: 10.1007/BF00756060
Figueroa, D. G., Rajantie, A., and Torrenti, F. (2018). Higgs field-curvature coupling and postinflationary vacuum instability. Phys. Rev. D98:023532. doi: 10.1103/PhysRevD.98.023532
Flanagan, E. E. (2004). The Conformal frame freedom in theories of gravitation. Class. Quant. Grav. 21:3817. doi: 10.1088/0264-9381/21/15/N02
Fumagalli, J. (2017). Renormalization group independence of cosmological attractors. Phys. Lett. B769, 451–459. doi: 10.1016/j.physletb.2017.04.017
Fumagalli, J., Mooij, S., and Postma, M. (2018). Unitarity and predictiveness in new Higgs inflation. J. High Ener. Phys. 03:038. doi: 10.1007/JHEP03(2018)038
Fumagalli, J., and Postma, M. (2016). UV (in)sensitivity of higgs inflation. J. High Ener. Phys. 05:049. doi: 10.1007/JHEP05(2016)049
Futamase, T., and Maeda, K.-i. (1989). Chaotic inflationary scenario in models having nonminimal coupling with curvature. Phys. Rev. D39, 399–404. doi: 10.1103/PhysRevD.39.399
Galante, M., Kallosh, R., Linde, A., and Roest, D. (2015). Unity of cosmological inflation attractors. Phys. Rev. Lett. 114:141302. doi: 10.1103/PhysRevLett.114.141302
Garcia-Bellido, J., Figueroa, D. G., and Rubio, J. (2009). Preheating in the standard model with the higgs-inflaton coupled to gravity. Phys. Rev. D79:063531. doi: 10.1103/PhysRevD.79.063531
Garcia-Bellido, J., Rubio, J., and Shaposhnikov, M. (2012). Higgs-dilaton cosmology: are there extra relativistic species? Phys. Lett. B718, 507–511. doi: 10.1016/j.physletb.2012.10.075
Garcia-Bellido, J., Rubio, J., Shaposhnikov, M., and Zenhausern, D. (2011). Higgs-dilaton cosmology: from the early to the late universe. Phys. Rev. D84:123504. doi: 10.1103/PhysRevD.84.123504
Garcia-Bellido, J., and Ruiz Morales, E. (2017). Primordial black holes from single field models of inflation. Phys. Dark Univ. 18, 47–54. doi: 10.1016/j.dark.2017.09.007
Ge, S.-F., He, H.-J., Ren, J., and Xianyu, Z.-Z. (2016). Realizing dark matter and higgs inflation in light of LHC diphoton excess. Phys. Lett. B757, 480–492. doi: 10.1016/j.physletb.2016.04.008
George, D. P., Mooij, S., and Postma, M. (2014). Quantum corrections in Higgs inflation: the real scalar case. J. Cosmol. Astropart. Phys. 1402:024. doi: 10.1088/1475-7516/2014/02/024
George, D. P., Mooij, S., and Postma, M. (2016). Quantum corrections in Higgs inflation: the standard model case. J. Cosmol. Astropart. Phys. 1604:006. doi: 10.1088/1475-7516/2016/04/006
Germani, C., and Kehagias, A. (2010a). Cosmological perturbations in the new higgs inflation. J. Cosmol. Astropart. Phys. 1005:019. doi: 10.1088/1475-7516/2010/05/019
Germani, C., and Kehagias, A. (2010b). New model of inflation with non-minimal derivative coupling of standard model higgs boson to gravity. Phys. Rev. Lett. 105:011302. doi: 10.1103/PhysRevLett.105.011302
Germani, C., and Prokopec, T. (2017). On primordial black holes from an inflection point. Phys. Dark Univ. 18, 6–10. doi: 10.1016/j.dark.2017.09.001
Gibbons, G. W., and Hawking, S. W. (1977). Action integrals and partition functions in quantum gravity. Phys. Rev. D15, 2752–2756. doi: 10.1103/PhysRevD.15.2752
Giudice, G. F., and Lee, H. M. (2011). Unitarizing higgs inflation. Phys. Lett. B694, 294–300. doi: 10.1016/j.physletb.2010.10.035
Gorbunov, D., and Tokareva, A. (2013). R2-inflation with conformal SM Higgs field. J. Cosmol. Astropart. Phys. 1312:021. doi: 10.1088/1475-7516/2013/12/021
Gorbunov, D. S., and Panin, A. G. (2011). Scalaron the mighty: producing dark matter and baryon asymmetry at reheating. Phys. Lett. B700, 157–162. doi: 10.1016/j.physletb.2011.04.067
Gorbunov, D. S., and Panin, A. G. (2012). Free scalar dark matter candidates in R2-inflation: the light, the heavy and the superheavy. Phys. Lett. B718, 15–20. doi: 10.1016/j.physletb.2012.10.015
Greenwood, R. N., Kaiser, D. I., and Sfakianakis, E. I. (2013). Multifield dynamics of higgs inflation. Phys. Rev. D87:064021. doi: 10.1103/PhysRevD.87.064021
Guth, A. H. (1981). The inflationary universe: a possible solution to the horizon and flatness problems. Phys. Rev. D23, 347–356. doi: 10.1103/PhysRevD.23.347
Hamada, Y., Kawai, H., and Oda, K.-Y. (2014a). Minimal Higgs inflation. Prog. Theor. Exp. Phys. 2014:023B02. doi: 10.1093/ptep/ptt116
Hamada, Y., Kawai, H., Oda, K.-Y., and Park, S. C. (2014b). Higgs inflation is still alive after the results from BICEP2. Phys. Rev. Lett. 112:241301. doi: 10.1103/PhysRevLett.112.241301
Hamada, Y., Kawai, H., Oda, K.-Y., and Park, S. C. (2015). Higgs inflation from Standard Model criticality. Phys. Rev. D91:053008. doi: 10.1103/PhysRevD.91.053008
Hawking, S. W. (1982). The development of irregularities in a single bubble inflationary universe. Phys. Lett., 115B:295. doi: 10.1016/0370-2693(82)90373-2
He, H.-J., and Xianyu, Z.-Z. (2014). Extending higgs inflation with TeV Scale new physics. J. Cosmol. Astropart. Phys. 1410:019. doi: 10.1088/1475-7516/2014/10/019
He, M., Starobinsky, A. A., and Yokoyama, J. (2018). Inflation in the mixed Higgs-R2 model. J. Cosmol. Astropart. Phys. 1805:064. doi: 10.1088/1475-7516/2018/05/064
Herranen, M., Markkanen, T., Nurmi, S., and Rajantie, A. (2014). Spacetime curvature and the Higgs stability during inflation. Phys. Rev. Lett. 113:211102. doi: 10.1103/PhysRevLett.113.211102
Hertzberg, M. P. (2010). On Inflation with Non-minimal Coupling. J. High Ener. Phys. 11:023. doi: 10.1007/JHEP11(2010)023
Hertzberg, M. P. (2012). Can inflation be connected to low energy particle physics? J. Cosmol. Astropart. Phys. 1208:008. doi: 10.1088/1475-7516/2012/08/008
Isidori, G., Rychkov, V. S., Strumia, A., and Tetradis, N. (2008). Gravitational corrections to standard model vacuum decay. Phys. Rev. D77:025034. doi: 10.1103/PhysRevD.77.025034
Jalmuzna, J., Rostworowski, A., and Bizon, P. (2011). A comment on AdS collapse of a scalar field in higher dimensions. Phys. Rev. D84:085021. doi: 10.1103/PhysRevD.84.085021
Jarv, L., Kannike, K., Marzola, L., Racioppi, A., Raidal, M., Runkla, M., et al. (2017). Frame-independent classification of single-field inflationary models. Phys. Rev. Lett. 118:151302. doi: 10.1103/PhysRevLett.118.151302
Jarv, L., Kuusk, P., Saal, M., and Vilson, O. (2015a). Invariant quantities in the scalar-tensor theories of gravitation. Phys. Rev. D91:024041. doi: 10.1103/PhysRevD.91.024041
Jarv, L., Kuusk, P., Saal, M., and Vilson, O. (2015b). Transformation properties and general relativity regime in scalar-tensor theories. Class. Quant. Grav. 32:235013. doi: 10.1088/0264-9381/32/23/235013
Kaiser, D. I. (1995). Primordial spectral indices from generalized Einstein theories. Phys. Rev. D52, 4295–4306. doi: 10.1103/PhysRevD.52.4295
Kaiser, D. I. (2010). Conformal transformations with multiple scalar fields. Phys. Rev. D81:084044. doi: 10.1103/PhysRevD.81.084044
Kaiser, D. I., Mazenc, E. A., and Sfakianakis, E. I. (2013). Primordial bispectrum from multifield inflation with nonminimal couplings. Phys. Rev. D87:064004. doi: 10.1103/PhysRevD.87.064004
Kaiser, D. I., and Sfakianakis, E. I. (2014). Multifield inflation after Planck: the case for nonminimal couplings. Phys. Rev. Lett. 112:011302. doi: 10.1103/PhysRevLett.112.011302
Kajantie, K., Laine, M., Rummukainen, K., and Shaposhnikov, M. E. (1996). Generic rules for high temperature dimensional reduction and their application to the standard model. Nucl. Phys. B458, 90–136. doi: 10.1016/0550-3213(95)00549-8
Kallosh, R., Linde, A., and Roest, D. (2013). Superconformal inflationary α-Attractors. J. High Ener. Phys. 11:198. doi: 10.1007/JHEP11(2013)198
Kamada, K. (2015a). Inflationary cosmology and the standard model Higgs with a small Hubble induced mass. Phys. Lett. B742, 126–135. doi: 10.1016/j.physletb.2015.01.024
Kamada, K. (2015b). On the strong coupling scale in Higgs G-inflation. Phys. Lett. B744, 347–351. doi: 10.1016/j.physletb.2015.04.012
Kamada, K., Kobayashi, T., Takahashi, T., Yamaguchi, M., and Yokoyama, J. (2012). Generalized higgs inflation. Phys. Rev. D86:023504. doi: 10.1103/PhysRevD.86.023504
Kamada, K., Kobayashi, T., Yamaguchi, M., and Yokoyama, J. (2011). Higgs G-inflation. Phys. Rev. D83:083515. doi: 10.1103/PhysRevD.83.083515
Kanemura, S., Matsui, T., and Nabeshima, T. (2013). Higgs inflation in a radiative seesaw model. Phys. Lett. B723, 126–131. doi: 10.1016/j.physletb.2013.05.002
Kannike, K., Marzola, L., Raidal, M., and Veermae, H. (2017). Single field double inflation and primordial black holes. J. Cosmol. Astropart. Phys. 1709:020. doi: 10.1088/1475-7516/2017/09/020
Karam, A., Pappas, T., and Tamvakis, K. (2017). Frame-dependence of higher-order inflationary observables in scalar-tensor theories. Phys. Rev. D96:064036. doi: 10.1103/PhysRevD.96.064036
Karamitsos, S., and Pilaftsis, A. (2018a). Frame covariant nonminimal multifield inflation. Nucl. Phys. B927, 219–254. doi: 10.1016/j.nuclphysb.2017.12.015
Karamitsos, S., and Pilaftsis, A. (2018b). “On the cosmological Frame Problem,” in 17th Hellenic School and Workshops on Elementary Particle Physics and Gravity (CORFU2017) Corfu, Greece, September 2-28, 2017. Available online at: https://pos.sissa.it/318/036
Karananas, G. K., and Monin, A. (2016a). Weyl and Ricci gauging from the coset construction. Phys. Rev. D93:064013. doi: 10.1103/PhysRevD.93.064013
Karananas, G. K., and Monin, A. (2016b). Weyl vs. Conformal. Phys. Lett. B757, 257–260. doi: 10.1016/j.physletb.2016.04.001
Karananas, G. K., and Rubio, J. (2016). On the geometrical interpretation of scale-invariant models of inflation. Phys. Lett. B761, 223–228. doi: 10.1016/j.physletb.2016.08.037
Koh, S. (2006). Non-gaussianity in nonminimally coupled scalar field theory. J. Korean Phys. Soc. 49, S787–S790. Available online at: http://inspirehep.net/record/693829
Komatsu, E., and Futamase, T. (1998). Constraints on the chaotic inflationary scenario with a nonminimally coupled ‘inflaton’ field from the cosmic microwave background radiation anisotropy. Phys. Rev. D58:023004. doi: 10.1103/PhysRevD.58.023004
Komatsu, E., and Futamase, T. (1999). Complete constraints on a nonminimally coupled chaotic inflationary scenario from the cosmic microwave background. Phys. Rev. D59:064029. doi: 10.1103/PhysRevD.59.064029
Kuusk, P., Jarv, L., and Vilson, O. (2016). Invariant quantities in the multiscalar-tensor theories of gravitation. Int. J. Mod. Phys. A31:1641003. doi: 10.1142/S0217751X16410037
Lazarides, G., and Pallis, C. (2015). Shift symmetry and higgs inflation in supergravity with observable gravitational waves. J. High Ener. Phys. 11:114. doi: 10.1007/JHEP11(2015)114
Lerner, R. N., and McDonald, J. (2010). A unitarity-conserving higgs inflation model. Phys. Rev. D82:103525. doi: 10.1103/PhysRevD.82.103525
Lerner, R. N., and McDonald, J. (2011). Distinguishing higgs inflation and its variants. Phys. Rev. D83:123522. doi: 10.1103/PhysRevD.83.123522
Linde, A. D. (1979). Phase transitions in gauge theories and cosmology. Rept. Prog. Phys. 42:389. doi: 10.1088/0034-4885/42/3/001
Linde, A. D. (1982). A new inflationary universe scenario: a possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. 108B, 389–393. doi: 10.1016/0370-2693(82)91219-9
Linde, A. D. (1983). Chaotic inflation. Phys. Lett. 129B, 177–181. doi: 10.1016/0370-2693(83)90837-7
Makino, N., and Sasaki, M. (1991). The density perturbation in the chaotic inflation with nonminimal coupling. Prog. Theor. Phys. 86, 103–118. doi: 10.1143/ptp/86.1.103
Marian, I. G., Defenu, N., Trombettoni, A., and Nandori, I. (2017). Pseudo Periodic Higgs Inflation, arXiv:1705.10276.
Masina, I. (2018). Ruling out critical higgs inflation? Phys. Rev. D98:043536. doi: 10.1103/PhysRevD.98.043536
Matsumura, T., Akiba, Y., Arnold, K., Borrill, J., Chendra, R., Chinone, Y., et al. (2016). LiteBIRD: mission overview and focal plane layout. J. Low. Temp. Phys. 184, 824–831. doi: 10.1007/s10909-016-1542-8
Minkowski, P. (1977). On the spontaneous origin of Newton's constant. Phys. Lett. 71B, 419–421. doi: 10.1016/0370-2693(77)90256-8
Moss, I. G. (2015). Higgs boson cosmology. Contemp. Phys. 56, 468–476. doi: 10.1080/00107514.2015.1058543
Mukhanov, V. F. (1988). Quantum theory of gauge invariant cosmological perturbations. Sov. Phys. JETP 67, 1297–1302.
Mukhanov, V. F., and Chibisov, G. V. (1981). Quantum fluctuations and a nonsingular universe. JETP Lett. 33, 532–535.
Mukhanov, V. F., Feldman, H. A., and Brandenberger, R. H. (1992). Theory of cosmological perturbations. Part 1. Classical perturbations. Part 2. Quantum theory of perturbations. Part 3. Extensions. Phys. Rept. 215, 203–333. doi: 10.1016/0370-1573(92)90044-Z
Oda, I., and Tomoyose, T. (2014a). Conformal Higgs inflation. J. High Ener. Phys. 09:165. doi: 10.1007/JHEP09(2014)165
Oda, I., and Tomoyose, T. (2014b). Quadratic chaotic inflation from Higgs inflation. Adv. Stud. Theor. Phys. 8:551. doi: 10.12988/astp.2014.4572
Okada, N., and Raut, D. (2017). Inflection-point Higgs inflation. Phys. Rev. D95:035035. doi: 10.1103/PhysRevD.95.035035
Okada, N., and Shafi, Q. (2015). Higgs inflation, seesaw physics and Fermion dark matter. Phys. Lett. B747, 223–228. doi: 10.1016/j.physletb.2015.06.001
Olive, K. A., Agashe, K., Amsler, C., Antonelli, M., Arguin, J.-F., Asner, D. M., et al. (2014). Review of particle physics. Chin. Phys. C38:090001. doi: 10.1088/1674-1137/38/9/090001
Pattison, C., Vennin, V., Assadullahi, H., and Wands, D. (2017). Quantum diffusion during inflation and primordial black holes. J. Cosmol. Astropart. Phys. 1710:046. doi: 10.1088/1475-7516/2017/10/046
Polyakov, A. M. (2010). Decay of vacuum energy. Nucl. Phys. B834, 316–329. doi: 10.1016/j.nuclphysb.2010.03.021
Popa, L. A., and Caramete, A. (2010). Cosmological constraints on higgs boson mass. Astrophys. J. 723, 803–811. doi: 10.1088/0004-637X/723/1/803
Postma, M., and Volponi, M. (2014). Equivalence of the Einstein and Jordan frames. Phys. Rev. D90:103516. doi: 10.1103/PhysRevD.90.103516
Rasanen, S. (2018). Higgs inflation in the Palatini formulation with kinetic terms for the metric, arXiv: 1811:09514.
Rasanen, S., and Tomberg, E. (2018). Planck scale black hole dark matter from Higgs inflation, arXiv:1810:12608.
Rasanen, S., and Wahlman, P. (2017). Higgs inflation with loop corrections in the Palatini formulation. J. Cosmol. Astropart. Phys. 1711:047. doi: 10.1088/1475-7516/2017/11/047
Ren, J., Xianyu, Z.-Z., and He, H.-J. (2014). Higgs gravitational interaction, weak Boson scattering, and Higgs inflation in Jordan and Einstein frames. J. Cosmol. Astropart. Phys. 1406:032. doi: 10.1088/1475-7516/2014/06/032
Repond, J., and Rubio, J. (2016). Combined Preheating on the lattice with applications to Higgs inflation. J. Cosmol. Astropart. Phys. 1607:043. doi: 10.1088/1475-7516/2016/07/043
Rubio, J. (2015). Higgs inflation and vacuum stability. J. Phys. Conf. Ser. 631:012032. doi: 10.1088/1742-6596/631/1/012032
Rubio, J., and Shaposhnikov, M. (2014). Higgs-Dilaton cosmology: universality versus criticality. Phys. Rev. D90:027307. doi: 10.1103/PhysRevD.90.027307
Salopek, D. S., Bond, J. R., and Bardeen, J. M. (1989). Designing density fluctuation spectra in inflation. Phys. Rev. D40:1753. doi: 10.1103/PhysRevD.40.1753
Saltas, I. D. (2016). Higgs inflation and quantum gravity: an exact renormalisation group approach. J. Cosmol. Astropart. Phys. 1602:048. doi: 10.1088/1475-7516/2016/02/048
Salvio, A. (2013). Higgs inflation at NNLO after the Boson discovery. Phys. Lett. B727, 234–239. doi: 10.1016/j.physletb.2013.10.042
Salvio, A. (2018). Initial conditions for critical Higgs inflation. Phys. Lett. B780, 111–117. doi: 10.1016/j.physletb.2018.03.009
Sasaki, M. (1986). Large scale quantum fluctuations in the inflationary universe. Prog. Theor. Phys. 76:1036. doi: 10.1143/PTP.76.1036
Shaposhnikov, M., and Wetterich, C. (2010). Asymptotic safety of gravity and the Higgs boson mass. Phys. Lett. B683, 196–200. doi: 10.1016/j.physletb.2009.12.022
Shaposhnikov, M., and Zenhausern, D. (2009). Scale invariance, unimodular gravity and dark energy. Phys. Lett. B671, 187–192. doi: 10.1016/j.physletb.2008.11.054
Smolin, L. (1979). Towards a theory of space-time structure at very short distances. Nucl. Phys. B160, 253–268. doi: 10.1016/0550-3213(79)90059-2
Spokoiny, B. L. (1984). Inflation and generation of perturbations in broken symmetric theory of gravity. Phys. Lett. 147B, 39–43. doi: 10.1016/0370-2693(84)90587-2
Starobinsky, A. A. (1980). A new type of isotropic cosmological models without singularity. Phys. Lett. B91, 99–102. doi: 10.1016/0370-2693(80)90670-X
Starobinsky, A. A. (1982). Dynamics of phase transition in the new inflationary universe scenario and generation of perturbations. Phys. Lett. 117B, 175–178. doi: 10.1016/0370-2693(82)90541-X
Starobinsky, A. A., and Yokoyama, J. (1994). Equilibrium state of a selfinteracting scalar field in the De Sitter background. Phys. Rev. D50, 6357–6368. doi: 10.1103/PhysRevD.50.6357
Steinwachs, C. F. (2013). Non-minimal Higgs Inflation and Frame Dependence in Cosmology. Cham: Springer. doi: 10.1007/978-3-319-01842-3
Takahashi, F., and Takahashi, R. (2016). Renormalization group improved Higgs inflation with a running kinetic term. Phys. Lett. B760, 329–334. doi: 10.1016/j.physletb.2016.07.009
Tanabashi, M., Hagiwara, K., Hikasa, K., Nakamura, K., Sumino, Y., Takahashi, F., et al. (2018). Review of Particle Physics. Phys. Rev. D98:030001. doi: 10.1103/PhysRevD.98.030001
Trashorras, M., Nesseris, S., and Garcia-Bellido, J. (2016). Cosmological constraints on Higgs-dilaton inflation. Phys. Rev. D94:063511. doi: 10.1103/PhysRevD.94.063511
Tsamis, N. C., and Woodard, R. P. (1993). Relaxing the cosmological constant. Phys. Lett. B301, 351–357. doi: 10.1016/0370-2693(93)91162-G
Tsamis, N. C., and Woodard, R. P. (1995). Strong infrared effects in quantum gravity. Annals Phys. 238, 1–82. doi: 10.1006/aphy.1995.1015
Tsujikawa, S., and Gumjudpai, B. (2004). Density perturbations in generalized Einstein scenarios and constraints on nonminimal couplings from the cosmic microwave background. Phys. Rev. D69:123523. doi: 10.1103/PhysRevD.69.123523
van de Bruck, C., and Longden, C. (2016). Higgs inflation with a Gauss-Bonnet term in the Jordan frame. Phys. Rev. D93:063519. doi: 10.1103/PhysRevD.93.063519
Vennin, V., and Starobinsky, A. A. (2015). Correlation functions in stochastic inflation. Eur. Phys. J. C75:413. doi: 10.1140/epjc/s10052-015-3643-y
Weenink, J., and Prokopec, T. (2010). Gauge invariant cosmological perturbations for the nonminimally coupled inflaton field. Phys. Rev. D82:123510. doi: 10.1103/PhysRevD.82.123510
Wetterich, C. (2017). Graviton fluctuations erase the cosmological constant. Phys. Lett. B773, 6–19. doi: 10.1016/j.physletb.2017.08.002
Xianyu, Z.-Z., and He, H.-J. (2014). Asymptotically safe Higgs inflation. J. Cosmol. Astropart. Phys. 1410:083. doi: 10.1088/1475-7516/2014/10/083
Yoon, Y., and Yoon, Y. (1997). Asymptotic conformal invariance of SU(2) and standard models in curved space-time. Int. J. Mod. Phys. A12, 2903–2914. doi: 10.1142/S0217751X97001602
York, J. W. Jr (1972). Role of conformal three geometry in the dynamics of gravitation. Phys. Rev. Lett. 28, 1082–1085. doi: 10.1103/PhysRevLett.28.1082
Keywords: higgs, inflation, higgs inflation, vacuum stability, scale-invariance
Citation: Rubio J (2019) Higgs Inflation. Front. Astron. Space Sci. 5:50. doi: 10.3389/fspas.2018.00050
Received: 10 July 2018; Accepted: 20 December 2018;
Published: 22 January 2019.
Edited by:
Francesco Sannino, University of Southern Denmark, DenmarkReviewed by:
Sayantan Choudhury, Max-Planck-Institut für Gravitationsphysik, GermanyCopyright © 2019 Rubio. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Javier Rubio, ai5ydWJpb0B0aHBoeXMudW5pLWhlaWRlbGJlcmcuZGU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.