
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci. , 17 October 2018
Sec. Cosmology
Volume 5 - 2018 | https://doi.org/10.3389/fspas.2018.00034
This article is part of the Research Topic Imagining the Future of Astronomy and Space Science View all 10 articles
We review two decades of progress using the Enzo hydrodynamic cosmology code to simulate the Cosmic Dawn, a period of roughly 1 billion years beginning with the formation of the first stars in the universe, and ending with cosmic reionization. Using simulations of increasing size and complexity, working up in length and mass scale and to lower redshifts, a connected narrative is built up covering the entire epoch. In the first part of the paper, we draw on results we and our collaborators have achieved using the Enzo cosmological adaptive mesh refinement code. Topics include the formation of Population III stars, the transition to Population II star formation, chemical enrichment, the assembly of the first galaxies, their high redshift galaxy statistics, and their role in reionization. In the second part of the paper we highlight physical difficulties that will require new, more physically complex simulations to address, drawing from a broader literature survey. We discuss the healthy interplay between self-consistent numerical simulations and analytic and semi-analytic approaches. Finally, we discuss technical advances in hardware and software that will enable a new class of more realistic simulations to be carried out on exascale supercomputers in the future.
The Cosmic Dawn begins with the formation of the first star in the universe and ends about 1 billion years later when the intergalactic medium has been ionized by UV light from the first galaxies. The later half of Cosmic Dawn has only recently begun to be explored observationally by the Hubble Space Telescope (HST) and other observatories. While much has been learned in recent years (Stark, 2016), many fundamental questions remain unanswered. Our driving question is: how did the universe first light up with stars, and what happened subsequently to make the most distant galaxies seen by the HST? The very earliest phases are beyond the HST's reach, and unfortunately also beyond the reach of the James Webb Space Telescope (JWST), to be launched early in the next decade. Nonetheless a picture has emerged of how structures form and galaxies grow during this tumultuous time through theoretical and computational means. In this article, we present an unbroken narrative connecting the first stars to the first galaxies, ending with cosmic reionization based on our numerical explorations carried out over the past two decades with numerous collaborators. We do this not only to highlight the progress made, but also to highlight the areas of uncertainty that will drive a new generation of simulations using new codes on future high performance computing (HPC) platforms. This is in keeping with the topical theme of this issue,“Imagining the future of astronomy and space science.”
There are many excellent reviews of this subject that are not so narrowly focused on numerical simulations, as we are here. For a general theoretical introduction we recommend Barkana and Loeb (2001). The numerical challenges of simulating the first stars and galaxies, along with a comprehensive survey of results, is given in Greif (2015). The physics and numerical simulation of reionization is reviewed by Choudhury and Ferrara (2006) and Trac and Gnedin (2011), respectively. Finally, semi-analytic approaches have been successfully applied to a number of topics discussed below, which we will mention as we go along.
There are two compelling reasons for simulating the Cosmic Dawn. The first is scientific curiosity. It is intrinsically interesting to understand the origins of things, in this case, the first light in the universe. The second is that detailed numerical simulations provide an interpretive basis for understanding what is being observed. This is true of all types of computational astrophysics simulations, but especially true here where the observations are so close to the detection threshold and angular resolution of the instrument. To illustrate this, we show in Figure 1 a simulation of a dwarf galaxy at z = 15, its rest frame appearance, and its appearance if observed by the HST and the JWST. We can see that although the simulation provides a lot of detail about the galaxy's morphology and spectrum, this is smoothed over by the instruments. In the lower left corner, show the intrinsic stellar spectrum (thin blue line) and processed galactic spectrum with dust and gas absorption, re-emission, and emission lines (thick green line). The reprocessing of the stellar radiation by the galaxy's interstellar medium is clearly important for a spectroscopic interpretation of observed spectra.
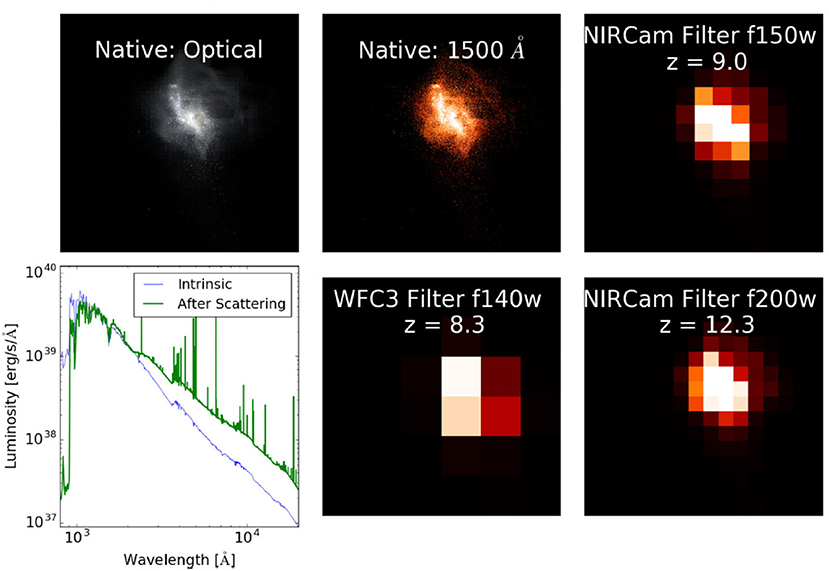
Figure 1. A simulated z = 15 high redshift protogalaxy and its photometric appearance with Hubble Space Telescope and the James Webb Space Telescope. A partial reproduction of Figure 12 from Barrow et al. (2017b).
Most of the simulations discussed in this article were carried out with the Enzo code (Bryan et al., 2014) over the past 18 years. The code, and the supercomputers employed, have both improved enormously over that timeframe. To a real extent, the exponential increase in supercomputer power over the past roughly 2 decades, coupled with Enzo's increasing software capabilities, is what has enabled us to build the narrative. On the hardware side, the empirical “Moore's law for supercomputers” (Denning and Lewis, 2016), states that peak supercomputer speed roughly doubles every 18 months. Over 18 years this translates into a speedup of 218/1.5 = 4, 096, which is a substantial factor. In fact, over the past half decade, Moore's law for supercomputers has actually sped up due to increased concurrency, making the speedup closer to 105. In astrophysics and cosmology, this increase in capability has been employed to increase the size and physical realism of the simulations undertaken.
The Enzo code1 is a widely used open-source software application that employs adaptive mesh refinement (AMR) to achieve high resolution where needed. Originally developed for numerical cosmology by Greg Bryan from 1994 to 1996 for his PhD thesis at the University of Illinois, Enzo is now a versatile, community-developed application with contributions from numerous authors (Bryan et al., 2014). Later in this article, we discuss how the open-source software movement was instrumental in the development of Enzo community and code.
Enzo solves the equations of hydrodynamic cosmology in an expanding universe within a cubic domain of size Lbox. The comoving “boxsize” is chosen to be large enough to encompass the objects of interest, but small enough to be computationally tractable. For simulations of the Cosmic Dawn, Lbox varies from as small as 1/8 comoving Mpc (cMpc) in the first star simulations to as large as 40 cMpc in the Renaissance Simulations. These are necessarily much smaller than typical boxes used to simulate galaxy large scale structure (100–1,000 cMpc) because we are interested in the smallest, earliest objects to form in the universe.
In its simplest form, Enzo integrates the Euler equations of gas dynamics and the Lagrangian N-body dynamics equations for the dark matter, which are coupled through their mutual self-gravity via the Poisson equation. Enzo's first important innovation was the introduction of structured AMR to numerical cosmology (Bryan and Norman, 1997; Norman and Bryan, 1999; cf. Figure 2), drawing on the the pioneering work of Berger and Colella (1989). Berger and Colella used structured AMR to improve resolution in problems of shock hydrodynamics. While this is also important in cosmological hydrodynamics, the main purpose for AMR is to maintain adequate numerical resolution in gravitationally collapsing and merging dark matter halos, and later, in gravitationally collapsing protostellar cloud cores (Abel et al., 2000).
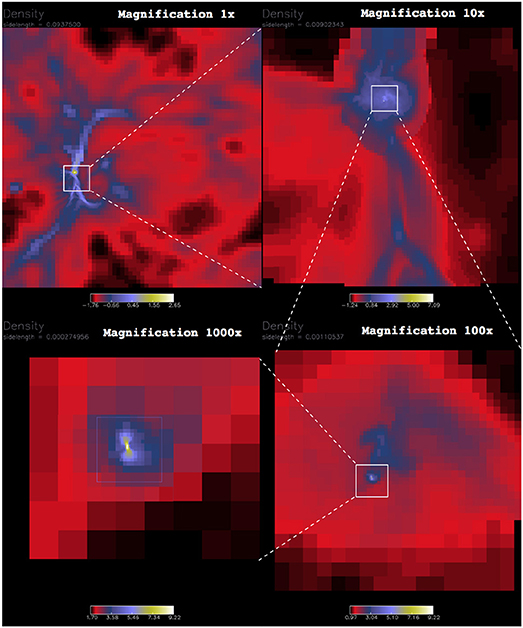
Figure 2. The first published zoom-in image from a cosmological AMR simulation of primordial star formation. Reproduced by permission of Figure 1 from Norman and Bryan (1999).
The second important innovation, essential for the first star simulations, was the incorporation of a model for primordial gas chemistry including H2, the primary coolant in dense primordial gas. A minimal model was developed by Tom Abel for his Masters thesis for the 9 chemical species H,H+,He,He+,He++,H−,H+2,H2, and e− (Abel et al., 1997). A modified backward-Euler numerical method for integrating the time-dependent rate equations for the 9 species was developed by Anninos et al. (1997). Bryan et al. were all together at the National Center for Supercomputing Applications at the University of Illinois in the 1994-1996 timeframe. A synthesis of Bryan's Enzo code, Abel's primordial chemistry model, and Anninos' efficient chemistry solver enabled the first fully cosmological simulations of the formation of the first stars in the universe (Abel et al., 2000, 2002), discussed in more detail below.
In subsequent years, a variety of additional physics capabilities were incorporated into the Enzo code, driven in large part by the physics of the Cosmic Dawn. Population III (hereafter Pop III) stars are predicted to be massive (section 3.1), and as such emit copious amounts of ionizing UV radiation. Therefore, 3D radiative transfer methods were developed and incorporated. The most accurate and flexible method based on adaptive ray tracing was developed by Wise and Abel (2011), although an alternative method based on flux-limited diffusion has also proven useful for reionization simulations (Norman et al., 2015). Chemical enrichment from Pop III supernovae drives the transition from primordial star formation to Population II star formation. This necessitates the ability for Enzo to track metallicity fields in expanding supernova remnants, and to correctly calculate the radiative cooling due to fine structure lines in a mixture of heavy elements. Since Pop II stars also chemically enrich their environments through winds and supernovae, multiple metallicity fields are needed. John Wise introduced two metallicity fields, one for metals ejected by Pop III supernovae, and one for metals returned to the ISM by Pop II stellar mass loss and supernovae in his “Birth of a Galaxy” simulations (Wise et al., 2012b), discussed below. Metal line cooling was introduced into Enzo by Britton Smith, Stein Sigurdsson, and Tom Abel who first explored the transition to metal-enriched star formation with AMR simulations (Smith et al., 2009), discussed in more detail below.
Two other physics ingredients are essential for simulating the Cosmic Dawn: a recipe for star formation and feedback in cases where it is unresolved, as in galaxy formation simulations, and cosmic radiation backgrounds (UV, Xray), that may modify the thermal, chemical, and ionization state of the gas. We defer discussion of these to the relevant sections below. Another piece of physics, magnetic fields, has been implemented in the Enzo code (Wang and Abel, 2009; Collins et al., 2010), but so far has not been much explored in the context of the Cosmic Dawn.
We conclude this section on simulations with a brief discussion about how Enzo is verified and validated. Verification, which asks “am I solving the equations correctly?” is done at the physics module level through an extensive test suite documented in Bryan et al. (2014), Wise and Abel (2011), and Norman et al. (2015). Many test problems have analytic solutions, which are compared against. Others have reference numerical solutions that are well established. Validation, which asks “am I solving the correct equations?” is done through comparison with observations as a part of the scientific process, and with the results of other codes through code-comparison campaigns. Enzo has participated in many such campaigns, validating its hydrodynamics (Agertz et al., 2007), magnetohydrodynamics (Kritsuk et al., 2011), cosmological hydrodynamics (Frenk et al., 1999; O'Shea et al., 2005), radiation transport (Iliev et al., 2006, 2009), and galaxy formation physics (Kim et al., 2014).
20 years on from the seminal paper by Tegmark et al. (1997), the story of how primordial gas collects in dark matter minihalos to form the first stars is well known, and the subject of a number of review articles and books (Loeb and Barkana, 2001; Bromm and Larson, 2004; Glover, 2005; Norman, 2008; Greif, 2015). As discussed by Tegmark et al. (1997), primordial gas becomes gravitationally bound to dark matter minihalos at high redshifts, and is able to radiatively cool by H2 if there is enough of it. Using an analytical model, they derived a minimum baryonic mass Mb that could cool as a function of redshift. They found that Mb is strongly redshift dependent, dropping from ~106M⊙ at z~15 to 5×103M⊙ at z~100 as molecular cooling becomes effective (multiply by 6 to get halo mass). They estimated “a fraction 10−3 of all baryons may have formed luminous objects by z = 30, which could be sufficient to reheat the universe.”
Tegmark et al.'s results were in good agreement with results from the first fixed grid 3D hydrodynamic cosmological models to incorporate H2 cooling by Abel et al. (1998a). However, neither the analytic model, nor the earliest simulations, could determine what the consequences of that cooling was. That is because star formation occurs on vastly smaller scales than the halo scale, which was only marginally resolved in Abel et al. (1998a). Speculations in the literature concerning what might form ranged from supermassive black holes to clusters of low mass stars. Our current understanding, based on 3D numerical simulations that span a vast range of spatial scales and densities, is that cooling and collapse results in the formation of a single massive star per halo (Abel et al., 2002; Yoshida et al., 2008), although massive binary stars may also be produced (Turk et al., 2009; Stacy et al., 2010). In a series of papers beginning in 1998 (Abel et al., 1998b, 1999, 2000, 2002; Norman and Bryan, 1999; Norman et al., 1999, 2000; Bryan et al., 2001), Abel et al. described numerical AMR simulations of increasingly higher resolution that established the following robust results.
• the analysis of Tegmark et al. (1997) is verified numerically, and the minimum mass to cool curve is a good estimate (Norman et al., 2000);
• H2 cooling produces a gravitationally unstable core of mass ~1, 000M⊙, density of ~104 cm−3 and temperature ~200K;
• once the molecular hydrogen fraction in the core exceeds fH2~5×10−4, it collapses rapidly in an inside-out fashion;
• collapse produces a fully molecular hydrogen core of less than a solar mass that accretes at a rate of ~10−3M⊙/year;
• the core does not fragment due to chemo-thermal instability to the highest densities achieved n~1012 cm−3.
These findings were independently verified by Bromm et al. (2002) and following work using smoothed particle hydrodynamics (SPH) simulations. The implication of the last two findings is that, absent fragmentation or radiation feedback shutting off accretion (McKee and Tan, 2008), the final star will be massive, as it would accrete ~100M⊙ in a Helmholtz time of 105 year (Abel et al., 2002). The first simulation to form a hydrostatic protostar starting from cosmological initial conditions was the SPH simulation of Yoshida et al. (2008). They found a single protostellar seed of 1% the Sun's mass is formed in the center of the parent minihalo, and speculated that it would grow to become a massive star. Other authors (Clark et al., 2011; Greif et al., 2012) have simulated a short way into the disk accretion phase of the protostar, and found that the disk fragments into numerous smaller accreting bodies. We return to the issue of fragmentation in a later section when we discuss future simulations.
The final masses of primordial stars is fundamental to how the Cosmic Dawn develops next. If the stars are massive, as simulations indicate, they will be very luminous in the UV, live only a few million years, chemically enrich the universe through their supernova explosions, and leave behind stellar remnants (neutron stars and black holes) (Heger and Woosley, 2002; Schaerer, 2002). This is the conventional wisdom, and the scenario most explored by us and others. Others have argued that the universe may contain low-mass primordial stars arising from primordial protostellar disk fragmentation (Stacy et al., 2010; Greif et al., 2011a). We know that at lease some primordial stars must have been massive enough to create the first heavy elements of the periodic table, as we have no other formation mechanism available. In the narrative that follows, we assume the conventional wisdom that primordial stars are primarily massive, but do not require that they are only massive.
A key complication that arises if primordial stars are primarily massive, is that they create a negative feedback effect on their subsequent formation as a result of the H2 dissociating radiation they emit in the Lyman-Werner band 10.2−13.6 eV. An extensive early population of massive primordial stars builds up a Lyman-Werner background (LWB) radiation field, that can suppress or limit subsequent primordial star formation by photodissociating the H2 molecule whose presence is required to form them in the first place. Using Enzo, Machacek et al. (2001) found that the minimum halo mass capable of cooling by H2 increases with the mean intensity of the LWB, and above a certain intensity, halos as massive has Mh=107M⊙ are unable to cool. The first numerical+semianalytic study to attempt to self-consistently model negative feedback in a cosmological setting was by Yoshida et al. (2003a). They found that the global Pop III star formation rate becomes self-regulating at z≈30 as minihalos below an increasing minimum mass to cool become suppressed. However, O'Shea and Norman (2008) showed, using high resolution Enzo AMR simulations, that even for very high LWB intensities, H2 formation and cooling is not suppressed, but merely delayed until halo virial temperatures increase enough so that H2 formation exceeds destruction. This occurs in halos of mass exceeding a few ×107M⊙.
The conclusion that Pop III stars were massive, based on the simulations discussed above, stands in contrast to what we know about metal-enriched stars in our Galaxy. For any observed group of stars, the distribution of stellar masses (the number of stars as a function of mass) follows a power-law with a slope of roughly −2.35, a quality first reported more than 60 years ago by Salpeter (1955). Below about a solar mass, the distribution function turns over and declines (Kroupa et al., 1993; Chabrier, 2003). In other words, there are far more low mass stars than high mass. This appears to hold almost universally over a broad range of physical conditions (Kroupa, 2012). This is itself very different from the case of Pop III, where even small changes to the properties of host halos result in stellar masses that can vary by up to two orders of magnitude (Hirano et al., 2014). How and when did this transition in star formation take place?
In their supernova explosions, Pop III stars introduced the first heavy elements (metals) to the universe. The addition of metals to a gas adds to the number of atomic and molecular transitions, increasing its ability to cool. Recalling that, to first order, Pop III stars are massive because metal-free gas clouds cease to cool (and, thus, fragment) as they collapse, one can then calculate the additional metals required for cooling and fragmentation to continue. From this exercise, two “critical metallicities” can be identified, at ~10−3.5Z⊙ due to fine-structure lines from C and O (Bromm and Loeb, 2003) and at ~10−5.5Z⊙ due to thermal emission from dust grains (Omukai, 2000). Numerous studies using three-dimensional simulations of homogeneously enriched gas clouds have shown that fragmentation does occur at these critical metallicities (Bromm et al., 2001; Smith and Sigurdsson, 2007; Clark et al., 2008; Smith et al., 2009; Dopcke et al., 2011). For example, Figure 3 shows density projections from Enzo simulations of gas clouds at different metallicities from Smith et al. (2009). These simulations did not include dust, but the change in morphology at Z=10−3.5Z⊙ is evident. Additionally, Smith et al. (2009) found that fragmentation was again reduced at even higher metallicities (Z>10−3Z⊙) as the gas was stabilized by reaching the temperature floor of the high-redshift CMB (almost 60 K at z~20). However, other simulations claimed that the ability of gas to fragment was extremely dependent on the initial setup of the simulation (Jappsen et al., 2009a,b; Meece et al., 2014). For example, simulations without rotation or turbulence in the cloud show no fragmentation at any metallicity. The only way to resolve this is to understand the true initial conditions of the first low mass stars.

Figure 3. Density projections of the central 0.5 pc in collapsing gas clouds at different metallicities from simulations using Enzo. At metallicities above 10−3.5Z⊙, the cloud is able to fragment due to enhanced cooling from metals. Below 10−3.5Z⊙, the gas reaches the CMB temperature floor at an early stage and becomes stabilized to fragmentation. Reproduced by permission of the American Astronomical Society, Figure 1 from Smith et al. (2009).
Addressing this issue is an extreme technical challenge. In place of simulations of gas at constant metallicities, we must now consider metals ejected by Pop III supernovae and their subsequent mixing into the surrounding medium. However, even before the explosion, the intense radiation emitted during the main-sequence lifetime of a Pop III star will remove most of the gas from its host halo (Whalen et al., 2004, 2008; Kitayama and Yoshida, 2005), in essence plowing the road before the supernova blast-wave sweeps through. This makes radiative transfer crucial to this effort. Additionally, a number of criteria conspire to place demands of extraordinary mass and spatial resolution on this type of simulation. The dark matter mass resolution must be high enough to resolve the smallest Pop III-forming minihalos, but the volume must also be large enough to contain a number of these halos. As well, extreme adaptive mesh-refinement is necessary in order to follow the collapse of metal-enriched gas to high densities.
Smith et al. (2015) presented PopIIPrime, the first simulation to begin from cosmological initial conditions, follow the creation and dispersal of metals by Pop III supernova, and end with the formation of metal-enriched stars. Run on the Blue Waters sustained petascale HPC system at the National Center for Supercomputing Applications, University of Illinois Urbana-Champaign, PopIIPrime combined Pop III star formation, radiation transport, and sophisticated chemistry (H2 chemistry with metal cooling and dust-grain effects) with a dark matter mass resolution of 1 M⊙ and a maximum AMR spatial resolution of nearly 1 AU. At its onset, the outcome of this enormous effort was entirely unknown. Would metal-enriched star formation have to wait for the heavy elements to fall back into their halos of origin? With minihalos, such a process can take up 100–200 Myr or more (Greif et al., 2010; Jeon et al., 2014). Would metals have to be pulled in during the hierarchical assembly of larger halos (Greif et al., 2007; Wise et al., 2012b)?
Somewhat surprisingly, metal-enriched star formation was found to occur only 25 Myr after the second Pop III supernova, at a redshift of roughly 16.5. Figure 4 illustrates the unexpected sequence of events. At z~19, a Pop III star forms in the minihalo denoted by circle “a” in the top, left panel of Figure 4. Circle “b” denotes a halo of nearly equal mass approximately 200 pc away. Columns 2 and 3 show the radiative feedback and initial explosion. The neighboring halo has been heavily disrupted by radiation from the star. Within 6 Myr of the initial explosion, the blast wave impacts the neighboring halo. The turbulent motions produced from a combination of the halo's own relaxation and the collision allow metals to mix into the densest gas in the halo's core. As the density continues to rise, the collapse time scale becomes shorter than the turbulent mixing time scale, and a runaway collapse begins within a pocket of gas enriched to a metallicity of about 2×10−5Z⊙. The collapse of this gas is shown in Figure 5. Because the low metallicity, the initial phases of collapse show no fragmentation. Eventually, at densities of roughly 1012cm−3, dust cooling triggers vigorous fragmentation on scales of ~100 AU, as shown in the bottom-left panel. To confirm that dust is the instigator of this, the collapse portion of the simulation is run again without the effects of dust, with the result shown in the bottom-left panel. This result showed the validity of a so-called “external enrichment mechanism” as a likely scenario for the formation of the earliest stars resembling those that are observed today. It also highlighted the need to continue to drive simulations to higher and higher resolution and sophistication.
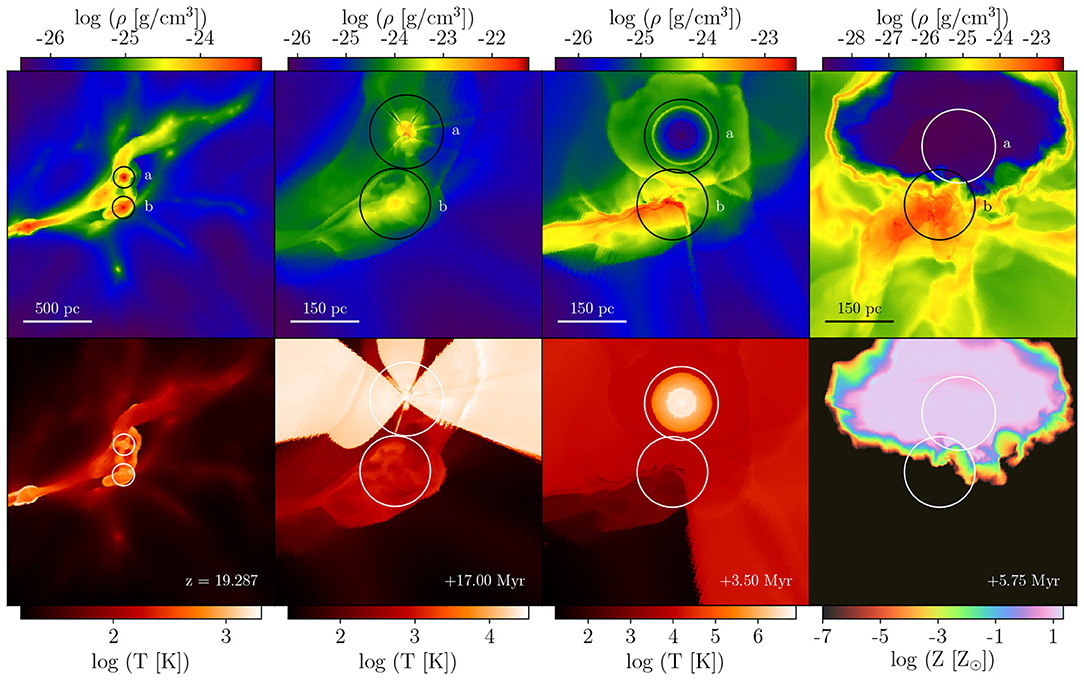
Figure 4. The external enrichment of a starless minihalo (halo b) by a Pop III supernova from a nearby minihalo (halo a). The top row shows slices of the gas density and the bottom shows gas temperature and metallicity in the right-most panel. Circles denote the virial radii of the two halos. Column 1: the two halos are shown at z~19, shortly before the formation of a Pop III star in halo a. Column 2: the star forms in halo a and ionizing radiation immediately escapes. Column 3: the star explodes in a core-collapse supernova. Radiation from the star has compressed the gas in halo b and its encompassing filament. Column 4: the metal-rich blast-wave impacts halo b. Turbulent motion will enable the metals to mix into the densest gas within halo b. A reproduction of Figure 1 from Smith et al. (2015).
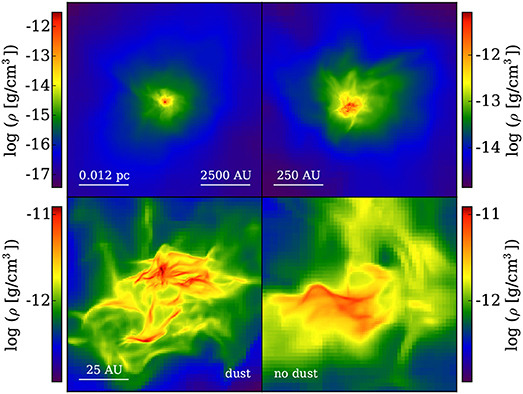
Figure 5. The collapse of metal-enriched gas from scales of 2000 AU down to 100 AU, where dust cooling cause the cloud to fragment. The bottom-right shows the result of the same collapse without the effects of dust. A reproduction of Figure 6 from Smith et al. (2015).
We learned in section 3.1 how the universe converts primordial gas into a primordial star in the cores of dark matter minihalos. And we have seen in section 3.2 how the heavy elements in the supernova ejecta of a primordial star can pollute neighboring minihalos, resulting in the formation of a small cluster of metal-enriched stars in some of them. Now we turn to the formation of the first objects in the universe that can rightfully be called galaxies. These are high redshift, dwarf galaxies like the one shown in Figure 1, composed of dark matter, metal-enriched gas, and stars. Ideally, we would like a numerical simulation that starts with linear matter fluctuations, self-consistently computes the formation of Pop III stars in their minihalos, as well as their feedback effects, computes the transition to Pop II star formation in chemically enriched gas, and produces one or more protogalaxies automatically. In the Birth of a Galaxy paper series (hereafter BOG), John Wise and his collaborators used an enhanced version of Enzo to accomplish that. Here we summarize some of their key findings.
Before we do, we must discuss a technical issue. A fundamental requirement of such simulations is a subgrid model for forming stars in regions of cool dense gas that are conducive to star formation, since we lack the resolution to form stars directly. Such models can be viewed as recipes that build in our knowledge about how star formation and stellar evolution works from both observations and theoretical models. Wise et al. (2012b) introduced the detailed model shown in Figure 6. It handles both Pop III and metal-enriched star formation and feedback, extending an earlier model which only handled Pop III star formation (Wise and Abel, 2008). It consists of a local test for collapse, building in criteria determined from Pop III star formation simulations discussed above, and two conditional branches depending on the value of the local gas metallicity. If Z/Z⊙<10−4, a star particle is created which represents an individual Pop III star with a mass drawn from a parameterized primordial initial mass function (PIMF). If Z/Z⊙>10−4, a star particle is created which represents a metal-enriched star cluster of mass 103M⊙, with an assumed Salpeter IMF. Stellar lifetimes, and their radiative, chemical, and kinetic feedbacks are all determined from the best available stellar models. Depending on the mass assigned to a Pop III star from the PIMF, its endpoint may be either a Type II supernova, a pair instability supernova (PISN), or a prompt black hole without an explosion according to the models of Heger and Woosley (2002). We mention this level of detail because it creates variety in the formation history of the first galaxies.
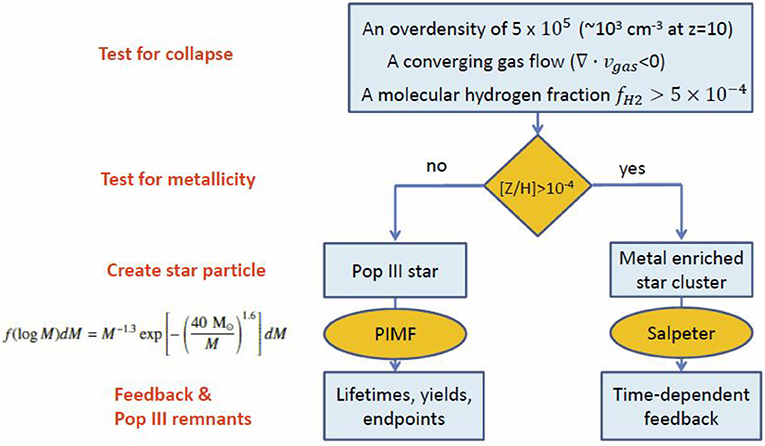
Figure 6. Recipe for making a numerical star or star cluster used in Enzo for Cosmic Dawn simulations. Based on description in Wise et al. (2012b).
The focus of the first Birth of a Galaxy paper (Wise et al., 2012b) is the evolution of the stellar populations in a small sample of high redshift dwarf galaxies 107<Mh/M⊙<109 taking into account chemical enrichment from Pop III supernovae. Achieving a maximum spatial resolution of 1 comoving parsec within a 1 cMpc box, individual molecular clouds were well resolved, and the history of star formation and chemical evolution could be simulated in detail. The entire simulation contained 38 galaxies with 3640 Pop II stellar clusters and captured the formation of 333 Pop III stars. The supernova blasts from Pop III stars first sweep baryons out of their parent minihalos. However the gas fraction recovers from 5% to nearly the cosmic fraction in halos above 107M⊙. The simulation showed that a single pair instability supernova is sufficient to enrich the host halo to a metallicity floor of 10−3Z⊙, triggering a transition to Population II star formation. Despite the small sample of galaxies, their individual star formation and chemical histories showed considerable variation. They found that stellar metallicities do not necessarily trace stellar ages, as mergers of halos with established stellar populations can create superpositions in the age-metallicity stellar tracks.
The second Birth of a Galaxy paper (Wise et al., 2012a) examined the role of radiation pressure on star formation in high-redshift dwarf galaxies, and found that it is significant. It was found that momentum input on neutral gas from ionizing radiation from young, massive stars raises the turbulent velocities in star forming clouds compared to a simulation that omits radiation pressure. The heightened level of turbulence is found to significantly reduce the star formation rate and lower the mean stellar metallicity, consistent with observed dwarfs in the Local Group. Radiation pressure is also found to help drive dense gas away from star forming regions, so that supernovae occur in a warmer and more diffuse medium. This launches metal-rich outflows and avoids the “overcooling problem” seen in some simulations.
The third Birth of a Galaxy paper (Wise et al., 2014) examined the contribution of the smallest galaxies to the process of cosmic reionization. The conventional wisdom is that galaxies in dark matter halos below ~108M⊙ contribute negligibly to cosmic reionization because they are unable to cool by atomic hydrogen lines and consequently they form stars very inefficiently. Our simulations revealed a new class of low mass halo, dubbed metal cooling halos (MCHs), with masses 106.5<Mh/M⊙<108.5, that have been chemically enriched by earlier Pop III supernovae (Figure 7). Although the MCHs form stars inefficiently, they are numerous. Moreover, we find that a high fraction of the ionizing radiation they produce escapes the host halo, decreasing from 50 to 5 percent in the mass range 107<Mh/M⊙<108.5. The combination of high space density and high ionizing escape fraction means that the MCHs contribute significantly to reionization, especially in the early stages of reionization. This possibility is further examined below.
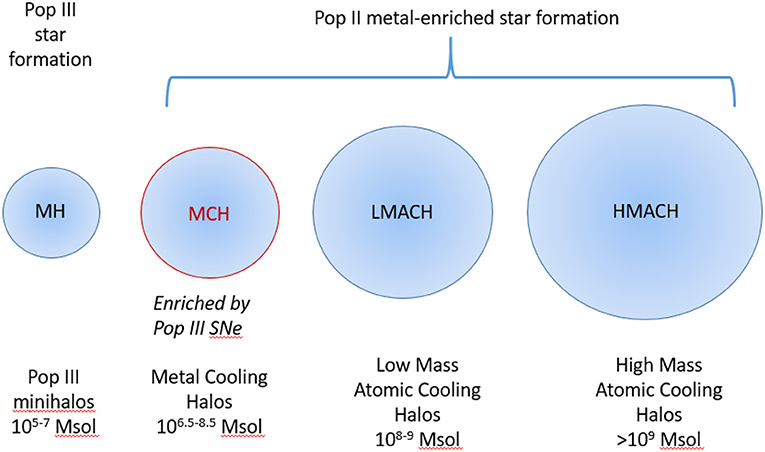
Figure 7. Four types of star-forming halos of importance during the Cosmic Dawn. The MHs, LMACHs, and HMACHs have been well-discussed in the literature. The MCHs, discovered in the Birth of a Galaxy simulations, represent a new, potentially important class.
So far, we have discussed phases of the Cosmic Dawn that are beyond the reach of our most powerful space telescopes. However, as the HST has probed ever-further into the past, and as numerical simulations deployed on ever more powerful supercomputers push to lower redshifts, they meet in the middle. Where they meet is the population of high redshift galaxies observed by the HST, at redshifts of z = 6−10. Stark (2016) provides an excellent summary of the observations to date. The James Webb Space Telescope is poised to revolutionize this area in the coming years.
The Birth of a Galaxy simulations lack the statistics to adequately predict the properties of the observed high redshift galaxy population due to the small volume simulated (1 cMpc)3. As emphasized by Barkana and Loeb (2004), such small volumes do not adequately sample the variance in the dark matter density field, resulting in an understimation of the formation redshifts of Pop III stars and galaxies in rare peaks and their clustering space. All the simulations discussed above have been carried out in very small volumes, and therefore suffer from these defects. For this reason, we have not been very precise about when certain phases of the Cosmic Dawn begin and end. To rectify these defects, in 2013 we began a new series of simulations called the Renaissance Simulations which are similar to the Birth of a Galaxy simulations but in a much larger volume–(40 cMpc)3. Rather than attempt to perform high resolution AMR throughout the entire volume, which would have been computationally prohibitive, we selected three regions of varing mean density for selective refinement (cf. Figure 8). The total volume of the 3 refinement regions is about 576 cMpc3–576 times the volume of the BOG simulations. The “Rare peak,” “Normal” and “Void” simulations were run to final redshifts of 15, 12.5, and 7.6, respectively. At their final redshifts, the three simulations produced a sample of nearly 10, 000 high redshift galaxies in the mass range 107<Mh/M⊙<108, nearly 500 galaxies in the mass range 108<Mh/M⊙<109, and 12 galaxies with Mh/M⊙>109. With this sample, we can begin to characterize the statistical properties of high redshift galaxies, and discuss their formation redshifts.
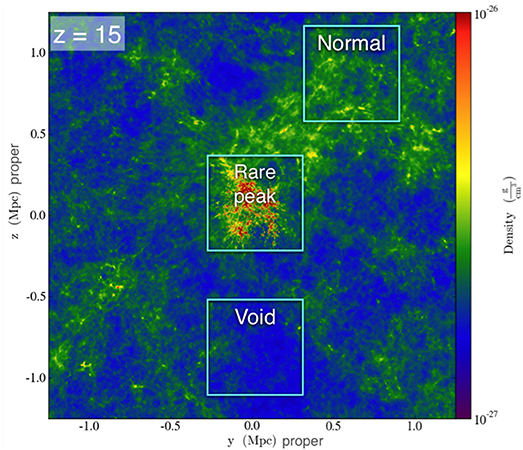
Figure 8. The Renaissance Simulations calculate star and galaxy formation in three regions with AMR and the full physics suite of the Birth of a Galaxy simulations: a high density region “Rare peak,” a region of average density “Normal,” and a low density region “Void.” The box size is 40 cMpc on a side, which at z = 15 is a few proper Mpc on a side.
The Renaissance Simulations represent the most comprehensive attempt yet to numerically simulate the detailed transition from a starless universe to one filled with galaxies. We have published 10 papers analyzing different aspects of the Renaissance Simulations (Xu et al., 2013, 2014, 2016a,b,c; Chen et al., 2014; Ahn et al., 2015; O'Shea et al., 2015; Barrow et al., 2017a,b). Here we highlight just a few of the more interesting findings that start to fill in the Cosmic Dawn narrative.
While this is well known from pure dark matter simulations and theory (Barkana and Loeb, 2004), Figure 9A shows this graphically. Plotted is the volume averaged Pop III star formation rate in the 3 regions. Primordial star formation starts earlier in the denser Rare peak simulation than in a region of average density, which in turn starts earlier that in a region of low density. The rates grow rapidly and then level out to rates that order themselves in the same way.
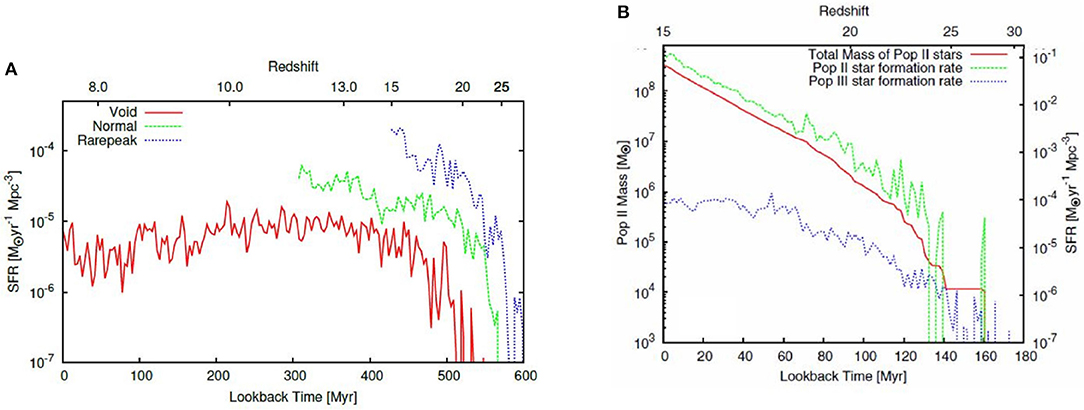
Figure 9. Star formation histories in the Renaissance Simulations. Lookback time is respect to the end of the simulation. Evolutionary time increases from right to left. (A) The volume-averaged Population III star formation rate density in Rarepeak, Normal, and Void regions. Due to the presence of a strong Lyman-Werner background, the onset of Pop III star formation is delayed, but begins earlier in denser regions. The curves end when the simulations were terminated. Reproduced by permission of the American Astronomical Society, Figure 1 from Xu et al. (2016a), (B) Pop III and Pop II star formation rates in the Rarepeak simulation. Pop II quickly overtakes Pop III. Reproduced by permission of the American Astronomical Society, Figure 2 from Xu et al. (2013).
Chemical enrichment from Pop III supernovae triggers the transition to Pop II star formation. As found in the BOG simulations, a single pair instability supernova is sufficient to raise a halo's metallicity above the critical threshold. In each of the three regions, the volume-averaged Pop II star formation rate begins to exceed the Pop III star formation rate within 20–30 Myr after the first Pop III star forms. Thereafter it grows quickly, and exceeds the Pop III star formation rate density by orders of magnitude (Figure 9B).
Interestingly, Pop III stars continue to form at low rates in each of the simulations as far as we can advance them. Our longest running simulation, the Void simulation, produces Pop III stars as late as z = 7.6 (Xu et al., 2016b). This is possible because chemical enrichment is local and slow, leaving more than 80% of the volume pristine by the end of the simulations.
A total of 14 Pop III galaxies are found in the Void simulation at z = 7.6 (Xu et al., 2016b). Some are found to have multiple active Pop III stars within them. This is a consequence of the fact that Pop III star formation is suppressed by the strong Lyman-Werner background until the halo becomes massive enough. Once the halo masses exceed about 107M⊙, as much as 103M⊙ pristine gas is able to cool and form multiple Pop III stars according to our recipe (Figure 10). The observational signatures of such galaxies has been analyzed by Barrow et al. (2017a).
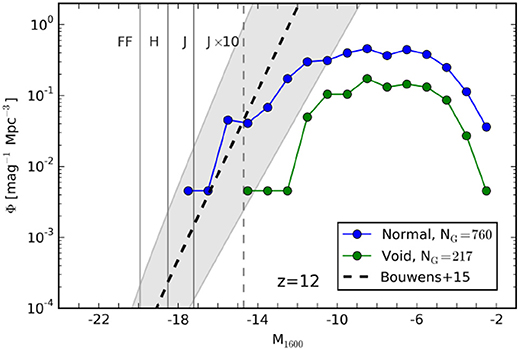
Figure 10. The predicted z = 12 ultraviolet luminosity functions (ULFs) for the Normal and Void Renaissance Simulations, showing flattening at faint magnitudes M1600>−15, which roughly corresponds to the transition from LMACHs to MCHs. At the bright end M1600 < −17, the Normal ULF is in good agreement with an extrapolation of observed ULF to z = 12 (shaded region). Reproduced by permission of the American Astronomical Society, Figure 1 from O'Shea et al. (2015).
HST observations of high redshift galaxies probe the brightest end of the luminosity function, whereas our simulations predict the faint end. Where they overlap, the agreement is good. However, at fainter magnitudes the ultraviolet luminosity function (ULF) flattens out and even drops, as it samples smaller halos incapable of forming stars efficiently and continuously (O'Shea et al., 2015).
The interest in the shape of the faint end of the ULF stems from the fact that a substantial population of galaxies fainter than those that HST can detect are required to complete reionization by z = 7, the latest best estimate for completion (Robertson et al., 2013). Therefore it is interesting to see whether the population of MCHs implied by the ULF shown in Figure 7 can indeed contribute to reionization, as suggested by Wise et al. (2014). We have carried out such a simulation using Enzo, and confirmed that the answer is yes. We imported the galaxy properties derived from the Renaissance Simulations into a radiation hydrodynamical simulation of hydrogen reionization. Using 11523 grid cells and particles in a small volume 10 Mpc/h on a side provides sufficient resolution to sample all halos down to a limiting mass of 107M⊙. Halo finding was run inline with the simulation at an interval of 20 Myr. Ionizing emissivities were assigned to halos according to their mass. The intermittency of star formation in low mass halos was included using a probabilistic method consistent with the ULF shown in Figure 10. The result is shown in Figure 11. The intermittency of star formation in such halos results in stochastic early reionization. However, more massive, luminous galaxies which form stars continuously dominate below redshift 10, and complete reionization around redshift 7. Because the ionizing emissivities assigned to halos were measured at the virial radius in the Renaissance Simulations–a scale well resolved here–there was no need to assume an ionizing escape fraction, as is done is other simulations of reionization. In a real sense, the simulation shown above had no adjustable parameters, save cosmological parameters. It is reassuring that the galaxies from the Renaissance Simulations both match the observed ULF where there is overlap, and succeed in reionizing the universe by z = 7, consistent with other observations.
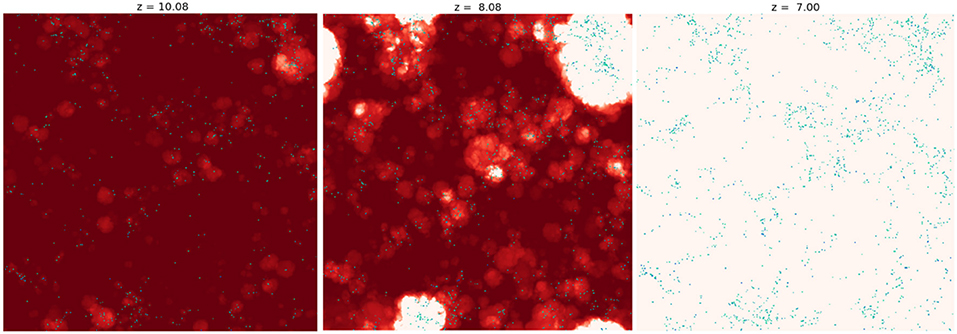
Figure 11. An Enzo simulation of cosmic reionization with sufficient resolution to include the MCH halos discussed above. Halo finding is done inline with the simulation, and their ionizing emissivities are assigned based on results from the Renaissance Simulations. The intermittency of star formation in such halos results in stochastic early reionization.
Complementing numerical simulations are analytic and semi-analytic models of the Cosmic Dawn. There is a rich interplay between these methodologies, which we briefly review here. The literature is too large for a comprehensive review; rather, we seek to illustrate how these approaches inform one another in the context of Cosmic Dawn topics of interest. An example of an analytic model is the use of the Press-Schechter formalism (Press and Schechter, 1974) to compute the halo population at high redshift, which is coupled with a parameterized model of how luminous objects form within these halos (e.g., Haiman and Loeb, 1997; Wise and Abel, 2005). An example of a semi-analytic model is one that post-processes halo catalogs or merger trees from N-body dark matter simulations, adding in baryon physics through physically motivated prescriptions (e.g., Somerville et al., 2008). Generally speaking, semi-analytic models are supplanting analytic models due to the tremendous advances in dark matter-only N-body simulations and the public availability of their data products (e.g., Springel et al., 2005; Skillman et al., 2014).
Once the minimum halo mass capable of hosting Pop III stars was determined analytically (Tegmark et al., 1997) and numerically (Abel et al., 2002; Bromm et al., 2002), two important questions came to the fore: (1) how many Pop III stars are there globally? (Pop III star formation rate density); (2) and how long do they continue to form (duration of the Pop III epoch)? It was soon realized that Pop III stars, through their copious production of UV radiation, could have a negative feedback effect on their own formation. If Pop III stars formed in every minihalo in the universe (and why wouldn't they?), they would quickly build up a photodissociating UV background (the Lyman-Werner background) that would inhibit subsequent H2 formation and cooling in minihalos. Machacek et al. (2001) used Enzo simulations to show that the level of the photodissociating background sets a minimum halo mass capable of cooling. This suggested that Pop III star formation would become self-regulated globally. This was demonstrated by Yoshida et al. (2003a), who constructed an analytic model of Pop III star formation informed by their own numerical simulations. They calculated the Pop III SFRD for two assumptions about the Pop III stellar mass (which is still uncertain), and concluded that Pop III star formation becomes self-regulated by z≈30.
Wise and Abel (2005) developed an analytic model based on the Press-Schechter formalism including self-regulated Pop III star formation in order to estimate how many Pop III supernovae might be observable. A byproduct of that is a model of the evolution of the LWB, that can be used as input to numerical simulations. The Renaissance Simulations described in section 3.4 used an updated version of the Wise and Abel (2005) LWB to account for physics occurring on smaller and larger scales than could be directly simulated. Such models show that Pop III stars make only a minor contribution of the UV photons required to reionize the universe (Haiman and Bryan, 2006).
Regarding the second question posed above, chemical pollution of the pristine gas by stellar evolution of any kind would terminate further Pop III star formation, and usher in the formation of metal-enriched stars (section 3.2). Although this process can be simulated locally, global models are needed to accurately estimate the duration of the Pop III epoch. The first attempt of this sort was by Schneider et al. (2006), who constructed a semi-analytic model of chemical enrichment by Pop III stars. They found that unless every pristine minihalo was internally enriched by a Pop III supernova, Pop III star formation would continue to redshifts as low as z = 2.5 since chemical feedback is highly localized. Hydrodynamic cosmological simulations by Tornatore et al. (2007) bore this out, and indicated that Pop III stars form preferentially at the periphery of metal-enriched zones. Analytic and semi-analytic models by Trenti and Stiavelli (2009) and Trenti et al. (2009) confirmed and refined these estimates. Our own Renaissance Simulations, which track the chemical enrichment of the IGM with high fidelity confirm this basic view. Xu et al. (2016b) carried the Void simulation to z = 7.6 and found 14 small Pop III galaxies in the 200 cMpc3 survey volume.
To conclude this subsection we draw attention to the recent work of Visbal et al. (2018) who use high resolution catalogs from N-body simulations to construct a semi-analytic model of the transition from Pop III to metal-enriched star formation. It includes self-regulated Pop III star formation by both the LWB and local sources in the volume, and uses analytic models of metal-enriched bubbles from supernovae to determine which neighboring halos are engulfed and enriched above the threshold for Pop II star formation. In many respects, it is like the Renaissance Simulations, minus the time-consuming radiation hydrodynamics. Its principal outputs are SFRDs vs. redshift for both Pop III and metal-enriched stars, with the ability to test dependencies on key input parameters. Models like this import insights from numerical simulations, and save numerical simulations from having to do expensive parameter surveys.
Semi-analytic models of galaxy formation are a mainstay of numerical cosmology to understand galaxy evolution in the post-reionization universe; e.g., Springel et al. (2005). Increasingly, this approach is being applied to high redshift galaxy evolution in the Cosmic Dawn era. The most ambitious project of this type is DRAGONS (Dark-ages Reionization and Galaxy-formation Observables from Numerical Simulations; Poole et al., 2016). Over a dozen papers have been published or submitted by the DRAGONS consortium covering many of the topics we have already touched on, including the dynamical state of high redshift galaxies (Poole et al., 2016), their UV luminosity function (Liu et al., 2016), and their spatial clustering (Park et al., 2017). Such semi-analytic models require redshift outputs with fine time resolution so that accurate merger trees can be constructed. Additionally, the semi-analytic recipes need to be modified to take into account processes which are ignorable at lower redshifts. Direct comparison with hydrodynamic simulations are indispensable to this end (Mitchell et al., 2018).
Semi-analytic approaches to modeling cosmic reionization are attractive because it is a global phenomenon amenable to simplification. Choudhury and Ferrara (2005) extended the general model of Miralda-Escudé et al. (2000) to include radiation sources from Pop III and Pop II stars, as well as QSOs. The ionization state and thermal state of the gas is modeled in a spatially averaged way, which allows the entire dynamical model to be embedded within an optimization loop subject to observational constraints. Inputs from numerical simulations include the minimum halo mass to cool, star formation efficiencies, and the size of H II regions inflated by Pop III stars in minihalos.
Furlanetto et al. (2004) introduced a model developed along similar lines to the above that took large scale density inhomogeneities into account. They calculated the evolution of ionized H II bubbles in a statistically averaged way. They showed that the characteristic bubble radius at overlap grows to ≥10 cMpc (Furlanetto et al., 2006). Subsequent enhancements of this approach by Furlanetto and his colleagues have made it a versatile tool for exploring many aspects of the IGM during Cosmic Dawn. The characteristic bubble size at overlap stimulated efforts to simulate this process directly (Iliev et al., 2007; Norman et al., 2015). The DRAGONS semi-analytic model discussed above has also been applied to model large-scale reionization topology and to identify observational probes connected to the galaxy population (Geil et al., 2016). A key unsettled question is the relative contribution of galaxies of difference size to the reionization photon budget.
Observations of the high redshift 21 cm signal will probe the earliest phases of Cosmic Dawn. These observations will be particularly sensitive to the thermal evolution of the IGM in the redshift interval that is coeval with early Pop III star formation. Sophisticated global semi-analytic models have been developed by Visbal et al. as recently reviewed by Barkana (2016). Key inputs from numerical simulations include the effect of the streaming velocity effect on suppressing Pop III star formation in the smallest minihalos (see section 5.7), the nature of the transition from Pop III to Pop II star formation, ionizing escape fractions in high redshift galaxies, and the potential formation of X-ray sources in such galaxies. As an example of the interplay between semi-analytic models and numerical simulations, Fialkov et al. (2014b) emphasized the importance of high-mass X-ray binaries (HMXB) produced by the first stars and galaxies to the 21cm signal. This stimulated us to consider the possible formation of Pop III HMXB, since many Pop III stars are expected to occur in binary systems. Xu et al. (2014) calculated the expected X-ray emission from galaxies in the Rare Peak Renaissance Simulation, assuming that half of all Pop III remnants were HMXBs. They showed that the preheating and preionization of the IGM is significant in such clustered regions. Moreover, Xu et al. (2016a) showed that because Pop III stars continue to form at a low rate to at least the epoch of reionization, their X-ray emitting remnants alone would build up an X-ray background of considerable intensity, one that could potentially alter the temperature of the IGM in the neutral regions between H IIbubbles.
As discussed above, a number of works have shown the accretion disk around a Pop III protostar to be prone to fragmentation (Clark et al., 2011; Greif et al., 2012). While it seems that a majority these fragments are re-accreted onto the primary object, a fraction may be ejected from the system to become low mass Pop III stars. These calculations have been limited by the extreme computational expense of following this and further stages in the evolution of the protostar. At the densities where fragmentation has been observed (n>1019 cm−3), chemical and hydrodynamic timescales become extremely short and the core is optically thick to its own cooling radiation. Later works have carried the torch forward by making sacrifices elsewhere. Hirano et al. (2014) introduced a method where Pop III-forming halos are excised from cosmological simulations and mapped into axisymmetric coordinates to be further evolved with a 2D radiation-hydrodynamics code. Hosokawa et al. (2016) improved on this with 3D rad-hydro simulations in spherical coordinates coupled to a stellar evolution code to model radiative output from the central zone. This is a significant advance, but as of the publication of that work, the simulations had not reached the resolution required for convergence. Additionally, the spherical geometry limits this approach to only following a single protostar and so cannot capture the evolution of any surviving clumps.
The PopIIPrime simulation showed that the external enrichment mechanism is a viable scenario for the formation of very low metallicity stars. In particular, this mechanism is important for explaining the origins of hyper metal-poor stars like SMSS J031300.36-670839.3 (Keller et al., 2014), which has an iron abundance of less that 10−7 of the solar value and appears consistent with enrichment from a single supernova. However, the frequency of such events is still not known. As well, what are the rates and eras of relevance for other mechanisms, like self-enrichment and the accretion of pre-enriched IGM during halo assembly? The Renaissance Simulations can provide a large enough sample from which to make statistical measurements, but their resolution is not high enough to capture the smallest Pop III minihalos of about 105M⊙. This leaves two challenges: (1) for larger simulations at the resolution of Pop2Prime that run past the first metal-enriched star, and (2) for a larger pool of researchers to mine the wealth of data available in works like the Renaissance Simulations. The response to the first is a relatively straightforward technical challenge for software and hardware. The second challenge is motivated by the large volume of complex data produced by cutting-edge simulations. Data releases by the consortia that run the simulations is becoming more commonplace (see section 6.2).
Another physical complication is the role of X-rays from accreting compact objects (neutron stars, black holes) produced by the first stars and galaxies on the early intergalactic medium. Because X-rays have long mean free paths, an early population of X-ray sources will build up an X-ray background that will preionize and preheat the IGM, potentially modifying its ability to cool and form stars (Machacek et al., 2003; Ricotti and Ostriker, 2004; Kuhlen and Madau, 2005). The major uncertainty is the source population. In the modern universe there are three astrophysical sources of X-rays that are well studied: active galactic nuclei, X-ray binary systems, and supernova remnants. Their relative importance as sources of X-rays in the early universe is poorly constrained by observations at the present time (Fialkov et al., 2017), leaving this a topic for speculation and simulation. One interesting possibility explored by Hao Xu et al. is that if some significant fraction of Pop III stars form in binary systems, as appears to be indicated by simulations (cf. section 3.1), they will evolve to form high mass X-ray binary systems (HMXB). Xu et al. (2014, 2016a) showed that because Pop III star formation begins at high redshift and is ongoing to at least z = 7.6, a significant hard X-ray background (Eγ>1 keV) is produced and redshifts to lower energies where it is absorbed and heats the IGM. Xu et al. (2016a) estimated the additional X-ray heating could be several hundred K by z = 6. Future high redshift 21cm observations will probe the thermal history of the IGM during the Cosmic Dawn, thereby helping to constrain the X-ray source population. Interpreting the observations will require detailed numerical simulations complementing semi-analytic approaches (Furlanetto et al., 2009; Fialkov et al., 2014a).
The theoretical literature on magnetic fields in the young universe is vast, and beyond the scope of this review. Here we focus on one specific topic that has received some attention, and for which some consensus has emerged. Namely, the role of magnetic fields in the formation of the first stars. The earliest simulations of Pop III star formation ignored the role, indeed the presence, of magnetic fields entirely. This stands in contrast to modern day star formation theory, where magnetic fields have been argued to have an important if not dominant role (Shu et al., 1987; McKee and Ostriker, 2007). The rationale for omitting magnetic fields was not simply one of convenience. It was argued that because Pop III star formation started from pristine initial conditions, unperturbed by previous generations of star formation and other astrophysical processes, one could ignore them because they were not present. However, this overlooked the possibility that minute seed fields pervading the universe from some early magneto-genesis process could be amplified by turbulence in the protostellar cloud, potentially modifying the dynamics of collapse and fragmentation. Moreover Kulsrud et al. (1997) argued that even in the absence of primordial seed fields, structure formation itself will generate seed fields via the Biermann battery mechanism, and that these will be quickly amplified to equipartition with the turbulent kinetic energy in the protogalactic cloud.
To investigate this possibility, Xu et al. (2008) carried out the first self-consistent AMR MHD simulations of Pop III star formation including the Biermann battery source term. The simulations were performed with the Enzo code, and were similar in design and dynamic range to the earlier simulations of Abel et al. (2002) and O'Shea and Norman (2007). Xu et al. found that from an initial state with no magnetic fields, a combination of the Biermann battery and compressional amplification can result in fields with strengths of 10−9 G at n = 1010 cm−3 at the center of a cosmological halo where a Pop III star will form. At these strengths, the B-field are dynamically unimportant. As this was the highest density obtained in the simulation, the dynamical importance of B-fields during later stages of collapse could not be addressed. In parallel investigations Banerjee et al. (2012) and Turk et al. (2012) showed that the Xu et al. simulations had inadequate spatial resolution to adequately capture the turbulence in the halo's core, and that when higher resolution was used, substantially higher peak magnetic field strengths resulted. They showed that a minimum resolution threshold is required to show any turbulent amplification at all, and that above this threshold the amplification growth rate is resolution-dependent. This motivated Schober et al. (2012) to approach the issue theoretically. Using the Kazantsev theory, which describes the so-called small-scale dynamo, they calculated the growth rate of the small-scale magnetic field for conditions appropriate to primordial halos. They confirmed what previous simulations had indicated: that assuming a seed field provided by the Biermann battery mechanism, small scale fields are amplified rapidly and can become dynamically important locally. They state that such fields are likely to become relevant after the formation of a protostellar disk and, thus, could influence the formation of the first stars and galaxies in the universe. Given what was said above about the uncertain fragmentation of the disk, this adds another layer of complexity to the subject, and calls out for detailed numerical investigation.
Dust is a complicating factor throughout astronomy with a wealth of literature and effort devoted to it. In the context of simulations of the high redshift universe, dust plays an important role in chemistry and cooling of low metallicity gas and is a source of opacity for stellar radiation. If the dust-to-gas ratio scales with the gas-phase metallicity, then the presence of dust can significantly enhance the formation of H2 in star forming gas for metallicities as low as 10−4Z⊙ and induce fragmentation in collapsing gas down to 10−5.5Z⊙ (Omukai, 2000). However, there is room for significant improvement in the modeling of dust at high redshift by taking into account dust production and size distributions from Pop III supernova models (e.g., Schneider et al., 2012) as well as dynamic evolution of the grain population (Chiaki et al., 2015), just as two examples. One of the challenges presented by improved modeling of dust grains is, of course, the technical one, in that the increased complexity comes at a greater computational cost. Though, perhaps a greater challenge is how the advances presented by works like those above can be incorporated into openly available simulation machinery and made available to research community. Some potential solutions to this are discussed below.
The matter power spectrum on small scales, and how dark matter interacts in bound structures, has a profound influence on early structure formation and therefore when and how Cosmic Dawn begins. An excellent discussion of this is found in Greif (2015). Here we summarize the main points. The most explored alternative to ΛCDM is the gavitino warm dark matter model (WDM), which truncates the matter power spectrum below a spatial scale determined by the particle mass. A mass below ~ 1 keV is ruled out observationally as it would suppress the Lyman-α forest. Yoshida et al. (2003b) showed that a mass of 10 keV would entirely suppress the formation of minihalos of mass ~106M⊙ at high redshift, delaying the formation of Pop III stars until more massive dark matter assemblies form. O'Shea et al. (2006) examined this further using Enzo for a range of WDM particle masses 10 keV ≤ mWDM ≤ 50 keV, and found that Pop III stars form substantially later than the mWDM = ∞ case via filament fragmentation. Importantly, however, they found that once primordial gas exceeds 105 cm−3 it cools and collapses identically to the CDM simulations. More recent work cited by Greif (2015) have confirmed these results.
Maio and Viel (2015) and Dayal et al. (2017) have shown that the early suppression of minihalos in light WDM particle scenarios has a cascading effect on subsequent structure formation, reducing star formation rate densities for Pop III and II, shifting the galaxy luminosity function, and potentially delaying reionization. They argue that the entire Cosmic Dawn era is a sensitive probe of dark matter physics. A running spectral index of the primordial power spectrum that suppresses power on small scales has a similar effect (Somerville et al., 2003). Villanueva-Domingo et al. (2018) have recently simulated reionization in a WDM cosmology, and caution that any conclusions on the nature of dark matter derived from reionization observables remain model-dependent.
On the flip side, sterile neutrino dark matter may produce X-rays that enhance the formation of H2 in minihalos, facilitating Pop III star formation (Biermann and Kusenko, 2006). Additionally, quintessence models with an evolving dark energy equation of state that satisfy observational constraints may have more dark matter minihalos at high redshift compared to ΛCDM (Maio et al., 2006).
A current laboratory for testing alternative dark matter models is Local Group dwarf galaxies (Bullock and Boylan-Kolchin, 2017). Given that it is generally believed that satellites of massive galaxies like the Milky Way are relics from the Cosmic Dawn, this may be the best place to do this. A variety of alternative dark matter models are being explored: self-interacting dark matter (SIDM; e.g., Elbert et al., 2015), fuzzy dark matter (FDM; e.g., Hui et al., 2017), and others. Insights obtained in the Local Group are being transferred to the high redshift universe (e.g., Lovell et al., 2018). With improved observations promised at both ultra-low and high redshifts, this is a stimulating time to be working in this subject.
The final physical complication we will discuss concerns the so-called supersonic streaming effect on the earliest generations of Pop III star formation. This relatively recent development in the theory of early structure formation was stimulated by a paper by Tseliakhovich and Hirata (2010), who showed that baryon acoustic oscillations (BAO) would result in a supersonic velocity offset between baryons and dark matter sufficient to alter how gas accretes into minihalos and possibly suppress the formation of the first bound objects that produce Pop III stars. The effect involves a quadratic term in the cosmological perturbation theory equations that was not included in studies based on linear perturbation theory. They showed that the effect leads to qualitative changes in the spatial distribution of the dark matter minihalos themselves, such as introducing scale-dependent bias and stochasticity. Naturally, this paper has generated a lot of interest among the high redshift structure formation community, and a cascade of follow-on investigations have resulted. As this is still a relatively new topic, many issues remain to be explored, and no broad consensus has emerged about the significance of the effect on later stages of structure formation. However, concerning the earliest stages of structure formation, some interesting results have been achieved, which can broadly be classified as small-scale effects and large-scale effects.
The small-scale effects concern the accretion of baryons into dark matter mini-halos in the presence of a supersonic velocity offset of the baryons relative to the dark matter. This has been simulated by several groups using high resolution cosmological simulations with somewhat divergent results. Stacy et al. (2011) performed SPH simulations initialized at redshift 100 with a range of relative streaming velocities and minihalo formation redshifts, and found that the typical streaming velocities have little effect on the gas evolution. They found that once the collapse begins, the subsequent evolution of the gas is nearly indistinguishable from the case of no streaming, and star formation will still proceed in the same way, with no change in the characteristic Pop III stellar masses. Conversely, Greif et al. (2011b) performed a series of higher-resolution moving-mesh calculations and show that these supersonic motions significantly influence the virialization of the gas in minihalos and delay the formation of the first stars by Δz~4. In addition, the streaming velocities increases the minimum halo mass capable of cooling by a factor of 3, which is partially responsible for the delay. They point out that becasue of the steepness of the halo mass function, that may reduce the number of minihalos capable of forming Pop III stars by an order of magnitude. Subsequent works by Richardson et al. (2013) and Naoz et al. (2012, 2013) find similar results to those of Greif et al. and conclude the effect is strongest for minihalos in the mass range M/M⊙<106 but becomes negligible above a halo mass of 107M⊙. We note in passing that a strong Lyman-Werner background suppresses H2 formation and cooling over the same halo mass range, and so these effects must be considered together before we have a complete understanding of the earliest stages of Pop III star formation. This becomes a severe numerical challenge because of large scale effects, discussed next.
The large-scale effects derive from the fact that the BAO modes which are responsible for the streaming velocities are themselves large-scale. The analysis of Tseliakhovich and Hirata (2010) showed that the streaming effect is negligible below several Mpc and above several 100 Mpc, but shows power everywhere in between. This means the streaming velocities are coherent on scales of a few Mpc–much larger than a minihalo's Lagrangian volume–but different in magnitude and direction on larger scales. The consequence is that the way in which minihalos form, accrete baryons, and cool to form Pop III stars is modulated on a range of scales between a few and a few hundred Mpc (comoving), with implications on formation epoch, spatial clustering, and radiative feedback to the IGM. In particular, the high redshift 21 cm signal, which is sensitive to the gas temperature, may show structure on these scales due to the spatial modulation of how sources form on these scales. The most comprehensive large-scale models taking this effect into account, albeit in a semi-analytic way, are those of the group of Fialkov et al., as recently reviewed by Barkana (2016) and Fialkov et al. (2017). Beyond the direct impact on 21 cm and reionization, the streaming velocity effect may leave imprints on galaxy clustering (Schmidt, 2016), CMB B-mode polarization (Ferraro et al., 2012), early supermassive black hole formation (Tanaka et al., 2013; Schauer et al., 2017), and may even have implications on the missing satellite problem (Bovy and Dvorkin, 2013). Recently, however, Ahn (2016) improved on the analysis of Tseliakhovich and Hirata (2010) by including second-order terms involving density fluctuations as well (Tseliakhovich and Hirata performed their analysis assuming uniform density), and showed that density-velocity correlations may enhance the streaming velocity effect, and suggested that the entire topic needs to be revisited with this result in mind. It is clear that much remains to be done both numerically and analytically in this fascinating aspect of the early Cosmic Dawn.
The Enzo simulations highlighted in this paper has been made possible by the combined effort of researchers across the world. The physical modules within the simulations, e.g., the chemistry solver, metal cooling, radiative transfer, star formation and feedback, have all resulted from separate projects performed by independent groups. As an open-source code, Enzo has provided both a means for distribution of and access to the latest methods for simulation. The value to the community is apparent in the number of citations (258 at the time of writing) the Enzo method paper (Bryan et al., 2014) has received in just three years. In fact, most of the latest work discussed here (e.g., the Renaissance Simulations, PopIIPrime, and Birth of a Galaxy) has used open-source software for its entire pipeline, from initial conditions (grafic, Bertschinger, 2001 and MUSIC Hahn and Abel, 2011), to simulation (Enzo), and analysis (yt, Turk et al., 2011). As discussed earlier, the sophistication and complexity of physical modules and solvers continues to increase rapidly, as in for example, the treatment of dust grain physics. Will researchers have to implement new published methods from scratch by following the relevant publications? Will this work have to be repeated for every research group and simulation code? When one considers that most scientific research is paid for by the public, the above appears especially undesirable. In recent years, open-source chemistry packages, like Grackle (Smith et al., 2017) and Krome (Grassi et al., 2014), have begun to serve as these community repositories for astrochemical work and their utility is evidenced by citations to those papers as well.
The simulations discussed here used tens of millions of CPU hours, a monetary value of at least a few million dollars. In general, the scientific potential contained within them far exceeds the available person-power within the group that ran them. The release of public data products, such as halo catalogs and merger trees from the Millennium Simulation (Springel et al., 2005; Lemson and Springel, 2006) has greatly increased the scientific return on the initial investment. More recently, large simulation efforts like Eagle (McAlpine et al., 2016; The EAGLE team, 2017) and Illustris (Nelson et al., 2015) have expanded their public releases beyond halo catalogs to include full or partial snapshots. The snapshots have a greater wealth of content, but also require significant computing facilities to store and process these large data sets. Services like the yt Hub (https://hub.yt/) and the Renaissance Simulation Laboratory will take this one step forward by hosting data along side publicly available compute resources accessible through browser-based interfaces. This will further decrease the necessity of expensive, local computing resources to scientific discovery.
Impressive as the advances that have been made over the past 2 decades, it is clear that even more ambitious simulations will be needed to address the physical complications discussed in section 5 and future observations. These complications, such as the large-scale effects of streaming velocities, result in an increasing scale separation that needs to be taken into account somehow. In addition, we have seen richer physical models might be required to deal with, e.g., the role of magnetic fields on Pop III protostellar disk fragmentation which will influence the Pop III stellar IMF. Finally, cosmological inferences rely on the ability to model large statistical samples of objects. The conclusion is that we need to continue moving down the track that we have already been on, namely toward larger and physically more comprehensive simulations. With the strong drive toward exascale computing systems happening worldwide, there will be adequate computer power to continue to meet growing simulation and data analysis needs. However, the architectures themselves are becoming increasingly complex, and the task of programming them is becoming a major problem. Here we briefly describe our effort to develop a version of Enzo for the coming exascale platforms.
The nominal exascale system will have something like a billion-way task or thread-level concurrency each running at a GigaHertz (109×109 = 1018). Systems will vary in their details as to how this will be accomplished, but are expected to begin showing up early in the next decade. Due to power constraints, each thread or task will need to operate out of a smaller amount of memory than we have been accustomed to (think memory per core). Also, due to power constraints, since it takes more energy to move data large distances in an HPC system, algorithms involving only local or nearest neighbor data will perform much better than algorithms that require global communication. The programmer's task therefore is to decompose the problem into of order 1 billion pieces of work that can be executed using mostly local or nearby data, and executed in such a way as to minimize the use of global synchronization or reductions. Ideally, each task would execute with its own locally-determined timestep when it has received all the data in needs to execute, i.e., asynchronously, as opposed to the bulk-synchronous programming paradigm prevalent in MPI codes. This approach is particularly advantageous for cosmological simulations where different regions of the universe evolve more or less separately from one another (gravity is the bug-bear).
We have designed and built such a code at UCSD called Enzo-P/Cello2. Enzo-P implements Enzo's physics solvers on top of the Cello extreme AMR software framework. Cello in turn is built on top of the Charm++ parallel object framework and runtime system developed at the University of Illinois, Urbana-Champaign. While MPI can be used to implement an asynchronous, task-parallel programming model, we chose Charm++ because it offers this capability out of the box, in addition to dynamic load balancing, fault tolerance, and parallel I/O which would otherwise fall to the application developer to implement. Charm++ is also a good fit for Enzo-P's object-oriented design. Finally, Charm++ interoperates with MPI, so libraries built with MPI can be exploited where needed. The software architecture is shown in Figure 12. We provide a thumbnail sketch of the salient features of each layer, going from bottom to top. The Charm++ parallel runtime insulates the application developer from the details of the hardware. It implements a collection of interacting objects called chares which execute user-defined tasks in a message-driven asynchronous manner. Charm++ maps the chares to processors dynamically to achieve locality and load balance. A standard aspect of Charm++ programs is the use of overdecomposition to generate many more chares (tasks) then there are processors. Overdecomposition is a good fit for exascale architectures because, as explained above, each thread or task should only operate on a small amount of data in local memory. Cello implements the array-of-octrees AMR algorithm pioneered by Burstedde et al. (2011). As the name implies, the computational domain is covered by an array of octrees, each of which have blocks of a fixed number of cells at their leaf nodes. Figure 12B illustrates a 3D array of size 2 × 2 × 2, where some of the trees are unrefined, and some are refined by 3 additional levels. In Cello, each block is a chare, and contains local field and particle data. Chares are elements of chare arrays, which are fully-distributed data structures supported by Charm++. The index space of a chare array is user-defined and very flexible. In Cello, the chare array combines both array level indexing and tree level indexing so that a given chare can determine its position and those of its nearest neighbors using simple bit operations. As currently implemented, Cello can support a 10243 array of 20-level octrees–i.e., many billions of tasks. Finally, Enzo-P is a collection of method objects which operate on the data contained in a chare (particles and fields). At the present time, Enzo-P implements most of the physics solvers in Enzo except for adaptive ray-tracing radiative transfer.
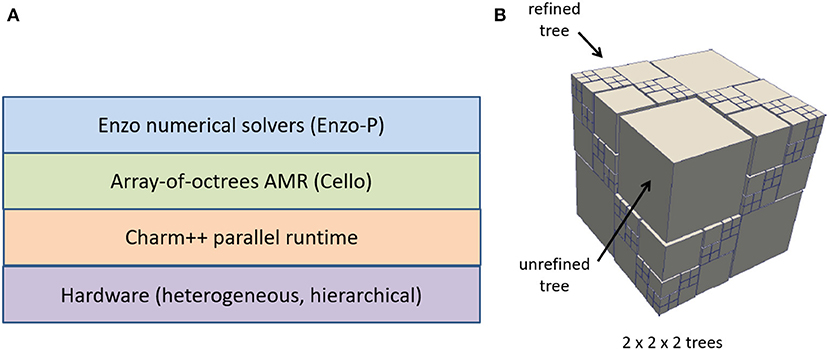
Figure 12. (A) Layered software architecture of the Enzo-P/Cello extreme scale hydrodynamic cosmology code. (B) Schematic illustration of the array-of-octree approach for adaptive mesh refinement used in Enzo-P/Cello.
The object-oriented design of Enzo-P/Cello results in a complete separation of concerns across the 4 layers of Figure 12. A key benefit of this is extensibility. To add a new physics capability to Enzo-P, it is as simple as adding the serial code that updates the field or particle data on a single block. AMR operations and parallel execution are handled automatically by the lower layers. Where things become somewhat more involved is implementing non-local solvers for gravity and radiation transfer which rely on linear system solvers that operate on the global adaptive mesh. In such cases Enzo-P and Cello need to be co-developed so that Cello provides the data structures and primitive operations Enzo-P methods access.
Weak scaling tests of Enzo-P/Cello performed on the Blue Waters sustained petascale system at the National Center for Supercomputing Applications (NCSA), University of Illinois have exhibited near-ideal scaling to 643 = 262 K cores on a hydrodynamic AMR test problem. The largest simulation performed involved an array of 643 octrees, each with some 6.5 M grid cells, for a total of 1.7 T cells. We have also carried out strong and weak scaling experiments on a hydrodynamic cosmology test problem without AMR, which exhibits excellent scaling to 128 K cores.
At the present time, Enzo-P is still under development. As a pure AMR hydrodynamics or MHD code, it is ready to use now. It is vastly superior to Enzo in terms of scalability. Cosmological hydrodynamics on a uniform mesh is also ready to use now, which exhibits superior weak and strong scaling compared to Enzo. The critical issue is the AMR gravity solver, which currently is a multigrid-preconditioned conjugate gradient algorithm. It is implemented and functioning, but needs additional tuning before it is ready for general use. We are considering implementing other approaches for gravity, such as the Fast Multipole Method, which have excellent scaling properties (Jabbar et al., 2014). Our goal is to have a feature compatible version of Enzo-P, with all of Enzo's capabilities, in 2 years time.
MN wrote the majority of the review based on published results with collaborators. BS wrote sections 3.2, 5.1, 5.2, 5.5 and the first two subsections of section 6 based on his published work. JB designed and developed Enzo-P/Cello described in section 6.3 and obtained the scaling results presented there.
This research has received many sources of institutional support and extramural funding over the past two decades, too many to recall. Here we acknowledge grants within the past 5 years to MN which have been most directly connected to the first galaxies research: National Science Foundation grants AST-1109243 and AST-1615848. Enzo-P/Cello is currently funded by NSF grant SI2-SSE-1440709, with previous funding through NSF grants PHY-1104819 and AST-0808184. The PopIIPrime and Renaissance simulations were performed using ENZO on the Blue Waters system operated by the National Center for Supercomputing Applications (NCSA) with PRAC allocation support by the NSF (award number ACI-0832662). Data analysis was performed on the Comet and Gordon supercomputers operated for XSEDE by the San Diego Supercomputer Center, and on the Blue Waters supercomputer.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We gratefully acknowledge our many wonderful collaborators over the years who have contributed so much to the research presented here. In alphabetical order they are: Tom Abel, Kyungjin Ahn, Peter Anninos, Kirk Barrow, Greg Bryan, Pengfei Chen, Dave Collins, Robert Harkness, Cameron Hummels, Sadegh Khochfar, Hui Li, Shengtai Li, Dan Reynolds, Jeff Oishi, Brian O'Shea, Stephen Skory, Geoffrey So, Matt Turk, Peng Wang, Dan Whalen, John Wise, Hao Xu, and Yu Zhang. The majority of the analysis and plots were done with YT (Turk et al., 2011). ENZO and YT are developed by a large number of independent researchers from numerous institutions around the world. Their commitment to open science has helped make this work possible.
Abel, T., Anninos, P., Norman, M. L., and Zhang, Y. (1998a). First Structure Formation. I. Primordial Star-forming Regions in Hierarchical Models. AStrophys. J. 508, 518–529. doi: 10.1086/306410
Abel, T., Anninos, P., Zhang, Y., and Norman, M. L. (1997). Modeling primordial gas in numerical cosmology. New Astronomy 2, 181–207. doi: 10.1016/S1384-1076(97)00010-9
Abel, T., Bryan, G., and Norman, M. (1999). “The formation and fragmentation of the first structures in the universe,” in H2 in Space, eds F. Combes and G. Pineau des Forêts. Available online at: http://adsabs.harvard.edu/abs/1999h2sp.confE.40A
Abel, T., Bryan, G. L., and Norman, M. L. (1998b). Numerical simulations of first structure formation. Mem. Soc. Astron. Ital. 69:377.
Abel, T., Bryan, G. L., and Norman, M. L. (2000). The formation and fragmentation of primordial molecular clouds. AStrophys. J. 540, 39–44. doi: 10.1086/309295
Abel, T., Bryan, G. L., and Norman, M. L. (2002). The formation of the first star in the universe. Science 295, 93–98. doi: 10.1126/science.1063991
Agertz, O., Moore, B., Stadel, J., Potter, D., Miniati, F., Read, J., et al. (2007). Fundamental differences 836 between SPH and grid methods. Month. Notices R. Astron. Soc. 380, 963–978. doi: 10.1111/j.1365-2966.2007.12183.x
Ahn, K. (2016). How the density environment changes the influence of the dark Matter-Baryon streaming velocity on cosmological structure formation. Astrophys. J. 830:68. doi: 10.3847/0004-637X/830/2/68
Ahn, K., Xu, H., Norman, M. L., Alvarez, M. A., and Wise, J. H. (2015). Spatially extended 21 cm signal from strongly clustered Uv and X-Ray Sources in the early Universe. Astrophys. J. 802:8. doi: 10.1088/0004-637X/802/1/8
Anninos, P., Zhang, Y., Abel, T., and Norman, M. L. (1997). Cosmological hydrodynamics with multi-species chemistry and nonequilibrium ionization and cooling. New Astron. 2, 209–224. doi: 10.1016/S1384-1076(97)00009-2
Banerjee, R., Sur, S., Federrath, C., Schleicher, D. R. G., and Klessen, R. S. (2012). Generation of strong magnetic fields via the small-scale dynamo during the formation of the first stars. arXiv [Pre-prints].
Barkana, R. (2016). The rise of the first stars: Supersonic streaming, radiative feedback, and 21-cm cosmology. Phys. Reports 645, 1–59. doi: 10.1016/j.physrep.2016.06.006
Barkana, R., and Loeb, A. (2001). In the beginning: the first sources of light and the reionization of the universe. Phys. Reports 349, 125–238. doi: 10.1016/S0370-1573(01)00019-9
Barkana, R., and Loeb, A. (2004). Unusually Large Fluctuations in the Statistics of Galaxy Formation at High Redshift. Astrophys. J. 609, 474–481. doi: 10.1086/421079
Barrow, K. S. S., Wise, J. H., Aykutalp, A., O'Shea, B. W., Norman, M. L., and Xu, H. (2017a). First Light II: Emission Line Extinction, Population III Stars, and X-ray Binaries. arXiv [Pre-prints].
Barrow, K. S. S., Wise, J. H., Norman, M. L., O'Shea, B. W., and Xu, H. (2017b). First light: exploring the spectra of high-redshift galaxies in the Renaissance Simulations. Monthly Notices R. Astron. Soc. 469, 4863–4878. doi: 10.1093/mnras/stx1181
Berger, M. J., and Colella, P. (1989). Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 82, 64–84. doi: 10.1016/0021-9991(89)90035-1
Bertschinger, E. (2001). Multiscale Gaussian random fields and their application to cosmological simulations. Astrophys. J. Suppl. 137, 1–20. doi: 10.1086/322526
Biermann, P. L., and Kusenko, A. (2006). Relic keV sterile neutrinos and reionization. Phys. Rev. Lett. 96:091301. doi: 10.1103/PhysRevLett.96.091301
Bovy, J., and Dvorkin, C. (2013). Low-mass suppression of the satellite luminosity function Due to the supersonic Baryon-Cold-dark-matter relative velocity. Astrophys. J. 768:70. doi: 10.1088/0004-637X/768/1/70
Bromm, V., Coppi, P. S., and Larson, R. B. (2002). The Formation of the First Stars. I. The Primordial Star-forming Cloud. Astrophys. J. 564, 23–51. doi: 10.1086/323947
Bromm, V., Ferrara, A., Coppi, P. S., and Larson, R. B. (2001). The fragmentation of pre-enriched primordial objects. Month. Notices R. Astron. Soc. 328, 969–976. doi: 10.1046/j.1365-8711.2001.04915.x
Bromm, V., and Larson, R. B. (2004). The First Stars. Ann. Rev. Astron. Astrophys. 42, 79–118. doi: 10.1146/annurev.astro.42.053102.134034
Bromm, V., and Loeb, A. (2003). The formation of the first low-mass stars from gas with low carbon and oxygen abundances. Nature 425, 812–814. doi: 10.1038/nature02071
Bryan, G. L., Abel, T., and Norman, M. L. (2001). Achieving extreme resolution in numerical cosmology using adaptive mesh refinement: resolving primordial star formation. arXiv [Pre-prints].
Bryan, G. L., and Norman, M. L. (1997). A Hybrid AMR Application for Cosmology and Astrophysics. arXiv [Pre-prints].
Bryan, G. L., Norman, M. L., O'Shea, B. W., Abel, T., Wise, J. H., Turk, M. J., et al. (2014). ENZO: an adaptive mesh refinement code for astrophysics. Astrophys. J. Suppl. 211:19. doi: 10.1088/0067-0049/211/2/19
Bullock, J. S., and Boylan-Kolchin, M. (2017). Small-Scale challenges to the ∧CDM Paradigm. Ann. Rev. Astron. Astrophys. 55, 343–387. doi: 10.1146/annurev-astro-091916-055313
Burstedde, C., Wilcox, L. C., and Gattas, O. (2011). p4est:Scalable algorithms for parallel adaptive mesh renement on forests of octrees. SIAM J. Sci. Comput. 33, 1103–1133. doi: 10.1137/100791634
Chabrier, G. (2003). Galactic Stellar and Substellar Initial Mass Function. Public. Astron. Soc. Pacific 115, 763–795. doi: 10.1086/376392
Chen, P., Wise, J. H., Norman, M. L., Xu, H., and O'Shea, B. W. (2014). Scaling relations for galaxies prior to reionization. Astrophys. J. 795:144. doi: 10.1088/0004-637X/795/2/144
Chiaki, G., Marassi, S., Nozawa, T., Yoshida, N., Schneider, R., Omukai, K., et al. (2015). Supernova dust formation and the grain growth in the early universe: the critical metallicity for low-mass star formation. Month. Notices R. Astron. Soc. 446, 2659–2672. doi: 10.1093/mnras/stu2298
Choudhury, T. R., and Ferrara, A. (2005). Experimental constraints on self-consistent reionization models. Month. Notices R. Astron. Soc. 361, 577–594. doi: 10.1111/j.1365-2966.2005.09196.x
Clark, P. C., Glover, S. C. O., and Klessen, R. S. (2008). The first stellar cluster. Astrophys. J. 672, 757–764. doi: 10.1086/524187
Clark, P. C., Glover, S. C. O., Smith, R. J., Greif, T. H., Klessen, R. S., and Bromm, V. (2011). The formation and fragmentation of disks around primordial protostars. Science 331:1040. doi: 10.1126/science.1198027
Collins, D. C., Xu, H., Norman, M. L., Li, H., and Li, S. (2010). Cosmological adaptive mesh refinement magnetohydrodynamics with Enzo. Astrophys. J. Suppl. 186, 308–333. doi: 10.1088/0067-0049/186/2/308
Dayal, P., Choudhury, T. R., Bromm, V., and Pacucci, F. (2017). Reionization and galaxy formation in warm dark matter cosmologies. Astrophys. J. 836:16. doi: 10.3847/1538-4357/836/1/16
Denning, P. J., and Lewis, T. G. (2016). Exponential laws of computing growth. Commun. ACM 60, 54–65. doi: 10.1145/2976758
Dopcke, G., Glover, S. C. O., Clark, P. C., and Klessen, R. S. (2011). The effect of dust cooling on low-metallicity star-forming clouds. Astrophys. J. Lett. 729:L3. doi: 10.1088/2041-8205/729/1/L3
Elbert, O. D., Bullock, J. S., Garrison-Kimmel, S., Rocha, M., Oñorbe, J., and Peter, A. H. G. (2015). Core formation in dwarf haloes with self-interacting dark matter: no fine-tuning necessary. Month. Notices R. Astron. Soc. 453, 29–37. doi: 10.1093/mnras/stv1470
Ferraro, S., Smith, K. M., and Dvorkin, C. (2012). Supersonic baryon-CDM velocities and CMB B-mode polarization. Phys. Rev. D 85:043523. doi: 10.1103/PhysRevD.85.043523
Fialkov, A., Barkana, R., Pinhas, A., and Visbal, E. (2014a). Complete history of the observable 21 cm signal from the first stars during the pre-reionization era. Month. Notices R. Astron. Soc. 437, L36–L40. doi: 10.1093/mnrasl/slt135
Fialkov, A., Barkana, R., and Visbal, E. (2014b). The observable signature of late heating of the Universe during cosmic reionization. Nature 506, 197–199. doi: 10.1038/nature12999
Fialkov, A., Cohen, A., Barkana, R., and Silk, J. (2017). Constraining the redshifted 21-cm signal with the unresolved soft X-ray background. Month. Notices R. Astron. Soc. 464, 3498–3508. doi: 10.1093/mnras/stw2540
Frenk, C. S., White, S. D. M., Bode, P., Bond, J. R., Bryan, G. L., Cen, R., et al. (1999). The Santa barbara cluster comparison project: a comparison of cosmological hydrodynamics solutions. Astrophys. J. 525, 554–582. doi: 10.1086/307908
Furlanetto, S. R., Lidz, A., Loeb, A., McQuinn, M., Pritchard, J. R., Shapiro, P. R., et al. (2009). “Cosmology from the Highly-Redshifted 21 cm Line,” in astro2010: The Astronomy and Astrophysics Decadal Survey, Vol. 2010 of Astronomy. Washington, DC: NAS Press.
Furlanetto, S. R., McQuinn, M., and Hernquist, L. (2006). Characteristic scales during reionization. Month. Notices R. Astron. Soc. 365, 115–126. doi: 10.1111/j.1365-2966.2005.09687.x
Furlanetto, S. R., Zaldarriaga, M., and Hernquist, L. (2004). Statistical probes of reionization with 21 centimeter tomography. Astrophys. J. 613, 16–22. doi: 10.1086/423028
Geil, P. M., Mutch, S. J., Poole, G. B., Angel, P. W., Duffy, A. R., Mesinger, A., et al. (2016). Dark-ages reionization and galaxy formation simulation V: morphology and statistical signatures of reionization. Month. Notices R. Astron. Soc. 462, 804–817. doi: 10.1093/mnras/stw1718
Glover, S. (2005). The formation Of the first stars in the universe. Space Sci. Rev. 117, 445–508. doi: 10.1007/s11214-005-5821-y
Grassi, T., Bovino, S., Schleicher, D. R. G., Prieto, J., Seifried, D., Simoncini, E., et al. (2014). KROME - a package to embed chemistry in astrophysical simulations. Month. Notices R. Astron. Soc. 439, 2386–2419. doi: 10.1093/mnras/stu114
Greif, T. H. (2015). The numerical frontier of the high-redshift Universe. Computat. Astrophys. Cosmol. 2:3. doi: 10.1186/s40668-014-0006-2
Greif, T. H., Bromm, V., Clark, P. C., Glover, S. C. O., Smith, R. J., Klessen, R. S., et al. (2012). Formation and evolution of primordial protostellar systems. Month. Notices R. Astron. Soc. 424, 399–415. doi: 10.1111/j.1365-2966.2012.21212.x
Greif, T. H., Glover, S. C. O., Bromm, V., and Klessen, R. S. (2010). The first galaxies: chemical enrichment, mixing, and star formation. Astrophys. J. 716, 510–520. doi: 10.1088/0004-637X/716/1/510
Greif, T. H., Johnson, J. L., Bromm, V., and Klessen, R. S. (2007). The first supernova explosions: energetics, feedback, and chemical enrichment. Astrophys. J. 670, 1–14. doi: 10.1086/522028
Greif, T. H., Springel, V., White, S. D. M., Glover, S. C. O., Clark, P. C., Smith, R. J., et al. (2011a). Simulations on a moving mesh: the clustered formation of population III protostars. Astrophys. J. 737:75. doi: 10.1088/0004-637X/737/2/75
Greif, T. H., White, S. D. M., Klessen, R. S., and Springel, V. (2011b). The delay of population III star formation by supersonic streaming velocities. Astrophys. J. 736:147. doi: 10.1088/0004-637X/736/2/147
Hahn, O., and Abel, T. (2011). Multi-scale initial conditions for cosmological simulations. Month. Notices R. Astron. Soc. 415, 2101–2121. doi: 10.1111/j.1365-2966.2011.18820.x
Haiman, Z., and Bryan, G. L. (2006). Was Star Formation Suppressed in High-Redshift Minihalos? Astrophys. J. 650, 7–11. doi: 10.1086/506580
Haiman, Z., and Loeb, A. (1997). Signatures of Stellar Reionization of the Universe. Astrophys. J. 483, 21–37. doi: 10.1086/304238
Heger, A., and Woosley, S. E. (2002). The nucleosynthetic signature of population III. Astrophys. J. 567, 532–543. doi: 10.1086/338487
Hirano, S., Hosokawa, T., Yoshida, N., Umeda, H., Omukai, K., Chiaki, G., et al. (2014). One hundred first stars: protostellar evolution and the final masses. Astrophys. J. 781:60. doi: 10.1088/0004-637X/781/2/60
Hosokawa, T., Hirano, S., Kuiper, R., Yorke, H. W., Omukai, K., and Yoshida, N. (2016). Formation of massive primordial tars: intermittent UV feedback with episodic mass accretion. Astrophys. J. 824:119. doi: 10.3847/0004-637X/824/2/119
Hui, L., Ostriker, J. P., Tremaine, S., and Witten, E. (2017). Ultralight scalars as cosmological dark matter. Phys. Rev. D 95:043541. doi: 10.1103/PhysRevD.95.043541
Iliev, I. T., Ciardi, B., Alvarez, M. A., Maselli, A., Ferrara, A., Gnedin, N. Y., et al. (2006). Cosmological radiative transfer codes comparison project - I. The static density field tests. Month. Notices R. Astron. Soc. 371, 1057–1086. doi: 10.1111/j.1365-2966.2006.10775.x
Iliev, I. T., Mellema, G., Shapiro, P. R., and Pen, U. (2007). Self-regulated reionization. Month. Notices R. Astron. Soc. 376, 534–548. doi: 10.1111/j.1365-2966.2007.11482.x
Iliev, I. T., Whalen, D., Mellema, G., Ahn, K., Baek, S., Gnedin, N. Y., et al. (2009). Cosmological radiative transfer comparison project - II. The radiation-hydrodynamic tests. Month. Notices R. Astron. Soc. 400, 1283–1316. doi: 10.1111/j.1365-2966.2009.15558.x
Jabbar, M. A., Yokota, R., and Keyes, D. (2014). Asynchronous execution of the fast multipole method using charm++. CoRR abs/1405.7487. arXiv:1405.7487
Jappsen, A.-K., Klessen, R. S., Glover, S. C. O., and Mac Low, M.-M. (2009a). Star Formation at Very Low Metallicity. IV. Fragmentation does not depend on metallicity for cold initial conditions. Astrophys. J. 696, 1065–1074. doi: 10.1088/0004-637X/696/2/1065
Jappsen, A.-K., Mac Low, M.-M., Glover, S. C. O., Klessen, R. S., and Kitsionas, S. (2009b). Star formation at very low metallicity. V. The greater importance of initial conditions compared to metallicity thresholds. Astrophys. J. 694, 1161–1170. doi: 10.1088/0004-637X/694/2/1161
Jeon, M., Pawlik, A. H., Bromm, V., and Milosavljevic, M. (2014). Recovery from population III supernova explosions and the onset of second generation star formation. arXiv [Pre-prints].
Keller, S. C., Bessell, M. S., Frebel, A., Casey, A. R., Asplund, M., Jacobson, H. R., et al. (2014). A single low-energy, iron-poor supernova as the source of metals in the star SMSS J031300.36-670839.3. Nature 506, 463–466. doi: 10.1038/nature12990
Kim, J.-H., Abel, T., Agertz, O., Bryan, G. L., Ceverino, D., Christensen, C., et al. (2014). The AGORA High-resolution Galaxy Simulations Comparison Project. Astrophys. J. Suppl. 210:14. doi: 10.1088/0067-0049/210/1/14
Kitayama, T., and Yoshida, N. (2005). Supernova explosions in the early universe: evolution of radiative remnants and the halo destruction efficiency. Astrophys. J. 630, 675–688. doi: 10.1086/432114
Kritsuk, A. G., Nordlund, Å., Collins, D., Padoan, P., Norman, M. L., Abel, T., et al. (2011). Comparing numerical methods for isothermal magnetized supersonic turbulence. Astrophys. J. 737:13. doi: 10.1088/0004-637X/737/1/13
Kroupa, P., Tout, C. A., and Gilmore, G. (1993). The distribution of low-mass stars in the Galactic disc. Month. Notices R. Astron. Soc. 262, 545–587. doi: 10.1093/mnras/262.3.545
Kuhlen, M., and Madau, P. (2005). The first miniquasar. Month. Notices R. Astron. Soc. 363, 1069–1082. doi: 10.1111/j.1365-2966.2005.09522.x
Kulsrud, R. M., Cen, R., Ostriker, J. P., and Ryu, D. (1997). The protogalactic origin for cosmic magnetic fields. Astrophys. J. 480, 481–491. doi: 10.1086/303987
Lemson, G., and Springel, V. (2006). “Cosmological simulations in a relational database: modelling and storing merger trees,” in Astronomical Data Analysis Software and Systems XV, vol. 351 of Astronomical Society of the Pacific Conference Series, eds C. Gabriel, C. Arviset, D. Ponz, and S. Enrique (San Francisco, CA: Astronomical Society of the Pacific), 212.
Liu, C., Mutch, S. J., Angel, P. W., Duffy, A. R., Geil, P. M., Poole, G. B., et al. (2016). Dark-ages reionization and galaxy formation simulation - IV. UV luminosity functions of high-redshift galaxies. Month. Notices R. Astron. Soc. 462, 235–249. doi: 10.1093/mnras/stw1015
Loeb, A., and Barkana, R. (2001). The Reionization of the universe by the first stars and quasars. Ann. Rev. Astron. Astrophys. 39, 19–66. doi: 10.1146/annurev.astro.39.1.19
Lovell, M. R., Zavala, J., Vogelsberger, M., Shen, X., Cyr-Racine, F.-Y., Pfrommer, C., et al. (2018). ETHOS - an effective theory of structure formation: predictions for the high-redshift Universe - abundance of galaxies and reionization. Month. Notices R. Astron. Soc. 477, 2886–2899. doi: 10.1093/mnras/sty818
Machacek, M. E., Bryan, G. L., and Abel, T. (2001). Simulations of pregalactic structure formation with radiative feedback. Astrophys. J. 548, 509–521. doi: 10.1086/319014
Machacek, M. E., Bryan, G. L., and Abel, T. (2003). Effects of a soft X-ray background on structure formation at high redshift. Month. Notices R. Astron. Soc. 338, 273–286. doi: 10.1046/j.1365-8711.2003.06054.x
Maio, U., Dolag, K., Meneghetti, M., Moscardini, L., Yoshida, N., Baccigalupi, C., et al. (2006). Early structure formation in quintessence models and its implications for cosmic reionization from first stars. Month. Notices R. Astron. Soc. 373, 869–878. doi: 10.1111/j.1365-2966.2006.11090.x1022
Maio, U., and Viel, M. (2015). The first billion years of a warm dark matter universe. Month. Notices R. Astron. Soc. 446, 2760–2775. doi: 10.1093/mnras/stu2304
McAlpine, S., Helly, J. C., Schaller, M., Trayford, J. W., Qu, Y., Furlong, M., et al. (2016). The EAGLE simulations of galaxy formation: Public release of halo and galaxy catalogues. Astron. Comput. 15, 72–89. doi: 10.1016/j.ascom.2016.02.004
McKee, C. F., and Ostriker, E. C. (2007). Theory of Star Formation. Ann. Rev. Astron. Astrophys. 45, 565–687. doi: 10.1146/annurev.astro.45.051806.110602
McKee, C. F., and Tan, J. C. (2008). The formation of the first stars. II. Radiative feedback processes and implications for the initial mass function. Astrophys. J. 681, 771–797. doi: 10.1086/587434
Meece, G. R., Smith, B. D., and O'Shea, B. W. (2014). Fragmentation in dusty low-metallicity star-forming halos. Astrophys. J. 783:75. doi: 10.1088/0004-637X/783/2/75
Miralda-Escudé, J., Haehnelt, M., and Rees, M. J. (2000). Reionization of the inhomogeneous universe. Astrophys. J. 530, 1–16. doi: 10.1086/308330
Mitchell, P. D., Lacey, C. G., Lagos, C. D. P., Frenk, C. S., Bower, R. G., Cole, S., et al. (2018). Comparing galaxy formation in semi-analytic models and hydrodynamical simulations. Month. Notices R. Astron. Soc. 474, 492–521. doi: 10.1093/mnras/stx2770
Naoz, S., Yoshida, N., and Gnedin, N. Y. (2012). Simulations of early baryonic structure formation with stream velocity. I. Halo abundance. Astrophys. J. 747:128. doi: 10.1088/0004-637X/747/2/128
Naoz, S., Yoshida, N., and Gnedin, N. Y. (2013). Simulations of early baryonic structure formation with stream velocity. II. The gas fraction. Astrophys. J. 763:27. doi: 10.1088/0004-637X/763/1/27
Nelson, D., Pillepich, A., Genel, S., Vogelsberger, M., Springel, V., Torrey, P., et al. (2015). The illustris simulation: Public data release. Astron. Comput. 13, 12–37. doi: 10.1016/j.ascom.2015.09.003
Norman, M. L. (2008). “Population III star formation and IMF,” in First Stars III, vol, 990 of American Institute of Physics Conference Series, eds B. W. O'Shea and A. Heger (Washington, DC: American Institute for Physics), 3–15.
Norman, M. L., Abel, T., and Bryan, G. (1999). “From cosmological initial conditions to primordial protostellar cloud cores,” in After the Dark Ages: When Galaxies were Young (the Universe at 2 lt Z lt 5) volume 470 of American Institute of Physics Conference Series, eds S. Holt, and E., Smith (Washington, DC: American Institute for Physics), 58–62.
Norman, M. L., Abel, T., and Bryan, G. (2000). “First structure formation and the first Stars,” in The First Stars, eds A. Weiss, T. G. Abel, and V. Hill (Heidelberg: Springer Verlag), 250.
Norman, M. L., and Bryan, G. L. (1999). “Cosmological Adaptive Mesh RefinementCD,” in Numerical Astrophysics, Vol. 240 of Astrophysics and Space Science Library eds S. M. Miyama, K. Tomisaka, and T. Hanawa (Boston, MA: Kluwer Academic), 19.
Norman, M. L., Reynolds, D. R., So, G. C., Harkness, R. P., and Wise, J. H. (2015). Fully coupled simulation of cosmic reionization. I. Numerical methods and tests. Astrophys. J. Suppl. 216:16. doi: 10.1088/0067-0049/216/1/16
Omukai, K. (2000). Protostellar collapse with various metallicities. Astrophys. J. 534, 809–824. doi: 10.1086/308776
O'Shea, B. W., Nagamine, K., Springel, V., Hernquist, L., and Norman, M. L. (2005). Comparing AMR and SPH cosmological simulations. I. Dark matter and adiabatic simulations. Astrophys. J. Suppl. 160, 1–27. doi: 10.1086/432645
O'Shea, B. W., and Norman, M. L. (2006). Population III Star Formation in a ?WDM Universe. Astrophys. J. 648, 31–46. doi: 10.1086/505684
O'Shea, B. W., and Norman, M. L. (2007). Population III Star formation in a LCDM Universe. I. The effect of formation redshift and environment on protostellar accretion rate. Astrophys. J. 654, 66–92. doi: 10.1086/509250
O'Shea, B. W., and Norman, M. L. (2008). Population III star formation in a ΛCDM Universe. II. effects of a photodissociating background. Astrophys. J. 673, 14–33. doi: 10.1086/524006
O'Shea, B. W., Wise, J. H., Xu, H., and Norman, M. L. (2015). Probing the ultraviolet luminosity function of the earliest galaxies with the renaissance simulations. Astrophys. J. Lett. 807:L12. doi: 10.1088/2041-8205/807/1/L12
Park, J., Kim, H.-S., Liu, C., Trenti, M., Duffy, A. R., Geil, P. M., et al. (2017). Dark-ages reionization and galaxy formation simulation-XI. Clustering and halo masses of high redshift galaxies. Month. Notices R. Astron. Soc. 472, 1995–2008. doi: 10.1093/mnras/stx1884
Poole, G. B., Angel, P. W., Mutch, S. J., Power, C., Duffy, A. R., Geil, P. M., et al. (2016). Dark-ages Reionization and Galaxy formation simulation - I. The dynamical lives of high-redshift galaxies. Month. Notices R. Astron. Soc. 459, 3025–3039. doi: 10.1093/mnras/stw674
Press, W. H., and Schechter, P. (1974). Formation of galaxies and clusters of galaxies by self-similar gravitational condensation. Astrophys. J. 187, 425–438. doi: 10.1086/152650
Richardson, M. L. A., Scannapieco, E., and Thacker, R. J. (2013). Hybrid cosmological simulations with stream velocities. Astrophys. J. 771:81. doi: 10.1088/0004-637X/771/2/81
Ricotti, M., and Ostriker, J. P. (2004). X-ray pre-ionization powered by accretion on the first black holes - I. A model for the WMAP polarization measurement. Month. Notices R. Astron. Soc. 352, 547–562. doi: 10.1111/j.1365-2966.2004.07942.x
Robertson, B. E., Furlanetto, S. R., Schneider, E., Charlot, S., Ellis, R. S., Stark, D. P., et al. (2013). New onstraints on cosmic reionization from the 2012 Hubble Ultra deep field campaign. Astrophys. J. 768:71. doi: 10.1088/0004-637X/768/1/71
Salpeter, E. E. (1955). The luminosity function and stellar evolution. Astrophys. J. 121:161. doi: 10.1086/145971
Schaerer, D. (2002). On the properties of massive Population III stars and metal-free stellar populations. Astron. Astrophys. 382, 28–42. doi: 10.1051/0004-6361:20011619
Schauer, A. T. P., Regan, J., Glover, S. C. O., and Klessen, R. S. (2017). The formation of direct collapse black holes under the influence of streaming velocities. Astronomy Astrophys. 471, 4878–4884. doi: 10.1093/mnras/stx1915
Schmidt, F. (2016). Effect of relative velocity and density perturbations between baryons and dark matter on the clustering of galaxies. Phys. Rev. D 94:063508. doi: 10.1103/PhysRevD.94.063508
Schneider, R., Omukai, K., Bianchi, S., and Valiante, R. (2012). The first low-mass stars: critical metallicity or dust-to-gas ratio? Month. Notices R. Astron. Soc. 419, 1566–1575. doi: 10.1111/j.1365-2966.2011.19818.x
Schneider, R., Salvaterra, R., Ferrara, A., and Ciardi, B. (2006). Constraints on the initial mass function of the first stars. Month. Notices R. Astron. Soc. 369, 825–834. doi: 10.1111/j.1365-2966.2006.10331.x
Schober, J., Schleicher, D., Federrath, C., Glover, S., Klessen, R. S., and Banerjee, R. (2012). The small-scale ynamo and non-ideal magnetohydrodynamics in primordial star formation. Astrophys. J. 754:99. doi: 10.1088/0004-637X/754/2/99
Shu, F. H., Adams, F. C., and Lizano, S. (1987). Star formation in molecular clouds - Observation and theory. Ann. Rev. Astron. Astrophys. 25, 23–81. doi: 10.1146/annurev.aa.25.090187.000323
Skillman, S. W., Warren, M. S., Turk, M. J., Wechsler, R. H., Holz, D. E., and Sutter, P. M. (2014). Dark Sky Simulations: Early Data Release. arXiv [Pre-prints].
Smith, B. D., Bryan, G. L., Glover, S. C. O., Goldbaum, N. J., Turk, M. J., Regan, J., et al. (2017). GRACKLE: a chemistry and cooling library for astrophysics. Month. Notices R. Astron. Soc. 466, 2217–2234. doi: 10.1093/mnras/stw3291
Smith, B. D., and Sigurdsson, S. (2007). The Transition from the First Stars to the Second Stars in the Early Universe. Astrophys. J. Lett. 661, L5–L8. doi: 10.1086/518692
Smith, B. D., Turk, M. J., Sigurdsson, S., O'Shea, B. W., and Norman, M. L. (2009). Three modes of metal-enriched star formation in the early universe. Astrophys. J. 691, 441–451. doi: 10.1088/0004-637X/691/1/441
Smith, B. D., Wise, J. H., O'Shea, B. W., Norman, M. L., and Khochfar, S. (2015). The first population II stars formed in externally enriched mini-haloes. Month. Notices R. Astron. Soc. 452, 2822–2836. doi: 10.1093/mnras/stv1509
Somerville, R. S., Bullock, J. S., and Livio, M. (2003). The epoch of reionization in models with reduced small-scale power. Astrophys. J. 593, 616–621. doi: 10.1086/376686
Somerville, R. S., Hopkins, P. F., Cox, T. J., Robertson, B. E., and Hernquist, L. (2008). A semi-analytic model for the co-evolution of galaxies, black holes and active galactic nuclei. Month. Notices R. Astron. Soc. 391, 481–506. doi: 10.1111/j.1365-2966.2008.13805.x
Springel, V., White, S. D. M., Jenkins, A., Frenk, C. S., Yoshida, N., Gao, L., et al. (2005). Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 435, 629–636. doi: 10.1038/nature03597
Stacy, A., Bromm, V., and Loeb, A. (2011). Effect of streaming motion of baryons relative to dark matter on the formation of the first stars. Astrophys. J. Lett. 730:L1. doi: 10.1088/2041-8205/730/1/L1
Stacy, A., Greif, T. H., and Bromm, V. (2010). The first stars: formation of binaries and small multiple systems. Month. Notices R. Astron. Soc. 403, 45–60. doi: 10.1111/j.1365-2966.2009.16113.x
Stark, D. P. (2016). Galaxies in the first billion years after the big bang. Ann. Rev. Astron. Astrophys. 54, 761–803. doi: 10.1146/annurev-astro-081915-023417
Tanaka, T. L., Li, M., and Haiman, Z. (2013). The effect of baryonic streaming motions on the formation of the first supermassive black holes. Month. Notices R. Astron. Soc. 435, 3559–3567. doi: 10.1093/mnras/stt1553
Tegmark, M., Silk, J., Rees, M. J., Blanchard, A., Abel, T., and Palla, F. (1997). How small were the first cosmological objects? Astrophys. J. 474, 1–12. doi: 10.1086/303434
The EAGLE team (2017). The EAGLE simulations of galaxy formation: public release of particle data. arXiv [Pre-prints].
Tornatore, L., Ferrara, A., and Schneider, R. (2007). Population III stars: hidden or disappeared? Month. Notices R. Astron. Soc. 382, 945–950. doi: 10.1111/j.1365-2966.2007.12215.x
Trac, H. Y., and Gnedin, N. Y. (2011). Computer simulations of cosmic reionization. Adv. Sci. Lett. 4, 228–243. doi: 10.1166/asl.2011.1214
Trenti, M., and Stiavelli, M. (2009). Formation rates of population III stars and chemical enrichment of halos during the reionization era. Astrophys. J. 694, 879–892. doi: 10.1088/0004-637X/694/2/879
Trenti, M., Stiavelli, M., and Michael Shull, J. (2009). Metal-free gas supply at the edge of reionization: late-epoch population III star formation. Astrophys. J. 700, 1672–1679. doi: 10.1088/0004-637X/700/2/1672
Tseliakhovich, D., and Hirata, C. (2010). Relative velocity of dark matter and baryonic fluids and the formation of the first structures. Phys. Rev. D 82:083520. doi: 10.1103/PhysRevD.82.083520
Turk, M. J., Abel, T., and O'Shea, B. (2009). The formation of population III binaries from cosmological initial Conditions. Science 325:601. doi: 10.1126/science.1173540
Turk, M. J., Oishi, J. S., Abel, T., and Bryan, G. L. (2012). Magnetic fields in population III star formation. Astrophys. J. 745:154. doi: 10.1088/0004-637X/745/2/154
Turk, M. J., Smith, B. D., Oishi, J. S., Skory, S., Skillman, S. W., Abel, T., et al. (2011). yt: A multi-code analysis toolkit for astrophysical simulation data. Astrophys. J. Suppl. 192:9. doi: 10.1088/0067-0049/192/1/9
Villanueva-Domingo, P., Gnedin, N. Y., and Mena, O. (2018). Warm dark matter and cosmic reionization. Astrophys. J. 852:139. doi: 10.3847/1538-4357/aa9ff5
Visbal, E., Haiman, Z., and Bryan, G. L. (2018). Self-consistent semi-analytic models of the first stars. Month. Notic. R. Astron. Soc. 475, 5246–5256. doi: 10.1093/mnras/sty142
Wang, P., and Abel, T. (2009). Magnetohydrodynamic simulations of disk galaxy formation: the magnetization of the cold and warm medium. Astrophys. J. 696, 96–109. doi: 10.1088/0004-637X/696/1/96
Whalen, D., Abel, T., and Norman, M. L. (2004). Radiation hydrodynamic evolution of primordial H II regions. Astrophys. J. 610, 14–22. doi: 10.1086/421548
Whalen, D., O'Shea, B. W., Smidt, J., and Norman, M. L. (2008). How the first stars regulated local star formation. I. Radiative feedback. Astrophys. J. 679, 925–941. doi: 10.1086/587731
Wise, J. H., and Abel, T. (2005). The Number of Supernovae from Primordial Stars in the Universe. Astrophys. J. 629, 615–624. doi: 10.1086/430434
Wise, J. H., and Abel, T. (2008). How very massive metal-free stars start cosmological reionization. Astrophys. J. 684, 1–17. doi: 10.1086/590050
Wise, J. H., and Abel, T. (2011). ENZO+MORAY: radiation hydrodynamics adaptive mesh refinement simulations with adaptive ray tracing. Month. Notices R. Astron. Soc. 414, 3458–3491. doi: 10.1111/j.1365-2966.2011.18646.x
Wise, J. H., Abel, T., Turk, M. J., Norman, M. L., and Smith, B. D. (2012a). The birth of a galaxy - II. The role of radiation pressure. Month. Notices R. Astron. Soc. 427, 311–326. doi: 10.1111/j.1365-2966.2012.21809.x
Wise, J. H., Demchenko, V. G., Halicek, M. T., Norman, M. L., Turk, M. J., Abel, T., et al. (2014). The birth of a galaxy - III. Propelling reionization with the faintest galaxies. Month. Notices R. Astron. Soc. 442, 2560–2579. doi: 10.1093/mnras/stu979
Wise, J. H., Turk, M. J., Norman, M. L., and Abel, T. (2012b). The birth of a galaxy: primordial metal enrichment and stellar populations. Astrophys. J. 745:50. doi: 10.1088/0004-637X/745/1/50
Xu, H., Ahn, K., Norman, M. L., Wise, J. H., and O'Shea, B. W. (2016a). X-Ray background at high redshifts from pop III remnants: results from pop III star formation rates in the renaissance simulations. Astrophys. J. Lett. 832:L5. doi: 10.3847/2041-8205/832/1/L5
Xu, H., Ahn, K., Wise, J. H., Norman, M. L., and O'Shea, B. W. (2014). Heating the ntergalactic medium by X-rays from population III binaries in high-redshift galaxies. Astrophys. J. 791:110. doi: 10.1088/0004-637X/791/2/110
Xu, H., Norman, M. L., O'Shea, B. W., and Wise, J. H. (2016b). Late pop III star formation during the epoch of reionization: results from the renaissance simulations. Astrophys. J. 823:140. doi: 10.3847/0004-637X/823/2/140
Xu, H., O'Shea, B. W., Collins, D. C., Norman, M. L., Li, H., and Li, S. (2008). The biermann battery in cosmological MHD simulations of population III star formation. Astrophys. J. Lett. 688:L57. doi: 10.1086/595617
Xu, H., Wise, J. H., and Norman, M. L. (2013). Population III stars and remnants in high-redshift galaxies. Astrophys. J. 773:83. doi: 10.1088/0004-637X/773/2/83
Xu, H., Wise, J. H., Norman, M. L., Ahn, K., and O'Shea, B. W. (2016c). Galaxy roperties and UV escape fractions during the epoch of reionization: results from the renaissance simulations. Astrophys. J. 833:84. doi: 10.3847/1538-4357/833/1/84
Yoshida, N., Abel, T., Hernquist, L., and Sugiyama, N. (2003a). Simulations of early structure formation: primordial gas clouds. Astrophys. J. 592, 645–663. doi: 10.1086/375810
Yoshida, N., Omukai, K., and Hernquist, L. (2008). Protostar formation in the early universe. Science 321:669. doi: 10.1126/science.1160259
Keywords: cosmology, structure formation, high redshift galaxies, reionization, exascale
Citation: Norman ML, Smith BD and Bordner J (2018) Simulating the Cosmic Dawn With Enzo. Front. Astron. Space Sci. 5:34. doi: 10.3389/fspas.2018.00034
Received: 23 November 2017; Accepted: 06 September 2018;
Published: 17 October 2018.
Edited by:
Lee Samuel Finn, Georgia Institute of Technology, United StatesReviewed by:
Paolo Salucci, Scuola Internazionale Superiore di Studi Avanzati (SISSA), ItalyCopyright © 2018 Norman, Smith and Bordner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael L. Norman, mlnorman@ucsd.edu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.